Geometrical optics formulaes for Helmholtz equation
|
|
|
- Λώτ Γλυκύς
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Geometrical optics formulaes for Helmholtz equation Francois Cuvelier To cite this version: Francois Cuvelier. Geometrical optics formulaes for Helmholtz equation <hal > HAL Id: hal Submitted on 7 Feb 013 HAL is a multi-disciplinary open access archive for the deposit and dissemination of scientific research documents, whether they are published or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers. L archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
2 GEOMETRICAL OPTICS FORMULAES FOR HELMHOLTZ EQUATION FRANÇOIS CUVELIER Abstract. The present work deals with high frequency Helmholtz equation resolution using geometrical optics. We give formulaes in dimension and 3 for mixed Dirichlet, Neumann and Robin boundaries conditions. 1. Introduction Let K j j1,,n be a set of regular, disjoint and strictly convex compacts in R d d or 3. We suppose that for j l, K j Kl. Let Ω j Kj c and Ω N Ω j. We note Γ j the boundary of K j and Γ N Γ j. j1 Let u inc be the incident wave given by u inc x e ikϕinc x a inc x 1.1 which satisfy Helmholtz equation in R d. We want to solve, at high frequency, Helmholtz equation u+k u 0, in Ω 1. j1 with boundaries conditions uγ u inc γ, γ Γ D, 1.3 u γ uinc n n γ, γ Γ N, 1.4 αk u αk n γ+βkuγ uinc n γ+βkuinc γ, γ Γ R, 1.5 and outgoing Sommerfeld radiation condition u r r iku bound for r x. 1.6 We assume that and αk βk j0 j 1 α j k j, α j C, 1.7 β j k j, β j C, 1.8 β 1 +ıα 0 µ 0 µ [0;1] 1.9 Here we take Γ D,Γ N and Γ R such that Γ Γ D Γ N Γ R, o Γ D o Γ N, o Γ D o Γ R and o Γ N o Γ R. Date: September 1, 01. 1
3 front of the incident wave Σ Γ D Γ D K j Γ R Γ N K i Γ N Γ R Figure 1. Exterior Helmholtz problem We assume that, Σ, the front of the incident wave is given by Σ { x R d ϕ inc x ϕ Σ } is a regular and orientable surface d 3 or curve d. We chose the orientation Nσ ϕinc σ ϕ inc σ. Let Σ + { x R d σ Σ, t > 0,x σ +t ϕ inc σ }, we also made following assumption : i N K j Σ + j1 ii curvature radius of Σ are negatives At high frequency means that wave length is small with respect to the obstacle boundary curvature radius, geometrical optics approximation for this problem is based on k 1 asymptotic expansion of vx ux + u inc x, where u is solution of problem 1.,1.3,1.4,1.5,1.6. The first term of the k 1 expansion is the geometrical optics ansatz.. Notations and results Definition 1 Geometrical optic ray. Let ρ σ,γ 1,...,γ l γ 0,γ 1,...,γ l Σ Γ l, we say that ρ is a geometrical optic ray coming from Σ, going through x γ l+1 and reflected l times if 1 γ j γ j 1, j {1,...,l+1}, l+1 ]γ j 1 ;γ j [ Γ, j1 γ 1 γ 0 3 γ 1 γ 0 ϕinc γ 0, 4 reflections conditions : j {1,...,l} γ j+1 γ j γ j+1 γ j γ j γ j 1 γ j γ j 1 5 non grazing conditions : j {1,...,l} γj γ j 1 γ j γ j 1,nγ j 0, where nγ note the exterior normal at Γ in γ. We note R l x a such set of ρ and Rx l N R l x. γj γ j 1 γ j γ j 1,nγ j nγ j,
4 Definition Grazing ray. Let ρ σ,γ 1,...,γ l γ 0,γ 1,...,γ l Σ Γ l, we say that ρ is a grazing ray coming from Σ, going through x γ l+1 and reflected l times if conditions 1 to 4 of definition 1 are satisfied and not condition 5. We note G l x a such set of ρ and Gx l N G l x. Definition 3 Propagation operator. Let t > 0, we note S d t R d d the set of matrix A such that I+tA is regular. We note S t the following application : S t : S d t R d d A AI+tA 1 Definition 4 Reflection operator. Let B R d d a symmetric matrix. Let η R d and ζ R d such that ζ,η 0. We note TB,η,ζ d : Rd d R d d given by : A R d d, x R d T d B,η,ζ Ax A ζ,η Bx η,x Aη [ +Bζ Aη +Bζ,x η + Aη,η Bζ,ζ ζ,η ] η,x η Definition 5 Reflection coefficient. Let η R d, we note b η the function defined on Γ by 1, if γ Γ D, 1, if γ Γ b η γ N, ıα 0 η,nγ +β 1, if γ Γ R. ıα 0 η,nγ β 1 Theorem 1. Let x Σ +, such that Gx, and ρ γ 0,γ 1,...,γ l R l x, l N. We note Bγ the curvature matrix of Γ at γ and nγ the exterior normal to Γ at γ. Let u G.O. ρ x be the ray contribution : with and for j l to 1, ϕ j u G.O. ρ x a ρ xe ikϕx;ρ ϕx;ρ ϕ l ρ γ l + x γ l a ρ x a l ρ γ l deti+ x γ l A l ρ γ l ρ γ j ϕ j 1 ρ γ j 1 + γ j γ j 1 a j 1 ρ γ j 1 a ρ j γ j b γ j γ j 1 γ j γ j γ j 1 det I+ γ j γ j 1 A j 1 ρ γ j 1 A ρ j γ j T d γ j γ j 1 S γj γ j 1 A j 1 ρ γ j 1 Bγ j,nγ j, γ j γ j 1 where ϕ 0 ρ γ 0 ϕ inc γ 0, A 0 ρ γ 0 Hessϕ inc γ 0 and a 0 ρ γ 0 a inc 0 γ 0. Then, we have and u inc x ρ R 0x ux ρ Rx u G.O. ρ x+o 1 k 1 u G.O. ρ x+o k 3. Proof To obtain theorem 1, we first give geometrical optics formulaes without obstacle, then with a stricly convox compact and finally with an union of stricly convex compacts. 3
5 3.1. Without obstacles. We want to solve, at high frequency, Helmholtz equation using an asymptotic expansion in k 1 of the solution u+k u 0 in R d 3.1 ux;k j N where we suppose that u is known on Σ. By substituting expansion 3. in Helmholtz equation, we obtain a j x k j e ıkϕx 3. k 1 ϕx [ a 0 x +k ı{ ϕx, a 0 x+a 0 x ϕx}+1 ϕx a 1 x + k j ı{ ϕx, a k+1 x+a k+1 x ϕx}+ a k x 0 j N Equating the coefficients of different powers of k, we have : Eikonal equation ϕx Transport equation for a 0 Transport equation for a j in function of a j 1 ϕx, a 0 x + 1 a 0x ϕx ϕx, a j x + 1 a jx ϕx ı a j 1x Solution of Eikonal equation 3.3. Derivating eikonal equation 3.3 give This equation can be solved by the caracteristics method : Let X t ϕxt with X0 σ Σ then we have : Hessϕx ϕx d dt ϕxt HessϕXtX t HessϕXt ϕxt 0 That is to say ϕxt ϕx0 hence Xt X0+t ϕx0. and ϕxt is constant along the line Xt X0+t ϕx0. Owing to the construction of Σ, we have Xt σ +tn σ with σ Σ and N σ ϕσ unitary normal vector to Σ at σ. We also have : d dt ϕxt ϕxt,x t ϕx0, ϕx0 1 Thus ϕxt ϕx0+t. We have proved following lemma : Lemma 1. 1 Caracteristic curves of Eikonal equation are geometrical optic rays, Phase is linear along geometrical optic rays : 3 We have σ Σ and σ Σ, t 0 ϕσ +tn σ ϕσ+t. 3.7 ϕσ N σ 3.8 HessϕσN σ
6 3.1.. Solution of transport equation 3.4. We want to solve { ϕx, a0 x + 1 a 0x ϕx 0 a 0 given on Σ 3.10 In fact, we only have to solve this equation along the ray σ +tn σ where σ Σ and N σ ϕσ. Thus, transport equation for a 0 becomes { d dt a 0σ +tn σ+ 1 ϕσ +tn σa 0 σ +tn σ 0, 3.11 a 0 σ given on Σ. We now have to compute ϕσ +tn σ TrHessϕσt. Letσ Σ,wenoteford 3resp. d B Σ σ {u,v,n}σresp. B Σ σ {u,n}σthedirect orthonormal curvature basis of Σ at σ. Here u and v are the direction of maximum and minimal principal curvature k 0 1 σ and k0 σ resp. u is the tangent vector and k0 σ the curvature. By hypothesis on Σ, we have k 0 σ k0 1 σ 0 resp. k0 σ 0. With these notations, we have in basis B Σ σ Hessϕσ 1 σ k 0 σ 0 resp. Hessϕσ k 0 Lemma. Let σ Σ. We note σt σ +tn σ then k 0 σ t 0, Hessϕσt S t Hessϕσ 3.1 In basis B Σ σ for d 3 resp. d k 0 1 σt 0 0 Hess ϕσt 0 k 0 σt 0 resp. Hessϕσt with Proof. To simplify notations, we note t 0 0 k 0 j σt k0 j σ 1 tk 0 j σ k0 j σ j 1, resp. 0 k 0 σt k0 σ 1 tk 0 σ k0 σ A t σ Hessϕσ +tn σ. Let Vσ R d be a neighborhood of σ Σ. We have, x Vσ k 0 σt ϕx ϕσ+a 0 σx σ+o x σ 3.13 Substituing ϕx by 3.13 in Eikonal equation 3.3 give, x Vσ : 1 ϕσ+a 0 σx σ+o x σ Thus Using A 0 σ symmetry, we obtain ϕσ + A 0 σx σ, ϕσ +O x σ 1+ A 0 σx σ,n σ +O x σ. x Vσ, A 0 σn σ,x σ 0 A 0 σn σ We now want to obtain a similar formula for A t σ. We know that A 0 σ is the curvature matrix of Σ at σ and in basis B Σ σ we have for d 3 resp. d k1 Σ σ 0 0 A 0 σ 0 k Σ σ 0 k resp. A 0 σ Σ σ
7 By hypothesis, curvature radius of Σ are negative and k Σ σ k Σ 1 σ 0 resp. k Σ σ 0 Thus, t 0, I+tA 0 σ is regular. Let x σ +tn σ with t > 0, then, there exists a neighborhood Vx R d of x such that x Vx, σ Vσ and t in a neighborhood of t verifying x σ +t N σ So we obtain by Taylor s developpement ϕx ϕx+a t σx x+o x x 3.15 Substituing ϕx for 3.15 in eikonal equation 3.3 give To prove formula 3.1 we write A t σn σ x x σ +t N σ σ tn σ σ σ +t tn σ+t N σ N σ. But, due to 3.13 N σ N σ A 0 σσ σ+o σ σ 3.17 and, thus x x σ σ +t tn σ+t A 0 σσ σ+o σ σ Substituing x x for 3.18 in 3.15 and using 3.16 give N σ N σ+a t σσ σ+t A t σa 0 σσ σ+o σ σ + t t. Now, with formula 3.17 we found A 0 σσ σ+o σ σ A t σσ σ+t A t σa 0 σσ σ+o σ σ + t t That is to say A 0 σ A t σ+ta t σa 0 σ A t σi+ta 0 σ. But, t 0, the matrix I+tA 0 σ is regular and formula 3.1 is proved. Lemma 3. Let σ Σ. Along the ray σt σ +tn σ, t 0, we have a 0 σt a 0 σ deti+thessϕσ 3.19 and t > 0, t 0 such that t > t a 0 σt a 0 σt. 3.0 The previous inegality becomes strict if, at least, one of the curvature radius of Σ is strictly negative. Proof. By definition of A t σ see proof of lemma Then we solve equation 3.11: a 0 σt a 0 σe 1 ϕσt TrA t σ t 0 TrAτσdτ t 0 Tr[A0σI+τA0σ 1 ]dτ a 0 σe 1 a 0 σe 1 [logdeti+τa0σ]t 0 a 0σ. deti+ta0σ We have seen, in proof of lemma, that eigenvalues of A 0 σ are positive, thus deti+t A 0 σ deti+ta 0 σ 1. and inequality 3.0 is immediatly prooved. We can remark that if, at least, one of the curvature of Σ at σ is strictly negative then, for d 3 resp. d k Σ σ < k Σ 1 σ 0 resp. k Σ σ < 0 and thus inequality 3.0 become strict. 6
8 Conclusion. The knowledge of a 0, ϕ, ϕ and Hessϕ on Σ is sufficient to compute them for all x in Σ + using formulaes along geometrical optic rays comming through x and we have Σ t Σ σ N σ σt σ +tn σ Figure. Wave Propagation Theorem. Let x Σ +, then there exist an unique σ Σ such that x σ + x σ N σ 3.1 and solution of is given by a 0 σ 1 ux;k e ikϕσ+ x σ +O deti+ x σ Hessϕσ k 3. Proof. By definition of Σ +, we have existence of σ Σ satisfying 3.1. For unicity, we suppose there exists σ 1 Σ and σ Σ satisfying 3.1. By convexity hypothesis on Σ, we have σ σ 1,N σ 1 0 and then But so we obtain By convexity hypothesis on Σ, we have σ σ 1,x σ 1 0. σ σ 1,x σ 1 σ σ 1,x σ + σ σ 1 σ σ 1,x σ σ 1 σ,n σ 0 7
9 and then σ 1 σ,x σ Thus, inequalities 3.3 and 3.4 give us σ 1 σ. Formula 3. is just an application of propagation Lemmas lemma 1 and lemma 3 along the ray σ R 0 x. 3.. Outside a strictly convex compact. Let K R d be a regular and stricly convex compact, Ω K c and Γ K be its boundary. Remark 1. Owing to the strict convexity of K and the hypotheses on Σ, we have There is only one reflexion on K. We denote by x Σ + Ω, l > 1, R l x. Γ s {γ Γ R 0 γ } and Γ e Γ s c Let γ Γ e and σ R 0 γ. Using previous formulas give us a 0 0, ϕ0, ϕ 0 and Hessϕ 0 on γ. If we can compute reflected wave on γ i.e. a 1 0, ϕ1, ϕ 1 and Hessϕ 1 on γ then we can use propagation formulaes along the reflected ray given by γ +t ϕ 1 γ, t > 0 a 0 0 σ ϕ Given 0 σ ϕ 0 σ Hessϕ 0 σ a 1 0 σ ϕ? 1 σ ϕ 1 σ Hessϕ 1 σ σ σ N σ nγ Σ 1 Σ γ Γ Figure 3. Wave reflection So, the local problem is only to find how to compute the reflected wave in γ. That is to say : a 0 0 γ ϕ 0 γ ϕ 0 γ Hessϕ 0 γ Computation of ϕ 1 and ϕ 1 in γ. Lemma 4. Let γ Γ, then given, how to compute Proof. Due to boundary condition : If γ Γ D, we have a 1 γe ikϕ1 γ a 0 γe ikϕ0 γ a 1 0 γ ϕ 1 γ ϕ 1 γ Hessϕ 1 γ ϕ 1 γ ϕ 0 γ 3.5 8? 3.6
10 If γ Γ N, we have a 1 n γ ıka1 γ ϕ1 n γ e ıkϕ1 γ a 0 n γ ıka0 γ ϕ0 n γ e ıkϕ0 γ If γ Γ R, we have [ ] a αk 1 n γ ıka1 γ ϕ1 n +βka γ 1 γ [ ] a αk 0 n γ ıka0 γ ϕ0 n +βka γ 0 γ By identification, we immediately obtain 3.5. e ikϕ1 γ e ikϕ0 γ Lemma 5. Let γ Γ, and nγ the exterior normal to Γ at γ. We have ϕ 1 γ ϕ 0 γ ϕ 0 γ,nγ nγ 3.9 Proof. Let B Γ γ {uγ,vγ,nγ} be the direct orthonormal curvature basis of Γ at γ. Then we have the local parametrization of Γ at γ : γu,v γ +u,v,gu,v with gu,v 1 kγ 1γu +k Γ γv +ou +v Taylor s expansion at order 1 of ϕ 0 and ϕ 1 on Γ at point γ are ϕ 0 γu,v ϕ 0 γ+ ϕ 0 γ,uuγ+vvγ ϕ 1 γu,v ϕ 1 γ+ ϕ 1 γ,uuγ+vvγ +Ou +v +Ou +v Due to relation 3.5 we obtain ϕ 1 γ ϕ 0 γ,uuγ+vvγ +Ou +v that is to say So, exists λ R such that ϕ 1 γ ϕ 0 γ,uγ ϕ 1 γ ϕ 0 γ,vγ 0 ϕ 1 γ ϕ 0 γ+λnγ Taking the norm of previous relation and using eikonal equation 3.6 give λ ϕ 0 γ,nγ. A similar proof will act in dimension Computation of a 1 0 in γ. Lemma 6. Let γ Γ e. If we know a 0 0 γ and ϕ0 γ then a 1 where the function b ϕ 0 γ is given in definition 5. Proof. If γ Γ D Γ e, formula 3.6 give 0 γ b ϕ γγa γ a 1 γ a 0 γ Using asymptotic expansions of a 0 and a 1 k j a 1 j γ k j a 0 j γ j N j N With high frequency hypothesis, we obtain the leading term in power of k: a 1 0 γ a0 0 γ 9
11 If γ Γ N Γ e, formula 3.7 give a 1 n γ ıka1 γ ϕ1 n γ Using asymptotic expansions of a 0 and a 1 a1 j j k j N j N k The leading term in power of k is But lemma 5 give ϕ1 n obtain a 1 a 0 n γ ıka0 γ ϕ0 n γ n γ ık j+1 a 1 j γ ϕ1 n γ a0 j j n γ ık j+1 a 0 j γ ϕ0 n γ 0 γ ϕ1 γ a0 0 n γ ϕ0 n γ γ ϕ0 n γ. Like γ Γe, we have ϕ 0 γ,nγ 0. So we a 1 0 γ a0 0 γ If γ Γ R Γ e, formula 3.8 give a 1 αk n γ ıka1 γ ϕ1 [ a 0 αk n γ +βka 1 γ n γ ıka0 γ ϕ0 n γ Using asymptotic expansions of a 0, a 1, αk and βk j Nk j α j j N + k j a1 j n γ ık j+1 a 1 j Nk j+1 β j 1 j Nk j a 1 j γ j γ ϕ1 ] +βka 0 γ n γ j Nk j α j k j a0 j n γ ık j+1 a 0 j γ ϕ0 n γ j N j Nk j+1 β j 1 j Nk j a 0 j γ The leading term in power of k is ıα 0 a 1 0 γ ϕ1 n γ+β 1a 1 0 γ ıα 0 a 0 0 γ ϕ0 n γ+β 1a 0 0 γ But ϕ1 n γ ϕ0 n γ, so a 1 0 γ β 1 +ıα 0 ϕ 0 n with hypothesis β 1 > α 0 we have So we obtain a 1 a 0 0 γ ϕ 0 β 1 ıα 0 n ϕ 0 β 1 +ıα 0 n 0 ϕ 0 γ β 1 ıα 0 0 n β 1 +ıα 0 ϕ 0 n 10 a 0 0 γ
12 We notice that γ Γ e b ϕ γγ This the case when there is no absorption in the boundary condition Calculus of Hessϕ 1 at γ Γ e. Lemma 7. Let γ Γ e. We note Bγ the curvature matrix of Γ at γ. Then, in dimension d or 3, we have Hessϕ 1 γ T d Bγ,nγ, ϕ 0 γ Hessϕ0 γ. 3.3 Proof. We have seen lemma 4 that ϕ 1 γ ϕ 0 γ. Let V Γ γ be a neighboorhood of γ in Γ. Taylor s expansion at order 1 of ϕ 0 and ϕ 1 are, for all γ V Γ γ, ϕ 0 γ ϕ 0 γ+hessϕ 0 γγ γ+o γ γ 3.33 and ϕ 1 γ ϕ 1 γ+hessϕ 1 γγ γ+o γ γ 3.34 Let γu,v be the local parametrization of Γ at γ define in section?? We compute now, Taylor s expansion at order 1 of nγu,v in dimension and 3. For that, we first evaluate γ u γ k1γu Γ u, v k Γ v γv +Ou +v, 1 We obtain B Γγ nγ+bγγu,v γ+ou +v. nγu,v nγ+bγγu,v γ +Ou +v. 1+k1 Γγu +k Γγv 1 But 1+k1γu Γ +kγv Γ 1 1+Ou +v so, we have nγ nγ+bγγ γ+o γ γ 3.35 In similar way, we obtain the same formula in dimension d. Using formulas 3.33 and 3.35 in equation 3.9 gives ϕ 1 γ ϕ 1 γ+hessϕ 0 γ ϕ 0 γ,nγ Bγγ γ ϕ 0 γ,bγγ γ nγ Hessϕ 0 γγ γ,nγ nγ+o γ γ So we obtain with formula 3.34, for all γ V Γ γ, Hessϕ 1 γγ γ Hessϕ 0 γ ϕ 0 γ,nγ Bγγ γ ϕ 0 γ,bγγ γ nγ Hessϕ 0 γγ γ,nγ nγ+o γ γ Now, we want to extend the previous formula for all x in Vγ R d, a neighborhood of γ. So we must add to previous formula a function from R d to R d which vanishes on Γ. That is to say at order, there exists a constant vector Cγ R d such that : for all x Vγ Hessϕ 1 γx γ Hessϕ 0 γ ϕ 0 γ,nγ Bγx γ ϕ 0 γ,bγx γ nγ Hessϕ 0 γx γ,nγ nγ + x γ,nγ Cγ+o x γ 3.36 To compute Cγ, we take x Vγ such that x γ ε ϕ 1 γ with ε > 0 and use 3.6 for ϕ 0 and ϕ 1 Hessϕ 0 x ϕ 0 x 0 and Hessϕ 1 x ϕ 1 x 0 11
13 So, formula 3.36 become Hessϕ 0 γ ϕ 0 γ,nγ Bγ ϕ 1 γ ϕ 0 γ,bγ ϕ 1 γ nγ Hessϕ 0 γ ϕ 1 γ,nγ nγ + ϕ 1 γ,nγ Cγ 0 Using 3.9 and Bγnγ 0 we obtain Bγ ϕ 1 γ Bγ ϕ 0 γ and so [ Bγ ϕ Cγ Hessϕ 0 0 γ, ϕ 0 γ γnγ,nγ ]nγ ϕ 0 γ,nγ [ Hessϕ 0 γnγ+bγ ϕ 0 γ ] Replacing Cγ by previous formula in 3.36 immediately give 3.3. These results are given in [ec89] Properties of Hessϕ 1 γ. Lemma 8. The matrix Hessϕ 1 γ is symmetric and Hessϕ 1 γ ϕ 1 γ In dimension d 3, eigenvalues of Hessϕ 1 γ are k 1 1 γ, k1 γ,0 and k 1 γ k1 1 γ < 0, k1 1 γ+k1 γ < k0 1 γ+k0 γ and k1 1 γk1 In dimension d, eigenvalues of Hessϕ 1 γ are k 1 γ,0 and k 1 γ < k 0 γ 0. γ < k0 1 γk0 γ. Proof. As we have seen in section 3.1., in dimension d 3 resp. d, eigenvalues of Hessϕ 0 γ are k 0 1 γ, k0 γ,0 resp. k0 γ,0 where k 0 γ k0 1 γ 0 resp. k0 γ 0. So we only have to apply lemma 1 in dimension or lemma 13 in dimension 3 to end the proof Conclusion. Outside a stricly convex compact, we proved following result Theorem 3. Let x Σ + Ω, such that Gx. Then #Rx #R 1 x 1, #R 0 x 1, and u inc x 1 u G.O. ρ x+o k and ρ R 0x ux ρ R 1x 1 u G.O. ρ x+o k 3.3. Outside an union of strictly convex compacts. To prove theorem 1, we just have to verify that we can use propagation and reflection lemmas along each ray coming through x. For that, we have Lemma 9. Let x Σ + Ω, such that Gx. Let l N such that R l x and ρ γ 0,γ 1,...,γ l R l x. In dimension d 3 resp. d, if eigenvalues of the symmetric matrix A 0 ρ γ 0 are λ 0 1 γ 0, λ 0 γ 0, 0 resp. λ 0 γ 0,0 where 0 λ 0 1 γ 0 λ 0 γ 0 resp. 0 λ 0 γ 0 then j {1,,l} eigenvalues of A j ρ γ j are λ j 1 γ j,λ j γ j,0 resp. λ j γ j,0 where 0 < λ j 1 γ j λ j γ j resp. 0 < λ j γ j 1
14 Proof. Due to hypothesis we can apply propagation lemma to obtain that A 0 ρ γ 1 S γ1 γ 0 A 0 ρ γ 0 is well defined. and its eigenvalues are λ 0 1 γ 1,λ 0 γ 1,0 where 0 λ 0 1 γ 1 λ 0 γ 1. By hypothesis ρ R l x so γ 1 γ 0,nγ 1 < 0 and we can apply reflection lemma 7 to obtain that A 1 ρ γ 1 T γ Bγ1,nγ 1, 1 γ 0 A 0 ρ γ 1 γ 1 γ 0 is well defined. Furthermore,lemma8giveusthatmatrixA 1 ρ γ 1 issymmetricanditseigenvaluesareλ 1 1 γ 1,λ 1 γ 1,0 where 0 < λ 1 1 γ 1 λ 1 γ 1. Then a simply recurrence proof give us lemma : Let j {1,,l 1} and suppose that A j ρ γ j is symmetric and its eigenvalues are λ j 1 γ j,λ j γ j,0 where 0 < λ j 1 γ j λ j γ j we can apply propagation lemma to obtain that A j ρ γ j+1 S γj+1 γ j A j ρ γ j is well defined. and its eigenvalues are λ j 1 γ j+1,λ j γ j+1,0 where 0 < λ j 1 γ j+1 λ j γ j+1. By hypothesis ρ R l x so γ j+1 γ j,nγ j+1 < 0 and we can apply reflection lemma 7 to obtain that A ρ j+1 γ j+1 T γ Bγj+1,nγ j+1 γ j A j j+1, ρ γ j+1 is well defined. Furthermore,lemma8giveusthatmatrixA ρ j+1 where and γ j+1 γ j 0 < λ j+1 1 γ j+1 λ j+1 γ j+1. A similar proof will act in dimension d. With theorem 1 hypothesis and this lemma, we immediatly have j {1,...,l}, det I+ γ j γ j 1 A j 1 ρ γ j 1 > 0 γ j+1 issymmetricanditseigenvaluesareλ j+1 1 γ j+1,λ j+1 γ j+1,0 det I+ x γ l A l ρ γ l > 0. So along each ray comming throug x we can apply propagation and reflection lemmas. Then, by adding the contribution of each ray we obtain theorem 1 results. Lemma 10. Let x Σ + Ω, such that Gx. Let l > 1 such that R l x and ρ γ 0,γ 1,...,γ l R l x. We have a 0 ρ γ 0 a ρ x < [ 1+dxλ Γ min 1+dmin λ Γ min l 1 ]d where and 0 < dx min x γ, γ Γ min λ 1γ if d 3, 0 < λ Γ γ Γ min min λγ if d,, γ Γ 0 < d min min i j min γ i γ j. γ i Γ i,γ j Γ j 13
15 Proof. Using 3.31 and definition of a j ρ γ j, we obtain j {1,,l}, a j+1 ρ γ j+1 where t j γ j+1 γ j and γ j+1 x. In dimension d, we can use equation 4.1 of lemma 1 to obtain λ j γ j λ j 1 γ j t j 1 λ Γ γ j nγ j,γ j γ j 1 But we have 1 t j 1 nγ j,γ j γ j 1 [ 1;0[ and then From proposition 1 we get and so λ j γ j λ j 1 γ j +λ Γ min > 0. λ j 1 γ j From equation 3.39, we immediately obtain and thus a j ργ j 3.39 det I+ γ j+1 γ j A j ρ γ j λ j 1 γ j 1 1+t j 1 λ j 1 γ j 1 λ j 1 γ j > 0 j {,,l} λ 0 γ 1 0 a 1 ρ γ 1 a 0 ρ γ 0 a ρ j+1 γ j+1 < a ρ j γ j 1+d min λmin Γ 1/ j {1,,l 1} a l ρ x a ρ x < a l ρ γ l 1+dxλ Γ 1/ min a 0 ρ γ 0 a ρ x < [. 1+dxλ ]1 Γ min 1+dmin λmin Γ l 1. In dimension d 3, We have det I+t j A ρ j γ j 1+λ j 1 γ j+λ j γ jt j +λ j 1 γ jλ j γ jt j and we can use equations 4.5 and 4.6 of lemma 13 to obtain λ j 1 γ j+λ j γ j λ j 1 1 γ j +λ j 1 γ j +4λ Γ min > 0, λ j 1 γ jλ j γ j λ j 1 1 γ j λ j 1 γ j +4λ Γ min > 0. So, with these inequalities, we have det I+t j A ρ j γ j 1+4λ Γ mint j +4λ Γ mint j + + λ j 1 1 γ j λ j 1 γ j From proposition 1 we get λ j 1 λ j 1 α γ j 1 α γ j 1+t j 1 λ j 1 α γ j 1, α {1,} t j λ j 1 1 γ j +λ j 1 γ j t j and, as λ j 1 γ j 1 λ j 1 1 γ j 1 > 0 for j {,,l +1} and λ 0 γ 0 λ 0 1 γ 0 0 see lemma 13 we have λ j 1 γ j λ j 1 1 γ j > 0 j {,,l} λ 0 γ 1 λ 0 1 γ. 1 0 With these inequalities, we have det I+t j A ρ j γ j > 1+λ Γ mint j if j > 1 det I+t 1 A 1 ρ γ 1 1+λ Γ mint 1 14
16 From equation 3.39, we immediately obtain and thus a 1 ρ γ 1 a 0 ρ γ 0 a ρ j+1 γ j+1 < a ρ j γ j 1+d min λmin Γ 1 j {1,,l 1} a l ρ x a ρ x < a l ρ γ l 1+dxλ Γ 1 min a ρ x < a 0 ρ γ 0 1+dxλ Γ min 1+dmin λ Γ min l Technical results Proposition 1. Let t > 0 and A S d t. Assume that λ is an eingenvalue of A with corresponding eingenvector ζ then λ 1+tλ is an eingenvalue of S ta with corresponding eingenvector ζ. Proof. By definition S t A AI+tA 1 and by hypothesis I+tAζ 1+tλζ with 1+tλ 0. So 1+tλI+tA 1 ζ ζ and we obtain Thus 1+tλAI+tA 1 ζ Aζ. AI+tA 1 ζ λ 1+tλ ζ. Lemma 11. Let η R d and ζ R d such that η 1 and η,ζ 0 Let A and B symmetric matrices in R d d. Assume Aζ 0 and Bη 0 then Proof. Note ξ ζ ζ,η η then, by definition, T d B,η,ζ Due to hypothesis, we have and So, we obtain T d B,η,ζ T d B,η,ζAζ ζ,η η 0 Aξ Aξ ζ,η Bξ η,ξ Aη [ +Bζ Aη +Bζ,ξ η + Aη,η Bζ,ζ ζ,η Aξ ζ,η Aη, Bξ Bζ, η,ξ ζ,η Aη +Bζ,ξ ζ,η Aη,η + Bζ,ζ. ] η,ξ η Aξ ζ,η Aη +Bζ+ ζ,η Aη [ +Bζ+4 ζ,η Aη,η η ] Bζ,ζ η η,ζ η 0. Aη,η Bζ,ζ ζ,η Lemma 1. Let B u,w and B I u I,w I two direct orthonormal basis of R such that w,w I < 0. Let B diagλ,0 in B basis and A I diagλ I,0 in B I basis. Then A R T B,w,w I A I is a symmetric matrix having for eingenvalues λ R,0 where λ R λ I λ w,w I 4.1 and If λ > 0 and λ I 0 then A R w I w,w I w 0 4. λ R > λ I
17 Proof. In basis B, we note u I u j j1, wi w j j1 and AI a ij i,j1. By hypothesis, AI is symmetric and A I w I 0. As w,w I 0, we can compute A R : x R A R x A I w,w I B x w,x A I w +Bw I A I w +Bw I,x w + [ A I w,w BwI,w I w,w I ] w,x w in basis B, x x j j1 and A R a11 a x 1 x1 λx1 a1 +λw w a 1 a x x 1 0 a [ ] a1 +λw 1 x1 0, + a a x 1 λw 1 0 x w 1 That is to say, A R a11 λw a 1 λw 1 a 1 λw 1 a λ w 1 w So we have A R symmetry. We can remark that formula 4. is a direct application of Lemma 11. Now, we study eingenvalues of A R. Let H be the normal matrix given by u1 w H 1 u w Then HA R H t is a similar to A R. Using A I u I λ I u I and A I w I 0 give a11 λw u 1 +a 1 +λw 1 u a 11 λw w 1 +a 1 +λw 1 w A R H a 1 +λw 1 u 1 a λ w 1 w u a 1 +λw 1 w 1 a λ w 1 w w λ I u 1 +λw 1 u w u 1 0 λ I u +λ w 1 w u w 1 u 1 0 But u I,w I is a direct and orthonormal basis, so Then H t A R H w u 1 w 1 u 1, w 1 u 1 +w u 0 and u 1 +u 1. [ ] λ I u 1 +u +λ w 1 u w u 1 u 1 w 1 w u +w 1 u 1 u λ I u 1 w 1 +u w +λw1u w u 1 w 1 w1u +w u 1 w 1 λ I λ w [w u 1 w 1 u ] λ I λ w Lemma 13. Let B u,v,w and B I u I,v I,w I two direct orthonormal basis of R 3 such that w,w I < 0. Let B diagλ 1,λ,0 in B basis and the symmetric matrix A I diagλ I 1,λI,0 in B I basis. Then A R T 3 A I is a symmetric matrix having for eingenvalues λ R B,w,w I 1,λ R,0 and A R w I w,w I w Under the hypothesis we have 0 0 < λ 1 λ and 0 λ I 1 λ I H λ R 1 +λ R λ I 1 +λ I +4λ 1 > 0, 4.5 λ R 1 λ R λ I 1 λi +4λ 1 >
18 and thus λ R 1 > 0, λ R > Proof. In basis B, u I u j 3 j1, vi v j 3 j1, wi w j 3 j1 and AI a ij 3 i,j1. By hypothesis, A I is symmetric and A I w I 0. As w,w I 0, we can compute A R : x R 3 in basis B, x x j 3 j1 and A R x A I w,w I B x w,x A I w +Bw I A I w +Bw I,x w A R x + [ A I w,w BwI,w I w,w I a 11 a 1 a 13 a 1 a a 3 a 13 a 3 a 33 a 13 +λ 1 w 1 x 3 a 3 +λ w a 33 x 1 x x 3 a 13 +λ 1 w 1 a 3 +λ w, a 33 ] w,x w λ 1 x 1 λ x 0 x 1 x x 3 [ + a 33 λ 1w1 +λ w ] 0 x That is to say, a 11 λ 1 a 1 a 13 λ 1 w 1 A R a 1 a λ a 3 λ w a 13 λ 1 w 1 a 3 λ w a 33 λ 1 w1 +λ w So we have A R symmetry. To proove formula 4.4, we make computation in basis B where w I w,w I w 1 w w So A R w R a 11 w 1 λ 1 w 1 +a 1 w +a 13 +λ 1 w 1 a 1 w 1 +a w λ w +a 3 +λ w a 13 w 1 λ 1 w1 a 3 w λ w a 33 +λ 1 w1 +λ w Then, using A I w I 0 give immediatly formula 4.4. To establish the formulas under the assumptions H, we will study the eigenvalues of matrix A R. For that, let H be the normal matrix given by u 1 v 1 w 1 H u v w u 3 v 3 Then HA R H t is similar to A R. Using that u I,v I,w I is a direct and orthonormal basis, we have u v 3 u 3 v w 1 u I v I w I u 1 v 3 +u 3 v 1 w 4.8 u 1 v u v 1 v I w I u I v v 3 w v 1 +v 3 w 1 u 1 u 4.9 v 1 w v w 1 u 3 17
19 w u 3 u v 1 w I u I v I w 1 u 3 + u 1 v 4.10 w 1 u w u 1 v 3 u I 1 u 1 +u +u v I 1 v 1 +v +v w I 1 w 1 +w +w Using A I u I λ I 1 ui, A I v I λ I 1 vi and A I w I 0 give { A R H λ I 1 u 1 +λ 1 w 1 u 3 u 1 λ I v 1 +λ 1 w 1 v 3 v 1 0 λ I 1 u +λ w u 3 u λ I v +λ w v 3 v 0 λ I 1 u 3 λ 1 w 1 u 1 u3w 1 λ w u u3w } { λ I v 3 λ 1 w 1 v 1 v3w 1 λ w v v3w } 0 To obtain H t A R H, we compute H t A R Hx,y x,y {u,v,w} We can remark that H t A R Hx,w 0 x {u,v,w} Now, we compute the six leading terms of matrix H t A R H Calculus of H t A R Hu,u H t A R Hu,u λ I 1 u 1 +λ 1 w 1 u 3 u 1 u 1 + λ I 1 u +λ w u 3 u u λ I 1 u 3 λ 1 w 1 u 1 u 3w1 λ w u u 3w u 3 By hypothesis u I 1 so H t A R Hu,u Using formula 4.10 give Calculus of H t A R Hu,v λ I 1 + λ 1 w3 w 1 u 3 u 1 w w 3u 1 w1u λ w3 w u u 3 w 3u w u 3 λ I 1 λ 1 u 1 w 1 u 3 λ u w u 3 H t A R Hu,u λ I 1 λ1 v +λ v 1 H t A R Hu,v λ I 1 u 1 +λ 1 w 1 u 3 u 1 v 1 + λ I 1 u +λ w u 3 u v λ I 1 u 3 λ 1 w 1 u 1 u 3w1 λ w u u 3w 18 v 3
20 By hypothesis u I,v I 0 so H t A R Hu,v λ 1 w3 w 1 u 3 v 1 w 3u 1 v 1 + w 1 u 1 v 3 w 1u 3 v 3 + λ w3 w u 3 v w 3u v + w u v 3 w u 3 v 3 λ 1 u 1 w 1 u 3 w 1 v 3 v 1 + λ u w u 3 w v 3 v Using formulas 4.9 and 4.10 give H t A R Hu,v λ 1 u v +λ u 1 v 1 Calculus of H t A R Hu,w H t A R Hu,w λ I 1 u 1 +λ 1 w 1 u 3 u 1 w 1 + λ I 1 u +λ w u 3 u w λ I 1 u 3 λ 1 w 1 u 1 u 3w1 λ w u u 3w By hypothesis u I,w I 0 so H t A R Hu,w 0 Calculus of H t A R Hv,u H t A R Hv,u λ I v 1 +λ 1 w 1 v 3 v 1 u 1 + λ I v +λ w v 3 v u λ I v 3 λ 1 w 1 v 1 v 3w1 λ w v v 3w u 3 By hypothesis u I,v I 0 so H t A R Hv,u λ 1 w1 u 1 v 3 w 3u 1 v 1 +w 1 u 3 v 1 w 1u 3 v 3 + λ w u v 3 w 3u v +w u 3 v w u 3 v 3 λ 1 u 1 w 1 u 3 w 1 v 3 v 1 + λ u w u 3 w v 3 v Using formulas 4.9 and 4.10 give H t A R Hv,u λ 1 u v +λ u 1 v 1 Calculus of H t A R Hv,v H t A R Hv,v λ I v 1 +λ 1 w 1 v 3 v 1 v 1 + λ I v +λ w v 3 v v λ I v 3 λ 1 w 1 v 1 v 3w1 λ w v v 3w 19 v 3
21 By hypothesis v I 1 so H t A R Hv,v λ I + λ 1 w1 v 1 v 3 w w 3v 1 w1v λ w v v 3 w 3v w v 3 λ I λ 1 v 1 w 1 v 3 λ v w v 3 Using formula 4.9 give H t A R Hv,v λ I λ1 u +λ u 1 Calculus of H t A R Hv,w H t A R Hv,w λ I v 1 +λ 1 w 1 v 3 v 1 w 1 + λ I v +λ w v 3 v w λ I v 3 λ 1 w 1 v 1 v 3w1 λ w v v 3w By hypothesis v I,w I 0 so H t A R Hu,w 0 With all these formulas we obtain : λ I H t A R 1 w λ1 3 v +λ v 1 λ 1 u v +λ u 1 v 1 0 H λ 1 u v +λ u 1 v 1 λ I w λ1 3 u +λ u As H t A R H is similar to A R, we refind that 0 is an eigenvalue of A R and the two others eigenvalues λ R 1 and λ R are also eingenvalues of λ I 1 A w λ1 3 v +λ v1 λ 1 u v +λ u 1 v 1 λ 1 u v +λ u 1 v 1 λ I w λ1 3 u +λ u 1 Furthermore, we have that TrA λ R 1 +λ R 4.15 deta λ R 1 λ R 4.16 To establish inequality 4.5, we use equation 4.15 under hypothesis H and < 0 to get We remark that and so, we obtain λ R 1 +λ R λ I 1 +λ I λ 1 u 1 +u +v 1 +v. u 1 +u +v 1 +v u 1 +v +u v 1 u 1 v u v 1 u 1 +v +u v 1 λ R 1 +λ R λ I 1 +λ I λ 1 u1 +v +u v 1 λ I 1 +λ I +4λ 1 +4λ 1 u1 +v +u v 1 λ I 1 +λ I +4λ 1. 0
22 To establish inequality 4.6, we use equation 4.16 to get λ R 1 λ R λ I 1 λ1 v +λ v 1 λ I λ1 u +λ u 1 4 w3 λ 1 u v +λ u 1 v 1 λ I 1 λi + 4 [ λ1 w3 v +λ v1 λ1 u +λ u 1 λ1 u v +λ u 1 v 1 ] λ1 v +λ v I 1 λ + λ 1 u +λ u I 1 λ 1 λ I 1 λi λ1 v +λ v I 1 λ + λ 1 u +λ u I 1 λ [ λ w3 1 u v +λ 1 λ u 1v +λ 1 λ v1u λ 1u v λ 1 λ u 1 v 1 u v λ 1 λ v1u ] λ I 1 λi λ1 v +λ v I 1 λ + λ 1 u +λ u I 1 λ [ w3λ 1 λ u 1 v u 1 v 1 u v +v1u ] λ I 1 λi λ1 v +λ v I 1 λ + λ 1 u +λ u I 1 λ w3 λ 1 λ u 1 v v 1 u From formula 4.8, we have u 1 v v 1 u and so we obtain λ R 1 λ R λ I 1 λi λ1 v +λ v I 1 λ + λ 1 u +λ u I 1 λ 1 +4λ 1 λ Under hypothesis H and < 0, we clearly have and we obtain formula 4.6. λ R 1 λ R λ I 1 λi +4λ 1 > 0 References [ec89] M.Balabane et C.Bardos. Equation des ondes : solutions asymptotiques et singularités. Compte Rendus INRIA de la session électromagnétisme, Université Paris XIII, Institut Galilée, LAGA CNRS UMR 7539,, 99, Av. J.-B. Clément F Villetaneuse, France address: cuvelier@math.univ-paris13.fr 1
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
DYNAMICS OF CHANGE WITHIN LIVESTOCK SUB-SECTOR IN CHAD : a key-study of raw milk commodity chain in N Djamena
 DYNAMICS OF CHANGE WITHIN LIVESTOCK SUB-SECTOR IN CHAD : a key-study of raw milk commodity chain in N Djamena Koussou Mian Oudanang To cite this version: Koussou Mian Oudanang. DYNAMICS OF CHANGE WITHIN
DYNAMICS OF CHANGE WITHIN LIVESTOCK SUB-SECTOR IN CHAD : a key-study of raw milk commodity chain in N Djamena Koussou Mian Oudanang To cite this version: Koussou Mian Oudanang. DYNAMICS OF CHANGE WITHIN
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Chemical and biological evaluations of an (111)in-labeled RGD-peptide targeting integrin alpha(v) beta(3) in a preclinical tumor model.
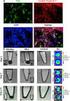 Chemical and biological evaluations of an (111)in-labeled RGD-peptide targeting integrin alpha(v) beta(3) in a preclinical tumor model. Mitra Ahmadi, Lucie Sancey, Arnaud Briat, Laurent Riou, Didier Boturyn,
Chemical and biological evaluations of an (111)in-labeled RGD-peptide targeting integrin alpha(v) beta(3) in a preclinical tumor model. Mitra Ahmadi, Lucie Sancey, Arnaud Briat, Laurent Riou, Didier Boturyn,
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Enzymatic Synthesis of Dithiolopyrrolone Antibiotics Using Cell-Free Extract of Saccharothrix
 Enzymatic Synthesis of Dithiolopyrrolone Antibiotics Using Cell-Free Extract of Saccharothrix algeriensis NRRL B-24137 and Biochemical Characterization of Two Pyrrothine N-Acyltransferases in This Extract.
Enzymatic Synthesis of Dithiolopyrrolone Antibiotics Using Cell-Free Extract of Saccharothrix algeriensis NRRL B-24137 and Biochemical Characterization of Two Pyrrothine N-Acyltransferases in This Extract.
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Multi-GPU numerical simulation of electromagnetic waves
 Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data
 Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data B. Renard, M. Lang, P. Bois To cite this version: B. Renard, M. Lang,
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data B. Renard, M. Lang, P. Bois To cite this version: B. Renard, M. Lang,
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
SPFC: a tool to improve water management and hay production in the Crau region
 SPFC: a tool to improve water management and hay production in the Crau region J.C. Mailhol, A. Merot To cite this version: J.C. Mailhol, A. Merot. SPFC: a tool to improve water management and hay production
SPFC: a tool to improve water management and hay production in the Crau region J.C. Mailhol, A. Merot To cite this version: J.C. Mailhol, A. Merot. SPFC: a tool to improve water management and hay production
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Couplage dans les applications interactives de grande taille
 Couplage dans les applications interactives de grande taille Jean-Denis Lesage To cite this version: Jean-Denis Lesage. Couplage dans les applications interactives de grande taille. Réseaux et télécommunications
Couplage dans les applications interactives de grande taille Jean-Denis Lesage To cite this version: Jean-Denis Lesage. Couplage dans les applications interactives de grande taille. Réseaux et télécommunications
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Jie He. To cite this version: HAL Id: halshs https://halshs.archives-ouvertes.fr/halshs
 Pollution haven hypothesis and Environmental impacts of foreign direct investment: The Case of Industrial Emission of Sulfur Dioxide (SO2) in Chinese provinces Jie He To cite this version: Jie He. Pollution
Pollution haven hypothesis and Environmental impacts of foreign direct investment: The Case of Industrial Emission of Sulfur Dioxide (SO2) in Chinese provinces Jie He To cite this version: Jie He. Pollution
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Consommation marchande et contraintes non monétaires au Canada ( )
 Consommation marchande et contraintes non monétaires au Canada (1969-2008) Julien Boelaert, François Gardes To cite this version: Julien Boelaert, François Gardes. Consommation marchande et contraintes
Consommation marchande et contraintes non monétaires au Canada (1969-2008) Julien Boelaert, François Gardes To cite this version: Julien Boelaert, François Gardes. Consommation marchande et contraintes
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
A Convolutional Neural Network Approach for Objective Video Quality Assessment
 A Convolutional Neural Network Approach for Objective Video Quality Assessment Patrick Le Callet, Christian Viard-Gaudin, Dominique Barba To cite this version: Patrick Le Callet, Christian Viard-Gaudin,
A Convolutional Neural Network Approach for Objective Video Quality Assessment Patrick Le Callet, Christian Viard-Gaudin, Dominique Barba To cite this version: Patrick Le Callet, Christian Viard-Gaudin,
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
 Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Jeux d inondation dans les graphes
 Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Développement de virus HSV-1 (virus de l herpes simplex de type 1) oncolytiques ciblés pour traiter les carcinomes hépatocellulaires
 Développement de virus HSV-1 (virus de l herpes simplex de type 1) oncolytiques ciblés pour traiter les carcinomes hépatocellulaires Aldo Decio Pourchet To cite this version: Aldo Decio Pourchet. Développement
Développement de virus HSV-1 (virus de l herpes simplex de type 1) oncolytiques ciblés pour traiter les carcinomes hépatocellulaires Aldo Decio Pourchet To cite this version: Aldo Decio Pourchet. Développement
Lecture 15 - Root System Axiomatics
 Lecture 15 - Root System Axiomatics Nov 1, 01 In this lecture we examine root systems from an axiomatic point of view. 1 Reflections If v R n, then it determines a hyperplane, denoted P v, through the
Lecture 15 - Root System Axiomatics Nov 1, 01 In this lecture we examine root systems from an axiomatic point of view. 1 Reflections If v R n, then it determines a hyperplane, denoted P v, through the
Pax8 and Pax2 are specifically required at different steps of Xenopus pronephros development
 Pax8 and Pax2 are specifically required at different steps of Xenopus pronephros development Isabelle Buisson, Ronan Le Bouffant, Mélinée Futel, Jean-François Riou, Muriel Umbhauer To cite this version:
Pax8 and Pax2 are specifically required at different steps of Xenopus pronephros development Isabelle Buisson, Ronan Le Bouffant, Mélinée Futel, Jean-François Riou, Muriel Umbhauer To cite this version:
Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat
 Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat Pierre Coucheney, Patrick Maillé, runo Tuffin To cite this version: Pierre Coucheney, Patrick
Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat Pierre Coucheney, Patrick Maillé, runo Tuffin To cite this version: Pierre Coucheney, Patrick
Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation
 Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation Florent Jousse To cite this version: Florent Jousse. Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation.
Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation Florent Jousse To cite this version: Florent Jousse. Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation.
Annulations de la dette extérieure et croissance. Une application au cas des pays pauvres très endettés (PPTE)
 Annulations de la dette extérieure et croissance. Une application au cas des pays pauvres très endettés (PPTE) Khadija Idlemouden To cite this version: Khadija Idlemouden. Annulations de la dette extérieure
Annulations de la dette extérieure et croissance. Une application au cas des pays pauvres très endettés (PPTE) Khadija Idlemouden To cite this version: Khadija Idlemouden. Annulations de la dette extérieure
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
The Pohozaev identity for the fractional Laplacian
 The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
ACI sécurité informatique KAA (Key Authentification Ambient)
 ACI sécurité informatique KAA (Key Authentification Ambient) Samuel Galice, Veronique Legrand, Frédéric Le Mouël, Marine Minier, Stéphane Ubéda, Michel Morvan, Sylvain Sené, Laurent Guihéry, Agnès Rabagny,
ACI sécurité informatique KAA (Key Authentification Ambient) Samuel Galice, Veronique Legrand, Frédéric Le Mouël, Marine Minier, Stéphane Ubéda, Michel Morvan, Sylvain Sené, Laurent Guihéry, Agnès Rabagny,
Modélisation de la réaction d alkylation du motif zinc-thiolate
 Modélisation de la réaction d alkylation du motif zinc-thiolate Delphine Picot To cite this version: Delphine Picot. Modélisation de la réaction d alkylation du motif zinc-thiolate. Chimie. Ecole Polytechnique
Modélisation de la réaction d alkylation du motif zinc-thiolate Delphine Picot To cite this version: Delphine Picot. Modélisation de la réaction d alkylation du motif zinc-thiolate. Chimie. Ecole Polytechnique
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis
 Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Émergence des représentations perceptives de la parole : Des transformations verbales sensorielles à des éléments de modélisation computationnelle
 Émergence des représentations perceptives de la parole : Des transformations verbales sensorielles à des éléments de modélisation computationnelle Anahita Basirat To cite this version: Anahita Basirat.
Émergence des représentations perceptives de la parole : Des transformations verbales sensorielles à des éléments de modélisation computationnelle Anahita Basirat To cite this version: Anahita Basirat.
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure
 Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure Hervé Rivano To cite this version: Hervé Rivano. Algorithmique et télécommunications
Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure Hervé Rivano To cite this version: Hervé Rivano. Algorithmique et télécommunications
Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques
 Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques Raphael Chenouard, Patrick Sébastian, Laurent Granvilliers To cite this version: Raphael
Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques Raphael Chenouard, Patrick Sébastian, Laurent Granvilliers To cite this version: Raphael
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2
![If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2 If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2](/thumbs/53/31933086.jpg) Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
The ε-pseudospectrum of a Matrix
 The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
If we restrict the domain of y = sin x to [ π 2, π 2
 Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Les gouttes enrobées
 Les gouttes enrobées Pascale Aussillous To cite this version: Pascale Aussillous. Les gouttes enrobées. Fluid Dynamics. Université Pierre et Marie Curie - Paris VI,. French. HAL Id: tel-363 https://tel.archives-ouvertes.fr/tel-363
Les gouttes enrobées Pascale Aussillous To cite this version: Pascale Aussillous. Les gouttes enrobées. Fluid Dynamics. Université Pierre et Marie Curie - Paris VI,. French. HAL Id: tel-363 https://tel.archives-ouvertes.fr/tel-363
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes.
 Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes. Diego Torres Machado To cite this version: Diego Torres Machado. Radio
Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes. Diego Torres Machado To cite this version: Diego Torres Machado. Radio
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
