(β) λ(g 1 g 2, p) = (g 1 g 2 )p = g 1 (g 2 p) = λ(g 1, λ(g 2, p)). (β ) φ(p, g 1 g 2 ) = p(g 1 g 2 ) = (pg 1 )g 2 = φ(φ(p, g 1 ), g 2 ),
|
|
|
- Ευάγγελος Δάβης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 10 Ομογενείς χώροι - Γεωμετρία κατά Klein Σύνοψη Σύμφωνα με τον F. Klein η γεωμετρία είναι η μελέτη εκείνων των ιδιοτήτων ενός χώρου οι οποίες παραμένουν αναλλοίωτες από την δράση μιας ομάδας μετασχηματισμών. Σε σύχγρονη γλώσσα, ο χώρος είναι μια λεία πολλαπλότητα και η ομάδα είναι μια ομάδα Lie, η οποία δρα στην πολλαπλότητα μεταβατικά. Διαφορετικές ομάδες Lie ορίζουν, μέσω των δράσεών τους, διαφορετικές γεωμετρίες σε μια πολλαπλότητα. Στο κεφάλαιο αυτό παρουσιάζουμε τα γενικά χαρακτηριστικά της θεωρίας των ομογενών χώρων, με έμφαση στους αναγωγικούς ομογενείς χώρους. Για έναν τέτοιο ομογενή χώρο δίνουμε τύπους για τη συνοχή Levi- Civita, τανυστή καμπυλότητας, καμπυλότητα Ricci και βαθμωτή καμπυλότητα. Τέλος, κάνουμε εφαρμογή σε ενδεικτικά παραδείγματα. Οι αναφορές μας με αύξοντα βαθμό δυσκολίας είναι τα βιβλία [1], [2], [5], [6], [9], [11], [3], [12], [16], [10], [7], καθώς και οι καλογραμμένες διπλωματικές εργασίες [15] και [18]. Προαπαιτούμενη γνώση Εισαγωγή στις πολλαπλότητες, εισαγωγή στις ομάδες Lie, γραμμική άλγεβρα, στοιχειώδης θεωρία αναπαραστάσεων. Ενας ομογενής χώρος είναι μια λεία πολλαπλότητα M στην οποία δρα μεταβατικά μια ομάδα Lie G. Οι ομογενείς χώροι αποτελούν μια φυσική επέκταση των ομάδων Lie και η βασική τους ιδιότητα είναι ότι, αν γνωρίζουμε την τιμή κάποιου γεωμετρικού αντικειμένου (π.χ. καμπυλότητα) σε ένα σημείο του χώρου, τότε χρησιμοποιώντας απεικονίσεις μεταφοράς, μπορούμε να υπολογίσουμε την τιμή του σε οποιοδήποτε σημείο του χώρου. Μια κλάση ομογενών χώρων είναι οι αναγωγικοί ομογενείς χώροι τους οποίους θα μελετήσουμε στη συνέχεια του κεφαλαίου. Οι ομογενείς χώροι είναι το μοντέλο της γεωμετρίας του Klein, σύμφωνα με το οποίο η γεωμετρία είναι η μελέτη εκείνων των γεωμετρικών αντικειμένων που παραμένουν αναλλοίωτα μέσω της δράσης μιας ομάδας σε ένα χώρο. Η ομάδα αυτή είναι γνωστή ως ομάδα μετασχηματισμών (transformation group). Θεωρώντας
2 2 Ομογενείς χώροι - Γεωμετρία κατά Klein διαφορετικές ομάδες κάθε φορά, οδηγούμαστε σε διαφορετικές γεωμετρίες. Τέλος, να αναφέρουμε ότι η θεωρία των ομογενών χώρων χρησιμοποιείται ευρέως στη μαθηματική φυσική, όπου μαζί με τη θεωρία συνοχών αποτελούν σημαντικό εργαλείο για την έρευνα στη σύγχρονη θεωρία στοιχειωδών σωματιδίων Δράσεις ομάδων Θα ξεκινήσουμε την ενότητα με τον ορισμό της δράσης μιας τοπολογικής ομάδας ή μιας ομάδας Lie σε ένα σύνολο, το οποίο μπορεί να είναι τοπολογικός χώρος, λεία πολλαπλότητα ή και διανυσματικός χώρος. Στη συνέχεια, θα δώσουμε μερικούς ορισμούς σχετικά με την έννοια της δράσης, για παράδειγμα θα δούμε πότε η δράση λέγεται μεταβατική και τέλος θα αναφέρουμε μερικά παραδείγματα. Ορισμός Εστω G μια τοπολογική ομάδα (αντίστ. ομάδα Lie) και M ένας τοπολογικός χώρος (αντίστ. λεία πολλαπλότητα). Μια αριστερή δράση (left action) της G στη M είναι μια συνεχής (αντίστ. λεία) απεικόνιση λ : G M M, (g, p) λ(g, p) = g p = gp, η οποία για κάθε g 1, g 2 G και p M ικανοποιεί τις παρακάτω συνθήκες: (α) λ(e, p) = ep = p και (β) λ(g 1 g 2, p) = (g 1 g 2 )p = g 1 (g 2 p) = λ(g 1, λ(g 2, p)). Παρόμοια, μπορούμε να ορίσουμε τη δεξιά δράση της G στη M, μέσω μιας συνεχούς (αντίστ. λείας) απεικόνισης φ : M G M, όπου κάθε ζεύγος (p, g) M G απεικονίζεται στο σημείο p g = pg το οποίο ανήκει στην M και ικανοποιεί τις ανάλογες συνθήκες: (α ) φ(p, e) = pe = p και (β ) φ(p, g 1 g 2 ) = p(g 1 g 2 ) = (pg 1 )g 2 = φ(φ(p, g 1 ), g 2 ), για κάθε g 1, g 2 G και p M. Πολλές φορές ο χώρος M με την δράση της G καλείται G-χώρος (G-space), ενώ η ομάδα G αναφέρεται και ως ομάδα μετασχηματισμών (transformation group) της M. Στο βιβλίο αυτό η G θα είναι μια ομάδα Lie και η M μια λεία πολλαπλότητα ενώ, επειδή κάθε αριστερή δράση μπορεί να γίνει δεξιά θέτοντας το g p να είναι p g 1 και αντιστρόφως, θα ασχοληθούμε μόνο με τις αριστερές δράσεις. Αν λ είναι μια αριστερή δράση της G στην M, τότε για κάθε g G η απεικόνιση λ g : M M με τύπο λ g (m) = λ(g, m) = gm είναι μια αμφιδιαφόριση της M. Πράγματι, παρατηρούμε ότι λ g1 λ g2 = λ g1 g 2, και λ e = Id κατά συνέπεια για κάθε g G, η αντίστροφη απεικόνιση της λ g είναι η λεία απεικόνιση λ g 1 = (λ g ) 1. Οπότε, μέσω των αριστερών δράσεων (αντίστ. δεξιών) μπορούμε να αναπαραστήσουμε την ομάδα G ως μια υποομάδα της ομάδας των αμφιδιαφορίσεων της πολλπαπλότητας M. Ας δούμε τώρα κάποιους ορισμούς σχετικά με μια δράση. Εστω M ένας G-χώρος.
3 Δράσεις ομάδων 3 Μια δράση λέγεται μεταβατική (transitive), αν για κάθε ζεύγος σημείων p, q M υπάρχει g G τέτοιο ώστε q = gp. Για κάθε m M, η ομάδα ισοτροπίας (isotropy group) του m, είναι το σύνολο εκείνων των στοιχείων της ομάδας, που διατηρούν το m σταθερό, δηλαδή είναι το σύνολο το οποίο συμβολίζουμε με G m, όπου G m = {g G : gm = m} G. Για κάθε m M, η τροχιά (orbit) του m, είναι το σύνολο G m = {g m : g G} M. 1 Μια δράση καλείται αποτελεσματική (effective), αν το e G είναι το μοναδικό στοιχείο που ορίζει την τετριμμένη δράση, δηλαδή αν gm = m για όλα τα m M, τότε g = e. Μια δράση καλείται ελεύθερη (free), αν η σχέση gm = m για κάποιο m M συνεπάγεται ότι g = e. Δηλαδή η δράση είναι ελεύθερη αν G m = {e}. Παρατηρήσεις. 1. Εύκολα προκύπτει ότι η ομάδα ισοτροπίας G m του m M είναι μια υποομάδα Lie της G. Πράγματι, παρατηρούμε ότι για κάθε g 1, g 2 G m είναι (g 1 g 2 ) m = g 1 (g 2 m) = g 1 m = m, δηλαδή g 1 g 2 G m, οπότε το σύνολο G m είναι κλειστό ως προς τον πολλαπλασιασμό της G. Το ουδέτερο στοιχείο e G ανήκει στην ομάδα ισοτροπίας του m, αφού e m = m. Τέλος, για κάθε g G m έχουμε g 1 G m, διότι m = e m = (g 1 g) m = g 1 (gm) = g 1 m. Άρα το G m είναι υποομάδα της G. Για να δείξουμε ότι είναι υποομάδα Lie της G, αρκεί να δείξουμε ότι είναι κλειστό (τοπολογικά) υποσύνολο της G. Παρατηρούμε ότι το G m είναι η αντίστροφη εικόνα της συνεχούς απεικόνισης f m : G M, με τιμή f m (g) = gm. Συνεπώς, η ομάδα ισοτροπίας του σημείου m M είναι μια υποομάδα Lie της G. 2. Αν M είναι ένας G-χώρος, τότε για m 1, m 2 M ορίζουμε m 1 m 2 εάν και μόνο εάν υπάρχει g G τέτοιο ώστε gm 1 = m 2. Τότε η σχέση είναι μια σχέση ισοδυναμίας. Πράγματι, για κάθε m M έχουμε em = m, άρα m m. Εστω m 1 m 2, δηλαδή gm 1 = m 2 για κάποιο g G. Τότε g 1 m 2 = g 1 (gm 1 ) = (g 1 g)m 1 = em 1 = m 1, άρα m 2 m 1. Τέλος αν m 1 m 2 και m 2 m 3 τότε g 1 m 1 = m 2 και g 2 m 2 = m 3, για κάποια g 1, g 2 G. Άρα (g 2 g 1 )m 1 = g 2 (g 1 m 1 ) = g 2 m 2 = m 3, δηλαδή m 1 m 3. Οι κλάσεις ισοδυναμίας της είναι ακριβώς οι τροχιές της δράσεις της ομάδας G. Κατά συνέπεια, οι τροχιές διαμερίζουν την πολλαπλότητα M. Με αυτόν τον τρόπο δημιουργείται ο χώρος πηλίκο M/G (χώρος τροχιών orbit space). 1 Μια μεταβατική δράση έχει μία και μοναδική τροχιά.
4 4 Ομογενείς χώροι - Γεωμετρία κατά Klein 3. Για κάθε g G ισχύει ότι G g x = gg x g 1. Πράγματι, αν h G g x, τότε h (g x) = g x. Πολλαπλασιάζουμε την προηγούμενη σχέση με το g 1 από αριστερά και έχουμε g 1 h (g x) = g 1 g x, δηλαδή (g 1 hg) x = e x = x. Άρα g 1 hg G x, ή h g 1 G x g. Επομένως, δείξαμε ότι G g x g 1 G x g. Μένει να δείξουμε ότι g 1 G x g G g x. Εστω h g 1 G x g. Τότε το g 1 hg ανήκει στο σύνολο G x, δηλαδή (g 1 hg) x = x. Πολλαπλασιάζοντας την τελευταία σχέση από αριστερά με g, θα πάρουμε g(g 1 hg) x = g x, ή eh(g x) = g x, δηλαδή h G g x. Αυτό μας λέει ότι, στην περίπτωση που δύο στοιχεία x, gx m M ανήκουν στην ίδια τροχιά, τότε οι ομάδες ισοτροπίας τους διαφέρουν μόνο κατά τον εσωτερικό αυτομορφισμό I g : G G, I g (α) = g 1 αg, ή ότι οι ομάδες ισοτροπίας είναι συζυγείς. Παραδείγματα. 1. Εχουμε δει στο Κεφάλαιο 8 ότι κάθε αναπαράσταση φ : G Aut(V ) ορίζει μια δράση της ομάδας G στον διανυσματικό χώρο V με τον εξής τρόπο: Φ : G V V, (g, v) φ(g)v gv. Τότε ισχύει Φ(g 1 g 2, v) = (g 1 g 2 )v = g 1 (g 2 v) = Φ(g 1, Φ(g 2, v)) και Φ(e, v) = ev = v, δηλαδή η απεικόνιση Φ είναι πράγματι μια δράση. 2. Η φυσική δράση της GL n R στον χώρο R n. Θεωρούμε έναν πίνακα A = [α ij ] GL n R και ένα διάνυσμα-στήλη u = (u i ) R n. Τότε η απεικόνιση GL n R R n R n με τιμή (A, u) A u, είναι μια αριστερή δράση της γενικής γραμμικής ομάδας στον Ευκλείδειο χώρο R n. Πράγματι, παρατηρούμε ότι για κάθε u R n και A, B GL n R έχουμε I n u = u και (AB) u = A (B u). Επίσης, η παραπάνω απεικόνιση είναι λεία, διότι τα στοιχεία του πίνακα A u είναι οι λείες συναρτήσεις, A u = j [α ij]u j. Η δράση αυτή δεν είναι μεταβατική, επειδή για κάθε A GL n R ισχύει ότι A 0 = 0. Η μεταβατικότητα ισχύει στην περίπτωση που η γενική γραμμική ομάδα δρά στον R n \{0}. Για παράδειγμα, όταν n = 2, τότε ( ) α θεωρούμε ένα μη μηδενικό διάνυσμα v = R 2, και ζητάμε έναν πίνακα A GL 2 R, τέτοιον ώστε β ( ) ( ) 1 α 0 A = v. Στην περίπτωση που έχουμε α 0, θεωρούμε τον πίνακα A =, ενώ αν β 0 0 β 1 ( ) α 1 τότε θεωρούμε τον πίνακα B =. Παρατηρούμε ότι οι πίνακες A, B ανήκουν στη γενική γραμμική β 0 ( ) 1 ομάδα και ο καθένας στέλνει το διάνυσμα στο v. Με το ίδιο σκεπτικό ορίζεται η μεταβατική δράση 0 των υποομάδων της GL n R στον Ευκλείδειο χώρο R n \{0}. 3. Κάθε ομάδα Lie G μπορεί να θεωρηθεί ως G-χώρος, αφού η G δρά στον ευατό της μέσω της απεικόνισης λ : G G G, (g 1, g 2 ) g 1 g 2.
5 Πολλαπλότητες πηλίκο 5 Επίσης, αν H είναι μια υποομάδα της G τότε η G είναι ένας H-χώρος μέσω της δράσης H G G, (h, g) hg. Η απεικόνιση I h : G G με τιμή I h (g) = hgh 1 για κάθε h H, ορίζει μια λεία δράση της υποομάδας H στην G. Πράγματι, για κάθε h 1, h 2 H και g G είναι I e = ege 1 = g και I h1 h 2 (g) = h 1 h 2 g(h 1 h 2 ) 1 = h 1 (h 2 gh 1 2 )h 1 1 = I h1 (I h2 (g)) Πολλαπλότητες πηλίκο Εστω G μια ομάδα Lie και K μια υποομάδα της G. Το σύνολο όλων των αριστερών συμπλόκων {gk : g G} της K στην G συμβολίζεται με G/K. Το σύνολο αυτό εφοδιασμένο με την τοπολογία πηλίκο (που ορίζεται μέσω της κανονικής προβολής π : G G/K, π(g) = gk), ονομάζεται χώρος πηλίκο (coset space). Γενικά, αν X είναι ένας τοπολογικός χώρος και είναι μια σχέση ισοδυναμίας στον X, τότε ο χώρος πηλίκο X/ είναι το σύνολο όλων των κλάσεων ισοδυναμίας, δηλαδή X/ = {[x] : x X} = {{y X : y x} : x X}. Ο χώρος αυτός εφοδιάζεται με την εξής τοπολογία. Εστω π : X X/, x [x] η κανονική προβολή (συμβολίζεται και αυτή με το ίδιο γράμμα). Τότε το U X/ ονομάζεται ανοικτό εάν και μόνο εάν το π 1 (U) είναι ανοικτό στο X. Προκειμένου ο χώρος πηλίκο να αποκτήσει δομή λείας πολλαπλότητας, η υποομάδα K απαιτείται να είναι κλειστή. Για την απόδειξη της παρακάτω πρότασης παραπέμπουμε στα βιβλία [7], [11], [16]. Θεώρημα Εστω G μια ομάδα Lie και K μια κλειστή υποομάδα της G. Τότε ο χώρος πηλίκο G/K επιδέχεται μία και μοναδική δομή λείας πολλαπλότητας, τέτοια ώστε η προβολή π : G G/K να είναι μια υπεμβάπτιση, δηλαδή το διαφορικό dπ g της π να είναι επί για κάθε g G. Υπάρχουν πολλές περιπτώσεις κατά τις οποίες η υποομάδα K μπορεί να είναι κλειστή. Για παράδειγμα, εάν η G είναι συνεκτική και απλά συνεκτική και η K είναι συνεκτική με ημιαπλή άλγεβρα Lie, τότε η K είναι κλειστή. Για περισσότερες πληροφορίες επί αυτού παραπέμπουμε στο βιβλίο [10]. Η λεία πολλαπλότητα G/K, που κατασκευάζεται σύμφωνα με το Θεώρημα 10.1, ονομάζεται πολλαπλότητα πηλίκο (coset manifold) ή ομογενής χώρος (homogeneous space). Επιπλέον, ισχύει ότι dim(g/k) = dim G dim K. Αν G/K είναι ένας ομογενής χώρος, τότε η απεικόνιση G G/K G/K, (a, gk) agk είναι μια δράση και ονομάζεται φυσική δράση της G στον G/K. Η δράση αυτή είναι μεταβατική. Για κάθε α G ορίζουμε την απεικόνιση τ a : G/K G/K με τ a (gk) = agk, η οποία ονομάζεται αριστερή μεταφορά (left translation) στον G/K. Αν a, b G και L a η αριστερή μεταφορά της ομάδας Lie G, τότε έχουμε ότι π L a = τ a π και τ ab = τ a τ b.
6 6 Ομογενείς χώροι - Γεωμετρία κατά Klein Η απεικόνιση τ a είναι μια αμφιδιαφόριση του G/K, αφού είναι λεία και έχει αντίστροφη τη λεία απεικόνιση τ a 1 = (τ a ) 1. Θα δούμε τώρα ότι κάθε μεταβατική δράση μπορεί να περιγραφεί με αυτόν τον τρόπο. Συγκεκριμένα, αν έχουμε μια μεταβατική δράση μιας ομάδας Lie G σε μια πολλαπλότητα M, τότε η M είναι ένας ομογενής χώρος. Συγκεκριμένα, ισχύει το εξής: Θεώρημα Εστω G M M μια μεταβατική δράση της ομάδας Lie G στη λεία πολλαπλότητα M και έστω K = G m η ομάδα ισοτροπίας του σημείου m M. Τότε (α) Η ομάδα ισοτροπίας K είναι μια κλειστή υποομάδα της G. (β) Η φυσική απεικόνιση j : G/K M με τιμή j(gk) = g m είναι μια G-ισοαναλλοίωτη αμφιδιαφόριση. (γ) Η τροχιά G m είναι αμφιδιαφορική με τον ομογενή χώρο G/K. Για την απόδειξη του θεωρήματος αυτού θα χρειαστούμε κάποια αποτελέσματα, για τις αποδείξεις των οποίων παραπέμπουμε στο βιβλίο [11]. Πρόταση Εστω M, N δύο λείες πολλαπλότητες και π : M N μια υπεμβάπτιση. Εστω P μια λεία πολλαπλότητα και F : M P λεία απεικόνιση, η οποία είναι σταθερή, όταν περιοριστεί στην υποπολλαπλότητα π 1 (p) για κάθε p N. Τότε υπάρχει μοναδική λεία απεικόνιση F : N P, τέτοια ώστε F π = F. M π N F F Επειδή η απεικόνιση π στο παραπάνω θεώρημα είναι καταβύθιση, τότε για κάθε p N το σύνολο π 1 (p) (κανονικό σύνολο στάθμης) είναι μια υποπολλαπλότητα της M διάστασης dimm dimn. Θυμίζουμε ότι (βλ. Κεφάλαιο 8), όταν έχουμε δύο G-χώρους V και W, τότε μια απεικόνιση A : V W λέγεται ισοαναλλοίωτη, αν για κάθε g G και v V ισχύει A(g v) = g A(v). Στην περίπτωση που η δράση της ομάδας G στο χώρο V είναι μεταβατική, τότε η τάξη της απεικόνισης A είναι σταθερή. Συγκεκριμένα ισχύει το εξής: Πρόταση Εστω M και N δύο λείες πολλαπλότητες και έστω G μια ομάδα Lie. Υποθέτουμε ότι η λεία απεικόνιση F : M N είναι ισοαναλλοίωτη ως προς μια μεταβατική δράση της G στη πολλαπλότητα M και ως προς οποιαδήποτε δράση της G στη N. Τότε η απεικόνιση F έχει σταθερή τάξη. P Απόδειξη. (του Θεωρήματος 10.2) (α) Θεωρούμε τη λεία απεικόνιση F : G M με τιμή F (g) = g m. Τότε παρατηρούμε ότι K = F 1 ({m}), δηλαδή η K είναι ένα κλειστό υποσύνολο της G ως αντίστροφη εικόνα του κλειστού συνόλου {m} M. Επομένως, σύμφωνα με το Θεώρημα 7.1 η ομάδα ισοτροπίας του σημείου m M είναι μια κλειστή υποομάδα Lie της G.
7 Πολλαπλότητες πηλίκο 7 (β) Θα δείξουμε πρώτα ότι η j είναι καλώς ορισμένη. Υποθέτουμε ότι g 1 K = g 2 K, δηλαδή g 1 1 g 2 K. Θέτουμε g 1 1 g 2 = k. Τότε είναι: j(g 2 K) = g 2 m = g 1 k m = j(g 1 kk) = j(g 1 K). Η τέταρτη ισότητα ισχύει, διότι το k K. Στη συνέχεια, θα δείξουμε ότι η απεικόνιση j είναι G- ισοαναλλοίωτη. Πράγματι, είναι j(g gk) = g g m = g (g m) = g j(gk). Επίσης, η j είναι λεία, διότι, αν περιορίσουμε την απεικόνιση F στην ομάδα ισοτροπίας K, δηλαδή F : K M, τότε είναι σταθερή, αφού για κάθε k K έχουμε F (k) = k m = m. Επομένως, από την Πρόταση 10.1 και επειδή ισχύει ότι π 1 (m) = K, θα υπάρχει μοναδική λεία απεικόνιση F, τέτοια ώστε F π = F. Στη συγκεκριμένη περίπτωση η F είναι η απεικόνιση j : G/K M. G F π G/K M j Άρα, αφού η j είναι λεία και ισοαναλλοίωτη, από την Πρόταση 10.2 θα έχει σταθερή τάξη. Για να είναι αμφιδιαφόριση, αρκεί να δείξουμε ότι η j είναι 1 1 (άσκηση, βλ. και []). Για το επί, έστω q M. Τότε υπάρχει κάποιο στοιχείο g G, τέτοιο ώστε j(gk) = g m = q. Η τελευταία ισότητα ισχύει, επειδή η δράση της G στην πολλαπλότητα M είναι μεταβατική. Τέλος, η απεικόνιση j είναι 1 1, αφού, αν j(g 1 K) = j(g 2 K), τότε g 1 m = g 2 m, δηλαδή g1 1 g 2 m = m κατ επέκταση g1 1 g 2 K, οπότε g 1 K = g 2 K. Το (γ) είναι άμεσο. Από το Θεώρημα 10.2 οδηγούμαστε στον παρακάτω ορισμό: Ορισμός Ενας ομογενής χώρος είναι μια λεία πολλαπλότητα M στην οποία δρά μεταβατικά μια ομάδα Lie G. Ισοδύναμα, είναι μια λεία πολλαπλότητα της μορφής G/K, όπου G είναι μια ομάδα Lie και K μια κλειστή υποομάδα της G. Αν (M, g) είναι μια πολλαπλότητα Riemann, τότε το σύνολο των ισομετριών I(M) είναι ομάδα με πράξη τη σύνθεση συναρτήσεων. Ενα θεώρημα των Myers-Steenrod αναφέρει ότι το σύνολο I(M) είναι ομάδα Lie. Επίσης, η ομάδα I(M) δρά μεταβατικά στην πολλαπλότητα Riemann M ως εξής: I(M) M M, (f, p) f(p). Η μεταβατικότητα σημαίνει ότι, για κάθε δύο σημεία p, q M υπάρχει μια ισομετρία f I(M), τέτοια ώστε f(p) = q. Σε αυτή την περίπτωση η M ονομάζεται ομογενής πολλαπλότητα Riemann. Επιπλέον, ισχυει το εξής:
8 8 Ομογενείς χώροι - Γεωμετρία κατά Klein Πρόταση Αν η M είναι μια ομογενής πολλαπλότητα Riemann, τότε η ομάδα ισοτροπίας σε κάποιο σημείο της είναι συμπαγής υποομάδα της I(M). Επιπλέον, η I(M) είναι συμπαγής εάν και μόνο εάν η M είναι συμπαγής. Ορισμός Μια γεωμετρία Klein είναι ένα ζεύγος (G, K) όπου G είναι μια ομάδα Lie και K μια κλειστη υποομάδα της G. Περισσότερα για τις γεωμετρίες Klein και για τη μετάβαση στη γεωμετρία κατά Cartan (μελέτη μιας συνοχής σε μια κύρια G-δέσμη), παραπέμπουμε στο βιβλίο [14]. Σε μια πολλαπλότητα ενδέχεται να δρούν μεταβατικά περισσότερες από μία ομάδες Lie, έτσι η ίδια πολλαπλότητα θα είναι αμφιδιαφορική με διαφορετικούς ομογενείς χώρους. Ενα χαρακτηριστικό παράδειγμα, όπως θα δούμε στη συνέχεια είναι η σφαίρα S n. Η εύρεση όλων ομάδων Lie, οι οποίες δρουν μεταβατικά σε μια πολλαπλότητα, αποτελεί ένα δύσκολο πρόβλημα της γεωμετρίας. Επίσης, πρέπει να αναφέρουμε ότι τα παραδείγματα που θα μελετήσουμε στη συνέχεια είναι όλα παραδείγματα ομογενών πολλαπλότητων Riemann. Το χαρακτηριστικό στοιχείο σε αυτά τα παραδείγματα είναι ότι δεν απαιτείται να δρά ολόκληρη η ομάδα των ισομετρίων της πολλαπλότητας, αλλά μια υποομάδα αυτής. Παραδείγματα. 1. Εστω G μια ομάδα Lie. Τότε η G εκφράζεται ως ομογενής χώρος με τους εξής δύο τρόπους: G = G/{e} = (G G)/G. Στην πρώτη περίπτωση η G δρα μεταβατικά στον ευατό της μέσω της αριστερής μεταφοράς L a : G G, για κάθε a G. Στη δεύτερη περίπτωση η ομάδα G G δρά στην G μέσω των αριστερών και δεξιών μεταφορών. εμφυτεύεται στην G G κατά διαγώνιο τρόπο. Η ομάδα ισοτροπίας στη δεύτερη περίπτωση είναι η G, η οποία 2. Εστω G μια ομάδα Lie διάστασης n και έστω g η άλγεβρα Lie της G. Θεωρούμε το σύνολο M όλων των εσωτερικών γινομένων της άλγεβρας g. Θα αποδείξουμε ότι το σύνολο M = { f : g g R, f διγραμμική, θετικά ορισμένη και συμμετρική απεικόνιση } είναι αμφιδιαφορικό με τον ομογενή χώρο GL n R/O(n). Συγκεκριμένα, θα δείξουμε ότι η γενική γραμμική ομάδα GL n R δρά μεταβατικά στο M. Εστω λ : GL n R M M, λ(a, f)(u, v) = ( A f ) (u, v) := f(a 1 u, A 1 v). (10.1) Η απεικόνιση (10.1) είναι μια δράση διότι, για κάθε (u, v) g g έχουμε Επίσης, ισχύει ότι λ(i, f)(u, v) = ( I f ) (u, v) = f(i 1 u, I 1 v) = f(u, v), λ(ab, f)(u, v) = ( AB f ) (u, v) = f ( (AB) 1 u, (AB) 1 v ) = f ( B 1 A 1 u, B 1 A 1 v ). λ ( A, λ(b, f) ) (u, v) = λ(b, f) ( A 1 u, A 1 v ) = f ( B 1 A 1 u, B 1 A 1 v ). Από τις παραπάνω ισότητες προκύπτει ότι λ(ab, f)(u, v) = λ ( A, λ(b, f) ) (u, v). Στη συνέχεια, θα δείξουμε ότι η δράση είναι μεταβατική, δηλαδή ότι για κάθε δύο εσωτερικά γινόμενα f, f M υπάρχει πίνακας
9 Πολλαπλότητες πηλίκο 9 g GL n R τέτοιος ώστε g f = f. Πράγματι, έστω f : g g R ένα εσωτερικό γινόμενο του οποίου ο πίνακας D ως προς μια τυχαία βάση του χώρου g είναι διαγώνιος και έστω f : g g R ένα άλλο εσωτερικό γινόμενο. Επειδή η απεικόνιση f είναι συμμετρική, υπάρχει ένας ορθογώνιος πίνακας P τέτοιος ώστε P 1 [f]p = P t [f]p = D, ισοδύναμα [f] = (P t ) 1 DP 1, όπου [f] είναι ο πίνακας της απεικόνισης f ως προς μια βάση του χώρου g. Επομένως, αν επιλέξουμε τον πίνακα g = P O(n) GL n R, τότε θα έχουμε P D = (P 1 ) t DP 1 = (P t ) 1 DP 1 = [f]. Πρέπει να σημειώσουμε ότι η δράση που ορίσαμε μέσω της απεικόνισης (10.1) με μορφή πινάκων, γράφεται ως A [f] = (A 1 ) t [f]a 1. Τέλος, θα υπολογίσουμε την ομάδα ισοτροπίας του εσωτερικού γινομένου h M ως προς το οποίο η βάση της άλγεβρας Lie g είναι ορθοκανονική, δηλαδή πρέπει να προσδιορίσουμε το σύνολο (GL n R) h = { ( ) } g GL n R : g h (u, v) = h(u, v). Γνωρίζουμε ότι κάθε πίνακας A GL n R ικανοποιεί τη σχέση Ax, y = x, A t y, οπότε αν υποθέσουμε ότι A O(n), τότε θα έχουμε Ax, Ay = x, A t Ay = x, y, δηλαδή οι ορθογώνιοι πίνακες αφήνουν αναλλοίωτο το εσωτερικό γινόμενο. Επομένως, για την ομάδα ισοτροπίας (GL n R) h, αν επιλέξουμε g O(n), τότε θα είναι ( ) ( g h (u, v) = h g 1 u, g 1 v ) = h ( u, (g 1 ) t g 1 v ) = h(u, v), άρα (GL n R) h = O(n). Από το Θεώρημα 10.2 η απεικόνιση j : GL n R/(GL n R) h M, με τιμή j(a(gl n R) h ) = ( A h ) (u, v) είναι αμφιδιαφόριση, οπότε GL n R/(GL n R) h = GL n R/O(n) = M. Τέλος, η διάσταση του M είναι dimm = dimgl n R dimo(n) = n n(n 1) = 1 n(n + 1) Εστω S n = { (x 1,..., x n+1 ) R n+1 : i x2 i = 1 } η μοναδιαία σφαίρα στον R n+1. Αν, είναι το κανονικό εσωτερικό γινόμενο του R n+1, τότε το σύνολο αυτό εκφράζεται και ως S n = { u R n+1 : u, u = 1 }, όπου u = (x 1,..., x n+1 ) R n+1. Θα δείξουμε ότι η σφαίρα S n είναι αμφιδιαφορική με τον ομογενή χώρο O(n+1)/O(n). Θα πρέπει δηλαδή να ορίσουμε μια μεταβατική δράση της ορθογώνιας ομάδας O(n+1) στην S n και στη συνέχεια να υπολογίσουμε την ομάδα ισοτροπίας σε κάποιο σημείο της σφαίρας. Για το πρώτο γνωρίζουμε ότι η GL n+1 R δρά με φυσικό
10 10 Ομογενείς χώροι - Γεωμετρία κατά Klein τρόπο στον Ευκλείδειο χώρο R n+1 μέσω του πολλαπλασιασμού πινάκων. Στην περίπτωση που A O(n+1), δηλαδή A t A = I, τότε είναι Au, Au = u, A t Au = u, u. Η πρώτη ισότητα ισχύει, διότι για κάθε πίνακα A GL n R n+1 το εσωτερικό γινόμενο ικανοποιεί τη σχέση Au, v = u, A t v. Η παραπάνω σχέση μας λέει ότι κάθε ορθογώνιος πίνακας διατηρεί τα μέτρα των διανυσμάτων του R n+1. Επομένως, μπορούμε να περιορίσουμε τη φυσική δράση της ειδικής γραμμικής ομάδας στον R n+1, στη δράση της ομάδας O(n + 1) στη μοναδιαία σφαίρα S n ως εξής: O(n + 1) S n S n, (A, u) A u. Θα αποδείξουμε ότι η δράση αυτή είναι μεταβατική. Πράγματι, αν e 1 = (1 0 0) t S n και v S n ένα άλλο μοναδιαίο διάνυσμα, αναζητάμε πίνακα A O(n+1) τέτοιον ώστε Ae 1 = v. Αρκεί να επιλέξουμε A = (v v 1... v n ), όπου {v, v 1,..., v n } είναι μια ορθοκανονική βάση του R n+1. Στη συνέχεια, θα υπολογίσουμε την ομάδα ισοτροπίας του σημείου e 1 S n, δηλαδή θα πρέπει να βρούμε το σύνολο Αν επιλέξουμε A = B 0 O(n + 1) e1 = { A O(n + 1) : Ae 1 = e 1 }., τότε Ae 1 = e 1. Θα πρέπει όμως ο A να ανήκει στην ορθογώνια ομάδα O(n + 1), δηλαδή deta = ±1, άρα αρκεί να πάρουμε B O(n). Επομένως, η ομάδα ισοτροπίας θα περιέχει πίνακες της παραπάνω μορφής. Λόγω της εμβύθισης O(n) B A = O(n + 1),. B 0 μπορούμε να ταυτίσουμε όλους τους πίνακες της ορθογώνιας ομάδας O(n) με πίνακες της O(n + 1), οπότε η ομάδα ισοτροπίας του σημείου e 1 S n είναι O(n + 1) e1 = { A O(n + 1) : Ae 1 = e 1 } = O(n), δηλαδή μια κλειστή υποομάδα της O(n + 1). Σύμφωνα με το Θεώρημα 10.2 η απεικόνιση είναι αμφιδιαφόριση, επομένως j : O(n + 1)/O(n + 1) e1 S n, με τιμή j(ao(n + 1) e1 ) = Ae 1 O(n + 1)/O(n + 1) e1 = O(n + 1)/O(n) = S n. Στην περίπτωση που θεωρήσουμε τη δράση της ειδικής ορθογώνιας ομάδας SO(n + 1) στη σφαίρα S n τότε θα έχουμε SO(n + 1)/SO(n) = S n.
11 Πολλαπλότητες πηλίκο 11 Σε αυτή την περίπτωση το μόνο που θα αλλάξει είναι ότι η ορθοκανονική βάση {v, v 1,, v n } του R n+1 είναι προσανατολισμένη, δηλαδή ο ορθογώνιος πίνακας A ικανοποιεί την σχέση deta = 1, οπότε A SO(n). 4. Το μιγαδικό ανάλογο του προηγούμενου παραδείγματος προέρχεται από τη φυσική δράση της GL n+1 C στον μιγαδικό χώρο C n+1. Σε αυτή την περίπτωση θα είναι S 2n+1 = { u C n+1 : u, u = 1 } R 2n+2, όπου u = (x 1,..., x n+1 ) C n+1. Το εσωτερικό γινόμενο ορίζεται ως u, v = i=1 ūiv i. Θα δείξουμε ότι η σφαίρα είναι αμφιδιαφορική με τον ομογενή χώρο U(n + 1)/U(n). Ενας ερμητιανός πίνακας A U(n + 1) διατηρεί τα μέτρα των διανυσμάτων του χώρου C n+1. Πράγματι, Au, Au = u, Āt Au = u, u, όπου η πρώτη ισότητα ισχύει από την ιδιότητα του εσωτερικού γινομένου στον C n+1, ενώ στη δεύτερη ισότητα χρησιμοποιήσαμε το γεγονός ότι A U(n + 1), δηλαδή Āt A = I. Συνεπώς, περιορίζοντας την δράση της GL n+1 C στη δράση της μοναδιαίας ομάδας U(n + 1) στη σφαίρα S n, δηλαδή U(n + 1) S 2n+1 S 2n+1, (A, u) A u και εργαζόμενοι όπως στο Παράδειγμα 3, προκύπτει ότι η δράση είναι μεταβατική. Επιπλέον, η ομάδα ισοτροπίας σε κάποιο σημείο της σφαίρας είναι η κλειστή υποομάδα U(n) της U(n + 1). Άρα η μοναδιαία σφαίρα S 2n+1 θα είναι αμφιδιαφορική με τον ομογενή χώρο U(n + 1)/U(n). Τέλος, λαμβάνοντας υπόψη τον προσανατολισμό των βάσεων στον C n+1, η S 2n+1 θα είναι αμφιδιαφορική με τον ομογενή χώρο SU(n + 1)/SU(n), άρα U(n + 1)/U(n) = SU(n + 1)/SU(n) = S 2n+1. Επίσης, υπάρχει και το υπερμιγαδικό ανάλογο του παραδείγματος αυτού, δηλαδή Sp(n + 1)/Sp(n) = S 4n+3. Μάλιστα, από τα παραπάνω προκύπτει ότι S 0 = O(1), S 1 = U(1) = SO(2) και S 3 = SU(2) = Sp(1) (και όπως έχουμε αναφέρει στο Κεφάλαιο 7 αυτές είναι οι μόνες σφαίρες που επιδέχονται δομή ομάδας Lie). 5. Ο πραγματικός προβολικός χώρος RP n είναι αμφιδιαφορικός με τον ομογενή χώρο SO(n + 1)/O(n) = O(n + 1)/O(n) O(1). Για την πρώτη περίπτωση θεωρούμε τη δράση της SO(n + 1) στον R n+1 \{0} μέσω του πολλαπλασιασμού πινάκων και την περιορίζουμε στον υπόχωρο RP n R n+1 \{0}, δηλαδή SO(n + 1) RP n RP n. Η δράση αυτή είναι μεταβατική, ενώ η ομάδα ισοτροπίας είναι η O(n), η οποία είναι μια κλειστή υποομάδα της SO(n+1), οπότε RP n = SO(n+1)/O(n). Στη δεύτερη περίπτωση θεωρούμε τη λεία δράση της ορθογώνιας ομάδας O(n+1) στον RP n. Αποδεικνύεται ότι η δράση είναι μεταβατική, ενώ η ομάδα ισοτροπίας σε κάποιο σημείο του προβολικού χώρου αποτελείται από τους πίνακες ( ) ±1 0 = O(n) O(1). 0 O(n)
12 12 Ομογενείς χώροι - Γεωμετρία κατά Klein Θα ισχύουν τα ίδια και για τον μιγαδικό προβολικό χώρο CP n, ο οποίος θα είναι αμφιδιαφορικός με τους ομογενείς χώρους SU(n + 1)/U(n) = U(n + 1)/U(n) U(1). 6. Οι πολλαπλότητες Grassmann Gr k R n. Μία πολλαπλότητα Grassmann αποτελείται από το σύνολο όλων των k-διάστατων υποχώρων του R n. Αποδεικνύεται ότι το σύνολο αυτο έχει δομή μιας λείας πολλαπλότητας (βλ. [4], [13]). Ενας k-διάστατος υπόχωρος W Gr k R n είναι δυνατόν να παράγεται από k ορθοκανονικά διανύσματα του R n, δηλαδή W = span{x 1,..., x k } x, όπου k n. Θεωρώντας τα x i, i = 1,..., k ως διανύσματα-στήλη, μπορούμε να γράψουμε το x ως έναν n k πίνακα ως x = (x 1,..., x k ). Θα δείξουμε ότι η πολλαπλότητα Gr k R n είναι αμφιδιαφορική με τον ομογενή χώρο O(n)/O(k) O(n k). Από το Παράδειγμα 2 γνωρίζουμε ότι ένας ορθογώνιος πίνακας A O(n) διατηρεί τα μέτρα των διανυσμάτων του R n, οπότε το σύνολο A W = { A ỹ : ỹ W }, (όπου A ỹ είναι πολλαπλασιασμός πινάκων), θα είναι ένας k-διάστατος υπόχωρος του R n. Επομένως, η δράση της ορθογώνιας ομάδας O(n) στην πολλαπλότητα Grassmann μπορεί να οριστεί ως εξής: O(n) Gr k R n Gr k R n, (A, W ) A W. Θα αποδείξουμε ότι η δράση είναι μεταβατική. Εστω V ένας k-διάστατος υπόχωρος του R n, ο οποίος παράγεται από τα πρώτα k διανύσματα της κανονικής βάσης του R n, ας τη συμβολίζουμε με B = {e 1,..., e k, e k+1,..., e n } και έστω W Gr k R n ένας άλλος k-διάστατος υπόχωρος, ο οποίος παράγεται από k ορθοκανονικά διανύσματα u 1,..., u k του R n. Από την γραμμική άλγεβρα γνωρίζουμε ότι μπορούμε να βρούμε διανύσματα u k+1,..., u n τέτοια ώστε το σύνολο B = {u 1,..., u k, u k+1,..., u n } να είναι μια ορθοκανονική βάση του R n. Επίσης, γνωρίζουμε ότι ο πίνακας μετάβασης από μια ορθοκανονική βάση σε μία άλλη είναι ορθογώνιος, οπότε στην περίπτωσή μας αρκεί να πάρουμε τον πίνακα μετάβασης από τη βάση B στην B, δηλαδή A = (u 1,..., u n ), όπου τα u i, i = 1,..., n είναι τα διανύσματα-στήλες του R n. Τότε θα είναι Ae i = u i, i = 1,..., n. Για παράδειγμα, αν υποθέσουμε ότι κάθε u i εκφράζεται ως u i = x 1i x 2i., τότε A = x 11 x x 1n x 21 x x 2n Οπότε, για παράδειγμα έχουμε: x ni x n1 x n2... x nn x 11 x x 1n x 21 x x 2n Ae 1 = x n1 x n2... x nn = x 11 x 21. x n1 = u 1. Τέλος, αν θέσουμε ẽ = (e 1..., e k ) και ũ = (u 1,..., u k ) ως τους n k πίνακες που αποτελούνται από τα διανύσματα-στήλες του R n τα οποία παράγουν τους υποχώρους V και W αντίστοιχα, τότε θα είναι
13 Πολλαπλότητες πηλίκο 13 Aẽ = (u 1,..., u k ) = ũ, δηλαδή A V = W. Επομένως, η δράση είναι μεταβατική. Η ομάδα ισοτροπίας του υπόχωρου V είναι το σύνολο το οποίο περιέχει πίνακες της μορφής { ( B 0 0 C ) : B O(k), C O(n k) Αυτό είναι μια κλειστή υποομάδα της O(n) και είναι ισόμορφο με την ομάδα O(k) O(n k). Επομένως, η απεικόνιση j : O(n)/O(k) O(n k) Gr k R n, } j ( A(O(k) O(n k)) ) = AV, είναι αμφιδιαφόριση, άρα Gr k R n = O(n)/O(k) O(n k). Στην περίπτωση που λάβουμε υπόψην τον προσανατολισμό των βάσεων και διαλέξουμε προσανατολισμένους υπόχωρους του Ευκλείδειου χώρου, τότε οδηγούμαστε σε μια μεταβατική δράση της SO(n) στην πολλαπλότητα Grassmann, οπότε με παρόμοιο σκεπτικό η πολλαπλότητα Gr k R n είναι αμφιδιαφορική με τον ομογενή χώρο SO(n)/SO(k) SO(n k). Τέλος, αξίζει να σημειώσουμε ότι η διάσταση της πολλαπλότητας Grassmann είναι: dimgr k R n = dimo(n) dim(o(k) O(n k)) = 1 2 n(n 1) (1 2 k(k 1) + 1 (n k)(n k 1)) = k(n k). 2 Παρόμοια, ορίζονται και οι μιγαδικές πολλαπλότητες Grassmann 7. Οι πολλαπλότητες Stiefel V k R n. Gr k C n = U(n)/U(k) U(n k) = SU(n)/S(U(k) U(n k)). Οι πολλαπλότητες Stiefel V k R n είναι το σύνολο όλων των ορθοκανονικών k-διάστατων πλαισίων (orthonormal k-frames) ũ = (u 1,..., u k ), k n, όπου u i, i = 1,..., k είναι ορθοκανονικά διανύσματα του R n. Αποδεικνύεται ότι το σύνολο αυτό έχει δομή λείας πολλαπλότητας (βλ. [4], [13]). Οπως και στο προηγούμενο παράδειγμα, αν θεωρήσουμε τα διανύσματα του R n ως διανύσματα-στήλες, τότε κάθε τέτοιο πλαίσιο μπορεί να εκφραστεί ως ένας n k πίνακας. Θα αποδείξουμε ότι ο χώρος V k R n είναι αμφιδιαφορικός με τον ομογενή χώρο O(n)/O(n k). Πρώτα θα ορίσουμε μια δράση της ορθογώνιας ομάδας στην πολλαπλότητα V k R n. Επειδή η ομάδα O(n) όταν δράσει στον χώρο R n διατηρεί τα μήκη των διανυσμάτων, θα έχουμε ότι το A ũ (όπου ũ είναι n k πίνακας), είναι ένα ορθοκανονικό πλαίσιο, αφού ισχύει ότι A ũ, A ũ = ũ, A t A ũ = ũ, ũ. Συνεπώς, ορίζουμε τη δράση της O(n) στην πολλαπλότητα V k R n, ως εξής: O(n) V k R n V k R n, (A, ũ) A ũ. Θα αποδείξουμε ότι η δράση αυτή είναι μεταβατική. V k R n.. Εστω ένα τυχαίο στοιχείο ũ = (u 1,..., u k ) Τότε ως γνωστόν μπορούμε να βρούμε διανύσματα u k+1,..., u n του R n, έτσι ώστε το σύνολο {u 1,..., u k, u k+1,..., u n } να είναι μια ορθοκανονική βάση του R n. Θεωρώντας κάθε u i, (i = 1,..., n) ως διάνυσμα-στήλη, ορίζουμε τον n n πίνακα A = (u 1... u n ). Προφανώς ο πίνακας A ανήκει στην O(n) και ικανοποιεί την σχέση Ae i = u i, i = 1,..., n,
14 14 Ομογενείς χώροι - Γεωμετρία κατά Klein όπου {e 1 = (1,..., 0),..., e n = (0,..., 1)} είναι η κανονική βάση του R n. Άρα, αν θέσουμε ẽ = (e 1,..., e k ), θα έχουμε A ẽ = ũ, επομένως η δράση είναι μεταβατική. Η ομάδα ισοτροπίας του ẽ = (e 1,..., e k ) είναι το σύνολο το οποίο αποτελείται από πίνακες της μορφής { ( ) } I k 0 : B O(n k). 0 B Το σύνολο αυτό αποτελεί κλειστή υποομάδα της O(n) και είναι ισόμορφο με την ομάδα O(n k). Άρα η απεικόνιση j : O(n)/O(n k) V k R n, j(ao(n k)) = A ẽ είναι μια αμφιδιαφόριση, οπότε V k R n = O(n)/O(n k). Στην περίπτωση που επιλέξουμε A SO(n), τότε με παρόμοιο τρόπο προκύπτει ότι Τέλος, η διάσταση της πολλαπλότητας V k R n είναι: V k R n = SO(n)/SO(n k) = O(n)/O(n k). dimv k R n = dimo(n) dimo(n k) = 1 2 n(n 1) 1 2 (n k)(n k 1) = 1 k(2n k 1). 2 Σημειώνουμε ότι ανάλογα ορίζονται οι μιγαδικές πολλαπλότητες Stiefel. Στην περίπτωση αυτή έχουμε V k C n = U(n)/U(n k) = SU(n)/SU(n k) Αναγωγικοί ομογενείς χώροι Προκειμένου να μελετήσουμε τη γεωμετρία ενός ομογενούς χώρου G/K, θα επιθυμούσαμε μια αποτελεσματική περιγραφή του εφαπτόμενου χώρου T o (G/K), όπου o = ek = K είναι το ουδέτερο σύμπλοκο του χώρου πηλίκο G/K. Μια τέτοια περίπτωση συμβαίνει όταν ο ομογενής χώρος είναι αναγωγικός. Επειδή η κανονική προβολή π : G G/K είναι υπεμβάπτιση, τότε T o (G/K) = g/k, όπου με o συμβολίζουμε το ουδέτερο σύμπλοκο ek = K του ομογενούς χώρου G/K. Στους αναγωγικούς ομογενείς χώρους, που θα παρουσιάσουμε στη συνέχεια, θα δούμε ότι ο πρηγούμενος ισομορφισμός γίνεται πολύ πιο απλός. Ορισμός Ενας ομογενής χώρος ονομάζεται αναγωγικός (reductive), εάν υπάρχει ένας υπόχωρος m της άλγεβρας Lie g, τέτοιος ώστε g = k m με την ιδιότητα Ad(k)m m για κάθε k K, δηλαδή ο υπόχωρος m είναι Ad(K)-αναλλοίωτος. Αν ισχύει Ad(k)m m, τότε προκύπτει ότι [k, m] m. Το αντίστροφο ισχύει μόνο στην περίπτωση που η ομάδα K είναι συνεκτική. Μια περίπτωση όπου ο ομογενής χώρος G/K είναι αναγωγικός, είναι αυτή κατά την οποία η ομάδα Lie G είναι συμπαγής και ημιαπλή. Πράγματι, τότε αρκεί να πάρουμε ως υπόχωρο m = k, το ορθογώνιο συμπλήρωμα της k στην άλγεβρα Lie g ως πρός το B, την αρνητική τιμή της μορφής Killing της g (γενικότερα μπορούμε να πάρουμε ένα οποιοδήποτε Ad(K)-αναλλοίωτο εσωτερικό γινόμενο της g). Άλλες περιπτώσεις κατά τις οποίες ένας ομογενής χώρος G/K αναγωγικός, είναι οι εξής (βλ. [10]):
15 Πολλαπλότητες πηλίκο 15 Η K να είναι συμπαγής. Η K να είναι συνεκτική και ημιαπλή. Η K να είναι διακριτή υποομάδα της G. Τότε έχουμε την τετριμμένη περίπτωση k = 0 και m = g. Πρόταση Εστω G/K ένας αναγωγικός ομογενής χώρος και g, k οι αντίστοιχες άλγεβρες Lie. Τότε το ορθογώνιο συμπλήρωμα k της k ως προς ένα Ad(K)-αναλλοίωτο εσωτερικό γινόμενο είναι ένας Ad(K)-αναλλοίωτος υπόχωρος της άλγεβρας Lie g. Απόδειξη. Θα δείξουμε ότι για κάθε k K είναι Ad(k)k = {Ad(k)X : X k } k. Εστω X k και Y k, οπότε X, Y = 0. Για κάθε h K θα έχουμε: Ad(k)X, Y = Ad(k 1 )Ad(k)X, Ad(k 1 )Y, επειδή το, είναι Ad(K)-αναλλοίωτο = X, Ad(k 1 )Y = 0, αφού Ad(k 1 )Y k και X k. Επομένως, αφού για κάθε k K ισχύει Ad(k)X, Y = 0, αυτό σημαίνει ότι το Ad(k)X είναι ορθογώνιο σε κάθε Y k, άρα είναι ορθογώνιο στον υπόχωρο k. Οπότε για κάθε X k και k K, έχουμε Ad(h)X k, δηλαδή ο υπόχωρος k είναι Ad(K)-αναλλοίωτος. Θεωρούμε τώρα την κανονική προβολή π : G G/K, π(g) = gk και υποθέτουμε ότι ο G/K είναι ένας αναγωγικός ομογενής χώρος. Τότε το διαφορικό (dπ) e : g T o (G/K) επάγει έναν γραμμικό ισομορφισμό μεταξύ του m και T o (G/K). Για να το αποδείξουμε, χρειαζόμαστε την παρακάτω πρόταση. Πρόταση Εστω M, N λείες πολλαπλότητες, f : M N λεία απεικόνιση, y N μια κανονική τιμή της f και Z = f 1 (y) η υποπολλαπλότητα της M διάστασης dim M dim N. Τότε ο πυρήνας του διαφορικού df x : T x M T y N σε κάθε σημείο x Z ισούται με τον εφαπτόμενο χώρο της υποπολλαπλότητας Z, δηλαδή Kerdf x = T x Z. Απόδειξη. Η απεικόνιση f είναι σταθερή στο σύνολο Z = f 1 (y) M, οπότε το διαφορικό της θα είναι μηδέν στον T x Z T x M, για κάθε x Z. Άρα ο T x Z είναι υπόχωρος του Kerdf x = {A T x M : df x A = 0}. Επίσης, έχουμε ότι για κάθε σημείο x Z η απεικόνιση df x : T x M T y N είναι επί. Επομένως, dim(t x M) = dim(kerdf x ) + dim(imdf x ) dim Kerdf x = dim(t x M) dim(imdf x ), (επειδή το df x είναι επί έχουμε Imdf x = T y N) = dim(m) dim(n) = dim(f 1 (y)) = dim(z). Η τέταρτη ισότητα ισχύει από υπόθεση. Οπότε, αφού dimkerdf x = dim(z) = dim(kert x Z) και επειδή ο T x Z είναι υπόχωρος του πυρήνα Kerdf x, θα έχουμε το ζητούμενο, δηλαδή Kerdf x = T x Z. Ο ισομορφισμός m = T o (G/K) προκύπτει τώρα ως εξής: Η π είναι υπεμβάπτιση οπότε το διαφορικό της είναι επί σε κάθε σημείο της G, άρα και στο ουδέτερο e. Το σημείο o = ek = K G/K είναι μια κανονική τιμή της προβολής π και π 1 (o) = K. Τότε, ο πυρήνας του διαφορικού (dπ) e, σύμφωνα με
16 16 Ομογενείς χώροι - Γεωμετρία κατά Klein την προηγούμενη πρόταση, θα είναι ο εφαπτόμενος χώρος της υποπολλαπλότητας K = π 1 (o), δηλαδή Ker(dπ) e = T e K = k. Συνεπώς έχουμε dim(ker(dπ) e ) = dim g dim(t o (G/K)), και επειδή ο ομογενής χώρος G/K είναι αναγωγικός, δηλαδή g = k m, η παραπάνω ισότητα γράφεται dim k = dim k + dim m dim(t o (G/K)), ή dim m = dim(t o (G/K)). Επειδή το διαφορικό (dπ) e είναι μια γραμμική και επί απεικόνιση, παίρνουμε τον κανονικό ισομορφισμό m = T o (G/K). Στην περίπτωση που ο ομογενής χώρος G/K δεν είναι αναγωγικός, ο παραπάνω ισομορφισμός είναι μόνο μεταξύ των g/k και T o (G/K). Σχήμα 10.1: Για έναν αναγωγικό ομογενή χώρο G/K με αναγωγική ανάλυση g = k m, ισχύει ο ισομορφισμός m = T o (G/K). Εστω G/K ένας αναγωγικός ομογενής χώρος και g = k m η αντίστοιχη αναγωγική ανάλυση της άλγεβρας Lie g. Αν X g και exptx η αντίστοιχη μονοπαραμετρική υποομάδα που παράγεται από το X τότε (dπ) e (X) = d dt (π(exptx)) t=0 = d dt (exptx)k t=0 = d dt (exptx)ek t=0 = d dt (exptx)o t=0. Το εφαπτόμενο διάνυσμα (dπ) e (X) T o (G/K) θα το συμβολίζουμε με X o, δηλαδή X o = d dt (exptx)o t=0.
17 Πολλαπλότητες πηλίκο 17 Αν g = k m τότε για κάθε X g γράφουμε X = X k + X m. (dπ) e (X k ) = 0 για κάθε X k k, οπότε Επειδή Ker(dπ) e = k τότε θα είναι (dπ) e (X) = (dπ) e (X k ) + (dπ) e (X m ) = (dπ) e (X m ), δηλαδή (dπ) e (X) = (dπ) e (X m ) = X o. Γενικά, για κάθε αριστερά αναλλοίωτο διανυσματικό πεδίο X g ορίζουμε το διανυσματικό πεδίο X στον ομογενή χώρο G/K μέσω της σχέσης X gk = d dt (exptx)gk t=0. Για την καλύτερη κατανόηση των παραπάνω εννοιών θα δώσουμε στη συνέχεια, ένα παράδειγμα υπολογισμού της αναγωγικής ανάλυσης ενός ομογενούς χώρου. Παράδειγμα. Θα βρούμε την αναγωγική ανάλυση του ομογενούς χώρου SU(3)/S(U(1) U(1) U(1)) = SU(3)/T, όπου T ο μεγιστικός δακτύλιος της SU(3). Ο συγκεκριμένος χώρος ονομάζεται πολλαπλότητα σημαιών (flag manifold) 2 και έχει διάσταση dim SU(3) dim T = (3 1) = 6. Η άλγεβρα Lie της SU(3) είναι το σύνολο su(3) = { A GL 3 C : A + Āt = 0, tra = 0 } = { ia x 2 + iy 2 x 3 + iy 3 x 2 + iy 2 ib a 3 + ib 3 x 3 + iy 3 a 3 + ib 3 ic : a + b + c = 0, a, b, c, x i, y i R, i = 2, 3 Η διάσταση της SU(3) είναι 8. Αντίστοιχα, για την άλγεβρα Lie της S(U(1) U(1) U(1)) έχουμε t = { ix iy iz { i 0 0 = span e 1 = } : x + y + z = i, e 2 = = { ix iy ix iy } 0 i i } : x, y R } (10.2). Προφανώς η διάσταση της S(U(1) U(1) U(1)) είναι 2. Για την εύρεση ενός Ad(S(U(1) U(1) U(1)))- αναλλοίωτου υποχώρου m, έτσι ώστε να ισχύει su(3) = t m, θα χρησιμοποιήσουμε την μορφή Killing της SU(3), η οποία δίνεται από την σχέση B(X, Y ) = 6tr(XY ). Επειδή η SU(3) είναι συμπαγής και ηπιαπλή, ένα εσωτερικό γινόμενο που ορίζεται στη άλγεβρα Lie su(3) είναι το, = B(, ), οπότε ως προς αυτό το γινόμενο θα έχουμε m = t = {A SU(3) : A, C = 0, για κάθε C t}. 2 Η ονομασία προέκυψε, επειδή είναι αμφιδιαφορικός με το σύνολο {f = {{0} V 1 V 2 C 3 } : dim V i = i, V i μιγαδικός υπόχωρος του C 3 }. Το στοιχείο f ονομάζεται σημαία (flag) στον C 3.
18 18 Ομογενείς χώροι - Γεωμετρία κατά Klein Για να προσδιορίσουμε το παραπάνω σύνολο παίρνουμε για C τους πίνακες e 1, e 2 και για A τον πίνακα που δίνεται από την έκφραση (10.2) και θα πρέπει A, C = tr(ac) = 0 για κάθε C {e 1, e 2 }. Εχουμε Ae 1 = ia x 2 + iy 2 x 3 + iy 3 i x 2 + iy 2 ib a 3 + ib 3 x 3 + iy 3 a 3 + ib 3 ic 0 0 i = άρα 0 = A, e 1 = tr(ae 1 ) = a + c, δηλαδή a = c. Τέλος, με όμοιο τρόπο είναι Ae 2 = ia x 2 + iy 2 x 3 + iy i 0 x 2 + iy 2 ib a 3 + ib 3 x 3 + iy 3 a 3 + ib 3 ic 0 0 i = a 0 c 0 b c Επομένως 0 = A, e 2 = tr(ae 2 ) = b + c, δηλαδή b = c. Ομως a + b + c = 0, οπότε c = 0 δηλαδή a = b = 0. Άρα ο υπόχωρος m θα έχει τη μορφή m = { 0 x 2 + iy 2 x 3 + iy 3 = span{ x 2 + iy 2 0 a 3 + ib 3 x 3 + iy 3 a 3 + ib i , i 0 0, , i 0 i 0 : a 3, b 3, x i, y i R, i = 2, , 0 0 i i 0 0 Επίσης, βλέπουμε ότι dim m = 6, άρα su(3) = t m. Τέλος, θα πρέπει να δείξουμε ότι υπόχωρος m είναι Ad(S(U(1) U(1) U(1)))-αναλλοίωτος. }. },, Επειδή η ομάδα U(1) είναι συνεκτική, το ίδιο ισχύει και το καρτεσιανό γινόμενο U(1) U(1) U(1), άρα η S(U(1) U(1) U(1)) θα είναι συνεκτική, οπότε αρκεί να δείξουμε ότι Παίρνουμε για X και Y τους πίνακες X = [t, m] m, ή ισοδύναμα [X, Y ] m για κάθε X t, Y m. ix iy iz και Y = Τότε μετά από πράξεις θα καταλήξουμε στο εξής: [X, Y ] = XY Y X = 0 x 2 + iy 2 x 3 + iy 3 x 2 + iy 2 0 a 3 + ib 3 x 3 + iy 3 a 3 + ib A + ib Γ + i A + ib 0 K + iλ Γ + i K + iλ 0., δηλαδή [X, Y ] m. Συνεπώς, έχουμε βρεί μια αναγωγική ανάλυση του ομογενούς χώρου SU(3)/S(U(1) U(1) U(1)) = SU(3)/T.
19 10.4. Η ΙΣΟΤΡΟΠΙΚ Η ΑΝΑΠΑΡ ΑΣΤΑΣΗ Η ισοτροπική αναπαράσταση Σε προηγούμενο κεφάλαιο ορίσαμε τη συζυγή αναπαράσταση Ad Ad G : G Aut(g) μιας ομάδας Lie G ως το διαφορικό του εσωτερικού αυτομορφισμού I g : G G, με I g (x) = gxg 1 στο ουδέτερο σημείο της ομάδας G, δηλαδή Ad(g) Ad G (g) = (di g ) e. Θα γενικεύσουμε τώρα αυτήν την έννοια για τους ομογενείς χώρους. Εστω M μια λεία πολλαπλότητα και G μια ομάδα Lie η οποία δρά από τα αριστερά στην M μέσω της απεικόνισης a : G M M, (g, m) gm. Θεωρούμε την αμφιδιαφόριση a g : M M και έστω H = {g G : gp = p} G η ομάδα ισοτροπίας του σημείου p M. Τότε η ισοτροπική αναπαράσταση (isotropy representation) της H στο p ορίζεται ως θ : H Aut(T p M) h (da h ) p : T p M T p M. Στην παραπάνω σχέση το διαφορικό της απεικόνισης a g αποτελεί έναν αυτομορφισμό του εφαπτόμενου χώρου T p M, διότι για κάθε h H έχουμε a g (h) = gh = h. Στη συνέχεια θα ορίσουμε την ισοτροπική αναπαράσταση του ομογενούς χώρου M = G/K, όπου G μια ομάδα Lie και K η ομάδα ισοτροπίας σε κάποιο σημείο της M. Θυμίζουμε ότι για κάθε α G η απεικόνιση τ α : G/K G/K με τύπο gk αgk είναι μια αμφιδιαφόριση. Επίσης, παρατηρούμε ότι για κάθε k K έχουμε τ k (o) = τ k (ek) = kek = ekk = ek = o. Συνεπώς, για κάθε k K το διαφορικό της απεικόνισης τ k αποτελεί έναν αυτομορφισμό του χώρου T o (G/K) = g/k. Επομένως, για την ισοτροπική αναπαράσταση δίνουμε τον εξής ορισμό. Ορισμός Η ισοτροπική αναπαράσταση (isotropy representation) ενός ομογενούς χώρου G/K είναι ο ομομορφισμός Ad G/K : K Aut(T o (G/K)) k (dτ k ) o : T o (G/K) T o (G/K). Δηλαδή για κάθε X T o (G/K) έχουμε Ad G/K (k)(x) = (dτ k ) o (X). Στην περίπτωση που ο ομογενής χώρος G/K είναι αναγωγικός, δηλαδή υπάρχει ένας Ad G (K)-αναλλοίωτος υπόχωρος m τέτοιος ώστε g = k m, τότε είναι δυνατόν να δοθεί μια ακριβής σχέση ανάμεσα στην ισοτροπική αναπαράσταση του ομογενούς χώρου G/K και της συζυγούς αναπαράστασης Ad G της ομάδας Lie G. Αρχικά θα συνοψίσουμε τις αναπαραστάσεις που έχουμε ορίσει μέχρι στιγμής Ad G : G Aut(g) Ad K : K Aut(k) Ad G/K : K Aut(m). Περιορίζοντας τη συζυγή αναπαράσταση Ad G της G στην υποομάδα Lie K, θα πάρουμε την αναπαράσταση Ad G K : K Aut(g), k Ad G K (k) : g g, δηλαδή Ad K (k) = Ad G (k) k. Ας έρθουμε τώρα στη σχέση μεταξύ της ισοτροπικής και της συζυγούς αναπαράστασης.
20 20 Ομογενείς χώροι - Γεωμετρία κατά Klein Πρόταση Εστω G/K ένας αναγωγικός ομογενής χώρος και g = k m η αναγωγική ανάλυση της g. Τότε για κάθε k K και X = X k X m g, όπου X k k και X m m ισχύει: δηλαδή, Ad G K = Ad K Ad G/K. Ad G (k)x = Ad G (k)(x k + X m ) = Ad K (k)x k + Ad G/K (k)x m, (10.3) Απόδειξη. Επειδή έχουμε ευθύ άθροισμα, αρκεί να αποδείξουμε την σχέση (10.3) για τις περιπτώσεις X k = 0 και X m = 0. Στη δεύτερη περίπτωση, δηλαδή X m = 0, η (10.3) ισοδυναμεί με την Ad G (k)x k = Ad K (k)x k. Αυτό πράγματι ισχύει, διότι, αν θεωρήσουμε τον περιορισμό της Ad G στην K, Ad G K : K Aut(g), τότε για κάθε k K έχουμε Ad K (k) = Ad G (k) k, αφού η K είναι υποομάδα Lie της G. Στην πρώτη περίπτωση αρκεί να δείξουμε ότι Ad G (k)x m = Ad G/K (k)x m, ή ισοδύναμα Ad G (k)x m = (dτ k ) o (X m ). Δηλαδή θα πρέπει να αποδείξουμε ότι η ισοτροπική αναπαράσταση του χώρου G/K είναι ισοδύναμη με τη συζυγή αναπαράσταση Ad G K στο χώρο m. Επομένως αρκεί να αποδειχθεί ότι το παρακάτω διάγραμμα είναι αντιμεταθετικό: (dπ) e m m Ad G (k) m (dπ) e m T o (G/K) (dτk ) o T o (G/K) Πριν προχωρήσουμε στην απόδειξη, διευκρινίζουμε τα εξής: Η πρώτη οριζόντια απεικόνιση του διαγράμματος προέρχεται από τον περιορισμό της Ad G (k) στον υπόχωρο m και από το γεγονός ότι Ad G (k)m m. Οι κάθετες απεικονίσεις είναι ισομορφισμοί και προέρχονται από τον περιορισμό της (dπ) e : g T o (G/K) στον m. Εστω λοιπόν k K και X m m. Θα δείξουμε ότι (dπ) e (Ad G (k)x m ) = (dτ k ) o ((dπ) e (X m )). Εχουμε: (dπ) e (Ad G (k)x m ) = d dt π(exp(tadg (k)x m )) = d t=0 dt exp(tadg (k)x m )K = d dt exp(adg (k)tx m )K = d t=0 dt (kexp(tx m)k 1 )K = d dt τ d k(exp(tx m )K) = (dτ k ) o t=0 dt exp(tx m)k t=0 = (dτ k ) o ((dπ) e (X m )). Στην τέταρτη ισότητα χρησιμοποιήσαμε ότι exp(ad(g)x) = gexp(tx)g 1 και στην πέμπτη ότι για κάθε k K ισχύει k 1 K = K. Από την παραπάνω απόδειξη προκύπτει το εξής: Πόρισμα Αν ο ομογενής χώρος είναι αναγωγικός, τότε η ισοτροπική αναπαράσταση του G/K είναι ισοδύναμη με τη συζυγή αναπαράσταση Ad G K στον υπόχωρο m. Στη περίπτωση που ο G/K δεν είναι αναγωγικός, το προηγούμενο πόρισμα ισχύει αν αντικαταστήσουμε τον m με τον g/k. t=0 t=0
21 Η ισοτροπική αναπαράσταση 21 Ορισμός Ενας ομογενής χώρος G/K καλείται ισοτροπικά μη αναγώγιμος (isotropy irreducible), αν η ισοτροπική αναπαράσταση Ad G/K είναι μη αναγώγιμη 3. Παρατήρηση. Εστω G/K ένας ομογενής χώρος και g = k m η αναγωγική ανάλυση της άλγεβρας Lie g. Τότε συνδυάζοντας τα όσα έχουμε αναφέρει μέχρι στιγμής καταλήγουμε στα ακόλουθα συμπεράσματα: 1. Αν η ισοτροπική αναπαράσταση Ad G/K : K Aut(m) είναι μη αναγώγιμη (δηλαδή οι μοναδικοί Ad G/K -αναλλοίωτοι υπόχωροι του m είναι ο τετριμμένος {0} και ο m), τότε ο εφαπτόμενος χώρος m = T o (G/K) δεν διασπάται σε μικρότερης διάστασης υποχώρους. 2. Στην περίπτωση που η ισοτροπική αναπαράσταση Ad G/K : K Aut(m) είναι αναγώγιμη, (δηλαδή υπάρχουν Ad G/K -αναλλοίωτοι υπόχωροι m i του m = T o (G/K)), τότε η ισοτροπική αναπαράσταση μπορεί να γραφεί ως ευθύ άθροισμα μη αναγώγιμων αναπαραστάσεων (ισοδύναμων ή μη ισοδύναμων) ϕ i : K Aut(m i ), i = 1, 2... l και l dim(m) ως εξής: Ad G/K = ϕ1 ϕ 2 ϕ l : K Aut(m 1 m 2 m l ), όπου m = m 1 m 2 m l. Παραδείγματα. 1. Θα υπολογίσουμε την ισοτροπική αναπαράσταση του ομογενούς χώρου SO(4)/SO(2) (πολλαπλότητα Stiefel διάστασης 5). Εστω λ 4 : SO(4) Aut(R 4 ) και Ad SO(4) = 2 λ 4 η συνήθης αναπαράσταση και η συζυγής αναπαράσταση αντίστοιχα, της SO(4). Γνωρίζουμε ότι η ισοτροπική αναπαράσταση Ad SO(4)/SO(2) : SO(2) Aut(m) του ομογενούς χώρου SO(4)/SO(2) συνδέεται με τη συζυγή αναπαράσταση της SO(4) μέσω της σχέσης Ad SO(4) SO(2) = Ad SO(2) Ad SO(4)/SO(2). Τότε θα έχουμε: Ad SO(4) SO(2) = 2 λ SO(2) 4 = 2 (λ 2 2) = 2 λ (λ 2 2) = 2 λ (λ 2 (1 1)) = 2 λ 2 1 ( (λ 2 1) (λ 2 1) ) = 2 λ 2 1 λ 2 λ 2. Στη δεύτερη ισότητα συμβολίζουμε με 2 το ευθύ άθροισμα 2 = 1 1, όπου 1 η τετριμμένη αναπαράσταση, και στην τρίτη ισότητα χρησιμοποίησαμε την αλγεβρική ταυτότητα k (V W ) = k ( i (V ) k i (W )), i=0 όπου V, W είναι διανυσματικοί χώροι πεπερασμένης διάστασης. Βλέπουμε ότι ο πρώτος όρος στην τελική έκφραση της περιορισμένης αναπαράστασης Ad SO(4) SO(2) είναι η συζυγής αναπαράσταση της SO(2), οπότε η ισοτροπική αναπαράσταση του ομογενούς χώρου είναι η Ad SO(4)/SO(2) = 1 λ 2 λ 2. (10.4) 3 Θυμίζουμε ότι μια αναπαράσταση φ : G Aut(V ) καλείται μη αναγώγιμη, εάν οι μοναδικοί G-αναλλοίωτοι υπόχωροι του V είναι {0} και V.
22 22 Ομογενείς χώροι - Γεωμετρία κατά Klein Παρατηρούμε ότι η ισοτροπική αναπαράσταση εκφράζεται ως ευθύ άθροισμα τριών μη αναγώγιμων αναπαραστάσεων διαστάσεων 1, 2 και 2 αντίστοιχα. Το παραπάνω άθροισμα επάγει έναν ισομορφισμό του εφαπτόμενου χώρου m = T o (G/K) με το ευθύ άθροισμα τριών πραγματικών υποχώρων 4 διαστάσεων 1, 2 και 2 αντίστοιχα, δηλαδή m = m 0 m 1 m 2. Πρέπει να σημειώσουμε εδώ ότι, επειδή στη σχέση (10.4) οι δύο τελευταίες αναπαραστάσεις είναι ισοδύναμες, η διάσπαση του m δεν είναι μοναδική. 2. Εστω ο ομογενής χώρος G/K = U(3)/U(1) U(1) U(1) (πολλαπλότητα σημαιών διάστασης 6). Θα υπολογίσουμε την ισοτροπική αναπαράσταση του χώρου G/K. Επειδή οι ομάδες Lie περιέχουν μιγαδικά στοιχεία, είναι πιο εύχρηστο να υπολογίσουμε τη μιγαδοποιημένη ισοτροπική αναπαράσταση. Εστω µ 3 : U(3) Aut(C 3 ) και µ 1 : U(1) Aut(C) οι κανονικές αναπαραστάσεις των U(3) και U(1) αντίστοιχα. Για τη μιγαδοποίηση της συζυγούς αναπαράστασης της U(n) ισχύει ότι Ad U(n) C = µ n C µ n. Εστω σ i : U(1) U(1) U(1) U(1), i = 1, 2, 3, η προβολή στην i-συνιστώσα. Τότε η σύνθεση p i = µ 1 σ i : U(1) U(1) U(1) Aut(C), είναι η κανονική αναπαράσταση της i-συνιστώσας του καρτεσιανού γινομένου K = U(1) U(1) U(1) (i = 1, 2, 3). Εχουμε: Ad U(3) C K = µ 3 µ 3 K = µ 3 K µ 3 K = (p 1 p 2 p 3 ) (p 1 p 2 p 3 ) = (p 1 p 2 p 3 ) ( p 1 p 2 p 3 ) = (p 1 p 1 p 2 p 2 p 3 p 3 ) ( 1 i j 3 p i p j ), όπου με p i p j συμβολίζουμε το τανυστικό γινόμενο p i p j. Το πρώτο μέλος του παραπάνω αθροίσματος είναι η μιγαδοποιημένη συζυγής αναπαράσταση της K = U(1) U(1) U(1). Ετσι, από την Πρόταση 10.3, συμπεραίνουμε ότι η μιγαδοποιημένη ισοτροπική αναπαράσταση του ομογενούς χώρου G/K είναι η Ad G/K C = p 1 p 2 p 1 p 3 p 2 p 1 p 2 p 3 p 3 p 1 p 3 p 2, Η παραπάνω αναπαράσταση είναι αναγώγιμη και εκφράζεται ως ευθύ άθροισμα έξι μη ισοδύναμων και μη αναγώγιμων μιγαδικών αναπαραστάσεων. Κάθε μία από αυτές είναι μονοδιάστατη. Γι αυτό, ο μιγαδοποιημένος εφαπτόμενος χώρος m C της G/K είναι ισόμορφος με το ευθύ άθροισμα έξι μονοδιάστατων μιγαδικών υποχώρων m C = K 12 K 13 K 21 K 23 K 31 K 32. Σημειώνουμε ότι αυτή η διάσπαση επάγει μια διάσπαση του m σε τρεις δισδιάστατους πραγματικούς υποχώρους, όπου m C ij = K ij K ji. m = m 12 m 13 m 23, Ο ομογενής χώρος G /K = SU(3)/S(U(1) U(1) U(1)) έχει διάσταση 6 και είναι ισόμορφος με τον G/K, συνεπώς ο μιγαδοποιημένος εφαπτόμενος χώρος του G /K (τον οποίο θα συμβολίζουμε επίσης με m C ), είναι ισόμορφος με το παραπάνω ευθύ άθροισμα των έξι μονοδιάστατων υποχώρων K ij. 4 Συγκεκριμένα Ad(SO(2))-προτύπων.
23 10.5. G-ΑΝΑΛΛΟ ΙΩΤΕΣ ΜΕΤΡΙΚ ΕΣ ΚΑΙ Η ΣΥΝΟΧ Η LEVI-CIVITA G-αναλλοίωτες μετρικές και η συνοχή Levi-Civita Ορισμός Εστω M = G/K ένας ομογενής χώρος. Μια μετρική Riemann g στην M καλείται G-αναλλοίωτη (G-invariant), εάν για κάθε a G, p M η αμφιδιαφόριση τ a : G/K G/K τ a (p) = ap είναι μια ισομετρία, δηλαδή g(x, Y ) = g(dτ a (X), dτ a (Y )), για κάθε X, Y T o (G/K), a G. Θα δώσουμε τώρα μια περιγραφή των G-αναλλοίωτων μετρικών σε έναν αναγωγικό ομογενή χώρο. Πρόταση Αν το διαφορικό (dπ) e : g T o (G/K) είναι μια ισομετρία, τότε υπάρχει μια 1 1 αντιστοιχία μεταξύ: 1. G-αναλλοίωτων μετρικών g στον ομογενή χώρο G/K και 2. Ad G/K Ad G (K)-αναλλοίωτων εσωτερικών γινομένων, στον m, δηλαδή για κάθε X, Y m, k K, ισχύει Ad G/K (k)x, Ad G/K (k)y = X, Y. Απόδειξη. Εστω g μια G-αναλλοίωτη μετρική στον ομογενή χώρο G/K. Ορίζουμε στον m ένα εσωτερικό γινόμενο, o με περιορισμό της μετρικής στον εφαπτόμενο χώρο T o (G/K) = m, δηλαδή X, Y o = g o (dτ k X, dτ k Y ) για κάθε X, Y T o (G/K). Επειδή η μετρική είναι G-αναλλοίωτη, η προηγούμενη σχέση γράφεται και ως X, Y o = g o (X, Y ). Το εσωτερικό αυτό γινόμενο είναι Ad G/K -αναλλοίωτο. Πράγματι, είναι X, Y o = dπ e X, dπ e Y o = g o (dτ k (dπ e X), dτ k (dπ e Y )) = g o (dπ e (Ad G/K (k)x), dπ e (Ad G/K (k)y )) = g o (Ad G/K (k)x, Ad G/K (k)y ) = Ad G/K (k)x, Ad G/K (k)y o. Στην πρώτη ισότητα χρησιμοποιήσαμε το γεγονός ότι η προβολή π είναι ισομετρία. Η τρίτη ισότητα ισχύει, διότι το διάγραμμα της Πρότασης 10.6 είναι αντιμεταθετικό και η τελευταία ισότητα ισχύει από τον ορισμό του εσωτερικού γινομένου, αφού για κάθε X T o (G/K) έχουμε ότι Ad G/K (k)x T o (G/K). Αντίστροφα, έστω, o ένα Ad G/K -αναλλοίωτο εσωτερικό γινόμενο στο χώρο m. Επεκτείνουμε αυτό το γινόμενο σε ολόκληρο τον ομογενή χώρο G/K, δηλαδή για κάθε σημείο gk G/K θέτουμε X, Y gk = (dτ g 1) gk (X), (dτ g 1) gk (Y ) o (gk G/K). (10.5) Λόγω του Ad G/K -αναλλοίωτου, αυτό το εσωτερικό γινόμενο δεν εξαρτάται από την επιλογή του αντιπροσώπου (άσκηση). Επίσης από τη σχέση (10.5) προκύπτει ότι η dτ k : m m είναι ισομετρία, επομένως η μετρική στον ομογενή χώρο είναι G-αναλλοίωτη. Κάθε εσωτερικό γινόμενο στον υπόχωρο m που ικανοποιεί τη Συνθήκη 2 της προηγούμενης πρότασης καλείται Ad(K)-αναλλοίωτο. Αν K = {e}, τότε ο ομογενής χώρος G/K είναι ουσιαστικά η ομάδα Lie G και σε αυτή την περίπτωση ο ισομορφισμός m = T o (G/K) γενικεύει τον ισομορφισμό g = T e G. Τότε οι G-αναλλοίωτες μετρικές στον ομογενή χώρο G/K αποτελούν τη γενίκευση των αριστερά αναλλοίωτων μετρικών στην ομάδα G. Η έννοια της αμφιαναλλοίωτης μετρικής σε μια ομάδα Lie G στους ομογενείς χώρους γενικεύται ως εξής:
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Ε Μέχρι 18 Μαΐου 2015.
 Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Τι είναι βαθμωτό μέγεθος? Ένα μέγεθος που περιγράφεται μόνο με έναν αριθμό (π.χ. πίεση)
 TETY Εφαρμοσμένα Μαθηματικά Ενότητα ΙΙ: Γραμμική Άλγεβρα Ύλη: Διανυσματικοί χώροι και διανύσματα, μετασχηματισμοί διανυσμάτων, τελεστές και πίνακες, ιδιοδιανύσματα και ιδιοτιμές πινάκων, επίλυση γραμμικών
TETY Εφαρμοσμένα Μαθηματικά Ενότητα ΙΙ: Γραμμική Άλγεβρα Ύλη: Διανυσματικοί χώροι και διανύσματα, μετασχηματισμοί διανυσμάτων, τελεστές και πίνακες, ιδιοδιανύσματα και ιδιοτιμές πινάκων, επίλυση γραμμικών
8.1 Διαγωνοποίηση πίνακα
 Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
Η ΜΕΤΡΙΚΗ ΤΟΥ ΧΩΡΟΥ. (στην περίπτωση, που γνωρίζουμε το πεδίον ορισμού του δείκτου, θα
 Η ΜΕΤΡΙΚΗ ΤΟΥ ΧΩΡΟΥ Η μετρική του χώρου Στην ορίσαμε το εσωτερικό γινόμενο δύο διανυσμάτων μέσω των συντεταγμένων τους, όταν οι συντεταγμένες αυτές λαβαίνονται σε ένα Καρτεσιανό σύστημα αναφοράς του Ερχόμαστε,
Η ΜΕΤΡΙΚΗ ΤΟΥ ΧΩΡΟΥ Η μετρική του χώρου Στην ορίσαμε το εσωτερικό γινόμενο δύο διανυσμάτων μέσω των συντεταγμένων τους, όταν οι συντεταγμένες αυτές λαβαίνονται σε ένα Καρτεσιανό σύστημα αναφοράς του Ερχόμαστε,
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Ο αναλυτικός δείκτης και η χαρακτηριστική του Euler 1
 Ο αναλυτικός δείκτης και η χαρακτηριστική του Euler 1 Ιάκωβος Ανδρουλιδάκης users.uoa.gr/ iandroul iandroul@math.uoa.gr Πανεπιστήμιο Αθηνών, Τμήμα Μαθηματικών, Τομέας Άλγεβρας-Γεωμετρίας Περίληψη Στη διάλεξη
Ο αναλυτικός δείκτης και η χαρακτηριστική του Euler 1 Ιάκωβος Ανδρουλιδάκης users.uoa.gr/ iandroul iandroul@math.uoa.gr Πανεπιστήμιο Αθηνών, Τμήμα Μαθηματικών, Τομέας Άλγεβρας-Γεωμετρίας Περίληψη Στη διάλεξη
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Ας ξεκινήσουμε υπενθυμίζοντας τον ορισμό της συνέχειας σε μετρικούς χώρους. διατυπώνεται και με τον ακόλουθο τρόπο: για κάθε σφαίρα
 33.4.Συνεχείς συναρτήσεις Η έννοια της συνεχούς συνάρτησης είναι θεμελιώδης και μελετάται κατ αρχήν για συναρτήσεις μιας και κατόπιν δύο ή περισσότερων μεταβλητών στα μαθήματα του Απειροστικού Λογισμού.
33.4.Συνεχείς συναρτήσεις Η έννοια της συνεχούς συνάρτησης είναι θεμελιώδης και μελετάται κατ αρχήν για συναρτήσεις μιας και κατόπιν δύο ή περισσότερων μεταβλητών στα μαθήματα του Απειροστικού Λογισμού.
3.5 Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους.
 7 3.5 Το θεώρημα Hah-Baach σε τοπολογικούς διανυσματικούς χώρους. Εξετάζουμε καταρχήν τη σχέση μεταξύ ενός μιγαδικού διανυσματικού χώρου E και του υποκείμενου πραγματικού χώρου E R. Έστω E μιγαδικός διανυσματικός
7 3.5 Το θεώρημα Hah-Baach σε τοπολογικούς διανυσματικούς χώρους. Εξετάζουμε καταρχήν τη σχέση μεταξύ ενός μιγαδικού διανυσματικού χώρου E και του υποκείμενου πραγματικού χώρου E R. Έστω E μιγαδικός διανυσματικός
n xt ( ) ( x( t),..., x( t)) U n, , i 1,..., n. Έτσι, η εξέλιξη του συστήματος των χημικών ουσιών διέπεται από το σύστημα των διαφορικών εξισώσεων:
 ΜΑΘΗΜΑ 1: ΑΠΟ ΤΟ ΠΕΙΡΑΜΑ ΣΤΟ ΜΑΘΗΜΑΤΙΚΟ ΝΤΕΤΕΡΜΙΝΙΣΤΙΚΟ ΠΡΟΤΥΠΟ Ας θεωρήσουμε ως παράδειγμα ένα σύστημα χημικών ουσιών που υπεισέρχονται σε μια χημική αντίδραση. Η στιγμιαία κατάσταση κάθε ουσίας χαρακτηρίζεται
ΜΑΘΗΜΑ 1: ΑΠΟ ΤΟ ΠΕΙΡΑΜΑ ΣΤΟ ΜΑΘΗΜΑΤΙΚΟ ΝΤΕΤΕΡΜΙΝΙΣΤΙΚΟ ΠΡΟΤΥΠΟ Ας θεωρήσουμε ως παράδειγμα ένα σύστημα χημικών ουσιών που υπεισέρχονται σε μια χημική αντίδραση. Η στιγμιαία κατάσταση κάθε ουσίας χαρακτηρίζεται
g (v + W ) = gv + W gv = 0.
 Ασκήσεις #1 Σε ότι ακολουθεί, G είναι πεπερασμένη ομάδα και V είναι C-διανυσματικός χώρος πεπερασμένης διάστασης. 1. Δείξτε ότι η απεικόνιση G G G που ορίζεται θέτοντας g x = gxg 1 για g, x G αποτελεί
Ασκήσεις #1 Σε ότι ακολουθεί, G είναι πεπερασμένη ομάδα και V είναι C-διανυσματικός χώρος πεπερασμένης διάστασης. 1. Δείξτε ότι η απεικόνιση G G G που ορίζεται θέτοντας g x = gxg 1 για g, x G αποτελεί
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Δώδεκα Αποδείξεις του. Θεμελιώδους Θεωρήματος της Άλγεβρας
 Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
ΚΕΦΑΛΑΙΟ 5: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5: 5. ΟΡΙΣΜΟΙ Έστω U και V δύο διανυσματικοί χώροι. Μια συνάρτηση F : U V θα λέγεται γραμμική απεικόνιση (ή ομομορφισμός, ή απλά μορφισμός εάν ικανοποιεί τις συνθήκες (i F ( u + = u + για κάθε
ΚΕΦΑΛΑΙΟ 5: 5. ΟΡΙΣΜΟΙ Έστω U και V δύο διανυσματικοί χώροι. Μια συνάρτηση F : U V θα λέγεται γραμμική απεικόνιση (ή ομομορφισμός, ή απλά μορφισμός εάν ικανοποιεί τις συνθήκες (i F ( u + = u + για κάθε
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. με νόρμα, με τις ακόλουθες νόρμες οι οποίες ορίζονται μέσω των νορμών των X και Y.
 2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω (, ) και (, ) {( x, ) : x και } χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται χώρος με
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω (, ) και (, ) {( x, ) : x και } χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται χώρος με
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Γεωµετρικη Θεωρια Ελεγχου
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων Τοµεας Γεωµετριας Γεωµετρικη Θεωρια Ελεγχου Πρώτη Εργασία, 2017-2018 1. ίνεται ϱοή φ(p, t). (αʹ) είξτε ότι το ω οριακό
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων Τοµεας Γεωµετριας Γεωµετρικη Θεωρια Ελεγχου Πρώτη Εργασία, 2017-2018 1. ίνεται ϱοή φ(p, t). (αʹ) είξτε ότι το ω οριακό
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. με νόρμα, με τις ακόλουθες νόρμες οι οποίες ορίζονται μέσω των νορμών των X και Y.
 2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω ( X, ) και (, ) X Y {( x, ) : x X και Y} Y χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω ( X, ) και (, ) X Y {( x, ) : x X και Y} Y χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii08/laii08.html Παρασκευή 4 Μαίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii08/laii08.html Παρασκευή 4 Μαίου
a b b < a > < b > < a >.
 Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1. Τελεστές και πίνακες. 1. Τελεστές και πίνακες Γενικά. Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
1 Χώροι πηλίκα { } x = y x y Y. Με τις πράξεις της πρόσθεσης και του βαθμωτού πολλαπλασιασμού που ορίζονται με τον
 Χώροι πηλίκα Έστω διανυσματικός χώρος και Y διανυσματικός υπόχωρος του. Για κάθε θεωρούμε το σύμπλοκο σχετικά με τον Y, = + y y Y = + Y ορ { : } δηλαδή το είναι η παράλληλη μεταφορά του Y κατά το διάνυσμα.
Χώροι πηλίκα Έστω διανυσματικός χώρος και Y διανυσματικός υπόχωρος του. Για κάθε θεωρούμε το σύμπλοκο σχετικά με τον Y, = + y y Y = + Y ορ { : } δηλαδή το είναι η παράλληλη μεταφορά του Y κατά το διάνυσμα.
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
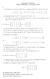 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii09/laii09.html Παρασκευή 0 Μαίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii09/laii09.html Παρασκευή 0 Μαίου
Τίτλος Μαθήματος: Διαφορική Γεωμετρία
 33 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Ο εφαπτόμενος χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 33 34 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
33 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Ο εφαπτόμενος χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 33 34 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Αλγεβρικές Δομές Ι. 1 Ομάδα I
 Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
ή κανονικός ( regular ), αν για κάθε x και κάθε κλειστό αντιπαραδείγματα με τα οποία αποδεικνύεται ότι οι αντίστροφες συνεπαγωγές δεν ισχύουν.
 93 4 Διαχωριστικά αξιώματα Στο κεφάλαιο αυτό εισάγουμε τα λεγόμενα διαχωριστικά αξιώματα και εξετάζουμε τις βασικές ιδιότητές τους. Ένα από αυτά το έχουμε ήδη εισαγάγει δηλαδή το αξίωμα Husdorff ( ορισμός
93 4 Διαχωριστικά αξιώματα Στο κεφάλαιο αυτό εισάγουμε τα λεγόμενα διαχωριστικά αξιώματα και εξετάζουμε τις βασικές ιδιότητές τους. Ένα από αυτά το έχουμε ήδη εισαγάγει δηλαδή το αξίωμα Husdorff ( ορισμός
6 Συνεκτικοί τοπολογικοί χώροι
 36 6 Συνεκτικοί τοπολογικοί χώροι Έστω R διάστημα και f : R συνεχής συνάρτηση τότε, όπως γνωρίζουμε από τον Απειροστικό Λογισμό, η f έχει την ιδιότητα της ενδιάμεσου τιμής. Η ιδιότητα αυτή δεν εξαρτάται
36 6 Συνεκτικοί τοπολογικοί χώροι Έστω R διάστημα και f : R συνεχής συνάρτηση τότε, όπως γνωρίζουμε από τον Απειροστικό Λογισμό, η f έχει την ιδιότητα της ενδιάμεσου τιμής. Η ιδιότητα αυτή δεν εξαρτάται
από t 1 (x) = A 1 x A 1 b.
 Σύνοψη Κεφαλαίου 2: Ομοπαραλληλική Γεωμετρία Γεωμετρία και μετασχηματισμοί 1. Μία ισομετρία του R 2 είναι μία απεικόνιση από το R 2 στο R 2 που διατηρεί αποστάσεις. Κάθε ισομετρία του R 2 έχει μία από
Σύνοψη Κεφαλαίου 2: Ομοπαραλληλική Γεωμετρία Γεωμετρία και μετασχηματισμοί 1. Μία ισομετρία του R 2 είναι μία απεικόνιση από το R 2 στο R 2 που διατηρεί αποστάσεις. Κάθε ισομετρία του R 2 έχει μία από
Αναπαραστάσεις οµάδων και Αλγεβρες Τελεστών
 6 Ιουλίου 2015 1 Οµάδες 2 3 οµάδες Οµάδες Παραδείγµατα (Z, +) (Z n, +) (R, +), (R, ), (R +, ) (T, ), T = {z C : z = 1} S n = {φ : N n N n, 1 1 και επί}, όπου N n = {1, 2,..., n}, µε πράξη την σύνθεση.
6 Ιουλίου 2015 1 Οµάδες 2 3 οµάδες Οµάδες Παραδείγµατα (Z, +) (Z n, +) (R, +), (R, ), (R +, ) (T, ), T = {z C : z = 1} S n = {φ : N n N n, 1 1 και επί}, όπου N n = {1, 2,..., n}, µε πράξη την σύνθεση.
ΠΛΗ ΛΥΣΕΙΣ ΕΡΓ_2 ΣΕΛ. 1/11
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
Παράρτηµα Β. Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης [ ) ( )
 Παράρτηµα Β Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης Β1 Χώροι Baach Βάσεις Schauder Στο εξής συµβολίζουµε µε Z,, γραµµικούς (διανυσµατικούς) χώρους πάνω απ το ίδιο σώµα K = ή και γράφουµε απλά
Παράρτηµα Β Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης Β1 Χώροι Baach Βάσεις Schauder Στο εξής συµβολίζουµε µε Z,, γραµµικούς (διανυσµατικούς) χώρους πάνω απ το ίδιο σώµα K = ή και γράφουµε απλά
X u, X u. Z = X u. W EG F 2 (X v F E X u). X u, X v X v, X v
 Κεφάλαιο 6 Το Θαυμαστό Θεώρημα Σύνοψη Στο Κεφάλαιο αυτό αποδεικνύουμε ένα από τα δύο κεντρικά θεωρήματα της θεωρίας επιφανειών το άλλο είναι το Θεώρημα των auss-bonnet. Το θεώρημα αυτό είναι γνωστό ως
Κεφάλαιο 6 Το Θαυμαστό Θεώρημα Σύνοψη Στο Κεφάλαιο αυτό αποδεικνύουμε ένα από τα δύο κεντρικά θεωρήματα της θεωρίας επιφανειών το άλλο είναι το Θεώρημα των auss-bonnet. Το θεώρημα αυτό είναι γνωστό ως
Σ Γιάννης Σακελλαρίδης Τελευταία ενημέρωση 11 Ιουνίου (Το αρχείο θα ενημερώνεται κατά τη διάρκεια του εξαμήνου.)
 Σ Γιάννης Σακελλαρίδης Τελευταία ενημέρωση 11 Ιουνίου 2016. (Το αρχείο θα ενημερώνεται κατά τη διάρκεια του εξαμήνου.) 1 Αντικείμενα: διανυσματικοί χώροι Ένας διανυσματικός χώρος (πάνω από το R, αλλά οι
Σ Γιάννης Σακελλαρίδης Τελευταία ενημέρωση 11 Ιουνίου 2016. (Το αρχείο θα ενημερώνεται κατά τη διάρκεια του εξαμήνου.) 1 Αντικείμενα: διανυσματικοί χώροι Ένας διανυσματικός χώρος (πάνω από το R, αλλά οι
V (F ) = {(u 1, u 2, u 3 ) P 2 K F (u 1, u 2, u 3 ) = 0}
 1 Θεώρημα BEZOU T Ο δακτύλιος K[x 1,..., x n ] είναι περιοχή μονοσήμαντης ανάλυσης. Άρα κάθε πολυώνυμο f K[x 1,..., x n ] (που δεν είναι σταθερά, δηλαδή f / K) αναλύεται σε γινόμενο αναγώγων πολυωνύμων,
1 Θεώρημα BEZOU T Ο δακτύλιος K[x 1,..., x n ] είναι περιοχή μονοσήμαντης ανάλυσης. Άρα κάθε πολυώνυμο f K[x 1,..., x n ] (που δεν είναι σταθερά, δηλαδή f / K) αναλύεται σε γινόμενο αναγώγων πολυωνύμων,
π B = B και άρα η π είναι ανοικτή απεικόνιση.
 3 Παράρτημα 2 Παρατηρήσεις, ασκήσεις και Διορθώσεις Παράγραφος ) Σελίδα, : Παρατηρούμε τα ακόλουθα για το χώρο πηλίκο / Y : Y = / Y και (α) { } (β) = Y / Y { } Επίσης από τον τύπο () έπεται ιδιαίτερα ότι
3 Παράρτημα 2 Παρατηρήσεις, ασκήσεις και Διορθώσεις Παράγραφος ) Σελίδα, : Παρατηρούμε τα ακόλουθα για το χώρο πηλίκο / Y : Y = / Y και (α) { } (β) = Y / Y { } Επίσης από τον τύπο () έπεται ιδιαίτερα ότι
Θεωρία Τελεστών. Ενότητα: Χώροι µε νόρµα - Χώροι Hilbert. Αριστείδης Κατάβολος. Τµήµα Μαθηµατικών
 Ενότητα: Χώροι µε νόρµα - Χώροι Hilbert Αριστείδης Κατάβολος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ενότητα: Χώροι µε νόρµα - Χώροι Hilbert Αριστείδης Κατάβολος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 5
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 12 Απριλίου 2019 Αν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 12 Απριλίου 2019 Αν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html ευτέρα 23 Απριλίου 2018 Αν C
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html ευτέρα 23 Απριλίου 2018 Αν C
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
= DX(0, 0)(ae 1 + be 2 ) = adx(0, 0)e 1 + bdx(0, 0)e 2 = ax u (0, 0) + bx v (0, 0).
 Κεφάλαιο 3 Ο εφαπτόμενος χώρος Σύνοψη Ο εφαπτόμενος χώρος μιας κανονικής επιφάνειας αποτελεί τη βέλτιση γραμμική προσέγγιση της επιφάνειας σε ένα σημείο της. Αποτελείται από όλα τα εφαπτόμενα διανύσματα
Κεφάλαιο 3 Ο εφαπτόμενος χώρος Σύνοψη Ο εφαπτόμενος χώρος μιας κανονικής επιφάνειας αποτελεί τη βέλτιση γραμμική προσέγγιση της επιφάνειας σε ένα σημείο της. Αποτελείται από όλα τα εφαπτόμενα διανύσματα
h(x, y) = card ({ 1 i n : x i y i
 Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
f I X i I f i X, για κάθεi I.
 47 2 Πράξεις σε τοπολογικούς χώρους 2. Η τοπολογία γινόμενο Σε προηγούμενη παράγραφο ορίσαμε την τοπολογία γινόμενο στο καρτεσιανό γινόμενο Y δύο τοπολογικών χώρων Y, ( παράδειγμα.33 () ). Στην παρούσα
47 2 Πράξεις σε τοπολογικούς χώρους 2. Η τοπολογία γινόμενο Σε προηγούμενη παράγραφο ορίσαμε την τοπολογία γινόμενο στο καρτεσιανό γινόμενο Y δύο τοπολογικών χώρων Y, ( παράδειγμα.33 () ). Στην παρούσα
Παναγιώτης Ψαρράκος Αν. Καθηγητής
 Ανάλυση Πινάκων Κεφάλαιο 1: Νόρμες Διανυσμάτων και Πινάκων Παναγιώτης Ψαρράκος Αν. Καθηγητής Δ.Π.Μ.Σ. Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών
Ανάλυση Πινάκων Κεφάλαιο 1: Νόρμες Διανυσμάτων και Πινάκων Παναγιώτης Ψαρράκος Αν. Καθηγητής Δ.Π.Μ.Σ. Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii9/laii9html Παρασκευή 9 Μαρτίου 9 Ασκηση Εστω (E,,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii9/laii9html Παρασκευή 9 Μαρτίου 9 Ασκηση Εστω (E,,
Αναπαραστάσεις οµάδων και Αλγεβρες Τελεστών
 8 Ιουλίου 2015 1 τοπολογικές οµάδες 2 3 4 τοπολογικές οµάδες Ορισµός Μια οµάδα G λέγεται τοπολογική οµάδα αν είναι εφοδιασµένη µε µια τοπολογία τ.ω. οι (x, y) xy και x x 1 να είναι συνεχείς. Παραδείγµατα
8 Ιουλίου 2015 1 τοπολογικές οµάδες 2 3 4 τοπολογικές οµάδες Ορισµός Μια οµάδα G λέγεται τοπολογική οµάδα αν είναι εφοδιασµένη µε µια τοπολογία τ.ω. οι (x, y) xy και x x 1 να είναι συνεχείς. Παραδείγµατα
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες
 ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-Art ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες *
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-Art ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες *
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ
 Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Στο πρώτο μέρος αυτού του κεφαλαίου συνοψίζουμε όσα είναι απαραίτητα για την εύρεση ιδιοτιμών και ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Στο δεύτερο μέρος αναπτύσσονται
Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Στο πρώτο μέρος αυτού του κεφαλαίου συνοψίζουμε όσα είναι απαραίτητα για την εύρεση ιδιοτιμών και ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Στο δεύτερο μέρος αναπτύσσονται
Je rhma John L mma Dvoretzky-Rogers
 Kefˆlaio 2 Je rhma Joh L mma Dvoretzky-Rogers 2.1 Elleiyoeidèc mègistou ìgkou eìc kurtoô s matoc Ορισμός 2.1.1. Ελλειψοειδές στον R είναι ένα κυρτό σώμα της μορφής { } (2.1.1) E = x R x, v i 2 : 1, όπου
Kefˆlaio 2 Je rhma Joh L mma Dvoretzky-Rogers 2.1 Elleiyoeidèc mègistou ìgkou eìc kurtoô s matoc Ορισμός 2.1.1. Ελλειψοειδές στον R είναι ένα κυρτό σώμα της μορφής { } (2.1.1) E = x R x, v i 2 : 1, όπου
1.2 Συντεταγμένες στο Επίπεδο
 1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
Πορίσματα της Κανονικής Μορφής Smith (συμπλήρωμα για την Ενότητα 4)
 Πορίσματα της Κανονικής Μορφής Smh (συμπλήρωμα για την Ενότητα 4 Θα δείξουμε εδώ ότι από την κανονική μορφή Smh πινάκων πάνω από περιοχή κυρίων ιδεωδών R, έπονται τα εξής Το Θεώρημα Βάσεων Το Θεώρημα Ανάλυσης
Πορίσματα της Κανονικής Μορφής Smh (συμπλήρωμα για την Ενότητα 4 Θα δείξουμε εδώ ότι από την κανονική μορφή Smh πινάκων πάνω από περιοχή κυρίων ιδεωδών R, έπονται τα εξής Το Θεώρημα Βάσεων Το Θεώρημα Ανάλυσης
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών
 Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 10
 Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
Γραμμική Αλγεβρα ΙΙ Διάλεξη 7 Βάσεις Διάσταση Χρήστος Κουρουνιώτης Πανεπισ τήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/ / 1
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 7 Διάσταση Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/2014 1 / 1 Εάν ένα υποσύνολο S του διανυσματικού χώρου V παράγει το V,
Γραμμική Άλγεβρα ΙΙ Διάλεξη 7 Διάσταση Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/2014 1 / 1 Εάν ένα υποσύνολο S του διανυσματικού χώρου V παράγει το V,
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT
 ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 4 Μαίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 6 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 4 Μαίου 2018 Ασκηση
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
n = dim N (A) + dim R(A). dim V = dim ker L + dim im L.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
= g(x e, Y e ) = g e (X, Y ) = g(x, Y )(e), = d(l (gα) 1 L g ) α u, d(l (gα) 1 L g ) α v
 Κεφάλαιο 9 Η γεωμετρία μιας ομάδας Le Σύνοψη Θα μελετήσουμε αριστερά αναλλοίωτες και αμφιαναλλοίωτες μετρικές Remann σε μια ομάδα Le. Θα παρουσιάσουμε τύπους για τη συνοχή Lev-Cvta, την καμπυλότητα τομής,
Κεφάλαιο 9 Η γεωμετρία μιας ομάδας Le Σύνοψη Θα μελετήσουμε αριστερά αναλλοίωτες και αμφιαναλλοίωτες μετρικές Remann σε μια ομάδα Le. Θα παρουσιάσουμε τύπους για τη συνοχή Lev-Cvta, την καμπυλότητα τομής,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 29 Μαρτίου 2019 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 29 Μαρτίου 2019 Ασκηση
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
Τα παρακάτω σύνολα θα τα θεωρήσουμε γενικά γνωστά, αν και θα δούμε πολλές από τις ιδιότητές τους: N Z Q R C
 Κεφάλαιο 1 Εισαγωγικές έννοιες Στο κεφάλαιο αυτό θα αναφερθούμε σε ορισμένες έννοιες, οι οποίες ίσως δεν έχουν άμεση σχέση με τους διανυσματικούς χώρους, όμως θα χρησιμοποιηθούν αρκετά κατά τη μελέτη τόσο
Κεφάλαιο 1 Εισαγωγικές έννοιες Στο κεφάλαιο αυτό θα αναφερθούμε σε ορισμένες έννοιες, οι οποίες ίσως δεν έχουν άμεση σχέση με τους διανυσματικούς χώρους, όμως θα χρησιμοποιηθούν αρκετά κατά τη μελέτη τόσο
Αναπαραστάσεις οµάδων: παραδείγµατα
 Φεβρουάριος-Μάρτιος 2016 1 τοπολογικές οµάδες 2 3 τοπολογικές οµάδες Ορισµός Μια οµάδα G λέγεται τοπολογική οµάδα αν είναι εφοδιασµένη µε µια τοπολογία τ.ω. οι (x, y) xy και x x 1 να είναι συνεχείς. Παραδείγµατα
Φεβρουάριος-Μάρτιος 2016 1 τοπολογικές οµάδες 2 3 τοπολογικές οµάδες Ορισµός Μια οµάδα G λέγεται τοπολογική οµάδα αν είναι εφοδιασµένη µε µια τοπολογία τ.ω. οι (x, y) xy και x x 1 να είναι συνεχείς. Παραδείγµατα
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
bca = e. H 1j = G 2 H 5j = {f G j : f(0) = 1}
 Αλγεβρα Ι, Χειμερινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Το [Α] συμβολίζει το φυλλάδιο ασκήσεων που θα βρείτε στην ιστοσελίδα του μαθήματος επιλέγοντας «Άλλες Ασκήσεις». 1. Πόσες
Αλγεβρα Ι, Χειμερινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Το [Α] συμβολίζει το φυλλάδιο ασκήσεων που θα βρείτε στην ιστοσελίδα του μαθήματος επιλέγοντας «Άλλες Ασκήσεις». 1. Πόσες
ΣΗΜΕΙΩΣΕΙΣ. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
4.2 Αυτοπάθεια και ασθενής συμπάγεια * * X, x X, είναι επί του. X. Σημειώνουμε ότι υπάρχουν παραδείγματα μη
 94 Ένας χώρος με νόρμα (, ( ( ( ϕ : : ϕ =, ( 4. Αυτοπάθεια και ασθενής συμπάγεια λέγεται αυτοπαθής ( refleive, αν η κανονική εμφύτευση,, είναι επί του, δηλαδή ϕ =. Παρατηρούμε ότι ένας αυτοπαθής χώρος
94 Ένας χώρος με νόρμα (, ( ( ( ϕ : : ϕ =, ( 4. Αυτοπάθεια και ασθενής συμπάγεια λέγεται αυτοπαθής ( refleive, αν η κανονική εμφύτευση,, είναι επί του, δηλαδή ϕ =. Παρατηρούμε ότι ένας αυτοπαθής χώρος
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii018/laii018html ευτέρα 3 Απριλίου 018 Αν C = x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii018/laii018html ευτέρα 3 Απριλίου 018 Αν C = x
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
B X Y : T X Y = U i V i : U i T X, V i T Y. (x, y) (U 1 V 1 ) (U 2 V 2 ) = (U 1 U 2 ) (V 1 V 2 ) B X Y. ((0, 2) (1, 3)) ((1, 3) (1, 2)) B X B Y
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΕΜ Χειμερινό εξάμηνο 2017-18 ΜΕΜ231-ΤΟΠΟΛΟΓΙΑ, 5Η ΔΙΑΛΕΞΗ ΤΟΠΟΛΟΓΙΑ ΓΙΝΟΜΕΝΟ ΚΑΙ ΕΠΑΓΟΜΕΝΗ ΤΟΠΟΛΟΓΙΑ ΔΙΔΑΣΚΩΝ: Ι.Δ. ΠΛΑΤΗΣ 1. Τοπολογια γινομενο και προβολες Εστω X, Y τοπολογικοί
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΕΜ Χειμερινό εξάμηνο 2017-18 ΜΕΜ231-ΤΟΠΟΛΟΓΙΑ, 5Η ΔΙΑΛΕΞΗ ΤΟΠΟΛΟΓΙΑ ΓΙΝΟΜΕΝΟ ΚΑΙ ΕΠΑΓΟΜΕΝΗ ΤΟΠΟΛΟΓΙΑ ΔΙΔΑΣΚΩΝ: Ι.Δ. ΠΛΑΤΗΣ 1. Τοπολογια γινομενο και προβολες Εστω X, Y τοπολογικοί
Παρουσία µηδενιστών στη θεωρία τοπολογικών αλγεβρών
 Παρουσία µηδενιστών στη θεωρία τοπολογικών αλγεβρών Μαρίνα Χαραλαµπίδου Τµήµα Μαθηµατικών Τοµέας Αλγεβρας και Γεωµετρίας Πανεπιστηµίο Αθηνών Σεµινάριο Τοµέα Αλγεβρας και Γεωµετρίας 11/12/2012 1 / 47 Περιεχόµενα
Παρουσία µηδενιστών στη θεωρία τοπολογικών αλγεβρών Μαρίνα Χαραλαµπίδου Τµήµα Μαθηµατικών Τοµέας Αλγεβρας και Γεωµετρίας Πανεπιστηµίο Αθηνών Σεµινάριο Τοµέα Αλγεβρας και Γεωµετρίας 11/12/2012 1 / 47 Περιεχόµενα
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες
 ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-rt ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες θεώρημα
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-rt ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες θεώρημα
Ε Μέχρι 31 Μαρτίου 2015.
 Ε Μέχρι 31 Μαρτίου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες
Ε Μέχρι 31 Μαρτίου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
Το φασματικό Θεώρημα
 Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Τανυστές στην Κβαντομηχανική Κβαντική Πληροφορική
 Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσική Τανυστές στην Κβαντομηχανική Κβαντική Πληροφορική Το ζήτημα των τανυστών είναι πολύ σημαντικό τόσο για την Κβαντομηχανική, όσο και για τη Σχετικότητα. Οι δύο
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσική Τανυστές στην Κβαντομηχανική Κβαντική Πληροφορική Το ζήτημα των τανυστών είναι πολύ σημαντικό τόσο για την Κβαντομηχανική, όσο και για τη Σχετικότητα. Οι δύο
R ισούται με το μήκος του. ( πρβλ. την ιστορική σημείωση 3.27 στο τέλος
 73 3. Συμπαγείς χώροι 3. Συμπαγείς χώροι και βασικές ιδιότητες Οι συμπαγείς χώροι είναι μια από τις πιο σημαντικές κλάσεις τοπολογικών χώρων. Η κλάση των συμπαγών χώρων περιλαμβάνει τα κλειστά διαστήματα,b
73 3. Συμπαγείς χώροι 3. Συμπαγείς χώροι και βασικές ιδιότητες Οι συμπαγείς χώροι είναι μια από τις πιο σημαντικές κλάσεις τοπολογικών χώρων. Η κλάση των συμπαγών χώρων περιλαμβάνει τα κλειστά διαστήματα,b
ι3.4 Παραδείγματα T ) έχει την ιδιότητα Heine-Borel, αν κάθε κλειστό και φραγμένο υποσύνολό του είναι συμπαγές.
 6 ι3.4 Παραδείγματα Στην παράγραφο αυτή θα μελετήσουμε κάποια σημαντικά παραδείγματα, για τις εφαρμογές, χώρων συναρτήσεων οι οποίοι είναι τοπικά κυρτοί και μετρικοποιήσιμοι αλλά η τοπολογία τους δεν επάγεται
6 ι3.4 Παραδείγματα Στην παράγραφο αυτή θα μελετήσουμε κάποια σημαντικά παραδείγματα, για τις εφαρμογές, χώρων συναρτήσεων οι οποίοι είναι τοπικά κυρτοί και μετρικοποιήσιμοι αλλά η τοπολογία τους δεν επάγεται
Μία απεικόνιση από ένα διανυσματικό χώρο V στον εαυτό του, L : V V την ονομάζουμε γραμμικό τελεστή στο V (ή ενδομορφισμό του V ). Ορισμός. L : V V γρα
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
