13. Συνήθεις διαφορικές εξισώσεις
|
|
|
- Ακακιος Ελευθερίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση ης οποίας οι παράγγοι εµφανίζοναι σην εξίσση είναι σνάρηση µιας ανεξάρηης µεαβληής, η εξίσση ονοµάζεαι σνήθης διαφορική εξίσση (Σ Ε) Γενικά, οποιαδήποε σνάρηση ν και y και ν παραγώγν ής y ς προς ορίζει µια σνήθη διαφορική εξίσση για ο dy d y,,,, y (3) d d y σναρήσει ο Μερικά παραδείγµαα: d d d y dy d y dy 3 m, a, a by c,, y f ( ) d d d d d d Οποιαδήποε σνάρηση ικανοποιεί µια Ε, ονοµάζεαι λύση ης Ε Μια σνάρηση η οποία εµπεριέχει όλες ις δναές λύσεις µιας Ε ονοµάζεαι γενική λύση ης Ε Ση διαύπση ν διαφορικών εξισώσεν χρησιµοποιούναι διάφορα σύµβολα, όπς: οι ελεσές d d και α σύµβολα y () και y () και d y d 3 d D για ην πράξη ης παραγώγισης (ς προς εδώ), d dy d για ην πρώη παράγγο ο για η δεύερη παράγγο, κοκ y() ς προς ο, ο σµβολισµός ο Νεύνα, σύµφνα µε ον οποίο µια ελεία πάν από ένα σύµβολο d d σηµαίνει παραγώγιση ς προς ο χρόνο :, d d Η άξη ης παραγώγο µεγαλύερης άξης πο εµφανίζεαι ση διαφορική εξίσση, ονοµάζεαι άξη ης διαφορικής εξίσσης Όαν η διαφορική εξίσση εκφρασεί ση µορφή πολνύµο, η δύναµη σην οποία εµφανίζεαι η µεγαλύερης άξης παράγγος ονοµάζεαι βαθµός ης διαφορικής εξίσσης Μια Σ Ε για ην y() ονοµάζεαι γραµµική, αν είναι γραµµική ς προς ην y() και ις παραγώγος ης Για παράδειγµα: d Η m είναι µια γραµµική Σ Ε πρώης άξης και πρώο βαθµού d d d y dy d y Οι a, a by c και είναι δεύερης άξης d d d d και πρώο βαθµού Και οι ρεις είναι γραµµικές 3 dy 3 Η y f ( ) είναι µια Σ Ε εξίσση πρώης άξης Είναι ρίο βαθµού, αφού d 3 dy 3 µπορεί να γραφεί ς ( f ( ) y ) Η µη γραµµικόηά ης οφείλεαι σον όρο d dy d 3, και σις δνάµεις ο y
2 68 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 3 Η παραγγή σνήθν διαφορικών εξισώσεν Έσ όι η σνάρηση y() περιέχει n παραµέρος Με n διαδοχικές παραγγίσεις ης αποκούµε n εξισώσεις Αν χρησιµοποιήσοµε αές ις εξισώσεις για να απαλείψοµε ις ( ) παραµέρος, βρίσκοµε µια σχέση πο περιέχει ις y (), y (),, y n ( ) και η µεαβληή Αποκούµε δηλαδή µια σνήθη διαφορική εξίσση n -οσής άξης για ην y() Παραδείγµαα: dy Αν y 4a( a) ( a σαθερά), παραγγίζονας βρίσκοµε όι y 4a d Απαλείφονας ην a από ις δύο αές εξισώσεις, βρίσκοµε η µη γραµµική διαφορική εξίσση πρώης άξης, Με ον ίδιο ρόπο, αν dy dy y y d d y, θα είναι dy d y και d d Η πρώη και η ρίη εξίσση δίνον η γραµµική διαφορική εξίσση δεύερης άξης: d y y, γνσή ς η εξίσση ο µονοδιάσαο απλού αρµονικού αλανή χρίς d απόσβεση ή εξερική διέγερση Η y λέγεαι όι είναι η γενική λύση ης Σ Ε d y y d Αποδεικνύεαι όι Για να είναι µια λύση η γενική λύση µιας Σ Ε n -οσής άξης, πρέπει να περιέχει n ανεξάρηες αθαίρεες σαθερές Οι λύσεις διαφορικών εξισώσεν πο περιγράφον φσικά προβλήµαα πρέπει να ικανοποιούν ορισµένες σνθήκες Αν οι σνθήκες αφορούν ις ιµές ης άγνσης σνάρησης και ν παραγώγν ης σε ένα µόνο σηµείο (µία ιµή ης ανεξάρηης µεαβληής), οι σνθήκες είναι γνσές ς αρχικές σνθήκες και ο πρόβληµα ονοµάζεαι πρόβληµα αρχικών ιµών Αν οι σνθήκες αφορούν ις ιµές ης άγνσης σνάρησης και ν παραγώγν ης σε περισσόερα ο ενός σηµεία, οι σνθήκες είναι γνσές ς σνοριακές σνθήκες και ο πρόβληµα ονοµάζεαι πρόβληµα σνοριακών ιµών Η ικανοποίηση αών ν σνθηκών, καθορίζει ις ιµές ν αθαίρεν σαθερών, και ξεχρίζει από ις άπειρες λύσεις πο περιγράφει η γενική λύση η µία λύση η οποία ισχύει για ο σγκεκριµένο πρόβληµα Θα εξεάσοµε παρακά µερικές σνήθεις διαφορικές εξισώσεις οι οποίες είναι σηµανικές σην περιγραφή φσικών σσηµάν Λόγ ο δεύερο νόµο ο Νεύνα, πολλές από ις διαφορικές εξισώσεις πο σνανά κανείς ση Μηχανική είναι πρώης ή δεύερης άξης Το ίδιο ισχύει και για προβλήµαα πο αναφέροναι σε αλανώσεις µηχανικών και ηλεκρικών σσηµάν Σε πολύπλοκα σσήµαα (µε πολλούς βαθµούς ελεθερίας) εµφανίζοναι σσήµαα διαφορικών εξισώσεν Για µια πληρέσερη µελέη ο θέµαος ν διαφορικών εξισώσεν ο αναγνώσης µπορεί να σµβολεθεί, µεαξύ πολλών άλλν, και ένα από α σγγράµµαα πο δίνοναι ση βιβλιογραφία 33 ιαφορικές εξισώσεις χριζόµενν µεαβληών Μια Ε η οποία µπορεί να αναχθεί ση διαφορική µορφή g ( y) dy f ( ) d, ονοµάζεαι διαφορική εξίσση χριζόµενν µεαβληών και µπορεί να λθεί µε απλή ολοκλήρση ν δύο µελών:
3 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 69 g ( y) dy f ( ) d c (3) όπο η c είναι µια κοινή σαθερά ολοκλήρσης για α δύο ολοκληρώµαα Οι εξισώσεις αές εξεάσηκαν σο Κεφάλαιο 9 34 Η γραµµική διαφορική εξίσση δεύερης άξης, µε σαθερούς σνελεσές Σις ενόηες πο ακολοθούν, θα θερήσοµε ο χρόνο ς ανεξάρηη µεαβληή, και ην y σνάρηση ο Η γραµµική διαφορική εξίσση δεύερης άξης µε σαθερούς σνελεσές έχει η γενική µορφή y p y p y f ( ) (33) όπο οι p, p είναι σαθεροί σνελεσές Αν f ( ), η εξίσση ονοµάζεαι οµογενής Ο γενικός ρόπος λύσης ης εξίσσης s y p y p y (34) είναι να ποεθεί η µορφή y για ις λύσεις και να ανικαασαθεί ση διαφορική εξίσση Αποκάαι έσι µια αλγεβρική εξίσση, η χαρακηρισική εξίσση, οι λύσεις ης οποίας δίνον si ις ιµές si ο s για ις οποίες οι σναρήσεις y i είναι λύσεις ης διαφορικής εξίσσης Η λύση ης µη οµογενούς εξίσσης βασίζεαι ση σµπλήρση ης γενικής λύσης ης οµογενούς εξίσσης Θα εξεάσοµε ις λύσεις ης γραµµικής διαφορικής εξίσσης δεύερης άξης µε σαθερούς σνελεσές, αρχίζονας από ην πιο απλή µορφή ης οµογενούς εξίσσης και σνεχίζονας µε πιο πολύπλοκες µορφές 34 Η εξίσση y p y s s s Αν ποθέσοµε λύσεις ης µορφής y έχοµε y s και y s Ανικαθισώνας ση διαφορική εξίσση έχοµε κοινό παράγονα s, βρίσκοµε η χαρακηρισική εξίσση s s p s και απλοποιώνας ον s p, ης οποίας λύσεις είναι οι s p και s p p Έχοµε λοιπόν δύο λύσεις ης διαφορικής εξίσσης, ις y και y Η γενική λύση ης διαφορικής εξίσσης είναι ο γραµµικός σνδασµός ν δύο λύσεν, p p y( ) c c (35) Η λύση έχει δύο ανεξάρηες αθαίρεες σαθερές και είναι η γενική λύση ης δοθείσας διαφορικής εξίσσης Ιδιαίερο ενδιαφέρον έχει η περίπση θεικού p Η εξίσση αή σνανάαι σχνά ς η διαφορική εξίσση ο απλού αρµονικού αλανή χρίς απόσβεση ή εξερική διέγερση (σύσηµα µάζας-ελαηρίο, αλανώσεις µικρού πλάος ο απλού ή φσικού εκκρεµούς, αλανώσεις ηλεκρικού κκλώµαος LC, κλπ) Η εξίσση γράφεαι ς y y, σαθ (36) p Υποθέονας λύσεις ης µορφής s y, βρίσκοµε η χαρακηρισική εξίσση s ης οποίας λύσεις είναι οι s i και s i (37) Οι αποδεκές λύσεις ης διαφορικής εξίσσης, πο ανισοιχούν σις δύο αές ιµές ης s, είναι οι
4 7 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής y i i και y (38) Η γενική λύση ης διαφορικής εξίσσης είναι ο γραµµικός σνδασµός ν δύο λύσεν, i y( ) c c i (39) Η λύση µπορεί να γραφεί σε πραγµαική µορφή κάνονας χρήση ο ύπο ο Όιλερ, οπόε έχοµε i i i και i y ) ( c ic ) ( c ic ), ή ( y ( ),, σαθ (3) Μια άλλη µορφή αής ης εξίσσης µπορεί να βρεθεί ς εξής: γράφονας, y( ) και ορίζονας ο πλάος φ a και η σαθερά φάσης φ έσι ώσε, φ έχοµε y( ) a (φ φ ), και ελικά, anφ (3) (3) y ( ) a ( φ) (33) για η λύση ης διαφορικής εξίσσης Οι σαθερές,, ή οι a, φ, µπορούν να προσδιορισούν για ένα σγκεκριµένο πρόβληµα από ις αρχικές ή άλλες σνθήκες ο προβλήµαος Σο Παράδειγµα πο ακολοθεί αό γίνεαι σαφές Παράδειγµα 3 Μια µάζα, σνδεδεµένη σο άκρο ενός ελαηρίο σαθεράς, εκελεί αλανώσεις χρίς απώλειες Να βρεθεί η κίνηση ης µάζας, αν αρχικά ( ) η µεαόπιση ης µάζας ήαν ( ) και η αχύηά ης ( ) Η εξίσση κίνησης ης µάζας είναι,, και η γενική ης λύση (µεαόπιση): ( ) d Η αχύηα ης µάζας είναι: ( ) d Θέονας Εποµένς, η, και χρησιµοποιώνας ις αρχικές σνθήκες, βρίσκοµε: ( ) και ( ) ( ) είναι η λύση πο ικανοποιεί ις δεδοµένες αρχικές σνθήκες
5 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 7 34 Η εξίσση y p y p y Η διαφορική εξίσση y p y p y έχει η χαρακηρισική εξίσση s p s p Η εξίσση αή έχει δύο ρίζες, ις και s, και γενική λύση ην s s s y( ) c c (34) (35) αν οι δύο ρίζες είναι διαφορεικές Αν οι σνελεσές p και p είναι έοιοι ώσε οι δύο ρίζες να είναι ίσες, s s s, η γενική λύση είναι s y ) ( c c ) (36) ( όπς µπορούµε να επιβεβαιώσοµε µε ανικαάσαση ση διαφορική εξίσση Θα µελεήσοµε η διαφορική αή εξίσση σο παράδειγµα πο ακολοθεί, µε αναφορά σον αρµονικό αλανή µε απόσβεση Παράδειγµα 4 Μια µάζα, σνδεδεµένη σο άκρο ενός ελαηρίο σαθεράς, κινείαι καά µήκος ο άξονα ν Ση µάζα ασκείαι επίσης µια δύναµη ριβής ανάλογη ης αχύηάς ης, b Να βρεθεί η λύση για η µεαόπιση ης µάζας () Σύµφνα µε ον δεύερο νόµο ο Νεύνα, η εξίσση κίνησης ης µάζας είναι: b Υποθέονας λύσεις ης µορφής, ή s y, (37) b, βρίσκοµε η χαρακηρισική εξίσση: s s, η οποία έχει ς ρίζες ις s, ± Ορίζοµε α µεγέθη: β και β, (38) οπόε οι δύο ρίζες γράφοναι ς: Αν s β i και β i, η γενική λύση είναι η i i ( ) c c (39) Χρησιµοποιώνας ον ύπο ο Όιλερ, γράφοµε η γενική λύση ση µορφή ή σην ισοδύναµη µορφή Οι σαθερές προβλήµαος s ( ) ( ) ( ) a, (3) ( φ) (3),, ή a, φ, προσδιορίζοναι από ις αρχικές ή άλλες σνθήκες ο Αναγνρίζοµε ις εξής ειδικές περιπώσεις: Μηδενική απόσβεση ( ) Η λύση ανάγεαι σην ( ) a ( φ), ης αµείης αλάνσης
6 7 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής Υποαπόσβεση ( > ) Οι ρίζες ης χαρακηρισικής εξίσσης είναι µιγαδικές και η λύση έχει η µορφή ( ) a ( φ) (3) a Η µάζα εκελεί αλανώσεις µε γνιακή σχνόηα, και πλάος πο φθίνει εκθεικά µε ο χρόνο Σην περίπση ης ασθενούς απόσβεσης, >>, η γνιακή σχνόηα είναι, και ) a ( φ) (33) 3 Κρίσιµη απόσβεση ( ) ( Σην περίπση αή η χαρακηρισική εξίσση γίνεαι s s, και έχει η διπλή ρίζα s Η λύση ης διαφορικής εξίσσης πο ανισοιχεί ση ρίζα αή είναι η ( ) C Αή όµς δεν µπορεί να είναι η γενική λύση ης διαφορικής εξίσσης, η οποία είναι δεύερης άξης και εποµένς έχει γενική λύση µε δύο ανεξάρηες σαθερές Αποδεικνύεαι, και ελέγχεαι µε ανικαάσαση ση διαφορική εξίσση, όι η ( ) D είναι επίσης λύση σην ειδική αή περίπση Εποµένς, η γενική λύση είναι: ( ) ( C D) (34) Αή είναι µια µη αλανική κίνηση Αν η αρχική µεαόπιση είναι αχύηα, η λύση εκφράζεαι ς [ ( ) ] και η αρχική ( ) (35) Η απόσαση ης µάζας από ο σηµείο γίνεαι µέγιση η χρονική σιγµή m Μεά, η µεαόπιση είνει ασµπικά σο µηδέν 4 Υπεραπόσβεση ( < ) Οι λύσεις ης χαρακηρισικής εξίσσης είναι πραγµαικές: Ορίζοµε α και γράφοµε η γενική λύση ς Η κίνηση είναι µη αλανική α α ( ) s, ± ( ) (36) 343 Η εξίσση y p y p y Πριν προχρήσοµε ση µελέη αής ης διαφορικής εξίσσης, θα αποδείξοµε µια πολύ σηµανική αρχή, πο ισχύει για όλες ις γραµµικές διαφορικές εξισώσεις µε σαθερούς σνελεσές, ην Αρχή ης πέρθεσης ή ης επαλληλίας: Αν η y είναι µια λύση ης εξίσσης y p y p y f( ) και η y είναι µια λύση ης εξίσσης y p y p y f( ), όε η y y y είναι µια λύση ης εξίσσης y p y p y f( ) f ( )
7 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 73 Απόδειξη: Επειδή y p y p y f( ) και y p y p y f( ), προσθέονας έχοµε ( y y ) p( y y) p( y y) f( ) f ( ) και εποµένς η y y y είναι λύση ης εξίσσης y p y p y f( ) f ( ) Η εξίσση y p y p y f ( ) είναι γνσή ση θερία ν αλανώσεν, και περιγράφει ην κίνηση ενός αρµονικού αλανή µε απόσβεση, ο οποίος φίσααι εξερική διέγερση ανάλογη ο f () Αν η y () είναι η γραµµική µεαόπιση µιας µάζας και ο χρόνος, όε η f () ισούαι µε ην εξερικά ασκούµενη δύναµη ανά µονάδα µάζας ο αλανή Η περίπση ης σαθερής διέγερσης δεν παροσιάζει ενδιαφέρον, αφού µια αλλαγή ης f µ εαβληής σε z y f p ανάγει ην εξίσση σην οµογενή εξίσση πο ήδη εξεάσαµε Η χρονικά µ εαβαλλόµενη διέγερση έχει εποµένς ενδιαφέρον, και ιδιαίερα η αρµονικά µ εαβαλλόµενη, δηλαδή ης µορφής ή Οι κύριοι λόγοι για η σηµασία ν αρµονικά µεαβαλλόµενν διεγέρσεν είναι οι εξής: Σα γραµµικά σσήµαα, αν η διέγερση είναι αρµονική και η απόκριση θα είναι αρµονική Ένα αθαίρεο περιοδικό σήµα διέγερσης, µε περίοδο T π, µπορεί να αναπχθεί σε σειρά Φοριέ, δηλαδή σε σειρά άπειρν όρν ης µορφής a a a a3 3 b b b3 3, αρµονικά µεαβαλλόµενν, µε σχνόηες πο είναι ακέραια πολλαπλάσια ης σχνόηας ο διεγείρονος σήµαος Αν βρεθεί η απόκριση ο σσήµαος σην κάθε µια σνισώσα ο σήµαος ξεχρισά, όε, σύµφνα µε ην αρχή ης επαλληλίας, η ολική απόκριση ο σσήµαος θα ισούαι µε ο άθροισµα ν επιµέρος αποκρίσεν Αν λοιπόν γνρίζοµε ην απόκριση ενός γραµµικού σσήµαος σε ηµιονικά ή σνηµ ιονικά σ ήµαα, γνρίζοµ ε και ην απόκρισή ο σε κάθε περιοδικό σήµα, και σο όριο πο η περίοδος αού ο σήµαος είνει σο άπειρο, σε κάθε σήµα, περιοδικό ή µη Θα προχρήσοµε ώρα ση λύση ης µη οµογενούς διαφορικής εξίσσης δεύερης άξης µ ε σαθερούς σνελεσές y p y p y, µε αναφορά σον µηχανικό αρµονικό αλανή µε απόσβεση ο οποίος φίσααι µια εξερικά ασκούµενη δύναµη ίση µε Για ο σύσηµα ης µάζας και ο ελαηρίο, η εξίσση κίνησης είναι: ή b, (37), (38) b Ας ποθέσο µε όι, µε οποιοδήποε ρόπο, έχοµε βρει µια λύση ης εξίσσης, ΕΟ, η οποία δεν περιέχει αθαίρεες σαθερές Η λύση αή ονοµάζεαι ειδικό ολοκλήρµα ης διαφορικής εξίσσης Εποµένς, Ε Ο Ε Ο Ε Ο (39) Έσ ώρα όι γράφοµε η γενική λύση ης εξίσσης ς Η ΣΣ ( ) Ε Ο Σ Σ ονοµάζεαι σµπληρµαική σνάρηση Ανικαθισώνας ση διαφορική εξίσση, βρίσκοµε (33) Ε Ο Σ Σ Ε Ο Σ Σ Ε Ο Σ Σ, (33) ( ) ( ) ( )
8 74 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής η οποία, σε σνδασµό µε ην Ε Ο Ε Ο Ε Ο, δίνει: Σ Σ Σ Σ Σ Σ (33) Η ΣΣ είναι η λύση ης οµογενούς εξίσσης, η οποία βρέθηκε σην Ενόηα 34 Η γενική λύση είναι εποµένς ( ) β ( ) (333) Ε Ο Σ Σ Ε Ο Η λύση αή ικανοποιεί η διαφορική εξίσση, και έχει δύο αθαίρεες σαθερές Είναι εποµένς η γενική λύση Σνοψίζονας, η µέθοδος λύσης ης Ε y p y p y f( ) είναι η εξής: Η γενική λύση ης Ε είναι ίση µε ο άθροισ µα ενός ειδικού ολοκληρώ µαος ης εξίσσης και η ς σµπληρµαικής σνάρησης, δηλαδή ης γενικής λύσης ης οµογενούς εξίσσης 343 Η εύρεση ο ειδικού ολοκληρώµαος Υπάρχον διάφοροι ρόποι εύρεσης ειδικών ολοκληρµάν Θα εξεάσοµε εδώ µόνο ην περίπση σην οποία είναι οκιµάζοµε η µορφή f ( ) Ε Ο E E, E, E σαθερές (334) Ανικαθισώνας ση διαφορική εξίσση Ε Ο Ε Ο Ε Ο, βρίσκοµε η σνθήκη ή ( E E ) ( E E ) ( E E ) E E E E E E (335) Η σνθήκη αή πρέπει να ισχύει για κάθε ιµή ο Εποµένς οι σνελεσ ές ν και πρέπει να είναι ίσοι µε µηδέν Έσι παίρνοµε E E E και E E E (336) Λύνονας για α και E, έχοµε για ο ειδικό ολοκλήρµα, E ( ) Ε Ο (337) ( ) ( ) Η λύση αή γράφεαι και ς Ε Ο ( φ) όπο anφ, (338) ( )
9 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 75 και η γενική λύση ης διαφορικής εξίσσης είναι: ( ) ( ) ( ) ( φ) (339) Ο πρώος όρος, ο οποίος φθίνει εκθεικά µε ο χρόνο και ελικά γίνεαι αµεληέος, περιγράφει η µεαβαική καάσαση ο σσήµαος Εξαράαι από ις αρχικές σνθήκες ο σσήµαος Ο δεύερος, ο οποίος αποµένει όαν µια δναµική ισορροπία έχει αποκαασαθεί, περιγράφει η µόνιµη καάσαση Η µόνιµη καάσαση δεν εξαράαι από ις αρχικές σνθήκες Η µεαβαική καάσαση περιγράφεαι από η σµπληρµαική σνάρηση και η µόνιµη καάσαση από ο ειδικό ολοκλήρµα 343 Η χρήση µιγαδικών σναρήσεν σην εύρεση ο ειδικού ολοκληρώµαος Η εύρεση ειδικού ολοκληρώµαος (ΕΟ) ης Ε µπορεί να γίνει ε κολόερη, και να σνδασεί µε ην εύρεση ΕΟ ης Ε, µε η χρήση µιγαδικών σναρήσεν Έσι, γράφοµε R R R και I I I (34) και ορίζοµε η µιγαδική σνάρηση R i I Πολλαπλασιάζονας επί i η διαφορική εξίσση για ην και προσθέονάς ην σε αήν για ο, βρίσκοµε I R i (34) Έσι, αν βρούµε ο ΕΟ αής ης διαφορικής εξίσσης, ο πραγµαικό ο µέρος θα είναι ο ΕΟ για η Ε µ ε ο και ο φανασικό ο µέρος θ α είναι ο ΕΟ για η Ε µε ο Το πλεονέκηµα είναι όι οι πράξεις µε εκθεικά είναι εκολόερες από αές µε ις ριγνοµερικές σναρήσεις i οκιµάζοµε η σνάρηση για ΕΟ ης ελεαίας αής Ε, όπο ο ενδεχοµένς να είναι µιγαδικό Ανικαθισώνας ση Ε (34), βρίσκοµε, µεά ην i απλοποίηση ο κοινού παράγονα, i ή Γράφονας, i iφ, i ( ) Έχοµε και anφ (34) ( ) Εποµένς είναι i iφ i i( φ ), (343) ο φανασικό µέρος ο οποίο µας δίνει ο ίδιο αποέλεσµα µε ην ενόηα 343
10 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 76 Μερικές κοινές εξισώσεις κίνησης και οι γενικές λύσεις ος Εξίσση Λύση ( ) ( ) ( ) ) ( ) ( ) ( C C C ) ( αρχική µεαόπιση, αρχική αχύηα b σαθερές,,, b ) ( ) ( ( ) C
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
8. Λύση απλών διαφορικών εξισώσεων και εξισώσεων κίνησης
 38 Κ Χριστοδολίδης: Μαθηµατικό Σµπλήρµα για τα Εισαγγικά Μαθήµατα Φσικής 8 Λύση απλών διαφορικών εξισώσεν εξισώσεν κίνησης 8 Εξισώσεις κίνησης πο οδηγούν σε διαφορικές εξισώσεις χριζόµενν µεταβλητών Η
38 Κ Χριστοδολίδης: Μαθηµατικό Σµπλήρµα για τα Εισαγγικά Μαθήµατα Φσικής 8 Λύση απλών διαφορικών εξισώσεν εξισώσεν κίνησης 8 Εξισώσεις κίνησης πο οδηγούν σε διαφορικές εξισώσεις χριζόµενν µεταβλητών Η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
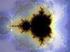 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
7. Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας
 7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
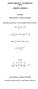 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 28 Απριλίου 2013 ιάρκεια Εξέτασης: 2 ώρες ΑΠΑΝΤΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 03 Ε_3.Φλ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΜΑ Α Ηµεροµηνία: Κριακή 8 Απριλίο 03 ιάρκεια Εξέτασης: ώρες Α. δ Α. γ Α3. β Α4. δ Α5. α Σ, β Λ, γ Σ, δ Σ, ε Λ. ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Β
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 03 Ε_3.Φλ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΜΑ Α Ηµεροµηνία: Κριακή 8 Απριλίο 03 ιάρκεια Εξέτασης: ώρες Α. δ Α. γ Α3. β Α4. δ Α5. α Σ, β Λ, γ Σ, δ Σ, ε Λ. ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Β
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΡΕΘΥΜΝΟΥ ΤΜΗΜΑ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΑΚΟΥΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ Τ.Ε.Ι. ΚΡΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΡΕΘΥΜΝΟΥ ΤΜΗΜΑ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΑΚΟΥΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΥΠΕΡΒΟΛΙΚΩΝ ΜΕΡΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. ΕΦΑΡΜΟΓΗ ΤΗΣ ΜΕΘΟΔΟΥ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ Τ.Ε.Ι. ΚΡΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΡΕΘΥΜΝΟΥ ΤΜΗΜΑ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΑΚΟΥΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΥΠΕΡΒΟΛΙΚΩΝ ΜΕΡΙΚΩΝ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. ΕΦΑΡΜΟΓΗ ΤΗΣ ΜΕΘΟΔΟΥ
, όπου οι σταθερές προσδιορίζονται από τις αρχικές συνθήκες.
 Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
5.15 Εφαρμογές της ομογενούς Δ.Ε. 2ης τάξης με σταθερούς συντελεστές
 4 ΚΕΦΑΛΑΙΟ 5 α) y -y +y e x /x 5 Aπ. u(/)x -3 e x β) y +ysecx Aπ. u[csx]ln csx +xsinx γ) y +4ysin x Aπ. u[cs (x)+]/ ) Γενικεύοντας την παραπάν πορεία για n>, δείξτε ότι τα v i (x) ικανοποιούν το σύστημα
4 ΚΕΦΑΛΑΙΟ 5 α) y -y +y e x /x 5 Aπ. u(/)x -3 e x β) y +ysecx Aπ. u[csx]ln csx +xsinx γ) y +4ysin x Aπ. u[cs (x)+]/ ) Γενικεύοντας την παραπάν πορεία για n>, δείξτε ότι τα v i (x) ικανοποιούν το σύστημα
1. Η αβαρής λεπτή ράβδος του διπλανού σχήµατος έχει
 Αβαρής ράβδος πο στο άκρο της έχει µικρό σώµα ή δίσκο ελεύθερο ή δίσκο σταθερό Τρεις παρόµοιες ασκήσεις πο εστιάζον στη διαφορετική σµπεριφορά λικού σηµείο ή σώµατος πο κινείται µεταφορικά και σώµατος
Αβαρής ράβδος πο στο άκρο της έχει µικρό σώµα ή δίσκο ελεύθερο ή δίσκο σταθερό Τρεις παρόµοιες ασκήσεις πο εστιάζον στη διαφορετική σµπεριφορά λικού σηµείο ή σώµατος πο κινείται µεταφορικά και σώµατος
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Επανάληψη Θεωρίας και Τυπολόγιο
 ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΠΡΟΕΤΟΙΜΑΣΙΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επανάληψη Θεωρίας και Τπολόγιο ΕΞΙΣΩΣΕΙΣ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ Γενικές έννοιες Περιοδική ονομάζεται η κίνηση πο επαναλαμβάνεται κατά τον
ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΠΡΟΕΤΟΙΜΑΣΙΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επανάληψη Θεωρίας και Τπολόγιο ΕΞΙΣΩΣΕΙΣ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ Γενικές έννοιες Περιοδική ονομάζεται η κίνηση πο επαναλαμβάνεται κατά τον
ΚΕΦΑΛΑΙΟ 8. Ροπή και Στροφορµή Μέρος δεύτερο
 ΚΕΦΑΛΑΙΟ 8 Ροπή και Στροφορµή Μέρος δεύτερο Στο προηγούµενο Κεφάλαιο εξετάσαµε την περιστροφή στερεού σώµατος περί σταθερό άξονα. Εδώ θα εξετάσοµε την εξίσωση κίνησης στερεού σώµατος γενικώς. Πριν το κάνοµε
ΚΕΦΑΛΑΙΟ 8 Ροπή και Στροφορµή Μέρος δεύτερο Στο προηγούµενο Κεφάλαιο εξετάσαµε την περιστροφή στερεού σώµατος περί σταθερό άξονα. Εδώ θα εξετάσοµε την εξίσωση κίνησης στερεού σώµατος γενικώς. Πριν το κάνοµε
Κίνηση φορτισµένου σωµατιδίου σε χώρο, όπου συνυπάρχουν ηλεκτρικό και µαγνητικό πεδίο οµογενή και χρονοανεξάρτητα
 Κίνηση φορτισµένο σµατιδίο σε χώρο, όπο σνπάρχον ηλεκτρικό και µαγνητικό πεδίο οµογενή και χρονοανεξάρτητα Α. Τι βλέπει ένας αδρανειακός παρατηρητής Σε ένα αδρανειακό σύστηµα σνπάρχον δύο οµογενή και χρονοανεξάρτητα
Κίνηση φορτισµένο σµατιδίο σε χώρο, όπο σνπάρχον ηλεκτρικό και µαγνητικό πεδίο οµογενή και χρονοανεξάρτητα Α. Τι βλέπει ένας αδρανειακός παρατηρητής Σε ένα αδρανειακό σύστηµα σνπάρχον δύο οµογενή και χρονοανεξάρτητα
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 2ο «ΓΕΩΜΕΤΡΙΑ»
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΣ ΜΘΗΜΤΙΚ ΥΜΝΣΙΟΥ ΜΕΡΟΣ ο «ΕΩΜΕΤΡΙ» Τι καλείται εμαδόν επίπεδης επιφάνειας; Το εμαδόν μιας επίπεδης επιφάνειας είναι ένας θετικός αριθμός, πο εκφράζει την έκταση πο καταλαμάνει η επιφάνεια
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΣ ΜΘΗΜΤΙΚ ΥΜΝΣΙΟΥ ΜΕΡΟΣ ο «ΕΩΜΕΤΡΙ» Τι καλείται εμαδόν επίπεδης επιφάνειας; Το εμαδόν μιας επίπεδης επιφάνειας είναι ένας θετικός αριθμός, πο εκφράζει την έκταση πο καταλαμάνει η επιφάνεια
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
Κίνηση φορτισµένου σωµατιδίου σε χώρο, όπου συνυπάρχουν ηλεκτρικό και µαγνητικό πεδίο οµογενή και χρονοανεξάρτητα
 Κίνηση φορτισµένο σωµατιδίο σε χώρο, όπο σνπάρχον ηλεκτρικό και µαγνητικό πεδίο οµογενή και χρονοανεξάρτητα Α. Τι βλέπει ένας αδρανειακός παρατηρητής Σε ένα αδρανειακό σύστηµα σνπάρχον δύο οµογενή και
Κίνηση φορτισµένο σωµατιδίο σε χώρο, όπο σνπάρχον ηλεκτρικό και µαγνητικό πεδίο οµογενή και χρονοανεξάρτητα Α. Τι βλέπει ένας αδρανειακός παρατηρητής Σε ένα αδρανειακό σύστηµα σνπάρχον δύο οµογενή και
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ ΑΣΚΗΣΗ 1 d x dx Η διαφορική εξίσωση κίνησης ενός ταλαντωτή δίνεται από τη σχέση: λ μx. Αν η μάζα d d του ταλαντωτή είναι ίση με =.5 kg, τότε να διερευνήσετε την κίνηση
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ ΑΣΚΗΣΗ 1 d x dx Η διαφορική εξίσωση κίνησης ενός ταλαντωτή δίνεται από τη σχέση: λ μx. Αν η μάζα d d του ταλαντωτή είναι ίση με =.5 kg, τότε να διερευνήσετε την κίνηση
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Ελαστική κρούση σώµατος µε ράβδο που µπορεί να στρέφεται γύρω από το άκρο της. Πότε µεγιστοποιείται η µεταφορά ενέργειας;
 . Μητρόπολος Μηχανική Στερεού σώµατος Ελαστική κρούση σώµατος µε ράβδο πο µπορεί να στρέφεται γύρ από το άκρο της. Πότε µεγιστοποιείται η µεταφορά ενέργειας; ο,, ΠΡΙΝ ΜΕΤ Η ράβδος το σχήµατος έχει µάζα,
. Μητρόπολος Μηχανική Στερεού σώµατος Ελαστική κρούση σώµατος µε ράβδο πο µπορεί να στρέφεται γύρ από το άκρο της. Πότε µεγιστοποιείται η µεταφορά ενέργειας; ο,, ΠΡΙΝ ΜΕΤ Η ράβδος το σχήµατος έχει µάζα,
3. ΑΠΟΚΡΙΣΗ ΚΑΤΑ ΣΥΧΝΟΤΗΤΑ
 3. 3. ΑΠΟΚΡΙΣΗ ΚΑΤΑ ΣΥΧΝΟΤΗΤΑ 3. Εισαγγή Στην μελέτη τν συστημάτν, μία από τις μεθόδους που χρησιμοποιούνται είναι η απόκριση κατά συχνότητα ή η συχνοτική απόκριση. Η μέθοδος αυτή μελετά την συμπεριφορά
3. 3. ΑΠΟΚΡΙΣΗ ΚΑΤΑ ΣΥΧΝΟΤΗΤΑ 3. Εισαγγή Στην μελέτη τν συστημάτν, μία από τις μεθόδους που χρησιμοποιούνται είναι η απόκριση κατά συχνότητα ή η συχνοτική απόκριση. Η μέθοδος αυτή μελετά την συμπεριφορά
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα : Συστήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Συστήματα Διακριτού Χρόνου Εξισώσεις Διαφορών Επίλυση Εξισώσεων Διαφορών με Γραμμικούς Συντελεστές
Ψηφιακή Επεξεργασία Σημάτων Ενότητα : Συστήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Συστήματα Διακριτού Χρόνου Εξισώσεις Διαφορών Επίλυση Εξισώσεων Διαφορών με Γραμμικούς Συντελεστές
Γενικές εξετάσεις Φυσική Γ λυκείου θετικής - τεχνολογικής κατεύθυνσης
 Γενικές εξετάσεις 00 Φσική Γ λκείο θετικής - τεχνολογικής κατεύθνσης Θέμα ο Να γράψετε ο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις - και δίπλα το γράμμα πο αντιοιχεί η σωή απάντηση..
Γενικές εξετάσεις 00 Φσική Γ λκείο θετικής - τεχνολογικής κατεύθνσης Θέμα ο Να γράψετε ο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις - και δίπλα το γράμμα πο αντιοιχεί η σωή απάντηση..
Φάση Αρχική φάση Διαφορά φάσης στην ταλάντωση
 Φάση Αρχική φάση Διαφορά φάσης στην ταλάντση Α. Προκαταρκτικά ) Οι κινήσεις στις οποίες θα αναφερθούµε είναι εθύγραµµες και άρα µονοδιάστατες. Πραγµατοποιούνται στον άξονα x και για την περιγραφή τος επιλέγοµε
Φάση Αρχική φάση Διαφορά φάσης στην ταλάντση Α. Προκαταρκτικά ) Οι κινήσεις στις οποίες θα αναφερθούµε είναι εθύγραµµες και άρα µονοδιάστατες. Πραγµατοποιούνται στον άξονα x και για την περιγραφή τος επιλέγοµε
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Κατσαλά Νικολέτα. Φυσικός. Γ Λυκείου. Τυπολόγιο
 Κατσαλά Νικολέτα Φσικός Γ Λκείο Τπολόγιο Εθύγραμμη Ομαλή Κίνηση Εθύγραμμη Ομαλά Μεταβαλλόμενη Κίνηση Ολικό Διάστημα και Ολικός Χρόνος στην Ομαλά Επιβραδνόμενη Μεταφορική Κίνηση Δ α, Δ Δ α σταθ, Δ α, Δ
Κατσαλά Νικολέτα Φσικός Γ Λκείο Τπολόγιο Εθύγραμμη Ομαλή Κίνηση Εθύγραμμη Ομαλά Μεταβαλλόμενη Κίνηση Ολικό Διάστημα και Ολικός Χρόνος στην Ομαλά Επιβραδνόμενη Μεταφορική Κίνηση Δ α, Δ Δ α σταθ, Δ α, Δ
ΑΝΑΛΥΣΗ ΤΟ ΓΕΝΙΚΟ ΠΛΑΝΟ 2019Κ7-1
 ΑΝΑΛΥΣΗ ΤΟ ΓΕΝΙΚΟ ΠΛΑΝΟ 19Κ7-1 ΤΟ ΜΑΥΡΟ ΚΟΥΤΙ Είσοδος ΜΑΥΡΟ ΚΟΥΤΙ Έξοδος 1. Το περιεχόμενο του μαύρου κουτιού (απλά ηλεκτρικά στοιχεία). Είσοδος: σήματα (κυματομορφές) διέγερσης 3. Έξοδος: απόκριση i.
ΑΝΑΛΥΣΗ ΤΟ ΓΕΝΙΚΟ ΠΛΑΝΟ 19Κ7-1 ΤΟ ΜΑΥΡΟ ΚΟΥΤΙ Είσοδος ΜΑΥΡΟ ΚΟΥΤΙ Έξοδος 1. Το περιεχόμενο του μαύρου κουτιού (απλά ηλεκτρικά στοιχεία). Είσοδος: σήματα (κυματομορφές) διέγερσης 3. Έξοδος: απόκριση i.
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΙΚΗΣ ΚΑΙ ΕΧΝΟΛΟΓΙΚΗΣ ΚΑΕΥΘΥΝΣΗΣ ΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΑ Η διάδοση μιας διαταραχής μέσα σ' ένα μέσο ονομάζεται κύμα. Για τη δημιοργία ενός μηχανικού κύματος
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΙΚΗΣ ΚΑΙ ΕΧΝΟΛΟΓΙΚΗΣ ΚΑΕΥΘΥΝΣΗΣ ΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΑ Η διάδοση μιας διαταραχής μέσα σ' ένα μέσο ονομάζεται κύμα. Για τη δημιοργία ενός μηχανικού κύματος
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 2008
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 8 ΘΕΜΑ ο Έστω, α,β, α β και ν α + + i = βi () β + αi α) Να αποδείξετε ότι ο δεν είναι πραγµατικός αριθµός. β) Να αποδείξετε
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 8 ΘΕΜΑ ο Έστω, α,β, α β και ν α + + i = βi () β + αi α) Να αποδείξετε ότι ο δεν είναι πραγµατικός αριθµός. β) Να αποδείξετε
Γραμμική Διαφορική Εξίσωση 2 ου βαθμού
 //04 Γραμμική Διαφορική Εξίσωση ου βαθμού, με τη βοήθεια του αορίστου ολοκληρώματος, της χρήσιμης γραμμικής διαφορικής εξίσωσης πρώτου βαθμού af ( ) f ( ) cf ( ) g( ), ac,, σταθεροί πραγματικοί αριθμοί
//04 Γραμμική Διαφορική Εξίσωση ου βαθμού, με τη βοήθεια του αορίστου ολοκληρώματος, της χρήσιμης γραμμικής διαφορικής εξίσωσης πρώτου βαθμού af ( ) f ( ) cf ( ) g( ), ac,, σταθεροί πραγματικοί αριθμοί
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
Μην χάσουμε τον σύνδεσμο ή τον κινηματικό περιορισμό!!!
 Μην χάσομε τον σύνδεσμο ή τον κινηματικό περιορισμό!!! Σε πάρα πολλές περιπτώσεις κατά τη µελέτη το στερεού, το πρόβληµα επιλύεται µε εφαρµογή το ο νό- µο το Νεύτωνα, τόσο για την περιστροφική κίνηση κάποιο
Μην χάσομε τον σύνδεσμο ή τον κινηματικό περιορισμό!!! Σε πάρα πολλές περιπτώσεις κατά τη µελέτη το στερεού, το πρόβληµα επιλύεται µε εφαρµογή το ο νό- µο το Νεύτωνα, τόσο για την περιστροφική κίνηση κάποιο
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
2. Στο σύστηµα αξόνων του πιο πάνω σχήµατος, να προσδιορίσετε τις συντεταγµένες. 3. Να βρεθεί το µέτρο της τελικής ταχύτητας υ Τ
 ιονύσης Μητρόπολος Β κείο Οριζόντια βολή Άσκηση στην οριζόντια βολή ο (0,0) x Η h Τ φ Μεταλλική σφαίρα µάζας m = 0,4kg εκτοξεύεται οριζόντια από την άκρη της ταράτσας κτιρίο ύψος Η = 0m, µε ταχύτητα µέτρο
ιονύσης Μητρόπολος Β κείο Οριζόντια βολή Άσκηση στην οριζόντια βολή ο (0,0) x Η h Τ φ Μεταλλική σφαίρα µάζας m = 0,4kg εκτοξεύεται οριζόντια από την άκρη της ταράτσας κτιρίο ύψος Η = 0m, µε ταχύτητα µέτρο
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
IΣΟΖΥΓΙΑ ΟΡΜΗΣ (SHELL MOMENTUM BALANCES) ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΑΣ (VELOCITY DUSTRIBUTION) ΣΤΡΩΤΗ ΡΟΗ (LAMINAR FLOW)
 IΣΟΖΥΓΙΑ ΟΡΜΗΣ (SHE MOMENTUM BAANCES ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΑΣ (VEOCITY DUSTIBUTION ΣΤΡΩΤΗ ΡΟΗ (AMINA FOW Σε αό ο κεφάλαιο θα εξεάσοµε πως µπορούµε να εφαρµόσοµε ο ισοζύγιο ορµής σε ένα διαφορικό όγκο (differential
IΣΟΖΥΓΙΑ ΟΡΜΗΣ (SHE MOMENTUM BAANCES ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΑΣ (VEOCITY DUSTIBUTION ΣΤΡΩΤΗ ΡΟΗ (AMINA FOW Σε αό ο κεφάλαιο θα εξεάσοµε πως µπορούµε να εφαρµόσοµε ο ισοζύγιο ορµής σε ένα διαφορικό όγκο (differential
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 2012 ΘΕΜΑΤΑ Α
 ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 0 ΘΕΜΑΤΑ Α Θέµα ο. Να βρεθεί (α) η γενική λύση yy() της διαφορικής εξίσωσης y' y + καθώς και (β) η µερική λύση που διέρχεται από το σηµείο y(/). (γ) Από ποια σηµεία του επιπέδου
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 0 ΘΕΜΑΤΑ Α Θέµα ο. Να βρεθεί (α) η γενική λύση yy() της διαφορικής εξίσωσης y' y + καθώς και (β) η µερική λύση που διέρχεται από το σηµείο y(/). (γ) Από ποια σηµεία του επιπέδου
Γενικές ασκήσεις σχ. βιβλίου σελίδας 47 49
 Γενικές ασκήσεις σχ. βιβλίο σελίδας 47 49. Αν µια σρµάτινη ράβδος είναι οµογενής, τότε η γραµµική της πκνότητα ρ ρ m και µετριέται σε χιλιόγραµµα l ορίζεται ως η µάζα της ανά µονάδα µήκος ( ) ανά µέτρο
Γενικές ασκήσεις σχ. βιβλίο σελίδας 47 49. Αν µια σρµάτινη ράβδος είναι οµογενής, τότε η γραµµική της πκνότητα ρ ρ m και µετριέται σε χιλιόγραµµα l ορίζεται ως η µάζα της ανά µονάδα µήκος ( ) ανά µέτρο
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
ΠΑΡΑΤΗΡΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ Στα προβλήματα ατού το κεφαλαίο, το πρώτο πο πρέπει να διακρίνομε είναι αν έχομε ισορροπία, μόνο στροφική κίνηση (δηλαδή γύρω από σταθερό άξονα περιστροφής)
ΠΑΡΑΤΗΡΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ Στα προβλήματα ατού το κεφαλαίο, το πρώτο πο πρέπει να διακρίνομε είναι αν έχομε ισορροπία, μόνο στροφική κίνηση (δηλαδή γύρω από σταθερό άξονα περιστροφής)
ΚΥΡΙΑ ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Εργαστηριακοί Συνεργάτες: Σ. ΒΑΣΙΛΕΙΑΔΟΥ, Α. ΟΙΚΟΝΟΜΙΔΗΣ,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Εργαστηριακοί Συνεργάτες: Σ. ΒΑΣΙΛΕΙΑΔΟΥ, Α. ΟΙΚΟΝΟΜΙΔΗΣ,
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
ΚΕΦΑΛΑΙΟ 4. ιατήρηση ορµής
 ΚΕΦΑΛΑΙΟ 4 ιατήρηση ορµής Ας θεωρήσοµε δυο υλικά σηµεία και µε µάζες και αντιστοίχως που βρίσκονται την τυχούσα χρονική στιγµή στις αντίστοιχες διανυσµατικές ακτίνες και και έχουν αντίστοιχες ταχύτητες
ΚΕΦΑΛΑΙΟ 4 ιατήρηση ορµής Ας θεωρήσοµε δυο υλικά σηµεία και µε µάζες και αντιστοίχως που βρίσκονται την τυχούσα χρονική στιγµή στις αντίστοιχες διανυσµατικές ακτίνες και και έχουν αντίστοιχες ταχύτητες
Σήματα και Συστήματα. Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
Εισαγωγή. Στο κεφάλαιο αυτό θα µελετηθεί ο τελεστικός ενισχυτής.
 Εισαγωγή Στο κεφάλαιο ατό θα µελετηθεί ο τελεστικός ενισχτής. Οι πρώτοι τελεστικοί ενισχτές ήταν κατασκεασµένοι από διακριτά στοιχεία (λχνίες κενού, και κατόπιν τρανζίστορ και αντιστάσεις) και το κόστος
Εισαγωγή Στο κεφάλαιο ατό θα µελετηθεί ο τελεστικός ενισχτής. Οι πρώτοι τελεστικοί ενισχτές ήταν κατασκεασµένοι από διακριτά στοιχεία (λχνίες κενού, και κατόπιν τρανζίστορ και αντιστάσεις) και το κόστος
x(t) 2 = e 2 t = e 2t, t > 0
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 216-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Σήµατα και Συστήµατα Ασκηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 216-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Σήµατα και Συστήµατα Ασκηση
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Κ. Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής. 9. ιανύσµατα
 46 Κ Χριστοδολίδης: Μαθηµατικό Σµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φσικής 9 ιανύσµατα 9 Σµβολισµός Ως ανεξάρτητο το σστήµατος σντεταγµένων, ένα διάνσµα σµβολίζεται στο τπωµένο κείµενο µε έντονο σύµβολο:
46 Κ Χριστοδολίδης: Μαθηµατικό Σµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φσικής 9 ιανύσµατα 9 Σµβολισµός Ως ανεξάρτητο το σστήµατος σντεταγµένων, ένα διάνσµα σµβολίζεται στο τπωµένο κείµενο µε έντονο σύµβολο:
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
10 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
5. Αυτεπαγωγή-Χωρητικότητα Inductance Capacitance
 5. Αυτεπαγγή-Χρητικότητα nucance Capaciance Εδώ εισάγουµε τα δύο τελευταία στοιχεία κυκλµάτν, τα πηνία και τους πυκντές. Οι τεχνικές ανάλυσης κυκλµάτν που εισήχθικαν νρίτερα ακόµα ισχύουν εδώ. Ένα πηνίο
5. Αυτεπαγγή-Χρητικότητα nucance Capaciance Εδώ εισάγουµε τα δύο τελευταία στοιχεία κυκλµάτν, τα πηνία και τους πυκντές. Οι τεχνικές ανάλυσης κυκλµάτν που εισήχθικαν νρίτερα ακόµα ισχύουν εδώ. Ένα πηνίο
Physica by Chris Simopoulos
 ΜΗΧΑΝΙΚΗ ΕΝΕΡΓΕΙΑ - ΘΜΚΕ Η μηχανική ενέργεια είναι το άθροισμα της κινητικής και της δναμικής ενέργειας το σώματος. Όπως είναι γνωστό οι σχέσεις πο δίνον τις ενέργειες ατές είναι: E = 1.m. (7) και Ε Δ
ΜΗΧΑΝΙΚΗ ΕΝΕΡΓΕΙΑ - ΘΜΚΕ Η μηχανική ενέργεια είναι το άθροισμα της κινητικής και της δναμικής ενέργειας το σώματος. Όπως είναι γνωστό οι σχέσεις πο δίνον τις ενέργειες ατές είναι: E = 1.m. (7) και Ε Δ
Δυναμική Μηχανών I. Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις. Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές
 Δυναμική Μηχανών I Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις 5 3 Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Δυναμική Μηχανών I Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις 5 3 Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
? Συμπεριφορά ψαθυρών υλικών 11/6/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας
 11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
