ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΣΤΙΣ ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΚΑΙ ΣΤΙΣ ΣΥΓΧΡΟΝΕΣ ΤΕΧΝΟΛΟΓΙΕΣ
|
|
|
- Πρίαμος Παπαδόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΣΤΙΣ ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΚΑΙ ΣΤΙΣ ΣΥΓΧΡΟΝΕΣ ΤΕΧΝΟΛΟΓΙΕΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΣΤΑ ΜΙΚΡΟΗΛΕΚΤΡΟΜΗΧΑΝΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΡΓΕΤΑΚΗ ΜΑΡΙΑ ΑΜ:33/53 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΙΟΥΝΙΟΣ 7 ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ ΧΡΗΣΤΟΣ ΝΙΚΟΛΟΠΟΥΛΟΣ
2 μου Στην μνήμη του παππού
3 ΠΕΡΙΕΧΟΜΕΝΑ Ευχαριστίες 4 Περίληψη 5 ΚΕΦΑΛΑΙΟ Εισαγωγή 6 Παρουσίαση του μοντέλου 9 Κανονικοποίηση σε συστήματα που κυριαρχούνται από αδράνεια 3 Κανονικοποίηση σε συστήματα στα οποία κυριαρχεί η εσωτερική τριβή 4 Κανονικοποίηση σε σύστημα στο οποίο εφαρμόζεται εναλλασσόμενο ρεύμα 3 5 Λύσεις σταθερής κατάστασης 4 6 Ευστάθεια των σταθερών καταστάσεων 8 ΚΕΦΑΛΑΙΟ Παραγωγή της κυματικής εξίσωσης Διατύπωση του μοντέλου σε ηλεκτροστατικό πεδίο 5 3 Επεκτάσεις του βασικού μοντέλου 9 3
4 4 3 Το όριο όταν το σύστημα κυριαρχείται από ιξώδες 5 Στάσιμες λύσεις 3 6 Δυναμική του συστήματος για λ λ 37 7 Δυναμική του συστήματος για λ > λ 38 8 Προσεγγιστική δομή των λύσεων στο σημείο επαφής 4 ΚΕΦΑΛΑΙΟ 3 3 Αριθμητική επίλυση του Μονοδιάστατου μοντέλου με μια απλή άμεση μέθοδο 45 3 Αριθμητική επίλυση με τη μέθοδο Crak-Nickolso 5 Συμπεράσματα 57 Βιβλιογραφία 58 4
5 Ευχαριστίες Θεωρώ χρέος μου να ευχαριστήσω όλους τους ανθρώπους που με διάφορους τρόπους με βοήθησαν στην εκπόνηση αυτής της εργασίας Θα ήθελα να ευχαριστήσω θερμά τον Επίκουρο Καθηγητή Χρήστο Νικολόπουλο για την ανάθεση της διπλωματικής εργασίας και για τη βοήθεια και την καθοδήγηση που μου παρ είχε καθ όλη τη διάρκεια της εκπόνησης της Ευχαριστώ τους Επίκουρους Καθηγητές κ Νίκο Καραχάλιο και κ Κώστα Χουσιάδα, οι οποίοι είχαν την καλή διάθεση να συμμετέχουν στην εξεταστική επιτροπή 5
6 6
7 Περίληψη Ίσως το πιο ευρέως διαδεδομένο φαινόμενο που σχετίζεται με MEMS (Microelectroical-mechaical-structures) συσκευές που κινούνται υπό τη δράση ηλεκτροστατικών δυνάμεων είναι η επονομαζόμενη ελκτική τάση αστάθειας (pull-i istabillity), δηλαδή η ηλεκτροστατική τάση η οποία προκαλεί επαφή μεταξύ των δύο συνιστωσών του συστήματος Στην εργασία αυτή κατασκευάσαμε ένα μοντέλο το οποίο αποτελείται από μια ελαστική μεμβράνη που αιωρείται πάνω από ένα σταθερό δίσκο Ανάμεσα στη μεμβράνη και το δίσκο εφαρμόζεται μια διαφορά δυναμικού (τάση) Όταν η τάση αυτή ξεπεράσει μια τιμή, την οποία ονομάζουμε κρίσιμη τιμή, τότε εμφανίζεται το φαινόμενο (touch dow), δηλαδή επαφή της ελαστικής μεμβράνης με τον δίσκο κάτι που γενικά είναι μη επιθυμητόστην περίπτωση της ελκτικής αστάθειας όταν οι εφαρμοσμένες τάσεις αυξάνονται πάνω από μια συγκεκριμένη κρίσιμη τιμή τότε δεν υπάρχει σχηματισμός σταθερής κατάστασης της συσκευής [] Αυτή η αστάθεια περιορίζει αυστηρά το πεδίο της σταθερής λειτουργίας πολλών συσκευών Στην εργασία αυτή κατασκευάζεται ένα μαθηματικό μοντέλο μιας εξιδανικευμένης συσκευής MEMS που κινείται ηλεκτροστατικά, με σκοπό την ανάλυση και καθορισμό των παραμέτρων, που προκαλούν η αποτρέπουν το φαινόμενο της επαφής (touch dow) Η ενσωμάτωση της συσκευής μας μέσα σε ένα κύκλωμα ελέγχου με πυκνωτή μετατρέπει ήδη το μη γραμμικό πρόβλημά μας σε μη τοπικό, το οποίο αναλύεται μέσα από μια ποικιλία ασυμπτωτικών, αναλυτικών και αριθμητικών μεθόδων Η ελκτική τάση αστάθειας διερευνάται με τη χρήση του διαγράμματος διακλάδωσης για το μαθηματικό μοντέλο Μεταβάλλοντας διάφορες παραμέτρους του συστήματος παρατηρούμε ότι προκύπτουν μεταβολές στο διάγραμμα διακλάδωσης, επηρεάζοντας την ελκτική τάση και ελκτική απόσταση, δηλαδή την ελάχιστη απόσταση μεταξύ δύο συνιστωσών του συστήματος όταν αυτές δεν έρχονται σε επαφή Επιπλέον δίνονται κάποιες εκτιμήσεις για ποιες τιμές των παραμέτρων έχουμε ελκτική τάση αστάθειας ή όχι και τα αποτελέσματα επαληθεύονται με κάποιες αριθμητικές προσομοιώσεις 7
8 Εισαγωγή Η έλευση των μίκρο-ηλεκτρομηχανικών συστημάτων (MEMS) έχει ανατρέψει πολυάριθμους κλάδους της επιστήμης και της βιομηχανίας Το πεδίο των ταχύτατα αναπτυσσόμενων νάνο-ηλεκτρομηχανικών NEMS (Nao-electroical-mechaicalstructures) συστημάτων υπόσχεται ακόμα περισσότερες ριζικές αλλαγές Στα MEMS και NEMS τα ηλεκτροστατικά φαινόμενα παίζουν ρόλο κλειδί Εξετάζοντας οι ερευνητές διάφορες συσκευές όπως επιταχυνσιόμετρα, μικροαντλίες, μικρολαβές, μικρομετρητές δυνάμεων και διατάξεις μετατροπής συνεχώς εξερευνούν νέες χρήσεις για τη δύναμη Coulomb [] Στην ηλεκτροστατική προσέγγιση διαφορετικές τάσεις εφαρμόζονται ανάμεσα στις μηχανικές συνιστώσες του συστήματος Η δύναμη Coulomb που προκαλείται ποικίλει σε ένταση με την αλλαγή της εφαρμοσμένης τάσης Η απλότητα και η σπουδαιότητα αυτής της τεχνικής έχει επηρεάσει πολυάριθμους ερευνητές να αναπτύξουν και να μελετήσουν μαθηματικά μοντέλα ηλεκτροστατικών και ελαστικών αλληλεπιδράσεων Στην εργασία αυτή εξετάζουμε με λεπτομέρεια ένα μοντέλο των συσκευών MEMS και NEMS που κινούνται ηλεκτροστατικά Συγκεκριμένα θα κατασκευάσουμε και θα αναλύσουμε ένα εξιδανικευμένο σύστημα το οποίο λειτουργεί όπως λειτουργεί ένα μοντέλο μάζας-ελατηρίου που κινείται ηλεκτροστατικά Στο κεφάλαιο θα μελετήσουμε το μοντέλο που παρουσιάζεται στο σχήμα Το μοντέλο αυτό αποτελείται από δύο πλάκες μια πάνω και μια κάτω και ένα ελατήριο πάνω στο οποίο στηρίζεται η πάνω πλάκα Ανάμεσα στις δύο πλάκες εφαρμόζεται κάποια τάση ΣΧΗΜΑ 8
9 Στο μοντέλο αυτό δεν λαμβάνουμε υπόψη γεωμετρικές μεταβολές δηλαδή παραμόρφωση των συνιστωσών του συστήματος Παράλληλες συνιστώσες του συστήματος υποτίθεται ότι παραμένουν παράλληλες καθ όλη τη διάρκεια του φαινομένου Αυτό συνεπάγεται ότι η μηχανική κατάσταση του συστήματος μπορεί να προσδιοριστεί από μια εξαρτημένη μεταβλητή u, όπου u η απόσταση η οποία είναι μια συνάρτηση του χρόνου Η σταθερά του ελατηρίου κ είναι μια παράμετρος που χαρακτηρίζει τις μηχανικές ιδιότητες του συστήματος [3] Θα υποθέσουμε ότι η ηλεκτροστατική δύναμη μπορεί να υπολογιστεί από τους παράλληλους δίσκους και θα εξετάσουμε την υπόθεση αυτή με περισσότερη λεπτομέρεια στο κεφάλαιο Θα κανονικοποιήσουμε το μοντέλο μας και η επιλογή της χρονικής κλίμακας που θα χρησιμοποιήσουμε εξαρτάται από το αν η συσκευή μας κυριαρχείται από εσωτερική τριβή ή αν στη συσκευή μας εφαρμόζεται εναλλασσόμενο ρεύμα Θα μελετήσουμε την κατάλληλη διαβάθμιση του συστήματος σε κάθε περίπτωση έχοντας σαν στόχο να αναπτύξουμε μια πρώτη αντίληψη της αστάθειας Σ αυτή την περίπτωση αστάθειας, όταν οι εφαρμοσμένες τάσεις αυξάνονται πάνω από ένα συγκεκριμένο σημείο, έχει αποδειχτεί ότι δεν υπάρχει σταθερή κατάσταση διαμόρφωσης της συσκευής στην οποία μηχανικά μέλη να παραμένουν χωριστά δηλαδή του φαινομένου κατά το οποίο οι δύο πλάκες έρχονται σε επαφή (touch dow) Η τάση για την οποία έχουμε έλξη των δύο πλακών (pull-i) αναφέρεται σαν ελκτική τάση και η μέγιστη απόσταση που επιτυγχάνεται όταν δεν έχουμε την παρουσία της ελκτικής αστάθειας αναφέρεται σαν ελκτική απόσταση Η ελκτική απόσταση για παράδειγμα στην περίπτωση ενός απλού μονοδιάστατου μοντέλου που θα αναλύσουμε στη συνέχεια είναι περίπου το /3 της απόστασης που έχουν οι πλάκες για μηδενική διαφορά δυναμικού[3] Στο κεφάλαιο περιγράφουμε πλήρως το εξιδανικευμένο μοντέλο Εδώ θεωρούμε ότι η άνω πλάκα η δίσκος επιδέχεται ελαστικής παραμόρφωσης Δείχνουμε πως το σύστημα μάζας-ελατηρίου μπορεί να χρησιμοποιηθεί σαν εργαλείο για περεταίρω εξερεύνηση συσκευών MEMS που κινούνται ηλεκτροστατικά Εδώ το μοντέλο αποτελείται από μια ελαστική μεμβράνη με πακτωμένα άκρα που αιωρείται πάνω από ένα σταθερό δίσκο Ανάμεσα στη μεμβράνη και το δίσκο εφαρμόζεται κάποια τάση Ξεκινάμε τη μελέτη μας αναλύοντας τις δυναμικές του εξιδανικευμένου ήλεκτρο-ελαστικού συστήματος που λειτουργεί σε καθεστώς που κυριαρχείται από εσώτερική τριβή, δηλαδή περιμένουμε οι επιρροές της απόσβεσης να είναι πιο σημαντικές από τις επιρροές της αδράνειας Αυτό σημαίνει ότι στο μαθηματικό μας μοντέλο επιτρέπουμε το σύστημα να μεταβάλλεται με το χρόνο αλλά αγνοούμε τις επιπτώσεις της αδράνειας Αυτό απλουστεύει το μαθηματικό μας μοντέλο και μας επιτρέπει να μελετήσουμε μια παραβολική εξίσωση του τύπου αντίδρασης διάχυσης Στην επόμενη παράγραφο επαναλαμβάνουμε τη διατύπωση του μοντέλου του οποίου η αναλογία των διαστάσεων της ελαστικής μεμβράνης που εκτρέπεται ηλεκτροστατικά είναι μικρή (small aspect ratio model), διατηρούμε την εξάρτηση από το χρόνο και παρουσιάζουμε το βασικό απλοποιημένο μοντέλο της ηλεκτροστατικής κίνησης Στη συνέχεια παρουσιάζουμε προεκτάσεις του βασικού μοντέλου και τις απλοποιήσεις που προκύπτουν από την θεώρηση μηδαμινών επιρροών αδράνειας, εισάγοντας το μοντέλο που μελετάμε σε ένα κύκλωμα χωρητικού ελέγχου Δείχνουμε πως η πρόσθεση αυτού του κυκλώματος στο μοντέλο αλλάζει την κυρίαρχη εξίσωση η οποία γίνεται μη τοπική Αναλύουμε την κυρίαρχη εξίσωση (τοπικό πρόβλημα) και μελετάμε τις συνέπειες του συστήματος στο κύκλωμα ελέγχου Στο υπόλοιπο της εργασίας εξετάζουμε τη συμπεριφορά σταθερής κατάστασης του συστήματος και μετά αναλύουμε τις δυναμικές του συστήματος σε δύο περιπτώσεις: 9
10 όταν λ > λ και όταν λ λ (pull-i ad o pull-i), όπου το λ είναι μια παράμετρος του συστήματος ανάλογη με το ηλεκτροστατικό δυναμικό που ασκείται στις δύο πλάκες Δηλαδή για λ λ υπάρχει τουλάχιστον μια λύση στο πρόβλημα σταθερής κατάστασης, ενώ για λ > λ δεν υπάρχει λύση για το πρόβλημα σταθερής κατάστασης Στην περίπτωση αυτή το πρόβλημα παρουσιάζει μεγαλύτερο ενδιαφέρον από ότι στην περίπτωση όπου λ < λ Στη σταθερή κατάσταση οι ελαστικές απομακρύνσεις του συστήματος που φαίνεται στο σχήμα 5 ικανοποιούν μια παραβολική εξίσωση ( βλ(4)) η οποία προκύπτει από μια υπερβολική εξίσωση (βλ(3)) Ένα κεντρικό αποτέλεσμα αυτής της εργασίας είναι ότι όταν η εφαρμοσμένη τάση είναι πάνω από την κρίσιμη τάση όπου λύσεις σταθερής κατάστασης σταματούν να υπάρχουν, οι λύσεις εμφανίζουν σημείο επαφής σε πεπερασμένο χρόνο[],[],[3] Στην περίπτωση μας η ελαστική μεμβράνη έρχεται σε επαφή με το δίσκο Επίσης υπολογίζουμε τα όρια του χρόνου στον οποίο γίνεται η επαφή (touch dow) Τέλος στο κεφάλαιο 3 θα μελετήσουμε τις πεπερασμένες διαφορές και το σχήμα Crak-Nickolso τα οποία θα χρησιμοποιήσουμε για να λύσουμε με αριθμητικές μεθόδους διάφορες εξισώσεις που προέκυψαν από τη μελέτη μας
11 ΚΕΦΑΛΑΙΟ Σ αυτό το κεφάλαιο θα παρουσιάσουμε ένα απλό μηχανικό μοντέλο που παρά την απλότητα του υποδεικνύει αρκετά χαρακτηριστικά της λειτουργίας μιας συσκευής MEMS Παρουσίαση του μοντέλου Το εξιδανικευμένο μοντέλο που θα εξετάσουμε αποτελείται από δύο δίσκους τοποθετημένους παράλληλα Ο πάνω δίσκος στηρίζεται από ένα ελατήριο ενώ ο κάτω είναι σταθερός Το μοντέλο αυτό λειτουργεί όπως το σύστημα μάζας ελατηρίου άρα ικανοποιεί το ο Νόμο του Νεύτωνα Ισχύει: d u m dt ' = forces
12 Όπου το m είναι η μάζα του πάνω δίσκου Οι δυνάμεις που ασκούνται στο σύστημα μας είναι η δύναμη του ελατηρίου που συμβολίζεται με Fs, η δύναμη της απόσβεσης που συμβολίζεται με Fd και η ηλεκτροστατική δύναμη Fe Η δύναμη του ελατηρίου ικανοποιεί το νόμο του Hooke και ισχύει: Fs= k( u l) όπου l είναι το μήκος του ελατηρίου όταν βρίσκεται σε ισορροπία, το u είναι η μετατόπιση από την κορυφή του δίσκου και k είναι η σταθερά του ελατηρίου Η δύναμη της απόσβεσης δίνεται από τον τύπο: du Fd= a dt ' όπου α είναι ο συντελεστής απόσβεσης Υποθέτουμε ότι η απόσβεση είναι γραμμικά ανάλογη της ταχύτητας Η ηλεκτροστατική δύναμη υπολογίζεται στο τμήμα xx ' και δίνεται από την σχέση: ε AV Fe= ( L u) όπου L είναι η απόσταση ανάμεσα στους δύο δίσκους, A είναι το εμβαδό των επιφανειών των δίσκων και V είναι η τάση που εφαρμόζεται ανάμεσα στους δύο δίσκους,
13 Επιπλέον υποθέτουμε ότι η μεταβολή της τάσης σε σχέση με το χρόνο είναι αρμονική και έχει τη μορφή V cos( ω t ') Η εξίσωση (4) γίνεται, αν προσθέσουμε τη συνημιτοειδή εξάρτηση της τάσης στην περίπτωση που έχουμε εναλλασσόμενο ρεύμα : ε AV Fe= cos ( ω t ') (5) ( L u) Εισάγουμε τις εξισώσεις (),(3 )και (5) στην εξίσωση () και παίρνουμε ε AV m a k u l t dt ' dt ' ( L u) d u du + + ( ) = cos ( ω ') (6) Στη συνέχεια θα παρουσιάσουμε δυνατές κανονικοποιήσεις για το μοντέλο της εξίσωσης (6) για 3 περιπτώσεις όταν το μοντέλο κυριαρχείται από αδράνεια, εσωτερική τριβή ή εναλλασσόμενο ρεύμα Κανονικοποίηση σε συστήματα που κυριαρχούνται από αδράνεια Εάν το σύστημα μας κυριαρχείται από αδράνεια δηλαδή εάν περιμένουμε οι επιρροές της αδράνειας να είναι πιο σημαντικές από τις επιρροές της απόσβεσης τότε θα πρέπει να διαβαθμίσουμε το σύστημα μας με τη φυσική συχνότητα της ταλάντωσης του μοντέλου μάζας ελατηρίου Έστω u το διαστατικό μήκος και v το αδιάστατο μήκος Αφού l < u < L για το αδιάστατο μήκος v θέλουμε < v < Τότε κανονικοποιώντας το u έχουμε : l l < u l < L l ή ισοδύναμα < u l < L l επομένως u L < < L l Άρα : u l v = L l Συνεπώς προκύπτουν οι παρακάτω σχέσεις: u l = v( L l) u = v( L l) + l, άρα 3
14 du = dv( L l), και d u = d v( L l), Έστω ότι ο διαστατικός χρόνος είναι t και ο αδιάστατος χρόνος είναι t Επειδή έχουμε μοντέλο μάζας ελατηρίου, ο διαστατικός χρόνος θα σχετίζεται με τη συχνότητα της ταλάντωσης Άρα t k t m Ά m tά = t k Επομένως dt ' = m dt k και m dt ' = dt k Αντικαθιστώντας τις ποσότητες (7),(8),(9) και () στην εξίσωση (6) έχουμε d v( L l) dv( L l) ε AV m m + a + k( v( L l) + l l) = cos ( ω t) m dt m [ L ( v( L l) + l) ] k, dt k k Επομένως d v( L l) k dv( L l) ε AV m + a + k[ v( L l)] = cos ( ω t) dt m [ L ( v( L l) l) ] k, + dt k διαιρούμε κάθε όρο της παραπάνω εξίσωσης με ( L l) k και παίρνουμε: d v dv ε AV m + a + v = cos ( ω t) dt dt mk ( L l) ( v) ( L l) k k α ε AV Θέτουμε â = m, λ = 3 και Ω = ω και η εξίσωση μας γίνεται: mk k( L l) k d v dv λ + aˆ + v = cos ( Ω t) dt dt ( v) Το λ γράφεται: ε AV λ = k( L l) ( L l) δηλαδή λ = η λ ε κ τ ρ ο σ τ α τ ι κ η& δ υ& ν α µ η α ν α φ ο ρ α& ς δ υ& ν α µ η α ν α φ ο ρ α& ς ε λ α τ η ρ & ι ο υ Το λ είναι μια παράμετρος που εκφράζει το λόγο της ηλεκτροστατικής δύναμης προς τη δύναμη επαναφοράς 4
15 3 Κανονικοποίηση σε συστήματα στα οποία κυριαρχεί η εσωτερική τριβή Εάν το σύστημα μας κυριαρχείται από εσωτερική τριβή δηλαδή εάν περιμένουμε οι επιρροές της απόσβεσης να είναι πιο σημαντικές από τις επιρροές της αδράνειας τότε θα πρέπει να διαβαθμίσουμε το σύστημα μας λαμβάνοντας υπόψη την απόσβεση του συστήματος Η αδιάστατη ποσότητα που θα χρησιμοποιήσουμε στην περίπτωση αυτή για το χρόνο θα πρέπει να είναι ανάλογη της σταθεράς του ελατηρίου k και αντιστρόφως k a ανάλογη με την απόσβεση άρα : t = t ' από την οποία προκύπτει t ' = t άρα a k a a dt ' = dt και dt ' = dt, η άλλη αδιάστατη μεταβλητή για την απόσταση είναι k k u l όπως προηγουμένως v = u = v( L l) + l άρα du = dv( L l) και L l d u = d v( L l) Αντικαθιστούμε αυτά στην εξίσωση (6) και έχουμε: d u du ε AV m + a + k( u l) = cos ( ω t ') dt ' dt ' ( L u) ε AV m + a + k v( L l) + l l = cos ( t ) d v( L l) dv( L l) a [ ] ω a a dt [ L ( v( L l) l) ] k dt + k k d v( L l) k dv( L l) k ε AV a m + a + k [ v( L l) ] = cos ( ω t ) a dt dta L ( v( L l) + l) k [ ] Διαιρούμε κάθε όρο της παραπάνω εξίσωσης με ( L l) k και παίρνουμε: d v dv ε AV a m k + + v = cos ( ω t ) a dt dt ( L l) ( u) ( L l) k k α dt dt ( v) όπου α = a ε AV, λ = mk k( L l) d v dv λ + + v = cos ( Ω t) 3 a και Ω = ω k 4 Κανονικοποίηση σε σύστημα στο οποίο εφαρμόζεται εναλλασσόμενο ρεύμα 5
16 Εάν στο σύστημα μας εφαρμόζεται εναλλασσόμενο ρεύμα τότε θα πρέπει να κανονικοποιήσουμε το σύστημα μας λαμβάνοντας υπόψη τη συχνότητα του ρεύματος Στην περίπτωση αυτή ο αδιάστατος χρόνος που παίρνουμε είναι: t = ω t ' t ' = t και ω μας δίνει: dt ' = dt και dt ' = dt Η αδιάστατη απόσταση είναι ίδια όπως τα προηγούμενα ω ω v = ( u l) ( L l) u = v( L l) + l άρα du = dv( L l) και d u = d v( L l) Εισάγοντας αυτές τις σχέσεις στην εξίσωση (6) παίρνουμε: d u du ε AV m + a + k ( u l ) = cos ( ω t ) dt dt L u ( ) ( ) ( ) d v L l dv L l ε AV m + a + k v ( L l ) l l cos t + = ω dt dt L ( v ( L l ) + l ) ω ω ω Διαιρούμε κάθε όρο της παραπάνω εξίσωσης με L l και παίρνουμε: d v dv ε AV mω + aω + kv = cos ( t ) dt dt ( L l ) ( v ) ( L l ) Διαιρούμε κάθε όρο της παραπάνω εξίσωσης με k και παίρνουμε: d v mω dv aω ε AV + + v = cos ( t ) dt k dt k ( L l ) ( v) ( L l ) k ω m a ε AV θέτουμε β =, γ = ω, και λ = 3 και η εξίσωση μας γίνεται: k k ( L l) k d v dv λ β + γ + v = cos ( t ) dt dt v ( ) Θα δούμε ότι οι εξισώσεις που παράχθηκαν μέχρι τώρα έχουν αρκετά κοινά χαρακτηριστικά με ένα πιο ακριβές μοντέλο για μια συσκευή MEMS (βλ Κεφάλαιο ) Παρατήρηση Υπάρχουν κάποιες συσκευές MEMS που έχουν τη δομή που φαίνεται στο σχήμα Ένας τρόπος για να δούμε τη μελέτη αυτού του μοντέλου είναι η θεώρηση μερικών βασικών χαρακτηριστικών τέτοιων συσκευών Στην πραγματικότητα θα προσπαθήσουμε να συσχετίσουμε τις παραμέτρους στο μοντέλο μάζας-ελατηρίου με κατάλληλες παραμέτρους για μια πραγματική συσκευή Το ελατήριο στο σχήμα αντικαθίσταται 6
17 από μία ελαστική δοκό ή μεμβράνη Σ αυτή την περίπτωση μπορούμε να γράψουμε το νόμο του Hooke s σε μια διάσταση για μια δοκό σαν: u σ = Ε x όπου εδώ Ε είναι το μέτρο Youg s, σ είναι η τάση της δοκού, u είναι η επιμήκυνση στην αξονική κατεύθυνση και x είναι η συντεταγμένη που μετράει την απόσταση κατά μήκος του άξονα της δοκού Με αυτό τον τρόπο βλέπουμε ότι το k μπορεί να αντικατασταθεί από το μέτρο Youg s E Το μέτρο του Youg s είναι γνωστό και εύκολο στον προσδιορισμό του για πολλά υλικά που χρησιμοποιούνται στην κατασκευή των MEMS Πρέπει να σημειωθεί ότι μια απλή αντικατάσταση του E από το k δεν είναι αρκετή Το μέτρο του Youg πρέπει να πολλαπλασιαστεί με ένα κατάλληλο παράγοντα για να ερμηνεύσει τη γεωμετρία του προβλήματος Στη συνέχεια θα θεωρήσουμε την εξίσωση που κυριαρχείται από την τριβή () για a > > και θα μελετήσουμε τις στάσιμες λύσεις του συστήματος ως προς την ευστάθεια τους 5 Λύσεις σταθερής κατάστασης Πολλές συσκευές MEMS λειτουργούν με συνεχές ρεύμα Στην περίπτωση αυτή τοποθετείται ένας διακόπτης στη συσκευή και εφαρμόζεται κάποια τάση Έτσι η συσκευή μας μετά από κάποιο χρόνο διαμορφώνεται σε μια στάσιμη κατάσταση Για να γίνουν αυτά πιο κατανοητά βάζουμε τη συχνότητα του εναλλασσόμενου ρεύματος ω να ισούται με μηδέν στην εξίσωση που ισχύει για το εναλλασσόμενο ρεύμα (6) Στη συνέχεια βάζουμε όλες τις χρονικές παραγώγους να είναι ίσες με μηδέν Άρα η εξίσωση μας γίνεται: ε AV k( u l) = ( L u) Σε αδιάστατη μορφή ανεξάρτητα από το χρόνο αναφοράς η εξίσωση μας γίνεται u l παίρνοντας ως αδιάστατη ποσότητα : v =, L l ε AV k [ v( L l) + l l ] =, L ( v( L l) + l) από την οποία παίρνουμε: v = ε [ ] [ ] AV L vl + vl + l k( L l), 7
18 η οποία ισοδύναμα γράφεται: ε AV v = ( L l) ( v) ( L l) k Θέτουμε λ = ε AV ( ) 3 L l k λ και παίρνουμε: v = ( v) Ορίζουμε f ( v) = λ v ( v) Από την εξίσωση (6) παίρνουμε τις λύσεις σταθερής κατάστασης Στο παρακάτω σχήμα σχεδιάζουμε τις ρίζες f ( v ) για διάφορες τιμές του λ ΣΧΗΜΑ 3 Από το σχήμα παρατηρούμε ότι η f παρουσιάζει ιδιομορφία στο v = Αυτό είναι αναμενόμενο καθώς το v = αντιστοιχεί στην περίπτωση όπου ο πάνω δίσκος συγκρούεται με τον κάτω δίσκο και τότε η ηλεκτροστατική δύναμη γίνεται άπειρη Στην περίπτωση όπου το v > σημαίνει ότι ο πάνω δίσκος έχει περάσει μέσα από το κάτω δίσκο το οποίο είναι αδύνατο να συμβεί και για το λόγο αυτό όποιες ρίζες του f είναι μεγαλύτερες του είναι μη φυσικές και χωρίς ενδιαφέρον Η τρίτη περίπτωση είναι όταν το v <, που αντιστοιχεί στην κίνηση του πάνω δίσκου μέχρι τον κάτω δίσκο χωρίς να τον ακουμπήσει Οι ρίζες του f που είναι μικρότερες του αντιστοιχούν σε λύσεις αποδεκτές με τη φυσική του προβλήματος Στο σχήμα μας βλέπουμε ότι η f είτε έχει ρίζες είτε είτε καμία Η αλλαγή συμβαίνει με τη μεταβολή του λ Όταν το λ είναι μικρό έχουμε ρίζες Αυτό συμβαίνει επειδή η ηλεκτροστατική δύναμη είναι αρκετά μικρή 8
19 έτσι ώστε να εξισορροπείται από τη γραμμικότητα της δύναμης του ελατηρίου δημιουργώντας μια σταθερή κατάσταση Όταν το λ αυξηθεί η ηλεκτροστατική δύναμη αυξάνεται και τότε υπερβαίνει τη γραμμικότητα της δύναμης του ελατηρίου με αποτέλεσμα όλες οι σταθερές καταστάσεις να εξαφανίζονται Αυτό ονομάζεται αρχή της ελκτικής τάσης αστάθειας Η εξαφάνιση των φυσικών λύσεων σημαίνει ότι ο πάνω δίσκος θα πρέπει να έχει καταρρεύσει ή να έχει τραβηχτεί μέσα στον κάτω δίσκο Λύνοντας την εξίσωση (6) ως προς λ παίρνουμε: λ = v( v) Το λ είναι συνάρτηση του v ορισμένη από την εξίσωση (7) και σχεδιάζουμε το λ ( v) ΣΧΗΜΑ4 Αν αναστρέψουμε τους άξονες και βάλουμε το v στη θέση του λ και το λ στη θέση του v παίρνουμε το παρακάτω σχήμα το οποίο ονομάζεται διάγραμμα διακλάδωσης για το μοντέλο μας 9
20 ΣΧΗΜΑ 5 Στον άξονα του λ διαλέγουμε την τιμή εκείνη που αντιστοιχεί στο πείραμα μας και μετά βρίσκουμε την τιμή του v για το λ που έχουμε διαλέξει και στη συνέχεια διαβάζουμε τις λύσεις σταθερής κατάστασης Από τη μελέτη αυτή παρατηρούμε ότι όταν το λ περάσει την τιμή λ (σχήμα 5) δεν υπάρχουν πια φυσικές λύσεις Γι αυτό το λόγο το λ είναι η κρίσιμη τιμή της τάσης Το λ υπολογίζεται με ακρίβεια Υπολογίζουμε την τετμημένη και το ύψος του πρώτου μέγιστου σημείου στο σχήμα 4 και βρίσκουμε 4 την τιμή του λ Έτσι σε αυτή την περίπτωση το λ = [3] Επίσης υπολογίζουμε και 7 την απόσταση στην οποία η συσκευή μας έχει απόκλιση ίση με vp όπου v p η απόκλιση που αντιστοιχεί στην τιμή λ Βρίσκουμε ότι το v p = [3] Το v p είναι η μέγιστη 3 απόκλιση και γι αυτό ονομάζεται αδιάστατη μέγιστη απόσταση Μπορούμε να υπολογίσουμε την αντίστοιχη ελκτική τάση V p χρησιμοποιώντας τον ορισμό του λ Από την σχέση: ε AV λ = p 3 k( L l) κάνουμε επίλυση τύπου ως προς V p και παίρνουμε : όπου λ = λ αν 4 λ = άρα 7 V λ k( L l) = ε AV ή V p p = 3 p 3 λ k( L l), ε A 3 8 k( L l) = 7 ε A
21 Μπορούμε χρησιμοποιώντας την κλίμακα μας για το v να υπολογίσουμε τη διαστατική τιμή της ελκτικής απόστασης u p : u p l vp = ή L l u = v ( L l) + l ή p p u p = ( L l ) 3 Άρα u p = της απόστασης των δύο πλακών όταν δεν εφαρμόζεται διαφορά δυναμικού 3 στο σύστημα 6 Ευστάθεια των σταθερών καταστάσεων Μελετώντας το σύστημα μας παρατηρούμε ότι υπάρχουν περισσότερες από μια στάσιμες καταστάσεις με φυσική σημασία και χρειάζεται να γνωρίζουμε την ευστάθεια των καταστάσεων αυτών Θα προσδιορίσουμε τη σταθερότητα του μοντέλου μας στην περίπτωση που κυριαρχεί η εσωτερική τριβή και με την απλουστευμένη υπόθεση ότι το a > > Σ αυτή την περίπτωση αγνοούμε τον αδρανιακό όρο στην εξίσωση () και εργαζόμαστε με το απλουστευμένο σύστημα πρώτης τάξης όπου θέτουμε ω = d v dv λ + + v = cos( Ω t) a dt dt ( v) ή για a < < παίρνουμε: dv λ + v = dt ( v) Αυτή η εξίσωση γράφεται : dv v dt = λ ( v) Το δεξί μέλος της (9) είναι το f ( v ) που ορίσαμε πιο πάνω άρα μπορούμε να ξαναγράψουμε την εξίσωση (9) έτσι: dv f ( v) dt = Η ευστάθεια μπορεί να προσδιοριστεί εξετάζοντας το σχήμα 3 Μελετώντας το παρατηρούμε ότι όταν το λ > λ τότε δεν υπάρχει καμία ρίζα του f μικρότερη του και το f ( v ) είναι πάντα θετικό Ξεκινώντας από οποιοδήποτε φυσικό σημείο για το v, η απόσταση του πάνω δίσκου συνέχεια θα αυξάνεται μέχρι τη στιγμή που θα συγκρουστεί με τον κάτω δίσκο όταν το v = Όταν το λ < λ τότε από το σχήμα 3 παίρνουμε ότι υπάρχουν ρίζες για το f Αν πάρουμε τη μικρότερη από αυτές τις ρίζες
22 παρατηρούμε ότι αριστερά της το f ( v ) > ενώ προς τα δεξιά, με την προϋπόθεση ότι είμαστε σε τιμή μικρότερη από τη δεύτερη ρίζα, το f ( v ) < Στο διάγραμμα διακλάδωσης (σχήμα 5) ο μικρότερος κλάδος των λύσεων, δηλαδή πριν την πρώτη πτυχή είναι ένας σταθερός κλάδος λύσεων Εξετάζοντας τη μεγαλύτερη από τις ρίζες είναι εύκολο να δούμε ότι είναι ασταθής, γιατί το δεξί μέλος της εξίσωσης () είναι είτε αρνητικό είτε θετικό ξεκινώντας προς τα αριστερά ή προς τα δεξιά Στο διάγραμμα διακλάδωσης αυτές οι λύσεις αντιστοιχούν στο δεύτερο κλάδο και άρα ο κλάδος αυτός είναι κλάδος με ασταθής λύσεις Την ανώτατη διακλάδωση για ( v > ) δε τη μελετάμε γιατί δεν έχει φυσική σημασία Για την εξίσωση () που είναι πρώτης τάξης έχουμε προσδιορίσει τη γενική δυναμική των λύσεων Αν πάρουμε μια αρχική τιμή για το λ και κοιτάξουμε την κίνηση πάνω στο διάγραμμα διακλάδωσης παρατηρούμε ότι για λ < λ οι λύσεις προσεγγίζουν μονότονα το χαμηλότερο ευσταθή κλάδο, με την προϋπόθεση ότι αυτές ξεκινούν από σημείο χαμηλότερο του μεσαίο κλάδου Στην περίπτωση όπου λ > λ η συσκευή μας επίσης έλκεται μονότονα Στη συνέχεια θα μελετήσουμε την ευστάθεια των λύσεων για το πλήρες μοντέλο δεύτερης τάξης δηλαδή για την εξίσωση () Στην περίπτωση αυτή τα αποτελέσματα της ευστάθειας δε παράγονται τόσο εύκολα όσο στην περίπτωση για την εξίσωση πρώτης τάξης Εδώ βασιζόμαστε σε ένα τοπικό αποτέλεσμα στη θεωρία της γραμμικής ευστάθειας η οποία μας λέει πως οι λύσεις σταθερής κατάστασης ανταποκρίνονται σε μικρές διαταραχές Η προσέγγιση που θα ακολουθήσουμε μοιάζει με την προσέγγιση που ακολουθούμε για να προσδιορίσουμε την ευστάθεια των λύσεων σταθερής κατάστασης σε μοντέλα που βασίζονται σε Μερικές Διαφορικές Εξισώσεις Εργαζόμαστε με την εξίσωση () Δηλώνουμε οποιαδήποτε ρίζα του f ( v ) με v και αναζητούμε μια λύση στην εξίσωση () της μορφής: t v( t) = v + ε e µ όπου ε < < και το µ μια θετική παράμετρος υπό προσδιορισμό Παρατηρούμε ότι αν µ > έχουμε γραμμική ευστάθεια και αν µ < έχουμε γραμμική αστάθεια Πράγματι εισάγοντας την () στη () μας δίνει: µ µ t µ t µ t ε e ε µ e = f ( v + ε e ) α Επεκτείνουμε την f σε μια σειρά Taylor γύρω από το ε = : µ t µ t µ t e f ( v + ε e ) = f ( v ) + ε e f '( v ) + ε f ''( v ) + Αγνοώντας τους όρους της τάξης ε η (3) μας δίνει: µ µ = f '( v ) α Λύνοντας αυτή τη δευτεροβάθμια εξίσωση υπολογίζουμε τις ρίζες: + 4 f '( v ) ± b ± b 4ac α α α + 4 f '( v ) µ, = = = ± a α α Από τις δύο αυτές ρίζες συμπεραίνουμε ότι το µ > f '( v ) <
23 Αυτό σημαίνει ότι η ευστάθεια των λύσεων σε αυτή την περίπτωση συνεπάγεται από το σχήμα 3 Η συνάρτηση f συναντά την μικρότερη ρίζα με αρνητική κλίση ( f Ά ( v ) < ) και άρα αυτή η λύση είναι ευσταθής Για την άλλη ρίζα με φυσική σημασία η κλίση είναι θετική και άρα είναι ασταθής λύση ΚΕΦΑΛΑΙΟ Στο κεφάλαιο αυτό θα παρουσιάσουμε τη γενική μορφή του μοντέλου το οποίο αποτελείται από ένα σταθερό δίσκο και μια ελαστική μεμβράνη που αιωρείται πάνω από το δίσκο Εφαρμόζουμε κάποια τάση ανάμεσα στη μεμβράνη και το δίσκο και τότε η μεμβράνη αρχίζει να λυγίζει προσεγγίζοντας προς το δίσκο Για να γίνει πιο κατανοητή η περιγραφή του μοντέλου μας και για να εξηγήσουμε καλύτερα τη συμπεριφορά του συστήματος λόγω της διαφοράς δυναμικού που δημιουργείται ανάμεσα στη μεμβράνη και το δίσκο θα χρησιμοποιήσουμε την εξίσωση της παλλόμενης χορδής Για την εξίσωση της παλλόμενης χορδής χρήσιμο είναι να παρουσιάσουμε την παραγωγή της Παραγωγή της κυματικής εξίσωσης 3
24 Στην παράγραφο αυτή θα δώσουμε μια πιο αναλυτική και πλήρη παραγωγή του μοντέλου με την παράγωγή της κυματικής εξίσωσης Θεωρούμε μια τέλεια εύκαμπτη χορδή μήκους α η οποία σε κατάσταση ισορροπίας είναι προεντεταμένη με σταθερά άκρα Επιλέγουμε καρτεσιανό σύστημα συντεταγμένων έτσι, ώστε τα δύο άκρα της χορδής να είναι στα σημεία (,,) και (α,,) Μπορούμε να χρησιμοποιήσουμε μία παράμετρο s, s a προκειμένου να παραμετρικοποιήσουμε μια καμπύλη με άκρα (,,) και (α,,) που αναπαριστά τη χορδή Σχηματική αναπαράσταση της χορδής Η κίνηση του σημείου s της χορδής, στον τρισδιάστατο χώρο κατά τη χρονική στιγμή t μπορεί να περιγραφεί από τη διανυσματική συνάρτηση r( s, t) = ( X ( s, t), Y ( s, t), Z( s, t)) r Το διάνυσμα αναπαριστά την ταχύτητα του σημείου s τη χρονική στιγμή t και t r εφάπτεται της χορδής στο σημείο s, ενώ το διάνυσμα μας δίνει την επιτάχυνση της t χορδής στο σημείο s Παραμόρφωση χορδής Εφαρμόζουμε τον δεύτερο νόμο του Newto σύμφωνα με τον οποίο η δύναμη σε κάθε τμήμα της χορδής ισούται με τη χρονική παράγωγο της ροπής αυτού του τμήματος Η μάζα της χορδής του τμήματος [α,β] δίνεται από τη συνάρτηση της πυκνότητας της μάζας ρ ( s), α < s < β Άρα έχουμε β ς α β ς α ρ ( s) ds = μάζα του τμήματος [α,β] της χορδής r( s, t) ρ ( s) ds = ροπή του τμήματος [α,β] της χορδής t Το τμήμα [α,β] της χορδής υφίσταται στα άκρα α και β τις δυνάμεις από το υπόλοιπο της χορδής (τάσεις) και τις εξωτερικές δυνάμεις από το περιβάλλον, όπως η βαρύτητα Οι 4
25 εξωτερικές δυνάμεις γραφόμενες ως μια διανυσματική συνάρτηση F( s, t) = ( F ( s, t), F ( s, t), F3 ( s, t)) παριστάνουν τη δύναμη ανά μονάδα μάζας στο σημείο s της χορδής Για να περιγράψουμε τις δυνάμεις επαφής, εισάγουμε την τάση Τ(s,t) Το τμήμα[β,a] ασκεί μια δύναμη επαφής επί του τμήματος [α,β] της χορδής στο σημείο s=β η οποία δίνεται από την πρόταση r ( β, t) + T ( β, t) s r ( β, t) s Η χορδή είναι τέλεια εύκαμπτη άρα η δύναμη επαφής έχει διεύθυνση κατά μήκος της εφαπτόμενης της χορδής στο σημείο s=β Κατ ανάλογο τρόπο έχουμε μία δύναμη που ασκείται από το [,α] στο τμήμα [α,β] της χορδής και στο σημείο s=α η οποία δίνεται από την παράσταση r ( a, t ) T ( a, t) s r ( a, t ) s Από το δεύτερο νόμο του Newto έχουμε r r β β ( β, t) ( a, t) r( s, t) + ρ ( s) ds ρ ( s) F( s, t) ds T ( β, t) s T ( a, t) s ς = + t ς r r α a ( β, t) ( a, t) s s Δυνάμεις επαφής Στο σημείο s=α η δύναμη είναι r ( β, t) + f ( b) = T ( β, t) s r ( β, t) s f ( a) = T ( a, t) r ( a, t ) s r ( a, t ) s και στο σημείο s=b, 5
26 + Εάν στην () πάρουμε το όριο β α προκύπτει ότι Τ ( α, t) = Τ ( α, t), έτσι + παραλείποντας το πρόσημο γράφουμε Τ ( α, t) = Τ ( α, t) = T ( s, t) Εάν παραγωγίσουμε ως προς β την () και θέσουμε β=s παίρνουμε την εξίσωση της παλλόμενης χορδής μ r ό ( s, t ) r( s, t) ο ( s) ( s) F( s, t) T ( s, t) s ο ρ = ρ + ν ύ t s ο r ( s, t) ο οξ s οώ Με s Ξ (, a) και t > Η διανυσματική διαφορική εξίσωση () ισοδυναμεί με τρεις βαθμωτές διαφορικές εξισώσεις ως προς τους άγνωστους X, Y, Z, T Για κάθε ελαστικό υλικό υπάρχει μια καλά ορισμένη συνάρτηση N που εκφράζει τη σχέση της τάσης T(s,t) και του παράγοντα r( s, t) η οποία γράφεται t ζ r( s, t) φ T ( s, t) = N η, s t χ θ ψ Η εξίσωση () είναι δύσκολο να λυθεί και έτσι καταφεύγουμε στη μελέτη μιας πρώτης προσέγγισης της, δηλαδή της γραμμικοποίησης της Αποδεικνύεται ότι οι λύσεις αυτής της γραμμικοποιημένης εξίσωσης δίνουν ικανοποιητικές απαντήσεις ειδικά σε φαινόμενα που αφορούν μικρές ταλαντώσεις Για να βρούμε τη πρώτη προσέγγιση του προβλήματος χρησιμοποιούμε τον ακόλουθο μετασχηματισμό X ( s, t) = s + ε x( s, t), Y ( s, t) = ε y( s, t), Z( s, t) = ε z( s, t), T ( s, t) = T + ε T ` ( s, t), F( s, t) = ε f ( s, t), όπου η παράμετρος ε έχει την ίδια τάξη μεγέθους με τη μέγιστη μετατόπιση της χορδής από τη θέση ουδέτερης ισορροπίας X=s, U=s, Z= Από τις εξισώσεις (3) και (4) έχουμε X x ( s, t) = + ε ( s, t), s s Y y ( s, t) = ε ( s, t), s s Z z ( s, t) = ε ( s, t), s s έτσι προκύπτει r ζ ( s, t) ε x φ ζ ( s, t) ε y φ ζ ( s, t) ε z φ = η + χ + η χ + η ( s, t) χ s θ s ψ θ s ψ θ s ψ Χρησιμοποιώντας το ανάπτυγμα Taylor έχουμε Άρα ισχύει r s x ( s, t) = + ε ( s, t) + O( ε ) s 6
27 r ( s, t ) s ζ y z φ = + O( ε ), ε ( s, t) + O( ε ), ε ( s, t) + O( ε ) r η χ s s ( s, t) θ ψ s Εισάγοντας την (5) στην () και χρησιμοποιώντας τους μετασχηματισμούς (3) και (4) παίρνουμε τις ακόλουθες γραμμικοποιημένες εξισώσεις για τις εγκάρσιες και διαμήκεις ταλαντώσεις, x( s, t) ρ ( s) = ρ ( s) f ( s, t) + T ( s, t), s Ξ (, α ), t > t s (, ) ( ) y s t y ρ s = ρ ( s) f ( s, t) + T ( s, t), s Ξ (, α ), t > t s (, ) ( ) z s t z ρ s = ρ ( s) f ( s, t) + T ( s, t), s Ξ (, α ), t > 3 t s Οι εξισώσεις που μας ενδιαφέρουν συνήθως είναι αυτές που περιγράφουν τις εγκάρσιες ταλαντώσεις δηλαδή η (7) και (8) Αυτές οι εξισώσεις είναι του ίδιου τύπου δηλαδή της λεγόμενης μονοδιάστατης κυματικής εξίσωσης U T U ( x, t) = ( x, t) + f ( x, t), x Ξ (, a), t > t ρ ( x) x Αν η μεμβράνη δεν είναι τέλεια ελαστική όπως στην περίπτωση μας τότε προστίθεται U στην εξίσωση (9) η δύναμη της τριβής a Προσθέτοντας τον όρο που εκφράζει t U την εσωτερική τριβή '' a " και θεωρώντας ότι η εξωτερική δύναμη είναι, t ε Φ f ( x, t) = ( ), δηλαδή η δύναμη που ασκείται στη μεμβράνη λόγω της διαφοράς z δυναμικού που εφαρμόζεται στη συσκευή, η εξίσωση (9) ξαναγράφεται: U U T U ε Φ + a = + ( ) () t t ρ ( x) x z ε Ο όρος εξαναγκασμού Φ ( ) προκύπτει από τη θεώρηση του συστήματος μέσα σε z ένα ηλεκτροστατικό πεδίο Η μελέτη και η παραγωγή του όρου εξαναγκασμού θα γίνει στην παράγραφο και προς το παρόν θεωρώντας το σα δεδομένο θα κανονικοποιήσουμε την εξίσωση Έστω t ο διαστατικός χρόνος και τ ο αδιάστατος χρόνος, U η διαστατική απόσταση και u η αδιάστατη απόσταση, x το διαστατικό μήκος και y το αδιάστατο μήκος, φ είναι το διαστατικό δυναμικό και ψ το αδιάστατο δυναμικό, z ' διαστατικό πλάτος και z το αδιάστατο πλάτος Τότε οι αδιάστατες μεταβλητές που παίρνω είναι: t x U τ = όπου t t ο χρόνος αναφοράς, x =, u = και ψ = φ Vs οι οποίες ισοδύναμα L l γράφονται: t = τ t, x = xl, U = ul καιφ = ψ Vs () 7
28 Εισάγω τις σχέσεις () στην εξίσωση () και παίρνουμε: ρ l u al u Tl u ε ψ V + = + s () t t t t L x z l u Επειδή θέλουμε ο συντελεστής του να είναι πολλαπλασιάζουμε κάθε όρο της t t () με al ρ l t u al t u Tl t u ε t + = + V ( ) s f u t al t t al t L al x l al (3) ζ ψ φ Θέτουμε f ( u) = η χ θ z ψ Η (3) γράφεται ισοδύναμα: ρ l u u Tt u ε Vs t + = + f ( u) 3 t a t t L a x al (4) u al Για να είναι ο συντελεστής του πρέπει t = και η εξίσωση (4) x T ξαναγράφεται: ρ T u u u ε Vs L + = + f ( u) 3 a L t t x Tl (5) ρ T ε L V Θέτουμε ε = και λ = s και η εξίσωση (5) παίρνει τη μορφή: 3 a L Tl u u u ε + = + λ f ( u) t t x (6) Στη συνέχεια αντί του συμβόλου x χρησιμοποιούμε το σύμβολο x,εννοώντας την αντίστοιχη κανονικοποιημένη μεταβλητή, όπου δε δημιουργείται σύγχυση Διατύπωση του μοντέλου σε ηλεκτροστατικό πεδίο Σ αυτή την ενότητα θα παρουσιάσουμε τις κυρίαρχες εξισώσεις για τη συμπεριφορά μιας συσκευής MEMS που κινείται σε ηλεκτροστατικό πεδίο Θα ξεκινήσουμε με τις εξισώσεις οι οποίες ελέγχουν το ηλεκτροστατικό πεδίο, δηλαδή τις ηλεκτροστατικές δυνάμεις στις συνιστώσες της συσκευής Για να γίνει ο προσδιορισμός της ηλεκτροστατικής δυναμικής για το μοντέλο μας είναι απαραίτητο να καθορίσουμε το ηλεκτροστατικό δυναμικό της συσκευής Η συσκευή μας αποτελείται από μια ελαστική 8
29 μεμβράνη που αιωρείται πάνω από ένα σταθερό δίσκο Η μεμβράνη όπως και ο δίσκος έχουν πλάτος w, μήκος L και η μεταξύ τους απόσταση είναι l Η συσκευή μας παρουσιάζεται στο (σχήμα 6) ΣΧΗΜΑ 6 Ανάμεσα στη μεμβράνη και το δίσκο εφαρμόζεται μια διαφορά δυναμικού Με όλα αυτά δημιουργούμε τις εξισώσεις που ικανοποιούν το ηλεκτροστατικό δυναμικό στην περιοχή γύρω από τη συσκευή και την ελαστική μετατόπιση της μεμβράνης Το ηλεκτροστατικό δυναμικό φ, ικανοποιεί την εξίσωση Laplace : φ φ φ φ = ισοδύναμα + + = x y z (7) Επίσης ικανοποιούνται οι ακόλουθες συνθήκες: ( x ', y ', l) x L, L y L, L, φ =, [ ], [ ] φ x y u = Vs f u l, x [ L, L ] [, ] (8) ( ', ', ') ( ' ) y L L (9), Το u '( x ') είναι η μετατόπιση από z ' = της μεμβράνης και V s είναι η αρχική τάση Η συνάρτηση f είναι μια αδιάστατη συνάρτηση και συμπεριλαμβάνει το γεγονός ότι η διαφορά δυναμικού στην περίπτωση που η συσκευή μας ενσωματώνεται σε ένα κύκλωμα μπορεί να εξαρτάται από το u ' Υποθέτουμε ότι το u ' είναι συνάρτηση του x ' Η μετατόπιση θεωρώντας μια χωρική διάσταση για απλότητα ικανοποιεί τη σχέση: d u ε T = φ dx ' () όπου το T είναι η ένταση του ηλεκτρικού δυναμικού και ε είναι διηλεκτρική σταθερά Υποθέτουμε ότι η μεμβράνη κρατιέται σταθερή στις άκρες στο x = ± L το οποίο μας δίνει τη συνοριακή συνθήκη: u '( L ) = u '( L ) = () Η υπόθεση που κάναμε ότι το u ' είναι συνάρτηση του x ' συνεπάγεται ότι τα εναπομένοντα άκρα είναι ελεύθερα Στη συνέχεια γράφουμε το πρόβλημα μας σε αδιάστατη μορφή Έστω ότι φ είναι το διαστατικό δυναμικό, u ' είναι η διαστατική 9
30 μετατόπιση της μεμβράνης, x ' είναι το διαστατικό μήκος, y ' είναι το διαστατικό πλάτος και z ' είναι το διαστατικό ύψος Αν συμβολίσουμε με ψ το αδιάστατο δυναμικό επειδή < φ < Vs και < ψ < παίρνουμε ψ = φ Vs Αν συμβολίσουμε με u την αδιάστατη απόσταση επειδή < u ' < l και < u < παίρνουμε u = u ' l Με τον ίδιο τρόπο αν συμβολίσουμε με x, y, z το αδιάστατο μήκος, πλάτος και ύψος αντίστοιχα και επειδή < x ' < l και < x <, < y ' < L, < y <, < z ' < l, < z < παίρνουμε x = x ' L, y = y ' w, z = z ' l Από αυτές τις αδιάστατες μεταβλητές παίρνουμε την παρακάτω σχέση : ψ = φ V s, u = u ' l, x = x ' L, y = y ' ω, z = z ' l () από την οποία παίρνουμε την παρακάτω σχέση : φ = ψ V s, u ' = ul, x ' = xl, y ' = yw, z ' = zl (3) άρα φ = ψ V s, u = ul, x ' = x L, y ' = y w, z ' = z l (4) Αντικαθιστώντας τις σχέσεις (),(3),(4) στις εξισώσεις (7)-() προκύπτει η εξίσωση μας και οι αρχικές συνθήκες σε αδιάστατη μορφή: φ φ φ + + = x y z ή ψ V ψ V ψ V x L x w z l s s s + + = πολλαπλασιάζουμε κάθε όρο της παραπάνω σχέσης με η οποία γράφεται: ψ V l ψ V l ψ V l, l V s s s + + = x L Vs x w Vs z l Vs ψ l ψ l ψ x L x w z + + = s και προκύπτει:, l L Επειδή θέλουμε να εμφανίσουμε τα αδιάστατα μεγέθη δ = και α = L w πολλαπλασιάζουμε το δεύτερο όρο της παραπάνω σχέσης με L και διαιρούμε με L και παίρνουμε: ψ l ψ l L ψ + + = x L x w L z Η οποία χρησιμοποιώντας τις σχέσεις l L δ = και α = γίνεται: L w 3
31 ψ ψ ψ x dy z δ + δ α + = (5) Οι συνοριακές συνθήκες παίρνουν τη μορφή: ( x, y, ), ή δ ψ =, x [ ], y [, ], ψ ( x, y, ) = f ( u), x [, ], [, ] ζ ψ ψ φ ψ θ x y ψ z η + α + = χ y Ενώ για το u η συνοριακή συνθήκη γίνεται: u( ) = u( ) = Στην εξίσωση () : d u ' ε T = Φ ή dx ' d u ' ε Φ Φ Φ = dx + + ' x y z Εισάγουμε τις αδιάστατες ποσότητες που είδαμε πιο πάνω και παίρνουμε: d ul ε ψ Vs ψ Vs ψ Vs T = dx L + + xl yw zl πολλαπλασιάζουμε κάθε όρο της πιο πάνω σχέσης με L και διαιρούμε με Tl d u ε L ι ζ ψ φ Vs ζ ψ φ V s ζ ψ φ V ω s = κ η χ + η χ + η χ ϊ dx Tl κλ θ x ψ L θ y ψ w θ z ψ l ϊϋ Διαιρούμε και πολλαπλασιάζουμε κάθε όρο της παραπάνω εξίσωσης με l και παίρνουμε: d u ε L V ι s ζ ψ φ l ζ ψ φ l ζ ψ φ l ω = κ 3 η χ + η χ + η χ ϊ dx Tl κλ θ x ψ L θ y ψ w θ z ψ l ϊϋ Θέτουμε όπου l δ =, L ε L V s Tl λ = και 3 l w α = και έχουμε: d u ψ ψ ψ = λ δ + α + dx x y z ψ ψ ψ = + x y και άρα η εξίσωση μας γίνεται: (6) 3
32 d u ι ζ ψ φ ω = λ δ ψ κ Ρ + η χ ϊ dx κλ θ z ψ ϊϋ Η σχέση αυτή ισχύει αν η μεμβράνη μετατοπίζεται μόνο στη μια διάσταση Από την εξίσωση της κυματικής [4] και την εξίσωση (6) θεωρώντας ότι μπορεί να έχουμε μετατόπιση και στις δύο (ή και τρείς ) διαστάσεις, οπότε θεωρούμε τον όρο " u " αντί του d u " " και η εξίσωση (6) γράφεται στην παρακάτω μορφή: dx u u ψ ε + u = λ [ δ Ρ ψ ( ) ] + (7) t t z Με τη συνοριακή συνθήκη: u( ) = u( ) = (8) Η παράμετρος ε = ρ T α l όπου ρ είναι η πυκνότητα της μεμβράνης και α είναι ο συντελεστής απόσβεσης Η παράμετρος ε παριστάνει τον παράγοντα ποιότητας ή το επονομαζόμενο Q του συστήματος Στη συνέχεια απλοποιούμε την εξίσωση μας υποθέτοντας ότι το δ είναι μικρό Επομένως θέτουμε δ = στην εξίσωση (7) και παίρνουμε: u u ψ ε + u = λ ( ) (9) t t z ζ ψ φ Μπορούμε να βρούμε μια εξάρτηση του όρου η χ θ z ψ από το u ως εξής: λύνουμε την εξίσωση: ψ z = Με αρχικές συνθήκες οι οποίες δίνονται από την εξίσωση (5): z =, ψ = και z = u, ψ = f ( u) Η λύση θα είναι της μορφής : ψ = Az + B Για z = και ψ = ή A + B = ή A = B Για z = u και ψ = f ( u) ή Au + B = f ( u) Από τις δυο αυτές σχέσεις προκύπτει: A( u + ) = f ( u) ή A = f ( u) u + Και τελικά παίρνουμε τη ζητούμενη λύση : ψ = f ( u)( z + ) u + Άρα η εξίσωση (7) μπορεί να ξαναγραφτεί: (3) 3
33 ε u u + u = ( ) t t + u λ (3) η οποία είναι μια μη γραμμική υπερβολική εξίσωση Η συνοριακή συνθήκη είναι πάλι όπως πριν u( ) = u ( ) = Οι εξισώσεις (8) και (3) μαζί με κατάλληλες αρχικές συνθήκες αποτελούν ένα απλοποιημένο μοντέλο ελαστικών παρεκτροπών στο ηλεκτροστατικό σύστημα του σχήματος 6 Σημειώνουμε ότι στη διαβάθμιση μας το u = αντιστοιχεί στη μη απομακρυσμένη μεμβράνη ενώ το u = αντιστοιχεί στην επαφή ανάμεσα στην μεμβράνη και στον κάτω δίσκο Η ηλεκτροστατική δύναμη γίνεται άπειρη στο u = 3 Επεκτάσεις του βασικού μοντέλου Επιπρόσθετες φυσικές επιρροές μπορούν να ενσωματωθούν μέσα στο βασικό μας μοντέλο που αποτελείται από τις εξισώσεις (8) και (3) Για παράδειγμα μεταβολή του χώρου στις διηλεκτρικές ιδιότητες της ελαστικής μεμβράνης εισάγουν ένα όρο στην εξίσωση (3) ο οποίος τοπικά διαφοροποιεί την ένταση της δύναμης Coulomb u u λ f ( x, y) ε + u = t t + u ( ) (3) Η συνάρτηση f ( x, y ) ικανοποιεί την σχέση < f ( x, y) και αναπαριστά μια αδιάστατη εκδοχή της διηλεκτρικής σταθεράς του υλικού Το Ω το παίρνουμε από τη συνοριακή συνθήκη και είναι Ω = [, ] Σαν δεύτερο παράδειγμα μπορούμε να ενσωματώσουμε τη βασική δομή του σχήματος 6 σε ένα κύκλωμα ελέγχου Αυτό μας διαφοροποιεί το δεξιό μέρος της εξίσωσης (3) προσθέτοντας ένα μη τοπικό όρο στην εξίσωση αυτή Η διαφοροποίηση εξαρτάται από τη φύση του κυκλώματος ελέγχου Αν χρησιμοποιήσουμε ένα σχήμα ελέγχου με πυκνωτή (capacitive cotrol scheme) τότε η τάση V διαμέσου της συσκευής εξαρτάται από άλλα στοιχεία του κυκλώματος και το σχηματισμό της συσκευής αυτής Εφαρμόζοντας τους κανόνες του Kirchoff στο σχήμα 7 βρίσκουμε ότι η τάση V διαμέσου της εξιδανικευμένης συσκευής MEMS δίνεται από τη σχέση : Q Vs = = Q( + ) C C C c f 33
34 Από την οποία προκύπτει: f ΣΧΗΜΑ 7 Vs Vs Q = = C f + C + C C C C Η τάση V της συσκευής μας δίνεται από τη σχέση: Vs Q V C s f Q = V = C f + C V = = = Vs C C f + C C f + C = C C C C C C Από τη σχέση αυτή παίρνουμε: Vs V = C + C f f f f Vs C f C f + C (33) Η εξίσωση αυτή μπορεί να χρησιμοποιηθεί για να καθορίσουμε την ηλεκτροστατική V δύναμη f γι αυτό το κύκλωμα θέτοντας f ( u) = Vs Άρα f ( u) = C + (34) C f Για να υπολογίσουμε το δυναμικό του κυκλώματος πρέπει να λύσουμε την εξίσωση (5) : ζ ψ ψ φ δ η + α ψ χ + θ x dy ψ z = Με συνοριακές συνθήκες : ( x, y, ), y, ψ =, x [ ], [ ] ψ ( x, y, ) = f ( u), x [, ], y [, ] Η συνοριακή συνθήκη για το u : u( ) = u( ) = 34
35 Για να υπολογίσουμε την χωρητικότητα του πυκνωτή C της συσκευής μας χρειαζόμαστε το δυναμικό για την περίπτωση που το f ( u ) = και υπολογίζουμε την χωρητικότητα C από το παρακάτω ολοκλήρωμα: ψ C = C ( x, y,) dxdy z Το C είναι η χωρητικότητα της( udeflected) συσκευής Υποθέτουμε ότι το δ είναι μικρό στην εξίσωση (5) και ότι α = Ο () Επομένως αγνοούμε τους όρους δ στην εξίσωση (5) και λύνουμε την εξίσωση που προκύπτει: ψ = (35) z Η λύση της (35) όπως υπολογίστηκε στην προηγούμενη ενότητα είναι η σχέση : f ( u)( z + ) ψ = (36) u + f ( u) = όπου το C + όπως ορίστηκε παραπάνω Άρα η προσεγγιστική χωρητικότητα C δίνεται από τη σχέση: C = C f Επομένως το f ( u) μπορεί να ξαναγραφτεί: f ( u) = + x + u (37) + u (38) C όπου το x = δηλαδή είναι ένας λόγος χωρητικότητας πυκνοτήτων (ratio of C capacitaces i the system) f Είδαμε ότι στην εξίσωση (6): d u ψ ψ ψ = λ δ + α + dx x y z με τις παραπάνω υποθέσεις καταλήγουμε στην εξίσωση (39) με συνοριακή συνθήκη: d u ψ = λ ( ), dx z u( ) = u( ) = Εισάγοντας τώρα τις σχέσεις (36)-(38) στην εξίσωση (39) παίρνουμε το μη τοπικό πρόβλημα 35
36 d u λ = dx ( + u) ( + xς ) + u Με τη συνοριακή συνθήκη να παραμένει ίδια: u( ) = u( ) = (4) Η αντίστοιχη εξίσωση της (3) παίρνει τη μορφή: u u λ + u = t t ε ζ φ ( + u ) η+ xς χ θ + u Ω ψ (4) Με συνοριακή συνθήκη: u( ) = u( ) = 4 Το όριο όταν το σύστημα κυριαρχείται από εσωτερική τριβή Εάν η εσωτερική τριβή (viscous) δηλαδή ο όρος du ή οι δυνάμεις απόσβεσης dt κυριαρχούν μέσα στο σύστημα πάνω στις δυνάμεις αδράνειας τότε είναι πιθανή μια περισσότερη απλοποίηση του βασικού μοντέλου Ειδικά στο όριο που κυριαρχείται από εσωτερική τριβή η παράμετρος ε < < Αυτό βέβαια δεν θα είναι το ίδιο για όλα τα συστήματα τα οποία λειτουργούν με αυτές τις προϋποθέσεις Ο επιτυχημένος σχεδιασμός τέτοιων συστημάτων απαιτεί χαμηλό Q, έτσι ονομάζονται συστήματα στα οποία κυριαρχεί η τριβή Στέλνοντας το ε στο στην εξίσωση (3) : u u λ ε + u = t t + u παίρνουμε την εξίσωση: u λ u = t + ( ) ( u ) (4) Η εξίσωση (4) είναι μια παραβολική εξίσωση της μορφής αντίδρασης-διάχυσης Στο υπόλοιπο της εργασίας μας θα περιορίσουμε την προσοχή μας στην εξίσωση (4) και θα αναλύσουμε τις δυναμικές των συσκευών των οποίων η συμπεριφορά 36
37 μοντελοποιείται από αυτή την εξίσωση Υποθέτουμε ότι συνοριακές συνθήκες είναι ίδιες με την εξίσωση (8), δηλαδή u = και εκμεταλλευόμαστε την αρχική συνθήκη u( x, y,) = (43) Αυτή η αρχική συνθήκη υποθέτει ότι το σύστημα ξεκινάει από τη βάση και ότι η τάση εφαρμόζεται στιγμιαία σε χρόνο t = 5 Στάσιμες λύσεις Στη σταθερή κατάσταση οι ελαστικές απομακρύνσεις του συστήματος που φαίνεται στο σχήμα 6 ικανοποιούν την εξίσωση: λ u = (44) + u ( ) η οποία προκύπτει από την εξίσωση: u λ u = t + u ( ) στέλνοντας την παράγωγο του χρόνου στο Στη συνέχεια θα παρουσιάσουμε την αρχή μεγίστου και το θεώρημα σύγκρισης, αποτελέσματα χρήσιμα για την απόδειξη των θεωρημάτων που ακολουθούν Συμβολίζουμε με Bu τη μορφή των πιθανών συνοριακών συνθηκών Δηλαδή Bu = u u αν έχουμε Dirichlet συνθήκες Bu = αν έχουμε Neuma και Bu = + au έχουμε Robi συνθήκες στο πρόβλημα μας u αν Θεώρημα: (Αρχή Μεγίστου-Ελαχίστου) Αν u( x, y) είναι μια αρμονική συνάρτηση στο πεδίο D (δηλαδή u = ) στο D, τότε η μέγιστη και η ελάχιστη τιμή της u( x, y) λαμβάνονται στο σύνορο D του πεδίου Ορισμός: Έστω u + f ( u) =, x Ξ Ω και Bu = στο Ω Τότε η v ονομάζεται κάτω λύση του προβλήματος αν ισχύει: v + f ( v) για x Ξ Ω και Bv στο Ω Αν για μια συνάρτηση w έχουμε w + f ( w) για x Ξ Ω και Bw στο Ω τότε η w ονομάζεται πάνω λύση Θεώρημα: (Σύγκρισης) Έστω Bu = u στο Ω Έστω v κάτω λύση του προβλήματος u + f ( u) =, x Ξ Ω και Bu = στο Ω και w πάνω λύση του προβλήματος u + f ( u) =, x Ξ Ω και Bu = στο Ω τέτοιες ώστε v( x) w( x) για κάθε x Ξ Ω Τότε υπάρχει λύση u του προβλήματος u + f ( u) =, x Ξ Ω και Bu = στο Ω τέτοια ώστε v u w 37
38 Λήμμα : Υπάρχει λ λ > τέτοιο ώστε η εξίσωση u = ( + u), u Ω = να έχει λύση για λ < λ Απόδειξη: λ Η u = είναι πάνω λύση αφού ( + u) λ Πρέπει να κατασκευάσουμε κάτω λύσεις Έστω u τέτοια ώστε u = στο Ω με u Ω = Από την αρχή μεγίστου έχουμε ότι u < στο Ω Έστω m : = if{ u ( x) / x Ξ Ω } και α = Για λ < m a / 4 λ παίρνουμε: ( α u ) a 4λ > ή u, και η au είναι κάτω λύση για ( + au) λ a / 4 Από θεώρημα σύγκρισης συμπεραίνουμε ότι υπάρχει μοναδική λύση της εξίσωσης για λ < λ Πόρισμα : Εάν Ω δίσκος ακτίνας R τότε υπάρχουν λύσεις για λ 4R Απόδειξη: Έχουμε για u ( ) ( x) = x i i R = Άρα για λ 4 R ε και a = R ότι λ ( α u ) a 4λ = 4 = R R 4 ( + α u ) υπάρχουν λύσεις του προβλήματος Θεώρημα 3: Υπάρχει για λ < λ και καμία για λ > λ λ > τέτοιο ώστε να υπάρχει τουλάχιστον μια στάσιμη λύση Απόδειξη: Εάν u στάσιμη λύση για λ = λ τότε για λ < λ ισχύει: λ λ u = > ( + u ) ( + u ) Άρα η u είναι κάτω λύση για κάθε λ < λ Έστω Ε = { λ > : να υπάρχει λύση} Από το προηγούμενο λήμμα Ε Ή Ζ Έστω λ : = sup Ε Θέλουμε να δείξουμε ότι λ < Έστω µ η πρώτη ιδιοτιμή για το πρόβλημα u = λ u, u Ω = Ισχυριζόμαστε ότι για 4 λ > µ το πρόβλημα δεν έχει λύση Πράγματι έστω u ιδιοσυνάρτηση με ιδιοτιμή 7 λ u λ µ δηλαδή u = µ u Τότε ς u[ u ] dx = µ [ u( + u) ] dx ( + u) ς ( + u) µ Ω Ω 38
39 Εάν 4 λ λ > µ ή [ u( + u) ] < 7 µ Για Ω = (, ) έχουμε πλήρη εικόνα για τις στάσιμες λύσεις της εξίσωσης (44) Πράγματι για ξ = λ x έχουμε u Ά = ( + u) u ( λ ) ± = ζ λ λ φ στο η, χ, με θ ψ Θέλουμε για λ = α µ το u( + u) a < ή u( + u) < a Θέτουμε f ( u) u( u) f Ά ( u) = 3u + 4u + Λύνοντας την f Ά ( u) = βρίσκουμε λύσεις u = και u = 3 ζ φ 4 4 Υπολογίζουμε το f ( u ), f η χ = Άρα a θ 3 ψ 7 7 = + άρα ζ λ λ Θεώρημα 4: Υπάρχει C τέτοιο ώστε η u Ά = στο, ( + u) η θ u ( λ ) ± = λ να έχει ή ή λύσεις, για >C λ, =C λ ή <C φ χ με ψ ζ u Ά=v φ η χ Απόδειξη: Στο διάγραμμα φάσεων (u,v) με v=uάτου συστήματος η v Ά= χ η ( +u ) χ θ ψ συμβολίζουμε με E την αρχική ενέργεια Οι ολοκληρωτικές καμπύλες ικανοποιούν τη v σχέση: E = + Μια καμπύλη από το ( u,) με < u < τέμνει τον άξονα v σε + u πεπερασμένο χρόνο στο (, v ) v Άρα E = + και οι ολοκληρωτικές καμπύλες έχουν τη μορφή : u v = ± v + όπου η v v ορίζεται για u = u + u + v Ο χρόνος μετάβασης από το ( u,) στο (, v ) δίνεται από την απεικόνιση Τ: du T ( v ) = ς u u v + + u Τότε T καθώς v ή v + Η Τ έχει μοναδικό μέγιστο (από αυτό βλέπουμε τη δομή των στάσιμων λύσεων) α Έστω a = v και β = τότε : + α 39
40 α + u a Τ ( α ) = du = + β si θ si θ dθ = F( a, θ ) dθ + α ς + ς ς π π β u β + a Όπου F( a, θ ) = + β si θ si θ Τώρα θεωρούμε την T% β ( a) : = ( + β si θ ) ( si θ ) dθ = G( a, θ ) dθ + a ς ς π π Αφού G = F και F > έχουμε ότι οι T και T % έχουν τα ίδια κρίσιμα σημεία Επιπλέον a T% ( a) = ι 3 λca ( c b) ( a ) + + ω π ϋ με c =, b = + c και + 4 dt% = ι ca + 4ba 4 4 ( a + b) ω da λ ϋ που γίνεται μηδέν για a = ι b ± b + ( c + b) c ω + a c λ ϋ ( ) Άρα η μοναδική θετική ρίζα είναι για ι ω c λ ϋ a = b + ( c + b) c b Στη συνέχεια θα θεωρήσουμε τη συμπεριφορά των λύσεων της εξίσωσης (44) Οι ποιοτικές μεταβολές του συστήματος εξαρτώνται από το αν το πρόβλημα σταθερής κατάστασης της εξίσωσης (44) έχει ή δεν έχει λύση Σε μια διάσταση όταν το Ω είναι μια ελαστική ταινία τότε η εξίσωση (44) απλοποιείται στην εξίσωση: d u λ = (45) dx + u με συνοριακή συνθήκη: ( ) u ( ) u ( ) = = (46) Αυτό το πρόβλημα έχει μελετηθεί από πολλούς [], [], [3] Έχει αποδειχτεί ότι υπάρχει μια τιμή λ τέτοια ώστε για λ < λ υπάρχουν ακριβώς δύο λύσεις στο σύστημα Για λ = λ υπάρχει ακριβώς μια λύση και για λ > λ καμία λύση δεν υπάρχει στο σύστημα [] Η τιμή λ ερμηνεύεται σαν την αδιάστατη κρίσιμη τιμή της τάσης (pull-i voltage) Χρησιμοποιώντας αριθμητική ανάλυση υπολογίζεται το λ =,4 [] Επιπλέον αποδείχτηκε ότι οι λύσεις της εξίσωσης (45) είναι αρνητικές και συμμετρικές ως προς το σημείο x = Στην περίπτωση όπου το Ω είναι ελαστικός δίσκος η κατάσταση είναι ίδια αλλά πιο περίπλοκη Σύμφωνα με το γνωστό θεώρημα Gidas-Ni-Niremberg, εφόσον το Ω είναι ένα κλειστό και φραγμένο χωρίο τότε όλες οι λύσεις στην εξίσωση (45) είναι ακτινικά συμμετρικές [] Επομένως μεταβολές στην κατεύθυνση θ μπορούν να αγνοηθούν στην εξίσωση (45) και η εξίσωση: 4
41 απλοποιημένη γίνεται: u = λ ( + u ) d u du λ + = dr r dr u ( + ) (47) με συνοριακές συνθήκες: du () = u() = (48) dr Όπως με την ελαστική ταινία έτσι και εδώ από το θεώρημα 3 αποδεικνύεται ότι υπάρχει μια τιμή για το λ τέτοια ώστε αν λ > λ τότε δεν υπάρχουν λύσεις για τις εξισώσεις (47) και (48) Όταν το λ λ τότε πολλαπλές λύσεις μπορούν να υπάρχουν Συγκεκριμένα όταν το λ = 4 9 υπάρχουν άπειρες λύσεις για τις εξισώσεις (47) και (48) [] Πάλι και εδώ το λ ερμηνεύεται σαν την αδιάστατη κρίσιμη τιμή για την τάση και χωρίζει τη συμπεριφορά σταθερής κατάστασης του συστήματος σε δύο περιοχές (regimes) Στο σχήμα 8 σχεδιάζουμε το διάγραμμα διακλάδωσης για την περίπτωση που το χωρίο Ω είναι ένας κυκλικός δίσκος ΣΧΗΜΑ 8 Στην περίπτωση αυτή από το θεώρημα 3 αποδεικνύεται η ύπαρξη μιας κρίσιμης τιμής λ Επιπλέον μπορούμε να αποκτήσουμε ανώτερα και κατώτερα όρια του λ Αν το Ω είναι μια φραγμένη περιοχή με τυχαία σύνορα και αν το µ είναι η πρώτη χαρακτηριστική ιδιοτιμή του πάνω στο Ω τότε από το θεώρημα 3 παίρνουμε ότι για λ > 4µ 7 και η εξίσωση (44) δεν έχει λύσεις Με τον ίδιο τρόπο βρίσκουμε ότι αν µ είναι η πρώτη χαρακτηριστική ιδιοτιμή του σε ένα κατάλληλα μεγενθυμένο 4
42 πεδίο ορισμού που περιέχει το Ω τότε μια λύση της εξίσωσης (44) υπάρχει για όλα τα λ < 4µ 7 Επομένως έχουμε ότι το λ ικανοποιεί τη σχέση: 4µ 7 < λ < 4µ 7 Αυτά τα όρια μπορούν να βελτιωθούν και η χρήση του μεγενθυμένου πεδίου ορισμού στον υπολογισμό του χαμηλότερου ορίου μπορεί να αφαιρεθεί Αυτά τα βελτιωμένα όρια ισχύουν για οποιοδήποτε πεδίο ορισμού φραγμένο ή περιορισμένο από ένα ελλειψοειδές Όταν το πεδίο ορισμού Ω είναι απλά συνεκτικό και έχει συμμετρία τότε το θεώρημα Gidas-Ni-Niremberg δίνει λύσεις στην εξίσωση (44) οι οποίες κληρονομούν τη συμμετρία του πεδίου ορισμού Όταν το πεδίο ορισμού δεν είναι απλά συνεκτικό τότε μπορεί να συμβεί σπάσιμο της συμμετρίας Το πιο ενδιαφέρον γεγονός σχετικά με την ανάλυση σταθερής κατάστασης είναι ο χωρισμός της συμπεριφοράς του συστήματος σε δύο περιοχές Αυτό είναι η ύπαρξη της τιμής λ που χωρίζει το διάστημα τιμών του λ σε μια περιοχή με λύσεις και μια περιοχή χωρίς λύσεις Στη συνέχεια θα δούμε ότι το διάστημα παραμέτρων χωρίζεται σε μια περιοχή όπου η γραφική παράσταση του λ εμφανίζει σημείο επαφής (touch dow) και σε μια περιοχή όπου δεν εμφανίζει σημείο επαφής (o-touch dow) 6 Δυναμική του συστήματος για λ λ Όπως αναφέραμε παραπάνω όταν το λ λ τότε τουλάχιστον μια λύση υπάρχει στο πρόβλημα μας όταν έχουμε σταθερή κατάσταση Το διάγραμμα διακλάδωσης που φαίνεται στο σχήμα 8 μας δείχνει ότι η μετάβαση από την ύπαρξη λύσης στη μη ύπαρξη οφείλεται σε μια πτυχή Επίσης το σχήμα 8 μας πληροφορεί ότι οι λύσεις μπορούν να φαίνονται σαν να υπάρχουν σε ευδιάκριτους κλάδους του διαγράμματος διακλάδωσης Ένα φυσικό αρχικό σημείο για μια ανάλυση της δυναμικής του συστήματος είναι να καθορίσουμε την ευστάθεια των διάφορων κλάδων Χρησιμοποιώντας τις εξισώσεις (8) και (3) μπορούμε να παρουσιάσουμε μια γραμμική ανάλυση της ευστάθειας και για την περίπτωση της ταινίας και για την περίπτωση του δίσκου Και στις δύο περιπτώσεις ο χαμηλότερος κλάδος των λύσεων είναι γραμμικά ευσταθής ενώ όλοι οι άλλοι είναι ασταθής Οι ιδιότητες ευστάθειας για λύσεις που ξεκινούν από το u = κοντά σε ένα δοσμένο κλάδο είναι όμοιες Μελετώντας τις εξισώσεις (8),(3) και (43) μπορούμε να δείξουμε ότι η λύση είναι αυστηρά αρνητική, μονότονα φθίνουσα και φραγμένη κάτω από το γραμμικό ευσταθή κλάδο των λύσεων σταθερής κατάστασης Από την ύπαρξη μιας συνάρτησης Lyapuov εξασφαλίζουμε συνθήκη σύγκλισης στη λύση της σταθερής κατάστασης [] Αριθμητική προσομοίωση των εξισώσεων (8), (3) και (43) μπορεί να παρουσιαστεί χρησιμοποιώντας ένα πεπλεγμένο σχήμα Crak-Nicholso για την περίπτωση όπου το Ω είναι μονοδιάστατο Μια χαρακτηριστική σειρά λύσεων που δείχνει την προσέγγιση στη σταθερή κατάσταση παρουσιάζεται στο σχήμα 9 για την περίπτωση όπου το λ = Η τιμή αυτή πρέπει να σημειωθεί ότι είναι χαμηλότερη από την κρίσιμη τιμή λ =,4 4
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
Υπολογισμός της σταθεράς ελατηρίου
 Εργαστηριακή Άσκηση 6 Υπολογισμός της σταθεράς ελατηρίου Βαρσάμης Χρήστος Στόχος: Υπολογισμός της σταθεράς ελατηρίου, k. Πειραματική διάταξη: Κατακόρυφο ελατήριο, σειρά πλακιδίων μάζας m. Μέθοδος: α) Εφαρμογή
Εργαστηριακή Άσκηση 6 Υπολογισμός της σταθεράς ελατηρίου Βαρσάμης Χρήστος Στόχος: Υπολογισμός της σταθεράς ελατηρίου, k. Πειραματική διάταξη: Κατακόρυφο ελατήριο, σειρά πλακιδίων μάζας m. Μέθοδος: α) Εφαρμογή
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
4 ΣΥΝΕΧΗ ΣΤΟ ΧΡΟΝΟ ΔΥΝΑΜΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 4 ΣΥΝΕΧΗ ΣΤΟ ΧΡΟΝΟ ΔΥΝΑΜΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Τα συνεχή στο χρόνο δυναμικά συστήματα, γνωστά και ως συστήματα διαφορικών εξισώσεων, περιγράφουν φαινόμενα που μεταβάλλονται συνεχώς στο χρόνο.
4 ΣΥΝΕΧΗ ΣΤΟ ΧΡΟΝΟ ΔΥΝΑΜΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Τα συνεχή στο χρόνο δυναμικά συστήματα, γνωστά και ως συστήματα διαφορικών εξισώσεων, περιγράφουν φαινόμενα που μεταβάλλονται συνεχώς στο χρόνο.
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
E = 1 2 k. V (x) = Kx e αx, dv dx = K (1 αx) e αx, dv dx = 0 (1 αx) = 0 x = 1 α,
 Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Κεφάλαιο 11 ΣΥΝΤΗΡΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Επανεξέταση του αρμονικού ταλαντωτή
 Κεφάλαιο 11 ΣΥΝΤΗΡΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Μία ειδική κατηγορία διδιάστατων δυναμικών συστημάτων είναι τα λεγόμενα συντηρητικά συστήματα. Ο όρος προέρχεται από την μηχανική, όπου για υλικό σημείο που δέχεται δύναμη
Κεφάλαιο 11 ΣΥΝΤΗΡΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Μία ειδική κατηγορία διδιάστατων δυναμικών συστημάτων είναι τα λεγόμενα συντηρητικά συστήματα. Ο όρος προέρχεται από την μηχανική, όπου για υλικό σημείο που δέχεται δύναμη
ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ
 ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΤΑΛΑΝΤΩΣΕΙΣ ΚΥΛΙΝΔΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ ΛΟΓΩ ΔΙΝΩΝ Γ. Σ. ΤΡΙΑΝΤΑΦYΛΛΟΥ ΚΑΘΗΓΗΤΗΣ ΕΜΠ Διατύπωση των εξισώσεων Θεωρούμε κύλινδρο διαμέτρου D, μήκους l, και μάζας m. Ο κύλινδρος συγκρατειται
ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΤΑΛΑΝΤΩΣΕΙΣ ΚΥΛΙΝΔΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ ΛΟΓΩ ΔΙΝΩΝ Γ. Σ. ΤΡΙΑΝΤΑΦYΛΛΟΥ ΚΑΘΗΓΗΤΗΣ ΕΜΠ Διατύπωση των εξισώσεων Θεωρούμε κύλινδρο διαμέτρου D, μήκους l, και μάζας m. Ο κύλινδρος συγκρατειται
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες
 Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
2o ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ
 2o ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Θέμα 1 ο Α. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
2o ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Θέμα 1 ο Α. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES
 ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
Κυκλώματα με ημιτονοειδή διέγερση
 Κυκλώματα με ημιτονοειδή διέγερση Κυκλώματα με ημιτονοειδή διέγερση ονομάζονται εκείνα στα οποία επιβάλλεται τάση της μορφής: = ( ω ϕ ) vt V sin t όπου: V το πλάτος (στιγμιαία μέγιστη τιμή) της τάσης ω
Κυκλώματα με ημιτονοειδή διέγερση Κυκλώματα με ημιτονοειδή διέγερση ονομάζονται εκείνα στα οποία επιβάλλεται τάση της μορφής: = ( ω ϕ ) vt V sin t όπου: V το πλάτος (στιγμιαία μέγιστη τιμή) της τάσης ω
Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο
 Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο Στο σχήμα φαίνεται μια γνώριμη διάταξη δύο παράλληλων αγωγών σε απόσταση, που ορίζουν οριζόντιο επίπεδο, κάθετο σε ομογενές μαγνητικό πεδίο έντασης.
Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο Στο σχήμα φαίνεται μια γνώριμη διάταξη δύο παράλληλων αγωγών σε απόσταση, που ορίζουν οριζόντιο επίπεδο, κάθετο σε ομογενές μαγνητικό πεδίο έντασης.
ΚΕΦΑΛΑΙΟ 1ο: ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
απόσβεσης, με τη βοήθεια της διάταξης που φαίνεται στο διπλανό σχήμα. Η σταθερά του ελατηρίου είναι ίση με k = 45 N/m και η χρονική εξίσωση της
 1. Ένα σώμα μάζας m =, kg εκτελεί εξαναγκασμένη ταλάντωση μικρής απόσβεσης, με τη βοήθεια της διάταξης που φαίνεται στο διπλανό σχήμα. Η σταθερά του ελατηρίου είναι ίση με k = 45 N/m και η χρονική εξίσωση
1. Ένα σώμα μάζας m =, kg εκτελεί εξαναγκασμένη ταλάντωση μικρής απόσβεσης, με τη βοήθεια της διάταξης που φαίνεται στο διπλανό σχήμα. Η σταθερά του ελατηρίου είναι ίση με k = 45 N/m και η χρονική εξίσωση
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73
 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
,..., xn) Οι συναρτήσεις που ορίζουν αυτό το σύστημα υποτίθενται παραγωγίσιμες με συνεχείς παραγώγους:
 ΜΑΘΗΜΑ 6 ο : ΕΥΣΤΑΘΕΙΑ ΤΩΝ ΚΑΤΑΣΤΑΣΕΩΝ ΙΣΟΡΡΟΠΙΑΣ (ΣΥΝΑΡΤΗΣΕΙΣ LYAPUNOV) O Aleksadr Lyapuv (857-98) έθεσε τις βάσεις της μαθηματικής θεωρίας της ευστάθειας που φέρει το όνομά του εμπνευσμένος από μια απλή
ΜΑΘΗΜΑ 6 ο : ΕΥΣΤΑΘΕΙΑ ΤΩΝ ΚΑΤΑΣΤΑΣΕΩΝ ΙΣΟΡΡΟΠΙΑΣ (ΣΥΝΑΡΤΗΣΕΙΣ LYAPUNOV) O Aleksadr Lyapuv (857-98) έθεσε τις βάσεις της μαθηματικής θεωρίας της ευστάθειας που φέρει το όνομά του εμπνευσμένος από μια απλή
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
γ /ω=0.2 γ /ω=1 γ /ω= (ω /g) v. (ω 2 /g)(x-l 0 ) ωt. 2m.
 Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 015-016 Ν. Βλαχάκης 1. Σώμα μάζας m και φορτίου q κινείται σε κατακόρυφο άξονα x, δεμένο σε ελατήριο σταθεράς k = mω του οποίου το άλλο άκρο είναι σταθερό. Το σύστημα
Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 015-016 Ν. Βλαχάκης 1. Σώμα μάζας m και φορτίου q κινείται σε κατακόρυφο άξονα x, δεμένο σε ελατήριο σταθεράς k = mω του οποίου το άλλο άκρο είναι σταθερό. Το σύστημα
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55
 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Προτεινόμενες Λύσεις Πρόβλημα - ( μονάδες) Ένα όχημα, μαζί με ένα κανόνι που είναι ακλόνητο πάνω σε αυτό,
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Προτεινόμενες Λύσεις Πρόβλημα - ( μονάδες) Ένα όχημα, μαζί με ένα κανόνι που είναι ακλόνητο πάνω σε αυτό,
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Γενικευμένα Mονοβάθμια Συστήματα
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΧΩΡΙΣ ΑΠΟΣΒΕΣΗ ΑΣΚΗΣΗ 6.1
 ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΧΩΡΙΣ ΑΠΟΣΒΕΣΗ ΑΣΚΗΣΗ 6. Σώμα μάζας gr έχει προσδεθεί στην άκρη ενός ελατηρίου και ταλαντώνεται επάνω σε οριζόντιο δάπεδο χωρίς τριβή. Εάν η σταθερά του ελατηρίου είναι 5N / και το πλάτος
ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΧΩΡΙΣ ΑΠΟΣΒΕΣΗ ΑΣΚΗΣΗ 6. Σώμα μάζας gr έχει προσδεθεί στην άκρη ενός ελατηρίου και ταλαντώνεται επάνω σε οριζόντιο δάπεδο χωρίς τριβή. Εάν η σταθερά του ελατηρίου είναι 5N / και το πλάτος
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου
 A A N A B P Y A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου Στερεό σώμα με κυλινδρική συμμετρία (κύλινδρος, σφαίρα, σφαιρικό κέλυφος, κυκλική στεφάνη κλπ) μπορεί να
A A N A B P Y A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου Στερεό σώμα με κυλινδρική συμμετρία (κύλινδρος, σφαίρα, σφαιρικό κέλυφος, κυκλική στεφάνη κλπ) μπορεί να
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
1. Τετραγωνικές μορφές. x y 0. 0x y 0 1α 1β 2α 2β 3. 0x + y 0
 Β4. ΕΣΣΙΑΝΟΣ ΠΙΝΑΚΑΣ-ΚΥΡΤΟΤΗΤΑ 1.Τετραγωνικές μορφές.χαρακτηρισμός συμμετρικών πινάκων 3.Δεύτερες μερικές παράγωγοι-εσσιανός πίνακας 4.Συνθήκες για ακρότατα 5.Κυρτές/κοίλες συναρτήσεις 6.Ολικά ακρότατα
Β4. ΕΣΣΙΑΝΟΣ ΠΙΝΑΚΑΣ-ΚΥΡΤΟΤΗΤΑ 1.Τετραγωνικές μορφές.χαρακτηρισμός συμμετρικών πινάκων 3.Δεύτερες μερικές παράγωγοι-εσσιανός πίνακας 4.Συνθήκες για ακρότατα 5.Κυρτές/κοίλες συναρτήσεις 6.Ολικά ακρότατα
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
ΔΙΑΓΩΝΙΣΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ
 ΔΙΑΓΩΝΙΣΜΑ ο ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά.. Το μέτρο της
ΔΙΑΓΩΝΙΣΜΑ ο ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά.. Το μέτρο της
ΤΑΛΑΝΤΩΣΗ ΗΛΕΚΤΡΙΚΟΥ ΦΟΡΤΙΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ
 A A N A B P Y T A ΡΑΛΛΟΥ ΦΑΣΟΥΡΑΚΗ (Β4) ΜΑΡΤΙΟΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 9 5 ΤΑΛΑΝΤΩΣΗ ΗΛΕΚΤΡΙΚΟΥ ΦΟΡΤΙΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ Γενίκευση της άσκησης (σελ 4) του σχολικού βιβλίου Φυσικής Κατεύθυνσης Β Λυκείου
A A N A B P Y T A ΡΑΛΛΟΥ ΦΑΣΟΥΡΑΚΗ (Β4) ΜΑΡΤΙΟΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 9 5 ΤΑΛΑΝΤΩΣΗ ΗΛΕΚΤΡΙΚΟΥ ΦΟΡΤΙΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ Γενίκευση της άσκησης (σελ 4) του σχολικού βιβλίου Φυσικής Κατεύθυνσης Β Λυκείου
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
Theory Greek (Cyprus) Μη γραμμική δυναμική σε Ηλεκτρικά Κυκλώματα (10 μονάδες)
 Q2-1 Μη γραμμική δυναμική σε Ηλεκτρικά Κυκλώματα (10 μονάδες) Παρακαλείστε, να διαβάσετε τις Γενικές Οδηγίες που βρίσκονται σε ξεχωριστό φάκελο πριν ξεκινήσετε την επίλυση αυτού του προβλήματος. Εισαγωγή
Q2-1 Μη γραμμική δυναμική σε Ηλεκτρικά Κυκλώματα (10 μονάδες) Παρακαλείστε, να διαβάσετε τις Γενικές Οδηγίες που βρίσκονται σε ξεχωριστό φάκελο πριν ξεκινήσετε την επίλυση αυτού του προβλήματος. Εισαγωγή
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Εισαγωγή στις Φυσικές Επιστήμες ( ) Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1. x x. x x x ( ) + ( 20) + ( + 4) = ( + ) + ( 10 + ) + ( )
 Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
Το ελαστικο κωνικο εκκρεμε ς
 Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Εργασία 2. Παράδοση 20/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες
 Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
Εργασία Παράδοση 0/1/08 Οι ασκήσεις είναι βαθμολογικά ισοδύναμες 1. Υπολογίστε τα παρακάτω όρια: Α. Β. Γ. όπου x> 0, y > 0 Δ. όπου Κάνετε απευθείας τις πράξεις χωρίς να χρησιμοποιήσετε παραγώγους. Επιβεβαιώστε
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΩΝ ΔΑΣΟΛΟΓΙΑΣ
 Ασκήσεις ΜΑΘΗΜΑΤΙΚΩΝ ΔΑΣΟΛΟΓΙΑΣ για Γενική Επανάληψη Πολυχρόνη Μωυσιάδη, Καθηγητή ΑΠΘ ΟΜΑΔΑ 1. Συναρτήσεις 1. Δείξτε ότι: και υπολογίστε την τιμή 2. 2. Να υπολογισθούν οι τιμές και 3. Υπολογίστε τις τιμές
Ασκήσεις ΜΑΘΗΜΑΤΙΚΩΝ ΔΑΣΟΛΟΓΙΑΣ για Γενική Επανάληψη Πολυχρόνη Μωυσιάδη, Καθηγητή ΑΠΘ ΟΜΑΔΑ 1. Συναρτήσεις 1. Δείξτε ότι: και υπολογίστε την τιμή 2. 2. Να υπολογισθούν οι τιμές και 3. Υπολογίστε τις τιμές
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Κεφάλαιο 5. Ενέργεια συστήματος
 Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
Δυναμική Μηχανών I. Διάλεξη 11. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 11 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Γραμμικοποίηση Ευστάθεια Απόκριση Συστημάτων 1 Β.Ε. που περιγράφονται από ΣΔΕ 1 ης τάξης 2 Πρόβλημα/Ερώτημα
Δυναμική Μηχανών I Διάλεξη 11 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Γραμμικοποίηση Ευστάθεια Απόκριση Συστημάτων 1 Β.Ε. που περιγράφονται από ΣΔΕ 1 ης τάξης 2 Πρόβλημα/Ερώτημα
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός)
 4 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός) Κυριακή, 5 Απριλίου, 00, Ώρα:.00 4.00 Προτεινόμενες Λύσεις Άσκηση ( 5 μονάδες) Δύο σύγχρονες πηγές, Π και Π, που απέχουν μεταξύ τους
4 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός) Κυριακή, 5 Απριλίου, 00, Ώρα:.00 4.00 Προτεινόμενες Λύσεις Άσκηση ( 5 μονάδες) Δύο σύγχρονες πηγές, Π και Π, που απέχουν μεταξύ τους
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Πεπερασμένες Διαφορές.
 Κεφάλαιο 1 Πεπερασμένες Διαφορές. 1.1 Προσέγγιση παραγώγων. 1.1.1 Πρώτη παράγωγος. Από τον ορισμό της παραγώγου για συναρτήσεις μιας μεταβλητής γνωρίζουμε ότι η παράγωγος μιας συνάρτησης f στο σημείο x
Κεφάλαιο 1 Πεπερασμένες Διαφορές. 1.1 Προσέγγιση παραγώγων. 1.1.1 Πρώτη παράγωγος. Από τον ορισμό της παραγώγου για συναρτήσεις μιας μεταβλητής γνωρίζουμε ότι η παράγωγος μιας συνάρτησης f στο σημείο x
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
A2. Θεωρήστε ότι d << r. Να δώσετε μια προσεγγιστική έκφραση για τη δυναμική ενέργεια συναρτήσει του q,d, r και των θεμελιωδών σταθερών.
 Γ Λυκείου 26 Απριλίου 2014 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα
Γ Λυκείου 26 Απριλίου 2014 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα
( ) ( r) V r. ( ) + l 2. Τι είδαμε: m!! r = l 2. 2mr 2. 2mr 2 + V r. q Ξεκινήσαμε την συζήτηση για το θέμα κεντρικής δύναμης
 ΦΥΣ 2 - Διαλ.4 Τι είδαμε: q Ξεκινήσαμε την συζήτηση για το θέμα κεντρικής δύναμης ü Ανάγαμε το πρόβλημα 2 σωμάτων σε πρόβλημα κεντρικής δύναμης ü διατήρηση ορμής CM μετατρέπει το πρόβλημα από 6 DoF σε
ΦΥΣ 2 - Διαλ.4 Τι είδαμε: q Ξεκινήσαμε την συζήτηση για το θέμα κεντρικής δύναμης ü Ανάγαμε το πρόβλημα 2 σωμάτων σε πρόβλημα κεντρικής δύναμης ü διατήρηση ορμής CM μετατρέπει το πρόβλημα από 6 DoF σε
υναµική Μηχανών Ι Ακαδηµαϊκό έτος : Ε. Μ. Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 22.
 υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι -. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 Cprigh ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 0. Με επιφύλαξη παντός
υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι -. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 Cprigh ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 0. Με επιφύλαξη παντός
ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) 1ο σετ - Μέρος Β ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 1 Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) 1ο σετ - Μέρος Β Ερώτηση 1. ΘΕΜΑ Β Σώμα εκτελεί Α.Α.Τ. με εξίσωση απομάκρυνσης
ΚΕΦΑΛΑΙΟ 1 Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) 1ο σετ - Μέρος Β Ερώτηση 1. ΘΕΜΑ Β Σώμα εκτελεί Α.Α.Τ. με εξίσωση απομάκρυνσης
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ*
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ* διατυπώνουν τον ορισμό του μαγνητικού πεδίου διατυπώνουν και να εφαρμόζουν τον ορισμό της έντασης του μαγνητικού πεδίου διατυπώνουν
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΦΥΣΙΚΗ, Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΝΟΤΗΤΑ 1: ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ* διατυπώνουν τον ορισμό του μαγνητικού πεδίου διατυπώνουν και να εφαρμόζουν τον ορισμό της έντασης του μαγνητικού πεδίου διατυπώνουν
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ ΑΣΚΗΣΗ 1 d x dx Η διαφορική εξίσωση κίνησης ενός ταλαντωτή δίνεται από τη σχέση: λ μx. Αν η μάζα d d του ταλαντωτή είναι ίση με =.5 kg, τότε να διερευνήσετε την κίνηση
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ ΑΣΚΗΣΗ 1 d x dx Η διαφορική εξίσωση κίνησης ενός ταλαντωτή δίνεται από τη σχέση: λ μx. Αν η μάζα d d του ταλαντωτή είναι ίση με =.5 kg, τότε να διερευνήσετε την κίνηση
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
Theory Greek (Greece) Μη Γραμμική Δυναμική σε Ηλεκτρικά Κυκλώματα (10 Μονάδες)
 Q2-1 Μη Γραμμική Δυναμική σε Ηλεκτρικά Κυκλώματα (10 Μονάδες) Παρακαλείστε να διαβάσετε τις Γενικές Οδηγίες στον ξεχωριστό φάκελο πριν ξεκινήσετε το πρόβλημα αυτό. Εισαγωγή Τα δισταθή μη γραμμικά ημιαγώγιμα
Q2-1 Μη Γραμμική Δυναμική σε Ηλεκτρικά Κυκλώματα (10 Μονάδες) Παρακαλείστε να διαβάσετε τις Γενικές Οδηγίες στον ξεχωριστό φάκελο πριν ξεκινήσετε το πρόβλημα αυτό. Εισαγωγή Τα δισταθή μη γραμμικά ημιαγώγιμα
Εφαρμοσμένα Μαθηματικά
 Εφαρμοσμένα Μαθηματικά ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ενότητα 6: Διπλά Ολοκληρώματα Δρ. Περικλής Παπαδόπουλος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε κλικ για
Εφαρμοσμένα Μαθηματικά ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ενότητα 6: Διπλά Ολοκληρώματα Δρ. Περικλής Παπαδόπουλος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε κλικ για
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
 ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής κ. Σ. Νατσιάβας Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων Στοιχεία Φοιτητή Ονοματεπώνυμο: Νατσάκης Αναστάσιος Αριθμός Ειδικού Μητρώου:
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής κ. Σ. Νατσιάβας Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων Στοιχεία Φοιτητή Ονοματεπώνυμο: Νατσάκης Αναστάσιος Αριθμός Ειδικού Μητρώου:
dy df(x) y= f(x) y = f (x), = dx dx θ x m= 1
 I. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ d df() = f() = f (), = d d.κλίση ευθείας.μεταολές 3.(Οριακός) ρυθμός μεταολής ή παράγωγος 4.Παράγωγοι ασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία 8.Στάσιμα
I. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ d df() = f() = f (), = d d.κλίση ευθείας.μεταολές 3.(Οριακός) ρυθμός μεταολής ή παράγωγος 4.Παράγωγοι ασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία 8.Στάσιμα
Κεφάλαιο 10 Περιστροφική Κίνηση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόμενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσματικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναμική της Περιστροφικής Κίνησης, Ροπή και
Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόμενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσματικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναμική της Περιστροφικής Κίνησης, Ροπή και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ. ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΙI Ιούνιος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΙI Ιούνιος 2004 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε στα 4 θέματα με σαφήνεια συντομία. Η πλήρης απάντηση θέματος εκτιμάται ιδιαίτερα. Καλή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΙI Ιούνιος 2004 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε στα 4 θέματα με σαφήνεια συντομία. Η πλήρης απάντηση θέματος εκτιμάται ιδιαίτερα. Καλή
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
Ασκήσεις κέντρου μάζας και ροπής αδράνειας. αν φανταστούμε ότι το χωρίζουμε το στερεό σώμα σε μικρά κομμάτια, μόρια, μάζας m i και θέσης r i
 Κέντρο μάζας Ασκήσεις κέντρου μάζας και ροπής αδράνειας Η θέση κέντρου μάζας ορίζεται ως r r i i αν φανταστούμε ότι το χωρίζουμε το στερεό σώμα σε μικρά κομμάτια, μόρια, μάζας i και θέσης r i. Συμβολίζουμε
Κέντρο μάζας Ασκήσεις κέντρου μάζας και ροπής αδράνειας Η θέση κέντρου μάζας ορίζεται ως r r i i αν φανταστούμε ότι το χωρίζουμε το στερεό σώμα σε μικρά κομμάτια, μόρια, μάζας i και θέσης r i. Συμβολίζουμε
ΘΕΜΑ 1ο. Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1 Ένα σώμα εκτελεί αρμονική ταλάντωση με ακραίες θέσεις που
ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1 Ένα σώμα εκτελεί αρμονική ταλάντωση με ακραίες θέσεις που
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Κεφάλαιο 0 Μιγαδικοί Αριθμοί
 Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
1. Κίνηση Υλικού Σημείου
 1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Κεφάλαιο ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Στη διαδικασία σχεδιασμού των Συστημάτων Αυτομάτου Ελέγχου, η απαραίτητη και η πρώτη εργασία που έχουμε να κάνουμε, είναι να
Κεφάλαιο ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Στη διαδικασία σχεδιασμού των Συστημάτων Αυτομάτου Ελέγχου, η απαραίτητη και η πρώτη εργασία που έχουμε να κάνουμε, είναι να
Όταν το ελατήριο έχει μάζα
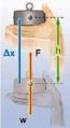 Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής y = αx 2 + βx + γ με α 0.
 ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ,α 0 337. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ ME α 0 Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής = α + β + γ με α 0. Η συνάρτηση = α +β+γ με α > 0 Η γραφική παράσταση της συνάρτησης
ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ,α 0 337. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ ME α 0 Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής = α + β + γ με α 0. Η συνάρτηση = α +β+γ με α > 0 Η γραφική παράσταση της συνάρτησης
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ η εξεταστική περίοδος 0-3 Σελίδα - - ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείου Τμήμα: Βαθμός: Ημερομηνία: 8-0-0 Διάρκεια: 3 ώρες Ύλη: Ταλαντώσεις Καθηγητής: ΑΤΡΕΙΔΗΣ
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ η εξεταστική περίοδος 0-3 Σελίδα - - ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείου Τμήμα: Βαθμός: Ημερομηνία: 8-0-0 Διάρκεια: 3 ώρες Ύλη: Ταλαντώσεις Καθηγητής: ΑΤΡΕΙΔΗΣ
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 17 Μαρτίου 2017 1 Βασικά μεγέθη Μηχανικών
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 17 Μαρτίου 2017 1 Βασικά μεγέθη Μηχανικών
