Απειροστικός Λογισμός Ι Ασκήσεις
|
|
|
- Ευγένιος Κωνσταντόπουλος
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης
2
3 . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο των για τα οποία αυτή είναι αληθής. Λύση. (i) Η ανισότητα + > λέει ότι η απόσταση του από το είναι μεγαλύτερη από. Άρα αληθεύει για τα στοιχεία του συνόλου (, 3) (, + ). Η αλγεβρική λύση έχει ως εξής: + > + < ή + > < 3 ή >. (ii) Η ανισότητα + λέει ότι η απόσταση του από το είναι μικρότερη ή ίση της απόστασης του από το. Άρα αληθεύει για τα στοιχεία του συνόλου [0, + ). Αλγεβρικά: + ( ) ( + ) Με άλλον, αλλά λιγότερο βολικό, τρόπο: και + ( + και + ) ή ( + και + ) ή ( + και + ) ή ( + και + ) 0 ή = > +3 (iii) Θα χειριστούμε την ανισότητα 3+ αλγεβρικά. Δεν θα πολλαπλασιάσουμε με το γινόμενο των παρονομαστών για να αποφύγουμε τις περιπτώσεις με το πρόσημό του. + > > 0 ( 3) (+)(3+) > 0 ( 3)(+) (+)(3+) > 0 ( 3)( + )( + )(3 + ) > 0. Η τελευταία πολυωνυμική παράσταση μηδενίζεται στα διαδοχικά σημεία,, 3, 3. Άρα η ανισότητα αληθεύει για τα στοιχεία του συνόλου (, ) (, 3 ) (3, + ). (iv) Θα χειριστούμε και την ανισότητα ( )( 3) 0 αλγεβρικά. Αυτή η ανισότητα είναι πιο ( ) απλή από την προηγούμενη. Κατ αρχάς πρέπει να είναι και άρα ( ) > 0. Άρα ( )( 3) ( ) 0 ( )( 3) 0 και. Άρα η ανισότητα αληθεύει για τα στοιχεία του συνόλου [, ) (, 3].. Λύστε τις εξισώσεις cos =, si = 3, cot =, ta = 3. Λύση. (i) Η συνάρτηση cos είναι π-περιοδική. Στο διάστημα [0, π) η εξίσωση cos = έχει δύο λύσεις, τις 3π 4 και π 3π 4 = 5π 4. Άρα η εξίσωση έχει λύσεις τις 3π 4 + kπ για k Z και + kπ για k Z. τις 5π 4 (ii) Η συνάρτηση si είναι π-περιοδική. Στο διάστημα [0, π) η εξίσωση si = έχει δύο λύσεις, τις π 3 και π π 3 = π 3. Άρα η εξίσωση έχει λύσεις τις π 3 + kπ για k Z και τις π 3 + kπ για k Z. 3
4 (iii) Η συνάρτηση cot είναι π-περιοδική. Στο διάστημα (0, π) η εξίσωση cot = έχει μία λύση, την 3π 4. Άρα η εξίσωση έχει λύσεις τις 3π 4 + kπ για k Z. (iv) Η συνάρτηση ta είναι π-περιοδική. Στο διάστημα ( π, π ) η εξίσωση ta = 3 έχει μία λύση, την π 3. Άρα η εξίσωση έχει λύσεις τις π 3 + kπ για k Z. 3. Αποδείξτε ότι cos = ta (/) +ta (/), si si y = cos( y) cos( + y). Λύση. (i) (ii) ta (/) +ta (/) = cos (/) si (/) cos (/)+si (/) = cos ( ) si ( ) = cos. cos( y) cos( + y) = (cos cos y + si si y cos cos y + si si y) = si si y.
5 4. Βρείτε τα πεδία ορισμού και τα σύνολα τιμών των συναρτήσεων y = +4, y = +, y = log 0 + 4, y = e + e + 3. Λύση. (i) Το πεδίο ορισμού της y = +4 είναι το (, 4) ( 4, + ). Το σύνολο τιμών της συνάρτησης αποτελείται από εκείνα τα y για τα οποία η εξίσωση +4 = y με άγνωστο το έχει τουλάχιστον μία λύση στο πεδίο ορισμού της συνάρτησης. Θεωρούμε δοσμένο το y και λύνουμε με άγνωστο το 4 την εξίσωση: +4 = y = y + 4y ( y) = + 4y. Αν y = τότε η εξίσωση δεν έχει λύση. Αν y τότε η εξίσωση έχει την λύση = +4y y και ελέγχουμε εύκολα ότι αυτή η λύση είναι 4. Άρα το σύνολο τιμών είναι το (, ) (, + ). (ii) Το πεδίο ορισμού της y = + είναι το (, ) (, ) (, + ). Το σύνολο τιμών της συνάρτησης αποτελείται από εκείνα τα y για τα οποία η εξίσωση + = y με άγνωστο το έχει τουλάχιστον μία λύση στο πεδίο ορισμού της συνάρτησης. Θεωρούμε δοσμένο το y και λύνουμε με άγνωστο το ± την εξίσωση: + = y + = y y (y ) = y +. Αν y = τότε η εξίσωση δεν έχει λύση. Αν y τότε η εξίσωση γράφεται ισοδύναμα = y+ y. Αν y+ y+ y < 0 τότε η εξίσωση δεν έχει λύση. Αν y 0 τότε η εξίσωση έχει τις λύσεις = ± y+ y και ελέγχουμε εύκολα ότι αυτές οι λύσεις είναι ±. Άρα το σύνολο τιμών περιέχει τα y για τα οποία ισχύει y+ y 0 ή, ισοδύναμα, (y + )(y ) > 0 και y. Επομένως το σύνολο τιμών είναι το (, ] (, + ). (iii) Το πεδίο ορισμού της y = log είναι το (0, + ). Το σύνολο τιμών της συνάρτησης περιέχει εκείνα τα y για τα οποία η εξίσωση log = y με άγνωστο το έχει τουλάχιστον μία λύση στο πεδίο ορισμού της συνάρτησης. Θεωρούμε δοσμένο το y και λύνουμε με άγνωστο το > 0 την εξίσωση: log = y log 0 = y 4 = 0 y 4. Η λύση = 0 y 4 είναι προφανώς > 0 για κάθε y. Άρα το σύνολο τιμών είναι το (, + ). (iv) Το πεδίο ορισμού της y = e + e + 3 είναι το (, + ). Το σύνολο τιμών της συνάρτησης περιέχει εκείνα τα y για τα οποία η εξίσωση e +e +3 = y με άγνωστο το έχει τουλάχιστον μία λύση στο πεδίο ορισμού της συνάρτησης. Θεωρούμε δοσμένο το y και λύνουμε με άγνωστο το την εξίσωση: e + e + 3 = y e + e + = y (e + ) = y. Αν y < τότε η εξίσωση δεν έχει λύση. Αν y τότε η εξίσωση γράφεται ισοδύναμα e + = ± y e + = y e = y. Αν y τότε η τελευταία εξίσωση δεν έχει λύση. Αν y > τότε η εξίσωση έχει την λύση = log( y ). Άρα το σύνολο τιμών περιέχει τα y για τα οποία ισχύει y > ή, ισοδύναμα, y >. Επομένως το σύνολο τιμών είναι το (3, + ). 3
6 5. Έστω αριθμοί a, b, c με a 0. Βάσει του γραφήματος της y =, περιγράψτε μέθοδο σχεδίασης του γραφήματος της y = a + b + c. Σε ποιά περίπτωση είναι η συνάρτηση άνω φραγμένη και σε ποιά περίπτωση είναι κάτω φραγμένη στο (, + ); Ποιό είναι το σύνολο τιμών της; Ειδικότερα, σχεδιάστε το γράφημα της y = και από αυτό να διακρίνετε το πεδίο ορισμού της συνάρτησης, το σύνολο τιμών της, τα διαστήματα μονοτονίας της και τα αντίστοιχα σύνολα τιμών. Λύση. (i) Γράφουμε y = a + b + c = a( + b a ) + 4ac b 4a. Ξεκινάμε από το γράφημα της y =. Η συνάρτηση είναι γνησίως φθίνουσα στο (, 0] και γνησίως αύξουσα στο [0, + ). Το σύνολο τιμών της είναι το [0, + ), είναι κάτω φραγμένη και έχει ελάχιστη τιμή 0. Μεταφέρουμε οριζόντια το γράφημα της y = κατά b a και βρίσκουμε το γράφημα της y = ( + b a ). Η συνάρτηση είναι γνησίως φθίνουσα στο (, b a ] και γνησίως αύξουσα στο [ b a, + ). Το σύνολο τιμών της είναι το [0, + ), είναι κάτω φραγμένη και έχει ελάχιστη τιμή 0. Πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του γραφήματος της y = ( + b a ) με a και βρίσκουμε το γράφημα της y = a( + b a ). Τώρα έχουμε δύο περιπτώσεις. Αν a > 0 τότε η συνάρτηση είναι γνησίως φθίνουσα στο (, b a ] και γνησίως αύξουσα στο, + ), έχει σύνολο τιμών το [0, + ) και είναι κάτω φραγμένη με ελάχιστη τιμή 0. [ b a Αν a < 0 τότε η συνάρτηση είναι γνησίως αύξουσα στο (, b a, + ), έχει σύνολο τιμών το (, 0] και είναι άνω φραγμένη με μέγιστη τιμή 0. [ b a ] και γνησίως φθίνουσα στο Μεταφέρουμε κατακόρυφα κατά 4ac b 4a το τελευταίο γράφημα και βρίσκουμε το γράφημα της y = a + b + c. Οπότε πάλι έχουμε δύο αντίστοιχες περιπτώσεις. Αν a > 0 τότε η συνάρτηση είναι γνησίως φθίνουσα στο (, b a ] και γνησίως αύξουσα στο [ b 4ac b a, + ), έχει σύνολο τιμών το [ 4a, + ) και είναι κάτω φραγμένη με ελάχιστη τιμή 4ac b 4a. Αν a < 0 τότε η συνάρτηση είναι γνησίως αύξουσα στο (, b a 4ac b, + ), έχει σύνολο τιμών το (, 4a (ii) Στην περίπτωση της y = έχουμε [ b a ] και γνησίως φθίνουσα στο ] και είναι άνω φραγμένη με μέγιστη τιμή 4ac b 4a. y = = 4( ) +. 4
7 Η συνάρτηση είναι γνησίως αύξουσα στο (, ] και γνησίως φθίνουσα στο [, + ), έχει σύνολο τιμών το (, ] και είναι άνω φραγμένη με μέγιστη τιμή. 6. Έστω αριθμοί a, b, c, d με c 0. Βάσει του γραφήματος της y =, περιγράψτε μέθοδο σχεδίασης του γραφήματος της y = a+b + c+d. Ειδικότερα, σχεδιάστε το γράφημα της y = και από αυτό να διακρίνετε το πεδίο ορισμού της συνάρτησης, το σύνολο τιμών της, τα διαστήματα μονοτονίας της και τα αντίστοιχα σύνολα τιμών. Λύση. (i) Γράφουμε y = a+b c+d = a c (c+d)+b ad c c+d = bc ad c + d c + a c. Ξεκινάμε από το γράφημα της y =. Η συνάρτηση είναι γνησίως φθίνουσα στο (, 0) με σύνολο τιμών το (, 0) και γνησίως φθίνουσα στο (0, + ) με σύνολο τιμών το (0, + ). Μεταφέρουμε οριζόντια το γράφημα της y = κατά d c και βρίσκουμε το γράφημα της y =. + d c Η συνάρτηση είναι γνησίως φθίνουσα στο (, d c ) με σύνολο τιμών το (, 0) και γνησίως φθίνουσα στο ( d c, + ) με σύνολο τιμών το (0, + ). Πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του γραφήματος της y = + d c βρίσκουμε το γράφημα της y = bc ad. Τώρα έχουμε τρεις περιπτώσεις. c + d c Αν bc ad = 0 τότε η συνάρτηση είναι σταθερή 0 στο (, d c c ) ( d c, + ). με bc ad c Αν bc ad > 0 τότε η συνάρτηση είναι γνησίως φθίνουσα στο (, d c c ) με σύνολο τιμών το (, 0) και γνησίως φθίνουσα στο ( d c, + ) με σύνολο τιμών το (0, + ). Αν bc ad < 0 τότε η συνάρτηση είναι γνησίως αύξουσα στο (, d c c ) με σύνολο τιμών το (0, + ) και γνησίως αύξουσα στο ( d c, + ) με σύνολο τιμών το (, 0). Μεταφέρουμε κατακόρυφα κατά a c το τελευταίο γράφημα και βρίσκουμε το γράφημα της y = a+b c+d. Οπότε πάλι έχουμε τρεις αντίστοιχες περιπτώσεις. Αν bc ad = 0 τότε η συνάρτηση είναι σταθερή a c c στο (, d c ) ( d c, + ). Αν bc ad > 0 τότε η συνάρτηση είναι γνησίως φθίνουσα στο (, d c c ) με σύνολο τιμών το (, a c ) και γνησίως φθίνουσα στο ( d c, + ) με σύνολο τιμών το ( a c, + ). Αν bc ad < 0 τότε η συνάρτηση είναι γνησίως αύξουσα στο (, d c c ) με σύνολο τιμών το ( a c, + ) και γνησίως αύξουσα στο ( d c, + ) με σύνολο τιμών το (, a c ). και 5
8 (ii) Στην περίπτωση της y = + έχουμε y = + = 3 +. Η συνάρτηση είναι γνησίως φθίνουσα στο (, ) με σύνολο τιμών το (, ) και γνησίως φθίνουσα στο (, + ) με σύνολο τιμών το (, + ). 7. Θεωρήστε την y = 3+. Βρείτε το πεδίο ορισμού, το σύνολο τιμών και τα διαστήματα μονοτονίας της και σχεδιάστε το γράφημά της. Βρείτε την αντίστροφη συνάρτηση, καθώς και το πεδίο ορισμού, το σύνολο τιμών και τα διαστήματα μονοτονίας της και σχεδιάστε το γράφημά της. Λύση. Το πεδίο ορισμού της y = 3+ είναι το (, 3 ) ( 3, + ). Είναι γνησίως φθίνουσα στο (, 3 ) και γνησίως φθίνουσα στο ( 3, + ) και, παρά το ότι δεν είναι γνησίως φθίνουσα στο (, 3 ) ( 3, + ), είναι ένα-προς-ένα στο (, 3 ) ( 3, + ) και άρα είναι αντιστρέψιμη. Το γράφημα της y = μπορούμε να το σχεδιάσουμε κατά το πρότυπο της άσκησης 6: γράφουμε 3+ y = 3+ =
9 Η συνάρτηση είναι γνησίως φθίνουσα στο (, 3 ) με σύνολο τιμών το (, 0) και γνησίως φθίνουσα στο ( 3, + ) με σύνολο τιμών το (0, + ). Άρα το σύνολο τιμών της συνάρτησης είναι το (, 0) (0, + ). Επομένως η αντίστροφη συνάρτηση έχει πεδίο ορισμού το (, 0) (0, + ) (το σύνολο τιμών της αρχικής συνάρτησης) και σύνολο τιμών το (, 3 ) ( 3, + ) (το πεδίο ορισμού της αρχικής συνάρτησης). Ο τύπος της αντίστροφης συνάρτησης προκύπτει όταν λύσουμε την εξίσωση 3+ = y με δοσμένο y και άγνωστο : y+ 3+ = y = 3y + y 3y = y + = 3y. Δηλαδή η αντίστροφη συνάρτηση είναι η = y+ 3y. Το γράφημά της το σχεδιάζουμε πάλι βάσει της άσκησης 6: γράφουμε = y+ 3y = 3 y 3. Εναλλακτικά, το γράφημα της = y+ 3y προκύπτει από το γράφημα της y = 3+ με ανάκλαση ως προς την ευθεία y =. Η αντίστροφη συνάρτηση είναι γνησίως φθίνουσα στο (, 0) με σύνολο τιμών το (, 3 ) και γνησίως φθίνουσα στο (0, + ) με σύνολο τιμών το ( 3, + ). 8. Θεωρήστε την y = +. Βρείτε το πεδίο ορισμού, το σύνολο τιμών και τα διαστήματα μονοτονίας της και σχεδιάστε το γράφημά της. Ορίζεται η αντίστροφη συνάρτηση; Χωρίζοντας το πεδίο ορισμού σε διαστήματα μονοτονίας της συνάρτησης, μοιράστε την σε γνησίως μονότονες συναρτήσεις, βρείτε τις αντίστροφες συναρτήσεις τους, τα πεδία ορισμού τους και τα σύνολα τιμών τους και σχεδιάστε τα γραφήματά τους. Λύση. Το πεδίο ορισμού της y = + είναι το (, + ) και μπορούμε να σχεδιάσουμε το γράφημά της κατά το πρότυπο της άσκησης 5: γράφουμε y = + = ( + ). Η συνάρτηση είναι γνησίως φθίνουσα στο (, ] με σύνολο τιμών το [, + ) και γνησίως αύξουσα στο [, + ) με σύνολο τιμών το [, + ). Αν περιορίσουμε την y = ( + ) στο (, ] τότε είναι αντιστρέψιμη (ως γνησίως φθίνουσα) με πεδίο ορισμού το (, ] και σύνολο τιμών το [, + ). Άρα η αντίστροφη συνάρτηση είναι γνησίως φθίνουσα με πεδίο ορισμού το [, + ) και σύνολο τιμών το (, ]. Ο τύπος της προκύπτει αφού λύσουμε την ( + ) = y ως εξίσωση με δοσμένο y και άγνωστο : ( + ) = y ( + ) = y + = ± y +. 7
10 Από τις δύο λύσεις εκείνη η οποία ανήκει στο (, ] είναι η = y +. Άρα η αντίστροφη συνάρτηση είναι η = y +. Αν περιορίσουμε την y = ( + ) στο [, + ) τότε είναι αντιστρέψιμη (ως γνησίως αύξουσα) με πεδίο ορισμού το [, + ) και σύνολο τιμών το [, + ). Άρα η αντίστροφη συνάρτηση είναι γνησίως αύξουσα με πεδίο ορισμού το [, + ) και σύνολο τιμών το [, + ). Ο τύπος της προκύπτει όπως πριν αφού λύσουμε την ( + ) = y ως εξίσωση με δοσμένο y και άγνωστο. Από τις δύο λύσεις τις οποίες βρήκαμε προηγουμένως εκείνη η οποία ανήκει στο [, + ) είναι η = + y +. Άρα η αντίστροφη συνάρτηση είναι η = + y Βάσει των γραφημάτων των y = και y = σχεδιάστε τα γραφήματα των y = ( ) 3 και y = 3 +. Από τα γραφήματα να διακρίνετε τα πεδία ορισμού, τα σύνολα τιμών, τα (+) 4 διαστήματα μονοτονίας και τα αντίστοιχα σύνολα τιμών. Λύση. (i) Ξεκινάμε με το γράφημα της y = και το μεταφέρουμε οριζόντια κατά. Κατόπιν 3 πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του νέου γραφήματος με (δηλαδή βρίσκουμε το συμμετρικό του ως προς τον -άξονα) και τέλος μεταφέρουμε το τελευταίο γράφημα κατακόρυφα κατά 4. Έτσι προκύπτει το γράφημα της y = 4. Από το γράφημα φαίνεται ( ) 3 καθαρά ότι η συνάρτηση είναι γνησίως αύξουσα στο (, ) με σύνολο τιμών το (4, + ) και γνησίως αύξουσα στο (, + ) με σύνολο τιμών το (, 4). Το πεδίο ορισμού της συνάρτησης είναι το (, ) (, + ) και το σύνολο τιμών της είναι το (, 4) (4, + ). (ii) Ξεκινάμε με το γράφημα της y = και το μεταφέρουμε οριζόντια κατά. Πολλαπλασιάζουμε τις -συντεταγμένες των σημείων του νέου γραφήματος με 4. Κατόπιν πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του νέου γραφήματος με 3 και τέλος μεταφέρουμε το τελευταίο γράφημα κατακόρυφα κατά. Έτσι προκύπτει το γράφημα της y = 3 +. Από το (+) 4 γράφημα διακρίνουμε ότι η συνάρτηση είναι γνησίως φθίνουσα στο (, ) με σύνολο τιμών το (, ) και γνησίως αύξουσα στο (, + ) με σύνολο τιμών το (, ). Το πεδίο ορισμού 8
11 της συνάρτησης είναι το (, ) (, + ) και το σύνολο τιμών της είναι το (, ). 0. Βάσει των γραφημάτων των y = και y = 5 σχεδιάστε τα γραφήματα των y = και y = 5 3. Ποιά είναι τα πεδία ορισμού και τα σύνολα τιμών τους; Λύση. (i) Μεταφέρουμε οριζόντια κατά το γράφημα της y = και προκύπτει το γράφημα της y =. Από το γράφημα βλέπουμε ότι η συνάρτηση είναι γνησίως αύξουσα στο [, + ) με σύνολο τιμών το [0, + ). (ii) Μεταφέρουμε οριζόντια το γράφημα της y = 5 κατά 3. Κατόπιν πολλαπλασιάζουμε με τις -συντεταγμένες των σημείων του νέου γραφήματος (δηλαδή βρίσκουμε το συμμετρικό του ως προς τον y-άξονα). Κατόπιν μεταφέρουμε το τελευταίο γράφημα κατακόρυφα κατά. Έτσι προκύπτει το γράφημα της y = 5 3. Από το γράφημα διακρίνουμε ότι η συνάρτηση είναι γνησίως φθίνουσα στο (, 3] με σύνολο τιμών το [, + ).. Σχεδιάστε στο ίδιο σχήμα τα γραφήματα των y = /3, y = /3, y = 3/, y = 3/, y =, y =. Λύση. Όλα τα γραφήματα βρίσκονται στο πρώτο τεταρτημόριο του y-επιπέδου και όλα διέρχονται από το σημείο (, ). Τα γραφήματα των συναρτήσεων με θετικό εκθέτη περιέχουν το σημείο 9
12 (0, 0) και ανεβαίνουν απεριόριστα προς δεξιά και πάνω. Τα γραφήματα των συναρτήσεων με αρνητικό εκθέτη προσεγγίζουν προς πάνω τον y-άξονα και προς δεξιά τον -άξονα. Στο διάστημα (0, ) όσο πιο μεγάλος είναι ο εκθέτης τόσο πιο ψηλά βρίσκεται το αντίστοιχο γράφημα. Αντιθέτως, στο διάστημα (, + ) όσο πιο μεγάλος είναι ο εκθέτης τόσο πιο χαμηλά βρίσκεται το αντίστοιχο γράφημα.. Σχεδιάστε το γράφημα της y = 3 cos + si. Λύση. Η τετραγωνική ρίζα του αθροίσματος των τετραγώνων των συντελεστών των cos, si είναι (( 3) + ) / = οπότε γράφουμε: 3 cos + si = ( 3 cos + si ) = ( si π 3 cos + cos π 3 si ) = si ( + π 3 ). Άρα για να βρούμε το γράφημα της y = 3 cos + si ξεκινάμε με το γράφημα της y = si, το μεταφέρουμε οριζόντια κατά π 3, και πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του νέου γραφήματος με το : 3. Βρείτε τα πεδία ορισμού και τα σύνολα τιμών των y = si, y = +si. Λύση. (i) Το πεδίο ορισμού της y = si είναι η ένωση των διαστημάτων [kπ, (k + )π] για k Z. Το σύνολο τιμών αποτελείται από τα y για τα οποία η εξίσωση si = y με άγνωστο το έχει μία τουλάχιστον λύση στο πεδίο ορισμού της συνάρτησης. Αν y < 0 ή αν y > τότε η εξίσωση si = y δεν έχει λύση. Αν 0 y τότε έχουμε si = y si = y. Επειδή 0 y, η εξίσωση αυτή έχει ακριβώς μία λύση στο διάστημα [0, π] και άρα υπάρχει ακριβώς μία λύση σε κάθε διάστημα [kπ, (k + )π] για k Z. Άρα το σύνολο τιμών της συνάρτησης είναι το [0, ]. (ii) Το πεδίο ορισμού της y = +si είναι η ένωση των διαστημάτων ( π + kπ, 3π + kπ) για k Z. Το σύνολο τιμών αποτελείται από τα y για τα οποία η εξίσωση = y με άγνωστο +si το έχει μία τουλάχιστον λύση στο πεδίο ορισμού της συνάρτησης. Αν y = 0 τότε η εξίσωση = y δεν έχει λύση. Αν y 0 τότε έχουμε +si +si = y + si = y si = y y. Προφανώς η εξίσωση αυτή έχει λύση αν και μόνο αν y y [, ]. Είναι εύκολο να δούμε ότι y y για κάθε y 0. Άρα η εξίσωση έχει λύση αν και μόνο αν y y (, ]. Τώρα είναι εύκολο να δούμε ότι < y y y. 0
13 Άρα όταν y < τότε y y / [, ] και άρα η εξίσωση si = y y y y τότε y (, ] και άρα η εξίσωση si = y y από τα διαστήματα ( π + kπ, 3π + kπ) για k Z. Άρα το σύνολο τιμών της συνάρτησης y = +si είναι το [, + ). 4. Σχεδιάστε τα γραφήματα των y = si, y = si. Λύση. (i) Ισχύει si για 0. δεν έχει λύση. Και όταν έχει τουλάχιστον μία λύση σε καθένα Άρα το γράφημα της y = si βρίσκεται ανάμεσα στα γραφήματα των y = και y =. Στις λύσεις της εξίσωσης si =, δηλαδή στα π + kπ με k = 0,,,..., το γράφημα της y = si ακουμπά το γράφημα της y = ενώ στις λύσεις της εξίσωσης si =, δηλαδή στα 3π + kπ με k = 0,,,..., το γράφημα της y = si ακουμπά το γράφημα της y =. Σε κάθε άλλο > 0 το γράφημα της y = si βρίσκεται γνησίως ανάμεσα στα γραφήματα των y = και y =. Στις λύσεις της εξίσωσης si = 0, δηλαδή στα kπ με k = 0,,,..., το γράφημα της y = si τέμνει τον -άξονα. Προσέχοντας πώς όλα αυτά τα σημεία (οι λύσεις των τριών εξισώσεων si =, si = και si = 0) διαδέχονται το ένα το άλλο, σχεδιάζουμε το γράφημα της y = si. Αν προσέξετε την μορφή του γραφήματος κοντά στο 0 θα παρατηρήσετε ότι εφάπτεται στον - άξονα. Αυτό δικαιολογείται με γνώσεις τις οποίες θα αποκτήσουμε αργότερα: η παράγωγος της y = si στο 0 είναι ίση με 0. (ii) Κατ αρχάς θεωρούμε την y = si στο (0, + ). Λόγω της ανισότητας si για > 0, το γράφημα της y = si βρίσκεται ανάμεσα στις ευθείες y = και y =. Στις λύσεις της εξίσωσης si =, δηλαδή στα (π/)+kπ με k = 0,,,..., το γράφημα της y = si ακουμπά την ευθεία y = και στις λύσεις της εξίσωσης si =, δηλαδή στα (3π/)+kπ με k = 0,,,..., το γράφημα της y = si ακουμπά την ευθεία y =. Σε κάθε άλλο > 0 το γράφημα της y = si βρίσκεται γνησίως ανάμεσα στις ευθείες y = και y =. Στις λύσεις της εξίσωσης si = 0, δηλαδή στα kπ με k =,,..., το γράφημα της y = si τέμνει τον -άξονα. Όλα αυτά τα σημεία (οι λύσεις των τριών εξισώσεων si =, si = και si = 0) διαδέχονται το ένα το άλλο και προσεγγίζουν το 0. Αυτές οι παρατηρήσεις μας βοηθούν να σχεδιάσουμε
14 το γράφημα της y = si το οποίο αντιστοιχεί στο (0, + ). Κατόπιν, χρησιμοποιώντας το ότι η y = si είναι άρτια, σχεδιάζουμε και το γράφημά της το οποίο αντιστοιχεί στο (, 0): είναι το συμμετρικό του προηγούμενου ως προς τον y-άξονα. Ένα ακόμη βοηθητικό στοιχείο είναι η ανισότητα si < για > 0 η οποία προκύπτει από την si t < t για t > 0 την οποία θα αποδείξουμε αργότερα. Από αυτήν παίρνουμε ότι si < για > 0 οπότε το γράφημα της y = si βρίσκεται κάτω από την οριζόντια ευθεία y =. Μάλιστα, το γράφημα προσεγγίζει προς δεξιά την ευθεία y = λόγω του ορίου + si = το οποίο θα δούμε αργότερα. Παρόμοιες παρατηρήσεις έχουμε και για το συμμετρικό κομμάτι του γραφήματος (δηλαδή για < 0). 5. Βρείτε τα arccos και arcsi των 0, ±, ±, ± 3, ±. Λύση. Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και άρα κατά αύξουσα διάταξη των ημιτόνων τους): si( π ) =, si( π 3 ) = 3, si( π 4 ) =, si( π 6 ) =, si 0 = 0, si π 6 =, si π 4 =, si π 3 = 3, si π =.
15 Άρα έχουμε αντιστοίχως: arcsi( ) = π, arcsi( 3 ) = π 3, arcsi( ) = π 4, arcsi( ) = π 6, arcsi 0 = 0, arcsi = π 6, arcsi = π 4, arcsi 3 = π 3, arcsi = π. Στο διάστημα [0, π] είναι (κατά αύξουσα διάταξη των γωνιών και άρα κατά φθίνουσα διάταξη των συνημιτόνων τους): Άρα έχουμε αντιστοίχως: arccos = 0, cos 0 =, cos π 6 = 3, cos π 4 =, cos π 3 =, cos π = 0, cos π 3 =, cos 3π 4 =, cos 5π 6 = 3, cos π =. arccos 3 = π 6, arccos = π 4, arccos = π 3, arccos 0 = π, arccos( ) = π 3, arccos( ) = 3π 4, arccos( 3 ) = 5π 6, arccos( ) = π. 6. (i) Αποδείξτε ότι arccos y + arcsi y = π για κάθε y [, ]. (ii) Αποδείξτε ότι arcta y + arccot y = π για κάθε y. Λύση. (i) Έστω y [, ] και = arcsi y. Αυτό σημαίνει ότι [ π, π ] και si = y. Ορίζουμε το z = π. Τότε z [0, π] και cos z = cos( π ) = si = y. Αρα arccos y = z = π = π arcsi y. (ii) Έστω = arcta y. Αυτό σημαίνει ότι ( π, π ) και ta = y. Ορίζουμε το z = π. Τότε z (0, π) και cot z = cot( π ) = ta = y. Αρα arccot y = z = π = π arcta y. 7. Σχεδιάστε τα γραφήματα των = arccos(y + ), = arcta y+. Λύση. (i) Μεταφέρουμε οριζόντια το γράφημα της = arccos y κατά και έτσι προκύπτει το γράφημα της = arccos(y + ). Πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του τελευταίου γραφήματος με και προκύπτει το γράφημα της = arccos(y + ). Τέλος, πολλαπλασιάζουμε τις -συντεταγμένες των σημείων του τελευταίου γραφήματος με και προκύπτει το γράφημα της = arccos(y + ). 3
16 (ii) Ξεκινάμε από το γράφημα της = arcta y και πολλαπλασιάζουμε τις y-συντεταγμένες των σημείων του με και προκύπτει το γράφημα της = arcta y. Μεταφέρουμε το τελευταίο γράφημα οριζόντια κατά και προκύπτει το γράφημα της = arcta y+. 8. Βρείτε το πεδίο ορισμού και το σύνολο τιμών της y = arcsi +. Λύση. Το + πρέπει να ανήκει στο [, ]. Εύκολα βλέπουμε ότι +. Άρα το πεδίο ορισμού της y = arcsi + είναι το (, ]. Το σύνολο τιμών της συνάρτησης = y με άγνωστο το έχει του- + ] τότε η εξίσωση arcsi = y δεν έχει αποτελείται από εκείνα τα y για τα οποία η εξίσωση arcsi + λάχιστον μία λύση στο πεδίο ορισμού. Αν y / [ π, π λύση. Αν y [ π, π ] τότε arcsi + = y + = si y (si y ) = si y +. Αν si y = δηλαδή αν y = π τότε η τελευταία εξίσωση δεν έχει λύση. Αν si y δηλαδή αν y [ π, π si y+ ) τότε η εξίσωση έχει λύση: = si y. Βλέπουμε εύκολα ότι η λύση αυτή ανήκει στο πεδίο ορισμού (, ] της συνάρτησης οπότε το σύνολο τιμών της είναι το [ π, π ). 9. Ποιά είναι η αντίστροφη συνάρτηση της y = arcsi ; Ποιό είναι το πεδίο ορισμού της και το σύνολο τιμών της; Λύση. Η συνάρτηση = si y με πεδίο ορισμού το [ π, π ] και σύνολο τιμών το [, ] έχει αντίστροφη συνάρτηση την y = arcsi με πεδίο ορισμού το [, ] και σύνολο τιμών το [ π, π ]. Άρα η αντίστροφη συνάρτηση της y = arcsi με πεδίο ορισμού το [, ] και σύνολο τιμών το [ π, π ] είναι η = si y με πεδίο ορισμού το [ π, π ] και σύνολο τιμών το [, ]. Προσοχή: η αντίστροφη συνάρτηση της y = arcsi δεν είναι η συνηθισμένη συνάρτηση = si y η οποία έχει πεδίο ορισμού το (, + ). 0. Σχεδιάστε τα γραφήματα των y = arcsi(si ), y = arcta(ta ). Λύση. (i) Έστω [ π + kπ, π + kπ] για k Z. Τότε το z = si ανήκει στο [, ] και το y = arcsi(si ) = arcsi z ορίστηκε ως ο (μοναδικός) αριθμός στο [ π, π ] για τον οποίο ισχύει 4
17 si y = z, δηλαδή si y = si. Από την εξίσωση αυτή προκύπτει το y από το. Η εξίσωση έχει δύο λύσεις: y = + mπ ή y = π + mπ με m Z. () Επειδή y [ π, π ], από την πρώτη δυνατότητα στην () έχουμε ή, ισοδύναμα, π + mπ π π mπ π mπ. Από την αρχική μας υπόθεση π + kπ π + kπ βλέπουμε ότι πρέπει να είναι k = m, δηλαδή ότι το k είναι άρτιος ακέραιος και ότι το y δίνεται από την y = kπ όταν το k είναι άρτιος ακέραιος. Πάλι, επειδή y [ π, π ], από την δεύτερη δυνατότητα στην () έχουμε π π + mπ π ή, ισοδύναμα, π + (m + )π π + (m + )π. Από την αρχική μας υπόθεση π + kπ π + kπ βλέπουμε ότι πρέπει να είναι k = m +, δηλαδή ότι το k είναι περιττός ακέραιος και ότι το y δίνεται από την y = + kπ όταν το k είναι περιττός ακέραιος. Όταν το k διατρέχει το Z τα αντίστοιχα διαστήματα [ π + kπ, π + kπ] είναι διαδοχικά και καλύπτουν ολόκληρο το (, + ) οπότε το γράφημα της y = arcsi(si ) είναι το: (ii) Έστω ( π + kπ, π + kπ) για k Z. Τότε το z = ta ανήκει στο (, + ) και το y = arcta(ta ) = arcta z ορίστηκε ως ο (μοναδικός) αριθμός στο ( π, π ) για τον οποίο ισχύει ta y = z, δηλαδή ta y = ta. Από την εξίσωση αυτή προκύπτει το y από το. Η εξίσωση έχει μία λύση: y = + mπ με m Z. Επειδή y ( π, π ), έχουμε ή, ισοδύναμα, π < + mπ < π π mπ < < π mπ. 5
18 Από την αρχική μας υπόθεση π + kπ < < π + kπ βλέπουμε ότι πρέπει να είναι k = m και ότι το y δίνεται από την y = kπ. Όταν το k διατρέχει το Z τα αντίστοιχα διαστήματα ( π + kπ, π + kπ) είναι διαδοχικά και καλύπτουν ολόκληρο το (, + ) (εκτός από τα σημεία π + kπ με k Z) και παίρνουμε το γράφημα της y = arcta(ta ): 6
19 . Βρείτε τα σύνολα των όρων των ακολουθιών ΑΚΟΛΟΥΘΙΕΣ ΚΑΙ ΟΡΙΑ ΑΚΟΛΟΥΘΙΩΝ ( +( ) ), ( a+b + ( ) a b ), ( [ ]), ( 3[ 3 ]). Λύση. (i) Για άρτιο έχουμε ότι +( ) = 0 και για περιττό ότι +( ) =. Άρα το σύνολο των όρων της ακολουθίας είναι το δισύνολο {0, }. (ii) Για άρτιο έχουμε ότι a+b a b + ( ) = b και για περιττό ότι a+b a b + ( ) = a. Άρα το σύνολο των όρων της ακολουθίας είναι το δισύνολο {a, b}. (iii) Αν το = k είναι άρτιος, τότε το = k είναι ακέραιος, οπότε [ ] = [k] = k και άρα [ ] = k k = 0. Αν το = k + είναι περιττός, τότε το = k + είναι ανάμεσα στους ακέραιους k και k +, οπότε [ ] = [k + ] = k και άρα [ ] = k + k =. Άρα το σύνολο των όρων της ακολουθίας είναι το δισύνολο {0, }. (iv) Αν = 3k με ακέραιο k, τότε το 3 = k είναι ακέραιος, οπότε [ 3 ] = [k] = k και άρα 3[ 3 ] = 3k 3k = 0. Αν = 3k + με ακέραιο k, τότε το 3 = k + 3 είναι ανάμεσα στους ακέραιους k και k +, οπότε [ 3 ] = [k + 3 ] = k και άρα 3[ 3 ] = 3k + 3k =. Αν = 3k + με ακέραιο k, τότε το 3 = k + 3 είναι ανάμεσα στους ακέραιους k και k +, οπότε [ 3 ] = [k + 3 ] = k και άρα 3[ 3 ] = 3k + 3k =. Άρα το σύνολο των όρων της ακολουθίας είναι το τρισύνολο {0,, }.. Υπολογίστε τον -οστό όρο καθεμίας από τις τέσσερις ακολουθίες οι οποίες ορίζονται από τους (κοινούς και για τις τέσσερις) πρώτους όρους = = και από τους αναδρομικούς τύπους + = 3, + = + +, + = 4 + 4, + = +. (Υπόδειξη: Διαβάστε την άσκηση..4.) Λύση. (i) Βάσει του αναδρομικού τύπου + = 3 κάθε όρος της ακολουθίας προσδιορίζει τον μεθεπόμενο όρο: από τον προσδιορίζονται οι όροι με περιττούς δείκτες και από τον προσδιορίζονται οι όροι με άρτιους δείκτες. Έχουμε διαδοχικά: =, 3 = 3 = 3 = 3, 5 = 3 3 = 3, 7 = 3 5 = 3 3, 9 = 3 7 = 3 4. Υποψιαζόμαστε ότι k = 3 k για κάθε k N και το αποδεικνύουμε επαγωγικά. Το k = 3 k ισχύει για k = αφού είναι το ίδιο με το =. Έστω ότι ισχύει k = 3 k για κάποιο m N. Τότε (m+) = m+ = 3 m = 3 3 m = 3 m = 3 (m+). Άρα το k = 3 k ισχύει και για το m +. Επίσης έχουμε διαδοχικά: =, 4 = 3 = 3 = 3, 6 = 3 4 = 3, 8 = 3 6 = 3 3, 0 = 3 8 = 3 4. Υποψιαζόμαστε ότι k = 3 k για κάθε k N και το αποδεικνύουμε επαγωγικά. Το k = 3 k ισχύει για k = αφού είναι το ίδιο με το =. Έστω ότι ισχύει k = 3 k για κάποιο m N. Τότε (m+) = m+ = 3 m = 3 3 m = 3 m = 3 (m+). 7
20 Άρα το k = 3 k ισχύει και για το m +. Καταλήγουμε στον τύπο { 3 (/) αν το είναι άρτιο = 3 ( )/ αν το είναι περιττό Επίσης ισχύει και ο τύπος = 3 [( )/]. (ii) Θεωρούμε την εξίσωση = +. Αυτή έχει τις λύσεις ρ = + 5 και ρ = 5 Προσδιορίζουμε κ, λ ώστε Αυτά είναι τα: κ = + 5 και λ = Τώρα μπορούμε να αποδείξουμε επαγωγικά ότι κ + λ = = κρ + λρ = = = κρ + λρ για κάθε N. Η σχέση αυτή ισχύει για = και για = αφού για = γίνεται κ + λ = = και για = γίνεται κρ + λρ = =. Τώρα έστω ότι για κάποιο N η σχέση ισχύει για το και για το +. Τότε + = + + = (κρ + λρ ) + (κρ + λρ ) = κρ (ρ + ) + λρ (ρ + ) = κρ + + λρ + οπότε η σχέση ισχύει και για το + και άρα ισχύει για κάθε N. Πιο συγκεκριμένα, έχουμε ότι: = ( + 5 ) 5 5 ( 5 ) ( = ) 5 ( 5 ) για κάθε N. (iii) Θεωρούμε την εξίσωση = 4 4. Αυτή έχει την μοναδική λύση ρ =. Προσδιορίζουμε κ, λ ώστε Αυτά είναι τα: κ = και λ =. Τώρα μπορούμε να αποδείξουμε επαγωγικά ότι κ = = κρ + λρ = = = κρ + λ( )ρ για κάθε N. Η σχέση αυτή ισχύει για = και για = αφού για = γίνεται κ = = και για = γίνεται κρ + λρ = =. Τώρα έστω ότι για κάποιο N η σχέση ισχύει για το και για το +. Τότε + = = 4(κρ + λρ ) 4(κρ + λ( )ρ ) = κρ (4ρ 4) + λρ (4ρ 4( )) = κρ + + λ( + )ρ + οπότε η σχέση ισχύει και για το + και άρα ισχύει για κάθε N. Πιο συγκεκριμένα (με κ =, λ = και ρ = ), έχουμε ότι: = ( ) = ( 3) για κάθε N. 8.
21 (iv) Θεωρούμε την εξίσωση =. Αυτή έχει τις λύσεις ρ = +i 3 και ρ = i 3 οι οποίες είναι μιγαδικές. Παρατηρούμε ότι cos π 3 = και si π 3 = 3, οπότε ρ = cos π 3 + i si π 3 και ρ = cos π 3 i si π 3. Προσδιορίζουμε κ, λ ώστε Αυτά είναι τα: κ = και λ = 3. Τώρα μπορούμε να αποδείξουμε επαγωγικά ότι κ = = κ cos π 3 + λ si π 3 = = = κ cos ( )π 3 + λ si ( )π 3 για κάθε N. Η σχέση αυτή ισχύει για = και για = αφού για = γίνεται κ = = και για = γίνεται κ cos π 3 + λ si π 3 = =. Τώρα έστω ότι για κάποιο N η σχέση ισχύει για το και για το +. Τότε + = + = ( κ cos π 3 + λ si π ) ( 3 κ cos ( )π 3 + λ si ( )π ) 3 = κ ( cos π ( )π ) ( 3 cos 3 + λ si π ( )π ) 3 si 3 = κ cos (+)π 3 + λ si (+)π 3 οπότε η σχέση ισχύει και για το + και άρα ισχύει για κάθε N. Πιο συγκεκριμένα, έχουμε ότι: = cos ( )π si ( )π 3 για κάθε N. 3. Ποιες από τις ακολουθίες (( 3) ), (( ) ) είναι άνω φραγμένες; κάτω φραγμένες; φραγμένες; Λύση. (i) Οι όροι της πρώτης ακολουθίας είναι { ( 3) 3 αν το είναι άρτιο = 3 αν το είναι περιττό Αν η ακολουθία έχει κάποιο άνω φράγμα u τότε ισχύει 3 u και άρα log 3 u για κάθε άρτιο. Επομένως ισχύει k log 3 u και άρα k log 3 u για κάθε φυσικό k. Αυτό σημαίνει ότι το σύνολο N είναι άνω φραγμένο και γνωρίζουμε ότι αυτό δεν ισχύει. Άρα η ακολουθία δεν έχει κανένα άνω φράγμα. Αν η ακολουθία έχει κάποιο κάτω φράγμα l τότε ισχύει 3 l και άρα log 3 ( l) για κάθε περιττό. Επομένως ισχύει k log 3 ( l) και άρα k (log 3 ( l) + ) για κάθε φυσικό k. Πάλι καταλήγουμε στο ότι το σύνολο N είναι άνω φραγμένο και άρα η ακολουθία δεν έχει κανένα κάτω φράγμα. (ii) Οι όροι της δεύτερης ακολουθίας είναι { ( ) 0 αν το είναι άρτιο = αν το είναι περιττό Το 0 είναι άνω φράγμα της ακολουθίας. Αν η ακολουθία έχει κάποιο κάτω φράγμα l τότε ισχύει l και άρα l για κάθε περιττό. Άρα ισχύει k l και επομένως k l 4 + για κάθε φυσικό k. Αυτό είναι άτοπο οπότε η ακολουθία δεν έχει κανένα κάτω φράγμα. 4. Αποδείξτε ότι οι ακολουθίες ( 4 / ) και (8 /!) δεν είναι μονότονες αλλά και ότι είναι μονότονες από κάποια τιμή του δείκτη και πέρα. Είναι φραγμένες; 9
22 Λύση. (i) Έστω = 4. Ελέγχουμε την γνήσια μονοτονία της ακολουθίας: Ομοίως, Άρα < + 4 < (+)4 + < ( + )4 < > + 4 > (+)4 + > ( + )4 > < < 3 < 4 < 5 < 6 > 7 > 8 >.... Δηλαδή η ακολουθία είναι γνησίως αύξουσα μέχρι τον έκτο όρο της και γνησίως φθίνουσα από τον έκτο όρο της και πέρα. Η ακολουθία είναι φραγμένη: όλοι οι όροι της βρίσκονται ανάμεσα στο 0 και στον έκτο όρο της. (ii) Έστω = 8!. Ελέγχουμε την γνήσια μονοτονία της ακολουθίας: Ομοίως, Άρα < + 8! < 8+ (+)! + < 8 < 7. > + 8! > 8+ (+)! + > 8 > 7. < < 3 < 4 < 5 < 6 < 7 = 8 > 9 > 0 > >.... Δηλαδή η ακολουθία είναι γνησίως αύξουσα μέχρι τον έβδομο όρο της και γνησίως φθίνουσα από τον όγδοο όρο της και πέρα. Η ακολουθία είναι φραγμένη: όλοι οι όροι της βρίσκονται ανάμεσα στο 0 και στον έβδομο όρο της. 5. Χρησιμοποιώντας τον ορισμό του ορίου, δηλαδή παίρνοντας ϵ > 0 και υπολογίζοντας κατάλληλο 0 N συναρτήσει του ϵ, αποδείξτε ότι ( ) 0, 0, , si 0, Λύση. (i) Παίρνουμε τυχαίο ϵ > 0 και θα βρούμε 0 N ώστε: 0 < ϵ. Λύνουμε την ανισότητα < ϵ, δηλαδή την < ϵ, ως προς : Άρα αρκεί να βρούμε 0 N ώστε: < ϵ > ϵ. 0 > ϵ. Αυτή η συνεπαγωγή ισχύει αν θεωρήσουμε ως 0 οποιονδήποτε φυσικό μεγαλύτερο από τον αριθμό. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό δίνεται από τον ϵ ϵ τύπο [ ] ϵ +. Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό 0 [ ϵ ] +. (ii) Παίρνουμε τυχαίο ϵ > 0 και θα βρούμε 0 N ώστε: 0 ( ) < ϵ. Λύνουμε την ανισότητα ( ) < ϵ, δηλαδή την < ϵ, ως προς : < ϵ > ϵ > log ϵ. 0
23 Άρα αρκεί να βρούμε 0 N ώστε: 0 > log ϵ. Αυτή η συνεπαγωγή ισχύει αν θεωρήσουμε ως 0 οποιονδήποτε φυσικό μεγαλύτερο από τον αριθμό log ϵ {. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό log ϵ δίνεται [log από τον τύπο ϵ ] + αν 0 < ϵ Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό αν < ϵ 0 { [log ϵ ] + αν 0 < ϵ αν < ϵ (iii) Παίρνουμε τυχαίο ϵ > 0 και θα βρούμε 0 N ώστε: 0 +3 < ϵ Λύνουμε την ανισότητα < ϵ ως προς : < ϵ 3(3+5) < ϵ > 9ϵ 5 3. Άρα αρκεί να βρούμε 0 N ώστε: 0 > 9ϵ 5 3. Όπως στις προηγούμενες περιπτώσεις, αυτή η συνεπαγωγή ισχύει αν θεωρήσουμε ως 0 οποιονδήποτε φυσικό μεγαλύτερο από τον αριθμό 9ϵ 5 3. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος {[ από τον αριθμό 9ϵ 5 3 δίνεται από τον τύπο 9ϵ 5 3 ] + αν 0 < ϵ 5 αν 5 < ϵ Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό { [ 0 9ϵ 5 3 ] + αν 0 < ϵ 5 αν 5 < ϵ (iv) Παίρνουμε τυχαίο ϵ > 0 και θα βρούμε 0 N ώστε: 0 si < ϵ. Η ανισότητα si si < ϵ, δηλαδή η έχει. Βρίσκουμε κάποια παράσταση του μεγαλύτερη και απλούστερη από την Άρα αρκεί να βρούμε 0 N ώστε: Λύνουμε την ανισότητα < ϵ ως προς : Άρα αρκεί να βρούμε 0 N ώστε: < ϵ, δεν λύνεται ως προς λόγω της μορφής την οποία si. 0 < ϵ. < ϵ > ϵ /3. 0 > ϵ /3. si :
24 Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό [ ] ϵ +. Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό /3 0 [ ϵ /3 ] +. (v) Παίρνουμε τυχαίο ϵ > 0 και θα βρούμε 0 N ώστε: 0 < ϵ. +3 ϵ /3 δίνεται από τον τύπο Η ανισότητα +3 < ϵ, δηλαδή η +3 < ϵ, δεν λύνεται ως προς λόγω της μορφής την οποία έχει. Βρίσκουμε κάποια παράσταση του μεγαλύτερη και απλούστερη από την Άρα αρκεί να βρούμε 0 N ώστε: < ϵ. +3 : Λύνουμε την ανισότητα < ϵ ως προς : < ϵ > ϵ. Άρα αρκεί να βρούμε 0 N ώστε: 0 > ϵ. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό ϵ δίνεται από τον τύπο [ ϵ ] +. Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό 0 [ ϵ ] Χρησιμοποιώντας τους ορισμούς των ορίων, δηλαδή παίρνοντας M > 0 και υπολογίζοντας το κατάλληλο 0 N συναρτήσει του M, αποδείξτε ότι (5/3) +, + ( ) +, , ( + cos ) +. Λύση. (i) Παίρνουμε τυχαίο M > 0 και θα βρούμε 0 N ώστε: 0 ( 5 3) > M. Λύνουμε την ανισότητα (5/3) > M ως προς : ( 5 ) 3 > M > log5/3 M. Άρα αρκεί να βρούμε 0 N ώστε: 0 > log 5/3 M. Αυτή η συνεπαγωγή ισχύει αν θεωρήσουμε ως 0 οποιονδήποτε φυσικό μεγαλύτερο από τον αριθμό log 5/3 M. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό log 5/3 M { [log5/3 M] + αν M δίνεται από τον τύπο Άρα μπορούμε να θεωρήσουμε οποιονδήποτε αν 0 < M < φυσικό { [log5/3 M] + αν M 0 αν 0 < M <
25 (ii) Παίρνουμε τυχαίο M > 0 και θα βρούμε 0 N ώστε: 0 + ( ) > M. Παρατηρούμε ότι η ανισότητα + ( ) > M είναι σχετικά δύσκολο να λυθεί ως προς επειδή η παράσταση + ( ) έχει διπλό τυπο: + αν το είναι άρτιο και αν το είναι περιττό. Βρίσκουμε μία ποσότητα μικρότερη και απλούστερη από την + ( ) : Άρα αρκεί να βρούμε 0 N ώστε: + ( ). 0 > M. Λύνουμε την ανισότητα > M ως προς : Επομένως > M M > 0 < +4M ή > + +4M. Άρα αρκεί να βρούμε 0 N ώστε: > + +4M > M. 0 > + +4M. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό + +4M δίνεται από τον τύπο [ + +4M ] +. Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό 0 [ + +4M ] +. (iii) Παίρνουμε τυχαίο M > 0 και θα βρούμε 0 N ώστε: > M. Η ανισότητα > M δεν λύνεται ως προς επειδή καταλήγει σε ανισότητα τρίτου βαθμού ως προς. Βρίσκουμε κάποια παράσταση του μικρότερη και απλούστερη από την : Άρα αρκεί να βρούμε 0 N ώστε: =. 0 > M. Λύνουμε την ανισότητα > M ως προς : Επομένως Άρα αρκεί να βρούμε 0 N ώστε: > M < M ή > M. > M > M. 0 > M Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό M δίνεται από τον τύπο [ M] +. Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό 0 [ M ] +. 3
26 (iv) Παίρνουμε τυχαίο M > 0 και θα βρούμε 0 N ώστε: 0 ( + cos ) > M. Η ανισότητα (+cos ) > M δεν λύνεται ως προς λόγω της μορφής την οποία έχει. Βρίσκουμε κάποια παράσταση του μικρότερη και απλούστερη από την ( + cos ): Άρα αρκεί να βρούμε 0 N ώστε: ( + cos ) ( ) =. 0 > M. Ο μικρότερος φυσικός ο οποίος είναι μεγαλύτερος από τον αριθμό M δίνεται από τον τύπο [M]+. Άρα μπορούμε να θεωρήσουμε οποιονδήποτε φυσικό 0 [M] +. ανάλογα με την τιμή της πα- (+) 7. Διερευνήστε την ύπαρξη και την τιμή του ορίου + ( ) ραμέτρου. Λύση. Η παράσταση (+) ( ) γράφεται ( + ) οπότε η ακολουθία μας είναι γεωμετρική πρόοδος με λόγο +. Η συμπεριφορά της είναι γνωστή και εξαρτάται από την σχετική θέση του λόγου ως προς τους αριθμούς και. Κάνοντας την απαιτούμενη διερεύνηση, καταλήγουμε στο ότι + αν 0 < < (+) ( ) αν = 0 0 αν < 0 δεν έχει όριο αν > 8. Χρησιμοποιώντας ιδιότητες των ορίων, βρείτε τα όρια των ακολουθιών με τους παρακάτω - οστούς όρους. ( + ( ) ) 4 (, 3 + ), ( ) Λύση. (i) Για την υπακολουθία των περιττών δεικτών έχουμε ότι ( k (k )) 4 (0 (+ )) 4 = ( ) 4 = +. Για την υπακολουθία των άρτιων δεικτών έχουμε ότι ( k + k) 4 (0 + (+ )) 4 = (+ ) 4 = +. Άρα ( + ( ) ) 4 +. (ii) Για την υπακολουθία των περιττών δεικτών έχουμε ότι ( 3 ) k ( = k ( 6) = ) k ( 36 6) 0( 6) = 0. Για την υπακολουθία των άρτιων δεικτών έχουμε ότι ( 3 + ) k = ( 5 6 )k = ( 5 k 36) 0. 4
27 Άρα ( 3 + ) ( ) 0. (iii) Χρησιμοποιούμε την αλγεβρική ταυτότητα = { + αν + αν = Άρα = ( ( ) ) 3 = (/3) 3 (/3) = ( ( ) 3) ( 0) =. 9. Αποδείξτε ότι δεν υπάρχουν τα όρια των ακολουθιών με τους εξής -οστούς όρους: +( ) (+) 3, 3 ( ), 3 ( ), ( + ), ( ) ( ). Λύση. (i) Για τις υπακολουθίες των περιττών και των άρτιων δεικτών έχουμε αντιστοίχως: (k +) 3(k ) = k 6k 3 = 6 (3/k) 3, +(k+) 3(k) = k+3 6k = 3 + k 3. Άρα η ακολουθία δεν έχει όριο. (ii) Για τις υπακολουθίες των περιττών και των άρτιων δεικτών έχουμε αντιστοίχως: 3 ( )k = 3 3 = 3, 3( )k = 3 3 = 3. Άρα η ακολουθία δεν έχει όριο. (iii) Για τις υπακολουθίες των περιττών και των άρτιων δεικτών έχουμε αντιστοίχως: 3 (k ) = 3 k = 3 9 k 0, 3 k = 9 k +. Άρα η ακολουθία δεν έχει όριο. (iv) Για τις υπακολουθίες των περιττών και των άρτιων δεικτών έχουμε αντιστοίχως: ( + 3 )k = ( 6 )k = 6 ( ) k 36 0, ( + 3 )k = ( 7 6 )k = ( 49 k 36) +. Άρα η ακολουθία δεν έχει όριο. (v) Πάλι χρησιμοποιούμε τον γνωστό τύπο για το άθροισμα των πρώτων όρων γεωμετρικής προόδου: + + ( ) = ( )+ ( ) = ( )+ 3. Τώρα για τις υπακολουθίες των περιττών και των άρτιων δεικτών έχουμε αντιστοίχως: ( ) k 3 = 4k 3, Άρα η ακολουθία δεν έχει όριο. ( ) k+ 3 = + 4k (i) Βρείτε ακολουθίες ( ), (y ) οι οποίες δεν έχουν όριο ώστε η ( + y ) να έχει όριο. (ii) Βρείτε ακολουθίες ( ), (y ) οι οποίες δεν έχουν όριο ώστε η ( y ) να έχει όριο. Λύση. (i) Παίρνουμε οποιαδήποτε ( ) η οποία δεν έχει όριο και ως (y ) παίρνουμε την αντίθετη της ( ), δηλαδή y = για κάθε N. Για παράδειγμα, = ( ) και y = ( ) για κάθε N. Οι ( ) και (y ) δεν έχουν όριο, αλλά + y = 0 0. (ii) Παίρνουμε οποιαδήποτε ( ) η οποία δεν έχει όριο και ως (y ) παίρνουμε την αντίστροφη της ( ), δηλαδή y = για κάθε N. Πρέπει μόνο να προσέξουμε ώστε να είναι 0 για κάθε N. Για παράδειγμα, = ( ) και y = ( ) = ( ) για κάθε N. Οι ( ) και (y ) δεν έχουν όριο, αλλά y =. 5
28 3. Βρείτε τα όρια των ακολουθιών με τους εξής -οστούς όρους: ( +, 3 ) 4 + 8, ( ) , (+3) (+)( 5, 3 +7, +) 5 + +log( ) 7 log, +, ( ), ( ) , + + 3, ( ) + ( ),, ( +, 3 si, [ ], ), ( + + ( (+) + 3 +) 3, + 3 +, ), ( ), ( +. ) Λύση. (i) Έχουμε πολυωνυμική παράσταση του. Άρα το όριο είναι αφού ο συντελεστής τού μεγιστοβάθμιου όρου είναι αρνητικός. Πιο αναλυτικά: = 3( ) (+ )( ) =. (ii) Έχουμε ρητή παράσταση του οπότε Άρα (iii) Όπως πριν: και = = (+ )( 3 ( 3 ) ( ) 8 = +. = = ( ) 3 ( ) 3 =. 3 ) =. (iv) Η μέγιστη δύναμη του στον αριθμητή είναι η. Το ίδιο και στον παρονομαστή. Άρα (+3) 7 (+)( +) = (+ 3 ) 7 (+ )(+ ) 0 (+0) 0 (+0)(+0) =. (v) Ο όρος με την μεγαλύτερη τάξη μεγέθους στον αριθμητή και στον παρονομαστή είναι ο 5. Άρα = ( ) ( 5 ) = 5. (vi) Έχουμε ότι +log( ) 7 log = + 3 log 7 log = log log log log = 3 4. (vii) Επειδή + + και +, προκύπτει απροσδιόριστη μορφή. Όμως, + = ( +) ++ = ++ = =. (viii) Όπως στο προηγούμενο όριο, πολλαπλασιάζοντας με συζυγείς παραστάσεις, παίρνουμε = ( + + ) ( + ) Επομένως = = = ( ++ +)( ++ )( ++ ). + ( ++ +)( ++ ) ( ) = ( ++ +)( ++ )( ++ ) = ( )( + + )( + + ) 4.
29 (i) Επειδή (+) + = και 3 +, προκύπτει απροσδιόριστη μορφή. Όμως, + (+) = ( +)( +) 3 (+) (+)( +) = Άρα ( (+) ) ( ) 3 =. () Με την γνωστή αλγεβρική ταυτότητα = + για έχουμε ότι ( ) = ( + ) (i) Απλοποιούμε: = 3 (+ ) 4 + = ) 4 + ( 3 ( 0) = 3. + = 3 ( ) (+) (+) = (+) (+) 0. (ii) Από την ανισότητα 3 si 3 για κάθε N και από το ότι 3 = + έχουμε ότι 3 si +. (iii) Επειδή η παράσταση η οποία βρίσκεται μέσα στο σύμβολο του ακέραιου μέρους έχει όριο +, χρησιμοποιούμε την ανισότητα [a] a < [a] + ή την ισοδύναμη a < [a] a και έχουμε ότι < [ ] οπότε < [ ] για κάθε N. Επειδή 0, από τον κανόνα παρεμβολής παίρνουμε ότι [ ]. (iv) Από τις ανισότητες < < = 5 έχουμε ότι < < 5 οπότε ( ) < < 5 ( ) για κάθε N. Επειδή 5 και, από τον κανόνα παρεμβολής παίρνουμε ότι (v) Από τις ανισότητες 3 < + 3 < = 3 έχουμε ότι 3 < + 3 < 3 για κάθε N. Επειδή, από τον κανόνα παρεμβολής παίρνουμε (vi) Από την ανισότητα του Beroulli έχουμε ότι ( ) + + = + για κάθε N. Επειδή + +, συνεπάγεται ( + ) +. (vii) Κατ αρχάς είναι ( ) < για κάθε N. Επίσης, από την ανισότητα του Beroulli έχουμε ότι ( ) = για κάθε N. Από την διπλή ανισότητα ( ) < και από τον κανόνα παρεμβολής συνεπάγεται ( ). 7
30 (viii) Είναι ( ) = ( ) και θεωρούμε την αντίστροφη ακολουθία: ( ). (Προσοχή: αυτή ορίζεται για.) Από την ανισότητα του Beroulli έχουμε ότι ( ) ( ) = + + για κάθε N,. Από + + συνεπάγεται ( ) ( + οπότε ) 0. (i) Επειδή (+ ) e, έχουμε ότι (+ + )+ e. (Είναι ο γνωστός κανόνας ότι αν τότε +k.) Άρα ( + + ) = ( + + )+ ( + + ) e = e. () Πάλι κάνουμε αναγωγή στο γνωστό όριο ( + ) e ως εξής: ( ) ( = ) = ( (i) Όπως πριν: ( + = = ) (+ ) (+ ) (+ ) ) ( = + ) ( = + + = ( ) + ( + + ) ( = + ) ( + + ) ) ( + ) e e = e. e = e. 3. Έστω για κάθε και. Αποδείξτε ότι αν και μόνο αν + +. Λύση. Το ότι από συνεπάγεται + προκύπτει από τους γνωστούς αλγεβρικούς κανόνες ορίων. Για την αντίστροφη συνεπαγωγή γράφουμε y = + και y = + οπότε η υπόθεσή μας είναι ότι y y. Τώρα λύνουμε τους τύπους ως προς και και βρίσκουμε + = y y +, = y y+. (Από τους τύπους οι οποίοι ορίζουν τα y, y είναι εύκολο να δούμε ότι y και y.) Τώρα, όπως πριν, από τους γνωστούς αλγεβρικούς κανόνες ορίων προκύπτει ότι από y y συνεπάγεται y y y + y+ και άρα. 33. Έστω > 0 για κάθε N. Αποδείξτε ότι + αν και μόνο αν log 0 +. Λύση. Έστω +. Για να αποδείξουμε ότι log 0 + παίρνουμε M > 0 και πρέπει να δούμε ότι αν το 0 γίνει αρκετά μεγάλο τότε θα γίνει log 0 > M. Τώρα, το log 0 > M είναι ισοδύναμο με το > 0 M. Άρα πρέπει να δούμε ότι αν το 0 γίνει αρκετά μεγάλο τότε θα γίνει > 0 M. Όμως αυτό είναι σωστό επειδή +. Άρα log 0 +. Αντιστρόφως, έστω log 0 +. Για να αποδείξουμε ότι + παίρνουμε M > 0 και πρέπει να δούμε ότι αν το 0 γίνει αρκετά μεγάλο τότε θα γίνει > M. Όπως πριν, το > M είναι ισοδύναμο με το log 0 > log 0 M οπότε πρέπει να δούμε ότι αν το 0 γίνει αρκετά μεγάλο τότε θα γίνει log 0 > log 0 M. Όμως αυτό είναι σωστό διότι log 0 +. Επομένως Βρείτε ακολουθία ( ) ώστε όλοι οι όροι της να περιέχονται στο διάστημα (, ] και ώστε το + να υπάρχει αλλά να μην περιέχεται στο (, ]. Λύση. Η ακολουθία με τύπο = Βρείτε το όριο της ( ) αν ισχύει < για κάθε. 8
31 Λύση. Bλέπουμε ότι και συμπεραίνουμε ότι. 36. Βρείτε τα όρια των ακολουθιών με τους εξής -οστούς όρους: si + cos, ( 3 + ), ( ) Λύση. (i) Έχουμε 0 si + cos si + cos + =. Επειδή 0 συνεπάγεται si + cos 0 και άρα si + cos 0. (ii) Παρατηρούμε ότι 3 + ( ) = οπότε ( 3 + ) ( ) ( 4 5 ). 4 για κάθε. Επειδή (5/4) + συνεπάγεται ότι ( 3 + ) ( ) 4 +. (iii) Το άθροισμα αποτελείται από όρους στην μορφή με k από τους οποίους +k ο μικρότερος όρος είναι ο τελευταίος (με k = ) και ο μεγαλύτερος είναι ο πρώτος (με k = ). Επομένως Τώρα, + και οπότε από τον κανόνα παρεμβολής έχουμε ότι Αν ισχύει για κάθε αποδείξτε ότι. Λύση. Από + συνεπάγεται +. Ομοίως, από + + συνεπάγεται + (για ). Άρα + + για κάθε. Από τον κανόνα παρεμβολής έχουμε ότι. 38. Αν ισχύει ( ) για κάθε αποδείξτε ότι. Λύση. Λύνουμε την ανισότητα δεύτερου βαθμού ( ) με άγνωστο το και βρίσκουμε ότι 3 + για κάθε. Από τον κανόνα παρεμβολής συνεπάγεται. 39. Έστω a 0 και ακολουθία ( ) ώστε 0 και ώστε να ισχύει a για άπειρα. Αποδείξτε ότι a = 0. Λύση. Έστω, για να καταλήξουμε σε άτοπο, ότι a > 0. Επειδή 0, αν το είναι αρκετά μεγάλο τότε θα γίνει < a. Όμως αυτό αντιφάσκει με το ότι ισχύει a για άπειρα. 40. (i) Ισχύει 4 < < αν το είναι αρκετά μεγάλο; (ii) Ισχύει < για άπειρα ; Λύση. (i) Ναι, διότι και 4 < 3 <. (ii) Έχουμε και <. Άρα ισχύει 3 < αν το είναι αρκετά μεγάλο οπότε δεν είναι δυνατό να ισχύει η αντίθετη ανισότητα για άπειρα. 9
32 4. Έστω > 0 και έστω ότι οι όροι της ( ) ικανοποιούν τον αναδρομικό τύπο 3 + = + για κάθε. Μελετήστε την μονοτονία της ( ) και εξετάστε αν έχει όριο και ποιό είναι αυτό. Λύση. Κατ αρχάς παρατηρούμε ότι όλοι οι όροι της ( ) είναι θετικοί διότι ο πρώτος όρος είναι θετικός και, επίσης, κάθε όρος από τον δεύτερο και πέρα είναι θετικός λόγω του αναδρομικού τύπου. Για να δούμε αν η ακολουθία είναι γνησίως αύξουσα ή γνησίως φθίνουσα εξετάζουμε αν ισχύει < + ή η αντίθετη ανισότητα. Λόγω του αναδρομικού τύπου έχουμε ότι < + 3 < + ( )( ) > 0 < ή < και ομοίως > + ( )( ) < 0 < <. Βλέπουμε λοιπόν ότι το αν ισχύει < + ή όχι εξαρτάται από την θέση του σε σχέση με τα σημεία και. Θα αρχίσουμε κάνοντας μία υπόθεση για την θέση του σε σχέση με τα και και θα δούμε ότι, λόγω του αναδρομικού τύπου, από αυτήν καθορίζεται η θέση όλων των επόμενων όρων σε σχέση με τα και. Κατ αρχάς, αν = τότε βλέπουμε αμέσως ότι, λόγω του αναδρομικού τύπου, προκύπτει = και μετά 3 = κ.τ.λ. οπότε η ακολουθία είναι σταθερή και άρα συγκλίνει στο. Παρομοίως, αν = τότε, λόγω του αναδρομικού τύπου, προκύπτει = και μετά 3 = κ.τ.λ. οπότε η ακολουθία είναι σταθερή και άρα συγκλίνει στο. Τώρα, έστω 0 < <. Θα δούμε με επαγωγή ότι ισχύει 0 < < για κάθε. Πράγματι, αν 0 < < για κάποιο τότε 3 + = + < 3 και άρα + <. Αποδείξαμε λοιπόν ότι ισχύει 0 < < για κάθε. Τότε όμως ισχύει και < + για κάθε. Άρα έχουμε ότι η ( ) είναι γνησίως αύξουσα και άνω φραγμένη με άνω φράγμα το. Επομένως η ( ) συγκλίνει, δηλαδή για κάποιον αριθμό. Παίρνοντας όρια στον αναδρομικό τύπο 3 + = +, βρίσκουμε 3 = + οπότε = ή =. Η περίπτωση = απορίπτεται διότι όλοι οι όροι της ακολουθίας είναι <. Άρα. Κατόπιν, έστω < <. Τώρα θα δούμε με επαγωγή ότι ισχύει < < για κάθε. Πράγματι, αν < < για κάποιο τότε 3 + = + > 3 και 3 + = + < 6 και άρα < + <. Άρα ισχύει < < για κάθε οπότε ισχύει και > + για κάθε. Άρα έχουμε ότι η ( ) είναι γνησίως φθίνουσα και κάτω φραγμένη με κάτω φράγμα το. Επομένως η ( ) συγκλίνει, δηλαδή για κάποιον αριθμό. Όπως πριν, παίρνοντας όρια στον αναδρομικό τύπο 3 + = +, βρίσκουμε 3 = + οπότε = ή =. Η περίπτωση = αποκλείεται διότι όλοι οι όροι της ακολουθίας είναι < και φθίνουν. Άρα. Τέλος, έστω <. Αποδείξτε τώρα εσείς ακριβώς όπως πριν, με επαγωγή, ότι ισχύει < και άρα < + για κάθε, δηλαδή ότι η ( ) είναι γνησίως αύξουσα. Άρα η ( ) είτε συγκλίνει είτε αποκλίνει στο +. Αν υποθέσουμε ότι για κάποιον αριθμό τότε, παίρνοντας όρια στον αναδρομικό τύπο, βρίσκουμε όπως πριν ότι = ή =. Και οι δύο περιπτώσεις αποκλείονται διότι όλοι οι όροι της ακολουθίας είναι > και αυξάνονται. Άρα Έστω + = + 6 για κάθε. (i) Αν 0 < < 3 αποδείξτε ότι η υπακολουθία ( k ) είναι γνησίως αύξουσα και άνω φραγμένη και η ( k ) είναι γνησίως φθίνουσα και κάτω φραγμένη και ότι 3. (ii) Τί γίνεται αν > 3; 30
33 Λύση. Κατ αρχάς παρατηρούμε ότι όλοι οι όροι της ( ) είναι θετικοί διότι ο πρώτος όρος είναι θετικός και, επίσης, κάθε όρος από τον δεύτερο και πέρα είναι θετικός λόγω του αναδρομικού τύπου. (i) Για να μελετήσουμε τις υπακολουθίες των περιττών και των άρτιων δεικτών είναι λογικό να αναζητήσουμε μία αναδρομική σχέση ανάμεσα στον γενικό όρο της ακολουθίας και στον μεθεπόμενο όρο της: + = = Άρα για την υπακολουθία των περιττών δεικτών ισχύει k+ = 7 k +6 k +6. Μπορούμε να απλοποιήσουμε λίγο τα σύμβολα ορίζοντας y k = k. = = Δηλαδή y =, y = 3, y 3 = 5, y 4 = 7 και ούτω καθ εξής. Οπότε είναι 0 < y < 3 και ο τελευταίος αναδρομικός τύπος γράφεται y k+ = 7y k+6 y k +6. Θα αποδείξουμε ότι η (y k ) είναι γνησίως αύξουσα και ότι y k 3. Τώρα, χρησιμοποιώντας το ότι y k = k > 0, έχουμε ότι y k < y k+ y k < 7y k+6 y k +6 (y k 3)(y k + ) < 0 y k < 3. Τώρα θα αποδείξουμε επαγωγικά ότι ισχύει y k < 3 για κάθε k και έτσι θα προκύψει και ότι η (y k ) είναι άνω φραγμένη αλλά και ότι είναι γνησίως αύξουσα. Είναι y < 3 και αν υποθέσουμε ότι ισχύει y k < 3 για κάποιο k τότε εύκολα προκύπτει αλγεβρικά ότι y k+ = 7y k+6 y k +6 < 3. Αφού λοιπόν η (y k ) είναι αύξουσα και άνω φραγμένη, συνεπάγεται ότι συγκλίνει: y k y για κάποιον αριθμό y. Παίρνοντας όρια στον αναδρομικό τύπο, βρίσκουμε y = 7y+6 y+6 και άρα y = ή y = 3. Η περίπτωση y = αποκλείεται διότι όλοι οι όροι της (y k ) είναι θετικοί. Άρα y k 3, δηλαδή k 3. Για την υπακολουθία των άρτιων δεικτών ισχύει Πάλι για απλούστευση ορίζουμε k+ = 7 k+6 k +6. y k = k. Δηλαδή y =, y = 4, y 3 = 6, y 4 = 8 και ούτω καθ εξής. Τώρα, από 0 < < 3 και από = + 6 προκύπτει εύκολα ότι 3 <. Οπότε είναι 3 < y και ο τελευταίος αναδρομικός τύπος γράφεται y k+ = 7y k+6 y k +6. Θα αποδείξουμε ότι η (y k ) είναι γνησίως φθίνουσα και ότι y k 3. Όπως πριν, έχουμε ότι y k > y k+ y k > 7y k+6 y k +6 (y k 3)(y k + ) > 0 y k > 3. 3
34 Τώρα θα αποδείξουμε επαγωγικά ότι ισχύει y k > 3 για κάθε k οπότε η (y k ) είναι κάτω φραγμένη αλλά και γνησίως φθίνουσα. Είναι y > 3 και αν υποθέσουμε ότι ισχύει y k > 3 για κάποιο k τότε y k+ = 7y k+6 y k +6 > 3. Άρα η (y k ) είναι φθίνουσα και κάτω φραγμένη οπότε συγκλίνει: y k y για κάποιον αριθμό y. Παίρνοντας πάλι όρια στον αναδρομικό τύπο, βρίσκουμε y = 7y+6 y+6 και άρα y = ή y = 3. Πάλι η περίπτωση y = αποκλείεται διότι όλοι οι όροι της (y k ) είναι θετικοί και άρα y k 3, δηλαδή k 3. Από k 3 και k 3 συνεπάγεται 3. (ii) Αν > 3 τότε, επαναλαμβάνοντας τα προηγούμενα, βλέπουμε ότι η υπακολουθία ( k ) είναι γνησίως φθίνουσα και κάτω φραγμένη και η ( k ) είναι γνησίως αύξουσα και άνω φραγμένη και ότι 3. 3
35 ΟΡΙΑ ΣΥΝΑΡΤΗΣΕΩΝ 43. Παρατηρήστε ότι τα παρακάτω όρια δεν έχουν νόημα. Προσέξτε: δεν εξετάζουμε αν τα όρια υπάρχουν ή ποιά είναι η τιμή τους. Εξετάζουμε αν έχουν νόημα. log 0, 3,, ( + )( ), + +. Λύση. (i) Το πεδίο ορισμού της log είναι το (0, + ) οπότε δεν μπορούμε να προσεγγίσουμε το 0 από αριστερά του με στοιχεία του πεδίου ορισμού (ώστε να ορίζεται το log ) διαφορετικά από το 0. Άρα το όριο 0 log δεν έχει νόημα. (ii) Η συνάρτηση 3 δεν ορίζεται για < 0 οπότε το δεν μπορεί να πλησιάσει το 0 από αριστερά του μέσα από το πεδίο ορισμού της συνάρτησης. Άρα δεν έχει νόημα το 0 3. (iii) Το πεδίο ορισμού της είναι το (, 0) (3, + ) οπότε δεν μπορούμε να προσεγγίσουμε το με στοιχεία του πεδίου ορισμού διαφορετικά από το. Άρα το όριο 3 3 δεν έχει νόημα. (iv) Το πεδίο ορισμού της 4 ( + )( ) είναι το [, ] {}. Άρα το δεν μπορεί να πλησιάσει το και να είναι μέσα από το πεδίο ορισμού της συνάρτησης. Άρα το όριο 4 ( + )( ) δεν έχει νόημα. (v) Επειδή + < 0 για >, το δεν μπορεί να πλησιάσει το από δεξιά του και να είναι μέσα στο πεδίο ορισμού της συνάρτησης +. Άρα το όριο + + δεν έχει νόημα. 44. Αποδείξτε βάσει των ορισμών ότι ( + 4) = 8, log = log, + =, + e = +, log =, =, Λύση. (i) Παίρνουμε τυχαίο ϵ > 0 και πρέπει να βρούμε δ > 0 ώστε: Λύνουμε την ( + 4) 8 < ϵ ως προς το : 0 < < δ ( + 4) 8 < ϵ. ( + 4) 8 < ϵ 4 < ϵ < ϵ. + =. Τώρα είναι προφανές ότι αν πάρουμε οποιοδήποτε δ το οποίο ικανοποιεί την 0 < δ ϵ τότε: 0 < < δ ϵ ( + 4) 8 < ϵ. 33
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις πρώτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9.. Για καθεμία από τις ανισότητες Λύσεις πρώτου φυλλαδίου ασκήσεων. x + > 2, x x +, x x+2 > x+3 3x+, (x )(x 3) (x 2) 2 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις δεύτερου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε τα arccos και arcsin των 0, ±, ±, ±, ±. Λύση: Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις δεύτερου φυλλαδίου ασκήσεων.. Βρείτε τα arccos και arcsin των 0, ±, ±, ±, ±. Λύση: Στο διάστημα [ π, π ] είναι (κατά αύξουσα διάταξη των γωνιών και
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις τέταρτου φυλλαδίου ασκήσεων. ( n(n+1) e 1 (
 . Αποδείξτε ότι: Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις τέταρτου φυλλαδίου ασκήσεων. +) 7 +) +), 5 +7 5 5, +log ) 7 log 4, +, ++ + + ) +4+4 + +4, + si +, +) +), + [ ], + + 0, + +, ) +,,
. Αποδείξτε ότι: Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 08-9. Λύσεις τέταρτου φυλλαδίου ασκήσεων. +) 7 +) +), 5 +7 5 5, +log ) 7 log 4, +, ++ + + ) +4+4 + +4, + si +, +) +), + [ ], + + 0, + +, ) +,,
ProapaitoÔmenec gn seic.
 ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έκτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
II. Συναρτήσεις. math-gr
 II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έβδομου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 2018-19. Λύσεις έβδομου φυλλαδίου ασκήσεων. 1. Έχουν οι παρακάτω συναρτήσεις μέγιστη ή ελάχιστη τιμή στο διάστημα (0, 1); Στο διάστημα (, + ); Στο διάστημα [0,
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 2018-19. Λύσεις έβδομου φυλλαδίου ασκήσεων. 1. Έχουν οι παρακάτω συναρτήσεις μέγιστη ή ελάχιστη τιμή στο διάστημα (0, 1); Στο διάστημα (, + ); Στο διάστημα [0,
Για την κατανόηση της ύλης αυτής θα συμβουλευθείτε επίσης το: βοηθητικό υλικό που υπάρχει στη
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: Φεβρουαρίου Ημερομηνία παράδοσης της Εργασίας: 6 Μαρτίου Πριν από την λύση κάθε άσκησης καλό είναι να
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: Φεβρουαρίου Ημερομηνία παράδοσης της Εργασίας: 6 Μαρτίου Πριν από την λύση κάθε άσκησης καλό είναι να
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 3 η Ημερομηνία Αποστολής στον Φοιτητή: 12 Ιανουαρίου 2009
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Ιανουαρίου 009 Ημερομηνία παράδοσης της Εργασίας: Φεβρουαρίου 009. Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Ιανουαρίου 009 Ημερομηνία παράδοσης της Εργασίας: Φεβρουαρίου 009. Πριν
Συναρτήσεις Όρια Συνέχεια
 Κωνσταντίνος Παπασταματίου Μαθηματικά Γ Λυκείου Κατεύθυνσης Συναρτήσεις Όρια Συνέχεια Συνοπτική Θεωρία Μεθοδολογίες Λυμένα Παραδείγματα Επιμέλεια: Μαθηματικός Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με
Κωνσταντίνος Παπασταματίου Μαθηματικά Γ Λυκείου Κατεύθυνσης Συναρτήσεις Όρια Συνέχεια Συνοπτική Θεωρία Μεθοδολογίες Λυμένα Παραδείγματα Επιμέλεια: Μαθηματικός Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με
ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ. f : A R και στη συνέχεια δίνουμε τον τύπο της συνάρτησης, π.χ.
 Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις ενδέκατου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 8-9. Λύσεις ενδέκατου φυλλαδίου ασκήσεων.. (i) Βρείτε μία παράγουσα της + στο (, + ). Ποιές είναι όλες οι παράγουσες της + στο (, + ); (ii) Βρείτε μία παράγουσα
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 8-9. Λύσεις ενδέκατου φυλλαδίου ασκήσεων.. (i) Βρείτε μία παράγουσα της + στο (, + ). Ποιές είναι όλες οι παράγουσες της + στο (, + ); (ii) Βρείτε μία παράγουσα
f(x) = και στην συνέχεια
 ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. 2x 1. είναι Τότε έχουμε: » τον χρησιμοποιούμε κυρίως σε θεωρητικές ασκήσεις.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
g(x) =α x +β x +γ με α= 1> 0 και
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
Ρητοί αριθμοί λέγονται οι αριθμοί που έχουν ή μπορούν να πάρουν τη μορφή
 ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΜΑΘΗΜΑ, 9-10-13 Μ. Παπαδημητράκης. 1 ΠΡΟΤΑΣΗ. Αν ισχύει y n για άπειρους n και x R και y n y R, τότε x y. Απόδειξη. Υποθέτουμε (για άτοπο) ότι y < x. Γνωρίζουμε ότι υπάρχει κάποιος αρκετά
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΜΑΘΗΜΑ, 9-10-13 Μ. Παπαδημητράκης. 1 ΠΡΟΤΑΣΗ. Αν ισχύει y n για άπειρους n και x R και y n y R, τότε x y. Απόδειξη. Υποθέτουμε (για άτοπο) ότι y < x. Γνωρίζουμε ότι υπάρχει κάποιος αρκετά
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β, 8B, 9 Έστω Α ένα υποσύνολο του Ονομάζουμε
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β, 8B, 9 Έστω Α ένα υποσύνολο του Ονομάζουμε
Επαναληπτικά θέματα στα Μαθηματικά προσανατολισμού-ψηφιακό σχολείο ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΚΕΦΑΛΑΙΟ 1 ο -ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απο το Ψηφιακό Σχολείο του ΥΠΠΕΘ Επιμέλεια: Συντακτική Ομάδα mathpgr Συντονιστής:
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΚΕΦΑΛΑΙΟ 1 ο -ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απο το Ψηφιακό Σχολείο του ΥΠΠΕΘ Επιμέλεια: Συντακτική Ομάδα mathpgr Συντονιστής:
Λύσεις Διαγωνισμάτος 1 Ενότητα: Ακολουθίες-Σειρές
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegea.gr Λύσεις Διαγωνισμάτος Ενότητα: Ακολουθίες-Σειρές Άσκηση. Έστω ακολουθία (a ), για την οποία ισχύει ότι Θεωρούμε
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegea.gr Λύσεις Διαγωνισμάτος Ενότητα: Ακολουθίες-Σειρές Άσκηση. Έστω ακολουθία (a ), για την οποία ισχύει ότι Θεωρούμε
n 5 = 7 ε (π.χ. ορίζοντας n0 = 1+ ε συνεπώς (σύμϕωνα με τις παραπάνω ισοδυναμίες) an 5 < ε. Επομένως a n β n 23 + β n+1
 Θέμα 1 (α) Υποθέτουμε (προς απαγωγή σε άτοπο) ότι το σύνολο A έχει μέγιστο στοιχείο, έστω a = max A Τότε, εϕόσον a A, έχουμε a R Q και a M Ομως ο αριθμός μητρώου M είναι ρητός αριθμός, άρα (εϕόσον ο a
Θέμα 1 (α) Υποθέτουμε (προς απαγωγή σε άτοπο) ότι το σύνολο A έχει μέγιστο στοιχείο, έστω a = max A Τότε, εϕόσον a A, έχουμε a R Q και a M Ομως ο αριθμός μητρώου M είναι ρητός αριθμός, άρα (εϕόσον ο a
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Όριο και συνέχεια πραγματικής συνάρτησης
 ΚΕΦΑΛΑΙΟ 4 Όριο και συνέχεια πραγματικής συνάρτησης Αγνοώ το πώς με βλέπει ο κόσμος αλλά στον εαυτό μου, φαίνομαι σαν να μην ήμουν τίποτα άλλο από ένα αγοράκι που παίζει στην ακρογιαλιά και κατά καιρούς
ΚΕΦΑΛΑΙΟ 4 Όριο και συνέχεια πραγματικής συνάρτησης Αγνοώ το πώς με βλέπει ο κόσμος αλλά στον εαυτό μου, φαίνομαι σαν να μην ήμουν τίποτα άλλο από ένα αγοράκι που παίζει στην ακρογιαλιά και κατά καιρούς
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
π x = κπ + με κ. Στην παράγραφο αυτή θα ασχοληθούμε με συναρτήσεις οι οποίες έχουν 2
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 3: ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο.3 Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Συνάρτηση Όταν
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 3: ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο.3 Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Συνάρτηση Όταν
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
2.3 Πολυωνυμικές Εξισώσεις
 . Πολυωνυμικές Εξισώσεις η Μορφή Ασκήσεων: Ασκήσεις που μας ζητούν να λύσουμε μια πολυωνυμική εξίσωση.. Να λυθούν οι εξισώσεις: i. + + + 6 = 0 ii. 7 = iii. ( + ) + 7 = 0 iv. 8 + 56 = 0 i. + + + 6 = 0 (
. Πολυωνυμικές Εξισώσεις η Μορφή Ασκήσεων: Ασκήσεις που μας ζητούν να λύσουμε μια πολυωνυμική εξίσωση.. Να λυθούν οι εξισώσεις: i. + + + 6 = 0 ii. 7 = iii. ( + ) + 7 = 0 iv. 8 + 56 = 0 i. + + + 6 = 0 (
,, δηλαδή στο σημείο αυτό παρουσιάζει τη μέγιστη τιμή της αν α < 0 2α 4α και την ελάχιστη τιμή της αν α > 0. β Στο διάστημα,
 Γενικής Παιδείας 1.4 Εφαρμογές των παραγώγων Το κριτήριο της πρώτης παραγώγου Στην Άλγεβρα της Α Λυκείου μελετήσαμε τη συνάρτηση f(x) = αx + βx + γ, α 0 και είδαμε ότι η γραφική της παράσταση είναι μία
Γενικής Παιδείας 1.4 Εφαρμογές των παραγώγων Το κριτήριο της πρώτης παραγώγου Στην Άλγεβρα της Α Λυκείου μελετήσαμε τη συνάρτηση f(x) = αx + βx + γ, α 0 και είδαμε ότι η γραφική της παράσταση είναι μία
Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β.
 Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
7. Αν υψώσουμε και τα δύο μέλη μιας εξίσωσης στον κύβο (και γενικά σε οποιαδήποτε περιττή δύναμη), τότε προκύπτει
 8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
ΣΥΝΑΡΤΗΣΕΩΝ. f3 x = και
 7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
Φίλη μαθήτρια, φίλε μαθητή,
 Φίλη μαθήτρια, φίλε μαθητή, Το βιβλίο αυτό, εναρμονισμένο με την πρόσφατα καθορισμένη ύλη, απευθύνεται στους μαθητές της Γ Λυκείου που έχουν επιλέξει τον προσανατολισμό Θετικών Σπουδών ή Σπουδών Πληροφορικής
Φίλη μαθήτρια, φίλε μαθητή, Το βιβλίο αυτό, εναρμονισμένο με την πρόσφατα καθορισμένη ύλη, απευθύνεται στους μαθητές της Γ Λυκείου που έχουν επιλέξει τον προσανατολισμό Θετικών Σπουδών ή Σπουδών Πληροφορικής
sin(5x 2 ) sin(4x) e 5t 2 1 (ii) lim x 0 10x 3 (iii) lim (iv) lim. 10t sin(ax) = 1. = 1 1 a lim = sin(5x2 ) = 2. f (x) = sin x. = e5t 1 = 1 0 = 0.
 ΑΣΚΗΣΕΙΣ ΑΠΕΙΡΟΣΤΙΚΟΥ ΛΟΓΙΣΜΟΥ Ι, Φυλλάδιο 3 Λύσεις Ασκήσεων. Να υπολογίσετε τα παρακάτω όρια. sia) i) ποιες συνθήκες πρέπει να ισχύουν για τα a, β ώστε να έχει νόημα το όριο;) 0 siβ) si5 ) si4) cos cos
ΑΣΚΗΣΕΙΣ ΑΠΕΙΡΟΣΤΙΚΟΥ ΛΟΓΙΣΜΟΥ Ι, Φυλλάδιο 3 Λύσεις Ασκήσεων. Να υπολογίσετε τα παρακάτω όρια. sia) i) ποιες συνθήκες πρέπει να ισχύουν για τα a, β ώστε να έχει νόημα το όριο;) 0 siβ) si5 ) si4) cos cos
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΟΙ πιο πάνω έννοιες εκφράζουν όπως λέμε τη μονοτονία της συνάρτησης.
 3 Μονοτονία συναρτήσεων 3 Μονοτονία συναρτήσεων 3Α Μονοτονία συνάρτησης Έστω f μία συνάρτηση με πεδίο ορισμού Γνησίως αύξουσα συνάρτηση Η συνάρτηση f λέγεται γνησίως αύξουσα στο Δ αν για κάθε, Δ, με
3 Μονοτονία συναρτήσεων 3 Μονοτονία συναρτήσεων 3Α Μονοτονία συνάρτησης Έστω f μία συνάρτηση με πεδίο ορισμού Γνησίως αύξουσα συνάρτηση Η συνάρτηση f λέγεται γνησίως αύξουσα στο Δ αν για κάθε, Δ, με
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
ΑΝΑΛΥΣΗ 1 ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, 15-10-13 Μ. Παπαδημητράκης. 1 Παράδειγμα. Ως εφαρμογή της Αρχιμήδειας Ιδιότητας θα μελετήσουμε το σύνολο { 1 } A = n N = {1, 1 n 2, 1 } 3,.... Κατ αρχάς το σύνολο A έχει προφανώς
ΑΝΑΛΥΣΗ 1 ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, 15-10-13 Μ. Παπαδημητράκης. 1 Παράδειγμα. Ως εφαρμογή της Αρχιμήδειας Ιδιότητας θα μελετήσουμε το σύνολο { 1 } A = n N = {1, 1 n 2, 1 } 3,.... Κατ αρχάς το σύνολο A έχει προφανώς
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, 6-12-13 Μ. Παπαδημητράκης. 1 Τώρα θα δούμε την απόδειξη του Θεωρήματος που διατυπώσαμε στο τέλος του προηγούμενου μαθήματος. Απόδειξη. [α] Θεωρούμε συνάρτηση f : A R και
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, 6-12-13 Μ. Παπαδημητράκης. 1 Τώρα θα δούμε την απόδειξη του Θεωρήματος που διατυπώσαμε στο τέλος του προηγούμενου μαθήματος. Απόδειξη. [α] Θεωρούμε συνάρτηση f : A R και
Κεφάλαιο 4: Διαφορικός Λογισμός
 ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 8. Πότε το γινόμενο δύο ή περισσοτέρων αριθμών παραγόντων είναι ίσο με το μηδέν ;
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ B ΛΥΚΕΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ B ΛΥΚΕΙΟΥ 1 ln 4 i Να βρείτε το πεδίο ορισμού της ii Να δείξετε ότι η παραπάνω συνάρτηση γράφεται: ln iii Να λύσετε την εξίσωση ln 5 ln 3 4 a a1 4,, a i Να βρείτε τον αριθμό
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ B ΛΥΚΕΙΟΥ 1 ln 4 i Να βρείτε το πεδίο ορισμού της ii Να δείξετε ότι η παραπάνω συνάρτηση γράφεται: ln iii Να λύσετε την εξίσωση ln 5 ln 3 4 a a1 4,, a i Να βρείτε τον αριθμό
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α. , έχει κατακόρυφη ασύμπτωτη την x 0.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ
 ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ 9η Κατηγορία: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Για να βρούμε τη μονοτονία μιας συνάρτησης ακολουθούμε την εξής διαδικασία: Θεωρούμε, Δ, όπου Δ διάστημα του πεδίου ορισμού
ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ 9η Κατηγορία: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Για να βρούμε τη μονοτονία μιας συνάρτησης ακολουθούμε την εξής διαδικασία: Θεωρούμε, Δ, όπου Δ διάστημα του πεδίου ορισμού
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: 5 Φεβρουαρίου 008 Ημερομηνία παράδοσης της Εργασίας: 4 Μαρτίου 008
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 4 η Ημερομηνία Αποστολής στον Φοιτητή: 5 Φεβρουαρίου 008 Ημερομηνία παράδοσης της Εργασίας: 4 Μαρτίου 008
ΜΑΘΗΜΑ 14 1.3 ΜΟΝΟΤΟΝΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΜΑΘΗΜΑ 4. ΜΟΝΟΤΟΝΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ Μονοτονία συνάρτησης Ακρότατα συνάρτησης Θεωρία Σχόλια Μέθοδοι Ασκήσεις ΘΕΩΡΙΑ. Ορισµός Συνάρτηση f λέγεται γνησίως αύξουσα σε διάστηµα, όταν για οποιαδήποτε,
ΜΑΘΗΜΑ 4. ΜΟΝΟΤΟΝΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ Μονοτονία συνάρτησης Ακρότατα συνάρτησης Θεωρία Σχόλια Μέθοδοι Ασκήσεις ΘΕΩΡΙΑ. Ορισµός Συνάρτηση f λέγεται γνησίως αύξουσα σε διάστηµα, όταν για οποιαδήποτε,
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ
 1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Για να μελετήσουμε και να χαράξουμε τη γραφική παράταση μιας συνάρτησης ακολουθούμε τα παρακάτω βήματα: 1. Βρίσκουμε το πεδίο ορισμού της.. Εξετάζουμε την
ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Για να μελετήσουμε και να χαράξουμε τη γραφική παράταση μιας συνάρτησης ακολουθούμε τα παρακάτω βήματα: 1. Βρίσκουμε το πεδίο ορισμού της.. Εξετάζουμε την
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών... 37 3.1 Αριθμητικά σύνολα... 37 3.2 Ιδιότητες... 37 3.3 Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
Μονοτονία - Ακρότατα - 1 1 Αντίστροφη Συνάρτηση
 4 Μονοτονία - Ακρότατα - Αντίστροφη Συνάρτηση Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Μονοτονία συνάρτησης Μια συνάρτηση f λέγεται: Γνησίως αύξουσα σ' ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε,
4 Μονοτονία - Ακρότατα - Αντίστροφη Συνάρτηση Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Μονοτονία συνάρτησης Μια συνάρτηση f λέγεται: Γνησίως αύξουσα σ' ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε,
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ
 ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
APEIROSTIKOS LOGISMOS I
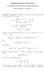 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών Αριθμητικά σύνολα Ιδιότητες Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ & ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ ΜΑΘΗΜΑΤΙΚΟΣ
 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ & ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ ΜΑΘΗΜΑΤΙΚΟΣ . ΣΥΝΟΛΑ ΑΡΙΘΜΩΝ Τα σύνολα των αριθμών είναι τα εξής : i. Φυσικοί αριθμοί : 0,,,,......,,,,0,,,,...
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ & ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ ΜΑΘΗΜΑΤΙΚΟΣ . ΣΥΝΟΛΑ ΑΡΙΘΜΩΝ Τα σύνολα των αριθμών είναι τα εξής : i. Φυσικοί αριθμοί : 0,,,,......,,,,0,,,,...
< και δεδομένου ότι η f είναι γνησίως μονότονη, συμπεραίνουμε ότι
 _1696 α) f ( 5) = f ( 4) = 9 Αφού
_1696 α) f ( 5) = f ( 4) = 9 Αφού
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
αβ (, ) τέτοιος ώστε f(x
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΘΕΜΑ Α Άσκηση α) Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ αβ., ] Αν η f είναι συνεχής στο [ αβ, ]
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΘΕΜΑ Α Άσκηση α) Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ αβ., ] Αν η f είναι συνεχής στο [ αβ, ]
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου]. ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].](/thumbs/52/29746903.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
Γιώργος Καριπίδης-Ανθούλα Σοφιανοπούλου ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΑ ΟΡΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Γιώργος Καριπίδης-Ανθούλα Σοφιανοπούλου ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΑ ΟΡΙΑ ΣΥΝΑΡΤΗΣΗΣ ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ του ορίου συνάρτησης όταν χ χ Για να έχει νόημα το όριο συνάρτησης f με πεδίο
Γιώργος Καριπίδης-Ανθούλα Σοφιανοπούλου ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΑ ΟΡΙΑ ΣΥΝΑΡΤΗΣΗΣ ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ του ορίου συνάρτησης όταν χ χ Για να έχει νόημα το όριο συνάρτησης f με πεδίο
ΜΙΓΑ ΙΚΟΙ. 3. Για κάθε z 1, z 2 C ισχύει z1 + z2 = z1 + z2. 4. Για κάθε z C ισχύει z z 2 z. 5. Για κάθε µιγαδικό z ισχύει: 6.
 ΜΙΓΑ ΙΚΟΙ 1 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 1 2 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 3 Για κάθε z 1, z 2 C ισχύει z1 + z2 = z1 + z2 4 Για κάθε z C ισχύει z z 2 z 5 Για κάθε µιγαδικό z ισχύει:
ΜΙΓΑ ΙΚΟΙ 1 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 1 2 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 3 Για κάθε z 1, z 2 C ισχύει z1 + z2 = z1 + z2 4 Για κάθε z C ισχύει z z 2 z 5 Για κάθε µιγαδικό z ισχύει:
Περιεχόμενα μεθόδευση του μαθήματος
 Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
V. Διαφορικός Λογισμός. math-gr
 V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
ΚΑΡΑΓΙΑΝΝΗΣ ΙΩΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών Μ Α Θ Η Μ Α Τ Ι Κ Α
 ΚΑΡΑΓΙΑΝΝΗΣ ΙΩΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών Μ Α Θ Η Μ Α Τ Ι Κ Α ΜΑΘΗΜΑΤΑ Π Ρ Ο Σ Α Ν Α Τ Ο Λ Ι Σ Μ Ο Υ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν, ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΣΥΝΑΡΤΗΣΕΙΣ
ΚΑΡΑΓΙΑΝΝΗΣ ΙΩΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών Μ Α Θ Η Μ Α Τ Ι Κ Α ΜΑΘΗΜΑΤΑ Π Ρ Ο Σ Α Ν Α Τ Ο Λ Ι Σ Μ Ο Υ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν, ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΣΥΝΑΡΤΗΣΕΙΣ
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ, 28--3 Μ. Παπαδημητράκης. ΚΡΙΤΗΡΙΟ ΑΠΟΛΥΤΗΣ ΣΥΓΚΛΙΣΗΣ. Αν η σειρά + = x συγκλίνει απολύτως, τότε συγκλίνει και + x x. = = Δεν θα παρουσιάσω την απόδειξη. Διαβάστε την στο βιβλίο.
ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ, 28--3 Μ. Παπαδημητράκης. ΚΡΙΤΗΡΙΟ ΑΠΟΛΥΤΗΣ ΣΥΓΚΛΙΣΗΣ. Αν η σειρά + = x συγκλίνει απολύτως, τότε συγκλίνει και + x x. = = Δεν θα παρουσιάσω την απόδειξη. Διαβάστε την στο βιβλίο.
Πραγματικές συναρτήσεις πραγματικής μεταβλητής
 ΚΕΦΑΛΑΙΟ Πραγματικές συναρτήσεις πραγματικής μεταβλητής Δεν υπάρχει πρόβλημα που δεν μπορεί να επιλυθεί François Viète (540-603) Υπάρχει το πρόβλημα, αναζητήστε τη λύση του, η ορθότητα των προτάσεων είναι
ΚΕΦΑΛΑΙΟ Πραγματικές συναρτήσεις πραγματικής μεταβλητής Δεν υπάρχει πρόβλημα που δεν μπορεί να επιλυθεί François Viète (540-603) Υπάρχει το πρόβλημα, αναζητήστε τη λύση του, η ορθότητα των προτάσεων είναι
ΣΗΜΕΙΩΣΕΙΣ. f (x) =, x 0, (1), x. lim f (x) = lim = +. x
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 2.9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ ΑΣΥΜΠΤΩΤΕΣ-ΚΑΝΟΝΑΣ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 2.9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ ΑΣΥΜΠΤΩΤΕΣ-ΚΑΝΟΝΑΣ
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. Γεώργιος Α. Κόλλιας - μαθηματικός. 150 ασκήσεις επανάληψης. και. Θέματα εξετάσεων
 Γεώργιος Α. Κόλλιας - μαθηματικός Περιέχονται 50 συνδυαστικές ασκήσεις επανάληψης και θέματα εξετάσεων. Δεν συμπεριλαμβάνεται το κεφάλαιο των πιθανοτήτων, της γεωμετρικής προόδου, της μονοτονίας συνάρτησης,
Γεώργιος Α. Κόλλιας - μαθηματικός Περιέχονται 50 συνδυαστικές ασκήσεις επανάληψης και θέματα εξετάσεων. Δεν συμπεριλαμβάνεται το κεφάλαιο των πιθανοτήτων, της γεωμετρικής προόδου, της μονοτονίας συνάρτησης,
Ακολουθίες & Σειρές. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ακολουθίες, Σειρές, Δυναμοσειρές. τεχνικές.
 Ακολουθίες & Σειρές Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ακολουθίες Σειρές Δυναμοσειρές τεχνικές 0 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / / 0 9 εκδόσεις Καλό
Ακολουθίες & Σειρές Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ακολουθίες Σειρές Δυναμοσειρές τεχνικές 0 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / / 0 9 εκδόσεις Καλό
2.1 ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ
 ΚΕΦΑΛΑΙΟ : ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ Ρητός ονομάζεται κάθε αριθμός που έχει ή μπορεί να πάρει τη μορφή κλάσματος, όπου, είναι ακέραιοι με 0. Ρητοί αριθμοί : Q /, 0. Έτσι π.χ.
ΚΕΦΑΛΑΙΟ : ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ Ρητός ονομάζεται κάθε αριθμός που έχει ή μπορεί να πάρει τη μορφή κλάσματος, όπου, είναι ακέραιοι με 0. Ρητοί αριθμοί : Q /, 0. Έτσι π.χ.
ΑΝΑΛΥΣΗ 1 ΣΕ 39 ΜΑΘΗΜΑΤΑ
 ΑΝΑΛΥΣΗ ΣΕ 39 ΜΑΘΗΜΑΤΑ Μ. Παπαδημητράκης. ΠΡΩΤΟ ΜΑΘΗΜΑ Κατ αρχάς θα δούμε μια πολλή απλή πρόταση. l 0xx x x ΠΡΟΤΑΣΗ. Έστω ότι ο l έχει την εξής ιδιότητα: l x για κάθε x > 0. Τότε l 0. Απόδειξη. Για να
ΑΝΑΛΥΣΗ ΣΕ 39 ΜΑΘΗΜΑΤΑ Μ. Παπαδημητράκης. ΠΡΩΤΟ ΜΑΘΗΜΑ Κατ αρχάς θα δούμε μια πολλή απλή πρόταση. l 0xx x x ΠΡΟΤΑΣΗ. Έστω ότι ο l έχει την εξής ιδιότητα: l x για κάθε x > 0. Τότε l 0. Απόδειξη. Για να
Ακουλουθίες ρ. Κωνσταντίνα Παναγιωτίδου
 Ακουλουθίες ρ. Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Μονοτονία Ακολουθίας Φραγµένη Ακολουθία Υπακολουθίες Σύγκλιση - Απόκλιση Ακολουθιών N = {1, 2,
Ακουλουθίες ρ. Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Μονοτονία Ακολουθίας Φραγµένη Ακολουθία Υπακολουθίες Σύγκλιση - Απόκλιση Ακολουθιών N = {1, 2,
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5
 Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
Κεφάλαιο 2 ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012) Τμήμα Θ. Αποστολάτου & Π. Ιωάννου 1 Σειρές O Ζήνων ο Ελεάτης (490-430 π.χ.) στη προσπάθειά του να υποστηρίξει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012) Τμήμα Θ. Αποστολάτου & Π. Ιωάννου 1 Σειρές O Ζήνων ο Ελεάτης (490-430 π.χ.) στη προσπάθειά του να υποστηρίξει
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες
 Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
ΑΝΑΛΥΣΗ 1 ΕΝΑΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΕΝΑΤΟ ΜΑΘΗΜΑ, 5-10-13 Μ. Παπαδημητράκης. 1 Τώρα θα μιλήσουμε για την έννοια της περιοχής, η οποία έχει κεντρικό ρόλο στη μελέτη της έννοιας του ορίου (ακολουθίας και συνάρτησης). Αν > 0, ονομάζουμε
ΑΝΑΛΥΣΗ 1 ΕΝΑΤΟ ΜΑΘΗΜΑ, 5-10-13 Μ. Παπαδημητράκης. 1 Τώρα θα μιλήσουμε για την έννοια της περιοχής, η οποία έχει κεντρικό ρόλο στη μελέτη της έννοιας του ορίου (ακολουθίας και συνάρτησης). Αν > 0, ονομάζουμε
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
13 Μονοτονία Ακρότατα συνάρτησης
 3 Μονοτονία Ακρότατα συνάρτησης Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σ ένα διάστημα Δ, τότε: Αν f ( ) > 0για κάθε εσωτερικό του Δ, η f είναι γνησίως αύξουσα στο Δ. Αν
3 Μονοτονία Ακρότατα συνάρτησης Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σ ένα διάστημα Δ, τότε: Αν f ( ) > 0για κάθε εσωτερικό του Δ, η f είναι γνησίως αύξουσα στο Δ. Αν
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ. Να εξετάσετε αν είναι ίσες οι συναρτήσεις f, g όταν: x x 2 x x. x x g x. ln x ln x 1 και
 Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
