ΠΑΝΔΠΙΣΗΜΙΟ ΠΔΙΡΑΙΑ ΣΜΗΜΑ ΣΑΣΙΣΙΚΗ ΚΑΙ ΑΦΑΛΙΣΙΚΗ ΔΠΙΣΗΜΗ ΜΔΣΑΠΣΤΥΙΑΚΗ ΔΡΓΑΙΑ
|
|
|
- Βασίλης Ζερβός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΔΠΙΣΗΜΙΟ ΠΔΙΡΑΙΑ ΣΜΗΜΑ ΣΑΣΙΣΙΚΗ ΚΑΙ ΑΦΑΛΙΣΙΚΗ ΔΠΙΣΗΜΗ ΜΔΣΑΠΣΤΥΙΑΚΗ ΔΡΓΑΙΑ Πξνζδηνξηζηηθνί παξάγνληεο δηαρξνληθά κεηαβαιιόκελνπ ζπζηεκαηηθνύ θηλδύλνπ (βήηα). Η πεξίπησζε ηεο Διιάδαο θαη ηεο Κύπξνπ. Μαξία Γεκεηξίνπ (ΜΑΔ921) ΔΞΔΣΑΣΙΚΗ ΔΠΙΣΡΟΠΗ Μ. Γθιεδάθνο (Καζεγεηήο) Α. Παλνπνύινπ (Δπηθ. Καζεγήηξηα) Δπηβιέπνπζα. Βξόληνο (Λέθηνξαο) ΠΔΙΡΑΙΑ Γεθέκβξηνο 211
2 Δπραξηζηώ, Σελ επηβιέπνπζα θαζεγήηξηά κνπ γηα ηε ζπλεξγαζία, ηε γλώζε θαη ηελ πνιύηηκε θαζνδήγεζή ηεο. Σελ νηθνγέλεηά κνπ. 1
3 ΠΔΡΙΔΥΟΜΔΝΑ ΔΗΑΓΩΓΖ... 3 ΚΔΦΑΛΑΗΟ 1: ΣΟ ΤΠΟΓΔΗΓΜΑ ΣΗΜΟΛΟΓΖΖ ΠΔΡΗΟΤΗΑΚΩΝ ΣΟΗΥΔΗΩΝ (Capital Asset Pricing Model CAPM) Γεληθά Τπνζέζεηο ηνπ CAPM Δμίζσζε CAPM πληειεζηήο beta θαη CAPM ΚΔΦΑΛΑΗΟ 2: MULTIVARIATE ΜΟΝΣΔΛΑ ΓΗΑΚΤΜΑΝΖ πληειεζηήο beta κέζσ CAPM Μνληέια ARCH(p), GARCH(p, q) Σν κνληέιν ΒΔΚΚ-GARCH(1, 1) ΚΔΦΑΛΑΗΟ 3: ΔΚΣΗΜΖΖ ΓΗΑΥΡΟΝΗΚΑ ΜΔΣΑΒΑΛΛΟΜΔΝΟΤ ΤΣΖΜΑΣΗΚΟΤ ΚΗΝΓΤΝΟΤ Δ ΔΛΛΑΓΑ & ΚΤΠΡΟ Πεξηγξαθή Γεδνκέλσλ Πεξίπησζε Διιάδαο Υξνληθή εμέιημε ησλ θιαδηθώλ δεηθηώλ θαη ηεο αγνξάο Πεξηγξαθηθά ζηαηηζηηθά απνηειέζκαηα ηεο απόδνζεο ησλ θιαδηθώλ δεηθηώλ Δθηίκεζε ζπληειεζηή beta Δβδνκαδηαία αλάιπζε απνδόζεσλ Πεξίπησζε Κύπξνπ Υξνληθή εμέιημε ησλ θιαδηθώλ δεηθηώλ θαη ηεο αγνξάο Πεξηγξαθηθά ζηαηηζηηθά απνηειέζκαηα ηεο απόδνζεο ησλ θιαδηθώλ δεηθηώλ Δθηίκεζε ζπληειεζηή beta Δβδνκαδηαία αλάιπζε απνδόζεσλ πθξηηηθή αμηνιόγεζε Διιάδαο - Κύπξνπ...75 ΚΔΦΑΛΑΗΟ 4 : ΠΡΟΓΗΟΡΗΣΗΚΟΗ ΠΑΡΑΓΟΝΣΔ Δηζαγσγή Μεζνδνινγία Πεξίπησζε Διιάδαο Γεδνκέλα καθξάο δηάξθεηαο Γεδνκέλα κηθξήο δηάξθεηαο Πεξίπησζε Κύπξνπ ΓΔΝΗΚΑ ΤΜΠΔΡΑΜΑΣΑ ΒΗΒΛΗΟΓΡΑΦΗΑ
4 ΔΙΑΓΩΓΗ Ζ εξγαζία κειεηά ην δηαρξνληθά κεηαβαιιόκελν ζπζηεκαηηθό θίλδπλν βήηα (beta) κέζσ ηνπ ππνδείγκαηνο BEKK-GARCH(1,1) θαη πξαγκαηεύεηαη πξνζδηνξηζηηθνύο παξάγνληεο πνπ ην επεξεάδνπλ. πγθεθξηκέλα εζηηάδεηαη ζηελ πεξίπησζε Διιάδαο θαη Κύπξνπ. ην θεθάιαην 1 γίλεηαη κηα αλαθνξά ζην ππόδεηγκα ηηκνιόγεζεο πεξηνπζηαθώλ ζηνηρείσλ (CAPM), δίλεηαη ε εμίζσζή ηνπ θαη ζρνιηάδεηαη ν ζπληειεζηήο beta. ην θεθάιαην 2 εηζάγνληαη ηα multivariate κνληέια δηαθύκαλζεο. ηε ζπλέρεηα γίλεηαη εθηελή αλαθνξά ζην bivariate κνληέιν BEKK πνπ ρξεζηκνπνηείηαη ζηε παξνύζα εξγαζία. ην θεθάιαην 3 αλαιύνληαη κε ην EVIEWS ηα δεδνκέλα νθηώ Διιεληθώλ θαη νθηώ Κππξηαθώλ θιαδηθώλ δεηθηώλ. ην θεθάιαην 4 γίλεηαη κηα πξνζπάζεηα λα κειεηεζνύλ θάπνηνη πξνζδηνξηζηηθνί παξάγνληεο πνπ επηδξνύλ ζηε δηακόξθσζε ηνπ ζπληειεζηή βήηα. Σέινο δίλνληαη ηα ζπκπεξάζκαηα ηεο εξγαζίαο θαη θαηεπζύλζεηο πξνο κειινληηθή έξεπλα. 3
5 ΚΔΦΑΛΑΙΟ 1 ΣΟ ΤΠΟΓΔΙΓΜΑ ΣΙΜΟΛΟΓΗΗ ΠΔΡΙΟΤΙΑΚΩΝ ΣΟΙΥΔΙΩΝ (Capital Asset Pricing Model CAPM) 1.1 Γεληθά Σν ππόδεηγκα CAPM απνηειεί έλα ζεη πξνβιέςεσλ ζε ό,ηη αθνξά ζηηο ηζνξξνπίεο κεηαμύ ησλ πξνζδνθώκελσλ απνδόζεσλ θαη θηλδύλνπ. Με ην CAPM κπνξεί λα δνζεί αθξηβή απάληεζε ζην εξώηεκα «πόζε απόδνζε απαηηείηαη γηα λα αληηζηαζκίζεη δεδνκέλν επίπεδν θηλδύλνπ;». Ζ ηππηθή ηνπ κνξθή αλαπηύρζεθε αλεμάξηεηα από ηνπο Sharpe (1964), Lintner (1965) θαη Mossin (1966) εμειίζζνληαο ηελ εξγαζία ηνπ Markowitz (1952) θαη απνηειεί ηελ πξώηε γεληθή ζρέζε ηζνξξνπίαο γηα ηελ απόδνζε πεξηνπζηαθώλ ζηνηρείσλ. πρλά αλαθέξεηαη σο κνξθή Sharpe-Lintner-Mossin γηα ην ππόδεηγκα απνηίκεζεο πεξηνπζηαθώλ ζηνηρείσλ ησλ θεθαιαίσλ. Σν κνληέιν έρεη αλαπηπρζεί κε κηα πνηθηιία κνξθώλ πνπ πεξηιακβάλνπλ δηαθνξεηηθό βαζκό απζηεξόηεηαο θαη καζεκαηηθήο πνιππινθόηεηαο. ηε ζπλέρεηα αλαπηύζζνπκε ηελ εμίζσζε ηνπ standard CAPM (γλσζηό θαη σο CAPM ελόο παξάγνληα) (Elton and Gruber (1995), chapter 13). 1.2 Τπνζέζεηο ηνπ CAPM Σν CAPM βαζίδεηαη ζηελ πην απζηεξή δέζκε πεξηνξηζκώλ πνπ ζε πνιιέο πεξηπηώζεηο δελ αληαπνθξίλνληαη ζηελ πξαγκαηηθόηεηα. Παξ όια απηά θαη πέξαλ ηεο απιόηεηάο ηνπ, ην κνληέιν έρεη δείμεη όηη πεξηγξάθεη αξθεηά θαιά ηηο ηηκέο ζηηο αγνξέο θεθαιαίνπ. Οη ππνζέζεηο ζηηο νπνίεο βαζίδεηαη είλαη νη αθόινπζεο: 1) Γελ ππάξρνπλ έμνδα ζπλαιιαγήο. Γειαδή, δελ ππάξρεη θόζηνο, ζηελ αγνξά ή πώιεζε νπνηνπδήπνηε πεξηνπζηαθνύ ζηνηρείνπ. Σν θόζηνο ζπλαιιαγώλ ζα αύμαλε ηελ πνιππινθόηεηα ηνπ κνληέινπ, θαζώο ε απόδνζε νπνηνπδήπνηε πεξηνπζηαθνύ ζηνηρείνπ ζα ήηαλ ζπλάξηεζε ηνπ θαηά πόζνλ ή όρη ν επελδπηήο θαηείρε ην πεξηνπζηαθό ζηνηρείν πξηλ από ηελ πεξίνδν απόθαζεο. Σπρόλ εηζαγσγή ηνπ θόζηνπο ζπλαιιαγώλ εμαξηάηαη από ηε ζεκαζία ηνπ ζηηο απνθάζεηο ησλ επελδπηώλ. Γεδνκέλνπ ηνπ κεγέζνπο ηνπ, ε ζεκαζία ηνπ κπνξεί λα ζεσξεζεί ακειεηέα. 2) Σα πεξηνπζηαθά ζηνηρεία είλαη απείξσο δηαηξεηά. Απηό ζεκαίλεη όηη νη επελδπηέο ζα κπνξνύζαλ λα ιάβνπλ νπνηαδήπνηε ζέζε ζε κηα επέλδπζε, αλεμάξηεηα από ην κέγεζνο ηνπ πινύηνπ ηνπο. Γηα παξάδεηγκα, έλαο επελδπηήο κπνξεί λα αγνξάζεη κεηνρή ηεο ΗΒΜ αμίαο ελόο δνιαξίνπ. 4
6 3) Απνπζία θόξνπ εηζνδήκαηνο θπζηθώλ πξνζώπσλ. Απηό ζεκαίλεη, γηα παξάδεηγκα, όηη ην άηνκν δελ ελδηαθέξεηαη γηα ηε κνξθή (κεξίζκαηα ή θέξδε θεθαιαίσλ), κε ηελ νπνία ιακβάλεηαη ε απόδνζε ηεο επέλδπζεο. 4) Έλα άηνκν δελ κπνξεί λα επεξεάζεη ηελ ηηκή κηαο κεηνρήο πξνβαίλνληαο ζηελ αγνξά ή πώιεζή ηεο. Απηό είλαη αλάινγν κε ηελ ππόζεζε ηνπ ηέιεηνπ αληαγσληζκνύ. Παξ όιν πνπ θαλέλαο κεκνλσκέλνο επελδπηήο δελ κπνξεί λα επεξεάζεη ηηο ηηκέο από κηα κεκνλσκέλε δξάζε, νη ηηκέο θαζoξίδνληαη από ηηο πξάμεηο ησλ επελδπηώλ ζην ζύλνιό ηνπο. 5) Οη επελδπηέο επηιέγνπλ ραξηνθπιάθην κε γλώκνλα ηε κεγηζηνπνίεζε ηεο ζρέζεο ηεο πξνζδνθώκελεο απόδνζεο θαη δηαθύκαλζεο (θίλδπλνο) όπσο θαη ε ζεσξία ηνπ Markowitz. 6) Δπηηξέπνληαη απεξηόξηζηεο αλνηρηέο πσιήζεηο (short-selling). Ο κεκνλσκέλνο επελδπηήο κπνξεί λα πσιήζεη αλνηρηά νπνηνδήπνηε πνζό νπνηνλδήπνηε κεηνρώλ. 7) Απεξηόξηζηε δαλεηνδόηεζε θαη δαλεηνιεςία ζε αθίλδπλν επηηόθην. Ο επελδπηήο κπνξεί λα δαλείδεη ή λα δαλείδεηαη νπνηνδήπνηε πνζόηεηα θεθαιαίσλ επηζπκεί κε επηηόθην ίζν κε απηό ηεο επέλδπζεο αθίλδπλσλ ρξενγξάθσλ. 8) Οη επελδπηέο έρνπλ νκνηνγελείο πξνζδνθίεο. Όινη νη επελδπηέο έρνπλ ηηο ίδηεο εθηηκήζεηο γηα ηηο αλακελόκελεο απνδόζεηο, δηαθπκάλζεηο (θίλδπλνο) θαη ζπζρεηίζεηο κεηαμύ ησλ απνδόζεσλ όισλ ησλ πεξηνπζηαθώλ ζηνηρείσλ. 9) Όινη νη επελδπηέο έρνπλ ηνλ ίδην επελδπηηθό ρξνληθό νξίδνληα. Δπίζεο ε πιεξνθόξεζή ηνπο ζεσξείηαη άκεζε θαη ρσξίο θόζηνο. Απηή ε ππόζεζε έρεη λα θάλεη νπζηαζηηθά κε ηνλ νξηζκό ηεο απνηειεζκαηηθόηεηαο ηεο αγνξάο. 1) Όια ηα πεξηνπζηαθά ζηνηρεία είλαη ξεπζηνπνηήζηκα. Όια ηα πεξηνπζηαθά ζηνηρεία, ζπκπεξηιακβαλνκέλσλ ηνπ αλζξώπηλνπ θεθαιαίνπ, κπνξνύλ λα πσινύληαη θαη λα αγνξάδνληαη ζηελ αγνξά. 1.3 Δμίζσζε CAPM ηελ πεξίπησζε παξνπζίαο αλνηρηώλ πσιήζεσλ, αιιά ρσξίο δπλαηόηεηα ρνξήγεζεο θαη ιήςεο δαλείσλ, θάζε επελδπηήο γηα ηελ επηινγή ραξηνθπιαθίνπ κε θίλδπλν αληηκεησπίδεη έλα απνηειεζκαηηθό ζύλνξν, όπσο απηό θαίλεηαη ζην ζρήκα
7 Πξνζδνθώκελε απόδνζε E(Ri) Δ Ε Ζ Γ Γ Β Α Σππηθή απόθιηζε σ (θίλδπλνο) ρήκα 1.1: Κακπύιε απνηειεζκαηηθώλ ραξηνθπιαθίσλ Ζ θακπύιε ΑΒΖ αληηπξνζσπεύεη ην ζύλνιν ησλ ραξηνθπιαθίσλ κε ηελ ειάρηζηε δηαζπνξά. Σν ηκήκα ΒΖ θαιείηαη θακπύιε ή ζύλνξν απνηειεζκαηηθώλ ραξηνθπιαθίσλ (efficient frontier) θαη απνηειεί ην αλώηεξν ηκήκα όισλ ησλ ζπλδπαζκώλ ραξηνθπιαθίσλ. Γηα ηα ραξηνθπιάθηα πάλσ ζην ζύλνξν, ηα νπνία είλαη αλώηεξα απηώλ πνπ βξίζθνληαη ζην εζσηεξηθό ηεο θακπύιεο, είλαη γλσζηέο νη κεηνρέο πνπ ηα απαξηίδνπλ, θαζώο θαη ην πνζνζηό ζπκκεηνρήο θάζε κεηνρήο ζηελ αμία ηνπ ραξηνθπιαθίνπ. Υαξηνθπιάθηα ζην εμσηεξηθό άλσ κέξνο ηνπ ζπλόξνπ είλαη αδύλαηνλ λα δεκηνπξγεζνύλ κε βάζε ηηο δπλαηόηεηεο ηεο αγνξάο. Γεληθά, ηα απνηειεζκαηηθά ζύλνξα ζα δηαθέξνπλ κεηαμύ ησλ επελδπηώλ, ιόγσ ησλ δηαθνξεηηθώλ πξνζδνθηώλ ησλ ηειεπηαίσλ. ηελ πεξίπησζε πνπ επηηξέπεηαη ε ρνξήγεζε θαη ιήςε δαλείσλ κε αθίλδπλν επηηόθην, κπνξεί λα ζπλδπαζηεί έλα από ηα ραξηνθπιάθηα ηνπ ζπλόξνπ απνηειεζκαηηθώλ ραξηνθπιαθίσλ κε κηα επέλδπζε κεδεληθνύ θόζηνπο, γηα παξάδεηγκα βξαρππξόζεζκα έληνθα γξακκάηηα δεκνζίνπ. Έζησ R f ην επηηόθην ηεο επέλδπζεο ρσξίο θίλδπλν (risk free rate), ηόηε ην άξηζην ραξηνθπιάθην είλαη απηό πνπ αληηζηνηρεί ζην ζεκείν P i, πνπ ζηελ πξάμε απνηειεί ην ραξηνθπιάθην ηεο αγνξάο. Σν ραξηνθπιάθην ηεο αγνξάο είλαη απηό πνπ δηαζέηεη ηηο κεηνρέο ηνπ γεληθνύ δείθηε θαηά ην πνζνζηό πνπ απηέο ζπκκεηέρνπλ ζε απηόλ. Σν ζεκείν απηό αληηζηνηρεί ζην ζεκείν επαθήο ηεο επζείαο πνπ μεθηλά από ηελ απόδνζε R f θαη εθάπηεηαη κε ην ζύλνξν ησλ απνηειεζκαηηθώλ ραξηνθπιαθίσλ, όπσο απεηθνλίδεηαη ζην ζρήκα
8 Πξνζδνθώκελε απόδνζε E(Ri) Ε(R i ) P i R f Β σ i Σππηθή απόθιηζε σ (θίλδπλνο) ρήκα 1.2: Γξακκή θεθαιαηαγνξάο Ζ επηινγή ηνπ ραξηνθπιαθίνπ P i έγθεηηαη ζην όηη απηό ζπλδπαδόκελν κε κηα επέλδπζε κεδεληθνύ θηλδύλνπ παξνπζηάδεη ηε κεγαιύηεξε πξνζδνθώκελε απόδνζε γηα ηνλ ίδην βαζκό θηλδύλνπ, ζπγθξηλόκελν κε ηα ππόινηπα ραξηνθπιάθηα ηνπ ζπλόξνπ απνηειεζκαηηθώλ ραξηνθπιαθίσλ. Με άιια ιόγηα, ην κεηνρηθό ραξηνθπιάθην P i έρεη ηνλ πςειόηεξν δείθηε αληακνηβήο θηλδύλνπ πνπ είλαη ίζνο κε ην ιόγν (θιίζε ηεο επζείαο): E ( R i ) R i f. Ζ επζεία γξακκή ηνπ ζρήκαηνο 1.2 θαιείηαη γξακκή θεθαιαηαγνξάο (capital market line, CML) θαη δελ πεξλά από ηελ αξρή ησλ αμόλσλ, αιιά ηέκλεη ηνλ θάζεην άμνλα ησλ απνδόζεσλ ζην ζεκείν R f πνπ παξηζηάλεη ηελ απόδνζε ηεο επέλδπζεο ρσξίο θίλδπλν. Σα απνηειεζκαηηθά ραξηνθπιάθηα επί ηεο γξακκήο παξηζηάλνπλ ελαιιαθηηθνύο ζπλδπαζκνύο θηλδύλνπ-απόδνζεο θαη ζπλδπάδνπλ κόλν δύν ραξηνθπιάθηα, απηό ηεο αγνξάο θαη ελόο αθίλδπλνπ ραξηνθπιαθίνπ. Απηό αλαθέξεηαη θαη σο ζεώξεκα ησλ δύν ακνηβαίσλ θεθαιαίσλ (two mutual fund theorem), δηόηη όινη νη επελδπηέο ζα είλαη ηθαλνπνηεκέλνη κε ην θεθάιαην ηεο αγνξάο, κε επηπιένλ ηε δπλαηόηεηα λα δαλείδνπλ ή λα δαλείδνληαη ζε αθίλδπλα ρξεόγξαθα. Σα ραξηνθπιάθηα επί ηεο γξακκήο θεθαιαηαγνξάο δηαθέξνπλ ζην πνζνζηό ζπκκεηνρήο ηνπ ραξηνθπιαθίνπ P i θαη ηνπ κεδεληθνύ θηλδύλνπ ραξηνθπιαθίνπ ζην ζπλνιηθό ραξηνθπιάθην. Έηζη κε δύν πεξηνπζηαθά ζηνηρεία, κπνξνύλ λα ζρεκαηηζηνύλ πνιιά ραξηνθπιάθηα ιόγσ ηεο δηαθνξεηηθήο ζύλζεζεο σο πξνο ηα πνζνζηά επέλδπζεο ζε θάζε πεξηνπζηαθό ζηνηρείν. Ζ εμίζσζε ηεο γξακκήο θεθαιαηαγνξάο είλαη E E ( R ) R m f ( R e ) R f e (1.1) m 7
9 Πξνζδνθώκελε απόδνζε E(Ri) όπνπ ν δείθηεο e ππνδειώλεη απνηειεζκαηηθό ραξηνθπιάθην, Ε(R e ) είλαη ε πξνζδνθώκελε απόδνζε ηνπ κηθηνύ ραξηνθπιαθίνπ, σ m είλαη ε ηππηθή απόθιηζε (θίλδπλνο) ηνπ ραξηνθπιαθίνπ ηεο αγνξάο θαη σ e είλαη ε ηππηθή απόθιηζε (θίλδπλνο) ηνπ κηθηνύ ραξηνθπιαθίνπ (νπζηαζηηθά ηνπ κεηνρηθνύ ραξηνθπιαθίνπ) Ο πξώηνο όξνο ηνπ δεμηνύ κέινπο ηεο εμίζσζεο (1.1) κπνξεί λα εξκελεπζεί σο ε απόδνζε ηνπ ρξόλνπ πνπ απαηηείηαη γηα ηελ θαζπζηέξεζε ηεο πηζαλήο θαηαλάισζεο, ζε κηα πεξίνδν θάησ από απόιπηε βεβαηόηεηα ησλ κειινληηθώλ ηακεηαθώλ ξνώλ. Ο όξνο E ( R m ) R m f κπνξεί λα εξκελεπζεί σο ε αληαπόδνζε ηνπ θηλδύλνπ ηεο αγνξάο γηα όια ηα απνηειεζκαηηθά ραξηνθπιάθηα. Δίλαη δειαδή, ε επηπιένλ απόδνζε πνπ κπνξεί λα απνθηεζεί γηα θάπνην απνηειεζκαηηθό ραξηνθπιάθην κε αύμεζε ηνπ θηλδύλνπ (ηππηθή απόθιηζε) θαηά κία κνλάδα. Ο δεύηεξνο όξνο ζην δεμί κέινο ηεο (1.1), είλαη ην γηλόκελν ηεο αληακνηβήο ηνπ θηλδύλνπ ηεο αγνξάο επί ην ύςνο ηνπ θηλδύλνπ ηνπ ραξηνθπιαθίνπ θαη αληηπξνζσπεύεη ην ζηνηρείν ηεο απαηηνύκελεο απόδνζεο πνπ νθείιεηαη ζε θίλδπλν. πλνςίδνληαο, ε εμίζσζε (1.1) κπνξεί λα γξαθεί σο: (αλακελόκελε απόδνζε) = (απόδνζε ρξόλνπ) + (απόδνζε θηλδύλνπ) (ύςνο θηλδύλνπ) ηελ ηειηθή επηινγή ηνπ ραξηνθπιαθίνπ θαζνξηζηηθό ξόιν ζα παίμεη ε ζηάζε ηνπ θάζε επελδπηή απέλαληη ζηνλ επελδπηηθό θίλδπλν, ε νπνία εθθξάδεηαη κέζα από ηε κνξθή ησλ θακππιώλ αδηαθνξίαο ηνπ επελδπηή απέλαληη ζηνλ θίλδπλν, όπσο γηα παξάδεηγκα θαίλνληαη ζην ζρήκα 1.3. CML P i R f Σππηθή απόθιηζε σ (θίλδπλνο) ρήκα 1.3: Κακπύιεο αδηαθνξίαο θαη άξηζην ραξηνθπιάθην γηα ηνλ επελδπηή i 8
10 Οη θακπύιεο αδηαθνξίαο ηνπ επελδπηή είλαη παξάιιειεο κεηαμύ ηνπο θαη όζν πςειόηεξα βξίζθνληαη ζην ζρήκα, ηόζν κεγαιύηεξε ρξεζηκόηεηα πξνζθέξνπλ ζηνλ επελδπηή. Κάζε ζεκείν κηαο θακπύιεο ζπλεπάγεηαη ίδηα ρξεζηκόηεηα γηα ηνλ επελδπηή. Ζ κνξθή ηεο θακπύιεο δείρλεη πόζν δέρεηαη ν θάζε επελδπηήο λα θηλδπλεύζεη επηπιένλ γηα λα βειηηώζεη ηελ πξνζδνθώκελε απόδνζή ηνπ. Δπεηδή θάζε επελδπηήο έρεη δηαθνξεηηθέο θακπύιεο αδηαθνξίαο, δελ ζπλζέηνπλ όινη νη επελδπηέο ην ίδην ραξηνθπιάθην. Ζ γξακκή θεθαιαηαγνξάο (CML) πεξηέρεη ηα απνηειεζκαηηθόηεξα ραξηνθπιάθηα πνπ είλαη θαη εθηθηά. Σν άξηζην ραξηνθπιάθην γηα θάπνηνλ επελδπηή είλαη απηό πνπ πξνέξρεηαη από ην ζεκείν επαθήο P i ζην νπνίν ε CML εθάπηεηαη ζηελ θακπύιε αδηαθνξίαο ηνπ επελδπηή απέλαληη ζηνλ θίλδπλν. ην ελ ιόγσ ζεκείν ν επελδπηήο επηηπγράλεη ηε κέγηζηε δπλαηή απόδνζε γηα δεδνκέλν θίλδπλν θαη, αληίζηξνθα, ην κηθξόηεξν δπλαηό θίλδπλν γηα δεδνκέλε απόδνζε. Καλέλα άιιν ζεκείν ηεο CML δελ πξνζθέξεη πςειόηεξε ρξεζηκόηεηα ζηνλ ζπγθεθξηκέλν επελδπηή. Ζ εμίζσζε (1.1) εθθξάδεη ηε ζρέζε ηζνξξνπίαο κεηαμύ ηεο αλακελόκελεο απόδνζεο θαη θηλδύλνπ απνηειεζκαηηθώλ ραξηνθπιαθίσλ. Παξ όια απηά δελ πεξηγξάθεη ηελ ηζνξξνπία απνδόζεσλ-θηλδύλνπ γηα κε απνηειεζκαηηθά ραξηνθπιάθηα ή γηα ζπγθεθξηκέλεο κεηνρέο. Σελ αδπλακία απηή ηεο CML ήξζε λα επηιύζεη ν Sharpe κε ηελ εηζαγσγή ηνπ ζπληειεζηή βήηα (beta). Κάησ από ηηο ππνζέζεηο ηνπ CAPM ε επηθηλδπλόηεηα κηαο κεηνρήο κεηξάηαη κε ην ζπληειεζηή βήηα (beta coefficient). Δθαξκόδνληαο ηηο ππνζέζεηο ηνπ CAPM, όινη νη επελδπηέο ζα επηιέμνπλ ην ίδην κεηνρηθό ραξηνθπιάθην (πνζνζηό ζπλνιηθνύ ραξηνθπιαθίνπ πνπ πεξηέρεη θίλδπλν) ην νπνίν ζα είλαη ην ραξηνθπιάθην ηεο αγνξάο Μ, ζαλ ζπλέπεηα ηεο επθακςίαο ησλ ηηκώλ ζε κηα απνηειεζκαηηθή αγνξά. Σα ραξηνθπιάθηα ησλ επελδπηώλ ζα δηαθέξνπλ κόλν σο πξνο ην πνζνζηό ζπκκεηνρήο ηνπ κεηνρηθνύ ραξηνθπιαθίνπ ζην ζπλνιηθό ραξηνθπιάθην. Ζ ζρέζε κεηαμύ θηλδύλνπ κηαο κεηνρήο ή ελόο ραξηνθπιαθίνπ θαη ηεο απόδνζεο ηεο κεηνρήο ή ηνπ ραξηνθπιαθίνπ δίλεηαη από ηε Security Market Line, SML. Ζ SML ζην ζύζηεκα ησλ αμόλσλ ηεο αλακελόκελεο απόδνζεο (θάζεηνο άμνλαο) θαη ηνπ ζπληειεζηή ζπζηεκαηηθνύ θηλδύλνπ (νξηδόληηνο άμνλαο) δίλεηαη ζην ζρήκα 1.4. Σν ζεκείν Μ αληηζηνηρεί ζην ραξηνθπιάθην ηεο αγνξάο, ην νπνίν έρεη beta ίζν κε έλα θαη αλακελόκελε απόδνζε E(R m ). 9
11 Πξνζδνθώκελε απόδνζε E(Ri) E(R m ) M R f β m = 1. πζηεκαηηθόο θίλδπλνο β i ρήκα 1.4: Security Market Line (SML) beta version Ζ εμίζσζε ηεο επζείαο γξακκήο έρεη ηε κνξθή: Ε(R i ) = α + b β i (1.2) Γηα ηνλ πξνζδηνξηζκό ησλ ζπληειεζηώλ α θαη b αξθνύλ δύν ζεκεία. Έλα ζεκείν είλαη ην αθίλδπλν πεξηνπζηαθό ζηνηρείν, δειαδή, απηό κε beta ίζν κε κεδέλ. Έηζη, R f = α + b ή α = R f Έλα δεύηεξν ζεκείν ηεο επζείαο είλαη ην ραξηνθπιάθην ηεο αγνξάο πνπ έρεη beta ίζν κε έλα. Έηζη, E(R m ) = α + b 1 ή b = E(R m ) α Αληηθαζηζηώληαο ηηο δύν παξαπάλσ εθθξάζεηο ζηελ εμίζσζε (1.2), πξνθύπηεη όηη Ε(R i ) = R f + β i [E(R m ) R f ] (1.3) όπνπ, νη εκπιεθόκελνη όξνη ζηελ εμίζσζε απηή είλαη αλαιπηηθά: Ε(R i ) είλαη ε πξνζδνθώκελε απόδνζε ηεο κεηνρήο (ή κεηνρηθνύ ραξηνθπιαθίνπ) i R f είλαη ε απόδνζε ηεο επέλδπζεο ρσξίο θίλδπλν β i είλαη ν ζπληειεζηήο επαηζζεζίαο (beta) γηα ηε κεηνρή i E(R m ) είλαη ε αλακελόκελε απόδνζε ηεο αγνξάο Αλαγξάθνληαο ηελ ζρέζε (1.3) παίξλνπκε: Ε(R i ) R f = β i [E(R m ) R f ] (1.4) 1
12 Όπνπ, E(R i ) R f είλαη ε ππεξβάιινπζα απόδνζε ή ππεξαπόδνζε ελόο ρξενγξάθνπ (risk premium) θαη E(R m ) R f είλαη ε ππεξβάιινπζα απόδνζε ή ππεξαπόδνζε ηνπ γεληθνύ δείθηε ηηκώλ (market premium). Ζ παξαπάλσ έθθξαζε ηεο εμίζσζεο CAPM δειώλεη όηη ην πξηκ ηνπ θηλδύλνπ είλαη ίζν κε ην πξηκ ηεο αγνξάο πνιιαπιαζηαζκέλν κε ην beta ηεο κεηνρήο. Ζ εμίζσζε (1.3) απνηειεί κία από ηηο πην ζεκαληηθέο αλαθαιύςεηο ζηνλ ηνκέα ηεο ρξεκαηνδόηεζεο. Πξόθεηηαη γηα κηα απιή εμίζσζε, πνπ πεξηγξάθεη ηελ Security Market Line θαη ε νπνία πεξηγξάθεη ηελ αλακελόκελε απόδνζε νπνηνπδήπνηε πεξηνπζηαθνύ ζηνηρείνπ ή ραξηνθπιαθίνπ θαη κπνξεί λα θαζνξίζεη εάλ είλαη απνηειεζκαηηθή ή όρη. Καζώο ν ζπλνιηθόο θίλδπλνο κπνξεί λα δηαηξεζεί ζε ζπζηεκαηηθό (ή θίλδπλνο ηεο αγνξάο) θαη κε ζπζηεκαηηθό θίλδπλν, ην beta απνηειεί ην δείθηε επαηζζεζίαο ηνπ ζπζηεκαηηθνύ θηλδύλνπ. Ο ζπζηεκαηηθόο θίλδπλνο δελ κπνξεί λα κεησζεί κέζσ δηαθνξνπνίεζεο, δειαδή είλαη κε-δηαθνξνπνηήζηκνο, ζε αληίζεζε κε ηνλ κε ζπζηεκαηηθό θίλδπλν ν νπνίνο κπνξεί λα κεησζεί κέζσ δηαθνξνπνίεζεο. Ζ εμίζσζε (1.3) δειώλεη όηη ν ζεκαληηθόο θίλδπλνο είλαη ν ζπζηεκαηηθόο (κε δηαθνξνπνηήζηκνο) θαη άξα ε αλακελόκελε απόδνζε ηεο κεηνρήο ή ηνπ ραξηνθπιαθίνπ ζπλδέεηαη γξακκηθά κε ην βαζκό ζπζηεκαηηθνύ θηλδύλνπ θαη όρη κε ην ζπλνιηθό θίλδπλν. Ζ εμίζσζε (1.3) ιέεη όηη γηα λα επηηεπρζεί πξνζδνθώκελε απόδνζε κεγαιύηεξε ηεο πξνζδνθώκελεο απόδνζεο ηνπ Γείθηε Αγνξάο, απαηηείηαη παξάιιειε αύμεζε ηνπ θηλδύλνπ. Όζν πςειόηεξν είλαη ην beta γηα θάπνην ηίηιν, ηόζν κεγαιύηεξνο είλαη ν ζπζηεκαηηθόο θίλδπλνο, θαη ηόζν πςειόηεξε είλαη ε αλακελόκελε απόδνζε πνπ απαηηείηαη από ηνπο επελδπηέο. ην ζεκείν απηό αμίδεη λα αλαθεξζεί κία θαηλνκεληθή πιάλε πνπ κπνξεί λα δεκηνπξγήζεη ε ρξήζε ηνπ CAPM. Κάπνηνο επελδπηήο ελδερνκέλσο λα δηαπηζηώζεη όηη κηα κεηνρή κε πςειό beta απέδσζε ηελ πξνεγνύκελε ρξνληθή πεξίνδν ιηγόηεξν από θάπνηεο άιιεο κεηνρέο νη νπνίεο είραλ κηθξόηεξν beta. Δπηζεκαίλεηαη όηη ην CAPM είλαη κηα ζρέζε ηζνξξνπίαο. Οη κεηνρέο κε πςειό beta αλακέλεηαη λα δώζνπλ πςειόηεξε απόδνζε από ηηο κεηνρέο κε κηθξόηεξν beta, επεηδή είλαη πην επηθίλδπλεο. Απηό δελ ζεκαίλεη όηη ζα δώζνπλ κηα πςειόηεξε απόδνζε ζε όια ηα δηαζηήκαηα ηνπ ρξόλνπ. ηελ πξαγκαηηθόηεηα, εάλ έδηλαλ πάληα κηα πςειόηεξε απόδνζε, ζα ήηαλ ιηγόηεξν επηθίλδπλεο, θαη όρη πην επηθίλδπλεο, από ηηο κεηνρέο κε ρακειό beta. Έηζη, επεηδή είλαη πην επηθίλδπλεο, ζα παξάγνπλ κεξηθέο θνξέο ρακειόηεξεο απνδόζεηο. Ωζηόζν, γηα κεγάιν ρξνληθό δηάζηεκα, ζα πξέπεη θαηά κέζν όξν λα παξάγνπλ πςειόηεξεο απνδόζεηο. Ζ Security Market Line (SML) δίλεη επηπιένλ έλα κέηξν ππνηηκεκέλσλ ή ππεξηηκεκέλσλ κεηνρώλ, (ζρήκα 1.5). 11
13 Πξνζδνθώκελε απόδνζε E(Ri) A B Γ R f Γ beta ρήκα 1.5: Τπνηηκεκέλεο θαη ππεξηηκεκέλεο κεηνρέο κέζσ ηεο SML Δάλ κηα κεηνρή ή γεληθόηεξα έλα πεξηνπζηαθό ζηνηρείν βξίζθεηαη πάλσ από ηελ SML ζεσξείηαη ππνηηκεκέλν (ζην ζρήκα ηα ζηνηρεία Α, Β). Απηό γηαηί ζα ππόζρεηαη θαιύηεξε ζρέζε θηλδύλνπ-αλακελόκελεο απόδνζεο, δειαδή απόδνζε κεγαιύηεξε από απηή πνπ δίλεη ε αγνξά δνζέληνο ηνπ ζπζηεκαηηθνύ θηλδύλνπ. Έηζη, ζύκθσλα κε ην CAPM, ζα παξνπζηάδεη απμεκέλε δήηεζε από ηνπο επελδπηέο, κε απνηέιεζκα λα απμεζεί ε ηηκή ηνπ κέρξη ην ζεκείν εθείλν όπνπ ε αλακελόκελε απόδνζε ζα κεηώλεηαη θαη ηειηθά ε ηηκή ζα πέζεη πάλσ ζηελ SML. ηελ αληίζεηε πεξίπησζε, κεηνρέο πνπ βξίζθνληαη θάησ από ηελ SML (ζην ζρήκα, ηα ζηνηρεία Γ, Γ) ζεσξνύληαη ππεξηηκεκέλεο. Ζ εμίζσζε ηνπ CAPΜ ζπλαληάηαη επίζεο θαη σο: E E ( R ) R m f ( R i ) R f im (1.5) 2 m Απηή είλαη ε εμίζσζε ηεο επζείαο SML αλ ζεσξήζνπκε ην ζύζηεκα αμόλσλ κε θάζεην άμνλα ηελ αλακελόκελε απόδνζε, θαη νξηδόληην άμνλα ηελ ζπλδηαθύκαλζε ησλ απνδόζεσλ ηεο κεηνρήο θαη ησλ απνδόζεσλ ηεο αγνξάο σ im, όπσο θαίλεηαη ζην ζρήκα
14 Πξνζδνθώκελε απόδνζε E(Ri) E(R m ) M R f 2 πλδηαθύκαλζε σ im m ρήκα 1.6: Security Market Line (SML) covariance version 2 H δηαθύκαλζε (θίλδπλνο) ησλ απνδόζεσλ ηεο αγνξάο είλαη m = cov(r m, R m ) = σ mm. Ο ιόγνο E ( R m ) R 2 m f αλαθέξεηαη σο ε ηηκή ηνπ ξίζθνπ ηεο αγνξάο. cov( R, R i m im Ο ζπληειεζηήο beta γξάθεηαη επίζεο σο i 2 var( R m ) ) m. Αληηθαζηζηώληαο ζηελ εμίζσζε (1.3) παίξλνπκε ηελ εμήο έθθξαζε γηα ηε γξακκή θεθαιαηαγνξάο, E E ( R ) R m f i m ( R i ) R f (1.6) Ζ ζρέζε (1.6) είλαη ε εμίζσζε κηαο επζείαο πνπ βξίζθεηαη ζην ζύζηεκα αμόλσλ κε θάζεην άμνλα ηελ αλακελόκελε απόδνζε ηεο κεηνρήο ή ραξηνθπιαθίνπ i, θαη κε νξηδόληην άμνλα ην m m ιόγν im m. Ο όξνο E ( R m ) R m f ραξαθηεξίδεηαη σο ε ηηκή ηνπ ξίζθνπ ηεο αγνξάο. Γεδνκέλνπ όηη o ιόγνο i m m είλαη ν νξηζκόο ηνπ θηλδύλνπ νπνηνπδήπνηε ηίηινπ, ή ραξηνθπιαθίνπ, κπνξνύκε λα δνύκε όηη ε Security Market Line (SML), όπσο θαη ε γξακκή απνηειεζκαηηθώλ ραξηνθπιαθίσλ (CML), εθθξάδεη όηη ε αλακελόκελε απόδνζε θάπνηνπ ηίηινπ είλαη ην αθίλδπλν επηηόθην πξνζαπμεκέλν κε ην γηλόκελν ηεο ηηκήο ηνπ ξίζθνπ ηεο αγνξάο επί ην πνζό ηνπ θηλδύλνπ ηνπ ρξενγξάθνπ ή ραξηνθπιαθίνπ. Ζ έθθξαζε ηεο ζρέζεο (1.6) είλαη ίζσο πην θαηάιιειε γηα λα πεξηγξάςεη ηνλ θίλδπλν ρξενγξάθνπ θαζώο εκθαλίδεηαη ν ιόγνο i m m πνπ απνηειεί έλα κέηξν γηα ην πώο ν θίλδπλνο ελόο ρξενγξάθνπ επεξεάδεη ηνλ θίλδπλν ηνπ ραξηνθπιαθίνπ αγνξάο. 13
15 Ζ εμίζσζε (1.3) απνηειεί ηελ πην ζπρλά ρξεζηκνπνηνύκελε γηα ην ππόδεηγκα CAPM, θαη απηή πνπ ππόθεηηαη ζε εκπεηξηθνύο ειέγρνπο. 1.4 πληειεζηήο beta θαη CAPM Κάζε κεηνρή ελέρεη θάπνην θίλδπλν ν νπνίνο δηαθξίλεηαη ζην ζπζηεκαηηθό θαη ζην κε ζπζηεκαηηθό κέξνο ηνπ. Ο ζπζηεκαηηθόο θίλδπλνο είλαη απηόο πνπ απνξξέεη από ηηο εμειίμεηο ζην εμσηεξηθό πεξηβάιινλ ηεο εηαηξίαο, όπσο ζηα νηθνλνκηθά κεγέζε ηεο νηθνλνκίαο, πνιηηηθέο εμειίμεηο θιπ. Ο κε ζπζηεκαηηθόο θίλδπλνο είλαη απηόο πνπ απνξξέεη από ηηο εμειίμεηο πνπ αθνξνύλ ζηελ ίδηα ηελ εηαηξία. Ο ζπληειεζηήο beta απνηειεί έλα κέηξν ηνπ ζπζηεκαηηθνύ (κε δηαθνξνπνηήζηκνπ) θηλδύλνπ ελόο ρξενγξάθνπ ή ραξηνθπιαθίνπ. Μεηξάεη ην βαζκό ζηνλ νπνίν νη απνδόζεηο κηαο κεηνρήο i ζπλδηαθπκαίλνληαη κε ηηο απνδόζεηο ηνπ ραξηνθπιαθίνπ ηεο αγνξάο Μ (γεληθόο δείθηεο όισλ ησλ κεηνρώλ). Γειαδή εθθξάδεη ηελ επαηζζεζία ηεο ηηκήο ηεο κεηνρήο ζε θάζε κεηαβνιή ηνπ γεληθνύ δείθηε ηηκώλ. Ζ έθθξαζή ηνπ δίλεηαη από ηε ζρέζε: cov( var( R, R i ) ) i m (1.7) i R ην ζρήκα 1.7 θαίλνληαη πσο κεηαβιήζεθαλ ζην παξειζόλ νη ηηκέο δύν κεηνρώλ Α θαη Β ζε ζρέζε κε ηηο κεηαβνιέο ηνπ Γεληθνύ Γείθηε Σηκώλ. Οη επζείεο πξνζδηνξίδνληαη κε εθαξκνγή ηεο κεζόδνπ παιηλδξόκεζεο ζεσξώληαο γηα παξάδεηγκα ηηο εκεξήζηεο (ή άιιεο ρξνληθήο κνλάδαο) απνδόζεηο κεηνρήο θαη ηνπ ΓΓΣ. Ο ζπληειεζηήο beta ηεο κεηνρήο είλαη ε θιίζε ηεο επζείαο: beta = R M. Μεηνρέο κε πςειό ζπληειεζηή beta ζεσξνύληαη πην επαίζζεηεο ζηηο απόηνκεο κεηαβνιέο ηεο αγνξάο. Απηό γηαηί όζν εύθνια κπνξνύλ λα απνθνκίζνπλ θέξδε, ηόζν εύθνια επίζεο κπνξνύλ λα ηα απσιέζνπλ. ην ζρήκα 1.7, ην beta ηεο κεηνρήο Β είλαη κεγαιύηεξν από ην beta ηεο κεηνρήο Α, δειαδή ε θιίζεο ηεο Β είλαη πην απόηνκε από ηελ θιίζε ηεο Α θαη ζπλεπώο, ζεσξείηαη κεηνρή πςειόηεξνπ θηλδύλνπ. Οη ζπληειεζηέο beta κπνξνύλ λα ιάβνπλ είηε ζεηηθή είηε αξλεηηθή ηηκή, αιιά ηηο πεξηζζόηεξεο θνξέο ε ηηκή ηνπο είλαη ζεηηθή. 14
16 Απόδνζε κεηνρήο R Μεηνρή Β ΓR Μεηνρή Α ΓΜ Γεληθόο Γείθηεο (απόδνζε αγνξάο Μ) ρήκα 1.7: Beta κεηνρήο Ο γεληθόο δείθηεο πνπ κεηξά ηελ επίδνζε κηαο ζπγθεθξηκέλεο αγνξάο, έρεη εμ νξηζκνύ ζπληειεζηή beta ίζν κε ηε κνλάδα. ηελ πεξίπησζε πνπ νη απνδόζεηο κηαο κεηνρήο δηαθπκαίλνληαη ζηνλ ίδην βαζκό κε ηηο απνδόζεηο ηνπ ραξηνθπιαθίνπ ηεο αγνξάο, ν ζπληειεζηήο beta ηνπ ρξενγξάθνπ είλαη κνλαδηαίνο (β = 1). Έλα beta κεγαιύηεξν ηεο κνλάδαο (β > 1) ζεκαίλεη όηη ε κεηνρή επεξεάδεηαη πεξηζζόηεξν από ηελ αγνξά, δειαδή δηαθπκαίλεηαη πεξηζζόηεξν από ηνλ γεληθό δείθηε θαη γη απηό αθξηβώο έρεη πεξηζζόηεξν ζπζηεκαηηθό θίλδπλν. Σέηνηεο κεηνρέο ραξαθηεξίδνληαη επηζεηηθέο, θαζώο επηθέξνπλ κεγάιεο απνδόζεηο ζε πεξηόδνπο αλόδνπ ηεο αγνξάο επηηείλνληαο όκσο ηε δεκία ζε πεξίνδν πηώζεο. Σν αληίζεην ζπκβαίλεη κε κεηνρέο ή ραξηνθπιάθηα κε beta κηθξόηεξν ηεο κνλάδαο (β < 1). Σόηε, ηα ρξεόγξαθα πνπ ζεσξνύκε, δελ επεξεάδνληαη πνιύ από ηηο θηλήζεηο ηεο αγνξάο, δειαδή δηαθπκαίλνληαη ιηγόηεξν από ηνλ γεληθό δείθηε θαη ζπλεπώο είλαη κηθξόηεξεο επηθηλδπλόηεηαο. Σέηνηεο κεηνρέο ραξαθηεξίδνληαη ακπληηθέο, αθνύ πξαγκαηνπνηνύλ κηθξά θέξδε θαη κηθξέο δεκηέο. πληειεζηήο beta ραξηνθπιαθίνπ Ο ζπληειεζηήο beta ελόο ραξηνθπιαθίνπ ππνινγίδεηαη σο ν ζηαζκηθόο κέζνο ησλ ζπληειεζηώλ beta ησλ επηκέξνπο κεηνρώv πνπ απαξηίδνπλ ην ελ ιόγσ ραξηνθπιάθην. Έλα παξάδεηγκα θαίλεηαη ζηνλ πίλαθα
17 Μεηνρή Σηκή κεηνρήο (λνκ. κνλ.) Αξηζκόο κεηνρώλ πλνιηθή αμία κεηνρήο Πνζνζηό ζπκκεηνρήο κεηνρήο beta κεηνρήο Α %.75 Β % 1.2 Γ %.9 Γ % 1.4 Αμία ραξηνθπιαθίνπ beta ραξηνθπιαθίνπ 84 1% Πίλαθαο 1.1: Παξάδεηγκα εύξεζεο beta ραξηνθπιαθίνπ 1.23 Σν beta ηνπ ραξηνθπιαθίνπ ππνινγίδεηαη σο εμήο: beta ραξηνθπιαθίνπ = = Ζ εξκελεία ηνπ beta ραξηνθπιαθίνπ είλαη ίδηα κε απηήλ ηνπ beta κεηνρήο. Μεηξά ηελ επαηζζεζία ηεο απόδνζεο ηνπ ραξηνθπιαθίνπ ζηηο κεηαβνιέο ηεο αγνξάο. Ζ ηηκή beta = 1.23 ηνπ παξαδείγκαηνο ζεκαίλεη όηη ζε πεξίπησζε αλόδνπ ηνπ Γεληθνύ Γείθηε Αγνξάο θαηά 1% ε απόδνζε ηνπ ραξηνθπιαθίνπ ζα είλαη επίζεο ζεηηθή θαηά 12.3%. 16
18 ΚΔΦΑΛΑΙΟ 2 MULTIVARIATE ΜΟΝΣΔΛΑ ΓΙΑΚΤΜΑΝΗ ην θεθάιαην απηό αλαιύνληαη ηα νηθνλνκεηξηθά κνληέια πνπ ρξεζηκνπνηνύληαη ζηελ εξγαζία γηα ηνλ θαζνξηζκό ηνπ ζπληειεζηή beta. 2.1 πληειεζηήο beta κέζσ CAPM ην θεθάιαην 1 αλαθέξζεθε όηη ζύκθσλα κε ηελ εμίζσζε CAPM ην beta γηα ηε κεηνρή i πξνθύπηεη από έλα απιό γξακκηθό κνληέιν παιηλδξόκεζεο θαη ζπγεθξηκέλα [Ε(R i ) R f ] t = α i + β i [E(R m ) R f ] t + ε it, t = 1,, T (2.1) ή επίζεο από ηε κνξθή R it = α i + β i R mt + ε it, t = 1,, T (2.2) όπνπ R it είλαη νη απνδόζεηο ηεο κεηνρήο i ζηελ πεξίνδν t R mt είλαη ε απόδνζε ηνπ γεληθνύ δείθηε ηεο αγνξάο ζηελ πεξίνδν t α i είλαη ν ζηαζεξόο όξνο ηεο γξακκηθήο παιηλδξόκεζεο β i είλαη ν ζπληειεζηήο επαηζζεζίαο (beta) ηνπ ρξενγξάθνπ i ε it είλαη ν δηαηαξαθηηθόο όξνο ηεο γξακκηθήο παιηλδξόκεζεο ηεο κεηνρήο i ζηελ πεξίνδν t Τ είλαη νη ρξνληθέο πεξίνδνη ησλ δεδνκέλσλ πνπ εμεηάδνπκε Σν CAPM ππνζέηεη όηη νη παξάκεηξνη α i θαη β i ζεσξνύληαη ζηαζεξνί ζε ζρέζε κε ην ρξόλν. Πνιύ ζπρλά όκσο παξαηεξείηαη ην θαηλόκελν ην beta κηαο κεηνρήο λα κεηαβάιιεηαη ξηδηθά όηαλ κεηαβάιιεηαη ε ρξνληθή πεξίνδνο ππνινγηζκνύ ηνπ. Έηζη πξνθύπηεη ην πξόβιεκα ηεο δηαρξνληθήο κεηαβνιήο ηνπ ζπζηεκαηηθνύ θηλδύλνπ β θαζώο ζην ππόδεηγκα CAPM, ην β είλαη ζηαζεξό ζην ρξόλν. Ζ θαηαζθεπή απνηειεζκαηηθώλ ραξηνθπιαθίσλ, νη πξνβιέςεηο ησλ απνδόζεσλ ησλ κεηνρώλ θαη άιισλ πεξηνπζηαθώλ ζηνηρείσλ βαζίδνληαη ζηελ αλάιπζε δηαθπκάλζεσλ θαη ζπλδηαθπκάλζεσλ. ηε ζπλέρεηα αλαθεξόκαζηε ζε δηάθνξα κνληέια δηαζπνξώλ πνπ έρνπλ πξνηαζεί. Βαζηθέο πεγέο ήηαλ νη Tsay (21) θαη Sheppard (21). 17
19 2.2 Μνληέια ARCH(p), GARCH(p, q) Σν γξακκηθό κνληέιν ARCH(p) (Autoregressive Conditional Heteroskedasticity απηνπαιίλδξνκν ππό ζπλζήθε εηεξνζθεδαζηηθό) πξνηάζεθε από ηνλ Engle (1982) θαη ζεσξεί όηη ε ππό ζπλζήθε δηαθύκαλζε εμαξηάηαη από ην ζύλνιν ηεο πιεξνθόξεζεο θαηά έλα απηνπαιίλδξνκν ηξόπν: p 2 2 t i t i (2.3) i 1 ε πνιιέο από ηηο εθαξκνγέο γηα ην γξακκηθό κνληέιν ARCH(p) εκθαλίζηεθε ε αλάγθε λα ρξεζηκνπνηεζεί έλαο κεγάινο αξηζκόο πζηεξήζεσλ, κε απνηέιεζκα λα κεηώλνληαη ζεκαληηθά νη βαζκνί ειεπζεξίαο ησλ εθηηκώκελσλ κνληέισλ. Μηα ελαιιαθηηθή κνξθή κνληεινπνίεζεο ηεο δηαθύκαλζεο είλαη ην γξακκηθό πνιπκεηαβιεηό κνληέιν GARCH(p, q) (Generalized Autoregressive Conditional Heteroskedasticity γεληθεπκέλν απηνπαιίλδξνκν ππό ζπλζήθε εηεξνζθεδαζηηθό) πνπ δόζεθε από ηνλ Bollerslev (1986), πνπ επηηξέπεη παξειζνληηθέο ηηκέο ηεο ππό ζπλλζήθεο δηαθύκαλζεο λα εκθαλίδνληαη ζηελ εμίζσζε ηεο ππό ζπλζήθεο δηαθύκαλζεο: p t i t i i t i (2.4) i 1 i 1 Σν απιό κνληέιν GARCH(1, 1) πξνηάζεθε μερσξηζηά από ηνλ Taylor (1986). p Πνιιέο πεξηπηώζεηο ηηκνιόγεζεο θαη δηαρείξηζεο ραξηνθπιαθίνπ επηβάιινπλ ηελ αλάιπζε ζε έλα πνιπκεηαβιεηό πιαίζην. ην κνληέιν GARCH(p, q) (Βollerslev θ.ά. 1988) ε δηαζπνξά δίλεηαη από ηε δηαλπζκαηηθή ζρέζε vec( t ) = vec(c) + Avec( ε t 1ε ) + Bvec( t 1 t 1 ) (2.5) όπνπ C είλαη έλαο ζεηηθά νξηζκέλνο πίλαθαο. Ο ζπκβνιηζκόο vec() απνηειεί ηνλ ηειεζηή πνπ ζηνηρεηνζεηεί έλαλ nn πίλαθα ζε (n 2 1) δηάλπζκα. Γηα παξάδεηγκα, vec a c a b b d c d. 18
20 2.3 Σν κνληέιν ΒΔΚΚ-GARCH(1, 1) Σν πξόζεκα ΒΔΚΚ νθείιεηαη ζηνπο Baba, Engle, Kraft θαη Kroner. Θέηνληαο p = q = 1 ζην GARCH (p, q) πξνθύπηεη ην δηκεηαβιεηό ππόδεηγκα ΒΔΚΚ GARCH (1, 1) ζην νπνίν ε παξακεηξνπνίεζε ηνπ πίλαθα δηαζπνξώλ-ζπλδηαζπνξώλ δίλεηαη από ηε ζρέζε t = CC + A ε t ε A + B t 1 Β (2.6) 1 t 1 όπνπ C είλαη k k θάησ ηξηγσληθόο πίλαθαο θαη νη Α, Β είλαη πίλαθεο παξακέηξσλ δηάζηαζεο k k. ηελ πεξίπησζε πνπ εμεηάδνπκε ζηελ παξνύζα εξγαζία, ην κνληέιν BEKK-GARCH(1, 1) ζρεκαηίδεηαη σο εμήο. Έζησ R t = (R 1t, R 2t ) ην δηάλπζκα ησλ ηηκώλ ησλ απνδόζεσλ, όπνπ R 1t ε απόδνζε ελόο θιαδηθνύ δείθηε, θαη R 2t ε απόδνζε ηνπ γεληθνύ δείθηε ηεο αγνξάο Ζ δηαδηθαζία είλαη R t = C + M R t 1 + E t (2.7) όπνπ C είλαη έλα 21 δηάλπζκα κε ζηαζεξέο, Μ είλαη 22 πίλαθαο ζπληειεζηώλ θαη Δ t = (ε 1t, ε 2t ) ην δηάλπζκα δηαηαξαθηηθώλ όξσλ, όπνπ ε 1t αλαθέξεηαη ζηνλ θιαδηθό δείθηε, θαη ε 2t αλαθέξεηαη ζηελ αγνξά. ρεηηθά κε ηνπο δηαηαξαθηηθνύο όξνπο είλαη ε i,t I t 1 ~ N(, t ) δειαδή ην δηάλπζκα ε i,t είλαη δεζκεπκέλν δνζέληνο I t 1, δειαδή ηεο πιήξνπο πιεξνθνξίαο κέρξη ηε ρξνληθή ζηηγκή t 1, θαη είλαη θαλνληθά θαηαλεκεκέλν κε κέζε ηηκή κεδέλ θαη δεζκεπκέλν πίλαθα δηαζπνξώλ t. Αλαιπηηθά θαη γηα k = 1 έρνπκε γηα ηνλ πίλαθα ησλ ζπλδηαζπνξώλ: ε ε 1, t 2, t 1 1, t 1 1, t 1 2, t 1 t 1 t 1 1, t 1 2, t 1 2 θαη 1 2 2, t 1 1, t 1 2, t 1 c c 11, t 12, t , t 22, t 21 c 22 c c 21 c 22 a a a a , t 1 2, t 1 1, t 1 1, t 1 2 2, t 1 2, t 1 a a a a b b b b , t 1 21, t 1 12, t 1 22, t 1 b b b b
21 Τινπνηώληαο ηνλ πνιιαπιαζηαζκό ησλ κεηξώλ πξνθύπηεη ε κνξθή , t c11 a11 1, t 1 2 a11 a12 1, t 1 2, t 1 a12 2, t 1 b11 11, t 1 2b11 b12 12, t 1 b12 22, t c c a a ( a a a a ) a a 12, t , t , t 1 2, t , t 1 b b ( b b b b ) b b , t , t , t c c a 2 a a a b 2 b b b 22, t , t , t 1 2, t , t , t , t , t 1 ρεηηθά κε ηελ εξκελεία ησλ όξσλ ηνπ ππνδείγκαηνο κπνξεί λα αλαθεξζεί όηη: α) εάλ νη όξνη α ij είλαη ζηαηηζηηθά ζεκαληηθνί, ε κεηαβιεηόηεηα ηεο απόδνζεο ηεο αγνξάο επεξεάδεη ηε κεηαβιεηόηεηα ησλ απνδόζεσλ ηνπ θιαδηθνύ δείθηε θαη αληίζηξνθα (crosseffects). β) εάλ νη όξνη b ij είλαη ζηαηηζηηθά ζεκαληηθνί, κηα πηζαλή δηαηαξαρή ζηελ ππό ζπλζήθε δηαθύκαλζε ηεο απόδνζεο ηεο αγνξάο ζα έρεη ζαλ απνηέιεζκα κηα δηαξθή επίδξαζε (persistence) ζηελ ππό ζπλζήθε δηαθύκαλζε ησλ απνδόζεσλ ηνπ θιαδηθνύ δείθηε, θαη αληίζηξνθα. Σν δηαγώλην ΒΔΚΚ-GARCH(1,1) ππόδεηγκα πξνζπαζεί λα αληηκεησπίζεη ην πξόβιεκα ηνπ κεγάινπ αξηζκνύ παξακέηξσλ πνπ εκθαλίδεηαη, θαη πξνο ηνύην ζεσξεί όηη νη πίλαθεο Α θαη Β είλαη δηαγώληνη. ηελ πεξίπησζε απηή, ν πίλαθαο ζπλδηαζπνξώλ δηακνξθώλεηαη σο ~ ~ ~ ~ C C A ε ε A B B (2.8) t t 1 t 1 t 1 όπνπ C είλαη k k θάησ ηξηγσληθόο πίλαθαο θαη νη A ~ θαη B ~ είλαη δηαγώληνη πίλαθεο παξακέηξσλ δηάζηαζεο k k. Αλαιπηηθά είλαη: 11, t 21, t 12, t 22, t c c c 22 c c c 22 a 11 a 22 1, t 1 2, t 1 1, t 2 1 1, t 1 2 2, t 1 2, t 1 a 11 a 22 b 11 b 22 11, t 1 21, t 1 12, t 1 22, t 1 b11 b 22 από ην νπνίν πξνθύπηνπλ νη ζρέζεηο , t c11 a11 1, t 1 b11 11, t 1 12, t c 11 c 21 a 11 a 22 1, t 1 2, t 1 b11 b 22 12, t , t c 21 c 22 a 22 2, t 1 b 22 22, t 1 2
22 Σν δηκεηαβιεηό ππόδεηγκα ΒΔΚΚ-GARCH(1,1) εθηηκά ηε κήηξα δηαζπνξώλ-ζπλδηαζπνξώλ 21, t 22, t 11, t 12, t. Σα κεγέζε t 11, t θαη απνηεινύλ δηαρξνληθέο εθηηκήζεηο ηεο 22, t δηαθύκαλζεο ηνπ θιαδηθνύ δείθηε θαη αγνξάο αληίζηνηρα. Σν κέγεζνο είλαη ε 12, t δηαρξνληθή εθηίκεζε ηεο ζπλδηαθύκαλζεο κεηαμύ θιαδηθνύ δείθηε θαη αγνξάο. Έηζη ε εθηίκεζε ηνπ ζπληειεζηή beta ζα δίλεηαη από ηε ζρέζε: it cov( R, R it mt 12, t (2.9) var( R it ) ) 22, t Ζ παξαπάλσ ζρέζε παξέρεη ηελ εθηίκεζε ηνπ ρξνληθά κεηαβαιιόκελνπ ζπζηεκαηηθνύ θηλδύλνπ beta κε ρξήζε ηνπ δηκεηαβιεηνύ ππνδείγκαηνο ΒΔΚΚ-GARCH(1,1). ην επόκελν θεθάιαην γίλεηαη δηεξεύλπζε θαηά πόζν ν ζπληειεζηήο beta κεηαβάιιεηαη δηαρξνληθά θαη εάλ ην δπλακηθό ππόδεηγκα ΒΔΚΚ-GARCH(1,1) είλαη θαηάιιειν γηα ηελ πεξηγξαθή ηηκώλ ζηελ πεξίπησζε νξηζκέλσλ θιαδηθώλ δεηθηώλ ζηελ Διιάδα θαη ζηελ Κύπξν. 21
β) (βαζκνί: 2) Έζησ όηη ε ρξνλνινγηθή ζεηξά έρεη κέζε ηηκή 0 θαη είλαη αληηζηξέςηκε. Δίλεηαη ην αθόινπζν απνηέιεζκα από ην EViews γηα ηε :
 1 ΝΑ ΑΠΑΝΤΗΘΟΥΝ 2 ΑΠΟ ΤΑ 3 ΘΕΜΑΤΑ ΘΕΜΑ 1 α) (βαζκνί: 3) Έζησ όηη ε ρξνλνινγηθή ζεηξά είλαη ζηάζηκε, αληηζηξέςηκε θαη αθνινπζεί ην ΑR(1) ππόδεηγκα. Να βξεζνύλ ε κέζε ηηκή, ε δηαζπνξά θαη ε απηνζπζρέηηζε
1 ΝΑ ΑΠΑΝΤΗΘΟΥΝ 2 ΑΠΟ ΤΑ 3 ΘΕΜΑΤΑ ΘΕΜΑ 1 α) (βαζκνί: 3) Έζησ όηη ε ρξνλνινγηθή ζεηξά είλαη ζηάζηκε, αληηζηξέςηκε θαη αθνινπζεί ην ΑR(1) ππόδεηγκα. Να βξεζνύλ ε κέζε ηηκή, ε δηαζπνξά θαη ε απηνζπζρέηηζε
Ενδεικτικά Θέματα Στατιστικής ΙΙ
 Ενδεικτικά Θέματα Στατιστικής ΙΙ Θέματα. Έζησ όηη ζε δείγκα 35 θαηνηθηώλ πνπ ελνηθηάδνληαη ζε θνηηεηέο ζηελ Κνδάλε βξέζεθε ην κέζν κεληαίν κίζζσκα ζηα 5 επξώ, ελώ ζην Ζξάθιεην ην κέζν κεληαίν κίζζσκα ζε
Ενδεικτικά Θέματα Στατιστικής ΙΙ Θέματα. Έζησ όηη ζε δείγκα 35 θαηνηθηώλ πνπ ελνηθηάδνληαη ζε θνηηεηέο ζηελ Κνδάλε βξέζεθε ην κέζν κεληαίν κίζζσκα ζηα 5 επξώ, ελώ ζην Ζξάθιεην ην κέζν κεληαίν κίζζσκα ζε
Κεθάιαην 20. Ελαχιστοποίηση του κόστους
 Κεθάιαην 0 Ελαχιστοποίηση του κόστους Ειαρηζηνπνίεζε ηνπ θόζηνπο Μηα επηρείξεζε ειαρηζηνπνηεί ην θόζηνο ηεο αλ παξάγεη νπνηνδήπνηε δεδνκέλν επίπεδν πξντόληνο y 0 ζην κηθξόηεξν δπλαηό ζπλνιηθό θόζηνο. Τν
Κεθάιαην 0 Ελαχιστοποίηση του κόστους Ειαρηζηνπνίεζε ηνπ θόζηνπο Μηα επηρείξεζε ειαρηζηνπνηεί ην θόζηνο ηεο αλ παξάγεη νπνηνδήπνηε δεδνκέλν επίπεδν πξντόληνο y 0 ζην κηθξόηεξν δπλαηό ζπλνιηθό θόζηνο. Τν
Μονοψϊνιο. Αγνξά κε ιίγνπο αγνξαζηέο. Δύναμη μονοψωνίος Η ηθαλόηεηα πνπ έρεη ν αγνξαζηήο λα επεξεάζεη ηελ ηηκή ηνπ αγαζνύ.
 Μονοψϊνιο Ολιγοψώνιο Αγνξά κε ιίγνπο αγνξαζηέο. Δύναμη μονοψωνίος Η ηθαλόηεηα πνπ έρεη ν αγνξαζηήο λα επεξεάζεη ηελ ηηκή ηνπ αγαζνύ. Οπιακή αξία Δπηπξόζζεηα νθέιε από ηελ ρξήζε/θαηαλάισζε κηαο επηπξόζζεηε
Μονοψϊνιο Ολιγοψώνιο Αγνξά κε ιίγνπο αγνξαζηέο. Δύναμη μονοψωνίος Η ηθαλόηεηα πνπ έρεη ν αγνξαζηήο λα επεξεάζεη ηελ ηηκή ηνπ αγαζνύ. Οπιακή αξία Δπηπξόζζεηα νθέιε από ηελ ρξήζε/θαηαλάισζε κηαο επηπξόζζεηε
ΓΗΑΓΩΝΗΣΜΑ ΣΤΑ ΜΑΘΖΜΑΤΗΚΑ. Ύλη: Μιγαδικοί-Σσναρηήζεις-Παράγωγοι Θεη.-Τετν. Καη Εήηημα 1 ο :
 ΓΗΑΓΩΝΗΣΜΑ ΣΤΑ ΜΑΘΖΜΑΤΗΚΑ Ον/μο:.. Γ Λσκείοσ Ύλη: Μιγαδικοί-Σσναρηήζεις-Παράγωγοι Θεη.-Τετν. Καη. 11-1-11 Εήηημα 1 ο : Α. Γηα ηελ ζπλάξηεζε f, λα βξείηε ην δηάζηεκα ζην νπνίν είλαη παξαγσγίζηκε θαζώο θαη
ΓΗΑΓΩΝΗΣΜΑ ΣΤΑ ΜΑΘΖΜΑΤΗΚΑ Ον/μο:.. Γ Λσκείοσ Ύλη: Μιγαδικοί-Σσναρηήζεις-Παράγωγοι Θεη.-Τετν. Καη. 11-1-11 Εήηημα 1 ο : Α. Γηα ηελ ζπλάξηεζε f, λα βξείηε ην δηάζηεκα ζην νπνίν είλαη παξαγσγίζηκε θαζώο θαη
Κευάλαιο 8 Μονοπωλιακή Συμπεριφορά- Πολλαπλή Τιμολόγηση
 Κευάλαιο 8 Μονοπωλιακή Συμπεριφορά- Πολλαπλή Τιμολόγηση Πώς πρέπει να τιμολογεί ένα μονοπώλιο; Μέρξη ζηηγκήο ην κνλνπώιην έρεη ζεσξεζεί ζαλ κηα επηρείξεζε ε νπνία πσιεί ην πξντόλ ηεο ζε θάζε πειάηε ζηελ
Κευάλαιο 8 Μονοπωλιακή Συμπεριφορά- Πολλαπλή Τιμολόγηση Πώς πρέπει να τιμολογεί ένα μονοπώλιο; Μέρξη ζηηγκήο ην κνλνπώιην έρεη ζεσξεζεί ζαλ κηα επηρείξεζε ε νπνία πσιεί ην πξντόλ ηεο ζε θάζε πειάηε ζηελ
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ ΠΑΓΚΤΠΡΙΟ ΓΙΑΓΩΝΙ ΜΟ
 ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ ΠΑΓΚΤΠΡΙΟ ΓΙΑΓΩΝΙ ΜΟ Α ΛΤΚΔΙΟΤ Ζμεπομηνία: 18/12/10 Ώπα εξέτασηρ: 09:30-12:30 ΠΡΟΣΕΙΝΟΜΕΝΕ ΛΤ ΕΙ 1. Δίλεηαη ην πνιπώλπκν Αλ θαη., λα βξείηε ην ηειεπηαίν ςεθίν ηνπ αξηζκνύ έρνπκε:
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ ΠΑΓΚΤΠΡΙΟ ΓΙΑΓΩΝΙ ΜΟ Α ΛΤΚΔΙΟΤ Ζμεπομηνία: 18/12/10 Ώπα εξέτασηρ: 09:30-12:30 ΠΡΟΣΕΙΝΟΜΕΝΕ ΛΤ ΕΙ 1. Δίλεηαη ην πνιπώλπκν Αλ θαη., λα βξείηε ην ηειεπηαίν ςεθίν ηνπ αξηζκνύ έρνπκε:
ΑΡΥΔ ΟΙΚΟΝΟΜΙΚΗ ΘΔΩΡΙΑ ΛΤΔΙ ΓΙΑΓΩΝΙΜΑΣΟ ΚΔΦΑΛΑΙΟΤ 2
 ΑΥΔ ΟΙΚΟΝΟΜΙΚΗ ΘΔΩΙΑ ΛΤΔΙ ΙΑΩΝΙΜΑΣΟ ΚΔΦΑΛΑΙΟΤ 2 1: Λάζος (είλαη ηζνζθειήο ππεξβνιή) Α2: Λάζος (ην ζεηηθό πξόζεκν ζεκαίλεη όηη ε Πνζνζηηαία Μεηαβνιή Δηζνδήκαηνο θαη ε Πνζνζηηαία Μεηαβνιή Πνζόηεηαο ήηαλ
ΑΥΔ ΟΙΚΟΝΟΜΙΚΗ ΘΔΩΙΑ ΛΤΔΙ ΙΑΩΝΙΜΑΣΟ ΚΔΦΑΛΑΙΟΤ 2 1: Λάζος (είλαη ηζνζθειήο ππεξβνιή) Α2: Λάζος (ην ζεηηθό πξόζεκν ζεκαίλεη όηη ε Πνζνζηηαία Μεηαβνιή Δηζνδήκαηνο θαη ε Πνζνζηηαία Μεηαβνιή Πνζόηεηαο ήηαλ
ΔΕΟ 13. Ποσοτικές Μέθοδοι. θαη λα ππνινγίζεηε ην θόζηνο γηα 10000 παξαγόκελα πξντόληα. Να ζρεδηαζηεί γηα εύξνο πξντόλησλ έσο 30000.
 ΔΕΟ 13 Ποσοτικές Μέθοδοι Σσνάρηηζη Κόζηοσς C(), μέζο κόζηος C()/. Παράδειγμα 1 Μηα εηαηξεία δαπαλά γηα θάζε πξντόλ Α πνπ παξάγεη 0.0 λ.κ. Τα πάγηα έμνδα ηεο εηαηξείαο είλαη 800 λ.κ. Ζεηείηαη 1) Να πεξηγξάςεηε
ΔΕΟ 13 Ποσοτικές Μέθοδοι Σσνάρηηζη Κόζηοσς C(), μέζο κόζηος C()/. Παράδειγμα 1 Μηα εηαηξεία δαπαλά γηα θάζε πξντόλ Α πνπ παξάγεη 0.0 λ.κ. Τα πάγηα έμνδα ηεο εηαηξείαο είλαη 800 λ.κ. Ζεηείηαη 1) Να πεξηγξάςεηε
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ ΠΑΓΚΤΠΡΙΟ ΓΙΑΓΩΝΙΜΟ Α ΛΤΚΔΙΟΤ. Ημεπομηνία: 10/12/11 Ώπα εξέτασηρ: 09:30-12:30 ΠΡΟΣΔΙΝΟΜΔΝΔ ΛΤΔΙ
 ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ ΠΑΓΚΤΠΡΙΟ ΓΙΑΓΩΝΙΜΟ Α ΛΤΚΔΙΟΤ Ημεπομηνία: 10/12/11 Ώπα εξέτασηρ: 09:30-12:30 ΠΡΟΣΔΙΝΟΜΔΝΔ ΛΤΔΙ Πρόβλημα 1: α) Να δείμεηε όηη αλ ζεηηθνί πξαγκαηηθνί αξηζκνί ηζρύεη: β) Αλ είλαη
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ ΠΑΓΚΤΠΡΙΟ ΓΙΑΓΩΝΙΜΟ Α ΛΤΚΔΙΟΤ Ημεπομηνία: 10/12/11 Ώπα εξέτασηρ: 09:30-12:30 ΠΡΟΣΔΙΝΟΜΔΝΔ ΛΤΔΙ Πρόβλημα 1: α) Να δείμεηε όηη αλ ζεηηθνί πξαγκαηηθνί αξηζκνί ηζρύεη: β) Αλ είλαη
Κεθάλαιο 7. Πξνζθνξά ηνπ θιάδνπ Μ. ΨΥΛΛΑΚΗ
 Κεθάλαιο 7 Πξνζθνξά ηνπ θιάδνπ 1 Προζθορά ανηαγωνιζηικού κλάδοσ Πώο πξέπεη λα ζπλδπαζηνύλ νη απνθάζεηο πξνζθνξάο ησλ πνιιώλ επηκέξνπο επηρεηξήζεσλ ελόο αληαγσληζηηθνύ θιάδνπ γηα λα βξνύκε ηελ θακπύιε πξνζθνξάο
Κεθάλαιο 7 Πξνζθνξά ηνπ θιάδνπ 1 Προζθορά ανηαγωνιζηικού κλάδοσ Πώο πξέπεη λα ζπλδπαζηνύλ νη απνθάζεηο πξνζθνξάο ησλ πνιιώλ επηκέξνπο επηρεηξήζεσλ ελόο αληαγσληζηηθνύ θιάδνπ γηα λα βξνύκε ηελ θακπύιε πξνζθνξάο
H ΜΑΓΕΙΑ ΤΩΝ ΑΡΙΘΜΩΝ
 H ΜΑΓΕΙΑ ΤΩΝ ΑΡΙΘΜΩΝ Φξεζηκόηεηα καζεκαηηθώλ Αξρή θαηακέηξεζεο Όζα έδσζαλ νη Έιιελεο... Τξίγσλνη αξηζκνί Τεηξάγσλνη αξηζκνί Δπηκήθεηο αξηζκνί Πξώηνη αξηζκνί Αξηζκνί κε μερσξηζηέο ηδηόηεηεο Γίδπκνη πξώηνη
H ΜΑΓΕΙΑ ΤΩΝ ΑΡΙΘΜΩΝ Φξεζηκόηεηα καζεκαηηθώλ Αξρή θαηακέηξεζεο Όζα έδσζαλ νη Έιιελεο... Τξίγσλνη αξηζκνί Τεηξάγσλνη αξηζκνί Δπηκήθεηο αξηζκνί Πξώηνη αξηζκνί Αξηζκνί κε μερσξηζηέο ηδηόηεηεο Γίδπκνη πξώηνη
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ ΚΑΗ ΔΠΑΛ ΣΔΣΑΡΣΖ 25 ΜΑΨΟΤ 2016 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΑΡΥΔ ΟΗΚΟΝΟΜΗΚΖ ΘΔΧΡΗΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ - ΔΠΗΛΟΓΖ
 ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ ΚΑΗ ΔΠΑΛ ΣΔΣΑΡΣΖ 25 ΜΑΨΟΤ 2016 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΑΡΥΔ ΟΗΚΟΝΟΜΗΚΖ ΘΔΧΡΗΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ - ΔΠΗΛΟΓΖ (Δλδεηθηηθέο Απαληήζεηο) ΘΔΜΑ Α Α1. α. Σωζηό β. Λάζνο
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ ΚΑΗ ΔΠΑΛ ΣΔΣΑΡΣΖ 25 ΜΑΨΟΤ 2016 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΑΡΥΔ ΟΗΚΟΝΟΜΗΚΖ ΘΔΧΡΗΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ - ΔΠΗΛΟΓΖ (Δλδεηθηηθέο Απαληήζεηο) ΘΔΜΑ Α Α1. α. Σωζηό β. Λάζνο
Q Η ζσνάρηηζη μέζοσ κόζηοσς μας δίνει ηο κόζηος ανά μονάδα παραγωγής. Q Η ζσνάρηηζη μέζοσ κόζηοσς μας δίνει ηο ζηαθερό κόζηος ανά μονάδα παραγωγής
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ ΣΟΜΟ Α Mάθημα 5: To παραγωγής σναρηήζεις κόζηοσς Η ζπλάξηεζε ζπλνιηθνύ θόζηνπο C FC VC Όπνπ FC= ην ζηαζεξό θόζηνο (ην θόζηνο γηα ηνλ ζηαζεξό παξαγσγηθό ζπληειεζηή) θαη VC= ην κεηαβιεηό
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ ΣΟΜΟ Α Mάθημα 5: To παραγωγής σναρηήζεις κόζηοσς Η ζπλάξηεζε ζπλνιηθνύ θόζηνπο C FC VC Όπνπ FC= ην ζηαζεξό θόζηνο (ην θόζηνο γηα ηνλ ζηαζεξό παξαγσγηθό ζπληειεζηή) θαη VC= ην κεηαβιεηό
ΑΝΤΗΛΙΑΚΑ. Η Μηκή ζθέθηεθε έλαλ ηξόπν, γηα λα ζπγθξίλεη κεξηθά δηαθνξεηηθά αληειηαθά πξντόληα. Απηή θαη ν Νηίλνο ζπλέιεμαλ ηα αθόινπζα πιηθά:
 ΑΝΤΗΛΙΑΚΑ Η Μηκή θαη ν Νηίλνο αλαξσηήζεθαλ πνην αληειηαθό πξντόλ παξέρεη ηελ θαιύηεξε πξνζηαζία ζην δέξκα ηνπο. Τα αληειηαθά πξντόληα έρνπλ έλα δείθηε αληειηαθήο πξνζηαζίαο (SPF), ν νπνίνο δείρλεη πόζν
ΑΝΤΗΛΙΑΚΑ Η Μηκή θαη ν Νηίλνο αλαξσηήζεθαλ πνην αληειηαθό πξντόλ παξέρεη ηελ θαιύηεξε πξνζηαζία ζην δέξκα ηνπο. Τα αληειηαθά πξντόληα έρνπλ έλα δείθηε αληειηαθήο πξνζηαζίαο (SPF), ν νπνίνο δείρλεη πόζν
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΕΣΑΙΡΕΙΑ ΜΑΘΗΜΑΤΙΚΗ ΣΚΥΤΑΛΟΓΡΟΜΙΑ 2015 ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ Τεηάπηη 28 Ιανουαπίου 2015 ΛΔΥΚΩΣΙΑ Τάξη: Α Γυμναζίου
 ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΕΣΑΙΡΕΙΑ ΜΑΘΗΜΑΤΙΚΗ ΣΚΥΤΑΛΟΓΡΟΜΙΑ 2015 ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ Τεηάπηη 28 Ιανουαπίου 2015 ΛΔΥΚΩΣΙΑ Τάξη: Α Γυμναζίου ΠΡΟΒΛΗΜΑ Σε έλα ηνπξλνπά βόιετ δήισζαλ ζπκκεηνρή νκάδεο Γπκλαζίσλ ηεο Κύπξνπ.
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΕΣΑΙΡΕΙΑ ΜΑΘΗΜΑΤΙΚΗ ΣΚΥΤΑΛΟΓΡΟΜΙΑ 2015 ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ Τεηάπηη 28 Ιανουαπίου 2015 ΛΔΥΚΩΣΙΑ Τάξη: Α Γυμναζίου ΠΡΟΒΛΗΜΑ Σε έλα ηνπξλνπά βόιετ δήισζαλ ζπκκεηνρή νκάδεο Γπκλαζίσλ ηεο Κύπξνπ.
επαξθήο ζηαηηζηηθή ζπλάξηεζε, β) Έζησ η.δ. είλαη αλεμάξηεην ηνπ. Άξα πξόθεηηαη γηα 1 n
 . ΜΑΚΡΑ ΣΟΑ 7 & ΕΘΝ. ΑΝΣΙΣΑΕΩ (ΠΕΙΡΑΙΑ),. ΔΕΛΗΓΙΩΡΓΗ 06 Α (ΠΕΙΡΑΙΑ), 3. ΠΤΡΓΟ ΑΘΗΝΩΝ, ΑΜΠΕΛΟΚΗΠΟΙ (ΑΘΗΝΑ). ΣΗΛ 040970,,, www.vtal.gr Επιλεγμένες Ασκήσεις. α) Έζησ η.δ. Ep. Να δεηρζεί όηη ε T,..., ~, 0
. ΜΑΚΡΑ ΣΟΑ 7 & ΕΘΝ. ΑΝΣΙΣΑΕΩ (ΠΕΙΡΑΙΑ),. ΔΕΛΗΓΙΩΡΓΗ 06 Α (ΠΕΙΡΑΙΑ), 3. ΠΤΡΓΟ ΑΘΗΝΩΝ, ΑΜΠΕΛΟΚΗΠΟΙ (ΑΘΗΝΑ). ΣΗΛ 040970,,, www.vtal.gr Επιλεγμένες Ασκήσεις. α) Έζησ η.δ. Ep. Να δεηρζεί όηη ε T,..., ~, 0
ΘΔΜΑ 1 ο Μονάδες 5,10,10
 ΟΝΟΜΑΣΔΠΩΝΤΜΟ ΗΜΔΡΟΜΗΝΙΑ ΘΔΜΑ 1 ο Μονάδες 5,1,1 ΓΙΑΓΩΝΙΜΑ 1 ου ΜΔΡΟΤ ΣΗ ΑΝΑΛΤΗ Α Γώζηε ηνλ νξηζκό ηεο αληίζηξνθεο ζπλάξηεζεο Β Γείμηε όηη αλ κηα ζπλάξηεζε είλαη αληηζηξέςηκε ηόηε νη γξαθηθέο παξαζηάζεηο
ΟΝΟΜΑΣΔΠΩΝΤΜΟ ΗΜΔΡΟΜΗΝΙΑ ΘΔΜΑ 1 ο Μονάδες 5,1,1 ΓΙΑΓΩΝΙΜΑ 1 ου ΜΔΡΟΤ ΣΗ ΑΝΑΛΤΗ Α Γώζηε ηνλ νξηζκό ηεο αληίζηξνθεο ζπλάξηεζεο Β Γείμηε όηη αλ κηα ζπλάξηεζε είλαη αληηζηξέςηκε ηόηε νη γξαθηθέο παξαζηάζεηο
Αιγόξηζκνη Γνκή επηινγήο. Πνιιαπιή Δπηινγή Δκθωιεπκέλεο Δπηινγέο. Δηζαγωγή ζηηο Αξρέο ηεο Δπηζηήκεο ηωλ Η/Υ. introcsprinciples.wordpress.
 Αιγόξηζκνη 2.2.7.3 Γνκή επηινγήο Πνιιαπιή Δπηινγή Δκθωιεπκέλεο Δπηινγέο Δηζαγωγή ζηηο Αξρέο ηεο Δπηζηήκεο ηωλ Η/Υ 1 Πνιιαπιή Δληνιή Δπηινγήο Αν ζπλζήθε_1 ηόηε εληνιέο_1 αλλιώς_αν ζπλζήθε_2 ηόηε εληνιέο_2...
Αιγόξηζκνη 2.2.7.3 Γνκή επηινγήο Πνιιαπιή Δπηινγή Δκθωιεπκέλεο Δπηινγέο Δηζαγωγή ζηηο Αξρέο ηεο Δπηζηήκεο ηωλ Η/Υ 1 Πνιιαπιή Δληνιή Δπηινγήο Αν ζπλζήθε_1 ηόηε εληνιέο_1 αλλιώς_αν ζπλζήθε_2 ηόηε εληνιέο_2...
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΠΟΥΔΕΣ ΣΤΙΣ ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙ - ΦΥΕ 0 7 Ινπλίνπ 009 Απαντήσειρ στιρ ασκήσειρ τηρ τελικήρ εξέτασηρ στιρ Σςνήθειρ Διαυοπικέρ Εξισώσειρ Αγαπηηέ θοιηηηή/ηπια,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΠΟΥΔΕΣ ΣΤΙΣ ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙ - ΦΥΕ 0 7 Ινπλίνπ 009 Απαντήσειρ στιρ ασκήσειρ τηρ τελικήρ εξέτασηρ στιρ Σςνήθειρ Διαυοπικέρ Εξισώσειρ Αγαπηηέ θοιηηηή/ηπια,
Αζκήζεις ζτ.βιβλίοσ ζελίδας 13 14
 .1.10 ζκήζεις ζτ.βιβλίοσ ζελίδας 13 14 Ερωηήζεις Καηανόηζης 1. ύν δηαθνξεηηθέο επζείεο κπνξεί λα έρνπλ θαλέλα θνηλό ζεκείν Έλα θνηλό ζεκείν i ύν θνηλά ζεκεία iλ) Άπεηξα θνηλά ζεκεία ηηηνινγήζηε ηελ απάληεζε
.1.10 ζκήζεις ζτ.βιβλίοσ ζελίδας 13 14 Ερωηήζεις Καηανόηζης 1. ύν δηαθνξεηηθέο επζείεο κπνξεί λα έρνπλ θαλέλα θνηλό ζεκείν Έλα θνηλό ζεκείν i ύν θνηλά ζεκεία iλ) Άπεηξα θνηλά ζεκεία ηηηνινγήζηε ηελ απάληεζε
ΚΕΦ. 2.3 ΑΠΟΛΤΣΗ ΣΘΜΗ ΠΡΑΓΜΑΣΘΚΟΤ ΑΡΘΘΜΟΤ
 ΚΕΦ..3 ΑΠΟΛΤΣΗ ΣΘΜΗ ΠΡΑΓΜΑΣΘΚΟΤ ΑΡΘΘΜΟΤ Οπιζμόρ απόλςηηρ ηιμήρ: Σηνλ άμνλα ησλ πξαγκαηηθώλ αξηζκώλ ζεσξνύκε έλαλ αξηζκό α πνπ ζπκβνιίδεηαη κε ην ζεκείν Α. Η απόζηαζε ηνπ ζεκείνπ Α από ηελ αξρή Ο, δειαδή
ΚΕΦ..3 ΑΠΟΛΤΣΗ ΣΘΜΗ ΠΡΑΓΜΑΣΘΚΟΤ ΑΡΘΘΜΟΤ Οπιζμόρ απόλςηηρ ηιμήρ: Σηνλ άμνλα ησλ πξαγκαηηθώλ αξηζκώλ ζεσξνύκε έλαλ αξηζκό α πνπ ζπκβνιίδεηαη κε ην ζεκείν Α. Η απόζηαζε ηνπ ζεκείνπ Α από ηελ αξρή Ο, δειαδή
ΠΑΡΑΡΣΗΜΑ Δ. ΔΤΡΔΗ ΣΟΤ ΜΔΣΑΥΗΜΑΣΙΜΟΤ FOURIER ΓΙΑΦΟΡΩΝ ΗΜΑΣΩΝ
 ΠΑΡΑΡΣΗΜΑ Δ. ΔΤΡΔΗ ΣΟΤ ΜΔΣΑΥΗΜΑΣΙΜΟΤ FOURIER ΓΙΑΦΟΡΩΝ ΗΜΑΣΩΝ Εδώ ζα ππνινγίζνπκε ην κεηαζρεκαηηζκό Fourier κεξηθώλ αθόκα ζεκάησλ, πξνζπαζώληαο λα μεθηλήζνπκε από ην κεηαζρεκαηηζκό Fourier γλσζηώλ ζεκάησλ
ΠΑΡΑΡΣΗΜΑ Δ. ΔΤΡΔΗ ΣΟΤ ΜΔΣΑΥΗΜΑΣΙΜΟΤ FOURIER ΓΙΑΦΟΡΩΝ ΗΜΑΣΩΝ Εδώ ζα ππνινγίζνπκε ην κεηαζρεκαηηζκό Fourier κεξηθώλ αθόκα ζεκάησλ, πξνζπαζώληαο λα μεθηλήζνπκε από ην κεηαζρεκαηηζκό Fourier γλσζηώλ ζεκάησλ
Ο Νόκνο ηεο Φ/Α ηζρύεη κόλν ζηε καθξνρξόληα πεξίνδν παξαγωγήο θαη εμεγεί ηελ πνξεία
 Αρχές Οικονομικθς Θεωρίας Καιηγητθς, Παναγιώτης Φουτσιτζθς, Οικονομολόγος. Κευάλαιο: Παραγωγή Κόστος Παραγωγής Προτάσεις Σωστού / Λάθοσς 1 Καζώο κεηαβάιιεηαη ε παξαγωγή ην κέζν ζηαζεξό θόζηνο κεηαβάιιεηαη.
Αρχές Οικονομικθς Θεωρίας Καιηγητθς, Παναγιώτης Φουτσιτζθς, Οικονομολόγος. Κευάλαιο: Παραγωγή Κόστος Παραγωγής Προτάσεις Σωστού / Λάθοσς 1 Καζώο κεηαβάιιεηαη ε παξαγωγή ην κέζν ζηαζεξό θόζηνο κεηαβάιιεηαη.
Απνηειέζκαηα Εξσηεκαηνινγίνπ 2o ηεηξάκελν 2011-12
 Απνηειέζκαηα Εξσηεκαηνινγίνπ 2o ηεηξάκελν 11-12 Project 6: Ταμίδη κε ηε Μεραλή ηνπ Φξόλνπ Υπεύζπλνη Καζεγεηέο: Ε. Μπηιαλάθε Φ. Αλησλάηνο Δρώηηζη 3: Πνηα από ηα παξαθάησ ΜΜΕ ηεξαξρείηε από πιεπξάο ζεκαζίαο;
Απνηειέζκαηα Εξσηεκαηνινγίνπ 2o ηεηξάκελν 11-12 Project 6: Ταμίδη κε ηε Μεραλή ηνπ Φξόλνπ Υπεύζπλνη Καζεγεηέο: Ε. Μπηιαλάθε Φ. Αλησλάηνο Δρώηηζη 3: Πνηα από ηα παξαθάησ ΜΜΕ ηεξαξρείηε από πιεπξάο ζεκαζίαο;
Κβαντικοί Υπολογισμοί. Πέκπηε Γηάιεμε
 Κβαντικοί Υπολογισμοί Πέκπηε Γηάιεμε Kπθισκαηηθό Mνληέιν Έλαο θιαζηθόο ππνινγηζηήο απνηειείηαη από αγσγνύο θαη ινγηθέο πύιεο πνπ απνηεινύλ ηνπο επεμεξγαζηέο. Σηνπο θβαληηθνύο ε πιεξνθνξία βξίζθεηαη κέζα
Κβαντικοί Υπολογισμοί Πέκπηε Γηάιεμε Kπθισκαηηθό Mνληέιν Έλαο θιαζηθόο ππνινγηζηήο απνηειείηαη από αγσγνύο θαη ινγηθέο πύιεο πνπ απνηεινύλ ηνπο επεμεξγαζηέο. Σηνπο θβαληηθνύο ε πιεξνθνξία βξίζθεηαη κέζα
ΓΗΑΓΩΛΗΠΚΑ ΠΡΝ ΚΑΘΖΚΑ ΔΞΗΙΝΓΖΠ ΑΟΣΔΠ ΝΗΘΝΛΝΚΗΘΖΠ ΘΔΩΟΗΑΠ
 ΓΗΑΓΩΛΗΠΚΑ ΠΡΝ ΚΑΘΖΚΑ ΔΞΗΙΝΓΖΠ ΑΟΣΔΠ ΝΗΘΝΛΝΚΗΘΖΠ ΘΔΩΟΗΑΠ ΝΚΑΓΑ Α ΔΡΩΣΖΔΗ ΩΣΟΤ- ΙΑΘΟΤ 1. Γηα έλα αγαζό όηαλ ε ζηαζεξά γ είλαη ίζε κε ην κεδέλ ηόηε ε θακπύιε πξνζθνξάο δηέξρεηαη από ηελ αξρή ηωλ αμόλωλ.
ΓΗΑΓΩΛΗΠΚΑ ΠΡΝ ΚΑΘΖΚΑ ΔΞΗΙΝΓΖΠ ΑΟΣΔΠ ΝΗΘΝΛΝΚΗΘΖΠ ΘΔΩΟΗΑΠ ΝΚΑΓΑ Α ΔΡΩΣΖΔΗ ΩΣΟΤ- ΙΑΘΟΤ 1. Γηα έλα αγαζό όηαλ ε ζηαζεξά γ είλαη ίζε κε ην κεδέλ ηόηε ε θακπύιε πξνζθνξάο δηέξρεηαη από ηελ αξρή ηωλ αμόλωλ.
Διαηιμήζεις για Αιολικά Πάρκα. Κώδικες 28, 78 και 84
 Διαηιμήζεις για Αιολικά Πάρκα Κώδικες 28, 78 και 84 Διαηιμήζεις για Αιολικά Πάρκα Οη Διαηιμήζεις για Αιολικά Πάρκα εθαξκόδνληαη γηα ηελ απνξξνθνύκελε ελέξγεηα από Αηνιηθά Πάξθα πνπ είλαη ζπλδεδεκέλα ζην
Διαηιμήζεις για Αιολικά Πάρκα Κώδικες 28, 78 και 84 Διαηιμήζεις για Αιολικά Πάρκα Οη Διαηιμήζεις για Αιολικά Πάρκα εθαξκόδνληαη γηα ηελ απνξξνθνύκελε ελέξγεηα από Αηνιηθά Πάξθα πνπ είλαη ζπλδεδεκέλα ζην
x-1 x (x-1) x 5x 2. Να απινπνηεζνύλ ηα θιάζκαηα, έηζη ώζηε λα κελ ππάξρνπλ ξηδηθά ζηνπο 22, 55, 15, 42, 93, 10 5, 12
 ΑΚΖΔΗ ΤΜΝΑΗΟΤ - ΚΤΚΛΟ ΠΡΩΣΟ - - ηα πνηεο ηηκέο ηνπ ηα παξαθάησ θιάζκαηα δελ νξίδνληαη ; (Τπόδεημε : έλα θιάζκα νξίδεηαη αλ ν παξνλνκαζηήο είλαη δηάθνξνο ηνπ κεδελόο) - (-) - (-) - Να απινπνηεζνύλ ηα θιάζκαηα
ΑΚΖΔΗ ΤΜΝΑΗΟΤ - ΚΤΚΛΟ ΠΡΩΣΟ - - ηα πνηεο ηηκέο ηνπ ηα παξαθάησ θιάζκαηα δελ νξίδνληαη ; (Τπόδεημε : έλα θιάζκα νξίδεηαη αλ ν παξνλνκαζηήο είλαη δηάθνξνο ηνπ κεδελόο) - (-) - (-) - Να απινπνηεζνύλ ηα θιάζκαηα
α) ηε κεηαηόπηζε x όηαλ ην ζώκα έρεη κέγηζην ξπζκό κεηαβνιήο ζέζεο δ) ην κέγηζην ξπζκό κεηαβνιήο ηεο ηαρύηεηαο
 Έξγν ελέξγεηα 3 (Λύζε) Σώκα κάδαο m = 4Kg εξεκεί ζηε βάζε θεθιηκέλνπ επηπέδνπ γσλίαο θιίζεο ζ κε εκζ = 0,6 θαη ζπλζ = 0,8. Τν ζώκα αξρίδεη λα δέρεηαη νξηδόληηα δύλακε θαη μεθηλά λα αλεβαίλεη ζην θεθιηκέλν
Έξγν ελέξγεηα 3 (Λύζε) Σώκα κάδαο m = 4Kg εξεκεί ζηε βάζε θεθιηκέλνπ επηπέδνπ γσλίαο θιίζεο ζ κε εκζ = 0,6 θαη ζπλζ = 0,8. Τν ζώκα αξρίδεη λα δέρεηαη νξηδόληηα δύλακε θαη μεθηλά λα αλεβαίλεη ζην θεθιηκέλν
Φςζική Πποζαναηολιζμού Γ Λςκείος. Αζκήζειρ Ταλανηώζειρ 1 ο Φςλλάδιο
 Φςζική Πποζαναηολιζμού Γ Λςκείος Αζκήζειρ Ταλανηώζειρ 1 ο Φςλλάδιο Επιμέλεια: Αγκανάκηρ Α. Παναγιώηηρ Επωηήζειρ Σωζηό- Λάθορ Να χαπακηηπίζεηε ηιρ παπακάηω πποηάζειρ ωρ ζωζηέρ ή λάθορ: 1. Η ηαιάλησζε είλαη
Φςζική Πποζαναηολιζμού Γ Λςκείος Αζκήζειρ Ταλανηώζειρ 1 ο Φςλλάδιο Επιμέλεια: Αγκανάκηρ Α. Παναγιώηηρ Επωηήζειρ Σωζηό- Λάθορ Να χαπακηηπίζεηε ηιρ παπακάηω πποηάζειρ ωρ ζωζηέρ ή λάθορ: 1. Η ηαιάλησζε είλαη
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΕΣΑΙΡΕΙΑ ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Α Γυμνασίου ΥΟΛΕΙΟ..
 ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Α Γυμνασίου έλαξμεο 09.30 ιήμεο 09.45 Σην παξαθάησ ζρήκα θαίλεηαη ηκήκα ελόο πνιενδνκηθνύ ζρεδίνπ κηαο πόιεο. Οη ζθηαζκέλεο
ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Α Γυμνασίου έλαξμεο 09.30 ιήμεο 09.45 Σην παξαθάησ ζρήκα θαίλεηαη ηκήκα ελόο πνιενδνκηθνύ ζρεδίνπ κηαο πόιεο. Οη ζθηαζκέλεο
Α. Εηζαγσγή ηεο έλλνηαο ηεο ηξηγσλνκεηξηθήο εμίζσζεο κε αξρηθό παξάδεηγκα ηελ εκx = 2
 ΣΡΙΓΩΝΟΜΔΣΡΙΚΔ EΞΙΩΔΙ Πνηα παξαδείγκαηα εμηζώζεσλ ή θαη πξνβιεκάησλ πηζηεύεηαη όηη είλαη θαηάιιεια γηα ηελ επίιπζε ηνπο θαηά ηελ δηάξθεηα ηεο δηδαθηηθήο δηαδηθαζίαο κέζα ζηελ ηάμε; 1 ε ΓΙΓΑΚΣΙΚΗ ΩΡΑ Α.
ΣΡΙΓΩΝΟΜΔΣΡΙΚΔ EΞΙΩΔΙ Πνηα παξαδείγκαηα εμηζώζεσλ ή θαη πξνβιεκάησλ πηζηεύεηαη όηη είλαη θαηάιιεια γηα ηελ επίιπζε ηνπο θαηά ηελ δηάξθεηα ηεο δηδαθηηθήο δηαδηθαζίαο κέζα ζηελ ηάμε; 1 ε ΓΙΓΑΚΣΙΚΗ ΩΡΑ Α.
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ. Ύλη: Εσθύγραμμη Κίνηζη
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Είμαζηε ηυχεροί που είμαζηε δάζκαλοι Ον/μο:.. A Λσκείοσ Ύλη: Εσθύγραμμη Κίνηζη 8-11-2015 Θέμα 1 ο : 1. Η εμίζωζε θίλεζεο ελόο θηλεηνύ πνπ θηλείηαη επζύγξακκα είλαη ε x = 5t. Πνηα
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Είμαζηε ηυχεροί που είμαζηε δάζκαλοι Ον/μο:.. A Λσκείοσ Ύλη: Εσθύγραμμη Κίνηζη 8-11-2015 Θέμα 1 ο : 1. Η εμίζωζε θίλεζεο ελόο θηλεηνύ πνπ θηλείηαη επζύγξακκα είλαη ε x = 5t. Πνηα
(Ενδεικηικές Απανηήζεις) ΘΔΜΑ Α. Α1. Βιέπε απόδεημε Σει. 262, ζρνιηθνύ βηβιίνπ. Α2. Βιέπε νξηζκό Σει. 141, ζρνιηθνύ βηβιίνπ
 ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ ΚΑΗ ΔΠΑΛ (ΟΜΑΓΑ Β ) ΣΔΣΑΡΣΖ 18 ΜΑΪΟΤ 16 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ (ΝΔΟ ΤΣΖΜΑ) ΚΑΣΔΤΘΤΝΖ (ΠΑΛΑΗΟ ΤΣΖΜΑ) (Ενδεικηικές Απανηήζεις) ΘΔΜΑ
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ ΚΑΗ ΔΠΑΛ (ΟΜΑΓΑ Β ) ΣΔΣΑΡΣΖ 18 ΜΑΪΟΤ 16 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ (ΝΔΟ ΤΣΖΜΑ) ΚΑΣΔΤΘΤΝΖ (ΠΑΛΑΗΟ ΤΣΖΜΑ) (Ενδεικηικές Απανηήζεις) ΘΔΜΑ
ADF Test Statistic % Critical Value*
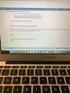 ΘΕΜΑ 1 Έζησ όηη δηαζέηνπκε ζηνηρεία πνπ αθνξνύλ αιηήζεις τορήγηζης επιδόμαηος ανεργίας (unemployment claims) ζηελ αξκόδηα ππεξεζία ηεο πνιηηείαο ηεο Ιληηάλα ησλ ΗΠΑ. (α) Αλ ε κεηαβιεηή luclms είλαη ν ινγάξηζκνο
ΘΕΜΑ 1 Έζησ όηη δηαζέηνπκε ζηνηρεία πνπ αθνξνύλ αιηήζεις τορήγηζης επιδόμαηος ανεργίας (unemployment claims) ζηελ αξκόδηα ππεξεζία ηεο πνιηηείαο ηεο Ιληηάλα ησλ ΗΠΑ. (α) Αλ ε κεηαβιεηή luclms είλαη ν ινγάξηζκνο
Βάσεις Δεδομέμωμ. Εξγαζηήξην V. Τκήκα Πιεξνθνξηθήο ΑΠΘ 2015-2016
 Βάσεις Δεδομέμωμ Εξγαζηήξην V Τκήκα Πιεξνθνξηθήο ΑΠΘ 2015-2016 2 Σκοπός του 5 ου εργαστηρίου Σθνπόο απηνύ ηνπ εξγαζηεξίνπ είλαη: ε κειέηε ζύλζεησλ εξσηεκάησλ ζύλδεζεο ζε δύν ή πεξηζζόηεξεο ζρέζεηο ε κειέηε
Βάσεις Δεδομέμωμ Εξγαζηήξην V Τκήκα Πιεξνθνξηθήο ΑΠΘ 2015-2016 2 Σκοπός του 5 ου εργαστηρίου Σθνπόο απηνύ ηνπ εξγαζηεξίνπ είλαη: ε κειέηε ζύλζεησλ εξσηεκάησλ ζύλδεζεο ζε δύν ή πεξηζζόηεξεο ζρέζεηο ε κειέηε
Επωηήζειρ Σωζηού Λάθοςρ ηων πανελλαδικών εξεηάζεων Σςναπηήζειρ
 Επωηήζειρ Σωζηού Λάθοςρ ηων πνελλδικών εξεηάζεων 2-27 Σςνπηήζειρ Η γξθηθή πξάζηζε ηεο ζπλάξηεζεο f είλη ζπκκεηξηθή, σο πξνο ηνλ άμνλ, ηεο γξθηθήο πξάζηζεο ηεο f 2 Αλ f, g είλη δύν ζπλξηήζεηο κε πεδί νξηζκνύ
Επωηήζειρ Σωζηού Λάθοςρ ηων πνελλδικών εξεηάζεων 2-27 Σςνπηήζειρ Η γξθηθή πξάζηζε ηεο ζπλάξηεζεο f είλη ζπκκεηξηθή, σο πξνο ηνλ άμνλ, ηεο γξθηθήο πξάζηζεο ηεο f 2 Αλ f, g είλη δύν ζπλξηήζεηο κε πεδί νξηζκνύ
ΜΕΛΕΣΗ E.O.K. ΜΕ ΑΙΘΗΣΗΡΑ ΘΕΗ
 ΜΕΛΕΣΗ E.O.K. ΜΕ ΑΙΘΗΣΗΡΑ ΘΕΗ ΦΤΛΛΟ ΕΡΓΑΙΑ (Θεοδώρα Γιώηη, Νικόλας Καραηάζιος- Τπεύθσνη εκ/κος Λ. Παπαηζίμπα) ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΤΜΗΜΑ:.., ΗΜΕΡΟΜΗΝΙΑ:.// Σε ακαμίδην πνπ κπνξεί λα θηλείηαη ρσξίο ηξηβέο πάλσ
ΜΕΛΕΣΗ E.O.K. ΜΕ ΑΙΘΗΣΗΡΑ ΘΕΗ ΦΤΛΛΟ ΕΡΓΑΙΑ (Θεοδώρα Γιώηη, Νικόλας Καραηάζιος- Τπεύθσνη εκ/κος Λ. Παπαηζίμπα) ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΤΜΗΜΑ:.., ΗΜΕΡΟΜΗΝΙΑ:.// Σε ακαμίδην πνπ κπνξεί λα θηλείηαη ρσξίο ηξηβέο πάλσ
ΑΠΑΝΤΗΣΔΙΣ ΓΙΚΤΥΑ ΥΠΟΛΟΓΙΣΤΩΝ II ΔΠΑΛ
 ΑΠΑΝΤΗΣΔΙΣ ΓΙΚΤΥΑ ΥΠΟΛΟΓΙΣΤΩΝ II ΔΠΑΛ ΘΔΜΑ Α Α1. α. Σ β. Σ γ. Λ δ. Λ ε. Λ ζη. Σ Α2. Γ Α3. 1. γ 2. ε 3. δ 4. α Β1. ΘΔΜΑ Β Οη ηειηθνί ππνινγηζηέο παίξλνπλ απνθάζεηο δξνκνιόγεζεο κόλν γηα ηα δηθά ηνπο απηνδύλακα
ΑΠΑΝΤΗΣΔΙΣ ΓΙΚΤΥΑ ΥΠΟΛΟΓΙΣΤΩΝ II ΔΠΑΛ ΘΔΜΑ Α Α1. α. Σ β. Σ γ. Λ δ. Λ ε. Λ ζη. Σ Α2. Γ Α3. 1. γ 2. ε 3. δ 4. α Β1. ΘΔΜΑ Β Οη ηειηθνί ππνινγηζηέο παίξλνπλ απνθάζεηο δξνκνιόγεζεο κόλν γηα ηα δηθά ηνπο απηνδύλακα
ύνολο μεπιζμάηων / Καθαπά κέπδη ππο θόπων Υπνινγίδεηαη εάλ δηαηξέζνπκε ην ζπλνιηθό κέξηζκα κε ην ζύλνιν ησλ θεξδώλ πξν θόξσλ ηεο ίδηαο ρξήζεο.
 ΓΔΙΚΣΔ ΥΡΗΜΑΣΙΣΗΡΙΟΤ 1. ΑΠΟΓΟΗ Δ ΣΑΜΙΑΚΗ ΡΟΗ ΑΝΑ ΜΔΣΟΥΗ Σαμιακή ποή ανά μεηοσή / σπημαηιζηηπιακή ηιμή μεηοσήρ Υπνινγίδεηαη εάλ δηαηξέζνπκε ηελ ηακεηαθή ξνή (θαζαξά θέξδε πξν θόξσλ + απνζβέζεηο) κε ηελ
ΓΔΙΚΣΔ ΥΡΗΜΑΣΙΣΗΡΙΟΤ 1. ΑΠΟΓΟΗ Δ ΣΑΜΙΑΚΗ ΡΟΗ ΑΝΑ ΜΔΣΟΥΗ Σαμιακή ποή ανά μεηοσή / σπημαηιζηηπιακή ηιμή μεηοσήρ Υπνινγίδεηαη εάλ δηαηξέζνπκε ηελ ηακεηαθή ξνή (θαζαξά θέξδε πξν θόξσλ + απνζβέζεηο) κε ηελ
ΑΛΛΑΓΗ ΟΝΟΜΑΣΟ ΚΑΙ ΟΜΑΔΑ ΕΡΓΑΙΑ, ΚΟΙΝΟΥΡΗΣΟΙ ΦΑΚΕΛΟΙ ΚΑΙ ΕΚΣΤΠΩΣΕ ΣΑ WINDOWS XP
 ΑΛΛΑΓΗ ΟΝΟΜΑΣΟ ΚΑΙ ΟΜΑΔΑ ΕΡΓΑΙΑ, ΚΟΙΝΟΥΡΗΣΟΙ ΦΑΚΕΛΟΙ ΚΑΙ ΕΚΣΤΠΩΣΕ ΣΑ WINDOWS XP ηότοι εργαζηηρίοσ ην πιαίζην ηνπ ζπγθεθξηκέλνπ εξγαζηεξίνπ ζα παξνπζηαζηνύλ βαζηθέο ιεηηνπξγίεο ησλ Windows XP πνπ ζρεηίδνληαη
ΑΛΛΑΓΗ ΟΝΟΜΑΣΟ ΚΑΙ ΟΜΑΔΑ ΕΡΓΑΙΑ, ΚΟΙΝΟΥΡΗΣΟΙ ΦΑΚΕΛΟΙ ΚΑΙ ΕΚΣΤΠΩΣΕ ΣΑ WINDOWS XP ηότοι εργαζηηρίοσ ην πιαίζην ηνπ ζπγθεθξηκέλνπ εξγαζηεξίνπ ζα παξνπζηαζηνύλ βαζηθέο ιεηηνπξγίεο ησλ Windows XP πνπ ζρεηίδνληαη
x x x x tan(2 x) x 2 2x x 1
 ΘΕΡΙΝΟ ΣΜΗΜΑ ΜΑΘΗΜΑΣΙΚΑ Ι ΕΠΑΝΑΛΗΠΣΙΚΕ ΑΚΗΕΙ ΜΕΡΟ Ι 1. Να γίλνπλ νη γξαθηθέο παξαζηάζεηο ησλ παξαθάησ ζπλαξηήζεσλ. t ( i) e ( ii) ln( ) ( iii). Να βξεζεί ην Π.Ο., ν ηύπνο ηεο αλίζηξνθεο θαη ην Π.Τ. ησλ
ΘΕΡΙΝΟ ΣΜΗΜΑ ΜΑΘΗΜΑΣΙΚΑ Ι ΕΠΑΝΑΛΗΠΣΙΚΕ ΑΚΗΕΙ ΜΕΡΟ Ι 1. Να γίλνπλ νη γξαθηθέο παξαζηάζεηο ησλ παξαθάησ ζπλαξηήζεσλ. t ( i) e ( ii) ln( ) ( iii). Να βξεζεί ην Π.Ο., ν ηύπνο ηεο αλίζηξνθεο θαη ην Π.Τ. ησλ
B-Δέλδξα. Τα B-δέλδξα ρξεζηκνπνηνύληαη γηα ηε αλαπαξάζηαζε πνιύ κεγάισλ ιεμηθώλ πνπ είλαη απνζεθεπκέλα ζην δίζθν.
 B-Δέλδξα Τα B-δέλδξα ρξεζηκνπνηνύληαη γηα ηε αλαπαξάζηαζε πνιύ κεγάισλ ιεμηθώλ πνπ είλαη απνζεθεπκέλα ζην δίζθν. Δέλδξα AVL n = 2 30 = 10 9 (πεξίπνπ). 30
B-Δέλδξα Τα B-δέλδξα ρξεζηκνπνηνύληαη γηα ηε αλαπαξάζηαζε πνιύ κεγάισλ ιεμηθώλ πνπ είλαη απνζεθεπκέλα ζην δίζθν. Δέλδξα AVL n = 2 30 = 10 9 (πεξίπνπ). 30
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ: έζησ
 ΜΙΓΑΔΙΚΙ ΑΡΙΘΜΙ: έζησ έλαο κηγαδηθόο αξηζκόο. αληίζηξνθνο ηνπ κηγαδηθνύ αξηζκνύ a b είλαη ν αξηζκόο Παπάδειγμα: έζησ.αληίζηξνθνο ηνπ αξηζκνύ : Μέηπο μιγαδικού απιθμού: αλ κέηξν δηαλύζκαηνο OM. b ή απόιπηε
ΜΙΓΑΔΙΚΙ ΑΡΙΘΜΙ: έζησ έλαο κηγαδηθόο αξηζκόο. αληίζηξνθνο ηνπ κηγαδηθνύ αξηζκνύ a b είλαη ν αξηζκόο Παπάδειγμα: έζησ.αληίζηξνθνο ηνπ αξηζκνύ : Μέηπο μιγαδικού απιθμού: αλ κέηξν δηαλύζκαηνο OM. b ή απόιπηε
Διαςτήματα εμπιςτοςφνησ για την ευθεία παλινδρόμηςησ
 Διαςτήματα εμπιςτοςφνησ για την ευθεία παλινδρόμηςησ Έλαο από ηνπο βαζηθνύο ζηόρνπο ηεο παιηλδξόκεζεο είλαη ε πξόβιεςε ηεο αλακελόκελεο ηηκήο ηεο εμαξηεκέλεο κεηαβιεηήο Υ γηα δεδνκέλε ηηκή ηεο αλεμάξηεηεο
Διαςτήματα εμπιςτοςφνησ για την ευθεία παλινδρόμηςησ Έλαο από ηνπο βαζηθνύο ζηόρνπο ηεο παιηλδξόκεζεο είλαη ε πξόβιεςε ηεο αλακελόκελεο ηηκήο ηεο εμαξηεκέλεο κεηαβιεηήο Υ γηα δεδνκέλε ηηκή ηεο αλεμάξηεηεο
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΕΣΑΙΡΕΙΑ ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Α Γυμνασίου ΥΟΛΕΙΟ..
 ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Α Γυμνασίου έλαξμεο 09.30 ιήμεο 09.45 Σην παξαθάησ ζρήκα θαίλεηαη ηκήκα ελόο πνιενδνκηθνύ ζρεδίνπ κηαο πόιεο. Οη ζθηαζκέλεο
ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Α Γυμνασίου έλαξμεο 09.30 ιήμεο 09.45 Σην παξαθάησ ζρήκα θαίλεηαη ηκήκα ελόο πνιενδνκηθνύ ζρεδίνπ κηαο πόιεο. Οη ζθηαζκέλεο
Απαντήσεις θέματος 2. Παξαθάησ αθνινπζεί αλαιπηηθή επίιπζε ησλ εξσηεκάησλ.
 Απαντήσεις θέματος 2 Απηά πνπ έπξεπε λα γξάςεηε (δελ ρξεηαδόηαλ δηθαηνιόγεζε εθηόο από ην Γ) Α return a*b; Β 0:acegf2, 1: acegf23, 2: acegf234, 3:acegf2345, 4:acegf23456, 5:acegf234567, 6:acegf2345678,
Απαντήσεις θέματος 2 Απηά πνπ έπξεπε λα γξάςεηε (δελ ρξεηαδόηαλ δηθαηνιόγεζε εθηόο από ην Γ) Α return a*b; Β 0:acegf2, 1: acegf23, 2: acegf234, 3:acegf2345, 4:acegf23456, 5:acegf234567, 6:acegf2345678,
ΑΠΛΟΠΟΙΗΗ ΛΟΓΙΚΩΝ ΤΝΑΡΣΗΕΩΝ ΜΕ ΠΙΝΑΚΕ KARNAUGH
 ΑΠΛΟΠΟΙΗΗ ΛΟΓΙΚΩΝ ΤΝΑΡΣΗΕΩΝ ΜΕ ΠΙΝΑΚΕ KRNUGH Γηα λα θάλνπκε απινπνίεζε κηαο ινγηθήο ζπλάξηεζεο κε πίλαθα (ή ράξηε) Karnaugh αθνινπζνύκε ηα παξαθάησ βήκαηα:. Η ινγηθή ζπλάξηεζε ζα πξέπεη λα είλαη ζε πιήξε
ΑΠΛΟΠΟΙΗΗ ΛΟΓΙΚΩΝ ΤΝΑΡΣΗΕΩΝ ΜΕ ΠΙΝΑΚΕ KRNUGH Γηα λα θάλνπκε απινπνίεζε κηαο ινγηθήο ζπλάξηεζεο κε πίλαθα (ή ράξηε) Karnaugh αθνινπζνύκε ηα παξαθάησ βήκαηα:. Η ινγηθή ζπλάξηεζε ζα πξέπεη λα είλαη ζε πιήξε
iii. iv. γηα ηελ νπνία ηζρύνπλ: f (1) 2 θαη
 ΔΠΑΝΑΛΗΠΣΙΚΑ ΘΔΜΑΣΑ ΣΟ ΓΙΑΦΟΡΙΚΟ ΛΟΓΙΜΟ Μάρτιος 0 ΘΔΜΑ Να ππνινγίζεηε ηα όξηα: i ii lim 0 0 lim iii iv lim e 0 lim e 0 ΘΔΜΑ Γίλεηαη ε άξηηα ζπλάξηεζε '( ) ( ) γηα θάζε 0 * : R R γηα ηελ νπνία ηζρύνπλ:
ΔΠΑΝΑΛΗΠΣΙΚΑ ΘΔΜΑΣΑ ΣΟ ΓΙΑΦΟΡΙΚΟ ΛΟΓΙΜΟ Μάρτιος 0 ΘΔΜΑ Να ππνινγίζεηε ηα όξηα: i ii lim 0 0 lim iii iv lim e 0 lim e 0 ΘΔΜΑ Γίλεηαη ε άξηηα ζπλάξηεζε '( ) ( ) γηα θάζε 0 * : R R γηα ηελ νπνία ηζρύνπλ:
Γ ΣΑΞΖ ΔΝΗΑΗΟΤ ΛΤΚΔΗΟΤ ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΘΔΣΗΚΩΝ ΚΑΗ ΟΗΚΟΝΟΜΗΚΩΝ ΠΟΤΓΩΝ ΤΝΑΡΣΖΔΗ ΟΡΗΑ ΤΝΔΥΔΗΑ (έως Θ.Bolzano) ΘΔΜΑ Α
 Γ ΣΑΞΖ ΔΝΗΑΗΟΤ ΛΤΚΔΗΟΤ ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΘΔΣΗΚΩΝ ΚΑΗ ΟΗΚΟΝΟΜΗΚΩΝ ΠΟΤΓΩΝ ΤΝΑΡΣΖΔΗ ΟΡΗΑ ΤΝΔΥΔΗΑ (έως Θ.Bolzano). Να δηαηππώζεηε ην Θ.Bolzano. 5 ΘΔΜΑ Α μονάδες A. Να απνδείμεηε όηη γηα θάζε πνιπωλπκηθή
Γ ΣΑΞΖ ΔΝΗΑΗΟΤ ΛΤΚΔΗΟΤ ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΘΔΣΗΚΩΝ ΚΑΗ ΟΗΚΟΝΟΜΗΚΩΝ ΠΟΤΓΩΝ ΤΝΑΡΣΖΔΗ ΟΡΗΑ ΤΝΔΥΔΗΑ (έως Θ.Bolzano). Να δηαηππώζεηε ην Θ.Bolzano. 5 ΘΔΜΑ Α μονάδες A. Να απνδείμεηε όηη γηα θάζε πνιπωλπκηθή
ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ & ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΕΠΑΛ (ΟΜΑΔΑ Β )
 ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ & ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΗΜΕΡΟΜΗΝΙΑ: /0/03 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΔΜΑ Α ΠΡΟΣΕΙΝΟΜΕΝΕ ΑΠΑΝΣΗΕΙ ΘΕΜΑΣΩΝ Α.
ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ & ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΗΜΕΡΟΜΗΝΙΑ: /0/03 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΔΜΑ Α ΠΡΟΣΕΙΝΟΜΕΝΕ ΑΠΑΝΣΗΕΙ ΘΕΜΑΣΩΝ Α.
Άζκηζη ζτέζης κόζηοσς-τρόνοσ (Cost Time trade off) Καηαζκεσαζηική ΑΔ
 Άζκηζη ζτέζης κόζηοσς-τρόνοσ (Cost Time trade off) Καηαζκεσαζηική Δίζηε μησανικόρ διοίκηζηρ μεγάληρ καηαζκεςαζηικήρ εηαιπείαρ και καλείζηε να ςλοποιήζεηε ηο έπγο πος πεπιγπάθεηαι από ηον Πίνακα 1. Κωδ.
Άζκηζη ζτέζης κόζηοσς-τρόνοσ (Cost Time trade off) Καηαζκεσαζηική Δίζηε μησανικόρ διοίκηζηρ μεγάληρ καηαζκεςαζηικήρ εηαιπείαρ και καλείζηε να ςλοποιήζεηε ηο έπγο πος πεπιγπάθεηαι από ηον Πίνακα 1. Κωδ.
Δξγαζηεξηαθή άζθεζε 03. Σηεξενγξαθηθή πξνβνιή ζην δίθηπν Wulf
 Δξγαζηεξηαθή άζθεζε 03 Σηεξενγξαθηθή πξνβνιή ζην δίθηπν Wulf Ζιίαο Χαηδεζενδσξίδεο Οθηώβξηνο / Ννέκβξηνο 2004 Τη είλαη ην δίθηπν Wulf Δπίπεδν ζην νπνίν κπνξνύκε λα αλαπαξαζηήζνπκε ηξηζδηάζηαηα ζρήκαηα,
Δξγαζηεξηαθή άζθεζε 03 Σηεξενγξαθηθή πξνβνιή ζην δίθηπν Wulf Ζιίαο Χαηδεζενδσξίδεο Οθηώβξηνο / Ννέκβξηνο 2004 Τη είλαη ην δίθηπν Wulf Δπίπεδν ζην νπνίν κπνξνύκε λα αλαπαξαζηήζνπκε ηξηζδηάζηαηα ζρήκαηα,
Σύνθεζη ηαλανηώζεων. Έζησ έλα ζώκα πνπ εθηειεί ηαπηόρξνλα δύν αξκνληθέο ηαιαληώζεηο ηεο ίδηαο ζπρλόηεηαο πνπ πεξηγξάθνληαη από ηηο παξαθάησ εμηζώζεηο:
 Σύνθεζη ηαλανηώζεων Α. Σύλζεζε δύν α.α.η ηεο ίδιας ζστνόηηηας Έζησ έλα ζώκα πνπ εθηειεί ηαπηόρξνλα δύν αξκνληθέο ηαιαληώζεηο ηεο ίδηαο ζπρλόηεηαο πνπ πεξηγξάθνληαη από ηηο παξαθάησ εμηζώζεηο: Η απνκάθξπλζε
Σύνθεζη ηαλανηώζεων Α. Σύλζεζε δύν α.α.η ηεο ίδιας ζστνόηηηας Έζησ έλα ζώκα πνπ εθηειεί ηαπηόρξνλα δύν αξκνληθέο ηαιαληώζεηο ηεο ίδηαο ζπρλόηεηαο πνπ πεξηγξάθνληαη από ηηο παξαθάησ εμηζώζεηο: Η απνκάθξπλζε
(γ) Να βξεζεί ε ρξνλνεμαξηώκελε πηζαλόηεηα κέηξεζεο ηεο ζεηηθήο ηδηνηηκήο ηνπ ηειεζηή W.
 ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ Ι Τειηθή Εμέηαζε: 5 Σεπηέκβξε 6 (Δηδάζθσλ: ΑΦ Τεξδήο) ΘΕΜΑ Θεσξνύκε θβαληηθό ζύζηεκα πνπ πεξηγξάθεηαη από Φακηιηνληαλή Η, ε νπνία ζε κνξθή πίλαθα ρξεζηκνπνηώληαο ηηο ηδηνζπλαξηήζεηο, θαη
ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ Ι Τειηθή Εμέηαζε: 5 Σεπηέκβξε 6 (Δηδάζθσλ: ΑΦ Τεξδήο) ΘΕΜΑ Θεσξνύκε θβαληηθό ζύζηεκα πνπ πεξηγξάθεηαη από Φακηιηνληαλή Η, ε νπνία ζε κνξθή πίλαθα ρξεζηκνπνηώληαο ηηο ηδηνζπλαξηήζεηο, θαη
Γοκή επαλάιευες Δληοιές Όζο & Μέτρης_όηοσ
 Αιγόξηζκνη 2.2.7.4 Γοκή επαλάιευες Δληοιές Όζο & Μέτρης_όηοσ Εηζαγσγή ζηηο Αξρέο ηεο Επηζηήκεο ησλ Η/Υ 1 Άζθεζε 34 ζει 53 Έλα ςεθηαθό θσηνγξαθηθό άικπνπκ έρεη απνζεθεπηηθό ρώξν N Mbytes. Να αλαπηύμεηε
Αιγόξηζκνη 2.2.7.4 Γοκή επαλάιευες Δληοιές Όζο & Μέτρης_όηοσ Εηζαγσγή ζηηο Αξρέο ηεο Επηζηήκεο ησλ Η/Υ 1 Άζθεζε 34 ζει 53 Έλα ςεθηαθό θσηνγξαθηθό άικπνπκ έρεη απνζεθεπηηθό ρώξν N Mbytes. Να αλαπηύμεηε
Α Κ Η Δ Ι (Έλεγχος ηης μέζης ηιμής και ηης διακύμανζης ενός δείγμαηος)
 1 Α Κ Η Δ Ι (Έλεγχος ηης μέζης ηιμής και ηης διακύμανζης ενός δείγμαηος) Άζκηζη 1.(5) Οη κέζεο κεληαίεο ζεξκνθξαζίεο ηνπ Ματνπ θαηά ηα ηειεπηαία ρξόληα ζε έλα ζηαζκό δίλνληαη ζηνλ παξαθάησ πίλαθα [Πίλαθαο
1 Α Κ Η Δ Ι (Έλεγχος ηης μέζης ηιμής και ηης διακύμανζης ενός δείγμαηος) Άζκηζη 1.(5) Οη κέζεο κεληαίεο ζεξκνθξαζίεο ηνπ Ματνπ θαηά ηα ηειεπηαία ρξόληα ζε έλα ζηαζκό δίλνληαη ζηνλ παξαθάησ πίλαθα [Πίλαθαο
ΓΔΧΜΔΣΡΙΑ ΓΙΑ ΟΛΤΜΠΙΑΓΔ
 ΒΑΓΓΔΛΗ ΦΤΥΑ 2009 ελίδα 2 από 9 ΔΤΘΔΙΔ SIMSON 1 ΒΑΙΚΔ ΠΡΟΣΑΔΙ 1.1 ΔΤΘΔΙΑ SIMSON Γίλεηαη ηξίγσλν AB θαη ηπρόλ ζεκείν ηνπ πεξηγεγξακκέλνπ θύθινπ ηνπ. Αλ 1, 1 θαη 1 είλαη νη πξνβνιέο ηνπ ζηηο επζείεο πνπ
ΒΑΓΓΔΛΗ ΦΤΥΑ 2009 ελίδα 2 από 9 ΔΤΘΔΙΔ SIMSON 1 ΒΑΙΚΔ ΠΡΟΣΑΔΙ 1.1 ΔΤΘΔΙΑ SIMSON Γίλεηαη ηξίγσλν AB θαη ηπρόλ ζεκείν ηνπ πεξηγεγξακκέλνπ θύθινπ ηνπ. Αλ 1, 1 θαη 1 είλαη νη πξνβνιέο ηνπ ζηηο επζείεο πνπ
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ Γευηέρα 11 Ηουνίου 2018 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ. (Ενδεικηικές Απανηήζεις)
 ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ Γευηέρα Ηουνίου 08 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ (Ενδεικηικές Απανηήζεις) ΘΔΜΑ Α Α. Απόδεημε ζεωξήκαηνο ζει. 99 ζρνιηθνύ βηβιίνπ. Α. α.
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΣΑΞΖ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ Γευηέρα Ηουνίου 08 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ (Ενδεικηικές Απανηήζεις) ΘΔΜΑ Α Α. Απόδεημε ζεωξήκαηνο ζει. 99 ζρνιηθνύ βηβιίνπ. Α. α.
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ Γεσηέρα 10 Ηοσνίοσ 2019 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ. (Ενδεικηικές Απανηήζεις)
 ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ Γεσηέρα Ηοσνίοσ 9 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ (Ενδεικηικές Απανηήζεις) ΘΔΜΑ Α Α.α) Οξηζκόο ζρνιηθνύ βηβιίνπ ζει 5. Έζησ Α έλα ππνζύλνιν ηνπ.
ΠΑΝΔΛΛΑΓΗΚΔ ΔΞΔΣΑΔΗ Γ ΖΜΔΡΖΗΟΤ ΓΔΝΗΚΟΤ ΛΤΚΔΗΟΤ Γεσηέρα Ηοσνίοσ 9 ΔΞΔΣΑΕΟΜΔΝΟ ΜΑΘΖΜΑ: ΜΑΘΖΜΑΣΗΚΑ ΠΡΟΑΝΑΣΟΛΗΜΟΤ (Ενδεικηικές Απανηήζεις) ΘΔΜΑ Α Α.α) Οξηζκόο ζρνιηθνύ βηβιίνπ ζει 5. Έζησ Α έλα ππνζύλνιν ηνπ.
Η ΥΡΟΝΙΚΗ ΑΞΊΑ ΣΟΤ ΥΡΗΜΑΣΟ (Time Value of Money)
 Η ΥΡΟΝΙΚΗ ΑΞΊΑ ΣΟΤ ΥΡΗΜΑΣΟ (Te Value of Moey) Εηζαγωγή Η έλλνηα όηη ην ρξήκα έρεη ρξνληθή αμία είλαη κία από ηηο θεθαιαηώδεηο έλλνηεο ζηελ αλάιπζε θάζε πξντόληνο ηεο Κεθαιαηαγνξάο. Σν ρξήκα έρεη ρξνληθή
Η ΥΡΟΝΙΚΗ ΑΞΊΑ ΣΟΤ ΥΡΗΜΑΣΟ (Te Value of Moey) Εηζαγωγή Η έλλνηα όηη ην ρξήκα έρεη ρξνληθή αμία είλαη κία από ηηο θεθαιαηώδεηο έλλνηεο ζηελ αλάιπζε θάζε πξντόληνο ηεο Κεθαιαηαγνξάο. Σν ρξήκα έρεη ρξνληθή
Α Σ Κ Ζ Σ Δ Η Σ. Τν βάξνο ησλ 28 καζεηώλ κηαο ηάμεο δίλεηαη ζηνλ παξαθάησ πίλαθα 1.(2).
 1 Α Σ Κ Ζ Σ Δ Η Σ ΑΣΚΗΣΗ 1.() Τν βάξνο ησλ 8 καζεηώλ κηαο ηάμεο δίλεηαη ζηνλ παξαθάησ πίλαθα 1.(). ΠΗΝΑΚΑΣ 1.().Βάξε καζεηώλ κηαο ηάμεο 77.4 75.8 75.8 74.5 71.5 68.8 66.6 73.9 70.1 73.0 71.9 66.6 73.4
1 Α Σ Κ Ζ Σ Δ Η Σ ΑΣΚΗΣΗ 1.() Τν βάξνο ησλ 8 καζεηώλ κηαο ηάμεο δίλεηαη ζηνλ παξαθάησ πίλαθα 1.(). ΠΗΝΑΚΑΣ 1.().Βάξε καζεηώλ κηαο ηάμεο 77.4 75.8 75.8 74.5 71.5 68.8 66.6 73.9 70.1 73.0 71.9 66.6 73.4
Βέιηηζηε επηινγή ραξηνθπιαθίνπ
 ΔΛΛΗΝΙΚΗ ΓΗΜΟΚΡΑΣΙΑ ΠΑΝΔΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΣΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΔΠΙΣΗΜΩΝ Διπλωματική Εργασία : Βέιηηζηε επηινγή ραξηνθπιαθίνπ ΠΑΠΑΝΙΚΟΛΑΟΤ ΑΠΟΣΟΛΟ Α.Μ. 0724 Δπηβιέπωλ θαζεγεηήο: ΟΓΙΑΚΑ ΒΑΙΛΔΙΟ Σξηκειήο επηηξνπή:
ΔΛΛΗΝΙΚΗ ΓΗΜΟΚΡΑΣΙΑ ΠΑΝΔΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΣΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΔΠΙΣΗΜΩΝ Διπλωματική Εργασία : Βέιηηζηε επηινγή ραξηνθπιαθίνπ ΠΑΠΑΝΙΚΟΛΑΟΤ ΑΠΟΣΟΛΟ Α.Μ. 0724 Δπηβιέπωλ θαζεγεηήο: ΟΓΙΑΚΑ ΒΑΙΛΔΙΟ Σξηκειήο επηηξνπή:
Παιχνίδι γλωζζικής καηανόηζης με ζχήμαηα!
 Cpyright 2013 Λόγος & Επικοινωνία // All rights Reserved Παιχνίδι γλωζζικής καηανόηζης με ζχήμαηα! Αυηό ηο παιχνίδι έχει ζηόχους: 1. ηελ εθγύκλαζε ηεο αθνπζηηθήο κλήκεο ησλ παηδηώλ 2. ηελ εμάζθεζε ζηελ
Cpyright 2013 Λόγος & Επικοινωνία // All rights Reserved Παιχνίδι γλωζζικής καηανόηζης με ζχήμαηα! Αυηό ηο παιχνίδι έχει ζηόχους: 1. ηελ εθγύκλαζε ηεο αθνπζηηθήο κλήκεο ησλ παηδηώλ 2. ηελ εμάζθεζε ζηελ
ΚΔΦ. 2.4 ΡΗΕΔ ΠΡΑΓΜΑΣΗΚΩΝ ΑΡΗΘΜΩΝ
 ΚΔΦ.. ΡΗΕΔ ΠΡΑΓΜΑΣΗΚΩΝ ΑΡΗΘΜΩΝ Οξηζκόο ηεηξαγσληθήο ξίδαο: Αλ 0 ηόηε νλνκάδνπκε ηεηξαγσληθή ξίδα ηνπ ηελ κε αξλεηηθή ιύζε ηεο εμίζσζεο:. Γειαδή ηεηξαγσληθή ξίδα ηνπ 0 ιέγεηαη ν αξηζκόο 0 πνπ όηαλ πςσζεί
ΚΔΦ.. ΡΗΕΔ ΠΡΑΓΜΑΣΗΚΩΝ ΑΡΗΘΜΩΝ Οξηζκόο ηεηξαγσληθήο ξίδαο: Αλ 0 ηόηε νλνκάδνπκε ηεηξαγσληθή ξίδα ηνπ ηελ κε αξλεηηθή ιύζε ηεο εμίζσζεο:. Γειαδή ηεηξαγσληθή ξίδα ηνπ 0 ιέγεηαη ν αξηζκόο 0 πνπ όηαλ πςσζεί
ΛΙΜΝΗ ΤΣΑΝΤ. Σρήκα 1. Σρήκα 2
 ΛΙΜΝΗ ΤΣΑΝΤ Τν Σρήκα 1 δείρλεη ηελ αιιαγή ηεο ζηάζκεο ηεο Λίκλεο Τζαλη, ζηε Σαράξα ηεο Βόξεηαο Αθξηθήο. Η Λίκλε Τζαλη εμαθαλίζηεθε ηειείσο γύξσ ζην 20.000 π.χ., θαηά ηε δηάξθεηα ηεο ηειεπηαίαο επνρήο ησλ
ΛΙΜΝΗ ΤΣΑΝΤ Τν Σρήκα 1 δείρλεη ηελ αιιαγή ηεο ζηάζκεο ηεο Λίκλεο Τζαλη, ζηε Σαράξα ηεο Βόξεηαο Αθξηθήο. Η Λίκλε Τζαλη εμαθαλίζηεθε ηειείσο γύξσ ζην 20.000 π.χ., θαηά ηε δηάξθεηα ηεο ηειεπηαίαο επνρήο ησλ
ΔΦΑΡΜΟΜΔΝΑ ΜΑΘΗΜΑΣΙΚΑ ΣΗ ΧΗΜΔΙΑ Ι ΘΔΜΑΣΑ Α επηέκβξηνο 2009. 1. Να ππνινγηζηνύλ νη κεξηθέο παξάγσγνη πξώηεο ηάμεο ηεο ζπλάξηεζεο f(x,y) =
 ΘΔΜΑΣΑ Α επηέκβξηνο 9. Να ππνινγηζηνύλ νη κεξηθέο παξάγσγνη πξώηεο ηάμεο ηεο ζπλάξηεζεο f(,y) = y.. Να ππνινγηζηνύλ ηα νινθιεξώκαηα: a) ln b) a) 3cos b) e sin 4. Να ππνινγηζηεί ην νινθιήξσκα: S ( y) 3
ΘΔΜΑΣΑ Α επηέκβξηνο 9. Να ππνινγηζηνύλ νη κεξηθέο παξάγσγνη πξώηεο ηάμεο ηεο ζπλάξηεζεο f(,y) = y.. Να ππνινγηζηνύλ ηα νινθιεξώκαηα: a) ln b) a) 3cos b) e sin 4. Να ππνινγηζηεί ην νινθιήξσκα: S ( y) 3
1. Η απιή αξκνληθή ηαιάλησζε πνπ εθηειεί έλα κηθξό ζώκα κάδαο m = 1 kg έρεη πιάηνο Α = 20 cm θαη
 ΛΤΜΔΝΔ ΑΚΖΔΗ ΣΖΝ ΔΤΡΔΖ ΑΡΥΗΚΖ ΦΑΖ 1. Η αιή αξκνληθή ηαιάλησζε ν εθηειεί έλα κηθξό ζώκα κάδαο m = 1 kg έρεη ιάηνο Α = cm θαη ζρλόηεηα f = 5 Hz. Τε ρξνληθή ζηηγκή = ην κηθξό ζώκα δηέξρεηαη αό ηε ζέζε ανκάθξλζεο
ΛΤΜΔΝΔ ΑΚΖΔΗ ΣΖΝ ΔΤΡΔΖ ΑΡΥΗΚΖ ΦΑΖ 1. Η αιή αξκνληθή ηαιάλησζε ν εθηειεί έλα κηθξό ζώκα κάδαο m = 1 kg έρεη ιάηνο Α = cm θαη ζρλόηεηα f = 5 Hz. Τε ρξνληθή ζηηγκή = ην κηθξό ζώκα δηέξρεηαη αό ηε ζέζε ανκάθξλζεο
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ. Οξηδόληηα θαη θαηαθόξπθε κεηαηόπηζε παξαβνιήο
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Οξηδόληηα θαη θαηαθόξπθε κεηαηόπηζε παξαβνιήο 1 ε Δξαζηεξηόηεηα Αλνίμηε ην αξρείν «Μεηαηόπηζε παξαβνιήο.ggb». Με ηε καύξε γξακκή παξηζηάλεηαη ε γξαθηθή παξάζηαζε ηεο f(x)=αx 2 πνπ ζα ηελ
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Οξηδόληηα θαη θαηαθόξπθε κεηαηόπηζε παξαβνιήο 1 ε Δξαζηεξηόηεηα Αλνίμηε ην αξρείν «Μεηαηόπηζε παξαβνιήο.ggb». Με ηε καύξε γξακκή παξηζηάλεηαη ε γξαθηθή παξάζηαζε ηεο f(x)=αx 2 πνπ ζα ηελ
Η ηηκή κηαο κεηνρήο ζα πξέπεη λα ηζνύηαη κε ην άζξνηζκα ηωλ πξνεμνθιεκέλωλ κεξηζκάηωλ. ...
 ΓΔΟ31 ΧΡΗΜΑΣΟΟΙΚΟΝΟΜΙΚΗ ΓΙΟΙΚΗΗ ΣΟΜΟ Β: Γιατείριζη Χαρηοθσλακίοσ Μάθημα 8: Μετοχές Η ηηκή κηαο κεηνρήο ζα πξέπεη λα ηζνύηαη κε ην άζξνηζκα ηωλ πξνεμνθιεκέλωλ κεξηζκάηωλ. D D D 1 k (1 k) (1 k) 1 2 3 0...
ΓΔΟ31 ΧΡΗΜΑΣΟΟΙΚΟΝΟΜΙΚΗ ΓΙΟΙΚΗΗ ΣΟΜΟ Β: Γιατείριζη Χαρηοθσλακίοσ Μάθημα 8: Μετοχές Η ηηκή κηαο κεηνρήο ζα πξέπεη λα ηζνύηαη κε ην άζξνηζκα ηωλ πξνεμνθιεκέλωλ κεξηζκάηωλ. D D D 1 k (1 k) (1 k) 1 2 3 0...
Έλαο πίνακας σσμβόλων ππνζηεξίδεη δύν βαζηθέο ιεηηνπξγίεο:
 Πίνακες Σσμβόλων Έλαο πίνακας σσμβόλων ππνζηεξίδεη δύν βαζηθέο ιεηηνπξγίεο: Εηζαγσγή ελόο ζηνηρείνπ Αλαδήηεζε ζηνηρείνπ κε δεδνκέλν θιεηδί Άιιεο ρξήζηκεο ιεηηνπξγίεο είλαη: Δηαγξαθή ελόο θαζνξηζκέλνπ ζηνηρείνπ
Πίνακες Σσμβόλων Έλαο πίνακας σσμβόλων ππνζηεξίδεη δύν βαζηθέο ιεηηνπξγίεο: Εηζαγσγή ελόο ζηνηρείνπ Αλαδήηεζε ζηνηρείνπ κε δεδνκέλν θιεηδί Άιιεο ρξήζηκεο ιεηηνπξγίεο είλαη: Δηαγξαθή ελόο θαζνξηζκέλνπ ζηνηρείνπ
Μέζνδνη ραξαθηεξηζκνύ πιηθώλ Δξγαζηεξηαθή άζθεζε 8: Μαγλεηηθέο Μεηξήζεηο Ηκεξνκελία δηεμαγσγήο: 26/5/2010
 Μέζνδνη ραξαθηεξηζκνύ πιηθώλ Δξγαζηεξηαθή άζθεζε 8: Μαγλεηηθέο Μεηξήζεηο Ηκεξνκελία δηεμαγσγήο: 26/5/2010 ΕΙΑΓΩΓΗ: Τα δηάθνξα πιηθά, αλάινγα κε ηε ζπκπεξηθνξά ηνπο εληόο καγλεηηθνύ πεδίνπ δηαθξίλνληαη
Μέζνδνη ραξαθηεξηζκνύ πιηθώλ Δξγαζηεξηαθή άζθεζε 8: Μαγλεηηθέο Μεηξήζεηο Ηκεξνκελία δηεμαγσγήο: 26/5/2010 ΕΙΑΓΩΓΗ: Τα δηάθνξα πιηθά, αλάινγα κε ηε ζπκπεξηθνξά ηνπο εληόο καγλεηηθνύ πεδίνπ δηαθξίλνληαη
ΟΠΤΙΚΗ Α. ΑΝΑΚΛΑΣΖ - ΓΗΑΘΛΑΣΖ
 ΟΠΤΙΚΗ Α. ΑΝΑΚΛΑΣΖ - ΓΗΑΘΛΑΣΖ. Μία αθηίλα θωηόο πξνζπίπηεη κε κία γωλία ζ ζηε επάλω επηθάλεηα ελόο θύβνπ από πνιπεζηέξα ν νπνίνο έρεη δείθηε δηάζιαζεο ε =,49 (ζρήκα ). Βξείηε πνηα ζα είλαη ε κέγηζηε γωλία
ΟΠΤΙΚΗ Α. ΑΝΑΚΛΑΣΖ - ΓΗΑΘΛΑΣΖ. Μία αθηίλα θωηόο πξνζπίπηεη κε κία γωλία ζ ζηε επάλω επηθάλεηα ελόο θύβνπ από πνιπεζηέξα ν νπνίνο έρεη δείθηε δηάζιαζεο ε =,49 (ζρήκα ). Βξείηε πνηα ζα είλαη ε κέγηζηε γωλία
ΔΡΔΤΝΑ ΚΑΣΑΝΑΛΩΣΙΚΗ ΔΜΠΙΣΟΤΝΗ
 ΔΡΔΤΝΑ ΚΑΣΑΝΑΛΩΣΙΚΗ ΔΜΠΙΣΟΤΝΗ Έξεπλεο Οηθνλνκηθήο πγθπξίαο ΙΟΒΔ - DG ECFIN Μάηνο 2011 H Έξεπλα θαηαλαισηώλ ηεο Δπξσπατθήο Δπηηξνπήο (1) Μέξνο ηνπ Δλαξκνληζκέλνπ Πξνγξάκκαηνο Δξεπλώλ ηεο ΔΔ από ην 1972
ΔΡΔΤΝΑ ΚΑΣΑΝΑΛΩΣΙΚΗ ΔΜΠΙΣΟΤΝΗ Έξεπλεο Οηθνλνκηθήο πγθπξίαο ΙΟΒΔ - DG ECFIN Μάηνο 2011 H Έξεπλα θαηαλαισηώλ ηεο Δπξσπατθήο Δπηηξνπήο (1) Μέξνο ηνπ Δλαξκνληζκέλνπ Πξνγξάκκαηνο Δξεπλώλ ηεο ΔΔ από ην 1972
Μνλνδηάζηαηνη Πίλαθεο Λπκέλεο Αζθήζεηο. Άζθεζε 1. Πνηά ζα είλαη ηα πεξηερόκελα ηνπ πίλαθα Α κεηά ηελ εθηέιεζε ηνπ παξαθάησ αιγνξίζκνπ;
 Μνλνδηάζηαηνη Πίλαθεο Λπκέλεο Αζθήζεηο Άζθεζε 1. Πνηά ζα είλαη ηα πεξηερόκελα ηνπ πίλαθα Α κεηά ηελ εθηέιεζε ηνπ παξαθάησ αιγνξίζκνπ; Αιγόξηζκνο Γεκηνπξγία_Πίλαθα Γηα i από 1 κέρξη 5 Α[i] i Γηα i από 2
Μνλνδηάζηαηνη Πίλαθεο Λπκέλεο Αζθήζεηο Άζθεζε 1. Πνηά ζα είλαη ηα πεξηερόκελα ηνπ πίλαθα Α κεηά ηελ εθηέιεζε ηνπ παξαθάησ αιγνξίζκνπ; Αιγόξηζκνο Γεκηνπξγία_Πίλαθα Γηα i από 1 κέρξη 5 Α[i] i Γηα i από 2
Σήκαηα Β Α Γ Γ Δ Λ Η Σ Ο Ι Κ Ο Ν Ο Μ Ο Υ Γ Ι Α Λ Δ Ξ Η - ( 2 ) ΕΙΣΑΓΨΓΗ ΣΤΙΣ ΤΗΛΕΠΙΚΟΙΝΨΝΙΕΣ
 Σήκαηα 1 Β Α Γ Γ Δ Λ Η Σ Ο Ι Κ Ο Ν Ο Μ Ο Υ Γ Ι Α Λ Δ Ξ Η - ( 2 ) Σήκαηα Οξηζκόο ζήκαηνο Ταμηλόκεζε ζεκάησλ Σεηξέο Fourier Μεηαζρεκαηηζκόο Fourier Σπλέιημε Σπζρέηηζε θαη Φαζκαηηθή Ππθλόηεηα 2 Οξηζκόο Σήκαηνο
Σήκαηα 1 Β Α Γ Γ Δ Λ Η Σ Ο Ι Κ Ο Ν Ο Μ Ο Υ Γ Ι Α Λ Δ Ξ Η - ( 2 ) Σήκαηα Οξηζκόο ζήκαηνο Ταμηλόκεζε ζεκάησλ Σεηξέο Fourier Μεηαζρεκαηηζκόο Fourier Σπλέιημε Σπζρέηηζε θαη Φαζκαηηθή Ππθλόηεηα 2 Οξηζκόο Σήκαηνο
Η/Υ A ΤΑΞΕΩΣ ΑΕ 2010-2011. Συστήματα Αρίθμησης. Υποπλοίαρχος Ν. Πετράκος ΠΝ
 Συστήματα Αρίθμησης Υποπλοίαρχος Ν. Πετράκος ΠΝ 1 Ειζαγωγή Τν bit είλαη ε πην βαζηθή κνλάδα κέηξεζεο. Είλαη κία θαηάζηαζε on ή off ζε έλα ςεθηαθό θύθισκα. Άιιεο θνξέο είλαη κία θαηάζηαζε high ή low voltage
Συστήματα Αρίθμησης Υποπλοίαρχος Ν. Πετράκος ΠΝ 1 Ειζαγωγή Τν bit είλαη ε πην βαζηθή κνλάδα κέηξεζεο. Είλαη κία θαηάζηαζε on ή off ζε έλα ςεθηαθό θύθισκα. Άιιεο θνξέο είλαη κία θαηάζηαζε high ή low voltage
Δξγαιεία Καηαζθεπέο 1 Σάμε Σ Δ.Κ.Φ.Δ. ΥΑΝΙΧΝ ΠΡΧΣΟΒΑΘΜΙΑ ΔΚΠΑΙΓΔΤΗ. ΔΝΟΣΗΣΑ 11 ε : ΦΧ ΔΡΓΑΛΔΙΑ ΚΑΣΑΚΔΤΔ. Καηαζθεπή 1: Φαθόο κε ζσιήλα.
 Δξγαιεία Καηαζθεπέο 1 Δ.Κ.Φ.Δ. ΥΑΝΙΧΝ ΠΡΧΣΟΒΑΘΜΙΑ ΔΚΠΑΙΓΔΤΗ ΔΝΟΣΗΣΑ 11 ε : ΦΧ ΔΡΓΑΛΔΙΑ ΚΑΣΑΚΔΤΔ Καηαζθεπή 1: Φαθόο κε ζσιήλα Γηαθξάγκαηα Δξγαιεία Καηαζθεπέο 2 Η θαηαζθεπή πεξηγξάθεηαη ζηελ αληίζηνηρε ελόηεηα
Δξγαιεία Καηαζθεπέο 1 Δ.Κ.Φ.Δ. ΥΑΝΙΧΝ ΠΡΧΣΟΒΑΘΜΙΑ ΔΚΠΑΙΓΔΤΗ ΔΝΟΣΗΣΑ 11 ε : ΦΧ ΔΡΓΑΛΔΙΑ ΚΑΣΑΚΔΤΔ Καηαζθεπή 1: Φαθόο κε ζσιήλα Γηαθξάγκαηα Δξγαιεία Καηαζθεπέο 2 Η θαηαζθεπή πεξηγξάθεηαη ζηελ αληίζηνηρε ελόηεηα
ΓΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 133. Ύλη: Σσναρηήζεις-Σηαηιζηική Θέμα 1
 ΓΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 1 Ον/μο:.. Γ Λσκείοσ Ύλη: Σσναρηήζεις-Σηαηιζηική Γεν. Παιδείας 9-1-1 Θέμα 1 Α. Αο ππνζέζνπκε όηη x 1,x,...,x k είλαη νη ηηκέο κηαο κεηαβιεηήο x πνπ αθνξά ηα άηνκα ελόο δείγκαηνο
ΓΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 1 Ον/μο:.. Γ Λσκείοσ Ύλη: Σσναρηήζεις-Σηαηιζηική Γεν. Παιδείας 9-1-1 Θέμα 1 Α. Αο ππνζέζνπκε όηη x 1,x,...,x k είλαη νη ηηκέο κηαο κεηαβιεηήο x πνπ αθνξά ηα άηνκα ελόο δείγκαηνο
ΚΤΠΡΙΑΚΗ ΜΑΘΗΜΑΣΙΚΗ ΕΣΑΙΡΕΙΑ ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Γ Γυμνασίου ΥΟΛΕΙΟ..
 ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Γ Γυμνασίου ιήμεο 11.00 Κάπνηνο άξρηζε λα δηαβάδεη έλα βηβιίν ηελ 1 ε Δεθεκβξίνπ. Κάζε κέξα δηάβαδε ηνλ ίδην αξηζκό ζειίδσλ
ΜΑΘΗΜΑΣΙΚΗ ΚΤΣΑΛΟΓΡΟΜΙΑ 2007 ΓΙΑ ΣΟ ΓΤΜΝΑΙΟ Παπασκευή 26 Ιανουαπίου 2007 Σάξη: Γ Γυμνασίου ιήμεο 11.00 Κάπνηνο άξρηζε λα δηαβάδεη έλα βηβιίν ηελ 1 ε Δεθεκβξίνπ. Κάζε κέξα δηάβαδε ηνλ ίδην αξηζκό ζειίδσλ
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ στα ΚΕΦΑΛΑΙΑ 1.2 και 1.3 ΟΝΟΜΑΤΕΠΩΝΥΜΟ : ΗΜΕΡΟΜΗΝΙΑ : ΘΕΜΑ 1 A. Να δηαηππώζεηε ην δεύηεξν λόκν ηνπ Νεύησλα κε ιόγηα θαη λα γξάςεηε ηελ αληίζηνηρε καζεκαηηθή ζρέζε (ηύπν) πνπ
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ στα ΚΕΦΑΛΑΙΑ 1.2 και 1.3 ΟΝΟΜΑΤΕΠΩΝΥΜΟ : ΗΜΕΡΟΜΗΝΙΑ : ΘΕΜΑ 1 A. Να δηαηππώζεηε ην δεύηεξν λόκν ηνπ Νεύησλα κε ιόγηα θαη λα γξάςεηε ηελ αληίζηνηρε καζεκαηηθή ζρέζε (ηύπν) πνπ
ΔΝΓΔΙΚΤΙΚΔΣ ΛΥΣΔΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΔΥΘΥΝΣΗΣ Γ ΛΥΚΔΙΟΥ ΓΔΥΤΔΡΑ 27 ΜΑΪΟΥ 2013
 ΔΝΓΔΙΚΤΙΚΔΣ ΛΥΣΔΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΔΥΘΥΝΣΗΣ Γ ΛΥΚΔΙΟΥ ΓΔΥΤΔΡΑ 7 ΜΑΪΟΥ 13 ΘΔΜΑ Α : (Α1) Σρνιηθό βηβιίν ζειίδα 33-335 (Α) Σρνιηθό βηβιίν ζειίδα 6 (Α3) Σρνιηθό βηβιίν ζειίδα (Α) α) Λάζνο β) Σωζηό γ) Σωζηό
ΔΝΓΔΙΚΤΙΚΔΣ ΛΥΣΔΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΔΥΘΥΝΣΗΣ Γ ΛΥΚΔΙΟΥ ΓΔΥΤΔΡΑ 7 ΜΑΪΟΥ 13 ΘΔΜΑ Α : (Α1) Σρνιηθό βηβιίν ζειίδα 33-335 (Α) Σρνιηθό βηβιίν ζειίδα 6 (Α3) Σρνιηθό βηβιίν ζειίδα (Α) α) Λάζνο β) Σωζηό γ) Σωζηό
Λεκηική έκθραζη, κριηική, οικειόηηηα και ηύπος δεζμού ζηις ζηενές διαπροζωπικές ζτέζεις
 Λεκηική έκθραζη, κριηική, οικειόηηηα και ηύπος δεζμού ζηις ζηενές διαπροζωπικές ζτέζεις Μαξία-Ησάλλα Αξγπξνπνύινπ Βαζίιεο Παπιόπνπινο Τνκέαο Ψπρνινγίαο, Παλεπηζηήκην Αζελώλ Αλαθνίλσζε ζην 5 ν Παλειιήλην
Λεκηική έκθραζη, κριηική, οικειόηηηα και ηύπος δεζμού ζηις ζηενές διαπροζωπικές ζτέζεις Μαξία-Ησάλλα Αξγπξνπνύινπ Βαζίιεο Παπιόπνπινο Τνκέαο Ψπρνινγίαο, Παλεπηζηήκην Αζελώλ Αλαθνίλσζε ζην 5 ν Παλειιήλην
ΙNCOFRUIT - (HELLAS).
 Πξνο ΟΛΑ ΤΑ ΜΔΛΗ Κε Σπλάδειθε Θέκα: Ιζπαλία & Γεξκαλία 5 ε ΔΒΓΟΜΑΓΑ 2011 (31 Ιαλ έσο 30 Φεβξ.2011) Παξαζέηνπκε θαησηέξσ: Αλαζθόπεζε ηεο 4 εο εβδνκάδνο 2011 κε ηηο ηηκέο ησλ εζπεξηδνεηδώλ πνπ δηακνξθώζεθαλ
Πξνο ΟΛΑ ΤΑ ΜΔΛΗ Κε Σπλάδειθε Θέκα: Ιζπαλία & Γεξκαλία 5 ε ΔΒΓΟΜΑΓΑ 2011 (31 Ιαλ έσο 30 Φεβξ.2011) Παξαζέηνπκε θαησηέξσ: Αλαζθόπεζε ηεο 4 εο εβδνκάδνο 2011 κε ηηο ηηκέο ησλ εζπεξηδνεηδώλ πνπ δηακνξθώζεθαλ
Αντισταθμιστική ανάλυση
 Θεσξήζηε έλαλ αιγόξηζκν Α πνπ ρξεζηκνπνηεί κηα δνκή δεδνκέλσλ Γ : Καηά ηε δηάξθεηα εθηέιεζεο ηνπ Α ε Γ πξαγκαηνπνηεί κία αθνινπζία από πξάμεηο. Παξάδεηγκα: Θπκεζείηε ην πξόβιεκα ηεο εύξεζεο-έλσζεο Δίρακε
Θεσξήζηε έλαλ αιγόξηζκν Α πνπ ρξεζηκνπνηεί κηα δνκή δεδνκέλσλ Γ : Καηά ηε δηάξθεηα εθηέιεζεο ηνπ Α ε Γ πξαγκαηνπνηεί κία αθνινπζία από πξάμεηο. Παξάδεηγκα: Θπκεζείηε ην πξόβιεκα ηεο εύξεζεο-έλσζεο Δίρακε
Πολυεπίπεδα/Διασυμδεδεμέμα Δίκτυα
 Πολυεπίπεδα/Διασυμδεδεμέμα Δίκτυα Κοιμωμικά δίκτυα (multiplex network) Έρεηε ινγαξηαζκό ζην Facebook? Έρεηε ινγαξηαζκό ζην LinkedIn? Έρεηε ινγαξηαζκό ζην Twitter? Αεροπορικές γραμμές της Ευρώπης(multiplex
Πολυεπίπεδα/Διασυμδεδεμέμα Δίκτυα Κοιμωμικά δίκτυα (multiplex network) Έρεηε ινγαξηαζκό ζην Facebook? Έρεηε ινγαξηαζκό ζην LinkedIn? Έρεηε ινγαξηαζκό ζην Twitter? Αεροπορικές γραμμές της Ευρώπης(multiplex
ΔΝΓΔΙΚΣΙΚΔ ΛΤΔΙ ΣΑ ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ 2017
 α: κολάδα β: κολάδες Σειίδα από 8 ΔΝΓΔΙΚΣΙΚΔ ΛΤΔΙ ΣΑ ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ 7 ΘΔΜΑ Α Α Έζηω, κε Θα δείμνπκε όηη f ( ) f ( ) Πξάγκαηη, ζην δηάζηεκα [, ] ε f ηθαλνπνηεί ηηο πξνϋπνζέζεηο ηνπ ΘΜΤ Επνκέλωο,
α: κολάδα β: κολάδες Σειίδα από 8 ΔΝΓΔΙΚΣΙΚΔ ΛΤΔΙ ΣΑ ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ 7 ΘΔΜΑ Α Α Έζηω, κε Θα δείμνπκε όηη f ( ) f ( ) Πξάγκαηη, ζην δηάζηεκα [, ] ε f ηθαλνπνηεί ηηο πξνϋπνζέζεηο ηνπ ΘΜΤ Επνκέλωο,
ΗΜΔΡΟΜΗΝΙΑ. ΟΝΟΜΑΣΔΠΩΝΤΜΟ.. ΒΑΘΜΟΛΟΓΙΑ..
 ΗΜΔΡΟΜΗΝΙΑ. ΟΝΟΜΑΣΔΠΩΝΤΜΟ.. ΒΑΘΜΟΛΟΓΙΑ.. ΘΔΜΑ Α Σηηο εκηηειείο πξνηάζεηο Α.1 Α.4 λα γξάςεηε ζην ηεηξάδην ζαο ηνλ αξηζκό ηεο πξόηαζεο θαη, δίπια, ην γξάκκα πνπ αληηζηνηρεί ζηε θξάζε ε νπνία ηε ζπκπιεξώλεη
ΗΜΔΡΟΜΗΝΙΑ. ΟΝΟΜΑΣΔΠΩΝΤΜΟ.. ΒΑΘΜΟΛΟΓΙΑ.. ΘΔΜΑ Α Σηηο εκηηειείο πξνηάζεηο Α.1 Α.4 λα γξάςεηε ζην ηεηξάδην ζαο ηνλ αξηζκό ηεο πξόηαζεο θαη, δίπια, ην γξάκκα πνπ αληηζηνηρεί ζηε θξάζε ε νπνία ηε ζπκπιεξώλεη
f '(x)g(x)h(x) g'(x)f (x)h(x) h'(x) f (x)g(x)
 ΓΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 54 Υλη: Παράγωγοι Γ Λσκείοσ Ον/μο:.. 6--4 Θεη-Τετν. ΘΔΜΑ Α.. Αλ f, g, h ηξεηο παξαγωγίζηκεο ζπλαξηήζεηο ζην λα απνδείμεηε όηη : f () g() h() ' f '()g()h() g'()f ()h() h'() f ()g()
ΓΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 54 Υλη: Παράγωγοι Γ Λσκείοσ Ον/μο:.. 6--4 Θεη-Τετν. ΘΔΜΑ Α.. Αλ f, g, h ηξεηο παξαγωγίζηκεο ζπλαξηήζεηο ζην λα απνδείμεηε όηη : f () g() h() ' f '()g()h() g'()f ()h() h'() f ()g()
ΓΗΜΟΙΑ ΟΙΚΟΝΟΜΙΚΗ ΣΟΜΟ Γ
 1 ΓΗΜΟΙΑ ΟΙΚΟΝΟΜΙΚΗ ΣΟΜΟ Γ Μάθημα 19: Φόροι ΦΟΡΟΛΟΓΙΚΑ ΤΣΗΜΑΣΑ: Προοδεσηικό, Αναλογικά και ανηίζηροθα προοδεσηικό θορολογικό ζύζηημα Μέζος και οριακός θορολογικός ζσνηελεζηής Ο κέζνο θνξνινγηθόο ζπληειεζηήο
1 ΓΗΜΟΙΑ ΟΙΚΟΝΟΜΙΚΗ ΣΟΜΟ Γ Μάθημα 19: Φόροι ΦΟΡΟΛΟΓΙΚΑ ΤΣΗΜΑΣΑ: Προοδεσηικό, Αναλογικά και ανηίζηροθα προοδεσηικό θορολογικό ζύζηημα Μέζος και οριακός θορολογικός ζσνηελεζηής Ο κέζνο θνξνινγηθόο ζπληειεζηήο
ΔΠΙΣΡΟΠΗ ΓΙΑΓΩΝΙΜΩΝ 74 ος ΠΑΝΔΛΛΗΝΙΟ ΜΑΘΗΣΙΚΟ ΓΙΑΓΩΝΙΜΟ ΣΑ ΜΑΘΗΜΑΣΙΚΑ Ο ΘΑΛΗ 19 Οκηωβρίοσ Δνδεικηικές λύζεις
 ΔΛΛΗΝΙΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ Παλεπηζηεκίνπ (Διεπζεξίνπ Βεληδέινπ) 34 06 79 ΑΘΖΝΑ Τει. 36653-367784 - Fax: 36405 e-mail : info@hms.gr www.hms.gr GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Δleftheriou
ΔΛΛΗΝΙΚΗ ΜΑΘΗΜΑΣΙΚΗ ΔΣΑΙΡΔΙΑ Παλεπηζηεκίνπ (Διεπζεξίνπ Βεληδέινπ) 34 06 79 ΑΘΖΝΑ Τει. 36653-367784 - Fax: 36405 e-mail : info@hms.gr www.hms.gr GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Δleftheriou
Να ζρεδηάζεηο ηξόπνπο ζύλδεζεο κηαο κπαηαξίαο θαη ελόο ιακπηήξα ώζηε ν ιακπηήξαο λα θσηνβνιεί.
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: Απλό ηλεκτπικό κύκλυμα Η δηδαζθαιία ηνπ απινύ ειεθηξηθνύ θπθιώκαηνο ππάξρεη ζην κάζεκα «Φπζηθά» ηεο Ε ηάμεο ηνπ δεκνηηθνύ θαη επαλαιακβάλεηαη ζην κάζεκα ηεο Φπζηθήο ζηε Γ ηάμε ηνπ Γπκλαζίνπ.
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: Απλό ηλεκτπικό κύκλυμα Η δηδαζθαιία ηνπ απινύ ειεθηξηθνύ θπθιώκαηνο ππάξρεη ζην κάζεκα «Φπζηθά» ηεο Ε ηάμεο ηνπ δεκνηηθνύ θαη επαλαιακβάλεηαη ζην κάζεκα ηεο Φπζηθήο ζηε Γ ηάμε ηνπ Γπκλαζίνπ.
ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. καινούργιο σχολ. σελ 35 / παλιό σχολ. 53 Α. Ψευδής, σελ.99 / παλιό σχολ. σελ. 7 αντιπαράδειγμά, f ( ) Α3. σελ 73, παλιό σχολ. σελ. 9 Α. α) Λάθος β)
ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. καινούργιο σχολ. σελ 35 / παλιό σχολ. 53 Α. Ψευδής, σελ.99 / παλιό σχολ. σελ. 7 αντιπαράδειγμά, f ( ) Α3. σελ 73, παλιό σχολ. σελ. 9 Α. α) Λάθος β)
Μηα ζπλάξηεζε κε πεδίν νξηζκνύ ην Α, ζα ιέκε όηη παξνπζηάδεη ηοπικό μέγιζηο ζην, αλ ππάξρεη δ>0, ηέηνην ώζηε:
 1 ΟΡΙΜΟΙ MONOTONIA AKΡOTATA Μηα ζπλάξηεζε κε πεδίν νξηζκνύ ην Α, ζα ιέκε όηη παξνπζηάδεη ηοπικό μέγιζηο ζην, αλ ππάξρεη δ>0, ηέηνην ώζηε: Σν ιέγεηαη ζέζε ή ζεκείν ηνπ ηνπηθνύ κεγίζηνπ θαη ην ( ηνπηθό κέγηζην.
1 ΟΡΙΜΟΙ MONOTONIA AKΡOTATA Μηα ζπλάξηεζε κε πεδίν νξηζκνύ ην Α, ζα ιέκε όηη παξνπζηάδεη ηοπικό μέγιζηο ζην, αλ ππάξρεη δ>0, ηέηνην ώζηε: Σν ιέγεηαη ζέζε ή ζεκείν ηνπ ηνπηθνύ κεγίζηνπ θαη ην ( ηνπηθό κέγηζην.
Α Ο Κ Η Α Μ Α Ζ Η Η Ρ Η ( S E A R C H )
 Ξ G O O G L E S C H O L A R Α Ο Ξ Ε Κ Ε Θ Λ Θ Α Λ Η Τ Α Μ Η Α Μ Α Ζ Η Η Ρ Η Ρ Οξαγκαηνπνηώληαο αλαδήηεζε ζην GoogleScholar (http://scholar.google.com/) ν ρξήζηεο κπνξεί λα εληνπίζεη πιηθό αθαδεκαϊθνύ θαη
Ξ G O O G L E S C H O L A R Α Ο Ξ Ε Κ Ε Θ Λ Θ Α Λ Η Τ Α Μ Η Α Μ Α Ζ Η Η Ρ Η Ρ Οξαγκαηνπνηώληαο αλαδήηεζε ζην GoogleScholar (http://scholar.google.com/) ν ρξήζηεο κπνξεί λα εληνπίζεη πιηθό αθαδεκαϊθνύ θαη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΗΛΕΚΤΡΟΛΟΓΙΑ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 08/09/2014
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 204-205 ΜΑΘΗΜΑ / ΤΑΞΗ : ΗΛΕΚΤΡΟΛΟΓΙΑ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 08/09/204 A ΟΜΑΓΑ Οδηγία: Να γράυεηε ζηο ηεηράδιο ζας ηον αριθμό κάθε μιας από ηις παρακάηφ ερφηήζεις Α.-Α.8 και
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 204-205 ΜΑΘΗΜΑ / ΤΑΞΗ : ΗΛΕΚΤΡΟΛΟΓΙΑ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 08/09/204 A ΟΜΑΓΑ Οδηγία: Να γράυεηε ζηο ηεηράδιο ζας ηον αριθμό κάθε μιας από ηις παρακάηφ ερφηήζεις Α.-Α.8 και
Constructors and Destructors in C++
 Constructors and Destructors in C++ Σύνθεζη Πνιύ ζπρλά ζηε C++ κία θιάζε κπνξεί λα πεξηέρεη ζαλ κέιεδεδνκέλα αληηθείκελα άιισλ θιάζεσλ. Πνηα είλαη ε ζεηξά κε ηελ νπνία δεκηνπξγνύληαη θαη θαηαζηξέθνληαη
Constructors and Destructors in C++ Σύνθεζη Πνιύ ζπρλά ζηε C++ κία θιάζε κπνξεί λα πεξηέρεη ζαλ κέιεδεδνκέλα αληηθείκελα άιισλ θιάζεσλ. Πνηα είλαη ε ζεηξά κε ηελ νπνία δεκηνπξγνύληαη θαη θαηαζηξέθνληαη
ΘΔΜΑΤΑ ΤΔΛΙΚΩΝ ΔΞΔΤΑΣΔΩΝ ΣΤΗ ΦΥΣΙΚΟΦΗΜΔΙΑ - ΘΔΩΡΙΑ ΦΡΟΝΙΚΗ ΓΙΑΡΚΔΙΑ: 1 ώρα (14:00-15:00) Α. Φημική Θερμοδσναμική
 ΘΔΜΑΤΑ ΤΔΛΙΚΩΝ ΔΞΔΤΑΣΔΩΝ ΣΤΗ ΦΥΣΙΚΟΦΗΜΔΙΑ - ΘΔΩΡΙΑ 2011-12 ΦΡΟΝΙΚΗ ΓΙΑΡΚΔΙΑ: 1 ώρα (14:00-15:00) Α. Φημική Θερμοδσναμική Βξείηε κηα εθθξαζε γηα ηνλ παξάγνληα ζπκπηεζηόηεηαο ελόο αεξίνπ πνπ αθνινπζεί ηελ
ΘΔΜΑΤΑ ΤΔΛΙΚΩΝ ΔΞΔΤΑΣΔΩΝ ΣΤΗ ΦΥΣΙΚΟΦΗΜΔΙΑ - ΘΔΩΡΙΑ 2011-12 ΦΡΟΝΙΚΗ ΓΙΑΡΚΔΙΑ: 1 ώρα (14:00-15:00) Α. Φημική Θερμοδσναμική Βξείηε κηα εθθξαζε γηα ηνλ παξάγνληα ζπκπηεζηόηεηαο ελόο αεξίνπ πνπ αθνινπζεί ηελ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΦΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Μάθημα: Πιθανόηηηες και Σηαηιζηική Διδάζκων: Σ. Γ.
 ΤΕΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Τρίπολη 06/07/2007 Τα θέμαηα 1-5 είναι σποτρεωηικά και έτοσν ηοσς ίδιοσς (ίζοσς) ζσνηελεζηές βαρύηηηας Το θέμα 6 δίνει επιπλέον βαθμούς με βαρύηηηα 10% για βεληίωζη ηης βαθμολογίας ΘΕΜΑΤΑ
ΤΕΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Τρίπολη 06/07/2007 Τα θέμαηα 1-5 είναι σποτρεωηικά και έτοσν ηοσς ίδιοσς (ίζοσς) ζσνηελεζηές βαρύηηηας Το θέμα 6 δίνει επιπλέον βαθμούς με βαρύηηηα 10% για βεληίωζη ηης βαθμολογίας ΘΕΜΑΤΑ
