Φώτη Ψωμόπουλου του Ευαγγέλου
|
|
|
- Πάνδαρος Βουρδουμπάς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Παράλληλοι Αλγόριθμοι Εξόρυξης και Ανάλυσης Δεδομένων σε Πλέγματα Υπολογιστών με εφαρμογές στη Βιοπληροφορική Διδακτορική Διατριβή που εκπονήθηκε ως μερική εκπλήρωση των απαιτήσεων για την απονομή του τίτλου του Διδάκτορα Μηχανικού του Φώτη Ψωμόπουλου του Ευαγγέλου Δ Η Μ Μ Υ Α Π Θ Επιβλέπων Περικλής Α. Μήτκας Καθηγητής Συμβουλευτική Επιτροπή Μιχαήλ Γ. Στρίντζης Καθηγητής Αναστάσιος Ν. Ντελόπουλος Επίκουρος Καθηγητής Υποστηρίχθηκε δημόσια στη Θεσσαλονίκη στις 18/06/2010
2 ii Εξεταστική Επιτροπή Περικλής Α. Μήτκας Μιχαήλ Γ. Στρίντζης Αναστάσιος Ν. Ντελόπουλος Καθηγητής Καθηγητής Επίκουρος Καθηγητής Χρήστος Α. Ουζούνης Γεώργιος Δ. Χασάπης Νικόλαος Κ. Μαγκλαβέρας Καθηγητής Καθηγητής Καθηγητής... Ιωάννης Ν. Δημητρόπουλος Καθηγητής
3 Wyrd bið ful ãræd
4 Αντί Προλόγου Η συγγραφή αυτής της διατριβής αποτελεί το επισφράγισμα μιας επίπονης και μακροχρόνιας πορείας. Κάνοντας μια αποτίμηση αυτού του ταξιδιού διαπιστώνω ότι σε κάθε βήμα υπήρχαν γύρω μου άνθρωποι οι οποίοι συνεισέφεραν καθοριστικά, ο καθένας με τον δικό του τρόπο, στην επιτυχή ολοκλήρωση αυτής της διαδρομής. Δεν θα ήταν λοιπόν δυνατόν να μην τους ευχαριστήσω και να μην αναγνωρίσω τη συνδρομή τους. Αρχικά θα πρέπει να ευχαριστήσω τον επιβλέποντα Καθηγητή μου, Περικλή Μήτκα, για την εμπιστοσύνη που μου έδειξε με την ανάθεση αυτού του θέματος, και για την υποστήριξή του όλα αυτά τα χρόνια. Τον Καθηγητή Ιωάννη Δημητρόπουλο για τη στενή μας συνεργασία και τις πολύτιμες συμβουλές του σε διάφορα τμήματα της προσπάθειάς μου. Τον Καθηγητή Χρήστο Ουζούνη για την προθυμία και την διάθεση να μου αφιερώσει το χρόνο του, ώστε να μου εξηγήσει λεπτομέρειες σε πολλά θέματα Βιολογίας και Βιοπληροφορικής. Την Ελένη Πολυχρονιάδου, την Ιωάννα Μπρούζα, το Χρήστο Γκέκα και τον Κώστα Καραγιάννη για τη συνεργασία μας και την καθοριστική συνεισφορά τους σε διάφορα τμήματα αυτής της εργασίας. Τους γονείς μου, για την αγάπη τους, την ενθάρρυνση, την υπομονή και την επιμονή τους σε πολλά σημεία της πορείας μου. Τη Φανή Τζήμα για τη φιλία της όλα αυτά τα χρόνια, τη συνεισφορά της σε αναρίθμητα σημεία της δουλειάς μου στο Εργαστήριο, την υπομονή, και κυρίως την αμεσότητά της. Τέλος, θα πρέπει να ευχαριστήσω τους φίλους μου Βίκυ, Χρήστο, Κυριάκο, Κώστα, Ανδρέα, Θανάση, Δημήτρη, Μάρω, Μαρία, Αλέξανδρο και Μανόλη για τις συζητήσεις εντός και εκτός Εργαστηρίου και επί παντός επιστητού, την υπομονή τους, και τη στήριξή τους στις δύσκολες στιγμές. Σε όλους αυτούς θα ήθελα να αφιερώσω τη διατριβή μου και να δώσω τις ολόψυχες ευχαριστίες μου. Φώτης Ψωμόπουλος
5 v Περίληψη Αν και οι επιστήμες της Βιοπληροφορικής και της Υπολογιστικής Βιολογίας συχνά συγχέονται ως το ίδιο διεπιστημονικό πεδίο, παρουσιάζουν αρκετά σημεία που τις διαφοροποιούν σε σημαντικό βαθμό. Η Βιοπληροφορική αφορά κυρίως την ανάλυση και την επεξεργασία των βιολογικών δεδομένων και, κατά συνέπεια, την προώθηση της έρευνας σε αλγοριθμικό και τεχνικό επίπεδο, τόσο των μεθόδων όσο και της θεωρίας για την επίλυση τυπικών προβλημάτων διαχείρισης δεδομένων. Από την άλλη πλευρά, η επιστήμη της Υπολογιστικής Βιολογίας στοχεύει στην επίλυση συγκεκριμένων προβλημάτων Βιολογίας, αξιοποιώντας τις εντυπωσιακές δυνατότητες των υπολογιστών για τη δοκιμή και την αξιολόγηση υποθέσεων. Αυτό βέβαια δε σημαίνει ότι δεν υπάρχουν αρκετές περιοχές σύγκλισης των δύο πεδίων. Ο χώρος της πρωτεομικής, δηλαδή της μελέτης των πρωτεϊνών, είναι ένας από αυτούς τους χώρους, ο οποίος ταυτόχρονα αποτελεί και ένα από τα σημεία εκτενούς έρευνας αυτή τη στιγμή. Η πρωτεομική είναι στην ουσία η μελέτη σε μεγάλη κλίμακα των πρωτεϊνών, από τον προσδιορισμό και την ανάλυση της δομής τους έως την πρόβλεψη της λειτουργίας τους και την κατασκευή μεταβολικών μονοπατιών. Τα τελευταία χρόνια υπήρξε μια μετατόπιση του ερευνητικού ενδιαφέροντος στη Βιοπληροφορική, από την ανάλυση γενετικών δεδομένων στην πρωτεομική, η οποία θεωρείται από πολλούς ως το επόμενο βήμα στη μελέτη των βιολογικών συστημάτων. Ενώ η γενετική πληροφορία σε ένα οργανισμό είναι λίγο πολύ αμετάβλητη τόσο στο χρόνο όσο και ανάμεσα στα διαφορετικά κύτταρα του ιδίου οργανισμού, το σύνολο των πρωτεϊνών που εκφράζονται κάθε χρονική στιγμή παρουσιάζει τεράστιες διαφορές μεταξύ κυττάρων. Επίσης, στα προηγούμενα έτη, μελέτες τόσο του γονιδιώματος όσο και των πρωτεϊνών μπορούσαν να επικεντρωθούν μόνο σε μία πρωτεΐνη ή γονίδιο τη φορά. Ωστόσο, η πρόοδος της τεχνολογίας στις βιοεπιστήμες οδήγησε σε μια εκθετικά αυξανόμενη ποσότητα δεδομένων. Για αυτό το λόγο υπήρξε μια στροφή στην έρευνα, από μελέτες γύρω από υποθέσεις προς μελέτες με γνώμονα τα διαθέσιμα δεδομένα. Καθώς η ζήτηση για αυτοματοποιημένη ανάλυση μεγάλου και κατανεμημένου όγκου δεδομένων αυξάνεται διαρκώς, αναδύονται νέες προκλήσεις τόσο στη μοντελοποίηση των προσεγγίσεων όσο και στην ανάπτυξη αλγορίθμων και τεχνικών ανάλυσης δεδομένων υψηλής ρυθμαπόδοσης. Στα πλαίσια της διατριβής παρουσιάζεται μια γενικευμένη μεθοδολογία ανάπτυξης αλγορίθμων σε περιβάλλοντα Πλέγματος Υπολογιστών, η οποία στοχεύει σε ακριβώς αυτές τις προκλήσεις. Ένα Πλέγμα Υπολογιστών μπορεί να θεωρηθεί ως μια εικονική υπολογιστική αρχιτεκτονική, η οποία παρέχει τη δυνατότητα εκτέλεσης εφαρμογών με υψηλότερη απόδοση, αξιοποιώντας πολλούς υπολογιστικούς πόρους γεωγραφικά κατανεμημένους και συνδεδεμένους μέσω δικτύου. Οι εφαρμογές Βιοπληροφορικής είναι ιδιαιτέρως κατάλληλες για ένα τέτοιο περιβάλλον, από άποψη διαθεσιμότητας, αξιοπιστίας και αποτελεσματικότητας των υπολογιστικών πόρων.
6 vi Υπάρχει ήδη σημαντική πρόοδος στην έρευνα όσον αφορά την εφαρμογή παράλληλων υπολογιστικών τεχνικών σε προσεγγίσεις Βιοπληροφορικής, όπως οι Πολλαπλές Συστοιχίσεις Ακολουθιών, η ανάλυση Γονιδιακών Εκφράσεων και οι Φυλογενετικές Μελέτες. Για να αντιμετωπισθεί ο όγκος δεδομένων σε αυτές τις περιπτώσεις, οι περισσότερες μέθοδοι μηχανικής μάθησης επικεντρώνονται σε συγκεκριμένες ομάδες δεδομένων, είτε μειώνοντας το μέγεθος των αρχικών δεδομένων, είτε μειώνοντας τον αριθμό των χαρακτηριστικών που συμμετέχουν στη μελέτη. Τα Πλέγματα Υπολογιστών μπορούν δυνητικά να αποτελέσουν μια εναλλακτική λύση για το πρόβλημα αυτό, συνδυάζοντας πολλαπλές προσεγγίσεις με ομοιογενή τρόπο. Η γενικευμένη μεθοδολογία που αναπτύχθηκε στα πλαίσια της διατριβής γεφυρώνει την απόσταση μεταξύ των Πλεγμάτων Υπολογιστών και των ιδιαίτερων αναγκών και προβλημάτων που εμφανίζει η πλειοψηφία των προσεγγίσεων Βιοπληροφορικής. Για να αξιολογηθεί η Γενικευμένη Μεθοδολογία εφαρμόσθηκε σε υπάρχοντες αλγορίθμους καθώς και σε μια σειρά νέων αλγορίθμων που αναπτύχθηκαν τόσο στο χώρο της Βιοπληροφορικής όσο και σε χώρους εκτός αυτού του ερευνητικού πεδίου. Οι αλγόριθμοι που κατασκευάσθηκαν ανήκουν κυρίως στο πεδίο της πρωτεομικής, και στοχεύουν στα προβλήματα της κατηγοριοποίησης και πρόβλεψης της λειτουργίας πρωτεϊνών, καθώς και την ομαδοποίησή τους με στόχο τον εντοπισμό μη-κανονικοτήτων σε διάφορους οργανισμούς. Τέλος, η Γενικευμένη Μεθοδολογία αξιοποιήθηκε και για την επίλυση ενός προβλήματος Υπολογιστικής Μοριακής Επιστήμης, και συγκεκριμένα στο πρόβλημα εντοπισμού μοριακών διαμορφώσεων, οι οποίες σχηματίζουν τοπολογία κόμβου στον τρισδιάστατο χώρο. Σε κάθε περίπτωση, αποδεικνύεται τόσο θεωρητικά όσο και πειραματικά, ότι η νέα προσέγγιση υπερτερεί των κλασικών προσεγγίσεων, από άποψη χρονικής επίδοσης και ευρωστίας.
7 Doctoral Disserta on vii Title Parallel Data Mining and Analysis Algorithms in a Grid environment and applica ons in Bioinforma cs Abstract Although Bioinforma cs and Computa onal Biology are o en confused as the same mul disciplinary field, there exist several differences that dis nguish them. Bioinforma- cs focuses on analysis and processing of biological data and consequently the promo on of research in algorithms and technical level of both the methods and theory to solve formal problems of data management. On the other hand, Computa onal Biology aims to solve specific problems in Biology, u lizing the poten al of computers for tes ng and evalua ng hypothesis. Nevertheless the two fields share several areas of convergence. Proteomics is one of these areas and is also the focus of extensive ongoing research. Proteomics is essen ally the large-scale study of proteins, ranging from the identifica on and analysis of their structure to the predic on of their func onality and the construc on of metabolic pathways. In recent years there has been a shi in research interest in Bioinforma cs from genomics to proteomics, which is widely considered as the next step in the study of biological systems. While the genome of an organiza on remains fairly constant in different cells of the same organiza on, the proteome of a species is highly differen ated from cell to cell. In previous years, genomics and proteomics could only focus on one gene or protein at a me. However, the technological advancements in Life Sciences has led to an exponen ally growing amount of data. For this reason there has been a shi in research, from hypothesis-driven to data-driven studies. As the demand for automated analysis of large and distributed data grows, new challenges emerge both regarding the modeling and the development of algorithms for high throughput data analysis. This thesis presents a general methodology for Bioinforma cs Algorithm Development in Grid Environments (BADGE) aiming at precisely these challenges. Grid Compu ng can be viewed as a virtual compu ng architecture that provides the ability to perform higher throughput processing by taking advantage of many computers geographically dispersed and connected by a network. Bioinforma cs applica ons can benefit greatly from the increased availability, reliability and efficiency of computa onal resources, in such a distributed environment. There is already considerable research in progress toward applying parallel compu- ng techniques on bioinforma cs methods, such as mul ple sequence alignment, gene
8 viii expression analysis and phylogene c studies. In order to cope with the dimensionality issue, most machine learning methods focus on specific groups of proteins or reduce either the size of the original data set or the number of a ributes involved. Grid Compu- ng can poten ally provide an alterna ve solu on to this problem, by combining mul ple approaches in a seamless way. The BADGE methodology presented in this thesis, couples the strengths of the Grid with the specific needs and constraints of proven bioinforma cs approaches. In order to evaluate the BADGE methodology, we applied it on several exis ng algorithms and on a series of new algorithms, which were developed to address issues both in Bioinforma cs and in other research areas as well. The bioinforma cs algorithms we designed mainly focus on proteomics and aim to provide solu on to the problems of protein classifica on, predic on of protein func on, and abnormal gene detec on. Finally, the methodology was also used in the development of an algorithm in Computa onal Chemistry, addressing the problem of iden fying molecular knots in three dimensional space. In every case, it was shown, both theore cally and experimentally, that the new approach presents clear advantages over conven onal approaches in terms of me performance and robustness. Fo s E. Psomopoulos Department of Electrical and Computer Engineering Aristotle University of Thessaloniki June 2010
9 Περιεχόμενα Αντί Προλόγου Περίληψη Abstract Περιεχόμενα Κατάλογος Σχημάτων Κατάλογος Πινάκων Κατάλογος Πλαισίων Κώδικα v vii ix xii xiv xv xvii 1 Εισαγωγή Γενική Περιγραφή του Πεδίου Εφαρμογής Τρέχουσα Κατάσταση Νέες Προκλήσεις στην Περιοχή της Βιοπληροφορικής Σκοπός και Επιμέρους Στόχοι της Διατριβής Συμβολή της Διατριβής Διάρθρωση της Διατριβής Βιοπληροφορική και Πλέγματα Υπολογιστών Βιολογικές Έννοιες Το Κύτταρο Το Κεντρικό Δόγμα της Βιολογίας Πρωτεΐνες Τομείς Έρευνας της Βιοπληροφορικής Κατηγοριοποίηση Πρωτεϊνών Παράλληλος Προγραμματισμός Διαδικασία Ανάπτυξης Παράλληλου Αλγορίθμου Προβλήματα Παράλληλου Προγραμματισμού
10 x Περιεχόμενα 2.4 Πλέγματα Υπολογιστών Αρχιτεκτονική Πλέγματος Υπολογιστών EGEE Πλεονεκτήματα και Μειονεκτήματα Πλεγμάτων Υπολογιστών Εξόρυξη Δεδομένων στη Βιοπληροφορικη Εξόρυξη Δεδομένων Εξόρυξη Δεδομένων στην Πρωτεομική Κατηγοριοποίηση Πρωτεϊνών Γενικευμένη Μεθοδολογία BADGE Ροή Εργασίας σε Πλέγματα Υπολογιστών Ροή Εργασίας σε Κατηγοριοποίηση Πρωτεϊνών Γενικευμένη Μεθοδολογία Ανάπτυξης Αλγορίθμων σε Πλέγματα Υπολογιστών Ανάλυση Πολυπλοκότητας Το Εργαλείο BADGE Αξιολόγηση Μεθοδολογίας BADGE GridBLAST g-class Proteas Fuzzy PhyloProf g-molknot Ποιοτική Σύγκριση του BADGE με άλλα συστήματα ροής εργασιών Ο Αλγόριθμος g-class Ο Αλγόριθμος Συνοπτικά Διάσπαση Δεδομένων Εισόδου Εκπαίδευση των Μοντέλων Κατηγοριοποίησης Συνδυασμός των Μοντέλων Ταξινόμησης Πολυπλοκότητα Αλγορίθμου g-class Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών Επιλογή Αλγορίθμου Κατηγοριοποίησης Επίδραση της διάσπασης των δεδομένων εισόδου στην κατανομή των πρωτεϊνών σε κατηγορίες BADGE και g-class Ο Αλγόριθμος Proteas Ο Αλγόριθμος Συνοπτικά Σχηματισμός Δεδομένων Εισόδου
11 Περιεχόμενα xi Κατασκευή Μοντέλων Πρόβλεψη Λειτουργίας Πρωτεϊνών Πολυπλοκότητα Αλγορίθμου Proteas Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών Στατιστικά Στοιχεία των Δεδομένων Εκπαίδευση και Κατασκευή Μοντέλων BADGE και Proteas Ο Αλγόριθμος Fuzzy PhyloProf Ο Αλγόριθμος Συνοπτικά Φυλογενετικά Προφίλ και Ασαφή Φυλογενετικά Προφίλ Ορισμός και χρήση της Ανάλυσης Ιδιαζουσών Τιμών Ορισμός Μετρικών Απόστασης σε Φυλογενετικά Προφίλ Ανάλυση του Διαγράμματος Ομαδοποίησης Πολυπλοκότητα Αλγορίθμου Fuzzy PhyloProf Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών Φυλογενετικά χαρακτηριστικά των πέντε οργανισμών αναφοράς Ασαφή Συνολικά Προφίλ και Ομαδοποίηση Γονιδίων Συσχέτιση Οργανισμών με Διακριτοποίηση των Ασαφών Προφίλ BADGE και Fuzzy PhyloProf Ο Αλγόριθμος g-molknot Ο Αλγόριθμος Συνοπτικά Αλγόριθμος GMK και Αλγόριθμος g-molknot Πολυπλοκότητα Αλγορίθμου g-molknot Αποτελέσματα Πειραματική Εκτίμηση Χρονικής Πολυπλοκότητας του g-molknot BADGE και g-molknot Συμπεράσματα Ανακεφαλαίωση Μελλοντικές Επεκτάσεις Μετά τη Μεθοδολογία BADGE Βιοπληροφορική και Πλέγματα Υπολογιστών Παραρτήματα 139 Παράρτημα Α: Βασικές Έννοιες Βιολογίας 141 Α.1 Ορισμοί Α.2 Μοτίβα σε Πρωτεϊνικές Αλυσίδες
12 xii Περιεχόμενα Α.3 Φυλογενετικά Δένδρα Παράρτημα Β: Τυπική Ροή Εργασίας σε Πλέγμα 147 Παράρτημα Γ: Σύνταξη JDL Αρχείων 151 Βιβλιογραφία 166
13 Κατάλογος Σχημάτων 1.1 Βάση Δεδομένων PDB Βάση Δεδομένων GenBank Η κατάρα της διαστατικότητας Αναπαράσταση της δομής ενός κυττάρου Κεντρικό δόγμα της Βιολογίας Τέσσερεις δομές μιας πρωτεΐνης Σχηματικό διάγραμμα ενός Πλέγματος Υπολογιστών Παγκόσμιος χάρτης με τις χώρες που συμμετέχουν στο EGEE EGEE στην Ευρώπη Τυπική Διαδικασία Κατηγοριοποίησης Πρωτεϊνών Τυπική Διαδικασία Κατηγοριοποίησης Πρωτεϊνών με χρήση Πλέγματος Ροή Δεδομένων σε Πλέγματα Υπολογιστών σύμφωνα με τη μεθοδολογία BADGE Διαφορετικοί λόγοι παράλληλου και σειριακού τμήματος Εσωτερική Λειτουργία Εργαλείου BADGE Λογικό Διάγραμμα για την Ανάκτηση Δεδομένων στο Εργαλείο BADGE Λογικό Διάγραμμα για τον ορισμό Εκτελέσιμου στο Εργαλείο BADGE Ροή Εργασίας Εξωτερικά του Πλέγματος Ροή Εργασίας σε Πλέγμα Διάγραμμα ροής του αλγορίθμου g-class Κατανομή πρωτεϊνών σε κατηγορίες για διαφορετικό πλήθος διασπάσεων και κατηγοριών Πειραματικά Αποτελέσματα του g-class με χρήση της μεθοδολογίας BADGE Διάγραμμα ροής του αλγορίθμου Proteas Κατασκευή μοντέλων με τη μέθοδο Proteas Πλήθος πρωτεϊνών σε σχέση με το πλήθος των μοτίβων Συγκεντρωτικό Ποσοστό πρωτεϊνών σε σχέση με το πλήθος μοτίβων Χρόνος Κατασκευής μοντέλων για διαφορετικό αριθμό πρωτεϊνών
14 xiv ΚΑΤΑΛΟΓΟΣ ΣΧΗΜΑΤΩΝ 6.6 Χρόνος Εκτέλεσης του Proteas Ακρίβεια πρόβλεψης μοντέλων του Proteas Χαρακτηριστικές περιοχές σε ένα διάγραμμα ομαδοποίησης της μεθόδου Fuzzy PhyloProf Διάγραμμα ροής του αλγορίθμου Fuzzy PhyloProf Πλήρες Φυλογενετικό Δένδρο Απλοποιημένο Φυλογενετικό Δένδρο των 5 οργανισμών Διάγραμμα Διατήρησης Γονιδίων για τα 5 είδη Ασαφή Συνολικά Προφίλ για τα 5 είδη Ομαδοποίηση όλων των γονιδίων των 5 οργανισμών Διακριτοποιημένα Ασαφή Προφίλ οργανισμών (α = 0.2) Διακριτοποιημένα Ασαφή Προφιλ οργανισμών (α = 0.99) Παραδείγματα κόμβου Διάγραμμα ροής του g-molknot Χρονική επίδοση του αλγορίθμου g-molknot Διάγραμμα μέσου χρόνου για τις 100 διεργασίες του g-molknot Παραγωγή κόμβων g-molknot B.1 Πιθανές καταστάσεις μιας εργασίας (job)
15 Κατάλογος Πινάκων 2.1 Αντιστοιχία μεταξύ του ηλεκτρικού δικτύου και του πλέγματος υπολογιστών Ελληνικοί κόμβοι EGEE Βήματα Μεθοδολογίας BADGE Πεδία Εσωτερικής Αναπαράστασης Εργαλείου BADGE Χρόνοι Συνολικής Εκτέλεσης του GridBLAST Σύγκριση των σεναρίων χρήσης Σύγκριση των συστημάτων ροής εργασιών Σύγκριση Πολυπλοκότητας Προσεγγίσεων στο g-class Αποτελέσματα Κατηγοριοποίησης 1,000 πρωτεϊνών για διαφορετικούς αλγορίθμους Αρχική Ανάλυση Πολυπλοκότητας στον Proteas Πολυπλοκότητα του Proteas Πολυπλοκότητα του αλγορίθμου Fuzzy PhyloProf Πίνακας Διατήρησης Γονιδίων για τα 5 είδη Πολυπλοκότητα του αλγορίθμου g-molknot Πλήθος παραγόμενων διαμορφώσεων σε διάφορους υποχώρους B.1 Ορισμοί κατάστασης εργασιών (jobs)
16 xvi ΚΑΤΑΛΟΓΟΣ ΠΙΝΑΚΩΝ
17 Κατάλογος Πλαισίων Κώδικα 4.1 Παράδειγμα εσωτερικής αναπαράστασης μιας διαδικασίας στη μεθοδολογία BADGE Εσωτερική Αναπαράσταση Διαδικασίας gridblast στη μεθοδολογία BADGE Ψευδοκώδικας Αλγορίθμου Διάσπασης Δεδομένων Ψευδοκώδικας Αλγορίθμου Συνδυασμού Ταξινομητών Εσωτερική αναπαράσταση διαδικασίας g-class στη μεθοδολογία BADGE Αρχείο XML από το εργαλείο InterProScan για την πρωτεΐνη P Ψευδοκώδικας Αλγορίθμου Κατασκευής PTA Ψευδοκώδικας Αλγορίθμου ProteasClassifier Εσωτερική Αναπαράσταση Διαδικασίας Proteas στη μεθοδολογία BADGE Παράδειγμα φυλογενετικών προφίλ Εσωτερική Αναπαράσταση Αλγορίθμου Fuzzy PhyloProf στη μεθοδολογία BADGE Εσωτερική Αναπαράσταση Αλγορίθμου g-molknot στη μεθοδολογία BADGE131
18 Κεφάλαιο 1 Εισαγωγή Στις 26 Ιουνίου 2000, οι επιστήμες της Βιολογίας και της Ιατρικής άλλαξαν ριζικά. Ο πρωθυπουργός της Αγγλίας και ο πρόεδρος της Αμερικής, σε μία κοινή συνέντευξη τύπου μέσω δορυφόρου, ανακοίνωσαν την ολοκλήρωση της πρώτης καταγραφής του ανθρώπινου γονιδιώματος. Η ακολουθία τριών δισεκατομμυρίων βάσεων ήταν το επιστέγασμα της δεκαετούς προσπάθειας της διεθνούς συνεργασίας έξι χωρών, είκοσι ερευνητικών κέντρων και χιλίων επιστημόνων. Από την ανακάλυψη της δομής του DNA από τους James Watson και Francis Crick το 1953, ή ακόμα από την επιβεβαίωση των νόμων του Mendel στην αρχή του 20 ου αιώνα, οι επιστήμονες είχαν χαράξει τον δρόμο για την κατανόηση της γενετικής πληροφορίας. Την τελευταία πλέον δεκαετία, ο στόχος ήταν ορατός και υλοποιήσιμος και το μόνο ερώτημα που απέμενε ήταν ο χρόνος επίτευξής του, άμεση συνάρτηση της ταχύτητας εξέλιξης της τεχνολογίας. Δίπλα στο Διαστημικό Πρόγραμμα που έστειλε τον άνθρωπο στη Σελήνη και στο Σχέδιο Manha an που κατασκεύασε την ατομική βόμβα, το Πρόγραμμα του Ανθρώπινου Γονιδιώματος (Human Genome Project) κερδίζει επάξια τη θέση του ως ένα από τα μεγάλα τεχνολογικά επιτεύγματα του 20 ου αιώνα, καθώς φαίνεται να συνδυάζει τις προοπτικές του πρώτου με τους κινδύνους του δεύτερου. Παρά τους κινδύνους που ελλοχεύουν από την κακή χρήση της κλωνοποίησης και της γενετικής μηχανικής, το Πρόγραμμα του Ανθρώπινου Γονιδιώματος δεν παύει να αποτελεί το ορόσημο στην εξέλιξη της βιολογίας και της ιατρικής, αλλά και ένα πολυδάπανο και μεγάλης κλίμακας έργο των σύγχρονων τεχνολογιών πληροφορίας. Η βάση του ανθρώπινου γονιδιώματος είναι η πληροφορία. Τόσο ο προσδιορισμός της ακολουθίας, όσο και οι εφαρμογές της βιολογίας που θα τη χρησιμοποιούσαν, απαιτούσαν τη χρήση των υπολογιστών. Η επιστήμη των υπολογιστών παρείχε την τεχνολογία και τα μέσα για την αποθήκευση των δεδομένων, την υπολογιστική ισχύ για τη μαζική επεξεργασία τους, καθώς και τα πολύπλοκα και εξειδικευμένα μαθηματικά εργαλεία για την εύρεση των αποτελεσμάτων. Η συνεργασία αυτή της βιολογίας και της πληροφορικής οδήγησε στη γένεση μιας νέας επιστήμης, της βιοπληροφορικής. Το 1965 έχουμε τον πρώτο άτλαντα της αλληλουχίας και δομής πρωτεϊνών (Atlas of Protein Sequence and Structure) από την Dr. Margaret Oakley Dayhoff ( , η
19 2 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ οποία ήταν καθηγήτρια βιοχημείας και ερευνήτρια στο Ιατρικό Κέντρο (Medical Center) του Πανεπιστημίου της Georgetown. Ήταν η πρώτη γυναίκα στον τομέα της Βιοπληροφορικής και ανήκει στους ιδρυτές αυτής της ενδιαφέρουσας επιστήμης. Η Margaret Dayhoff είχε γνώσεις Χημείας, Μαθηματικών, Βιολογίας και Πληροφορικής, τις οποίες αξιοποίησε και συνδύασε κατάλληλα, ώστε να προσφέρει στην κοινωνία των επιστημόνων τον πρώτο άτλαντα με πληροφορίες 65 πρωτεϊνών. Επιστήμονες από όλο τον κόσμο είχαν το βιβλίο της Dr. Dayhoff [DECS65] ως σημείο αναφοράς για τα πειράματά τους. Είναι αυτή που εισήγαγε μεθόδους σύγκρισης πρωτεϊνικών αλληλουχιών με τη χρήση ηλεκτρονικών υπολογιστών. 1.1 Γενική Περιγραφή του Πεδίου Εφαρμογής Η Βιοπληροφορική πρακτικά γεννήθηκε όταν η χρήση υπολογιστών έγινε απαραίτητη στα πειράματα και στις μελέτες των βιολόγων. Η τεράστια εξέλιξη που γνώρισε η επιστήμη των υπολογιστών τις τελευταίες δεκαετίες και η δημιουργία του διαδικτύου έχουν αλλάξει ριζικά τον τρόπο με τον οποίο διεξάγεται η έρευνα στις μέρες μας. Μέσα στο σύντομο αυτό χρονικό διάστημα, οι υπολογιστές έχουν πολλαπλασιάσει την υπολογιστική τους ισχύ και πλέον χρησιμοποιούνται για τη συλλογή, την διαχείριση και την ανάλυση βιολογικών δεδομένων. Ταυτόχρονα έχουν δημιουργηθεί δεκάδες βάσεις βιολογικών δεδομένων στο διαδίκτυο, οι οποίες είναι συνεχώς διαθέσιμες στους επιστήμονες. Ο όγκος των δεδομένων σε αυτές τις βάσεις αυξάνεται εκθετικά, όπως φαίνεται και στα Σχήματα 1.1 και 1.2 για τις βάσεις δεδομένων PDB [RCS10] [BWF + 00] και GenBank [Gen10a] [BKML + 08]. x 10 4 Growth of PDB ( ) 6 deposited structures for this year total available structures 5 PDB Structures Year Σχήμα 1.1: Ο ρυθμός αύξησης δεδομένων στη βάση δεδομένων PDB [PDB10]. Τα στοιχεία για το έτος 2010 είναι μέχρι και το Μάιο.
20 1.1 Γενική Περιγραφή του Πεδίου Εφαρμογής 3 Σχήμα 1.2: Το μέγεθος της βάσης δεδομένων GenBank [Gen10b] Οι βάσεις βιολογικών δεδομένων περιέχουν συνήθως πληροφορίες που αφορούν ακολουθίες νουκλεϊκών οξέων, ακολουθίες αμινοξέων, δομές πρωτεϊνών και λειτουργίες πρωτεϊνών. Εκτός από δεδομένα, ενσωματώνουν επίσης διάφορα εργαλεία που βοηθούν τους χρήστες να εντοπίζουν τις ζητούμενες πληροφορίες εύκολα και γρήγορα [RLB00]. Αυτά τα εργαλεία είναι απολύτως απαραίτητα λόγω του τεράστιου όγκου των δεδομένων. Χωρίς αυτά η ζητούμενη πληροφορία μπορεί εύκολα να χαθεί μέσα στον όγκο των διαθέσιμων δεδομένων. Κατά συνέπεια, η πλειοψηφία των βάσεων βιολογικών δεδομένων έχουν σχεδιαστεί με τέτοια εσωτερική οργάνωση η οποία επιτρέπει την εξυπηρέτηση πολλαπλών και σύνθετων ερωτημάτων, ενώ παραμένει διάφανη (transparent) προς τον τελικό χρήστη.
21 4 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ 1.2 Τρέχουσα Κατάσταση Παρόλο που η Υπολογιστική Βιολογία και η Βιοπληροφορική συχνά αντιμετωπίζονται ως συνώνυμα του ίδιου διεπιστημονικού χώρου, παρουσιάζουν αρκετές σημαντικές διαφοροποιήσεις. Η κύρια ενασχόληση της Βιοπληροφορικής είναι η ανάλυση και η επεξεργασία των βιολογικών δεδομένων, και επομένως ενδιαφέρει η ανάπτυξη τόσο στο αλγοριθμικό όσο και το τεχνικό μέρος της θεωρίας και των τεχνικών για την επίλυση τυπικών και πρακτικών προβλημάτων διαχείρισης δεδομένων. Από την άλλη πλευρά, η Υπολογιστική Βιολογία στοχεύει στην επίλυση συγκεκριμένων βιολογικών προβλημάτων, χρησιμοποιώντας υπολογιστές για τον έλεγχο και την αξιολόγηση υποθέσεων. Οι τρέχοντες ορισμοί των δύο αυτών επιστημονικών χώρων, όπως έχουν διατυπωθεί από το Na onal Ins tute of Health, είναι οι εξής [NIH08]: Bioinforma cs: Research, development, or applica on of computa onal tools and approaches for expanding the use of biological, medical, behavioral or health data, including those to acquire, store, organize, archive, analyze, or visualize such data. Computa onal Biology: The development and applica on of data-analy cal and theore cal methods, mathema cal modeling and computa onal simula on techniques to the study of biological, behavioral, and social systems. Παρόλα αυτά όμως, πρέπει να τονισθεί ότι ενώ οι δύο επιστήμες είναι διακριτές, εμφανίζουν αρκετές επικαλύψεις με σημαντική και ουσιαστική δραστηριότητα. Η Πρωτεομική (Proteomics) είναι μία από τις περιοχές-κλειδιά που εδράζεται στην επικάλυψή τους. Συνοπτικά, η πρωτεομική είναι η μεγάλης κλίμακας μελέτη πρωτεϊνών, ξεκινώντας από τη δομική και λειτουργική ανάλυση, μέχρι την κατασκευή δικτύων αλληλεπίδρασης πρωτεϊνών (protein-protein interac on networks) και φυλογενετικών δένδρων. Οι πρωτεΐνες είναι οργανικά μόρια μεγάλου μήκους αποτελούμενα από αμινοξέα δομημένα σε μορφή αλυσίδας και τα οποία ενώνονται με πεπτιδικούς δεσμούς. Αποτελούν αναγκαίο τμήμα κάθε οργανισμού, καθώς συμμετέχουν σε όλες τις λειτουργίες εντός των κυττάρων: στην κατάλυση βιοχημικών αντιδράσεων (ένζυμα), στη διατήρηση του σχήματος του κυττάρου ως κυτταρικός σκελετός, ως μέσο επικοινωνίας μεταξύ κυττάρων, κτλ. Ο όρος πρωτέωμα (proteome), κατ αντιστοιχία με το γονιδίωμα, περιγράφει το σύνολο των πρωτεϊνών που εκφράζονται από ένα γονιδίωμα σε κάποια δεδομένη στιγμή και υπό συγκεκριμένες και καθορισμένες συνθήκες. Τελευταία παρατηρείται μια μετατόπιση του ερευνητικού ενδιαφέροντος από τη γενομική στην πρωτεομική, κυρίως γιατί η πρωτεομική θεωρείται από πολλούς ως το επόμενο βήμα στη μελέτη των βιολογικών συστημάτων. Το γονιδίωμα ενός οργανισμού είναι επί το πλείστο σταθερό, παρουσιάζοντας πολύ μικρές διαφοροποιήσεις στα διά-
22 1.3 Νέες Προκλήσεις στην Περιοχή της Βιοπληροφορικής 5 φορα κύτταρα του ιδίου οργανισμού, σε αντίθεση με το πρωτέωμα, το οποίο διαφοροποιείται σε μεγάλο βαθμό μεταξύ κυττάρων. Μια από τις πιο σημαντικές πληροφορίες που έχουν προκύψει από το χώρο της πρωτεομικής είναι η φύση της σχέσης μεταξύ γονιδίων και πρωτεϊνών. Η μελέτη του πρωτεώματος του ποντικιού [GKL + 99] έδειξε ότι μια πρωτεΐνη μπορεί να θεωρηθεί ως έκφραση όχι ενός αλλά συνδυασμού πολλών γονιδίων [Klo99]. Κατ αντιστοιχία, μια μόνο μετάλλαξη σε ένα γονίδιο μπορεί να επηρεάσει πολλές πρωτεΐνες. Επιπλέον, χρησιμοποιώντας το πρωτέωμα της μαγιάς (yeast), το δίκτυο αλληλεπίδρασης των αναγκαίων πρωτεϊνών (essen al-essen al protein interac on network) θεωρείται ότι αποτελεί ένα γενικευμένο υπόβαθρο γύρω από το οποίο συγκλίνουν τόσο πρωτεΐνες του ίδιου οργανισμού όσο και πρωτεΐνες της ίδια ομοταξίας [PLAPAO05]. 1.3 Νέες Προκλήσεις στην Περιοχή της Βιοπληροφορικής Σε προηγούμενα χρόνια, η έρευνα τόσο στη γενομική όσο και στην πρωτεομική μπορούσε να εστιαστεί μόνο σε ένα γονίδιο ή πρωτεΐνη τη φορά. Παρόλα αυτά, η εξέλιξη των τεχνικών στις βιοεπιστήμες έχει αρχίσει να παρέχει ένα εκθετικά αυξανόμενο όγκο δεδομένων. Εξαιτίας αυτού του φαινομένου παρατηρείται μια μετάβαση στην έρευνα από μελέτες ωθούμενες από υπόθεση (hypothesis-driven) προς μελέτες ωθούμενες από δεδομένα (data-driven). Η μετατόπιση αυτή φέρνει αντιμέτωπους τους επιστήμονες με νέες προκλήσεις στην ανάλυση δεδομένων. Από τη μια πλευρά, οι περισσότερες μελέτες στη Βιοπληροφορική και ιδιαίτερα στην πρωτεομική εμφανίζουν περιορισμένο αριθμό N περιπτώσεων (δηλαδή δειγμάτων ή εγγραφών). Συνήθως, το N κυμαίνεται από δεκάδες έως εκατοντάδες, πολύ πιο περιορισμένο συγκριτικά με τις χιλιάδες ή εκατομμύρια περιπτώσεις που υπάρχουν σε τυπικές εφαρμογές πληροφορικής ή οικονομικών. Από την άλλη πλευρά, τεχνικές υψηλής απόδοσης στις βιοεπιστήμες καταγράφουν πολλές χιλιάδες παραμέτρους P σε κάθε περίπτωση, το οποίο έρχεται σε ισχυρή αντίθεση με κλασικά σενάρια εξόρυξης δεδομένων. Το πρόβλημα αυτό είναι γνωστό ως η κατάρα της διαστατικότητας ( curse of dimensionality ) ή small-n-large-p problem [BGD07] (Σχήμα 1.3). Παραδείγματος χάριν, σε ένα τυπικό σύνολο δεδομένων σε πρόβλημα πρωτεομικής, το πλήθος P των μεταβλητών ανά περίπτωση είναι της τάξης των 10⁴, ενώ το ίδιο το πλήθος N των περιπτώσεων είναι της τάξης του 10². Επίσης, εδώ θα πρέπει να σημειωθεί ότι μελέτες πάνω σε πρωτεϊνικά δεδομένα παρουσιάζουν σημαντικά μεγαλύτερη πολυπλοκότητα από ότι μελέτες πάνω σε γονιδιώματα. Οι πρωτεΐνες εμφανίζουν πιο σύνθετες μορφές, έχουν πολλαπλές λειτουργίες ενώ υπάρχουν πολλές περιπτώσεις όπου μεταβάλλονται ενεργά από το περιβάλλον στο οποίο βρίσκονται (πχ υπάρχουν πρωτεΐνες οι οποίες δεν ενεργοποιούνται εάν δεν βρεθούν σε περιβάλλον υψηλής συγκέντρωσης σε φώσφορο). Για να αντιμετωπισθεί αυτό το πρόβλημα, η πλειοψηφία των προσεγγίσεων μηχανι-
23 6 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ (α) (β) N N P P Σχήμα 1.3: Η κατάρα της διαστατικότητας. N είναι το πλήθος των εγγραφών, και P το πλήθος των γνωρισμάτων. (α) Κλασικό πρόβλημα (β) Πρόβλημα Βιοπληροφορικής κής μάθησης είτε εστιάζουν την έρευνα σε συγκεκριμένες περιπτώσεις (πχ συγκεκριμένη κατηγορία πρωτεϊνών, όπως είναι τα ένζυμα) είτε μειώνουν το πλήθος των μεταβλητών που λαμβάνονται υπόψιν σε κάθε περίπτωση (πχ μέσω ανάλυσης πρωτευουσών συνιστωσών - Principal Component Analysis). Ενώ αυτές οι προσεγγίσεις δίνουν ικανοποιητικά αποτελέσματα στην εκάστοτε ερευνητική περιοχή, είναι εμφανής στη βιβλιογραφία η έλλειψη μεθόδων οι οποίες μπορούν να αντιμετωπίσουν με ένα γενικευμένο τρόπο την ανάλυση όλων των δεδομένων σε ικανοποιητικό χρόνο και με συγκρίσιμη απόδοση. Οι τεχνολογίες Υπολογιστικής Πλέγματος (Grid Compu ng) μπορούν ενδεχομένως να παράσχουν μια εναλλακτική προσέγγιση στο πρόβλημα, αναλύοντας πολλαπλές μεθόδους με ομοιογενή τρόπο. 1.4 Σκοπός και Επιμέρους Στόχοι της Διατριβής Στα πλαίσια της παρούσας διατριβής γίνεται μια μελέτη του συγκερασμού δύο ερευνητικών περιοχών: της Βιοπληροφορικής (με έμφαση σε ανάλυση πρωτεΐνικών δεδομένων) και της Υπολογιστικής Πλέγματος. Από αυτή τη μελέτη προκύπτει μια γενικευμένη μεθοδολογία η οποία εφαρμόζεται σε Πλέγματα Υπολογιστών ενώ ταυτόχρονα λαμβάνει υπόψη τις ιδιαιτερότητες και τους περιορισμούς που παρουσιάζουν τα προβλήματα Βιοπληροφορικής.
24 1.4 Σκοπός και Επιμέρους Στόχοι της Διατριβής 7 Καθώς η απαίτηση για αυτοματοποιημένη ανάλυση μεγάλου και κατανεμημένου όγκου βιολογικών δεδομένων αυξάνεται διαρκώς, εμφανίζονται νέες προκλήσεις τόσο στο χώρο των Πλεγμάτων Υπολογιστών όσο και στην ίδια τη συνεργασία μεταξύ επιστημόνων διάφορων πεδίων. Ένας μέσος ερευνητής συνήθως ενδιαφέρεται και αντιλαμβάνεται έννοιες, ζητήματα, υποθέσεις και απαιτήσεις που προέρχονται από το δικό του πεδίο εφαρμογών, και δεν τον απασχολούν σε βάθος τα ιδιαίτερα χαρακτηριστικά των μέσων ή των πόρων που θα είναι διαθέσιμοι για χρήση στις εφαρμογές του. Ενώ η κατάσταση αυτή είναι ευρύτερα αποδεκτή ως αναγκαίο κακό, είναι γεγονός ότι μία τυποποίηση των χαρακτηριστικών που βρίσκονται στην τομή των δύο ερευνητικών πεδίων θα επιτρέψει αφενός την καλύτερη καταγραφή και κατανόηση των αναγκών που υπάρχουν και αφετέρου θα καταστήσει δυνατή την κατασκευή αυτόματων ή ημι-αυτόματων εργαλείων τα οποία θα γεφυρώνουν με ένα διαφανή τρόπο τις δύο περιοχές βελτιώνοντας ταυτόχρονα τόσο την απόδοση όσο και την ταχύτητα των μελετών. Διατυπώνοντας την υπόθεση της διατριβής, υποστηρίζεται ότι: Μια γενικευμένη μεθοδολογία η οποία α) θα εκμεταλλεύεται τα πλεονεκτήματα των Πλεγμάτων Υπολογιστών, β) θα λαμβάνει υπόψη τις ιδιαιτερότητες και τους περιορισμούς των εφαρμογών Βιοπληροφορικής, και γ) θα ικανοποιεί την απαίτηση του μέσου ερευνητή για ευχρηστία και απλότητα, είναι δυνατόν να αποτελέσει το επόμενο βήμα στην ανάλυση βιολογικών δεδομένων μεγάλης κλίμακας καθώς: 1. θα αυτοματοποιήσει τη διαδικασία ανάλυσης βιολογικών δεδομένων, 2. θα επιτρέψει τη βελτίωση της απόδοσης μέσω της ταυτόχρονης χρήσης πολλαπλών υπολογιστικών πόρων, και 3. θα αποτελέσει ένα βασικό υπόβαθρο για τον περαιτέρω σχεδιασμό και ανάπτυξη μεθόδων υψηλών επιδόσεων στη Βιοπληροφορική. Πιο συγκεκριμένα, οι επιμέρους στόχοι της διατριβής είναι οι εξής: 1. Η καταγραφή και η τυποποίηση των κοινών χαρακτηριστικών στα ερευνητικά πεδία της Βιοπληροφορικής με έμφαση στο χώρο της πρωτεομικής, 2. Η θεωρητική μελέτη των επιμέρους βημάτων στα οποία μπορεί να αναλυθεί μια τυπική προσέγγιση Βιοπληροφορικής, 3. Ο έλεγχος και η βέλτιστη κατανομή των βημάτων στα πλαίσια ενός περιβάλλοντος Πλέγματος Υπολογιστών, 4. Η αυτοματοποίηση της μεθοδολογίας με χρήση ημι-αυτόματων εργαλείων λογισμικού,
25 8 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ 5. Η αξιολόγηση της μεθοδολογίας με εφαρμογή της σε πραγματικά προβλήματα Βιοπληροφορικής, 6. Η διερεύνηση της γενίκευσης της μεθοδολογίας με χρήση ερευνητικών προβλημάτων εκτός Βιοπληροφορικής. 1.5 Συμβολή της Διατριβής Στα πλαίσια της διατριβής ορίστηκε και αναπτύχθηκε η γενικευμένη μεθοδολογία ανάπτυξης αλγορίθμων βιοπληροφορικής σε περιβάλλοντα Πλέγματος Υπολογιστών, η οποία καλείται BADGE (Bioinforma cs Algorithm Development for Grid Environments). Η μεθοδολογία BADGE απαρτίζεται από πέντε φάσεις: 1. Ανάκτηση Δεδομένων, όπου προσδιορίζονται οι πηγές δεδομένων (τοπικές ή κατανεμημένες), οι οποίες θα χρησιμοποιηθούν στη συνέχεια, 2. Προεπεξεργασία Δεδομένων, όπου καθορίζεται ο τρόπος προετοιμασίας των δεδομένων που θα αναλυθούν και μπορεί να περιλαμβάνει είτε γνωστές μεθόδους προεπεξεργασίας είτε αλγορίθμους προσαρμοσμένους από τον χρήστη για την εκάστοτε μελέτη, 3. Διαμόρφωση Αλγορίθμου, όπου γίνεται η μεταγλώττιση του πηγαίου κώδικα της τελικής εφαρμογής, εάν αυτό απαιτείται, καθώς και ο ορισμός των παραμέτρων εκτέλεσης, 4. Καθορισμός Τύπου και Εκτέλεση της Εφαρμογής, όπου, ανάλογα με την παραμετροποίηση των προηγούμενων βημάτων, η τελική εφαρμογή κατατάσσεται σε μία από τις τρεις κατηγορίες: Μίας Διεργασίας, Πολλαπλών Διεργασιών, ή Παράλληλη (MPI) και οι αντίστοιχες εργασίες υποβάλλονται στο Πλέγμα Υπολογιστών, και 5. Αξιολόγηση των Αποτελεσμάτων, όπου επιλέγεται είτε η καταλληλότερη μέθοδος από ένα σύνολο προκαθορισμένων αλγορίθμων είτε κάποια προσαρμοσμένη στην εκάστοτε μελέτη. Για την ανάδειξη και αξιολόγηση της μεθοδολογίας BADGE αναπτύχθηκαν κάποιοι νέοι αλγόριθμοι βιοπληροφορικής ή προσαρμόστηκαν κατάλληλα υπάρχοντες αλγόριθμοι. Συγκεκριμένα αναπτύχθηκε ο αλγόριθμος g-class για το πρόβλημα της κατηγοριοποίησης πρωτεϊνών. Ο αλγόριθμος στοχεύει στην ταξινόμηση πρωτεϊνών σε πολλαπλές οικογένειες αξιοποιώντας μια τεχνική διαίρει-και-βασίλευε. Το αρχικό σύνολο δεδομένων εισόδου διασπάται σε ένα πλήθος ξένων συνόλων, τα οποία ο αλγόριθμος επεξεργάζεται παράλληλα για την κατασκευή των κατάλληλων μοντέλων. Ένας άλλος αλγόριθμος που αναπτύχθηκε είναι ο Proteas, ο οποίος στοχεύει στην επίλυση του προβλήματος
26 1.5 Συμβολή της Διατριβής 9 κατηγοριοποίησης πρωτεϊνών με βάση τα χαρακτηριστικά τους σύμφωνα με την Gene Ontology. Τα δεδομένα αντλούνται από διαφορετικές και κατανεμημένες βάσεις δεδομένων, ενώ η εκπαίδευση των διαφορετικών μοντέλων γίνεται με παράλληλη επεξεργασία συγκεκριμένων συνόλων δεδομένων εισόδου. Ο Proteas αξιοποιεί σε βάθος τεχνικές παράλληλου προγραμματισμού, αλλά ταυτόχρονα εφαρμόζεται σε Πλέγμα Υπολογιστών παρουσιάζοντας αισθητή βελτίωση στο χρόνο εκτέλεσής του. Ο τρίτος αλγόριθμος που αναπτύχθηκε, ο Fuzzy PhyloProf, παρουσιάζει μια ιδιαιτερότητα τόσο στη φύση των δεδομένων εισόδου που χρησιμοποιεί, όσο και το πρόγραμμα υλοποίησής του. Τα δεδομένα εισόδου χαρακτηρίζονται από μεγάλο όγκο καθώς και από παρουσία θορύβου. Η υλοποίηση του αλγορίθμου από την άλλη πλευρά, εξαρτάται από την ύπαρξη ενός συγκεκριμένου πακέτου λογισμικού για μαθηματική μοντελοποίηση (Octave), αλλά ταυτόχρονα, με χρήση της γενικευμένης μεθοδολογίας, αξιοποιεί σε βάθος την αρχιτεκτονική των Πλεγμάτων Υπολογιστών. Τέλος, η μεθοδολογία εφαρμόσθηκε και στο ερευνητικό πεδίο της Υπολογιστικής Μοριακής Επιστήμης, ώστε να γίνει αξιολόγηση της ικανότητας της μεθοδολογίας να αξιοποιείται σε ευρύτερο φάσμα εφαρμογών. O αλγόριθμος g- MolKnot, που αποτελεί επέκταση του αλγόριθμου GMK για την αναζήτηση τοπολογιών κόμβου σε οργανικά μόρια με συγκεκριμένες ιδιότητες, τροποποιήθηκε για εκτέλεση σε πλέγμα υπολογιστών. Εφαρμόζει μια τακτική διαίρει-και-βασίλευε στο πρόβλημα, διασπώντας το χώρο αναζήτησης σε πολλούς διακριτούς και ανεξάρτητους υποχώρους, και συνδυάζοντας στο τέλος τα αποτελέσματα πολλαπλών διεργασιών. Χρησιμοποιώντας το g-molknot κατέστη για πρώτη φορά εφικτός σε λογικό χρόνο ο υπολογισμός μιας κομβικής τοπολογίας τεσσάρων διασταυρώσεων του μορίου C 36 H 74. Πέρα από το θεωρητικό υπόβαθρο, αναπτύχθηκε και ένα ημι-αυτόματο εργαλείο το οποίο υλοποιεί τη γενικευμένη μεθοδολογία και διευκολύνει την υποβολή ολοκληρωμένων εργασιών στο Πλέγμα Υπολογιστών. Με χρήση αυτού του εργαλείου έγινε η αξιολόγηση του BADGE με την εφαρμογή του σε μια σειρά από προβλήματα που προέρχονται από το χώρο της Βιοπληροφορικής. Η επιστημονική συμβολή της παρούσας διατριβής συνίσταται στα εξής: Ανάλυση και τυποποίηση των επιμέρους βημάτων σε προσεγγίσεις ανάλυσης δεδομένων σε εφαρμογές Βιοπληροφορικής Ορισμός της γενικευμένης μεθοδολογίας BADGE Ανάπτυξη νέων αλγορίθμων εξόρυξης δεδομένων με στόχο την άμεση εφαρμογή τους σε Πλέγματα Υπολογιστών Σύγκριση νέων και υπαρχόντων αλγορίθμων με χρήση της γενικευμένης μεθοδολογίας Τα αποτελέσματα που εξήχθησαν κατά τη διάρκεια της εκπόνησης της παρούσας διδακτορικής διατριβής υποβλήθηκαν, εγκρίθηκαν και παρουσιάστηκαν σε διεθνή πε-
27 10 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ ριοδικά και συνέδρια του πεδίου. Ως εκ τούτου, θεωρούμε πως τα συμπεράσματα και η συμβολή της διατριβής επικυρώθηκαν, ενώ παράλληλα διασφαλίστηκε η επιστημονική τους ορθότητα. Συνολικά, στο πλαίσιο εκπόνησης της διδακτορικής διατριβής έγιναν: δύο δημοσιεύσεις σε περιοδικά με σύστημα κριτών: [PM10a] και [PMKD09] μια δημοσίευση υπό εξέταση σε περιοδικό με σύστημα κριτών μια δημοσίευση σε βιβλίο με σύστημα κριτών (book chapter): [PM09b] έξι δημοσιεύσεις σε πρακτικά διεθνών συνεδρίων με σύστημα κριτών (conference paper): [PM10b], [PM09a], [PPM06], [PM06], [PM05] και [PDM04] εννιά ανακοινώσεις σε διεθνή συνέδρια χωρίς πρακτικά με σύστημα κριτών: [CPM10], [TPM10], [KPM09], [PM08], [GPM08b], [PMKD08], [GPM07], [MPM07] και [MDSP06] τρεις δημοσιεύσεις σε άλλα συνέδρια: [GPM08c], [MPM08] και [GPM08a] 1.6 Διάρθρωση της Διατριβής H διδακτορική διατριβή αποτελείται από εννέα κεφάλαια. Στη συνέχεια, παρατίθενται εν συντομία τα θέματα που αυτή πραγματεύεται. Στο Κεφάλαιο 1 παρουσιάζεται μια σύντομη επισκόπηση της ερευνητικής περιοχής της Βιοπληροφορικής και των τεχνολογιών Πλεγμάτων Υπολογιστών. Στη συνέχεια, ορίζεται το αντικείμενο της διατριβής, οριοθετούνται οι επιμέρους στόχοι της και επεξηγείται συνοπτικά η επιστημονική της συμβολή στην κατανόηση και αντιμετώπιση του προβλήματος. Στο Κεφάλαιο 2 παρουσιάζονται οι έννοιες που συνθέτουν το αναγκαίο υπόβαθρο για την κατανόηση της διατριβής. Συγκεκριμένα γίνεται μια συνοπτική αναφορά στις βασικές έννοιες Βιολογίας και Βιοπληροφορικής, καθώς επίσης και στις τεχνολογίες Πλέγματος Υπολογιστών. Στο Κεφάλαιο 3 γίνεται μια πρώτη προσπάθεια καταγραφής της διαδικασίας ανάλυσης δεδομένων και εξόρυξης γνώσης στο χώρο της Βιοπληροφορικής. Παρουσιάζονται οι κυριότερες μελέτες στο χώρο αυτό, και συνοψίζονται τα κοινά χαρακτηριστικά και οι ελλείψεις που διαπιστώνονται. Το υλικό αυτού του κεφαλαίου δημοσιεύθηκε στα [PM09b] και [PM08]. Το Κεφάλαιο 4 παρουσιάζει και αναλύει τη μεθοδολογία BADGE, η οποία αναπτύχθηκε στα πλαίσια της διατριβής. Στη συνέχεια παρουσιάζονται σε βάθος τα επιμέρους βήματα της μεθοδολογίας και αναλύεται η πολυπλοκότητα τόσο σε κάθε επίπεδο όσο και συνολικά. Η ενότητα κλείνει με περιγραφή του εργαλείου BADGE και μια σύντομη
28 1.6 Διάρθρωση της Διατριβής 11 παρουσίαση των εφαρμογών που αναπτύχθηκαν. Το υλικό του κεφαλαίου δημοσιεύθηκε στα [PM10a], [PM09b], [PM09a] και [PM08]. Το Κεφάλαιο 5 περιγράφει τον αλγόριθμο ανάλυσης δεδομένων g-class που αναπτύχθηκε για το πρόβλημα της κατηγοριοποίησης πρωτεϊνών με χρήση μοτίβων. Στην ενότητα γίνεται η περιγραφή τόσο του ίδιου του αλγορίθμου, όσο και του τρόπου που αυτός γενικεύθηκε με χρήση της μεθοδολογίας. Ο στόχος του κεφαλαίου είναι να τονιστεί η δυνατότητα της γενικευμένης μεθοδολογίας να αξιοποιεί ήδη υπάρχοντες αλγορίθμους για την ανάλυση ως τώρα απαγορευτικά μεγάλου όγκου δεδομένων, βελτιώνοντας ταυτόχρονα τη συνολική απόδοσή τους. Το υλικό του κεφαλαίου δημοσιεύθηκε στο [PPM06]. Στο Κεφάλαιο 6 παρουσιάζεται ο αλγόριθμος εξόρυξης γνώσης Proteas και ο τρόπος εφαρμογής του με τη χρήση της γενικευμένης μεθοδολογίας. Σε αυτή την περίπτωση, ο αλγόριθμος σχεδιάστηκε εξαρχής με βάση την γενικευμένη μεθοδολογία που παρουσιάστηκε στο Κεφάλαιο 4. Το υλικό του κεφαλαίου δημοσιεύθηκε στα [PM06], [PM05], [PDM04], [GPM08b], [GPM07], [GPM08c] και [GPM08a]. Το Κεφάλαιο 7 παρουσιάζει έναν τρίτο αλγόριθμο επεξεργασίας φυλογενετικών δεδομένων, που ονομάζεται Fuzzy PhyloProf. Ο αλγόριθμος διαχειρίζεται ένα μεγάλο όγκο δεδομένων εισόδου, τα οποία χαρακτηρίζονται από θόρυβο, και εξαρτάται από ένα εξωτερικό πακέτο λογισμικού για τη μαθηματική μοντελοποίηση. Το υλικό αυτού του κεφαλαίου δημοσιεύθηκε στα [PM10b] και [KPM09]. Στο Κεφάλαιο 8 περιγράφεται ο αλγόριθμος g-molknot, ο οποίος αποτελεί μια προσπάθεια εφαρμογής της γενικευμένης μεθοδολογίας σε ερευνητικό πεδίο εκτός του χώρου της Βιοπληροφορικής. Το υλικό αυτής της ενότητας δημοσιεύθηκε στα [PMKD08] και [PMKD09]. Το Κεφάλαιο 9 συνοψίζει τα αποτελέσματα της διατριβής και προτείνει μελλοντικές κατευθύνσεις της έρευνας στον χώρο αυτό. Η διατριβή περιλαμβάνει και μια σειρά από επεξηγηματικά Παραρτήματα.
29 12 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ
30 Κεφάλαιο 2 Βιοπληροφορική και Πλέγματα Υπολογιστών Σε αυτό το κεφάλαιο γίνεται μια καταγραφή βασικών εννοιών της Βιολογίας και παρουσιάζονται οι επιμέρους κλάδοι της Βιοπληροφορικής με ιδιαίτερη έμφαση στην περιοχή της πρωτεομικής και στο πρόβλημα της κατηγοριοποίησης πρωτεϊνών. Ακολουθεί λεπτομερής αναφορά στο θεωρητικό υπόβαθρο, τις πειραματικές διαδικασίες και στη βιβλιογραφία πάνω σε υπάρχουσες μεθόδους στο χώρο της πρωτεομικής. Μετά την παρουσίαση του Βιολογικού υπόβαθρου, γίνεται μια εισαγωγή στις τεχνικές Υπολογισμού Υψηλών Επιδόσεων (High Performance Compu- ng) και Πλεγμάτων Υπολογιστών ως μεθόδων αντιμετώπισης των προβλημάτων Βιοπληροφορικής. Αρχικά περιγράφεται η θεωρία της Υπολογιστικής Υψηλών Επιδόσεων με έμφαση σε παράλληλα και κατανεμημένα συστήματα. Στη συνέχεια γίνεται περιγραφή της λογικής των Πλεγμάτων Υπολογιστών, σε επίπεδο φιλοσοφίας, αρχιτεκτονικής και πρακτικής εφαρμογής. Τέλος γίνεται αναφορά στα πλεονεκτήματα που παρουσιάζει αυτή η τεχνολογία, καθώς και στα εμφανή προβλήματα ευχρηστίας. 2.1 Βιολογικές Έννοιες Το Κύτταρο Το κύτταρο αποτελεί δομικό στοιχείο κάθε οργανισμού. Ορατό με οπτικό μικροσκόπιο, αποτελεί ένα μικροσκοπικό αλλά πολύπλοκο χημικό εργοστάσιο (Σχήμα 2.1). Είναι ικανό να λειτουργήσει και να αναπαραχθεί μόνο του στους μονοκύτταρους οργανισμούς, αλλά και να συνεργαστεί με μια ποικιλόμορφη πληθώρα άλλων κυττάρων για να επιτελέσει όλες τις λειτουργίες ενός πολύπλοκου πολυκύτταρου οργανισμού. Οι άνθρωποι έχουν κατά προσέγγιση 100 τρισεκατομμύρια κύτταρα. Το μέγεθος ενός χαρακτηριστικού κυττάρου είναι 10 μm και η μάζα του 1 ng.
31 14 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ Σχήμα 2.1: Αναπαράσταση της δομής ενός κυττάρου [The10] Υπάρχουν δύο τύποι κυττάρων: τα προκαρυωτικά και τα ευκαρυωτικά. με ουσιαστικότερη διαφορά μεταξύ τους την οργάνωση στο εσωτερικό τους. Τα προκαρυωτικά κύτταρα είναι μονοκύτταροι οργανισμοί χωρίς ευδιάκριτο πυρήνα και χωρίς διαμερισματοποίηση. Ούτε το DNA τους, ούτε οποιαδήποτε άλλη περιοχή μεταβολικής δραστηριότητάς τους συγκεντρώνεται σε μία ιδιαίτερη εσωκλειόμενη από μεμβράνη περιοχή. Το γενετικό υλικό των προκαρυωτικών κυττάρων είναι ένα δίκλωνο κυκλικό μόριο DNA, με ένα μόνο αντίγραφο του γονιδιώματος. Τα ευκαρυωτικά κύτταρα από την άλλη πλευρά έχουν πιο περίπλοκη εσωτερική δομή. Χαρακτηρίζονται από τον επιμερισμό πολλών λειτουργιών σε διαφορετικές περιοχές τους, τα ονομαζόμενα οργανίδια. Κάθε τύπος οργανιδίου διαδραματίζει έναν μοναδικό ρόλο στην αύξηση και το μεταβολισμό του κυττάρου και ορισμένα περιέχουν μια συλλογή συγκεκριμένων ενζύμων που καταλύουν τις απαραίτητες βιοχημικές αντιδράσεις. Τέλος, αξίζει να σημειωθεί ότι τα προκαρυωτικά κύτταρα διαβιούν συνήθως ανεξάρτητα, ενώ τα ευκαρυωτικά κύτταρα συγκροτούν συχνά πολυκύτταρους οργανισμούς.
32 2.1 Βιολογικές Έννοιες Το Κεντρικό Δόγμα της Βιολογίας Η διαδικασία μεταφοράς πληροφορίας μεταξύ βιοπολυμερών στους ζωντανούς οργανισμούς μπορεί να αναλυθεί στις εξής τρεις περιπτώσεις: 1. αντιγραφή (replica on), 2. μεταγραφή (transcrip on), και 3. μετάφραση (transla on) Τα βιοπολυμερή είναι βιολογικά πολυμερή, δηλαδή μόρια αποτελούμενα από δομικές μονάδες γνωστές ως μονομερή. Υπάρχουν τρεις σημαντικές κατηγορίες βιοπολυμερών: τα δύο νουκλεϊκά οξέα (DNA και RNA) και οι πρωτεΐνες. Τα νουκλεϊκά οξέα είναι γραμμικά πολυμερή μόρια αποτελούμενα από νουκλεοτίδια, ενώ οι πρωτεΐνες είναι γραμμικά πολυμερή μόρια αποτελούμενα από αμινοξέα. Το κεντρικό δόγμα της βιολογίας παρουσιάζεται σχηματικά στο Σχήμα 2.2. Υπάρχουν συνολικά 9 (3 3) κατανοητές άμεσες μεταφορές πληροφορίας που μπορούν να εμφανιστούν. Οι συνεχόμενες γραμμές αντιπροσωπεύουν τις γενικές μεταφορές, δηλαδή μεταφορές πληροφορίας οι οποίες λαμβάνουν χώρα κανονικά στα περισσότερα κύτταρα. Οι διακεκομμένες γραμμές αντιπροσωπεύουν τις ειδικές μεταφορές, δηλαδή μεταφορές πληροφορίας οι οποίες είναι γνωστό ότι συμβαίνουν, αλλά μόνο υπό ειδικές συνθήκες. Τέλος, οι γραμμές οι οποίες δεν εμφανίζονται στο Σχήμα αντιπροσωπεύουν τις μεταφορές πληροφορίας οι οποίες θεωρούνται σχετικά απίθανο να συμβούν, όπως η μεταφορά από πρωτεΐνη σε πρωτεΐνη. Οι γενικές μεταφορές περιγράφουν την κανονική ροή της βιολογικής πληροφορίας: το DNA μπορεί να αντιγραφεί παράγοντας νέα μόρια DNA (αντιγραφή DNA), η πληροφορία του DNA μπορεί να μεταγραφεί σε RNA (μεταγραφή) και οι πρωτεΐνες μπορούν να συντεθούν χρησιμοποιώντας την πληροφορία του mrna ως πρότυπο (μετάφραση). Εδώ θα πρέπει να σημειωθεί το εξής: οι μεταφορές της πληροφορίας που περιγράφονται από το κεντρικό δόγμα είναι πιστές, αιτιοκρατικές μεταφορές, όπου ένα βιοπολυμερές χρησιμοποιείται ως πρότυπο για την κατασκευή ενός άλλου βιοπολυμερούς, η ακολουθία του οποίου εξαρτάται εξ ολοκλήρου από το αρχικό βιοπολυμερές [Σοφία Κοσσίδα08] Πρωτεΐνες Οι πρωτεΐνες είναι μεγάλες οργανικές ενώσεις που αποτελούνται από μια σειρά αμινοξέων, τα οποία ενώνονται μεταξύ τους με πεπτιδικούς δεσμούς. Η ακριβής ακολουθία των αμινοξέων καθορίζεται από το αντίστοιχο γονίδιο του DNA που κωδικοποιεί κάθε πρωτεΐνη. Η λέξη πρωτεΐνη προέρχεται από το επίθετο πρώτος, τονίζοντας με τον
33 16 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ Σχήμα 2.2: Κεντρικό δόγμα της Βιολογίας [Cen10] τρόπο αυτό την πρωταρχική σημασία που έχουν τα μόρια αυτά στη λειτουργία του κυττάρου. Οι πρωτεΐνες είναι τα μόρια που καθορίζουν τις περισσότερες δραστηριότητες και τη δομή ενός οργανισμού. Μεταξύ άλλων, αποτελούν τους δομικούς λίθους όλων των ιστών και των οργάνων, καταλύουν χημικές αντιδράσεις (ένζυμα), και μεταφέρουν σήματα ανάμεσα στα κύτταρα. Είναι απαραίτητες για την ανάπλαση των κατεστραμμένων κυττάρων, αλλά και για το σχηματισμό νέων, κυρίως κατά τη διάρκεια της ανάπτυξης. Είναι χαρακτηριστικό ότι ένα 3-5% της συνολικής πρωτεΐνης του ανθρώπινου σώματος αναπλάθεται κάθε μέρα. Κατά τη δημιουργία της πρωτεΐνης, το ριβόσωμα διαβάζει τις βάσεις του mrna ανά τριάδες και έτσι καθορίζεται ποιο αμινοξύ θα χρησιμοποιηθεί. Όπως αναφέρθηκε προηγούμενα, η διαδικασία αυτή ονομάζεται μετάφραση. Ο ρυθμός σύνθεσης της πρωτεΐνης μπορεί να φτάσει στα προκαρυωτικά κύτταρα έως και τα 20 αμινοξέα ανά δευτερόλεπτο, ενώ στα ευκαρυωτικά κύτταρα είναι λίγο μικρότερος. Το μέγεθος της πρωτεΐνης μπορεί να μετρηθεί είτε από τον αριθμό αμινοξέων που αυτή περιέχει είτε από την ολική μοριακή της μάζα. Η διαδικασία της παραγωγής πρωτεϊνών (ή με άλλα λόγια, της έκφρασης γονιδίων) δεν ολοκληρώνεται όταν ο γενετικός κώδικας έχει χρησιμοποιηθεί για να δημιουργήσει την ακολουθία αμινοξέων που αποτελούν μια πρωτεΐνη. Για να είναι χρήσιμη στο κύτταρο, η νέα πολυπεπτιδική αλυσίδα πρέπει να αναδιπλωθεί προς μία μοναδική τρισδιάστατη διαμόρφωση, να δεσμεύσει τους μικρο-μοριακούς συμπαράγοντες που απαιτούνται για τη δραστηριότητά της, να τροποποιηθεί κατάλληλα ή να αλληλεπιδράσει με τις
34 2.1 Βιολογικές Έννοιες 17 άλλες πρωτεϊνικές υπομονάδες, με τις οποίες αποτελεί λειτουργικό μόριο. Η αλληλουχία των αμινοξέων που αποτελούν την πρωτεΐνη ονομάζεται πρωτοταγής δομή της πρωτεΐνης. Η μοναδική τρισδιάστατη διαμόρφωσή της στο χώρο ονομάζεται τριτοταγής δομή της πρωτεΐνης. Μεταξύ πρωτοταγούς και τριτοταγούς δομής, υπάρχει η έννοια της δευτεροταγούς δομής μιας πρωτεΐνης: είναι το σύνολο των σαφώς καθορισμένων ενδιάμεσων δομών, όπως έλικες (helices) και φύλλα (sheets), οι οποίες παρουσιάζονται στην τρισδιάστατη δομή της. Τέλος, το τελικό μοριακό σύμπλεγμα το οποίο προκύπτει από την αλληλεπίδραση πολλών πρωτεϊνών, ονομάζεται τεταρτοταγής δομή. Εδώ πρέπει να σημειωθεί ότι η ακολουθία αμινοξέων κάθε πρωτεΐνης έχει επιλεγεί κατά τη διάρκεια πολλών εκατομμυρίων ετών, όχι μόνο για τη διαμόρφωση που υιοθετεί, αλλά και για τη δυνατότητα να αναδιπλωθεί γρήγορα [BO01]. Οι τέσσερεις αυτές διαφορετικές δομές εμφανίζονται στο Σχήμα 2.3. Σχήμα 2.3: Τέσσερεις δομές μιας πρωτεΐνης [Pro10]
35 18 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ 2.2 Τομείς Έρευνας της Βιοπληροφορικής Όπως έχει αναφερθεί ήδη, ο όρος Βιοπληροφορική αφορά τη μελέτη και την υλοποίηση τεχνικών και εργαλείων για την επεξεργασία βιολογικών δεδομένων. Χρησιμοποιεί υπολογιστικές μεθόδους για να μελετήσει και να χειριστεί τα βιολογικά δεδομένα που υπάρχουν διαθέσιμα. Περιγράφει τη δημιουργία και την πρόοδο των αλγορίθμων, των υπολογιστικών και στατιστικών και της θεωρίας για να επιλύσει τα πρακτικά προβλήματα που δημιουργούνται από τη διαχείριση και την ανάλυση των βιολογικών δεδομένων. Η Βιοπληροφορική, επομένως, παίζει ουσιαστικό ρόλο στην ανάπτυξη των στατιστικών μεθόδων για την ανάλυση των μεγάλων συνόλων δεδομένων και για την ανάπτυξη των μεθόδων διαχείρισης πληροφοριών για τους νέους τύπους δεδομένων που παράγονται. Σημαντικές ερευνητικές προσπάθειες στον τομέα περιλαμβάνουν τη συστοίχιση ακολουθιών, την εύρεση γονιδίων, την υπέρθεση των πρωτεϊνικών δομών, την πρόγνωση των πρωτεϊνικών δομών από τις ακολουθίες, την πρόβλεψη της έκφρασης γονιδίων, των αλληλεπιδράσεων μεταξύ πρωτεϊνών και τη διερεύνηση της εξελικτικής διαδικασίας [CN07]. Μερικοί από τους πιο σημαντικούς τομείς της έρευνας στη Βιοπληροφορική είναι οι εξής: Ανάπτυξη Βάσεων Δεδομένων Περιγράφονται οι βάσεις δεδομένων και οι μηχανές αναζήτησής τους. Οι βιολογικές βάσεις δεδομένων έχουν γίνει ένα σημαντικό εργαλείο στην ενίσχυση των επιστημόνων για την κατανόηση και την ερμηνεία ενός πλήθους βιολογικών φαινομένων από τη δομή των βιομορίων και την αλληλεπίδρασή τους, μέχρι την κατανόηση της εξέλιξης των ειδών. Ανάλυση και Συστοίχιση Ακολουθιών Η συνεχόμενη αύξηση του ποσού των διαθέσιμων ακολουθιών έχει καταστήσει αδύνατη την ανάλυσή τους με το χέρι. Σήμερα, τα προγράμματα υπολογιστών χρησιμοποιούνται για τη διερεύνηση του γονιδιώματος πολλών οργανισμών. Οι συστοιχίσεις μας εμφανίζουν ποιά κομμάτια είναι μεταβλητά και ποιά συντηρούνται. Αυτά δείχνουν τις θέσεις πιθανών μεταλλάξεων, προσθήκης, αφαίρεσης ή και αντικατάστασης νουκλεοτιδίων ή αμινοξέων, και επομένως επιτρέπουν τον προσδιορισμό σημαντικών λειτουργικών στοιχείων. Φυλογενετική Ανάλυση Η εξελικτική βιολογία ασχολείται με τη μελέτη της προέλευσης και καταγωγής των ειδών, καθώς και της αλλαγής των έμβιων όντων με το πέρασμα του χρόνου. Η πληροφορική έχει βοηθήσει τους εξελικτικούς βιολόγους με διάφορους τρόπους,
36 2.2 Τομείς Έρευνας της Βιοπληροφορικής 19 όπως η αποκρυπτογράφηση του ρυθμού εξέλιξης ενός μεγάλου αριθμού γονιδίων με τη μέτρηση των αλλαγών στο DNA τους, καθώς και η δημιουργία σύνθετων υπολογιστικών προτύπων των πληθυσμών, με σκοπό την πρόβλεψη της κατάστασης ενός οικοσυστήματος με το πέρασμα του χρόνου. Ρυθμιστική Ανάλυση Η ρύθμιση είναι η σύνθετη ενορχήστρωση των ενδοκυτταρικών γεγονότων, αρχίζοντας από ένα εξωκυτταρικό σήμα, που καταλήγει σε αύξηση ή μείωση της δραστηριότητας μίας ή περισσότερων πρωτεϊνών. Πρωτεϊνική Ανάλυση Η πρόγνωση πρωτεϊνικών δομών από την αλληλουχία τους και η οπτικοποίηση της δομής τους είναι κάποιες από τις σημαντικότερες εφαρμογές της βιοπληροφορικής. Επιπλέον, ένα ενδιαφέρον πεδίο είναι η πρόβλεψη των πιθανών αλληλεπιδράσεων μεταξύ πρωτεϊνών. Πρωτεομική Η πρωτεομική είναι μια ευρείας κλίμακας μελέτη των πρωτεϊνών, ιδιαίτερα όσον αφορά τις δομές και λειτουργίες τους. Η πρωτεομική θεωρείται συχνά το επόμενο βήμα στη μελέτη των βιολογικών συστημάτων, μετά από τη γονιδιωματική. Επιπλέον, είναι πιο περίπλοκη από τη γονιδιωματική, καθώς, ενώ το γονιδίωμα ενός οργανισμού παραμένει σταθερό (με κάποιες εξαιρέσεις όπως η προσθήκη γενετικού υλικού που προκαλείται από ένα ιό, ή οι γρήγορες μεταλλαγές, μεταθέσεις και επεκτάσεις που μπορούν να εμφανιστούν σε έναν όγκο), το πρωτέωμα διαφέρει από κύτταρο σε κύτταρο ενός οργανισμού Κατηγοριοποίηση Πρωτεϊνών Το πρόβλημα της κατάρας της διαστατικότητας είναι ιδιαίτερα εμφανές στις μελέτες κατηγοριοποίησης πρωτεϊνών. Ερευνητικά κέντρα σε όλο τον κόσμο καταγράφουν νέες πρωτεϊνικές ακολουθίες και παράγουν δεδομένα με διαρκώς αυξανόμενους ρυθμούς. Πολλές από αυτές τις ακολουθίες δεν έχουν πλήρως καταγεγραμμένες τις ιδιότητες ή τις λειτουργίες τους, δημιουργώντας την ανάγκη για αυτόματα ή ήμι-αυτόματα εργαλεία οργάνωσης και ανάλυσης δεδομένων. Παρόλο που υπάρχει μια πληθώρα εργαλείων, τεχνικών και βάσεων δεδομένων για ανάλυση πρωτεϊνικών δεδομένων που έχουν προκύψει από τεχνικές φασματομετρίας μάζας (Mass Spectrometry) [Mat07], υπάρχουν σημαντικά λιγότερες υπολογιστικές μέθοδοι διαθέσιμες για επεξεργασία δεδομένων σε υψηλότερο επίπεδο. Έχοντας δεδομένη μια νέα πρωτεϊνική ακολουθία, η συνήθης προσέγγιση για την πρόβλεψη της λειτουργικότητας και των ιδιοτήτων της βασίζεται στην
37 20 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ σύγκριση ανά ζεύγη (pairwise comparison) με άλλες, πλήρως καταγεγραμμένες πρωτεϊνικές ακολουθίες. Παρόλα αυτά υπάρχουν πάρα πολλές πρωτεΐνες οι οποίες εμφανίζουν ίδια ή παρόμοια λειτουργικότητα, αλλά παρουσιάζουν εξαιρετικά μικρή ομοιότητα σε επίπεδο ακολουθιών. Σε αυτές τις περιπτώσεις η σύγκριση ανά ζεύγη αποτυγχάνει να δώσει χρήσιμες πληροφορίες σχετικά με τις ιδιότητες της υπό εξέταση πρωτεΐνης. Για αυτό το λόγο, έχουν γίνει πολλές προσπάθειες προς την αναζήτηση σημαντικών προτύπων σε πρωτεϊνικές αλληλουχίες. Οι διαφορετικές μεθοδολογίες οδήγησαν σε πολλές διαφορετικές απεικονίσεις μοτίβων και προτύπων, και επομένως προέκυψαν αρκετά διαφορετικά σχήματα κατηγοριοποίησης. Από τη μια πλευρά υπάρχουν μέθοδοι, όπως η PROSITE [HBFB99], η PRINTS [AFL + 00], η Blocks [HHP00], και η IDENTIFY [NMWB98], η οποίες στοχεύουν στην ανακάλυψη μικρών προτύπων και μοτίβων σε μια ακολουθία αμινοξέων. Άλλες μέθοδοι στοχεύουν στην αναζήτηση και ταυτοποίηση ολόκληρων συμπλεγμάτων (domains) ή αλληλεπιδράσεων συμπλεγμάτων, όπως η Pfam [BBD + 00], η ProDom [CGK00], η Domo [GA98] και η SMART [PSMB99]. Τέλος υπάρχουν μελέτες οι οποίες στοχεύουν στην εξαγωγή πληροφορίας σε υψηλότερο επίπεδο. Σε αυτές τις μελέτες περιλαμβάνονται προσεγγίσεις όπου γίνεται εξ ολοκλήρου ανάλυση όλων των πρωτεϊνικών ακολουθιών, όπως είναι τα COGs [TED97], η PIR [BPG96] και η Systers [KV98], καθώς και μελέτες όπου συνδυάζονται μετρικές ομοιότητας μεταξύ πρωτεϊνικών ακολουθιών, ομάδων ομόλογων πρωτεϊνών (σμηνών) και ομάδων σχετικών σμηνών, όπως είναι η μέθοδος ProtoMap [YLL00]. Γενικά, οι κυριότερες μέθοδοι κατηγοριοποίησης πρωτεϊνών μπορούν να διαχωρισθούν στις εξής τρεις βασικές κατηγορίες: αλγόριθμοι σύγκρισης ακολουθιών ανά ζεύγη [A + 90, SW81], αλγόριθμοι παραγωγής μοντέλων για οικογένειες πρωτεϊνών [K + 94, P + 98, PM05] και αλγόριθμοι ταξινομητών διάκρισης (discrimina ve classifiers) [J + 00, L + 02, WLI + 05]. Αν και όλες οι μέθοδοι χρησιμοποιούν πληροφορία είτε χαμηλού επιπέδου (δηλαδή την αλληλουχία αμινοξέων των πρωτεϊνών) είτε υψηλού επιπέδου (δηλαδή τα μοτίβα που εμφανίζονται στην πρωτεϊνική αλυσίδα), όλες έχουν ένα κοινό χαρακτηριστικό: η κατασκευή ενός συστήματος κατηγοριοποίησης εξαρτάται στενά από την ορθή αναπαράσταση και εκπροσώπηση των δεδομένων εισόδου, είτε αυτά είναι πρωταρχικά (αμινοξέα) είτε μέτα-δεδομένα (μοτίβα). Επιπρόσθετα, το πλήθος των πλήρως καταγεγραμμένων πρωτεϊνικών ακολουθιών είναι σχετικά μικρό (65,378 εγγραφές [RCS10]) σε αντίθεση με τις πρωτεΐνες στις οποίες είναι γνωστές μόνο η ακολουθία και οι οποίες έχουν πλήθος κοντά στα διακόσια εκατομμύρια (185,231,366 εγγραφές [EMB10]). Εδώ θα πρέπει να σημειωθεί ότι σε κάθε εγγραφή το πλήθος των διαθέσιμων μεταβλητών κυμαίνεται από αρκετές δεκάδες (σε περίπτωση των μέτα-δεδομένων, όπως είναι τα μοτίβα) έως αρκετές εκατοντάδες (όταν γίνεται απευθείας χρήση της αλληλουχίας αμινοξέων). Για να αντιμετωπισθεί αυτό το πρόβλημα, οι περισσότερες μέθοδοι μηχανικής μάθησης εστιάζουν σε συγκεκριμένες ομάδες ή σύνολα πρωτεϊνών, αγνοώντας τις υπόλοι-
38 2.3 Παράλληλος Προγραμματισμός 21 πες, ή απλά μειώνοντας τον όγκο είτε των αρχικών δεδομένων είτε των μεταβλητών που λαμβάνονται υπόψη. Τα Παράλληλα Συστήματα και τα Πλέγματα Υπολογιστών έχουν την δυνατότητα να δώσουν μια εναλλακτική λύση στο πρόβλημα αυτό, συνδυάζοντας ένα πλήθος προσεγγίσεων με ένα ομοιογενή τρόπο. 2.3 Παράλληλος Προγραμματισμός Υπάρχουν γενικά δύο ειδών παράλληλα συστήματα [Slo04]: α) τα συστήματα κοινής μνήμης (Shared memory), όπου όλες οι διεργασίες χρησιμοποιούν κάποια κοινή μνήμη, και β) τα συστήματα ανταλλαγής μηνυμάτων (Message Passing), όπου κάθε διεργασία χρησιμοποιεί τον δικό της χώρο στη μνήμη και ανταλλάσσονται μηνύματα ανάμεσα στις διεργασίες για τη μεταφορά δεδομένων και για τον καλύτερο συντονισμό τους. Γενικά, το χρονικό διάστημα που απαιτείται για την εκτέλεση ενός προγράμματος περιλαμβάνει δύο εντελώς διαφορετικές έννοιες. Έτσι λοιπόν είναι δυνατή η διάκριση ανάμεσα στον χρόνο εκτέλεσης του προγράμματος (WCT - Wall Clock Time) και στον χρόνο επεξεργαστή (CPU Time). Σύμφωνα με την ονομασία του, ο χρόνος εκτέλεσης του προγράμματος αναφέρεται στο χρονικό διάστημα που πρέπει να περιμένει ο χρήστης του υπολογιστή για να αποκτήσει τα επιθυμητά αποτελέσματα. Αντίθετα, ο χρόνος επεξεργαστή αναφέρεται στο χρόνο που πρέπει να εργαστεί η CPU για να εκτελέσει το πρόγραμμα. Η διαφορά ανάμεσα στα δύα αυτά χρονικά διαστήματα προκύπτει από το γεγονός ότι όλα τα σύγχρονα λειτουργικά συστήματα μοιράζουν το χρόνο του επεξεργαστή σε πολλές διεργασίες και έτσι δημιουργείται στον χρήστη η αίσθηση ότι αυτές τρέχουν παράλληλα, ενώ κατά βάση όλοι οι σύγχρονοι επεξεργαστές είναι σειριακοί. Εφόσον λοιπόν ο διαθέσιμος χρόνος επεξεργαστή μοιράζεται σε πολλές διεργασίες, είναι λογικό πως ο χρόνος εκτέλεσης του προγράμματος θα είναι μεγαλύτερος ή ίσος με το χρόνο επεξεργαστή. Στην πράξη υπάρχουν περιπτώσεις όπου σειριακοί αλγόριθμοι μπορούν εύκολα να παραλληλοποιηθούν και περιπτώσεις που κάτι τέτοιο δεν είναι εφικτό, οπότε η εύρεση κάποιου άλλου παράλληλου αλγορίθμου είναι αναγκαία. Είναι γεγονός ότι οι παράλληλοι αλγόριθμοι είναι πιο πολύπλοκοι από τους σειριακούς. Ένας σειριακός αλγόριθμος είναι μία καθορισμένη αλληλουχία βημάτων τα οποία εκτελούνται το ένα μετά το άλλο. Αντίθετα, κατά τη σχεδίαση και υλοποίηση παράλληλων προγραμμάτων θα πρέπει να ληφθούν κρίσιμες αποφάσεις που αφορούν την σωστή κατανομή των διαφόρων υποεργασιών, τον έλεγχο των διεργασιών, το συγχρονισμό των διεργασιών μέσω ανταλλαγής μηνυμάτων, την κατανομή των δεδομένων εισόδου στις διάφορες διεργασίες, την αποφυγή προβλημάτων που δημιουργούνται λόγω της παράλληλης φύσης του προγράμματος κοκ.
39 22 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ Διαδικασία Ανάπτυξης Παράλληλου Αλγορίθμου Το κυριότερο στάδιο στη διαδικασία σχεδίασης ενός παράλληλου αλγορίθμου είναι η ανάλυση του προβλήματος που στοχεύει να επιλύσει ο αλγόριθμος. Ένα μεγάλο πρόβλημα μπορεί να χωριστεί σε διάφορες εργασίες (jobs), οι οποίες λογίζονται ως κομμάτια του προβλήματος που μπορούν να εκτελεσθούν αυτόνομα [Slo04]. Όλες αυτές οι εργασίες είναι υποψήφιες προς παραλληλοποίηση. Ανάλογα με τη φύση του προβλήματος που εξετάζεται, αυτό μπορεί να αποτελείται από εργασίες μικρού μεγέθους, μεγάλου μεγέθους, ή από ένα μείγμα εργασιών και από τις δύο προαναφερθείσες κατηγορίες. Μία εργασία λέγεται ότι έχει μεγάλο μέγεθος όταν ο χρόνος επεξεργαστή που απαιτείται για την αποπεράτωσή της είναι σχετικά μεγάλος. Το ακριβώς αντίθετο ισχύει για μια εργασία μικρού μεγέθους. Είναι προφανές ότι όσο πιο μεγάλες είναι οι εργασίες, τόσο μικρότερο κόστος επικοινωνίας μεταξύ των διεργασιών εμφανίζει το πρόγραμμα. Παρόλα αυτά όμως, υπάρχει το ενδεχόμενο να μη γίνεται σωστή χρήση των επεξεργαστών, δηλαδή μερικοί από τους επεξεργαστές να παραμένουν σε αδράνεια και να αναμένουν τους υπόλοιπους να ολοκληρώσουν την εκτέλεση της εργασίας που έχουν αναλάβει. Αντίθετα, στην περίπτωση που οι εργασίες είναι σχετικά μικρές, εμφανίζεται μεγάλο κόστος στην επικοινωνία μεταξύ των διαφόρων διεργασιών, πράγμα που καθυστερεί αρκετά τον τερματισμό του προγράμματος. Συμπερασματικά λοιπόν, θα πρέπει να γίνει σωστή επιλογή του μεγέθους των εργασιών, στα πλαίσια του δυνατού, ούτως ώστε να αποφευχθούν τα προβλήματα που προαναφέρθηκαν. Ένας παράλληλος αλγόριθμος μπορεί να παρασταθεί γραφικά χρησιμοποιώντας γράφους. Οι εργασίες παριστάνονται ως κόμβοι που συνδέονται μεταξύ τους με βέλη, τα οποία με τη σειρά τους εκφράζουν τη ροή δεδομένων μεταξύ δύο ή περισσοτέρων διεργασιών. Η γραφική παράσταση ενός αλγορίθμου βοηθάει σημαντικά στον εντοπισμό εργασιών που είναι ανεξάρτητες μεταξύ τους, και μπορούν πιθανώς να εκτελεσθούν παράλληλα. Επιπρόσθετα, διευκολύνει την καλύτερη κατανομή των διαθέσιμων υπολογιστικών πόρων, τη βέλτιστη διάθεση των απαραίτητων δεδομένων εισόδου για κάθε διεργασία και την εύρεση του κρίσιμου μονοπατιού. Το κρίσιμο μονοπάτι (cri cal path) ορίζεται ως η αλληλουχία εργασιών (μονοπάτι στο γράφο) που θα χρειαστεί τον περισσότερο χρόνο για να ολοκληρωθεί [Slo04]. Ουσιαστικά καθορίζει το ελάχιστο χρονικό διάστημα το οποίο απαιτείται για την ολοκλήρωση της εκτέλεσης του αλγορίθμου. Κατά συνέπεια, κάθε προσπάθεια μείωσης του χρόνου εκτέλεσης θα πρέπει να επικεντρώνεται στη μείωση το χρόνου που απαιτείται για την ολοκλήρωση των εργασιών του κρίσιμου μονοπατιού. Επιστρέφοντας και πάλι στη διαδικασία αποσύνθεσης του προβλήματος, αξίζει να αναφερθεί ότι υπάρχουν διάφορες στρατηγικές που ακολουθούνται και χρησιμοποιούνται ανάλογα με την περίπτωση. Οι στρατηγικές αυτές ανήκουν σε μία από τις εξής δύο κατηγορίες: Διαμοιρασμός Δεδομένων και Διαμοιρασμός Εργασιών. Οι περισσότεροι παράλληλοι αλγόριθμοι που χρησιμοποιούνται στην πράξη εμφανίζουν χαρακτηριστικά
40 2.3 Παράλληλος Προγραμματισμός 23 και από τις δύο κατηγορίες. 1. Διαμοιρασμός Δεδομένων (Data Decomposi on) Όταν χρησιμοποιείται η τεχνική του διαμοιρασμού δεδομένων, τα δεδομένα εισόδου D i χωρίζονται σε n ξένα μεταξύ τους σύνολα D i 1 D i 2 D i 3... D i n = και κατανέμονται στις διάφορες διεργασίες p (processes). Στην περίπτωση αυτή οι διεργασίες είναι πανομοιότυπες, αλλά επεξεργάζονται διαφορετικό τμήμα των αρχικών δεδομένων. 2. Διαμοιρασμός Εργασιών (Task Decomposi on) Η τεχνική του διαμοιρασμού εργασιών συνίσταται στο διαχωρισμό του αρχικού προβλήματος σε k εργασίες Job i, i = 1,..., k και η ανάθεση των εργασιών αυτών σε m διακριτές διεργασίες (processes) p j, όπου j = 1,..., m. Στη γενικότερη περίπτωση k m. Αυτό συνεπάγεται ότι οι διεργασίες θα πρέπει να είναι διαφορετικές μεταξύ τους και ειδικά σχεδιασμένες ούτως ώστε να μπορούν να αναλάβουν την εκτέλεση της κάθε εργασίας. Συγκρίνοντας τις δύο προαναφερθείσες τεχνικές μπορεί κανείς εύλογα να συμπεράνει πως ο διαμοιρασμός των δεδομένων είναι πολύ πιο εύκολο να χρησιμοποιηθεί και επιτυγχάνει καλύτερο έλεγχο του παράλληλου προγράμματος. Ουσιαστικά στην περίπτωση του διαμοιρασμού δεδομένων σχεδιάζεται και υλοποιείται κάθε διεργασία μία φορά και απλά της ανατίθενται διαφορετικά τμήματα των αρχικών δεδομένων. Επιπλέον, ο προγραμματιστής μπορεί πολύ εύκολα να υπολογίσει το χρονικό διάστημα που απαιτείται για την εκτέλεση ενός στοιχειώδους τμήματος δεδομένων από μία διεργασία, οπότε με τον τρόπο αυτό αποκτά καλύτερη αίσθηση του φορτίου που έχει η κάθε διεργασία και έτσι μπορεί να αποφύγει πολλά προβλήματα που εισάγει η παράλληλη φύση του προγράμματος. Τέλος,ο διαμοιρασμός δεδομένων δίνει πολύ καλά αποτελέσματα για προβλήματα που έχουν δεδομένα εισόδου τα οποία συνεχώς αυξάνονται, όπως είναι τα περισσότερα προβλήματα Βιοπληροφορικής. Η κατάσταση αυτή μπορεί να αντιμετωπισθεί εύκολα και απλά εάν αυξηθεί ο αριθμός των παράλληλων διεργασιών που εκτελούνται, οπότε τελικά επιτυγχάνεται ο (σχεδόν) ίδιος χρόνος εκτέλεσης παρόλο που τα δεδομένα εισόδου έχουν αυξηθεί Προβλήματα Παράλληλου Προγραμματισμού Ο παράλληλος προγραμματισμός εισάγει από τη φύση του ορισμένα προβλήματα τα οποία συνήθως αφορούν το συγχρονισμό και την επικοινωνία μεταξύ των διαφόρων διεργασιών. Παρακάτω γίνεται μια προσπάθεια καταγραφής των πιο τυπικών προβλημάτων τα οποία προκύπτουν κατά την ανάλυση ενός παράλληλου προγράμματος.
41 24 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ 1. Καθυστέρηση επικοινωνίας Σε κάθε παράλληλο πρόγραμμα υπάρχει η ανάγκη επικοινωνίας και συντονισμού μεταξύ των διεργασιών που εκτελούνται σε διαφορετικούς επεξεργαστές. Η επικοινωνία αυτή εισάγει σημαντική καθυστέρηση, η οποία μπορεί να αποτελέσει μεγάλο πρόβλημα στην περίπτωση που είναι επιθυμητή η βελτιστοποίηση του χρόνου εκτέλεσης του προγράμματος. Εύλογα λοιπόν μπορεί κανείς να συμπεράνει ότι όσο λιγότερη επικοινωνία χρειάζεται μεταξύ των διεργασιών, τόσο μικρότερες καθυστερήσεις θα υπάρχουν. Η ιδανική περίπτωση είναι τα εκ φύσεως παράλληλα προβλήματα (Embarrassingly parallel problems) όπου η κάθε διεργασία είναι απολύτως ανεξάρτητη των υπολοίπων. Επομένως, ο κύριος στόχος κατά τον σχεδιασμό ενός παράλληλου αλγορίθμου είναι η αύξηση του αριθμού των διεργασιών με ταυτόχρονη μείωση των αναγκών επικοινωνίας μεταξύ τους. 2. Κατανομή φορτίου Μία από τις κυριότερες πηγές καθυστέρησης είναι και η λανθασμένη κατανομή φορτίου ανάμεσα στις διεργασίες. Η καθυστέρηση οφείλεται στο γεγονός ότι μερικοί επεξεργαστές παραμένουν ανενεργοί περιμένοντας κάποια υπερβολικά σύνθετη και χρονοβόρα διεργασία να τελειώσει. Ο καλύτερος τρόπος εξάλειψης αυτού του προβλήματος είναι η σωστή εκτίμηση των υπολογιστικών αναγκών του προβλήματος και κατάλληλη ανάθεση των εργασιών στους διαθέσιμους υπολογιστικούς πόρους. Σωστή κατανομή φορτίου σημαίνει αρχικά διάσπαση του προβλήματος σε κατά το δυνατόν ισομεγέθεις εργασίες και κατανομή τους στους διαθέσιμους επεξεργαστές. Αυτό βέβαια δεν ισχύει στην περίπτωση που οι υπολογιστικοί κόμβοι (computa onal nodes) δεν είναι ισοδύναμοι (πχ διαφορετική συχνότητα επεξεργαστή, πιο γρήγορη μνήμη κοκ.) ή όταν μερικοί από αυτούς είναι υπερφορτωμένοι. Επίσης δεν ισχύει όταν οι καθυστερήσεις επικοινωνίας ανάμεσα στους υπολογιστικούς κόμβους δεν είναι ομοιόμορφες. Άρα λοιπόν, πριν καταλήξει κανείς σε κάποια απόφαση σχετικά με τη δομή του παράλληλου προγράμματος, θα πρέπει να λάβει σοβαρά υπόψη του τις υποδομές υπολογιστών πάνω στις οποίες θα εκτελεσθεί τελικά ο αλγόριθμος. Μία δομή που χρησιμοποιείται συχνά σε αυτές τις περιπτώσεις είναι η δεξαμενή εργασιών (work pool). Στη δεξαμενή αποθηκεύονται προσωρινά όλες οι εργασίες του παράλληλου προγράμματος που πρέπει να εκτελεσθούν. Στη συνέχεια κάθε επεξεργαστής του συστήματος που είναι σε αδράνεια τροφοδοτείται με μια νέα εργασία. Όμως πρέπει να ληφθεί υπόψη ότι η δομή δεξαμενής εργασιών είναι ιδανική όταν τα δεδομένα που χρειάζεται να αποσταλούν για κάθε εργασία είναι πολύ μικρότερα σε σχέση με τους υπολογισμούς που απαιτούνται για την εύρεση του τελικού αποτελέσματος. Επίσης ιδιαίτερη προσοχή χρειάζεται ώστε μια
42 2.3 Παράλληλος Προγραμματισμός 25 διεργασία (συνήθως η διεργασία συντονισμού) να μην αποτελέσει αναχαιτιστικό παράγοντα (bo leneck) προς όλη τη διαδικασία. 3. Πλεονάζοντες υπολογισμοί Σε πολλά παράλληλα προγράμματα συχνά εμφανίζεται το πρόβλημα των πλεοναζόντων υπολογισμών. Γενικά ο διαχωρισμός ενός αλγορίθμου σε πολλές παράλληλες διεργασίες δεν είναι μια εύκολη υπόθεση, διότι πολλές φορές η ίδια η φύση του προβλήματος δημιουργεί εμπόδια. Σαν αποτέλεσμα, οι διάφορες εργασίες που δημιουργούνται δεν είναι εντελώς αυτόνομες, αλλά είναι απαραίτητη η εκτέλεση των ίδιων πράξεων ή λειτουργιών σε περισσότερες της μίας εργασίας. Παρόλα αυτά σε ορισμένες περιπτώσεις οι πλεονάζοντες υπολογισμοί μπορεί όχι μόνο να μην αποτελούν πρόβλημα, αλλά να συμβάλλουν στη μείωση του συνολικού χρόνου εκτέλεσης του παράλληλου προγράμματος. Αυτό ισχύει διότι με τον τρόπο αυτό περιορίζεται η καθυστέρηση που θα υπήρχε στη μετάδοση των αποτελεσμάτων εάν οι υπολογισμοί αυτοί γινόταν σε μία διεργασία και στη συνέχεια αποστέλλονταν σε όλες τις άλλες. 4. Συγχρονισμός Τα σειριακά προγράμματα έχουν κατά βάση ντετερμινιστικό χαρακτήρα, δηλαδή κάθε γραμμή του κώδικα εκτελείται με τη σειρά κατά την οποία γράφηκε. Αντιθέτως, στα παράλληλα προγράμματα οι διάφορες εργασίες κατανέμονται στους διαθέσιμους επεξεργαστές, οπότε εμφανίζονται διαφοροποιήσεις στη σειρά με την οποία εκτελούνται. Επιπροσθέτως, ο φόρτος εργασιών κάθε επεξεργαστή αλλάζει δυναμικά και οι διάφορες διεργασίες ανταγωνίζονται μεταξύ τους για την απόκτηση επικοινωνιακών πόρων. Όλα αυτά δημιουργούν διαφορετικές συνθήκες κάθε φορά που το πρόγραμμα εκτελείται, οπότε εμφανίζονται διαφοροποιήσεις και στο συνολικό χρόνο εκτέλεσης. Ένα σωστά δομημένο παράλληλο πρόγραμμα θα πρέπει να προβλέπει το πρόβλημα της έλλειψης συγχρονισμού ανάμεσα στις διεργασίες και να το αντιμετωπίζει αποτελεσματικά. 5. Αδιέξοδα Ένα αδιέξοδο (deadlock) συμβαίνει όταν δύο ή παραπάνω διεργασίες περιμένουν η μία την άλλη για κάποιο λόγο. Για παράδειγμα, ενδέχεται η διεργασία Α να περιμένει αποστολή δεδομένων από τη διεργασία Β και το αντίστροφο. Στην περίπτωση αυτή καμία διαδικασία δεν μπορεί να προχωρήσει, οπότε το πρόγραμμα φτάνει σε αδιέξοδο. Παρόλο που το πρόβλημα αυτό φαίνεται πως μπορεί να επιλυθεί εύκολα, η πραγματικότητα δεν είναι έτσι καθώς πολλές φορές τα αδιέξοδα αφορούν μια αλυσίδα αλληλεξαρτώμενων διεργασιών που στις περισσότερες περιπτώσεις είναι δύσκολο να εντοπισθεί.
43 26 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ 2.4 Πλέγματα Υπολογιστών Για μια σχετικά καινούργια έννοια όπως το Πλέγμα Υπολογιστών είναι δύσκολο κανείς να δώσει έναν ολοκληρωμένο και καθολικά αποδεκτό ορισμό. Συνήθως η ποικιλία απαντήσεων είναι ανάλογη του πλήθους των ερωτηθέντων. Μία εικόνα για τα πλέγματα και τους πιθανούς ορισμούς τους μπορεί να δώσει μία γρήγορη αναζήτηση στην αστείρευτη βάση δεδομένων του διαδικτύου με τη βοήθεια της μηχανής αναζήτησης Google και της υπηρεσίας Googlism. Ένα τμήμα των αποτελεσμάτων αυτής της αναζήτησης παρουσιάζεται παρακάτω [Wha10]: grid compu ng is the next big thing grid compu ng is no longer just a buzzword grid compu ng is not years away but rather here today grid compu ng is the next evolu onary wave a er the internet grid compu ng is the next genera on IT infrastructure that promises to transform the way organiza ons and individuals compute grid compu ng is too great for anyone not to be interested in grid compu ng is a key area where we will need more exper se soon grid compu ng is going to enable things we can t even imagine grid compu ng is a step up from distributed compu ng grid compu ng is based on the idea that the unused computa onal power of desktop PCs can be harnessed to create an aggregate computa onal resource grid compu ng is applying the resources of many computers in a network to a single problem at the same me grid compu ng is a way to create a virtual supercomputer by connec ng large numbers of PCs in different loca ons over a shared network grid compu ng is an emerging technology that allows seamless sharing of geographically distributed computa onal resources and networked instrumenta on grid compu ng is the convergence of high end compu ng and bandwidth the grid is the worldwide network of networks
44 2.4 Πλέγματα Υπολογιστών 27 the grid is virtual; in fact they may never actually see or even know where exactly these resources are located... Σε μια προσπάθεια ορισμού της έννοιας του Πλέγματος Υπολογιστών με τρόπο που να καλύπτει όλες τις διαφορετικές πτυχές και όψεις της νέας τεχνολογίας, θα μπορούσε να ειπωθεί ότι: Τα Πλέγματα Υπολογιστών αποτελούν δυναμικά και κατανεμημένα σύνολα ατόμων, οργανισμών και πόρων που μοιράζονται ασφαλώς, ευέλικτα και συντονισμένα πόρους μέσω της χρήσης ανοιχτών και γενικών προτύπων και πρωτοκόλλων για να ικανοποιήσουν τις αυξημένες σε υπολογιστική ισχύ και δεδομένα απαιτήσεις μιας μεγάλης ποικιλίας εφαρμογών. Το όνομα Πλέγμα Υπολογιστών (Computer Grid) προήλθε από μια παρομοίωση που έκαναν οι Ian Foster και Carl Kesselman μεταξύ ενός δικτύου συστοιχιών υπολογιστών που θα παρέχει στους χρήστες υπολογιστική ισχύ και του ηλεκτρικού δικτύου που παρέχει στους χρήστες ηλεκτρική ισχύ [FK98]. Στον Πίνακα 2.1 παρέχεται μία αντιστοιχία μεταξύ των ιδιοτήτων του Πλέγματος Υπολογιστών και του Ηλεκτρικού Δικτύου, η οποία αιτιολογεί εν μέρει και την επιλογή του όρου Αρχιτεκτονική Πλέγματος Υπολογιστών Στο Σχήμα 2.4 παρουσιάζεται σχηματικά η αρχιτεκτονική ενός τυπικού Πλέγματος Υπολογιστών. Λειτουργεί γενικά με παρόμοιο τρόπο όπως οι Συστοιχίες Υπολογιστών (Computer Cluster), με τη διαφορά ύπαρξης ενός ειδικευμένου λογισμικού που ονομάζεται middleware, το οποίο αναλαμβάνει τα εξής καθήκοντα: Ανεύρεση κατάλληλων υπολογιστικών πόρων για την εκτέλεση της δεδομένης εργασίας Βελτιστοποίηση της χρήσης των διαφόρων γεωγραφικά κατανεμημένων πόρων Εξασφάλιση της πρόσβασης σε δεδομένα που βρίσκονται αποθηκευμένα σε ειδικό αποθηκευτικό χώρο του Πλέγματος Εκτέλεση της εργασίας Παρακολούθηση της εξέλιξης της εργασίας Εντοπισμός λαθών κατά την εκτέλεση και επιδιόρθωσή τους Επιστροφή των τελικών αποτελεσμάτων στο χρήστη
45 28 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ Πίνακας 2.1: Αντιστοιχία μεταξύ του ηλεκτρικού δικτύου και του πλέγματος υπολογιστών Ηλεκτρικό Δίκτυο Παροχή ηλεκτρικής ισχύος με αξιόπιστο τρόπο. Η ηλεκτρική ενέργεια είναι διαθέσιμη 24/7 και προσιτή σε όλους με την καταβολή κάποιων χρημάτων. Τεράστια υποδομή που περιλαμβάνει ετερογενή συστήματα παραγωγής και διάθεσης ηλεκτρικής ενέργειας. Οι ηλεκτρικές συσκευές χρησιμοποιούνται εάν απλά συνδεθούν στο ηλεκτρικό δίκτυο με την τοποθέτησή τους στην πρίζα. Πλέγμα Υπολογιστών Παροχή υπολογιστικής ισχύος και αποθηκευτικού χώρου με αξιόπιστο τρόπο. Οι υπηρεσίες είναι διαθέσιμες 24/7 και προσιτές σε όλους, μέχρι στιγμής δωρεάν. Τεράστια υποδομή που περιλαμβάνει ετερογενή υπολογιστικά συστήματα και υπηρεσίες. Πρόσβαση σε απομακρυσμένους υπολογιστικούς πόρους μέσω του διαδικτύου από οποιαδήποτε πλατφόρμα. Όπως φαίνεται και από το διάγραμμα του Σχήματος 2.4, τα κυριότερα στοιχεία μιας αρχιτεκτονικής Πλέγματος είναι η Διεπαφή Χρήστη (User Interface), ο Διαμεσολαβητής Πόρων (Resource Broker), ο Κατάλογος Πληροφοριών (Informa on Index), οι Υπολογιστικοί Κόμβοι (Computa onal Nodes), τα Υπολογιστικά Τμήματα (Compu ng Elements - CE), οι Αποθηκευτικοί Χώροι (Storage Elements - SE) και οι Κόμβοι Εργασίας (Worker Nodes - WN). Ακολουθεί μια σύντομη περιγραφή της λειτουργίας καθενός από τα στοιχεία αυτά. Διεπαφή Χρήστη Για να χρησιμοποιήσει ένας χρήστης τις δυνατότητες που του παρέχει ένα Πλέγμα Υπολογιστών θα πρέπει αρχικά να αποκτήσει έναν προσωπικό λογαριασμό και να συνδεθεί στη Διεπαφή Χρήστη. Με τον τρόπο αυτό γίνεται η πιστοποίηση του χρήστη και η ταυτοποίησή του κάθε φορά που ζητά υπολογιστικούς πόρους. Αφού ο χρήστης συνδεθεί στη Διεπαφή Χρήστη, τότε μπορεί να δημιουργήσει μια εργασία και να εντοπίσει τους υπολογιστικούς πόρους του Πλέγματος όπου αυτή η εργασία μπορεί να εκτελεσθεί. Αν υποβάλει την εργασία, μπορεί να παρακολουθήσει την εξέλιξή της, να την ακυρώσει εάν το επιθυμεί, και να λάβει τα αποτελέσματα
46 2.4 Πλέγματα Υπολογιστών 29 Replica Catalog Information Index Computational Node User Interface Resource Broker Storage Element Computing Element Worker Nodes Σχήμα 2.4: Σχηματικό διάγραμμα ενός Πλέγματος Υπολογιστών. Μόνο ένας Υπολογιστικός Κόμβος φαίνεται. και τα δεδομένα εξόδου στην περίπτωση που η εκτέλεση της εργασίας έχει ολοκληρωθεί με επιτυχία. Διαμεσολαβητής Πόρων Ο Διαμεσολαβητής Πόρων αποτελεί ένα από τα πιο σημαντικά στοιχεία του Πλέγματος. Ρόλος του είναι να λαμβάνει τις εργασίες που υποβάλλουν οι χρήστες και στη συνέχεια να εντοπίζει τους κατάλληλους υπολογιστικούς πόρους που χρειάζονται για την εκτέλεση της κάθε εργασίας. Εξετάζοντας τους Καταλόγους Πληροφοριών, ο Διαμεσολαβητής Πόρων μπορεί να κατανέμει τις υποβληθείσες εργασίες στους διαθέσιμους Υπολογιστικούς Κόμβους. Κατάλογος Πληροφοριών Ο Κατάλογος Πληροφοριών παρέχει πληροφορίες σχετικά με τον κάθε Υπολογιστικό Κόμβο του Πλέγματος. Συγκεκριμένα, για κάθε κόμβο αναφέρει τα χαρακτη-
47 30 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ ριστικά του (αριθμός επεξεργαστών, διαθέσιμος αποθηκευτικός χώρος κοκ), το είδος των εργασιών που είναι διατεθειμένος να αναλάβει, και την πληρότητά του, δηλαδή κατά πόσο είναι ήδη φορτωμένος με άλλες εργασίες. Υπολογιστικοί Κόμβοι Ο Υπολογιστικός Κόμβος είναι η οργανωτική μονάδα του Πλέγματος. Αποτελείται από τρία συστατικά: τα Υπολογιστικά Τμήματα, τον Αποθηκευτικό Χώρο και τους Κόμβους Εργασίας. Υπολογιστικά Τμήματα Το Υπολογιστικό Τμήμα διαχειρίζεται την υποδομή ολόκληρου του Υπολογιστικού Κόμβου και αποτελεί το σημείο εισόδου των διαφόρων εργασιών από το Πλέγμα. Στο Υπολογιστικό Τμήμα εκτελείται ειδικό λογισμικό για τη διαχείριση της ουράς εργασιών, τη μεταφορά κάποιας εργασίας προς εκτέλεση σε έναν ή περισσότερους Κόμβους Εργασίας, και την παρακολούθηση της εξέλιξης της εργασίας. Μόλις κάποια εργασία εκτελεσθεί με επιτυχία, τότε το Υπολογιστικό Τμήμα αναλαμβάνει να συλλέξει το δεδομένα εξόδου και να τα μεταφέρει μέσω του Διαμεσολαβητή Πόρων στη Διεπαφή Χρήστη του τελικού χρήστη. Αποθηκευτικοί Χώροι Ο Αποθηκευτικός Χώρος χρησιμοποιείται για την αποθήκευση δεδομένων που απαιτούνται για την εκτέλεση πολλών εργασιών. Με τον τρόπο αυτό τα δεδομένα βρίσκονται σε ένα κεντρικό σημείο και δεν χρειάζεται να μεταφέρονται κάθε φορά που υποβάλλεται μια νέα εργασία. Πρόσβαση σε αυτόν τον χώρο έχουν όλοι οι χρήστες του Πλέγματος, οι οποίοι τον χρησιμοποιούν συνήθως για την αποθήκευση δεδομένων εισόδου που απαιτούνται από τις διάφορες εργασίες που καταθέτουν στο Πλέγμα προς εκτέλεση. Κόμβοι Εργασίας Κάθε Κόμβος Εργασίας αναλαμβάνει να εκτελέσει τις εργασίες που του αναθέτει το Υπολογιστικό Τμήμα και να αποδώσει σε αυτόν τα τελικά αποτελέσματα. Στην περίπτωση που πρόκειται για παράλληλη εργασία, η οποία χρησιμοποιεί κάποια βιβλιοθήκη παράλληλου προγραμματισμού (π.χ. Message Passing Interface - MPI) για την ανταλλαγή μηνυμάτων μεταξύ των διαφόρων επεξεργαστών, τότε ο κόμβος εργασίας έχει τη δυνατότητα συνεργασίας με άλλους κόμβους, ούτως ώστε να επιτευχθεί το επιδιωκόμενο αποτέλεσμα. Τέλος, κάθε Κόμβος Εργασίας θα πρέπει να είναι εξοπλισμένος με το απαραίτητο λογισμικό (π.χ. βιβλιοθήκες προγραμματισμού) έτσι ώστε να μπορεί να υποστηρίξει την εκτέλεση των εργασιών που του ανατίθενται.
48 2.4 Πλέγματα Υπολογιστών EGEE Το πρόγραμμα EGEE - Enabling Grids for E-sciencE χρηματοδοτήθηκε από το 6 Κοινοτικό Πλαίσιο Στήριξης της Ευρωπαϊκής Επιτροπής και συνδέει πάνω από 260 ιδρύματα και ινστιτούτα σε 55 χώρες του κόσμου [EGE09] ¹. Στοχεύει στην παροχή αξιόπιστων υπηρεσιών πλέγματος που θα είναι διαθέσιμες στους επιστήμονες σε 24ωρη βάση, ανεξαρτήτως γεωγραφικής θέσης. Επί του παρόντος (Μάιος 2010), οι υποδομές του EGEE περιλαμβάνουν άνω των 150,000 επεξεργαστών και περίπου 28 Petabytes αποθηκευτικού χώρου. Είναι προφανές ότι η ύπαρξη τέτοιου είδους υπολογιστικών πόρων έχει αλλάξει σημαντικά τον τρόπο με τον οποίο γίνεται η έρευνα στις μέρες μας. Το EGEE ξεκίνησε το Μάρτιο του 2004 ως ένα καθαρά ευρωπαϊκό πρόγραμμα, στη συνέχεια όμως επεκτάθηκε για να συμπεριλάβει ιδρύματα και ινστιτούτα που βρίσκονται εκτός Ευρώπης (π.χ. Ηνωμένες Πολιτείες Αμερικής, Ασία κοκ). Κύριοι στόχοι του προγράμματος είναι η δημιουργία μίας σταθερής και αξιόπιστης υποδομής πλέγματος, η προσέλκυση χρηστών τόσο από την ακαδημαϊκή κοινότητα όσο και από τη βιομηχανία και η συνένωση των εθνικών υποδομών πλέγματος των διαφόρων χωρών που συμμετέχουν στο πρόγραμμα ούτως ώστε να αυξηθεί το μέγεθος και η αξιοπιστία του συνολικού συστήματος. Στο Σχήμα 2.5 παρουσιάζεται ο παγκόσμιος χάρτης στον οποίο διακρίνονται με έντονο χρώμα οι χώρες που συμμετέχουν στο πρόγραμμα, ενώ στο Σχήμα 2.6 παρουσιάζονται τα σημεία που δραστηριοποιείται το πρόγραμμα στην Ευρώπη. Σχήμα 2.5: Παγκόσμιος χάρτης με τις χώρες που συμμετέχουν στο EGEE (Μάιος 2010) Οι διαθέσιμες υποδομές χρησιμοποιούνται σήμερα για μία πληθώρα εφαρμογών που απορρέουν από διάφορες επιστημονικές περιοχές, όπως για παράδειγμα τη Βιο- ¹Το πρόγραμμα EGEE ολοκληρώθηκε στις 30 Απριλίου του Η κατανεμημένη υπολογιστική υποδομή και οι υπηρεσίες που αναπτύχθηκαν στα πλαίσια του EGEE συνεχίζονται αυτή τη στιγμή στα πλαίσια του EGI - European Grid Ini a ve [EGI10].
49 32 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ Σχήμα 2.6: Τα σημεία όπου δραστηριοποιείται το EGEE στην Ευρώπη (Μάιος 2010) πληροφορική, την Υπολογιστική Χημεία, την Αστροφυσική, τη Βιοϊατρική, τη Γεωλογία και πολλές άλλες. Το περιβάλλον που παρέχει το EGEE είναι ιδανικό για κάθε είδους έρευνα, ιδίως όπου απαιτείται η χρήση πόρων που αδυνατεί να παράσχει κάποιο ινστιτούτο από μόνο του. Για να αποκτήσει κάποιος πρόσβαση στο EGEE απαιτούνται δύο βήματα. Το πρώτο βήμα αφορά την έκδοση ψηφιακού πιστοποιητικού από μία ενδεδειγμένη Αρχή Πιστοποίησης (CA - Cer fica on Authority) ². Αυτό το βήμα είναι απαραίτητο ούτως ώστε να διαφυλαχθεί ένα στοιχειώδες επίπεδο ασφαλείας και να αποφευχθούν περιπτώσεις κακόβουλης χρήσης του Πλέγματος από διάφορους χρήστες. Το δεύτερο βήμα συνίσταται στην ένταξη του υποψήφιου χρήστη σε έναν Εικονικό Οργανισμό (VO - Virtual Organiza on) ³. Ένας Εικονικός Οργανισμός περιλαμβάνει χρήστες που είτε εργάζονται πάνω στον ίδιο επιστημονικό κλάδο, είτε βρίσκονται στην ίδια γεωγραφική περιοχή. Στην πρώτη περίπτωση, ο Εικονικός Οργανισμός λαμβάνει το όνομα του επιστημονικού κλάδου στον οποίο αναφέρεται (πχ. biomed - Biomedicine, compchem - Computa onal ²Οι αρχές πιστοποίησης χωρίζονται ανά κράτος. Μία πλήρης λίστα μπορεί να βρεθεί στον εξής σύνδεσμο: h p:// ³Μία πλήρης λίστα με όλους τους Εικονικούς Οργανισμούς που υπάρχουν αυτή τη στιγμή στο EGEE μπορεί να βρεθεί στον ακόλουθο σύνδεσμο: h p://clc.gridops.org/index.php?sec on=home&page=volist
50 2.4 Πλέγματα Υπολογιστών 33 Chemistry, esr - Earth Sciences κοκ), ενώ στη δεύτερη περίπτωση λαμβάνει το όνομα της γεωγραφικής περιοχής στην οποία αναφέρεται (πχ. SEE - South Eastern Europe, VOCE - Central Europe, Grid-IT - Italy κοκ). Η Ελλάδα συμμετέχει στο πρόγραμμα EGEE τόσο με τις υποδομές που αναπτύχθηκαν μέσω του εθνικού προγράμματος HellasGrid, όσο και με υποδομές που έχουν αναπτύξει μόνα τους κάποια πανεπιστήμια και ερευνητικά ινστιτούτα. Στον Πίνακα 2.2 παρουσιάζεται συνοπτικά η κατάσταστη των ελληνικών κόμβων. Όπως φαίνεται, πολλά πανεπιστημιακά ιδρύματα επέλεξαν να υλοποιήσουν τις δικές τους Συστοιχίες Υπολογιστών και να τα εντάξουν στο EGEE ως ξεχωριστούς κόμβους. Πίνακας 2.2: Οι ελληνικοί κόμβοι που συμμετέχουν στο πρόγραμμα EGEE. Κόμβος Όνομα CPUs Storage (GB) Τοποθεσία HG-01-GRNET isabella.grnet.gr Αθήνα HG-02-IASA marie.hellasgrid.gr Αθήνα HG-03-AUTH afrodi.hellasgrid.gr Θεσσαλονίκη HG-04-CTI-CEID kallisto.hellasgrid.gr Πάτρα HG-05-FORTH ariagni.hellasgrid.gr Ηράκλειο HG-06-EKT athena.hellasgrid.gr Αθήνα GR-01-AUTH grid.auth.gr Θεσσαλονίκη GR-03-HEPNTUA hep.ntua.gr Αθήνα GR-04-FORTH-ICS ics.forth.gr 8 0 Ηράκλειο GR-05-DEMOKRITOS inp.demokritos.gr Αθήνα GR-06-IASA ce02.marie.hellasgrid.gr Αθήνα GR-07-UOI-HEPLAB physics.uoi.gr Ιωάννινα Σύνολο Πηγή:h p://goc.grid.sinica.edu.tw/gstat//index.html Πλεονεκτήματα και Μειονεκτήματα Πλεγμάτων Υπολογιστών Όπως διαφαίνεται και από την προηγούμενη περιγραφή, υπάρχουν αρκετές διαφορές μεταξύ ενός Πλέγματος Υπολογιστών και ενός Υπερυπολογιστή. Η κυριότερη από
51 34 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ αυτές είναι ότι σε έναν υπερυπολογιστή η επικοινωνία μεταξύ επεξεργαστών επιτυγχάνεται μέσω τοπικού διαύλου υψηλής ταχύτητας. Αντίθετα, ένα Πλέγμα Υπολογιστών χρησιμοποιεί το διαδίκτυο υπολογιστών για την επικοινωνία των διαφόρων μονάδων μεταξύ τους. Μία άλλη πολύ σημαντική διαφορά είναι το γεγονός ότι σε ένα Πλέγμα Υπολογιστών κάθε κόμβος αποτελείται από ένα σύνολο απλών ηλεκτρονικών υπολογιστών του εμπορίου, που μπορούν να αγοραστούν σε σχετικά χαμηλή τιμή. Συνδυάζοντας πολλούς τέτοιους απλούς υπολογιστές μπορεί κανείς να κατασκευάσει μια υποδομή αντίστοιχη ενός υπερυπολογιστή, αλλά σε πολύ μικρότερο κόστος. Το κυριότερο μειονέκτημα των Πλεγμάτων σε σύγκριση με τους Υπερυπολογιστές είναι ότι η ταχύτητα σύνδεσης μεταξύ κόμβων είναι σαφώς μικρότερη. Είναι προφανές πως η ταχύτητα μεταφοράς δεδομένων που προσφέρει ένας τοπικός δίαυλος υψηλής ταχύτητας είναι πολύ μεγαλύτερη σε σύγκριση με αυτή που προσφέρει ένα δίκτυο Ethernet. Αν και στα Πλέγματα υπάρχει διαθέσιμο ένα πλήθος από Συστοιχίες Υπολογιστών, η πραγματική δύναμη των Πλεγμάτων Υπολογιστών διαφαίνεται σε εφαρμογές που δεν απαιτούν την συνεχή επικοινωνία μεταξύ των επεξεργαστών, αλλά μπορούν να εκτελεσθούν παράλληλα σε διαφορετικούς κόμβους με την ελάχιστη δυνατή επικοινωνία μεταξύ τους. Παρόλο που στην πράξη ένα περιβάλλον Πλέγματος Υπολογιστών μπορεί να θεωρηθεί ως μια εικονική υπολογιστική αρχιτεκτονική, η οποία δίνει τη δυνατότητα εκτέλεσης υπολογισμών υψηλών επιδόσεων, αξιοποιώντας ένα πλήθος επεξεργαστών γεωγραφικά κατανεμημένων και συνδεδεμένων μέσω δικτύου, τα Πλέγματα Υπολογιστών δεν είναι απαραίτητα ισοδύναμα με περιβάλλοντα Παράλληλου Προγραμματισμού. Τα Παράλληλα Συστήματα είναι μια μορφή υπολογισμών όπου πολλές εντολές εκτελούνται ταυτόχρονα, και ο παραλληλισμός εμφανίζεται σε πολλά διαφορετικά επίπεδα: σε επίπεδο bit (bit-level parallelism), σε επίπεδο εντολών (instruc on-level parallelism), σε επίπεδο δεδομένων (data parallelism), σε επίπεδο διεργασιών (task parallelism) και σε επίπεδο συστήματος. Κλασικά Παράλληλα Συστήματα υφίστανται σε ένα περιβάλλον Πλέγματος Υπολογιστών με τη μορφή Συστοιχιών Υπολογιστών, τα οποία είναι διαθέσιμα ως πόροι. Από την άλλη πλευρά, επειδή οι πόροι σε ένα Πλέγμα Υπολογιστών είναι συνδεδεμένοι με δίκτυο χαμηλής σχετικά ταχύτητας, τα Πλέγματα δείχνουν τις πραγματικές τους δυνατότητες σε περιπτώσεις εκ φύσεως παράλληλων εφαρμογών. Επομένως, μπορεί κανείς να ισχυρισθεί ότι το Πλέγμα Υπολογιστών είναι ένα υπερσύνολο, το οποίο εμπεριέχει τις δυνατότητες των Παράλληλων Συστημάτων (μέσω χρήσης των Συστοιχιών Υπολογιστών που είναι διαθέσιμα) και τη δυνατότητα αξιοποίησης γεωγραφικά κατανεμημένων υπολογιστικών πόρων. Εδώ αξίζει να σημειωθεί ότι η βασική έννοια ενός Πλέγματος είναι η δυνατότητα διαπραγμάτευσης διακανονισμών στην κατανομή πόρων μεταξύ ενός συνόλου συμμετεχόντων, και στη συνέχεια η χρήση του συνόλου πόρων που προκύπτει για την ικανοποίηση κάποιου συγκεκριμένου στόχου. Σύμφωνα με τον ορισμό που δόθηκε από τον
52 2.4 Πλέγματα Υπολογιστών 35 Ian Foster [FKT01], ισχύει ότι: The sharing that we are concerned with is not primarily file exchange but rather direct access to computers, so ware, data, and other resources, as is required by a range of collabora ve problem-solving in industry, science and engineering. This sharing is, necessarily, highly controlled, with resource providers and consumers defining clearly and carefully just what is shared, who is allowed to share, and the condi ons under which sharing occurs. A set of individuals and/or ins tu ons defined by such sharing rules form what we call a virtual organiza on. Από τα παραπάνω είναι εμφανές ότι οι εφαρμογές Βιοπληροφορικής μπορούν να κερδίσουν πολλά σε ένα περιβάλλον Πλέγματος Υπολογιστών, όχι μόνο όσον αφορά διαθέσιμους υπολογιστικούς πόρους, αλλά και όσον αφορά αξιοπιστία και συνολική απόδοση. Ήδη υπάρχει στη διεθνή βιβλιογραφία αρκετή δουλειά προς την κατεύθυνση συγκερασμού παράλληλων συστημάτων με εφαρμογές βιοπληροφορικής, όπως στην πολλαπλή συστοίχιση ακολουθιών (Mul ple Sequence Alignment) [Dat06], στην ανάλυση γονιδιακών εκφράσεων (Gene Expression Analysis) [Mar06] και στην φυλογενετική ανάλυση (Phylogene c Studies) [Sta06], μεταξύ άλλων. Επιπλέον, υπάρχει μια πρόσφατη τάση στην αξιοποίηση του Πλέγματος Υπολογιστών είτε ως πλατφόρμα διεξαγωγής πολύπλοκων προσεγγίσεων σε προβλήματα Βιοπληροφορικής, όπως η αντίστροφη σχεδίαση δικτύων γονιδιακού ελέγχου (Reverse-engineering gene-regulatory networks) [SHM + 05] και το εργαλείο Τοπικής Συστοίχισης Ακολουθιών σε Πλέγμα (Grid Basic Local Alignment Search Tool - Grid-BLAST) [Kri05], είτε με την κατασκευή πλαισίων εργασίας που στοχεύουν σε συγκεκριμένα ερευνητικά ζητήματα γονιδιωματικής ή πρωτεομικής, όπως το πρόγραμμα Bio-GRID (Biotechnology Informa on and Knowledge Grid) [BAG + 02] και το πρόγραμμα BIGGER (Bioinforma cs and Genomics Grid for European Research) [Cam03]. Από την κατεύθυνση της έρευνας στο χώρο αυτό είναι προφανές ότι υπάρχουν σημαντικές δυνατότητες περαιτέρω αξιοποίησης του Πλέγματος Υπολογιστών για την ενίσχυση της πλειοψηφίας των προσεγγίσεων στα προβλήματα ανάλυσης της Βιοπληροφορικής.
53 36 ΚΕΦΑΛΑΙΟ 2. ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΠΛΕΓΜΑΤΑ ΥΠΟΛΟΓΙΣΤΩΝ
54 Κεφάλαιο 3 Εξόρυξη Δεδομένων στη Βιοπληροφορικη Σε αυτό το κεφάλαιο γίνεται μια σύντομη αναφορά στο χώρο της Εξόρυξης Δεδομένων (Data Mining). Επειδή το πρόβλημα της κατηγοριοποίησης πρωτεϊνών αναφέρθηκε στο προηγούμενο κεφάλαιο, σε αυτό το σημείο είναι χρήσιμη μια περιγραφή του γενικότερου προβλήματος κατηγοριοποίησης (classifica on). Πέρα από το βασικό θεωρητικό υπόβαθρο της Εξόρυξης Γνώσης λοιπόν, δίνεται έμφαση στη θεωρία πίσω από το πρόβλημα της κατηγοριοποίησης και γίνεται συγκεκριμένη αναφορά στο χώρο της κατηγοριοποίησης πρωτεϊνών με έμφαση στα χαρακτηριστικά που το διαφοροποιούν από ένα κλασσικό πρόβλημα κατηγοριοποίησης, καθώς και στα ιδιαίτερα προβλήματα που αυτά προκαλούν. 3.1 Εξόρυξη Δεδομένων Η Εξόρυξη Δεδομένων ορίζεται ως η διαδικασία ανακάλυψης προτύπων και συσχετίσεων μέσα σε συνήθως πολύ μεγάλο όγκο δεδομένων. Η διαδικασία αυτή πρέπει να είναι αυτόματη ή, όπως συμβαίνει συχνά, ημιαυτόματη. Με άλλα λόγια, η Εξόρυξη Δεδομένων είναι μια επαγωγική, επαναληπτική διαδικασία η οποία εξάγει πληροφορία ή γνώση από μεγάλους όγκους δεδομένων [WF05]. Αν και πολλοί αντιμετωπίζουν την Εξόρυξη Δεδομένων ως μια προχωρημένη μορφή στατιστικής ανάλυσης, η αλήθεια είναι ότι υπάρχουν σημαντικές διαφορές μεταξύ αυτών των δύο ερευνητικών πεδίων. Συνήθως η Στατιστική ασχολείται με την αξιολόγηση υποθέσεων πάνω σε ένα καθορισμένο σύνολο δεδομένων, ενώ η Εξόρυξη Δεδομένων συχνά εστιάζει στην αναζήτηση ενός γενικευμένου μοντέλου το οποίο περιλαμβάνει ένα σύνολο υποθέσεων υπό διερεύνηση. Από την άλλη θα ήταν μια υπεραπλούστευση ο ισχυρισμός ότι τα δύο αυτά πεδία δεν έχουν πολλά κοινά σημεία. Αντιθέτως, υπάρχουν πολλές προσεγγίσεις που αναπτύχθηκαν εκ παραλλήλου στους τομείς της Εξόρυξης Δεδομένων και της Στατιστικής, με πολλές κοινά αποδεκτές μεθόδους της Στατιστικής να έχουν γίνει αναπόσπαστο
55 38 ΚΕΦΑΛΑΙΟ 3. ΕΞΟΡΥΞΗ ΔΕΔΟΜΕΝΩΝ ΣΤΗ ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ τμήμα της Εξόρυξης Δεδομένων και το αντίστροφο. Ένας τρόπος ερμηνείας του προβλήματος της Εξόρυξης Δεδομένων, που ταυτόχρονα τη διαφοροποιεί από τις προσεγγίσεις της Στατιστικής, είναι ο εξής: έχουμε ένα τεράστιο σύνολο, μέσα στο οποίο αναζητούμε όλες τις δυνατές περιγραφές κάποιων εννοιών, που εκφράζονται με τη μορφή κανόνων, και οι οποίες ικανοποιούν τα δεδομένα. Η διαδικασία της γενίκευσης μπορεί να αντιμετωπισθεί ως μια αναζήτηση μέσα σε ένα τεράστιο, αλλά πεπερασμένο χώρο αναζήτησης. Η βασική αρχή είναι ότι κάθε πρόβλημα μπορεί να επιλυθεί εάν κάποιος απαριθμήσει όλες τις δυνατές περιγραφές, απορρίπτοντας αυτές που δεν ικανοποιούν τις εγγραφές που δόθηκαν ως δεδομένα. Οι περιγραφές που θα παραμείνουν στο τέλος αυτής της διαδικασίας μπορούν να αξιοποιηθούν για την κατασκευή ενός μοντέλου των αρχικών δεδομένων. Στην πράξη είναι συνήθως ανεπαρκής, έως αδύνατη, η απαρίθμηση όλων των δυνατών περιγραφών που μπορούν να εξαχθούν από ένα συγκεκριμένο σύνολο δεδομένων. Εάν κάθε εγγραφή αναπαρασταθεί με ένα διάνυσμα x = (a 1, a 2,..., a p ) αποτελούμενο από P παραμέτρους (ή αλλιώς χαρακτηριστικά γνωρίσματα), τότε το πλήθος όλων των πιθανών συνδυασμών για κάθε κανόνα είναι a i, όπου a i είναι το πλήθος των διαφορετικών τιμών που μπορεί να πάρει το γνώρισμα a i. Είναι εμφανές ότι το μέγεθος του χώρου αναζήτησης αυξάνει δραματικά με το πλήθος των γνωρισμάτων που λαμβάνονται υπόψη. Επίσης, υπάρχουν πολλά προβλήματα, και ιδιαίτερα σε προσεγγίσεις πρωτεομικής και μεθόδους κατηγοριοποίησης πρωτεϊνών, όπου τα γνωρίσματα δεν έχουν διακριτές τιμές, αλλά αντίθετα λαμβάνουν τιμές από ένα συνεχή χώρο. Σε αυτές τις περιπτώσεις η απευθείας απαρίθμηση του χώρου κανόνων είναι αδύνατη, εάν δεν γίνει πρώτα μια διακριτοποίηση των σχετικών γνωρισμάτων. Η διαδικασία γενίκευσης στην Εξόρυξη Δεδομένων, όπως έχει παρουσιασθεί ως τώρα, δείχνει ξεκάθαρα ότι οι πιο σημαντικές αποφάσεις σε ένα τέτοιο σύστημα είναι οι εξής: 1. Η γλώσσα περιγραφής των εννοιών 2. Η σειρά και ο τρόπος με τον οποίο διασχίζεται ο χώρος αναζήτησης 3. Ο τρόπος με τον οποίο αποφεύγεται η υπερεκπαίδευση (overfi ng) πάνω στα δεδομένα 3.2 Εξόρυξη Δεδομένων στην Πρωτεομική Εστιάζοντας στο ερευνητικό πεδίο της πρωτεομικής, με έμφαση στο πρόβλημα της κατηγοριοποίησης πρωτεϊνών, οι αποφάσεις που αναφέρθηκαν προηγουμένως μπορούν να αναλυθούν περισσότερο. Πρώτα από όλα, όπως έχει αναφερθεί ήδη, όλες οι προσεγγίσεις κατηγοριοποίησης πρωτεϊνών αντιμετωπίζουν το πρόβλημα της κατάρας της διαστατικότητας. Αυτό είναι ισοδύναμο με έναν αχανή χώρο αναζήτησης κανόνων
56 3.2 Εξόρυξη Δεδομένων στην Πρωτεομική 39 μαζί με ένα συγκριτικά πολύ μικρότερο σύνολο δεδομένων, γύρω από τα οποία πρέπει να γίνει η επαλήθευση του τελικού μοντέλου. Η συνήθης προσέγγιση σε μελέτες πρωτεομικής είναι η απόπειρα προσδιορισμού ενός υποσυνόλου σημαντικών γνωρισμάτων, τα οποία στη συνέχεια χρησιμοποιούνται για την κατασκευή του μοντέλου αγνοώντας όλα τα υπόλοιπα. Παρόλα αυτά, πειράματα και μελέτες υψηλής ρυθμαπόδοσης (throughput) έχουν συνήθως εξερευνητικό χαρακτήρα στα δεδομένα εισόδου, οπότε προσεγγίσεις που περιστρέφονται γύρω από υπερβολικά εστιασμένες υποθέσεις συχνά δεν είναι επιθυμητές ή πολλές φορές ακόμα και αδύνατες. Για αυτό το λόγο, η γλώσσα περιγραφής των εννοιών θα πρέπει να κυμαίνεται από τις πληροφορίες χαμηλού επιπέδου που είναι διαθέσιμες για τα πρωτεϊνικά δεδομένα (δεδομένα ακολουθιών), έως την υψηλού επιπέδου αναπαράσταση πρωτεϊνικών δεδομένων με τη μορφή μοτίβων. Από την άλλη πλευρά όμως, λαμβάνοντας υπόψη όλη τη δυνατή και διαθέσιμη πληροφορία κατά την κατασκευή του μοντέλου δημιουργείται ο κίνδυνος υπερεκπαίδευσης του μοντέλου. Ιδιαίτερα όταν γίνεται χρήση των αλληλουχιών αμινοξέων των πρωτεϊνικών αλυσίδων, ο κίνδυνος είναι εμφανώς μεγαλύτερος καθώς η πληροφορία χαμηλού επιπέδου είναι εκ φύσεως αρκετά θορυβώδης. Για να υπάρχει μια ισορροπία μεταξύ της πολυπλοκότητας του χώρου αναζήτησης και της αποδοτικότητας του μοντέλου, διατηρώντας ταυτόχρονα μια αναπαράσταση των αρχικών δεδομένων, η οποία έχει νόημα για τον ειδικό ερευνητή, η περιγραφή των δεδομένων με χρήση των μοτίβων, που εμφανίζονται σε αυτά, φαίνεται να είναι η πλέον ελπιδοφόρα λύση. Η αντικατάσταση των αλυσίδων αμινοξέων με αλληλουχίες μοτίβων στα πρωτεϊνικά δεδομένα, επιτρέπει την κατασκευή ενός μικρότερου χώρου αναζήτησης (αν και παραμένει το πρόβλημα της διαστατικότητας) ενώ ταυτόχρονα υπάρχουν συγκριτικά ελάχιστες απώλειες πληροφορίας. Τέλος, ένα από τα πιο σημαντικά ζητήματα στο πρόβλημα της κατηγοριοποίησης πρωτεϊνών είναι η έλλειψη ενός κοινά αποδεκτού σχήματος κατηγοριοποίησης. Στα πλαίσια της κατηγοριοποίησης, οι κατηγορίες μπορούν να θεωρηθούν ως μια διακριτή μεταβλητή. Δεδομένου ενός συνόλου N εγγραφών (πρωτεϊνικών αλυσίδων), το σύνολο των k κατηγοριών C = {c 1, c 2, c 3,..., c k } συνήθως ορίζεται αυθαίρετα και ανάλογα με το εκάστοτε πρόβλημα που αντιμετωπίζεται. Για παράδειγμα, οι οικογένειες πρωτεϊνών ορίζονται διαφορετικά στην περίπτωση κατηγοριοποίησης ενζύμων και τελείως διαφορετικά στην περίπτωση κατηγοριοποίησης ομολόγων. Καθώς το συνολικό πλήθος των καταγεγραμμένων ακολουθιών αυξάνεται και το ενδιαφέρον επεκτείνεται στο χώρο της ανάλυσης του πρωτεώματος, γίνεται μια παγκόσμια προσπάθεια οργάνωσης των πρωτεϊνών σε οικογένειες και καταγραφής των μοτίβων και των συμπλεγμάτων που αυτές περιλαμβάνουν, όπως είναι το πρόγραμμα Gene Ontology [Con00, GO07]. Επιπρόσθετα, σε ισχυρή αντίθεση με τα κλασικά σενάρια κατηγοριοποίησης, η μεγάλη πλειοψηφία των πρωτεϊνών δεν ανήκουν σε μία μόνο λειτουργική ομάδα, καθώς μπορούν να διαφοροποιηθούν σε πολλά διαφορετικά επίπεδα λειτουργικότητας και επεξεργασίας.
57 40 ΚΕΦΑΛΑΙΟ 3. ΕΞΟΡΥΞΗ ΔΕΔΟΜΕΝΩΝ ΣΤΗ ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ 3.3 Κατηγοριοποίηση Πρωτεϊνών Στην προσπάθεια τυπικού ορισμού του προβλήματος κατηγοριοποίησης πρωτεϊνών, έστω ότι κάθε πρωτεΐνη x i περιγράφεται από P γνωρίσματα - χαρακτηριστικά, τα οποία και εκπροσωπούν το χώρο αναζήτησης, δηλαδή x i = (x i1, x i2, x i3,..., x ip ). Σε κάθε εγγραφή αντιστοιχίζεται ένα πλήθος m < k ετικετών (κατηγοριών), δηλαδή (x i, c i1, c i2,..., c im ). Η κατηγοριοποίηση περιλαμβάνει μια διαδικασία εκμάθησης από παραδείγματα, κατά την οποία στόχος είναι η κατάταξη κάθε εγγραφής σε μία ή περισσότερες από τις k κατηγορίες, έχοντας ως βάση ένα σύνολο παρατηρήσεων. Με άλλα λόγια, ο στόχος είναι η πρόβλεψη του (c i1, c i2,..., c im ) από το x i. Συνοψίζοντας τα ιδιαίτερα θέματα που προκύπτουν από το χώρο της κατηγοριοποίησης πρωτεϊνών, προκύπτουν τα εξής ζητήματα: 1. Δεν υπάρχει κάποιο κοινά αποδεκτό σχήμα κατηγοριοποίησης πρωτεϊνών. Οι οικογένειες πρωτεϊνών ορίζονται κάθε φορά ανάλογα με το εκάστοτε πρόβλημα. 2. Κάθε πρωτεΐνη μπορεί να ανήκει σε περισσότερες της μίας κατηγορίες (πρόβλημα πολλαπλών ετικετών - mul -labeling problem). 3. Το πλήθος των γνωρισμάτων που εμπλέκονται είναι τεράστιο (small-n-large-p problem). Περισσότερο στην περίπτωση της αναπαράστασης ως αλληλουχία αμινοξέων και λιγότερο στην περίπτωση αναπαράστασης με τη χρήση μοτίβων. Ένα άλλο θέμα που προκύπτει από την αναπαράσταση των δεδομένων εισόδου είναι ότι σε κάθε εγγραφή το πλήθος των γνωρισμάτων είναι μεταβλητό. Από την παραδοσιακή άποψη της Εξόρυξης Γνώσης, αυτό υποδηλώνει ότι το σύνολο δεδομένων εισόδου θα περιέχει πολλά γνωρίσματα με κενές τιμές, ιδίως στα επιλεγμένα γνωρίσματα. Πάλι, οι κοινά αποδεκτές προσεγγίσεις είναι ο μετασχηματισμός των λεκτικών χαρακτηριστικών σε δυαδικά ή η εισαγωγή μιας κενής τιμής για τη συμμετρική πλήρωση των μικρότερων ακολουθιών τόσο στην αρχή όσο και στο τέλος τους. Μια εναλλακτική προσέγγιση είναι η χρήση προσαρμοσμένων αλγορίθμων εξόρυξης δεδομένων, οι οποίοι μπορούν να επεξεργαστούν εγγραφές με διατεταγμένες ακολουθίες, όπου η σειρά εμφάνισης των γνωρισμάτων έχει σημασία, σε αντίθεση με τις εγγραφές συνόλων, όπου η γνώση ότι ένα γνώρισμα εμφανίζεται στη συγκεκριμένη πρωτεΐνη είναι αρκετή. Υπάρχουν πολλοί αλγόριθμοι κατηγοριοποίησης στη διεθνή βιβλιογραφία, οι οποίοι εστιάζουν στο πρόβλημα κατηγοριοποίησης πρωτεϊνών. Κάθε ένας χαρακτηρίζεται από ένα σύνολο ιδιότυπων απαιτήσεων όσον αφορά την προ-επεξεργασία δεδομένων εισόδου, τη διαμόρφωση των εσωτερικών παραμέτρων, και την αξιολόγηση και ερμηνεία των αποτελεσμάτων. Παρόλα αυτά, όπως έχει δηλωθεί και από το θεώρημα του No Free Lunch [WM97], κανένας ταξινομητής δεν είναι εγγενώς ανώτερος από τον οποιοδήποτε άλλο. Το πρώτο βήμα σε κάθε προσέγγιση εξόρυξης δεδομένων είναι η αλυσίδα
58 3.3 Κατηγοριοποίηση Πρωτεϊνών 41 Ερώτηση Διεργασία Μέθοδος (Ques on Task Method). Είναι η ίδια η φύση του προβλήματος και το εκάστοτε υπό μελέτη σύνολο δεδομένων, τα οποία καθορίζουν ποιός ταξινομητής είναι καλύτερα προσαρμοσμένος για τη συγκεκριμένη προσέγγιση. Παρόλα αυτά, μια από τις βασικές αρχές στις προσεγγίσεις Εξόρυξης Δεδομένων, η οποία εφαρμόζεται απόλυτα στην περίπτωση της κατηγοριοποίησης πρωτεϊνών, είναι το αξίωμα γνωστό ως Λεπίδα του Όκαμ ( Occam s Razor ), ή αλλιώς lex parsimoniae, το οποίο δηλώνει ότι συνήθως είναι σκόπιμο να επιλέγεται το απλούστερο μοντέλο το οποίο ικανοποιεί το σύνολο δεδομένων. Οι Μηχανές Διανυσμάτων Υποστήριξης (Support Vector Machines - SVM) θεωρούνται από πολλούς ως μια από τις πιο εξεζητημένες αλλά και πιο αποτελεσματικές μεθόδους, και αυτό αποδεικνύεται εμπειρικά από εξαιρετικά καλά αποτελέσματα σε πολύπλοκα σύνολα δεδομένων που περιλαμβάνουν δύο κατηγορίες. Παρόλα αυτά όμως, στη θεωρία δεν υπάρχουν ακόμα ικανοποιητικές αποδείξεις, που να ενισχύουν την πεποίθηση ότι οι Μηχανές Διανυσμάτων υπερέχουν έναντι άλλων ταξινομητών σε περιπτώσεις όπου υπάρχει το ζήτημα της διαστατικότητας [HTJ02]. Ωστόσο, το πρόβλημα της κατηγοριοποίησης πρωτεϊνών είναι ένα υπολογιστικά απαιτητικό ζήτημα εξαιτίας της πολυπλοκότητάς του. Η χρήση απλών ταξινομητών, όπως ο 0-R, ο k-nearest neighbours ή ο C4.5, συνήθως αποφέρουν φτωχά αποτελέσματα σε αντίθεση με πιο σύνθετες μεθόδους, όπως τα SVM. Από την άλλη όμως, οι χρόνοι εκτέλεσης τείνουν να αυξάνουν σημαντικά με τους πιο σύνθετους ταξινομητές, υποχρεώνοντας τους ερευνητές στην αναζήτηση της χρυσής τομής μεταξύ ακριβών αποτελεσμάτων και αποδοτικού χρόνου επεξεργασίας. Σε αυτό το σημείο πρέπει να σημειωθεί ότι στην πλειοψηφία των παραδοσιακών συστημάτων ταξινομητών υπάρχει ένα στάδιο προ-επεξεργασίας, όπου το σύνολο των πρωτεϊνικών δεδομένων πρέπει να μετασχηματιστεί, και στην ουσία να απλοποιηθεί, ούτως ώστε να μπορέσει να εφαρμοσθεί ο ταξινομητής. Αυτό εγκυμονεί τον κίνδυνο της απώλειας πληροφορίας, το οποίο είναι ένα σημαντικό μειονέκτημα ιδιαίτερα στις περιπτώσεις αραιών δεδομένων εισόδου. Για αυτό το λόγο υπάρχει σημαντική συνεχιζόμενη έρευνα προς την κατεύθυνση της ανάπτυξης εξειδικευμένων αλγορίθμων στο χώρο της πρωτεομικής, με στόχο την καλύτερη κατηγοριοποίηση πρωτεϊνών. Υπάρχουν στη βιβλιογραφία αρκετές τεχνικές που μπορούν να εφαρμοσθούν τόσο στο επίπεδο της πρωταρχικής αλληλουχίας αμινοξέων, όπως είναι οι αλγόριθμοι που προκύπτουν από τη θεωρία πυρήνων (Kernel Theory) [WLI + 05, L + 02], όσο και στο επίπεδο αναπαράστασης με χρήση μοτίβων, όπως οι αλγόριθμοι που προκύπτουν από τη θεωρία στοχαστικών πεπερασμένων αυτομάτων (Stochas c Finite State Automata) [PDM04]. Παρόλα αυτά, όλοι οι ταξινομητές που αναφέρθηκαν εμφανίζουν ένα κοινό χαρακτηριστικό μειονέκτημα: εξαιτίας της πολυπλοκότητας του προβλήματος της κατηγοριοποίησης πρωτεϊνών, και του γεγονότος ότι τα πρωτεϊνικά δεδομένα εισόδου βρίσκονται σε πολλές, γεωγραφικά κατανεμημένες τοποθεσίες, η συνολική διαδικασία εκπαίδευσης και κατασκευής του μοντέλου παραμένει εξαιρετικά χρονοβόρα. Από αυτή την άποψη,
59 42 ΚΕΦΑΛΑΙΟ 3. ΕΞΟΡΥΞΗ ΔΕΔΟΜΕΝΩΝ ΣΤΗ ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ το περιβάλλον Πλέγματος Υπολογιστών είναι ιδιαίτερα προσαρμοσμένο για αυτά τα συστήματα. Υπάρχουν αρκετές πρόσφατες προσπάθειες για τη συνέργια και ολοκλήρωση με ομοιόμορφο τρόπο αυτών των δύο πεδίων: της Εξόρυξης Δεδομένων και των τεχνικών Πλέγματος Υπολογιστών [SSK + 08]. Ωστόσο, μια ενοποιητική μεθοδολογία, η οποία θα συνδυάζει τα δύο αυτά πεδία, ενώ ταυτόχρονα θα λαμβάνει υπόψη τις συγκεκριμένες ανάγκες και τους ιδιαίτερους περιορισμούς του προβλήματος της κατηγοριοποίησης πρωτεϊνών, μπορεί δυνητικά να αποτελέσει το πρώτο βήμα προς τη γενίκευση των τεχνικών στη Βιοπληροφορική, και να δώσει το έναυσμα για τη στενότερη και αποτελεσματικότερη συνεργασία μεταξύ ειδικών των δύο χώρων.
60 Κεφάλαιο 4 Γενικευμένη Μεθοδολογία Ανάπτυξης Αλγορίθμων σε Πλέγματα Υπολογιστών Αυτό το Κεφάλαιο έχει αποκλειστικό στόχο την αναλυτική παρουσίαση και περιγραφή της γενικευμένης μεθοδολογίας που αναπτύχθηκε στα πλαίσια της διατριβής. Αρχικά τονίζεται η γενικότητα της προσέγγισης, αλλά η ανάγκη για επικύρωση οδήγησε στην επιλογή του προβλήματος κατηγοριοποίησης πρωτεϊνών ως το χώρο ελέγχου. Τα βήματα που αποτελούν τη μεθοδολογία εξηγούνται σε βάθος, τόσο θεωρητικά (π.χ. μέση πολυπλοκότητα βημάτων κτλ), όσο και πρακτικά. Επιπλέον γίνεται μια παρουσίαση του ημιαυτόματου εργαλείου που αναπτύχθηκε ως υλοποίηση της γενικευμένης μεθοδολογίας. Τέλος, γίνεται αναφορά σε περιπτώσεις χρήσης (use cases) που αναπτύχθηκαν με αυτή τη λογική, και τα οποία περιγράφονται σε επόμενα κεφάλαια. 4.1 Ροή Εργασίας σε Πλέγματα Υπολογιστών Αποτελεί μια γενικότερη πραγματικότητα η τάση να προτιμούν οι ερευνητές λογισμικό με το οποίο νοιώθουν εξοικείωση, ενώ ταυτόχρονα επιζητούν τη μέγιστη διαθέσιμη υπολογιστική ισχύ, χωρίς όμως να επιθυμούν να απασχοληθούν με τις λεπτομέρειες υλοποίησης. Ο στόχος λοιπόν είναι η τυποποίηση της διαδικασίας εκτέλεσης μιας εφαρμογής Βιοπληροφορικής σε ένα Πλέγμα Υπολογιστών, παρέχοντας ένα επίπεδο αφαιρετικότητας μεταξύ επιστήμονα και Πλέγματος. Αυτό το επίπεδο, υπό τη μορφή ενός σχεδιαστή ροής εργασίας, στοχεύει στο να βοηθήσει τον ερευνητή: αʹ. να οργανώσει την εκτέλεση ενός υπολογιστικού πειράματος, βʹ. να αποφασίσει για την καλύτερη κατανομή των διαθέσιμων πόρων, και γʹ. να πάρει μια αρχική εκτίμηση της επιτάχυνσης (speed-up) χωρίς να έχει ιδιαίτερες γνώσεις της υποδομής του Πλέγματος Υπολογιστών.
61 44 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Για την κάλυψη αυτής της ανάγκης, αναπτύχθηκε στα πλαίσια της διατριβής η Γενικευμένη Μεθοδολογία Ανάπτυξης Αλγορίθμων Βιοπληροφορικής σε Πλέγματα Υπολογιστών, με το όνομα BADGE (Bioinforma cs Algorithm Development for Grid Environments). Μία διαδικασία ροής εργασίας μπορεί να αναλυθεί σε τέσσερα διακριτά στοιχεία [YB05]: 1. τη σχεδίαση της ροής εργασίας (workflow design), 2. τον προγραμματισμό της ροής εργασίας (workflow scheduling), 3. τη διαδικασία χειρισμού σφαλμάτων (fault-tolerance), και 4. τη διαδικασία μετακίνησης δεδομένων (data movement). Η σχεδίαση της ροής εργασίας προσδιορίζει τον τρόπο με τον οποίο θα ορισθούν και θα κατασκευασθούν τα επιμέρους στοιχεία της εργασίας. Ο προγραμματισμός εστιάζει στην αντιστοίχιση και διαχείριση των διαδικασιών της ροής στους εκάστοτε κοινά διαθέσιμους πόρους, οι οποίοι δεν βρίσκονται απαραίτητα υπό τον άμεσο έλεγχο του συστήματος ροής εργασίας. Σε κάθε διαδικασία, ιδίως στην περίπτωση ενός περιβάλλοντος Πλέγματος Υπολογιστών, η εκτέλεση μια ροής μπορεί να ανασταλεί για πολλούς λόγους, όπως εξαιτίας σφαλμάτων επικοινωνίας μέσω δικτύου, ή μη διαθεσιμότητας του απαιτούμενου λογισμικού. Για αυτό το λόγο, οι τεχνικές διαχείρισης σφαλμάτων αποτελούν ένα αναγκαίο τμήμα κάθε συστήματος ροής εργασίας. Τέλος, ο τρόπος διαχείρισης δεδομένων εισόδου / εξόδου σε υπολογισμούς μεγάλης κλίμακας είναι ένα κρίσιμο στοιχείο της διαδικασίας, ιδιαίτερα σε κατανεμημένα συστήματα. Αυτή τη στιγμή υφίστανται αρκετές προσεγγίσεις σε συστήματα ροής εργασίας σε Πλέγματα Υπολογιστών, όπως η Triana [TSW03], η Taverna [OAF + 04], ο Pegasus [DBG + 03], και ο Kepler [LAB + 05] μεταξύ άλλων. Κάθε σύστημα έχει ορισμένα μοναδικά χαρακτηριστικά όσον αφορά τη συνολική υλοποίηση της ροής εργασίας: τόσο η Taverna όσο και ο Pegasus αξιοποιούν μία σχεδίαση ροής με βάση Κατευθυνόμενους Άκυκλους Γράφους (DAG - Directed Acyclic Graph), σε αντίθεση με τις προσεγγίσεις των Triana και Kepler. Η Taverna αντιμετωπίζει τη διαδικασία διαχείρισης και μετακίνησης δεδομένων με μια συγκεντρωτική προσέγγιση, ανταλλάσσοντας ενδιάμεσα δεδομένα διαμέσου ενός κεντρικού κόμβου, ενώ ο Pegasus υιοθετεί μία διαμεσολαβητική προσέγγιση, με την οποία οι τοποθεσίες των ενδιάμεσων δεδομένων ελέγχονται απευθείας από ένα κατανεμημένο σύστημα διαχείρισης δεδομένων. Τέλος, η Triana προσφέρει μια αποκεντρωμένη αρχιτεκτονική προγραμματισμού ροής εργασίας, σε αντίθεση με τον Kepler ο οποίος είναι ειδικά σχεδιασμένος για να επιτρέπει την άμεση επίβλεψη του χρήστη. Παρόλα αυτά, ένα κοινό χαρακτηριστικό της συντριπτικής πλειοψηφίας των συστημάτων διαχείρισης ροής εργασίας είναι ότι είναι σχεδιασμένα για εκτέλεση στον προσωπικό υπολογιστή
62 4.1 Ροή Εργασίας σε Πλέγματα Υπολογιστών 45 του χρήστη, δηλαδή εξωτερικά ενός περιβάλλοντος Πλέγματος Υπολογιστών. Μία ποιοτική σύγκριση των γενικότερων χαρακτηριστικών του BADGE με αντιπροσωπευτικά συστήματα ροής εργασίας θα γίνει στη συνέχεια (Ενότητα 4.4). Η γενικευμένη μεθοδολογία BADGE σχεδιάστηκε εξαρχής με τη λογική της εκτέλεσης εξ ολοκλήρου εντός ενός Πλέγματος Υπολογιστών. Η μεθοδολογία στοχεύει στο να βοηθήσει στο σχεδιασμό εφαρμογών ανάλυσης δεδομένων, και στην προαγωγή της διαδικασίας μεταφοράς υπαρχόντων εφαρμογών στο Πλέγμα. Πέρα από τη θεωρητική μεθοδολογία αναπτύχθηκε και ένα ημι-αυτόματο εργαλείο, το οποίο λειτουργεί εντός της υποδομής του Πλέγματος και εφαρμόσθηκε σε ένα πλήθος πραγματικών σεναρίων χρήσης, επιδεικνύοντας κάθε φορά μια σημαντική βελτίωση στην χρονική απόδοση και την αξιοποίηση των διαθέσιμων πόρων Ροή Εργασίας σε Κατηγοριοποίηση Πρωτεϊνών Για να γίνει πιο κατανοητή η ανάλυση μιας ροής εργασίας ανάλυσης δεδομένων στη Βιοπληροφορική, θα μελετηθεί το πρόβλημα της κατηγοριοποίησης πρωτεϊνών χωρίς απώλεια της γενίκευσης. Αναλύοντας μια τυπική διαδικασία κατηγοριοποίησης πρωτεϊνών, προκύπτουν πέντε διακριτές φάσεις: 1. Ανάκτηση Δεδομένων 2. Προεπεξεργασία Δεδομένων 3. Κατασκευή Ταξινομητή 4. Αξιολόγηση Μοντέλου 5. Ερμηνεία Αποτελεσμάτων Τα παραπάνω βήματα εμφανίζονται στο Σχήμα 4.1. Με την εξαίρεση της τελευταίας φάσης, η οποία συνήθως εκπληρώνεται από τον ίδιο τον ερευνητή, σε κάθε φάση ο ερευνητής έρχεται αντιμέτωπος με συγκεκριμένα ερωτήματα, τα οποία βασίζονται στα χαρακτηριστικά που έχουν συζητηθεί ως τώρα: 1. Τα δεδομένα προέρχονται από μία ή από πολλαπλές πηγές; 2. Τα δεδομένα πρέπει να τυποποιηθούν σε κάποια συγκεκριμένη μορφή; Είναι όλα τα γνωρίσματα αναγκαία στη μελέτη; Εάν όχι, είναι αναγκαία η εφαρμογή κάποιου αλγορίθμου αυτόματης επιλογής χαρακτηριστικών ή η επιλογή θα γίνει απευθείας από τον ίδιο το χρήστη;
63 46 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Δημόσιες Βάσεις Δεδομένων Αρχείο Χρήστη Ανάκτηση Δεδομένων Προεπεξεργασία Δεδομένων Κατασκευή Ταξινομητή Αξιολόγηση Μοντέλου Σχήμα 4.1: Τυπική Διαδικασία Κατηγοριοποίησης Πρωτεϊνών. Το βήμα Κατασκευής Ταξινομητή είναι στην ουσία η εκτέλεση του αντίστοιχου αλγορίθμου. 3. Ποιός είναι ο επιθυμητός τύπος μοντέλου (π.χ. βασισμένος σε κανόνες, δένδρα, ή νευρωνικά δίκτυα); Ποιά είναι η φύση της εφαρμογής που υλοποιεί τον αλγόριθμο (μίας ή πολλαπλών διεργασιών); Με βάση ποιό σχήμα ταξινόμησης θα γίνει η κατηγοριοποίηση των πρωτεϊνών; 4. Ποιά είναι η επιθυμητή μέθοδος αυτόματης αξιολόγησης των αποτελεσμάτων (π.χ. έλεγχος στατιστικής υπόθεσης ή πολλαπλή επικύρωση); Στις υπάρχουσες προσεγγίσεις Εξόρυξης Δεδομένων, η επιτυχία ή η αποτυχία μιας κατανεμημένης εφαρμογής κατηγοριοποίησης εξαρτάται στενά από ένα συγκεκριμένο εργαλείο ή μέθοδο. Έτσι, η διαδικασία αυτή απαιτεί την ύπαρξη τυποποιημένων πρωτοκόλλων αναφορικά με τη μεθοδολογία και τις τεχνικές που χρησιμοποιούνται. Ο στόχος αυτής της τυποποίησης είναι η διευκόλυνση των ερευνητών Βιοπληροφορικής στο μετασχηματισμό ενός προβλήματος κατηγοριοποίησης πρωτεϊνών σε ένα σύνολο διεργασιών Εξόρυξης Δεδομένων σε μεγαλύτερο επίπεδο αφαιρετικότητας και με λιγότερη προσπάθεια. Στην προσπάθεια ορισμού μιας ροής εργασίας για το σχεδιασμό ενός πειράματος, θα πρέπει να ληφθούν υπόψη τα διαφορετικά πρότυπα εκτέλεσης εφαρμογών, τα οποία είναι δυνατόν να υπάρχουν σε ένα περιβάλλον Πλέγματος Υπολογιστών. Εφαρμογές Μίας Διεργασίας (Single Process Applica ons) Αυτή η κατηγορία περιλαμβάνει σενάρια χρήσης, όπου η εφαρμογή αποτελείται από μία μοναδική διεργασία με υψηλές υπολογιστικές απαιτήσεις. Περιλαμβάνει
64 4.1 Ροή Εργασίας σε Πλέγματα Υπολογιστών 47 την πλειοψηφία των αλγορίθμων Εξόρυξης Δεδομένων. Προγράμματα σε αυτήν την κατηγορία έχουν την τάση να παρουσιάζουν οριακά καλύτερη απόδοση (κυρίως σε χρόνο εκτέλεσης) κατά την εκτέλεσή τους σε Πλέγμα Υπολογιστών, συγκριτικά με την εκτέλεσή τους σε απλό προσωπικό υπολογιστή. Παρόλα αυτά, αποτελούν επίσης την κατηγορία η οποία εμφανίζεται συχνότερα σε Πλέγμα Υπολογιστών κυρίως εξαιτίας της ευκολίας μεταφοράς και εκτέλεσής τους στο περιβάλλον αυτό. Εφαρμογές Πολλαπλών Διεργασιών (Mul ple Process Applica ons) Αυτό το πρότυπο εκτέλεσης εφαρμογών περιλαμβάνει όλα τα προγράμματα, τα οποία μπορούν να αναλυθούν σε ένα πλήθος επαναληπτικών διαδικασιών, με μικρή έως μηδενική εξάρτηση μεταξύ επαναλήψεων και διεργασιών. Χαρακτηριστικά παραδείγματα αυτής της κατηγορίας είναι οι εφαρμογές σάρωσης παραμέτρων ή οι εφαρμογές μίας-διεργασίας-πολλαπλών-δεδομένων (Single-Process- Mul ple-data / SPMD). Συνήθως είναι αλγόριθμοι και εφαρμογές εκ φύσεως παράλληλες (embarassingly parallel). Οι εφαρμογές αυτές συχνά εμφανίζουν τη μέγιστη ευελιξία για τον τελικό χρήση-ερευνητή, επιτρέποντας πολλαπλές πειραματικές διατάξεις να εκτελούνται συγχρόνως αντί σειριακά σε ένα προσωπικό υπολογιστή. Όμως απαιτούν ταυτόχρονα ο χρήστης να έχει κάποιες βασικές γνώσεις για την υποβολή εργασιών στο Πλέγμα Υπολογιστών. Εφαρμογές Παράλληλου Προγραμματισμού (Parallel Applica ons) Αυτή η ομάδα αλγορίθμων περιέχει όλες τις περιπτώσεις που εμφανίζουν παραλληλία λεπτού κόκκου (fine-grained parallelism). Τυπικά πρόκειται για υλοποιήσεις παράλληλων αλγορίθμων με χρήση της βιβλιοθήκης MPI ή κάποιας αντίστοιχης, και απαιτούν ένα ιδιαίτερο περιβάλλον Συστοιχίας Υπολογιστών (Computer Cluster) για την εκτέλεσή τους. Ένα χαρακτηριστικό μέλος αυτής της κατηγορίας είναι η παράλληλη υλοποίηση του αλγορίθμου CLUSTALW [Li03]. Αν και αυτές οι εφαρμογές είναι και οι πιο αποδοτικές ανάμεσα στις κατηγορίες, από άποψη χρόνου εκτέλεσης, είναι ταυτόχρονα και οι σπανιότερα χρησιμοποιούμενες. Ο κυριότερος λόγος είναι ότι απαιτούν ιδιαίτερη υλοποίηση, και επομένως εξειδικευμένες γνώσεις από πλευράς τελικού χρήστη. Παρόλο που υπάρχουν αρκετοί αλγόριθμοι Βιοπληροφορικής ήδη διαθέσιμοι σε Πλέγμα Υπολογιστών, είναι γεγονός ότι οι τελικοί χρήστες θα πρέπει να έχουν τις αναγκαίες γνώσεις για την αποτελεσματική χρήση τους. Από τα παραπάνω είναι προφανές ότι το ιδανικό σενάριο θα ήταν ο συνδυασμός της ευελιξίας των Εφαρμογών Πολλαπλών Διεργασιών, με την αποδοτικότητα των Εφαρμογών Παράλληλου Προγραμματισμού και την ευκολία χρήσης των Εφαρμογών Μίας Διεργασίας. Αν και αυτός ο συνδυασμός είναι αρκετά δύσκολο να επιτευχθεί, είναι λογικό να
65 48 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE επιδιώξει κανείς το συνδυασμό ευελιξίας με ευκολία για τον τελικό χρήστη. Σε κάθε περίπτωση, ευσταθεί ο ισχυρισμός ότι η εκτέλεση πολλών διαφορετικών διαμορφώσεων του ίδιου πειράματος ταυτόχρονα σε απομακρυσμένους υπολογιστικούς πόρους, αντί σειριακά στον προσωπικό υπολογιστή, αποφέρει ένα σημαντικό κέρδος. Στο Σχήμα 4.2 παρουσιάζεται μια τροποποίηση της τυπικής διαδικασίας κατηγοριοποίησης πρωτεϊνών, αξιοποιώντας το Πλέγμα Υπολογιστών μόνο ως το χώρο εκτέλεσης της εφαρμογής. Όλα τα υπόλοιπα βήματα εκτελούνται στον προσωπικό υπολογιστή του χρήστη. Δημόσιες Βάσεις Δεδομένων Ανάκτηση Δεδομένων Αρχείο Χρήστη Προεπεξεργασία Δεδομένων Κατασκευή Ταξινομητή Αξιολόγηση Μοντέλου Grid Σχήμα 4.2: Τυπική Διαδικασία Κατηγοριοποίησης Πρωτεϊνών με χρήση Πλέγματος Υπολογιστών. Σε αυτή την περίπτωση μόνο η εκτέλεση του αλγορίθμου λαμβάνει χώρα εντός του Πλέγματος Υπολογιστών. 4.2 Γενικευμένη Μεθοδολογία Ανάπτυξης Αλγορίθμων σε Πλέγματα Υπολογιστών Το πρώτο βήμα στον καθορισμό μιας ροής εργασίας για την εκτέλεση μιας σειράς εφαρμογών σε Πλέγμα Υπολογιστών είναι ο προσδιορισμός των δεδομένων που θα χρησιμοποιηθούν. Σε αυτό το σημείο πρέπει να υπογραμμισθεί η σημασία της ύπαρξης πρωτεϊνικών Βάσεων Δεδομένων διαθέσιμων στο κοινό μέσω χρήσης προγραμμάτων. Αν και υπάρχουν αρκετές Βάσεις Δεδομένων Πρωτεϊνών προσβάσιμων με τη χρήση παρεχόμενων υπηρεσιών δικτύου, όπως η InterProScan [ZA01] και η efamily, ο αριθμός τους είναι πολύ μικρότερος συγκριτικά με το πλήθος των εξαιρετικά λεπτομερών και
66 4.2 Γενικευμένη Μεθοδολογία Ανάπτυξης Αλγορίθμων σε Πλέγματα Υπολογιστών 49 πλήρως τεκμηριωμένων διαθέσιμων Βάσεων Δεδομένων. Αυτό το γεγονός ωθεί τους ερευνητές είτε να διατηρούν ένα τοπικό αντίγραφο όλων των δεδομένων που χρησιμοποιούν (οικονομικά ασύμφορο καθώς πλέον αναφερόμαστε σε Petabytes δεδομένων), είτε να περιορίζονται μόνο στις Βάσεις που παρέχουν προγραμματιστική πρόσβαση, αναιρώντας έτσι στην ουσία το δυναμικό μιας εφαρμογής Πλέγματος Υπολογιστών. Σε κάθε περίπτωση, για τη διαδικασία εκτέλεσης σε Πλέγμα, τα δεδομένα εισόδου μπορούν να προέλθουν, μεταξύ άλλων, και από τις εξής πηγές: i. Από αρχείο που παρέχει ο ίδιος ο χρήστης (είτε απλό είτε ειδικά διαμορφωμένο αρχείο). ii. Από Βάση Δεδομένων που διατηρεί ο ίδιος ο χρήστης, χρησιμοποιώντας παραδοσιακά πρωτόκολλα προγραμματιστικής πρόσβασης σε Βάση Δεδομένων. iii. Από εξωτερική, προσβάσιμη από το κοινό, Βάση Δεδομένων, χρησιμοποιώντας υπηρεσίες δικτύου (web-services) για την προγραμματιστική πρόσβαση σε αυτή. iv. Από αρχείο το οποίο υφίσταται ήδη σε χώρο αποθήκευσης του Πλέγματος Υπολογιστών, χρησιμοποιώντας το μοναδικό αναγνωριστικό πλέγματος (grid iden fier - guid). Σε όλες αυτές τις περιπτώσεις δεν υπάρχει όριο στο πλήθος των πηγών δεδομένων που θα συμπεριληφθούν, δεδομένου ότι είτε έχουν την ίδια διαμόρφωση, είτε ότι υπάρχει διαθέσιμος ένας μετατροπέας διαμορφώσεων. Στην πράξη όμως, η τελευταία περίπτωση είναι ένα σπάνιο φαινόμενο, καθώς η πλειοψηφία των βιολογικών Βάσεων Δεδομένων επιστρέφουν έξοδο είτε σε XML, είτε σε FASTA διαμόρφωση. Το επόμενο βήμα είναι ο έλεγχος, εάν απαιτείται κάποια προεπεξεργασία των δεδομένων. Πάλι, μπορούν να διακριθούν αρκετές περιπτώσεις, όπως: Όλα τα γνωρίσματα των πρωτεϊνικών δεδομένων πρέπει να ληφθούν υπόψη. Θα πρέπει να γίνει αυτόματη επιλογή σημαντικών γνωρισμάτων, με χρήση μεθόδων Principal Component Analysis (PCA) ή Singular Value Decomposi on (SVD) μεταξύ άλλων. Θα γίνει επιλογή γνωρισμάτων από τον ίδιο το χρήστη. Όλες αυτές οι περιπτώσεις μπορούν να ληφθούν υπόψη κατά τη διάρκεια υποβολής μιας εργασίας στο Πλέγμα, με την εισαγωγή ενός αντίστοιχου πεδίου κατά τη διαδικασία σχεδιασμού της ροής εργασίας. Ειδικότερα στην τελευταία περίπτωση, ο χρήστης θα πρέπει να προσθέσει επιπλέον και μια λίστα με τα γνωρίσματα τα οποία θα ληφθούν υπόψη κατά την κατασκευή του μοντέλου ταξινομητή.
67 50 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Μετά τον ορισμό των δεδομένων και των επιλογών προεπεξεργασίας, η κύρια φάση της μεθοδολογίας είναι ο προσδιορισμός της μεθόδου που θα χρησιμοποιηθεί για την κατασκευή του ταξινομητή. Εδώ πρέπει να σημειωθεί ότι στις περισσότερες περιπτώσεις αυτό το βήμα σχετίζεται άμεσα με τις προηγούμενες φάσεις. Αρκετοί αλγόριθμοι εξόρυξης δεδομένων απαιτούν συγκεκριμένους τύπους δεδομένων στις τιμές των γνωρισμάτων (για παράδειγμα, ορισμένοι αλγόριθμοι είναι σχεδιασμένοι ώστε να χρησιμοποιούν μόνο πραγματικές τιμές), κτλ. Επιπλέον, αν και ο χρήστης μπορεί να δώσει τη δική του βιβλιοθήκη αλγορίθμων, αυτή τη στιγμή υπάρχουν αρκετοί αλγόριθμοι διαθέσιμοι στο Πλέγμα Υπολογιστών ως πόροι συστήματος. Αυτό το γεγονός δίνει αφενός μεγαλύτερη ευελιξία, και αφετέρου τη δυνατότητα χρήσης μιας πληθώρας εργαλείων χωρίς να είναι αναγκαία η σε βάθος γνώση της κάθε μεθόδου. Πέρα από την επιλογή της μεθόδου του ταξινομητή, πρέπει να ορισθούν τόσο οι οικογένειες των πρωτεϊνών, με βάση τις οποίες θα γίνει και η κατασκευή του τελικού μοντέλου, όσο και ο τύπος της τελικής εφαρμογής. Οι κατηγορίες των πρωτεϊνών μπορούν να επιλεχθούν εύκολα ανάμεσα από τα γνωρίσματα που προσδιορίσθηκαν σε προηγούμενο βήμα. Ο τύπος της εφαρμογής μπορεί είτε να ορισθεί ρητά από το χρήστη, είτε να εξαχθεί αυτόματα από την επιλογή του συστήματος ταξινομητή. Παρόλα αυτά όμως, ορίζοντας ρητά τον τύπο της εφαρμογής, ο χρήστης μπορεί υπό συνθήκες να επιτρέψει μια εφαρμογή Μίας Διεργασίας να εκτελεσθεί ως εφαρμογή Πολλαπλών Διεργασιών. Αν και αυτή η αλλαγή γίνεται κατόπιν αίτησης του χρήστη, στην πράξη ο μετασχηματισμός γίνεται κατά τη διάρκεια της εκτέλεσης στο Πλέγμα, όπου το σύνολο δεδομένων εισόδου διασπάται σε μικρότερα τμήματα, τα οποία εκτελούνται ταυτόχρονα. Το τελικό βήμα της μεθοδολογίας είναι η επιλογή της μεθόδου αξιολόγησης. Καθώς τα περισσότερα συστήματα ταξινομητών εμπεριέχουν ένα πλήθος μεθόδων αξιολόγησης, το βήμα αυτό είναι περισσότερο μια απλή επιλογή μεθόδου. Όμως είναι δυνατόν ο χρήστης να ζητήσει η αξιολόγηση του μοντέλου να γίνει πάνω σε ένα συγκεκριμένο, κατασκευασμένο από τον ίδιο, σύνολο δεδομένων. Μετά τον ορισμό όλων των παραμέτρων της μεθοδολογίας, η εφαρμογή υποβάλλεται στο Πλέγμα Υπολογιστών, το οποίο με τη σειρά του αναλαμβάνει την εκτέλεσή της και την επιστροφή των ζητούμενων αποτελεσμάτων στον τελικό χρήστη. Εδώ να σημειωθεί ότι στην περίπτωση όπου επιλέγονται πολλές οικογένειες πρωτεϊνών, και ο συγκεκριμένος ταξινομητής δεν έχει τη δυνατότητα διαχείρισης πολλών κατηγοριών, η εφαρμογή μετατρέπεται αυτόματα σε εφαρμογή Πολλαπλών Διεργασιών, έτσι ώστε να αντιμετωπισθεί το πρόβλημα των πολλαπλών ετικετών. Σε αυτό το σενάριο, κάθε διεργασία αναλαμβάνει να κατασκευάσει ένα μοντέλο ταξινομητή που θα διακρίνει μία μόνο από τις οικογένειες πρωτεϊνών που επιλέχθηκαν κατά την περιγραφή της εφαρμογής, και τα μοντέλα συνδυάζονται τελικά είτε με μεθόδους ενορχήστρωσης (ensemble methods), είτε με απλές μεθόδους ψηφοφορίας (vo ng mechanisms). Η συνολική ροή δεδομένων παρουσιάζεται στο Σχήμα 4.3.
68 4.2 Γενικευμένη Μεθοδολογία Ανάπτυξης Αλγορίθμων σε Πλέγματα Υπολογιστών 51 Δημόσιες Βάσεις Δεδομένων Αρχείο Χρήστη Συλλογή Δεδομένων Προεπεξεργασία Δεδομένων Αξιολόγηση Αποτελεσμάτων Επιλογή Ταξινομητή Grid Σχήμα 4.3: Ροή Δεδομένων σε Πλέγματα Υπολογιστών σύμφωνα με τη μεθοδολογία BADGE. Όλα τα βήματα της διαδικασίας εκτελούνται στο εσωτερικό του Πλέγματος Υπολογιστών. Αν και ως αυτό το σημείο η περιγραφή της μεθοδολογίας έγινε έχοντας ως σημείο αναφοράς το πρόβλημα κατηγοριοποίησης πρωτεϊνών, μπορεί κανείς να παρατηρήσει ότι εύκολα γενικεύεται για το μεγαλύτερο πλήθος αλγορίθμων ανάλυσης δεδομένων στο χώρο της Βιοπληροφορικής. Ο Πίνακας 4.1 παρουσιάζει τα βήματα της γενικευμένης μεθοδολογίας BADGE. Σε αυτό το σημείο πρέπει να τονισθεί ότι δεν υπάρχει ρητά ορισμένη μια διαδικασία διαχείρισης σφαλμάτων στη μεθοδολογία. Καθώς το BADGE έχει σχεδιαστεί με στόχο την εφαρμογή του απευθείας στο εσωτερικό της υποδομής Πλέγματος, η διαδικασία διαχείρισης σφαλμάτων μεταβιβάζεται στο λογισμικό middleware του Πλέγματος. Η πιο συνήθης τεχνική που περιλαμβάνεται στην πλειοψηφία των διαθέσιμων λογισμικών τύπου middleware, είναι ο συνδυασμός της επαναπροσπάθειας και του εναλλακτικού πόρου (retry and alternate resource). Η τεχνική αντιμετωπίζει την εμφάνιση σφάλματος σε οποιοδήποτε σημείο της εκτέλεσης με την επανεκτέλεση του συγκεκριμένου βήματος, ή τη μεταπήδηση σε κάποιο εναλλακτικό πόρο μετά από ένα αριθμό προσπαθειών που ορίζεται από το χρήστη. Το γεγονός ότι κάθε βήμα της γενικευμένες μεθοδολογίας είναι διακριτό και ανεξάρτητο των υπολοίπων κάνει την εφαρμογή της συγκεκριμένης τεχνικής διαχείρισης σφαλμάτων ιδιαίτερα αποτελεσματική στην περίπτωση του BADGE.
69 52 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Πίνακας 4.1: Βήματα Μεθοδολογίας BADGE Βήμα Φάση Παραδείγματα Επιλογών Α. Αρχείο Α1. Τοπικό Α2. Πλέγμα Ανάκτηση Δεδομένων Β. Βάση Δεδομένων (Data Acquisi on) Β1. Χρήστη Β2. Δημόσια Γ. Πρόσβαση μέσω διεπαφής Γ1. Υπηρεσίες Δικτύου Α. Αποθορυβοποίηση Δεδομένων Προεπεξεργασία Δεδομένων Β. Επιλογή Χαρακτηριστικών (Data Preprocessing) Β1. PCA Β2. SVD Γ. Χωρίς Προεπεξεργασία Διαμόρφωση Αλγορίθμου (Algorithm Configura on) - Βήμα Μεταγλώττισης συνήθεις παράμετροι μεταγλώττισης - Βήμα Διαμόρφωσης Α. Μίας Διεργασίας Εκτέλεση Εφαρμογής Β. Πολλαπλών Διεργασιών (Applica on Execu on) Γ. Παράλληλη (MPI) Φάση Αξιολόγησης Α. Διαδικασία Ελέγχου (Evalua on Method) Β. Επαναληπτική Διαδικασία 4.3 Ανάλυση Πολυπλοκότητας Έστω F i (ˆn i ), i = 1, 2,..., 5 η χρονική πολυπλοκότητα του καθενός από τα 5 βήματα της γενικευμένης μεθοδολογίας BADGE. Η συνολική σειριακή πολυπλοκότητα F s (n t ) οποιασδήποτε διαδικασίας η οποία εκτελείται σε έναν μόνο επεξεργαστή, θα είναι ίση
70 4.3 Ανάλυση Πολυπλοκότητας 53 με: F s (n t ) = 5 F i (ˆn i ) (4.1) i=1 όπου n t είναι μία συνάρτηση των ˆn i, i = 1, 2,..., 5. Παρόλα αυτά, αρκετά στάδια στη διαδικασία μπορούν να αναλυθούν περαιτέρω για να καταστεί δυνατός ο διαχωρισμός σε σειριακό και παράλληλο κομμάτι. Η πολυπλοκότητα F 1 () του Βήματος 1 (Ανάκτηση Δεδομένων - Data Acquisi on) μπορεί να ξαναγραφεί ως εξής: F 1 (n 1, p 1 ) = I d s (n 1 ) + Id p(n 1 ) p 1 (4.2) όπου I d s (n 1 ) είναι το τμήμα της λήψης δεδομένων το οποίο είναι αναγκαία σειριακό, I d p(n 1 ) είναι το τμήμα της διαδικασίας που μπορεί να εκτελεσθεί παράλληλα, και p 1 είναι το πλήθος των επεξεργαστών που θα χρησιμοποιηθούν στο παράλληλο τμήμα (n 1, όσον αφορά την προσπέλαση δεδομένων, συνήθως αναφέρεται στο μέγεθος των τμημάτων μνήμης - data blocks). Προφανώς, το χειρότερο σενάριο είναι να μην υπάρχει καθόλου παράλληλο τμήμα, δηλαδή I d p(n 1 ) = 0. Σχηματικά, η πολυπλοκότητα παρουσιάζεται στο Σχήμα 4.4 για διαφορετικούς λόγους σειριακού και παράλληλου τμήματος σε μία διεργασία All Serial All Parallel Both with different ratios 7 6 F(n) n Σχήμα 4.4: Διαφορετικοί λόγοι παράλληλου και σειριακού τμήματος σε μία διεργασία Το βήμα της Προεπεξεργασίας Δεδομένων μπορεί να αναλυθεί σε σειριακό και παράλληλο τμήμα με παρόμοιο τρόπο. Εάν F 2 () είναι η πολυπλοκότητα του δεύτερου βή-
71 54 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE ματος, τότε η συνάρτηση μπορεί να κατατμηθεί ως εξής: F 2 (n 2, p 2 ) = I r s (n 2 ) + Ir s (n 2 ) p 2 (4.3) Για άλλη μια φορά, το χειρότερο σενάριο είναι όταν κανένα τμήμα του αλγορίθμου προεπεξεργασίας των δεδομένων δε μπορεί να εκτελεσθεί παράλληλα, δηλαδή I r p(n 2 ) = 0. Η παράμετρος n 2 είναι γενικής χρήσης, καθώς εξαρτάται άμεσα από το συγκεκριμένο αλγόριθμο που θα αξιοποιηθεί σε αυτή τη φάση. Η φάση Διαμόρφωσης Αλγορίθμου (Algorithm Configura on) (Βήμα 3) έχει μελετηθεί σε μεγάλο βαθμό όσον αφορά τη χρονική πολυπλοκότητα. Δεδομένων n 3 γραμμών κώδικα, ένας συμβολομεταφραστής (assembler) απαιτεί σχεδόν O(n 3 ) χρόνο, με την υπόθεση ότι η αναζήτηση στον πίνακα συμβόλων γίνεται με χρήση κάποιας συνήθους συνάρτησης κατακερματισμού. Για προγραμματιστικές γλώσσες υψηλότερου επιπέδου, όπως η C++ ή η Java, η διαδικασία είναι πολύ πιο περίπλοκη. Η πολυπλοκότητα κυμαίνεται από O(n 3 log(n 3 )) για γρήγορες μεθόδους περάσματος (fast parsing methods), για παράδειγμα γραμματικές ενιαίας σάρωσης χαρακτηριστικών (single-sweep a ribute grammars) και μια πλήρη σημασιολογική δομή στη γλώσσα, έως O(n 2 3) όταν εισάγονται τα προβλήματα γράφων στους βελτιστοποιητές. Χωρίς απώλεια της γενικότητας, η πολυπλοκότητα του τρίτου βήματος μπορεί να γραφτεί ως εξής: F 3 (n 3 ) = f[n 2 3 log(n 3 )] (4.4) Το τέταρτο βήμα στη μεθοδολογία BADGE είναι στην ουσία αυτή καθαυτή η εκτέλεση του προγράμματος στο περιβάλλον Πλέγματος Υπολογιστών. Αν και στη θεωρία υπάρχουν τρία διαφορετικά πρότυπα επεξεργασίας και εκτέλεσης, η συντριπτική πλειοψηφία των προσεγγίσεων στη Βιοπληροφορική εντάσσονται στο πρότυπο των Πολλαπλών Διεργασιών (Mul ple Process paradigm). Ενώ υπάρχει μια πληθώρα αλγορίθμων Βιοπληροφορικής που παρουσιάζουν παραλληλία λεπτού κόκκου (fine-grained parallelism), είναι κοινή γνώση ότι η πλειοψηφία των σχεδιασμών πειραμάτων απαιτούν πολλαπλές εκτελέσεις M του ιδίου αλγορίθμου με παρεμφερή διαμόρφωση παραμέτρων και την ίδια είσοδο. Θεωρητικά η πολυπλοκότητα αυτού του βήματος είναι αυτή που παρουσιάζεται στην Εξίσωση 4.5. F theory 4 (n 4, p 4 ) = I e s(n 4 ) + p 4 I e p(n 4 ) (4.5) όπου p 4 είναι το τμήμα της εφαρμογής που μπορεί να εκτελεσθεί παράλληλα. Στην πράξη όμως, το πλήθος M των εκτελέσεων του ιδίου αλγορίθμου, αποτελεί ένα κρίσιμο παράγοντα στη διαμόρφωση της συνολικής πολυπλοκότητας αυτού του βήμα-
72 4.3 Ανάλυση Πολυπλοκότητας 55 τος. Στην πράξη επομένως, η πολυπλοκότητα F 4 (n 4, M) δίνεται από την Εξίσωση 4.6. F 4 (n 4, p 4, M) = M [ ] Is(n e 4 ) + p 4 Ip(n e 4 ) (4.6) όπου M είναι το πλήθος επαναλήψεων ολόκληρης της εκτέλεσης του προγράμματος. Τέλος, η χρονική πολυπλοκότητα του πέμπτου βήματος (Φάση Αξιολόγησης) μπορεί να εκφρασθεί με τρόπο παρόμοιο της πολυπλοκότητας της φάσης Προεπεξεργασίας Δεδομένων, όπως φαίνεται στην Εξίσωση 4.7. F 5 (n 5, p 5 ) = I v s (n 5 ) + Iv p (n 5 ) p 5 (4.7) Σε αυτό το σημείο, θα πρέπει να ληφθεί υπόψη ο επιπλέον χρόνος αναμονής που υφίσταται πάντα σε κάθε υποβολή εργασίας σε Πλέγμα Υπολογιστών. Αν και αυτός ο χρόνος αναμονής τείνει να εξαφανισθεί όσο βελτιώνεται το middleware, είναι γνωστό ότι ο χρόνος αναμονής αυξάνεται γραμμικά με το πλήθος των επεξεργαστών (p 0 ) που δεσμεύονται κατά την υποβολή της εργασίας (Εξίσωση 4.8): F 0 (p 0 ) = I o (p 0 ) (4.8) Αντικαθιστώντας τις συναρτήσεις πολυπλοκότητας κάθε βήματος στην Εξίσωση 4.1, η συνολική πολυπλοκότητα της κάθε διαδικασίας στη μεθοδολογία BADGE και σε ένα μόνο επεξεργαστή, είναι η ακόλουθη: F s (n t ) =I d s (n 1 ) + p 1 I d p(n 1 )+ I r s (n 2 ) + p 2 I r p(n 2 )+ f[n 2 3 log(n 3 )]+ [ ] M Is(n e 4 ) + p 4 Ip(n e 4 ) + (4.9) I v s (n 5 ) + p 5 I v p (n 5 ) όπου n t = g(n 1, n 2, n 3, n 4, n 5 ), p 1, p 2, p 3 και p 4 είναι εσωτερικές παράμετροι των αλγορίθμων, και M είναι μια παράμετρος οριζόμενη από το χρήστη. Από την άλλη πλευρά, η πολυπλοκότητα μιας διαδικασίας του BADGE σε ένα περιβάλλον Πλέγματος Υπολογι-
73 56 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE στών, θα είναι η εξής: F grid (n t, p nodes ) =I o (p nodes )+ I d s (n 1 ) + Id p(n 1 ) p 1 + I r s (n 2 ) + Ir p(n 2 ) p 2 + f[n 2 3 log(n 3 )]+ M p nodes I v s (n 5 ) + Iv p (n 5 ) p 5 [ I e s(n 4 ) + p 4 I e p(n 4 ) ] + (4.10) Εάν p nodes = M p 1 p 2 p 5, τότε η επιτάχυνση (speedup) θα είναι η ιδανική, σε αναλογία πάντα με τη σειριακή προσέγγιση. Από την άλλη, εάν M = 1 και δεν υπάρχουν παράλληλα τμήματα σε οποιοδήποτε βήμα της ροής εργασίας, τότε η προσέγγιση με χρήση Πλέγματος Υπολογιστών θα είναι οριακά χειρότερη από τη σειριακή. Παρόλα αυτά, στην πράξη η συντριπτική πλειοψηφία των προσεγγίσεων Βιοπληροφορικής είναι κυρίως επαναληπτικές διαδικασίες, επιτρέποντας συνεπώς σημαντικό κέρδος στο χρόνο εκτέλεσης. 4.4 Το Εργαλείο BADGE Η γενικευμένη μεθοδολογία BADGE μπορεί να αξιοποιηθεί από σχεδιαστές λογισμικού ως ένα θεωρητικό υπόβαθρο για τη σχεδίαση και ανάπτυξη εφαρμογών Βιοπληροφορικής σε Πλέγματα Υπολογιστών, γρηγορότερα και καταβάλλοντας λιγότερη προσπάθεια. Πέρα από αυτό όμως, μια υλοποίηση αυτής της μεθοδολογίας μπορεί να χρησιμοποιηθεί ως ένα εργαλείο λογισμικού, υποβοηθώντας μη έμπειρους χρήστες στην χρήση πόρων Πλέγματος Υπολογιστών. Το εργαλείο BADGE που αναπτύχθηκε ακολουθεί την ίδια δομή με τη γενικευμένη μεθοδολογία BADGE, και επιτρέπει τη σταδιακή κατασκευή των αναγκαίων αρχείων για την υποβολή μιας εργασίας στο Πλέγμα Υπολογιστών, ακολουθώντας μια σειρά επιλογών (όπως προσδιορισμός δεδομένων εισόδου, αρχείο εκτελέσιμου κτλ). Το εργαλείο BADGE αναπτύχθηκε για να λειτουργήσει ως πόρος του Πλέγματος, διαθέσιμος στο επίπεδο της Διεπαφής Χρήστη του περιβάλλοντος. Αν και έχει σχεδιαστεί ως ένα εργαλείο γενικής χρήσης, η τρέχουσα υλοποίηση εξαρτάται άμεσα από το λογισμικό middleware glite, το οποίο αποτελεί τη βάση της υποδομής του EGEE. Το εργαλείο BADGE λειτουργεί με παρόμοιο τρόπο όπως μια εφαρμογή οδηγού (wizard),
74 4.4 Το Εργαλείο BADGE 57 1 AppType = M u l t i p l e ; 2 NumCPU = 1 0 ; 3 P r e P r o c = NaN ; 4 C l a s s = { F a m i l y } ; 5 A l g o r i t h m = weka. c l a s s i f i e r s. t r e e s. J48 ; 6 L o c a l D a t a = { P r o s i t e. a r f f } ; 7 RemoteData = { l f n : / g r i d / see / fpsom / weka. j a r } ; 8 Output = { g C l a s s _ m o d e l s. t a r. gz } ; 9 E v a l = { { c r o s s v a l i d a t i o n, 1 0 } } ; Πλαίσιο 4.1: Παράδειγμα εσωτερικής αναπαράστασης μιας διαδικασίας στη μεθοδολογία BADGE όπου ο χρήστης επιλέγει τις επιθυμητές παραμέτρους για μια συγκεκριμένη διαδικασία, και στη συνέχεια το εργαλείο αναλαμβάνει να κατασκευάσει και να υποβάλλει τα απαραίτητα αρχεία για την εργασία στο Πλέγμα. Το Πλαίσιο 4.1 παρουσιάζει ένα παράδειγμα της εσωτερικής αναπαράστασης του εργαλείου BADGE για μία ροή εργασίας πολλαπλών διεργασιών (πεδίο AppType) η οποία θα εκτελεσθεί ταυτόχρονα σε 10 CPUs (πεδίο NumCPU). Η ροή εργασίας δεν περιλαμβάνει κάποιο βήμα προεπεξεργασίας δεδομένων (πεδίο PreProc), και η συγκεκριμένη εφαρμογή είναι ο αλγόριθμος κατηγοριοποίησης J48 (πεδίο Algorithm). Εξαιτίας της επιλογής του συγκεκριμένου αλγορίθμου, το πεδίο Class είναι επίσης απαραίτητο. Η διαδικασία μεταφοράς δεδομένων εισόδου / εξόδου προσδιορίζεται από τα πεδία LocalData, RemoteData και Output. Τέλος, ο χρήστης επιθυμεί να υπάρξει μια φάση αξιολόγησης των αποτελεσμάτων, και επομένως προσδιορίζεται η τιμή του πεδίου Eval. Στο Σχήμα 4.5 παρουσιάζεται η εσωτερική λειτουργία του εργαλείου. Ο χρήστης ορίζει με ένα τυποποιημένο τρόπο όλες τις σχετικές παραμέτρους για την εκτέλεση της εργασίας, όπως για παράδειγμα το όνομα του εκτελέσιμου, τα αρχεία εισόδου, όποιες εξωτερικές εξαρτήσεις υπάρχουν κτλ. Κατά τη διάρκεια αυτής της διαδικασίας, το εργαλείο καταγράφει αυτές τις παραμέτρους σε ένα αρχείο εσωτερικής αναπαράστασης της ροής εργασίας. Μετά την ολοκλήρωση της διαδικασίας, παράγονται αυτόματα από το αρχείο εσωτερικής αναπαράστασης όλα τα απαραίτητα αρχεία JDL, και στη συνέχεια υποβάλλεται η εργασία στο Πλέγμα. Όταν ολοκληρωθεί η εκτέλεση, τα αποτελέσματα της εκτέλεσης επιστρέφονται απευθείας στο χρήστη. Στον Πίνακα 4.2 παρουσιάζεται μια ενδεικτική λίστα από τα πεδία που εμφανίζονται στην εσωτερική αναπαράσταση μια ροής εργασίας στο εργαλείο BADGE. Τέλος, στα Σχήματα 4.6 και 4.7 παρουσιάζονται τα λογικά διαγράμματα δύο βασικών διαδικασιών στο εργαλείο BADGE. Στο Σχήμα 4.6 καταγράφεται η διαδικασία ανάκτησης δεδομένων, δηλαδή το πρώτο βήμα της γενικευμένης μεθοδολογίας. Στο Σχήμα 4.7 καταγράφεται η διαδικασία προσδιορισμού του εκτελέσιμου, καθώς
75 58 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Βιβλιοθήκες Εκτελέσιμο Υποβολή Χρήστης BADGE Εσωτερική Αναπαράσταση Ροής Παραγόμενα Αρχεία (JDL) Grid Δεδομένα Επιστροφή Αποτελεσμάτων Σχήμα 4.5: Εσωτερική Λειτουργία Εργαλείου BADGE και του τρόπου εκτέλεσής του στο Πλέγμα. 4.5 Αξιολόγηση Μεθοδολογίας BADGE Για να γίνει μια πρακτική αξιολόγηση της μεθοδολογίας BADGE, στα πλαίσια της διατριβής ορίσθηκε μια σειρά σεναρίων χρήσης, τα οποία αναπτύχθηκαν και εφαρμόσθηκαν στο περιβάλλον Πλέγματος Υπολογιστών EGEE [EGE09]. Αν και στα επόμενα κεφάλαια θα γίνει αναλυτική περιγραφή ορισμένων από αυτά, καθώς πέρα από εφαρμογές της μεθοδολογίας παρουσιάζουν συγκεκριμένες καινοτομίες και ερευνητικό ενδιαφέρον στον εκάστοτε χώρο τους, για λόγους πληρότητας ακολουθεί μια σύντομη αναφορά όλων των σεναρίων. Για να αποφευχθεί η επανάληψη των ίδιων στοιχείων, κάθε περίπτωση εκτελέσθηκε με χρήση της γενικευμένης μεθοδολογίας BADGE, και όλα τα δεδομένα, εργαλεία και αλγόριθμοι που αναφέρονται στα σενάρια βρίσκονται αποθηκευμένα στα Αποθηκευτικά Στοιχεία του Πλέγματος και λαμβάνονται κατά ζήτηση, εκτός εάν δηλώνεται το αντίθετο. Το περιβάλλον εκτέλεσης όλων των εφαρμογών ήταν το Πλέγμα Υπολογιστών EGEE.
76 4.5 Αξιολόγηση Μεθοδολογίας BADGE 59 Πίνακας 4.2: Πεδία Εσωτερικής Αναπαράστασης Εργαλείου BADGE Όνομα Πεδίου AppType NumCPU PreProc Class Algorithm Args LocalData RemoteData Output Eval Παραδείγματα Τιμών Εκπροσωπεί τον τύπο εκτέλεσης της εφαρμογής. Μπορεί να είναι Single, Mul ple ή MPI Η τιμή του πεδίου δηλώνει το πλήθος επεξεργαστών που απαιτούνται. Περιέχει το όνομα του αλγορίθμου που θα χρησιμοποιηθεί για την προεπεξεργασία των δεδομένων. Εάν δεν θα υπάρξει, τότε μπαίνει η τιμή NaN. Στην περίπτωση που δηλωθεί ως εκτελέσιμο ένας αλγόριθμος κατηγοριοποίησης, το πεδίο περιέχει το όνομα του a ribute που θα χρησιμοποιηθεί ως ετικέτα. Το όνομα του εκτελέσιμου. Περιέχει μια λίστα με ορίσματα εισόδου του εκτελέσιμου (όταν υπάρχουν). Περιέχει μια λίστα με ονόματα αρχείων εισόδου που υπάρχουν τοπικά και απαιτούνται για την τελική εκτέλεση. Περιέχει μια λίστα με ονόματα αρχείων εισόδου που υπάρχουν στο Πλέγμα και απαιτούνται για την τελική εκτέλεση. Περιέχει μια λίστα με ονόματα αρχείων εξόδου που θα πρέπει να επιστραφούν. Περιέχει μια λίστα με ζευγάρια αλγορίθμων και παραμέτρων που θα εφαρμοσθούν στα αρχεία εξόδου πριν την επιστροφή τους στο χρήστη GridBLAST Το πρώτο σενάριο χρήσης είναι η εκτέλεση μιας πολύ κοινής, αλλά αρκετά χρονοβόρας, διαδικασίας στη Βιοπληροφορική, και συγκεκριμένα η εκτέλεση του αλγορίθμου BLAST για ένα πλήθος πρωτεϊνικών ακολουθιών. Το υπολογιστικό πακέτο BLAST (Basic Local Alignment Sequence Tool) [A + 90] περιλαμβάνει προγράμματα για την εύρεση τοπικών ομοιοτήτων μεταξύ μιας ακολουθίας που αποτελεί το όρισμα του ερωτήματος (query sequence) και μιας βάσης δεδομένων. Το BLAST μπορεί να χειρίζεται τόσο πρω-
77 60 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Αρχή Ναι Δεδομενα Εισόδου; Όχι Ναι Δεδομένα Εξόδου; Τοπικά Πλήρες Path Τοπικού Αρχείου Όχι Web-service Βάση Δεδομένων Πλέγμα WSDL του Web- Service URL, username και password της Βάσης Δεδομένων LFN Αρχείου στο Πλέγμα Να αποθηκευθούν στο Πλέγμα; Όχι Ναι Ρύθμιση Σημαίας Καταγραφή Ονόματος Αρχείου Ναι Απαιτούνται άλλα Δεδομένα; Όχι Τέλος Σχήμα 4.6: Λογικό Διάγραμμα για την Ανάκτηση Δεδομένων στο Εργαλείο BADGE τεϊνικές όσο και νουκλεοτιδικές ακολουθίες. Η βασική αρχή του αλγορίθμου BLAST είναι ότι οι βέλτιστες συστοιχίσεις περιέχουν μικρές περιοχές (λέξεις) όπου η βαθμολογία της συστοίχισης είναι μεγαλύτερη από μια τιμή κατωφλίου. Αυτές οι λέξεις θεωρούνται πιθανά σημεία έναρξης μιας καλής τοπικής συστοίχισης. Το τυπικό τους μήκος είναι 3 για πρωτεϊνικές ακολουθίες και 28 για νουκλεοτιδικές. Ο αλγόριθμος τις εντοπίζει και προσπαθεί να επεκτείνει τη συστοίχιση και
78 4.5 Αξιολόγηση Μεθοδολογίας BADGE 61 Αρχή Αρχείο Εκτελέσιμου Ορίσθηκε το αρχείο; Ναι Όχι Μεταγλώττιση Ναι Όχι Ορίσθηκε το αρχείο; Όχι Μεταγλωττιστής Ναι Εξωτερικό Περιβάλλον Ναι Όνομα Βιβλιοθήκης Όχι Όνομα Περιβάλλοντος Ναι Βιβλιοθήκες; Όχι Ορίσματα Εισόδου Εκτελέσιμου Τύπος Εκτελέσιμου Πλήθος Επεξεργαστών Πήγαινε στην Ανάκτηση Δεδομένων Τέλος Σχήμα 4.7: Λογικό Διάγραμμα για τον ορισμό Εκτελέσιμου στο Εργαλείο BADGE προς τις δύο κατευθύνσεις, όσο η βαθμολογία αυξάνεται. Οι περιοχές που προκύπτουν έτσι είναι τα λεγόμενα ζεύγη υψηλής βαθμολογίας (High Scoring Pairs, HSPs), από τα οποία επιλέγονται εκείνα που έχουν βαθμολογία μεγαλύτερη από ένα κατώφλι και εμφανίζουν υψηλή στατιστική σημαντικότητα (δηλαδή θεωρείται ότι δεν έχουν προκύψει τυχαία). Η βασική υλοποίηση του αλγορίθμου BLAST εντοπίζει τοπικές συστοιχίσεις χωρίς κενά, ωστόσο έχουν αναπτυχθεί διάφορες εξειδικευμένες παραλλαγές που δίνουν
79 62 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE και τοπικές συστοιχίσεις με κενά [AG96, A + 97]. Καθώς το πακέτο BLAST δεν είναι εγκατεστημένο σε όλους τους κόμβους του Πλέγματος, σε κάθε νέα εκτέλεση της εφαρμογής GridBLAST το πακέτο πρέπει να ληφθεί και να εγκατασταθεί εκ νέου στον κόμβο εκτέλεσης. Επιπλέον, καθώς το BLAST απαιτεί την ύπαρξη κάποιας βάσης δεδομένων μέσα στην οποία θα γίνει η αναζήτησης της καλύτερης στοίχισης, έπρεπε επίσης να ληφθεί και να σταλεί η βάση δεδομένων SWISS-PROT [BA00], μία από τις τρεις βάσεις που αποτελούν την UniProt [Apw04]. Η SWISS-PROT είναι η παγκοσμίως πιο αναλυτική αποθήκη δομικών, λειτουργικών και άλλων πληροφοριών για τις ακολουθίες πρωτεϊνών. Στα πειράματα που έγιναν, χρησιμοποιήθηκε η τελευταία έκδοση της βάσης SWISS- PROT (Μάϊος 2009), η έκδοση του πακέτου BLAST και ένα σύνολο δεδομένων από 100 ακολουθίες πρωτεϊνών με μήκη που κυμαίνονταν από 500 έως 2500 αμινοξέα. Αρχικά η διαδικασία εκτελέσθηκε σε ένα προσωπικό υπολογιστή (Intel Core 2 Duo CPU 2.40 GHz, 4.00 GByte RAM) όπου υπήρχαν ήδη εγκατεστημένα το πακέτο και η βάση, ενώ στη συνέχεια η διαδικασία εκτελέσθηκε σε ένα διαφορετικό πλήθος κόμβων, όπου έπρεπε κάθε φορά να γίνει λήψη και εγκατάσταση των βιβλιοθηκών. Ο Πίνακας 4.3 παρουσιάζει τους συνολικούς χρόνους εκτέλεσης σε όλες τις περιπτώσεις. Πίνακας 4.3: Χρόνοι Συνολικής Εκτέλεσης του GridBLAST Πλήθος Χρόνος Εκτέλεσης Επιτάχυνση Κόμβων σε second (Speedup) PC Grid Grid Grid Grid Από τον Πίνακα 4.3 είναι εμφανές ότι αυτός ο τύπος προβλήματος είναι ο ιδανικός υποψήφιος για την εκτέλεση σε ένα περιβάλλον Πλέγματος Υπολογιστών. Επίσης, με τη χρήση της γενικευμένης μεθοδολογίας BADGE η διαδικασία διαμόρφωσης και υποβολής της εργασίας στο Πλέγμα απλοποιείται σημαντικά σε σχέση με τον παραδοσιακό τρόπο υποβολής εργασιών. Στο Πλαίσιο 4.2 εμφανίζεται η εσωτερική αναπαράσταση που έχει η μέθοδος gridblast μέσω της γενικευμένης μεθοδολογίας BADGE.
80 4.5 Αξιολόγηση Μεθοδολογίας BADGE 63 1 AppType = M u l t i p l e ; 2 NumCPU = 1 0 ; 3 P r e P r o c = NaN ; 4 C l a s s = { NaN } ; 5 A l g o r i t h m = b l a s t p ; 6 L o c a l D a t a = { p r o t. f a s t a } ; 7 RemoteData = { g u i d : a09dd806 a59e 448e 9558 e323c462f24e } ; 8 Output = { p r o t. out } ; 9 E v a l = { NaN } ; Πλαίσιο 4.2: Εσωτερική Αναπαράσταση Διαδικασίας gridblast στη μεθοδολογία BADGE g-class Η g-class είναι μια διαίρει-και-βασίλευε μεθοδολογία Εξόρυξης Δεδομένων, η οποία αξιοποιεί υπάρχοντες αλγορίθμους κατηγοριοποίησης σε ένα περιβάλλον Πλέγματος Υπολογιστών, ούτως ώστε να κατασκευάσει ένα μοναδικό μοντέλο κατηγοριοποίησης πρωτεϊνών [PPM06]. Χρησιμοποιώντας μια αναπαράσταση πρωτεϊνών με χρήση των μοτίβων που εμφανίζονται στις ακολουθίες τους, ο στόχος είναι η αξιολόγηση της επίδρασης της παραλληλοποίησης στη συνολική απόδοση, ακρίβεια και επίδοση του τελικού ταξινομητή. Αναλυτική περιγραφή του g-class θα γίνει στο Κεφάλαιο Proteas Ο Proteas είναι μια παράλληλη μεθοδολογία για την πρόβλεψη της λειτουργίας πρωτεϊνών [GPM08a, GPM07]. Το πρώτο στάδιο της μεθοδολογίας περιλαμβάνει την εφαρμογή τεχνικών εξόρυξης δεδομένων σε πρωτεϊνικά δεδομένα με στόχο τη δημιουργία ενός μοντέλου για κάθε όρο της Οντολογίας Γονιδίων (Gene Ontology [Con00, GO07]). Στη συνέχεια αυτά τα μοντέλα μπορούν να χρησιμοποιηθούν για την πρόβλεψη της λειτουργίας νέων πρωτεϊνικών αλυσίδων. Η εφαρμογή που αναπτύχθηκε μπορεί να εκτελεσθεί σε Συστοιχία Υπολογιστών και χρησιμοποιεί τη βιβλιοθήκη MPI για την επικοινωνία μεταξύ των διαφόρων διεργασιών. Αναλυτική περιγραφή του Proteas θα γίνει στο Κεφάλαιο Fuzzy PhyloProf Τα φυλογενετικά προφίλ δηλώνουν την έκφραση των γονιδίων, ή ομολόγων των γονιδίων, επί ενός πλήθους πλήρως καταγεγραμμένων γονιδιωμάτων. Έχουν αναδειχθεί ως ένας δημοφιλής τρόπος αναπαράστασης για τον προσδιορισμό και την αναζήτηση λειτουργικά διασυνδεδεμένων γονιδίων ή μεταβολικών μονοπατιών. Παρόλα αυτά υπάρχει μια αυξημένη ζήτηση για υπολογιστικές μεθόδους, οι οποίες θα χρησι-
81 64 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE μοποιούν αποδοτικά την πληροφορία των φυλογενετικών προφίλ, κυρίως εξαιτίας της πολυπλοκότητας του προβλήματος. Το Fuzzy PhyloProf είναι μια μέθοδος ανίχνευσης ιδιοσυγκρασιών σε γονιδιώματα, δηλαδή γονίδια τα οποία εκφράζονται σε συγκεκριμένους οργανισμούς αλλά ταυτόχρονα παρουσιάζουν ενδιαφέρουσες ιδιότητες, όσον αφορά τη συσχέτισή τους, είτε εντός είτε εκτός του ίδιου του οργανισμού. Αναλυτική περιγραφή του Fuzzy PhyloProf θα γίνει στο Κεφάλαιο g-molknot Τέλος, η μεθοδολογία αξιολογήθηκε και σε ένα χώρο εκτός Βιοπληροφορικής, και συγκεκριμένα στην Υπολογιστική Χημεία. Οι περισσότερες μοριακές ιδιότητες είναι ιδιαίτερα ευαίσθητες στην τοπολογία που εμφανίζει το μόριο. Ο αλγόριθμος General Molecular Kno ng algorithm - GMK [SD07] και το σχετικό πακέτο MolKnot είναι μια εφαρμογή Υπολογιστικής Χημείας στην περιοχή της Στερεοχημείας - ενός κλάδου της χημείας που συσχετίζει την τρισδιάστατη μοριακή δομή με τη σύνθεση και τη λειτουργία ενός μορίου. Ο αλγόριθμος είναι αρκετά αποδοτικός για μικρά μόρια, εκεί όπου άλλες μέθοδοι αποτυγχάνουν. Όμως, καθώς ο αλγόριθμος εκτελεί μια εξαντλητική αναζήτηση στο χώρο διαμόρφωσης των μορίων, ο χρόνος εκτέλεσης αυξάνεται εκθετικά με το μέγεθος του μορίου. Προς αυτή την κατεύθυνση ο αλγόριθμος τροποποιήθηκε ώστε να να είναι δυνατή η εκτέλεσή του σε περιβάλλον Πλέγματος Υπολογιστών, δίνοντας ενδιαφέροντα αποτελέσματα όσον αφορά τη συνολική απόδοση της μεθοδολογίας. Η μέθοδος g-molknot εφαρμόζει μια τακτική διαίρει-και-βασίλευε στο πρόβλημα, διασπώντας το χώρο αναζήτησης σε πολλούς διακριτούς και ανεξάρτητους υποχώρους, και συνδυάζοντας τα αποτελέσματα πολλαπλών διεργασιών στο τέλος [PMKD09]. Αναλυτική περιγραφή του g-molknot θα γίνει στο Κεφάλαιο 8. Στον Πίνακα 4.4 παρουσιάζονται συνοπτικά τα γενικά χαρακτηριστικά των πέντε σεναρίων χρήσης, σε σχέση με τη μεθοδολογία BADGE. 4.6 Ποιοτική Σύγκριση του BADGE με άλλα συστήματα ροής εργασιών Με μια αρχική σύγκριση της μεθοδολογίας BADGE και άλλων συστημάτων ροής εργασίας, όπως η Triana [TSW03], η Taverna [OAF + 04], ο Pegasus [DBG + 03], και ο Kepler [LAB + 05] μεταξύ άλλων, διαπιστώνεται ότι η σημαντικότερη διαφορά τους είναι το γεγονός ότι η γενικευμένη μεθοδολογία έχει σχεδιαστεί ούτως ώστε να υπάρχει εξ ολοκλήρου εντός ενός περιβάλλοντος Πλέγματος Υπολογιστών. Πιο συγκεκριμένα, στο Σχήμα 4.8 παρουσιάζεται η ροή εργασίας σε ένα τυπικό σύστημα διαχείρισης, το οποίο εκτελείται στον προσωπικό υπολογιστή του χρήστη. Σε αυτή την περίπτωση, όλα τα δεδομένα
82 4.6 Ποιοτική Σύγκριση του BADGE με άλλα συστήματα ροής εργασιών 65 Πίνακας 4.4: Σύγκριση των σεναρίων χρήσης σε σχέση με τη γενικευμένη μεθοδολογία BADGE Σενάριο Προϋπήρχε Δεδομένα Απαιτήθηκε Τύπος Χρήσης Αλγόριθμος Προεπεξεργασία Εκτέλεσης gridblast Ναι Τοπικά και στο Πλέγμα Όχι Πολλαπλές Διεργασίες g-class Ναι Τοπικά Ναι Πολλαπλές Διεργασίες Proteas Όχι Βάση Δεδομένων Όχι MPI Fuzzy PhyloProf Όχι Παράγονται Όχι Πολλαπλές Διεργασίες g-molknot Ναι Παράγονται Όχι Πολλαπλές Διεργασίες συγκεντρώνονται στον προσωπικό υπολογιστή του χρήστη, και στη συνέχεια υποβάλλονται στο Πλέγμα υπό τη μορφή ενός πακέτου εργασίας. Καθώς όμως τα περισσότερα συστήματα ροής εργασιών δεν είναι σχεδιασμένα για απευθείας διεπαφή με το Πλέγμα, το βήμα της τελικής υποβολής της εργασίας απαιτεί σε αρκετά μεγάλο βαθμό μικροδιαχείριση από πλευράς χρήστη. Στο Σχήμα 4.9 παρουσιάζεται η ίδια ακριβώς διαδικασία, αλλά από την πλευρά της γενικευμένης μεθοδολογίας BADGE. Σε αυτή την περίπτωση, όλα τα δεδομένα συγκεντρώνονται απευθείας μέσα στο Πλέγμα, και συγκεκριμένα στο επίπεδο Διεπαφής Χρήστη. Καθώς το BADGE βρίσκεται ήδη εντός του Πλέγματος, η διαδικασία υποβολής μιας εργασίας μπορεί να γίνει αυτόματα και αόρατα από τον τελικό χρήστη. Επιπρόσθετα, αυτός ο τρόπος διαχείρισης δεδομένων επιτρέπει τη διατήρηση ογκωδών δεδομένων μόνιμα στο Πλέγμα, και επομένως μειώνεται σημαντικά ο χρόνος της αρχικής διαμόρφωσης μιας νέας εργασίας. Από αυτή την άποψη λοιπόν, η γενικευμένη μεθοδολογία BADGE έχει σαφές πλεονέκτημα έναντι των υπολοίπων συστημάτων. Τέλος, ο Πίνακας 4.5 παρουσιάζει τα βασικότερα χαρακτηριστικά του BADGE και ενδεικτικών συστημάτων ροής εργασίας.
83 66 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE Προσωπικός Υπολογιστής Grid 3 Αποτελέσματα Network Εκτελέσιμο 1 2 Αρχείο Χρήστη 1 Πακέτο υποβολής εργασίας 1 1 Αρχεία στο Grid Εκτέλεση Εργασίας Δημόσιες Βάσεις Δεδομένων Σχήμα 4.8: Ροή Εργασίας Εξωτερικά του Πλέγματος. Η τυπική προσέγγιση της πλειοψηφίας των συστημάτων διαχείρισης ροής εργασίας.
84 4.6 Ποιοτική Σύγκριση του BADGE με άλλα συστήματα ροής εργασιών 67 Προσωπικός Υπολογιστής Grid Αποτελέσματα 3 Network Αρχείο Χρήστη 1 1 Πακέτο υποβολής εργασίας 2 1 Εκτέλεση Εργασίας Εκτελέσιμο 1 Αρχεία στο Grid Δημόσιες Βάσεις Δεδομένων Σχήμα 4.9: Ροή Εργασίας σε Πλέγμα. Η προσέγγιση του BADGE.
85 Πίνακας 4.5: Σύγκριση των συστημάτων ροής εργασιών Σύστημα Ροής Δομή Αρχιτεκτονική Χειρισμός Μετακίνηση Εργασίας Σχεδίασης Ροής Προγραμματισμού Σφαλμάτων Δεδομένων Ροής Pegasus DAG Centralized Βασισμένη Διαμεσολαβητική στον DAGMan Triana DAG Decentralized Βασισμένη Peer-to-Peer στον CAT Manager Επίπεδο Διεργασιών Taverna DAG Centralized - Retry Συγκεντρωτική - Alternate Resource Επίπεδο Διεργασιών - Alternate Resource - Συγκεντρωτική Kepler non-dag Centralized Επίπεδο Ροής - Διαμεσολαβητική - έλεγχος εξαιρέσεων - Peer-to-Peer από τον χρήστη - διάσωση ροής Επίπεδο Διεργασιών BADGE non-dag Decentralized - Retry - Διαμεσολαβητική - Alternate Resource - Peer-to-Peer 68 ΚΕΦΑΛΑΙΟ 4. ΓΕΝΙΚΕΥΜΕΝΗ ΜΕΘΟΔΟΛΟΓΙΑ BADGE
86 Κεφάλαιο 5 Κατηγοριοποίηση Πρωτεϊνών: Ο Αλγόριθμος g-class Αυτό το κεφάλαιο περιγράφει τον αλγόριθμο ανάλυσης δεδομένων g- Class που αναπτύχθηκε για το πρόβλημα της κατηγοριοποίησης πρωτεϊνών με χρήση μοτίβων. Ο αλγόριθμος στοχεύει στην ταξινόμηση πρωτεϊνών σε πολλαπλές οικογένειες αξιοποιώντας μια τεχνική διαίρει-και-βασίλευε. Το αρχικό σύνολο δεδομένων εισόδου διασπάται σε ένα πλήθος ξένων συνόλων, τα οποία ο αλγόριθμος επεξεργάζεται παράλληλα για την κατασκευή των κατάλληλων μοντέλων. Στην ενότητα γίνεται η περιγραφή τόσο του ίδιου του αλγορίθμου, όσο και του τρόπου που αυτός γενικεύθηκε με χρήση της μεθοδολογίας BADGE. Ο στόχος του κεφαλαίου είναι να αναδείξει τη δυνατότητα της γενικευμένης μεθοδολογίας να αξιοποιεί ήδη υπάρχοντες αλγορίθμους για την ανάλυση ως τώρα απαγορευτικά μεγάλου όγκου δεδομένων, βελτιώνοντας ταυτόχρονα τη συνολική απόδοσή τους. 5.1 Ο Αλγόριθμος Συνοπτικά Ο αλγόριθμος g-class επιτυγχάνει την παραλληλοποίηση της κατηγοριοποίησης πρωτεϊνών βασιζόμενη στη λογική του διαίρει-και-βασίλευε και στην ύπαρξη ενός αρχικού συνόλου δεδομένων S T, που περιλαμβάνει ήδη ταξινομημένες πρωτεΐνες. Το σύνολο S T διασπάται σε p μικρότερα διακριτά σύνολα S j, επιλεγμένου μεγέθους, τα οποία όμως διατηρούν την κατανομή κλάσεων του αρχικού συνόλου δεδομένων. Στη συνέχεια, το καθένα από τα μικρότερα αυτά σύνολα χρησιμοποιείται ως σύνολο εκπαίδευσης για τη δημιουργία ενός μοντέλου ταξινόμησης M j. Η εκπαίδευση μπορεί να πραγματοποιηθεί με οποιονδήποτε συμβατό αλγόριθμο ταξινόμησης, παρέχοντας με αυτόν τον τρόπο μεγάλη ευελιξία στις απαιτήσεις του χρήστη. Η εκπαίδευση του κάθε μοντέλου είναι επίσης ανεξάρτητη από τα άλλα, με αποτέλεσμα τη δυνατότητα παράλληλης επεξεργασίας. Τέλος, συνδυάζονται όλα τα μεμονωμένα μοντέλα για την εξαγωγή των τελικών κανόνων ταξινόμησης, που χρησιμοποιούνται για τον έλεγχο της απόδοσης του αλγορίθμου
87 70 ΚΕΦΑΛΑΙΟ 5. Ο ΑΛΓΟΡΙΘΜΟΣ G-CLASS και την ταξινόμηση νέων πρωτεϊνών. Ο αλγόριθμος, που απεικονίζεται συνοπτικά στο Σχήμα 5.1, μπορεί να χωρισθεί στα εξής τρία στάδια: Protein.arff Data Splitting P1.arff P2.arff P3.arff Pn.arff Classifier Training Classifier Training Classifier Training Classifier Training Model 1 Model 2 Model 3 Model n Classifier Combination Total Classifier Σχήμα 5.1: Διάγραμμα ροής του αλγορίθμου g-class 1. Διάσπαση των δεδομένων εισόδου (Data Spli ng) Διάσπαση του συνόλου δεδομένων εισόδου S T σε p ξένα μεταξύ τους υποσύνολα S j. 2. Εκπαίδευση ταξινομητή (Classifier Training) Εκπαίδευση p μοντέλων κατηγοριοποίησης από τα p σύνολα δεδομένων. 3. Συνδυασμός ταξινομητών (Classifier Combining) Συνδυασμός των p μοντέλων M j για την εξαγωγή των συνολικών κανόνων κατηγοριοποίησης (συνολικό μοντέλο M).
88 5.1 Ο Αλγόριθμος Συνοπτικά Διάσπαση Δεδομένων Εισόδου Στο πρώτο στάδιο του αλγορίθμου g-class, διασπάται το αρχικό σύνολο δεδομένων S T σε p υποσύνολα. Το βασικό θέμα που έχει να αντιμετωπίσει αυτή η διαδικασία είναι ο τρόπος με τον οποίο θα γίνει η διάσπαση των δεδομένων εκπαίδευσης. Ιδιαίτερη προσοχή δόθηκε ώστε τα διασπασμένα τμήματα που θα αποτελέσουν τα δεδομένα εκπαίδευσης των μοντέλων κατηγοριοποίησης να μην είναι πολωμένα (biased), να μην εμφανίζουν δηλαδή προτίμηση υπέρ κάποιων κλάσεων, έτσι ώστε και τα αποτελέσματα του συνδυασμού τους να μπορούν να είναι αξιόπιστα. Επιλέχθηκε ως βέλτιστη λύση ο διαχωρισμός των πρωτεϊνών ανάλογα με τις κατηγορίες στις οποίες ανήκουν, και η τοποθέτηση ίσου πλήθους πρωτεϊνών από κάθε κατηγορία σε κάθε επιμέρους σύνολο δεδομένων. Στόχος είναι, με άλλα λόγια, να διασφαλιστεί στο μέτρου του δυνατού πως η κατανομή κλάσεων σε κάθε υποσύνολο δε θα διαφέρει πολύ από την κατανομή κλάσεων του αρχικού συνόλου. Για να γίνει αυτό ακολουθείται μια λογική Round Robin κατά την κατασκευή των υποσυνόλων S j. Ο αλγόριθμος, κατά τη διάρκεια ανάγνωσης των δεδομένων, ταξινομεί τις εγγραφές ανά κατηγορία και τις αναδιατάσσει, ομαδοποιώντας τις πρωτεΐνες που ανήκουν στην ίδια κατηγορία. Στην περίπτωση που μία πρωτεΐνη ανήκει σε παραπάνω από μία κατηγορίες, τότε για κάθε μία από τις m κατηγορίες δημιουργείται μια νέα εγγραφή η οποία αντιστοιχίζεται σε μία μόνο κατηγορία. Τελικά, παράγεται μια λίστα η οποία περιέχει όλες τις αρχικές εγγραφές, ομαδοποιημένες ανά κατηγορίες και τοποθετημένες τυχαία εντός της ίδιας κατηγορίας. Στη συνέχεια, ακολουθώντας μια Round Robin λογική, τοποθετείται η πρωτεΐνη i στο (i mod n) σύνολο δεδομένων. Με άλλα λόγια, τοποθετεί την πρώτη εγγραφή-πρωτεΐνη της λίστας στο υποσύνολο S 1, τη δεύτερη στο S 2 κ.ο.κ., μέχρι να τοποθετηθεί μία πρωτεΐνη σε κάθε υποσύνολο. Μετά τοποθετεί την επόμενη πάλι στο πρώτο, την επόμενη στο δεύτερο, κ.ο.κ. Συνοπτικά, σε κάθε ενδιάμεσο σύνολο δεδομένων S j τοποθετούνται οι πρωτεΐνες που βρίσκονται στις θέσεις (j, n + j, 2n + j, 3n + j,...) της μετασχηματισμένης αρχικής λίστας. Ο αλγόριθμος που εκτελεί αυτή τη διαδικασία παρουσιάζεται με τη μορφή ψευδοκώδικα στο Πλαίσιο Εκπαίδευση των Μοντέλων Κατηγοριοποίησης Το δεύτερο βήμα του αλγορίθμου g-class είναι αυτό στο οποίο επιτελείται η εκπαίδευση των μοντέλων κατηγοριοποίησης. Έχοντας ως είσοδο τα νέα σύνολα δεδομένων S j που δημιουργήθηκαν στο προηγούμενο βήμα, κατασκευάζονται οι ταξινομητές επιλέγοντας κάποιον αλγόριθμο κατηγοριοποίησης. Εδώ πρέπει να σημειωθεί ότι στο στάδιο αυτό μπορεί να χρησιμοποιηθεί οποιοσδήποτε αλγόριθμος κατηγοριοποίησης, ανάλογα με τις ανάγκες της εκάστοτε εφαρμογής. Το σύστημα έχει διατηρηθεί εντελώς ανεξάρτητο από τον αλγόριθμο ταξινόμησης, ακριβώς για λόγους προσαρμοστικότητας σε
89 72 ΚΕΦΑΛΑΙΟ 5. Ο ΑΛΓΟΡΙΘΜΟΣ G-CLASS 1 a l g o r i t h m D a t a S p l i t t e r 2 i n p u t : 3 S T : the i n i t i a l d a t a s e t 4 p : number of s p l i t s e t s S j 5 output : 6 n d i s j o i n t d a t a s e t s S j 7 begin 8 read S T 9 re order and randomize S T by p r o t e i n c l a s s 10 do ( i [1, p] ) 11 c r e a t e S i 12 end do 13 do ( i i n s t a n c e s i n the re ordered S T ) 14 s e t i n s t a n c e i to S i mod p 15 end do 16 end a l g o r i t h m D a t a S p l i t t e r Πλαίσιο 5.1: Ψευδοκώδικας Αλγορίθμου Διάσπασης Δεδομένων οποιοδήποτε σύνολο δεδομένων. Με αυτόν τον τρόπο μπορεί να επιτευχθεί βέλτιστο αποτέλεσμα σύμφωνα με τις απαιτήσεις του κάθε χρήστη. Το στάδιο της Εκπαίδευσης των Ταξινομητών είναι αυτό στο οποίο βασίζεται η παραλληλοποίηση του αλγορίθμου. Η εκπαίδευση του κάθε μοντέλου είναι ανεξάρτητη από τα υπόλοιπα, οπότε καθίσταται δυνατή η παράλληλη εκπαίδευσή τους είτε σε πολλούς υπολογιστές, είτε σε ένα περιβάλλον Πλέγματος Υπολογιστών. Η παραλληλοποίηση αυτή επιτυγχάνει σημαντική μείωση του χρόνου που απαιτείται για την εξαγωγή κανόνων από το αρχικό σύνολο δεδομένων Συνδυασμός των Μοντέλων Ταξινόμησης Το τρίτο στάδιο του αλγορίθμου είναι αυτό που παραλαμβάνει τα μοντέλα και είναι υπεύθυνο για την εξαγωγή των τελικών κανόνων κατηγοριοποίησης. Δέχεται ως είσοδο τα n μοντέλα που εκπαιδεύτηκαν στο προηγούμενο στάδιο και τα συνδυάζει με σκοπό τη δημιουργία κανόνων που θα χρησιμοποιηθούν για τη μετέπειτα ταξινόμηση νέων άγνωστων πρωτεϊνών. Ο αλγόριθμος που ακολουθεί το στάδιο αυτό στηρίζεται σε μία λογική ψηφοφορίας, όπου για κάθε πρωτεΐνη προσμετρώνται οι ψήφοι που δίνει το κάθε μοντέλο για την εκάστοτε κατηγορία. Αρχικά, στο σύστημα εισάγονται τα p μοντέλα κατηγοριοποίησης και το σύστημα τα διαβάζει υπολογίζοντας για το καθένα και για την κάθε πρωτεΐνη το αντίστοιχο διάνυσμα κατανομής (distribu on vector). Αυτό αποτελεί ένα διάνυσμα που περιλαμβάνει τις πιθανότητες που δίνει το μοντέλο για την ένταξη της πρωτεΐνης σε κάθε κατηγορία.
90 5.2 Πολυπλοκότητα Αλγορίθμου g-class 73 Συμβολικά μπορεί να γραφεί ως εξής: D pr,j =< a 1, a 2, a 3,..., a k > (5.1) όπου D pr,j το διάνυσμα κατανομής του μοντέλου M j, j = 1,..., p για την πρωτεΐνη pr και a i, i = 1,...,..., k η πιθανότητα που δίνει το μοντέλο M j να ανήκει η πρωτεΐνη pr στην κατηγορία k. Σκοπός του αλγορίθμου είναι να υπολογίσει το συνολικό αποτέλεσμα όλων των διανυσμάτων κατανομής. Αυτό πραγματοποιείται ουσιαστικά με τον υπολογισμό του μέσου όρου όλων των διανυσμάτων. Θεωρώντας μία πρωτεΐνη, ο αλγόριθμος προσθέτει τα διανύσματα κατανομής που προκύπτουν από το κάθε μοντέλο για τη συγκεκριμένη πρωτεΐνη, προσθέτοντας τις αντίστοιχες πιθανότητες της κάθε κατηγορίας. Το συνολικό διάνυσμα που προκύπτει διαιρείται με το πλήθος των μοντέλων, και το αποτέλεσμα είναι ο μέσος όρος των διανυσμάτων κατανομής για την πρωτεΐνη, δηλαδή το διάνυσμα D pr όπως φαίνεται παρακάτω: D pr = p j=1 D pr,j p (5.2) Η διαδικασία αυτή επαναλαμβάνεται για την κάθε πρωτεΐνη του συνόλου δεδομένων και τα τελικά διανύσματα κατανομής που προκύπτουν είναι αυτά που προσδιορίζουν σε ποιές κατηγορίες ανήκουν οι πρωτεΐνες και με ποιά πιθανότητα στην κάθε μία. Μπορεί να εξαχθεί με αυτόν τον τρόπο η επικρατέστερη ή επικρατέστερες κατηγορίες για την κάθε εγγραφή και ο βαθμός αξιοπιστίας του αποτελέσματος. Ο αλγόριθμος με μορφή ψευδοκώδικα παρουσιάζεται στο Πλαίσιο Πολυπλοκότητα Αλγορίθμου g-class Στην ανάλυση πολυπλοκότητας του αλγορίθμου υπάρχουν δύο περιπτώσεις: η σειριακή και η παράλληλη προσέγγιση στο πρόβλημα. Για να υπάρχει ένα μέτρο σύγκρισης, και οι δύο περιπτώσεις θα αντιμετωπισθούν αναλύοντας τα βήματα που καταγράφηκαν στα πλαίσια της γενικευμένης μεθοδολογίας BADGE (Κεφάλαιο 4). Μια αντιστοίχιση των βημάτων της μεθοδολογίας BADGE με τις πολυπλοκότητες των φάσεων που περιγράφηκαν για τη μέθοδο g-class παρουσιάζεται στον Πίνακα 5.1. Στον υπολογισμό των συναρτήσεων πολυπλοκότητας του Πίνακα 5.1 έγιναν οι εξής παραδοχές: Θεωρήθηκε ότι η ανάκτηση δεδομένων έγινε απευθείας σε μορφή ικανοποιητική για τον αλγόριθμο κατηγοριοποίησης. Επομένως, εάν n είναι το πλήθος εγγραφών
91 74 ΚΕΦΑΛΑΙΟ 5. Ο ΑΛΓΟΡΙΘΜΟΣ G-CLASS 1 a l g o r i t h m C l a s s i f i e r C o m b i n e r 2 i n p u t : 3 S T : the i n i t i a l d a t a s e t 4 p : number of i n t e r m e d i a t e models M j 5 output : 6 R : the f i n a l r u l e s e t 7 begin 8 do ( p r o t e i n pr S T ) 9 do ( c l a s s i f i e r models M j ) 10 c a l c u l a t e the D i s t r i b u t i o n V e c t o r D pr,j f o r pr 11 D pr,j =< a 1, a 2, a 3,..., a k > 12 end do 13 c a l c u l a t e the f i n a l V e c t o r f o r pr p j=1 D pr,j 14 D pr = p 15 end do 16 end a l g o r i t h m C l a s s i f i e r C o m b i n e r Πλαίσιο 5.2: Ψευδοκώδικας Αλγορίθμου Συνδυασμού Ταξινομητών Πίνακας 5.1: Σύγκριση Πολυπλοκότητας Προσεγγίσεων στο g-class Βήμα Σειριακή Προσέγγιση Παράλληλη Προσέγγιση Ανάκτηση Δεδομένων O(n) O(n) Προεπεξεργασία Δεδομένων - O(n p) Διαμόρφωση Αλγορίθμου - - Τύπος Εφαρμογής O(f(n)) O(f( n )) + O(n p) p Φάση Αξιολόγησης O(g(p)) O(g(p)) Σύνολο O(n + f(n) + g(p)) O(n p + f( n p ) + g(p)) στο σύνολο δεδομένων εισόδου, η χειρότερη περίπτωση χρονικής πολυπλοκότητας για την ανάκτησή τους είναι O(n). ¹ Προεπεξεργασία δεδομένων δεν απαιτείται στην περίπτωση της σειριακής προσέγγισης. Αντίθετα, στην προσέγγιση του g-class εφαρμόζεται η διαδικασία Διά- ¹Εάν θεωρηθεί ότι το n είναι αρκετά μεγάλο ώστε να δημιουργείται πρόβλημα στη σελιδοποίηση μνήμης, τότε η πολυπλοκότητα αυτή αυξάνεται σημαντικά. Παρόλα αυτά, καθώς η μεταβολή θα είναι κοινή και στις δύο περιπτώσεις, η γενίκευση της προσέγγισης δεν αναιρείται.
92 5.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 75 σπασης Δεδομένων με τη συγκεκριμένη πολυπλοκότητα. Θεωρούμε ότι η υλοποίηση του επιλεγμένου αλγορίθμου κατηγοριοποίησης έχει διαθέσιμο το εκτελέσιμο αρχείο, οπότε δεν είναι αναγκαίο το βήμα Διαμόρφωσης Αλγορίθμου. Και στις δύο περιπτώσεις γίνεται χρήση του ιδίου αλγορίθμου κατηγοριοποίησης. Επομένως η χρονική πολυπλοκότητα εκτέλεσής του περιγράφεται και στις δύο περιπτώσεις από την ίδια συνάρτηση f(). Η διαφορά είναι αφενός στο πλήθος των δεδομένων εισόδου που χρησιμοποιούνται σε κάθε περίπτωση, και αφετέρου στη διαδικασία συνδυασμού των μοντέλων που γίνεται στην παράλληλη περίπτωση. Τέλος, η αξιολόγηση των αποτελεσμάτων γίνεται με την ίδια μέθοδο (πχ. με ένα νέο σύνολο δεδομένων ελέγχου), επομένως η πολυπλοκότητα είναι κοινή και στις δύο περιπτώσεις. Αν και από τον Πίνακα 5.1 φαίνεται εκ πρώτης όψεως ότι η πολυπλοκότητα της σειριακής προσέγγισης O(n + f(n) + g(p)) είναι συγκριτικά μικρότερη της προσέγγισης του αλγορίθμου g-class O(n p + f( n ) + g(p)), πρέπει να σημειωθούν τα εξής: Πρώτον, ενώ το πλήθος δεδομένων n είναι της τάξης των δεκάδων χιλιάδων, το πλήθος των p διεργασιών p στις οποίες θα διασπασθεί η διαδικασία (όπου κάθε διεργασία παράγει και ένα μοντέλο κατηγοριοποίησης) είναι της τάξης των δεκάδων (n >> p). Επιπλέον, ο χρόνος εκτέλεσης της συντριπτικής πλειοψηφίας των αλγορίθμων κατηγοριοποίησης αυξάνει (συχνά εκθετικά, καθώς πρόκειται για αλγορίθμους κυρίας μνήμης) με τον όγκο δεδομένων εισόδου, ή αλλιώς με το πλήθος n των εγγραφών εκπαίδευσης, δηλαδή f(n) >> f( n ). Τελικά, μπορεί κανείς να ισχυριστεί ότι ο καταλυτικός παράγοντας στη p σύγκριση των δύο προσεγγίσεων είναι η συνάρτηση f(), δηλαδή ο χρόνος εκτέλεσης του αλγορίθμου κατηγοριοποίησης. Το συμπέρασμα αυτό επιβεβαιώνεται και από τα πειραματικά αποτελέσματα της μεθόδου. 5.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών Επιλογή Αλγορίθμου Κατηγοριοποίησης Για την πειραματική επαλήθευση της διαδικασίας g-class χρησιμοποιήθηκαν πρωτεϊνικά δεδομένα από τη βάση δεδομένων PROSITE [HBFB99], η οποία επιτρέπει την αναπαράσταση πρωτεϊνικών αλυσίδων ως αλληλουχίες μοτίβων. Επίσης, για την κατασκευή του μοντέλου ταξινομητή επιλέχθηκε η υλοποίηση του αλγορίθμου C4.5 [Qui93], που περιλαμβάνεται στο δημοφιλές πακέτο αλγορίθμων εξόρυξης δεδομένων WEKA [WF05]. Η επιλογή έγινε μετά από εκτενή πειράματα με ένα πλήθος διαθέσιμων αλγορίθμων κατηγοριοποίησης που προσφέρει το πακέτο. Συγκεκριμένα, κάνοντας χρήση
93 76 ΚΕΦΑΛΑΙΟ 5. Ο ΑΛΓΟΡΙΘΜΟΣ G-CLASS ενός μικρού χαρακτηριστικού συνόλου δεδομένων με περίπου 1000 εγγραφές, έγινε προσπάθεια δημιουργίας ενός μοντέλου ταξινόμησης με τη διαδικασία του 10-fold stra- fied cross-valida on. Οι αλγόριθμοι που χρησιμοποιήθηκαν για αυτή τη σύγκριση είναι οι εξής: αʹ. ο Ibk [AK91] και ο KStar [CT95] από την κατηγορία των instance-based αλγορίθμων κατηγοριοποίησης, βʹ. ο NaiveBayes [JL95] από την κατηγορία των Bayesian αλγορίθμων, γʹ. ο PART [FW98], ο JRip [Coh95] και ο DecisionTable [Koh95] από τους αλγορίθμους που βασίζονται σε κανόνες, και δʹ. ο J48 [Qui93] από τα δένδρα αποφάσεων. Στον Πίνακα 5.2 παρατίθενται η επιτυχία της ταξινόμησης και ο χρόνος εκτέλεσης (με σειριακή προσέγγιση) για κάθε έναν από τους παραπάνω αλγορίθμους. Η στήλη Train αναφέρεται στο ποσοστό επιτυχίας της εκπαίδευσης ως ποσοστό % των επιτυχώς ταξινομημένων πρωτεϊνών προς τις συνολικές και η στήλη Test στο ποσοστό επιτυχίας του stra fied cross-valida on. Η τιμή Test αποτελεί το πιο αποδεκτό μέτρο της επιτυχίας της κατηγοριοποίησης, ενώ η τιμή Train μπορεί να θεωρηθεί ως ένα άνω όριό της. Για να διασφαλισθεί ότι οι μετρήσεις είναι αντιπροσωπευτικές, διενεργήθηκε μια σειρά πειραμάτων για τον κάθε αλγόριθμο, ενώ οι τιμές που αναγράφονται στον Πίνακα 5.2 είναι ο μέσος όρος τιμών (εδώ αξίζει να σημειωθεί ότι η ακρίβεια της κατηγοριοποίησης παρουσίασε ελάχιστη διακύμανση στα πειράματα του ιδίου αλγορίθμου, σε αντίθεση με το χρόνο εκτέλεσής του). Με βάση τα αποτελέσματα που προέκυψαν, επιλέχθηκε τελικά ο αλγόριθμος J48 (C4.5) καθώς εμφανίζει τη δεύτερη μεγαλύτερη ακρίβεια ταξινόμησης αλλά με πολύ καλύτερο χρόνο εκτέλεσης από τον πρώτο Επίδραση της διάσπασης των δεδομένων εισόδου στην κατανομή των πρωτεϊνών σε κατηγορίες Με βάση τον αλγόριθμο διάσπασης δεδομένων που περιγράφηκε προηγουμένως, έγινε μια προσπάθεια πειραματικού προσδιορισμού της απόδοσής του. Χρησιμοποιώντας δύο διαφορετικού μεγέθους σύνολα δεδομένων (με 5 και 70 τυχαίες κατηγορίες πρωτεϊνών, αντίστοιχα), ο αλγόριθμος εκτελέσθηκε για δύο διαφορετικά πλήθη διασπάσεων. Όπως φαίνεται και από τα διαγράμματα κατανομής του Σχήματος 5.2, η κατανομή των πρωτεϊνών σε κατηγορίες διατηρείται σε όλες τις περιπτώσεις, ενώ μειώνεται σημαντικά ο όγκος δεδομένων σε κάθε νέο υποσύνολο.
94 5.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 77 Πίνακας 5.2: Αποτελέσματα Κατηγοριοποίησης 1,000 πρωτεϊνών για διαφορετικούς αλγορίθμους Αλγόριθμος Χρόνος Εκτέλεσης (min) Ποσοστό Επιτυχίας % Training Test Ibk KStar NaiveBayes PART JRip DecisionTable J BADGE και g-class Όπως αναφέρθηκε προηγουμένως, η διαδικασία g-class χρησιμοποίησε πρωτεϊνικά δεδομένα από τη βάση δεδομένων PROSITE. Συνολικά, έγιναν δύο σειρές πειραμάτων, και στις δύο περιπτώσεις αξιοποιώντας υπολογιστικούς πόρους διαθέσιμους στο περιβάλλον Πλέγματος Υπολογιστών EGEE. Αρχικά χρησιμοποιήθηκαν τα τρία σύνολα δεδομένων για τα οποία υπάρχουν γνωστά αποτελέσματα στη βιβλιογραφία [HDAM03]. Αυτά τα σύνολα δεδομένων περιέχουν πρωτεΐνες που ανήκουν σε 10, 20 και 30 χαρακτηριστικές οικογένειες (για να υπάρχει ένα μέτρο σύγκρισης, στην PROSITE υπάρχουν καταγεγραμμένες 1100 οικογένειες πρωτεϊνών - Μάιος 2009). Εδώ θα πρέπει να σημειωθεί ότι οικογένεια είναι το σύνολο όλων των πρωτεϊνών που ανήκουν στην ίδια βιολογικά ορισμένη κατηγορία, ενώ κατηγορία είναι ένα σύνολο πρωτεϊνών που έχουν χαρακτηρισθεί με την ίδια ετικέτα. Με άλλα λόγια, όταν έχουμε το σύνολο όλων των πρωτεϊνών μιας οικογένειας, τότε αναφερόμαστε σε οικογένεια, ενώ εάν δεν περιέχονται όλες οι πρωτεΐνες, τότε αναφερόμαστε σε κατηγορία. Σε αντίθεση με τη βιβλιογραφία όμως, η προσέγγιση του g-class λαμβάνει υπόψη και τις επικαλύψεις οικογενειών που παρατηρούνται στα σύνολα δεδομένων εισόδου. Έτσι το σύνολο δεδομένων με 10 οικογένειες στην πραγματικότητα περιέχει 662 πρωτεΐνες, που ανήκουν σε 27 επικαλυπτόμενες κατηγορίες, το σύνολο δεδομένων με 20 οικογένειες περιέχει 2214 πρωτεΐνες, που ανήκουν σε 64 επικαλυπτόμενες κατηγορίες, ενώ το σύνολο δεδομένων με 30 οικογένειες περιέχει 2788 πρωτεΐνες, που ανήκουν σε 105 επικαλυπτόμενες κατηγορίες. Εδώ πρέπει να σημειωθεί ότι το τρίτο σύνολο δεδομένων (με τις 30 οικογένειες πρω-
95 78 ΚΕΦΑΛΑΙΟ 5. Ο ΑΛΓΟΡΙΘΜΟΣ G-CLASS Σχήμα 5.2: Κατανομή πρωτεϊνών σε κατηγορίες για διαφορετικό πλήθος διασπάσεων σε δύο σύνολα με 5 και 70 κατηγορίες τεϊνών) είναι το μεγαλύτερο σε μέγεθος και όγκο πληροφοριών που μπορεί να διαχειριστεί το πακέτο WEKA με τη μορφή ενός ενιαίου συνόλου δεδομένων εισόδου. Για αυτό το λόγο, έγινε μια νέα σειρά πειραμάτων με δύο νέα σύνολα δεδομένων εισόδου, με τις 5 και 10 πολυπληθέστερες οικογένειες πρωτεϊνών. Για την ακρίβεια, το σύνολο δεδομένων με τις 5 οικογένειες περιέχει συνολικά 4380 πρωτεϊνικές αλυσίδες που ανήκουν σε 66 συνολικά κατηγορίες, ενώ το σύνολο δεδομένων με τις 10 οικογένειες περιέχει 7027 σε 96 κατηγορίες. Προφανώς, τα δύο αυτά σύνολα δεδομένων δεν ήταν δυνατόν να υποστούν επεξεργασία με σειριακό τρόπο από το πακέτο WEKA. Τα αποτελέσματα των δύο αυτών σειρών πειραμάτων παρουσιάζονται στα διαγράμ-
96 5.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών [a] Accuracy for Presets class dataset 20 class dataset 30 class dataset # of Splits Time (sec) [b] Processing time for Presets 10 class dataset 20 class dataset 30 class dataset # of Splits 85 [c] Accuracy for Larger Classes 5 most populated classes 10 most populated classes [d] Processing time for Larger Classes 5 most populated classes 10 most populated classes # of Splits Time (sec) # of Splits Σχήμα 5.3: Πειραματικά Αποτελέσματα του g-class με χρήση της μεθοδολογίας BADGE [a] Ακρίβεια g-class στην περίπτωση χρήσης των τριών προκαθορισμένων συνόλων δεδομένων. [b] Συνολικός χρόνος εκτέλεσης g-class στην περίπτωση χρήσης των τριών προκαθορισμένων συνόλων δεδομένων. [c] Ακρίβεια g-class στην περίπτωση χρήσης των δύο συνόλων δεδομένων με τις πολυπληθέστερες οικογένειες πρωτεϊνών. [d] Συνολικός χρόνος εκτέλεσης g-class στην περίπτωση χρήσης των δύο συνόλων δεδομένων με τις πολυπληθέστερες οικογένειες πρωτεϊνών. ματα του Σχήματος 5.3. Είναι εμφανές ότι υπάρχει σημαντική βελτίωση στο χρόνο εκτέλεσης της διαδικασίας εκπαίδευσης, ενώ η ακρίβεια του συνολικού μοντέλου κατηγοριοποίησης παραμένει σχεδόν αμετάβλητη. Πιο συγκεκριμένα, μπορεί κανείς να εκτιμήσει ότι ο χρόνος επεξεργασίας και κατασκευής των μοντέλων ακολουθεί την καμπύλη e α p όπου το α εξαρτάται από το μέγεθος του αρχικού συνόλου δεδομένων εισόδου, ενώ το p είναι το πλήθος των διασπάσεων που γίνονται στο σύνολο αυτό. Η μικρή διακύμανση που παρουσιάζει η ακρίβεια του μοντέλου κατηγοριοποίησης μπορεί να αποδοθεί στην κατανομή που έχουν οι δευτερεύουσες (επικαλυπτόμενες) οικογένειες στα ενδιάμεσα σύνολα δεδομένων. Τέλος, για λόγους πληρότητας, στο Πλαίσιο 5.3 εμφανίζεται η εσωτερική αναπαράσταση που έχει η μέθοδος g-class μέσω της γενικευμένης μεθοδολογίας BADGE.
97 80 ΚΕΦΑΛΑΙΟ 5. Ο ΑΛΓΟΡΙΘΜΟΣ G-CLASS 1 AppType = M u l t i p l e ; 2 NumCPU = 1 0 ; 3 P r e P r o c = NaN ; 4 C l a s s = { F a m i l y } ; 5 A l g o r i t h m = weka. c l a s s i f i e r s. t r e e s. J48 ; 6 L o c a l D a t a = { P r o s i t e. a r f f } ; 7 RemoteData = { l f n : / g r i d / see / fpsom / weka. j a r } ; 8 Output = { g C l a s s _ m o d e l s. t a r. gz } ; 9 E v a l = { { c r o s s v a l i d a t i o n, 1 0 } } ; Πλαίσιο 5.3: Εσωτερική αναπαράσταση διαδικασίας g-class στη μεθοδολογία BADGE
98 Κεφάλαιο 6 Κατηγοριοποίηση Πρωτεϊνών: Ο Αλγόριθμος Proteas Σε αυτό το κεφάλαιο παρουσιάζεται ο αλγόριθμος εξόρυξης γνώσης Proteas και ο τρόπος εφαρμογής του με τη χρήση της γενικευμένης μεθοδολογίας BADGE. Ο αλγόριθμος στοχεύει στην επίλυση του προβλήματος κατηγοριοποίησης πρωτεϊνών με βάση τα χαρακτηριστικά τους σύμφωνα με την Gene Ontology. Τα δεδομένα αντλούνται από διαφορετικές και κατανεμημένες βάσεις δεδομένων, ενώ η εκπαίδευση των διαφορετικών μοντέλων γίνεται με παράλληλη επεξεργασία συγκεκριμένων συνόλων δεδομένων εισόδου. Σε αυτή την περίπτωση, ο αλγόριθμος σχεδιάστηκε εξ αρχής με βάση τη μεθοδολογία BADGE. Ο Proteas αξιοποιεί σε βάθος τεχνικές παράλληλου προγραμματισμού, αλλά ταυτόχρονα εφαρμόζεται σε Πλέγμα Υπολογιστών παρουσιάζοντας αισθητή βελτίωση στο χρόνο εκτέλεσής του. 6.1 Ο Αλγόριθμος Συνοπτικά Ο αλγόριθμος Proteas λαμβάνει αρχικά ως είσοδο ένα σύνολο DS πρωτεϊνικών δεδομένων που αποτελείται από μία πληθώρα αρχείων XML, κάθε ένα από τα οποία περιέχει πληροφορίες για την αλληλουχία μοτίβων, τους όρους Gene Ontology [Con00] [GO07] και τα διάφορα άλλα χαρακτηριστικά μίας πρωτεΐνης. Τα αρχεία αυτά προέρχονται από την υπηρεσία InterProScan [ZA01] [Int07] που χρησιμοποιείται για τη διενέργεια ερωτημάτων σχετικά με μία πρωτεΐνη σε πολλές βάσεις πρωτεϊνικών δεδομένων. Στη συνέχεια τα δεδομένα χωρίζονται σε δύο επιμέρους σύνολα που είναι ξένα μεταξύ τους: α) το σύνολο δεδομένων εκπαίδευσης DS train (Training Set) και β) το σύνολο δεδομένων ελέγχου DS test (Test Set). Το σύνολο DS train χρησιμοποιείται για τη δημιουργία ενός μοντέλου για κάθε όρο Gene Ontology, και το σύνολο DS test χρησιμοποιείται για την εκτίμηση της ακρίβειας των αποτελεσμάτων που παράγει ο αλγόριθμος. Για τη δημιουργία του μοντέλου του εκάστοτε όρου της Gene Ontology λαμβάνονται υπόψη μόνο οι πρωτεΐνες οι οποίες χαρακτηρίζονται με τον συγκεκριμένο όρο.
99 82 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS Αυτές οι εγγραφές εισάγονται σε μια διαδικασία κατασκευής ενός Δένδρου Αποδοχής Προθεμάτων (Prefix Tree Acceptor). Στη συνέχεια, το δένδρο αυτό μετατρέπεται σε ένα Στοχαστικό Πεπερασμένο Αυτόματο, το οποίο και αποτελεί και το ζητούμενο μοντέλο αναπαράστασης του δεδομένου όρου. Το τελικό στάδιο περιλαμβάνει την αξιοποίηση των μοντέλων που κατασκευάστηκαν στο προηγούμενο βήμα για την πρόβλεψη της λειτουργίας νέων πρωτεϊνών. Η πρόβλεψη γίνεται μέσω μιας διαδικασίας, η οποία δέχεται όλα τα μοντέλα και την αλληλουχία μοτίβων της υπό εξέταση πρωτεΐνης ως είσοδο, και επιστρέφει ένα σύνολο τιμών πιθανότητας, μία για κάθε όρο Gene Ontology. Εάν εφαρμοσθούν κατάλληλα κριτήρια ποιότητας, είναι εφικτό το φιλτράρισμα των αποτελεσμάτων του αλγορίθμου, ούτως ώστε στο τέλος να παραμείνουν μονάχα εκείνα που έχουν τη μεγαλύτερη πιθανότητα να είναι σωστά. Για τη μείωση του χρόνου εκτέλεσης του Proteas, η εφαρμογή υλοποιήθηκε χρησιμοποιώντας τεχνικές παράλληλου προγραμματισμού ώστε να είναι δυνατή η εκτέλεσή της σε περιβάλλον Συστοιχίας Υπολογιστών (Computer Cluster). Αξιοποιεί το μοντέλο master - slave για την κατανομή των διαφόρων εργασιών στους διαθέσιμους επεξεργαστές. Συγκεκριμένα, ο αλγόριθμος χωρίζεται σε πολλές μικρές εργασίες, τις οποίες ο επεξεργαστής-συντονιστής (master) αναλαμβάνει να προωθήσει στους επεξεργαστέςεργάτες (slave) προς εκτέλεση. Μόλις κάποιος επεξεργαστής-εργάτης ολοκληρώσει την εργασία που έχει αναλάβει, τότε στέλνει τα αποτελέσματα στον επεξεργαστή-συντονιστή και εν συνεχεία αναλαμβάνει κάποια άλλη εργασία. Όταν όλες οι διαθέσιμες εργασίες τελειώσουν, τότε το πρόγραμμα παρουσιάζει τα αποτελέσματα στον τελικό χρήστη και τερματίζεται. Το συνολικό διάγραμμα ροής του Proteas παρουσιάζεται στο Σχήμα 6.1. Η κύρια διαφορά της προσέγγισης του Proteas σε σχέση με άλλους αλγορίθμους που έχουν αναπτυχθεί τόσο από την κοινότητα Αναγνώρισης Προτύπων (Pa ern Recogni on), όσο και από την κοινότητα Μηχανικής Μάθησης (Machine Learning) είναι το γεγονός ότι γίνεται χρήση Μηχανών Πεπερασμένων Καταστάσεων για την επίλυση του προβλήματος της πρόβλεψης της λειτουργίας πρωτεϊνών. Αντιθέτως, οι υπόλοιποι αλγόριθμοι που έχουν αναπτυχθεί χρησιμοποιούν στατιστικά μοντέλα [DH73], νευρωνικά δίκτυα [Bis95], ή δέντρα αποφάσεων [Qui93] [WWHD01]. Αν και στη βιβλιογραφία υπάρχουν αναφορές με αλγορίθμους που κάνουν επίσης χρήση πεπερασμένων αυτομάτων σε αυτή την κατεύθυνση [PDM04] [PM05] [PM06], στην περίπτωση του Proteas η όλη διαδικασία εκτελείται με παράλληλο τρόπο, μειώνοντας σημαντικά το συνολικό χρόνο εκτέλεσης Σχηματισμός Δεδομένων Εισόδου Το πρώτο βήμα του αλγορίθμου αφορά τον σχηματισμό του αρχικού συνόλου πρωτεϊνικών δεδομένων, το οποίο θα πρέπει για κάθε πρωτεΐνη να περιέχει τόσο την αλληλουχία μοτίβων της, όσο και τους όρους Gene Ontology που της έχουν αποδοθεί. Για το σκοπό αυτό χρησιμοποιείται ο κωδικός UNIPROT [Apw04] της κάθε πρωτεΐνης σε
100 6.1 Ο Αλγόριθμος Συνοπτικά 83 Q63425 P57001 P23671 Q45356 P57435 PTACreation Algorithm PTACreation Algorithm PTACreation Algorithm Alergia Algorithm (PTA to FSA) Alergia Algorithm (PTA to FSA) Alergia Algorithm (PTA to FSA) Protein Classifier Protein Classifier Protein Classifier Probability that protein belongs to GO:XXXXXXX Probability that protein belongs to GO:YYYYYYY Probability that protein belongs to GO:ZZZZZZZ Σχήμα 6.1: Διάγραμμα ροής του αλγορίθμου Proteas
101 84 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS συνδυασμό με το εργαλείο InterProScan. Με τον τρόπο αυτό λαμβάνονται υπόψη όλες οι συσχετισμένες βάσεις δεδομένων πρωτεϊνικών ακολουθιών, όπως για παράδειγμα η PROSITE [HBFB99], ProDom [CGK00], PRINTS [AFL + 00], PFAM [BBD + 00]. Τελικά, το αρχικό σύνολο δεδομένων απαρτίζεται από έναν συγκεκριμένο αριθμό αρχείων XML (έξοδος του εργαλείου InterProScan), κάθε ένα από τα οποία αντιστοιχεί σε μία πρωτεΐνη, και περιέχει όλη την απαιτούμενη πληροφορία για τη σωστή λειτουργία του αλγορίθμου. Στο Πλαίσιο 6.1 παρουσιάζεται ενδεικτικά το αρχείο εισόδου που αντιστοιχεί στην πρωτεΐνη P Συγκεκριμένα, στο πρώτο τμήμα του αρχείου εμφανίζονται οι εννιά βάσεις δεδομένων οι οποίες χρησιμοποιήθηκαν για την ανάκτηση των σχετικών πληροφοριών, ενώ στη συνέχεια αναφέρονται στη γενικότερη περίπτωση σε μορφή λίστας όλες οι πληροφορίες για την εκάστοτε πρωτεΐνη. Στην περίπτωση της πρωτεΐνης P38371 εντοπίσθηκε μόνο ένα μοτίβο, το PS00013, από την βάση δεδομένων PROFILE, και το οποίο ξεκινά από τη θέση 12 της πρωτεϊνικής ακολουθίας και ολοκληρώνεται στη θέση 22.
102 1 <? xml v e r s i o n = 1. 0 encoding = ISO ?> 2 < E B I I n t e r P r o S c a n R e s u l t s xmlns = h t t p : / /www. e b i. ac. uk / schema 3 xmlns : x s i = h t t p : / /www. w3. org /2001/ XMLSchema i n s t a n c e 4 x s i : nonamespaceschemalocation = h t t p : / /www. e b i. ac. uk / schema / I n t e r P r o S c a n R e s u l t. xsd > 5 <Header > 6 <program name= I n t e r P r o S c a n v e r s i o n = 4. 0 c i t a t i o n = PMID : / > 7 < parameters > 8 < sequences t o t a l = 1 / > 9 < databases t o t a l = 9 > 10 < database number= 1 name= PRODOM type = sequences / > 11 < database number= 2 name= PRINTS type = m a t r i x / > 12 < database number= 3 name= PIR type = model / > 13 < database number= 4 name= PFAM type = model / > 14 < database number= 5 name= SMART type = model / > 15 < database number= 6 name= TIGRFAMs type = model / > 16 < database number= 7 name= PROFILE type = s t r i n g s / > 17 < database number= 8 name= PROSITE type = s t r i n g s / > 18 < database number= 9 name= SUPERFAMILY type = model / > 19 </ databases > 20 </ parameters > 21 </ Header > 22 < i n t e r p r o _ m a t c h e s > 23 < p r o t e i n i d = u n i p r o t P38371 MLPA_MYXXA l e n g t h = 236 c r c 6 4 = 6 EC63BE102CC1E70 > 24 < i n t e r p r o i d = IPR name= P r o k a r y o t i c membrane l i p o p r o t e i n l i p i d attachment s i t e 25 type = PTM > 26 <match i d = PS00013 name= PROKAR_LIPOPROTEIN dbname= PROFILE > 27 < l o c a t i o n s t a r t = 12 end= 22 s c o r e =. s t a t u s = T e v i d e n c e = P r o f i l e S c a n / > 28 </ match > 29 </ i n t e r p r o > 30 </ p r o t e i n > 31 </ i n t e r p r o _ m a t c h e s > 32 </ E B I I n t e r P r o S c a n R e s u l t s > Πλαίσιο 6.1: Αρχείο XML από το εργαλείο InterProScan για την πρωτεΐνη P Ο Αλγόριθμος Συνοπτικά 85
103 86 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS Τα δεδομένα αυτά χωρίζονται στη συνέχεια σε δύο σύνολα: το σύνολο δεδομένων εκπαίδευσης, DS train, και το σύνολο δεδομένων ελέγχου, DS test. Στο σημείο αυτό θα πρέπει να σημειωθεί ότι τα δύο αυτά σύνολα θα πρέπει να είναι ξένα μεταξύ τους, δηλαδή να ισχύει η Εξίσωση 6.1: DS train DStest = (6.1) Επίσης, για κάθε πρωτεΐνη που ανήκει στο σύνολο δεδομένων εκπαίδευσης θα πρέπει να είναι γνωστά το όνομά της, η ακολουθία μοτίβων της και οι όροι Gene Ontology που της έχουν αποδοθεί. Άλλα στοιχεία, όπως για παράδειγμα η αλληλουχία αμινοξέων της πρωτεΐνης, δεν απαιτούνται για τη λειτουργία του Proteas οπότε κατά το στάδιο προεπεξεργασίας των δεδομένων μπορούν να απαλειφθούν. Σημαντικό ρόλο παίζει ο τρόπος με τον οποίο γίνεται ο διαχωρισμός του αρχικού συνόλου δεδομένων. Η διαδικασία αυτή θα πρέπει να διασφαλίσει την ομοιογένεια μεταξύ του αρχικού συνόλου δεδομένων και των παραγόμενων υποσυνόλων, πράγμα που σημαίνει ότι κάθε όρος του Gene Ontology θα πρέπει να εκπροσωπείται ισότιμα στα δύο σύνολα DS train και DS test. Εάν ο διαχωρισμός του αρχικού συνόλου δεδομένων δεν γίνει με καθαρά τυχαίο τρόπο, τότε στα δύο παραγόμενα υποσύνολα υπάρχει η πιθανότητα κάποιος όρος να υπερεκπροσωπείται έναντι κάποιων άλλων. Αυτό θα καταστήσει ελλειματικά και ανεπαρκή τα μοντέλα που θα παραχθούν για τους όρους που υποεκπροσωπούνται, οπότε η αξιοπιστία της μεθόδου θα μειωθεί σημαντικά. Το τελικό βήμα στη διαδικασία σχηματισμού των δεδομένων εισόδου είναι η περαιτέρω διαίρεση του συνόλου εκπαίδευσης σε μικρά υποσύνολα, κάθε ένα από τα οποία έχει το εξής χαρακτηριστικό: οι πρωτεΐνες pr i που το απαρτίζουν έχουν χαρακτηρισθεί με ένα συγκεκριμένο όρο Gene Ontology g j. Άρα λοιπόν για κάθε όρο g j, j = 1,..., m που υπάρχει στην Οντολογία σχηματίζεται και το αντίστοιχο σύνολο δεδομένων GO j, το οποίο περιέχει μονάχα εκείνες τις πρωτεΐνες pr i που ανήκουν στο DS train και τους έχει αποδοθεί ο συγκεκριμένος όρος g j, δηλαδή GO j = {pr i DS train : pr i g j }. Δεδομένου ότι μία πρωτεΐνη κατά κανόνα χαρακτηρίζεται από πολλούς όρους Gene Ontology, συνεπάγεται ότι μπορεί ταυτόχρονα να ανήκει σε παραπάνω από ένα σύνολα δεδομένων, δηλαδή pr i GO 1, GO 2,..., GO k. Τέλος, καθώς το ίδιο σύνολο δεδομένων μπορεί να χρησιμοποιηθεί αυτούσιο για τη διεξαγωγή των διαφόρων πειραμάτων, είναι λογικό να ισχυρισθεί κανείς ότι το στάδιο αυτό μπορεί να εκτελεσθεί μία φορά και στη συνέχεια να ανανεώνεται περιοδικά Κατασκευή Μοντέλων Η διαδικασία κατασκευής των μοντέλων στον Proteas μπορεί να αναλυθεί στη διαδοχική χρήση των δύο παρακάτω αλγορίθμων για κάθε ένα από τα υποσύνολα των δεδομένων εκπαίδευσης:
104 6.1 Ο Αλγόριθμος Συνοπτικά Αλγόριθμος κατασκευής δένδρου αποδοχής προθεμάτων - PTACrea on Ο αλγόριθμος αυτός χρησιμοποιεί τα δεδομένα εισόδου για να κατασκευάσει ένα δένδρο αποδοχής προθεμάτων. Για το σκοπό αυτό εξετάζεται κάθε μία πρωτεΐνη που ανήκει στα δεδομένα εισόδου και αρχικά εξάγεται η ακολουθία των μοτίβων της. Στη συνέχεια δημιουργείται ένας κόμβος που αποτελεί τη ρίζα του δένδρου αποδοχής προθεμάτων και στη συνέχεια προστίθεται κάθε μία από τις ακολουθίες μοτίβων ξεχωριστά. Όταν πλέον έχουν προστεθεί οι ακολουθίες μοτίβων από όλες τις πρωτεΐνες του συγκεκριμένου συνόλου εισόδου, τότε θεωρείται ότι έχει τερματίσει η διαδικασία κατασκευής του δένδρου, το οποίο παραδίδεται και ως είσοδος στον επόμενο αλγόριθμο για περαιτέρω επεξεργασία. 2. Αλγόριθμος κατασκευής στοχαστικού πεπερασμένου αυτομάτου - Alergia Ο αλγόριθμος Alergia [CO94] λαμβάνει ως είσοδο ένα δένδρο αποδοχής προθεμάτων και στόχος του είναι η μείωση της περιττής πληροφορίας που υπάρχει μέσα στο δένδρο, ούτως ώστε να προκύψει ένα συμπαγές και στατιστικά ισοδύναμο μοντέλο. Η μείωση της περιττής πληροφορίας επιτυγχάνεται μέσα από τη συγχώνευση δύο η περισσοτέρων κόμβων που θεωρούνται στατιστικά ισοδύναμοι. Στο τέλος, ο αλγόριθμος επιστρέφει ως έξοδο ένα Στοχαστικό Αυτόματο Πεπερασμένων Καταστάσεων (Stochas c Finite State Automaton), το οποίο αποτελεί ουσιαστικά και το ζητούμενο μοντέλο. Η συνολική διαδικασία παρουσιάζεται στο Σχήμα 6.2. Για την καλύτερη κατανόηση των χαρακτηριστικών και της λειτουργίας ενός δένδρου αποδοχής προθεμάτων, ισχύει ο εξής ορισμός της έννοιας του προθέματος: Πρόθεμα (Prefix) μιας ακολουθίας χαρακτήρων T = t 1...t n θεωρείται οποιαδήποτε ακολουθία χαρακτήρων ˆT = t 1...t m όπου m < n. Ένα πρόθεμα λέγεται κανονικό εάν δεν έχει ισάριθμους χαρακτήρες σε σχέση με την αρχική ακολουθία χαρακτήρων και επίσης δεν είναι κενό. Άρα λοιπόν, για ένα κανονικό πρόθεμα θα πρέπει να ισχύει: 0 < m < n [DPG06] [LP97]. Εάν θεωρήσουμε ένα σύνολο συμβολοσειρών, τότε είναι δυνατή η δημιουργία ενός αντίστοιχου συνόλου προθεμάτων. Κάθε ένα από αυτά τα προθέματα θα έχει μήκος μεγαλύτερο του μηδενός και μικρότερο ή ίσο με το μήκος της συμβολοσειράς από την οποία προήλθε. Στη συνέχεια, βάσει των προθεμάτων, είναι δυνατή η δημιουργία ενός πεπερασμένου αυτομάτου που θα χρησιμεύει στην αναγνώριση των αρχικών συμβολοσειρών. Αυτό το πεπερασμένο αυτόματο ονομάζεται Δένδρο Αποδοχής Προθεμάτων (PTA - Prefix Tree Acceptor). Ο αλγόριθμος δημιουργίας του Δένδρου είναι σχετικά απλός και λειτουργεί με τον εξής τρόπο: Αρχικά λαμβάνει ως είσοδο ένα σύνολο πρωτεϊνών και για κάθε μία από
105 88 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS Βάση Δεδομένων Ν πρωτεϊνών με γνωστά μοτίβα και γνωστές οικογένειες Σύνολο δεδομένων εκπαίδευσης με Ν Τ πρωτεΐνες Σύνολο δεδομένων εκπαίδευσης με Τ < Ν πρωτεΐνες PTACreator Algorithm Κατασκευάζει το Δένδρο Αποδοχής Προθεμάτων PTA Rules ProbExtractor Algorithm Υπολογίζει Πιθανότητες από FSA Σύγκριση πραγματικής κατάταξης πρωτεϊνών με κατάταξη συστήματος Απόδοση Συστήματος ALERGIA Algorithm Μετατρέπει ένα PTA σε FSA FSA Σχήμα 6.2: Κατασκευή μοντέλων με τη μέθοδο Proteas αυτές εξετάζει την ακολουθία μοτίβων της και την εισάγει στο δένδρο, δημιουργώντας καινούργιους κόμβους και κλάδους όπου αυτό είναι απαραίτητο. Εάν κατά την εισαγωγή μιας ακολουθίας διαπιστωθεί ότι κάποια μετάβαση υπάρχει, τότε την χρησιμοποιεί και δεν δημιουργεί μία καινούργια. Ο ψευδοκώδικας του αλγορίθμου αυτού παρουσιάζεται στο Πλαίσιο 6.2. Το επόμενο βήμα είναι η μετατροπή των Δένδρων Αποδοχής Προθεμάτων σε Στοχαστικά Πεπερασμένα Αυτόματα. Η μετατροπή αυτή γίνεται με χρήση του αλγορίθμου Alergia [CO94] [CO99]. Πριν γίνει όμως μια συνοπτική περιγραφή του αλγορίθμου, ακολουθεί ο ορισμός της έννοιας του πεπερασμένου αυτομάτου. Ένα Αιτιοκρατικό Πεπερασμένο Αυτόματο (DFSA - Determinis c Finite State Automaton) είναι μια πεντάδα της μορφής M = (K, Σ, δ, s, F ) όπου: K είναι ένα πεπερασμένο σύνολο καταστάσεων Σ είναι ένα αλφάβητο δ είναι η συνάρτηση μετάβασης μεταξύ καταστάσεων, δηλαδή δ : K Σ K
106 6.1 Ο Αλγόριθμος Συνοπτικά 89 1 a l g o r i t h m P T A C r e a t i o n 2 i n p u t : 3 S p : p r o t e i n m o t i f sequence d a t a s e t 4 output : 5 P T A : the f i n a l PTA 6 begin 7 i n i t i a l i z e P T A ( s e t r o o t node ) 8 do ( p r o t e i n pr S p ) 9 s e t currentnode = P T A ( r o o t ) 10 do ( m o t i f s m pr ) 11 i f ( node = P T A ( currentnode, m ) ) 12 then 13 currentnode = P T A ( currentnode, m ) 14 e l s e 15 add s t a t e = P T A ( currentnode, m ) 16 currentnode = s t a t e 17 end i f 18 end do 19 end do 20 end a l g o r i t h m P T A C r e a t i o n Πλαίσιο 6.2: Ψευδοκώδικας Αλγορίθμου Κατασκευής PTA s K είναι η αρχική κατάσταση F K είναι το σύνολο των τελικών καταστάσεων Διαισθητικά μπορεί κανείς να πει ότι ένα αιτιοκρατικό πεπερασμένο αυτόματο είναι ένας υπολογιστής που δέχεται ως είσοδο μια συμβολοσειρά και στην έξοδο παράγει μια ένδειξη κατά πόσο η συμβολοσειρά αυτή είναι αποδεκτή ή όχι. Η συμβολοσειρά θα πρέπει να αποτελείται από χαρακτήρες που ανήκουν στο αλφάβητο Σ. Το αυτόματο εξετάζει στη συμβολοσειρά που του δίνεται ένα χαρακτήρα τη φορά. Ανάλογα με τον χαρακτήρα που διαβάζεται, το αυτόματο μεταβαίνει σε μια νέα κατάσταση από το σύνολο K των δυνατών καταστάσεων. Οι κανόνες βάσει των οποίων γίνονται οι διάφορες μεταβάσεις κωδικοποιούνται στη συνάρτηση μετάβασης (transi on func on) δ. Θα πρέπει στο σημείο αυτό να σημειωθεί ότι η κάθε μετάβαση εξαρτάται αποκλειστικά και μόνο από την τρέχουσα κατάσταση στην οποία βρίσκεται το αυτόματο και από το σύμβολο που μόλις διάβασε. Η διαδικασία ανάγνωσης συμβόλων και μετάβασης σε νέες καταστάσεις επαναλαμβάνεται διαρκώς έως ότου αναγνωσθεί και το τελευταίο σύμβολο της συμβολοσειράς εισόδου. Εάν η κατάσταση στην οποία βρίσκεται τότε ανήκει στο σύνολο F, τότε και μόνο τότε η συμβολοσειρά θεωρείται αποδεκτή. Τα Στοχαστικά Πεπερασμένα Αυτόματα διαφέρουν από τα απλά Αιτιοκρατικά στο γεγονός ότι διαθέτουν πιθανότητα μετάβασης από μία κατάσταση σε κάποια επόμενη, δηλαδή μερικές μεταβάσεις κατα-
107 90 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS στάσεων ενδέχεται να είναι πιο πιθανές σε σχέση με τις άλλες. Ο αλγόριθμος Alergia χρησιμοποιείται στον Proteas για την μετατροπή των Δένδρων Αποδοχής Προθεμάτων σε Στοχαστικά Αιτιοκρατικά Πεπερασμένα Αυτόματα. Το αυτόματο που παράγεται μέσα από αυτή τη διαδικασία εκφράζει μία γενικευμένη άποψη της δομής των πρωτεϊνών (όσον αφορά την ακολουθία μοτίβων τους), και δεν αποτελεί μια απλή απεικόνιση του συνόλου δεδομένων εκπαίδευσης. Άρα μπορεί να χρησιμοποιηθεί ως μοντέλο που περιγράφει επαρκώς τις πρωτεΐνες που χαρακτηρίζονται με κάποιον συγκεκριμένο όρο Gene Ontology. Η λειτουργία του αλγορίθμου βασίζεται στη συστηματική συγχώνευση κόμβων - καταστάσεων του Δένδρου Αποδοχής Προθεμάτων, όταν αυτοί θεωρούνται στατιστικά ισοδύναμοι. Σύμφωνα με τη θεωρία του Alergia, δύο καταστάσεις είναι ισοδύναμες μόνο εάν έχουν τις ίδιες πιθανότητες μετάβασης για κάθε σύμβολο και οι επόμενες καταστάσεις είναι επίσης ισοδύναμες. Δηλαδή, δύο καταστάσεις S i και S j θεωρούνται ισοδύναμες εάν για κάθε σύμβολο m ισχύει: p i (m) = p j (m) S i S j δ m (i) δ m (j) m (6.2) Συμπερασματικά λοιπόν, ο αλγόριθμος Alergia λαμβάνει ως είσοδο ένα Δένδρο Αποδοχής Προθεμάτων και συγκρίνει τις καταστάσεις του ανά ζεύγη. Εάν δύο καταστάσεις θεωρηθούν στατιστικά ισοδύναμες, σύμφωνα με όσα ειπώθηκαν προηγουμένως, τότε συγχωνεύονται. Η διαδικασία αυτή συνεχίζει έως ότου ολοκληρωθούν όλοι οι έλεγχοι. Στο τέλος παράγεται ένα Στοχαστικό Πεπερασμένο Αυτόματο, το οποίο αποτελεί και το ζητούμενο μοντέλο. Προφανώς, είναι κατανοητό ότι οι διαδικασίες από υποσύνολο δεδομένων έως κατασκευή μοντέλου είναι ανεξάρτητες μεταξύ τους και επομένως μπορούν να εκτελεσθούν παράλληλα Πρόβλεψη Λειτουργίας Πρωτεϊνών Στο σημείο αυτό του αλγορίθμου έχουν πλέον δημιουργηθεί όλα τα απαιτούμενα μοντέλα, ένα για κάθε όρο της Gene Ontology. Το στάδιο αυτό έχει ως στόχο την αξιοποίηση αυτών των μοντέλων για την πρόβλεψη της λειτουργίας άγνωστων πρωτεϊνών. Επιγραμματικά η λειτουργία αυτού του σταδίου έχει ως εξής: Για κάθε πρωτεΐνη pd i υπό εξέταση καθορίζεται αρχικά η ακολουθία pm i =< m k > k 1 μοτίβων της και υπολογίζονται όλες οι υποακολουθίες pm s i =< m kj > kj 1 όπου k j < k j+1, j 1 αυτής της ακολουθίας. Στη συνέχεια οι υποακολουθίες pm s i χρησιμοποιούνται ως είσοδος σε κάθε μοντέλο που έχει κατασκευασθεί και προσδιορίζεται εκείνη η υποακολουθία που για το δεδομένο μοντέλο δίνει τη μέγιστη πιθανότητα. Μετά το πέρας αυτής της διαδικασίας ο χρήστης έχει στη διάθεσή του για κάθε μοντέλο Gene Ontology μία τιμή πιθανότητας,
108 6.2 Πολυπλοκότητα Αλγορίθμου Proteas 91 1 a l g o r i t h m P r o t e a s C l a s s i f i e r 2 i n p u t : 3 pr[ ] : p r o t e i n m o t i f sequence 4 S m : s e t of SFSA models 5 output : 6 P : p r o b a b i l i t y v e c t o r 7 begin 8 do ( m S m ) 9 s e t P (m) = 1 10 do ( permutation perm i of pr ) 11 i f ( p r o b a b i l i t y (S m, perm i ) > P (m) ) 12 then 13 P (m) = (S m, perm i ) 14 end i f 15 end do 16 end do 17 end a l g o r i t h m P r o t e a s C l a s s i f i e r Πλαίσιο 6.3: Ψευδοκώδικας Αλγορίθμου ProteasClassifier οπότε εφαρμόζοντας ειδικά κριτήρια και φίλτρα μπορεί να επιλέξει εκείνα τα μοντέλα που παρουσιάζουν τη μεγαλύτερη πιθανότητα να είναι σωστά. Ο αλγόριθμος που εκτελεί αυτή τη διαδικασία παρουσιάζεται στο Πλαίσιο 6.3. Αρχικά υπολογίζονται όλες οι υποακολουθίες της υπό εξέτασης πρωτεϊνικής ακολουθίας. Στη συνέχεια, για κάθε συνδυασμό υποακολουθίας και μοντέλου Gene Ontology γίνεται χρήση των εξισώσεων υπολογισμού πιθανότητας ακολουθίας σε στοχαστικό αυτόματο [Hin02] για την εκτίμηση της σχέσης του εκάστοτε όρου της οντολογίας με την αρχική ακολουθία. Τελικά, στην έξοδο επιστρέφονται N τιμές πιθανότητας, όπου N είναι ίσο με τον αριθμό των μοντέλων που εξετάσθηκαν. Το σημαντικό σε αυτή τη διαδικασία είναι για άλλη μία φορά η ανεξαρτησία μεταξύ της κάθε διεργασίας. Αυτό σημαίνει ότι ο έλεγχος κάθε πρωτεϊνικής ακολουθίας μπορεί να γίνεται παράλληλα με τις υπόλοιπες. 6.2 Πολυπλοκότητα Αλγορίθμου Proteas Καθώς ο αλγόριθμος του Proteas σχεδιάσθηκε εξαρχής έχοντας υπόψη την υλοποίησή του με τεχνικές παράλληλου προγραμματισμού, δεν έχει νόημα να αναφερόμαστε σε σειριακή και παράλληλη προσέγγιση. Παρόλα αυτά, μπορεί να γίνει ανάλυση της πολυπλοκότητάς του χρησιμοποιώντας το μοντέλο ανάλυσης της γενικευμένης μεθοδολογίας BADGE, όπως φαίνεται στον Πίνακα 6.1. Στην ανάλυση της πολυπλοκότητας χρησιμοποιούνται οι εξής συμβολισμοί:
109 92 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS n είναι το πλήθος πρωτεϊνικών αλληλουχιών, g είναι το πλήθος των μοντέλων Gene Ontology, m είναι το πλήθος των μοτίβων σε μία συγκεκριμένη ακολουθία, και I είναι το πλήθος όλων των δυνατών διαθέσιμων μοτίβων. Πίνακας 6.1: Αρχική Ανάλυση Πολυπλοκότητας στον Proteas Βήμα Πολυπλοκότητα Ανάκτηση Δεδομένων O(n) Προεπεξεργασία Δεδομένων O(n g) Διαμόρφωση Αλγορίθμου - Τύπος Εφαρμογής O(n m I) + O(f(n 3 )) Φάση Αξιολόγησης O(n g (2 m 1) e m ) Σύνολο O (n (g + m I + g (2 m 1) e m )) + O (f(n 3 )) Στη συνέχεια θα γίνει μια πιο λεπτομερής ανάλυση της πολυπλοκότητας για κάθε βήμα. Όσον αφορά την ανάκτηση και προεπεξεργασία των δεδομένων (δηλαδή τη λήψη n δεδομένων μέσω του εργαλείου InterProScan και τη διάσπασή τους σε ένα πλήθος μικρότερων συνόλων δεδομένων, όσα και οι όροι g στην Gene Ontology), ο υπολογισμός της πολυπλοκότητας είναι προφανής και ίσος με O(n) και O(n g) αντίστοιχα. Για την κατασκευή του Δένδρου Αποδοχής Προθεμάτων, έστω ότι στο σύνολο δεδομένων που εξετάζουμε υπάρχουν n πρωτεΐνες, κάθε πρωτεΐνη έχει m μοτίβα στην ακολουθία της ενώ υπάρχουν συνολικά I διαφορετικά μοτίβα. Με βάση τον ψευδοκώδικα του Πλαισίου 6.2, η πολυπλοκότητα του αλγορίθμου είναι ίση με: O theory P T ACreator = O(n m I) (6.3) Παρόλα αυτά όμως μπορούμε να κάνουμε τις εξής αποδοχές: Το πλήθος των μοτίβων που διαθέτει η αλυσίδα κάθε πρωτεΐνης είναι συγκριτικά πολύ μικρότερο τόσο του πλήθους των πρωτεϊνών όσο και του συνολικού πλήθους των μοτίβων. Επίσης, η συντριπτική πλειοψηφία των πρωτεϊνικών ακολουθιών μπορεί να αναπαρασταθεί με ακολουθία μοτίβων που το μήκος της δεν ξεπερνά ένα σταθερό αριθμό α (πειραματικά φάνηκε ότι α = 20), και επομένως μπορεί να αντιμετωπισθεί ως ένας σταθερός αριθμός. Επιπλέον, ο αριθμός των διαθέσιμων μοτίβων I μεταβάλλεται σπάνια (συνήθως σε
110 6.2 Πολυπλοκότητα Αλγορίθμου Proteas 93 κάθε σημαντική ενημέρωση των σχετικών Βάσεων Δεδομένων), οπότε μπορεί να θεωρηθεί επίσης ως σταθερός αριθμός. Αυτές οι δύο παραδοχές οδηγούν στο συμπέρασμα ότι η πολυπλοκότητα του αλγορίθμου εξαρτάται γραμμικά από τον αριθμό των πρωτεϊνών που λαμβάνονται υπόψη κατά τη δημιουργία του Δένδρου Αποδοχής Προθεμάτων, δηλαδή: O P T ACreator = O(n) (6.4) Ο αλγόριθμος Alergia έχει μελετηθεί σε βάθος τόσο θεωρητικά όσο και πειραματικά [CO94]. Διαπιστώνεται λοιπόν ότι στη χειρότερη περίπτωση η πολυπλοκότητα είναι πολυωνυμική συνάρτηση τρίτου βαθμού σε σχέση με το πλήθος καταστάσεων του αρχικού Δένδρου Αποδοχής Προθεμάτων, κάτι που είναι αναμενόμενο δεδομένου ότι πρόκειται για έναν αναδρομικό αλγόριθμο. Με άλλα λόγια, καθώς το πλήθος καταστάσεων είναι συνάρτηση του πλήθους των πρωτεϊνικών ακολουθιών που δόθηκαν ως είσοδος, η πολυπλοκότητα εκτιμάται ότι είναι: O theory Allergia = O(f(n3 )) (6.5) Παρόλα αυτά, στην πράξη η πολυπλοκότητα του αλγορίθμου εμφανίζεται να είναι αυστηρά γραμμική σε σχέση με το μέγεθος του αρχικού Δένδρου, με άλλα λόγια, η πολυπλοκότητα του αλγορίθμου Alergia στην πράξη είναι ίση με: O Allergia = O(f(n)) (6.6) Τέλος, η εξαγωγή πιθανοτήτων συσχέτισης μιας πρωτεϊνικής ακολουθίας με έναν όρο της Gene Ontology είναι η πιο χρονοβόρος διαδικασία στον Proteas. Αρχικά για κάθε πρωτεΐνη n παράγονται όλες οι δυνατές υποακολουθίες (και μεταθέσεις υποακολουθιών) της αλληλουχίας μοτίβων της, δηλαδή εκτελούνται n (2 m 1) επαναλήψεις. Στη συνέχεια, σε κάθε επανάληψη γίνεται ο υπολογισμός της πιθανότητας για τη συγκεκριμένη υποακολουθία για κάθε όρο g της Gene Ontology η οποία έχει πολυπλοκότητα O(e m ) [Hin02]. Επομένως, η συνολική πολυπλοκότητα αυτού του βήματος είναι ίση με: O theory Classifier = O(n (2m 1) g e m ) (6.7) Ακόμα και με τις παραδοχές ότι m και g είναι κατά προσέγγιση σταθεροί αριθμοί, η πολυπλοκότητα εξακολουθεί να είναι αρκετά μεγάλη. Καθώς όμως η κάθε διεργασίαεπανάληψη είναι εντελώς ανεξάρτητη από τις υπόλοιπες, όλη η διαδικασία μπορεί να εκτελεσθεί παράλληλα σε p διεργασίες. Επομένως, στην πράξη η τελική πολυπλοκότητα αυτού του βήματος είναι: O Classifier = O( n em ) (6.8) p
111 94 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS Αντικαθιστώντας τις πολυπλοκότητες του Πίνακα 6.1 με τις παραπάνω εκφράσεις προκύπτει ο Πίνακας 6.2. Πίνακας 6.2: Πολυπλοκότητα του Proteas Βήμα Ανάκτηση Δεδομένων Πολυπλοκότητα O(n) Προεπεξεργασία Δεδομένων O(n g) Διαμόρφωση Αλγορίθμου - Τύπος Εφαρμογής Φάση Αξιολόγησης Σύνολο O(n) + O(f(n)) O( n em p ) (n g + f(n) + n em p ) 6.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών Στατιστικά Στοιχεία των Δεδομένων Για όλα τα πειράματα που έγιναν χρησιμοποιήθηκαν 39,211 πρωτεϊνικές ακολουθίες, οι οποίες μπορούν να ενταχθούν σε 1,712 όρους της Gene Ontology. Κατά συνέπεια, κατασκευάστηκαν 1,712 μοντέλα, ένα για κάθε όρο, και η διαδικασία κατηγοριοποίησης κάθε νέας πρωτεΐνης γίνεται με σύγκριση και με τα 1,712 μοντέλα και την εξαγωγή ισάριθμων τιμών πιθανότητας. Στο Σχήμα 6.3 παρουσιάζεται ένα διάγραμμα που απεικονίζει το ποσοστό των πρωτεϊνικών αλυσίδων σε σχέση με το πλήθος μοτίβων που περιγράφουν την κάθε μία. Η τιμή για τα 50 μοτίβα εμπεριέχει και όλες τις τιμές άνω των 50 μοτίβων, για αυτό το λόγο παρουσιάζει αυτή την αύξηση σε σχέση με τις γειτονικές τιμές. Από το διάγραμμα μπορεί κανείς να παρατηρήσει ότι η συντριπτική πλειοψηφία των πρωτεϊνών μπορούν να αναπαρασταθούν με ακολουθίες μοτίβων που το μήκος τους δεν ξεπερνά τα 20 μοτίβα. Μια πιο ξεκάθαρη εικόνα που ενισχύει αυτή την παρατήρηση δίνεται στο Σχήμα 6.4, όπου παρουσιάζεται το διάγραμμα του συγκεντρωτικού ποσοστού των πρωτεϊνών σε σχέση με το πλήθος των μοτίβων. Από το διάγραμμα αυτό φαίνεται ότι περίπου το 9% των πρωτεϊνών έχει πάνω από 20 μοτίβα, ενώ το 51% διαθέτει 8 ή λιγότερα μοτίβα. Με βάση τις δύο παραπάνω παρατηρήσεις, σε όλα τα πειράματα τα οποία έγιναν χρησιμοποιήθηκαν πρωτεϊνικές αλυσίδες οι οποίες εμφανίζουν το πολύ έως 8 μοτίβα.
112 6.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 95 Σχήμα 6.3: Πλήθος πρωτεϊνών σε σχέση με το πλήθος των μοτίβων Σχήμα 6.4: Συγκεντρωτικό Ποσοστό πρωτεϊνών σε σχέση με το πλήθος μοτίβων Φυσικά ο Proteas λειτουργεί για οποιονδήποτε αριθμό μοτίβων, αλλά η επιβολή αυτού του ορίου κρίθηκε απαραίτητη ούτως ώστε να μπορούν να διεξαχθούν ομαλά τα
113 96 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS διάφορα πειράματα Εκπαίδευση και Κατασκευή Μοντέλων Όπως αναφέρθηκε και προηγούμενα, η διαδικασία κατασκευής των συνόλων δεδομένων εισόδου, αν και εκτελείται παράλληλα, δεν είναι αναγκαίο να επιτελείται σε κάθε εκτέλεση της εφαρμογής. Το επόμενο βήμα είναι ο έλεγχος παραλληλοποίησης της διαδικασίας κατασκευής των μοντέλων. Σύμφωνα με την ανάλυση της πολυπλοκότητας που έγινε στην προηγούμενη ενότητα, αναμένεται ο χρόνος κατασκευής να είναι γραμμικός σε σχέση με το πλήθος των δεδομένων εισόδου. Στο Σχήμα 6.5 παρουσιάζονται σχηματικά οι χρόνοι κατασκευής όλων των δυνατών μοντέλων για διαφορετικό πλήθος πρωτεϊνών στο σύνολο δεδομένων εισόδου. Σχήμα 6.5: Χρόνος Κατασκευής μοντέλων για διαφορετικό αριθμό πρωτεϊνών Από το διάγραμμα φαίνεται ότι για ολόκληρο το σύνολο των διαθέσιμων πρωτεϊνών (39,211) χρειάστηκαν κατά προσέγγιση 322 δευτερόλεπτα (δηλαδή 5 λεπτά και 22 δευτερόλεπτα) για την επεξεργασία και κατασκευή 1,712 μοντέλων, ένα για κάθε όρο Gene Ontology. Κατά συνέπεια είναι ασφαλής η υπόθεση ότι στο στάδιο αυτό του Proteas δεν είναι απαραίτητη η χρήση πολλαπλών επεξεργαστών, ακριβώς λόγω του γεγονότος ότι το χρονικό διάστημα που χρειάζεται για την ολοκλήρωση της διαδικασίας κατασκευής των μοντέλων είναι πολύ μικρό. Στην πραγματικότητα, η χρήση πολλών επεξεργαστών μπορεί να επιβραδύνει την εκτέλεση του προγράμματος αντί να την επιταχύνει, διότι στην περίπτωση αυτή απαιτείται επιπρόσθετος χρόνος για την επικοινωνία μεταξύ των επεξεργαστών (π.χ. ανταλλαγή μηνυμάτων). Με βάση αυτές τις παρατηρήσεις, ο αλγόριθμος Proteas εκτελέσθηκε εξ ολοκλήρου σε Πλέγμα Υπολογιστών, με κάποιες διαφοροποιήσεις ανάλογα με το εκάστοτε βήμα. Το
114 6.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 97 βήμα κατασκευής συνόλων δεδομένων εισόδου εκτελέσθηκε μία μόνο φορά, αξιοποιώντας πολλαπλούς επεξεργαστές παράλληλα. Το βήμα κατασκευής μοντέλων εκτελείται σε κάθε περίπτωση, αλλά αξιοποιώντας ένα μόνο επεξεργαστή του Πλέγματος, ενώ το τελικό βήμα εκτελείτε κάθε φορά παράλληλα σε πολλαπλούς επεξεργαστές BADGE και Proteas Ο αλγόριθμος Proteas εφαρμόσθηκε σε πρωτεϊνικά δεδομένα από όλες τις διαθέσιμες Βάσεις Δεδομένων (σύνολο 13, Μάιος 2009) που είναι συνδεδεμένες με το εργαλείο InterProScan (ProDom, PRINTS, PIR, PFAM, SMART, TIGRFAMs, PROFILE, PROSITE, SUPERFAMILY, SIGNALP, TMHMM, PANTHER, GENE3D). Έγινε μία σειρά πειραμάτων για ένα μεγάλο σύνολο δεδομένων 20,000 πρωτεϊνικών ακολουθιών αξιοποιώντας υπολογιστικούς πόρους διαθέσιμους στο περιβάλλον Πλέγματος Υπολογιστών EGEE. Χρησιμοποιώντας τη γενικευμένη μεθοδολογία BADGE για τη διαμόρφωση και την υποβολή των εργασιών στο Πλέγμα Υπολογιστών, έγινε ο πειραματικός έλεγχος τόσο της ακρίβειας κατηγοριοποίησης του Proteas (Σχήμα 6.7) όσο και της απόδοσής του σε χρόνο εκτέλεσης (Σχήμα 6.6). Σε κάθε περίπτωση χρησιμοποιήθηκε το ίδιο σύνολο δεδομένων εισόδου, αλλά διαφορετικά ποσοστά στα σύνολα δεδομένων εκπαίδευσης και ελέγχου. Τέλος, το κάθε πείραμα εκτελέσθηκε δέκα φορές και στα διαγράμματα παρουσιάζεται ο μέσος όρος των τιμών που προέκυψαν από τις μετρήσεις Execution Time 1 CPU 4 CPU 8 CPU 16 CPU 10 5 Time (sec) Test Set (%) Σχήμα 6.6: Χρόνος Εκτέλεσης του Proteas Από τα διαγράμματα είναι εμφανές ότι υπάρχει σημαντικό κέρδος στο χρόνο εκτέλεσης της εφαρμογής, ιδιαίτερα στις περιπτώσεις όπου γίνεται χρήση 8 και 16 CPUs, ενώ η
115 98 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS ακρίβεια στην πρόβλεψη της λειτουργίας των πρωτεϊνών του συνόλου ελέγχου παρουσιάζει μικρές διακυμάνσεις. Το διάγραμμα της Εικόνας 6.6 παρουσιάζει το χρόνο που απαιτήθηκε για την κατηγοριοποίηση όλων των πρωτεϊνών που ανήκουν στο σύνολο δεδομένων ελέγχου. Είναι προφανές ότι όσο μεγαλύτερο είναι το σύνολο ελέγχου τόσο περισσότερο χρόνο απαιτεί η εφαρμογή για τη κατηγοριοποίηση των πρωτεϊνών. Παρόλα αυτά σημειώνεται σημαντική βελτίωση του χρόνου κατηγοριοποίησης όταν η εφαρμογή αξιοποιεί περισσότερους του ενός επεξεργαστές. Συγκεκριμένα, ο χρόνος εκτέλεσης των πειραμάτων στην περίπτωση των 8 επεξεργαστών είναι κατά προσέγγιση ο μισός σε σχέση με το χρόνο που απαιτήθηκε σε 4 επεξεργαστές. Παρόμοια σχέση εμφανίζεται μεταξύ των πειραμάτων σε 16 και 8 επεξεργαστές αντίστοιχα Accuracy Plot 1 CPU 4 CPU 8 CPU 16 CPU 0.8 Accuracty Test Set (%) Σχήμα 6.7: Ακρίβεια πρόβλεψης μοντέλων του Proteas Η μέση τιμή της ακρίβειας κατηγοριοποίησης για κάθε αναλογία Συνόλου Εκπαίδευσης προς Σύνολο Ελέγχου παρουσιάζεται στο διάγραμμα του Σχήματος 6.7. Παρατηρείται πολύ μικρή διακύμανση της τιμής της ακρίβειας με τη μεταβολή του ποσοστού, με τις τιμές να κυμαίνονται μεταξύ και Το γεγονός ότι η ακρίβεια παραμένει πρακτικά σταθερή για διάφορες αναλογίες Εκπαίδευσης / Ελέγχου υποδεικνύει ότι η μέθοδος του Proteas παράγει εξαιρετικά ακριβή αποτελέσματα, ακόμα και όταν το μέγεθος του συνόλου εκπαίδευσης είναι συγκριτικά πολύ μικρότερο του συνόλου ελέγχου. Επομένως μπορεί κανείς να ισχυρισθεί ότι ο αλγόριθμος μπορεί να δίνει ικανοποιητικά αποτελέσματα ακόμα και σε περιπτώσεις σχετικής έλλειψης πληροφορίας. Τέλος, για λόγους πληρότητας, στο Πλαίσιο 6.4 εμφανίζεται η εσωτερική αναπαράσταση που έχει η μέθοδος Proteas μέσω της γενικευμένης μεθοδολογίας BADGE. Αυτή
116 6.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 99 1 AppType = MPI ; 2 NumCPU = 1 6 ; 3 P r e P r o c = NaN ; 4 C l a s s = { GO } ; 5 A l g o r i t h m = l f n : / g r i d / see / fpsom / p r o t e a s ; 6 L o c a l D a t a = { NaN } ; 7 RemoteData = { l f n : / g r i d / see / fpsom / i n p u t _ d a t a. t a r. j a r } ; 8 Output = { Proteas_models. t a r. gz } ; 9 E v a l = { { t e s t _ r a t i o, 2 0 } } ; Πλαίσιο 6.4: Εσωτερική Αναπαράσταση Διαδικασίας Proteas στη μεθοδολογία BADGE τη φορά, τόσο τα δεδομένα όσο και ο αλγόριθμος υφίστανται ως πόροι του Πλέγματος. Η εφαρμογή ορίζεται ως Παράλληλη Εφαρμογή, πράγμα που σημαίνει ότι απαιτεί ένα περιβάλλον Συστοιχίας Υπολογιστών (MPI) για την εκτέλεσή της. Η αξιολόγηση των αποτελεσμάτων, στην περίπτωση που περιγράφει το συγκεκριμένο Πλαίσιο, γίνεται με χρήση του 20% του αρχικού συνόλου δεδομένων, ενώ το υπόλοιπο (80%) χρησιμοποιείται για την κατασκευή και εκπαίδευση των μοντέλων.
117 100 ΚΕΦΑΛΑΙΟ 6. Ο ΑΛΓΟΡΙΘΜΟΣ PROTEAS
118 Κεφάλαιο 7 Επεξεργασία Φυλογενετικών Προφίλ: Ο Αλγόριθμος Fuzzy PhyloProf Αυτό το κεφάλαιο παρουσιάζει έναν αλγόριθμο επεξεργασίας φυλογενετικών δεδομένων, που ονομάζεται Fuzzy PhyloProf. Ο αλγόριθμος αυτός εμφανίζει μια ιδιαιτερότητα τόσο στη φύση των δεδομένων εισόδου που χρησιμοποιεί, όσο και το πρόγραμμα υλοποίησής του. Τα δεδομένα εισόδου χαρακτηρίζονται από μεγάλο όγκο καθώς και από παρουσία θορύβου. Η υλοποίηση του αλγορίθμου από την άλλη πλευρά, εξαρτάται από την ύπαρξη ενός συγκεκριμένου πακέτου λογισμικού για μαθηματική μοντελοποίηση (Octave), αλλά ταυτόχρονα, με χρήση της γενικευμένης μεθοδολογίας BADGE, αξιοποιεί σε βάθος την αρχιτεκτονική των Πλεγμάτων Υπολογιστών. 7.1 Ο Αλγόριθμος Συνοπτικά Τα φυλογενετικά προφίλ έχουν χρησιμοποιηθεί εκτενώς στη βιβλιογραφία για πολλούς σκοπούς. Μεταξύ άλλων, στην τεκμηρίωση γονιδίων και την εξαγωγή δικτύων γονιδίων [WHD06], στην πρόβλεψη γονιδίων στις περιπτώσεις ορφανών μεταβολικών λειτουργιών [CV06] και στην ανίχνευση και προσδιορισμό λειτουργικά συνδεδεμένων πρωτεϊνών [CMP07]. Ο αλγόριθμος Fuzzy PhyloProf είναι μία προσπάθεια προς την κατεύθυνση εντοπισμού γενομικών ιδιοσυγκρασιών, χρησιμοποιώντας απευθείας σύγκριση φυλογενετικών προφίλ γονιδίων με το συνολικό προφίλ ολόκληρων γονιδιωμάτων. Με άλλα λόγια, στόχος του αλγορίθμου Fuzzy PhyloProf είναι ο προσδιορισμός γονιδίων τα οποία παρουσιάζουν ενδιαφέρουσες ιδιότητες, όσον αφορά τη σχέση τους είτε με τα υπόλοιπα γονίδια του ιδίου είδους (intra-genome correla on) είτε με γονίδια άλλων ειδών (inter-genome correla on). Ο αλγόριθμος αποτελείται συνοπτικά από τα εξής βήματα: 1. Λήψη των φυλογενετικών δεδομένων για όλα τα γονίδια (genes) των ειδών (species ή genomes) υπό μελέτη.
119 102 ΚΕΦΑΛΑΙΟ 7. Ο ΑΛΓΟΡΙΘΜΟΣ FUZZY PHYLOPROF 2. Κατασκευή των ασαφών συνολικών προφίλ για όλα τα είδη υπό εξέταση. 3. Αποθορυβοποίηση των φυλογενετικών δεδομένων με χρήση της μεθόδου Ανάλυσης Ιδιαζουσών Τιμών (Singular Value Decomposi on - SVD). 4. Υπολογισμός συσχέτισης μεταξύ φυλογενετικών προφίλ και ασαφών προφίλ, με χρήση μετρικών απόστασης, όπως Jaccard και Cosine. 5. Εντοπισμός φυλογενετικών προφίλ (γονιδίων) που παρουσιάζουν ιδιαιτερότητες στις συσχετίσεις τους. Πέρα από τα αποτελέσματα που παράγει ο αλγόριθμος Fuzzy PhyloProf, η τεχνική που ακολουθεί παρουσιάζει ορισμένες καινοτομίες, οι οποίες την ξεχωρίζουν έναντι άλλων προσεγγίσεων στη βιβλιογραφία: Είναι μια ιδιαίτερα αποδοτική, σε ακρίβεια και ταχύτητα, μέθοδος. Παρουσιάζει χαμηλότερη πολυπλοκότητα σε σχέση με παρόμοιες προσεγγίσεις. Μπορεί να χρησιμοποιηθεί για την παραγωγή βιβλιοθήκης συνολικών προφίλ, τα οποία μπορούν αφενός να επαναχρησιμοποιηθούν και αφετέρου να ενημερωθούν εύκολα. Μπορεί να χρησιμοποιηθεί ως μέθοδος επικύρωσης άλλων μελετών. Κλιμακώνεται εύκολα σε μεγαλύτερα σύνολα δεδομένων, τόσο από τη φύση της όσο και με την αξιοποίηση Πλεγμάτων Υπολογιστών. Στη συνέχεια ακολουθεί μια λεπτομερής περιγραφή του κάθε βήματος της μεθόδου Φυλογενετικά Προφίλ και Ασαφή Φυλογενετικά Προφίλ Το φυλογενετικό προφίλ ενός γονιδίου (ή με άλλα λόγια μιας πρωτεΐνης) περιγράφει την ύπαρξη ή όχι ενός ομολόγου του στους οργανισμούς που περιλαμβάνονται [PMT + 99]. Πρωτεΐνες οι οποίες αποτελούν δομικά συμπλέγματα πολλαπλών μερών είναι πιθανόν να παρουσιάζουν όμοια προφίλ. Επίσης, πρωτεΐνες οι οποίες είναι γνωστό ότι συμμετέχουν σε ένα δεδομένο βιοχημικό μονοπάτι είναι πολύ πιθανό να είναι γειτονικές στο χώρο των φυλογενετικών προφίλ. Με άλλα λόγια, τα φυλογενετικά προφίλ είναι ένα χρήσιμο εργαλείο για τον προσδιορισμό των λειτουργιών στις οποίες συμμετέχει μια πρωτεΐνη, όπως το δομικό σύμπλεγμα ή το μεταβολικό μονοπάτι μεταξύ άλλων. Η υπόθεση πίσω από τις μεθόδους που αξιοποιούν τα φυλογενετικά προφίλ είναι ότι πρωτεΐνες, οι οποίες λειτουργούν μαζί, έχουν την τάση να εμφανίζονται μαζί στα
120 7.1 Ο Αλγόριθμος Συνοπτικά MGEN G MGEN G MGEN G Πλαίσιο 7.1: Παράδειγμα φυλογενετικών προφίλ γονιδιώματα των οργανισμών. Έτσι, ομάδες πρωτεϊνών με παρόμοια προφίλ αντιστοιχούν σε μονοπάτια και συμπλέγματα, και η συμμετοχή σε μια τέτοια ομάδα μπορεί να χρησιμοποιηθεί ως απόδειξη ότι μια άγνωστη πρωτεΐνη έχει επίσης την ίδια λειτουργία. Ένα φυλογενετικό προφίλ μπορεί να εκφρασθεί ως ένα δυαδικό διάνυσμα pp j το οποίο περιέχει n τιμές, όσο είναι και το πλήθος των οργανισμών που συμμετέχουν στο προφίλ. Με άλλα λόγια ισχύει ότι: pp j = [pp 1j pp 2j pp 3j... pp nj ], pp 1j, pp 2j, pp 3j,, pp nj {0, 1} (7.1) Στο Πλαίσιο 7.1 παρουσιάζονται τα φυλογενετικά προφίλ τριών γονιδίων. Η διαδικασία ορισμού ενός ασαφούς προφίλ οργανισμού (ή εναλλακτικά ενός προφίλ συναίνεσης - consensus profile) είναι η εξής. Έστω το γονιδίωμα ενός οργανισμού s i, το οποίο ανακτάται από μια βάση δεδομένων n οργανισμών (i = 1, 2,..., n), και τα m i φυλογενετικά προφίλ pp j (όπου j = 1, 2,..., m i ) όλων των γονιδίων που περιέχονται στο s i. Όπως αναφέρθηκε προηγούμενως, το συνολικό πλήθος των γονιδιωμάτων (οργανισμών) που συμμετέχουν στην κατασκευή των φυλογενετικών προφίλ είναι n. Το ασαφές φυλογενετικό προφίλ f i για τον οργανισμό s i ορίζεται ως: m i j=1 f i = pp 1j m i m i pp 2j j=1 m i m i pp 3j j=1 m i m i pp nj j=1 m i (7.2) Είναι προφανές ότι το ασαφές προφίλ είναι ένα διάνυσμα n πραγματικών τιμών. Καθώς οι τιμές pp ij είναι δυαδικές, κάθε στοιχείο του διανύσματος f i θα παίρνει τιμές στο διάστημα [0, 1). Επιπλέον, κάθε τιμή f ii του ασαφούς προφίλ αντιστοιχεί στο ποσοστό των γονιδίων (πρωτεϊνών) του οργανισμού s i τα οποία εκφράζονται ή έχουν ομόλογα στον οργανισμό s i. Το επόμενο βήμα είναι ο υπολογισμός ενός ζεύγους αποστάσεων dist ppj = (x, y) για κάθε φυλογενετικό προφίλ των οργανισμών που περιλαμβάνονται στο εκάστοτε πείραμα. Η πρώτη συντεταγμένη x εκφράζει την απόσταση μεταξύ του φυλογενετικού προφίλ pp j κάθε γονιδίου του οργανισμού s i και του ασαφούς προφίλ f i του ιδίου οργανισμού, δηλαδή x = dist(pp j, f i ). Η δεύτερη συντεταγμένη y εκφράζει την απόσταση μεταξύ του φυλογενετικού προφίλ pp j και μιας μετρικής των ασαφών προφίλ όλων των
121 104 ΚΕΦΑΛΑΙΟ 7. Ο ΑΛΓΟΡΙΘΜΟΣ FUZZY PHYLOPROF άλλων οργανισμών. Εάν η μετρική αυτή είναι η ελάχιστη απόσταση, τότε θα ισχύει ότι y = min(dist(pp j, f k ), k i). Με άλλα λόγια: dist ppj = (dist(pp j, f i ), min(dist(pp j, f k ), k i)) (7.3) Πέρα από τη συνάρτηση min, μπορούν να χρησιμοποιηθούν και άλλες συναρτήσεις όπως η average ή weighted συναρτήσεις. Πειραματικά όμως, η min έδωσε τα καλύτερα αποτελέσματα. Για να γίνει εφικτή μια πιο διακριτή ομαδοποίηση, το επόμενο βήμα είναι ο μετασχηματισμός του ασαφούς προφίλ f i ενός οργανισμού σε ένα διακριτό προφίλ συναίνεσης f di (ή ψηφιακό σε αντίθεση με το αναλογικό). Αυτή η διαδικασία μπορεί να γίνει ως εξής: 0, if f ij < α f di = [f di1 f di2 f di3... f din ], f dij = 1, if f ij α (7.4) Παρόλα αυτά, εδώ πρέπει να σημειωθεί ότι τα δεδομένα φυλογενετικών προφίλ χαρακτηρίζονται από υψηλά επίπεδα θορύβου. Έχοντας ως στόχο λοιπόν να εμφανιστούν έντονα οι διαφορές που υπάρχουν στα αρχικά δεδομένα, μετά την κατασκευή των ασαφών προφίλ των οργανισμών θα εφαρμοσθεί Ανάλυση Ιδιαζουσών Τιμών πάνω στα φυλογενετικά προφίλ των γονιδίων Ορισμός και χρήση της Ανάλυσης Ιδιαζουσών Τιμών Έστω A ένας m n πίνακας με βαθμό (rank) r. Υποθέτουμε χωρίς άρση της γενικότητας ότι m n, και έστω: λ 1 λ 2 λ 3... λ r > λ r+1 = λ r+2 =... = λ n = 0 (7.5) οι ιδιοτιμές του πίνακα AA T. (Αν ισχύει m n, τότε αντικαθιστούμε τον A με τον A T ). Οι τιμές σ i = λ i, όπου i = 1, 2,..., min(m, n), λέγονται ιδιάζουσες τιμές (singular values) του πίνακα A. Τότε υπάρχουν δύο ορθογώνιοι πίνακες U m m = (u 1, u 2,..., u m ) και V n n = (v 1, v 2,..., v n ) τέτοιοι, ώστε να ισχύει: A = UΣV T = r ( ) ui σ i vi T i=1 όπου ο m n διαγώνιος πίνακας Σ = (σ i ) έχει στοιχεία που δίνονται από τις σχέσεις: 0, όταν i j σ ij = λi, όταν i = j (7.6) (7.7)
122 7.1 Ο Αλγόριθμος Συνοπτικά 105 και έχει ακριβώς r μη μηδενικά στοιχεία στις θέσεις (i, i), όπου i = 1, 2,..., min(m, n). Η Εξίσωση 7.6 αποτελεί την Ανάλυση Ιδιαζουσών Τιμών του πίνακα A. Επιλέγοντας τις πρώτες k < n τιμές σ i του Σ (σ 1 σ 2... σ n ) και θέτωντας τις υπόλοιπες ίσες με 0, είναι δυνατή η κατασκευή ενός προσεγγιστικού πίνακα. Στην περίπτωση των φυλογενετικών προφίλ, ως προσεγγιστικός πίνακας θεωρείται ένας πίνακας με λιγότερο περιεχόμενο σε θόρυβο. Η επιλογή της τιμής του k μπορεί να γίνει κανονικοποιώντας τις τιμές των σ i στο διάστημα [0, 1] και θέτωντας ένα κατώφλι κάλυψης λ, ή αλλιώς κατώφλι SVD. Σε αυτή την περίπτωση ισχύει η θεώρηση ότι επιλέγοντας k τιμές των σ i οι οποίες δίνουν ποσοστιαίο άθροισμα λ, γίνεται μια καλή εκπροσώπηση του λ% των αρχικών φυλογενετικών δεδομένων. Προφανώς, ο αντίστροφος μετασχηματισμός θα επιστρέψει τελικά ένα νέο πίνακα ο οποίος θα περιέχει πραγματικές τιμές (σε αντίθεση με τις δυαδικές τιμές που είχε πριν την Ανάλυση SVD). Τέλος, για να ανακατασκευασθεί η δυαδική απεικόνιση των αρχικών δεδομένων, αρκεί να ορισθεί ένα κατώφλι α: τιμές a ij που είναι μεγαλύτερες από το κατώφλι α θέτωνται ίσες με 1, ενώ όλες οι υπόλοιπες ορίζονται ίσες με 0 (η λογική είναι ακριβώς αντίστοιχη με τη διαδικασία της Εξίσωσης 7.4). Το κατώφλι α ονομάζεται κατώφλι διακριτοποίησης Ορισμός Μετρικών Απόστασης σε Φυλογενετικά Προφίλ Στη βιβλιογραφία χρησιμοποιούνται διάφορες μετρικές απόστασης για την αξιολόγηση της γειτνίασης φυλογενετικών προφίλ, όπως η απόσταση Hamming, η συσχέτιση Pearson [CV06] και το μέτρο αμοιβαίας πληροφορίας (mutual informa on) [CV06]. Στην περίπτωση του αλγορίθμου Fuzzy PhyloProf χρησιμοποιήθηκαν δύο μετρικές οι οποίες παρουσιάζουν συγκριτικά πιο εύρωστα αποτελέσματα: η απόσταση συνημιτόνου (Cosine distance metric) και η απόσταση Jaccard. Παρακάτω ακολουθούν οι τυπικοί ορισμοί των δύο μετρικών. Η απόσταση συνημιτόνου (Cosine distance) μεταξύ δύο διανυσμάτων x r και x s είναι ισοδύναμη με ένα μείον το συνημίτονο της εσωτερικής γωνίας μεταξύ των δύο σημείων, θεωρούμενα ως διανύσματα. Σε περίπτωση ομαδοποίησης, το κεντροειδές είναι ο μέσος όρος των σημείων στη συγκεκριμένη ομάδα, μετά την κανονικοποίησή τους σε μοναδιαίο Ευκλείδειο μήκος. Ο μαθηματικός ορισμός της απόστασης συνημιτόνου είναι ο εξής: d rs = ( ) x r x s 1 (x rx r ) 1/2 (x sx s ) 1/2 (7.8) Η απόσταση Jaccard είναι ίση με ένα μείον το συντελεστή Jaccard. Πρακτικά εκπροσωπεί το ποσοστό των μη-μηδενικών συντεταγμένων των δύο σημείων που διαφέρουν
123 106 ΚΕΦΑΛΑΙΟ 7. Ο ΑΛΓΟΡΙΘΜΟΣ FUZZY PHYLOPROF μεταξύ τους. Ο μαθηματικός ορισμός της απόστασης Jaccard είναι ο εξής: d rs = [(x rj x sj ) ((x rj 0) (x sj 0))] [(x rj 0) (x sj 0)] (7.9) Στην πράξη η μετρική της απόστασης συνημιτόνου εξυπηρετεί περισσότερο σε περιπτώσεις όπου τα σημεία-διανύσματα ανήκουν στον πραγματικό χώρο, ενώ η μετρική της απόστασης Jaccard έχει αποδειχθεί ότι έχει πολύ καλά αποτελέσματα σε περιπτώσεις διακριτών σημείων [SGM + 06] Ανάλυση του Διαγράμματος Ομαδοποίησης Εφαρμόζοντας τον αλγόριθμο στο επιλεγμένο σύνολο γονιδίων, παράγεται το αντίστοιχο διάγραμμα ομαδοποίησης όπου στον οριζόντιο άξονα ορίζεται η ενδο- γονιδιωματική απόσταση, ενώ στον κατακόρυφο άξονα εμφανίζεται η απόσταση του κάθε γονιδίου από τα υπόλοιπα γονιδιώματα. Ανεξαρτήτως της μετρικής απόστασης που θα χρησιμοποιηθεί για την ανίχνευση των εντός και εκτός γονιδιωμάτων αποστάσεων, σε ένα γενικό διάγραμμα ομαδοποίησης που παράγεται από τον αλγόριθμο Fuzzy PhyloProf (Σχήμα 7.1) μπορούν να διαχωρισθούν οι εξής περιοχές: Σχήμα 7.1: Χαρακτηριστικές περιοχές σε ένα διάγραμμα ομαδοποίησης της μεθόδου Fuzzy PhyloProf
124 7.2 Πολυπλοκότητα Αλγορίθμου Fuzzy PhyloProf Η περιοχή a στην κάτω αριστερή γωνία Σε αυτή την περιοχή, τα γονίδια που αναπαριστώνται έχουν μικρή απόσταση τόσο από το συνολικό προφίλ του οργανισμού στον οποίο ανήκουν, όσο και από το συνολικό προφίλ άλλων οργανισμών. Με άλλα λόγια, είναι γονίδια που μπορεί να είναι υπεύθυνα για λειτουργίες κοινές σε όλους τους οργανισμούς. 2. Η περιοχή b εκατέρωθεν της κυρίας διαγωνίου Τα γονίδια σε αυτή την περιοχή παρουσιάζουν αυξανόμενη απόσταση τόσο από τον ίδιο τον οργανισμό όσο και από τους υπόλοιπους. Η τρέχουσα εικασία για αυτήν την περίπτωση είναι ότι πρόκειται για γονίδια τα οποία επιτελούν λειτουργίες στον εκάστοτε οργανισμό οι οποίες τον διαφοροποιούν από τους υπόλοιπους, αλλά δεν αποτελούν και ιδιαίτερο χαρακτηριστικό του. 3. Η περιοχή c πάνω από την κύρια διαγώνιο Τα γονίδια που εμφανίζονται σε αυτή την περιοχή έχουν ιδιαίτερα υψηλή απόσταση από τα συνολικά προφίλ άλλων οργανισμών, αλλά πολύ μικρή απόσταση από τον ίδιο οργανισμό. Με άλλα λόγια, πρόκειται για γονίδια τα οποία είναι χαρακτηριστικά του εκάστοτε οργανισμού. 4. Η περιοχή d κάτω από την κύρια διαγώνιο Τα γονίδια που εντοπίζονται σε αυτή την περιοχή έχουν πολύ μικρή απόσταση από τα προφίλ άλλων οργανισμών, ενώ η απόστασή τους από τον ίδιο οργανισμό είναι μεγάλη. Με άλλα λόγια, πρόκειται για ανώμαλα γονίδια, τα οποία είναι πιθανόν να έχουν προέλθει από οριζόντια μεταφορά γονιδίων ανάμεσα σε οργανισμούς. Ένα συνολικό διάγραμμα ροής του αλγορίθμου Fuzzy PhyloProf παρουσιάζεται στο Σχήμα Πολυπλοκότητα Αλγορίθμου Fuzzy PhyloProf Η ανάλυση της πολυπλοκότητας του αλγορίθμου Fuzzy PhyloProf διαφέρει από τα προηγούμενα σενάρια χρήσης, καθώς αποτελεί μια αλληλουχία μαθηματικών συναρτήσεων πάνω στα δεδομένα εισόδου. Παρόλα αυτά, με χρήση των βημάτων της γενικευμένης μεθοδολογίας, μπορεί να γίνει μια προσπάθεια προσδιορισμού και αντιστοίχισης της πολυπλοκότητας σε κάθε φάση. Στον Πίνακα 7.1 παρουσιάζεται η ανάλυση της πολυπλοκότητας του αλγορίθμου ανά φάση. Σύμφωνα με την περιγραφή του αλγορίθμου, όπως έγινε προηγουμένως, τα δύο πρώτα βήματα είναι η ανάκτηση των m φυλογενετικών δεδομένων όλων των γονιδίων
125 108 ΚΕΦΑΛΑΙΟ 7. Ο ΑΛΓΟΡΙΘΜΟΣ FUZZY PHYLOPROF Genome S 1 Genome S 2 Genome S 3 Genome S n Load Data (Phylogenetic Profiles) Create Fuzzy Profiles Data Denoise (SVD) Discretize Fuzzy Profiles Discretize denoised data Determine Profile Distances Σχήμα 7.2: Διάγραμμα ροής του αλγορίθμου Fuzzy PhyloProf υπό εξέταση και στη συνέχεια η κατασκευή των ασαφών προφίλ όλων των n οργανισμών που συμμετέχουν στη μελέτη. Επομένως, όπως φαίνεται και από τον Πίνακα 7.1, οι πολυπλοκότητες είναι O(m) και O(n m) αντίστοιχα.
126 7.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 109 Πίνακας 7.1: Πολυπλοκότητα του αλγορίθμου Fuzzy PhyloProf Βήμα Πολυπλοκότητα Ανάκτηση Δεδομένων O(m) Προεπεξεργασία Δεδομένων O(n m) Διαμόρφωση Αλγορίθμου O(m n 2 + m 2 n + n 3 ) Τύπος Εφαρμογής O(n m) Φάση Αξιολόγησης - Σύνολο O(m + n m + m n 2 + m 2 n + n 3 ) Το σημείο στο οποίο καθυστερεί η όλη διαδικασία είναι η συνάρτηση Ανάλυσης Ιδιαζουσών Τιμών (SVD). Από τη βιβλιογραφία [GvL96] είναι γνωστό ότι η πολυπλοκότητα της μεθόδου στη γενική περίπτωση είναι O(m n 2 +m 2 n+n 3 ). Αυτό καθιστά την επεξεργασία μεγάλων όγκων δεδομένων δύσκολη έως ανέφικτη. Παρόλα αυτά, εάν είναι εκ των προτέρων γνωστός ο βαθμός r true του πίνακα, τότε η πολυπλοκότητα της συνάρτησης SVD γίνεται ίση με O(m n rtrue). 2 Στην περίπτωση των φυλογενετικών δεδομένων, ο βαθμός του πίνακα των δεδομένων είναι γνωστός και ίσος (στη γενική περίπτωση) με το πλήθος n των οργανισμών που συμμετέχουν στην κατασκευή των προφίλ. Επομένως, στον αλγόριθμο Fuzzy PhyloProf η πολυπλοκότητα της μεθόδου SVD είναι ίση με O(m n 3 ). Τέλος, η ομαδοποίηση των δεδομένων γίνεται με απλή εφαρμογή της μετρικής απόστασης για κάθε συνδυασμό των n συνολικών μοτίβων οργανισμών με τα m φυλογενετικά προφίλ των γονιδίων. Προφανώς, η διαδικασία αυτή μπορεί να εκτελεσθεί εκ παραλλήλου σε p διεργασίες για κάθε ένα οργανισμό, οπότε η πολυπλοκότητα αυτού του βήματος είναι ίση με O( n m ). Επομένως, η πολυπλοκότητα του αλγορίθμου Fuzzy p PhyloProf δίνεται από την παράσταση της Εξίσωσης 7.10: C F P P (m, n, p) = O(m + m n + m n 3 + n m ) (7.10) p 7.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών Όλα τα πειράματα έγιναν με χρήση δεδομένων φυλογενετικών προφίλ από τη βάση ProfUse [GJA + 05]. Τα δεδομένα που περιέχονται στη βάση περιγράφουν τα φυλογενετικά προφίλ 915,554 γονιδίων τα οποία ανήκουν συνολικά σε 243 διαφορετικούς οργανισμούς. Για να είναι δυνατή η επαλήθευση της αξιοπιστίας των αποτελεσμάτων χρη-
127 110 ΚΕΦΑΛΑΙΟ 7. Ο ΑΛΓΟΡΙΘΜΟΣ FUZZY PHYLOPROF σιμοποιήθηκαν στα πειράματα πέντε οργανισμοί αναφοράς, οι οποίοι έχουν μελετηθεί σε βάθος στη βιβλιογραφία [KAG + 05] Φυλογενετικά χαρακτηριστικά των πέντε οργανισμών αναφοράς Τα 5 διαφορετικά είδη τα οποία χρησιμοποιήθηκαν στα πειράματα είναι τα εξής: 1. MGEN-G27-01 (mg) Mycoplasma genitalium, G-37 (Bacteria; Firmicutes; Mollicutes; Mycoplasmatales; Mycoplasmataceae; Mycoplasma). Αποτελείται από 479 γονίδια καταγεγραμμένα στη βάση COGENT [JEA + 03] 2. UURE-SV3-01 (uu) Ureaplasma urealy cum, serovar 3 (Bacteria; Firmicutes; Mollicutes; Mycoplasmatales; Mycoplasmataceae; Ureaplasma). Αποτελείται από 613 γονίδια καταγεγραμμένα στη βάση COGENT [JEA + 03] 3. SPYO-SF3-01 (sp) Streptococcus pyogenes M1, SF370 (Bacteria; Firmicutes; Bacilli; Lactobacillales; Streptococcaceae; Streptococcus). Αποτελείται από 1696 γονίδια καταγεγραμμένα στη βάση COGENT [JEA + 03] 4. BAPH-XSG-01 (ba) Buchnera aphidicola, SG (Bacteria; Proteobacteria; Gammaproteobacteria; Enterobacteriales; Enterobacteriaceae; Buchnera). Αποτελείται από 545 γονίδια καταγεγραμμένα στη βάση COGENT [JEA + 03] 5. NEQU-N4M-0 (ne) Nanoarchaeum equitans, Kin4-M (Archaea; Nanoarchaeota; Nanoarchaeum). Αποτελείται από 563 γονίδια καταγεγραμμένα στη βάση COGENT [JEA + 03] Το πλήρες φυλογενετικό δένδρο το οποίο δείχνει τις θέσεις των 5 αυτών οργανισμών παρουσιάζεται στο Σχήμα 7.3. Μια απλοποιημένη μορφή του ίδιου δένδρου, με μόνο αυτούς τους 5 οργανισμούς φαίνεται στο Σχήμα 7.4. Από τη βιβλιογραφία [KAG + 05] ο πίνακας διατήρησης γονιδίων (Gene Conserva on Matrix) για αυτά τα 5 είδη παρουσιάζεται στον Πίνακα 7.2 καθώς και στο διάγραμμα του Σχήματος 7.5. Σε αυτόν τον πίνακα, όσο μικρότερη είναι η τιμή του κάθε στοιχείου a ij τόσο μεγαλύτερη είναι η συγγένεια μεταξύ των ειδών s i και s j. Προφανώς a ii = 0, αφού κάθε οργανισμός έχει τη μεγαλύτερη δυνατή συγγένεια με τον εαυτό του.
128 7.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 111 Σχήμα 7.3: Πλήρες Φυλογενετικό Δένδρο Σχήμα 7.4: Απλοποιημένο Φυλογενετικό Δένδρο των 5 οργανισμών
129 112 ΚΕΦΑΛΑΙΟ 7. Ο ΑΛΓΟΡΙΘΜΟΣ FUZZY PHYLOPROF Πίνακας 7.2: Πίνακας Διατήρησης Γονιδίων για τα 5 είδη MGEN UURE SPYO BAPH NEQU MGEN UURE SPYO BAPH NEQU Σχήμα 7.5: Διάγραμμα Διατήρησης Γονιδίων για τα 5 είδη Ασαφή Συνολικά Προφίλ και Ομαδοποίηση Γονιδίων Ακολουθώντας τη διαδικασία που περιγράφηκε προηγουμένως, τα ασαφή προφίλ των 5 διαφορετικών οργανισμών παρουσιάζονται στα διαγράμματα του Σχήματος 7.6. Με βάση τις πραγματικές φυλογενετικές αποστάσεις των 5 ειδών, όπως παρουσιάζονται στα Σχήματα 7.3 και 7.4, είναι ενδιαφέρον να παρατηρήσει κανείς ότι οι διαφορές μεταξύ των ασαφών συνολικών προφίλ γίνονται πιο έντονες όταν οι αντίστοιχοι οργανισμοί απέχουν μεγαλύτερη απόσταση στο φυλογενετικό δένδρο. Για παράδειγμα, η διαφορά μεταξύ του προφίλ του MGEN και του NEQU είναι πιο έντονη από τη διαφορά μεταξύ του MGEN και του UURE. Μια πιο ποσοτική απεικόνιση αυτής της διαφοράς απεικονίζεται στον Πίνακα 7.2. Αξιοποιώντας απευθείας τα ασαφή προφίλ για τον ορισμό της βάσης στη σύγκριση
130 7.3 Αποτελέσματα στην Κατηγοριοποίηση Πρωτεϊνών 113 Σχήμα 7.6: Ασαφή Συνολικά Προφίλ για τα 5 είδη των φυλογενετικών προφίλ των 3896 γονιδίων που συμμετέχουν στα πειράματα, και χρησιμοποιώντας τη μετρική της απόστασης συνημιτόνου για τον προσδιορισμό της γειτνίασης των προφίλ, προκύπτουν τα διαγράμματα ομαδοποίησης που παρουσιάζονται στο Σχήμα 7.7.
Φώτη Ψωμόπουλου του Ευαγγέλου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Παράλληλοι Αλγόριθμοι Εξόρυξης και Ανάλυσης Δεδομένων σε Πλέγματα Υπολογιστών με εφαρμογές
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Παράλληλοι Αλγόριθμοι Εξόρυξης και Ανάλυσης Δεδομένων σε Πλέγματα Υπολογιστών με εφαρμογές
Εξόρυξη Γνώσης από Βιολογικά εδομένα
 Παρουσίαση Διπλωματικής Εργασίας Εξόρυξη Γνώσης από Βιολογικά εδομένα Καρυπίδης Γεώργιος (Μ27/03) Επιβλέπων Καθηγητής: Ιωάννης Βλαχάβας MIS Πανεπιστήμιο Μακεδονίας Φεβρουάριος 2005 Εξόρυξη Γνώσης από Βιολογικά
Παρουσίαση Διπλωματικής Εργασίας Εξόρυξη Γνώσης από Βιολογικά εδομένα Καρυπίδης Γεώργιος (Μ27/03) Επιβλέπων Καθηγητής: Ιωάννης Βλαχάβας MIS Πανεπιστήμιο Μακεδονίας Φεβρουάριος 2005 Εξόρυξη Γνώσης από Βιολογικά
ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ. 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
 ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στόχος Θεματικής Ενότητας Οι μαθητές να περιγράφουν τους βασικούς τομείς της Επιστήμης των Υπολογιστών και να μπορούν
ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στόχος Θεματικής Ενότητας Οι μαθητές να περιγράφουν τους βασικούς τομείς της Επιστήμης των Υπολογιστών και να μπορούν
Βιοπληροψορική, συσιημική βιολογία και εξατομικευμένη θεραπεία
 Βιοπληροψορική, συσιημική βιολογία και εξατομικευμένη θεραπεία Φραγκίσκος Κολίσης Καθηγητής Βιοτεχνολογίας, Σχολή Χημικών Μηχανικών ΕΜΠ, Διευθυντής Ινστιτούτου Βιολογικών Ερευνών και Βιοτεχνολογίας, EIE
Βιοπληροψορική, συσιημική βιολογία και εξατομικευμένη θεραπεία Φραγκίσκος Κολίσης Καθηγητής Βιοτεχνολογίας, Σχολή Χημικών Μηχανικών ΕΜΠ, Διευθυντής Ινστιτούτου Βιολογικών Ερευνών και Βιοτεχνολογίας, EIE
Βιοπληροφορική. Μαργαρίτα Θεοδωροπούλου. Πανεπιστήμιο Θεσσαλίας, Λαμία 2016
 Βιοπληροφορική Μαργαρίτα Θεοδωροπούλου Πανεπιστήμιο Θεσσαλίας, Λαμία 2016 Βιοπληροφορική Εισαγωγή στη Μοριακή Βιολογία, Γενωμική και Βιοπληροφορική. Βάσεις Βιολογικών Δεδομένων. Ακολουθίες Πρωτεϊνών και
Βιοπληροφορική Μαργαρίτα Θεοδωροπούλου Πανεπιστήμιο Θεσσαλίας, Λαμία 2016 Βιοπληροφορική Εισαγωγή στη Μοριακή Βιολογία, Γενωμική και Βιοπληροφορική. Βάσεις Βιολογικών Δεδομένων. Ακολουθίες Πρωτεϊνών και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΕΠΛ 450 ΥΠΟΛΟΓΙΣΤΙΚΗ ΒΙΟΛΟΓΙΑ. Παύλος Αντωνίου
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΕΠΛ 450 ΥΠΟΛΟΓΙΣΤΙΚΗ ΒΙΟΛΟΓΙΑ Παύλος Αντωνίου Με μια ματιά: Εισαγωγή στη Βιολογία Ευθυγράμμιση Ακολουθιών Αναζήτηση ομοίων ακολουθιών από βάσεις δεδομενων Φυλογενετική πρόβλεψη Πρόβλεψη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΕΠΛ 450 ΥΠΟΛΟΓΙΣΤΙΚΗ ΒΙΟΛΟΓΙΑ Παύλος Αντωνίου Με μια ματιά: Εισαγωγή στη Βιολογία Ευθυγράμμιση Ακολουθιών Αναζήτηση ομοίων ακολουθιών από βάσεις δεδομενων Φυλογενετική πρόβλεψη Πρόβλεψη
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΚΕΦΑΛΑΙΟ 2 ο 1. Με ποιο μηχανισμό αντιγράφεται το DNA σύμφωνα με τους Watson και Crick; 2. Ένα κύτταρο που περιέχει ένα μόνο χρωμόσωμα τοποθετείται σε θρεπτικό υλικό που περιέχει ραδιενεργό
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΚΕΦΑΛΑΙΟ 2 ο 1. Με ποιο μηχανισμό αντιγράφεται το DNA σύμφωνα με τους Watson και Crick; 2. Ένα κύτταρο που περιέχει ένα μόνο χρωμόσωμα τοποθετείται σε θρεπτικό υλικό που περιέχει ραδιενεργό
Πανεπιστήμιο Θεσσαλίας Τμήμα βιοχημείας και βιοτεχνολογίας
 Πανεπιστήμιο Θεσσαλίας Τμήμα βιοχημείας και βιοτεχνολογίας Διδακτική με έμφαση στις βιοεπιστήμες Μαρία Ευαγγελία Βασιλογιάννη Στοιχεία Μαθήματος 1. Μάθημα : Βιολογία 2. Τίτλος ενότητας: Η ροή της γενετικής
Πανεπιστήμιο Θεσσαλίας Τμήμα βιοχημείας και βιοτεχνολογίας Διδακτική με έμφαση στις βιοεπιστήμες Μαρία Ευαγγελία Βασιλογιάννη Στοιχεία Μαθήματος 1. Μάθημα : Βιολογία 2. Τίτλος ενότητας: Η ροή της γενετικής
Τα χημικά στοιχεία που είναι επικρατέστερα στους οργανισμούς είναι: i..
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «XHMIKH ΣΥΣΤΑΣΗ ΤΟΥ ΚΥΤΤΑΡΟΥ» ΕΙΣΑΓΩΓΗ ΚΑΙ Η ΧΗΜΕΙΑ ΤΗΣ ΖΩΗΣ Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ 1. Όταν αναφερόμαστε στον όρο «Χημική Σύσταση του Κυττάρου», τί νομίζετε ότι
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «XHMIKH ΣΥΣΤΑΣΗ ΤΟΥ ΚΥΤΤΑΡΟΥ» ΕΙΣΑΓΩΓΗ ΚΑΙ Η ΧΗΜΕΙΑ ΤΗΣ ΖΩΗΣ Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ 1. Όταν αναφερόμαστε στον όρο «Χημική Σύσταση του Κυττάρου», τί νομίζετε ότι
Γονιδιωματική. G. Patrinos
 Γονιδιωματική Η μεταγονιδιωματική εποχή... Σημαντικότερα επιτεύγματα POST GENOME ERA Ολοκλήρωση της αποκρυπτογράφησης της αλληλουχίας των γονιδιωμάτων πολλών οργανισμών. Προτύπωση μεθοδολογιών για προσδιορισμό
Γονιδιωματική Η μεταγονιδιωματική εποχή... Σημαντικότερα επιτεύγματα POST GENOME ERA Ολοκλήρωση της αποκρυπτογράφησης της αλληλουχίας των γονιδιωμάτων πολλών οργανισμών. Προτύπωση μεθοδολογιών για προσδιορισμό
Βιολογία Γενικής Παιδείας Β Λυκείου
 Απρίλιος Μάιος 12 Βιολογία Γενικής Παιδείας Β Λυκείου Βιολογία Γενικής Παιδείας Β Λυκείου (Ερωτήσεις που παρουσιάζουν ενδιαφέρον) 1. Τι είναι τα βιομόρια και ποια είναι τα βασικά χαρακτηριστικά τους; Βιομόρια
Απρίλιος Μάιος 12 Βιολογία Γενικής Παιδείας Β Λυκείου Βιολογία Γενικής Παιδείας Β Λυκείου (Ερωτήσεις που παρουσιάζουν ενδιαφέρον) 1. Τι είναι τα βιομόρια και ποια είναι τα βασικά χαρακτηριστικά τους; Βιομόρια
Βιοπληροφορική Ι (ΜΕΡΟΣ Α) Βιοπληροφορική Ανάλυση Γονιδιωμάτων. Εισαγωγή στης Βιολογικές Βάσεις Δεδομένων
 Βιοπληροφορική Ι (ΜΕΡΟΣ Α) Βιοπληροφορική Ανάλυση Γονιδιωμάτων Εισαγωγή στης Βιολογικές Βάσεις Δεδομένων Η επιστήμη της Βιολογίας έχει μετατραπεί τα τελευταία χρόνια σε μια υπερπλούσια σε πληροφορίες επιστήμη.
Βιοπληροφορική Ι (ΜΕΡΟΣ Α) Βιοπληροφορική Ανάλυση Γονιδιωμάτων Εισαγωγή στης Βιολογικές Βάσεις Δεδομένων Η επιστήμη της Βιολογίας έχει μετατραπεί τα τελευταία χρόνια σε μια υπερπλούσια σε πληροφορίες επιστήμη.
αποτελούν το 96% κ.β Ποικιλία λειτουργιών
 ΧΗΜΙΚΑ ΣΤΟΙΧΕΙΑ ΠΟΥ ΣΥΝΘΕΤΟΥΝ ΤΟΥΣ ΟΡΓΑΝΙΣΜΟΥΣ 92 στοιχεία στο φλοιό της Γης 27 απαραίτητα για τη ζωή H, Ο, Ν, C αποτελούν το 96% κ.β S, Ca, P, Cl, K, Na, Mg αποτελούν το 4% κ.β. Fe, I Ιχνοστοιχεία αποτελούν
ΧΗΜΙΚΑ ΣΤΟΙΧΕΙΑ ΠΟΥ ΣΥΝΘΕΤΟΥΝ ΤΟΥΣ ΟΡΓΑΝΙΣΜΟΥΣ 92 στοιχεία στο φλοιό της Γης 27 απαραίτητα για τη ζωή H, Ο, Ν, C αποτελούν το 96% κ.β S, Ca, P, Cl, K, Na, Mg αποτελούν το 4% κ.β. Fe, I Ιχνοστοιχεία αποτελούν
NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS SCHOOL OF SCIENCE FACULTY OF INFORMATICS AND TELECOMMUNICATIONS
 NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS SCHOOL OF SCIENCE FACULTY OF INFORMATICS AND TELECOMMUNICATIONS INTERDICIPLINARY POSTGRADUATE PROGRAMME "INFORMATION TECHNOLOGIES IN MEDICINE AND BIOLOGY"
NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS SCHOOL OF SCIENCE FACULTY OF INFORMATICS AND TELECOMMUNICATIONS INTERDICIPLINARY POSTGRADUATE PROGRAMME "INFORMATION TECHNOLOGIES IN MEDICINE AND BIOLOGY"
ΑΝΑΠΤΥΞΗ ΛΟΓΙΣΜΙΚΟΥ ΓΙΑ ΤΗ ΔΙΕΝΕΡΓΕΙΑ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΜΕΛΕΤΩΝ
 ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΝΑΠΤΥΞΗ ΛΟΓΙΣΜΙΚΟΥ ΓΙΑ ΤΗ ΔΙΕΝΕΡΓΕΙΑ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΜΕΛΕΤΩΝ ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ Α.Μ. 123/04 ΕΠΙΒΛΕΠΩΝ: ΣΑΜΑΡΑΣ ΝΙΚΟΛΑΟΣ ΘΕΣΣΑΛΟΝΙΚΗ, ΙΟΥΝΙΟΣ 2007 Περιεχόμενα
ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΝΑΠΤΥΞΗ ΛΟΓΙΣΜΙΚΟΥ ΓΙΑ ΤΗ ΔΙΕΝΕΡΓΕΙΑ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΜΕΛΕΤΩΝ ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ Α.Μ. 123/04 ΕΠΙΒΛΕΠΩΝ: ΣΑΜΑΡΑΣ ΝΙΚΟΛΑΟΣ ΘΕΣΣΑΛΟΝΙΚΗ, ΙΟΥΝΙΟΣ 2007 Περιεχόμενα
ΜΕΤΑΓΡΑΦΗ ΤΟΥ DNA ΣΕ RNA
 ΓΥΜΝΑΣΙΟ ΚΕΡΑΤΕΑΣ ΕΡΓΑΣΙΑ ΒΙΟΛΟΓΙΑΣ Β ΤΡΙΜΗΝΟΥ Γ 4 23.1.12 ΜΕΤΑΓΡΑΦΗ ΤΟΥ DNA ΣΕ RNA ΕΡΓΑΣΤΗΚΑΝ: ΑΛΕΞΑΝΔΡΟΣ ΔΕΛΗΜΙΧΑΛΗΣ ΑΡΤΕΜΗΣ ΑΝΑΣΤΑΣΙΑΔΗΣ 1 ΕΙΣΑΓΩΓΗ Το δεοξυριβονουκλεϊκό οξύ (Deoxyribonucleic acid -
ΓΥΜΝΑΣΙΟ ΚΕΡΑΤΕΑΣ ΕΡΓΑΣΙΑ ΒΙΟΛΟΓΙΑΣ Β ΤΡΙΜΗΝΟΥ Γ 4 23.1.12 ΜΕΤΑΓΡΑΦΗ ΤΟΥ DNA ΣΕ RNA ΕΡΓΑΣΤΗΚΑΝ: ΑΛΕΞΑΝΔΡΟΣ ΔΕΛΗΜΙΧΑΛΗΣ ΑΡΤΕΜΗΣ ΑΝΑΣΤΑΣΙΑΔΗΣ 1 ΕΙΣΑΓΩΓΗ Το δεοξυριβονουκλεϊκό οξύ (Deoxyribonucleic acid -
ΒΙΟΛΟΓΙΑ Γ ΛΥΚΕΙΟΥ, ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΙΚΟΝΑ 2.4 ΣΤΑΔΙΑ ΜΕΤΑΦΡΑΣΗΣ σ ε λ ί δ α 1 ΕΙΚΟΝΑ 4.2β ΕΡΩΤΗΣΕΙΣ 1. Να συμπληρώσετε τα κενά πλαίσια της εικόνας με την κατάλληλη λέξη ή φράση 2. Να γράψετε τον προσανατολισμό της μετακίνησης του ριβοσώματος
ΕΙΚΟΝΑ 2.4 ΣΤΑΔΙΑ ΜΕΤΑΦΡΑΣΗΣ σ ε λ ί δ α 1 ΕΙΚΟΝΑ 4.2β ΕΡΩΤΗΣΕΙΣ 1. Να συμπληρώσετε τα κενά πλαίσια της εικόνας με την κατάλληλη λέξη ή φράση 2. Να γράψετε τον προσανατολισμό της μετακίνησης του ριβοσώματος
Θέματα πριν τις εξετάσεις. Καλό διάβασμα Καλή επιτυχία
 Θέματα πριν τις εξετάσεις Καλό διάβασμα Καλή επιτυχία 2013-2014 Θέματα πολλαπλής επιλογής Μετουσίωση είναι το φαινόμενο α. κατά το οποίο συνδέονται δύο αμινοξέα για τον σχηματισμό μιας πρωτεΐνης β. κατά
Θέματα πριν τις εξετάσεις Καλό διάβασμα Καλή επιτυχία 2013-2014 Θέματα πολλαπλής επιλογής Μετουσίωση είναι το φαινόμενο α. κατά το οποίο συνδέονται δύο αμινοξέα για τον σχηματισμό μιας πρωτεΐνης β. κατά
Μάθημα 16 ο ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ
 Μάθημα 16 ο ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ Περιεχόμενα Παρουσίασης Βιολογικό υπόβαθρο Το κεντρικό αξίωμα Σύνοψη της Βιοπληροφορικής Ερευνητικές περιοχές Πηγές πληροφοριών Τι είναι η Βιοπληροφορική Βιο Πληροφορική μοριακή
Μάθημα 16 ο ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ Περιεχόμενα Παρουσίασης Βιολογικό υπόβαθρο Το κεντρικό αξίωμα Σύνοψη της Βιοπληροφορικής Ερευνητικές περιοχές Πηγές πληροφοριών Τι είναι η Βιοπληροφορική Βιο Πληροφορική μοριακή
Κεφ. 4 DNA, RNA και η ροή των γενετικών πληροφοριών
 Κεφ. 4 DNA, RNA και η ροή των γενετικών πληροφοριών Η οικογενειακή ομοιότητα, οφείλεται στα κοινά γονίδια. Τα γονίδια πρέπει να εκφραστούν για να έχουν αποτέλεσμα, και η έκφραση αυτή ρυθμίζεται από πρωτεΐνες.
Κεφ. 4 DNA, RNA και η ροή των γενετικών πληροφοριών Η οικογενειακή ομοιότητα, οφείλεται στα κοινά γονίδια. Τα γονίδια πρέπει να εκφραστούν για να έχουν αποτέλεσμα, και η έκφραση αυτή ρυθμίζεται από πρωτεΐνες.
KΕΦΑΛΑΙΟ 1ο Χημική σύσταση του κυττάρου. Να απαντήσετε σε καθεμιά από τις παρακάτω ερωτήσεις με μια πρόταση:
 KΕΦΑΛΑΙΟ 1ο Χημική σύσταση του κυττάρου Ενότητα 1.1: Χημεία της ζωής Ενότητα 2.1: Μακρομόρια Να απαντήσετε σε καθεμιά από τις παρακάτω ερωτήσεις με μια πρόταση: 1. Για ποιο λόγο θεωρείται αναγκαία η σταθερότητα
KΕΦΑΛΑΙΟ 1ο Χημική σύσταση του κυττάρου Ενότητα 1.1: Χημεία της ζωής Ενότητα 2.1: Μακρομόρια Να απαντήσετε σε καθεμιά από τις παρακάτω ερωτήσεις με μια πρόταση: 1. Για ποιο λόγο θεωρείται αναγκαία η σταθερότητα
ΤΟ DNA ΚΑΙ RNA. Θανος Εξαρχου Γ1
 ΤΟ DNA ΚΑΙ RNA Θανος Εξαρχου Γ1 ΤΟ DNA Το δε(σ)οξυριβο(ζο)νουκλεϊ(νι)κό οξu είναι νουκλεϊκό οξύ που περιέχει τις γενετικές πληροφορίες που καθορίζουν τη βιολογική ανάπτυξη όλων των κυτταρικών μορφών ζωής
ΤΟ DNA ΚΑΙ RNA Θανος Εξαρχου Γ1 ΤΟ DNA Το δε(σ)οξυριβο(ζο)νουκλεϊ(νι)κό οξu είναι νουκλεϊκό οξύ που περιέχει τις γενετικές πληροφορίες που καθορίζουν τη βιολογική ανάπτυξη όλων των κυτταρικών μορφών ζωής
1. Πού πραγματοποιούνται η αντιγραφή και η μεταγραφή; ΘΩΜΑΣ ΑΠΑΝΤΗΣΗ. 2. Ποιες είναι οι κατηγορίες γονιδίων με κριτήριο το προϊόν της μεταγραφής τους;
 Βιολογία Γ Ενιαίου Λυκείου / Θετική Κατεύθυνση κεφαλαιο 2ο: αντιγραφη, εκφραση και ρυθμιση τησ ΓενετικηΣ ΠληροφοριαΣ 1. Πού πραγματοποιούνται η αντιγραφή και η μεταγραφή; Ευκαρυωτικά κύτταρα: στον πυρήνα,
Βιολογία Γ Ενιαίου Λυκείου / Θετική Κατεύθυνση κεφαλαιο 2ο: αντιγραφη, εκφραση και ρυθμιση τησ ΓενετικηΣ ΠληροφοριαΣ 1. Πού πραγματοποιούνται η αντιγραφή και η μεταγραφή; Ευκαρυωτικά κύτταρα: στον πυρήνα,
Βιοτεχνολογία Φυτών. Μοριακοί Δείκτες (Εισαγωγή στη Μοριακή Βιολογία)
 Βιοτεχνολογία Φυτών ΔΠΘ / Τμήμα Αγροτικής Ανάπτυξης ΠΜΣ Αειφορικά Συστήματα Παραγωγής και Περιβάλλον στη Γεωργία Μοριακοί Δείκτες (Εισαγωγή στη Μοριακή Βιολογία) Αριστοτέλης Χ. Παπαγεωργίου Εργαστήριο
Βιοτεχνολογία Φυτών ΔΠΘ / Τμήμα Αγροτικής Ανάπτυξης ΠΜΣ Αειφορικά Συστήματα Παραγωγής και Περιβάλλον στη Γεωργία Μοριακοί Δείκτες (Εισαγωγή στη Μοριακή Βιολογία) Αριστοτέλης Χ. Παπαγεωργίου Εργαστήριο
Τμήμα Βιολογίας Μάθημα: ΒΙΟΛΟΓΙΑ ΚΥΤΤΑΡΟΥ Γ εξάμηνο 2014-2015 Διαλέξεις κάθε Τρίτη 13-15 μ.μ. και Παρασκευή 11-13
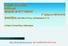 Τμήμα Βιολογίας Μάθημα: ΒΙΟΛΟΓΙΑ ΚΥΤΤΑΡΟΥ Γ εξάμηνο 2014-2015 Διαλέξεις κάθε Τρίτη 13-15 μ.μ. και Παρασκευή 11-13 Ισιδώρα Παπασιδέρη, Καθηγήτρια...για περισσότερα... http://kyttariki.biol.uoa.gr, ttp://multimedia.biol.uoa.gr
Τμήμα Βιολογίας Μάθημα: ΒΙΟΛΟΓΙΑ ΚΥΤΤΑΡΟΥ Γ εξάμηνο 2014-2015 Διαλέξεις κάθε Τρίτη 13-15 μ.μ. και Παρασκευή 11-13 Ισιδώρα Παπασιδέρη, Καθηγήτρια...για περισσότερα... http://kyttariki.biol.uoa.gr, ttp://multimedia.biol.uoa.gr
Αρχιτεκτονική της τρισδιάστατης δομής πρωτεϊνών
 Αρχιτεκτονική της τρισδιάστατης δομής πρωτεϊνών Βασίλης Προμπονάς, PhD Ερευνητικό Εργαστήριο Βιοπληροφορικής Τμήμα Βιολογικών Επιστημών Νέα Παν/πολη, Γραφείο B161 Πανεπιστήμιο Κύπρου Ταχ.Κιβ. 20537 1678,
Αρχιτεκτονική της τρισδιάστατης δομής πρωτεϊνών Βασίλης Προμπονάς, PhD Ερευνητικό Εργαστήριο Βιοπληροφορικής Τμήμα Βιολογικών Επιστημών Νέα Παν/πολη, Γραφείο B161 Πανεπιστήμιο Κύπρου Ταχ.Κιβ. 20537 1678,
ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΟΙΚΗΣΗ της ΥΓΕΙΑΣ» ΑΞΙΟΛΟΓΗΣΗ ΑΠΟΔΟΣΗΣ ΠΡΟΣΩΠΙΚΟΥ: ΜΕΛΕΤΗ ΠΕΡΙΠΤΩΣΗΣ ΙΔΙΩΤΙΚΟΥ ΝΟΣΟΚΟΜΕΙΟΥ ΠΑΡΑΓΙΟΥΔΑΚΗ ΜΑΓΔΑΛΗΝΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΟΙΚΗΣΗ της ΥΓΕΙΑΣ» ΑΞΙΟΛΟΓΗΣΗ ΑΠΟΔΟΣΗΣ ΠΡΟΣΩΠΙΚΟΥ: ΜΕΛΕΤΗ ΠΕΡΙΠΤΩΣΗΣ ΙΔΙΩΤΙΚΟΥ ΝΟΣΟΚΟΜΕΙΟΥ ΠΑΡΑΓΙΟΥΔΑΚΗ ΜΑΓΔΑΛΗΝΗ Διπλωματική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΟΙΚΗΣΗ της ΥΓΕΙΑΣ» ΑΞΙΟΛΟΓΗΣΗ ΑΠΟΔΟΣΗΣ ΠΡΟΣΩΠΙΚΟΥ: ΜΕΛΕΤΗ ΠΕΡΙΠΤΩΣΗΣ ΙΔΙΩΤΙΚΟΥ ΝΟΣΟΚΟΜΕΙΟΥ ΠΑΡΑΓΙΟΥΔΑΚΗ ΜΑΓΔΑΛΗΝΗ Διπλωματική
Βιοπληροφορική Ι. Παντελής Μπάγκος. Παν/µιο Στερεάς Ελλάδας
 Βιοπληροφορική Ι Παντελής Μπάγκος Παν/µιο Στερεάς Ελλάδας Λαµία 2006 1 Βιοπληροφορική Ι Εισαγωγή: Ορισµός της Βιοπληροφορικής, Υποδιαιρέσεις της Βιοπληροφορικής, Τα είδη των δεδοµένων στη Βιοπληροφορική.
Βιοπληροφορική Ι Παντελής Μπάγκος Παν/µιο Στερεάς Ελλάδας Λαµία 2006 1 Βιοπληροφορική Ι Εισαγωγή: Ορισµός της Βιοπληροφορικής, Υποδιαιρέσεις της Βιοπληροφορικής, Τα είδη των δεδοµένων στη Βιοπληροφορική.
Βιοπληροφορική και Πολυµέσα. Ειρήνη Αυδίκου Αθήνα
 Βιοπληροφορική και Πολυµέσα Αθήνα 1.2.2009 ΠΕΡΙΕΧΟΜΕΝΑ 1. Πως σχετίζεται µε τα Πολυµέσα 2. Τι είναι η Βιοπληροφορική 3. Χρήσεις 4. Συµπεράσµατα 5. Βιβλιογραφία Βιοπληροφορική και Πολυµέσα 2 1. Τι είναι
Βιοπληροφορική και Πολυµέσα Αθήνα 1.2.2009 ΠΕΡΙΕΧΟΜΕΝΑ 1. Πως σχετίζεται µε τα Πολυµέσα 2. Τι είναι η Βιοπληροφορική 3. Χρήσεις 4. Συµπεράσµατα 5. Βιβλιογραφία Βιοπληροφορική και Πολυµέσα 2 1. Τι είναι
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ "ΤΕΧΝΟΛΟΓΙΕΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΗΝ ΙΑΤΡΙΚΗ ΚΑΙ ΤΗ ΒΙΟΛΟΓΙΑ" ΔΙΠΛΩΜΑΤΙΚΗ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ "ΤΕΧΝΟΛΟΓΙΕΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΗΝ ΙΑΤΡΙΚΗ ΚΑΙ ΤΗ ΒΙΟΛΟΓΙΑ" ΔΙΠΛΩΜΑΤΙΚΗ
Splice site recognition between different organisms
 NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS SCHOOL OF SCIENCE DEPARTMENT OF INFORMATICS AND TELECOMMUNICATIONS INTERDEPARTMENTAL POSTGRADUATE PROGRAM "INFORMATION TECHNOLOGIES IN MEDICINE AND BIOLOGY"
NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS SCHOOL OF SCIENCE DEPARTMENT OF INFORMATICS AND TELECOMMUNICATIONS INTERDEPARTMENTAL POSTGRADUATE PROGRAM "INFORMATION TECHNOLOGIES IN MEDICINE AND BIOLOGY"
Εισαγωγή στη Γενετική και στη Γονιδιωματική Τι είναι η κληρονομικότητα, και πώς μεταβιβάζεται η πληροφορία από γενιά σε γενιά;
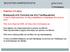 ΒΙΟΛΟΓΙΚΗ ΑΝΘΡΩΠΟΛΟΓΙΑ 12 26/10/2016 Κεφάλαιο 3 Α μέρος Εισαγωγή στη Γενετική και στη Γονιδιωματική Τι είναι η κληρονομικότητα, και πώς μεταβιβάζεται η πληροφορία από γενιά σε γενιά; Ποια είναι η δομή
ΒΙΟΛΟΓΙΚΗ ΑΝΘΡΩΠΟΛΟΓΙΑ 12 26/10/2016 Κεφάλαιο 3 Α μέρος Εισαγωγή στη Γενετική και στη Γονιδιωματική Τι είναι η κληρονομικότητα, και πώς μεταβιβάζεται η πληροφορία από γενιά σε γενιά; Ποια είναι η δομή
Γουλή Ευαγγελία. 1. Εισαγωγή. 2. Παρουσίαση και Σχολιασµός των Εργασιών της Συνεδρίας
 1. Εισαγωγή Σχολιασµός των εργασιών της 16 ης παράλληλης συνεδρίας µε θέµα «Σχεδίαση Περιβαλλόντων για ιδασκαλία Προγραµµατισµού» που πραγµατοποιήθηκε στο πλαίσιο του 4 ου Πανελλήνιου Συνεδρίου «ιδακτική
1. Εισαγωγή Σχολιασµός των εργασιών της 16 ης παράλληλης συνεδρίας µε θέµα «Σχεδίαση Περιβαλλόντων για ιδασκαλία Προγραµµατισµού» που πραγµατοποιήθηκε στο πλαίσιο του 4 ου Πανελλήνιου Συνεδρίου «ιδακτική
ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ. «ΔΙΟΙΚΗΣΗ της ΥΓΕΙΑΣ» ΑΞΙΟΛΟΓΗΣΗ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗ ΝΟΣΟΚΟΜΕΙΑΚΟΥ ΠΡΟΣΩΠΙΚΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΟΙΚΗΣΗ της ΥΓΕΙΑΣ» ΑΞΙΟΛΟΓΗΣΗ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗ ΝΟΣΟΚΟΜΕΙΑΚΟΥ ΠΡΟΣΩΠΙΚΟΥ Μαστρογιάννη Μαρία Διπλωματική Εργασία υποβληθείσα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΟΙΚΗΣΗ της ΥΓΕΙΑΣ» ΑΞΙΟΛΟΓΗΣΗ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗ ΝΟΣΟΚΟΜΕΙΑΚΟΥ ΠΡΟΣΩΠΙΚΟΥ Μαστρογιάννη Μαρία Διπλωματική Εργασία υποβληθείσα
ΒΙΟΧΗΜΕΙΑ Ι. ΚΕΦΑΛΑΙΟ 2 ο Βιοχημική εξέλιξη
 ΒΙΟΧΗΜΕΙΑ Ι ΚΕΦΑΛΑΙΟ 2 ο Βιοχημική εξέλιξη ΣΥΝΔΕΣΗ ΜΕ ΤΑ ΠΡΟΗΓΟΥΜΕΝΑ Τι είναι ΒΙΟΧΗΜΕΙΑ DNA ΠΡΩΤΕΙΝΕΣ ΑΛΛΑ ΣΥΝΔΕΣΗ ΒΙΟΛΟΓΙΑΣ ΚΑΙ ΧΗΜΕΙΑΣ (Δεσμοί, ενέργεια, δομή) ΕΞΕΛΙΞΗ ΤΗΣ ΖΩΗΣ Υπάρχει μια συνεχή εξελικτική
ΒΙΟΧΗΜΕΙΑ Ι ΚΕΦΑΛΑΙΟ 2 ο Βιοχημική εξέλιξη ΣΥΝΔΕΣΗ ΜΕ ΤΑ ΠΡΟΗΓΟΥΜΕΝΑ Τι είναι ΒΙΟΧΗΜΕΙΑ DNA ΠΡΩΤΕΙΝΕΣ ΑΛΛΑ ΣΥΝΔΕΣΗ ΒΙΟΛΟΓΙΑΣ ΚΑΙ ΧΗΜΕΙΑΣ (Δεσμοί, ενέργεια, δομή) ΕΞΕΛΙΞΗ ΤΗΣ ΖΩΗΣ Υπάρχει μια συνεχή εξελικτική
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΜΑΘΗΜΑΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΑΝΑΛΥΣΗ ΠΙΣΤΟΠΟΙΗΤΙΚΩΝ ΕΝΕΡΓΕΙΑΚΗΣ ΑΠΟΔΟΣΗΣ ΚΤΙΡΙΩΝ Εβελίνα Θεμιστοκλέους
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΜΑΘΗΜΑΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΑΝΑΛΥΣΗ ΠΙΣΤΟΠΟΙΗΤΙΚΩΝ ΕΝΕΡΓΕΙΑΚΗΣ ΑΠΟΔΟΣΗΣ ΚΤΙΡΙΩΝ Εβελίνα Θεμιστοκλέους
Πτυχιακή διατριβή. Η επίδραση της τασιενεργής ουσίας Ακεταλδεΰδης στη δημιουργία πυρήνων συμπύκνωσης νεφών (CCN) στην ατμόσφαιρα
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η επίδραση της τασιενεργής ουσίας Ακεταλδεΰδης στη δημιουργία πυρήνων συμπύκνωσης νεφών (CCN)
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η επίδραση της τασιενεργής ουσίας Ακεταλδεΰδης στη δημιουργία πυρήνων συμπύκνωσης νεφών (CCN)
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 16 IOYNIOY 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 16 IOYNIOY 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. δ Α2. δ Α3. β Α4. γ Α5. α ΘΕΜΑ Β Β1. Α I Β IV Γ VI
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 16 IOYNIOY 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. δ Α2. δ Α3. β Α4. γ Α5. α ΘΕΜΑ Β Β1. Α I Β IV Γ VI
Βάσεις δομικών δεδομένων βιολογικών μακρομορίων
 Βάσεις δομικών δεδομένων βιολογικών μακρομορίων Vasilis Promponas Bioinformatics Research Laboratory Department of Biological Sciences University of Cyprus Εισαγωγή Βασικές αρχές δομής πρωτεϊνών και νουκλεϊκών
Βάσεις δομικών δεδομένων βιολογικών μακρομορίων Vasilis Promponas Bioinformatics Research Laboratory Department of Biological Sciences University of Cyprus Εισαγωγή Βασικές αρχές δομής πρωτεϊνών και νουκλεϊκών
Περιεχόμενα. 1 Η ιστορία της εξελικτικής βιολογίας: Εξέλιξη και Γενετική 2 Η Προέλευση της Μοριακής Βιολογίας 3 Αποδείξεις για την εξέλιξη 89
 Περιεχόμενα Οι Συγγραφείς Πρόλογος της Ελληνικής Έκδοσης Πρόλογος της Αμερικανικής Έκδοσης Σκοπός και Αντικείμενο του Βιβλίου ΜΕΡΟΣ Ι ΜΙΑ ΕΠΙΣΚΟΠΗΣΗ ΤΗΣ ΕΞΕΛΙΚΤΙΚΗΣ ΒΙΟΛΟΓΙΑΣ 1 Η ιστορία της εξελικτικής
Περιεχόμενα Οι Συγγραφείς Πρόλογος της Ελληνικής Έκδοσης Πρόλογος της Αμερικανικής Έκδοσης Σκοπός και Αντικείμενο του Βιβλίου ΜΕΡΟΣ Ι ΜΙΑ ΕΠΙΣΚΟΠΗΣΗ ΤΗΣ ΕΞΕΛΙΚΤΙΚΗΣ ΒΙΟΛΟΓΙΑΣ 1 Η ιστορία της εξελικτικής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΒΙΟΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΒΙΟΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ (ΒΙΟ 003) Εισαγωγή στη Βιοπληροφορική Διδάσκων: Βασίλειος Ι. Προμπονάς, Ph.D. Λέκτορας Βιοπληροφορικής ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ Διαλέξεις Φροντιστήριο Τρίτη και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΒΙΟΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ (ΒΙΟ 003) Εισαγωγή στη Βιοπληροφορική Διδάσκων: Βασίλειος Ι. Προμπονάς, Ph.D. Λέκτορας Βιοπληροφορικής ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ Διαλέξεις Φροντιστήριο Τρίτη και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΒΙΟΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΒΙΟΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ (ΒΙΟ 003) Εισαγωγή στη Βιοπληροφορική Διδάσκοντες: Χρήστος Ουζούνης, Βασίλειος Ι. Προµπονάς ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ Διαλέξεις Τρίτη και Παρασκευή 10:30 12:00,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΒΙΟΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ (ΒΙΟ 003) Εισαγωγή στη Βιοπληροφορική Διδάσκοντες: Χρήστος Ουζούνης, Βασίλειος Ι. Προµπονάς ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ Διαλέξεις Τρίτη και Παρασκευή 10:30 12:00,
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ Κ Υ Κ Λ Ο Υ Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ Κ Α Ι Υ Π Η Ρ Ε Σ Ι Ω Ν Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ Κ Υ Κ Λ Ο Υ Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ Κ Α Ι Υ Π Η Ρ Ε Σ Ι Ω Ν Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η
Δασική Γενετική Εισαγωγή: Βασικές έννοιες
 Δασική Γενετική Εισαγωγή: Βασικές έννοιες Χειμερινό εξάμηνο 2014-2015 Γενετική Πειραματική επιστήμη της κληρονομικότητας Προέκυψε από την ανάγκη κατανόησης της κληρονόμησης οικονομικά σημαντικών χαρακτηριστικών
Δασική Γενετική Εισαγωγή: Βασικές έννοιες Χειμερινό εξάμηνο 2014-2015 Γενετική Πειραματική επιστήμη της κληρονομικότητας Προέκυψε από την ανάγκη κατανόησης της κληρονόμησης οικονομικά σημαντικών χαρακτηριστικών
TreeTOPS. ένα εισαγωγικό παιχνίδι για τα φυλογενετικά δέντρα. Teacher s Guide. ELLS European Learning Laboratory for the Life Sciences
 TreeTOPS ένα εισαγωγικό παιχνίδι για τα φυλογενετικά δέντρα Teacher s Guide ELLS European Learning Laboratory for the Life Sciences 1 Γενικός σκοπός Το συγκεκριμένο παιχνίδι έχει ως στόχο να εισάγει τους
TreeTOPS ένα εισαγωγικό παιχνίδι για τα φυλογενετικά δέντρα Teacher s Guide ELLS European Learning Laboratory for the Life Sciences 1 Γενικός σκοπός Το συγκεκριμένο παιχνίδι έχει ως στόχο να εισάγει τους
ΜΕΘΟΔΟΛΟΓΙΑ ΕΡΕΥΝΑΣ. 1 η ΠΑΡΟΥΣΙΑΣΗ. Ι. Δημόπουλος Τμήμα Διοίκησης Επιχειρήσεων και Οργανισμών. ΤΕΙ Πελοποννήσου
 ΜΕΘΟΔΟΛΟΓΙΑ ΕΡΕΥΝΑΣ 1 η ΠΑΡΟΥΣΙΑΣΗ Ι. Δημόπουλος Τμήμα Διοίκησης Επιχειρήσεων και Οργανισμών. ΤΕΙ Πελοποννήσου Κάποιες έννοιες Επιστήμη : κάθε συστηματικό πεδίο μελέτης ή σύστημα γνώσης που έχει ως σκοπό
ΜΕΘΟΔΟΛΟΓΙΑ ΕΡΕΥΝΑΣ 1 η ΠΑΡΟΥΣΙΑΣΗ Ι. Δημόπουλος Τμήμα Διοίκησης Επιχειρήσεων και Οργανισμών. ΤΕΙ Πελοποννήσου Κάποιες έννοιες Επιστήμη : κάθε συστηματικό πεδίο μελέτης ή σύστημα γνώσης που έχει ως σκοπό
Κεφάλαιο 7 - Ένζυμα, οι μηχανισμοί της ζωής
 1 Απόσπασμα από το βιβλίο «Πως να ζήσετε 150 χρόνια» του Dr. Δημήτρη Τσουκαλά Κεφάλαιο 7 - Ένζυμα, οι μηχανισμοί της ζωής Μικροσκοπικοί οργανισμοί που ρυθμίζουν τη λειτουργία του ανθρώπινου σώματος σε
1 Απόσπασμα από το βιβλίο «Πως να ζήσετε 150 χρόνια» του Dr. Δημήτρη Τσουκαλά Κεφάλαιο 7 - Ένζυμα, οι μηχανισμοί της ζωής Μικροσκοπικοί οργανισμοί που ρυθμίζουν τη λειτουργία του ανθρώπινου σώματος σε
Πειραματική και θεωρητική μελέτη της χημικής απόθεσης από ατμό χαλκού και αλουμινίου από αμιδικές πρόδρομες ενώσεις. Ιωάννης Γ.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ Πειραματική και θεωρητική μελέτη της χημικής απόθεσης από ατμό χαλκού και αλουμινίου από αμιδικές πρόδρομες ενώσεις Ιωάννης Γ. Αβιζιώτης ΣΤΟΙΧΕΙΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ Πειραματική και θεωρητική μελέτη της χημικής απόθεσης από ατμό χαλκού και αλουμινίου από αμιδικές πρόδρομες ενώσεις Ιωάννης Γ. Αβιζιώτης ΣΤΟΙΧΕΙΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΕΠΙΛΥΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΧΡΟΝΟΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕΤΑΔΟΣΗΣ ΣΕ ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ ΜΕ ΣΥΣΚΕΥΕΣ ΔΙΑΚΡΙΤΩΝ ΤΙΜΩΝ ΙΣΧΥΟΣ ΜΕ ΤΗ ΧΡΗΣΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΕΠΙΛΥΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΧΡΟΝΟΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΜΕΤΑΔΟΣΗΣ ΣΕ ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ ΜΕ ΣΥΣΚΕΥΕΣ ΔΙΑΚΡΙΤΩΝ ΤΙΜΩΝ ΙΣΧΥΟΣ ΜΕ ΤΗ ΧΡΗΣΗ
Φάσμα group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι.
 σύγχρονο Φάσμα group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. µαθητικό φροντιστήριο Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ 50.51.557 50.56.296 25ης Μαρτίου 74 ΠΛ.ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990
σύγχρονο Φάσμα group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. µαθητικό φροντιστήριο Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ 50.51.557 50.56.296 25ης Μαρτίου 74 ΠΛ.ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990
τρόπος για να εμπεδωθεί η θεωρία. Για την επίλυση των παραδειγμάτων χρησιμοποιούνται στατιστικά πακέτα, ώστε να είναι δυνατή η ανάλυση μεγάλου όγκου
 ΠΡΟΛΟΓΟΣ Η γραμμική παλινδρόμηση χρησιμοποιείται για την μελέτη των σχέσεων μεταξύ μετρήσιμων μεταβλητών. Γενικότερα, η γραμμική στατιστική συμπερασματολογία αποτελεί ένα ευρύ πεδίο της στατιστικής ανάλυσης
ΠΡΟΛΟΓΟΣ Η γραμμική παλινδρόμηση χρησιμοποιείται για την μελέτη των σχέσεων μεταξύ μετρήσιμων μεταβλητών. Γενικότερα, η γραμμική στατιστική συμπερασματολογία αποτελεί ένα ευρύ πεδίο της στατιστικής ανάλυσης
Κεφάλαιο 1: Το Γενετικό Υλικό 1.
 Κεφάλαιο 1: Το Γενετικό Υλικό 1. Ο πνευμονιόκοκκος είναι: α. μύκητας β. βακτήριο γ. ιός δ. πρωτόζωο 2. Στο πείραμα του Griffith τι αποτελέσματα είχε ο εμβολιασμός με βακτήρια, θάνατο(θ) ή επιβίωση (Ε),
Κεφάλαιο 1: Το Γενετικό Υλικό 1. Ο πνευμονιόκοκκος είναι: α. μύκητας β. βακτήριο γ. ιός δ. πρωτόζωο 2. Στο πείραμα του Griffith τι αποτελέσματα είχε ο εμβολιασμός με βακτήρια, θάνατο(θ) ή επιβίωση (Ε),
ΟΜΑΔΑ Λ. Αναστασίου Κωνσταντίνος Δεληγιάννη Ισαβέλλα Ζωγοπούλου Άννα Κουκάκης Γιώργος Σταθάκη Αρετιάννα
 ΟΜΑΔΑ Λ Αναστασίου Κωνσταντίνος Δεληγιάννη Ισαβέλλα Ζωγοπούλου Άννα Κουκάκης Γιώργος Σταθάκη Αρετιάννα ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ Τι είναι η βιοπληροφορική; Αποκαλείται ο επιστημονικός κλάδος ο οποίος προέκυψε από
ΟΜΑΔΑ Λ Αναστασίου Κωνσταντίνος Δεληγιάννη Ισαβέλλα Ζωγοπούλου Άννα Κουκάκης Γιώργος Σταθάκη Αρετιάννα ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ Τι είναι η βιοπληροφορική; Αποκαλείται ο επιστημονικός κλάδος ο οποίος προέκυψε από
Το ΔΕΠΠΣ- ΑΠΣ των Φυσικών Επιστημών της Ε και Στ Δημοτικού Τα Νέα Διδακτικά Βιβλία των Φυσικών Επιστημών της Ε και Στ Δημοτικού
 Το ΔΕΠΠΣ- ΑΠΣ των Φυσικών Επιστημών της Ε Τα Νέα Διδακτικά Βιβλία των Φυσικών Επιστημών της Ε Ειδικοί σκοποί ΑΠΣ Κατανόηση: φυσικού κόσμου νόμων που τον διέπουν φυσικών φαινομένων διαδικασιών που οδηγούν
Το ΔΕΠΠΣ- ΑΠΣ των Φυσικών Επιστημών της Ε Τα Νέα Διδακτικά Βιβλία των Φυσικών Επιστημών της Ε Ειδικοί σκοποί ΑΠΣ Κατανόηση: φυσικού κόσμου νόμων που τον διέπουν φυσικών φαινομένων διαδικασιών που οδηγούν
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ
 ΠΕΡΙΓΡΑΜΜΑ 2.1 ΒΑΣΙΚΑ ΟΡΓΑΝΙΚΑ ΜΟΡΙΑ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΑΠΌ ΤΟΥΣ ΖΩΝΤΕΣ ΟΡΓΑΝΙΣΜΟΥΣ 2.2 Η ΕΞΕΛΙΞΗ ΧΡΕΙΑΖΕΤΑΙ ΑΝΑΠΑΡΑΓΩΓΗ, ΠΟΙΚΙΛΟΜΟΡΦΙΑ, ΚΑΙ ΕΞΕΛΙΚΤΙΚΗ ΠΙΕΣΗ 2.3 ΕΝΕΡΓΕΙΑΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΊΝΑΙ ΑΠΑΡΑΙΤΗΤΟΙ
ΠΕΡΙΓΡΑΜΜΑ 2.1 ΒΑΣΙΚΑ ΟΡΓΑΝΙΚΑ ΜΟΡΙΑ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΑΠΌ ΤΟΥΣ ΖΩΝΤΕΣ ΟΡΓΑΝΙΣΜΟΥΣ 2.2 Η ΕΞΕΛΙΞΗ ΧΡΕΙΑΖΕΤΑΙ ΑΝΑΠΑΡΑΓΩΓΗ, ΠΟΙΚΙΛΟΜΟΡΦΙΑ, ΚΑΙ ΕΞΕΛΙΚΤΙΚΗ ΠΙΕΣΗ 2.3 ΕΝΕΡΓΕΙΑΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΊΝΑΙ ΑΠΑΡΑΙΤΗΤΟΙ
Σχεδιασμός Οικολογικού Διαμεσολαβητή για την εποπτεία και διαχείριση δικτύου διανομής ηλεκτρικής ενέργειας
 Σχεδιασμός Οικολογικού Διαμεσολαβητή για την εποπτεία και διαχείριση δικτύου διανομής ηλεκτρικής ενέργειας Σωτηρία Δριβάλου Εθνικό Μετσόβιο Πολυτεχνείο Μονάδα Εργονομίας Συστήματα διανομής ηλεκτρικής ενέργειας
Σχεδιασμός Οικολογικού Διαμεσολαβητή για την εποπτεία και διαχείριση δικτύου διανομής ηλεκτρικής ενέργειας Σωτηρία Δριβάλου Εθνικό Μετσόβιο Πολυτεχνείο Μονάδα Εργονομίας Συστήματα διανομής ηλεκτρικής ενέργειας
1. Ο Griffith στα πειράματά του χρησιμοποίησε:
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΒΙΟΛΟΓΙΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 27/11/11 ΘΕΜΑ 1 Ο Α. Να επιλέξετε τη φράση που συμπληρώνει ορθά κάθε μία από τις ακόλουθες προτάσεις: 1. Ο Griffith στα πειράματά
ΜΑΘΗΜΑ / ΤΑΞΗ : ΒΙΟΛΟΓΙΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 27/11/11 ΘΕΜΑ 1 Ο Α. Να επιλέξετε τη φράση που συμπληρώνει ορθά κάθε μία από τις ακόλουθες προτάσεις: 1. Ο Griffith στα πειράματά
ΑΠΑΝΤΗΣΕΙΣ. ΘΕΜΑ Α Α1. β Α2. γ Α3. δ Α4. γ Α5. β
 ΘΕΜΑ Α Α1. β Α2. γ Α3. δ Α4. γ Α5. β 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΤΕΤΑΡΤΗ 10 ΣΕΠΤΕΜΒΡΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ:
ΘΕΜΑ Α Α1. β Α2. γ Α3. δ Α4. γ Α5. β 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΤΕΤΑΡΤΗ 10 ΣΕΠΤΕΜΒΡΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ:
ΘΕΜΑ Α Α1. γ Α2. γ Α3. α Α4. β Α5. β ΘΕΜΑ B B1. B2.
 ΘΕΜΑ Α Α1. γ (το πριμόσωμα) Α2. γ (οι υποκινητές και οι μεταγραφικοί παράγοντες κάθε γονιδίου) Α3. α (μεταφέρει ένα συγκεκριμένο αμινοξύ στο ριβόσωμα) Α4. β (αποδιάταξη των δύο συμπληρωματικών αλυσίδων)
ΘΕΜΑ Α Α1. γ (το πριμόσωμα) Α2. γ (οι υποκινητές και οι μεταγραφικοί παράγοντες κάθε γονιδίου) Α3. α (μεταφέρει ένα συγκεκριμένο αμινοξύ στο ριβόσωμα) Α4. β (αποδιάταξη των δύο συμπληρωματικών αλυσίδων)
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή διατριβή
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η ΣΥΓΚΕΝΤΡΩΣΗ ΤΩΝ ΒΑΡΕΩΝ ΜΕΤΑΛΛΩΝ ΣΤΟ ΕΔΑΦΟΣ ΚΑΙ ΜΕΘΟΔΟΙ ΠΡΟΣΔΙΟΡΙΣΜΟΥ ΤΟΥΣ Μιχαήλ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η ΣΥΓΚΕΝΤΡΩΣΗ ΤΩΝ ΒΑΡΕΩΝ ΜΕΤΑΛΛΩΝ ΣΤΟ ΕΔΑΦΟΣ ΚΑΙ ΜΕΘΟΔΟΙ ΠΡΟΣΔΙΟΡΙΣΜΟΥ ΤΟΥΣ Μιχαήλ
Β. ΚΑΜΙΝΕΛΛΗΣ ΒΙΟΛΟΓΙΑ. Είναι η επιστήμη που μελετά τους ζωντανούς οργανισμούς. (Αποτελούνται από ένα ή περισσότερα κύτταρα).
 ΒΙΟΛΟΓΙΑ Είναι η επιστήμη που μελετά τους ζωντανούς οργανισμούς. (Αποτελούνται από ένα ή περισσότερα κύτταρα). Είδη οργανισμών Υπάρχουν δύο είδη οργανισμών: 1. Οι μονοκύτταροι, που ονομάζονται μικροοργανισμοί
ΒΙΟΛΟΓΙΑ Είναι η επιστήμη που μελετά τους ζωντανούς οργανισμούς. (Αποτελούνται από ένα ή περισσότερα κύτταρα). Είδη οργανισμών Υπάρχουν δύο είδη οργανισμών: 1. Οι μονοκύτταροι, που ονομάζονται μικροοργανισμοί
ΕΝΟΤΗΤΑ 14: Ο ΦΟΡΕΑΣ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ (DNA) 14.1 ΕΙΣΑΓΩΓΗ
 1 ΕΝΟΤΗΤΑ 14: Ο ΦΟΡΕΑΣ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ (DNA) 14.1 ΕΙΣΑΓΩΓΗ Οι δύο πολυνουκλεοτιδικές αλυσίδες του DNA αποτελούνται από νουκλεοτίδια τα οποία ενώνονται με φωσφοδιεστερικούς δεσμούς. Πιο συγκεκριμένα
1 ΕΝΟΤΗΤΑ 14: Ο ΦΟΡΕΑΣ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ (DNA) 14.1 ΕΙΣΑΓΩΓΗ Οι δύο πολυνουκλεοτιδικές αλυσίδες του DNA αποτελούνται από νουκλεοτίδια τα οποία ενώνονται με φωσφοδιεστερικούς δεσμούς. Πιο συγκεκριμένα
ΚΕΦΑΛΑΙΟ 5. Διατήρηση και συνέχεια της ζωής
 ΚΕΑΛΑΙΟ 5 ιατήρηση και συνέχεια της ζωής 5.2 H ροή της γενετικής πληροφορίας 3 Πώς βρέθηκε η δομή του DNA στο χώρο; Η ανακάλυψη της δομής του DNA πραγματοποιήθηκε το 1953 από τους Watson και Crick. Από
ΚΕΑΛΑΙΟ 5 ιατήρηση και συνέχεια της ζωής 5.2 H ροή της γενετικής πληροφορίας 3 Πώς βρέθηκε η δομή του DNA στο χώρο; Η ανακάλυψη της δομής του DNA πραγματοποιήθηκε το 1953 από τους Watson και Crick. Από
ΔΙΑΚΡΙΣΗ ΣΤΟΙΧΕΙΩΝ ΜΑΚΡΟΘΡΕΠΤΙΚΑ (C, H, N, O) 96% ΜΙΚΡΟΘΡΕΠΤΙΚΑ (πχ. Na, K, P, Ca, Mg) 4% ΙΧΝΟΣΤΟΙΧΕΙΑ (Fe, I) 0,01%
 ΔΙΑΚΡΙΣΗ ΣΤΟΙΧΕΙΩΝ ΜΑΚΡΟΘΡΕΠΤΙΚΑ (C, H, N, O) 96% ΜΙΚΡΟΘΡΕΠΤΙΚΑ (πχ. Na, K, P, Ca, Mg) 4% ΙΧΝΟΣΤΟΙΧΕΙΑ (Fe, I) 0,01% Ο άνθρακας, το υδρογόνο, το οξυγόνο και το άζωτο συμμετέχουν, σε σημαντικό βαθμό, στη
ΔΙΑΚΡΙΣΗ ΣΤΟΙΧΕΙΩΝ ΜΑΚΡΟΘΡΕΠΤΙΚΑ (C, H, N, O) 96% ΜΙΚΡΟΘΡΕΠΤΙΚΑ (πχ. Na, K, P, Ca, Mg) 4% ΙΧΝΟΣΤΟΙΧΕΙΑ (Fe, I) 0,01% Ο άνθρακας, το υδρογόνο, το οξυγόνο και το άζωτο συμμετέχουν, σε σημαντικό βαθμό, στη
ΠΟΩΤΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΔΤΝΑΜΙΚΗΣ ΜΗΧΑΝΩΝ
 ΡΙΣΤΟΤΕΩΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΟΕΣΣΑΩΟΝΙΚΗΣ ΠΟΩΤΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΤΑΣΚΕΤΑΣΤΙΚΟΣ ΤΟΜΕΑΣ ΕΡΓΑΣΤΗΡΙΟ ΔΤΝΑΜΙΚΗΣ ΜΗΧΑΝΩΝ Γεωργία N. Γεωργίου Διπλ. Μηχανολόγος Μηχανικός A.Π.O. ΙΖΡΟΣΔΙΟΡΙΣΜΟΣ
ΡΙΣΤΟΤΕΩΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΟΕΣΣΑΩΟΝΙΚΗΣ ΠΟΩΤΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΤΑΣΚΕΤΑΣΤΙΚΟΣ ΤΟΜΕΑΣ ΕΡΓΑΣΤΗΡΙΟ ΔΤΝΑΜΙΚΗΣ ΜΗΧΑΝΩΝ Γεωργία N. Γεωργίου Διπλ. Μηχανολόγος Μηχανικός A.Π.O. ΙΖΡΟΣΔΙΟΡΙΣΜΟΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΟΜΟΣΤΑΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΕΤΑΛΛΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΑΥΤΟΜΑΤΟ ΕΛΕΓΧΟ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Ανεµόµετρο AMD 1 Αισθητήρας AMD 2 11 ος όροφος Υπολογιστής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΟΜΟΣΤΑΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΕΤΑΛΛΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΑΥΤΟΜΑΤΟ ΕΛΕΓΧΟ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Ανεµόµετρο AMD 1 Αισθητήρας AMD 2 11 ος όροφος Υπολογιστής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΑΜΕΣΕΣ ΞΕΝΕΣ ΕΠΕΝΔΥΣΕΙΣ ΣΕ ΕΥΡΩΠΑΙΚΕΣ ΧΩΡΕΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΣΤΡΑΤΗΓΙΚΗ ΑΜΕΣΕΣ ΞΕΝΕΣ ΕΠΕΝΔΥΣΕΙΣ ΣΕ ΕΥΡΩΠΑΙΚΕΣ ΧΩΡΕΣ Αθανάσιος Νταραβάνογλου Διπλωματική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΣΤΡΑΤΗΓΙΚΗ ΑΜΕΣΕΣ ΞΕΝΕΣ ΕΠΕΝΔΥΣΕΙΣ ΣΕ ΕΥΡΩΠΑΙΚΕΣ ΧΩΡΕΣ Αθανάσιος Νταραβάνογλου Διπλωματική
ΠΑΝΕΛΛAΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ
 ΠΑΝΕΛΛAΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 16-06-2017 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. δ Α2. δ Α3. β Α4. γ Α5. α ΘΕΜΑ Β Β1. Α. φωσφορική ομάδα (Ι) E. υδροξύλιο (II) Β. mrna
ΠΑΝΕΛΛAΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 16-06-2017 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. δ Α2. δ Α3. β Α4. γ Α5. α ΘΕΜΑ Β Β1. Α. φωσφορική ομάδα (Ι) E. υδροξύλιο (II) Β. mrna
Βιολογία Β Λυκείου θέματα
 Ι. Οι υδατάνθρακες διακρίνονται σε μονοσακχαρίτες, δισακχαρίτες και πολυσακχαρίτες. α) Να αναφέρετε από δύο παραδείγματα μονοσακχαριτών, δισακχαριτών και πολυσακχαριτών. (6μ) β) Σε ένα κύτταρο συναντώνται
Ι. Οι υδατάνθρακες διακρίνονται σε μονοσακχαρίτες, δισακχαρίτες και πολυσακχαρίτες. α) Να αναφέρετε από δύο παραδείγματα μονοσακχαριτών, δισακχαριτών και πολυσακχαριτών. (6μ) β) Σε ένα κύτταρο συναντώνται
ΒΙΟΛΟΓΙΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 16-2-2014 ΘΕΜΑ 1 ο Α. Να βάλετε σε κύκλο το γράμμα που αντιστοιχεί στη σωστή απάντηση. (Μονάδες 25)
 ΤΣΙΜΙΣΚΗ &ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 270727 222594 ΑΡΤΑΚΗΣ 12 - Κ. ΤΟΥΜΠΑ THΛ: 919113 949422 ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:... ΒΙΟΛΟΓΙΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 16-2-2014 ΘΕΜΑ 1 ο Α. Να βάλετε σε
ΤΣΙΜΙΣΚΗ &ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 270727 222594 ΑΡΤΑΚΗΣ 12 - Κ. ΤΟΥΜΠΑ THΛ: 919113 949422 ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:... ΒΙΟΛΟΓΙΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 16-2-2014 ΘΕΜΑ 1 ο Α. Να βάλετε σε
ΣΥΜΠΥΚΝΩΣΗ: αφαίρεση ενός μορίου νερού - σύνθεση ενός διμερούς ΥΔΡΟΛΥΣΗ : προσθήκη ενός μορίου νερού - διάσπαση του διμερούς στα συστατικά του
 ΣΥΜΠΥΚΝΩΣΗ: αφαίρεση ενός μορίου νερού - σύνθεση ενός διμερούς ΥΔΡΟΛΥΣΗ : προσθήκη ενός μορίου νερού - διάσπαση του διμερούς στα συστατικά του ΤΑ ΜΟΝΟΜΕΡΗ ΣΥΝΔΕΟΝΤΑΙ ΜΕ ΟΜΟΙΟΠΟΛΙΚΟ ΔΕΣΜΟ. 1. ΠΡΩΤΕΪΝΕΣ
ΣΥΜΠΥΚΝΩΣΗ: αφαίρεση ενός μορίου νερού - σύνθεση ενός διμερούς ΥΔΡΟΛΥΣΗ : προσθήκη ενός μορίου νερού - διάσπαση του διμερούς στα συστατικά του ΤΑ ΜΟΝΟΜΕΡΗ ΣΥΝΔΕΟΝΤΑΙ ΜΕ ΟΜΟΙΟΠΟΛΙΚΟ ΔΕΣΜΟ. 1. ΠΡΩΤΕΪΝΕΣ
τα Λεπτά Υμένια στις Νανοδομές και στις Νανο- & Mεγάλης κλίμακας κατασκευές.
 Από τα Λεπτά Υμένια στις Νανοδομές και στις Νανο- & Mεγάλης κλίμακας κατασκευές. Η εξέλιξη της επιστημονικής έρευνας, πέρα της ικανοποίησης της έμφυτης ανάγκης του ανθρώπου για γνώση, είχε και ως παράλληλο
Από τα Λεπτά Υμένια στις Νανοδομές και στις Νανο- & Mεγάλης κλίμακας κατασκευές. Η εξέλιξη της επιστημονικής έρευνας, πέρα της ικανοποίησης της έμφυτης ανάγκης του ανθρώπου για γνώση, είχε και ως παράλληλο
ΕΠΙΣΤΗΜΟΝΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ: Μια ενδιαφέρουσα σταδιοδρομία
 ΕΠΙΣΤΗΜΟΝΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ: Μια ενδιαφέρουσα σταδιοδρομία N. Μισυρλής (e-mail: nmis@di.uoa.gr) Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Parallel Scientific Computing Laboratory (PSCL)
ΕΠΙΣΤΗΜΟΝΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ: Μια ενδιαφέρουσα σταδιοδρομία N. Μισυρλής (e-mail: nmis@di.uoa.gr) Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Parallel Scientific Computing Laboratory (PSCL)
Αλγόριθμοι Εύρεσης Ομοιοτήτων Ακολουθιών
 Αλγόριθμοι Εύρεσης Ομοιοτήτων Ακολουθιών Μέρος Ι: Στοιχίσεις ακολουθιών κατά ζεύγη Βασίλης Προμπονάς, PhD Ερευνητικό Εργαστήριο Βιοπληροφορικής Τμήμα Βιολογικών Επιστημών Νέα Παν/πολη, Γραφείο B161 Πανεπιστήμιο
Αλγόριθμοι Εύρεσης Ομοιοτήτων Ακολουθιών Μέρος Ι: Στοιχίσεις ακολουθιών κατά ζεύγη Βασίλης Προμπονάς, PhD Ερευνητικό Εργαστήριο Βιοπληροφορικής Τμήμα Βιολογικών Επιστημών Νέα Παν/πολη, Γραφείο B161 Πανεπιστήμιο
ΔΟΜΗ ΚΑΙ ΑΝΑΛΥΣΗ ΒΙΟΜΟΡΙΩΝ
 ΔΟΜΗ ΚΑΙ ΑΝΑΛΥΣΗ ΒΙΟΜΟΡΙΩΝ Διδάσκοντες: Δ.Δ. Λεωνίδας, Α.-Μ. Ψαρρά Κωδικός e-class: SEYC194 28/9/2015 Δ.Δ. Λεωνίδας 28/9/2015 Δ.Δ. Λεωνίδας Βιοχημεία είναι η Χημεία που εμφανίζεται μέσα στους ζώντες οργανισμούς
ΔΟΜΗ ΚΑΙ ΑΝΑΛΥΣΗ ΒΙΟΜΟΡΙΩΝ Διδάσκοντες: Δ.Δ. Λεωνίδας, Α.-Μ. Ψαρρά Κωδικός e-class: SEYC194 28/9/2015 Δ.Δ. Λεωνίδας 28/9/2015 Δ.Δ. Λεωνίδας Βιοχημεία είναι η Χημεία που εμφανίζεται μέσα στους ζώντες οργανισμούς
Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015
 Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015 Μάθηση και γνώση: μια συνεχής και καθοριστική αλληλοεπίδραση Αντώνης Λιοναράκης Στην παρουσίαση που θα ακολουθήσει θα μιλήσουμε
Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015 Μάθηση και γνώση: μια συνεχής και καθοριστική αλληλοεπίδραση Αντώνης Λιοναράκης Στην παρουσίαση που θα ακολουθήσει θα μιλήσουμε
Νουκλεϊκά οξέα: νήµατα και αγγελιαφόροι της ζωής
 Νουκλεϊκά οξέα: νήµατα και αγγελιαφόροι της ζωής Αριστοτέλης Κωτίτσας Οι λειτουργίες των οργανισµών πραγµατοποιούνται χάρη στις πρωτεΐνες. Ο βιολογικός ρόλος των πρωτεϊνών καθορίζεται από τη µορφή τους.
Νουκλεϊκά οξέα: νήµατα και αγγελιαφόροι της ζωής Αριστοτέλης Κωτίτσας Οι λειτουργίες των οργανισµών πραγµατοποιούνται χάρη στις πρωτεΐνες. Ο βιολογικός ρόλος των πρωτεϊνών καθορίζεται από τη µορφή τους.
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ. Πτυχιακή εργασία ΟΛΙΣΘΗΡΟΤΗΤΑ ΚΑΙ ΜΑΚΡΟΥΦΗ ΤΩΝ ΟΔΟΔΤΡΩΜΑΤΩΝ ΚΥΚΛΟΦΟΡΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΟΛΙΣΘΗΡΟΤΗΤΑ ΚΑΙ ΜΑΚΡΟΥΦΗ ΤΩΝ ΟΔΟΔΤΡΩΜΑΤΩΝ ΚΥΚΛΟΦΟΡΙΑΣ Χριστοδούλου Αντρέας Λεμεσός 2014 2 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΟΛΙΣΘΗΡΟΤΗΤΑ ΚΑΙ ΜΑΚΡΟΥΦΗ ΤΩΝ ΟΔΟΔΤΡΩΜΑΤΩΝ ΚΥΚΛΟΦΟΡΙΑΣ Χριστοδούλου Αντρέας Λεμεσός 2014 2 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΓΩΝΙΕΣ φ, ψ ΚΑΙ ΕΠΙΤΡΕΠΤΕΣ ΔΙΑΜΟΡΦΩΣΕΙΣ ΤΗΣ ΠΟΛΥΠΕΠΤΙΔΙΚΗΣ ΑΛΥΣΙΔΑΣ
 ΓΩΝΙΕΣ φ, ψ ΚΑΙ ΕΠΙΤΡΕΠΤΕΣ ΔΙΑΜΟΡΦΩΣΕΙΣ ΤΗΣ ΠΟΛΥΠΕΠΤΙΔΙΚΗΣ ΑΛΥΣΙΔΑΣ ΜΕΤΡΗΣΗ ΤΗΣ ΓΩΝΙΑΣ φ φ Ccarbonyl n Ccarbonyl n N Cα n Ccarbonyl n-1 Cα n N φ Ccarbonyl n-1 ΜΕΤΡΗΣΗ ΤΗΣ ΓΩΝΙΑΣ ψ φ ψ Ccarbonyl n N (Ca
ΓΩΝΙΕΣ φ, ψ ΚΑΙ ΕΠΙΤΡΕΠΤΕΣ ΔΙΑΜΟΡΦΩΣΕΙΣ ΤΗΣ ΠΟΛΥΠΕΠΤΙΔΙΚΗΣ ΑΛΥΣΙΔΑΣ ΜΕΤΡΗΣΗ ΤΗΣ ΓΩΝΙΑΣ φ φ Ccarbonyl n Ccarbonyl n N Cα n Ccarbonyl n-1 Cα n N φ Ccarbonyl n-1 ΜΕΤΡΗΣΗ ΤΗΣ ΓΩΝΙΑΣ ψ φ ψ Ccarbonyl n N (Ca
Λίγα λόγια για τους συγγραφείς 16 Πρόλογος 17
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς 16 Πρόλογος 17 1 Εισαγωγή 21 1.1 Γιατί χρησιμοποιούμε τη στατιστική; 21 1.2 Τι είναι η στατιστική; 22 1.3 Περισσότερα για την επαγωγική στατιστική 23 1.4 Τρεις
Περιεχόμενα Λίγα λόγια για τους συγγραφείς 16 Πρόλογος 17 1 Εισαγωγή 21 1.1 Γιατί χρησιμοποιούμε τη στατιστική; 21 1.2 Τι είναι η στατιστική; 22 1.3 Περισσότερα για την επαγωγική στατιστική 23 1.4 Τρεις
Μεταπτυχιακή Διατριβή
 Μεταπτυχιακή Διατριβή ΣΧΗΜΑΤΙΣΜΟΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΣ ΒΙΟΦΙΛΜ ΣΤΙΣ ΜΕΜΒΡΑΝΕΣ ΑΝΤΙΣΤΡΟΦΗΣ ΩΣΜΩΣΗΣ ΣΤΗΝ ΑΦΑΛΑΤΩΣΗ ΛΕΜΕΣΟΥ ΚΥΠΡΟΣ ΜΙΧΑΗΛ Λεμεσός, Μάιος 2017 1 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ
Μεταπτυχιακή Διατριβή ΣΧΗΜΑΤΙΣΜΟΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΣ ΒΙΟΦΙΛΜ ΣΤΙΣ ΜΕΜΒΡΑΝΕΣ ΑΝΤΙΣΤΡΟΦΗΣ ΩΣΜΩΣΗΣ ΣΤΗΝ ΑΦΑΛΑΤΩΣΗ ΛΕΜΕΣΟΥ ΚΥΠΡΟΣ ΜΙΧΑΗΛ Λεμεσός, Μάιος 2017 1 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ
Πρόγνωση δομής πρωτεϊνών (Μέρος Ι)
 Πρόγνωση δομής πρωτεϊνών (Μέρος Ι) Βασίλης Προμπονάς, PhD Ερευνητικό Εργαστήριο Βιοπληροφορικής Τμήμα Βιολογικών Επιστημών Νέα Παν/πολη, Γραφείο B161 Πανεπιστήμιο Κύπρου Ταχ.Κιβ. 20537 1678, Λευκωσία ΚΥΠΡΟΣ
Πρόγνωση δομής πρωτεϊνών (Μέρος Ι) Βασίλης Προμπονάς, PhD Ερευνητικό Εργαστήριο Βιοπληροφορικής Τμήμα Βιολογικών Επιστημών Νέα Παν/πολη, Γραφείο B161 Πανεπιστήμιο Κύπρου Ταχ.Κιβ. 20537 1678, Λευκωσία ΚΥΠΡΟΣ
Ενδεικτικές απαντήσεις
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΑΡΑΣΚΕΥΗ 8 ΣΕΠΤΕΜΒΡΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ενδεικτικές απαντήσεις
ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΑΡΑΣΚΕΥΗ 8 ΣΕΠΤΕΜΒΡΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ενδεικτικές απαντήσεις
Κεφάλαιο 4: Ανασυνδυασμένο DNA
 Κεφάλαιο 4: Ανασυνδυασμένο DNA 1. Η ανάπτυξη της γενετικής μηχανικής επέτρεψε: α. την κατανόηση των μηχανισμών αντιγραφής του γενετικού υλικού β. την απομόνωση των πλασμιδίων από τα βακτήρια γ. την πραγματοποίηση
Κεφάλαιο 4: Ανασυνδυασμένο DNA 1. Η ανάπτυξη της γενετικής μηχανικής επέτρεψε: α. την κατανόηση των μηχανισμών αντιγραφής του γενετικού υλικού β. την απομόνωση των πλασμιδίων από τα βακτήρια γ. την πραγματοποίηση
Να επιλέξετε τη φράση που συμπληρώνει ορθά κάθε μία από τις ακόλουθες προτάσεις:
 ΒΙΟΛΟΓΙΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 04/11/2018 Νότα Λαζαράκη Αλέξανδρος Παπαγιαννακόπουλος ΘΕΜΑ Α Να επιλέξετε τη φράση που συμπληρώνει ορθά κάθε μία από τις ακόλουθες προτάσεις: Α1. Σε ένα
ΒΙΟΛΟΓΙΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 04/11/2018 Νότα Λαζαράκη Αλέξανδρος Παπαγιαννακόπουλος ΘΕΜΑ Α Να επιλέξετε τη φράση που συμπληρώνει ορθά κάθε μία από τις ακόλουθες προτάσεις: Α1. Σε ένα
«Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής»
 ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΧΡΗΣΤΟΣ ΚΑΚΑΒΑΣ 1 ΚΑΘΗΓΗΤΗΣ ΒΙΟΛΟΓΟΣ Μ.Δ.Ε
 ΚΕΦΑΛΑΙΟ 2 ον. ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΤΙ ΠΡΕΠΕΙ ΝΑ ΞΕΡΩ. 1. Τη δομή της δίκλωνης έλικας πάρα πολύ καλά. 2. Τους δεσμούς υδρογόνου μεταξύ των συμπληρωματικών βάσεων και την επίπτωσή
ΚΕΦΑΛΑΙΟ 2 ον. ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΤΙ ΠΡΕΠΕΙ ΝΑ ΞΕΡΩ. 1. Τη δομή της δίκλωνης έλικας πάρα πολύ καλά. 2. Τους δεσμούς υδρογόνου μεταξύ των συμπληρωματικών βάσεων και την επίπτωσή
Απομόνωση ανθρώπινου DNA γονιδιώματος & ποιοτικός και ποσοτικός προσδιορισμός
 Απομόνωση ανθρώπινου DNA γονιδιώματος & ποιοτικός και ποσοτικός προσδιορισμός Ευαγγελία - Ειρήνη Τσερμπίνι 1. Σκοπός Σκοπός της παρούσας άσκησης είναι η απομόνωση ανθρώπινου DNA γονιδιώματος από δείγμα
Απομόνωση ανθρώπινου DNA γονιδιώματος & ποιοτικός και ποσοτικός προσδιορισμός Ευαγγελία - Ειρήνη Τσερμπίνι 1. Σκοπός Σκοπός της παρούσας άσκησης είναι η απομόνωση ανθρώπινου DNA γονιδιώματος από δείγμα
Μελέτη και Υλοποίηση Αλγορίθμων για Βιολογικές Εφαρμογές σε MapReduce Περιβάλλον
 Μελέτη και Υλοποίηση Αλγορίθμων για Βιολογικές Εφαρμογές σε MapReduce Περιβάλλον Δανάη Κούτρα Eργαστήριο Συστημάτων Βάσεων Γνώσεων και Δεδομένων Εθνικό Μετσόβιο Πολυτεχνείο Θέματα Σκοπός της διπλωματικής
Μελέτη και Υλοποίηση Αλγορίθμων για Βιολογικές Εφαρμογές σε MapReduce Περιβάλλον Δανάη Κούτρα Eργαστήριο Συστημάτων Βάσεων Γνώσεων και Δεδομένων Εθνικό Μετσόβιο Πολυτεχνείο Θέματα Σκοπός της διπλωματικής
ΔΟΜΗ ΚΑΙ ΔΡΑΣΗ ΠΡΩΤΕΙΝΩΝ
 ΔΟΜΗ ΚΑΙ ΔΡΑΣΗ ΠΡΩΤΕΙΝΩΝ ΠPΩTEINEΣ Οι πρωτεΐνες παίζουν σημαντικό ρόλο σε όλες σχεδόν τις βιολογικές διεργασίες. H σημασία τους φαίνεται στις παρακάτω περιπτώσεις: 1. Κατάλυση (πχ. ένζυμα) 2. Μεταφορά
ΔΟΜΗ ΚΑΙ ΔΡΑΣΗ ΠΡΩΤΕΙΝΩΝ ΠPΩTEINEΣ Οι πρωτεΐνες παίζουν σημαντικό ρόλο σε όλες σχεδόν τις βιολογικές διεργασίες. H σημασία τους φαίνεται στις παρακάτω περιπτώσεις: 1. Κατάλυση (πχ. ένζυμα) 2. Μεταφορά
ΕΙΣΑΓΩΓΗ ΣΤΗ ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ Σελίδα 1 Διδάσκοντες Ηλίας Ηλιόπουλος Τριάς Θηραίου Βασιλική Κουμάντου Σχετικά με το μάθημα Σημειώσεις διδασκόντων / εργαστηριακές ασκήσεις http://www.biotech.aua.gr/ Αποστολή εργασιών auabioinf@gmail.com
ΕΙΣΑΓΩΓΗ ΣΤΗ Σελίδα 1 Διδάσκοντες Ηλίας Ηλιόπουλος Τριάς Θηραίου Βασιλική Κουμάντου Σχετικά με το μάθημα Σημειώσεις διδασκόντων / εργαστηριακές ασκήσεις http://www.biotech.aua.gr/ Αποστολή εργασιών auabioinf@gmail.com
ΘΕΜΑ Α. 1. δ 2. δ 3. β 4. γ 5. α ΘΕΜΑ Β Β1. Α I Β IV Γ VI Δ VII Ε II ΣΤ III Ζ V Η -
 ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2017 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΙΜΕΛΕΙΑ: Π. ΚΡΥΣΤΑΛΛΙΔΗΣ 1. δ 2. δ 3. β 4. γ 5. α ΘΕΜΑ Α Β1. Α I Β IV Γ VI Δ VII Ε II ΣΤ III Ζ V Η - ΘΕΜΑ Β Β2. Η εικόνα αντιστοιχεί
ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2017 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΙΜΕΛΕΙΑ: Π. ΚΡΥΣΤΑΛΛΙΔΗΣ 1. δ 2. δ 3. β 4. γ 5. α ΘΕΜΑ Α Β1. Α I Β IV Γ VI Δ VII Ε II ΣΤ III Ζ V Η - ΘΕΜΑ Β Β2. Η εικόνα αντιστοιχεί
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ. Σπύρος Τσιπίδης. Περίληψη διατριβής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ Σπύρος Τσιπίδης Γεω - οπτικοποίηση χωρωχρονικών αρχαιολογικών δεδομένων Περίληψη διατριβής H παρούσα εργασία
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ Σπύρος Τσιπίδης Γεω - οπτικοποίηση χωρωχρονικών αρχαιολογικών δεδομένων Περίληψη διατριβής H παρούσα εργασία
ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΕΝΙΣΧΥΣΗ ΤΩΝ ΚΟΜΒΩΝ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΜΕ ΒΑΣΗ ΤΟΥΣ ΕΥΡΩΚΩΔΙΚΕΣ
 Σχολή Μηχανικής και Τεχνολογίας Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΕΝΙΣΧΥΣΗ ΤΩΝ ΚΟΜΒΩΝ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΜΕ ΒΑΣΗ ΤΟΥΣ ΕΥΡΩΚΩΔΙΚΕΣ Σωτήρης Παύλου Λεμεσός, Μάιος 2018 i ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
Σχολή Μηχανικής και Τεχνολογίας Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΕΝΙΣΧΥΣΗ ΤΩΝ ΚΟΜΒΩΝ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΜΕ ΒΑΣΗ ΤΟΥΣ ΕΥΡΩΚΩΔΙΚΕΣ Σωτήρης Παύλου Λεμεσός, Μάιος 2018 i ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Επιβλέπων Καθηγητής: Δρ. Νίκος Μίτλεττον Η ΣΧΕΣΗ ΤΟΥ ΜΗΤΡΙΚΟΥ ΘΗΛΑΣΜΟΥ ΜΕ ΤΗΝ ΕΜΦΑΝΙΣΗ ΣΑΚΧΑΡΩΔΗ ΔΙΑΒΗΤΗ ΤΥΠΟΥ 2 ΣΤΗΝ ΠΑΙΔΙΚΗ ΗΛΙΚΙΑ Ονοματεπώνυμο: Ιωσηφίνα
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Επιβλέπων Καθηγητής: Δρ. Νίκος Μίτλεττον Η ΣΧΕΣΗ ΤΟΥ ΜΗΤΡΙΚΟΥ ΘΗΛΑΣΜΟΥ ΜΕ ΤΗΝ ΕΜΦΑΝΙΣΗ ΣΑΚΧΑΡΩΔΗ ΔΙΑΒΗΤΗ ΤΥΠΟΥ 2 ΣΤΗΝ ΠΑΙΔΙΚΗ ΗΛΙΚΙΑ Ονοματεπώνυμο: Ιωσηφίνα
ΛΥΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΓΙΑ Β ΛΥΚΕΙΟΥ)
 ΛΥΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΓΙΑ Β ΛΥΚΕΙΟΥ) ΘΕΜΑ 1 ο Α. Να γράψετε στο τετράδιο σας τον αριθμό κάθε μιας από τις παρακάτω ημιτελείς προτάσεις 1 έως 5 και δίπλα το γράμμα που αντιστοιχεί
ΛΥΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΓΙΑ Β ΛΥΚΕΙΟΥ) ΘΕΜΑ 1 ο Α. Να γράψετε στο τετράδιο σας τον αριθμό κάθε μιας από τις παρακάτω ημιτελείς προτάσεις 1 έως 5 και δίπλα το γράμμα που αντιστοιχεί
ΘΕΜΑΤΑ ΒΙΟΛΟΓΙΑΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΛΥΚΕΙΟΥ ΑΠΟ ΤΟ ΒΙΒΛΙΟ ΜΟΥ (YΠΟ ΕΚ ΟΣΗ): ΒΙΟΛΟΓΙΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΒΙΟΛΟΓΙΑΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΛΥΚΕΙΟΥ ΑΠΟ ΤΟ ΒΙΒΛΙΟ ΜΟΥ (YΠΟ ΕΚ ΟΣΗ): ΒΙΟΛΟΓΙΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΛΥΚΕΙΟΥ (Περιέχει 67 ερωτήσεις θεωρίας µε απαντήσεις, 116 ασκήσεις ανοικτού- κλειστού τύπου µε µ
ΘΕΜΑΤΑ ΒΙΟΛΟΓΙΑΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΛΥΚΕΙΟΥ ΑΠΟ ΤΟ ΒΙΒΛΙΟ ΜΟΥ (YΠΟ ΕΚ ΟΣΗ): ΒΙΟΛΟΓΙΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΛΥΚΕΙΟΥ (Περιέχει 67 ερωτήσεις θεωρίας µε απαντήσεις, 116 ασκήσεις ανοικτού- κλειστού τύπου µε µ
ΒΕΛΤΙΩΣΗ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟΥ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΡΓΑΛΕΙΩΝ ΔΙΑΣΦΑΛΙΣΗΣ ΠΟΙΟΤΗΤΑΣ ΣΕ ΜΕΤΑΛΛΟΒΙΟΜΗΧΑΝΙΑ
 Σχολή Mηχανικής και Τεχνολογίας Πτυχιακή εργασία ΒΕΛΤΙΩΣΗ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟΥ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΡΓΑΛΕΙΩΝ ΔΙΑΣΦΑΛΙΣΗΣ ΠΟΙΟΤΗΤΑΣ ΣΕ ΜΕΤΑΛΛΟΒΙΟΜΗΧΑΝΙΑ Στέλιος Καράσαββας Λεμεσός, Μάιος 2017
Σχολή Mηχανικής και Τεχνολογίας Πτυχιακή εργασία ΒΕΛΤΙΩΣΗ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟΥ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΡΓΑΛΕΙΩΝ ΔΙΑΣΦΑΛΙΣΗΣ ΠΟΙΟΤΗΤΑΣ ΣΕ ΜΕΤΑΛΛΟΒΙΟΜΗΧΑΝΙΑ Στέλιος Καράσαββας Λεμεσός, Μάιος 2017
Π Τ Υ Χ Ι Α Κ Η Ε Ρ Γ Α Σ Ι Α
 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΟΜΕΑΣ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ Η/Υ, ΠΛΗΡΟΦΟΡΙΚΗΣ & ΔΙΚΤΥΩΝ Εργ. Τεχνολογίας Λογισμικού & Υπηρεσιών S 2 E Lab Π Τ Υ Χ Ι
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΟΜΕΑΣ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ Η/Υ, ΠΛΗΡΟΦΟΡΙΚΗΣ & ΔΙΚΤΥΩΝ Εργ. Τεχνολογίας Λογισμικού & Υπηρεσιών S 2 E Lab Π Τ Υ Χ Ι
Τεχνολογία Λογισμικού. Ενότητα 1: Εισαγωγή στην UML Καθηγητής Εφαρμογών Ηλίας Γουνόπουλος Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά)
 Τεχνολογία Λογισμικού Ενότητα 1: Εισαγωγή στην UML Καθηγητής Εφαρμογών Ηλίας Γουνόπουλος Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τεχνολογία Λογισμικού Ενότητα 1: Εισαγωγή στην UML Καθηγητής Εφαρμογών Ηλίας Γουνόπουλος Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
