Δεδομένα και Μέθοδοι Θεωρία και Πράξη. Ιορδάνης Μπιπέρης Δρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών

Transcript

1 Δεδομένα και Μέθοδοι Θεωρία και Πράξη Ιορδάνης Μπιπέρης Δρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών

2 Εισαγωγή - γενικά χαρακτηριστικά βιομετρικών συστημάτων Κλασικές τεχνικές αναγνώρισης προτύπων Πρόσωπο, δακτυλικό αποτύπωμα και ίριδα Σύντηξη βιομετρικών Ανθεκτικότητα και περιορισμοί

3

4 Υψίστης σημασίας: Σχέσεις πολιτείας-πολίτη Έλεγχος πρόσβασης σε εγκαταστάσεις και εξοπλισμό ασφαλείας Απομακρυσμένες εμπορικές συναλλαγές Εγκληματολογικές έρευνες

5 Βασισμένοι σε κάτι που έχεις Δελτίο ταυτότητας Έξυπνη κάρτα RFID τσιπ Βασισμένοι σε κάτι που ξέρεις Κωδικός Προβλήματα Πλαστογράφηση Υποκλοπή Απώλεια

6 Βιομετρικά: Τα χαρακτηριστικά γνωρίσματα της μορφολογίαςκαιτηςσυμπεριφοράςενός ατόμου που το διαφοροποιούν από τα υπόλοιπα. Πλεονεκτήματα: Αναγνώριση βάσει του τι είσαι. Δύσκολο να ξεχαστεί, να χαθεί, να μιμηθεί.

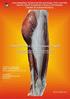
7 Δακτυλικό αποτύπωμα Παλαμικό αποτύπωμα Γεωμετρία χεριού και δακτύλων Αγγεία χεριού Εικόνα προσώπου Γεωμετρία προσώπου

8 Θερμικές εικόνες προσώπου Αμφιβληστροειδής χιτώνας Ίριδα Γεωμετρία αφτιού DNA

9 Υπογραφή Φωνή Βάδισμα Πληκτρολόγηση

10 Τέσσερις βασικές υπομονάδες Αισθητήρας: Καταγραφή του βιομετρικού. Π.χ. κάμερα, μικρόφωνο, scanner κ.τ.λ. Παράγει τα πρωτογενή δεδομένα (raw data). Εξαγωγέας βιομετρικού προτύπου: Ποσοτικοποίηση βιομετρικού. Συνήθως δημιουργία ενός διανύσματος μετρήσεων.

11 Συγκριτής: Συγκρίνει τα βιομετρικά πρότυπα, εγκαθιδρύει ένα είδος ομοιότητας ή απόστασης μεταξύ τους και αποφασίζει για την ταξινόμηση. Βάση δεδομένων: Χώρος αποθήκευσης γνωστών βιομετρικών προτύπων. Κεντρική ή αποκεντρωμένη (π.χ. σε μαγνητική ταινία που κατέχει ο χρήστης).

12 Δημογραφικές πληροφορίες X1 X2 X3 Xn Αισθητήρας Πρωτογενή δεδομένα Βιομετρικό πρότυπο Βάση δεδομένων

13 Αυθεντικοποίηση Απαντά στο ερώτημα: «Είναι πράγματι αυτός που ισχυρίζεται ότι είναι;» Ταυτοποίηση Απαντά στο ερώτημα: «Ποιος είναι;» Πρόβλημα κλειστού συνόλου. Πρόβλημα ανοιχτού συνόλου.

14 Ισχυριζόμενη ταυτότητα X1 X2 X3 Xn Υ1 Υ2 Υ3 Υn Αισθητήρας Πρωτογενή δεδομένα Παρουσιαζόμενο βιομετρικό Συγκριτής (κανόνας) Αποθηκευμένο βιομετρικό Βάση δεδομένων Αποδοχή/άρνηση

15 Αισθητήρας Πρωτογενή δεδομένα Παρουσιαζόμενο βιομετρικό X1 X2 X3 Xn Αποθηκευμένα βιομετρικά Τ1 Τ2 Ζ1 Ζ2 Υ1 Υ2 Υ3 Υn Βάση δεδομένων Συγκριτής (κανόνας) Ταυτότητα/άγνωστο

16 Αυθεντικοποίηση Παροχή βιομετρικού και ισχυρισμός μιας ταυτότητας. Σύγκριση 1:1 Απάντηση «αποδοχή» ή «άρνηση» Ταυτοποίηση Παροχή μόνο του βιομετρικού Σύγκριση 1:Ν Απάντηση «ταυτότητα» ή/και «άγνωστο»

17 Τα 4 πρώτα αφορούν το ίδιο το βιομετρικό, ενώ τα επόμενα 3 αφορούν το βιομετρικό σύστημα. Καθολικότητα (universality): Αν το έχουν όλοι άνθρωποι. Διακριτικότητα (distinctiveness): Αν μπορούν οι άνθρωποι να διακριθούν με βάση αυτό το χαρακτηριστικό. Μονιμότητα (permanence): Πόσο μόνιμο είναι το χαρακτηριστικό.

18 Συλλεξιμότητα (collectability): Πόσο καλά μπορεί να αποκτηθεί και να ποσοτικοποιηθεί το βιομετρικό. Απόδοση (performance): Ταχύτητα και ακρίβεια συστήματος. Αποδεκτικότητα (acceptability): Πόσο πρόθυμοι είναι οι άνθρωποι να το χρησιμοποιούν. Εξαπάτηση (circumvention): Πόσο εύκολο είναι να εξαπατηθεί το σύστημα.

19

20 Δεν υπάρχει τέλειο βιομετρικό. Εξαρτάται από την εφαρμογή, το επίπεδο ασφάλειας, το κόστος, την φιλικότητα προς τον χρήστη Ορισμένα είναι προσφορότερα για μια εφαρμογή από κάποια άλλα. Π.χ. για αναγνώριση από απόσταση προσφέρεται το βάδισμα.

21 Τα βιομετρικά πρότυπα διαφορετικών ατόμων είναι διαφορετικά. (Η βάσηόληςτηςθεωρίας!) Δια-ατομική μεταβλητότητα. Τα καταγραφόμενα βιομετρικά πρότυπα του ίδιου ατόμου δεν είναι πάντα ίδια. Ενδοατομική μεταβλητότητα. Εγγενείς αιτίες: Αλλαγή μεγέθους, γήρανση, τραύματα, υπογραφή μετά από μέθη, βάδισμα κατά την εγκυμοσύνη, διαβητική αμφιβληστροειδοπάθεια. Εξωγενείς αιτίες: Εξωτερικές συνθήκες, εργονομία εξοπλισμού, προβλήματα αισθητήρων, συνεργασία χρήστη.

22 Πυκνότητα πιθανότητας Ενδο-ατομικές αποστάσεις Κατώφλι σύγκρισης Δια-ατομικές αποστάσεις Positive Negative Απόσταση βιομετρικών προτύπων

23 Ρυθμός αποτυχίας καταγραφής Εξαρτάται από τον αισθητήρα και τη διαδικασία καταγραφής. Ρυθμός αποτυχίας εγγραφής Εξαρτάται από την διεπαφή και τη συμπεριφορά του χρήστη. Χωρητικότητα βιομετρικών προτύπων Ρυθμός αναγνώρισης Εξαρτάται κυρίως από την ακολουθούμενη μέθοδο.

24 Ποσοστό ορθής αναγνώρισης R: Το απλούστερο μέτρο. Ελλιπείς πληροφορίες. Προσέγγιση λίστας υπόπτων (watch-list): Θέλουμε η ορθή ταυτότητα να βρίσκεται μέσα στις k καλύτερες (top-k) θέσεις που επιστρέφει το σύστημα. Το k επιλέγεται αυθαίρετα από 1 ως τον αριθμό των ατόμων. Για k=1 ταυτίζεται με το ποσοστό ορθής αναγνώρισης R.

25 Διάγραμμα του ποσοστού R(k) ορθής ένταξης της σωστής ταυτότητας στις k- καλύτερες θέσεις, για κάθε k. 100% R k Ν (αριθμός χρηστών)

26 Πίνακας σύγχυσης Νόμιμη προσπάθεια (βιομετρικά ίδιου ατόμου) Παράνομη προσπάθεια (βιομετρικά διαφορετικών ατόμων) Αποδοχή True Positive (TP) False Positive (FP) Άρνηση False Negative (FN) True Negative (TN) False Accept Rate: Ποσοστό των παράνομων προσπαθειών που γίνονται αποδεκτές. False Reject Rate: Ποσοστό των νόμιμων προσπαθειών που απορρίπτονται. FAR= FRR= FP FP + ΤΝ FN TP + FΝ

27 Πυκνότητα πιθανότητας Κατώφλι Μικρό FAR σύγκρισηςμικρό FRR TP Ενδο-ατομικές αποστάσεις TN Δια-ατομικές αποστάσεις FP Positive FN FP FN FP FN Negative Απόσταση βιομετρικών προτύπων

28 FRR Ασφαλές αλλά δύσχρηστο σύστημα Χαμηλό κατώφλι Equal Error Rate Υψηλό κατώφλι Διάτρητο αλλά φιλικό σύστημα FAR

29 Ένα σύστημα αυθεντικοποίησης μπορεί να τεθεί σε λειτουργία ταυτοποίησης. Εγγεγραμμένοι χρήστες Χ 1, Χ 2,, Χ Ν To σύστημα αναγνωρίζει τους Χ 1 Χ Ν την ταυτότητα τους. χωρίς να δίνουν Η ταυτοποίηση γίνεται με κατάταξη των σκορ. FAR ID : Η πιθανότηταναπαρουσιαστείμη εγγεγραμμένος Υ και το σύστημα να τον αποδεχτεί ως κάποιον από τους Χ 1 Χ Ν. FRR ID : Η πιθανότητα να παρουσιαστεί κάποιος από τους Χ 1 Χ Ν και το σύστημα να τον απορρίψει.

30

31

32 FRR ID : Ποια η πιθανότητα να εμφανιστεί κάποιος X i και να απορριφθεί; FRR ID =P{X 1 }*P{R(X 1 ) X 1 } + P{X 2 }*P{R(X 2 ) X 2 } + P{X N }* P{R(X N ) X N } =1/N*FRR + 1/N*FRR 1/N*FRR FRR ID =FRR

33

34 Απαίτηση ενός συνόλου δειγμάτων εκπαίδευσης για καθένα από τα οποία είναι εκ των προτέρων γνωστή η κλάση στην οποία ανήκει. Συνήθως απαραίτητος ο μετασχηματισμός των δειγμάτων. Εκπαίδευση κατάλληλου ταξινομητή που αναγνωρίζει την κλάση νέων άγνωστων δειγμάτων (supervised machine learning). Πρώτα η φάση της εκπαίδευσης και μετά η φάση της αναγνώρισης.

35 Σύνηθες φαινόμενο η διανυσματική αναπαράσταση. Π.χ.: Στοίβαγμα διαφόρων μετρήσεων σε ένα διάνυσμα. Χρήση τοπικών περιγραφέων. Ευκολότερη διαχείριση. Στιβαρό μαθηματικό υπόβαθρο και εδραιωμένες έννοιες.

36 Π.χ. αναδιάταξη της εικόνας σε ένα διάνυσμα (στοίβαγμα γραμμών ή στηλών). Μεγαλύτερη ανάλυση περισσότερες λεπτομέρειες, αλλά έκρηξη μεγέθους. Π.χ. μια εικόνα γίνεται διάνυσμα διάστασης Ανάγκη διαχωρισμού χρήσιμης πληροφορίας από θόρυβο και πλεονάζουσα πληροφορία.

37 y w 2 w 1 Εύρεση αξόνων μέγιστης διασποράς. Επιλογή κάποιων αξόνων με μέγιστη διασπορά. Προβολή σε νέους άξονες, αλλαγή διανυσματικής βάσης. Μείωση διάστασης. x Βάση, τα ιδιοδιανύσματα του πίνακα συμμεταβλητότητας. Γνώση του ποσοστού πληροφορίας που χάνεται από τις ιδιοτιμές λ 1 και λ 2.

38 w2 w 1 w 2 w 1 Στην πράξη έχουμε μια δομή (manifold) 2 εσωτερικών διαστάσεων ενσωματωμένη σε ένα 3Δ ευκλείδειο χώρο.

39 Τα πρώτα 6 ιδιοπρόσωπα y λ 2 w 2 λ 1 w 1 x Τα ιδιοδιανύσματα (w i ) είναι ίδιας διάστασης και φύσης με τα δείγματα. Αποτελούν βάση του διανυσματικού χώρου. Οι συντελεστές είναι το νέο διάνυσμα μικρότερης διάστασης. Π.χ. για εικόνα, με ανακατασκευή των ιδιοδιανυσμάτων προκύπτουν τα ιδιοπρόσωπα.

40 Σκοπός του PCA η μείωσητηςδιάστασηςμε κατά το δυνατό πιστότερη αναπαράσταση (least squares sense). Δεν εγγυάται την καλύτερη διάκριση των προτύπων. Πιθανόν οι λεπτομέρειες που διαχωρίζουν τα πρότυπα να χάνονται. Παράδειγμα ο διαχωρισμός των γραμμάτων Q και Ο. Ανάγκη εξεύρεσης βέλτιστης διανυσματικής βάσης διαχωρισμού.

41 Κριτήριο: Να βρεθεί η βάση για την οποία, μετά την προβολή των δειγμάτων, η ενδοταξιακή διασπορά ελαχιστοποιείται, ενώ ηδιαταξιακήμεγιστοποιείται. Πρόβλημα: Για να είναι καλώς ορισμένοι οι πίνακες διασποράς, πρέπει ο αριθμός των διανυσμάτων να είναι μεγαλύτερος από τη διάστασή τους. (Χρειάζεται τεράστιες βάσεις δειγμάτων). Μείωση διάστασης με PCA με διατήρηση κατά το δυνατόν μέγιστου ποσοστού πληροφορίας.

42 w PCA w LDA

43 Τα 6 πρώτα Fisherfaces. Παράδειγμα: Όπωςτα ιδιοπρόσωπα, με ανακατασκευή των διανυσμάτων βάσης προκύπτουν τα Fisherfaces.

44 Ταξινόμηση: αλγόριθμος αυτόματης κατάταξης κάθε δείγματος σε μια από τις θεωρούμενες κλάσεις. Διάφορες μέθοδοι ταξινόμησης. Κυρίως: Βάσει αποστάσεων μεταξύ διανυσμάτων Πιθανοτικά κριτήρια Συνήθως χρειάζεται η ρύθμιση παραμέτρων. Απαιτείται δείγμα εκπαίδευσης (supervised learning). Ακολουθία από διανύσματα εισόδου και επιθυμητές εξόδους.

45 Ταξινόμηση βάση επιφανειών διαχωρισμού: Διαχωρισμός ανά δύο κλάσεων σε ημιχώρους. Απλούστευση: γραμμικός διαχωρισμός. Εύρεση υπερεπιπέδων βάσει αποστάσεων. Κέντρα βάρους κλάσεων κυψελίδες Voronoi Perceptron Support Vector Machines (SVM) Βελτιστοποίηση άλλων κριτηρίων

46 περιοχή C + x 2 w 1 x 1 + w 2 x 2 + b > 0 σύνορο απόφασης περιοχή C - w 1 x 1 + w 2 x 2 + b <= 0 x 1 w 1 x 1 + w 2 x 2 + b = 0 Σύνορο: Ημιχώρος 1: Ημιχώρος 2: g g g ( x ) = w T x + b = ( x ) = w T x + b > ( x ) = w T x + b < 0 0 0

47 b x w x w g N N =... ) ( 1 1 x [ ] b w w w N T K 2 1 = w [ ] N T x x x K = x x w x T g = ) ( i k k i i T k i k k i i T k C C x w w x x w x w w x x w λ λ = > + = < τότε, και 0 Αν τότε, και 0 Αν Τυχαία αρχικοποίηση και μετά διόρθωση βαρών με κάθε x i, ώσπου κανένα λάθος. Αν οι κλάσεις είναι γραμμικώς διαχωρίσιμες, η σύγκλιση είναι εγγυημένη.

48 w Τ x+b =0 περιθώριο Απειρία λύσεων στον perceptron. Διαμόρφωση ως πρόβλημα βελτιστοποίησης. Κριτήριο η μεγιστοποίηση του περιθωρίου.

49 Διαμόρφωση ως προβλήματος βελτιστοποίησης κατάλληλου κριτηρίου J (w) και επαναληπτική διόρθωση βάσει κανόνα J w k + 1 = w k λ w Έστω y = i y x i i όπου 1 όταν 1 όταν C C + i = x i Σύνορο διαχωρισμού το υπερεπίπεδο που T ικανοποιεί w y > 0, y. i i y i Επίλυση συστήματος εξισώσεων αντί ανισώσεων. Περισσότερο κατανοητό και μελετημένο x

50 ΈστωΥτοσύνολοτωνδειγμάτωνπου κατατάσσονται εσφαλμένα. Δηλαδή Κριτήριο προς ελαχιστοποίηση w T y i < 0 J p = y Y w Μηδενίζεται όταν δεν υπάρχουν λάθη. Η παράγωγος του σφάλματος και ο κανόνας διόρθωσης είναι J p w = y Y y w T y k + 1 = w k + λ y i Y Perceptron! y i

51 Άλλα κριτήρια J q = ( T w y) ( ) 2 T 1 w y θ J = r 2 y Y Όλα τα παραπάνω έχουν λύση όταν οι κλάσεις είναι γραμμικά διαχωρίσιμες. Με άλλα κριτήρια αντιμετωπίζονται και μη διαχωρίσιμες κλάσεις. Βασίζονται σε όλα τα δείγματα. 2 y Y y 2 J LMS ( T w y θ ) = i 2

52 Τικάνουμεσεπεριπτώσειςμηγραμμικού διαχωρισμού; x Ψάχνουμε καμπύλες επιφάνειες διαχωρισμού αντί υπερεπιπέδων. 2 2 g (x ) w x + w x x + w x + w x + w x + = x 1 b

53 Απεικονίζουμετααρχικάδιανύσματασε χώρο μεγαλύτερης διάστασης. w T = y T = [ w w w w w b ] x1 x 2 x 2 x1 x 2 [ x 1] g ( y ) = w T y Πρόβλημα γραμμικού διαχωρισμού στο χώρο μεγαλύτερης διάστασης! Καμπυλώνουμε τον χώρο αντί να καμπυλώνουμε την επιφάνεια διαχωρισμού!

54 Μονοδιάστατες μη γραμμικά διαχωρίσιμες κλάσεις R 1 και R 2. Διαχωρισμός με τριώνυμο 2 w x w x b

55

56 Παρατήρηση: Γιαταβάρηw χρειάζονται μόνο τα εσωτερικά γινόμενα Kernel trick! Για κάθε συμμετρική και θετικά ημιορισμένη συνάρτηση Κ(x,y) υπάρχει συνάρτηση φ(.) ώστε: Κ(x,y)=<φ(x),φ(y)> Άρα αν επιλέξεις την φ(.) ως απεικόνιση, μπορείς να υπολογίσεις το εσωτερικό γινόμενο χωρίς να χρειάζεται καν να απεικονίσεις το διάνυσμα! Μπορεί να εφαρμοστεί επίσης σε PCA και LDA.

57 Πολυωνυμικός Gaussian (απεικόνιση φ σε χώρο άπειρης διάστασης!) Σιγμοειδής (δεν καλύπτει τις συνθήκες αλλά δουλεύει στην πράξη) p T d K ) ( ), ( y x y x + = 2 2 ) ( ) ( ), ( σ y x y x y x = T e K ( 1 ) ), ( β +β + = y x y x T e K

58 Η υπολογιστική ισχύς του εγκεφάλου οφείλεται στη λειτουργία ενός νευρωνικού δικτύου. Οι νευρώνες αποτελούνται από το σώμα, τους δενδρίτες και τον άξονα. Ο άξονας ενός νευρώνα μπορεί να συνδεθεί με τους δενδρίτες άλλων νευρώνων μέσω των συνάψεων.

59 Μέσω των δενδριτών λαμβάνονται ηλεκτροχημικά σήματα από άλλους νευρώνες (είσοδοι). Η "ένταση" των σημάτων εισόδου εξαρτάται από την "αντίσταση" των συνάψεων. Στο σώμα υπολογίζεται κατά προσέγγιση το άθροισμα των σημάτων εισόδου. Αν το άθροισμα είναι πάνω από ένα κατώφλι, ο νευρώνας ενεργοποιείται και στέλνει στον άξονά του ένα ηλεκτροχημικό σήμα (έξοδος).

60 w 0 x 1 x 2 x N w 1 w 2 w N Σ f(.) y N = f w + 0 i= 1 w i x i f ( x) = x Συνάρτηση ενεργοποίησης 1 f ( x) = f ( x) = 1+ exp( x) exp( x) exp( x) exp( x) + exp( x)

61 σύνορο απόφασης x 2 g περιοχή C + ( x ) = w T x + b > 0 g περιοχή C - = w T x + b 0 g ( x ) = w T x + b = 0 ( x ) < x 1 Η συνάρτηση απόφασης: ( ) T g ( x ) = sign ( w + ) h ( x ) = sign x b ένας νευρώνας! (perceptron)

62 Συνδυάζοντας νευρώνες μπορούμε να διαχωρίσουμε κλάσεις που εκτείνονται σε πολύπλοκες περιοχές. x x1 x 2 x 1 Νευρωνικό δίκτυο

63 Δομή Τύπος περιοχής απόφασης Exclusive-OR Πρόβλημα Παράδειγμα κλάσεων Γενική περιοχή απόφασης Ένας νευρώνας Δύο ημιχώροι χωρισμένοι με υπερεπίπεδο A B B A B A Δύο στρώματα Κυρτές ανοιχτές ή κλειστές περιοχές A B B A B A Τρία στρώματα Τυχαίες (εξαρτάται από αριθμό νευρώνων) A B B A B A

64 Χαρακτηριστικά Ένα κρυφό στρώμα και ένας νευρώνας εξόδου για κάθε κλάση. Ενεργοποίηση αν το διάνυσμα εισόδου είναι κοντά σε Έξοδοι ένα πρότυπο διάνυσμα. Radial units o i Φ ( x) = ( ) x c j K j = 1 w ij = exp Φ ( ) x c x c σ j j 2 j Είσοδοι

65 Ταξινόμηση MLPs υπερεπίπεδα RBFs υπερσφαίρες x 2 MLP Δομή MLPs: ένα ή περισσότερα κρυφά στρώματα RBFs: ένα μόνο κρυφό στρώμα RBFs: απαιτούν περισσότερους νευρώνες. x 2 x 1 x 1 RBF

66 Η επιλογή του δικτύου (τοπολογία, στρώματα, αριθμός νευρώνων, συνάρτηση ενεργοποίησης, διανύσματα στόχοι) εξαρτάται από το εκάστοτε πρόβλημα. Οσυντονισμόςτωνβαρώνw γίνεται με επαναληπτική εκπαίδευση του δικτύου. Τα βάρη αρχικοποιούνται τυχαία και διορθώνονται προοδευτικά. Παρουσιάζεται ένα σύνολο δειγμάτων με γνωστές κλάσεις και υπολογίζονται τα σφάλματα των πραγματικών εξόδων σε σχέση με τις επιθυμητές. Τα βάρη διορθώνονται ώστε να μειωθούν τα σφάλματα.

67 Τα σφάλματα δίνονται αναλυτικά ως προς τα βάρη. Υπολογισμός παραγώγου σφάλματος ως προς τα βάρη (κάποιες τοπολογίες βοηθούν πολύ π.χ. MPLs back propagation). Steepest descent: Δw = λ E w 0<λ<1, Ε: τετραγωνικό σφάλμα πραγματικής-επιθυμητής εξόδου Momentum, ε 0.7 Δ ( t) f w = Δ ( t 1) w+ εδ ( t) w

68 Ο άνθρωπος γεννιέται με περίπου 10 δισ. νευρώνες, οι οποίοι δεν ανανεώνονται. Κάθε νευρώνας συνδέεται κατά μέσο όρο με χιλιάδες άλλους νευρώνες. Ο χρόνος ενεργοποίησης είναι ~0.001 sec. Πόσες κλάσεις μπορεί να αναγνωρίσει;!

69 Πολλά βιομετρικά πρότυπα κείτονται σε ένα manifold. To manifold (πολλαπλότητα, πολύπτυχο;) είναι ένας τοπολογικός χώρος που τοπικά μοιάζει με ευκλείδειο. Π.χ. μια επιφάνεια στον 3Δ χώροείναιένα manifold. Το submanifold είναι ένα υποσύνολο ενός manifold που είναι και αυτό manifold αλλά μικρότερης διάστασης. Π.χ. η γη και ο ισημερινός της.

70 Στόχος το ξεδίπλωμα του manifold! Ταυτόχρονη μείωση της διάστασης. Διατήρηση "συνοχής" και εφαρμογή προηγούμενων μεθόδων.

71 Multidimensional scaling (MDS) Locally linear embedding (LLE) ISOMAP, Spectral clustering, Laplacian eigenmaps Ιδέα MDS Έστω διανύσματα x i με ανά ζεύγη αποστάσεις d. Να βρεθούν y ij i (μικρότερης διάστασης) ώστε y i y j S Πρόβλημα βελτιστοποίησης: d ij ( ) yi j dij E( y) = y i< j S 2

72 Ιδέα LLE Κάθε x i μπορεί να περιγραφεί ως γραμμικός συνδυασμός των γειτόνων του. Βρες ταw ij ώστε να ελαχιστοποιείται ( ) E w = xi w ij x j i j w y Με γνωστά τα, βρες τα που ελαχιστοποιούν ij ( ) Φ y = y i wijy j i j i 2 2

73 p( x ω j ) P( ω j ) Θεώρημα Bayes P( j x), όπου p( x) οι κλάσεις. Έστω λij το κόστος απόφασης ωi ( a i ) ενώ ισχύει. Τα μέσα κόστη είναι: R( a R( a ω j Υιοθέτηση 1 2 p( x ω1) p( x ω ) x) = λ P( ω x) + λ P( ω x) 11 x) = λ P( ω x) + λ P( ω x) 2 21 ω 1 λ12 λ αν M.A.P. λ 12 = λ21, λ11 = λ M.L. P ω ) = P( ) λ λ ( 1 ω2 ω ω = j P( ω2) P( ω )

74

75 Ο κατεξοχήν τρόπος αναγνώρισης μεταξύ των ανθρώπων. Η αναγνώριση ενός προσώπου μπορεί να γίνει σε 0.1 sec. Θεωρείται το πιο αποδεκτό βιομετρικό. Ανθρώπινη αντίληψη: Τα νεογνά αναγνωρίζουν τη μητέρα τους από την 4η ημέρα και νέα πρόσωπα που μοιάζουν (φύλο, ηλικία, φυλή) από τον 3ο μήνα. Τα πρόσωπα αναγνωρίζονται δυσκολότερα όταν είναι αναποδογυρισμένα. Για οικεία πρόσωπα, η αναγνώριση βασίζεται περισσότερο στις εσωτερικές περιοχές του προσώπου παρά στις εξωτερικές με μαλλιά. Για μη οικεία, ισχύει το αντίστροφο.

76 Ανθρώπινη αντίληψη: Τα πρόσωπα της ίδιας φυλής αναγνωρίζονται ευκολότερα. Αντίληψη του προσώπου ως σύνολο και όχι τμηματικά. Δύο διαφορετικά χαρακτηριστικά (π.χ. μύτες) εντοπίζονται καλύτερα όταν παρουσιάζονται με όλο το πρόσωπο παρά μόνα τους. Για την αναγνώριση ενός προσώπου ενεργοποιούνται σχεδόν τόσοι νευρώνες όσοι για την επίλυση ενός μαθηματικού προβλήματος. Η ατρακτοειδής έλικα θεωρείται ότι είναι το τμήμα του εγκεφάλου όπου γίνεται η αναγνώριση των προσώπων, όχι όμως και των εκφράσεων. Άτομα με προσωπαγνωσία αναγνωρίζουν άλλα αντικείμενα, αλλά όχι πρόσωπα.

77 Διάφορα χαρακτηριστικά του προσώπου (modalities). Ασπρόμαυρη εικόνα Έγχρωμη εικόνα Υπέρυθρη (ή σχεδόν υπέρυθρη) εικόνα Θερμική εικόνα Χάρτης βάθους Πλήρες 3Δ μοντέλο Ακολουθούν την πρόοδο της τεχνολογίας των αισθητήρων. Δύο βασικές προσεγγίσεις Εικόνα (2D modalities) - προσέγγιση πίνακα τιμών Επιφάνεια με/χωρίς υφή (2.5D, 3D modalities)

78 Ασπρόμαυρη εικόνα Έγχρωμη εικόνα Υπέρυθρη εικόνα Θερμική εικόνα Χάρτης βάθους Επιφάνεια

79 Μετατροπή εικόνας σε διάνυσμα και εφαρμογή κλασικών μεθόδων αναγνώρισης προτύπων. Ανάλυση πρωτευουσών συνιστωσών Ανάλυση γραμμικού διαχωρισμού Support Vector Machines Χρήση χώρων και υποχώρων (manifolds) Πιθανοτικά μοντέλα Χρήση τοπικών περιγραφέων (π.χ. αποκρίσεις φίλτρων). Προσαρμογή μοντέλων και σύγκριση παραμέτρων.

80 Βασικό πρόβλημα οι αλλαγές στις συνθήκες φωτισμού, οι αλλαγές στην πόζα, οι εκφράσεις, η προσθήκη εξαρτημάτων (γυαλιά, σκουφιά, κασκόλ κ.τ.λ.) στέρεες και μη στέρεες παραμορφώσεις. Μελέτες έδειξαν ότι οι εικόνες των προσώπων κείτονται σε ένα manifold. Οι διάφορες παραλλαγές που οφείλονται π.χ. σε πόζα ή εκφράσεις δημιουργούν ένα submanifold.

81 Γραμμικό μοντέλο PCA ένα σετ παραμέτρων που εξαρτάται από την ταυτότητα του χρήστη. Πολυγραμμικά μοντέλα. Ένα σετ παραμέτρων για κάθε πηγή μεταβλητότητας. Διγραμμικά μοντέλα (ταυτότητα-εκφράσεις) Higher Order Singular Value Decomposition Tensorfaces Όσο πιο ασυσχέτιστοι οι συντελεστές, τόσο καλύτερο το μοντέλο.

82 Σημεία εμπιστοσύνης τα οποία συνδέονται με έναν ελαστικά παραμορφώσιμο γράφο. Σε κάθε σημείο υπολογίζεται ένας τοπικός περιγραφέας: Οι συντελεστές του μτσχ Gabor σε διάφορες κλίμακες και προσανατολισμούς. Ο γράφος προσαρμόζεται στο πρόσωπο με τοπική παραμόρφωση ελαχιστοποιώντας μια συνάρτηση κόστους.

83 Δύο γραμμικά μοντέλα (PCA): Για το σχήμα του προσώπου (απαιτεί ανατομικά σημεία και Προκρούστεια ανάλυση) Για την εμφάνιση ανεξαρτήτου σχήματος (warping). Η προσαρμογή του μοντέλου σε άγνωστο πρόσωπο γίνεται με ελαχιστοποίηση του σφάλματος

84

85 Οι χάρτες βάθους άλλοτε μεταχειρίζονται ως εικόνα (2D μέθοδοι) και άλλοτε για τη δημιουργία μιας επιφάνειας. Μεταχείριση επιφάνειας: Καμπυλότητα επιφάνειας. Τοπικοί περιγραφείς. Ευθυγράμμιση μέσω Iterative Closest Point (ICP). Μέθοδοι ανθεκτικές στην παραμόρφωση λόγω εκφράσεων.

86 Τομή επιφάνειας με διαδοχικά επίπεδα κάθετα στη διεύθυνση του βλέμματος. Σύγκριση ισοϋψών καμπυλών (ροπές, CSS, EFD) για τον υπολογισμό της ομοιότητας. Πρόσωπο A Πρόσωπο B

87 Διάφορα μέτρα καμπυλότητας : πρωτεύουσες καμπυλότητες γκαουσιανή και μέση καμπυλότητα δείκτης σχήματος Η καμπυλότητα δεν εξαρτάται από τον προσανατολισμό και την μετατόπιση. Χρήσιμη για κατάτμηση της επιφάνειας σε κυρτές και κοίλες περιοχές και εντοπισμός ανατομικών σημείων.

88 Τοπικά γεωμετρικά χαρακτηριστικά. Αμετάβλητοι στους στέρεους μετασχηματισμούς. Μονοδιάστατα ή δισδιάστατα ιστογράμματα ανθεκτικότητα στο θόρυβο. Δεν αντιμετωπίζουν τις μη στέρεες παραμορφώσεις (π.χ. λόγω εκφράσεων).

89

90

91 Ευθυγράμμιση επιφανειών με επαναληπτικά βήματα. 1.Καθορισμός κοντινότερων σημείων. 2.Υπολογισμός στροφής και μετατόπισης. Άμεσος υπολογισμός ομοιότητας.

92 Η επιφάνεια είναι αμετάβλητη στον φωτισμό, τον προσανατολισμό και την μετατόπιση. Ευαισθησία στις παραμορφώσεις εξαιτίας των εκφράσεων. Αντιμετώπισημεαπόρριψητων παραμορφώσιμων περιοχών. Ανθεκτικοί τοπικοί περιγραφείς. Μοντέλο ισομετρικής παραμόρφωσης: το δέρμα κάμπτεται, δεν συμπιέζεται, δεν επιμηκύνεται.

93 Οι γεωδαισιακές αποστάσεις των σημείων της επιφάνειας παραμένουν σταθερές κατά τις ισομετρικές παραμορφώσεις. Υπολογισμός γεωδαισιακών αποστάσεων και απεικόνιση με MDS σε ευκλείδειο χώρο, 2-σφαίρα, 3-σφαίρα.

94 Απεικόνιση στο επίπεδο των πολικών γεωδαισιακών συντεταγμένων. "Εξαφανίζονται" οι εκφράσεις.

95 Προσαρμογή ενός ελαστικά παραμορφώσιμου μοντέλου στην επιφάνεια του προσώπου. Οι κόμβοι έχουν ανατομική σημασία διανυσματική περιγραφή. Προσαρμογή με κατευθυνόμενο ICP. v xp k = I J i= 1 j= 1 w ijk a x i b p j Ένα σετ παραμέτρων ελέγχει την ταυτότητα και ένα άλλο την έκφραση.

96

97

98 Το αποτύπωμα των πτυχώσεων της επιδερμίδας του δακτύλου. Μοναδικό για κάθε άνθρωπο και μάλιστα για κάθε δάκτυλο. Ορολογία: θηλοειδείς γραμμές, θηλόγραμμα, ακρολοφίες και αύλακες, ράχες και κοιλάδες.

99 Διαμορφώνεται κατά τον έβδομο μήνα της κύησης και παραμένει σταθερό μέχρι το θάνατο (μέχρι την αποσύνθεση). Αποτέλεσμα γενετικών και επιγενετικών παραγόντων (θέση εμβρύου και σύσταση αμνιακού υγρού). Αναγεννάται με πανομοιότυπο τρόπο σε περίπτωση μικροτραυματισμού (προϋπόθεση να μην πληγεί ο υποδόριος ιστός-υπόδερμα).

100 Αποτυπώματα σε πλήθος αρχαιολογικών ευρημάτων. 1686: ο Marcello Malpighi παρατηρεί τους διαφόρους σχηματισμούς. 1880: οι Fauld και Herschel προτείνουν την μοναδικότητα του δακτυλικού αποτυπώματος. 1888: ο Sir Francis Galton παρουσιάζει την μέθοδο σύγκρισης βάσει μικρολεπτομερειών (minutiae). 1899: ο Edward Henry παρουσιάζει το πρώτο σύστημα ταξινόμησης.

101 Τρεις βασικές κατηγορίες Τοξωτά (arch), ~5% των δακτύλων Κολποειδή (loop), ~65% των δακτύλων Σπειροειδή (whorl), ~30% των δακτύλων Δέλτα Εστία

102 Plain arch Tented arch

103 Radial loop Ulnar loop

104 Plain whorl Central pocket whorl Double loop whorl Accidental whorl

105 Μικρολεπτομέρειες

106

107 Το 1924 η βάσητουfbi διέθετε περίπου 810Κ κάρτες αποτυπωμάτων. Το 2007 η βάσητουfbi διέθετε πάνω από 200Μ κάρτες αποτυπωμάτων. Η ανάγκη για αυτόματη αναγνώριση είναι πασιφανής. Automatic Fingerprint Identification Systems (AFIS) διαθέτουν σχεδόν όλα τα σύγχρονα κράτη.

108 Οπτικοί: Τεχνική Frustrated Total Internal Reflection (FTIR). Φωτισμός μέσω πρίσματος. Το φως ανακλάται στις κοιλάδες και απορροφάται στις ράχες. Εικόνα καταγράφεται με CCD ή CMOS. Στερεάς κατάστασης: Συστοιχία αισθητήρων (χωρητικών, ηλεκτρικών, θερμικών, πιεζοηλεκτρικών) επάνω σε βάση πυριτίου που έρχονται σε άμεση επαφή με το δάκτυλο.

109 Κατάτμηση Χάρτης τοπικών κατευθύνσεων Χάρτης τοπικών συχνοτήτων Βελτίωση εικόνας: contextual filters Εντοπισμός ανωμαλιών (εστίες, δέλτα): δείκτης Poincare Εντοπισμός μικρολεπτομερειών: λέπτυνση και εφαρμογή μάσκας.

110 Cross-correlation Στόχος η εύρεση της σχετικής μετατόπισης και στροφής που ευθυγραμμίζει τα πρότυπα Υπολογιστικά δαπανηρή διαδικασία Μη ανθεκτική στις μη γραμμικές παραμορφώσεις Επηρεάζεται από μεταβολές πίεσης εντυπώματος, φωτεινότητας, κοντράστ

111 Τριπλέτες (x, y, θ) Point pattern matching Προσέγγιση με μετασχηματισμό Hough Κερδίζει σε απλότητα, χάνει σε διακριτικότητα

112 Τοπικοί περιγραφείς υποβοηθούμενοι από χαρακτηριστικά σημεία Φίλτρα ή σχέσεις θηλογράμμων

113

114 Ίριδα Άνω βλέφαρο Κόρη Η ίριδα αποτελείται από δυο περιοχές, την central pupillary zone και την outer ciliary zone. Το σύνορο τους ονομάζεται collarette. Σκληρός χιτώνας Κάτω βλέφαρο

115 Οι μικρολεπτομέρειες της ίριδας καθορίζονται τυχαία κατά την εμβρυική ανάπτυξη. Είναι διαφορετικές σε κάθε άτομο ακόμα και στα δυο μάτια του ίδιου ατόμου. Το χρώμα αλλάζει αυξάνεται κατά την παιδική ηλικία. Μετά παραμένει σχετικά σταθερή.

116 1885: Ο Γάλλος γιατρός Alphonse Bertillon την προτείνει ως αναγνωριστικό μοναδικότητας. 1949: Ο Βρετανός οφθαλμίατρος James Doggart παρατηρεί ότι η μοναδικότητα της ίριδας προσομοιάζει αυτή των δακτυλικών αποτυπωμάτων. 1987: Οι οφθαλμίατροι Flom και Safir πατεντάρουν την ιδέα της αναγνώρισης ίριδας! : Πρώτες αναφορές από Johnston και Daugman. 2001: Big bang!

117 Stop and stare: συσκευή καταγραφής με ΝΙ φωτισμό. Διαδικασία εστίασης με ηχητική ανάδραση. Εντοπισμός ίριδας μέσα στην εικόνα του ματιού. Εξαγωγή χαρακτηριστικών κατάλληλων για σύγκριση (αντιμετώπιση απόστασης από κάμερα, συστολής/διαστολής λόγω φωτισμού)

118 Καθοδήγηση χρήστη με φωνητικές οδηγίες. Διάμετρος ίριδας 200 pixels.

119 Εντοπισμός ίριδας Προσέγγιση ορίων με κύκλους. Χρήση Active Contours (snakes).

120 Eξαγωγή χαρακτηριστικών Απεικόνιση ίριδας σε ένα κανονικοποιημένο σύστημα συντεταγμένων. Συνέλιξη με φίλτρα Gabor οι συντελεστές το βιομετρικό πρότυπο. Κβαντισμός συντελεστών 256 byte IrisCode Σύγκριση βάσει απόστασης Hamming.

121 Daugman Wildes Φωτισμός LED και κάμερα Διάχυτο πολωμένο φως και κάμερα χαμηλού φωτισμού Active Contours Gabor φίλτρα Απόσταση Hamming Hough Transform Laplacian of Gaussian φίλτρα Κανονικοποιημένη συσχέτιση

122 Ακολουθούν τις προσεγγίσεις Daugman, Wildes. Χρήση εναλλακτικών φίλτρων και μετασχηματισμών: Log Gabor φίλτρα Wavelets σε 1Δ κύκλους γύρω από την κόρη Wavelet packet Discrete Cosine Transform Hilbert Transform+αυθεντική εικόνα

123 Τοπική ισοστάθμιση ιστογράμματος Συνδυασμοί PCA, LDA, DLDA, SVM Linear Prediction Cepstral Coefficients (αναγνώριση φωνής) Υποζώνες και μέτρηση αυτοομοιότητας με εκτίμηση της κλασματικής διάστασης (fractal dimension) Διαμέριση σε blocks και δημιουργία Local Binary Patterns 4 δυαδικές εικόνες από τα 4 MSBs, εφαρμογή connected components και υπολογισμός αριθμού Euler.

124 Ηπεριοχήτηςίριδαςκοντάστηκόρηείναι η πιο χρήσιμη για αναγνώριση. Θόρυβος από βλεφαρίδες Περισσότερο χαρακτηριστικοί σχηματισμοί Τα λάθη δεν κατανέμονται ομοιόμορφα στους ανθρώπους. Το φύλο μπορεί να εκτιμηθεί με ακρίβεια 80%. Ηκαλύτερηαπόδοση(NIST, Authenticorp, International Biometrics Group) είναι FRR 0.01με FAR

125

126 Πολλαπλοί αισθητήρες Πολλαπλά βιομετρικά Πολλαπλές προσπάθειες Πολυβιομετρικά συστήματα Πολλαπλά μέρη Πολλαπλοί αλγόριθμοι

127 Σύντηξη: Ενοποίηση διαφορετικών βιομετρικών. Αλληλοκάλυψη ευπαθειών. Ανθεκτικότερο σύστημα με χρήση πολλαπλών βιομετρικών. Ισχυρότερη ένδειξη φυσικής παρουσίας. Σωστή σχεδίαση, αλλιώς χειρότερη επίδοση, ανώφελη αύξηση κόστους και ταλαιπωρίας του χρήστη.

128 Επίπεδο αισθητήρων Επίπεδο εξαγωγής βιομετρικού προτύπου Επίπεδο σύγκρισης βιομετρικών προτύπων υπολογισμός ομοιότητας ή απόστασης απόφαση (κατάταξη ή αποδοχή)

129 X1 X2 X3 Xn Τ1 Τ2 Ζ1 Ζ2 Υ1 Υ2 Υ3 Υn Αισθητήρας Παρουσιαζόμενο Πρωτογενή βιομετρικό δεδομένα Αποθηκευμένο βιομετρικό Βάση δεδομένων Συγκριτής (κανόνας) Ταυτότητα/άγνωστο Αποδοχή/άρνηση

130 Διαφορετικά αλλά συμβατά βιομετρικά. Π.χ. εικόνα προσώπου και γεωμετρία προσώπου συνδυάζονται για τη δημιουργία 3Δ μοντέλουμευφή. Π.χ. έγχρωμη και θερμική εικόνα προσώπου συνδυάζονται για τη δημιουργία σύνθετης εικόνας προσώπου.

131 Συνδυάζονται δύο ή περισσότερα βιομετρικά πρότυπα για τη δημιουργία ενός νέου προτύπου που αντιπροσωπεύει το άτομο. Π.χ. οι διάφορες αποστάσεις της γεωμετρίας του χεριού να συγχωνευτούν με τους ιδιο-συντελεστές του προσώπου. X1 X2 X3 Xn Υ1 Υ2 Υ3 Υm X1 Xn Υ1 Υm

132 Σύντηξη των αποστάσεων ή των σκορ ομοιότητας Σύντηξη των αποστάσεων ή των σκορ ομοιότητας καθενός συγκριτή για τη δημιουργία μιας τελικής απόστασης ή ενός τελικού σκορ ομοιότητας. Π.χ. σε ένα σύστημα προσώπου και φωνής, συνδυάζονται τα σκορ ομοιότητας με ένα κανόνα αθροίσματος (μέσοςόροςή σταθμισμένο άθροισμα).

133 Σύντηξη των κανόνων απόφασης Σύντηξη των επιμέρους λιστών κατάταξης για τη δημιουργία μιας τελικής λίστας. Π.χ. μέθοδος Borda count. (Ταυτοποίηση) Σύντηξη των ετικετών κλάσης στις οποίες κατατάσσει κάθε συγκριτής (π.χ. «αποδοχή», «άρνηση», «Ιορδάνης», «Γιάννης») σε μια τελική ετικέτα κλάσης. Π.χ. Majority voting. (Αυθεντικοποίηση και ταυτοποίηση)

134 Γενικός κανόνας: όσο νωρίτερα τόσο καλύτερα. Καθώς το βιομετρικό επεξεργάζεται χάνεται πληροφορία. Προσφορότερη η σύντηξη σε επίπεδο αισθητήρων. Συνήθως είναι δυνατή μόνο η σύντηξη κατά τη σύγκριση, λόγω ασύμβατων ή κλειστών συστημάτων (ο κανόνας στα εμπορικά).

135

136 Κωδικές λέξεις: Το δίλλημα, μεγάλες λέξεις που ξεχνάς εύκολα ή μικρές λέξεις που μαντεύονται εύκολα; Μελέτη το 2001 στη Βρετανία: οι μισοί περίπου από 1200 υπαλλήλους διάλεξαν ως κωδικό το όνομα τους, το όνομα του κατοικιδίου τους ή μέλους της οικογένειας τους. Το 20-50% των αιτημάτων βοήθειας αφορούν επανέκδοση κωδικών (Gartner Group). Το μέσο κόστος επανέκδοσης κωδικού είναι περίπου 38$. (Forester Research) Συνηθίζεται να χρησιμοποιείται ο ίδιος κωδικός σε όλες τις εφαρμογές.

137 Αποκάλυψη με μεθόδους social engineering. Οι κάρτες χάνονται και πλαστογραφούνται εύκολα. Η ασφάλεια του συστήματος είναι τόσο καλή όσο του χειρότερου κωδικού - κάρτας.

138 Δεν χάνονται και δεν ξεχνιούνται. Δύσκολο να πλαστογραφηθούν και να φτιαχτούν τεχνητά βιομετρικά. Η πιθανότητα να παρακαμφθεί κάποιος χρήστης είναι η ίδια για όλους. Φιλικές προς τον χρήστη. Η μόνη λύση για αρνητική αναγνώριση, όπου το σύστημα απαντά αν ο παρουσιαζόμενος είναι αυτός που (εμμέσως) αρνείται ότι είναι.

139 Μυστικότητα Ένας κωδικός είναι ασφαλής όσο είναι κρυφός. Τα βιομετρικά μπορούν να είναι κρυφά; Μεγάλη σημασία η φυσική παρουσία και η ακεραιότητα του βιομετρικού. Δημοσίευση βιομετρικών αλγορίθμων Στην κρυπτογραφία είναι γνωστοί οι αλγόριθμοι και η ασφάλεια προέρχεται από την μυστικότητα του κλειδιού. Στη βιομετρία η γνώση των αλγορίθμων μειώνει την ασφάλεια. (π.χ. Hill climbing attach) Ανάκληση βιομετρικών προτύπων Αν μαθευτεί ένας κωδικός τον ανακαλείς και εκδίδεις καινούριο. Αν μαθευτεί ένα βιομετρικό πρότυπο, τι κάνεις; Εξαπάτηση (Spoofing) Πώς αντιμετωπίζεται η δημιουργία πλαστών βιομετρικών; (π.χ. φωτογραφίες υψηλής ανάλυσης, εκμαγεία προσώπου, συνθετικά δακτυλικά αποτυπώματα κ.τ.λ) Απάντηση ο έλεγχος ζωντάνιας.

140 Βάση δεδομένων 7. Μεταβολή δεδομένων 3. Παράκαμψη εξαγωγέα 6. Υποκλοπή δεδομένων Αισθητήρας Εξαγωγέας βιομετρικού Συγκριτής Ελεγχόμενη συσκευή 1. Ψεύτικο βιομετρικό 2. Επανάληψη υποκλεμμένου βιομετρικού 4. Συνθετικό πρότυπο 5. Παράκαμψη συγκριτή 8. Παράκαμψη τελικής απόφασης