KURS ZA ENERGETSKI AUDIT 1.1
|
|
|
- Κόρη Αγγελόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 KURS ZA ENERGETSKI AUDIT 1.1 TEORIJSKE OSNOVE Priremio: Dr Nenad Kažić 1
2 Osnovni ojmovi Sistemi mjera i jedinice ISM - INTERNACIONALNI SISTEM MJERA ASM - ANGLOSAKSONSKI SISTEM MJERA 2
3 ISM ASM DUŽINA Metar - m fit ft = m MASA Kilogram - kg Libra mase lb = kg TEMPERATURA t C=(t F-32) 5/9 VRIJEME Celzijus - C Kelvin - K Sekunda - s Farenhajt F =5/9 C Rankin - R Sekunda - s 3
4 ISM SPECIFIČNA ZAPREMINA v [m 3 /kg ] JE ZAPREMINA 1 kg SUPSTANCE. v=v/m [m 3 /kg] 1 kg v=v (1kg) GUSTINA ρ [kg/m 3 ] JE MASA 1m 3 SUPSTANCE 1 m 3 ρ = m (1m3) V [m 3 ] m[kg] ρ=m/v [kg/m 3 ] 4
5 ISM ASM F SILA=MASA*UBRZANJE F[N]=ma a [m/s 2 ] - ubrzanje N (Njutn)=kg*m/s 2 PRITISAK=SILA/POVRŠINA Libra Sile (Libre Force) lb F =mg=0.454*9.81=4.45 N lb m G=mg [Pa]=F/A Pa (Paskal)=1N / 1 m 2 1 bar = 10 5 Pa PSI Pound_Square_Inch= =1 lb F / 1sq in, sq in=in 2 = 4.45 / = 6897 Pa 5
6 RAD [J] = SILA [N]*POMJERANJE [m] RAD [J] = SNAGA [W]*VRIJEME [s] TOPLOTA [J] = TOPLOTNI FLUKS [W]*VRIJEME [s] SNAGA [W] = RAD [J] / VRIJEME [s] TOPLOTNI FLUKS [W] = TOPLOTA [J] / VRIJEME [s] 6
7 ISM Rad, Tolota [J, kj, Wh, kwh] Snaga P [W]=Rad/Vrijeme 1 W= 1 J/s Fluks Q [W]=Tolota/Vrijeme 1 W= 1 J/s Tolota: ASM Britanska Tolotna jedinica [BTU]: Britiche Thermal Unit Tolota otrebna da se 1 lb m vode zagrije za 1 F. 1 BTU mc w Δt =0.454*4180*5/9 1 BTU 1055 J Tolotni Fluks [BTU/h] 1 BTU/h 1055/3600 W=0.293 W Snaga [HP] 1 HP Konjska snaga 1HP=75*9.81=736 W 7
8 8
9 I ELEKTRIČNA STRUJA JAČINA STRUJE A (Amer) I U NAPON V (Volt) R R OTPOR Ω (Om) U P SNAGA =U I W (Vat) I=U / R OMOV ZAKON I=U / R 9
10 q Δφ R PROTOK RAZLIKA POTENCIJALA OTPOR ELEKTRIČNA ANALOGIJA Mnogi fenomeni u rirodi se onašaju analogno električnoj struji, odnosno mogu se okarakterisati Generalizovanim Omovim Zakonom. q R Δφ q=δφ / R q= Δφ / R GENERALIZOVANI OMOV ZAKON PROTOK NEKE VELIČINE IZAZIVA RAZLIKA POTENCIJALA (POKRETAČKA SILA) A PROTIVI MU SE OTPOR 10
11 Primjer Koliko energije (E el ) sadrži naunjen olovni akumulator u automobilu kaaciteta 50 Ah (naon 12 V, m =20 kg)? E el =P[W]*τ[h]=(U*I)* τ =U*(I* τ) =12*50=600 Wh,(VAh) e=600/20=30 Wh/kg=0.033 kwh/kg (Litijum-jonske e=120 Wh/kg, skulje 10 uta) Sa druge strane 1 kg goriva sadrži oko 40 MJ / kwh. Na točkove automobila (dizel), od toga dodje oko 30%, dakle oko 3 kwh. Dakle 20 kg olovnog akumulatora sadrži 0.66 kwh električne (mehaničke) energije, a 1kg goriva 3 kwh. 11
12 VELIČINE STANJA TO SU FIZIKALNE VELIČINE KOJE DEFINIŠU STANJE (ZOVU SE I TERMODINAMIČKE KOORDINATE STANJA) Zaremina V [m 3 ] Stanje Pritisak [Pa] T Temeratura t [C], T [K] V 12
13 VELIČINE STANJA Zaremina V [m 3 ] Secifična zaremina v [m 3 / kg] (zaremina 1 kg) FLUID V [m 3 ] m [kg] v [m 3 / kg]= V/m Gustina ρ [kg/m 3 ] (masa 1 m 3 ) ρ [kg/m 3 ]=m/v=1/ v 13
14 Pritisak [Pa] VELIČINE STANJA Pritisak se javlja kao osledica udara molekula u zidove suda (instrumenta). Pritisak je uvjek veći ili jednak nuli (vakuum). Pritisak ne može biti manji od nule. =F/A A F w w 14
15 Pritisak [Pa] Manometarski ritisak (nadritisak) m [Pa] okazuje koliko je ritisak veći od atmosferskog (nadritisak). Manometar = 0 m > 0 VELIČINE STANJA m =- 0 Asolutni ritisak [Pa] = 0 + m 0 Elastična membrana 15
16 Pritisak [Pa] Podritisak ( vakuum ) v [Pa] daje informaciju o tome koliko je ritisak manji od atmosferskog (odritisak ili vakuum ). < 0 v = 0 VELIČINE STANJA v = 0 - Asolutni ritisak [Pa] 0 = 0 - v = 0 - v Elastična membrana 16
17 VELIČINE STANJA Pritisak [Pa] =G/A=mg/A =(ρv)g/a=ρ(v/a)g =ρgh U- cijev A 0 Hidrostatički ritisak [Pa] G =ρ g h h h Δ= =- 0 =ρ g h Δ= =- 0 =ρ g h = 0 + Δ 17
18 VELIČINE STANJA Bernulijeva jednačina redstavlja zakon o održanju mehaničke energije ri strujanju fluida (zanemaren ad ritiska usled trenja). 1 2 z 1 z 2 / /ρ 2 w w ρ + + gz = / ρ w 2 resjek1 2 + gz resjek 2 Unutrašnji mehanički otencijal (vidi definiciju ENTALPIJE) 2 Kinetička energija gz Potencijalna energija (ρ gustina, W brzina strujanja) = const 18
19 VELIČINE STANJA Bernulijeva jednačina (omnožena rethodna sa gustinom, ρ) 2 2 w w + ρ + ρ gz = + ρ + ρ gz = 2 2 t1 1 t2 1 TRENJE 2 z 1 x d Statički ritisak 2 w = ρ M 2 t [Pa] = + d tx z 2 t 2 const Totalni (zaustavni) ritisak Dinamički ritisak TOTALNI (ZAUSTAVNI) PRITISAK t je zbir statićkog i dinamičkog ritiska. Manometar na slici će okazivati vrijednost totalnog ritiska jer je struja zaustavljena (w x =0) na mjestu mjerenja (x), a iz Bern. jed. slijedi da je ( + ρw 2 / 2) 1 = ( + ρw 2 / 2) x,wx=0 = tx. 19
20 VELIČINE STANJA Kako izmjeriti brzinu strujanja fluida? w w d = w ρ 2 2 statički 1. Izmjerimo statički () i totalni ( t ) ritisak (Sl. gore), 2. Odredimo dinamički ritisak ( d ) kao razliku totalnog i statičkog, 3. Izračunamo brzinu iz dinamičkog ritiska M w m s d = t - totalni = Pito-cijev (tube) M t 2 ρ d [ ] Pa 20
21 VELIČINE STANJA t t [Pa] = + d Totalni t w Za mjerenje totalnog ( t ) i statičkog () ritiska koristi se Pito-cijev (tube) (na slici) koja se ostavlja rema struji fluida. Centralni otvor detektuje totalni ritisak ( t ) a otvor sa strane statički (). Razlika ova dva redstavlja dinamički ritisak. Statički t d = t - t 21
22 VELIČINE STANJA Asolutna Temeratura T [K] je roorcionalna kinetičkoj energiji molekula T~ μ w 2 /2. Voda ključa μ masa molekula w brzina 100 C Relativna tem. t C 0 C Voda+Led 373 K Asolutna tem. 273 K T [K]=t [C] C CELZIJUS - KELVIN o =1 bar 0 K 22
23 VELIČINE STANJA Entalija I [J], i [J/kg] U- Unutrašnja energija je energija molekula A [m 2 ] I [J]=U + V i [J/kg]=u + v =G/A=const G=A G [N], T z[m] m V=Az V I [J]=U + A z=u + Gz TERMIČKI POTENCIJAL MEHANIČKI POTENCIJAL ( UNUTRAŠNJI ) V=Gz=mgZ I Entalija je veličina stanja koja ima termički (U) i mehanički (V) otencijal (ovaj mehanički - unutrašnji otencijal se javlja u Bernulijevoj jednačini, stim što su 23 članovi u njoj svedeni na jedinicu zaremine, V=1 m 3 ). G
24 Jednačina stanja Šta je Jednačina Stanja (JS) materije? T Jednačina Stanja F(,V,T)=0 T Površ Stanja V V Jednačina Stanja je funkcionalna veza izmedju veličina stanja. To je formula koja definiše ovrš stanja na slici. 24
25 Idealni gasovi (IG) Osnovne karakteristike IG Ne ostoje medjumolekulske sile F m Zaremina molekula je zanemarljiva Posledica Nema AGREGATNIH stanja Realni gasovi liče na idealne kada su razrijedjeni 25
26 Idealan gas (IG) Jednačna stanja F(,V, T)=0 Površ(ina) stanja IG Jednačina Stanja F(,V,T)=0 T T 1 T 2 T 3 T V T 1 T 2 T 3 V V 1 V 2 V3 V T 26
27 Idealan gas (IG) Jednačna stanja F(,V, T)=0 T 1 T 2 T 3 T V=m R T V/m= RT v = R T R=(MR)/M ρ= /R T Površina stanja V [Pa], T [K], V [m 3 ], v [m 3 /kg] Univerzalna gasna konstanta (MR)=8314[J/kmol K] M [kg/kmol] Molarna masa 29 Vazduh 18 Voda 27
28 Primjer Idealan gas (IG) U sudu zaremine V=1 m 3 se nalazi vazduh na ritisku =2 bar i temeraturi t = 120 C. Odrediti masu i gustinu vazduha u sudu. Podaci: molekulska masa vazduha je M=29 kg/kmol, univerzalna gasna konstanta je (MR)=8314 J/kgK. Rešenje m T V V=m R T m=v/ (R T ) R=8314/M = 8314/29 = J / kgk T= t +273= = 393 K m= x 1 /(286.7 x 393 )=1.78 kg ρ=m/v=1.78/1=1.78 kg/m 3 28
29 Realni gasovi Pare (RG-P) Osnovne karakteristike RG-P w Postoje medjumolekulske sile Zaremina molekula nije zanemarljiva Posledica Pojava AGREGATNIH stanja Gas Tečnost F m F m Fm Čvrsto w w 29
30 Realni gasovi - Pare Kako izgleda roces dobijanja are ri =const? A B ZAGRIJAVANJE TEČNOSTI *=const Tečnost Q T C T BC T A T (Temeratura) *=const T=const A Tečnost B C Para *,T=cons Q D * Para B C PROMJENA FAZE (ISPARAVANJE) τ (Vrijeme) C D PREGRIJAVANJE PARE Promjena B-C je isaravanje (romjena faze) Promjena C B je kondenzacija (romjena faze) PRI FAZNOM PRELAZU T=const 30
31 Realni gasovi - Pare Jednačina Stanje F(,V,T)=0 V T S c S+G V S + L L ga L+G B T=const T k =const K =const S- Solid (Čvrsto) L- Likquid (Tečno) G- Gas-Para (Gasovito) G C D T Površ(ina) stanja 31
32 -V, i -s, -i dijagrami -V - i S + x=0 Realni gasovi Pare (RG-P) K A B C T k D LS + L G+L L S S+L+G x=1 G S S+G K T=const V S Molierov i-s c S+G V S + L L ga L+S B G T=const T=const T k =const K C =const D i K C =const x=0 B TKR=const x=1 D T A B C A B C D D x=0.5 x=0 x=1 T A i T BC T D s - Entroija 32
33 Izobare 33 Izoterme Steen suvoće Izobare - Izoterme Entalija (h, i [ kj/kg] )
34 Izoterme 34 Izentroe Izobare Steen suvoće Izoterme PRITISAK ()-ENTALPIJA (h, i) Izoterme
35 Proces od B do C je isaravanje Proces od C do B je kondenzacija Realni gasovi Pare (RG-P) x=m /(m +m l ) B *,T=const Para Tečnost C x=const S c S+G V S + L L ga B L+S T=const T k =const K G C =const Fazni relaz B u C (isaravanje) je skokovit, jer kad tečnost redje u aru oveća joj se zaremina ~ 1000 uta. Tečnost iz B skoči u aru C. Izmedju njih nema medju-stanja. Pri tome se sva tolota troši na slom strukture tečne u gasnu. To je latentna tolota isaravanja r 2500 kj/kg. U sudu tokom rocesa imamo istovremeno tečnost B i aru C. Udio mase are u ukunoj masi u sudu se izražava reko 35 steena suvoće are x=m are/(m are+m tečnosti). D T
36 Realni gasovi Pare (RG-P) Površina stanja Pritisak ključanja (ravnoteže) Kriva naona (ključanja) 1 bar A B C K Pokazuje vezu izmedju ritiska i temerature ključanja t D 100 C Temeratura ključanja (ravnoteže) S c S+G V S + L L ga L+S B G T=const T k =const K C =const D T S- Solid (Čvrsto) L- Liquid (Tečno) G- Gas-Para (Gasovito) 36
37 t [C] P[kPa] t [C] P[kPa] t [C] Realni gasovi Pare (VODA) P[kPa] Pritisak ključanja (ravnoteže) Kriva naona (ključanja) kpa K 100 C Temeratura ključanja (ravnoteže) t 37
38 Vlažan vazduh ž Smješa suvog vazduha (L, SV ) i vlage (W, H2O) se naziva vlažan vazduh: m vv [kg]=l+w Vlažan vazduh L+W V,T Vlaga-Para V,T = + W Suvi vazduh L V,T DALTONOV ZAKON: KOMPONENTE SMJEŠE SE PONAŠAJU NEZAVISNO JEDNA OD DRUGE (KAO DA NE VIDE JEDNA DRUGU), TAKO DA IH MOŽEMO POSMATRATI RAZDVOJENO (Sl. GORE). TO JE PRINCIP SUPERPOZICIJE. Pri tome komonente imaju istu temeraturu T (jer su u kontaktu jedna sa drugom) i zauzimaju istu zareminu V. 38
39 Vlažan vazduh ž Vlažan vazduh V,T L+W Vlaga-Para V,T = + W Suvi vazduh V,T L 1 kg SV 1 kg SV x kg vlage x kg vlage 39
40 x ž Asolutna vlažnost (x ) daje informaciju o sastavu smješe, tj. koliko ima vlage u 1 kg suvog vazduha (kg vlage / kg suvog vazduha), odnosno o koncentraciji vlage u suvom vazduhu = masa vlage masa suvog vazduha Vlažnost vazduha = W L kgw kgsv Lkg SV Wkg vlage W m VV = L + W = L (1 + ) = L (1 + L W L W W L W x) G L S x = = + + = xg + xl + L GAS-PARA TEČNOST L LED x S m vv kg 40
41 Vlažnost vazduha ž ć t Vlazan vazduh V,T L+W Vlaga V,T d = + W Suvi vazduh V,T L L ϕ = d d ' Ukuan ritisak smješe () je jednak zbiru arcijalnih ritisaka suvog vazduha ( L ) i arcijalnog ritiska vodene are ( d ). 41
42 Vlažnost vazduha ž ć t Nezasićen V,T d Zasićen V,T d Kondenzacija ć ć To je maximalni ritisak vodene are ri zadatoj temeraturi (to je ritisak koji odgovara temeraturi ravnoteže za H 2 O). Analogija sa rastvorima u hemiji: Zasićen rastvor (na rimjer voda i šećer) redstavlja rastvor sa maximalnom koncentracijom rastvorene sustance (šećera u vodi). Dalje dodavanje šećera dovodi do njegovog izdvajanja na dnu. Zasićen vazduh ne može više da rastvori (rimi) vodene are. Svako dalje dodavanje H 2 O dovodi do izdvajanja (kondenzacije) vode. 42
43 Vlažan vazduh ENTALPIJA Tačka rose stanja vazduha A (Kondenzacija) i t t d φ A NEZASIĆEN VAZDUH φ=1 (100 %) ZASIĆEN VAZDUH Zasićen odručje vlažne magle V,t d d x 43 APSOLUTNAVLAŽNOST
44 V& [ m / s] Zareminski rotok je zaremina koja rodje kroz odredjeni resjek u 1 sec. 3 Dakle, ako kroz neki resjek ovršine A [m 2 ] "rotekne" fluid zaremine ΔV za vrijeme Δτ, tada se zareminski rotok, 3 dobija kao količnik, tj. 3 ΔV[ m ] V& [ m / s] = Δτ[ s] A [m 2 ] je ovršina orečnog resjeka cijevi, w [m/s] je brzina strujanja. - Presjek A w 1 2 Δ x w = Δ τ Δ V Δτ 3 3 ΔV[ m ] AΔ x V &[ m / s] = = = Δτ[ s] Δτ Δ x Δ V= A Δx A[ m 2 ] w[ m / s] 44
45 Primjer Kroz orečni resjek cijevi ovršine A=0.5 m 2 za vrijeme Δτ =5 s rotekne zaremina fluida ΔV =6 m 3. Odrediti zareminski rotok i brzinu strujanja u tom resjeku. Δ V= A Δx - Presjek Δ V V& [ m / s] 3 ΔV[ m ] Δτ[ s] 6 3 = = = Δ x Δx ΔV / A ΔV / Δτ V& 1.2 w[ m / s] = = = = = = Δτ Δτ A A
46 m& [ kg / s] Maseni rotok ( ) je masa koja rodje kroz odredjeni resjek u jednoj sekundi. A Δ m Δx Ako kroz neki resjek rotekne masa fluida (Δm) za vrijeme Δτ, tada je maseni rotok, količnik m& [ kg / s] m & Δm[kg] Δτ[s] GUSTINA ρ=m/v m& [ kg / s] = Δm[ kg] Δτ[ s] = ρ [ kg 3 / m ] ΔV[ Δτ[ s] m 3 ] = ρv& 46
47 Primjer Koliki je maseni rotok u rethodnom rimjeru ako je gustina fluida ρ [kg /m 3 ]=1.2? A Δ m Δx V& [ m GUSTINA ρ=m/v MASA m= ρv / s] 3 ΔV[ m ] Δτ[ s] 6 3 = = = m& [ kg / s] = Δm[ kg] Δτ[ s] = ρ [ kg 3 / m ] ΔV[ Δτ[ s] m 3 ] = ρv& m &[ kg / s] = ρv& = =
48 MJERENJE PROTOKA BLENDA (loča sa otvorom u sredini) Pad ritiska (Δ) ri roticanju kroz blendu je roorcionalan dinamičkom ritisku struje ( d ): Δ = ( ) ~ 1 2 w ρ 2 2 A 1 2 w ( m / s ) = K Δ B [ ] m 3 s Aw V & / = Δ Blenda 48
49 MJERENJE PROTOKA ULTRAZVUČNI MJERAČ PROTOKA Emiter Brzina zvuka je različita uz i niz struju. Na osnovu te razlike se odredjuje brzina struje fluida. Ultrazvučni talasi 49
50 ENERGIJA: OBLICI - KVALITET ŠTA JE ENERGIJA? ENERGIJA JE VELIČINA STANJA! KINETIČKA ENERGIJA POTENCIJALNA ENERGIJA UNUTRAŠNJA ENERGIJA m W m Ek=mw 2 /2 E=mgH H MAKROSKOPSKI OBLICI E M = E k +E MIKROSKOPSKI OBLICI E m = U 50
51 Unutrašnja energija U [J],u[J/kg] MIKROSKOPSKI OBLIK ENERGIJE Energija translatornog kretanja molekula w Energija rotacije usled rotiranja molekula Energija vibracije molekula 51
52 ENERGIJA JE SKALARNA VELIČINA ŠTA JE ENERGIJA? M 2 M 1 E 2 E 1 M=M 1 +M 2 ANALOGIJA E=E 1 +E 2 E [J]=m e m [kg], e [J/kg]=E/m ENERGIJA IMA OSOBINU ADITIVNOSTI E Sistem =E A +E B +E C A B C Sistem 52
53 TOPLOTA Q [J] Q Gas Haotično kretanje molekula Tolota je transfer dezorganizovane energije. 53
54 Secifična tolota c [J/ kg K] Q ΔT m Tolota otrebna da se tijelo mase m zagrije za ΔT (c je secifična tolota) je: Q = m c ΔT Za čvrsta i tečna tijela c ~ const. Za gasove c = const. Secifična tolota nije karakteristika materije, odnosno može imati različite vrijednosti. 54
55 Primjer Secifična tolota c [J/ kg K] Koliko je tolote otrebno dovesti da bi m=100 kg (l) vode zagrijali za Δt=10 C. Secifična tolota vode je c=4.18 kj/kgk. Q m ΔT Q = m c ΔT Za čvrsta i tečna tijela c ~ const. Q=100 x 4.18 x 10 = 4180 kj 1 kwh=3.6 MJ=3600 kj Q=4180 / 3600=1.16 kwh 55
56 Idealan gas Secifične tolote gasova: c (ri =const)i c v (ri V=const) Q v = m c v ΔT c v = Q v /m ΔT Q = m c ΔT c = Q /m ΔT A G Q v m V=const ΔT Q z =const z1 m ΔT z 2 =G/A=const Promjena ri V=const Promjena ri =const Očigledno je da je c >c v jer je Q >Q V ri istoj masi m i romjeni ΔT 56
57 Idealan gas Unutrašnja energija U [J]=m c v T u [J /kg] =c v T Entalija I [J]=m c T i [J /kg] =c T Za vazduh: c v =720 J/kgK c =1055 J/kgK 57
58 RAD W [J] Rad redstavlja skalarni roizvod sile i uta. Rad je transfer organizovane energije F Δx ΔW=F x Δx x F x Ukuan rad: W ΣF x Δx, 58
59 RAD - W POJAVNI OBLICI RADA Asolutni zareminski rad (romjena zaremine) Rad W L Wt F Δx F=A ΔL =FΔx ΔL=(A)Δx ΔL=ΔV Tehnički rad (Obrtanje osovine) 59
Slično važi i za bilo koje druge kombinacije nekondenzujućih ( O
 8. Vlažni gasovi 8.1 Uvod - smeše realnog i idealnog gasa - smeše kondenzujućeg i nekondenzujućeg gasa - arno gasne smeše - najoznatiji redstavnik ažan vazduh - smeša (suvog) vazduha idealnog gasa i age
8. Vlažni gasovi 8.1 Uvod - smeše realnog i idealnog gasa - smeše kondenzujućeg i nekondenzujućeg gasa - arno gasne smeše - najoznatiji redstavnik ažan vazduh - smeša (suvog) vazduha idealnog gasa i age
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
TERMODINAMIKA. Vježbe II
 ERMODINAMIKA Vježbe II Zadatak br. 9 kg neke materije mijenja stanje kvazistatički o zakonu = ks, gdje je od stanja ( 00K ) do stanja ( k kg K kj 900K ). Potrebna količina tolote dovodi se od tolotnog
ERMODINAMIKA Vježbe II Zadatak br. 9 kg neke materije mijenja stanje kvazistatički o zakonu = ks, gdje je od stanja ( 00K ) do stanja ( k kg K kj 900K ). Potrebna količina tolote dovodi se od tolotnog
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
TOPLOTA. Primjeri. * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem.
 1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
C 273,15, T 273,15, 1 1 C 1 50 C 273,15 K 50K 323,15K 50K 373,15K C 40 C 40 K
 1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
4. VLAZAN VAZDUH. Ukupan pritisak vlaznog vazduha jednak je zbiru parcijalnih pritisaka suvog vazduha i vodene pare.
 4. VLAZAN VAZDUH Vlazan vazduh je dvo-komonentna mesavina, suvog vazduha i vodene are. Za suv vazduh kao komonentu vlaznog vazduha vaze zakonitosti idealnog gasa. Za vodenu aru kao komonentu vlaznog vazduha
4. VLAZAN VAZDUH Vlazan vazduh je dvo-komonentna mesavina, suvog vazduha i vodene are. Za suv vazduh kao komonentu vlaznog vazduha vaze zakonitosti idealnog gasa. Za vodenu aru kao komonentu vlaznog vazduha
Λύση: Ισολογισµός ισχύος στο Λέβητα Καυσαερίων: (1)
 6 η Οµάδα Ασκήσεων Άσκηση 6.1 Η πρόωση πλοίου επιτυγχάνεται µε Βραδύστροφο, -Χ κινητήρα Dieel µέγιστης συνεχούς ισχύος στον άξονα 6100 PS. Η ειδική κατανάλωση του κινητήρα είναι 15 gr/psh σε φορτίο 100
6 η Οµάδα Ασκήσεων Άσκηση 6.1 Η πρόωση πλοίου επιτυγχάνεται µε Βραδύστροφο, -Χ κινητήρα Dieel µέγιστης συνεχούς ισχύος στον άξονα 6100 PS. Η ειδική κατανάλωση του κινητήρα είναι 15 gr/psh σε φορτίο 100
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
KURS ZA ENERGETSKI AUDIT 1.2
 KURS ZA ENERGETSKI AUDIT. TEORIJSKE OSNOVE Pripremio: Dr Nenad Kažić I ZAKON TERMODINAMIKE ZA OTVOREN SISTEM Prema Zakonu o održanju energije, promjena energije (ΔE) neizolovanog sistema jednaka je "čistom"
KURS ZA ENERGETSKI AUDIT. TEORIJSKE OSNOVE Pripremio: Dr Nenad Kažić I ZAKON TERMODINAMIKE ZA OTVOREN SISTEM Prema Zakonu o održanju energije, promjena energije (ΔE) neizolovanog sistema jednaka je "čistom"
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
13. и 14. novembar godine
 3. и 4. novembar 0. godine Kretanje fluida je znatno komlikovanije od kretanja čvrstog tela. Kretanje fluida se naziva strujanje fluida = nastaje zbog težine fluida ili razlike ritisaka razmatramo strujanje:
3. и 4. novembar 0. godine Kretanje fluida je znatno komlikovanije od kretanja čvrstog tela. Kretanje fluida se naziva strujanje fluida = nastaje zbog težine fluida ili razlike ritisaka razmatramo strujanje:
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa
 .vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
TERMOENERGETIKA. Boričić Aleksandra
 TERMOENERGETIKA Boričić Aleksandra Šta proučava termodinamika? Termodinamika je nauka koja proučava pojave vezane za međusobno pretvaranje jednog oblika energije u drugi. Termodinamika analizira i definiše
TERMOENERGETIKA Boričić Aleksandra Šta proučava termodinamika? Termodinamika je nauka koja proučava pojave vezane za međusobno pretvaranje jednog oblika energije u drugi. Termodinamika analizira i definiše
RAD, SNAGA I ENERGIJA
 RAD, SNAGA I ENERGIJA SADRŢAJ 1. MEHANIĈKI RAD SILE 2. SNAGA 3. MEHANIĈKA ENERGIJA a) Kinetiĉka energija b) Potencijalna energija c) Ukupna energija d) Rad kao mera za promenu energije 4. ZAKON ODRŢANJA
RAD, SNAGA I ENERGIJA SADRŢAJ 1. MEHANIĈKI RAD SILE 2. SNAGA 3. MEHANIĈKA ENERGIJA a) Kinetiĉka energija b) Potencijalna energija c) Ukupna energija d) Rad kao mera za promenu energije 4. ZAKON ODRŢANJA
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE)
 Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
=1), što znači da će duljina cijevi L odgovarati kritičnoj duljini Lkr. koji vlada u ulaznom presjeku, tako da vrijedi
 Primjer. Zrak (R=87 J/(kg K), κ=,4) se iz atmosfere ( =, bar, T =88 K) usisava oz cijev romjera D = mm, duljine L = m, rema slici. Treba odrediti maksimalno mogući maseni rotok m max oz cijev uz retostavku
Primjer. Zrak (R=87 J/(kg K), κ=,4) se iz atmosfere ( =, bar, T =88 K) usisava oz cijev romjera D = mm, duljine L = m, rema slici. Treba odrediti maksimalno mogući maseni rotok m max oz cijev uz retostavku
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2011 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος B Λυκείου
 Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ B Λυκείου Μαρτίου Θεωρητικό Μέρος Θέμα ο A. Στα δύο όμοια δοχεία του σχήματος υπάρχουν ίσες ποσότητες νερού, με την ίδια αρχική θερμοκρασία θ =4 ο
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ B Λυκείου Μαρτίου Θεωρητικό Μέρος Θέμα ο A. Στα δύο όμοια δοχεία του σχήματος υπάρχουν ίσες ποσότητες νερού, με την ίδια αρχική θερμοκρασία θ =4 ο
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
BIOFIZIKA TERMO-FIZIKA
 BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2003 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος.
 Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 00 Β Λυκείου 5 Μαρτίου 00 Θεωρητικό Μέρος Θέμα ο Α. Δίνεται ένα ομοιόμορφα φορτισμένο λεπτό τεταρτημόριο δαχτυλιδιού ακτίνας R, με φορτίο λ ανά μονάδα
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 00 Β Λυκείου 5 Μαρτίου 00 Θεωρητικό Μέρος Θέμα ο Α. Δίνεται ένα ομοιόμορφα φορτισμένο λεπτό τεταρτημόριο δαχτυλιδιού ακτίνας R, με φορτίο λ ανά μονάδα
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Tip ureappleaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 656
 TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
OSNOVI ELEKTRONIKE. Vežbe (2 časa nedeljno): mr Goran Savić
 OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία
 Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία LBNL, Report 2268E Οδηγοί εξοικονόμησης ενέργειας LBNL, Report 2268E Πλαίσιο και στόχος των διαλέξεων Οι δράσεις
Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία LBNL, Report 2268E Οδηγοί εξοικονόμησης ενέργειας LBNL, Report 2268E Πλαίσιο και στόχος των διαλέξεων Οι δράσεις
TEHNIƒKA MEHANIKA 2 Osnovne akademske studije, III semestar
 TEHNIƒKA MEHANIKA 2 Osnovne akademske studije, III semestar Prof. dr Stanko Br i Prof. dr Rastislav Mandi Doc. dr Stanko ori email: cstanko@grf.bg.ac.rs Graževinski fakultet Univerzitet u Beogradu k. god.
TEHNIƒKA MEHANIKA 2 Osnovne akademske studije, III semestar Prof. dr Stanko Br i Prof. dr Rastislav Mandi Doc. dr Stanko ori email: cstanko@grf.bg.ac.rs Graževinski fakultet Univerzitet u Beogradu k. god.
Masa i gustina. zadaci
 Masa i gustina zadaci 1.)Vaga je u ravnote i dok je na jednom njenom tasu telo, a na drugom su tegovi od: 10 g, 2 g, 500 mg i 200 mg.kolika je masa ovog tela? 2.)Na jednom tasu vage se nal azi telo i teg
Masa i gustina zadaci 1.)Vaga je u ravnote i dok je na jednom njenom tasu telo, a na drugom su tegovi od: 10 g, 2 g, 500 mg i 200 mg.kolika je masa ovog tela? 2.)Na jednom tasu vage se nal azi telo i teg
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
GASNO STANJE.
 GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Ι Ο Λ Ο Γ Ι Μ Ο - Α Π Ο Λ Ο Γ Ι Μ Ο Μ Η Ν Ο Γ Δ Κ Δ Μ Β Ρ Ι Ο Υ 2 0 1 5
 Μ Ρ : 0 9 / 0 1 / 2 0 1 6 Ρ. Ρ Ω. : 7 Λ Γ Μ - Λ Γ Μ Μ Η Γ Δ Κ Δ Μ Β Ρ Υ 2 0 1 5 Δ Γ Ρ Ϋ Λ Γ Θ Δ ΚΔ Μ Β Δ Β Ω Θ Δ Δ Ρ Υ Θ Δ 0111 Χ / Γ Δ Θ Μ Θ Δ Ρ Ω Κ - - - 0112 Χ / Γ Λ Ρ Γ Κ Δ 2 3. 2 1 3. 0 0 0, 0 0-2
Μ Ρ : 0 9 / 0 1 / 2 0 1 6 Ρ. Ρ Ω. : 7 Λ Γ Μ - Λ Γ Μ Μ Η Γ Δ Κ Δ Μ Β Ρ Υ 2 0 1 5 Δ Γ Ρ Ϋ Λ Γ Θ Δ ΚΔ Μ Β Δ Β Ω Θ Δ Δ Ρ Υ Θ Δ 0111 Χ / Γ Δ Θ Μ Θ Δ Ρ Ω Κ - - - 0112 Χ / Γ Λ Ρ Γ Κ Δ 2 3. 2 1 3. 0 0 0, 0 0-2
PRAVAC. riješeni zadaci 1 od 8 1. Nađite parametarski i kanonski oblik jednadžbe pravca koji prolazi točkama. i kroz A :
 PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
nvt 1) ukoliko su poznate struje dioda. Struja diode D 1 je I 1 = I I 2 = 8mA. Sada je = 1,2mA.
 IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
2 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ
 2 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Διαθέτουμε τροχό ο οποίος αποτελείται από έναν ομογενή λεπτό δακτύλιο μάζας m = 1 kg και ακτίνας R και τέσσερις λεπτές ομογενείς ράβδους μάζας Μ ρ = ¾m και μήκους l = 2R η
2 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Διαθέτουμε τροχό ο οποίος αποτελείται από έναν ομογενή λεπτό δακτύλιο μάζας m = 1 kg και ακτίνας R και τέσσερις λεπτές ομογενείς ράβδους μάζας Μ ρ = ¾m και μήκους l = 2R η
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Trigonometrijske nejednačine
 Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu.
 VISKOZNOST VISKOZNOST Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu. VISKOZNOST Da li očekujete da će glicerol imati veću ili manju
VISKOZNOST VISKOZNOST Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu. VISKOZNOST Da li očekujete da će glicerol imati veću ili manju
1. Ένα σώμα m=1 kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα.
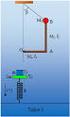 . Ένα σώμα m= kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα. α. Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή. β. Να γράψετε τις εξισώσεις
. Ένα σώμα m= kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα. α. Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή. β. Να γράψετε τις εξισώσεις
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
ΣΥΝΤΟΜΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΑΤΡΑΚΤΩΝ ΑΞΟΝΩΝ ΚΑΤΑ DIN 743 : 2000-10 V1.4
 3 ΣΥΝΤΟΜΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΑΤΡΑΚΤΩΝ ΑΞΟΝΩΝ ΚΑΤΑ DIN 743 : 000-0 V.4 4 Περιεχόμενα 5 Ειαγωγή...9 Ανοχή χαλύβων...9 3 Φόριη... 4 Υπολογιμός ε δυναμική θραύη... 4. Ονομαικές άεις (ημιεύρος δυναμικής
3 ΣΥΝΤΟΜΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΑΤΡΑΚΤΩΝ ΑΞΟΝΩΝ ΚΑΤΑ DIN 743 : 000-0 V.4 4 Περιεχόμενα 5 Ειαγωγή...9 Ανοχή χαλύβων...9 3 Φόριη... 4 Υπολογιμός ε δυναμική θραύη... 4. Ονομαικές άεις (ημιεύρος δυναμικής
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
