Δυαδικές Μονάδες Μνήμης: Μανδαλωτής SR, D και JK Flip-Flops Σχεδιασμός Μετρητή Ριπής

Transcript

1 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡOY ΗΜΥ Δυαδικές Μονάδες Μνήμης: Μανδαλωτής SR, D και JK Flip-Flops Σχεδιασμός Μετρητή Ριπής Εισαγωγή ΕΡΓΑΣΤΗΡΙΟ ΛΟΓΙΣΜΙΚΟΥ/ΥΛΙΚΟΥ 4 Στις προηγούμενες εργαστηριακές ασκήσεις μελετήσαμε την ανάπτυξη και την υλοποίηση συνδυαστικών λογικών συναρτήσεων. Στην άσκηση αυτή μελετούμε τα δυαδικά στοιχεία μνήμης, τα οποία ονομάζονται μανδαλωτές (latches) και flip-flops και τα οποία, μαζί με τα συνδυαστικά κυκλώματα, επιτρέπουν τον σχεδιασμό ακολουθιακών λογικών κυκλωμάτων. Αρχικά, εξετάζουμε τρία από τα πιο γνωστά στοιχεία μνήμης: τoν μανδαλωτή SR και τα flip-flops D και JK (βλέπε σελ , του βιβλίου των Mano&Kime). Ακολούθως, χρησιμοποιούμε τα JK flip-flops για να σχεδιάσουμε ένα modulo 16/10 μετρητή ριπής (ripple counter, βλέπε σελ του βιβλίου των Mano&Kime). Θα κληθείτε να αλλάξετε αυτό τον μετρητή σε modulo 16/N, όπου το N θα είναι μεταξύ Τέλος, ο μετρητής modulo 16/10 θα περιγραφεί με κώδικα VHDL και θα προσομοιωθεί με τον QUARTUS II simulator. Σημειώστε: Βαθμολογείστε και κατά τη διάρκεια του εργαστηρίου (λογισμικού και υλικού). Βεβαιωθείτε ότι ένας από τους υπεύθυνους του εργαστηρίου έχει δει το τελικό αποτέλεσμα για κάθε μέρος της άσκησης, το οποίο σάς ζητείτε να παραδώσετε ή να παρουσιάσετε. Οι ακόλουθες εκτυπώσεις και συμπληρωμένες σελίδες (και από τις δύο εβδομάδες) είναι απαραίτητες και θα πρέπει να υπογραφούν από τους υπεύθυνους του εργαστηρίου και να συμπεριληφθούν στη γραπτή αναφορά: Την κυματομορφή από το βήμα Α.Ι.6, και την εξήγηση από το βήμα Α.Ι.7. Τον σχεδιασμό του μετρητή ριπής και του σήματος Clear (CLRN), με τον πίνακα αληθείας, τον χάρτη Karnaugh, και την ελαχιστοποιημένη εξίσωση με τις πύλες NAND 3-εισόδων (καθαρογραμμένα στον διαθέσιμο χώρο στο τέλος της εκφώνησης) για το μέρος Α.ΙΙ. Το σχηματικό από το βήμα Α.ΙΙ.3, και τις δύο εξόδους προσομοίωσης από το βήμα Α.ΙΙ.6. Το τροποποιημένο κύκλωμα του σήματος Clear (CLRN) των τεσσάρων flip-flops (καθαρογραμμένο στον διαθέσιμο χώρο στο τέλος της εκφώνησης) για το μέρος Α.ΙΙΙ. Το τροποποιημένο σχηματικό από το βήμα Α.ΙΙΙ.4 και τα αποτελέσματα της προσομοίωσης για διάφορες τιμές N από το βήμα Α.ΙΙΙ.8. Τις κυματομορφές με τα αποτελέσματα της προσομοίωσης, καθώς και τον κώδικα του αρχείου lab4d.vhd, από το βήμα A.IV.4. Το σχηματικό με τα pins από το βήμα B.I.15. Την προεργασία και το διάγραμμα συνδεσμολογίας του κυκλώματος από το βήμα Β.ΙΙ.1. Ακολουθίες απαρίθμησης από τα βήματα Β.ΙΙ.3, Β.ΙΙ.5, και Β.ΙΙ.6. 1

2 Μέρος Α (πρώτη εβδομάδα) Σημείωση: Τα πιο κάτω αρχεία θα χρησιμοποιηθούν στην άσκηση αυτή. Πριν ξεκινήσετε, κατεβάστε τα αρχεία αυτά από την ιστοσελίδα του μαθήματος (στο σύνδεσμο Πρόγραμμα/Σημειώσεις), ή ακολουθήστε τις οδηγίες των υπευθύνων του εργαστηρίου. Αντιγράψτε τα αρχεία αυτά στον κατάλογο, όπου θα αποθηκεύσετε τους σχεδιασμούς σας για αυτή την άσκηση. lab4a.bdf lab4a.vwf lab4b.vwf lab4d.vhd lab4d.vwf Α.I. Μανδαλωτές (Latches) και Flip-Flops για τον σχεδιασμό στοιχείων μνήμης Στο σχηματικό του Graphic Editor στην επόμενη σελίδα φαίνονται τέσσερεις διαφορετικές διατάξεις μνήμης ενός bit. Το κύκλωμα των πυλών NAND (σύμβολα 5 έως 10) αποτελούν μια SSI υλοποίηση ενός θετικής λογικής ακμοπυροδότητου (positive edge-triggered) D flip-flop, με ασύγχρονη είσοδο clear αρνητικής λογικής (active-low) και συμπληρωματικές εξόδους. Αυτό είναι ισοδύναμο, σε επίπεδο πύλης, με μια μονάδα MSI 7474A, που φαίνεται στην πάνω, δεξιά γωνιά του σχηματικού, με μόνη διαφορά ότι το τελευταίο έχει μιαν επιπλέον είσοδο αρνητικής λογικής για ασύγχρονο preset (καθορισμό της τιμής του). Οι πύλες NOR, που είναι συνδεδεμένες χιαστή (σύμβολα 14 και 15), συνιστούν ένα Μανδαλωτή Set-Reset (SR Latch) με συμπληρωματικές εξόδους. Στην κάτω αριστερή γωνία φαίνεται ένα ολοκληρωμένο MSI 7473A που είναι ένα αρνητικής λογικής ακμοπυροδότητο (negative edge-triggered) JK flip-flop με ασύγχρονη είσοδο clear αρνητικής λογικής (active-low) και συμπληρωματικές εξόδους. Στο μέρος A.I, θα προσομοιωθεί το σχηματικό της επόμενης σελίδας. Το 7476Α JK flip-flop, το οποίο διαθέτει τόσο clear όσο και preset εισόδους, θα χρησιμοποιηθεί στα μέρη Α.ΙΙ, Α.ΙΙΙ, και Β. Ο χαρακτηριστικός πίνακας του SR Latch που φαίνεται στη σελίδα 4 δηλώνει ότι αν και οι δύο είσοδοι (S και R) είναι High (1), τότε και οι δύο έξοδοι είναι Low (0). Αυτή η λειτουργία είναι αντίθετη με την κανονική λειτουργία των δύο εξόδων, που τις θέλει να είναι συμπληρωματικές (Q = (QB) ). Για το λόγο αυτό, και για την αποφυγή ταλαντώσεων (oscillations) στις τιμές εξόδου όταν αλλάζει η κατάσταση αυτή, ο σχεδιαστής πρέπει να διασφαλίσει ότι οι είσοδοι S και R δεν είναι ποτέ High (1) ταυτόχρονα. Οι πίνακες λειτουργίας για τα D και JK flip-flops φαίνονται επίσης στη σελίδα 4. Σημειώστε ότι αυτά είναι flip-flops με ρολόι (clock), τα οποία ενεργοποιούνται με ακμή (ακμοπυροδοτούνται = edgetriggered) στην είσοδο clock. Οι άλλες είσοδοι πρέπει να παραμένουν σταθερές για συγκεκριμένα χρονικά διαστήματα μετά την ενεργοποίηση του ρολογιού. 2

3 Δυαδικές Μονάδες Μνήμης 3

4 SR Latch S R Q + QB Q QB Μανδαλωτής με θετικής λογικής Set και Reset 7474a D Flip-Flop Θετικής Λογικής Ακμοπυροδότητο (Positive edge-triggered) με ασύγχρονα Preset (PREN) και Clear (CLRN) αρνητικής λογικής (active-low) CLRN PREN D CLK Q + QN X X X X X X X Q QN a (*χωρίς είσοδο PREN) και 7476a JK Flip-Flops Αρνητικής Λογικής Ακμοπυροδότητα (Negative edge-triggered) με ασύγχρονα Clear (CLRN) και Preset(PREN*) αρνητικής λογικής (active-low) CLRN PREN* J K CLKN Q + QN X X X X X X X X X Q QN (Q) (QN) 1 1 X X Q QN 4

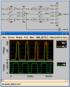
5 Προσομοίωση με το QUARTUS II: 1. Δημιουργήστε στο χώρο εργασίας σας ένα νέο φάκελο (folder) με το όνομα Lab4, κάτω από τον κατάλογο του μαθήματος. Αντιγράψτε το αρχείο σχεδιασμού του graphic editor, lab4a.bdf, καθώς και το αρχείο κυματομορφών, lab4a.vwf, από την ιστοσελίδα του μαθήματος, όπως περιγράφηκε πιο πριν στη σελίδα Ανοίξετε το QUARTUS II. Ανοίξετε το αρχείο lab4a.bdf από τον φάκελο σας, και συμπεριλάβετε το σε ένα νέο project, lab4, το οποίο πρέπει να δημιουργήσετε. Ο σχεδιασμός που υπάρχει στη σελίδα 3 πρέπει να ανοίξει στον Graphic Editor. 3. Καθορίστε το αρχείο lab4a.bdf ως Top-Level Entity και μεταφράστε τον σχεδιασμό. 4. Ανοίξετε το Simulator Tool και καθορίστε το αρχείο lab4a.vwf σαν είσοδο. Επιλέξετε Timing στο πεδίο Simulation mode. 5. Τρέξτε την προσομοίωση για 1000ns και μετά ανοίξετε το αρχείο κυματομορφών (Report) για να δείτε τα αποτελέσματα. 6. Κρατήστε μία εκτύπωση της κυματομορφής (με το όνομα και τον αριθμό ταυτότητάς σας και την ημέρα εργαστηρίου). 7. Μελετήστε την έξοδο της προσομοίωσης και σχολιάστε τα αποτελέσματα. Σημειώστε κυρίως τις διαφορές ανάμεσα σε θετικά και αρνητικά ακμοπυροδότητα flip-flops και μεταξύ των flip-flops με ρολόι και των μανδαλωτών (latches). Σημειώστε τις διακυμάνσεις στις εξόδους του μανδαλωτή SR και τις συνθήκες για τις οποίες συμβαίνουν. Σημειώστε ότι οι καθυστερήσεις που έχουν να κάνουν με την NAND υλοποίηση του D flip-flop είναι διαφορετικές από αυτές του 7474A flip-flop. Ποιο από τα δύο στοιχεία μνήμης παρουσιάζει πραγματικά συμπληρωματική συμπεριφορά στις εξόδους Q και QN για όλες τις χρονικές στιγμές; (Μεγεθύνετε τα συγκεκριμένα χρονικά σημεία που θέλετε να παρατηρήσετε στο παράθυρο αποτελεσμάτων της προσομοίωσης και χρησιμοποιήστε τα βέλη του Master Time Bar στο πάνω μέρος του παραθύρου για να βρείτε τις χρονικές διαφορές. Σημειώστε τις στην κυματομορφή.) Σημείωση: Θα πρέπει να έχετε κατανοήσει τα πιο πάνω και να μπορείτε να τα εξηγήσετε σε έναν υπεύθυνο εργαστηρίου, πριν σάς υπογράψει την εκτύπωση. 8. Κλείστε όλα τα παράθυρα, αλλά παραμείνετε στο QUARTUS II. Α.II. Μετρητής Ριπής modulo 16/10 (Modulo 16/10 Ripple Counter) με JK flip-flops Ένα JK flip-flop μετατρέπεται σε Τ flip-flop (από την λέξη Toggle που σημαίνει εναλλάσσει κατάσταση) όταν και οι δύο είσοδοι J και K κρατηθούν High (1). Με αυτές τις συνθήκες, το flip-flop αλλάζει κατάσταση (από 0 σε 1, ή από 1 σε 0) σε κάθε ακμή του σήματος του ρολογιού. Στο μέρος αυτό θα σχεδιάσετε ένα μετρητή ριπής με τη χρήση τεσσάρων αρνητικής λογικής ακμοπυροδότητα (negative edge-triggered) JK flip-flops (7476Α) με ασύγχρονα preset και clear αρνητικής λογικής (active-low). Ένα σήμα ρολογιού (clock) με το όνομα CLK θα οδηγεί την είσοδο του ρολογιού του πρώτου flip-flop (το πρώτο flip-flop αντιστοιχεί στο λιγότερο σημαντικό ψηφίο LSB), ενώ η έξοδος Q του πρώτου flip- 5

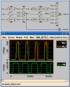
6 flop θα οδηγεί την είσοδο του ρολογιού του δεύτερου flip-flop (επόμενου σημαντικού ψηφίου), και το ίδιο για τα επόμενα δύο flip-flops. Όλες οι J και K είσοδοι, καθώς και τα presets θα τεθούν σταθερά στο High (Vcc). Έτσι, όταν η έξοδος κάποιου flip-flop πάει από High σε Low (negative edge), θα προκαλεί μια αλλαγή κατάστασης στο επόμενο flip-flop, και η ομάδα των τεσσάρων flip-flop θα λειτουργεί σαν ένας δυαδικός μετρητής ριπής τεσσάρων bit. Άλλη μια είσοδος, με όνομα CLRB, θα θέτει ασύγχρονα όλα τα flip-flops στο 0, όταν το CLRB είναι Low (active-low clear). Θα υπάρχει, επίσης, και μια τρίτη είσοδος, η MOD10, η οποία καθορίζει πότε τα flipflops θα μηδενιστούν. Όταν το MOD10 είναι High, ο μετρητής θα μηδενίζεται όταν η μέτρηση φτάνει στον δυαδικό αριθμό Έτσι, όταν το MOD10 είναι Low και το CLRB είναι High ο μετρητής θα απαριθμεί κυκλικά και τις 16 δυαδικές τιμές που μπορούν να αναπαρασταθούν με 4 bit, ενώ όταν και τα δύο σήματα (MOD10 και CLRB) είναι High, ο μετρητής θα απαριθμεί κυκλικά μόνο τους αριθμούς από το 0000 έως το 1001 (γίνεται δηλαδή modulo 10 μετρητής). Η έξοδος του κυκλώματος είναι το σύνολο των τεσσάρων εξόδων των flip-flops, συνδεδεμένες με ένα δίαυλο σε μία και μόνο έξοδο, την CNT[3..0]. Η έξοδος του πρώτου flip-flop (που οδηγείται από το CLK) είναι το λιγότερο σημαντικό ψηφίο (LSB) του μετρητή, δηλαδή το CNT[0]. 1. Κατασκευάστε ένα κύκλωμα στον διαθέσιμο χώρο στο τέλος της εκφώνησης, το οποίο να συμφωνεί με τις προδιαγραφές που τέθηκαν στις προηγούμενες παραγράφους, με τη χρήση μόνο δύο ολοκληρωμένων 7476A (τα οποία περιέχουν συνολικά 4 flip-flops) και ενός ολοκληρωμένου 7410 (το οποίο περιέχει 3 NAND 3-εισόδων). Για να σχεδιάσετε το σήμα Clear (CLRN) των τεσσάρων flip-flops, μπορείτε να χρησιμοποιήσετε πίνακα αληθείας και μετά χάρτη Karnaugh για να βρείτε την απλοποιημένη εξίσωση συναρτήσει των CNT[3..0], MOD10, και CLRB. Ακολούθως, υλοποιείστε τη με τρεις NAND τριών εισόδων. Δείξετε όλη την εργασία σας στον διαθέσιμο χώρο στο τέλος της εκφώνησης. 2. Δημιουργήστε ένα νέο αρχείο σχεδιασμού, το lab4b.bdf, και αποθηκεύσετε το στο φάκελο σας, Lab4. Καθορίστε το ως top-level-entity στο τρέχον project. Σχεδιάστε σε αυτό το κύκλωμα που έχετε φτιάξει στο προηγούμενο βήμα. Ο σχεδιασμός σας θα περιέχει μία σύνδεση διαύλου στη θύρα εξόδου. Ανατρέξετε στην εργαστηριακή άσκηση 3 για υπενθύμιση της χρήσης διαύλων. Επίσης, μπορείτε να χρησιμοποιήσετε την ονομασία κόμβων ώστε να εξοικονομήσετε χώρο και να κάνετε το κύκλωμα σας πιο ξεκάθαρο και ευανάγνωστο. 3. Αποθηκεύσετε και μεταφράστε τον σχεδιασμός σας. Κρατήστε μια εκτύπωση του (με το όνομα και τον αριθμό ταυτότητάς σας, και την ημέρα εργαστηρίου). 4. Αντιγράψετε το αρχείο με τις κυματομορφές, lab4b.vwf, από την ιστοσελίδα του μαθήματος στο φάκελο σας, Lab4. (Για σωστή προσομοίωση, βεβαιωθείτε ότι τα ονόματα των εισόδων και εξόδων του σχεδιασμού σας είναι ακριβώς όπως αυτά έχουν καθοριστεί στις πιο πάνω προδιαγραφές και στο αρχείο κυματομορφών.) 5. Προσομοιώστε τον σχεδιασμό του μετρητή, με το πιο πάνω αρχείο για 3000ns, με την επιλογή για χρονική προσομοίωση (Timing). Μεγεθύνετε το αποτέλεσμα της κυματομορφής και παρατηρήστε τη μετάβαση από το 7 στο 8. Σχολιάστε. 6. Κρατήστε δύο εκτυπώσεις του αποτελέσματος της προσομοίωσης (με το όνομα και τον αριθμό ταυτότητάς σας και την ημέρα εργαστηρίου). Μια συνολική από το 0ns έως3000ns και μια από το 1370ns έως 1720ns. 6

7 Α.III. Μετρητής Ριπής modulo 16/N (Modulo 16/N Ripple Counter) με JK flip-flops Σε αυτό το μέρος θα τροποποιήσετε τον προηγούμενο σχεδιασμό, από το Μέρος Α.II, για να υλοποιήσετε ένα μετρητή ριπής modulo 16/Ν, όπου το N θα παίρνει τιμές από το 0 ως 15. Η τιμή modulo N θα είναι μια νέα είσοδος, σε μορφή διαύλου, του τροποποιημένου σχεδιασμού, και ο μετρητής θα απαριθμεί κυκλικά από το 0 ως το Ν-1 (θα γίνεται δηλαδή μετρητής modulo N) όταν τα δύο σήματα MODN και CLRB είναι High (λογικό 1). Θα πρέπει να γίνεται σύγκριση ανά δυαδικό ψηφίο μεταξύ του N[3..0] και του CNT[3..0]. Όποτε ισούνται, δηλαδή το CNT[3..0] θα έχει φτάσει στον αριθμό Ν (έστω και στιγμιαία), ο μετρητής θα αρχικοποιείται στο μηδέν όταν το MODN είναι High (λογικό 1). 1. Δημιουργήστε ένα αντίτυπο του προηγούμενου σχεδιασμού σας στο φάκελο Lab4 και ονομάστε το lab4b_modn.bdf. 2. Ανοίξετε το lab4b_modn.bdf στο QUARTUS II και θέστε το ως top-level entity στο τρέχον project. 3. Τροποποιήστε τον σχεδιασμό σας ούτως ώστε να υλοποιεί ένα μετρητή ριπής modulo 16/N, όπου η τιμή N θα καθορίζεται από μια επιπρόσθετη θύρα εισόδου σε μορφή διαύλου, Ν[3..0]. (Αλλάξετε επίσης το όνομα της εισόδου MOD10 σε MODN.) Ακολούθως, αλλάξτε το κύκλωμα για το Clear (CLRN) των τεσσάρων flip-flops, ούτως ώστε να συνάδει με τις πιο πάνω προδιαγραφές. Όπως έχει αναφερθεί, θα πρέπει να γίνεται σύγκριση ανά δυαδικό ψηφίο μεταξύ του N[3..0] και του CNT[3..0]. Όταν ισούνται, και το MODN είναι High (λογικό 1), ο μετρητής θα μηδενίζεται. 4. Αποθηκεύσετε και μεταφράστε τον σχεδιασμό σας. Κρατήστε μια εκτύπωση του (με το όνομα και τον αριθμό ταυτότητάς σας, και την ημέρα εργαστηρίου). 5. Δημιουργήστε ένα αντίτυπο του αρχείου κυματομορφών lab4b.vwf στο φάκελο Lab4 και ονομάστε το lab4b_modn.vwf. 6. Ανοίξετε το lab4b_modn.vwf στο QUARTUS II και εισαγάγετε σ αυτό το σήμα εισόδου N[3..0]. (Κάντε δεξί κλικ στην στήλη Name: στα αριστερά του παραθύρου του Waveform Editor και επιλέξτε Insert Insert Node or Bus. Στο καινούργιο παράθυρο διαλόγου καθορίστε το όνομα του νέου διαύλου ως N, τον τύπο ως INPUT, το πλάτος (bus width) ως 4, και το Radix ως Unsigned Decimal.) Καθορίστε μια συγκεκριμένη τιμή στο N[3..0] για όλη τη διάρκεια της προσομοίωσης. Μετονομάστε, επίσης, το MOD10 σε MODN, και καθορίστε την τιμή του ούτως ώστε να είναι 1 για σχεδόν όλη την διάρκεια της προσομοίωσης. (Το πιο πιθανό να μπορέσετε να προσομοιώσετε μόνο μια τιμή του N για χρονική διάρκεια γύρω στα 3000ns. Η διάρκεια πρέπει να διαφοροποιείται αναλόγως του Ν για να φαίνονται όλα τα βήματα της απαρίθμησης. Μπορείτε να προσομοιώσετε ταυτόχρονα περισσότερες από μία τιμή για το N, αλλά αυτό ενδεχομένως να συνεπάγεται μεγαλύτερης διάρκειας προσομοίωση.) 7. Προσομοιώστε τον σχεδιασμό του μετρητή ριπής modulo 16/N, με το τροποποιημένο αρχείο κυματομορφών, με την επιλογή για χρονική (timing) προσομοίωση. Δοκιμάστε δύο τουλάχιστον ξεχωριστές τιμές για το N (εκτός του 10). 8. Κρατήστε εκτυπώσεις των αποτελεσμάτων των προσομοιώσεων (με το όνομα και τον αριθμό ταυτότητάς σας, και την ημέρα εργαστηρίου). 7

8 Α.IV. Προσομοίωση σε VHDL του Μετρητή Ριπής Modulo 16/10 Στην άσκηση αυτή θα χρησιμοποιήσετε ένα σχεδόν έτοιμο αρχείο VHDL που περιγράφει τη δομή (structural description) ενός μετρητή ριπής modulo 16/10, θα το συμπληρώσετε όπου έχει κενά, θα το μεταφράσετε, και θα το προσομοιώσετε. Με την άσκηση αυτή θα δείτε τις δυνατότητες που έχει το λογισμικό σας για την προσομοίωση αρχείων VHDL που περιγράφουν λογικούς σχεδιασμούς, όπως ακριβώς γίνεται και με τα αρχεία του graphic editor. Επίσης, μπορούν να προσομοιωθούν projects που περιέχουν, τόσο σχηματικές περιγραφές, όσο και περιγραφές σε VHDL, πράγμα το οποίο όμως δεν θα δείξουμε σε αυτή την εργαστηριακή άσκηση. 1. Αντιγράψετε τα αρχεία lab4d.vhd και lab4d.vwf από την ιστοσελίδα, όπως περιγράφηκε πιο πριν, στον κατάλογο σας Lab4. 2. Ανοίξετε το lab4d.vhd στο QUARTUS II και αναθέστε το σε ένα νέο project, lab4d. Το VHDL αρχείο θα ανοίξει στην εφαρμογή Text Editor. Παρατηρήστε για λίγο τον VHDL κώδικα. Οι λέξεις-κλειδιά της VHDL είναι με διαφορετικό χρώμα, κάτι που επιτρέπει καλύτερη ανάγνωση και αποσφαλμάτωση (debugging) του κώδικα. Παρόλο που γενικά ένα αρχείο VHDL μπορεί να δημιουργηθεί με οποιονδήποτε editor, το QUARTUS II προσφέρει διάφορα εργαλεία τα οποία διευκολύνουν τη διαδικασία σχεδιασμού. Όταν θα κληθείτε να αναπτύξετε μόνοι σας κώδικα VHDL, θα βοηθηθείτε πολύ χρησιμοποιώντας τα templates της VHDL (Edit Insert Template), καθώς και την επιλογή Auto- Indent (Tools Options, και μετά επιλέξτε Category: Text Editor), επιπλέον του χρωματισμού του κώδικα που είδαμε στο σημείο αυτό. 3. Συμπληρώστε τα κενά του κώδικα VHDL στο αρχείο lab4d.vhd, ούτως ώστε ο κώδικας να πληροί τις προδιαγραφές ενός μετρητή ριπής modulo 16/10. Χρησιμοποιήστε για βοήθεια τον σχεδιασμό σας lab4b.bdf από το μέρος Α.ΙΙ. 4. Μεταφράστε και ακολούθως προσομοιώστε το project lab4d, με τη χρήση του αρχείου lab4d.vwf, που έχετε αντιγράψει στο βήμα 1. Κρατήστε μιαν εκτύπωση του κώδικα, καθώς και των αποτελεσμάτων της προσομοίωσης (με το όνομα και τον αριθμό ταυτότητάς σας, και την ημέρα εργαστηρίου). Αναφορά Μέρους Α Μέρος I. Συμπεριλάβετε τις προσομοιώσεις από το βήμα Α.Ι.6 και τη συζήτηση από το βήμα Α.Ι.7. Μέρος II. Σχολιάστε τα αποτελέσματα σας, συμπεριλαμβανομένων και των πλεονεκτημάτων και των μειονεκτημάτων ενός μετρητή ριπής, έναντι ενός σύγχρονου μετρητή (synchronous counter) (βλέπε σχετική ύλη στο βιβλίο των Mano&Kime, σελ ), καθώς και τη χρήση των τριών NAND για παραλλαγές στο υπόλοιπο (modulus variations). Συμπεριλάβετε τις εκτυπώσεις από το σχηματικό του βήματος Α.ΙΙ.3, και από τις δύο εξόδους προσομοίωσης του βήματος Α.ΙΙ.6. Μέρος III. Συμπεριλάβετε τις εκτυπώσεις από το τροποποιημένο σχηματικό του βήματος Α.ΙΙΙ.4 και των αποτελεσμάτων της προσομοίωσης για διάφορες τιμές N από το βήμα Α.ΙΙΙ.8. Μέρος IV. Συμπεριλάβετε τις κυματομορφές με τα αποτελέσματα της προσομοίωσης, καθώς και τον κώδικα του αρχείου lab4d.vhd, από το βήμα A.IV.4. 8

9 Μέρος Β.Ι (Δεύτερη εβδομάδα) Σε αυτή την εργαστηριακή άσκηση υλικού θα επαληθεύσετε πειραματικά τη λειτουργία του modulo 16/N μετρητή ριπής, που σχεδιάσατε και προσομοιώσατε στα μέρη Α.ΙI και Α.III. Η πλακέτα DE1 περιλαμβάνει ταλαντωτές (oscillators) για παραγωγή παλμών συχνότητας 24, 27 και 50 MHz. Οι ταλαντωτές αυτοί είναι συνδεδεμένοι με το ολοκληρωμένο Cyclone II και επιτρέπουν την υλοποίηση ακολουθιακών κυκλωμάτων, αφού χρησιμοποιούνται σαν το ρολόι του κυκλώματος. Η έξοδος του μετρητή θα φαίνεται στο SSD, αφού πρώτα μετατρέψετε τις εξόδους του με ένα αποκωδικοποιητή δεκαεξαδικό-σε-ssd (Hex to Seven-Segment Display decoder), όπως κάνατε στην προηγούμενη άσκηση υλικού (3). Παρόλα αυτά, το ρολόι είναι πολύ γρήγορο και δεν θα μπορέσετε να ελέγξετε τη λειτουργία του μετρητή, γι αυτό σάς παρέχετε μια συνάρτηση για μείωση (διαίρεση) της συχνότητας του ρολογιού. 1. Ανοίξετε το project, lab4.qpf, που έχετε δημιουργήσει στο προηγούμενο εργαστήριο λογισμικού, επιλέγοντας File Open Project, ή κάνοντας διπλό κλικ στο αρχείο στο φάκελο σας. Ανοίξετε, επίσης, στο ίδιο project το σχηματικό lab4b_modn.bdf, επιλέγοντας File Open. 2. Αντιγράψετε τα περιεχόμενα του καταλόγου της βιβλιοθήκης DE1core library functions στον κατάλογο σας, Lab4, όπως κάνατε στο προηγούμενο εργαστήριο υλικού. Προσθέστε τον κατάλογο αυτό στις διαθέσιμες βιβλιοθήκες του QUARTUS II. (Επιλέξτε Assignments Settings και μετά την κάρτα Libraries.) 3. Τοποθετήστε μια πύλη not στην είσοδο MODN. Ο μετρητής θα μετρά μέχρι το N-1, όταν ο διακόπτης πίεσης 1 (push button KEY1) είναι πατημένος. 4. Εισαγάγετε ένα σύμβολο dec_7seg και ένα σύμβολο clk_div στο σχηματικό σας. Το clk_div είναι υλοποιημένο σε VHDL. Κάντε Doubleclick στο σύμβολο για να ανοίξετε τον περιγραφή του σε VHDL και παρατηρήστε πώς η συνάρτηση διαιρεί το σήμα του ρολογιού σε μικρότερες συχνότητες. 5. Συνδέστε τη θύρα εισόδου CLK στην είσοδο του συμβόλου clk_div και την έξοδο του clock_1hz στην είσοδο του ρολογιού του πρώτου flip-flop. (Η συχνότητα 1 Hz είναι αρκετά αργή για να σάς επιτρέψει να δείτε την έξοδο του μετρητή.) 6. Διαγράψετε την έξοδο CNT[3..0] και τραβήξετε μια γραμμή (δίαυλο) στην είσοδο του συμβόλου dec_7seg. Ονομάστε τον κόμβο (δίαυλο) αυτό CNT[3..0]. 7. Εισαγάγετε 7 νέες θύρες εξόδου και ονομάστε τις με τα λατινικά γράμματα a έως g. Συνδέστε με καλώδιο τις 7 θύρες εξόδου στις αντίστοιχες εξόδους του συμβόλου dec_7seg. 8. Επιλέξτε Project Set as Top-Level Entity και μεταφράστε τον σχεδιασμό σας. 9. Επιλέξτε Assignments Pins για να αναθέσετε τα pins στις εισόδους και εξόδους. 10. Αναθέστε τον ταλαντωτή 24 MHz στην είσοδο CLK. 11. Αναθέστε τον δεξιό διακόπτη πίεσης (push button) KEY0 στην είσοδο CLRB. 12. Αναθέστε τον δεύτερο διακόπτη πίεσης από τα δεξιά KEY1 στην είσοδο MODN. 13. Αναθέστε τους διακόπτες SW3 έως SW0 στις εισόδους Ν[3] έως Ν[0], αντίστοιχα. 14. Αναθέστε τα 7 pins (0-6) του πρώτου SSD από τα δεξιά (HEX0) στις εξόδους a έως g. 9

10 15. Αποθηκεύσετε και μεταφράστε τον σχεδιασμό σας, μετά την ανάθεση των pins. Κρατήστε μια εκτύπωση του (με το όνομα και τον αριθμό ταυτότητάς σας, και τη μέρα εργαστηρίου). 16. Κατεβάστε τον σχεδιασμό σας στο ολοκληρωμένο Cyclone II της πλακέτας DE1 με την εφαρμογή Tools Programmer (όπως έχετε δει στα προηγούμενα εργαστήρια υλικού). 17. Ελέγξετε τον σχεδιασμό σας. Δοκιμάστε διάφορες τιμές στο Ν (με τους διακόπτες SW3 έως SW0 και τον διακόπτη πίεσης KEY1). Σχολιάστε τα αποτελέσματα και εξηγήστε γιατί ο μετρητής ονομάζεται μετρητής ριπής (ripple counter). Επίδειξη σε έναν από τους υπεύθυνους του μαθήματος απαραίτητη. Μέρος Β.ΙΙ (Δεύτερη εβδομάδα) Σε αυτή την άσκηση θα επαληθεύσετε πειραματικά τη λειτουργία του μετρητή ριπής modulo 16/10 που προσομοιώθηκε στα μέρη Α.II και Α.IV. Φέρτε το σχηματικό lab4b.bdf στο εργαστήριο κάνοντας την προετοιμασία που περιγράφεται πιο κάτω: Προετοιμασία: Σημειώστε στα στοιχεία του σχηματικού lab4b.bdf τα ονόματα των ολοκληρωμένων και τους αριθμούς των pins που θα χρησιμοποιήσετε. Ανατρέξετε στα διαγράμματα των ολοκληρωμένων πιο κάτω για τη σωστή ανάθεση των pins στις εισόδους και τις εξόδους στο σχηματικό σας. Σημειώστε, επίσης, και τα Vcc και GND στο σχηματικό σας. Το ολοκληρωμένο 74LS10 έχει το GND στο Pin 7 και το Vcc στο Pin 14, όπως συνήθως. Αντιθέτως, το 74LS76A διπλό flip-flop έχει στο Pin 5 το Vcc και στο Pin 13 το GND. Εισαγάγετε ένα 74LS04 Hex Inverter στη δεύτερη στήλη διαχωριστικού της πλακέτας ETS-7000 (κάτω από το V2). Εισαγάγετε δύο 74LS76A JK Flip-Flops (με δύο FFs σε κάθε ολοκληρωμένο) στην τρίτη στήλη της πλακέτας, και τέλος ένα 74LS10, τριπλή NAND τριών εισόδων, στην τέταρτη στήλη. Η διάταξη και η αρίθμηση των pins των ολοκληρωμένων φαίνεται πιο κάτω. 1. Χρησιμοποιήστε τους διακόπτες SW0 και SW1 ως τις εισόδους CLRB και MOD10, αντίστοιχα. Το σήμα CLK θα το πάρετε από την έξοδο ενός αντιστροφέα 74LS04, του οποίου η είσοδος θα ενωθεί στην έξοδο TTL Mode της γεννήτριας παλμών, όπου πρώτα έχετε επιλέξει τετραγωνικό παλμό και θέσατε το πλάτος κατάλληλα (μεταξύ ¼ και ½). Χρησιμοποιήστε τους λαμπτήρες L7, L6, L5 και L4 για τις εξόδους CNT[3:0]. (Επίσης, δείξτε τις εξόδους στο δεξί SSD, ενώνοντας το D2 στο GND, και το L4 στο A, το L5 στο B, το L6 στο C και το L7 στο D του D1.) Σχεδιάστε αυτές τις συνδέσεις, καθώς και τις αναθέσεις των pins, στο διάγραμμα κυκλώματος στο τέλος της εκφώνησης. Επίσης, δείξετε την τροφοδοσία Vcc και τη γείωση GND στα αντίστοιχα pins. 2. Συνδέστε το κύκλωμα όπως το διάγραμμα συνδεσμολογίας του βήματος Θέστε τη συχνότητα ρολογιού στα 2 Hz και παρατηρήστε τη συμπεριφορά του κυκλώματος σε σχέση με τις εισόδους. Καταγράψετε στον διαθέσιμο χώρο στο τέλος της εκφώνησης την ακολουθία απαρίθμησης και για τις δύο τιμές του MOD10 (SW1). Σημειώστε ότι το SSD παρουσιάζει μόνο τις τιμές που αντιστοιχούν στα δεκαδικά ψηφία 0 έως Σχολιάστε τα αποτελέσματα και εξηγήστε γιατί αυτός ο μετρητής ονομάζεται μετρητής ριπής. (Επίδειξη σε έναν από τους υπεύθυνους του μαθήματος απαραίτητη.) 5. Δείξετε πώς μπορείτε να δημιουργήσετε παραλλαγές στο υπόλοιπο (modulus variations) στον μετρητή ριπής. Με μόνο τις κατάλληλες τροποποιήσεις στη συνδεσμολογία καλωδίων, 10

11 υλοποιήστε μερικά παραδείγματα μετρητή ριπής modulo 16/N (όπου Ν διαφορετικό από το 10) και καταγράψτε στον διαθέσιμο χώρο στο τέλος της εκφώνησης τις ακολουθίες απαρίθμησης. Πόσα διαφορετικά modulo N θα μπορούσατε να υλοποιήσετε με το παρόν κύκλωμα; 6. Δείξετε πώς μπορείτε να υλοποιήσετε έναν αντίστροφο μετρητή ριπής. Υλοποιήστε τον με μόνο τις κατάλληλες τροποποιήσεις στη συνδεσμολογία καλωδίων και καταγράψτε την ακολουθία απαρίθμησης στον διαθέσιμο χώρο στο τέλος της εκφώνησης. Λίστα με στοιχεία και όργανα που θα χρησιμοποιηθούν: A/A Qty Part No Description 1 1 WK-1 Wire Kit LS04 Hex Inverter LS10 Triple 3-Input NAND Gate LS76A Dual JK Flip Flop 5 1 ETS-7000 Digital Analog Training System unit 11

12 Όνομα: Αρ. Ταυτότητας: Ημέρα:

13 Όνομα: Αρ. Ταυτότητας: Ημέρα:

14 Όνομα: Αρ. Ταυτότητας: Ημέρα:

15 Όνομα: Αρ. Ταυτότητας: Ημέρα: