1.1. Μηχανικές Ταλαντώσεις. Ομάδα Δ.
|
|
|
- Ἐλιούδ Ασπάσιος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1.1. Μηχανικές. Ομάδα Δ Συνάντηση σωμάτων που ταλαντώνονται. Τα σώματα Α και Β του σχήματος έχουν ίσες μάζες m 1 =m 2 =m=1kg. Τα δύο σώματα ισορροπούν πάνω στο λείο οριζόντιο δάπεδο, με τα ελατήρια να έχουν το φυσικό τους μήκος. Τα ελατήρια έχουν ίσες σταθερές σκληρότητας k 1 =k 2 =k= =100 N/m. Η απόσταση μεταξύ των σωμάτων είναι ίση με d=10cm. Απομακρύνουμε προς τα αριστερά το σώμα Α κατά x=20cm και το αφήνουμε ελεύθερο να κινηθεί από την ηρεμία. Το σώμα Α συγκρούεται με το σώμα Β, με αποτέλεσμα κατά την κρούση των δύο σωμάτων να πραγματοποιηθεί ανταλλαγή ταχυτήτων. i) Πόση είναι η μέγιστη συσπείρωση του κάθε ελατηρίου μετά την κρούση και ποια χρονική στιγμή εμφανίζεται; ii) Πότε θα συναντηθούν για πρώτη φορά μετά την κρούση τα δύο σώματα και σε ποια θέση; Ποια η ταχύτητα κάθε σώματος οριακά πριν τη συνάντηση; Αρχή μέτρησης του χρόνου t=0 θεωρούμε τη στιγμή της 1ης κρούσης και αρχή του άξονα χ χ, ο οποίος συμπίπτει με τον κοινό άξονα των δύο ελατήριων, την αρχική θέση του σώματος Α. Δίνεται: συν(α+β)=συνασυνβ-ημαημβ Δυο ταλαντώσεις που ξεκινούν ταυτόχρονα Τα σώματα Σ1, Σ2 του σχήματος, έχουν μάζες m1 = d = 0, 2m Σ 2 Σ 1 k 1 x = 0 +A 1 kg, m2 = 4 kg αντίστοιχα, και ηρεμούν σε ισορροπία πάνω σε λείο οριζόντιο επίπεδο. Τα σώματα, είναι δεμένα στα άκρα δυο οριζόντιων ιδανικών ελατηρίων με σταθερές Κ1 = Κ2 =100 N/m και παράλ- k 2 ληλους άξονες που βρίσκονται στο φυσικό τους μήκος. Τα άλλα άκρα των ελατηρίων είναι ακλόνητα. Μετατοπίζουμε τα σώματα κατά μήκος της διεύθυνσης των ελατηρίων, προς την ίδια κατεύθυνση κατά d = 0,2 m, και την χρονική στιγμή t = 0, τα αφήνουμε ελεύθερα ταυτόχρονα και τα δύο από την ηρεμία. Να υπολογίσετε: i) Τη χρονική στιγμή tσ, τα δυο σώματα θα συναντηθούν στη θέση x = +A για πρώτη φορά. ii) Το πλήθος των ταλαντώσεων που θα έχει εκτελέσει κάθε σώμα από t = 0 μέχρι t = tσ. iii) Την περίοδο του φαινόμενου, της συνάντησης των δυο σωμάτων στη θέση x = +A. iv) Τις συναρτήσεις απομάκρυνσης χρόνου για τις ταλαντώσεις που εκτελούν τα σώματα, με θετική τη φορά της αρχικής εκτροπής από τη θέση ισορροπίας, και να τις παραστήσετε γραφικά σε κοινό διάγραμμα. 1
2 v) Πόσες φορές πριν τη χρονική στιγμή tσ έχουν συναντηθεί και σε ποιες θέσεις της τροχιάς τους έχει συμβεί αυτό. vi) Πόσες φορές θα συναντιούνται σε κάθε ταλάντωση του Σ1, πόσες σε κάθε ταλάντωση του Σ2, και σε ποιες θέσεις ΑΑΤ και εγκατάλειψη του ελατηρίου. Ένα κατακόρυφο ελατήριο, σταθεράς k=200ν/m, στηρίζεται στο έδαφος με το κάτω άκρο του, ενώ στο πάνω άκρο του ηρεμεί ένα σώμα μάζας m=8kg, χωρίς να είναι δεμένο με το ελατήριο. Ασκώντας κατάλληλη κατακόρυφη δύναμη, εκτρέπουμε το σώμα κατακόρυφα προς τα κάτω κατά y 1 =0,8m και για t=0 το αφήνουμε να κινηθεί. i) Ν αποδειχθεί ότι για όσο χρόνο το σώμα βρίσκεται σε επαφή με το ε- λατήριο, εκτελεί απλή αρμονική ταλάντωση. ii) Ποια χρονική στιγμή το σώμα εγκαταλείπει το ελατήριο; Τι κίνηση θα πραγματοποιήσει από κει και πέρα; iii) Πόσο θα απέχει το σώμα από το πάνω άκρο του ελατηρίου, τη στιγμή που θα μηδενιστεί στιγμιαία η ταχύτητά του; Δίνεται g=10m/s Ένα σύστημα σωμάτων και μια γραφική παράσταση. Ένα σώμα Σ ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, όπως στο σχήμα. Εκτρέπουμε το σώμα κατακόρυφα και για t=0 το αφήνουμε να ταλαντωθεί (με σταθερά επαναφοράς D=k). Τη χρονική στιγμή t 1 πάνω στο σώμα αφήνουμε ένα δεύτερο σώμα Γ μάζας 2kg, οπότε η ταλάντωση συνεχίζεται με το σύστημα των σωμάτων. Στο διάγραμμα δίνεται η γραφική παράσταση της απομάκρυνσης από την αρχική θέση ισορροπίας (y=0) του σώματος Σ, σε συνάρτηση με το χρόνο. Δίνεται ότι t 2 =t 1 + 1s, π 2 10 και g=10m/s 2. Να χαρακτηρίσετε ως σωστές ή λανθασμένες τις παρακάτω προτάσεις. i) Η ενέργεια ταλάντωσης του συστήματος είναι τετραπλάσια της αρχικής ενέργειας ταλάντωσης του σώματος Σ. 2
3 ii) Η δύναμη Ν (δύναμη στήριξης) που δέχεται το σώμα Γ από το σώμα Σ τη χρονική στιγμή t 2 έχει φορά προς τα πάνω και μέτρο 28Ν. iii) Η δύναμη που ασκεί το σώμα Γ στο σώμα Σ τη στιγμή t 3 έχει φορά προς τα κάτω και μέτρο 16Ν Ένα πρόβλημα δύο ταλαντώσεων Σώμα είναι κρεμασμένο από κατακόρυφο ελατήριο και εκτελεί Γ.Α.Τ. πλάτους Α 1 =12cm. Δίπλα βρίσκεται δεύτερο ίδιο σύστημα που εκτελεί Γ.Α.Τ. πλάτους Α 2 =4 3 cm ώστε οι θέσεις ισορροπίας να βρίσκονται στο ίδιο οριζόντιο επίπεδο. Τα δύο σώματα φτάνουν ταυτόχρονα και με την ίδια φορά σε απομάκρυνση y=6cm. Χρησιμοποιώντας στρεφόμενα διανύσματα να βρείτε τα εξής: i) Τη διαφορά φάσης των δύο ταλαντώσεων. ii) Κάθε πότε γίνονται ίσες οι απομακρύνσεις των δύο σωμάτων; Δυναμική ενέργεια ελατηρίου Σώμα μάζας m=1kg ισορροπεί δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, το άλλο άκρο του οποίου είναι στερεωμένο σε οροφή. Εκτρέπουμε το σώμα κατακόρυφα προς τα κάτω κατά d, και την χρονική στιγμή t=0 το αφήνουμε ελεύθερο, οπότε το σώμα εκτελεί απλή αρμονική ταλάντωση. Στο παρακάτω διάγραμμα δίνεται η γραφική παράσταση της δυναμικής ενέργειας ελατηρίου συναρτήσει της α- πομάκρυνσης από την θέση ισορροπίας του σώματος. Uελ(J) Α 0 +Α x(m) i) Να υπολογιστεί η παραμόρφωση Δl ο του ελατηρίου στη θέση ισορροπίας του σώματος και το πλάτος της ταλάντωσης. 3
4 ii) Να βρεθεί η σταθερά k του ελατηρίου και η περίοδος της ταλάντωσης. iii) Να γραφούν οι χρονικές εξισώσεις απομάκρυνσης του σώματος από την θέση ισορροπίας και της δυναμικής ενέργειας του ελατηρίου, θεωρώντας ως θετική την φορά της αρχικής εκτροπής. iv) Να υπολογιστούν τα έργα της δύναμης του ελατηρίου και της δύναμης επαναφοράς κατά την μετάβαση του σώματος από την κάτω ακραία στην πάνω ακραία θέση της ταλάντωσης του. v) Να βρεθεί για πόσο χρονικό διάστημα στη διάρκεια μίας περιόδου το ελατήριο είναι επιμηκυμένο περισσότερο από 0,2m; Δίνεται: g=10m/s Ταλάντωση δύο σωμάτων Δύο υλικά σημεία εκτελούν Α.Α.Τ πάνω στην ίδια διεύθυνση, γύρω από την ίδια θέση ισορροπίας. Οι ταλαντώσεις έχουν ίδιο πλάτος Α και ίδια περίοδο Τ. Οι απομακρύνσεις από τη Θ.Ι δίνονται από τις σχέσεις: x 1 =Αημ(ωt+π/2) και x 2 = Αημ(ωt+π). υ 2 Ο υ 1 i) Να σχεδιάσετε σε κοινό σύστημα αξόνων τις γραφικές παραστάσεις x 1 -t, x 2 -t. ii) Πόση είναι η μέγιστη απόσταση μεταξύ των υλικών σημείων; iii) Ποιες χρονικές στιγμές η απόσταση μεταξύ των υλικών σημείων είναι μέγιστη για πρώτη και πότε για έβδομη φορά; Απλή Αρμονική Ταλάντωση και Τεντωμένο Νήμα Ένα σώμα μάζας m, κρέμεται από το ελεύθερο άκρο κατακόρυφου ελατηρίου σταθεράς k (αμελητέας μάζας) με τη βοήθεια ενός μη εκτατού νήματος, όπως φαίνεται στο παρακάτω σχήμα. i) Να δείξετε ότι το σύστημα εκτελεί απλή αρμονική ταλάντωση και να υπολογίσετε την περίοδο της. ii) Να προσδιορίσετε τη μέγιστη απομάκρυνση του ελατηρίου, ώστε το νήμα να είναι διαρκώς τεντωμένο. Δίνεται g=10m/s Μια σανίδα αναρτημένη από δυο κατακόρυφα ελατήρια Μια ομογενής σανίδα Σ μάζας Μ, είναι δεμένη στα κάτω άκρα δυο κατακόρυφων όμοιων ιδανικών ελατηρίων, και ηρεμεί σε ισορροπία όπως φαίνεται στο σχήμα, σε οριζόντια θέση. Τα επάνω άκρα των ελατηρίων είναι ακλόνητα στερεωμένα. Τοποθετούμε στο μέσον της σανίδας σώμα Σ1 μάζας m1= 12 kg, και παρατηρούμε ότι, το σύστημα σταματά στιγμιαία για πρώτη φορά σε χρόνο Δt1 = k k π/5 s, αφού διανύσει διάστημα S1= 0,6 m. Αν αντί του Σ1, τοποθετήσουμε στο ίδιο σημείο της σανίδας, σώμα Σ2 μάζας Σ 4
5 m2, το σύστημα σταματά στιγμιαία για πρώτη φορά, σε χρόνο Δt2 = 3π/10 s. Να υπολογίσετε : i) Τις σταθερές των ελατηρίων. ii) Τη μάζα Μ της σανίδας. iii) Τη μάζα m2. iv) Τη μέγιστη τιμή της κινητικής ενέργειας του συστήματος, όταν πάνω στη σανίδα είναι τοποθετημένο το σώμα Σ2. Δίνεται g = 10 m/s² Ταλάντωση με τη βοήθεια νήματος Σώμα μάζας m=0.2kg, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και ισορροπεί δεμένο στο άκρο οριζοντίου ελατηρίου σταθεράς k=20n/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Κάποια χρονική στιγμή, που θεωρείται αρχή των χρόνων, το σώμα δέχεται, μέσω νήματος αντοχής F F o =30Ν, οριζόντια δύναμη F=10+20x, (S.I.), όπου x η μετατόπιση του σώματος, που έχει διεύθυνση τον άξονα του ελατηρίου και φορά όπως φαίνεται στην εικόνα. Α. i) να δειχτεί ότι το σώμα θα αρχίσει να κινείται ii) να βρεθεί η μετατόπιση και η χρονική στιγμή που σπάζει το νήμα iii) να γραφεί η εξίσωση της μετατόπισης και της ταχύτητας του σώματος σε συνάρτηση με τον χρόνο Β. μετά το σπάσιμο του νήματος v) να δειχτεί ότι το σώμα θα πραγματοποιήσει γραμμική αρμονική ταλάντωση vi) να βρεθεί η περίοδος, η κυκλική συχνότητα και το πλάτος αυτής της ταλάντωσης vii) να γραφεί η εξίσωση της απομάκρυνσης και της ταχύτητας του σώματος σε συνάρτηση με τον χρόνο Ταλάντωση με μακρύτερο λάστιχο. Κρατώ στο χέρι μου ένα λάστιχο στο οποίο έχω κρεμάσει ένα σώμα. Το θέτω σε ταλάντωση και διαπιστώνω ότι η περίοδος είναι 0,8 s. Αν τετραπλασιάσω το μήκος του λάστιχου ποια θα είναι η περίοδος. Η μάζα του λάστιχου είναι αμελητέα. 5
6 Δυο ταλαντώσεις πάνω σε λείο οριζόντιο επίπεδο Τα σώματα Σ 1, Σ 2 του σχήματος, έχουν μάζες m 1 = 1 kg, m 2 = 4 kg d = 0, 2 m αντίστοιχα και ηρεμούν σε ισορροπία πάνω σε λείο οριζόντιο k 2 Σ 2 Σ 1 k 1 x = 0 επίπεδο. Τα σώματα, είναι δεμένα στα άκρα δυο οριζόντιων ιδανικών ελατηρίων με σταθερές k 1 = k 2 =100 N/m και παράλληλους άξονες, που βρίσκονται στο φυσικό τους μήκος. Τα άλλα άκρα των ελατηρίων είναι ακλόνητα. Μετατοπίζουμε τα σώματα κατά +A μήκος της διεύθυνσης των ελατηρίων, προς την ίδια κατεύθυνση κατά d = 0,2 m, και την χρονική στιγμή t = 0, τα αφήνουμε ε- λεύθερα ταυτόχρονα και τα δύο από την ηρεμία. Α. Να υπολογίσετε: i) Την συνολική ενέργεια Ε δ που δαπανήθηκε για την αρχική εκτροπή και των δύο σωμάτων από τη θέση ισορροπίας τους. ii) Το ποσοστό επί τοις εκατό της ενέργειας Ε δ που μετατρέπεται σε μέγιστη κινητική ενέργεια κάθε σώματος ξεχωριστά. Β. Κάποια χρονική στιγμή t 1 τα σώματα Σ 1, Σ 2 κινούνται με ταχύτητες υ 1, υ2 και απέχουν ίσες αποστάσεις από το σημείο ισορροπίας των. Να υπολογίσετε την τιμή που έχει το κλάσμα υ 1 / υ 2 τη χρονική στιγμή t 1. Γ. Κάποια χρονική στιγμή t 2 οι απομακρύνσεις των Σ 1, Σ 2 είναι x 1 = x 2 = -0,1 m. Να υπολογίσετε τους ρυθμούς μεταβολής των κινητικών τους ενεργειών την χρονική στιγμή t Σε πόση απόσταση και πότε; Δυο κατακόρυφα ελατήρια σταθερών k 1 =200/3Ν/m και k 2 =200Ν/m, βρίσκονται όπως στο πρώτο σχήμα, με τον άξονά τους στην ίδια ευθεία και τα ελεύθερα άκρα τους να απέχουν κατά d=0,3m. Σε μια στιγμή δένουμε στο κάτω άκρο του πάνω ελατηρίου, μια λεπτή πλάκα μάζας Μ=2kg και την αφήνουμε να κινηθεί. Μόλις η πλάκα έρθει σε επαφή με το κάτω ελατήριο, το πάνω αποσυνδέεται, οπότε η πλάκα ταλαντώνεται πλέον στο πάνω άκρο του κάτω ελατηρίου. i) Πόση συνολικά απόσταση διανύει η πλάκα κινούμενη προς τα κάτω; ii) Πόσο χρόνο διαρκεί η προς τα κάτω κίνηση της πλάκας; Δίνεται ότι η κίνηση ενός σώματος στο άκρο κατακόρυφου ελατηρίου είναι ΑΑΤ και g=10m/s
7 Πλαστική κρούση-ταλάντωση-χάσιμο επαφής Δύο σώματα Σ 1 και Σ 2 με μάζες m 1 =3kg και m 2 =4kg είναι δεμένα στα άκρα κατακόρυφου ιδανικού ελατηρίου σταθεράς k, έτσι ώστε το Σ 2 να ακουμπά στο έ- δαφος και το Σ 1 να ισορροπεί ακίνητο στο πάνω άκρο του ελατηρίου. Τρίτο σώμα Σ μάζας m=1kg αφήνεται από ύψος h, στη διεύθυνση του άξονα του ελατηρίου, πάνω από το σώμα Σ 1 στην με το οποίο συγκρούεται μετωπικά και πλαστικά. Το συσσωμάτωμα που δημιουργείται ταλαντώνεται με χρονική εξίσωση απομάκρυνσης της μορφής 5π x Αημ ωt (S.I.) θεωρώντας ως t=0 την στιγμή αμέ- 6 σως μετά την κρούση και θετική την φορά προς τα πάνω. Αν το μέτρο της δύναμης του ελατηρίου μεγιστοποιείται για 1 η φορά μετά την κρούση την χρονική στιγμή t = s, να υπολογιστούν: α. η περίοδος ταλάντωσης Τ του συσσωματώματος. β. η σταθερά k του ελατηρίου και το πλάτος A της ταλάντωσης. γ. το ύψος h από το οποίο αφήνεται το σώμα. δ. η μέγιστη και η ελάχιστη τιμή της δύναμης που ασκείται στο σώμα Σ 2 από το οριζόντιο επίπεδο κατά την διάρκεια ταλάντωσης του συσσωματώματος. ε. το μέγιστο ύψος h από το οποίο μπορεί να αφεθεί το σώμα Σ χωρίς να χάσει την επαφή του με το οριζόντιο επίπεδο το σώμα Σ 2 κατά την ταλάντωση του συσσωματώματος που θα δημιουργηθεί. Δίνεται g=10m/s 2. Θεωρήστε αμελητέα τη χρονική διάρκεια της κρούσης καθώς και τις πάσης φύσεως τριβές κατά την κίνηση των σωμάτων Ταλάντωση και ρυθμός μεταβολής της ορμής Ένα υλικό σημείο, μάζας m=0,2kg, εκτελεί ΑΑΤ και η εξίσωση της ταχύτητάς του είναι υ=2συν(5t+π/3) (μονάδες στο S.Ι.). i) Να βρεθεί ποιες χρονικές στιγμές το σώμα περνά για πρώτη και δεύτερη φορά από την θέση x= -0,2m. ii) Να υπολογιστεί ο ρυθμός μεταβολής της ορμής του σώματος τις παραπάνω χρονικές στιγμές. h Θ.Ι. k Σ Σ 1 Σ 2 m (+) Εξασκούμαι με τη δυναμική της ταλάντωσης. Ένα σώμα μάζας 2kg είναι δεμένο στα άκρα δύο κατακόρυφων ελατηρίων, όπως στο σχήμα και ισορροπεί, έχοντας επιμηκύνει το πάνω ελατήριο κατά 10cm. Εκτρέπουμε το σώμα κατακόρυφα προς τα κάτω κατά 20cm και το αφήνουμε να κινηθεί, τη στιγμή t=0. Αν δίνονται οι σταθερές των ελατηρίων k 1 =200Ν/m και k 2 =600Ν/m, ενώ g=10m/s 2, ζητούνται; i) Να αποδειχθεί ότι το σώμα θα εκτελέσει ΑΑΤ και να υπολογιστεί η περίοδος ταλάντωσης. ii) Να βρεθεί η εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο, θεωρώντας την προς τα πάνω κατεύθυνση θετική. k 1 k2 7
8 iii) Να υπολογιστεί ο ρυθμός με τον οποίο το κάτω ελατήριο προσφέρει ενέργεια στο σώμα τη χρονική στιγμή t 1 =7π/80 s Ταλάντωση και κόψιμο νήματος. Τα σώματα Σ 1 και Σ 2 που φαίνονται στο σχήμα έχουν μάζες m 1 =1kg και m 2 =3kg αντίστοιχα και είναι δεμένα μεταξύ τους με αβαρές και μη εκτατό νήμα μήκους l=0,7m. Το σώμα Σ 1 είναι δεμένο στο ένα άκρο κατακόρυφου ελατηρίου σταθεράς k=100n/m, το άλλο άκρο του οποίου είναι στερεωμένο στην οροφή. Εκτρέπουμε το σύστημα από τη θέση ισορροπίας του κατακόρυφα προς τα κάτω κατά d=0,3m και την χρονική στιγμή t=0 το αφήνουμε ελεύθερο να ταλαντωθεί. Α. i) Να αποδείξετε ότι το σύστημα εκτελεί α.α.τ. ii) Να γραφεί η χρονική εξίσωση απομάκρυνσης του σώματος Σ 2 από τη θέση ισορροπίας του και η χρονική εξίσωση της δύναμης που ασκεί το νήμα στο σώμα Σ 2, θεωρώντας ως θετική τη φορά προς τα πάνω. iii) Να υπολογιστεί η επιτάχυνση των σωμάτων τη στιγμή που η δυναμική ενέργεια του ελατηρίου ι- σούται με τη δυναμική ενέργεια ταλάντωσης. iv) Να βρείτε τη μέγιστη απόσταση d max που μπορούμε να εκτρέψουμε αρχικά το σύστημα, ώστε το νήμα να παραμένει διαρκώς τεντωμένο κατά τη διάρκεια της ταλάντωσης. Β. Κάποια στιγμή που το σύστημα βρίσκεται στην κάτω ακραία θέση της ταλάντωσής του, κόβουμε το νήμα. i) Να βρεθεί το νέο πλάτος ταλάντωσης του Σ 1. ii) Να υπολογιστεί η απόσταση των σωμάτων, όταν το Σ 1 ακινητοποιηθεί για 1 η φορά μετά το κόψιμο του νήματος. Δίνονται: g=10m/s 2, π 2 =10, και η αντίσταση του αέρα είναι αμελητέα Δυο γραφικές παραστάσεις για σώμα στο άκρο νήματος. Ένα σώμα Σ ηρεμεί όπως στο σχήμα, δεμένο στο άκρο νήματος μήκους l=2d=20cm, έχοντας επιμηκύνει το ελατήριο κατά d=10cm, Εκτρέπουμε το σώμα κατακόρυφα προς τα κάτω κατά 2d και τη στιγμή t=0 το αφήνουμε να ταλαντωθεί. i) Σε ποια θέση μηδενίζεται η τάση του νήματος; Δικαιολογήστε την α- πάντησή σας. ii) Να γίνει η γραφική παράσταση της επιτάχυνσης του σώματος σε συνάρτηση με απομάκρυνση από την θέση ισορροπίας του. iii) ii) Να βρεθεί η εξίσωση της ταχύτητας του σώματος σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση. Θεωρείστε την προς τα πάνω κατεύθυνση σαν θετική, ενώ g=10m/s Μια ταλάντωση και η τάση του νήματος. 8
9 Σε λείο οριζόντιο επίπεδο ηρεμούν δύο σώματα Α και Β, με μάζες m 1 =1kg και m 2 =3kg, δεμένα στα άκρα δύο οριζόντιων ελατηρίων με σταθερές k 1 =100Ν/m και k 2 =300Ν/m. Τα σώματα θεωρούνται αμελητέων διαστάσεων και απέχουν d=1m. Σύρουμε το σώμα Α προς τα δεξιά, δένουμε τα σώματα με νήμα μήκους l=0,2m και κατόπιν, κάποια στιγμή που θεωρούμε t=0, αφήνουμε το σύστημα ελεύθερο να κινηθεί. i) Να αποδειχθεί ότι το σύστημα των σωμάτων εκτελεί ΑΑΤ και να υπολογιστεί η ενέργεια ταλάντωσης. ii) Θεωρώντας την προς τα δεξιά κατεύθυνση θετική, να βρεθεί η εξίσωση της δύναμης που ασκεί το Α σώμα στο Β, μέσω του νήματος, σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση Ένα ελατήριο και ένα λάστιχο. k 1 50 N m k N m 0, 2m Ένα σώμα μάζας 2kg τοποθετείται σε λείο οριζόντιο επίπεδο και συνδέεται όπως δείχνει το σχήμα με οριζόντιο ελατήριο και οριζόντιο λάστιχο που βρίσκονται στην ίδια με το σώμα ευθεία. Τα ελατήριο και το λάστιχο έχουν στη θέση μηδέν τα φυσικά τους μήκη. Εκτρέπουμε το σώμα προς τα αριστερά κατά 0,2 m και το αφήνουμε ελεύθερο. Να θεωρήσετε ως δεδομένο ότι όταν το λάστιχο είναι τεντωμένο το σύστημα εκτελεί α.α.τ. με D = k 1 +k 2. i) Να γίνουν οι γραφικές παραστάσεις της θέσης και της ταχύτητας του σώματος συναρτήσει του χρόνου. ii) Χρονική στιγμή μηδέν είναι αυτή που αφέθηκε και θετική κατεύθυνση η προς τα δεξιά Μια κρούση στη διάρκεια της ταλάντωσης. Το σώμα Σ μάζας Μ=3kg ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ελατηρίου σταθεράς k=300ν/m. Μετακινούμε το σώμα Σ προς τα αριστερά κατά 0,2m και σε μια στιγμή το αφήνουμε να ταλαντωθεί, ενώ ταυτόχρονα αφήνουμε από ορισμένο ύψος h μια μικρή σφαίρα, μάζας m=1kg, να πέσει. Τα σώματα συγκρούονται πλαστικά, αφού το Σ μετακινηθεί κατά s=0,3m. Τα σώματα θεωρούνται υλικά σημεία, αμελητέων διαστάσεων, ενώ g=10m/s 2. i) Να υπολογιστεί το ύψος h. ii) Πόση είναι η απώλεια της μηχανικής ενέργειας κατά την κρούση; iii) Να βρεθεί η μείωση της ενέργειας ταλάντωσης που οφείλεται στην κρούση. 9
10 iv) Επαναλαμβάνουμε το πείραμα, αλλά η σφαίρα αφήνεται από μεγαλύτερο ύψος. Πόση είναι η ελάχιστη απόσταση y, κατά την οποία πρέπει να ανυψώσουμε τη σφαίρα, σε σχέση με την αρχική της θέση, ώστε τα δυο σώματα να ξανασυγκρουσθούν στην ίδια θέση με πριν; v) Για την παραπάνω περίπτωση να υπολογιστούν: α) Η απώλεια της μηχανικής ενέργειας και β) Η μείωση της ενέργειας ταλάντωσης Μια πλαστική κρούση και ενέργειες ταλάντωσης. Ένα σώμα Σ 1 μάζας m 1 =2kg ηρεμεί σε λείο οριζόντιο επίπεδο, στο άκρο οριζόντιου ελατηρίου σταθεράς k=20ν/m. Μετακινούμε το σώμα Σ 1 συσπειρώνοντας το ελατήριο κατά Δl=0,5m, φέρνοντάς το στη θέση Γ. Για t=0 αφήνουμε το σώμα Σ ελεύθερο να ταλαντωθεί, (δεχόμαστε ότι αυτό εκτελεί α.α.τ.) ενώ τη στιγμή αυτή απέχει απόσταση (ΓΔ)= d=5m από ένα δεύτερο σώμα μάζας m 2 =3kg, το οποίο κινείται αντίθετα κατά μήκος του άξονα του ελατηρίου. Τη χρονική στιγμή t 1 =1s τα δύο σώματα συγκρούονται μετωπικά και πλαστικά. i) Σε ποια θέση συγκρούσθηκαν τα δύο σώματα και με ποια ταχύτητα υ 2 κινείτο το δεύτερο σώμα Σ 2 ; ii) Ποια η ενέργεια ταλάντωσης πριν και μετά την κρούση; iii) Με ποια ταχύτητα το συσσωμάτωμα θα φτάσει στη θέση Γ; iv) Ποιο το πλάτος ταλάντωσης μετά την κρούση; Θεωρείστε ότι και το σώμα Σ 2 κινείται χωρίς τριβές, η κίνηση μετά την κρούση είναι απλή αρμονική ταλάντωση και π Μια ΑΑΤ. τμήμα μιας ταλάντωσης. 0 Ένα κατακόρυφο ιδανικό ελατήριο, σταθεράς k=200ν/m, στηρίζεται στο έδαφος με το κάτω άκρο του, ενώ στο πάνω άκρο του ηρεμεί ένα σώμα μάζας m=8kg, χωρίς να είναι δεμένο με το ελατήριο. Ασκώντας κατάλληλη κατακόρυφη δύναμη, εκτρέπουμε το σώμα κατακόρυφα προς τα κάτω κατά y 1 =0,8m και για t=0 το αφήνουμε να κινηθεί. i) Ν αποδειχθεί ότι, για όσο χρόνο το σώμα βρίσκεται σε επαφή με το ελατήριο, εκτελεί απλή αρμονική 10
11 ταλάντωση. ii) Ποια χρονική στιγμή το σώμα εγκαταλείπει το ελατήριο; Τι κίνηση θα πραγματοποιήσει από κει και πέρα; iii) Πόσο θα απέχει το σώμα από το πάνω άκρο του ελατηρίου, τη στιγμή που θα μηδενιστεί στιγμιαία η ταχύτητά του; iv) Ποια χρονική στιγμή το σώμα θα επιστρέψει ξανά στην αρχική του θέση, για πρώτη φορά; Δίνεται g=10m/s Μια ταλάντωση με κρούση. Ορμή και ενέργειες. Το σώμα Σ μάζας m 1 ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο B άκρο ιδανικού ελατηρίου σταθεράς k, µε πλάτος Α και περίοδο Τ. Όταν το σώμα µάζας Σ διέρχεται από τη θέση ισορροπίας συγκρούεται πλαστικά µε Σ το σώμα Β, μάζας m 2 που έπεφτε ελεύθερα από ύψος h, και το σύστημα συνεχίζει να ταλαντώνεται. i) Ποιες προτάσεις είναι σωστές και ποιες λανθασμένες: α) Η θέση ισορροπίας της ταλάντωσης έμεινε η ίδια. β) Κατά τη διάρκεια της κρούσης ισχύει η αρχή διατήρησης της ορμής. γ) Η ορμή του συστήματος στην οριζόντια διεύθυνση, ελάχιστα πριν την κρούση, είναι ίση με την ορμή του ελάχιστα µετά την κρούση. δ) Η περίοδος της ταλάντωσης αυξήθηκε. ε) Η ενέργεια της ταλάντωσης μειώθηκε. ii) Να υπολογίσετε την απώλεια της μηχανικής ενέργειας κατά την κρούση, σε συνάρτηση με το ύψος h. Πότε η απώλεια αυτή είναι ελάχιστη; iii) Αν η κρούση δεν πραγματοποιηθεί στη θέση ισορροπίας, αλλά σε απομάκρυνση x, να βρεθεί η συνθήκη για την ελάχιστη μείωση της ενέργειας ταλάντωσης Οι δύο αισθητήρες. Το σώμα του σχήματος κρέμεται σε ελατήριο. Το κρατάμε με το χέρι μας ώστε το ελατήριο να έχει το φυσικό του μήκος και του δίνουμε ώθηση προς τα κάτω. Με τη βοήθεια δύο αισθητήρων καταγράφουμε την δύναμη του ελατηρίου (ας θεωρηθεί αμελητέας μάζας) και τη θέση του σώματος. Περνάμε τις μετρήσεις σε λογιστικό φύλλο και κάνουμε τη γραφική παράσταση της δύναμης του ελατηρίου συναρτήσει της θέσης του αναφορικά με τον αισθητήρα θέσης. Η ένδειξη του αισθητήρα δύναμης είναι θετική όταν το σώμα δέχεται δύναμη από το ελατήριο προς τα πάνω. g 10 m s 2 Η γραφική παράσταση που κάναμε παρατίθεται. 11
12 Βρείτε: i) Το πλάτος της ταλάντωσης. ii) Τη σταθερά του ελατηρίου. iii) Τη μάζα του σώματος. iv) Την ταχύτητα που προσδώσαμε στο σώμα όταν αυτό βρισκόταν στη θέση φυσικού μήκους του. v) Την εξίσωση θέσης του σώματος ως προς τον αισθητήρα θέσης Μηχανική ενέργεια και ενέργεια Ταλάντωσης. Ένα σώμα μάζας 3kg ηρεμεί στο κάτω άκρο ενός κατακόρυφου ελατηρίου k d h Θ.Ι. σταθεράς k 1 = k=100ν/m, όπως στο σχήμα, ευρισκόμενο σε ύψος h=0,7m από το έδαφος. Ασκώντας πάνω του μια εξωτερική δύναμη F 1, το μετακινούμε κατακόρυφα ανεβάζοντάς το κατά d=0,3m και το αφήνουμε να ταλαντωθεί, εκτελώντας ΑΑΤ. Θεωρείστε ότι το σώμα, αμελητέων διαστάσεων, έχει μηδενική δυναμική ενέργεια όταν βρίσκεται στο έδαφος και g=10m/s 2. i) Να υπολογίσετε την αρχική μηχανική ενέργεια του συστήματος σώμα -Γη-ελατήριο καθώς και το έργο της εξωτερικής δύναμης F 1 για την εκτροπή του σώματος. Πόση είναι τελικά η μηχανική ενέργεια του συστήματος και πόση η ενέργεια ταλάντωσης; ii) Επαναλαμβάνουμε το πείραμα, αλλά τώρα τοποθετούμε κάτω από το σώμα ένα δεύτερο κατακόρυφο ελατήριο, σταθεράς k 2 =k και φυσικού μήκους l 0 =0,9m, με τον άξονά του να ταυτίζεται με τον άξονα του πάνω ελατηρίου και αφήνουμε το σώμα να κινηθεί. Να αποδείξτε ότι μόλις το σώμα έρθει σε ε- παφή με το κάτω ελατήριο, θα ξεκινήσει μια νέα ταλάντωση, η οποία είναι επίσης ΑΑΤ, υπολογίζοντας την ενέργεια ταλάντωσής της. iii) Να υπολογίστε τη μηχανική ενέργεια του συστήματος σώμα-γη-ελατήριο στη διάρκεια της δεύτερης ταλάντωσης
13 Δυο κινήσεις ενός δοκαριού, μια ΑΑΤ Ένα δοκάρι μάζας Μ=1,6kg και μήκους l=1m βρίσκεται σε λείο οριζόντιο επίπεδο δεμένο στο ένα άκρο οριζόντιου ελατηρίου σταθεράς k=75n/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Ένα μικρό σώμα μάζας m=1kg βρίσκεται ακίνητο στο μέσο του δοκαριού. Ασκούμε στο σώμα σταθερή οριζόντια δύναμη F=20N, οπότε αυτό αρχίζει να κινείται πάνω στο δοκάρι, με το οποίο παρουσιάζει συντελεστή τριβής ολίσθησης μ=0,5. Τη στιγμή που το ελατήριο έχει επιμήκυνση Δl=0,1m, το σώμα εγκαταλείπει το δοκάρι και απομακρύνεται κατάλληλα. φμ F υ1 υ2 Α. Να υπολογίστε την ταχύτητα του σώματος τη στιγμή που εγκαταλείπει το δοκάρι. Β. Να υπολογίσετε την κινητική ενέργεια του δοκαριού την ίδια στιγμή. Γ. Να υπολογίστε τη μέγιστη συσπείρωση που θα υποστεί στη συνέχεια το ελατήριο. Δ. Σε πόσο χρόνο από τη στιγμή που το σώμα θα εγκαταλείψει τη σανίδα το ελατήριο θα έχει τη μέγιστη συσπείρωσή του για πρώτη φορά; Δίνεται g=10m/s 2 και π 2 = Άλλη μια κρούση κατά τη διάρκεια ταλάντωσης. Τα σώμα Β και Γ με μάζες m 1 =0,1kg και m 2 =2m 1 =0,2kg ηρεμούν σε λείο οριζόντιο επίπεδο, δεμένα στα άκρα οριζόντιων ελατηρίων με σταθερές k 1 =30Ν/m και k 2 =2k 1 = 60Ν/m αντίστοιχα, όπως στο σχήμα, όπου οι άξονες των δύο ελατηρίων συμπίπτουν. Τα σώματα που θεωρούνται υλικά σημεία, αμελητέων διαστάσεων απέχουν κατά d=0,3m. Ασκώντας κατάλληλες δυνάμεις στα σώματα, συσπειρώνουμε κάθε ελατήριο κατά 0,3m και αφήνουμε ταυτόχρονα τα σώματα να εκτελέσουν ΑΑΤ. Μετά από λίγο τα σώματα συγκρούονται πλαστικά, οπότε το συσσωμάτωμα εκτελεί μια νέα ΑΑΤ με σταθερά D=k 1 +k 2. Ζητούνται: i) Η ενέργεια ταλάντωσης κάθε σώματος πριν την κρούση. ii) Η ενέργεια ταλάντωσης του συσσωματώματος. iii) Η απώλεια της μηχανικής ενέργειας (η ενέργεια που εμφανίζεται ως αύξηση της θερμικής ενέργειας των σωμάτων, συν ενέργεια μόνιμης παραμόρφωσης των σωμάτων, συν ενέργεια ήχου ), που οφεί- 13
14 λεται στην κρούση Μια ταλάντωση σε ανελκυστήρα. Ένα σώμα Σ μάζας 1kg, βρίσκεται δεμένο στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου, το οποίο κρέμεται μέσα σε έναν ανελκυστήρα (ασανσέρ) το οποίο κατέρχεται με σταθερή επιτάχυνση α=2m/s 2. Στη διάρκεια της κίνησης το σώμα παραμένει «ακίνητο» ως προς το θάλαμο του ανελκυστήρα, απέχοντας 1m από τη βάση του. Σε μια στιγμή και ενώ η ταχύτητά του είναι υ=4m/s, ο θάλαμος συγκρούεται με το έδαφος, όπου και ακινητοποιείται ακαριαία. Δίνεται η σταθερά του ελατηρίου k=20ν/m και η επιτάχυνση της βαρύτητας g=10m/s 2. i) Στη διάρκεια της πτώσης του θαλάμου, το ελατήριο έχει το φυσικό του μήκος ή όχι; ii) Να περιγράψετε την κίνηση που θα κάνει το σώμα Σ, μετά την ακινητοποίηση του ανελκυστήρα. iii) Να αποδειχτεί ότι η κίνηση αυτή θα είναι ΑΑΤ. iv) Να εξετάσετε αν το σώμα Σ θα φτάσει στο δάπεδο του θαλάμου Και μια και δύο ΑΑΤ. Ένα σώμα μάζας 2kg, είναι δεμένο στο άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 =200Ν/m. Ανεβάζουμε το σώμα κατακόρυφα προς τα πάνω φέρνοντάς το σε μια θέση Θ, όπου το ελατήριο έχει συσπειρωθεί κατά Δl=0,1m. Κάτω ακριβώς από το σώμα Θ υπάρχει ένα δεύτερο ιδανικό ελατήριο, το πάνω άκρο του οποίου απέχει κατά d=0,2m από το σώμα, όπως στο σχήμα. Σε μια στιγμή t ο =0, αφήνουμε το σώμα ελεύθερο να κινηθεί και παρατηρούμε ότι σταματά την προς τα κάτω κίνησή του, αφού μετατοπισθεί κατά 0,3m. i) Να αποδείξετε ότι το σώμα θα εκτελέσει ΑΑΤ, μέχρι να έρθει σε επαφή με το κάτω ελατήριο, υπολογίζοντας το πλάτος και την περίοδο ταλάντωσης. ii) Να αποδείξτε ότι η κίνηση του σώματος, όταν βρίσκεται σε επαφή με το κάτω ελατήριο είναι μια νέα ΑΑΤ, υπολογίζοντας επίσης το πλάτος και την περίοδο ταλάντωσης. iii) Ποια χρονική στιγμή το σώμα θα επανέρθει για πρώτη φορά στη θέση Θ; iv) Να υπολογιστούν οι ρυθμοί μεταβολής της ορμής του σώματος στην ανώτερη και στην κατώτερη θέση της τροχιάς του. Δίνεται g=10m/s 2. k 1 k 2 d 14
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ.
 1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 .. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
.. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
4. Σώμα Σ 1 μάζας m 1 =1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ=30 ο. Το σώμα Σ 1 είναι δεμένο στην άκρη
 1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
4.1. Κρούσεις. Κρούσεις. 4.1.Ταχύτητες κατά την ελαστική κρούση Η Ορμή είναι διάνυσμα. 4.3.Κρούση και Ενέργεια.
 4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
1.1. Μηχανικές Ταλαντώσεις.
 1.1. Μηχανικές. 1) Εξισώσεις ΑΑΤ Ένα υλικό σηµείο κάνει α.α.τ. µε πλάτος 0,1m και στην αρχή των χρόνων, βρίσκεται σε σηµείο Μ µε απο- µάκρυνση 5cm, αποµακρυνόµενο από τη θέση ισορροπίας. Μετά από 1s περνά
1.1. Μηχανικές. 1) Εξισώσεις ΑΑΤ Ένα υλικό σηµείο κάνει α.α.τ. µε πλάτος 0,1m και στην αρχή των χρόνων, βρίσκεται σε σηµείο Μ µε απο- µάκρυνση 5cm, αποµακρυνόµενο από τη θέση ισορροπίας. Μετά από 1s περνά
Κρούσεις. Ομάδα Γ. Κρούσεις Ενέργεια Ταλάντωσης και Ελαστική κρούση Κρούση και τριβές Κεντρική ανελαστική κρούση
 . Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
. Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
Κρούσεις. Ομάδα Δ. Κρούσεις Μια κρούση και οι τριβές Κρούση σφαίρας με άλλη ακίνητη.
 . Ομάδα Δ. 4.1.41. Μια κρούση και οι τριβές. Σε οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m=1kg και Μ=3kg αντίστοιχα, τα οποία απέχουν απόσταση d=4,75m. Το Β είναι δεμένο στο άκρο ιδανικού
. Ομάδα Δ. 4.1.41. Μια κρούση και οι τριβές. Σε οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m=1kg και Μ=3kg αντίστοιχα, τα οποία απέχουν απόσταση d=4,75m. Το Β είναι δεμένο στο άκρο ιδανικού
3.2. Διατήρηση της Ορμής. Ομάδα Γ.
 3.2. Διατήρηση της Ορμής. Ομάδα Γ. 3.21. Η ορμή και ένα σύστημα σωμάτων. Δυο σώματα Α και Β με μάζες m 1 =2kg και m 2 =1kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει ένα ιδανικό ελατήριο
3.2. Διατήρηση της Ορμής. Ομάδα Γ. 3.21. Η ορμή και ένα σύστημα σωμάτων. Δυο σώματα Α και Β με μάζες m 1 =2kg και m 2 =1kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει ένα ιδανικό ελατήριο
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
3.1. Διατήρηση της Ορμής.
 3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. i) Υπολογίστε την ορμή του
3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. i) Υπολογίστε την ορμή του
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
1. Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα.
 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
4.1.α. Κρούσεις. Κρούσεις. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. 4.1.22. Κρούση και τριβές. 4.1.23. Κεντρική ανελαστική κρούση
 4.1.α.. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα µάζας Μ=4kg ηρεµεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουµε
4.1.α.. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα µάζας Μ=4kg ηρεµεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουµε
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ
 ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
Σάββατο 12 Νοεμβρίου Απλή Αρμονική Ταλάντωση - Κρούσεις. Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες. Θέμα Α.
 Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]
![ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%] ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]](/thumbs/65/53613594.jpg) 1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
3.1. Διατήρηση της Ορμής.
 3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. υ Γ Ο Α i) Υπολογίστε την ορμή
3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. υ Γ Ο Α i) Υπολογίστε την ορμή
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ F 2 F 3 F 1 F 4
 1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ. =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1. =8m /s συγκρούεται κεντρικά
 ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
2) Ορμή και ρυθμός μεταβολής της στην κυκλική κίνηση. 3) Ένα σύστημα σωμάτων σε πτώση. 4) Ένα σύστημα επιταχύνεται. Γ) Ορμή και διατήρηση ορμής
 Γ) Ορμή και διατήρηση ορμής 1) Στο ταβάνι, στον τοίχο ή στο πάτωμα; Βρισκόμαστε σε ένα δωμάτιο όπου ταβάνι τοίχος και δάπεδο έχουν φτιαχτεί από το ίδιο υλικό και κάνουμε το εξής πείραμα. Εκτοξεύουμε μπαλάκι
Γ) Ορμή και διατήρηση ορμής 1) Στο ταβάνι, στον τοίχο ή στο πάτωμα; Βρισκόμαστε σε ένα δωμάτιο όπου ταβάνι τοίχος και δάπεδο έχουν φτιαχτεί από το ίδιο υλικό και κάνουμε το εξής πείραμα. Εκτοξεύουμε μπαλάκι
α. β. γ. δ. Μονάδες 5 α. β. γ. δ. Μονάδες 5 α. ελαστική β. ανελαστική γ. πλαστική δ. έκκεντρη
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
Εκφώνηση 1. α). β). γ). Επιλέξτε τη σωστή πρόταση και αιτιολογείστε.
 Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ - ΑΣΚΗΣΕΙΣ
 ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
προς ένα ακίνητο σωμάτιο α (πυρήνας Ηe), το οποίο είναι ελεύθερο να κινηθεί,
 ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 24/09/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. Α1. Κατά τη διάρκεια μιας
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. Α1. Κατά τη διάρκεια μιας
0. Ασκήσεις επανάληψης.
 0. Ασκήσεις επανάληψης. 1. Κίνηση με μεταβλητή κατακόρυφη δύναμη Ένα σώμα μάζας 2kg βρίσκεται ακίνητο στο έδαφος. Σε μια στιγμή δέχεται την επίδραση μιας μεταβλητής κατακόρυφης δύναμης F, το μέτρο της
0. Ασκήσεις επανάληψης. 1. Κίνηση με μεταβλητή κατακόρυφη δύναμη Ένα σώμα μάζας 2kg βρίσκεται ακίνητο στο έδαφος. Σε μια στιγμή δέχεται την επίδραση μιας μεταβλητής κατακόρυφης δύναμης F, το μέτρο της
ΘΕΜΑΤΑ. Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν. Α2. Όταν δυο σώματα συγκρούονται πλαστικά:
 ΔΙΑΓΩΝΙΣΜΑ Μάθημα : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Ονοματεπώνυμο: Τμήμα: ΘΕΜΑΤΑ Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν απομακρύνεται
ΔΙΑΓΩΝΙΣΜΑ Μάθημα : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Ονοματεπώνυμο: Τμήμα: ΘΕΜΑΤΑ Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν απομακρύνεται
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
7. Ένα σώμα εκτελεί ταυτόχρονα δύο αρμονικές ταλαντώσεις με εξισώσεις,
 1. Κάθε ελατήριο του σχήματος έχει το ένα άκρο του στερεωμένο σε ακίνητο σημείο και το άλλο του άκρο προσδεμένο στο σώμα Σ. Οι σταθερές των δύο ελατηρίων είναι Κ 1 =120Ν/m και Κ 2 =80N/m. To σώμα Σ, έχει
1. Κάθε ελατήριο του σχήματος έχει το ένα άκρο του στερεωμένο σε ακίνητο σημείο και το άλλο του άκρο προσδεμένο στο σώμα Σ. Οι σταθερές των δύο ελατηρίων είναι Κ 1 =120Ν/m και Κ 2 =80N/m. To σώμα Σ, έχει
Δυναμική. Ομάδα Γ. Δυναμική Κατακόρυφη βολή και γραφικές παραστάσεις Κατακόρυφη βολή και κάποια συμπεράσματα.
 . Ομάδα Γ. 1.2.21. Κατακόρυφη βολή και γραφικές παραστάσεις Από ένα σημείο Ο σε ύψος Η=25m από το έδαφος εκτοξεύεται κατακόρυφα προς τα πάνω ένα σώμα με αρχική ταχύτητα υ 0 =20m/s. Αν g=10m/s 2, ενώ η
. Ομάδα Γ. 1.2.21. Κατακόρυφη βολή και γραφικές παραστάσεις Από ένα σημείο Ο σε ύψος Η=25m από το έδαφος εκτοξεύεται κατακόρυφα προς τα πάνω ένα σώμα με αρχική ταχύτητα υ 0 =20m/s. Αν g=10m/s 2, ενώ η
ΤΑΛΑΝΤΩΣΕΙΣ. . Ερωτήσεις αντιστοίχισης. Σχήμα 2 από τη θέση ισορροπίας του δίνεται από την εξίσωση x = Aημωt.
 ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β.
 ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
Ποιο είναι το πλάτος της ταλάντωσης ;
 Ποιο είναι το πλάτος της ταλάντωσης ; 1. Ένα σώμα είναι δεμένο στο δεξιό άκρο οριζόντιου ιδανικού ελατηρίου και στο αριστερό άκρο οριζόντιου νήματος και ηρεμεί σε ισορροπία όπως δείχνει το σχήμα. Το ελατήριο
Ποιο είναι το πλάτος της ταλάντωσης ; 1. Ένα σώμα είναι δεμένο στο δεξιό άκρο οριζόντιου ιδανικού ελατηρίου και στο αριστερό άκρο οριζόντιου νήματος και ηρεμεί σε ισορροπία όπως δείχνει το σχήμα. Το ελατήριο
Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον)
 Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον) 1. Σε μια φθίνουσα ταλάντωση ποιο από τα παρακάτω μεγέθη παραμένει σταθερό: α) το πλάτος
Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον) 1. Σε μια φθίνουσα ταλάντωση ποιο από τα παρακάτω μεγέθη παραμένει σταθερό: α) το πλάτος
1.1 Κινηματική προσέγγιση
 1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
υ r 1 F r 60 F r A 1
 2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
1.4. Σύνθεση Ταλαντώσεων. Ομάδα Γ.
 1.4. Σύνθεση Ταλαντώσεων. Ομάδα Γ. 1.4.1. Σύνθετη ταλάντωση και περιστρεφόμενα διανύσματα. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση, της οποίας η απομάκρυνση από τη θέση ισορροπίας είναι x=0, + (..) και
1.4. Σύνθεση Ταλαντώσεων. Ομάδα Γ. 1.4.1. Σύνθετη ταλάντωση και περιστρεφόμενα διανύσματα. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση, της οποίας η απομάκρυνση από τη θέση ισορροπίας είναι x=0, + (..) και
Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Όλα τα θέματα των πανελληνίων στις μηχανικές ταλαντώσεις έως και το 2014 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ. Ερωτήσεις Πολλαπλής Επιλογής
 έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
Θέμα Α(25 Μονάδες) Α1. (5 μονάδες) Α2. (5 μονάδες) Α3. (5 μονάδες) Α4. (5 μονάδες)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ ΣΕΠΤΕΜΒΡΙΟΥ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 13 ΣΕΠΤΕΜΒΡΙΟΥ 018 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) Θέμα
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ ΣΕΠΤΕΜΒΡΙΟΥ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 13 ΣΕΠΤΕΜΒΡΙΟΥ 018 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) Θέμα
Δυναμική στο επίπεδο. Ομάδα Γ.
 .3.2. Η τριβή και η κίνηση. στο επίπεδο. Ομάδα Γ. Ένα σώμα μάζας 2kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστές τριβής μ=μ s =0,2. Σε μια στιγμή t 0 =0 στο σώμα ασκείται μεταβλητή
.3.2. Η τριβή και η κίνηση. στο επίπεδο. Ομάδα Γ. Ένα σώμα μάζας 2kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστές τριβής μ=μ s =0,2. Σε μια στιγμή t 0 =0 στο σώμα ασκείται μεταβλητή
5. Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με τον χρόνο.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
κριτήρια αξιολόγησης ΚΕΦΑΛΑΙΟ 5 1o Κριτήριο αξιολόγησης
 1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης
 4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης 1 ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά κινείται με ταχύτητα
4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης 1 ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά κινείται με ταχύτητα
2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ
 2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ 207-208 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΝΟΕΜΒΡΙΟΥ 207 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΟΝΟΜΑΤΕΠΩΝΥΜΟ Τμήμα Γθετ.
2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ 207-208 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΝΟΕΜΒΡΙΟΥ 207 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΟΝΟΜΑΤΕΠΩΝΥΜΟ Τμήμα Γθετ.
Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή
 Θέμα ο. Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή 4--06 Στα θέματα Α, Α, Α3,Α4 επιλέξτε το γράμμα που απαντά στην ερώτηση και γράψτε το
Θέμα ο. Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή 4--06 Στα θέματα Α, Α, Α3,Α4 επιλέξτε το γράμμα που απαντά στην ερώτηση και γράψτε το
ΚΕΦΑΛΑΙΟ 1ο: ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Έργο-Ενέργεια Ασκήσεις Έργου-Ενέργειας Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ Μεταβλητή δύναµη και κίνηση
 2.2. Ασκήσεις Έργου-Ενέργειας. 2.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 2.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 1
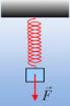
 1. Ένα βλήμα μάζας 0,1 kg που κινείται οριζόντια με ταχύτητα 100 m/s σφηνώνεται σε ακίνητο ξύλο μάζας 1,9 kg. Να βρεθεί η απώλεια ενέργειας που οφείλεται στην κρούση, όταν το ξύλο είναι: α. πακτωμένο στο
1. Ένα βλήμα μάζας 0,1 kg που κινείται οριζόντια με ταχύτητα 100 m/s σφηνώνεται σε ακίνητο ξύλο μάζας 1,9 kg. Να βρεθεί η απώλεια ενέργειας που οφείλεται στην κρούση, όταν το ξύλο είναι: α. πακτωμένο στο
Φυσική Γ Λυκείου Θετικού Προσανατολισμού Σχ. έτος ο Διαγώνισμα Κρούσεις - Ταλαντώσεις Θέμα 1ο
 1ο Διαγώνισμα Κρούσεις - Ταλαντώσεις Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη ϕράση που τη συμπληρώνει σωστά.
1ο Διαγώνισμα Κρούσεις - Ταλαντώσεις Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη ϕράση που τη συμπληρώνει σωστά.
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 4. α. β. ii. iii. 6. α.
 Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16
 ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16 Θέμα Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που
ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16 Θέμα Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που
2. Σώμα εκτελεί Α.Α.Τ. και η εξίσωση της απομάκρυνσης σε σχέση με το χρόνο είναι:
 1. Σώμα εκτελεί Α.Α.Τ. με περίοδο 2 s και πλάτος ταλάντωσης 0,1 m. Τη χρονική στιγμή 0 το σώμα διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Να υ πολογιστούν: α) η συχνότητα και η γωνιακή συχνότητα
1. Σώμα εκτελεί Α.Α.Τ. με περίοδο 2 s και πλάτος ταλάντωσης 0,1 m. Τη χρονική στιγμή 0 το σώμα διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Να υ πολογιστούν: α) η συχνότητα και η γωνιακή συχνότητα
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
Κρούσεις. 5. Σε μια ελαστική κρούση δεν διατηρείται α. η ολική κινητική ενέργεια του συστήματος. β. η ορμή του συστήματος.
 ο ΘΕΜΑ Κρούσεις Α Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σε κάθε κρούση ισχύει α η
ο ΘΕΜΑ Κρούσεις Α Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σε κάθε κρούση ισχύει α η
ΔΙΑΓΩΝΙΣΜΑ 01 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α
 Σελίδα από ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ () ΘΕΜΑ Α Α. Με την πάροδο του χρόνου και καθώς τα αμορτισέρ ενός αυτοκινήτου παλιώνουν και φθείρονται:
Σελίδα από ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ () ΘΕΜΑ Α Α. Με την πάροδο του χρόνου και καθώς τα αμορτισέρ ενός αυτοκινήτου παλιώνουν και φθείρονται:
ΟΡΟΣΗΜΟ Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση x 5 3 cm. Να βρείτε την αρχική φάση φ 0
 Απλή Αρμονική Ταλάντωση ΚΕΦΑΛΑΙΟ 1 Σώμα που εκτελεί απλή αρμονική ταλάντωση και χρησιμοποιούμε τις εξισώσεις. 1.56 Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση
Απλή Αρμονική Ταλάντωση ΚΕΦΑΛΑΙΟ 1 Σώμα που εκτελεί απλή αρμονική ταλάντωση και χρησιμοποιούμε τις εξισώσεις. 1.56 Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση
2 ο Διαγώνισμα Γ Λυκείου
 ο Διαγώνισμα Γ Λυκείου 03-09-08 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ερωτήσεις Α ως και Α4 επιλέξτε την σωστή απάντηση: Α. Όταν ένα κινούμενο σώμα συγκρουστεί κεντρικά και ελαστικά
ο Διαγώνισμα Γ Λυκείου 03-09-08 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ερωτήσεις Α ως και Α4 επιλέξτε την σωστή απάντηση: Α. Όταν ένα κινούμενο σώμα συγκρουστεί κεντρικά και ελαστικά
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
5. Ένα σώµα ταλαντώνεται µεταξύ των σηµείων Α και Ε. Στο σχήµα φαίνονται πέντε θέσεις Α,Β,Γ, και Ε, οι οποίες ισαπέχουν µεταξύ 1
 1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
ΠΕΝΤΕΛΗ ΒΡΙΛΗΣΣΙΑ. 1. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση. Αν διπλασιάσουμε το πλάτος της
 Τάξη Μάθημα Εξεταστέα ύλη Γ Λυκείου Φυσικη κατευθυνσης ΠΕΝΤΕΛΗ Κτίριο 1 : Πλ. Ηρώων Πολυτεχνείου 13, Τηλ. 210 8048919 / 210 6137110 Κτίριο 2 : Πλ. Ηρώων Πολυτεχνείου 29, Τηλ. 210 8100606 ΒΡΙΛΗΣΣΙΑ Καθηγητής
Τάξη Μάθημα Εξεταστέα ύλη Γ Λυκείου Φυσικη κατευθυνσης ΠΕΝΤΕΛΗ Κτίριο 1 : Πλ. Ηρώων Πολυτεχνείου 13, Τηλ. 210 8048919 / 210 6137110 Κτίριο 2 : Πλ. Ηρώων Πολυτεχνείου 29, Τηλ. 210 8100606 ΒΡΙΛΗΣΣΙΑ Καθηγητής
ΠΕΝΤΕΛΗ. Κτίριο 1 : Πλ. Ηρώων Πολυτεχνείου 13, Τηλ. 210 8048919 / 210 6137110 Κτίριο 2 : Πλ. Ηρώων Πολυτεχνείου 29, Τηλ. 210 8100606 ΒΡΙΛΗΣΣΙΑ
 Τάξη Μάθημα Εξεταστέα ύλη Γ Λυκείου Φυσικη κατευθυνσης ΠΕΝΤΕΛΗ Κτίριο 1 : Πλ. Ηρώων Πολυτεχνείου 13, Τηλ. 210 8048919 / 210 6137110 Κτίριο 2 : Πλ. Ηρώων Πολυτεχνείου 29, Τηλ. 210 8100606 ΒΡΙΛΗΣΣΙΑ Καθηγητής
Τάξη Μάθημα Εξεταστέα ύλη Γ Λυκείου Φυσικη κατευθυνσης ΠΕΝΤΕΛΗ Κτίριο 1 : Πλ. Ηρώων Πολυτεχνείου 13, Τηλ. 210 8048919 / 210 6137110 Κτίριο 2 : Πλ. Ηρώων Πολυτεχνείου 29, Τηλ. 210 8100606 ΒΡΙΛΗΣΣΙΑ Καθηγητής
Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις
 Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις Θέμα Α. (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις Θέμα Α. (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΟΡΟΣΗΜΟ. 1ο Κριτήριο αξιολόγησης στα κεφ Θέμα 1. Κριτήρια αξιολόγησης Ταλαντώσεις - Κύματα.
 1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
Ημερομηνία: Τετάρτη 26 Οκτωβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ 6/0/06 ΕΩΣ 30/0/06 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 6 Οκτωβρίου 06 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ 6/0/06 ΕΩΣ 30/0/06 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 6 Οκτωβρίου 06 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
2.2. Ασκήσεις Έργου-Ενέργειας. Οµάδα Γ.
 2.2. Ασκήσεις Έργου-Ενέργειας. Οµάδα Γ. 2.2.21. Έργο και µέγιστη Κινητική Ενέργεια. Ένα σώµα µάζας 2kg κινείται σε οριζόντιο επίπεδο και σε µια στιγµή περνά από την θέση x=0 έχοντας ταχύτητα υ 0 =8m/s,
2.2. Ασκήσεις Έργου-Ενέργειας. Οµάδα Γ. 2.2.21. Έργο και µέγιστη Κινητική Ενέργεια. Ένα σώµα µάζας 2kg κινείται σε οριζόντιο επίπεδο και σε µια στιγµή περνά από την θέση x=0 έχοντας ταχύτητα υ 0 =8m/s,
3.6. Σύνθετα θέματα στερεού. Ομάδα Δ.
 3.5.61. Μια κινούμενη τροχαλία. 3.6. Σύνθετα θέματα στερεού. Ομάδα Δ. Γύρω από μια τροχαλία μάζας Μ=0,8kg έχουμε τυλίξει ένα αβαρές νήμα, στο άκρο του οποίου έχουμε δέσει ένα σώμα Σ μάζας m=0,1kg. Συγκρατούμε
3.5.61. Μια κινούμενη τροχαλία. 3.6. Σύνθετα θέματα στερεού. Ομάδα Δ. Γύρω από μια τροχαλία μάζας Μ=0,8kg έχουμε τυλίξει ένα αβαρές νήμα, στο άκρο του οποίου έχουμε δέσει ένα σώμα Σ μάζας m=0,1kg. Συγκρατούμε
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΡΟΥΣΕΙΣ-ΤΑΛΑΝΤΩΣΕΙΣ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΡΟΥΣΕΙΣ-ΤΑΛΑΝΤΩΣΕΙΣ 5/11/2017 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΡΟΥΣΕΙΣ-ΤΑΛΑΝΤΩΣΕΙΣ 5/11/2017 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 02/10/2016 ΔΙΑΡΚΕΙΑ: 3 ΩΡΕΣ ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 0/0/06 ΔΙΑΡΚΕΙΑ: 3 ΩΡΕΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις -5 να γράψετε στο φύλλο απαντήσεών σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 0/0/06 ΔΙΑΡΚΕΙΑ: 3 ΩΡΕΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις -5 να γράψετε στο φύλλο απαντήσεών σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
των δύο σφαιρών είναι. γ.
 ΘΕΜΑ B Σφαίρα µάζας κινούµενη µε ταχύτητα µέτρου υ συγκρούεται κεντρικά και ελαστικά µε ακίνητη σφαίρα ίσης µάζας Να βρείτε τις σχέσεις που δίνουν τις ταχύτητες των δύο σφαιρών, µετά την κρούση, µε εφαρµογή
ΘΕΜΑ B Σφαίρα µάζας κινούµενη µε ταχύτητα µέτρου υ συγκρούεται κεντρικά και ελαστικά µε ακίνητη σφαίρα ίσης µάζας Να βρείτε τις σχέσεις που δίνουν τις ταχύτητες των δύο σφαιρών, µετά την κρούση, µε εφαρµογή
ΔΙΑΡΚΕΙΑ: 180min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ 1 ο ΘΕΜΑ 2 ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ
 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 80min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΜΟΝΑΔΕΣ ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΘΕΜΑ Α:. Κατά την διάρκεια της φθίνουσας ταλάντωσης ενός αντικειμένου, το
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 80min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΜΟΝΑΔΕΣ ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΘΕΜΑ Α:. Κατά την διάρκεια της φθίνουσας ταλάντωσης ενός αντικειμένου, το
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο.
 1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
Κρούσεις. 1 ο ΘΕΜΑ. Φυσική Γ Θετ. και Τεχν/κης Κατ/σης. Θέματα εξετάσεων
 ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ΚΕΦΑΛΑΙΟ 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΚΕΦΑΛΑΙΟ 2.1 91 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Α. ΈΡΓΟ ΣΤΑΘΕΡΗΣ ΔΥΝΑΜΗΣ 1. Το σώμα του σχήματος μετακινείται πάνω στο οριζόντιο επίπεδο κατά x=2m. Στο σώμα εκτός του βάρους του και της αντίδρασης του
ΚΕΦΑΛΑΙΟ 2.1 91 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Α. ΈΡΓΟ ΣΤΑΘΕΡΗΣ ΔΥΝΑΜΗΣ 1. Το σώμα του σχήματος μετακινείται πάνω στο οριζόντιο επίπεδο κατά x=2m. Στο σώμα εκτός του βάρους του και της αντίδρασης του
