Πηγές Πληροφορίας και Κωδικοποίηση Πηγής
|
|
|
- Καλόγερος Γεννάδιος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Πηγές Πληροφορίας και Κωδικοποίηση Πηγής Τηλεπικοινωνιακά συστήµατα Τα τηλεπικοινωνιακά συστήµατα είναι σχεδιασµένα για να διαβιβάζουν πληροφορία. Σε κάθε τηλεπικοινωνιακό σύστηµα υπάρχει µια πηγή που παράγει την πληροφορία, και σκοπός του συστήµατος είναι η διαβίβαση της εξόδου της πηγής στονπροορισµότης. Πληροφορία κοινή αντίληψη Σεραφείµ Καραµπογιάς Η διαισθητική και κοινή αντίληψη της πληροφορίας παραπέµπει σε κάθε καινούριαγνώσηγιακάτι (πληροφορία = νέαγνώση). Η έξοδος µιας πηγής πληροφορίας είναι µια χρονικά-µεταβαλλόµενη συνάρτηση, χωρίς δυνατότητα πρόβλεψης (εάν ήταν δυνατή η πρόβλεψή της, δεν θαυπήρχελόγοςµετάδοσήςτης), µπορείναθεωρηθείωςµιατυχαίαδιαδικασία. Ο σχεδιαστής τηλεπικοινωνιακών συστηµάτων σχεδιάζει ένα σύστηµα που διαβιβάζει την έξοδο µιας τυχαίας διαδικασίας (πηγή πληροφορίας) σ' έναν προορισµό µέσα από ένα τυχαία συµπεριφερόµενο µέσο (κανάλι) εξασφαλίζοντας µικρή παραµόρφωση.
2 Πληροφορία µία διαισθητική προσέγγιση Καθέναςαντιλαµβάνεταιδιαισθητικάτηνέννοιατηςπληροφορίας. Η ποιοτική περιγραφή της πληροφορίας δεν είναι αρκετή απαιτείται ένα ποσοτικό µέτρο της πληροφορίας και µαθηµατική µοντελοποίηση των πηγών πληροφορίας. Πληροφορία προσέγγιση µηχανικού Η πληροφορία σε ένα µήνυµα είναι ο χρόνος που απαιτείται για την µετάδοσή του. Μηνύµατα µε µεγάλη πιθανότητα εµφάνισης µπορούν να µεταδοθούν σε συντοµότερο χρόνο από ότι µηνύµατα µε µικρή πιθανότητα εµφάνισης. Η έξοδος µιας πηγής πληροφορίας µπορεί να γίνει πιο συµπαγής, και συνεπώς να διαβιβασθεί ή να αποθηκευθεί ευκολότερα. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-2
3 Πηγές Πληροφορίας Η έξοδος µιας πηγής πληροφορίας είναι µία χρονικά-µεταβαλλόµενη συνάρτηση χωρίς δυνατότητα πρόβλεψης. Οι πηγές πληροφορίας µπορούν να µοντελοποιηθούν µε τυχαίες διαδικασίες, των οποίων οι ιδιότητες εξαρτώνται από τη φύση της πηγής. Οι πηγές πληροφορίας µπορούν να ταξινοµηθούν σε δύο κατηγορίες: αναλογικές (ή συνεχών τιµών) διακριτές Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-3
4 Όταν µοντελοποιούµε σήµατα οµιλίας, το φάσµα ισχύος της προκύπτουσας τυχαίας διαδικασίας καλύπτει περίπου την περιοχή των 3 34 Hz, κι αυτό διότι η φασµατική πυκνότητα ισχύος του σήµατος οµιλίας καταλαµβάνει αυτή τη ζώνη συχνοτήτων. S X ( f ) Σεραφείµ Καραµπογιάς f Τυπικό φάσµα ισχύος σήµατος οµιλίας Όλες οι πηγές έχουν πεπερασµένο εύρος ζώνης, εποµένως είναι δυνατή η δειγµατολήπτηση µε ρυθµό Nyquist ή µεγαλύτερο και να ανακατασκευασθούν από τις τιµές των δειγµάτων. Ηπηγήµοντελοποιείταιωςµιατυχαίαδιαδικασίαδιακριτούχρόνου{ X } i i= Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-4
5 Το απλούστερο µοντέλο πηγής πληροφορίας που µελετάµε, είναι η διακριτή πηγή χωρί-µνήµη (Discrete Memoryless Source, DMS). Η DMS είναι µια τυχαία διαδικασία διακριτού-χρόνου και διακριτού-πλάτους, στην οποία όλα τα X i δηµιουργούνταιανεξάρτηταµεταξύτουςαλλάµετηνίδιακατανοµήπιθανότητας. Εποµένως, µία DMS δηµιουργεί µία σειρά από ανεξάρτητες πανοµοιότυπης κατανοµής (independent and identically distributed i.i.d.) τυχαίες µεταβλητές που λαµβάνουν τιµή από ένα διακριτό σύνολο. Το σύνολο των τιµών της τυχαίας µεταβλητής X είναι A = { a a K }, 2, a N Η συνάρτηση πιθανότητας µάζας (PMF) για τη διακριτή τυχαία µεταβλητή X είναι ( X = a ) γιακάθε i=, 2, K N pi = p i, Πηγή πληροφορίας K X X, X, X,, K 2, X 2 Μαθηµατικό Μοντέλο για µια πηγή διακριτού χρόνου Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-5
6 Το Πληροφοριακό Περιεχόµενο ενός Μηνύµατος Όταν δίνεται µια πηγή πληροφορίας πώς να υπολογίσουµε το ρυθµό µε τον οποίο η πηγή παράγει την πληροφορία. Σε διαισθητική βάση, η ποσότητα πληροφορίας που δεχόµαστε µε την γνώση της εµφάνισης ενός γεγονότος σχετίζεται µε την πιθανότητα εµφάνισης του γεγονότος. Ένα λογικό µέτρο της πληροφορίας µιας εξόδου της πηγής πρέπει να είναι φθίνουσα και συνεχής συνάρτηση της πιθανότητας της εξόδου αυτής. Όσο πιο απίθανο είναι το γεγονός, τόσο πιο µεγάλη πληροφορία µεταφέρει. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-6
7 Ηποσότητατηςπληροφορίαςπουπαρέχειµίαέξοδος (σύµβολο) α j µεπιθανότητα p j ικανοποιείτιςσυνθήκες: Το περιεχόµενο της πληροφορίας της εξόδου α j εξαρτάται µόνο από την πιθανότητατηςα j καιόχιαπότηντιµήτηςα j. Συµβολίζουµεαυτήτησυνάρτησηµε I(p j ) καιτηνονοµάζουµειδία-πληροφορίαήπληροφοριακόπεριεχόµενο. Ηιδία-πληροφορίαείναιµίασυνεχήςσυνάρτησητης p j. Η ιδία-πληροφορία είναι µία φθίνουσα συνάρτηση του ορίσµατός της. ( pk ) > I( p j ) αν pk p j I < Όταν δεχόµαστε δύο ανεξάρτητες εξόδους, η ολική ιδία-πληροφορία που παίρνουµε είναι το άθροισµα των ιδίων-πληροφοριών που µεταφέρει κάθε µία από τις δύο εξόδους Αν p j = ( j) ( j 2 ) ( j) ( j 2 ) ( p ) I( p ) p p τότε I ( p ) = I + j Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-7
8 Μια συνεχής συνάρτηση της p k που ικανοποιεί τις παραπάνω συνθήκες είναι η λογαριθµική συνάρτηση, µπορούµε λοιπόν να ορίσουµε ιδία-πληροφορία µε την I( p k ) = log = log ( p k p k ) Η βάση του λογαρίθµου ορίζει τη µονάδα µέτρησης της πληροφορίας Ότανηβάσηείναιτο 2, ηπληροφορίαµετριέταισε bit. Όταν χρησιµοποιείται φυσικός λογάριθµος, η πληροφορία µετριέται σε nap. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-8
9 Η πληροφορία που παρέχεται από µία µη αναγνωρισθείσα έξοδο που αποτελείται από Μ σύµβολα θα είναι ίση µε το άθροισµα της συνεισφοράς καθ ενόςαπότανσύµβολατουαλφάβητουτηςπηγήςκαιδίνεταιαπότησχέση I total = N i= ( M p ) log( p ) ( bit) i i Η µέση ιδία-πληροφορία ανά σύµβολο λέγεται και εντροπία της πηγής (ρυθµός της πηγής). Γενικά η εντροπία µιας διακριτής τυχαίας µεταβλητής X ορίζεται από τη σχέση H I M N total ( X ) = = p I ( p ) = p log( p ) i= i i N i= i i bits symbol Η H(X) είναι µία συνάρτηση του PMF της τυχαίας µεταβλητής. Η εντροπία αποτελεί ένα µέτρο της αβεβαιότητας για έξοδο της πηγής (κατά µέσο όρο). Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-9
10 Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή, ( X ) = E[ log ( )] H 2 p i Σεραφείµ Καραµπογιάς Η εντροπία µιας πηγής πληροφορίας είναι ένα µέτρο της αβεβαιότητας ή ισοδύναµα του πληροφοριακού περιεχοµένου της πηγής. Επίσης η εντροπία αποτελεί ένα µέτρο του αριθµού των bits πληροφορίας που χρειάζονται κατά µέσο όρο για να µεταδώσουµε την πληροφορία που περιέχεται στην µεταβλητή X, υπό την προϋπόθεση ότι έχει χρησιµοποιηθεί ένα βέλτιστος αλγόριθµος κωδικοποίησης. Με άλλα λόγια κάθε έξοδος της πηγής απαιτεί H(X) bits για ουσιαστικά χωρίς σφάλµατα αναπαράσταση. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-
11 Για µία πηγή µε ένα αλφάβητο από Ν σύµβολα, η µέγιστη εντροπία κατορθώνεται όταν οι πιθανότητες των συµβόλων είναι ίσες οπότε p p p = 2 = L = N = N H = max log 2 N bits ( ) symbol Αν symbols r S sec είναι ο σταθερός ρυθµός µε τον οποίο εκπέµπονται τα σύµβολα από την πηγή, ορίσουµε το µέσο ρυθµό (παροχής) της πληροφορίας από της πηγής ως R = r S H bits sec Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-
12 Παράδειγµα Να βρεθεί η εντροπία µιας πηγής που εκπέµπει ένα από τα τρία σύµβολα Α, Β και C σε στατιστικάανεξάρτητηακολουθίαµεπιθανότητααντίστοιχα /2, /4 και /4. Απάντηση: H=, 5 bits symbol Παράδειγµα Μια διακριτή πηγή εκπέµπει ένα από πέντε σύνβολα κάθε msec. Οι πιθανότητες των συµβόλων είναι /2, /4, /8, /6, και /6 αντίστοιχα. Να βρεθεί η εντροπία της πηγής και ο µέσος ρυθµός πληροφορίας. Απάντηση: H=, 875 bits symbol R=875 bits sec Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-2
13 Στη δυαδική πηγή χωρίς µνήµη µε πιθανότητες p και p, αντίστοιχα έχουµε H = p ( p) log ( ) log ( p) 2 2 p Η συνάρτηση αυτή, που συµβολίζεται µε H b (p), είναι γνωστή ως η συνάρτηση δυαδικής εντροπίας. Η συνάρτηση δυαδικής εντροπίας µεγιστοποιείται όταν p =,5. Η µέγιστη τιµής της είναι H b (,5) =, δηλαδή,τοαποτέλεσµαµπορείναµεταφερθείµε bit. H b ( p),5, 5 p Η συνάρτηση δυαδικής εντροπίας Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-3
14 Για δύο ή περισσότερες τυχαίες µεταβλητές εισάγουµε τη συνδυασµένη και την υποσυνθήκη εντροπία. Έννοιες ιδιαίτερα σηµαντικές για πηγές µε µνήµη. Η συνδυασµένη εντροπία δύο διακριτών τυχαίων µεταβλητών (X,Υ) ορίζεται από τη σχέση H = ( X, Y) p ( x, y ) log( p( x, y )) x, y Η σχέση γενικεύεται για περισσότερες τυχαίες µεταβλητές Σεραφείµ Καραµπογιάς Η συνδυασµένη εντροπία είναι απλά η εντροπία µιας τυχαίας διανυσµατικής µεταβλητής Παράδειγµα ύο δυαδικές τυχαίες µεταβλητές X και Y κατανέµονται σύµφωνα µε τη συνδυασµένηκατανοµή p(x = Y = ) = p(x =, Y = ) = p(x = Y = ) = /3. Υπολογίστε τις H(X), H(Y) και H(X,Y). Απάντηση: H(X) =,983, H(Y) =,983και H(X,Y) =,585. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-4
15 Υποσυνθήκη εντροπία Η PMF της τυχαίας µεταβλητής X δεδοµένης της τιµής y της τυχαίας µεταβλητής Y είναι p (x y) Η υποσυνθήκη εντροπία της τυχαίας µεταβλητής X δεδοµένης της τιµής y της τυχαίας µεταβλητής Y ορίζεται από τη σχέση H = ) ( X Y = y) p ( x y ) log( p ( x y ) x η οποια διαισθητικά είναι η ποσότητα αβεβαιότητας στη Χ όταν γνωρίζουµε ότι Υ = y. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-5
16 Η υποσυνθήκη εντροπία είναι η σταθµισµένη µέση τιµή των παραπάνω ποσοτήτων για όλα τα y και υποδηλώνει την εντροπία (ή την αβεβαιότητα) της τυχαίας µεταβλητής X όταν είναι γνωστή η τυχαία µεταβλητή Y, δηλαδή, Η υποσυνθήκη εντροπία µιας διακριτής τυχαίας µεταβλητής X δεδοµένης της τυχαίας µεταβλητής Y ορίζεται από τη σχέση H ( X Y) = p( x y) p( y) log( p( x y) ) = x, y x, y p( x, Αποδεικνύεταιότι H(X,Y) = H(Y) + H(X Y). y) log ( p( x y) ) Σεραφείµ Καραµπογιάς Επειδή η Y µπορεί να παρέχει κάποια πληροφορία για τη X είναι H(X Y) H(X). Το περιεχόµενο της πληροφορίας του ζεύγους (X,Y) είναι ίσο προς το πληροφοριακό περιεχόµενο της Y συν το πληροφοριακό περιεχόµενο της X όταν είναι γνωστή η Y Η σχέση αυτή επίσης δηλώνει ότι η ίδια πληροφορία µεταφέρεται είτε εµφανίζοντας το ζεύγος (X,Y), ή αποκαλύπτοντας πρώτα το Y και στη συνέχεια την αποµένουσα πληροφορία στο Χ. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-6
17 Αν X n δηλώνειτηνέξοδοµιαςδιακριτήςπηγήςτηχρονικήστιγµή n, τότε ΗΗ(Χ 2 Χ ) υποδηλώνειτηνκαινούργιαπληροφορίαπουπαρέχειηέξοδος X 2 της πηγήςσεκάποιονπουγνωρίζειτηνέξοδο X. Γενικά Η (Χ n Χ, Χ 2,, Χ n- ) δηλώνειτηνκαινούργιαπληροφορίαπουπαρέχειη έξοδος X n τηςπηγήςσεκάποιονπουέχειπαρατηρήσειτηνακολουθία (Χ, Χ 2,, Χ n- ). Ο ρυθµός εντροπίας µιας στατικής τυχαίας διαδικασίας διακριτού χρόνου ορίζεται από την H ( X X, X K X ) = lim H n 2,, n n Αποδεικνύεται ότι ένας εναλλακτικός ορισµός του ρυθµού εντροπίας για πηγές µε µνήµη είναι H = lim H 2, K, n n ( X, X X ) Ορυθµόςτηςεντροπίαςπαίζειτορόλοτηςεντροπίαςγιαπηγέςµεµνήµη. n Σεραφείµ Καραµπογιάς Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-7
18 ΘΕΩΡΗΜΑ ΚΩ ΙΚΟΠΟΙΗΣΗΣ ΠΗΓΗΣ Τοθεώρηµααυτόκαθορίζειέναθεµελιώδεςόριοστορυθµό, µετονοποίοηέξοδος µιας πηγής πληροφορίας µπορεί να συµπιεστεί χωρίς να προκληθεί µεγάλη πιθανότητα σφάλµατος. Σε ακολουθίες από εξόδους µιας DMS µήκους n κάθε γράµµα α ι i =, 2,, N επαναλαµβάνεταιµευψηλήπιθανότητα (πουφτάνειτο καθώςτο n ) περίπου np i φορές. Μεάλλαλόγιαασυµπτωτικά σχεδόνόλεςοιακολουθίεςείναιπερίπου ισοπίθανες. Οιακολουθίες xπουέχουντηνπαραπάνωδοµήονοµάζονταιτυπικέςακολουθίες. Η πιθανότητα µιας τυπικής ακολουθίας είναι P n p log p i= i 2 i= N n p N n p p i i i i i i n H( X ) ( = ) p = 2 log X x = 2 = = Παρατηρούµε ότι για µεγάλο n σχεδόν όλες οι ακολουθίες εξόδου µήκους n της n H( X ) πηγής (τυπικέςακολουθίες) είναιισοπίθανεςµεπιθανότηταπερίπου 2. Ο συνολικός αριθµός των τυπικών ακολουθιών είναι σχεδόν 2. Η πιθανότητα του συνόλου των µη τυπικών ακολουθιών είναι αµελητέα.. N Σεραφείµ Καραµπογιάς n H ( X ) Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-8
19 Παρατηρούµε ότι παρόλο που µία πηγή µε µέγεθος αλφαβήτου N µπορεί να παράγει N n ακολουθίες µήκους n, µπορούµε να λάβουµε υπόψιν το σύνολο των τυπικών ακολουθιών και να αµελήσουµε τις άλλες εξόδους και η πιθανότητα να έχουµε χάσει κάτι πλησιάζει στο µηδέν καθώς το n τείνει στο άπειρο. Το σύνολο των τυπικών ακολουθιώνµε 2 n H (X ) Τοσύνολοτωντυπικώνκαιτωνµητυπικών ακολουθιών. Αυτή είναι η ουσία της συµπίεσης δεδοµένων, δηλαδή, της πρακτικής της αναπαράστασης της εξόδου της πηγής µε ένα αριθµό ακολουθιών µικρότερο από εκείνο που η πηγή παράγει στην πραγµατικότητα. Επειδή ο συνολικός αριθµός των τυπικών ακολουθιών (µε µήκος n) είναι περίπου 2 n H ( X ) χρειαζόµαστε n H ( X ) bits γιανατιςαναπαραστήσουµε. Παρατηρούµεότικατάµέσοόρο, κάθεέξοδοςτηςπηγήςαπαιτεί H ( X ) bits γιαµία ουσιαστικά χωρίς σφάλµατα αναπαράσταση. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-9
20 Για µία πηγή της οποίας η PMF είναι οµοιόµορφα κατανεµηµένη έχουµε H ( X) = log N έτσι το πλήθος των τυπικών ακολουθιών είναι n H( X ) n log N n 2 = 2 Αυτό σηµαίνει ότι ο αριθµός των τυπικών ακολουθίων της πηγής µήκους n είναι ίσοςπροςτοσυνολικόαριθµότωνεξόδων τηςπηγήςκαικαµίασυµπίεσηδενείναι δυνατή. = N Σεραφείµ Καραµπογιάς Εάν η πηγή έχει µνήµη τότε οι έξοδοι δεν είναι ανεξάρτητες και για αυτό φανερώνουν πληροφορία για τις επόµενες εξόδους. Σεµίαπηγήµεµνήµηορυθµόςµετονοποίοπαράγεταιηκαινούργιαπληροφορία ελαττώνεταικαθώςόλοκαιπερισσότερεςέξοδοιτηςπηγήςεµφανίζονται. Γενικά γιαπηγέςµεµνήµηµαςενδιαφέρειορυθµόςεντροπίαςη(χ n Χ, Χ 2,, Χ n- ) Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-2
21 Θεώρηµα κωδικοποίησης πηγής Σεραφείµ Καραµπογιάς Θεώρηµα Κωδικοποίησης Πηγής. Μία πηγή εντροπίας (ή ρυθµού εντροπίας) H µπορεί να κωδικοποιηθεί µε αυθαίρετα αυθέρετα µικρή πιθανότητα σφάλµατος σε οποιοδήποτερυθµό R (bits / έξοδοπηγής) εφόσον R > H. Αντίστροφα, αν R < H, η πιθανότητα σφάλµατος θα παραµένει µακριά από το µηδέν, ανεξάρτητα από την πολυπλοκότητα του κωδικοποιητή και του αποκωδικοποιητή που χρησιµοποιούνται Ο κωδικοποιητής πηγής αντιστοιχεί δυαδικές κωδικές λέξεις στα πακέτα συµβόλων της πηγής και παράγει στην έξοδο του µια δυαδική ακολουθία. Το θεώρηµα κωδικοποίησης πηγής δίνει µόνο αναγκαίες και ικανές συνθήκες για τηνύπαρξηκωδίκωνπηγής. ίνει επίσης ένα φράγµα στο ρυθµό µε τον οποίο η πηγή µπορεί να συµπιεσθεί (κωδικοποιηθεί) γιααξιόπιστηανακατασκευή. εν προσφέρει συγκεκριµένους αλγορίθµους για να σχεδιασθούν κώδικες που να προσεγγίζουν αυτό το φράγµα. Υπάρχουν δύο γνωστοί αλγόριθµοι που οι επίδοσείς τους είναι πολύ κοντά στο φράγµα της εντροπίας. Ο αλγόριθµος κωδικοποίησης πηγής του Huffman Ο αλγόριθµος κωδικοποίησης πηγής του Lempel-Ziv. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-2
22 Ο Αλγόριθµος Huffman Κωδικοποίησης Πηγής Στην κωδικοποίηση Huffman µπλοκ συµβόλων σταθερού µήκους από τη έξοδο της πηγής απεικονίζονται σε µεταβλητού µήκους µπλοκ δυαδικών συµβόλων. Αυτό καλείται κωδικοποίηση από σταθερό σε µεταβλητό µπλοκ. Οι συχνότερα εµφανιζόµενες ακολουθίες εξόδου σε βραχύτερες δυαδικές ακολουθίες Στην κωδικοποίηση µεταβλητού µήκους πρέπει να υπάρχει ένας και µοναδικός τρόπος για να διαχωρίζουµε τη λαµβανόµενη δυαδική ακολουθία σε κωδικές λάξεις Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-22
23 Κωδικές Λέξεις Σύµβολο a a 2 a 3 a 4 a 5 Πιθανότητα p = 2 p 2 = p 4 3 = p 8 4 = p 6 5 = 6 Κώδικας Κώδικας 2 Κώδικας 3 Κώδικας 4 αυτό-συγχρονιζόµενοι κώδικες άµεσος µονοσήµαντα αποκωδικοποιήσιµοι µη µονοσήµαντα αποκωδικοποιήσιµος Στουςκώδικες και 3 καµίακωδικήλέξηδενείναιπρόθεµαµιαςάλληςλέµεότι ικανοποιούν τη συνθήκη προθέµατος. Γιατοκώδικα τοµέσοµήκοςλέξηςείναι E(L) = 3/6. Ενώγιατοκώδικα 3 το µέσο µήκος λέξης είναι E(L) = 3/6. Ο ποιο ενδιαφέρων είναι ο κώδικας 3 και είναι ένα παράδειγµα κώδικα Huffman. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-23
24 ιατάξτε τις εξόδους της πηγής κατά φθίνουσα σειρά των πιθανοτήτων τους Σεραφείµ Καραµπογιάς Συγχωνεύστε τις δύο λιγότερο πιθανές εξόδους σε µία µοναδική έξοδο, και θέστε ως πιθανότητα της το άθροισµα των δύο πιθανοτήτων Αν ο αριθµός των εξόδων που αποµένουν είναι 2, τότε προχωρήστε στο επόµενο βήµα. ιαφορετικά, επανέλθετε στο βήµα. Αυθαίρετα αντιστοιχίστε το και το ως κωδικές λέξεις για τις δύο εξόδους που αποµένουν Αν µια έξοδος είναι το αποτέλεσµα της συγχώνευσης δύο εξόδων σε προηγούµενο βήµα, προσαρτήστεστηντρέχουσακωδικήλέξη καιτο γιανααποκτήσετετηνκωδικήλέξηγια τις προηγούµενες εξόδους το βήµα 5. Αν καµία έξοδος δεν προηγείται άλλης σταµατήστε. p = 2 p 2 = p 3 = p 4 = p 5 = Πηγές Πληροφορίας και Κωδικοποίηση Πηγής
25 Έχουµεήδηδειότιοικώδικες Huffmanείναιβέλτιστοιµετηνέννοιαότιγιαµια δεδοµένηπηγήπαρέχουνκώδικα µεελάχιστοµέσοµήκοςκωδικήςλέξης. Οι κώδικες Huffman παρουσιάζουν ισχυρή εξάρτηση από τις πιθανότητες (τη στατιστική) της πηγής. Η στατιστική της πηγής πρέπει να είναι γνωστή από πριν για νασχεδιάσουµεένανκώδικα Huffman. Το άλλο πρόβληµα µε τους κώδικες Huffman είναι ότι αν ο κώδικας είναι σχεδιασµένος για µπλοκ µήκους ενός συµβόλου αξιοποιεί µόνο τη συχνότητα εµφάνισηςτωνσυµβόλωντηςπηγήςκαιόχιτηµνήµητης. Ο αλγόριθµος Lempel-Ziv Ο αλγόριθµος Lempel-Ziv ανήκει στην κατηγορία των καθολικών (universal) αλγορίθµων κωδικοποίησης πηγής, δηλαδή αλγορίθµων που είναι ανεξάρτητοι από τη στατιστική της πηγής. Ο αλγόριθµος αυτός είναι ένα σχήµα κωδικοποίησηςαπόµπλοκµεταβλητούµήκουςσεσταθερούµήκους. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-25
26 ... Περιεχόµενο Λεξικού Κωδική Λέξη ιευθύνσεις Λεξικού Σεραφείµ Καραµπογιάς Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-26
27 Η αµοιβαία πληροφορία µεταξύ δύο διακριτών µεταβλητών X και Y δηλώνεται µε I(X;Y) και ορίζεται από την I ( X ; Y) = H ( X ) H ( X Y ) Η H(X) - H(X Y) είναι η ποσότητα πληροφορίας που παρέχεται από την τυχαία µεταβλητήυγιατηντυχαίαµεταβλητή X. Με άλλα λόγια αποτελεί ένα µέτρο της πληροφορίας της τυχαίας µεταβλητής X που περιέχεται στη µεταβλητή Y. Μίασηµαντικήιδιότηταείναι I ( X; Y ) = H ( X ) + H ( Y ) H ( X, Y ). Παράδειγµα Έστω X και Y δυαδικέςτυχαίεςµεταβλητέςµε P( X =, Y= ) = P( X =,Y = ) = P( X =, Y = ) = /3. ΝαβρεθείηI( X; Y ) Παρατηρούµεότι P( X = ) = P( Y = ) = 2/3, εποµένωςη( Χ ) = Η( Y ) =,99. Το ζεύγος (X,Y) είναι ένα τυχαίο διάνυσµα κατανεµηµένο οµοιόµορφα σε τιµές (,), (,) και (,) εποµένωςη( Χ, Υ ) = log3 =,585 καιη(χ Υ ) = Η ( Χ, Υ ) Η ( Υ ) =,666. Άρα I ( X; Y ) = H ( X ) H ( X Y ) =,253. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-27
28 Κωδικοποίηση µε απώλειες - Προβλήµατα Σεραφείµ Καραµπογιάς Αν η έξοδος µιας συνεχούς πηγής αναπαρασταθεί µε πεπερασµένο αριθµό bits/σύµβολο τότε πόσο κοντά µπορεί να είναι η συµπιεσµένη έκδοση µε την αρχική; Ανοαριθµόςτωνδιαθέσιµων bits/έξοδοείναιµικρότεροςαπό H ( X ), δενείναι δυνατή η ανάκτηση της πηγής χωρίς σφάλµατα και µερικά σφάλµατα θα είναι αναπόφευκτα. Για δεδοµένο αριθµό bits/σύµβολο, ποιος είναι ο ελάχιστος ρυθµός σφαλµάτων που µπορεί να επιτευχθεί; Ποιος είναι ο ελάχιστος αριθµών bits/έξοδο που απαιτείται για να αναπαραγάγουµε την πηγή µε καθορισµένο επίπεδο παραµόρφωσης. Ένα καλό µέτρο παραµόρφωσης, δηλαδή, ένα µέτρο της πιστότητας ή εγγύτητας της αναπαραγόµενης προς την αρχική έξοδο της πηγής, πρέπει να ικανοποιεί τις ιδιότητες Πρέπει να είναι µια καλή προσέγγιση της διαδικασίας αντίληψης Πρέπει να είναι απλό, ώστε να είναι µαθηµατικά εύχρηστο. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-28
29 Παραµόρφωση Hamming Σεραφείµ Καραµπογιάς Γενικά, ένα µέτρο παραµόρφωσης είναι η απόσταση µεταξύ του x και της αναπαραγωγής του x. ˆ Στη διακριτή περίπτωση ένα µέτρο παραµόρφωσης, είναι η παραµόρφωση Hamming, µεταξύ του και της αναπαραγωγής του, που ορίζεται από την x ) ), x x d H ( x, x) =, αλλιώς x ) Στη συνεχή περίπτωση χρησιµοποιείται η παραµόρφωση του τετραγωνικού σφάλµατος. ) ) d H ( x, x) = ( x x) 2 Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-29
30 Συνάρτηση Ρυθµού-Παραµόρφωσης Μέτρο παραµόρφωσης ανά γράµµα µιας ακολουθίας συµβόλων είναι d n n ) n ( ) = ) x, x d( x, x ) n i= Αφού η έξοδος µιας πηγής είναι µία τυχαία διαδικασία, το τυχαία µεταβλητή. i i d n n (, X ) X ) είναι µία Ορίζουµε ως παραµόρφωση για την πηγή την αναµενόµενη τιµή της τυχαίας αυτής µεταβλητής, δηλαδή, ) n n n ) ) D= E[ d( X, X )] = E[ d( X i, X i) ] = E[ d( X, X) ] n i= Σεραφείµ Καραµπογιάς στο τελευταίο βήµα χρησιµοποιήθηκε η παραδοχή της στατικότητας της πηγής Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-3
31 Η αρχική µας ερώτηση µπορεί να επαναδιατυπωθεί ως εξής: Για µια δεδοµένη πηγή πληροφορίας χωρίς µνήµη µε αλφάβητο X και κατανοµή πιθανότητας p(x), ένα αλφάβητο ανακατασκευής X και ένα µέτρο παραµόρφωσης d(x, x) πουορίζεταιγιαόλατα x X και x X, ποιος είναι ο ελάχιστος αριθµός των bits/έξοδο, R, της πηγής που απαιτείται για να εξασφαλίζει ότι η µέση παραµόρφωση µεταξύ της ακολουθίας εξόδου της πηγής και της αντίστοιχης ανακτηθείσας εξόδου της πηγής δεν υπερβαίνει κάποια συγκεκριµένη D. O R είναι µία φθίνουσα συνάρτηση της D. Η σχέση µεταξύ R και D δίνεται από τη συνάρτηση ρυθµού-παραµόρφωσης R ( D) = p ( X X) min ) I ; ) ( x x) : E[ d( X, X )] D ) Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-3
32 n X R R 2 R 2 nr R R 3 4 R i nr i 2 nr bits K Κωδικοποιητής Αποκωδικοποιητής ) ) x i X n x ) i n x X Ο χώρος των ακολουθιών εξόδου µήκους n, δηλαδή ο X n nr χωρίζεται σε 2 περιοχές n Ανηέξοδος x τηςπηγήςανήκειστηνπεριοχή i, ηδυαδικήαναπαράστασητου i διαβιβάζεται στον αποκωδικοποιητή. nr Επειδή i 2, η δυαδική αναπαράσταση είναι µήκους nr, εποµένως η κωδικοποίηση γίνεται σ ένα ρυθµό R bits/έξοδο πηγής. Ο αποκωδικοποιητής, αφού λάβει τη δυαδική αναπαράσταση του i, παράγει µια προκαθορισµένη ακολουθία x ) n τέτοια ώστε η µέση απόσταση (παραµόρφωση) από τις x ακολουθίες στην περιοχή i να είναι ελάχιστη. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6-32
( ) log 2 = E. Σεραφείµ Καραµπογιάς
 Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
ιαφορική εντροπία Σεραφείµ Καραµπογιάς
 ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
Θεώρημα κωδικοποίησης πηγής
 Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Ψηφιακές Τηλεπικοινωνίες. Θεωρία Ρυθμού Παραμόρφωσης
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Σεραφείµ Καραµπογιάς. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6.3-1
 Ο αλγόριθµος Lempel-iv Ο αλγόριθµος Lempel-iv ανήκει στην κατηγορία των καθολικών universal αλγορίθµων κωδικοποίησης πηγής δηλαδή αλγορίθµων που είναι ανεξάρτητοι από τη στατιστική της πηγής. Ο αλγόριθµος
Ο αλγόριθµος Lempel-iv Ο αλγόριθµος Lempel-iv ανήκει στην κατηγορία των καθολικών universal αλγορίθµων κωδικοποίησης πηγής δηλαδή αλγορίθµων που είναι ανεξάρτητοι από τη στατιστική της πηγής. Ο αλγόριθµος
Εισαγωγή στη θεωρία πληροφορίας
 Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Τι είναι σήµα; Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές.
 Τι είναι σήµα; Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές. Παραδείγµατα: Σήµα οµιλίας x 1 Πίεση x P(t) t Σήµα εικόνας
Τι είναι σήµα; Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές. Παραδείγµατα: Σήµα οµιλίας x 1 Πίεση x P(t) t Σήµα εικόνας
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Κωδικοποίηση Πηγής Ψηφιακή Μετάδοση Υπάρχουν ιδιαίτερα εξελιγμένες τεχνικές αναλογικής μετάδοσης (που ακόμη χρησιμοποιούνται σε ορισμένες εφαρμογές) Επίσης,
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Κωδικοποίηση Πηγής Ψηφιακή Μετάδοση Υπάρχουν ιδιαίτερα εξελιγμένες τεχνικές αναλογικής μετάδοσης (που ακόμη χρησιμοποιούνται σε ορισμένες εφαρμογές) Επίσης,
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πιθανότητες Πληροφορία Μέτρο
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πιθανότητες Πληροφορία Μέτρο
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
Θεωρία πληροφοριών. Τεχνολογία Πολυµέσων 07-1
 Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 4η διάλεξη (4η έκδοση, 11/3/2013)
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 4η διάλεξη (4η έκδοση, 11/3/2013) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 5 Μαρτίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 4η διάλεξη (4η έκδοση, 11/3/2013) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 5 Μαρτίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
0, αλλιώς. Σεραφείµ Καραµπογιάς. Παράδειγµα 1 Η πηγή X(t) είναι στατική Gaussian µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος.
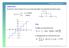 Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πληροφορία Μέτρο πληροφορίας Μέση πληροφορία ή Εντροπία Από κοινού εντροπία
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πληροφορία Μέτρο πληροφορίας Μέση πληροφορία ή Εντροπία Από κοινού εντροπία
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
( x) Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ. Βασικά αξιώµατα και ιδιότητες της πιθανότητας. Σεραφείµ Καραµπογιάς
 Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ Βασικά αξιώµατα και ιδιότητες της πιθανότητας Σεραφείµ Καραµπογιάς Η αθροιστική συνάρτηση κατανοµής cumulaive diribuio ucio CDF µίας τυχαίας µεταβλητής X ορίζεται
Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ Βασικά αξιώµατα και ιδιότητες της πιθανότητας Σεραφείµ Καραµπογιάς Η αθροιστική συνάρτηση κατανοµής cumulaive diribuio ucio CDF µίας τυχαίας µεταβλητής X ορίζεται
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 2η διάλεξη (3η έκδοση, 11/3)
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 2η διάλεξη (3η έκδοση, 11/3) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 19 Φεβρουαρίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 2η διάλεξη (3η έκδοση, 11/3) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 19 Φεβρουαρίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
Τεχνολογία Πολυμέσων. Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια. Παράδοση: Έως 22/6/2015
 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ
 ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ 5. Εισαγωγή Ο σκοπός κάθε συστήματος τηλεπικοινωνιών είναι η μεταφορά πληροφορίας από ένα σημείο (πηγή) σ ένα άλλο (δέκτης). Συνεπώς, κάθε μελέτη ενός τέτοιου συστήματος
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ 5. Εισαγωγή Ο σκοπός κάθε συστήματος τηλεπικοινωνιών είναι η μεταφορά πληροφορίας από ένα σημείο (πηγή) σ ένα άλλο (δέκτης). Συνεπώς, κάθε μελέτη ενός τέτοιου συστήματος
Αναλογικές και Ψηφιακές Επικοινωνίες
 Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
Ασκήσεις στο µάθηµα «Επισκόπηση των Τηλεπικοινωνιών»
 Ασκήσεις στο µάθηµα «Επισκόπηση των Τηλεπικοινωνιών» Άσκηση 1 Πρόκειται να µεταδώσουµε δυαδικά δεδοµένα σε RF κανάλι µε. Αν ο θόρυβος του καναλιού είναι Gaussian - λευκός µε φασµατική πυκνότητα W, να βρεθεί
Ασκήσεις στο µάθηµα «Επισκόπηση των Τηλεπικοινωνιών» Άσκηση 1 Πρόκειται να µεταδώσουµε δυαδικά δεδοµένα σε RF κανάλι µε. Αν ο θόρυβος του καναλιού είναι Gaussian - λευκός µε φασµατική πυκνότητα W, να βρεθεί
Θεωρία Πληροφορίας. Διάλεξη 5: Διακριτή πηγή πληροφορίας με μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 5: Διακριτή πηγή πληροφορίας με μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Διακριτές πηγές πληροφορίας με μνήμη Μαρκοβιανές αλυσίδες Τάξη μακροβιανών αλυσίδων
Θεωρία Πληροφορίας Διάλεξη 5: Διακριτή πηγή πληροφορίας με μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Διακριτές πηγές πληροφορίας με μνήμη Μαρκοβιανές αλυσίδες Τάξη μακροβιανών αλυσίδων
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ. Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Z
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o
 Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 12η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 12η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 2 Ιουνίου 2015 ηµήτρης-αλέξανδρος Τουµπακάρης Προχ. Θέµατα Θεωρίας Πληροφορίας 12η
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 12η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 2 Ιουνίου 2015 ηµήτρης-αλέξανδρος Τουµπακάρης Προχ. Θέµατα Θεωρίας Πληροφορίας 12η
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Θ.Ε. ΠΛΗ22 (2012-13) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #4. Έκδοση v2 με διόρθωση τυπογραφικού λάθους στο ερώτημα 6.3 Στόχος: Βασικό στόχο της 4 ης εργασίας αποτελεί η εξοικείωση με τα μέτρα ποσότητας πληροφορίας τυχαίων
Θ.Ε. ΠΛΗ22 (2012-13) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #4. Έκδοση v2 με διόρθωση τυπογραφικού λάθους στο ερώτημα 6.3 Στόχος: Βασικό στόχο της 4 ης εργασίας αποτελεί η εξοικείωση με τα μέτρα ποσότητας πληροφορίας τυχαίων
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 5: Βασική Θεωρία Πληροφορίας Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θέματα Συστημάτων Πολυμέσων Ενότητα # 5: Βασική Θεωρία Πληροφορίας Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Βασικά στοιχεία της θεωρίας πιθανοτήτων
 Η έννοια του Πειράµατος Τύχης. 9 3 6 Το σύνολο των πιθανών εκβάσεων ενός πειράµατος τύχης καλείται δειγµατοχώρος ή δειγµατικόςχώρος (sample space)καισυµβολίζεταιµεωήµε S.Έναστοιχείοωήsτου δειγµατικού χώρου
Η έννοια του Πειράµατος Τύχης. 9 3 6 Το σύνολο των πιθανών εκβάσεων ενός πειράµατος τύχης καλείται δειγµατοχώρος ή δειγµατικόςχώρος (sample space)καισυµβολίζεταιµεωήµε S.Έναστοιχείοωήsτου δειγµατικού χώρου
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 17 Μαΐου 2011 (2η έκδοση, 21/5/2011) ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 17 Μαΐου 2011 (2η έκδοση, 21/5/2011) ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
Θεωρία της Πληροφορίας 3 ο Εξάμηνο
 Σμήμα Πληροφορικής & Επικοινωνιών Θεωρία της Πληροφορίας 3 ο Εξάμηνο Τομέας Τηλεπικοινωνιών και Δικτύων Δρ. Αναστάσιος Πολίτης Καθηγητής Εφαρμογών 1 Διεξαγωγή και Εξέταση του Μαθήματος Μάθημα Πώς? 13 Διαλέξεις.
Σμήμα Πληροφορικής & Επικοινωνιών Θεωρία της Πληροφορίας 3 ο Εξάμηνο Τομέας Τηλεπικοινωνιών και Δικτύων Δρ. Αναστάσιος Πολίτης Καθηγητής Εφαρμογών 1 Διεξαγωγή και Εξέταση του Μαθήματος Μάθημα Πώς? 13 Διαλέξεις.
Πρόλογος 1. 1 Μαθηµατικό υπόβαθρο 9
 Πρόλογος 1 Μαθηµατικό υπόβαθρο 7 1 Μαθηµατικό υπόβαθρο 9 1.1 Η αριθµητική υπολοίπων.............. 10 1.2 Η πολυωνυµική αριθµητική............ 14 1.3 Θεωρία πεπερασµένων οµάδων και σωµάτων.... 17 1.4 Πράξεις
Πρόλογος 1 Μαθηµατικό υπόβαθρο 7 1 Μαθηµατικό υπόβαθρο 9 1.1 Η αριθµητική υπολοίπων.............. 10 1.2 Η πολυωνυµική αριθµητική............ 14 1.3 Θεωρία πεπερασµένων οµάδων και σωµάτων.... 17 1.4 Πράξεις
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής. Εντροπία Shannon
 Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής Εντροπία Shannon Ένα από τα βασικά ερωτήματα της θεωρίας της πληροφορίας ήταν ανέκαθεν το πώς θα μπορούσε να ποσοτικοποιηθεί η πληροφορία, ώστε να μπορούμε
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής Εντροπία Shannon Ένα από τα βασικά ερωτήματα της θεωρίας της πληροφορίας ήταν ανέκαθεν το πώς θα μπορούσε να ποσοτικοποιηθεί η πληροφορία, ώστε να μπορούμε
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Μάθημα Επισκόπηση των Τηλεπικοινωνιών
 Μάθημα Επισκόπηση των Τηλεπικοινωνιών Κωδικοποίηση Πηγής & Καναλιού Μάθημα 8 ο 9 ο ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Επισκόπηση των Τηλεπικοινωνιών Κωδικοποίηση Πηγής & Καναλιού Μάθημα 8 ο 9 ο ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Συμπίεση χωρίς Απώλειες
 Συμπίεση χωρίς Απώλειες Στόχοι της συμπίεσης δεδομένων: Μείωση του απαιτούμενου χώρου αποθήκευσης των δεδομένων. Περιορισμός της απαιτούμενης χωρητικότητας διαύλου επικοινωνίας για την μετάδοση. μείωση
Συμπίεση χωρίς Απώλειες Στόχοι της συμπίεσης δεδομένων: Μείωση του απαιτούμενου χώρου αποθήκευσης των δεδομένων. Περιορισμός της απαιτούμενης χωρητικότητας διαύλου επικοινωνίας για την μετάδοση. μείωση
Δίαυλος Πληροφορίας. Η λειτουργία του περιγράφεται από:
 Δίαυλος Πληροφορίας Η λειτουργία του περιγράφεται από: Πίνακας Διαύλου (μαθηματική περιγραφή) Διάγραμμα Διαύλου (παραστατικός τρόπος περιγραφής της λειτουργίας) Πίνακας Διαύλου Χρησιμοποιούμε τις υπό συνθήκη
Δίαυλος Πληροφορίας Η λειτουργία του περιγράφεται από: Πίνακας Διαύλου (μαθηματική περιγραφή) Διάγραμμα Διαύλου (παραστατικός τρόπος περιγραφής της λειτουργίας) Πίνακας Διαύλου Χρησιμοποιούμε τις υπό συνθήκη
Βασικά στοιχεία της θεωρίας πιθανοτήτων
 Η έννοια του Πειράµατος Τύχης. 9 3 Το σύνολο των πιθανών εκβάσεων ενός πειράµατος τύχης καλείται δειγµατοχώρος ήδειγµατικόςχώρος (sample space)καισυµβολίζεταιµεωήµε S.Έναστοιχείοω ή s του δειγµατικού χώρου
Η έννοια του Πειράµατος Τύχης. 9 3 Το σύνολο των πιθανών εκβάσεων ενός πειράµατος τύχης καλείται δειγµατοχώρος ήδειγµατικόςχώρος (sample space)καισυµβολίζεταιµεωήµε S.Έναστοιχείοω ή s του δειγµατικού χώρου
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 10η διάλεξη (2η έκδοση, 7/5/2013)
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 10η διάλεξη (2η έκδοση, 7/5/2013) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 23 Απριλίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 10η διάλεξη (2η έκδοση, 7/5/2013) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 23 Απριλίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
Ο Βέλτιστος Φωρατής. Σεραφείµ Καραµπογιάς
 Ο Βέλτιστος Φωρατής Ο φωρατής σήµατος, µε τη βοήθεια ενός κανόνα απόφασης, βασιζόµενος στην παρατήρηση του διανύσµατος, λαµβάνει µία απόφαση ως προς το µεταδιδόµενο σύµβολο, έτσι ώστε να µεγιστοποιείται
Ο Βέλτιστος Φωρατής Ο φωρατής σήµατος, µε τη βοήθεια ενός κανόνα απόφασης, βασιζόµενος στην παρατήρηση του διανύσµατος, λαµβάνει µία απόφαση ως προς το µεταδιδόµενο σύµβολο, έτσι ώστε να µεγιστοποιείται
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Τυχαίες μεταβλητές Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ Η απεικόνιση των εκβάσεων ενός πειράματος
Επεξεργασία Στοχαστικών Σημάτων Τυχαίες μεταβλητές Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ Η απεικόνιση των εκβάσεων ενός πειράματος
Κεφάλαιο 2 Πληροφορία και εντροπία
 Κεφάλαιο 2 Πληροφορία και εντροπία Άσκηση. Έστω αλφάβητο Α={0,} και δύο πηγές p και q. Έστω οτι p(0)=-r, p()=r, q(0)=-s και q()=s. Να υπολογιστούν οι σχετικές εντροπίες Η(Α,p/q) και Η(Α,q/p). Να γίνει
Κεφάλαιο 2 Πληροφορία και εντροπία Άσκηση. Έστω αλφάβητο Α={0,} και δύο πηγές p και q. Έστω οτι p(0)=-r, p()=r, q(0)=-s και q()=s. Να υπολογιστούν οι σχετικές εντροπίες Η(Α,p/q) και Η(Α,q/p). Να γίνει
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Κώστας Μπερμπερίδης Εργαστήριο Σημάτων & Τηλεπικοινωνιών Τμήμα Μηχανικών Η/Υ & Πληροφορικής Ψηφιακή Αναπαράσταση Συμπίεση
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Κώστας Μπερμπερίδης Εργαστήριο Σημάτων & Τηλεπικοινωνιών Τμήμα Μηχανικών Η/Υ & Πληροφορικής Ψηφιακή Αναπαράσταση Συμπίεση
KΕΦΑΛΑΙΟ 1 ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ. { 1,2,3,..., n,...
 KΕΦΑΛΑΙΟ ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ Βασικές έννοιες διαιρετότητας Θα συµβολίζουµε µε, τα σύνολα των φυσικών αριθµών και των ακεραίων αντιστοίχως: {,,3,,, } { 0,,,,, } = = ± ± ± Ορισµός Ένας φυσικός αριθµός
KΕΦΑΛΑΙΟ ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ Βασικές έννοιες διαιρετότητας Θα συµβολίζουµε µε, τα σύνολα των φυσικών αριθµών και των ακεραίων αντιστοίχως: {,,3,,, } { 0,,,,, } = = ± ± ± Ορισµός Ένας φυσικός αριθµός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
Μοντέλο Επικοινωνίας Δεδομένων. Επικοινωνίες Δεδομένων Μάθημα 6 ο
 Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
1 1 c c c c c c = 1 c = 1 28 P (Y < X) = P ((1, 2)) + P ((4, 1)) + P ((4, 3)) = 2 1/ / /28 = 18/28
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-17: Πιθανότητες -Χειµερινό Εξάµηνο 01 ιδάσκων : Π. Τσακαλίδης Λύσεις : Πέµπτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 14/11/01 Ηµεροµηνία Παράδοσης : 8/11/01
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-17: Πιθανότητες -Χειµερινό Εξάµηνο 01 ιδάσκων : Π. Τσακαλίδης Λύσεις : Πέµπτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 14/11/01 Ηµεροµηνία Παράδοσης : 8/11/01
Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Πληροφορικής ΠΜΣ Κρυπτογραφία και Εφαρμογές
 Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Πληροφορικής ΠΜΣ Κρυπτογραφία και Εφαρμογές Μαριάς Ιωάννης Μαρκάκης Ευάγγελος marias@aueb.gr markakis@gmail.com Περίληψη Shannon theory Εντροπία Μελέτη κρυπτοσυστηµάτων
Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Πληροφορικής ΠΜΣ Κρυπτογραφία και Εφαρμογές Μαριάς Ιωάννης Μαρκάκης Ευάγγελος marias@aueb.gr markakis@gmail.com Περίληψη Shannon theory Εντροπία Μελέτη κρυπτοσυστηµάτων
Τυχαία μεταβλητή (τ.μ.)
 Τυχαία μεταβλητή (τ.μ.) Τυχαία μεταβλητή (τ.μ.) είναι μια συνάρτηση X ( ) με πεδίο ορισμού το δειγματικό χώρο Ω του πειράματος και πεδίο τιμών ένα υποσύνολο πραγματικών αριθμών που συμβολίζουμε συνήθως
Τυχαία μεταβλητή (τ.μ.) Τυχαία μεταβλητή (τ.μ.) είναι μια συνάρτηση X ( ) με πεδίο ορισμού το δειγματικό χώρο Ω του πειράματος και πεδίο τιμών ένα υποσύνολο πραγματικών αριθμών που συμβολίζουμε συνήθως
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣΟΡ Κεφάλαιο 1 : Εισαγωγή στη Θεωρία ωία Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Έννοια της πληροφορίας Άλλες βασικές έννοιες Στόχος
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣΟΡ Κεφάλαιο 1 : Εισαγωγή στη Θεωρία ωία Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Έννοια της πληροφορίας Άλλες βασικές έννοιες Στόχος
Απαντήσεις σε απορίες
 Ερώτηση Η µέση ποσότητα πληροφορίας κατά Shannon είναι Η(Χ)=-Σp(xi)logp(xi)...σελ 28 Στο παραδειγµα.3 στη σελιδα 29 στο τέλος δεν καταλαβαίνω πως γίνεται η εφαρµογή του παραπάνω τύπου ηλαδη δεν βλεπω συντελεστη
Ερώτηση Η µέση ποσότητα πληροφορίας κατά Shannon είναι Η(Χ)=-Σp(xi)logp(xi)...σελ 28 Στο παραδειγµα.3 στη σελιδα 29 στο τέλος δεν καταλαβαίνω πως γίνεται η εφαρµογή του παραπάνω τύπου ηλαδη δεν βλεπω συντελεστη
Συστήµατα Πολυµέσων Ενδιάµεση Εξέταση: Οκτώβριος 2004
 Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Παλµοκωδική ιαµόρφωση
 Παλµοκωδική ιαµόρφωση Η παλµοκωδική διαµόρφωση (PCM) είαι το απλούστερο και αρχαιότερο σχήµα κωδικοποίησης κυµατοµορφής. Έας παλµοκωδικός διαµορφωτής αποτελείται από τρία βασικάµέρη: έαδειγµατολήπτηση,
Παλµοκωδική ιαµόρφωση Η παλµοκωδική διαµόρφωση (PCM) είαι το απλούστερο και αρχαιότερο σχήµα κωδικοποίησης κυµατοµορφής. Έας παλµοκωδικός διαµορφωτής αποτελείται από τρία βασικάµέρη: έαδειγµατολήπτηση,
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 10η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 10η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 21 Μαΐου 2015 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 10η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 21 Μαΐου 2015 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
Επεξεργασία Πολυµέσων. Δρ. Μαρία Κοζύρη Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας
 Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Τεράστιες ανάγκες σε αποθηκευτικό χώρο
 ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 6η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 6η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 24 Μαρτίου 2010 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 6η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 24 Μαρτίου 2010 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
Σημείωμα Αδειοδότησης
 Μελέτη Περιπτώσεων στη Λήψη Αποφάσεων Σημείωμα Αδειοδότησης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Μελέτη Περιπτώσεων στη Λήψη Αποφάσεων Σημείωμα Αδειοδότησης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια της τυχαίας ιαδικασίας Η έννοια της τυχαίας διαδικασίας, βασίζεται στην επέκταση της έννοιας της τυχαίας µεταβλητής, ώστε να συµπεριλάβει το χρόνο. Σεκάθεαποτέλεσµα s k ενόςπειράµατοςτύχης αντιστοιχούµε,
Η Έννοια της τυχαίας ιαδικασίας Η έννοια της τυχαίας διαδικασίας, βασίζεται στην επέκταση της έννοιας της τυχαίας µεταβλητής, ώστε να συµπεριλάβει το χρόνο. Σεκάθεαποτέλεσµα s k ενόςπειράµατοςτύχης αντιστοιχούµε,
Παράδειγµα ενός ηλεκτρικού συστήµατος
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός aplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος A R B i( ) i
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός aplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος A R B i( ) i
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
1 Βασικές Έννοιες Θεωρίας Πληροφορίας
 1 Βασικές Έννοιες Θεωρίας Πληροφορίας Εντροπία τυχαίων μεταβλητών X, Y : H(X) = E [log Pr(x)] (1) H(X, Y ) = E [log Pr(x, y)] (2) H(X Y ) = E [log Pr(x y)] (3) Ιδιότητες Εντροπίας: Νόμος Bayes: Pr(y x)
1 Βασικές Έννοιες Θεωρίας Πληροφορίας Εντροπία τυχαίων μεταβλητών X, Y : H(X) = E [log Pr(x)] (1) H(X, Y ) = E [log Pr(x, y)] (2) H(X Y ) = E [log Pr(x y)] (3) Ιδιότητες Εντροπίας: Νόμος Bayes: Pr(y x)
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
 Πολύγωνο αθροιστικών σχετικών συχνοτήτων και διάµεσος µιας τυχαίας µεταβλητής ρ. Παναγιώτης Λ. Θεοδωρόπουλος πρώην Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Πρόλογος Στην εργασία αυτή αναλύονται
Πολύγωνο αθροιστικών σχετικών συχνοτήτων και διάµεσος µιας τυχαίας µεταβλητής ρ. Παναγιώτης Λ. Θεοδωρόπουλος πρώην Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Πρόλογος Στην εργασία αυτή αναλύονται
Ευρυζωνικά δίκτυα (2) Αγγελική Αλεξίου
 Ευρυζωνικά δίκτυα (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Σήματα και πληροφορία Βασικές έννοιες 2 Αναλογικά και Ψηφιακά Σήματα Στις τηλεπικοινωνίες συνήθως χρησιμοποιούμε περιοδικά αναλογικά σήματα και
Ευρυζωνικά δίκτυα (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Σήματα και πληροφορία Βασικές έννοιες 2 Αναλογικά και Ψηφιακά Σήματα Στις τηλεπικοινωνίες συνήθως χρησιμοποιούμε περιοδικά αναλογικά σήματα και
Ψηφιακές Τηλεπικοινωνίες. Βέλτιστος Δέκτης
 Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Τηλεπικοινωνίες. Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων. Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ
 Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
22Α004 - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Τελική Εξέταση
 22A004 (eclass EE278) Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 11 Δ. Τουμπακάρης 6 Ιουνίου 2013 22Α004 - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Τελική Εξέταση Διάρκεια Εξέτασης: 3 ώρες. 4 ασκήσεις
22A004 (eclass EE278) Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 11 Δ. Τουμπακάρης 6 Ιουνίου 2013 22Α004 - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Τελική Εξέταση Διάρκεια Εξέτασης: 3 ώρες. 4 ασκήσεις
X(t) = A cos(2πf c t + Θ) (1) 0, αλλού. 2 cos(2πf cτ) (9)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
Στοχαστικές Στρατηγικές
 Στοχαστικές Στρατηγικές 3 η ενότητα: Εισαγωγή στα στοχαστικά προβλήματα διαδρομής Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές 3 η ενότητα: Εισαγωγή στα στοχαστικά προβλήματα διαδρομής Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Πίνακες Διασποράς. Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h. Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση
 Πίνακες Διασποράς Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση κλειδί k T 0 1 2 3 4 5 6 7 U : χώρος πιθανών κλειδιών Τ : πίνακας μεγέθους
Πίνακες Διασποράς Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση κλειδί k T 0 1 2 3 4 5 6 7 U : χώρος πιθανών κλειδιών Τ : πίνακας μεγέθους
Σήματα και Συστήματα. Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Μάθημα 7 ο. Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
ΚΑΤΑΝΟΜΕΣ ΠΙΘΑΝΟΤΗΤΑΣ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια)
 ΚΑΤΑΝΟΜΕΣ ΠΙΘΑΝΟΤΗΤΑΣ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια) Χαράλαµπος Α. Χαραλαµπίδης 9 Νοεµβρίου 2009 ΣΥΝΑΡΤΗΣΗ ΠΥΚΝΟΤΗΤΑΣ ΠΙΘΑΝΟΤΗΤΑΣ Ορισµός Μία τυχαία µεταβλητή X καλείται διακριτή ή απαριθµητή αν παίρνει
ΚΑΤΑΝΟΜΕΣ ΠΙΘΑΝΟΤΗΤΑΣ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια) Χαράλαµπος Α. Χαραλαµπίδης 9 Νοεµβρίου 2009 ΣΥΝΑΡΤΗΣΗ ΠΥΚΝΟΤΗΤΑΣ ΠΙΘΑΝΟΤΗΤΑΣ Ορισµός Μία τυχαία µεταβλητή X καλείται διακριτή ή απαριθµητή αν παίρνει
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 25 Απριλίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 25 Απριλίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
cov(x, Y ) = E[(X E[X]) (Y E[Y ])] cov(x, Y ) = E[X Y ] E[X] E[Y ]
![cov(x, Y ) = E[(X E[X]) (Y E[Y ])] cov(x, Y ) = E[X Y ] E[X] E[Y ] cov(x, Y ) = E[(X E[X]) (Y E[Y ])] cov(x, Y ) = E[X Y ] E[X] E[Y ]](/thumbs/52/30692583.jpg) Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-317: Εφαρµοσµένες Στοχαστικές ιαδικασίες-εαρινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης Συνδιασπορά - Συσχέτιση Τυχαίων Μεταβλητών Επιµέλεια : Κωνσταντίνα
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-317: Εφαρµοσµένες Στοχαστικές ιαδικασίες-εαρινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης Συνδιασπορά - Συσχέτιση Τυχαίων Μεταβλητών Επιµέλεια : Κωνσταντίνα
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές
 Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Συστήµατα τα οποία χαρακτηρίζονται από γραµµικές εξισώσεις διαφορών µε σταθερούς συντελεστές x h γραµµική εξίσωση διαφορών µε σταθερούς συντελεστές της µορφής x µπορεί να θεωρηθεί ως ένας αλγόριθµος υπολογισµού
Σεραφείµ Καραµπογιάς ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
Μέρος ΙΙ. Τυχαίες Μεταβλητές
 Μέρος ΙΙ. Τυχαίες Μεταβλητές Ορισμοί Συναρτήσεις κατανομής πιθανότητας και πυκνότητας πιθανότητας Διακριτές τυχαίες μεταβλητές Ειδικές κατανομές διακριτών τυχαίων μεταβλητών Συνεχείς τυχαίες μεταβλητές
Μέρος ΙΙ. Τυχαίες Μεταβλητές Ορισμοί Συναρτήσεις κατανομής πιθανότητας και πυκνότητας πιθανότητας Διακριτές τυχαίες μεταβλητές Ειδικές κατανομές διακριτών τυχαίων μεταβλητών Συνεχείς τυχαίες μεταβλητές
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Παρεµβολή και Προσέγγιση Συναρτήσεων
 Κεφάλαιο 4 Παρεµβολή και Προσέγγιση Συναρτήσεων 41 Παρεµβολή µε πολυώνυµο Lagrage Εστω ότι γνωρίζουµε τις τιµές µιας συνάρτησης f (x), f 0, f 1,, f ν σε σηµεία x 0, x 1,, x ν, και Ϲητάµε να υπολογίσουµε
Κεφάλαιο 4 Παρεµβολή και Προσέγγιση Συναρτήσεων 41 Παρεµβολή µε πολυώνυµο Lagrage Εστω ότι γνωρίζουµε τις τιµές µιας συνάρτησης f (x), f 0, f 1,, f ν σε σηµεία x 0, x 1,, x ν, και Ϲητάµε να υπολογίσουµε
5.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
Κωδικοποίηση Πηγής. Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα):
 Κωδικοποίηση Πηγής Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα): Coder Decoder Μεταξύ πομπού-καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας
Κωδικοποίηση Πηγής Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα): Coder Decoder Μεταξύ πομπού-καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 2004., η οποία όµως µπορεί να γραφεί µε την παρακάτω µορφή: 1 e
 ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
Περιεχόµενα ΕΠΛ 422: στα Συστήµατα Πολυµέσων. Βιβλιογραφία. ειγµατοληψία. ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων
 Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Ψηφιακή Αναπαράσταση Σήµατος: ειγµατοληψία Βιβλιογραφία ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων Βασικές Έννοιες Επεξεργασίας Σηµάτων Ψηφιοποίηση
Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Ψηφιακή Αναπαράσταση Σήµατος: ειγµατοληψία Βιβλιογραφία ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων Βασικές Έννοιες Επεξεργασίας Σηµάτων Ψηφιοποίηση
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Αρχές κωδικοποίησης. Τεχνολογία Πολυµέσων 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Γραφική αναπαράσταση ενός ψηφιακού σήµατος
 γ) Ψηφιακάτα x (n) 3 2 1 1 2 3 n Γραφική αναπαράσταση ενός ψηφιακού σήµατος Αφού δειγµατοληπτηθεί και κβαντιστεί η έξοδος µιας αναλογικής πηγής πληροφορίας, δηµιουργείταιµιαακολουθίααπόκβαντισµένεςτιµές
γ) Ψηφιακάτα x (n) 3 2 1 1 2 3 n Γραφική αναπαράσταση ενός ψηφιακού σήµατος Αφού δειγµατοληπτηθεί και κβαντιστεί η έξοδος µιας αναλογικής πηγής πληροφορίας, δηµιουργείταιµιαακολουθίααπόκβαντισµένεςτιµές
