ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
|
|
|
- Ἁλκυόνη Μακρή
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ VII. ΣΤΟΙΧΕΙΑ ΘΡΑΥΣΕΟΜΗΧΑΝΙΚΗΣ. Εισαγωγή Θραύση (fracture) ονοµάζεται ο διαχωρισµός, ή θρυµµατισµός, ενός στερεού σώµατος σε δύο ή περισσότερα κοµµάτια, κάτω από την επίδραση µηχανικών τάσεων. Η διαδικασία της θραύσης µπορεί να θεωρηθεί ότι αποτελείται από δύο διακριτά στάδια: την πυρήνωση (initiation) και την προώθηση (propagation) ρηγµάτων. Η θραύση των υλικών γενικά διακρίνεται σε δύο µεγάλες κατηγορίες: όλκιµη (ductile) και ψαθυρή (brittle). Η όλκιµη θραύση χαρακτηρίζεται από το µεγάλο ποσοστό πλαστικής παραµόρφωσης που υφίσταται το υλικό, πριν και κατά τη διάρκεια προώθησης των ρηγµάτων, τα οποία τελικά επιφέρουν τη θραύση. Αντίθετα, η ψαθυρή θραύση χαρακτηρίζεται από την µεγάλη ταχύτητα µε την οποία προωθούνται τα ρήγµατα στο υλικό, χωρίς να προκαλέσουν πλαστική παραµόρφωση. Η πιθανότητα εµφάνισης ψαθυρής θραύσης αυξάνεται µε µείωση της θερµοκρασίας, µε αύξηση της ταχύτητας φόρτισης και µε την παρουσία εγκοπών ή άλλων ασυνεχειών στο υλικό. Η ψαθυρή θραύση, ακριβώς επειδή συµβαίνει ακαριαία και χωρίς προειδοποίηση, είναι συνήθως ιδιαίτερα καταστροφική και ο σχεδιασµός κατασκευών πρέπει να γίνεται µε βασικό κριτήριο την αποφυγή της. Στην ενότητα αυτή θα εξετάσουµε µερικές από τις βασικές αρχές που διέπουν την µηχανική συµπεριφορά µεταλλικών υλικών που περιέχουν ρήγµατα (cracks). Θα εξετάσουµε δηλαδή τις βασικές αρχές του κλάδου της µηχανικής που ασχολείται µε τη θραύση και είναι γενικότερα γνωστός µε τον όρο θραυσεοµηχανική (fracture mechanics). Όµως, πριν περάσουµε στη συζήτηση για την συµπεριφορά των µεταλλικών υλικών παρουσία ρηγµάτων, έχει ενδιαφέρον να δούµε επιγραµµατικά τις µεταβολές που επιφέρει στην εντατική κατάσταση ενός υλικού η ύπαρξη ασυνεχειών (discontinuities). 39
2 . Συγκέντρωση Τάσεων σε Ασυνέχειες Η ύπαρξη µιας γεωµετρικής ασυνέχειας σε ένα υλικό, όπως για παράδειγµα µία τρύπα ή µία εγκοπή, έχει σαν αποτέλεσµα την δηµιουργία ανοµοιόµορφης κατανοµής της τάσης κοντά στην περιοχή της ασυνέχειας. Αυτό σηµαίνει ότι κοντά στην ασυνέχεια οι τάσεις έχουν πολύ µεγαλύτερη τιµή, από ότι σε σηµεία του υλικού που βρίσκονται µακριά από την ασυνέχεια. Εποµένως, στις περιοχές ασυνέχειας του υλικού εµφανίζεται συγκέντρωση τάσεων (stress concentration). Το Σχ. δείχνει ένα έλασµα που καταπονείται σε µονοαξονικό εφελκυσµό και το οποίο περιέχει µία οπή κυκλικής γεωµετρίας. Εάν δεν υπήρχε η οπή, τότε η ορθή εφελκυστική τάση θα ήταν οµοιόµορφα κατανεµηµένη σε όλη την επιφάνεια διατοµής του ελάσµατος και θα είχε παντού την τιµή σ nom που φαίνεται στο Σχ.. Η παρουσία της οπής επιφέρει ανοµοιόµορφη κατανοµή της ορθής εφελκυστικής τάσης, η οποία ακριβώς στα όρια της οπής εµφανίζει ένα µέγιστο σ max και καθώς αποµακρυνόµαστε από την οπή µειώνεται σταδιακά, µέχρις ότου φτάσει στην τιµή σ nom, Σχ.. Σχ. : Συγκέντρωση τάσεων σε έλασµα µε κυκλική οπή. 40
3 Η ποσοτικοποίηση της συγκέντρωσης τάσεων γίνεται µε τη χρήση ενός θεωρητικού συντελεστή συγκέντρωσης τάσεων, K t. Γενικά, ο συντελεστής K t εκφράζει τον λόγο της µέγιστης τάσης που εµφανίζεται κοντά στην ασυνέχεια, ως προς την τάση που επικρατεί µακριά από αυτήν. Χρησιµοποιώντας τα σύµβολα του Σχ., ο συντελεστής K t ορίζεται ως εξής: K t σ = max () σ nom Εκτός του ότι µία ασυνέχεια δηµιουργεί συγκέντρωση τάσεων κοντά της, µεταβάλλει τοπικά και την εντατική κατάσταση του υλικού. Ακόµη δηλαδή και αν γενικά στο υλικό η εντατική κατάσταση είναι απλός µονοαξονικός εφελκυσµός, κοντά στην ασυνέχεια η εντατική κατάσταση γίνεται σύνθετη (διαξονική ή τριαξονική). Για παράδειγµα, στην περίπτωση του Σχ., όπου η εντατική κατάσταση είναι απλός µονοαξονικός εφελκυσµός, κοντά στην οπή η εντατική κατάσταση είναι σύνθετη, αφού αναπτύσσονται οι ορθές τάσεις σ r (µε φορά ακτινικά προς την οπή) και σ θ (µε φορά εφαπτοµενικά προς την οπή) και η διατµητική τάση τ θr. (Κάτι αντίστοιχο συµβαίνει και στην περιοχή του λαιµού σε ένα δοκίµιο εφελκυσµού.) Για το συγκεκριµένο παράδειγµα του Σχ. έχει αποδειχθεί ότι η εντατική κατάσταση κοντά στην κυκλική οπή περιγράφεται από τις εξής σχέσεις: 4 σ α σ α α σ = 3 4 cos θ r r r r () 4 σ α σ α σ θ = 3 cos θ r r (3) 4 σ α α τ θ = 3 sin θ 4 + r r r (4) όπου σ η οµοιόµορφη τάση που επικρατεί µακριά από την οπή (δηλαδή στο παράδειγµά µας η σ nom ), α η ακτίνα της κυκλικής οπής και r και θ οι συντεταγµένες οποιουδήποτε σηµείου του υλικού σε σχέση µε το κέντρο της οπής. 4
4 Εξετάζοντας τις Εξ. () (4) διαπιστώνουµε ότι η µέγιστη τάση εµφανίζεται στο σηµείο Α του Σχ., για το οποίο θ = π/ και r = α. Στο σηµείο εκείνο η εντατική κατάσταση είναι σ θ = 3σ = σ max, σ r = 0 και τ θr = 0. Εποµένως, ο συντελεστής συγκέντρωσης τάσεων για την περίπτωση ελάσµατος (πλάκας) µε κυκλική οπή σε µονοαξονικό εφελκυσµό είναι K t = 3. Περαιτέρω εξέταση των Εξ. () (4) µας δείχνει ότι για θ = 0 και r = α, που αντιστοιχεί στο σηµείο Β του Σχ., έχουµε σ θ = -σ, σ r = 0 και τ θr = 0. Άρα, το σηµείο Β του υλικού υφίσταται θλίψη σε µία διεύθυνση κάθετη προς το επιβαλλόµενο εξωτερικό εφελκυστικό φορτίο. Μία άλλη ενδιαφέρουσα περίπτωση είναι αυτή του Σχ., όπου έχουµε ένα έλασµα σε µονοαξονικό εφελκυσµό, στο οποίο υπάρχει ελλειψοειδής εγκοπή µε ηµιάξονες a και b. Η µέγιστη τάση στα άκρα της εγκοπής δίδεται από τη σχέση: a σ + max = σ (5) b σ σ Σχ. : Έλασµα µε ελλειψοειδή εγκοπή σε µονοαξονικό εφελκυσµό. 4
5 Παρατηρήστε ότι όταν a = b (όταν δηλαδή έχουµε κυκλική οπή) τότε σ max = 3σ, αποτέλεσµα που βρήκαµε και παραπάνω. Παρατηρήστε ακόµη ότι στην Εξ. (5) η τιµή της µέγιστης τάσης είναι ευθέως ανάλογη του λόγου a/b. Εποµένως, για µία πολύ στενή και επιµήκη εγκοπή (a >> b), κάτι που για παράδειγµα ισχύει στα ρήγµατα, δηµιουργείται πολύ υψηλή συγκέντρωση τάσεων στα άκρα της εγκοπής (δηλαδή, αν ήταν ρήγµα, στις αιχµές του ρήγµατος). υστυχώς, αναλυτικές λύσεις για τον καθορισµό της συγκέντρωσης τάσεων υπάρχουν διαθέσιµες µόνο για πολύ απλές γεωµετρίες ασυνεχειών και για σχετικά απλές εντατικές καταστάσεις, σαν αυτές που είδαµε παραπάνω. Στην πράξη, για πιο περίπλοκες περιπτώσεις, αναγκαζόµαστε να καταφύγουµε στο πείραµα. Ωστόσο, στο Σχ. 3 συνοψίζονται διαγράµµατα που δίνουν το K t σαν συνάρτηση των γεωµετρικών χαρακτηριστικών, για ορισµένα είδη ασυνεχειών και εντατικών καταστάσεων. 3. Θεωρητική Αντοχή Θραύσης Τα µεταλλικά υλικά έχουν τεράστια τεχνολογική αξία, επειδή καταφέρνουν να συνδυάζουν σε ικανοποιητικό βαθµό υψηλή µηχανική αντοχή και ολκιµότητα. Γενικά, η υψηλή αντοχή των µετάλλων οφείλεται στις δυνάµεις συνοχής (cohesive forces) που αναπτύσσονται µεταξύ των ατόµων τους. Οι δυνάµεις συνοχής είναι ουσιαστικά οι δυνάµεις του χηµικού δεσµού µεταξύ των ατόµων, οι οποίες αντιστέκονται στις εξωτερικές δυνάµεις και προσπαθούν να συγκρατήσουν τα άτοµα στις θέσεις ισορροπίας τους. Όπως είδαµε στην τεχνολογία υλικών, η δύναµη συνοχής µεταξύ δύο ατόµων µεταβάλλεται ανάλογα µε την απόσταση που τα χωρίζει. Το διάγραµµα του Σχ. 4 δείχνει τη µεταβολή αυτή. ύο άτοµα κανονικά ισορροπούν σε απόσταση r o (θέση ισορροπίας), όπου εκεί η δύναµη συνοχής µηδενίζεται. Αν κάποιος προσπαθήσει να αποµακρύνει τα άτοµα από τη θέση αυτή, επιβάλλοντας για παράδειγµα ένα εξωτερικό εφελκυστικό φορτίο, τότε ο χηµικός δεσµός που τα συνδέει προβάλλει αντίσταση και η δύναµη συνοχής αυξάνεται. Σε κάποια συγκεκριµένη απόσταση διαχωρισµού η δύναµη συνοχής παίρνει µία µέγιστη τιµή (σ th ). Αν η απόσταση των ατόµων αυξηθεί ακόµη περισσότερο, η δύναµη συνοχής µειώνεται και µετά από κάποια απόσταση µηδενίζεται, γεγονός που υποδηλώνει το σπάσιµο του δεσµού. 43
6 44 Σχ. 3
7 Εποµένως, η σ th εκφράζει ουσιαστικά την θεωρητική αντοχή σε θραύση ενός υλικού. Κι αυτό διότι για να πραγµατοποιηθεί η θραύση πρέπει το υλικό να αποσπαστεί σε δύο τουλάχιστον ξεχωριστά κοµµάτια, γεγονός που σηµαίνει ότι θα πρέπει να σπάσουν οι δεσµοί ανάµεσα στα άτοµα των δύο κοµµατιών. Εποµένως, για να συµβεί αυτό θα πρέπει η εξωτερικά επιβαλλόµενη τάση να ξεπεράσει την σ th. r o σ th Σχ. 4 Παρατηρήστε ακόµη ότι η σ th εκφράζει την θεωρητική αντοχή δύο γειτονικών κρυσταλλικών επιπέδων απέναντι σε µία ορθή τάση που προσπαθεί να τα αποµακρύνει κάθετα το ένα από το άλλο. Στην ενότητα της µικροπλαστικότητας των κρυστάλλων είχαµε δει την θεωρητική αντοχή µονοκρυστάλλου σε διάτµηση, τ th. Αυτή ήταν η αντίσταση που προέβαλε ένας τέλειος κρύσταλλος απέναντι σε µία διατµητική τάση που προσπαθούσε να προκαλέσει ολίσθηση ανάµεσα σε δύο παράλληλα κρυσταλλικά επίπεδα (βλ. σελ σηµειώσεων). Εκεί είχαµε παρατηρήσει ότι µία ορθή τάση δεν µπορούσε να προκαλέσει ολίσθηση, παρά µόνο κάθετη αποµάκρυνση των δύο επιπέδων µεταξύ τους. Ακριβώς αυτή την αντίσταση σε ορθές τάσεις που προσπαθούν να διαχωρίσουν δύο κρυσταλλικά επίπεδα εκφράζει η σ th. 45
8 Η θεωρητική αντοχή σε θραύση των περισσοτέρων υλικών έχει υπολογιστεί προσεγγιστικά σε σ th E/0, όπου Ε το µέτρο ελαστικότητας του υλικού. Η τιµή αυτή αντιστοιχεί σε µία πάρα πολύ υψηλή τάση (θυµηθείτε ότι το Ε των περισσοτέρων µετάλλων και κεραµικών είναι της τάξεως των µερικών δεκάδων GPa). Στην πραγµατικότητα, όµως, τα περισσότερα υλικά υφίστανται θραύση σε τάσεις από 0 έως και 000 φορές µικρότερες από την σ th. Η απόκλιση αυτή οφείλεται στο γεγονός ότι τα πραγµατικά υλικά περιέχουν ρήγµατα, στα οποία εµφανίζεται µεγάλη συγκέντρωση τάσεων. Έτσι, παρότι γενικά σε µία κατασκευή οι τάσεις µπορεί να είναι πολύ µικρότερες από την σ th, κοντά στα ρήγµατα οι τοπικές τάσεις είναι δυνατόν να ξεπερνούν την σ th, µε αποτέλεσµα να επέρχεται ψαθυρή θραύση του υλικού. Το πόσο πολύ εξασθενεί την αντίσταση ενός υλικού σε θραύση η παρουσία ρηγµάτων µπορεί να φανεί µε ένα απλό παράδειγµα. Ας υποθέσουµε ότι έχουµε ένα µεγάλο έλασµα που καταπονείται σε µονοαξονικό εφελκυσµό, στο οποίο υπάρχει ένα ελλειψοειδές ρήγµα, Σχ. 5. Το ρήγµα έχει µήκος α και η ακτίνα καµπυλότητας στις αιχµές του είναι ρ t. Σύµφωνα µε τα όσα είπαµε σε προηγούµενη παράγραφο, κοντά στο ρήγµα υπάρχει συγκέντρωση τάσεων. Η µέγιστη τάση εµφανίζεται στις αιχµές του ρήγµατος και ισούται µε: a a σ max = σ + σ ρ (6) t ρt Εποµένως, εάν το ρήγµα είναι αρκετά αιχµηρό (δηλαδή αν ρ t << α) η σ max µπορεί εύκολα να πάρει πολύ µεγάλη τιµή, ακόµη και αν η τάση µακριά από το ρήγµα (σ) είναι µικρή. Σχ. 5 46
9 4. Θεωρία Griffith για την Ψαθυρή Θραύση Πρώτος ο A. Griffith το 90 προσπάθησε να εξηγήσει την απόκλιση, ανάµεσα στην θεωρητική και στην πειραµατικά παρατηρούµενη αντοχή των υλικών σε θραύση. Παρότι σήµερα αναγνωρίζεται ότι η θεωρία Griffith ισχύει απόλυτα µόνο για πολύ ψαθυρά υλικά, όπως για παράδειγµα το γυαλί, οι ιδέες που εισήγαγε η θεωρία αυτή ήταν πολύ διαφωτιστικές και για την θραύση πιο όλκιµων υλικών, όπως είναι τα µέταλλα. Σύµφωνα µε την θεωρία αυτή, κάθε ψαθυρό υλικό περιέχει ένα πλήθος λεπτών ρηγµάτων, στα οποία δηµιουργείται συγκέντρωση τάσεων, έτσι ώστε οι τάσεις κοντά στα ρήγµατα να ξεπερνούν την θεωρητική αντοχή του υλικού σε θραύση, παρότι µακριά από τα ρήγµατα οι τάσεις µπορεί να βρίσκονται σε αρκετά χαµηλές τιµές. Όταν οποιοδήποτε από τα ρήγµατα αυτά προωθείται µέσα στο υλικό, τότε δηµιουργούνται δύο νέες ελεύθερες επιφάνειες, δηλαδή οι πλευρικές επιφάνειες του ρήγµατος. Όπως είναι γνωστό, κάθε ελεύθερη επιφάνεια χαρακτηρίζεται από ένα ποσό ενέργειας που λέγεται επιφανειακή ενέργεια (surface energy), η φυσική προέλευση της οποίας οφείλεται στο γεγονός ότι τα άτοµα στις ελεύθερες επιφάνειες έχουν ανικανοποίητους (δηλ. σπασµένους) χηµικούς δεσµούς και είναι πιο ευκίνητα απ ότι τα άτοµα στο εσωτερικό του υλικού. Κατά συνέπεια, µε την προώθηση του ρήγµατος και την αύξηση της ελεύθερης επιφάνειάς του, η συνολική ενέργεια του συστήµατος (δηλ. του υλικού) αυξάνεται κατά ένα ποσό, ίσο µε την επιφανειακή ενέργεια των νέων ελεύθερων επιφανειών που δηµιουργήθηκαν. Εποµένως, αφού γνωρίζουµε ότι κάθε φυσικό σύστηµα τείνει αυθόρµητα προς καταστάσεις όπου ελαχιστοποιείται η συνολική του ενέργεια, θα περίµενε κανείς ότι σε κανένα υλικό δεν θα έπρεπε να συµβαίνει αυθόρµητη προώθηση ρηγµάτων (δηλαδή θραύση), αφού έτσι θα αυξανόταν η συνολική ενέργεια του συστήµατος. Ωστόσο, το σπάσιµο χηµικών δεσµών που προκαλείται κατά την προώθηση ενός ρήγµατος οδηγεί σε µείωση µίας άλλης µορφής ενέργειας του υλικού, της ελαστικής ενέργειας παραµόρφωσης (elastic strain energy). Η ενέργεια αυτή οφείλεται στο έργο που παράγουν τα εξωτερικά φορτία που καταπονούν και παραµορφώνουν ελαστικά το υλικό. Η ενέργεια αυτή είναι αποθηκευµένη στο υλικό και όταν εκλείψουν τα εξωτερικά φορτία µηδενίζεται. Όταν ένα ρήγµα που προωθείται περάσει από ένα σηµείο του υλικού και το χωρίσει σε δύο τµήµατα, τα τµήµατα αυτά παύουν πλέον να βρίσκονται υπό τάση, µε αποτέλεσµα να απελευθερώνεται η ελαστική ενέργεια παραµόρφωσης που βρισκόταν αποθηκευµένη εκεί. 47
10 Εποµένως, η προώθηση ενός ρήγµατος στο υλικό επιφέρει µείωση της αποθηκευµένης ελαστικής ενέργειας και αύξηση της επιφανειακής ενέργειας στο σύστηµα. Εάν η µείωση της ελαστικής ενέργειας είναι µεγαλύτερη από την αύξηση της επιφανειακής ενέργειας, τότε η προώθηση του ρήγµατος οδηγεί σε µείωση της συνολικής ενέργειας του συστήµατος και εποµένως το σύστηµα τείνει αυθόρµητα προς την κατεύθυνση αυτή. Όταν συµβαίνει αυτό δηλαδή, το υλικό θέλει να υποστεί θραύση για να ελαχιστοποιήσει την συνολική του ενέργεια. Ας δούµε τώρα πώς µπορούµε να εκφράσουµε µε µαθηµατικό τρόπο το παραπάνω κριτήριο θραύσης. Για το σκοπό αυτό θα χρησιµοποιήσουµε το µοντέλο του Σχ. 6, που δείχνει ένα έλασµα µε πολύ µικρό πάχος σε σχέση µε τις υπόλοιπες διαστάσεις του, το οποίο περιέχει ένα ελλειπτικό εσωτερικό ρήγµα µήκους α (ή ένα ηµιελλειπτικό επιφανειακό ρήγµα µήκους α) και καταπονείται σε απλό εφελκυσµό. Σχ. 6 Η µείωση της ελαστικής ενέργειας παραµόρφωσης που οφείλεται στην ύπαρξη του ρήγµατος ισούται µε: 48
11 π α σ U el = (7) E όπου σ η τάση µακριά από το ρήγµα και Ε το µέτρο ελαστικότητας του υλικού. Αντίθετα, η αύξηση της επιφανειακής ενέργειας που οφείλεται στην ύπαρξη του ρήγµατος (δηλ. η ενέργεια των πλευρικών του επιφανειών) δίδεται από τη σχέση: U = 4 α γ (8) s s όπου γ s είναι η επιφανειακή ενέργεια ανά µονάδα επιφανείας του υλικού. Η µεταβολή της συνολικής ενέργειας του υλικού λόγω της ύπαρξης του ρήγµατος είναι: U = U el + U s (9) Σύµφωνα µε την θεωρία του Griffith, το ρήγµα θα προωθηθεί υπό σταθερή τάση σ εάν µια απειροστή αύξηση του µήκους του ρήγµατος dα τείνει να µειώσει ή έστω (οριακά) να αφήσει αµετάβλητη την συνολική ενέργεια του συστήµατος. ηλαδή: ( U ) d dα = d π α σ dα E f π α σ + 4α γ s = 0 E f + 4γ s = 0 (0) σ f = E γ s π α Η Εξ. (0) δίνει την τιµή της (µακροσκοπικής) τάσης που απαιτείται, για να προκαλέσει την προώθηση ενός µικροσκοπικού ρήγµατος σε ένα ψαθυρό υλικό, σαν συνάρτηση του µεγέθους του ρήγµατος. Παρατηρείστε ότι, όσο µεγαλύτερο είναι το µήκος του ρήγµατος, τόσο µικρότερη είναι η τάση που απαιτείται για να προκληθεί ψαθυρή θραύση του υλικού, δηλαδή τόσο µικρότερη η αντοχή του υλικού σε θραύση, σ f. Παρόµοιες σχέσεις, που υπολογίζουν την αντοχή σε θραύση σαν συνάρτηση του µεγέθους του ρήγµατος, προκύπτουν και σε προβλήµατα διαφορετικής γεωµετρίας ή εντατικής κατάστασης. Για παράδειγµα, εάν θεωρήσουµε ένα έλασµα µε πάχος πολύ µεγαλύτερο από 49
12 το µέγεθος του ρήγµατος (σε αντίθεση δηλαδή µε το παράδειγµα του Σχ. 0, όπου το πάχος του ελάσµατος θεωρήθηκε αµελητέο), τότε η εξίσωση Griffith παίρνει τη µορφή: σ f E γ s = ( ν ) π α () Όπως αναφέρθηκε και προηγουµένως, η θεωρία Griffith προβλέπει µε ικανοποιητική ακρίβεια την αντοχή σε θραύση ενός τέλεια ψαθυρού υλικού, δηλαδή ενός υλικού που δεν επιδέχεται καθόλου πλαστική παραµόρφωση. Τέτοια υλικά είναι το γυαλί και αρκετά ακόµη κεραµικά υλικά. Ωστόσο, όσον αφορά τα µέταλλα, ακόµη και τα πιο σκληρά µεταλλικά υλικά δεν είναι τελείως ψαθυρά, από την άποψη ότι πάντοτε επιδέχονται έστω και ένα πολύ µικρό ποσοστό πλαστικής παραµόρφωσης. Κατά συνέπεια, η εξίσωση Griffith δεν προβλέπει ποσοτικά µε µεγάλη ακρίβεια την αντοχή σε θραύση των µετάλλων. Έτσι, ο E. Orowan πρότεινε µία τροποποίηση της εξίσωσης Griffith για τα µεταλλικά υλικά, η οποία περιλαµβάνει έναν επιπλέον όρο, που αφορά την ενέργεια (γ p ) που απορροφά το µέταλλο όταν παραµορφώνεται πλαστικά κατά την προώθηση του ρήγµατος: σ f E ( γ s + γ p ) = π α E γ p α () Το γ s στο τελευταίο µέλος της Εξ. () µπορεί να απαλειφθεί, επειδή είναι πολύ µικρότερο του γ p. Αυτό συµβαίνει επειδή οι συνήθεις τιµές του γ p είναι της τάξεως των J/m, ενώ η επιφανειακή ενέργεια γ s κυµαίνεται συνηθέστερα µεταξύ J/m. 5. Ρυθµός Απελευθέρωσης Ενέργειας Παραµόρφωσης Όπως είδαµε προηγουµένως, η Εξ. () προβλέπει καλύτερα την αντοχή θραύσης στα µεταλλικά υλικά, αφού λαµβάνει υπόψη την ενέργεια γ p που απορροφά το υλικό που βρίσκεται µπροστά στις αιχµές του ρήγµατος για να παραµορφωθεί πλαστικά, καθώς αυτό προωθείται και σχηµατίζονται νέες επιφάνειες θραύσης. Ωστόσο, επειδή η ποσότητα γ p είναι πολύ δύσκολο να µετρηθεί πειραµατικά, καθώς συνδέεται µε ένα πολύ µικροσκοπικό φαινόµενο όπως είναι η προώθηση τόσο µικρών ρηγµάτων, ο G. Irwin το 958 εισήγαγε µία άλλη ποσότητα, που είναι απευθείας µετρήσιµη. Η ποσότητα αυτή συµβολίζεται µε G, 50
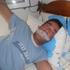
13 ονοµάζεται ρυθµός απελευθέρωσης ενέργειας παραµόρφωσης (strain-energy release rate) και εκφράζει τον ρυθµό µε τον οποίο απελευθερώνεται ελαστική ενέργεια από το υλικό κατά την διαδικασία προώθησης του ρήγµατος. Οι µονάδες µέτρησης του G είναι επίσης J/m, όπως και του γ p. Όταν το G πάρει µία κρίσιµη τιµή, τότε το ρήγµα γίνεται ασταθές, προωθείται ταχύτατα και προκαλεί θραύση του υλικού. Η κρίσιµη αυτή τιµή συµβολίζεται µε G c και ονοµάζεται κρίσιµος ρυθµός απελευθέρωσης ενέργειας παραµόρφωσης ή ενεργειακή δυσθραυστότητα (fracture toughness) του υλικού. Έτσι, η Εξ. () µπορεί τώρα να γραφτεί ως εξής: σ f = E Gc π α (3) όπου σ f η αντοχή του υλικού σε θραύση. Ας δούµε τώρα µε ποιο πείραµα µπορεί να µετρηθεί ο ρυθµός απελευθέρωσης ενέργειας παραµόρφωσης. Για την µέτρηση αυτή προετοιµάζεται ένα δοκίµιο του υλικού µε µία προκατασκευασµένη εγκοπή µήκους α, Σχ. 7α. Το δοκίµιο αρχικά υποβάλλεται σε ορισµένους κύκλους εναλλασσόµενης φόρτισης, µε σκοπό στην ρίζα της εγκοπής να δηµιουργηθεί ένα µικρό αρχικό ρήγµα λόγω κόπωσης. Στη συνέχεια, το δοκίµιο υποβάλλεται σε εφελκυσµό µε ένα συνεχώς αυξανόµενο εφελκυστικό φορτίο P. Με κάποιο κατάλληλο όργανο (σήµερα συνήθως χρησιµοποιείται κάποια δέσµη laser) καταγράφεται συνεχώς η αποµάκρυνση των πλευρικών επιφανειών του ρήγµατος, δ, σε σχέση µε το επιβαλλόµενο εφελκυστικό φορτίο. Μετρώντας το πόσο αποµακρύνονται µεταξύ τους οι πλευρικές επιφάνειες µας δείχνει ουσιαστικά και την κατά µήκος προώθηση του ρήγµατος, αφού όσο περισσότερο ανοίγει το ρήγµα τόσο αναπτύσσεται και προς τα εµπρός. Η φωτογραφία του Σχ. 8 δείχνει ένα πραγµατικό δοκίµιο κατά τη στιγµή εκτέλεσης του πειράµατος. Τα αποτελέσµατα του πειράµατος εκφράζονται σε διαγράµµατα P δ, σαν αυτό που φαίνεται στο Σχ. 7β. Στο συγκεκριµένο διάγραµµα υπάρχουν δύο γραµµές, οι οποίες αντιστοιχούν σε δύο δοκίµια µε διαφορετικό αρχικό µήκος ρήγµατος, α και α. Βλέπουµε ότι η σχέση µεταξύ φορτίου και µετατόπισης των πλευρικών επιφανειών του ρήγµατος είναι γραµµική, P = Μ δ, όπου Μ η κλίση της γραµµικής αυτής σχέσης. Η ελαστική ενέργεια 5
14 παραµόρφωσης (U o ) ισούται µε το εµβαδόν της επιφάνειας που βρίσκεται κάτω από την γραµµή, δηλαδή: P U o = P δ = (4) M (α) (β) Σχ. 7 Σχ. 8 5
15 Ας εξετάσουµε τώρα την περίπτωση του Σχ. 7β. Αν κατασκευάσουµε δοκίµιο µε ρήγµα αρχικού µήκους α, το φορτίο που απαιτείται ώστε να αποµακρυνθούν οι πλευρικές επιφάνειες του ρήγµατος κατά δ ισούται µε P. Ας υποθέσουµε ότι στη συνέχεια βάζουµε ένα άλλο δοκίµιο του ίδιου υλικού, µε ρήγµα αρχικού µήκους α > α. Το φορτίο που χρειάζεται για να αποµακρυνθούν οι πλευρικές επιφάνειες του ρήγµατος κατά µία απόσταση δ = δ είναι τώρα P < P. ηλαδή, τώρα που α > α αρκεί ένα µικρότερο φορτίο P για να προωθήσει εξίσου το ρήγµα. Έχουµε ότι: P = M δ P δ = M P = M δ δ P = M Όµως, δ = δ και εποµένως P /M = P /M. Βλέπουµε δηλαδή ότι ο λόγος P/M είναι σταθερός, ανεξάρτητα από το αρχικό µήκος ρήγµατος. Κατά συνέπεια, ισχύει ότι: ( P ) ( ) ( ) M α P P = 0 + P M = 0 = P M M (5) α M α α α Εξ ορισµού, ο ρυθµός απελευθέρωσης ενέργειας παραµόρφωσης G ισούται µε: U o P P G = = + P α M α ( ) M α (6) Αντικαθιστώντας το P/ α από την Εξ. (5) στην Εξ. (6) προκύπτει ότι: ( ) G = P M (7) α Για να καθορίσουµε την ενεργειακή δυσθραυστότητα ενός υλικού, πραγµατοποιούµε µια σειρά τέτοιων πειραµάτων σε δοκίµια µε διαφορετικό αρχικό µήκος εγκοπής, καθορίζουµε για κάθε δοκίµιο τον συντελεστή Μ και στη συνέχεια κατασκευάζουµε ένα διάγραµµα /Μ 53
16 α, από το οποίο µπορούµε να υπολογίσουµε το (/Μ)/ α. Η ενεργειακή δυσθραυστότητα υπολογίζεται µέσω της Εξ. (7), αν όπου P βάλουµε την τιµή P max, το φορτίο δηλαδή στο οποίο το ρήγµα γίνεται ασταθές και προωθείται ταχύτατα, προκαλώντας θραύση του δοκιµίου: ( ) Pmax G = M C (8) α 6. Ο Παράγοντας Έντασης Τάσεων Στην παράγραφο που µιλήσαµε για ασυνέχειες, είδαµε ότι κοντά σε αυτές η εντατική κατάσταση είναι ριζικά διαφορετική από εκείνη που επικρατεί σε άλλα τµήµατα του υλικού, που βρίσκονται µακριά από τις ασυνέχειες. Ακριβώς το ίδιο φαινόµενο παρατηρείται και στην περίπτωση των ρηγµάτων. Η εντατική κατάσταση που επικρατεί κοντά στις αιχµές ενός ρήγµατος, το οποίο βρίσκεται σε ένα λεπτό έλασµα που υποβάλλεται σε εφελκυσµό, Σχ. 9, δίδεται από τις παρακάτω σχέσεις: σ x α = σ r θ θ 3θ cos sin sin σ y α = σ r θ θ 3θ cos + sin sin (9) τ xy α = σ r θ θ sin cos cos 3θ 54
17 Σχ. 9 Οι Εξ. (9) ισχύουν όταν α > r > ρ, δηλαδή ισχύουν για αιχµηρά ρήγµατα και περιγράφουν τις τάσεις σε απόσταση από το ρήγµα µεγαλύτερη από την ακτίνα καµπυλότητας της αιχµής του. Ακριβώς µπροστά από την αιχµή του ρήγµατος (θ = 0) το τασικό πεδίο που αναπτύσσεται α είναι σ x = σ y = σ και τ xy = 0. r Οι Εξ. (9) δείχνουν ότι οι τοπικές τάσεις που επικρατούν κοντά σε ένα ρήγµα εξαρτώνται από το γινόµενο της (µακροσκοπικής) τάσης σ µακριά από το ρήγµα και της τετραγωνικής ρίζας του µεγέθους του ρήγµατος. Το γινόµενο αυτό ονοµάστηκε από τον Irwin παράγοντας έντασης τάσεων (stress intensity factor) Κ. Για ένα αιχµηρό ρήγµα σε ένα µεγάλο έλασµα (όπως αυτό του Σχ. 9) ο παράγοντας έντασης τάσεων ορίζεται ως εξής: K = σ π α (0) Όπως φαίνεται από την Εξ. (0), ο παράγοντας έντασης τάσεων έχει σαν µονάδες µέτρησης το Ν/m 3/ ή το Pa m /. Χρησιµοποιώντας αυτό τον ορισµό του παράγοντα έντασης τάσεων, οι Εξ. (9) µπορούν να γραφούν ως εξής: 55
18 σ x = K π r θ θ 3θ cos sin sin σ y = K π r θ θ 3θ cos + sin sin () τ xy = K π r θ θ sin cos cos 3θ Ο παράγοντας έντασης τάσεων αποτελεί έναν εύχρηστο τρόπο για την περιγραφή της εντατικής κατάστασης που επικρατεί γύρω από ένα ρήγµα. Εάν δύο ρήγµατα διαφορετικής γεωµετρίας έχουν τον ίδιο παράγοντα έντασης τάσεων, τότε το τασικό πεδίο γύρω από τα ρήγµατα αυτά θα είναι το ίδιο. Τιµές του παράγοντα έντασης τάσεων Κ για διάφορες γεωµετρίες ρηγµάτων και για διάφορες εντατικές καταστάσεις µπορούν να υπολογιστούν µέσω της θεωρίας ελαστικότητας. Στη γενική περίπτωση ο παράγοντας έντασης τάσεων δίδεται από την εξίσωση: K = f σ π α () όπου το f ονοµάζεται παράγοντας σχήµατος ή γεωµετρίας (shape ή geometry factor) και εξαρτάται από τη µορφή του ρήγµατος (ελλειπτικό, ηµιελλειπτικό, ηµικυκλικό, κ.ο.κ.), τη θέση του στο υλικό (επιφανειακό, εσωτερικό), τη γεωµετρία και τις διαστάσεις του δοµικού στοιχείου ή εξαρτήµατος στο οποίο βρίσκεται το ρήγµα, καθώς και από την εντατική κατάσταση. Για παράδειγµα, για ένα έλασµα πολύ µεγάλου µήκους και πλάτους w, που καταπονείται σε µονοαξονικό εφελκυσµό και στο οποίο υπάρχει ένα ελλειπτικό ρήγµα µήκους α στο κέντρο του, ο παράγοντας έντασης τάσεων δίδεται από τη σχέση: w π α K = tan σ π α (3) π α w Όπως φαίνεται στην Εξ. (3), στη συγκεκριµένη περίπτωση ο παράγοντας σχήµατος είναι: 56
19 f w π α = tan π α w Ανάλογες εκφράσεις του παράγοντα σχήµατος υπάρχουν για διάφορες γεωµετρίες και εντατικές καταστάσεις και διατίθενται σε πιο εξειδικευµένη βιβλιογραφία. 7. Τρόποι (modes) Προώθησης Ρήγµατος Ένα ρήγµα µπορεί να προωθηθεί µε διάφορους τρόπους µέσα σε ένα υλικό, σε σχέση µε τις τάσεις που προσπαθούν να ανοίξουν τις πλευρικές του επιφάνειες (δηλαδή τις επιφάνειες θραύσης). Οι τρόποι αυτοί έχουν καταταγεί σε τρεις βασικές κατηγορίες, που ονοµάζονται mode I, mode II και mode III και φαίνονται παραστατικά στο Σχ. 0. Για κάθε έναν από τους τρεις αυτούς τρόπους ορίζεται και ο αντίστοιχος παράγοντας έντασης τάσεων, δηλαδή K I, K II και K III. Στο mode I οι πλευρικές επιφάνειες του ρήγµατος αποµακρύνονται η µία από την άλλη (κι έτσι προωθείται το ρήγµα) κάτω από την επίδραση εφελκυστικής ορθής τάσης κάθετης στις επιφάνειες αυτές. Στο mode II η προώθηση του ρήγµατος γίνεται µε την επίδραση διατµητικής τάσης παράλληλης στις πλευρικές του επιφάνειες, ενώ στο mode III έχουµε και πάλι διατµητική τάση παράλληλη στις πλευρικές επιφάνειες αλλά µε φορά κάθετη σε σχέση µε το mode II. Σχ. 0 57
20 8. υσθραυστότητα Κ Ιc Από τους τρεις τρόπους προώθησης ρήγµατος που είδαµε στη προηγούµενη παράγραφο, το mode I έχει τη µεγαλύτερη πρακτική σηµασία, καθώς µπορεί ευκολότερα να προωθήσει ένα ρήγµα. Υπάρχουν δύο ακραίες περιπτώσεις για το mode I. Η µία περίπτωση είναι όταν το υλικό έχει λεπτό πάχος διατοµής, οπότε µπροστά στις αιχµές του ρήγµατος επικρατεί επίπεδη εντατική κατάσταση (plane stress). Η άλλη ακραία περίπτωση είναι όταν έχει µεγάλο πάχος διατοµής, οπότε µπροστά στις αιχµές του ρήγµατος επικρατεί εντατική κατάσταση επίπεδης παραµόρφωσης (plane strain). Όπως θα δούµε παρακάτω, η περίπτωση της επίπεδης παραµόρφωσης είναι πιο σηµαντική, επειδή τότε οι τιµές του κρίσιµου παράγοντα έντασης τάσεων Κ Ι είναι χαµηλότερες, σε σύγκριση µε την επίπεδη εντατική κατάσταση. Από τα παραπάνω συνάγεται ότι η κρίσιµη τιµή του παράγοντα έντασης τάσεων Κ Ι ενός συγκεκριµένου υλικού, στην οποία επέρχεται η θραύση του, δεν είναι σταθερή, αλλά εξαρτάται σηµαντικά από το πάχος του δοκιµίου και κατ επέκταση από την εντατική κατάσταση που επικρατεί κοντά στο ρήγµα. Αυτό σηµαίνει ότι το κρίσιµο Κ Ι δεν µπορεί να θεωρηθεί σαν ιδιότητα του υλικού, αφού δεν εξαρτάται µόνο από το υλικό, αλλά και από την γεωµετρία και τις διαστάσεις του. Ωστόσο, η κρίσιµη αυτή τιµή σταθεροποιείται από κάποιο πάχος δοκιµίου και πάνω. Αυτό φαίνεται χαρακτηριστικά στο διάγραµµα του Σχ., το οποίο δείχνει την µεταβολή του κρίσιµου παράγοντα έντασης τάσεων Κ Ι σαν συνάρτηση του πάχους διατοµής του υλικού. Όπως φαίνεται, η κρίσιµη τιµή του Κ Ι αρχικά αυξάνεται όσο αυξάνεται το πάχος δοκιµίου και φτάνει σε µία µέγιστη τιµή σε πάχος Α. Από εκεί και πέρα αρχίζει να µειώνεται, µέχρις ότου από κάποιο πάχος δοκιµίου Β και πάνω σταθεροποιείται. ηλαδή, από το πάχος Β και πάνω το κρίσιµο Κ Ι παραµένει σταθερό. Στο ίδιο διάγραµµα φαίνεται και η εντατική κατάσταση που επικρατεί µπροστά στις αιχµές του ρήγµατος. Σε πολύ λεπτά δοκίµια και µέχρι το πάχος Α επικρατεί επίπεδη εντατική κατάσταση (plane stress). Σε πάχη µεταξύ Α και Β η εντατική κατάσταση είναι µικτή, ενώ σε πάχη µεγαλύτερα του Β (εκεί που σταθεροποιείται η κρίσιµη τιµή του Κ Ι ) επικρατεί εντατική κατάσταση επίπεδης παραµόρφωσης (plane strain). Αυτή η σταθερή κρίσιµη τιµή του Κ Ι είναι ιδιότητα του υλικού, ονοµάζεται δυσθραυστότητα (fracture toughness) ή κρίσιµος παράγοντας έντασης τάσεων σε επίπεδη παραµόρφωση και συµβολίζεται µε το K Ic. Αυτή ακριβώς είναι η ιδιότητα που χρησιµοποιείται στον σχεδιασµό κατασκευών για αντοχή σε θραύση και όπως βλέπουµε είναι µία µάλλον συντηρητική εκτίµηση της δυσθραυστότητας του υλικού. 58
21 επίπεδη εντατική κατάσταση (plane stress) max. κρίσιµο Κ Ι εντατική κατάσταση επίπεδης παραµόρφωσης (plane strain) Κ Ι (κρίσιµο) µικτή εντατική κατάσταση 0 Α Β πάχος δοκιµίου Σχ. Από ένα πολύ µεγάλο πλήθος πειραµατικών αποτελεσµάτων της µορφής του Σχ., έχει διαπιστωθεί ότι το πάχος Β, για τα περισσότερα µεταλλικά υλικά µε τεχνολογική σηµασία, ισούται περίπου µε: K,5 B = Ic σ o (4) όπου σ ο το όριο διαρροής του υλικού σε µονοαξονικό εφελκυσµό. Για παράδειγµα, σε ένα κράµα αλουµινίου υψηλής αντοχής 7075 µε K Ic = 8 MPa m / και σ ο = 50 MPa το κρίσιµο πάχος Β είναι περίπου 7,5 mm. Το πάχος Α στο διάγραµµα του Σχ., εκεί δηλαδή όπου εµφανίζεται η µέγιστη κρίσιµη τιµή του Κ Ι, έχει διαπιστωθεί πειραµατικά ότι ισούται κατά προσέγγιση µε: 59
22 K A = Ic π σ o (5) Έτσι, για το παράδειγµα του κράµατος Al 7075, το πάχος Α ισούται περίπου µε 0,9 mm. Αυτό που αξίζει να παρατηρήσει κανείς είναι ότι τα πάχη Α και Β εξαρτώνται ισχυρά από το όριο διαρροής σ ο. Όπως φαίνεται από τις Εξ. (4) και (5), όσο υψηλότερη µηχανική αντοχή έχει ένα µεταλλικό υλικό (σ ο ), τόσο µικρότερο είναι το χαρακτηριστικό πάχος Β. Εποµένως, σε υλικά µε υψηλό σ ο, ακόµη και όταν αυτά είναι λεπτόπαχα, είναι δυνατόν να δηµιουργούνται συνθήκες εντατικής κατάστασης επίπεδης παραµόρφωσης. 9. Πειραµατικός Καθορισµός του K Ic Ο κρίσιµος παράγοντας έντασης τάσεων σε επίπεδη παραµόρφωση, ή πιο απλά η δυσθραυστότητα Κ Ic, είναι µία ιδιότητα των υλικών µε πολύ µεγάλη σηµασία για τον µηχανικό που σχεδιάζει κατασκευές. Κατά συνέπεια, η πειραµατική της µέτρηση έχει εξίσου µεγάλη σηµασία. Αυτός είναι και ο λόγος για τον οποίο οι σηµαντικότεροι εθνικοί και διεθνείς οργανισµοί προδιαγραφών (ASTM, DIN, κ.τ.λ.) έχουν αναπτύξει λεπτοµερείς προδιαγραφές για τον τρόπο πειραµατικού καθορισµού του K Ic. Η συνηθισµένη πρακτική αφορά την διενέργεια µιας δοκιµής σαν αυτή που είδαµε στην παράγραφο 5 (Σχ. 7). Πρώτα κατασκευάζεται ένα δοκίµιο από το υλικό του οποίου θέλουµε να µετρήσουµε το K Ic, στο οποίο δηµιουργείται τεχνητά µία εγκοπή. Η γεωµετρία και οι διαστάσεις ενός χαρακτηριστικού δοκιµίου (σύµφωνα µε την προδιαγραφή ASTM E 399) φαίνονται στο Σχ.. Το δοκίµιο αρχικά υποβάλλεται σε ορισµένους κύκλους εναλλασσόµενης φόρτισης, µε σκοπό στην ρίζα της εγκοπής να δηµιουργηθεί ένα µικρό αρχικό ρήγµα λόγω κόπωσης. Στη συνέχεια, το δοκίµιο υποβάλλεται σε εφελκυσµό µε συνεχώς αυξανόµενο φορτίο P, γεγονός που προκαλεί την προώθηση του ρήγµατος, µέχρις ότου το δοκίµιο να σπάσει. Η δυσθραυστότητα K Ic του υλικού υπολογίζεται µέσω της παρακάτω σχέσης: 60
23 K Ic P = f ( α / W ) (6) B W όπου P το φορτίο τη στιγµή της θραύσης, B και W το πάχος και το πλάτος του δοκιµίου, αντίστοιχα, και f(α/w) µία συνάρτηση βαθµονόµησης (calibration function). Εδώ πρέπει να σηµειωθεί ότι σαν α στον λόγο α/w λαµβάνεται το µήκος του αρχικού ρήγµατος, δηλαδή στο τέλος των κύκλων κόπωσης. Ο Πίνακας περιέχει τιµές της συνάρτησης αυτής. Σχ. 6
24 Πίνακας : Τιµές της συνάρτησης βαθµονόµησης f(α/w) 0. Εκτίµηση του K Ic από οκιµή Κρούσης Όπως έγινε φανερό στην προηγούµενη παράγραφο, η πειραµατική µέτρηση του K Ic προϋποθέτει µία ορισµένη διαδικασία. Ωστόσο, πολλές φορές δεν υπάρχει η δυνατότητα για την διενέργεια τέτοιας δοκιµής. Αντίθετα, η γνωστή µας δοκιµή κρούσης (impact test), στην οποία ένα δοκίµιο µε προκατασκευασµένη εγκοπή σχήµατος V (V-notch) χτυπιέται µε ένα ειδικό σφυρί στη µηχανή κρούσης και µετριέται η ενέργεια που απορροφάται κατά την θραύση του δοκιµίου, είναι µία µηχανική δοκιµή πολύ πιο γρήγορη, απαιτεί λιγότερη προετοιµασία και γενικά παρουσιάζει µεγαλύτερη ευκολία στην εκτέλεση. Έτσι λοιπόν, έχουν αναπτυχθεί διάφορες εµπειρικές σχέσεις, που προσπαθούν να δώσουν µία εκτίµηση του K Ic του υλικού από αποτελέσµατα δοκιµών κρούσης. ύο τυπικές καµπύλες από δοκιµή κρούσης φαίνονται στο διάγραµµα του Σχ. 3. Το διάγραµµα αυτό δείχνει την ενέργεια που απορροφά το δοκίµιο κατά την θραύση του, σαν συνάρτηση της θερµοκρασίας στην οποία πραγµατοποιείται η δοκιµή κρούσης. Όσο χαµηλότερη είναι η ενέργεια που απορροφά το υλικό για να σπάσει τόσο πιο ψαθυρό είναι. Ορισµένα υλικά (π.χ. ωστενιτικοί ανοξείδωτοι χάλυβες) παρουσιάζουν µία οµαλή καµπύλη, 6
25 ενώ άλλα (π.χ. απλοί ανθρακοχάλυβες) παρουσιάζουν µία µετάβαση από όλκιµη σε ψαθυρή θραύση σε χαµηλές θερµοκρασίες. Σχ. 3 Υπάρχουν διάφορες µέθοδοι µε τις οποίες µπορεί να γίνει µία εκτίµηση του K Ic ενός µεταλλικού υλικού από αποτελέσµατα δοκιµών κρούσης, κάθε µία από τις οποίες ισχύει κάτω από ορισµένες προϋποθέσεις. Για την κατάλληλη επιλογή και τα όρια ισχύος κάθε µεθόδου ο µηχανικός θα πρέπει πάντοτε να συµβουλεύεται τις κατάλληλες προδιαγραφές (π.χ. API 579). Εδώ θα αναφέρουµε µία από τις µεθόδους αυτές σαν παράδειγµα. Ας υποθέσουµε ότι έχουµε µία πλήρη καµπύλη κρούσης (δηλαδή σε διάφορες θερµοκρασίες) για έναν χάλυβα µε 0,60% C, σαν αυτόν του Σχ. 3, που εµφανίζει µετάβαση. Πρώτα πρέπει να καθορίσουµε την ενέργεια κρούσης, CVN, σαν συνάρτηση της θερµοκρασίας. Για να το κάνουµε αυτό χρησιµοποιούµε την εξής συνάρτηση: 63
ΣΗΜΕΙΩΣΕΙΣ Ε ΑΦΟΜΗΧΑΝΙΚΗΣ
 ΤΕΙ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΣΗΜΕΙΩΣΕΙΣ Ε ΑΦΟΜΗΧΑΝΙΚΗΣ Σύνταξη σηµειώσεων : Πλαστήρα Β. ΑΙΓΑΛΕΩ, 2010 2 3 ΠΡΟΛΟΓΟΣ Στις σηµειώσεις αυτές έχουν καταγραφεί θεµελιώδεις
ΤΕΙ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΣΗΜΕΙΩΣΕΙΣ Ε ΑΦΟΜΗΧΑΝΙΚΗΣ Σύνταξη σηµειώσεων : Πλαστήρα Β. ΑΙΓΑΛΕΩ, 2010 2 3 ΠΡΟΛΟΓΟΣ Στις σηµειώσεις αυτές έχουν καταγραφεί θεµελιώδεις
Καµπτική Ενίσχυση οκών µε Ελάσµατα και FRP κατά ΚΑΝ.ΕΠΕ.
 Καµπτική Ενίσχυση οκών µε Ελάσµατα και FRP κατά ΚΑΝ.ΕΠΕ. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΟΚΩΝ ΜΕ ΕΛΑΣΜΑΤΑ ΚΑΙ FRP ΚΑΤΑ ΚΑΝ.ΕΠΕ. ΠΑΝΑΓΙΩΤΑΤΟΥ ΕΛΠΙ Α ΚΩΤΣΟΒΙΝΟΣ ΑΝΑΣΤΑΣΙΟΣ Περίληψη Η παρούσα εργασία έχει ως στόχο να εξετάσει
Καµπτική Ενίσχυση οκών µε Ελάσµατα και FRP κατά ΚΑΝ.ΕΠΕ. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΟΚΩΝ ΜΕ ΕΛΑΣΜΑΤΑ ΚΑΙ FRP ΚΑΤΑ ΚΑΝ.ΕΠΕ. ΠΑΝΑΓΙΩΤΑΤΟΥ ΕΛΠΙ Α ΚΩΤΣΟΒΙΝΟΣ ΑΝΑΣΤΑΣΙΟΣ Περίληψη Η παρούσα εργασία έχει ως στόχο να εξετάσει
ΣΥΓΧΡΟΝΑ ΥΛΙΚΑ Ι ΣΗΜΕΙΩΣΕΙΣ. Δρ. ΚΩΝΣΤΑΝΤΙΝΟΣ Γ. ΚΟΛΟΒΟΣ
 ΣΥΓΧΡΟΝΑ ΥΛΙΚΑ Ι ΣΗΜΕΙΩΣΕΙΣ Δρ. ΚΩΝΣΤΑΝΤΙΝΟΣ Γ. ΚΟΛΟΒΟΣ ΧΗΜΙΚΟΣ ΜΗΧΑΝΙΚΟΣ Ε.Μ.Π. ΔΙΔΑΚΤΩΡ ΜΗΧΑΝΙΚΟΣ Ε.Μ.Π. ΛΕΚΤΟΡΑΣ Π.Δ. 407/80 Σ.Σ.Ε. ΕΡΕΥΝΗΤΗΣ ΤΟΥ Ε.Κ.Ε.Ο «ΑΘΗΝΑ» ΒΑΡΗ 2012 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 2 1.
ΣΥΓΧΡΟΝΑ ΥΛΙΚΑ Ι ΣΗΜΕΙΩΣΕΙΣ Δρ. ΚΩΝΣΤΑΝΤΙΝΟΣ Γ. ΚΟΛΟΒΟΣ ΧΗΜΙΚΟΣ ΜΗΧΑΝΙΚΟΣ Ε.Μ.Π. ΔΙΔΑΚΤΩΡ ΜΗΧΑΝΙΚΟΣ Ε.Μ.Π. ΛΕΚΤΟΡΑΣ Π.Δ. 407/80 Σ.Σ.Ε. ΕΡΕΥΝΗΤΗΣ ΤΟΥ Ε.Κ.Ε.Ο «ΑΘΗΝΑ» ΒΑΡΗ 2012 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 2 1.
KΕΦΑΛΑΙΟ 1 0 : ΕΙΣΑΓΩΓΗ ΣΤΑ ΜΙΚΡΟΚΥΜΑΤΑ
 KΕΦΑΛΑΙΟ 1 0 : ΕΙΣΑΓΩΓΗ ΣΤΑ ΜΙΚΡΟΚΥΜΑΤΑ 1.1 Εισαγωγή Η επιστήµη των Μικροκυµάτων ξεκίνησε µε την ανάπτυξη του ραντάρ και επεκτάθηκε κατά τη διάρκεια του 2 ου Παγκοσµίου Πολέµου. Η ανακάλυψη των µικροκυµατικών
KΕΦΑΛΑΙΟ 1 0 : ΕΙΣΑΓΩΓΗ ΣΤΑ ΜΙΚΡΟΚΥΜΑΤΑ 1.1 Εισαγωγή Η επιστήµη των Μικροκυµάτων ξεκίνησε µε την ανάπτυξη του ραντάρ και επεκτάθηκε κατά τη διάρκεια του 2 ου Παγκοσµίου Πολέµου. Η ανακάλυψη των µικροκυµατικών
ΕΝΑ ΝΕΟ ΤΡΑΝΖΙΣΤΟΡ ΒΑΣΙΣΜΕΝΟ ΣΤΟ ΥΠΟΞΕΙ ΙΟ ΤΟΥ ΧΑΛΚΟΥ (Cu 2 O)
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΣΤΗ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΕΝΑ ΝΕΟ ΤΡΑΝΖΙΣΤΟΡ ΒΑΣΙΣΜΕΝΟ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΣΤΗ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΕΝΑ ΝΕΟ ΤΡΑΝΖΙΣΤΟΡ ΒΑΣΙΣΜΕΝΟ
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ Δρ. ΕΥΘΥΜΙΟΣ ΜΠΑΚΑΡΕΖΟΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ
 ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ Δρ. ΕΥΘΥΜΙΟΣ ΜΠΑΚΑΡΕΖΟΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ ΜΟΝΑΔΕΣ ΜΕΓΕΘΟΣ ΣΥΜΒΟΛΟ ΜΟΝΑΔΕΣ S.. Φορτίο, q oulomb, Ηλεκτρικό ρεύμα, i Ampére, A Ηλεκτρικό δυναμικό olt, Ενέργεια
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ Δρ. ΕΥΘΥΜΙΟΣ ΜΠΑΚΑΡΕΖΟΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ ΜΟΝΑΔΕΣ ΜΕΓΕΘΟΣ ΣΥΜΒΟΛΟ ΜΟΝΑΔΕΣ S.. Φορτίο, q oulomb, Ηλεκτρικό ρεύμα, i Ampére, A Ηλεκτρικό δυναμικό olt, Ενέργεια
Κατασκευαστικές Τεχνολογίες 1
 Κατασκευαστικές Τεχνολογίες 1 Κατασκευαστικές Τεχνολογίες 1. ΕΙΣΑΓΩΓΙΚΑ Στο πρώτο κεφάλαιο της εργασίας περιλαμβάνονται ο πρόλογος, μια σύντομη ιστορική αναδρομή για την εξέλιξη των μηχανικών διαμορφώσεων
Κατασκευαστικές Τεχνολογίες 1 Κατασκευαστικές Τεχνολογίες 1. ΕΙΣΑΓΩΓΙΚΑ Στο πρώτο κεφάλαιο της εργασίας περιλαμβάνονται ο πρόλογος, μια σύντομη ιστορική αναδρομή για την εξέλιξη των μηχανικών διαμορφώσεων
Σηµειώσεις Ατοµικής και Μοριακής Φυσικής
 Σηµειώσεις Ατοµικής και Μοριακής Φυσικής Ε. Φωκίτης ΠΕΡΙΕΧΟΜΕΝΑ Ατοµική και Μοριακή Φυσική 1. Εισαγωγή 2. Πολυηλεκτρονιακά άτοµα: Ταυτόσηµα σωµατίδια,συµµετρικές και αντισυµµετρικές κυµατοσυναρτήσεις.
Σηµειώσεις Ατοµικής και Μοριακής Φυσικής Ε. Φωκίτης ΠΕΡΙΕΧΟΜΕΝΑ Ατοµική και Μοριακή Φυσική 1. Εισαγωγή 2. Πολυηλεκτρονιακά άτοµα: Ταυτόσηµα σωµατίδια,συµµετρικές και αντισυµµετρικές κυµατοσυναρτήσεις.
K4: Η Εξίσωση Schrödinger & ο Κβαντικός Μικρόκοσμος
 Σύγχρονη Φυσική Ι, Μέρος Δεύτερο Περιεχόμενα K0. Εισαγωγή Π1: Παράρτημα Οπτικής K1: Σωματιδιακή Φύση των ΗΜ Κυμάτων Π: Παράρτημα (Η Δυναμική Ενέργεια σε Σταθερό Ηλεκτρικό Πεδίο) K: Σωματιδιακή Φύση της
Σύγχρονη Φυσική Ι, Μέρος Δεύτερο Περιεχόμενα K0. Εισαγωγή Π1: Παράρτημα Οπτικής K1: Σωματιδιακή Φύση των ΗΜ Κυμάτων Π: Παράρτημα (Η Δυναμική Ενέργεια σε Σταθερό Ηλεκτρικό Πεδίο) K: Σωματιδιακή Φύση της
Μηχανικά και Κλασσικά Ανάλογα της Σύγχρονης Φυσικής
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Μεταπτυχιακή Ειδίκευση Καθηγητών Φυσικών Επιστηµών ιπλωµατική Εργασία της Ευθυµίας- Βικτωρίας Σιούτα Σύµβουλος Καθηγητής: ΣΠΥΡΟΣ ΕΥΣΤ. ΤΖΑΜΑΡΙΑΣ Μηχανικά και Κλασσικά Ανάλογα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Μεταπτυχιακή Ειδίκευση Καθηγητών Φυσικών Επιστηµών ιπλωµατική Εργασία της Ευθυµίας- Βικτωρίας Σιούτα Σύµβουλος Καθηγητής: ΣΠΥΡΟΣ ΕΥΣΤ. ΤΖΑΜΑΡΙΑΣ Μηχανικά και Κλασσικά Ανάλογα
Οπτική, Σύγχρονη, Ατομική & Μοριακή Φυσική για Βιολόγους
 Οπτική, Σύγχρονη, Ατομική & Μοριακή Φυσική για Βιολόγους 011 Σαμουήλ Κοέν Μέρος Α. Οπτική Κ0. Εισαγωγικό Σημείωμα Κυματικής Σελίδα 1. Απλή Αρμονική Ταλάντωση.... Κ0-1 1.1 Ορισμοί... Κ0-1 1. Η Αρχή της
Οπτική, Σύγχρονη, Ατομική & Μοριακή Φυσική για Βιολόγους 011 Σαμουήλ Κοέν Μέρος Α. Οπτική Κ0. Εισαγωγικό Σημείωμα Κυματικής Σελίδα 1. Απλή Αρμονική Ταλάντωση.... Κ0-1 1.1 Ορισμοί... Κ0-1 1. Η Αρχή της
1. Εισαγωγή στις Μεθόδους Μη Καταστροφικού Ελέγχου
 1. Εισαγωγή στις Μεθόδους Μη Καταστροφικού Ελέγχου Ο όρος «μη καταστροφική αξιολόγηση» (NDE) περιλαμβάνει πολλές επιμέρους έννοιες που χρησιμοποιούνται για να περιγράψουν διάφορες δραστηριότητες του εν
1. Εισαγωγή στις Μεθόδους Μη Καταστροφικού Ελέγχου Ο όρος «μη καταστροφική αξιολόγηση» (NDE) περιλαμβάνει πολλές επιμέρους έννοιες που χρησιμοποιούνται για να περιγράψουν διάφορες δραστηριότητες του εν
«ΤΕΧΝΙΚΕΣ ΜΕΤΡΗΣΗΣ ΧΡΟΝΩΝ ΜΑΓΝΗΤΙΚΗΣ ΑΠΟΚΑΤΑΣΤΑΣΗΣ (Τ1, Τ2, Τ2*) ΜΕ ΧΡΗΣΗ ΟΜΟΙΩΜΑΤΩΝ ΠΡΟΣΟΜΟΙΩΣΗΣ ΑΝΘΡΩΠΙΝΩΝ ΙΣΤΩΝ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΟΦΙΑ ΒΕΝΕΤΗ
 «ΤΕΧΝΙΚΕΣ ΜΕΤΡΗΣΗΣ ΧΡΟΝΩΝ ΜΑΓΝΗΤΙΚΗΣ ΑΠΟΚΑΤΑΣΤΑΣΗΣ (Τ1, Τ2, Τ2*) ΜΕ ΧΡΗΣΗ ΟΜΟΙΩΜΑΤΩΝ ΠΡΟΣΟΜΟΙΩΣΗΣ ΑΝΘΡΩΠΙΝΩΝ ΙΣΤΩΝ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΟΦΙΑ ΒΕΝΕΤΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΡΙΚΗ ΣΧΟΛΗ, ΔΠΜΣ ΙΑΤΡΙΚΗΣ ΦΥΣΙΚΗΣ
«ΤΕΧΝΙΚΕΣ ΜΕΤΡΗΣΗΣ ΧΡΟΝΩΝ ΜΑΓΝΗΤΙΚΗΣ ΑΠΟΚΑΤΑΣΤΑΣΗΣ (Τ1, Τ2, Τ2*) ΜΕ ΧΡΗΣΗ ΟΜΟΙΩΜΑΤΩΝ ΠΡΟΣΟΜΟΙΩΣΗΣ ΑΝΘΡΩΠΙΝΩΝ ΙΣΤΩΝ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΟΦΙΑ ΒΕΝΕΤΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΡΙΚΗ ΣΧΟΛΗ, ΔΠΜΣ ΙΑΤΡΙΚΗΣ ΦΥΣΙΚΗΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΛΑΜΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΛΑΜΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΘΕΩΡΙΑ ΑΣΥΡΜΑΤΕΣ ΖΕΥΞΕΙΣ- ΙΑ ΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΚΥΜΑΤΩΝ Ο Ι ΑΣΚΩΝ ΒΑΡΖΑΚΑΣ ΠANAΓΙΩΤΗΣ ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ Ασύρµατες
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΛΑΜΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΘΕΩΡΙΑ ΑΣΥΡΜΑΤΕΣ ΖΕΥΞΕΙΣ- ΙΑ ΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΚΥΜΑΤΩΝ Ο Ι ΑΣΚΩΝ ΒΑΡΖΑΚΑΣ ΠANAΓΙΩΤΗΣ ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ Ασύρµατες
ÅÉÓÁÃÙÃÇ ÓÔÇÍ ÁÑÉÈÌÇÔÉÊÇ ÁÍÁËÕÓÇ
 ÐÁÍÅÐÉÓÔÇÌÉÏ ÉÙÁÍÍÉÍÙÍ ÓïöïêëÞò Ä. ÃáëÜíçò ÁíáðëçñùôÞò ÊáèçãçôÞò ÅÉÓÁÃÙÃÇ ÓÔÇÍ ÁÑÉÈÌÇÔÉÊÇ ÁÍÁËÕÓÇ É Ù Á Í Í É Í Á 0 0 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ. Γενικά. Αλγόριθμος του Συμπληρώματος 6.3
ÐÁÍÅÐÉÓÔÇÌÉÏ ÉÙÁÍÍÉÍÙÍ ÓïöïêëÞò Ä. ÃáëÜíçò ÁíáðëçñùôÞò ÊáèçãçôÞò ÅÉÓÁÃÙÃÇ ÓÔÇÍ ÁÑÉÈÌÇÔÉÊÇ ÁÍÁËÕÓÇ É Ù Á Í Í É Í Á 0 0 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ. Γενικά. Αλγόριθμος του Συμπληρώματος 6.3
Σηµειώσεις στις σειρές
 . ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
. ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
Πρόλογος. Η νέα έκδοση των παρόντων σημειώσεων θα ολοκληρωθεί κατά το εαρινό εξάμηνο του ακαδημαϊκού έτους 2008-2009. Αύγουστος 2008.
 Πρόλογος Οι παρούσες σημειώσεις αποτελούν το μεγαλύτερο μέρος του υλικού που διδάχτηκε στις παραδόσεις του προπτυχιακού μαθήματος της Αριθμητικής Ανάλυσης, το εαρινό εξάμηνο 7-8, στο Μαθηματικό τμήμα του
Πρόλογος Οι παρούσες σημειώσεις αποτελούν το μεγαλύτερο μέρος του υλικού που διδάχτηκε στις παραδόσεις του προπτυχιακού μαθήματος της Αριθμητικής Ανάλυσης, το εαρινό εξάμηνο 7-8, στο Μαθηματικό τμήμα του
Διάδοση Κυμάτων στα Υλικά. Δ. Ευταξιόπουλος
 Διάδοση Κυμάτων στα Υλικά Δ. Ευταξιόπουλος 14 Φεβρουαρίου 01 Περιεχόμενα 1 Διάδοση κυμάτων σε ελαστικό μέσο άπειρων διαστάσεων 5 1.1 Τάσεις και παραμορφώσεις...................... 5 1. Ο νόμος Hooke για
Διάδοση Κυμάτων στα Υλικά Δ. Ευταξιόπουλος 14 Φεβρουαρίου 01 Περιεχόμενα 1 Διάδοση κυμάτων σε ελαστικό μέσο άπειρων διαστάσεων 5 1.1 Τάσεις και παραμορφώσεις...................... 5 1. Ο νόμος Hooke για
Κεφάλαιο 17. Σύγκριση συχνοτήτων κατηγοριών: Το στατιστικό κριτήριο χ 2 17.1. ΠΡΟΫΠΟΘΕΣΕΙΣ ΓΙΑ ΤΗ ΧΡΗΣΗ ΤΟΥ ΚΡΙΤΗΡΙΟΥ 17.2.
 Κεφάλαιο 17 Σύγκριση συχνοτήτων κατηγοριών: Το στατιστικό κριτήριο χ 2 17.1. ΠΡΟΫΠΟΘΕΣΕΙΣ ΓΙΑ ΤΗ ΧΡΗΣΗ ΤΟΥ ΚΡΙΤΗΡΙΟΥ 17.2. ΕΙΣΑΓΩΓΗ 17.3. ΤΟ χ 2 ΓΙΑ ΜΙΑ ΠΟΙΟΤΙΚΗ ΜΕΤΑΒΛΗΤΗ 17.3.1. Ένα ερευνητικό παράδειγμα
Κεφάλαιο 17 Σύγκριση συχνοτήτων κατηγοριών: Το στατιστικό κριτήριο χ 2 17.1. ΠΡΟΫΠΟΘΕΣΕΙΣ ΓΙΑ ΤΗ ΧΡΗΣΗ ΤΟΥ ΚΡΙΤΗΡΙΟΥ 17.2. ΕΙΣΑΓΩΓΗ 17.3. ΤΟ χ 2 ΓΙΑ ΜΙΑ ΠΟΙΟΤΙΚΗ ΜΕΤΑΒΛΗΤΗ 17.3.1. Ένα ερευνητικό παράδειγμα
Η θερµότητα και η θερµοκρασία
 Η θερµότητα και η θερµοκρασία Επιστηµονικό µέρος Η θερµοκρασία και η θερµότητα Η θερµοκρασία και η θερµότητα αποτελούν δύο βασικές έννοιες Της Φυσικής οι οποίες σχετίζονται µε την έννοια της ενέργειας
Η θερµότητα και η θερµοκρασία Επιστηµονικό µέρος Η θερµοκρασία και η θερµότητα Η θερµοκρασία και η θερµότητα αποτελούν δύο βασικές έννοιες Της Φυσικής οι οποίες σχετίζονται µε την έννοια της ενέργειας
Τµήµα Ηλεκτρονικών Μηχανικών Τ.Ε. του Τεχνολογικού Εκπαιδευτικού Ιδρύµατος Κρήτης
 ΑΡΧΕΣ ΤΗΣ ΜΗ ΓΡΑΜΜΙΚΗΣ ΟΠΤΙΚΗΣ Τµήµα Ηλεκτρονικών Μηχανικών Τ.Ε. του Τεχνολογικού Εκπαιδευτικού Ιδρύµατος Κρήτης ιπλωµατική εργασία των φοιτητών Αγαθοκλέους Θεόφιλος Περικλεούς Τζούλια Χαραλάµπους Σωτήρης
ΑΡΧΕΣ ΤΗΣ ΜΗ ΓΡΑΜΜΙΚΗΣ ΟΠΤΙΚΗΣ Τµήµα Ηλεκτρονικών Μηχανικών Τ.Ε. του Τεχνολογικού Εκπαιδευτικού Ιδρύµατος Κρήτης ιπλωµατική εργασία των φοιτητών Αγαθοκλέους Θεόφιλος Περικλεούς Τζούλια Χαραλάµπους Σωτήρης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ "ΜΕΤΡΗΣΕΙΣ ΡΑ ΙΟΝΟΥΚΛΙ ΙΩΝ ΣΤΟΝ ΑΕΡΑ. ΕΦΑΡΜΟΓΗ ΜΕ ΜΕΤΡΗΣΕΙΣ Be-7 ΣΤΟΝ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ "ΜΕΤΡΗΣΕΙΣ ΡΑ ΙΟΝΟΥΚΛΙ ΙΩΝ ΣΤΟΝ ΑΕΡΑ. ΕΦΑΡΜΟΓΗ ΜΕ ΜΕΤΡΗΣΕΙΣ Be-7 ΣΤΟΝ
ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 ΔΗΜΗΤΡΗΣ ΣΟΥΡΛΑΣ ΑΝΑΠΛΗΡΩΤΗΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑΤΟΣ ΦΥΣΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 3 ( ) ( ) ( ) = 4( ) d d ΕΚΔΟΣΕΙΣ ΣΥΜΜΕΤΡΙΑ ΑΘΗΝΑ 00 Email: dsourlas@phsics.upatras.gr www.phsics.upatras.gr
ΔΗΜΗΤΡΗΣ ΣΟΥΡΛΑΣ ΑΝΑΠΛΗΡΩΤΗΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑΤΟΣ ΦΥΣΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 3 ( ) ( ) ( ) = 4( ) d d ΕΚΔΟΣΕΙΣ ΣΥΜΜΕΤΡΙΑ ΑΘΗΝΑ 00 Email: dsourlas@phsics.upatras.gr www.phsics.upatras.gr
Πρόχειρες Σηµειώσεις Φυσικής Γ Λυκείου
 Πρόχειρες Σηµειώσεις Φυσικής Γ Λυκείου Θετικής & Τεχνολογικής Κατεύθυνσης Μιχάλης Ε. Καραδηµητριου MSc Φυσικός Ηράκλειο Κρήτης 2η Εκδοση - Ιούλης 2013 2 Μιχάλης Ε. Καραδηµητρίου Περιεχόµενα 1 Ταλαντώσεις
Πρόχειρες Σηµειώσεις Φυσικής Γ Λυκείου Θετικής & Τεχνολογικής Κατεύθυνσης Μιχάλης Ε. Καραδηµητριου MSc Φυσικός Ηράκλειο Κρήτης 2η Εκδοση - Ιούλης 2013 2 Μιχάλης Ε. Καραδηµητρίου Περιεχόµενα 1 Ταλαντώσεις
ιανυσµατική ανάλυση Κεφάλαιο 1 1.1 ιανυσµατική άλγεβρα 1.1.1 Πράξεις µε διανύσµατα
 Κεφάλαιο 1 ιανυσµατική ανάλυση 1.1 ιανυσµατική άλγεβρα 1.1.1 Πράξεις µε διανύσµατα Αν περπατήσετε 4 µίλια προς τον βορρά και µετά 3 µίλια προς την ανατολή (Σχ. 1.1), θα έχετε διανύσει συνολικά 7 µίλια,
Κεφάλαιο 1 ιανυσµατική ανάλυση 1.1 ιανυσµατική άλγεβρα 1.1.1 Πράξεις µε διανύσµατα Αν περπατήσετε 4 µίλια προς τον βορρά και µετά 3 µίλια προς την ανατολή (Σχ. 1.1), θα έχετε διανύσει συνολικά 7 µίλια,
ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕΛΕΤΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΣΥΣΤΗΜΑΤΟΣ ΟΔΗΓΗΣΗΣ ΚΙΝΗΤΗΡΑ Σ.Ρ. ΜΕΣΩ ΜΟΝΟΦΑΣΙΚΗΣ ΠΛΗΡΩΣ ΕΛΕΓΧΟΜΕΝΗΣ ΓΕΦΥΡΑΣ
 2014 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕΛΕΤΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΣΥΣΤΗΜΑΤΟΣ ΟΔΗΓΗΣΗΣ ΚΙΝΗΤΗΡΑ Σ.Ρ. ΜΕΣΩ ΜΟΝΟΦΑΣΙΚΗΣ ΠΛΗΡΩΣ ΕΛΕΓΧΟΜΕΝΗΣ ΓΕΦΥΡΑΣ DESIGN AND CONSTRUCTION
2014 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕΛΕΤΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΣΥΣΤΗΜΑΤΟΣ ΟΔΗΓΗΣΗΣ ΚΙΝΗΤΗΡΑ Σ.Ρ. ΜΕΣΩ ΜΟΝΟΦΑΣΙΚΗΣ ΠΛΗΡΩΣ ΕΛΕΓΧΟΜΕΝΗΣ ΓΕΦΥΡΑΣ DESIGN AND CONSTRUCTION
Μια µατιά στην Κβαντοµηχανική 0.1 Εισαγωγή
 Μια µατιά στην Κβαντοµηχανική 0.1 Εισαγωγή Είναι χρήσιµο να ξεκινήσουµε πρώτα µε κάποιες γενικές παρατηρήσεις και υπενθυµίσεις. Η Φυσική είναι η επιστήµη που µελετάει τη δοµή της ύλης και τις αλληλεπιδράσεις
Μια µατιά στην Κβαντοµηχανική 0.1 Εισαγωγή Είναι χρήσιµο να ξεκινήσουµε πρώτα µε κάποιες γενικές παρατηρήσεις και υπενθυµίσεις. Η Φυσική είναι η επιστήµη που µελετάει τη δοµή της ύλης και τις αλληλεπιδράσεις
ΑΝΑΚΟΙΝΩΣΗ ΥΛΗΣ. Ο διδάσκων. Θ. Παπαδόγγονας
 ΑΝΑΚΟΙΝΩΣΗ ΥΛΗΣ Ανακοινώνεται στους σπουδαστές του 1ου εξαμήνου του Τμήματος Διοίκησης Επιχειρήσεων ότι η ύλη της τελικής εξέτασης του μαθήματος «Μικροοικονομική» αφορά τις εξής ενότητες: Οικονομική Επιστήμη
ΑΝΑΚΟΙΝΩΣΗ ΥΛΗΣ Ανακοινώνεται στους σπουδαστές του 1ου εξαμήνου του Τμήματος Διοίκησης Επιχειρήσεων ότι η ύλη της τελικής εξέτασης του μαθήματος «Μικροοικονομική» αφορά τις εξής ενότητες: Οικονομική Επιστήμη
ΣΥΝ ΥΑΣΜΟΣ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΗΣ ΑΝΑΛΥΣΗΣ ΜΕ ΕΝ ΡΑ ΑΠΟΦΑΣΕΩΝ ΓΙΑ ΗΜΙΟΥΡΓΙΑ ΧΑΡΤΟΦΥΛΑΚΙΟΥ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΥΝ ΥΑΣΜΟΣ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΗΣ ΑΝΑΛΥΣΗΣ ΜΕ ΕΝ ΡΑ ΑΠΟΦΑΣΕΩΝ ΓΙΑ ΗΜΙΟΥΡΓΙΑ ΧΑΡΤΟΦΥΛΑΚΙΟΥ ιπλωµατική Εργασία του Παπαβασιλείου
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΥΝ ΥΑΣΜΟΣ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΗΣ ΑΝΑΛΥΣΗΣ ΜΕ ΕΝ ΡΑ ΑΠΟΦΑΣΕΩΝ ΓΙΑ ΗΜΙΟΥΡΓΙΑ ΧΑΡΤΟΦΥΛΑΚΙΟΥ ιπλωµατική Εργασία του Παπαβασιλείου
