ΑΝΑΛΥΤΙΚΗ ΜΕΛΕΤΗ ΕΠΙΠΕΔΩΝ ΚΑΙ ΣΦΗΝΟΕΙΔΩΝ ΔΙΑΤΑΞΕΩΝ ΔΙΠΛΟ-ΑΡΝΗΤΙΚΩΝ ΥΛΙΚΩΝ
|
|
|
- Ζένα Βλαχόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΔΗΜΗΤΡΙΟΥ Λ. ΣΟΥΝΑ Διπλ. Ηλεκτρολόγου Μηχανικού και Μηχανικού Υπολογιστών Α.Π.Θ. ΑΝΑΛΥΤΙΚΗ ΜΕΛΕΤΗ ΕΠΙΠΕΔΩΝ ΚΑΙ ΣΦΗΝΟΕΙΔΩΝ ΔΙΑΤΑΞΕΩΝ ΔΙΠΛΟ-ΑΡΝΗΤΙΚΩΝ ΥΛΙΚΩΝ ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ Θεσσαλονίκη, Μάιος 2009
2
3 Η διδακτορική διατριβή προέκυψε από το πρόγραμμα ΠΕΝΕΔ 2003, το οποίο συγχρηματοδοτήθηκε από εθνικούς πόρους και την Ευρωπαϊκή Επιτροπή Ευρωπαϊκό Κοινωνικό Ταμείο.
4 Δημήτριος Λ. Σουνάς Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης ΑΝΑΛΥΤΙΚΗ ΜΕΛΕΤΗ ΕΠΙΠΕΔΩΝ ΚΑΙ ΣΦΗΝΟΕΙΔΩΝ ΔΙΑΤΑΞΕΩΝ ΔΙΠΛΟ-ΑΡΝΗΤΙΚΩΝ ΥΛΙΚΩΝ ΤΡΙΜΕΛΗΣ ΣΥΜΒΟΥΛΕΥΤΙΚΗ ΕΠΙΤΡΟΠΗ Θ. Δ. Τσιμπούκης Καθηγητής Χ. Σ. Αντωνόπουλος Αναπληρωτής Καθηγητής Α. Γ. Παπαγιαννάκης Αναπληρωτής Καθηγητής ΕΠΤΑΜΕΛΗΣ ΕΞΕΤΑΣΤΙΚΗ ΕΠΙΤΡΟΠΗ Θ. Δ. Ξένος Καθηγητής Θ. Δ. Τσιμπούκης Καθηγητής Δ. Π. Χρυσουλίδης Καθηγητής Χ. Σ. Αντωνόπουλος Αναπληρωτής Καθηγητής Ε. Ε. Κριεζής Αναπληρωτής Καθηγητής Α. Γ. Παπαγιαννάκης Αναπληρωτής Καθηγητής Τ. Β. Γιούλτσης Επίκουρος Καθηγητής «Η έγκριση της παρούσης Διδακτορικής Διατριβής από το Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης δεν υποδηλώνει αποδοχή των γνωμών του συγγραφέως» (Ν. 5343/1932, άρθρο 202, παρ. 2)
5 Στους γονείς και στον αδερφό μου
6
7 Π Η διδακτορική αυτή διατριβή εκπονήθηκε κατά το χρονικό διάστημα από τον Οκτώβριο του 2004 ως τον Μάιο του 2009 στον τομέα Τηλεπικοινωνιών του τμήματος Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης. Στο σημείο αυτό, θεωρώ υποχρέωση να ευχαριστήσω τον επιβλέποντα καθηγητή κ. Θεόδωρο Τσιμπούκη για την εμπιστοσύνη που έδειξε προς το πρόσωπό μου και την ευκαιρία που μου έδωσε να αποτελέσω μέλος του Εργαστηρίου Ηλεκτρομαγνητικών Εφαρμογών και Υπολογισμών. Οι συμβουλές του τόσο σε επιστημονικά όσο και σε θέματα γενικότερου ενδιαφέροντος αποτελούν πολύτιμη παρακαταθήκη για το μέλλον. Επίσης, θερμές ευχαριστίες εκφράζω στον διδάκτορα κ. Νικόλαο Κανταρτζή, η άρτια επιστημονική κατάρτιση και η μεθοδικότητα του οποίου αποτελούν πρότυπο για μένα. Η αμέριστη συμπαράστασή που μου προσέφερε σε στιγμές δυσκολίας υπήρξε καταλυτική για την επίτευξη του σκοπού μου. Επιθυμώ, επίσης, να ευχαριστήσω τα άλλα δύο μέλη της τριμελούς συμβουλευτικής επιτροπής, αναπληρωτές καθηγητές κ.κ. Χρήστο Αντωνόπουλο και Αντώνιο Παπαγιαννάκη, για τις εύστοχες παρεμβάσεις και τη συνεργασία τους κατά τη διάρκεια εκπόνησης της διατριβής. Ακόμη, θα ήταν παράλειψη να μην εξέφραζα τις ευχαριστίες μου στον αναπληρωτή καθηγητή κ. Εμμανουήλ Κριεζή και στον επίκουρο καθηγητή κ. Τραϊανό Γιούλτση για τις γόνιμες συζητήσεις καθ όλη τη διάρκεια της διδακτορικής διατριβής. Η παρουσία μου όλα αυτά τα χρόνια στον Τηλεπικοινωνιακό Τομέα μου παρείχε τη δυνατότητα συναναστροφής με εκλεκτούς φίλους και συναδέλφους. Για τον λόγο αυτό, θα ήθελα να ευχαριστήσω τους διδάκτορες Θεόδωρο Ζυγκιρίδη, Δημήτριο Ζωγραφόπουλο, Ελισσάβετ Κοσμίδου, Κωνσταντίνο Προκοπίδη και Αθανάσιο Πολυμερίδη, όπως επίσης τους διπλωματούχους μηχανικούς Βασίλειο Παπαντωνίου, Αντώνιο Λάλα, Γεώργιο Μπουζιανά και Αλέξανδρο Δημητριάδη. Τέλος, θα ήθελα να εκφράσω την ευγνωμοσύνη μου προς τους γονείς μου, Λεμονή και Γεωργία, και τον αδερφό μου Απόστολο, για την ηθική και υλική στήριξη που, ακούραστα, μου παρείχαν σε όλη τη διάρκεια της προσπάθειας αυτής. Θεσσαλονίκη, Μάιος 2009 Δημήτριος Σουνάς
8
9 Π Πρόλογος i 1 Εισαγωγή Ιστορική και βιβλιογραφική αναδρομή Διάρθρωση και συμβολή της εργασίας Ηλεκτροδυναμική των Διπλο-Αρνητικών Υλικών Εισαγωγή Ιδιότητες των διπλοαρνητικών υλικών Καταστατικές παράμετροι και διασπορά Επίπεδο κύμα σε διπλοαρνητικό υλικό Αρνητική διάθλαση και συντελεστές Fresnel Επιφανειακά κύματα Αντίστροφο φαινόμενο Goos-Hänchen Αντίστροφο φαινόμενο Doppler Αντίστροφη ακτινοβολία Vavilov-Čerenkov Επίπεδη πλάκα διπλο-αρνητικού υλικού Πεδίο που δημιουργεί άπειρη γραμμική πηγή Διακριτό φάσμα ρυθμών Επιφανειακά κύματα Διαρρέοντα κύματα Τέλειος φακός Η μέθοδος FDTD στα διπλο-αρνητικά υλικά Α Ρυθμοί στην επιφάνεια διπλο-αρνητικού υλικού με απώλειες Η Επίπεδη Πλάκα Διπλο-Αρνητικού Υλικού ως Διάταξη Εστίασης Εισαγωγή Συντελεστής μετάδοσης Επίδραση απωλειών Επίδραση αποκλίσεων από τη συνθήκη τέλειου φακού Κριτήρια συσχέτισης Το πρόβλημα εύρεσης του βέλτιστου εστιακού επιπέδου
10 iv Περιεχόμενα Θεωρητική διαμόρφωση Δυναμική συμπεριφορά του πεδίου Περιγραφή του προβλήματος Βροχοτομές και πόλοι της K(ω, k x ) Υπολογισμός του I K Ολοκλήρωμα γύρω από τη βροχοτομή Έκφραση του Ẽ 3y (x, z, t, k x ) Εύρεση του E 3y (x, z, t) Α Απόδειξη των (3.39) Β Υπολογισμός των b n της (3.52) Γ Απόδειξη των (3.55), (3.56) Eπίλυση του Προβλήματος Σκέδασης από Σφηνοειδή Δομή Διπλο-Αρνητικού Υλικού Εισαγωγή Ο μετασχηματισμός Kontorovich-Lebedev Σφηνοειδής δομή διπλο-αρνητικού υλικού Περιγραφή του προβλήματος Ο μετασχηματισμός KL του πεδίου Πόλοι του μετασχηματισμού KL Εκφράσεις του πεδίου στο χώρο Φυσική ερμηνεία της λύσης Έλεγχος της λύσης Επέκταση του συνόλου των ρυθμών της διάταξης Η περίπτωση ϵ r = µ r = Συμπεράσματα και Μελλοντικές Προεκτάσεις 133 Βιβλιογραφία 137 Abstract περίληψη στα Αγγλικά 145
11 Κ 1 Ε 1.1 Ιστορική και βιβλιογραφική αναδρομή Η πρώτη βιβλιογραφική αναφορά των διπλο-αρνητικών υλικών, δηλαδή των υλικών με αρνητικές και τις δύο καταστατικές παραμέτρους, ανάγεται στην εργασία [Veselago, 1968] του Ρώσου φυσικού Veselago, ο οποίος, αφού, αρχικά, απέδειξε τη συμβατότητα των διπλο-αρνητικών υλικών με τις εξισώσεις Maxwell, μελέτησε, θεωρητικά, μερικές βασικές ιδιότητες τους, όπως είναι οι αντιπαράλληλες διευθύνσεις κυματικού διανύσματος και διανύσματος Poyn ng, η αντιστροφή της ακτινοβολίας Vavilov-Čerenkov και του φαινόμενου Doppler, η αρνητική διάθλαση και η υποχρεωτική παρουσία χρονικής διασποράς. Παρ όλα αυτά, το ενδιαφέρον της επιστημονικής κοινότητας για τα διπλοαρνητικά υλικά παρέμεινε, σχεδόν, μηδαμινό κατά τη διάρκεια των επόμενων τριών δεκαετιών, εξαιτίας της ανυπαρξίας τους στη φύση και της αδυναμίας πρακτικής υλοποίησής τους. Νέα ώθηση στο αντικείμενο δόθηκε από τις εργασίες [Pendry et al., 1996], [Pendry et al., 1999], όπου παρουσιάστηκε ένας τρόπος υλοποίησης τεχνητών υλικών¹ στις μικροκυματικές συχνότητες με μία καταστατική παράμετρο αρνητική. Συγκεκριμένα, αποδείχθηκε ότι η περιοδική τοποθέτηση λεπτών συρμάτων στο χώρο οδηγεί σε μία ισοδύναμη διηλεκτρική σταθερά που ακολουθεί το μοντέλο διασποράς Drude, δηλαδή λαμβάνει αρνητικές τιμές για συχνότητες μικρότερες της συχνότητας πλάσματος. Ανάλογα, η χρήση συντονιστών διακεκομμένου δακτυλίου (split-ring resonators, SRR) έχει ως αποτέλεσμα την εμφάνιση μαγνητικού συντονισμού στις μικροκυματικές συχνότητες και την επίτευξη αρνητικών τιμών μαγνητικής διαπερατότητας για συχνότητες μεγαλύτερες από τη συχνότητα συντονισμού. Συνδυάζοντας τα υλικά που προέκυψαν από την έρευνα του Pendry, οι Smith et al. πρότειναν το πρώτο πρακτικά υλοποιήσιμο διπλο-αρνητικό υλικό [Smith et al., 2000] και απέδειξαν ότι έχει αρνητικό δείκτη διάθλασης σε συγκεκριμένη συχνοτική περιοχή [Smith and Kroll, 2000]. Τόσο τα υλικά του Pendry όσο και αυτά του Smith επικράτησαν να ονομάζονται με τον γενικό όρο μεταϋλικά, ο οποίος χρησιμοποιείται για τεχνητά υλικά με ιδιότητες που, συνήθως, δεν απαντώνται στη φύση. Την πρώτη και, ίσως, από τις πιο ενδιαφέρουσες εφαρμογές των διπλο-αρνητικών υλικών αποτέλεσε ο τέλειος φακός [Pendry, 2000], ο οποίος συνίσταται από μία επίπεδη πλάκα με καταστατικές παραμέτρους αντίθετες από αυτές του περιβάλλοντα χώρου, η οποία έχει την ιδιότητα να εστιάζει τέλεια μία σημειακή πηγή. Τα ευρήματα αυτά των Smith και Pendry σηματοδότησαν την έναρξη μιας σειράς θεωρητικών, αριθμητικών και πειραματικών μελετών, προκειμένου να διαπιστωθεί η ορθότητά τους. Σε μικρό χρονικό διάστημα από τη δημοσίευση της έρευνας των Smith et al., πραγματοποιήθηκε ¹Τεχνητά υλικά είναι περιοδικές ή μη διατάξεις όμοιων διηλεκτρικών ή μεταλλικών στοιχείων, οι οποίες συμπεριφέρονται ως ομογενή μέσα κατά τη διέλευση ηλεκτρομαγνητικών κυμάτων μέσα από αυτές. Απαραίτητη προϋπόθεση για να χαρακτηριστεί μία διάταξη ως τεχνητό υλικό είναι οι διαστάσεις των στοιχείων που την αποτελούν και οι μεταξύ τους αποστάσεις να είναι πολύ μικρότερες από το μήκος κύματος.
12 2 Κεφάλαιο 1 η πρώτη θεωρητική μελέτη των διπλο-αρνητικών υλικών [Lindell et al., 2001], στην οποία εξετάστηκε η διάδοση επίπεδων ηλεκτρομαγνητικών κυμάτων μέσα από ισοτροπικά και ανισοτροπικά υλικά και προτάθηκε ο όρος μέσα οπισθοκατευθυντικού κύματος, αντί του υλικά αρνητικού δείκτη διάθλασης, ως περισσότερου αντιπροσωπευτικού της θεμελιώδους ιδιότητας των υλικών αυτών ότι το κυματικό διάνυσμα και το διάνυσμα Poyn ng έχουν αντίθετες διευθύνσεις. Στην ίδια περίοδο, αποδείχτηκε η δυνατότητα οδήγησης πλασμονικών ρυθμών από μία διεπιφάνεια διπλο-αρνητικού υλικού και συμβατικού υλικού, δηλαδή ενός υλικού με θετικές καταστατικές παραμέτρους, [Ruppin, 2000] και μελετήθηκαν τα χαρακτηριστικά των ρυθμών αυτών στην περίπτωση της επίπεδης πλάκας [Ruppin, 2001]. Παράλληλα, μία αρχική επιβεβαίωση των θεωρητικών ευρημάτων, τόσο αυτών που προκύπτουν μέσω του ομογενοποιημένου μέσου όσο και αυτών που σχετίζονται με το τεχνητό υλικό του Smith, επετεύχθη μέσω αριθμητικών προσομοιώσεων, πρώτα με τη μέθοδο των πεπερασμένων διαφορών στο πεδίο του χρονου (finite-difference me-domain, FDTD) [Ziolkowski and Heyman, 2001] και έπειτα με τις μεθόδους των πεπερασμένων στοιχείων [Caloz et al., 2001] και του πίνακα μεταφοράς [Markoš and Soukoulis, 2001], [Markoš and Soukoulis, 2002]. Επιστέγασμα των παραπάνω μελετών αποτέλεσε η κατασκευή του πρώτου διπλο-αρνητικού υλικού και η πρώτη πειραματική επιβεβαίωση του αντίστροφου νόμου του Snell [Shelby et al., 2001]. Στα πρώτα στάδια έρευνας των διπλο-αρνητικών υλικών, οι μοναδικές ιδιότητες τους που δεν απαντώνται στη φύση προκάλεσαν τον έντονο σκεπτικισμό ενός μέρους της επιστημονικής κοινότητας. Συγκεκριμένα, αμφισβητήθηκε η δυνατότητα επίτευξης αρνητικής διάθλασης για πραγματικούς διαμορφωμένους παλμούς στο πεδίο του χρόνου και θεωρήθηκαν λανθασμένα τα συμπεράσματα των αρχικών πειραματικών μελετών σχετικά με την αντιστροφή του νόμου του Snell [Valanju et al., 2002]. Επιπλέον, εκφράστηκαν έντονες διαφωνίες για την ορθότητα της ανάλυσης του Pendry, που προέβλεπε ενίσχυση των αποσβεννύμενων (evanescent) κυμάτων κατά τη διέλευσή τους μέσα από μία επίπεδη πλάκα διπλο-αρνητικού υλικού [ t Hoo, 2001], [Williams, 2001], [Garcia and Nieto-Vesperinas, 2002]. Οι ισχυρισμοί αυτοί είχαν ως συνέπεια την εμφάνιση ενός μεγάλου αριθμού μελετών για την επιβεβαίωση ή την απόρριψή τους. Έτσι, το φαινόμενο της αρνητικής διάθλασης αποδείχθηκε ότι υφίσταται, ακόμη, και για κύματα με πεπερασμένο συχνοτικό περιεχόμενο μέσω μιας σειράς θεωρητικών [Smith et al., 2002b], [Pacheco et al., 2002], [Thomas and Ishimaru, 2005], [Scalora et al., 2005], αριθμητικών [Moss et al., 2002], [Foteinopoulou et al., 2003], [Kolinko and Smith, 2003], [Cummer, 2003] και πειραματικών [Parazzoli et al., 2003], [Houck et al., 2003], [Aydin et al., 2005b] μελετών. Από την άλλη πλευρά, κατανοήθηκε, μέσω θεωρητικής ανάλυσης, η ενίσχυση των αποσβεννύμενων κυμάτων ως μία αργή διαδικασία στο πεδίο του χρόνου [Gómez-Santos, 2003] και επιβεβαιώθηκαν οι ισχυρισμοί του Pendry. Επίσης, διαπιστώθηκε, μέσω αριθμητικών προσομοιώσεων, η δυνατότητα της επίπεδης πλάκας διπλο-αρνητικού υλικού να εστιάζει το διαδιδόμενο [Loschialpo et al., 2003], [Loschialpo et al., 2004] και το αποσβεννύμενο [Rao and Ong, 2003], [Rao and Ong, 2003] φάσμα μιας σημειακής πηγής, συμπεριφορά που, αργότερα, επαληθεύτηκε πειραματικά [Lagarkov and Kissel, 2004]. Η αποσαφήνιση των ζητημάτων που αφορούν τις βασικές ιδιότητες των διπλο-αρνητικών υλικών επέτρεψε την ανάπτυξη της έρευνας σε περισσότερο εξειδικευμένα αντικείμενα. Έτσι, εξετάστηκε το πρόβλημα του στρωματοποιημένου μέσου [Kong, 2002], [Ishimaru et al., 2005], [Chew, 2005] και αντιμετωπίστηκε πλήρως η γεωμετρία της επίπεδης πλάκας διπλο-αρνητικού υλικού [Zhang et al., 2002]. Στο ίδιο θεωρητικό πλαίσιο, διερευνήθηκε η συμβατότητα των διπλο-αρνητικών υλικών με την αρχή της αιτιότητας [Ziolkowski and Kipple, 2003], [Cui and Kong, 2004a] και βρέθηκαν αναλυτικές εκφράσεις για την ενέργεια, όταν οι καταστατικές παράμετροι ακολουθούν τα μοντέλα διασποράς Drude
13 1.1. Ιστορική και βιβλιογραφική αναδρομή 3 και Lorentz [Cui and Kong, 2004b], [Tretyakov, 2005], [Boardman and Marinov, 2006]. Στην ίδια περίοδο, αποδείχθηκε το φαινόμενο Goos-Hänchen για τα διπλο-αρνητικά υλικά, σύμφωνα με το οποίο η μετατόπιση που υφίσταται μία γκαουσιανή δέσμη που προσπίπτει σε διπλο-αρνητικό υλικό είναι αντίθετη από αυτήν σε ένα συμβατικό μέσο [Kong et al., 2002], [Berman, 2002], [Shadrivov et al., 2003b], [Lakhakia, 2003]. Επιπλέον, η αντιστροφή της ακτινοβολίας Vavilov-Čerenkov, η οποία είχε προβλεφθεί, ήδη, από τον Veselago, εξάγεται μέσω μιας αυστηρής μαθηματικής ανάλυσης [Lu et al., 2003]. Από την άλλη πλευρά, μία προσομοιωτική και πειραματική μελέτη οδήγησε στο συμπέρασμα ότι η κλιμάκωση που υπάρχει, αναπόφευκτα, στις επιφάνειες διατάξεων από μεταϋλικά, εξαιτίας των πεπερασμένων διαστάσεων των στοιχείων που τα αποτελούν, συνεπάγεται την εμφάνιση σημαντικών φαινομένων σκέδασης, εκτός από την αναμενόμενη διάθλαση [Smith et al., 2004]. Από την αρχή, ακόμη, της ενασχόλησης με τα μεταϋλικά, υπήρξε αυξημένο ενδιαφέρον για τη βελτιστοποίηση του υλικού του Smith. Ένα από τα πρώτα επιτεύγματα στη θεματική αυτή περιοχή ήταν η υλοποίηση ισοτροπικών συντονιστών διακεκομμένου δακτυλίου, με την τοποθέτηση δυο συμβατικών SRR σε κάθετα επίπεδα [Gay-Balmaz and Mar n, 2002]. Παράλληλα, διερευνήθηκαν σε βάθος οι ιδιότητες του SRR και αποδείχθηκε η παρουσία διανισοτροπικής συμπεριφοράς [Marqués et al., 2002]. Το γεγονός αυτό οδήγησε στην υλοποίηση ενός νέου τύπου SRR, στον οποίο οι διακεκομμένοι δακτύλιοι είναι τοποθετημένοι σε παράλληλα επίπεδα και ο οποίος δεν παρουσιάζει διανισοτροπικές ιδιότητες [Marqués et al., 2003]. Ταυτόχρονα, αναλύθηκε η δυνατότητα επίτευξης μαγνητικής δραστηριότητας στις μικροκυματικές συχνότητες με τη χρήση μαγνητο-διηλεκτρικών σφαιριδίων σε ένα διηλεκτρικό υλικό [Holloway et al., 2003], [Jylhä et al., 2006]. Επιπλέον, τα μεταλλικά στοιχεία σχήματος Ω, τα οποία είχαν, παλαιότερα, χρησιμοποιηθεί για τα διανισοτροπικά τους χαρακτηριστικά, αποδείχθηκαν θεωρητικά [Simovski and He, 2003] και πειραματικά [Huangfu et al., 2004] ότι μπορούν να αξιοποιηθούν στην κατασκευή ισοτροπικών διπλο-αρνητικών υλικών. Αναφέρεται, ακόμη, η δυνατότητα χρήσης μεταλλικών στοιχείων σχήματος S, με πλεονέκτημα το μεγαλύτερο εύρος ζώνης και τη δυνατότητα εμφάνισης πολλαπλών μαγνητικών συντονισμών [Chen et al., 2004a], [Chen et al., 2005a], [Chen et al., 2005b]. Παρά την ύπαρξη προσεγγιστικών εκφράσεων για τις ομογενοποιημένες καταστατικές παραμέτρους των μεταϋλικών, από νωρίς κατανοήθηκε η ανάγκη εξαγωγής ακριβέστερων μοντέλων. Σημειώνεται ότι η χρήση ομογενοποιημένων μοντέλων είναι απαραίτητη τόσο στις θεωρητικές όσο και στις αριθμητικές μελέτες, για τη διερεύνηση των σχετικών φυσικών μηχανισμών τη μείωση του υπολογιστικού φόρτου. Η απλούστερη και, ίσως, η περισσότερο διαδεδομένη τεχνική ομογενοποίησης υπολογίζει τις καταστατικές παραμέτρους από τους συντελεστές ανάκλασης και μετάδοσης μιας επίπεδης πλάκας μεταϋλικού, για κάθετη πρόσπτωση επίπεδου κύματος [Smith et al., 2002a]. Μία περισσότερο εκτενής μελέτη πάνω στην τεχνική αυτή, που διαπραγματεύεται τις γρήγορες μεταβολές των παραμέτρων γύρω από τις συχνότητες συντονισμού και τον καθορισμό των επιφανειών της ομογενοποιημένης πλάκας, παρουσιάστηκε στην εργασία [Ziolkowski, 2003], μαζί με ένα πλήθος παραδειγμάτων εφαρμογής της. Η τεχνική αυτή βελτιώθηκε ακόμη περισσότερο [Chen et al., 2004c] και επεκτάθηκε, επιπλέον, στην περίπτωση των διανισοτροπικών υλικών [Chen et al., 2005c]. Παρ όλη την απλότητά της, η παραπάνω μέθοδος οδηγεί σε μη-τοπικές παραμέτρους, με αποτέλεσμα στο άρθρο [Smith et al., 2005] να προτείνεται ο διαχωρισμός του φάσματος σε περιοχές όπου η υπόθεση τοπικότητας είναι αποδεκτή και σε άλλες όπου πρέπει να ληφθεί υπόψη ο περιοδικός χαρακτήρας της διάταξης. Ένας άλλος ακριβέστερος τρόπος για την υπέρβαση του προβλήματος αυτού στηρίζεται στον αρχικό υπολογισμό Bloch παραμέτρων από τους συντελεστές ανάκλασης και διάδοσης και,
14 4 Κεφάλαιο 1 έπειτα, στην εξαγωγή των καταστατικών παραμέτρων, μέσω αυτών [Simovski and Tretyakov, 2007], [Simovski, 2007]. Παράλληλα, αναπτύχθηκε μία εντελώς διαφορετική τεχνική ομογενοποίησης, στην οποία χρησιμοποιούνται οι μέσοι όροι των πεδιακών μεγεθών στον όγκο ενός μοναδιαίου κελιού και εξάγεται μία γενικευμένη, μη-τοπική, διηλεκτρική σταθερά, στην οποία συμπεριλαμβάνεται και η μαγνητική δραστηριότητα του υλικού [Silveirinha and Fernandes, 2005], [Silveirinha, 2006], [Silveirinha, 2007]. Αναφέρεται, επίσης, ότι έχουν προταθεί και άλλες τεχνικές ομογενοποίησης, οι οποίες στηρίζονται σε μέσες τιμές των πεδιακών μεγεθών κατά μήκος των ακμών του μοναδιαίου κελιού ή πάνω στις έδρες του [Smith and Pendry, 2006], [Lerat et al., 2006], [Liu et al., 2007]. Ακόμη, ως μέθοδος ομογενοποίησης, κατά μία γενικότερη έννοια, θα μπορούσε να θεωρηθεί η αντικατάσταση των στοιχείων που αποτελούν τα μεταϋλικά με κατάλληλα μοντέλα διπολικών σκεδαστών, η οποία έχει χρησιμοποιηθεί επιτυχώς σε διάφορα προβλήματα [Belov and Simovski, 2005], [Belov and Silveirinha, 2006], [Belov and Simovski, 2006]. Η επίπεδη πλάκα διπλο-αρνητικού υλικού αποτέλεσε το αντικείμενο μελέτης πολλών επιστημόνων, λόγω της ικανότητάς της να εστιάζει το διαδιδόμενο και το αποσβεννύμενο φάσμα μιας πηγής. Μετά την υπέρβαση των αρχικών θεωρητικών διαφωνιών σχετικά με τη λειτουργία της διάταξης, εξετάστηκε ο ρόλος των απωλειών, της διασποράς και της εγγενούς περιοδικότητας που υπάρχει σε κάθε πρακτικό μεταϋλικό και διαπιστώθηκε ο περιορισμός της αναλυτικότητας σε πεπερασμένες τιμές αντίθετα από την άπειρη αναλυτικότητα του τέλειου φακού που πρότεινε ο Pendry μεγαλύτερες, ωστόσο, από το όριο περίθλασης των συμβατικών φακών [Smith et al., 2003], [Ye, 2003], [Marqués et al., 2003], [Merlin, 2004]. Από την άλλη πλευρά, η ανάλυση της επίπεδης πλάκας πεπερασμένου μήκους, μέσω της μεθόδου FDTD, οδήγησε στο συμπέρασμα ότι η αναλυτικότητά της είναι ιδιαίτερα ευαίσθητη σε μεταβολές του μήκους, εξαιτίας των ρυθμών που αναπτύσσονται στις επιφάνειές της [Chen et al., 2004b]. Παρ όλα αυτά, μερικά χρόνια αργότερα, τα φαινόμενα που περιγράφονται στην εργασία [Chen et al., 2004b] αποδόθηκαν στην μη-ορθή μοντελοποίηση των οριακών συνθηκών στο πλαίσιο της μεθόδου FDTD και διατυπώθηκε ο ισχυρισμός ότι η αναλυτικότητα της επίπεδης πλάκας διπλο-αρνητικού υλικού μένει, πρακτικά, ανεπηρέαστη από το μήκος της [Zhao et al., 2007]. Τα ίδια αποτελέσματα είχαν προκύψει, ήδη ένα χρόνο νωρίτερα, με τη βοήθεια μαθηματικής ανάλυσης, βασισμένης στην αρχή του Huygens [Chen et al., 2006]. Μία σημαντική παρατήρηση που αφορά τα εστιακά χαρακτηριστικά της επίπεδης πλάκας διπλο-αρνητικού υλικού και περιγράφεται στην εργασία [Mesa et al., 2005] είναι η αδυναμία πλήρους εστίασης του πεδίου στον τρισδιάστατο χώρο. Πιο συγκεκριμένα, αποδεικνύεται, αριθμητικά και πειραματικά, ότι είναι αδύνατη η ταυτόχρονη εξαγωγή από το διαδιδόμενο πεδίο της θέσης της πηγής και της μορφής της. Στο ίδιο πλαίσιο, εκφράστηκε από τον Veselago η άποψη ότι η επίπεδη πλάκα μπορεί να θεωρηθεί ως φακός μόνο για πλάτη μεγαλύτερα του μήκους κύματος, στα οποία δεν παρατηρείται ενίσχυση των αποσβεννύμενων κυμάτων, ενώ για μικρότερα πλάτη λειτουργεί, περισσότερο, ως προσαρμοστική διάταξη [Veselago, 2005]. Η έντονη διασπορά των διπλο-αρνητικών υλικών καθιστά χρήσιμη τη διερεύνηση της επίδρασης του φάσματος της πηγής στις εστιακές της ικανότητες. Έτσι, η μελέτη που παρουσιάστηκε στο άρθρο [Marqués et al., 2003] οδήγησε στο συμπέρασμα ότι η διαδικασία εστίασης συνοδεύεται από μία ελάχιστη χρονική διάρκεια, θέτοντας ένα άνω όριο στο εύρος φάσματος της πηγής. Αργότερα, μέσω μιας αυστηρότερης ανάλυσης, διαπιστώθηκε ότι για πηγές με πεπερασμένο φάσμα υφίσταται ένα άνω όριο στο πάχος της πλάκας, πάνω από το οποίο αποσβεννύμενα κύματα με συγκεκριμένη φασική σταθερά δεν μπορούν να ενισχυθούν [de Wolf, 2005]. Από την άλλη πλευρά, η δυναμική συμπεριφορά του πεδίου για μονοχρωματική πηγή που αρχίζει να ακτινοβολεί κάποια συγκεκριμένη
15 1.1. Ιστορική και βιβλιογραφική αναδρομή 5 χρονική στιμή υπολογίστηκε στην εργασία [Zhou et al., 2005], μέσω διπλής αριθμητικής ολοκλήρωσης ως προς τη φασική σταθερά και τη συχνότητα, αποκαλύπτοντας την ύπαρξη έντονων μεταβατικών φαινομένων, τα οποία αποδόθηκαν στη διέγερση επιφανειακών ρυθμών. Τα μεταβατικά αυτά φαινόμενα, που προκαλούν σημαντικές διακυμάνσεις του πλάτους του πεδίου, θεωρήθηκαν υπεύθυνα για την ασυμφωνία μεταξύ των αρχικών αριθμητικών διερευνήσεων που χρησιμοποίησαν τη μέθοδο FDTD [Zhou and Chan, 2005]. Η καταστολή των ταλαντώσεων αυτών του πεδίου επιτυγχάνεται είτε εισάγοντας απώλειες, με την ταυτόχρονη υποβάθμιση όμως της εστιακής ικανότητας της πλάκας, είτε ρυθμίζοντας κατάλληλα τον χρόνο ανόδου της πηγής [Huang et al., 2006]. Η πρώτη πρακτική υλοποίηση του επίπεδου φακού βασίστηκε σε σπειροειδείς συντονιστές για την επίτευξη αρνητικής μαγνητικής διαπερατότητας και σε παράλληλα λεπτά σύρματα για την αρνητική διηλεκτρική σταθερά και χρησιμοποίησε δύο δίπολα ως πηγές για τον έλεγχο της αναλυτικότητας της διάταξης [Lagarkov and Kissel, 2004]. Την ίδια περίοδο, κατασκευάστηκε η πρώτη πλάκα τρισδιάστατου μεταϋλικού, αποτελούμενου από συντονιστές τύπου Ω, με ικανοποιητικά αποτελέσματα [Verney et al., 2004]. Ακολούθησε μία σειρά από πειραματικές μελέτες, από τις οποίες φάνηκε ότι μία πλάκα φτιαγμένη από το υλικό του Smith πετυχαίνει αναλυτικότητα μεγαλύτερη από το όριο περίθλασης [Aydin et al., 2005a], [Aydin et al., 2007], [Aydin and Ozbay, 2007]. Παράλληλα, ένα μέρος της έρευνας επικεντρώθηκε στην επαλήθευση του φαινομένου ενίσχυσης των αποσβεννύμενων κυμάτων. Προς τον σκοπό αυτό, στην εργασία [Baena et al., 2005] περιγράφηκε μία γενική μεθοδολογία μέτρησης του βαθμού ενίσχυσης των αποσβεννύμενων κυμάτων με τη χρήση των αποσβεννύμενων ρυθμών ενός ορθογωνικού κυματοδηγού και δόθηκαν αποτελέσματα μέσω αριθμητικών προσομοιώσεων. Με βάση τη μέθοδο αυτή, ένα χρόνο μετά, δημοσιεύτηκαν μετρήσεις του πεδίου γύρω και εντός μιας πλάκας ισοτροπικού μεταϋλικού από SRR, από τις οποίες φαίνεται, ξεκάθαρα, ενίσχυση του πλάτους [Popa and Cummer, 2006]. Τα ίδια συμπεράσματα προέκυψαν, επίσης, μέσω μιας διαφορετικής προσέγγισης, που βασίστηκε στη επίπεδη υλοποίηση μεταϋλικών τύπου γραμμής μεταφοράς [Liu et al., 2006], [Cui et al., 2006]. Ένα από τα πιο ενδιαφέροντα φαινόμενα που σχετίζονται με την επίπεδη πλάκα διπλο-αρνητικού υλικού είναι η υποστήριξη ενός μεγάλου φάσματος ρυθμών. Μάλιστα, όπως αποδείχθηκε στην εργασία [Ruppin, 2001], εμφανίζονται πλασμονικοί ρυθμοί, οι οποίοι κανονικά απαντώνται στις επιφάνειες των μετάλλων στις οπτικές συχνότητες και έχουν αποσβεννύμενη μορφή τόσο εκτός όσο και εντός της πλάκας. Τα χαρακτηριστικά των ρυθμών αυτών, ως συνάρτηση των γεωμετρικών και ηλεκτρομαγνητικών παραμέτρων της πλάκας, παρουσιάστηκαν αναλυτικά στο άρθρο [Shadrivov et al., 2003a], όπου διαπιστώθηκε η δυνατότητα οδήγησής τους για αυθαίρετα μικρά πλάτη της πλάκας και συγκεκριμένες τιμές καταστατικών παραμέτρων. Παράλληλα, αποδείχθηκε η ανάπτυξη ρυθμών με ημιτονοειδή μορφή στο εσωτερικό της πλάκας, παρόμοιας φύσης με τους ρυθμούς που οδηγούνται από μία πλάκα συμβατικού υλικού [Wu et al., 2003]. Οι πλασμονικοί ρυθμοί που υποστηρίζονται από μία πλάκα διπλο-αρνητικού υλικού αξιοποιήθηκαν για τη βελτίωση των χαρακτηριστικών των κυματοδηγών. Συγκεκριμένα, η εισαγωγή στρώματος διπλο-αρνητικού υλικού σε κυμματοδηγό παράλληλων πλακών συνεπάγεται την εμφάνιση αργών ρυθμών με πολύ μεγάλη κυματική σταθερά [Nefedov and Tretryakov, 2003], όπως επίσης την εξασφάλιση μονόρυθμης λειτουργίας για μεγάλα πλάτη του κυματοδηγού και την υποστήριξη TE πολωμένων ρυθμών, ακόμη, και όταν το πλάτος τείνει στο 0 [Alù and Engheta, 2004]. Την ίδια περίοδο, μελετήθηκε με τη βοήθεια της μεθόδου FDTD η φύση των επιφανειακών ρυθμών σε μία πλάκα πεπερασμένου μήκους και διαπιστώθηκε η ύπαρξη ενός μηχανισμού κυκλικής κυκλοφορίας της ενέργειας ανάμεσα στο διπλο-αρνητικό και στο συμβατικό μέσο [Schelleng
16 6 Κεφάλαιο 1 et al., 2004]. Επιπλέον, μία λεπτομερής περιγραφή των διαγραμμάτων διασποράς των επιφανειακών ρυθμών που αναπτύσσονται σε ένα στρώμα διπλο-αρνητικού υλικού πάνω από ένα άπειρα αγώγιμο επίπεδο αποκάλυψε την ύπαρξη ζωνών αποκοπής και τη δυνατότητα χρήσης διπλο-αρνητικών υλικών ως υποστρώματα κεραιών για την καταστολή επιφανειακών κυμάτων [Baccarelli et al., 2005a], [Mahmoud and Viitanen, 2005]. Αντίθετα με ότι συμβαίνει στα συμβατικά υλικά, μία πλάκα διπλοαρνητικού υλικού υποστηρίζει διαρρέοντα κύματα με εκθετική μείωση του πλάτους εκτός αυτής, ιδιότητα που μπορεί να αξιοποιηθεί στην κατασκευή κατευθυντικών κεραιών με κωνικά διαγράμματα ακτινοβολίας [Baccarelli et al., 2005b], [Li et al., 2005]. Ο ρόλος των επιφανειακών και των διαρρεόντων κυμάτων κατά την πρόσπτωση μιας γκαουσιανής δέσμης σε πλάκα διπλο-αρνητικού υλικού αναλύθηκε στην εργασία [Shadrivov et al., 2005] και διαπιστώθηκε μεγάλη μετατόπιση της ανακλώμενης δέσμης σε σχέση με την προσπίπτουσα. Οι πλασμονικοί ρυθμοί επιβεβαιώθηκαν πειραματικά για την περίπτωση ενός μονομαγνητικού υλικού υλικό με αρνητική μόνο τη μαγνητική διαπερατότητα από SRR, μέσω της τεχνικής ολικής ανάκλασης, φανερώνοντας ταυτόχρονα μία πολύ καλή συμφωνία μεταξύ πειραματικών και θεωρητικών διαγραμμάτων διασποράς [Gollub et al., 2005]. Μία αναλυτική περιγραφή των πόλων που αντιστοιχούν τόσο στα επιφανειακά όσο και στα διαρρέοντα κύματα στο μιγαδικό επίπεδο για ολόκληρο το φάσμα συχνοτήτων και την περίπτωση απωλειών δόθηκε στην εργασία [Lovat et al., 2008]. Η σφηνοειδής ή πρισματική δομή είναι μία συχνά απαντώμενη γεωμετρία σε προσομοιωτικές και πειραματικές μελέτες διπλο-αρνητικών υλικών. Μία πρώτη προσπάθεια προσέγγισης της ηλεκτροδυναμικής της συμπεριφοράς παρουσιάστηκε στο άρθρο [Monzon et al., 2005], όπου, μέσω της τεχνικής χωρισμού των μεταβλητών και του διαχωρισμού της λύσης σε ένα συμμετρικό και ένα αντισυμμετρικό μέρος, προέκυψαν εκφράσεις του πεδίου σε κλειστή μορφή για την άπειρη σφηνοειδή δομή με καταστατικές παραμέτρους που ικανοποιούν τη συνθήκη τέλειου φακού, όταν ως διέγερση χρησιμοποιείται άπειρη γραμμική πηγή. Σημειώνεται ότι η λύση ισχύει για θέσεις της πηγής εκτός ενός συγκεκριμένου κυκλικού τομέα και φανερώνει την ύπαρξη ενός μηχανισμού εστίασης του πεδίου, παρόμοιου με αυτό του τέλειου φακού. Λίγο αργότερα, εξετάστηκε, από την ίδια ερευνητική ομάδα, η περίπτωση πρόσπτωσης επίπεδου κύματος και διαπιστώθηκε φαινομενική ακτινοβολία από την κορυφή της διάταξης και η παρουσία μιας νέας μορφής στάσιμου κύματος [Monzon et al., 2006b]. Παράλληλα, η ειδική περίπτωση πρόσπτωσης επίπεδου κύματος σε σφηνοειδή γεωμετρία ανοίγματος 90 αποδείχθηκε ότι συνοδεύεται από ένα μοναδικό φαινόμενο οπισθοανάκλασης, χωρίς, ταυτόχρονη παρουσία μηχανισμού περίθλασης, όπως συμβαίνει σε συμβατικούς δίεδρους ανακλαστήρες [Monzon et al., 2006a]. Παρόμοια συμπεράσματα περιγράφονται στην εργασία [Uslenghi, 2006], ωστόσο, μέσω μιας ανάλυσης βασισμένης στη γεωμετρική οπτική. Μία διαφορετική προσέγγιση του προβλήματος σκέδασης από σφηνοειδή δομή ιδανικού διπλο-αρνητικού υλικού, βασισμένη στη μέθοδο χωρισμού των μεταβλητών και στον προσδιορισμό των άγνωστων συντελεστών ως υπολοίπων κατάλληλης μερομορφικής συνάρτησης μπορεί, επίσης, να βρεθεί στο άρθρο [Daniele and Uslenghi, 2007a]. Την ίδια περίοδο, χρησιμοποιώντας τη θεωρία του Meixner [Meixner, 1972], αποδείχθηκε η αδυναμία σύγκλισης της μεθόδου FDTD κατά την προσομοίωση σφηνοειδών γεωμετριών ομογενοποιημένων διπλο-αρνητικών υλικών, γεγονός που αποδόθηκε στη διέγερση, στην περιοχή της κορυφής, ρυθμών με αυθαίρετα μεγάλη συχνότητα ταλάντωσης [Sukhorukov et al., 2006]. Η ύπαρξη των ρυθμών αυτών διαπιστώθηκε και μέσω μιας ακριβούς στατικής ανάλυσης, η οποία εμπλέκει την επίλυση της εξίσωσης Laplace και θεωρείται ακριβής στην περιοχή της κορυφής της σφηνοειδούς δομής [Wallén et al., 2008]. Η ανάλυση αυτή φανέρωσε, επίσης, τον απειρισμό της ενέργειας των ρυθμών
17 1.2. Διάρθρωση και συμβολή της εργασίας 7 αυτών και τη, μη-φυσική, διέγερσή τους, ακόμη, και στην περίπτωση απωλειών. Επιπλέον επιβεβαίωσε την αδυναμία σύγκλισης αριθμητικών τεχνικών (στην προκειμένη περίπτωση, της μεθόδου των πεπερασμένων στοιχείων), τόσο στο κοντινό όσο και στο μακρινό πεδίο, και πρότεινε, ως τρόπο αντιμετώπισης του προβλήματος, την ομαλοποίηση της κορυφής της γωνίας. Τέλος, πρόσφατα, προτάθηκε μία νέα μέθοδος ακριβούς επίλυσης της γενικής περίπτωσης που οι καταστατικές παράμετροι λαμβάνουν αυθαίρετες τιμές, κεντρική ιδέα της οποίας είναι η εξαγωγή ιδιόμορφων ολοκληρωτικών εξισώσεων, μέσω του μετασχηματισμού Kontorovich-Lebedev, και η αριθμητική επίλυσή τους με τη χρήση αναπτυγμάτων Neumann [Salem and Kamel, 2008b]. 1.2 Διάρθρωση και συμβολή της εργασίας Αντικείμενο της παρούσας διατριβής είναι η αναλυτική μελέτη επίπεδων και σφηνοειδών διατάξεων από διπλο-αρνητικά υλικά. Κίνητρο για την ενασχόληση με τα διπλο-αρνητικά υλικά υπήρξε η ραγδαία ανάπτυξή τους την τελευταία δεκαετία, η οποία είχε ως αποτέλεσμα μία πληθώρα πρακτικών εφαρμογών. Η επίπεδη διάταξη που εξετάζεται είναι η πλάκα διπλο-αρνητικού υλικού, που, εκτός από τη σημαντικότερη ιδιότητά της να εστιάζει το διαδιδόμενο και το αποσβεννύμενο φάσμα μιας πηγής, έχει χρησιμοποιηθεί ως διάταξη κυματοδήγησης και ως υπόστρωμα κεραιών. Από την άλλη πλευρά, ενώ η σφηνοειδής δομή εμφανίζεται, πάντοτε, σε πεπερασμένες γεωμετρίες και έχει χρησιμοποιηθεί για την επιβεβαίωση πολλών βασικών ιδιοτήτων των διπλο-αρνητικών υλικών, όπως είναι η αρνητική διάθλαση, έχει ερευνηθεί σε περιορισμένο βαθμό, κυρίως, εξαιτίας της πολυπλοκότητάς της. Για τη μελέτη των παραπάνω προβλημάτων επιλέχθηκε μία αναλυτική προσέγγιση, λόγω της γενικότητας των αποτελεσμάτων που προκύπτουν μέσω αυτής και της δυνατότητας καλύτερης κατανόησης των φυσικών μηχανισμών που διέπουν τις ερευνώμενες διατάξεις. Στην συνέχεια, παρουσιάζεται μία περίληψη του περιεχομένου και της συμβολής της παρούσας εργασίας. Στο δεύτερο κεφάλαιο περιγράφονται τα πιο αντιπροσωπευτικά στοιχεία της ηλεκτροδυναμικής συμπεριφοράς των διπλο-αρνητικών υλικών. Συγκεκριμένα, αφού πραγματοποιηθεί μία σύντομη αναφορά στην ορολογία για τα διπλο-αρνητικά υλικά, αποδεικνύεται η υποχρεωτική παρουσία χρονικής διασποράς, ως αποτέλεσμα του β θερμοδυναμικού νόμου. Ακολούθως, εξετάζεται η διάδοση επίπεδου κύματος μέσα σε διπλο-αρνητικό υλικό και παρουσιάζεται η θεμελιώδης ιδιότητα αντιπαράλληλων διευθύνσεων κυματικού διανύσματος και διανύσματος Poyn ng. Στο ίδιο πλαίσιο, αναλύεται η πρόσπτωση επίπεδου κύματος στη διαχωριστική επιφάνεια ενός συμβατικού και ενός διπλοαρνητικού υλικού, με το, συνεπαγόμενο, φαινόμενο της αρνητικής διάθλασης και περιγράφονται οι έννοιες του επίπεδου φακού και του τέλεια προσαρμοσμένου μέσου. Παραμένοντας στη γεωμετρία των δύο μέσων, αποδεικνύεται η δυνατότητα οδήγησης επιφανειακών πλασμονικών ρυθμών και παρέχονται τα διαγράμματα διασποράς τους. Παράλληλα, αναφέρονται τα φαινόμενα της αρνητικής ολίσθησης Goos-Hänchen, της αντίστροφης μετατόπισης Doppler και της αντίστροφης ακτινοβολίας Vavilov-Čerenkov. Η επόμενη γεωμετρία που μελετάται είναι η επίπεδη πλάκα διπλο-αρνητικού υλικού, μέσω του προβλήματος ακτινοβολίας άπειρης γραμμικής πηγής και της αναπαράστασης του πεδιου μέσω κατάλληλων ολοκληρωμάτων Sommerfeld. Το πλήρες διακριτό φάσμα ρυθμών, που περιλαμβάνει τα επιφανειακά και τα διαρρέοντα κύματα, προσδιορίζεται από τους πόλους των συντελεστών ανάκλασης και μετάδοσης που βρίσκονται και στα δύο φύλλα Riemann του προβλήματος. Κατόπιν, διερευνάται η συμπεριφορά της πλάκας προσαρμοσμένου διπλο-αρνητικού υλικού ως τέλειου φακού και περιγράφεται το φαινόμενο της ενίσχυσης των αποσβεννύμενων κυμάτων. Επιπλέον,
18 8 Κεφάλαιο 1 πραγματοποιείται μία συνοπτική αναφορά στη μορφή που λαμβάνει η μέθοδος FDTD στην περίπτωση των διπλο-αρνητικών υλικών και τονίζονται τα σημεία που πρέπει να προσεχθούν κατά την εφαρμογή της. Το κεφάλαιο ολοκληρώνεται με ένα παράρτημα το οποίο ασχολείται με τη μορφή των πλασμονικών ρυθμών στη διεπιφάνεια συμβατικού και διπλο-αρνητικού υλικού όταν υπάρχουν απώλειες. Στο τρίτο κεφάλαιο, πραγματοποιείται μία συστηματική μελέτη της επίπεδης πλάκας διπλο-αρνητικού υλικού ως διάταξης εστίασης. Δεδομένης της απουσίας στη βιβλιογραφία ενός γενικού τρόπου αποτίμησης των εστιακών χαρακτηριστικών της διάταξης αυτής, παρουσιάζεται μία νέα ολοκληρωμένη μέθοδος για τον ακριβή προσδιορισμό των δύο βασικότερων παραμέτρων που σχετίζονται με το φαινόμενο εστίασης, δηλαδή της αναλυτικότητας και της θέσης του εστιακού επιπέδου. Ο προσδιορισμός της αναλυτικότητας, δηλαδή της ελάχιστης διάστασης της πηγής που μπορεί να αναπαραχθεί στο εστιακό επίπεδο, επιτυγχάνεται μέσω του συντελεστή μετάδοσης ενός επίπεδου κύματος από το επίπεδο της πηγής στο επίπεδο εστίασης. Μέσω μιας σειράς γραφικών παραστάσεων του συντελεστή μετάδοσης ως προς τον παράλληλο στην πλάκα κυματικό αριθμό για διαφορές τιμές των παραμέτρων της διάταξης, διαπιστώνεται η ύπαρξη ενός άνω ορίου για τον κυματικό αριθμό, πάνω από το οποίο δεν είναι δυνατή η αναπαραγωγή του κυματικού πλάτους στο εστιακό επίπεδο. Ο προσδιορισμός του ορίου αυτού επιτυγχάνεται, επίσης, μέσω μιας προσεγγιστικής σχέσης, η ορθότητα της οποίας ελέγχεται μέσω συγκρίσεων με τις ακριβείς τιμές του ορίου που προκύπτουν από τα διαγράμματα. Από την άλλη πλευρά, η θέση του βέλτιστου επιπέδου εστίασης βρίσκεται μέσω δύο νέων κριτηρίων συσχέτισης του πεδίου στο επίπεδο της πηγής και σε ένα τυχαίο επίπεδο παράλληλο προς αυτό, τα οποία βασίζονται στις έννοιες του συντελεστή συσχέτισης και του μέσου τετραγωνικού σφάλματος. Συγκεκριμένα, το βέλτιστο επίπεδο εστίασης είναι αυτό στο οποίο μεγιστοποιείται ο συντελεστής συσχέτισης και ελαχιστοποιείται το μέσο τετραγωνικό σφάλμα. Με τον τρόπο αυτό, επιτυγχάνεται ο ακριβής προσδιορισμός του εστιακού επιπέδου και αίρονται οι ασάφειες των υπαρχουσών μεθόδων, που βασίζονται, κατά κύριο λόγο, στην οπτική παρατήρηση της χωρικής κατανομής του πεδίου. Για την εξασφάλιση της ακρίβειας της μεθόδου απαιτείται η συμφωνία των αποτελεσμάτων που εξάγονται μέσω των δύο κριτηρίων. Η ανάλυση φανερώνει μία εγγενή αδυναμία στο ορισμό του μέσου τετραγωνικού σφάλματος, η οποία αντιμετωπίζεται με την εισαγωγή ενός βελτιωμένο μέσου τετραγωνικού σφάλματος, από το οποίο αφαιρείται η φάση του πεδίου στα σημεία του κάθετου στην πλάκα άξονα, διατηρείται, ωστόσο, η σχετική φάση στα επίπεδα που είναι κάθετα προς αυτόν. Η ευρωστία του νέου κριτηρίου αποδεικνύεται τόσο μέσω αριθμητικών αποτελεσμάτων όσο και μέσω μιας μαθηματικής ανάλυσης του προβλήματος κάθετης πρόσπτωσης γκαουσιανής δέσμης στην πλάκα. Στο δεύτερο μέρος του τρίτου κεφαλαίου μελετάται η δυναμική συμπεριφορά του πεδίου της πλάκας όταν η χρονική μεταβολή της πηγής καθορίζεται από μία κατά πλάτος διαμορφωμένη ημιτονοειδή συνάρτηση, και εξάγονται, για πρώτη φορά, αναλυτικές εκφράσεις για την ηλεκτρική πεδιακή ένταση στο πεδίο του χρόνου. Αντί της συνήθους προσέγγισης, με βάση την οποία το ολοκλήρωμα που δίνει την ηλεκτρική πεδιακή ένταση υπολογίζεται με ολοκλήρωση, πρώτα, ως προς τον κυματικό αριθμό και στη συνέχεια ως προς τη συχνότητα, στην παρούσα εργασία πραγματοποιείται, αρχικά, η ολοκλήρωση ως προς τη συχνότητα. Με τον τρόπο αυτό, παρακάμπτεται το πρόβλημα απειρισμού του πεδίου στη συχνότητα που οι καταστατικές παράμετροι ικανοποιούν τη συνθήκη τέλειου φακού και καθίσταται δυνατή η εξαγωγή εκφράσεων σε κλειστή μορφή. Παράλληλα, αποφεύγεται η διπλή αριθμητική ολοκλήρωση, η οποία είναι απαραίτητη στη συνήθη προσέγγιση. Το ολοκλήρωμα ως προς τη συχνότητα βρίσκεται, κατόπιν, μέσω μιας αυστηρής μαθηματικής διαδικασίας, η οποία εμπλέκει τον καθορισμό βροχοτομών και τη μελέτη των θέσεων των πόλων στο μιγαδικό επίπεδο συχνοτήτων.
19 1.2. Διάρθρωση και συμβολή της εργασίας 9 Το ζητούμενο ολοκλήρωμα εκφράζεται ως άθροισμα των υπολοίπων της ολοκληρωτέας ποσότητας στους πόλους της και ενός ολοκληρώματος γύρω από τη μία βροχοτομή. Για την εύρεση του τελευταίου ολοκληρώματος εισάγεται ένας μετασχηματισμός από το επίπεδο συχνοτήτων σε ένα νέο μιγαδικό επίπεδο, ο οποίος έχει την ιδιότητα απεικόνισης και των δύο φύλλων Riemann του αρχικού επιπέδου σε ένα φύλλο του νέου επιπέδου. Με το τρόπο αυτό, εξάγονται εκφράσεις σε κλειστή μορφή, η ακρίβεια των οποίων αποδεικνύεται ιδιαίτερα ικανοποιητική, μέσω συγκρίσεων με την ακριβή τιμή του ολοκληρώματος, όπως αυτή προκύπτει με αριθμητική ολοκλήρωση. Η αποτελεσματικότητα της προτεινόμενης τεχνικής αποδεικνύεται, επίσης, μέσω συγκρίσεων με αποτελέσματα που προκύπτουν χρησιμοποιώντας τη μέθοδο FDTD. Επόμενο βήμα είναι ο υπολογισμός του ολοκληρώματος ως προς τον κυματικό αριθμό, ο οποίος επιτυγχάνεται αξιοποιώντας την τεχνική στάσιμης φάσης. Όπως και πριν, η ακρίβεια των εκφράσεων ελέγχεται πραγματοποιώντας συγκρίσεις με τις ακριβείς τιμές που προκύπτουν μέσω αριθμητικής ολοκλήρωσης. Σε όλες τις περιπτώσεις παρέχεται η φυσική ερμηνεία των αποτελεσμάτων, η οποία βοηθά στην κατανόηση του φαινομένου εστίασης του αποσβεννύμενου φάσματος της πηγής. Στο σημείο αυτό, κρίνεται σκόπιμο να τονιστεί ο γενικός χαρακτήρας της παραπάνω μεθοδολογίας, καθώς μπορεί να χρησιμοποιηθεί σε κάθε επίπεδα στρωματοποιημένο μέσο. Τα παραρτήματα που παρατίθενται στο τέλος του κεφαλαίου περιέχουν τις αποδείξεις συγκεκριμένων σχέσεων που απαιτούνται κατά τη διάρκεια της ανάλυσης. Αντικείμενο του τέταρτου κεφαλαίου είναι η αναλυτική επίλυση του προβλήματος της άπειρης σφηνοειδούς δομής διπλο-αρνητικού υλικού με δείκτη διάθλασης ίσο με αυτόν του περιβάλλοντα χώρου. Το πρόβλημα αυτό είναι ανάλογο του προβλήματος της ισοδιαθλαστικής δομής στα συμβατικά υλικά και επιδέχεται αναλυτική λύση, λόγω του σταθερού πλάτους του κυματικού αριθμού σε ολόκληρο τον χώρο. Παρ όλα αυτά, η δυσκολία στην περίπτωση των διπλο-αρνητικών υλικών είναι αυξημένη σε σχέση με τα συμβατικά υλικά, εξαιτίας των οπισθοκατευθυντικών κυμάτων και της μη ακριβούς γνώσης της συνθήκης ακτινοβολίας. Η ανάλυση πραγματοποιείται με τη βοήθεια του μετασχηματισμού Kontorovich-Lebedev (KL), μία λεπτομερής παρουσίαση του οποίου περιλαμβάνεται στο πρώτο μέρος του κεφαλαίου. Στο μέρος αυτό, εισάγονται τα δύο είδη του ευθέος και του αντίστροφου μετασχηματισμού και εξάγεται μία νέα ιδιότητά του, που φανερώνει την άμεση σύνδεση του είδους του μετασχηματισμού KL με τη συνθήκη ακτινοβολίας. Επίσης, επιδεικνύεται ο τρόπος χρήσης του, μέσω του προβλήματος εύρεσης της συνάρτησης Green του ελεύθερου χώρου. Στη συνέχεια, μελετάται το πρόβλημα της σφηνοειδούς δομής και αποδεικνύεται ότι το πεδίο εκφράζεται ως γραμμικός συνδυασμός στοιχειωδών συμμετρικών και αντισυμμετρικών ρυθμών, οι οποίοι αντιστοιχούν στους πόλους του μετασχηματισμού KL και εμπλέκουν τις συναρτήσεις Hankel β είδους. Αντίθετα με την περίπτωση των συμβατικών υλικών, προκύπτει η ύπαρξη φανταστικών και μιγαδικών πόλων, οι οποίοι αντιστοιχούν σε ρυθμούς παρόμοιας μορφής με αυτή των επιφανειακών κυμάτων στις επίπεδες γεωμετρίες. Μάλιστα, αποδεικνύεται ότι οι ρυθμοί που αντιστοιχούν στους φανταστικούς πόλους έχουν άπειρη ενέργεια στην περιοχή της κορυφής της διάταξης, συμπεριφορά που αποδίδεται στην ιδιομορφία της γεωμετρίας στο σημείο αυτό. Μέσω ενός ελέγχου συμβατότητας των αποτελεσμάτων με την αρχή διατήρησης της ενέργειας, φανερώνεται η μη πληρότητα του συνόλου των ρυθμών. Για τον λόγο αυτό, πραγματοποιείται η επέκταση του συνόλου αυτού, λαμβάνοντας υπόψη τους ρυθμούς που εμπλέκουν τις συναρτήσεις Hankel α είδους. Η παραπάνω θεωρία εφαρμόζεται επιτυχώς στην περίπτωση προσαρμοσμένου διπλο-αρνητικού υλικού, η οποία αποδεικνύεται ότι βρίσκεται σε πλήρη αναλογία με την επίπεδη πλάκα από αυτό το υλικό. Η ορθότητα της προτεινόμενης μεθόδου επαληθεύεται από την πολύ καλή συμφωνία των αναλυτικών αποτελεσμάτων με αυτά που εξάγονται
20 10 Κεφάλαιο 1 μέσω της μεθόδου FDTD. Μία από τις σημαντικότερες καινοτομίες της τεχνικής που παρουσιάζεται στο τέταρτο κεφάλαιο, πέρα από το γεγονός ότι αποτελεί την πληρέστερη ανάλυση της σφηνοειδούς δομής διπλο-αρνητικού υλικού (η μόνη περίπτωση που έχει μελετηθεί μέχρις στιγμής είναι η δομή προσαρμοσμένου διπλορνητικού υλικού για συγκεκριμένες θέσεις της πηγής), είναι η εύρεση μιας πλήρους αντιστοιχίας μεταξύ της σφηνοειδούς και της επίπεδης δομής. Συγκεκριμένα, το πεδίο στη σφηνοειδή δομή εκφράζεται ως άθροισμα ρυθμών που προκύπτουν από τους πόλους του μετασχηματισμού KL, όπως, ακριβώς, στην επίπεδη πλάκα εκφράζεται ως γραμμικός συνδυασμός ρυθμών που αντιστοιχούν στις ιδιομορφίες (πόλοι και βροχοτομές) του χωρικού μετασχηματισμού Fourier. Μάλιστα, οι ρυθμοί στους πραγματικούς πόλους της σφηνοειδούς δομής αντιστοιχούν στο συνεχές φάσμα της επίπεδης πλάκας, ενώ οι ρυθμοί στους φανταστικούς και μιγαδικούς πόλους της σφηνοειδούς δομής έχουν παρόμοια χαρακτηριστικά με τα επιφανειακά και διαρρέοντα κύματα της επίπεδης περίπτωσης. Σημειώνεται ότι η αναλογία αυτή δεν μπορεί να φανεί από τη σφηνοειδή δομή συμβατικού υλικού, καθώς η τελευταία δεν υποστηρίζει επιφανειακά κύματα. Το πέμπτο και τελευταίο κεφάλαιο συνίσταται από μία συνοπτική περιγραφή των κυριότερων σημείων της διατριβής και παρουσιάζει τα συμπεράσματα που εξάγονται από αυτήν. Ακόμη, αναφέρεται σε πιθανές μελοντικές προεκτάσεις που θα μπορούσε να έχει η παρούσα εργασία.
21 Κ 2 Η Δ -Α Υ 2.1 Εισαγωγή Στο κεφάλαιο αυτό αναλύεται η ηλεκτροδυναμική συμπεριφορά των διπλο-αρνητικών υλικών, δηλαδή των μεταϋλικών με αρνητικές και τις δύο καταστατικές παραμέτρους. Αρχικά, εξετάζονται οι πιο βασικές ιδιότητές τους, όπως η υποχρεωτική παρουσία χρονικής διασποράς, η διάδοση οπισθοκατευθυντικών κυμάτων και το φαινόμενο της αρνητικής διάθλασης κατά την πρόσπτωση επίπεδου κύματος σε διπλο-αρνητικό υλικό, η αξιοποίηση του οποίου επιτρέπει την κατασκευή επίπεδων φακών. Επίσης, διερευνάται η δυνατότητα οδήγησης πλασμονικών ρυθμών κατά μήκος της διαχωριστικής επιφάνειας ενός συμβατικού και ενός διπλο-αρνητικού υλικού και περιγράφεται η μορφή των φαινομένων Doppler, Goos-Hänchen και Vavilov-Čerenkov μέσα στα διπλο-αρνητικά υλικά. Στη συνέχεια, η ανάλυση επικεντρώνεται στην επίπεδη πλάκα διπλο-αρνητικού υλικού και προσδιορίζεται, πλήρως, το φάσμα των επιφανειακών και των διαρρεόντων ρυθμών που υποστηρίζει. Στο πλαίσιο αυτό, περιγράφεται η αρχή λειτουγίας του τέλειου φακού, δηλαδή μιας επίπεδης πλάκας διπλο-αρνητικού υλικού που είναι προσαρμοσμένη στον περιβάλλοντα χώρο, η οποία επιτρέπει την ανακατασκευή αντικειμένων με άπειρη αναλυτικότητα. Τέλος, παρουσιάζονται μερικά βασικά στοιχεία για την προσομοίωση διατάξεων από διπλο-αρνητικά υλικά με τη μέθοδο FDTD. Ένα πρόβλημα που συναντάται στη βιβλιογραφία και σχετίζεται με τα υλικά που έχουν αρνητικές καταστατικές παραμέτρους είναι η έλλειψη μιας κοινώς χρησιμοποιούμενης ονομασίας. Έτσι, οι όροι διπλο-αρνητικά υλικά (double-nega ve materials), υλικά Veselago, αριστερόστροφα υλικά (le -handed materials), υλικά οπισθοκατευθυντικού κύματος (backward-wave materials) και υλικά αρνητικού δείκτη διάθλασης (nega ve refrac ve index materials) περιγράφουν, όλοι, ένα μέσο με αρνητικές καταστατικές παραμέτρους. Από αυτούς, ο πρώτος αποτυπώνει το πρόσημο των καταστατικών παραμέτρων και ο δεύτερος το γεγονός ότι ο πρώτος που αναφέρθηκε στις ιδιότητες των υλικών αυτών είναι ο Ρώσος φυσικός Veselago. Από την άλλη πλευρά, οι τρεις τελευταίοι όροι είναι απόρροια συγκεκριμένων ιδιοτήτων (αριστερόστροφο σύστημα συντεταγμένων που δημιουργείται από τις πεδιακές εντάσεις και το κυματικό διάνυσμα, διάδοση οπισθοκατευθυντικού κύματος, αρνητική διάθλαση). Επειδή όμως οι ιδιότητες αυτές εμφανίζονται και σε άλλες διατάξεις (π.χ. φωτονικούς κρυστάλλους), θα ήταν χρήσιμο να διευκρινηστεί ότι μόνο οι όροι διπλο-αρνητικά υλικά και υλικά Veselago προσδιορίζουν μονοσήμαντα τα υλικά αυτά. Μάλιστα, ο όρος αριστερόστροφα υλικά είναι δυνατό να παρανοηθεί με τον αντίστοιχο όρο που χρησιμοποιείται για την περιγραφή μιας συγκεκριμένης κατηγορίας χειρόμορφων υλικών. Στην παρούσα διατριβή, υιοθετείται η ονομασία διπλοαρνητικά υλικά, καθώς ο όρος υλικά Veselago απαντάται σε πολύ μικρό βαθμό στη σχετική βιβλιογραφία.
22 12 Κεφάλαιο Ιδιότητες των διπλοαρνητικών υλικών Καταστατικές παράμετροι και διασπορά Μία από τις θεμελιωδέστερες ιδιότητες των διπλοαρνητικών υλικών είναι η παρουσία χρονικής διασποράς, δηλαδή η εξάρτηση των καταστατικών παραμέτρων ϵ, µ από την κυκλική συχνότητα ω. Η συμπεριφορά αυτή επιβάλλεται από το γεγονός ότι η ενέργεια του ηλεκτρομαγνητικού πεδίου πρέπει να είναι θετική, το όποιο, με τη σειρά του, απορρέει από το β θερμοδυναμικό αξίωμα.¹ Πιο συγκεκριμένα, είναι γνωστό ότι, σε ένα μέσο χωρίς διασπορά, η πυκνότητα ενέργειας δίνεται από τη σχέση U = 1 4 ( Re{ϵ} E 2 + Re{µ} H 2) (2.1) Αν Re{ϵ}, Re{µ} < 0, όπως συμβαίνει στα διπλοαρνητικά ϋλικά, προκύπτει ότι U < 0. Κατά συνέπεια, ένα διπλοαρνητικό υλικό πρέπει να εμφανίζει πάντα διασπορά. Τότε, υποθέτοντας ότι οι απώλειες είναι αμελητέες, η πυκνότητα ενέργειας για ένα πεδίο με φασματικό περιεχόμενο σε μια στενή ζώνη γύρω από την κυκλική συχνότητα ω είναι [Landau et al., 1984] U = 1 4 [ (ωϵ) ω Προκειμένου η U να είναι θετική, πρέπει να ισχύει E 2 + (ωµ) ] ω H 2 (2.2) (ωϵ) ω > 0, (ωµ) > 0, (2.3) ω από όπου εύκολα διαπιστώνει κανείς ότι, όταν ϵ, µ < 0, οι ϵ, µ είναι αύξουσες συναρτήσεις της συχνότητας. Οι (2.3) καλούνται συνθήκες εντροπίας, ισχύουν, μόνο, στην περίπτωση αμελητέων απωλειών και καταδεικνύουν την ισχυρή εξάρτηση των καταστατικών παραμέτρων από τη συχνότητα. Ας θεωρήσουμε, τώρα, μια περιοχή V με συνορο S που καταλαμβάνεται από διπλοαρνητικό υλικό και δεν περιέχει πηγές. Τότε, σύμφωνα με την ολοκληρωτική διατύπωση του θεωρήματος Poyn ng [Balanis, 1989],² η μέση ισχύς που εισέρχεται στην περιοχή αυτή στη μόνιμη κατάσταση είναι { } P in = Re E H ( ˆn ds = ω Im{ϵ} H 2 + Im{µ} H 2) dv (2.4) S V Επειδή δεν υπάρχουν πηγές στο εσωτερικό της S, όλη η ισχύς που εισέρχεται θα πρέπει να μετατρέπεται σε θερμότητα, δηλαδή P in > 0 και Im{ϵ} < 0, Im{µ} < 0 (2.5) ¹Η αποθηκευμένη ενέργεια ενός πεδίου που έχει φτάσει στη μόνιμη κατάσταση (steady state) ισούται με τη θερμότητα που παράγεται όταν αφαιρεθεί η διέγερση. Η θερμότητα, όμως, σύμφωνα με το β θερμοδυναμικό νόμο, είναι μη αρνητική ποσότητα. ²Αντίθετα με την έκφραση που δίνει την ενέργεια του πεδιου, το θεώρημα Poyn ng δεν επηρεάζεται από την ύπαρξη της διασποράς, καθώς είναι άμεση συνέπεια των εξισώσεων Maxwell. Η μόνη αλλαγή σε σχέση με την περίπτωση υλικών που δεν έχουν διασπορά είναι ότι οι όροι 1 4 V Re{µ} H 2 dv, 1 Re{ϵ} E 2 dv 4 V δεν αντιστοιχούν, πλέον, στην μέση τιμή της μαγνητικής και της ηλεκτρικής ενέργειας, αντίστοιχα.
23 2.2. Ιδιότητες των διπλοαρνητικών υλικών 13 (α) (β) Σχήμα 2.1: Πραγματικό και φανταστικό μέρος (α) του ϵ για ω p = 10 9 rad/s, Γ = 0.01ω p και (β) του µ για ω 0 = 10 9 rad/s, ω p = rad/s, Γ = 0.01ω 0. Παρατηρούμε, δηλαδή, ότι το πρόσημο των Im{ϵ}, Im{µ} στα διπλοαρνητικά υλικά είναι το ίδιο με την περίπτωση των συμβατικών υλικών.³ Ένα πολύ διαδεδομένο μοντέλο διασποράς που χρησιμοποιείται στις πρακτικές εφαρμογές για την περιγραφή της διηλεκτρικής σταθεράς είναι το μοντέλο Drude, που δίνεται από την εξίσωση ϵ(ω) = ϵ 0 + ω 2 p ω 2 + jωγ, (2.6) με ω p τη συχνότητα πλάσματος και Γ τον παράγοντα απωλειών. Στην πραγματικότητα, η (2.6) αναπαριστά τη διηλεκτρική σταθερά του μέσου λεπτών συρμάτων (thin wires), που χρησιμοποιείται πολύ συχνά στις πρακτικές υλοποιήσεις διπλο-αρνητικών υλικών. Εύκολα διαπιστώνεται ότι, απουσία απωλειών, αρνητικές τιμές για την ϵ λαμβάνονται όταν ω < ω p. Από την άλλη πλευρά, η μαγνητική διαπερατότητα περιγράφεται, συνήθως, μέσω ενός μοντέλου Lorentz, όπως φαινεται από τη σχέση µ(ω) = µ 0 (1 + ω 2 p ω 2 0 ω 2 + ω jωγ Πάλι, ω p, Γ είναι η συχνότητα πλάσματος και ο παράγοντας απωλειών, αντίστοιχα, ενώ ω 0 είναι η συχνότητα συντονισμού. Το μοντέλο Lorentz περιγράφει ικανοποιητικά την απόκριση των συντονιστών διακεκομμένου δακτυλίου (split-ring resonators, SRR), που συνιστούν την πιο κοινή γεωμετρία για την παραγωγή μαγνητικής δραστηριότητας στα μεταϋλικά. Αν ο Γ θεωρηθεί αμελητέος, η µ γίνεται αρνητική στο διάστημα ω 0 < ω < ω p. Σημειώνεται ότι το μοντέλο Lorentz καταλήγει στο αντίστοιχο Drude για ω 0 = 0. Στο σχήμα 2.1 παριστάνεται η μεταβολή του πραγματικού και του φανταστικού μέρους των ϵ, µ με τη συχνότητα, όταν ω p = 10 9 rad/s, Γ = 0.01ω p (μοντέλο Drude) και ω 0 = 10 9 rad/s, ω p = 2ω 0, Γ = 0.01ω 0 (μοντέλο Lorentz). Αξίζει να παρατηρηθεί η σημαντική αύξηση των απωλειών στις συχνότητες γύρω από τον συντονισμό του μοντέλου Lorentz. ) (2.7) Επίπεδο κύμα σε διπλοαρνητικό υλικό Είναι γνωστό ότι οποιοδήποτε κύμα μπορεί να αναλυθεί ως άθροισμα επίπεδων κυμάτων. Επομένως, η μελέτη της διάδοσης ενός επίπεδου κύματος μέσα από ένα υλικό είναι αναγκαία για την ³Από εδώ και στο εξής συμβατικά θα ονομάζουμε τα υλικά στα οποία Re{ϵ}, Re{µ} > 0.
24 14 Κεφάλαιο 2 κατανόηση των ιδιοτήτων του υλικού. Η γενική μορφή της ηλεκτρικής και της μαγνητικής πεδιακής έντασης ενός επίπεδου κύματος είναι, αντίστοιχα, E 0 e jk r και H 0 e jk r, με E 0, H 0 τα αντίστοιχα πλάτη, r το διάνυσμα θέσης και k το κυματικό διάνυσμα, που περιέχει την πληροφορία για τη διεύθυνση και την ταχύτητα διάδοσης. Είναι απλό να αποδειχθεί ότι οι εξισώσεις Maxwell στην περίπτωση αυτή γράφονται k E = ωµh k H = ωϵe (2.8α) (2.8β) Αντικαθιστώντας την (2.8β) στην (2.8α) προκύπτει, μετά από μερικές πράξεις, ότι k 2 = k 2 = ω 2 µϵ ή k 2 = ω 2 [(Re{µ} Re{ϵ} Im{µ} Im{ϵ}) + j(re{µ} Im{ϵ} + Re{ϵ} Im{µ})]. Κατά συνέπεια, αν το υλικό που γεμίζει τον χώρο είναι διπλοαρνητικό, Im{k 2 } > 0 και Re{k} > 0, Im{k} > 0, ή Re{k} < 0, Im{k} < 0 (2.9) Οι παραπάνω σχέσεις αποκτούν φυσικό νόημα όταν το επίπεδο κύμα παράγεται από μία ρευματική κατανομή, οπότε η επιλογή του προσήμου των Re{k}, Im{k} πρέπει να συμβαδίζει με την απαίτηση το πλάτος του κύματος να μειώνεται καθώς απομακρυνόμαστε από την πηγή. Για παράδειγμα, αν θεωρήσουμε μία πηγή στο επίπεδο z = 0, η οποία δημιουργεί εκατέρωθέν της επίπεδα κύματα με διεύθυνση διάδοσης παράλληλη προς τον άξονα z γεγονός που δηλώνει ότι k = kẑ η σωστή επιλογή για z > 0 είναι Re{k} < 0, Im{k} < 0, ενώ για z < 0 είναι Re{k} > 0, Im{k} > 0. Αξίζει να σημειωθεί ότι σε ένα συμβατικό μέσο οι αντίστοιχες επιλογές είναι Re{k} > 0, Im{k} < 0 και Re{k} < 0, Im{k} > 0. Η σημασία αυτού του γεγονότος θα κατανοηθεί πλήρως στην επόμενη παράγραφο. Στη συνέχεια θα επικεντρωθούμε στην περίπτωση αμελητέων απωλειών, δηλαδή όταν Im{k} = 0. Τότε, επειδή ϵ, µ < 0, οι (2.8α), (2.8β) γράφονται ως k E = ω µ H k H = ω ϵ E (2.10α) (2.10β) Είναι φανερό ότι τα διανύσματα E, H και k διαμορφώνουν ένα αριστερόστροφο σύστημα συντεταγμένων, αντίθετα από ό,τι συμβαίνει στα συμβατικά υλικά. Από την άλλη πλευρά, το πραγματικό διάνυσμα Poyn ng είναι P = 1 2 Re {E H } = E 2 k, (2.11) ω µ δηλαδή έχει φορά αντίθετη από αυτήν του k. Με άλλα λόγια, στα διπλοαρνητικά υλικά η διεύθυνση ροής της ισχύος είναι αντίθετη προς τη διεύθυνση διάδοσης των μετώπων κύματος. Η ιδιότητα αυτή είναι ιδιαίτερα σημαντική, καθώς σχετίζεται με την εμφάνιση πολλών από τα ενδιαφέροντα χαρακτηριστικά των υλικών αυτών. Επίσης, έχει ωθήσει μία μερίδα επιστημόνων στην υιοθέτηση του όρου μέσα οπισθοκατευθυντικού κύματος (backward-wave media) για να περιγράψει τα υλικά με ϵ, µ < 0. Η παραπάνω ανάλυση αποτυπώνεται στο σχήμα 2.2, που δείχνει τις σχετικές διευθύνσεις των διανυσμάτων E, H, k, P σε ένα συμβατικό και ένα διπλοαρνητικό μέσο. Αναφορικά με το παράδειγμα της προηγούμενης παραγράφου, στον χώρο z > 0 η ισχύς ρέει προς τη διεύθυνση των θετικών z, απομακρυνόμενη από την πηγή, και συνεπώς το P έχει την ίδια φορά με το ẑ. Άρα, k = k ẑ, δηλαδή Re{k} < 0, όπως ακριβώς προβλέφθηκε. Ανάλογα συμπεράσματα ισχύουν για τον χώρο z < 0.
25 2.2. Ιδιότητες των διπλοαρνητικών υλικών 15 (α) (β) Σχήμα 2.2: Σχετικές διευθύνσεις των διανυσμάτων E, H, k, P σε ένα (α) συμβατικό και (β) διπλοαρνητικό μέσο Μέχρι στιγμής η μελέτη περιορίστηκε σε μονοχρωματικά κύματα. Ωστόσο, ενδιαφέρον έχει η διάδοση παλμών πεπερασμένου φάσματος. Για ευκολία, η ανάλυση που ακολουθεί αναφέρεται σε κύματα που διαδίδονται παράλληλα με τον άξονα z (k = kẑ). Όταν το εύρος ζώνης του παλμού είναι μικρό συγκριτικά με την κεντρική συχνότητά του, οριζεται η ταχύτητα ομάδας v g = dω/dk, η οποία δίνει την ταχύτητα διάδοσης του παλμού ως συνόλου. Αντίθετα, η ταχύτητα των μετώπων κύματος στο εσωτερικό του παλμού είναι η ταχύτητα φάσης v p = ω/k. Παραγωγίζοντας την έκφραση k 2 = ω 2 µϵ ως προς ω και αξιοποιώντας τις (2.3), λαμβάνουμε 2k dk d(ωµ) d(ωϵ) = ωϵ + ωµ dω dω dω < 0 (2.12) Χρησιμοποιώντας τους ορισμούς των v p, v g στην (2.12) προκύπτει v p v g < 0, (2.13) δηλαδή οι ταχύτητες φάσης και ομάδας έχουν αντίθετη φορά. Το αποτέλεσμα αυτό είναι απόλυτα λογικό, αφού η v g εκφράζει, ουσιαστικά, την ταχύτητα ροής της ισχύος, η οποία, όπως αποδείχθηκε προηγουμένως, διαδίδεται προς την αντίθετη κατεύθυνση από αυτήν που διαδίδονται τα μέτωπα κύματος Αρνητική διάθλαση και συντελεστές Fresnel Έστω ότι ο χώρος χωρίζεται στις περιοχές z < 0 και z > 0, οι οποίες καταλαμβάνονται, αντίστοιχα, από ένα συμβατικό υλικό με καταστατικές παραμέτρους ϵ 1, µ 1 και ένα διπλο-αρνητικό με παραμέτρους ϵ 2, µ 2. Ένα επίπεδο κύμα προσπίπτει από το συμβατικό υλικό στο διπλο-αρνητικό με γωνία θ i ως προς τον άξονα z, όπως φαίνεται στο σχήμα 2.3. Τότε, τα κυματικά διανύσματα του προσπίπτοντος και του ανακλώμενου κύματος είναι, αντίστοιχα, k i = k 1x ˆx + k 1z ẑ και k r = k 1x ˆx k 1z ẑ, όπου k 1x = k 1 sin θ i, k 1z = k 1 cos θ i και k 1 = ω µ 1 ϵ 1. Επίσης, θεωρούμε ότι το κυματικό διάνυσμα του διαθλώμενου κύματος είναι k t = k 2x ˆx + k 2z ẑ. Από τη συνέχεια των εφαπτομενικών συνιστωσών της ηλεκτρικής πεδιακής έντασης στη διαχωριστική επιφάνεια προκύπτει ότι η εφαπτομενική συνιστώσα του k t ισούται με την εφαπτομενική συνιστώσα των k i, k r, δηλαδή k 2x = k 1 sin θ i. Έτσι, χρησιμοποιώντας τη σχέση διασποράς k t 2 = k 2 2x + k2 2z = ω2 µ 2 ϵ 2, εξάγεται ότι k 2z = ±ω µ 2 ϵ 2 µ 1 ϵ 1 sin 2 θ i (2.14) Υποθέτοντας ότι µ 2 ϵ 2 µ 1 ϵ 1 sin 2 θ i > 0, δηλαδή ότι δεν υπάρχουν απώλειες και δεν βρισκόμαστε στην περιπτωση της ολικής ανάκλασης, το πρόσημο στην (2.14) προσδιορίζεται από την αρχή διατήρησης της ενέργειας στην επιφάνεια z = 0. Πιο συγκεκριμένα, η ισχύς στο συμβατικό υλικό ρέει
26 16 Κεφάλαιο 2 Σχήμα 2.3: Πρόσπτωση επίπεδου κύματος από ένα συμβατικό υλικό (z < 0) σε ένα διπλο-αρνητικό (z > 0). Σχήμα 2.4: Κυματικό διάνυσμα και διάνυσμα Poyn ng του προσπίπτοντος, ανακλώμενου και διαθλώμενου κύματος, για πρόσπτωση από ένα συμβατικό υλικό σε ένα διπλοαρνητικό. προς την κατεύθυνση του θετικού άξονα z και το ίδιο πρέπει να συμβαίνει στο διπλο-αρνητικό υλικό. Όμως, επειδή σε κάθε διπλο-αρνητικό μέσο η φορά διάδοσης της ισχύος είναι αντίθετη από αυτή του κυματικού διανύσματος, έπεται ότι k 2z < 0 και στην (2.14) πρέπει να επιλεγεί το αρνητικό προσημο. Λαμβάνοντας υπόψη το αποτέλεσμα αυτό και τις αντίθετες φορές του κυματικού διανύσματος και του διανύσματος Poyn ng μέσα στο διπλοαρνητικό υλικό, το σχήμα 2.4 απεικονίζει το κυματικό διάνυσμα και το διάνυσμα Poyn ng του προσπίπτοντος, ανακλώμενου και διαθλώμενου κύματος. Αν ορίσουμε ως θετική φορά μέτρησης των γωνιών από τον άξονα z την αντίθετη των δεικτών του ρολογιού, η γωνία διάθλασης θ t είναι αρνητική, αντίθετα με ότι συμβαίνει κατά την πρόσπτωση σε ένα συμβατικό μέσο, όπου η γωνία διάθλασης είναι πάντα θετική. Το φαινόμενο αυτό καλείται αρνητική διάθλαση (nega ve refrac on) και αποτελεί χαρακτηριστική ιδιότητα των διπλο-αρνητικών υλικών. Η παραπάνω ανάλυση μας επιτρέπει να εκφράσουμε τον νόμο του Snell στην περίπτωση πρόσπτωσης σε διπλο-αρνητικό υλικό. Από το σχήμα 2.4, προκύπτει ότι η γωνία διάθλασης υπολογίζεται
27 2.2. Ιδιότητες των διπλοαρνητικών υλικών 17 Σχήμα 2.5: Εστίαση μέσω επίπεδης πλάκας διπλοαρνητικού υλικού, δείκτη διάθλασης n = 1. από την εξίσωση sin θ t = k 2x k t (2.15) Επιπλέον, k t = k 2 = ω µ 2 ϵ 2 και k 2x = k 1 sin θ i = ω µ 1 ϵ 1 sin θ i, οπότε η (2.15) καταλήγει στην sin θ t ϵ1 µ 1 = (2.16) sin θ i ϵ2 µ 2 Η διαφορά της παραπάνω σχέσης από τον νόμο του Snell που ισχύει όταν και τα δύο μέσα είναι συμβατικά έγκειται στο πρόσημο μείον που εμφανίζεται στο δεύτερο μέλος. Υπενθυμίζεται ότι ο νόμος του Snell στα συμβατικά μέσα είναι sin θ t = n 1, (2.17) sin θ i n 2 με n 1 = µ 1 ϵ 1, n 2 = µ 2 ϵ 2 τους δείκτες διάθλασης στα δύο μέσα. Η (2.17) σε συνδυασμό με την (2.16) μας οδηγεί στον ορισμό του δείκτη διάθλασης ενός διπλο-αρνητικού υλικού χωρίς απώλειες ως n = µϵ, προκειμένου να μην αλλάζει η μορφή του νόμου του Snell. Οι αρνητικές τιμές που λαμβάνει ο δείκτης διάθλασης, σύμφωνα με τον ορισμό αυτό, οδήγησαν ένα μέρος της επιστημονικής κοινότητας στην υιοθέτηση της ονομασίας υλικά αρνητικού δεικτη διάθλασης (nega ve refrac ve index materials) για τα υλικά με ϵ, µ < 0. Βασιζόμενος στο φαινόμενο της αρνητικής διάθλασης, ο Veselago [Veselago, 1968] κατέληξε στο συμπέρασμα ότι μία επίπεδη πλάκα με δείκτη διάθλασης n = 1 που περιβάλλεται από αέρα μπορεί να εστιάσει πλήρως το διαδιδόμενο φάσμα μιας σημειακής πηγής.⁴ Η πρόταση αυτή συμπυκνώνεται στο σχήμα 2.5, το οποίο παριστάνει τις διαδρομές των ακτίνων σύμφωνα με μία προσέγγιση γεωμετρικής οπτικής. Κάθε ακτίνα που προσπίτει στην αριστερή πλευρά της πλάκας με γωνία θ i ως προς την κάθετη ευθεία στην πλευρά αυτή (θετική φορά θεωρείται, ξανά, η αντίθετη των δεικτών του ρολογιού) διαθλάται σε μία γωνία θ t, που, με βάση τον νόμο του Snell, ισούται με θ i. Είναι φανερό ότι με τον τρόπο αυτό οι ακτίνες συγκλίνουν σε δύο σημεία F 1 και F 2 εντός και εκτός της πλάκας, αντίστοιχα, με την προϋπόθεση ότι d s < d, όπου d είναι το πλάτος της πλάκας και d s η απόσταση της πηγής από ⁴Όπως θα φανεί καλύτερα στην ενότητα 2.3, το πεδίο που παράγεται από μία πηγή μπορεί να εκφραστεί ως υπέρθεση επίπεδων κυμάτων. Τα κύματα αυτά μπορεί να είναι είτε διαδιδόμενα, οπότε ανήκουν στο διαδιδόμενο φάσμα της πηγής, είτε αποσβεννύμενα, οπότε ανήκουν στον αποσβεννύμενο φάσμα.
28 18 Κεφάλαιο 2 Σχήμα 2.6: Εστίαση μέσω επίπεδης πλάκας διπλοαρνητικού υλικού, δείκτη διάθλασης n = 1. Η μεταβλητή s δηλώνει την απόσταση από την αριστερή πλευρά της πλάκας του σημείου στο οποίο συγκλίνει η κόκκινη ακτίνα με τη συμμετρική της ως προς τον άξονα z. αυτήν. Οι αποστάσεις των F 1 και F 2 από την πηγή είναι 2d s και 2d αντίστοιχα. Η διάταξη αυτή, συνήθως, ονομάζεται επίπεδος φακός (flat lens), παρόλο που στην πραγματικότητα, όπως έχει τονιστεί ήδη από τον Veselago, δεν αποτελεί φακό με την αυστηρή εννοια του όρου, καθώς δεν μπορεί να εστιάσει μία παράλληλη δέσμη ακτίνων. Η ιδιότητα της πλήρους εστίασης που περιγράφηκε προηγουμένως παύει να ισχυει όταν n = 1. Τότε, η γωνία διάθλασης μιας ακτίνας είναι θ t = sin 1 (sin θ i /n) και η απόσταση από την αριστερή πλευρά της πλάκας στην οποία η ακτίνα συγκλίνει με τη συμμετρική της ως προς τον άξονα z (σχήμα 2.6) είναι tan θ s = i d s tan θ t = d n2 sin 2 θ i s (2.18) cos θ i Η απόσταση αυτή είναι διαφορετική για κάθε ζεύγος ακτίνων και, επομένως, η εστίαση δεν πραγματοποιείται σε ένα σημείο αλλά σε μία περιοχή (χρωματισμένες περιοχές του σχήματος 2.6). Σημειώνεται ότι τα αποτελέσματα των δύο τελευταίων παραγράφων μπορούν να επεκταθούν στην περίπτωση που το μέσο που περιβάλλει την πλάκα έχει δείκτη διάθλασης n R = 1, με τη διαφορά ότι η πλήρης εστίαση παρατηρείται όταν ο δείκτης διάθλασης του διπλο-αρνητικού υλικού είναι n L = n R. Επιστρέφοντας στο πρόβλημα της πρόσπτωσης επίπεδου κύματος στη διεπιφάνεια ενός συμβατικού και ενός διπλο-αρνητικού υλικού, θα μελετηθούν στη συνέχεια οι συντελεστές ανάκλασης και διάθλασης. Παραλείποντας τις μαθηματικές λεπτομέρειες, που είναι γνωστές από την κλασική θεωρία του ηλεκτρομαγνητικού πεδίου, οι συντελεστές ανάκλασης και διάθλασης στην παράλληλη πόλωση (ηλεκτρική πεδιακή ένταση στο επίπεδο πρόσπτωσης)⁵ είναι [Balanis, 1989] R = ϵ 1k 2z ϵ 2 k 1z ϵ 1 k 2z + ϵ 2 k 1z, T = 2ϵ 1 k 2z ϵ 1 k 2z + ϵ 2 k 1z cos θ i cos θ t (2.19α) (2.19β) ⁵Εναλλακτικά, η πόλωση αυτή ονομάζεται εγκάρσια ηλεκτρική TE y, καθώς η ηλεκτρική πεδιακή ένταση είναι κάθετη στον άξονα y.
29 2.2. Ιδιότητες των διπλοαρνητικών υλικών 19 Οι αντίστοιχοι συντελεστές για την κάθετη πόλωση (ηλεκτρική πεδιακή ένταση κάθετη στο επίπεδο πρόσπτωσης)⁶ είναι R = µ 2k 1z µ 1 k 2z µ 2 k 1z + µ 1 k 2z, (2.20α) T = 2µ 2 k 1z µ 2 k 1z + µ 1 k 2z (2.20β) Οι συντελεστές αυτοί έχουν την ίδια τιμή με την περίπτωση που ο χώρος z < 0 καταλαμβάνεται από ένα συμβατικό μέσο με καταστατικές παραμέτρους ϵ 2 και µ 2, καθώς αλλάζει μόνο το πρόσημο των θ t και k 2z. Επίσης, όταν ϵ 2 = ϵ 1 και µ 2 = µ 1, ισχύει R = R = 0 και T = T = 1, δηλαδή, ανεξάρτητα της γωνίας πρόσπτωσης, δεν υπάρχει ανακλώμενο κύμα και το διπλο-αρνητικό μέσο είναι απόλυτα προσαρμοσμένο στο συμβατικό. Σε έναν επίπεδο φακό από υλικό που είναι τέλεια προσαρμοσμένο στον περιβάλλοντα χώρο, οι ακτίνες μεταφέρουν στα εστιακά σημεία το ίδιο ποσό ενέργειας που έχουν καθώς πηγάζουν από την πηγή. Με άλλα λόγια, μια τέτοια διάταξη πετυχαίνει να αναπαράγει στα εστιακά επίπεδα (τα επίπεδα που διέρχονται από τα εστιακά σημεία και είναι παράλληλα προς τις επιφάνειες της πλάκας) τέλεια το διαδιδόμενο φάσμα της πηγής. Στις επόμενες ενότητες θα αποδειχθεί ότι η διάταξη αυτή μπορεί, ακόμη, να αναπαράγει πλήρως το αποσβεννύμενο φάσμα της πηγής και με τον τρόπο αυτό να λειτουργήσει ως ένας τέλειος φακός. Η ανάλυση των προηγούμενων παραγράφων πραγματοποιήθηκε με την υπόθεση ότι δεν υπάρχουν απώλειες. Παρ όλα αυτά, οι απώλειες είναι αναπόφευκτες σε κάθε πραγματικό μέσο. Αν, λοιπόν, Im{ϵ 2 }, Im{µ 2 } = 0, το σωστό πρόσημο στην (2.14) είναι αυτό που δίνει ένα αποσβεννύμενο κύμα κατά τη διεύθυνση του θετικού άξονα z (διεύθυνση κατά την οποία απομακρυνόμαστε από την διαχωριστική επιφάνεια των δυο μέσων). Πιο συγκεκριμένα, κάθε συνιστώσα του πεδίου είναι ανάλογη του όρου e jk 2xx jk 2z z, ο οποίος, επειδή ο k 2x είναι πραγματικός και ο k 2z μιγαδικός, γράφεται e jk 2xx j Re{k 2z }z e Im{k 2z}z (2.21) Επομένως, το πλάτος του πεδίου μειώνεται για αυξανόμενα z όταν Im{k 2z } < 0. Από την άλλη πλευρά, βρίσκεται εύκολα, μέσω της (2.14), ότι Im{k 2 2z } > 0, το οποίο μπορεί να ισχύει μόνο όταν οι Re{k 2z }, Im{k 2z } είναι ομόσημοι. Τελικά, συμπεραίνουμε ότι η αποδεκτή τιμή του k 2z είναι αυτή για την οποία Re{k 2z }, Im{k 2z } < 0. Η διεύθυνση διάδοσης της ισχύος καθορίζεται από το πραγματικό διάνυσμα Poyn ng, το οποίο για τις περιπτώσεις της κάθετης και της παράλληλης πόλωσης είναι, αντίστοιχα, P = E t0 2 2ω µ 2 2 e2 Im{k 2z}z (Re{µ 2 } Re{k t } + Im{µ 2 } Im{k t }), P = H t0 2 2ω ϵ 2 2 e2 Im{k 2z}z (Re{ϵ 2 } Re{k t } + Im{ϵ 2 } Im{k t }), (2.22α) (2.22β) με E t0, H t0 τα πλάτη της ηλεκτρικής και της μαγνητικής πεδιακής έντασης του διαθλώμενου κύματος. Στο σχήμα 2.7 απεικονίζονται τα κυματικά διανύσματα και τα διανύσματα Poyn ng στα δύο μέσα και για τα δύο είδη πόλωσης, από όπου γίνεται φανερή η παρουσία του φαινομένου της αρνητικής διάθλασης. Η διαφορά με τη διάταξη χωρίς απώλειες είναι ότι το διάνυσμα Poyn ng του διαθλώμενου ⁶Για την πόλωση αυτή χρησιμοποιείται και ο όρος εγκάρσια μαγνητική TM y, επειδή η μαγνητική πεδιακή ένταση είναι κάθετη στον άξονα y.
30 20 Κεφάλαιο 2 Σχήμα 2.7: Κυματικό διάνυσμα και διάνυσμα Poyn ng του προσπίπτοντος, ανακλώμενου και διαθλώμενου κύματος, για πρόσπτωση από ένα συμβατικό υλικό σε ένα διπλοαρνητικό με απώλειες. κύματος δεν είναι παράλληλο με το Re{k t }, που δίνει τη διεύθυνση διάδοσης των μετώπων κύματος, αλλά σχηματίζει μία γωνία ως προς αυτό. Σημειώνεται, επίσης, ότι το διάνυσμα Im{k t } δίνει τη διεύθυνση μείωσης του κυματικού πλάτους Επιφανειακά κύματα Ένα αξιοσημείωτο φαινόμενο που εντοπίζεται στη διαχωριστική επιφάνεια ενός συμβατικού και ενός διπλο-αρνητικού υλικού είναι η ανάπτυξη επιφανειακών κυμάτων με πλάτος που μειώνεται εκθετικά κατά μήκος του κάθετου άξονα στην διαχωριστική επιφάνεια, τόσο μέσα στο συμβατικό όσο και στο διπλο-αρνητικό υλικό. Η μορφή των κυμάτων αυτών είναι παρόμοια με την αντίστοιχη των επιφανειακών πλασμονικών ρυθμών (surface plasmons) που οδηγούνται παράλληλα στη διαχωριστική επιφάνεια ενός συμβατικού υλικού και ενός υλικού με αρνητική διηλεκτρική σταθερά (π.χ. μέταλλα στις οπτικές συχνότητες). Η ανάλυση που θα ακολουθήσει βασίζεται στη γεωμετρία του σχήματος 2.3 και θεωρεί ότι η διάδοση συμβαίνει παράλληλα στον άξονα x, γεγονός που επιτρέπει τη διάκριση των επιφανειακών ρυθμών σε TM y και TE y πολωμένους. Επιπροσθέτως, λαμβάνεται ότι το διπλο-αρνητικό υλικό δεν έχει απώλειες. Η περίπτωση των απωλειών διερευνάται διεξοδικά στο παράρτημα 2.Α. Αναφορικά με την περίπτωση της TM y πόλωσης, η ηλεκτρική πεδιακή ένταση διαθέτει μία μοναδική συνιστωσα παράλληλη στον άξονα y, η οποία δίνεται από τις εκφράσεις E 1y = A 1 e jβx e a 1z, E 2y = A 2 e jβx e a 2z, (2.23α) (2.23β) για το συμβατικό και το διπλο-αρνητικό μέσο, αντίστοιχα. Σημειώνεται ότι β είναι η σταθερά διάδοσης κατά τη διεύθυνση του άξονα x, a 1 και a 2 είναι οι σταθερές απόσβεσης στο συμβατικό και στο διπλοαρνητικό μέσο, ενώ A 1, A 2 είναι τα αντίστοιχα κυματικά πλάτη. Τονίζεται ότι a 1, a 2 > 0 προκειμένου το πεδίο να μειώνεται καθώς απομακρυνόμαστε από την επιφάνεια z = 0 και β 2 a 2 1 = ω2 µ 1 ϵ 1, β 2 a 2 2 = ω 2 µ 2 ϵ 2, (2.24α) (2.24β)
31 2.2. Ιδιότητες των διπλοαρνητικών υλικών 21 ως αποτέλεσμα του γεγονότος ότι οι (2.23) είναι λύσεις της εξίσωσης Helmholtz. Είναι φανερό ότι για να είναι δυνατή η ανάπτυξη επιφανειακού κύματος πρέπει β 2 > ω 2 µ 1 ϵ 1 και β 2 > ω 2 µ 2 ϵ 2, ώστε οι a 1, a 2 να είναι πραγματικοί αριθμοί. Επιπλέον, στη διαχωριστική επιφάνεια των δύο μέσων απαιτείται να ικανοποιούνται οι συνθήκες E z=0 1y = E z=0 1 E 1y 2y, = 1 E 2y, (2.25) µ 1 z µ 2 z z=0 z=0 οι οποίες είναι αποτέλεσμα της συνέχειας των εφαπτομενικών συνιστωσών της ηλεκτρικής και της μαγνητικής πεδιακής έντασης. Με αντικατάσταση των (2.23) στις (2.25) λαμβάνουμε a 1 µ 1 + a 2 µ 2 = 0 (2.26) Είναι προφανές ότι, επειδή a 1, a 2 > 0, η τελευταία εξίσωση έχει λύση μόνο αν οι µ 1, µ 2 είναι ετερόσημοι. Η διαπίστωση αυτή καταδεικνύει τη δυνατότητα οδήγησης επιφανειακού κύματος κατά μήκος της διεπιφάνειας ενός συμβατικού και ενός διπλο-αρνητικού υλικού. Αντίθετα, επιφανειακά κύματα δεν υποστηρίζονται στην διεπιφάνεια δύο συμβατικών ή δύο διπλο-αρνητικών υλικών. Συνδυάζοντας την (2.26) με τις (2.24), λαμβάνουμε τη σχέση διασποράς β 2 = ω 2 µ2 1 µ 2ϵ 2 µ 2 2 µ 1ϵ 1 µ 2 1 µ2 2 (2.27) Οι συνθήκες ύπαρξης επιφανειακού κύματος, οι οποίες καθορίζονται από την απαίτηση β 2 > ω 2 µ 1 ϵ 1 και β 2 > ω 2 µ 2 ϵ 2, είναι, τότε, µ 2 < µ 1 < µ 2 ϵ 2 ϵ 1 ή µ 1 < µ 2 < µ 1 ϵ 1 ϵ 2 (2.28) Ενδιαφέρον παρουσιάζει, επιπλέον, η μελέτη του πραγματικού διανύσματος Poyn ng, το οποίο δίνεται από τις εκφράσεις P 1 = β E 1y 2 ˆx, 2ωµ 1 (2.29α) P 2 = β E 2y 2 ˆx, 2ωµ 2 (2.29β) για το συμβατικό και το διπλο-αρνητικό υλικό, αντίστοιχα. Λαμβάνοντας υπόψη ότι µ 1 > 0 και µ 2 < 0, εξάγεται ότι η ροή της ισχύος και το διάνυσμα βˆx, που καθορίζει τη διεύθυνση διάδοσης των μετώπων κύματος, έχουν την ίδια φορά στο συμβατικό υλικό και αντίθετη στο διπλο-αρνητικό. Παρ όλα αυτά, η συνολική ισχύς που ρέει παράλληλα προς τον άξονα x μπορεί να έχει την ίδια ή αντίθετη φορά από το διάνυσμα β ˆx. Πιο συγκεκριμένα, η συνολική ισχύς υπολογίζεται ότι είναι P tot = β A 1 2 µ 2 2 µ2 1 2ωa 1 µ 1 µ 2 ˆx, (2.30) 2 μέσω ολοκλήρωσης του πραγματικού διανύσματος Poyn ng πάνω στον άξονα z. Είναι ξεκάθαρο ότι το P tot δείχνει προς τα θετικά x όταν µ 2 > µ 1 και προς τα αρνητικά όταν µ 1 > µ 2. Με άλλα λόγια, οι επιφανειακοί ρυθμοί που υποστηρίζονται στη διεπιφάνεια ενός συμβατικού και ενός διπλοαρνητικού υλικού μπορούν να είναι είτε εμπροσθοκατευθυντικοί είτε οπισθοκατευθυντικοί. Τα
32 22 Κεφάλαιο 2 (α) (β) Σχήμα 2.8: (α) Διάνυσμα Poyn ng και κυματικό διάνυσμα βˆx ενός επιφανειακού κύματος που αναπτύσσεται στην διαχωριστική επιφάνεια ενός συμβατικού και ενός διπλο-αρνητικού υλικού. (β) Πεδιακό πλάτος Σχήμα 2.9: Διάγραμμα διασποράς των επιφανειακών ρυθμών που αναπτύσσονται στην διεπιφάνεια του αέρα και ενός διπλο-αρνητικού υλικού, η διηλεκτρική σταθερά του οποίου ακολουθεί το μοντέλο Drude με ω p = rad/s και Γ = 0 rad/s, ενώ η μαγνητική του διαπερατότητα ακολουθεί το μοντέλο Lorentz με ω 0 = rad/s, ω p = rad/s και Γ = 0 rad/s. Ο οριζόντιος άξονας κανονικοποιείται ως προς τον κυματικό αριθμό του αέρα k 0 στην κυκλική συχνότητα 10 9 rad/s. Οι κυκλικές συχνότητες ω 1 = rad/s και ω 2 = rad/s είναι αυτές στις οποίες ϵ 2 = ϵ 0 και µ 2 = µ 0, αντίστοιχα. παραπάνω συμπεράσματα αποτυπώνονται στο σχήμα 2.8, όπου απεικονίζεται το διάνυσμα Poyn ng, το κυματικό διάνυσμα βˆx και η μορφή του πεδίου στα δύο μέσα. Με ανάλογη διαδικασία αντιμετωπίζεται η περίπτωση της TE y πόλωσης. Αναφέρεται μόνο ότι η αντίστοιχη εξίσωση της (2.26) είναι η από την οποία προκύπτει η σχέση διασποράς a 1 ϵ 1 + a 2 ϵ 2 = 0, (2.31) β 2 = ω 2 ϵ2 2 µ 1ϵ 1 ϵ 2 1 µ 2ϵ 2 ϵ 2 2 ϵ2 1 (2.32)
33 2.2. Ιδιότητες των διπλοαρνητικών υλικών 23 και η συνθήκη ϵ 1 < ϵ 2 < ϵ 1 µ 1 µ 2 ή ϵ 2 < ϵ 1 < ϵ 2 µ 2 µ 1, (2.33) που πρέπει να ικανοποιείται για να είναι δυνατή η ανάπτυξη επιφανειακών ρυθμών. Το σχήμα 2.9 παρουσιάζει το διάγραμμα διασποράς των ρυθμών και των δύο πολώσεων, όταν το συμβατικό μέσο είναι ο αέρας, η διηλεκτρική σταθερά του διπλο-αρνητικού υλικού δίνεται από την (2.6) με ω p = rad/s και Γ = 0 rad/s, ενώ η μαγνητική διαπερατότητα ακολουθεί το μοντέλο Lorentz της (2.7) με ω 0 = rad/s, ω p = rad/s και Γ = 0 rad/s. Στο διάγραμμα σημειώνονται, επίσης, οι κυκλικές συχνότητες ω 1 = rad/s και ω 2 = rad/s, στις οποίες ϵ 2 = ϵ 0 και µ 2 = µ 0. Παρατηρούμε ότι TM y ρυθμοί εμφανίζονται μόνο σε συχνότητες όπου µ 2 < 0 (σκουρόχρωμη σκιασμένη περιοχή) ενώ TE y ρυθμοί διεγείρονται στις συχνότητες όπου ϵ 2 < 0 (ανοιχτόχρωμη και σκουρόχρωμη σκιασμένη περιοχή). Επιπλέον, η καμπύλη διασποράς του TM y ρυθμού τείνει ασυμπτωτικά στην ευθεία ω = ω 2 ενώ οι αντίστοιχες των TE y ρυθμών τείνουν στις ω = ω 0 και ω = ω 1. Η συμπεριφορά αυτή είναι γενική με την έννοια ότι ο TM y ρυθμός με β διεγείρεται στη συχνότητα όπου µ 2 = µ 1, ενώ οι TE y ρυθμοί με β διεγείρονται στις συχνότητες όπου ϵ 2 = ϵ 1 ή µ 2 (η απόδειξη είναι άμεση συνέπεια των (2.27), (2.32)). Επιπροσθέτως, είναι φανερό ότι κάθε καμπύλη διασποράς βρίσκεται δεξιά του κώνου φωτός για το συμβατικό υλικό,⁷ το οποίο είναι απόλυτα αναμενόμενο, καθώς μόνο έτσι το κύμα στο συμβατικό μέσο είναι αποσβεννύμενο. Μάλιστα, στη συχνοτική περιοχή όπου µ 2, ϵ 2 < 0, οι καμπύλες διασποράς τέμνουν τον κώνο φωτός στη συχνότητα όπου µ 2 ϵ 2 = 1, όπως προκύπτει εύκολα από τις (2.27) και (2.32). Μερικά χρήσιμα συμπεράσματα που μπορεί να προκύψουν από τη μελέτη του διαγράμματος διασποράς αφορούν στην ταχύτητα ομάδας v g = dω/dβ των επιφανειακών ρυθμών. Από τον ορισμό της v g φαίνεται αμέσως ότι η ταχύτητα ομάδας ενός ρυθμού ισούται με την κλίση της αντίστοιχης καμπύλης διασποράς. Από το σχήμα 2.9 παρατηρούμε ότι η κλίση των καμπύλων διασποράς, και κατά συνέπεια η v g, είναι πάντα μικρότερη από την κλίση του κώνου φωτός, η οποία ισούται με την ταχύτητα διάδοσης ενός επίπεδου κύματος στο συμβατικό μέσο. Το γεγονός αυτό δικαιολογεί τον όρο αργά κύματα (slow waves) που χρησιμοποιείται, συχνά, για να περιγράψει τα επιφανειακά κύματα. ⁸ Μάλιστα, μπορεί να διακρίνει κανείς ότι v g 0 καθώς β, δηλαδή για μεγάλα β οι επιφανειακοί ρυθμοί δεν μεταφέρουν, σχεδόν, καθόλου ενέργεια κατά μήκος της διεπιφάνειας των υλικών. Επιπροσθέτως, v g < 0 για τον ρυθμό TM y, πράγμα που σημαίνει ότι ο ρυθμός αυτός είναι οπισθοκατευθυντικός. Στο ίδιο αποτέλεσμα καταλήγουμε χρησιμοποιώντας την (2.30), επειδή σε συχνότητες ω > ω 2 το μοντέλο Lorentz δίνει µ 2 < µ 0. Aπό την άλλη πλευρά, οι TE y ρυθμοί είναι εμπροσθοκατευθυντικοί, εφόσον v g > 0, ένα συμπέρασμα που μπορεί, πάλι, να εξαχθεί μέσω της συνολικής ροής ισχύος. Μια ειδική, ωστόσο ενδιαφέρουσα, περίπτωση προκύπτει όταν υπάρχει συχνότητα ω m στην οποία το διπλο-αρνητικό υλικό είναι τέλεια προσαρμοσμένο στο συμβατικό, δηλαδή ϵ 2 = ϵ 1 και µ 2 = µ 1. Τότε, a 1 = a 2, επειδή µ 1 ϵ 1 = µ 2 ϵ 2, και οι (2.27), (2.32) ικανοποιούνται για κάθε β > ω m µ1 ϵ 1. Κατά συνέπεια, η καμπύλη διασποράς είναι η ευθεία ω = ω m και η ταχύτητα ομάδας είναι 0, γεγονός που σημαίνει ότι δεν μπορεί να μεταφερθεί ισχύς κατά μήκος της επιφάνειας. ⁷Κώνος φωτός είναι η ευθεία ω = β/ µ 1 ϵ 1, δηλαδή η καμπύλη διασποράς ενός επίπεδου κύματος που διαδίδεται παράλληλα στον άξονα x στο συμβατικό υλικό. ⁸Εκτός από την ταχύτητα ομάδας, η ταχύτητα φάσης v p = ω/β είναι και αυτή μικρότερη από την ταχύτητα διάδοσης στο συμβατικό υλικό.
34 24 Κεφάλαιο 2 (α) (β) Σχήμα 2.10: Φαινόμενο Goos-Hänchen για πρόσπτωση δέσμης (α) σε συμβατικό υλικό και (β) σε διπλο-αρνητικό υλικό Αντίστροφο φαινόμενο Goos-Hänchen Το φαινόμενο Goos-Hänchen είναι άρρηκτα συνδεδεμένο με το φαινόμενο της ολικής ανάκλασης, το οποίο παρατηρείται κατά την πρόσπτωση ενός επίπεδου κύματος από ένα πυκνότερο σε ένα αραιότερο μέσο (δηλαδή από ένα μέσο με μεγαλύτερο δείκτη διάθλασης σε ένα μέσο με μικρότερο), με γωνία μεγαλύτερη από μία συγκεκριμένη τιμή που ονομάζεται κρίσιμη γωνία. Έχοντας ως αναφορά το σχήμα 2.3 και θεωρώντας ότι n 2 < n 1 ( µ 2 ϵ 2 < µ 1 ϵ 1 ), η κρίσιμη γωνία θ c ορίζεται ως η γωνία πρόσπτωσης για την οποία θ t = π/2 και υπολογίζεται από τη σχέση θ c = sin 1 ( n 1 / n 2 ). Για θ i > θ c, ο k 2z γίνεται μιγαδικός αριθμός και το κύμα στο μέσο 2 (μέσο με καταστατικές παραμέτρους ϵ 2, µ 2 ) διαδίδεται παράλληλα στο άξονα x, με πλάτος που μειώνεται εκθετικά κατά τη διεύθυνση του άξονα z. Επίσης, ο συντελεστής ανάκλασης έχει μέτρο 1 και όλη η προσπίπτουσα ενέργεια ανακλάται. Το φαινόμενο Goos-Hänchen εμφανίζεται κατά την πρόσπτωση μίας δέσμης φωτός από το πυκνότερο στο αραιότερο μέσο, με γωνία μεγαλύτερη της θ c. Τότε, η ανακλώμενη δέσμη εμφανίζει μία ολίσθηση ως προς την προσπίπτουσα, κατά την παράλληλη διεύθυνση προς τον άξονα x, όπως φαίνεται στο σχήμα 2.10(α). Αν το πλάτος της δέσμης είναι μεγάλο σε σχέση με το μήκος κύματος και η γωνία πρόσπτωσης δε βρίσκεται κοντά στις οριακές τιμές θ c και π/2, αποδεικνύεται ότι = φ r k x, (2.34) με φ r το όρισμα του συντελεστή ανάκλασης. Χρησιμοποιώντας την (2.19), βρίσκεται ότι ( 2ϵ = 1 ϵ 2 k x k2z ϵ2 2k2 1z + ϵ2 1 k + k ) 1z 2z 2, (2.35) k 2z για την περίπτωση της παράλληλης πόλωσης. Η αντίστοιχη σχέση που ισχύει για την κάθετη πόλωση προκύπτει από την (2.34) με αντικατάσταση των ϵ 1, ϵ 2 από τα µ 1, µ 2. Είναι φανερό ότι όταν και τα δύο μέσα είναι συμβατικά (ϵ 1, ϵ 2 > 0), > 0. Όταν, όμως, το μέσο 2 γίνει διπλο-αρνητικό (ϵ 2 < 0), < 0 και η δέσμη ανακλάται όπως δείχνει το σχήμα 2.10(β). Σημειώνεται ότι η ολίσθηση της δέσμης είναι, επίσης, αρνητική όταν η πόλωση είναι παράλληλη και ϵ 2 < 0, µ 2 > 0, ή η πόλωση είναι κάθετη και ϵ 2 > 0, µ 2 < 0. Μια ποιοτική ερμηνεία της αντιστροφής του φαινομένου Goos-Hänchen στην περίπτωση πρόσπτωσης σε διπλο-αρνητικό υλικό μπορεί να δοθεί μέσω της ροής της ισχύος. Πιο συγκεκριμένα, εί- k 1z
35 2.2. Ιδιότητες των διπλοαρνητικών υλικών 25 ναι δυνατο να θεωρηθεί ότι η ισχύς της προσπίπτουσας δέσμης, πριν ανακλαστεί, διαδίδεται στο μέσο 2 κατά μία απόσταση. Όταν το μέσο αυτό είναι συμβατικό, τα κύματα που υποστηρίζει είναι εμπροσθοκατευθυντικά και η ισχύς ρέει προς την κατεύθυνση του κυματικού διανύσματος. Επιπλέον, η εφαπτομενική συνιστώσα του κυματικού διανύσματος στο μέσο 2 έχει φορά προς τα θετικά x, καθώς είναι ίδια με αυτήν της προσπίπτουσας δέσμης, με συνέπεια η ισχύς να μεταφέρεται προς τα θετικά x και να ισχύει > 0. Αντίθετα, αν το μέσο 2 είναι διπλο-αρνητικό, υποστηρίζει οπισθοκατευθυντικά κύματα, με αποτέλεσμα η ισχύς να ρέει προς τα αρνητικά x και να ισχύει < Αντίστροφο φαινόμενο Doppler Ένα χαρακτηριστικό των διπλο-αρνητικών υλικών, στο οποίο είχε αναφερθεί ο Veselago στο κλασικό άρθρο του [Veselago, 1968], είναι η αντιστροφή της ολίσθησης Doppler. Υπενθυμίζεται ότι η ολίσθηση Doppler είναι η διαφορά ανάμεσα στη συχνότητα που ακτινοβολεί μία πηγή και σε αυτήν που μετράει ένας παρατηρητής, όταν αυτός βρίσκεται σε σχετική κίνηση ως προς την πηγή. Ας υποθέσουμε ότι η συχνότητα της πηγής είναι f και ότι ο παρατηρητής κινείται πάνω σε μία ευθεία που διέρχεται από την πηγή, με φορά προς την πηγή και σταθερή ταχύτητα v. Η συχνότητα f που μετράει ο παρατηρητής καθορίζεται από τον χρόνο T που χρειάζεται για να συναντήσει ένα μέτωπο κύματος με διαφορά φάσης 2π από αυτό στο οποίο βρίσκεται μία συγκεκριμένη στιγμή.⁹ Σε ένα συμβατικό υλικό, τα μέτωπα κύματος διαδίδονται απομακρυνόμενα από την πηγή, δηλαδή με φορά αντίθετη από τη φορά κίνησης του παρατηρητή. Επομένως, T = λ/(v + v p ), με v p την φασική ταχύτητα του υλικού μέσα στο οποίο ακτινοβολεί η πηγή και λ το μήκος κύματος που μετράει ένας ακίνητος παρατηρητής. Έτσι, βρίσκεται ότι η ολίσθηση Doppler είναι f = f f = v v p f (2.36) Όταν η πηγή βρίσκεται μέσα σε διπλο-αρνητικό υλικό, τα κύματα που ακτινοβολεί είναι οπισθοκατευθυντικά και τα μέτωπα κύματος διαδίδονται με φορά προς την πηγή, δηλαδή με την ίδια φορά που κινείται ο παρατηρητής. Τότε, T = λ/(v v p ) και f = f f = v v p f (2.37) Παρατηρούμε, λοιπόν, ότι σε ένα συμβατικό μέσο η συχνότητα που μετράει ένας παρατηρητής που προσεγγίζει την πηγή είναι μεγαλύτερη από αυτήν της πηγής, ενώ σε ένα διπλο-αρνητικό είναι μικρότερη. Η συμπεριφορά αυτή αντιστρέφεται όταν ο παρατηρητής απομακρύνεται από την πηγή Αντίστροφη ακτινοβολία Vavilov-Čerenkov Ο όρος ακτινοβολία Vavilov-Čerenkov αναφέρεται στο φαινόμενο κατά το οποίο ένα κινούμενο φορτισμένο σωματίδιο ακτινοβολεί ισχύ, όταν η ταχύτητά του είναι μεγαλύτερη από την ταχύτητα του φωτός του περιβάλλοντος μέσου. Τυπική περίπτωση όπου παρατηρείται το φαινόμενο αυτό είναι σε υγρά που βομβαρδίζονται με ταχέως κινούμενα φορτισμένα σωματίδια (π.χ. το νερό που περιβάλει έναν πυρηνικό αντιδραστήρα), οπότε εκπέμπεται ηλεκτρομαγνητική ακτινοβολία στην περιοχή του ορατού φωτός. Έστω ένα σωματίδιο με φορτίο q, το οποίο κινείται με ταχύτητα v πάνω στον άξονα z ⁹Ουσιαστικά, ο T είναι η περίοδος που μετράει ο παρατηρητής.
36 26 Κεφάλαιο 2 (α) (β) Σχήμα 2.11: Ακτινοβολία Vavilov-Čerenkov ενός σωματιδίου με φορτίο q και ταχύτητα v = vẑ μέσα (α) σε συμβατικό υλικό και (β) σε διπλο-αρνητικό υλικό. Στο σχήμα απεικονίζονται, επίσης, το κυματικό διάνυσμα k και το πραγματικό διάνυσμα Poyn ng P. και με φορά προς τα αυξανόμενα z. Αν τη χρονική στιγμή t = 0 το σωματίδιο βρίσκεται στο σημείο z = 0, η κίνησή του αντιστοιχεί στη ρευματική κατανομή J (r, t) = ẑqvδ(x)δ(y)δ(z vt), (2.38) όπου δ( ) είναι η συνάρτηση δέλτα Dirac και r το διάνυσμα θέσης. Ο μετασχηματισμός Fourier της παραπάνω εξίσωσης είναι J(r) = ẑqδ(x)δ(y)e jβz, (2.39) με β = ω/v. Στην πραγματικότητα, η (2.39) δίνει τη ρευματική κατανομή που δημιουργεί το σωματίδιο στην κυκλική συχνότητα ω. Παραλείποντας την ενδιάμεση μαθηματική ανάλυση, η ηλεκτρική πεδιακή ένταση του κύματος που παράγεται από την J(r) σε ένα συμβατικό μέσο δίνεται, σε κυλινδρικές συντεταγμένες, από την έκφραση E(r) = q ( k2ẑ jβ ) H (2) 0 (k ρ ρ)e jβz, (2.40) 4ωϵ όπου µ, ϵ οι καταστατικές παράμετροι του μέσου, k 2 = ω 2 µϵ, k ρ = k 2 β 2 και H (2) 0 ( ) η συνάρτηση Hankel β είδους και μηδενικής τάξης. Η χρήση του β είδους της συνάρτησης Hankel είναι απόρροια της ασυμπτωτικής της έκφρασης j2/(πk ρ ρ)e jkρρ για k ρ ρ 1, η οποία δίνει ένα κύμα με διεύθυνση διάδοσης της φάσης (και άρα και της ισχύος, αφού βρισκόμαστε σε συμβατικό μέσο) προς αυξανόμενα ρ. Σημειώνεται ότι, σύμφωνα με την αρχή διατήρησης της ενέργειας, η ισχύς πρέπει να ρέει από την πηγή πρός το άπειρο, δηλαδή προς αυξανόμενα ρ. Για μεγάλα ρ η (2.40) λαμβάνει την ασυμπτωτική μορφή E(r) = q j2k ρ ( β ˆρ kρ ẑ ) e j(k ρρ+βz) (2.41) 4ωϵ πρ Είναι φανερό ότι ισχύς ακτινοβολείται μόνο όταν ο k ρ είναι πραγματικός αριθμός, δηλαδή όταν β < k ή v > 1/ µϵ. Επιβεβαιώνεται, έτσι, το γεγονός πως το σωματίδιο ακτινοβολεί μόνο αν η ταχύτητά του είναι μεγαλύτερη από την ταχύτητα τους φωτός στο μέσο όπου κινείται. Επίσης, παρατηρούμε ότι η J(r) δημιουργεί ένα κύμα με κυματικό διάνυσμα k = k ρ ˆρ + βẑ, το οποίο σχηματίζει γωνία θ = cos 1 (v p /v) με τον άξονα z, όπως απεικονίζεται στο σχήμα 2.11(α). Την ίδια γωνία με τον άξονα z σχηματίζει και το πραγματικό διάνυσμα Poyn ng, ως παράλληλο με το k. Αξίζει να σημειωθεί ότι η
37 2.3. Επίπεδη πλάκα διπλο-αρνητικού υλικού 27 θ είναι ανεξάρτητη της συχνότητας και κατά συνέπεια δίνει τη διεύθυνση κατά την οποία ακτινοβολεί το σωματίδιο. Αν το υλικό μέσα στο οποίο πραγματοποιείται η κίνηση είναι διπλο-αρνητικό, η φάση διαδίδεται προς την αντίθετη κατεύθυνση από την ισχύ και άρα προς μειούμενα ρ (η ισχύς ρέει, πάλι, προς την κατεύθυνση των αυξανόμενων ρ). Κατά συνέπεια, τη θέση της συνάρτησης Hankel β είδους στην (2.40) λαμβάνει η αντίστοιχη α είδους, καθώς η τελευταία έχει ασυμπτωτική έκφραση 2/(jπk ρ ρ)e jk ρρ για k ρ ρ 1. Τότε, για μεγάλα ρ, η ηλεκτρική πεδιακή ένταση λαμβάνει την ασυμπτωτική μορφή E(r) = q 2k ρ ( β ˆρ + kρ ẑ ) e j( k ρρ+βz) 4ωϵ jπρ (2.42) Επομένως, το κύμα που δημιουργείται από την J(r) έχει κυματικό διάνυσμα k = k ρ ˆρ + βẑ, ενώ η ισχύς του ρέει προς την κατεύθυνση του k, σχηματίζοντας γωνία θ = π cos 1 (v p /v) με τον άξονα z (σχήμα 2.11(β)). Παρατηρούμε, λοιπόν, ότι ένα φορτισμένο σωματίδιο που κινείται μέσα σε διπλο-αρνητικό μέσο ακτινοβολεί ισχύ με φορά αντίθετη προς τη φορά της κίνησής του. Στην πραγματικότητα, βέβαια, επειδή κάθε διπλο-αρνητικό μέσο εμφανίζει διασπορά, θα υπάρχει πάντοτε ισχύς η οποία θα οδεύει προς την κατεύθυνση που κινείται το σωματίδιο. Μάλιστα, όπως αναλύεται στην εργασία [Lu et al., 2003], η ισχύς αυτή αντιστοιχεί στις συχνότητες στις οποίες οι καταστατικές παράμετροι του υλικού είναι θετικές. 2.3 Επίπεδη πλάκα διπλο-αρνητικού υλικού Πεδίο που δημιουργεί άπειρη γραμμική πηγή Στην ενότητα αυτή, θα μελετηθούν οι ιδιότητες της επίπεδης πλάκας διπλο-αρνητικού υλικού, η οποία, όπως αναφέρθηκε στο κεφάλαιο 1, βρίσκει εφαρμογή σε πολλές πρακτικές διατάξεις. Η ανάλυση πραγματοποιείται μέσω του προβλήματος σκέδασης κύματος που παράγεται από άπειρη γραμμική ρευματική πηγή, παράλληλη προς τις επιφάνειες της πλάκας. Η γεωμετρία του προβλήματος παρουσιάζεται στο σχήμα 2.12, όπου d ειναι το πάχος της πλάκας, (x, z ) είναι το σημείο από το οποίο διέρχεται η πηγή, η οποία θεωρείται ότι είναι παράλληλη στον άξονα y και διαρρέεται από ρεύμα έντασης I, ϵ 2, µ 2 οι καταστατικές παράμετροι της πλάκας και ϵ 1, µ 1 οι αντίστοιχες του περιβάλλοντα χώρου. Είναι γνωστό ότι το πεδίο που δημιουργεί η πηγή κατά την απουσία της πλάκας είναι TM y πολωμένο και η ηλεκτρική πεδιακή ένταση έχει μία μοναδική συνιστώσα παράλληλη στον άξονα y, που δίνεται από το ολοκλήρωμα Sommerfeld E y (x, z) = Iωµ 1 4π ˆ e jk x(x x ) e jk 1z z z k 1z dk x, (2.43) με k 1z = k 2 1 k2 x και k 1 = ω µ 1 ϵ 1. Αξίζει να παρατηρηθεί ότι η ολοκληρωτέα ποσότητα στην (2.43) αντιστοιχεί στην ηλεκτρική πεδιακή ένταση ενός επίπεδου κύματος με κυματικό διάνυσμα k x ˆx ± k 1z ẑ (το + ισχύει για z > 0 και το για z < 0), φανερώνοντας τη δυνατότητα έκφρασης του πεδίου ως αθροίσματος επίπεδων κυμάτων. Στη συνέχεια, χάριν της απλότητας των εκφράσεων, θα θεωρήσουμε ότι η πηγή βρίσκεται πάνω στο επίπεδο x = 0, δηλαδή x = 0. Επειδή η γεωμετρία είναι αμετάβλητη κατά μήκος του άξονα y, το σκεδαζόμενο πεδίο θα είναι, επίσης, TM y πολωμένο.
38 28 Κεφάλαιο 2 Σχήμα 2.12: Επίπεδη πλάκα διπλο-αρνητικού υλικού (καταστατικές παράμετροι ϵ 2, µ 2 ), πάχους d, μέσα σε χώρο συμβατικού υλικού (καταστατικές παράμετροι ϵ 1, µ 1 ). Για τη διέγερση της διάταξης χρησιμοποιείται γραμμική πηγή που διέρχεται από το σημείο (x, z ). Αν οι περιοχές z < d/2, d/2 < z < d/2 και z > d/2 ονομαστούν 1, 2 και 3, αντίστοιχα, η ηλεκτρική πεδιακή ένταση σε κάθε μία από αυτές γράφεται E 1y (x, z) = Iωµ 1 4π E 2y (x, z) = Iωµ 1 4π ˆ ˆ ˆ e jk xx k 1z [ e jk 1z z z + Re jk 1z(z+d/2) e jk 1z z +d/2 ] dk x, (2.44α) e jk xx k 1z e jk 1z z +d/2 ( Ae jk 2zz + Be jk 2zz ) dk x, (2.44β) E 3y (x, z) = Iωµ 1 e jk xx Te jk 1z z +d/2 e jk1z(z d/2) dk x (2.44γ) 4π k 1z με k 2z = k 2 2 k2 x και k 2 = ω µ 2 ϵ 2. Οι συντελεστές R, A, B και T είναι συναρτήσεις του k x και υπολογίζονται μέσω των E z= 1y d = E z= 1 E 1y 2y d, 2 2 µ 1 z = 1 E 2y z= d µ 2 z, (2.45α) 2 z= d 2 E z= 2y d = E z= 1 E 2y 3y d, = 1 E 3y 2 2 µ 2 z µ 1 z, (2.45β) z= d 2 οι οποίες συνιστούν τη μαθηματική διατύπωση της συνέχειας των εφαπτομενικών συνιστωσών του πεδίου στις επιφάνειες της πλάκας. Αντικαθιστώντας τις (2.44) στις (2.45), εξάγεται, μετά από μία σειρά αλγεβρικών πράξεων, ότι R = R ( 1 e j2k 2z d ) ( ) 1 R 2 1 R 2, T = e jk 2z d e j2k 2zd 1 R 2 (2.46α) e j2k 2zd A = (1 + R )e jk 2zd/2 1 R 2 e j2k 2zd z= d 2, B = R (1 + R )e j3k 2zd/2 1 R 2, (2.46β) e j2k 2zd όπου R είναι ο συντελεστής ανάκλασης από ημιάπειρο χώρο διπλο-αρνητικού υλικού, όπως δίνεται από την (2.20α). Έχοντας κατά νου τη φυσική ερμηνεία που δόθηκε για την (2.43), οι R, T είναι οι
39 2.3. Επίπεδη πλάκα διπλο-αρνητικού υλικού 29 (α) (β) Σχήμα 2.13: Βροχοτομές του k 1z στο k x -επίπεδο για συμβατικό υλικό (α) με απώλειες και (β) χωρίς απώλειες. Η συνεχής κόκκινη γραμμή δείχνει τον δρόμο ολοκλήρωσης για τον υπολογισμό των ολοκληρωμάτων Sommerfeld. συντελεστές ανάκλασης και μετάδοσης ενός επίπεδου κύματος με συνιστώσα του κυματικού διανύσματος κατά τη διεύθυνση του άξονα x ίση με k x. Η εμφάνιση της τετραγωνικής ρίζας στον ορισμό των k 1z, k 2z τους καθιστά πλειότιμες συναρτήσεις του k x με δύο κλάδους. Σχετικά με το k 2z, είναι δυνατό να αποδειχθεί ότι οι R, T και Ae jk 2zz + Be jk 2zz παραμένουν αναλλοίωτοι μετά την αντικατάσταση του k 2z από το k 2z και κατά συνέπεια, η επιλογή του κλάδου του k 2z δεν επηρεάζει τον υπολογισμό των ολοκληρωμάτων (2.44). Από την άλλη πλευρά, για τον προσδιορισμό του αποδεκτού κλάδου του k 1z, θεωρείται ότι το συμβατικό μέσο που περιβάλλει την πλάκα έχει απώλειες, δηλαδή οι ϵ 1, µ 1 είναι μιγαδικοί αριθμοί με Im{ϵ 1 }, Im{µ 1 } < 0. Τότε, το πεδίο θα πρέπει να τείνει στο 0 καθώς z ±, πράγμα που ικανοποιείται μόνο όταν Im{k 1z } < 0. Λαμβάνοντας ως βροχοτομές για το k 1z τις καμπύλες Im{k 1z } = 0 του k x -επιπέδου, η ολοκλήρωση των (2.44) πραγματοποιείται στο φύλλο Riemann στο οποίο Im{k 1z } < 0. Οι βροχοτομές, ο δρόμος ολοκλήρωσης και το πρόσημο του Re{k 1z } σε διάφορες περιοχές του k x -επιπέδου, το οποίο θα φανεί απαραίτητο αργότερα κατά τη μελέτη των ρυθμών που υποστηρίζει η διάταξη, απεικονίζονται στο σχήμα 2.13(α). Αν Im{ϵ 1 }, Im{µ 1 } 0, δηλαδή το συμβατικό μέσο δεν έχει απώλειες, οι βροχοτομές διαμορφώνονται όπως δείχνει το σχήμα 2.13(β), ενώ το φύλλο Riemann πάνω στο οποίο γίνεται η ολοκλήρωση παραμένει το ίδιο. Μία περισσότερο ολοκληρωμένη περιγραφή της διαδικασίας μέσω της οποίας βρίσκονται οι βροχοτομές και τα φύλλα Riemann μπορεί να βρεθεί στο παράρτημα 2.Α Διακριτό φάσμα ρυθμών Διακριτό φάσμα ρυθμών μιας διάταξης ορίζεται το σύνολο των ρυθμών που μπορούν να υπάρχουν χωρίς την παρουσία εξωτερικής διέγερσης. Στην περίπτωση της επίπεδης πλάκας, η εξωτερική διέγερση είναι το προσπίπτον κύμα και το διακριτό φάσμα ρυθμών προσδιορίζεται από τους πόλους του R και κατ επέκταση των T, A, B δηλαδή από τις τιμές των k x για τις οποίες είναι δυνατό να υπάρχει κύμα στις περιοχές 1, 2, 3 χωρίς προσπίπτον.¹⁰ Για την εύρεση των πόλων αυτών, η έκφραση ¹⁰Εκτός από το διακριτό φάσμα ρυθμών, που προσδιορίζεται από τους πόλους του συντελεστή ανάκλασης, υπάρχει και το συνεχές φάσμα, το οποίο συνίσταται από κύματα με k x πάνω στις βροχοτομές του k 1z. Σε αντίθεση με το διακριτό, κάθε
40 30 Κεφάλαιο 2 του R, όπως δίνεται στην (2.20α), αντικαθίσταται στην πρώτη από τις (2.46α), οπότε λαμβάνεται R = µ 2 2 k2 1z µ2 1 k2 2z [µ 2 k 1z jµ 1 k 2z cot(k 2z d/2)] [µ 2 k 1z + jµ 1 k 2z tan(k 2z d/2)] (2.47) Κατά συνέπεια, οι ζητούμενοι πόλοι είναι οι ρίζες των εξισώσεων µ 2 k 1z = jµ 1 k 2z cot(k 2z d/2), (2.48α) µ 2 k 1z = jµ 1 k 2z tan(k 2z d/2) (2.48β) Ακολούθως, θα δείξουμε ότι οι πόλοι που προκύπτουν από τις (2.48α), (2.48β) οδηγούν σε αντισυμμετρικούς και σε συμμετρικούς ρυθμούς, αντίστοιχα. Σημειώνεται ότι ένας ρυθμός ονομάζεται συμμετρικός (αντισυμμετρικός), όταν η ηλεκτρική πεδιακή ένταση είναι συμμετρική (αντισυμμετρική) ως προς το επίπεδο z = 0. Επειδή για έναν ρυθμό που ανήκει στο διακριτό φάσμα δεν υφίσταται προσπίπτον κύμα, η ηλεκτρική πεδιακή ένταση στις περιοχές 1, 2 και 3 δίνεται, αντίστοιχα, από τις σχέσεις E 0 e jk xx e jk 1z(z+d/2), (A/R)E 0 e jk xx e jk 2zz + (B/R)E 0 e jk xx e jk 2zz και (T/R)E 0 e jk xx e jk 1z(z d/2), με E 0 το πλάτος του πεδίου στην περιοχή 1. Συνεπώς, συμμετρικός ρυθμός σημαίνει ότι A = B ή R e jk 2zd = 1, όπως προκύπτει μέσω των (2.46β). Η τελευταία εξίσωση αποδεικνύεται εύκολα ότι είναι ισοδύναμη με την (2.48β). Ανάλογα, αν ο ρυθμός είναι αντισυμμετρικός, A = B ή R e jk 2zd = 1, η οποία είναι ισοδύναμη με την (2.48α) Επιφανειακά κύματα Εφόσον τα υλικά που διαμορφώνουν τη διάταξη δεν έχουν απώλειες, οι πραγματικοί πόλοι του συντελεστή ανάκλασης αντιστοιχούν σε παγιδευμένα επιφανειακά κύματα. Το πλάτος κάθε τέτοιου κύματος μειώνεται εκθετικά όσο αυξάνεται ο z στον χώρο εκτός της πλάκας, πράγμα που σημαίνει ότι αυτά τα κύματα διεγείρονται όταν k x > k 1, οπότε k 1z = ja 1z, με a 1z = k 2 x k 2 1. Τα επιφανειακά κύματα μπορούν να χωριστούν σε δύο κατηγορίες, ανάλογα αν k x > k 2 ή k x < k 2. Στην πρώτη κατηγορία, ο k 2z είναι φανταστικός αριθμός και το κύμα έχει αποσβεννύμενη μορφή στο εσωτερικό της πλάκας. Στη δεύτερη κατηγορία, ο k 2z είναι πραγματικός αριθμός και το κύμα μέσα στην πλάκα έχει στάσιμο χαρακτήρα. Σημειώνεται ότι, όπως θα δειχθεί στη συνέχεια, μία πλάκα από συμβατικό υλικό υποστηρίζει μόνο τα κύματα της δεύτερης κατηγορίας. Έστω ότι k x > k 2. Τότε, k 2z = ja 2z, με a 2z = k 2 x k 2 2 > 0¹¹ και οι (2.48) γίνονται µ 2 a 1z = µ 1 a 2z coth(a 2z d/2), (2.49α) µ 2 a 1z = µ 1 a 2z tanh(a 2z d/2) (2.49β) Είναι φανερό ότι οι παραπάνω εξισώσεις έχουν λύση μόνο όταν οι µ 1, µ 2 είναι ετερόσημοι, γεγονός που δηλώνει ότι αυτού του είδους οι ρυθμοί μπορούν να διεγερθούν σε μία διπλο-αρνητική πλάκα, όχι, όμως, σε μία συμβατική. Επίσης, εξαιτίας των υπερβολικών συναρτήσεων, κάθε μία από τις (2.49) έχει μοναδική λύση.¹² Στην πραγματικότητα, η ύπαρξη των ρυθμών αυτών είναι άμεση συνέπεια της ρυθμός του συνεχούς φάσματος δεν μπορει να υπάρχει χωρίς προσπίπτον κύμα. Το διακριτό μαζί με το συνεχές φάσμα αποτελούν ένα πλήρες σύνολο ρυθμών για την περιγραφή του πεδίου που δημιουργείται από οποιαδήποτε πηγή. ¹¹Όπως αναλύθηκε στην υποενότητα 1.3.1, το πρόσημο του k 2z δεν επηρεάζει τα αποτελέσματα και για τον λόγο αυτό επιλέχθηκε, αυθαίρετα, θετικό. ¹²Μία γραφική απόδειξη της πρότασης αυτής παρέχεται στην εργασία [Wu et al., 2003].
41 2.3. Επίπεδη πλάκα διπλο-αρνητικού υλικού 31 Σχήμα 2.14: Ροή ισχύος ενός επιφανειακού ρυθμού σε μία επίπεδη πλάκα διπλο-αρνητικού υλικού. Τα διανύσματα P 1, P 2, P 3 συμβολίζουν το πραγματικό διάνυσμα Poyn ng στις περιοχές 1, 2 και 3. δυνατότητας που έχει μία διεπιφάνεια συμβατικού και διπλο-αρνητικού υλικού να οδηγεί πλασμονικούς ρυθμούς, δηλαδή κύματα με πλάτος που μειώνεται εκθετικά εκατέρωθεν της επιφάνειας. Πιο συγκεκριμένα, κάθε μία από τις επιφάνειες της πλάκας υποστηρίζει από έναν πλασμονικό ρυθμό, οι οποίοι, γενικά, αλληλεπιδρούν μεταξύ τους. Αν αυτοί οι ρυθμοί βρίσκονται σε φάση, δημιουργείται ο συμμετρικός ρυθμός της πλάκας, ενώ όταν έχουν αντίθετες φάσεις προκύπτει ο αντισυμμετρικός ρυθμός. Η αλληλεπίδραση αυτή χάνεται αν a 2z d/2 1, το οποίο ισχύει είτε όταν a 2z 1 (k x k 2 ) είτε όταν d 1. Στην περίπτωση αυτή, οι (2.49) καταλήγουν στην µ 2 a 1z = µ 1 a 2z, (2.50) η οποία ταυτίζεται με την (2.26), δηλαδή την εξίσωση διασποράς του επιφανειακού κύματος που αναπτύσσεται στη διαχωριστική επιφάνεια ενός συμβατικού με ένα διπλο-αρνητικό υλικό. Με άλλα λόγια, όταν αυξηθεί ο k x ή το πάχος της πλάκας, οι πλασμονικοί ρυθμοί που αναπτύσσονται σε καθεμία από τις επιφάνειες της πλάκας αποσυμπλέκονται εντελώς, καθώς το πεδίο του καθενός από αυτούς είναι, σχεδόν, μηδέν στην περιοχή όπου αναπτύσσεται ο άλλος. Από την άλλη πλευρά, η διέγερση των κυμάτων της δεύτερης κατηγορίας προϋποθέτει ότι k 1 < k x < k 2, το οποίο ισχύει όταν µ 1 ϵ 1 < µ 2 ϵ 2, δηλαδή όταν το διπλο-αρνητικό υλικό είναι πυκνότερο από το συμβατικό. Λαμβάνοντας υπόψη το γεγονός αυτό και τη στάσιμη μορφή του πεδίου αυτών των ρυθμών στο εσωτερικό της πλάκας, συμπεραίνουμε ότι ο φυσικός μηχανισμός που ευθύνεται για την εμφάνιση των κυμάτων αυτών είναι η ολική ανάκλαση, όπως ακριβώς συμβαίνει σε μία συμβατική πλάκα. Αντίθετα, όμως, με μία συμβατική πλάκα, όπου τα επιφανειακά κύματα είναι πάντοτε εμπροσθοκατευθυντικά, τα κύματα σε μία διπλο-αρνητική πλάκα μπορεί να είναι είτε εμπροσθοκατευθυντικά είτε οπισθοκατευθυντικά. Η συμπεριφορά αυτή, που θα φανεί ξεκάθαρα μέσω των διαγραμμάτων διασποράς, είναι συνέπεια του γεγονότος ότι μέσα στο διπλο-αρνητικό υλικό η ισχύς ρέει προς την αντίθετη κατεύθυνση του διανύσματος k x ˆx, το οποίο δίνει τη φορά διάδοσης των μετώπων κύματος και τη φορά ροής της ισχύος στο συμβατικό υλικό. Πιο συγκεκριμένα, αν η συνολική ισχύς που ρέει παράλληλα προς τον άξονα x μέσα στην πλάκα είναι μεγαλύτερη από την αντίστοιχη εκτός της πλάκας, η συνολική ισχύς του επιφανειακού κύματος ρέει αντίθετα από το k x ˆx και το κύμα είναι οπισθοκατευθυντικό. Η συμπεριφορά αυτή, η οποία ισχύει και στην περίπτωση των κυμάτων της πρώτης κατηγορίας, παρουσιάζεται, γραφικά, στο σχημα Το διάγραμμα διασποράς των τεσσάρων πρώτων συμμετρικών και αντισυμμετρικών ρυθμών μιας
42 32 Κεφάλαιο 2 (α) (β) Σχήμα 2.15: Διάγραμμα διασποράς των ρυθμών του διακριτού φάσματος μιας πλάκας διπλο-αρνητικού υλικού πάχους d = 3 cm, που περιβάλλεται από αέρα. Η διηλεκτρική σταθερά της πλάκας ακολουθεί το μοντέλο Drude με ω p = rad/s και Γ = 0 rad/s, ενώ η μαγνητική της διαπερατότητα ακολουθεί το μοντέλο Lorentz με ω 0 = rad/s, ω p = rad/s και Γ = 0 rad/s. Υπόμνημα: συνεχής μπλε γραμμή: συμμετρικοί φυσικοί επιφανειακοί ρυθμοί, συνεχής κόκκινη γραμμή: αντισυμμετρικοί φυσικοί επιφανειακοί ρυθμοί, διακεκομμένη μπλε γραμμή: συμμετρικοί μη-φυσικοί επιφανειακοί ρυθμοί, διακεκομμένη κόκκινη γραμμή: αντισυμμετρικοί μη-φυσικοί επιφανειακοί ρυθμοί, συνεχής μαύρη γραμμή: συμμετρικοί φυσικοί διαρρέοντες ρυθμοί, συνεχής πράσινη γραμμή: αντισυμμετρικοί φυσικοί διαρρέοντες ρυθμοί. πλάκας με d = 3 cm που περιβάλλεται από αέρα απεικονίζεται στο σχήμα 2.15(α) με τις μπλε και κόκκινες συνεχείς γραμμές, αντίστοιχα. Οι καταστατικές παράμετροι της πλάκας ακολουθούν τα μοντέλα Drude και Lorentz με τις παραμέτρους που χρησιμοποιήθηκαν στο σχήμα 2.9. Είναι εμφανές ότι η καμπύλη κάθε ρυθμού μπορεί να έχει θετική ή αρνητική κλίση, πράγμα που σημαίνει ότι ο ρυθμός μπορει να είναι είτε εμπροσθοκατευθυντικός είτε οπισθοκατευθυντικός. Μάλιστα, είναι δυνατό σε μία συγκεκριμένη συχνότητα να διεγείρεται ο ίδιος ρυθμός ως εμπροσθοκατευθυντικός για μία τιμή
43 2.3. Επίπεδη πλάκα διπλο-αρνητικού υλικού 33 (α) (β) (γ) (δ) (ε) (στ) Σχήμα 2.16: Μορφή του πεδίου στο επίπεδο x = 0 των επιφανειακών ρυθμών (α) TM 0, (β) TM 2, (γ) TM 4, (δ) TM 1, (ε) TM 3, (στ) TM 5. του k x και ως οπισθοκατευθυντικός για μία άλλη, ένα φαινόμενο που απουσιάζει εντελώς από τα συμβατικά συστήματα κυματοδήγησης. Προκειμένου να κατανοηθεί πληρέστερα η φύση των ρυθμών, το σχήμα 2.16 παρουσιάζει τη μορφή σε ένα επίπεδο σταθερού x των τριών πρώτων, από πάνω προς τα κάτω, συμμετρικών και αντισυμμετρικών ρυθμών του διαγράμματος διασποράς. Όπως είναι αναμενόμενο, ο πρώτος συμμετρικός και αντισυμμετρικός ρυθμός είναι αποσβεννύμενοι στο εσωτερικό της πλάκας, ενώ οι υπόλοιποι ακολουθούν μία ημιτονοειδή μεταβολή. Επίσης, ονομάζοντας ως TM n τον ρυθμό το πεδίο του οποίου έχει n μηδενισμούς μέσα στο διπλο-αρνητικό υλικό, οι τρεις πρώτοι συμμετρικοί ρυθμοί είναι κατά σειρά οι TM 0, TM 2, TM 4 ενώ οι τρεις πρώτοι αντισυμμετρικοί είναι οι TM 1, TM 3, TM 5. Σημειώνεται ότι, επειδή η (2.50) είναι η εξίσωση διασποράς των ρυθμών TM 0, TM 1 για μεγάλα k x, οι καμπύλες διασποράς τους, πρακτικά, ταυτίζονται μετά από κάποιο k x και τείνουν ασυμπτωτικά στην ευθεία ω = ω 1, με ω 1 τη συχνότητα στην οποία µ 2 = µ 1. Όλοι οι ρυθμοί που εξετάστηκαν έως τώρα προκύπτουν από πόλους του συντελεστή ανάκλασης στο α φύλλο Riemann και, επομένως, το πεδίο τους μειώνεται εκθετικά καθώς απομακρυνόμαστε από την πλάκα. Ωστόσο, ο συντελεστής ανάκλασης είναι δυνατό να έχει πόλους στο β φύλλο Riemann, οι οποίοι αντιστοιχούν σε ρυθμούς με εκθετικά αυξανόμενο πλάτος εκτός του διπλο-αρνητικού υλικού. Οι ρυθμοί αυτοί καλούνται μη-φυσικοί (improper), σε αντίθεση με τους πρώτους που ονομάζονται φυσικοί (proper), καθώς παραβιάζουν τη βασική φυσική αρχή ότι το πεδίο σε άπειρη απόσταση από τους διάφορους σκεδαστές πρέπει να είναι μηδενικό. Στο διάγραμμα διασποράς του σχηματος 2.15(α) οι μη-φυσικοί ρυθμοί παριστάνονται με τις μπλε και κόκκινες διακεκομμένες γραμμές. Παρατηρούμε ότι, όπως και οι φυσικοί, διεγείρονται στην περιοχή k x > k 1, οπότε το k 1z είναι φανταστικός αριθμός, όμως, με Im{k 1z } > 0.
44 34 Κεφάλαιο 2 (α) (β) Σχήμα 2.17: Ροή ισχύος σε μία πλάκα διπλο-αρνητικού υλικού για ένα διαρρέον κύμα που αντιστοιχεί σε πόλο στην περιοχή (α) Γ και (β) Δ. Με P 1, P 2, P 3 συμβολίζεται το πραγματικό διάνυσμα Poyn ng στις περιοχές 1, 2 και 3, αντίστοιχα, ενώ k 1, k 3 είναι το κυματικό διάνυσμα στις περιοχές 1 και Διαρρέοντα κύματα Οι (2.48), εκτός από τις πραγματικές ρίζες που μελετήθηκαν στην προηγούμενη υποενότητα, έχουν και μιγαδικές ρίζες στο α φύλλο Riemann. Οι τελευταίες οδηγούν σε κύματα με πλάτος που μειώνεται κατά μήκος της πλάκας, καθώς ένα μέρος της ενέργειας που μεταφέρουν ακτινοβολείται στον περιβάλλοντα χώρο, και για τον λόγο αυτό καλούνται διαρρέοντα κύματα (leaky waves). Επίσης, εφόσον οι πόλοι βρίσκονται στο α φύλλο Riemann, ισχύει Im{k 1z } < 0 και το πλάτος τους μειώνεται όσο απομακρυνόμαστε από την πλάκα πάνω στον άξονα z. Σημειώνεται ότι όταν η πλάκα αποτελείται από συμβατικό υλικό, οι μιγαδικοί πόλοι εντοπίζονται πάντοτε στο β φύλλο Riemann, με συνέπεια τα κύματα που αντιστοιχούν σε αυτούς να είναι μη-φυσικά. Η διέγερση διαρρεόντων κυμάτων μπορεί να φανεί χρήσιμη στην υλοποίηση κατευθυντικών κεραιών, με μέγιστο του κύριου λοβού στην κατεύθυνση κατά την οποία ακτινοβολείται ισχύς από το διαρρέον κύμα. Δεδομένου ότι δεν υπάρχουν απώλειες, δηλαδή ότι οι ϵ 1, µ 1, ϵ 2, µ 2 είναι πραγματικοί αριθμοί, αν k x είναι ρίζα των (2.48), το ίδιο συμβαίνει και για τους k x, ±k x. Επομένως, ρίζες εντοπίζονται σε κάθε τεταρτημόριο του k x -επιπέδου και το πρόσημο του φανταστικού μέρους τους μπορεί να είναι θετικό ή αρνητικό. Έχοντας υπόψη ότι οι διευθύνσεις διάδοσης της ισχύος και μείωσης του πλάτους πρέπει να ταυτίζονται, θετικό Im{k x } δηλώνει διάδοση κατά τα θετικά x και αρνητικό Im{k x } κατά τα αρνητικά. Στη συνέχεια εξετάζονται κύματα με διεύθυνση διάδοσης τον θετικό ημιάξονα x, ώστε οι πόλοι στους οποίους αντιστοιχούν να βρίσκονται στις περιοχές Γ ή Δ του σχήματος 2.13(β). Αν ο πόλος βρίσκεται στην περιοχή Γ, ισχύει Re{k x } < 0, Re{k 1z } > 0 και το πραγματικό μέρος των κυματικών διανυσμάτων k 1 και k 3 στις περιοχές 1 και 3 σχηματίζει γωνία θ > π/2 με τον θετικό ημιάξονα x, όπως φαίνεται στο σχήμα 2.17(α). Την ίδια γωνία σχηματιζει, επίσης, η ακτινοβολούμενη ισχύς, καθώς σε ένα συμβατικό μέσο το πραγματικό μέρος του κυματικού διανύσματος δίνει τη διεύθυνση ροής της ισχύος. Από την άλλη πλευρά, ένας ρυθμός που προκύπτει από πόλο στην περιοχή Δ έχει Re{k x } > 0, Re{k 1z } < 0, με αποτέλεσμα το κυματικό διάνυσμα και το πραγματικό διάνυσμα Poyn ng να έχουν τις διευθύνσεις που παρουσιάζονται στο σχήμα 2.17(β). Στην περίπτωση αυτή, δεν υπάρχει ακτινοβολία ισχύος από την πλάκα στον περιβάλλοντα χώρο αλλά είσοδος ισχύος στην πλάκα. Η ισχύς αυτή μεταφέρεται, στη συνέχεια, μέσω του διπλο-αρνητικού υλικού προς την κατεύθυνση του αρνητικού άξονα x, δηλαδή αντίθετα από τη διεύθυνση διάδοσης του κύματος (κατεύθυνση προς την πηγή). Η
45 2.3. Επίπεδη πλάκα διπλο-αρνητικού υλικού 35 συμπεριφορά αυτή φανερώνει ότι ο όρος διαρρέον δεν αντικατοπτρίζει τη φύση ενός κύματος αυτού του είδους και χρησιμοποιείται μόνο καταχρηστικά για να δηλώσει ότι το κύμα προέρχεται από μιγαδικό πόλο. Στο σχήμα 2.15 απεικονίζονται τα Re{k x }, Im{k x } για τους συμμετρικούς (μαύρες γραμμές) και τους αντισυμμετρικούς (πράσινες γραμμές) ρυθμούς που αντιστοιχούν στους τέσσερις πιο κοντινούς πόλους στον πραγματικό άξονα της περιοχής Δ.¹³ Είναι φανερό ότι κάθε διαρρέον κύμα αντιστοιχεί σε ένα επιφανειακό, με την καμπύλη διασποράς του πρώτου να αγγίζει αυτήν του δεύτερου στο σημείο του ωk x επιπέδου που η τελευταία έχει μηδενική κλίση. Πιο συγκεκριμένα, παρατηρούμε ότι καθώς μειώνεται η συχνότητα, η σταθερά απόσβεσης ενός διαρρέοντος κύματος ελαττώνεται και γίνεται μηδέν όταν το κύμα μετατρέπεται από διαρρέον σε επιφανειακό. Στη συχνότητα μετάβασης η ταχύτητα ομάδας του κύματος είναι μηδέν. Υπενθυμίζεται ότι σε μία συμβατική πλάκα η σταθερά απόσβεσης των διαρρεόντων ρυθμών μειώνεται με την αύξηση της συχνότητας και τα σημεία μετάβασης βρίσκονται, πάντα, πάνω στον κώνο φωτός του περιβάλλοντος μέσου, δηλαδή στο κλαδικό σημείο k x = k 1 του k x -επιπέδου. Με άλλα λόγια, σε μία συμβατική πλάκα το σημείο στο οποίο οι διαρρέοντες ρυθμοί γίνονται επιφανειακοί είναι αυτό στο οποίο οι πόλοι τους αλλάζουν φύλλο Riemann, κάτι που δεν συμβαίνει σε μία διπλο-αρνητική πλάκα, όπου οι μιγαδικοί και οι πραγματικοί πόλοι βρίσκονται στο ίδιο φύλλο Riemann Τέλειος φακός Ήδη από το 1968, ο Veselago είχε προβλέψει μέσω μιας ακτινικής προσέγγισης, ότι μία πλάκα με καταστατικές παραμέτρους ϵ 2 = ϵ 1, µ 2 = µ 1 μπορεί να εστιάσει, πλήρως, το διαδιδόμενο φάσμα μιας σημειακής πηγής [Veselago, 1968]. Την πρόταση αυτή επεξέτεινε ο Pendry το 2000, αποδεικνύοντας ότι μία τέτοια πλάκα μπορεί, επίσης, να εστιάσει το αποσβεννύμενο φάσμα μιας σημειακής πηγής και να αναπαράγει στο επίπεδο εστίασης τέλεια τη μορφή που έχει το πεδίο στο επίπεδο της πηγής [Pendry, 2000]. Για τον λόγο αυτό, η διάταξη αυτή καθιερώθηκε με την ονομασία τέλειος φακός, καθώς παρέχει τη δυνατότητα επίτευξης άπειρης αναλυτικότητας εστίασης, σε αντιδιαστολή με τους συμβατικούς φακούς, των οποίων η αναλυτικότητα καθορίζεται από το μήκος κύματος. Ο τέλειος φακός αποτελεί, ουσιαστικά, την πρώτη εφαρμογή των διπλο-αρνητικών υλικών¹⁴ και έχει συγκεντρώσει αυξημένο θεωρητικό και πειραματικό ενδιαφέρον προκειμένου να διαπιστωθεί η δυνατότητα πρακτικής υλοποίησής του. Στην ενότητα αυτή θα περιγραφούν οι γενικές αρχές που διέπουν τον τέλειο φακό, καθώς μία ενδελεχής μελέτη του θα πραγματοποιηθεί στο κεφάλαιο 4. Όπως αναφέρθηκε στην αρχή της ενότητας, το πεδίο που παράγει μία γραμμική πηγή εκφράζεται ως άθροισμα επίπεδων κυμάτων. Η ηλεκτρική πεδιακή ένταση ενός τέτοιου κύματος δίνεται, σύμφωνα με την (2.43), από την έκφραση e jk xx e jk 1z z z, (2.51) όπου, για λόγους σαφήνειας, το πλάτος 1/k 1z παραλείπεται και x = 0, δηλαδή η πηγή θεωρείται ότι βρίσκεται στο επίπεδο x = 0. Υπενθυμίζεται ότι, επειδή η ολοκλήρωση πραγματοποιείται στο α ¹³Οι πόλοι της περιοχής Γ και οι αντίστοιχοι ρυθμοί προκύπτουν από τους συζυγείς των πόλων της περιοχής Δ, εφόσον είμαστε στην περίπτωση χωρίς απώλειες, και για τον λόγο αυτό δεν παρουσιάζονται. ¹⁴Το άρθρο του Pendry δημοσιεύτηκε, περίπου, 4 μήνες μετά την πρώτη πρακτική υλοποίηση διπλο-αρνητικού υλικού από τους Smith et al. [Smith et al., 2000].
46 36 Κεφάλαιο 2 Σχήμα 2.18: Εστίαση του πεδίου που παράγεται από γραμμική πηγή μέσω συμβατικού φακού. φύλλο Riemann, ισχύει k 2 1 k 1z = k2 x, αν k x k 1 j k 2 x k 21, αν k (2.52) x > k 1 Από τις (2.51), (2.52) εύκολα διαπιστώνεται ότι k x < k 1 αντιστοιχεί σε διαδιδόμενα κύματα, ενώ k x > k 1 σε αποσβεννύμενα, με πλάτος που μειώνεται εκθετικά καθώς ο z z αυξάνει. Το πεδίο στο επίπεδο της πηγής είναι E y (x, z ) = Iωµ 1 4π ˆ e jk xx k 1z dk x, (2.53) από όπου φαίνεται ότι προκύπτει από την υπέρθεση όλων των διαδιδόμενων και αποσβεννύμενων κυμάτων. Όσο, όμως, αυξάνεται η απόσταση z z από το επίπεδο της πηγής, ο όρος e jk 1z z z για k x > k 1 τείνει γρήγορα στο 0, με αποτέλεσμα το πεδίο να γράφεται ως γραμμικός συνδυασμός μόνο των διαδιδόμενων ρυθμών, σύμφωνα με τη σχέση E y (x, z) = Iωµ 1 4π ˆ k1 k 1 e jkxx e jk1z z z k 1z dk x, (2.54) Ας υποθέσουμε, τώρα, ότι η πηγή βρίσκεται σε μία από τις εστίες ενός συμβατικού συγκλίνοντος φακού, όπως παριστάνεται στο σχήμα 2.18.¹⁵ Τότε η λειτουργία του φακού συνοψίζεται στο γεγονός ότι, στην καλύτερη περίπτωση, όλοι οι ρυθμοί του διαδιδόμενου φάσματος της πηγής αποκτούν στο εστιακό επίπεδο (το επίπεδο που είναι κάθετο στον άξονα του φακού και διέρχεται από την εστία του) την ίδια διαφορά φάσης, έστω φ, σε σχέση με το επίπεδο της πηγής (το επίπεδο που είναι κάθετο στον άξονα του φακού και πάνω στο οποίο βρίσκεται η πηγή). Από την άλλη πλευρά, ο φακός δεν έχει καμία επίδραση πάνω στο αποσβεννύμενο φάσμα της πηγής, με αποτέλεσμα το πεδίο στο εστιακό ¹⁵Αν και δεν αναφέρεται ρητά, ο φακός που θεωρούμε είναι δισδιάστατος. Με τον όρο δισδιάστατος φακός εννοείται μία διάταξη που είναι άπειρη κατά τη διεύθυνση του άξονα y και η διατομή της στο επίπεδο xz είναι η ίδια με τη διατομή ενός τρισδιάστατου φακού. Ουσιαστικά, ένας δισδιάστατος φακός δεν έχει εστιακά σημεία αλλά εστιακούς άξονες. Παρ όλα αυτά, λειτουργεί ακριβώς όπως ένας τρισδιάστατος, με την προϋπόθεση ότι σε μία από τις εστίες του τοποθετείται μία γραμμική πηγή, αντί της σημειακής που χρησιμοποιείται στις τρεις διαστάσεις.
47 2.3. Επίπεδη πλάκα διπλο-αρνητικού υλικού 37 (α) (β) Σχήμα 2.19: (α) Φάση ενός διαδιδόμενου κύματος στο επίπεδο x = 0, για μία επίπεδη πλάκα με ϵ 2 = ϵ 1, µ 2 = µ 1. (β) Πλάτος ενός αποσβεννύμενου κύματος στο επίπεδο x = 0, για μία επίπεδη πλάκα με ϵ 2 = ϵ 1, µ 2 = µ 1. επίπεδο z = z f να είναι E y (x, z f ) = Iωµ 1e j φ 4π ˆ k1 k 1 e jkxx k 1z dk x, (2.55) Η τελευταία εξίσωση φανερώνει ότι το χωρικό εύρος φάσματος του E y (x, z f ) είναι k 1, σε αντίθεση με αυτό του E y (x, z ), το οποίο είναι άπειρο. Επομένως, το χωρικό εύρος του πεδιου στο εστιακό επίπεδο, όπως προκύπτει μέσω του θεωρήματος της αβεβαιότητας για τον μετασχηματισμό Fourier, είναι 2π/k 1 = λ 1, όπου λ 1 είναι το μήκος κύματος στον χώρο που περιβάλλει το φακό. Με άλλα λόγια, το είδωλο μιας σημειακής πηγής στο εστιακό επίπεδο είναι μία κουκκίδα με διάμετρο το λιγότερο ίση με το μήκος κύματος στο υλικό μέσα στο οποίο βρίσκεται η πηγή. Αν, λοιπόν, τοποθετηθούν δύο σημειακές πηγές σε απόσταση μικρότερη του λ 1, τα είδωλά τους είναι αδύνατο να διαχωριστούν, γεγονός που καθορίζει ότι η αναλυτικότητα της διάταξης είναι της τάξης του ενός μήκους κύματος. Η συμπεριφορά αυτή αλλάζει στην περίπτωση που η πηγή ακτινοβολεί παρουσία μιας επίπεδης πλάκας που αποτελείται από διπλο-αρνητικό υλικό προσαρμοσμένο στον περιβάλλοντα χώρο. Τότε, ϵ 2 = ϵ 1, µ 2 = µ 1 και k 2 1 = k2 2, k2 2z = k2 1z. Το γεγονός ότι το πρόσημο του k 2z δεν επηρεάζει τον υπολογισμό των ολοκληρωμάτων (2.44) επιτρέπει να θεωρήσουμε ότι k 2z = k 1z, οπότε R 1 = 0 και R = 0, T = e jk1zd, A = 0, B = e jk1zd/2. Ο απειρισμός του R δεν έρχεται σε αντίθεση με το γεγονός ότι το διπλο-αρνητικό υλικό είναι τέλεια προσαρμοσμένο στο συμβατικό υλικό που το περιβάλλει, καθώς ο R χάνει τη φυσική του σημασία στις (2.46), αποκτώντας αποκλειστικά φορμαλιστικό ρόλο. Κατά συνέπεια, το πεδίο στις περιοχές 1, 2 και 3 που προκαλείται από την πρόσπτωση του επίπεδου κύματος (2.51) είναι, αντίστοιχα, e jk xx e jk 1z z z, e jk xx e jk 1z(z+z +d), e jk xx e jk 1z(z z 2d) (2.56α) (2.56β) (2.56γ) Αν το κύμα είναι διαδιδόμενο (k x k 1 ), η φάση του μειώνεται κατά τη διεύθυνση των αυξανόμενων z μέσα στο συμβατικό υλικό και αυξάνεται στο εσωτερικό της πλάκας, όπως δείχνει το σχήμα 2.19(α). Η αύξηση της φάσης μέσα στο διπλο-αρνητικό υλικό είναι απόλυτα αναμενόμενη, αν ληφθεί
48 38 Κεφάλαιο 2 υπόψη ότι η ισχύς ρέει προς την κατεύθυνση του θετικού ημιάξονα z και το κύμα είναι οπισθοκατευθυντικό. Από το σχήμα 2.19(α) καθίσταται φανερή η ύπαρξη δύο επιπέδων σταθερού z, το ένα από τα οποία βρίσκεται στο εσωτερικό και το άλλο στο εξωτερικό της πλάκας, στα οποία η φάση του κύματος συμπίπτει με αυτή που έχει στο επίπεδο της πηγής. Τα επίπεδα προσδιορίζονται από τις εξισώσεις z f 1 = z d, z f 2 = z + 2d και η αναγκαία συνθήκη για την ύπαρξη τους είναι z < 3d/2, δηλαδή η απόσταση της πηγής από την πλάκα να μην υπερβαίνει το πάχος της πλάκας. Είναι εύκολο να διαπιστώσει κανείς ότι τα επίπεδα αυτά συμπίπτουν με τα εστιακά επίπεδα που προσδιορίστηκαν από τον Veselago μέσω της ακτινικής προσέγγισης. Όσον αφορά τους αποσβεννύμενους ρυθμούς (k x > k 1 ), το σχήμα 2.19(β) απεικονίζει τη μεταβολή του πλάτους τους κατά μήκος του άξονα z. Πέρα από την αναμενόμενη μείωση του πλάτους στο συμβατικό υλικό, παρατηρείται αύξηση του στο εσωτερικό του διπλο-αρνητικού υλικού. Με τον τρόπο αυτό, αντισταθμίζεται η εξασθένηση του πεδίου των αποσβεννύμενων ρυθμών στο συμβατικό υλικό, ώστε το πλάτος τους στα επίπεδα z = z f 1, z = z f 2 να ισούται με το πλάτος τους στο επίπεδο της πηγής. Κατά συνέπεια, τόσο οι διαδιδόμενοι όσο και οι αποσβεννύμενοι ρυθμοί αποκτούν στα επίπεδα z = z f 1, z = z f 2 το ίδιο μέτρο και φάση με το επίπεδο z = z. Συμπεραίνουμε, λοιπόν, ότι η πλάκα του διπλο-αρνητικού υλικού επιτυγχάνει να αναπαράγει στα επίπεδα z = z f 1, z = z f 2 τέλεια τη μορφή που έχει το πεδίο στο επίπεδο της πηγής. Με άλλα λόγια, η σημειακή πηγή αναπαριστάνεται ως σημείο στα εστιακά επίπεδα z = z f 1, z = z f 2 και η αναλυτικότητα που προσφέρει η διάταξη είναι άπειρη. Ενδιαφέρον, επίσης, παρουσιάζει η μελέτη του πεδίου στον χώρο, γενικά. Προς τον σκοπό αυτό, χρησιμοποιούνται οι (2.44), οι οποίες για την περίπτωση του τέλειου φακού λαμβάνουν τη μορφή E 1y (x, z) = Iωµ 1 4π E 2y (x, z) = Iωµ 1 4π E 3y (x, z) = Iωµ 1 4π ˆ ˆ ˆ e jk xx k 1z e jk 1z z z dk x, (2.57α) e jk xx k 1z e jk 1z(z z f 1 ) dk x, (2.57β) e jk xx k 1z e jk 1z(z z f 2 ) dk x, (2.57γ) με τον k 1z να δίνεται από την (2.52). Οι παραπάνω εξισώσεις μπορούν να απλοποιηθούν, περαιτέρω, μέσω της σχέσης H (2) 0 (k 1 R) = 1 ˆ e jk xx e jk 1z z z dk x, (2.58) π k 1z όπου R = x 2 + (z z ) 2. Τότε, θέτοντας R 1 = x 2 + (z z ) 2, R 2 = R 3 = x 2 + (z z f 2 ) 2, έχουμε x 2 + (z z f 1 ) 2 και E 1y (x, z) = Iωµ 1 H (2) 0 (k 1 R 1 ), (2.59α) 4 E 2y (x, z) = Iωµ 1 H (2) 0 (k 1 R 2 ), (2.59β) 4 E 3y (x, z) = Iωµ 1 H (2) 0 (k 1 R 3 ) (2.59γ) 4 Για την ακρίβεια, οι (2.59β), (2.59γ) ισχύουν μόνο όταν z < z f 1 και z > z f 2, αντίστοιχα, καθώς στα υπόλοιπα τμήματα των περιοχών 2 και 3 τα ολοκληρώματα (2.57β), (2.57γ) αποκλίνουν. Πράγματι, αν z > z f 1 και k x k 1, το δεύτερο εκθετικό της ολοκληρωτέας ποσότητας στην (2.57β) γράφεται e jk 1z(z z f 1 ) = e k x z z f 1, από όπου φαίνεται ότι τείνει στο άπειρο καθώς k x. Παρόμοια, το
49 2.4. Η μέθοδος FDTD στα διπλο-αρνητικά υλικά 39 ολοκλήρωμα της (2.57γ) αποδεικνύεται ότι αποκλίνει για z < z f 2. Αξίζει να παρατηρήσει κανείς ότι το πεδίο στην περιοχή z > z f 2 συμπίπτει με αυτό που παράγει μία γραμμική πηγή τοποθετημένη στο σημείο z = z f 2 του άξονα z. Κρίνεται, ωστόσο, απαραίτητο να τονιστεί ότι η επίπεδη πλάκα διπλο-αρνητικού υλικού πετυχαίνει εστίαση μόνο σε δύο διαστάσεις ή, διαφορετικά, αναπαράγει στο επίπεδο εστίασης τη μορφή που έχει το πεδίο στο επίπεδο της πηγής χωρίς, όμως, να εστιάζει την ενέργεια στον τρισδιάστατο χώρο (το πεδίο στην περιοχή z < z f 2 διαφέρει εντελώς από το αντίστοιχο στην περιοχή z < z ). Για τον λόγο αυτό, έχει διατυπωθεί η άποψη ότι η επίπεδη πλάκα διπλοαρνητικού υλικού με µ 2 = µ 1, ϵ 2 = ϵ 1 ανήκει περισσότερο στην κατηγορία των προσαρμοστικών διατάξεων παρά σε αυτήν των φακών. 2.4 Η μέθοδος FDTD στα διπλο-αρνητικά υλικά Μία από τις πρώτες αριθμητικές τεχνικές που χρησιμοποιήθηκαν για την προσομοίωση διατάξεων από διπλο-αρνητικά υλικά είναι η μέθοδος FDTD. Επειδή η μέθοδος αυτή υπολογίζει τη χρονική εξέλιξη του πεδίου, η εισαγωγή στο πλαίσιο του αλγορίθμου των καταστατικών παραμέτρων των διπλοαρνητικών υλικών είναι απαραίτητο να πραγματοποιηθεί μέσω των αιτιατών μοντέλων διασποράς που περιγράφηκαν στην υποενότητα 2.2.1, προκειμένου να εξασφαλιστεί η ευστάθεια στις προσομοιώσεις. Εντούτοις, οι εξισώσεις ανανέωσης του πεδίου δεν αλλάζουν σε σχέση με την περίπτωση των συμβατικών υλικών με διασπορά. Ως παράδειγμα, στη συνέχεια εξάγoνται η εξίσωση ανανέωσης στην περίπτωση που η διηλεκτρική σταθερά δίνεται από το μοντέλο Drude της (2.6) και η μαγνητική διαπερατότητα από το μοντέλο Lorentz της (2.7). Προς τον σκοπό αυτό, χρησιμοποιείται η τεχνική της βοηθητικής διαφορικής εξίσωσης (auxiliary differen al equa on, ADE), η οποία είναι η πιο διαδεδομένη τεχνική σε εφαρμογές διπλο-αρνητικών υλικών, χωρίς, ωστόσο, να αποκλείεται ο αλγόριθμος της επαναληπτικής συνέλιξης. Αφετηρία για την διαμόρφωση των εξισώσεων ανανέωσης της μαγνητικής πεδιακής έντασης αποτελει ο νόμος του Faraday E = B t, (2.60) όπου E, B δηλώνουν την ηλεκτρική πεδιακή ένταση και τη μαγνητική επαγωγή στο πεδίο του χρόνου. Θεωρώντας ότι η ηλεκτρική πεδιακή ένταση και η μαγνητική επαγωγή δειγματοληπτούνται στις χρονικές στιγμές n t και (n + 0.5) t, αντίστοιχα, με n ακέραιο και t το χρονικό βήμα του αλγορίθμου, η (2.60) διακριτοποιείται ως B n+0.5 = B n 0.5 t( E) n, (2.61) από όπου η B n+0.5 υπολογίζεται, άμεσα, από τις τιμές των B και E σε προηγούμενες χρονικές στιγμές. Σημειώνεται ότι ο συμβολισμός F n δηλώνει την τιμή του μεγέθους F τη χρονική στιγμή n t και η παράγωγος ( F / t) n αντικαθίσταται από την κεντρική διαφορά (F n+0.5 F n 0.5 )/ t. Επόμενο βήμα είναι η μετατροπή της καταστατικής εξίσωσης B = µh, με µ να δίνεται από την (2.7), στο πεδίο του χρόνου. Κάνοντας χρήση του γεγονότος ότι πολλαπλασιασμός με jω στο πεδίο της συχνότητας ισοδυναμεί με διαφόριση στο πεδίο του χρόνου, προκύπτει 2 B t 2 + Γ B ( t + ω2 0B = 2 H µ 0 t 2 + Γ H t ) + ω 2 ph, (2.62)
50 40 Κεφάλαιο 2 όπου H είναι η μαγνητική πεδιακή ένταση στο πεδίου του χρόνου. Η διακριτοποιημένη μορφή της παραπάνω εξίσωσης είναι B n+0.5 2B n + B n 0.5 t 2 µ 0 ( H n+0.5 2H n + H n 0.5 t 2 + Γ B n+0.5 B n t + H n+0.5 H n t + ω0 2 B n B n + B n H n H n + H n ) = (2.63) Αξίζει να προσεχθεί ότι για την εξασφάλιση της ευστάθειας του αλγορίθμου η B στη διακριτοποιημένη εξίσωση αντικαθίσταται από τον μέσο όρο (B n B n + B n 0.5 )/4 και όχι από την τιμή B n. Η (2.63) επιτρέπει την εύρεση του H n+0.5 χρησιμοποιώντας τις τιμές των B, H σε προηγούμενες χρονικές στιγμές και την τιμή B n+0.5 που υπολογίστηκε μέσω της (2.61). Με παρόμοιο τρόπο, οι εξισώσεις ανανέωσης της ηλεκτρικής πεδιακής έντασης εξάγονται από τις εξισώσεις 2 D t 2 H = D t, + Γ D t = ϵ 0 ( 2 E t 2 (2.64α) + Γ E ) t + ω2 pe, (2.64β) από τις οποίες η πρώτη είναι ο νόμος του Ampère και η δεύτερη η μετασχηματισμένη στο πεδίο του χρόνου καταστατική εξίσωση D = ϵe, με ϵ όπως αυτό της (2.6). Σημειώνεται ότι το D συμβολίζει την διηλεκτρική μετατόπιση στο πεδίο του χρόνου. Παρ όλα αυτά, είναι δυνατή η εξαγωγή ενός εναλλακτικού σχήματος πεπερασμένων διαφορών που βασίζεται στο ρεύμα πόλωσης και εμπλέκει μικρότερο αριθμό πεδιακών τιμών σε περασμένες χρονικές στιγμές, μειώνοντας, έτσι, τις απαιτήσεις για μνήμη. Το ρεύμα πόλωσης ορίζεται από τη σχέση και μετατρέπει τις (2.64) στις J p = t (D ϵ 0E) (2.65) E H = ϵ 0 t + J p, (2.66α) J p + ΓJ p = ω 2 t pe, (2.66β) πετυχαίνοντας να ελαττώσει την τάξη της βοηθητικής διαφορικής εξίσωσης. Για την διακριτοποίηση των εξισώσεων αυτών, θεωρείται ότι το J p δειγματοληπτείται τις χρονικές στιγμές (n + 0.5) t, οπότε λαμβάνουμε ( H) n+0.5 E = n+1 E n ϵ 0 + J p n+0.5, t (2.67α) J p n+0.5 J p n Γ J p n J p n 0.5 = ω 2 t 2 pe n (2.67β) Για τον υπολογισμό του E n+1, βρίσκεται, πρώτα, το J p n+0.5 από την (2.67β) και στη συνέχεια αντικαθίσταται στην (2.67α).
51 2.4. Η μέθοδος FDTD στα διπλο-αρνητικά υλικά 41 Σχήμα 2.20: Πλέγμα της μεθόδου FDTD γύρω από τη διαχωριστική επιφάνεια ενός συμβατικού και ενός διπλοαρνητικού μέσου. Το συμβατικό μέσο καταλαμβάνει την κίτρινη περιοχή, ενώ το διπλο-αρνητικό τη γκριζα. Οι πλασμονικοί ρυθμοί που αναπτύσσονται στις διεπιφάνειες διπλο-αρνητικών και συμβατικών υλικών είναι έντονα συντονιζόμενοι ρυθμοί και, επομένως, ιδιαίτερα ευαίσθητοι σε μεταβολές των γεωμετρικών χαρακτηριστικών. Για τον λόγο αυτό, μεγάλη προσοχή πρέπει να δίνεται κατά τη διαμόρφωση των εξισώσεων που αφορούν πεδιακές συνιστώσες οι οποίες βρίσκονται πάνω σε διαχωριστικές επιφάνειες, ώστε να είναι συμβατές με τις οριακές συνθήκες. Η κατανόηση του γεγονότος αυτού θα πραγματοποιηθεί μέσω του δισδιάστατου προβλήματος της διαχωριστικής επιφάνειας ενός συμβατικού υλικού με καταστατικές παραμέτρους µ 1, ϵ 1 και ενός διπλο-αρνητικού με παραμέτρους µ 2, ϵ 2, όπως παρουσιάζεται στο σχήμα Τα χωρικά βήματα του πλέγματος κατά τις διευθύνσεις των αξόνων x, y είναι x, y και η αρχή του συστήματος συντεταγμένων βρίσκεται στον κόμβο O. Η διαχωριστική επιφάνεια βρίσκεται στα αριστερά της ευθείας x = x και απέχει απόσταση f x από αυτήν, με 0 f 0.5. Η εφαρμογή του νόμου του Ampère στην κλειστή διαδρομή που σημειώνεται με κόκκινη διακεκομμένη γραμμή δίνει ˆ 1.5 x 0.5 x ˆ 1.5 y 0.5 y ˆ 1.5 y H x (x, 0.5 y) dx + H y (0.5 x, y) dx = t ˆ 1.5 x H y (1.5 x, y) dx 0.5 y ˆ 1.5 x ˆ 1.5 y 0.5 x 0.5 y 0.5 x H x (x, 1.5 y) dx D z (x, y) dx dy (2.68) Επειδή η E z, ως εφαπτομενική συνιστώσα στη διαχωριστική επιφάνεια, είναι συνεχής πάνω σε αυτήν, το επιφανειακό ολοκλήρωμα του δεύτερου μέλους της (2.68) γράφεται ˆ 1.5 x ˆ 1.5 y 0.5 x 0.5 y D z (x, y) dx dy = ˆ (1 f ) x ˆ 1.5 y x ˆ 1.5 x (1 f ) x 0.5 y ˆ 1.5 y 0.5 y ϵ 1 E z (x, y) dx dy ϵ 2 E z (x, y) dx dy [(0.5 f )ϵ 1 + (0.5 + f )ϵ 2 ]E z ( x, y) x y (2.69) Επομένως, στον κόμβο ( x, y) πρέπει να οριστεί η ισοδύναμη διηλεκτρική σταθερά ϵ e f f = (0.5 f )ϵ 1 + (0.5 + f )ϵ 2 (2.70) Από την άλλη πλευρά, λαμβάνοντας υπόψη ότι η B x είναι συνεχής πάνω στη διαχωριστική επιφάνεια,
52 42 Κεφάλαιο 2 το πρώτο ολοκλήρωμα της (2.68) παίρνει τη μορφή ˆ 1.5 x 0.5 x H x (x, 0.5 y) dx = 1 ˆ (1 f ) x B x (x, 0.5 y) dx µ x + 1 µ 2 ˆ 1.5 x (1 f ) x ( 0.5 f µ f µ 2 B x (x, 0.5 y) dx ) B x ( x, 0.5 y) x (2.71) Έτσι, η ισοδύναμη μαγνητική διαπερατότητα στη θέση ( x, 0.5 y) ορίζεται από τη σχέση 1 = 0.5 f f, (2.72) µ e f f µ 1 µ 2 ώστε να ισχύει ˆ 1.5 x 0.5 x H x (x, 0.5 y) dx H x ( x, 0.5 y) x (2.73) 2.Α Ρυθμοί στην επιφάνεια διπλο-αρνητικού υλικού με απώλειες Σκοπός του παραρτήματος αυτού είναι η μελέτη των ρυθμών που αναπτύσσονται στη διεπιφάνεια ενός συμβατικού και ενός διπλο-αρνητικού υλικού με απώλειες. Η γεωμετρία του προβλήματος είναι αυτή του σχήματος 2.3 και ο συμβολισμός που χρησιμοποιείται είναι ο ίδιος με αυτόν της υποενότητας Η μέθοδος που εφαρμόζεται συνίσταται στην εύρεση των πόλων των συντελεστών ανάκλασης και διάθλασης, οι οποίοι, όπως είναι γνωστό από την κλασική θεωρία του ηλεκτρομαγνητικού πεδίου, παρέχουν την παράλληλη στη διαχωριστική επιφάνεια σταθερά διάδοσης (στην προκειμένη περίπτωση k x ) των ζητούμενων ρυθμών. Η φυσική ερμηνεία του φαινομένου αυτού έγκειται στο γεγονός ότι όταν η k x του προσπίπτοντος κύματος είναι πόλος των συντελεστών ανάκλασης και διάθλασης, το πλάτος του ανακλώμενου και του διαθλώμενου κύματος απειρίζεται. Με άλλα λόγια, είναι δυνατή η ύπαρξη ανακλώμενου και διαθλώμενου κύματος χωρίς την ύπαρξη προσπίπτοντος κύματος, αν η k x είναι πόλος των συντελεστών ανάκλασης και διάθλασης. Θα μπορούσε να ισχυριστεί κανείς ότι οι επιφανειακοί ρυθμοί αποτελούν, κατά κάποιο τρόπο, τους φυσικούς ρυθμούς της διάταξης, σε αναλογία με τους φυσικούς ρυθμούς ενός κυκλωματικού δικτύου, οι οποίοι προκύπτουν από τους πόλους της συνάρτησης μεταφοράς. Ως επιβεβαίωση των παραπάνω συμπερασμάτων, οι ρίζες της ϵ 1 k 2z + ϵ 2 k 1z (παρονομαστής των R, T ) δίνονται από την k 2 x = ω 2 ϵ2 2 µ 1ϵ 1 ϵ1 2µ 2ϵ 2 ϵ2 2, (2.74) ϵ2 1 η οποία είναι ίδια με την (2.32). Παρόμοιο αποτέλεσμα προκύπτει και για την κάθετη πόλωση. Στη συνέχεια, θα επικεντρωθούμε στην παράλληλη (TE y ) πόλωση, καθώς ο χειρισμός του άλλου είδους πόλωσης πραγματοποιείται με ανάλογο τρόπο. Όπως ήδη διατυπώθηκε, οι πόλοι του συντελεστή ανάκλασης πρέπει να αναζητηθούν ανάμεσα στις τιμές του k x που υπολογίζονται μέσω της (2.74). Παρόλο που κάθε πόλος ικανοποιεί υποχρεωτικά την (2.74), δεν ισχύει το αντίστροφο, καθώς ο μηδενισμός του αριθμητή του R οδηγεί, επίσης, στην
53 2.Α. Ρυθμοί στην επιφάνεια διπλο-αρνητικού υλικού με απώλειες 43 (α) (β) Σχήμα 2.21: (α) Βροχοτομές του k 2z στο k x -επίπεδο και πρόσημο του Re{k 2z } στο α φύλλο Riemann. (β) Βροχοτομές του k 1z στο k x -επίπεδο και πρόσημο του Re{k 1z } στο α φύλλο Riemann. (2.74). Σημειώνεται ότι τα μηδενικά του R αντιστοιχούν στη γνωστή γωνία Brewster μηδενικής ανάκλασης και για τον λόγο αυτό θα καλούνται από εδώ και στο εξής μηδενικά Brewster.¹⁶ Από την άλλη πλευρά, η (2.74) υποδηλώνει ότι ο k x μπορεί να λάβει δύο διαφορετικές τιμές: μία με Im{k x } > 0 και μία με Im{k x } < 0, οι οποίες είναι αποδεκτές για διάδοση της ισχύος κατά τη διεύθυνση του αρνητικού και του θετικού άξονα x, αντίστοιχα. Σε αντίθεση, όμως, με τον k x, το πρόσημο του οποίου καθορίζεται από τη διεύθυνση διάδοσης, ο Re{k x } μπορεί να είναι είτε θετικός είτε αρνητικός αριθμός. Μάλιστα, όταν οι Re{k x }, Im{k x } είναι ομόσημοι, ο ρυθμός είναι εμπροσθοκατευθυντικός, ενώ όταν είναι ετερόσημοι, ο ρυθμός είναι οπισθοκατευθυντικός. Εκτός από τον υπολογισμό του k x, η εύρεση της πλήρους μορφής των ρυθμών απαιτεί τη γνώση των k 1z, k 2z. Επιπλέον, οι k 1z, k 2z είναι απαραίτητοι για τον έλεγχο του k x αν αντιστοιχεί σε πόλο ή σε μηδενικό του συντελεστή ανάκλασης. Τονίζεται ότι οι k 1z, k 2z είναι πλειότιμες συναρτήσεις του k x και για τον λόγο αυτό η ανάλυση διευκολύνεται κατασκευάζοντας τις βροχοτομές τους στο μιγαδικό k x -επίπεδο. Επειδή το πρόσημο των Im{k 1z }, Im{k 2z } καθορίζει αν κάποιος ρυθμός είναι φυσικός ή όχι, δηλαδή αν το πεδίο του μειώνεται καθώς απομακρυνόμαστε από τη διαχωριστική επιφάνεια, οι βροχοτομές λαμβάνονται κατά μήκος των καμπύλων Im{k 1z } = 0 και Im{k 2z } = 0. Σημειώνεται ότι ένας ρυθμός είναι φυσικός (proper) όταν Im{k 1z }, Im{k 2z } < 0 και μη-φυσικός (improper) διαφορετικά.¹⁷ Εξετάζοντας, αρχικά, τον k 2z, υπενθυμίζεται ότι δίνεται από τη σχέση k 2z = k 2 2 k2 x, (2.75) με k 2 2 = ω2 µ 2 ϵ 2. Σύμφωνα με την (2.9), ο k 2 μπορεί να λάβει δύο αντίθετες τιμές στα α και γ τεταρτημόρια του k x -επιπέδου, όπως φαίνεται στο σχήμα 2.21 (ακολούθως θεωρούμε ότι ο k 2 βρίσκεται στο α τεταρτημόριο και ο k 2 στο γ ). Τότε, η συνθήκη Im{k 2z } επαληθεύεται στα τμήματα της υπερβολής Re{k x } Im{k x } = Re{k 2 } Im{k 2 } για τα οποία Re{k x } < Re{k 2 }. Οι καμπύλες αυτές, που στο σχήμα 2.21(α) παριστάνονται με την ακανόνιστη γραμμή, συνιστούν τη βροχοτομή για ¹⁶Για την ακρίβεια, η γωνία Brewster συνδέεται με τα μηδενικά Brewster μόνο όταν δεν υπάρχουν απώλειες και k x < ω µ 1 ϵ 1. ¹⁷Το γεγονός ότι ένας ρυθμός είναι φυσικός όταν Im{k 1z }, Im{k 2z } < 0 κατανοείται καλύτερα αν λάβουμε υπόψη ότι η ηλεκτρική πεδιακή ένταση έχει τη μορφή E r0 e jk xx e jk 1zz για z < 0 (ανακλώμενο κύμα) και την E t0 e jk xx e jk 2zz για z > 0 (διαθλώμενο κύμα), όπου E r0, E t0 σταθερά μιγαδικά διάνυσματα.
54 44 Κεφάλαιο 2 Σχήμα 2.22: Βροχοτομές για το πρόβλημα της διεπιφάνειας συμβατικού και διπλο-αρνητικού υλικού και προσημο των Re{k 1z }, Re{k 2z } στο α φύλλο Riemann. το k 2z. Κάθε φορά που διαπερνάμε τη βροχοτομή, περνάμε σε διαφορετικό φύλλο Riemann, δηλαδή αλλάζει το πρόσημο του Im{k 2z }. Από την άλλη πλευρά το πρόσημο του Im{k 2z } διατηρείται σταθερό σε όλα τα σημεία του k x -επιπέδου, όταν ανήκουν στο ίδιο φύλλο Riemann. Αναφορικά με το Re{k 2z }, αλλάζει πρόσημο εκατέρωθεν της υπερβολής Re{k x } Im{k x } = Re{k 2 } Im{k 2 } (ακανόνιστη και διακεκομμένη γραμμή στο σχήμα 2.21), με την προυπόθεση ότι βρισκόμαστε στο ίδιο φύλο Riemann. Επικεντρώνοντας στο φύλλο Riemann για το οποίο Im{k 2z } < 0, δηλαδή στην περίπτωση που μας ενδιαφέρει, Re{k 2z } > 0 στη σκιασμένη περιοχή του σχήματος 2.21 και Re{k 2z } < 0 στο υπόλοιπο επίπεδο. Το γεγονός αυτό μπορεί να εξαχθεί άμεσα από την παρατήρηση ότι αν k x = 0, k 2z = k 2 και Re{k 2 } < 0. Με παρόμοιο τρόπο εξάγονται οι βροχοτομές του k 1z, που παρουσιάζονται στο σχήμα 2.21(β) μαζί με το πρόσημο του Re{k 1z } στο φύλλο Riemann Im{k 1z } < 0. Ο συνδυασμός των 2.21(α), 2.21(β) δίνει τις βροχοτομές για το πρόβλημα της διεπιφάνειας συμβατικού και διπλοαρνητικού υλικού, όπως φαίνεται στο σχήμα Στο ίδιο σχήμα παριστάνεται επίσης το πρόσημο των Re{k 1z }, Re{k 2z } στο φύλλο Riemann Im{k 1z }, Im{k 2z } < 0 (α φύλλο Riemann). Στην ανάλυση που ακολουθεί θα προσδιοριστούν οι περιοχές του α φύλλου Riemann στις οποίες μπορούν να εμφανίζονται πόλοι και τα χαρακτηριστικά των κυμάτων που αντιστοιχούν στους πόλους αυτούς. Λαμβάνοντας το πραγματικό μέρος της εξίσωσης ϵ 1 k 2z + ϵ 2 k 1z = 0, που δίνει τους πόλους του συντελεστή ανάκλασης, προκύπτει Re{ϵ 1 } Re{k 2z } + Re{ϵ 2 } Re{k 1z } = Im{ϵ 1 } Im{k 2z } + Im{ϵ 2 } Im{k 1z } (2.76) Επειδή Re{ϵ 1 } > 0, Re{ϵ 2 }, Im{ϵ 1 }, Im{ϵ 2 } < 0 και Im{k 1z }, Im{k 2z } < 0 στο α φύλλο Riemann, έπεται, από την (2.77), ότι δεν μπορεί να ισχύει Re{k 1z } > 0 και Re{k 2z } < 0. Επομένως πόλοι που δίνουν φυσικούς ρυθμούς εντοπίζονται στις περιοχές A, B, Γ και του σχήματος 2.22, ενώ στην περιοχή E μπορούν να υπάρχουν μηδενικά Brewster. Επίσης, στις περιοχές A και Γ οι ρυθμοί είναι οπισθοκατευθυντικοί, αφού οι Re{k x }, Im{k x } είναι ετερόσημοι, ενώ στις B και είναι εμπροσθοκατευθυντικοί. Από την άλλη πλευρά, οι πόλοι στις περιοχές, B δίνουν κύματα που διαδίδονται κατά την κατεύθυνση του αρνητικού άξονα x σε αντίθεση με αυτούς στις περιοχές Γ, που αντιστοιχούν σε κύματα διαδιδόμενα προς τα θετικά x. Τα παραπάνω συμπεράσματα αποτυπώνονται γραφικά στο σχήμα 2.23, στο οποίο μπορεί να δει κανείς τα κυματικά διανύσματα και τα πραγματικά διανύσματα
55 2.Α. Ρυθμοί στην επιφάνεια διπλο-αρνητικού υλικού με απώλειες 45 (α) (β) Σχήμα 2.23: Κυματικά διανύσματα k 1, k 2 και πραγματικά διανύσματα Poyn ng P 1, P 2 ενός (α) εμπροσθοκατευθυντικού και (β) οπισθοκατευθυντικού ρυθμού, με διεύθυνση διάδοσης αυτήν του θετικού άξονα x, για την περίπτωση της διεπιφάνειας ενός συμβατικού και ενός διπλο-αρνητικού υλικού. Poyn ng ενός εμπροσθοκατευθυντικού και ενός οπισθοκατευθυντικού ρυθμού με διεύθυνση διάδοσης αυτήν του θετικού άξονα x. Σημειώνεται ότι το πραγματικό διάνυσμα Poyn ng στο συμβατικό και στο διπλο-αρνητικό υλικό είναι, αντίστοιχα, P 1 = H y0 2 2ω ϵ 1 2 e2 Im{k 1} r (Re{ϵ 1 } Re{k 1 } + Im{ϵ 1 } Im{k 2 }), P 2 = H y0 2 2ω ϵ 2 2 e2 Im{k 2} r (Re{ϵ 2 } Re{k 2 } + Im{ϵ 2 } Im{k 2 }), (2.77α) (2.77β) με k 1 = k x ˆx k 1z ẑ, k 2 = k x ˆx + k 2z ẑ, r = xˆx + zẑ και H y0 το πλάτος της μαγνητικής πεδιακής έντασης. Για την εξαγωγή των (2.77) χρησιμοποιήθηκε το γεγονός ότι η μαγνητική πεδιακή ένταση είναι κάθετη στα k 1 και k 2, καθώς, για την περίπτωση της TE y πόλωσης που εξετάζουμε, η μαγνητική πεδιακή ένταση είναι παράλληλη στον άξονα y ενώ τα k 1, k 2 βρίσκονται πάνω στο xz επίπεδο. Στη συνέχεια θα επιχειρήσουμε να κατηγοροποιήσουμε τους ρυθμούς στη διεπιφάνεια ενός συμβατικού και ενός διπλο-αρνητικού υλικού με βάση τις κατηγορίες που παρουσιάζονται στη σελίδα 48 του [Ishimaru, 1991]. Καταρχήν, όταν δεν υπάρχουν απώλειες, ο ρυθμός χαρακτηρίζεται ως παγιδευμένο επιφανειακό κύμα (trapped surface wave), καθώς η ισχύς ρέει παράλληλα προς την επιφάνεια, το πλάτος του πεδίου παραμένει σταθερό κατά μήκος της επιφάνειας και μειώνεται εκθετικά καθώς απομακρυνόμαστε από αυτήν. Όταν υπάρχουν απώλειες και ο ρυθμός είναι εμπροσθοκατευθυντικός, η μορφή του μοιάζει με τη μορφή ενός κύματος Zenneck, αφού ισχύς εισέρχεται από το συμβατικό στο διπλο-αρνητικό υλικό. Αντίθετα, όταν το ρυθμός είναι οπισθοκατευθυντικός, ανήκει στην κατηγορία των οπισθοκατευθυντικών διαρρεόντων κυμάτων (backward leaky waves), καθώς ισχύς ρέει από την διαχωριστική επιφάνεια προς το άπειρο. Μέχρι στιγμής, μελετήθηκαν οι πόλοι του συντελεστή ανάκλασης και οι ρυθμοί που προκύπτουν από αυτούς στο α φύλλο Riemann. Παρόλο που μόνο οι πόλοι αυτοί οδηγούν σε φυσικές λύσεις, έχει ενδιαφέρον να δούμε τι συμβαίνει στα άλλα φύλλα Riemann. Αν k x είναι ένας πόλος στο α φύλλο Riemann, τότε ο ίδιος k x στο δ φύλλο Riemann, στο οποίο Im{k 1z }, Im{k 2z } > 0 είναι επίσης πόλος, επειδή οι τιμές k 1z, k 2z σε ένα σημείο του δ φύλλου Riemann είναι αντίθετες των τιμών που έχουν στο ίδιο σημείο του α φύλλου Riemann. Από την άλλη πλευρά, ο ίδιος k x στο β φύλλο (Im{k 1z } > 0, Im{k 2z } < 0) ή στο γ φύλλο (Im{k 1z } < 0, Im{k 2z } > 0) Riemann είναι μηδενικό του συντελεστή ανάκλασης, καθώς αλλάζει πρόσημο μόνο ένας από τους k 1z, k 2z. Παρόμοια συμπεράσματα ισχύουν
56 46 Κεφάλαιο 2 (α) (β) Σχήμα 2.24: Διάγραμμα διασποράς επιφανειακών ρυθμών που αναπτύσσονται στη διεπιφάνεια αέρα και διπλο-αρνητικού υλικού. Το διπλο-αρνητικό έχει διηλεκτρική σταθερά που ακολουθεί το μοντέλο Drude με ω p = rad/s, Γ = 10 8 rad/s και μαγνητική διαπερατότητα που ακολουθεί το μοντέλο Lorentz με ω 0 = rad/s, ω p = rad/s και Γ = rad/s. Το σχήμα (α) παρουσιάζει τη φασική σταθερά διάδοσης και το (β) τη σταθερά απόσβεσης. Ο οριζόντιος άξονας κανονικοποιείται ως προς τον κυματικό αριθμό του αέρα στην κυκλική συχνότητα 10 9 rad/s. και για τα μηδενικά Brewster. Αν, δηλαδή, ο k x είναι μηδενικό στο α φύλλο Riemann τότε είναι, επίσης, μηδενικό στο δ φύλλο Riemann και πόλος στα β και γ φύλλο Riemann. Τονίζεται ότι οι ρυθμοί που προκύπτουν από τους πόλους στα φύλλα Riemann εκτός του α είναι μη-φυσικοί, αφού το πλάτος τους απειρίζεται όταν z ή/και z. Ως εφαρμογή της ανάλυσης που προηγήθηκε, το σχήμα 2.24 απεικονίζει το διάγραμμα διασποράς των επιφανειακών ρυθμών όταν το συμβατικό υλικό είναι ο αέρας και το διπλο-αρνητικό έχει διηλεκτρική σταθερά που ακολουθεί το μοντέλο Drude με ω p = rad/s, Γ = 10 8 rad/s και μαγνητική διαπερατότητα που ακολουθεί το μοντέλο Lorentz με ω 0 = rad/s, ω p = rad/s και Γ = rad/s. Για όλους τους ρυθμούς έχει θεωρηθεί ότι Re{k x } > 0, οπότε εμπροσθοκατευθυντικοί είναι αυτοί με Im{k x } < 0 και οπισθοκατευθυντικοί αυτοί με Im{k x } > 0. Αν και εμφανίζονται πόλοι δεξιά του κώνου φωτός του συμβατικού υλικού (δηλαδή σε περιοχές όπου είναι αδύνατη η ανάπτυξη επιφανειακών κυμάτων στην περίπτωση χωρίς απώλειες), το μιγαδικό τους μέρος είναι αρκετά μεγάλο ώστε αποσβένυνται πολύ γρήγορα με την απόσταση. Στην πραγματικότητα, οι ρυθμοί με Im{k x } κοντά στο 0, οι οποίοι είναι πρακτικά διαδόσιμοι, συμπίπτουν, σχεδόν, με τους αντίστοιχους της περίπτωσης χωρίς απώλειες (σχήμα 2.9).
57 Κ 3 Η Ε Π Δ -Α Υ Δ Ε 3.1 Εισαγωγή Σκοπός του παρόντος κεφαλαίου είναι η λεπτομερής μελέτη της επίπεδης πλάκας διπλο-αρνητικού υλικού ως διάταξης εστίασης ηλεκτρομαγνητικών κυμάτων. Αρχικά, η εστιακή ικανότητα μιας πλάκας με καταστατικές παραμέτρους που αποκλίνουν από τη συνθήκη του τέλειου φακού, είτε λόγω απωλειών είτε εξαιτίας διασποράς του διπλο-αρνητικού υλικού, αναλύεται μέσω του συντελεστή μετάδοσης ενός επίπεδου κύματος από το επίπεδο της πηγής στο επίπεδο εστίασης. Με τον τρόπο αυτό εξάγεται, τόσο μέσω διαγραμμάτων όσο και μέσω μιας θεωρητικής ανάλυσης, ένα άνω όριο για την παράλληλη με την πλάκα συνιστώσα του κυματικού διανύσματος, πάνω από το οποίο δεν είναι δυνατή η αναπαραγωγή του κυματικού πλάτους στο επίπεδο εστίασης. Στη συνέχεια, διερευνάται το πρόβλημα προσδιορισμού του βέλτιστου επιπέδου εστίασης, το οποίο, στη γενική περίπτωση, διαφέρει από αυτό του τέλειου φακού. Προς τον σκοπό αυτό, αναπτύσσεται μία νέα τεχνική, η οποία επιχειρεί τη συσχέτιση του πεδίου στο επίπεδο της πηγής με αυτό σε ένα τυχαίο επίπεδο, παράλληλο προς την επιφάνεια της πλάκας, μέσω κατάλληλων κριτηρίων βασισμένων στις έννοιες του συντελεστή συσχέτισης και του μέσου τετραγωνικού σφάλματος. Η αποδοτικότητα των κριτηρίων αυτών ερευνάται διεξοδικά μέσω αριθμητικών παραδειγμάτων και μιας αναλυτικής προσέγγισης του προβλήματος πρόσπτωσης γκαουσιανής δέσμης στην πλάκα. Η ανάλυση αποκαλύπτει την ύπαρξη μιας εγγενούς αδυναμίας στον ορισμό του μέσου τετραγωνικού σφάλματος, η οποία αντιμετωπίζεται επιτυχώς με την εισαγωγή ενός νέου τροποποιημένου μέσου τετραγωνικού σφάλματος. Στο υπόλοιπο μέρος του κεφαλαίου, εξετάζονται τα χαρακτηριστικά της πλάκας διπλο-αρνητικού υλικού στο πεδίο του χρόνου, όταν αυτή διεγείρεται από μία επίπεδη πηγή ρεύματος, η οποία τίθεται σε λειτουργία κάποια συγκεκριμένη χρονική στιγμή, έχει αρμονική χρονική εξάρτηση και αργά μεταβαλλόμενο πλάτος. Προς τον σκοπό αυτό, το πεδίο εκφράζεται ως ένα διπλό ολοκλήρωμα με μεταβλητές ολοκλήρωσης τη συχνότητα ω και τη φασική σταθερά k x. Αντί της συνήθους τεχνικής ολοκλήρωσης πρώτα ως προς k x και έπειτα ως προς ω, που απαντάται στη βιβλιογραφία και η οποία, στις περισσότερες περιπτώσεις, υλοποιείται αριθμητικά, προτιμάται η πραγματοποίηση, αρχικά, της ολοκλήρωσης ως προς ω. Με τον τρόπο αυτό, εξάγεται σε κλειστή μορφή το πεδίο που παράγεται από μία κατανεμημένη πηγή με χωρική συχνότητα k x και χρονική εξάρτηση ίδια με αυτήν της αρχικής πηγής, μέσω μιας αυστηρής ανάλυσης στο μιγαδικό ω-επίπεδο. Κατόπιν, το πεδίο που δημιουργεί η αρχική πηγή υπολογίζεται με εφαρμογή της τεχνικής στάσιμης φάσης στο υπολοιπόμενο ολοκλήρωμα ως προς k x. Οι αναλυτικές εκφράσεις ελέγχονται προσεχτικά ως προς την ακρίβειά τους και συγκρίνονται με αποτελέσματα που προκύπτουν μέσω της μεθόδου FDTD. Επίσης, παρουσιάζεται η φυσική
58 48 Κεφάλαιο 3 Σχήμα 3.1: Πλάτος του T s f για διάφορες μη-μηδενικές τιμές των ϵ ri, µ ri και d = 0.2λ 1. σημασία τους, μέσα από την οποία καθίσταται δυνατή η κατανόηση των μηχανισμών που διέπουν τη λειτουργία της επίπεδης πλάκας διπλο-αρνητικού υλικού. 3.2 Συντελεστής μετάδοσης Επίδραση απωλειών Όπως αναλύθηκε στο κεφάλαιο 2, μία επίπεδη πλάκα διπλο-αρνητικού υλικού με καταστατικές παραμέτρους ϵ 0, µ 0 που περιβάλλεται από αέρα μπορεί να πετύχει άπειρη αναλυτικότητα κατά την εστίαση μιας σημειακής πηγής. Επίσης, αποδείχθηκε ότι στην περιοχή μεταξύ των εστιακών επιπέδων εντός και εκτός της πλάκας το πεδίο, και κατ επέκταση η ενέργεια, απειρίζεται. Βεβαίως, η παρουσία απωλειών, η οποία είναι αναπόφευκτη σε κάθε πρακτική διάταξη, λύνει το πρόβλημα απειρισμού της λύσης, θέτοντας, όμως, όρια στην αναλυτικότητα της εστίασης. Παρ όλα αυτά, είναι δυνατή, με κατάλληλη επιλογή των παραμέτρων της διάταξης, η επίτευξη αναλυτικότητας μεγαλύτερης του μήκους κύματος. Ουσιαστικά, ο τέλειος φακός που περιγράφηκε στο κεφάλαιο 2 μετατρέπεται σε υπερ-φακό (super lens) στην περίπτωση ύπαρξης απωλειών. Η ανάλυση που ακολουθεί βασίζεται στο σχήμα 2.12, με ϵ 1 = ϵ 0, µ 1 = µ 0, ϵ 2 = ϵ 0 (1 + jϵ ri ) και µ 2 = µ 0 (1 + jµ ri ), όπου ϵ ri, µ ri > 0. Ο συντελεστής μετάδοσης ενός επίπεδου κύματος από το επίπεδο της πηγής z = z στο εστιακό επίπεδο z = z + 2d είναι T s f = e jk 1z( d/2 z ) Te jk 1z(z +2d d/2) = Te jk1zd, με T τον συντελεστή μετάδοσης της πλάκας, όπως δίνεται από την (2.46α). Όταν δεν υπάρχουν απώλειες (ϵ ri = µ ri = 0), ισχύει T = e jk1zd και T s f = 1, δηλαδή κάθε επίπεδο κύμα φθάνει στο εστιακό επίπεδο με το ίδιο πλάτος και φάση που έχει στο επίπεδο της πηγής. Η συμπεριφορά αυτή αλλάζει όταν προστεθούν απώλειες, όπως φαινεται στο σχήμα 3.1, που απεικονίζει το πλάτος του T s f για διάφορες μη-μηδενικές τιμές των ϵ ri, µ ri και d = 0.2λ 1 (λ 1 είναι το μήκος κύματος στο μέσο που περιβάλλει την πλάκα). Θεωρώντας ότι ένα κύμα αναπαράγεται στο επίπεδο εστίασης όταν T s f > 0.5, είναι φανερό ότι εστιάζονται κύματα με k x < k x,max, όπου k x,max είναι η τιμή του k x για την οποία T s f = 0.5, η οποία εξαρτάται από τα ϵ ri, µ ri και είναι μεγαλύτερη του k 1. Επομένως, η επίπεδη πλάκα με απώλειες επιτυγχάνει αναλυτικότητα = 2π/k x,max, η οποία, ωστόσο, είναι μικρότερη ή ίση του λ 1, αφού k x,max k 1. Όπως είναι αναμενόμενο, αύξηση των ϵ ri, µ ri συνεπάγεται
59 3.2. Συντελεστής μετάδοσης 49 μείωση του k x,max, δηλαδή αύξηση του και υποβάθμιση της εστιακής ικανότητας της διάταξης. Αναφορικά με τα αποσβεννύμενα κύματα (k x > k 1 ), η επίδραση των μαγνητικών απωλειών σε αυτά είναι πολύ ισχυρότερη από αυτήν των ηλεκτρικών απωλειών. Το συμπέρασμα αυτό προκύπτει, άμεσα, από τη σύγκριση των καμπυλών του σχήματος 3.1 που αντιστοιχούν στα ζεύγη παραμέτρων ϵ ri = 0, µ ri = 0.01 και ϵ ri = 0.01, µ ri = 0, τα οποία οδηγούν στον ίδιο κυματικό αριθμό k 2. Παρόμοια συμπεριφορά εμφανίζουν και οι καμπύλες που προκύπτουν από τα ζεύγη ϵ ri = 0, µ ri = 0.1 και ϵ ri = 0.1, µ ri = 0. Επίσης, αξίζει να παρατηρήσει κανείς ότι, στην περιοχή του αποσβεννύμενου φάσματος, οι καμπύλες για ϵ ri = 0.01, µ ri = 0.01 και ϵ ri = 0, µ ri = 0.01, όπως επίσης και αυτές που αντιστοιχούν σε ϵ ri = 0.1, µ ri = 0.1 και ϵ ri = 0, µ ri = 0.1, βρίσκονται πολύ κοντά η μία στην άλλη. Επομένως, το πλάτος των αποσβεννύμενων κυμάτων καθορίζεται από τον µ ri, εκτός και αν µ ri ϵ ri. Η φυσική ερμηνεία του φαινομένου αυτού στηρίζεται στο γεγονός ότι η ενίσχυση των αποσβεννύμενων κυμάτων επιτυγχάνεται μέσω της διέγερσης πλασμονικών επιφανειακών ρυθμών, οι οποίοι ως TM y πολωμένοι εξαρτώνται κυρίως από τη μαγνητική διαπερατότητα. Μία πλήρης περιγραφή του μηχανισμού αυτού θα καταστεί δυνατή αργότερα στο παρόν κεφάλαιο, όταν θα μελετηθούν τα χαρακτηριστικά λειτουργίας της πλάκας στο πεδίο του χρόνου. Στα συμπεράσματα της προηγούμενης παραγράφου είναι, επίσης, δυνατό να καταλήξουμε μέσω μιας αναλυτικής μελέτης του συντελεστή ανάκλασης. Πιο συγκεκριμένα, αν k x k 1, μπορούν να χρησιμοποιηθούν οι προσεγγίσεις Από τις παραπάνω σχέσεις προκύπτει και k 1z = jkx (1 k2 1 2k 2 x k 2z = jkx [1 k2 1 2k 2 j k2 1 x 2k 2 (ϵ ri + µ ri ) x ), (3.1α) ] (3.1β) R 2 = ( ) (3.2) j µ ri + k2 1 ϵ 2k 2 ri x T s f 4 = ( ) 2, (3.3) 4 + µ ri + k2 1 ϵ 2k 2 ri e 2k x d x από όπου εξάγεται ότι ο k x,max επαληθεύει την εξίσωση ( ) µ ri + k2 1 2k 2 ϵ ri e kx,maxd = 2 (3.4) x,max Τονίζεται ότι η παραπάνω εξίσωση ισχύει υπο την προϋπόθεση ότι k x,max k 1.¹ Για τον έλεγχο ορθότητας της (3.4), ο πίνακας 3.1 περιέχει τις ακριβείς και τις προσεγγιστικές τιμές του k x,max για διάφορα ϵ ri, µ ri, από όπου φαίνεται ότι, ακόμη και για, σχετικά, μεγάλες απώλειες και, κατά συνέπεια, μικρά k x,max, η (3.4) οδηγεί σε αξιόπιστα αποτελέσματα. Στο σχήμα 3.2 παριστάνοται διάφορες καμπύλες σταθερού k x,max στο ϵ ri µ ri επίπεδο. Τα σημεία στα οποία μία καμπύλη είναι οριζόντια είναι αυτά στα οποία πρωταρχικό ρόλο έχουν οι μαγνητικές απώλειες, αφού η μεταβολή του ϵ ri δεν επηρεάζει τον k x,max. Ανάλογα, οι ηλεκτρικές απώλειες καθίστανται κυρίαρχες στα σημεία όπου η καμπύλη αποκτά κατακόρυφη κλίση. Το σημείο μετάβασης από τη μία κατάσταση στην άλλη είναι το σημείο στο οποίο ¹Για την ακριβεια, η (3.4) προκύπτει με βάση την περισσότερο χαλαρή συνθήκη k 2 x,max k 2 1.
60 50 Κεφάλαιο 3 k x,max /k 1 ϵ ri µ ri Ακριβής τιμή Προσεγγιστική τιμή Πίνακας 3.1: Ακριβείς και προσεγγιστικές τιμές του k x,max για διάφορα ϵ ri, µ ri και d = 0.2λ 1. Σχήμα 3.2: Καμπύλες σταθερού k x,max στο επίπεδο ϵ ri µ ri για d = 0.2λ 1. η καμπύλη σπάει. Στο σημείο αυτό, η ϵ ri είναι μεγαλύτερη από την µ ri ως και δύο τάξεις μεγέθους, για όλους τους k x,max, γεγονός που δηλώνει την κύρια εξάρτηση των χαρακτηριστικών της διάταξης από τις μαγνητικές απώλειες. Εξετάζοντας το διαδιδόμενο φάσμα, δηλαδή την περιοχή k x < k 1 του σχήματος 3.1, παρατηρείται απότομη βύθιση του T s f για k x κοντά στον k 1 και μηδενισμός στη θέση k x = k 1, ακόμη και όταν οι απώλειες είναι μικρές. Η αιτία του φαινομένου αυτού είναι το γεγονός ότι, στην περίπτωση μητέλειας προσαρμογής,² ο συντελεστής ανάκλασης τείνει στο 1, καθώς ο k x τείνει στον k 1, δηλαδή κύματα με k x κοντά στον k 1 υφίστανται ισχυρή ανάκλαση και για τον λόγο αυτό φθάνουν με μειωμένο πλάτος στο επίπεδο εστίασης. Επιπροσθέτως, το πλάτος των κυμάτων αποσβέννυται κατά τη διάδοσή τους μέσα στο διπλο-αρνητικό υλικό, εξαιτίας των απωλειών. Η απόσβεση αυτή είναι ανάλογη του Im{k 2z }, δηλαδή εξαρτάται από το γινόμενο των καταστατικών παραμέτρων της πλάκας και όχι από τις απόλυτες τιμές τους. Η πρόταση αυτή επιβεβαιώνεται μέσω του σχήματος 3.3 μεγέθυνση της περιοχής k x < k 1 του σχήματος 3.1 από το οποίο φαίνεται η, σχεδόν, ταύτιση των καμπυλών που αντιστοιχούν στα ζεύγη παραμέτρων ϵ ri = 0, µ ri = 0.01 και ϵ ri = 0.01, µ ri = 0, όπως επίσης και αυτών που αντιστοιχούν σε ϵ ri = 0, µ ri = 0.1 και ϵ ri = 0.1, µ ri = 0. Ενδιαφέρον παρουσιάζει, επίσης, η επίδραση του πάχους της πλάκας στην εστιακή της ικανότητα. ²Υπενθυμίζεται ότι τέλεια προσαρμογή υπάρχει μόνο όταν ϵ 2 = ϵ 0 και µ 2 = µ 0. Συνεπώς, ακόμη και η προσθήκη ενός μικρού όρου απωλειών καταστρέφει τη συνθήκη αυτή.
61 3.2. Συντελεστής μετάδοσης 51 Σχήμα 3.3: Μεγέθυνση του σχήματος 3.1 στην περιοχή του διαδιδόμενου φάσματος. Σχήμα 3.4: Πλάτος του T s f για ϵ ri = µ ri = και μεταβλητό d. Για τον σκοπό αυτό, το σχήμα 3.4 παριστάνει το πλάτος του T s f για ϵ ri = µ ri = και μεταβλητό d. Αύξηση του d έχει ως αποτέλεσμα τη μείωση του k x,max και την υποβάθμιση της αναλυτικότητας του συστήματος. Αιτία του φαινομένου αυτού είναι το γεγονός ότι αύξηση του πάχους συνεπάγεται μείωση της αλληλεπίδρασης μεταξύ των επιφανειών της πλάκας και αδυναμία διέγερσης στην επιφάνεια που βρίσκεται εγγύτερα στο εστιακό επίπεδο πλασμονικών ρυθμών που αντιστοιχούν σε μεγάλες τιμές του k x, δηλαδή ρυθμών που παρουσιάζουν γρήγορη απόσβεση με την απόσταση. Υπενθυμίζεται ότι η ανάπτυξη πλασμονικών ρυθμών είναι αυτή που οδηγεί στην ενίσχυση των αποσβεννύμενων κυμάτων. Μία σημαντική παρατήρηση που προκύπτει από το σχημα 3.4 είναι ότι η ενίσχυση αποσβεννύμενων κυμάτων παύει να υφίσταται για πάχη μεγαλύτερα του μήκους κύματος, θέτοντας, ταυτόχρονα, περιορισμό στην απόσταση της πηγής από την πλάκα (η απόσταση της πηγής από την πλάκα πρέπει να είναι μικρότερη από το πάχος της πλάκας). Από την άλλη πλευρά, τα διαδιδόμενα κύματα φαίνεται να επηρεάζονται πολύ λίγο από τη μεταβολή του d, γεγονός που, στην πραγματικότητα, οφείλεται στις μικρές απώλειες. Μεγαλώνοντας τις απώλειες, παρατηρείται εμφανής εξάρτηση του πλάτους του διαδιδόμενου φάσματος από το d, όπως φαινεται στο σχήμα 3.5, που αντιστοιχεί
62 52 Κεφάλαιο 3 Σχήμα 3.5: Πλάτος του T s f για ϵ ri = µ ri = 0.01 και μεταβλητό d. στην περίπτωση ϵ ri = µ ri = 0.1. Μάλιστα, επειδή η απόσβεση ενός διαδιδόμενου κύματος είναι ανάλογη της απόστασης που διανύει μέσα στην πλάκα, διπλασιασμός του d συνεπάγεται διπλασιασμό της απόσβεσης (ύψωση στο τετράγωνο του T s f ). Ακολούθως, θα αποδειχτεί ότι το πρόβλημα απειρισμού του πεδίου στην περιοχή z f 1 < z < z f 2 ξεπερνιέται παρουσία απωλειών. Η ανάλυση θα πραγματοποιηθεί για z > d/2 καθώς η περίπτωση z < d/2 αντιμετωπίζεται με τον ίδιο, ακριβώς, τρόπο. Η ηλεκτρική πεδιακή ένταση για z > d/2 δίνεται από την (2.44γ). Χρησιμοποιώντας τις (3.1) και (3.2), η ολοκληρωτέα ποσότητα, εξαιρούμενου του όρου e jk xx /k 1z, που δεν παίζει ρόλο στη σύγκλιση του ολοκληρώματος, γράφεται 4 + 4e k x(2d+z z) για k x k 1. Αν, επιπλέον, k x k x,max, η (3.5) γράφεται ( ) 2, (3.5) µ ri + k2 1 ϵ 2k 2 ri e 2k x d x 4e k x(z z) η οποία τείνει εκθετικά στο 0 καθώς k x, αφού z > z. ( ) 2, (3.6) µ ri + k2 1 ϵ 2k 2 ri x Επίδραση αποκλίσεων από τη συνθήκη τέλειου φακού Οι καταστατικές παράμετροι κάθε διπλο-αρνητικού υλικού εμφανίζουν έντονη χρονική διασπορά. Επομένως, μικρές μετατοπίσεις της συχνότητας λειτουργίας μπορούν να επιφέρουν υπολογίσιμες αποκλίσεις από τη συνθήκη τέλειου φακού ϵ 2 = ϵ 0, µ 2 = µ 0 και σημαντικές διαφοροποιήσεις στη λειτουργία της διάταξης. Στη συνέχεια, θεωρείται ότι ϵ 2 = ϵ 0 (1 + δ ϵ ) και µ 2 = µ 0 (1 + δ µ ), όπου δ ϵ, δ µ είναι πραγματικοί αριθμοί, με μέτρο αρκετά μικρότερο του 1. Το σχήμα 3.6 απεικονίζει τον T s f για d = 0.2λ 1 και διάφορες τιμές των δ ϵ, δ µ. Είναι φανερός ο απειρισμός του T s f σε δύο τιμές του k x, μία πλησίον του k 1 και μία μακριά από αυτό, οι οποίες αντιστοιχούν σε επιφανειακούς ρυθμούς, που αναπτύσσονται κατά μήκος της πλάκας. Το γεγονός αυτό κατανοείται καλύτερα θεωρώντας ότι οι ϵ 2, µ 2 ακολουθούν τα μοντέλα διασποράς Drude και Lorentz, έτσι ώστε στις συχνότητες f 1, f 2
63 3.2. Συντελεστής μετάδοσης 53 Σχήμα 3.6: Πλάτος του T s f για διάφορα δ ϵ, δ µ και d = 0.2λ 1. (α) (β) (γ) Σχήμα 3.7: Μορφή των καμπυλών διασποράς των ρυθμών TM 0 (μπλε καμπύλη) και TM 1 (κόκκινη καμπύλη) για (α) f 1 = f 2 < f 0, (β) f 2 < f 1 = f 0 και f 1 < f 2 = f 0. Οι μεταβλητές f 1, f 2 δηλώνουν τις συχνότητες στις οποίες ϵ 2 = ϵ 0 και µ 2 = µ 0, αντίστοιχα. να ισχύει ϵ 2 = ϵ 0 και µ 2 = µ 0, αντίστοιχα. Τότε, δ ϵ > 0 αν f < f 1 και δ µ > 0 αν f < f 2. Η μορφή του διαγράμματος διασποράς των ρυθμών TM 0 και TM 1 παρουσιάζεται στο σχήμα 3.7 για τις περιπτώσεις f 1 = f 2, f 1 > f 2 και f 2 < f 1.³ Ακόμη, στο σχήμα αυτό σημειώνεται η συχνότητα λειτουργίας f 0 που οδηγεί στους διάφορους συνδυασμούς των δ ϵ, δ µ του σχηματος 3.6. Είναι φανερό ότι η ευθεία f = f 0 τέμνει την καμπύλη διασποράς του ρυθμού TM 0 σε δύο σημεία, τα οποία αντιστοιχούν στις θέσεις απειρισμών του T s f. Αν k x,max είναι η θέση του πιο απομακρυσμένου από τον k 1 απειρισμού του T s f, ο T s f είναι, περίπου, ίσος με 1 για k x < k x,max και μειώνεται εκθετικά για k x > k x,max. Άρα, ο k x,max είναι η μέγιστη χωρική συχνότητα που μπορεί να αναπαραχθεί στο εστιακό επίπεδο και η αναλυτικότητα του συστήματος είναι = 2π/k x,max. Μείωση των δ ϵ, δ µ (αύξηση της απόλυτης τιμής τους) συνεπάγεται μείωση του k x,max, συμπέρασμα στο οποίο, επίσης, καταλήγουμε παρατηρώντας τα διαγράμματα διασποράς του σχήματος 3.7. Πραγματι, μείωση των δ ϵ, δ µ σημαίνει αύξηση της f 0 και μετατόπιση προς τα αριστερά του δεξιότερου σημείου τομής της καμπύλης διασποράς με την ευθεία f = f 0. Ακολουθώντας παρόμοια πορεία με την περιπτωση των απωλειών, βρίσκεται ότι αν k x,max k 1, ³Για την εξαγωγή του σχήματος 3.7 χρησιμοποιήθηκαν συγκεκριμένες τιμές των f 1, f 2, f 0 και αριθμητική επίλυση της εξίσωσης διασποράς (2.49), οι οποίες παραλείπονται για λόγους συνοχής του κειμένου.
64 54 Κεφάλαιο 3 (α) (β) Σχήμα 3.8: (α) Πλάτος και (β) φάση του T s f για δ ϵ = δ µ = ±0.1 και d = 0.5λ 1 ή d = 3λ 1. ισχύει η προσεγγιστική σχέση ( ) δ µ + k2 1 2k 2 δ ϵ e kx,maxd = 2, (3.7) x,max με τα προσημα και + να εφαρμόζονται στους TM 0 και TM 1 ρυθμούς, αντίστοιχα. Επιπλέον, όπως και στην περίπτωση της πλάκας με απώλειες, ο δ µ έχει εντονότερη επίδραση στην εστιακή ικανότητα της διάταξης από τον δ ϵ. Μία προσεχτική παρατήρηση των διαγραμμάτων διασποράς του σχήματος 3.7 φανερώνει ότι οι αποσβεννύμενοι ρυθμοί που ενισχύονται από τη διάταξη αντιστοιχούν σε k x για τα οποία η ευθεία f = f 0 βρίσκεται μεταξύ των καμπυλών διασποράς των ρυθμών TM 0 και TM 1. Τότε, τα πλάτη των ρυθμών TM 0 και TM 1 που διεγείρονται είναι τέτοια ώστε η ενέργεια να συγκεντρώνεται στην επιφάνεια z = d/2 της πλάκας. Αντίθετα, όταν η ευθεία f = f 0 είναι πάνω από την καμπύλη του TM 0 ρυθμού ή κάτω από την καμπύλη του TM 1 ρυθμού, τα πλάτη των ρυθμών είναι τέτοια ώστε η ενέργεια συσσωρεύεται στην επιφάνεια z = d/2. Τα φαινόμενα αυτά θα γίνουν πλήρως κατανοητά στην ενότητα 3.4, όπου γίνεται λόγος για τα χαρακτηριστικά της πλάκας στο πεδίο του χρόνου. Αναφορικά με το διαδιδόμενο φάσμα, oι αποκλίσεις από τη συνθήκη τέλειου φακού δεν επηρεάζουν το πλάτος του T s f, καθώς τα κύματα στο εσωτερικό της πλάκας δεν υφίστανται απόσβεση. Εξαίρεση αποτελεί μία στενή ζώνη πριν τον k 1, όπου παρατηρειται ένα απότομο βύθισμα και το οποίο οφείλεται στις υψηλές τιμές (κοντά στο 1) του συντελεστή ανάκλασης. Μάλιστα, αν µ 2 ϵ 2 < µ 0 ϵ 0 (δ ϵ, δ µ < 0), τα επίπεδα κύματα με k 2 < k x < k 1 υφίστανται ολική ανάκλαση και αποσβέννυνται εκθετικά μέσα στο διπλο-αρνητικό υλικό. Το φαινόμενο αυτό καθίσταται έντονο όταν αυξηθεί ο d, οπότε η σύζευξη μεταξύ των κυμάτων στις περιοχές z < d/2 και z > d/2 καθίσταται πολύ μικρή. Ως παράδειγμα, ο T s f για δ ϵ = δ µ = ±0.1 και d = 0.5λ 1 ή d = 3λ 1 παριστάνεται στο σχήμα 3.8(α). Είναι εμφανής η απότομη πτώση του T s f για k x = 0.9, όταν d = 3λ 1 συγκριτικά με όταν d = 0.5λ 1, στην περίπτωση δ ϵ = δ µ = 0.1, στην οποία k 2 = 0.9k 1. Αντίθετα, όταν δ ϵ = δ µ = 0.1, κύματα με k x πολύ κοντά στον k 1 διαπερνούν την πλάκα με πολύ μικρή απόσβεση, ανεξάρτητα του d. Αν και το πλάτος του T s f για τα διαδιδόμενα κύματα δεν επηρεάζεται σε σημαντικό βαθμό από τις αποκλίσεις από τη συνθήκη τέλειου φακού δεν συμβαίνει το ίδιο με τη φάση του, όπως φαίνεται από το σχήμα 3.8(β), που απεικονίζει την arg{t s f } για τις παραμέτρους που χρησιμοποιήθηκαν στο σχήμα 3.8(α).
65 3.3. Κριτήρια συσχέτισης 55 Παρατηρεί κανείς ότι η arg{t s f } δεν είναι ομοιόμορφη για όλα τα k x, όπως θα έπρεπε να συμβαίνει ώστε να επιτυγχάνεται εστίαση. Με άλλα λόγια, υπάρχει πιθανότητα ένα επίπεδο διαφορετικό του z = z f 1 να αποτελεί το βέλτιστο επίπεδο εστίασης, ισχυρισμός που θα εξεταστεί διεξοδικά στην επόμενη ενότητα. Στο σημείο αυτό επισημαίνεται ότι η ύπαρξη πάνω στον πραγματικό k x -άξονα πόλου του T s f δεν οδηγεί σε απειρισμό του πεδίου, καθώς ο πόλος αυτός μπορεί να παρακαμφθεί με κατάλληλη αλλαγή του δρόμου ολοκλήρωσης στο μιγαδικό k x -επίπεδο. Επομένως, όσο κοντά στο 0 αλλά όχι 0 και να είναι οι δ ϵ, δ µ, η ενέργεια του πεδίου παραμένει πεπερασμένη. Η μόνη περίπτωση, λοιπόν, που παρατηρείται απειρισμός του πεδίου είναι ο ιδανικός, μη πρακτικά υλοποιήσιμος τέλειος φακός (ϵ 2 = ϵ 0, µ 2 = µ 0 ). Ακόμη και τότε, όμως, είναι δυνατόν να αρθεί ο απειρισμός αυτός μελετώντας την χρονική εξέλιξη των φαινομένων και όχι τη σταθερή κατάσταση ισορροπίας. Πιο συγκεκριμένα, αποδεικνύεται ότι ο απειρισμός του πεδίου συμβαίνει μετά από άπειρο χρόνο από τη στιγμή που ξεκινά η παρατήρηση του φαινομένου, μέσω της συνεχούς συσσώρευσης ενέργειας στην περιοχή z f 1 < z < z f 2. Περισσότερες λεπτομέρειες για το θέμα αυτό παρέχονται στην ενότητα Κριτήρια συσχέτισης Το πρόβλημα εύρεσης του βέλτιστου εστιακού επιπέδου Αν και ο συντελεστής μετάδοσης σχετίζεται, άμεσα, μέσω του k x,max, με την εστιακή ικανότητα μιας επίπεδης πλάκας διπλο-αρνητικού υλικού, δεν παρέχει πληροφορία για τη θέση του εστιακού επιπέδου. Σημειώνεται ότι στη γενική περίπτωση που οι ϵ 2, µ 2 αποκλίνουν από τις τιμές ϵ 0, µ 0, το εστιακό επίπεδο δεν συμπίπτει με το αντίστοιχο του τέλειου φακού. Επιπλέον, αν η πλάκα έχει πεπερασμένο μήκος, το κύμα που παράγεται κατά την πρόσπτωση ενός επίπεδου κύματος δεν είναι, πλέον, επίπεδο και ο συντελεστής μετάδοσης χάνει τη σημασία που έχει στην περίπτωση της άπειρης διάταξης. Για τους λόγους αυτούς, στην παρούσα ενότητα εισάγονται δύο νέα κριτήρια συσχέτισης του πεδίου ανάμεσα στο επίπεδο της πηγής και σε επίπεδα σταθερού z, μέσα από τα οποία μπορεί, αφενός, να εκτιμηθεί η εστιακή ικανότητα της πλάκας και, αφετέρου, να προσδιοριστεί με ακρίβεια το επίπεδο εστίασης [Sounas et al., 2006]. Για την ανάλυση που ακολουθεί, θεωρείται ότι πάνω στο επίπεδο z = z είναι τοποθετημένη μία επιφανειακή πηγή ρεύματος, η οποία δίνεται από την εξίσωση J(x, z) = e ( x w0 ) 2 δ(z z )ŷ (3.8) Τότε, το πεδίο που δημιουργείται προκύπτει από τη συνέλιξη της J(x, z) με τη συνάρτηση Green του προβλήματος της επίπεδης πλάκας διπλο-αρνητικού υλικού, η οποία, ουσιαστικά, αντιστοιχεί στο πεδίο που δίνεται από τις (2.44), με I = 1. Αν με G iy συμβολίσουμε τη συνάρτηση Green στην περιοχή i (i = 1, 2, 3), το πεδίο που παράγεται από την J(x, z) στην περιοχή αυτή είναι E iy (x, z) = ˆ f (x )G iy (x x, z) dx, (3.9)
66 56 Κεφάλαιο 3 (α) (β) Σχήμα 3.9: (α) Πλάτος και (β) πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης για ϵ 2 = 1.1ϵ 0, µ 2 = µ 0 και d = 0.5λ 1. όπου f (x) = e x2 /w 2 0. Εισάγοντας τις (2.44) με I = 1 στην (3.9), εξάγεται, μετά από μερικές πράξεις, E 1y (x, z) = ωµ 1 4π E 2y (x, z) = ωµ 1 4π E 3y (x, z) = ωµ 1 4π ˆ ˆ ˆ F(k x ) e jk xx k 1z [ e jk 1z z z + Re jk 1z(z+z +d) ] dk x, (3.10α) F(k x ) e jk xx k 1z e jk 1z(z +d/2) ( Ae jk 2zz + Be jk 2zz ) dk x, (3.10β) F(k x ) e jk xx k 1z Te jk 1z(z z d) dk x, (3.10γ) όπου F(k x ) = w 0 πe w 2 0 k2 x/4 είναι ο μετασχηματισμός Fourier της f (x). Είναι φανερό ότι η επιλογή του w 0 επιτρέπει τον καθορισμό του εύρους του διαδιδόμενου και αποσβεννύμενου φάσματος. Πιο συγκεκριμένα, θεωρώντας ότι ένας ρυθμός δεν διεγείρεται αν το πλάτος της F(k x ) είναι μικρότερο του 0.01w 0 π, ο μέγιστος kx που διεγείρεται είναι 4.3/w 0. Μείωση του w 0, δηλαδή στένεμα του πλάτους του γκαουσιανού παλμού, συνεπάγεται διεύρυνση του φάσματος των διεγειρόμενων ρυθμών, το οποίο συμφωνεί με το γεγονός ότι μία γραμμική πηγή (w 0 ) διεγείρει όλους τους διαδιδόμενους και αποσβεννύμενους ρυθμούς. Σημειώνεται ότι η επιλογή της (3.8) ως διέγερσης, αντί της γραμμικής πηγής, στηρίζεται στο γεγονός ότι, με τον τρόπο αυτό, αποφεύγονται τα άπειρα όρια ολοκλήρωσης κατά την εύρεση του πεδίου και ο απειρισμός του πεδίου πάνω στο επίπεδο της πηγής. Επίσης, δίνει τη δυνατότητα ελέγχου του βαθμού εστίασης αντικειμένων με διαφορετικές διαστάσεις (μικρότερες ή μεγαλύτερες του μήκους κύματος), μέσω της, κατάλληλης, προσαρμογής του w 0. Πρωτού προχωρήσουμε στην εισαγωγή των κριτηρίων συσχέτισης, κρίνεται χρήσιμη μία σύντομη περιγραφή της μορφής που έχει το πεδίο στον χώρο. Οι καταστατικές παράμετροι του διπλο-αρνητικού υλικού επιλέγονται ϵ 2 = 1.1ϵ 0, µ 2 = µ 0 και το πάχος της πλάκας d = 0.5λ 1. Επίσης, το εύρος της πηγής λαμβάνεται w 0 = 0.05λ 1, δηλαδή πολύ μικρότερο του μήκους κύματος, ώστε να είναι δυνατή η διέγερση τυχόν επιφανειακών ρυθμών. Στο σχήμα 3.9(α) απεικονίζεται το πλάτος της ηλεκτρικής πεδιακής έντασης. Είναι φανερό ότι, με μία πρώτη παρατήρηση, δεν μπορεί να εντοπιστεί κάποια περιοχή εστίασης, καθώς το πεδίο μεγιστοποιείται στις επιφάνειες της πλάκας και μειώνεται καθώς απομακρυνόμαστε από αυτές. Μάλιστα, εξαιρώντας μία στενή ζώνη εκατέρωθεν του άξονα z, το πλάτος του πεδίου παραμένει, σχεδόν, σταθερό κατά μήκος των επιφανειών της πλάκας, γεγονός που δηλώνει την ύπαρξη επιφανειακών κυμάτων. Η παρουσία επιφανειακών κυμάτων μπορει να γί-
67 3.3. Κριτήρια συσχέτισης 57 (α) (β) Σχήμα 3.10: (α) Πλάτος και (β) πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης για ϵ 2 = 1.1ϵ 0, µ 2 = µ 0 και d = 2λ 1. νει καλύτερα αντιληπτή μέσω του πραγματικού μέρους της ηλεκτρικής πεδιακής έντασης, το οποίο εκφράζει το στιγμιότυπο του πεδίου τη χρονική στιγμή 0 και παρουσιάζεται στο σχήμα 3.9(β). Είναι φανερή η ύπαρξη ενός κύματος το οποίο διαδίδεται παράλληλα προς τις επιφάνειες της πλάκας (τα μέτωπα κύματος είναι κάθετα σε αυτές) και έχει πλάτος που μειώνεται, γρήγορα, κατά τη διεύθυνση του άξονα z. Από το σχήμα αυτό, φαίνεται, επίσης, ότι το πεδίο είναι αντισυμμετρικό ως προς το επίπεδο z = 0, γεγονός που συμφωνεί, απόλυτα, με το διάγραμμα διασποράς 3.7, στο οποίο η ευθεία f = f 0 τέμνει την καμπύλη διασποράς του αντισυμμετρικού ρυθμού σε ένα σημείο, όταν f 0 = f 2 < f 1. Επιπλέον, αξίζει να σημειωθεί ότι το μήκος κύματος του ρυθμού αυτού, όπως μετράται από το σχήμα 3.9(β), είναι, περίπου, 2.5λ 1, το οποίο συμφωνεί με τη φασική σταθερά του ρυθμού όπως υπολογίζεται μέσω της εξίσωσης διασποράς (2.49). Η συμπεριφορά της πλάκας αλλάζει σε μεγάλο βαθμό όταν αυξηθεί το πάχος της. Στο συμπέρασμα αυτό καταλήγουμε μελετώντας το σχήμα 3.10, που παριστάνει το πλάτος και το πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης όταν d = 2λ 1. Σε αντίθεση με την προηγούμενη περίπτωση, είναι δυνατό, πλέον, να εντοπιστεί μία, σαφής, περιοχή εστίασης, όπου το πλάτος μεγιστοποιείται. Πιο συγκεκριμένα, καθώς το z αυξάνει από την τιμή d/2, το πλάτος αρχικά αυξάνεται, λαμβάνει μία μέγιστη τιμή και στη συνέχεια ελαττώνεται. Επιπλέον, τα μέτωπα κύματος έχουν κυλινδρική μορφή με κέντρο την περιοχή όπου εστιάζεται το πεδίο και το μήκος κύματος είναι ίσο με λ 1. Η μεταβολή αυτή στα χαρακτηριστικά της διάταξης οφείλεται στη μη-διέγερση επιφανειακών κυμάτων, η οποία ωστόσο, έχει ως συνέπεια τη μη-ενίσχυση του αποσβεννύμενου φάσματος της πηγής. Με τον τρόπο αυτό, επιτυγχάνεται αναλυτικότητα περίπου ίση με λ 1, γεγονός που φαίνεται, επίσης, από το εύρος της περιοχής εστίασης παράλληλα στον άξονα x, το οποίο είναι της τάξης του λ Θεωρητική διαμόρφωση Εφόσον η επίπεδη πλάκα διπλο-αρνητικού υλικού επιτυγχάνει δισδιάστατη εστίαση, είναι λογικό ότι, για την εύρεση του επιπέδου εστίασης, χρειάζεται να συγκριθεί το πεδιο σε διάφορα επίπεδα σταθερού z με το πεδίο του προσπίπτοντος κύματος στο επίπεδο z = z. Προσεγγιστικά, η θέση του επιπέδου εστίασης θα μπορούσε να βρεθεί μέσω της οπτικής απεικόνισης της μορφής που έχει το πεδίο σε ένα πεπερασμένο αριθμό επιπέδων σταθερού z και σύγκρισης των καμπυλών. Παραδείγ-
68 58 Κεφάλαιο 3 Σχήμα 3.11: Πλάτος του E 3y (x, z) σε διάφορα επίπεδα σταθερού z, για ϵ 2 = 1.1ϵ 0, µ 2 = µ 0 και d = 0.5λ 1. Οι μονάδες του κατακόρυφου άξονα είναι αυθαίρετες. ματος χάριν, στο σχήμα 3.11 σχεδιάζεται το πλάτος του πεδίου σε 5 επίπεδα, ισοκατανεμημένα στο διάστημα d/2 ως 3d/2, για μία πλάκα με ϵ 2 = 1.1ϵ 0, µ 2 = µ 0 και d = 0.5λ 1. Συγκρίνοντας τη μορφή των καμπυλών με την καμπύλη του προσπίπτοντος κύματος, που, επίσης, παρουσιάζεται στο ίδιο σχήμα, εξάγεται ότι το επίπεδο εστίασης είναι μεταξύ του z = 0.4λ 1 και του z = 0.5λ 1. Είναι φανερό ότι ο ακριβής προσδιορισμός του εστιακού επιπέδου δεν είναι δυνατό να πραγματοποιηθεί μέσω αυτής της οπτικής μεθόδου. Επίσης, η μέθοδος αυτή αγνοεί, εντελώς, τη φάση του πεδίου. Για τους λόγους αυτούς, κρίνεται απαραίτητη η ανάπτυξη κατάλληλων μαθηματικών κριτηρίων που να παρέχουν το βαθμό συσχέτισης του πεδίου σε ένα τυχαίο επίπεδο με το προσπίπτον πεδίο στο επίπεδο της πηγής. Τότε, το εστιακό επίπεδο είναι αυτό στο οποίο τα κριτήρια αυτά δίνουν τη μέγιστη συσχέτιση. Τα κριτήρια που θα χρησιμοποιηθούν για την εύρεση του επιπέδου εστίασης βασίζονται στις έννοιες του συντελεστή συσχέτισης και του μέσου τετραγωνικού σφάλματος. Πιο συγκεκριμένα, αν E sy (x, z) είναι το πεδίο που δημιουργεί η πηγή απουσία της πλάκας, το οποίο υπολογίζεται από την εξίσωση E sy (x, z) = ωµ 1 4π ο συντελεστής συσχέτισης ορίζεται ως corr(z, z ) = και το μέσο τετραγωνικό σφάλμα ως ˆ xm ˆ F(k x ) e jk xx k 1z e jk 1z z z dk x, (3.11) ˆ xm E sy (x, z )E 3y(x, z) dx x m x m E sy (x, z ) 2 dx ˆ xm x m E 3y (x, z) 2 dx 2 (3.12) mse(z, z ) = ˆ xm x m Esy (x, z ) E 3y (x, z) 2 dx ˆ xm x m E sy (x, z ) 2 dx (3.13)
69 3.3. Κριτήρια συσχέτισης 59 Σχήμα 3.12: Κριτήρια συσχέτισης για τέλειο φακό με d = 0.5λ 1 ή d = λ 1. Τότε, το επίπεδο εστίασης είναι αυτό στο οποίο μεγιστοποιείται ο corr και ελαχιστοποιείται το mse. Σημειώνεται ότι corr(z, z ) 1, με την ισότητα να ισχύει όταν E 3y (x, z) = ae sy (x, z ), όπου a μία μιγαδική σταθερά.⁴ Αντίστοιχα, mse(z, z ) 0, με την ισότητα να ισχύει όταν E 3y (x, z) = E sy (x, z ). Επομένως, το mse είναι ισχυρότερο κριτήριο από τον corr, καθώς το δεύτερο θεωρεί ότι υπάρχει πλήρης συσχέτιση των E sy (x, z ), E 3y (x, z) όταν έχουν την ίδια μορφή, ανεξάρτητα του πλάτους, ενώ το πρώτο απαιτεί να υπάρχει πλήρης ταύτιση. Το διάστημα ολοκλήρωσης [ x m, x m ] πρέπει, θεωρητικά, να εκτείνεται από το ως το. Στην πράξη, ωστόσο, αρκεί να είναι αρκετά μεγαλύτερο από τις διαστάσεις της πηγής, ώστε να εμπεριέχει όλες τις λεπτομέρειες της. Στα αποτελέσματα που ακολουθούν λαμβάνεται x m = 2λ 1, καθώς το εύρος της πηγής είναι πάντα μικρότερο του λ 1, δηλαδή w 0 λ 1. Αν και θα ήταν δυνατό να ισχυριστεί κανείς ότι μόνο το ένα κριτήριο αρκεί για τη εξέταση των χαρακτηριστικών εστίασης της πλάκας, η χρήση και των δύο κριτηρίων κρίνεται απαραίτητη για τη διασφάλιση της αξιoπιστίας των αποτελεσμάτων. Με άλλα λόγια, η θέση του βέλτιστου επιπέδου εστίασης όπως προσδιορίζεται μέσω του corr θα πρέπει να βρίσκεται κοντά στην αντίστοιχη που προκύπτει μέσω του mse, ώστε οι υπολογισμοί να θεωρηθούν σωστοί. Ως πρώτο παράδειγμα εφαρμογής των corr, mse επιλέγεται ο τέλειος φακός (ϵ 2 = ϵ 0, µ 2 = µ 0 ) με d = 0.5λ 1 ή d = λ 1, z = d και w 0 = 0.05λ 1. Τα κριτήρια συσχέτισης παρουσιάζονται στο σχήμα 3.12 ως συναρτήσεις του z, από όπου φαίνεται ότι corr(d, z ) = 1 και mse(d, z ) = 0. Τα αποτελέσματα αυτά είναι, απόλυτα, αναμενόμενα, καθώς είναι γνωστό ότι ο τέλειος φακός επιτυγχάνει τέλεια εστίαση στο επίπεδο z = z + 2d = d. Αξίζει, ωστόσο, να παρατηρηθεί η γρήγορη απόκλιση, για z < d, των corr και mse από τις τιμές τους στο επίπεδο εστίασης, η οποία επιβεβαιώνει το γεγονός ότι ο τέλειος φακός εστιάζει μόνο στις δύο διαστάσεις. Εισάγοντας απώλειες στις καταστατικές παραμέτους, ώστε ϵ 2 = (1 + j0.01)ϵ 0, µ 2 = (1 + j0.01)µ 0, προκύπτει το διάγραμμα του σχήματος Είναι φανερό ότι η μέγιστη τιμή του corr (απο εδώ και στο εξής θα συμβολίζεται corr max ) είναι, πλέον, μικρότερη του 1 και η ελάχιστη τιμή του mse (απο εδώ και στο εξής θα συμβολίζεται mse min ) ⁴Το γεγονός ότι corr(z, z ) 1 είναι άμεση συνέπεια την ανισότητας Schwarz-Hölder, σύμφωνα με την οποία ισχύει ˆ f (x) g 2 ˆ (x) dx ˆ f (x) 2 dx g(x) 2 dx, για οποιεσδήποτε συναρτήσεις f, g. Η ισότητα επαληθεύεται όταν f (x) = ag(x), με a έναν μιγαδικό αριθμό.
70 60 Κεφάλαιο 3 Σχήμα 3.13: Κριτήρια συσχέτισης για μία πλάκα με ϵ 2 = (1 + j0.01)ϵ 0, µ 2 = (1 + j0.01)µ 0 και d = 0.5λ 1 ή d = λ 1. Σχήμα 3.14: Πλάτος του E 3y (x, z) σε διάφορα επίπεδα σταθερού z, για ϵ 2 = (1 + j0.01)ϵ 0, µ 2 = (1 + j0.01)µ 0 και d = 0.5λ 1. Οι μονάδες του κατακόρυφου άξονα είναι αυθαίρετες. είναι μεγαλύτερη του 0, ως αποτέλεσμα της πεπερασμένης αναλυτικότητας της πλάκας. Μάλιστα, ο corr max αυξάνεται και το mse min μειώνεται με την αύξηση του d, επειδή, όπως δείχτηκε στην ενότητα 3.2, ο k x,max μειώνεται με την αυξηση του d. Παρ όλα αυτά, η θέση του βέλτιστου επιπέδου εστίασης δεν μεταβάλλεται σημαντικά σε σχέση με την περίπτωση του τέλειου φακού. Από την άλλη πλευρά, αντίθετα με ότι συμβαίνει στην περίπτωση χωρίς απώλειες, τόσο ο corr όσο και το mse έχουν μία, περίπου, συμμετρική μορφή εκατέρωθεν του εστιακού επιπέδου, γεγονός που θα μπορούσε να οδηγήσει στο συμπέρασμα ότι επιτυγχάνεται τρισδιάστατη εστίαση. Εντούτοις, παρατηρώντας τη μορφή του πεδίου σε διάφορα επίπεδα εκατέρωθεν του εστιακού επιπέδου, όπως απεικονίζεται στο σχήμα 3.14 για d = 0.5λ 1, φαίνεται ότι το πεδίο παρουσιάζει μία μονότονη μείωση του πλάτους για αυξανόμενα z, αντί να έχει μία συμμετρική μεταβολή, όπως θα έπρεπε να ισχύει αν εστιάζονταν σε μία περιοχή του τρισδιάστατου χώρου. Κατά συνέπεια, ο δισδιάστος χαρακτήρας των κριτηρίων συσχέτι-
71 3.3. Κριτήρια συσχέτισης 61 Σχήμα 3.15: Κριτήρια συσχέτισης για μία πλάκα με ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 0.2λ 1, z = d και w 0 = 0.05λ 1. σης δεν επιτρέπει την εξαγωγή συμπερασμάτων για τη μορφή του πεδίου στον τρισδιάστατο χώρο. Μεγαλύτερο ενδιαφέρον παρουσιάζει η μελέτη των κριτηρίων συσχέτισης στην περίπτωση που οι καταστατικές παράμετροι του διπλο-αρνητικού υλικού αποκλίνουν από τη συνθήκη τέλειου φακού. Τότε, η ευθεία f = f 0 ( f 0 είναι η συχνότητα λειτουργίας) τέμνει τις καμπύλες διασποράς των ρυθμών TM 0, TM 1, με συνέπεια την ανάπτυξη επιφανειακών κυμάτων. Τα κύματα αυτά, που κυρίως εμφανίζονται για μικρά d, έχουν αρνητική επίδραση στην ποιότητα της εστίασης, αφού οδηγούν σε δυσανάλογη ενίσχυση των χωρικών συχνοτήτων που αντιστοιχούν σε αυτά. Το σχήμα 3.15 απεικονίζει τον συντελεστή συσχέτισης και το μέσο τετραγωνικό σφάλμα όταν ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 0.2λ 1, z = d και w 0 = 0.05λ 1. Αν και οι θέσεις των corr max, mse min βρίσκονται κοντά η μία στην άλλη, η απόστασή τους από την πλάκα είναι διπλάσια σε σχέση με την περίπτωση του τέλειου φακού. Παρ όλο που αναμένεται απόκλιση από τη θέση εστίασης του τέλειου φακού, η μεγάλη αυτή διαφορά οφείλεται στην έντονη παρουσία των επιφανειακών κυμάτων σε επίπεδα που βρίσκονται πιο κοντά στην πλάκα. Το γεγονός αυτό ξεκαθαρίζεται μέσω του σχήματος 3.16, που παρουσιάζει το πλάτος της ηλεκτρικής πεδιακής έντασης σε διάφορα επίπεδα σταθερού z. Είναι φανερό ότι, αν και εντοπίζεται μία κεντρική κορυφή για x = 0, η ύπαρξη των επιφανεικών κυμάτων έχει ως αποτέλεσμα τη σημαντική διαφοροποίηση της μορφής του πεδίου σε σύγκριση με αυτήν του προσπίπτοντος κύματος. Η επίδραση των επιφανειακών κυμάτων εξασθενεί όταν απομακρυνθούμε από την πλάκα, με την ταυτόχρονη, όμως, απώλεια εστίασης των υπόλοιπων ρυθμών του φάσματος της πηγής, όπως φαίνεται από το άνοιγμα της καμπύλης του πλάτους. Για την υπέρβαση του προβλήματος που περιγράφηκε παραπάνω είναι αναγκαίος ο περιορισμός της επίδρασης του επιφανειακού κύματος. Ένας τρόπος για να επιτευχθεί αυτός ο σκοπός, χωρίς την αλλαγή των παραμέτρων της διάταξης (π.χ., χωρίς εισαγωγή απωλειών), είναι η αύξηση του w 0 και ο περιορισμός του φάσματος της πηγής σε χωρικές συχνότητες μικρότερες από αυτήν που αντιστοιχεί στο επιφανειακό κύμα. Μία δυνατή επιλογή είναι w 0 = π/k x,sw, δεδομένου ότι το επιφανανειακό κύμα εμφανίζεται στην χωρική συχνότητα k x,sw. Είναι αναγκαίο να τονιστεί ότι η αύξηση του w 0 με τον τρόπο αυτό δεν επηρεάζει την αναλυτικότητα, καθώς αυτή καθορίζεται από τον k x,sw. Με άλλα λόγια, η μείωση του w 0 έχει ως συνέπεια μόνο την ελάττωση του πλάτος του ανεπιθύμητου επιφα-
72 62 Κεφάλαιο 3 Σχήμα 3.16: Πλάτος της E 3y (x, z) σε διάφορα επίπεδα σταθερού z, για ϵ 2 = 1, 1ϵ 0, µ 2 = 1.1µ 0, d = 0.2λ 1, z = d και w 0 = 0.05λ 1. Οι μονάδες του κατακόρυφου άξονα είναι αυθαίρετες. (α) (β) Σχήμα 3.17: (α) Κριτήρια συσχέτισης για μία πλάκα με ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 0.2λ 1, z = d και w 0 = 0.2λ 1. (β) Πλάτος των E 3y (x, 1.05d), E sy (x, z) για την ίδια διάταξη. Οι μονάδες του κατακόρυφου άξονα είναι αυθαίρετες. νειακού ρυθμού ώστε να είναι ευδιάκριτη η μορφή του πεδίου που είναι αποτέλεσμα των άλλων ρυθμών του φάσματος της πηγής. Κάτω από αυτές τις προϋποθέσεις, το σχήμα 3.17(α) απεικονίζει τα κριτήρια συσχέτισης για μία πλάκα με ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 0.2λ 1, z = d και w 0 = 0.2λ 1, από όπου είναι εμφανής η μετατόπιση του corr max σε μικρότερες τιμές του z. Η διαφωνία μεταξύ των θέσεων των corr max και mse min, η οποία για την περίπτωση αυτή είναι μικρή λόγω του μικρού d, θα εξηγηθεί αναλυτικά στην επόμενη παράγραφο. Για επιβεβαίωση της ορθότητας της θέσης του εστιακού επιπέδου όπως προκύπτει από τον corr max, το σχήμα 3.17(β) παριστάνει το πλάτος του προσπίπτοντος πεδίου στο επίπεδο z = z και το πλάτος του σκεδαζόμενου πεδίου στο επίπεδο z = 1.05d, από όπου είναι φανερή η πολύ καλή συμφωνία μεταξύ των δύο καμπυλών. Στη συνέχεια, θα διερευνηθεί η ασυμφωνία ανάμεσα στον corr και το mse αναφορικά με τη θέση του επιπέδου εστίασης. Αντί να χρησιμοποιήσουμε τις παραμέτρους της προηγούμενης παραγρά-
73 3.3. Κριτήρια συσχέτισης 63 Σχήμα 3.18: Κριτήρια συσχέτισης για μία πλάκα με ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 2λ 1, z = d και w 0 = 0.5λ 1. φου, θεωρούμε ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 2λ 1, z = d και w 0 = 0.5λ 1, για τις οποίες η ασυμφωνία μεταξύ των κριτηρίων συσχέτισης είναι εντονότερη. Σημειώνεται ότι η αναλυτικότητα της πλάκας αυτής είναι λ 1, δηλαδή δεν μπορεί να ενισχύσει αποσβεννύμενα κύματα. Τα κριτήρια συσχέτισης για την περίπτωση αυτή αναπαρίστανται στο σχήμα Παρατηρεί κανείς ότι στη θέση του corr max το mse μεγιστοποιείται, ενώ, κανονικά, θα έπρεπε να ελαχιστοποιείται. Επιπλέον, είναι εμφανής η ύπαρξη πολλαπλών ελαχίστων και μιας περιοδικής μορφής για την καμπύλη του mse, με περίοδο ίση, περίπου, με λ 1. Η συμπεριφορά αυτή μας οδηγεί στο συμπέρασμα ότι η διαφορά μεταξύ του corr και του mse είναι αποτέλεσμα της φάσης του πεδίου και πιο συγκεκριμένα του όρου e jk 1z που εκφράζει τη διάδοση του κύματος στον χώρο. Προκειμένου να κατανοηθεί καλύτερα το γεγονός αυτό, θα υπολογιστεί, ακολούθως, το mse όταν το προσπίπτον κύμα είναι γκαουσιανή δέσμη με ηλεκτρική πεδιακή ένταση [Kojima and Yanagiuchi, 1979] όπου z 1 = z z και Ey inc (x, z 1 ) = w0 w(z 1 ) e x2 w 2 (z 1) e j k 0 x2 R(z 1) e j(k 0z 1 θ), (3.14) [ ( ) ] 2 ( w 2 (z 1 ) = w0 2 2z1 k0 w 1 + k 0 w0 2, R(z 1 ) = z 1 [1 2 ) 2 ] 0 +, θ = 1 ( ) 2z1 2z 1 2 tan 1 k 0 w0 2 (3.15) Αν w 0 0.5λ 1 και η αναλυτικότητα της διάταξης είναι της τάξης του λ 1, μπορεί να θεωρηθεί ότι το κύμα που διαπερνά την πλάκα είναι E 3y (x, z) = ae jφ E inc y (x, z z f 2 ), (3.16) με a έναν συντελεστή που εκφράζει την απόσβεση του πλάτους, φ τη φάση που εισάγει η πλάκα και z f 2 τη θέση του εστιακού επιπέδου. Θεωρώντας ότι x m, ο αριθμητής στο δεύτερο μέλος της
74 64 Κεφάλαιο 3 (3.13) γράφεται I 1 = + ˆ ˆ E inc Λαμβάνοντας υπόψη την ταυτότητα y (x, 0) E 3y (x, z) 2 dx = E3y (x, z) 2 dx 2 ˆ ˆ e ax2 dx = οι όροι του δεξιού μέλους της (3.17) γράφονται ˆ I 2 = Ey inc (x, 0) 2 π dx = w 0 2, I 3 = I 4 = ˆ ˆ E3y (x, z) 2 dx = a 2 w 0 π 2, { Re E inc cos ˆ Ey inc (x, 0) 2 dx { } Re Ey inc (x, 0)E3y(x, z) } y (x, 0)E3y(x, aw 0 π z) dx = 4 ζ4 + 8ζ [ k 1 (z z f 2 ) φ tan 1 ζ tan 1 όπου ζ = 2(z z f 2 )/(k 1 w0 2 ). Επομένως, εξάγεται ότι mse(z, z ) = I 2 + I 3 2I 4 I 2 cos dx (3.17) π a, (3.18) (3.19α) (3.19β) ] 2ζ 2 + ζ 2, (3.19γ) = 1 + a 2 2 2a 4 ζ4 + 8ζ [ k 1 (z z f 2 ) φ tan 1 ζ + 1 ] 2ζ 2 tan ζ 2 (3.20) Είναι προφανές ότι η περιοδική συμπεριφορά του mse οφείλεται στον όρο του cos. Επίσης, εύκολα βρίσκεται ότι mse(z f 2, z ) = 1 + a 2 2a cos φ, δηλαδή, ακόμη και όταν a = 1 (το προσπίπτον κύμα δεν υφίσταται καθόλου απόσβεση κατά τη διέλευση του μέσα από την πλάκα), το mse στο εστιακό επίπεδο είναι δυνατό να είναι μεγαλύτερο από 0, ανάλογα με την τιμή του φ. Μάλιστα, αν φ = π, mse(z f 2, z ) = 1 + a > 1, το οποίο έρχεται σε αντίθεση με το γεγονός ότι η δέσμη εστιάζεται στο επίπεδο z = z f 2. Με άλλα λόγια, το mse αδυνατεί να παρέχει τη σωστή θέση του εστιακού επιπέδου. Αξίζει να σημειωθεί ότι τέτοιο πρόβλημα δεν αντιμετωπίζεται στον corr, ο οποίος για την περίπτωση της προσπίπτουσας γκαουσιανής δέσμης παίρνει τη μορφή corr(z, z ) = 2 ζ4 + 8ζ (3.21) Είναι εύκολο να διαπιστώσει κανείς ότι corr(z f 2, z ) = 1, δηλαδή ο corr μεγιστοποιείται στο επίπεδο z = z f 2, όπως θα έπρεπε να συμβαίνει. Εφόσον το πρόβλημα με το mse εντοπίζεται στη μεταβολή της φάσης του κύματος κατά τη διάδοσή του παράλληλα προς τον άξονα z, η επίλυσή του συνίσταται στην απαλειφή του όρου που δίνει τη φάση αυτή. Πιο συγκεκριμένα, εισάγεται το τροποποιημένο μέσο τετραγωνικό σφάλμα mse m (z, z ) = ˆ xm Esy (x, z ) Ĕ 3y (x, z) 2 dx x m ˆ xm E sy (x, z ), (3.22) 2 dx x m
75 3.3. Κριτήρια συσχέτισης 65 Σχήμα 3.19: Κριτήρια συσχέτισης για μία πλάκα με ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 2λ 1, z = d και w 0 = 0.5λ 1. με Ĕ 3y (x, z) = E 3y (x, z)e j[arg{e sy(0,z )} arg{e 3y (x,z)}], δηλαδή αφαιρείται από τη φάση του πεδίου η διαφορά ανάμεσα στη φάση του πεδίου για τα σημεία του άξονα z και στην αντίστοιχη φάση του προσπίπτοντος κύματος. Αναφερόμενοι στην περίπτωση της γκαουσιανής δέσμης, αφαιρείται η ποσότητα φ jk 1 (z z f 2 ). Παρ όλα αυτά, διατηρείται η σχετική φάση του πεδίου στα σημεία ενός επιπέδου σταθερού z. Για τη διέγερση με γκαουσιανή δέσμη, αποδεικνύεται ότι το mse m λαμβάνει τη μορφή mse m (z, z ) = 1 + a 2 2a 2 + ζ 2 + ζ 4 + 8ζ ζ 4 + 8ζ 2, (3.23) + 4 από όπου φαίνεται ότι δεν περιέχει τον ταλαντούμενο τριγωνομετρικό όρο που περιλαμβάνεται στο mse. Επιπλέον, mse m (z f 2, z ) = 0 για a = 1, δηλαδή το τροποποιημένο σφάλμα ελαχιστοποιείται στο επίπεδο εστίασης. Στο σχήμα 3.19 παρουσιάζεται ο corr και το mse m για τη διάταξη με ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0, d = 2λ 1, z = d και w 0 = 0.5λ 1. Είναι εμφανής η συμφωνία μεταξύ των δύο κριτηρίων αναφορικά με τη θέση του εστιακού επιπέδου, επιβεβαιώνοντας την ορθότητα της ανάλυσης. Ολοκληρώνοντας την παρούσα υποενότητα, τα κριτήρια συσχέτισης για διαφορετικούς συνδυασμούς των ϵ 2, µ 2 και d παριστάνονται στο σχήμα Παρατηρεί κανείς ότι, όταν ϵ 2 < ϵ 0, µ 2 < µ 0, το επίπεδο εστίασης μετατοπίζεται προς την πλάκα, σε σχέση με την περίπτωση του τέλειου φακού, και απομακρύνεται από αυτήν όταν ϵ 2 > ϵ 0, µ 2 > µ 0. Το γεγονός αυτό είναι, κατά μία έννοια, παράδοξο, καθώς, όταν το υλικό της πλάκας είναι πυκνότερο από τον περιβάλλοντα χώρο, ένα επίπεδο κύμα αποκτά τη φάση που έχει στο επίπεδο της πηγής για z > z + 2d. Πράγματι, είναι απλό να αποδειχθεί ότι το επίπεδο πάνω στο οποίο αναπαράγεται η φάση είναι k 2 z = z k2 x k 2 1 k2 x d, (3.24) το οποίο βρίσκεται δεξιότερα του z = z + 2d αν k 2 > k 1, δηλαδή αν µ 2 ϵ 2 > µ 1 ϵ 1. Η συμπεριφορά αυτή καθιστά σαφέστερη τη χρησιμότητα των corr, mse m στην εκτίμηση της θέσης του εστιακού επιπέδου. Από την άλλη πλευρά, αύξηση του d οδηγεί σε μεγαλύτερες αποκλίσεις της θέσης του εστιακού
76 66 Κεφάλαιο 3 (α) (β) Σχήμα 3.20: (α) Συντελεστής συσχέτισης για d = 3.2λ 1 και μεταβλητά ϵ 2, µ 2. (β) Τροποποιημένο μέσο τετραγωνικό σφάλμα για ϵ 2 = 1.1ϵ 0, µ 2 = 1.1µ 0 και μεταβλητό d. επιπέδου από την αντίστοιχη του τέλειου φακού, επειδή μεγαλώνει η φάση που εισάγεται στο κύμα κατά τη διέλευσή του μέσα από το διπλο-αρνητικό υλικό. Υπενθυμίζεται ότι για μεγάλα d (πρακτικά μεγαλύτερα του λ 1 ) δεν ενισχύεται το αποσβεννύμενο φάσμα της πηγής και το φαινόμενο της εστίασης οφείλεται, αποκλειστικά, στην αρνητική διάθλαση που υφίστανται τα διαδιδόμενα κύματα στις επιφάνειες της πλάκας. 3.4 Δυναμική συμπεριφορά του πεδίου Η μέχρι στιγμής ανάλυση της πλάκας διπλο-αρνητικού υλικού αναφέρεται, αποκλειστικά, στο πεδίο της συχνότητας, καθώς λαμβάνει υπόψη τις τιμές των καταστατικών παραμέτρων, μόνο, σε μία συγκεκριμένη συχνότητα f 0. Στην πραγματικότητα, βέβαια, κάθε πηγή δημιουργεί ένα φάσμα συχνοτήτων γύρω από μία κεντρική συχνότητα, εξαιτίας της πεπερασμένης διάρκειας των κυματομορφών που παράγει. Το πεπερασμένο αυτό φάσμα συνδέεται άμεσα με τα μεταβατικά φαινόμενα που εμφανίζονται σε μία διάταξη, δηλαδή την απόκριση της διάταξης από τη στιγμή που η πηγή τίθεται σε λειτουργία μέχρι την αποκατάσταση της μόνιμης κατάστασης ισορροπίας. Σε συμβατικές διατάξεις, τα μεταβατικά φαινόμενα είναι, συνήθως, αποτέλεσμα διαδοχικών ανακλάσεων του κύματος στις διάφορες ασυνέχειες της γεωμετρίας και διαρκούν ένα μικρό χρονικό διάστημα σε σχέση με το συνολικό χρόνο λειτουργίας. Αντίθετα, σε μία πλάκα διπλο-αρνητικού υλικού, η διέγερση επιφανειακών πλασμονικών ρυθμών έχει ως συνέπεια την εμφάνιση ισχυρών μεταβατικών φαινομένων, που μπορούν να διαρκέσουν εκατοντάδες περιόδους (από εδώ και στο εξής, όταν αναφέρεται η περίοδος χωρίς κάποια άλλη επεξήγηση θα εννοείται αυτή που αντιστοιχεί στην κεντρική συχνότητα λειτουργίας), επηρεάζοντας αρνητικά την απόδοση της διάταξης. Υπενθυμίζεται ότι οι ρυθμοί αυτοί έχουν έντονα συντονιζόμενο χαρακτήρα, λόγω της μικρής ταχύτητας ομάδας, που τους καθιστά, σχεδόν, στατικούς. Από την άλλη πλευρά, η ύπαρξη πλασμονικών ρυθμών είναι απαραίτητη για την ενίσχυση του αποσβεννύμενου φάσματος της πηγής και την επίτευξη αναλυτικότητας μικρότερης από το μήκος κύματος. Με άλλα λόγια, η ανάπτυξη επιφανειακών ρυθμών οδηγεί σε δύο αλληλοσυγκρουόμενα φαινόμενα: τη βελτίωση της αναλυτικότητας της πλάκας στην κεντρική συχνότητα, εξαιτίας της ενίσχυσης των αποσβεννύμενων κυμάτων, και την υποβάθμιση της στον χρόνο, λόγω των έντονων
77 3.4. Δυναμική συμπεριφορά του πεδίου 67 μεταβατικών φαινομένων. Σκοπός της παρούσας ενότητας είναι η αξιολόγηση της επίδρασης της ταλαντούμενης συμπεριφοράς των επιφανειακών ρυθμών στις εστιακές ιδιότητες της επίπεδης πλάκας διπλο-αρνητικού υλικού. Προς τον σκοπό αυτό, εξάγονται αναλυτικές εκφράσεις για τη δυναμική συμπεριφορά του πεδίου μέσω μιας αυστηρής μαθηματικής ανάλυσης. Επίσης, καθίσταται δυνατή η κατανόηση των φυσικών μηχανισμών που συντελούν στην εστίαση του αποσβεννύμενου φάσματος της πηγής Περιγραφή του προβλήματος Η γεωμετρία του προβλήματος συμπίπτει με αυτήν του σχήματος 2.12, με τις καταστατικές παραμέτρους, ωστόσο, του διπλο-αρνητικού υλικού να ακολουθούν τα μοντέλα Drude ) ω 2 pe ϵ 2 (ω) = ϵ 0 (1 + ω 2 + jωγ e, (3.25α) ) ω 2 pm µ 2 (ω) = µ 0 (1 + ω 2 + jωγ m (3.25β) Η επιλογή του μοντέλου Drude για τη μαγνητική διαπερατότητα, αντί του ορθότερου μοντέλου Lorentz, προτιμάται για λόγους απλότητας των εκφράσεων και δεν αλλάζει τα τελικά συμπεράσματα, αφού τα δύο μοντέλα βρίσκονται κοντά το ένα στο άλλο σε συχνότητες μακριά του μαγνητικού συντονισμού, όπως είναι αυτές στις οποίες λειτουργεί ο επίπεδος φακός. Η πηγή που διεγείρει τη διάταξη βρίσκεται πάνω στο επίπεδο z = z και δίνεται από την εξίσωση J s (x, z, t) = f (x)p(t)δ(z z )ŷ, με f (x) τη χωρική κατανομή της πηγής και p(t) τη χρονική της εξάρτηση. Αν η κεντρική συχνότητα λειτουργίας είναι f 0, λαμβάνεται p(t) = p on (t) sin(2π f 0 t), με p on (t) ένα σήμα διαμόρφωσης, το οποίο ισούται με 0, για t < 0, και με 1, για t > T on, όπου T on ο χρόνος ανόδου. Στη συνέχεια, εξετάζονται μερικές ιδιότητες του μετασχηματισμού Fourier P(ω) της p(t), οι οποίες θα φανούν χρήσιμες στον υπολογισμό του πεδίου. Σύμφωνα με τον ορισμό του μετασχηματισμού Fourier ισχύει P(ω) = ˆ p(t)e jωt dt = ˆ Ton 0 ˆ p(t)e jωt dt + sin(ω 0 t)e jωt dt T on (3.26) Το δεύτερο ολοκλήρωμα του δεύτερου μέλους της παραπάνω εξίσωσης, το οποίο θα συμβολίζεται P 2 (ω), είναι ίσο με P 2 (ω) = ˆ T on sin(ω 0 t)e jωt dt = e jωton ω 2 + ω0 2 [jω sin(ω 0 T on ) + ω 0 cos(ω 0 T on )], (3.27) δηλαδή η P 2 (ω) έχει δύο πόλους στα σημεία ±ω 0, με ω 0 = 2π f 0. Σχετικά με το πρώτο ολοκλήρωμα του δεξιού μέλους της (3.27), για το οποίο θα χρησιμοποιείται ο συμβολισμός P 1 (ω), δεν μπορεί να βρεθεί αναλυτική έκφραση, καθώς είναι άγνωστη η ακριβής μορφή της p(t) στο διάστημα [0, T on ]. Εντούτοις, είναι δυνατό να προσδιοριστεί ένα άνω φράγμα, με την προϋπόθεση ότι η p(t) είναι φραγμένη. Πράγματι, αν p(t) < M, με M έναν θετικό πραγματικό αριθμό, ισχύει P 1 (ω) ˆ Ton 0 ˆ Ton p(t) e Im{ω}t dt M e Im{ω}t dt = M eim{ω}t on 1 0 Im{ω} (3.28)
78 68 Κεφάλαιο 3 Σχήμα 3.21: Δρόμος ολοκλήρωσης για τον υπολογισμό του αντίστροφου μετασχηματισμού Fourier της P(ω). Επιπλέον, αν η p(t) έχει πεπερασμένο πλήθος σημείων ασυνέχειας εντός του διαστήματος [0, T on ], η P 1 (ω) είναι αναλυτική, σύμφωνα με το θεώρημα της σελίδας 108 του [Copson, 1972]. Από τις (3.27), (3.28) εύκολα διαπιστώνεται ότι P(ω) 0 καθώς ω και Im{ω} < 0, ενώ αν ω και Im{ω} > 0, ισχύει e jωτ P(ω) 0, για τ > T on. Στο σημείο αυτό χρειάζεται να τονιστεί ότι το ολοκλήρωμα που δίνει την P 2 (ω), και κατ επέκταση το ολοκλήρωμα του μετασχηματισμού Fourier, συγκλίνει μόνο στο ημιεπίπεδο Im{ω} < 0. Παρ όλα αυτά, οι P 1 (ω), P(ω) επεκτείνονται σε ολόκληρο το μιγαδικό επίπεδο μέσω αναλυτικής συνέχειας. Ο αντίστροφος μετασχηματισμός Fourier της P(ω) υπολογίζεται από το ολοκλήρωμα p(t) = 1 ˆ P(ω)e jωt dω, (3.29) 2π όπου ο δρόμος ολοκλήρωσης είναι αυτός που συμβολίζεται με C στο σχήμα 3.21, δηλαδή ανήκει στην περιοχή σύγκλισης του ολοκληρώματος Fourier. Η ορθότητα επιλογής αυτού του δρόμου ολοκλήρωσης επιβεβαιώνεται από το γεγονός ότι οδηγεί στον μηδενισμό του p(t) για t < 0, όπως θα έπρεπε να ισχύει, αφού το σήμα p(t) είναι αιτιατό. Πράγματι, επειδή η P(ω) είναι αναλυτική στο ημιεπίπεδο Im{ω} < 0, ισχύει ˆ ˆ P(ω) e jωt dt = P(ω)e jωt dt, (3.30) C 1 C με C 1 το ημικύκλιο του άπειρου κύκλου που ανήκει στο ημιεπίπεδο Im{ω} < 0. Επειδή, όμως, P(ω) 0 πάνω στο C 1, σύμφωνα με το λήμμα του Jordan, το δεξιό ολοκλήρωμα της (3.29), και κατ επέκταση το αριστερό ολοκλήρωμα και η p(t), είναι 0, αν t < 0. Σύμφωνα με την (3.29), η πηγή J s εκφράζεται ως υπέρθεση των πηγών J s (x, z, ω) = f (x)p(ω) δ(z z )ŷ, που έχουν αρμονική εξάρτηση στον χρόνο με κυκλική συχνότητα ω. Επομένως, και το πεδίο που παράγει η J s εκφράζεται ως υπέρθεση των πεδίων που δημιουργούν οι J s. Ακολουθώντας την (3.10), η ηλεκτρική πεδιακή ένταση στην περιοχή 3 του σχήματος 2.12 περιοχή στην οποία εστιάζεται, κυρίως, η προσοχή μας που οφείλεται στην J s είναι E 3y (x, z, ω) = ωµ 1P(ω) 4π ˆ F(k x ) e jk xx k 1z Te jk 1z(z z d) dk x, (3.31)
79 3.4. Δυναμική συμπεριφορά του πεδίου 69 όπου F(k x ) είναι ο μετασχηματισμός Fourier της f (x).⁵ Κατά συνέπεια, το πεδίο που δημιουργεί η J s είναι E 3y (x, z, t) = 1 ˆ E 3y (x, z, ω)e jωt dω (3.32) 2π Αντικαθιστώντας την (3.32) και την (2.46α) στην παραπάνω εξίσωση λαμβάνουμε όπου E 3y (x, z, t) = µ 1 8π 2 ˆ ˆ ( k2z d S(ω, k x ) = k 1z cos 2 ( k2z d A(ω, k x ) = cos 2 F(k x ) ej[ωt k xx k 1z (z z d)] S(ω, k x )A(ω, k x ) P(ω)ω dk x dω, (3.33) ) + j k 2z ) + jk 1z µ r k 2z sin ( ) k2z d sin, (3.34α) µ r 2 ( ) k2z d (3.34β) 2 και µ r = µ 2 /µ 1. Σημειώνεται ότι η επίλυση των S(ω, k x ) = 0, A(ω, k x ) = 0 ως προς k x και ω σταθερό δίνει τις φασικές σταθερές των συμμετρικών και αντισυμμετρικών ρυθμών, αντίστοιχα. Από την άλλη πλευρά η επίλυση τους ως προς ω με k x σταθερό οδηγεί στις συχνότητες των ρυθμών που έχουν ως φασική σταθερά τη συγκεκριμένη τιμή του k x. Η πιο συνηθισμένη μέθοδος υπολογισμού του διπλού ολοκληρώματος της (3.33) συνίσταται στην ολοκλήρωση πρώτα ως προς k x, ώστε να βρεθεί το πεδίο σε μία συγκεκριμένη συχνότητα, και κατόπιν ως προς ω. Ωστόσο, το ολοκλήρωμα ως προς k x για τα σημεία που βρίσκονται κοντά στην πλάκα και τα οποία μας ενδιαφέρουν περισσότερο υπολογίζεται μόνο αριθμητικά, με αποτέλεσμα και το ολοκλήρωμα ως προς ω να υπολογίζεται, μόνο, αριθμητικά. Επιπλέον, στην περίπτωση του τέλειου φακού, η ολοκλήρωση ως προς k x αποκλίνει στην περιοχή d/2 < z < z + 2d. Από την άλλη πλευρά, ο t μπορεί να λάβει αυθαίρετα μεγάλες τιμές σε όλα τα σημεία του χώρου, συμπεριλαμβανομένων εκείνων που αντιστοιχούν σε μικρά x, z. Συνεπώς, το ολοκλήρωμα ως προς ω και k x σταθερό θα ήταν, ίσως, δυνατό να προσεγγιστεί με μία ασυμπτωτική έκφραση, που θα ίσχυε για t μεγαλύτερο μιας συγκεκριμένης τιμής, αποφεύγοντας με τον τρόπο αυτό, τουλάχιστον, μία αριθμητική ολοκλήρωση. Για τον λόγο αυτό, στην παρούσα ανάλυση επιλέγεται να πραγματοποιηθεί πρώτα η ολοκλήρωση ως προς ω και μετά ως προς k x [Sounas et al., 2007]. Πιο συγκεκριμένα, αφού, αρχικά, βρεθεί η ποσότητα Ẽ 3y (x, z, t, k x ) = µ 1e jk xx το πεδίο υπολογίζεται μέσω της σχέσης 4π E 3y (x, z, t) = 1 2π ˆ ˆ e j[ωt k 1z(z z d)] P(ω)ω dω, (3.35) S(ω, k x )A(ω, k x ) F(k x )Ẽ 3y (x, z, t, k x ) dk x (3.36) Ουσιαστικά, Ẽ 3y (x, z, t, k x ) είναι το πεδίο που δημιουργείται από την πηγή J s (x, z, t, k x ) = e jk xx p(t)δ(z z )ŷ. Επομένως, αναμένεται να συμπεριλαμβάνει τα επιφανειακά κύματα με φασική σταθερά k x, τα οποία ευθύνονται για την ενίσχυση του αποσβεννύμενου κύματος με κυματικό αριθμό κατά τη διεύθυνση του άξονα x ίσο με k x. Χάριν της σαφήνειας, από εδώ και στο εξής η ολοκληρωτέα ποσότητα στην (3.36) θα συμβολίζεται K(ω, k x ) και το αντίστοιχο ολοκλήρωμα I K. ⁵Ο μετασχηματισμός Fourier για συναρτήσεις που περιγράφουν χωρική μεταβολή ορίζεται ως ˆ F(k x ) = f (x)e jkxx dx και διαφέρει από τον μετασχηματισμό Fourier της (3.26), ο οποίος χρησιμοποιείται για συναρτήσεις στο πεδίο του χρόνου, στο πρόσημο της εκθετικής συνάρτησης που περιέχει τη μεταβλητή του μετασχηματισμού.
80 70 Κεφάλαιο 3 Σχήμα 3.22: Δρόμος ολοκλήρωσης για τον υπολογισμό του I K Βροχοτομές και πόλοι της K(ω, k x ) Η παρουσία της τετραγωνικής ρίζας στις σχέσεις ορισμού των k 1z, k 2z τις καθιστά πλειότιμες συναρτήσεις του ω. Επομένως, πριν τον υπολογισμό του I K, είναι απαραίτητο να καθοριστούν οι αποδεκτοί κλάδοι των k 1z, k 2z. Στην πραγματικότητα, επειδή η K(ω, k x ) είναι άρτια συνάρτηση της k 2z, το πρόβλημα περιορίζεται στον προσδιορισμό των κλάδων της k 1z. Έχοντας ως κριτήριο τη διατήρηση της καμπύλης C του σχήματος 3.21 ως δρόμο ολοκλήρωσης και λαμβάνοντας υπόψη ότι τα κλαδικά σημεία του k 1z είναι ω = ±ck x, με c = 1/ µ 0 ϵ 0, επιλέγονται ως βροχοτομές οι ημιευθείες Re{ω} = ±ck x, Im{ω} 0, όπως φαίνονται στο σχήμα 3.22 με τις ακανόνιστες συνεχείς γραμμές. Γράφοντας τον k 1z ως k 1z = (1/c) ω ck x ω + ckx, είναι απλό να διαπιστώσει κανείς ότι η επιλογή αυτή για τις βροχοτομές είναι ισοδύναμη με την επιλογή του θετικού φανταστικού άξονα z ως βροχοτομή της συνάρτησης z. Ορίζοντας θ 1 = arg{ω ck x } και θ 2 = arg{ω + ck x }, το α φύλλο Riemann είναι αυτό στο οποίο 3π/2 < θ 1, θ 2 π/2 ή π/2 < θ 1, θ 2 5π/2 και το β φύλλο εκείνο όπου 3π/2 < θ 1 π/2 και π/2 < θ 2 5π/2 ή π/2 < θ 1 5π/2 και 3π/2 < θ 2 π/2. Ένα πολύ σημαντικό επακόλουθο της επιλογής αυτής των βροχοτομών είναι ότι στο α φύλλο Riemann, όπου πραγματοποιείται η ολοκλήρωση, όλοι οι πόλοι της K(ω, k x ) βρίσκονται στο ημιεπίπεδο Im{ω} 0. Για την απόδειξη της πρότασης αυτής θα χρησιμοποιηθεί η συνθήκη Ẽ(x, z, t, k x ) = 0 για t < (z z )/c, η οποία απορρέει από την αρχή της αιτιότητας και το γεγονός ότι η μέγιστη ταχύτητα διάδοσης της ηλεκτρομαγνητικής ενέργειας είναι c. Aν δεν υπάρχουν πόλοι στο ημιεπίπεδο Im{ω} < 0, δηλαδή η K(ω, k x ) είναι αναλυτική συνάρτηση στο ημιεπίπεδο αυτό, από το θεώρημα του Cauchy προκύπτει ˆ ˆ K(ω, k x ) dω = K(ω, k x ) dω, (3.37) Γ 2 Γ με Γ τον δρόμο ολοκλήρωσης και Γ 2 το τμήμα του άπειρου κύκλου που βρίσκεται κάτω από τον πραγματικό άξονα, όπως απεικονίζονται στο σχήμα Επιπλέον, αν t < (z z )/c, το δεύτερο ολοκλήρωμα στην (3.37) είναι 0, λόγω του ότι ισούται με Ẽ(x, z, t, k x ), γεγονός που πρέπει να ισχύει και για το πρώτο. Πράγματι, κατά μήκος της Γ 2 ισχύει k 1z = k2z = ω/c και µr = ϵr = 1, με συνέπεια
81 3.4. Δυναμική συμπεριφορά του πεδίου 71 (α) (β) Σχήμα 3.23: Πόλοι της K(ω, k x ) στο ω-επίπεδο για ω pe = ω pm = ω 0 2, Γe = Γ m = ω 0, k x = 2k 0 και (α) d = 0.2λ 0 (β) d = 0.8λ 0. Με k 0, λ 0 συμβολίζονται ο κυματικός αριθμός και το μήκος κύματος του συμβατικού υλικού στη συχνότητα f 0. K(ω, k x ) = P(ω)e jω[t (z z )/c]. Όμως, το δεύτερο ολοκλήρωμα της (3.30) είναι 0 αν t < 0 και, άρα, το ολοκλήρωμα της K(ω, k x ) κατά μήκος της Γ 2 είναι 0 για t < (z z )/c. Όπως θα φανει αργότερα, οι θέσεις των πόλων της K(ω, k x ) στο μιγαδικό ω-επίπεδο έχουν σημαντικό ρόλο στον υπολογισμό του I K και για τον λόγο αυτό πραγματοποιείται, στη συνέχεια, μία συνοπτική περιγραφή τους. Εκτός από τους πόλους ±ω 0, που οφείλονται στη διέγερση, οι υπόλοιποι πόλοι είναι οι ρίζες των S(ω, k x ), A(ω, k x ) και αντιστοιχούν στις συχνότητες των υποστηριζόμενων επιφανειακών ρυθμών. Πιο συγκεκριμένα, οι συχνότητες αυτές μπορούν να προσδιοριστούν από το διάγραμμα διασποράς των επιφανειακών ρυθμών της πλάκας ως οι τομές των καμπυλών διασποράς με την ευθεία που είναι κάθετη στον οριζόντιο άξονα (άξονας k x ) στο σημείο με τιμή αυτήν του k x στην οποία ζητείται να υπολογιστεί το I K.⁶ Υπενθυμίζεται ότι οι επιφανειακοί ρυθμοί μιας πλάκας διπλο-αρνητικού υλικού είναι άπειρου πλήθους και ονομάζονται TM n, με n = 0, 1, 2,... να εκφράζει το πλήθος των μηδενισμών του πεδίου εντός της πλάκας. Ανάλογα, οι συχνότητες συντονισμού των ρυθμών, δηλαδή οι ρίζες των S(ω, k x ), A(ω, k x ), θα συμβολίζονται ωn sw,⁷ με τα άρτια n να αντιστοιχούν στην S(ω, k x ) και τα περιττά στην A(ω, k x ). Σημειώνεται ότι, όταν η πλάκα έχει απώλειες, οι ωn sw είναι μιγαδικοί αριθμοί με Im{ωn sw } > 0, όπου το φανταστικό μέρος εκφράζει τη μείωση του πλάτους στον χρόνο εξαιτίας των απωλειών. Επίσης, Re{ω0 sw} > Re{ωsw 1 } > Re{ωsw 2 } >.... Επειδή οι S(ω, k x ), A(ω, k x ) είναι συμμετρικές ως προς τον φανταστικό άξονα, οι αριθμοί (ω sw n είναι και αυτοί πόλοι της K(ω, k x ). Εκτός από τους επιφανειακούς ρυθμούς, μία πλάκα υποστηρίζει διαρρέοντα κύματα, τα οποία αντιστοιχούν σε μιγαδικές συχνότητες, ακόμα και στην περίπτωση μηδενικών απωλειών, ως αποτέλεσμα της μείωσης του πλάτους λόγω της διαρροής ενέργειας στο υλικό που περιβάλλει την πλάκα. Ο συμβολισμός που θα χρησιμοποιηθεί για τις συχνότητες των διαρρεόντων κυμάτων είναι ωn lw,⁸ με n = 0, 1, 2,... και Re{ω0 lw} < Re{ωlw 1 } < Re{ωlw 2 } <.... Σε αντίθεση με τα επιφανειακά κύματα, ο δείκτης n στα διαρρέοντα κύματα δεν έχει κάποια φυσική ⁶Αναφερόμενοι στο σχήμα 2.15, όπου ο οριζόντιος άξονα είναι η κανονικοποιημένη φασική σταθερά n = k x /k 1, οι συχνότητες των επιφανειακών ρυθμών προσδιορίζονται από τα σημεία τομής των καμπυλών διασποράς με την υπερβολή ω = ck x /n. ⁷Ο εκθέτης sw είναι συντομογραφία του surface wave. ⁸Ο εκθέτης lw είναι συντομογραφία του leaky wave. )
82 72 Κεφάλαιο 3 σημασία. Όπως και πριν, οι αριθμοί (ωn lw ) είναι επίσης πόλοι της K(ω, k x ). Στο σχήμα 3.23 παριστάνονται οι πόλοι για μία πλάκα με ω pe = ω pm = ω 0 2 και Γe = Γ m = ω 0, τιμές που οδηγούν σε ϵ 2 = (1 + j0.001)ϵ 0 και µ 2 = (1 + j0.001)µ 0, στην κεντρική συχνότητα. Αξίζει να παρατηρηθεί η μεγάλη εγγύτητα των ω0 sw, ωsw 1 με την ω 0, που γίνεται εντονότερη καθώς αυξάνεται το d. Επιπλέον, οι συχνότητες των διαρρέοντων κυμάτων βρίσκονται δεξιότερα του κλαδικού σημείου ck x, δηλαδή η φασική τους σταθερά k x είναι μικρότερη από τον κυματικό αριθμό k 1, στις συχνότητες στις οποίες διεγείρονται. Μία πολύ σημαντική ιδιότητα των ρυθμών μιας πλάκας διπλο-αρνητικού υλικού, η οποία διαδραματίζει κυρίαρχο ρόλο στον υπολογισμό του I K, είναι η ύπαρξη φασικών σταθερών αποκοπής για κάθε έναν από αυτούς, δηλαδή η μη διέγερση ενός ρυθμού όταν ο k x είναι μεγαλύτερος ή μικρότερος από κάποια συγκεκριμένη τιμή. Η κατανόηση αυτού του φαινομένου επιτυγχάνεται, καλύτερα, μέσω του διαγράμματος διασποράς των ρυθμών του σχήματος Είναι φανερό ότι οι καμπύλες διασποράς των επιφανειακών κυμάτων βρίσκονται δεξιά του κώνου φωτός του μέσου που περιβάλλει την πλάκα (ευθεία n = 1) και οι φασικές σταθερές αποκοπής προσδιορίζονται από τα σημεία τομής των καμπυλών διασποράς με τον κώνο φωτός. Πιο συγκεκριμένα, επειδή σε κάθε σημείο του κώνου φωτός k 1z = 0, έπεται από τις εξισώσεις διασποράς S(ω, k x ) = 0 και A(ω, k x ) = 0 ότι, για την περίπτωση χωρίς απώλειες, η φασική σταθερά αποκοπής k c xn του ρυθμού TM n επαληθεύει την εξίσωση k 2z = nπ/d. Ειδικότερα, ισχύει k c xn = ωn/c, c όπου ωn c είναι η συχνότητα αποκοπής του ρυθμού, η οποία υπολογίζεται από την εξίσωση (ωn) c 2 [µ 2 (ωn)ϵ c 2 (ωn) c µ 0 ϵ 0 ] = (nπ/d) 2. Η τιμή του k c xn αλλάζει στην περίπτωση απωλειών, η γενική, όμως, συμπεριφορά παραμένει η ίδια. Από την άλλη πλευρά, τα διαρρέοντα κύματα έχουν άνω φασική σταθερά αποκοπής, δηλαδή εμφανίζονται όταν ο k x είναι μικρότερος από συγκεκριμένες τιμές. Παρ όλα αυτά, δεν πρόκειται να δοθούν περισσότερες λεπτομέρειες στο θέμα αυτό, μιας και, όπως θα αποδειχθεί στη συνέχεια, τα διαρρέοντα κύματα έχουν πολύ μικρή επίδραση στην τιμή του πεδίου Υπολογισμός του I K Έχοντας υπόψη τις παρατηρήσεις της προηγούμενης υποενότητας, μπορούμε, πλέον, να προχωρήσουμε στον υπολογισμό του I K. Προκειμένου να αποφευχθεί η ύπαρξη πόλων με πολλαπλότητα μεγαλύτερη του 1,⁹ θεωρείται ότι το διπλο-αρνητικό υλικό έχει απώλειες. Η περίπτωση χωρίς απώλειες προκύπτει από το όριο της λύσης με απώλειες, όταν οι συντελεστές απωλειών Γ e, Γ m τείνουν στο 0. Αν Γ 1 είναι το ημικύκλιο του άπειρου κύκλου που βρίσκεται στο ημιεπίπεδο Im{ω} > 0 και Γ b1, Γ b2 είναι οι καμπύλες που περιβάλλουν τις βροχοτομές, όπως φαίνεται στο σχήμα 3.22, η εφαρμογή του ολοκληρωτικού τύπου του Cauchy στην κλειστή καμπύλη που διαμορφώνεται από τις καμπύλες Γ, Γ 1, Γ b1, Γ b2 οδηγεί στην εξίσωση ˆ ˆ ˆ ˆ K(ω, k x ) dω K(ω, k x ) dω K(ω, k x ) dω K(ω, k x ) dω Γ Γ 1 Γ b1 Γ b2 = j2π Res{K(ω, k x )}, (3.38) p ω p με Res z0 { f (z)} το ολοκληρωτικό υπόλοιπο της f (z) στο σημείο z 0. Το άθροισμα στο δεύτερο μέλος της (3.38) αναφέρεται σε όλους τους πόλους ω p της K(ω, k x ), που βρίσκονται στο ημιεπίπεδο ⁹Πόλος με πολλαπλότητα μεγαλύτερη του 1 εμφανίζεται όταν η ω 0 συμπίπτει με τη συχνότητα συντονισμού ενός επιφανειακού ρυθμού.
83 3.4. Δυναμική συμπεριφορά του πεδίου 73 Im{ω} 0. Σημειώνεται ότι ο ω p λαμβάνει τιμές από το σύνολο {ωn sw, (ωn sw ), ωn lw, (ωn lw ), ±ω 0 /n = 0, 1, 2,...}. Επιπλέον, ισχύει K( ω ) = K (ω) και ( ) Res {K(ω, k x )} = Res {K(ω, k x )}, (3.39α) ω p ω p ˆ (ˆ ) K(ω) dω = K(ω) dω, (3.39β) Γ b2 Γ b1 ιδιότητες που αποδεικνύονται στο παράρτημα 3.Α. Έτσι, η (3.38) γράφεται ˆ ˆ K(ω, k x ) dω K(ω, k x ) dω Γ Γ {ˆ 1 } { } = 2 Re K(ω, k x ) dω 4π Im Res{K(ω, k x )}, (3.40) Γ b1 p ω p όπου η άθροιση αναφέρεται, τώρα, στους πόλους στο τεταρτημόριο Im{ω} 0, Re{ω} > 0. Αν ω p = ω 0, το ολοκληρωτικό υπόλοιπο δίνεται από τη σχέση Res ω 0 {K(ω)} = ej[ω0t k1z(ω0)(z z d)] 2S(ω 0, k x )A(ω 0, k x ) ω 0 (3.41) Αντίθετα, αν ω p είναι ρίζα των S(ω, k x ) ή A(ω, k x ), το ολοκληρωτικό υπόλοιπο δίνεται, αντίστοιχα, από τις εξισώσεις Res ω p {K(ω, k x )} = Res ω p {K(ω, k x )} = ej[ωpt k1z(ωp)(z z d)] ω S(ω p, k x ) A(ω p, k x ) P(ω p)ω p, ej[ωpt k1z(ωp)(z z d)] S(ω p, k x ) ω A(ω p, k x ) P(ω p)ω p (3.42α) (3.42β) Για τον υπολογισμό του δεύτερου ολοκληρώματος του πρώτου μέλους της (3.40) απαιτείται η εύρεση της ασυμπτωτικής έκφρασης της K(ω, k x ) στην Γ 1. Προς τον σκοπό αυτό, η Γ 1 χωρίζεται στα τμήματα Re{ω} < ck x (τμήμα α), Re{ω} < ck x (τμήμα β) και Re{ω} > ck x (τμήμα γ). Η ασυμπτωτική έκφραση της k 1z στα τμήματα α, β είναι k 1z = ω/c, ενώ στο τμήμα γ είναι k1z = ω/c. Αντίθετα, k 2z = ω/c σε ολόκληρη την Γ1. Με βάση τις παρατηρήσεις αυτές, προκύπτει ότι K(ω, k x ) = cp(ω)e jω[t (z z )/c] στα τμήματα α, γ και K(ω, k x ) = cp(ω)e jω[t+(z z )/c] στο τμήμα β. Επομένως, αν P(ω)e jωt on, αν Re{ω} > ck x Q(ω) = (3.43) P(ω)e jωt on e j2ω(z z )/c, αν Re{ω} < ck x K(ω, k x ) = Q(ω)e jω[t T on (z z )/c] κατά μήκος του ημικυκλίου Γ 1. Όμως, σύμφωνα με τις (3.27), (3.28), η Q(ω) τείνει στο 0 πάνω στο Γ 1. Κατά συνέπεια, αν t > T on + (z z )/c, από το λήμμα του Jordan εξάγεται ότι το δεύτερο ολοκλήρωμα της (3.40) είναι 0 και {ˆ } I K = 2 Re K(ω, k x ) dω Γ b1 4π Im p { Res ω p {K(ω, k x )} } (3.44) Κρίνεται σκόπιμο να τονιστεί ότι μέχρι στιγμής δεν πραγματοποιήθηκε καμία προσέγγιση για τον υπολογισμό του I K. Επίσης, το γεγονός ότι η (3.44) ισχύει μόνο όταν t > T on + (z z )/c δεν αποτελεί
84 74 Κεφάλαιο 3 Σχήμα 3.24: Περιοχές του w-επιπέδου. Η έντονα σκιασμένη περιοχή αντιστοιχεί στο α φύλλο Riemann του ω-επιπέδου και η ελαφρά σκιασμένη περιοχή στο β φύλλο Riemann. μειονέκτημα της λύσης, καθώς η ποσότητα T on + (z z )/c είναι της τάξης του 10T 0, με T 0 = 1/ f 0, δηλαδή, όπως θα φανεί αργότερα, πολύ μικρότερη από τη συνολική διάρκεια του φαινομένου.¹⁰ Ολοκλήρωμα γύρω από τη βροχοτομή Ακολούθως, θα επιχειρηθεί ο υπολογισμός του ολοκληρώματος της (3.44) κατά μήκος της καμπύλης Γ b1 του σχήματος 3.22, που περικλείει τη βροχοτομή η οποία διέρχεται από το κλαδικό σημείο ω b = ck x. Προς τον σκοπό αυτό, εισάγεται μία νέα συνάρτηση Λ(ω) = K(ω, k x )e jωt, με t = t T on (z z )/c, έτσι ώστε το ζητούμενο ολοκλήρωμα να λάβει τη μορφή ˆ I b = Λ(ω)e jωt dω (3.45) Γ b1 Χαρακτηριστικό της Λ(ω) είναι ότι εξαρτάται, μόνο, από τη συχνότητα, σε αντίθεση με την K(ω, k x ), η οποία εξαρτάται και από τον χρόνο. Επίσης, αν ω και Im{ω} > 0, Λ(ω) = Q(ω) και Λ(ω) 0 στο άνω ημικύκλιο του άπειρου κύκλου. Μάλιστα, Λ(ω) O(ω 1 e j2ω(z z )/c ) στην περιοχή ω b Re{ω} < ω b και Λ(ω) O(ω 1 ) εκτός αυτής. Η βασική ιδέα για τον υπολογισμό του I b είναι η απεικόνιση του ω-επιπέδου σε ένα νέο επίπεδο, μέσω του του μετασχηματισμού w = ω ω b. Με τον τρόπο αυτό, η Γ b του ω-επιπέδου αντιστοιχίζεται στην ευθεία w = se jπ/4, με < s <, του w-επιπέδου, όπως φαίνεται στο σχήμα Επίσης, ο k 1z λαμβάνει τη μορφή k 1z = w w 2 + 2ω b /c στο w-επίπεδο, από όπου προκύπτει ότι έχει δύο κλάδους με κλαδικά σημεία ±j 2ω b. Ως βροχοτομές επιλέγονται τα τμήματα της υπερβολής (Im{w}) 2 (Re{w}) 2 = 2ω b που βρίσκονται στο πρώτο και τρίτο τεταρτημόριο, δηλαδή στα τεταρτημόρια όπου Re{w} Im{w} 0.¹¹ Με βάση τις βροχοτομές αυτές, ¹⁰Ο T on είναι, συνήθως, της τάξης του 10T 0 και ο (z z )/c, περίπου, ίσος με T 0, για μία συνηθισμένη απόσταση μεταξύ πηγής και σημείου παρατήρησης της τάξης του μήκους κύματος. ¹¹Οι βροχοτομές αυτές προκύπτουν, όπως και στην περίπτωση του ω-επιπέδου, θεωρώντας ως βροχοτομή της τετραγωνικής ρίζας τον θετικό φανταστικό άξονα. Εύκολα διαπιστώνεται ότι οι βροχοτομές του w-επιπέδου είναι απεικόνιση της βροχοτομής Re{ω} = ω b, Im{ω} 0 του ω-επιπέδου.
85 3.4. Δυναμική συμπεριφορά του πεδίου 75 στο α φύλλο Riemann του w-επιπέδου ισχύει 3π/4 < arg{ w 2 + 2ω b } π/4 και στο β π/4 < arg{ w 2 + 2ω b } 3π/4. Στο πρώτο από αυτά τα φύλλα, τα ημιεπίπεδα 3π/4 < arg{w} π/4 και π/4 < arg{w} 5π/4 είναι απεικονίσεις των α και β φύλλων Riemann του ω-επιπέδου, αντίστοιχα, συμπεριφορά που αντιστρέφεται στο β φύλλο Riemann του w-επιπέδου. Από την άλλη πλευρά, στο α φύλλο Riemann του w-επιπέδου το I b γράφεται ως και στο β φύλλο Riemann ως ˆ I b = j2e jω bt sλ 1 (se jπ/4) e s2 t ds (3.46) ˆ I b = j2e jω bt sλ 1 (se jπ/4) e s2 t ds, (3.47) με Λ 1 (w) = Λ(w 2 + ω b ). Οι (3.46) και (3.47) είναι ισοδύναμες και οδηγούν στο ίδιο αποτέλεσμα. Στη συνέχεια, επιλέγεται να χρησιμοποιηθεί η (3.46), δηλαδή θεωρούμε ότι βρισκόμαστε στο α φύλλο Riemann. Mία γραφική απεικόνιση αυτού του φύλλου παρουσιάζεται στο σχήμα 3.24, όπου οι ακανόνιστες συνεχείς γραμμές συμβολίζουν τις βροχοτομές της w 2 + 2ω b, η έντονα σκιασμένη περιοχή αντιστοιχεί στο α φύλλο Riemann του ω-επιπέδου, ενώ η ελαφρά σκιασμένη περιοχή στο β φύλλο Riemann του ω-επιπέδου. Από την ασυμπτωτική συμπεριφορά της Λ(ω) στο ω-επίπεδο εξάγεται ότι για s ισχύει Λ 1 (se jπ/4 ) O(s 2 ), ενώ για s ισχύει Λ 1 (se jπ/4 ) O(s 2 e 2s2 (z z )/c ). Το γεγονός αυτό και η παρουσία του όρου e s2 t στην ολοκληρωτέα ποσότητα καθιστά φανερό ότι η τιμή του ολοκληρώματος καθορίζεται κυρίως από τις τιμές της ολοκληρωτέας ποσότητας σε μία περιοχή γύρω από το σημείο s = 0. Επομένως, για την εύρεση του I b θα ήταν αρκετή η γνώση του αναπτύγματος Taylor της Λ 1 (w) σε μία περιοχή του σημείου w = 0, με ακτίνα R ίση με την απόσταση του σημείου w = 0 από τον πλησιέστερο πόλο της Λ 1 (w). Σημειώνεται ότι αν ω p είναι ένας πόλος της Λ(ω), ο αντίστοιχος πόλος της Λ 1 (w) είναι w p = ω p ω b. Η μέγιστη R που θα μπορούσε να επιτευχθεί είναι 2ωb, δηλαδή ίση με την απόσταση του σημείου w = 0 από τις βροχοτομές του w-επιπέδου, στην περίπτωση που δεν υπήρχε πόλος εντός του κύκλου w < 2ω b. Παρ όλα αυτά, ακόμη και στην περίπτωση ύπαρξης πόλων, είναι δυνατό να επιτευχθεί αυτή η μέγιστη ακτίνα σύγκλισης, με κατάλληλη εισαγωγή τους στο ανάπτυγμα της Λ 1 (w). Έστω ότι η Λ 1 (w) έχει N απλούς πόλους w 1, w 2,..., w N, με το N να μπορεί να είναι άπειρο, στο εσωτερικό του κύκλου w < 2ω b, κανένας από τους οποίους δεν συμπίπτει με το σημείο w = 0. Τότε, η συνάρτηση Λ 2 (w) = Λ 1 (w) N n=1 a n w w n, (3.48) όπου a n το ολοκληρωτικό υπόλοιπο της Λ 1 (w) στον πόλο w n, είναι αναλυτική στο εσωτερικό του κύκλου w < 2ω b και αναπτύσσεται σε μία σειρά Taylor Λ 2 (w) = b n w n, (3.49) n=0 με b n = Λ (n) 2 (0)/n!. Επομένως, το πλήρες ανάπτυγμα της Λ 1 (w), το οποίο ισχύει για κάθε w εντός του κύκλου w < 2ω b, είναι Λ 1 (w) = N n=1 a n w w n + n=0 b n w n (3.50)
86 76 Κεφάλαιο 3 Σχήμα 3.25: Σχετικό σφάλμα μεταξύ της ακριβούς τιμής του I b, όπως υπολογίζεται μέσω αριθμητικής ολοκλήρωσης, και της αντίστοιχης προσεγγιστικής, που υπολογίζεται μέσω των (3.53), (3.55) και (3.57), για διάφορες τιμές των k x, d και ω pe = ω pm = ω 0 2, Γe = Γ m = 0. Οι συντελεστές a n δίνονται από την εξίσωση ενώ οι b n από την a n = lim w w n (w w n )Λ 1 (w) = b n = Λ(n) 2 (0) n! = Λ(n) 1 (0) n! ω n ω b Res ω n {Λ(ω)}, (3.51) N m=1 a m ( ω m ω b ) n+1 (3.52) Στο σημείο αυτό πρέπει να τονιστεί ότι στο ανάπτυγμα (3.50) υπεισέρχονται τόσο οι πόλοι της Λ(ω) που ανήκουν στο α όσο και αυτοί που ανήκουν στο β φύλλο Riemann. Για παράδειγμα, ο πόλος ω = ω 0 που οφείλεται στη διέγερση υπάρχει και στα δύο φύλλα Riemann, και μάλιστα έχει την ίδια απόσταση από το κλαδικό σημείο. Επομένως, αναμένεται η συνεισφορά του στο ανάπτυγμα (3.50) να είναι της ίδιας τάξης, με την όποια διαφορά να οφείλεται στην τιμή του ολοκληρωτικού υπολοίπου. Μία διαδικασία υπολογισμού των b n περιττής τάξης, που, όπως θα αποδειχθεί, είναι τα μοναδικά που επηρεάζουν την τιμή του I b, περιγράφεται στο παράρτημα 3.Β. Μετά τις παραπάνω παρατηρήσεις, είμαστε, πλέον, σε θέση να υπολογίσουμε το I b. Αντικαθιστώντας την (3.50) στην (3.46), προκύπτει ) ( N I b = j2e jω bt a n I (1) bn + b n e jnπ/4 I (2) bn n=1 n=0, (3.53) με I (1) bn I (2) bn = ˆ se s2 t se jπ/4 w n ds, ˆ = s n+1 e s2 t ds Αν w n = w n e jπ/4, το πρώτο από τα παραπάνω ολοκληρώματα είναι ( ) I (1) π bn = e jπ/4 t + π w w n t, αν Im{w n} 0 ω n ω b w ( w t ), αν Im{w n} < 0 n (3.54α) (3.54β) (3.55)
87 3.4. Δυναμική συμπεριφορά του πεδίου 77 όπου w(z) = e z2 erfc( jz). Αν, επιπλέον, t, ισχύει I (1) bn = m=1 e j(2m 1)π/4 Γ(m + 1/2) w 2m n t m+1/2 (3.56) Μία πλήρης απόδειξη των παραπάνω εξισώσεων παρέχεται στο παράρτημα 3.Β. Από την άλλη πλευρά, το I (2) bn δίνεται από την [Abramowitz and Stegun, 1972] I (2) bn = 0, αν n άρτιος Γ(1 + n/2) t 1+n/2, αν n πέριττος (3.57) Παρατηρούμε ότι μόνο οι όροι του αναπτύγματος Taylor που αντιστοιχούν σε περιττά n συνεισφέρουν στην τιμή του I b. Σημειώνεται ότι I (2) b,n+2 /I(2) bn t 1, δηλαδή ένα μικρό πεπερασμένο πλήθος όρων του δεύτερου αθροίσματος της (3.53) αρκεί για την επίτευξη ικανοποιητικής ακρίβειας. Από τις (3.52), (3.53), (3.56) και (3.57), εύκολα, προκύπτει ότι για μεγάλα t I b = j2e jω b t n=1 Λ (2n 1) 1 (0) (2n 1)! ej(2n 1)π/4 Γ(n + 1/2) t n+1/2, (3.58) δηλαδή ο I b μειώνεται όπως η 1/t 3/2. Στο σχήμα 3.25 απεικονίζεται το σχετικό σφάλμα μεταξύ της ακριβούς τιμής του I b, όπως υπολογίζεται μέσω αριθμητικής ολοκλήρωσης, και της αντίστοιχης προσεγγιστικής, που υπολογίζεται μέσω των (3.53), (3.55) και (3.57), για διάφορες τιμές των k x, d. Για τον προσεγγιστικό υπολογισμό του πρώτου αθροίσματος της (3.53) χρησιμοποιήθηκαν, σε όλες τις περιπτώσεις, οι πόλοι ω 0, ω0 sw, ωsw 1 του α φύλλου Riemann, όπως επίσης ο ω 0 και αυτός που αντιστοιχεί στον μη-φυσικό TM 0 ρυθμό του β φύλλου Riemann. Από την άλλη πλευρά, για την εύρεση του δεύτερου αθροίσματος της (3.53) απαιτήθηκε η γνώση του όρου n = 1, όταν k x = 1.01k 1, d = 0.2λ 0, των όρων μέχρι n = 3 όταν k x = 1.01k 1 και d = 0.2λ 0 ή d = 0.5λ 0, και μέχρι n = 5, όταν d = λ 0. Σε όλες τις περιπτώσεις η συμφωνία της προσεγγιστικής λύσης με την ακριβή τιμή είναι ιδιαίτερα ικανοποιητική και γίνεται καλύτερη με την αύξηση του t. Η σταθερή τιμή που αποκτά το σχετικό σφάλμα μετά από κάποιο t είναι συνέπεια του γεγονότος ότι η ακρίβεια της αριθμητικής ολοκλήρωσης καθορίστηκε στα 8 δεκαδικά ψηφία, δηλαδή η σύγκριση παύει να έχει νόημα όταν το απόλυτο σφάλμα γίνει μικρότερο του Στο σημείο αυτό κρίνεται σκόπιμο να τονιστεί ότι το σφάλμα κατά την εύρεση του I b είναι το μοναδικό σφάλμα που υπεισέρχεται στον υπολογισμό του I K. Επομένως το σχετικό σφάλμα στην εύρεση του I K αναμένεται να είναι μικρότερο, αφού το απόλυτο σφάλμα παραμένει το ίδιο και η ακριβής τιμή του I K είναι μεγαλύτερη από την αντίστοιχη του I b Έκφραση του Ẽ 3y (x, z, t, k x ) Συνοψίζοντας την ανάλυση των προηγούμενων ενοτήτων, η ηλεκτρική πεδιακή ένταση που παράγεται από την πηγή J (x, z, t, k x ) είναι ( Ẽ 3y (x, z, t, k x ) = µ 1e jk xx T 0 + 4π n=0 T n sw + n=0 T lw n + T b ), (3.59)
88 78 Κεφάλαιο 3 (α) (β) (γ) (δ) Σχήμα 3.26: Πλάτος των όρων του δεύτερου μέλους της (3.59) για d = 0.2λ 0, ω pe = ω pm = ω 0 2, Γe = Γ m = 0.01ω pe και (α) k x = 1.01k 0, (β) k x = 1.1k 0, (γ) k x = 1.5k 0 (δ) k x = 0.9k 0. όπου { } T 0 = 4π Im Res{K(ω, k x )}, (3.60α) ω 0 { } = 4π Im Res{K(ω, k x )}, (3.60β) ωn { sw } = 4π Im Res{K(ω, k x )}, (3.60γ) T sw n T lw n T b = 2 Re{I b } ω lw n (3.60δ) Εξυπακούεται ότι στα αθροίσματα της (3.59) λαμβάνονται υπόψη μόνο οι πόλοι των ρυθμών που διεγείρονται για τον k x στον οποίο πραγματοποιείται ο υπολογισμός του πεδιου. Ο όρος T 0 εκφράζει το επιθυμητό πεδίο στην κεντρική συχνότητα της πηγής και έχει αρμονική χρονική μεταβολή με συχνότητα f 0. Οι όροι T n sw αντιστοιχούν στα επιφανειακά κύματα και η δυναμική τους συμπεριφορά καθορίζεται από τη συνάρτηση e jωsw n t. Αν το διπλο-αρνητικό υλικό δεν έχει απώλειες, το πλάτος των κυμάτων αυτών παραμένει σταθερό, ενώ υπό την παρουσία απωλειών μειώνεται με συντελεστή απόσβεσης Im{ωn sw }. Ανάλογα, οι T n lw δίνουν το πεδίο των διαρρεόντων κυμάτων, το πλάτος των οποίων,
89 3.4. Δυναμική συμπεριφορά του πεδίου 79 (α) (β) (γ) (δ) Σχήμα 3.27: Σύγκριση της μεθόδου FDTD με την εξίσωση (3.59) για (α) k x = 1.01k 0 και (β) k x = 1.5k 0. Οι παράμετροι της διάταξης είναι ω pe = ω pm = ω 0 2, Γe = Γ m = 0, d = 0.2λ 0 και T on = 0. Οι μονάδες του κατακόρυφου άξονα είναι αυθαίρετες. ωστόσο, αποσβέννυται γρήγορα, ακόμη και στην περίπτωση μηδενικών απωλειών. Τέλος, ο όρος T b, που προκύπτει από την ολοκλήρωση γύρω από τη βροχοτομή, έχει χρονική εξάρτηση e jω bt /t 3/2 για μεγάλα t. Ο όρος αυτός αποτυπώνει τη συμπεριφορά των κυμάτων των οποίων η διεύθυνση διάδοσης σχηματίζει μικρές γωνίες με τον άξονα x και τα οποία διαδίδονται με πολύ μικρή ταχύτητα κατά μήκος του άξονα z. Μεγάλο ενδιαφέρον παρουσιάζει η μελέτη του βαθμού που καθένας από τους όρους που περιγράφηκαν στην προηγούμενη παράγραφο συνεισφέρει στην τιμή του πεδίου. Για τον λόγο αυτό, το σχήμα 3.26 απεικονίζει το πλάτος μερικών από τους όρους αυτούς ως συνάρτηση του χρόνου, για διάφορες τιμές του k x. Είναι φανερό ότι η επίδραση του T b καθίσταται υπολογίσιμη για k x κοντά στον k 1, δηλαδή όταν o ω 0 βρίσκεται πλησίον του ω b. Επίσης, σε όλες τις περιπτώσεις, το πλάτος των όρων που αντιστοιχούν σε διαρρέοντα κύματα ελαττώνεται πολύ γρήγορα με την παρέλευση του χρόνου, ώστε να μην έχουν σημαντικό ρόλο στο τελικό αποτέλεσμα. Αναφορικά με τους επιφανειακούς ρυθμούς, η συνεισφορά τους στο άθροισμα μειώνεται καθώς αυξάνει η τάξη τους, επειδή το φασματικό πλάτος της πηγής στις συχνότητες συντονισμού τους μειώνεται, ως αποτέλεσμα της απομάκρυνσης των τελευταίων από την f 0. Ακολούθως, η ορθότητα της (3.59) ελέγχεται μέσω συγκρίσεων με αποτελέσματα που προκύπτουν
90 80 Κεφάλαιο 3 (α) (β) (γ) (δ) Σχήμα 3.28: Κανονικοποιημένο πλάτος της ηλεκτρικής πεδιακής έντασης στα επίπεδα z = d/2 (μπλε καμπύλες) και z = z + 2d (κόκκινες κάμπυλες), για d = 0.2λ 0, ω pe = ω pm = ω 0 2, Γe = Γ m = 0 και (α) k x = 2k 0, (β) k x = 4k 0, (γ) k x = 6k 0, (δ) k x = 8k 0. με τη μέθοδο FDTD. Στο πλαίσιο της μεθόδου αυτής, η προσομοίωση της άπειρης πλάκας που διεγείρεται από την πηγή J (x, z, t, k x ) επιτυγχάνεται με τη χρήση περιοδικών οριακών συνθηκών στα οριακά επίπεδα του υπολογιστού χώρου που είναι κάθετα στον άξονα x. Από την άλλη πλευρά, οι άπειρες διαστάσεις κατά τη διεύθυνση του άξονα z μοντελοποιούνται μέσω κατάλληλων στρωμάτων PML. Το χωρικό βήμα επιλέγεται λ 0 /100, με σκοπό την ορθή προσομοίωση των αποσβεννύμενων κυμάτων. Το σχήμα 3.27 παρουσιάζει τη χρονική εξέλιξη του πεδίου, όπως υπολογίζεται αναλυτικά από την (3.59) και αριθμητικά μέσω της μεθόδου FDTD, για k x = 1.01k 0 και k x = 1.5k 0. Παρατηρεί κανείς μία, σχεδόν, ταύτιση των καμπυλών, γεγονός που αφενός μαρτυρεί την ορθότητα της αναλυτικών εκφράσεων, αφετέρου επιβεβαιώνει την αξιοπιστία της μεθόδου FDTD. Στη συνέχεια, θα παρουσιαστεί πως, μέσω της (3.59), μπορούν να κατανοηθούν οι φυσικοί μηχανισμοί που εμπλέκονται στην ενίσχυση των αποσβεννύμενων κυμάτων. Προς τον σκοπό αυτό, θεωρείται ότι k x > k 0 και ω pe = ω pm = ω 0 2, δηλαδή Re{ϵ2 } = ϵ 0 και Re{µ 2 } = µ 0 στην κεντρική συχνότητα ω 0. Υπό αυτές τις προϋποθέσεις οι όροι του δεύτερου μέλους της (3.59) που, κυρίως, καθορίζουν την τιμή του πρώτου μέλους είναι οι T 0, T 0 sw και T 1 sw. Τότε, επειδή οι ω0 sw, ωsw 1 είναι πολύ κοντά στην ω 0, η Ẽ 3y (x, z, t, k x ) εκφράζεται ως το γινόμενο μιας αργά μεταβαλόμενης περιβάλλουσας με μία γρήγορα μεταβαλόμενη αρμονική συνάρτηση στη συχνότητα ω 0. Μάλιστα, αν
91 3.4. Δυναμική συμπεριφορά του πεδίου 81 (α) (β) (γ) (δ) Σχήμα 3.29: Κανονικοποιημένο πλάτος της ηλεκτρικής πεδιακής έντασης στα επίπεδα z = d/2 (μπλε καμπύλες) και z = z + 2d (κόκκινες κάμπυλες), για d = 0.2λ 0, ω pe = ω pm = ω 0 2, Γe = Γ m = 0.001ω pe και (α) k x = 2k 0, (β) k x = 4k 0, (γ) k x = 6k 0, (δ) k x = 8k 0. k x k 0, είναι δυνατό να αποδειχθεί [Gómez-Santos, 2003] ότι ω sw 0 ω 0 = ω sw 1 ω 0 και η συχνότητα ταλάντωσης της περιβάλλουσας είναι ω = ω sw 0 ω 0 = ω sw 1 ω 0. Καθώς αυξάνει ο k x, οι ω sw 0, ωsw 1 προσεγγίζουν την ω 0 και η ω μειώνεται. Τα παραπάνω συμπεράσματα επιβεβαιώνονται από το σχήμα 3.28, που απεικονίζει το πλάτος της περιβάλλουσας για διάφορα k x στα επίπεδα z = d/2 (δεξιά επιφάνεια πλάκας) και z = z + 2d (επίπεδο εστίασης), όταν δεν υπάρχουν απώλειες και d = 0.2λ 0. Ο κατακόρυφος άξονας είναι κανονικοποιημένος έτσι ώστε η τιμή 1 να αντιστοιχεί στο πλάτος του προσπίπτοντος κύματος στη θέση της πηγής. Είναι φανερό ότι το πλάτος του πεδιου ταλαντώνεται με συχνότητα η οποία μειώνεται καθώς μεγαλώνει ο k x. Ο χρόνος που απαιτείται για να αποκτήσει για πρώτη φορά το πλάτος στο επίπεδο z = z + 2d την τιμή 1, δηλαδή να γίνει ίσο με το πλάτος του προσπίπτοντος κύματος στο επίπεδο της πηγής, είναι αντίστροφα ανάλογος της ω. Το γεγονός αυτό ισοδυναμεί με τη συγκέντρωση μεγαλύτερου ποσού ενέργειας γύρω από τη δεξιά επιφάνεια της πλάκας για μεγαλύτερο k x, όπως, εξάλλου, φαίνεται από την αύξηση της μέγιστης τιμής του πλάτους στο επίπεδο z = d/2. Με άλλα λόγια, η ενίσχυση των αποσβεννύμενων κυμάτων επιτυγχάνεται μέσω της συσσώρευσης ενέργειας στην περιοχή της δεξιάς επιφάνειας της πλάκας, εξαιτίας της ανάπτυξης επιφανειακών πλασμονικών ρυθμών. Στο όριο k x, ισχύει ω 0, με συνέπεια τη γραμμική αύξηση του πλάτους και τη συνεχή συσσώρευση ενέργειας στη περιοχή του
92 82 Κεφάλαιο 3 Σχήμα 3.30: Πλάτος των T sw 0, T sw 1 ως συνάρτηση του k x, για d = 0.2λ 0, ω pe = ω pm = ω 0 2, Γe = Γ m = 0.001ω pe. επιπέδου z = z + 2d.¹² Η συμπεριφορά αυτή ερμηνεύει τον απειρισμό του πεδίου στην περιοχή z f 1 < z < z f 2 του τέλειου φακού, ο οποίος, στην πραγματικότητα, εμφανίζεται μετά από άπειρο χρόνο από τη στιγμή που η πηγή τίθεται σε λειτουργία. Από την παραπάνω ανάλυση εξάγεται το συμπέρασμα ότι αν ο χρόνος λειτουργίας της πηγής είναι πεπερασμένος, τίθεται ένα άνω όριο στον k x των αποσβεννύμενων κυμάτων, το πλάτος των οποίων μπορεί να αποκατασταθεί στο επίπεδο εστίασης. Επειδή πεπερασμένη διάρκεια ισοδυναμεί με διεύρυνση του φάσματος, οι εστιακές ικανότητες της πλάκας διπλο-αρνητικού υλικού επηρεάζονται, άμεσα, από το φάσμα της πηγής. Θεωρώντας πεπερασμένες απώλειες για την πλάκα, και πιο συγκεκριμένα Γ e = Γ m = 0.001ω pe, το πλάτος του πεδίου στα επίπεδα z = d/2 και z = z + 2d αποκτά τη μορφή που παρουσιάζεται στο σχήμα Πλέον, οι ταλαντώσεις αποσβέννυνται και αποκαθίσταται η μόνιμη κατάσταση ισορροπίας μετά από ένα πεπερασμένο χρονικό διάστημα. Παρ όλα αυτά, αξίζει να παρατηρηθεί ότι ο χρόνος απόσβεσης είναι της τάξης των εκατοντάδων περιόδων, γεγονός που μαρτυρεί τον έντονα συντονιζόμενο χαρακτήρα των επιφανειακών πλασμονικών ρυθμών. Όταν ο k x υπερβεί μία συγκεκριμένη τιμή (στην περίπτωση του σχήματος 3.29, την τιμή 6), η οποία συμπίπτει με τον k x,max της διάταξης, αλλάζει η μορφή του πλάτους και η τιμή του στην κατάσταση ισορροπίας. Στην πραγματικότητα, η μεταβολή αυτή δηλώνει την αδυναμία της πλάκας να ενισχύει αποσβεννύμενα κύματα με k x > k x,max. Σύμφωνα με την ανάλυση της εργασίας [Gómez-Santos, 2003], το φαινόμενο αυτό οφείλεται στο γεγονός ότι για k x > k x,max ο χρόνος που απαιτείται για την αποκατάσταση του πλάτους του πεδίου, δηλαδή ο χρόνος που απαιτείται για τη συγκέντρωση στη δεξιά επιφάνεια της πλάκας της ενέργειας που απαιτείται για την αποκατάσταση του πλάτους του αποσβεννύμενου κύματος, είναι μεγαλύτερος από τον χρόνο απόσβεσης των επιφανειακών ρυθμών. Επιπλέον, χρησιμοποιώντας την (3.60β), μπορεί να βρεθεί ότι και το πλάτος των επιφανεικών ρυθμών μειώνεται με την αύξηση του k x. Ο ισχυρισμός αυτός επιβεβαιώνεται από το σχήμα 3.30, στο οποίο απεικονίζονται τα πλάτη των T 0 sw, T 1 sw ως συνάρτηση του k x για τις παραμέτρους του σχήματος ¹²Το γεγονός αυτό κατανοείται πληρέστερα παρατηρώντας ότι η συνάρτηση sin( ωt), η οποία θα μπορούσε να θεωρηθεί ότι περιγράφει την μεταβολή του πλάτους, είναι περίπου ίση με ωt, αν ωt 1, δηλαδή για χρονικές στιγμές πολύ μικρότερες της περιόδου 2π/ ω.
93 3.4. Δυναμική συμπεριφορά του πεδίου Εύρεση του E 3y (x, z, t) Έχοντας προσδιορίσει το Ẽ 3y (x, z, t, k x ), μπορούμε να προχωρήσουμε στον υπολογισμό του E 3y (x, z, t) μέσω της (3.36). Πιο συγκεκριμένα, λαμβάνοντας υπόψη την (3.59), ισχύει ( ) T 0 + Tn lw + T b, (3.61) με E 3y (x, z, t) = µ 1 8π 2 T 0 = T sw n = T lw n = T b = ˆ ˆ ˆ ˆ n=0 Tn sw + n=0 F(k x ) T 0 e jk xx dk x, (3.62α) F(k x ) T sw n e jk xx dk x, (3.62β) F(k x ) T lw n e jk xx dk x, (3.62γ) F(k x ) T b e jk xx dk x (3.62δ) Επειδή K(ω, k x ) = K(ω, k x ),¹³ το ίδιο ισχύει και για τους T n sw, T n lw, T b. Ακόμη, F( k x ) = F (k x ), ως μετασχηματισμός Fourier πραγματικής συνάρτησης. Έτσι, οι (3.62β)-(3.62δ) μετασχηματίζονται στις T sw n = 2 T lw n = 2 T b = 2 ˆ 0 ˆ 0 ˆ 0 { } Re F(k x )e jk xx T sw { } Re F(k x )e jk xx T lw { } Re F(k x )e jk xx T b dk x n dk x, (3.63α) n dk x, (3.63β) (3.63γ) Ο όρος T 0 παρέχει το πεδίο της σημειακής πηγής στην κεντρική συχνότητα f 0 και υπολογίζεται αριθμητικά, όπως ένα τυπικό ολοκλήρωμα Sommerfeld. Το πεδίο αυτό αντιστοιχεί στη σταθερή κατάσταση ισορροπίας, η οποία, θεωρητικά, αποκαθίσταται μετά την παρέλευση άπειρου χρόνου από τη στιγμή εκίνησης της πηγής, οπότε τα μεταβατικά φαινόμενα μηδενίζονται. Από την άλλη πλευρά οι όροι T sw T lw n, T b προσδιορίζουν τα μεταβατικά φαινόμενα. Στη συνέχεια, θα επιχειρηθεί η εξαγωγή προσεγγιστικών εκφράσεων για τους όρους αυτούς. Σημειώνεται ότι στην ανάλυση αμελούνται οι όροι που αντιστοιχούν στα διαρρέοντα κύματα, καθώς το πλάτος τους μειώνεται πολύ γρήγορα με τον χρόνο και η συνεισφορά τους στο τελικό αποτέλεσμα είναι αμελητέα. Όπως αναφέρθηκε σε προηγούμενες ενότητες, ένα επιφανειακό κύμα συνεισφέρει στην τιμή του πεδίου όταν ο k x είναι μεγαλύτερος από τη φασική σταθερά αποκοπής του k c xn και επομένως T n sw = 0, αν k x < k c xn. Με άλλα λόγια, η ολοκληρωτέα ποσότητα στην (3.63α) παρουσιάζει σημείο ασυνέχειας στο διάστημα ολοκλήρωσης. Επιπλέον, η T n sw έχει πόλο k sw xn, ο οποίος ικανοποιεί την εξίσωση S(ω 0, k sw xn ) = 0, εξαιτίας του όρου (ωn sw ) 2 ω0 2 στον παρονομαστή του ολοκληρωτικού υπολοίπου που εμπλέκεται στην έκφραση της T n sw. Στην πραγματικότητα, ο πόλος αυτός είναι ένας από τους πόλους της T 0 και προκύπτει από την τομή της καμπύλης διασποράς του ρυθμού TM n με την ευθεία ¹³Για την απόδειξη της ιδιότητας αυτής αρκεί να παρατηρήσει κανείς ότι ο k 1z = (1/c) ω k x ω + kx παραμένει αμετάβλητος κατά την αντικατάσταση του k x από το k x. Επιπλέον, ο k 2z είναι άρτια συνάρτηση του k x. n,
94 84 Κεφάλαιο 3 Σχήμα 3.31: Γεωμετρικός τόπος των συχνοτήτων συντονισμού του φυσικού και μη-φυσικού TM 0 ρυθμού στο w-επίπεδο, για 0.8k 0 k x 1.1k 0. Οι παράμετροι της πλάκας είναι d = 0.2λ 0, ω pe = ω pm = 0.96ω 0 2, Γ e = Γ m = 0.01ω pe. Η διακεκκομένη γραμμή αντιστοιχεί στην καμπύλη Γ b1 του ω-επιπέδου. ω = ω 0.¹⁴ O πόλος αυτός βρίσκεται πάνω στον πραγματικό k x άξονα μόνο αν η διάταξη δεν έχει απώλειες. Όσον αφορά τον T b, θεωρούμενο ως συνάρτηση του k x, είναι, επίσης, ασυνεχής στα σημεία k c xn. Για να γίνει κατανοητό αυτό το γεγονός, το σχήμα 3.31 απεικονίζει στο w-επίπεδο τον γεωμετρικό τόπο των πόλων που αντιστοιχούν στον TM 0 φυσικό και μη-φυσικό ρυθμό, για μεταβολή του k x από 1.1k 0 μέχρι 0.8k 0 και παραμέτρους της διάταξης αυτές που αναγράφονται στη λεζάντα του σχήματος. Είναι φανερό ότι, για k x = k c x0 = 0.966k 0, ο πόλος του TM 0 φυσικού ρυθμού, ο οποίος θα συμβολίζεται w 0, βρίσκεται πάνω στην ευθεία arg{w} = 3π/4, η οποία αντιστοιχεί στη βροχοτομή Re{ω} = ω b, Im{ω} 0 του ω-επιπέδου. Αν k x > k c x0, ο πόλος εντοπίζεται στο ημιεπίπεδο 3π/4 < arg{w} < π/4, που είναι απεικόνιση του α φύλλου Riemann του ω-επιπέδου, ενώ αν k x < k c x0, ο w 0 βρίσκεται στο ημιεπίπεδο π/4 < arg{w} < 5π/4, το οποίο αντιστοιχεί στο β φύλλο Riemann του ω-επιπέδου. Κατά συνέπεια, θέτοντας w 0 = w 0e jπ/4, ισχύει π < arg{w 0 } < 0, αν k x > k c x0 και 0 < arg{w 0 } < π, αν k x < k c x0. Έτσι, προκύπτει ( ) π b0 = w w 0 t, αν k x < k c e jπ/4 x0 t + πw 0 w (, (3.64) w 0 t ), αν k x > k c x0 I (1) δηλαδή η I (1) b0 είναι ασυνεχής στο σημείο kc x0. Μάλιστα, λαμβάνοντας υπόψη ότι Re{w(x)} = e x2, για x πραγματικό αριθμό [Abramowitz and Stegun, 1972], αποδεικνύεται ότι η ασυνέχεια αυτή ισούται με ¹⁴Για να είμαστε ακριβείς, η T n sw μονότονη συνάρτηση του k x. I (1) b0 k c I (1) b0 x0 k c+ x0 = 2πw 0 (k c x0)e jw2 0 (kc x0 )t, (3.65) μπορεί να έχει δύο τέτοιους πόλους, μιας και η καμπύλη διασποράς δεν είναι, πάντα,
95 3.4. Δυναμική συμπεριφορά του πεδίου 85 με w 0 (k c x0 ) τον πόλο όταν k x = k c x0 και kc+ x0 (kc x0 ) να δηλώνει ότι ο k x τείνει στον k c x0 από δεξιά (αριστερά). Από την άλλη πλευρά, οι I (2) bn είναι συνεχείς συναρτήσεις του k x, καθώς οι συντελεστές b n είναι οι συντελεστές του αναπτύγματος Taylor της Λ 2 (w), η οποία είναι η ίδια για k x = k c+ x0 και k x = k c x0. Αρα, ο I b έχει ασυνέχεια στη θέση k x = k c x0, η οποία δίνεται από την εξίσωση I k b c I k b c+ = j2πe jωsw x0 x0 0 (k c x0 )t Res ω sw 0 (kc x0 = j2π Res ){Λ(ω)} ω0 sw(kc ){K(ω, kc x0)} (3.66) x0 Πλέον, είμαστε σε θέση να προχωρήσουμε στον υπολογισμό των ολοκληρωμάτων (3.63α), (3.63γ). Προς τον σκοπό αυτό, θα χρησιμοποιηθεί η τεχνική της στάσιμης φάσης [Felsen and Marcuvitz, 1994], η οποία παρέχει μία προσεγγιστική τιμή του ολοκληρώματος I = ˆ xb x a g(x)e jωq(x) dx, (3.67) όπου Ω > 0, q(x) είναι πραγματική συνάρτηση και g(x) είναι ομαλή συνάρτηση του x. Τότε, αν υπάρχει x s που ανήκει στο διάστημα (x a, x b ) και στο οποίο q (x s ) = 0, ισχύει I 2π = Ω q (x s ) g(x s)e jωq(xs)±jπ/4 + 1 [ g(xb ) jω q (x b ) ejωq(xb) g(x ] a) q (x a ) ejωq(x a), (3.68) με το + να εφαρμόζεται όταν q (x s ) > 0 και το όταν q (x s ) < 0. Αν κάποιο από τα όρια τείνει στο άπειρο, ο αντίστοιχος όρος παραλείπεται. Τονίζεται ότι η παραπάνω έκφραση εφαρμόζεται όταν ο Ω είναι ένας μεγάλος θετικός αριθμός (Ω ). Στην περίπτωση των ολοκληρωμάτων που μας ενδιαφέρουν, τον ρόλο του Ω τον έχει ο t, ο οποίος μπορεί να λάβει αυθαίρετα μεγάλες τιμές. Εξετάζοντας, αρχικά, το ολοκλήρωμα (3.63γ), αυτό εκφράζεται, μέσω της (3.60δ), ως {ˆ T b = 4 Re Re {F(k } } x )e jk xx I b dk x (3.69) 0 Όμως, σύμφωνα με την (3.66), ο I b είναι ασυνεχής στα σημεία ±k c xn, με n = 0, 1, 2,.... Άρα, ο ασυμπτωτικός υπολογισμός της (3.69) πρέπει να πραγματοποιηθεί ξεχωριστά στα διαστήματα (k c x,n+1, kc xn), με n = 0, 1, 2,.... Λαμβάνοντας υπόψη ότι στην περίπτωση του ολοκληρώματος (3.69) τη θέση της q(x) έχει η ω b = ck x, η οποία δεν διαθέτει στασιμοποιητικό σημείο, εξάγεται ότι { T b 1 { = 4 Re jct } ( } Re F(k c ) xn)e jkc xnx I k b c I k b c+ (3.70) x0 x0 n=0 Η τελευταία εξίσωση γράφεται, μέσω της (3.66), ως Όσον αφορά τον T sw n { T b 8π { = ct Re Re n=0 T sw n F(k c xn)e jkc xnx } Res {K(ω, 0 (kc xn) kc xn)} ω sw, οι (3.63α), (3.60β) οδηγούν στην {ˆ { } } = 8π Im Re F(k c xn)e jkc xnx Res{K(ω, k x )} dk x k c xn ωn sw } (3.71) (3.72) Στην περίπτωση αυτή, τον ρόλο της q(x) έχει η Re{ω sw n (k x )}, η οποία μπορεί να έχει ένα στασιμοποιητικό σημείο, έστω k st xn, ως αποτέλεσμα της μη-μονότονης μεταβολής των καμπυλών διασποράς
96 86 Κεφάλαιο 3 (α) (β) Σχήμα 3.32: Ακριβής, μέσω αριθμητικής ολοκλήρωσης, και προσεγγιστική, μέσω της (3.73), τιμή της T sw 0, όταν ω pe = ω pm = 0.96ω 0 2, Γe = Γ m = 0.001ω pe και d = 0.2λ 0. των ρυθμών. Επιπλέον, αν θεωρηθεί ότι το διπλο-αρνητικό υλικό έχει απώλειες, ακόμη και μικρές, η ολοκληρωτέα ποσότητα είναι ομαλή σε όλο το διάστημα ολοκλήρωσης και ισχύει Tn sw 8π { = } { } t Re{ωn sw (k st xn)} Re F(k c xn)e jkc xnx Re Res {K(ω, ω0 sw(kc xn) kc xn)} 2π { } 8π t Re{ωn sw (k st xn)} Re F(k st xn)e jkst xnx { } Im Res {K(ω, kst xn)}e ±jπ/4 (3.73) ω sw n (k st xn) Αν η διάταξη δεν έχει απώλειες, ωn sw (k st xn) = c, καθώς η καμπύλη διασποράς εφάπτεται του κώνου φωτός στην φασική σταθερά αποκοπής. Η συνθήκη αυτή μπορεί να θεωρηθεί ότι ισχύει, προσεγγιστικά, και στην περίπτωση μικρών απωλειών, οπότε, από τις (3.71), (3.73), προκύπτει T b + Tn sw n=0 = 8π 2π t Re{ωn sw (k st xn)} Re { } Im Res {K(ω, kst xn)}e ±jπ/4 n=0 ω sw n (k st xn) { } F(k st xn)e jkst xnx (3.74) Επομένως, το μεταβατικό φαινόμενο συνίσταται από όρους της μορφής e jωsw n (k st xn)t / t, δηλαδή από κύματα που το πλάτος τους μειώνεται όπως η 1/ t και παρουσιάζουν αρμονική χρονική μεταβολή στις στασιμοποιητικές συχνότητες των ρυθμών. Στην πράξη, βέβαια, τη σημαντικότερη επίδραση έχουν οι ρυθμοί TM 0 και TM 1, οι οποίοι έχουν το μεγαλύτερο πλάτος, καθώς οι συχνότητες συντονισμού τους είναι οι πιο κοντινές στην κεντρική συχνότητα της πηγής. Το σχήμα 3.32 απεικονίζει την τιμή του T0 sw όπως υπολογίζεται με αριθμητική ολοκλήρωση και μέσω της (3.73), από όπου φαίνεται ότι η συμφωνία μεταξύ των αποτελεσμάτων βελτιώνεται με την παρέλευση του χρόνου. Η διαφορά στο πλάτος που παρατηρείται για μικρά t οφείλεται στην μη μηδενική τιμή του ολοκληρώματος κοντά στους πόλους της T 0 sw, η οποία αγνοείται στο πλαίσιο της τεχνικής στάσιμης φάσης. Κρίνεται απαραίτητο να τονιστεί ότι ο πόλος αυτός βρίσκεται πολύ κοντά στον πραγματικό άξονα, καθώς οι απώλειες του διπλοαρνητικού υλικού έχουν ληφθεί πολύ μικρές (Γ e = Γ m = 0.001ω pe ).
97 3.4. Δυναμική συμπεριφορά του πεδίου 87 Σχήμα 3.33: Πλάτος του E 3y (0, z + 2d, t), για ω pe = ω pm = ω 0 2 και μεταβλητά d, γ, με γ = Γe /ω pe = Γ m /ω pm. Οι μονάδες του κατακόρυφου άξονα είναι αυθαίρετες. Αξίζει να σημειωθεί ότι η (3.74) είναι σε πλήρη συμφωνία με τα αποτελέσματα των [Zhou and Chan, 2005], [Huang et al., 2006], όπου το πεδίο υπολογίστηκε μέσω αριθμητικής ολοκλήρωσης πρώτα ως προς k x και έπειτα ως προς ω. Πιο συγκεκριμένα, στις παραπάνω εργασίες αποδεικνύεται, αριθμητικά, ότι το πλάτος του πεδίου παρουσιάζει ταλαντεύσεις, οι οποίες οφείλονται στον συμμετρικό επιφανειακό ρυθμό με μηδενική ταχύτητα ομάδας. Στο ίδιο ακριβώς συμπέρασμα καταλήγουμε μέσω της (3.74), από όπου φαίνεται ότι το μεταβατικό φαινόμενο οφείλεται στους ρυθμούς με φασικές σταθερές k st xn, δηλαδή στους ρυθμούς με ταχύτητα ομάδας v gn = Re{ω sw n (k st xn)} = 0. Στην πράξη, οι όροι που, κυρίως, καθορίζουν την τιμή του αθροίσματος της (3.74) είναι αυτοί που αντιστοιχούν στα επιφανειακά κύματα TM 0 και TM 1, καθώς το πλάτος των όρων μεγαλύτερης τάξης είναι αμελητέο, εξαιτίας του μικρού φασματικού περιεχομένου της πηγής στις συχνότητες συντονισμού των αντίστοιχων ρυθμών. Αν οι συχνότητες f 1, f 2 στις οποίες ϵ 2 = ϵ 0 και µ 2 = µ 0 συμπίπτουν, τότε μόνο ο συμμετρικός ρυθμός έχει στασιμοποιητικό σημείο. Αν, όμως, f 1 = f 2, είναι δυνατό να υπάρχει στασιμοποιητικό σημείο και για τον αντισυμμετρικό ρυθμό, όπως είναι η περίπτωση του σχήματος Μία φυσική ερμηνεία του φαινομένου αυτού βασίζεται στο γεγονός ότι όλοι οι ρυθμοί με μημηδενική ταχύτητα ομάδας διαδίδονται με κατεύθυνση παράλληλη προς τον άξονα x, από το σημείο x = 0 προς το άπειρο, με συνέπεια το πλάτος τους σε ένα συγκεκριμένο σημείο να μειώνεται γρήγορα με τον χρόνο. Αντίθετα, οι ρυθμοί με μηδενική ταχύτητα ομάδας είναι στάσιμοι, υπό την έννοια ότι η ενέργειά τους δεν διαδίδεται στον χώρο, δημιουργώντας τις διακυμάνσεις στο πλάτος του πεδιου. Στην πραγματικότητα, όπως εξάλλου φαίνεται μέσω της τεχνικής στάσιμης φάσης, στο μεταβατικό φαινόμενο συνεισφέρουν όλες οι φασικές σταθερές που βρίσκονται πολύ κοντά στην k sw xn, στις οποίες η ταχύτητα ομάδας είναι πολύ μικρή, ωσόσο μη-μηδενική. Για τον λόγο αυτό, το πλάτος του όρου που δίνει το μεταβατικό φαινόμενο μειώνεται σύμφωνα με τη συνάρτηση 1/ t, όταν δεν υπάρχουν απώλειες. Αντίθετα, παρουσία απωλειών το πλάτος μειώνεται σύμφωνα με έναν εκθετικό όρο, ο οποίος οδηγεί σε πολύ γρηγορότερο ρυθμό απόσβεσης από τον 1/ t. Ως παράδειγμα εφαρμογής της ανάλυσης της παρούσας υποενότητας, το σχήμα 3.33 απεικονίζει το πλάτος του πεδίου για διάφορα d, ω pe = ω pm = ω 0 2 και μεταβλητό συντελεστή απωλειών. Είναι φανερό ότι η διάρκεια του μεταβατικού φαινομένου είναι της τάξης των εκατοντάδων περιόδων και μειώνεται είτε εισάγοντας μεγαλύτερες απώλειες είτε αυξάνοντας το d.
98 88 Κεφάλαιο 3 3.Α Απόδειξη των (3.39) Οι βασικές ιδιότητες πάνω στις οποίες θα βασιστεί η απόδειξη των (3.39) είναι arg{ z} = arg{z} + (2n + 1)π, arg{z } = arg{z} + 2nπ, (3.75α) (3.75β) όπου n είναι ακέραιος αριθμός. Από τις παραπάνω εξισώσεις προκύπτει, άμεσα, ότι και, επομένως, arg{ z } = arg{z} + (2n + 1)π (3.76) arg{ ω ck x } = arg{ω + ck x } + (2n + 1)π, arg{ ω + ck x } = arg{ω ck x } + (2m + 1)π (3.77α) (3.77β) Εφόσον η ανάλυση πραγματοποιείται στο α φύλλο Riemann ισχύει 3π 2 < arg{ω ± ck x} π 2 ή π 2 < arg{ω ± ck x} 5π 2 (3.78) και 3π 2 < arg{ ω ± ck x } π π ή 2 2 < arg{ ω ± ck x } 5π (3.79) 2 Αν εξαιρέσουμε τα σημεία των βροχοτομών, οι (3.77)-(3.79) συνεπάγονται n = m = 1 ή n = m = 0. Κατά συνέπεια, k 1z ( ω ) = 1 ω c ck x ω + ck x = 1 ω ck x ω + ck x e 1 2 (arg{ω+ck x}+arg{ω ck x }) e j(m+n+1)π c = k 1z(ω) (3.80) Επιπλέον, µ 2 ( ω ) = µ 2 (ω), ϵ 2( ω ) = ϵ 2 (ω), P( ω ) = P (ω) και k 2z ( ω ) = ±k 2z (ω). Άρα, από τους ορισμούς (3.34), προκύπτει S( ω, k x ) = S (ω, k x ), A( ω, k x ) = A (ω, k x ) και K( ω, k x ) = K (ω, k x ). Έστω ω p πόλος της K(ω, k x ). Τότε, σύμφωνα με τις προηγούμενες ιδιότητες, ο ω p είναι, επίσης, πόλος. Το ολοκληρωτικό υπόλοιπο της K(ω, k x ) στον ω p είναι Res{K(ω, k x )} = lim (ω + ω p)k(ω, k x ) ω p ω ω p = lim ( ω + ω ω ω p p)k( ω, k x ) ( ) ( ) = lim (ω ω p )K(ω, k x ) = Res{K(ω, k x )} (3.81) ω ω p ω p Από την άλλη πλευρά, η εφαρμογή του μετασχηματισμού ω ω στην καμπύλη Γ b2 του σχήματος 3.22 δίνει την καμπύλη Γ b1, με αντίθετη φορά διαγραφής. Επομένως, ˆ ˆ (ˆ ) K(ω, k x ) dω = K( ω, k x ) d( ω ) = K(ω, k x ) dω (3.82) Γ b2 Γ b1 Γ b1
99 3.Β. Υπολογισμός των b n της (3.52) 89 3.Β Υπολογισμός των b n της (3.52) Στο παράρτημα αυτό θα παρουσιαστεί μία διαδικασία εύρεσης των συντελεστών b n του αναπτύγματος της Λ 2 (w). Προς τον σκοπό αυτό και σύμφωνα με την (3.52), αρκεί να βρεθούν οι Λ (n) 1 (0). Αφετηρία θα αποτελέσει η παρατήρηση ότι η Λ(ω) μπορεί να εκφραστεί ως συνάρτηση δύο μεταβλητών x, y, με x = ω και y = ω ω b, δηλαδή Λ(ω) = Λ(x, y). Τότε, επειδή w = ω ω b, Λ 1 (w) = Λ(w 2 + ω b, w). Επομένως, Λ 1(w) = 2w Λ x + Λ y (3.83) Όμως, αν η Λ(ω) δεν έχει πόλο στο κλαδικό σημείο, η x Λ είναι πεπερασμένη στο σημείο ω = ω b (x = ω b, y = 0), το οποίο αντιστοιχεί στο w = 0. Άρα, Λ 1(0) = Λ (3.84) y x=ωb y=0 Παρόμοια, υπολογίζονται και οι ανώτερες παράγωγοι της Λ 1 (w). Ενδεικτικά, αναφέρεται ότι Λ (3) 1 (0) = 6 2 Λ x y + 3 Λ x=ωb y 3, (3.85α) x=ωb y=0 y=0 Λ (5) 1 (0) = 60 3 Λ x Λ y x y Λ y 5 (3.85β) 3.Γ Απόδειξη των (3.55), (3.56) όπου Το ολοκλήρωμα της (3.54α) γράφεται I (1) bn x=ωb y=0 ˆ ˆ = e jπ/4 e s2 t ds jw n I = ˆ x=ωb y=0 x=ωb y=0 e s2 t π ds = e jπ/4 s w n e jπ/4 t jw n I, (3.86) e s2 t ds (3.87) s w n e jπ/4 Για τον υπολογισμό του I θα χρησιμοποιηθούν οι ταυτότητες [Abramowitz and Stegun, 1972] ˆ ˆ ye t2 (x t) 2 dt = π Re{w(x + jy)}, (3.88α) + y2 (x t)e t2 (x t) 2 dt = π Im{w(x + jy)}, (3.88β) + y2 οι οποίες ισχύουν για x πραγματικό και y > 0. Σημειώνεται ότι w(z) = e z2 erfc( jz). Τότε, αν w n = w n e jπ/4 = p + jq, ισχύει ˆ e s2 t ˆ I = (s p) jq ds = ( ˆ p ) t s e s2 = (s p ) 2 t + (q ) 2 ds + j t (p s)e s2 t ˆ (s p) 2 + q 2 ds + j ˆ qe s2 t (s p) 2 + q 2 ds q t e s2 (s p t ) 2 + (q t ) 2 ds (3.89)
100 90 Κεφάλαιο 3 Αν q > 0, ˆ I = ( p ) t s e s2 (s p ) 2 t + (q ) 2 ds + j t ˆ q t e s2 (s p t ) 2 + (q t ) 2 ds { ( )} { ( )} ( ) = π Im w w n t + jπ Re w w n t = jπw w n t, (3.90) ενώ αν q < 0, ˆ I = { ( = π Im w ( p ) t s e s2 (s p ) 2 t + ( q ) 2 ds j t w n { ( t )} jπ Re w w n ˆ t )} q t e s2 (s p t ) 2 + ( q t ) 2 ds Αντικαθιστώντας τις (3.90), (3.91) στην (3.86) εξάγεται η (3.55). Για την απόδειξη της (3.56) θα χρησιμοποιηθεί η ασυμπτωτική έκφραση πze z 2 erfc(z) = 1 + n=1 = jπw ( w n t ), (3.91) n (2n 1) ( 1) (2z 2 ) n, (3.92) η οποία ισχύει για arg{z} < 3π/4 [Abramowitz and Stegun, 1972]. Τότε, από τον ορισμό της w(z) και την ταυτότητα (2n 1) Γ(n + 1/2) = π (3.93) 2 n προκύπτει [ ] w(z) = j z Γ(n + 1/2) π π z n=1 2n, (3.94) υπό την προϋπόθεση ότι π 4 < arg{z} < 5π 4 (3.95) Αν Im{w n} 0, ο w n ικανοποιεί την (3.95), οπότε εφαρμόζοντας την (3.95) στην (3.55) καταλήγουμε στην (3.56). Παρόμοια, αν Im{w n} < 0, ο w n ικανοποιεί την (3.95) και η (3.55) μετατρέπεται, ξανά, στην (3.56).
101 Κ 4 E Π Σ Σ Δ Δ -Α Υ 4.1 Εισαγωγή Η σφηνοειδής δομή αποτελεί μία από τις συχνότερα απαντώμενες γεωμετρίες σε πρακτικές διαταξεις και ταυτόχρονα ένα από τα περισσότερο απαιτητικά προβλήματα της μαθηματικής φυσικής. Ενώ η περίπτωση των στατικών πεδίων έχει αντιμετωπιστεί επιτυχώς [Scharstein, 1993], [Nikoskinen and Lindell, 1995], δεν έχει υπάρξει, μέχρι στιγμής, μία γενική λύση για τη δυναμική περίπτωση. Εξαίρεση αποτελεί η γεωμετρία με αδιαπέρατα τοιχώματα (π.χ. ηλεκτρικά αγώγιμα τοιχώματα), η οποία επιλύθηκε, πλήρως, από τις αρχές, ακόμη, του περασμένου αιώνα [Macdonald, 1902]. Το βασικό πρόβλημα που εμφανίζεται σε μία δομή που αποτελείται από διαπερατό υλικό είναι η αδυναμία χωρισμού των μεταβλητών στην εξίσωση Helmholtz, όπως αυτή εκφράζεται στις κυλινδικές συντεταγμένες. Πιο συγκεκριμένα, η διαφορά στην τιμή του κυματικού αριθμού εντός και εκτός της σφηνοειδούς δομής δυσκολεύει την εφαρμογή των οριακών συνθηκών πάνω στις διαχωριστικές επιφάνειες των υλικών, εξαιτίας των διαφορετικών ορισμάτων που έχουν οι συναρτήσεις Bessel και Hankel.¹ Διάφορες προσεγγιστικές μέθοδοι που βασίζονται σε αναλυτικούς [Meixner, 1972], [Andersen and Solodukhov, 1978], [Joo et al., 1984] ή αριθμητικούς [Marx, 1990], [Marx, 1993] υπολογισμούς έχουν κατά καιρούς αναπτυχθεί προκειμένου να αντιμετωπίσουν το πρόβλημα. Ανάμεσα σε αυτές ξεχωρίζει μία πρόσφατη μέθοδος [Rawlins, 1999], [Salem et al., 2006], [Salem and Kamel, 2008a] που βασίζεται στον μετασχηματισμό Kontorovich-Lebedev (KL) και στη χρήση αναπτυγμάτων Neumann για την επίλυση ιδιαζουσών ολοκληρωτικών εξισώσεων. Μία ειδική περίπτωση κατά την οποία είναι δυνατή η εξαγωγή αναλυτικών εκφράσεων για το πεδίο είναι η σφηνοειδής δομή ισοδιαθλαστικού υλικού, δηλαδή η γεωμετρία στην οποία ο δείκτης διάθλασης είναι σταθερός παντού στον χώρο. Τονίζεται ότι αν και ο δείκτης διάθλασης δεν αλλάζει, οι καταστατικές παράμετροι μπορούν να μεταβάλλονται με μία σχέση εξάρτησης μεταξύ τους. Ουσιαστικά, ο λόγος για τον οποίο μπορεί να βρεθεί λύση σε κλειστή μορφή είναι ότι στην περίπτωση αυτή η εξίσωση Helmholtz επιδέχεται χωρισμό μεταβλητών. Το πρόβλημα της ισοδιαθλαστικής δομής μελετήθηκε λεπτομερώς στις εργασίες [Knockaert et al., 1997], [Daniele and Uslenghi, 2007b]. Η επέκταση του προβλήματος αυτού στην περιοχή των διπλο-αρνητικών υλικών είναι μία δομή κατασκευασμένη από διπλο-αρνητικό υλικό στο οποίο η απόλυτη τιμή του δείκτη διάθλασης είναι ίση με τον δείκτη διάθλασης του υλικού που την περιβάλλει. Στην πραγματικότητα, επειδή κάθε διπλο-αρνητικό υλικό έχει αρνητικό δείκτη διάθλασης, οι δείκτες διάθλασης εντός και εκτός της σφηνοειδούς δομής είναι ¹Ο κυματικός αριθμός εισέρχεται στο όρισμα των συναρτήσεων Bessel και Hankel, που αποτελούν θεμελιώδεις λύσεις της εξίσωσης Helmholtz σε κυλινδρικες συντεταγμένες.
102 92 Κεφάλαιο 4 αντίθετοι. Παρ όλα αυτά, είναι πάλι δυνατός ο χωρισμός μεταβλητών στην εξίσωση Helmholtz και η εύρεση αναλυτικής λύσης. Οι πρώτες προσπάθειες ενασχόλησης με το πρόβλημα αυτό περιγράφονται στις εργασίες [Monzon et al., 2005], [Daniele and Uslenghi, 2007a], όπου μελετάται η σφηνοειδής δομή διπλο-αρνητικού υλικού με σχετικές καταστατικές παραμέτρους ίσες με 1 και συγκεκριμένες θέσεις της πηγής. Αν και εκ πρώτης όψεως φαίνεται ότι ο τρόπος αντιμετώπισης της σφηνοειδούς γεωμετρίας διπλοαρνητικού υλικού πρέπει να είναι ίδιος με αυτόν που χρησιμοποιείται στην ισοδιαθλαστική δομή υπάρχουν σημαντικές διαφορές μεταξύ τους. Η βασικότερη είναι ότι στην περίπτωση του διπλοαρνητικού υλικού υπάρχουν περιοχές του χώρου όπου η ενέργεια ρέει προς την κορυφή της διάταξης, εξαιτίας του φαινομένου της αρνητικής διάθλασης στην διεπιφάνεια ενός συμβατικού υλικού με θετικό δείκτη διάθλασης και ενός διπλο-αρνητικού υλικού. Κατά συνέπεια, ενώ στην ισοδιαθλαστική γεωμετρία γνωρίζουμε επακριβώς τη συνθήκη ακτινοβολίας στο άπειρο, δεν συμβαίνει το ίδιο και στη δομή που εμπλέκει το διπλο-αρνητικό υλικό. Το γεγονός αυτό εισάγει μία σοβαρή δυσκολία στον υπολογισμό του πεδίου, καθώς ο καθορισμός της συνθήκης ακτινοβολίας είναι απαραίτητη προϋπόθεση για την εξασφάλιση της μοναδικότητας της λύσης. Σε ένα πρόβλημα σφηνοειδούς δομής το πεδίο εκφράζεται ως ο γραμμικός συνδυασμός στοιχειωδών ρυθμών, οι οποίοι αντιστοιχίζονται στις ρίζες μιας υπερβατικής εξίσωσης, χαρακτηριστικής για τη συγκεκριμένη διάταξη. Σημειώνεται ότι η συμπεριφορά αυτή ισχύει τόσο στη στατική όσο και στη δυναμική περίπτωση. Επίσης, η συνάρτηση Bessel ή Hankel που εισέρχεται στην έκφραση του πεδίου ενός ρυθμού έχει ως τάξη τη ρίζα στην οποία αντιστοιχεί ο ρυθμός αυτός. Όταν η δομή είναι κατασκευασμένη από συμβατικά υλικά, όλες οι ρίζες είναι πραγματικοί αριθμοί. Παρουσία, όμως, διπλο-αρνητικού υλικού, εμφανίζονται μιγαδικές ρίζες και οι αντίστοιχοι ρυθμοί έχουν τη μορφή επιφανειακών κυμάτων με το πεδίο τους συγκεντρωμένο σε μια περιοχή γύρω από την επιφάνεια του διπλο-αρνητικού υλικού. Ακόμη, αξίζει να σημειωθεί ότι, ενώ στην περίπτωση των συμβατικών υλικών το σύνολο των ρυθμών που εμπλέκουν το β είδος των συναρτήσεων Hankel αρκεί για να περιγράψει πλήρως τη λύση, στα διπλο-αρνητικά υλικά πρέπει να χρησιμοποιηθούν και τα δύο είδη των συναρτήσεων Hankel, εξαιτίας της ροής ενέργειας προς το εσωτερικό της διάταξης, όπως αναφέρθηκε στην προηγούμενη παράγραφο. Στο κεφάλαιο αυτό διερευνάται το πρόβλημα της σφηνοειδούς δομής διπλο-αρνητικού υλικού με διέγερση από μία άπειρη γραμμική πηγή ρεύματος. Η συμμετρία της διάταξης και η μορφή της πηγής, ουσιαστικά, ανάγει το πρόβλημα στην εύρεση της συνάρτησης Green σε δύο διαστάσεις. Η μέθοδος που χρησιμοποιείται περιλαμβάνει τον απευθείας μετασχηματισμό της εξίσωσης Helmholtz και των οριακών συνθηκών μέσω ενός κατάλληλου μετασχηματισμού KL. Η προσέγγιση αυτή διαφέρει από την αντίστοιχη της εργασίας [Knockaert et al., 1997], όπου ο μετασχηματισμός KL εφαρμόζεται σε ολοκληρωτικές εξισώσεις που διαμορφώνονται για τα σημεία της διαχωριστικής επιφάνειας των υλικών. Ο τρόπος χρήσης του μετασχηματισμού KL επιδεικνύεται μέσω του υπολογισμού της δισδιάστατης συνάρτησης Green του ελεύθερου κενού χώρου. Στο πλαίσιο αυτό, αποδεικνύεται η άμεση σύζευξη μεταξύ του μετασχηματισμού και της συνθήκης ακτινοβολίας και εισάγονται τα δύο είδη του μετασχηματισμού ανάλογα με το είδος της συνάρτησης Hankel. Ακολούθως, βρίσκεται ο μετασχηματισμός KL β είδους του πεδίου και πραγματοποιείται μία λεπτομερής παραμετρική διερεύνηση των πόλων του, η οποία είναι απαραίτητη για την σωστή εφαρμογή της σχέσης αντιστροφής και τη φυσική ερμηνεία της λύσης. Τα αποτελέσματα ελέγχονται αν ικανοποιούν την αρχή διατήρησης της ενέργειας και διαπιστώνεται ότι το σύνολο των ρυθμών που προκύπτουν μέσω του μετασχηματισμού KL β είδους
103 4.2. Ο μετασχηματισμός Kontorovich-Lebedev 93 είναι ελλειπές. Για τον λόγο αυτό, το συγκεκριμένο σύνολο επεκτείνεται με τους ρυθμούς που προκύπτουν μέσω του μετασχηματισμού α είδους, με αποτέλεσμα να γίνει πλήρες και να μπορεί, έτσι, να χρησιμοποιηθεί σε κάθε πρόβλημα, ανοικτού ή κλειστού ορίου, που εμπλέκει σφηνοειδή δομή διπλοαρνητικού υλικού. Η παραπάνω θεωρία εφαρμόζεται, επιτυχώς, στην περίπτωση της προσαρμοσμένης διάταξης και πραγματοποιούνται συγκρίσεις με αριθμητικά αποτελέσματα που προκύπτουν μέσω της μεθόδου FDTD. 4.2 Ο μετασχηματισμός Kontorovich-Lebedev Μια από τις πιο κατάλληλες μεθόδους για την αντιμετώπιση προβλημάτων σκέδασης από σφηνοειδείς γεωμετρίες είναι ο μετασχηματισμός Kontorovich-Lebedev (KL). Η αρχική μορφή του μετασχηματισμού, όπως διατυπώθηκε από τους Kontorovich και Lebedev [Kontorovich and Lebedev, 1938], εμπλέκει τις τροποποιημένες συναρτήσεις Bessel δεύτερου είδους και φανταστικής τάξης (συναρτήσεις Macdonald), και εφαρμόζεται, κατά κύριο λόγο, σε στατικά προβλήματα. Στις περιπτώσεις, ωστόσο, όπου υπάρχει αρμονική χρονική μεταβολή και ζητείται η λύση της εξίσωσης Helmholtz, συνιστάται η χρήση της μορφής που προτάθηκε από τον Jones [Jones, 1980], η οποία αξιοποιεί τις συναρτήσεις Hankel μιγαδικής τάξης. Σύμφωνα με αυτήν, ο μετασχηματισμός KL μιας συνάρτησης f (x) ορισμένης στον θετικό πραγματικό ημιάξονα x δίνεται από τη σχέση KL i { f (x)}(ν) = ˆ 0 f (x) x H(i) ν (kx) dx, (4.1) όπου H (i) ν (kx) είναι η συνάρτηση Hankel ν-οστής τάξης και i-οστού είδους (i = 1, 2), ενώ k είναι ένας μιγαδικός αριθμός, που, όπως θα φανεί στη συνέχεια, συμπίπτει με τον κυματικό αριθμό ο οποίος εμφανίζεται στην εξίσωση Helmholtz. Από την (4.1) προκύπτει ότι, ανάλογα με το είδος της συνάρτησης Hankel, μπορούν να οριστούν δυο είδη μετασχηματισμού KL. Ακόμη, το ολοκλήρωμα του μετασχηματισμού συγκλίνει πάνω στον φανταστικό άξονα Re{ν} = 0 όταν η f (x) ικανοποιεί τις συνθήκες ˆ 1 0 ˆ c f (x) x f (x) x ln x dx <, (4.2α) e ( 1)i+1 jkx x dx <, (4.2β) με c μια αυθαίρετη θετική σταθερά. Να σημειωθεί ότι αν f (x) O(x α ) όταν x 0 + και f (x) O(x β ) καθώς x, οι (4.2α) και (4.2β) οδηγούν στις α > 0 και β < 3/2, αντίστοιχα. Επιπλέον, χρησιμοποιώντας την ιδιότητα H ν(kx) (i) = e ( 1)i+1jνπ H (i) ν (kx) των συναρτήσεων Hankel, μπορεί να εξαχθεί η συμμετρική ιδιότητα του μετασχηματισμού KL ως KL i { f (x)}( ν) = e ( 1)i+1 jνπ KL i { f (x)}(ν) (4.3) Ο αντίστροφος μετασχηματισμός KL μιας συνάρτησης f (ν) παρέχεται από την εξίσωση IKL i { f (ν)}(x) = ( 1) i lim ε 0 + ˆ j j νe εν2 J ν (kx) f (ν) dν, (4.4) όπου J ν (kx) είναι η συνάρτηση Bessel πρώτου είδους και ν-οστής τάξης. Ο όρος e εν2 εισάγεται για την εξασφάλιση της σύγκλισης του ολοκληρώματος και, όπως θα φανεί στη συνέχεια της ενότητας
104 94 Κεφάλαιο 4 μέσω ενός παραδείγματος, έχει σαν αποτέλεσμα την αλλαγή του δρόμου ολοκλήρωσης. Αξίζει να παρατηρηθεί ότι, σε αντίθεση με άλλους μετασχηματισμούς που εμπλέκουν συναρτήσεις Bessel, όπως ειναι ο μετασχηματισμός Fourier-Bessel, ο αντίστροφος μετασχηματισμός KL υπολογίζεται μέσω ενός μιγαδικού ολοκληρώματος ως προς την τάξη της συνάρτησης Bessel και όχι ως προς το όρισμά της. Επιπλέον, πρέπει να τονιστεί ότι το ζεύγος του ευθέος μετασχηματισμού KL και του αντίστροφού του, όπως δίνονται από τις (4.1) και (4.4), δεν είναι αμοιβαίο, με την έννοια ότι σωστά αποτελέσματα εξασφαλίζονται μόνο όταν ακολουθείται η φορά f (x) KL i f (ν) IKL i f (x) (4.5) Με άλλα λόγια, υπάρχουν συναρτήσεις f (ν) οι οποίες δεν αναπαράγονται μετά την κατά σειρά εφαρμογή ενός αντίστροφου και ενός ευθέος μετασχηματισμού KL. Ως παράδειγμα αναφέρεται η f (ν) = e jνπ/2, για την οποία το ολοκλήρωμα του αντίστροφου μετασχηματισμού KL είναι 0 (η απόδειξη της πρότασης αυτής θα καταστεί δυνατή αργότερα, αφού περιγραφεί ο τρόπος υπολογισμού του ολοκληρώματος (4.4)). Παρόλα αυτά, προκύπτει άμεσα από τον ορισμό ότι ο ευθύς μετασχηματισμός της μηδενικής συνάρτησης είναι 0, το οποίο, προφανώς, διαφέρει από τη συνάρτηση f (ν) που θεωρήθηκε αρχικά. Επομένως, κάθε φορά που εφαρμόζεται η (4.4) είναι απαραίτητο να γίνεται έλεγχος της ορθότητας των αποτελεσμάτων με την εφαρμογή ενός ευθέος μετασχηματισμού KL. Η μη αμοιβαιότητα είναι ακόμη μία σημαντική διαφορά του μετασχηματισμού KL από άλλους ολοκληρωτικούς μετασχηματισμούς (π.χ. μετασχηματισμός Fourier). Η ανάπτυξη του διαφορικού τελεστή Laplace σε κυλινδρικές συντεταγμένες εμφανίζει στην εξίσωση Helmholtz έναν όρο της μορφής x 2 f (x) + x f (x) + k 2 x 2 f (x). Επομένως, είναι κρίσιμο να εξεταστεί πως αυτός ο όρος μετασχηματίζεται μέσω του μετασχηματισμού KL. Από τη σχέση ορισμού (4.1) και με τη διπλή εφαρμογή ολοκλήρωσης κατά παράγοντες, προκύπτει και [ KL i {x 2 f (x) + x f (x)}(ν) = x + f (x)h (i) ν [ ˆ 0 f (x) (kx) k f (x)h (i) ν k 2 xh (i) ν ] (kx) (kx) + kh (i) ν (kx) 0 ] dx (4.6) KL i {x 2 f (x) + x f (x) + k 2 x 2 f (x)}(ν) ˆ f (x) [ = k 2 x 2 H (i) ν (kx) + kxh (i) ν 0 x [ + x f (x)h (i) ν (kx) k f (x)h (i) ν (kx) (kx) + k 2 x 2 H (i) ν ] 0 ] (kx) dx (4.7) Στη συνέχεια, αξιοποιείται το γεγονός ότι η H (i) ν (kx) επαληθεύει την εξίσωση Bessel k 2 x 2 H (i) ν ώστε η (4.7) να λάβει τη μορφή (kx) + kxh (i) ν (kx) + (k 2 x 2 ν 2 )H (i) ν (kx) = 0 (4.8) KL i {x 2 f (x) + x f (x) + k 2 x 2 f (x)}(ν) = ν 2 KL i { f (x)}(ν) [ ] + x f (x)h (i) ν (kx) k f (x)h (i) ν (kx) 0 (4.9)
105 4.2. Ο μετασχηματισμός Kontorovich-Lebedev 95 Αν ληφθεί υπόψη ότι x f (x), f (x) O(x α ), με α > 0, για x 0 + και ότι, όταν Re{ν} = 0, η H (i) ν (kx) συμπεριφέρεται στη χειρότερη περίπτωση ν = 0 όπως η ln x, αποδεικνύεται ότι ο δεύτερος όρος του δεξιού μέλους της (4.9) είναι μηδεν στην οριακή τιμή x = 0. Επιπλέον, είναι γνωστό ότι αν x, H (i) ν (kx) 2 = e( 1)i+1 j(kx 1 2 νπ 1 π) 4, (4.10) πkx με αποτέλεσμα η (4.9) να γραφεί KL i {x 2 f (x) + x f (x) + k 2 x 2 f (x)}(ν) = ν 2 KL i { f (x)}(ν) 2 { + πk lim [ ] x f (x) + ( 1) i jk f (x) e ( 1)i+1 j(kx 2 1 νπ 1 π)} 4 (4.11) x Μπορεί να παρατηρήσει κανείς ότι στην ειδική περίπτωση [ ] x f (x) + ( 1) i jk f (x) = 0 (4.12) ισχύει lim x KL i {x 2 f (x) + x f (x) + k 2 x 2 f (x)}(ν) = ν 2 KL i { f (x)}(ν) (4.13) Αξίζει να σημειωθεί ότι για αρμονική χρονική μεταβολή e jωt η (4.12) συμπίπτει με τη συνθήκη ακτινοβολίας για εισερχόμενα (i = 1) ή εξερχόμενα (i = 2) κυλινδρικά κύματα. Με άλλα λόγια, η εφαρμογή του μετασχηματισμού KL απαιτεί τη γνώση της συνθήκης ακτινοβολίας, μία παρατήρηση που είναι απόλυτα συμβατή με το γεγονός ότι η μοναδικότητα λύσης της εξίσωσης Helmholtz εξασφαλίζεται από τη γνώση των οριακών συνθηκών στα όρια της περιοχής επίλυσης. Επισημαίνεται ότι η συνθήκη ακτινοβολίας επιβάλλεται πάνω στην άπειρη σφαίρα που αποτελεί το εξωτερικό όριο στα προβλήματα ανοικτού χώρου. Τα παραπάνω συμπεράσματα θα φανούν ιδιαίτερα χρήσιμα κατά την αντιμετώπιση του προβλήματος της σφηνοειδούς γεωμετρίας από διπλο-αρνητικό υλικό, όταν θα κληθούμε να επιλέξουμε το είδος του μετασχηματιμού KL που είναι κατάλληλο για την κάθε περιοχή του χώρου. Ο τρόπος χρήσης του μετασχηματισμού KL μπορει να γίνει καλύτερα κατανοητός μέσω ενός παραδείγματος. Για τον λογο αυτό, στη συνέχεια, θα προσπαθήσουμε να προσδιορίσουμε τη δισδιάστατη βαθμωτή συνάρτηση Green G(ρ, φ) σε έναν ομογενή χώρο με κυματικό αριθμό k. Η G(ρ, φ) επαληθεύει την εξίσωση (ρ 2 2 ρ 2 + ρ ) ρ + 2 φ 2 + k2 ρ 2 G(ρ, φ) = ρδ(ρ ρ )δ(φ φ ), (4.14) μαζί με τις οριακές συνθήκες και τη συνθήκη ακτινοβολίας G(ρ, 0) = G(ρ, 2π), G φ = G φ=0 φ (4.15) φ=2π [ ] G(ρ, φ) lim ρ + jkg(ρ, φ) = 0 (4.16) ρ ρ Να σημειωθεί ότι ρ, φ δηλώνουν τις συντεταγμένες της πηγής και ότι δ(x) είναι η συνάρτηση δέλτα Dirac. Η λύση της παραπάνω εξίσωσης, η οποία θα αντιπαρατεθεί με το αποτέλεσμα που εξάγεται μέσω του μετασχηματισμού KL, είναι γνωστό ότι δίνεται από την έκφραση [Balanis, 1989] G(ρ, φ) = j 4 H(2) 0 (k ρ ρ ) = j 2 ε n J n (kρ < )H (2) n (kρ > ) cos[n(φ φ )], (4.17) n=0
106 96 Κεφάλαιο 4 με ρ, ρ τα διανύσματα θέσης στα σημεία παρατήρησης και πηγής, αντίστοιχα, ρ < = min{ρ, ρ }, ρ > = max{ρ, ρ } και 0.5, αν n = 0 ε n = (4.18) 1, αν n > 0 Η (4.16) υποδηλώνει ότι για τον μετασχηματισμό της (4.14) πρέπει να χρησιμοποιηθεί ο μετασχηματισμός KL β ειδους. Τότε, σύμφωνα με την (4.13), έχουμε ( 2 φ 2 + ν2 ) G(ν; φ) = H (2) ν (kρ )δ(φ φ ), (4.19) όπου G(ν; φ) = KL 2 {G(ρ, φ)}(ν). Παρόμοια, οι (4.15) μετατρέπονται στις G(ν; 0) = G(ν; 2π), G φ = G φ=0 φ (4.20) φ=2π Η (4.19) είναι μια κανονική διαφορική εξίσωση β τάξης με οριακές συνθήκες αυτές που παρουσιάζονται στην (4.20) και γενική λύση a(ν) cos(νφ) + b(ν) sin(νφ), αν 0 < φ < φ G(ν;, φ) = (4.21) c(ν) cos(νφ) + d(ν) sin(νφ), αν φ < φ < 2π Η G(ν; φ) έχει δύο κλάδους εξαιτίας της συνάρτησης δ(φ φ ) στο δεξιό μέλος της (4.19), η οποία εισάγει μία ασυνέχεια στη θέση φ = φ. Για τον υπολογισμό των άγνωστων συναρτήσεων a(ν), b(ν), c(ν), d(ν) αντικαθιστούμε την (4.21) στις (4.20), οπότε λαμβάνουμε a(ν) = c(ν) cos(2νπ) + d(ν) sin(2νπ) b(ν) = c(ν) sin(2νπ) + d(ν) cos(2νπ) (4.22α) (4.22β) Επιπλέον, η G(ν; φ) πρέπει να είναι συνεχής στο σημείο φ = φ, αφού διαφορετικά η δεύτερη παράγωγός της ως προς φ θα περιείχε τη συνάρτηση δ (φ φ ), η οποία δεν συμπεριλαμβάνεται στο δεξιό μέλος της (4.19). Επομένως, ισχύει G φ=φ = G φ=φ + (4.23) και, μέσω της (4.21), a(ν) cos(νφ ) + b(ν) sin(νφ ) = c(ν) cos(νφ ) + d(ν) sin(νφ ) (4.24) Ολοκληρώνοντας, ακόμη, την (4.19) ως προς φ στο διάστημα (φ, φ + ) εξάγεται ότι και G φ φ=φ + G φ φ=φ = H (2) ν (kρ ) (4.25) c(ν) sin(νφ ) + d(ν) cos(νφ ) + a(ν) sin(νφ ) b(ν) cos(νφ ) = H(2) ν (kρ ) ν (4.26)
107 4.2. Ο μετασχηματισμός Kontorovich-Lebedev 97 Οι (4.22), (4.24) και (4.26) σχηματίζουν ένα σύστημα 4 εξισώσεων με 4 αγνώστους, του οποίου η λύση είναι a(ν) = H(2) ν (kρ ) 2ν sin(νπ) cos[ν(π φ )] b(ν) = H(2) ν (kρ ) 2ν sin(νπ) sin[ν(π φ )] c(ν) = H(2) ν (kρ ) 2ν sin(νπ) cos[ν(π + φ )] d(ν) = H(2) ν (kρ ) 2ν sin(νπ) sin[ν(π + φ )] (4.27α) (4.27β) (4.27γ) (4.27δ) Με αυτόν τον τρόπο, προκύπτει ότι G(ν; φ) = H(2) ν (kρ ) 2ν sin(νπ) cos[ν(π φ φ )] (4.28) Το επόμενο βήμα ειναι ο υπολογισμός του αντίστροφου μετασχηματισμού KL της G(ν; φ), ο οποίος, συμφωνα με την (4.4), δίνεται από το ολοκλήρωμα G(ρ, φ) = 1 ˆ j 2 lim e εν2 J ν (kρ)h (2) ε 0 + ν (kρ ) cos[ν(π φ φ )] dν (4.29) j 2 sin(νπ) Για τον σκοπό αυτό, θα χρειαστεί να πραγματοποιήσουμε ολοκλήρωση πάνω στο μιγαδικό ν-επίπεδο και θα πρέπει να γνωρίζουμε την ασυμπτωτική συμπεριφορά των συναρτήσεων Bessel και Hankel για μεγάλες μιγαδικές τάξεις. Υποθέτοντας ότι x > 0 και ν = ν e jψ, όπου ν, ισχύει [Felsen and Marcuvitz, 1994] όταν ψ < π και J ν (x) H (2) ν ( 1 e ν cos ψ ln 2 ν ex ), ψ sin ψ (4.30) 2π ν (x) 2 π ν e ν ( cos ψ ln 2 ν ex ψ sin ψ ), (4.31) όταν π/2 < ψ π/2. Επίσης, αν α είναι πραγματικός αριθμός, μπορεί να αποδειχθεί ότι cos(να), sin(να) 1 2 e να sin ψ (4.32) Με βάση τις προαναφερθείσες ασυμπτωτικές εκφράσεις και τη σχέση e εν2 = e ε ν 2 cos(2ψ), η ολοκληρωτέα ποσότητα στην (4.29), που στο εξής θα συμβολίζεται ως K(ν), λαμβάνει τη μορφή K(ν) 1 [ ] 2π ν e ν ε ν cos(2ψ)+cos ψ ln ρ ρ +( π φ φ π) sin ψ (4.33) Επειδή ε > 0, φαίνεται, αμέσως, ότι ο εκθέτης στην τελευταία εξίσωση είναι ένας μεγάλος αρνητικός αριθμός όταν cos(2ψ) < 0 ή π/4 < ψ < π/2. Το γεγονός αυτό οδηγεί στο συμπέρασμα ότι το ολοκλήρωμα της K(ν) πάνω στα ημικύκλια C 1, C 2 του σχήματος 4.1 είναι μηδέν και ο δρόμος ολοκλήρωσης για τον υπολογισμό της (4.29) μπορεί να εκτραπεί κατά μήκος της C, η οποία αποτελείται από τις ευθείες ψ = a και ψ = a, με π/4 < a < π/2. Επιπροσθέτως, εφόσον 0 < φ, φ < 2π,
108 98 Κεφάλαιο 4 Σχήμα 4.1: Δρόμος ολοκλήρωσης για τον αντίστροφο μετασχηματισμό KL. ισχύει φ φ < 2π και π φ φ < π. Κατά συνέπεια, αν ρ < ρ, το ολοκλήρωμα της K(ν) πάνω στην C συγκλίνει ακόμη και όταν ε = 0, πράγμα που σημαίνει ότι το όριο και ο όρος e εν2 που εμφανίζονται στην (4.29) μπορούν να παραλειφθούν, ώστε να πάρουμε G(ρ, φ) = 1 2 ˆ C J ν (kρ)h (2) ν (kρ ) cos[ν(π φ φ )] dν (4.34) 2 sin(νπ) Ανατρέχοντας στην (4.33), παρατηρούμε ότι για ε = 0 και ρ < ρ η συνάρτηση K(ν) μηδενίζεται πάνω στο τόξο C 3, το οποίο ορίζεται από τη σχέση a < ψ < a. Άρα, συμφωνα με το θεώρημα των ολοκληρωτικών υπολοίπων, η G(ρ, φ) εκφράζεται ως το άθροισμα των υπολοίπων της ολοκληρωτέας ποσότητας στους πόλους που περιέχονται μεταξύ της C και της C 3, οι οποίοι συμπίπτουν με τις ρίζες του sin(νπ). Τελικά, μετά από μερικές αλγεβρικές πράξεις έχουμε G(ρ, φ) = j 2 ε n J n (kρ)h (2) n (kρ ) cos[n(φ φ )], (4.35) n=0 η οποία είναι ίδια με την (4.17) όταν ρ < ρ. Ο χειρισμός της περίπτωσης ρ > ρ πραγματοποιείται με την αντικατάσταση J ν (kρ) = [H (1) ν (kρ) + H (2) ν (kρ)]/2 στην (4.29) και την παρατήρηση ότι η ποσότητα e εν2 H (1) ν (kρ)h (2) ν (kρ ) cos[ν(π φ φ )] 2 sin(νπ) (4.36) είναι περιττή συνάρτηση του ν. Το γεγονός αυτό απορρέει από την ιδιότητα των συναρτήσεων Hankel H ν(z) (i) = e ( 1)i+1jνπ H (i) ν (z) και οδηγεί στο συμπέρασμα ότι το ολοκλήρωμα της (4.36) κατά μήκος του φανταστικού άξονα είναι μηδέν. Ως αποτέλεσμα, η G(ρ, φ) υπολογίζεται από την εξίσωση G(ρ, φ) = 1 4 lim ε 0 + ˆ j j e εν2 H (2) ν (kρ)h (2) ν (kρ ) cos[ν(π φ φ )] dν (4.37) 2 sin(νπ) Αν, στη συνέχεια, χρησιμοποιηθεί η ταυτότητα H (2) ν (kρ ) = 2J ν (kρ ) H (1) ν (kρ ), η G(ρ, φ) γράφεται ως άθροισμα δύο ολοκληρωμάτων, το ένα από τα οποία είναι όμοιο με αυτό της (4.29) με
109 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 99 Σχήμα 4.2: Γεωμετρία σφηνοειδούς δομής διπλο-αρνητικού υλικού, που διεγείρεται από μια γραμμική πηγή στο σημείο S. εναλαγμένες, ωστόσο, τις θέσεις των ρ, ρ, ενώ το άλλο έχει ως ολοκληρωτέα ποσότητα την (4.36), με εξαίρεση τις διαφορετικές θέσεις των ρ, ρ. Αυτό το δεύτερο ολοκλήρωμα είναι μηδέν για τους ίδιους λόγους που το ολοκλήρωμα της (4.36) μηδενίζεται. Άρα, πάλι μέσω του θεωρήματος ολοκληρωτικών υπολοίπων, προκύπτει ότι το πρώτο ολοκλήρωμα είναι ίσο με G(ρ, φ) = j 2 ε n J n (kρ )H (2) n (kρ) cos[n(φ φ )] (4.38) n=0 και ταυτίζεται με την (4.17) όταν ρ > ρ. Στο σημείο αυτό, χρειάζεται να τονιστεί ότι η διαδικασία εύρεσης του αντίστροφου μετασχηματισμού KL που περιγράφηκε στο παραπάνω παράδειγμα ειναι γενική. Μάλιστα, προκύπτει ότι ο ουσιαστικός ρόλος του όρου e εν2 και του ορίου στον ορισμό (4.4) είναι η εκτροπή του δρόμου ολοκλήρωσης κατά μήκος της καμπύλης C που φαινεται στο σχήμα 4.1. Με παρόμοιο τρόπο αποδεικνύεται ότι το ολοκλήρωμα του αντίστροφου μετασχηματισμού KL για τη συνάρτηση f (ν) = e jνπ/2 είναι μηδέν, καθώς αυτή δεν έχει πόλους στο μιγαδικό επίπεδο. Υπενθυμίζεται ότι η συνάρτηση αυτή χρησιμοποιήθηκε για να αποδείξει τον ισχυρισμό ότι οι σχέσεις (4.1) και (4.4) δεν είναι μεταξύ τους αμοιβαίες. 4.3 Σφηνοειδής δομή διπλο-αρνητικού υλικού Περιγραφή του προβλήματος Έχοντας περιγράψει τα απαραίτητα μαθηματικά εργαλεία, μπορούμε να προχωρήσουμε στην ανάλυση του προβλήματος σκέδασης από τη σφηνοειδή δομή διπλο-αρνητικού υλικού. Η γεωμετρία του προβλήματος απεικονίζεται στο σχήμα 4.2. H σφηνοειδής δομή έχει άνοιγμα 2φ 0 και καταλαμβάνει τον τομέα φ 0 < φ < φ 0. Η διάταξη είναι άπειρη κατά τη διεύθυνση του άξονα z και διεγείρεται από μια άπειρη γραμμική πηγή παράλληλη με τον άξονα z, η οποία διέρχεται από το σημείο (ρ, φ ) και διαρρέεται από ρεύμα έντασης I 0. Το διπλο-αρνητικό υλικό έχει αρνητικές σχετικές καταστατικές παραμέτρους ϵ r, µ r, οι οποίες ικανοποιούν τη συνθήκη ϵ r µ r = 1. Ο λόγος που χρησιμοποιείται αυτή
110 100 Κεφάλαιο 4 Σχήμα 4.3: Ακτινική προσέγγιση για τη ροή της ισχύος όταν φ > 3φ 0. η συνθήκη είναι ότι το μέτρο του κυματικού αριθμού παραμένει σταθερό παντού στον χώρο και είναι δυνατή η εξαγωγή αναλυτικής λύσης. Εξαιτίας της συμμετρίας του προβλήματος και της μορφής της διέγερσης υποστηρίζονται πεδία μόνο με εγκάρσια μαγνητική πόλωση, πράγμα που σημαίνει πως η ηλεκτρική πεδιακή ένταση διαθέτει μία μοναδική συνιστώσα E z (ρ, φ) παράλληλη με τον άξονα z. Η συνιστώσα αυτή επαληθεύει την εξίσωση Helmholtz (4.14), με τη διαφορά ότι το δεξιό μέλος γίνεται jωµ 0 I 0 ρδ(ρ ρ )δ(φ φ ). Παρ όλα αυτά, για λόγους απλότητας, στο υπόλοιπο της ανάλυσης θεωρούμε ότι jωµ 0 I 0 = 1. Επιπλέον, η E z ικανοποιεί τις οριακές συνθήκες E z φ= φ 0 = E z φ= φ + 0, E z φ=φ 0 = E z φ=φ + 0, E z φ E z φ φ= φ 0 φ=φ 0 = 1 µ r E z φ = 1 µ r E z φ, φ= φ + 0, φ=φ + 0 (4.39α) (4.39β) οι οποίες είναι άμεση συνέπεια της συνέχειας των εφαπτομενικών συνιστωσών της ηλεκτρικής και της μαγνητικής πεδιακής έντασης πάνω στη διαχωριστική επιφάνεια αέρα και διπλο-αρνητικού υλικού. Όπως, ήδη, αναφέρθηκε στην προηγούμενη ενότητα, η μοναδικότητα της λύσης σε ένα πρόβλημα ανοικτού ορίου απαιτεί τον καθορισμό της συνθήκης ακτινοβολίας. Για τον λόγο αυτό, στη συνέχεια της ενότητας θα επιχειρηθεί ο προσδιορισμός της συνθήκης ακτινοβολίας στην περίπτωση της σφηνοειδούς δομής διπλο-αρνητικού υλικού, μέσω μιας ακτινικής προσέγγισης για τη ροή της ισχύος. Στο πλαίσιο αυτής της προσέγγισης, η ακτίνα που διέρχεται από κάθε σημείο θεωρείται ότι είναι παράλληλη προς το διάνυσμα Poyn ng στο σημείο αυτό και έχει την ίδια φορά με το εν λόγω διάνυσμα. Επίσης, οι ακτίνες έχουν ως αρχή το σημείο (ρ, φ ) της πηγής και υφίστανται αλλαγή κλίσης στη διεπιφάνεια αέρα και διπλο-αρνητικού υλικού συμφωνα με τον νόμο του Snell. Το τελευταίο γεγονός
111 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 101 σημαίνει ότι, αν θ i, θ r είναι οι γωνίες που σχηματίζει μια τυχαία ακτίνα με το κάθετο διάνυσμα στη διαχωριστική επιφάνεια πριν και μετά την πρόσπτωση, ισχύει θ r = θ i. Με βάση την παρατήρηση αυτή, το σχήμα 4.3 παριστάνει το ακτινικό διάγραμμα για την περίπτωση φ > 3φ 0. Είναι φανερό ότι οι ακτίνες αποκλίνουν μεταξύ τους από τη στιγμή που αναδύονται από την πηγή έως ότου φθάσουν στην επιφάνεια φ = φ 0. Στη συνέχεια, συγκλίνουν μέσα στο διπλο-αρνητικό υλικό, χωρίς, ωστόσο, να σχηματίσουν κάποια εστία πριν αγγίξουν την επιφάνεια φ = φ 0, μετά την οποία αποκλίνουν, ξανά. Αναφορικά με την ισχύ και για ρ > ρ, αυτή ρέει προς το άπειρο στην περιοχή φ 0 < φ < 2π φ 0 (περιοχή 1), που καταλαμβάνεται από αέρα, και προς την αρχή του συστήματος συντεταγμένων στον τομέα φ 0 < φ < φ 0 (περιοχή 2), ο οποίος περιέχει το διπλο-αρνητικό υλικό. Ως αποτέλεσμα, στην περιοχή 1 και για μεγάλα ρ, ο όρος που δίνει τη μεταβολή της φάσης του πεδιου πρέπει να είναι της μορφής e jk0ρ και η συνθήκη ακτινοβολίας δίνεται από την εξίσωση [ ] Ez (ρ, φ) lim ρ + jk 0 E z (ρ, φ) = 0 (4.40) ρ ρ Η (4.40) συμπίπτει με τη συνηθισμένη συνθήκη ακτινοβολίας που εφαρμόζεται σε συμβατικά υλικά με θετικές καταστατικές παραμέτρους. Από την άλλη πλευρά, ο προσδιορισμός της συνθήκης ακτινοβολίας στην περιοχή 2 απαιτεί να λάβουμε υπόψη, εκτός από τη φορά ροής της ισχύος, το γεγονός πως στα διπλο-αρνητικά υλικά η κατεύθυνση μείωσης της φάσης (κατεύθυνση της φασικής ταχύτητας) είναι αντίθετη από την κατεύθυνση ροής της ισχύος (κατεύθυνση της ταχύτητας ομάδας). Επομένως, εφόσον το μέτρο του κυματικού αριθμού μέσα στο διπλο-αρνητικό υλικό ειναι k 0, ο όρος φάσης για απομακρυσμένα σημεία από την αρχή του συστήματος είναι, πάλι, e jk 0ρ και η συνθήκη ακτινοβολίας που εφαρμοζεται μέσα στο διπλο-αρνητικό υλικό είναι, πάλι, η (4.40). Στο σημείο αυτό, είναι απαραίτητο να τονιστεί ότι η ακτινική προσέγγιση που περιγράφηκε στην προηγούμενη παράγραφο δεν λαμβάνει υπόψη τα φαινόμενα περίθλασης από την κορυφή της γεωμετρίας καθώς και πιθανές ανακλάσεις στα τοιχώματα του διπλο-αρνητικού υλικού. Επίσης, καλύπτει μόνο την περίπτωση φ > 3φ 0. Ο λόγος που χρησιμοποιήθηκε ειναι γιατί παρέχει ενδείξεις σχετικά με τη συνθήκη ακτινοβολίας που πρέπει να εφαρμοστεί στον τομέα ο οποίος καταλαμβάνεται από διπλο-αρνητικό υλικό. Κατά συνέπεια, η λύση που θα υπολογιστεί με βάση τη συνθήκη ακτινοβολίας (4.40) θα πρέπει να εξεταστεί για τη συμβατότητά της με θεμελιώδεις φυσικές αρχές, όπως είναι η αρχή διατήρησης της ενέργειας, κάτι που πραγματοποιείται στην ενότητα Ο μετασχηματισμός KL του πεδίου Αντικείμενο της παρούσας ενότητας είναι ο υπολογισμός του μετασχηματισμού KL του πεδίου, με την προϋπόθεση ότι ισχύει η συνθήκη ακτινοβολίας (4.40). Παρόλο που ειναι δυνατή η απευθείας επίλυση του προβλήματος, θα επιλέξουμε να υπολογίσουμε, πρώτα, την συμμετρική και την αντισυμμετρική λύση και, στη συνέχεια, να εκφράσουμε τη συνολική λύση ως το άθροισμά τους. Ο λόγος που προτιμάται αυτή η προσέγγιση είναι αφενός ότι απαιτεί μικρότερο όγκο αλγεβρικών πράξεων και αφετέρου ότι προσφέρει μεγαλύτερη ευκολία στην φυσική ερμηνεία των τελικών αποτελεσμάτων. Σημειώνεται ότι η αντισυμμετρική λύση προκύπτει από την τοποθέτηση δυο πηγών που διαρρέονται από ρεύματα πλάτους I 0 /2 και I 0 /2 στις θέσεις (ρ, φ ) και (ρ, 2π φ ), αντίστοιχα, ή, ισοδύναμα, από την τοποθέτηση ενός άπειρα ηλεκτρικά αγώγιμου υλικού στο επίπεδο συμμετριας y = 0. Από την άλλη πλευρά, για τη διέγερση της συμμετρικής λύσης απαιτείται η ύπαρξη δύο πηγών ίδιου πλάτους ρεύματος I 0 /2 στις θέσεις (ρ, φ ), (ρ, 2π φ ), ή, διαφορετικά, η επικάλυψη του επιπέδου y = 0
112 102 Κεφάλαιο 4 με ένα άπειρα μαγνητικά αγώγιμο μέσο. Επισημαίνεται ότι ο διαχωρισμός της συνολικής λύσης σε ένα συμμετρικό και ένα αντισυμμετρικό μέρος δίνει τη δυνατότητα επίλυσης του προβλήματος στον μισό χώρο, που περιγράφεται από τη συνθήκη 0 < φ < π. Η ανάλυση που ακολουθεί αναφέρεται στην αντισυμμετρική διέγερση. Συμβολίζοντας με E1z a (ρ, φ), E2z a (ρ, φ) την κατά z συνιστώσα της ηλεκτρικής πεδιακής έντασης στις περιοχές φ 0 < φ < π και 0 < φ < φ 0, αντίστοιχα, οι οριακές συνθήκες στη διαχωριστική επιφάνεια αέρα και διπλο-αρνητικού υλικού, και στο επίπεδο y = 0 γράφονται E1z a φ=φ0 = E2z a φ=φ0, E1z a φ=π = 0, E a 1z φ E a 2z = 1 E a 2z φ=φ0 µ r φ, φ=φ0 φ=0 = 0 (4.41α) (4.41β) Επειδή και στις δύο περιοχές ισχύει η συνθήκη ακτινοβολίας (4.40), πρέπει να χρησιμοποιηθεί ο μετασχηματισμός KL β είδους με κυματικό αριθμό k 0. Τότε, αν Ẽiz a (ν; φ) = KL 2{Eiz a (ρ, φ)}(ν), με i = 1, 2, η εξίσωση Helmholtz μετασχηματίζεται στις διαφορικές εξισώσεις ( 2 φ 2 + ν2 ( 2 φ 2 + ν2 ) Ẽ1z a (ν; φ) = H(2) ν (k 0 ρ )δ(φ φ ), (4.42α) ) Ẽ a 2z(ν; φ) = 0 (4.42β) Επίσης, οι οριακές συνθήκες (4.41α) και (4.41β) μετασχηματίζονται στις Ẽ1z a φ=φ0 = Ẽ2z a φ=φ0, Ẽ1z a φ=π = 0, Ẽ a 1z φ Ẽ a 2z = 1 Ẽ a 2z φ=φ0 µ r φ, φ=φ0 φ=0 = 0 (4.43α) (4.43β) Οι λύσεις των (4.42α),(4.43β) δίνονται από τις σχέσεις Ẽ1z a (ν; φ) = a(ν) sin[ν(π φ)], αν φ < φ < π (4.44α) b(ν) cos(νφ) + c(ν) sin(νφ), αν φ 0 < φ < φ Ẽ a 2z(ν; φ) = d(ν) sin(νφ) (4.44β) Αξίζει να προσεχθεί ότι η έκφραση για το Ẽ1z a (ν; φ) έχει δύο κλάδους εξαιτίας της συνάρτησης δ(φ φ ) που υπεισέρχεται στο δεξιό μέλος της (4.42α) και εισάγει ασυνέχεια στη θέση φ = φ. Επίσης, οι συνθήκες (4.43β) έχουν ήδη ληφθεί υπόψη με την εισαγωγή της συνάρτησης sin[ν(π φ)] στον κλάδο της Ẽ1z a (ν; φ) που ισχύει για φ > φ και τη χρήση, μόνο, της sin(νφ) στην έκφραση που δίνει την Ẽ2z a (ν; φ). Για τον υπολογισμό των άγνωστων συναρτήσεων a(ν), b(ν), c(ν), d(ν) οι (4.44) αντικαθίστανται στις (4.43α), οπότε παίρνουμε b(ν) cos(νφ 0 ) + c(ν) sin(νφ 0 ) = d(ν) sin(νφ 0 ), b(ν) sin(νφ 0 ) + c(ν) cos(νφ 0 ) = 1 µ r d(ν) cos(νφ 0 ) (4.45α) (4.45β)
113 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 103 Οι δύο επιπλέον εξισώσεις που είναι απαραίτητες για την εύρεση των a(ν), b(ν), c(ν), d(ν) είναι αντίστοιχες των (4.23) και (4.25), και πιο συγκεκριμένα Ẽ 1z φ=φ = Ẽ 1z φ=φ +, Ẽ 1z φ φ=φ + Ẽ 1z φ φ=φ Η εισαγωγή των (4.44) στις (4.46) έχει ως αποτέλεσμα (4.46α) = H (2) ν (k 0 ρ ) (4.46β) a(ν) sin[ν(π φ )] = b(ν) cos(νφ ) + c(ν) sin(νφ ), a(ν) cos[ν(π φ )] = b(ν) sin(νφ ) + c(ν) cos(νφ ) + H(2) ν (k 0 ρ ) ν Μετά από πράξεις εξάγεται ότι η λύση του συστήματος των εξισώσεων (4.45) και (4.47) είναι a(ν) = H(2) ν (k 0 ρ ) sin(νφ ) + Λ a sin[ν(φ 2φ 0 )] ν sin(νπ) + Λ a sin[ν(π 2φ 0 )], b(ν) = H(2) ν (k 0 ρ ) Λ a sin(2νφ 0 ) sin[ν(π φ )] ν sin(νπ) + Λ a sin[ν(π 2φ 0 )], c(ν) = H(2) ν (k 0 ρ ) ν (4.47α) (4.47β) (4.48α) (4.48β) sin[ν(π φ )][1 + Λ a cos(2νφ 0 )] sin(νπ) + Λ a, (4.48γ) sin[ν(π 2φ 0 )] d(ν) = H(2) ν (k 0 ρ ) (1 Λ a ) sin[ν(π φ )] ν sin(νπ) + Λ a sin[ν(π 2φ 0 )], όπου Λ a = (1 µ r )/(1 + µ r ). Τελικά, οι (4.44) σε συνδυασμό με τις (4.48) οδηγούν στις Ẽ a 1z H(2) ν (k 0 ρ (ν; φ) = ) sin(νφ < ) + Λ a sin[ν(φ < 2φ 0 )] ν sin(νπ) + Λ a sin[ν(π φ > )], sin[ν(π 2φ 0 )] Ẽ2z(ν; a φ) = H(2) ν (k 0 ρ ) (1 Λ a ) sin[ν(π φ )] sin(νφ) ν sin(νπ) + Λ a sin[ν(π 2φ 0 )], (4.48δ) (4.49α) (4.49β) με φ > = max{φ, φ } και φ < = min{φ, φ }. Η διαδικασία που πρέπει να ακολουθηθεί για την εύρεση του μετασχηματισμού KL στην περίπτωση της συμμετρικής διέγερσης ειναι ακριβώς ίδια με αυτήν που χρησιμοποιήθηκε στην αντισυμμετρική διέγερση. Χρησιμοποιώντας τον συμβολισμό E1z s (ρ, φ), Es 2z (ρ, φ) για τη z συνιστώσα της ηλεκτρικής πεδιακής έντασης στις περιοχές φ 0 < φ < π και 0 < φ < φ 0, αντίστοιχα, οι συνθήκες στις διαχωριστικές επιφάνειες παίρνουν τη μορφή E1z s φ=φ0 = E2z s φ=φ0, E s 1z φ = 0, φ=π Ο μετασχηματισμός KL των παραπάνω εξισώσεων δίνει Ẽ1z s φ=φ0 = Ẽ2z s φ=φ0, Ẽ s 1z φ = 0, φ=π E s 1z φ E s 2z φ Ẽ s 1z φ Ẽ s 2z φ = 1 E s 2z φ=φ0 µ r φ, φ=φ0 = 0 φ=π = 1 Ẽ s 2z φ=φ0 µ r φ, φ=φ0 = 0, φ=π (4.50α) (4.50β) (4.51α) (4.51β)
114 104 Κεφάλαιο 4 όπου Ẽ1z s (ν; φ) = KL 2{E1z s (ρ, φ)}(ν) και Ẽs 2z (ν; φ) = KL 2{E2z s (ρ, φ)}(ν). Οι Ẽs 1z (ν; φ), Ẽs 2z (ν; φ) επαληθεύουν τις (4.42α), (4.42β) και λαμβάνονται από τις σχέσεις Ẽ1z s (ν; φ) = a(ν) cos[ν(π φ)], αν φ < φ < π (4.52α) b(ν) cos(νφ) + c(ν) sin(νφ), αν φ 0 < φ < φ Ẽ s 2z(ν; φ) = d(ν) cos(νφ), (4.52β) με το cos[ν(π φ)] και το cos(νφ) να εισάγονται στις (4.52) για την ικανοποίηση των (4.51β). Οι συναρτήσεις a(ν), b(ν), c(ν), d(ν) υπολογίζονται με την αντικατάσταση των (4.52) στις (4.51α) και στις αντίστοιχες εξισώσεις των (4.46), οι οποίες προκύπτουν με την αλλαγή του εκθέτη a σε s. Με τον τρόπο αυτό, δημιουργείται ένα συστημα εξισώσεων η λύση του οποίου είναι a(ν) = H(2) ν (k 0 ρ ) cos(νφ ) + Λ s cos[ν(φ 2φ 0 )] ν sin(νπ) + Λ s sin[ν(π 2φ 0 )], b(ν) = H(2) ν (k 0 ρ ) ν (4.53α) cos[ν(π φ )] [1 + Λ s cos(2νφ 0 )] sin(νπ) + Λ s, (4.53β) sin[ν(π 2φ 0 )] c(ν) = H(2) ν (k 0 ρ ) Λ s cos[ν(π φ )] sin(2νφ 0 ) ν sin(νπ) + Λ s sin[ν(π 2φ 0 )], d(ν) = H(2) ν (k 0 ρ ) (1 + Λ s ) cos[ν(π φ )] ν sin(νπ) + Λ s sin[ν(π 2φ 0 )], όπου Λ s = (µ r 1)/(µ r + 1). Η εισαγωγή των παραπάνω εκφράσεων στις (4.52) δίνει, τελικά, (4.53γ) (4.53δ) Ẽ s 1z H(2) ν (k 0 ρ (ν; φ) = ) cos(νφ < ) + Λ s cos[ν(φ < 2φ 0 )] ν sin(νπ) + Λ s cos[ν(π φ > )], sin[ν(π 2φ 0 )] Ẽ2z(ν; s φ) = H(2) ν (k 0 ρ ) (1 + Λ s ) cos[ν(π φ )] cos(νφ) ν sin(νπ) + Λ s sin[ν(π 2φ 0 )] (4.54α) (4.54β) Πόλοι του μετασχηματισμού KL Όπως έγινε, ήδη, φανερό στην ανάλυση της ενότητας 4.2, οι πόλοι του μετασχηματισμού KL μιας συνάρτησης έχουν σημαντικό ρόλο κατά την εφαρμογή της σχέσης αντιστροφής (4.4). Για το λόγο αυτό, στη συνέχεια, θα μελετηθούν οι πόλοι των Ẽ1z a (ν; φ), Ẽa 2z (ν; φ), Ẽs 1z (ν; φ), Ẽs 2z (ν; φ), οι οποίοι προκύπτουν από τη λύση της εξίσωσης sin(νπ) + Λ sin[ν(π 2φ 0 )] = 0, (4.55) όπου Λ = Λ a ή Λ = Λ s. Παρόλο που η τελευταία εξίσωση μπορει να λυθεί αριθμητικά για οποιοαδήποτε γωνία φ 0 με τη χρήση ενός αλγόριθμου εύρεσης μιγαδικών ριζών (π.χ. αλγόριθμος Muller), θα υποθέσουμε ότι η φ είναι ένα ρητό πολλαπλάσιο του π, δηλαδή φ 0 = mπ/n, όπου m, n φυσικοί αριθμοί. Η θεώρηση αυτή δεν είναι αυθαίρετη καθώς σε κάθε πρακτικό υπολογισμό οι πραγματικοί αριθμοί παριστάνονται με ένα πεπερασμένο πλήθος δεκαδικών ψηφίων ή, διαφορετικά, προσεγγίζονται με ρητούς αριθμούς. Από την άλλη πλευρά, λαμβάνοντας υπόψη ότι για έναν φυσικό αριθμό n ισχύει η ταυτότητα n+1 sin(nx) = sin x 2 k=1 ( 1) k+1 2 n 2k+1 ( n k k 1 ) cos n 2k+1 x, (4.56)
115 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 105 όπου x είναι το ακέραιο μέρος του x, είναι δυνατό η (4.55) να μετατραπεί σε μία πολυωνυμική εξίσωση ως προς cos x. Πράγματι, εισάγοντας στην (4.55) την φ 0 = mπ/n και πραγματοποιώντας την αντικατάσταση x = νπ/n εξάγεται ότι Χρησιμοποιώντας, κατόπιν, την (4.56) καταλήγουμε στην n+1 2 ( ) n k sin x ( 1) k+1 2 n 2k+1 cos n 2k+1 x k 1 k=1 n 2m+1 +Λ 2 k=1 sin(nx) + Λ sin[(n 2m)x] = 0 (4.57) ( 1) k+1 2 n 2m 2k+1 ( n 2m k k 1 ) cos n 2m 2k+1 x = 0, (4.58) Παρατηρούμε ότι το μέλος που βρίσκεται μέσα στις αγκύλες είναι ένα πολυώνυμο βαθμού n 1 ως προς cos x. Αν r i, όπου i = 1, 2,..., n 1, είναι οι ρίζες αυτού του πολυωνύμου, οι ρίζες της αρχικής εξίσωσης (4.55) είναι ±(n/π) cos 1 r i + 2nk, με k = 0, ±1, ±2,..., καθώς επίσης και οι ρίζες nk του sin x.² Μια σημαντική ιδιότητα των ριζών της (4.55) ειναι η περιοδικότητά τους στο μιγαδικό επίπεδο. Πράγματι, αντικαθιστώντας στο δεξιό μέλος της (4.55) όπου ν το ν ± n και χρησιμοποιώντας το γεγονός ότι φ 0 = mπ/n έχουμε sin[(ν ± n)π] + Λ sin[(ν ± n)(π 2φ 0 )] = ( 1) n {sin(νπ) + Λ sin[ν(π 2φ 0 )]} (4.59) Επομένως, αν το ν είναι ρίζα της εξίσωσης το ίδιο θα συμβαίνει και για το ν ± n, το οποίο σημαίνει ότι οι ρίζες επαναλαμβάνονται με περίοδο n. Από την άλλη πλευρά, επειδή 0 Re{cos 1 z} π, όπου z ένας μιγαδικός αριθμός, έπεται ότι 0 Re{(n/π) cos 1 r i } n (i = 1, 2,..., n 1) και ο αριθμός των ριζών στο διάστημα [0, n) είναι n, συμπεριλαμβανομένης της τετριμμένης ρίζας στο 0. Αν συμβολίσουμε αυτές τις ρίζες με ν i,0, όπου i = 1, 2,..., n, τότε, εξαιτίας της περιοδικότητας, κάθε άλλη ρίζα εκτός του διαστήματος [0, n) μπορει να γραφεί ως ν i,k = ν i,0 + nk, με k = ±1, ±2,.... Ένα από τα πιο ουσιώδη κομμάτια της ανάλυσης, το οποίο θα φανεί χρήσιμο στην κατανόηση της φυσικής σημασίας της λύσης, είναι η μελέτη της επίδρασης που έχουν οι γεωμετρικές και οι ηλεκτρομαγνητικές παράμετροι της διάταξης πάνω στους πόλους του μετασχηματισμού KL του πεδίου. Για τον λόγο αυτό, στο σχήμα 4.4 παρουσιάζεται ο γεωμετρικός τόπος των ριζών της (4.55) για τις περιπτώσεις φ 0 = π/13, 2π/13, 3π/13, 4π/13, όταν 10 < Λ < 10. Οι κύκλοι και τα τετράγωνα αναπαριστούν τις ρίζες στις τιμές Λ = 1 και Λ = 1, αντίστοιχα, και η διάταξή τους καθορίζει τη φορά των καμπυλών για αυξανόμενα Λ. Πιο συγκεκριμένα, επειδή κάθε ζεύγος κύκλου-τετραγώνου ίδιου χρώματος αντιστοιχεί στην καμπύλη που έχει το χρώμα αυτό, η ζητούμενη φορά είναι αυτή που δείχνει από τον κύκλο προς το τετράγωνο. Μία πρώτη παρατήρηση που εξάγεται από τα διαγράμματα είναι ότι οι πόλοι ειναι, γενικά, μιγαδικοί αριθμοί πλήθους n στο διάστημα [0, n). Ακόμη, διακρίνουμε ότι για 1 < Λ < 1, όπως συμβαίνει όταν µ r > 0, όλες οι ρίζες είναι πραγματικοί αριθμοί, το οποίο είναι σύμφωνο με τα αποτελέσματα της βιβλιογραφίας σχετικά με συμβατικά υλικά θετικών καταστατικών παραμέτρων. Αντίθετα, αν Λ > 1, το οποίο ισχύει μόνο για µ r < 0, εμφανίζονται ²Οι r i υπολογίζονται εύκολα μέσω έτοιμων συναρτήσεων επίλυσης πολυωνυμικών εξισώσεων που περιέχονται σε υπολογιστικά πακέτα.
116 106 Κεφάλαιο 4 (α) (β) (γ) (δ) Σχήμα 4.4: Γεωμετρικός τόπος των ριζών για γωνία φ 0 ίση με (α) π/13, (β) 2π/13, (γ) 3π/13 και (δ) 4π/13. μιγαδικές ρίζες, μερικές από τις οποίες βρίσκονται πάνω στις ευθείες ν = nk και ν = nk + n/2, με k = 0, ±1, ±2,..., ενώ οι υπόλοιπες τείνουν να βρεθούν πάνω στους άξονες ν = nl/(2m) + nk, με l = 1,..., m 1, m + 1,..., 2m 1, καθώς το Λ προσεγγίζει τις ακραίες τιμές,. Αξίζει να σημειωθεί ότι στην αντισυμμετρική περίπτωση ενώ στη συμμετρική lim µ r 1 Λa =, lim + µ r 1 Λa =, (4.60) lim µ r 1 + Λs =, lim µ r 1 Λs = (4.61) Από όλους τους μιγαδικούς πόλους θα επικεντρωθούμε σε αυτούς που βρίσκονται σε συμμετρικές θέσεις πάνω στον φανταστικό άξονα, ο οποίος είναι ο δρόμος ολοκλήρωσης για τον αντίστροφο μετασχηματισμό KL. Είναι φανερό ότι οι πόλοι αυτοί τείνουν προς το άπειρο όταν Λ. Καθώς το Λ αυξάνεται, προσεγγίζουν την αρχή των αξόνων και καθίστανται πραγματικοί αριθμοί όταν το Λ υπερβεί μια οριακή τιμή Λ 0. Για Λ = Λ 0, ο τετριμμένος πόλος ν = 0 και οι δύο προαναφερθέντες πόλοι ταυτίζονται, δηλαδή το 0 είναι μηδενικό τρίτης τάξης. Ως αποτέλεσμα, σε μία περιοχή γύρω από το ν = 0 το αριστερό μέλος της (4.55) γράφεται ν 3 f (ν), όπου f (ν) μία αναλυτική συνάρτηση, το οποίο, με τη σειρά του, σημαίνει ότι η παράγωγός της sin(νπ) + Λ 0 sin[ν(π 2φ 0 )] στο 0 είναι 0. Έτσι, προκύπτει ότι Λ 0 = π/(π 2φ 0 ).
117 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού Εκφράσεις του πεδίου στο χώρο Έχοντας υπολογίσει τους πόλους των Ẽ1z a (ν; φ), Ẽa 2z (ν; φ), Ẽs 1z (ν; φ), Ẽs 2z (ν; φ), είναι δυνατό, πλέον, να προχωρήσουμε στην αντιστροφή τους με την εφαρμογή της (4.4). Οι λεπτομερειες υπολογισμού του ολοκληρώματος του αντίστροφου μετασχηματισμού έχουν δοθεί στην ενότητα 4.2 και για τον λόγο αυτό δεν πρόκειται να επαναληφθούν. Αναφέρεται, μόνο, ότι ο αντίστροφος μετασχηματισμός KL μιας συνάρτησης f (ν) εκφράζεται ως άθροισμα των υπολοίπων της συνάρτησης νj ν (k 0 ρ) f (ν) στους πόλους της που βρίσκονται στο δεξιό μιγαδικό ημιεπίπεδο, με την προϋπόθεση ότι το ολοκλήρωμά της κατά μήκος του τόξου C 3 του σχήματος 4.1 συγκλίνει. Σημειώνεται ότι η ανάλυση που ακολουθεί αναφέρεται σε πεπερασμένες τιμές των Λ a, Λ s, δηλαδή δεν καλύπτει την περίπτωση µ r = 1, η οποία θα εξεταστεί ξεχωριστά. Σχετικά με την Ẽ1z a (ν; φ), βασιζόμενοι στις (4.30)-(4.32) και (4.49α), βρίσκεται ότι η ασυμπτωτική έκφραση της νj ν (k 0 ρ)ẽ1z a (ν; φ), για ν και ψ = arg{ν} είναι νj ν (k 0 ρ)ẽ1z a (ν; φ) 1 [ ] π ν e ν cos ψ ln ρ ρ +(φ < φ > ) sin ψ (4.62) Άρα, όταν ρ < ρ και επειδή φ < φ > < 0 το ολοκλήρωμα της νj ν (k 0 ρ)ẽ a 1z (ν; φ) πάνω στην C 3 συγκλίνει και, κατά συνέπεια, εξάγεται ότι E a 1z (ρ, φ) = jλ 0 k=0 n i=1 ε(ν a i,k )J ν a i,k (k 0ρ < )H (2) ν a i,k (k 0 ρ > ) sin(νa i,k φ <) + Λ a sin[ν a i,k (φ < 2φ 0 )] Λ 0 cos(ν a i,k π) + Λa cos[ν a i,k (π 2φ 0)] sin[νa i,k (π φ >)], (4.63) όπου νi,k a είναι οι ρίζες της (4.55) με Λ = Λa και 0.5, αν Re{z} = 0 ε(z) = 1, αν Re{z} = 0 (4.64) Είναι, επιπλέον, δυνατό να δειχτεί ότι, αν ν είναι ρίζα της (4.55), ισχύει sin(νφ) + Λ sin[ν(φ 2φ 0 )] = {cos(νπ) + Λ cos[ν(π 2φ 0 )]} sin[ν(π φ)], (4.65) Συμπεραίνουμε, λοιπόν, ότι E a 1z (ρ, φ) = jλ 0 k=0 n i=1 ε(ν a i,k )J ν a i,k (k 0ρ < )H (2) ν a i,k (k 0 ρ > ) cos(νa i,k π) + Λa cos[νi,k a (π 2φ 0)] Λ 0 cos(νi,k a π) + Λa cos[νi,k a (π 2φ 0)] sin[νa i,k (π φ )] sin[νi,k a (π φ)], (4.66) Παρόμοια, λαμβάνοντας υπόψη την (4.49β), προκύπτει νj ν (k 0 ρ)ẽ a 2z(ν; φ) 1 π ν 1 Λa e ν [ ] cos ψ ln ρ ρ +(φ φ ) sin ψ (4.67) για ν και το ολοκλήρωμα της νj ν (k 0 ρ)ẽ a 2z (ν; φ) κατά μήκος της C 3 συγκλίνει. Επομένως, ισχύει E a 2z(ρ, φ) = jλ 0 k=0 n i=1 ε(ν a i,k )J ν a i,k (k 0ρ < )H (2) ν a i,k (k 0 ρ > ) (Λa 1) sin[ν a i,k (π φ )] sin(ν a i,k φ) Λ 0 cos(ν a i,k π) + Λa cos[ν a i,k (π 2φ 0)] (4.68)
118 108 Κεφάλαιο 4 Όπως, ήδη, αναλύθηκε στην ενότητα 4.2, η μη αμοιβαιότητα μεταξύ του ευθέος και του αντίστροφου μετασχηματισμού KL επιβάλλει την επαλήθευση των αποτελεσμάτων που προκύπτουν με τη χρήση της (4.4) μέσω της εφαρμογής ενός ευθέος μετασχηματισμού KL. Στην περίπτωση που μελετάμε, η εφαρμογή ενός ευθέος μετασχηματισμού KL β είδους στις E1z a (ρ, φ), Ea 2z (ρ, φ) θα πρέπει να δώσει τις Ẽ1z a (ν; φ), Ẽa 2z (ν; φ). Η επαλήθευση πραγματοποιειται μόνο για την Ea 1z (ρ, φ) καθώς η E2z a (ρ, φ) αντιμετωπίζεται με ανάλογο τρόπο. Μια παρατήρηση του αθροίσματος της (4.63) φανερώνει ότι ο μόνος όρος που εξαρτάται από το ρ είναι ο J ν a i,k (k 0 ρ < )H (2) νi,k a (k 0 ρ > ). Συνεπώς, σαν πρώτο βήμα θα υπολογιστεί ο μετασχηματισμός της συνάρτησης u µ (ρ) = J µ (k 0 ρ < )H (2) µ (k 0 ρ > ). Γράφοντας τη συνάρτηση αυτή ως u µ (ρ) = J µ (k 0 ρ)h (2) µ (k 0 ρ )[H(ρ) H(ρ ρ )] + J µ (k 0 ρ )H (2) µ (k 0 ρ)h(ρ ρ ), (4.69) με H(x) τη συνάρτηση Heaviside, αποδεικνύεται ότι ρ 2 u µ(ρ) + ρu µ(ρ) + k 2 0 ρ2 u µ (ρ) = µ 2 u µ (ρ) j2 π ρ δ(ρ ρ ) (4.70) Επειδή η u µ (ρ) ικανοποιεί την (4.12), η εφαρμογή του μετασχηματισμού KL β είδους στην (4.70) έχει ως αποτέλεσμα { KL 2 uµ (ρ) } (ν) = j2 H (2) ν (k 0 ρ ) π ν 2 µ 2 (4.71) Η χρήση της τελευταίας σχέσης στην (4.63) δίνει KL 2 {E a 1z (ρ, φ)} (ν) = 2Λ 0 π k=0 n i=1 ε(ν a i,k ) H(2) ν (k 0 ρ ) ν 2 (ν a i,k )2 sin(νa i,k φ <) + Λ a sin[ν a i,k (φ < 2φ 0 )] Λ 0 cos(ν a i,k π) + Λa cos[ν a i,k (π 2φ 0)] sin[νa i,k (π φ >)], (4.72) Η ισότητα των (4.49α), (4.72) είναι, πλέον, απόρροια του γεγονότος ότι η συνάρτηση sin(νφ < ) + Λ a sin[ν(φ < 2φ 0 )] sin(νπ) + Λ a sin[ν(π 2φ 0 )] sin[ν(π φ > )] (4.73) είναι μερομορφική (δεν έχει πόλο στο άπειρο) και μπορεί να εκφραστεί ως ένα άθροισμα μερικών κλασμάτων A i,k /(ν νi,k a ) στους πόλους της νa i,k, με πλάτη A i,k τα ολοκληρωτικά υπόλοιπα σε αυτούς. Στη συμμετρική διέγερση είναι δυνατό να παρατηρήσει κανείς ότι οι Ẽ1z s (ν; φ), Ẽs 2z (ν; φ) ικανοποιούν τις ασυμπτωτικές εκφράσεις (4.62), (4.67). Έτσι, μετά την εφαρμογή του αντίστροφου μετασχηματισμού KL και την παρατήρηση ότι cos(νφ) + Λ cos[ν(φ 2φ 0 )] = {cos(νπ) + Λ cos[ν(π 2φ 0 )]} cos[ν(π φ)], (4.74) όταν το ν είναι ρίζα της (4.55), οι E1z s (ρ, φ), Es 2z (ρ, φ) υπολογίζονται από τις εξισώσεις E s 1z (ρ, φ) = jλ 0 k=0 n i=1 ε(ν s i,k )J ν s i,k (k 0ρ < )H (2) ν s i,k (k 0 ρ > ) cos(νs i,k π) + Λs cos[νi,k s (π 2φ 0)] Λ 0 cos(νi,k s π) + Λs cos[νi,k s (π 2φ 0)] cos[νs i,k (π φ )] cos[νi,k s (π φ)], (4.75α) E s 2z(ρ, φ) = jλ 0 k=0 n i=1 ε(ν s i,k )J ν s i,k (k 0ρ < )H (2) ν s i,k (k 0 ρ > ) (1 + Λs ) cos[ν s i,k (π φ )] cos(ν s i,k φ) Λ 0 cos(ν s i,k π) + Λs cos[ν s i,k (π 2φ 0)] (4.75β)
119 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 109 Στις παραπάνω εξισώσεις νi,k s είναι οι ρίζες της (4.55) με Λ = Λs. Όπως και στην περίπτωση της αντισυμμετρικής διέγερσης, είναι δυνατό να αποδειχθεί και εδώ ότι ο μετασχηματισμός KL β είδους των (4.75), συμπίπτει με τις (4.54). Η εύρεση των E1z a (ρ, φ), Ea 2z (ρ, φ), Es 1z (ρ, φ), Es 2z (ρ, φ) ολοκληρώνει το μαθηματικό πρόβλημα της επίλυσης της εξίσωσης Helmholtz με τις οριακές συνθήκες (4.41), (4.50) και τη συνθήκη ακτινοβολίας (4.40). Από μαθηματικής απόψεως η λύση που προέκυψε είναι πλήρως αποδεκτή και δεν απαιτεί περαιτέρω διερεύνηση. Από φυσικής απόψεως, ωστόσο, μένει να ελεγχθεί αν η λύση είναι συμβατή με θεμελιώδεις αρχές, όπως η αρχή διατήρησης της ενέργειας και η απαίτηση η συνολική ισχύς που ρέει προς το άπειρο να είναι θετική (απαίτηση μη ύπαρξης πηγών πέρα από τον άπειρο κύλινδρο). Ο έλεγχος αυτός ανάγεται, ουσιαστικά, σε έλεγχο των υποθέσεων που πραγματοποιήθηκαν σχετικά με τη συνθήκη ακτινοβολίας και γίνεται στην υποενότητα Φυσική ερμηνεία της λύσης Όπως έγινε φανερό από την ανάλυση της υποενότητας 4.3.4, το πεδίο εκφράζεται ως άθροισμα όρων οι οποίοι υπολογίζονται στις ρίζες της (4.55). Ο κάθε ένας από αυτούς τους όρους μπορεί να θεωρηθεί ως ένας θεμελιώδης ρυθμός της διάταξης, ο οποίος, όπως θα αποδειχθεί στη συνέχεια, μπορει να έχει κατανεμημένο (κύμα χώρου) ή τοπικό (επιφανειακό κύμα) χαρακτήρα, σε αναλογία με τους ρυθμούς που υποστηρίζονται από ένα επίπεδο στρωματοποιημένο μέσο. Σε αντίθεση, όμως, με το επίπεδα στρωματοποιημένο μέσο στο οποίο, εξαιτίας των βροχοτομών που υπεισέρχονται στα ολοκληρώματα Sommerfeld, οι κατανεμημένοι ρυθμοί διαμορφώνουν ένα συνεχές φάσμα, όλοι οι ρυθμοί που αναπτύσσονται στη σφηνοειδή γεωμετρία ανήκουν σε ένα διακριτό φάσμα. Ένα επιπλέον χαρακτηριστικό των ρυθμών αυτών είναι ότι μπορούν να χωριστούν σε συμμετρικούς και αντισυμμετρικούς, με βάση τη μορφή της ηλεκτρικής πεδιακής έντασης ως προς το επίπεδο y = 0. Έτσι, η ηλεκτρική πεδιακή ένταση για έναν τυχαίο αντισυμμετρικό και συμμετρικό ρυθμό δίνονται, αντίστοιχα, από E a,(2) z,ν a i,k E s,(2) z,ν s i,k (ρ, φ) = Y (2) νi,k a (k 0, ρ, ρ )ψν a i,k a (φ), (4.76α) (ρ, φ) = Y (2) νi,k s (k 0, ρ, ρ )ψν s i,k s (φ), (4.76β) όπου Y (i) ν (k 0, ρ, ρ ) = J ν (k 0 ρ < )H (i) ν (k 0 ρ > ), (4.77) με i = 1, 2, και Λ a 1 Λ 0 cos(ν ψν a i,k a (φ) = i,k a π) + Λa cos[νi,k a (π 2φ 0)] sin(νa i,k φ), αν 0 < φ < φ 0 cos(νi,k a π) + Λa cos[νi,k a (π 2φ 0)] Λ 0 cos(νi,k a π) + Λa cos[νi,k a (π 2φ 0)] sin[νa i,k (π φ)], αν φ 0 < φ < π Λ s + 1 Λ 0 cos(ν ψν s i,k s (φ) = i,k s π) + Λs cos[νi,k s (π 2φ 0)] cos(νs i,k φ), αν 0 < φ < φ 0 cos(νi,k s π) + Λs cos[νi,k s (π 2φ 0)] Λ 0 cos(νi,k s π) + Λs cos[νi,k s (π 2φ 0)] cos[νs i,k (π φ)], αν φ 0 < φ < π (4.78α) (4.78β)
120 110 Κεφάλαιο 4 Σημειώνεται ότι στις (4.76) k = 0, 1, 2,... και i = 1, 2,..., n. Οι συνιστώσες της μαγνητικής πεδιακής έντασης προκύπτουν, μέσω του νόμου του Faraday, ότι είναι H a,(2) ρ,νi,k a (ρ, φ) = H a,(2) φ,νi,k a (ρ, φ) = 1 H s,(2) ρ,νi,k s (ρ, φ) = H s,(2) φ,νi,k s (ρ, φ) = 1 j ωµ 0 ρ Y (2) νi,k a X (2) jη ν a 0 i,k j ωµ 0 ρ Y (2) νi,k s X (2) jη ν s 0 i,k (k 0, ρ, ρ ) w(φ) ψ a ν a i,k (φ), (4.79α) (k 0, ρ, ρ ) w(φ) ψν a i,k a (φ), (4.79β) (k 0, ρ, ρ ) w(φ) ψ a ν s i,k (φ), (4.79γ) (k 0, ρ, ρ ) w(φ) ψν a i,k s (φ), (4.79δ) με µ r 1, αν 0 < φ < φ 0 w(φ) = 1, αν φ 0 < φ < π (4.80) και X (i) ν (k 0, ρ, ρ ) = J ν(k 0 ρ) H (i) ν (k 0 ρ), αν ρ < ρ J ν (k 0 ρ ) H (i) ν (k 0 ρ), αν ρ > ρ (4.81) Μια σημαντική ιδιότητα των συναρτήσεων Y (i) ν (k 0, ρ, ρ ) και X (i) ν (k 0, ρ, ρ ), η οποία θα φανεί χρήσιμη στο υπόλοιπο της ανάλυσης, είναι η Y (2) ν (k 0, ρ, ρ ) = Y (1) ν (k 0, ρ, ρ ), (4.82α) X (2) ν (k 0, ρ, ρ ) = X (1) ν (k 0, ρ, ρ ) (4.82β) Η απόδειξή της στηρίζεται στη σχέση ( z ) ( ν 1 J ν (z) = 2 4 z2) k k! Γ(ν + k + 1), (4.83) k=0 όπου Γ(z) είναι η συνάρτηση Γάμμα, και στις εξισώσεις ορισμού H (1) ν [ (z) = j csc(νπ) H (2) ν (z) = j csc(νπ) ] e jνπ J ν (z) J ν (z), (4.84α) [ ] J ν (z) e jνπ J ν (z) (4.84β) Όταν το όρισμα της συνάρτησης Bessel είναι πραγματικός αριθμός και δεδομένου ότι Γ(z ) = Γ (z), προκύπτει ότι J ν (z) = Jν (z) και H (2) ν (z) = H(1) ν (z). Το υπόλοιπο της απόδειξης είναι άμεση απόρροια των ορισμών (4.77) και (4.81). Οι ρυθμοί που περιγράφηκαν προηγουμένως μπορεί να δειχθεί ότι είναι ορθογώνιοι μεταξύ τους.
121 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 111 Αφετηρία της ανάλυσης θα αποτελέσει η παρατήρηση ψ ν a ai,k, ψa ν ai,k = ˆ π = π 2φ 0 2 ˆ π ψ ν s si,k, ψs ν si,k = = π 2φ 0 2 ˆ π ψ ν a ai,k, ψs ν si,k = w(φ) ψν a i,k a (φ) ψa ν a (φ) dφ i,k cos(ν a i,k π) + Λa cos[ν a i,k (π 2φ 0)] Λ 0 cos(ν a i,k π) + Λa cos[ν a i,k (π 2φ 0)] δ ν a i,k ±νa i,k, w(φ) ψν s i,k s (φ) ψs ν s (φ) dφ i,k cos(ν s i,k π) + Λs cos[ν s i,k (π 2φ 0)] Λ 0 cos(ν s i,k π) + Λs cos[ν s i,k (π 2φ 0)] δ ν s i,k ±νs i,k, w(φ) ψν a i,k a (φ) ψs ν s (φ) dφ = 0, (4.85γ) i,k (4.85α) (4.85β) Για την εξαγωγή των (4.85) χρησιμοποιήθηκαν οι εξισώσεις { cos(ν a i,k π) + Λ a cos[ν a i,k (π 2φ 0)] } sin[ν a i,k (π φ 0)] = (Λ a 1) sin(ν a i,k φ 0), (4.86α) { cos(ν a i,k π) + Λ a cos[ν a i,k (π 2φ 0)] } cos[ν a i,k (π φ 0)] = (Λ a + 1) cos(ν a i,k φ 0), (4.86β) και οι αντίστοιχες με τα ν s i,k, Λs στη θέση των ν a i,k, Λa, οι οποίες απορρέουν από τις (4.65), (4.74). Κατά συνέπεια, προκύπτει ˆ π 0 ˆ π 0 ˆ π 0 E a,(2) z,ν a i,k E s,(2) z,ν s i,k (ρ, φ) H a,(2) j φ,ν a (ρ, φ) dφ = i,k (ρ, φ) H s,(2) j φ,ν s (ρ, φ) dφ = i,k Y (2) η ν a 0 i,k Y (2) η ν s 0 i,k ˆ π E a,(2) z,νi,k a (ρ, φ) H s,(2) φ,ν s (ρ, φ) dφ = i,k 0 E s,(2) z,ν s i,k (k 0, ρ, ρ ) X (1) ν a i,k ψν a i,k a, ψa νi,k a (k 0, ρ, ρ ) X (1) ν s i,k ψν s i,k s, ψs νi,k s (k 0, ρ, ρ ) δ ν a i,k ±ν a i,k, (k 0, ρ, ρ ) δ ν s i,k ±ν s, i,k, (ρ, φ) H a,(2) φ,ν a (ρ, φ) dφ = 0 (4.87γ) i,k (4.87α) (4.87β) Παρατηρούμε, καταρχήν, ότι κάθε αντισυμμετρικός ρυθμός είναι ορθογώνιος προς κάθε συμμετρικό ρυθμό. Επίσης, ένας ρυθμός που αντιστοιχεί σε μια πραγματική ρίζα είναι ορθογώνιος προς όλους τους άλλους ρυθμούς. Αντίθετα, ένας ρυθμός που αντιστοιχεί σε μία μιγαδική ρίζα είναι μη ορθογώνιος μόνο με τον ρυθμό που αντιστοιχεί στη συζυγή ρίζα. Το γεγονός αυτό οδηγεί στο συμπέρασμα ότι κάθε ζεύγος ρυθμών που αντιστοιχεί σε συζυγείς ρίζες πρέπει να λαμβάνεται ως ένας ρυθμός, με πεδίο ίσο με το άθροισμα των πεδίων των αρχικών ρυθμών. Τότε, ο νέος σύνθετος ρυθμός είναι μη ορθογώνιος μόνο με τον εαυτό του. Οι σχέσεις ορθογωνικότητας που παρουσιάστηκαν θα φανούν χρήσιμες κατά τον υπολογισμό της συνολικής ισχύος που διαπερνά μια κυλινδρική επιφάνεια με άξονα τον άξονα z. Στη συνέχεια, θα μελετηθεί η κατανομή του πεδιου και η ροή της ισχύος στον χώρο για όλα τα είδη των ρυθμών. Στο σχήμα 4.5 απεικονίζεται το πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης για τέσσερις ρυθμούς που υποστηρίζονται από μία δομή με φ 0 = π/12, µ r = 2, ρ = 4λ 0 και αντιστοιχούν στους πόλους , , , 6. Οι δύο πρώτοι από τους πόλους ισχύουν για αντισυμμετρική διέγερση, ενώ οι δύο τελευταίοι για συμμετρική. Είναι φανερό ότι για ρ > ρ το πεδιο έχει τη μορφή στάσιμου κύματος κατά τη διεύθυνση των φ και διαδιδόμενου κατά τη διεύθυνση
122 112 Κεφάλαιο 4 (α) (β) (γ) (δ) Σχήμα 4.5: Πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης σε σφηνοειδή δομή με φ0 = π/12, ρ = 4λ0, µr = 2 για τους ρυθμούς που αντιστοιχούν στους αντισυμμετρικούς πόλους (α) , (β) και τους συμμετρικούς πόλους (γ) και (δ) 6. των ρ. Το πλήθος και οι θέσεις των μηδενισμών της ηλεκτρικής πεδιακής έντασης πάνω σε επιφάνειες σταθερού ρ καθορίζεται από την τιμή του πόλου. Μάλιστα, μπορεί να αποδειχθεί, μέσω των αναλυτικών εκφράσεων που δίνουν το πεδίο των ρυθμών, ότι η γωνία που σχηματίζεται μεταξύ δύο διαδοχικών μηδενισμών είναι π/ν, όπου ν είναι ο πόλος που αντιστοιχεί στον συγκεκριμένο ρυθμό. Από την άλλη πλευρά, το πεδίο στην περιοχή ρ < ρ είναι στάσιμο τόσο κατά τη διεύθυνση του φ όσο κατά τη διεύθυνση του ρ. Παρόμοια συμπεράσματα μπορούν να εξαχθούν και μέσω του πραγματικού μέρους του διανύσματος Poyn ng, το οποίο απεικονίζεται στο σχήμα 4.6 για τους τέσσερις ρυθμούς που αναφέρθηκαν προηγουμένως. Πιο συγκεκριμένα, τα διανύσματα δείχνουν τη φορά του διανύσματος Poyn ng και η χρωματική απεικόνιση το πλάτος του. Όταν ρ > ρ, το διάνυσμα Poyn ng έχει τη διεύθυνση των ρ με φορά προς το άπειρο στον αέρα και προς την αρχή του συστήματος συντεταγμένων μέσα στο διπλο-αρνητικό υλικό. Η συμπεριφορά αυτή είναι άμεση συνέπεια της συνθήκης ακτινοβολίας που επιβλήθηκε, η οποία στον αέρα αντιστοιχεί σε κύματα που κατευθύνονται προς το εξωτερικό του χώρου, ενώ μέσα στο διπλο-αρνητικό υλικό, όπου οι ταχύτητες ομάδας και φάσης είναι αντίθετες, υποδηλώνει την ύπαρξη κυμάτων που ρέουν προς την αρχή του συστήματος συντεταγμένων. Από την άλλη πλευρά, το πλάτος του πραγματικού διανύσματος Poyn ng στο εσωτερικό του κυλίνδρου ρ = ρ είναι μηδέν, το οποίο είναι απόλυτα συμβατό με την ύπαρξη στάσιμων κυμάτων, όπως αναφέρθηκε προηγουμένως. Τα διανύσματα που υπάρχουν στην περιοχή αυτή και φαίνεται να έχουν τυχαίο προσανατολισμό οφείλονται στα αριθμητικά σφάλματα κατά τον υπολογισμό των αναλυτικών εκφράσεων του πεδίου, τα οποία παίζουν σημαντικό ρόλο εξαιτίας της μηδενικής τιμής του
123 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 113 (α) (β) (γ) (δ) Σχήμα 4.6: Πραγματικό διάνυσμα Poyn ng σε σφηνοειδή δομή με φ0 = π/12, ρ = 4λ0, µr = 2 για τους ρυθμούς που αντιστοιχούν στους αντισυμμετρικούς πόλους (α) , (β) και τους συμμετρικούς πόλους (γ) και (δ) 6. Η χρωματική κλίμακα μετράται σε db και η άσπρη συμπαγής γραμμή δείχνει την διεπιφάνεια αέρα και διπλο-αρνητικού υλικού. διανύσματος Poyn ng. Ενδιαφέρον έχει, επίσης, η μορφή του πεδίου στην κορυφή της σφηνοειδούς γεωμετρίας. Οι εκφράσεις που δίνουν το πεδίο δείχνουν ότι τόσο η ηλεκτρική όσο και η μαγνητική πεδιακή ένταση του αντισυμμετρικού ρυθμού που αντιστοιχεί στον πόλο 0 είναι μηδενικές παντού στον χώρο. Σχετικά με τον συμμετρικό ρυθμό στον μηδενικό πόλο, προκύπτει ότι η ηλεκτρική πεδιακή ένταση για ρ 0 μεταβάλεται όπως η J0 (k0 ρ), δηλαδή παραμένει, περίπου σταθερή. Η κατά ρ συνιστώσα της μαγνητικής πεδιακής έντασης είναι 0 σε όλο τον χώρο, ενώ η κατά φ συνιστώσα της μαγνητικής έντασης για μικρά ρ συμπεριφέρεται όπως η J1 (k0 ρ), δηλαδή τείνει γραμμικά στο 0. Αναφορικά με τους ρυθμούς σε θετικούς πραγματικούς πόλους, αξιοποιώντας την ασυμπτωτική έκφραση Jν ( x ) x ν /[2ν Γ(ν + 1)] της συνάρτηση Bessel α είδους για x 0, εξάγεται ότι a/s,(2) Ez,ν (ρ, φ) ρν, a/s,(2) H φ,ν (4.88α) φ ) ρ ν 1, (4.88β) (ρ, φ) ρν 1, (4.88γ) a/s,(2) Hρ,ν (ρ, a ή ν = νs. Επειδή οι ν a, νs είναι θετικοί πραγματικοί αριθμοί, η ηλεκτρική πεδιακή όπου ν = νi,k i,k i,k i,k a, νs > 1, ένταση τείνει μονότονα στο 0. Η μαγνητική πεδιακή ένταση τείνει μονότονα στο 0 όταν νi,k i,k a, νs < 1, απειρίζεται στην κορυφή της διάταξης. Από τις εκφράσεις (4.88α)-(4.88γ) ενώ για 0 < νi,k i,k
124 114 Κεφάλαιο 4 (α) (β) (γ) (δ) Σχήμα 4.7: Πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης σε σφηνοειδή δομή με φ 0 = π/12, ρ = 4λ 0 για τους ρυθμούς που αντιστοιχούν στους αντισυμμετρικούς πόλους (α) ±j (µ r = 2), (β) ±j (µ r = 1.2) και στους συμμετρικούς πόλους (γ) ±j (µ r = 0.7) και (δ) ±j (µ r = 0.9). μπορεί να ελεγχθεί η τετραγωνική ολοκληρωσιμότητα της ηλεκτρικής και μαγνητικής πεδιακής έντασης σε μία περιοχή της κορυφής O της σφηνοειδούς δομής, η οποία συνδέεται άμεσα με τη συνολική ενέργεια του πεδιου στην περιοχή αυτή. Υπενθυμίζεται ότι μία συνάρτηση f (ρ, φ) είναι τετραγωνικά ολοκληρώσιμη σε μια περιοχή της αρχής του συστήματος αν ˆ a ˆ 2π 0 0 f (ρ, φ) 2 ρ dρ dφ <, (4.89) με a > 0. Αντικαθιστώντας τις (4.88α)-(4.88γ) στην παραπάνω εξίσωση προκύπτει ότι τοσο η ηλεκτρική πεδιακή ένταση όσο και η μαγνητική είναι τετραγωνικά ολοκληρώσιμες σε μια περιοχή του O, ακόμα και αν η τελευταία απειρίζεται στο O. Με άλλα λόγια, η ηλεκτρική και η μαγνητική ενέργεια γύρω από το O των ρυθμών που αντιστοιχούν σε πραγματικούς πόλους ειναι πεπερασμένη. Σημαντικοί ρυθμοί που εμφανίζονται σε δομές από διπλο-αρνητικά υλικά και απουσιάζουν εντελώς στις δομές από συμβατικά υλικά με θετικές καταστατικές παραμέτρους είναι αυτοί που αντιστοιχούν σε μιγαδικούς πόλους. Υπενθυμίζεται ότι κάθε τέτοιος ρυθμός θεωρείται ότι αντιστοιχεί σε ένα ζεύγος ενός μιγαδικού πόλου με τον συζυγή του. Από όλους αυτούς τους ρυθμούς, μεγάλο ενδιαφέρον έχει αυτός με πόλους πάνω στον φανταστικό άξονα. Η συνθήκη ύπαρξης φανταστικών πόλων είναι, όπως αποδείχθηκε στην υποενότητα 4.3.3, Λ a, Λ s < Λ 0. Επειδή Λ 0 < 1, συνάγεται ότι για αντισυμμετρικούς ρυθμούς αυτό συμβαίνει όταν µ r < 1 και για συμμετρικούς όταν µ r > 1. Το σχήμα 4.7 παρουσιάζει το πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης για τους αντισυμμετρικούς πόλους ±j2.0982, ±j4.5796, που προκύπτουν όταν µ r = 2, 1.2, και τους συμμετρικούς
125 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 115 (α) (β) (γ) (δ) Σχήμα 4.8: Πραγματικό διάνυσμα Poyn ng σε σφηνοειδή δομή με φ 0 = π/12, ρ = 4λ 0 για τους ρυθμούς που αντιστοιχούν στους αντισυμμετρικούς πόλους (α) ±j (µ r = 2), (β) ±j (µ r = 1.2) και στους συμμετρικούς πόλους (γ) ±j (µ r = 0.7) και (δ) ±j (µ r = 0.9). Η χρωματική κλίμακα μετράται σε db και η άσπρη συμπαγής γραμμή δείχνει την διεπιφάνεια αέρα και διπλο-αρνητικού υλικού. ±j3.3128, ±j5.6235, οι οποίοι εμφανίζονται αν επιλεγεί µ r = 0.7, 0.9. Σε όλες τις περιπτώσεις θεωρείται φ 0 = π/12 και ρ = 4λ 0. Σε αντίθεση με την περίπτωση των πραγματικών πόλων, το πεδίο εμφανίζει έντονα τοπικό χαρακτήρα και είναι συγκεντρωμένο σε μια περιοχή γύρω από την διεπιφάνεια αέρα και διπλο-αρνητικού υλικού. Η αύξηση της απόλυτης τιμής του πόλου έχει ως αποτέλεσμα την αύξηση του πλάτους του πεδίου πάνω στην επιφάνεια αυτή και τη συρρίκνωση της περιοχής μέσα στην οποία κατανέμεται. Σημειώνεται ότι παρόμοια συμπεριφορά έχουν οι επιφανειακοί ρυθμοί σε μία επίπεδη πλάκα διπλο-αρνητικού υλικού. Στο σχήμα 4.8 απεικονίζεται το πραγματικό διάνυσμα Poyn ng, το οποίο έχει συνιστώσα μόνο κατά ρ, που έχει φορά προς το άπειρο στον αέρα και προς την κορυφή της διάταξης στο διπλο-αρνητικό υλικό. Το πλάτος του διανύσματος Poyn ng είναι μέγιστο πάνω στην διεπιφάνεια αέρα και διπλο-αρνητικού υλικού και μειώνεται καθώς απομακρυνόμαστε απο αυτήν. Αν και για γωνίες φ κοντά στην τιμή π υπάρχει ροή ισχύος προς το άπειρο, το πλάτος είναι τόσο μικρό ώστε πρακτικά είναι μη υπολογίσιμη. Η ασυμπτωτική συμπεριφορά των ρυθμών σε φανταστικούς πόλους βρίσκεται, όπως και στην περίπτωση των πραγματικών πόλων, μέσω της ασυμπτωτικής έκφρασης της συνάρτησης Bessel για
126 116 Κεφάλαιο 4 (α) (β) Σχήμα 4.9: Πραγματικό μέρος της ηλεκτρικής πεδιακής έντασης σε σφηνοειδή δομή με φ0 = 2π/13, ρ = 4λ0, µr = 1.1 για τους ρυθμούς που αντιστοιχούν (α) στους αντισυμμετρικούς πόλους 6.5 ± j και (β) στους συμμετρικούς πόλους (β) 3.25 ± j (α) (β) Σχήμα 4.10: Πραγματικό διάνυσμα Poyn ng σε σφηνοειδή δομή με φ0 = 2π/13, ρ = 4λ0, µr = 1.1 για τους ρυθμούς που αντιστοιχούν (α) στους αντισυμμετρικούς πόλους 6.5 ± j και (β) στους συμμετρικούς πόλους 3.25 ± j Η χρωματική κλίμακα μετράται σε db και η άσπρη συμπαγής γραμμή δείχνει την διεπιφάνεια αέρα και διπλο-αρνητικού υλικού. όρισμα κοντά στο 0. Αν ο φανταστικός πόλος είναι ν = j ν, τότε ισχύει a/s,(2) (ρ, φ) ρ± j ν e± j ν ln ρ, (4.90α) a/s,(2) (ρ, φ) ρ 1 ρ± j ν ρ 1 e± j ν ln ρ, (4.90β) a/s,(2) (ρ, φ) ρ 1 ρ± j ν ρ 1 e± j ν ln ρ (4.90γ) Ez,ν Hρ,ν H φ,ν Παρατηρούμε ότι όλες οι συνιστώσες του πεδίου περιέχουν τον όρο e± j ν ln ρ, ο οποίος περιγράφει μία ταλαντούμενη συνάρτηση με συχνότητα που τείνει στο άπειρο καθώς ρ 0. Από την άλλη πλευρά, το πλάτος της ηλεκτρικής πεδιακής έντασης παραμένει σταθερό σε μια περιοχή του O, σε αντίθεση με αυτό της μαγνητικής πεδιακής έντασης που απειρίζεται για ρ = 0. Επίσης, αποδεικνύεται ότι η ηλεκτρική πεδιακή ένταση είναι τετραγωνικά ολοκληρώσιμη γύρω από το O, ενώ η μαγνητική δεν είναι. Έτσι, καταλήγουμε στο μη φυσικό συμπέρασμα ότι η συνολική μαγνητική ενέργεια σε μια περιοχή του O απειρίζεται. Παρόμοια συμπεράσματα έχουν διατυπωθεί και στην εργασία [Wallén et al., 2008] και η αφύσικη αυτή συμπεριφορά του πεδίου αποδίδεται στη μη ρεαλιστική υπόθεση ότι η διάταξη είναι άπειρα αιχμηρή στην κορυφή της.
127 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 117 Τέλος, εξετάζεται η μορφή των ρυθμών σε μιγαδικούς πόλους με μη μηδενικό πραγματικό μέρος. Το πραγματικό μέρος της ηλεκτρικής πεδιακής και το πραγματικό διάνυσμα Poyn ng παρουσιάζονται στα σχήματα 4.9 και 4.10, αντίστοιχα, για τους πόλους 6.5 ± j και 3.25 ± j3.1496, ο πρώτος από τους οποίους εξάγεται για αντισυμμετρική διέγερση, ενώ ο δεύτερος για συμμετρική. Οι πόλοι αυτοί υπολογίστηκαν θεωρώντας ότι φ 0 = 2π/13 και µ r = 1.1. Η συμπεριφορά των ρυθμών αυτών είναι, σε γενικές γραμμές, ίδια με αυτήν των ρυθμών που αντιστοιχούν σε καθαρά φανταστικούς πόλους, με εξαίρεση μία περιοχή γύρω από την κορυφή της διάταξης. Συγκεκριμένα, αν ν = ν r + jν i είναι ο μιγαδικός πόλος, με ν r, ν i > 0, οι ασυμπτωτικές εκφράσεις του πεδίου για μικρά ρ δίνονται από E a/s,(2) z,ν (ρ, φ) ρ ν r ρ ±jν i = ρ ν r e ±jν i ln ρ, (4.91α) H a/s,(2) ρ,ν (ρ, φ) ρ ν r 1 ρ ±jν i = ρ ν r 1 e ±jν i ln ρ, (4.91β) H a/s,(2) φ,ν (ρ, φ) ρ νr 1 ρ ±jν i = ρ νr 1 e ±jν i ln ρ (4.91γ) Επομένως, αντίθετα με την περίπτωση φανταστικών πόλων, η ηλεκτρική πεδιακή ένταση των ρυθμών σε μιγαδικούς πόλους τείνει στο 0 καθώς προσεγγίζουμε την κορυφή O. Ίδια συμπεριφορά παρουσιάζει και η μαγνητική πεδιακή ένταση, με εξαίρεση την περίπτωση 0 < ν i < 1, κατά την οποία το πλάτος της τείνει προς το άπειρο όταν ρ 0. Παρ όλα αυτά, σε κάθε περίπτωση η ηλεκτρική και η μαγνητική ένταση ειναι τετραγωνικά ολοκληρώσιμες συναρτήσεις σε μια περιοχή του O και η συνολική ενέργεια του πεδίου στην περιοχή αυτή παραμένει πεπερασμένη Έλεγχος της λύσης Ακολούθως, πραγματοποιείται ένας αρχικός έλεγχος συμβατότητας της λύσης με βασικές φυσικές αρχές. Μία από αυτές είναι ότι η συνολική ισχύς που διαπερνά τον άπειρο κύλινδρο με κατεύθυνση προς το εξωτερικό του πρέπει να είναι θετική και ίση με την ισχύ που εξέρχεται από την πηγή. Η πρόταση αυτή είναι συνέπεια του γεγονότος πως δεν υπάρχουν πηγές στο άπειρο και ότι τα υλικά που διαμορφώνουν τη διάταξη δεν έχουν απώλειες. Η ισχύς που διέρχεται από την επιφάνεια S ρ ενός κυλίδρου με άξονα τον άξονα z, ακτίνα ρ και μοναδιαίο μήκος κατά τη διεύθυνση του άξονα z δίνεται από τη σχέση P ρ = 1 2 S ρ Re {E H } ˆρ ds = 1 2 ˆ π 0 { } Re E z (ρ, φ) Hφ(ρ, φ) ρ dφ, (4.92) στην οποία το άνω όριο του δεύτερου ολοκληρώματος λαμβάνεται π γιατί οι αντισυμμετρικοί και οι συμμετρικοί ρυθμοί εξετάζονται στον μισό χώρο. Επικεντρώνοντας την προσοχή μας στην αντισυμμετρική διέγερση, το συνολικό πεδιο που παράγεται από τη γραμμική πηγή γράφεται ως άθροισμα των πεδίων των ρυθμών της διάταξης ως εξής E a z(ρ, φ) = jλ 0 k=0 H a φ(ρ, φ) = jλ 0 k=0 n i=1 n i=1 ε ( νi,k a ) a,(2) E z,νi,k a (ρ, φ) sin [ νi,k a (π φ ) ], (4.93α) ε ( νi,k a ) a,(2) H φ,ν φ) i,k(ρ, a sin [ νi,k a (π φ ) ] (4.93β)
128 118 Κεφάλαιο 4 Αντικαθιστώντας τις (4.90) στην (4.89) και χρησιμοποιώντας τις ορθογωνικές ιδιότητες (4.87), προκύπτει P a ρ = Λ2 0 2η 0 k=0 n i=1 ε ( ν a i,k ) Re {jρ Y (2) ν a i,k (k 0, ρ, ρ )X (1) νi,k a (k 0, ρ, ρ ) ψ a ν a i,k, ψa ν a i,k sin 2 [ ν a i,k (π φ ) ]} (4.94) Αξιοποιώντας την ασυμπτωτική έκφραση (4.10) της συνάρτησης Hankel, βρίσκεται ότι η συνολική ισχύς που διαπερνά τον άπειρο κύλινδρο είναι P a = Λ2 0 2πωµ 0 k=0 n i=1 ε ( νi,k a ) { Re Jν 2 i,k a (k 0ρ ) ψν a i,k a, ψa νi,k a sin 2 [ νi,k a (π φ ) ]} (4.95) Ακολουθώντας την ίδια ακριβώς διαδικασία, αποδεικνύεται ότι στη συμμετρική διέγερση η συνολική ισχυς που διαπερνά την επιφάνεια S ρ ειναι P s ρ = Λ2 0 2η 0 k=0 n i=1 ε ( ν s i,k ενώ η ισχύς που φθάνει στο άπειρο είναι P s = Λ2 0 2πωµ 0 k=0 n i=1 ) Re {jρ Y (2) ν s i,k (k 0, ρ, ρ )X (1) νi,k s (k 0, ρ, ρ ) ψ s ν s i,k, ψs ν s i,k cos 2 [ ν s i,k (π φ ) ]}, (4.96) ε ( νi,k s ) { Re Jν 2 i,k s (k 0ρ ) ψν s i,k s, ψs νi,k s cos 2 [ νi,k s (π φ ) ]} (4.97) Η ισχύς που εξέρχεται από την πηγή δίνεται, σύμφωνα με την ολοκληρωτική διατύπωση του θεωρήματος του Poyn ng, από τον τύπο P s = 1 Re {E J s } dv, (4.98) 2 V όπου J s είναι η ρευματική κατανομή της πηγής και V είναι ένας χώρος που την περιβάλει. H P s είναι, τότε, η ισχυς που διαπερνά το σύνορο του V. Στο πρόβλημα που εξετάζουμε J s (ρ, φ) = (I 0 /ρ)δ(ρ ρ )δ(φ φ )ẑ, οπότε η (4.98) γίνεται P s = 1 2 Re { I 0 E z (ρ, φ ) } (4.99) Για την εξαγωγή της παραπάνω σχέσης θεωρήθηκε ότι ο όγκος V είναι το εσωτερικό ενός κυλίνδρου με άξονα συμμετρίας την ευθεία ρ = ρ, φ = φ, ακτίνα που τείνει στο 0 και μοναδιαίο ύψος. Ειδικότερα, στην αντισυμμετρική διέγερση, ο συνδυασμός της (4.93α) με την (4.99) και το γεγονός ότι I 0 = 1/jωµ 0 δίνουν P a s = Λ 0 2ωµ 0 k=0 n i=1 ε ( ν a i,k ) Re {Y (2) νi,k a (k 0, ρ, ρ ) ψν a i,k a (φ ) sin [ νi,k a (π φ ) ]} (4.100) Λαμβάνοντας υπόψη την ταυτότητα H (2) ν (z) = J ν (z) jy ν (z), με Y ν (z) τη συνάρτηση Neumann, και το γεγονός ότι οι συναρτήσεις Bessel και Neumann ειναι πραγματικές για πραγματική τάξη και όρισμα, προκύπτει { Re Y (2) ν a i,k (k 0, ρ, ρ ) ψ a ν a i,k (φ ) sin [ ν a i,k (π φ ) ]} = J 2 ν a i,k (k 0ρ ) ψ a ν a i,k (φ ) sin [ ν a i,k (π φ ) ], (4.101)
129 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 119 (α) (β) Σχήμα 4.11: Συνολική ισχυς που διαπερνά τον άπειρο κύλινδρο ως συνάρτηση της φ για φ 0 = π/12 και διάφορες τιμές του µ r, όταν χρησιμοποείται (α) αντισυμμετρική διέγερση και (β) συμμετρική διέγερση. Η τιμή της ισχύος είναι κανονικοποιημένη ως προς τη μέγιστη τιμή της στο διάστημα (φ 0, π). υπό την προϋπόθεση ότι ο νi,k a είναι πραγματικός. Όταν ο νa i,k είναι μιγαδικός και επειδή είναι γνωστό ότι ο συζυγής του είναι, επίσης, πόλος του μετασχηματισμού KL μπορεί να αποδειχτεί { Re Y (2) νi,k a (k 0, ρ, ρ ) ψν a i,k a (φ ) sin [ νi,k a (π φ ) ] + Y (2) νi,k a (k 0, ρ, ρ ) ψν a i,k a (φ ) sin [ νi,k a (π φ ) ]} { = 2 Re Jν 2 i,k a (k 0ρ ) ψν a i,k a (φ ) sin [ νi,k a (π φ ) ]} (4.102) Κατά συνέπεια, η (4.100) μετασχηματίζεται στην P a s = Λ 0 2ωµ 0 k=0 n i=1 ε ( νi,k a ) { Re Jν 2 i,k a (k 0ρ ) ψν a i,k a (φ ) sin [ νi,k a (π φ ) ]}, (4.103) η οποία διαπιστώνεται εύκολα ότι συμπίπτει με την (4.95). Αποδείχτηκε, λοιπόν, αναλυτικά ότι η ισχύς που δίνει η πηγή ισούται με την ισχύ που οδεύει προς το άπειρο, όπως απαιτεί η αρχή διατήρησης της ενέργειας. Ο χειρισμός της συμμετρικής περίπτωσης γίνεται με παρόμοιο τρόπο και οδηγεί στα ίδια συμπεράσματα. Η συνολική ισχύς που ρέει προς το άπειρο, όπως δίνεται από τις (4.95), (4.97), παρουσιάζεται στο σχήμα 4.11 ως συνάρτηση της φ, κανονικοποιημένη ως προς τη μέγιστη τιμή της στο διάστημα (φ 0, π), για φ 0 = π/12 και διάφορες τιμές του µ r. Παρατηρούμε ότι ενώ για µ r > 0 η ισχύς είναι θετική για κάθε τιμή της φ, όταν µ r < 0 υπάρχουν περιοχές στις οποίες αποκτά αρνητικές τιμές. Με άλλα λόγια, στις περιοχές αυτές η ισχύς ρέει από το άπειρο προς το εσωτερικό της διάταξης και απορροφάται από την πηγή. Το γεγονός αυτό καθιστά τη λύση ασυμβίβαστη με την αρχή διατήρησης της ενέργειας, η οποία επιβάλλει η ροή ισχύος να συμβαίνει προς το άπειρο, εφόσον οι πηγές βρίσκονται εντός του άπειρου κυλίνδρου. Για να κατανοηθεί η παράδοξη αυτή συμπεριφορά θα μελετηθούν, στη συνέχεια, οι όροι που διαμορφώνουν τα αθροίσματα των (4.95) και (4.97). Να σημειωθεί ότι κάθε ένας από αυτούς τους όρους είναι η ισχύς του ρυθμού που αντιστοιχεί στον πόλο στον οποίο υπολογίζεται ο όρος αυτός. Εξετάζοντας, πρώτα, τους όρους σε πραγματικούς πόλους, διαπιστώνεται ότι το πρόσημό τους εξαρτάται από το πρόσημο της ποσότητας ψ a/s ν, ψ a/s ν = π 2φ 0 2 cos(νπ) + Λ cos[ν(π 2φ 0 )] Λ 0 cos(νπ) + Λ a cos[ν(π 2φ 0 )], (4.104)
130 120 Κεφάλαιο 4 Σχήμα 4.12: Πρόσημο της ποσότητας A που δίνεται από την (4.105) ως συνάρτηση των ν, φ 0 Το κόκκινο χρώμα αντιστοιχεί στην τιμή 1 και το μπλε στην τιμή 1. όπου ν = ν a i,k ή ν = νs i,k και Λ = Λa ή Λ = Λ s. Λαμβάνοντας υπόψη ότι το ν είναι ρίζα της (4.55) και, κατά συνέπεια, Λ = sin(νπ)/ sin[ν a i,k π 2φ 0)], προκύπτει, μετά από πράξεις, ότι το πρόσημο της (4.104) είναι ίδιο με το πρόσημο της ποσότητας A = sin(2νφ 0 ) (π 2φ 0 ) sin(2νφ 0 ) 2φ 0 cos(νπ) sin[ν(π 2φ 0 )] (4.105) Το πρόσημο της A ως συνάρτηση των ν, φ 0 παριστάνεται στο σχήμα Παρατηρούμε ότι υπάρχουν περιοχές στις οποίες το A είναι αρνητικός αριθμός, δηλαδή η συνολική ισχύς που διαπερνά τον άπειρο κύλινδρο έχει φορά προς την κορυφή της διάταξης για τους ρυθμούς που αντιστοιχούν σε πόλους μέσα στις περιοχές αυτές. Από την άλλη πλευρά, η ισχύς ενός ρυθμού που αντιστοιχεί σε έναν μιγαδικό πόλο ν είναι Re { Jν 2 (k 0 ρ ) ψ a/s ν, ψν a/s { }} sin 2 [ν(π φ )] cos 2 [ν(π φ, (4.106) )] όπου το sin χρησιμοποιείται για τους αντισυμμετρικούς ρυθμούς και το cos για τους συμμετρικούς. Βλέπουμε ότι όταν ο πόλος είναι μιγαδικός, σε αντίθεση με την περίπτωση των πραγματικών πόλων, το πρόσημο της ισχύος εξαρτάται από τη θέση της πηγής. Το σχήμα 4.13 απεικονίζει την ισχύ αυτή ως συνάρτηση της φ, για τους ρυθμούς που αντιστοιχούν στους φανταστικούς πόλους και στους μιγαδικούς με το μικρότερο πραγματικό μέρος. Η ισχύς είναι κανονικοποιημένη ως προς τη μέγιστη τιμή της στο διάστημα (φ 0, π), η γωνία της σφηνοειδούς δομής λαμβάνεται φ 0 = π/12, ενώ το µ r μεταβάλλεται. Είναι εμφανής η ύπαρξη περιοχών όπου η ισχύς γίνεται αρνητική, παραβιάζοντας, έτσι, την αρχή διατήρησης της ενέργειας. H παραπάνω ανάλυση μας οδηγεί στο συμπέρασμα ότι το σύνολο των ρυθμών που προέκυψε με την χρήση της συνθήκης ακτινοβολίας (4.40) δεν αρκεί για να δώσει μία φυσικά αποδεκτή λύση. Για κάθε ρυθμό, συγκεκριμένοι συνδυασμοί πλάτους του πεδίου και τιμών των γεωμετρικών παραμέτρων έχουν σαν αποτέλεσμα την εισροή ισχύος από το άπειρο μέσα στο χώρο που βρίσκεται η διάταξη και την απορρόφησή της από την πηγή. Η αντιμετώπιση του προβλήματος αυτού πραγματοποιείται στην
131 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 121 (α) (β) Σχήμα 4.13: Συνολική ισχυς που διαπερνά τον άπειρο κύλινδρο ως συνάρτηση της φ για (α) αντισυμμετρικούς ρυθμούς και (β) συμμετρικούς ρυθμούς που αντιστοιχούν σε μιγαδικούς πόλους. Η τιμή της ισχύος είναι κανονικοποιημένη ως προς τη μέγιστη τιμή της στο διάστημα (φ 0, π) και φ 0 = π/12. επόμενη υποενότητα μέσω της επέκτασης του συνόλου των ρυθμών, έτσι ώστε ο γραμμικός τους συνδυαμός να δίνει το συνολικό πεδίο που παράγεται από μία γραμμική πηγή Επέκταση του συνόλου των ρυθμών της διάταξης Πρωτού προχωρήσουμε στην εύρεση των ρυθμών που συμπληρώνουν το σύνολο αυτών που παρουσιάστηκαν στην υποενότητα 4.3.5, θα υπολογίσουμε τις ισοδύναμες πηγές που παράγουν τον κάθε ρυθμό. Είναι γνωστό ότι όπου υπάρχουν πηγές ρεύματος εμφανίζεται ασυνέχεια στην εφαπτομενική συνιστώσα της μαγνητικής πεδιακής έντασης. Επίσης, από τις (4.79) φαίνεται ότι η κατά φ συνιστώσα της μαγνητικής πεδιακής έντασης είναι ασυνεχής πάνω στην επιφάνεια ρ = ρ και, επομένως, υπάρχει πάνω σε αυτήν μια ρευματική κατανομή. Το πλάτος και η φορά της κατανομής αυτής υπολογίζονται από την οριακή συνθήκη που συνδέει τις επιφανειακές συνιστώσες της μαγνητικής πεδιακής έντασης εκατέρωθεν της επιφάνειας. Πιο συγκεκριμένα, αν με J a,(2) νi,k a συμβολίσουμε την ρευματική κατανομή που παράγει τον αντισυμμετρικό ρυθμό στον πόλο νi,k a, ισχύει J a,(2) νi,k a (ρ, φ) = ˆρ ( H a,(2) ν a i,k ρ=ρ + H a,(2) ν a i,k ρ=ρ ) δ(ρ ρ ) = 2 πωµ 0 ρ w(φ) ψa ν a i,k (φ) δ(ρ ρ ) ẑ (4.107) Με ανάλογο τρόπο βρίσκεται ότι η ρευματική κατανομή που διεγείρει τον συμμετρικό ρυθμό στον πόλο ν s i,k είναι J s,(2) νi,k s (ρ, φ) = 2 πωµ 0 ρ w(φ) ψs νi,k s (φ) δ(ρ ρ ) ẑ (4.108) Αξίζει να σημειωθεί ότι, σύμφωνα με την αρχή της υπέρθεσης, το άθροισμα των J a,(2) νi,k a (ρ, φ), J s,(2) νi,k s (ρ, φ) πολλαπλασιασμένων με τα πλάτη των ρυθμών που εμφανίζονται στην έκφραση του συνολικού πεδίου
132 122 Κεφάλαιο 4 δίνει την ρευματική κατανομή της γραμμικής πηγής. Επομένως, για 0 < φ, φ < π, ισχύει δ(φ φ 2 ) = π 2φ 0 δ(φ φ 2 ) = π 2φ 0 k=0 k=0 n i=1 n i=1 ε(ν a i,k )w(φ)ψa ν a i,k (φ) sin [ ν a i,k (π φ ) ], ε(ν s i,k )w(φ)ψs ν s i,k (φ) cos [ ν s i,k (π φ ) ] (4.109α) (4.109β) Οι δύο παραπάνω εξισώσεις αποδεικνύουν ότι τα σύνολα B a = {ψ a ν a i,k(φ)/k = 0, 1,..., ; i = 1, 2,..., n} και B s = {ψ s ν s i,k(φ)/k = 0, 1,..., ; i = 1, 2,..., n} είναι πλήρεις βάσεις των συναρτήσεων f (φ) που ορίζονται στο διάστημα [0, π] και ικανοποιούν τις οριακές συνθήκες f (0) = f (π) = 0, f (φ + 0 ) = f (φ+ 0 ), f (φ + 0 ) = µ 1 r f (φ + 0 ), (4.110α) f (0) = f (π) = 0, f (φ + 0 ) = f (φ+ 0 ), f (φ + 0 ) = µ 1 r f (φ + 0 ) (4.110β) Όπως διαπιστώθηκε στην προηγούμενη ενότητα, το σύνολο των ρυθμών που υπολογίστηκαν έως τώρα δεν αρκεί για να δώσει μία φυσικά αποδεκτή περιγραφή του πεδίου. Ο λόγος είναι ότι υπάρχουν ρυθμοί που για συγκεκριμένες τιμές των παραμέτρων της διάταξης οδηγούν στην είσοδο ισχύος από το άπειρο και στην απορρόφησή της από τις πηγές. Προκειμένου να δοθεί λύση στο πρόβλημα αυτό, είναι απαραιτητο να κατανοηθεί, πρώτα, η αιτία που το δημιουργεί. Η συνθήκη ακτινοβολίας (4.40) που χρησιμοποιήθηκε για την εξαγωγή του πεδίου έχει σαν αποτέλεσμα η ροή της ισχύος να έχει φορά προς το εξωτερικό του χώρου στον αέρα και προς το εσωτερικό στο διπλο-αρνητικό. Συνεπώς, όταν για έναν ρυθμό η ισχύς που ρέει μέσα στο διπλο-αρνητικό είναι μεγαλύτερη από αυτήν που ρέει στον αέρα, η συνολική ισχύς που διαπερνά τον άπειρο κύλινδρο είναι αρνητική. Αν, ωστόσο, αλλάζαμε τη μορφή του ρυθμού ώστε η ροή της ισχύος να αντιστρέφονταν τόσο μέσα στον αέρα όσο και μέσα στο διπλο-αρνητικό υλικό, θα πετυχαίναμε θετικό πρόσημο στη συνολική ισχύ που ρέει προς το άπειρο. Μαθηματικά, το γεγονός αυτό ισοδυναμεί με την επιβολή στον άπειρο κύλινδρο της συνθήκης ακτινοβολίας [ ] Ez (ρ, φ) lim ρ jk 0 E z (ρ, φ) = 0 (4.111) ρ ρ Η συνθήκη ακτινοβολίας (4.111) καθορίζει ότι για τον μετασχηματισμό του πεδίου πρέπει να χρησιμοποιηθεί ο μετασχηματισμός KL α είδους, ο οποίος εμπλέκει τη συνάρτηση Hankel α είδους. Εφαρμόζοντας, ακριβώς, την ίδια ανάλυση που παρουσιάστηκε στις υποενότητες 4.3.2, και 4.3.5, προκύπτει ότι το πεδίο εκφράζεται ως γραμμικός συνδυασμός των αντισυμμετρικών ρυθμών με πεδιακές συνιστώσες E a,(1) z,ν a i,k (ρ, φ) = Y (1) νi,k a (k 0, ρ, ρ )ψν a i,k a (φ) (4.112α) j H a,(1) ρ,νi,k a (ρ, φ) = H a,(1) φ,νi,k a (ρ, φ) = 1 ωµ 0 ρ Y (1) νi,k a X (1) jη ν a 0 i,k και των συμμετρικών με πεδιακές συνιστώσες E s,(1) z,ν a i,k (k 0, ρ, ρ )w(φ)ψ a ν a i,k (φ) (4.112β) (k 0, ρ, ρ )w(φ)ψν a i,k a (φ) (4.112γ) (ρ, φ) = Y (1) νi,k s (k 0, ρ, ρ )ψν s i,k s (φ), (4.113α) j H s,(1) ρ,νi,k s (ρ, φ) = H s,(1) φ,νi,k s (ρ, φ) = 1 ωµ 0 ρ Y (1) νi,k s X (1) jη ν s 0 i,k (k 0, ρ, ρ )w(φ)ψ s ν s i,k (φ), (4.113β) (k 0, ρ, ρ )w(φ)ψν s i,k s (φ) (4.113γ)
133 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 123 Τονίζεται ότι οι πόλοι νi,k a, νs i,k που καθορίζουν τον κάθε ρυθμό είναι ακριβώς ίδιοι με αυτούς που προσδιορίστικαν στις υποενότητες και Στη συνέχεια, θα ονομάζουμε τους ρυθμούς αυτούς α είδους για να τους διακρίνουμε από αυτούς που υπολογίστηκαν στις προηγούμενες ενότητες, οι οποίοι θα χαρακτηρίζονται ως β ειδους. Οι σχέσεις ορθογωνικότητας που ισχύουν για τους ρυθμούς α είδους είναι παρόμοιες με τις αντίστοιχες των ρυθμών β είδους και δίνονται από τις εξισώσεις ˆ π 0 ˆ π 0 ˆ π 0 E a,(1) z,ν a i,k E s,(1) z,ν s i,k (ρ, φ) H a,(1) 1 φ,ν a (ρ, φ) dφ = i,k (ρ, φ) H s,(1) 1 φ,ν s (ρ, φ) dφ = i,k ˆ π E a,(1) z,νi,k a (ρ, φ) H s,(1) φ,ν s (ρ, φ) dφ = i,k 0 Y (1) jη ν a 0 i,k Y (1) jη ν s 0 i,k E s,(1) z,ν s i,k (k 0, ρ, ρ ) X (2) ν a i,k ψν s i,k s, ψs νi,k s (k 0, ρ, ρ ) X (2) ν s i,k ψν s i,k s, ψs νi,k s (k 0, ρ, ρ ) δ ν s i,k ±ν s, i,k (k 0, ρ, ρ ) δ ν s i,k ±ν s, i,k (ρ, φ) H a,(1) φ,ν a (ρ, φ) dφ = 0, (4.114γ) i,k (4.114α) (4.114β) Επίσης, είναι εύκολο να αποδειχθεί ότι κάθε αντισυμμετρικός ρυθμός α είδους είναι ορθογώνιος προς κάθε συμμετρικό ρυθμό β είδους και το αντίστροφο. Οι ρευματικές κατανομές που παράγουν τους ρυθμούς α ειδους είναι οι αντίθετες αυτών που δημιουργούν τους ρυθμούς β είδους, δηλαδή J a,(1) ν a i,k (ρ, φ) = J a,(2) νi,k a (ρ, φ), J s,(1) ν s i,k (ρ, φ) = J s,(2) νi,k s (ρ, φ) (4.115) Η συνολική ισχύς που διαπερνά τον άπειρο κύλινδρο ενός αντισυμμετρικού ρυθμού α είδους που αντιστοιχεί στον πόλο ν a i,k είναι³ P a,(1),ν = 1 { } i,k a Re Jν 2 πωµ a (k 0ρ ) ψ a 0 i,k νi,k a, ψa νi,k a (4.116) Η αντίστοιχη ισχύς του αντισυμμετρικού ρυθμού β είδους στον ίδιο πόλο νi,k a και ίδιου πλάτους, ο οποίος όπως φαίνεται από την (4.114) διεγείρεται από την ίδια ρευματική κατανομή (το πρόσημο δεν παίζει κανένα ρόλο στην ισχύ) προκύπτει, μέσω των (4.76α), (4.79β), ότι είναι P a,(2),ν = 1 { } i,k a Re Jν 2 πωµ a (k 0ρ ) ψ a 0 i,k νi,k a, ψa νi,k a (4.117) Όπως είναι αναμενόμενο, οι P a,(1),νi,k a και P a,(2),νi,k a είναι αντίθετες. Το γεγονός ότι η συνολική ισχύς ενός ρυθμού α είδους μπορεί να είναι θετική είναι πιθανό να οδηγήσει στο συμπέρασμα ότι το πεδίο του ρυθμού συμπίπτει με αυτό που παράγει η αντίστοιχη ρευματική κατανομή. Ωστόσο, το συμπέρασμα αυτό δεν είναι ορθό, επειδή κάθε ρυθμός α είδους συνεπάγεται είσοδο ισχύος σε όλον τον χώρο που καταλαμβάνεται από αέρα και, κατά συνέπεια, ακόμη και σε περιοχές που βρίσκονται μακριά από την διεπιφάνεια αέρα και διπλο-αρνητικού υλικού, όπου η ισχύς πρέπει να ρέει προς το άπειρο. Ως παράδειγμα αναφέρεται η περιοχή όπου η γωνία φ προσεγγίζει την τιμή π, στην οποία δεν υπάρχει λόγος εισόδου ισχύος από το άπειρο, όταν φ 0 < π/2. Στην πραγματικότητα, το πεδίο που δημιουργείται από κάθε μία από τις ρευματικές κατανομές των ³Για την ακρίβεια, τόσο η (4.115) όσο και η (4.116) δίνουν την ισχύ στην περίπτωση ενός πραγματικού πόλου. Όταν ο πόλος είναι μιγαδικός αριθμός, θα πρέπει να προηγηθεί ένας συντελεστής 2, καθώς στο πεδίο του ρυθμού συνεισφέρει τόσο ο πόλος αυτός όσο και ο συζυγής του.
134 124 Κεφάλαιο 4 (4.107), (4.108) προκύπτει από την υπέρθεση των ρυθμών σε όλους τους πόλους. Τα πλάτος, παρ όλα αυτά, ενός ρυθμού α είδους σε έναν πόλο διαφορετικό από αυτόν της ρευματικής κατανομής θα πρέπει να είναι ίσο με το πλάτος του αντίστοιχου ρυθμού β είδους, προκειμένου να ικανοποιούνται οι οριακές συνθήκες πάνω στην επιφάνεια της πηγής. Γενικά, όταν χρησιμοποιείται γραμμική πηγή, η ηλεκτρική πεδιακή ένταση στην αντισυμμετρική και στη συμμετρική διέγερση δίνονται, αντίστοιχα, από E a z(ρ, φ) = E s z(ρ, φ) = n k=0 i=1 n k=0 i=1 με τα πλάτη Ai,k a, Ba i,k, As i,k, Bs i,k να ικανοποιούν τις σχέσεις [ [ ] Ai,k a Ea,(1) z,νi,k a (ρ, φ) + Bi,k a Ea,(2) z,νi,k a (ρ, φ), (4.118α) ] Ai,k s Es,(1) z,νi,k s (ρ, φ) + Bi,k s Es,(2) z,νi,k s (ρ, φ), (4.118β) A a i,k Ba i,k = 1, As i,k Bs i,k = 1 (4.119) Για τον προσδιορισμό των Ai,k a, Ba i,k, As i,k, Bs i,k πρέπει να είναι γνωστή, επακριβώς, η συνθήκη ακτινοβολίας στο άπειρο. Συμπερασματικά, αναφέρεται ότι αν και δεν κατέστη δυνατό να ολοκληρωθεί η επίλυση του γενικού προβλήματος της σφηνοειδούς γεωμετρίας μεταϋλικού άπειρων διαστάσεων εξαιτίας της μη γνώσης της συνθήκης ακτινοβολίας, προσδιορίστηκε, ωστόσο, ένα σύνολο συναρτήσεων που μπορεί να περιγράψει πλήρως το πεδίο. Τονίζεται ότι η γνώση των στοιχειωδών ρυθμών που υποστηρίζει μια γεωμετρία είναι απαραίτητη προϋπόθεση για την κατανόηση των φυσικών μηχανισμών που τη διέπουν και την ανάπτυξη σύνθετων διατάξεων που βασίζονται πάνω σε αυτήν. Επίσης, το σύνολο αυτό των συναρτήσεων μπορεί άμεσα να χρησιμοποιηθεί σε προβλήματα κλειστού ορίου που εμπλέκουν τη σφηνοειδή δομή, υπό την προϋπόθεση ότι είναι γνωστές οι οριακές συνθήκες Η περίπτωση ϵ r = µ r = 1 Μια ειδική, ωστόσο ενδιαφέρουσα, περίπτωση που δεν καλύπτεται από την ανάλυση των προηγούμενων ενοτήτων είναι η σφηνοειδής δομή διπλο-αρνητικού υλικού με καταστατικές παραμέτρους ϵ r = µ r = 1. Σημειώνεται ότι ένα τέτοιο διπλο-αρνητικό υλικό είναι τέλεια προσαρμοσμένο στον αέρα, δηλαδή ο συντελεστής ανάκλασης κάθε κύματος που προσπίπτει πάνω του είναι 0. Συνεπώς, το ακτινικό διάγραμμα του σχήματος 4.3 είναι ακριβές για φ > 3φ 0, με αποτέλεσμα να μπορεί να θεωρηθεί ότι παντού στον χώρο ισχύει η συνθήκη ακτινοβολίας (4.40). Ο μετασχηματισμός KL β είδους στην περίπτωση αυτή δίνεται για τη συμμετρική και την αντισυμμετρική διέγερση από τις σχέσεις sin[ν(π φ )] Ẽ a,(2) z Ẽ s,(2) z (ν; φ) = H(2) ν (k 0 ρ ) sin[ν(π 2φ 0 )] sin(νφ), αν 0 < φ < φ 0 ν sin[ν(φ < 2φ 0 )] sin[ν(π φ > )], αν φ 0 < φ < π sin[ν(π 2φ 0 )] cos[ν(π φ )] (ν; φ) = H(2) ν (k 0 ρ ) sin[ν(π 2φ 0 )] cos(νφ), αν 0 < φ < φ 0 ν cos[ν(φ < 2φ 0 )] cos[ν(π φ > )], αν φ 0 < φ < π sin[ν(π 2φ 0 )] (4.120α) (4.120β)
135 4.3. Σφηνοειδής δομή διπλο-αρνητικού υλικού 125 Σχήμα 4.14: Πραγματικό διάνυσμα Poyn ng σε μία δομή με παραμέτρους φ 0 = 15, φ = 55, ρ = 4λ 0 και ϵ r = µ r = 1. Η λευκή άσπρη γρμμή δηλωνει την επιφάνεια αέρα-μεταϋλικού και η χρωματική κλίμακα είναι βαθμονομημένη σε db. Σε πλήρη αναλογία με την (4.55), η εξίσωση sin[ν(π 2φ 0 )] = 0 δίνει τους πόλους του μετασχηματισμού KL, οι οποίοι είναι ν n = nπ/(π 2φ 0 ), με n = 0, ±1, ±2,.... Επίσης, υποθέτωντας ότι ν = ν e jψ και ν, η παράσταση που βρίσκεται δεξιά του όρου H (2) ν (k 0 ρ )/ν λαμβάνει την ασυμπτωτική έκφραση e ν sin ψ ( φ < 2φ 0 φ > +2φ 0 ), αν π > φ > φ 0, και e ν sin ψ (2φ 0 φ +φ), αν 0 < φ < φ 0. Κάθε μία από αυτές τις εκφράσεις είναι δυνατό να αποδειχθεί ότι τείνει εκθετικά προς το μηδέν, υπό την προϋπόθεση ότι φ > 3φ 0. Κατά συνέπεια, οι συναρτήσεις E a,(2) z (ν; φ), E s,(2) z (ν; φ) πολλαπλασιασμένες με τον όρο νj ν (k 0 ρ) μηδενίζονται πάνω στην καμπύλη C 3 του σχήματος 4.1 και το ολοκλήρωμα του αντίστροφου μετασχηματισμού KL συγκλίνει. Παραλείποντας τις λεπτομέρειες, αναφέρεται ότι το συνολικό πεδίο που παράγεται από τη γραμμική πηγή είναι το άθροισμα της αντισυμμετρικής και της συμμετρικής λύσης και δίνεται από την εξίσωση E z (ρ, φ) = jλ 0 2 ε(ν n )J νn (k 0 ρ < )H (2) n=0 ν n (k 0 ρ > ) cos[ν n (φ φ )], αν φ 0 < φ < 2π φ 0, (4.121) cos[ν n (2φ 0 φ φ )], αν φ < φ 0 Να σημειωθεί στο σημείο αυτό ότι το σύνολο των ρυθμών β ειδους περιγράφει πλήρως τη λύση λόγω της συνθήκης ακτινοβολίας (4.40) (με διαφορετικά λόγια, δεν χρειάζεται να χρησιμοποιήσουμε τους ρυθμούς α είδους στο ανάπτυγμα του πεδίου). Ακόμη, εύκολα εξάγεται ότι η συνολική ισχύς που ρέει προς το άπειρο είναι P = Λ 0 4ωµ 0 ε(ν n )Jν 2 n (k 0 ρ ), (4.122) n=0 ισούται με την ισχύ που εξέρχεται από την πηγή και είναι θετικός αριθμός. Το σχήμα 4.14 απεικονίζει το πραγματικό διάνυσμα Poyn ng μιας δομής με παραμέτρους φ 0 = 15, φ = 55, ρ = 4λ 0. Είναι φανερό πως η ροή της ισχύος είναι σε πολύ καλή συμφωνία με την ακτινική προσέγγιση.
11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ
 xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
Ασύρματη Μεταφορά Ενέργειας Αξιοποιώντας την Τεχνολογία των Μεταϋλικών
 1 st Energy Tech Forum Ανοικτή Συζήτηση για την Ενεργειακή Τεχνολογία και την Καινοτομία Ασύρματη Μεταφορά Ενέργειας Αξιοποιώντας την Τεχνολογία των Μεταϋλικών Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής
1 st Energy Tech Forum Ανοικτή Συζήτηση για την Ενεργειακή Τεχνολογία και την Καινοτομία Ασύρματη Μεταφορά Ενέργειας Αξιοποιώντας την Τεχνολογία των Μεταϋλικών Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής
Αξιοποίηση της Τεχνολογίας των Μεταϋλικών για Αποδοτικότερη Ασύρματη Μεταφορά Ενέργειας
 3 o Technology Forum Αξιοποίηση της Τεχνολογίας των Μεταϋλικών για Αποδοτικότερη Ασύρματη Μεταφορά Ενέργειας Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής 2, Δημήτριος Τζοβάρας 1 και Θεόδωρος Τσιμπούκης 2 1
3 o Technology Forum Αξιοποίηση της Τεχνολογίας των Μεταϋλικών για Αποδοτικότερη Ασύρματη Μεταφορά Ενέργειας Αντώνιος Λάλας 1, 2, Νικόλαος Κανταρτζής 2, Δημήτριος Τζοβάρας 1 και Θεόδωρος Τσιμπούκης 2 1
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΥΑΓΓΕΛΙΑΣ Π. ΛΟΥΚΟΓΕΩΡΓΑΚΗ Διπλωματούχου Πολιτικού Μηχανικού ΟΛΟΚΛΗΡΩΜΕΝΟ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΥΑΓΓΕΛΙΑΣ Π. ΛΟΥΚΟΓΕΩΡΓΑΚΗ Διπλωματούχου Πολιτικού Μηχανικού ΟΛΟΚΛΗΡΩΜΕΝΟ
ΚΕΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της FDTD
 ΚΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της DTD 4.. ισαγωγή Από τις τρεις µεθόδους πρόβλεψης των επενεργειών της ηλεκτροµαγνητικής ακτινοβολίας πειραµατική αναλυτική υπολογιστική- η υπολογιστική είναι η νεότερη
ΚΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της DTD 4.. ισαγωγή Από τις τρεις µεθόδους πρόβλεψης των επενεργειών της ηλεκτροµαγνητικής ακτινοβολίας πειραµατική αναλυτική υπολογιστική- η υπολογιστική είναι η νεότερη
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
«Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής»
 ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ. 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες... 7
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι. Για το 3ο εξάμηνο. ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ
 ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας)
 ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
Μεταϋλικά: μαθαίνοντας στο φως καινούργιες διαδρομές
 Μεταϋλικά: μαθαίνοντας στο φως καινούργιες διαδρομές Βασίλης Γιαννόπαπας Τμήμα Επιστήμης των Υλικών, Πανεπιστήμιο Πατρών Ημερίδα ΣΥ.ΚΑ.ΦΥ/ Ε.Κ.Φ., Λευκωσία, Κύπρος, 23-1-2012 Μεταϋλικά: μαθαίνοντας στο
Μεταϋλικά: μαθαίνοντας στο φως καινούργιες διαδρομές Βασίλης Γιαννόπαπας Τμήμα Επιστήμης των Υλικών, Πανεπιστήμιο Πατρών Ημερίδα ΣΥ.ΚΑ.ΦΥ/ Ε.Κ.Φ., Λευκωσία, Κύπρος, 23-1-2012 Μεταϋλικά: μαθαίνοντας στο
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
Βασικές διαδικασίες παραγωγής πολωμένου φωτός
 Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Συμπεράσματα Κεφάλαιο 7.
 7. ΣΥΜΠΕΡΑΣΜΑΤΑ Ο κύριος στόχος της παρούσας διατριβής ήταν η προσομοίωση της σεισμικής κίνησης με τη χρήση τρισδιάστατων προσομοιωμάτων για τους εδαφικούς σχηματισμούς της ευρύτερης περιοχής της Θεσσαλονίκης.
7. ΣΥΜΠΕΡΑΣΜΑΤΑ Ο κύριος στόχος της παρούσας διατριβής ήταν η προσομοίωση της σεισμικής κίνησης με τη χρήση τρισδιάστατων προσομοιωμάτων για τους εδαφικούς σχηματισμούς της ευρύτερης περιοχής της Θεσσαλονίκης.
Παρουσίαση 2 η : Αρχές εκτίμησης παραμέτρων Μέρος 1 ο
 Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Δ.-Θ. Κακλαμάνη, Καθηγήτρια ΕΜΠ Δρ. Σ. Καπελλάκη,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Δ.-Θ. Κακλαμάνη, Καθηγήτρια ΕΜΠ Δρ. Σ. Καπελλάκη,
ΑΣΚΗΣΗ 1. Περίληψη. Θεωρητική εισαγωγή. Πειραματικό μέρος
 ΑΣΚΗΣΗ 1 Περίληψη Σκοπός της πρώτης άσκησης ήταν η εξοικείωση μας με τα όργανα παραγωγής και ανίχνευσης των ακτίνων Χ και την εφαρμογή των κανόνων της κρυσταλλοδομής σε μετρήσεις μεγεθών στο οεργαστήριο.
ΑΣΚΗΣΗ 1 Περίληψη Σκοπός της πρώτης άσκησης ήταν η εξοικείωση μας με τα όργανα παραγωγής και ανίχνευσης των ακτίνων Χ και την εφαρμογή των κανόνων της κρυσταλλοδομής σε μετρήσεις μεγεθών στο οεργαστήριο.
ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διδάσκουσα: Δ.-Θ. Κακλαμάνη Web Sites: http://olympos.esd.ece.ntua.gr
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΓΙΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διδάσκουσα: Δ.-Θ. Κακλαμάνη Web Sites: http://olympos.esd.ece.ntua.gr
Δυναμική Μηχανών I. Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις. Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές
 Δυναμική Μηχανών I Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις 5 3 Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Δυναμική Μηχανών I Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις 5 3 Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Σήματα και Συστήματα
 Σήματα και Συστήματα Διάλεξη 12: Ιδιότητες του Μετασχηματισμού aplace Ο αντίστροφος Μετασχηματισμός aplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού aplace 1. Ιδιότητες
Σήματα και Συστήματα Διάλεξη 12: Ιδιότητες του Μετασχηματισμού aplace Ο αντίστροφος Μετασχηματισμός aplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού aplace 1. Ιδιότητες
Experiments are the only means of knowledge. Anyother is poetry and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΤΟΠΟΓΡΑΦΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΑΣΚΟΠΗΣΗ ΘΕΩΡΙΑΣ ΣΥΝΟΡΘΩΣΕΩΝ
 ΤΟΠΟΓΡΑΦΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΑΣΚΟΠΗΣΗ ΘΕΩΡΙΑΣ ΣΥΝΟΡΘΩΣΕΩΝ Βασίλης Δ. Ανδριτσάνος Δρ. Αγρονόμος - Τοπογράφος Μηχανικός ΑΠΘ Επίκουρος Καθηγητής ΤΕΙ Αθήνας 3ο εξάμηνο http://eclass.teiath.gr Παρουσιάσεις,
ΤΟΠΟΓΡΑΦΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΑΣΚΟΠΗΣΗ ΘΕΩΡΙΑΣ ΣΥΝΟΡΘΩΣΕΩΝ Βασίλης Δ. Ανδριτσάνος Δρ. Αγρονόμος - Τοπογράφος Μηχανικός ΑΠΘ Επίκουρος Καθηγητής ΤΕΙ Αθήνας 3ο εξάμηνο http://eclass.teiath.gr Παρουσιάσεις,
ΠΕΡΙΕΧΟΜΕΝΑ Σελίδα 1. Εισαγωγή Βασικές έννοιες Αγωγή
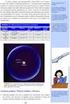 ΠΕΡΙΕΧΟΜΕΝΑ 1. Εισαγωγή Βασικές έννοιες 11 1.1 Εισαγωγή... 11 1.2 Μηχανισμοί μετάδοσης θερμότητας... 12 1.2.1 Αγωγή... 12 1.2.2 Συναγωγή... 13 1.2.3 Ακτινοβολία... 14 2. Αγωγή 19 2.1 Ο φυσικός μηχανισμός...
ΠΕΡΙΕΧΟΜΕΝΑ 1. Εισαγωγή Βασικές έννοιες 11 1.1 Εισαγωγή... 11 1.2 Μηχανισμοί μετάδοσης θερμότητας... 12 1.2.1 Αγωγή... 12 1.2.2 Συναγωγή... 13 1.2.3 Ακτινοβολία... 14 2. Αγωγή 19 2.1 Ο φυσικός μηχανισμός...
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ
 ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Φυσικής Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε Καλή αρχή Υπερηχογραφία Ανήκει στις τομογραφικές μεθόδους απεικόνισης Δεν έχει ιονίζουσα
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Φυσικής Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε Καλή αρχή Υπερηχογραφία Ανήκει στις τομογραφικές μεθόδους απεικόνισης Δεν έχει ιονίζουσα
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος.
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Πρόλογος. Κατάλογος Σχημάτων
 Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
Περιεχόμενα Πρόλογος Κατάλογος Σχημάτων v xv 1 ΜΔΕ πρώτης τάξης 21 1.1 Γενικότητες........................... 21 1.2 Εισαγωγή............................ 24 1.2.1 Γεωμετρικές θεωρήσεις στο πρόβλημα της
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΤΙΚΗ FOURIER. Γ. Μήτσου
 ΕΡΓΑΣΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΙΚΗΣ - ΟΠΟΗΛΕΚΡΟΝΙΚΗΣ & LASER ΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & /Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΙΚΗ FOURIER Γ. Μήτσου Μάρτιος 8 Α. Θεωρία. Εισαγωγή Η επεξεργασία οπτικών δεδοµένων, το φιλτράρισµα χωρικών συχνοτήτων
ΕΡΓΑΣΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΙΚΗΣ - ΟΠΟΗΛΕΚΡΟΝΙΚΗΣ & LASER ΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & /Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΙΚΗ FOURIER Γ. Μήτσου Μάρτιος 8 Α. Θεωρία. Εισαγωγή Η επεξεργασία οπτικών δεδοµένων, το φιλτράρισµα χωρικών συχνοτήτων
iωb = curl E. (Faraday s law) (2)
 Το φασματικό πρόβλημα σε μια διανισοτροπική κοιλότητα Ευτυχία Η. Αργυροπούλου, Ανδρέας Δ. Ιωαννίδης Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Linnaeus University, Σουηδία EME 2013, Καρδίτσα Ευτυχία
Το φασματικό πρόβλημα σε μια διανισοτροπική κοιλότητα Ευτυχία Η. Αργυροπούλου, Ανδρέας Δ. Ιωαννίδης Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Linnaeus University, Σουηδία EME 2013, Καρδίτσα Ευτυχία
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΑΝΑΛΥΣΗ FOURIER (H ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER) Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΑΝΑΛΥΣΗ FOURIER (H ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER) Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Χαρακτηρισμός και μοντέλα τρανζίστορ λεπτών υμενίων βιομηχανικής παραγωγής: Τεχνολογία μικροκρυσταλλικού πυριτίου χαμηλής θερμοκρασίας
 Χαρακτηρισμός και μοντέλα τρανζίστορ λεπτών υμενίων βιομηχανικής παραγωγής: Τεχνολογία μικροκρυσταλλικού πυριτίου χαμηλής θερμοκρασίας Υποψήφιος Διδάκτορας: Α. Χατζόπουλος Περίληψη Οι τελευταίες εξελίξεις
Χαρακτηρισμός και μοντέλα τρανζίστορ λεπτών υμενίων βιομηχανικής παραγωγής: Τεχνολογία μικροκρυσταλλικού πυριτίου χαμηλής θερμοκρασίας Υποψήφιος Διδάκτορας: Α. Χατζόπουλος Περίληψη Οι τελευταίες εξελίξεις
Περιοχές Ακτινοβολίας Κεραιών
 Κεραίες ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Δημοσθένης Βουγιούκας Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφοριακών & Επικοινωνιακών Συστημάτων Περιοχές Ακτινοβολίας Κεραιών 2 1 Σημειακή Πηγή 3 Κατακόρυφα Πολωμένο
Κεραίες ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Δημοσθένης Βουγιούκας Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφοριακών & Επικοινωνιακών Συστημάτων Περιοχές Ακτινοβολίας Κεραιών 2 1 Σημειακή Πηγή 3 Κατακόρυφα Πολωμένο
ΛΥΣΕΙΣ ΕΞΙΣΩΣΗΣ ΚΥΜΑΤΟΣ ΣΤΟΥΣ ΚΥΜΑΤΟΔΗΓΟΥΣ ΔΙΑΦΟΡΩΝ ΔΙΑΤΟΜΩΝ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
ΗΜ & Διάδοση ΗΜ Κυμάτων. Μηχανισμοί Διάδοσης ΗΜ Κυμάτων
 ΗΜ & Διάδοση ΗΜ Κυμάτων Μηχανισμοί Διάδοσης ΗΜ Κυμάτων Μηχανισμοί Διάδοσης Διάδοση Ελεύθερου Χώρου (Free Space ropagaton) Διάδοση ενός ΗΜ κύματος σε ένα ομοιογενές, χωρίς απώλειες και άπειρων διαστάσεων
ΗΜ & Διάδοση ΗΜ Κυμάτων Μηχανισμοί Διάδοσης ΗΜ Κυμάτων Μηχανισμοί Διάδοσης Διάδοση Ελεύθερου Χώρου (Free Space ropagaton) Διάδοση ενός ΗΜ κύματος σε ένα ομοιογενές, χωρίς απώλειες και άπειρων διαστάσεων
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών
 Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
Αριθμητική Ανάλυση & Εφαρμογές
 Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικής Ισχύος Εργαστήριο Υψηλών Τάσεων ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ (Αριθμητικές μέθοδοι υπολογισμού
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικής Ισχύος Εργαστήριο Υψηλών Τάσεων ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ (Αριθμητικές μέθοδοι υπολογισμού
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ. Ηλεκτροστατικοί και Μαγνητικοί Φακοί Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών
 ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ. Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής
 ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής Re Im V r V r i V r, όπου οι συναρτήσεις Re,Im V r V r είναι πραγματικές συναρτήσεις
ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής Re Im V r V r i V r, όπου οι συναρτήσεις Re,Im V r V r είναι πραγματικές συναρτήσεις
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Εφαρμοσμένη Οπτική. Περίθλαση Fraunhofer Περίθλαση Fresnel
 Εφαρμοσμένη Οπτική Περίθλαση Fraunhofer Περίθλαση Fresnel Περίθλαση - Ορισμός Περίθλαση είναι κάθε απόκλιση από την ευθύγραμμη διάδοση του φωτός, η οποία προκαλείται από παρεμβολή κάποιου εμποδίου. Στη
Εφαρμοσμένη Οπτική Περίθλαση Fraunhofer Περίθλαση Fresnel Περίθλαση - Ορισμός Περίθλαση είναι κάθε απόκλιση από την ευθύγραμμη διάδοση του φωτός, η οποία προκαλείται από παρεμβολή κάποιου εμποδίου. Στη
Αναγνώριση Προτύπων Ι
 Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Περιεχόμενα. σελ. Πρόλογος 1 ης Έκδοσης... ix Πρόλογος 2 ης Έκδοσης... xi Εισαγωγή... xiii
 Περιεχόμενα Πρόλογος 1 ης Έκδοσης... ix Πρόλογος 2 ης Έκδοσης... xi Εισαγωγή... xiii 1. Ειδικές συναρτήσεις 1.0 Εισαγωγή... 1 1.1 Εξίσωση του Laplace Συστήματα συντεταγμένων... 2 1.2 Συνάρτηση δ του Dirac...
Περιεχόμενα Πρόλογος 1 ης Έκδοσης... ix Πρόλογος 2 ης Έκδοσης... xi Εισαγωγή... xiii 1. Ειδικές συναρτήσεις 1.0 Εισαγωγή... 1 1.1 Εξίσωση του Laplace Συστήματα συντεταγμένων... 2 1.2 Συνάρτηση δ του Dirac...
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55
 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
& Εφαρμογές. (εργαστήριο) Μικροκύματα
 Μικροκύματα & Εφαρμογές (εργαστήριο) ΜΙΚΡΟΚΥΜΑΤΙΚΑ ΣΤΟΙΧΕΙΑ Στο κεφάλαιο αυτό γίνεται παρουσίαση των κυριότερων μικροκυματικών στοιχείων, που συνήθως χρησιμοποιούνται σε μικροκυματικές εφαρμογές στην περιοχή
Μικροκύματα & Εφαρμογές (εργαστήριο) ΜΙΚΡΟΚΥΜΑΤΙΚΑ ΣΤΟΙΧΕΙΑ Στο κεφάλαιο αυτό γίνεται παρουσίαση των κυριότερων μικροκυματικών στοιχείων, που συνήθως χρησιμοποιούνται σε μικροκυματικές εφαρμογές στην περιοχή
Κεφάλαιο 15 ΚίνησηΚυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 ΚίνησηΚυµάτων ΠεριεχόµεναΚεφαλαίου 15 Χαρακτηριστικά Κυµατικής Είδη κυµάτων: ιαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της ιάδοσης κυµάτων ΗΕξίσωσητουΚύµατος Κανόνας
Κεφάλαιο 15 ΚίνησηΚυµάτων ΠεριεχόµεναΚεφαλαίου 15 Χαρακτηριστικά Κυµατικής Είδη κυµάτων: ιαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της ιάδοσης κυµάτων ΗΕξίσωσητουΚύµατος Κανόνας
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ. και σε κάθε γειτονιά του z
 7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
Ο Μετασχηματισμός Ζ. Ανάλυση συστημάτων με το μετασχηματισμό Ζ
 Ο Μετασχηματισμός Ζ Ανάλυση συστημάτων με το μετασχηματισμό Ζ Ο μετασχηματισμός Z (Ζ-Τransform: ZT) χρήσιμο μαθηματικό εργαλείο για την ανάλυση των διακριτών σημάτων και συστημάτων αποτελεί ό,τι ο μετασχηματισμός
Ο Μετασχηματισμός Ζ Ανάλυση συστημάτων με το μετασχηματισμό Ζ Ο μετασχηματισμός Z (Ζ-Τransform: ZT) χρήσιμο μαθηματικό εργαλείο για την ανάλυση των διακριτών σημάτων και συστημάτων αποτελεί ό,τι ο μετασχηματισμός
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
ΚΥΡΙΑ ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Εργαστηριακοί Συνεργάτες: Σ. ΒΑΣΙΛΕΙΑΔΟΥ, Α. ΟΙΚΟΝΟΜΙΔΗΣ,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Εργαστηριακοί Συνεργάτες: Σ. ΒΑΣΙΛΕΙΑΔΟΥ, Α. ΟΙΚΟΝΟΜΙΔΗΣ,
ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ 1 ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ( t ) Χρονική εξίσωση απομάκρυνσης a ( t ) με a Χρονική εξίσωση ταχύτητας a aa ( t ) με a a Χρονική εξίσωση επιτάχυνσης a Σχέση
ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ( t ) Χρονική εξίσωση απομάκρυνσης a ( t ) με a Χρονική εξίσωση ταχύτητας a aa ( t ) με a a Χρονική εξίσωση επιτάχυνσης a Σχέση
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2. ΣΤΟΙΧΕΙΑ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 1.1 Εισαγωγή 1.1 1.2 Συμβολισμοί και μονάδες 1.3 1.3 Φορτίο, τάση και ενέργεια 1.5 Φορτίο και ρεύμα 1.5 Τάση 1.6 Ισχύς και Ενέργεια 1.6 1.4 Γραμμικότητα 1.7 Πρόσθεση
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 1.1 Εισαγωγή 1.1 1.2 Συμβολισμοί και μονάδες 1.3 1.3 Φορτίο, τάση και ενέργεια 1.5 Φορτίο και ρεύμα 1.5 Τάση 1.6 Ισχύς και Ενέργεια 1.6 1.4 Γραμμικότητα 1.7 Πρόσθεση
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
ΠΟΩΤΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΔΤΝΑΜΙΚΗΣ ΜΗΧΑΝΩΝ
 ΡΙΣΤΟΤΕΩΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΟΕΣΣΑΩΟΝΙΚΗΣ ΠΟΩΤΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΤΑΣΚΕΤΑΣΤΙΚΟΣ ΤΟΜΕΑΣ ΕΡΓΑΣΤΗΡΙΟ ΔΤΝΑΜΙΚΗΣ ΜΗΧΑΝΩΝ Γεωργία N. Γεωργίου Διπλ. Μηχανολόγος Μηχανικός A.Π.O. ΙΖΡΟΣΔΙΟΡΙΣΜΟΣ
ΡΙΣΤΟΤΕΩΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΟΕΣΣΑΩΟΝΙΚΗΣ ΠΟΩΤΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΤΑΣΚΕΤΑΣΤΙΚΟΣ ΤΟΜΕΑΣ ΕΡΓΑΣΤΗΡΙΟ ΔΤΝΑΜΙΚΗΣ ΜΗΧΑΝΩΝ Γεωργία N. Γεωργίου Διπλ. Μηχανολόγος Μηχανικός A.Π.O. ΙΖΡΟΣΔΙΟΡΙΣΜΟΣ
AΠΟΦΑΣΗ της από 3/4/2012 Συνεδρίασης του Δ.Σ. του Τμήματος Φυσικής. ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Για το 5ο εξάμηνο
 ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Ι. Ηλεκτρικό φορτίο-διατήρηση φορτίου-κβάντωση φορτίου-νόμος Coulomb-Ενέργεια συστήματος φορτίων-ηλεκτρικό πεδίο-κατανομές φορτίου-ροή, Νόμος Gauss. ΙΙ. Ηλεκτρικό
ΕΞΕΤΑΣΤΕΑ ΥΛΗ ΦΥΣΙΚΗΣ ΙΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ) Ι. Ηλεκτρικό φορτίο-διατήρηση φορτίου-κβάντωση φορτίου-νόμος Coulomb-Ενέργεια συστήματος φορτίων-ηλεκτρικό πεδίο-κατανομές φορτίου-ροή, Νόμος Gauss. ΙΙ. Ηλεκτρικό
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
ΗΜ & Διάδοση ΗΜ Κυμάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα 3: Μηχανισμοί Διάδοσης ΗΜ Κυμάτων Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα 3: Μηχανισμοί Διάδοσης ΗΜ Κυμάτων Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
ΚΥΜΑΤΟ ΗΓΗΣΗ. «Μικροοπτικές διατάξεις-ολοκληρωµένα οπτικά»
 ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
«ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ»
 ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
6 Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας
 Πρόλογος Σ το βιβλίο αυτό περιλαμβάνεται η ύλη του μαθήματος «Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας» που διδάσκεται στους φοιτητές του Γ έτους σπουδών του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Πρόλογος Σ το βιβλίο αυτό περιλαμβάνεται η ύλη του μαθήματος «Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας» που διδάσκεται στους φοιτητές του Γ έτους σπουδών του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Μεταβατική Ανάλυση - Φάσορες. Κατάστρωση διαφορικών εξισώσεων. Μεταβατική απόκριση. Γενικό μοντέλο. ,, ( ) είναι γνωστές ποσότητες (σταθερές)
 Μεταβατική Ανάλυση - Φάσορες Πρόσθετες διαφάνειες διαλέξεων Αλέξανδρος Πίνο Δεκέμβριος 2017 Γενικό μοντέλο Απόκριση κυκλώματος πρώτης τάξης, δηλαδή με ένα μόνο στοιχείο C ή L 3 Μεταβατική απόκριση Ξαφνική
Μεταβατική Ανάλυση - Φάσορες Πρόσθετες διαφάνειες διαλέξεων Αλέξανδρος Πίνο Δεκέμβριος 2017 Γενικό μοντέλο Απόκριση κυκλώματος πρώτης τάξης, δηλαδή με ένα μόνο στοιχείο C ή L 3 Μεταβατική απόκριση Ξαφνική
Περιεχόμενα. 1. Ειδικές συναρτήσεις. 2. Μιγαδικές Συναρτήσεις. 3. Η Έννοια του Τελεστή. Κεφάλαιο - Ενότητα
 Περιεχόμενα Κεφάλαιο - Ενότητα σελ 1. Ειδικές συναρτήσεις 1.0 Εισαγωγή 1.1 Εξίσωση του Laplace Συστήματα συντεταγμένων 1.2 Συνάρτηση δ του Dirac 1.3 Συνάρτηση του Heaviside 1.4 Οι συναρτήσεις Β, Γ και
Περιεχόμενα Κεφάλαιο - Ενότητα σελ 1. Ειδικές συναρτήσεις 1.0 Εισαγωγή 1.1 Εξίσωση του Laplace Συστήματα συντεταγμένων 1.2 Συνάρτηση δ του Dirac 1.3 Συνάρτηση του Heaviside 1.4 Οι συναρτήσεις Β, Γ και
ΜΔΕ: Αναλυτικό πρόγραμμα - Ύλη Μαθήματος 2018
 1 ΚΕΦΑΛΑΙΟ 1 ΜΔΕ: Αναλυτικό πρόγραμμα - Ύλη Μαθήματος 2018 Αντικείμενο του μαθήματος είναι η μελέτη Μερικών Διαφορικών Εξισώσεων. Τον όρο Μερική Διαφορική Εξίσωση θα συμβολίζουμε με (ΜΔΕ). Η ιστοσελίδα
1 ΚΕΦΑΛΑΙΟ 1 ΜΔΕ: Αναλυτικό πρόγραμμα - Ύλη Μαθήματος 2018 Αντικείμενο του μαθήματος είναι η μελέτη Μερικών Διαφορικών Εξισώσεων. Τον όρο Μερική Διαφορική Εξίσωση θα συμβολίζουμε με (ΜΔΕ). Η ιστοσελίδα
Το μαθηματικό μοντέλο της FDTD (1)
 (Fe Dfferece - Tme Doma) Το μαθηματικό μοντέλο της FDTD () Η FDTD αποτελεί μια από τις πιο δημοφιλείς μεθόδους για την αριθμητική επίλυση των εξισώσεων του Mawell. Το μαθηματικό της μοντέλο βασίζεται στη
(Fe Dfferece - Tme Doma) Το μαθηματικό μοντέλο της FDTD () Η FDTD αποτελεί μια από τις πιο δημοφιλείς μεθόδους για την αριθμητική επίλυση των εξισώσεων του Mawell. Το μαθηματικό της μοντέλο βασίζεται στη
2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier
 2.1 2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier 2.1 Εισαγωγή Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια της μεθόδου Fourier συνίσταται στο ότι μία κυματομορφή μιας οποιασδήποτε
2.1 2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier 2.1 Εισαγωγή Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια της μεθόδου Fourier συνίσταται στο ότι μία κυματομορφή μιας οποιασδήποτε
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. ΜΕΡΟΣ Α : Άλγεβρα. Κεφάλαιο 2 ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Ειδικότερα:
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
