Θεώρημα κωδικοποίησης πηγής
|
|
|
- Δείμος Καρράς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Κωδικοποίηση
2 Kωδικοποίηση πηγής
3 Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα σφάλματος Shannon 1948
4 Τυπικές και μη τυπικές ακολουθίες Έξοδος πηγής DMS μεγάλου μήκους n Το σύμβολο x 1 επαναλαμβάνεται περίπου np 1 φορές Το σύμβολο x 2 επαναλαμβάνεται περίπου np 2 φορές Το σύμβολο x Ν επαναλαμβάνεται περίπου np Ν φορές
5 Τυπικές και μη τυπικές ακολουθίες Με πιθανότητα σχεδόν 1 όλες οι ακολουθίες έχουν την ίδια σύνθεση Σχεδόν όλες οι ακολουθίες είναι περίπου ισοπίθανες! (τυπικές ακολουθίες) p( X = x) i= 1 N n p log p np log p nh ( X ) i= 1 N p np i = = = i i i i i i= N
6 Τυπικές και μη τυπικές ακολουθίες Η πιθανότητα εμφάνισης των μη τυπικών ακολουθιών είναι αμελητέα Ο συνολικός αριθμός τυπικών ακολουθιών είναι ( ) περίπου 2 nh X παρόλο που η πηγή μπορεί να παράγει N n ακολουθίες Για πρακτικούς λόγους αρκεί να λάβουμε υπόψητοσύνολοτυπικών ακολουθιών αντί του συνόλου όλων των δυνατών ακολουθιών εξόδων της πηγής
7 Τυπικές και μη τυπικές ακολουθίες
8 Συμπίεση δεδομένων Επιλέγοντας αρκετά μεγάλο n, το σφάλμα που προκύπτει εάν αγνοήσουμε τις μη τυπικές ακολουθίες μπορεί να γίνει μικρότερο από κάθε ε>0 Συμπίεση δεδομένων Αναπαράσταση της εξόδου μια πηγής με ένα μικρότερο αριθμό ακολουθιών από ότι παράγει η πηγή στην πραγματικότητα
9 Συμπίεση δεδομένων Χρειαζόμαστε nh(x) bit για την αναπαράσταση του συνόλου των τυπικών ακολουθιών Πλήθος τυπικών ακολουθιών Πλήθος δυνατών ακολουθιών N n ( ) 2 nh X Απαιτούνται H(X) bit ανά σύμβολο! Ησυμπίεσηδενείναιδυνατήεάντασύμβολα είναι ισοπίθανα Για ισοπίθανα σύμβολα H(X)=log(N) και nh ( X ) = n log( N ) = N n 2 2
10 Πηγές με μνήμη Εάν η πηγή έχει μνήμη, τότε οι έξοδοι δεν είναι ανεξάρτητες και για αυτό φανερώνουν πληροφορία για τις επόμενες εξόδους Για παράδειγμα στην αγγλική γλώσσα το q σχεδόν πάντα ακολουθείται από u ένα γράμμα μεταξύ δύο κενών είναι το I ήτο a
11 Πηγές με μνήμη Για πηγές με μνήμη μας ενδιαφέρει ο ρυθμός εντροπίας H( Xn X1, X2,..., Xn 1) Στην αγγλική γλώσσα (26 γράμματα και το κενό διάστημα) για n=1 ηεντροπίαείναι4,03 bit/γράμμα και ο ρυθμός εντροπίας (n ) είναι 1,3 bit/γράμμα
12 Θεώρημα κωδικοποίησης πηγής Μια πηγή (ρυθμού) εντροπίας H μπορεί να κωδικοποιηθεί με αυθαίρετα μικρή πιθανότητα σφάλματος σε οποιοδήποτε ρυθμό R, εφόσον R>H Αντίστροφα, εάν R<H η πιθανότητα σφάλματος θα παραμένει μακριά από το μηδέν, ανεξάρτητα από την πολυπλοκότητα του κωδικοποιητή
13 Αλγόριθμοι κωδικοποίησης πηγής Το θεώρημα κωδικοποίησης πηγής δίνει μόνο αναγκαίες και ικανές συνθήκες για την ύπαρξη κωδίκων πηγής Δεν περιγράφει κανένα αλγόριθμο για τη σχεδίαση Δίνει ένα φράγμα στο ρυθμό με τον οποίο μπορεί να κωδικοποιηθεί μια πηγής Δύο γνωστοί αλγόριθμοι σχεδίασης κωδίκων που δίνουν αποτελέσματα κοντά στο φράγμα εντροπίας Huffman (1952) Lempel-Ziv (1977,1978) ZIP,ZOO,ARJ
14 Συνάρτηση ρυθμού - παραμόρφωσης
15 Κωδικοποίηση με απώλειες Έστω ότι μετάδοση με ρυθμούς κοντά σε αυτόν της εντροπίας δεν είναι δυνατή Μπορούμε να συμπιέσουμε την έξοδο μιας πηγής αποδεχόμενοι απώλειες και κάποια παραμόρφωση Παράδειγμα: η κωδικοποίηση της εξόδου αναλογικής πηγής Τα δείγματα είναι πραγματικοί αριθμοί Άπειρος αριθμός bit Κβάντιση και κωδικοποίηση των κβαντισμένων τιμών
16 Το βασικό πρόβλημα Υποθέστε ότι ζητείται να μεταδοθεί πληροφορία μετά από συμπίεση της εξόδου της πηγής σε ορισμένο ρυθμό bit/σύμβολο Πόσο κοντά είναι η συμπιεσμένη εκδοχή στην αρχική; Για δεδομένο ρυθμό, ποιος είναι ο ελάχιστος ρυθμός σφαλμάτων και πώς μπορεί να επιτευχθεί; Ποιος είναι ο ελάχιστος αριθμός bit ανά έξοδο για καθορισμένο επίπεδο παραμόρφωσης;
17 Παραμόρφωση Υπάρχουν διάφορα μέτρα της παραμόρφωσης, δηλαδή, τουπόσοαπέχειτοσήμααπότην αναπαραγωγή του Hamming d H (,) x xˆ 1, x xˆ = 0, αλλιώς Τετραγωνικού σφάλματος d ( x, xˆ) = ( x xˆ) H 2
18 Παραμόρφωση Για ακολουθία συμβόλων, ως παραμόρφωση ορίζουμε τη μέση παραμόρφωση ανά σύμβολο Η θέση του σφάλματος δεν είναι σημαντική Η παραμόρφωση δεν εξαρτάται από τα συμφραζόμενα ˆ 1 n d( XX, ) = d( X, Xˆ ) n = i 1 Η παραμόρφωση της πηγής είναι η αναμενόμενη τιμή της ως άνω τυχαίας μεταβλητής ˆ 1 D= Ed {( XX, )} = EdX {(, Xˆ )} = EdXX {(, ˆ)} n n i = 1 i i i i
19 Παραμόρφωση Hamming Στην περίπτωση που ως μέτρο χρησιμοποιείται η παραμόρφωση Hamming, η παραμόρφωση D της πηγής είναι η πιθανότητα σφάλματος D= E{ d ( X, Xˆ)} = 1 p{ X Xˆ} + 0 p{ X = Xˆ} H = px { Xˆ } = p{λάθος}
20 Συνάρτηση ρυθμού - παραμόρφωσης Δοθείσης μιας πηγής πληροφορίας χωρίς μνήμη, τουαλφάβητουπουπαράγει, του αλφάβητου αναπαραγωγής της και του μέτρου παραμόρφωσης, ποιος είναι ο ρυθμός R bit/σύμβολο για παραμόρφωση D; ΟρυθμόςR είναι ο ελάχιστος αριθμός bit ανά έξοδο της πηγής που εξασφαλίζει την απαιτούμενη μέση παραμόρφωση ΗσχέσημεταξύR και D είναι η συνάρτηση ρυθμού παραμόρφωσης R(D)
21 Θεώρημα ρυθμού - παραμόρφωσης Ο ελάχιστος αριθμός bit ανά έξοδο πηγής που απαιτείται για αναπαραγωγή μιας πηγής χωρίς μνήμη με παραμόρφωση μικρότερη από D είναι RD ( ) = min I( X; Xˆ ) p( xx ˆ ): E{ d( X, Xˆ )} D R(D) είναι φθίνουσα συνάρτηση της D Υψηλή πιστότητα (μικρή D) απαιτεί μεγάλο R
22 Θεώρημα ρυθμού - παραμόρφωσης Για δεδομένο ρυθμό ελάχιστη επιτεύξιμη παραμόρφωση Για δεδομένη παραμόρφωση ελάχιστος ρυθμός
23 Δυαδική πηγή χωρίς μνήμη Η συνάρτηση ρυθμού-παραμόρφωσης της δυαδικής πηγής χωρίς μνήμη είναι H ( p) H ( D), 0 D min{ p,1 p} b b RD ( ) = 0, αλλιώς Για μηδενική παραμόρφωση, ως αναμένεται R(0) = H ( p) b Για p<0,5 και D=p έχουμε R(D)=0 Δεν χρειάζεται μετάδοση (όλα μηδέν)
24 Δυαδική πηγή χωρίς μνήμη
25 Γκαουσιανή πηγή Η συνάρτηση ρυθμού-παραμόρφωσης της γκαουσιανής πηγής είναι 2 1 σ log, 0 D RD ( ) = 2 D 0, αλλιώς 2 σ 2 Για 0 D σ η αντίστροφη συνάρτηση παραμόρφωσης-ρυθμού είναι 2 2 DR ( ) = σ 2 R άρα αύξηση του R κατά ένα bit μειώνει την παραμόρφωση D κατά 4 (6 db)
26 Γκαουσιανή πηγή
27 Κβάντιση
28 Κβαντιστές Η ακριβής αναπαράσταση μιας αναλογικής πηγής απαιτεί άπειρο αριθμό bit ανά έξοδο Με την κβάντιση θα εμφανισθεί κάποια παραμόρφωση Ησυνάρτησηρυθμού-παραμόρφωσης δίνει ένα θεμελιώδες όριο Ανταλλαγή ρυθμού κωδικοποίησης και παραμόρφωσης Προσεγγίζεται μόνο ασυμπτωτικά με περίπλοκους κωδικοποιητές/αποκωδικοποιητές
29 Κβαντιστές Όσο μεγαλύτερη η τιμή του n τόσο πιο κοντά στο όριο της συνάρτησης ρυθμούπαραμόρφωσης Οι κβαντιστές πρέπει να κβαντίζουν τις εξόδους κατά μπλοκ και όχι χωριστά Διανυσματικοί κβαντιστές Κβάντιση των εξόδων σε μπλοκ Βαθμωτοί κβαντιστές Κβάντιση κάθε εξόδου χωριστά
30 Βαθμωτή κβάντιση Το σύνολο των πραγματικών αριθμών R διαμερίζεται σε Ν ξένα μεταξύ τους σύνολα R k, k=1,2,, N Για κάθε υποσύνολο R k επιλέγεται ένα αντιπροσωπευτικό του στοιχείο x i Εάν η έξοδος της πηγής τη χρονική στιγμή i ανήκει στο R k τότε αναπαρίσταται με x, που αποτελεί την ˆi κβαντισμένηεκδοχήτου x Το στη συνέχεια αναπαρίσταται με μια δυαδική ακολουθία, η ˆi οποία και μεταδίδεται Ο ρυθμός μετάδοσης είναι R = log Ν bit συνήθως το N επιλέγεται να είναι δύναμη του δύο x ˆi
31 Ομοιόμορφη κβάντιση
32 Λόγος σήματος προς θόρυβο κβάντισης Είναι η ισχύς του σήματος προς την ισχύ του σήματος θορύβου Qx ( ) = xˆ, x R i dxx (,) ˆ = x Qx () ( ) D= E{( d X, Xˆ )} = E X Q( X) i { 2 } {( ( 2 )) } {( ) 2 } EX P SNQR = = E X Q X P Μέτρο της επίδοσης του κβαντιστή 2 X Xˆ
33 Παραμόρφωση στην ομοιόμορφη κβάντιση Η παραμόρφωση του ομοιόμορφου κβαντιστή a D 1 x x 2 f x dx = ( ˆ ) ( ) + N ( ˆ ) ( ) + a1 + ( i 1) q i+ 1 x i= 1 1 a + iq 1 ( ˆ ) 2 ( ) a + ( N 2) q N x x x x f xdx + x x f x dx
34 Παραμόρφωση στην μη ομοιόμορφη κβάντιση Η παραμόρφωση του μη ομοιόμορφου κβαντιστή a D 1 x x 2 f x dx = ( ˆ ) ( ) + N 2 + i ai i+ 1 x i= 1 N 1 a 1 ( x xˆ ) f ( x) dx ( ˆ ) 2 ( ) a N x + x x f x dx x
35 Βέλτιστος κβαντιστής Για την ελαχιστοποίηση της D παραγωγίζοντας ως προς α i βρίσκουμε xˆ + xˆ a = i i+ i 2 1 Τα άκρα των περιοχών κβάντισης είναι η μέση τιμή των γειτονικών σταθμών κβάντισης
36 Βέλτιστος κβάντιστης Για τα προηγούμενα όρια περιοχών παραγωγίζοντας την D ως προς βρίσκουμε xˆ i = a a i i 1 a a i i 1 xf f x x ( x) dx ( x) dx = xf ( x a < x a ) dx x i 1 i = E{ x a < x a} i 1 Οι στάθμες κβάντισης είναι τα κέντρα μάζης των περιοχών κβάντισης i xˆi
37 Διανυσματική κβάντιση Λαμβάνουμε τα δείγματα σε ομάδες των n δειγμάτων κάθε φορά Ο χώρος των δειγμάτων είναι R n και χωρίζεται σε K περιοχές R i Απαιτούνται logk bit ανά ομάδα, οπότε ο ρυθμός είναι R log K = n Ο βέλτιστος διανυσματικός κβαντιστής προκύπτει επιλέγοντας τις περιοχές κβάντιστης και τις τιμές κβάντισης έτσι ώστε να ελαχιστοποιείται η παραμόρφωση
38 Παράδειγμα διανυσματικής κβάντισης K=37, n=2
39 Παράδειγμα διανυσματικής κβάντισης Βαθμωτός κβαντιστής 4 σταθμών και διανυσματικός κβαντιστής 4 σταθμών σε δύο δείγματα
Ψηφιακές Τηλεπικοινωνίες. Θεωρία Ρυθμού Παραμόρφωσης
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
ιαφορική εντροπία Σεραφείµ Καραµπογιάς
 ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
( ) log 2 = E. Σεραφείµ Καραµπογιάς
 Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Κωδικοποίηση Πηγής Ψηφιακή Μετάδοση Υπάρχουν ιδιαίτερα εξελιγμένες τεχνικές αναλογικής μετάδοσης (που ακόμη χρησιμοποιούνται σε ορισμένες εφαρμογές) Επίσης,
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Κωδικοποίηση Πηγής Ψηφιακή Μετάδοση Υπάρχουν ιδιαίτερα εξελιγμένες τεχνικές αναλογικής μετάδοσης (που ακόμη χρησιμοποιούνται σε ορισμένες εφαρμογές) Επίσης,
0, αλλιώς. Σεραφείµ Καραµπογιάς. Παράδειγµα 1 Η πηγή X(t) είναι στατική Gaussian µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος.
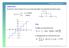 Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Εισαγωγή στη θεωρία πληροφορίας
 Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 5: Pulse Code Modulation (PCM) Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Γνωριμία με την περισσότερο εφαρμοζόμενη
Συστήματα Επικοινωνιών Ενότητα 5: Pulse Code Modulation (PCM) Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Γνωριμία με την περισσότερο εφαρμοζόμενη
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Κώστας Μπερμπερίδης Εργαστήριο Σημάτων & Τηλεπικοινωνιών Τμήμα Μηχανικών Η/Υ & Πληροφορικής Ψηφιακή Αναπαράσταση Συμπίεση
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Κώστας Μπερμπερίδης Εργαστήριο Σημάτων & Τηλεπικοινωνιών Τμήμα Μηχανικών Η/Υ & Πληροφορικής Ψηφιακή Αναπαράσταση Συμπίεση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
ΣΤOIΧΕΙΑ ΑΠΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και PCM
 ΣΤOIΧΕΙΑ ΑΠΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και PCM ΠΗΓΗ ΜΕ ΔΙΑΚΡΙΤΑ ΣΥΜΒΟΛΑ Τα στοιχεία της ακολουθίας των συμβόλων Διακριτή Πηγή Χωρίς Μνήμη-DMS Σύμβολα μεταξύ τους στατιστικά ανεξάρτητα: (X i =α k & X j =α l )=
ΣΤOIΧΕΙΑ ΑΠΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και PCM ΠΗΓΗ ΜΕ ΔΙΑΚΡΙΤΑ ΣΥΜΒΟΛΑ Τα στοιχεία της ακολουθίας των συμβόλων Διακριτή Πηγή Χωρίς Μνήμη-DMS Σύμβολα μεταξύ τους στατιστικά ανεξάρτητα: (X i =α k & X j =α l )=
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
Μάθημα 7 ο. Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
1 Βασικές Έννοιες Θεωρίας Πληροφορίας
 1 Βασικές Έννοιες Θεωρίας Πληροφορίας Εντροπία τυχαίων μεταβλητών X, Y : H(X) = E [log Pr(x)] (1) H(X, Y ) = E [log Pr(x, y)] (2) H(X Y ) = E [log Pr(x y)] (3) Ιδιότητες Εντροπίας: Νόμος Bayes: Pr(y x)
1 Βασικές Έννοιες Θεωρίας Πληροφορίας Εντροπία τυχαίων μεταβλητών X, Y : H(X) = E [log Pr(x)] (1) H(X, Y ) = E [log Pr(x, y)] (2) H(X Y ) = E [log Pr(x y)] (3) Ιδιότητες Εντροπίας: Νόμος Bayes: Pr(y x)
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Κωδικοποίηση καναλιού Τι θα δούμε στο μάθημα Σύντομη εισαγωγή Γραμμικοί κώδικες
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Κωδικοποίηση καναλιού Τι θα δούμε στο μάθημα Σύντομη εισαγωγή Γραμμικοί κώδικες
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια. Παράδοση: Έως 22/6/2015
 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 7 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 7 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας. Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
Τεχνολογία Πολυμέσων. Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Διαδικασία Ψηφιοποίησης (1/2)
 Διαδικασία Ψηφιοποίησης (1/2) Η διαδικασία ψηφιοποίησης περιλαμβάνει: Φιλτράρισμα και δειγματοληψία Κβαντισμό και κωδικοποίηση Φιλτράρισμα και δειγματοληψία Κβαντισμός και κωδικοποίηση Κβαντισμός Τα αναλογικά
Διαδικασία Ψηφιοποίησης (1/2) Η διαδικασία ψηφιοποίησης περιλαμβάνει: Φιλτράρισμα και δειγματοληψία Κβαντισμό και κωδικοποίηση Φιλτράρισμα και δειγματοληψία Κβαντισμός και κωδικοποίηση Κβαντισμός Τα αναλογικά
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Κβάντιση και Κωδικοποίηση ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Χειμερινό Εξάμηνο Τμήμα Πληροφορικής και Τηλεπικοινωνίων Νικόλαος Χ. Σαγιάς Αναπληρωτής Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Κβάντιση και Κωδικοποίηση ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Χειμερινό Εξάμηνο Τμήμα Πληροφορικής και Τηλεπικοινωνίων Νικόλαος Χ. Σαγιάς Αναπληρωτής Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 5: Βασική Θεωρία Πληροφορίας Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θέματα Συστημάτων Πολυμέσων Ενότητα # 5: Βασική Θεωρία Πληροφορίας Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o
 Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Θεωρία πληροφοριών. Τεχνολογία Πολυµέσων 07-1
 Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
Μετάδοση σήματος PCM
 Μετάδοση σήματος PCM Θόρυβος κατά τη μετάδοση Εύρος ζώνης μετάδοσης Το (διαμορφωμένο) σήμα PCM όταν μεταδίδεται μέσω του διαύλου είναι ένα σήμα συνεχούς χρόνου και έχει το δικό του εύρος ζώνης Το εύρος
Μετάδοση σήματος PCM Θόρυβος κατά τη μετάδοση Εύρος ζώνης μετάδοσης Το (διαμορφωμένο) σήμα PCM όταν μεταδίδεται μέσω του διαύλου είναι ένα σήμα συνεχούς χρόνου και έχει το δικό του εύρος ζώνης Το εύρος
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Θ.Ε. ΠΛΗ22 (2012-13) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #4. Έκδοση v2 με διόρθωση τυπογραφικού λάθους στο ερώτημα 6.3 Στόχος: Βασικό στόχο της 4 ης εργασίας αποτελεί η εξοικείωση με τα μέτρα ποσότητας πληροφορίας τυχαίων
Θ.Ε. ΠΛΗ22 (2012-13) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #4. Έκδοση v2 με διόρθωση τυπογραφικού λάθους στο ερώτημα 6.3 Στόχος: Βασικό στόχο της 4 ης εργασίας αποτελεί η εξοικείωση με τα μέτρα ποσότητας πληροφορίας τυχαίων
Δυαδικά Αντίποδα Σήματα. Προχωρημένα Θέματα Τηλεπικοινωνιών. Πιθανότητα Σφάλματος σε AWGN Κανάλι. r s n E n. P r s P r s.
 Προχωρημένα Θέματα Τηλεπικοινωνιών Πιθανότητα Σφάλματος σε AWGN Κανάλι Δυαδικά Αντίποδα Σήματα Δυαδικά Αντίποδα Σήματα Βασικής Ζώνης) : s (t)=-s (t) Παράδειγμα: Δυαδικό PA s (t)=g T (t) (παλμός με ενέργεια
Προχωρημένα Θέματα Τηλεπικοινωνιών Πιθανότητα Σφάλματος σε AWGN Κανάλι Δυαδικά Αντίποδα Σήματα Δυαδικά Αντίποδα Σήματα Βασικής Ζώνης) : s (t)=-s (t) Παράδειγμα: Δυαδικό PA s (t)=g T (t) (παλμός με ενέργεια
Μετάδοση πληροφορίας - Διαμόρφωση
 Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Σεραφείµ Καραµπογιάς. Πηγές Πληροφορίας και Κωδικοποίηση Πηγής 6.3-1
 Ο αλγόριθµος Lempel-iv Ο αλγόριθµος Lempel-iv ανήκει στην κατηγορία των καθολικών universal αλγορίθµων κωδικοποίησης πηγής δηλαδή αλγορίθµων που είναι ανεξάρτητοι από τη στατιστική της πηγής. Ο αλγόριθµος
Ο αλγόριθµος Lempel-iv Ο αλγόριθµος Lempel-iv ανήκει στην κατηγορία των καθολικών universal αλγορίθµων κωδικοποίησης πηγής δηλαδή αλγορίθµων που είναι ανεξάρτητοι από τη στατιστική της πηγής. Ο αλγόριθµος
Μετάδοση πληροφορίας - Διαμόρφωση
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πιθανότητες Πληροφορία Μέτρο
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πιθανότητες Πληροφορία Μέτρο
Καναλιού. Καναλιού. Προχωρημένα Θέματα Τηλεπικοινωνιών. Κατηγορίες Κωδικών Καναλιού. Τι πετυχαίνει η Κωδ. Καναλιού. Κωδικοποίηση Καναλιού.
 Προχωρημένα Θέματα Τηλεπικοινωνιών Πηγή Δεδομένων Κωδικοποίηση Καναλιού Κώδικας Πηγής Κώδικας Καναλιού Διαμόρφωση Κανάλι Δέκτης Δεδομένων Αποκωδ/ση Πηγής Αποκωδ/ση Καναλιού Αποδιαμόρφωση Κωδικοποίηση Καναλιού
Προχωρημένα Θέματα Τηλεπικοινωνιών Πηγή Δεδομένων Κωδικοποίηση Καναλιού Κώδικας Πηγής Κώδικας Καναλιού Διαμόρφωση Κανάλι Δέκτης Δεδομένων Αποκωδ/ση Πηγής Αποκωδ/ση Καναλιού Αποδιαμόρφωση Κωδικοποίηση Καναλιού
ΚΩΔΙΚΟΠΟΙΗΣΗ ΕΛΕΓΧΟΥ ΣΦΑΛΜΑΤΟΣ (2)
 ΚΩΔΙΚΟΠΟΙΗΣΗ ΕΛΕΓΧΟΥ ΣΦΑΛΜΑΤΟΣ () P e συνάρτηση των S/N και r b (B) Συμβάσεις κανονισμοί για τα S, B Φασματική πυκνότητα θορύβου καθορισμένη Πολυπλοκότητα και κόστος συστήματος ΚΩΔΙΚΟΠΟΙΗΣΗ ΚΑΝΑΛΙΟΥ Καλά
ΚΩΔΙΚΟΠΟΙΗΣΗ ΕΛΕΓΧΟΥ ΣΦΑΛΜΑΤΟΣ () P e συνάρτηση των S/N και r b (B) Συμβάσεις κανονισμοί για τα S, B Φασματική πυκνότητα θορύβου καθορισμένη Πολυπλοκότητα και κόστος συστήματος ΚΩΔΙΚΟΠΟΙΗΣΗ ΚΑΝΑΛΙΟΥ Καλά
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
Δεύτερη Σειρά Ασκήσεων
 Δεύτερη Σειρά Ασκήσεων ΑΣΚΗΣΗ 1 Από ένα αθόρυβο κανάλι 4 khz παίρνουμε δείγματα κάθε 1 msec. - Ποιος είναι ο μέγιστος ρυθμός μετάδοσης δεδομένων; - Πώς μεταβάλλεται ο μέγιστος ρυθμός μετάδοσης δεδομένων
Δεύτερη Σειρά Ασκήσεων ΑΣΚΗΣΗ 1 Από ένα αθόρυβο κανάλι 4 khz παίρνουμε δείγματα κάθε 1 msec. - Ποιος είναι ο μέγιστος ρυθμός μετάδοσης δεδομένων; - Πώς μεταβάλλεται ο μέγιστος ρυθμός μετάδοσης δεδομένων
Βασικές λειτουργίες Ανίχνευση πλαισίων Τι κάνει το επίπεδο ζεύξης Χρησιμοποιεί τις υπηρεσίες του φυσικού επιπέδου, ήτοι την (ανασφαλή) μεταφορά δεδομέ
 Αρχές σχεδιασμού, μοντέλα αναφοράς, τυποποίηση Μιλτιάδης Αναγνώστου 19 Μαΐου 2011 1/41 Βασικές λειτουργίες Ανίχνευση πλαισίων Επίδραση του θορύβου Παραδείγματα 2/41 Βασικές λειτουργίες Ανίχνευση πλαισίων
Αρχές σχεδιασμού, μοντέλα αναφοράς, τυποποίηση Μιλτιάδης Αναγνώστου 19 Μαΐου 2011 1/41 Βασικές λειτουργίες Ανίχνευση πλαισίων Επίδραση του θορύβου Παραδείγματα 2/41 Βασικές λειτουργίες Ανίχνευση πλαισίων
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣΟΡ Κεφάλαιο 1 : Εισαγωγή στη Θεωρία ωία Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Έννοια της πληροφορίας Άλλες βασικές έννοιες Στόχος
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣΟΡ Κεφάλαιο 1 : Εισαγωγή στη Θεωρία ωία Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Έννοια της πληροφορίας Άλλες βασικές έννοιες Στόχος
Μοντέλο Επικοινωνίας Δεδομένων. Επικοινωνίες Δεδομένων Μάθημα 6 ο
 Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Ήχος. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 04-1
 Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 2η διάλεξη (3η έκδοση, 11/3)
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 2η διάλεξη (3η έκδοση, 11/3) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 19 Φεβρουαρίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 2η διάλεξη (3η έκδοση, 11/3) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 19 Φεβρουαρίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
Τηλεπικοινωνίες. Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων. Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ
 Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Τεράστιες ανάγκες σε αποθηκευτικό χώρο
 ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α)
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
Ημιτονοειδή σήματα Σ.Χ.
 Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
Ψηφιακές Τηλεπικοινωνίες. Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση
 Ψηφιακές Τηλεπικοινωνίες Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση Σύνδεση με τα Προηγούμενα Σχεδιάστηκε ο βέλτιστος δέκτης για κανάλι AWGN Επειδή πάντοτε υπάρχει ο θόρυβος, ακόμη κι ο βέλτιστος δέκτης
Ψηφιακές Τηλεπικοινωνίες Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση Σύνδεση με τα Προηγούμενα Σχεδιάστηκε ο βέλτιστος δέκτης για κανάλι AWGN Επειδή πάντοτε υπάρχει ο θόρυβος, ακόμη κι ο βέλτιστος δέκτης
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής. Εντροπία Shannon
 Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής Εντροπία Shannon Ένα από τα βασικά ερωτήματα της θεωρίας της πληροφορίας ήταν ανέκαθεν το πώς θα μπορούσε να ποσοτικοποιηθεί η πληροφορία, ώστε να μπορούμε
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής Εντροπία Shannon Ένα από τα βασικά ερωτήματα της θεωρίας της πληροφορίας ήταν ανέκαθεν το πώς θα μπορούσε να ποσοτικοποιηθεί η πληροφορία, ώστε να μπορούμε
Θεωρία της Πληροφορίας 3 ο Εξάμηνο
 Σμήμα Πληροφορικής & Επικοινωνιών Θεωρία της Πληροφορίας 3 ο Εξάμηνο Τομέας Τηλεπικοινωνιών και Δικτύων Δρ. Αναστάσιος Πολίτης Καθηγητής Εφαρμογών 1 Διεξαγωγή και Εξέταση του Μαθήματος Μάθημα Πώς? 13 Διαλέξεις.
Σμήμα Πληροφορικής & Επικοινωνιών Θεωρία της Πληροφορίας 3 ο Εξάμηνο Τομέας Τηλεπικοινωνιών και Δικτύων Δρ. Αναστάσιος Πολίτης Καθηγητής Εφαρμογών 1 Διεξαγωγή και Εξέταση του Μαθήματος Μάθημα Πώς? 13 Διαλέξεις.
Η κωδικοποίηση των συντελεστών DC
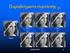 Η κωδικοποίηση των συντελεστών DC Γιακάθευποπίνακαηδιαφορά, d,του DC συντελεστήτουαπότοσυντελεστή DC τουπροηγούµενουυποπίνακαοδηγούνταιστονκωδικοποιητήεντροπίας (variable length coding VLC). Στονκωδικοποιητήηδιαφοράκατατάσσεταιανάλογαµετοµέγεθόςτηςστοακόλουθοπίνακα,
Η κωδικοποίηση των συντελεστών DC Γιακάθευποπίνακαηδιαφορά, d,του DC συντελεστήτουαπότοσυντελεστή DC τουπροηγούµενουυποπίνακαοδηγούνταιστονκωδικοποιητήεντροπίας (variable length coding VLC). Στονκωδικοποιητήηδιαφοράκατατάσσεταιανάλογαµετοµέγεθόςτηςστοακόλουθοπίνακα,
Ψηφιακές Τηλεπικοινωνίες. Κωδικοποίηση Κυματομορφής
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Κυματομορφής Σύνδεση με τα Προηγούμενα Οι τεχνικές κωδικοποίησης αναλογικής πηγής διακρίνονται σε τεχνικές κωδικοποίησης κυματομορφής τεχνικές ανάλυσης σύνθεσης Οι
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Κυματομορφής Σύνδεση με τα Προηγούμενα Οι τεχνικές κωδικοποίησης αναλογικής πηγής διακρίνονται σε τεχνικές κωδικοποίησης κυματομορφής τεχνικές ανάλυσης σύνθεσης Οι
Σημείωμα Αδειοδότησης
 Μελέτη Περιπτώσεων στη Λήψη Αποφάσεων Σημείωμα Αδειοδότησης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Μελέτη Περιπτώσεων στη Λήψη Αποφάσεων Σημείωμα Αδειοδότησης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Αρχές κωδικοποίησης. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Αναλογικές και Ψηφιακές Επικοινωνίες
 Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 10: Παλμοκωδική Διαμόρφωση, Διαμόρφωση Δέλτα και Πολύπλεξη Διαίρεσης Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Παλμοκωδική Διαμόρφωση (PCM) Παλμοκωδική Διαμόρφωση
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 10: Παλμοκωδική Διαμόρφωση, Διαμόρφωση Δέλτα και Πολύπλεξη Διαίρεσης Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Παλμοκωδική Διαμόρφωση (PCM) Παλμοκωδική Διαμόρφωση
Πίνακες Διασποράς. Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h. Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση
 Πίνακες Διασποράς Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση κλειδί k T 0 1 2 3 4 5 6 7 U : χώρος πιθανών κλειδιών Τ : πίνακας μεγέθους
Πίνακες Διασποράς Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση κλειδί k T 0 1 2 3 4 5 6 7 U : χώρος πιθανών κλειδιών Τ : πίνακας μεγέθους
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πληροφορία Μέτρο πληροφορίας Μέση πληροφορία ή Εντροπία Από κοινού εντροπία
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πληροφορία Μέτρο πληροφορίας Μέση πληροφορία ή Εντροπία Από κοινού εντροπία
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ. Ενότητα 6: Κωδικοποίηση & Συμπίεση Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 6: Κωδικοποίηση & Συμπίεση Εικόνας Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 6: Κωδικοποίηση & Συμπίεση Εικόνας Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ. Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Z
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης
 Πανεπιστήμιο Πατρών Τμήμα Μηχ. Η/Υ & Πληροφορικής Ακαδημαϊκό Έτος 009-010 Ψ Η Φ Ι Α Κ Ε Σ Τ Η Λ Ε Π Ι Κ Ο Ι Ν Ω Ν Ι ΕΣ η Εργαστηριακή Άσκηση: Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης Στην άσκηση
Πανεπιστήμιο Πατρών Τμήμα Μηχ. Η/Υ & Πληροφορικής Ακαδημαϊκό Έτος 009-010 Ψ Η Φ Ι Α Κ Ε Σ Τ Η Λ Ε Π Ι Κ Ο Ι Ν Ω Ν Ι ΕΣ η Εργαστηριακή Άσκηση: Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης Στην άσκηση
χωρίςναδηµιουργείταιαίσθησηαπώλειαςτηςποιότηταςτηςανακατασκευασµένηςεικόνας.
 Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Τεχνικές Κωδικοποίησης Πηγής Η Περίπτωση της Φωνής
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Τεχνικές Κωδικοποίησης Πηγής Η Περίπτωση της Φωνής
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Nέες Τεχνολογίες. στις Επικοινωνίες
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Nέες Τεχνολογίες στις Επικοινωνίες Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Κώδικες Διόρθωσης Λαθών Τεχνολογικό Εκπαιδευτικό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Nέες Τεχνολογίες στις Επικοινωνίες Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Κώδικες Διόρθωσης Λαθών Τεχνολογικό Εκπαιδευτικό
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 4η διάλεξη (4η έκδοση, 11/3/2013)
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 4η διάλεξη (4η έκδοση, 11/3/2013) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 5 Μαρτίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 4η διάλεξη (4η έκδοση, 11/3/2013) ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 5 Μαρτίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη
 ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 25 Απριλίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
ΕΕ728 Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας 11η διάλεξη ηµήτρης-αλέξανδρος Τουµπακάρης Τµήµα ΗΜ&ΤΥ, Πανεπιστήµιο Πατρών 25 Απριλίου 2013 ηµήτρης-αλέξανδρος Τουµπακάρης Προχωρηµένα Θέµατα Θεωρίας Πληροφορίας
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ
 ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ 5. Εισαγωγή Ο σκοπός κάθε συστήματος τηλεπικοινωνιών είναι η μεταφορά πληροφορίας από ένα σημείο (πηγή) σ ένα άλλο (δέκτης). Συνεπώς, κάθε μελέτη ενός τέτοιου συστήματος
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ 5. Εισαγωγή Ο σκοπός κάθε συστήματος τηλεπικοινωνιών είναι η μεταφορά πληροφορίας από ένα σημείο (πηγή) σ ένα άλλο (δέκτης). Συνεπώς, κάθε μελέτη ενός τέτοιου συστήματος
Τεχνολογία Πολυμέσων. Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
ΕΙΣ. ΣΥΣΤ. ΕΠΙΚΟΙΝΩΝΙΩΝ /2/ :09:46 µµ
 ΕΙΣ. ΣΥΣΤ. ΕΠΙΚΟΙΝΩΝΙΩΝ 013-14 18//014 1:09:46 µµ PULSE CODE MODULATION (PCM) 18//014 Το PCM είναι ένα σύστηµα, µε το οποίο µπορούµε να διαβιβάσουµε ένα αναλογικό (συνεχές) σήµα x(t) µέσω διακριτού καναλιού.
ΕΙΣ. ΣΥΣΤ. ΕΠΙΚΟΙΝΩΝΙΩΝ 013-14 18//014 1:09:46 µµ PULSE CODE MODULATION (PCM) 18//014 Το PCM είναι ένα σύστηµα, µε το οποίο µπορούµε να διαβιβάσουµε ένα αναλογικό (συνεχές) σήµα x(t) µέσω διακριτού καναλιού.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 6 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 6 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Κβάντιση-Κωδικοποίηση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Κβάντιση-Κωδικοποίηση
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 4 : Δειγματοληψία και κβάντιση (Sampling and Quantization) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 4 : Δειγματοληψία και κβάντιση (Sampling and Quantization) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 Κωδικοποίηση ζωνών συχνοτήτων Δρ. Ν. Π. Σγούρος 2 Φαινόμενο Μπλόκ (Blocking Artifact) Η χρήση παραθύρων για την εφαρμογή των μετασχηματισμών δημιουργεί το φαινόμενο μπλόκ Μειώνεται
Συμπίεση Δεδομένων 2013-2014 Κωδικοποίηση ζωνών συχνοτήτων Δρ. Ν. Π. Σγούρος 2 Φαινόμενο Μπλόκ (Blocking Artifact) Η χρήση παραθύρων για την εφαρμογή των μετασχηματισμών δημιουργεί το φαινόμενο μπλόκ Μειώνεται
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ψηφιακές Επικοινωνίες Εργαστήριο 4 ο : Κβάντιση-Κωδικοποίηση Βασική Θεωρία Κβάντιση Κατά την μετατροπή ενός αναλογικού
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ψηφιακές Επικοινωνίες Εργαστήριο 4 ο : Κβάντιση-Κωδικοποίηση Βασική Θεωρία Κβάντιση Κατά την μετατροπή ενός αναλογικού
Κεφάλαιο 2 Πληροφορία και εντροπία
 Κεφάλαιο 2 Πληροφορία και εντροπία Άσκηση. Έστω αλφάβητο Α={0,} και δύο πηγές p και q. Έστω οτι p(0)=-r, p()=r, q(0)=-s και q()=s. Να υπολογιστούν οι σχετικές εντροπίες Η(Α,p/q) και Η(Α,q/p). Να γίνει
Κεφάλαιο 2 Πληροφορία και εντροπία Άσκηση. Έστω αλφάβητο Α={0,} και δύο πηγές p και q. Έστω οτι p(0)=-r, p()=r, q(0)=-s και q()=s. Να υπολογιστούν οι σχετικές εντροπίες Η(Α,p/q) και Η(Α,q/p). Να γίνει
