ΥΠΟΛΟΓΙΣΜΟΣ ΠΑΡΑΜΕΤΡΩΝ ΚΑΙ ΕΚΤΙΜΗΣΗ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ R=H*V
|
|
|
- Τιτάνια Αναγνωστάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1
2 Εισαγωγή - Ορισµοί R=H*V Ο σεισµικός κίνδυνος (R-seismic risk) αποτελεί εκτιµήσεις της πιθανότητας να συµβούν απώλειες που σχετίζονται µε παράγοντες της σεισµικής επικινδυνότητας (ανθρώπινες, κοινωνικές, οικονοµικές, τεχνολογικές). Η σεισµική επικινδυνότητα (H-seismic hazard) περιγράφει το δυναµικό µιας περιοχής για την εκδήλωση επικίνδυνων φυσικών παραγόντων (εδαφική κίνηση, εδαφικές διαρρήξεις, ρευστοποίηση εδάφους, κατολισθήσεις) που σχετίζονται µε τη γένεση σεισµών. Η τρωτότητα (V-vulnerability) σχετίζεται µε τη σεισµική συµπεριφορά των κατασκευών και εξαρτάται κυρίως από την ποιότητα και τις αντισεισµικές προδιαγραφές των κατασκευών. Η σεισµική επικινδυνότητα αποτελεί µια φυσική παράµετρο που δεν επιδέχεται παρεµβάσεις ως προς τη µείωσή της. Εποµένως η ελάττωση του σεισµικού κινδύνου εξαρτάται από την ελάττωση της τρωτότητας. Όµως, ο αντισεισµικός σχεδιασµός των κατασκευών γίνεται κυρίως βάσει των παραµέτρων της σεισµικής επικινδυνότητας. Είναι λοιπόν απαραίτητη η εκτίµηση της σεισµικής επικινδυνότητας για την ελάττωση του σεισµικού κινδύνου.
3 Εισαγωγή - Ορισµοί R=H*V Πολύ συχνά οι όροι σεισµική επικινδυνότητα και σεισµικός κίνδυνος συγχέονται, συµβαίνει δηλαδή κάτι αντίστοιχο µε τις έννοιες του µεγέθους και της έντασης σεισµών. Η σεισµική επικινδυνότητα σχετίζεται µε εδαφικές παραµέτρους. Ο σεισµικός κίνδυνος σχετίζεται µε αποτελέσµατα των σεισµών στις κατασκευές, ανθρώπινες απώλειες κλπ. Δηλαδή θα µπορούσαµε να συσχετίσουµε τις παραπάνω έννοιες για τη δική µας ευκολία ως εξής: (Μέγεθος - Σεισµική Επικινδυνότητα) Ένταση - Σεισµικός Κίνδυνος Σε αυτήν την άσκηση θα ασχοληθούµε µόνο µε τη σεισµική επικινδυνότητα και τον υπολογισµό των παραµέτρων της σε περιοχές του Ελλαδικού χώρου.
4 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΠΙΘΑΝΟΛΟΓΙΚΗ PROBABILISTIC (PSHA) «Η σεισµική επικινδυνότητα στην περιοχή της Λευκάδας είναι της τάξης του 0.36g µε 5% πιθανότητα µη υπέρβασης για τα επόµενα 50 χρόνια». ΑΙΤΙΟΚΡΑΤΙΚΗ DETERMINISTIC (DSHA) «Η σεισµική επικινδυνότητα στην πόλη της Λευκάδας είναι 0.38g για σεισµό µε µέγεθος 6.4 στο ρήγµα Κεφαλονιάς-Λευκάδας σε απόσταση 10 km από την πόλη». Οι δύο βασικές µέθοδοι εκτίµησης της σεισµικής επικινδυνότητας χρησιµοποιούν τον ίδιο βασικό κορµό πληροφοριών. Η βασική διαφορά είναι ότι η πιθανολογική προσέγγιση εξετάζει συστηµατικά την πιθανότητα ενός «πραγµατικού» σεισµού που υπερβαίνει την εδαφική κίνηση σχεδιασµού. Όλα τα στοιχεία της αιτιοκρατικής ανάλυσης εµπεριέχονται στην πιθανολογική προσέγγιση. ΑΙΤΙΟΚΡΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Σεισµικές πηγές Σενάριο σεισµού (µέγεθος και επικεντρική απόσταση) PGA, PGV, PGD στην περιοχή µελέτης Απόσβεση σεισµικής κίνησης Σεισµός σχεδιασµού Πηγή
5 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΠΙΘΑΝΟΛΟΓΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Σεισµικές πηγές 2. Περίοδος επανάληψης 3. Απόσβεση σεισµικής κίνησης 4. Πιθανότητα υπέρβασης Στην πιθανολογική ανάλυση, η περίοδος επανάληψης (συχνότητα σεισµών Μ) θεωρείται ως αβεβαιότητα σε κάθε βήµα της διαδικασίας πιθανολογικής ανάλυσης. Το αποτέλεσµα είναι µια καµπύλη σεισµικής επικινδυνότητας η οποία συσχετίζει τις παραµέτρους σχεδιασµού της εδαφικής κίνησης µε την πιθανότητα υπέρβασης.
6 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΠΙΘΑΝΟΛΟΓΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Άλλοι παράγοντες αβεβαιότητας που υπεισέρχονται στην πιθανολογική ανάλυση είναι: 1.Οι νόµοι απόσβεσης 2.Η απόσταση από τη σεισµική πηγή
7 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΠΙΘΑΝΟΛΟΓΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Σχέση µεταξύ της περιόδου επανάληψης (Π.E.), περιόδου ενδιαφέροντος (Τ) και πιθανότητας υπέρβασης (P): Π.Ε. = -Τ / ln(1-p)
8 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΠΙΘΑΝΟΛΟΓΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Π.χ. εάν ένας µηχανικός θέλει να κατασκευάσει ένα φράγµα για να αντέχει σε σεισµική επιτάχυνση, η οποία έχει µόνο 2% πιθανότητα να ξεπεραστεί σε µια περίοδο 50 χρόνων (διάρκεια ζωής του φράγµατος), θα επιλέξει τη σεισµική επιτάχυνση από την καµπύλη σεισµικής επικινδυνότητας.
9 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΑΙΤΙΟΚΡΑΤΙΚΗ - ΠΙΘΑΝΟΛΟΓΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Η αιτιοκρατική προσέγγιση παρότι αποδίδει διακριτά αποτελέσµατα εκτίµησης της σεισµικής επικινδυνότητας, δεν αποδίδει δείκτες αβεβαιότητας. Έτσι, τα συµπεράσµατα της αιτιοκρατικής ανάλυσης είναι πολύ πιθανό να ανατραπούν από τη γένεση νέων σεισµών. Η πιθανολογική προσέγγιση περιλαµβάνει ένα µεγάλο εύρος πληροφοριών και παραγόντων αβεβαιότητας. Η πιο καλή λύση έχει αποδειχθεί ο συνδυασµός αιτιοκρατικής και πιθανολογικής ανάλυσης για την εκτίµηση της σεισµικής επικινδυνότητας σε µια περιοχή. Η αιτιοκρατική µπορεί να χρησιµοποιηθεί στα πλαίσια του «µέγιστου αναµενόµενου σεισµού», ενώ η πιθανολογική στα πλαίσια του «πιθανότερου σεισµού σχεδιασµού». Είναι δηλαδή οι δύο µέθοδοι συµπληρωµατικές η µια προς την άλλη.
10 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΣΤΗΝ ΕΥΡΩΠΗ
11 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΣΤΗΝ ΕΛΛΑΔΑ Στην περιοχή της Ελλάδας εκλύεται η 6η κατά σειρά σεισµική ενέργεια το χρόνο παγκοσµίως. Στον ευρύτερο Ελλαδικό χώρο συµβαίνουν 2 σεισµοί µε M=6.0 κάθε χρόνο, ένας µε M=7.0 κάθε 5.8 χρόνια, ένας µε M=7.5 κάθε 70 χρόνια και ένας µε M=8.0 κάθε 850 χρόνια. Η πλειονότητα των επιφανειακών (<60 km) σεισµών περιλαµβάνεται : 1.Σε µια ζώνη παράλληλη στο Ελληνικό Τόξο 2.Στον Κορινθιακό κόλπο 3.Στην Τάφρο του Βορείου Αιγαίου Σεισµοί ενδιαµέσου βάθους εντοπίζονται κυρίως στην περιοχή του οπισθοτόξου.
12 ΣΕΙΣΜΙΚΗ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑ ΣΤΗΝ ΕΛΛΑΔΑ Περίπου το 75% των σεισµών είναι υποθαλάσσιοι και αυτό ελαττώνει σηµαντικά την σεισµική επικινδυνότητα που όµως δεν παύει να είναι µεγάλη σε σχέση µε αυτήν της Ευρώπης. είναι υποθαλάσσιοι, µακριά από κατοικηµένες περιοχές. Ο αναθεωρηµένος αντισεισµικός κανονισµός (ΝΕΑΚ2004) χωρίζει την Ελλάδα σε τρεις σεισµικές ζώνες µε τιµές επιτάχυνσης σχεδιασµού 0.16g, 0.24g και 0.36g. Σεισµογενείς ζώνες στην Ελλάδα (Papazachos & Papazachou (1997. Καµπύλες απόσβεσης για Μ=7.6 και h=10 km (Papaioannou et al., 2008) Ζώνες σεισµικής επικινδυνότητας στην Ελλάδα (NEAK-2004).
13 ΣΧΕΣΗ GUTENBERG-RICHTER Ο ρυθµός επανάληψης σεισµών σχεδιασµού προκύπτει από την ανάλυση σεισµολογικών καταλόγων και συγκεκριµένα από τον υπολογισµό των σταθερών a και b της σχέσης Gutenberg-Richter: logn = a bm όπου Ν το πλήθος των σεισµών µε µέγεθος Μ
14 ΣΧΕΣΗ GUTENBERG-RICHTER Αιτίες σφαλµάτων στον υπολογισµό των a και b της σχέσης Gutenberg-Richter: 1.Μικρό πλήθος δεδοµένων 2.Η χρήση σεισµικών µεγεθών µικρότερων από το κατώφλι πληρότητας του σεισµικού καταλόγου. 3.Σφάλµατα στον υπολογισµό των µεγεθών του καταλόγου.
15 ΣΧΕΣΗ GUTENBERG-RICHTER Αιτίες σφαλµάτων στον υπολογισµό των a και b της σχέσης GutenbergRichter: Μικρό πλήθος δεδοµένων
16 ΣΧΕΣΗ GUTENBERG-RICHTER Αιτίες σφαλµάτων στον υπολογισµό των a και b της σχέσης GutenbergRichter: Χρήση σεισµικών µεγεθών µικρότερων από το κατώφλι πληρότητας του σεισµικού καταλόγου
17 ΣΧΕΣΗ GUTENBERG-RICHTER Αιτίες σφαλµάτων στον υπολογισµό των a και b της σχέσης GutenbergRichter: Σφάλµατα στον υπολογισµό των µεγεθών του καταλόγου
18 ΣΧΕΣΗ GUTENBERG-RICHTER Ο ακριβής υπολογισµός του b της σχέσης Gutenberg-Richter είναι σηµαντικός στην ανάλυση της σεισµικής επικινδυνότητας διότι: Μικρή απόκλιση του b µεγάλη απόκλιση στο πλήθος των σεισµών µεγάλου µεγέθους b= M 7.0 σεισµοί σεισµοί µε Μ 4.0 b= M 7.0 σεισµοί
19 ΣΧΕΣΗ GUTENBERG-RICHTER Κατάλογος σεισµικών παραµέτρων του Ελλαδικού χώρου (Makropoulos et al., 1989) Πληρότητα στοιχείων καταλόγου Τάξη Μεγέθους Μ 4.0 Μ 4.5 Μ 5.0 Μ 5.5 Μ 6.0 Μ 6.5 Χρονική Περίοδος με π λήρη δεδομένα
20 ΣΧΕΣΗ GUTENBERG-RICHTER Δεδοµένα της άσκησης 1.Κατάλογος εστιακών παραµέτρων σεισµών του Ελλαδικού χώρου ( Makropoulos et al., 1989). 2.Γεωγραφικές συντεταγµένες πόλεων της Ελλάδας Ζητούµενα της άσκησης 1.Οι συντελεστές at, a και b της σχέσης Gutenberg-Richter 2.Εκτίµηση της αβεβαιότητας των συντελεστών at, a και b 3.Οι ρυθµοί υπέρβασης Νt και Ν 4.Η περίοδος επανάληψης (ΠΕ) του µέγιστου παρατηρούµενου µεγέθους 5.Η µέγιστη αναµενόµενη σεισµική επιτάχυνση για: α) Την παρατηρούµενη ΠΕ β) Διαφορετικές παραµέτρους αβεβαιότητας (πιθανολογική ανάλυση)
21 ΣΧΕΣΗ GUTENBERG-RICHTER Βήµατα της άσκησης 1.Δίνεται κατάλογος εστιακών παραµέτρων σεισµών του Ελλαδικού χώρου ( Makropoulos et al., 1989). 2.Ανοίγετε το αρχείο µε το Excel. 3.Με κέντρο την περιοχή ενδιαφέροντος επιλέγετε επίκεντρα σε περιοχή ακτίνας Π.χ. αν ο τόπος έχει γεωγραφικές συντεταγµένες (38.50, 21.00) επιλέγετε επίκεντρα σε ένα τετράγωνο που οι κορυφές του έχουν συντεταγµένες ( , , , ). Η επιλογή γίνεται από το Menu: Δεδοµένα Φίλτρο Φίλτρα αριθµών Προσαρµοσµένο φίλτρο π.χ. 380 και 390 (το ίδιο γίνεται και για το Γ. µήκος). 4.Αντιγράφετε τα φιλτραρισµένα στοιχεία σε ένα νέο αρχείο µε όνοµα π.χ. Kastoria_mdl.xls Έτσι έχετε τον κατάλογο των σεισµών της περιοχής που σας ενδιαφέρει. 5.Σηµειώνετε τη διάρκεια σε έτη του καταλόγου σας (π.χ , 90 έτη) 6.Ταξινοµείτε τα δεδοµένα µε βάση τη στήλη των µεγεθών από το µικρότερο προς το µεγαλύτερο: (Δεδοµένα Ταξινόµηση Ταξινόµηση κατά στήλη J από το Α ως το Ω). 7.Με διαδοχική διαδικασία φιλτραρίσµατος των µεγεθών υπολογίζετε για κάθε µέγεθος Μi το πλήθος των µεγεθών Ν Μi.
22 ΣΧΕΣΗ GUTENBERG-RICHTER Βήµατα της άσκησης 8. Σε άλλο φύλλο αρχειοθετείτε τα παραπάνω στοιχεία ως εξής: Nt lognt M Κατασκευάζετε τη γραφική παράσταση της συνάρτησης y=lognt=f(m)=x 10.Χρησιµοποιείτε την επιλογή «Εισαγωγή γραφήµατος διασποράς» 11.Με δεξί κλικ πάνω σε ένα σηµείο επιλέγετε «προσθήκη γραµµής τάσης - τύπος τάσης γραµµική προβολή εξίσωσης στο γράφηµα». 12.Η εξίσωση είναι η σχέση Gutenberg-Richter και είναι της µορφής: y = -bx + at lognt = at - bm 13. Ο συντελεστής at αντιστοιχεί στο ρυθµό υπέρβασης για το χρονική διάρκεια του καταλόγου σας (π.χ. 90 έτη). Ο συντελεστής a που αντιστοιχεί στον ετήσιο ρυθµό υπέρβασης είναι: a = at - logt = at log100
23 ΣΧΕΣΗ GUTENBERG-RICHTER (ετήσιος ρυθµός υπέρβασης) Βήµατα της άσκησης 14. Με βάση τους συντελεστές a και b και για M1=Mmin και M2=Mmax κατασκευάζετε την ευθεία που αντιστοιχεί στον ετήσιο ρυθµό υπέρβασης: N = 10a - bm 15. Η περίοδος επανάληψης για κάθε µέγεθος Μ δίνεται από τη σχέση: Π.Ε.(Μ)=1/Ν 16. Υπολογίζετε την Π.Ε. (Μmax) του καταλόγου σας. 17. Με βάση τη γραφική παράσταση της N = 10a bm υπολογίζουµε την τιµή του ρυθµού υπέρβασης που αντιστοιχεί στο µέγιστο παρατηρούµενο µέγεθος (Μmax). (Π.Ε. = 1/10-3 = 1000 έτη) 10-3
24 ΕΚΤΙΜΗΣΗ ΠΙΘΑΝΟΛΟΓΙΚΗΣ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ 19. Χρησιµοποιώντας τη σχέση µεταξύ της περιόδου επανάληψης (Π.E.), περιόδου ενδιαφέροντος (Τ) και πιθανότητας υπέρβασης (P): Π.Ε. = -Τ / ln(1-p) Και την καµπύλη σεισµικής επικινδυνότητας Συµπληρώνετε τον παρακάτω πίνακα: Τ Ρ1 (%) Π.Ε. Ν Mmax
25 ΥΠΟΛΟΓΙΣΜΟΣ ΠΑΡΑΜΕΤΡΩΝ ΚΑΙ ΕΚΤΙΜΗΣΗ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΣΥΓΚΕΝΤΩΤΙΚΟΙ ΧΑΡΤΕΣ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΤΗΣ ΕΛΛΑΔΑΣ 20. Με την ανταλλαγή και τη συγκέντρωση όλων των στοιχείων των περιοχών που µελετήσατε, θα κατασκευάσετε χάρτες σεισµικής επικινδυνότητας της Ελλάδας σε περιβάλλον GIS.
Σεισμική Επικινδυνότητα Κεφ.21
 Σεισμική Επικινδυνότητα Κεφ.21 Αθήνα, 1999 Ε. Σώκος Εργαστήριο Σεισμολογίας Τμήμα Γεωλογίας Σεισμική επικινδυνότητα Ορισμοί Μεθοδολογίες Μοντέλα περιγραφής σεισμικότητας Εξασθένιση σεισμικής κίνησης Παραδείγματα
Σεισμική Επικινδυνότητα Κεφ.21 Αθήνα, 1999 Ε. Σώκος Εργαστήριο Σεισμολογίας Τμήμα Γεωλογίας Σεισμική επικινδυνότητα Ορισμοί Μεθοδολογίες Μοντέλα περιγραφής σεισμικότητας Εξασθένιση σεισμικής κίνησης Παραδείγματα
συνάρτηση κατανομής πιθανότητας
 Στατιστική των σεισμών Κεφ.13 Θ.Σώκος Εργαστήριο Σεισμολογίας Τμήμα Γεωλογίας Η στατιστική των σεισμών ασχολείται λί με τη μελέτη της κατανομής των σεισμών λαμβάνοντας υπ όψη σαν κύρια παράμετρο το σεισμικό
Στατιστική των σεισμών Κεφ.13 Θ.Σώκος Εργαστήριο Σεισμολογίας Τμήμα Γεωλογίας Η στατιστική των σεισμών ασχολείται λί με τη μελέτη της κατανομής των σεισμών λαμβάνοντας υπ όψη σαν κύρια παράμετρο το σεισμικό
ΕΠΙΔΡΑΣΗ ΤΗΣ ΓΕΩΛΟΓΙΑΣ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑΚΗ ΔΙΑΜΟΡΦΩΣΗ ΤΗΣ ΙΣΧΥΡΗΣ ΣΕΙΣΜΙΚΗΣ ΚΙΝΗΣΗΣ
 ΕΠΙΔΡΑΣΗ ΤΗΣ ΓΕΩΛΟΓΙΑΣ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑΚΗ ΔΙΑΜΟΡΦΩΣΗ ΤΗΣ ΙΣΧΥΡΗΣ ΣΕΙΣΜΙΚΗΣ ΚΙΝΗΣΗΣ Βασίλης Μάργαρης & Νίκος Θεοδουλίδης Δ/ντές Ερευνών ΙΤΣΑΚ 1 Σεισμική Μηχανική T.Σεισμολογία Εδαφικές Κινήσεις Απόκριση Εδάφους/Κατασκευής
ΕΠΙΔΡΑΣΗ ΤΗΣ ΓΕΩΛΟΓΙΑΣ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑΚΗ ΔΙΑΜΟΡΦΩΣΗ ΤΗΣ ΙΣΧΥΡΗΣ ΣΕΙΣΜΙΚΗΣ ΚΙΝΗΣΗΣ Βασίλης Μάργαρης & Νίκος Θεοδουλίδης Δ/ντές Ερευνών ΙΤΣΑΚ 1 Σεισμική Μηχανική T.Σεισμολογία Εδαφικές Κινήσεις Απόκριση Εδάφους/Κατασκευής
Εξάρτηση της σεισμικής κίνησης από τις τοπικές εδαφικές συνθήκες
 Εξάρτηση της σεισμικής κίνησης από τις τοπικές εδαφικές συνθήκες Μηχανικές ιδιότητες του εδάφους θεμελίωσης Πάχος και δυσκαμψία του επιφανειακού ιζηματογενούς στρώματος Κλίση των στρωμάτων και τοπογραφία
Εξάρτηση της σεισμικής κίνησης από τις τοπικές εδαφικές συνθήκες Μηχανικές ιδιότητες του εδάφους θεμελίωσης Πάχος και δυσκαμψία του επιφανειακού ιζηματογενούς στρώματος Κλίση των στρωμάτων και τοπογραφία
ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ
 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ 1 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ 2 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ 3 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ
ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ 1 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ 2 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ 3 ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ ΙΕΡΑ ΜΟΝΗ ΣΤΑΥΡΟΝΙΚΗΤΑ
7 ΚΕΦΑΛΑΙΟ ΣΥΝΟΨΗ ΑΠΟΤΕΛΕΣΜΑΤΑ ΠΡΟΟΠΤΙΚΗ
 7 ΚΕΦΑΛΑΙΟ ΣΥΝΟΨΗ ΑΠΟΤΕΛΕΣΜΑΤΑ ΠΡΟΟΠΤΙΚΗ 7.1 Σύνοψη Η παρούσα διατριβή είχε ως στόχο τη µελέτη του φαινοµένου της ρευστοποίησης στην ευρύτερη περιοχή του Αιγαίου και τη δηµιουργία νέων εµπειρικών σχέσεων
7 ΚΕΦΑΛΑΙΟ ΣΥΝΟΨΗ ΑΠΟΤΕΛΕΣΜΑΤΑ ΠΡΟΟΠΤΙΚΗ 7.1 Σύνοψη Η παρούσα διατριβή είχε ως στόχο τη µελέτη του φαινοµένου της ρευστοποίησης στην ευρύτερη περιοχή του Αιγαίου και τη δηµιουργία νέων εµπειρικών σχέσεων
Εισαγωγή στην Στατιστική (ΔΕ200Α-210Α)
 Τμήμα Διοίκησης Επιχειρήσεων (Αγ. Νικόλαος), Τ.Ε.Ι. Κρήτης Σελίδα 1 από 13 5η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση στοχεύει στην εκμάθηση κατασκευής γραφημάτων που θα παρουσιάζουν
Τμήμα Διοίκησης Επιχειρήσεων (Αγ. Νικόλαος), Τ.Ε.Ι. Κρήτης Σελίδα 1 από 13 5η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση στοχεύει στην εκμάθηση κατασκευής γραφημάτων που θα παρουσιάζουν
Κεφάλαιο 8 H ΣΕΙΣΜΙΚΗ ΔΡΑΣΗ ΤΗΣ ΓΗΣ ΚΑΙ Η ΚΑΤΑΝΟΜΗ ΤΗΣ
 Κεφάλαιο 8 H ΣΕΙΣΜΙΚΗ ΔΡΑΣΗ ΤΗΣ ΓΗΣ ΚΑΙ Η ΚΑΤΑΝΟΜΗ ΤΗΣ -Δεν υπάρχει συμφωνία μεταξύ των σεισμολόγων για τον όρο «σεισμική δράση». -Μία ποιοτική εικόνα της σεισμικής δράσης μπορούμε να αποκτήσουμε με την
Κεφάλαιο 8 H ΣΕΙΣΜΙΚΗ ΔΡΑΣΗ ΤΗΣ ΓΗΣ ΚΑΙ Η ΚΑΤΑΝΟΜΗ ΤΗΣ -Δεν υπάρχει συμφωνία μεταξύ των σεισμολόγων για τον όρο «σεισμική δράση». -Μία ποιοτική εικόνα της σεισμικής δράσης μπορούμε να αποκτήσουμε με την
Εισαγωγή στην Στατιστική (ΔΕ200Α-210Α)
 Τμήμα Διοίκησης Επιχειρήσεων (Αγ. Νικόλαος), Τ.Ε.Ι. Κρήτης Σελίδα 1 από 13 5η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση στοχεύει στην εκμάθηση κατασκευής γραφημάτων που θα παρουσιάζουν
Τμήμα Διοίκησης Επιχειρήσεων (Αγ. Νικόλαος), Τ.Ε.Ι. Κρήτης Σελίδα 1 από 13 5η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση στοχεύει στην εκμάθηση κατασκευής γραφημάτων που θα παρουσιάζουν
ΣΕΙΣΜΟΣ ΑΤΤΙΚΗΣ Μ5.3 ΤΗΣ 19/07/2019
 ΣΕΙΣΜΟΣ ΑΤΤΙΚΗΣ Μ5.3 ΤΗΣ 19/07/2019 ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΕΚΘΕΣΗ ΘΕΣΣΑΛΟΝΙΚΗ ΙΟΥΛΙΟΣ 2019 Η αναφορά στη χρήση του περιεχοµένου αυτής της έκθεσης είναι η εξής: ΙΤΣΑΚ (2019): Σεισµός ΒΔ Αττικής Μ5.3 της 19/7/2017
ΣΕΙΣΜΟΣ ΑΤΤΙΚΗΣ Μ5.3 ΤΗΣ 19/07/2019 ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΕΚΘΕΣΗ ΘΕΣΣΑΛΟΝΙΚΗ ΙΟΥΛΙΟΣ 2019 Η αναφορά στη χρήση του περιεχοµένου αυτής της έκθεσης είναι η εξής: ΙΤΣΑΚ (2019): Σεισµός ΒΔ Αττικής Μ5.3 της 19/7/2017
ΜΕΡΟΣ 1 ΠΕΡΙΕΧΟΜΕΝΑ. 1. Γεωλογείν περί Σεισμών...3. 2. Λιθοσφαιρικές πλάκες στον Ελληνικό χώρο... 15. 3. Κλάδοι της Γεωλογίας των σεισμών...
 ΜΕΡΟΣ 1 1. Γεωλογείν περί Σεισμών....................................3 1.1. Σεισμοί και Γεωλογία....................................................3 1.2. Γιατί μελετάμε τους σεισμούς...........................................
ΜΕΡΟΣ 1 1. Γεωλογείν περί Σεισμών....................................3 1.1. Σεισμοί και Γεωλογία....................................................3 1.2. Γιατί μελετάμε τους σεισμούς...........................................
Κεφαλονιά. Ινστιτούτο. Ληξουρίου, κόλπος
 Προκαταρκτική ανάλυση καταγραφών επιταχυνσιογράφων του Γεωδυναμικού Ινστιτούτου για το σεισμό της 26 Ιανουαρίουυ 2014 στην Κεφαλονιά Επιμέλεια και πληροφορίες Δρ. Ι. Καλογεράς (i.kalog@noa) Την 26 η Ιανουαρίουυ
Προκαταρκτική ανάλυση καταγραφών επιταχυνσιογράφων του Γεωδυναμικού Ινστιτούτου για το σεισμό της 26 Ιανουαρίουυ 2014 στην Κεφαλονιά Επιμέλεια και πληροφορίες Δρ. Ι. Καλογεράς (i.kalog@noa) Την 26 η Ιανουαρίουυ
Κεφάλαιο 7 ΜΕΓΕΘΟΣ ΚΑΙ ΕΝΕΡΓΕΙΑ ΣΕΙΣΜΩΝ
 Κεφάλαιο 7 ΜΕΓΕΘΟΣ ΚΑΙ ΕΝΕΡΓΕΙΑ ΣΕΙΣΜΩΝ Κατά την γένεση ενός σεισμού υπάρχει έκλυση ενέργειας λόγω παραμόρφωσης και μετατροπή της σε κυματική ενέργεια που είναι τα σεισμικά κύματα. ΜΕΓΕΘΟΣ Μ, ενός σεισμού
Κεφάλαιο 7 ΜΕΓΕΘΟΣ ΚΑΙ ΕΝΕΡΓΕΙΑ ΣΕΙΣΜΩΝ Κατά την γένεση ενός σεισμού υπάρχει έκλυση ενέργειας λόγω παραμόρφωσης και μετατροπή της σε κυματική ενέργεια που είναι τα σεισμικά κύματα. ΜΕΓΕΘΟΣ Μ, ενός σεισμού
Μέθοδος των γραμμών πόλωσης των εγκαρσίων κυμάτων
 Μέθοδος των γραμμών πόλωσης των εγκαρσίων κυμάτων Πρώτες αποκλίσεις των SH και SV κυμάτων καθορισμός των ορικών επιφανειών u V =0 και u H =0 Μειονέκτημα : η ανάλυση της πρώτης απόκλισης δεν είναι εύκολη
Μέθοδος των γραμμών πόλωσης των εγκαρσίων κυμάτων Πρώτες αποκλίσεις των SH και SV κυμάτων καθορισμός των ορικών επιφανειών u V =0 και u H =0 Μειονέκτημα : η ανάλυση της πρώτης απόκλισης δεν είναι εύκολη
Φαινόµενα ρευστοποίησης εδαφών στον Ελληνικό χώρο Κεφάλαιο 1
 1 ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ 1.1 Εισαγωγικό σηµείωµα Η προκαλούµενη, κατά τη διάδοση των σεισµικών κυµάτων, εφαρµογή κυκλικών διατµητικών τάσεων οδηγεί τους κορεσµένους χαλαρούς αµµώδεις σχηµατισµούς σε συµπύκνωση.
1 ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ 1.1 Εισαγωγικό σηµείωµα Η προκαλούµενη, κατά τη διάδοση των σεισµικών κυµάτων, εφαρµογή κυκλικών διατµητικών τάσεων οδηγεί τους κορεσµένους χαλαρούς αµµώδεις σχηµατισµούς σε συµπύκνωση.
ΟΝΟΜΑ: Ηµ/νία παραλαβής : Ηµ/νία παράδοσης :
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Πολυτεχνική Σχολή - Τµήµα Πολιτικών Μηχανικών Τοµέας : Γεωτεχνικής Μηχανικής Εργ/ριο : Εδαφοµηχανικής & Θεµελιώσεων Α. Σ. Τ. Ε. - 1 ΜΑΘΗΜΑ : «Τεχνική Σεισµολογία
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Πολυτεχνική Σχολή - Τµήµα Πολιτικών Μηχανικών Τοµέας : Γεωτεχνικής Μηχανικής Εργ/ριο : Εδαφοµηχανικής & Θεµελιώσεων Α. Σ. Τ. Ε. - 1 ΜΑΘΗΜΑ : «Τεχνική Σεισµολογία
Πρόλογος...vi 1 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ Εισαγωγικό σηµείωµα Στόχος της διατριβής οµή της διατριβής...4
 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...vi 1 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ...1 1.1 Εισαγωγικό σηµείωµα...1 1.2 Στόχος της διατριβής...3 1.3 οµή της διατριβής...4 2 ΚΕΦΑΛΑΙΟ - Ρευστοποίηση εδαφικών σχηµατισµών...8 2.1 Εισαγωγή...8
ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...vi 1 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ...1 1.1 Εισαγωγικό σηµείωµα...1 1.2 Στόχος της διατριβής...3 1.3 οµή της διατριβής...4 2 ΚΕΦΑΛΑΙΟ - Ρευστοποίηση εδαφικών σχηµατισµών...8 2.1 Εισαγωγή...8
Ν. Σαμπατακάκης Αν. Καθηγητής Εργαστήριο Τεχνικής Γεωλογίας Παν/μιο Πατρών
 ΚΕΦΑΛΑΙΟ 6 ΥΝΑΜΙΚΗ ΤΩΝ Ε ΑΦΩΝ - ΓΕΩΤΕΧΝΙΚΗ ΣΕΙΣΜΙΚΗ ΜΗΧΑΝΙΚΗ Με τον όρο «δυναμική» εννοείται η συμπεριφορά που παρουσιάζει το έδαφος υπό την επίδραση δυναμικών τάσεων που επιβάλλονται σε αυτό είδη δυναμικών
ΚΕΦΑΛΑΙΟ 6 ΥΝΑΜΙΚΗ ΤΩΝ Ε ΑΦΩΝ - ΓΕΩΤΕΧΝΙΚΗ ΣΕΙΣΜΙΚΗ ΜΗΧΑΝΙΚΗ Με τον όρο «δυναμική» εννοείται η συμπεριφορά που παρουσιάζει το έδαφος υπό την επίδραση δυναμικών τάσεων που επιβάλλονται σε αυτό είδη δυναμικών
Συστήματα Υποστήριξης Αποφάσεων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Υποστήριξης Αποφάσεων Άσκηση 1η: Αξιολόγηση σεισμογενών περιοχών της Ελλάδας Διονύσης Γιαννακόπουλος Τμήμα Διοίκησης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Υποστήριξης Αποφάσεων Άσκηση 1η: Αξιολόγηση σεισμογενών περιοχών της Ελλάδας Διονύσης Γιαννακόπουλος Τμήμα Διοίκησης
METΡΗΣΗ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΜΕ ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ
 ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΔΟΜΙΚΩΝ ΕΡΓΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τ. Ε. Ι. Σ Ε Ρ Ρ Ω Ν ΕΞΕΤΑΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΦΥΣΙΚΗΣ ΟΝΟΜΑTΕΠΩΝΥΜΟ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ METΡΗΣΗ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΜΕ ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ Χρησιμοποιώντας
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΔΟΜΙΚΩΝ ΕΡΓΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τ. Ε. Ι. Σ Ε Ρ Ρ Ω Ν ΕΞΕΤΑΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΦΥΣΙΚΗΣ ΟΝΟΜΑTΕΠΩΝΥΜΟ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ METΡΗΣΗ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΜΕ ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ Χρησιμοποιώντας
ΣΥΜΒΟΛΗ ΤΟΥ ΙΤΣΑΚ ΣΤΗΝ ΑΝΤΙΣΕΙΣΜΙΚΗ ΘΩΡΑΚΙΣΗ ΤΗΣ ΧΩΡΑΣ
 ΣΥΜΒΟΛΗ ΤΟΥ ΙΤΣΑΚ ΣΤΗΝ ΑΝΤΙΣΕΙΣΜΙΚΗ ΘΩΡΑΚΙΣΗ ΤΗΣ ΧΩΡΑΣ ΙΤΣΑΚ - TEE/TKM 30/5/2018 Συµβολή του ΙΤΣΑΚ στη Μελέτη της Ισχυρής Σεισµικής Κίνησης και Παροχή Αντίστοιχων Υπηρεσιών στην Κοινωνία Θεοδουλίδης Ν.,
ΣΥΜΒΟΛΗ ΤΟΥ ΙΤΣΑΚ ΣΤΗΝ ΑΝΤΙΣΕΙΣΜΙΚΗ ΘΩΡΑΚΙΣΗ ΤΗΣ ΧΩΡΑΣ ΙΤΣΑΚ - TEE/TKM 30/5/2018 Συµβολή του ΙΤΣΑΚ στη Μελέτη της Ισχυρής Σεισµικής Κίνησης και Παροχή Αντίστοιχων Υπηρεσιών στην Κοινωνία Θεοδουλίδης Ν.,
Το Πρώτο Δίκτυο Σεισμολογικών Σταθμών στη Σελήνη. Ιδιότητες των Σεισμικών Αναγραφών στη Σελήνη. Μηχανισμός και Αίτια Γένεσης των Σεισμών της Σελήνης
 Μάθημα 12ο Σεισμολογία της Σελήνης Το Πρώτο Δίκτυο Σεισμολογικών Σταθμών στη Σελήνη Ιδιότητες των Σεισμικών Αναγραφών στη Σελήνη Μέθοδοι Διάκρισης των Δονήσεων της Σελήνης Σεισμικότητα της Σελήνης Μηχανισμός
Μάθημα 12ο Σεισμολογία της Σελήνης Το Πρώτο Δίκτυο Σεισμολογικών Σταθμών στη Σελήνη Ιδιότητες των Σεισμικών Αναγραφών στη Σελήνη Μέθοδοι Διάκρισης των Δονήσεων της Σελήνης Σεισμικότητα της Σελήνης Μηχανισμός
ΣΕΙΣΜΟΣ ΛΗΜΝΟΥ-ΣΑΜΟΘΡΑΚΗΣ 24/05/2014
 ΣΕΙΣΜΟΣ ΛΗΜΝΟΥ-ΣΑΜΟΘΡΑΚΗΣ 24/05/2014 Στις 09:25 UTC (12:25 ώρα Ελλάδας) της 24/5/2014 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους 6,3 βαθμών στο θαλάσσιο χώρο μεταξύ Σαμοθράκης και Λήμνου. Την δόνηση ακολούθησε
ΣΕΙΣΜΟΣ ΛΗΜΝΟΥ-ΣΑΜΟΘΡΑΚΗΣ 24/05/2014 Στις 09:25 UTC (12:25 ώρα Ελλάδας) της 24/5/2014 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους 6,3 βαθμών στο θαλάσσιο χώρο μεταξύ Σαμοθράκης και Λήμνου. Την δόνηση ακολούθησε
3. ΣΕΙΣΜΙΚΟΤΗΤΑ ΜΕΛΕΤΗ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ
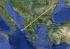 3. ΣΕΙΣΜΙΚΟΤΗΤΑ 3.1 ΕΙΣΑΓΩΓΗ Ο Ν. Μαγνησίας και η ευρύτερη περιοχή χαρακτηρίζονται από υψηλή σεισμικότητα. Ισχυροί σεισμοί έχουν πλήξει επανειλλημένα την περιοχή και ειδικά την πόλη του Βόλου. Τον τελευταίο
3. ΣΕΙΣΜΙΚΟΤΗΤΑ 3.1 ΕΙΣΑΓΩΓΗ Ο Ν. Μαγνησίας και η ευρύτερη περιοχή χαρακτηρίζονται από υψηλή σεισμικότητα. Ισχυροί σεισμοί έχουν πλήξει επανειλλημένα την περιοχή και ειδικά την πόλη του Βόλου. Τον τελευταίο
Καθορισμός του μηχανισμού γένεσης
 Καθορισμός του μηχανισμού γένεσης Σκοπός Σκοπός της άσκησης αυτής είναι ο καθορισμός του μηχανισμού γένεσης ενός σεισμού με βάση τις πρώτες αποκλίσεις των επιμήκων κυμάτων όπως αυτές καταγράφονται στους
Καθορισμός του μηχανισμού γένεσης Σκοπός Σκοπός της άσκησης αυτής είναι ο καθορισμός του μηχανισμού γένεσης ενός σεισμού με βάση τις πρώτες αποκλίσεις των επιμήκων κυμάτων όπως αυτές καταγράφονται στους
Ε.Μ. Σκορδύλης Καθηγητής Σεισμολογίας Τομέας Γεωφυσικής, Α.Π.Θ.
 Ε.Μ. Σκορδύλης Καθηγητής Σεισμολογίας Τομέας Γεωφυσικής, Α.Π.Θ. 223 Μa 200 Μa 135 Μa 35 Μa Present 2 Σχετικές Κινήσεις Λιθοσφαιρικών Πλακών 1. Απόκλισεις λιθοσφαιρικών πλακών (μεσο-ωκεάνιες ράχες) 2. Εφαπτομενικές
Ε.Μ. Σκορδύλης Καθηγητής Σεισμολογίας Τομέας Γεωφυσικής, Α.Π.Θ. 223 Μa 200 Μa 135 Μa 35 Μa Present 2 Σχετικές Κινήσεις Λιθοσφαιρικών Πλακών 1. Απόκλισεις λιθοσφαιρικών πλακών (μεσο-ωκεάνιες ράχες) 2. Εφαπτομενικές
Συμπεράσματα Κεφάλαιο 7.
 7. ΣΥΜΠΕΡΑΣΜΑΤΑ Ο κύριος στόχος της παρούσας διατριβής ήταν η προσομοίωση της σεισμικής κίνησης με τη χρήση τρισδιάστατων προσομοιωμάτων για τους εδαφικούς σχηματισμούς της ευρύτερης περιοχής της Θεσσαλονίκης.
7. ΣΥΜΠΕΡΑΣΜΑΤΑ Ο κύριος στόχος της παρούσας διατριβής ήταν η προσομοίωση της σεισμικής κίνησης με τη χρήση τρισδιάστατων προσομοιωμάτων για τους εδαφικούς σχηματισμούς της ευρύτερης περιοχής της Θεσσαλονίκης.
ΚΑΘΟΡΙΣΜΟΣ ΤΟΥ ΠΕΔΙΟΥ ΤΩΝ ΤΑΣΕΩΝ
 ΚΑΘΟΡΙΣΜΟΣ ΤΟΥ ΠΕΔΙΟΥ ΤΩΝ ΤΑΣΕΩΝ Εισαγωγή: Η σεισμικότητα μιας περιοχής χρησιμοποιείται συχνά για την εξαγωγή συμπερασμάτων σχετικών με τις τεκτονικές διαδικασίες που λαμβάνουν χώρα εκεί. Από τα τέλη του
ΚΑΘΟΡΙΣΜΟΣ ΤΟΥ ΠΕΔΙΟΥ ΤΩΝ ΤΑΣΕΩΝ Εισαγωγή: Η σεισμικότητα μιας περιοχής χρησιμοποιείται συχνά για την εξαγωγή συμπερασμάτων σχετικών με τις τεκτονικές διαδικασίες που λαμβάνουν χώρα εκεί. Από τα τέλη του
Θεσσαλονίκη 14/4/2006
 Θεσσαλονίκη 14/4/2006 ΘΕΜΑ: Καταγραφές δικτύου επιταχυνσιογράφων του ΙΤΣΑΚ από τη πρόσφατη δράση στη περιοχή της Ζακύνθου. Στις 01:05 (ώρα Ελλάδας) της 5 ης Απριλίου 2006 συνέβη στο θαλάσσιο χώρο της Ζακύνθου
Θεσσαλονίκη 14/4/2006 ΘΕΜΑ: Καταγραφές δικτύου επιταχυνσιογράφων του ΙΤΣΑΚ από τη πρόσφατη δράση στη περιοχή της Ζακύνθου. Στις 01:05 (ώρα Ελλάδας) της 5 ης Απριλίου 2006 συνέβη στο θαλάσσιο χώρο της Ζακύνθου
ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2019 ΜΑΘΗΜΑΤΙΚΑ ΚΟΙΝΟΥ ΚΟΡΜΟΥ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 6, Γραφείο 102, Στρόβολος 200, Λευκωσία Τηλέφωνο: 57 2278101, Φαξ: 57 2279122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2019 ΜΑΘΗΜΑΤΙΚΑ ΚΟΙΝΟΥ ΚΟΡΜΟΥ Ημερομηνία:
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 6, Γραφείο 102, Στρόβολος 200, Λευκωσία Τηλέφωνο: 57 2278101, Φαξ: 57 2279122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2019 ΜΑΘΗΜΑΤΙΚΑ ΚΟΙΝΟΥ ΚΟΡΜΟΥ Ημερομηνία:
Μηχανισμοί γένεσης σεισμών
 Μηχανισμοί γένεσης σεισμών Μέθοδοι προσδιορισμού ρ και σύνδεσή τους με σεισμοτεκτονικά μοντέλα στον Ελληνικό χώρο. Κεφ.10 http://seismo.geology.upatras.gr/seismology/ gy p g gy Σώκος Ευθύμιος Λέκτορας
Μηχανισμοί γένεσης σεισμών Μέθοδοι προσδιορισμού ρ και σύνδεσή τους με σεισμοτεκτονικά μοντέλα στον Ελληνικό χώρο. Κεφ.10 http://seismo.geology.upatras.gr/seismology/ gy p g gy Σώκος Ευθύμιος Λέκτορας
Σεισμική Πρόγνωση Κεφάλαιο 15. Σώκος Ευθύμιος Λέκτορας
 Σεισμική Πρόγνωση Κεφάλαιο 15 Σώκος Ευθύμιος Λέκτορας Σεισμική Πρόγνωση Από πολύ παλιά ο άνθρωπος προσπάθησε να προβλέψει τους σεισμούς Μετεωρολογικά φαινόμενα Ο Παυσανίας κατέγραψε «πρόδρομα» φαινόμενα
Σεισμική Πρόγνωση Κεφάλαιο 15 Σώκος Ευθύμιος Λέκτορας Σεισμική Πρόγνωση Από πολύ παλιά ο άνθρωπος προσπάθησε να προβλέψει τους σεισμούς Μετεωρολογικά φαινόμενα Ο Παυσανίας κατέγραψε «πρόδρομα» φαινόμενα
Εισαγωγή στην Στατιστική (ΔΕ200Α-210Α)
 Τμήμα Διοίκησης Επιχειρήσεων (Αγ. Νικόλαος), Τ.Ε.Ι. Κρήτης Σελίδα 1 από 10 6η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση στοχεύει στην εκμάθηση προσαρμογής διαφορετικών ειδών τάσης σε διαγράμματα
Τμήμα Διοίκησης Επιχειρήσεων (Αγ. Νικόλαος), Τ.Ε.Ι. Κρήτης Σελίδα 1 από 10 6η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση στοχεύει στην εκμάθηση προσαρμογής διαφορετικών ειδών τάσης σε διαγράμματα
The contribution of 3D recording networks of strong motion in the seismic risk of Thessaloniki
 The contribution of 3D recording networks of strong motion in the seismic risk of Thessaloniki Η συνεισφορά των τρισδιάστατων δικτύων καταγραφής της ισχυρής κίνησης στην σεισμική διακινδύνευση της Θεσσαλονίκης
The contribution of 3D recording networks of strong motion in the seismic risk of Thessaloniki Η συνεισφορά των τρισδιάστατων δικτύων καταγραφής της ισχυρής κίνησης στην σεισμική διακινδύνευση της Θεσσαλονίκης
ΠΡΟΚΑΤΑΡΚΤΙΚΟ ΔΕΛΤΙΟ Σεισμός της 8 ης Ιανουαρίου 2012 στο θαλάσσιο χώρο ΝΑ της Λήμνου Ι. Καλογεράς, Ν. Μελής & Χ. Ευαγγελίδης
 ΠΡΟΚΑΤΑΡΚΤΙΚΟ ΔΕΛΤΙΟ Σεισμός της 8 ης Ιανουαρίου 2012 στο θαλάσσιο χώρο ΝΑ της Λήμνου Ι. Καλογεράς, Ν. Μελής & Χ. Ευαγγελίδης Στις 16:16 τοπική ώρα της 8 ης Ιανουαρίου 2012 σημειώθηκε ισχυρή σεισμική δόνηση
ΠΡΟΚΑΤΑΡΚΤΙΚΟ ΔΕΛΤΙΟ Σεισμός της 8 ης Ιανουαρίου 2012 στο θαλάσσιο χώρο ΝΑ της Λήμνου Ι. Καλογεράς, Ν. Μελής & Χ. Ευαγγελίδης Στις 16:16 τοπική ώρα της 8 ης Ιανουαρίου 2012 σημειώθηκε ισχυρή σεισμική δόνηση
ΣΕΙΣΜΟΣ ΛΕΥΚΑΔΑΣ 17/11/2015
 ΣΕΙΣΜΟΣ ΛΕΥΚΑΔΑΣ 17/11/2015 Στις 07:10 UTC (09:10 ώρα Ελλάδας) της 17/11/2015 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M W =6.4 βαθμών Νοτιοδυτικά της πόλης της Λευκάδας. Την δόνηση ακολούθησε μετασεισμική
ΣΕΙΣΜΟΣ ΛΕΥΚΑΔΑΣ 17/11/2015 Στις 07:10 UTC (09:10 ώρα Ελλάδας) της 17/11/2015 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M W =6.4 βαθμών Νοτιοδυτικά της πόλης της Λευκάδας. Την δόνηση ακολούθησε μετασεισμική
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ ΑΣΚΗΣΗ 1 d x dx Η διαφορική εξίσωση κίνησης ενός ταλαντωτή δίνεται από τη σχέση: λ μx. Αν η μάζα d d του ταλαντωτή είναι ίση με =.5 kg, τότε να διερευνήσετε την κίνηση
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΑΠΟΣΒΕΣΗ ΚΑΙ ΔΙΕΓΕΡΣΗ ΑΣΚΗΣΗ 1 d x dx Η διαφορική εξίσωση κίνησης ενός ταλαντωτή δίνεται από τη σχέση: λ μx. Αν η μάζα d d του ταλαντωτή είναι ίση με =.5 kg, τότε να διερευνήσετε την κίνηση
Μια Κοντινή Ματιά στα Σεισμικά Φαινόμενα & στις Επιπτώσεις τους. Μανώλης Σκορδύλης Καθηγητής Σεισμολογίας Εργαστήριο Γεωφυσικής, Α.Π.Θ.
 1 Μια Κοντινή Ματιά στα Σεισμικά Φαινόμενα & στις Επιπτώσεις τους Μανώλης Σκορδύλης Καθηγητής Σεισμολογίας Εργαστήριο Γεωφυσικής, Α.Π.Θ. Ποια η εκπαίδευση για θέματα σεισμών που δίνουμε σήμερα στους αυριανούς
1 Μια Κοντινή Ματιά στα Σεισμικά Φαινόμενα & στις Επιπτώσεις τους Μανώλης Σκορδύλης Καθηγητής Σεισμολογίας Εργαστήριο Γεωφυσικής, Α.Π.Θ. Ποια η εκπαίδευση για θέματα σεισμών που δίνουμε σήμερα στους αυριανούς
Σεισμοί και Εκπαιδευτική Κοινότητα. Δρ. Ι. Καλογεράς Σεισμολόγος Διευθυντής Ερευνών Γεωδυναμικό Ινστιτούτο Εθνικού Αστεροσκοπείου Αθηνών
 Σεισμοί και Εκπαιδευτική Κοινότητα Δρ. Ι. Καλογεράς Σεισμολόγος Διευθυντής Ερευνών Γεωδυναμικό Ινστιτούτο Εθνικού Αστεροσκοπείου Αθηνών ΕΚΦΕ Ν. Φιλαδέλφειας, Οκτώβριος 2015 Συνειδητοποίηση Ευαισθητοποίηση
Σεισμοί και Εκπαιδευτική Κοινότητα Δρ. Ι. Καλογεράς Σεισμολόγος Διευθυντής Ερευνών Γεωδυναμικό Ινστιτούτο Εθνικού Αστεροσκοπείου Αθηνών ΕΚΦΕ Ν. Φιλαδέλφειας, Οκτώβριος 2015 Συνειδητοποίηση Ευαισθητοποίηση
ΣΕΙΣΜΟΣ ΛΕΥΚΑΔΑΣ 17/11/2015
 ΣΕΙΣΜΟΣ ΛΕΥΚΑΔΑΣ 17/11/2015 Στις 07:10 UTC (09:10 ώρα Ελλάδας) της 17/11/2015 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M W =6.4 βαθμών Νοτιοδυτικά της πόλης της Λευκάδας. Την δόνηση ακολούθησε μετασεισμική
ΣΕΙΣΜΟΣ ΛΕΥΚΑΔΑΣ 17/11/2015 Στις 07:10 UTC (09:10 ώρα Ελλάδας) της 17/11/2015 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M W =6.4 βαθμών Νοτιοδυτικά της πόλης της Λευκάδας. Την δόνηση ακολούθησε μετασεισμική
Μάθημα 7 ο. Μέγεθος Σεισμών
 Μάθημα 7 ο Μέγεθος Σεισμών Μέγεθος Σεισμού Σεισμική Ροπή Ενέργεια Σεισμού ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΕΙΣΜΟΛΟΓΙΑ Μάθημα 6ο: Σεισμομετρία ΤΟΜΕΑΣ ΓΕΩΦΥΣΙΚΗΣ Α.Π.Θ 1 Μέγεθος Σεισμού Ορισμός Το μέγεθος, Μ, ενός σεισμού,
Μάθημα 7 ο Μέγεθος Σεισμών Μέγεθος Σεισμού Σεισμική Ροπή Ενέργεια Σεισμού ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΕΙΣΜΟΛΟΓΙΑ Μάθημα 6ο: Σεισμομετρία ΤΟΜΕΑΣ ΓΕΩΦΥΣΙΚΗΣ Α.Π.Θ 1 Μέγεθος Σεισμού Ορισμός Το μέγεθος, Μ, ενός σεισμού,
ΕΚΤΙΜΗΣΗ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ & ΑΝΑΜΕΝΟΜΕΝΗΣ ΕΔΑΦΙΚΗΣ ΚΙΝΗΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΓΕΦΥΡΙΟΥ ΤΗΣ ΠΛΑΚΑΣ
 ΕΚΤΙΜΗΣΗ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ & ΑΝΑΜΕΝΟΜΕΝΗΣ ΕΔΑΦΙΚΗΣ ΚΙΝΗΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΓΕΦΥΡΙΟΥ ΤΗΣ ΠΛΑΚΑΣ Κωνσταντίνος Σπυράκος Δρ. Πολιτικός Μηχανικός, Καθηγητής ΕΜΠ, Δ/ντής Εργαστηρίου Αντισεισμικής Τεχνολογίας
ΕΚΤΙΜΗΣΗ ΣΕΙΣΜΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ & ΑΝΑΜΕΝΟΜΕΝΗΣ ΕΔΑΦΙΚΗΣ ΚΙΝΗΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΓΕΦΥΡΙΟΥ ΤΗΣ ΠΛΑΚΑΣ Κωνσταντίνος Σπυράκος Δρ. Πολιτικός Μηχανικός, Καθηγητής ΕΜΠ, Δ/ντής Εργαστηρίου Αντισεισμικής Τεχνολογίας
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2005
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 005 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Να αποδειχθεί ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει: P(A B) = P(A) + P(B) P(A B) Τα απλά ενδεχόµενα
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 005 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Να αποδειχθεί ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει: P(A B) = P(A) + P(B) P(A B) Τα απλά ενδεχόµενα
Χρήση του προγράμματος Excel για τον υπολογισμό της αντίστασης και της ισχύος, την κατασκευή χαρακτηριστικής I V, και της ευθείας φόρτου.
 Χρήση του προγράμματος Excel για τον υπολογισμό της αντίστασης και της ισχύος, την κατασκευή χαρακτηριστικής I V, και της ευθείας φόρτου. Στα παραδείγματα θα γίνει χρήση 12 πειραματικών μετρήσεων σε αντίσταση
Χρήση του προγράμματος Excel για τον υπολογισμό της αντίστασης και της ισχύος, την κατασκευή χαρακτηριστικής I V, και της ευθείας φόρτου. Στα παραδείγματα θα γίνει χρήση 12 πειραματικών μετρήσεων σε αντίσταση
Εργασία στο µάθηµα Ανάλυση εδοµένων
 Μεταπτυχιακό Υπολογιστικής Φυσικής Εργασία στο µάθηµα Ανάλυση εδοµένων ηµήτρης Κουγιουµτζής E-mail: dkugiu@auth.gr 30 Ιανουαρίου 2018 Οδηγίες : Σχετικά µε την παράδοση της εργασίας ϑα πρέπει : Το κείµενο
Μεταπτυχιακό Υπολογιστικής Φυσικής Εργασία στο µάθηµα Ανάλυση εδοµένων ηµήτρης Κουγιουµτζής E-mail: dkugiu@auth.gr 30 Ιανουαρίου 2018 Οδηγίες : Σχετικά µε την παράδοση της εργασίας ϑα πρέπει : Το κείµενο
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ
 Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΞΑΜΗΝΟ: 7 ο ΔΙΔΑΣΚΟΝΤΕΣ: Β. ΧΡΗΣΤΑΡΑΣ, Καθηγητής Β. ΜΑΡΙΝΟΣ,
Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΞΑΜΗΝΟ: 7 ο ΔΙΔΑΣΚΟΝΤΕΣ: Β. ΧΡΗΣΤΑΡΑΣ, Καθηγητής Β. ΜΑΡΙΝΟΣ,
Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο
 Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο Στο σχήμα φαίνεται μια γνώριμη διάταξη δύο παράλληλων αγωγών σε απόσταση, που ορίζουν οριζόντιο επίπεδο, κάθετο σε ομογενές μαγνητικό πεδίο έντασης.
Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο Στο σχήμα φαίνεται μια γνώριμη διάταξη δύο παράλληλων αγωγών σε απόσταση, που ορίζουν οριζόντιο επίπεδο, κάθετο σε ομογενές μαγνητικό πεδίο έντασης.
Πρακτική µε στοιχεία στατιστικής ανάλυσης
 Πρακτική µε στοιχεία στατιστικής ανάλυσης 1. Για να υπολογίσουµε µια ποσότητα q = x 2 y xy 2, µετρήσαµε τα µεγέθη x και y και βρήκαµε x = 3.0 ± 0.1και y = 2.0 ± 0.1. Να βρεθεί η ποσότητα q και η αβεβαιότητά
Πρακτική µε στοιχεία στατιστικής ανάλυσης 1. Για να υπολογίσουµε µια ποσότητα q = x 2 y xy 2, µετρήσαµε τα µεγέθη x και y και βρήκαµε x = 3.0 ± 0.1και y = 2.0 ± 0.1. Να βρεθεί η ποσότητα q και η αβεβαιότητά
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ 1 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1. Ένα σηµείο Α(χ, ψ) ανήκει στη γραφική παράσταση της f αν f(ψ)=χ. 2. Αν µια συνάρτηση είναι γνησίως αύξουσα σε ένα διάστηµα A,
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ 1 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1. Ένα σηµείο Α(χ, ψ) ανήκει στη γραφική παράσταση της f αν f(ψ)=χ. 2. Αν µια συνάρτηση είναι γνησίως αύξουσα σε ένα διάστηµα A,
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ
 ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
Μικροζωνικές Μελέτες. Κεφάλαιο 24. Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών
 Μικροζωνικές Μελέτες Κεφάλαιο 24 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Ορισμός Με τον όρο μικροζωνική μελέτη εννοούμε την εκτίμηση των αναμενόμενων εδαφικών κινήσεων σε μία περιοχή λαμβάνοντας υπ
Μικροζωνικές Μελέτες Κεφάλαιο 24 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Ορισμός Με τον όρο μικροζωνική μελέτη εννοούμε την εκτίμηση των αναμενόμενων εδαφικών κινήσεων σε μία περιοχή λαμβάνοντας υπ
Επίδραση Τοπικών Συνθηκών
 Επίδραση Τοπικών Συνθηκών και Αλληλεπίδραση Εδάφους-Ανωδοµής Ιωάννης Β. Κωνσταντόπουλος, ScD (MIT) Ioannis.Constantopoulos@ulb.ac.be Σχ. 1 Επίδραση Τοπικών Συνθηκών Ο όρος Επίδραση Τοπικών Συνθηκών αναφέρεται
Επίδραση Τοπικών Συνθηκών και Αλληλεπίδραση Εδάφους-Ανωδοµής Ιωάννης Β. Κωνσταντόπουλος, ScD (MIT) Ioannis.Constantopoulos@ulb.ac.be Σχ. 1 Επίδραση Τοπικών Συνθηκών Ο όρος Επίδραση Τοπικών Συνθηκών αναφέρεται
3 ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ
 ΚΩΝΙΚΕ ΤΟΜΕ ΕΡΩΤΗΕΙ ΑΞΙΟΟΓΗΗ ΕΡΩΤΗΕΙ ΑΞΙΟΟΓΗΗ 1. Να σημειώσετε το σωστό () ή το λάθος () στους παρακάτω ισχυρισμούς: 1. Η εξίσωση + = α (α > 0) παριστάνει κύκλο.. Η εξίσωση + + κ + λ = 0 µε κ, λ 0 παριστάνει
ΚΩΝΙΚΕ ΤΟΜΕ ΕΡΩΤΗΕΙ ΑΞΙΟΟΓΗΗ ΕΡΩΤΗΕΙ ΑΞΙΟΟΓΗΗ 1. Να σημειώσετε το σωστό () ή το λάθος () στους παρακάτω ισχυρισμούς: 1. Η εξίσωση + = α (α > 0) παριστάνει κύκλο.. Η εξίσωση + + κ + λ = 0 µε κ, λ 0 παριστάνει
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΏΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ Ε ΑΦΟΜΗΧΑΝΙΚΗΣ, ΘΕΜΕΛΙΩΣΕΩΝ ΚΑΙ ΓΕΩΤΕΧΝΙΚΗΣ ΣΕΙΣΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΏΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ Ε ΑΦΟΜΗΧΑΝΙΚΗΣ, ΘΕΜΕΛΙΩΣΕΩΝ ΚΑΙ ΓΕΩΤΕΧΝΙΚΗΣ ΣΕΙΣΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ Συμπεριφορά υπόγειων αγωγών Φυσικού Αερίου υπό σεισμική φόρτιση
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΏΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ Ε ΑΦΟΜΗΧΑΝΙΚΗΣ, ΘΕΜΕΛΙΩΣΕΩΝ ΚΑΙ ΓΕΩΤΕΧΝΙΚΗΣ ΣΕΙΣΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ Συμπεριφορά υπόγειων αγωγών Φυσικού Αερίου υπό σεισμική φόρτιση
1 και Ρ(Β) = τότε η Ρ (Α Β) είναι ίση µε: 2 δ και Ρ(Α Β) = 4
 ΘΕΜΑ ο Α.. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει ότι: Ρ (Α Β) Ρ (Α) Ρ (Α Β). Μονάδες 8, Α.. Να µεταφέρετε στο τετράδιό σας τις παρακάτω σχέσεις και να συµπληρώσετε
ΘΕΜΑ ο Α.. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει ότι: Ρ (Α Β) Ρ (Α) Ρ (Α Β). Μονάδες 8, Α.. Να µεταφέρετε στο τετράδιό σας τις παρακάτω σχέσεις και να συµπληρώσετε
ΣΕΙΣΜΙΚΗ ΤΡΩΤΟΤΗΤΑ ΔΙΚΤΥΩΝ ΚΟΙΝΗΣ ΩΦΕΛΕΙΑΣ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΕΙΣΜΙΚΗ ΤΡΩΤΟΤΗΤΑ ΔΙΚΤΥΩΝ ΚΟΙΝΗΣ ΩΦΕΛΕΙΑΣ ΡΟΥΜΠΑ ΔΗΜΗΤΡΑ Α.Μ. 2002.05.0042 ΤΡΙΜΕΛΗΣ ΕΠΙΤΡΟΠΗ ΤΣΟΜΠΑΝΑΚΗΣ ΙΩΑΝΝΗΣ Επίκουρος Καθηγητής
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΕΙΣΜΙΚΗ ΤΡΩΤΟΤΗΤΑ ΔΙΚΤΥΩΝ ΚΟΙΝΗΣ ΩΦΕΛΕΙΑΣ ΡΟΥΜΠΑ ΔΗΜΗΤΡΑ Α.Μ. 2002.05.0042 ΤΡΙΜΕΛΗΣ ΕΠΙΤΡΟΠΗ ΤΣΟΜΠΑΝΑΚΗΣ ΙΩΑΝΝΗΣ Επίκουρος Καθηγητής
Προσεισμικός Έλεγχος Κτιρίων Δημόσιας και Κοινωφελούς Χρήσης
 Προσεισμικός Έλεγχος Κτιρίων Δημόσιας και Κοινωφελούς Χρήσης Οργανισμός Αντισεισμικού Σχεδιασμού & Προστασίας (Ο.Α.Σ.Π.) Περιφερειακή Ενότητα Πειραιά και Περιφερειακή Ενότητα Νήσων Συνάντηση Εργασίας (workshop)
Προσεισμικός Έλεγχος Κτιρίων Δημόσιας και Κοινωφελούς Χρήσης Οργανισμός Αντισεισμικού Σχεδιασμού & Προστασίας (Ο.Α.Σ.Π.) Περιφερειακή Ενότητα Πειραιά και Περιφερειακή Ενότητα Νήσων Συνάντηση Εργασίας (workshop)
Στατιστική, Άσκηση 2. (Κανονική κατανομή)
 Στατιστική, Άσκηση 2 (Κανονική κατανομή) Στον πίνακα που ακολουθεί δίνονται οι μέσες παροχές όπως προέκυψαν από μετρήσεις πεδίου σε μια διατομή ενός ποταμού. Ζητείται: 1. Να αποδειχθεί ότι το δείγμα προσαρμόζεται
Στατιστική, Άσκηση 2 (Κανονική κατανομή) Στον πίνακα που ακολουθεί δίνονται οι μέσες παροχές όπως προέκυψαν από μετρήσεις πεδίου σε μια διατομή ενός ποταμού. Ζητείται: 1. Να αποδειχθεί ότι το δείγμα προσαρμόζεται
Επένδυση µέρους των ρευστών διαθεσίµων ύψους
 Case 03: Επιλογή Χαρτοφυλακίου Ι «ΖΗΤΑ A.E.» ΣΕΝΑΡΙΟ (Portfolio Selection) Επένδυση µέρους των ρευστών διαθεσίµων ύψους 600.000 Επένδυση Ετήσιο αναµενόµενο ποσοστό απόδοσης (%) ΤραπεζικήΜετοχήΑ 13,7 ΤραπεζικήΜετοχήΒ
Case 03: Επιλογή Χαρτοφυλακίου Ι «ΖΗΤΑ A.E.» ΣΕΝΑΡΙΟ (Portfolio Selection) Επένδυση µέρους των ρευστών διαθεσίµων ύψους 600.000 Επένδυση Ετήσιο αναµενόµενο ποσοστό απόδοσης (%) ΤραπεζικήΜετοχήΑ 13,7 ΤραπεζικήΜετοχήΒ
Παιδαγωγικό σενάριο : Μελέτη της συνάρτησης y=αx
 Παιδαγωγικό σενάριο : Μελέτη της συνάρτησης y=αx Στόχος: Το παιδαγωγικό σενάριο αναφέρεται στη μελέτη της συνάρτησης y=αx και στη κατανόηση της κλίσης ευθείας. Λογισμικό: Για την εφαρμογή του σεναρίου
Παιδαγωγικό σενάριο : Μελέτη της συνάρτησης y=αx Στόχος: Το παιδαγωγικό σενάριο αναφέρεται στη μελέτη της συνάρτησης y=αx και στη κατανόηση της κλίσης ευθείας. Λογισμικό: Για την εφαρμογή του σεναρίου
ΕΡΓΑΣΤΗΡΙΟ ΕΝΟΡΓΑΝΗΣ ΑΝΑΛΥΣΗΣ ΤΡΟΦΙΜΩΝ Οδηγός Συγγραφής Εργαστηριακών Αναφορών
 ΕΡΓΑΣΤΗΡΙΟ ΕΝΟΡΓΑΝΗΣ ΑΝΑΛΥΣΗΣ ΤΡΟΦΙΜΩΝ Οδηγός Συγγραφής Εργαστηριακών Αναφορών Βασιλεία Ι. Σινάνογλου Ειρήνη Φ. Στρατή Παναγιώτης Ζουμπουλάκης Σωτήρης Μπρατάκος Εξώφυλλο Εργαστηριακό Τμήμα (ημέρα ώρα)
ΕΡΓΑΣΤΗΡΙΟ ΕΝΟΡΓΑΝΗΣ ΑΝΑΛΥΣΗΣ ΤΡΟΦΙΜΩΝ Οδηγός Συγγραφής Εργαστηριακών Αναφορών Βασιλεία Ι. Σινάνογλου Ειρήνη Φ. Στρατή Παναγιώτης Ζουμπουλάκης Σωτήρης Μπρατάκος Εξώφυλλο Εργαστηριακό Τμήμα (ημέρα ώρα)
ΣΕΙΣΜΟΣ ΝΔ ΤΗΣ ΖΑΚΥΝΘΟΥ (M=6.8, 26/10/2018)
 ΣΕΙΣΜΟΣ ΝΔ ΤΗΣ ΖΑΚΥΝΘΟΥ (M=6.8, 26/10/2018) 1. ΓΕΝΙΚΑ Στις 01:54 ώρα Ελλάδας (22:54 UTC) της 25 ης Οκτωβρίου 2018 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους 6.8 στη θαλάσσια περιοχή ΝΔ της Ζακύνθου. Τη
ΣΕΙΣΜΟΣ ΝΔ ΤΗΣ ΖΑΚΥΝΘΟΥ (M=6.8, 26/10/2018) 1. ΓΕΝΙΚΑ Στις 01:54 ώρα Ελλάδας (22:54 UTC) της 25 ης Οκτωβρίου 2018 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους 6.8 στη θαλάσσια περιοχή ΝΔ της Ζακύνθου. Τη
Ε.Μ. Σκορδύλης Καθηγητής Σεισμολογίας Τομέας Γεωφυσικής, Α.Π.Θ.
 Ε.Μ. Σκορδύλης Καθηγητής Σεισμολογίας Τομέας Γεωφυσικής, Α.Π.Θ. 223 Μa 200 Μa 135 Μa 35 Μa Present 2 Σχετικές Κινήσεις Λιθοσφαιρικών Πλακών 1. Απόκλισεις λιθοσφαιρικών πλακών (μεσο-ωκεάνιες ράχες) 2. Εφαπτομενικές
Ε.Μ. Σκορδύλης Καθηγητής Σεισμολογίας Τομέας Γεωφυσικής, Α.Π.Θ. 223 Μa 200 Μa 135 Μa 35 Μa Present 2 Σχετικές Κινήσεις Λιθοσφαιρικών Πλακών 1. Απόκλισεις λιθοσφαιρικών πλακών (μεσο-ωκεάνιες ράχες) 2. Εφαπτομενικές
Z U REC (cm) (V) i =log(z) y i =log(u REC ) x i x i y i 10 74,306 1,000 1,871 1,000 1, ,528 1,079 1,796 1,165 1, ,085 1,146 1,749
 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΦΥΣΙΚΗ ΙΙ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ (ΑΣΚΗΣΗ 3) - set 00 ΣΤΟΙΧΕΙΑ ΦΟΙΤΗΤΗ Ονοµατεπώνυµο: Γηρούσης Θεόδωρος
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΦΥΣΙΚΗ ΙΙ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ (ΑΣΚΗΣΗ 3) - set 00 ΣΤΟΙΧΕΙΑ ΦΟΙΤΗΤΗ Ονοµατεπώνυµο: Γηρούσης Θεόδωρος
Σεισμικές παράμετροι. Κεφάλαιο 12
 Σεισμικές παράμετροι Κεφάλαιο 12 Σεισμικές παράμετροι Σεισμικό μέγεθος Σεισμική ενέργεια Σεισμική ροπή Σεισμική πτώση τάσης Σεισμικό μέγεθος Προέκυψε από την προσπάθεια εκτίμησης της εκλυόμενης ενέργειας.
Σεισμικές παράμετροι Κεφάλαιο 12 Σεισμικές παράμετροι Σεισμικό μέγεθος Σεισμική ενέργεια Σεισμική ροπή Σεισμική πτώση τάσης Σεισμικό μέγεθος Προέκυψε από την προσπάθεια εκτίμησης της εκλυόμενης ενέργειας.
Ο ΗΓΙΕΣ ΕΠΕΞΕΡΓΑΣΙΑΣ Ε ΟΜΕΝΩΝ ΚΑΙ ΣΥΓΓΡΑΦΗΣ ΤΗΣ ΤΕΛΙΚΗΣ ΕΡΓΑΣΙΑΣ ΤΟΥ ΕΡΓΑΣΤΗΡΙΟΥ ΦΥΣΙΚΗΣ ΙΙ
 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τ. Ε. Ι. Σ Ε Ρ Ρ Ω Ν Ο ΗΓΙΕΣ ΕΠΕΞΕΡΓΑΣΙΑΣ Ε ΟΜΕΝΩΝ ΚΑΙ ΣΥΓΓΡΑΦΗΣ ΤΗΣ ΤΕΛΙΚΗΣ ΕΡΓΑΣΙΑΣ ΤΟΥ ΕΡΓΑΣΤΗΡΙΟΥ ΦΥΣΙΚΗΣ ΙΙ Προετοιµασία ιαβάστε καλά
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τ. Ε. Ι. Σ Ε Ρ Ρ Ω Ν Ο ΗΓΙΕΣ ΕΠΕΞΕΡΓΑΣΙΑΣ Ε ΟΜΕΝΩΝ ΚΑΙ ΣΥΓΓΡΑΦΗΣ ΤΗΣ ΤΕΛΙΚΗΣ ΕΡΓΑΣΙΑΣ ΤΟΥ ΕΡΓΑΣΤΗΡΙΟΥ ΦΥΣΙΚΗΣ ΙΙ Προετοιµασία ιαβάστε καλά
ΣΤΑΤΙΣΤΙΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΓΙΑ ΤΗΝ ΑΠΟΤΙΜΗΣΗ ΤΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ
 ΣΤΑΤΙΣΤΙΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΓΙΑ ΤΗΝ ΑΠΟΤΙΜΗΣΗ ΤΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ Στατιστική ανάλυση του γεωχηµικού δείγµατος µας δίνει πληροφορίες για τον γεωχηµικό πληθυσµό που µελετάµε. Συνυπολογισµός σφαλµάτων Πειραµατικά
ΣΤΑΤΙΣΤΙΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΓΙΑ ΤΗΝ ΑΠΟΤΙΜΗΣΗ ΤΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ Στατιστική ανάλυση του γεωχηµικού δείγµατος µας δίνει πληροφορίες για τον γεωχηµικό πληθυσµό που µελετάµε. Συνυπολογισµός σφαλµάτων Πειραµατικά
ΦΥΣ 145 Μαθηµατικές Μέθοδοι στη Φυσική. 5 Μαίου 2012
 ΦΥΣ 145 Μαθηµατικές Μέθοδοι στη Φυσική 5 Μαίου 2012 Συµπληρώστε τα στοιχεία σας στο παρακάτω πίνακα τώρα Ονοµατεπώνυµο Αρ. Ταυτότητας Username Password Δηµιουργήστε ένα φάκελο στο home directory σας µε
ΦΥΣ 145 Μαθηµατικές Μέθοδοι στη Φυσική 5 Μαίου 2012 Συµπληρώστε τα στοιχεία σας στο παρακάτω πίνακα τώρα Ονοµατεπώνυµο Αρ. Ταυτότητας Username Password Δηµιουργήστε ένα φάκελο στο home directory σας µε
Φύλλο Εργασίας για την y=αx 2
 Πρόβλημα Σε ένα τετραγωνικό περιβόλι πλευράς 10m πρόκειται να χτιστεί μια αποθήκη σχήματος ορθογωνίου, όπως φαίνεται στο διπλανό σχήμα. Α) Να βρεθούν οι διαστάσεις της αποθήκης συναρτήσει του x, αν γνωρίζετε
Πρόβλημα Σε ένα τετραγωνικό περιβόλι πλευράς 10m πρόκειται να χτιστεί μια αποθήκη σχήματος ορθογωνίου, όπως φαίνεται στο διπλανό σχήμα. Α) Να βρεθούν οι διαστάσεις της αποθήκης συναρτήσει του x, αν γνωρίζετε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
ΣΚΑΡΛΑΤΟΥ ΗΣ Α. ΑΝ ΡΕΑΣ
 ΣΚΑΡΛΑΤΟΥ ΗΣ Α. ΑΝ ΡΕΑΣ ΕΠΑΝΥΠΟΛΟΓΙΣΜΟΣ ΥΠΟΚΕΝΤΡΙΚΩΝ ΠΑΡΑΜΕΤΡΩΝ ΣΕΙΣΜΩΝ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ ΜΕ ΤΗ ΧΡΗΣΗ Ε ΟΜΕΝΩΝ ΤΟΠΙΚΩΝ ΠΕΙΡΑΜΑΤΩΝ ΚΑΙ ΕΠΙ ΡΑΣΗ ΤΟΥΣ ΣΤΙΣ ΣΧΕΣΕΙΣ ΑΠΟΣΒΕΣΗΣ ΤΗΣ ΙΣΧΥΡΗΣ ΣΕΙΣΜΙΚΗΣ ΚΙΝΗΣΗΣ
ΣΚΑΡΛΑΤΟΥ ΗΣ Α. ΑΝ ΡΕΑΣ ΕΠΑΝΥΠΟΛΟΓΙΣΜΟΣ ΥΠΟΚΕΝΤΡΙΚΩΝ ΠΑΡΑΜΕΤΡΩΝ ΣΕΙΣΜΩΝ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ ΜΕ ΤΗ ΧΡΗΣΗ Ε ΟΜΕΝΩΝ ΤΟΠΙΚΩΝ ΠΕΙΡΑΜΑΤΩΝ ΚΑΙ ΕΠΙ ΡΑΣΗ ΤΟΥΣ ΣΤΙΣ ΣΧΕΣΕΙΣ ΑΠΟΣΒΕΣΗΣ ΤΗΣ ΙΣΧΥΡΗΣ ΣΕΙΣΜΙΚΗΣ ΚΙΝΗΣΗΣ
4.3. Γραµµικοί ταξινοµητές
 Γραµµικοί ταξινοµητές Γραµµικός ταξινοµητής είναι ένα σύστηµα ταξινόµησης που χρησιµοποιεί γραµµικές διακριτικές συναρτήσεις Οι ταξινοµητές αυτοί αναπαρίστανται συχνά µε οµάδες κόµβων εντός των οποίων
Γραµµικοί ταξινοµητές Γραµµικός ταξινοµητής είναι ένα σύστηµα ταξινόµησης που χρησιµοποιεί γραµµικές διακριτικές συναρτήσεις Οι ταξινοµητές αυτοί αναπαρίστανται συχνά µε οµάδες κόµβων εντός των οποίων
Βασικό Επίπεδο στο Modellus
 Βασικό Επίπεδο στο Modellus Το λογισµικό Modellus επιτρέπει στον χρήστη να οικοδοµήσει µαθηµατικά µοντέλα και να τα εξερευνήσει µε προσοµοιώσεις, γραφήµατα, πίνακες τιµών. Ο χρήστης πρέπει να γράψει τις
Βασικό Επίπεδο στο Modellus Το λογισµικό Modellus επιτρέπει στον χρήστη να οικοδοµήσει µαθηµατικά µοντέλα και να τα εξερευνήσει µε προσοµοιώσεις, γραφήµατα, πίνακες τιµών. Ο χρήστης πρέπει να γράψει τις
Κεφάλαιο 6 ΣΕΙΣΜΟΜΕΤΡΙΑ
 Κεφάλαιο 6 ΣΕΙΣΜΟΜΕΤΡΙΑ Στην σεισμολογία μετρούμε πάντα μήκος πάνω στα σεισμογράμματα. -Κατά την διεύθυνση του άξονα Χ μετρούμε χρόνο ή περίοδο -Κατά την διεύθυνση του άξονα Υ μετρούμε μετάθεση ή ταχύτητα
Κεφάλαιο 6 ΣΕΙΣΜΟΜΕΤΡΙΑ Στην σεισμολογία μετρούμε πάντα μήκος πάνω στα σεισμογράμματα. -Κατά την διεύθυνση του άξονα Χ μετρούμε χρόνο ή περίοδο -Κατά την διεύθυνση του άξονα Υ μετρούμε μετάθεση ή ταχύτητα
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων
 Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
ΣΕΙΣΜΟΣ ΛΕΣΒΟΥ Μ W 6.3 ΤΗΣ 12/06/2017
 ΣΕΙΣΜΟΣ ΛΕΣΒΟΥ Μ W 6.3 ΤΗΣ 12/06/2017 ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΕΚΘΕΣΗ Θ ΕΣ ΣΑΛΟΝΙΚΗ ΙΟΥΝΙΟΣ 2017 Η αναφορά στη χρήση του περιεχομένου αυτής της έκθεσης είναι η εξής: ΙΤΣΑΚ (2017): Σεισμός Λέσβου Μw 6.3 της 12/06/2017
ΣΕΙΣΜΟΣ ΛΕΣΒΟΥ Μ W 6.3 ΤΗΣ 12/06/2017 ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΕΚΘΕΣΗ Θ ΕΣ ΣΑΛΟΝΙΚΗ ΙΟΥΝΙΟΣ 2017 Η αναφορά στη χρήση του περιεχομένου αυτής της έκθεσης είναι η εξής: ΙΤΣΑΚ (2017): Σεισμός Λέσβου Μw 6.3 της 12/06/2017
ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017)
 ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017) Στις 12:28 UTC (15:28 ώρα Ελλάδας) της 12/06/2017 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M w =6.3 μεταξύ Λέσβου και Χίου, ~15χλμ Ν-ΝΔ των νότιων ακτών της
ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017) Στις 12:28 UTC (15:28 ώρα Ελλάδας) της 12/06/2017 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M w =6.3 μεταξύ Λέσβου και Χίου, ~15χλμ Ν-ΝΔ των νότιων ακτών της
ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017)
 ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017) Στις 12:28 UTC (15:28 ώρα Ελλάδας) της 12/06/2017 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M w =6.3 μεταξύ Λέσβου και Χίου, ~15χλμ Ν-ΝΔ των νότιων ακτών της
ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017) Στις 12:28 UTC (15:28 ώρα Ελλάδας) της 12/06/2017 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M w =6.3 μεταξύ Λέσβου και Χίου, ~15χλμ Ν-ΝΔ των νότιων ακτών της
ΣΕΙΣΜΟΣ ΚΕΦΑΛΟΝΙΑΣ 26/01/2014
 ΣΕΙΣΜΟΣ ΚΕΦΑΛΟΝΙΑΣ 26/01/2014 Στις 13:55 UTC (15:55 ώρα Ελλάδας) της 26/1/2014 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M W =6.1 βαθμών στις δυτικές ακτές της Κεφαλονιάς. Την δόνηση ακολούθησε μετασεισμική
ΣΕΙΣΜΟΣ ΚΕΦΑΛΟΝΙΑΣ 26/01/2014 Στις 13:55 UTC (15:55 ώρα Ελλάδας) της 26/1/2014 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M W =6.1 βαθμών στις δυτικές ακτές της Κεφαλονιάς. Την δόνηση ακολούθησε μετασεισμική
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
αx αx αx αx 2 αx = α e } 2 x x x dx καλείται η παραβολική συνάρτηση η οποία στο x
 A3. ΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ. εύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σηµεία καµπής ΠΑΡΑΡΤΗΜΑ 7. εύτερη πλεγµένη παραγώγιση 8.Χαρακτηρισµός
A3. ΕΥΤΕΡΗ ΠΑΡΑΓΩΓΟΣ-ΚΥΡΤΟΤΗΤΑ. εύτερη παράγωγος.παραβολική προσέγγιση ή επέκταση 3.Κυρτή 4.Κοίλη 5.Ιδιότητες κυρτών/κοίλων συναρτήσεων 6.Σηµεία καµπής ΠΑΡΑΡΤΗΜΑ 7. εύτερη πλεγµένη παραγώγιση 8.Χαρακτηρισµός
4. Μέθοδοι αναγνώρισης ταξινοµητές µε επόπτη
 ΑΕΙ Σερρών 4. Μέθοδοι αναγνώρισης ταξινοµητές µε επόπτη 4.. Αναγνώριση µε βάση τα κέντρα των τάξεων Είναι µια απλοϊκή µέθοδος αναγνώρισης µε επόπτη σύµφωνα µε την οποία κατά την εκµάθηση υπολογίζεται η
ΑΕΙ Σερρών 4. Μέθοδοι αναγνώρισης ταξινοµητές µε επόπτη 4.. Αναγνώριση µε βάση τα κέντρα των τάξεων Είναι µια απλοϊκή µέθοδος αναγνώρισης µε επόπτη σύµφωνα µε την οποία κατά την εκµάθηση υπολογίζεται η
Επεξεργασία Δεδομένων - Γραφικές Παραστάσεις
 1. Σκοπός Επεξεργασία Δεδομένων - Γραφικές Παραστάσεις Σκοπός της άσκησης είναι να εξοικειωθούν οι σπουδαστές με τη γραφική απεικόνιση των δεδομένων τους, την χρήση των γραφικών παραστάσεων για την εξαγωγή
1. Σκοπός Επεξεργασία Δεδομένων - Γραφικές Παραστάσεις Σκοπός της άσκησης είναι να εξοικειωθούν οι σπουδαστές με τη γραφική απεικόνιση των δεδομένων τους, την χρήση των γραφικών παραστάσεων για την εξαγωγή
Εισαγωγή στις Ηλεκτρικές Μετρήσεις
 Εισαγωγή στις Ηλεκτρικές Μετρήσεις Σφάλματα Μετρήσεων Συμβατικά όργανα μετρήσεων Χαρακτηριστικά μεγέθη οργάνων Παλμογράφος Λέκτορας Σοφία Τσεκερίδου 1 Σφάλματα μετρήσεων Επιτυχημένη μέτρηση Σωστή εκλογή
Εισαγωγή στις Ηλεκτρικές Μετρήσεις Σφάλματα Μετρήσεων Συμβατικά όργανα μετρήσεων Χαρακτηριστικά μεγέθη οργάνων Παλμογράφος Λέκτορας Σοφία Τσεκερίδου 1 Σφάλματα μετρήσεων Επιτυχημένη μέτρηση Σωστή εκλογή
µε την βοήθεια του Συστήµατος Συγχρονικής Λήψης Απεικόνισης.
 1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ () ΜΕ ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ µε την βοήθεια του Συστήµατος Συγχρονικής Λήψης Απεικόνισης. Το φύλλο εργασίας στηρίζεται στο αντίστοιχο του Παιδαγωγικού Ινστιτούτου που
1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ () ΜΕ ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ µε την βοήθεια του Συστήµατος Συγχρονικής Λήψης Απεικόνισης. Το φύλλο εργασίας στηρίζεται στο αντίστοιχο του Παιδαγωγικού Ινστιτούτου που
Επεξεργασία Δεδομένων - Γραφικές Παραστάσεις
 1. Σκοπός Επεξεργασία Δεδομένων - Γραφικές Παραστάσεις Σκοπός της άσκησης είναι να εξοικειωθούν οι σπουδαστές με τη γραφική απεικόνιση των δεδομένων τους, την χρήση των γραφικών παραστάσεων για την εξαγωγή
1. Σκοπός Επεξεργασία Δεδομένων - Γραφικές Παραστάσεις Σκοπός της άσκησης είναι να εξοικειωθούν οι σπουδαστές με τη γραφική απεικόνιση των δεδομένων τους, την χρήση των γραφικών παραστάσεων για την εξαγωγή
ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017)
 ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017) Στις 12:28 UTC (15:28 ώρα Ελλάδας) της 12/06/2017 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M w =6.3 μεταξύ Λέσβου και Χίου, ~15χλμ Ν-ΝΔ των νότιων ακτών της
ΣΕΙΣΜΟΣ Ν. ΤΗΣ ΛΕΣΒΟΥ (Μ w =6.3, 12/06/2017) Στις 12:28 UTC (15:28 ώρα Ελλάδας) της 12/06/2017 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους M w =6.3 μεταξύ Λέσβου και Χίου, ~15χλμ Ν-ΝΔ των νότιων ακτών της
ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΩΝ ΤΕΤΡΑΓΩΝΩΝ
 ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΩΝ ΤΕΤΡΑΓΩΝΩΝ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ Δημήτρης Στεφανάκης Η Μέθοδος των Ελαχίστων Τετραγώνων (ΜΕΤ) χρησιμοποιείται για την κατασκευή της γραφικής παράστασης που περιγράφει ένα φαινόμενο,
ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΩΝ ΤΕΤΡΑΓΩΝΩΝ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ Δημήτρης Στεφανάκης Η Μέθοδος των Ελαχίστων Τετραγώνων (ΜΕΤ) χρησιμοποιείται για την κατασκευή της γραφικής παράστασης που περιγράφει ένα φαινόμενο,
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο «ΑΛΓΕΒΡΑ»
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
Ευρασιατική, Αφρικανική και Αραβική
 Έχει διαπιστωθεί διεθνώς ότι τα περιθώρια τεκτονικών πλακών σε ηπειρωτικές περιοχές είναι πολύ ευρύτερα από τις ωκεάνιες (Ευρασία: π.χ. Ελλάδα, Κίνα), αναφορικά με την κατανομή των σεισμικών εστιών. Στην
Έχει διαπιστωθεί διεθνώς ότι τα περιθώρια τεκτονικών πλακών σε ηπειρωτικές περιοχές είναι πολύ ευρύτερα από τις ωκεάνιες (Ευρασία: π.χ. Ελλάδα, Κίνα), αναφορικά με την κατανομή των σεισμικών εστιών. Στην
Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΕΚΦΕ Ν.ΚΙΛΚΙΣ η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΕΞΕΡΓΑΣΙΑ : Κ. ΚΟΥΚΟΥΛΑΣ, ΦΥΣΙΚΟΣ - ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΟΣ [ Ε.Λ. ΠΟΛΥΚΑΣΤΡΟΥ ] ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ () ΜΕ ΤΗ ΒΟΗΘΕΙΑ
ΕΚΦΕ Ν.ΚΙΛΚΙΣ η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΕΞΕΡΓΑΣΙΑ : Κ. ΚΟΥΚΟΥΛΑΣ, ΦΥΣΙΚΟΣ - ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΟΣ [ Ε.Λ. ΠΟΛΥΚΑΣΤΡΟΥ ] ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ () ΜΕ ΤΗ ΒΟΗΘΕΙΑ
ΠΕΡΙΕΧΟΜΕΝΑ. ΠΡΟΛΟΓΟΣ... vii ΠΕΡΙΕΧΟΜΕΝΑ... ix ΓΕΝΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ... xv. Κεφάλαιο 1 ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΑΠΟ ΤΗ ΣΤΑΤΙΣΤΙΚΗ
 ΠΡΟΛΟΓΟΣ... vii ΠΕΡΙΕΧΟΜΕΝΑ... ix ΓΕΝΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ... xv Κεφάλαιο 1 ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΑΠΟ ΤΗ ΣΤΑΤΙΣΤΙΚΗ 1.1 Πίνακες, κατανομές, ιστογράμματα... 1 1.2 Πυκνότητα πιθανότητας, καμπύλη συχνοτήτων... 5 1.3
ΠΡΟΛΟΓΟΣ... vii ΠΕΡΙΕΧΟΜΕΝΑ... ix ΓΕΝΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ... xv Κεφάλαιο 1 ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΑΠΟ ΤΗ ΣΤΑΤΙΣΤΙΚΗ 1.1 Πίνακες, κατανομές, ιστογράμματα... 1 1.2 Πυκνότητα πιθανότητας, καμπύλη συχνοτήτων... 5 1.3
ΔΕΟ13 - Επαναληπτικές Εξετάσεις 2010 Λύσεις
 ΔΕΟ - Επαναληπτικές Εξετάσεις Λύσεις ΘΕΜΑ () Το Διάγραμμα Διασποράς εμφανίζεται στο επόμενο σχήμα. Από αυτό προκύπτει καταρχήν μία θετική σχέση μεταξύ των δύο μεταβλητών. Επίσης, από το διάγραμμα φαίνεται
ΔΕΟ - Επαναληπτικές Εξετάσεις Λύσεις ΘΕΜΑ () Το Διάγραμμα Διασποράς εμφανίζεται στο επόμενο σχήμα. Από αυτό προκύπτει καταρχήν μία θετική σχέση μεταξύ των δύο μεταβλητών. Επίσης, από το διάγραμμα φαίνεται
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/2014
 minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
ΠΑΡΟΥΣΙΑΣΗ ΣΤΟ ΝΟΤΙΟ ΔΥΤΙΚΟ ΑΙΓΑΙΟ ΑΠΟ ΤΟΥΣ ΣΕΙΣΜΟΥΣ ΤΗΣ 21/09/2012 ΣΤΗ ΘΑΛΑΣΣΙΑ ΠΕΡΙΟΧΗ ΤΟΥ ΝΔ ΑΙΓΑΙΟΥ
 ΠΑΡΟΥΣΙΑΣΗ ΚΑΤΑΓΡΑΦΩΝ ΤΟΥ ΔΙΚΤΥΟΥ ΕΠΙΤΑΧΥΝΣΙΟΓΡΑΦΩΝ ΙΤΣΑΚ-ΟΑΣΠ ΣΤΟ ΝΟΤΙΟ ΔΥΤΙΚΟ ΑΙΓΑΙΟ ΑΠΟ ΤΟΥΣ ΣΕΙΣΜΟΥΣ ΤΗΣ 21/09/2012 ΣΤΗ ΘΑΛΑΣΣΙΑ ΠΕΡΙΟΧΗ ΤΟΥ ΝΔ ΑΙΓΑΙΟΥ Την 21 η Σεπτεμβρίου 2012 και τοπική ώρα 11:47
ΠΑΡΟΥΣΙΑΣΗ ΚΑΤΑΓΡΑΦΩΝ ΤΟΥ ΔΙΚΤΥΟΥ ΕΠΙΤΑΧΥΝΣΙΟΓΡΑΦΩΝ ΙΤΣΑΚ-ΟΑΣΠ ΣΤΟ ΝΟΤΙΟ ΔΥΤΙΚΟ ΑΙΓΑΙΟ ΑΠΟ ΤΟΥΣ ΣΕΙΣΜΟΥΣ ΤΗΣ 21/09/2012 ΣΤΗ ΘΑΛΑΣΣΙΑ ΠΕΡΙΟΧΗ ΤΟΥ ΝΔ ΑΙΓΑΙΟΥ Την 21 η Σεπτεμβρίου 2012 και τοπική ώρα 11:47
Γεωγραφικά Πληροφοριακά Συστήµατα (GIS) στη διαχείριση καταστροφών
 Γεωγραφικά Πληροφοριακά Συστήµατα (GIS) στη διαχείριση καταστροφών Χρίστος Χαλκιάς ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ - ΜΠΣ, ΚΑΤΕΥΘΥΝΣΗ ΙΑΧΕΡΙΣΗΣ ΦΥΣΙΚΩΝ ΚΑΙ ΑΝΘΡΩΠΟΓΕΝΩΝ ΚΑΤΑΣΤΡΟΦΏΝ ΣΥΓΧΡΟΝΕΣ ΤΕΧΝΟΛΟΓΙΕΣ
Γεωγραφικά Πληροφοριακά Συστήµατα (GIS) στη διαχείριση καταστροφών Χρίστος Χαλκιάς ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ - ΜΠΣ, ΚΑΤΕΥΘΥΝΣΗ ΙΑΧΕΡΙΣΗΣ ΦΥΣΙΚΩΝ ΚΑΙ ΑΝΘΡΩΠΟΓΕΝΩΝ ΚΑΤΑΣΤΡΟΦΏΝ ΣΥΓΧΡΟΝΕΣ ΤΕΧΝΟΛΟΓΙΕΣ
