ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
|
|
|
- Πράξις Βουρδουμπάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων έσι ώσε να ικανοποιούναι συγκεκριμένες απαιήσεις με κριήριο συνήθως ο κόσος (και σπανιόερα ο βάρος). Για παράδειγμα, ο μηχανικός καλείαι να αποφασίσει για ις διασάσεις μίας δοκού (π.χ. πλάος και ύψος διαομής) ή για ο πάχος μίας πλάκας ώσε α σοιχεία αυά να παραλαμβάνουν α φορία για α οποία έχουν μελεηθεί χωρίς να ασοχήσουν αλλά και χωρίς να παραμορφωθούν σημανικά. Επίσης καλείαι να υπολογίσει ο φορίο που μπορεί να παραλάβει ένα υποσύλωμα προού λυγίσει, ή, όπως θα μάθουμε σο έλος ου παρόνος συγγράμμαος, προού βρεθεί σε καάσαση ασάθειας. Ανικείμενο ων μαθημάων μηχανικής ων υλικών, ή ανοχής ων υλικών, όπως παραδοσιακά ονομαζόαν σο παρελθόν, αποελεί η παρουσίαση αναλυικών μεθόδων προσδιορισμού ης ανοχής, ης παραμόρφωσης και ης ευσάθειας δομικών σοιχείων που παραλαμβάνουν φορία. Η μηχανική ων υλικών αποελεί παλαιό πεδίο ης επισήμης, ο οποίο ξεκίνησε να ίθεαι σε ορθολογισική βάση και να περιγράφεαι μέσω μαθημαικών σχέσεων από ις αρχές ου 17 ου αιώνα μέσω ων εργασιών ου Γαλιλαίου. Ο Γαλιλαίος μελέησε η συμπεριφορά δομικών σοιχείων σε εφελκυσμό, θλίψη, ακόμα και κάμψη, με σκοπό ην καασκευή πλοίων για ο Ιαλικό ναυικό. Έκοε πολλοί διακεκριμένοι επισήμονες συνέβαλαν σην περαιέρω ανάπυξη ου πεδίου, με γνωσόερους ους Γάλλους ερευνηές Coulomb, oisson, Nvier, St. Vennt και Cuch, οι οποίοι σις αρχές ου 19 ου αιώνα διεύπωσαν θεωρήμαα και μεθόδους που αποελούν σήμερα ης βάσεις ης μηχανικής. Σήμερα η μηχανική ων υλικών αποελεί κύριο πεδίο μελέης για όλες ις καηγορίες μηχανικών: πολιικών, μηχανολόγων, αεροναυπηγών, ναυπηγών, ηλεκρολόγων, ηλεκρονικών, εμβιομηχανικών κλπ. Η συμπεριφορά δομικών σοιχείων υπό φόριση εξαράαι αφενός από θεμελιώδεις νόμους ης μηχανικής, αφεέρου από α μηχανικά χαρακηρισικά ων υλικών ων σοιχείων, όπως αυά προκύπουν βάσει εργασηριακών δοκιμών. Σις δοκιμές αυές α υλικά κααπονούναι συνήθως με γνωσές δυνάμεις, ενώ παράλληλα κααγράφεαι η
2 2 απόκρισή ους σε όρους παραμορφώσεων, ανάπυξης ρωγμών ή άλλων μορφών ασοχίας. Αυό που ενδιαφέρει σα πλαίσια ου παρόνος συγγράμμμαος είναι κυρίως ο πρώο μήμα, δηλαδή η μαθημαική διαύπωση και καανόηση ων βασικών αρχών ης μηχανικής, χωρίς να δίνεαι ιδιαίερη έμφαση σε πειραμαικές μεθόδους και εχνικές. Σο κεφάλαιο αυό παρουσιάζοναι ρεις βασικές ενόηες: γενικές αρχές και ορισμοί για ις άσεις, απλές περιπώσεις κααπόνησης και (γ) η εφαρμογή απλών κριηρίων σχεδιασμού δομικών σοιχείων με βάση ην ανοχή. 1.2 Η μέθοδος ων ομών Ένα από α θεμελιώδη προβλήμαα ης μηχανικής είναι η μελέη ης φύσης ων δυνάμεων που αναπύσσοναι σο εσωερικό σερεών σωμάων ως αποέλεσμα ης δράσης εξωερικών φορίων. Για ο σκοπό αυό γίνεαι ένα σχέδιο ου κααπονούμενου σώμαος, πάνω σο οποίο δείχνοναι όλες οι ασκούμενες δυνάμεις αλλά και οι ανιδράσεις σις σηρίξεις. Το σχέδιο αυό είναι γνωσό ως διάγραμμα ελευθέρου σώμαος. Επισημαίνεαι όι σε ένα έοιο διάγραμμα, όπως π.χ. αυό ου Σχ. 1.1α, οι δυνάμεις ικανοποιούν ις συνθήκες σαικής ισορροπίας και ο σώμα ισορροπεί. (γ) Σχ. 1.1 ιάγραμμα ελευθέρου σώμαος και ομή σε σερεό σώμα. Ακολούθως φαναζόμασε μία υποθεική ομή (επίπεδο ABCD σο Σχ. 1.1α), η οποία χωρίζει ο σώμα σε δύο ξεχωρισά μήμαα, Σχ. 1.1β,γ. εδομένου όι ο αρχικό σώμα ήαν σε καάσαση ισορροπίας, ομοίως ισχύει και για οποιοδήποε από α
3 3 υποσύνολά ου. Για να καασεί ούο δυναό χρειάζεαι η παρουσία εσωερικών δυνάμεων ση θέση ης ομής, έσι ώσε οι εξωερικές δυνάμεις ση μία πλευρά ης ομής να εξισορροπούναι από ις εσωερικές δυνάμεις σην ομή. Η μέθοδος αυή, γνωσή ως μέθοδος ων ομών, επιρέπει ην εύρεση ων εσωερικών δυνάμεων για οποιαδήποε θέση ης υποθεικής ομής. Σο σημείο αυό αξίζει να σημειώσουμε όι κινούμενα σώμαα (π.χ. ένα κήριο καά η διάρκεια ενός σεισμού) βρίσκοναι σε καάσαση δυναμικής ισορροπίας, η οποία είναι όμως ουσιασικά ισοδύναμη με η σαική ισορροπία, αρκεί να εφαρμοσθεί σο κένρο μάζας ου σώμαος μία δύναμη F ίση με ην επιάχυνσή ου,, επί η μάζα ου, m, και με φορά ανίθεη προς αυή ης επιάχυνσης. Η διαύπωση αυή, που αποελεί ην αρχή ου d Alembert, επιρέπει η γενίκευση ης εφαρμογής ης μεθόδου ων ομών όσο σε σαικά όσο και σε δυναμικά προβλήμαα. 1.3 Ορισμός ης άσης Οι εσωερικές δυνάμεις που ασκούναι σε πολύ μικρές επιφάνειες Δ A μίας ομής έχουν μέγεθος και φορά που γενικά ποικίλλει, ανάλογα με η θέση ης μικρής αυής επιφάνειας. Τις δυνάμεις αυές μπορούμε να θεωρήσουμε ως διανύσμαα ( Δ σο Σχ. 1.2α), α οποία μπορούν να αναλυθούν κάθεα σο επίπεδο ης ομής ( Δ ) αλλά και πάνω σε αυό. Το διάνυσμα επί ου επιπέδου αναλύεαι περαιέρω σους άξονες και z ενός ρισορθογώνιου συσήμαος συνεαγμένων, δίνονας ις δυνάμεις (Σχ. 1.2β). Δ Δ και z Σχ. 1.2 Εσωερικές δυνάμεις σε ομή ελευθέρου σώμαος και μεγέθυνση με ις συνισώσες ης δύναμης.
4 4 Θεωρώνας ην επιφάνεια Δ A απειροσά μικρή, κααλήγουμε σον ορισμό ης άσης σε σημείο ης ομής, ως εξής: Δ σ = lim (1.1α) ΔA 0 ΔA Δ = lim (1.1β) ΔA 0 ΔA Δ z z = lim (1.1γ) ΔA 0 ΔA Η άση κάθεα σο επίπεδο ης ομής (ση διεύθυνση ου άξονα ) ονομάζεαι ορθή άση και συμβολίζεαι με ο γράμμα σ (ο δείκης δηλώνει η διεύθυνση), ενώ οι άση πάνω σο επίπεδο ης ομής ονομάζεαι διαμηική άση και συμβολίζεαι με ο γράμμα. Βάσει ης ανάλυσης ης διαμηικής άσης σους άξονες και z, οι δείκες ου δηλώνουν: ο πρώος ον άξονα που είναι κάθεος σο επίπεδο πάνω σο οποίο ασκείαι η διαμηική άση (άξονας ) και ο δεύερος η διεύθυνση ου διανύσμαος ης διαμηικής άσης ( ή z ). Τέλος, ορθές άσεις που προκαλούν μήκυνση, δηλαδή εφελκυσμό, ου σερεού ση διεύθυνση που ασκούναι ονομάζοναι εφελκυσικές, ενώ αυές που προκαλούν βράχυνση, δηλαδή θλίψη, ονομάζοναι θλιπικές. Αυό που αξίζει να γίνει καανοηό, πέρα από η μαθημαική διαύπωση ης άσης, είναι η φυσική σημασία ης: η άση σε κάθε σημείο ενός σερεού σώμαος καθορίζει ο βαθμό κααπόνησης ου υλικού, δηλαδή ο πόσο αλλά και ο πώς πονάει ο υλικό σο εν λόγω σημείο. Έχονας ορίσει ην άση ως δύναμη δια επιφάνεια, ως μονάδα άσης σο διεθνές σύσημα SI ορίζεαι ο N/m 2, γνωσό και ως (scl). Συνήθως όμως σην πράξη χρησιμοποιείαι ο M (megpscl, 1 M = 10 6 ), ο οποίο ισούαι με 1 ΜΝ/m 2, ή, ισοδύναμα, με 1 N/mm 2. Τέλος επισημαίνεαι όι ο γινόμενο άσης επί επιφάνεια σην οποία ασκείαι δίνει δύναμη. Σε μία υποθεική ομή, ο διανυσμαικό άθροισμα όλων αυών ων δυνάμεων, δηλαδή οι συνισαμένες ων άσεων, αποελεί αυό που συχνά ονομάζουμε εσωερικά εναικά μεγέθη (αξονική δύναμη, έμνουσα δύναμη, ροπή κάμψης κλπ). Ση μηχανική συνήθως πρώα προσδιορίζοναι α μεγέθη αυά (βάσει ισορροπίας) και ακολούθως, μέσω μαθημαικών σχέσεων, υπολογίζοναι οι άσεις.
5 5 1.4 Ο ανυσής ων άσεων Αν πλέον ης υποθεικής ομής ου Σχ. 1.2 θεωρήσουμε ακόμα ένα επίπεδο μέσω ου σερεού σώμαος σε απειροσή απόσαση d από ο αρχικό, απομονώνουμε μία σοιχειώδη φέα ου υλικού. Καόπιν, θεωρώνας δύο ακόμα ζεύγη επιπέδων κάθεα σα αρχικά αλλά και μεαξύ ους, απομονώνουμε έναν σοιχειώδη κύβο ου υλικού, ο οποίος δείχνεαι σο Σχ. 1.3α μαζί με ις ορθές και διαμηικές άσεις που ανισοιχούν σε κάθε επίπεδο. Σις κονινές πλευρές ου κύβου (δηλαδή σις πιο απομακρυσμένες από ο σύσημα αξόνων) οι άσεις θεωρούναι θεικές όαν η φορά ους συμπίπει με αυή ου συσήμαος αξόνων. Ανίθεα, σις απένανι πλευρές ου κύβου, προς ο σύσημα αξόνων, οι θεικές άσεις ασκούναι, λόγω ισορροπίας, με φορά ανίθεη αυής ων αξόνων. σ z σ ' σ σ σ z z σ z σ z z z z dz' ' σ z z d d z σ z dz σ d' σ z z' d' σ Σχ. 1.3 Ορθές και διαμηικές άσεις σε σοιχειώδες μήμα ου σερεού σώμαος με επίπεδα κάθεα σο σύσημα αξόνων --z (οι εικονιζόμενες άσεις είναι θεικές). Ορθές και διαμηικές άσεις σε σοιχειώδες μήμα ου σερεού σώμαος με επίπεδα κάθεα σε άλλο σύσημα αξόνων, ο οποίο έχει σραφεί ως προς ο --z. Σε κάποιο συγκεκριμένο σημείο ου σερεού σώμαος οι άσεις μπορούν να δειχθούν ως προς οποιοδήποε σύσημα αξόνων, z, ο οποίο έχει σραφεί σε σχέση με ο αρχικό z (Σχ. 1.3β). Οι νέες αυές άσεις είναι εν γένει διαφορεικές από αυές ου συσήμαος z, και ο υπολογισμός ους ονομάζεαι μεασχημαισμός άσεων (Κεφ. 4). Η εναική καάσαση (δηλαδή ο σύνολο ων άσεων) σε ένα σημείο ενός σερεού σώμαος περιγράφεαι πλήρως αν είναι γνωσές οι ρεις άσεις σα ρία κάθεα μεαξύ ους επίπεδα που ορίζοναι από ο σύσημα αξόνων σο εν λόγω σημείο. Σο Σχ. 1.3α
6 6 οι άσεις αυές είναι σ, και z,, σ και z, z, z και σ z, οι οποίες μπορούν να γραφούν σην παρακάω μηρωική μορφή, γνωσή ως ανυσής άσεων. σ z σ z z z σ z (1.2) Ση συνέχεια θα αποδείξουμε όι ο μηρώο (1.2) είναι συμμερικό, δηλαδή ij = ji. Αυό προκύπει από ην ισορροπία ου σοιχειώδους μήμαος ου Σχ. 1.3α, που θεωρείαι με πλευρές d, d και dz. Σο μήμα αυό, που δείχνεαι και πάλι σο Σχ. 1.4α (και για διευκόλυνση σε δύο διασάσεις σο Σχ. 1.4β) διαυπώνουμε ην εξίσωση ισορροπίας ροπών ως προς άξονα z (σο Σχ. 1.4 δείχνοναι μόνο οι άσεις που συμμεέχουν σην εξίσωση ισορροπίας ροπών): M C ( d dz) d ( d dz) d = = 0 = 0 (1.3) Με ο ίδιο ρόπο μπορεί να δειχθεί όι z = z και z = z. d B A B d z D dz O C D Σχ. 1.4 Οι (διαμηικές) άσεις που συμμεέχουν σην εξίσωση ισορροπίας ροπών ως προς ο σημείο C. Η εξ. (1.3) είναι εξαιρεικά σημανική: δείχνει αφενός όι οι διαμηικές άσεις σε κάθεα μεαξύ ους επίπεδα είναι ίσες, αφεέρου όι για ην ικανοποίηση ης ισορροπίας ροπών ως προς άξονα z χρειάζοναι και α δύο ζεύγη διαμηικών άσεων. Σο Σχ. 1.4β α ζεύγη άσεων είναι έοια ώσε η φορά ων διανυσμάων να συγκλίνει σε δύο διαμερικά ανίθεες γωνίες (πάνω δεξιά και κάω αρισερά).
7 7 Σην αρκεά συνηθισμένη περίπωση που οι άσεις αναπύσσοναι μόνο πάνω σε ένα επίπεδο, όπως π.χ. σο Σχ. 1.5, λέμε όι ο υλικό βρίσκεαι σε επίπεδη εναική καάσαση. Για απλόηα ορισμένες φορές παραλείπουμε ους δείκες σις διαμηικές άσεις, ις οποίες συμβολίζουμε πλέον με. σ σ σ σ σ d z d σ dz σ O σ Σχ. 1.5 Επίπεδη εναική καάσαση. Σε μηρωική μορφή η επίπεδη εναική καάσαση περιγράφεαι ως εξής: σ 0 σ (1.4) Εδώ αξίζει να αναφερθεί, όπως θα δούμε και σε άλλες ενόηες, όι με καάλληλη επιλογή ου συσήμαος συνεαγμένων θα μπορούσαμε να κααλήξουμε σε σοιχειώδες μήμα ου υλικού σο οποίο θα ασκούναν μόνο ορθές άσεις, ενώ οι διαμηικές θα ήαν μηδέν. Η ανίσοιχη μηρωική μορφή είναι σ σ σ 3 (1.5) και η συγκεκριμένη εναική καάσαση ονομάζεαι ριαξονική (οι άσεις σε ρεις άξονες αρκούν για να δώσουν ην πλήρη εικόνα κααπόνησης). Για ην επίπεδη εναική καάσαση σ 3 = 0, οπόε η ανίσοιχη εναική καάσαση ονομάζεαι διαξονική. Απλό παράδειγμα διαξονικής εναικής καάσασης αποελεί η κααπόνηση ενός λεπού
8 8 ελάσμαος σε δύο κάθεες μεαξύ ους διευθύνσεις. Τέλος, για αξονικά φοριζόμενα δομικά σοιχεία (π.χ. ράβδοι ενός δικυώμαος) εκός από ην σ 3 μηδενίζεαι και η σ 2, αφήνονας ως μόνη μη μηδενική άση η σ 1. Αυή η εναική καάσαση ονομάζεαι μονοαξονική. 1.5 Τάσεις σε δομικά σοιχεία υπό αξονική κααπόνηση Σην παρούσα ενόηα θα υπολογίσουμε ις άσεις που αναπύσσοναι σε μία υχαία διαομή ενός δομικού σοιχείου σε μονοαξονική φόριση, δηλαδή σοιχείου ύπου ράβδου. Θεωρούμε ην πρισμαική (δηλαδή με σαθερή διαομή καά μήκος, εμβαδού A ) ράβδο ου Σχ. 1.6α, σο δεξιό άκρο ης οποίας ασκείαι δύναμη με σημείο εφαρμογής ο κένρο βάρους ης διαομής. Αποέλεσμα ης δύναμης είναι η ίσου μεγέθους και ανίθεης φοράς ανίδραση σο αρισερό άκρο, που για λόγους καλύερης καανόησης θα σημειώνεαι από δω και πέρα με μία μικρή γραμμή που έμνει ο διάνυσμα ης ανίδρασης λοξά. Σα Σχ. 1.6β-γ δίνοναι α διαγράμμαα ελευθέρου σώμαος σοιχείων ης ράβδου από ο αρισερό άκρο μέχρι δύο υχούσες ομές, - και b-b, πάνω σις οποίες σημειώνεαι η δύναμη (με κυμαισή γραμμή) που απαιείαι για ην ισορροπία ων σοιχείων, καθώς και οι συνισώσες αυής σε σύσημα αξόνων z. Ας σημειώσουμε όι για ην περίπωση ομής σε επίπεδο κάθεο σο επίπεδο (Σχ. 1.6γ) η δύναμη αναλύεαι σε δύο συνισώσες, μία εξ αυών κάθεη σην ομή και άλλη μία πάνω σο επίπεδο ης ομής. b b z ' z' ' z (γ) z' ' b b ' Σχ. 1.6 Τομές σε αξονικά φοριζόμενη πρισμαική ράβδο και εσωερικές δυνάμεις.
9 9 Αν α επίπεδα ων ομών - και b-b είναι κάθεα μεαξύ ους (αλλά και κάθεα σο επίπεδο ), όπως δείχνεαι σο Σχ. 1.7α, η εσωερική δύναμη σε κάθε μία από αυές αναλύεαι σε cosθ και sinθ (Σχ. 1.7β-γ), όπου θ η γωνία (θεική αν είναι αρισερόσροφη) μεαξύ ου άξονα (κάθεος σον άξονα ης ράβδου) και ης ομής ο b b κένρο βάρους θ διαομή ' cosθ θ ' A/sinθ Κένρο βάρους ' cosθ A/cosθ θ sinθ (γ) ιαομή sinθ 90 ο -θ 90 ο -θ ' σ θ σ θ θ-90 ο θ θ σ θ-90ο (δ) (ε) (σ) (ζ) (/A)cos 2 θ (/A)sinθcosθ (/A)sin 2 θ Σχ. 1.7 Κάθεες ομές σε πρισμαική ράβδο και άσεις. Το εμβαδόν ης κεκλιμένης διαομής ης ράβδου ση θέση - ισούαι με A / cosθ, συνεπώς η ορθή άση σ θ και η διαμηική άση θ (Σχ. 1.7δ-ε) δίνοναι από ις παρακάω σχέσεις: cosθ = = cos θ (1.6) A / cosθ A σ θ 2 θ sinθ = = sinθ cosθ (1.7) A / cosθ A Το αρνηικό πρόσημο σην εξ. (1.7) εξηγείαι βάσει ου ορισμού που δόθηκε παραπάνω για η διαμηική άση, παραηρώνας δηλαδή όι η διαμηική δύναμη sinθ, άρα και η διαμηική άση, έχει φορά ανίθεη ση θεική ου άξονα.
10 10 Οι εξ. (1.6)-(1.7) δείχνουν όι οι ορθές και οι διαμηικές άσεις σε κάθε διαομή ης ράβδου εξαρώναι από η γωνία θ. Η ορθή άση σ θ γίνεαι μέγιση για θ = 0 ο, δηλαδή όαν η ομή γίνεαι κάθεα σον άξονα ης ράβδου. Η ανίσοιχη διαμηική άση είναι μηδέν. Συμπεραίνουμε όι η μέγιση ορθή άση σ m σε ράβδο υπό μονοαξονική κααπόνηση είναι σ = σ m = (1.8) A όπου η ασκούμενη δύναμη και A ο εμβαδόν ης διαομής ης ράβδου. Η εύρεση ης μέγισης διαμηικής άσης m ση ράβδο γίνεαι παραγωγίζονας ην εξ. (1.7) ως προς θ και θέονας ην παράγωγο ίση με μηδέν, οπόε προκύπει tn θ = ±1 (1.9) που οδηγεί σο συμπέρασμα όι η m εμφανίζεαι σε επίπεδα που σχημαίζουν γωνία +45 ο ή -45 ο με ον άξονα ης ράβδου. Επειδή δε ο πρόσημο ση διαμηική άση δεν παίζει κάποιο ρόλο, δηλαδή σερείαι φυσικής σημασίας, μπορούμε να γράψουμε σ m = = (1.10) 2A 2 Συνεπώς, η μέγιση διαμηική άση σε μονοαξονικά κααπονούμενη ράβδο ισούαι με ο μισό ης μέγισης ορθής άσης. Η παραπάνω διαδικασία μπορεί να εφαρμοσεί και για ην ομή b-b, αρκεί να εθεί σις παραπάνω σχέσεις όπου θ η γωνία -(90 ο - θ ) (βλ. Σχ. 1.7γ), δηλαδή θ - 90 ο. Οι άσεις που προκύπουν είναι sinθ 2 σ ο θ 90 = = sin θ (1.11) A / sinθ A cosθ ο θ 90 = = sinθ cosθ (1.12) A / sinθ A Εδώ παραηρούμε όι η διαμηική άση έχει φορά η θεική ου άξονα (Σχ. 1.7σ), γεγονός που επιβεβαιώνεαι και από ο θεικό πρόσημο σο αποέλεσμα ης εξ. (1.12). Συνδυάζονας α αποελέσμαα για ις ομές - και b-b σο απειροσά μικρό σοιχείο ου Σχ. 1.7ζ παραηρούμε όι οι ορθές άσεις σε κάθεα μεαξύ ους επίπεδα είναι άνισες, ενώ οι ανίσοιχες διαμηικές είναι ίσες [σε απόλυη συμφωνία με ην εξ. (1.3)]. Όπως ήδη αναφέρθηκε, σην περίπωση ομής σε επίπεδο κάθεο σον άξονα (Σχ. 1.8α), οι άσεις που αναπύσσοναι είναι μόνο ορθές, με μέγεθος σ = / A
11 11 (μπορούμε πλέον να παραλείψουμε ο δείκη, δεδομένου όι αναφερόμασε πάνα σε ορθές άσεις παράλληλα σον άξονα ης ράβδου). Σε κάθε διαομή καά μήκος ης ράβδου οι άσεις αυές είναι ίσες, λόγω ισορροπίας ων ανισοίχων ελευθέρων σωμάων, και λαμβάνοναι ως ομοιόμορφα καανεμημένες σε οποιοδήποε σημείο ης διαομής (Σχ. 1.8γ). Έσι αν θεωρήσουμε ένα υχαίο σοιχείο ης ράβδου μήκους d μεαξύ δύο ομών κάθεα σον άξονα, θα διαπισώσουμε όι οι άσεις σις δύο όψεις ου σοιχείου αυού είναι ίσες (και ομοιόμορφα καανεμημένες), όπως δείχνεαι σο Σχ. 1.8δ. Αυή η μονοαξονική εναική καάσαση μπορεί να παρασαθεί και με η βοήθεια ενός απειροσά μικρού κυβίσκου (Σχ. 1.8ε), ή ακόμα απλούσερα, με ο σοιχείο ου Σχ. 1.8σ. Άξονας ράβδου Κένρο βάρους (γ) σ da = A σ σ d σ = A (δ) σ σ σ σ d dz d (σ) (ε) Σχ. 1.8 ιαδοχικά βήμαα για ον προσδιορισμό ης μέγισης ορθής άσης σε ράβδο. Η σχέση σ = / A εφαρμόζεαι αυσηρά σε πρισμαικές ράβδους, αλλά καά καλή προσέγγιση και σε ράβδους σις οποίες η διαομή μεαβάλλεαι καά μήκος ου άξονα σχεικά ομαλά. Ένονες αλλαγές ση γεωμερία ης διαομής (π.χ. ξαφνική μείωση ου εμβαδού ης διαομής) προκαλούν ανωμαλίες σις άσεις, οι οποίες θα περιγραφούν σε επόμενη ενόηα. Τα παραπάνω ισχύουν ανεξαρήως ου προσήμου ης δύναμης, η οποία μπορεί να προκαλεί μήκυνση ή βράχυνση ης ράβδου, οπόε οι άσεις σ θα είναι εφελκυσικές ή θλιπικές, ανίσοιχα. Ση δεύερη περίπωση βέβαια θα πρέπει να εξασφαλίζεαι όι ση ράβδο δεν εμφανίζοναι φαινόμενα λυγισμού (μεγάλες πλευρικές παραμορφώσεις, όπως π.χ. θα γινόαν αν φορίζαμε σε θλίψη ένα λεπό σύρμα μεγάλου μήκους). Τέοια φαινόμενα θα περιγραφούν σο Κεφ. 11. Σε ορισμένες περιπώσεις έχουμε η δημιουργία θλιπικών άσεων λόγω ης μεαφοράς αξονικής δύναμης από ένα σοιχείο σε κάποιο άλλο, όπως δείχνεαι σο
12 12 παράδειγμα ου Σχ Σο παράδειγμα αυό η δύναμη που ασκείαι σο πάνω σοιχείο (κύβος) προκαλεί θλιπικές άσεις μεαξύ ου σοιχείου αυού και ου ακριβώς από κάω πρίσμαος, καθώς επίσης μεαξύ ης κάω επιφάνειας ου πρίσμαος και ου εδάφους. Οι άσεις αυές, που ονομάζοναι και άσεις επαφής, υπολογίζοναι από η σχέση σ = / A, όπου A ο εμβαδόν ης μικρόερης εκ ων δύο επιφανειών επαφής μεαξύ δύο σοιχείων. έδαφος Σχ. 1.9 Η δύναμη μεαφέρεαι από ον κύβο σο κάω πρίσμα και μέσω αυού σο έδαφος. Επίσης πρέπει να ονίσουμε όι η ισχύς ης σχέσης σ = / A προϋποθέει εξιδανικευμένα υλικά, σα οποία κάθε σοιχειώδες μήμα ης μικροδομής (π.χ. κόκκος ) συνεισφέρει με ον ίδιο ακριβώς ρόπο σην ανάληψη ης δύναμης. Τα υλικά αυά ονομάζοναι ομοιογενή και σην πραγμαικόηα δεν υπάρχουν. Τα πραγμαικά υλικά χαρακηρίζοναι από ανομοιογένεια (π.χ. ο σκυρόδεμα περιέχει αδρανή διαφόρων μεγεθών και σιμενοπολό με περίπλοκο σύσημα πόρων, ο ξύλο είναι ινώδες κλπ), με αποέλεσμα κάποιες περιοχές σε αυά να κααπονούναι περισσόερο από άλλες (Σχ. 1.10α). Βλέπονας όμως ο υλικό κάπως μακροσκοπικά, δηλαδή όχι σε επίπεδο κόκκου αλλά θεωρώνας σχεικά μεγάλες περιοχές ου, η σχέση σ = / A εξακολουθεί να ισχύει με πολύ ικανοποιηική ακρίβεια για ον υπολογισμό ης μέσης άσης σις περιοχές αυές. Εξίσου σημανικό να αναφερθεί είναι όι οι παραπάνω εξισώσεις για ον προσδιορισμό άσεων προϋποθέουν υλικά εξ αρχής αφόρισα. Σην πραγμαικόηα, σε ορισμένα υλικά οι άσεις προϋπάρχουν λόγω ης μεθόδου παραγωγής ους. Σο παράδειγμα ου Σχ. 1.10β βλέπουμε κάπως ποιοικά ις εφελκυσικές άσεις που αναπύσσοναι σε χαλύβδινα ελάσμαα καά η φάση θερμής εξέλασης, ενώ δηλαδή αυά ελκύοναι μεαξύ ζεύγους κυλίνδρων προκειμένου να μειωθεί ο πάχος ους. Η διαδικασία αυή (έλκυση ου ελάσμαος από η δεξιά πλευρά ου Σχ. 1.10β) προκαλεί εφελκυσικές άσεις με ιμές μεγαλύερες προς ις εξωερικές επιφάνειες συγκριικά με ο εσωερικό. Οι άσεις αυές έχουν μέση ιμή, ίση με η δύναμη έλκυσης δια ην σ v
13 13 επιφάνεια ου ελάσμαος (πλάος επί πάχος t ). Αμέσως μεά ον ερμαισμό ης λειουργίας ων κυλίνδρων η άση σ v αναιρείαι, δηλαδή αφαιρείαι από ις άσεις που αναπύσσοναι καά η διάρκεια ης εξέλασης, οπόε προκύπει η εναική καάσαση ου Σχ. 1.10γ, με εφελκυσικές άσεις σις εξωερικές επιφάνειες και θλιπικές σο εσωερικό. Οι άσεις αυές, που ονομάζοναι παραμένουσες άσεις, βρίσκοναι σε καάσαση ισορροπίας, δηλαδή ο άθροισμά ους σε οποιαδήποε διαομή ου ελάσμαος είναι μηδέν. Σις περιπώσεις που είναι σημανικές θα πρέπει να λαμβάνοναι υπόψη και να προσίθεναι σις άσεις λόγω φόρισης ου υλικού. Εφελκυσμός σ v t t σ v Θλίψη (γ) Σχ Ανομοιομόμορφη καανομή άσεων λόγω ανομοιογενούς δομής ου υλικού. Ανομοιόμορφη καανομή άσεων καά ην έννοια ου πάχους σε χαλύβδινο έλασμα καά η διάρκεια εξέλασης και (γ) παραμένουσες άσεις. Παράδειγμα 1.1 Θεωρούμε όι ο σοιχείο θεμελίωσης ου Σχ. 1.11α φέρει σην κορυφή ομοιόμορφα καανεμημένο φορίο 20 kn/m 2. Αν ο υλικό ου σοιχείου θεμελίωσης είναι σκυρόδεμα με βάρος 25 kn/m 3, να υπολογισεί η άση σο σκυρόδεμα σε ύψος 1 m από ο έδαφος. Το συνολικό βάρος ου σοιχείου είναι W = [( )/2] = 25 kn και η συνολική δύναμη σην κορυφή ου είναι = = 5 kn. H ανίδραση R ση βάση ου σοιχείου θεμελίωσης υπολογίζεαι βάσει ισορροπίας δυνάμεων ση διεύθυνση : F = 0 R = W + = 30 kn. Ο προσδιορισμός ης άσης ση διαομή - (1 m από η βάση) γίνεαι βάσει ου διαγράμμαος ελευθέρου σώμαος οποιουδήποε εκ ων δύο σοιχείων πάνω και κάω από η σάθμη αυή. Θεωρώνας ο πάνω μήμα ως ελεύθερο σώμα (Σχ. 1.11β), ο βάρος ου μήμαος αυού είναι W 1= (0.5+1)0.5125/2 = 9.4 kn και βάσει ισορροπίας καακόρυφων δυνάμεων είναι F = + W1 = 14.4 kn. Συνεπώς η (ορθή) άση σε
14 14 οποιοδήποε σημείο ης διαομής - είναι σ = F / A = 14.4/(0.51) = 28.8 kn/m 2. H δύναμη F έχει φορά προς η διαομή, συνεπώς η υπολογισθείσα άση είναι θλιπική. Αν θεωρήσουμε ο κάω μήμα ου σοιχείου θεμελίωσης ως ελεύθερο σώμα (Σχ. 1.11γ), ο βάρος ου μήμαος αυού είναι W 2 =(1+1.5)0.5125/2 = 15.6 kn, οπόε βάσει ισορροπίας καακόρυφων δυνάμεων είναι και πάλι F = R W2 = 14.4 kn. Ο υπολογισμός ης άσης γίνεαι όπως και παραπάνω. ιαομή - Πλάγια όψη (γ) Σχ Φοριζόμενο σοιχείο θεμελίωσης και διαγράμμαα ελευθέρου σώμαος πάνω και κάω από η διαομή Προσεγγισικός υπολογισμός διαμηικών άσεων σε συνδέσεις Σε πολλές περιπώσεις αξονικές δυνάμεις σε δομικά σοιχεία έχουν ως αποέλεσμα ην ανάπυξη διαμηικών άσεων σε διεπιφάνειες ή σε σοιχεία ύπου κοχλία ή βλήρου. Σις περιπώσεις αυές ο ακριβής υπολογισμός ων διαμηικών άσεων είναι σχεικά περίπλοκος, αλλά, καά προσέγγιση, η μέση διαμηική άση μπορεί να υπολογισεί διαιρώνας η συνολική έμνουσα δύναμη V σε μία επιφάνεια με ο εμβαδόν ης, δηλαδή V v = A (1.13)
15 15 Σο παράδειγμα ου Σχ. 1.12α θεωρούμε ένα μικρό εμάχιο ενός υλικού κολλημένο πάνω σε κάποιο μεγαλύερο. Η οριζόνια φόριση ου μικρού εμαχίου με δύναμη προκαλεί συνολική έμνουσα δύναμη ση διεπιφάνεια μεαξύ ων δύο εμαχίων ίση με, καθώς και ένα ζεύγος μικρών δυνάμεων, που συνήθως είναι αμεληέες, έσι ώσε να ικανοποιείαι η συνθήκη ισορροπίας δυνάμεων και ροπών σο ελεύθερο σώμα ου Σχ. 1.12β. ιαιρώνας ην έμνουσα δύναμη ση διεπιφάνεια με ο εμβαδόν ης υπολογίζεαι η μέση διαμηική άση v, που φαίνεαι παρασαικά σο Σχ. 1.12γ. Ανίσοιχη είναι και η καάσαση σο Σχ. 1.12δ-σ, ο οποίο δείχνει η μεαφορά δύναμης από ο φοριζόμενο εμάχιο (ση μέση) σα πάνω και κάω από αυό μέσω διάμησης σις διεπιφάνειες. (δ) (ε) (γ) v (σ) v Σχ Συνθήκες φόρισης σε κολλημένα εμάχια υλικών και διαμηικές άσεις σις διεπιφάνειες. Παραδείγμαα συνδέσεων μεαξύ ελασμάων με κοχλίες ανί για κόλλα δίνοναι σα Σχ. 1.13α-δ και 1.13ε-η, α οποία δείχνουν η σύνδεση δύο και ριών ελασμάων, ανίσοιχα. Αν θεωρήσουμε ους κοχλίες σχεικά χαλαρούς, έσι ώσε η δύναμη από έλασμα σε έλασμα να μεαφέρεαι μέσω άσεων επαφής και ακολούθως μέσω διαμηικών άσεων σους κοχλίες, και όχι μέσω ριβής μεαξύ ων ελασμάων (κάι που θα γινόαν αν οι κοχλίες ήαν αρκεά σφιγμένοι ), μπορούμε να υπολογίσουμε προσεγγισικά η μέση διαμηική άση σε κάθε κοχλία διαιρώνας η δύναμη σε v
16 16 κάθε διεπιφάνεια ( ση σύνδεση ου Σχ. 1.12α και / 2 ση σύνδεση ου Σχ. 1.13ε) με ο εμβαδόν ης διαομής ου κοχλία. (γ) (δ) v (ε) (σ) (ζ) (η) v Σχ Συνθήκες φόρισης σε ελάσμαα συνδεδεμένα με κοχλίες, άσεις επαφής και διαμηικές άσεις σους κοχλίες. Μονόμηος κοχλίας (απλή διάμηση), δίμηος κοχλίας (διπλή διάμηση). Μία ακόμα περίπωση σύνδεσης εμαχίων είναι η συγκόλληση (σα μέαλλα), που και αυή έχει ως κύριο χαρακηρισικό η μεαφορά ων αξονικών δυνάμεων από ο ένα μέαλλο σο άλλο μέσω διάμησης σο υλικό ης συγκόλλησης (Σχ. 1.14). Συγκόλληση Τομή Σχ Φόριση συγκολλημένων μεαλλικών ελασμάων με αποέλεσμα ην ανάπυξη διαμηικών άσεων σα επίπεδα - και b-b ης συγκόλλησης. Παράδειγμα 1.2 Τρία χαλύβδινα ελάσμαα συνδέοναι μεαξύ ους με δύο κοχλίες όπως φαίνεαι σο Σχ. 1.15α. Οι κοχλίες έχουν διάμερο 20 mm και ο συνολικό φορίο που μεαφέρει η σύνδεση είναι = 100 kn. Να υπολογισεί η μέση διαμηική άση σους κοχλίες.
17 17 Από ο Σχ. 1.13ζ η δύναμη που μεαφέρεαι σους δύο κοχλίες είναι 100/2 = 50 kn. Υποθέονας συμμερία η δύναμη αυή καανέμεαι εξ ίσου σε κάθε κοχλία, επομένως η μέση διαμηική άση σε κάθε κοχλία είναι v = = Μ 2 2 π / 4 ( 20) 3 v Σχ Φόριση ζεύγους δίμηων κοχλιών. 1.7 Εισαγωγή σο σχεδιασμό δομικών σοιχείων με βάση ην ανοχή Γενικά Βασικός σόχος ου υπολογισμού ων άσεων σε δομικά σοιχεία είναι η σύγκριση αυών (εκεί όπου είναι μέγισες) με ις ανοχές ων υλικών, οι οποίες προσδιορίζοναι βάσει πειραμάων επί δοκιμίων (ανιπροσωπευικά δείγμαα ου υλικού) σο εργασήριο. Ως απλό παράδειγμα πειράμαος αναφέρουμε η δοκιμή εφελκυσμού σε μέαλλα, η οποία συνίσααι σην εφαρμογή σαδιακά αυξανόμενης αξονικής δύναμης επί ράβδων κυκλικής διαομής μέχρι ο υλικό ης ράβδου να ασοχήσει (δηλαδή η ράβδος να σπάσει σε δύο μήμαα), Σχ ιαιρώνας η μέγιση δύναμη που απαιείαι για να προκληθεί ασοχία ης ράβδου με ο εμβαδόν ης (κυκλικής) διαομής προσδιορίζουμε ην εφελκυσική ανοχή ου υλικού. Ενδεικικές ιμές εφελκυσικής ανοχής για κοινά υλικά είναι π.χ. 650 M για ο χάλυβα οπλισμού σκυροδέμαος, 3 M για ο σκυρόδεμα, 30 M για ο ξύλο. Σις περιπώσεις που η κααπόνηση ενός δομικού σοιχείου είναι επαναλαμβανόμενη, ώσε ο υλικό να φορίζεαι, να αποφορίζεαι, να επαναφορίζεαι, να αποφορίζεαι εκ νέου κ.ο.κ. (π.χ. ο σκυρόδεμα σα υποσυλώμαα ενός κηρίου καά η διάρκεια ενός σεισμού, ο χάλυβας σα καλώδια ανάρησης ου καασρώμαος μίας γέφυρας λόγω κυκλοφορίας οχημάων), μας ενδιαφέρει η ανοχή ου υλικού για ο συγκεκριμένο ρόπο φόρισης, ο οποίος ονομάζεαι κόπωση.
18 18 Σχ Μηχανή εφελκυσμού και δοκίμια χάλυβα πριν η φόριση και μεά ην ασοχία. Οι δυνάμεις που ασκούναι σα δομικά σοιχεία αλλά και οι ανοχές ων υλικών αποελούν παραμέρους που δύσκολα προσδιορίζοναι επακριβώς και γενικά χαρακηρίζοναι από σημανική αβεβαιόηα. Η αβεβαιόηα αυή μπορεί να ληφθεί υπόψη είε βάσει ου λεγόμενου προσδιορισμικού σχεδιασμού (deterministic design), που κυριαρχούσε ση μελέη δομικών έργων μέχρι πριν από μερικές δεκαείες, είε βάσει ου λεγόμενου πιθανοικού σχεδιασμού (probbilistic design), που υιοθεείαι ση μελέη ων καασκευών σήμερα. Η λεπομερής παρουσίαση ων δύο αυών προσεγγίσεων ου προβλήμαος ξεφεύγει βεβαίως από ο σόχο ου παρόνος συγγράμμαος, αλλά για λόγους πληρόηας σις ακόλουθες δύο ενόηες θα παρουσιάσουμε η βασική φιλοσοφία ης κάθε μίας με ον απλούσερο δυναό ρόπο Προσδιορισμικός σχεδιασμός αξονικά κααπονούμενων σοιχείων Ο προσδιορισμικός σχεδιασμός ενός αξονικά φοριζόμενου σοιχείου γίνεαι υπολογίζονας αρχικά ην εσωερική αξονική δύναμη N και ακολούθως η μέγιση ορθή άση, σ m, διαιρώνας ην N με ην ελάχιση δυναή διαομή (για σοιχεία μεαβληής διαομής). Η άση αυή συγκρίνεαι με η λεγόμενη επιρεπόμενη άση για ο υλικό, σ επ, η οποία σην πραγμαικόηα αποελεί μία εξαιρεικά συνηρηική προσέγγιση ης ανοχής ου υλικού. Ο λόγος ης ανοχής ου υλικού προς ην επιρεπόμενη άση ονομάζεαι συνελεσής ασφάλειας (Σ.Α.). Αν θεωρείαι αποδεκός, ενώ για σ m < σ επ ο σχεδιασμός ου μέλους σm σεπ θεωρείαι όι έχει επέλθει ασοχία.
19 19 Παράδειγμα 1.3 Για ο δικύωμα ου Σχ. 1.17α να επιλεγούν οι ράβδοι FC και CB (δηλαδή να υπολογισεί ο απαιούμενο εμβαδόν διαομής για ην κάθε μία, A FC και A CB ) θεωρώνας ην επιρεπόμενη ορθή άση σο υλικό ων ράβδων ίση με 140 M (ισοδύναμα θα μπορούσε να δίνεαι η ανοχή ου υλικού, έσω 280 Μ, και ο συνελεσής ασφάλειας, έσω 2). Ν AC Ν FC Ν AB 6 ίσα μήμαα ου 0.5 m = 3 m (γ) Ν CG Ν AB Ν CB (δ) Σχ Σχεδιασμός μελών δικυώμαος. Αν ζηούμενο ου προβλήμαος ήαν ο σχεδιασμός όλων ων ράβδων ου δικυώμαος (δηλαδή η επιλογή ης καάλληλης διαομής για κάθε μία από αυές), θα έπρεπε να γίνει πρώα η σαική επίλυση ου φορέα, δηλαδή ο προσδιορισμός ων αξονικών δυνάμεων σε κάθε ράβδο (π.χ. με η μέθοδο ων κόμβων). Σο συγκεκριμένο πρόβλημα, όπου ενδιαφέρει ο σχεδιασμός μικρού αριθμού ράβδων, μπορεί να εφαρμοσεί για συνομία η μέθοδος ων ομών. Αρχικά προσδιορίζοναι οι ανιδράσεις (Σχ. 1.17β), βάσει ισορροπίας δυνάμεων και ροπών: F = 0 R 520 = 0 R = 520 kn D D
20 20 M = 0 R = 0 R = 325 kn E D M = 0 R = 0 R = 65 kn D E [Επαλήθευση: F = = 0 ] Από ο διάγραμμα ελευθέρου σώμαος ου Σχ. 1.17γ είναι: M = 0 N = 0 N = kn A FC A FC = N FC / σεπ = /140 = 620 mm 2 3 Από ο διάγραμμα ελευθέρου σώμαος ου Σχ. 1.17δ είναι: N ( N ) = ( N ) = F = kn CB ( ) / = = 13 3 CB N CB +391 kn CB A CB = N CB / σεπ = /140 = 2790 mm 2 3 D E FC Πιθανοικός σχεδιασμός Για να γίνουν καανοηές οι βασικές αρχές ου πιθανοικού σχεδιασμού, θεωρούμε ως παράδειγμα α πειραμαικά αποελέσμαα για η θλιπική ανοχή δύο διαφορεικών υλικών, ου ξύλου και ου χάλυβα, όπως δίνοναι σο Σχ Το πλάος κάθε ράβδου σα ισογράμμαα ανισοιχεί σε ένα μικρό εύρος ανοχής ενός πληθυσμού 538 συνολικά δοκιμίων ξύλου και 51 δοκιμίων χάλυβα, ενώ οι εσωερικοί καακόρυφοι άξονες ου Σχ δίνουν ον αριθμό δοκιμίων για κάθε εύρος ανοχής. Για κάθε υλικό θεωρούμε όι οι πειραμαικά μερημένες ιμές ανοχής έχουν μέση ιμή X, υπική απόκλιση S και διασπορά V = S / X. Ακολούθως, θεωρώνας όι η θλιπική ανοχή κάθε υλικού αποελεί υχαία μεαβληή (έσω με σύμβολο R, από ον όρο Resistnce) με κανονική πιθανοική καανομή (καανομή Guss), κάι που ισχύει με καλή προσέγγιση για ις ανοχές ων περισσοέρων υλικών, α πραγμαικά ισογράμμαα ανικαθίσαναι από καμπύλες, γνωσές από η Θεωρία Πιθανοήων ως συναρήσεις πυκνόηας πιθανόηας, f R (r ). Ουσιασικά, κάθε έοια καμπύλη δίνει ην πιθανόηα να λάβει η ανοχή ου υλικού συγκεκριμένη ιμή. Αυό που έχει ενδιαφέρον να επισημάνουμε, συγκρίνονας α Σχ. 1.18α και 1.18β, είναι όι οι καμπύλες για α δύο υλικά έχουν ην ίδια μορφή αλλά διαφορεικά χαρακηρισικά μεγέθη, δηλαδή διαφορεική μέση ιμή μ R και υπική απόκλιση σ R.
21 21 Ανηγμένη συχνόηα fr(r) Συχνόηα (αριθμός πειραμάων) ΞΥΛΟ 1 2πσ R Μέση ιμή 25.4 M 538 πειράμαα S=4.62 V=0.18 f R (r) Κανονική καανομή Ανηγμένη συχνόηα fr(r) Συχνόηα (αριθμός πειραμάων) ΧΑΛΥΒΑΣ 51 πειράμαα S=26.2 V=0.11 Μέση ιμή 238 M 1 2πσ R f R (r) Κανονική καανομή X X [M] X 300 X [M] Θλιπική ανοχή Θλιπική άση διαρροής 0 μ R -4σ R μ R μ R +4σ R r 0 μ R -4σ R μ R μ R +4σ R r Σχ Ισογράμμαα θλιπικής ανοχής για ξύλο και για χάλυβα. Πυκνόηα πιθανόηας f E (e) Αποέλεσμα φορίου (δράσης) f f R (r) Ανίσαση (ανοχή) 0 e ή r Φορίο ή ανίσαση Σχ Συναρήσεις πυκνόηας πιθανόηας για ις δύο υχαίες μεαβληές (φορίο και ανίσαση, ή άση και ανοχή). Αν εκός από ην ανοχή κάθε υλικού θεωρήσουμε όι και α εξωερικά φορία (οι δράσεις) είναι υχαίες μεαβληές (ακόμα και α γεωμερικά χαρακηρισικά ων διαομών, π.χ. ο εμβαδόν ης επιφάνειας, είναι υχαίες μεαβληές), ο αποέλεσμα ων δράσεων αυών, δηλαδή π.χ. η ορθή άση σε ένα αξονικά φοριζόμενο σοιχείο, θα είναι και αυό μία υχαία μεαβληή (με σύμβολο E ), με συνάρηση πυκνόηας πιθανόηας f E (e). Παραθέονας ις δύο καμπύλες πυκνόηας πιθανόηας, f R (r ) και
22 22 f E (e), σο ίδιο σύσημα αξόνων (Σχ. 1.19) και με βάση η θεώρηση όι ο υλικό ασοχεί αν η άση ξεπεράσει ην ανοχή, βλέπουμε όι η περιοχή ομής ων δύο συναρήσεων (σκιασμένο μήμα σο Σχ. 1.19) δίνει ην πιθανόηα ασοχίας ( f ) ου δομικού σοιχείου για η συγκεκριμένη κααπόνηση. Έσι λοιπόν γίνεαι σαφές όι όχι μόνο η μέση ιμή ης ανοχής ενός υλικού αλλά, γενικόερα, η μορφή ης συνάρησης πυκνόηας πιθανόηας για ην ανοχή αυή παίζει καθορισικό ρόλο για ο σχεδιασμό ου δομικού σοιχείου. Σον πιθανοικό σχεδιασμό η διασασιολόγηση ων δομικών σοιχείων γίνεαι έσι ώσε να πιθανόηα ασοχίας, ιμή. f, να λαμβάνει συγκεκριμένη
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Ενότητα Ζ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ
 Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
? Συμπεριφορά ψαθυρών υλικών 11/6/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας
 11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Κεφάλαιο 8: Μαγνητικά Υλικά και Ιδιότητες ΙΙ. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Μέθοδοι ανάλυσης οικονοµικής σκοπιµότητας έργων. Κοινωνικο- οικονοµικές. Ο ορισµός του έργου. Τεχνική αξιολόγησης έργων
 Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
4/11/2017. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Βασική αρχή εργαστηριακής άσκησης
 Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
5/14/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80)
 Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) 1 Βασική αρχή εργαστηριακής άσκησης Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία
Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) 1 Βασική αρχή εργαστηριακής άσκησης Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία
ΕΠΙΡΡΟΗ ΕΥΤΕΡΟΓΕΝΩΝ ΣΤΡΕΠΤΙΚΩΝ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΣΤΗΝ ΑΝΑΛΥΣΗ ΡΑΒ ΩΝ ΤΥΧΟΥΣΑΣ ΙΑΤΟΜΗΣ
 ΕΠΙΡΡΟΗ ΕΥΤΕΡΟΓΕΝΩΝ ΣΤΡΕΠΤΙΚΩΝ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΣΤΗΝ ΑΝΑΛΥΣΗ ΡΑΒ ΩΝ ΤΥΧΟΥΣΑΣ ΙΑΤΟΜΗΣ Ε.Ι. Σαπουνζάκης Αναπληρωής Καθηγηής Σχολή Πολιικών Μηχανικών, Εθνικό Μεσόβιο Πολυεχνείο Πολυεχνειούπολη Ζωγράφου, Αθήνα
ΕΠΙΡΡΟΗ ΕΥΤΕΡΟΓΕΝΩΝ ΣΤΡΕΠΤΙΚΩΝ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΣΤΗΝ ΑΝΑΛΥΣΗ ΡΑΒ ΩΝ ΤΥΧΟΥΣΑΣ ΙΑΤΟΜΗΣ Ε.Ι. Σαπουνζάκης Αναπληρωής Καθηγηής Σχολή Πολιικών Μηχανικών, Εθνικό Μεσόβιο Πολυεχνείο Πολυεχνειούπολη Ζωγράφου, Αθήνα
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΟΧΗΜΑΤΩΝ
 2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
Ολοκλήρωση διεργασίας χρησιμοποιώντας την τεχνολογία σύγκλισης (Pinch Technology)
 Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
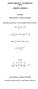 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
7. Στρέψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών. 7. Στρέψη/ Μηχανική Υλικών
 7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
(1A) Ε ΟΜΕΝΑ 2Φ10 Σ. Η. ΔΡΙΤΣΟΣ. Yλικά : Άνοιγµα δοκού: l 0-2 = l 2-3 = 4,40 m ΖΗΤΟΥΜΕΝΑ: Σ..Η ΔΡΙΤΣΟΣ
 (A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
(A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
Σημειώσεις του μαθήματος Μητρωϊκή Στατική
 ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Σημειώσεις του μαθήματος Μητρωϊκή Στατική Π. Γ. Αστερής Αθήνα, Μάρτιος 017 Περιεχόμενα Κεφάλαιο 1 Ελατήρια σε σειρά... 1.1 Επιλογή μονάδων και καθολικού
ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Σημειώσεις του μαθήματος Μητρωϊκή Στατική Π. Γ. Αστερής Αθήνα, Μάρτιος 017 Περιεχόμενα Κεφάλαιο 1 Ελατήρια σε σειρά... 1.1 Επιλογή μονάδων και καθολικού
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Η ΘΡΑΥΣΤΟΜΗΧΑΝΙΚΗ ΩΣ ΕΡΓΑΛΕΙΟ ΓΙΑ ΤΗΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟ ΕΝΙΣΧΥΣΗΣ ΡΗΓΜΑΤΩΜΕΝΩΝ ΚΑΤΑΣΚΕΥΩΝ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΟΛΟΓΙΑ» Η ΘΡΑΥΣΤΟΜΗΧΑΝΙΚΗ ΩΣ ΕΡΓΑΛΕΙΟ ΓΙΑ ΤΗΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟ ΕΝΙΣΧΥΣΗΣ ΡΗΓΜΑΤΩΜΕΝΩΝ ΚΑΤΑΣΚΕΥΩΝ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΟΛΟΓΙΑ» Η ΘΡΑΥΣΤΟΜΗΧΑΝΙΚΗ ΩΣ ΕΡΓΑΛΕΙΟ ΓΙΑ ΤΗΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟ ΕΝΙΣΧΥΣΗΣ ΡΗΓΜΑΤΩΜΕΝΩΝ ΚΑΤΑΣΚΕΥΩΝ
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Σειρά Ασκήσεων στην Αντοχή των Υλικών
 Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
10,2. 1,24 Τυπική απόκλιση, s 42
 Ασκηση 3.1 (a) Αν μία ράβδος οπλισμού θεωρηθεί ότι λυγίζει μεταξύ δύο διαδοχικών συνδετήρων με μήκος λυγισμού το μισό της απόστασης, s w, των συνδετήρων, να υπολογισθεί η απόσταση συνδετήρων, s w, πέραν
Ασκηση 3.1 (a) Αν μία ράβδος οπλισμού θεωρηθεί ότι λυγίζει μεταξύ δύο διαδοχικών συνδετήρων με μήκος λυγισμού το μισό της απόστασης, s w, των συνδετήρων, να υπολογισθεί η απόσταση συνδετήρων, s w, πέραν
ΘΕΩΡΙΕΣ ΑΣΤΟΧΙΑΣ ΥΛΙΚΩΝ
 105 Κεφάλαιο 5 ΘΕΩΡΙΕΣ ΑΣΤΟΧΙΑΣ ΥΛΙΚΩΝ 5.1 Εισαγωγή Στα προηγούμενα κεφάλαια αναλύσαμε την εντατική κατάσταση σε δομικά στοιχεία τα οποία καταπονούνται κατ εξοχήν αξονικά (σε εφελκυσμό ή θλίψη) ή πάνω
105 Κεφάλαιο 5 ΘΕΩΡΙΕΣ ΑΣΤΟΧΙΑΣ ΥΛΙΚΩΝ 5.1 Εισαγωγή Στα προηγούμενα κεφάλαια αναλύσαμε την εντατική κατάσταση σε δομικά στοιχεία τα οποία καταπονούνται κατ εξοχήν αξονικά (σε εφελκυσμό ή θλίψη) ή πάνω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
Στοιχεία Μηχανών. Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά
 Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ. Ασκήσεις προηγούμενων εξετάσεων ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
4/26/2016. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Βασική αρχή εργαστηριακής άσκησης
 Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Μηχανική Ι - Στατική
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μηχανική Ι - Στατική Ενότητα #6: Δικτυώματα (Μέθοδος Κόμβων) Δρ. Κωνσταντίνος Ι. Γιαννακόπουλος Τμήμα Μηχανολόγων Μηχανικών Τ.Ε.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μηχανική Ι - Στατική Ενότητα #6: Δικτυώματα (Μέθοδος Κόμβων) Δρ. Κωνσταντίνος Ι. Γιαννακόπουλος Τμήμα Μηχανολόγων Μηχανικών Τ.Ε.
ΜΗΧΑΝΙΚΕΣ ΚΑΤΕΡΓΑΣΙΕΣ. Υπολογισμοί συγκολλήσεων
 Σχήμα 1 Δυο ελάσματα πάχους h, συγκολλημένα σε μήκος L, με υλικό συγκόλλησης ορίου ροής S y, που εφελκύονται με δύναμη P. Αν το πάχος της συγκόλλησης είναι h, τότε η αναπτυσσόμενη στο υλικό της συγκόλλησης
Σχήμα 1 Δυο ελάσματα πάχους h, συγκολλημένα σε μήκος L, με υλικό συγκόλλησης ορίου ροής S y, που εφελκύονται με δύναμη P. Αν το πάχος της συγκόλλησης είναι h, τότε η αναπτυσσόμενη στο υλικό της συγκόλλησης
8. ΔΙΚΤΥΩΜΑΤΑ. 8.1 Ορισμοί:
 8. ΔΙΚΤΥΩΜΑΤΑ Σχ. 8.1 Παραδείγματα δικτυωμάτων 8.1 Ορισμοί: Δικτύωμα θα λέγεται ένας σύνθετος φορέας που όλα τα μέλη του είναι ράβδοι. Παραδείγματα δικτυωμάτων δίνονται στο σχήμα παραπάνω. Πλεονέκτημα
8. ΔΙΚΤΥΩΜΑΤΑ Σχ. 8.1 Παραδείγματα δικτυωμάτων 8.1 Ορισμοί: Δικτύωμα θα λέγεται ένας σύνθετος φορέας που όλα τα μέλη του είναι ράβδοι. Παραδείγματα δικτυωμάτων δίνονται στο σχήμα παραπάνω. Πλεονέκτημα
Γ. ΥΠΟΛΟΓΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M)
 . ΥΠΟΛΟΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M). Ορισμοί φορτίσεων μίας δοκού Οι φορτίσεις που μπορεί να εμφανισθούν σ'ένα σώμα είναι ο εφελκυσμός (ή η θλίψη με κίνδυνο λογισμού), η διάτμηση, η κάμψη και η στρέψη.
. ΥΠΟΛΟΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M). Ορισμοί φορτίσεων μίας δοκού Οι φορτίσεις που μπορεί να εμφανισθούν σ'ένα σώμα είναι ο εφελκυσμός (ή η θλίψη με κίνδυνο λογισμού), η διάτμηση, η κάμψη και η στρέψη.
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ- ΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕ Ο ΚΑΙ ΣΤΟ
 ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ- ΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕ Ο ΚΑΙ ΣΤΟ ΧΩΡΟ Στη συνέχεια θα δοθούν ορισμένες βασικές έννοιες μαθηματικών και φυσικήςμηχανικής που είναι απαραίτητες για την κατανόηση του μαθήματος
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ- ΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕ Ο ΚΑΙ ΣΤΟ ΧΩΡΟ Στη συνέχεια θα δοθούν ορισμένες βασικές έννοιες μαθηματικών και φυσικήςμηχανικής που είναι απαραίτητες για την κατανόηση του μαθήματος
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 A2. Δικτυώματα Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr A2. Δικτυώματα/ Μηχανική Υλικών 1 Τι είναι ένα δικτύωμα Είναι ένα σύστημα λεπτών,
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 A2. Δικτυώματα Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr A2. Δικτυώματα/ Μηχανική Υλικών 1 Τι είναι ένα δικτύωμα Είναι ένα σύστημα λεπτών,
1.1.1 Εσωτερικό και Εξωτερικό Γινόμενο Διανυσμάτων
 3 1.1 Διανύσματα 1.1.1 Εσωτερικό και Εξωτερικό Γινόμενο Διανυσμάτων ΑΣΚΗΣΗ 1.1 Να βρεθεί η γωνία που σχηματίζουν τα διανύσματα î + ĵ + ˆk και î + ĵ ˆk. z k i j y x Τα δύο διανύσματα που προκύπτουν από
3 1.1 Διανύσματα 1.1.1 Εσωτερικό και Εξωτερικό Γινόμενο Διανυσμάτων ΑΣΚΗΣΗ 1.1 Να βρεθεί η γωνία που σχηματίζουν τα διανύσματα î + ĵ + ˆk και î + ĵ ˆk. z k i j y x Τα δύο διανύσματα που προκύπτουν από
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ.
 Τίτλος Μαθήματος ΤΧΝΟΛΟΙΚΟ ΚΠΙΔΥΤΙΚΟ ΙΔΡΥΜ ΚΝΤΡΙΚΗΣ ΜΚΔΟΝΙΣ ΣΧΟΛΗ ΤΧΝΟΛΟΙΚΩΝ ΦΡΜΟΩΝ ΤΜΗΜ ΜΗΧΝΟΛΟΩΝ ΜΗΧΝΙΚΩΝ Τ ΜΗΧΝΙΚΗ Ι ΡΣΤΗΡΙΟ Καθηγητής Δρ. Μοσχίδης Νικόλαος ΣΡΡΣ, ΣΠΤΜΡΙΟΣ 2015 Άδειες Χρήσης Το παρόν
Τίτλος Μαθήματος ΤΧΝΟΛΟΙΚΟ ΚΠΙΔΥΤΙΚΟ ΙΔΡΥΜ ΚΝΤΡΙΚΗΣ ΜΚΔΟΝΙΣ ΣΧΟΛΗ ΤΧΝΟΛΟΙΚΩΝ ΦΡΜΟΩΝ ΤΜΗΜ ΜΗΧΝΟΛΟΩΝ ΜΗΧΝΙΚΩΝ Τ ΜΗΧΝΙΚΗ Ι ΡΣΤΗΡΙΟ Καθηγητής Δρ. Μοσχίδης Νικόλαος ΣΡΡΣ, ΣΠΤΜΡΙΟΣ 2015 Άδειες Χρήσης Το παρόν
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Μηχανική Στερεού Σώματος. Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ ΑΝΤΟΧΗ ΠΛΟΙΟΥ 5 ου ΕΞΑΜΗΝΟΥ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2016 ΗΜΕΡΟΜΗΝΙΑ 07 ΣΕΠΤΕΜΒΡΙΟΥ 2016
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΚΑΘΗΓΗΤΗΣ Μ. ΣΑΜΟΥΗΛΙΔΗΣ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ ΑΝΤΟΧΗ ΠΛΟΙΟΥ 5 ου ΕΞΑΜΗΝΟΥ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 016
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΚΑΘΗΓΗΤΗΣ Μ. ΣΑΜΟΥΗΛΙΔΗΣ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ ΑΝΤΟΧΗ ΠΛΟΙΟΥ 5 ου ΕΞΑΜΗΝΟΥ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 016
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
