ΚΕΦΑΛΑΙΟ 3 ΤΑΛΑΝΤΩΣΗ ΣΥΝΕΧΩΝ ΣΥΣΤΗΜΑΤΩΝ
|
|
|
- θάλασσα Λούπης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 3 ΤΑΛΑΝΤΩΣΗ ΣΥΝΕΧΩΝ ΣΥΣΤΗΜΑΤΩΝ 3. Ταλάντση χορδής. Η χορδή του σχήµατος έχει γνστό µήκος και ακίνητα άκρα. Η πυκνότητα της και το εµβαδόν της διατοµής είναι γνστά και παραµένουν σταθερά σε όλο το µήκος της. α) Να προσδιοριστεί η ελεύθερη ταλάντση της χορδής για αρχικές συνθήκες w(, ) = w( ) &w (, ) = wˆ ( ) β) Κατόπιν να εξεταστεί η ειδική περίπτση κατά την οποία το µέσο της χορδής προεκτείνεται µια γνστή απόσταση s και µετά αφήνεται η χορδή να ταλαντθεί ελεύθερα. z Λύση α) Για τη χορδή ισχύουν οι αρχικές συνθήκες w(,) = w ( ) () w& (,) = w ( ) () Επειδή τα άκρα της χορδής είναι πακτµένα καθώς οι συνοριακές συνθήκες είναι w(, t) = w(, t) = (3) w (, t) = w (, t) = (4) Η εξίσση κίνησης της χορδής είναι ˆ w(, t) w(, t) N + q(, t) = ρ( ) A( ) t (5) Επειδή δεν ασκείται εξτερική δύναµη, είναι q(, t ) = (6) Επίσης δίνεται ότι η χορδή έχει σταθερή πυκνότητα ρ() και σταθερό εµβαδόν Α() διατοµής σε όλο το µήκος της, δηλαδή 7
2 ρ( ) A( ) Με αντικατάσταση τν σχέσεν (6), (7), (8) στην (5) έχουµε = ρ (7) = A (8) N w(, t) w(, t) w(, t) ρ A w(, t) = ρ A = t N t Θέτουµε w(, t) w(, t) = N t ρ A (9) οπότε η (9) γράφεται N = () ρ A w(, t) w(, t) = () t Η εξίσση () είναι µια διαφορική εξίσση µε µερικές παραγώγους, γραµµική και οµογενής. Ζητάµε να τη λύσουµε, µε τον όρο η λύση της w(,t) να ικανοποιεί τις αρχικές και συνοριακές συνθήκες τν σχέσεν (), (), (3), (4). Για να λύσουµε την () χρησιµοποιούµε τη µέθοδο χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε ότι η () έχει µια µερική λύση της µορφής Με αντικατάσταση της () στην () έχουµε w (, t) = X ( ) T ( t) () [ X ( ) T ( t) ] = [ X ( ) T ( t) ] X ( ) T ( t) = X ( ) T& ( t) t ( ) ( ) = & X ( ) T ( t) X T t (3) Επειδή η µεταβλητή του πρώτου µέλους είναι η απόσταση ενώ του δεύτερου ο χρόνος t, η µόνη περίπτση για να ισχύει η ισότητα είναι το κάθε µέλος να ισούται µε µια σταθερά η οποία αναµένεται να είναι αρνητική έτσι ώστε η προκύπτουσα διαφορική εξίσση ς προς να περιγράφει ταλάντση. Έτσι θέτουµε οπότε ( ) &( ) = = X ( ) T ( t) X T t (4) 7
3 και X ( ) = X ( ) = X ( ) X ( ) = X ( ) X ( ) T& ( t) T ( t) X ( ) + X ( ) = = = + = (5) T& ( t) T ( t) T& ( t) T ( t) (6) Η εξίσση (5) ς γνστόν αντιστοιχεί σε ταλάντση και η γενική λύση της είναι X ( ) = a os + bsi (7) όπου τα α, b, θα προσδιοριστούν. Επειδή η () είναι λύση της () ισχύουν και για αυτή οι συνοριακές συνθήκες δηλαδή w (, t ) = (8) Από την () έχουµε αν θέσουµε = w (, t ) = (9) w (, t) = X () T ( t) = X () T ( t) = X () X () = () Όµοια αν θέσουµε = έχουµε w (, t) = X ( ) T ( t) = X ( ) T ( t) = X ( ) X ( ) = () Από την (7) για = έχουµε Άρα X () = a os + bsi X () = a = a a= () Από την (3) για = έχουµε X ( ) = bsi (3) X ( ) = bsi = bsi (4) Είναι προφανές ότι το b δεν µπορεί να είναι µηδέν γιατί τότε ολόκληρη η συνάρτηση X() θα είναι µηδέν, οπότε και η λύση w (, t ). Άρα π si = = π = για =,,3, (5) 73
4 όπου αντί για θέσαµε δεδοµένου ότι οι λύσεις της (4) είναι άπειρες. Παρατηρούµε ότι υπάρχουν άπειρες τιµές του που επαληθεύουν τη σχέση (4). Οι τιµές λέγονται ιδιοσυχνότητες της χορδής. Για κάθε µια από τις τιµές,,. του λύνουµε την (5) και βρίσκουµε όπς και την (3) τις αντίστοιχες λύσεις Χ (), X (), που έχουν γενική µορφή π π X ( ) = bsi X ( ) = bsi X ( ) = bsi για =,,3, (6) Οι συναρτήσεις X ( ) λέγονται ιδιοµορφές της χορδής. Για δύο διαφορετικές ιδιοµορφές της χορδής ισχύει η σχέση ορθογνιότητας X ( ) X s ( ) d= (7) Αν απαιτηθεί η σχέση ορθοκανονικότητας τότε για = s έχουµε ραx ( ) X s ( ) d = δ s (8) s s [ ] ραx ( ) X ( ) d= δ ρα X ( ) d= (9) Με αντικατάσταση από τη σχέση (6) έχουµε π π ρα bsi d= ραb si d= (3) Ισχύει η τριγνοµετρική ταυτότητα π π si = os (3) οπότε µε αντικατάσταση στην (3) έχουµε π π os = os = ραb ραb d d ραb ραb π d os d= ραb ραb = b= ρα (3) όπου χρησιµοποιήσαµε τη σχέση 74
5 π π π os d= si = si si = π π = [ si π si ] [ ] π = π = (33) Με αντικατάσταση της σχέσης (3) στην (6) έχουµε π X ( ) = si ρα για =, (34) Επίσης από την εξίσση (6) για κάθε µια τυχαία τιµή του προκύπτει ότι η γενική λύση είναι της µορφής T ( t) = Γ ost+ sit (35) Επειδή οι τιµές του είναι οι,, οι αντίστοιχες γενικές λύσεις θα είναι T ( t) = Γ os t+ si t (36) Επανερχόµενοι τώρα στη σχέση () όπου ζητήσαµε µια µερική λύση w (, t ) της () παρατηρούµε ότι βρήκαµε µια απειρία τέτοιν µερικών λύσεν, δεδοµένου ότι υπάρχουν άπειρες συναρτήσεις X(), T(t) που δίνονται από τις σχέσεις (34), (36). Η απειρία αυτών τν συναρτήσεν θα έχει γενική µορφή [ ] w (, t) = X ( ) T ( t) w (, t) = X ( ) Γ os t+ si t (37) όπου Γ, είναι σταθερές ποσότητες. Σύµφνα µε τη θερία τν γραµµικών διαφορικών εξισώσεν η γενική λύση µιας οµογενούς διαφορικής εξίσσης είναι ο γραµµικός συνδυασµός τν µερικών λύσεν. Άρα η γενική λύση της () είναι ( ) w(, t) = C w (, t) w(, t) = C X ( ) Γ os t+ si t = = Αν θέσουµε ( ) (38) w(, t) = X ( ) C Γ os t+ C si t = A = C Γ και B = C (39) τότε η γενική λύση θα είναι ( ) (4) w(, t) = X ( ) Α os t+ Β si t = 75
6 Οι σταθερές Α, B προσδιορίζονται µε τη βοήθεια τν αρχικών συνθηκών τν σχέσεν (), (). Συγκεκριµένα από τη σχέση (4) για t = έχουµε ( ) w(,) = X ( ) Α os + Β si w(,) = X ( ) Α = = ρ Aw(,) = ρ AX ( ) A ρ Aw(,) X ( ) = ρ AX ( ) X ( ) A = = ρ Aw(,) X ( ) d= ρ AX ( ) X ( ) d A = (4) Με αντικατάσταση τν σχέσεν (), (8) στην (4) έχουµε ρ Aw ( ) X ( ) d= δ A ρ Aw ( ) X ( ) d= A = A = ρ Aw ( ) X ( ) d (4) Για να βρούµε τα Β παραγγίζουµε την γενική λύση (4) ς προς t και θέτουµε =. Είναι = ( ) w(, t) = X ( ) A os t+ Β si t = ( ) w& (, t) = X ( ) A si t+ Β os t = ( ) w& (,) = X ( ) A si + Β os = ( ) w& (,) = X ( ) Β ρα w& (,) = ρax ( ) B ρaw& (,) X ( ) = ρax ( ) X ( ) B = = ρ Aw& (,) X ( ) d= ρ AX ( ) X ( ) d B (43) = Με αντικατάσταση τν σχέσεν (),(8) στη (43) έχουµε 76
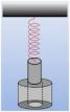
7 ρ Awˆ ( ) X ( ) d= δ B ρ Awˆ ( ) X ( ) d= B = B ˆ = ρ Aw ( ) X ( ) d (44) Άρα η γενική λύση w (,t) της αρχικής εξίσσης, που είναι και η ζητούµενη συνάρτηση κίνησης της χορδής δίνεται από τη σχέση (4) όπου τα Χ () δίνονται από τη σχέση (34) και τα, A, B από τις σχέσεις (5), (4),(44) αντίστοιχα. β) Στην ειδική περίπτση που το µέσο της χορδής αποµακρύνεται µια απόσταση s η αρχική παραµόρφση της χορδής θα είναι της µορφής του σχήµατος (). s Από το σχήµα () προκύπτει ότι η εξίσση της αρχικής παραµόρφσης είναι w ( ) = s / για (45) w ( ) = s( / ) για (46) Με αντικατάσταση της (45), (46) στην (4) έχουµε / Α = ραw ( ) X ( ) d Α = ρα s X ( ) d+ ραs / X ( ) d (47) Για την εύρεση τν ολοκληρµάτν δες στο παράρτηµα της άσκησης. Επίσης επειδή η αρχική ταχύτητα είναι µηδέν ισχύει w& (,) = w ( ) = (48) ˆ Με αντικατάσταση της wˆ ( ) από τη (48) στην (44) έχουµε 77
8 B = ρα X ( ) d = (49) Άρα στην περίπτση αυτή η γενική λύση είναι = ( ) w(, t) = X ( ) Α os t+ si t w(, t) = Α X ( )os t (5) = όπου τα, Χ, A δίνονται από τις σχέσεις (5), (34), (47). Παράρτηµα Είναι Α = ρα s X ( ) d+ ρα s X ( ) / d ραs ραs Α = X ( ) d+ ρα s X ( ) d X ( ) d / / Αρκεί να υπολογίσουµε τα ολοκληρώµατα =, A X ( ) d = B X ( ) d /, / Γ = X ( ) d Είναι π π π B= X ( ) d= si d= si d= os = / / ρα ρα / ρα π / / os π os π os π os π = ρα π ρα π Τα ολοκληρώµατα Α, Γ υπολογίζονται εφαρµόζοντας την ιδιότητα Σχόλιο b b = [ ] a a fg d fg f gd Θα πρέπει να διευκρινίσουµε ότι η απειρία τν συναρτήσεν X () οφείλεται στις άπειρες τιµές του που ικανοποιούν τη σχέση (4) και όχι στην εξίσση (5) η οποία για κάθε τιµή του έχει µια µόνο γενική λύση. Πιο αναλυτικά, η (5) για µια τιµή του, έστ την 3 γράφεται b a 78
9 3 ( ) ( ) X + X = (Σ ) όπου από τη σχέση (5) έχουµε ότι 3π = (Σ ) 3 Η διαφορική εξίσση (Σ ) έχει γενική λύση (µη καθορισµένη) την 3( ) = os + si (Σ 3 ) 3 3 X a b Αν στην γενική λύση Χ 3 () επιβάλουµε τη συνθήκη () τότε παίρνουµε τη µερική λύση 3 X 3( ) = bsi (Σ 4 ) (χρησιµοποιούµε το ίδιο σύµβολο για λόγους ευκολίας). Η λύση που δίνεται από τη σχέση (Σ 4 ) αν και µερική, δεν είναι καθορισµένη., δεδοµένου ότι το b είναι άγνστο. Εφαρµόζοντας όµς τη συνθήκη ορθογνιότητας (8) βρίσκουµε ότι b= (Σ 5 ) ρα οπότε = (Σ 6 ) ρα 3 X 3( ) si Άρα η Χ 3 () που δίνεται από τη σχέση (Σ 6 ) είναι µια µερική λύση της εξίσσης που δίνεται από τη σχέση (Σ ). Όµοια οι ιδιοµορφές X () που δίνονται από τη σχέση π X ( ) = si ρα είναι µερικές λύσεις τν αντίστοιχν διαφορικών εξισώσεν όπου X ( ) + X ( ) = (Σ7) π = µε =,, (Σ8) 79
10 . Στη χορδή του σχήµατος που έχει µήκος είναι m, η ακτίνα.5 mm, πυκνότητα 8 kg/m 3 ασκείται τάση Ν. Να βρεθούν οι δύο πρώτες ιδιοσυχνότητες και οι δύο πρώτες ιδιοµορφές. ίνονται τα µεγέθη = m, =.5 mm, ρ = 8 kg/m 3, N = N. z Λύση Οι ιδιοσυχνότητες και ιδιοµορφές προκύπτουν από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του προβλήµατος που είναι N w(, t) w(, t) = ρ( ) A( ) t () ίνεται ότι η χορδή έχει σταθερή πυκνότητα ρ() και σταθερό εµβαδόν Α() διατοµής σε όλο το µήκος της, δηλαδή ρ( ) A( ) Με αντικατάσταση τν σχέσεν (), (3) στην () έχουµε = ρ () = A (3) N w(, t) w(, t) w(, t) ρ A w(, t) = ρ A = t N t Θέτουµε w(, t) w(, t) = N t ρ A (4) N = (5) ρ A οπότε η (4) γράφεται w(, t) w(, t) = t (6) 8
11 Για να λύσουµε την (6) χρησιµοποιούµε τη µέθοδο χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε ότι η (6) έχει µια µερική λύση της µορφής Με αντικατάσταση της (7) στην (6) έχουµε w (, t) = X ( ) T ( t) ) (7) [ X ( ) T ( t) ] = [ X ( ) T ( t) ] X ( ) T ( t) = X ( ) T& ( t) t ( ) ( ) = & X ( ) T ( t) X T t (8) Επειδή η µεταβλητή του πρώτου µέλους είναι η απόσταση ενώ του δεύτερου ο χρόνος t, η µόνη περίπτση για να ισχύει η ισότητα είναι το κάθε µέλος να ισούται µε µια σταθερά η οποία αναµένεται να είναι αρνητική έτσι ώστε η προκύπτουσα διαφορική εξίσση ς προς να περιγράφει ταλάντση. Έτσι θέτουµε οπότε ( ) &( ) = = X ( ) T ( t) X T t X ( ) = X ( ) = X ( ) X ( ) = X ( ) X ( ) (9) X ( ) + X ( ) = () Επειδή η (7) είναι λύση της (6) ισχύουν και για αυτή οι συνοριακές συνθήκες δηλαδή Από την (7) έχουµε αν θέσουµε = Όµοια αν θέσουµε = w (, t ) = () w (, t ) = () w (, t) = X () T ( t) = X () T ( t) = X () X () = (3) w (, t) = X ( ) T ( t) = X ( ) T ( t) = X ( ) X ( ) = (4) Η εξίσση () ς γνστόν αντιστοιχεί σε ταλάντση και η γενική λύση της είναι 8
12 όπου τα α, b, θα προσδιοριστούν. Από την (5) για = έχουµε X ( ) = a os + bsi (5) Άρα X () = a os + bsi X () = a = a a= (5) X ( ) = bsi (6) Από την (6) για = έχουµε X ( ) = bsi = bsi (7) Είναι προφανές ότι το b δεν µπορεί να είναι µηδέν γιατί τότε ολόκληρη η συνάρτηση X() θα είναι µηδέν, οπότε και η λύση w (, t ). Άρα π si = = π = για =,,3, (8) όπου αντί για θέσαµε δεδοµένου ότι οι λύσεις της (7) είναι άπειρες. Από την (5) είναι N N = = = = 78.4 m / se ρ A ρπ ( ) (9) Με αντικατάσταση τν µεγεθών στη (8) έχουµε Οπότε π = = = 56. () = 56. = 56. ad / se () = 56. =. ad / se () Ως γνστόν b= = = = 7.8 ρ ρπ ( ) A 3 m kg () Οι διοµορφές δίνονται από τη σχέση 8
13 X ( ) si = b (3) Με αντικατάσταση τν (), () στην (3) έχουµε 56. X ( ) = bsi X ( ) = 7.8si X ( ) = 7.8si 3.4 (4) 78.4 Οπότε X ( ) = 7.8si 3.4 (5) X ( ) = 7.8si 6.8 (6) 83
14 3. Αξονική ταλάντση 3. Η ράβδος του σχήµατος στηρίζεται στο ένα άκρο της σε ελαστικό ελατήριο στιβαρότητας k, ενώ το άλλο άκρο της είναι ελεύθερο. Η πυκνότητα, το εµβαδόν διατοµής και το µέτρο ελαστικότητάς της είναι γνστά και παραµένουν σταθερά σε όλο το µήκος της. Επίσης η µάζα m και το µήκος της είναι γνστά. Η ράβδος εκτελεί αξονική ταλάντση. α) Να προσδιοριστεί η χαρακτηριστική εξίσση του µηχανικού συστήµατος και να εκφραστεί συναρτήσει τν αδιάστατν παραµέτρν k Κ = και λ = EA/ / β) Να υπολογιστεί η τιµή της θεµελιώδους συχνότητας αν K z ρ, Α, Ε O Λύση α) Η χαρακτηριστική εξίσση προκύπτει από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του προβλήµατος που είναι ρα( ) u& = EAu () ( ) / Επειδή τα Ε, Α είναι σταθερά, ανεξάρτητα του από την () έχουµε u u u u ραu& = EAu ρu& = Eu Eu = ρu& E = ρ = () t t όπου E = (3) ρ Το άκρο = στηρίζεται στο ελατήριο. Άρα όπς γνρίζουµε για την γενική λύση u(, t) ισχύει η συνοριακή συνθήκη u(, t) EA ku(, t) = (4) Το άκρο = είναι ελεύθερο. Άρα ισχύει η συνοριακή συνθήκη u(, t) = (5) 84
15 Στη συνέχεια προχράµε στην επίλυση της (). Η µέθοδος που χρησιµοποιούµε για τη λύση είναι η µέθοδος του χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε µια µερική λύση της µορφής u (, t) = X ( ) T ( t) (6) Με αντικατάσταση της (6) στη () έχουµε [ ( ) ( )] [ ( ) ( )] X T t X T t ( ) ( ) ( ) ( ) ( ) ( ) X T & = X T t = X T& t = t (7) t X ( ) T ( t) Για ισχύει η ισότητα (7) πρέπει κάθε µέλος να είναι ίσο µε µια σταθερά ποσότητα Θέτουµε X ( ) T& ( t) = = (8) X ( ) T ( t) Από την (8) έχουµε X = ( ) = ( ) ( ) + ( ) = ( ) X X X X X ( ) Όµοια από (8) έχουµε X + X = (9) T& ( t) T ( t) &( ) ( ) & () = T t + T t = T+ T = Η u (, t) ς µερική λύση ικανοποιεί τις ίδιες συνοριακές συνθήκες (4), (5) που ικανοποιεί και η αντίστοιχη γενική λύση u(, t) της οµογενούς γραµµικής διαφορικής εξίσσης (). Άρα ισχύουν οι συνοριακές συνθήκες u (, t) EA ku (, t) = u (, t) = () () Με αντικατάσταση της ( 6) στην (), έχουµε [ X () T ( t) ] EA kx () T ( t) = EAX () T ( t) kx () T ( t) = Όµοια από (6), () έχουµε EAX () kx () = (3) 85
16 [ X ( ) T ( t) ] EA = EAX ( ) T ( t) = X ( ) = (4) Η εξίσση (9) µαζί µε τις αντίστοιχες σχέσεις (3), (4) αποτελούν το λεγόµενο ιδιοπρόβληµα που επιλύουµε στη συνέχεια. Η γενική λύση της (9) είναι της µορφής X ( ) = a os + bsi (5) όπου η και µια από τις σταθερές α, b προσδιορίζονται µε την εφαρµογή τν συνοριακών συνθηκών. Από τη σχέση (5) για = έχουµε Παραγγίζοντας την (5) έχουµε Θέτουµε στην (5) = και παίρνουµε X () = a os + b si X () = a (6) X ( ) = a si + b os (7) X () = a si + b os X () = a + b X () = b (8) Αντικαθιστώντας τις σχέσεις (6), (8 ) στη (3) έχουµε Θέτουµε στην (7) = και παίρνουµε EA b ka= ka EA b= (9) X ( ) = a si + b os X ( ) = a si + b os () Από (4) και () προκύπτει ότι = a si + b os a si b os = () Οι σχέσεις (9), () είναι ένα σύστηµα µε άγνστα τα α, b. Το σύστηµα σε µορφή πινάκν γράφεται k EA a = () b si os 86
17 Για να έχει λύση διάφορη του µηδενός πρέπει η διακρίνουσα του πίνακα να είναι µηδενική, δηλαδή k EA k EA si = = os si os k os + EA si = k os + si = (3) EA Η σχέση (3) είναι η χαρακτηριστική εξίσση του µοντέλου δεδοµένου ότι όπς αναφέραµε η λύση της θα δώσει τις τιµές του. Θα την εκφράσουµε σε σχέση µε τις παραµέτρους Κ, λ. ίνεται ότι K = k K k k K EA / = EA EA = και λ= λ= = λ / (4) (5) Με αντικατάσταση τν σχέσεν (4), (5) στην (3) έχουµε K λ λ λ K λ os + si = osλ+ siλ= K osλ+ λ siλ= siλ K K λ siλ= K osλ = taλ = (6) osλ λ λ Η εξίσση (6) είναι η ζητούµενη χαρακτηριστική εξίσση του µοντέλου που εκφρασµένη σε σχέση µε τους παραµέτρους Κ, λ. Η παράµετρος Κ θερείται γνστή δεδοµένου ότι όπς παρατηρούµε από τη σχέση (4) εξαρτάται από τα γνστά µεγέθη k, E, A, ενώ η λ άγνστη δεδοµένου ότι φαίνεται από τη σχέση (5) εξαρτάται από το. Έτσι η άγνστη µεταβλητή της εξίσσης (6) είναι το λ. Αν βρούµε το λ τότε από τη σχέση (5) µπορούµε να βρούµε το. Η εξίσση (6) δεν έχει αναλυτική λύση ς προς λ και λύνεται µόνο αριθµητικά. Αποδεικνύεται ότι οι τιµές του λ που επαληθεύουν την (6) είναι άπειρες το πλήθος και για αυτό τις συµβολίζουµε µε λ. Με αντικατάσταση τν λ στην (5) βρίσκουµε τις αντίστοιχες ιδιοσυχνότητες που θα είναι λ λ = = (7) β) Αν K τότε από τη σχέση (6) προκύπτει ότι taλ (8) 87
18 Από τη σχέση (8) προκύπτει ότι taλ λ (9) δεδοµένου ότι όπς είναι γνστό από την τριγνοµετρία ισχύει η σχέση ta (3) όταν το είναι πολύ µικρό. Από τις (6), (9) προκύπτει ότι K λ= λ = K λ= K (3) λ Επειδή το Κ είναι πολύ µικρό, τείνει στο µηδέν, η τιµή του λ που δίνεται από την εξίσση (9) είναι η πιο µικρή τιµή του λ, δηλαδή η λ. Οπότε έχουµε Με αντικατάσταση του Κ από τη σχέση (4) στη (3) έχουµε λ = K (3) λ = k EA / (33) Επίσης από τη σχέση (7) για = παίρνουµε λ = λ = Από (33), (34) προκύπτει ότι k = EA / (34) (35) Επίσης εφαρµόζοντας τη σχέση (3) στη (35) έχουµε k ρ k ρ k k = = = = (36) E EA/ E EA E EA ρ A ρ Όµς ισχύει ρa = ρv = m (37) όπου V είναι ο όγκος και m η µάζα της ράβδου. Τελικά µε αντικατάσταση της σχέσης (37) στη (36) έχουµε k k = = (38) m m 88
19 4. Η ράβδος του σχήµατος έχει γνστό µήκος. Το αριστερό άκρο της είναι πακτµένο και το δεξιό άκρο της ελεύθερο. Η πυκνότητα, το εµβαδόν διατοµής και το µέτρο ελαστικότητάς της είναι γνστά και παραµένουν σταθερά σε όλο το µήκος της. Στο δεξιό άκρο ασκείται γνστή δύναµη F(t). Να υπολογιστεί η δυναµική απόκριση της ράβδου όταν η κίνησή της ξεκινά: α) Από γνστές αρχικές συνθήκες u(, ) = u ( ), u& (, ) = uˆ ( ). β) Από µηδενικές αρχικές συνθήκες. z ρ, Α, Ε F(t) O Λύση α) Στο πρώτο βήµα επίλυσης του προβλήµατος γράφουµε την εξίσση κίνησης του συστήµατος και τις αντίστοιχες αρχικές και συνοριακές συνθήκες. Επειδή στη ράβδο ασκείται η δύναµη F(t) θα εκτελέσει αξονική ταλάντση. Η εξίσση κίνησης είναι u u(, t) ρ A( ) = E( ) A( ) f (, t) + t () Το µέτρο ελαστικότητας η διατοµή και η πυκνότητα της ράβδου είναι σταθερά, δηλαδή Ε() = E () A()= A (3) οπότε η () γράφεται ρ() = ρ (4) u u (, t ) (, ) (, ) u ρ A = EA f t ρ A EA u t f (, t) + = + t t (5) Η δύναµη F(t) ασκείται στο άκρο της ράβδου, δηλαδή στο σηµείο =, ενώ η () ισχύει για τιµές µικρότερες του. Άρα επειδή στη ράβδο δεν ασκείται δύναµη για < < από την (5) έπεται ότι όπου u u(, t) u u(, t) u(, t) u ρ A = EA ρ = E = (6) t t t = (7) ρ E 89
20 Για το άκρο της ράβδου που αντιστοιχεί στη τιµή = επειδή είναι πακτµένο ισχύει η συνοριακή συνθήκη u(, t ) = (8) Οµοίς για το άκρο της ράβδο που αντιστοιχεί στη τιµή = ισχύει η σχέση u(, t) EA = F( t) (9) Η εξίσση (6) είναι η εξίσση κίνησης του συστήµατος ενώ οι σχέσεις (8), (9) αποτελούν τις αντίστοιχες συνοριακές συνθήκες της λύσης του u(, t ). Στο δεύτερο βήµα καταστρώνουµε και επιλύουµε το ιδιοπρόβληµα. Βρίσκουµε την οµογενή εξίσση και τις αντίστοιχες συνοριακές συνθήκες που διέπουν τη λύση της. Η εξίσση του προβλήµατος είναι οµογενής, άρα χρησιµοποιείται όπς είναι στο ιδιοπρόβληµα. Επίσης από τις συνοριακές συνθήκες (8), (9) αφαιρούµε τους όρους φόρτισης. Από αυτές µόνο η (9) έχει τέτοιο όρο και µετά την αφαίρεση γίνεται u(, t) EA = u (, t) = () Στη συνέχεια προχράµε στην επίλυση της (6) υπό τον όρο η γενική λύση της uh(, t ) να ικανοποιεί τις συνοριακές συνθήκες (8), (). Για το λόγο αυτό θερούµε µια µερική λύση της (6) είναι η u (, t) = X ( ) T ( t) () Με αντικατάσταση της () στην (6) έχουµε [ ( ) ( )] [ ( ) ( )] X T t X T t ( ) ( ) ( ) ( ) ( ) ( ) X T & = X T t = X T& t = t () t X ( ) T ( t) Για ισχύει η ισότητα () πρέπει κάθε µέλος να είναι ίσο µε µια σταθερά ποσότητα Θέτουµε X = X ( ) = X ( ) X ( ) + X ( ) = ( ) X ( ) X + X = (3) Όµοια T& ( t) = T& ( t) + T ( t) = T& + T = (4) T ( t) Η u (, t) ς µερική λύση ικανοποιεί τις συνοριακές συνθήκες (8), () που ικανοποιεί και η αντίστοιχη γενική λύση uh(, t) της οµογενούς γραµµικής διαφορικής εξίσσης (6). Από (8), () έχουµε u (, t) = X () T ( t) = X () = (5) 9
21 u (, t) = X ( ) T ( t) = X ( ) = (6) Η εξίσση (3) µαζί µε τις αντίστοιχες σχέσεις (5), (6) αποτελούν το λεγόµενο ιδιοπρόβληµα που επιλύουµε στη συνέχεια. Η γενική λύση της (3 είναι της µορφής Από την (7 για = έχουµε X ( t) = a os + bsi (7) X () = a os + bsi X () = a + b X () = a (8) Από (5) και (8) έπεται ότι Από (9) και (7 προκύπτει Παραγγίζοντας την () έχουµε a= (9) X ( ) = bsi () X ( t) = b os X ( ) = b os () Από (6) και () παίρνουµε b os = bos = () Η () είναι η χαρακτηριστική εξίσση του µηχανικού συστήµατος. Από την επίλυσή της βρίσκουµε τις ιδιοσυχνότητες του. Το b δεν µπορεί να είναι ίσο µε το µηδέν γιατί τότε θα είναι και X() =. Άρα π π os = = ( ) = ( ) (3) Άρα, σύµφνα µε την () οι ιδιοµορφές θα δίνονται από τη σχέση X ( ) si = b (4) όπου οι ιδιοσυχνότητες δίνονται από τη σχέση (3). Επίσης µε εφαρµογή της σχέσης (3) στην (4) οι ιδιοµορφές δίνονται και στη µορφή ( ) si ( π X = b ) ( ) ( ) si π X = b (5) Επίσης όπς έχουµε δείξει στην άσκηση () το b δίνεται από τη σχέση 9
22 b= = ρ A m (6) όπου m η µάζα της ράβδου. Έτσι επιλύσαµε και το λεγόµενο ιδιοπρόβληµα. Στο τελικό βήµα βρίσκοµε τη γενική λύση της εξίσσης του προβλήµατος που είναι (6) µε αντίστοιχες συνοριακές συνθήκες τις (8), (9). Παρατηρούµε ότι η συνοριακή συνθήκη (9) δεν είναι οµογενής και άρα η µέθοδος της ανάλυσης ιδιοµορφών δεν εφαρµόζεται άµεσα. Σε τέτοιες περιπτώσεις εφαρµόζουµε το εξής τέχνασµα. Θέτουµε f (, t) = F( t) δ ( ) (7) Η συνθήκη (9) σηµαίνει ότι το φορτίο είναι παντού µηδέν, εκτός από το άκρο της ράβδου που αντιστοιχεί στη τιµή =, όπου ισούται µε F(t). Με αυτό τον τρόπο η εξίσση κίνησης (6) της ράβδου τρέπεται στη µη οµογενή µορφή, δηλαδή u u(, t) ρα = EA + t f (, t) (8) Η συνοριακή συνθήκη (9), αν η δύναµη είναι της µορφής (7) γράφεται u(, t) EA = u (, t) = (9) δηλαδή είναι οµογενής. Η εξίσση κίνησης σύµφνα µε τη µέθοδο ανάλυσης ιδιοµορφών δέχεται λύση της µορφής u(, t) = X ( ) τ ( t) (3) = Οι ιδιοµορφές έχουν ήδη βρεθεί. Μένει να βρούµε τους χρονικούς συντελεστές τ (t). Με αντικατάσταση της (3) στη (8) έχουµε ρ A X ( ) ( ) ( ) ( ) (, ) t EA X t f t t τ τ = + = = και σε συνοπτική µορφή ρa X ( ) τ& ( t) = EA X ( ) τ ( t) + f (, t) (3) = = ρ A X τ& = EA X τ + f (, t) (3) = = Όµς η Χ ικανοποιεί την εξίσση (3), οπότε 9
23 + = = X X X X (33) Με αντικατάσταση της (33) στη (3) έχουµε = = ρ A X τ& = EA X τ + f (, t) (34) και µε αντικατάσταση του από τη σχέση (7) στη (34), ρ A X τ = EA X τ + f (, t) & E = = ρ & = = ρ A X τ = ρ A X τ + f (, t) & & = = ρ A X τ + τ = f (, t) ρ A X X τ + τ = X f (, t) Ισχύει ότι = οπότε η (35) γράφεται ρ AX X d τ + τ = & X f (, t) d (35) ρ AX X d= δ (36) = + = X f t d τ + τ = δ & τ τ (, ) & X f (, t) d (37) Αν θέσουµε η (37) γράφεται f ( t) = X f (, t) d (38) & τ + τ = f ( t) (39) Με αντικατάσταση του δείκτη µε το συνήθη δείκτη η (39) γράφεται & τ τ µε =,, (4) + = f ( t) Οι χρονικοί συντελεστές όπς έχουµε αναφέρει στην άσκηση (7) δίνονται από τη σχέση όπου t τ ( t) = A os t+ B si t+ f ( τ )si ( t τ) dτ (4) 93
24 και f ( t) = X f (, t) d (4) A = ρ Aw ( ) X ( ) d (43) B = ρ Awˆ ( ) X ( ) d (44) µε w( ), wˆ ( ) να είναι οι αρχικές συνθήκες, δηλαδή w( ) = u(,) (45) wˆ ( ) = u& (,) (46) Από τις σχέσεις (7), (38) προκύπτει ότι f ( t) = X F( t) δ ( ) d f ( t) = F( t) X δ ( ) d f ( t) = F( t) X ( ) (47) Από τη σχέση (4) για = προκύπτει X ( ) si = b (48) Από τις σχέσεις (47), (48) έχουµε f ( ) ( )si t = bf t (49) Τελικά η απόκριση του συστήµατος δίνεται από τη σχέση (3) όπου οι ιδιοµορφές X () δίνονται από τη σχέση (5) και οι χρονικοί συντελεστές τ (t) από τη σχέση (4). Επίσης για τον υπολογισµό τν τ (t) χρειάζονται και οι σχέσεις (3), (43), (44), (49). β) ίνεται ότι οι αρχικές συνθήκες είναι µηδενικές, οπότε από τις (45), (46) συνεπάγεται w( ) = u(,) = (5) wˆ ( ) = u& (,) = (5) Από τις (5), (5) και (43), (44) έπεται ότι Από τις σχέσεις (5), (53) και (4) έχουµε ότι A = (5) B = (53) 94
25 t τ ( t) = f ( τ )si ( t τ) dτ (54) Επίσης δίνεται ότι εξτερική δύναµη είναι σταθερή, δηλαδή Η (49) συνεπάγεται από την (55) F( t) = F (55) f( t) = bf si f( τ ) = bf si (56) Με αντικατάσταση της (56) στην (54) παίρνουµε τ t = bf t τ dτ τ t = bf t τ dτ t ( ) ( ) t ( ) si si ( ) si si τ ( t) = bf si os ( t τ) t τ ( t) = bf si os t t os t t ( ) ( ) τ ( t) = bf si [ ost] (57) Άρα στην προκειµένη περίπτση, η γενική λύση δίνεται από τη σχέση (3), όπου οι ιδιοµορφές δίνονται από τη σχέση (5) και οι χρονικοί συντελεστές από τη σχέση (57). 5. Μια οµοιόµορφη ράβδος µε µήκος, µε το ένα άκρο της πακτµένο και το άλλο ελεύθερο επιµηκύνεται οµοιόµορφα µέχρι το µήκος της να γίνει και αφήνεται ελεύθερη τη χρονική στιγµή t =, όπς δείχνεται στο σχήµα. Να υπολογιστεί η δυναµική της απόκριση. ίνονται η πυκνότητα, το εµβαδόν διατοµής και το µέτρο ελαστικότητάς της. z ρ, Α, Ε Λύση 95
26 Στο πρώτο βήµα επίλυσης του προβλήµατος γράφουµε την εξίσση κίνησης του συστήµατος και τις αντίστοιχες αρχικές και συνοριακές συνθήκες. Η ράβδος εκτελεί αξονική ταλάντση οπότε η εξίσση κίνησης είναι u(, t) u(, t) ρα ( ) = E( ) A( ) t () Επειδή τα Ε, Α είναι σταθερά, ανεξάρτητα του έχουµε u(, t) u(, t) u(, t) u(, t) ρα = EA ρ = E t t όπου u(, t) u(, t) = t () E = ρ (3) Βρίσκουµε τις αρχικές συνθήκες και συνοριακές συνθήκες Έστ u(,) είναι η µετατόπιση τη χρονική στιγµή t = ενός σηµείου της ράβδου που απέχει απόσταση από το σηµείο µηδέν. ίνεται ότι τη χρονική στιγµή t = το δεξιό άκρο από τη θέση = έχει µετατοπιστεί στη θέση, δηλαδή η θέση του έχει µεταβληθεί κατά. Αναλογικά έχουµε: Το σηµείο που απέχει απόσταση έχει µετατοπιστεί κατά Το σηµείο που απέχει απόσταση έχει µετατοπιστεί κατά u(,) Από την αναλογία προκύπτει ότι u(,) = (4) Για µια πιο αυστηρή απόδειξη της (4) δες στο σχόλιο, που παρατίθεται στο τέλος της άσκησης. Στην αρχή της ταλάντσης η ράβδος δεν έχει ταχύτητα, οπότε Οι σχέσεις (4), (5) αποτελούν τις αρχικές συνθήκες. Το άκρο = είναι πακτµένο, οπότε u (,) = (5) u(, t ) = (6) Το άκρο = είναι ελεύθερο, οπότε u (, t) = (7) Στο δεύτερο βήµα καταστρώνουµε και επιλύουµε το ιδιοπρόβληµα 96
27 Θερούµε µια µερική λύση της µορφής Με αντικατάσταση της (8) στη () έχουµε [ ( ) ( )] [ ( ) ( )] u (, t) = X ( ) T ( t) (8) X T t X T t ( ) ( ) ( ) ( ) ( ) ( ) X T & = X T t = X T& t = t (9) t X ( ) T ( t) Για ισχύει η ισότητα (9) πρέπει κάθε µέλος να είναι ίσο µε µια σταθερά ποσότητα Θέτουµε X ( ) T& ( t) = = () X ( ) T ( t) Από την () έχουµε X = X ( ) = X ( ) X ( ) + X ( ) = ( ) X ( ) X + X = () Όµοια από () έχουµε T& ( t) = T& ( t) + T ( t) = T& + T = () T ( t) Η u (, t) ς µερική λύση ικανοποιεί τις ίδιες συνοριακές συνθήκες (6), (7) που ικανοποιεί και η αντίστοιχη γενική λύση uh(, t) της οµογενούς γραµµικής διαφορικής εξίσσης (). Άρα ισχύει και u (, t) = X () T ( t) = X () = (3) u (, t) = X ( ) T ( t) = X ( ) = (4) Η εξίσση () µαζί µε τις αντίστοιχες σχέσεις (5),(6) αποτελούν το λεγόµενο ιδιοπρόβληµα που επιλύουµε στη συνέχεια. Η () έχει γενική λύση της µορφής X ( ) = a os + bsi (5) όπου η και µια από τις σταθερές α, b προσδιορίζονται µε την εφαρµογή τν συνοριακών συνθηκών. Από την (5) για = έχουµε Από τις (3), (6) προκύπτει ότι X () = a os + b si X () = a (6) 97
28 a= (7) οπότε η σχέση (5) γράφεται X ( ) = bsi (8) Με παραγώγιση της (8) παίρνουµε X ( ) = bsi X ( ) = bos X ( ) = bos (9) Από (4) και (9) συνεπάγεται = bos os = () Η () είναι η χαρακτηριστική εξίσση του προβλήµατος. Από την () έχουµε = ( ) π = ( ) π Από τις (8), () προκύπτει ότι οι αντίστοιχες ιδιοµορφές είναι () όπου ς γνστόν οπότε X ( ) = bsi X ( ) = bsi b= ρ A X ( ) = si ρ A ( ) π ( ) π () () (3) Τέλος βρίσκουµε τη γενική λύση. Σύµφνα µε τη µέθοδο ανάλυσης ιδιοµορρφών η u(, t) = X ( ) τ ( t) (4) = Με αντικατάσταση της (4) στη () έχουµε X ( ) ( ) ( ) ( ) τ t X τ t = = t = X ( ) τ ( t) = X ( ) τ ( t) & (5) = = Όµς η Χ ικανοποιεί την εξίσση (), οπότε + = = X X X X (6) 98
29 Με αντικατάσταση της (6) στην (5) έχουµε X ( t) = X ( ) &( t) τ τ = = X ( ) & τ ( t) X τ ( t) X & τ τ = = = + = + = ρ ΑX X d τ & + τ = (7) = Ισχύει ότι οπότε η (7) γράφεται ρ ΑX X d= δ (8) δ τ + τ = τ + τ = (9) = Με αντικατάσταση του δείκτη µε το συνήθη δείκτη η (8) γράφεται & τ + τ = µε =,, (3) Η γενική λύση της (3) ς γνστόν είναι τ ( t) = A os t+ B si t (3) όπου όπς έχουµε δείξει στην άσκηση () τα Α, B δίνονται από τις σχέσεις A = ρ Aw ( ) X ( ) d (3) και w( ), wˆ ( ) είναι οι αρχικές συνθήκες, δηλαδή B = ρ Awˆ ( ) X ( ) d (33) w( ) = u(,) (34) Από (5), (35) έπεται ότι Από (3), (36) συνεπάγεται ότι Από (3), (37) συνεπάγεται Από (5), (34) έπεται ότι wˆ ( ) = u& (,) (35) wˆ ( ) = (36) B = (37) τ ( t) = A os t (38) 99
30 Από (3), (39) είναι ˆ ( ) = w (39) A = ρ A X ( ) d A = ρ A X ( ) d (4) Με αντικατάσταση του Χ () από την (3) στη (4) έχουµε ( ) π = si ρ A A ρ A d ( ) π = ρ ρ A A A si d (4) Τελικά η απόκριση του συστήµατος δίνεται από τη σχέση (4) όπου οι ιδιοµορφές X () δίνονται από τη σχέση (3) και οι χρονικοί συντελεστές τ (t) από τη σχέση (38). Σχόλιο Έστ η ράβδος του σχήµατος της άσκησης που έχει µήκος. Αν στο δεξιό άκρο της ασκηθεί σταθερή δύναµη F θα προκαλέσει επιµήκυνση της ράβδου. Έστ ότι η ράβδος επιµηκύνεται µέχρι το µήκος της να γίνει. Στην κατάσταση αυτή, που είναι η αρχή της ταλάντσης και άρα αντιστοιχεί στη χρονική στιγµή t =, ένα τυχαίο σηµείο που απέχει απόσταση από την αρχή της ράβδου έχει µετατοπιστεί από την αρχική του θέση κατά µια απόσταση u(, ). Όπς αναµένεται η συνάρτηση u(,) θα είναι ανάλογη του, δεδοµένου ότι όσο πιο πολύ απέχει ένα σηµείο από την αρχή τόσο πιο πολύ µετατοπίζεται. Το σηµείο που απέχει απόσταση θα µετατοπιστεί κατά, ενώ το αριστερό άκρο της ράβδου που είναι πακτµένο δεν θα µετακινηθεί καθόλου. Ας βρούµε την σχέση u(,). Τη χρονική στιγµή t = που αντιστοιχεί στην κατάσταση που η ράβδος έχει επιµηκυνθεί και έχει µήκος, σε κάθε σηµείο της που απέχει απόσταση από την αρχή της ράβδου, σύµφνα µε τον νόµο ελαστικής παραµόρφσης του Hooke αναπτύσσεται εστερική ορθή τάση (δύναµη που οφείλεται στην ελαστικότητα της ράβδου), που δίνεται από τη σχέση du(,) N(,) = EA (4) d Όµς στην κατάσταση ισορροπίας τα σηµεία της ράβδου είναι ακίνητα, οπότε σε κάθε σηµείο που απέχει απόσταση θα πρέπει να ισχύει N(,) = F (43) Εδώ θα πρέπει να παρατηρήσουµε ότι η F αν και εφαρµόζεται µόνο στο δεξιό άκρο της ράβδου, µεταδίδεται σε κάθε σηµείο της. Από τις (4), (43) έπεται ότι
31 du(,) F = EA Fd= EAdu(,) Fd= EAdu(,) + C d (44) F d= EA du(,) + C F= EAu(,) + C Επειδή το αριστερό άκρο της ράβδου που είναι στη θέση = είναι πακτµένο δεν θα µετακινηθεί είναι u(,) =. Άρα από την (44) έχουµε F = EAu(, ) + C = EA + C C= (45) Από (44), (45) συνεπάγεται F F= EAu(,) u(,) = (46) EA Επίσης δίνεται ότι το σηµείο που απέχει απόσταση θα µετατοπιστεί κατά, δηλαδή ισχύει u (,) = (47) Από (46) αν θέσουµε = έχουµε F u(,) = (48) EA Από (47), (48) έπεται F F = = (49) EA EA Με αντικατάσταση της (49) στην (46) παίρνουµε τη σχέση u(,) = (5) Η σχέση (5) είναι η σχέση (4).
32 6. Μια στήλη µε διατοµή Α, µέτρο ελαστικότητας Ε, πυκνότητας ρ και µήκους στηρίζει µια µηχανή µάζας Μ µέσ µιας πλάκας S όπς δείχνεται στο σχήµα. Λόγ αζυγοσταθµικής περιστροφικής κίνησης της µηχανής αναπτύσσεται σ αυτή µια κατακόρυφη δύναµη της µορφής F( t) = FosΩt Αν το έδαφος είναι στέρεο, να υπολογιστεί η µόνιµη κατάσταση της αξονικής ταλάντσης της ράβδου. M S Λύση Η εξίσση κίνησης είναι u u(, t) ρα( ) = E( ) A( ) t () Το µέτρο ελαστικότητας η διατοµή και η πυκνότητα της ράβδου είναι σταθερά, δηλαδή Ε() = E () A()= A (3) ρ() = ρ (4) οπότε η () γράφεται u u(, t) u u(, t) ρα = EA ρα EA = t t όπου ρ u u(, t) u(, t) u = E = t t = (6) ρ Για το άκρο της ράβδου που αντιστοιχεί στη τιµή = επειδή είναι πακτµένο ισχύει η συνοριακή συνθήκη E (5)
33 u(, t ) = (7) To άκρο της ράβδο που αντιστοιχεί στη τιµή = υπάρχει η µηχανή µάζας Μ στην οποία ασκείται η δύναµη F( t) = F osωt (8) λόγ αζυγοσταθµίας και η δύναµη u(, t) F (, t) = EA (9) από την στήλη. Σύµφνα τον ο νόµο του Νεύτνα ισχύει u (, t ) (, ) (, ) ( ) (, ) u t M = F t F t M = F osωt EA u t t t () Μια επεξήγηση της () δίνεται στο τέλος της άσκησης στο σχόλιο. Οι σχέσεις (7), () είναι οι συνοριακές συνθήκες του προβλήµατος. Επειδή το ζητούµενο είναι να προσδιοριστεί η απόκριση στη µόνιµη κατάσταση η λύση της (5) θα είναι της µορφής u(, t) = U ( )osω t () Με αντικατάσταση της () στην (6) παίρνουµε U ( )os Ωt ( )os ( ) os = U Ωt os Ωt U = U ( ) Ωt t t os ΩtU ( ) = U ( ) Ω os Ωt U ( ) = U ( ) Ω Η () έχει λύση της µορφής Από την (9) για = έχουµε Ω U ( ) + U ( ) = () Ω Ω U ( ) = a os + bsi (3) u(, t) = U ()osωt (4) Με αντικατάσταση της (4) στη () παίρνουµε [ U () os Ωt] [ U () osωt] M = F osωt EA t = MΩ U () osωt F os Ωt EAU () osωt MΩ U F EAU () = () (5) Από την () για = προκύπτει u(, t) = U ( )osωt (6) και µε τη χρήση της (7) παίρνουµε 3
34 = U ( )os Ωt U ( ) = (7) Στη συνέχεια βρίσκουµε τις τιµές U (), U (), U ( ) µε τη βοήθεια της σχέσης (3) µε σκοπό να τα αντικαταστήσουµε στις (5), (7). Από (3) για = έχουµε U () = a os + b si U () = a (8) Από (3) µε παραγώγιση και θέτοντας = προκύπτει Ω Ω Ω Ω Ω Ω Ω U ( ) = a si + b os U () = a si + b os U () = b (9) Από (3) για = έχουµε Ω Ω U ( ) = a os + bsi () Με αντικατάσταση τν U (), U () από τις (8), (9) στη (5) παίρνουµε Ω = () MΩ a F EAb Με αντικατάσταση του U ( ) από την () στην (7) έχουµε Ω Ω a os + bsi = () Οι σχέσεις (), () είναι σύστηµα µε άγνστα τα α, b που λύνουµε. Από () προκύπτει Ω a os Ω Ω a os + bsi = b= Ω si (3) Με αντικατάσταση του b στην () βρίσκουµε το α. Είναι Ω Ω a os os Ω Ω MΩ a= F + EA MΩ a EA a= F Ω Ω si si Ω os Ω F a MΩ + EA F a Ω = = Ω si os Ω MΩ + EA Ω si 4
35 a= MΩ Ω F si Ω Ω Ω si + EA os (4) Από (3), (4) βρίσκουµε το b. Είναι Ω F si Ω os Ω Ω Ω MΩ si + EA os b= Ω si b= MΩ Ω F os Ω Ω Ω si + EA os (5) Τελικά η λύση του προβλήµατος από τις (), (3) θα είναι Ω Ω u(, t) = a os + bsi osωt (6) όπου τα α, b δίνονται από τις σχέσεις (4), (5). Σχόλιο Έστ έχουµε τη διάταξη του σχήµατος µε το ελατήριο. Αν ασκηθεί µια δύναµη F στο σώµα τότε το ελατήριο θα ασκήσει στο σώµα µια αντίθετη δύναµη F ελ. Όµοιο φαινόµενο συµβαίνει και στη διπλανή διάταξη µε τη κατακόρυφη στήλη που λόγ ελαστικότητας συµπεριφέρεται σαν ελατήριο. Αν ασκηθεί µια δύναµη F στο σώµα τότε η στήλη θα ασκήσει στο σώµα µια αντίθετη δύναµη F. F ελ F u F F Σχόλιο Το φυσικό νόηµα της λύσης δεν αλλάζει αν πάρουµε ς αρχή τν αξόνν τη βάση της στήλης. 5
36 7. Η ράβδος του σχήµατος στηρίζεται στο ένα άκρο της σε ελατήριο, ενώ το άλλο είναι πακτµένο. Η ράβδος έχει µήκος m, πυκνότητα 78 kg/m, εµβαδόν διατοµής 3-6 m και µέτρο ελαστικότητάς της 9 N/m. Η στιβαρότητα του ελατηρίου είναι 5 N/m. α) Να προσδιοριστεί η χαρακτηριστική εξίσση του µηχανικού συστήµατος όταν εκτελεί αξονική ταλάντση. β) Να βρεθεί η χαµηλότερη συχνότητα της ταλάντσης αν η µικρότερη λύση της εξίσσης taφ = -.5φ είναι η τιµή φ =.97 ad z ρ, Α, Ε O Λύση α) Η χαρακτηριστική εξίσση προκύπτει από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του προβλήµατος που είναι u(, t) u(, t) ρα( ) = E( ) A( ) t () Επειδή τα Ε, Α είναι σταθερά, ανεξάρτητα του έχουµε ρ u(, t) u(, t) u(, t) u(, t) Α = EA ρ = E t t όπου u(, t) u(, t) = t () E = ρ (3) Προσδιορίζουµε τις συνοριακές συνθήκες. Το άκρο = είναι πακτµένο και άρα ισχύει Το άκρο = στηρίζεται στο ελατήριο και άρα ισχύει u(, t ) = (4) 6
37 u(, t) EA = ku(, t) = (5) Για την εξαγγή της σχέσης (5) δες σχόλιο στο τέλος της άσκησης. Στη συνέχεια προχράµε στην επίλυση της (). Η µέθοδος που χρησιµοποιούµε για τη λύση είναι η µέθοδος του χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε µια µερική λύση της µορφής Με αντικατάσταση της (6) στη () έχουµε [ ( ) ( )] [ ( ) ( )] u (, t) = X ( ) T ( t) (6) X T t X T t ( ) ( ) ( ) ( ) ( ) ( ) X T & = X T t = X T& t = t (7) t X ( ) T ( t) Για ισχύει η ισότητα (7) πρέπει κάθε µέλος να είναι ίσο µε µια σταθερά ποσότητα Θέτουµε Από την (8) έχουµε ( ) &( ) = = X ( ) T ( t) X T t (8) X = X ( ) = X ( ) X ( ) + X ( ) = ( ) X ( ) Όµοια από (8) έχουµε X + X = (9) T& ( t) T ( t) T& ( t) T ( t) T& T () = + = + = Η u (, t) ς µερική λύση ικανοποιεί τις ίδιες συνοριακές συνθήκες (4), (5) που ικανοποιεί και η αντίστοιχη γενική λύση u(, t) της οµογενούς γραµµικής διαφορικής εξίσσης (). Άρα ισχύουν οι συνοριακές συνθήκες u (, t ) = () u (, t) u (, t) EA = ku (, t) = EA + ku (, t) = () Από (6), () έχουµε u (, t) = X () T ( t) = X () T ( t) X () = (3) 7
38 Όµοια µε αντικατάσταση της ( 6) στην (), έχουµε [ ] u (, t) X ( ) T ( t) EA + ku (, t) = EA + kx ( ) T ( t) = EAX ( ) T ( t) + kx ( ) T ( t) = EAX ( ) + kx ( ) = (4) Η εξίσση (9) µαζί µε τις αντίστοιχες σχέσεις (3), (4) αποτελούν το λεγόµενο ιδιοπρόβληµα που επιλύουµε στη συνέχεια. Η γενική λύση της (9) είναι της µορφής X ( ) = a os + bsi (5) όπου η και µια από τις σταθερές α, b προσδιορίζονται µε την εφαρµογή τν συνοριακών συνθηκών. Από τη σχέση (5) για = έχουµε X () = a os + b si X () = a (6) Από (3), (6) συνεπάγεται ότι Από (5), (7) έχουµε Από την (8) για = παίρνουµε a= (7) X ( ) = bsi (8) X ( ) = bsi (9) Παραγγίζοντας την (8) έχουµε X ( ) = b os () Από την () για = παίρνουµε X ( ) = b os () Αντικαθιστούµε τις (9), () στη (4) EAb os + kbsi = k si = EA os si os EA EA = ta = k k () 8
39 Με αντικατάσταση της από τη σχέση (3) στη σχέση () βρίσκουµε ta EA ρ A Eρ = ta = (3) E E E k k ρ ρ Η (3) είναι η χαρακτηριστική εξίσση της ταλάντσης. β) Θέτουµε Από την οποία προκύπτει ότι ρ = φ E (4) Eφ = ρ (5) Αντικαθιστούµε τις (4), (5) στην (3), οπότε Eφ A Eρ ρ AE taφ= taφ= φ k k (6) Με αντικατάσταση τν µεγεθών στην (6) βρίσκουµε 6 9 ( 3 )( ) 5 ( )( ) taφ= φ taφ=.5φ (7) ίνεται ότι η µικρότερη λύση της (7) είναι φ =.97 (8) Με αντικατάσταση στην (5) έχουµε Σχόλιο Eφ = = ρ = 4.83 ad/se (9) Η απόδειξη της συνοριακής συνθήκης (5) γίνεται ς εξής: z u(,t) ρ, Α, Ε F ελ O Μ Ν 9
40 Έστ στο άκρο = της ράβδου υπάρχει σώµα µάζας Μ. Όταν η ράβδος συσπειρώνεται κατά u(,t) τότε στο σώµα ασκείται µια ελκτική δύναµη F ελ από το ελατήριο και µια απθητική δύναµη Ν από τη ράβδο. Ισχύει Fελ = ku(, t) (3) και u(, t) N(, t) = EA (3) Σύµφνα µε το δεύτερο νόµο του Νεύτνα ισχύει u(, t) u(, t) u(, t) M = F N(, t) M ku(, t) EA ελ = (3) Αν η µάζα είναι πολύ µικρή (απειροστή), δηλαδή τότε παίρνουµε τη διάταξη της άσκησης. Η (3) συνεπάγεται από την (33) M ; (33) u(, t) u(, t) = ku(, t) EA EA = ku(, t) (34) Η (34) είναι η ζητούµενη συνοριακή σχέση (5).
41 3.3 Στρεπτική ταλάντση 8. Το σχήµα παρουσιάζει το µοντέλο µιας µηχανικής διάταξης, η οποία αποτελείται από άτρακτο µε γνστές ελαστικές και γεµετρικές ιδιότητες, (δηλαδή το µήκος, τη διατοµή Α, την πυκνότητα ρ, την πολική ροπή I και το µέτρο διάτµησης G) και από στρόβιλο µε γνστή ροπή αδράνειας Ι ς προς τον διαµήκη άξονα της ατράκτου. Οι ιδιότητες παραµένουν σταθερές σε όλη την έκταση του µήκους της. H ράβδος εκτελεί στρεπτική ταλάντση. α) Να προσδιοριστεί η χαρακτηριστική εξίσση του συστήµατος συναρτήσει τν αδιάστατν παραµέτρν I α = και β = ρi β) Να καθοριστούν οι ιδιοµορφές του. z G, I, ρ Ι O Σχήµα Λύση α) Η χαρακτηριστική εξίσση προκύπτει από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του προβλήµατος που είναι θ t θ t ( ) (, ) (, t) I ρ = GJ () Επειδή τα µεγέθη G, J είναι σταθερά η () γράφεται θ (, t) θ (, t) θ (, t) θ (, t) I ρ = GJ I ρ = GJ t t όπου I ρ θ t θ t θ t t = = θ (, ) (, ) (, ) (, ) GJ t t () GJ = (3) I ρ Το άκρο = είναι πακτµένο, οπότε ισχύει η συνοριακή συνθήκη θ(, t ) = (4) Στο άκρο = υπάρχει σώµα µε ροπή αδράνειας I, οπότε ισχύει η σχέση
42 θ (, t) I = M (, ) t t (5) t Θέτουµε το αρνητικό πρόσηµο στη ροπή γιατί η ροπή τείνει να στρέψει τη ράβδο σε αντίθετη κατεύθυνση από την γνία θ(,t) όπς δείχνεται στο σχήµα α. Στο σχήµα β δείχνεται το αντίστοιχο µοντέλο ελατηρίου όπου το σώµα δέχεται δύναµη µε αντίθετη διεύθυνση της συσπείρσης. Η ροπή Μ αντιστοιχεί στη δύναµη F και η γνία στροφής θ στη συσπείρση. Επίσης ισχύει η σχέση θ (, t) θ (, t) M t (, t) = GJ M t (, t) = GJ (6) Από (6) και (7) συνεπάγεται ότι ισχύει η συνοριακή συνθήκη θ (, t) θ (, t) θ (, t) θ (, t) I = GJ I + GJ = t t (7) (α) Μ (β) F θ Στη συνέχεια προχράµε στην επίλυση της (). Η µέθοδος που χρησιµοποιούµε για τη λύση είναι η µέθοδος του χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε µια µερική λύση της µορφής θ (, t) = X ( ) T ( t) (8) Με αντικατάσταση της (3) στη (4) έχουµε [ X ( ) T ( t) ] [ X ( ) T ( t) ] = X ( ) T ( t) = X ( ) T& ( t) t ( ) ( ) = & X ( ) T ( t) X T t (9) Επειδή τα µέλη της εξίσσης έχουν διαφορετικές µεταβλητές, το πρώτο έχει τη και το δεύτερο το t, για να είναι ίσα θα πρέπει να ισούται µε µια σταθερά, δηλαδή ( ) &( ) = = X ( ) T ( t) X T t ()
43 όπου θέσαµε τη σταθερά µε αρνητικό πρόσηµο για φυσικούς λόγους. Από την () έχουµε Όµοια X = X = X X + X = ( ) ( ) ( ) ( ) ( ) X ( ) T& ( t) T ( t) = T t + T t = () &( ) ( ) () Η θ (, t) ς µερική λύση ικανοποιεί τις ίδιες συνοριακές συνθήκες (4), (7) που ικανοποιεί και η αντίστοιχη γενική λύση u(, t) της οµογενούς γραµµικής διαφορικής εξίσσης (). Από την (8) για = προκύπτει θ (, t) = X () T ( t) (3) Επίσης η θ (, t) ς λύση του προβλήµατος ικανοποιεί την συνοριακή συνθήκη (4), δηλαδή Από (3) και (4) έπεται ότι Από την (8) µε παραγώγιση ς προς έχουµε και µε παραγώγιση ς προς t έχουµε θ (, t) = (4) = X () T ( t) X () = (5) θ (, t) θ (, t) = X ( ) T ( t) = X ( ) T ( t) (6) θ (, t) θ (, t) = X ( ) T& ( t) = X ( ) T& ( t) (7) t t Επίσης η θ (, t) ς λύση του προβλήµατος ικανοποιεί την συνοριακή συνθήκη (7), δηλαδή Αντικαθιστώντας τις (6), (7) στην (8) παίρνουµε I θ (, t) θ (, t) + GJ = (8) t I X ( ) T& ( t) + GJX ( ) T ( t) = (9) Από τη σχέση () έχουµε & ( ) = T ( t) () T t Με αντικατάσταση της () στην (9) προκύπτει 3
44 I X T t + GJX T t = I X GJX = () ( ) ( ) ( ) ( ) ( ) ( ) Η εξίσση () µαζί µε τις αντίστοιχες σχέσεις (5), () αποτελούν το λεγόµενο ιδιοπρόβληµα που επιλύουµε στη συνέχεια Η () έχει λύση της µορφής X ( ) = Aos + Bsi () Από την () για = έχουµε X () = Aos + B si X () = A (3) Από (5) (3) συνεπάγεται ότι A= (4) Από () και (4) προκύπτει X ( ) = Bsi (5) Από την (5) για = έχουµε X ( ) = Bsi (6) Παραγγίζουµε την (5) X ( ) = B os X ( ) = B os (7) Με αντικατάσταση τν (6), (7) στην () παίρνουµε I Bsi GJB os I si GJ os = = si os = GJ I GJ ta = (8) I Η (8) έχει ς άγνστη µεταβλητή το και είναι η χαρακτηριστική εξίσση του συστήµατος. Στη συνέχεια θα εκφράσουµε την (8) σε σχέση µε τις παραµέτρους α και β όπς ζητείται από την άσκηση. ίνεται ότι α α = α = (9) Με αντικατάσταση της σχέσης (9) στη σχέση (8) έχουµε α GJ GJ ta = taα = α I Iα (3) 4
45 Με αντικατάσταση της (3) στη (3) έχουµε GJ taα = taα = taα = GJ I I Iα α α I ρ I ρ I ρ taα = taα = (3) I αβ α I ρ Η σχέση (3) είναι η ζητούµενη χαρακτηριστική εξίσση και λύνεται αριθµητικά ς προς α. Από τη λύση βρίσκουµε ότι υπάρχουν άπειρες τιµές του α που τις συµβολίζουµε µε α οι οποίες την επαληθεύουν. Με αντικατάσταση αυτών τν τιµών του α στη σχέση (9) βρίσκουµε τις αντίστοιχες τιµές του σύµφνα µε την εξίσση a = (3) Με αντικατάσταση της (3) στην (5) βρίσκουµε τις ιδιοµορφές a X ( ) si = B (33) 9. Μια οµοιόµορφη ράβδος µε κυκλική διατοµή έχει µήκος, πυκνότητα ρ, µέτρο διάτµησης G και ακίνητα άκρα. Να βρεθούν: α) Η διαφορική εξίσση κίνησης για στρεπτική ταλάντση, β) Οι συνοριακές συνθήκες γ) Η χαρακτηριστική εξίσση και οι ιδιοσυχνότητες. z ρ, Α, G O Λύση α) Όταν µια ράβδος εκτελεί ελεύθερη ταλάντση η εξίσση κίνησης ( ) (, ) θ (, t) I = GJ t θ t ρ () Επειδή τα µεγέθη G, J είναι σταθερά η () γράφεται 5
46 (, t) (, t) (, t) (, t) I θ GJ θ I θ ρ = ρ = GJ θ t t µε ρ θ (, ) (, ) = GJ t I t θ t θ (, t) θ (, t) = () t GJ G = = (3) I ρ ρ όπου J=I δεδοµένου ότι η ράβδος έχει κυκλική διατοµή. Η () είναι η εξίσση κίνησης της ράβδου, όπου το δίνεται από τη σχέση (3). β) Το άκρο = είναι πακτµένο, οπότε ισχύει η συνοριακή συνθήκη θ(, t ) = (4) Το άκρο = είναι πακτµένο, οπότε ισχύει η συνοριακή συνθήκη Οι σχέσεις (4), (5) είναι οι συνοριακές συνθήκες. θ(, t ) = (5) γ) Η χαρακτηριστική εξίσση και οι ιδιοσυχνότητες προκύπτουν από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του που είναι η (). Για να λύσουµε την () χρησιµοποιούµε τη µέθοδο χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε ότι η () έχει µια µερική λύση της µορφής Με αντικατάσταση της (6) στην () έχουµε θ (, t) = X ( ) T ( t) ) (6) [ X ( ) T ( t) ] = [ X ( ) T ( t) ] X ( ) T ( t) = X ( ) T& ( t) t ( ) ( ) = & X ( ) T ( t) X T t (7) Επειδή η µεταβλητή του πρώτου µέλους είναι η απόσταση ενώ του δεύτερου ο χρόνος t, η µόνη περίπτση για να ισχύει η ισότητα είναι το κάθε µέλος να ισούται µε µια σταθερά η οποία αναµένεται να είναι αρνητική έτσι ώστε η προκύπτουσα διαφορική εξίσση ς προς να περιγράφει ταλάντση. Έτσι θέτουµε ( ) &( ) = = X ( ) T ( t) X T t (8) 6
47 οπότε X ( ) = X ( ) = X ( ) X ( ) = X ( ) X ( ) X ( ) + X ( ) = (9) Επειδή η (6) είναι λύση της () ισχύουν και για αυτή οι συνοριακές συνθήκες δηλαδή Από την (6) έχουµε αν θέσουµε = Όµοια αν θέσουµε = θ (, t) = () θ (, t) = () θ (, t) = X () T ( t) = X () T ( t) = X () X () = () θ (, t) = X ( ) T ( t) = X ( ) T ( t) = X ( ) X ( ) = (3) Η εξίσση (9) ς γνστόν αντιστοιχεί σε ταλάντση και η γενική λύση της είναι X ( ) = a os + bsi (4) όπου τα α, b, θα προσδιοριστούν. Από την (4) για = έχουµε X () = a os + bsi X () = a = a a= (5) Άρα X ( ) = bsi (6) Από την (6) για = έχουµε X ( ) = bsi = bsi (7) Είναι προφανές ότι το b δεν µπορεί να είναι µηδέν γιατί τότε ολόκληρη η συνάρτηση X() θα είναι µηδέν, οπότε και η λύση θ (, t). Άρα si = (8) Η εξίσση (8) που έχει ς άγνστη τη συχνότητα είναι η χαρακτηριστική εξίσση. Από τη λύση της βρίσκούµε τις ιδιοσυχνότητες. Είναι 7
48 π si = = π = για =,,3, (9) όπου αντί για θέσαµε δεδοµένου ότι οι λύσεις της (8) είναι άπειρες.. Να βρεθούν οι ιδιοσυχνότητες και ιδιοµορφές της στρεπτικής ταλάντσης µιας οµοιόµορφης ατράκτου µήκους, πυκνότητας ρ, µέτρου διάτµησης G και πολικής ροπής I. Το ένα άκρο της είναι πακτµένο και το άλλο ελεύθερο. z ρ, Α, G, I O Λύση Οι ιδιοσυχνότητες και ιδιοµορφές προκύπτουν από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του προβλήµατος που είναι ( ) (, ) θ (, t) I = GJ t θ t ρ () Επειδή τα µεγέθη G, J είναι σταθερά η () γράφεται (, t) (, t) (, t) (, t) I θ GJ θ I θ ρ = ρ = GJ θ t t µε ρ θ (, ) (, ) θ (, t) θ (, t) = = GJ t t I t θ t () GJ G = I ρ = ρ (3) όπου J=I δεδοµένου ότι η ράβδος έχει κυκλική διατοµή. Η () είναι η εξίσση κίνησης της ράβδου. Το άκρο = είναι πακτµένο, οπότε ισχύει η συνοριακή συνθήκη θ(, t ) = (4) Το άκρο = είναι ελεύθερο, οπότε ισχύει η συνοριακή συνθήκη 8
49 Οι σχέσεις (4), (5) είναι οι συνοριακές συνθήκες. θ (, t) = (5) Η χαρακτηριστική εξίσση και οι ιδιοσυχνότητες προκύπτουν από τη λύση του ιδιοπροβλήµατος. Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του που είναι η (). Για να λύσουµε την () χρησιµοποιούµε τη µέθοδο χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε ότι η () έχει µια µερική λύση της µορφής Με αντικατάσταση της (6) στην () έχουµε θ (, t) = X ( ) T ( t) (6) [ X ( ) T ( t) ] = [ X ( ) T ( t) ] X ( ) T ( t) = X ( ) T& ( t) t ( ) ( ) = & X ( ) T ( t) X T t (7) Επειδή η µεταβλητή του πρώτου µέλους είναι η απόσταση ενώ του δεύτερου ο χρόνος t, η µόνη περίπτση για να ισχύει η ισότητα είναι το κάθε µέλος να ισούται µε µια σταθερά η οποία αναµένεται να είναι αρνητική έτσι ώστε η προκύπτουσα διαφορική εξίσση ς προς να περιγράφει ταλάντση. Έτσι θέτουµε οπότε ( ) &( ) = = X ( ) T ( t) X T t X ( ) = X ( ) = X ( ) X ( ) = X ( ) X ( ) X ( ) + X ( ) = (8) (9) Επειδή η (6) είναι λύση της () ισχύουν και για αυτή οι συνοριακές συνθήκες δηλαδή Από την (6) έχουµε αν θέσουµε = έχουµε θ (, t) = () θ (, t) = () θ (, t) = X () T ( t) = X () T ( t) = X () X () = () Όµοια αν παραγγίσουµε την (6) ς προς και θέσουµε = έχουµε 9
50 θ (, t) = X ( ) T ( t) θ (, t) = X ( ) T ( t) = X ( ) T ( t) X ( ) = (3) Η εξίσση (9) ς γνστόν αντιστοιχεί σε ταλάντση και η γενική λύση της είναι X ( ) = a os + bsi (4) όπου τα α, b, θα προσδιοριστούν. Από την (4) για = έχουµε Άρα X () = a os + bsi X () = a = a a= (5) Παραγγίζοντας την (6) έχουµε X ( ) = bsi (6) X ( ) = b os X ( ) = b os = b os os = (7) Η εξίσση (7) που έχει ς άγνστη τη συχνότητα είναι η χαρακτηριστική εξίσση. Από τη λύση της βρίσκούµε τις ιδιοσυχνότητες. Είναι π os π = = ( ) = ( ) για =,,3, (8) όπου αντί για θέσαµε δεδοµένου ότι οι λύσεις της (8) είναι άπειρες. Από τις (3) και (8) έχουµε ( ) π os = = ( ) = Σύµφνα µε τη (6) οι ιδιοµορφές είναι της µορφής π G για =,,3, (9) ρ όπου η δίνεται από τη σχέση (9). Η σταθερά b όπς έχουµε δείξει βρίσκεται από τη σχέση X ( ) si = b () και την () και ισούται ρ I X m( ) X ( ) d= δ m () b= ρi ()
51 . Η άτρακτος του σχήµατος έχει κυκλική διατοµή, µήκος, πυκνότητα ρ, µέτρο διάτµησης G και πολικής ροπής I. Το ένα άκρο της είναι πακτµένο και το άλλο ελεύθερο. Στο ελεύθερο άκρο της ατράκτου ασκείται για µια στιγµή ροπή F t. Να προσδιοριστεί η ταλανττική συµπεριφορά της ατράκτου, δηλαδή α) Να γραφεί η εξίσση κίνησης της ατράκτου. β) Να γραφούν οι αρχικές και συνοριακές συνθήκες. γ) Να βρεθούν οι ιδιοσυχνότητες και ιδιοµορφές. δ) Να βρεθεί η λύση της εξίσσης κίνησης ατράκτου. z ρ, G, I F t O Λύση α) Στο πρώτο βήµα επίλυσης του προβλήµατος γράφουµε την εξίσση κίνησης του συστήµατος και τις αντίστοιχες αρχικές και συνοριακές συνθήκες. ( ) (, ) θ (, t) I = GJ t θ t ρ () Επειδή τα µεγέθη G, J είναι σταθερά η () γράφεται (, t) (, t) (, t) (, t) I θ GJ θ I θ ρ = ρ = GJ θ t t µε ρ θ (, ) (, ) = GJ t I t θ t θ (, t) θ (, t) = () t GJ G = I ρ = ρ (3) όπου J=I δεδοµένου ότι η ράβδος έχει κυκλική διατοµή. Η () είναι η εξίσση κίνησης της ράβδου. β) Γράφουµε τις εξισώσεις τν αρχικών συνθηκών. Στην αρχή της κίνησης, λόγ της ροπής F t η ράβδος θα έχει στραφεί. Έστ θ (,) είναι η γνία που έχει στραφεί ένα σηµείο της ατράκτου που απέχει απόσταση από την αρχή της ράβδου. Ισχύει Ft Ft θ (,) = θ (,) = (4) GJ GI
52 Για την απόδειξη της (4) δες στο σχόλιο που παρατίθεται στο τέλος της άσκησης. Η κίνηση της ράβδου ξεκινάει από την ηρεµία. Άρα η αρχική γνιακή ταχύτητα ενός σηµείου της ατράκτου που απέχει απόσταση από της ράβδου είναι µηδέν, δηλαδή Οι σχέσεις (4) και (5) είναι οι αρχικές συνθήκες. & θ (,) = (5) Στη συνέχεια γράφουµε τις συνοριακές συνθήκες. Το άκρο = είναι πακτµένο, οπότε ισχύει η συνοριακή συνθήκη θ(, t ) = (6) Το άκρο = είναι ελεύθερο, οπότε ισχύει η συνοριακή συνθήκη θ (, t) = (7) γ) Η κατάστρση του ιδιοπροβλήµατος αρχίζει από την αντίστοιχη οµογενή εξίσση του που είναι η (). Για να λύσουµε την () χρησιµοποιούµε τη µέθοδο χρισµού τν µεταβλητών. Συγκεκριµένα θερούµε ότι η () έχει µια µερική λύση της µορφής Με αντικατάσταση της (8) στη () έχουµε θ (, t) = X ( ) T ( t) ) (8) [ X ( ) T ( t) ] = [ X ( ) T ( t) ] X ( ) T ( t) = X ( ) T& ( t) t X ( ) T ( t) = & X ( ) T ( t) (9) Επειδή η µεταβλητή του πρώτου µέλους είναι η απόσταση ενώ του δεύτερου ο χρόνος t, η µόνη περίπτση για να ισχύει η ισότητα είναι το κάθε µέλος να ισούται µε µια σταθερά η οποία αναµένεται να είναι αρνητική έτσι ώστε η προκύπτουσα διαφορική εξίσση ς προς να περιγράφει ταλάντση. Έτσι θέτουµε οπότε ( ) &( ) = = X ( ) T ( t) X T t X ( ) = X ( ) = X ( ) X ( ) = X ( ) X ( ) () X ( ) + X ( ) = () Επειδή η (8) είναι λύση της () ισχύουν και για αυτή οι συνοριακές συνθήκες δηλαδή
53 θ (, t) = () θ (, t) = (3) Από την (8) αν θέσουµε = έχουµε θ (, t) = X () T ( t) = X () T ( t) = X () X () = (4) Όµοια αν παραγγίσουµε την (8) ς προς και θέσουµε = έχουµε θ (, t) = X ( ) T ( t) θ (, t) = X ( ) T ( t) = X ( ) T ( t) X ( ) = (5) Η εξίσση () ς γνστόν αντιστοιχεί σε ταλάντση και η γενική λύση της είναι X ( ) = a os + bsi (6) όπου τα α, b, θα προσδιοριστούν. Από την (6) για = έχουµε X () = a os + bsi X () = a = a a= (7) Άρα X ( ) = bsi (8) Παραγγίζοντας την (8) έχουµε X ( ) = b os X ( ) = b os = b os os = (9) Η εξίσση (9) που έχει ς άγνστη τη συχνότητα είναι η χαρακτηριστική εξίσση. Από τη λύση της βρίσκούµε τις ιδιοσυχνότητες. Είναι π os π = = ( ) = ( ) για =,,3, () όπου αντί για θέσαµε δεδοµένου ότι οι λύσεις της (9) είναι άπειρες. Από τις (3) και () έχουµε π os = = ( ) = ( ) π G για =,,3, () ρ 3
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
Εσωτερική Ροπή και Εσωτερική ύναµη
 Εστερική Ροπή και Εστερική ύναµη Η οµογενής ράβδος του σχήµατος έχει µάζα Μ=0,6 g και µήκος =, και στο ένα άκρο της είναι κολληµένο σώµα =0,g αµελητέν διαστάσεν, (σφαίρα). Το όλο σύστηµα µπορεί να στρέφεται
Εστερική Ροπή και Εστερική ύναµη Η οµογενής ράβδος του σχήµατος έχει µάζα Μ=0,6 g και µήκος =, και στο ένα άκρο της είναι κολληµένο σώµα =0,g αµελητέν διαστάσεν, (σφαίρα). Το όλο σύστηµα µπορεί να στρέφεται
ΚΕΦΑΛΑΙΑ 3,4. Συστήµατα ενός Βαθµού ελευθερίας. k Για E 0, η (1) ισχύει για κάθε x. Άρα επιτρεπτή περιοχή είναι όλος ο άξονας
 ΚΕΦΑΛΑΙΑ,4. Συστήµατα ενός Βαθµού ελευθερίας. Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα ' O για την απωστική δύναµη F, > και για ενέργεια Ε. (α) Είναι V και οι επιτρεπτές περιοχές της κίνησης
ΚΕΦΑΛΑΙΑ,4. Συστήµατα ενός Βαθµού ελευθερίας. Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα ' O για την απωστική δύναµη F, > και για ενέργεια Ε. (α) Είναι V και οι επιτρεπτές περιοχές της κίνησης
7. Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας
 7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
Ταλαντώσεις σώματος αλλά και συστήματος.
 σώματος αλλά και συστήματος. Μια καλοκαιρινή περιπλάνηση. Τα δυο σώµατα Α και Β µε ίσες µάζες g, ηρεµούν όπως στο σχήµα, ό- που το ελατήριο έχει σταθερά 00Ν/, ενώ το Α βρίσκεται σε ύψος h0,45 από το έδαφος.
σώματος αλλά και συστήματος. Μια καλοκαιρινή περιπλάνηση. Τα δυο σώµατα Α και Β µε ίσες µάζες g, ηρεµούν όπως στο σχήµα, ό- που το ελατήριο έχει σταθερά 00Ν/, ενώ το Α βρίσκεται σε ύψος h0,45 από το έδαφος.
Ποια μπορεί να είναι η κίνηση μετά την κρούση;
 Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ
 ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ Οι σηµαντικότερες αντιπρόσποι της κατηγορίας αυτής τν δυνάµεν είναι οι δυνάµεις βαρύτητος και οι ηλεκτροστατικές δυνάµεις, που είναι ανάλογες του αντιστρόφου τετραγώνου της
ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ Οι σηµαντικότερες αντιπρόσποι της κατηγορίας αυτής τν δυνάµεν είναι οι δυνάµεις βαρύτητος και οι ηλεκτροστατικές δυνάµεις, που είναι ανάλογες του αντιστρόφου τετραγώνου της
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση
 Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
2.1 Παραμορφώσεις ανομοιόμορφων ράβδων
 ΑΞΟΝΙΚΗ ΦΟΡΤΙΣΗ 9 Αξονική φόρτιση. Παραμορφώσεις ανομοιόμορφων ράβδων. Ελαστική ράβδος ΑΒ μήκους, Γ B μέτρου ελαστικότητας Ε και / συντελεστή θερμικής διαστολής α, είναι πακτωμένη στα σημεία Α και Β και
ΑΞΟΝΙΚΗ ΦΟΡΤΙΣΗ 9 Αξονική φόρτιση. Παραμορφώσεις ανομοιόμορφων ράβδων. Ελαστική ράβδος ΑΒ μήκους, Γ B μέτρου ελαστικότητας Ε και / συντελεστή θερμικής διαστολής α, είναι πακτωμένη στα σημεία Α και Β και
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
Οι τροχαλίες θεωρούνται κυλινδρικά σώµατα µε ροπή αδράνειας ως προς τον άξονα περιστροφής τους I. = mr και g=10m/s 2.
 Γιο Γιο σε Τροχαλία και µια Ολίσθηση που µετατρέπεται σε Κύλιση Η µεγάλη τροχαλία του διπλανού σχήµατος έχει µάζα Μ=4kg, ακτίνα R=0, και κρέµεται από σταθερό σηµείο. Η µικρή τροχαλία έχει µάζα =kg και
Γιο Γιο σε Τροχαλία και µια Ολίσθηση που µετατρέπεται σε Κύλιση Η µεγάλη τροχαλία του διπλανού σχήµατος έχει µάζα Μ=4kg, ακτίνα R=0, και κρέµεται από σταθερό σηµείο. Η µικρή τροχαλία έχει µάζα =kg και
Μάθηµα 1. Κεφάλαιο 1o: Συστήµατα. γ R παριστάνει ευθεία και καλείται γραµµική εξίσωση µε δύο αγνώστους.
 Μάθηµα 1 Κεφάλαιο 1o: Συστήµατα Θεµατικές Ενότητες: A. Συστήµατα Γραµµικών Εξισώσεων B. Συστήµατα 3x3 Α. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Ορισµοί Κάθε εξίσωση της µορφής α x+β =γ, µε α, β, γ R παριστάνει
Μάθηµα 1 Κεφάλαιο 1o: Συστήµατα Θεµατικές Ενότητες: A. Συστήµατα Γραµµικών Εξισώσεων B. Συστήµατα 3x3 Α. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Ορισµοί Κάθε εξίσωση της µορφής α x+β =γ, µε α, β, γ R παριστάνει
e-mail@p-theodoropoulos.gr
 Ασκήσεις Μαθηµατικών Κατεύθυνσης Γ Λυκείου Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος Μαθηµατικών e-mail@p-theodoropoulos.gr Στην εργασία αυτή ξεχωρίζουµε και µελετάµε µερικές περιπτώσεις ασκήσεων
Ασκήσεις Μαθηµατικών Κατεύθυνσης Γ Λυκείου Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος Μαθηµατικών e-mail@p-theodoropoulos.gr Στην εργασία αυτή ξεχωρίζουµε και µελετάµε µερικές περιπτώσεις ασκήσεων
Σχολικός Σύµβουλος ΠΕ03
 Ασκήσεις Μαθηµατικών Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου ρ. Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Στην εργασία αυτή ξεχωρίζουµε και µελετάµε µερικές περιπτώσεις
Ασκήσεις Μαθηµατικών Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου ρ. Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Στην εργασία αυτή ξεχωρίζουµε και µελετάµε µερικές περιπτώσεις
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Προτεινόμενες Λύσεις Πρόβλημα-1 (15 μονάδες) Μια
7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Προτεινόμενες Λύσεις Πρόβλημα-1 (15 μονάδες) Μια
A2. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ
 A. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ d df() = f() = f (), = d d.κλίση ευθείας.μεταβολές 3.(Οριακός) ρυθµός µεταβολής ή παράγωγος 4.Παράγωγοι βασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία
A. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ d df() = f() = f (), = d d.κλίση ευθείας.μεταβολές 3.(Οριακός) ρυθµός µεταβολής ή παράγωγος 4.Παράγωγοι βασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία
ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 93
 ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 93 ΚΕΦΑΛΑΙΟ 5 ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 5.. Εισαγωγή Η παρουσία εξωτερικών διεγέρσεων σε ένα σύστηµα πολλών Β.Ε. δηµιουργεί σ'
ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 93 ΚΕΦΑΛΑΙΟ 5 ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 5.. Εισαγωγή Η παρουσία εξωτερικών διεγέρσεων σε ένα σύστηµα πολλών Β.Ε. δηµιουργεί σ'
k c (1) F ελ f ( t) F απ http://www.didefth.gr/mathimata/ 1
 Την παρακάτω ανάλυση στο θέµα των Εξαναγκασµένων Ταλαντώσεων έκαναν οι : ρ. Μιχάλης Αθανασίου ρ. Απόστολος Κουιρουκίδης Φυσικοί, Επιστηµονικοί Συνεργάτες ΤΕΙ Σερρών, στα Τµήµατα Πληροφορικής -Επικοινωνιών
Την παρακάτω ανάλυση στο θέµα των Εξαναγκασµένων Ταλαντώσεων έκαναν οι : ρ. Μιχάλης Αθανασίου ρ. Απόστολος Κουιρουκίδης Φυσικοί, Επιστηµονικοί Συνεργάτες ΤΕΙ Σερρών, στα Τµήµατα Πληροφορικής -Επικοινωνιών
ίσκος µάζας Μ = 2Kg ισορροπεί σε κατακόρυφο ελατήριο k = 100 N/m, του οποίου το κάτω άκρο είναι στερεωµένο στο έδαφος. Από ύψος h = 60 cm πάνω από το
 ΦΥΣΙΚΗ ΆΣΚΗΣΗ - ΜΕΛΕΤΗ: ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ ΣΕ ΚΑΤΑ- ΚΟΡΥΦΟ ΕΛΑΤΗΡΙΟ ίσκος µάζας Μ = Kg ισορροπεί σε κατακόρυφο ελατήριο k = 00 N/m, του οποίου το κάτω άκρο είναι στερεωµένο στο έδαφος. Από ύψος
ΦΥΣΙΚΗ ΆΣΚΗΣΗ - ΜΕΛΕΤΗ: ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ ΣΕ ΚΑΤΑ- ΚΟΡΥΦΟ ΕΛΑΤΗΡΙΟ ίσκος µάζας Μ = Kg ισορροπεί σε κατακόρυφο ελατήριο k = 00 N/m, του οποίου το κάτω άκρο είναι στερεωµένο στο έδαφος. Από ύψος
8. Λύση απλών διαφορικών εξισώσεων και εξισώσεων κίνησης
 38 Κ Χριστοδολίδης: Μαθηµατικό Σµπλήρµα για τα Εισαγγικά Μαθήµατα Φσικής 8 Λύση απλών διαφορικών εξισώσεν εξισώσεν κίνησης 8 Εξισώσεις κίνησης πο οδηγούν σε διαφορικές εξισώσεις χριζόµενν µεταβλητών Η
38 Κ Χριστοδολίδης: Μαθηµατικό Σµπλήρµα για τα Εισαγγικά Μαθήµατα Φσικής 8 Λύση απλών διαφορικών εξισώσεν εξισώσεν κίνησης 8 Εξισώσεις κίνησης πο οδηγούν σε διαφορικές εξισώσεις χριζόµενν µεταβλητών Η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
Κεφάλαιο 14 Ταλαντώσεις. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 14 Ταλαντώσεις Ταλαντώσεις Ελατηρίου Απλή αρµονική κίνηση Ενέργεια απλού αρµονικού ταλαντωτή Σχέση απλού αρµονικού ταλαντωτή και κυκλικής κίνησης Το απλό εκκρεµές Περιεχόµενα 14 Το φυσικό εκκρεµές
Κεφάλαιο 14 Ταλαντώσεις Ταλαντώσεις Ελατηρίου Απλή αρµονική κίνηση Ενέργεια απλού αρµονικού ταλαντωτή Σχέση απλού αρµονικού ταλαντωτή και κυκλικής κίνησης Το απλό εκκρεµές Περιεχόµενα 14 Το φυσικό εκκρεµές
N/m, k 2 = k 4 = 6 N/m και m=2 kgr. (α) k 1 m k 3 k 4. (β) k 12 m k 34. k 12 = k 1 +k 2 = 3+6 = 9 N/m (1) k k = = = = 2 N/m (2) (3) k 2.
 ΚΕΦΑΛΑΙΟ ΤΑΛΑΝΤΩΣΗ ΥΝΑΜΙΚΏΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΕΝΑ ΒΑΘΜΟ ΕΛΕΥΘΕΡΙΑΣ. Ελεύθερη ταλάντωση χωρίς απόσβεση. Να βρεθεί η ιδιοσυχνότητα του συστήµατος στο σχήµα (α). ίνεται 3 3 N/m, 4 6 N/m και m gr. (α) m 3 4 (β)
ΚΕΦΑΛΑΙΟ ΤΑΛΑΝΤΩΣΗ ΥΝΑΜΙΚΏΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΕΝΑ ΒΑΘΜΟ ΕΛΕΥΘΕΡΙΑΣ. Ελεύθερη ταλάντωση χωρίς απόσβεση. Να βρεθεί η ιδιοσυχνότητα του συστήµατος στο σχήµα (α). ίνεται 3 3 N/m, 4 6 N/m και m gr. (α) m 3 4 (β)
ιαγωνισµός Ξανθόπουλου 2012 Μονάδες 3
 Κατακόρυφο ελατήριο σταθεράς k, έχει το άνω άκρο του σταθερά συνδεδεµένο, ενώ στο κάτω άκρο του έχει αναρτηθεί σώµα µάζας m kg. Το σώµα ισορροπεί στη θέση ισορροπίας και η επιµήκυνση του ελατηρίου είναι
Κατακόρυφο ελατήριο σταθεράς k, έχει το άνω άκρο του σταθερά συνδεδεµένο, ενώ στο κάτω άκρο του έχει αναρτηθεί σώµα µάζας m kg. Το σώµα ισορροπεί στη θέση ισορροπίας και η επιµήκυνση του ελατηρίου είναι
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
Συνταγολόγιο Φυσικής Μηχανική Στερεού Σώµατος. Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός.
 Συνταγολόγιο Φυσικής Μηχανική Στερεού Σώµατος Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός http://perifysikhs.wordpress.com 1 Κίνηση Ράβδου σε κατακόρυφο επίπεδο Εστω µια οµογενής ϱάβδος ΟΑ µάζας Μ
Συνταγολόγιο Φυσικής Μηχανική Στερεού Σώµατος Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός http://perifysikhs.wordpress.com 1 Κίνηση Ράβδου σε κατακόρυφο επίπεδο Εστω µια οµογενής ϱάβδος ΟΑ µάζας Μ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Προτεινόμενες Λύσεις Πρόβλημα - ( μονάδες) Ένα όχημα, μαζί με ένα κανόνι που είναι ακλόνητο πάνω σε αυτό,
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Προτεινόμενες Λύσεις Πρόβλημα - ( μονάδες) Ένα όχημα, μαζί με ένα κανόνι που είναι ακλόνητο πάνω σε αυτό,
Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ
 8 Παραβολή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισµός Παραβολή είναι ο γεωµετρικός τόπος των σηµείων Μ του επιπέδου τα οποία ισαπέχουν από µια σταθερή ευθεία (δ) που λέγεται διευθετούσα της παραβολής και από
8 Παραβολή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισµός Παραβολή είναι ο γεωµετρικός τόπος των σηµείων Μ του επιπέδου τα οποία ισαπέχουν από µια σταθερή ευθεία (δ) που λέγεται διευθετούσα της παραβολής και από
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55
 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
3.3 ΑΛΓΕΒΡΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΟΥ
 . ΑΛΓΕΒΡΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΘΕΩΡΙΑ. Μέθοδοι επίλυσης : Οι βασικές µέθοδοι αλγεβρικής επίλυσης ενός γραµµικού συστήµατος δύο εξισώσεων µε δύο αγνώστους είναι δύο η µέθοδος της αντικατάστασης
. ΑΛΓΕΒΡΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΘΕΩΡΙΑ. Μέθοδοι επίλυσης : Οι βασικές µέθοδοι αλγεβρικής επίλυσης ενός γραµµικού συστήµατος δύο εξισώσεων µε δύο αγνώστους είναι δύο η µέθοδος της αντικατάστασης
, g 10 m / s, / 2, / 2, Απάντηση
 Φυσική κατεύθυνσης Στη διάταξη του διπλανού σχήματος η ράβδος Σ 1 είναι ομογενής, έχει μάζα 1 =0,3kg, μήκος (ΑΓ) = l = 0,8 και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα κάθετο
Φυσική κατεύθυνσης Στη διάταξη του διπλανού σχήματος η ράβδος Σ 1 είναι ομογενής, έχει μάζα 1 =0,3kg, μήκος (ΑΓ) = l = 0,8 και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα κάθετο
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
, όπου οι σταθερές προσδιορίζονται από τις αρχικές συνθήκες.
 Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Απενεργοποιήστε τα κινητά σας τηλέφωνα!!! Παρακαλώ
7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Απενεργοποιήστε τα κινητά σας τηλέφωνα!!! Παρακαλώ
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ.
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ. Θα μελετήσουμε τώρα συστήματα που διεγείρονται σε ταλάντωση μέσω εξωτερικής ς που μπορεί να είναι (όπως θα δούμε παρακάτω) σταθερή, μεταβλητού
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ. Θα μελετήσουμε τώρα συστήματα που διεγείρονται σε ταλάντωση μέσω εξωτερικής ς που μπορεί να είναι (όπως θα δούμε παρακάτω) σταθερή, μεταβλητού
Κ. Ι. ΠΑΠΑΧΡΗΣΤΟΥ. Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ. Ιδιότητες & Εφαρµογές
 Κ Ι ΠΑΠΑΧΡΗΣΤΟΥ Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ Ιδιότητες & Εφαρµογές ΠΕΙΡΑΙΑΣ 2013 ΟΡΙΖΟΥΣΕΣ Έστω 2 2 πίνακας: a b A= c d Όπως γνωρίζουµε, η ορίζουσα του Α είναι ο αριθµός a
Κ Ι ΠΑΠΑΧΡΗΣΤΟΥ Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ Ιδιότητες & Εφαρµογές ΠΕΙΡΑΙΑΣ 2013 ΟΡΙΖΟΥΣΕΣ Έστω 2 2 πίνακας: a b A= c d Όπως γνωρίζουµε, η ορίζουσα του Α είναι ο αριθµός a
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
Υπολογισμός της σταθεράς ελατηρίου
 Εργαστηριακή Άσκηση 6 Υπολογισμός της σταθεράς ελατηρίου Βαρσάμης Χρήστος Στόχος: Υπολογισμός της σταθεράς ελατηρίου, k. Πειραματική διάταξη: Κατακόρυφο ελατήριο, σειρά πλακιδίων μάζας m. Μέθοδος: α) Εφαρμογή
Εργαστηριακή Άσκηση 6 Υπολογισμός της σταθεράς ελατηρίου Βαρσάμης Χρήστος Στόχος: Υπολογισμός της σταθεράς ελατηρίου, k. Πειραματική διάταξη: Κατακόρυφο ελατήριο, σειρά πλακιδίων μάζας m. Μέθοδος: α) Εφαρμογή
Δημήτρης Αγαλόπουλος Σελίδα 1
 ΛΥΣΗ Δ1. Η ράβδος διαγράφει γωνία μέχρι να συγκρουστεί με το σώμα (Σ 1 ). Τη χρονική στιγμή t=0 βρίσκεται στην οριζόντια θέση (Α), την χρονική στιγμή t 1 γίνεται κατακόρυφη θέση (Γ) και συγκρούεται με
ΛΥΣΗ Δ1. Η ράβδος διαγράφει γωνία μέχρι να συγκρουστεί με το σώμα (Σ 1 ). Τη χρονική στιγμή t=0 βρίσκεται στην οριζόντια θέση (Α), την χρονική στιγμή t 1 γίνεται κατακόρυφη θέση (Γ) και συγκρούεται με
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
Φυσική Ο.Π. Γ Λυκείου
 Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Δυναμική Μηχανών I. Δυναμικά Μοντέλα Συνεχούς Μέσου
 Δυναμική Μηχανών I 8 1 Δυναμικά Μοντέλα Συνεχούς Μέσου 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Μοντελοποίηση
Δυναμική Μηχανών I 8 1 Δυναμικά Μοντέλα Συνεχούς Μέσου 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Μοντελοποίηση
x(t) 2 = e 2 t = e 2t, t > 0
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 216-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Σήµατα και Συστήµατα Ασκηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 216-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Σήµατα και Συστήµατα Ασκηση
Εξίσωση Κίνησης Μονοβάθμιου Συστήματος (συνέχεια)
 Εξίσωση Κίνησης Μονοβάθμιου Συστήματος (συνέχεια) Εξίσωση Κίνησης Μονοβάθμιου Συστήματος: Επιρροή Μόνιμου Φορτίου Βαρύτητας Δ03-2 Μέχρι τώρα στη διατύπωση της εξίσωσης κίνησης δεν έχει ληφθεί υπόψη το
Εξίσωση Κίνησης Μονοβάθμιου Συστήματος (συνέχεια) Εξίσωση Κίνησης Μονοβάθμιου Συστήματος: Επιρροή Μόνιμου Φορτίου Βαρύτητας Δ03-2 Μέχρι τώρα στη διατύπωση της εξίσωσης κίνησης δεν έχει ληφθεί υπόψη το
5.15 Εφαρμογές της ομογενούς Δ.Ε. 2ης τάξης με σταθερούς συντελεστές
 4 ΚΕΦΑΛΑΙΟ 5 α) y -y +y e x /x 5 Aπ. u(/)x -3 e x β) y +ysecx Aπ. u[csx]ln csx +xsinx γ) y +4ysin x Aπ. u[cs (x)+]/ ) Γενικεύοντας την παραπάν πορεία για n>, δείξτε ότι τα v i (x) ικανοποιούν το σύστημα
4 ΚΕΦΑΛΑΙΟ 5 α) y -y +y e x /x 5 Aπ. u(/)x -3 e x β) y +ysecx Aπ. u[csx]ln csx +xsinx γ) y +4ysin x Aπ. u[cs (x)+]/ ) Γενικεύοντας την παραπάν πορεία για n>, δείξτε ότι τα v i (x) ικανοποιούν το σύστημα
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 2ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73
 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΦΥΣ. 211 Τελική Εξέταση 10-Μάη-2014
 ΦΥΣ. 211 Τελική Εξέταση 10-Μάη-2014 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
ΦΥΣ. 211 Τελική Εξέταση 10-Μάη-2014 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
Ελεύθερη Ταλάντωση Μονοβάθμιου Συστήματος
 Ελεύθερη Ταλάντωση Μονοβάθμιου Συστήματος Εισαγωγή Ελεύθερη Ταλάντωση Μονοβάθμιου Συστήματος: Δ05-2 Μία κατασκευή λέγεται ότι εκτελεί ελεύθερη ταλάντωση όταν μετακινηθεί από τη θέση στατικής ισορροπίας
Ελεύθερη Ταλάντωση Μονοβάθμιου Συστήματος Εισαγωγή Ελεύθερη Ταλάντωση Μονοβάθμιου Συστήματος: Δ05-2 Μία κατασκευή λέγεται ότι εκτελεί ελεύθερη ταλάντωση όταν μετακινηθεί από τη θέση στατικής ισορροπίας
ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
Γιο Γιο σε Τροχαλία και μια Ολίσθηση που μετατρέπεται σε Κύλιση
 Γιο Γιο σε Τροχαλία και μια Ολίσθηση που μετατρέπεται σε Κύλιση Απάντηση α) Επειδή το νήµα δεν ολισθαίνει στις τροχαλίες και παραµένει τεντµένο, όλα τα σηµεία του έχουν την ίδια ταχύτητα. Το σηµείο Α συµµετέχει
Γιο Γιο σε Τροχαλία και μια Ολίσθηση που μετατρέπεται σε Κύλιση Απάντηση α) Επειδή το νήµα δεν ολισθαίνει στις τροχαλίες και παραµένει τεντµένο, όλα τα σηµεία του έχουν την ίδια ταχύτητα. Το σηµείο Α συµµετέχει
ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2017
 ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2017 ΘΕΜΑ Α Α1. Δ Α2. Γ Α3. Α Α4. Δ Α5. α) Λ β) Σ γ) Σ δ) Σ ε) Λ ΘΕΜΑ Β Β1. α) Σωστή η ii. β) Στη θέση ισορροπίας (Θ.Ι.) του σώματος ισχύει η συνθήκη ισορροπίας: ΣF=0
ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2017 ΘΕΜΑ Α Α1. Δ Α2. Γ Α3. Α Α4. Δ Α5. α) Λ β) Σ γ) Σ δ) Σ ε) Λ ΘΕΜΑ Β Β1. α) Σωστή η ii. β) Στη θέση ισορροπίας (Θ.Ι.) του σώματος ισχύει η συνθήκη ισορροπίας: ΣF=0
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
m i r i z i Αν είναι x, y, z τα µοναδιαία διανύσµατα των τριών αξόνων, τότε τα διανύσµατα ω r και r i µπορούν αντίστοιχα να γραφούν: r r x i y i ω x
 ΓΕΝΙΚΗ ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΤΡΟΦΟΡΜΗ, ΤΑΝΥΣΤΗΣ Α ΡΑΝΕΙΑΣ, ΚΥΡΙΟΙ ΑΞΟΝΕΣ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ Έστ ότι το στερεό του σχήµατος στρέφεται µε γνιακή ταχύτητα (,, γύρ από άξονα που διέρχεται από σταθερό σηµείο Ο. Αν
ΓΕΝΙΚΗ ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΤΡΟΦΟΡΜΗ, ΤΑΝΥΣΤΗΣ Α ΡΑΝΕΙΑΣ, ΚΥΡΙΟΙ ΑΞΟΝΕΣ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ Έστ ότι το στερεό του σχήµατος στρέφεται µε γνιακή ταχύτητα (,, γύρ από άξονα που διέρχεται από σταθερό σηµείο Ο. Αν
δ) µειώνεται το µήκος κύµατός της (Μονάδες 5)
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 30/1/11 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 30/1/11 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση 19-05-08 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Συµπαγής κύλινδρος µάζας Μ συνδεδεµένος σε ελατήριο σταθεράς k = 3. N / και αµελητέας µάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Συµπαγής κύλινδρος µάζας Μ συνδεδεµένος σε ελατήριο σταθεράς k = 3. N / και αµελητέας µάζας, κυλίεται, χωρίς να
ΦΥΣ. 211 Τελική Εξέταση 10-Μάη-2014
 ΦΥΣ. 211 Τελική Εξέταση 10-Μάη-2014 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
ΦΥΣ. 211 Τελική Εξέταση 10-Μάη-2014 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
Μεταξύ της τάσης και της ελαστικής παραμόρφωσης ενός σώματος υπάρχει μια απλή σχέση, ο νόμος του Hooke:
 Άσκηση Μ Σπειροειδές ελατήριο Νόμος του Hooe και εξίσωση δυνάμεων Μεταξύ της τάσης και της ελαστικής παραμόρφωσης ενός σώματος υπάρχει μια απλή σχέση, ο νόμος του Hooe: Οι ελαστικές τάσεις και οι παραμορφώσεις
Άσκηση Μ Σπειροειδές ελατήριο Νόμος του Hooe και εξίσωση δυνάμεων Μεταξύ της τάσης και της ελαστικής παραμόρφωσης ενός σώματος υπάρχει μια απλή σχέση, ο νόμος του Hooe: Οι ελαστικές τάσεις και οι παραμορφώσεις
ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Κεφάλαιο ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Στη διαδικασία σχεδιασμού των Συστημάτων Αυτομάτου Ελέγχου, η απαραίτητη και η πρώτη εργασία που έχουμε να κάνουμε, είναι να
Κεφάλαιο ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Στη διαδικασία σχεδιασμού των Συστημάτων Αυτομάτου Ελέγχου, η απαραίτητη και η πρώτη εργασία που έχουμε να κάνουμε, είναι να
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 10 ΑΠΡΙΛΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
 ΦΥΣΙΗ Γ ΛΥΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΩΝ ΣΠΟΥΔΩΝ 10 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΗ Γ ΛΥΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΩΝ ΣΠΟΥΔΩΝ 10 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
5. Στερεό σώµα. (5.1) Το µέτρο της ταχύτητας είναι ίσο µε υ = ω a, όπου a είναι η απόσταση του σωµατιδίου από τον άξονα περιστροφής.
 5 Στερεό σώµα Βιβλιογραφία C Kttel, W D Knght, A Ruderman, A C Helmholz και B J oyer, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 998) Κεφ 8 R Spegel, Θερητική Μηχανική (Εκδόσεις ΕΣΠΙ, Αθήνα, 985) Κεφ 9 5
5 Στερεό σώµα Βιβλιογραφία C Kttel, W D Knght, A Ruderman, A C Helmholz και B J oyer, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 998) Κεφ 8 R Spegel, Θερητική Μηχανική (Εκδόσεις ΕΣΠΙ, Αθήνα, 985) Κεφ 9 5
ΕΝΟΣ ΒΑΘΜΟΥ ΕΛΕΥΘΕΡΙΑΣ
 ΣΥΣΤΗΜΑ ΕΝΟΣ ΒΑΘΜΟΥ ΕΛΕΥΘΕΡΙΑΣ 11 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΝΟΣ ΒΑΘΜΟΥ ΕΛΕΥΘΕΡΙΑΣ.1. Ελεύθερη ταλάντση συστήματος ενός βαθμού ελευθερίας Φυσική συχνότητα και απόκριση Ο αρμονικός ταλανττής (βλ. σχήμα.1.α) είναι
ΣΥΣΤΗΜΑ ΕΝΟΣ ΒΑΘΜΟΥ ΕΛΕΥΘΕΡΙΑΣ 11 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΝΟΣ ΒΑΘΜΟΥ ΕΛΕΥΘΕΡΙΑΣ.1. Ελεύθερη ταλάντση συστήματος ενός βαθμού ελευθερίας Φυσική συχνότητα και απόκριση Ο αρμονικός ταλανττής (βλ. σχήμα.1.α) είναι
ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗ. Εφαπτοµένη ευθεία
 ΜΑΘΗΜΑ 5.. ΠΑΡΑΓΩΓΙΣΙΜΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗ Εφαπτοµένη ευθεία Παράγωγος βασικών συναρτήσεων ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ Αθροίσµατος γινοµένου - πηλίκου Θεωρία Σχόλια Μέθοδοι Ασκήσεις ΘΕΩΡΙΑ. Εξίσωση
ΜΑΘΗΜΑ 5.. ΠΑΡΑΓΩΓΙΣΙΜΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗ Εφαπτοµένη ευθεία Παράγωγος βασικών συναρτήσεων ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ Αθροίσµατος γινοµένου - πηλίκου Θεωρία Σχόλια Μέθοδοι Ασκήσεις ΘΕΩΡΙΑ. Εξίσωση
Εξαναγκασμένη Ταλάντωση. Τυχαία Φόρτιση (Ολοκλήρωμα Duhamel)
 Εξαναγκασμένη Ταλάντωση Τυχαία Φόρτιση (Ολοκλήρωμα Duhamel) Εξαναγκασμένη Ταλάντωση: Τυχαία Φόρτιση: Απόκριση σε Τυχαία Φόρτιση: Βασική Ιδέα Δ10-2 Το πρόβλημα της κίνησης μονοβάθμιου συστήματος σε τυχαία
Εξαναγκασμένη Ταλάντωση Τυχαία Φόρτιση (Ολοκλήρωμα Duhamel) Εξαναγκασμένη Ταλάντωση: Τυχαία Φόρτιση: Απόκριση σε Τυχαία Φόρτιση: Βασική Ιδέα Δ10-2 Το πρόβλημα της κίνησης μονοβάθμιου συστήματος σε τυχαία
Μέθοδος των Δυνάμεων
 Μέθοδος των Δυνάμεων Εισαγωγή Μέθοδος των Δυνάμεων: Δ07-2 Η Μέθοδος των Δυνάμεων ή Μέθοδος Ευκαμψίας είναι μία μέθοδος για την ανάλυση γραμμικά ελαστικών υπερστατικών φορέων. Ανκαιημέθοδοςμπορείναεφαρμοστείσεπολλάείδηφορέων
Μέθοδος των Δυνάμεων Εισαγωγή Μέθοδος των Δυνάμεων: Δ07-2 Η Μέθοδος των Δυνάμεων ή Μέθοδος Ευκαμψίας είναι μία μέθοδος για την ανάλυση γραμμικά ελαστικών υπερστατικών φορέων. Ανκαιημέθοδοςμπορείναεφαρμοστείσεπολλάείδηφορέων
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ 3 Ο : ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ η Κατηγορία : Ο Κύκλος και τα στοιχεία
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ 3 Ο : ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ η Κατηγορία : Ο Κύκλος και τα στοιχεία
Η διάταξη εξαναγκασμένων ταλαντώσεων του σχολικού βιβλίου
 Η ιάταξη εξαναγκασμένν ταλαντώσεν του σχολικού βιβλίου Εισαγγή Κατά την μαθηματική μελέτη της εξαναγκασμένης ταλάντσης με αρμονικό ιεγέρτη θερούμε ένα σώμα στο οποίο, εκτός από την ύναμη επαναφοράς Dx
Η ιάταξη εξαναγκασμένν ταλαντώσεν του σχολικού βιβλίου Εισαγγή Κατά την μαθηματική μελέτη της εξαναγκασμένης ταλάντσης με αρμονικό ιεγέρτη θερούμε ένα σώμα στο οποίο, εκτός από την ύναμη επαναφοράς Dx
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 4 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε µε σαφήνεια και συντοµία. Η ορθή πλήρης απάντηση θέµατος εκτιµάται περισσότερο από τη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 4 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε µε σαφήνεια και συντοµία. Η ορθή πλήρης απάντηση θέµατος εκτιµάται περισσότερο από τη
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2016 Β ΦΑΣΗ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 06 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Απριλίου 06 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από -4 να γράψετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 06 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Απριλίου 06 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από -4 να γράψετε
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ ÅÐÉËÏÃÇ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 017 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Μ Τετάρτη 1 Απριλίου 017 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 017 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Μ Τετάρτη 1 Απριλίου 017 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
4 η Εργασία (Ηµεροµηνία Παράδοσης: 10-5-2004)
 Άσκηση (Μονάδες ) 4 η Εργασία (Ηµεροµηνία Παράδοσης: -5-4) Α) Αστροναύτης µάζας 6 Κg βρίσκεται µέσα σε διαστηµόπλοιο που κινείται µε σταθερή ταχύτητα προς τον Άρη. Σε κάποιο σηµείο του ταξιδιού βρίσκεται
Άσκηση (Μονάδες ) 4 η Εργασία (Ηµεροµηνία Παράδοσης: -5-4) Α) Αστροναύτης µάζας 6 Κg βρίσκεται µέσα σε διαστηµόπλοιο που κινείται µε σταθερή ταχύτητα προς τον Άρη. Σε κάποιο σηµείο του ταξιδιού βρίσκεται
ΜΕΛΕΤΗ ΑΠΟΚΡΙΣΗΣ ΔΟΚΑΡΙΟΥ TIMOSHENKO
 ΜΕΛΕΤΗ ΑΠΟΚΡΙΣΗΣ ΟΚΑΡΙΟΥ TIOSHENKO ILE::\NTU\y Documets\ΤΑΛΑΝΤΩΣΕΙΣ ΓΑΣΤΡΑΣ\SHIP IBRTIONS 4 5\οκάρι Timosheko Uit C\Uit C Timosheko.doc σελίδα /4 ΜΕΛΕΤΗ ΑΠΟΚΡΙΣΗΣ ΟΚΑΡΙΟΥ TIOSHENKO Στην ενότητα αυτή μελετάται
ΜΕΛΕΤΗ ΑΠΟΚΡΙΣΗΣ ΟΚΑΡΙΟΥ TIOSHENKO ILE::\NTU\y Documets\ΤΑΛΑΝΤΩΣΕΙΣ ΓΑΣΤΡΑΣ\SHIP IBRTIONS 4 5\οκάρι Timosheko Uit C\Uit C Timosheko.doc σελίδα /4 ΜΕΛΕΤΗ ΑΠΟΚΡΙΣΗΣ ΟΚΑΡΙΟΥ TIOSHENKO Στην ενότητα αυτή μελετάται
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
Όταν το ελατήριο έχει μάζα
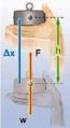 Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
Επαναληπτικη άσκηση στην Μηχανική Στερεού-Κρούσεις
 Επαναληπτικη άσκηση στην Μηχανική Στερεού-Κρούσεις Σφαίρα Σ 2 µάζας m 2 =m=2kg ηρεµεί στερεωµένη στο αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m το άλλο άκρο του οποίου είναι στερεωµένο
Επαναληπτικη άσκηση στην Μηχανική Στερεού-Κρούσεις Σφαίρα Σ 2 µάζας m 2 =m=2kg ηρεµεί στερεωµένη στο αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m το άλλο άκρο του οποίου είναι στερεωµένο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: ) Είναι πολύ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: ) Είναι πολύ
Ζεύγος δυνάµεων Κύλιση - Κρούση
 Ζεύγος δυνάµεων Κύλιση - Κρούση Οµογενής σφαίρα µάζας Μ=2kg και ακτίνας R=0,5m ηρεµεί πάνω σε λείο οριζόντιο δάπεδο, µε την κατακόρυφη διάµετρό της να απέχει απόσταση s=60,5m από λείο κατακόρυφο τοίχωµα.
Ζεύγος δυνάµεων Κύλιση - Κρούση Οµογενής σφαίρα µάζας Μ=2kg και ακτίνας R=0,5m ηρεµεί πάνω σε λείο οριζόντιο δάπεδο, µε την κατακόρυφη διάµετρό της να απέχει απόσταση s=60,5m από λείο κατακόρυφο τοίχωµα.
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 2 o ΔΙΑΓΩΝΙΣΜΑ ΔΕΚΕΜΒΡΙΟΣ 2018: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΤΑΛΑΝΤΩΣΕΙΣ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Αα. (α) Αα. (γ) Α3α. (α) Α4α. (γ) Αβ. (γ) Αβ. (δ) Α3β. (β) Α4β. (β) Α0. α.λ β.λ γ.σ δ.λ ε.σ ΘΕΜΑ B
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΤΑΛΑΝΤΩΣΕΙΣ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Αα. (α) Αα. (γ) Α3α. (α) Α4α. (γ) Αβ. (γ) Αβ. (δ) Α3β. (β) Α4β. (β) Α0. α.λ β.λ γ.σ δ.λ ε.σ ΘΕΜΑ B
ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΓΕΝΙΚΗ ΜΟΡΦΗ
 ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΓΕΝΙΚΗ ΜΟΡΦΗ Κάθε εξίσωση της µορφής α + β = γ όπου α + β 0 ( α, β όχι συγχρόνως 0) παριστάνει ευθεία. (Η εξίσωση λέγεται : ΓΡΑΜΜΙΚΗ) ΕΙ ΙΚΑ γ Αν α = 0 και β 0έχουµε =. ηλαδή µορφή = c.
ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΓΕΝΙΚΗ ΜΟΡΦΗ Κάθε εξίσωση της µορφής α + β = γ όπου α + β 0 ( α, β όχι συγχρόνως 0) παριστάνει ευθεία. (Η εξίσωση λέγεται : ΓΡΑΜΜΙΚΗ) ΕΙ ΙΚΑ γ Αν α = 0 και β 0έχουµε =. ηλαδή µορφή = c.
ΦΥΣ η ΠΡΟΟΔΟΣ 2-Απρίλη-2016
 ΦΥΣ. 211 2 η ΠΡΟΟΔΟΣ 2-Απρίλη-2016 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
ΦΥΣ. 211 2 η ΠΡΟΟΔΟΣ 2-Απρίλη-2016 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
ΦΥΣ η ΠΡΟΟΔΟΣ 2-Απρίλη-2016
 ΦΥΣ. 211 2 η ΠΡΟΟΔΟΣ 2-Απρίλη-2016 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
ΦΥΣ. 211 2 η ΠΡΟΟΔΟΣ 2-Απρίλη-2016 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2003
 ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Ταλάντωση, γραφικές παραστάσεις και ρυθµοί µεταβολής
 Ταλάντωση, γραφικές παραστάσεις και ρυθµοί µεταβολής Σώµα µάζας m=kg ισορροπεί δεµένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=00 N/m, το άλλο άκρο του οποίου είναι στερεωµένο ακλόνητα στο
Ταλάντωση, γραφικές παραστάσεις και ρυθµοί µεταβολής Σώµα µάζας m=kg ισορροπεί δεµένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=00 N/m, το άλλο άκρο του οποίου είναι στερεωµένο ακλόνητα στο
1 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ
 1 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Αβαρές και μη εκτατό νήμα είναι δεμένο στο ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m, το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος. Το ελεύθερο άκρο
1 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Αβαρές και μη εκτατό νήμα είναι δεμένο στο ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m, το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος. Το ελεύθερο άκρο
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2003
 ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ 12) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ 3
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Άσκηση. ( µον.). Έστω z ο µιγαδικός αριθµός z i, µε, R. (α) ίνεται η εξίσωση: z
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Άσκηση. ( µον.). Έστω z ο µιγαδικός αριθµός z i, µε, R. (α) ίνεται η εξίσωση: z
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Γ έκδοση Στις ηµιτελείς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Γ έκδοση Στις ηµιτελείς
Σύνθεση ή σύζευξη ταλαντώσεων;
 Σύνθεση ή σύζευξη ταλαντώσεων; Σώμα Σ μάζας προσδένεται στο ένα άκρο οριζόντιου ελατηρίου σταθεράς το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Πάνω στο πρώτο σώμα στερεώνεται δεύτερο ελατήριο σταθεράς,
Σύνθεση ή σύζευξη ταλαντώσεων; Σώμα Σ μάζας προσδένεται στο ένα άκρο οριζόντιου ελατηρίου σταθεράς το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Πάνω στο πρώτο σώμα στερεώνεται δεύτερο ελατήριο σταθεράς,
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ( εύτερη Φάση) Κυριακή, 03 Απριλίου, 0 Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: ) Είναι
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ( εύτερη Φάση) Κυριακή, 03 Απριλίου, 0 Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: ) Είναι
