ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ( 2.1)
|
|
|
- Αλάστωρ Λαγός
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦ 2 ο : H υθία στο πίπδο ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ( 2.1) Εξίσση γραµµής C του πιπέδου: Είναι µια ξίσση µ δύο αγνώστους x, που έχι τις ιδιότητς i) Oι συντταγµένς κάθ σηµίου της γραµµής C παληθύουν την ξίσση και αντίστροφα: ii) Αν οι συντταγµένς νός σηµίου παληθύουν την ξίσση, τότ το σηµίο ανήκι στην γραµµή C ηλαδή αν συµβολίσουµ φ(x, )=, την ξίσση της γραµµής C,τότ: Aν το Μ(x 1, 1 ) ίναι σηµίο της C, θα ισχύι φ(x 1, 1 )= Αν ισχύι φ(α, β)=,τότ το Ν(α, β) ίναι σηµίο της C C M( x1, 1) ο N(α,β) C :φ(x,)= Στα πόµνα θα µλτήσουµ τις ιδιότητς της απλούστρης τν γραµµών που ίναι η υθία Συντλστής διύθυνσης υθίας Γνία της υθίας µ τον άξονα χ χ: Λέγται η κυρτή γνία που διαγράφι ο άξονας χ χ στρφόµνος κατά τη θτική φορά γύρ από το σηµίο τοµής του µ την υθία και µέχρι να συµπέσι µ αυτή. Ισχύι < 18 ή σ ακτίνια <π. Αν // χ χ τότ = χ χ χ χ χ χ χ χ <9 >9 = =9 Συντλστής διύθυνσης λ υθίας: Λέγται η τριγνοµτρική φαπτοµένη της γνίας που σχηµατίζι η υθία µ τον άξονα χ χ. ηλαδή λ=φ συντλστής διύθυνσης λέγται και κλίση της υθίας, γιατί καθορίζι πλήρς την διύθυνση της υθίας Αν = τότ λ = φ = Αν οξία γνία τότ λ > χ λ=φ χ Αν αµβλία γνία τότ λ < Αν χ χ δν ορίζται συντλστής διύθυνσης της υθίας
2 ΚΕΦ 2 ο : H υθία στο πίπδο Σχέση τν συντλστών διύθυνσης υθίας και παράλληλου διανύσµατος «Μία υθία και ένα παράλληλο διάνυσµα έχουν ίσους συντλστές διύθυνσης» ηλ. αν //δ τότ Απόδιξη λ =λ δ δ φ φ= δ φ φ=π+ Συντλστής διύθυνσης υθίας από δύο σηµία της Αν υθία διέρχται από τα σηµία Α(x 1, 1 ) και Β(x 2, 2 ), µ x x 2 τότ έχι συντλστή διύθυνσης λ= x x 2 1 Απόδιξη B 2 A 1 x 1 x 2 Συνθήκς καθτότητας και παραλληλίας υθιών Έστ οι υθίς 1, 2 µ συντλστές διύθυνσης λ 1, λ 2 αντίστοιχα ύο υθίς ίναι παράλληλς όταν έχουν ίσους συντλστές διύθυνσης (και αντιστρόφς) δ1 δηλαδή: 1 // 2 λ 1 =λ 2 1 δ2 2 ύο υθίς ίναι κάθτς όταν οι συντλστές διύθυνσης (φόσον υπάρχουν) έχουν γινόµνο -1 (και αντιστρόφς) δηλαδή 1 2 λ 1 λ 2 = -1 1 δ1 2 δ2
3 ΚΕΦ 2 ο : H υθία στο πίπδο Εξίσση υθίας Ένας τρόπος για να ορίσουµ µία υθία ίναι να γνρίζουµ δύο σηµία της Α, Β. Επιδή όµς το διάνυσµα ΑΒ καθορίζι τον συντλστή διύθυνσης λ, δηλαδή την κλίση της υθίας, µπορούµ να πούµ ότι η υθία ορίζται από ένα σηµίο της π.χ. το Α και τον συντλστή διύθυνσής της λ. Και για τις δύο αυτές πριπτώσις θα δώσουµ την ξίσση της υθίας Η υθία που διέρχται από το σηµίο Α(x, ) και έχι συντλστή διύθυνσης λ, έχι ξίσση: - = λ(x-x ) Aπόδιξη M(x,) A(x, ) φ Η µη κατακόρυφη υθία που διέρχται από τα σηµία Α(x 1, 1 ) και Β(x 2, 2 ), έχι ξίσση: = (x x ) x2 x1 A(x 1, 1) φ B(x2, 2) Η υθία που διέρχται από το σηµίο Α(x, ) και ίναι κάθτη στον άξονα χ χ έχι ξίσση: x =x (κατακόρυφη υθία) Ειδικά ο άξονας έχι ξίσση x= Α(x, ) x Ειδικές πριπτώσις ξίσσης υθίας Η υθία που διέρχται από το σηµίο Α(, β) του άξονα και έχι συντλστή διύθυνσης λ, έχι ξίσση: =λx+β φ λ=φφ Α(,β) 9 ο 3
4 ΚΕΦ 2 ο : H υθία στο πίπδο Η υθία που διέρχται από την αρχή τν αξόνν και έχι συντλστή διύθυνσης λ, έχι ξίσση: =λx λ=φφ φ (,) i) Η διχοτόµος της 1 ης και 3 ης γνίας, έχι ξίσση: =x ii) Η διχοτόµος της 2 ης και 4 ης γνίας, έχι ξίσση: =-x χ 45 =x χ =-x χ 135 χ H υθία που διέρχται από το σηµίο Α(x, ) και ίναι παράλληλη στον άξονα Α(x, ) x x, έχι ξίσση: = (οριζόντια υθία) Ειδικά ο άξονας χ χ έχι ξίσση = Άσκηση 1 ίνονται τα σηµία Α(2,-1), Β(4,1), Γ(5,). α) Να βρθί ο συντλστής διύθυνσης της υθίας ΑΓ Αν γνρίζουµ το λ µπορούµ να βρούµ την γνία από την σχέση φ=λ β) Να δίξτ ότι η υθία ΑΓ ίναι παράλληλη στο διάνυσµα δ =(6α 2, 2α 2 ), α γ) Να βρθί η γνία κάθ µιας από τις υθίς ΑΒ και ΒΓ µ τον χ χ Αν το γινόµνο τν συντλστών ίναι -1, τότ οι υθίς ίναι κάθτς Βρίσκουµ την ξίσση υθίας όταν δ) Να διχθί ότι οι υθίς ΑΒ και ΒΓ ίναι κάθτς Γνρίζουµ ένα σηµίο της υθίας και τον συντλστή διύθυνσής της ή ) Να βρθούν οι ξισώσις τν υθιών ΑΒ και ΒΓ Γνρίζουµ δύο σηµία της στ) Ποιά υθία διέρχται από το Α και ίναι παράλληλη στον χ χ; ζ) Ποιά υθία διέρχται από το Γ και ίναι κάθτη στον χ χ; η) Ποιά υθία πρνά από την αρχή τν αξόνν και το σηµίο Β; θ) Να βρθί η ξίσση της υθίας που διέρχται από το Α και ίναι παράλληλη στην υθία =-2x+1 ι) Να βρθί η ξίσση της υθίας που διέρχται από το Γ και ίναι κάθτη στην υθία = 1 3 x συντλστής διύθυνσης µιας υθίας µπορί να βρθί έµµσα: Από µια υθία παράλληλη στην Από µια υθία κάθτη στην Θέτοντας στην ξίσση της υθίας: x=, βρίσκουµ την τοµή της µ τον =, βρίσκουµ την τοµή της µ τον χ χ ια) Να βρθούν τα σηµία τοµής της υθίας ΑΒ µ τους άξονς ιβ) Να βρθί το σηµίο τοµής της υθίας ΒΓ µ την 1 η διχοτόµο. ιγ) Να δίξτ ότι τα σηµία Α, Β και (1, -2) ίναι συνυθιακά. Τρία σηµία ίναι συνυθιακά όταν το ένα ανήκι στην υθία που ορίζουν τα άλλα δύο
5 ιδ) Αν το σηµίο Ε(-1,β) ανήκι στην υθία ΑΓ να βρθί το β. ΚΕΦ 2 ο : H υθία στο πίπδο Άσκηση 2 ίνται τρίγνο ΑΒΓ µ κορυφές τα σηµία Α(2, 1), Β(-1, -1), Γ(-3, 2). Να βρθούν οι ξισώσις : i) Tου φορέα του ύψους Β. ii) Tου φορέα της διαµέσου ΑΜ iii) Της µσοκαθέτου της πλυράς ΒΓ. Άσκηση 3 Έστ ΑΒΓ παραλληλόγραµµο µ κέντρο το σηµίο Κ(2,1) και ξισώσις τν πλυρών ΑΒ, ΑΓ τις =x+1 και =-2x+4 αντιστοίχς. Να βρθούν οι ξισώσις τν άλλν δύο πλυρών. Άσκηση 4 Έστ η υθία : =x+1 και το σηµίο Α(2, 1) α) Να βρθούν οι συντταγµένς της προβολής του σηµίου Α πάν στην. β) Να βρθούν οι συντταγµένς του συµµτρικού του Α ς προς την. Άσκηση 5 Να βρίτ τις ξισώσις τν πλυρών του ττραγώνου του οποίου οι διαγώνις βρίσκονται πάν στους άξονς και η πλυρά του έχι µήκος ίσο µ 2. Άσκηση 6 Tα σηµία Α(2, ) και Β(-1, 4) ίναι διαδοχικές κορυφές ττραγώνου. Να βρθούν οι ξισώσις τν πλυρών του. Άσκηση 7 Να βρίτ τις ξισώσις τν υθιών που διέρχονται από το σηµίο Μ(1, 2) και σχηµατίζουν µ τους άξονς ισοσκλές τρίγνο. Άσκηση 8 Να βρίτ την ξίσση της υθίας που διέρχται από το σηµίο Μ(1, 4) και τέµνι τις υθίς 1 : =-x+4 και 2 : =2x+3 στα σηµία Α και Β αντιστοίχς, έτσι ώστ το Μ να ίναι το µέσο του ΑΒ. Άσκηση 9 Να βρίτ την ξίσση της υθίας που διέρχται από το σηµίο Μ(, 1) και τέµνι τις υθίς 1 : = 1 2 x και 2: = 1 x+1 στα σηµία Α και Β αντιστοίχς, έτσι ώστ να 2 Εύρση υθίας που διέρχται από ισχύι ΑΒ=1. γνστό σηµίο Κάθ υθία που διέρχται από το σηµίο Α(x, ) έχι ξίσση της µορφής: - = λ(x-x ) ή x =x Έτσι λοιπόν πρέπι Να βρούµ το λ, άρα και την υθία Να ξτάσουµ αν η υθία x =x ίναι λύση του προβλήµατος
6 ΚΕΦ 2 ο : H υθία στο πίπδο ΓΕΝΙΚΗ ΜΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ ( 2.2) Όλς οι πριπτώσις ξίσσης υθίας µπορούν να πάρουν µια νιαία µορφή, την οποία συνηθίζουµ να λέµ: γνική ξίσση υθίας i) Κάθ υθία του πιπέδου έχι ξίσση της µορφής Αx+B+Γ=, µ Α ή Β ii) H ξίσση Αx+B+Γ=, µ Α ή Β παριστάνι υθία του πιπέδου ( ηλαδή µία ξίσση 1 ου βαθµού ς προς x, παριστάνι υθία όταν δν µηδνίζονται συγχρόνς οι συντλστές τν αγνώστν) Απόδιξη Σ(,β) Ρ(x, ) Παρατήρησις Η ξίσση Αx+B+Γ=, µ Α ή Β στην ιδική πρίπτση που: i) Α= παριστάνι υθία παράλληλη στον χ χ. ii) Β= παριστάνι υθία παράλληλη στον. Για να βρούµ τον συντλστή διύθυνσης της υθίας Αx+B+Γ=, λύνουµ την ξίσση ς προς και την φέρνουµ στην µορφή =λx+β Άσκηση 1 Να δίξτ ότι, η ξίσση (λ+2)x+( λ-3)+(3λ 2-8λ+5)= για κάθ λ Rπαριστάνι υθία. Πότ η υθία ίναι παράλληλη στον χ χ, πότ παράλληλη στον και πότ διέρχται από το (,); Αν δίξουµ ότι οι συντλστές τν x, δν µηδνίζονται ταυτόχρονα, τότ η ξίσση παριστάνι υθία Άσκηση 11 Να ξτάστ για ποιές τιµές του λ R η ξίσση (λ 2 -λ)x+( λ 2-1)+(λ+3)= παριστάνι υθία. Πότ η υθία αυτή ίναι παράλληλη στον χ χ και πότ ίναι παράλληλη στον ; ιρύνηση της παραµτρικής ξίσσης Αx+B+Γ= Αν µηδνίσουµ ταυτόχρονα τους συντλστές τν x και, θα βρούµ για ποιές τιµές της παραµέτρου λ η ξίσση δν παριστάνι υθία
7 ΚΕΦ 2 ο : H υθία στο πίπδο Άσκηση 12 Να βρθί η ξίσση της µσοπαράλληλης τν υθιών 1 : 2x+-8= και 2 : 4x+2-8=. Άσκηση 13 Τριγώνου ΑΒΓ η κορυφή Α έχι συντταγµένς (1,2), η υθία του ύψους ΒΕ έχι ξίσση 1 : x+3=3 και η υθία της διαµέσου ΓΜ έχι ξίσση 2 : x--11=. Να βρίτ τις δύο άλλς κορυφές του Άσκηση 14 Να δίξτ ότι για κάθ α Rοι υθίς:(2α 2 +α+1)x-(α 2 -α+1)-(α 2 +2α)= (1), διέρχονται από το ίδιο σηµίο. Μσοπαράλληλη δύο υθιών 1, 2 Παίρνουµ δύο σηµία Α, Β πάν στις 1, 2 Βρίσκουµ το µέσο Μ του τµήµατος ΑΒ Η µσοπαράλληλη τν 1, 2 διέρχται από το Μ και έχι το ίδιο λ µ τις 1, 2 Παραµτρική υθία διρχοµένη από σταθρό σηµίο i) ίνουµ δύο αυθαίρτς τιµές στην παράµτρο και βρίσκουµ δύο υθίς 1, 2 ii) Βρίσκουµ το σηµίο τοµής A τν υθιών 1, 2 iii) ίχνουµ ότι οι συντταγµένς του Μ παληθύουν την παραµτρική ξίσση Άσκηση 15 Nα δίξτ ότι για κάθ τιµή του λ R, η ξίσση (x+2-5)+λ(3x-2+1)= (1) παριστάνι υθία. Στη συνέχια να δίξτ ότι όλς οι υθίς που ορίζονται από την (1) πρνάν από το ίδιο σηµίο. Τέλος να βρίτ ποιά από τις παραπάν υθίς της ξίσσης (1) : i) ιέρχται από το σηµίο Α(3,-1) ii) Είναι παράλληλη στον χ χ iii) Είναι παράλληλη στον iv) Είναι παράλληλη στην υθία 4x+3-5= v) Είναι κάθτη στην υθία x+3+7=. Η δέσµη υθιών 1 +λ 2 Αν 1, 2 οι ξισώσις δύο υθιών τότ: Για να δίξουµ ότι η ξίσση 1 +λ 2 παριστάνι υθία, την φέρνουµ στην µορφή Αx+Β+Γ= κ.λ.π. Για να δίξουµ ότι οι υθίς 1 +λ 2 διέρχονται από το ίδιο σηµίο: 1 ος τρόπος: Όπς στην Άσκ ος τρόπος: Η ξίσση 1 +λ 2 ισχύι για κάθ λ R (ταυτότητα) άρα πρέπι να µηδνίζονται συχρόνς οι συντλστές 1 και 2 Η λύση του συστήµατος τν ξισώσν τν 1 και 2 ίναι το σηµίο από το οποίο διέρχονται όλς οι υθίς. Παρατήρηση ι ξισώσις ς προς x, µ βαθµό µγαλύτρο του πρώτου γνικώς παριστάνουν καµπύλς γραµµές. Είναι δυνατόν όµς να παριστάνουν και µία ή πρισσότρς υθίς Άσκηση 16 Να βρίτ τις γραµµές που παριστάνουν οι ξισώσις : α) x= β) x 2-5x+6= γ) x - = δ) x 2-2 = ) x x+12-8=
8 ΚΕΦ 2 ο : H υθία στο πίπδο Πώς βρίσκουµ ένα παράλληλο και ένα κάθτο διάνυσµα σ υθία Ένα διάνυσµα παράλληλο στην υθία Αx+Β+Γ= ίναι το δ =(Β,-Α). Απόδιξη Ax+B+Γ= δ=(β,-α) Ένα διάνυσµα κάθτο στην υθία Αx+Β+Γ= ίναι το η =(Α,Β) Απόδιξη Ax+B+Γ= η=(α,β) Άσκηση 17 Να βρθί η οξία γνία τν υθιών 1 : x=3 και 2 : x++1= Εύρση της Γνίας δύο υθιών Παίρνουµ δύο διανύσµατα παράλληλα στις υθίς Η γνία τν διανυσµάτν ίναι και η γνία τν υθιών Άσκηση 18 M τη βοήθια τν διπλανών σχηµάτν : α) Να κφράστ την γνία τν υθιών 1 και 2 συναρτήσι τν γνιών τους 1 και 2 β) Να κφράστ την φ συναρτήσι τν συντλστών διύθυνσης λ 1, λ 2 τν υθιών 1, 2 Σχτική θέση δύο υθιών ι υθίς 1 : Α 1 x+β 1 +Γ 1 = και 2 : Α 2 x+β 2 +Γ 2 = Α1 Β1 Τέµνονται αν και µόνον αν Α Β 2 2 Α1 Β1 Γ1 Είναι παράλληλς αν και µόνον αν = Α Β Γ 2 2 Α1 Β1 Γ1 Συµπίπτουν αν και µόνον αν = = Α Β Γ 2 2 Άσκηση 19 α) Για τις διάφορς τιµές του λ να βρθούν οι σχτικές θέσις τν υθιών 1 : λx-(λ+1)-1=, 2 : x-2+λ-2= β) Αν οι υθίς τέµνονται να δίξτ ότι το σηµίο τοµής τους Α κινίται σ υθία 2 2 Για τις σχτικές θέσις δύο παραµτρικών υθιών κάνουµ διρύνηση στο σύστηµα τν ξισώσών τους
9 ΚΕΦ 2 ο : H υθία στο πίπδο ΑΠΣΤΑΣΗ ΣΗΜΕΙΥ ΑΠ ΕΥΘΕΙΑ ( 2.3) Η απόσταση του σηµίου Μ (x, ) από την υθία : Αx+Β+Γ= συµβολίζται d(m, ) και δίνται από τον τύπο: Αx +B +Γ d(m,)= 2 2 Α +Β d Μ (x, ) Αx+B+Γ= Άσκηση 2 α) Να βρθί η απόσταση του σηµίου Μ(2, -3) από την υθία 4 2 = x+ 3 3 ίδια υθία β) Να βρθί η απόσταση της αρχής τν αξόνν από την 4 2 = x+ 3 3 Φέρνουµ την υθία στην µορφή Αx+Β+Γ= και φαρµόζουµ τον τύπο της απόστασης Άσκηση 21 Να βρθί το σηµίο του άξονα χ χ που ισαπέχι από την αρχή τν αξόνν και από την υθία : 3x-4-24=. Άσκηση 22 Να βρίτ τις ξισώσις τν υθιών που ιέρχονται από την αρχή (,) και απέχουν από το σηµίο Α(1, 2) απόσταση ίση µ 1. Άσκηση 23 Να βρθί η ξίσση της υθίας που διέρχται από το σηµίο Α(-2, 1) και απέχι από την αρχή τν αξόνν 2 µονάδς. Προσδιορισµός σηµίου Θέτουµ Μ(x,) το ζητούµνο σηµίο και κφράζουµ αναλυτικά τις συνθήκς Εύρση υθίας που διέρχται από γνστό σηµίο Κάθ υθία που διέρχται από το σηµίο Α(x, ) έχι ξίσση της µορφής: - = λ(x-x ) ή x =x Έτσι λοιπόν πρέπι Να βρούµ το λ, άρα και την υθία Να ξτάσουµ αν η υθία x =x ίναι λύση του προβλήµατος Άσκηση 24 Να βρίτ την απόσταση τν υθιών 1 : 4x -6+5= και 2 : = 2 3 x+1. Απόσταση δύο παραλλήλν υθιών Παίρνουµ ένα τυχαίο σηµίο στη µία υθία και βρίσκουµ την απόστασή του από την άλλη ΕΜΒΑ ΤΡΙΓΩΝΥ ( 2.3) Το µβαδό του τριγώνου µ κορυφές Α(x 1, 1 ), B(x 2, 2 ), Γ(x 3, 3 ) δίνται από τον τύπο: (ΑΒΓ)= 1 det(αβ, A Γ) 2 Α(x, ) 1 1 B(x2, 2) Γ(x, ) 3 3
10 ΚΕΦ 2 ο : H υθία στο πίπδο Άσκηση 25 Ενός παραλληλογράµµου ΑΒΓ οι τρις κορυφές του έχουν συντταγµένς (-3, 1), (-2, 3) και (4, -5). Να υπολογίστ το µβαδό του παραλληλογράµµου. Άσκηση 26 Έστ τα σηµία Α(1,1) και Β(5,5) και η υθία : x-2-1=. Nα βρθί σηµίο Γ της υθίας, ώστ το µβαδό του τριγώνου ΑΒΓ να ίναι ίσο µ 4. Άσκηση 27 Έστ τα σηµία Α(1,2), Β(-3,4), Γ(2λ+1,-λ+1), λ R. i) Να διχθί ότι τα σηµία Α, Β, Γ ίναι κορυφές τριγώνου µ σταθρό µβαδό για κάθ λ R. ii) Nα δίξτ ότι το σηµίο Γ κινίται πάν σ υθία της οποίας να βρίτ την ξίσση iii) Nα βρίτ το λ R ώστ το σηµίο Γ(2λ+1, -λ+1) να απέχι από την αρχή τν αξόνν την λάχιστη απόσταση Άσκηση 28 α) Να βρθούν οι ξισώσις της διχοτόµου τν γνιών που σχηµατίζουν οι υθίς: 1 : 3x-4+1= και 2 : 5x+12+4= β) Να βρθί η ξίσση της µσοπαράλληλης τν υθιών 1 : 2x+-8= και 2 : 4x+2-8= Γµτρικοί τόποι i) Θρούµ τυχαίο σηµίο Μ(x,) του γ. τόπου ii) Εκφράζουµ µ αλγβρικές σχέσις την ιδιότητα που έχι το σηµίο Μ iii) Εκτλούµ τις πράξις και παίρνουµ µία ξίσση ς προς x, Άσκηση 29 Να δίξτ ότι οι υθίς λx+(λ-2)=λ-1 και (λ+2)x+λ=λ τέµνονται για όλς τις τιµές του λ R. Στη συνέχια να βρίτ τον γµτρικό τόπο του σηµίου τοµής τους Άσκηση 3 Σ ορθογώνιο σύστηµα αναφοράς x δίνται το ορθογώνιο ΑΒΓ, του οποίου οι κορυφές Α και Γ κινούνται στους θτικούς ηµιάξονς Ox και O αντίστοιχα και ίναι Β (α, β) µ α-β=1. Να δίξτ ότι η κάθτη που φέρουµ από το Β στην ΑΓ διέρχται από σταθρό σηµίο το οποίο και να βρθί. Παραµτρικές ξισώσις γραµµής του πιπέδου Όταν οι συντταγµένς νός σηµίου Μ(x,) της γραµµής C δίνονται ς συναρτήσις µιας µταβλητής t ( η οποία καλίται παράµτρος), τότ λέµ ότι έχουµ τις παραµτρικές ξισώσις της γραµµής C ηλαδή οι παραµτρικές ξισώσις έχουν µορφή: x=x(t), =(t), όπου η µταβλητή t ανήκι σ ένα σύνολο Α Από τις παραµτρικές ξισώσις µ απαλοιφή του t βρίσκουµ µία ξίσση ς προς x, που ίναι η αναλυτική ξίσση της γραµµής C. Άσκηση 31 Να δίξτ ότι τα σηµία Μ(2t-1, 5-6t), t Rανήκουν σ υθία της οποίας να βρίτ την ξίσση.
11 ΚΕΦ 2 ο : H υθία στο πίπδο ν ίναι δυνατόν! Κι άλλς ασκήσις 32. ίνονται τα σηµία Α(7, 5), Β(6, -7) και Γ(2, 3). Να αποδίξτ ότι το τρίγνο ΑΒΓ ίναι ορθογώνιο. 33. Σ τρίγνο ΑΒΓ έχουµ: Α (-8, 2), Β (7, 4), και Η (5, 2) το ορθόκντρό του. Να βρίτ : α) την ξίσση της πλυράς ΒΓ β) τις συντταγµένς της κορυφής Γ γ) τις ξισώσις τν πλυρών του 34. Να βρίτ τις ξισώσις τν υθιών που ίναι παράλληλς προς την υθία : 2x 3 12= και οι οποίς ορίζουν µ τους άξονς τρίγνο µ µβαδόν 12 τ.µ. 35. ίνται η υθία : =3x-2. Na βρθί η συµµτρική της : i) ς προς τον άξονα xx ii) ς προς τον άξονα iii) ς προς το σηµίο (,) iv) ς προς την υθία δ : 2x+-3= και v) ς προς το σηµίο Κ(2,1) 36. ίνονται τα σηµία Α (λ,). Β(2λ,3λ), λ. Αν η κάθτη στην ΑΒ στο σηµίο Α τέµνι την υθία x= -2λ στο Γ, να αποδιχθί ότι το τρίγνο ΑΒΓ ίναι ισοσκλές. [ Απ: ΑΒ=ΑΓ ] 37. ίνονται οι υθίς 1 : (λ+2)x+λψ+3λ-1= και 2 : (λ-1)x+λ+5=. Nα βρίτ τον λ ώστ να ίναι: 1 // ίνονται οι υθίς 1 : (µ+1)x+(µ+2)ψ= και 2 : µx-(3µ+2)+7=. Nα βρίτ το µ ώστ η γνία τν 1 και 2 να ίναι 9 ο. 39. Να βρθί ο γµτρικός τόπος τν σηµίν Μ(λ-1, 2λ+3), λ R 4. Έστ οι υθίς 1 : 2x-3+1=, 2 : -x+4+3= και το σηµίο Α (1,-2). Να βρθί σηµίο Μ της 2, ώστ το µέσο του ΑΜ να ανήκι στην 1. [ Απ : M(-49/5, -16/5) ] 41. ίνονται τα σηµία A(4, 2), B(3, -1) και η υθία : =-3x. Να βρθί σηµίο Γ της υθίας, ώστ το τρίγνο ΑΒΓ να ίναι ισοσκλές µ κορυφή το Β. 42. Na βρίτ τις ξισώσις τν πλυρών νός τριγώνου ΑΒΓ όπου Α(4, 1) και ένα ύψος του και µια διάµσός του από διαφορτικές κορυφές του έχουν ξισώσις =-x-1 και = x+ αντίστοιχα. [ Απ : = x+, = x , =x-3 ] 43. Να αποδιχθί ότι η ξίσση x 2 2 4λ 2λx- 3λ 2 = παριστάνι δύο υθίς κάθτς µταξύ τους. Να βρθί ο γµτρικός τόπος του σηµίου τοµής τν δύο αυτών υθιών.
12 ΚΕΦ 2 ο : H υθία στο πίπδο 44. Να αποδίξτ ότι η ξίσση: 2 2 3x 2x 2 = παριστάνι ζύγος δύο υθιών. Ποια ίναι η σχτική θέση τν δύο υθιών που βρήκατ; 45. ίνονται τα σηµία Α(4,2) και Β(3,-5) και η υθία : 7x+-23=. Na βρθί σηµίο Μ της τέτοιο ώστ το τρίγνο ΑΜΒ να ίναι ορθογώνιο στο Μ. 46. Φτινή ακτίνα διρχόµνη από το σηµίο Σ(2, 3) και προσπίπτουσα στην υθία x++1=, µτά την ανάκλασή της διέρχται από το σηµίο Μ(1, 1). Να βρθούν οι ξισώσις της προσπίπτουσας και της ανακλώµνης ακτίνας. 47. Τριγώνου ΑΒΓ δίνονται η κορυφή Α (1, 2) και οι ξισώσις : x = και 1 = δύο διαµέσν του. Να βρίτ τις ξισώσις τν πλυρών του τριγώνου ΑΒΓ 48. Na βρθί η ξίσση της υθίας που διέρχται από το σηµίο Μ(2,-1) και σχηµατίζι µ 1 3 την υθία 2x-3-6= γνία 45 ο. [ Απ : =5x-11 ή = x- ] Έστ Α(3,-2) και Γ(-5,4) οι δύο κορυφές ττραγώνου ΑΒΓ. Να βρθούν οι συντταγµένς τν κορυφών Β,. [Απ : B(2,5), (-4,-3) ] 5. Να βρθί το µβαδόν του ττραπλύρου που έχι κορυφές τα σηµία: Α(1, -2), Β(-2, 3), Γ(-1, -4), (5, ). 51. Να βρίτ το γµτρικό τόπο τν σηµίν του πιπέδου τν οποίν ο λόγος τν αποστάσν από τις υθίς 1 : x-2= και 2 : x+2= ίναι ίσος µ ίνονται τα σηµία Α(-1,2) και Β(3,-2). Να βρθί σηµίο Ρ της υθίας : 2x-+3=, ώστ να ίναι : Ε(ΡΑΒ)=Ε(ΑΒ). [Απ : (1/3, 11/3) ή (-5/3, -1/3) ] 53. Να αποδίξτ ότι η ξίσση x x-3x-3+2= παριστάνι δύο παράλληλς υθίς και στη συνέχια να βρίτ το µβαδόν του τραπζίου που σχηµατίζουν οι υθίς αυτές µ τους άξονς. [ Ε=3/2 τµ. ] 54. Έστ Α(3, 5) η κορυφή ισοσκλούς τριγώνου ΑΒΓ µ Ε(ΑΒΓ)=2 τµ. και του οποίου η βάση ΒΓ βρίσκται πί της υθίας : x+2=3. Na βρθούν οι ξισώσις τν άλλν δύο πλυρών του τριγώνου. [Απ : =5, 3-4x=3 ]
Γωνία που σχηματίζει η ε με τον άξονα. Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα
 ΕΥΘΕΙΑ Γωνία που σχηματίζι η μ τον άξονα. Έστω O ένα σύστημα συντταγμένων στο πίπδο και μια υθία που τέμνι τον άξονα στο σημίο Α. Α ω Α ω Τη γωνία ω που διαγράφι ο άξονας όταν στραφί γύρω από το Α κατά
ΕΥΘΕΙΑ Γωνία που σχηματίζι η μ τον άξονα. Έστω O ένα σύστημα συντταγμένων στο πίπδο και μια υθία που τέμνι τον άξονα στο σημίο Α. Α ω Α ω Τη γωνία ω που διαγράφι ο άξονας όταν στραφί γύρω από το Α κατά
Η θεωρία στην ευθεία σε ερωτήσεις - απαντήσεις
 Η θρία στην υθία σ ρτήσις - απαντήσις Τι ονομάζουμ ξίσση γραμμής Μια ξίσση μ δύο αγνώστους λέγται ξίσση μιας γραμμής C, όταν οι συντταγμένς τν σημίν της C, και μόνο αυτές, την παληθύουν Ποιό ίναι το βασικό
Η θρία στην υθία σ ρτήσις - απαντήσις Τι ονομάζουμ ξίσση γραμμής Μια ξίσση μ δύο αγνώστους λέγται ξίσση μιας γραμμής C, όταν οι συντταγμένς τν σημίν της C, και μόνο αυτές, την παληθύουν Ποιό ίναι το βασικό
# Κάθε σημείο που οι συντεταγμένες του. Μεθοδολογία στην ευθεία γραμμή ΜΕΘΟΔΟΛΟΓΙΑ ΓΡΑΜΜΗ
 Μθοδολογία στην υθία γραμμή Κοινά σημία δύο γραμμών. Για να βρούμ τις συντταγμένς του σημίου δύο γραμμών, λύνουμ το σύστημα των ξισώσών τους. ΓΡΑΜΜΗ Μια ξίσωση της μορφής φ(χ,ψ)= λέγται ξίσωση μιας πίπδης
Μθοδολογία στην υθία γραμμή Κοινά σημία δύο γραμμών. Για να βρούμ τις συντταγμένς του σημίου δύο γραμμών, λύνουμ το σύστημα των ξισώσών τους. ΓΡΑΜΜΗ Μια ξίσωση της μορφής φ(χ,ψ)= λέγται ξίσωση μιας πίπδης
ΚΕΦΑΛΑΙΟ 2ο Διαφορικός Λογισμός (Νο 6) ΕΠΙΜΕΛΕΙΑ : Π. Δ. ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ
 ΚΕΦΑΛΑΙΟ ο Διαφορικός Λογισμός (Νο 6) Λ Υ Κ Ε Ι Ο Α Ν Α Λ Υ Σ Η 1Ο Κ Ε Φ Α Λ Α Ι Ο ΕΠΙΜΕΛΕΙΑ : Π. Δ. ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Θτική Τχνολογική Κατύθυνση ασκήσις (ΝΑ ΛΥΘΟΥΝ ΜΕΤΑ ΑΠΟ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΤΟΥ ΒΙΒΛΙΟΥ)
ΚΕΦΑΛΑΙΟ ο Διαφορικός Λογισμός (Νο 6) Λ Υ Κ Ε Ι Ο Α Ν Α Λ Υ Σ Η 1Ο Κ Ε Φ Α Λ Α Ι Ο ΕΠΙΜΕΛΕΙΑ : Π. Δ. ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Θτική Τχνολογική Κατύθυνση ασκήσις (ΝΑ ΛΥΘΟΥΝ ΜΕΤΑ ΑΠΟ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΤΟΥ ΒΙΒΛΙΟΥ)
6.3 Η ΣΥΝΑΡΤΗΣΗ f(x) = αx + β
 1 6.3 Η ΣΥΝΡΤΗΣΗ f() = α + β ΘΕΩΡΙ 1. Η πρίφηµη γωνία ω Έστω υθία που τέµνι τον άξονα σ σηµίο. Στρέφουµ την ηµιυθία κατά θτική φορά µέχρι να πέσι πάνω στην. Η γωνία ω που διαγράφται λέγται γωνία που σχηµατίζι
1 6.3 Η ΣΥΝΡΤΗΣΗ f() = α + β ΘΕΩΡΙ 1. Η πρίφηµη γωνία ω Έστω υθία που τέµνι τον άξονα σ σηµίο. Στρέφουµ την ηµιυθία κατά θτική φορά µέχρι να πέσι πάνω στην. Η γωνία ω που διαγράφται λέγται γωνία που σχηµατίζι
4.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ Έστω A ένα υποσύνολο του Ονομάζουμ πραγματική συνάρτηση μ πδίο ορισμού το A, μια διαδικασία f, μ την οποία, κάθ στοιχίο A αντιστοιχίζται σ ένα μόνο πραγματικό αριθμό Το
Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ Έστω A ένα υποσύνολο του Ονομάζουμ πραγματική συνάρτηση μ πδίο ορισμού το A, μια διαδικασία f, μ την οποία, κάθ στοιχίο A αντιστοιχίζται σ ένα μόνο πραγματικό αριθμό Το
2 1 1+ ΜΑΘΗΜΑΤΙΚΑ Ο.Π. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΚΕΦΑΛΑΙΟ:2 ο - ΠΑΡΑΓΡΑΦΟΣ: 2.1 2.2. Γιάννης Ζαµπέλης Μαθηµατικός
 ΚΕΦΑΛΑΙΟ: ο - ΠΑΡΑΓΡΑΦΟΣ:.. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 4 5 Γιάννης Ζαµπέλης Μαθηµατικός 8575 Β (Αναρτήθηκ 8 4 ) ίνονται τα σηµία Α(,) και Β(5,6). α) Να βρίτ την ξίσωση της υθίας που διέρχται από τα σηµία Α και B.
ΚΕΦΑΛΑΙΟ: ο - ΠΑΡΑΓΡΑΦΟΣ:.. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 4 5 Γιάννης Ζαµπέλης Μαθηµατικός 8575 Β (Αναρτήθηκ 8 4 ) ίνονται τα σηµία Α(,) και Β(5,6). α) Να βρίτ την ξίσωση της υθίας που διέρχται από τα σηµία Α και B.
Θεώρηµα ( ) x x. f (x)
 Η ΣΥΝΡΤΗΣΗ f() = α + ΓΩΝΙ ΕΥΘΕΙΣ ΜΕ ΤΝ ΞΝ Η ΣΥΝΡΤΗΣΗ f() = α + Έστ ( ) µία υθία στ καρτσιανό πίπδ η πία τέµνι τν άξνα στ σηµί A. Γνία της υθίας ( ) µ τν άξνα λέγται η γνία πυ διαγράφι η ηµιυθία, αν στραφί
Η ΣΥΝΡΤΗΣΗ f() = α + ΓΩΝΙ ΕΥΘΕΙΣ ΜΕ ΤΝ ΞΝ Η ΣΥΝΡΤΗΣΗ f() = α + Έστ ( ) µία υθία στ καρτσιανό πίπδ η πία τέµνι τν άξνα στ σηµί A. Γνία της υθίας ( ) µ τν άξνα λέγται η γνία πυ διαγράφι η ηµιυθία, αν στραφί
2 Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ. Εισαγωγή
 Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Εισαγωγή Η ιδέα της χρησιμοποίησης νός συστήματος συντταγμένων για τον προσδιορισμό της θέσης νός σημίου πάνω σ μια πιφάνια προέρχται από την Γωγραφία και ήταν γνωστή στους αρχαίους
Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Εισαγωγή Η ιδέα της χρησιμοποίησης νός συστήματος συντταγμένων για τον προσδιορισμό της θέσης νός σημίου πάνω σ μια πιφάνια προέρχται από την Γωγραφία και ήταν γνωστή στους αρχαίους
2018 Φάση 1 ιαγωνίσµατα Προετοιµασίας ΜΑΘΗΜΑΤΙΚΑ. Β' Γενικού Λυκείου. Θετικών Σπουδών. Παρασκευή 5 Ιανουαρίου 2018 ιάρκεια Εξέτασης: 2 ώρες ΘΕΜΑΤΑ
 ΘΕΜΑ Α 018 Φάση 1 ιαγωνίσµατα Προτοιµασίας ΜΑΘΗΜΑΤΙΚΑ Β' νικού Λυκίου Θτικών Σπουδών Παρασκυή 5 Ιανουαρίου 018 ιάρκια Εξέτασης: ώρς Α1. Δίνονται τα διανύσματα α, β, γ ΘΕΜΑΤΑ. Να δίξτ ότι ισχύι α β + γ
ΘΕΜΑ Α 018 Φάση 1 ιαγωνίσµατα Προτοιµασίας ΜΑΘΗΜΑΤΙΚΑ Β' νικού Λυκίου Θτικών Σπουδών Παρασκυή 5 Ιανουαρίου 018 ιάρκια Εξέτασης: ώρς Α1. Δίνονται τα διανύσματα α, β, γ ΘΕΜΑΤΑ. Να δίξτ ότι ισχύι α β + γ
Σχεδίαση µε τη χρήση Η/Υ
 Σχδίαση µ τη χρήση Η/Υ Ε Φ Α Λ Α Ι Ο 1 0 Ο Σ Τ Ο Ι Χ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α Σ Τ Ο Υ Χ Ω Ρ Ο Υ Ρ Λ Ε Ω Ν Ι Α Σ Α Ν Θ Ο Π Ο Υ Λ Ο Σ, Ε Π Ι Ο Υ Ρ Ο Σ Α Θ Η Γ Η Τ Η Σ Τ Μ Η Μ Α Ι Ο Ι Η Σ Η Σ Α Ι Ι Α Χ Ε Ι
Σχδίαση µ τη χρήση Η/Υ Ε Φ Α Λ Α Ι Ο 1 0 Ο Σ Τ Ο Ι Χ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α Σ Τ Ο Υ Χ Ω Ρ Ο Υ Ρ Λ Ε Ω Ν Ι Α Σ Α Ν Θ Ο Π Ο Υ Λ Ο Σ, Ε Π Ι Ο Υ Ρ Ο Σ Α Θ Η Γ Η Τ Η Σ Τ Μ Η Μ Α Ι Ο Ι Η Σ Η Σ Α Ι Ι Α Χ Ε Ι
4.1 ΕΥΘΕΙΕΣ ΚΑΙ ΕΠΙΠΕ Α ΣΤΟ ΧΩΡΟ
 1 4.1 ΥΙΣ ΚΙ Ι ΣΤΟ ΧΩΡΟ ΩΡΙ 1. Το πίπδο: ίναι έννοια πρωταρχική για τα µαθηµατικά δηλαδή έννοια που δν πιδέχται ορισµό. H ικόνα του πιπέδου ίναι γνωστή από την µπιρία µας. Την έχουµ ταυτίσι µ τη µορφή
1 4.1 ΥΙΣ ΚΙ Ι ΣΤΟ ΧΩΡΟ ΩΡΙ 1. Το πίπδο: ίναι έννοια πρωταρχική για τα µαθηµατικά δηλαδή έννοια που δν πιδέχται ορισµό. H ικόνα του πιπέδου ίναι γνωστή από την µπιρία µας. Την έχουµ ταυτίσι µ τη µορφή
Στοιχεία από τη Γεωμετρία του χώρου (αναλυτικά στο βιβλίο: Ευκλείδεια Γεωμετρία Α και Β Ενιαίου Λυκείου)
 Στοιχία από τη Γωμτρία του χώρου (αναλυτικά στο βιβλίο: Ευκλίδια Γωμτρία Α και Β Ενιαίου Λυκίου) Σχήματα των οποίων τα σημία δν βρίσκονται όλα στο ίδιο πίπδο ονομάζονται γωμτρικά στρά (π.χ. σφαίρα, κύλινδρος,
Στοιχία από τη Γωμτρία του χώρου (αναλυτικά στο βιβλίο: Ευκλίδια Γωμτρία Α και Β Ενιαίου Λυκίου) Σχήματα των οποίων τα σημία δν βρίσκονται όλα στο ίδιο πίπδο ονομάζονται γωμτρικά στρά (π.χ. σφαίρα, κύλινδρος,
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 2ο ΓΕΩΜΕΤΡΙΑ ΑΣΚΗΣΕΙΣ ΛΥΜΕΝΕΣ 1 ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΜΕΡΣ ο ΕΩΜΕΤΡΙ ΣΚΗΣΕΙΣ ΛΥΜΕΝΕΣ 1 ΕΠΙΜΕΛΕΙ : ΥΕΡΙΝΣ ΣΙΛΗΣ ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΣΚΗΣΕΙΣ ΜΕΡΣ 1ο : ΕΩΜΕΤΡΙ ΚΕΦΛΙ 1ο ΣΙΚΕΣ ΕΩΜΕΤΡΙΚΕΣ ΕΝΝΙΕΣ νακφαλαίωση σημίο άπιρς υθίς από υθύγραμμο τμήμα Δ παράλληλα
ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΜΕΡΣ ο ΕΩΜΕΤΡΙ ΣΚΗΣΕΙΣ ΛΥΜΕΝΕΣ 1 ΕΠΙΜΕΛΕΙ : ΥΕΡΙΝΣ ΣΙΛΗΣ ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΣΚΗΣΕΙΣ ΜΕΡΣ 1ο : ΕΩΜΕΤΡΙ ΚΕΦΛΙ 1ο ΣΙΚΕΣ ΕΩΜΕΤΡΙΚΕΣ ΕΝΝΙΕΣ νακφαλαίωση σημίο άπιρς υθίς από υθύγραμμο τμήμα Δ παράλληλα
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ΘΕΜΑ 2 ο. Α. 1. Θεωρία σχολικό βιβλίο σελ Θεωρία σχολικό βιβλίο σελ. 61
 ΛΥΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ 5 / / 0 ΘΕΜΑ ο Α Θωρία σχολικό βιβλίο σλ 7 Θωρία σχολικό βιβλίο σλ 6 Β Λ, Σ, Λ, 4 Λ, 5 Λ, 6 Λ, 7 Λ, 8 Σ, 9 Λ, 0 Σ Γ Β,, Α, 4 Α, 5 Α ΘΕΜΑ ο A λ, µ Β µ, λ 6 α xa
ΛΥΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ 5 / / 0 ΘΕΜΑ ο Α Θωρία σχολικό βιβλίο σλ 7 Θωρία σχολικό βιβλίο σλ 6 Β Λ, Σ, Λ, 4 Λ, 5 Λ, 6 Λ, 7 Λ, 8 Σ, 9 Λ, 0 Σ Γ Β,, Α, 4 Α, 5 Α ΘΕΜΑ ο A λ, µ Β µ, λ 6 α xa
ΕΞΙΣΩΣΗ ΣΦΑΙΡΑΣ. είναι όλοι ίσοι και επιπλέον δεν υπάρχουν οι όροι xy, yz, zx. Γενικά µια εξίσωση της µορφής: 0 + Β + Α.
 Suies & Publishing ΣΟΛΩΜΟΥ 9 ΠΟΛΥΤΕΧΝΕΙΟ ΤΗΛ.:.38..57 www.arnοs.gr 3 Ο γωµτρικός τόπος των σηµίων που έχουν σταθρή απόσταση από το σηµίο,, του 3 ονοµάζται σφαίρα. Η σφαίρα µ κέντρο το,, και ακτίνα έχι
Suies & Publishing ΣΟΛΩΜΟΥ 9 ΠΟΛΥΤΕΧΝΕΙΟ ΤΗΛ.:.38..57 www.arnοs.gr 3 Ο γωµτρικός τόπος των σηµίων που έχουν σταθρή απόσταση από το σηµίο,, του 3 ονοµάζται σφαίρα. Η σφαίρα µ κέντρο το,, και ακτίνα έχι
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Α ΒΑΘΜΟΥ
 Πριοδικό ΕΥΚΛΕΙΔΗΣ Β Ε.Μ.Ε. ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Α ΒΑΘΜΟΥ A. ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ ΜΕ ΔΥΟ ΑΓΝΩΣΤΟΥΣ Γραμμική ξίσωση μ δύο αγνώστους ονομάζται κάθ ξίσωση της μορφής: α + βψ = γ (), μ α,β,γ π.χ. ψ =, =, ψ =, κλπ.
Πριοδικό ΕΥΚΛΕΙΔΗΣ Β Ε.Μ.Ε. ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Α ΒΑΘΜΟΥ A. ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ ΜΕ ΔΥΟ ΑΓΝΩΣΤΟΥΣ Γραμμική ξίσωση μ δύο αγνώστους ονομάζται κάθ ξίσωση της μορφής: α + βψ = γ (), μ α,β,γ π.χ. ψ =, =, ψ =, κλπ.
ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΑΞΟΝΑ
 1 1-2 ΣΥΜΜΕΤΡΙ ΩΣ ΠΡΣ ΞΝ ΞΝΣ ΣΥΜΜΕΤΡΙΣ ΘΕΩΡΙ Συµµτρικό σηµίου ως προς υθία Όταν το ν βρίσκται πάνω στην νοµάζουµ συµµτρικό του ως προς την υθία το σηµίο µ το οποίο συµπίπτι το όταν ιπλώσουµ το σχήµα κατά
1 1-2 ΣΥΜΜΕΤΡΙ ΩΣ ΠΡΣ ΞΝ ΞΝΣ ΣΥΜΜΕΤΡΙΣ ΘΕΩΡΙ Συµµτρικό σηµίου ως προς υθία Όταν το ν βρίσκται πάνω στην νοµάζουµ συµµτρικό του ως προς την υθία το σηµίο µ το οποίο συµπίπτι το όταν ιπλώσουµ το σχήµα κατά
φ = ω Β=Γ Α= Β=Ε Γ=Ζ φ Ο
 1 Η Π ΕΙΞΗ ΣΤΗΝ ΕΥΚΛΕΙ ΕΙ ΕΩΜΕΤΡΙ. ΩΝΙΕΣ ΙΣΕΣ ια να αποδίξουμ ότι δύο γωνίς ίναι ίσς πρέπι να αποδίξουμ: 1. Ότι ίναι άθροισμα ή διαφορά γωνιών αντίστοια ίσων. α = β α+ γ = β + δ ν τότ γ = δ α γ = β δ.
1 Η Π ΕΙΞΗ ΣΤΗΝ ΕΥΚΛΕΙ ΕΙ ΕΩΜΕΤΡΙ. ΩΝΙΕΣ ΙΣΕΣ ια να αποδίξουμ ότι δύο γωνίς ίναι ίσς πρέπι να αποδίξουμ: 1. Ότι ίναι άθροισμα ή διαφορά γωνιών αντίστοια ίσων. α = β α+ γ = β + δ ν τότ γ = δ α γ = β δ.
ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 3 Ευθεία - Επίπεδο ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ/2010-11
 ΛΥΣΕΙΣ ΦΥΛΛΔΙΥ 3 Ευθία - Επίπδο ΣΧΛΗ ΠΛΙΤΙΚΩΝ ΜΗΧΝΙΚΩΝ/00-.(α) Τα διανύσματα Β = (,, ), Γ = (,, 3) ίναι μη συγγραμμικά και παράλληλα προς το πίπδο Π, νώ το σημίο (,,3) μ διάνυσμα θέσης r = (,,3) ίναι σημίο
ΛΥΣΕΙΣ ΦΥΛΛΔΙΥ 3 Ευθία - Επίπδο ΣΧΛΗ ΠΛΙΤΙΚΩΝ ΜΗΧΝΙΚΩΝ/00-.(α) Τα διανύσματα Β = (,, ), Γ = (,, 3) ίναι μη συγγραμμικά και παράλληλα προς το πίπδο Π, νώ το σημίο (,,3) μ διάνυσμα θέσης r = (,,3) ίναι σημίο
ΓΕΩΜΕΤΡΙΑ ΘΕΩΡΙΑ. ΚΕΦΑΛΑΙΟ 1ο: ΒΑΣΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ
 ΕΩΜΕΤΡΙ ΘΕΩΡΙ ΚΕΦΛΙ ο: ΣΙΚΕΣ ΕΩΜΕΤΡΙΚΕΣ ΕΝΝΙΕΣ. Ποια η έννοια του σημίου,του υθυγράμμου τμήματος, τι ονομάζουμ άκρα του τμήματος,τι ορίζουν αυτά και πως κατασκυάζουμ ένα τμήμα; πάντηση Η άκρη του μολυβιού
ΕΩΜΕΤΡΙ ΘΕΩΡΙ ΚΕΦΛΙ ο: ΣΙΚΕΣ ΕΩΜΕΤΡΙΚΕΣ ΕΝΝΙΕΣ. Ποια η έννοια του σημίου,του υθυγράμμου τμήματος, τι ονομάζουμ άκρα του τμήματος,τι ορίζουν αυτά και πως κατασκυάζουμ ένα τμήμα; πάντηση Η άκρη του μολυβιού
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 2ο ΓΕΩΜΕΤΡΙΑ
 ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΜΕΡΣ ο ΕΩΜΕΤΡΙ ΕΠΙΜΕΛΕΙ : ΥΕΡΙΝΣ ΣΙΛΗΣ ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΘΕΩΡΙ ΜΕΡΣ ο : ΕΩΜΕΤΡΙ ΚΕΦΛΙ ο ΣΙΚΕΣ ΕΩΜΕΤΡΙΚΕΣ ΕΝΝΙΕΣ. Ποια η έννοια του σημίου,του υθυγράμμου τμήματος, τι ονομάζουμ άκρα του τμήματος,τι
ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΜΕΡΣ ο ΕΩΜΕΤΡΙ ΕΠΙΜΕΛΕΙ : ΥΕΡΙΝΣ ΣΙΛΗΣ ΜΘΗΜΤΙΚ ΥΜΝΣΙΥ ΘΕΩΡΙ ΜΕΡΣ ο : ΕΩΜΕΤΡΙ ΚΕΦΛΙ ο ΣΙΚΕΣ ΕΩΜΕΤΡΙΚΕΣ ΕΝΝΙΕΣ. Ποια η έννοια του σημίου,του υθυγράμμου τμήματος, τι ονομάζουμ άκρα του τμήματος,τι
Μαθηµατικά Κατεύθυνσης Β Λυκείου Ευθεία. Ασκήσεις Ευθεία
 Ασκήσεις Ευθεία 1. Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σηµείο τοµής των ευθειών 3x + 4y 11 = 0 και 2x 3y + 21 = 0 και να γίνει η γραφική της παράσταση όταν είναι: i) παράλληλη στην
Ασκήσεις Ευθεία 1. Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σηµείο τοµής των ευθειών 3x + 4y 11 = 0 και 2x 3y + 21 = 0 και να γίνει η γραφική της παράσταση όταν είναι: i) παράλληλη στην
ΕΝΟΤΗΤΑ Β.2.1. Συμμετρία ως προς άξονα
 ΕΝΟΤΗΤΑ Β.2.1. Συμμτρία ως προς άξονα ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / Δραστηριότητα 1 Βρίτ το συμμτρικό του Α ως προς την υθία Βρίτ το συμμτρικό του Β ως προς την υθία 1 Α Β Βρίτ το συμμτρικό του Α ως προς
ΕΝΟΤΗΤΑ Β.2.1. Συμμτρία ως προς άξονα ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / Δραστηριότητα 1 Βρίτ το συμμτρικό του Α ως προς την υθία Βρίτ το συμμτρικό του Β ως προς την υθία 1 Α Β Βρίτ το συμμτρικό του Α ως προς
5 Γενική µορφή εξίσωσης ευθείας
 5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
ΚΑΤΕΥΘΥΝΣΗ Β ΛΥΚΕΙΟΥ EΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ των Κώστα Βακαλόπουλου, Βασίλη Καρκάνη, Άννας Βακαλοπούλου
 ΚΑΤΕΥΘΥΝΣΗ Β ΛΥΚΕΙΟΥ EΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ των Κώστ Βκλόπουλου, Βσίλη Κρκάνη, Άννς Βκλοπούλου Άσκηση η Δίνοντι τ δινύσμτ, β διάφορ του μηδνικού γι τ οποί ισχύι: β, β κι β i) Ν βρθούν τ μέτρ των δινυσμάτων,
ΚΑΤΕΥΘΥΝΣΗ Β ΛΥΚΕΙΟΥ EΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ των Κώστ Βκλόπουλου, Βσίλη Κρκάνη, Άννς Βκλοπούλου Άσκηση η Δίνοντι τ δινύσμτ, β διάφορ του μηδνικού γι τ οποί ισχύι: β, β κι β i) Ν βρθούν τ μέτρ των δινυσμάτων,
ÏÌÉÊÑÏÍ ÖÑÏÍÔÉÓÔÇÑÉÏ ÊÏÑÄÅËÉÏ
 ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (ΟΕΦΕ) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 01 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ / ΚΑΤΕΥΘΥΝΣΗΣ Ηµροµηνία: Κυριακή Μαΐου 01 ιάρκια Εξέτασης: ώρς ΑΠΑΝΤΗΣΕΙΣ
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (ΟΕΦΕ) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 01 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ / ΚΑΤΕΥΘΥΝΣΗΣ Ηµροµηνία: Κυριακή Μαΐου 01 ιάρκια Εξέτασης: ώρς ΑΠΑΝΤΗΣΕΙΣ
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ
 Ευθεία ΣΥΝΤΕΛΕΣΤΗΣ ΔΙΕΥΘΥΝΣΗΣ ΕΥΘΕΙΑΣ ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ 1. Να βρεθεί ο συντελεστής διεύθυνσης της ευθείας ε, αν αυτή έχει εξίσωση: 5x 6 i) y = x- 1 ii) y = 3 5x iii) y iv) x = y + 3 10 v) 18x-6y
Ευθεία ΣΥΝΤΕΛΕΣΤΗΣ ΔΙΕΥΘΥΝΣΗΣ ΕΥΘΕΙΑΣ ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ 1. Να βρεθεί ο συντελεστής διεύθυνσης της ευθείας ε, αν αυτή έχει εξίσωση: 5x 6 i) y = x- 1 ii) y = 3 5x iii) y iv) x = y + 3 10 v) 18x-6y
ΕΥΘΕΙΑ. Κεφάλαιο 2ο: Ερωτήσεις του τύπου «Σωστό-Λάθος»
 Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος». * Συντελεστής διεύθυνσης µιας ευθείας (ε) είναι η εφαπτοµένη της γωνίας που σχηµατίζει η ευθεία (ε) µε τον άξονα x x. Σ Λ. * Ο συντελεστής διεύθυνσης
Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος». * Συντελεστής διεύθυνσης µιας ευθείας (ε) είναι η εφαπτοµένη της γωνίας που σχηµατίζει η ευθεία (ε) µε τον άξονα x x. Σ Λ. * Ο συντελεστής διεύθυνσης
1. * Να βρείτε τον συντελεστή διεύθυνσης µιας ευθείας ε, που σχηµατίζει µε τον άξονα x x γωνία: 2π 3
 Ερωτήσεις ανάπτυξης 1. * Να βρείτε τον συντελεστή διεύθυνσης µιας ευθείας ε, που σχηµατίζει µε τον άξονα x x γωνία: α) ω = 3 π β) ω = 2π 3 γ) ω = π 2. * Να βρείτε τη γωνία ω που σχηµατίζει µε τον άξονα
Ερωτήσεις ανάπτυξης 1. * Να βρείτε τον συντελεστή διεύθυνσης µιας ευθείας ε, που σχηµατίζει µε τον άξονα x x γωνία: α) ω = 3 π β) ω = 2π 3 γ) ω = π 2. * Να βρείτε τη γωνία ω που σχηµατίζει µε τον άξονα
Ασκήσεις στην ευθεία. 2. Θεωρούµε την γραµµή µε εξίσωση x 2 +y 2-2x+y-5=0. Βρείτε τα σηµεία της καµπύλης, αν υπάρχουν, µε τετµηµένη -1.
 Ασκήσεις στην ευθεία 1. Να βρείτε τα σηµεία τοµής των γραµµών µε εξισώσεις : α) 7x-11y+1=0, x+y-=0 β) y-3x-=0, x +y =4 γ) x +y =α, 3x+y+α=0. Θεωρούµε την γραµµή µε εξίσωση x +y -x+y-5=0. Βρείτε τα σηµεία
Ασκήσεις στην ευθεία 1. Να βρείτε τα σηµεία τοµής των γραµµών µε εξισώσεις : α) 7x-11y+1=0, x+y-=0 β) y-3x-=0, x +y =4 γ) x +y =α, 3x+y+α=0. Θεωρούµε την γραµµή µε εξίσωση x +y -x+y-5=0. Βρείτε τα σηµεία
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 2 ΕΥΘΕΙΑ ΑΣΚΗΣΕΙΣ Πηγή: KEE
 1. Να βρείτε τον συντελεστή διεύθυνσης µιας ευθείας ε, που σχηµατίζει µε τον άξονα x x γωνία: α) ω = 3 π β) ω = π 3 γ) ω = π. Να βρείτε τη γωνία ω που σχηµατίζει µε τον άξονα x x µια ευθεία ε, η οποία
1. Να βρείτε τον συντελεστή διεύθυνσης µιας ευθείας ε, που σχηµατίζει µε τον άξονα x x γωνία: α) ω = 3 π β) ω = π 3 γ) ω = π. Να βρείτε τη γωνία ω που σχηµατίζει µε τον άξονα x x µια ευθεία ε, η οποία
ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΚΑΙ
 1.1.. ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΕΜΑ ΟΝ ΤΡΙΓΩΝΟΥ ΘΕΩΡΙΑ 1. Εξίσωση γραµµής C Μια εξίσωση µε δύο αγνώστους x, y λέγεται εξίσωση µιας γραµµής C, όταν οι συντεταγµένες των σηµείων της C, και µόνον αυτές, την επαληθεύουν..
1.1.. ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΕΜΑ ΟΝ ΤΡΙΓΩΝΟΥ ΘΕΩΡΙΑ 1. Εξίσωση γραµµής C Μια εξίσωση µε δύο αγνώστους x, y λέγεται εξίσωση µιας γραµµής C, όταν οι συντεταγµένες των σηµείων της C, και µόνον αυτές, την επαληθεύουν..
9o Γεν. Λύκειο Περιστερίου ( 3.1) ΚΥΚΛΟΣ. ΚΕΦΑΛΑΙΟ 3 ο : KΩΝΙΚΕΣ ΤΟΜΕΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΚΕΦΑΛΑΙ 3 ο : KΩΝΙΚΕΣ ΤΜΕΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΥ ( 3.) ΚΥΚΛΣ Γνωρίζουµε ότι ένας κύκλος (, ρ) είναι ο γεωµετρικός τόπος των σηµείων του επιπέδου τα οποία απέχουν µια ορισµένη απόσταση ρ από ένα
ΚΕΦΑΛΑΙ 3 ο : KΩΝΙΚΕΣ ΤΜΕΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΥ ( 3.) ΚΥΚΛΣ Γνωρίζουµε ότι ένας κύκλος (, ρ) είναι ο γεωµετρικός τόπος των σηµείων του επιπέδου τα οποία απέχουν µια ορισµένη απόσταση ρ από ένα
Επαναληπτικά συνδυαστικα θέµατα
 Επαναληπτικά συνδυαστικα θέµατα A. Αν α, β i. αβ Θέµα ο µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: και ii. Αν α β τότε ισχύει α + β =. B. Να βρεθούν οι τιµές του λ ώστε η εξίσωση
Επαναληπτικά συνδυαστικα θέµατα A. Αν α, β i. αβ Θέµα ο µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: και ii. Αν α β τότε ισχύει α + β =. B. Να βρεθούν οι τιµές του λ ώστε η εξίσωση
11. Η έννοια του διανύσµατος 22. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο
 Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Η γενική μορφή της εξίσωσης ευθείας είναι η από τα Α, Β διάφορο του μηδενός
 ΕΥΘΕΙΑ Να προσέχεις ότι: Η γενική μορφή της εξίσωσης ευθείας είναι η από τα Α, Β διάφορο του μηδενός Ax+By+Γ=0, με κάποιο Η εξίσωση της ευθείας που διέρχεται από ένα σημείο Α(x 0,y 0 ) και έχει συντελεστή
ΕΥΘΕΙΑ Να προσέχεις ότι: Η γενική μορφή της εξίσωσης ευθείας είναι η από τα Α, Β διάφορο του μηδενός Ax+By+Γ=0, με κάποιο Η εξίσωση της ευθείας που διέρχεται από ένα σημείο Α(x 0,y 0 ) και έχει συντελεστή
ΘΕΜΑ ίνονται τα διανύσµαταα, β. α) Να υπολογίσετε τη γωνία. β) Να αποδείξετε ότι 2α+β= β) το συνηµίτονο της γωνίας των διανυσµάτων
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ! ΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΘΕΜΑ 005 Θεωρούµε τα σηµεία Ρ, Λ, Κ και Μ του επιπέδου για τα οποία ισχύει η σχέση 5ΡΛ
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ! ΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΘΕΜΑ 005 Θεωρούµε τα σηµεία Ρ, Λ, Κ και Μ του επιπέδου για τα οποία ισχύει η σχέση 5ΡΛ
Ερωτήσεις αντιστοίχισης
 Ερωτήσεις αντιστοίχισης 1. ** Να αντιστοιχίσετε κάθε ευθεία που η εξίσωσή της βρίσκεται στη του πίνακα (Ι) µε τον συντελεστή της που βρίσκεται στη, συµπληρώνοντας τον πίνακα (ΙΙ) (α, β 0). 1. ε 1 : y =
Ερωτήσεις αντιστοίχισης 1. ** Να αντιστοιχίσετε κάθε ευθεία που η εξίσωσή της βρίσκεται στη του πίνακα (Ι) µε τον συντελεστή της που βρίσκεται στη, συµπληρώνοντας τον πίνακα (ΙΙ) (α, β 0). 1. ε 1 : y =
Εφαρµογές στη δυναµική του κέντρου µάζας στερεού σώµατος
 Εφαρµογές στη δυναµική του κέντρου µάζας στρού σώµατος Εφαρµογή 1η Οµογνής δίσκος ακτίνας R ηρµί στην άκρη οριζόντιου τραπζιού µ το κέντρο του Κ να βρίσκται στην κατακόρυφη που διέρχται από την ία Ο του
Εφαρµογές στη δυναµική του κέντρου µάζας στρού σώµατος Εφαρµογή 1η Οµογνής δίσκος ακτίνας R ηρµί στην άκρη οριζόντιου τραπζιού µ το κέντρο του Κ να βρίσκται στην κατακόρυφη που διέρχται από την ία Ο του
2.2 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ
 63 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ Η Εξίσωση Αx + Βy + Γ = 0, με Α 0 ή Β 0 Έστω ε μια ευθεία στο καρτεσιανό επίπεδο Αν η ευθεία ε τέμνει τον άξονα yy στο σημείο Σ (, 0 β ) και έχει συντελεστή διεύθυνσης
63 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ Η Εξίσωση Αx + Βy + Γ = 0, με Α 0 ή Β 0 Έστω ε μια ευθεία στο καρτεσιανό επίπεδο Αν η ευθεία ε τέμνει τον άξονα yy στο σημείο Σ (, 0 β ) και έχει συντελεστή διεύθυνσης
Ονοµάζουµε παραβολή µε εστία σηµείο Ε και διευθετούσα ευθεία (δ) το γεωµετρικό τόπο των σηµείων του επιπέδου τα οποία ισαπέχουν από το Ε και τη (δ)
 3. Η ΠΑΡΑΒΟΛΗ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµε παραβολή µε εστία σηµείο Ε και διευθετούσα ευθεία (δ) το γεωµετρικό τόπο των σηµείων του επιπέδου τα οποία ισαπέχουν από το Ε και τη (δ). Εξίσωση παραβολής p, όπου
3. Η ΠΑΡΑΒΟΛΗ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµε παραβολή µε εστία σηµείο Ε και διευθετούσα ευθεία (δ) το γεωµετρικό τόπο των σηµείων του επιπέδου τα οποία ισαπέχουν από το Ε και τη (δ). Εξίσωση παραβολής p, όπου
c 2 b b Λύση Το δυναµικό οµογενούς ηλεκτρικού πεδίου έντασης ε είναι V( x)
 ΑΣΚΗΣΗ 8 Φορτισµένος αρµονικός ταλανττής βρίσκται µέσα σ οµογνές ηλκτρικό πδίο έντασης. Τη χρονική στιγµή t= ο ταλανττής βρίσκται στη βασική κατάσταση. Να υπολογιστί η πιθανότητα ο ταλανττής να παραµίνι
ΑΣΚΗΣΗ 8 Φορτισµένος αρµονικός ταλανττής βρίσκται µέσα σ οµογνές ηλκτρικό πδίο έντασης. Τη χρονική στιγµή t= ο ταλανττής βρίσκται στη βασική κατάσταση. Να υπολογιστί η πιθανότητα ο ταλανττής να παραµίνι
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙ ΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ. Ιωάννης Βανδουλάκης Χαράλαμπος Καλλιγάς Νικηφόρος Μαρκάκης Σπύρος Φερεντίνος
 ΥΠΥΡΕΙ ΕΘΝΙΚΗΣ ΠΙ ΕΙΣ ΚΙ ΘΡΗΣΚΕΥΜΤΩΝ ΠΙ ΩΙΚ ΙΝΣΤΙΤΥΤ Ιωάννης ανδουλάκης Χαράλαμπος Καλλιγάς Νικηφόρος Μαρκάκης Σπύρος Φρντίνος ΜΘΗΜΤΙΚ υμνασίου ΜΕΡΣ ωμτρία Τόμος 2ος Μαθηματικά ΥΜΝΣΙΥ ΜΕΡΣ ωμτρία Τόμος
ΥΠΥΡΕΙ ΕΘΝΙΚΗΣ ΠΙ ΕΙΣ ΚΙ ΘΡΗΣΚΕΥΜΤΩΝ ΠΙ ΩΙΚ ΙΝΣΤΙΤΥΤ Ιωάννης ανδουλάκης Χαράλαμπος Καλλιγάς Νικηφόρος Μαρκάκης Σπύρος Φρντίνος ΜΘΗΜΤΙΚ υμνασίου ΜΕΡΣ ωμτρία Τόμος 2ος Μαθηματικά ΥΜΝΣΙΥ ΜΕΡΣ ωμτρία Τόμος
Νόμος του Gauss 1. Ηλεκτρική Ροή ( πλήθος δυναμικών γραμμών). είναι διάνυσμα μέτρου Α και κατεύθυνσης κάθετης στην επιφάνεια. Στην γενική περίπτωση:
 Νόμος του Gauss 1. Ηλκτρική Ροή ( πλήθος δυναμικών γραμμών). ( a) cosφ ( b) ίναι διάνυσμα μέτρου Α και κατύθυνσης κάθτης στην πιφάνια. Στην γνική πρίπτωση: d d d ( ) (πιφανιακό ολοκλήρωμα) Νόμος του Gauss
Νόμος του Gauss 1. Ηλκτρική Ροή ( πλήθος δυναμικών γραμμών). ( a) cosφ ( b) ίναι διάνυσμα μέτρου Α και κατύθυνσης κάθτης στην πιφάνια. Στην γνική πρίπτωση: d d d ( ) (πιφανιακό ολοκλήρωμα) Νόμος του Gauss
ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. ΘΕΜΑ 2ο
 Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε = 5 + 2 α) Να γράψετε το διάνυσμα β) Να δείξετε
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε = 5 + 2 α) Να γράψετε το διάνυσμα β) Να δείξετε
Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ
 2ο κεφάλαιο: Ευθείες Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Μαθηµατικά Προσανατολισµού Β Λυκείου Αποστόλου Γιώργος Μαθηµατικός Copyright 2015 Αποστόλου Γιώργος Αποστόλου
2ο κεφάλαιο: Ευθείες Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Μαθηµατικά Προσανατολισµού Β Λυκείου Αποστόλου Γιώργος Μαθηµατικός Copyright 2015 Αποστόλου Γιώργος Αποστόλου
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ Διανύσματα-Ευθεία-Κύκλος Αναλυτική Θεωρία 500 Ασκήσεις Επιμέλεια : ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ Σελίδα 2 1. Η Έννοια του Διανύσματος Ορισμός Διανύσματος Το διάνυσμα ορίζεται ως
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ Διανύσματα-Ευθεία-Κύκλος Αναλυτική Θεωρία 500 Ασκήσεις Επιμέλεια : ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ Σελίδα 2 1. Η Έννοια του Διανύσματος Ορισμός Διανύσματος Το διάνυσμα ορίζεται ως
6.2 ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ
 1 6. ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ ΘΕΩΡΙΑ 1. Οι συντεταγµένες σηµείου Ο Ο άξονας τετµηµένων άξονας τεταγµένων (ΟΚ) µε πρόσηµο = α, η τετµηµένη του Μ (ΟΛ) µε πρόσηµο = β, η τεταγµένη του Μ Το ζευγάρι (α,
1 6. ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ ΘΕΩΡΙΑ 1. Οι συντεταγµένες σηµείου Ο Ο άξονας τετµηµένων άξονας τεταγµένων (ΟΚ) µε πρόσηµο = α, η τετµηµένη του Μ (ΟΛ) µε πρόσηµο = β, η τεταγµένη του Μ Το ζευγάρι (α,
π (α,β). Έστω τα διανύσματα π (α,β) να βρεθούν:
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΚΑΤΕΥΘΥΝΣΗΣ 1. Για τα διανύσματα α, β δίνεται ότι α =1, β = και u α β, v α - β.να υπολογίσετε: π (α,β). Έστω τα διανύσματα α. το εσωτερικό γινόμενο α β β. τα μέτρα u, v των διανυσμάτων
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΚΑΤΕΥΘΥΝΣΗΣ 1. Για τα διανύσματα α, β δίνεται ότι α =1, β = και u α β, v α - β.να υπολογίσετε: π (α,β). Έστω τα διανύσματα α. το εσωτερικό γινόμενο α β β. τα μέτρα u, v των διανυσμάτων
Συµπάγεια και οµοιόµορφη συνέχεια
 35 Συµπάγια και οµοιόµορφη συνέχια Μια πολύ σηµαντική έννοια στην Ανάλυση ίναι αυτή της συµπάγιας. Όπως θα δούµ τα συµπαγή υποσύνολα του Ευκλίδιου χώρου R συµπριφέρονται λίγο πολύ ως ππρασµένα σύνολα.
35 Συµπάγια και οµοιόµορφη συνέχια Μια πολύ σηµαντική έννοια στην Ανάλυση ίναι αυτή της συµπάγιας. Όπως θα δούµ τα συµπαγή υποσύνολα του Ευκλίδιου χώρου R συµπριφέρονται λίγο πολύ ως ππρασµένα σύνολα.
( ) Ασκήσεις σχολικού βιβλίου σελίδας A Oµάδας
 3.3 Ασκήσις σχολικού ιλίου σλίδς 3 A Oµάδς. Ν ρίτ τη ξίσωση της έλλιψης σ κθµιά πό τις πρκάτω πριπτώσις : (i Ότ έχι στίς τ σηµί Ε (, 0 κι Ε(, 0 κι µγάλο άξο 0 (ii Ότ έχι στίς τ σηµί Ε (0, 5 κι Ε(0, 5 κι
3.3 Ασκήσις σχολικού ιλίου σλίδς 3 A Oµάδς. Ν ρίτ τη ξίσωση της έλλιψης σ κθµιά πό τις πρκάτω πριπτώσις : (i Ότ έχι στίς τ σηµί Ε (, 0 κι Ε(, 0 κι µγάλο άξο 0 (ii Ότ έχι στίς τ σηµί Ε (0, 5 κι Ε(0, 5 κι
Επαναληπτικά συνδυαστικα θέµατα
 Επαναληπτικά συνδυαστικα θέµατα Θέµα ο A. Αν α, β µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: i. αβ και ii. Αν α β τότε ισχύει α + β =. 4 4 B. Να βρεθούν οι τιµές του λ ώστε η
Επαναληπτικά συνδυαστικα θέµατα Θέµα ο A. Αν α, β µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: i. αβ και ii. Αν α β τότε ισχύει α + β =. 4 4 B. Να βρεθούν οι τιµές του λ ώστε η
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ 3 Ο : ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ η Κατηγορία : Ο Κύκλος και τα στοιχεία
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ 3 Ο : ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ η Κατηγορία : Ο Κύκλος και τα στοιχεία
ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
Τράπεζα συναρτήσει των διανυσμάτων α,β,γ. Μονάδες 13 β) να αποδείξετε ότι τα σημεία Α, Β, Γ είναι συνευθειακά. Μονάδες 12
 Τράπεζα 0- Πολλαπλασιασμός αριθμού με διάνυσμα.58 Θεωρούμε τα διανύσματα α,β,γ και τυχαίο σημείο Ο. Αν α β 5γ, α 3β 4γ και 3α β 6γ, τότε: α) να εκφράσετε τα διανύσματα, συναρτήσει των διανυσμάτων α,β,γ.
Τράπεζα 0- Πολλαπλασιασμός αριθμού με διάνυσμα.58 Θεωρούμε τα διανύσματα α,β,γ και τυχαίο σημείο Ο. Αν α β 5γ, α 3β 4γ και 3α β 6γ, τότε: α) να εκφράσετε τα διανύσματα, συναρτήσει των διανυσμάτων α,β,γ.
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
3.2. Ασκήσεις σχολικού βιβλίου σελίδας A Οµάδας
 3. Ασκήσεις σχολικού βιβλίου σελίδας 99 A Οµάδας. Να βρεθεί η εξίσωση της παραβολής που έχει κορυφή την αρχή των αξόνων και άξονα συµµετρίας τον άξονα σε καθεµιά από τις παρακάτω περιπτώσεις : (i) Όταν
3. Ασκήσεις σχολικού βιβλίου σελίδας 99 A Οµάδας. Να βρεθεί η εξίσωση της παραβολής που έχει κορυφή την αρχή των αξόνων και άξονα συµµετρίας τον άξονα σε καθεµιά από τις παρακάτω περιπτώσεις : (i) Όταν
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
Ανοικτά και κλειστά σύνολα
 5 Ανοικτά και κλιστά σύνολα Στην παράγραφο αυτή αναπτύσσται ο µηχανισµός που θα µας πιτρέψι να µλτήσουµ τις αναλυτικές ιδιότητς των συναρτήσων πολλών µταβλητών. Θα χριαστούµ τις έννοις της ανοικτής σφαίρας
5 Ανοικτά και κλιστά σύνολα Στην παράγραφο αυτή αναπτύσσται ο µηχανισµός που θα µας πιτρέψι να µλτήσουµ τις αναλυτικές ιδιότητς των συναρτήσων πολλών µταβλητών. Θα χριαστούµ τις έννοις της ανοικτής σφαίρας
Τάξη B. Μάθημα: Η Θεωρία σε Ερωτήσεις. Επαναληπτικά Θέματα. Επαναληπτικά Διαγωνίσματα. Επιμέλεια: Κώστας Κουτσοβασίλης. α Ε
 Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
Κατοίκον Εργασία 2. (γ) το ολικό φορτίο που βρίσκεται στον κύβο. (sd p.e 4.9 p146)
 Κατοίκον Εργασία. Ένα σημιακό φορτίο (point charge) 5 mc και ένα - mc βρίσκονται στα σημία (,0,4) και (-3,0,5) αντίστοιχα. (α) Υπολογίστ την δύναμη πάνω σ ένα φορτίο (point charge) nc που βρίσκται στο
Κατοίκον Εργασία. Ένα σημιακό φορτίο (point charge) 5 mc και ένα - mc βρίσκονται στα σημία (,0,4) και (-3,0,5) αντίστοιχα. (α) Υπολογίστ την δύναμη πάνω σ ένα φορτίο (point charge) nc που βρίσκται στο
ΣΕΤ ΑΣΚΗΣΕΩΝ
 ΣΕΤ ΑΣΚΗΣΕΩΝ 4.4.07. α) Ποια ίναι η σχέση μταξύ των οικονομιών κλίμακας και αποδόσων κλίμακας; β) Πως μτράμ την έκταση των οικονομιών κλίμακας; ΛΥΣΗ α) Οι οικονομίς κλίμακας και οι αποδόσις κλίμακας ίναι
ΣΕΤ ΑΣΚΗΣΕΩΝ 4.4.07. α) Ποια ίναι η σχέση μταξύ των οικονομιών κλίμακας και αποδόσων κλίμακας; β) Πως μτράμ την έκταση των οικονομιών κλίμακας; ΛΥΣΗ α) Οι οικονομίς κλίμακας και οι αποδόσις κλίμακας ίναι
ΜΑΘΗΜΑΤΙΚΑ Ο.Π. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΝ ΥΑΣΤΙΚΑ ΘΕΜΑΤΑ. Γιάννης Ζαµπέλης Μαθηµατικός
 ΣΥΝ ΥΑΣΤΙΚΑ ΘΕΜΑΤΑ 4 5 Γιάννης Ζαµπέλης Μαθηµατικός 867 (Αναρτήθηκε 8 4 ) ίνονται τα διανύσµατα a και b µε µέτρα, 6 αντίστοιχα και ϕ [, π] a b+ x+ a b y 5= () δίνεται η εξίσωση ( ) ( ) α) Να αποδείξετε
ΣΥΝ ΥΑΣΤΙΚΑ ΘΕΜΑΤΑ 4 5 Γιάννης Ζαµπέλης Μαθηµατικός 867 (Αναρτήθηκε 8 4 ) ίνονται τα διανύσµατα a και b µε µέτρα, 6 αντίστοιχα και ϕ [, π] a b+ x+ a b y 5= () δίνεται η εξίσωση ( ) ( ) α) Να αποδείξετε
ΜΑΘΗΜΑ 7. 2.3 Μέτρο µιγαδικού Ασκήσεις Γεωµετρικών τόπων ΑΣΚΗΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑ 7.3 Μέτρο µιγαδικού Ασκήσεις Γεωµετρικών τόπων. Να βρείτε το γεωµετρικό τόπο των µιγαδικών z, για τους οποίους οι εικόνες των µιγαδικών z, i, iz είναι συνευθειακά σηµεία. Έστω z = x + i,
ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑ 7.3 Μέτρο µιγαδικού Ασκήσεις Γεωµετρικών τόπων. Να βρείτε το γεωµετρικό τόπο των µιγαδικών z, για τους οποίους οι εικόνες των µιγαδικών z, i, iz είναι συνευθειακά σηµεία. Έστω z = x + i,
Ερωτήσεις ανάπτυξης 1. ** 2. ** 3. ** 4. ** 5. ** 6. **
 Ερωτήσεις ανάπτυξης 1. ** ίνονται επίπεδο p και τρία µη συνευθειακά σηµεία του Α, Β και Γ καθώς και ένα σηµείο Μ, που δεν συµπίπτει µε το Α. Αν η ευθεία ΑΜ τέµνει την ευθεία ΒΓ, να δείξετε ότι το Μ είναι
Ερωτήσεις ανάπτυξης 1. ** ίνονται επίπεδο p και τρία µη συνευθειακά σηµεία του Α, Β και Γ καθώς και ένα σηµείο Μ, που δεν συµπίπτει µε το Α. Αν η ευθεία ΑΜ τέµνει την ευθεία ΒΓ, να δείξετε ότι το Μ είναι
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2016 Β ΦΑΣΗ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 016 Ε_.ΜλΘ(ε) ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ηµεροµηνία: Κυριακή 17 Απριλίου 016 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Έστω a, v
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 016 Ε_.ΜλΘ(ε) ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ηµεροµηνία: Κυριακή 17 Απριλίου 016 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Έστω a, v
Χαρακτηρίστε τις παρακάτω προτάσεις ως σωστό (Σ) ή λάθος (Λ)
 ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ ΕΥΘΕΙΑ Χαρακτηρίστε τις παρακάτω προτάσεις ως σωστό (Σ) ή λάθος (Λ) 1. Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία με τον
ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ ΕΥΘΕΙΑ Χαρακτηρίστε τις παρακάτω προτάσεις ως σωστό (Σ) ή λάθος (Λ) 1. Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία με τον
Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Μέρος Α : Θεωρία
 1 Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Μέρος Α : Θεωρία ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ Εξίσωση Γραμμής Μια εξίσωση με δύο αγνώστους, λέγεται εξίσωση μιας γραμμής C, όταν οι συντεταγμένες των σημείων της C, και μόνο αυτές, την επαληθεύουν.
1 Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Μέρος Α : Θεωρία ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ Εξίσωση Γραμμής Μια εξίσωση με δύο αγνώστους, λέγεται εξίσωση μιας γραμμής C, όταν οι συντεταγμένες των σημείων της C, και μόνο αυτές, την επαληθεύουν.
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρηµα του Θαλή και οι Συνέπειές του
 ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρηµα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήµα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν Α ΒΓ, Ε ΑΒ τότε το τρίγωνο
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρηµα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήµα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν Α ΒΓ, Ε ΑΒ τότε το τρίγωνο
Συμπλήρωμα 2 εδαφίου 3.3: Το γενικό μεταβολικό πρόβλημα για συναρτησιακό ολοκληρωτικού τύπου με ολοκληρωτέα συνάρτηση F κατά 2
 ΚΕΦ. 3 Η Αρχή των Ήρωνος-Fermat 3.3-8 Συμπλήρωμα 2 δαφίου 3.3: Το νικό μταβολικό πρόβλημα ια συναρτησιακό ολοκληρωτικού τύπου μ ολοκληρωτέα συνάρτηση F κατά 2 τμήματα C, ορισμένο πί καμπυλών που τέμνουν
ΚΕΦ. 3 Η Αρχή των Ήρωνος-Fermat 3.3-8 Συμπλήρωμα 2 δαφίου 3.3: Το νικό μταβολικό πρόβλημα ια συναρτησιακό ολοκληρωτικού τύπου μ ολοκληρωτέα συνάρτηση F κατά 2 τμήματα C, ορισμένο πί καμπυλών που τέμνουν
2 η δεκάδα θεµάτων επανάληψης
 η δεκάδα θεµάτων επανάληψης. ίνεται ο κύκλος x + y = 5 και οι εφαπτόµενες σ αυτόν από το σηµείο Μ(0, 0). Αν Α και Β είναι τα σηµεία επαφής, να βρείτε Τις εξισώσεις των εφαπτόµενων Τις συντεταγµένες των
η δεκάδα θεµάτων επανάληψης. ίνεται ο κύκλος x + y = 5 και οι εφαπτόµενες σ αυτόν από το σηµείο Μ(0, 0). Αν Α και Β είναι τα σηµεία επαφής, να βρείτε Τις εξισώσεις των εφαπτόµενων Τις συντεταγµένες των
2 ΕΥΘΕΙΑ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ
 ΕΥΘΕΙΑ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να βρείτε τον συντελεστή διεύθυνσης μιας ευθείας ε, που σχηματίζει με τον άξονα x x γωνία: π 3 α) ω = β) ω = γ) ω = π 3. Να βρείτε τη γωνία ω που σχηματίζει με
ΕΥΘΕΙΑ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να βρείτε τον συντελεστή διεύθυνσης μιας ευθείας ε, που σχηματίζει με τον άξονα x x γωνία: π 3 α) ω = β) ω = γ) ω = π 3. Να βρείτε τη γωνία ω που σχηματίζει με
2 Ο ΚΕΦΑΛΑΙΟ Ενότητα 5.
 Ευθεία Ο ΚΕΦΑΛΑΙΟ Ενότητα 5. Εξίσωση γραμμής Συντελεστής διεύθυνσης ευθείας Συνθήκες καθετότητας και παραλληλίας ευθειών Εξίσωση ευθείας ειδικές περιπτώσεις Σχόλιο Το σημείο είναι ο θεμελιώδης λίθος της
Ευθεία Ο ΚΕΦΑΛΑΙΟ Ενότητα 5. Εξίσωση γραμμής Συντελεστής διεύθυνσης ευθείας Συνθήκες καθετότητας και παραλληλίας ευθειών Εξίσωση ευθείας ειδικές περιπτώσεις Σχόλιο Το σημείο είναι ο θεμελιώδης λίθος της
ΜΕΘΟΔΙΚΗ ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ Β ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΔΙΑΝΥΣΜΑΤΑ ΜΕΘΟΔΙΚΗ ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ Β ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1) Δίνονται διανύσματα α και β, με α π = 4 και (α, β ) = 3 Αν ισχύει ότι το α (α + 2β ) = 28, να βρείτε: α) το εσωτερικό γινόμενο α β, β) το μέτρο
ΔΙΑΝΥΣΜΑΤΑ ΜΕΘΟΔΙΚΗ ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ Β ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1) Δίνονται διανύσματα α και β, με α π = 4 και (α, β ) = 3 Αν ισχύει ότι το α (α + 2β ) = 28, να βρείτε: α) το εσωτερικό γινόμενο α β, β) το μέτρο
3.5 ΣΧΕΤΙΚΗ ΘΕΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΚΩΝΙΚΗΣ
 1 3.5 ΣΧΕΤΙΚΗ ΘΕΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΚΩΝΙΚΗΣ ΘΕΩΡΙΑ 1. Σχετική θέση ευθείας και κωνικής τοµής Έστω η ευθεία ε : y = λx + β και µία κωνική τοµή C µε εξίσωση την φ(x, y) =. Το πλήθος των κοινών σηµείων της ε και
1 3.5 ΣΧΕΤΙΚΗ ΘΕΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΚΩΝΙΚΗΣ ΘΕΩΡΙΑ 1. Σχετική θέση ευθείας και κωνικής τοµής Έστω η ευθεία ε : y = λx + β και µία κωνική τοµή C µε εξίσωση την φ(x, y) =. Το πλήθος των κοινών σηµείων της ε και
( )( ) ( )( ) Βασικές γνώσεις A 2
 Βασικές γνώσεις Ευθεία που τέµνει τους άξονες : yλx+β. Ευθεία που διέρχεται από την αρχή των αξόνων : yλx. Ευθεία παράλληλη στον άξονα x x και τέµνει τον y y στο (0, y 0 ) : y y0. Ευθεία παράλληλη στον
Βασικές γνώσεις Ευθεία που τέµνει τους άξονες : yλx+β. Ευθεία που διέρχεται από την αρχή των αξόνων : yλx. Ευθεία παράλληλη στον άξονα x x και τέµνει τον y y στο (0, y 0 ) : y y0. Ευθεία παράλληλη στον
ΘΕΜΑ 1. Α. Να δείξετε ότι η ευθεία ε: αx + βy + γ = 0, ( α + β 0), είναι παράλληλη στο. (Μονάδες: 5) Β. ΣΩΣΤΟ ΛΑΘΟΣ
 Ε4 ΘΕΜΑ 1 Α. Να δείξετε ότι η ευθεία ε: αx + βy + γ = 0, ( α + β 0), είναι παράλληλη στο δ = ( β, α). (Μονάδες: 5) Β. ΣΩΣΤΟ ΛΑΘΟΣ 1. Η απόσταση του 0(0,0) από την x + y + = 0 είναι.. Η εξίσωση y = xy παριστάνει
Ε4 ΘΕΜΑ 1 Α. Να δείξετε ότι η ευθεία ε: αx + βy + γ = 0, ( α + β 0), είναι παράλληλη στο δ = ( β, α). (Μονάδες: 5) Β. ΣΩΣΤΟ ΛΑΘΟΣ 1. Η απόσταση του 0(0,0) από την x + y + = 0 είναι.. Η εξίσωση y = xy παριστάνει
Μαθηματικά Προσανατολισμού Β Λυκείου Ασκήσεις από την Τράπεζα θεμάτων Ευθεία Εξίσωση ευθείας
 Μαθηματικά Προσανατολισμού Β Λυκείου Ασκήσεις από την Τράπεζα θεμάτων Ευθεία - 1-1. 2-18575 Εξίσωση ευθείας Δίνονται τα σημεία Α(1,2) και Β (5,6 ). α) Να βρείτε την εξίσωση της ευθείας που διέρχεται από
Μαθηματικά Προσανατολισμού Β Λυκείου Ασκήσεις από την Τράπεζα θεμάτων Ευθεία - 1-1. 2-18575 Εξίσωση ευθείας Δίνονται τα σημεία Α(1,2) και Β (5,6 ). α) Να βρείτε την εξίσωση της ευθείας που διέρχεται από
ΚΕΦΑΛΑΙΟ 2 Ο ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ
 Σχδίαση μ τη χρήση Η/Υ ΚΕΦΛΙ 2 ΓΕΩΜΕΤΡΙΚΕΣ ΚΤΣΚΕΥΕΣ ΔΡ ΛΕΩΝΙΔΣ ΝΘΠΥΛΣ, ΕΠΙΚΥΡΣ ΚΘΗΓΗΤΗΣ ΤΜΗΜ ΔΙΙΚΗΣΗΣ ΚΙ ΔΙΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΡΙΣΣ Θέμα 16 ο : αρμονική σωτρική ρική διαίρση υθύγραμμου τμήματος σ λόγο
Σχδίαση μ τη χρήση Η/Υ ΚΕΦΛΙ 2 ΓΕΩΜΕΤΡΙΚΕΣ ΚΤΣΚΕΥΕΣ ΔΡ ΛΕΩΝΙΔΣ ΝΘΠΥΛΣ, ΕΠΙΚΥΡΣ ΚΘΗΓΗΤΗΣ ΤΜΗΜ ΔΙΙΚΗΣΗΣ ΚΙ ΔΙΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΡΙΣΣ Θέμα 16 ο : αρμονική σωτρική ρική διαίρση υθύγραμμου τμήματος σ λόγο
3.3 Η ΕΛΛΕΙΨΗ. 2. Άµεση συνέπεια (ΜΕ ) + (ΜΕ) = 2α Ο γ.τ του σηµείου Μ είναι έλλειψη µε εστίες Ε και Ε. Περιορισµός : Αν ( ΕΕ ) = 2γ, πρέπει γ < α
 3.3 Η ΕΛΛΕΙΨΗ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµ έλλιψη µ στίς τ σηµί Ε ι Ε, το γωµτριό τόπο των σηµίων του πιπέδου των οποίων το άθροισµ των ποστάσων πό τ Ε ι Ε ίνι στθρό ι µγλύτρο του Ε Ε.. Άµση συνέπι (ΜΕ )
3.3 Η ΕΛΛΕΙΨΗ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµ έλλιψη µ στίς τ σηµί Ε ι Ε, το γωµτριό τόπο των σηµίων του πιπέδου των οποίων το άθροισµ των ποστάσων πό τ Ε ι Ε ίνι στθρό ι µγλύτρο του Ε Ε.. Άµση συνέπι (ΜΕ )
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο
 . ΣΥΝΤΕΤΑΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο ΘΕΩΡΙΑ. Άξονας (Ο, i ) λέγεται κάθε ευθεία εφοδιασµένη µε αρχή Ο και µοναδιαίο διάνυσµα i.. Τετµηµένη σηµείου Μ που ανήκει σε άξονα (Ο, i ) λέγεται ο αριθµός, για τον οποίο ισχύει
. ΣΥΝΤΕΤΑΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο ΘΕΩΡΙΑ. Άξονας (Ο, i ) λέγεται κάθε ευθεία εφοδιασµένη µε αρχή Ο και µοναδιαίο διάνυσµα i.. Τετµηµένη σηµείου Μ που ανήκει σε άξονα (Ο, i ) λέγεται ο αριθµός, για τον οποίο ισχύει
= π 3 και a = 2, β =2 2. a, β
 1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 x και y = - λx είναι κάθετες
 Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
( ) y ) άγνωστη συνάρτηση, f (, )
 6. Ι ΙΑΣΑΑ ΠΡΟΒΛΗΜΑΑ ΣΥΝΟΡΙΑΚΝ ΙΜΝ 6. Πρόβληµατα πδίου σ διαστάσις Η νότητα αυτή αναφέρται σ προβλήµατα πδίου, όπου άγνωστη συνάρτηση ίναι µία βαθµωτή συνάρτηση. α προβλήµατα αυτά έχουν σηµαντικές φαρµογές
6. Ι ΙΑΣΑΑ ΠΡΟΒΛΗΜΑΑ ΣΥΝΟΡΙΑΚΝ ΙΜΝ 6. Πρόβληµατα πδίου σ διαστάσις Η νότητα αυτή αναφέρται σ προβλήµατα πδίου, όπου άγνωστη συνάρτηση ίναι µία βαθµωτή συνάρτηση. α προβλήµατα αυτά έχουν σηµαντικές φαρµογές
ΜΑΘΗΜΑ 8. B 2.3 Χρησιµοποιώντας Ευκλείδεια Γεωµετρία
 ΜΑΘΗΜΑ 8. B.3 Χρησιµοποιώντας Ευκλείδεια Γεωµετρία Θεωρία Ασκήσεις γ. τόπου και µεγιστο ελάχιστου Στις ασκήσεις αυτού του µαθήµατος χρησιµοποιούµε ανισωτικές σχέσεις από την Ευκλείδεια Γεωµετρία. Θυµίζουµε
ΜΑΘΗΜΑ 8. B.3 Χρησιµοποιώντας Ευκλείδεια Γεωµετρία Θεωρία Ασκήσεις γ. τόπου και µεγιστο ελάχιστου Στις ασκήσεις αυτού του µαθήµατος χρησιµοποιούµε ανισωτικές σχέσεις από την Ευκλείδεια Γεωµετρία. Θυµίζουµε
β = (9, x) να είναι ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια ( ) ΤΑΞΗ...Β ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΣΗΣ...
 Αµυραδάκη 0, Νίκαια (104903576) ΝΟΕΜΒΡΙΟΣ 01 ΘΕΜΑ 1 ο i) Αν Α( x 1, y 1 ) και Β(x, y ) δυο σηµεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγµένες του µέσου Μ του ΑΒ, να αποδείξετε ότι : x 1 + x x
Αµυραδάκη 0, Νίκαια (104903576) ΝΟΕΜΒΡΙΟΣ 01 ΘΕΜΑ 1 ο i) Αν Α( x 1, y 1 ) και Β(x, y ) δυο σηµεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγµένες του µέσου Μ του ΑΒ, να αποδείξετε ότι : x 1 + x x
ΚΩΝΙΚΕΣ ΤΟΜΕΣ. Κεφάλαιο 4ο: Ερωτήσεις του τύπου «Σωστό - Λάθος» k R
 Κεφάλαιο 4ο: ΚΩΝΙΚΕΣ ΤΟΜΕΣ Α. ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. * Η εξίσωση ( x x ) + ( y y ) = k, k R είναι πάντοτε εξίσωση κύκλου. o o. * Η εξίσωση x + y + Ax + By + Γ = 0 παριστάνει κύκλο
Κεφάλαιο 4ο: ΚΩΝΙΚΕΣ ΤΟΜΕΣ Α. ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. * Η εξίσωση ( x x ) + ( y y ) = k, k R είναι πάντοτε εξίσωση κύκλου. o o. * Η εξίσωση x + y + Ax + By + Γ = 0 παριστάνει κύκλο
Σημειώσεις Μαθηματικών 1
 Σημειώσεις Μαθηματικών 1 Αναλυτική Γεωμετρία Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 4 Αναλυτική Γεωμετρία 4.1 Εξίσωση Καμπύλης Έστω C μια καμπύλη στο R. H C αποτελείται από άπειρα σημεία Μ(x,y). Έξίσωση μιας
Σημειώσεις Μαθηματικών 1 Αναλυτική Γεωμετρία Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 4 Αναλυτική Γεωμετρία 4.1 Εξίσωση Καμπύλης Έστω C μια καμπύλη στο R. H C αποτελείται από άπειρα σημεία Μ(x,y). Έξίσωση μιας
1 η δεκάδα θεµάτων επανάληψης
 1 1 η δεκάδα θεµάτων επανάληψης 1. Α. Έστω α = (x 1, y 1 ) και β = (x, y ) δύο διανύσµατα Να γράψετε την αναλυτική έκφραση του εσωτερικού γινοµένου τους i Αν τα διανύσµατα δεν είναι παράλληλα προς τον
1 1 η δεκάδα θεµάτων επανάληψης 1. Α. Έστω α = (x 1, y 1 ) και β = (x, y ) δύο διανύσµατα Να γράψετε την αναλυτική έκφραση του εσωτερικού γινοµένου τους i Αν τα διανύσµατα δεν είναι παράλληλα προς τον
ΜΑΘΗΜΑΤΟΣ & ΕΡΓΑΣΙΑΣ
 ΦΥΛΛΟ ΓΕΩΜΕΤΡΙΑ ΜΑΘΗΜΑΤΟΣ & ΕΡΓΑΣΙΑΣ Α ΕΠΑΛ ΚΕΦΑΛΑΙΟ 4 4.1, 4., 4.3, 4.4, 4.5 Παράλληλς υθίς ΤΕΜΝΟΥΣΑ ΔΥΟ ΕΥΘΕΙΩΝ Ο γίς α, δ, ζ, η λέγοα ός Ο γίς β, γ,, θ λέγοα κός Δύο γίς που βρίσκοα προς ο ίδο μέρος
ΦΥΛΛΟ ΓΕΩΜΕΤΡΙΑ ΜΑΘΗΜΑΤΟΣ & ΕΡΓΑΣΙΑΣ Α ΕΠΑΛ ΚΕΦΑΛΑΙΟ 4 4.1, 4., 4.3, 4.4, 4.5 Παράλληλς υθίς ΤΕΜΝΟΥΣΑ ΔΥΟ ΕΥΘΕΙΩΝ Ο γίς α, δ, ζ, η λέγοα ός Ο γίς β, γ,, θ λέγοα κός Δύο γίς που βρίσκοα προς ο ίδο μέρος
Ο κύκλος με κέντρο την αρχή των αξόνων και ακτίνα ρ έχει εξίσωση: B,- 2 A 2
 3 0 ΛΥΚΕΙΟ ΚΕΡΑΤΣΙΝΙΟΥ Λ. ΒΟΥΛΓΑΡΗ ΜΑΘΗΜΑΤΙΚΟΣ ΚΥΚΛΟΣ Κύκλος είναι ο γεωμετρικός τόπος των σημείων του επιπέδου που απέχουν σταθερή απόσταση από ένα σταθερό σημείο του επιπέδου αυτού. Το σταθερό σημείο
3 0 ΛΥΚΕΙΟ ΚΕΡΑΤΣΙΝΙΟΥ Λ. ΒΟΥΛΓΑΡΗ ΜΑΘΗΜΑΤΙΚΟΣ ΚΥΚΛΟΣ Κύκλος είναι ο γεωμετρικός τόπος των σημείων του επιπέδου που απέχουν σταθερή απόσταση από ένα σταθερό σημείο του επιπέδου αυτού. Το σταθερό σημείο
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
: y=x+3, εξίσωση διαµέσου µ. : y= 2x+3 και κορυφή Β(4,1). Να προσδιορίσετε τις κορυφές Α και Γ του τριγώνου y= x+ 7 7 και y= 7x 5 αντίστοιχα.
 Κεφάλαιο ο : Η ευθεία στο επίπεδο Θέµατα «Ανάπτυξης» Να βρείτε τις εξισώσεις των πλευρών τριγώνου ΑΒΓ του οποίου η κορυφή Α έχει συντεταγµένες (,5) και οι διάµεσοι ΒΕ και ΓΖ έχουν εξισώσεις x 4y + = 0
Κεφάλαιο ο : Η ευθεία στο επίπεδο Θέµατα «Ανάπτυξης» Να βρείτε τις εξισώσεις των πλευρών τριγώνου ΑΒΓ του οποίου η κορυφή Α έχει συντεταγµένες (,5) και οι διάµεσοι ΒΕ και ΓΖ έχουν εξισώσεις x 4y + = 0
Λέγεται κάθε προσανατολισμένη ευθεία x x στην οποία ορίζουμε ως αρχή ένα σημείο. Ο και το μοναδιαίο διάνυσμα i ( i = 1)
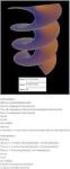 α.. Άξονας Λέγεται κάθε προσανατολισμένη ευθεία στην οποία ορίζουμε ως αρχή ένα σημείο Ο και το μοναδιαίο διάνυσμα i ( i 1). Ο i I Οι ημιευθείες Ο και O λέγονται αντίστοιχα θετικός ημιάξονας και αρνητικός
α.. Άξονας Λέγεται κάθε προσανατολισμένη ευθεία στην οποία ορίζουμε ως αρχή ένα σημείο Ο και το μοναδιαίο διάνυσμα i ( i 1). Ο i I Οι ημιευθείες Ο και O λέγονται αντίστοιχα θετικός ημιάξονας και αρνητικός
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ
 ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Β MΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α Α1. Αν Α(x 1, y 1 ) και Β(x, y ) είναι σημεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγμένες
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Β MΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α Α1. Αν Α(x 1, y 1 ) και Β(x, y ) είναι σημεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγμένες
ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΕΥΘΕΙΑ Β ΛΥΚΕΙΟΥ. i) Μία ευθεία με συντελεστή διεύθυνσης ίσο με το μηδέν, θα είναι παράλληλη στον άξονα των y.
 ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΕΥΘΕΙΑ Β ΛΥΚΕΙΟΥ Θέμα Α. Να αποδείξετε ότι ο συντελεστής διεύθυνσης ευθείας στο επίπεδο της μορφής x y 0, με 0, 0 θα δίνεται από τον τύπο. ( μονάδες) Β. Να γράψετε τους τύπους του εμβαδού
ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΕΥΘΕΙΑ Β ΛΥΚΕΙΟΥ Θέμα Α. Να αποδείξετε ότι ο συντελεστής διεύθυνσης ευθείας στο επίπεδο της μορφής x y 0, με 0, 0 θα δίνεται από τον τύπο. ( μονάδες) Β. Να γράψετε τους τύπους του εμβαδού
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2004 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Α ίνονται τα διανύσµατα α και β, τα οποία δεν είναι παράλληλα προς τον άξονα y y και έχουν συντελεστές διεύθυνσης λ και λ αντίστοιχα
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Α ίνονται τα διανύσµατα α και β, τα οποία δεν είναι παράλληλα προς τον άξονα y y και έχουν συντελεστές διεύθυνσης λ και λ αντίστοιχα
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ
 6ο κεφάλαιο: Συναρτήσεις ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Copyright 2014 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoo.com άδεια χρήσης 3η Εκδοση, Αύγουστος 2014 Περιεχόµενα
6ο κεφάλαιο: Συναρτήσεις ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Copyright 2014 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoo.com άδεια χρήσης 3η Εκδοση, Αύγουστος 2014 Περιεχόµενα
