БИЕ ДААЛТЫН БОДЛОГО Цалин Татвар 10.
|
|
|
- Ναβαδίας Οικονόμου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 БИЕ ДААЛТЫН БОДЛОГО. ax bx c 0 квадрат тэгшитгэлийн бодит шийдийг олох алгоритм зохиох. Хэрэв төсвийн байгууллагын ажилтан нь доорхи хүснэгтэнд өгсөн цалинтай бол татварыг тооцох программ зохио. Цалин Татвар 5000 хүртэлх 3% 0000 хүртэлх 5% 5000 хүртэлх 8% 5000-аас дээш 0% 3. Улам (Ulam)-ын дарааллыг хэвлэх программ зохио. Уламын дараалал нь - Xэрэв тухайн бүхэл тоо нь тэгш тоо бол дараагийн тоо нь түүний хагас байна. - Хэрэв а нь сондгой бол дараагийн тоо нь 3а+ байна. - Дараалал нь гэсэн утгыг авбал дуусна. 4. Гурвалжны оройг (x,y ), (x,y ), (x 3,y 3 ) координатаар өгөгдсөн бол гурвалжны периметр, талбайг тодорхойлох. 5. Хоѐр тоо өгөгджээ. Хэрэв -р нь -р тооноос бага буюу тэнцүү бол -р тоог нойллох эсрэг тохиолдолд өөрчлөлтгүй үлдээх 6. Банкинд төгрөгийг сар бүр 3%-ийн хүүтэй хадгалуулбал хэдэн сарын дараа хоѐр дахин өсөх вэ? 7. Y=+/+/4+/8+/ цувааны нийлбэрийг нарийвчлал тай тодорхойлох 8. Үнээ 0 төгрөг, бяруу 5 төгрөг, тугал төгрөгийн үнэтэй бол 00 төгрөгт хэдэн үнээ, бяруу, тугал худалдаж авч болох вэ? 9. Өгсөн тооны хамгийн их хуваагчийг олох. 0.!+!+3!+...n!-ыг тодорхойлох программ зохиох.
2 . a тодорхойлох. y x x x 4 8 x... x 56 x утгыг өгөгдсөн Х-ийн хувьд тодорхойлох. 3. Х i, С i =(,,3 n) хэмжилтийн утгаар М ба D-г тодорхойлох программ зохиох. M n n x ; D n i i n ( X M ) 4.Цифрийн квадратын нийлбэр нь 5-д хуваагддаг гурван оронтой хичнээн тоо байх вэ? 5. Өгөгдсөн А бүхэл тоо хэдэн оронтой вэ? 6. Өгөгдсөн тэмдэгт мөрөнд байгаа ижил тэмдгийн тоог тодорхойлох. 7. Өгөгдсөн тэмдэгт мөрөөс зай үлдээх тэмдгийг зайлуулж шахах 8. N хүртэлх тооноос анхны тоонуудыг тодорхойлох. 9. а,а,а 3...а n- ын нийлбэрийг олох. S n a i i 0. а,а,а 3...а n -аас -оос их 5-аас бага утгуудын тоог олох.. Квадрат матрицын гол диагоналиас доошхи элементүүдээс хамгийн бага утгыг тодорхойлох. Тэгш өнцөгт матрицын мөр бүрээс хамгийн их утгыг олж, эдгээрээс хамгийн бага утгыг тодорхойлох.
3 3. Квадрат матрицын гол ба эсрэг диагоналын элементүүдийг хооронд байраар нь солих программ зохио. 4.A(N,N), B(N,N) матрицын нийлбэрийг олох. 5. A(N,N) матрицын гол диагоналын элементүүдийн нийлбэр тодорхойлох. 6. A(N,N) матрицын эсрэг диагоналын элементүүдээс хамгийн их утгатай (max) элементийг тодорхойлох. 7. A(n,n) матрицын гол диагнолаас дээшхи элементийн нийлбэр олох 8. Хавтгай дээр (х i,у i ) координаттай n ширхэг цэг өгөгджээ.эдгээр цэгүүдийн хоорондох зай нь хамгийн бага цэгийг координатын хамт тодорхойлох. 9. Автобусны билет 4 оронтой номертой (abcd). Азтай билет хичнээн ширхэг байх вэ? (a+b=c+d). 30. А матриц хөрвүүлэх /транспирование/ 3. S n... язгуур тодорхойлох 3. а 0,а,а...а n коэффициентууд өгөгдсөн бол х-ийн тодорхой утганд y=а n,x n +a n- x n a x+a 0 полиномын утгыг тодорхойлох. 33. Урт настан (00-аас дээш) тэрний насны цифрийн квадратын нийлбэр дээр түүний төрсөн өдрийг нэмбэл (-3) түүний нас гардагийг олжээ. Хичнээн настай вэ? 34. Тэмдэгт мөрөөс зай үлдээх тэмдгийг зайлуулж шахах программ зохиох. Тэмдгийн дараалал хэвээр үлдээнэ. 35. Өгсөн 3 оронтой тооны хамгийн их утгатай цифрийг тодорхойлох алгоритм зохиох
4 .Долоо хоногийн гаригуудыг оролцуулсан өгөгдлийн тоочих төрлийг үүсгэн ашиглах программ зохио.. Хоѐр хэмжээст хоѐр матрицыг үржүүлэх программ зохио. 3. Тэмдэгт мөрөөс өгөгдсөн тэмдэгтийг хайн байрлалыг буцаах функц бүхий программ зохио. 4.Ангийн оюутнуудын рейтингийн оноог бодох функц бүхий программыг бүтэц ашиглан зохио. Ангийн дундаж оноо, хамгийн өндөр оноотой оюутанг тус тус ол. 5. Шатрын хөлгийг морины нүүдлээр дүүрэг. 6. Өгөгдсөн 3 оронтой тооны цифрүүдийн нийлбэрийг олох программ зохио. 7. Х секунд өгөгдөв. Түүнийг цаг, минут, секундэд шилжүүлэх программ зохио. 8.Өгөгдсөн 4 оронтой тооны цифрүүдийн ихийг ол. 9.Гурван оронтой тоонуудаас М-д хуваагдах тоо хэд байгааг ол. 0.Өгөгдсөн 3 оронтой тоонуудын цифрүүдийг өсөх эрэмбээр эрэмбэлсэн тоог хэвлэ..гуравдугаар эрэмбийн тодорхойлогч бод..гауссын аргыг программчил. 3.А,В бүхэл тоо өгөгдөв. А-ын В зэрэгтийг олох программ зохио. 4.А-аас В хүртэлх тоон завсар орших тоонуудын нийлбэрийг ол. 5.А,В,С талуудтай хайрцаг Х, Ү талуудтай цонхоор багтах уу олох программ зохио олох программ зохио 8. cosx+cosx +cosx 3 + cosx 30 Нийлбэрийг ол 9.!+!+3!+...n! нийлбэрийг ол. 0.А,В,С,D гэсэн бүхэл тоо өгч дараах хуулиар эхний гурван тонуудыг өөрчлөөд байя. Хэдийд D тоо гарах вэ?. (a,b,c) (a+b,b+c,c+a).өгсөн 3 оронтой тооны хөрвөсөн тоог ол. 3 3.Өөрийнхөө бүх цифрт хуваагддаг 3 оронтой тоо хэд байгааг тоол. 3.Хоѐр бүхэл тооны ХИЕХ-ийг ол. 4.Өгөгдсөн үгэнд А үсэг хэд орсныг тоол.
5 5.Өгөгдсөн өгүүлбэрийн хамгийн урт үгийг ол. 6.А(N,M) массиваас хамгийн их элементийг олж байрыг заа. 7.Хэсэглэл бодох программ зохио. Өгөгдсөн өгүүлбэр хэдэн үгтэй болохыг ол. 8.Шугаман хүснэгтэд өгөгдсөн тоо хэд орсныг тоолох программ зохио. 9.-М хүртэлх тоонудаас квадратуудын нийлбэрт тавигдах тоо хэд байна вэ? 30.5&6? Илэрхийллийн үр дүнг ол &&9=? 5 8=? a=8<<
6 . Бодит А,В,С тоонууд өгөгджээ. Эдгээр тоонууд а в с нөцлийг хангаж байвал утгыг нь дахин нэмэгдүүл, биелэгдэхгүй бол абсолют утгаар нь сольж хэвлэ.. Х,Ү ялгаатай бүхэл тонууд өгөгджээ. Энэ хоѐр тооны багыг нь нийлбэрийнх нь хагасаар, ихийг нь дахин үржүүлсэн үржвэрээр сольж хэвлэ..3 N натураль тоо өгөгджээ. (N 00) a) N тоо хэдэн цифртэй вэ? Б) түүний цифрийн нийлбэр хэд вэ? В) N тооны сүүлчийн цифрийг ол Г) N тооны эхний хоѐр цифрийн нийлбэрийг ол..4 Өгсөн 3 оронтой дурын тооны цифрүүдийг өсөхөөр эрэмбэл..5 Хэрэв Х,Ү,Z ялгаатай хос бодит тоонуудын хос хосоор олсон нийлбэрийн утга нэгээс бага бол эдгээр нийлбэрүүдийн хамгийн ихийг үлдсэн хоѐрын нийлбэрийн хагасаар соль, эсрэг тохиолдолд Х ба Ү-ийн нийлбэрийн хагасаар үлдсэн хоѐр нийлбэрийг сольж хэвлэ..6 N натураль тоо өгөгджээ. (n>=00) N тоог хүний нас гэж үзвэл N тооны утгад год, года, лет -ийн аль нь тохирох вэ? Жишээ нь: год, 3 года, 45 лет n тоо өгөгдөв. (n>=99) n нь n тооны цифрүүдийн нийлбэрийн кубтэй тэнцэх үү?.8. Х гэсэн бодит тоо өгөгджээ. F(x) функцийн утгыг дараахь нөхцөлүүдийн хувьд а) f(x)={- x< бол х эсрэг тохиолдолд б) f(x)={х бол х +4х+5 эсрэг тохиолдолд в) f(x)={х бол 0 эсрэг тохиолдолд х -sinπх г) f(x)={x 0 бол 0 эсрэг тохиолдолд x 4.9. h-бодит тоо өгөгджээ. ax +bx+c=0 Тэгшитгэлийн бодит шийд дараахь утгуудын хувьд орших уу? Хэрэв бодит шийдтэй бол тэдгээрийг ол, эсрэг тохиолдолд шийдгүй гэсэн мэдээлэл хэвлэ..0 Дурын бүхэл тоо К өгөгджээ. К-ын утга [,3] интервалд орших уу?
7 . Өгөгдсөн тоо нь L нь сарыг төлөөлсөн утга бол жилийн дөрвөн улиралын алинд багтах вэ?, Дурын бүхэл тоо Р өгөгдсөн. Хэрэв Р нь ) оронтой бол уг тоонуудын цифрүүдийн квадратын нийлбэрийг )3 оронтой бол цифрүүдийн нийлбэрийн кубыг 3)4 оронтой бол цифрүүдийн геометр дундажийг ол..3 -ээс 5 хүртэлх тоог Ром тоогоор илэрхийл..4 Q, W эерэг бүхэл тоонуудын хувьд хамгийн их ерөнхий хуваагч байгаа эсэхийг олдог Евклидийн алгоритм. М ба N тоонууд нь сөрөг биш, тэгтэй тэнцүү биш бөгөөд M>N нөхцлийг хангаж байвал: Хэрэв n=0 бол XUEX(n,m), харин n=0 бол XUEX(m,n), XUEX(n,r) нөхцөл хангагдах ѐстой. R нь М-ийг N-д хуваахад гарах үлдэгдэл. Жишээ: XUEX(5.6)-XUEX(6.3)=3. Дурын M,N тооны хувьд XUEX-ийг Евклидийн алгоритмаар ол..5 Дараахь st хувьсагчид байгаа утгуудыг сар хувьсагчид байгаа харгалзах утгуудад олгож хэвлэ. Type улс=(австри, Болгар, Грек, Итали, Норвеги, Франц); Нийслэл=(Вена, Софи, Афин, Рим, Осло, Париж, Бонн);.6 Эртний Японы хуанлид жилийн 5 дэд давталт бүхий 60 жилийн давталт хэрэглэгддэг байжээ. Дэд давталтууд нь Ногоон, Улаан, Шар, Цагаан ба Хар гэсэн өнгөөр илэрхийлэгддэг байв. Дэд давталт бүрийн жилүүд нт Хулгана, Үхэр, бар, туулай, луу, могой, Морь, Хонь, Бич, Тахиа, Нохой ба гахай гэж нэрлэгддэг. (984 он бол ногоон хулгана жил байсан бөгөөд давталтын эхлэл байв) он хүртэлх хуцгацааны оныг оруулахад тухайн жилийн нэрийг Японы эртний хуанлийн нэрээр хэвлэн гаргадаг программ бич..7 К тоо нь бодит тоо бөгөөд уг тоонд ойролцоо орших утгыг, уг тооны бутархай хэсгийг ялган авч модулийг нь олж тэгш сондгойг тодорхойл..8 Гурван оронтой бүх тоонууд дотроос өгөгдсөн дурын К тоонд хуваагдах хэдэн ширхэг ямар тоонууд байгааг ол. Илэрхийллийн утгыг ол..9 Зуугийн факториалын сүүлчийн 3 цифрийг хэвлэ.0 A,N дурын бүхэл тоо өгөгдөв. -с N хүртэлх тоонууд дотор A=x! байх Х тоо олдох уу?
8 N=00 үед илэрхийллийн утгыг ол. а,в гэсэн нэг хэмжээст массивын ижил индекстэй элементүүдээс хоорондоо ялгаатай элемент байвал тоонийг олох. Массивын элемент дээр ердийн хувьсагч шиг арифметик үйлдэл хийж болно. +,/,*,- дэрэг үйлдлүүдийг. Мөн нэг массивын утгыг нөгөөд олгож болно..3 Тогтмол Х,Ү гэсэн хэмжээст массив өгөгдсөн бол массивын харгалзах элементүүдийг хооронд нь нэмж шинэ массив үүсгэх..4 A(N)-д К-тай хамгийн ойр байх утгатай элементийг хэвлэж байрлалыг тодорхойл..5 A(N,N) өгөгдсөн бол массивын мөр тус бүрийн max олж тэдгээрийн дотроос min-ийг ол..6 Массивын мөр бүрийг эрэмбэл.7 Массивт 3<T<50 тоо хичнээн байгааг тоол..8 А,В квадрат матрицууд А-ийн maх-ийг олж, В-ийн min-ийг олоод уг min-ийн байранд maх-ийг байрлуул..9 Массивын к-р мөрийн элементүүдийг эрэмбэл..30 Массивын maх оршиж буй багана мөрийн элементүүдийн нийлбэрийг олж, ихийг нь тодорхойл..3 N урттай цувааны голын элемент уг цуваанд хичнээн удаа орсныг тоол..3 Өгөгдсөн үг нь палиндром эсэхийг шалга..33 Өгөгдсөн өгүүлбэр дотроос тэгш урттай тоотой үгнүүдийг хэвлэх..34 N,M натурал тоонууд өгөгдсөн цифрүүдийн нийлбэрийн квадрат нь м-тэй тэнцэх, n-ээс хэтрэхгүй бүх натурал тоог ол..35 Эхний цифрийн нийлбэр нь сүүлийн цифрийн нийлбэртэй тэнцэх 4 оронтой бүх анхны тоог ол..36 Тоо өгөгдөхөд анхны тоо эсэхийг шалга..37 Квадрат нь цифрүүдийнхээ нийлбэрийн кубтэй тэнцэх бүх оронтой тоог ол..38 Нэг нь нөгөөгийнхөө бүх хуваагчуудын нийлбэртэй тэнцэх 3 оронтой хос тоонуудыг ол..39 A(N), B(N) гэсэн бодит тоон утга бүхий массив өгөгджээ. N<0, A,B массивын харгалзах элементүүдийг хооронд нь сольж программ зохио.
9 .40 N ба A,B-ийн утгыг шивүүр картнаас оруулж, өөрчлөлтийн өмнөх ба дараахи А,В массивын утгуудыг хэвлэж гаргах..4 A(N,N) массивын гол диагональ дээр элементүүдийн дотор ижил утгатай элемент байгаа эсэхийг шалга, байвал байрлалтай нь хэвлэ..4 3 ба 5-аас өөр анхны хуваагчгүй эхний 00 тоог өмөх эрэмбээр байрлуулах N,M натурал тоонууд өгөгджээ. Цифрүүдийн нийлбэрийн квадрат нь М-тэй тэнцэж, N-ээс хэтрэхгүй байх бүх натурал тоог олж хэвлэ..43 Эхний цифрийн нийлбэр нь сүүлийн цифрийн нийлбэртэй тэнцэх 4 оронтой бүх анхны тоог олж хэвлэ..44 Нэг нь нөгөөгийнхөө бүх хуваагчуудын нийлбэртэй тэнцэх 3 оронтой хос тоонууд ол..45 N натурал тоо өгөгджээ. Дараах илэрхийллүүдийг программчил. N натурал тоо өгөгджээ. А: n тоо хэдэн цифртэй вэ? Давталттай алгоритм Нэг ба хэд хэдэн үйлдлийг тодорхой тооны дотор буюу тодорхой нөхцөл биелэгдтэл давтан гүйцэтгэхийг давталтын алгоритм гэнэ. Давталттай алгоритмд. Давталтын параметр. Давталтын параметрийн эхлэлийн утга 3. Давталтын параметрийн төгсгөлийн утга 4. Давталтын параметрийн өөрчлөлтийн алхам гэсэн ойлголтуудыг хэрэглэдэг. Хэрэв давтах тоо нь тодорхой бус, давталтын өөрчлөлтийн алхам нь -ээс ялгаатай тохиолдолд нөхцөлтэй давталт гэж нэрлэдэг.
10 Хэрэв давтах тоо нь тодорхой бол параметртай давталт гэж нэрлэнэ. Харин давталтын тоо нь тодорхой бус, давталтын өөрчлөлтийн алхам нь -ээс ялгаатай тохиолдолд нөхцөлтэй давталт гэж нэрлэдэг. Жишээ. -N хүртлэх сондгой тоонуудын үржвэрийг олох алгоритм зохиоѐ.
11 сарын 7-нд етуяагийн т/одор
Шалгалтын бодлогуудын бодолтод øаардагдах çàðèì тоìüёо = = 7. 1 AB BC AC AB BC AC. цэгийг дайрсан шулууны тэгшитгэл = ХУВИЛБАР А
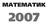 МАТЕМАТИК 007 Шалгалтын бодлогуудын бодолтод øаардагдах çàðèì тоìüёо Математикийн хичээлийн даалгавар - 007 (a + a n ) n. a ± b = ( a± b)( a ab+ b ). -í - S n =. b sin + = 4.. lim = 5. Виетиéн теорåм
МАТЕМАТИК 007 Шалгалтын бодлогуудын бодолтод øаардагдах çàðèì тоìüёо Математикийн хичээлийн даалгавар - 007 (a + a n ) n. a ± b = ( a± b)( a ab+ b ). -í - S n =. b sin + = 4.. lim = 5. Виетиéн теорåм
Шалгалтын бодлогуудын бодолтод øаардагдах çàðèì тоìüёо. (магадлалын сонгодог тодорхойлолт) AB = ( x x ) + ( y y ) ХУВИЛÁАР А ÍÝÃÄ ÃÝÝÐ ХЭСЭГ
 МАТЕМАТИК 006 Шалгалтын бодлогуудын бодолтод øаардагдах çàðèì тоìüёо Математикийн хичээлийн даалгавар - 006. 0 0 sin(90 - α )= cos α; cos α(90 - α )= sinα. { k } a арифметик прогресс бол (a + a n ) n
МАТЕМАТИК 006 Шалгалтын бодлогуудын бодолтод øаардагдах çàðèì тоìüёо Математикийн хичээлийн даалгавар - 006. 0 0 sin(90 - α )= cos α; cos α(90 - α )= sinα. { k } a арифметик прогресс бол (a + a n ) n
ШИНЖЛЭХ УХААН ТЕХНОЛОГИЙН ИХ СУРГУУЛЬ U.MT101-МАТЕМАТИК I ХИЧЭЭЛИЙН СЕМИНАРЫН ЗӨВЛӨМЖ он
 ШИНЖЛЭХ УХААН ТЕХНОЛОГИЙН ИХ СУРГУУЛЬ ХЭРЭГЛЭЭНИЙ ШИНЖЛЭХ УХААНЫ СУРГУУЛЬ U.MT-МАТЕМАТИК ХИЧЭЭЛИЙН СЕМИНАРЫН ЗӨВЛӨМЖ 5 он . КОМПЛЕКС ТОО, ТҮҮН ДЭЭР ХИЙХ ҮЙЛДЛҮҮД Жишээ. A i( + i) + (7 i) +i илэрхийллийг
ШИНЖЛЭХ УХААН ТЕХНОЛОГИЙН ИХ СУРГУУЛЬ ХЭРЭГЛЭЭНИЙ ШИНЖЛЭХ УХААНЫ СУРГУУЛЬ U.MT-МАТЕМАТИК ХИЧЭЭЛИЙН СЕМИНАРЫН ЗӨВЛӨМЖ 5 он . КОМПЛЕКС ТОО, ТҮҮН ДЭЭР ХИЙХ ҮЙЛДЛҮҮД Жишээ. A i( + i) + (7 i) +i илэрхийллийг
Бодолт: ( ) ,2
 46. AOB = 9, Rрадиустай секторын AO, OB хэрчмүүд болон AB нумыг шүргэсэн тойрог багтсан бол тойргийн радиусыг ол. Бодолт: MO = x, OO = OK OK OO = R x, OO M = 45 = OMO OM = OM = O K = x, x + Rx R = ( )
46. AOB = 9, Rрадиустай секторын AO, OB хэрчмүүд болон AB нумыг шүргэсэн тойрог багтсан бол тойргийн радиусыг ол. Бодолт: MO = x, OO = OK OK OO = R x, OO M = 45 = OMO OM = OM = O K = x, x + Rx R = ( )
8x100. 8x100. 8x100. 8x100
 1 ЭЕШ 01 A хувилбарын бодлого, бодолт 1-р хэсэг. 1. x = [1.6] =? x = [1.6] = 1. Хариу B. A. 13 B. 1 C. 1. D. 1 E. 13. 500000 тоог стандарт хэлбэрт бич. A. 500000 B. 0.5 10 7 C. 50 10 D. 5 10 5 E. 5. 10
1 ЭЕШ 01 A хувилбарын бодлого, бодолт 1-р хэсэг. 1. x = [1.6] =? x = [1.6] = 1. Хариу B. A. 13 B. 1 C. 1. D. 1 E. 13. 500000 тоог стандарт хэлбэрт бич. A. 500000 B. 0.5 10 7 C. 50 10 D. 5 10 5 E. 5. 10
Математикийн хичээлийн даалгавар. Эрхэм шалгуулагч танд амжилт хүсье.
 Эрхэм шалгуулагч танд амжилт хүсье. Шалгалтын бодлого бодоход ашиглагдах зарим томьёонууд: 1. Конусын хажуу гадаргуу нь SS х.г = ππ RR ll байна. Үүнд ll нь байгуулагч.. log aa kk bb = 1 kk log aa bb 3.
Эрхэм шалгуулагч танд амжилт хүсье. Шалгалтын бодлого бодоход ашиглагдах зарим томьёонууд: 1. Конусын хажуу гадаргуу нь SS х.г = ππ RR ll байна. Үүнд ll нь байгуулагч.. log aa kk bb = 1 kk log aa bb 3.
8x100. 8x100. 8x100. 8x100
 1 1-р хэсэг. Элсэлтийн ерөнхий шалгалт 016-С 1. 6 7 тооны урвуу тоог олоорой. A. 6 7 B. 7 6 C. 1 1 6 1 D. 6 7 1 E. 0.86 A нь A тооны эсрэг тоо. 1 тоо нь A тооны урвуу тоо юм. Иймд зөв хариу A нь 7 6 =11
1 1-р хэсэг. Элсэлтийн ерөнхий шалгалт 016-С 1. 6 7 тооны урвуу тоог олоорой. A. 6 7 B. 7 6 C. 1 1 6 1 D. 6 7 1 E. 0.86 A нь A тооны эсрэг тоо. 1 тоо нь A тооны урвуу тоо юм. Иймд зөв хариу A нь 7 6 =11
S.PH102 Физик-2. Семинар 7. Сэдэв : Квант механикийн үндэс, Атомын физик. Тест оны намар
 S.PH102 Физик-2 Семинар 7 Сэдэв : Квант механикийн үндэс, Атомын физик Тест 2015-2016 оны намар Физик -2 7.1 Устөрөгчийн атом фотон шингээсэн бол түүний электроны орбитын радиус............. А. Багасна.
S.PH102 Физик-2 Семинар 7 Сэдэв : Квант механикийн үндэс, Атомын физик Тест 2015-2016 оны намар Физик -2 7.1 Устөрөгчийн атом фотон шингээсэн бол түүний электроны орбитын радиус............. А. Багасна.
615 АВС гурвалжны багтаасан тойргийн төв нь О. ( А>90 ) AL биссектрисийн үргэлжлэл нь багтаасан тойргийг F цэгт огтолно. OA радиус ВС талыг Е цэгээр
 615 АВС гурвалжны багтаасан тойргийн төв нь О. ( А>90 ) AL биссектрисийн үргэлжлэл нь багтаасан тойргийг F цэгт огтолно. OA радиус ВС талыг Е цэгээр огтолно. АН нь уг гурвалжны өндөр ба АН AF3 ÐAEH30 бол
615 АВС гурвалжны багтаасан тойргийн төв нь О. ( А>90 ) AL биссектрисийн үргэлжлэл нь багтаасан тойргийг F цэгт огтолно. OA радиус ВС талыг Е цэгээр огтолно. АН нь уг гурвалжны өндөр ба АН AF3 ÐAEH30 бол
МАТЕМАТИК ХУВИЛБАР D. 8x100. 8x100. 8x100
 МАТЕМАТИК ХУВИЛБАР D ЭЛСЭЛТИЙН ЕРӨНХИЙ ШАЛГАЛТ - 07 МАТЕМАТИК ХУВИЛБАР D Хувилбар D - Математик. 0.5 бутархайг энгийн бутархай болгож бич. A. B. C. 40 4 5 0.5 = 5 00 = 4. A = 6 бол A =? D. 5 99 E. 5 90
МАТЕМАТИК ХУВИЛБАР D ЭЛСЭЛТИЙН ЕРӨНХИЙ ШАЛГАЛТ - 07 МАТЕМАТИК ХУВИЛБАР D Хувилбар D - Математик. 0.5 бутархайг энгийн бутархай болгож бич. A. B. C. 40 4 5 0.5 = 5 00 = 4. A = 6 бол A =? D. 5 99 E. 5 90
ТУХАЙН ДИФФЕРЕНЦИАЛТ ТЭГШИТГЭЛ. Contents Bibliography 11 References 11 Index 12
 ТУХАЙН ДИФФЕРЕНЦИАЛТ ТЭГШИТГЭЛ ҮҮЕЭ ОТГОНБАЯР Contents 1. 2 2. 5 3. 8 Bibliography 11 References 11 Index 12 Date: August 23, 2008. 1 2 ҮҮЕЭ ОТГОНБАЯР 1 Бид Nakhlé H. Asmar-ийн Partial Differential Equations
ТУХАЙН ДИФФЕРЕНЦИАЛТ ТЭГШИТГЭЛ ҮҮЕЭ ОТГОНБАЯР Contents 1. 2 2. 5 3. 8 Bibliography 11 References 11 Index 12 Date: August 23, 2008. 1 2 ҮҮЕЭ ОТГОНБАЯР 1 Бид Nakhlé H. Asmar-ийн Partial Differential Equations
Физикийн даалгавар 10-р анги оны хичээлийн жил Нэгдүгээр хэсэг (тест)
 Нэгдүгээр хэсэг (тест) Утгат оронг алдагдуулахгүй тооцоол. Тестийн дугаар 1 2 3 4 25.05+37.5= 54-22.4= 12 15.5 = 18.75 7.5 = A 62.55 31.6 186 2.5 B 62.5 31 190 2.50 C 62.6 32 180 3.0 D 63 30 186.0 2.0
Нэгдүгээр хэсэг (тест) Утгат оронг алдагдуулахгүй тооцоол. Тестийн дугаар 1 2 3 4 25.05+37.5= 54-22.4= 12 15.5 = 18.75 7.5 = A 62.55 31.6 186 2.5 B 62.5 31 190 2.50 C 62.6 32 180 3.0 D 63 30 186.0 2.0
S.PH101 ФИЗИК-1 ЛЕКЦ 13
 ЛЕКЦ 3 S.PH0 ФИЗИК- ПОТЕНЦИАЛ, ЦАХИЛГААН ОРНЫ ХҮЧЛЭГ БА ПОТЕНЦИАЛЫН ХОЛБОО, ЦАХИЛГААН ОРОН ДАХЬ ДАМЖУУЛАГЧ, ДАМЖУУЛАГЧ ДАХЬ ЦЭНЭГҮҮДИЙН ТЭНЦВЭР, ГАДНЫ ЦАХИЛГААН ОРОН ДАХЬ ДАМЖУУЛАГЧ, ЦАХИЛГААН БАГТААМЖ,
ЛЕКЦ 3 S.PH0 ФИЗИК- ПОТЕНЦИАЛ, ЦАХИЛГААН ОРНЫ ХҮЧЛЭГ БА ПОТЕНЦИАЛЫН ХОЛБОО, ЦАХИЛГААН ОРОН ДАХЬ ДАМЖУУЛАГЧ, ДАМЖУУЛАГЧ ДАХЬ ЦЭНЭГҮҮДИЙН ТЭНЦВЭР, ГАДНЫ ЦАХИЛГААН ОРОН ДАХЬ ДАМЖУУЛАГЧ, ЦАХИЛГААН БАГТААМЖ,
Тухайн Дифференциал Тэгшитгэл. Үүеэ Отгонбаяр
 Тухайн Дифференциал Тэгшитгэл Үүеэ Отгонбаяр Гарчиг Бүлэг 1. 1 Хичээл 1. 1 Хичээл 2. 4 Хичээл 3. 8 Хичээл 4. 11 Хичээл 5. 15 Бүлэг 2. 19 Хичээл 1. 19 Хичээл 2. 21 Ишлэл 23 Товъёг 25 iii БҮЛЭГ 1 Хичээл
Тухайн Дифференциал Тэгшитгэл Үүеэ Отгонбаяр Гарчиг Бүлэг 1. 1 Хичээл 1. 1 Хичээл 2. 4 Хичээл 3. 8 Хичээл 4. 11 Хичээл 5. 15 Бүлэг 2. 19 Хичээл 1. 19 Хичээл 2. 21 Ишлэл 23 Товъёг 25 iii БҮЛЭГ 1 Хичээл
ГУРАВДУГААР АЖИЛ Гэрлийн туйлшрал судлан Малюсын хуулийг шалгах
 ГУРАВДУГААР АЖИЛ Гэрлийн туйлшрал судлан Малюсын хуулийг шалгах Ажлын зорилго: Энэхүү ажлаар гэрлийн туйлшралын үзэгдэлтэй танилцан, туршлагаар Малюсын хуулийг шалгахад оршино. Хэрэглэгдэх багаж: Гэрэл
ГУРАВДУГААР АЖИЛ Гэрлийн туйлшрал судлан Малюсын хуулийг шалгах Ажлын зорилго: Энэхүү ажлаар гэрлийн туйлшралын үзэгдэлтэй танилцан, туршлагаар Малюсын хуулийг шалгахад оршино. Хэрэглэгдэх багаж: Гэрэл
S.МТ200 Математик Тооцооллын Үндэс
 Батлав: Математикийн салбарын эрхлэгч.................. /Д.Цэдэнбаяр/ 208-209 оны хичээлийн жил. I улиpал. Жишиг даалгавар. A ВАРИАНТ -Р ХЭСЭГ. arcsin(2x 3 илэрхийлэх кодыг сонго. S.МТ200 Математик Тооцооллын
Батлав: Математикийн салбарын эрхлэгч.................. /Д.Цэдэнбаяр/ 208-209 оны хичээлийн жил. I улиpал. Жишиг даалгавар. A ВАРИАНТ -Р ХЭСЭГ. arcsin(2x 3 илэрхийлэх кодыг сонго. S.МТ200 Математик Тооцооллын
АЖЛЫН СХЕМ 9 ДҮГЭЭР АНГИ
 АЖЛЫН СХЕМ 9 ДҮГЭЭР АНГИ Заавар III улирлын хувьд төлөвлөсөн төлөвлөгөө өөрчлөгдөж байна. Иймд гарын авлагад байгаа суралцахуйн зорилтоор ажлын схемээ ашиглана уу. 1 Бүлэг 1: Тоо тоолол ба алгебр Код Суралцахуйн
АЖЛЫН СХЕМ 9 ДҮГЭЭР АНГИ Заавар III улирлын хувьд төлөвлөсөн төлөвлөгөө өөрчлөгдөж байна. Иймд гарын авлагад байгаа суралцахуйн зорилтоор ажлын схемээ ашиглана уу. 1 Бүлэг 1: Тоо тоолол ба алгебр Код Суралцахуйн
11-р ангийн математикийн хөтөлбөр. 2-р хувилбар (2012/08/05)
 11-р ангийн математикийн хөтөлбөр -р хувилбар (01/08/05) Танилцуулга 11, 1 дугаар ангийн хөтөлбөр боловсруулах ажил болон сургалтын үеэр энэхүү материалыг ашиглана. 11 дүгээр ангийн Математик Хөтөлбөрийн
11-р ангийн математикийн хөтөлбөр -р хувилбар (01/08/05) Танилцуулга 11, 1 дугаар ангийн хөтөлбөр боловсруулах ажил болон сургалтын үеэр энэхүү материалыг ашиглана. 11 дүгээр ангийн Математик Хөтөлбөрийн
S.PH101 ФИЗИК-1 ЛЕКЦ 12
 ЛЕКЦ 12 S.PH101 ФИЗИК-1 ЦАХИЛГААН ЦЭНЭГ, КУЛОНЫ ХУУЛЬ, ЦАХИЛГААН ОРОН, ОРНЫ ХҮЧЛЭГ, СИСТЕМ ЦЭНЭГҮҮДИЙН ХАРИЛЦАН ҮЙЛЧЛЭЛ, ДИПОЛЬ, СИСТЕМ ЦЭНЭГҮҮДИЙН ОРНЫГ ХОЛ ЗАЙД ТООЦОХ, ЦАХИЛГААН СТАТИК ОРНЫ ЦИРКУЛЯЦ,
ЛЕКЦ 12 S.PH101 ФИЗИК-1 ЦАХИЛГААН ЦЭНЭГ, КУЛОНЫ ХУУЛЬ, ЦАХИЛГААН ОРОН, ОРНЫ ХҮЧЛЭГ, СИСТЕМ ЦЭНЭГҮҮДИЙН ХАРИЛЦАН ҮЙЛЧЛЭЛ, ДИПОЛЬ, СИСТЕМ ЦЭНЭГҮҮДИЙН ОРНЫГ ХОЛ ЗАЙД ТООЦОХ, ЦАХИЛГААН СТАТИК ОРНЫ ЦИРКУЛЯЦ,
МОНГОЛ КЕМБРИЖИЙН БОЛОВСРОЛЫН САНААЧИЛГА. Монголын ерөнхий боловсролын 12 жилийн сургуулийн 6 8 р ангийн математикийн хичээлийн хөтөлбөр
 1 МОНГОЛ КЕМБРИЖИЙН БОЛОВСРОЛЫН САНААЧИЛГА Монголын ерөнхий боловсролын 12 жилийн сургуулийн 6 8 р ангийн математикийн хичээлийн хөтөлбөр 2 ГАРЧИГ 1. 6 8 р ангийн математик хөтөлбөрийн зорилго... 3 2.
1 МОНГОЛ КЕМБРИЖИЙН БОЛОВСРОЛЫН САНААЧИЛГА Монголын ерөнхий боловсролын 12 жилийн сургуулийн 6 8 р ангийн математикийн хичээлийн хөтөлбөр 2 ГАРЧИГ 1. 6 8 р ангийн математик хөтөлбөрийн зорилго... 3 2.
ГАЛИЛЕЙН ХАРЬЦАНГУЙ ЗАРЧИМ, ИНЕРЦИАЛ БИШ ТООЛЛЫН СИСТЕМ, ИНЕРЦИЙН ХҮЧНҮҮД, ХАРЬЦАНГУЙН ТУСГАЙ ОНОЛ, ЛОРЕНЦЫН ХУВИРГАЛТ БА ТҮҮНИЙ МӨРДЛӨГӨӨ
 ЛЕКЦ 5 S.PH101 ФИЗИК-1 ГАЛИЛЕЙН ХАРЬЦАНГУЙ ЗАРЧИМ, ИНЕРЦИАЛ БИШ ТООЛЛЫН СИСТЕМ, ИНЕРЦИЙН ХҮЧНҮҮД, ХАРЬЦАНГУЙН ТУСГАЙ ОНОЛ, ЛОРЕНЦЫН ХУВИРГАЛТ БА ТҮҮНИЙ МӨРДЛӨГӨӨ Бэлтгэсэн: О.СҮХ, Б.ОДОНТУЯА 2 S.PH101
ЛЕКЦ 5 S.PH101 ФИЗИК-1 ГАЛИЛЕЙН ХАРЬЦАНГУЙ ЗАРЧИМ, ИНЕРЦИАЛ БИШ ТООЛЛЫН СИСТЕМ, ИНЕРЦИЙН ХҮЧНҮҮД, ХАРЬЦАНГУЙН ТУСГАЙ ОНОЛ, ЛОРЕНЦЫН ХУВИРГАЛТ БА ТҮҮНИЙ МӨРДЛӨГӨӨ Бэлтгэсэн: О.СҮХ, Б.ОДОНТУЯА 2 S.PH101
МИКРОКОНТРОЛЛЕРИЙН ХЯЛБАР ДАСГАЛУУД
 3.1. ГЭРЭЛТЭГЧ ДИОДЫГ УДИРДАХ МИКРОКОНТРОЛЛЕРИЙН ХЯЛБАР ДАСГАЛУУД Гэрэлтэгч диодуудыг төрөл бүрийн эффекттэйгээр асааж унтраах эдгээр дасгалууд нь портоор мэдээллийг хэрхэн гаргах талаар үзэх хичээл юм.
3.1. ГЭРЭЛТЭГЧ ДИОДЫГ УДИРДАХ МИКРОКОНТРОЛЛЕРИЙН ХЯЛБАР ДАСГАЛУУД Гэрэлтэгч диодуудыг төрөл бүрийн эффекттэйгээр асааж унтраах эдгээр дасгалууд нь портоор мэдээллийг хэрхэн гаргах талаар үзэх хичээл юм.
АДРОНЫ КЛАСТЕРЫГ ЯЛГАХАД ЗОРИУЛСАН ПАРАМЕТРИЙГ ТОДОРХОЙЛСОН НЬ
 DOI: http://dx.doi.org/10.5564/pmas.v54i2.657 АДРОНЫ КЛАСТЕРЫГ ЯЛГАХАД ЗОРИУЛСАН ПАРАМЕТРИЙГ ТОДОРХОЙЛСОН НЬ Р.Тогоо 1, Ж.Шинэбаяр 2, Д.Отгонсүрэн 1 1) ШУА, Физик технологийн хүрээлэн 2) МУБИС, Боловсрол
DOI: http://dx.doi.org/10.5564/pmas.v54i2.657 АДРОНЫ КЛАСТЕРЫГ ЯЛГАХАД ЗОРИУЛСАН ПАРАМЕТРИЙГ ТОДОРХОЙЛСОН НЬ Р.Тогоо 1, Ж.Шинэбаяр 2, Д.Отгонсүрэн 1 1) ШУА, Физик технологийн хүрээлэн 2) МУБИС, Боловсрол
Тухайн Дифференциал Тэгшитгэл ба Түүний Нийтлэг Хэрэглээ
 Тухайн Дифференциал Тэгшитгэл ба Түүний Нийтлэг Хэрэглээ Сүхболдын Төгөлдөр 2012 оны 1р сарын 23 1 Өмнөх Үг Юуны өмнө энэ семинарт оролцох боломжийг олгосон Төмөр ахдаа баярлалаа. Миний бие астрофизикийн
Тухайн Дифференциал Тэгшитгэл ба Түүний Нийтлэг Хэрэглээ Сүхболдын Төгөлдөр 2012 оны 1р сарын 23 1 Өмнөх Үг Юуны өмнө энэ семинарт оролцох боломжийг олгосон Төмөр ахдаа баярлалаа. Миний бие астрофизикийн
Физикийн даалгавар 11-р анги оны хичээлийн жил Нэгдүгээр хэсэг( Тест )
 Нэгдүгээр хээг( Тет ) 1-5-р бодлогод утга, цифр анхаар. 1. Дэлхий дээрх бүх хүмүүийн маийг үнэл. A. 4 10 12 кг B. 1 10 9 кг C. 2 10 10 кг D. 3 10 11 кг 2. Сүүн зам хэмээх манай глактикийн диаметрийн хэмжээ
Нэгдүгээр хээг( Тет ) 1-5-р бодлогод утга, цифр анхаар. 1. Дэлхий дээрх бүх хүмүүийн маийг үнэл. A. 4 10 12 кг B. 1 10 9 кг C. 2 10 10 кг D. 3 10 11 кг 2. Сүүн зам хэмээх манай глактикийн диаметрийн хэмжээ
Компьютер графикийн файлын формат
 Компьютер графикийн файлын формат Лекц 13-14 МУИС-МТС-КМТТ багш П.Гантуяа Bit dept Энэ нь зурагын 1 пикселд хичнээн тооны өнгө байхыг тодорхойлж өгдөг. Их bit depth-тэй бол илүү олон тооны өнгөний сонголттой
Компьютер графикийн файлын формат Лекц 13-14 МУИС-МТС-КМТТ багш П.Гантуяа Bit dept Энэ нь зурагын 1 пикселд хичнээн тооны өнгө байхыг тодорхойлж өгдөг. Их bit depth-тэй бол илүү олон тооны өнгөний сонголттой
Ерөнхий эмиттертэй транзисторт өсгөгч Унших материал
 ажил7 Ерөнхий эмиттертэй транзисторт өсгөгч Унших материал Electronic Deices and ircuits, 4 th edition: Section 5-1, Ac amplifier Fundamentals; Section 5-3, Amplifier Analysis Usg Small-Signal Models,
ажил7 Ерөнхий эмиттертэй транзисторт өсгөгч Унших материал Electronic Deices and ircuits, 4 th edition: Section 5-1, Ac amplifier Fundamentals; Section 5-3, Amplifier Analysis Usg Small-Signal Models,
Рекурсив Хамгийн бага Квадратын аргаар MIMO сувгийг дагах алгоритм
 Рекурсив Хамгийн бага Квадратын аргаар MIMO сувгийг дагах алгоритм Б.Золбоо, А.Мөнхбаясгалан, М.Баярпүрэв МУИС, Хэрэглээний Шинжлэх Ухаан, Инженерчлэлийн Сургууль Электроник, Холбооны Инженерчлэлийн Тэнхим
Рекурсив Хамгийн бага Квадратын аргаар MIMO сувгийг дагах алгоритм Б.Золбоо, А.Мөнхбаясгалан, М.Баярпүрэв МУИС, Хэрэглээний Шинжлэх Ухаан, Инженерчлэлийн Сургууль Электроник, Холбооны Инженерчлэлийн Тэнхим
Физикийн даалгавар 12-р анги оны хичээлийн жил
 Утгат оронг алдагдуулахгүй тооцоол. Тестийн дугаар 1 2 3 4 25.05+37.5= 54-22.4= 12 15.5 = 18.75 7.5 = A 62.55 31.6 186 2.5 B 62.5 31 190 2.50 C 62.6 32 180 3.0 D 63 30 186.0 2.0 Абсольют алдаагаар өгөгдсөн
Утгат оронг алдагдуулахгүй тооцоол. Тестийн дугаар 1 2 3 4 25.05+37.5= 54-22.4= 12 15.5 = 18.75 7.5 = A 62.55 31.6 186 2.5 B 62.5 31 190 2.50 C 62.6 32 180 3.0 D 63 30 186.0 2.0 Абсольют алдаагаар өгөгдсөн
ªÐÕ ÄÝÄ Ó ÐÀÕ ÈÍÔËßÖÈÉÍ ÄÀÐÀÌÒ
 ªÐÕ ÄÝÄ Ó ÐÀÕ ÈÍÔËßÖÈÉÍ ÄÀÐÀÌÒ Хураангуй Эдийн засгийн судалгаа, эрдэм шинжилгээний хүрээлэн Боловсруулсан: Судалгааны багийн ахлагч Г.Рагчаасүрэн Судалгааны багийн гишүүн: Б.Цолмон 2015 оны 4-р сар Энэхүү
ªÐÕ ÄÝÄ Ó ÐÀÕ ÈÍÔËßÖÈÉÍ ÄÀÐÀÌÒ Хураангуй Эдийн засгийн судалгаа, эрдэм шинжилгээний хүрээлэн Боловсруулсан: Судалгааны багийн ахлагч Г.Рагчаасүрэн Судалгааны багийн гишүүн: Б.Цолмон 2015 оны 4-р сар Энэхүү
КИНЕМАТИК, МЕХАНИК ХӨДӨЛГӨӨН, ХУРД, ХУРДАТГАЛ, ЭРГЭХ ХӨДӨЛГӨӨН
 ЛЕКЦ 1 S.PH101 ФИЗИК-1 КИНЕМАТИК, МЕХАНИК ХӨДӨЛГӨӨН, ХУРД, ХУРДАТГАЛ, ЭРГЭХ ХӨДӨЛГӨӨН Бэлтгэсэн: О.СҮХ, Б.ОДОНТУЯА S.PH101 Физик-1 [Лекц-1] КИНЕМАТИК 1-1 МЕХАНИК ХӨДӨЛГӨӨН Материйн хамгийн энгийн хөдөлгөөн
ЛЕКЦ 1 S.PH101 ФИЗИК-1 КИНЕМАТИК, МЕХАНИК ХӨДӨЛГӨӨН, ХУРД, ХУРДАТГАЛ, ЭРГЭХ ХӨДӨЛГӨӨН Бэлтгэсэн: О.СҮХ, Б.ОДОНТУЯА S.PH101 Физик-1 [Лекц-1] КИНЕМАТИК 1-1 МЕХАНИК ХӨДӨЛГӨӨН Материйн хамгийн энгийн хөдөлгөөн
1. Атомын нарийн нийлмэл бүтэц 19 -р зууны эцэс. Физикийн шинжлэх ухааны нээлтүүд Атомын бүтцийн загварууд Атомын бүтцийн онолууд
 CHEM101: Органик биш хими I Ëåêö ¹4 1. Атомын нарийн нийлмэл бүтэц 19 -р зууны эцэс. Физикийн шинжлэх ухааны нээлтүүд Атомын бүтцийн загварууд Атомын бүтцийн онолууд. Атомын электрон давхраат бүтэц, түүнийг
CHEM101: Органик биш хими I Ëåêö ¹4 1. Атомын нарийн нийлмэл бүтэц 19 -р зууны эцэс. Физикийн шинжлэх ухааны нээлтүүд Атомын бүтцийн загварууд Атомын бүтцийн онолууд. Атомын электрон давхраат бүтэц, түүнийг
Барилгын дулаалгын материалын шинэ стандартууд
 Барилгын дулаалгын материалын шинэ стандартууд MNS EN 13162 2011 MW MNS EN 13163 2011 EPS MNS EN 13163 2011 XPS MNS EN 13163 2011 PUR АГУУЛГА 1. Хамрах хүрээ 2. Норматив ишлэл 3. Нэр томъёо, тодорхойлолт,
Барилгын дулаалгын материалын шинэ стандартууд MNS EN 13162 2011 MW MNS EN 13163 2011 EPS MNS EN 13163 2011 XPS MNS EN 13163 2011 PUR АГУУЛГА 1. Хамрах хүрээ 2. Норматив ишлэл 3. Нэр томъёо, тодорхойлолт,
АРГА ТЕХНОЛОГИЙН НЭР: Физикийн хичээлээр сурагчдыг ЕШ-д амжилттай бэлтгэх - арга технологи.
 АРГА ТЕХНОЛОГИЙН НЭР: Физикийн хичээлээр сурагчдыг ЕШ-д амжилттай бэлтгэх - арга технологи. ЭЕШ- ийн сэдвийн хүрээ нь бүрэн дунд боловсролын стандартын агуулгын хүрээнд байж, их дээд сургуульд элсэхийг
АРГА ТЕХНОЛОГИЙН НЭР: Физикийн хичээлээр сурагчдыг ЕШ-д амжилттай бэлтгэх - арга технологи. ЭЕШ- ийн сэдвийн хүрээ нь бүрэн дунд боловсролын стандартын агуулгын хүрээнд байж, их дээд сургуульд элсэхийг
ПРОПАНТ ХӨӨСТ КАМЕРТ БҮРТГЭГДСЭН ХАРИМХАЙ БУС ХАРИЛЦАН ҮЙЛЧЛЭЛЭЭР ҮҮССЭН ЭЕРЭГ ЦЭНЭГТ БӨӨМИЙГ ЯЛГАН ТАНИХ НЭГЭН БОЛОМЖ
 Proceedings of the Mongolian Academy of Sciences Vol. 56 No 01 (217) 2016 DOI: http://dx.doi.org/10.5564/pmas.v56i01.671 ПРОПАНТ ХӨӨСТ КАМЕРТ БҮРТГЭГДСЭН ХАРИМХАЙ БУС ХАРИЛЦАН ҮЙЛЧЛЭЛЭЭР ҮҮССЭН ЭЕРЭГ ЦЭНЭГТ
Proceedings of the Mongolian Academy of Sciences Vol. 56 No 01 (217) 2016 DOI: http://dx.doi.org/10.5564/pmas.v56i01.671 ПРОПАНТ ХӨӨСТ КАМЕРТ БҮРТГЭГДСЭН ХАРИМХАЙ БУС ХАРИЛЦАН ҮЙЛЧЛЭЛЭЭР ҮҮССЭН ЭЕРЭГ ЦЭНЭГТ
Физикийн даалгавар 8-р анги оны хичээлийн жил
 8-р анги физик 1. 100м-н гүн усандахь даралтыг ол. Агаарын даралтыг тооцохгүй A) 10 5 Па B) 10 4 Па C) 10 3 Па D) 10 6 Па 2. 10атм даралт ойролцоогоор хэдэн Па даралттай тэнцэх вэ? A) 10 5 B) 10 4 C) 10
8-р анги физик 1. 100м-н гүн усандахь даралтыг ол. Агаарын даралтыг тооцохгүй A) 10 5 Па B) 10 4 Па C) 10 3 Па D) 10 6 Па 2. 10атм даралт ойролцоогоор хэдэн Па даралттай тэнцэх вэ? A) 10 5 B) 10 4 C) 10
Хадан Дээрх Тамганы Дүрсийг Адууны Тамганы Дүрстэй Машин Сургалтын Аргуудаар Харьцуулах
 Хадан Дээрх Тамганы Дүрсийг Адууны Тамганы Дүрстэй Машин Сургалтын Аргуудаар Харьцуулах Пэрэнлэйлхүндэв Гантуяа*, Батсуурь Сувдаа*, Дамдинсүрэн Цэвээндорж** *Монгол Улсын Их Сургууль, Мэдээлэл, Компьютерийн
Хадан Дээрх Тамганы Дүрсийг Адууны Тамганы Дүрстэй Машин Сургалтын Аргуудаар Харьцуулах Пэрэнлэйлхүндэв Гантуяа*, Батсуурь Сувдаа*, Дамдинсүрэн Цэвээндорж** *Монгол Улсын Их Сургууль, Мэдээлэл, Компьютерийн
Физикийн даалгавар 9-р анги оны хичээлийн жил
 9р анги физик Бодолгод анхаарах зүйл. асуултын ард дөрвөлжин хаалтан доторхи нэгжээр хариуг илэрхийлнэ.[ ] хаалтан дотор тухайн хариуны нэгж байна. Жишээ нь чиний бодсон бодлого 1000м гарав гэтэл хаалтан
9р анги физик Бодолгод анхаарах зүйл. асуултын ард дөрвөлжин хаалтан доторхи нэгжээр хариуг илэрхийлнэ.[ ] хаалтан дотор тухайн хариуны нэгж байна. Жишээ нь чиний бодсон бодлого 1000м гарав гэтэл хаалтан
Лекц:5 Эрсдэл, өгөөж ба түүхэн тоон мэдээлэл
 Лекц:5 Эрсдэл, өгөөж ба түүхэн тоон мэдээлэл 2017 оны 3-р сарын 9 Лекц 5: Эрсдэл, өгөөж ба түүхэн тоон мэдээлэл c Г.Гүнбилэг 2017 МУИС-БС 1 Агуулга 1 ХТ-г тодорхойлогчид 2 Өгөөжүүдийг харьцуулах нь 3 ЗГБХҮЦ
Лекц:5 Эрсдэл, өгөөж ба түүхэн тоон мэдээлэл 2017 оны 3-р сарын 9 Лекц 5: Эрсдэл, өгөөж ба түүхэн тоон мэдээлэл c Г.Гүнбилэг 2017 МУИС-БС 1 Агуулга 1 ХТ-г тодорхойлогчид 2 Өгөөжүүдийг харьцуулах нь 3 ЗГБХҮЦ
802.11b утасгүй сүлжээн дээгүүр TCP протоколын дамжуулах чадамжийг үнэлэх математик загвар
 MMT-013 80.11b утасгүй сүлжээн дээгүүр TCP протоколын дамжуулах чадамжийг үнэлэх математик загвар Я.Дашдорж, П. Минж Шинжлэх Ухаан Технологын Их Сургуулийн Компюьтерийн Техник Менежментийн Сургууль эмайл:
MMT-013 80.11b утасгүй сүлжээн дээгүүр TCP протоколын дамжуулах чадамжийг үнэлэх математик загвар Я.Дашдорж, П. Минж Шинжлэх Ухаан Технологын Их Сургуулийн Компюьтерийн Техник Менежментийн Сургууль эмайл:
Барилгын эрчим хүч хэмнэлтийн төв БАРИЛГЫН БИТҮҮМЖЛЭЛ ТҮҮНИЙГ ТООЦОХ БОЛОН ТОДОРХОЙЛОХ АРГАЧЛАЛ. Менежер: Б. Билгүүн
 Барилгын эрчим хүч хэмнэлтийн төв БАРИЛГЫН БИТҮҮМЖЛЭЛ ТҮҮНИЙГ ТООЦОХ БОЛОН ТОДОРХОЙЛОХ АРГАЧЛАЛ Менежер: Б. Билгүүн Агуулга 1.Агаар нэвтрүүлэлт түүний нөлөөлөл 2.Агаар нэвтрүүлэлтийн стандарт 3.Барилгын
Барилгын эрчим хүч хэмнэлтийн төв БАРИЛГЫН БИТҮҮМЖЛЭЛ ТҮҮНИЙГ ТООЦОХ БОЛОН ТОДОРХОЙЛОХ АРГАЧЛАЛ Менежер: Б. Билгүүн Агуулга 1.Агаар нэвтрүүлэлт түүний нөлөөлөл 2.Агаар нэвтрүүлэлтийн стандарт 3.Барилгын
:xeu 2+ - ИЙГ ГАРГАН АВАХ БОЛОН ТҮҮНИЙ ГЭРЛИЙН ЦАЦАРГАЛТЫН СУДАЛГАА
 DOI: https://doi.org/10.5564/pmas.v57i3.888 :xeu 2+ - ИЙГ ГАРГАН АВАХ БОЛОН ТҮҮНИЙ ГЭРЛИЙН ЦАЦАРГАЛТЫН СУДАЛГАА Н.Төвжаргал 1, *, Б. Алтантулга 1, н.цогхүү 2, О.Төгс 2, Ж.Даваасамбуу 1 1 МУИС-ийн Физикийн
DOI: https://doi.org/10.5564/pmas.v57i3.888 :xeu 2+ - ИЙГ ГАРГАН АВАХ БОЛОН ТҮҮНИЙ ГЭРЛИЙН ЦАЦАРГАЛТЫН СУДАЛГАА Н.Төвжаргал 1, *, Б. Алтантулга 1, н.цогхүү 2, О.Төгс 2, Ж.Даваасамбуу 1 1 МУИС-ийн Физикийн
Химийн даалгавар 11-р анги оны хичээлийн жил
 Нэгдүгээр хэсэг: Санамж: Нэгдүгээр хэсэг нийт 40 оноотой бөгөөд даалгавар тус бүр 1 оноо болно. Даалгавар бүрээс зөвхөн нэг хариултыг 1. Дараах томьёо бүхий бодисуудын нэр хаяггүй гурван уусмалыг нихром
Нэгдүгээр хэсэг: Санамж: Нэгдүгээр хэсэг нийт 40 оноотой бөгөөд даалгавар тус бүр 1 оноо болно. Даалгавар бүрээс зөвхөн нэг хариултыг 1. Дараах томьёо бүхий бодисуудын нэр хаяггүй гурван уусмалыг нихром
Валютын ханшийн эрсдэлээс хамгаалах санхүүгийн хэрэгсэл
 Валютын ханшийн эрсдэлээс хамгаалах санхүүгийн хэрэгсэл Эдийн Засгийн Судалгаа, Эрдэм Шинжилгээний Хүрээлэн 2013 оны 8-р сар 1 Валютын опцион ханшийн хэлбэлзлээс хамгаалах хэрэгсэл Манай Засгийн газрын
Валютын ханшийн эрсдэлээс хамгаалах санхүүгийн хэрэгсэл Эдийн Засгийн Судалгаа, Эрдэм Шинжилгээний Хүрээлэн 2013 оны 8-р сар 1 Валютын опцион ханшийн хэлбэлзлээс хамгаалах хэрэгсэл Манай Засгийн газрын
Өгөгдөл(Data) and Дохио(signal)
 Мэдээллийн сүлжээ профессорын баг Өгөгдөл(Data) and Дохио(signal) Семинар 2 Багш (Доктор Ph.D) Л.Одончимэг Оюутан юу эзэмших вэ: Өгөгдөл гэж юу вэ? Өгөгдөл ба Дохионы ялгаа Аналог ба Тоон дохионы ялгаа
Мэдээллийн сүлжээ профессорын баг Өгөгдөл(Data) and Дохио(signal) Семинар 2 Багш (Доктор Ph.D) Л.Одончимэг Оюутан юу эзэмших вэ: Өгөгдөл гэж юу вэ? Өгөгдөл ба Дохионы ялгаа Аналог ба Тоон дохионы ялгаа
НЭГДҮГЭЭР ХЭСЭГ C-н температур хэдэн кельвины температур болох вэ?. A. 281 B. 265 C. 8 D. 16 A B C. 726 D. 12
 НЭГДҮГЭЭР ХЭСЭГ 1. 8 0 C-н температур хэдэн кельвины температур болох вэ?. A. 281 B. 265 C. 8 D. 16 2. 1273 0 К температур хэдэн цельсын температур болох вэ? A. 1523 B. 20 C. 0 D. 1000 Бодлого: (3-7) 1кг
НЭГДҮГЭЭР ХЭСЭГ 1. 8 0 C-н температур хэдэн кельвины температур болох вэ?. A. 281 B. 265 C. 8 D. 16 2. 1273 0 К температур хэдэн цельсын температур болох вэ? A. 1523 B. 20 C. 0 D. 1000 Бодлого: (3-7) 1кг
ҮЙЛ АЖИЛЛАГААНЫ ЭРСДЭЛИЙГ ТООЦОХ ЗӨВЛӨМЖ
 Ìîíãîëáàíêíû Åðºíõèéëºã èéí 006 îíû -ð ñàðûí 7-íû ºäðèéí 537 äóãààð òóøààëûí õàâñðàëò ҮЙЛ АЖИЛЛАГААНЫ ЭРСДЭЛИЙГ ТООЦОХ ЗӨВЛӨМЖ НЭГ. НИЙТЛЭГ ҮНДЭСЛЭЛ Санхүүгийн байгууллагуудын үйл ажиллагааны эрсдэлийг
Ìîíãîëáàíêíû Åðºíõèéëºã èéí 006 îíû -ð ñàðûí 7-íû ºäðèéí 537 äóãààð òóøààëûí õàâñðàëò ҮЙЛ АЖИЛЛАГААНЫ ЭРСДЭЛИЙГ ТООЦОХ ЗӨВЛӨМЖ НЭГ. НИЙТЛЭГ ҮНДЭСЛЭЛ Санхүүгийн байгууллагуудын үйл ажиллагааны эрсдэлийг
МОНГОЛ УЛСЫН СТАНДАРТ. Стандартчилал, Хэмжилзүйн Үндэсний Зөвлөлийн 2009 оны 12 дугаар сарын 24- ний өдрийн 52 дугаар тогтоолоор батлав.
 МОНГОЛ УЛСЫН СТАНДАРТ Ангилалтын код 91.040.30 Орон сууцны барилгын доторх сууцны талбай тооцох аргачлал Methodology of housing unit area calculation in residential buildings Стандартчилал, Хэмжилзүйн
МОНГОЛ УЛСЫН СТАНДАРТ Ангилалтын код 91.040.30 Орон сууцны барилгын доторх сууцны талбай тооцох аргачлал Methodology of housing unit area calculation in residential buildings Стандартчилал, Хэмжилзүйн
Дан болон давхар урвуу дүүжингийн тэнцвэржилт
 Дан болон давхар урвуу дүүжингийн тэнцвэржилт Б.Луубаатар, А.Батмөнх ШУТИС-МХТС-ийн ахлах багш, ШУТИС-МХТС-ийн профессор Хураангуй Энэхүү өгүүлэлд дан болон давхар урвуу дүүжингийн загварчлал, тэдгээрийн
Дан болон давхар урвуу дүүжингийн тэнцвэржилт Б.Луубаатар, А.Батмөнх ШУТИС-МХТС-ийн ахлах багш, ШУТИС-МХТС-ийн профессор Хураангуй Энэхүү өгүүлэлд дан болон давхар урвуу дүүжингийн загварчлал, тэдгээрийн
ÍÄÝÑÍÈÉ ÑÒÀÒÈÑÒÈÊÈÉÍ ÕÎÐÎÎ EVIEWS 9 ÏÐÎÃÐÀÌÛÃ ØÈÍÆÈËÃÝÝÍÄ ÀØÈÃËÀÕ ÍÜ ÃÀÐÛÍ ÀÂËÀÃÀ
 ÍÄÝÑÍÈÉ ÑÒÀÒÈÑÒÈÊÈÉÍ ÕÎÐÎÎ EVIEWS 9 ÏÐÎÃÐÀÌÛÃ ØÈÍÆÈËÃÝÝÍÄ ÀØÈÃËÀÕ ÍÜ ÃÀÐÛÍ ÀÂËÀÃÀ ÓËÀÀÍÁÀÀÒÀÐ 2018 ДАА 005.1 ННА 32.973-018 E-93 EVIEWS 9 ПРОГРАМЫГ ШИНЖИЛГЭЭНД АШИГЛАХ НЬ Гарын авлага Хянан тохиолдуулсан:
ÍÄÝÑÍÈÉ ÑÒÀÒÈÑÒÈÊÈÉÍ ÕÎÐÎÎ EVIEWS 9 ÏÐÎÃÐÀÌÛÃ ØÈÍÆÈËÃÝÝÍÄ ÀØÈÃËÀÕ ÍÜ ÃÀÐÛÍ ÀÂËÀÃÀ ÓËÀÀÍÁÀÀÒÀÐ 2018 ДАА 005.1 ННА 32.973-018 E-93 EVIEWS 9 ПРОГРАМЫГ ШИНЖИЛГЭЭНД АШИГЛАХ НЬ Гарын авлага Хянан тохиолдуулсан:
Физикийн хичээлийн даалгавар (үндэсний хөтөлбөр)
 Нэгдүгээр хэсэг: Сонгох даалгавар Дараах даалгаврууд нь 5 сонгох хариулттай. Тэдгээрийн зөвхөн нэг нь зөв. Хамгийн зөв гэсэн хариултыг сонгож хариултын хуудсанд будаж тэмдэглэнэ. Нийт 46 сонгох даалгавар
Нэгдүгээр хэсэг: Сонгох даалгавар Дараах даалгаврууд нь 5 сонгох хариулттай. Тэдгээрийн зөвхөн нэг нь зөв. Хамгийн зөв гэсэн хариултыг сонгож хариултын хуудсанд будаж тэмдэглэнэ. Нийт 46 сонгох даалгавар
Физикийн хичээлийн даалгавар (үндэсний хөтөлбөр)
 Нэгдүгээр хэсэг: Сонгох даалгавар Дараах даалгаврууд нь 5 сонгох хариулттай. Тэдгээрийн зөвхөн нэг нь зөв. Хамгийн зөв гэсэн хариултыг сонгож хариултын хуудсанд будаж тэмдэглэнэ. Нийт 46 сонгох даалгавар
Нэгдүгээр хэсэг: Сонгох даалгавар Дараах даалгаврууд нь 5 сонгох хариулттай. Тэдгээрийн зөвхөн нэг нь зөв. Хамгийн зөв гэсэн хариултыг сонгож хариултын хуудсанд будаж тэмдэглэнэ. Нийт 46 сонгох даалгавар
7 Цаг уур, агаарын чанарын мониторингийн өгөгдлийн дүн шинжилгээ 7.1 Цаг уурын өгөгдлийн анализ
 7 Цаг уур, агаарын чанарын мониторингийн өгөгдлийн дүн шинжилгээ 7.1 Цаг уурын өгөгдлийн анализ 7.1.1 Олж авсан цаг уурын өгөгдлийг боловсруулах болон алдааг шалгах Цаг уурын жилийн тайланг боловсруулсанаар
7 Цаг уур, агаарын чанарын мониторингийн өгөгдлийн дүн шинжилгээ 7.1 Цаг уурын өгөгдлийн анализ 7.1.1 Олж авсан цаг уурын өгөгдлийг боловсруулах болон алдааг шалгах Цаг уурын жилийн тайланг боловсруулсанаар
2012/05/23 / ХАВАР/ Радио Холбооны Системүүд J.RC215. a. 48 хиймэл дагуул, 8 тойрог зам b. 24 хиймэл дагуул, 6 тойрог зам
 Батлав:/.../Сургалт хариуцсан Дэд захирал С.Долгорсүрэн Батлав:/.../УХӨНТ-ийн багийн профессор (h.) Б.Отгонбаяр // / ХАВАР/ Радио Холбооны Системүүд J.C. FM радио телевиз ямар радио долгионы цараанд тархдаг
Батлав:/.../Сургалт хариуцсан Дэд захирал С.Долгорсүрэн Батлав:/.../УХӨНТ-ийн багийн профессор (h.) Б.Отгонбаяр // / ХАВАР/ Радио Холбооны Системүүд J.C. FM радио телевиз ямар радио долгионы цараанд тархдаг
ДИНАМИК, НЬЮТОНЫ ХУУЛИУД, МАСС БА ИМПУЛЬС, ИМПУЛЬС ХАДГАЛАГДАХ ХУУЛЬ, ХҮЧНҮҮД, ХУВЬСАХ МАССТАЙ БИЕИЙН ХӨДӨЛГӨӨН, МАССЫН ТӨВ
 ЛЕКЦ 2 S.PH101 ФИЗИК-1 ДИНАМИК, НЬЮТОНЫ ХУУЛИУД, МАСС БА ИМПУЛЬС, ИМПУЛЬС ХАДГАЛАГДАХ ХУУЛЬ, ХҮЧНҮҮД, ХУВЬСАХ МАССТАЙ БИЕИЙН ХӨДӨЛГӨӨН, МАССЫН ТӨВ Бэлтгэсэн: О.СҮХ, Б.ОДОНТУЯА 2 S.PH101 Физик-1 [Лекц-2]
ЛЕКЦ 2 S.PH101 ФИЗИК-1 ДИНАМИК, НЬЮТОНЫ ХУУЛИУД, МАСС БА ИМПУЛЬС, ИМПУЛЬС ХАДГАЛАГДАХ ХУУЛЬ, ХҮЧНҮҮД, ХУВЬСАХ МАССТАЙ БИЕИЙН ХӨДӨЛГӨӨН, МАССЫН ТӨВ Бэлтгэсэн: О.СҮХ, Б.ОДОНТУЯА 2 S.PH101 Физик-1 [Лекц-2]
МОНГОЛ ОРНЫ ЭНДЕМИК УРГАМАЛ МОНГОЛ ДОГАР- CARYOPTERIS MONGOLICA BGE.-ИЙГ IN VITRO НӨХЦӨЛД ҮРЖҮҮЛСЭН ДҮНГЭЭС
 Proceedings of the Mongolian Academy of Sciences Vol. 52 No 2 (202) 2012 МОНГОЛ ОРНЫ ЭНДЕМИК УРГАМАЛ МОНГОЛ ДОГАР- CARYOPTERIS MONGOLICA BGE.-ИЙГ IN VITRO НӨХЦӨЛД ҮРЖҮҮЛСЭН ДҮНГЭЭС Д.Бямбасүх ШУА, Ботаникийн
Proceedings of the Mongolian Academy of Sciences Vol. 52 No 2 (202) 2012 МОНГОЛ ОРНЫ ЭНДЕМИК УРГАМАЛ МОНГОЛ ДОГАР- CARYOPTERIS MONGOLICA BGE.-ИЙГ IN VITRO НӨХЦӨЛД ҮРЖҮҮЛСЭН ДҮНГЭЭС Д.Бямбасүх ШУА, Ботаникийн
ТААМАГЛАЛЫН ТОДОРХОЙ БУС БАЙДАЛ: ИНФЛЯЦИЙН ТААМАГЛАЛЫН FAN CHART, ТҮҮНД ҮНДЭСЛЭСЭН ШИНЖИЛГЭЭ
 ТААМАГЛАЛЫН ТОДОРХОЙ БУС БАЙДАЛ: ИНФЛЯЦИЙН ТААМАГЛАЛЫН FAN CHART, ТҮҮНД ҮНДЭСЛЭСЭН ШИНЖИЛГЭЭ Д.Ган-Очир 1 gan_ochir.d@mongolbank.mn П.Авралт-Од Avralod@mongolbank.mn Б.Даваадалай davaadalai@mongolbank.mn
ТААМАГЛАЛЫН ТОДОРХОЙ БУС БАЙДАЛ: ИНФЛЯЦИЙН ТААМАГЛАЛЫН FAN CHART, ТҮҮНД ҮНДЭСЛЭСЭН ШИНЖИЛГЭЭ Д.Ган-Очир 1 gan_ochir.d@mongolbank.mn П.Авралт-Од Avralod@mongolbank.mn Б.Даваадалай davaadalai@mongolbank.mn
MOНГОЛЫН ҮНЭТ ЦААСНЫ АРИЛЖАА ЭРХЛЭГЧДИЙН ХОЛБОО ӨЗБ ҮНЭТ ЦААСААР ХИЙХ ХӨРӨНГӨ ОРУУЛАЛТЫН ЭРСДЭЛИЙГ ТООЦОХ АРГАЧЛАЛ
 MOНГОЛЫН ҮНЭТ ЦААСНЫ АРИЛЖАА ЭРХЛЭГЧДИЙН ХОЛБОО ӨЗБ ҮНЭТ ЦААСААР ХИЙХ ХӨРӨНГӨ ОРУУЛАЛТЫН ЭРСДЭЛИЙГ ТООЦОХ АРГАЧЛАЛ Агуулга Эрсдэл гэж юу вэ? Эрсдэлийн менежментийн олон улсын стандарт Эрсдэлийн төрлүүд
MOНГОЛЫН ҮНЭТ ЦААСНЫ АРИЛЖАА ЭРХЛЭГЧДИЙН ХОЛБОО ӨЗБ ҮНЭТ ЦААСААР ХИЙХ ХӨРӨНГӨ ОРУУЛАЛТЫН ЭРСДЭЛИЙГ ТООЦОХ АРГАЧЛАЛ Агуулга Эрсдэл гэж юу вэ? Эрсдэлийн менежментийн олон улсын стандарт Эрсдэлийн төрлүүд
АРВАНГУРАВДУГААР АЖИЛ Тасалгааны цацрагийн дэвсгэр түвшинг тодорхойлох нь
 АРВАНГУРАВДУГААР АЖИЛ Тасалгааны цацрагийн дэвсгэр түвшинг тодорхойлох нь Ажлын зорилго: Тасалгааны цацрагийн дэвсгэр түвшинг тодорхойлон хэмжихэд оршино. Хэрэглэгдэх багаж: PASCO- Гейгер-Мюллерийн тоолуур,
АРВАНГУРАВДУГААР АЖИЛ Тасалгааны цацрагийн дэвсгэр түвшинг тодорхойлох нь Ажлын зорилго: Тасалгааны цацрагийн дэвсгэр түвшинг тодорхойлон хэмжихэд оршино. Хэрэглэгдэх багаж: PASCO- Гейгер-Мюллерийн тоолуур,
НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР
 НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 69 оноотой бөгөөд - дүгээр тест тус бүр оноо, -7 дугаар тест тус бүр оноо, 8- дүгээр тест тус бүр - хүртэлх оноотой болно. Даалгавар бүрээс
НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 69 оноотой бөгөөд - дүгээр тест тус бүр оноо, -7 дугаар тест тус бүр оноо, 8- дүгээр тест тус бүр - хүртэлх оноотой болно. Даалгавар бүрээс
НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР
 НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 69 оноотой бөгөөд - дүгээр тест тус бүр оноо, -7 дугаар тест тус бүр оноо, 8- дүгээр тест тус бүр - хүртэлх оноотой болно. Даалгавар бүрээс
НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 69 оноотой бөгөөд - дүгээр тест тус бүр оноо, -7 дугаар тест тус бүр оноо, 8- дүгээр тест тус бүр - хүртэлх оноотой болно. Даалгавар бүрээс
Сонгуулийн прогноз хийх арга зүй: асуудал, хувилбар, арга. Ц.Болд, Ч.Тамир /МУИС-ийн Социологийн тэнхмийн багш нар/
 Сонгуулийн прогноз хийх арга зүй: асуудал, хувилбар, арга.сонгуулийн прогноз хийх үндсэн нөхцөл, хүчин зүйлс Ц.Болд, Ч.Тамир /МУИС-ийн Социологийн тэнхмийн багш нар/ Сонгуулийн дүнг прогнозчилох явдал
Сонгуулийн прогноз хийх арга зүй: асуудал, хувилбар, арга.сонгуулийн прогноз хийх үндсэн нөхцөл, хүчин зүйлс Ц.Болд, Ч.Тамир /МУИС-ийн Социологийн тэнхмийн багш нар/ Сонгуулийн дүнг прогнозчилох явдал
МОНГОЛ ХОНИНЫ НООСНЫ БҮТЭЦ, ШИНЖ ЧАНАРЫГ ЭЛЕКТРОН МИКРОСКОПИЙН АРГААР СУДЛАХ
 82 МОНГОЛ ХОНИНЫ НООСНЫ БҮТЭЦ, ШИНЖ ЧАНАРЫГ ЭЛЕКТРОН МИКРОСКОПИЙН АРГААР СУДЛАХ Г.Ганбат 1, Ц.Хишигжаргал 1, Ч.Ганзориг 2, Э.Оюунсүрэн 1, Л.Ганчимэг 2 1-ХААИС, Биологийн нөөцийн менежментийн сургууль 2-МУИС,
82 МОНГОЛ ХОНИНЫ НООСНЫ БҮТЭЦ, ШИНЖ ЧАНАРЫГ ЭЛЕКТРОН МИКРОСКОПИЙН АРГААР СУДЛАХ Г.Ганбат 1, Ц.Хишигжаргал 1, Ч.Ганзориг 2, Э.Оюунсүрэн 1, Л.Ганчимэг 2 1-ХААИС, Биологийн нөөцийн менежментийн сургууль 2-МУИС,
Физикийн ерөнхий шалгалтын тест нийт 57 даалгавартай. Хоёр хэсэгтэй. Нийлбэр оноо 100.
 ФИЗИК 2010 Боловсролын Үнэлгээний Төв ХУВИЛБАР A НЭГДҮГЭЭР ХЭСЭГ Физикийн ерөнхий шалгалтын тест нийт 57 даалгавартай. Хоёр хэсэгтэй. Нийлбэр оноо 100. Дараах даалгаврууд нь 5 сонгох хариулттай. Тэдгээрийн
ФИЗИК 2010 Боловсролын Үнэлгээний Төв ХУВИЛБАР A НЭГДҮГЭЭР ХЭСЭГ Физикийн ерөнхий шалгалтын тест нийт 57 даалгавартай. Хоёр хэсэгтэй. Нийлбэр оноо 100. Дараах даалгаврууд нь 5 сонгох хариулттай. Тэдгээрийн
S.PH102 Физик-2. Семинар 2. Сэдэв : Цахилгаан соронзон индукц. Тест оны намар
 S.PH102 Физик-2 Семинар 2 Сэдэв : Цахилгаан соронзон индукц Тест 2015-2016 оны намар 2.1 Доорхи хэлхээгээр гүйх хувьсах гүйдлийг ихэсгэхийн тулд гүйдлийн давтамжийг яаж өөрчилбөл зохих вэ? А. Давтамжийг
S.PH102 Физик-2 Семинар 2 Сэдэв : Цахилгаан соронзон индукц Тест 2015-2016 оны намар 2.1 Доорхи хэлхээгээр гүйх хувьсах гүйдлийг ихэсгэхийн тулд гүйдлийн давтамжийг яаж өөрчилбөл зохих вэ? А. Давтамжийг
г усанд 10 г давсыг уусгахад үүссэн уусмалын процентын концентрацыг бодож олно уу. A. 5% B. 10% C. 15% D. 20% E. 25%
 НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 68 оноотой бөгөөд 1 5 дугаар тест тус бүр 1 оноо, 6 0 дугаар тест тус бүр оноо, 1 1 дүгээр тест тус бүр оноо болно. Даалгавар бүрээс зөвхөн
НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 68 оноотой бөгөөд 1 5 дугаар тест тус бүр 1 оноо, 6 0 дугаар тест тус бүр оноо, 1 1 дүгээр тест тус бүр оноо болно. Даалгавар бүрээс зөвхөн
50 th IChO 2018 ОНОЛЫН ТЭМЦЭЭН BACK TO WHERE IT ALL BEGAN оны 7-р сарын Братислав, СЛОВАК Праг, ЧЕХ
 2018 оны 7-р сарын 19 29 Братислав, СЛОВАК Праг, ЧЕХ www.50icho.eu ОНОЛЫН ТЭМЦЭЭН Country: Name as in passport: Mongolia - MNG Student code: Language: Mongolian 50 th IChO 2018 International Chemistry
2018 оны 7-р сарын 19 29 Братислав, СЛОВАК Праг, ЧЕХ www.50icho.eu ОНОЛЫН ТЭМЦЭЭН Country: Name as in passport: Mongolia - MNG Student code: Language: Mongolian 50 th IChO 2018 International Chemistry
ЭДИЙН ЗАСГИЙН ИДЭВХТЭЙ БАЙДАЛД НӨЛӨӨЛӨГЧ ХҮЧИН ЗҮЙЛИЙН ЭКОНОМЕТРИК ШИНЖИЛГЭЭ
 ЭДИЙН ЗАСГИЙН ИДЭВХТЭЙ БАЙДАЛД НӨЛӨӨЛӨГЧ ХҮЧИН ЗҮЙЛИЙН ЭКОНОМЕТРИК ШИНЖИЛГЭЭ МБДС, Бизнесийн удирдлага мэдээлэл зүйн тэнхимийн оюутан Г.Нямдорж, Б. Болортуяа Хураангуй Монгол Улсын ажиллах хүчний оролцоо
ЭДИЙН ЗАСГИЙН ИДЭВХТЭЙ БАЙДАЛД НӨЛӨӨЛӨГЧ ХҮЧИН ЗҮЙЛИЙН ЭКОНОМЕТРИК ШИНЖИЛГЭЭ МБДС, Бизнесийн удирдлага мэдээлэл зүйн тэнхимийн оюутан Г.Нямдорж, Б. Болортуяа Хураангуй Монгол Улсын ажиллах хүчний оролцоо
1-Биотехнологи, үржүүлгийн тэнхим, МААБС, ХААИС, 2-Кантогийн их сургуулийн ХАА-н коллеж, БНВУ. *
 110 N.V.Ay ба бусад (2017) ÕÀÀ-í øèíæëýõ óõààí ñýòã ë ¹20 (01): 110-115 ИХ ТАВАН САЛАА (PLANTAGO MAJOR L.) УРГАМЛЫН ХОРТ ХАВДРЫН ЭСРЭГ ИДЭВХИЙГ ТОДОРХОЙЛСОН ДҮН N.V. Ay 1, 2, O. Дүүриймаа 1, Х. Алтанцэцэг
110 N.V.Ay ба бусад (2017) ÕÀÀ-í øèíæëýõ óõààí ñýòã ë ¹20 (01): 110-115 ИХ ТАВАН САЛАА (PLANTAGO MAJOR L.) УРГАМЛЫН ХОРТ ХАВДРЫН ЭСРЭГ ИДЭВХИЙГ ТОДОРХОЙЛСОН ДҮН N.V. Ay 1, 2, O. Дүүриймаа 1, Х. Алтанцэцэг
LATEX 2ε-ийн гарын авлага
 LATEX 2ε-ийн гарын авлага буюу L A TEX 2ε-г 141 минутад Тобиас Оетикер Хьюберт Партл, Ирэн Хина, Элизабет Шлегл Хувилбар 4.26, 2008 оны 09-р сарын 25 Орчуулсан: Доржготовын Батмөнх ii Зохиогчийн эрх 1995-2005
LATEX 2ε-ийн гарын авлага буюу L A TEX 2ε-г 141 минутад Тобиас Оетикер Хьюберт Партл, Ирэн Хина, Элизабет Шлегл Хувилбар 4.26, 2008 оны 09-р сарын 25 Орчуулсан: Доржготовын Батмөнх ii Зохиогчийн эрх 1995-2005
ВАЛЮТЫН ХАНШИЙН ИНФЛЯЦИД ҮЗҮҮЛЭХ АСИММЕТР НӨЛӨӨГ ШАЛГАХ НЬ
 ВАЛЮТЫН ХАНШИЙН ИНФЛЯЦИД ҮЗҮҮЛЭХ АСИММЕТР НӨЛӨӨГ ШАЛГАХ НЬ Б.Даваадалай /МБХ-ийн эдийн засагч/ П.Авралт-Од /МБХ-ийн эдийн засагч/ 2010 оны 9 дүгээр сар Хураангуй Энэхүү судалгааны ажлын зорилго нь Монголын
ВАЛЮТЫН ХАНШИЙН ИНФЛЯЦИД ҮЗҮҮЛЭХ АСИММЕТР НӨЛӨӨГ ШАЛГАХ НЬ Б.Даваадалай /МБХ-ийн эдийн засагч/ П.Авралт-Од /МБХ-ийн эдийн засагч/ 2010 оны 9 дүгээр сар Хураангуй Энэхүү судалгааны ажлын зорилго нь Монголын
III. Химийн бодисын харилцан үйлчлэл
 CHEM101: Органик биш хими I Лекц 11 III. Химийн бодисын харилцан үйлчлэл III.1 ТЕРМОДИНАМИК, ХИМИЙН УРВАЛЫН ЧИГЛЭЛ Аяндаа явагдах өөрчлөлт. Термодинамикийн II хууль. Энтропи (S), стандарт энтропи. Термодинамикийн
CHEM101: Органик биш хими I Лекц 11 III. Химийн бодисын харилцан үйлчлэл III.1 ТЕРМОДИНАМИК, ХИМИЙН УРВАЛЫН ЧИГЛЭЛ Аяндаа явагдах өөрчлөлт. Термодинамикийн II хууль. Энтропи (S), стандарт энтропи. Термодинамикийн
Õóðààíãóé. Түлхүүр үг: GPS тропосфер Монголд, усны уурын агууламж, агаар мандлын зайнаас тандалт
 АГААР МАНДАЛ ДАХЬ УСНЫ УУРЫН АГУУЛАМЖИЙГ GPS ХЭМЖИЛТЭЭС ТОДОРХОЙЛСОН ДҮН Ш. Амаржаргал 1, Г. Даваахүү 1, Д. Лхагвасүрэн 1, С. Санжжав 1, Н. Хишигжаргал 2, Ч. Мөнхчимэг 2, 1 Одон Орон Геофизикийн Судалгааны
АГААР МАНДАЛ ДАХЬ УСНЫ УУРЫН АГУУЛАМЖИЙГ GPS ХЭМЖИЛТЭЭС ТОДОРХОЙЛСОН ДҮН Ш. Амаржаргал 1, Г. Даваахүү 1, Д. Лхагвасүрэн 1, С. Санжжав 1, Н. Хишигжаргал 2, Ч. Мөнхчимэг 2, 1 Одон Орон Геофизикийн Судалгааны
Химийн даалгавар 11-р анги оны хичээлийн жил
 Нэгдүгээр хэсэг: Санамж: Нэгдүгээр хэсэг нийт 68 оноотой бөгөөд даалгавар тус бүр 1 оноо болно. Даалгавар бүрээс зөвхөн нэг хариултыг 1. Азотын атомын электронт бүтцийн томьёог. 1s 2 2s 2 2p 1. 1s 2 2s
Нэгдүгээр хэсэг: Санамж: Нэгдүгээр хэсэг нийт 68 оноотой бөгөөд даалгавар тус бүр 1 оноо болно. Даалгавар бүрээс зөвхөн нэг хариултыг 1. Азотын атомын электронт бүтцийн томьёог. 1s 2 2s 2 2p 1. 1s 2 2s
ЗҮРХ СУДАСНЫ ҮНДЭСНИЙ КОНФЕРЕНЦИ Зүрх судасны өвчний хяналт ба менежментийг сайжруулахад
 ЗҮРХ СУДАСНЫ ҮНДЭСНИЙ КОНФЕРЕНЦИ 2011 Зүрх судасны өвчний хяналт ба менежментийг сайжруулахад 1 Тохиолдолд суурилсан тахиаритмийн ялган оношлогоо Д.Зулгэрэл, PhD, дэд профессор ЭМШУИСийн зүрх судасны тэнхмийн
ЗҮРХ СУДАСНЫ ҮНДЭСНИЙ КОНФЕРЕНЦИ 2011 Зүрх судасны өвчний хяналт ба менежментийг сайжруулахад 1 Тохиолдолд суурилсан тахиаритмийн ялган оношлогоо Д.Зулгэрэл, PhD, дэд профессор ЭМШУИСийн зүрх судасны тэнхмийн
II бүлэг. Химийн элементийн геохимийн тархалт
 CHEM 323: Геохимийн үндэс Атом ба химийн элемент Лекц 5 II бүлэг. Химийн элементийн геохимийн тархалт Химийн элементийн үүслийн тухай таамаглал Цацраг идэвх чанар. Цацараг идэвхт изотоп, түүний задрал
CHEM 323: Геохимийн үндэс Атом ба химийн элемент Лекц 5 II бүлэг. Химийн элементийн геохимийн тархалт Химийн элементийн үүслийн тухай таамаглал Цацраг идэвх чанар. Цацараг идэвхт изотоп, түүний задрал
Орон сууцны зээлийн эдийн засагт үзүүлэх нөлөө
 Орон сууцны зээлийн эдийн засагт үзүүлэх нөлөө Д.Гансүлд (СЭЗИС) Б.Түвшинтөгс (ЭЗСЭШХ) 2018 оны 03-р сарын 13 Д.Гансүлд (СЭЗИС), Б.Түвшинтөгс (ЭЗСЭШХ) Орон сууцны зээлийн эдийн засагт үзүүлэх нөлөө2018
Орон сууцны зээлийн эдийн засагт үзүүлэх нөлөө Д.Гансүлд (СЭЗИС) Б.Түвшинтөгс (ЭЗСЭШХ) 2018 оны 03-р сарын 13 Д.Гансүлд (СЭЗИС), Б.Түвшинтөгс (ЭЗСЭШХ) Орон сууцны зээлийн эдийн засагт үзүүлэх нөлөө2018
МОНГОЛЫН МЭДЭЭЛЛИЙН ТЕХНОЛОГИ-2018
 МОНГОЛЫН МЭДЭЭЛЛИЙН ТЕХНОЛОГИ-2018 ЭРДЭМ ШИНЖИЛГЭЭНИЙ ХУРАЛ Улаанбаатар хот Ерөнхий зохион байгуулагч: Монгол Улсын Их Сургууль Хамтран зохион байгуулагч: Монголын Мэдээллийн Технологийн Консорциум Шинжлэн
МОНГОЛЫН МЭДЭЭЛЛИЙН ТЕХНОЛОГИ-2018 ЭРДЭМ ШИНЖИЛГЭЭНИЙ ХУРАЛ Улаанбаатар хот Ерөнхий зохион байгуулагч: Монгол Улсын Их Сургууль Хамтран зохион байгуулагч: Монголын Мэдээллийн Технологийн Консорциум Шинжлэн
ÑÍ 2. NH 2 -òîñíû õ èë 4-àìèíáóòàíû õ èë ÑÍ 3 ÑÍ ÑÍ 2 ÑÎÎÍ ÑÍ 2 ÑÍ 2 ÑÎÎÍ HOOC CH 2 CH COOH NH 2
 ЛЕКЦ 15 АМИН ХҮЧИЛ БА УУРАГ Амьд организмын найрлаганд ордог, түүний үйл ажиллагаанд чухал үүрэг гүйцэтгэдэг, нийлмэл бүтэцтэй органик бодисыг протеин гэх бөгөөд энэ нь анхдагч гэсэн утгатай грек үгнээс
ЛЕКЦ 15 АМИН ХҮЧИЛ БА УУРАГ Амьд организмын найрлаганд ордог, түүний үйл ажиллагаанд чухал үүрэг гүйцэтгэдэг, нийлмэл бүтэцтэй органик бодисыг протеин гэх бөгөөд энэ нь анхдагч гэсэн утгатай грек үгнээс
Төгрөгийн гадаад валюттай харьцах ханшийн тэнцвэрт түвшний судалгаа
 Төгрөгийн гадаад валюттай харьцах ханшийн тэнцвэрт түвшний судалгаа Д.Ган-Очир doojav_ganochir@yahoo.com Т. Оюунбаатар _oyuka@yahoo.com 2010 оны 3 дугаар сар Монголбанкны мөнгөний бодлого, судалгааны газрын
Төгрөгийн гадаад валюттай харьцах ханшийн тэнцвэрт түвшний судалгаа Д.Ган-Очир doojav_ganochir@yahoo.com Т. Оюунбаатар _oyuka@yahoo.com 2010 оны 3 дугаар сар Монголбанкны мөнгөний бодлого, судалгааны газрын
Зохиогч: Ч. Ганбаатар Удирдагч: Доктор (Ph.D) Б. Батзолбоо. ШУТИС-Компьютерийн Техник Менежментийн Сургуулийн Програмчлалын профессорын баг.
 АВТОМАШИНЫ ДУГААР ИЛРҮҮЛЭХ СИСТЕМИЙГ ХӨГЖҮҮЛЭХ АСУУДАЛД: Зохиогч: Ч. Ганбаатар Удирдагч: Доктор (Ph.D) Б. Батзолбоо ШУТИС-Компьютерийн Техник Менежментийн Сургуулийн Програмчлалын профессорын баг. Хураангуй:
АВТОМАШИНЫ ДУГААР ИЛРҮҮЛЭХ СИСТЕМИЙГ ХӨГЖҮҮЛЭХ АСУУДАЛД: Зохиогч: Ч. Ганбаатар Удирдагч: Доктор (Ph.D) Б. Батзолбоо ШУТИС-Компьютерийн Техник Менежментийн Сургуулийн Програмчлалын профессорын баг. Хураангуй:
Химийн даалгавар 12-р анги оны хичээлийн жил. D. d судлах шингэн = m ус d ус
 Нэгдүгээр хэсэг: Санамж: Нэгдүгээр хэсэг нийт 68 оноотой бөгөөд даалгавар тус бүр 1 оноо болно. Даалгавар бүрээс зөвхөн нэг хариултыг 1. Урвалын тэгшитгэлүүдээс ногоон ургамал шим бодис нийлэгжүүлэх урвалыг
Нэгдүгээр хэсэг: Санамж: Нэгдүгээр хэсэг нийт 68 оноотой бөгөөд даалгавар тус бүр 1 оноо болно. Даалгавар бүрээс зөвхөн нэг хариултыг 1. Урвалын тэгшитгэлүүдээс ногоон ургамал шим бодис нийлэгжүүлэх урвалыг
O 8. ), жонш (KAlSi 3
 Шинжлэх Ухааны Академийн Мэдээ 2013 оны 03 (207) Полиминералын post IR-IR болон кварцын кристаллын люминесценцийн аргыг хослуулан олдворын он цагийг тогтоох нь С.Саран 1,2, С.Тэнгис 1, Б. Оргил 1, Р.Мөнхтулга
Шинжлэх Ухааны Академийн Мэдээ 2013 оны 03 (207) Полиминералын post IR-IR болон кварцын кристаллын люминесценцийн аргыг хослуулан олдворын он цагийг тогтоох нь С.Саран 1,2, С.Тэнгис 1, Б. Оргил 1, Р.Мөнхтулга
МЭДЭЭЛЭЛ, ХОЛБООНЫ САЛБАРЫН ХӨГЖИЛД БИДНИЙ ГҮЙЦЭТГЭХ ҮҮРЭГ-2017
 МОНГОЛ УЛСЫН ШИНЖЛЭХ УХААН,ТЕХНОЛОГИЙН ИХ СУРГУУЛЬ МЭДЭЭЛЭЛ, ХОЛБООНЫ ТЕХНОЛОГИЙН СУРГУУЛЬ ДОКТОР, ПРОФЕССОР Г. ЦОГБАДРАХЫН НЭРЭМЖИТ МЭДЭЭЛЭЛ, ХОЛБООНЫ САЛБАРЫН ХӨГЖИЛД БИДНИЙ ГҮЙЦЭТГЭХ ҮҮРЭГ-2017 2016/2017
МОНГОЛ УЛСЫН ШИНЖЛЭХ УХААН,ТЕХНОЛОГИЙН ИХ СУРГУУЛЬ МЭДЭЭЛЭЛ, ХОЛБООНЫ ТЕХНОЛОГИЙН СУРГУУЛЬ ДОКТОР, ПРОФЕССОР Г. ЦОГБАДРАХЫН НЭРЭМЖИТ МЭДЭЭЛЭЛ, ХОЛБООНЫ САЛБАРЫН ХӨГЖИЛД БИДНИЙ ГҮЙЦЭТГЭХ ҮҮРЭГ-2017 2016/2017
НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР
 Элсэлтийн ерөнхий шалгалт-07 он Элсэлтийн ерөнхий шалгалт-07 он Хувилбар А - Хими НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 7 оноотой бөгөөд -8 дугаар даалгавар тус бүр оноотой, 9-40
Элсэлтийн ерөнхий шалгалт-07 он Элсэлтийн ерөнхий шалгалт-07 он Хувилбар А - Хими НЭГДҮГЭЭР ХЭСЭГ. СОНГОХ ДААЛГАВАР Санамж: Нэгдүгээр хэсэг нийт 7 оноотой бөгөөд -8 дугаар даалгавар тус бүр оноотой, 9-40
J.RC322 Бичил долгионы хэрэгсэл Хувилбар B. Хувилбар B.
 J.RC322 Бичил долгионы хэрэгсэл Хувилбар B 2016-2017 оны хичээлийн жилийн хаврын улирлын шалгалт Батлав:...МХТС-ийн дэд захирал /З. Буянхишиг/ Хянасан:...Холбооны салбарын эрхлэгч /Н. Эрдэнэхүү/ Хувилбар
J.RC322 Бичил долгионы хэрэгсэл Хувилбар B 2016-2017 оны хичээлийн жилийн хаврын улирлын шалгалт Батлав:...МХТС-ийн дэд захирал /З. Буянхишиг/ Хянасан:...Холбооны салбарын эрхлэгч /Н. Эрдэнэхүү/ Хувилбар
4-6-р асуултын хариултыг дараах томьёоноос сонгоно уу. A. B. C. D. E.
 ФИЗИК 006 5 Боловсролын Үнэлгээний Төв ХУВИЛБАР А НЭГДҮГЭЭР ХЭСЭГ. Биеийн хүндийн хүч Н-той тэнцүү байв. Биеийн масс ямар байх вэ? A. кг B. 0 кг C. 0. кг D. г E. 0. Н. Дараах хэмжигдэхүүнүүдэд тохирох
ФИЗИК 006 5 Боловсролын Үнэлгээний Төв ХУВИЛБАР А НЭГДҮГЭЭР ХЭСЭГ. Биеийн хүндийн хүч Н-той тэнцүү байв. Биеийн масс ямар байх вэ? A. кг B. 0 кг C. 0. кг D. г E. 0. Н. Дараах хэмжигдэхүүнүүдэд тохирох
БИЛЭЭ СУЛ ҮГИЙН УТГА, ХЭРЭГЛЭЭ
 Беньямин Брозиг (Benjamin Brosig). 2012. БИЛЭЭ СУЛ ҮГИЙН УТГА, ХЭРЭГЛЭЭ (The meaning and usage of the particle bilee ). Хэл зохиол судлал V (37): 10-18. The wording of the text should be as published.
Беньямин Брозиг (Benjamin Brosig). 2012. БИЛЭЭ СУЛ ҮГИЙН УТГА, ХЭРЭГЛЭЭ (The meaning and usage of the particle bilee ). Хэл зохиол судлал V (37): 10-18. The wording of the text should be as published.
Transmission of Analog Signal
 Шинжлэх Ухаан Технологийн Их Сургууль Мэдээлэл Холбооны Технологийн Сургууль Мэдээллийн сүлжээний профессорын баг Transmission of Analog Signal Лекц 5 Багш (Ph.D)Л.Одончимэг Аналог дохио дамжуулал Агуулга:
Шинжлэх Ухаан Технологийн Их Сургууль Мэдээлэл Холбооны Технологийн Сургууль Мэдээллийн сүлжээний профессорын баг Transmission of Analog Signal Лекц 5 Багш (Ph.D)Л.Одончимэг Аналог дохио дамжуулал Агуулга:
ARTICLES ФОТОЭМУЛЬСИЙН АРГААР ХЭМЖСЭН НЕЙТРОНЫ ЭНЕРГИЙН СПЕКТРИЙГ GEANT4 БАГЦ ПРОГРАМААР ЗАГВАРЧИЛЖ ХАРЬЦУУЛСАН НЬ
 02 01 (226) (225) ARTICLES ФОТОЭМУЛЬСИЙН АРГААР ХЭМЖСЭН НЕЙТРОНЫ ЭНЕРГИЙН СПЕКТРИЙГ GEANT4 БАГЦ ПРОГРАМААР ЗАГВАРЧИЛЖ ХАРЬЦУУЛСАН НЬ Д.Отгонсүрэн 1 *, Р.Тогоо 1, А.Төрсүх 1 1 Физик технологийн хүрээлэн,
02 01 (226) (225) ARTICLES ФОТОЭМУЛЬСИЙН АРГААР ХЭМЖСЭН НЕЙТРОНЫ ЭНЕРГИЙН СПЕКТРИЙГ GEANT4 БАГЦ ПРОГРАМААР ЗАГВАРЧИЛЖ ХАРЬЦУУЛСАН НЬ Д.Отгонсүрэн 1 *, Р.Тогоо 1, А.Төрсүх 1 1 Физик технологийн хүрээлэн,
ТӨСВИЙН БА УРСГАЛ ТЭНЦЛИЙН АЛДАГДЛЫН ЭДИЙН ЗАСАГТ ҮЗҮҮЛЭХ НӨЛӨӨ
 ТӨСВИЙН БА УРСГАЛ ТЭНЦЛИЙН АЛДАГДЛЫН ЭДИЙН ЗАСАГТ ҮЗҮҮЛЭХ НӨЛӨӨ Судалгааны хэлтсийн эдийн засагч Д.Энхзаяа Хураангуй Энэ судалгааны ажлаар хос алдагдлын эдийн засагт үзүүлэх нөлөөг тодорхойлохыг зорьсон.
ТӨСВИЙН БА УРСГАЛ ТЭНЦЛИЙН АЛДАГДЛЫН ЭДИЙН ЗАСАГТ ҮЗҮҮЛЭХ НӨЛӨӨ Судалгааны хэлтсийн эдийн засагч Д.Энхзаяа Хураангуй Энэ судалгааны ажлаар хос алдагдлын эдийн засагт үзүүлэх нөлөөг тодорхойлохыг зорьсон.
Монголд уул уурхайн өсөн нэмэгдэж буй үйлдвэрлэл хөдөө аж ахуйн салбарт хэрхэн нөлөөлж байгаа тухай
 Монголын бэлчээрийн нөхөн сэргэх чадамжийг бэхжүүлэх нь Салбар хөрвөсөн эрдэм шинжилгээний судалгааны хурлын бүтээл, Улаанбаатар хот, Монгол Улс, 2015 оны 6-р сарын 9-10 Монголд уул уурхайн өсөн нэмэгдэж
Монголын бэлчээрийн нөхөн сэргэх чадамжийг бэхжүүлэх нь Салбар хөрвөсөн эрдэм шинжилгээний судалгааны хурлын бүтээл, Улаанбаатар хот, Монгол Улс, 2015 оны 6-р сарын 9-10 Монголд уул уурхайн өсөн нэмэгдэж
Õàâòãàé òýãø ºíöºãò ìåòàëëûí êîìïëåêñ íýãäýë äýõ õàëàëöàà. 1-р хэсэг
 Õàâòãàé òýãø ºíöºãò ìåòàëëûí êîìïëåêñ íýãäýë äýõ õàëàëöàà 1-р хэсэг Åðºíõèé óðâàëûí õóðä: Õàëàëöëûí õóðäàä íºëººëºõ õ чèí ç éë ä Õàëàãч á ëãèéí íºëºº Õàëàãäàãч á ëãèéí íºëºº Êîìïëåêñ íýãäýë äэõü áóñàä
Õàâòãàé òýãø ºíöºãò ìåòàëëûí êîìïëåêñ íýãäýë äýõ õàëàëöàà 1-р хэсэг Åðºíõèé óðâàëûí õóðä: Õàëàëöëûí õóðäàä íºëººëºõ õ чèí ç éë ä Õàëàãч á ëãèéí íºëºº Õàëàãäàãч á ëãèéí íºëºº Êîìïëåêñ íýãäýë äэõü áóñàä
ХӨДӨЛМӨРИЙН БҮТЭЭМЖ, ЦАЛИНГИЙН СТАТИСТИК ШИНЖИЛГЭЭ
 МОНГОЛ УЛСЫН ИХ СУРГУУЛЬ ЭДИЙН ЗАСГИЙН СУРГУУЛЬ СТАТИСТИКИЙН ТЭНХИМ БААТАРЫН ОЮУН-ЭРДЭНЭ ХӨДӨЛМӨРИЙН БҮТЭЭМЖ, ЦАЛИНГИЙН СТАТИСТИК ШИНЖИЛГЭЭ Мэргэжлийн индекс : E310900 Эдийн засгийн ухааны магистрын зэрэг
МОНГОЛ УЛСЫН ИХ СУРГУУЛЬ ЭДИЙН ЗАСГИЙН СУРГУУЛЬ СТАТИСТИКИЙН ТЭНХИМ БААТАРЫН ОЮУН-ЭРДЭНЭ ХӨДӨЛМӨРИЙН БҮТЭЭМЖ, ЦАЛИНГИЙН СТАТИСТИК ШИНЖИЛГЭЭ Мэргэжлийн индекс : E310900 Эдийн засгийн ухааны магистрын зэрэг
Барилгын хашлага бүтээцийн дулаан техникийн тооцооны программ суулгаж тохиргоо хийх тухай
 Барилгын хашлага бүтээцийн дулаан техникийн тооцооны программ суулгаж тохиргоо хийх тухай Барилгын хашлага бүтээцийн дулаан техникийн тооцооны программ ыг компьютерт суурилуулахад доорх техник, тоног төхөөрөмж
Барилгын хашлага бүтээцийн дулаан техникийн тооцооны программ суулгаж тохиргоо хийх тухай Барилгын хашлага бүтээцийн дулаан техникийн тооцооны программ ыг компьютерт суурилуулахад доорх техник, тоног төхөөрөмж
= 120 м/мин бол тэдгээрийг жишнэ үү. (1 оноо) A. v 1. > v 1
 ФИЗИК 2009 Боловсролын Үнэлгээний Төв ХУВИЛБАР A НЭГДҮГЭЭР ХЭСЭГ 1. Зөв харгалзуулна уу. (1оноо) 1. Үзэгдэл a. Гэрлийн цацраг À. 1e2b3c4a5d 2. Загвар b. Хүчдэл B. 1е2а3с4d5b 3. Хэмжигдэхүүн c. Люкс C.
ФИЗИК 2009 Боловсролын Үнэлгээний Төв ХУВИЛБАР A НЭГДҮГЭЭР ХЭСЭГ 1. Зөв харгалзуулна уу. (1оноо) 1. Үзэгдэл a. Гэрлийн цацраг À. 1e2b3c4a5d 2. Загвар b. Хүчдэл B. 1е2а3с4d5b 3. Хэмжигдэхүүн c. Люкс C.
ARTICLES МОНГОЛЫН ГОВЬД АЖИГЛАГДСАН ШОРООН ШУУРГАНЫ ҮЕИЙН ТООСНЫ БОСОО УРСГАЛЫГ ҮНЭЛСЭН НЬ
 02 01 (226) (225) ARTICLES МОНГОЛЫН ГОВЬД АЖИГЛАГДСАН ШОРООН ШУУРГАНЫ ҮЕИЙН ТООСНЫ БОСОО УРСГАЛЫГ ҮНЭЛСЭН НЬ Д.Жүгдэр* Ус, цаг уур, орчны судалгаа мэдээллийн хүрээлэн, Монгол улс --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
02 01 (226) (225) ARTICLES МОНГОЛЫН ГОВЬД АЖИГЛАГДСАН ШОРООН ШУУРГАНЫ ҮЕИЙН ТООСНЫ БОСОО УРСГАЛЫГ ҮНЭЛСЭН НЬ Д.Жүгдэр* Ус, цаг уур, орчны судалгаа мэдээллийн хүрээлэн, Монгол улс --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
ИСЛАНД УЛСЫН БАГА ТЕМПЕРАТУРТАЙ, ГАЗРЫН ГҮНИЙ ДУЛААНЫ ИЛЭРЦТЭЙ ТАЛБАЙ ДЭЭРХ ТЕМ БА МТ АРГУУДЫН ХЭРЭГЛЭЭ
 Шинжлэх Ухааны Академийн Мэдээ 2017 оны 02 (222) DOI: http://dx.doi.org/10.5564/pmas.v57i2.849 ИСЛАНД УЛСЫН БАГА ТЕМПЕРАТУРТАЙ, ГАЗРЫН ГҮНИЙ ДУЛААНЫ ИЛЭРЦТЭЙ ТАЛБАЙ ДЭЭРХ ТЕМ БА МТ АРГУУДЫН ХЭРЭГЛЭЭ Л.Саранцэцэг
Шинжлэх Ухааны Академийн Мэдээ 2017 оны 02 (222) DOI: http://dx.doi.org/10.5564/pmas.v57i2.849 ИСЛАНД УЛСЫН БАГА ТЕМПЕРАТУРТАЙ, ГАЗРЫН ГҮНИЙ ДУЛААНЫ ИЛЭРЦТЭЙ ТАЛБАЙ ДЭЭРХ ТЕМ БА МТ АРГУУДЫН ХЭРЭГЛЭЭ Л.Саранцэцэг
Компьютерийн шинжлэх ухаан Computer science Натурал компьютер: онол ба хэрэглээ Natural computing: theory and aplication
 ЗУНЫ ЛЕКЦ 2010 MyPhone Компьютерийн шинжлэх ухаан Computer science Натурал компьютер: онол ба хэрэглээ Natural computing: theory and aplication И. Цэрэн Онолт Цр 23 07 2010, Улаанбаатар computation is
ЗУНЫ ЛЕКЦ 2010 MyPhone Компьютерийн шинжлэх ухаан Computer science Натурал компьютер: онол ба хэрэглээ Natural computing: theory and aplication И. Цэрэн Онолт Цр 23 07 2010, Улаанбаатар computation is
MNS ISO TR 25107:2013
 9. СОРОНЗОН БӨӨМИЙН СОРИЛ - ТҮВШИН I, II БА III MNS ISO TR 25107:2013 Ардаа тоотой E ба P үсгэн тэмдэглэгээ нь харгалзан онолын (education) ба дадлагын (pratical) сургалтын цагийг тэмдэглэгээ болно. Агуулга
9. СОРОНЗОН БӨӨМИЙН СОРИЛ - ТҮВШИН I, II БА III MNS ISO TR 25107:2013 Ардаа тоотой E ба P үсгэн тэмдэглэгээ нь харгалзан онолын (education) ба дадлагын (pratical) сургалтын цагийг тэмдэглэгээ болно. Агуулга
