«Oδηγώντας στην πόλη»
|
|
|
- Ὀφιοῦχος Δημαράς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ «Oδηγώντας στην πόλη» Κωνσταντίνα Τσάση 1, Έλλη Τσενέ 2 1 MSc Φιλόλογος nantiatsasi@yahoo.gr 2 MSc Φιλόλογος, Aμερικανικό Κολλέγιο Ελλάδος elli_tsene@yahoo.gr ΠΕΡΙΛΗΨΗ Το παρόν διδακτικό σενάριο αποτελεί μια διαθεματική πρόταση για τη διδασκαλία της Κυκλοφοριακής Αγωγής, που απευθύνεται κυρίως στην Πρωτοβάθμια Εκπαίδευση αλλά και τη βαθμίδα του Γυμνασίου. Οι δραστηριότητες στις οποίες θα εμπλακούν οι μαθητές πραγματοποιούνται σε ένα ανοιχτό μαθησιακό περιβάλλον, το εκπαιδευτικό παιχνίδι «Οδηγώντας στην πόλη», το οποίο σχεδιάστηκε με το λογισμικό MicroWorlds Pro. Ο μαθητής ελέγχοντας και καθοδηγώντας την πορεία και την ταχύτητα ενός από τα αυτοκίνητα του προγράμματος καλείται να μετακινηθεί με ασφάλεια στους δρόμους. Ο ίδιος οφείλει να κινείται σύμφωνα με τους κανόνες οδικής κυκλοφορίας, οι οποίοι καθορίζονται από τα αντίστοιχα σήματα που έχουν ενταχθεί μέσα στο πρόγραμμα. Τυχόν λανθασμένες του επιλογές θα δημιουργήσουν συγκρούσεις, ενώ παράλληλα ο ίδιος ενημερώνεται από το παιχνίδι σχετικά με τον λόγο για τον οποίο προέκυψε η προσωρινή διακοπή στη ροή του προγράμματος. Στη συνέχεια, οι μαθητές καλούνται να διορθώσουν κάποιες «ελλείψεις» του προγράμματος και τελικά να το εμπλουτίσουν, με σκοπό να κατασκευάσουν ένα παιχνίδι το οποίο θα δημοσιευτεί στο διαδίκτυο και θα έχει ως προτεινόμενο στόχο την απόκτηση «διπλώματος» από τον χρήστη. Οι μαθητές, από απλοί χρήστες του παιχνιδιού θα μετατραπούν σε προγραμματιστές, αξιοποιώντας τις γνώσεις τους σχετικά με τους κανόνες οδικής κυκλοφορίας αλλά και φυσικής και μαθηματικών, καθώς ασχολούνται με έννοιες όπως η ταχύτητα και οι αρνητικές τιμές. Μέσα από την προσπάθεια γραπτής έκφρασης στη γλώσσα προγραμματισμού Logo, ο μαθητής πειραματίζεται, οργανώνει τις εντολές του, δομεί τη σκέψη του και αναστοχάζεται σε σχέση με τις λανθασμένες του επιλογές, καλλιεργώντας με αυτόν τον τρόπο στρατηγικές επίλυσης προβλημάτων. ΛΕΞΕΙΣ ΚΛΕΙΔΙΑ: Ανοιχτό μαθησιακό περιβάλλον, γλώσσα προγραμματισμού Logo ΕIΣΑΓΩΓΗ Τα τελευταία χρόνια κοινή είναι η παραδοχή πως η ανάπτυξη της επιστήμης και της τεχνολογίας έχουν επηρεάσει τον τρόπο με τον οποίο αντιλαμβάνεται και προσεγγίζει ο άνθρωπος τη γνώση. Η γρήγορη ροή των πληροφοριών [1495]
2 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» αλλά και η άμεση πρόσβαση σε αυτή μέσα από το διαδίκτυο έχουν καταστήσει πλέον σημαντικά για τη μαθησιακή διαδικασία όχι τη συγκράτηση της γνώσης, αλλά την ικανότητα αναζήτησης, ανάλυσης και έκθεσης της πληροφορίας (Κynigos, 1995). Aντίστοιχα, όσον αφορά στον ρόλο των μαθητών στη σύγχρονη εποχή, στόχος μας δεν είναι να έχουμε μαθητές που γνωρίζουν σωρεία πληροφοριών αλλά ευέλικτους και προσαρμόσιμους μαθητές, που προσεγγίζουν και οικοδομούν σταδιακά τη γνώση (Soloway, 1990, στο Κynigos, 1995). Αναφερόμαστε, επομένως, σε μια διδακτική διαδικασία η οποία στηρίζεται στις αρχές της διερευνητικής μάθησης και χρησιμοποιεί τα υπολογιστικά εργαλεία ως μέσο πειραματισμού, διερεύνησης και αναζήτησης στα χέρια των μαθητών (ο.π.). Παράλληλα, μιλάμε για μια μαθησιακή διαδικασία η οποία επιδιώκει να εμπλέξει τους μαθητές σε διαδικασίες που έχουν προσωπικό νόημα για τους ίδιους και να τους καταστήσει αυτόνομους, έχοντας οι ίδιοι τον έλεγχο της μάθησής τους. Με βάση τις παραπάνω παραδοχές αποφασίσαμε να προσεγγίσουμε ένα από τα σύγχρονα καθημερινά προβλήματα των ανθρώπων, την εσφαλμένη οδική συμπεριφορά. Πολύ συχνά, οδηγοί και πεζοί παραπονούνται για έλλειψη σωστής κυκλοφοριακής αγωγής των συμπολιτών τους, με αποτέλεσμα να προκύπτουν διαταραχές στην ομαλή και ασφαλή μετακίνησή τους. Λαμβάνοντας υπόψη τα δεδομένα αυτά έντονα ακούγεται στον εκπαιδευτικό χώρο η ανάγκη να αποκτήσουν οι νέοι κυκλοφοριακή συνείδηση. Στη συγκεκριμένη διδακτική πρόταση, οι μαθητές αναλαμβάνουν ρόλο ενεργητικό για να κατανοήσουν βασικούς κανόνες οδικής κυκλοφορίας. Οι ίδιοι εργάζονται σε ομάδες, πειραματίζονται όσον αφορά τους δυνατούς τρόπους μετακίνησής τους και τις συνέπειες των αποφάσεων που λαμβάνουν, παρεμβαίνουν για να αλλάξουν την πορεία των πραγμάτων με στόχο τη βελτίωση της κυκλοφορίας. Η συγκεκριμένη διδακτική πρόταση θα μπορούσε να εφαρμοστεί στο πλαίσιο του μαθήματος «Αγωγή του Πολίτη», καθώς και στη «Μελέτη Περιβάλλοντος» που διδάσκονται στο δημοτικό σχολείο. Παράλληλα, το Πρόγραμμα της «Ευέλικτης Ζώνης», το οποίο εφαρμόζεται τα τελευταία χρόνια τόσο στα Δημοτικά όσο και στα Γυμνάσια, θα μπορούσε να φιλοξενήσει και να εντάξει αυτήν την πρόταση στις θεματικές ενότητες τις οποίες διαπραγματεύεται. [1496]
3 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ Σχήμα 1: Η κεντρική σελίδα ΠΕΡΙΓΡΑΦΗ ΔΙΔΑΚΤΙΚΗΣ ΠΡΟΤΑΣΗΣ ΣΤΟΧΟΙ Α) Γνωστικό αντικείμενο Να είναι οι μαθητές σε θέση να ερμηνεύσουν τη λειτουργία τριών σημάτων οδικής κυκλοφορίας: στοπ, απαγορεύεται δεξιά, διάβαση πεζών. Να κατανοήσουν τις δύο βασικές ιδιότητες της χελώνας (θέσηπροσανατολισμός) και να τις συσχετίσουν με την πραγματική κίνηση στον χώρο. Β) Μαθησιακή διαδικασία Να διατυπώσουν υποθέσεις και να πειραματιστούν προκειμένου να ελέγξουν την ορθότητά τους. Να είναι σε θέση να αναλύουν ένα πρόβλημα σε επιμέρους υποπροβλήματα και να τα ανασυνθέτουν σε ενιαίο όλο. Να συζητήσουν εναλλακτικές λύσεις για την επίλυση κάποιου προβλήματος και τη λήψη απόφασης. Να αναστοχαστούν με αφορμή τις συνέπειες των ενεργειών τους. Να καλλιεργήσουν στρατηγικές διόρθωσης σφαλμάτων. Γ) Στόχοι σε σχέση με τη χρήση του εργαλείου Να ερμηνεύσουν και να διορθώσουν προγράμματα σε γλώσσα προγραμματισμού Logo που περιέχουν διαδικασίες με μεταβλητές για τον έλεγχο της ταχύτητας. Να επεκτείνουν τη γλώσσα προγραμματισμού δημιουργώντας νέες διαδικασίες (δευτερογενείς εντολές) για να εμπλουτίσουν το εκπαιδευτικό παιχνίδι. 1 η ΦΑΣΗ: ΓΝΩΡΙΜΙΑ ΜΕ ΤΟ ΠΑΙΧΝΙΔΙ Σε αυτή τη φάση οι μαθητές έρχονται σε πρώτη επαφή με το παιχνίδι, «κινούνται» στους δρόμους και αντιμετωπίζουν ό,τι τους προκύπτει. Ο [1497]
4 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» εκπαιδευτικός, συγκεκριμένα, πληροφορεί τους μαθητές για το θέμα του παιχνιδιού, δίνει σύντομες διευκρινίσεις για τον τρόπο λειτουργίας του, τους παροτρύνει να το παίξουν δοκιμάζοντας ποικίλες διαδρομές και τους ζητά να παρατηρήσουν τα αποτελέσματα των ενεργειών τους. Στη συνέχεια, τους ζητά να καταγράψουν τα σχόλια τους σχετικά με αυτά που συμβαίνουν και να προβούν σε ανάλογες κρίσεις όσον αφορά τους κανόνες ορθής οδικής συμπεριφοράς. Σε ένα δεύτερο επίπεδο, οι μαθητές συγκεντρωμένοι στο κεντρικό τραπέζι θα συζητήσουν με τους συμμαθητές και τον διδάσκοντα για όσα συνάντησαν κατά την ενάσχόληση τους με το παιχνίδι (ερμηνεία σημάτων, ανακοινώσεων κτλ). Σκόπιμο είναι σε αυτή τη φάση να σχολιαστούν οι λανθασμένες ενέργειες στις οποίες προέβησαν οι μαθητές ενώ έπαιζαν το παιχνίδι, προκειμένου να προκύψουν μέσα από αυτή τη διαδικασία ορισμένοι βασικοί κανόνες οδικής συμπεριφοράς. Σε αυτή τη φάση, ο εκπαιδευτικός βοηθά τους μαθητές να αναστοχαστούν πάνω στον τρόπο που ενήργησαν, τονίζει και οργανώνει τα συμπεράσματα που προκύπτουν. Στο συγκεκριμένο παιχνίδι υπάρχει εσκεμμένα μια ατέλεια όσον αφορά την ταχύτητα με την οποία μπορεί να κινηθεί το αυτοκίνητο που ελέγχει ο μαθητής. Η παρατήρηση αυτή είναι δυνατόν να γίνει αντιληπτή από κάποιους μαθητές κατά την ενασχόλησή τους. Εάν, ωστόσο, αυτό δε γίνει αντιληπτό, ο εκπαιδευτικός προτείνεται να ενθαρρύνει τους μαθητές να παρατηρήσουν τι συμβαίνει όταν τα αυτοκίνητό τους κινείται με πολύ μεγάλη ταχύτητα ή με πολύ μικρή. 2 η ΦΑΣΗ: ΔΙΑΤΥΠΩΣΗ ΥΠΟΘΕΣΕΩΝ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ Οι μαθητές καλούνται να διαπιστώσουν το πρόβλημα και να προσπαθήσουν να το επιλύσουν κάνοντας τις απαραίτητες παρεμβάσεις στον κώδικα (προγραμματισμός). Σε αυτό το σημείο οι μαθητές ξαναχωρίζονται σε ομάδες, διατυπώνουν τις πρώτες υποθέσεις και ξεκινούν τη διερεύνηση του προβλήματος. Αφού «τεμαχίσουν» το πρόβλημα στα επιμέρους, δοκιμάζουν εντολές, παρατηρούν άμεσα τα αποτελέσματα των προσπαθειών τους και ελέγχουν τις υποθέσεις τους μέχρι να οδηγηθούν στο επιθυμητό αποτέλεσμα. Στο τέλος της φάσης, οι ομάδες θα ξανασυναντηθούν για να συζητήσουν την πορεία που ακολούθησαν, τις δυσκολίες που ενδεχομένως συνάντησαν και τους εναλλακτικούς τρόπους που βρήκαν για την αντιμετώπισή τους. 3 η ΦΑΣΗ: ΕΠΕΚΤΑΣΗ ΛΟΓΙΣΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η τελευταία αυτή φάση της συγκεκριμένης διδακτικής πρότασης εμπλέκει ενεργά το μαθητή στον ρόλο του προγραμματιστή. Κάθε ομάδα καλείται να εμπλουτίσει σε μία νέα σελίδα το παιχνίδι με καινούρια δεδομένα, όπως για παράδειγμα σήματα, αυτοκίνητα, πεζούς, διαβάσεις. Στη συνέχεια, ο μαθητής χρειάζεται να ορίσει νέες διαδικασίες και να αλλάξει το σκεπτικό του παιχνιδιού έχοντας ως κίνητρο τη δημοσίευσή του στην ιστοσελίδα του σχολείου. Στο σημείο αυτό απαραίτητος κρίνεται ο ενισχυτικός ρόλος του διδάσκοντα, καθώς οι μαθητές θα χρειαστεί να αξιοποιήσουν εντολές που ίσως δεν έχουν χρησιμοποιήσει ξανά. Τελικός στόχος του παιχνιδιού θα είναι η απόκτηση διπλώματος. [1498]
5 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ 4 η ΦΑΣΗ: ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΕΡΓΟΥ ΤΩΝ ΜΑΘΗΤΩΝ Σε συζήτηση εφ όλης της ύλης, οι μαθητές παρουσιάζουν στην τάξη το τελικό προϊόν, αναπτύσσουν το σκεπτικό πάνω στο οποίο κινήθηκαν, αναφέρουν τα σημεία που τους δυσκόλεψαν και εκφράζουν τις τελικές τους εντυπώσεις. To τελικό προϊόν μπορεί πλέον να δημοσιευθεί στην ιστοσελίδα του σχολείου. ΤΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΠΑΧΝΙΔΙ: «ΟΔΗΓΩΝΤΑΣ ΣΤΗΝ ΠΟΛΗ» Το «Οδηγώντας στην πόλη» είναι ένα εκπαιδευτικό παιχνίδι κατασκευασμένο με το λογισμικό MicroWorlds Pro. Το συγκεκριμένο λογιμσικό είναι ένα ανοιχτό αλληλεπιδραστικό περιβάλλον, το οποίο αξιοποιεί ως κύριο μέσο έκφρασης τη γλώσα προγραμματισμού Logo. Από την ενασχόληση των μαθητών με τη συγκεκριμένη γλώσσα θεωρούμε ότι μπορούν να προκύψουν σημαντικά μαθησιακά οφέλη, στα οποία και θα αναφερθούμε εκτενώς στην παρούσα ενότητα. Α. ΑΞΙΟΠΟΙΗΣΗ ΔΙΑΙΣΘΗΤΙΚΗΣ ΓΝΩΣΗΣ Ξεκινώντας την αναφορά μας στις διαισθητικές ιδέες θα θέλαμε να παραπέμψουμε σε αυτό που ο Penner αναφέρει, ότι δηλαδή «οι διαισθήσεις θα πρέπει να χρησιμοποιούνται ως βάση για τη δόμηση της γνώσης» (Pener, 2001, όπως αναφέρεται στο Γιαννούτσου, 2005). Για να γίνει ωστόσο αυτό, θα πρέπει εκείνες να έρθουν στο προσκήνιο, να γίνουν αντιληπτές από τους μαθητές, τόσο ως έννοιες αλλά και ως λειτουργίες. Η γλώσσα προγραμματισμού Logo προσφέρει τη δυνατότητα αυτή στους μαθητές, καθώς τους παρέχει το έναυσμα για να εστιάσουν σε έννοιες και αντιλήψεις που ήδη κατέχουν αλλά δεν έχουν συνειδητοποιήσει, να τις εκφράσουν, να τις συστηματοποιήσουν αλλά και να μετασχηματίσουν τυχόν λανθασμένες (disessa, 1993, 2000 όπως αναφέρεται στο Γιαννούτσου, 2005). Για να γίνει αυτό κατανοητό, ας αναφερθούμε στη λειτουργία της γλώσσας στη ζωή των ανθρώπων. Η πιο γνωστή είναι αυτή ως μέσο έκφρασης ιδεών και επικοινωνίας των ανθρώπων. Μια δεύτερη ωστόσο λειτουργία που συχνά δεν αναφέρεται είναι αυτή της χρήσης της ως μέσο για να αντιληφθεί κανείς την πραγματικότητα. Η φυσική γλώσσα θα μπορούσε να χαρακτηρισθεί ως περιγραφική. Η γλώσσα προγραμματισμού, ωστόσο, που χρησιμοποείται στο συγκεκριμένο περιβάλλον απαιτεί ακρίβεια και περιεκτικότητα. Ο μαθητής χρειάζεται να δώσει οδηγίες, να διδάξει τον υπολογιστή, να τον κάνει να σκεφτεί. Για να γίνουν αυτά, όμως, χρειάζεται ο ίδιος να μάθει τον προσωπικό του τρόπο σκέψης (Papert, 1991). Με βάση αυτή τη λογική, οι μαθητές χρειάζεται να κοινοποιήσουν και να κωδικοποιήσουν τις διαισθητικές τους ιδέες, ερχόμενοι βεβαίως αντιμέτωποι με τις «συνέπειες» των επιλογών τους (Hoyles & Sutherland, 1992, Sherin& disessa, 1993 όπως αναφέρεται στο Γιαννούτσου, 2005). Αυτό σημαίνει ότι πολλές φορές οι ίδιοι θα έρθουν αντιμέτωποι με ένα αποτέλεσμα το οποίο οι ίδιοι αρχικά δεν είχαν επιδιώξει. Θα χρειαστεί να το παρατηρήσουν, να το συγκρίνουν με αυτό που αρχικά είχαν υποθέσει ως σωστό, να προβούν στους [1499]
6 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» κατάλληλους συσχετισμούς και τελικά να το ερμηνεύσουν. Οι ίδιοι χρειάζεται να αιτιολογήσουν τις επιλογές που υιοθέτησαν, να αναλύσουν το φαινόμενο το οποίο διαπραγματεύονται σε επιμέρους διαδικασίες. Η διαδικασία αυτή συμβάλλει σημαντικά στο να μπορέσει να αντιληφθεί κανείς την πραγματικότητα. Ένα διδακτικό παράδειγμα που επεξηγεί τις παραπάνω παραδοχές είναι το εξής. Όταν η χελώνα-αυτοκίνητο στο εκπαιδευτικό παιχνίδι «Οδηγώντας στην πόλη» άλλαζε κατεύθυνση, αρχικά δεν είχαμε ορίσει να αλλάζει και σχήμα το αυτοκίνητο, έτσι ώστε να δείχνει τη σωστή κατεύθυνση της χελώνας. Φυσικό επακόλουθο ήταν λοιπόν η χελώνα να στρίβει δεξιά, ενώ το σχήμα της έδειχνε ευθεία κίνηση. Επομένως, έπρεπε με κάποιον τρόπο να συνδέσουμε την αλλαγή του σχήματος με την κατεύθυνση της χελώνας. Αρχικά, λοιπόν, συνδέσαμε την κατεύθυνση της χελώνας με τα αντίστοιχα πλήκτρα-βέλη από το πληκτρολόγιο. Με το πάτημα κάθε βέλους, η χελώνα θα έπρεπε να προχωρά ευθεία σε 0 μοίρες ή να στρίβει 90 μοίρες ή 180 ή 270. Αυτό σημαίνει ότι μπορεί να πάει ευθεία, αριστερά, δεξιά και να επιστρέψει και στην αρχική της θέση. Ωστόσο, αυτό που μπορέσαμε διαισθητικά να αντιληφθούμε ήταν ότι εάν συνδέαμε και τα διαφορετικά σχήματα του αυτοκινήτου με τα βέλη θα είχαμε σε κάθε στροφή και το σωστό σχήμα. Ο μοναδικός τρόπος να ελέγξουμε κατά πόσο η άποψη αυτή ήταν σωστή ήταν να τη διατυπώσουμε σε κώδικα και να δούμε τα αποτελέσματα. Πράγματι, η υπόθεσή μας ήταν σωστή και η ο προσανατολισμός της χελώνας με την αλλαγή των σχημάτων εκτελείτο σε αντιστοιχία, κατά έναν τρόπο κυκλικό. Μετά από όλα αυτά είναι φανερό πως η έννοια των διαισθητικών ιδεών συνδέεται άρρηκτα με τις αρχές της θεωρίας του Κονστρουκτιβισμού. Συγκεκριμένα, καθώς ο μαθητής αντιλαμβάνεται και συνειδητοποιεί τις διαισθητικές του ιδέες βρίσκεται σε θέση να επαναδομήσει τα γνωστικά του σχήματα και να τα εμπλουτίσει με νέες έννοιες που συνδέονται μεταξύ τους δυναμικά και μετασχηματίζουν τον αρχικό τρόπο με τον οποίο αντιλαμβανόταν μέχρι τώρα την πραγματικότητα. Αυτή ακριβώς η διαδικασία είναι που σύμφωνα με τη συγκεκριμένη θεωρία μάθησης αιτιολογεί το χαρακτηρισμό που έχει αποδοθεί στη μαθησιακή διαδικασία ως ενεργή διαδικασία «χτισίματος» νοημάτων (Ράπτης, 1998). Έμφαση δίνεται σε αυτό το σημείο και στην έννοια του υποκειμενικού στοιχείου όσον αφορά τη δόμηση των γνωστικών αναπαραστάσεων κάθε ανθρώπου, καθώς η προσωπική αντίληψη και κατανόηση των πραγμάτων οδηγεί στην οικοδόμηση διαφορετικών σχημάτων με προσωπικό νόημα για τον καθένα. Β. ΑΝΑΣΤΟΧΑΣΜΟΣ Αφήνοντας το κεφάλαιο των διαισθητικών ιδεών, ενδιαφέρον κρίνεται σε αυτό το σημείο να αναφερθεί η άποψη ότι όταν η διαίσθηση γίνεται συμβολική έκφραση, τότε την ίδια στιγμή γίνεται και πιο ανοιχτή στον αναστοχασμό (Hoyles 1995, Papert 1980, Penner 2001, disessa 1995 όπως αναφέρεται στο Γιαννούτσου, 2005). Η υπολογιστική τεχνολογία θεωρείται ότι συμβάλλει σε διαδικασίες αναστοχασμού, καθώς γνώσεις και διαδικασίες έρχονται στην [1500]
7 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ επιφάνεια λόγω της χρήσης του διερευνητικού λογισμικού. Ειδικότερα, ο αναστοχασμός συνδέεται στενά με το είδος ανατροφοδότησης την οποία προσφέρει το υπολογιστικό εργαλείο. Ένα βασικό στοιχείο του συγκεκριμένου διερευνητικού περιβάλλοντος είναι το ότι παρουσιάζει άμεσα τις «συνέπειες» των αποφάσεων των μαθητών. Αυτό τους δίνει τη δυνατότητα να εντοπίσουν τη διαφορά ανάμεσα σε αυτό που περίμεναν ότι θα συμβεί και αυτό που τελικά πραγματοποιήθηκε, να την κατανοήσουν, να τη διορθώσουν. Η έννοια του αναστοχασμού αλλάζει ριζικά τον τρόπο που κανείς αντιλαμβάνεται το λάθος και το ρόλο του στη μαθησιακή διαδικασία. Σημασία δεν έχει πλέον το γιατί έκανε κανείς λάθος αλλά να το μελετήσει και να εξετάσει το πώς μπορεί να το διορθώσει (Papert, 1991). Eίναι απαραίτητο, δηλαδή, να αναπτύξει ο μαθητής στρατηγικές «διόρθωσης σφαλμάτων», τις οποίες είναι επιθυμητό να χρησιμοποιεί γενικότερα σε οποιαδήποτε ανάλογη περίσταση. Παρόλο που οι στρατηγικές διόρθωσης σφαλμάτων υπήρχαν και πριν τη χρήση του υπολογιστή στη διδακτική διαδικασία, o Papert αναφέρει ότι «το σημαντικό είναι το ότι σκεφτόμαστε σχετικά με τη μάθηση σε αναλογία με την ανάπτυξη προγράμματος, πράγμα το οποίο είναι ένας εφικτός τρόπος για να αντιμετωπίζουμε πιο ξεκάθαρα τις στρατηγικές μας «διόρθωσης σφάλματος» και να τις βελτιώνουμε» (Papert, 1991). Συγκεκριμένα, ο ίδιος χρειάζεται να εντοπίσει που βρίσκεται το πρόβλημα, (η γλώσσα Logo διευκολύνει σε αυτόν τον τομέα, καθώς ο μαθητής μπορεί να δει το γραφικό αποτέλεσμα για κάθε επιμέρους τμήμα του κώδικα που έχει γράψει) και να το αντιμετωπίσει. Αυτό μπορεί να γίνει με το να αναλογιστεί και παλι πάνω στις σχέσεις που διέπουν τον συμβολικό κώδικα, εξετάζοντας όλες τις παραμέτρους, να αναδομήσει τα νοήματα και τελικά να εμπλακεί σε μια συνεχή ενεργητική διαδικασία δόμησης αλλά και επανελέγχου της γνώσης. H ικανότητα αυτή του αναστοχασμού είναι ένα από εκείνα τα στοιχεία που τελικά συμβάλλουν στο να πάρει ο μαθητής τον έλεγχο της μάθησης στα χέρια του και να κατευθύνει ο ίδιος τη διαδικασία. Η έννοια αυτή του ελέγχου της μαθησιακής διαδικασίας είναι ιδιαίτερα σημαντική εάν αναλογιστεί κανείς ότι λίγοι είναι εκείνοι οι οποίοι μπορούν να έχουν τον έλεγχο της τεχνολογίας (Papert 1980, disessa & Abelson, 1986 στο Κynigos, 1995). Με βάση αυτό το σκεπτικό, το λάθος δεν έχει νόημα να ποινικοποιείται και να επικρίνεται αλλά να γίνεται αντικείμενο συζήτησης, να χρησιμοποιείται ως μέσο για να αναδομηθεί η γνώση του μαθητή και να αναχθεί σε σωστότερα και καταλληλότερα γνωστικά σχήματα. Η διαδικασία αυτή «αναπτύσσει στο μαθητή μια αρθρωμένη και ξεκάθαρη γλώσσα για να ζητήσουν οι μαθητές βοήθεια όταν τη χρειάζονται» (Papert, 1991). Παράλληλα, η διαδικασία αυτή δίνει προσωπικό νόημα στο μαθητή για να εμπλακεί στη διαδικασία του προγραμματισμού, εφόσον ο ίδιος πειραματίζεται πάνω σε προσωπικά του σενάρια και έχει τη δυνατότητα να δομήσει τις ιδέες του με τον δικό τρόπο (Kynigos, 1997). H έμφαση που δίνεται σε δραστηριότητες που οι μαθητές τις αισθάνονται προσωπικές και σημαντικές ανοίγει σύμφωνα με τον Papert τον δρόμο «...για ένα πιο κατανοητό και συντονισμένο είδος μάθησης» (Papert, 1991). Eξάλλου, σύμφωνα με τον Bruner, τα εσωτερικά κίνητρα είναι εκείνα τα οποία [1501]
8 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» ενεργοποιούν το μαθητή και του καλλιεργούν τη διάθεση για συμμετοχή στη μαθησιακή διαδικασία. Ένα χαρακτηριστικό παράδειγμα σχετικά με τον αναστοχασμό αποτελεί το εξής πρόβλημα που προέκυψε κατά τον προγραμματισμό στο «Οδηγώντας στην πόλη». Σε συγκεκριμένο σημείο θέσαμε το σήμα που απαγορεύει τη στροφή προς τα δεξιά. Παράλληλα, ορίσαμε πως εάν το αυτοκίνητο στρίψει δεξιά θα πρέπει να εμφανιστεί μια ειδοποίηση που να τονίζει στον μαθητή ότι έχει διαπράξει παράβαση. Το πρόγραμμα καταλαβαίνει ότι το αυτοκίνητο έστριψε σε αυτό το σημείο λόγω μιας κρυμμένης χελώνας που βρίσκεται σε αυτό το σημείο. Ενώ λοιπόν φαινόταν πως όλα λειτουργούν σωστά, προέκυψε στην πορεία πως όταν το αυτοκίνητο βρίσκεται στο ίδιο σημείο από την αντίθετη κατεύθυνση, τότε ξαναεμφανίζεται η ειδοποίηση ότι έχει κάνει παράβαση, γεγονός το οποίο στη συγκεκριμένη περίπτωση δεν υφίσταται καθώς η στροφή προς τα δεξιά στο συγκεκριμένο σημείο επιτρέπεται. Χρειάστηκε λοιπόν να αναλογιστούμε σχετικά με το γιατί εμφανίζεται σε αυτό το σημείο η ειδοποίηση. Μελετώντας το αντίστοιχο σημείο του κώδικα προκύπτει ότι η ειδοποίηση βγαίνει όταν το αυτοκίνητο αγγίζει τη συγκεκριμένη χελώνα ανεξάρτητα από την κατεύθυνσή του. Χρειάζεται, λοιπόν, να προσθέσουμε μια νέα συνθήκη στον κώδικά, που να επιτρέπει την εμφάνιση της ειδοποίησης μόνο όταν το αυτοκίνητο ακουμπά την κρυμμένη χελώνα και έχει το σχήμα εκείνο που δείχνει κατεύθυνση προς τα κάτω. Γ. ΣΤΡΑΤΗΓΙΚΕΣ ΕΠΙΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΟΣ Έχουμε ήδη αναφεθεί στο κεφάλαιο της διασθητικής γώσης στο γεγονός ότι η η γλώσσα Logo είναι διαδικαστική. Με αφορμή αυτό το χαρακτηριστικό θα μιλήσουμε για τη συμβολή της συγκεκριμένης γλώσσας προγραμματισμού στην ανάπτυξη από τον μαθητή στρατηγικών επίλυσης προβλημάτων. Όταν αναφερόμαστε στον όρο διαδικαστική γνώση εννούμε τη δυνατότητα που έχει ο μαθητής να χωρίσει ένα αρχικό πρόβλημα σε επιμέρους τμήματα, αντιμετωπίζοντας το καθένα από αυτά ξεχωριστά. Αναφερόμαστε στην έννοια του δομημένου προγραμματισμού, που δίνει έμφαση στα στάδια μιας διαδικασίας, τις υποδιαδικασίες (Papert, 1991) αλλά και ακολούθως στη σύνθεση των επιμέρους διαδικασίων σε ένα ενιαίο όλο, την επαναδόμησή τους, με τελικό στόχο να αντιμετωπισθεί το αρχικό πρόβλημα. (disessa, 2000 όπως αναφέρεται στο Γιαννούτσου, 2005). Όπως αναφέρεται από τον Papert, το περιβάλλον μπορεί να λειτουργήσει ως ένα είδος «νοητικής σκαλωσιάς», καθώς ο μαθητής «τεμαχίζοντας» το πρόβλημα μπορεί να ασχοληθεί προοδευτικά απο το πιο απλό στο πιο σύνθετο μέρος του, αναπτύσσοντας εξελικτικά την αφαιρετική του σκέψη (Papert, 1980, όπως αναφέρεται στο Αργύρης, 2002). Ειδικότερα, καθώς ο μαθητής ασχολείται με το επιμέρους πρόβλημα και στη συνέχεια επιχειρεί να συνδέσει τις επιμέρους λύσεις σε ένα ενιαίο και δυναμικό σύνολο, είναι πιο εύκολο να συνειδητοποιήσει ότι υπάρχει αυτό που αποκαλούμε «τρόπος σκέψης». Το γεγονός αυτό διευκολύνει το μαθητή, καθώς μειώνει το επίπεδο πολυπλοκότητας του προβλήματος αλλά και της [1502]
9 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ απαιτούμενης αφαίρεσης. Οι μαθητές βιώνουν τη διαδικασία επίλυσης ενός προβλήματος και έχουν την ευκαιρία να διαλέξουν τρόπους, να κάνουν τη μαθητεία τους ως επιστήμονες, δηλαδή, να μάθουν να σκέφτονται καθαρά σχετικά με τη σκέψη (Papert, 1991). Σε αυτό το σημείο διαφαίνεται και η ευκαιρία που παρέχεται στο μέσα από τη χρήση της γλώσσας προγραμματισμού να ενεργήσει ως ενήλικας και επιστήμονας σε σχέση με τις εργασίες που αναλαμβάνει να φέρει εις πέρας αλλά και τον εαυτό του (ο.π.). Η διαδικασία αυτή τονίζεται από το χώρο της Γνωστικής Ψυχολογίας και τον Bruner, καθώς εκτός των άλλων επιδρά θετικά ως προς την αντίληψη που έχει ο μαθητής για τον εαυτό του και την αυτοεκτίμηση που νιώθει (Ράπτης, 1998). Ένα δεύτερο σημείο στο οποίο θα θέλαμε να δώσουμε έμφαση είναι στην έννοια «διαδικασία» κατά την επίλυση κάποιου προβλήματος. Ο όρος αυτός δηλώνει τόσο τη διάρκεια όσο και τη σταδιακή εξέλιξη. Τα στοιχεία αυτά είναι ιδιαιτέρως σημαντικά για το μαθητή, καθώς ο ίδιος βλέπει συνεχώς την πρόοδο στην εργασία του, την πορεία της. Με αυτόν τον τρόπο καλλιεργείται η άποψη ότι τα πράγματα δεν είναι εντελώς σωστά ή λάθος αλλά συνεχόμενα, γεγονός το οποίο αντικατοπτρίζει την έννοια της μαθητειακής στρατηγικής στην οποία επιθυμούμε να ασκηθούν οι μαθητές (Papert, 1991). Ο Papert τονίζει ακόμη πως πρέπει να δημιουργούνται στην τάξη συνθήκες για να χρησιμοποιεί ο μαθητής τη διαδικαστική σκέψη και πως η υπολογιστική τεχνολογία αποτελεί ένα δυναμικό διανοητικό εργαλείο που μπορεί να χρησιμοποιηθεί ως μέσο για την επίτευξη του παραπάνω στόχου (Papert, 1991). Έμφαση δίνεται, δηλαδή, στην έννοια του κοινωνικού πλαισίου, το οποίο σύμφωνα με τον Vygotsky και τις αρχές του κοιωνικού δομητισμού ασκεί μεγάλη επίδραση στον τρόπο με τον οποίο ο άνθρωπος αντιλαμβάνεται την πραγματικότητα (Μπασέτας, 2002). Αυτή η κοινωνικο-πολιτιστική διάσταση στη θεωρία του Vygotsky αποτελεί και μια σημαντική διαφορά σε σχέση με την αμιγώς γνωστική θεωρία και τον Piaget, καθώς δίνει έμφαση στη μετατροπή των κοινωνικών σχέσεων σε νοητικές διεργασίες μέσω διαμεσολαβητικών εργαλείων, όπως είναι στη συγκεκριμένη περίπτωση το προαναφερόμενο ανοιχτό διερευνητικό περιβάλλον (Ράπτης, 1998). Συμπληρωματικά, αναφέρουμε ότι ο ρόλος της γλώσσας πραγραμματισμού σύμφωνα με τα προαναφερόμενα στοιχεία φαίνεται να είναι παρωθητικός, καθώς ο μαθητής αντικρίζει και καρπώνεται άμεσα τα αποτελέσματα των ενεργειών του και βιώνει το αίσθημα της προσωπικής ικανοποίησης. Παράλληλα η γλώσσα προγραμματισμού Logo λειτουργεί και ανατροφοδοτικά, καθώς ο μαθητής μπορεί αμέσως να ελέγξει κατά πόσο ενήργησε σωστά ή όχι και να συνεχίσει αναλόγως. Ακόμη, χρειάζεται να αναφερθεί το γεγονός ότι κατά τη διαδικασία επίλυσης ενός προβλήματος χρειάζεται να ξεκινήσει κανείς από κάτι που ήδη καταλαβαίνει ή κάτι το οποίο θα μοιάζει με αυτό που ήδη καταλαβαίνει (Polya, όπως αναφέρεται στο Papert, 1991). Το γεγονός αυτό είναι σημαντικό, γιατί φανερώνει ότι τα πράγματα δεν είναι ασύνδετα μεταξύ τους. Αντιθέτως, ο προγραμματισμός έχει τη βάση του στα δομικά στοιχεία των πραγμάτων, στην ανάλυση και σύνθεση της δομής των σχέσεων που διέπουν τις εντολές, στην επισήμανση κανονικοτήτων, στον [1503]
10 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» εντοπισμό και την αξιοποίηση των στοιχείων εκείνων που επαναλαμβάνονται σε παρόμοιες συνθήκες με κοινά χαρακτηριστικά (μοτίβα). Συνοψίζοντας, θα λέγαμε πως οι διαδικασίες αυτές βοηθούν τον μαθητή να εσωτερικεύει τη διαδικασία της μάθησης και επίλυσης κάποιας κατάστασης προβληματισμού και αυτό γιατί προγραμματίζοντας, χρειάζεται ο ίδιος να συγκεκριμενοποιήσει το στόχο του, να διαχωρίσει τα βασικά στοιχεία και τα υποπροβλήματα, να τα επανασυνδέσει με τρόπο που να αναδεικνύεται η μεταξύ τους σχέση (Hoyles & Sutherland, 1992 όπως αναφέρεται στο Γιαννούτσου, 2005). Όλα αυτά προϋποθέτουν, ωστόσο, ότι ο μαθητής θα αλλάξει την οπτική γωνία που αντιλαμβάνεται τα πράγματα και θα προσπαθήσει να μπει στη θέση της χελώνας για να κατανοήσει το λόγο για τον οποίο συμβαίνουν τα πράγματα, με τον τρόπο που συμβαίνουν. Στη συνέχεια, όλα αυτά θα τα εκφράσει με έναν τρόπο που να μπορέσει να καταλάβει ο υπολογιστής. Ένα χαρακτηριστικό παράδειγμα σχετικά με τον επιμερισμό του αρχικού προβλήματος στα δομικά του στοιχεία και η επανασύνθεσή τους είναι το εξής. Κατά την κατασκευή του εκπαιδευτικού παιχνιδιού «Οδηγώντας στην πόλη» θελήσαμε να υπάρχει ένα αυτοκίνητο το οποίο θα καθοδηγούσε ο μαθητής στον χώρο. Αυτό ήταν και το αρχικό ζητούμενο. Για να υλοποιηθεί όμως αυτή η διαδικασία χρειάστηκε να ασχοληθούμε διεξοδικά με τα εξής υποπροβλήματα. Αρχικά, χρειάστηκε να σχοληθούμε με την κίνηση του αυτοκινήτου, να ορίσουμε δηλαδή πόσα βήματα θα προχωρά και με ποια συχνότητα, προκειμένου να είναι η κίνησή του φυσική. Στη συνέχεια, επειδή η χελώνα άλλαζε κατεύθυνση χρειάστηκε να προσδιορίσουμε και το σχήμα που θα έπαιρνε αυτή σε κάθε στροφή. Ένα τρίτο στάδιο ήταν να προγραμματίσουμε το αυτοκίνητο κατά τέτοιον τρόπο, ώστε να χειρίζεται ο μαθητής την κίνηση και τον προσανατολισμό της από το πληκτρολόγιο. Τέλος, επειδή η ταχύτητα ενός αυτοκινήτου στην πραγματικότητα δεν είναι σταθερή αλλά επιδέχεται αυξομοιώσεις, χρειάστηκε να προγραμματίσουμε τη χελώνα να αυξομειώνει ταχύτητα μέσα από το πληκτρολόγιο που χρησιμοποιεί ο μαθητής. Όλες αυτές οι υποδιαδικασίες βρέθηκαν τελικά μέσα στο πλαίσιο της εντολής «για καθοδηγηση». Σύμφωνα με τον Piaget, το τελευταίο στάδιο γνωστικής ανάπτυξης στο οποίο μπορεί να φτάσει ο άνθρωπος είναι αυτό της τυπικής-αφηρημένης σκέψης. Κάποιοι, ωστόσο, παρόλο που το στάδιο αυτό είναι δυνατόν να εμφανιστεί από το δωδέκατο έτος ζωής του ανθρώπου, μπορεί και να μην το φτάσουν ποτέ (Μπασέτας, 2002). Γίνεται, λοιπόν, κατανοητό το πόσο σημαντικό είναι να υπάρχουν κατά τη μαθησιακή διαδικασία εργαλεία τα οποία υποστηρίζουν την καλλιέργεια αφηρημένης σκέψης και η υπολογιστική τεχνολογία θεωρείται πως μπορεί να είναι ένα από αυτά. Eνα βασικό στοιχείο το οποίο υποστηρίζει την άποψη αυτή είναι το γεγονός ότι, μέσα από τη χρήση της γλώσσας προγραμματισμού, ο μαθητής συνδέει δυναμικά το συγκεκριμένο με το αφηρημένο. Για παράδειγμα, η πραγμάτωση της έννοιας που εκφράζεται μέσα από μια συγκεκριμένη εντολή στο συμβολικό κώδικα αναπαρίσταται μέσα από το γραφικό αποτέλεσμα (disessa, 1992, όπως [1504]
11 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ αναφέρεται στο Γιαννούτσου, 2005). Από μια διαφορετική σκοπιά, θα λέγαμε πως ο προγραμματισμός και η δυναμική διασύνδεση των αναπαραστάσεων οπτικοποιεί αυτό που σκέφτεται ο μαθητής (Ντέμπορα, 1995, όπως αναφέρεται στο Papert, 1991). To γεγονός αυτό είναι ιδιαίτερα χρήσιμο για τον εκπαιδευτικό, καθώς μπορεί να διαπιστώσει τον τρόπο με τον οποίο σκέπτονται οι μαθητές του, τις ιδέες τους και να παρέμβει επιβοηθητικά στο κατάλληλο σημείο. Παράλληλα, με τη χρήση της γλώσσας εισάγεται η έννοια της «ενταγμένης αφαίρεσης» (Hoyles, 1992 στο Γιαννούτσου, 2005). Ο μαθητής, δηλαδή, μέσα από τη μελέτη συγκεκριμένων καταστάσεων μπορεί να διατυπώσει γενικές και αφηρημένες σχέσεις. Ο ίδιος, καθώς προγραμματίζει, χρησιμοποιεί συνδυαστικά διαδικασίες και εντολές, εφόσον μπορεί να ενσωματώνει τη μια μέσα στην άλλη. Το γεγονός αυτό ενισχύει τη μετάβαση από το συγκεκριμένο στο αφηρημένο, ενώ ταυτόχρονα η σταδιακή αυτή δόμηση του κώδικα από τον μαθητή οδηγεί και στην παράλληλη δόμηση της δικής του προσωπικής γνώσης (Hoyles & Noss όπως αναφέρεται στο Γιαννούτσου, 2005). Eξάλλου, για να διδάξει ο μαθητής τη χελώνα να «σκεφτεί», απαραίτητη προϋπόθεση είναι να οδηγηθεί και ο ίδιος σε συλλογισμό για τις δικές του πράξεις. Επιπρόσθετα, κατά τη διάρκεια του προγραμματισμού ο μαθητής δεν εμπλέκεται μόνο σε γνωστικές διεργασίες αλλά αντιμετωπίζει παράλληλα τους φόβους του, τις ανησυχίες του, τα λογικά αναμενόμενα αδιέξοδα στα οποία συχνά βρίσκεται. Το γεγονός αυτό αναδεικνύει και την ψυχολογική πλευρά της διαδικασίας και όχι μόνο της κοινωνικής (Kynigos, 1995) Δ. ΠΕΙΡΑΜΑΤΙΣΜΟΣ Σύμφωνα με τον ορισμό που δίνεται από την Edwards, «μικρόκοσμος» είναι: «...ένα υπολογιστικό περιβάλλον όπου μέσα βρίσκονται ενσωματωμένες συγκεκριμένες έννοιες γνωστικού αντικειμένου, υπό μορφή δυναμικών αναπαραστάσεων (Edwards 1995, όπως αναφέρεται στο Αργύρης, 2002). Ο ορισμός αυτός φανερώνει πως η γνώση δεν αναγράφεται πουθενά, ούτε ανακοινώνεται αλλά βρίσκεται ενσωματωμένη και διάχυτη μέσα στον μικρόκοσμο, περιμένοντας να ανακαλυφθεί από τον χρήστη. Τα στοιχεία αυτά, τα οποία χαρακτηρίζουν και το μικρόκοσμο «Οδηγώντας στην πόλη», φανερώνουν πως η εμπλοκή με ένα τέτοιο παιχνίδι σχετίζεται άμεσα με το είδος της διερευνητικής μάθησης και θέλουν το μαθητή να εμπλακεί σε μια διαδικασία ενεργούς αναζήτησης της γνώσης. Η διερευνητική και επομένως ανακαλυπτική μάθηση, η οποία επιδιώκεται από το προαναφερόμενο σενάριο ενέχει την έννοια του πειραματισμού, την οποία και θα αναλύσουμε στη συνέχεια αυτού του κεφαλαίου. Κατά την ενασχόληση τους με το υπό μελέτη πρόβλημα, οι μαθητές διατυπώνουν υποθέσεις σχετικά με την επίλυση κάποιου προβλήματος και καλούνται να ελέγξουν την ορθότητα της σκέψης τους. Για τον σκοπό αυτό κατασκευάζουν πράγματα και δοκιμάζουν πιθανές λύσεις. Σε περίπτωση που τα αποτελέσμτα δεν έιναι αυτά που οι ίδιοι είχαν θέσει ως αρχικό στόχο, έχουν τη δυνατότητα να αλλάξουν τις παραμέτρους και να επαναλάβουν τη διαδικασία όσε φορές εκείνοι επιθυμούν και κρίνουν απαραίτητο. Οι αλλαγές [1505]
12 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» αυτές είναι δυνατόν αλλά και επιθυμητό παράλληλα να οδηγήσουν σε επαναδιατύπωση των υποθέσεων και επανέλεγχο αυτών (Hoyles & Sutherland, 1989 όπως αναφέρεται στο Γιαννούτσου, 2005). Η διαδικασία αυτή μάλιστα θεωρείται πως οδηγεί τους μαθητές βήμα βήμα προς τη γενίκευση και την τελική διατύπωση ορθών υποθέσεων (Αrcavi & Handos, 2000 ο.π.). Παράλληλα, λόγω του γεγονότος ότι οι μαθητές δοκιμάζουν εναλλακτικές λύσεις σχετικά με μια κατάσταση προβληματισμού και δοκιμάζουν τη ορθότητα του προσωπικού τους τρόπου σκέψης, η διαδικασία αυτή αποκτά προσωπικό νόημα για εκείνους και λειτουργεί παρωθητικά για την εμπλοκή τους με τον προγραμματισμό. Μάλιστα, η ευκαιρία αυτή που έχουν οι μαθητές για να εκφράσουν το δικό τους τρόπο σκέψης δίνει τη δυνατότητα να αναπτυχθούν και να προκύψουν διαφορετικές στρατηγικές για την αντιμετώπιση του προβλήματος (Hoyles & Noss, 1999 όπως αναφέρεται στο Αργύρης, 2002). Χρειάζεται επιπρόσθετα να αναφερθεί, ότι η διαδικασία αυτή του πειραματισμού, η οποία λόγω της φύσης του υπολογιστικού εργαλείου ανατροφοδοτείται άμεσα, προσφέρει μεγαλύτερη πιθανότητα μετασχηματισμού των αρχικών και εσφαλμένων ιδεών του μαθητή (Sherin&diSessa, όπως αναφέρεται στο Αργύρης, 2002). Σε αυτό το σημείο, θα δώσουμε ένα πράδειγμα από το «Οδηγώντας στην πόλη», το οποίο δείχει πως πειραματιστήκαμε για την επιλογή κατάλληλου «trigger», έτσι ώστε όταν το πρόγραμμα ξεκινά, η μηχανή να μπορεί αλλάξει κατεύθυνση και να προχωρά είτε ευθεία, είτε να στρίβει στο πρώτο στενό αριστερά. Αρχικά, επιλέξαμε για trigger το χρώμα και κατασκευάσαμε ένα ορθογώνιο, στο οποίο όταν η μηχανή ακουμπούσε θα έστριβε αριστερά. Σχήμα 2: Το πρόβλημα με τη μηχανή Στην πράξη, ωστόσο, διαπιστώσαμε ότι επειδή το σχήμα ήταν μικρό το αυτοκίνητο με το βήμα που του είχαμε ορίσει (μπροστά 30) το προσπερνούσε και η εντολή δεν ενεργοποιείτο. Αποφασίσαμε, λοιπόν, να μεγαλώσουμε το [1506]
13 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ σχήμα. Αποτέλεσμα ήταν η μηχανή να ακουμπά συνέχεια στο χρώμα και επομένως να στρίβει σε λάθος σημείο και να πέφτει πάνω στο οικοδομικό τετράγωνο. Για το λογο αυτό, αποφασίστηκε το «trigger» να μην είναι χρώμα αλλά μια χελώνα η οποία θα είχε το σχήμα ορθογωνίου που εμείς θα κατασκευάζαμε στα γραφικά. Για να μη φαίνεται, ωστόσο, του δώσαμε τελικά χρώμα ίδιο με αυτό του δρόμου. ΣΥΜΠΕΡΑΣΜΑ Στην παρούσα εισήγηση παρουσιάστηκε μια διδακτική εφαρμογή η οποία στηρίζεται στην αξιοποίηση της γλώσσας προγραμματισμού Logo. Ο μαθητής, μέσα από την ενασχόλησή του με ένα εκπαιδευτικό παιχνίδι, είχε τη δυνατότητα να κατανοήσει βασικούς κανόνες οδικής συμπεριφοράς, ενώ παράλληλα έγινε ο ίδιος ο προγραμματιστής ενός ανοιχτού μαθησιακού περιβάλλοντος. Η συγκεκριμένη διαδικασία είχε ως στόχο να εντάξει τον μαθητή σε μια ενεργητική διαδικασία μάθησης, κατά την οποία ο ίδιος αξιοποίησε τις διαισθητικές του γνώσεις και πειραματίστηκε σε σχέση με αυτές. Παράλληλα, τα αποτελέσματα των αποφάσεών του ήταν εκείνα τα οποία τον οδήγησαν σε αναστοχασμό όσον αφορά την πορεία της σκέψης του και την υλοποίησή της. Επιπρόσθετα, ο μαθητής επιδίωξε να λύσει τα προβλήματα που προέκυψαν ακολουθώντας σταδιακά διαφορετικά βήματα, τα οποία και ο ίδιος καθόρισε. Μέσα σε αυτό το πλαίσιο, ο μαθητής-προγραμματιστής μαθαίνει να αντιμετωπίζει τα μαθησιακά αδιέξοδα, τους προβληματισμούς του, με τρόπο μεθοδικό και επιστημονικό, ικανότητα την οποία αναμφισβήτητα το σύγχρονο σχολείο οφείλει να επιδιώκει. ΒΙΒΛΙΟΓΡΑΦΙΑ 1. Edwards (1998), Embodying Mathematics and Science: Microworldsas representation, Journal of Mathematical Behavior, Vol. 17, Issuel, pp 53-78, Ablex Publishing Corp 2. Kynigos C., (1995), Programming as a means of expressing and exploring ideas: Three case studies situated in a directive educational system, In A. disessa, C. Hoyles and R. Noss with L. Edwards (Eds), Computers for exploratory Learning (pp ), Nato ASI Series, Berlin: Springer-Verlag 3. Kynigos C., Koutlis, M.& Hatzilacos, T.(1997), Mathematics with component-oriented exploratory software, International Journal of Computers for Mathematical Learning, 2, Papert S. (1991), «Νοητικές Θύελλες, Παιδιά, Υπολογιστές και Δυναμικές ιδέες, τα πάντα γύρω από τη Logo», εκδ. Οδυσσέας 5. Papert S. (1993), The Children s Machine. Rethinking School in the Age of the Computer, Harvester Wheatsheaf 6. Αργύρης Μ. (2001), «Η διαμόρφωση της εκπαιδευτικής πρακτικής δασκάλων σε περιβάλλον σχεδιασμένο για συνεργατική, διερευνητική μάθηση με χρήση ανάλογων υπολογιστικών εργαλείων», Αδημοσίευτη [1507]
14 «Ψηφιακές και Διαδικτυακές εφαρμογές στην Εκπαίδευση» διδακτορική διατριβή, Τομέας Παιδαγωγικής, Φιλοσοφική Σχολή, Πανεπιστήμιο Αθηνών 7. Αργύρης Μ. (2002), «Διερευνητική μάθηση με χρήση υπολογιστικών εργαλείων: Μια εναλλακτική πρόταση διδασκαλίας», στο «Νοητικά Εργαλεία και Πληροφοριακά Μέσα», επιμ. Κυνηγός Χ., Δημαράκη Ε.Β., εκδ. Καστανιώτη, Αθήνα 8. Γιαννούτσου Ν. (2005), «Αναπαραστάσεις εννοιών του χώρου: Μαθησιακή διαδικασία στα πλαίσια συνεργατικού περιβάλλοντος βασισμένου στη χρήση νέων Τεχνολογιών», Αδημοσίευτη διδακτορική διατριβή, Τομέας Παιδαγωγικής, Φιλοσοφική Σχολή, Πανεπιστήμιο Αθηνών 9. Κυνηγός Χ. (1995), «Η ευκαιρία που δεν πρέπει να χαθεί: Η υπολογιστική Τεχνολογία ως Εργαλείο Έκφρασης και Διερεύνησης στη Γενική Παιδεία», στο Καζαμίας, Κασσωτάκης (επιμ.) Ελληνική Εκπαίδευση, Προοπτικές Αναπτυξης και Εκσυγχρονισμού, εκδ. Σείριος, Αθήνα 10. Ματσαγγούρας Η. (2003), «Στρατηγικές διδασκαλίας», εκδ. Gutenberg, Αθήνα 11. Μπασέτας Κ. (2002), «Ψυχολογία της Μάθησης», εκδ. Ατραπός, Αθήνα 12. Ράπτης Α., Ράπτη Α. (1998), «Πληροφορική και Εκπαίδευση, Συνολική Προσέγγιση», Αθήνα [1508]
Παιδαγωγικές δραστηριότητες μοντελοποίησης με χρήση ανοικτών υπολογιστικών περιβαλλόντων
 Παιδαγωγικές δραστηριότητες μοντελοποίησης με χρήση ανοικτών υπολογιστικών περιβαλλόντων Βασίλης Κόμης, Επίκουρος Καθηγητής Ερευνητική Ομάδα «ΤΠΕ στην Εκπαίδευση» Τμήμα Επιστημών της Εκπαίδευσης και της
Παιδαγωγικές δραστηριότητες μοντελοποίησης με χρήση ανοικτών υπολογιστικών περιβαλλόντων Βασίλης Κόμης, Επίκουρος Καθηγητής Ερευνητική Ομάδα «ΤΠΕ στην Εκπαίδευση» Τμήμα Επιστημών της Εκπαίδευσης και της
Η διάρκεια πραγματοποίησης της ανοιχτής εκπαιδευτικής πρακτικής ήταν 2 διδακτικές ώρες
 ΣΧΟΛΕΙΟ Η εκπαιδευτική πρακτική αφορούσε τη διδασκαλία των μεταβλητών στον προγραμματισμό και εφαρμόστηκε σε μαθητές της τελευταίας τάξης ΕΠΑΛ του τομέα Πληροφορικής στα πλαίσια του μαθήματος του Δομημένου
ΣΧΟΛΕΙΟ Η εκπαιδευτική πρακτική αφορούσε τη διδασκαλία των μεταβλητών στον προγραμματισμό και εφαρμόστηκε σε μαθητές της τελευταίας τάξης ΕΠΑΛ του τομέα Πληροφορικής στα πλαίσια του μαθήματος του Δομημένου
Άθροισµα γωνιών τριγώνου, γωνίες ισοπλεύρου, ισοσκελούς τριγώνου και εξωτερική γωνία τριγώνου στην Α Γυµνασίου
 ΣΕΝΑΡΙΟ «Προσπάθησε να κάνεις ένα τρίγωνο» Άθροισµα γωνιών τριγώνου, γωνίες ισοπλεύρου, ισοσκελούς τριγώνου και εξωτερική γωνία τριγώνου στην Α Γυµνασίου Ηµεροµηνία: Φλώρινα, 6-5-2014 Γνωστική περιοχή:
ΣΕΝΑΡΙΟ «Προσπάθησε να κάνεις ένα τρίγωνο» Άθροισµα γωνιών τριγώνου, γωνίες ισοπλεύρου, ισοσκελούς τριγώνου και εξωτερική γωνία τριγώνου στην Α Γυµνασίου Ηµεροµηνία: Φλώρινα, 6-5-2014 Γνωστική περιοχή:
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ
 ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ Κατερίνα Σάλτα ΔιΧηΝΕΤ 2017-2018 Θέματα Διδακτικής Φυσικών Επιστήμων 1. ΟΙ ΙΔΕΕΣ ΤΩΝ ΜΑΘΗΤΩΝ 2. ΤΑ ΜΟΝΤΕΛΑ ΚΑΙ Η ΜΟΝΤΕΛΟΠΟΙΗΣΗ 3. ΤΟ ΕΡΓΑΣΤΗΡΙΟ & ΤΟ ΠΕΙΡΑΜΑ 4. ΔΙΔΑΚΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ Κατερίνα Σάλτα ΔιΧηΝΕΤ 2017-2018 Θέματα Διδακτικής Φυσικών Επιστήμων 1. ΟΙ ΙΔΕΕΣ ΤΩΝ ΜΑΘΗΤΩΝ 2. ΤΑ ΜΟΝΤΕΛΑ ΚΑΙ Η ΜΟΝΤΕΛΟΠΟΙΗΣΗ 3. ΤΟ ΕΡΓΑΣΤΗΡΙΟ & ΤΟ ΠΕΙΡΑΜΑ 4. ΔΙΔΑΚΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ
ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO
 1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
Αναλυτικό Πρόγραμμα Μαθηματικών
 Αναλυτικό Πρόγραμμα Μαθηματικών Σχεδιασμός... αντιμετωπίζει ενιαία το πλαίσιο σπουδών (Προδημοτική, Δημοτικό, Γυμνάσιο και Λύκειο), είναι συνέχεια υπό διαμόρφωση και αλλαγή, για να αντιμετωπίζει την εξέλιξη,
Αναλυτικό Πρόγραμμα Μαθηματικών Σχεδιασμός... αντιμετωπίζει ενιαία το πλαίσιο σπουδών (Προδημοτική, Δημοτικό, Γυμνάσιο και Λύκειο), είναι συνέχεια υπό διαμόρφωση και αλλαγή, για να αντιμετωπίζει την εξέλιξη,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΦΛΩΡΙΝΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΦΛΩΡΙΝΑ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΥΛΙΚΟΥ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΧΡΗΣΗ ΤΠΕ ΘΕΜΑ ΕΡΓΑΣΙΑΣ: ΜΕΤΑΤΡΟΠΗ ΤΟΥ ΣΕΝΑΡΙΟΥ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΦΛΩΡΙΝΑ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΥΛΙΚΟΥ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΧΡΗΣΗ ΤΠΕ ΘΕΜΑ ΕΡΓΑΣΙΑΣ: ΜΕΤΑΤΡΟΠΗ ΤΟΥ ΣΕΝΑΡΙΟΥ
«Ψηφιακά δομήματα στα μαθηματικά ως εργαλεία μάθησης για το δάσκαλο και το μαθητή»
 Ψηφιακό σχολείο: Το γνωστικό πεδίο των Μαθηματικών «Ψηφιακά δομήματα στα μαθηματικά ως εργαλεία μάθησης για το δάσκαλο και το μαθητή» ΕΛΕΝΗ ΚΑΛΑΪΤΖΙΔΟΥ Πληροφορικός ΠΕ19 (1 ο Πρότυπο Πειραματικό Γυμνάσιο
Ψηφιακό σχολείο: Το γνωστικό πεδίο των Μαθηματικών «Ψηφιακά δομήματα στα μαθηματικά ως εργαλεία μάθησης για το δάσκαλο και το μαθητή» ΕΛΕΝΗ ΚΑΛΑΪΤΖΙΔΟΥ Πληροφορικός ΠΕ19 (1 ο Πρότυπο Πειραματικό Γυμνάσιο
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ»
 ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ» Νικόλαος Μπαλκίζας 1. ΕΙΣΑΓΩΓΗ Σκοπός του σχεδίου μαθήματος είναι να μάθουν όλοι οι μαθητές της τάξης τις έννοιες της ισοδυναμίας των κλασμάτων,
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ» Νικόλαος Μπαλκίζας 1. ΕΙΣΑΓΩΓΗ Σκοπός του σχεδίου μαθήματος είναι να μάθουν όλοι οι μαθητές της τάξης τις έννοιες της ισοδυναμίας των κλασμάτων,
ΣΕΝΑΡΙΟ: Εφαπτομένη οξείας γωνίας στη Β Γυμνασίου
 ΣΕΝΑΡΙΟ: Εφαπτομένη οξείας γωνίας στη Β Γυμνασίου Συγγραφέας: Κοπατσάρη Γεωργία Ημερομηνία: Φλώρινα, 5-3-2014 Γνωστική περιοχή: Μαθηματικά (Γεωμετρία) Β Γυμνασίου Προτεινόμενο λογισμικό: Προτείνεται να
ΣΕΝΑΡΙΟ: Εφαπτομένη οξείας γωνίας στη Β Γυμνασίου Συγγραφέας: Κοπατσάρη Γεωργία Ημερομηνία: Φλώρινα, 5-3-2014 Γνωστική περιοχή: Μαθηματικά (Γεωμετρία) Β Γυμνασίου Προτεινόμενο λογισμικό: Προτείνεται να
Τρίτη 24 και Τετάρτη 25 Οκτωβρίου 2017
 Τρίτη 24 και Τετάρτη 25 Οκτωβρίου 2017 Παιδαγωγικές προσεγγίσεις και διδακτικές πρακτικές - η σχέση τους με τις θεωρίες μάθησης Παρατηρώντας τη μαθησιακή διαδικασία Τι είδους δραστηριότητες παρατηρήσατε
Τρίτη 24 και Τετάρτη 25 Οκτωβρίου 2017 Παιδαγωγικές προσεγγίσεις και διδακτικές πρακτικές - η σχέση τους με τις θεωρίες μάθησης Παρατηρώντας τη μαθησιακή διαδικασία Τι είδους δραστηριότητες παρατηρήσατε
Τα Διδακτικά Σενάρια και οι Προδιαγραφές τους. του Σταύρου Κοκκαλίδη. Μαθηματικού
 Τα Διδακτικά Σενάρια και οι Προδιαγραφές τους του Σταύρου Κοκκαλίδη Μαθηματικού Διευθυντή του Γυμνασίου Αρχαγγέλου Ρόδου-Εκπαιδευτή Στα προγράμματα Β Επιπέδου στις ΤΠΕ Ορισμός της έννοιας του σεναρίου.
Τα Διδακτικά Σενάρια και οι Προδιαγραφές τους του Σταύρου Κοκκαλίδη Μαθηματικού Διευθυντή του Γυμνασίου Αρχαγγέλου Ρόδου-Εκπαιδευτή Στα προγράμματα Β Επιπέδου στις ΤΠΕ Ορισμός της έννοιας του σεναρίου.
Εκπαιδευτικό λογισμικό: Αβάκιο Χελωνόκοσμος Δραστηριότητα 1: «Διερευνώντας τα παραλληλόγραμμα»
 Εκπαιδευτικό λογισμικό: Αβάκιο Χελωνόκοσμος Δραστηριότητα 1: «Διερευνώντας τα παραλληλόγραμμα» Φύλλο δασκάλου 1.1 Ένταξη δραστηριότητας στο πρόγραμμα σπουδών Τάξη: Ε και ΣΤ Δημοτικού. Γνωστικά αντικείμενα:
Εκπαιδευτικό λογισμικό: Αβάκιο Χελωνόκοσμος Δραστηριότητα 1: «Διερευνώντας τα παραλληλόγραμμα» Φύλλο δασκάλου 1.1 Ένταξη δραστηριότητας στο πρόγραμμα σπουδών Τάξη: Ε και ΣΤ Δημοτικού. Γνωστικά αντικείμενα:
Σενάριο 5. Μετασχηµατισµοί στο επίπεδο. Γνωστική περιοχή: Γεωµετρία Α' Λυκείου. Συµµετρία ως προς άξονα. Σύστηµα συντεταγµένων.
 Σενάριο 5. Μετασχηµατισµοί στο επίπεδο Γνωστική περιοχή: Γεωµετρία Α' Λυκείου. Συµµετρία ως προς άξονα. Σύστηµα συντεταγµένων. Απόλυτη τιµή πραγµατικών αριθµών. Συµµεταβολή σηµείων. Θέµα: Στο περιβάλλον
Σενάριο 5. Μετασχηµατισµοί στο επίπεδο Γνωστική περιοχή: Γεωµετρία Α' Λυκείου. Συµµετρία ως προς άξονα. Σύστηµα συντεταγµένων. Απόλυτη τιµή πραγµατικών αριθµών. Συµµεταβολή σηµείων. Θέµα: Στο περιβάλλον
Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού
 Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού Πέτρος Κλιάπης kliapis@sch.gr 1 Ο Ρόλος του εκπαιδευτικού Αξιολογεί την αρχική μαθηματική κατάσταση κάθε παιδιού, ομαδοποιεί τα παιδιά σύμφωνα με
Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού Πέτρος Κλιάπης kliapis@sch.gr 1 Ο Ρόλος του εκπαιδευτικού Αξιολογεί την αρχική μαθηματική κατάσταση κάθε παιδιού, ομαδοποιεί τα παιδιά σύμφωνα με
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά. Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων
 Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Εκπαιδευτικό Σενάριο 2
 Εκπαιδευτικό Σενάριο 2 Τίτλος: Τα συνεργατικά περιβάλλοντα δημιουργίας και επεξεργασίας υπολογιστικών φύλλων Εκτιμώμενη διάρκεια εκπαιδευτικού σεναρίου: Προβλέπεται να διαρκέσει συνολικά 3 διδακτικές ώρες.
Εκπαιδευτικό Σενάριο 2 Τίτλος: Τα συνεργατικά περιβάλλοντα δημιουργίας και επεξεργασίας υπολογιστικών φύλλων Εκτιμώμενη διάρκεια εκπαιδευτικού σεναρίου: Προβλέπεται να διαρκέσει συνολικά 3 διδακτικές ώρες.
ΡΟΜΠΟΤΙΚΗ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ
 ΡΟΜΠΟΤΙΚΗ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ Γιατί η Ρομποτική στην Εκπαίδευση; A) Τα παιδιά όταν σχεδιάζουν, κατασκευάζουν και προγραμματίζουν ρομπότ έχουν την ευκαιρία να μάθουν παίζοντας και να αναπτύξουν δεξιότητες Η
ΡΟΜΠΟΤΙΚΗ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ Γιατί η Ρομποτική στην Εκπαίδευση; A) Τα παιδιά όταν σχεδιάζουν, κατασκευάζουν και προγραμματίζουν ρομπότ έχουν την ευκαιρία να μάθουν παίζοντας και να αναπτύξουν δεξιότητες Η
Τα σχέδια μαθήματος 1 Εισαγωγή
 Τα σχέδια μαθήματος 1 Εισαγωγή Τα σχέδια μαθήματος αποτελούν ένα είδος προσωπικών σημειώσεων που κρατά ο εκπαιδευτικός προκειμένου να πραγματοποιήσει αποτελεσματικές διδασκαλίες. Περιέχουν πληροφορίες
Τα σχέδια μαθήματος 1 Εισαγωγή Τα σχέδια μαθήματος αποτελούν ένα είδος προσωπικών σημειώσεων που κρατά ο εκπαιδευτικός προκειμένου να πραγματοποιήσει αποτελεσματικές διδασκαλίες. Περιέχουν πληροφορίες
Ξεκινώντας τον Προγραµµατισµό στις τάξεις του ηµοτικού Παίζοντας µε το Scratch
 Ξεκινώντας τον Προγραµµατισµό στις τάξεις του ηµοτικού Παίζοντας µε το Scratch Κωνσταντίνος Χαρατσής ρ. Ηλεκτρολόγος Μηχανικός ΠΕ 19 Εκπαιδευτικός Πληροφορικής Ενότητα Προγραµµατισµός στο ηµοτικό (Ε και
Ξεκινώντας τον Προγραµµατισµό στις τάξεις του ηµοτικού Παίζοντας µε το Scratch Κωνσταντίνος Χαρατσής ρ. Ηλεκτρολόγος Μηχανικός ΠΕ 19 Εκπαιδευτικός Πληροφορικής Ενότητα Προγραµµατισµός στο ηµοτικό (Ε και
3 βήματα για την ένταξη των ΤΠΕ: 1. Εμπλουτισμός 2. Δραστηριότητα 3. Σενάριο Πέτρος Κλιάπης-Όλγα Κασσώτη Επιμόρφωση εκπαιδευτικών
 3 βήματα για την ένταξη των ΤΠΕ: 1. Εμπλουτισμός 2. Δραστηριότητα 3. Σενάριο Πέτρος Κλιάπης-Όλγα Κασσώτη Επιμόρφωση εκπαιδευτικών Παρουσίαση βασισμένη στο κείμενο: «Προδιαγραφές ψηφιακής διαμόρφωσης των
3 βήματα για την ένταξη των ΤΠΕ: 1. Εμπλουτισμός 2. Δραστηριότητα 3. Σενάριο Πέτρος Κλιάπης-Όλγα Κασσώτη Επιμόρφωση εκπαιδευτικών Παρουσίαση βασισμένη στο κείμενο: «Προδιαγραφές ψηφιακής διαμόρφωσης των
Σενάριο 1. Σκιτσάροντας µε Παραλληλόγραµµα. Γνωστική περιοχή: Γεωµετρία (και σχέσεις µεταξύ γενικευµένων αριθµών).
 Σενάριο 1. Σκιτσάροντας µε Παραλληλόγραµµα Γνωστική περιοχή: Γεωµετρία (και σχέσεις µεταξύ γενικευµένων αριθµών). Θέµα: Η διερεύνηση µερικών βασικών ιδιοτήτων των παραλληλογράµµων από τους µαθητές µε χρήση
Σενάριο 1. Σκιτσάροντας µε Παραλληλόγραµµα Γνωστική περιοχή: Γεωµετρία (και σχέσεις µεταξύ γενικευµένων αριθµών). Θέµα: Η διερεύνηση µερικών βασικών ιδιοτήτων των παραλληλογράµµων από τους µαθητές µε χρήση
ΔΙΔΑΚΤΙΚΉ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ
 ΔΙΔΑΚΤΙΚΉ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ 2. Εκπαιδευτικό Λογισμικό για τα Μαθηματικά 2.1 Κύρια χαρακτηριστικά του εκπαιδευτικού λογισμικού για την Διδακτική των Μαθηματικών 2.2 Κατηγορίες εκπαιδευτικού λογισμικού για
ΔΙΔΑΚΤΙΚΉ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ 2. Εκπαιδευτικό Λογισμικό για τα Μαθηματικά 2.1 Κύρια χαρακτηριστικά του εκπαιδευτικού λογισμικού για την Διδακτική των Μαθηματικών 2.2 Κατηγορίες εκπαιδευτικού λογισμικού για
ΣΕΝΑΡΙΟ ΤΠΕ ΓΕΝΙΚΕΥΜΕΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ - ΝΟΜΟΣ ΣΥΝΗΜΙΤΟΝΩΝ
 ΣΕΝΑΡΙΟ ΤΠΕ ΓΕΝΙΚΕΥΜΕΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ - ΝΟΜΟΣ ΣΥΝΗΜΙΤΟΝΩΝ Γνωστική Περιοχή: Γεωμετρία Β Λυκείου Θέμα Το Πυθαγόρειο Θεώρημα είναι γνωστό στους μαθητές από το Γυμνάσιο. Το προτεινόμενα θέμα αφορά την
ΣΕΝΑΡΙΟ ΤΠΕ ΓΕΝΙΚΕΥΜΕΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ - ΝΟΜΟΣ ΣΥΝΗΜΙΤΟΝΩΝ Γνωστική Περιοχή: Γεωμετρία Β Λυκείου Θέμα Το Πυθαγόρειο Θεώρημα είναι γνωστό στους μαθητές από το Γυμνάσιο. Το προτεινόμενα θέμα αφορά την
Διδακτικές προσεγγίσεις στην Πληροφορική. Η εποικοδομιστική προσέγγιση για τη γνώση. ως ενεργητική και όχι παθητική διαδικασία
 Διδακτικές προσεγγίσεις στην Πληροφορική Η εποικοδομιστική προσέγγιση για τη γνώση ως ενεργητική και όχι παθητική διαδικασία ως κατασκευή και όχι ως μετάδοση ως αποτέλεσμα εμπειρίας και όχι ως μεταφορά
Διδακτικές προσεγγίσεις στην Πληροφορική Η εποικοδομιστική προσέγγιση για τη γνώση ως ενεργητική και όχι παθητική διαδικασία ως κατασκευή και όχι ως μετάδοση ως αποτέλεσμα εμπειρίας και όχι ως μεταφορά
«Το Λογισμικό Αράχνη Επικουρικό Εργαλείο στην Διδασκαλία του Προγραμματισμού»
 2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ «Το Λογισμικό Αράχνη Επικουρικό Εργαλείο στην Διδασκαλία του Προγραμματισμού» Αθανάσιος Βρακόπουλος 1, Ολυμπία Βρακοπούλου 2, Γιώργος Μακρής 3 1 Καθηγητής
2o Πανελλήνιο Εκπαιδευτικό Συνέδριο Ημαθίας ΠΡΑΚΤΙΚΑ «Το Λογισμικό Αράχνη Επικουρικό Εργαλείο στην Διδασκαλία του Προγραμματισμού» Αθανάσιος Βρακόπουλος 1, Ολυμπία Βρακοπούλου 2, Γιώργος Μακρής 3 1 Καθηγητής
6.5 Ανάπτυξη, εφαρμογή και αξιολόγηση εκπαιδευτικών σεναρίων και δραστηριοτήτων ανά γνωστικό αντικείμενο
 6.5 Ανάπτυξη, εφαρμογή και αξιολόγηση εκπαιδευτικών σεναρίων και δραστηριοτήτων ανά γνωστικό αντικείμενο Το εκπαιδευτικό σενάριο Η χρήση των Τ.Π.Ε. στην πρωτοβάθμια εκπαίδευση θα πρέπει να γίνεται με οργανωμένο
6.5 Ανάπτυξη, εφαρμογή και αξιολόγηση εκπαιδευτικών σεναρίων και δραστηριοτήτων ανά γνωστικό αντικείμενο Το εκπαιδευτικό σενάριο Η χρήση των Τ.Π.Ε. στην πρωτοβάθμια εκπαίδευση θα πρέπει να γίνεται με οργανωμένο
Η λογαριθµική συνάρτηση και οι ιδιότητές της
 ΕΚΦΩΝΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ Η λογαριθµική συνάρτηση και οι ιδιότητές της Η διδασκαλία της λογαριθµικής συνάρτησης, στο σχολικό εγχειρίδιο της Β Λυκείου, έχει σαν βάση την εκθετική συνάρτηση και την ιδιότητα
ΕΚΦΩΝΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ Η λογαριθµική συνάρτηση και οι ιδιότητές της Η διδασκαλία της λογαριθµικής συνάρτησης, στο σχολικό εγχειρίδιο της Β Λυκείου, έχει σαν βάση την εκθετική συνάρτηση και την ιδιότητα
Κοινωνικοπολιτισμικές. Θεωρίες Μάθησης. & Εκπαιδευτικό Λογισμικό
 Κοινωνικοπολιτισμικές Θεωρίες Μάθησης & Εκπαιδευτικό Λογισμικό Κοινωνικοπολιτισμικές προσεγγίσεις Η σκέψη αναπτύσσεται (προϊόν οικοδόμησης και αναδόμησης γνώσεων) στα πλαίσια συνεργατικών δραστηριοτήτων
Κοινωνικοπολιτισμικές Θεωρίες Μάθησης & Εκπαιδευτικό Λογισμικό Κοινωνικοπολιτισμικές προσεγγίσεις Η σκέψη αναπτύσσεται (προϊόν οικοδόμησης και αναδόμησης γνώσεων) στα πλαίσια συνεργατικών δραστηριοτήτων
Πειραματιζόμενοι με αριθμούς στο περιβάλλον του Microworlds Pro: διαθεματική προσέγγιση περί «πολλαπλασίων και διαιρετών»
 Πειραματιζόμενοι με αριθμούς στο περιβάλλον του Microworlds Pro: διαθεματική προσέγγιση περί «πολλαπλασίων και διαιρετών» μια Νίκος Δαπόντες Φυσικός Δευτεροβάθμιας Εκπαίδευσης Το περιβάλλον Microworlds
Πειραματιζόμενοι με αριθμούς στο περιβάλλον του Microworlds Pro: διαθεματική προσέγγιση περί «πολλαπλασίων και διαιρετών» μια Νίκος Δαπόντες Φυσικός Δευτεροβάθμιας Εκπαίδευσης Το περιβάλλον Microworlds
ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΟΡΙΟΥ ΣΥΝΑΡΤΗΣΗΣ
 ΕΠΙΜΟΡΦΩΣΗ ΤΩΝ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΩΝ ΤΠΕ ΣΤΗ ΔΙΔΑΚΤΙΚΗ ΠΡΑΞΗ ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΟΡΙΟΥ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΕΞ ΑΡΙΣΤΕΡΩΝ ΚΑΙ ΕΚ ΔΕΞΙΩΝ ΣΥΓΓΡΑΦΕΑΣ: ΚΟΥΤΙΔΗΣ ΙΩΑΝΝΗΣ
ΕΠΙΜΟΡΦΩΣΗ ΤΩΝ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΩΝ ΤΠΕ ΣΤΗ ΔΙΔΑΚΤΙΚΗ ΠΡΑΞΗ ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΟΡΙΟΥ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΕΞ ΑΡΙΣΤΕΡΩΝ ΚΑΙ ΕΚ ΔΕΞΙΩΝ ΣΥΓΓΡΑΦΕΑΣ: ΚΟΥΤΙΔΗΣ ΙΩΑΝΝΗΣ
Εκπαιδευτική Τεχνολογία και Θεωρίες Μάθησης
 Θεωρίες Μάθησης Εκπαιδευτική Τεχνολογία και Θεωρίες Μάθησης Κάθε εκπαιδευτικός (εκούσια ή ακούσια) υιοθετεί μια θεωρία μάθησης. Το ίδιο ισχύει και για τις διάφορες εκπαιδευτικές τεχνολογίες. Για την εισαγωγή
Θεωρίες Μάθησης Εκπαιδευτική Τεχνολογία και Θεωρίες Μάθησης Κάθε εκπαιδευτικός (εκούσια ή ακούσια) υιοθετεί μια θεωρία μάθησης. Το ίδιο ισχύει και για τις διάφορες εκπαιδευτικές τεχνολογίες. Για την εισαγωγή
«ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ «ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Διδάσκουσες:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ «ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Διδάσκουσες:
Φύλλα εργασίας. MicroWorlds Pro. Πολυμεσικές Εφαρμογές με την χρήση της γλώσσας LOGO Στο Γυμνάσιο. Β. Χ. Χρυσοχοΐδης
 Φύλλα εργασίας MicroWorlds Pro Πολυμεσικές Εφαρμογές με την χρήση της γλώσσας LOGO Στο Γυμνάσιο Β. Χ. Χρυσοχοΐδης Πρόεδρος Συλλόγου Εκπαιδευτικών Πληροφορικής Φλώρινας 2 «Σχεδίαση και ανάπτυξη δραστηριοτήτων
Φύλλα εργασίας MicroWorlds Pro Πολυμεσικές Εφαρμογές με την χρήση της γλώσσας LOGO Στο Γυμνάσιο Β. Χ. Χρυσοχοΐδης Πρόεδρος Συλλόγου Εκπαιδευτικών Πληροφορικής Φλώρινας 2 «Σχεδίαση και ανάπτυξη δραστηριοτήτων
Cabri II Plus. Λογισμικό δυναμικής γεωμετρίας
 Cabri II Plus Λογισμικό δυναμικής γεωμετρίας Cabri II Plus Ο Jean-Marie LABORDE ξεκίνησε το 1985 το πρόγραμμα με σκοπό να διευκολύνει τη διδασκαλία και την εκμάθηση της Γεωμετρίας Ο σχεδιασμός και η κατασκευή
Cabri II Plus Λογισμικό δυναμικής γεωμετρίας Cabri II Plus Ο Jean-Marie LABORDE ξεκίνησε το 1985 το πρόγραμμα με σκοπό να διευκολύνει τη διδασκαλία και την εκμάθηση της Γεωμετρίας Ο σχεδιασμός και η κατασκευή
Έννοιες Φυσικών Επιστημών Ι
 Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία Έννοιες Φυσικών Επιστημών Ι Ενότητα 4: Θεωρίες διδασκαλίας μάθησης στη διδακτική των Φ.Ε. Σπύρος Κόλλας (Βασισμένο στις σημειώσεις του Βασίλη Τσελφέ)
Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία Έννοιες Φυσικών Επιστημών Ι Ενότητα 4: Θεωρίες διδασκαλίας μάθησης στη διδακτική των Φ.Ε. Σπύρος Κόλλας (Βασισμένο στις σημειώσεις του Βασίλη Τσελφέ)
Αναγκαιότητα - Χρησιμότητα
 Διδακτικά Σενάρια Σενάρια Ως διδακτικό σενάριο θεωρείται η περιγραφή μιας διδασκαλίας- παρέμβασης με εστιασμένο γνωστικό αντικείμενο, συγκεκριμένους εκπαιδευτικούς στόχους, διδακτικές αρχές και πρακτικές.
Διδακτικά Σενάρια Σενάρια Ως διδακτικό σενάριο θεωρείται η περιγραφή μιας διδασκαλίας- παρέμβασης με εστιασμένο γνωστικό αντικείμενο, συγκεκριμένους εκπαιδευτικούς στόχους, διδακτικές αρχές και πρακτικές.
Σε ποιους απευθύνεται: Χρόνος υλοποίησης: Χώρος υλοποίησης: Κοινωνική ενορχήστρωση της τάξης Στόχοι:... 4
 Περιεχόμενα Νικόλαος Μανάρας... 2 Σενάριο για διδασκαλία/ εκμάθηση σε μια σύνθεση μεικτής μάθησης (Blended Learning) με τη χρήση του δυναμικού μαθηματικού λογισμικού Geogebra σε διαδραστικό πίνακα και
Περιεχόμενα Νικόλαος Μανάρας... 2 Σενάριο για διδασκαλία/ εκμάθηση σε μια σύνθεση μεικτής μάθησης (Blended Learning) με τη χρήση του δυναμικού μαθηματικού λογισμικού Geogebra σε διαδραστικό πίνακα και
Η έννοια της κάλυψης του επιπέδου με κανονικά πολύγωνα.
 9.1.3 Σενάριο 3. Διερεύνηση των κανονικών πολυγώνων σε περιβάλλον που αξιοποιεί λογισμικό συμβολικής έκφρασης, την κοινωνική δικτύωση και τη συλλογική διαπραγμάτευση. Γνωστική περιοχή: Μαθηματικά Β Γυμνασίου.
9.1.3 Σενάριο 3. Διερεύνηση των κανονικών πολυγώνων σε περιβάλλον που αξιοποιεί λογισμικό συμβολικής έκφρασης, την κοινωνική δικτύωση και τη συλλογική διαπραγμάτευση. Γνωστική περιοχή: Μαθηματικά Β Γυμνασίου.
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000)
 Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΟΛΙΤΙΣΜΙΚΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΝΕΩΝ ΤΕΧΝΟΛΟΓΙΩΝ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΙΜΕΛΕΙΑ: ΘΕΟΔΩΡΟΥ ΕΛΕΝΗ ΑΜ:453 ΕΞ.: Ζ ΕΙΣΗΓΗΤΗΣ: ΔΡ. ΔΗΜΗΤΡΗΣ ΤΣΩΛΗΣ ΚΟΛΟΜΒΟΥ ΑΦΡΟΔΙΤΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΟΛΙΤΙΣΜΙΚΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΝΕΩΝ ΤΕΧΝΟΛΟΓΙΩΝ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΙΜΕΛΕΙΑ: ΘΕΟΔΩΡΟΥ ΕΛΕΝΗ ΑΜ:453 ΕΞ.: Ζ ΕΙΣΗΓΗΤΗΣ: ΔΡ. ΔΗΜΗΤΡΗΣ ΤΣΩΛΗΣ ΚΟΛΟΜΒΟΥ ΑΦΡΟΔΙΤΗ
Λογισμικό διδασκαλίας των μαθηματικών της Γ Τάξης Γυμνασίου
 Λογισμικό διδασκαλίας των μαθηματικών της Γ Τάξης Γυμνασίου Δρ. Βασίλειος Σάλτας 1, Αλέξης Ηλιάδης 2, Ιωάννης Μουστακέας 3 1 Διδάκτωρ Διδακτικής Μαθηματικών, Επιστημονικός Συνεργάτης ΑΣΠΑΙΤΕ Σαπών coin_kav@otenet.gr
Λογισμικό διδασκαλίας των μαθηματικών της Γ Τάξης Γυμνασίου Δρ. Βασίλειος Σάλτας 1, Αλέξης Ηλιάδης 2, Ιωάννης Μουστακέας 3 1 Διδάκτωρ Διδακτικής Μαθηματικών, Επιστημονικός Συνεργάτης ΑΣΠΑΙΤΕ Σαπών coin_kav@otenet.gr
Οι συζητήσεις Δρ Δημήτριος Γκότζος
 Οι συζητήσεις Δρ Δημήτριος Γκότζος Οι διαφάνειες αποτελούν προϊόν μελέτης και αποδελτίωσης του Ι.Ε.Π. (2017). Οδηγός Εκπαιδευτικού για την Περιγραφική Αξιολόγηση στο Δημοτικό http://iep.edu.gr/images/iep/epistimoniki_ypiresia/epist_monades/a_kyklos/evaluation/2017/2a_perigrafiki_d
Οι συζητήσεις Δρ Δημήτριος Γκότζος Οι διαφάνειες αποτελούν προϊόν μελέτης και αποδελτίωσης του Ι.Ε.Π. (2017). Οδηγός Εκπαιδευτικού για την Περιγραφική Αξιολόγηση στο Δημοτικό http://iep.edu.gr/images/iep/epistimoniki_ypiresia/epist_monades/a_kyklos/evaluation/2017/2a_perigrafiki_d
Προσχολική Παιδαγωγική Ενότητα 8: Σχεδιασμός Ημερησίων Προγραμμάτων
 Προσχολική Παιδαγωγική Ενότητα 8: Σχεδιασμός Ημερησίων Προγραμμάτων Διδάσκουσα: Μαρία Καμπεζά Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην Προσχολική Ηλικία Σκοποί ενότητας Να συζητήσουν και να
Προσχολική Παιδαγωγική Ενότητα 8: Σχεδιασμός Ημερησίων Προγραμμάτων Διδάσκουσα: Μαρία Καμπεζά Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην Προσχολική Ηλικία Σκοποί ενότητας Να συζητήσουν και να
Γεωµετρία Γ' Γυµνασίου: Παραλληλία πλευρών, αναλογίες γεωµετρικών µεγεθών, οµοιότητα
 Σενάριο 3. Τα µέσα των πλευρών τριγώνου Γνωστική περιοχή: Γεωµετρία Γ' Γυµνασίου: Παραλληλία πλευρών, αναλογίες γεωµετρικών µεγεθών, οµοιότητα τριγώνων, τριγωνοµετρικοί αριθµοί περίµετρος και εµβαδόν.
Σενάριο 3. Τα µέσα των πλευρών τριγώνου Γνωστική περιοχή: Γεωµετρία Γ' Γυµνασίου: Παραλληλία πλευρών, αναλογίες γεωµετρικών µεγεθών, οµοιότητα τριγώνων, τριγωνοµετρικοί αριθµοί περίµετρος και εµβαδόν.
Εκπαιδευτικό Σενάριο Τίτλος: Δημιουργία κόμικ
 Εκπαιδευτικό Σενάριο Τίτλος: Δημιουργία κόμικ Τάξη: Γ Δημοτικού Ενότητα: Δημιουργώ με τον κειμενογράφο Εμπλεκόμενες έννοιες: Δημιουργία και πληκτρολόγηση εγγράφου, αποθήκευση, μορφοποίηση γραμματοσειράς,
Εκπαιδευτικό Σενάριο Τίτλος: Δημιουργία κόμικ Τάξη: Γ Δημοτικού Ενότητα: Δημιουργώ με τον κειμενογράφο Εμπλεκόμενες έννοιες: Δημιουργία και πληκτρολόγηση εγγράφου, αποθήκευση, μορφοποίηση γραμματοσειράς,
H Συμβολή της Υπολογιστικής Σκέψης στην Προετοιμασία του Αυριανού Πολίτη
 H Συμβολή της Υπολογιστικής Σκέψης στην Προετοιμασία του Αυριανού Πολίτη Κοτίνη Ι., Τζελέπη Σ. Σχ. Σύμβουλοι Κ. Μακεδονίας στην οικονομία, στη τέχνη, στην επιστήμη, στις ανθρωπιστικές και κοινωνικές επιστήμες.
H Συμβολή της Υπολογιστικής Σκέψης στην Προετοιμασία του Αυριανού Πολίτη Κοτίνη Ι., Τζελέπη Σ. Σχ. Σύμβουλοι Κ. Μακεδονίας στην οικονομία, στη τέχνη, στην επιστήμη, στις ανθρωπιστικές και κοινωνικές επιστήμες.
«Ανάλογα ποσά Γραφική παράσταση αναλογίας» ΠΡΟΤΕΙΝΟΜΕΝΟ ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ
 ΠΡΟΤΕΙΝΟΜΕΝΟ ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΜΑΘΗΜΑ: Μαθηματικά ΤΑΞΗ: Α Γυμνασίου ΕΝΟΤΗΤΕΣ: 1. Ανάλογα ποσά Ιδιότητες αναλόγων ποσών 2. Γραφική παράσταση σχέσης αναλογίας ΕΙΣΗΓΗΤΕΣ: Άγγελος Γιαννούλας Κωνσταντίνος Ρεκούμης
ΠΡΟΤΕΙΝΟΜΕΝΟ ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΜΑΘΗΜΑ: Μαθηματικά ΤΑΞΗ: Α Γυμνασίου ΕΝΟΤΗΤΕΣ: 1. Ανάλογα ποσά Ιδιότητες αναλόγων ποσών 2. Γραφική παράσταση σχέσης αναλογίας ΕΙΣΗΓΗΤΕΣ: Άγγελος Γιαννούλας Κωνσταντίνος Ρεκούμης
ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ:
 ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ: σύγχρονες αναγνώσεις Καβάλα 14/11/2015 ΜΑΡΙΑΝΝΑ ΤΖΕΚΑΚΗ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 2 Γιατί αλλαγές; 1 3 Για ουσιαστική μαθηματική ανάπτυξη, Σύγχρονο πρόγραμμα
ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ: σύγχρονες αναγνώσεις Καβάλα 14/11/2015 ΜΑΡΙΑΝΝΑ ΤΖΕΚΑΚΗ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 2 Γιατί αλλαγές; 1 3 Για ουσιαστική μαθηματική ανάπτυξη, Σύγχρονο πρόγραμμα
Το σενάριο προτείνεται να διεξαχθεί με τη χρήση του Cabri Geometry II.
 9.2.3 Σενάριο 6. Συμμεταβολές στο ισοσκελές τρίγωνο Γνωστική περιοχή: Γεωμετρία Β Λυκείου. Συμμεταβολή μεγεθών. Εμβαδόν ισοσκελούς τριγώνου. Σύστημα συντεταγμένων. Γραφική παράσταση συνάρτησης. Μέγιστη
9.2.3 Σενάριο 6. Συμμεταβολές στο ισοσκελές τρίγωνο Γνωστική περιοχή: Γεωμετρία Β Λυκείου. Συμμεταβολή μεγεθών. Εμβαδόν ισοσκελούς τριγώνου. Σύστημα συντεταγμένων. Γραφική παράσταση συνάρτησης. Μέγιστη
Μαθηματικά: Οι τάσεις στη διδακτική και τα Προγράμματα Σπουδών. Πέτρος Κλιάπης Σχολικός Σύμβουλος Π.Ε.
 Μαθηματικά: Οι τάσεις στη διδακτική και τα Προγράμματα Σπουδών Πέτρος Κλιάπης Σχολικός Σύμβουλος Π.Ε. Στάσεις απέναντι στα Μαθηματικά Τι σημαίνουν τα μαθηματικά για εσάς; Τι σημαίνει «κάνω μαθηματικά»;
Μαθηματικά: Οι τάσεις στη διδακτική και τα Προγράμματα Σπουδών Πέτρος Κλιάπης Σχολικός Σύμβουλος Π.Ε. Στάσεις απέναντι στα Μαθηματικά Τι σημαίνουν τα μαθηματικά για εσάς; Τι σημαίνει «κάνω μαθηματικά»;
Η ανοικτή αυτή πρακτική έχει διάρκεια 2 διδακτικών ωρών και λαμβάνει μέρος στο εργαστήριο πληροφορικής του σχολείου.
 ΣΧΟΛΕΙΟ Η συγκεκριμένη εκπαιδευτική πρακτική υλοποιήθηκε από τους μαθητές της Ε τάξης δημοτικού κατά την διάρκεια των παρεμβάσεων «εφαρμογής στην τάξη» της 6ης περιόδου επιμόρφωσης Β επιπέδου ΤΠΕ, αξιοποιώντας
ΣΧΟΛΕΙΟ Η συγκεκριμένη εκπαιδευτική πρακτική υλοποιήθηκε από τους μαθητές της Ε τάξης δημοτικού κατά την διάρκεια των παρεμβάσεων «εφαρμογής στην τάξη» της 6ης περιόδου επιμόρφωσης Β επιπέδου ΤΠΕ, αξιοποιώντας
Χρήση ρομποτικής στη διδασκαλία δομών προγραμματισμού: «Εύκολο παρκάρισμα»
 5ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ- ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 1 Χρήση ρομποτικής στη διδασκαλία δομών προγραμματισμού: «Εύκολο παρκάρισμα» Χάρος Σταύρος Πληροφορικός stcharos@yahoo.gr Τρακαντζίδης Ιωάννης Ηλεκτρολόγος, 1ο
5ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ- ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 1 Χρήση ρομποτικής στη διδασκαλία δομών προγραμματισμού: «Εύκολο παρκάρισμα» Χάρος Σταύρος Πληροφορικός stcharos@yahoo.gr Τρακαντζίδης Ιωάννης Ηλεκτρολόγος, 1ο
Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές
 Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές Σκοποί ενότητας Να συζητηθούν βασικές παιδαγωγικές αρχές της προσχολικής εκπαίδευσης Να προβληματιστούμε για τους τρόπους με τους οποίους μπορεί
Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές Σκοποί ενότητας Να συζητηθούν βασικές παιδαγωγικές αρχές της προσχολικής εκπαίδευσης Να προβληματιστούμε για τους τρόπους με τους οποίους μπορεί
ΔΙΔΑΚΤΙΚΗ της ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΔΙΔΑΚΤΙΚΗ της ΠΛΗΡΟΦΟΡΙΚΗΣ Μ. Γρηγοριάδου Ρ. Γόγουλου Ενότητα: Η Διδασκαλία του Προγραμματισμού Περιεχόμενα Παρουσίασης
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΔΙΔΑΚΤΙΚΗ της ΠΛΗΡΟΦΟΡΙΚΗΣ Μ. Γρηγοριάδου Ρ. Γόγουλου Ενότητα: Η Διδασκαλία του Προγραμματισμού Περιεχόμενα Παρουσίασης
ΠΑΙΖΟΝΤΑΣ ΜΕ ΙΣΟΠΛΕΥΡΑ ΤΡΙΓΩΝΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ 13/11/2016 ΠΑΙΖΟΝΤΑΣ ΜΕ ΙΣΟΠΛΕΥΡΑ ΤΡΙΓΩΝΑ ΜΑΘΗΜΑ ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΥΛΙΚΟΥ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΗ ΧΡΗΣΗ ΤΠΕ ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ 13/11/2016 ΠΑΙΖΟΝΤΑΣ ΜΕ ΙΣΟΠΛΕΥΡΑ ΤΡΙΓΩΝΑ ΜΑΘΗΜΑ ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΥΛΙΚΟΥ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΗ ΧΡΗΣΗ ΤΠΕ ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ:
ΠΑΙΔΑΓΩΓΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Η/Υ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΑΙΔΑΓΩΓΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Η/Υ ΘΕΜΑΤΑ ΕΝΟΤΗΤΑΣ ΣΙΑΣΙΑΚΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΕΥΘΥΝΟΣ ΕΝΟΤΗΤΑΣ «ΠΑΙΔΑΓΩΓΙΚΗ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΑΙΔΑΓΩΓΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Η/Υ ΘΕΜΑΤΑ ΕΝΟΤΗΤΑΣ ΣΙΑΣΙΑΚΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΕΥΘΥΝΟΣ ΕΝΟΤΗΤΑΣ «ΠΑΙΔΑΓΩΓΙΚΗ
Ι ΑΚΤΙΚΟ ΣΕΝΑΡΙΟ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ
 1. Τίτλος Ι ΑΚΤΙΚΟ ΣΕΝΑΡΙΟ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ «Φτιάχνω γεωµετρικά σχήµατα», (Μαθηµατικά Β ηµοτικού) 2. Εµπλεκόµενες γνωστικές περιοχές Κατά την υλοποίηση του διδακτικού σεναρίου θα αξιοποιηθούν κατά κύριο
1. Τίτλος Ι ΑΚΤΙΚΟ ΣΕΝΑΡΙΟ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ «Φτιάχνω γεωµετρικά σχήµατα», (Μαθηµατικά Β ηµοτικού) 2. Εµπλεκόµενες γνωστικές περιοχές Κατά την υλοποίηση του διδακτικού σεναρίου θα αξιοποιηθούν κατά κύριο
Οδηγίες για αξιολόγηση στο πλαίσιο ομότιμης συνεργατικής μάθησης
 Οδηγίες για αξιολόγηση στο πλαίσιο ομότιμης συνεργατικής μάθησης Τι είναι το PeLe; Το PeLe είναι ένα διαδικτυακό περιβάλλον που ενθαρρύνει την αξιολόγηση στο πλαίσιο της ομότιμης συνεργατικής μάθησης και
Οδηγίες για αξιολόγηση στο πλαίσιο ομότιμης συνεργατικής μάθησης Τι είναι το PeLe; Το PeLe είναι ένα διαδικτυακό περιβάλλον που ενθαρρύνει την αξιολόγηση στο πλαίσιο της ομότιμης συνεργατικής μάθησης και
222 Διδακτική των γνωστικών αντικειμένων
 222 Διδακτική των γνωστικών αντικειμένων 8. Χελωνόκοσμος (απαιτεί να είναι εγκατεστημένο το Αβάκιο) (6 ώρες) Τίτλος: Ιδιότητες παραλληλογράμμων Δημιουργός: Μιχάλης Αργύρης ΕΜΠΛΕΚΟΜΕΝΕΣ ΓΝΩΣΤΙΚΕΣ ΠΕΡΙΟΧΕΣ
222 Διδακτική των γνωστικών αντικειμένων 8. Χελωνόκοσμος (απαιτεί να είναι εγκατεστημένο το Αβάκιο) (6 ώρες) Τίτλος: Ιδιότητες παραλληλογράμμων Δημιουργός: Μιχάλης Αργύρης ΕΜΠΛΕΚΟΜΕΝΕΣ ΓΝΩΣΤΙΚΕΣ ΠΕΡΙΟΧΕΣ
Γεωµετρία Β' Λυκείου. Συµµεταβολή µεγεθών. Εµβαδόν ισοσκελούς τριγώνου. Σύστηµα. συντεταγµένων. Γραφική παράσταση συνάρτησης. Μέγιστη - ελάχιστη τιµή.
 Σενάριο 6. Συµµεταβολές στο ισοσκελές τρίγωνο Γνωστική περιοχή: Γεωµετρία Β' Λυκείου. Συµµεταβολή µεγεθών. Εµβαδόν ισοσκελούς τριγώνου. Σύστηµα συντεταγµένων. Γραφική παράσταση συνάρτησης. Μέγιστη - ελάχιστη
Σενάριο 6. Συµµεταβολές στο ισοσκελές τρίγωνο Γνωστική περιοχή: Γεωµετρία Β' Λυκείου. Συµµεταβολή µεγεθών. Εµβαδόν ισοσκελούς τριγώνου. Σύστηµα συντεταγµένων. Γραφική παράσταση συνάρτησης. Μέγιστη - ελάχιστη
Εκπαιδευτική Τεχνολογία - Πολυμέσα. Ελένη Περιστέρη, Msc, PhD
 Εκπαιδευτική Τεχνολογία - Πολυμέσα Ελένη Περιστέρη, Msc, PhD Τι είναι η «Εκπαιδευτική Τεχνολογία» (1) Εκπαιδευτική Τεχνολογία είναι «η εφαρμογή τεχνολογικών διαδικασιών και εργαλείων που μπορούν να χρησιμοποιηθούν
Εκπαιδευτική Τεχνολογία - Πολυμέσα Ελένη Περιστέρη, Msc, PhD Τι είναι η «Εκπαιδευτική Τεχνολογία» (1) Εκπαιδευτική Τεχνολογία είναι «η εφαρμογή τεχνολογικών διαδικασιών και εργαλείων που μπορούν να χρησιμοποιηθούν
Τσικολάτας Α. (2011) Οι ΤΠΕ ως Εκπαιδευτικό Εργαλείο στην Ειδική Αγωγή. Αθήνα
 Οι ΤΠΕ ως Εκπαιδευτικό Εργαλείο στην Ειδική Αγωγή Τσικολάτας Αλέξανδρος Αναπληρωτής Καθηγητής, ΕΕΕΕΚ Παμμακαρίστου, tsikoman@hotmail.com Περίληψη Στην παρούσα εργασία γίνεται διαπραγμάτευση του ρόλου των
Οι ΤΠΕ ως Εκπαιδευτικό Εργαλείο στην Ειδική Αγωγή Τσικολάτας Αλέξανδρος Αναπληρωτής Καθηγητής, ΕΕΕΕΚ Παμμακαρίστου, tsikoman@hotmail.com Περίληψη Στην παρούσα εργασία γίνεται διαπραγμάτευση του ρόλου των
Μοντεσσόρι: Ένας κόσμος επιτευγμάτων. Το πρώτο μου βιβλίο για τους ΑΡΙΘΜΟΥΣ. με πολλά φανταστικά αυτοκόλλητα
 Μοντεσσόρι: Ένας κόσμος επιτευγμάτων Το πρώτο μου βιβλίο για τους ΑΡΙΘΜΟΥΣ με πολλά φανταστικά αυτοκόλλητα ΤΟ ΠΡΩΤΟ ΜΟΥ ΒΙΒΛΙΟ ΓΙΑ ΤΟΥΣ ΑΡΙΘΜΟΥΣ Η απόκτηση μιας δεξιότητας ή η ανάπτυξη της γνώσης απαιτεί
Μοντεσσόρι: Ένας κόσμος επιτευγμάτων Το πρώτο μου βιβλίο για τους ΑΡΙΘΜΟΥΣ με πολλά φανταστικά αυτοκόλλητα ΤΟ ΠΡΩΤΟ ΜΟΥ ΒΙΒΛΙΟ ΓΙΑ ΤΟΥΣ ΑΡΙΘΜΟΥΣ Η απόκτηση μιας δεξιότητας ή η ανάπτυξη της γνώσης απαιτεί
Η ανάλυση της κριτικής διδασκαλίας. Περιεχόμενο ή διαδικασία? Βασικό δίλημμα κάθε εκπαιδευτικού. Περιεχόμενο - η γνώση ως μετάδοση πληροφορίας
 Η ανάλυση της κριτικής διδασκαλίας Περιεχόμενο ή διαδικασία? Βασικό δίλημμα κάθε εκπαιδευτικού Περιεχόμενο - η γνώση ως μετάδοση πληροφορίας Διαδικασία η γνώση ως ανάπτυξη υψηλών νοητικών λειτουργιών (
Η ανάλυση της κριτικής διδασκαλίας Περιεχόμενο ή διαδικασία? Βασικό δίλημμα κάθε εκπαιδευτικού Περιεχόμενο - η γνώση ως μετάδοση πληροφορίας Διαδικασία η γνώση ως ανάπτυξη υψηλών νοητικών λειτουργιών (
ΕΚΠΑΙΔΕΥΤΙΚΗ ΨΥΧΟΛΟΓΙΑ
 ΕΚΠΑΙΔΕΥΤΙΚΗ ΨΥΧΟΛΟΓΙΑ 2016-2017 Μάθημα 1 ο Εισαγωγή στις βασικές έννοιες Προτεινόμενη Βιβλιογραφία Elliot, S. N., Kratochwill, T. R., Cook, J. L., & Travers, J. F. (2008). Εκπαιδευτική Ψυχολογία: Αποτελεσματική
ΕΚΠΑΙΔΕΥΤΙΚΗ ΨΥΧΟΛΟΓΙΑ 2016-2017 Μάθημα 1 ο Εισαγωγή στις βασικές έννοιες Προτεινόμενη Βιβλιογραφία Elliot, S. N., Kratochwill, T. R., Cook, J. L., & Travers, J. F. (2008). Εκπαιδευτική Ψυχολογία: Αποτελεσματική
Ταυτότητα εκπαιδευτικού σεναρίου
 Ταυτότητα εκπαιδευτικού σεναρίου Τίτλος: Συμβάντα και ενέργειες - Το πολύχρωμο σκαθάρι Σύντομη περιγραφή: Ένα εκπαιδευτικό σενάριο για την διδασκαλία των συμβάντων και ενεργειών στον προγραμματισμό, με
Ταυτότητα εκπαιδευτικού σεναρίου Τίτλος: Συμβάντα και ενέργειες - Το πολύχρωμο σκαθάρι Σύντομη περιγραφή: Ένα εκπαιδευτικό σενάριο για την διδασκαλία των συμβάντων και ενεργειών στον προγραμματισμό, με
Σχεδιάζοντας τη διδασκαλία των Μαθηματικών: Βασικές αρχές
 Σχεδιάζοντας τη διδασκαλία των Μαθηματικών: Βασικές αρχές Φοιτητής: Σκαρπέντζος Γεώργιος Καθηγήτρια: Κολέζα Ευγενία ΠΕΡΙΕΧΟΜΕΝΑ Βασικές θεωρίες σχεδιασμού της διδασκαλίας Δραστηριότητες και κατανόηση εννοιών
Σχεδιάζοντας τη διδασκαλία των Μαθηματικών: Βασικές αρχές Φοιτητής: Σκαρπέντζος Γεώργιος Καθηγήτρια: Κολέζα Ευγενία ΠΕΡΙΕΧΟΜΕΝΑ Βασικές θεωρίες σχεδιασμού της διδασκαλίας Δραστηριότητες και κατανόηση εννοιών
ΕΠΙΜΟΡΦΩΣΗ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΣΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΟ ΝΗΠΙΑΓΩΓΕΙΟ
 ΕΠΙΜΟΡΦΩΣΗ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΣΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΟ ΝΗΠΙΑΓΩΓΕΙΟ 2011 ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΟ ΝΗΠΙΑΓΩΓΕΙΟ Τα σύγχρονα
ΕΠΙΜΟΡΦΩΣΗ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΣΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΟ ΝΗΠΙΑΓΩΓΕΙΟ 2011 ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΟ ΝΗΠΙΑΓΩΓΕΙΟ Τα σύγχρονα
Βασικές εντολές σχεδίασης στη γλώσσα προγραμματισμού Logo Εντολή επανάληψης
 Βασικές εντολές σχεδίασης στη γλώσσα προγραμματισμού Logo Εντολή επανάληψης Επαρκές Σενάριο Γνωστικό αντικείμενο: Πληροφορική Δημιουργός: Αθηνά Κοκκόρη ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ,
Βασικές εντολές σχεδίασης στη γλώσσα προγραμματισμού Logo Εντολή επανάληψης Επαρκές Σενάριο Γνωστικό αντικείμενο: Πληροφορική Δημιουργός: Αθηνά Κοκκόρη ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ,
Διαφοροποίηση στρατηγικών διδασκαλίας ανάλογα με το περιεχόμενο στα μαθήματα των φυσικών επιστημών
 Διαφοροποίηση στρατηγικών διδασκαλίας ανάλογα με το περιεχόμενο στα μαθήματα των φυσικών επιστημών Κων/νος Στεφανίδης Σχολικός Σύμβουλος Πειραιά kstef2001@yahoo.gr Νικόλαος Στεφανίδης Φοιτητής ΣΕΜΦΕ, ΕΜΠ
Διαφοροποίηση στρατηγικών διδασκαλίας ανάλογα με το περιεχόμενο στα μαθήματα των φυσικών επιστημών Κων/νος Στεφανίδης Σχολικός Σύμβουλος Πειραιά kstef2001@yahoo.gr Νικόλαος Στεφανίδης Φοιτητής ΣΕΜΦΕ, ΕΜΠ
ΕΚΠΑΙΔΕΥΤΙΚΗ ΨΥΧΟΛΟΓΙΑ
 ΕΚΠΑΙΔΕΥΤΙΚΗ ΨΥΧΟΛΟΓΙΑ Μάθημα 1 ο Εισαγωγή στις βασικές έννοιες Προτεινόμενη Βιβλιογραφία Elliot, S. N., Kratochwill, T. R., Cook, J. L., & Travers, J. F. (2008). Εκπαιδευτική Ψυχολογία: Αποτελεσματική
ΕΚΠΑΙΔΕΥΤΙΚΗ ΨΥΧΟΛΟΓΙΑ Μάθημα 1 ο Εισαγωγή στις βασικές έννοιες Προτεινόμενη Βιβλιογραφία Elliot, S. N., Kratochwill, T. R., Cook, J. L., & Travers, J. F. (2008). Εκπαιδευτική Ψυχολογία: Αποτελεσματική
5.34 Αξιοποίηση κοινοτήτων μάθησης στο πλαίσιο προγράμματος προπτυχιακής εκπαίδευσης εν δυνάμει εκπαιδευτικών
 5.34 Αξιοποίηση κοινοτήτων μάθησης στο πλαίσιο προγράμματος προπτυχιακής εκπαίδευσης εν δυνάμει εκπαιδευτικών συντελεστές Σπυρίδων Δουκάκης sdoukakis@rhodes.aegean.gr ΠΤΔΕ Πανεπιστημίου Αιγαίου Μαρία Μοσκοφόγλου-
5.34 Αξιοποίηση κοινοτήτων μάθησης στο πλαίσιο προγράμματος προπτυχιακής εκπαίδευσης εν δυνάμει εκπαιδευτικών συντελεστές Σπυρίδων Δουκάκης sdoukakis@rhodes.aegean.gr ΠΤΔΕ Πανεπιστημίου Αιγαίου Μαρία Μοσκοφόγλου-
Μέρος B: Εισαγωγή στις έννοιες παιδαγωγικής αξιοποίησης των ΤΠΕ με εφαρμογή στη διδακτική της Πληροφορικής Οργάνωση και Σχεδίαση Μαθήματος
 Μέρος: Θέμα: Μέρος B: Εισαγωγή στις έννοιες παιδαγωγικής αξιοποίησης των ΤΠΕ με εφαρμογή στη διδακτική της Πληροφορικής Οργάνωση και Σχεδίαση Μαθήματος Φύλλα Δραστηριότητας L1 - Εύκολες L2 - Μέτριες L3
Μέρος: Θέμα: Μέρος B: Εισαγωγή στις έννοιες παιδαγωγικής αξιοποίησης των ΤΠΕ με εφαρμογή στη διδακτική της Πληροφορικής Οργάνωση και Σχεδίαση Μαθήματος Φύλλα Δραστηριότητας L1 - Εύκολες L2 - Μέτριες L3
Το σενάριο προτείνεται να υλοποιηθεί με το λογισμικό Geogebra.
 9.3. Σενάριο 9. Μελέτη της συνάρτησης f(x) = αx +βx+γ Γνωστική περιοχή: Άλγεβρα Α Λυκείου. Η συνάρτηση ψ= αχ +βχ+γ (γραφική παράσταση, μονοτονία, ακρότατα). Θέμα: Το προτεινόμενο θέμα αφορά την κατασκευή
9.3. Σενάριο 9. Μελέτη της συνάρτησης f(x) = αx +βx+γ Γνωστική περιοχή: Άλγεβρα Α Λυκείου. Η συνάρτηση ψ= αχ +βχ+γ (γραφική παράσταση, μονοτονία, ακρότατα). Θέμα: Το προτεινόμενο θέμα αφορά την κατασκευή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ. ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Διδακτική της Πληροφορικής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Διδακτική της Πληροφορικής Η Πληροφορική ως αντικείμενο και ως εργαλείο μάθησης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Διδακτική της Πληροφορικής Η Πληροφορική ως αντικείμενο και ως εργαλείο μάθησης
ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την
 1 ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την παλαιότερη γνώση τους, σημειώνουν λεπτομέρειες, παρακολουθούν
1 ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την παλαιότερη γνώση τους, σημειώνουν λεπτομέρειες, παρακολουθούν
ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ ΣΧΟΛΕΙΟΥ
 ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ ΣΧΟΛΕΙΟΥ Τι είναι Μαθηματικά; Ποια είναι η αξία τους καθημερινή ζωή ανάπτυξη λογικής σκέψης αισθητική αξία και διανοητική απόλαυση ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ
ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ ΣΧΟΛΕΙΟΥ Τι είναι Μαθηματικά; Ποια είναι η αξία τους καθημερινή ζωή ανάπτυξη λογικής σκέψης αισθητική αξία και διανοητική απόλαυση ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ
Διδακτικές Τεχνικές (Στρατηγικές)
 Διδακτικές Τεχνικές (Στρατηγικές) Ενδεικτικές τεχνικές διδασκαλίας: 1. Εισήγηση ή διάλεξη ή Μονολογική Παρουσίαση 2. Συζήτηση ή διάλογος 3. Ερωταποκρίσεις 4. Χιονοστιβάδα 5. Καταιγισμός Ιδεών 6. Επίδειξη
Διδακτικές Τεχνικές (Στρατηγικές) Ενδεικτικές τεχνικές διδασκαλίας: 1. Εισήγηση ή διάλεξη ή Μονολογική Παρουσίαση 2. Συζήτηση ή διάλογος 3. Ερωταποκρίσεις 4. Χιονοστιβάδα 5. Καταιγισμός Ιδεών 6. Επίδειξη
Κοινωνικογνωστικές θεωρίες μάθησης. Διδάσκουσα Φ. Αντωνίου
 Κοινωνικογνωστικές θεωρίες μάθησης Διδάσκουσα Φ. Αντωνίου Περίγραμμα Νοοκατασκευαστική θεώρηση της μάθησης Ιστορικό υπόβαθρο Top-down * bottom up Ομαδοσυνεργατική μάθηση Νοοκατασκευαστικές μέθοδοι στην
Κοινωνικογνωστικές θεωρίες μάθησης Διδάσκουσα Φ. Αντωνίου Περίγραμμα Νοοκατασκευαστική θεώρηση της μάθησης Ιστορικό υπόβαθρο Top-down * bottom up Ομαδοσυνεργατική μάθηση Νοοκατασκευαστικές μέθοδοι στην
Σχεδίαση και ανάπτυξη δραστηριοτήτων στο προγραμματιστικό περιβάλλον MicroWorlds Pro
 «Σχεδίαση και ανάπτυξη δραστηριοτήτων στο προγραμματιστικό περιβάλλον MicroWorlds Pro» Φύλλο Εργασίας 1 Ο μαθητής εξοικειώνεται με το περιβάλλον της Logo και του Microworlds Pro και μαθαίνει να δημιουργεί
«Σχεδίαση και ανάπτυξη δραστηριοτήτων στο προγραμματιστικό περιβάλλον MicroWorlds Pro» Φύλλο Εργασίας 1 Ο μαθητής εξοικειώνεται με το περιβάλλον της Logo και του Microworlds Pro και μαθαίνει να δημιουργεί
O φάκελος μαθητή/-τριας
 O φάκελος μαθητή/-τριας Δρ Δημήτριος Γκότζος Οι διαφάνειες 1-14 και 18-20 αποτελούν προϊόν μελέτης και αποδελτίωσης του Ι.Ε.Π. (2017). Οδηγός Εκπαιδευτικού για την Περιγραφική Αξιολόγηση στο Δημοτικό http://iep.edu.gr/images/iep/epistimoniki_ypiresia/epist_monades/a_kyklos/evaluation/2017/2a_perigrafiki_dhmotiko.pdf
O φάκελος μαθητή/-τριας Δρ Δημήτριος Γκότζος Οι διαφάνειες 1-14 και 18-20 αποτελούν προϊόν μελέτης και αποδελτίωσης του Ι.Ε.Π. (2017). Οδηγός Εκπαιδευτικού για την Περιγραφική Αξιολόγηση στο Δημοτικό http://iep.edu.gr/images/iep/epistimoniki_ypiresia/epist_monades/a_kyklos/evaluation/2017/2a_perigrafiki_dhmotiko.pdf
Διδακτική της Πληροφορικής ΙΙ
 Διδακτική της Πληροφορικής ΙΙ Ομάδα Γ Βότσης Ευστάθιος Γιαζιτσής Παντελής Σπαής Αλέξανδρος Τάτσης Γεώργιος Προβλήματα που αντιμετωπίζουν οι αρχάριοι προγραμματιστές Εισαγωγή Προβλήματα Δυσκολίες Διδακτικό
Διδακτική της Πληροφορικής ΙΙ Ομάδα Γ Βότσης Ευστάθιος Γιαζιτσής Παντελής Σπαής Αλέξανδρος Τάτσης Γεώργιος Προβλήματα που αντιμετωπίζουν οι αρχάριοι προγραμματιστές Εισαγωγή Προβλήματα Δυσκολίες Διδακτικό
ΘΕΜΑΤΑ ΓΙΑ ΑΣΕΠ ΝΗΠΙΑΓΩΓΩΝ
 ΘΕΜΑΤΑ ΓΙΑ ΑΣΕΠ ΝΗΠΙΑΓΩΓΩΝ Στις ερωτήσεις πολλαπλών επιλογών για την ειδικότητα των νηπιαγωγών των εκπαιδευτικών πρέπει να δοθεί ιδιαίτερη έμφαση, ακριβώς λόγω του μεγάλου ανταγωνισμού και των υψηλών βαθμολογιών
ΘΕΜΑΤΑ ΓΙΑ ΑΣΕΠ ΝΗΠΙΑΓΩΓΩΝ Στις ερωτήσεις πολλαπλών επιλογών για την ειδικότητα των νηπιαγωγών των εκπαιδευτικών πρέπει να δοθεί ιδιαίτερη έμφαση, ακριβώς λόγω του μεγάλου ανταγωνισμού και των υψηλών βαθμολογιών
1. Η σκοπιμότητα της ένταξης εργαλείων ψηφιακής τεχνολογίας στη Μαθηματική Εκπαίδευση
 1. Η σκοπιμότητα της ένταξης εργαλείων ψηφιακής τεχνολογίας στη Μαθηματική Εκπαίδευση Στη βασική παιδεία, τα μαθηματικά διδάσκονται με στατικά μέσα α) πίνακα/χαρτιού β) κιμωλίας/στυλού γ) χάρτινου βιβλίου.
1. Η σκοπιμότητα της ένταξης εργαλείων ψηφιακής τεχνολογίας στη Μαθηματική Εκπαίδευση Στη βασική παιδεία, τα μαθηματικά διδάσκονται με στατικά μέσα α) πίνακα/χαρτιού β) κιμωλίας/στυλού γ) χάρτινου βιβλίου.
Κάθε επιλογή, κάθε ενέργεια ή εκδήλωση του νηπιαγωγού κατά τη διάρκεια της εκπαιδευτικής διαδικασίας είναι σε άμεση συνάρτηση με τις προσδοκίες, που
 ΕΙΣΑΓΩΓΗ Οι προσδοκίες, που καλλιεργούμε για τα παιδιά, εμείς οι εκπαιδευτικοί, αναφέρονται σε γενικά κοινωνικά χαρακτηριστικά και παράλληλα σε ατομικά ιδιοσυγκρασιακά. Τέτοια γενικά κοινωνικο-συναισθηματικά
ΕΙΣΑΓΩΓΗ Οι προσδοκίες, που καλλιεργούμε για τα παιδιά, εμείς οι εκπαιδευτικοί, αναφέρονται σε γενικά κοινωνικά χαρακτηριστικά και παράλληλα σε ατομικά ιδιοσυγκρασιακά. Τέτοια γενικά κοινωνικο-συναισθηματικά
Μοντέλα Εκπαίδευσης με σκοπό τη Διδασκαλία με χρήση Ψηφιακών Τεχνολογιών
 1ο Κεφάλαιο Μοντέλα Εκπαίδευσης με σκοπό τη Διδασκαλία με χρήση Ψηφιακών Τεχνολογιών Τις τελευταίες δεκαετίες, οι επιστημονικές ενώσεις, οι συνδικαλιστικοί φορείς και εκπαιδευτικοί της πράξης μέσω συνεδρίων
1ο Κεφάλαιο Μοντέλα Εκπαίδευσης με σκοπό τη Διδασκαλία με χρήση Ψηφιακών Τεχνολογιών Τις τελευταίες δεκαετίες, οι επιστημονικές ενώσεις, οι συνδικαλιστικοί φορείς και εκπαιδευτικοί της πράξης μέσω συνεδρίων
Πληροφορική Γυμνασίου. Δρ. Κοτίνη Ισαβέλλα Σχ. Σύμβουλος Πληροφορικής Πέλλας, Ημαθίας και Πιερίας
 Πληροφορική Γυμνασίου Δρ. Κοτίνη Ισαβέλλα Σχ. Σύμβουλος Πληροφορικής Πέλλας, Ημαθίας και Πιερίας Εκπαιδευτικό υλικό Ο εκπαιδευτικός μπορεί να σχεδιάσει τις δικές του δραστηριότητες, να αξιοποιήσει αξιόλογο
Πληροφορική Γυμνασίου Δρ. Κοτίνη Ισαβέλλα Σχ. Σύμβουλος Πληροφορικής Πέλλας, Ημαθίας και Πιερίας Εκπαιδευτικό υλικό Ο εκπαιδευτικός μπορεί να σχεδιάσει τις δικές του δραστηριότητες, να αξιοποιήσει αξιόλογο
Στρατηγική επίλυσης προβλημάτων: Διερεύνηση περιμέτρου κι εμβαδού με τη βοήθεια του Ms Excel.
 Στρατηγική επίλυσης προβλημάτων: Διερεύνηση περιμέτρου κι εμβαδού με τη βοήθεια του Ms Excel. Έντυπο Α Φύλλα εργασίας Μαθητή Διαμαντής Κώστας Τερζίδης Σωτήρης 31/1/2008 Φύλλο εργασίας 1. Ομάδα: Ημερομηνία:
Στρατηγική επίλυσης προβλημάτων: Διερεύνηση περιμέτρου κι εμβαδού με τη βοήθεια του Ms Excel. Έντυπο Α Φύλλα εργασίας Μαθητή Διαμαντής Κώστας Τερζίδης Σωτήρης 31/1/2008 Φύλλο εργασίας 1. Ομάδα: Ημερομηνία:
ΕΦΑΠΤΟΜΕΝΗ ΓΩΝΙΑΣ ΚΑΙ ΚΛΙΣΗ ΕΥΘΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β' ΓΥΜΝΑΣΙΟΥ
 184 1 ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΕΦΑΠΤΟΜΕΝΗ ΓΩΝΙΑΣ ΚΑΙ ΚΛΙΣΗ ΕΥΘΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β' ΓΥΜΝΑΣΙΟΥ Ιωάννου Στυλιανός Εκπαιδευτικός Μαθηματικός Β θμιας Εκπ/σης Παιδαγωγική αναζήτηση Η τριγωνομετρία
184 1 ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΕΦΑΠΤΟΜΕΝΗ ΓΩΝΙΑΣ ΚΑΙ ΚΛΙΣΗ ΕΥΘΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β' ΓΥΜΝΑΣΙΟΥ Ιωάννου Στυλιανός Εκπαιδευτικός Μαθηματικός Β θμιας Εκπ/σης Παιδαγωγική αναζήτηση Η τριγωνομετρία
Η LOGO ΩΣ ΕΡΓΑΛΕΙΟ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΚΥΚΛΟΥ
 3 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ-ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 677 Η LOGO ΩΣ ΕΡΓΑΛΕΙΟ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΚΥΚΛΟΥ Καρατράντου Ανθή Δρ. Πληροφορικής, Εκπαιδευτικός ΠΕ19 Ε-mail: a.karatrantou@eap.gr Αλιμήσης Δημήτρης
3 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ-ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 677 Η LOGO ΩΣ ΕΡΓΑΛΕΙΟ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΚΥΚΛΟΥ Καρατράντου Ανθή Δρ. Πληροφορικής, Εκπαιδευτικός ΠΕ19 Ε-mail: a.karatrantou@eap.gr Αλιμήσης Δημήτρης
ΕΚΠΑΙΔΕΥΤΙΚΟ ΣΕΝΑΡΙΟ. pagioti@sch.gr
 ΕΚΠΑΙΔΕΥΤΙΚΟ ΣΕΝΑΡΙΟ Αγιώτης Πέτρος pagioti@sch.gr Εκπαιδευτικός Πληροφορικής Τίτλος διδακτικού σεναρίου Η έννοια των σταθερών και της καταχώρησης στη Visual Basic Εμπλεκόμενες γνωστικές περιοχές Στοιχεία
ΕΚΠΑΙΔΕΥΤΙΚΟ ΣΕΝΑΡΙΟ Αγιώτης Πέτρος pagioti@sch.gr Εκπαιδευτικός Πληροφορικής Τίτλος διδακτικού σεναρίου Η έννοια των σταθερών και της καταχώρησης στη Visual Basic Εμπλεκόμενες γνωστικές περιοχές Στοιχεία
Διδάσκοντας Φυσικές Επιστήμες με την υποστήριξη των ΤΠΕ. Καθηγητής T. A. Μικρόπουλος Πανεπιστήμιο Ιωαννίνων
 Διδάσκοντας Φυσικές Επιστήμες με την υποστήριξη των ΤΠΕ Καθηγητής T. A. Μικρόπουλος Πανεπιστήμιο Ιωαννίνων 1. Οι ψηφιακές τεχνολογίες ως γνωστικά εργαλεία στην υποστήριξη της διδασκαλίας και της μάθηση
Διδάσκοντας Φυσικές Επιστήμες με την υποστήριξη των ΤΠΕ Καθηγητής T. A. Μικρόπουλος Πανεπιστήμιο Ιωαννίνων 1. Οι ψηφιακές τεχνολογίες ως γνωστικά εργαλεία στην υποστήριξη της διδασκαλίας και της μάθηση
το σύστηµα ελέγχει διαρκώς το µαθητή,
 Α/Α Τύπος Εκφώνηση Απαντήσεις Ένας νηπιαγωγός, προκειµένου να διδάξει σε παιδιά προσχολικής ηλικίας το λεξιλόγιο των φρούτων Σωστό και λαχανικών που συνδέονται µε τις διατροφικές συνήθειες µας, δε ζητάει
Α/Α Τύπος Εκφώνηση Απαντήσεις Ένας νηπιαγωγός, προκειµένου να διδάξει σε παιδιά προσχολικής ηλικίας το λεξιλόγιο των φρούτων Σωστό και λαχανικών που συνδέονται µε τις διατροφικές συνήθειες µας, δε ζητάει
εργαλείο δυναμικής διαχείρισης γεωμετρικών σχημάτων και αλγεβρικών παραστάσεων δυνατότητα δυναμικής αλλαγής των αντικειμένων : είναι δυνατή η
 εργαλείο δυναμικής διαχείρισης γεωμετρικών σχημάτων και αλγεβρικών παραστάσεων δυνατότητα δυναμικής αλλαγής των αντικειμένων : είναι δυνατή η μετακίνηση, περιστροφή, αυξομείωση, ανάκλαση και απόκρυψη του
εργαλείο δυναμικής διαχείρισης γεωμετρικών σχημάτων και αλγεβρικών παραστάσεων δυνατότητα δυναμικής αλλαγής των αντικειμένων : είναι δυνατή η μετακίνηση, περιστροφή, αυξομείωση, ανάκλαση και απόκρυψη του
Η έννοια της μεταβλητής και της λίστας με την βοήθεια του λογισμικού Scratch
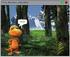 Η έννοια της μεταβλητής και της λίστας με την βοήθεια του λογισμικού Scratch Επαρκές Σενάριο Γνωστικό αντικείμενο: Πληροφορική Δημιουργός: Ουρανία Καλαντζή ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ
Η έννοια της μεταβλητής και της λίστας με την βοήθεια του λογισμικού Scratch Επαρκές Σενάριο Γνωστικό αντικείμενο: Πληροφορική Δημιουργός: Ουρανία Καλαντζή ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ
ΤΟ ΠΡΟΣΗΜΟ ΤΟΥ ΤΡΙΩΝΥΜΟΥ
 ΣΕΝΑΡΙΟ του Κύπρου Κυπρίδηµου, µαθηµατικού ΤΟ ΠΡΟΣΗΜΟ ΤΟΥ ΤΡΙΩΝΥΜΟΥ Περίληψη Στη δραστηριότητα αυτή οι µαθητές καλούνται να διερευνήσουν το πρόσηµο του τριωνύµου φ(x) = αx 2 + βx + γ. Προτείνεται να διδαχθεί
ΣΕΝΑΡΙΟ του Κύπρου Κυπρίδηµου, µαθηµατικού ΤΟ ΠΡΟΣΗΜΟ ΤΟΥ ΤΡΙΩΝΥΜΟΥ Περίληψη Στη δραστηριότητα αυτή οι µαθητές καλούνται να διερευνήσουν το πρόσηµο του τριωνύµου φ(x) = αx 2 + βx + γ. Προτείνεται να διδαχθεί
Εφαρμογές Προσομοίωσης
 Εφαρμογές Προσομοίωσης H προσομοίωση (simulation) ως τεχνική μίμησης της συμπεριφοράς ενός συστήματος από ένα άλλο σύστημα, καταλαμβάνει περίοπτη θέση στα πλαίσια των εκπαιδευτικών εφαρμογών των ΤΠΕ. Μπορούμε
Εφαρμογές Προσομοίωσης H προσομοίωση (simulation) ως τεχνική μίμησης της συμπεριφοράς ενός συστήματος από ένα άλλο σύστημα, καταλαμβάνει περίοπτη θέση στα πλαίσια των εκπαιδευτικών εφαρμογών των ΤΠΕ. Μπορούμε
ΕΠΙΜΟΡΦΩΤΙΚΗ ΗΜΕΡΙΔΑ «Η ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΜΑΘΗΤΗ ΣΥΜΦΩΝΑ ΜΕ ΤΑ ΝΕΑ ΠΡΟΓΡΑΜΜΑΤΑ ΣΠΟΥΔΩΝ»
 ΕΠΙΜΟΡΦΩΤΙΚΗ ΗΜΕΡΙΔΑ «Η ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΜΑΘΗΤΗ ΣΥΜΦΩΝΑ ΜΕ ΤΑ ΝΕΑ ΠΡΟΓΡΑΜΜΑΤΑ ΣΠΟΥΔΩΝ» ΕΙΣΗΓΗΣΗ: «Πρακτικές αξιολόγησης κατά τη διδασκαλία των Μαθηματικών» Γιάννης Χριστάκης Σχολικός Σύμβουλος 3ης Περιφέρειας
ΕΠΙΜΟΡΦΩΤΙΚΗ ΗΜΕΡΙΔΑ «Η ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΜΑΘΗΤΗ ΣΥΜΦΩΝΑ ΜΕ ΤΑ ΝΕΑ ΠΡΟΓΡΑΜΜΑΤΑ ΣΠΟΥΔΩΝ» ΕΙΣΗΓΗΣΗ: «Πρακτικές αξιολόγησης κατά τη διδασκαλία των Μαθηματικών» Γιάννης Χριστάκης Σχολικός Σύμβουλος 3ης Περιφέρειας
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΗ ΜΑΘΗΣΗ ΚΑΙ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΕΚΠΑΙΔΕΥΣΗ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΗ ΜΑΘΗΣΗ ΚΑΙ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΕΚΠΑΙΔΕΥΣΗ ΑΝΑΓΝΩΡΙΖΟΝΤΑΣ ΤΗ ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ & ΑΝΑΠΤΥΣΣΟΝΤΑΣ ΔΙΑΦΟΡΟΠΟΙΗΜΕΝΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Διαστάσεις της διαφορετικότητας Τα παιδιά προέρχονται
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΗ ΜΑΘΗΣΗ ΚΑΙ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΕΚΠΑΙΔΕΥΣΗ ΑΝΑΓΝΩΡΙΖΟΝΤΑΣ ΤΗ ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ & ΑΝΑΠΤΥΣΣΟΝΤΑΣ ΔΙΑΦΟΡΟΠΟΙΗΜΕΝΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Διαστάσεις της διαφορετικότητας Τα παιδιά προέρχονται
