... λέγονται στοιχεία του πίνακα Α και οι δείκτες δηλώνουν τη γραµµή και τη στήλη, αντίστοιχα, που ανήκει το στοιχείο α. . Για παράδειγµα, οι πίνακες
|
|
|
- Φυλλίδος Παπακωνσταντίνου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούµε µε το ορισµό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθµώ ή άλλω στοιχείω Οι πίακες εµφαίζοται στη θεωρία τω γραµµικώ συστηµάτω, στη θεωρία τω γραµµικώ απεικοίσεω και σήµερα πλέο χρησιµοποιούται σε όλους τους κλάδους τω µαθηµατικώ Θα ορίσουµε τις πράξεις µεταξύ τω πιάκω και θα µελετήσουµε τις ιδιότητές τους Οι πίακες που θα θεωρήσουµε στη συέχεια έχου στοιχεία πραγµατικούς ή µιγαδικούς αριθµούς Ότα ααφερόµαστε στο σώµα Κ, εοούµε ότι Κ= ή Κ= Βασικοί ορισµοί Ορισµός Μία ορθογώια παράταξη µ στοιχείω από το σώµα Κ σε µ οριζότιες σειρές, που λέγοται γραµµές, και σε κατακόρυφες σειρές, που λέγοται στήλες, της µορφής α α α α α α αµ αµ αµ λέγεται πίακας τύπου µ Συήθως συµβολίζεται µε έα από τα κεφαλαία γράµµατα ή µε το γεικό στοιχείο α σε παρέθεση, δηλαδή γράφουµε Α= ( α ) ή ( α ) µ Α=, α ο τύπος του πίακα είαι γωστός Οι αριθµοί α λέγοται στοιχεία του πίακα Α και οι δείκτες δηλώου τη γραµµή και τη στήλη, ατίστοιχα, που αήκει το στοιχείο α Για παράδειγµα, οι πίακες 3 Α=, Β= είαι τύπου 3 και, ατίστοιχα, και έχουµε i και j
2 8 Κεφάλαιο Πίακες α =, α =, α3 = 5, β = 4, β = 5, κλπ Ότα είαι µ =, τότε ο πίακας λέγεται τετραγωικός Έας πίακας τύπου (ατ, µ ) λέγεται πίακας-γραµµή (ατ, πίακας - στήλη) Το σύολο όλω τω πιάκω τύπου µ µε στοιχεία από το σώµα Κ συµ- βολίζεται µε Μµ ( Κ ) ή Μ µ τω τετραγωικώ πιάκω συµβολίζεται µε ( ), α το σώµα Κ θεωρείται γωστό Το σύολο Μ Μ Κ ή απλά Τα στοιχεία α, α,, α ορίζου τη κύρια διαγώιο του τετραγωικού πίακα Α= ( α ) Ο τετραγωικός πίακας Α= ( α ) λέγεται τριγωικός άω, α όλα τα στοιχεία του που βρίσκοται κάτω από τη κύρια διαγώιο είαι 0, δηλαδή είαι 0, για i > j Οµοίως ο πίακας Α= α λέγεται α = ( ) τριγωικός κάτω, α όλα τα στοιχεία του που βρίσκοται πάω από τη κύρια διαγώιο είαι 0, δηλαδή ισχύει ότι α = 0, για i < j Η σχέση της ισότητας στο σύολο ( ) ( β ) Β=, ορίζεται ως εξής: µ Μ µ Κ, α είαι ( α ) µ Α=Β α = β, για κάθε i =,,, µ, j =,,, Α= και Πράξεις στο σύολο τω µ πιάκω Η πρόσθεση πιάκω Ορισµός Στο σύολο Μ µ τω µ πιάκω µε στοιχεία στο σώµα Κ= ή η πρόσθεση είαι µία εσωτερική πράξη, που ορίζεται ως εξής: ( a b ) + : Μ µ Μµ Μµ,( Α, Β) Α+Β : = +, όπου Α= ( a ) και Β= ( b ) Ο πίακας Α +Β λέγεται άθροισµα τω πιάκω Α, Β και κάθε του στοιχείο προκύπτει ως άθροισµα τω ατίστοιχω στοιχείω τω πιάκω Α και Β Για παράδειγµα, α είαι 0 Α= 3 3, Β= , τότε Α+Β=
3 Οι πράξεις στο σύολο τω µ πιάκω 9 Θεώρηµα Η πράξη της πρόσθεσης ικαοποιεί τις ακόλουθες ιδιότητες: (i) Α+Β=Β+Α, για κάθε ΑΒ Μ, µ (ατιµεταθετική ιδιότητα) (ii) ( Α+Β ) +Γ=Α+ ( Β+Γ), για κάθε ΑΒΓ Μ,, µ (προσεταιριστική ιδιότητα) (iii) Υπάρχει το ουδέτερο στοιχείο για τη πρόσθεση και είαι ο µηδεικός πίακας Ο= (0) µ, που όλα τα στοιχεία του είαι 0 Ισχύει ότι Α +Ο=Ο+Α=Α, για κάθε Α Μ µ (iv) Για κάθε πίακα ( a υπάρχει ο ατίθετος πίακας που είαι τέτοιος ώστε Α+ ( Α ) = ( Α ) +Α=Ο Έτσι, το σύολο Απόδειξη Α= ) Α = ( a ) Μ µ γίεται αβελιαή προσθετική οµάδα Α= Β=, (i) Σύµφωα µε το ορισµό της πρόσθεσης, α είαι ( a ), ( b ) (ii) Α έχουµε (iii) Α (iv) Α Α+Β= ( a + b ) = ( b a + ) =Β+Α Α= ( a ), Β= ( b ) και Γ= ( c ) είαι µ ( ) (( a b ) c ) ( a ( b c )) ( Α= ( a ) τότε: Ο+ Α=Α+Ο= ( a + 0) = ( a ) =Α Α= ) τότε: ( ) ( ) (( a ) a ) ( 0) πίακες, τότε Α+Β +Γ= + + = + + =Α+ Β+Γ) ( a Α+ Α = Α +Α= + = =Ο Η πράξη της αφαίρεσης στο σύολο Μ µ ορίζεται µέσω της πρόσθεσης από τη ισότητα Α Β : =Α+ ( Β) Από το ορισµό και τις ιδιότητες της πρόσθεσης εύκολα προκύπτει ότι το άθροισµα τριώ ή περισσότερω πιάκω του ιδίου τύπου είαι το ίδιο µε οποιαδήποτε σειρά και α εκτελεστού οι επιµέρους προσθέσεις Για παράδειγµα, ισχύει Α+Β+Γ+ = ( Α+Β ) + ( Γ+ ) = [( Α+Β ) +Γ ] + = + [ Β+ ( Γ+Α)] Η εξίσωση πιάκω Α+Χ=Β έχει µοαδική λύση Χ =Β Α, αφού Α+Χ=Β Α+ ( Α+Χ ) = ( Α ) +Β [( Α ) +Α ] +Χ =Β+ ( Α) Ο+Χ=Β Α Χ=Β Α
4 0 Κεφάλαιο Πίακες Ο πολλαπλασιασµός αριθµού µε πίακα Ορισµός Στο σύολο Κ= ή Μ µ τω µ πιάκω µε στοιχεία στο σώµα ο πολλαπλασιασµός αριθµού µε πίακα είαι µία εξωτε- ρική πράξη µε συτελεστές στο σώµα Κ, που, α Α= ( a ) και λ Κ, ορίζεται ως εξής: λ Α= ( λa ) Συήθως γράφουµε λα, ατί του τυπικού συµβόλου λ Α Για παράδειγµα, α είαι Θεώρηµα Για κάθε, 0 Α= 3 3, τότε Α= 4 Α = a, Β= b Μµ( Κ λ µ Κ και ( ) ( ) ) ισχύου: (i) λ ( Α+Β ) = λ Α+ λ Β, (ii) ( λ + µ ) Α= λ Α+ µ Α, (iii) λ ( µ Α ) = ( λµ ) Α, (iv) Α=Α, όπου είαι η µοάδα τω πραγµατικώ αριθµώ Απόδειξη (i) ( ) ( ( a b )) ( a b ) ( a ) ( b ) (ii) ( ) (( ) a ) ( a a ) ( a ) ( a ) (iii) λ ( µ Α ) = λ ( µ a ) ( ( ) ) ( ( ) ) = λ µ a = λµ a = ( λµ ) Α Α= ( a ) = ( a ) =Α λ Α+Β = λ + = λ + λ = λ + λ = λ Α+ λ Β λ + µ Α = λ + µ = λ + µ = λ + µ = λ Α+ µ Α (iv) Παρατήρηση Το σύολο Μ ( Κ) µ εφοδιασµέο µε τις πράξεις της πρόσθεσης και του πολλαπλασιασµού αριθµού µε πίακα, όπως θα µάθουµε στο κεφάλαιο 8, αποκτά τη δοµή διαυσµατικού χώρου πάω στο σώµα Κ Πολλαπλασιασµός πιάκω Η πράξη του πολλαπλασιασµού πιάκω δε είαι εσωτερική πράξη στο σύολο Μ ( Κ), είαι όµως εσωτερική πράξη στο σύολο Μ ( Κ ) Η αφετη- µ ρία του ορισµού του πολλαπλασιασµού πιάκω είαι η θεωρία τω γραµ-
5 Οι πράξεις στο σύολο τω µ πιάκω µικώ απεικοίσεω που θα µελετήσουµε στο κεφάλαιο 9 Θα δούµε ότι σε κάθε γραµµική απεικόιση ατιστοιχίζεται έας πίακας και ατιστρόφως Επιπλέο, α οι πίακες Α και Β είαι ατίστοιχοι τω γραµµικώ απεικοίσεω f και g, τότε ο πίακας που ορίζουµε ως γιόµεο ΑΒ είαι ο ατίστοιχος της απεικόισης f g Έτσι οδηγούµεθα στο ακόλουθο ορισµό: Ορισµός 3 Α Α= ( a ) Μµ ( Κ), Β= ( b ) Μ ρ( Κ ), το γιόµεο Α Β ή απλά ΑΒ είαι έας πίακας τύπου µ ρ µε γεικό στοιχείο ibj ai b j i j ik kj k = που προκύπτει από το πολλαπλασιασµό τω στοιχείω της i- γραµµής του πίακα Α µε τα ατίστοιχα στοιχεία της j στήλης του πίακα Β και άθροιση τω γιοµέω που προκύπτου 3 0 Για παράδειγµα, α Α= 4, Β= 9, τότε ΑΒ = , εώ ορίζεται και ο πίακας + ( 3) 0+ ( 3) + ( 3) ΒΑ = = Παρατηρήσεις Το γιόµεο ΑΒ ορίζεται µόο ότα ο αριθµός τω στηλώ του πίακα Α ισούται µε το αριθµό τω γραµµώ του πίακα Β Σχηµατικά έχουµε Α Β ΑΒ, µ ρ µ ρ εώ για τους παραπάω πίακες το γιόµεο ΒΑ ορίζεται, µόο ότα µ = ρ και ε γέει έχουµε ΑΒ ΒΑ Θεώρηµα 3 Α οι πίακες Α, ΒΓ, είαι κατάλληλου τύπου, ώστε α ορίζοται οι πράξεις που εµφαίζοται, τότε ισχύου: (i) ( ΑΒ ) Γ = Α(ΒΓ) (προσεταιριστική ιδιότητα) ii) ΑΒ ( +Γ) =ΑΒ+ΑΓ ( Β+ Γ) Α=ΒΑ+ΓΑ (iii) ΑΒ = Ο Α =Οή Β= Ο c a a b a b = =,, (επιµεριστικές ιδιότητες)
6 Κεφάλαιο Πίακες Απόδειξη (i) Α είαι Α= ( a ), Β= ( b ), Γ= ( c ) µ ρ ρ τ a το γεικό στοιχείο του πίακα ως = Α κλπ, τότε έχουµε Α ( ), και γράψουµε ρ ρ ρ ( ΑΒ) Γ = ( ΑΒ) ik c kj = a i σbσ k c kj = a i σ bσ k c kj k= k= σ= σ= k= = a i σ( ΒΓ) σ j = Α( ΒΓ ) σ = (ii) Α είαι Α= ( a ), Β= ( b ), Γ= ( c ) µ ρ ρ, τότε έχουµε ΑΒ+Γ ( ) = a ( b + c ) = a b + a c =ΑΒ+ΑΓ ik kj kj ik kj ik kj k= k= k= Οµοίως, α Α= ( a ), Β= ( b ), Γ= ( c ) ρ µ µ, τότε έχουµε ( Β+Γ) Α= ( b + c ) a = b a + c a =ΒΑ+ΓΑ ik ik kj ik kj ik kj k= k= k= (iii) Αρκεί α βρούµε έα ατιπαράδειγµα µε πίακες για τους οποίους ισχύει ότι ΑΒ = Ο µε Α Ο και Β Ο Τέτοιοι είαι, για παράδειγµα, οι πίακες Α= και Β= 3 Ο µοαδιαίος πίακας Ο πίακας Ι = ( δ ) =, όπου δ 0 0, α i = = 0, α i j j είαι η συάρτηση δέλτα του Kronecker, οοµάζεται µοαδιαίος πίακας και έχει τις ιδιότητες: ΑΙ =Ι Α = Α, για κάθε πίακα Α τύπου, ΑΙ = Α,για κάθε πίακα Α τύπου µ, Ι Α=Α, για κάθε πίακα Α τύπου ρ
7 Οι πράξεις στο σύολο τω µ πιάκω 3 Ο ατίστροφος πίακας Ορισµός 4 Α ο πίακας Α είαι τετραγωικός τύπου και υπάρχει πίακας Χ τέτοιος ώστε ΑΧ = ΧΑ = Ι, τότε λέµε ότι ο πίακας Α είαι ατιστρέψιµος και ο πίακας Χ είαι ο ατίστροφος πίακας του Α Γράφουµε τότε Χ =Α Θεώρηµα 4 Α οι πίακες Α, Β είαι ατιστρέψιµοι, τότε ισχύου: (i) Απόδειξη ( Α ) = Α (i) Από το ορισµό 4 έχουµε ότι ΑΑ (ii) = Α Α =Ι, οπότε προκύπτει άµεσα το ζητούµεο (ii) ( ΑΒ)( Β Α ) = Α( ΒΒ ) Α = ΑΙ Α = ΑΑ = Ι και οµοίως αποδεικύεται ότι: ( ΑΒ ) =Β Α Β Α ΑΒ =Ι ( )( ) Στα επόµεα κεφάλαια θα θεωρήσουµε δύο τρόπους εύρεσης του ατίστροφου εός πίακα, α αυτός υπάρχει Σηµειώουµε ότι δε έχου όλοι οι τετραγωικοί πίακες ατίστροφο πίακα Στο παρό κεφάλαιο θα δώσουµε έα τύπο για το υπολογισµό του ατίστροφου εός πίακα Α είαι Α= a a x y και a a Χ= z w είαι ο ζητούµεος ατίστροφος του πίακα,τότε από τις ισότητες ΑΧ =ΧΑ=Ι και τη επίλυση τω Α γραµµικώ συστηµάτω µε δύο εξισώσεις και δύο αγώστους που προκύπτου, µε τη προϋπόθεση ότι aa aa 0, λαµβάουµε: a a a a Χ= a a = a a a a a a Οι δυάµεις εός πίακα Για κάθε τετραγωικό πίακα Α ορίζουµε τις δυάµεις του ως εξής: 0 Α =Ι, n n * Α =Α και Α = Α Α, για κάθε n µε n
8 4 Κεφάλαιο Πίακες Επιπλέο, α πίακας Α είαι ατιστρέψιµος, τότε ορίζουµε n Α = ( Α ) n *, για κάθε n Με βάση τις ιδιότητες που ικαοποιεί η πράξη του πολλαπλασιασµού πιάκω προκύπτου αµέσως οι ιδιότητες: m n n m m+ n Α Α = Α Α = Α, για κάθε mn, m ( ) n Α = Α mn, για κάθε mn, ( ) n n 3 λα = λ Α n, για κάθε n (Για n < 0 απαιτείται η ισότητα ( λ ) 4 ( Α ) ( Α ) =, για κάθε n n n 5 ( Α+Β ) = ( Α+Β) ( Α+Β ) =Α +ΑΒ+ΒΑ+Β 6 Α ΑΒ = ΒΑ, τότε ισχύου: ( Α±Β ) =Α ± ΑΒ+Β 3 3 ( Α ±Β ) =Α ± 3Α Β+ 3ΑΒ ±Β ( Α +Β) ( Α Β ) =Α Β Α = λ Α, για κάθε λ 0 ) n n n n k k * ( Α+Β) = Α Β, για κάθε k = 0 k n Ο αάστροφος πίακας Ορισµός 5 Α ( a ) µ 3 Α= Μ, τότε ο πίακας που προκύπτει από το Α µε εαλλαγή µεταξύ γραµµώ και στηλώ του λέγεται αάστροφος πίακας του Α και συµβολίζεται µε Α, έχουµε δηλαδή Για παράδειγµα, α είαι ( ji ) Α = Μ a µ Α= 3, 0 5 Β =, τότε Α = και [ 3] Β = Από το ορισµό του αάστροφου πίακα άµεσα προκύπτου οι ιδιότητες:
9 Οι πράξεις στο σύολο τω µ πιάκω 5 ( Α+Β ) =Α +Β, γιακάθε Α, Β Μ, µ ( λα ) = λα, για κάθε λ Κ, Α Μ µ, 3 ( ΑΒ ) = Β Α, για κάθε Α Μ, Β Μ, 4 Ι =Ι, ( ) 5 Α = Α, για κάθε Α Μ µ και 6 ( Α ) = ( Α ) µ ρ Απόδειξη Η απόδειξη τω περισσοτέρω από τις παραπάω ιδιότητες είαι απλή εφαρµογή του ορισµού Ειδικότερα για τη 3, α µε ( Α συµβο- λίσουµε το γεικό στοιχείο του πίακα Α, έχουµε : (( ) ) ( ) ( ) ( ΑΒ = ΑΒ ji = ajkbki = Β ik Α ) kj = ( Β Α ) Για τη 6 έχουµε k= k= ( ) ( ) ( ) ( ) ΑΑ = Α Α = Ι ΑΑ = Α Α = Ι Α Α = Α Α = Ι, οπότε, λόγω της µοαδικότητας του ατίστροφου εός πίακα, θα ισχύει ότι ( ) ( ) Ορισµός 6 Ο τετραγωικός πίακας Α = ( a ) (i) συµµετρικός, α (ii) ατισυµµετρικός, α i, j =,,, Για παράδειγµα, από τους πίακες Α = Α Μ λέγεται: Α = Α, δηλαδή, α a = a, για κάθε i, j =,,,, Α = Α, δηλαδή α ji 4 0 Α= 3, Β= 0, ji a ) = a, για κάθε ο Α είαι συµµετρικός, εώ ο Β είαι ατισυµµετρικός Παρατηρούµε ότι τα στοιχεία της κυρίας διαγωίου του πίακα Β είαι όλα µηδέ Αυτό δε είαι τυχαίο, αλλά ισχύει σε κάθε ατισυµµετρικό πίακα, αφού από τη ισότητα a για προκύπτει ότι i = = a i= j a = 0, για κάθε,,, ji ii
10 6 Κεφάλαιο Πίακες 3 Ειδικοί τύποι πιάκω Κατ αρχή σηµειώουµε ότι, σε µία γραµµή που δε έχει όλα τα στοιχεία της 0 (µη µηδεική γραµµή), το ηγετικό στοιχείο της είαι το πρώτο, από αριστερά προς τα δεξιά, µη µηδεικό στοιχείο της Ορισµός 3 (α) Ο πίακας ( a ) Α= Μ λέγεται κλιµακωτός ή κλιµακωτής µορφής, ότα ισχύου τα ακόλουθα: (i) οι µηδεικές γραµµές, α υπάρχου, βρίσκοται στη σειρά µετά τις µη µηδεικές γραµµές και (ii) α γ, γ,, γκ, κ µ είαι οι µη µηδεικές γραµµές του πίακα Α, τότε το ηγετικό στοιχείο της γ i + - γραµµής βρίσκεται δεξιότερα από το ηγετικό στοιχείο της γ i -γραµµής (β) Ο πίακας ( a ) Α= Μ λέγεται αηγµέος κλιµακωτός ή αηγ- µ µέης κλιµακωτής µορφής, α ισχύου τα ακόλουθα: (i) είαι κλιµακωτός, (ii) το ηγετικό στοιχείο κάθε µη µηδεικής γραµµής είαι και (iii) σε µία στήλη που περιέχει το ηγετικό στοιχείο κάποιας γραµµής, όλα τα άλλα στοιχεία της είαι 0 Για παράδειγµα, οι παρακάτω πίακες είαι κλιµακωτοί Α= και Β=, εώ αηγµέοι κλιµακωτοί είαι οι πίακες Γ= 0 και = Στοιχειώδεις πράξεις και πίακες Στο σύολο τω µ πιάκω θεωρούµε απεικοίσεις της µορφής τ: Μ Μ, Α τ( Α), µ µ που λέγοται στοιχειώδεις πράξεις γραµµώ ή γραµµοπράξεις Ο πίακας τ ( Α ) προκύπτει από το πίακα Α µε εφαρµογή µιας από τις ακόλουθες διαδικασίες: µ
11 3 Ειδικοί τύποι πιάκω 7 II III γ γ, εαλλαγή της i γραµµής µε τη I i j j γραµµή γ λγ, λ 0, πολλαπλασιασµός της i γραµµής επί λ 0 i i γ γ + λγ, λ 0, ατικατάσταση της i γραµµής από το άθροισµα i i j αυτής και του λ πλασίου της j γραµµής Οι πίακες Α και τ ( Α ) λέγοται γραµµοϊσοδύαµοι Όµοια, ορίζοται και οι στοιχειώδεις πράξεις στηλώ ή στηλοπράξεις και συµβολίζοται µε σ: Μ Μ, Α σ( Α) µ µ σ σ, σ λσ, σ σ + λσ, λ 0 i j i i i i j Σε κάθε µία από τις στοιχειώδεις πράξεις γραµµώ (ατίστοιχα, στηλώ) ατιστοιχίζουµε έα στοιχειώδη πίακα Έτσι, στη στοιχειώδη πράξη γραµµώ τ που εφαρµόζεται σε µ πίακα, ατιστοιχίζουµε το στοιχειώδη πίακα τ ( Ι µ ) που προκύπτει από τη εφαρµογή της τ στο µοαδιαίο πίακα Ι µ, εώ στη στοιχειώδη πράξη στηλώ σ που εφαρµόζεται σε µ πίακα, ατιστοιχίζουµε το στοιχειώδη πίακα σ ( Ι ) που προκύπτει από τη εφαρµογή της σ στο µοαδιαίο πίακα Ι Για παράδειγµα, στις στοιχειώδεις πράξεις γ γ, σ 3 σ, γ3 γ3 + γ, ότα εφαρµόζοται σε 3 4 πίακα, ατιστοιχίζοται οι παρακάτω στοιχειώδεις πίακες: ,, Ααγωγή πίακα σε αηγµέο κλιµακωτό Θεωρούµε έα πίακα ( a ) Α= Μ Αυτός µε διαδοχική εφαρµογή στοιχειωδώ πράξεω γραµµώ αάγεται αρχικά σε κλιµακωτό και στη συέχεια σε αηγµέο κλιµακωτό πίακα Η διαδικασία ααγωγής είαι αλγοριθµική (αλγόριθµος τω Gauss-Jordan) και περιγράφεται ως εξής: µ
12 8 Κεφάλαιο Πίακες Ι Με εαλλαγή γραµµώ, α είαι αάγκη, κάουµε το πρώτο στοιχείο της πρώτης µη µηδεικής στήλης διάφορο του 0 Το στοιχείο αυτό το οοµάζου- µε βασικό (pivot), όπως και το ηγετικό στοιχείο κάθε µη µηδεικής γραµµής ΙΙ Με εφαρµογή της γραµµοπράξης γ ( ) γ a το στοιχείο a γίεται ίσο µε Στη συέχεια µε εφαρµογή τω γραµµοπράξεω γ γ a γ,, γ γ a γ µ µ µ µηδείζουµε όλα τα στοιχεία της πρώτης στήλης εκτός του βασικού Α όλα τα στοιχεία της πρώτης στήλης είαι 0, τότε εφαρµόζουµε τη διαδικασία που περιγράψαµε στη πρώτη από τις επόµεες στήλες που έχει µη µηδεικά στοιχεία, κοκ ΙΙΙ Αγοώτας τη πρώτη γραµµή και τη πρώτη στήλη του πίακα που έχει προκύψει, επααλαµβάουµε τη παραπάω διαδικασία για α κάουµε το στοιχείο a ίσο µε και τα στοιχεία a3,,a µ της δεύτερης στήλης που βρίσκοται κάτω από το a ίσα µε 0 Συεχίζουµε τη ίδια διαδικα- σία µέχρις ότου ο πίακας Α γίει κλιµακωτός και µε τα ηγετικά στοιχεία τω γραµµώ του ίσα µε ΙVΜε στοιχειώδεις πράξεις γραµµώ τύπου ΙΙΙ µετατρέπουµε τα µη µηδεικά στοιχεία κάθε στήλης που περιέχει το ηγετικό µιας γραµµής σε µηδεικά αρχίζοτας από αυτή που είαι δεξιότερα Παρατηρήσεις Με τα βήµατα Ι και ΙΙ ο πίακας µετατρέπεται σε κλιµακωτό, χωρίς α είαι ααγκαίο α γίου τα ηγετικά στοιχεία τω γραµµώ ίσα µε Γεικά ο κλιµακωτός πίακας που προκύπτει δε είαι µοαδικός έχει όµως πάτοτε το ίδιο αριθµό µη µηδεικώ γραµµώ Ο αριθµός αυτός έχει µεγάλη σηµασία για έα πίακα και στα επόµεα κεφάλαια θα δούµε ότι οοµάζεται βαθµός του πίακα Ο αηγµέος κλιµακωτός πίακας που προκύπτει µε το παραπάω αλγόριθµο είαι µοαδικός 3 Τα τρία πρώτα βήµατα της παραπάω µεθόδου αποτελού τη µέθοδο απαλοιφής του Gauss, εώ η πλήρης µέθοδος είαι η µέθοδος απαλοιφής τω Gauss-Jordan Η ααγωγή πίακα σε αηγµέο κλιµακωτό είαι πολύ χρήσιµη για τη εύρεση του βαθµού πίακα, αλλά και για τη επίλυση γραµµικώ συστηµάτω Παράδειγµα 4 Να µετατραπεί σε αηγµέο κλιµακωτό ο πίακας Α=
13 4 Ααγωγή πίακα σε αηγµέο κλιµακωτό 9 Λύση Ο πίακας Α γίεται: γ γ γ γ γ γ4 γ4 3γ ( 4) γ γ3 0 γ3 γ3 4γ 0 γ γ3 γ4 γ4 8γ γ3 γ 0 4 γ4 γ4 0γ 0 3 γ3 ( ) γ3 4 ( γ 4) γ γ γ γ γ γ + γ3 γ γ+ 5γ4 γ γ γ Στη συέχεια θα δούµε µερικές προτάσεις σχετικές µε τις στοιχειώδεις πράξεις, τους στοιχειώδεις πίακες και τη εύρεση του ατίστροφου εός πίακα Πρόταση 4 (α) Α τ : Μµ Μ µ είαι µία στοιχειώδης πράξη γραµµώ και Α Μ µ, τότε ( ) τ( Α ) = τ Ιµ Α (β) Α σ : Μµ Μ µ είαι µία στοιχειώδης πράξη στηλώ και Α Μ µ, τότε σ( Α ) =Ασ( Ι ) Απόδειξη (α) Θα εξετάσουµε µόο τις στοιχειώδεις πράξεις τύπου Ι, ( γ γ ) Οι άλλες δύο περιπτώσεις και το ερώτηµα (β) αποδεικύοται αάλογα Ο στοιχειώδης πίακας που ατιστοιχεί στη γραµµοπράξη τ ( γ γ ) είαι i i j j
14 30 Κεφάλαιο Πίακες ( µ ) µ ii jj ji, τ Ι =Ι Ε Ε +Ε +Ε όπου Ε είαι µ µ πίακας που έχει το στοιχείο του ίσο µε και όλα τα υπόλοιπα στοιχεία του είαι 0 Έστω ότι ο πίακας ( a ) =, γραµµές γ k aka k ak k Επίσης έχουµε µ Τότε θα είαι i jγ i+, j i j + µ τ( Α ) = γ γ γ γ γ γ γ τ ( Ιµ ) Α = ( µ ) Α= έχει ii jj ji ii jj ji µ Ι Ε Ε +Ε +Ε Α=Α Ε Α Ε Α+Ε Α+Ε Α γ γ γi γ 0 a i j 0 γ j = + + = = τ ( Α) γ j 0 γ j 0 γ i γ i γµ 0 a µ γµ 0 γµ Παρατήρηση Σηµειώουµε ότι οι στοιχειώδεις πίακες που ατιστοιχίζοται στις στοιχειώδεις πράξεις γ i λγ i και γ γ + λγ, λ 0 είαι οι diag(,, λ,) και Ι µ + λε, ατίστοιχα i i j Πρόταση 4 Κάθε στοιχειώδης πίακας είαι ατιστρέψιµος Απόδειξη Έστω P και Q οι στοιχειώδεις πίακες που ατιστοιχού σε µία γραµµοπράξη τ και στη ατίστροφή της, έστω τ Σύµφωα µε τη πρόταση 4 έχουµε ( ( )) ( ) ( ) ( ) τ µ τ τ µ τ µ µ Ι = Ι = PΙ = Q PΙ = QP, ( ) ( ) ( ) Ι = τ τ Ι = QΙ = P QΙ = PQ µ µ µ µ Άρα έχουµε τη ισότητα PQ = QP =Ι µ, οπότε ο πίακας P είαι ατιστρέψιµος µε P = Q
15 5 Εύρεση του ατίστροφου πίακα 3 5 Εύρεση του ατίστροφου πίακα Από τις προτάσεις 4 και 4 έπεται ότι ο πίακας που προκύπτει µε διαδοχική εφαρµογή γραµµοπράξεω σε έα µ πίακα Α είαι της µορφής PΑ, όπου ο P είαι ατιστρέψιµος µ µ πίακας ως γιόµεο στοιχειωδώ πιάκω Ειδικότερα, για τετραγωικούς πίακες έχουµε: Πρόταση 5 Έστω ότι ο πίακας Α Μ ( Κ ) µε διαδοχική εφαρµογή γραµµοπράξεω τ, τ,, τ s µε ατίστοιχους στοιχειώδεις πίακες P,, P µ, P s µετασχηµατίζεται στο αηγµέο κλιµακωτό πίακα Α R Τότε ισχύου: I Α ο ΑR έχει µία τουλάχιστο µηδεική γραµµή, τότε ο πίακας Α είαι µη ατιστρέψιµος II Α ο Α δε έχει µηδεικές γραµµές, τότε Α =Ι, ο πίακας Α είαι R R µ ατιστρέψιµος και Α = P PP Ι µ s Απόδειξη Ι Έστω ότι ο πίακας έχει µία τουλάχιστο µηδεική γραµµή και ας Α R είαι ατιστρέψιµος Τότε θα υπάρχει πία- υποθέσουµε ότι ο πίακας Α κας Χ τέτοιος ώστε ΑΧ = ΧΑ = Ι µ () Από τη πρόταση 4, θα υπάρχει ατιστρέψιµος πίακας τέτοιος, ώστε α ισχύει s R P = P PP P PPΑ = PΑ = Α () Από τις () και () έχουµε Ι = PP = PΑΧ P = Α ΧP από τις οποίες προκύπτει ότι δηλαδή ο πίακας Α R Α R µ R Ι = ΧΑ = ΧP PΑ = ΧP Α, µ ( ) ( ) ΑR Χ P = ΧP Α =Ι µ, είαι ατιστρέψιµος, που είαι άτοπο, γιατί ο πίακας έχει µία τουλάχιστο µηδεική γραµµή και το γιόµεό του µε οποιοδήποτε πίακα θα περιέχει επίσης µία τουλάχιστο µηδεική γραµ- µή και έτσι δε µπορεί α είαι ο µοαδιαίος πίακας Άρα ο πίακας Α δε είαι ατιστρέψιµος R s
16 3 Κεφάλαιο Πίακες ΙΙ Α ο πίακας Α R δε έχει µηδεική γραµµή, τότε αυτός θα περιέχει µ ηγετικά καταεµηµέα σε µ µη µηδεικές γραµµές, που το καθέα βρίσκεται δεξιότερα από το ηγετικό της προηγούµεης γραµµής, οπότε θα είαι Α R =Ι µ Επιπλέο θα ισχύει s R µ s P PPΑ= PΑ=Α =Ι Α = P PP = P Α γράψουµε δίπλα στο πίακα Α Μµ ( Κ ) το µοαδιαίο πίακα Ι µ και εφαρµόσουµε και στους δύο ταυτόχροα τις ίδιες στοιχειώδεις πράξεις γραµµώ, ώστε ο πίακας Α α µετασχηµατιστεί στο αηγµέο κλιµακωτό πίακα, τότε θα έχουµε Α R [ ] Α Ιµ ΑR Β Από τη πρόταση 5 συµπεραίουµε ότι: Α ΑR Ι µ, τότε ο πίακας Α δε ατιστρέφεται Α Α R =Ι µ, τότε ο πίακας Α ατιστρέφεται και Α =Β Παράδειγµα 5 Να βρεθεί ο ατίστροφος του πίακα 3 Α= Λύση Έχουµε [ Α Ι γ γ γ 3] = γ3 γ3 3γ γ3 γ3 γ γ γ γ γ ( ) γ γ γ 3γ γ γ γ = Ι3 Β 0 0 Άρα ο πίακας Α είαι ατιστρέψιµος και ο ατίστροφός του είαι ο 0 Α =Β= 0 3
17 6 Εισαγωγή στα γραµµικά συστήµατα 33 6 Εισαγωγή στα γραµµικά συστήµατα Κάθε εξίσωση της µορφής λx+ λx + + λ x = β, (),,, όπου λ, λ,, λ, β Κ = ή και x x x άγωστοι αριθµοί από το σώµα Κ, λέγεται γραµµική εξίσωση µε αγώστους Ο αριθµός β λέγεται σταθερός όρος της εξίσωσης, εώ οι αριθµοί λ, λ,, λ λέγοται συτελεστές τω αγώστω Λύση της γραµµικής εξίσωσης () λέγεται κάθε διατεταγµέη -άδα ω, ω,, ω ) Κ τέτοια ώστε ( λω+ λω + + λω = β, δηλαδή επαληθεύεται η εξίσωση, α θέσουµε xi = ωi, i =,,, Γραµµικό σύστηµα µε µ εξισώσεις και αγώστους ή µ - γραµµικό σύστηµα είαι έα (πεπερασµέο) πλήθος µ γραµµικώ εξισώσεω µε αγώστους, δηλαδή έχει τη µορφή αx + αx + + α x = β x x x α + α + + α = β α µ x+ αµ x+ + αµx = βµ Α θεωρήσουµε τους πίακες () α α α α α α Α=, αµ αµ αµ x β x β Χ=, Β= x βµ τότε το γραµµικό σύστηµα () γράφεται ως µία εξίσωση πιάκω ΑΧ =Β, (3) όπου ο πίακας Α είαι πίακας τω συτελεστώ, ο πίακας Χ είαι ο πίακας τω αγώστω και ο πίακας Β είαι πίακας τω σταθερώ όρω Λύση της γραµµικού συστήµατος () λέγεται κάθε διατεταγµέη -άδα (,,, ) ξ ξ ξ Κ που επαληθεύει και τις µ εξισώσεις του συστήµατος ()
18 34 Κεφάλαιο Πίακες Το γραµµικό σύστηµα () λέγεται συµβιβαστό, α έχει µία τουλάχιστο λύση, εώ λέγεται αδύατο, α δε έχει λύση Για λόγους συµβατότητας µε τους συµβολισµούς µας θα συµβολίζουµε τη λύση ( ξ, ξ,, ξ ) και µε το πίακα-στήλη [ ] ξ ξ ξ ξ = ύο γραµµικά συστήµατα µε µ εξισώσεις και αγώστους ΑΧ=Β και Α Χ=Β, λέγοται ισοδύαµα, α έχου ακριβώς τις ίδιες λύσεις Η επίλυση εός γραµµικού συστήµατος, δηλαδή η διαδικασία εύρεσης όλω τω λύσεω του συστήµατος, βασίζεται στη εύρεση άλλω γραµµικώ συστηµάτω ισοδυάµω προς το αρχικό, αλλά απλούστερης µορφής Α ο πίακας Β τω σταθερώ όρω είαι ο µηδεικός πίακας, δηλαδή α είαι Β= [ 0 0 0], τότε το γραµµικό σύστηµα γίεται ΑΧ =Ο (4) και λέγεται οµογεές Ο πίακας ΑΒ Μµ ( + ) που είαι ο πίακας Α συµπληρωµέος µε µία τελευταία στήλη, αυτή που ορίζει ο πίακας Β τω σταθερώ όρω λέγεται επαυξηµέος πίακας του συστήµατος ΑΧ =Β 7 Η µέθοδος απαλοιφής του Gauss Η βασική µέθοδος επίλυσης του γραµµικού συστήµατος ΑΧ =Β, (Σ) όπου Α= ( α ) Μ µ, Χ= [ x x x ], Β= β β β µ, είαι η µέθοδος απαλοιφής του Gauss Η µέθοδος αυτή ουσιαστικά συίσταται στο µετασχηµατισµό του επαυξη- µέου πίακα ΑΒ του συστήµατος (Σ) σε αηγµέο κλιµακωτό µε χρήση µόο στοιχειωδώ πράξεω γραµµώ, ακολουθώτας το αλγόριθµο τω Gauss-Jordan που περιγράψαµε παραπάω στη παράγραφο 4, ως εξής: Ι Με εαλλαγή γραµµώ, α είαι αάγκη κάουµε το πρώτο στοιχείο της πρώτης µη µηδεικής στήλης διάφορο του 0 Το στοιχείο αυτό το οοµάζουµε βασικό (pivot), όπως και το ηγετικό στοιχείο κάθε µη µηδεικής γραµµής
19 7 Η µέθοδος απαλοιφής του Gauss 35 ΙΙ Με εφαρµογή της γραµµοπράξης γ ( ) γ a το στοιχείο a γίεται ίσο µε Στη συέχεια µε εφαρµογή τω γραµµοπράξεω γ γ aγ,, γµ γµ aµ γ, µηδείζουµε όλα τα στοιχεία της πρώτης στήλης εκτός του βασικού Α όλα τα στοιχεία της πρώτης στήλης είαι 0, τότε η διαδικασία που περιγράψαµε εφαρµόζεται στη πρώτη από τις επόµεες στήλες που έχει µη µηδεικά στοιχεία, κοκ III Αγοώτας τη πρώτη γραµµή και τη πρώτη στήλη του πίακα που έχει προκύψει, επααλαµβάουµε τη παραπάω διαδικασία για α κάου- µε το στοιχείο ίσο µε και τα στοιχεία a της δεύτερης στη- a 3,,a µ λης που βρίσκοται κάτω από το a ίσα µε 0 Συεχίζουµε τη ίδια δια- δικασία µέχρις ότου ο πίακας Α γίει κλιµακωτός και µε τα ηγετικά στοιχεία τω γραµµώ του ίσα µε IV Με στοιχειώδεις πράξεις γραµµώ τύπου ΙΙΙ µετατρέπουµε τα µη µηδεικά στοιχεία κάθε στήλης που περιέχει το ηγετικό µιας γραµµής σε µηδεικά, αρχίζοτας από αυτή που είαι δεξιότερα Είαι φαερό ότι µε διαδοχική εφαρµογή στοιχειωδώ πράξεω γραµ- µώ στο επαυξηµέο πίακα του συστήµατος (Σ), τα προκύπτοτα συστή- µατα έχου εξισώσεις που είαι γραµµικοί συδυασµοί τω εξισώσεω του αρχικού συστήµατος (Σ) Έτσι, τα συστήµατα που προκύπτου είαι ισοδύαµα προς το αρχικό σύστηµα, δηλαδή έχου το ίδιο σύολο λύσεω µε το σύστηµα (Σ) Μετά τη ααγωγή του επαυξηµέου πίακα [ Α Β ] σε αηγµέο κλιµακωτό διακρίουµε τις περιπτώσεις: Α στο αηγµέο κλιµακωτό πίακα υπάρχει γραµµή της µορφής β, β 0, τότε το σύστηµα είαι αδύατο Α δε υπάρχου γραµµές της µορφής β, β 0 και έχουµε συολικά κ µη µηδεικές γραµµές, κ min{ µ, }, τότε θεωρούµε τους κ αγώστους που ατιστοιχού σε στήλες του αηγµέου κλιµακωτού πίακα, που δε περιέχου κάποιο από τα ηγετικά, ως αυθαίρετους και εκφράζουµε τους υπόλοιπους αγώστους ως συαρτήσεις τω αυθαίρετω αγώστω Παράδειγµα Να προσδιορίσετε το σύολο τω λύσεω του γραµµικού συστήµατος: x+ y+ 3z+ w= 3, y z+ w= 4, x+ 3y+ z+ 3w= 7 { }
20 36 Κεφάλαιο Πίακες Λύση Με στοιχειώδεις πράξεις γραµµώ µετασχηµατίζουµε το επαυξηµέο πίακα του συστήµατος σε αηγµέο κλιµακωτό Έχουµε: γ γ γ γ3 γ3 γ γ γ γ Από τη µορφή του αηγµέου κλιµακωτού πίακα που προκύπτει συ- µπεραίουµε ότι το σύστηµα είαι συµβιβαστό Οι άγωστοι z και w που ατιστοιχού στις δύο τελευταίες στήλες, οι οποίες δε περιέχου κάποιο από τα ηγετικά τω µη µηδεικώ γραµµώ, επιλέγοται ως αεξάρτητοι (αυθαίρετοι) άγωστοι, εώ οι άγωστοι x και y που ατιστοιχού στις δύο πρώτες στήλες, οι οποίες περιέχου τα ηγετικά τω µη µηδεικώ γραµ- µώ, είαι οι εξαρτηµέοι άγωστοι Έτσι έχουµε το ισοδύαµο σύστηµα x+ 5z 3w= 5 x = 5 5z+ 3w y z + w = 4 y = 4 + z w, z, w Εποµέως, η τυχούσα από τις άπειρες λύσεις του συστήµατος είαι ( xyzw,,, ) = ( 5 5κ + 3 λ,4+ κ λ, κ, λ) = ( 5, 4, 0, 0) + κ( 5,,, 0) + λ(3,, 0,), κ, λ, εώ το σύολο τω λύσεω του συστήµατος είαι το Λ= ( 5 5κ+ 3 λ,4+ κ λκλ,, ): κλ, { } Παράδειγµα Να προσδιορίσετε το σύολο τω λύσεω του οµογεούς συστήµατος: x + x + 3x + 4x = x + 3x + 4x + 5x = Λύση Ο επαυξηµέος πίακας του συστήµατος γίεται : γ γ γ γ γ γ και το σύστηµα είαι ισοδύαµο µε το
21 7 Η µέθοδος απαλοιφής του Gauss 37 x + x + x = 0 x = x x x + x3 + x4 = 0 x = x3 x4, x3, x4 Εποµέως το σύολο τω λύσεω του δεδοµέου οµογεούς συστήµατος είαι {( κ λ, κ λκλ,, ) : κλ, } { κ λ κ λ } Λ= = (,,, 0) + (,, 0,):, Παράδειγµα 3 Να προσδιορίσετε τις τιµές της παραµέτρου a για τις οποίες έχει λύση το σύστηµα x+ 3y+ 5z = x+ 4z = x y+ z = a, a και στη συέχεια α βρείτε τη λύση του συστήµατος Λύση Ο επαυξηµέος πίακας του συστήµατος γίεται: γ γ γ ΑΒ = γ3 γ3 γ a a γ γ 6 γ3 γ3+ 4γ γ γ 3γ a a 3 Εποµέως το σύστηµα είαι συµβιβαστό, ότα a = 0 a = 3 3 Για a =, το σύστηµα είαι ισοδύαµο µε το σύστηµα 3 x+ z = x = z, z y+ z = y = z 6 6 οπότε το σύολο τω λύσεω του είαι Λ= c, c, c : c 6
22 38 Κεφάλαιο Πίακες 8 Η LU παραγοτοποίηση πίακα Όπως ξέρουµε, η µέθοδος απαλοιφής του Gauss για τη επίλυση του γραµµικού συστήµατος ΑΧ =Β (Σ) Α Β σε αηγµέο βασίζεται στη µετατροπή του επαυξηµέου πίακα [ ] κλιµακωτό Στη παράγραφο αυτή θα περιγράψουµε µία διαφορετική µεθοδο επίλυσης του γραµµικού συστήµατος (Σ) η οποία βασίζεται στη παραγοτοποίηση του πίακα Α τω συτελεστώ σε γιόµεο δύο πιάκω, εός κάτω τριγωικού και εός κλιµακωτού πίακα Η µέθοδος αυτή είαι ιδιαίτερα χρήσιµη ότα έχουµε α λύσουµε πολλά γραµµικά συστήµατα µε το ίδιο πίακα συτελεστώ και διαφορετικό πίακα σταθερώ όρω, είαι κατάλληλη για ηλεκτροικούς υπολογιστές και αποτελεί τη βάση πολλώ υπολογιστικώ πακέτω Ας υποθέσουµε ότι έχουµε α λύσουµε το γραµµικό σύστηµα (Σ) και ότι έχουµε παραγοτοποιήσει το πίακα Α Μ ( Κ), Κ = ή τω συτελεστώ σε γιόµεο δύο πιάκω της µορφής Α = LU, () όπου ο L είαι m m κάτω τριγωικός µε τα στοιχεία της κυρίας διαγωίου ίσα µε, εώ ο U είαι κλιµακωτός m n πίακας Έχουµε ΑΧ=Β LU Χ=Β L U Χ =Β, m n ( ) ( ) οπότε, α θέσουµε Y = U Χ, τότε έχουµε α επιλύσουµε τα απλά γραµµικά συστήµατα µε πίακα κλιµακωτής µορφής L Y =Β και U Χ = Y Επιλύουµε το σύστηµα L Y =Β µε ατικατάσταση προς τα εµπρός και στη συέχεια επιλύουµε το σύστηµα U Χ = Y µε ατικατάσταση προς τα πίσω Για παράδειγµα, ας υποθέσουµε ότι έχουµε προς λύση το σύστηµα x 0 x ΑΧ = = = Β x x4 και ότι έχουµε βρει τη παραγοτοποίηση Α= = 00 = LU Επιλύουµε πρώτα το σύστηµα
23 8 Η LU- παραγοτοποίηση πίακα y y 0 y = Y= y = 3 3 y y 3 Στη συέχεια προκύπτει το σύστηµα x x 7,75 + 0,5α 0 x x 0 0 = 3 Χ = =, α x 3, 5 3 x + α x4 x α 4 Ο αλγόριθµος της LU -παραγοτοποίησης ( ) Θεωρούµε πίακα Α Μm n Κ και µε διαδοχικές στοιχειώδεις πράξεις γραµµώ, χωρίς α κάουµε εαλλαγή γραµµώ, µετατρέπουµε το πίακα σε κλιµακωτό, οπότε έχουµε Ρ Ρ Ρ Α = U, (),, s s όπου Ρ Ρ Ρ είαι οι ατίστοιχοι στοιχειώδεις πίακες Επειδή όλοι οι στοιχειώδεις πίακες είαι ατιστρέψιµοι έχουµε Α=Ρ U LU Ρ Ρ s =, (3) όπου έχουµε θέσει s L =Ρ Ρ Ρ Επιπλέο λαµβάουµε Ρ Ρ Ρ L =Ι, (4) s οπότε παρατηρούµε ότι οι ίδιες γραµµοπράξεις µετατρέπου το πίακα L στο µοαδιαίο πίακα Για παράδειγµα, ας θεωρήσουµε το πίακα 0 Α= τω συτελεστώ του συστήµατος που λύσαµε προηγουµέως Έχουµε 0 0 γ γ γ γ3 γ3 γ Μέχρι τώρα χρησιµοποιήσαµε ως βασικό (pivot) στοιχείο το a = (συµβολίζεται µε παχύ µαύρο) και παρατηρούµε ότι οι ίδιες στοιχειώδεις πράξεις δίου
24 40 Κεφάλαιο Πίακες γ γ γ 0 0 γ3 γ3 γ * 0 * Στη συέχεια έχουµε 0 0 γ3 γ+ γ = U, όπου χρησιµοποιήσαµε ως βασικό το στοιχείο a = Παρατηρούµε ότι η ίδια στοιχειώδης πράξη δίει γ γ + γ 0 0, οπότε πλέο είαι φαερό ότι ο κατάλληλος πίακας L που µε τις ίδιες γραµµοπράξεις µετατρέπεται στο µοαδιαίο πίακα είαι ο 0 0 L = 0 3 Μπορούµε πλέο α περιγράψουµε τη διαδικασία παραγοτοποίησης του πίακα Α ως εξής: (i) (ii) Μετατρέπουµε το πίακα Α µε στοιχειώδεις πράξεις γραµµώ, χωρίς εαλλαγές γραµµώ, σε κλιµακωτό, οπότε προκύπτει ο πίακας U ιαµορφώουµε κάθε στήλη του Α που έχει βασικό στοιχείο, κάθε φορά που εµφαίζεται, µε µηδεικά πάω από το βασικό στοιχείο και διαιρώτας τα υπόλοιπα στοιχεία της µε το βασικό στοιχείο Οι στήλες που διαµορφώοται µαζί µε µία τελευταία στήλη της µορφής [ 0 0 ] αποτελού τις στήλες του πίακα L 9 ιαµερίσεις πιάκω Θεωρούµε πίακα ( a ) Α= και τους φυσικούς αριθµούς µ µ, µ,, µ r,,,, s έτσι, ώστε µ + µ + + µ r = µ και s =
25 9 ιαµερίσεις πιάκω 4 Στη συέχεια µε διακεκοµµέες οριζότιες και κατακόρυφες γραµµές απoκόβουµε τις µ πρώτες γραµµές µετά τις µ επόµεες γραµµές κοκ, τις πρώτες στήλες κοκ Έτσι από το πίακα Α σχηµατίζουµε rs πίακες, έστω Α, κ =,,, r, λ = κλ,,, s, τύπου µ κ λ Οι πίακες Α κλ αποτελού µία r s διαµέριση του πίακα Α που ατιστοιχεί στους αριθµούς ( µ, µ,, µ ) και ( r,,, s ) Συµβολικά γράφουµε Α= ( Α κλ Για παράδειγµα, ο 3 5 πίακας ) r s 3 5 Α= µπορεί α διαµεριστεί σε 6 υποπίακες ως εξής 3 5 Α Α Α3 Α= ( Αλµ ) = = Α Α Α 3 0 Ας θεωρήσουµε τώρα το 5 4πίακα Β µε µία 3 διαµέριση Β Β 4 Β= Β Β = 0 0 Β 3 Β Το γιόµεο τω δύο πιάκω Α και Β είαι ο πίακας ΑΒ = ΑikΒkj = k = 6 4 Σηµειώουµε ότι για α είαι γεικά δυατός ο παραπάω πολλαπλασιασµός διαµερισµέω πιάκω πρέπει και αρκεί α είαι δυατός ο πολλαπλασιασµός όλω τω ατίστοιχω υποπιάκω Α και Β Με κατάλληλη επιλογή τω διαµερίσεω, συήθως γίεται ευκολότερα ο πολλαπλασιασµός δύο πιάκω Στο προηγούµεο παράδειγµα, ατί α κάουµε απ ευθείας το πολλαπλασιασµό τω δύο πιάκω, πολλαπλασιάζουµε υποπίακες που έχου µικρότερο αριθµό γραµµώ και στηλώ Αυτό ik kj
26 4 Κεφάλαιο Πίακες είαι σηµατικό, κυρίως ότα οι δεδοµέοι πίακες έχου µεγάλο αριθµό γραµµώ και στηλώ Μία ιδιαίτερη περίπτωση έχουµε, ότα ο πίακας Α µπορεί α διαµεριστεί σε υποπίακες Α, Α,, Αr, πιθαώς διαφορετικώ τάξεω, έτσι ώστε Α Ο Ο Ο Α Ο Α= = diag ( Α, Α,, Αr ) Ο Ο Α r Επιπλέο, α [ ], Α= Α Α Β= Β Β, τότε ΑΒ =ΑΒ +ΑΒ, ότα βέβαια ορίζοται οι πολλαπλασιασµοί και οι προσθέσεις υποπιάκω που εµφαίζοται, π χ = και = + = = + = Πίακες µε στοιχεία συαρτήσεις [ ] Πολλές φορές θεωρούµε πίακες µε στοιχεία συαρτήσεις µιας ή περισσοτέρω πραγµατικώ µεταβλητώ, όπως οι πίακες a() t a () t a () t x () t a() t a () t a () t x () t Α () t =, Χ () t = aµ () t aµ () t aµ() t x () t
27 0 Πίακες µε στοιχεία συαρτήσεις 43 Ορισµός 0 (i) Ο πίακας () t ( a () t ) Α = είαι συεχής για t = t0, α κάθε συάρτηση a () t είαι συεχής για t = t0 Ο πίακας Α () t είαι συεχής στο διάστηµα [ α, β ], α είαι συεχής σε κάθε σηµείο του διαστή- µατος [ α, β ] ( (ii) Ο πίακας Α () t = a () t ) είαι παραγωγίσιµος στο διάστηµα [ α, β ], α κάθε µία από τις συαρτήσεις a () t είαι παραγωγίσιµη στο διάστηµα [ α, β ] και η παράγωγός του είαι ο πίακας dα Α () t : = ( a () t ) dt (iii) Όµοια ορίζουµε το ολοκλήρωµα του πίακα Α () t = ( a () t ) β β α Α () tdt: = ( α a () tdt) Για παράδειγµα, ο πίακας t t Α e e t = () cos t sin t είαι συεχής στο και ισχύει π t t e e e Α () t = sin t cos t και e π π Α() tdt = 0 0 Μερικές από τις βασικές ιδιότητες της παραγώγισης πιάκω µε στοιχεία συαρτήσεις παραθέτουµε παρακάτω, όπου ( a () t ), ( b () t ) Α= Β= και Γ= ( c () t ) (σταθερός πίακας) είαι πίακες κατάλληλου τύπου, ώστε α ορίζοται οι εµφαιζόµεες πράξεις πιάκω : d dα d dα dβ ΑΒ = Β + Α dt dt dt dt dt d dα dβ d dα Α+Β = + 4 ( Α ) = Α Α dt dt dt dt dt ( ΓΑ ) = Γ 3 ( ) ( )
28 44 Κεφάλαιο Πίακες ΑΣΚΗΣΕΙΣ Ο πίακας Α Μ ( Κ) είαι τέτοιος ώστε ( Α + Ι ) =Ο (α) Να αποδείξετε ότι ο πίακας Α είαι ατιστρέψιµος και α εκφρά- σετε το πίακα Α ως πολυώυµο του Α (β) Να αποδείξετε ότι ο πίακας Α +Ι είαι ατιστρέψιµος Α ΑΒ Μ, ( Κ), α χαρακτηρίσετε τις επόµεες προτάσεις ως αληθείς ή ψευδείς, δικαιολογώτας τη απάτησή σας µε απόδειξη ή µε κάποιο ατιπαράδειγµα : (i) Α ΑΒ = Α Β και ΑΒ, ατιστρέψιµοι, τότε Α =Β (ii) Α ΑΒ, ατιστρέψιµοι, τότε και Α +Β ατιστρέψιµος (iii) Α ΑΒ = Ο και Α Ο, τότε Α, Β µη ατιστρέψιµοι (iv) Α ΑΒΑ = Ο και Β µη ατιστρέψιµος, τότε ( ) 3 Α ο πίακας Α Μ είαι τέτοιος ώστε υπάρχου xy, έτσι, ώστε α ισχύει xy Α= y Ισχύει το ίδιο, ότα Α Μ ; ( ( ) x xy Α =Ο Α =Ο, α αποδείξετε ότι 4 Οι πίακες ΑΒ Μ Κ) είαι τέτοιοι ώστε Α =ΑΒ, =Β και ( ), Α+Β =Α+Β Να αποδείξετε ότι: ΑΒ= ΒΑ=Ο 5 Α οι πίακες Α, Β είαι συµµετρικοί, α αποδείξετε ότι: (α) ΑΒ συµµετρικός ΑΒ=ΒΑ (β) Ο πίακας ΑΒ ΒΑ είαι ατισυµµετρικός k 6 Α Α = Ο για κάποιο k, α αποδείξετε ότι: * ( ) k Ι Α =Ι+Α+ +Α 7 Ο πίακας J έχει όλα τα στοιχεία του ίσα µε Θεωρούµε α, β µε α + β 0 (Α) Να αποδείξετε ότι: (i) J = J (ii) ο πίακας Χ= αι + β J είαι ατιστρέψιµος, ααζητώτας το
29 Ασκήσεις 45 ατίστροφό του στη µορφή ( γ J ) α Ι + (Β) Να βρείτε το ατίστροφο του πίακα (i) Α οι πίακες ΑΒ, και Ρ είαι τέτοιοι, ώστε ΑΡ =ΡΒ και * ο Ρ είαι ατιστρέψιµος, α αποδείξετε ότι για κάθε n ισχύει: n n Α =ΡΒ Ρ 4 (ii) Έστω Α= 3, Β= 0 0 και Ρ Μ ( ) Κ Να αποδείξετε ότι: x y ΑΡ = ΡΒ Ρ =, x, y x 3y * Θεωρώτας x = y =, βρείτε το πίακα Α n, n Ν 9 Οι πίακες ΑΒ Μ ( Κ) είαι τέτοιοι ώστε ( ), ΑΒ =Ι Να αποδείξετε ότι οι πίακες Α, Β είαι ατιστρέψιµοι και ( ΒΑ ) =Ι 0 Α ΑΒ Μ, ( Κ ) µε Α+Β=ΑΒ, α αποδείξετε ότι: Α Α είαι πίακας τέτοιος, ώστε Α Α=Ι = [ ] ΑΒ =ΒΑ, τότε ο πίακας Η=Ι ΑΑ είαι ο ατίστοιχος πίακας Householder, που οοµάστηκε έτσι προς τιµή του Αµερικαού µαθηµατικού A Householder (i) Α Α = Α Α=Ι = και α υπολογίσετε το ατίστοιχο πίακα του Householder (ii) Α Η είαι πίακας Householder, α αποδείξετε ότι: Η=Η και Η Η=Ι, α επαληθεύσετε ότι [ ] Με τη υπόθεση ότι όλοι οι ατίστροφοι πίακες που εµφαίζοται υπάρχου, α αποδείξετε ότι: (i) ( ) ( ) (ii) ( ) (iii) ( Α+ΒΒ ) Β=Α Β( Ι+Β Α Β) Α +Β = Α Α+Β Β Ι +ΑΒ Α=Α( Ι+ΒΑ )
30 46 Κεφάλαιο Πίακες 3 Να βρεθεί αηγµέος κλιµακωτός πίακας που είαι γραµµοϊσοδύα- µος µε καθέα από τους παρακάτω πίακες: Α= 4, Β= Να βρεθεί ο ατίστροφος, α υπάρχει, τω παρακάτω πιάκω: 0 Α= 3 4, Β= Ο επαυξηµέος πίακας εός γραµµικού συστήµατος είαι ο a 0 b a a a b Να εξετάσετε για ποιες τιµές τω παραµέτρω ab, το σύστηµα: (i) Έχει µοαδική λύση (ii) Έχει µοοπαραµετρική απειρία λύσεω (iii) Έχει διπαραµετρική απειρία λύσεω (iv) ε έχει λύση 6 Να λύσετε τα γραµµικά συστήµατα x+ x + 3x3 = x 3x + x3 = 0 (i) (ii) x + x3 = 4 x + x 3x3 = 0 x x + x3 = 9x + x3 5x4 = 0 x x + 3x3 = (iii) x+ x 4x4 = 0 (iv) x3 + 8x4 = 0 3x 3x + 7x3 = 0 0 x 0x + 4x3 = Α είαι Α Μ4 ( ), Β Μ 4( ) και ΑΒ =, α προσδιορίσετε το πίακα ΒΑ
... λέγονται στοιχεία του πίνακα Α και οι δείκτες i και j δηλώνουν τη γραμμή και τη στήλη, αντίστοιχα, που ανήκει το στοιχείο α
 ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούε ε το ορισό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθώ ή άλλω στοιχείω Οι πίακες εφαίζοται στη θεωρία τω γραικώ συστηάτω,
ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούε ε το ορισό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθώ ή άλλω στοιχείω Οι πίακες εφαίζοται στη θεωρία τω γραικώ συστηάτω,
(πολλδ β) = πολλδ + ( 1) ν β ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΘΟ ΙΚΟ ΙΑΙΡΕΤΟΤΗΤΑ
 ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΑΛΓΕΒΡΑ. Για να βρούµε την δύναµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωνα µε την ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ
 ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
β± β 4αγ 2 x1,2 x 0.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Λυµένες Ασκήσεις * * *
 Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικών αριθµών. Μιγαδικό επίπεδο. Γεωµετρική παράσταση του αθροίσµατος µιγαδικών αριθµών.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Α. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
Ε 1. Διαφορικός λογισμός (Κανόνες παραγώγισης)
 Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
ΜΑΘΗΜΑ 9 Γενικές ασκήσεις µιγαδικών
 ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
1. [0,+ , >0, ) 2. , >0, x ( )
 Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
(Καταληκτική ημερομηνία αποστολής 15/11/2005)
 η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Θεωρία - Μέθοδοι
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Ι δ ι ο τ η τ ε ς Π ρ ο σ θ ε σ η ς - Π ο λ λ α π λ α σ ι α σ μ ο υ ΙΔΙΟΤΗΤΑ ΠΡΟΣΘΕΣΗ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
ΛΥΚΕΙΟ ΜΕΤΑΜΟΡΦΩΣΗΣ 2014 ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
Παρατηρήσεις 1 Για α ααζητήσουµε το όριο της f στο, πρέπει η f α ορίζεται όσο θέλουµε κοτά στο, δηλαδή η f α είαι ορισµέη σ έα σύολο της µορφής ( α, )
 Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
2.2 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ Ασκήσεις : 1, 2, 3, σελ. 107.
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεων
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
Ασκήσεις7 80. AU διαγώνιο. αποτελούμενη από ιδιοδιανύσματα του A. Πρόσθετες ιδιότητες κανονικών πινάκων: Έστω A o
 Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
1. Το σύνολο των μιγαδικών αριθμών
 Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
+ + = + + α ( β γ) ( )
 ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ Αριθµητική παράσταση Αριθµητική παράσταση λέγεται µια σειρά αριθµώ που συδέοται µεταξύ τους µε πράξεις. Η σειρά τω πράξεω σε µια αριθµητική παράσταση είαι η εξής: 1. Υπολογίζουµε
ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ Αριθµητική παράσταση Αριθµητική παράσταση λέγεται µια σειρά αριθµώ που συδέοται µεταξύ τους µε πράξεις. Η σειρά τω πράξεω σε µια αριθµητική παράσταση είαι η εξής: 1. Υπολογίζουµε
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ = Γ. β1 = β2
 Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος
 Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
5.3 ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ
 5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
ν ν Άσκηση 1. Α =Α, Β =Β. Λύση Άσκηση Α Β =Β Α, Α Β=ΒΑ. Β Α= ( Β Β)( ΑΒ ) Β Α=Ι( ΑΒ ) Β Α=ΑΒ. Άσκηση = Α Α Α Α=.
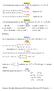 Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Μαθηματικά κατεύθυνσης Γ Λυκείου. Όλη η θεωρία και οι ασκήσεις των πανελλαδικών εξετάσεων. Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς
 Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
0..1 ΒΑΣΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΝΝΟΙΕΣ
 Εισαγωγικό Κεφάλαιο: Ρητοί Αριθµοί ΜΑΘΗΜΑ 0 Υποεότητα 1: Βασικές Επααληπτικές Έοιες (Επααλήψεις-Συµπληρώσεις) Θεµατικές Εότητες: 1. Ρητοί αριθµοί-βασικές επααληπτικές έοιες.. Πρόσθεση ρητώ αριθµώ. 3. Άθροισµα
Εισαγωγικό Κεφάλαιο: Ρητοί Αριθµοί ΜΑΘΗΜΑ 0 Υποεότητα 1: Βασικές Επααληπτικές Έοιες (Επααλήψεις-Συµπληρώσεις) Θεµατικές Εότητες: 1. Ρητοί αριθµοί-βασικές επααληπτικές έοιες.. Πρόσθεση ρητώ αριθµώ. 3. Άθροισµα
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι x 1,x,,x k είαι οι τιµές µιας µεταβλητής Χ, που αφορά τα άτοµα εός δείγµατος µεγέθους, όπου
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι x 1,x,,x k είαι οι τιµές µιας µεταβλητής Χ, που αφορά τα άτοµα εός δείγµατος µεγέθους, όπου
1.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ
 ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι 1,,, k είαι οι τιµές µιας µεταβλητής Χ, που αφορά Β.1. τα άτοµα εός δείγµατος µεγέθους,
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι 1,,, k είαι οι τιµές µιας µεταβλητής Χ, που αφορά Β.1. τα άτοµα εός δείγµατος µεγέθους,
ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συνδυασμός ν στοιχείων ανά κ είναι μια μη διατεταγμένη συλλογή κ στοιχείων από τα ν.
 13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ
 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ονοµάζεται γεωµετρική πολλαπλότητα αυτής. Τα ιδιοδιανύσµατα αυτά είναι βάση του διανυσµατικού υποχώρου E ( λ 0 ), που ονοµάζεται ιδιόχωρος
 Γραµµική Άγεβρα ΙΙ Σείδα από 5 Μάθηµα 5 ο Ι ΙΟΤΙΜΕΣ ΚΑΙ Ι ΙΟ ΙΑΝΥΣΜΑΤΑ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άγεβρα : εδάφιο, σε 33 (όχι Πρόταση 63) εδάφιο, σε 4, Πρόταση 65, (χωρίς απόδειξη) και Πρόταση 66 εδάφιο
Γραµµική Άγεβρα ΙΙ Σείδα από 5 Μάθηµα 5 ο Ι ΙΟΤΙΜΕΣ ΚΑΙ Ι ΙΟ ΙΑΝΥΣΜΑΤΑ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άγεβρα : εδάφιο, σε 33 (όχι Πρόταση 63) εδάφιο, σε 4, Πρόταση 65, (χωρίς απόδειξη) και Πρόταση 66 εδάφιο
Η παραπάνω ιδιότητα γενικεύεται και για περισσότερους από δύο πραγµατικούς αριθµούς. Έτσι έχουµε: αβγ α β γ = β β. d a β = α
 ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να γωρίζει τη έοια της ακολουθίας, τους τρόπους που ορίζεται, τις διαφορές της από μία συάρτηση. Να γωρίζει τους ορισμούς της αριθμητικής και γεωμετρικής
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να γωρίζει τη έοια της ακολουθίας, τους τρόπους που ορίζεται, τις διαφορές της από μία συάρτηση. Να γωρίζει τους ορισμούς της αριθμητικής και γεωμετρικής
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2003 ΕΚΦΩΝΗΣΕΙΣ
 ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
Γραμμική Άλγεβρα ΙΙ. Εξέταση Σεπτεμβρίου Επώνυμο συνοπτικές ενδεικτικές λύσεις. Όνομα. ΑΜ_(13 ψηφία) Σύνολο
 Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 00 Επώυμο συοπτικές εδεικτικές λύσεις Όομα ΑΜ_( ψηφία) Ημ/ία Αίθουσα Α 4 Σύολο Η εξέταση αποτελείται από 4 Θέματα Κάθε θέμα αξίζει μοάδες Το άριστα είαι 0 μοάδες
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 00 Επώυμο συοπτικές εδεικτικές λύσεις Όομα ΑΜ_( ψηφία) Ημ/ία Αίθουσα Α 4 Σύολο Η εξέταση αποτελείται από 4 Θέματα Κάθε θέμα αξίζει μοάδες Το άριστα είαι 0 μοάδες
Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ. Λυµένες Ασκήσεις
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5 σελ 9 Ασκήσεις : 3 4 8 9 σελ 98 Λυµέες Ασκήσεις Άσκηση 8 Να βρείτε τη ιδιάζουσα παραγοτοποίηση
Αάλυση Πιάκω και Εφαρµογές Σελίδα από Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5 σελ 9 Ασκήσεις : 3 4 8 9 σελ 98 Λυµέες Ασκήσεις Άσκηση 8 Να βρείτε τη ιδιάζουσα παραγοτοποίηση
Λύση. Λύση Άσκηση 3. Λύση. ( Α Α Α Ι ) Α. Α Α=Ιν. Άσκηση 4. επαληθεύει τη σχέση Χ. Λύση.
 Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
z = =5 ενώ z 1 z 2. (µε απόδειξη) z = z z I. z = z. z 1 z z όπου z 1 =x 1 +y 1 i και z 2 =x 2 +y 2 i σταθεροί z παριστάνει υπερβολή µε z 2
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ A =. Σύµφωνα µε την Πρόταση 5.7 (σελ. 119), η συµπληρωµατική (δυϊκή)
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
στους μιγαδικούς αριθμούς
 Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 ΚΕΦΑΛΑΙΟ ο. Τι οοµάζεται συάρτηση ; Είαι µια διαδικασία µε τη οποία κάθε στοιχείο εός συόλου Α ατιστοιχίζεται σε έα ακριβώς στοιχείο κάποιου άλλου συόλου Β.. Ποιες είαι οι κυριότερες γραφικές παραστάσεις
ΚΕΦΑΛΑΙΟ ο. Τι οοµάζεται συάρτηση ; Είαι µια διαδικασία µε τη οποία κάθε στοιχείο εός συόλου Α ατιστοιχίζεται σε έα ακριβώς στοιχείο κάποιου άλλου συόλου Β.. Ποιες είαι οι κυριότερες γραφικές παραστάσεις
είναι οι τιμές μιας μεταβλητής Χ, που αφορά τα άτομα ενός δείγματος μεγέθους v,. Συχνότητα (απόλυτη) νi
 ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός λέγεται έα σύολο που θέλουμε α εξετάσουμε τα στοιχεία του ως προς έα ή περισσότερα χαρακτηριστικά τους Μεταβλητές λέγοται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε
ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός λέγεται έα σύολο που θέλουμε α εξετάσουμε τα στοιχεία του ως προς έα ή περισσότερα χαρακτηριστικά τους Μεταβλητές λέγοται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε
x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ
![x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ](/thumbs/53/30835179.jpg) Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
xf(y) + yf(x) = (x + y)f(x)f(y)
 ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
Δυνάμεις πραγματικών αριθμών
 Κεφάλαιο 1 ο 45 Β. Δυάμεις πραγματικώ αριθμώ Α έχουμε έα γιόμεο της μορφής (-) (-) (-) (-) όπου κάθε παράγοτας είαι (δηλαδή ο ίδιος ο αριθμός) μπορούμε α το συμβολίσουμε με μια πιο απλή μορφή : (-) 4.
Κεφάλαιο 1 ο 45 Β. Δυάμεις πραγματικώ αριθμώ Α έχουμε έα γιόμεο της μορφής (-) (-) (-) (-) όπου κάθε παράγοτας είαι (δηλαδή ο ίδιος ο αριθμός) μπορούμε α το συμβολίσουμε με μια πιο απλή μορφή : (-) 4.
Δ/νση Β /θµιας Εκπ/σης Φλώρινας Κέντρο ΠΛΗ.ΝΕ.Τ. (Πρόοδοι) ΠΡΟΟΔΟΙ
 ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ AA A A
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
ΑΛΓΕΒΡΑ Α' ΛΥΚΕΙΟΥ. Η ΕΞΙΣΩΣΗ αx+β=0
 Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Σ
 ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Σ υ δ υ α σ τ ι κ ή Πειραιάς 7 Μάθημα 8ο ΣΥΝΔΥΑΣΤΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ Μ. Κούτρας Συδυαστική 7-8 8 Το διωυμικό θεώρημα μπορεί α αποτελέσει τη βάση για τη απόδειξη
ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Σ υ δ υ α σ τ ι κ ή Πειραιάς 7 Μάθημα 8ο ΣΥΝΔΥΑΣΤΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ Μ. Κούτρας Συδυαστική 7-8 8 Το διωυμικό θεώρημα μπορεί α αποτελέσει τη βάση για τη απόδειξη
εδάφιο 3, σελ. 181 υπερβολή ή παραβολή. Η ταξινόµηση αυτή παρουσιάζεται στον 1 ο πίνακα, T
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 9 ο ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 7, εδάφιο, σελ 75, εδάφιο 3, σελ 8 Ασκήσεις :,, 3, 4, 5, 6, 7, 8, σελ 75,, 4, 8, σελ 8, II, IV, σελ
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 9 ο ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 7, εδάφιο, σελ 75, εδάφιο 3, σελ 8 Ασκήσεις :,, 3, 4, 5, 6, 7, 8, σελ 75,, 4, 8, σελ 8, II, IV, σελ
Τι είναι εκτός ύλης. Σχολικό έτος
 Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών z για τους οποίους ισχύει:
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
4.3 ΔΙΑΙΡΕΤΟΤΗΤΑ. Εισαγωγή
 49 43 ΔΙΑΙΡΕΤΟΤΗΤΑ Εισαγωγή Στα Στοιχεία του Ευκλείδη, βιβλία VII, VIII και IX (περίπου 300 πχ), οι θετικοί ακέραιοι παριστάοται ως ευθύγραμμα τμήματα και η έοια της διαιρετότητας συδέεται άμεσα με τη
49 43 ΔΙΑΙΡΕΤΟΤΗΤΑ Εισαγωγή Στα Στοιχεία του Ευκλείδη, βιβλία VII, VIII και IX (περίπου 300 πχ), οι θετικοί ακέραιοι παριστάοται ως ευθύγραμμα τμήματα και η έοια της διαιρετότητας συδέεται άμεσα με τη
Κι όµως, τα Ρολόγια «κτυπούν» και Εξισώσεις: Η Άλγεβρα των εικτών του Ρολογιού
 Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
5.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C
 5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
www.fr-anodos.gr (, )
 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
78 Ερωτήσεις Θεωρίας Στα Μαθηματικά Γενικής Παιδείας
 Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
a lim x 1.7 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ ( x ) ΒΑΣΙΚΑ ΟΡΙΑ , a R * ΠΑΡΑΤΗΡΗΣΗ : Ενώ αν f(x) < g(x) κοντά στο x 0, τότε lim f(x) lim g(x)
 7 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ ( ) ΒΑΣΙΚΑ ΟΡΙΑ + - - a v α άρτιος α περιττός 0 ar * ΠΑΡΑΤΗΡΗΣΗ : Εώ α f() < g() κοτά στο 0 τότε f() g() ότα + εώ f()
7 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ ( ) ΒΑΣΙΚΑ ΟΡΙΑ + - - a v α άρτιος α περιττός 0 ar * ΠΑΡΑΤΗΡΗΣΗ : Εώ α f() < g() κοτά στο 0 τότε f() g() ότα + εώ f()
2.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
ΓΙΑ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΥΛΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Μαθηµατική Επαγωγή 175.
 Μαθηµατική Επαγωγή 75. Μαθηµατική Επαγωγή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Στο κεφάλαιο τω προόδω έχει αποδειχθεί ότι ο ισχυρισµός v( v+ ) P( v ):+ + 3 +... + v, v N είαι αληθής (ως άθροισµα
Μαθηµατική Επαγωγή 75. Μαθηµατική Επαγωγή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Στο κεφάλαιο τω προόδω έχει αποδειχθεί ότι ο ισχυρισµός v( v+ ) P( v ):+ + 3 +... + v, v N είαι αληθής (ως άθροισµα
f(x) < g(x) (α), f(x) g(x) (α ), f(x) > g(x) (β) και f(x) g(x) (β ) β β
 Σελίδα από ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Ατώης Κυριακόπουλος a_kiriak@otenetgr Η γεική έοια της αίσωσης Ορισµός Θεωρούµεα έα διατεταγµέο σώµα Σ, έα µη κεό σύολο Ω και δύο συαρτήσεις f :Α Σ και g :Β Σ µιας µεταβλητής
Σελίδα από ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Ατώης Κυριακόπουλος a_kiriak@otenetgr Η γεική έοια της αίσωσης Ορισµός Θεωρούµεα έα διατεταγµέο σώµα Σ, έα µη κεό σύολο Ω και δύο συαρτήσεις f :Α Σ και g :Β Σ µιας µεταβλητής
4. Δεσμευμένη Πιθανότητα - Ανεξαρτησία Ενδεχομένων
 Δεσμευμέη Πιθαότητα Αεξαρτησία Εδεχομέω 4 Δεσμευμέη Πιθαότητα - Αεξαρτησία Εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας Η πιθαότητα, ως έα μέτρο του βαθμού βεβαιότητας που έχουμε
Δεσμευμέη Πιθαότητα Αεξαρτησία Εδεχομέω 4 Δεσμευμέη Πιθαότητα - Αεξαρτησία Εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας Η πιθαότητα, ως έα μέτρο του βαθμού βεβαιότητας που έχουμε
ΑΠΑΝΤΗΣΕΙΣ. Επιµέλεια: Οµάδα Μαθηµατικών της Ώθησης
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Τετάρτη, 3 Μα ου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α Α. Α οι συαρτήσεις f, g είαι παραγωγίσιμες στο
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Τετάρτη, 3 Μα ου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α Α. Α οι συαρτήσεις f, g είαι παραγωγίσιμες στο
ΟΡΙΑ. 0 : Παραγοντοποιώ αριθµητή και παρονοµαστή και διώχνω τους παράγοντες x, x 0 που προκύπτουν.
 ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
ΜΑΘΗΜΑ Η έννοια του µιγαδικού αριθµού Πράξεις
 ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
(c f (x)) = c f (x), για κάθε x R
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
 ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου
ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
Γραµµική Αλγεβρα Ι. Ενότητα: Εισαγωγικές Εννοιες. Ευάγγελος Ράπτης. Τµήµα Μαθηµατικών
 Ενότητα: Εισαγωγικές Εννοιες Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα: Εισαγωγικές Εννοιες Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ. ΘΕΜΑ Ι ίνεται η συνεχής συνάρτηση f : R
 ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
Πανελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γενικης Παιδειας
 ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
c f(x) = c f (x), για κάθε x R
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
5 η ΕΚΑ Α ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 41.
 ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 5 η ΕΚΑ Α 4. Έστω Ω { ω, ω, ω, ω 4 } ο δειγµατικός χώρος εός πειράµατος τύχης και τα εδεχόµεα Α {ω, ω }, Β {ω, ω 4 } + Α είαι P(A B) και Ρ( Β Α ), όπου θετικός ακέραιος τότε + 4 Να αποδείξετε
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 5 η ΕΚΑ Α 4. Έστω Ω { ω, ω, ω, ω 4 } ο δειγµατικός χώρος εός πειράµατος τύχης και τα εδεχόµεα Α {ω, ω }, Β {ω, ω 4 } + Α είαι P(A B) και Ρ( Β Α ), όπου θετικός ακέραιος τότε + 4 Να αποδείξετε
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ. 1. Τι ονομάζουμε σύνολο Μιγαδικών Αριθμών; Τι ονομάζουμε πραγματικό μέρος - φανταστικό μέρος ενός μιγαδικού αριθμού z = α + βi.
 ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]
![ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β] ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]](/thumbs/20/426829.jpg) ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
Ευκλείδειοι Χώροι. Ορίζουµε ως R n, όπου n N, το σύνολο όλων διατεταµένων n -άδων πραγµατικών αριθµών ( x
 Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
 015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ( ) Να αποδείξετε ότι για κάθε θετικό ακέραιο ν ισχύει : ! + 2 2! + 3 3! + +ν ν! = (ν + 1)!
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να αποδείξετε ότι για κάθε θετικό ακέραιο ισχύει : 1 + 1 1! +! +! + +! = ( + 1)!. Να αποδείξτε ότι 6 10 [ ( 1) ] = ( + 1) ( + ) ( + ) (), για κάθε θετικό ακέραιο.. Να αποδείξετε ότι
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να αποδείξετε ότι για κάθε θετικό ακέραιο ισχύει : 1 + 1 1! +! +! + +! = ( + 1)!. Να αποδείξτε ότι 6 10 [ ( 1) ] = ( + 1) ( + ) ( + ) (), για κάθε θετικό ακέραιο.. Να αποδείξετε ότι
4.7 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ
 174 47 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ Το ζήτημα της διαιρετότητας τω αεραίω είαι υρίαρχο θέμα στη Θεωρία τω Αριθμώ Μια έοια που βοηθάει στη μελέτη αι επίλυση προβλημάτω διαιρετότητας είαι η έοια τω ισοϋπόλοιπω αριθμώ
174 47 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ Το ζήτημα της διαιρετότητας τω αεραίω είαι υρίαρχο θέμα στη Θεωρία τω Αριθμώ Μια έοια που βοηθάει στη μελέτη αι επίλυση προβλημάτω διαιρετότητας είαι η έοια τω ισοϋπόλοιπω αριθμώ
ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ. ορισµοί. Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 )
 ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ 1 ορισµοί Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 ) Γησίως αύξουσα: σε έα διάστηµα του πεδίου ορισµού της λέγεται µια συάρτηση f ότα για κάθε χ 1,χ 2 µε χ 1
ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ 1 ορισµοί Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 ) Γησίως αύξουσα: σε έα διάστηµα του πεδίου ορισµού της λέγεται µια συάρτηση f ότα για κάθε χ 1,χ 2 µε χ 1
Γραπτές ανακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις
 Γραπτές αακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις Δρ. Πααγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύμβουλος κλάδου ΠΕ03 www.p-theodoropoulos.gr Για το υπολογισμό του βαθμού της ετήσιας επίδοσης τω
Γραπτές αακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις Δρ. Πααγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύμβουλος κλάδου ΠΕ03 www.p-theodoropoulos.gr Για το υπολογισμό του βαθμού της ετήσιας επίδοσης τω
Α. Οι Πραγματικοί Αριθμοί
 ΠΑΡΑΡΤΗΜΑ Α Οι Πραγματικοί Αριθμοί Α1 Να τοποθετήσετε σε φθίουσα σειρά τους αριθμούς: 01 0 15, 0 15,, 01 5 5 A Να υπολογίσετε τη τιμή της παράστασης 4 1 A Να ρεθού το πηλίκο και το υπόλοιπο της διαίρεσης
ΠΑΡΑΡΤΗΜΑ Α Οι Πραγματικοί Αριθμοί Α1 Να τοποθετήσετε σε φθίουσα σειρά τους αριθμούς: 01 0 15, 0 15,, 01 5 5 A Να υπολογίσετε τη τιμή της παράστασης 4 1 A Να ρεθού το πηλίκο και το υπόλοιπο της διαίρεσης
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
Εκφωνήσεις Λύσεις των θεμάτων
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΜΙΓΑΔΙΚΟΙ 9o ΓΕΛ ΠΕΡΙΣΤΕΡΙΟΥ είναι τέλεια, να υπολογίσετε την τιμή της παράστασης: Α = (1 + i) v - (1 - i) v. 15. Αν z μιγαδικός και f (ν) = i
 Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο TEI
 Βασικές γώσεις Μαθηµατικώ Α και Β Λυκείου που πρέπει α ξέρουµε για α ξεκιήσουµε τις σπουδές µας στο TEI Επιµέλεια Όµηρος Κορακιαίτης Προσθήκες διορθώσεις: Θεολόγος Πααγιωτίδης Άλγεβρα και πράξεις: (ή το
Βασικές γώσεις Μαθηµατικώ Α και Β Λυκείου που πρέπει α ξέρουµε για α ξεκιήσουµε τις σπουδές µας στο TEI Επιµέλεια Όµηρος Κορακιαίτης Προσθήκες διορθώσεις: Θεολόγος Πααγιωτίδης Άλγεβρα και πράξεις: (ή το
Επαναληπτικό Διαγώνισμα Μαθηματικών Γενικής Παιδείας Γ Λυκείου
 Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)

 ΜΑΘΗΜΑΤΙΚΑ α x +β
ΜΑΘΗΜΑΤΙΚΑ α x +β