i) Να βρεθεί η ελάχιστη επιτρεπόµενη απόσταση των Α 1, Α 2, όταν το µήκος της ράβδου είναι L=20 L *.
|
|
|
- Ἀμβρόσιος Πρωτονοτάριος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Στην διάταξη του σχήµατος (1) η οµογενής λεπτή ράβδος ΑΒ έχει στε ρεωθεί στις άκρες Α 1, Α δύο κατακόρυφων ιδανικών ελατηρίων µε αντίστοιχες σταθερές k και 3k. Η ράβδος ισορροπεί οριζόντια όταν οι αποστάσεις των Α 1, Α από το µέσον Ο της ράβδου είναι ακέραια πολ λαπλάσια της µονάδας µήκους L * της ράβδου. i) Να βρεθεί η ελάχιστη επιτρεπόµενη απόσταση των Α 1, Α, όταν το µήκος της ράβδου είναι L= L *. ii) Με την βοήθεια µιας κατακόρυφης δύναµης που ενεργεί στο Ο επί πολύ µικρό χρονικό διάστηµα, δίνουµε στην ράβδο ταχύτητα προς τα κάτω µέτρου gx, όπου g η επιτάχυνση της βαρύτητας και x η συσ πείρωση των δύο ελατηρίων από την φυσική τους κατάσταση, όταν η ράβδος ισορροπεί. Να εκφράσετε σε συνάρτηση µε τον χρόνο την τα χύτητα µεταβολής της κινητικής ενέργειας της ράβδου και να δώσετε την γραφική παράσταση της σχέσεως που θα βρείτε. iii) Εάν η βαρυτική δυναµική ενέργεια της ράβδου µετράται µε επίπε δο αναφοράς την αρχική της θέση, να δείξετε ότι κάθε στιγµή η δυνα µική ενέργεια ταλάντωσης U ταλ. της ράβδου και η δυναµική ενέργεια U συστ. του συστήµατος ράβδος-ελατήρια, συνδέονται µε την σχέση: U "#. = U #$%. + kx ΛΥΣΗ: i) Ας δεχθούµε ότι η απόσταση των δύο κατακόρυφων ελατηρίων έχει κατάλληλη τιµή που εξασφαλίζει την ισορροπία της ράβδου σε οριζόντια θέση. Στην θέση αυτή η ράβδος δέχεται το βάρος της w και τις δυνάµεις F 1,, F, από τα συµπιεσµένα ελατήρια σταθερών k και 3k αντιστοίχως. Λόγω της ισορ ροπίας της ράβδου η συνισταµένη των ροπών των δυνάµεων αυτών περί το κεν τρο µάζας Ο της ράβδου είναι µηδέν, δηλαδή ισχύει: " (O) = F 1, ( A 1 O) - F, ( A O) = kx ( 1 L * ) - 3kx ( L * ) = 1-3 = 1 / = 3/1 (1)
2 όπου ρ 1, ρ θετικοί ακέραιοι αριθµοί, καθόσον τα µήκη Α 1 Ο και Α Ο είναι ακέ ραια πολλαπλάσια της µονάδας µήκους L * της ράβδου. Επειδή το κλάσµα 3/1 είναι ανάγωγο, από την (1) προκύπτει ότι οι πιο µικρές τιµές που µπορούν να πάρουν οι ακέραιοι ρ 1, ρ είναι 3 και 1 αντιστοίχως, οπότε: Άρα ( A 1 O) min = 3L * και ( A O) min = L * ( A 1 O) min + ( A O) min = 4L * ( A 1 A ) min = 4L * = 4L/ = L/5 () Σχήµα 1 ii) Επειδή η κατακόρυφη δύναµη ενεργεί στο κέντρο µάζας της ράβδου, αυτή δεν περιστρέφεται περί το Ο αλλά εκτελεί µεταφορική κίνηση παραµένουσα συνεχώς οριζόντια. Εξετάζοντας την ράβδο κάποια τυχαία στιγµή που η απο µάκρυνσή της από την θέση ισορροπίας της είναι x, παρατηρούµε ότι η ράβδος δέχεται το βάρος της w και τις κατακόρυφες δύναµεις F 1, F από τα παραµορ Σχήµα φωµένα ελατήρια. Αν δεχθούµε ως θετική φορά επί της κατακόρυφης διεύ θυνσης την προς τα κάτω, τότε η αλγεβρική τιµή της συνισταµένης δύναµης επί της ράβδου είναι: F (x) = mg - F 1 - F = mg - ( F 1, + 3kx) - ( F, + kx) F (x) = mg - F 1, - F, - 4kx = -4kx (3)
3 H σχέση (3) εγγυάται ότι η µεταφορική κίνηση της ράβδου είναι απλή αρµονική ταλάντωση µε σταθερά ταλάντωσης 4k, που σηµαίνει ότι η γωνιακή συχνότητα ω της ράβδου θα ικανοποιεί την σχέση: 4k = m 4gk = mg 4gk = ( 3kx + kx ) 4gk = 4kx = g/x (4) Επειδή κατά την έναρξη της ταλάντωσης της ράβδου (t=) η αποµάκρυνσή της από την θέση ισορροπίας της είναι x= και η ταχύτητά της είναι θετική, η εξίσωση κίνησης της ράβδου έχει την µορφή: x = Aµ"t (5) Όµως το πλάτος Α της ταλάντωσης σχετίζεται µε την µέγιστη ταχύτητα gx της ράβδου µέσω της σχέσεως: (4) gx = A gx = A g/x A = x οπότε η (5) γράφεται: " x = x µ $ # g % t x ' (6) & Εξάλλου η εξίσωση της ταχύτητας της ράβδου έχει την µορφή: % v = x "#$' & g ( g % t x * = x "#$ ) x ' & g ( t x * ) v = $ x g"# & % g ' t x ) (7) ( Aκόµη εάν dk είναι η µεταβολή της κινητικής ενέργειας της ράβδου µεταξύ των χρονικών στιγµών t και t+dt και dx η αντίστοιχη µετατόπισή της, θα έχουµε µε βάση το θεώρηµα κινητικής ενέργειας-έργου την σχέση: (3) dk = F (x) dx dk = -4kxdx dk dt (6),(7) dx = -4kx dt = -4kxv dk dt = -4kx " µ $ # g % " t x ' x g ()* $ & # g % t x ' &
4 dk dt = -kx " x gµ g % $ t # x ' (8) & όπου dk/dt η ταχύτητα µεταβολής της κινητικής ενέργειας της ράβδου κατά την τυχαία χρονική στιγµή t. H γραφική παράτσαση της (8) είναι η ηµιτονο ειδής καµπύλη του σχήµατος (3). Σχήµα 3 iii) Χωρίς να βλάπτει την γενικότητα δεχόµαστε ότι κάποια στιγµή t η ράβδος βρίσκεται κάτω από την θέση ισορροπίας της σε απόσταση x από αυτήν. Η δυνα µική ενέργεια U συστ. του συστήµατος ράβδος-ελατήρια είναι: U "#. = 3k ( x + x ) + k ( x + x ) - mgx U "#. = k( x + x) - ( 3kx + kx )x U "#. = k( x + x $µ%t) - 4kx x $µ%t U "#. = kx ( 1 + $µ%t) - 4kx $µ%t U "#. = kx ( 1 + $µ %t + $µ%t - $µ%t) U "#. = kx + kx $µ %t (9) Την ίδια στιγµή η δυναµική ενέργεια ταλάντωσης U ταλ. της ράβδου είναι: U "#. = 4k x = kx $µ %t (1) Συνδυάζοντας τις σχέσεις (9) και (1) παίρνουµε την αποδεικτέα σχέση:
5 U "#. = U #$%. + kx P.M. fysikos Ένα µικρό σφαιρίδιο µάζας m, µπορεί να ολισθαίνει χωρίς τριβή κατα µήκος ενός ευθύγραµµου σωλήνα που είναι στερεώµενος σε οριζόν τιο επίπεδο. Το σφαιρίδιο έλκεται από σταθερό κέντρο Ο, που βρίσκε ται εκτός σωλήνος σε απόσταση α από αυτόν, µε δύναµη F της οποί ας το µέτρο περιγράφεται από την σχέση F = kr, όπου k θετική σταθε ρή ποσότητα και r η απόσταση του σφαιριδίου από το ελκτικό κέντρο Ο. Την στιγµή t= το σφαιρίδιο αφήνεται σε σηµείο Μ του σωλήνα που απέχει από το Ο απόσταση 5. i) Να βρείτε την ταχύτητα του σφαιριδίου όταν για πρώτη φορά η από στασή του από το Ο γίνεται ίση µε α, καθώς και τον αντίστοιχο χρόνο κινήσεώς του. ii) Εάν µεταξύ του σφαιριδίου και των τοιχωµάτων του σωλήνα υπάρχει τριβή µε συντελεστή τριβής ολισθήσεως n=1, να δείξετε ότι το σφαιρίδιο δεν µπορεί να υπερβεί το σηµείο Ο του σωλήνα που βρίσκε ται εγγύτερα προς το ελκτικό κέντρο Ο. Να αγνοήσετε το βαρυτικό πεδίο της Γης, ΛΥΣΗ: i) Κάθε στιγµή t η θέση Μ του σφαιριδίου καθορίζεται από το διάνυσ µα x που έχει αρχή την προβολή Ο του ελκτικού κέντρου Ο στην διεύθυνση του σωλήνα και πέρας το σφαιρίδιο. Το σφαιρίδιο δέχεται την δύναµη F από το ελκτικό κέντρο Ο, η οποία αναλύεται στην κάθετη προς τον σωλήνα συνιστώσα F y και στην συγραµµική προς τον σωλήνα συνιστώσα F x. Η F y εξουδετερώνε ται από την κάθετη αντίδραση N των τοιχωµάτων του σωλήνα, οπότε η F x απο Σχήµα 4 τελεί την συνισταµένη δύναµη που δέχεται το σφαιρίδιο (σχ. 4). Θεωρώντας ως θετική φορά στην διεύθυνση x x του σωλήνος την φορά του διανύσµατος O M θα έχουµε για το σφαίριδιο, συµφωνα µε τον δεύτερο νόµο κίνησης του Νεύτωνα την σχέση:
6 F (x) = -F x = -F"µ# F (x) = -kr"µ# = -kx (1) Η σχέση (1) εγγυάται ότι το σφαιρίδιο εκτελεί απλή αρµονική ταλάντση µε κέν τρο ταλάντωσης το Ο και σταθερά ταλάντωσης k. H γωνιακή συχνότητα ω της ταλάντωσης ικανοποιεί την σχέση: k = m = k/m () Eάν Τ * είναι η περίοδος ταλάντωσης του σφαιριδίου, τότε ο χρόνος t κίνησής του από την αρχική του θέση Μ µεχρι την εγγύτερη προς το Ο θέση του Ο είναι ίσος µε Τ * /4, δηλαδή ισχύει: t = T * 4 = 4" () t = m k (3) Eξάλλου το µέτρο της ταχύτητας του σφαιριδίου στην θέση Ο είναι: v = ( O " M ) = ( OM ) - ( O " O) v = ( 5" ) - " = " k m (4) ii) Όταν µεταξύ του σφαιριδίου και των τοιχωµάτων υπάρχει τριβή, τότε η εκ κίνηση του σφαιρίδιου είναι δυνατή εφ όσον το µέτρο της συνιστώσας F x στην αρχική του θέση Μ υπερβαίνει το µέτρο της τριβής ολισθήσεως T. Όµως έχου µε: T= nn = nf y = nf"#$ T= kr"#$ = k% (5) και F x O M ( ) M = k ( ) = k" (6) Σχήµα 5 Από (5) και (6) προκύπτει ότι ( F x ) M > T, που σηµαίνει ότι το σφαιρίδιο θα εκκι νήσει όταν αφεθεί ελεύθερο στο Μ. Είναι σηµαντικό να παρατηρήσουµε ότι κατα την κίνηση του σφαιριδίου η δύναµη F x προσοµοιάζει µε την δύναµη που θα δεχόταν το σφαιρίδιο από ιδανικό ελατήριο σταθεράς k και περίπου µηδενικού φυσικού µήκους, που το ένα του άκρο είναι στερεωµένο στο Ο και το άλλο του άκρο προσδε δεµένο στο σφαιρίδιο. Αυτό σηµαίνει ότι µπορούµε να αποδώσουµε στο σφαιρίδιο δυναµική ενέργεια που απορρέει από την δύναµη F x η οποία
7 εκφράζεται µέσω της σχέσεως U=kx /. Ας δεχθούµε τώρα ότι το σφαιρίδιο φθάνει στο Ο µε ταχύτητα v *. Εφαρµόζοντας για την κίνηση του σφαιριδίου το θεώρηµα µηχανικής ενέργειας-έργου κατά την κινησή του από την αρχική του θέση Μ στην θέση Ο παίρνουµε: U + K = W T - k ( ) + mv * - k ( O M ) + mv * ( ) - = -T O M = -nn -k + mv * / = -(k) mv * / = k - k = v * = Δηλαδή το σφαιρίδιο δεν µπορεί να υπερβεί το σηµείο Ο του σωλήνα. P.M. fysikos Ένας τροχός, µάζας m ακτίνας R και ακτίνας αδράνειας Κ, ακινητεί επί οριζοντίου εδάφους όπως φαίνεται στο σχήµα (1). Στην περιφέ ρεια του τροχού έχει περιτυλιχθεί λεπτό και µη εκτατό νήµα στο ελεύ θερο άκρο του οποίου εφαρµόζεται η οριζόντια δύναµη F. i) Είναι δυνατόν ο τροχός να κυλίεται πάνω στο οριζόντιο έδαφος, εάν αυτό είναι λείο; ii) Εάν ο τροχός έχει την µορφή τροχαλίας (K =R /) και ο συντελε στής οριακής τριβής µεταξύ εδάφους και τροχαλίας είναι n=1/, να βρεθεί η µέγιστη επιτρεπόµενη τιµή του µέτρου της F, ώστε η τροχα λία να κυλίεται. iii) Εάν F=mg/ να βρεθεί η ταχύτητα του κέντρου µάζας της τρο χαλίας, όταν έχει ξετυλιχθεί νήµα µήκους L. Πόση γίνεται η ταχύτη τα αυτή, αν F=3mg; Δίνεται η επιτάχυνση g της βαρύτητας. ΛΥΣΗ: i) Εάν το οριζόντιο έδαφος είναι λείο, τότε η αντίδραση N του εδάφους επί του τροχού είναι κατακόρυφη µε φορά προς τα πάνω και ο φορέας της διέρχεται από το κέντρο του τροχού. Επειδή η δύναµη F έχει ροπή περί τον άξονα που διέρχεται από το κέντρο C του τροχού και είναι κάθετος στο επίπεδό του, ο τροχός θ αποκτήσει περιστροφική κίνηση περί τον άξονα αυτόν, µε γωνιακή επιτάχυνση ' για την οποία ισχύει ο θεµελιώδης νόµος της στρο φικής κίνησης, δηλαδη ισχύει: FR = I C ' FR = mk ' '= FR/mK (1)
8 Όµως ο τροχός έχει και µεταφορική κίνηση, λόγω της οποίας ο άξονας περισ τροφής του µετατοπίζεται οριζόντια, η δε επιτάχυνσή του a C συµφωνα µε τον δεύτερο νόµο κίνησης του Νευτωνα ικανοποιεί την σχέση: F = ma C a C = F/m () Για να κυλίεται ο τροχός πρέπει το σηµείο επαφής Α µε το έδαφος να έχει µηδενική επιτρόχια επιτάχυνση, δηλαδή πρέπει: (1),() a C - 'R = a C = 'R F m = FR mk K = R (3) που σηµαίνει ότι ο τροχός πρέπει να έχει τη µορφή λεπτής στεφάνης. ii) Εάν ο τροχός έχει την µορφή τροχαλίας (K =R /) τότε είναι αδύνατη η κύλισή του, όταν το έδαφος είναι λείο, είναι όµως δυνατή όταν υπάρχει τριβή µεταξύ τροχού και εδάφους, µε την πρoυπόθεση ότι η F δεσµεύεται, ώστε η τριβή αυτή να είναι στατική. Ας δεχθούµε ότι η τριβή T έχει την ίδια φορά µε Σχήµα 6 την F και ότι το µέτρο της είναι τέτοιο, ώστε η τροχαλία να κυλίεται. Τότε για την µεταφορική κίνηση της τροχαλίας θα ισχύει, συµφωνα µε τον δεύτερο νόµο κίνησης του Νεύτωνα η σχέση: F + T = ma C (4) όπου a C η επιτάχυνση του κέντρου µάζας της τροχαλίας. Εφαρµόζοντας εξάλ λου για την περιστροφική κίνηση της τροχαλίας τον θεµελιώδη νόµο της στροφικής κίνησης παίρνουµε την σχέση: (F - T)R = I C ' (F - T)R = mr '/ F - T = mr'/ F - T = ma C / (5) όπου ' η γωνιακή επιτάχυνση της τροχαλίας. Διαιρώντας κατά µέλη τις σχέσεις (4) και (5) έχουµε: F + T F - T = F + T = F - T T = F/3 (6) Όµως η T είναι στατική τριβή, οπότε το µέτρο της ικανοποιεί την σχέση:
9 (6) T nn T nmg F/3 nmg F 3nmg F max = 3mg/ (7) iii) Εάν F=mg/, τότε η τροχαλία θα κυλίεται, διότι ικανοποιείται η (7), το δε κέντρο της θα έχει επιτάχυνση a C, της οποίας το µέτρο υπολογίζεται από την σχέση: F + F / 3 = ma C 4F / 3 = ma C mg / 3 = ma C a C = 3g/ Εφαρµόζοντας για την τροχαλία το θεώρηµα κινητικής ενέργειας-έργου κατά τον χρόνο που απαιτείται να ξετυλιχθεί νήµα µήκους L, παίρνουµε: mv C + I = FL mv C + mr 4 = FL 3mv C 4 = mgl v C = gl 3 v C = gl 3 όπου v C η ζητούµενη ταχύτητα του κέντρου µάζας της τροχαλίας και η γωνιακή της ταχύτητα. Εάν F= 3mg, τότε η τροχαλία δεν κυλίεται, διότι δεν ικανοποιείται η (7), που σηµαίνει ότι η τριβή T είναι τριβή ολίσθησης και το µέτρο της είναι: T = nn = nmg = mg/ Σύµφωνα µε τον δεύτερο νόµο κίνησης του Νεύτωνα θα ισχύει: F + T = ma C 3mg + mg/ = ma C a C = 5g/ Εξάλλου, σύµφωνα µε τον θεµελιώδη νόµο της στροφικής κίνησης έχουµε: (F - T)R = I C ' 3mgR - mgr/ = mr '/ 5g/ = 'R '= 5g/R Η επιτρόχια επιτάχυνση του σηµείου Β της τροχαλίας έχει µέτρο: a B = a C + 'R = 5g/ + 5g/ = 5g Eάν t * είναι ο χρόνος για να ξετυλιχθεί νήµα µήκους L, θα ισχύει: L = a B t * / = 5gt * / L/5g = t * t * = L/5g Η ταχύτητα v C του κέντρου της τροχαλίας την χρονική στιγµή t * είναι: (8)
10 v C = a C t * = 5g L 5g = 5gL P.M. fysikos Ένα µικρό σώµα µάζας m, κρατείται σε επαφή µε κατακόρυφο τοίχο µε την βοήθεια µιας δύναµης της οποίας ο φορέας σχηµατίζει γωνία φ µε την οριζόντια διεύθυνση. Να βρείτε για ποια τιµή του µέτρου της δύναµης επίκειται η ολίσθη ση του σώµατος επί του τοίχου. Nα διερευνήσετε τι συµβαίνει, όταν η γωνία φ µεταβάλλεται. Δίνεται ο συντελεστής οριακής τριβής n µεταξύ του σώµατος και του τοίχου και η επιτάχυνση g της βαρύτητας. ΛΥΣΗ: α) Θα εξετάσουµε αρχικά την περίπτωση που το σώµα ισορροπεί µε τάση να ολισθήσει προς τα πάνω. Τότε η τριβή που δέχεται από τον τοίχο έχει φορά προς τα κάτω και για να συγκρατείται το σώµα επί του τοίχου πρέπει αναγκαστικά η δύναµη F να κατευθύνεται όπως στο σχήµα (7). Το σώµα εκτός από την δύναµη F δέχεται το βάρος του m g και την δύναµη επαφής από τον τοίχο που αναλύεται στην κάθετη αντίδραση N και στην στατική τριβή T. Λό γω της ισορροπίας του σώµατος ισχύουν οι σχέσεις: Σχήµα 7 και F (x) = F x - N = N = F"#$ (1) F (y) = F y - mg - T = T = Fµ" - mg ()
11 όπου F x, F y η οριζόντια και η κατακόρυφη συνιστώσα αντιστοίχως της F. Όταν επίκειται η ολίσθηση του σώµατος η τριβή είναι ίση µε την οριακή στα τική τριβή, δηλαδή το µέτρο της γίνεται ίσο µε nn και η σχέση () γράφεται: (1) nn = Fµ" - mg nf"#$ = F%µ$ - mg Fµ" - nf#$%" = mg F = mg µ" - n#$%" (3) Θέτοντας n=εφφ η (3) γράφεται: F = mg µ" - #$" %&'" = mg µ" - µ" %&'" /%&'" F = mg"#$ %µ$"#$ - %µ$ "#$"#$ = mg"#$ %µ $ - $ ( ) (4) Η σχέση (4) έχει νόηµα για φ>φ, ενώ η τιµή φ=φ είναι µη επιτρεπτή διότι οδηγεί σε απειρισµό του µέτρου της F. β) Αν το σώµα ισορροπεί µε τάση να ολισθήσει προς τα κάτω, τότε η τριβή κα τευθύνεται προς τα πάνω και η συγκράτηση του σώµατος επί του τοίχου επιτυγχάνεται ή όταν η δύναµη είναι οριζόντια ή όταν κατευθύνεται όπως στο σχήµα (8). Στην περίπτωση αυτή θα έχουµε τις σχέσεις: Σχήµα 8 και F (x) = F x - N = N = F"#$ (5) F (y) = - F y - mg + T = T = Fµ" + mg (6) Όταν επίκειται η ολίσθηση του σώµατος είναι Τ=nN και η (6) γράφεται: (5) nn = Fµ" + mg nf"#$ = F%µ$ + mg
12 nf"#$ - F%µ$ = mg F = mg n"#$ - %µ$ (7) Θέτοντας πάλι n=εφφ η (7) γράφεται: F = mg "# $%&# - 'µ# = mg 'µ# $%&# /$%&# - 'µ# F = mg"#$ = mg"#$ %µ$ "#$ - %µ$"#$ %µ $ - $ ( ) (8) Η σχέση (8) έχει νόηµα για,φ<φ ενώ η τιµή φ=φ οδηγεί πάλι σε απειρισµό του µέτρου της F. Παρατήρηση: Mπορούµε να παρακάµψουµε τους πολλαπλούς υπολογισµούς κάνοντας χρήση της έννοιας του κώνου τριβής και της γωνίας τριβής. Στην περίπτωση που το σώµα ισορροπεί οριακά τεινοντας να ολισθήσει προς τα πάνω η αντίδραση R του τοίχου κατευθύνεται όπως φαίνεται στο σχήµα (9) ο δε φορέας της βρίσκε Σχήµα 9 ται στην παράπλευρη επιφάνεια του κώνου τριβής, που σηµαίνει ότι σχηµατίζει µε την οριζόντια διεύθυνση γωνία ίση µε την γωνία τριβής φ (εφφ =n). Εξάλ λου πρέπει η συνισταµένη του βάρους του σώµατος και της δύναµης F που το ακινητοποιεί επί του τοίχου να είναι αντίθετη της R και το γεγονός αυτό µας επιτρέπει χρησιµοποιώντας το διαγραµµισµένο δυναµοτρίγωνο να γράψου µε τις σχέσεις: mg µ (" - " ) = F µ # / - " ( ) F = mg"#$ %µ $ - $ ( ) Εξετάζοντας µε το ίδιο σκεπτικό την περίπτωση που το σώµα ισορροπεί οριακά τεινοντας να ολισθήσει προς τα πάνω παρατηρούµε ότι τώρα η αντίδραση R του τοιχου κατευθύνεται όπως φαίνεται στο σχήµα (1) ο δε φορέας της βρίσκε ται πάλι στην παράπλευρη επιφάνεια του κώνου τριβής, που σηµαίνει ότι σχη
13 µατίζει µε την οριζόντια διεύθυνση γωνία ίση µε την γωνία τριβής φ (εφφ =n). Εξάλλου η συνισταµένη του βάρους m g και της δύναµης F είναι αντίθετη Σχήµα 1 της R και αυτό µας επιτρέπει χρησιµοποιώντας το διαγραµµισµένο δυναµο τρίγωνο να γράψουµε τις σχέσεις: mg µ (" - " ) = F µ # / - " ( ) F = mg"#$ %µ $ - $ ( ) Δηλαδή καταλήξαµε στο ίδιο συµπέρασµα για το µέτρο της δύναµης F, αλλά συντοµότερα. P.M. fysikos Στην περιφέρεια λεπτoύ δίσκου µάζας m και ακτίνας R έχει τυλιχ θεί αβαρές νήµα και ο δίσκος αφήνεται να κινηθεί κατά µήκος λείου κεκλιµένου επιπέδου γωνίας κλίσεως φ ως προς τον ορίζον τα. Το ένα άκρο του νήµατος είναι στερεωµένο στην κορυφή του κεκλιµένου επιπέδου (σχ. 11), µε αποτέλεσµα να ξετυλίγεται καθώς ο δίσκος µετα τοπίζεται προς τα κάτω. Να βρείτε: i) τον ρυθµό µεταβολής της στροφορµής του δίσκου, περί το κέντρο του και ii) τον ρυθµό µεταβολής της κινητικής του ενέργειας. Δίνεται η ροπή αδράνειας I C =mr / του δίσκου ως προς άξονα κά θετο στο επίπεδό του και διερχόµενο από το κέντρο του και η επι τάχυνση g της βαρύτητας. ΛΥΣΗ: i) Επί του δίσκου ενεργεί το βάρος του w, που αναλύεται στην παράλληλη προς το κεκλιµένο επίπεδο συνιστώσα w 1 και στην κάθετη προς
14 αυτό συνιστώσα w, η κάθετη αντίδραση N του λείου κεκλιµένου επιπέδου και η τάση T του νήµατος. Λόγω της ροπής που εµφανίζει η T περί τον άξονα που διέρχεται από το κέντρο µάζας C του δίσκου και είναι κάθετος στο επίπεδό του, ο δίσκος αποκτά περιστροφική κίνηση περί τον άξονα αυτόν µε γωνιακή επιτάχυνση ', η οποία σύµφωνα µε τον θεµελιώδη νόµο της στροφικής κίνησης ικανοποιεί την σχέση: TR= I C ' TR= mr '/ T= mr'/ (1) Σχήµα 11 Όµως ο δίσκος εκτελεί και µεταφορική κίνηση, µε αποτέλεσµα το κέντρο του C να έχει επιτάχυνση a C, η οποία σύµφωνα µε τον δεύτερο νόµο κίνησης του Νεύτωνα ικανοποιεί την σχέση: w 1 - T = ma C mgµ" - T = ma C () Eπειδή το σηµείο επαφής Α του δίσκου µε το κεκλιµένο επίπεδο έχει µηδενι κή ταχύτητα (το νήµα είναι ακίνητο) θα ισχύει: v A = v C - R = v C = R όπου v C η ταχύτητα του κέντρου του δίσκου κατά την στιγµή που τον εξετά ζουµε. Αν µεταξύ των χρονικών στιγµών t και t+dt το µέτρο της ταχύτητας v C µεταβάλλεται κατά dv C και το µέτρο της κατά dω, τοτε από την προηγού µενη σχέση προκύπτει: dv C = Rd dv C /dt = Rd / dt a C = R' (3) oπότε η σχέση (1) γράφεται: T= ma C / (4) Συνδυάζοντας τις σχέσεις () και (3) παίρνουµε: mgµ" - ma C / = ma C mgµ" = 3ma C / a C = gµ" /3 (5) Άρα το µέτρο της T είναι:
15 T = m gµ" 3 = mgµ" 3 (6) Εφαρµόζοντας για τον δίσκο τον νόµο µεταβολής της στροφορµής κατά την χρο νική στιγµή t, παίρνουµε την σχέση: d L dt = TR k d L dt = mgrµ" 3 k (7) όπου k το µοναδιαίο κάθετο διάνυσµα στην επιφάνεια του δίσκου, του οποί ου η φορά ελήφθη συµβατικά ίδια µε τη φορά της γωνιακής του ταχυτητας (σχ. 11) και d L /dt ο ζητούµενος ρυθµός µεταβολής της στροφορµής του δίσκου. ii) Στην διάρκεια που ο δίσκος κινείται, η µηχανική του ενέργεια παραµένει σταθερή, αφού δεν υπάρχει τριβή µεταξύ αυτού και του κεκλιµένου επιπέδου. Έτσι, αν µεταξύ των χρονικών στιγµών t και t+dt η κινητική και η βαρυτική δυναµίκη ενέργεια του δίσκου µεταβάλλονται κατά dk και du αντιστοίχως, θα ισχύει η σχέση: dk + du = dk dt + du dt = dk dt = - du dt (8) Όµως για την µεταβολή du έχουµε: du = -mgµ"ds du dt = -mgµ" ds dt du dt = -mgv C µ" (9) όπου ds η µετατόπιση του κέντρου του δίσκου στον χρόνο dt και du/dt ο ρυθµός µεταβολής της βαρυτικής δυναµικής ενέργειας του δίσκου κατά την χρονική στιγµή t. Συνδυάζοντας εξάλλου τις σχέσεις (8) και (9) παίρνουµε: dk dt = mgv C µ" (1) όπου dk/dt ο αντίστοιχος ρυθµός µεταβολής της κινητικής ενέργειας του δίσκου. Όµως παρατηρούµε από την (5) ότι η µεταφορική κίνηση του δίσκου είναι οµαλά επιταχυνόµενη, αφού η a C είναι σταθερή, οπότε ισχύει v C =a C t και η προηγούµενη σχέση (9) γράφεται: dk dt = mga C tµ" (5) dk dt = mg # % $ 3 gµ" & ( tµ" = ' 3 mg tµ " P.M. fysikos
16 Μια σφαίρα µάζας m και ακτίνας R ηρεµεί επί οριζοντίου εδάφους και κάποια στιγµή προσπίπτει πάνω της µε ταχύτητα v ξύλινος κύ βος ακµής R. Η κρούση του κύβου µε την σφαίρα είναι µετωπική και τελείως ελαστική, ο συντελεστής τριβής ολίσθησης µεταξύ του εδάφους και των δύο σωµάτων είναι n και η επιτάχυνση της βαρύ τητας g. Να βρείτε: i) την θερµότητα που ελευθερώνεται εξ αιτίας της τριβής και ii) την µορφή του διαγράµµατος της απόστασης κύβου-σφαίρας σε συνάρτηση µε τον χρόνο. Δίνεται η ροπή αδράνειας Ι=mR /5 της σφαίρας ως προς άξονα που διέρχεται από το κέντρο της. ΛΥΣΗ: i) Eπειδή η σφαίρα και ο κύβος έχουν την ίδια µάζα και η κρούση τους είναι µετωπική και τελείως ελαστική, συµβαίνει ανταλλαγή των ταχύτη των των κέντρων µάζας τους, δηλαδή αµέσως µετά την κρούση µηδενίζεται η ταχύτητα του κύβου, ενώ η σφαίρα αποκτά µεταφορική ταχύτητα v. Επί της σφαίρας ενεργεί το βάρος της w και η δύναµη από το οριζόντιο έδαφος, η οποία αναλύεται στην τριβή ολισθήσεως T και στην κάθετη αντίδραση N. H τριβή T επιβραδύνει την µεταφορική κίνηση της σφαίρας, ενώ προκαλεί δεξιόστροφη περιστροφική κίνηση αυτής περί οριζόντιο άξονα που διέρχεται από το κέντρο µάζας της C. Εφαρµόζοντας για την µεταφορική κίνηση τον δεύτερο νόµο του Νεύτωνα και για την περιστροφική της κίνηση τον θεµελιώδη νόµο της στροφι κής κίνησης, παίρνουµε τις σχέσεις: T = ma C " # TR = I' $ nmg = ma " C # nmgr = mr '/$ a = ng " C # '= 5ng/R $ (1) Σχήµα 1 όπου a C η επιτάχυνση του κέντρου µάζας C της σφαίρας και ' η γωνιακή της επιτάχυνση. Το σηµείο επαφής Α της σφαίρας µε το οριζόντιο έδαφος θα έχει την χρονική στιγµή t, λόγω της µεταφορικής κίνησης της σφαίρας ταχύτητα (µ v ) A οµόρροπη της v, µε µέτρο: (1) (µ v ) A = v - a C t v A (µ ) = v - ngt ()
17 Όµως την ίδια στιγµή το σηµείο Α θα έχει λόγω της περιστροφής της σφαίρας ταχύτητα v ( ) A αντίρροπη της v, µε µέτρο: (1) ( v ) A = "R = "'Rt v A ( ) = 5ngt/ (3) όπου η αντίστοιχη γωνιακή ταχύτητα της σφαίρας. Παρατηρούµε από τις σχέσεις () και (3) ότι υπάρχει χρονική στιγµή t * για την οποία ισχύει v (µ) A =v (π) Α, που σηµαίνει ότι την στιγµή αυτή µηδενίζεται η ταχύτητα του σηµείου Α ως προς το ακίνητο έδαφος, δηλαδή τη στιγµή αυτή µηδενίζεται η τριβή T αφού η σφαίρα δεν παρουσιάζει πλέον τάση προς ολίσθηση. Έτσι από τη στιγµή t * και µετά η σφαίρα θα κυλίεται ισοταχώς επί του εδάφους µε µεταφορική ταχύτητα v *, της οποίας το µέτρο δίνεται από την σχέση: v * = 5ngt * / (4) Εξάλλου ο χρόνος t * θα υπολογιστεί από την σχέση: v A (µ ) = v A ( ) (1),(3) v - ngt * = 5ngt * / v - ngt * = 5ngt * t * = v /7ng (5) Συνδυάζοντας τις σχέσεις (4) και (5) παίρνουµε: v * = 5ng v 7ng = 5v 7 (6) Κατά τον χρόνο t * ελευθερώνεται λόγω τριβής θερµότητα Q, η οποία σύµφω να µε την αρχή διατήρησης της ενέργειας θα ικανοποιεί την σχέση: K "# = K $%& + Q Q = K "# - K $%& (7) όπου Κ αρχ, Κ τελ η αρχική και η τελική κινητική ενέργεια της σφαίρας. Όµως ισχύουν και οι σχέσεις: K "# = mv και K "# = mv * + I$ * K "# = mv * + 5mR v * = 7mv * R 4 (6) K "# = 7m 4 $ & % v 7 ' ) ( = mv 7 οπότε η (7) γράφεται: Q = mv - mv 7 = 5mv 7 ii) Στο χρονικό διάστηµα [, t * ] η απόσταση S των κέντρων του κύβου και της σφαίρας µεταβάλλεται µε τον χρόνο t σύµφωνα µε την σχέση:
18 S = v t- a C t / = v t - ngt / Για t t * η απόσταση αυτή δίνεται από την σχέση: S = S * + v * (t - t * ) = v t * - ngt * / + v * (t - t * ) (5),(6) S = (v - v * )t * - ngt * / + v * t S = v 49ng + 5v 7 t = v 49 v # " ng + 35t $ & (8) % Σχήµα 13 Mε βάση τα παραπάνω η σχέση S=f(t) που δίνει την απόσταση S σε συνάρτη ση µε τον χρόνο t έχει την µορφή: ) v t- a C t, t v + 7ng S = * v " v 49 $ # ng + 35t % + ' &, t ( v, + 7ng η δε γραφική της παράσταση φαίνεται στο σχήµα (13). P.M. fysikos Οµογενής κύλινδρος µάζας m και ακτίνας R εφάπτεται µε την παρά πλευρη επιφάνεία του σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Με την βοήθεια επίπεδου εµποδίου (ε), το οποίο εφάπτεται του κυλίνδρου, εξασκούµε σ αυτόν δύναµη κατά την διεύ θυνση του κεκλιµένου επιπέδου, που τον ωθεί προς τα πάνω (σχ. 14). i) Εάν ο συντελεστής τριβής ολίσθησης σε όλες τις επαφές είναι κοι νός, να βρεθεί η αναγκαία συνθήκη, ώστε κατά την έναρξη της κίνη
19 σης του κυλίνδρου αυτός να ολισθαίνει επί του εµποδίου και να κυλί εται χωρίς ολίσθηση επί του κεκλιµένου επιπέδου. ii) Στην περίπτωση που είναι φ=π/6, να εξετάσετε αν ο κύλινδρος µπο ρεί να ανέρχεται κυλιόµενος χωρίς ολίσθηση µε επιτάχυνση µέτρου g/, όπου g η επιτάχυνση της βαρύτητας. Δίνεται η ροπή αδράνειας Ι C =mr / του κυλίνδρου ως προς τον γεωµετρικό του άξονα. ΛΥΣΗ: i) Ας δεχθούµε ότι ο κύλινδρος είναι έτοιµος να εκκινήσει και ότι επί κειται η ολίσθησή του επί του εµποδίου και η κύλισή του χωρίς ολίσθηση επί του κεκλιµένου επιπέδου. Την στιγµή αυτή ο κύλινδρος ισορροπεί οριακά υπό την επίδραση του βάρους του w που αναλύεται στην παράλληλη προς το κεκλιµένο επίπεδο συνιστώσα w x και στην κάθετη προς αυτό συνιστώσα w y, της αντίδρασης του κεκλιµένου επιπέδου που αναλύεται στην κάθετη αντίδρα ση N και στην στατική τριβή T και τέλος της δύναµης επαφής από το εµπό Σχήµα 14 διο που αναλύεται στην κάθετη αντίδραση F και την οριακή τριβή T. Μπορού µε εποµένως να γράψουµε τις σχέσεις: F (x) = F - T - w x = F = T + mg"µ# (1) F (y) = N - T - w y = N = nf + mg"#$ () " (C) = T R - T " R = T - nf = T = nf (3) H (1) λόγω της (3) γράφεται: F = nf + mgµ" F( 1 - n) = mgµ" F = mgµ" 1 - n (4) µε αποτέλεσµα η () να παίρνει την µορφή: N = nmgµ" 1 - n + mg#$%" (5)
20 Όµως η T είναι στατική τριβή και εποµένως το µέτρο της ικανοποιει την σχέ ση Τ κ <nn, η οποία λόγω των (3) και (5) γράφεται: & nf < n( nmgµ" ' 1 - n (4) ) + mg#$%" + * mgµ" 1 - n < nmgµ" 1 - n + mg#$%" µ" 1 - n - nµ" 1 - n < #$%" µ" < #$%" "# < 1 < " / 4 (6) H (6) αποτελεί την ζητούµενη αναγκαία συνθήκη. ii) Αν η γωνία κλίσεως φ είναι π/6 η συνθήκη (6) ικανοποιείται, που σηµαίνει ότι ο κύλινδρος ωθούµενος κατάλληλα από το εµπόδιο (ε) ξεκινάει κυλιόµενος προς τα πάνω χωρίς ολίσθηση επί του κεκλιµένου επιπέδου και έστω ότι το κέν τρο µάζας του C έχει επιτάχυνση µέτρου g/. Η κίνηση του κυλίνδρου είναι συνδυασµός µιας µεταφορικής και µιας περιστροφικής κίνησης περί τον γεω µετρικό του άξονα, συµφωνα δε µε τον δεύτερο νόµο κίνησης του Νεύτωνα και τον θεµελιώδη νόµο της στροφικής κίνησης θα έχουµε τις σχέσεις: F - T - w x = mg/ F = T + mg"µ(# / 6) + mg/ και F = T + mg (7) T R - T " R = I C $ # T R - nfr = mr #" / T - nf = mr #" / T = nf + mr #" / όπου " η γωνιακή επιτάχυνση του κυλίνδρου,όµως λόγω της κυλίσεως του κυλίνδρου ισχύει g/=ω R, οπότε η προηγούµενη σχέση γράφεται: T = nf + mg / 4 (8) Συνδυάζοντας τις (7) και (8) παίρνουµε την σχέση: F = nf + mg / 4 + mg F( 1 - n) = 5mg / 4 F= Επειδή η τριβή T είναι στατική πρέπει να ικανοποιεί την σχέση: 5mg ( ) n (9) (),(8) T " nn nf + mg 4 n " $ nf + 3 # mg % ' & F( 1 - n) - mg (9) mg 5mg 1 - n ( ) ( ) mg$ n 3 # n " % ' & n 3 3 n 3 n 3 (1)
21 H σχέση (1) αποτελεί την αναγκαία συνθήκη, ώστε όταν ο κυλινδρος ωθείται από το εµπόδιο να ανέρχεται κυλιόµενος πάνω στο κεκλιµένο επίπεδο, µε επι τάχυνση µέτρου g/. P.M. fysikos Ένα σώµα µάζας m, κινείται πάνω σε οριζόντιο επίπεδο µε το οποίο παρουσιάζει συντελεστή τριβής ολίσθησης n. Tο σώµα κάποια στιγµή συναντά το ελεύθερο άκρο ιδανικού οριζόντιου ελατηρίου, του οποίου το άλλο άκρο είναι ακλόνητο, µε ταχύτητα µέτρου v της οποίας ο φο ρέας συµπίπτει µε τον άξονα του ελατηρίου. Aν ο µέγιστος ρυθµός µε ταβολής της ορµής του σώµατος έχει µέτρο (dp/dt) max =P *, να βρείτε: i) την σταθερά του ελατηρίου, ii) την συσπείρωση του ελατηρίου, την στιγµή που ο ρυθµός µεταβο λής της ορµής του σώµατος είναι ίσος µε µηδέν και iii) την αντίστοιχη ταχύτητα µεταβολής της κινητικής του ενέργειας. Δίνεται η επιτάχυνση g της βαρύτητας. ΛΥΣΗ: i) To σώµα στην διάρκεια που συµπιέζει το ελατήριο δέχεται το βάρος του m g, την δύναµη επαφής από το οριζόντιο επίπεδο που αναλύεται στην τριβή ολισθήσεως T και στην κάθετη αντίδραση N που εξουδετερώνει το βάρος του και τέλος την δύναµη F " από το συµπιεσµένο ελατήριο. Σύµφωνα µε τον γενικευµένο νόµο κίνησης του Νεύτωνα, ο ρυθµός µεταβολής της ορµής του Σχήµα 15 σώµατος αποκτά το µεγαλύτερο µέτρο, όταν η συνισταµένη δύναµη που δέχε ται αποκτήσει αντίστοιχα το µεγαλύτερο µέτρο της. Αυτό θα συµβεί λίγο πριν το ελατήριο υποστεί την µέγιστη συσπειρωσή του x max, διότι την στιγµή αυτή το µέτρο της συνισταµένης δύναµης θα λάβει την µέγιστη τιµή του Τ+kx max. όπου k η σταθερά του ελατηρίου. Έτσι θα έχουµε την σχέση: ( dp/ dt) max = T + kx max P * = nmg + kx max kx max = P * - nmg (1)
22 Εφαρµόζοντας για το σώµα το θεώρηµα µηχανικής ενέργειας-έργου στην διάρκεια που το ελατήριο συµπιέζεται, παίρνουµε την σχέση: ( K "# + U "# ) - ( K $%& + U $%& ) = W T # " + kx max $ & - # % " -mv + kx max + $ & = -nmgx max % mv (1) = -nmgx max -mv + x max ( P * - nmg) = -nmgx max ( P * + nmg)x max = mv x max = mv P * + nmg () H (1) λόγω της () γράφεται: kmv P * + nmg = P * - nmg k = ( P * - nmg )( P * + nmg) mv k = P * - ( nmg) (3) mv όπου τα δεδοµένα πρέπει να ικανοποιούν την σχέση P * >nmg. Σχήµα 16 ii) Στην θέση όπου ο ρυθµός µεταβολής της ορµής του σώµατος είναι µηδέν η δύναµη από το συµπιεσµένο ελατήριο είναι αντίθετη της τριβής (αυτό συµβαίνει κατά την αποσυσπείρωση του ελατηρίου), οπότε θα ισχύει: T = kx nmg = kx x = nmg / k (3) x = ngm v ( ) (4) P * - nmg όπου x η ζητούµενη συσπείρωση του ελατηρίου.
23 iii) O ρυθµός µεταβολής της κινητικής ενέργειας του σώµατος είναι κάθε στιγ µή ίσος µε την ισχύ της συνισταµένης δύναµης που δέχεται το σώµα, δηλαδή ισχύει: dk / dt = F " v ( ) (5) όπου η v η ταχύτητα του σώµατος την στιγµή που το εξετάζουµε. Η (5) την στιγµή που το ελατήριο είναι συσπειρωµένο κατά x δίνει: ( dk / dt) x = διότι F = P.M. fysikos Δύο ακριβώς όµοιες λείες σφαίρες κινούνται πάνω σε λείο οριζόντιο επίπεδο η µία προς την άλλη, οι δε ταχύτητες των κέντρων τους είναι v και - v. Οι φορείς των ταχυτήτων αυτών απέχουν µεταξύ τους από σταση ίση προς την ακτίνα των σφαιρών, οπότε οι σφαίρες κάποια στιγµή θα συγκρουσθούν. i) Εάν η κρούση τους είναι ελαστική να βρεθούν οι ταχύτητες των σφαιρών µετά την κρούση τους. ii) Χωρίς να χρησιµοποιήσετε τον δεύτερο νόµο του Νεύτωνα, να δεί ξετε ότι η µεταβολή της ορµής κάθε σφαίρας έχει φορέα την διάκεν τρο των σφαιρών. ΛΥΣΗ: i) Κάτα την κρούση των δύο σφαιρών η ορµή του συστήµατος δεν µεταβάλλεται, δηλαδή ισχύει η σχέση: m v + m(- v ) = m V 1 + m V V 1 + V = V 1 = - V (1) Σχήµα 17 Σχήµα 18 όπου V 1, V οι ταχύτητες των σφαιρών µετά την κρούση και m η µάζα κάθε
24 σφαίρας. Εξάλλου, επειδή η κρούση είναι ελαστική η κινητική ενέργεια του συστήµατος πριν και µετά την κρούση είναι ίδια, δηλαδή ισχύει: mv + mv = mv 1 + mv v = V 1 + V (1) v = V 1 (1) V 1 = V = v () Επειδή κατά τον χρόνο που οι σφαίρες είναι σε επαφή οι δυνάµεις κρούσεως είναι κάθετες στο κοινό εφαπτόµενο επίπεδό τους, η ταχύτητα κάθε σφαίρας κατά την κάθετη προς την διάκεντρο διεύθυνση y δεν µεταβάλλεται, δηλαδή θα έχουµε τις σχέσεις: v,y = V 1,y " -v,y = -V,y # v µ" = V 1 µ# 1 $ % v µ" = V µ# & () µ" = µ# 1 $ % µ" = µ# & 1 = = " (3) όπου φ η γωνία των φορέων των ταχυτήτων v, - v µε την διάκεντρο των σφαιρών κατά τον χρόνο της επαφής τους και θ 1, θ οι γωνίες των ταχυτήτων V 1, V αντιστοίχως µε την διάκεντρο αυτή (σχ. 17, 18). Όµως από την Γεωµετ ρία του σχήµατος (17) προκύπτει ότι ηµφ=r/r δηλαδή φ=π/6, οπότε θα είναι και θ 1 =θ =π/6. Από την όλη ανάλυση προκύπτει ότι µετά την κρούση τα κέντρα των δύο σφαιρών θα κινούνται µε αντίθετες ταχύτητες επί παραλλήλων ευθείων που βρίσκονται σε απόσταση d=rηµθ 1 =R µεταξύ τους (σχ. 18). ii) Aν εστιάσουµε την προσοχή µας στην αριστερή σφαίρα παρατηρούµε ότι η µεταβολή P 1 της ορµής της κατά τον χρόνο της κρούσεως είναι: ( v ) P 1 = m V 1 - m v = m V 1 + -m Σχήµα 19 Όµως το παραλληλόγραµµο των διανυσµάτων m V 1 και -m v είναι ρόµβος (σχ. 19) που σηµαίνει ότι η συνισταµένη τους P 1 θα διχοτοµεί την γωνία τους φ+θ 1, δηλαδή σχηµατίζει µε το διάνυσµα -m v γωνία φ που σηµαίνει ότι ο φορέας της βρίσκεται επί της διακέντρου των σφαιρών. Ανάλογα ισχύουν και για την δεξιά σφαίρα. P.M. fysikos
25 Ένα σφαιρίδιο Σ 1 µάζας m, είναι δεµένο στο ένα άκρο αβαρούς και µη εκτατού νήµατος µήκους L, του οποίου το άλλο άκρο έχει στερεω θεί σε ακλόνητο σηµείο, όπως φαίνεται στο σχήµα ( ). Κάποια στιγµή προσκρούει επί του σφαιριδίου Σ 1 δεύτερο σφαιρίδιο Σ µάζας m, µε ταχύτητα v της οποίας ο φορέας διέρχεται από κέντρο του Σ 1 και σχηµατίζει µε την οριζόντια διεύθυνση γωνία φ=π/4. i) Eάν τα δύο σφαιρίδια συγκρούονται ελαστικά, να βρείτε τις ταχύ τητές τους αµέσως µετά την κρούση. ii) Nα βρείτε για ποια τιµή του µέτρου της v το νήµα µετά την κρού ση θα χαλαρώσει την στιγµή που υπέρκειται του οριζόντιου επιπέδου κατα γωνία θ=π/6. Να θεωρήσετε λείες τις επιφάνειες των δύο σφαιρι δίων και τις ακτίνες τους πολύ µικρές σε σχέση µε το µήκος L. ΛΥΣΗ: i) Eπειδή οι επιφάνειες των σφαιριδίων είναι λείες, οι δυνάµεις κρού σεως διευθύνονται κατά την διάκεντρό τους, που σηµαίνει ότι το σφαιρίδιο Σ αµέσως µετά την κρούση θ αποκτήσει ταχύτητα v συγγραµµική της v (σχ. 1). Τα σφαιρίδια κατα τον µικρό χρόνο Δt (Δt ) που βρίσκονται σ επαφή δεν δέχονται οριζόντιες εξωτερικές δυνάµεις, oπότε η ορµή του συστήµατος κατά την οριζόντια διεύθυνση x x δεν µεταβάλλεται, δηλαδή ισχύει η σχέση: mv,x = mv - mv x v "#$ = V - v"#$ "#$( v + v) = V v + v = V "#$ v + v = V "#($ / 4) = 4V (1) Σχήµα Σχήµα 1 όπου V η ταχύτητα του σφαιριδίου Σ 1 αµέσως µετά την κρούση, της οποίας ο φορέας είναι οριζόντιος λόγω του δεσµού κίνησης που του επιβάλλει το κατα κόρυφο νήµα, ενώ δεχθήκαµε ότι η ταχύτητα v είναι αντίρροπη της v. Εξάλ
26 λου επειδή η κρούση των σφαιριδίων είναι ελαστική η κινητική τους ενέργεια λίγο πριν και αµέσως µετά την κρούση είναι ίδια, δηλαδή ισχύει: mv = mv + mv v - v v - v = V ( )( v + v) = V () Συνδυάζοντας την (1) µε την () παίρνουµε: ( v - v) 4V = V v - v = V (3) Προσθέτοντας κατά µέλη τις (1) και (3) έχουµε: v = V + 4V v = V ( + 4 ) V = 4v 5 = v 5 (4) Aπό την σχέση (1) έχουµε: v = 4V (4) - v v = 4 v 5 - v = 8v 5 - v = 3v 5 (5) ii) Έστω ότι το µέτρο της v έχει επιλεγεί, ώστε το νήµα να χαλαρώνει στην θέση Μ του σφαιριδίου Σ 1, η οποία καθορίζεται από την γωνία θ=π/6 (σχ. ). Στην θέση αυτή το σφαιρίδιο δέχεται µόνο το βάρος του w, του οποίου η ακτι Σχήµα νική συνιστώσα w r ενεργεί επί του σφαιριδίου ως κεντροµόλος δύναµη, δηλα δή µπορούµε να γράψουµε την σχέση: w r = mv L mgµ" = mv " L
27 # gµ " & % ( = v ) $ 6' L v = gl όπου v η ταχύτητα του σφαιριδίου στην θέση Μ. Εξάλλου κατά την κίνηση του σφαιριδίου από την θέση κρούσεως Α στην θέση Μ η µηχανική του ενέρ γεια διατηρείται, οπότε ισχύει: (6) K A + U A = K M + U M mv + = mv + mg( L + L"µ ) (6) V = v + gl( 1 + 1/) V = gl + gl 3 $ # & " % = 7gL (4) # " v 5 $ & % = 7gL 8v 5 = 7gL v = 5 7gL 4 (7) P.M. fysikos Mια σφαίρα µάζας m 1, κινείται πάνω σε λείο οριζόντιο επίπεδο µε ταχύτητα v και συγκρούεται ελαστικά αλλά όχι µετωπικά µε µια ακίνητη σφαίρα µάζας m, µε αποτέλεσµα να εκτρέπεται της αρχικής διεύθυνσης κινήσεώς της κατά γωνία φ. i) Eάν m 1 <m και φ=π/, να δείξετε ότι η κινητική ενέργεια Κ 1 της µάζας m 1 µετά την κρούση ικανοποιεί την σχέση: K 1 = m v 1 m - m 1 $ # & " m 1 + m % ii) Eάν m 1 >m, να δείξετε ότι η γωνία φ δεσµεύεται µε την σχέση: µ" # m / m 1 iii) Eάν m 1 =m να δείξετε ότι oι κινητικές ενέργειες Κ 1, Κ των µαζών m 1 και m αντιστοίχως µετά την κρούση, ικανοποιούν την σχέση: K 1 / K = " # ΛΥΣΗ: Eάν P 1, P είναι οι ορµές των σφαιρών µε µάζες m 1 και m αντι στοίχως µετά την κρούση και P η ορµή της µάζας m 1 πριν την κρούση, τότε συµφωνα µε την αρχή διατήρησης της ορµής θα ισχύει η διανυσµατική σχέση:
28 P 1 + P = P m 1 v 1 + m v = m 1 v (1) όπου v 1, v οι ταχύτητες των µαζών m 1 και m αντιστοίχως µετά την κρού ση. Εφαρµόζοντας στο σκιασµένο τρίγωνο του σχήµατος (3) τον νόµο του συνηµιτόνου παίρνουµε την σχέση: Σχήµα 3 P = P 1 + P - P 1 P "#$ m v = m 1 v 1 + m 1 v - m 1 v v 1 "#$ () Όµως λόγω της ελαστικής κρούσεως των δύο σφαιρών η κινητική ενερ γεια του συστήµατος τελικώς δεν µεταβάλλεται, δηλαδή θα έχουµε: m 1 v = m v m v m v = m 1 v - m 1 v 1 m v = m 1 m v - m 1 m v 1 (3) Η () λόγω της (3) γράφεται: m 1 v 1 + m 1 v - m 1 v v 1 "#$ = m 1 m v - m 1 m v 1 m 1 v 1 + m 1 v - m 1 v v 1 "#$ = m v - m v 1 ( m 1 + m )v 1 - m 1 v "#$ v 1 + ( m 1 - m )v = (4) H (4) είναι εξίσωση δεύτερου βαθµού ως προς v 1 για την οποία παρατη ρούµε τα εξής: i) Eάν m 1 <m, τότε το γινόµενο των ριζών της είναι αρνητικό και εποµέ νως οι ρίζες της είναι πραγµατικές και ετερόσηµες και φυσικά δεκτή είναι η θετική ρίζα: v 1 = m 1v "#$ + m 1v "# $ - ( m 1 - m )( m 1 + m )v m 1 + m m 1 + m
29 v 1 = m 1v "#$ + m 1 v "# $ - m ( 1 - m )v (5) m 1 + m Για φ=π/ η (5) δίνει: v 1 = v - m ( 1 - m ) = v m - m 1 (6) m 1 + m m 1 + m H κινητική ενέργεια K 1 της µάζας m 1 µετά την κρούση είναι: K 1 = m 1v 1 (6) K 1 = m 1v m # - m 1 # " m 1 + m ( ) $ & & % = m 1v ' m - m 1 * ), (7) ( m 1 + m + ii) Eάν m 1 >m, τότε η ταχύτητα v 1 είναι αποδεκτή εφ όσον οι ρίζες της (4) είναι πραγµατικές, δηλαδή η διακρίνουσά της είναι µη αρνητική. Πρέ πει εποµένως να ισχύει: 4m 1 v "# $ - 4( m 1 - m )( m 1 + m )v % m 1 "# $ - m ( 1 - m ) % m "# ( $ ) % m m 1 µ " # m µ" # m / m 1 (8) iii) Eάν m 1 =m τότε η (4) γράφεται: ( m 1 + m )v 1 - m 1 v "#$ v 1 = v 1 ( v 1 - v "#$) = από την οποία προκύπτει v 1 = (κεντρική κρούση) ή v 1 =v συνφ (έκκεντρη κρούση). Στην περίπτωση της έκκεντρης κρούσεως θα έχουµε P 1 =P συνφ οπότε η () παίρνει την µορφή: P = P "# $ + P - P "# $ = P %µ $ Παρατηρούµε ότι στην περίπτωση αυτή το σκιασµένο τρίγωνο είναι ορθο γώνιο, που σηµαίνει ότι οι σφαίρες µετά την κρούση κινούνται επί καθέ των διευθύσεων. Οι κινητικές ενέργειες Κ 1, Κ των σφαιρών είναι: K 1 = P 1 / m 1 = P "# $ / m 1 & ' K = P / m = P %µ $ / m ( (:) K 1 = P "# $ / m 1 = & $ K P %µ $ / m P.M. fysikos
i) Να δείξετε ότι: F max = (m 1 + m 2 όπου! g η επιτάχυνση της βαρύτητας.
 Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
της οποίας ο φορέας σχηµατί ζει γωνία φ=π/6 µε την κατακόρυφη διεύθυνση και ανακλάται µε αντίστοιχη γωνία φ=π/4.
 Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
i) Nα δείξετε ότι, κάθε στιγµή οι ταχύτητες των δύο πιθήκων ως προς το ακίνητο έδαφος είναι ίσες.
 Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δίνεται η ροπή αδράνειας I=mL 2 /3 της ράβδου ως προς τον άξονα περιστροφής της, η επιτάχυνση! g της βαρύτητας και ότι π 2!10.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
, της οποίας το µέτρο ικανοποιεί τη σχέση:
 Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
ΛΥΣΗ: Έστω O η θέση ισορροπίας του σφαιριδίου. Στη θέση αυτή το σφαι ρίδιο δέχεται το βάρος του w!, τη δύναµη F
 Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
από τον κατακόρυφο τοίχο, της οποίας ο φορέας είναι οριζόντιος και την δύναµη επα φής N!
 Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
(τρίτος νόµος του Νεύτωνα) και την πλάγια αντίδραση του οριζόντιου εδάφους, η οποία αναλύεται στην τριβή ολίσθησης T!
 Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση.
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
i) Nα βρεθεί η επιτάχυνση του κέντρου Κ της τροχαλίας την στιγµή t=0 αµέσως µετά την θραύση του νήµατος.
 H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
ii) Να δείξετε ότι το σφαιρίδιο εκτελεί µια µη αρµονική περιοδική ταλάντωση, της οποίας να υπολογίσετε την περίοδο.
 Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
διέρχεται από το σηµείο τοµής Ο των φορέων του βάρους w! της ράβδου και της οριζόντιας αντίδρασης A!
 Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
i) Nα βρείτε την επιτάχυνση του κέντρου της τροχαλίας τ 1.
 Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
. Αυτό σηµαίνει ότι το κέντρο µάζας κινείται ευθύγραµµα µε σταθερή επιτάχυνση a! = F!
 Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
ii) Nα υπολογιστεί η κινητική ενέργεια του συστήµατος σε συνάρτηση µε τον χρόνο. Δίνεται η επιτάχυνση! g της βαρύτητας.
 Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
Q του νήµατος που το συγκρατεί, συµφωνα δε µε τον δεύτερο νό µο κίνησης του Νεύτωνα θα ισχύει η σχέση: της τάσεως!
 Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
ακτινικής διεύθυνσης και στην οριακή τριβή T!"
 Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V!
 Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή
 Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
i) το πλάτος ταλάντωσης του καροτσιού µετά την ενσωµάτωση του σφαιριδίου σ' αυτό και
 Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
i) Nα βρείτε την ταχύτητα του κέντρου της στεφάνης αµέσως µετά την κρού ση, η οποία θεωρείται βραχείας διάρκειας.
 Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
i) την ενέργεια που πρέπει να προσφερθεί στο σφαιρίδιο,
 Tο σφαιρίδιο του σχήµατος ισορροπεί πάνω στο λείο οριζόντιο δαπεδο, ενώ τα οριζόντια ελατήρια είναι τεντωµένα. H απόσταση των σηµείων στήριξης των δύο ελατηρίων είναι 3α, ενώ τα ελατήρια έχουν το ίδιο
Tο σφαιρίδιο του σχήµατος ισορροπεί πάνω στο λείο οριζόντιο δαπεδο, ενώ τα οριζόντια ελατήρια είναι τεντωµένα. H απόσταση των σηµείων στήριξης των δύο ελατηρίων είναι 3α, ενώ τα ελατήρια έχουν το ίδιο
Οµογενής σφαίρα µάζας m και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση!!
 Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
όπου Α το πλάτος της ταλάντωσης, φ η αρχική της φάση και ω η γωνιακή της συχνότητα. Οι σχέσεις (2) εφαρµοζόµενες τη χρονική στιγµή t=0 δίνουν:
 Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
(σχ. 1). Εφαρ µόζοντας για την µεταφορική συνιστώσα της κύλισης του δίσκου τον
 Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
όπου Μ η µάζα της Γης την οποία θεωρούµε σφαίρα οµογενή, G η παγκόσµια σταθερά της βαρύτητας και L!
 Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου.
 Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος. και Α 2
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
i) Nα αποδείξετε ότι το σώµα τελικά θα ηρεµήσει ως προς το δοκάρι και να βρείτε την κοινή τους ταχύτητα στο σύστηµα αναφοράς του εδάφους.
 Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
Eάν L 1, L 2 είναι τα αντίστοιχα φυσικά µήκη των ελατηρίων ε 1 και ε 2 τότε για την απόσταση ΑΒ των σηµείων στήριξης των ελατηρίων θα έχουµε:
 Tο µικρό σώµα του σχήµατος (1) έχει µάζα m και συγκρατείται στο λείο οριζόντιο έδαφος σε τέτοια θέση, ώστε τα ελατήρια ε 1 και ε να είναι τεντωµένα κατά α απο την φυσική τους κατάσταση. i) Eάν k, k είναι
Tο µικρό σώµα του σχήµατος (1) έχει µάζα m και συγκρατείται στο λείο οριζόντιο έδαφος σε τέτοια θέση, ώστε τα ελατήρια ε 1 και ε να είναι τεντωµένα κατά α απο την φυσική τους κατάσταση. i) Eάν k, k είναι
περί το κέντρο της σφαίρας, ονοµάζεται δε τριβή κυλίσεως. Tο µέτρο της τρι βής κυλίσεως είναι προφανώς ανάλογο του µέτρου της N,!
 Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
από την άρθρωση και της δύναµης επαφής από τον τοίχο που αναλύεται στην στατική τριβη T!
 Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
ii) ii) Nα καθορίσετε το είδος της ισορροπίας της ράβδου.
 Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
! =A'B=C!! C! = R" (1)
 Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
i) Να γράψετε τη διαφορική εξίσωση κίνησης του σώµατος και να δείξετε ότι δέχεται λύση της µορφής:
 Μικρό σώµα µάζας m στερεώνεται στο ένα άκρο οριζόντιου ιδα νικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο προσδένε ται σε κατακόρυφο τοίχωµα όπως φαίνεται στο σχήµα. Το σώµα µπορεί να ολισθαίνει πάνω
Μικρό σώµα µάζας m στερεώνεται στο ένα άκρο οριζόντιου ιδα νικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο προσδένε ται σε κατακόρυφο τοίχωµα όπως φαίνεται στο σχήµα. Το σώµα µπορεί να ολισθαίνει πάνω
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
1. Για το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και. = (x σε μέτρα).
 Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
ii) Nα βρείτε την µέγιστη γωνιακή ταχύτητα της ράβδου.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
Τροχός ακτίνας R κυλίεται χωρίς ολίσθηση κατά µήκος οριζόντιου αυλακιού, το δε κέντρο µάζας του C έχει σταθερή ταχύτητα v!
 Τροχός ακτίνας R κυλίεται χωρίς ολίσθηση κατά µήκος οριζόντιου αυλακιού, το δε κέντρο µάζας του C έχει σταθερή ταχύτητα v C. Σε σηµείο της περιφέρειας του τροχου έχει αρθρωθεί το ένα άκρο Β µιας λεπτής
Τροχός ακτίνας R κυλίεται χωρίς ολίσθηση κατά µήκος οριζόντιου αυλακιού, το δε κέντρο µάζας του C έχει σταθερή ταχύτητα v C. Σε σηµείο της περιφέρειας του τροχου έχει αρθρωθεί το ένα άκρο Β µιας λεπτής
θα επιβρα δύνεται. Επειδή η F! /Μ και θα ισχύει η σχέση: /t!
 Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από
Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από
την αρχή Ο του ΟΧY, που είναι ένα αδρανειακό σύστηµα αναφοράς. Εάν
 Ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε, παραµένουν αµετάβλητες µε τον χρόνο. Για την µελέτη της επίπεδης κίνησης στερεού
Ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε, παραµένουν αµετάβλητες µε τον χρόνο. Για την µελέτη της επίπεδης κίνησης στερεού
. Εάν η σφαίρα κυλίεται πάνω στο δοκάρι να βρείτε: i) την επιτάχυνση του δοκαριού και του κέντρου της σφαίρας, στο σύστηµα αναφοράς του δαπέδου και
 Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
, σταθερής κατεύθυνσης, της οποίας το µέτρο µεταβάλλεται µε τον χρόνο t, σύµφωνα µε την σχέση:
 Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
i) Nα δείξετε ότι αν το σύστηµα αφεθεί ελεύθερο η τροχαλία τ 1 δεν µπορεί να κυλίεται, άλλά µόνο να ισσρροπεί ή να ολισθαίνει.
 Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
του σφαιριδίου κατευθύνεται προς τα κάτω και σχηµατίζει µε την κατακόρυφη διεύθυνση γωνία φ.
 Μικρό σφαιρίδιο µάζας m, προσπίπτει σε σηµεί ο Α της περιφέρειας ενός δακτυλιδιού ακτίνας R, το οποίο µπορεί να περιστρέφεται περί οριζόντιο άξονα που διέρχεται από ένα σηµείο του Ο. Η ταχύτητα πρόσπτωσης
Μικρό σφαιρίδιο µάζας m, προσπίπτει σε σηµεί ο Α της περιφέρειας ενός δακτυλιδιού ακτίνας R, το οποίο µπορεί να περιστρέφεται περί οριζόντιο άξονα που διέρχεται από ένα σηµείο του Ο. Η ταχύτητα πρόσπτωσης
i) Να δείξετε ότι η κίνηση του συστήµατος των δύο σφαιριδίων είναι περιοδική και να υπολογίσετε την περίοδο της.
 Ένα σφαιρίδιο Σ 1 µάζας m, είναι στερεωµένο στο άκρο ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο είναι ακλόνητο όπως φαίνεται στο σχήµα (α). Το σφαιρίδιο µπορεί να κινείται χωρίς τριβή πάνω
Ένα σφαιρίδιο Σ 1 µάζας m, είναι στερεωµένο στο άκρο ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο είναι ακλόνητο όπως φαίνεται στο σχήµα (α). Το σφαιρίδιο µπορεί να κινείται χωρίς τριβή πάνω
ΦΥΣΙΚΗ Ο.Π Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
( ) ( ) 2 1 K = K = m 2. ! = v 2 + v 1 R + r (3) H (1) λόγω της (3) γράφεται: R - v 2. + v 1. v 2. r > 0 (4) ! v K. + v 1 )R - v 2. = v 2. - v.
 Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
i) Το επίπεδο της τροχαλίας είναι οριζόντιο και το έδαφος λείο.
 Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
τα µοναδιαία διανύσµατα των αξόνων Οx, Oy, Oz αντιστοί χως. Η αντίστοιχη στροφορµή L!
 Στο ένα άκρο ράβδου µήκους L και αµελητέας µά ζας, έχει στερεωθεί σφαιρίδιο µάζας m. Η ράβδος είναι ακίνητη πάνω σε λείο οριζόντιο επίπεδο Οxy, µε το σφαιρίδιο στο σηµείο, και το άλλο της άκρο στο σηµείο
Στο ένα άκρο ράβδου µήκους L και αµελητέας µά ζας, έχει στερεωθεί σφαιρίδιο µάζας m. Η ράβδος είναι ακίνητη πάνω σε λείο οριζόντιο επίπεδο Οxy, µε το σφαιρίδιο στο σηµείο, και το άλλο της άκρο στο σηµείο
Θέμα 1ο Να σημειώσετε τη σωστή απάντηση σε καθεμία από τις παρακάτω ερωτήσεις πολλαπλής επιλογής.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΚΡΙΤΗΡΙΑ ΑΞΙΟΛΟΓΗΣΗΣ o ΕΠΑΝΑΛΗΠΤΙΚΟ ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ Θέμα ο Να σημειώσετε τη σωστή απάντηση σε καθεμία από τις παρακάτω ερωτήσεις πολλαπλής επιλογής. ) Σώμα εκτελεί ταυτόχρονα δύο απλές
ΕΠΑΝΑΛΗΠΤΙΚΑ ΚΡΙΤΗΡΙΑ ΑΞΙΟΛΟΓΗΣΗΣ o ΕΠΑΝΑΛΗΠΤΙΚΟ ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ Θέμα ο Να σημειώσετε τη σωστή απάντηση σε καθεμία από τις παρακάτω ερωτήσεις πολλαπλής επιλογής. ) Σώμα εκτελεί ταυτόχρονα δύο απλές
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
. Εάν η κρούση της ράβ δου µε το οριζόντιο έδαφος είναι τελείως ελαστική, να βρείτε:
 Μια λεπτή λαστιχένια ράβδος ΑΒ µήκους L και µάζας m, εκτελεί ελεύθερη πτώση χώρίς να περιστρέφεται και κάποια στιγµή το άκρο της Α συναντά λείο οριζόντιο έδαφος. Την στιγµή αυτή η ράβδος έχει κλίση φ ως
Μια λεπτή λαστιχένια ράβδος ΑΒ µήκους L και µάζας m, εκτελεί ελεύθερη πτώση χώρίς να περιστρέφεται και κάποια στιγµή το άκρο της Α συναντά λείο οριζόντιο έδαφος. Την στιγµή αυτή η ράβδος έχει κλίση φ ως
διέρχεται από το σηµείο Ο της ράβδου, υπό την επίδραση των βαρών m 1 από τον άξονα περιστροφής, που αναλύεται στην οριζόντια συνιστώσα!
 Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1. ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου
![% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου % ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου](/thumbs/53/30956495.jpg) 1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
i) την µέγιστη ροπή του ζεύγους δυνάµεων που επιτρέπεται να ενερ γήσει επί του κυλίνδρου, ώστε αυτός να ισορροπεί και
 Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
) ω ω. L λίγο πριν. . Nα βρεθούν:
 Δύο σφαιρίδια A, B µάζας m το καθένα συνδέονται µεταξύ τους µε αβαρές και µη εκτατό νήµα µήκους L, ηρεµούν δε πάνω σε οριζόντιο τραπέζι ευρισκόµενα σε απόσταση α
Δύο σφαιρίδια A, B µάζας m το καθένα συνδέονται µεταξύ τους µε αβαρές και µη εκτατό νήµα µήκους L, ηρεµούν δε πάνω σε οριζόντιο τραπέζι ευρισκόµενα σε απόσταση α
Προτεινόμενα ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ
 ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
(ΘΕΜΑ 17ο)
 Εισαγωγικά: Με το πρόβληµα της αλληλεπίδρασης δύο µαζών, µέσω αβαρούς και µη εκτατού νήµατος παρουσία οµογενούς βαρυτικού πεδίου, είχα ασχοληθεί και στο παρελθόν παρουσιάζοντάς το στην ιστοσελίδα µου µε
Εισαγωγικά: Με το πρόβληµα της αλληλεπίδρασης δύο µαζών, µέσω αβαρούς και µη εκτατού νήµατος παρουσία οµογενούς βαρυτικού πεδίου, είχα ασχοληθεί και στο παρελθόν παρουσιάζοντάς το στην ιστοσελίδα µου µε
i) Nα εκφράσετε σε συνάρτηση µε τον χρόνο την γωνιακή ταχύτητα της τροχαλίας.
 Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
µε φορά προς το κυρτό µέρος του σύρµατος (σχήµα α) η οποία µαζί µε την ακτινική συνιστώσα w!
 Το κυκλικό σύρµα του σχήµατος έχει µάζα m/ και είναι κρεµασµένο από κατακόρυφο σπάγκο αµελητέας µάζας αλλά επαρκούς αντοχής. Δύο όµοιες σηµειακές χάντρες, καθε µιά µε µάζα m, αφήνονται ταυτόχρονα από την
Το κυκλικό σύρµα του σχήµατος έχει µάζα m/ και είναι κρεµασµένο από κατακόρυφο σπάγκο αµελητέας µάζας αλλά επαρκούς αντοχής. Δύο όµοιες σηµειακές χάντρες, καθε µιά µε µάζα m, αφήνονται ταυτόχρονα από την
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΜΕΡΟΣ Γ! 2η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα
 Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
που δέχεται από την παράπλευρη επιφάνεια του κώνου, της οποίας ο φορέας είναι κάθετος στην επιφάνεια αυτή, αφού θεωρείται λεία και των δυνάµεων T
 Mιά κυκλική σπείρα εύκαµπτης αλυσίδας βάρους w, είναι τοποθετηµένη πάνω σε λείο ορθό κώνο ύψους h, του οποίου η βάση έχει ακτίνα R (σχ. 9). O κατακόρυφος άξονας του κώνου διέρ χεται από το κέντρο της αλυσίδας
Mιά κυκλική σπείρα εύκαµπτης αλυσίδας βάρους w, είναι τοποθετηµένη πάνω σε λείο ορθό κώνο ύψους h, του οποίου η βάση έχει ακτίνα R (σχ. 9). O κατακόρυφος άξονας του κώνου διέρ χεται από το κέντρο της αλυσίδας
Nα δείξετε τις εξής προτάσεις:
 Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
Κρούσεις. 1 ο ΘΕΜΑ.
 ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
# $ + L " = ml " ml! = ML " $ + ml " $ L " = ML/2(M + m) # $ (1) Eξάλλου, εάν L' α, L' σ είναι οι τελικές αποστάσεις του κέντρου µάζας C του
 Mία σανίδα, µήκους L καί µάζας M, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Στο ένα άκρο της σανίδας πατάει άνθ ρωπος µάζας m και αρχίζει να κινείται προς το άλλο άκρο της. Kατά πόσο θα µετατοπιστεί η
Mία σανίδα, µήκους L καί µάζας M, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Στο ένα άκρο της σανίδας πατάει άνθ ρωπος µάζας m και αρχίζει να κινείται προς το άλλο άκρο της. Kατά πόσο θα µετατοπιστεί η
Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση
 Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση α) Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση λίγο πριν και αμέσως μετά το κόψιμο του νήματος, Η ομογενής και ισοπαχής ράβδος
Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση α) Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση λίγο πριν και αμέσως μετά το κόψιμο του νήματος, Η ομογενής και ισοπαχής ράβδος
 ΘΕΜΑ Α 018 Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση. A1. Δύο μικρά σώματα με
ΘΕΜΑ Α 018 Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση. A1. Δύο μικρά σώματα με
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
, που είναι στατική τριβή µε κατεύθυνση αντίθετη της ταχύτητας του κέντρου µάζας C 1 της σφαίρας (σχήµα 1) και η δύναµη επαφής!
 Δύο οµογενείς σφαίρες Α και Β, της ίδιας ακτίνας R µε αντίστοιχες µάζες m και m είναι ακίνητες επί οριζοντίου εδάφους και εφάπ τονται µεταξύ τους. Κάποια στιγµή που λαµβάνεται ως αρχή µέτρη σης του χρόνου
Δύο οµογενείς σφαίρες Α και Β, της ίδιας ακτίνας R µε αντίστοιχες µάζες m και m είναι ακίνητες επί οριζοντίου εδάφους και εφάπ τονται µεταξύ τους. Κάποια στιγµή που λαµβάνεται ως αρχή µέτρη σης του χρόνου
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Προτεινόμενες Λύσεις Πρόβλημα-1 (15 μονάδες) Μια
7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α ΦΑΣΗ) ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 7 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 01 Προτεινόμενες Λύσεις Πρόβλημα-1 (15 μονάδες) Μια
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ
 Ονοµατεπώνυµο: Διάρκεια: (3 45)+5=50 min Τµήµα: ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ Ζήτηµα ο Ένα στερεό µπορεί να στρέφεται γύρω από σταθερό άξονα και αρχικά ηρεµεί. Σε µια στιγµή δέχεται (ολική) ροπή
Ονοµατεπώνυµο: Διάρκεια: (3 45)+5=50 min Τµήµα: ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ Ζήτηµα ο Ένα στερεό µπορεί να στρέφεται γύρω από σταθερό άξονα και αρχικά ηρεµεί. Σε µια στιγµή δέχεται (ολική) ροπή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Προτεινόμενες Λύσεις Πρόβλημα - ( μονάδες) Ένα όχημα, μαζί με ένα κανόνι που είναι ακλόνητο πάνω σε αυτό,
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Προτεινόμενες Λύσεις Πρόβλημα - ( μονάδες) Ένα όχημα, μαζί με ένα κανόνι που είναι ακλόνητο πάνω σε αυτό,
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ii) Nα βρεθεί η κινητική ενέργεια της σφαίρας, όταν το δοκάρι έχει µετατοπιστεί κατά S ως προς το έδαφος.
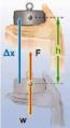 Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
Ασκήσεις (διάφορες, στροφορμής και δυναμικής συστήματος σωματιδίων)
 Προσπαθείστε να λύσετε τις: Ασκήσεις (διάφορες, στροφορμής και δυναμικής συστήματος σωματιδίων Διάφορες: l. inn: : 7.6, 7.76, 7.78 Serwy: Κεφ.. 9:, 55, 65, 8, 85 Στροφορμή: : : 7.5, 7.8, 7., 7.6 Δυν. Συστ.
Προσπαθείστε να λύσετε τις: Ασκήσεις (διάφορες, στροφορμής και δυναμικής συστήματος σωματιδίων Διάφορες: l. inn: : 7.6, 7.76, 7.78 Serwy: Κεφ.. 9:, 55, 65, 8, 85 Στροφορμή: : : 7.5, 7.8, 7., 7.6 Δυν. Συστ.
