ΠΡΟΣΑΡΜΟΣΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΙΚΑΝΟΠΟΙΗΣΗΣ ΠΕΡΙΟΡΙΣΜΩΝ
|
|
|
- Ἀκελδαμά Ιωαννίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΠΡΟΣΑΡΜΟΣΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΙΚΑΝΟΠΟΙΗΣΗΣ ΠΕΡΙΟΡΙΣΜΩΝ Η Διπλωματική Εργασία παρουσιάστηκε ενώπιον του Διδακτικού Προσωπικού του Πανεπιστημίου Αιγαίου Σε Μερική Εκπλήρωση των Απαιτήσεων για το Δίπλωμα του Μηχανικού Πληροφοριακών και Επικοινωνιακών Συστημάτων του Βογιατζή Αρτεμίου ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2007
2 Η ΤΡΙΜΕΛΗΣ ΕΠΙΤΡΟΠΗ ΔΙΔΑΣΚΟΝΤΩΝ ΕΠΙΚΥΡΩΝΕΙ ΤΗ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΒΟΓΙΑΤΖΗ ΑΡΤΕΜΙΟΥ : Στεργίου Κωνσταντίνος, Επιβλέπων Ημερομηνία Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Βούρος Γεώργιος, Μέλος Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Σταματάτος Ευστάθιος, Μέλος Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2007 ii
3 ΠΕΡΙΛΗΨΗ Η παρούσα εργασία έχει σαν αντικείμενο την μελέτη αλγορίθμων και ευριστικών μεθόδων για προβλήματα ικανοποίησης περιορισμών. Ο στόχος αυτών των αλγορίθμων είναι η επίλυση των προβλημάτων, δηλαδή η συνεπής (ή μη) ανάθεση μίας τιμής σε κάθε μία από τις μεταβλητές που συμμετέχουν στο πρόβλημα, ή απόδειξη ότι δεν υπάρχει λύση. Οι γνωστοί αλγόριθμοι που εξετάζονται είναι οι MAC και Forward Checking, που ανήκουν στην κατηγορία των look- ahead αλγορίθμων [11]. Οι αλγόριθμοι αυτοί επιλέγουν τις μεταβλητές με κάποια σειρά και κάνουν ανάθεση τιμών σε αυτές έως ότου όλες να έχουν από μία έγκυρη τιμή σύμφωνα με τους περιορισμούς. Μετά από κάθε προσωρινή ανάθεση τιμής σε μία μεταβλητή ο MAC αλγόριθμος εφαρμόζει έλεγχο συνέπειας τόξου (arc consistency) σε ολόκληρο το πρόβλημα, ενώ ο Forward Checking ελέγχει την συμβατότητα μεταξύ της συγκεκριμένης μεταβλητής και των γειτονικών της στις οποίες δεν έχει ανατεθεί τιμή. Αυτό αποτελεί, ουσιαστικά, μία περιορισμένη μορφή ελέγχου συνέπειας τόξου. Σε περίπτωση ασυμβατότητας μελλοντικών τιμών, οι αλγόριθμοι αυτοί αφαιρούν αυτές τις τιμές καθώς δεν θα μπορούν να συμμετέχουν στη λύση του αρχικού προβλήματος. Λόγω κατασκευής λοιπόν, ο ΜΑC αλγόριθμος χρησιμοποιεί το μέγιστο επίπεδο διάδοσης συνέπειας τόξου και ο Forward Checking ένα ασθενέστερο μοντέλο ελέγχου συνέπειας. Σε πολύ εύκολα προβλήματα, ο Forward Checking είναι πιο αποδοτικός του MAC λόγω του λιγότερου χρόνου που χρειάζεται για την επίλυσή τους, καθώς ο MAC εφαρμόζει πάντα πλήρη έλεγχο συνέπειας τόξου και καθυστερεί χωρίς να υπάρχει πραγματική ανάγκη [6]. Σε δύσκολα προβλήματα, ωστόσο, ο Forward Checking αργεί να ανακαλύψει τις ασυνέπειες με αποτέλεσμα ο MAC να είναι αποδοτικότερος μια και εξερευνεί πολύ μικρότερο κομμάτι του χώρου αναζήτησης από ότι ο Forward Checking. Παρουσιάζει ενδιαφέρον να εξετάσουμε αλγορίθμους που κάνουν έλεγχο για παραπάνω από μία μεταβλητή σε κάθε επανάληψη (όπως ο Forward Checking) αλλά δεν εξετάζουν ολόκληρο το πρόβλημα όπως ο MAC. Αυτοί οι αλγόριθμοι εφαρμόζουν έλεγχο συνέπειας τόξου για περιοχές που αποτελούνται από λιγότερες ή το πολύ ίδιες μεταβλητές με τις συνολικές του προβλήματος. Eφαρμόζουν, δηλαδή, λιγότερο ισχυρή διάδοση συνέπειας από αυτήν που χρησιμοποιεί ο MAC και ταυτόχρονα είναι πιο «ισχυροί» του Forward Checking. Οι αλγόριθμοι αυτοί εφαρμόζουν έλεγχο συνέπειας για ένα υποδίκτυο μόνο του αρχικού προβλήματος. Το μέγεθος του υποδικτύου που εξετάζεται βασίζεται στην έννοια της «γειτονιάς», δηλαδή στο σύνολο των μεταβλητών και περιορισμών που βρίσκονται σε κάποια προκαθορισμένη απόσταση από την εκάστοτε μεταβλητή που εξετάζεται. Για την επιλογή της επόμενης, κάθε φορά, μεταβλητής προς εξέταση, μπορεί να εφαρμοστεί μία ευριστική συνάρτηση ώστε να επιλέγεται η μεταβλητή που εμφανίζεται ως η πιο «περιορισμένη». Εξετάζονται δύο τέτοιες συναρτήσεις σε συνδυασμό με τους αλγορίθμους. Η μία βασίζεται σε χαρακτηριστικά κάθε μεταβλητής ξεχωριστά (η ευριστική συνάρτηση dom/deg ) και η άλλη λαμβάνει υπ όψιν πληροφορίες για κάποιο τμήμα του συνολικού προβλήματος. Στο παρόν κείμενο παρουσιάζονται τα αποτελέσματα των πειραμάτων για διάφορους συνδυασμούς αλγορίθμων/ ευριστικών συναρτήσεων του ΒΟΓΙΑΤΖΗ ΑΡΤΕΜΙΟΥ iii
4 Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ iv
5 ABSTRACT This work includes examination of algorithms used to solve Constraint Satisfaction Problems (CSPs). These problems are considered to be solved when each variable of which they consist is assigned a valid value, thus satisfying all constraints. We use two known algorithms, Forward Checking and MAC. They both belong to lookahead category of algorithms. These algorithms eliminate inconsistencies found in a subnetwork of the whole problem, since an inconsistent partial instantiation cannot be a part of the problem s solution. We also examine another kind of algorithms, which are more powerful than Forward Checking but weaker than MAC as far as propagation is considered. Forward Checking only checks compatibility between each current variable and its future neighbors. MAC performs a full arc- consistency check (AC- 3) to the whole problem for each variable that is assigned a value. The new kind of algorithms perform a full arc consistency check only for a subnetwork of the whole problem, designated as neighborhood of level- i, meaning the consistency check has a scope of all variables that can be reached from current variable with up to i hops from it. The effectiveness of these algorithms can be improved with the use of variable ordering heuristics. The heuristics are usually based on characteristics of each variable apart. There are other heuristics, though, which are based on characteristics of a wider subset of variables. In this work, we examine one heuristic for each category, dom/deg and heuristic proposed in [1] respectively. The results are based on experiments done using various combinations of algorithms and heuristics VOGIATZIS ARTEMIOS Department of Information and Communication Systems Engineering UNIVERSITY OF THE AEGEAN v
6 ΕΥΧΑΡΙΣΤΙΕΣ - ΑΦΙΕΡΩΣΕΙΣ Κατ αρχάς θα ήθελα να ευχαριστήσω τον επιβλέποντα καθηγητή μου, κύριο Κωνσταντίνο Στεργίου για την βοήθεια και την στήριξη που μου παρείχε καθ όλη την προσπάθεια της εκπόνησης της παρούσης εργασίας. Επίσης, ευχαριστώ την οικογένειά μου που με στήριξε ψυχολογικά κατά την συγγραφή του παρόντος. vi
7 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΠΕΡΙΛΗΨΗ...iii ABSTRACT...v ΕΥΧΑΡΙΣΤΙΕΣ - ΑΦΙΕΡΩΣΕΙΣ...vi ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ...7 ΚΕΦΑΛΑΙΟ 1 - ΕΙΣΑΓΩΓΗ Παρουσίαση προβλημάτων ικανοποίησης περιορισμών Γενικά για τα προβλήματα ικανοποίησης περιορισμών Γνωστά παραδείγματα προβλημάτων ικανοποίησης περιορισμών Αναπαράσταση Προβλημάτων Ικανοποίησης Περιορισμών Λύση Προβλημάτων Μέθοδοι Επίλυσης Προβλημάτων Ικανοποίησης Περιορισμών Αλγόριθμοι Διάδοσης Συνέπειας Αλγόριθμοι Αναζήτησης Ευριστικές Συναρτήσεις (heuristics) DOM/DEG [15] H_k_dom/futdeg_x [2]...25 ΚΕΦΑΛΑΙΟ 2 - ΠΑΡΟΥΣΙΑΣΗ ΕΡΓΑΣΙΑΣ Κύριο πρόγραμμα Δομές που χρησιμοποιήθηκαν Λειτουργία του προγράμματος Λειτουργία και υλοποίηση των αλγορίθμων και των ευριστικών συναρτήσεων Λειτουργία και υλοποίηση αλγορίθμων Υλοποίηση heuristics...38 ΚΕΦΑΛΑΙΟ 3 - ΠΕΙΡΑΜΑΤΑ Σύγκριση αλγορίθμων με χρήση DOM/DEG Πυκνότητα περιορισμών p= 5% Πυκνότητα περιορισμών p = 20% Σύγκριση heuristics με χρήση MAC Πυκνότητα περιορισμών p = 5% Πυκνότητα περιορισμών p = 20% Σύγκριση αλγορίθμων clac- x με χρήση heuristics Πυκνότητα περιορισμών p = 5% Πυκνότητα περιορισμών p = 20%...63 ΚΕΦΑΛΑΙΟ 4 - ΣΥΜΠΕΡΑΣΜΑΤΑ...70 ΒΙΒΛΙΟΓΡΑΦΙΑ
8 ΚΕΦΑΛΑΙΟ 1 - ΕΙΣΑΓΩΓΗ Περιορισμός είναι μία συσχέτιση μεταξύ κάποιων παραγόντων η οποία περιορίζει τις διαθέσιμες επιλογές για κάποια κατάσταση. Για παράδειγμα το πλήθος των πλευρών ενός τετραγώνου είναι πάντα τέσσερα, οι διαθέσιμες ώρες μίας ημέρας είναι 24, το σύνολο της μνήμης RAM σε έναν υπολογιστή είναι συγκεκριμένο. Η έννοια της επίλυσης περιορισμών παρουσιάζεται συχνά σε καθημερινές καταστάσεις της ζωής του ανθρώπου. Οι αγορές με βάση ένα δεδομένο χρηματικό ποσό στην τράπεζα, ο καθορισμός των καλεσμένων σε μία αίθουσα με συγκεκριμένη χωρητικότητα, ο χωρισμός των παικτών σε ισοδύναμες ομάδες σε ένα παιχνίδι ποδοσφαίρου μεταξύ φίλων, αποτελούν κάποια απλά παραδείγματα καταστάσεων στις οποίες επιλύουμε κάποιους περιορισμούς προκειμένου να επιτύχουμε την πραγμάτωσή τους. Πιο σύνθετα προβλήματα αποτελούν η ανάθεση ωρών διδασκαλίας σε ένα πανεπιστήμιο, η κατασκευή του προγράμματος αγώνων μίας αγωνιστικής περιόδου και άλλα. Στο παράδειγμα του πανεπιστημίου, προκύπτουν διάφοροι περιορισμοί όπως: ένας καθηγητής δεν μπορεί να κάνει ταυτόχρονα μάθημα σε δύο διαφορετικές αίθουσες, όπως επίσης μία αίθουσα πρέπει να χρησιμοποιείται σε κάθε χρονική στιγμή από ένα συγκεκριμένο μάθημα και η χωρητικότητα της να καλύπτει τον αριθμό φοιτητών που παρακολουθούν το μάθημα. Κάποια μαθήματα δεν επιτρέπεται να διδάσκονται την ίδια ώρα, ενώ κανένα μάθημα δεν μπορεί να διδάσκεται μετά τις δέκα το βράδυ. Στον προγραμματισμό αγώνων μπορεί να θέλουμε κάθε ομάδα να παίζει κάθε δεύτερη εβδομάδα εκτός έδρας (η αγωνιστική είναι μία φορά την εβδομάδα), και όλες οι ομάδες να έχουν παίξει τον ίδιο αριθμό εντός και εκτός έδρας παιχνίδια, και σε όλα τα γήπεδα. Εδώ προκύπτουν περιορισμοί όπως: Μία ομάδα δεν μπορεί να παίζει εντός έδρας δύο συνεχόμενες φορές, ούτε και εκτός. Σε κάθε παιχνίδι θα πρέπει να συμμετέχει μία ομάδα που έχει σειρά να παίξει εντός έδρας και μία που έχει σειρά να παίξει εκτός, εκτός αν επιτρέπεται ο αγώνας σε δανεικό γήπεδο, οπότε μπορούν να αγωνιστούν δύο ομάδες που έχουν σειρά να παίξουν εκτός έδρας. Δεν επιτρέπεται να επαναληφθεί ο ίδιος αγώνας ούτε να μείνουν κάποιες ομάδες χωρίς παιχνίδι κάποια αγωνιστική. Όπως γίνεται αντιληπτό, καθώς η δυσκολία των προβλημάτων αυξάνεται, είναι αδύνατο να επιλυθούν αποτελεσματικά και σε λογικό χρονικό διάστημα χωρίς την βοήθεια κάποιων μεθόδων και την χρήση υπολογιστών [1]. Ένας τρόπος επίλυσης τέτοιων συνδυαστικών προβλημάτων βασίζεται στην τεχνολογία προγραμματισμού με περιορισμούς (Constraint Programming). Ακολουθώντας τη μεθοδολογία αυτή, τα προβλήματα μοντελοποιούνται ως προβλήματα επίλυσης περιορισμών (Constraint Satisfaction Problems). 8
9 1.1 Παρουσίαση προβλημάτων ικανοποίησης περιορισμών Γενικά για τα προβλήματα ικανοποίησης περιορισμών Τα προβλήματα ικανοποίησης περιορισμών (CSPs) αποτελούνται από ένα σύνολο μεταβλητών, ένα σύνολο δυνατών τιμών για κάθε μία από αυτές (πεδίο τιμών) και ένα σύνολο από περιορισμούς. Ένας περιορισμός είναι μία σχέση που καθορίζει τους έγκυρους συνδυασμούς τιμών μεταξύ ενός υποσυνόλου των μεταβλητών. Η λύση σε ένα τέτοιο πρόβλημα θεωρείται η ανάθεση μιας τιμής σε κάθε μεταβλητή από το αντίστοιχο πεδίο τιμών της, ώστε να μη παραβιάζεται κανένας περιορισμός. Ένα πρόβλημα μπορεί να έχει μία, πολλές ή καμία λύση. Τα προβλήματα αυτά ανήκουν στην κατηγορία (NP-hard), δηλαδή οι χρησιμοποιούμενοι αλγόριθμοι επίλυσης δεν μπορούν να εξασφαλίσουν αποδοτικότητα για οποιοδήποτε μέγεθος προβλήματος [1].Σε όλη την έκταση της εργασίας ασχολούμαστε με δυαδικούς περιορισμούς, δηλαδή την περίπτωση προβλημάτων στα οποία κάθε περιορισμός περιλαμβάνει το πολύ δύο μεταβλητές. Επιστρέφοντας στο παράδειγμα της ανάθεσης ωρών διδασκαλίας, η μοντελοποίησή του μπορεί να γίνει ως εξής. Οι ημέρες διδασκαλίας μπορούν να αναπαραστούνται με ένα σύνολο μεταβλητών, οι οποίες ως τιμές μπορούν να έχουν τριπλέτες (μάθημα- καθηγητής- αίθουσα). Καθώς κάποια μαθήματα δεν επιτρέπεται να διδάσκονται την ίδια μέρα, προκύπτουν αυτόματα περιορισμοί για κάθε μεταβλητή. Επίσης, λόγω του περιορισμού της αδυναμίας ταυτόχρονης παρουσίας ενός καθηγητή σε δύο μαθήματα την ίδια ώρα, προκύπτουν περιορισμοί που αφορούν κάποιους συνδυασμούς τιμών σε μία ή περισσότερες μεταβλητές. Αντίστοιχα προκύπτουν περισσότεροι περιορισμοί με βάση τον ορισμό του προβλήματος Υπάρχουν διάφορες κατηγορίες περιορισμών. Για παράδειγμα, υπάρχουν οι αριθμητικοί (numeric) και οι περιορισμοί που ακολουθούν την άλγεβρα Boole (Boolean). Οι αριθμητικοί περιορισμοί αναπαριστούν τους περιορισμούς με αριθμητικές εκφράσεις, για παράδειγμα η έκφραση ( 6x + 2y 20) (4x 7 y 12) είναι ένας περιορισμός μεταξύ των μεταβλητών x και y. Στην κατηγορία των Boolean, οι μεταβλητές έχουν πεδίο τιμών {0,1} ή {αληθές, ψευδές}. Για παράδειγμα η έκφραση ( A B) ( C A) αναπαριστά 3 μεταβλητές με μία σύζευξη δύο διαζευκτικών περιορισμών. Ο στόχος της ενασχόλησης με ένα πρόβλημα μπορεί να είναι η εξασφάλιση της ύπαρξης μίας τουλάχιστον λύσης, η εύρεση μίας ή όλων των λύσεων εάν υπάρχουν είτε η εύρεση της καλύτερης δυνατής λύσης (ή ένα σύνολο από καλύτερες λύσεις). Η καλύτερη λύση ορίζεται βάσει προκαθορισμένης απαίτησης από την λεγόμενη συνάρτηση κόστους. Αυτού του είδους τα προβλήματα ονομάζονται προβλήματα βελτιστοποίησης. Μία απλή αναπαράσταση ενός δυαδικού προβλήματος ικανοποίησης περιορισμών είναι ένας γράφος, στον οποίο οι μεταβλητές αναπαραστούνται με κόμβους και οι περιορισμοί με ακμές. Για παράδειγμα ένα απλοποιημένο πρόβλημα με μεταβλητές α, β, γ, δ, πεδίο τιμών {0,1} και 9
10 περιορισμούς α β, β = γ, δ = α, δ β παίρνει την μορφή: α β = = δ γ Σχήμα 1.1 Το παραπάνω πρόβλημα μπορεί να αναπαριστά μία πραγματική κατάσταση. Για παράδειγμα οι μεταβλητές είναι οι πιθανοί καλεσμένοι σε μία γιορτή, η τιμή 1 αναπαριστά ότι κάποιος θα καλεστεί, η 0 ότι δεν θα καλεστεί και οι περιορισμοί την υποχρεωτική συμβατότητα καλεσμένων μεταξύ τους. Εάν καλεστεί ο α, αυτόματα καλείται ο δ, ο β αποκλείεται και σε συνέχεια αποκλείεται και ο γ. Εάν καλεστεί ο γ, αυτόματα καλείται ο β και στη συνέχεια αποκλείονται ο α και ο β Γνωστά παραδείγματα προβλημάτων ικανοποίησης περιορισμών Το πρόβλημα των n- Βασιλισσών Ο στόχος σε αυτό το πρόβλημα είναι η τοποθέτηση n βασιλισσών σε μία σκακιέρα διάστασης n x n ώστε καμία να μην απειλείται. Οι μεταβλητές εδώ μπορεί να είναι οι στήλες και το πεδίο τιμών τους ο αριθμός της γραμμής στην οποία βρίσκεται η βασίλισσα για κάθε στήλη. Ο περιορισμός για κάθε ζεύγος μεταβλητών είναι ότι οι βασίλισσες δεν πρέπει να βρίσκονται στην ίδια γραμμή ή διαγώνιο. Σχήμα
11 Χρωματισμός Χάρτη Στο πρόβλημα αυτό θεωρούμε έναν χάρτη χωρισμένο σε περιοχές και η επίλυσή του θεωρείται ο χρωματισμός όλων των περιοχών με έναν τρόπο ώστε οποιεσδήποτε δύο γειτονικές περιοχές να μην έχουν το ίδιο χρώμα. Ως μεταβλητές θεωρούμε τις περιοχές και σαν πεδίο τιμών τα διαθέσιμα χρώματα. Στο παραπάνω πρόβλημα, οι μεταβλητές είναι οι A,B,C,D,E,F,G και το πεδίο τιμών για κάθε μεταβλητή είναι π.χ. D= {κόκκινο, πράσινο, μπλε}. Ο περιορισμός για κάθε ζεύγος μεταβλητών x i και x j είναι πως αν η x i είναι γειτονική με την x j, τότε x i xj. Σχήμα Αναπαράσταση Προβλημάτων Ικανοποίησης Περιορισμών Θεωρούμε ένα πεπερασμένο σύνολο από μεταβλητές X = {x 1, x 2,, x n } με αντίστοιχα πεδία τιμών D = {D 1, D 2,, Dn} που αναπαριστούν τις πιθανές τιμές για κάθε μεταβλητή- D i = { v 1, v 2,, v n }. Οι περιορισμοί είναι το σύνολο C = {C 1, C 2,, Cn}. Ολόκληρο το πρόβλημα λοιπόν μπορεί να αναπαρασταθεί συνοπτικά ως (X, D, C). Κάθε περιορισμός είναι μία σχέση ανάμεσα σε κάποιο υποσύνολο μεταβλητών του X, S i. Ουσιαστικά μας υποδεικνύει τις έγκυρες ταυτόχρονες αναθέσεις τιμών αυτών των μεταβλητών. Το εύρος του περιορισμού είναι το σύνολο των μεταβλητών στις οποίες έχει εφαρμογή. Το πλήθος των μεταβλητών που εμπλέκονται σε έναν περιορισμό καθορίζει και τον βαθμό του περιορισμού. Εάν ο περιορισμός αναφέρεται σε μία μεταβλητή λέγεται μοναδιαίος, σε δύο δυαδικός κ.ο.κ. Το σύνολο των S i ονομάζεται σχήμα (scheme) του προβλήματος. 4. Σαν παράδειγμα, στη συνέχεια αναπαριστούμε το πρόβλημα των n- βασιλισσών για n = 11
12 Σχήμα 1.3 Οι μεταβλητές είναι οι στήλες, X = { x 1, x 2, x 3, x 4 }. Το πεδίο τιμών είναι ο αριθμός της γραμμής για κάθε στήλη, D i = {1, 2, 3, 4} για i = Όπως είδαμε, οι περιορισμοί είναι πως μετά την τοποθέτηση τους, καμία βασίλισσα δεν πρέπει να απειλείται, ή διαφορετικά να μην είναι στην ίδια γραμμή ή διαγώνιο με κάποια άλλη. Οι περιορισμοί είναι δυαδικοί, με στιγμιότυπα της μορφής (v i, v j ), με vi και vj τις επιτρεπτές θέσεις της βασίλισσας κάθε στήλης. Αφού κάθε μεταβλητή έχει περιορισμό με όλες τις υπόλοιπες, το σύνολο θα είναι έξι περιορισμοί. Συγκεκριμένα, R 12 = { (1,3), (1,4), (2,4), (3,1), (4,1), (4,2) } R 13 = { (1,2), (1,4), (2,1), (2,3), (3,2), (3,4), (4,1), (4,3) } R 14 = { (1,2), (1,3), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,2), (4,3) } R 23 = { (1,3), (1,4), (2,4), (3,1), (4,1), (4,2) } R 24 = { (1,2), (1,4), (2,1), (2,3), (3,2), (3,4), (4,1), (4,3) } R 34 = { (1,3), (1,4), (2,4), (3,1), (4,1), (4,2) } Κάθε σχέση R ij υποδεικνύει τους επιτρεπτούς συνδυασμούς τιμών για τις μεταβλητές i και j από τα αντίστοιχα πεδία τιμών τους Λύση Προβλημάτων Η ανάθεση τιμών σε ένα υποσύνολο των μεταβλητών Χ είναι μία σειρά διατεταγμένων ζευγών μεταβλητών- τιμών. Για παράδειγμα στο πρόβλημα των βασιλισσών, μία ανάθεση για το υποσύνολο μεταβλητών {x 1, x 2, x3} μπορεί να είναι η a = { (x 1,2), (x 2, 3), (x3,1) }. Η ανάθεση τιμών ελέγχεται εάν παραβιάζει κάποιον περιορισμό. Για την ανάθεση του παραδείγματος, φαίνεται εύκολα πως η ανάθεση των x 1 και x2 με τιμές 2 και 3 παραβιάζει την σχέση R 12, καθώς αυτές οι τιμές είναι ασύμβατες μεταξύ τους. Δηλαδή a[{ x1, x2}] = (2,3) αλλά ( 2,3) R 12 Μία ανάθεση τιμών σε ένα υποσύνολο μεταβλητών, (εύρος S) είναι συνεπής ως προς αυτό μόνο εάν για όλα τα S i που ανήκουν στο S, η ανάθεση a[ S i ] R S i, δηλαδή δεν παραβιάζεται περιορισμός. Για παράδειγμα, η μερική ανάθεση τιμών για τις μεταβλητές x1, x 2, 12
13 x 3, a ={ (x 1,1), (x2,4), (x 3,2) } είναι συνεπής, καθώς δεν παραβιάζεται κάποιος περιορισμός ανάμεσά τους. Όμως, αυτή η ανάθεση δεν οδηγεί σε λύση. Η λύση ενός προβλήματος R = (X, D, C) είναι, τελικά, η ανάθεση τιμών σε όλες τις μεταβλητές με τρόπο που ικανοποιούνται όλοι οι περιορισμοί. Η λύση ορίζεται τυπικά ως: sol ( R) { a = ( a1..., a ) a D, S scheme of R a[ S i ] R } [1] = n i i i, i Για το πρόβλημα των βασιλισσών, οι δύο λύσεις είναι οι (2,4,1,3) και (3,1,4,2) 1.2 Μέθοδοι Επίλυσης Προβλημάτων Ικανοποίησης Περιορισμών Οι τρόποι επίλυσης των προβλημάτων χωρίζονται σε δύο κύριες κατηγορίες, την διάδοση συνέπειας και την αναζήτηση Αλγόριθμοι Διάδοσης Συνέπειας Η διάδοση συνέπειας βασίζεται στη λογική ότι ένα πρόβλημα μπορεί να μετατραπεί μέσω εξαγωγής συμπερασμάτων (inference) σε μία πιο σαφή και περιορισμένη μορφή, ώστε ο χώρος αναζήτησης να γίνει μικρότερος [12][13][5]. Ένα απλό παράδειγμα είναι το εξής πρόβλημα ανάθεσης τιμών. Έστω τρεις μεταβλητές x, y, z με πεδίο τιμών {0,1} και τους περιορισμούς x = y, x = z και z y. Μπορούμε να συμπεράνουμε ότι το πρόβλημα δεν έχει λύση (inconsistent). Εφ όσον x = y και x = z, μπορούμε να εξάγουμε σαν συμπέρασμα ότι και z = y, αυτό όμως παραβιάζει τον τρίτο περιορισμό σε κάθε περίπτωση. Η χρήση τεχνικών διάδοσης συνέπειας μπορεί να οδηγήσει στην εύρεση πλήρους λύσης ενός προβλήματος, έχοντας περιορίσει το αρχικό πρόβλημα σε μορφή απ την οποία μία λύση είναι ευθέως ορατή, είτε βρίσκοντας ασυνέπεια (οπότε δεν έχει λύση). Αναλυτικότερα, οι αλγόριθμοι που εξετάζουν συνέπεια σε ένα πρόβλημα διαφοροποιούνται, κατ αρχάς, από το επίπεδο του υποπροβλήματος στο οποίο εφαρμόζουν την τεχνική εξαγωγής συμπερασμάτων. Το επίπεδο ορίζεται ως ο αριθμός των μεταβλητών οι οποίες εξετάζονται κάθε φορά σε συνδυασμό για συνέπεια (υποστήριξη). Οι αλγόριθμοι που εξετάζουν ένα υποπρόβλημα (ή υποδίκτυο) μεγέθους 2 ονομάζονται αλγόριθμοι συνέπειας τόξου (arc consistency algorithms). Οι αλγόριθμοι αυτοί ελέγχουν την ύπαρξη συνέπειας μεταξύ δύο κάθε φορά μεταβλητών, δηλαδή ελέγχουν εάν οποιαδήποτε έγκυρη τιμή (που δεν έχει διαγραφεί δηλαδή) από το πεδίο τιμών μιας μεταβλητής είναι συμβατή με τουλάχιστον μία τιμή από το πεδίο τιμών κάθε άλλης μεταβλητής [12][13][5]. Οι αλγόριθμοι που εξετάζουν και εξασφαλίζουν ότι ένας έγκυρος συνδυασμός τιμών μεταξύ ενός ζεύγους μεταβλητών μπορεί να επεκταθεί σε όλες τις υπόλοιπες μεταβλητές μία προς 13
14 μία ονομάζονται αλγόριθμοι συνέπειας μονοπατιού (path consistency algorithms). Σε αυτήν την περίπτωση το επίπεδο είναι 3, καθώς ελέγχεται το συνεπές ζεύγος με μία τρίτη μεταβλητή. Σημειώνεται πως για να είναι συνεπές σε επίπεδο 3 ένα πρόβλημα, πρέπει όλα τα δυνατά μονοπάτια μεγέθους 3 να είναι συνεπή [5][7]. Οι αλγόριθμοι που εξετάζουν παραπάνω επίπεδα ονομάζονται αλγόριθμοι επιπέδου συνέπειας i, όπου i θεωρούμε τον αριθμό επιπέδου. Οι αλγόριθμοι επιπέδου συνέπειας- i εξασφαλίζουν ότι η ανάθεση τιμών i-1 μεταβλητών μπορεί να επεκταθεί σε οποιαδήποτε i- οστή μεταβλητή [7]. Εάν ένα πρόβλημα είναι i- συνεπές για κάθε τιμή του i τότε ονομάζεται καθολικά συνεπές και μπορεί να βρεθεί λύση με ανάθεση τιμών χωρίς την ανάγκη οπισθοδρόμησης (απουσία αδιεξόδων). Η δυσκολία στην επίλυση (από πλευράς χρόνου και χώρου) αυξάνεται εκθετικά όσο αυξάνεται το επίπεδο εστίασης. Η χρονική και χωρική πολυπλοκότητα αυτών των αλγορίθμων για προβλήματα n μεταβλητών είναι Ο(n i ). Στη συνέχεια θα παρουσιαστούν αναλυτικότερα οι αλγόριθμοι συνέπειας τόξου Συνέπεια τόξου (Arc Consistency) [13] Η συνέπεια τόξου ελέγχει για κάθε δύο μεταβλητές x και y που σχετίζονται με περιορισμό εάν κάθε τιμή a από το πεδίο της x είναι συμβατή με τουλάχιστον μία τιμή από το πεδίο τιμών της y. (Το πεδίο τιμών αναφέρεται πάντα στις έγκυρες κάθε φορά τιμές). Σε αυτήν την περίπτωση λέμε ότι η τιμή a της x έχει υποστήριξη στην y. Γνωστοί αλγόριθμοι συνέπειας τόξου είναι οι AC- 1, AC- 3 και AC- 4. Έχουν προταθεί πιο εξελιγμένοι αλγόριθμοι, όπως οι AC- 6 και AC-7. Ορισμός: Δεδομένου ενός προβλήματος R= (X, D, C), με R ij C, μία μεταβλητή x i λέγεται συνεπής τόξου (arc-consistent) αν και μόνο αν για κάθε τιμή α i Di και για κάθε μεταβλητή xj, όπου x j υπάρχει μία τιμή α j D j τέτοια ώστε (α i, α j ) R ij. Το υποδίκτυο {x i, x j } είναι arcconsistent αν και μόνο αν η x i είναι arc-consistent σε σχέση με την xj και η x j είναι arc-consistent σε σχέση με την x i. Το συνολικό δίκτυο των μεταβλητών (το πρόβλημα) ονομάζεται arcconsistent εάν και μόνο αν όλα τα υποδίκτυα μεγέθους 2 (τόξα) είναι arc- consistent [12]. Η λογική στην εφαρμογή της συνέπειας τόξου είναι η απαλοιφή κάθε τιμής από το πεδίο τιμών της εξεταζόμενης μεταβλητής όταν δεν έχει υποστήριξη από καμία τιμή της μεταβλητής με την οποία ελέγχεται για συνέπεια. Αφού αυτή η τιμή δεν αποτελεί λύση για το συγκεκριμένο υποδίκτυο μεγέθους 2, δεν θα αποτελεί λύση και για το συνολικό δίκτυο Αλγόριθμος REVISE [13] Ένας απλός αλγόριθμος που υλοποιεί τα παραπάνω, είναι ο εξής Αλγόριθμος REVISE: REVISE((xi), xj) 14
15 Input: A subnetwork defined by two variables X= {x i, x j }, a distinguished variable x i, domains Di and D j, constraint R ij. Output: Di, such that xi is arc-consistent relative to xj. 1. for each a i Di 2. if there is no aj Dj such that (ai, aj) Rij 3. delete ai from Di 4. endif 5. endfor Όπως βλέπουμε, ο αλγόριθμος επιστρέφει κάθε φορά το πεδίο τιμών για την x i μεταβλητή ενημερωμένο για πιθανές ασυμβατότητες με την μεταβλητή x j έχοντας δηλαδή διαγράψει όποιες τιμές παραβιάζουν τον περιορισμό R ij. 2 Η πολυπλοκότητα του αλγορίθμου REVISE είναι Ο(d ), με d το μέγεθος του πεδίου τιμών. Πράγματι, στην χειρότερη περίπτωση θα ελεγχθούν όλες οι τιμές της x i με όλες τις τιμές της x j, δηλαδή d x d = d 2 έλεγχοι. Παράδειγμα: Σχήμα 1.5 Έστω ότι ελέγχουμε την μεταβλητή x με την y, και οι γραμμές αντιπροσωπεύουν τα επιτρεπόμενα ζευγάρια τιμών βάσει κάποιου περιορισμού. Φτάνοντας στον έλεγχο της τιμής 2 για την x μεταβλητή, διαπιστώνουμε ότι καμία τιμή από το πεδίο τιμών της y δεν την υποστηρίζει, άρα παραβιάζεται ο περιορισμός. Η τιμή 2 διαγράφεται, και πλέον το πεδίο τιμών της x περιλαμβάνει μόνο τις τιμές 0 και 1. Τώρα η μεταβλητή x είναι συνεπής σε σχέση με την y. Η μεταβλητή y είναι συνεπής σε σχέση με την x (εάν τρέξουμε τον αλγόριθμο REVISE για το ζεύγος {y,x} θα διαπιστώσουμε ότι κάθε τιμή της y έχει υποστήριξη σε κάποια τιμή της x) άρα το υποδίκτυο είναι πλέον συνεπές. Σε κάποιες περιπτώσεις όμως, η εφαρμογή του αλγορίθμου REVISE θα δημιουργεί ασυνέπειες στο υπόλοιπο πρόβλημα λόγω αλλαγής του πεδίου τιμών μίας μεταβλητής η οποία συμμετέχει σε κάποιον άλλο περιορισμό. Ένα παράδειγμα είναι το ακόλουθο. 15
16 Σχήμα 1.6 Καλώντας τον αλγόριθμο REVISE για τις μεταβλητές y και x, διαπιστώνουμε πως η y είναι συνεπής σε σχέση με την x, και αντίστοιχα αν ελέγξουμε την x ως προς y, η x είναι συνεπής ως προς την y. Εάν καλέσουμε στη συνέχεια τον αλγόριθμο για να εξετάσουμε την συνέπεια της x ως προς την z, θα αφαιρεθεί η τιμή 0 της x, με αποτέλεσμα η μεταβλητή y να μην είναι πλέον συνεπής ως προς την x. Η τιμή 0 της y δεν θα έχει υποστήριξη από καμία τιμή της x, άρα θα πρέπει και αυτή να διαγραφεί από το πεδίο τιμών της y. (Παρατηρούμε ότι στη συνέχεια και η τιμή 0 της z θα μείνει χωρίς υποστήριξη στο πεδίο τιμών της y). Θα πρέπει λοιπόν με κάποιον τρόπο να είμαστε σίγουροι πως γίνεται ενημέρωση για πιθανές ασυνέπειες που μπορεί να δημιουργηθούν με τη διαγραφή τιμών από το πεδίο τιμών μίας μεταβλητής κατά την διαδικασία ελέγχου συνέπειας Αλγόριθμος AC- 1 [13] Ο αλγόριθμος AC-1 ελέγχει όλα τα ζεύγη μεταβλητών που συμμετέχουν σε έναν περιορισμό (προς αμφότερες κατευθύνσεις) με τον αλγόριθμο REVISE έως ότου μετά το τέλος ενός πλήρους κύκλου να μην έχει αλλαχθεί κανένα πεδίο τιμών [1]. Εάν διαπιστωθεί στην πορεία του αλγορίθμου ότι το πεδίο τιμών κάποιας μεταβλητής μένει κενό, τότε το πρόβλημα δεν έχει λύση. Αλγόριθμος AC-1: AC-1 (R) Input: A network of constraints R = (X, D, C). Output: R, which is the loosest arc-consistent network euivalent to R. 1. repeat 2. for every pair {xi, xj} that participates in a constraint 3. REVISE((xi), xj) 4. REVISE((xj), xi) 5. endfor 16
17 6. until no domain is changed Για μέγεθος πεδίου τιμών d, n μεταβλητές και k δυαδικούς περιορισμούς η πολυπλοκότητα του αλγορίθμου AC- 1 είναι Ο(knd 3 ). Πράγματι, εάν ελέγξουμε όλους τους περιορισμούς σε ένα κύκλο του αλγορίθμου, φτάνουμε το Ο(kd 2 ). Εφ όσον όλες οι δυνατές τιμές είναι nd (και στην χειρότερη περίπτωση διαγράφεται το πολύ μία τιμή ενός πεδίου τιμών σε κάθε κύκλο), θα χρειαστούμε nd κύκλους, συνεπώς Ο(knd 3 ). Στο παράδειγμα, έστω η σειρά ελέγχου R xy, R xz, R zy. O αλγόριθμος ελέγχει τις μεταβλητές x και y και προς τις δύο κατευθύνσεις. Δεν θα αφαιρέσει καμία τιμή από τα πεδία τιμών τους. Ελέγχοντας μετά το υποδίκτυο {x, z}, θα αφαιρέσει την τιμή 0 της x. Ελέγχοντας το {z, y} δεν θα αφαιρέσει καμία τιμή. Αφού κάποιο πεδίο τιμών άλλαξε, ο αλγόριθμος μπαίνει ξανά στο loop (1.), και ελέγχει ξανά όλα τα ζευγάρια τιμών. Κατά τον έλεγχο του περιορισμού R xy, θα αφαιρεθεί η τιμή 0 της y κατά τον έλεγχο από y σε x. Κατά τον έλεγχο R xz δεν θα αφαιρεθεί καμία τιμή. Κατά τον έλεγχο R zy θα αφαιρεθεί η τιμή 0 της z αφού πλέον δεν έχει υποστήριξη στην y. Ο αλγόριθμος θα ξαναμπεί στο loop. Κατά τον έλεγχο R xy δεν θα γίνει κάποια αλλαγή. Κατά τον έλεγχο R xz δεν θα αφαιρεθεί κάποια τιμή (η τιμή 1 της x εξακολουθεί να έχει υποστήριξη στην z στην τιμή 1). Τέλος κατά τον έλεγχο του R zy δεν αφαιρείται καμία τιμή και ο αλγόριθμος τερματίζει καθώς έκανε έναν πλήρη κύκλο χωρίς να αλλαχθεί το πεδίο τιμών κάποιας μεταβλητής. Σχηματικά, Σχήμα
18 Παρατηρούμε ότι ο αλγόριθμος AC- 1 έχει ένα «περιττό» χαρακτηριστικό. Σε κάθε κύκλο ελέγχει όλους τους περιορισμούς ανάμεσα στις μεταβλητές (και προς τις δύο κατευθύνσεις) ανεξάρτητα από το ποιος περιορισμός ευθύνεται για τη διαγραφή τιμών από το πεδίο τιμών κάποιας μεταβλητής στο προηγούμενο βήμα. Ένας αλγόριθμος που ξεπερνά αυτό το χαρακτηριστικό είναι ο AC Αλγόριθμος AC- 3 [13] Ο αλγόριθμος AC- 3 αποτελεί μία βελτιωμένη εκδοχή του ΑC- 1 [13][1]. Αντί να ελέγχει σε κάθε κύκλο όλα τα ζεύγη που έχουν περιορισμό μεταξύ τους, διατηρεί μία λίστα με τα ζεύγη μεταβλητών τα οποία πρέπει να εξεταστούν (συμμετέχουν σε περιορισμό). Αρχικά όλα τα ζεύγη τοποθετούνται σε αυτήν την λίστα (η οποία συνήθως υλοποιείται ως ουρά ή σωρός). Υπενθυμίζεται ότι ο έλεγχος γίνεται προς τις δύο κατευθύνσεις, οπότε το κάθε ζεύγος για x i και x j μεταβλητές που συμμετέχουν σε έναν περιορισμό θα αποθηκευτεί μία φορά ως (x i, xj) και μία φορά ως (x j, x i ). Κάθε ζεύγος βγαίνει από τη λίστα, εξετάζεται με τον αλγόριθμο REVISE και ξαναμπαίνει μόνο εάν κατά την πορεία του αλγορίθμου αλλάξει το πεδίο τιμών της δεύτερης μεταβλητής αυτού του περιορισμού. Αλγόριθμος AC- 3 AC- 3(R) Input: A network of constraints R = (X, D, C). Output: R, which is the largest arc- consistent network euivalent to R. 1. for every pair {x i, x j } that participates in a constraint R ij R 2. ueue ueue { (xi, xj), (x j, x i) } 3. endfor 4. while ueue {} 5. select and delete (x i, x j ) from ueue 6. REVISE((x i ), x j ) 7. if REVISE((x i ), x j ) causes a change in D i 8. ueue ueue { (xk, x i), k i, k j } 9. endif 10. end while 3 Η χρονική πολυπλοκότητα του AC- 3 είναι Ο(kd ). Ο κάθε περιορισμός ελέγχεται το πολύ 2d φορές, αφού σε περίπτωση επανεξέτασης ενός περιορισμού σίγουρα έχει αφαιρεθεί μία τουλάχιστον τιμή, με 2d το σύνολο των τιμών. Έχοντας k περιορισμούς, απαιτούνται O(2kd) κλήσεις στη REVISE, συνεπώς η πολυπλοκότητα είναι Ο(kd 3 ). Στο παρόν παράδειγμα, ο αλγόριθμος τοποθετεί στην λίστα όλα τα ζεύγη μεταβλητών που συμμετέχουν σε περιορισμό, δηλαδή ueue: { (x, y), (y,x), (x, z), (z,x), (y, z), (z, y) }. 18
19 Βγαίνει το ζευγάρι (x, y), δεν γίνεται καμία αλλαγή. Συνεπώς ο αλγόριθμος συνεχίζει βγάζοντας το (y, x). Πάλι μετά το REVISE δεν υπάρχει διαγραφή τιμής και απ την λίστα βγαίνει το (x, z). Από το πεδίο τιμών της μεταβλητής x διαγράφεται η τιμή 0. Το ζεύγος (y, x) ξαναμπαίνει στη λίστα. Το (z, x) βγαίνει από τη λίστα και δεν υπάρχει αλλαγή, στη συνέχεια το (y, z) βγαίνει από τη λίστα και πάλι δεν υπάρχει αλλαγή. Το ζεύγος (z, y) βγαίνει από τη λίστα και δεν υπάρχει αλλαγή. Το ζεύγος (y, x) βγαίνει (πάλι) από τη λίστα και η τιμή 0 της y διαγράφεται. Στη λίστα ξαναμπαίνουν τα (x, y) και (z, y). Βγαίνει το (x, y) από τη λίστα, δεν υπάρχει αλλαγή, και τέλος βγαίνει το (z, x) και πάλι δεν υπάρχει αλλαγή, οπότε τερματίζεται και ο αλγόριθμος. Ο αλγόριθμος έχει καταλήξει σε λύση ελέγχοντας 9 περιορισμούς με τον αλγόριθμο REVISE έναντι 18 που χρειάστηκε ο AC- 1. Οι αλγόριθμοι συνέπειας τόξου δεν είναι ικανοί να λύσουν από μόνοι τους όλα τα προβλήματα ικανοποίησης περιορισμών. Οπότε χρησιμοποιούνται για να μειώσουν τα πεδία τιμών (και άρα τον χώρο αναζήτησης). Συνδυάζεται, δηλαδή, ο έλεγχος συνέπειας τόξου με κάποιον αλγόριθμο αναζήτησης (αναφέρονται στη συνέχεια). Με αυτόν τον τρόπο επιτυγχάνεται μία εξισορρόπηση μεταξύ του χρόνου που χρειάζεται ο αλγόριθμος συνέπειας τόξου και ο αλγόριθμος αναζήτησης [7] Αλγόριθμοι Αναζήτησης Οι αλγόριθμοι αναζήτησης προχωρούν στην επίλυση ενός προβλήματος αναθέτοντας σε κάθε βήμα μία τιμή σε μία μεταβλητή (συχνά η επιλογή γίνεται με τη βοήθεια μίας ευριστικής συνάρτησης). Ουσιαστικά πραγματοποιείται μία κατά βάθος αναζήτηση, καθώς μετά από κάθε επιτυχή ανάθεση τιμής σε μία μεταβλητή, οι αλγόριθμοι συνεχίζουν στην ανάθεση τιμής στην επόμενη, θεωρώντας πως όλες οι προηγούμενες μεταβλητές έχουν από μία έγκυρη τιμή. Ο χώρος αναζήτησης που εξερευνά ένας αλγόριθμος μπορεί να αναπαρασταθεί από ένα δέντρο (που ονομάζεται δέντρο αναζήτησης). Οι κόμβοι στο δέντρο αντιστοιχούν σε συνδυασμούς αναθέσεων τιμών στις μεταβλητές [1]. Υπάρχει βέβαια το ενδεχόμενο η προσπάθεια ανάθεσης τιμής σε κάποια μεταβλητή να μην είναι επιτυχής, δηλαδή να μην υπάρχει υποστήριξη για καμία έγκυρη τιμή της σε κάποια από τις προηγούμενες (που έχουν ήδη τιμή) μεταβλητές. Ο πιο απλός αλγόριθμος που επιλύει αυτό το θέμα, και στον οποίο βασίζονται πολλοί από τους πιο εξελιγμένους αλγόριθμους, είναι η χρονική οπισθοδρόμηση (backtracking). Ο αλγόριθμος οπισθοδρόμησης επεκτείνει μία μερική λύση (ένα υποσύνολο μεταβλητών στις οποίες έχει γίνει ανάθεση τιμών) αναθέτοντας τιμές σε άλλες μεταβλητές [1][9]. Σε κάθε βήμα εξασφαλίζεται ότι η τιμή που ανατίθεται σε μία μεταβλητή έχει υποστήριξη σε όλες τις προηγούμενες μεταβλητές. Εάν για κάποια μεταβλητή που εξετάζεται δεν υπάρχει καμία διαθέσιμη τιμή η οποία να έχει υποστήριξη σε όλες τις προηγούμενες τιμές παρουσιάζεται «αδιέξοδο». Σε αυτήν την περίπτωση, ο αλγόριθμος οπισθοδρομεί, αλλάζοντας την τιμή την οποία ανέθεσε στην αμέσως προηγούμενη μεταβλητή (εάν υπάρχει άλλη διαθέσιμη), και συνεχίζει την αναζήτηση. Ο αλγόριθμος τερματίζει όταν βρεθεί λύση (ανάθεση τιμών σε όλες τις μεταβλητές) ή όταν συμπεράνει ότι δεν υπάρχει λύση. Όπως γίνεται αντιληπτό, η ένδειξη ότι ένα πρόβλημα δεν έχει λύση είναι ο αλγόριθμος να φτάσει στο σημείο να εξετάσει ανεπιτυχώς όλες τις τιμές στο πεδίο τιμών της πρώτης μεταβλητής που επέλεξε,δηλαδή η οπισθοδρόμηση να φτάσει πέραν της πρώτης μεταβλητής. Αυτό σημαίνει ότι λόγω αδιεξόδων, έχουν απορριφθεί όλοι οι πιθανοί συνδυασμοί τιμών για τις μεταβλητές. Εάν όλες οι τιμές της αρχικής οδηγούν σε 19
20 αδιέξοδο, δεν μπορεί να γίνει ανάθεση τιμής σε αυτήν την μεταβλητή και το πρόβλημα δεν έχει λύση. Υπάρχουν αλγόριθμοι που «κοιτούν μπροστά» (look ahead) και αλγόριθμοι που «κοιτούν προς τα πίσω» (look back). Όπως γίνεται αντιληπτό από τις ονομασίες τους, οι τεχνικές look ahead εστιάζουν στον τρόπο με τον οποίο θα γίνει η μελλοντική ανάθεση τιμών/επιλογή μεταβλητών και οι τεχνικές look back αποσκοπούν στην καλύτερη ανάκαμψη από μία κατάσταση αδιεξόδου κατά την επίλυση ενός προβλήματος. Στο παρόν κείμενο θα εξεταστούν οι αλγόριθμοι Forward Checking (FC) και MAC (Maintaining Arc Consistency), οι οποίοι ανήκουν στην κατηγορία των look ahead αλγορίθμων Αλγόριθμος Forward Checking Ο αλγόριθμος Forward Checking είναι η πιο απλή μορφή αυτής της κατηγορίας αλγορίθμων. Κατά την εκτέλεσή του, αναθέτει μία τιμή σε μία μεταβλητή (την ονομάζουμε τρέχουσα) και ελέγχει εάν όλες οι τιμές όλων των μελλοντικών μεταβλητών υποστηρίζονται από την τρέχουσα ανάθεση. Με αυτήν την τεχνική, σε κάθε βήμα είμαστε σίγουροι ότι το υποπρόβλημα έως και την τρέχουσα μεταβλητή είναι συνεπές [9]. Κατά τον έλεγχο διαγράφονται μελλοντικές τιμές που δημιουργούν ασυνέπεια (δηλαδή δεν υποστηρίζονται από την τρέχουσα ανάθεση) και εάν το πεδίο τιμών κάποιας από τις μελλοντικές μεταβλητές μείνει άδειο (domain wipeout), τότε η επιλεγμένη τιμή της τρέχουσας μεταβλητής απορρίπτεται και επιλέγεται άλλη. Εάν για όλες τις δυνατές τιμές της τρέχουσας μεταβλητής παρουσιάζεται κενό πεδίο τιμών σε κάποια μελλοντική μεταβλητή, τότε είμαστε σίγουροι πως δεν υπάρχει λύση που να περιλαμβάνει την τρέχουσα ανάθεση τιμών. Συνεπώς ο αλγόριθμος οπισθοδρομεί στην αμέσως προηγούμενη μεταβλητή και της αναθέτει διαφορετική τιμή. Ένα απλό παράδειγμα είναι το εξής. a 1, 2 b 1, 2 1, 2 d 1, 2 c Σχήμα 1.8 Οι μεταβλητές είναι οι a, b, c, d. Έστω ότι οι περιορισμοί μεταξύ τους δίνουν τους ακόλουθους συνδυασμούς επιτρεπτών τιμών. R ab = { (2,2) } 20
21 R ac = { (2,1) } R bc = { (2,1) } R bd = { (2,1) } R cd = { (2,1) } Έστω ότι η σειρά επίσκεψης των μεταβλητών για το παράδειγμα ακολουθεί λεξικογραφική σειρά, δηλαδή σειρά επίσκεψης a,b,c,d. Ο αλγόριθμος ξεκινά από την μεταβλητή a. Επιλέγοντας την τιμή 1, δεν ικανοποιείται κανένας περιορισμός και η τιμή 1 απορρίπτεται (δεν υπάρχει καμία τιμή σε καμία μελλοντική μεταβλητή γειτονική με την a που να είναι συμβατή με την ανάθεση a = 1, δηλαδή πρακτικά η ανάθεση της τιμής 1 οδηγεί σε αδιέξοδο είτε διαλέξουμε να εξετάσουμε το Rac είτε το Rab πρώτα). Ο αλγόριθμος επιλέγει την τιμή 2. Κατά συνέπεια, διαγράφει την τιμή 1 από το πεδίο τιμών της b και την τιμή 2 από το πεδίο τιμών της c. Ο αλγόριθμος συνεχίζει εξετάζοντας την μεταβλητή b. Η τιμή 2 της b έχει υποστήριξη από την τιμή 1 της c και την τιμή 1 της d. Η τιμή 2 της d διαγράφεται. Ο αλγόριθμος εξετάζει την μεταβλητή c. Έχοντας μόνο την τιμή 1 διαθέσιμη (η τιμή 2 διαγράφηκε κατά τον έλεγχο της b) η μεταβλητή c δεν έχει υποστήριξη από την μεταβλητή d (που είναι η μοναδική επόμενη μεταβλητή). Παρουσιάζεται λοιπόν αδιέξοδο και ο αλγόριθμος οπισθοδρομεί στην προηγούμενη μεταβλητή που είναι η b. Το πεδίο τιμών της b δεν έχει άλλη διαθέσιμη τιμή, οπότε ο αλγόριθμος οπισθοδρομεί ξανά, και ελέγχει την a. Η a δεν έχει άλλη διαθέσιμη τιμή, οπότε παρουσιάζεται αδιέξοδο στην αρχική μεταβλητή και ο αλγόριθμος τερματίζει, καταλήγοντας στο συμπέρασμα πως δεν υπάρχει λύση στο πρόβλημα Αλγόριθμος MAC Ο αλγόριθμος αυτός λειτουργεί παρόμοια με τον FC, αλλά είναι πιο ισχυρός, καθώς σε κάθε βήμα του μπορεί να διαγράψει περισσότερες τιμές από μελλοντικές μεταβλητές. Αφού επιλεχθεί μία τιμή για την τρέχουσα μεταβλητή, εφαρμόζεται έλεγχος συνέπειας τόξου σε ολόκληρο το πρόβλημα (χρησιμοποιώντας τον αλγόριθμο AC- 3 για την παρούσα εργασία). Εάν παρατηρηθεί εξάλειψη πεδίου τιμών κάποιας μεταβλητής, η τιμή που δόθηκε απορρίπτεται (διαγράφεται από το πεδίο τιμών) και επιλέγεται άλλη. Εφαρμόζεται πλήρης έλεγχος συνέπειας με το καινούριο πεδίο τιμών, κ.ο.κ. Με αυτόν τον τρόπο σε κάθε βήμα ελέγχουμε όχι μόνο τους περιορισμούς μεταξύ της τρέχουσας μεταβλητής και όλων των μελλοντικών μεταβλητών με τις οποίες σχετίζεται με περιορισμό, αλλά και όλους τους περιορισμούς μεταξύ όλων των μεταβλητών [1][6]. Έχουμε δηλαδή εξασφάλιση συνέπειας τόξου όχι μόνο για τις προηγούμενες μεταβλητές (όπως με την χρήση FC), αλλά και για τις μελλοντικές (μεταβλητές που ακόμα δεν έχουμε επισκεφτεί). Εάν σε κάποιο βήμα παρουσιαστεί εξάλειψη του πεδίου τιμών συμπεραίνουμε πως το υπόλοιπο πρόβλημα πέραν της τρέχουσας μεταβλητής δεν έχει λύση και, όπως κατά την εφαρμογή Forward Checking, πραγματοποιείται οπισθοδρόμηση στην αμέσως προηγούμενη μεταβλητή. Ο αλγόριθμος θα τερματίσει είτε βρίσκοντας λύση, είτε φτάνοντας στο συμπέρασμα ότι το πρόβλημα δεν έχει λύση. Για το παράδειγμα του σχήματος 1.8, ο αλγόριθμος MAC σε συνδυασμό με εφαρμογή AC- 3 θα πραγματοποιήσει τα εξής. Επιλέγει την τιμή 1 για την μεταβλητή a. Ελέγχοντας τον περιορισμό με την b, θα διαγράψει όλες τις τιμές της b, κατά συνέπεια ο αλγόριθμος θα επαναφέρει το πεδίο τιμών της b και η a θα πάρει την επόμενη τιμή, 2. Εφαρμόζεται πάλι έλεγχος συνέπειας. Εξετάζοντας την b, 21
22 θα διαγράψει την τιμή 1 από το πεδίο τιμών της (b) και την τιμή 2 της c. Οι δύο μεταβλητές προστίθενται στη λίστα προς εξέταση. Βγάζοντας από την λίστα και εξετάζοντας την b, διαγράφεται η τιμή 2 της d, η οποία προστίθεται στην λίστα. Στη συνέχεια βγαίνει η c από τη λίστα. Η τιμή της (1) δεν είναι συμβατή με κάποια τιμή της d (έχει μείνει η 1), με αποτέλεσμα να παρουσιάζεται αδιέξοδο (η μεταβλητή d μένει με άδειο πεδίο τιμών). Ο αλγόριθμος δεν μπορεί να αναθέσει άλλη τιμή στην τρέχουσα μεταβλητή (a), και δεν υπάρχει άλλο περιθώριο οπισθοδρόμησης καθώς η a είναι η πρώτη μεταβλητή που εξετάστηκε. Συνεπώς το πρόβλημα δεν έχει λύση Αλγόριθμος clac Όπως είδαμε, ο αλγόριθμος MAC είναι ένας αλγόριθμος που εφαρμόζει πλήρη συνέπεια τόξου σε κάθε βήμα του. Ο Forward Checking (FC) ελέγχει σε κάθε βήμα μόνο τους άμεσους περιορισμούς κάθε μεταβλητής. Ως αποτέλεσμα της κατασκευής τους, σε κάποιες περιπτώσεις προβλημάτων η χρήση MAC είναι «περιττή» καθώς ο απλός έλεγχος Forward Checking, ο οποίος είναι «φθηνός» σε CPU time καταλήγει στην επίλυση πολύ γρήγορα. Σε κάποια άλλα προβλήματα ο «φθηνός» Forward Checking αδυνατεί να βρει γρήγορα αδιέξοδα (αφού διαγράφει λιγότερες τιμές από ότι ο MAC σε κάθε βήμα), με αποτέλεσμα να είναι χειρότερος χρονικά από τον MAC. Το ενδιαφέρον μας εστιάζεται στο να εξετάσουμε τι συμβαίνει για ενδιάμεσες καταστάσεις. Κάποια προβλήματα δηλαδή όπου η εφαρμογή Forward Checking δεν είναι αποδοτική λόγω της αδυναμίας γρήγορου εντοπισμού αδιεξόδων, αλλά ταυτόχρονα η εφαρμογή MAC μπορεί να είναι περιττή. Οι νέοι αλγόριθμοι οι οποίοι εξετάζονται είναι πιο «ισχυροί» από τον απλό Forward Checking και πιο «αδύναμοι» από τον MAC. Η «ισχύς» αναφέρεται στον αριθμό τιμών που μπορεί δυνητικά να διαγράψει ο αλγόριθμος από τα πεδία τιμών μελλοντικών μεταβλητών σε κάθε βήμα. Κατά συνέπεια, αφορά τον αριθμό επισκέψεων κόμβων. Είναι εύκολα αντιληπτό ότι για κάθε πρόβλημα η εφαρμογή MAC υπερκαλύπτει τον έλεγχο που θα γινόταν με εφαρμογή Forward Checking. Οι αλγόριθμοι οι οποίοι εξετάζονται παρακάτω εξασφαλίζουν σε κάθε βήμα περισσότερες διαγραφές τιμών από μελλοντικά πεδία τιμών από ότι ο Forward Checking και λιγότερες ή το πολύ ίσες με αυτές που θα επιτύχει η εφαρμογή MAC στο πρόβλημα Γενική Περιγραφή Αλγορίθμου clac Ο αλγόριθμος clac (custom level Arc consistency) αποτελεί μία υβριδική μέθοδο η οποία εφαρμόζει έλεγχο συνέπειας τόξου (Arc Consistency- AC) σε ένα υποδίκτυο του αρχικού προβλήματος. Συγκεκριμένα, ανάλογα με το επιθυμητό επίπεδο γειτονιάς, έστω i, που καθορίζεται από τον χρήστη, εφαρμόζεται πλήρης έλεγχος συνέπειας (AC- 3) για όλες τις μεταβλητές σε απόσταση i από την τρέχουσα μεταβλητή. Η απόσταση δύο μεταβλητών ορίζεται από το πλήθος των ακμών (περιορισμών) που μεσολαβούν μεταξύ τους στο γράφο περιορισμών. Ονομάζουμε αυτόν τον χώρο γειτονιά επιπέδου i. Σχηματικά, ένα απλό παράδειγμα που απεικονίζει τη διαφορά της προσέγγισης MAC, FC και clac για επίπεδο γειτονιάς 1 και 2. 22
23 c d c α b b β a a γ δ z 1. MAC 2. FC 3. clac clac- 2 Σχήμα 1.9 Η τρέχουσα μεταβλητή απεικονίζεται με μαύρο χρώμα. Ο αλγόριθμος MAC θα ελέγξει με την χρήση του AC-3 όλους τους περιορισμούς της τρέχουσας και σε περίπτωση που αλλοιωθεί το πεδίο τιμών μίας γειτονικής μεταβλητής, τότε αυτή θα προστεθεί στην στοίβα που αποθηκεύονται οι προς επίσκεψη κόμβοι. Σε επόμενο βήμα μπορεί να προστίθενται μεταβλητές που βρίσκονται σε οσοδήποτε μεγάλη απόσταση από την τρέχουσα. (Για παράδειγμα, μπορεί να προστεθεί η μεταβλητή α, και στη συνέχεια, κατά τον έλεγχό της να προστεθεί η β, και σε συνέχεια οι γ και δ, λόγω διαγραφής τιμών από την β). Ο αλγόριθμος Forward Checking θα ελέγξει όλους τους περιορισμούς της τρέχουσας μεταβλητής με τις γειτονικές της, όχι όμως και τους περιορισμούς μεταξύ των γειτονικών μεταβλητών της. Στο παράδειγμα του σχήματος, ο περιορισμός μεταξύ a και b δεν θα ελεγχθεί σε αυτόν τον κύκλο (σχ ). Αν επιλέξουμε να γίνεται έλεγχος σε γειτονιές μεγέθους 1, το υποδίκτυο στο οποίο θα εφαρμοστεί ο AC- 3 απεικονίζεται στο (σχ ). Σε κάθε κύκλο του αλγορίθμου, εξετάζεται εάν η προς εξέταση γειτονική μεταβλητή της μεταβλητής που μόλις βγήκε από την λίστα είναι επίσης γειτονική σε επίπεδο 1 με την τρέχουσα. Για παράδειγμα, έστω ότι ελέγχεται ο περιορισμός μεταξύ της τρέχουσας και της b. (H b είναι γειτονική με την τρέχουσα, οπότε ο έλεγχος του περιορισμού θα γίνει. Έστω τώρα ότι η μεταβλητή b χάνει κάποιες τιμές από το πεδίο της. Θα προστεθεί στην στοίβα με τις προς εξέταση μεταβλητές. Ας υποθέσουμε ότι η τρέχουσα μεταβλητή δε δημιουργεί αλλοιώσεις στα πεδία τιμών των υπόλοιπων γειτονικών μεταβλητών της, οπότε η επόμενη προς εξέταση μεταβλητή είναι η b. Ο περιορισμός μεταξύ της b και της a θα εξεταστεί, καθώς η a βρίσκεται σε απόσταση 1 από την τρέχουσα. Αντίθετα, ο περιορισμός της b με την c δεν θα εξεταστεί καθώς η c βρίσκεται σε απόσταση μεγαλύτερη από 1 από την τρέχουσα. Αντίστοιχα εφαρμόζουμε κατά απαίτηση του χρήστη για επίπεδο 2 έως n-1, όπου n ο αριθμός των μεταβλητών, ή (συνηθέστερα) έως επίπεδο i, με i το μέγιστο επίπεδο γειτόνων. Το μέγιστο επίπεδο γειτόνων δηλώνει την απόσταση των πιο απομακρυσμένων ζευγαριών μεταβλητών. Για παράδειγμα μέγιστο επίπεδο 3 σημαίνει ότι η μεγαλύτερη απόσταση ανάμεσα σε δύο οποιοσδήποτε μεταβλητές είναι ίση με 3. Μπορεί να υπάρχουν δηλαδή μεταβλητές που έχουν επίπεδο γειτόνων 1 (συνδέονται απ ευθείας με όλες τις άλλες μεταβλητές), κάποιες με επίπεδο 2 (χρειάζονται 2 hops για να συναντήσουν όλες τις μεταβλητές του προβλήματος) και κάποιες με επίπεδο Χαρακτηριστικά της μεθόδου clac 23
24 Το παράδειγμα μας δείχνει πως ο αλγόριθμος clac είναι σε κάθε περίπτωση ισχυρότερος του FC και ασθενέστερος ή ισοδύναμος του MAC (όπως είδαμε), για έλεγχο από επίπεδο 1 έως και επίπεδο ίσο με το μέγιστο επίπεδο γειτόνων -1. Στην περίπτωση της εφαρμογής του αλγορίθμου για επίπεδο 1 (clac-1), είμαστε βέβαιοι ότι θα ελεγχθούν περισσότεροι περιορισμοί από ότι με την εφαρμογή FC, καθώς εφαρμόζοντας τον AC-3 ελέγχονται όχι μόνο οι περιορισμοί μεταξύ τρέχουσας και των γειτονικών της, αλλά και όλοι οι περιορισμοί μεταξύ των γειτονικών τιμών μεταξύ τους. Όπως γίνεται αντιληπτό, μπορεί να υπάρχουν το πολύ n-1 επίπεδα γειτόνων. Η επίλυση με επιλογή εξέτασης γειτονιών επιπέδου n-1 ισοδυναμεί εξ ορισμού με εφαρμογή MAC. Σε όλα τα πειράματα ελέγχεται εάν το επιθυμητό επίπεδο γειτονιάς από τον χρήστη οδηγεί, τελικά, σε επίλυση με έλεγχο συνέπειας σε υποπρόβλημα ίδιο με το αρχικό (ισοδύναμο με ΜΑC). Για παράδειγμα εάν το μεγαλύτερο επίπεδο γειτονιάς είναι 7 και ο χρήστης επιλέξει ο έλεγχος να γίνεται σε γειτονιές μεγέθους 7, τότε η επίλυση είναι ουσιαστικά ίδια με την εφαρμογή MAC. Στην περίπτωση του παραδείγματος, το καθολικό μέγιστο επίπεδο γειτόνων είναι ίσο με 5. Εάν επιλέξουμε να γίνεται έλεγχος για γειτονιές επιπέδου 4, θα υπάρξουν περιπτώσεις κατά την διαδικασία επίλυσης όπου ο έλεγχος θα είναι ισοδύναμος με τον MAC και περιπτώσεις όπου ένα μέρος του δικτύου δεν θα ελέγχεται για συνέπεια τόξου. Εάν η τρέχουσα μεταβλητή είναι η z (σχ ) και το επίπεδο 4, τότε ο περιορισμός μεταξύ c και d δεν θα εξεταστεί. Εάν όμως η τρέχουσα είναι η προεπιλεγμένη για το παράδειγμά μας (κόμβος με μαύρο χρώμα), τότε ο έλεγχος είναι ίδιος με την εφαρμογή πλήρους MAC για αυτόν τον κύκλο. Αφού το μέγιστο επίπεδο γειτόνων για την μεταβλητή αυτή είναι 3 και ελέγχονται όλοι οι περιορισμοί σε επίπεδο 4, ελέγχονται στην ουσία όλοι οι περιορισμοί του αρχικού προβλήματος. 1.3 Ευριστικές Συναρτήσεις (heuristics) Οι ευριστικές συναρτήσεις χρησιμοποιούνται για την βελτίωση της διαδικασίας επιλογής της επόμενης κάθε φορά μεταβλητής ή/και τιμής προς εξέταση κατά την επίλυση ενός προβλήματος. Στην παρούσα εργασία έγινε χρήση heuristics για επιλογή μεταβλητών. Η επιλογή τιμών ακολουθεί λεξικογραφική διάταξη, δηλαδή η επιλογή της τιμής γίνεται κατά αύξουσα διάταξη. Γενικά είναι επιθυμητό να βρούμε γρήγορα τα πιθανά αδιέξοδα σε ένα πρόβλημα. Εάν επιλέγουμε μεταβλητές που έχουν μεγαλύτερη πιθανότητα να μειώσουν τα πεδία τιμών των υπόλοιπων μεταβλητών, το δίκτυό μας θα γίνει πολύ πιο περιορισμένο και κατά συνέπεια θα κερδίσουμε χρόνο κατά τον έλεγχο των επόμενων μεταβλητών. Επίσης το πιθανό συμπέρασμα ότι το πρόβλημα είναι άλυτο θα αποδειχθεί συντομότερα (λόγω ακριβώς της γρήγορης εξάλειψης πεδίων τιμών) [14][9]. Τα heuristics που προσπαθούν να πετύχουν γρήγορο εντοπισμό αδιεξόδων βασίζονται σε χαρακτηριστικά του δικτύου του προβλήματος. Για παράδειγμα, λαμβάνουν υπ όψιν το μέγεθος του πεδίου τιμών, ή τον αριθμό των περιορισμών στους οποίους μετέχει η κάθε μεταβλητή, ή - συνηθέστερα- έναν συνδυασμό αυτών. Υπάρχουν ευριστικές συναρτήσεις που υπολογίζουν δυναμικά κάποιες πληροφορίες, όπως για παράδειγμα τον τρέχοντα αριθμό έγκυρων τιμών στα πεδία τιμών. Οι τελευταίες ονομάζονται δυναμικές ευριστικές συναρτήσεις (Dynamic Variable Ordering heuristics). Οι δύο ευριστικές συναρτήσεις που χρησιμοποιήθηκαν είναι οι εξής. 24
25 1.3.1 DOM/DEG [15] Η συνάρτηση αυτή διαιρεί τον αριθμό των έγκυρων τιμών (στον τρέχων κύκλο) με τον αριθμό των περιορισμών στους οποίους συμμετέχει η κάθε μεταβλητή. Η ποσότητα αυτή υπολογίζεται για όλες τις μελλοντικές μεταβλητές και η μεταβλητή που επιλέγεται είναι εκείνη για την οποία η ευριστική συνάρτηση επιστρέφει την χαμηλότερη τιμή. Με αυτόν τον τρόπο προσπαθούμε να επιλέξουμε μεταβλητές που συνδυάζουν μικρό πεδίο τιμών και συμμετοχή σε πολλούς περιορισμούς. Ο λόγος που επιθυμούμε την ελαχιστοποίηση της ποσότητας αυτής είναι ο εξής. Όσο λιγότερες έγκυρες τιμές έχει μία μεταβλητή, τόσο πιο πιθανό είναι να οδηγήσει σε αδιέξοδο, καθώς σε πιθανή διαγραφή της τρέχουσας τιμής θα μένουν λίγες μέχρι την πιθανή εξάλειψη του πεδίου της. Οι δυνατές επιλογές για υποστήριξη θα είναι περιορισμένες σε σχέση με μια μεταβλητή που έχει περισσότερες διαθέσιμες τιμές. Όσο μεγαλύτερος είναι ο αριθμός των μεταβλητών με τις οποίες έχει περιορισμό μία μεταβλητή (ο παρανομαστής) τόσο πιο «περιοριστική» είναι, δηλαδή έχει περισσότερες πιθανότητες να προκαλέσει πολλές αλλαγές πεδίων τιμών λόγω διαγραφών σε περισσότερες μεταβλητές σε έναν κύκλο H_k_dom/futdeg_x [2] Αυτή η ευριστική συνάρτηση αποτελεί την γενικευμένη μορφή (για k επίπεδα) της ευριστικής συνάρτησης όπως περιγράφεται στο [2]. Η συνάρτηση αυτή επιλέγει την επόμενη μεταβλητή βάσει πληροφορίας για την ίδια την μεταβλητή καθώς και για τις μεταβλητές σε απόσταση k από αυτήν. Συγκεκριμένα υπολογίζει μία συνδυασμένη μορφή της DOM/DEG. Η αναδρομική μορφή της για αριθμό επιπέδου k, πλήθος τιμών και περιορισμών dom και futdeg αντίστοιχα είναι H ( k, dom / fut deg) ( a( X ) H X j Γ ( X i ) i ( k 1) = 2 Γ( X i ) ( X j )) Ο πίνακας Γ(i) κρατά όλους τους γείτονες για κάθε i μεταβλητή (αντίστοιχο του deg). Η D( X i ) ποσότητα α(χi ) είναι ίση με, δηλαδή με την τιμή DOM/DEG της τρέχουσας Γ( X ) i μεταβλητής. Αν επιλέξουμε μηδενικό επίπεδο βάθους, θα λάβουμε ακριβώς αυτήν την ποσότητα σαν αποτέλεσμα. Για επίπεδο 1, για παράδειγμα, θα λάβουμε την ποσότητα H (1, dom / fut deg) = D( X i ) Γ( X X j Γ ( X i ) i ) 3 D( X Γ( X j j ) ) 25
26 Η ευριστική συνάρτηση υπολογίζει για όλες τις μεταβλητές έως και k επίπεδα μακριά από την τρέχουσα αυτήν την παραλλαγή της DOM/DEG, δίνοντας βάρος και στην αρχική ποσότητα αυτής. Για παράδειγμα, για k = 1 η ποσότητα που υπολογίζεται είναι: η ποσότητα dom[τρέχουσας μεταβλητής]/ deg[τρέχουσας μεταβλητής]^3 επί το άθροισμα των (dom/deg) ποσοτήτων όλων των γειτόνων της τρέχουσας μεταβλητής. Για επίπεδο k = 2, θα υπολογίσει την ποσότητα dom[τρέχουσας μεταβλητής]/ deg[τρέχουσας μεταβλητής]^3 επί το άθροισμα της ποσότητας του H 1 για όλους τους γείτονες της τρέχουσας. (Θα φτάσει να υπολογίσει δηλαδή τις τιμές dom/deg των μεταβλητών που είναι γειτονικές των γειτονικών της τρέχουσας). Ουσιαστικά τα heuristics που προκύπτουν, όταν ελέγχουν τις μεταβλητές για να επιλέξουν την επόμενη που θα πάρει τιμή λαμβάνουν υπ όψιν πληροφορία σχετικά με τα πεδία τιμών και το πλήθος των περιορισμών και των γειτονικών (σε απόσταση k) μεταβλητών. Έτσι προσπαθούν να κάνουν μια πιο ακριβή πρόβλεψη για το ποια είναι η πιο περιοριστική μεταβλητή. Η διαρρύθμιση των κεφαλαίων που ακολουθούν έχει ως εξής. Στο κεφάλαιο 2 γίνεται η παρουσίαση της παρούσης μελέτης και της υλοποίησης του προγράμματος. Παρουσιάζεται η λειτουργία και η δομή των αλγορίθμων και των ευριστικών συναρτήσεων που χρησιμοποιήθηκαν. Στο κεφάλαιο 3 παρουσιάζονται και αναλύονται τα αποτελέσματα των πειραμάτων και στο κεφάλαιο 4 τα συμπεράσματα και η μελλοντική μελέτη. 26
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Ικανοποίηση Περιορισμών Κατηγορία προβλημάτων στα οποία είναι γνωστές μερικές
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Ικανοποίηση Περιορισμών Κατηγορία προβλημάτων στα οποία είναι γνωστές μερικές
Επίλυση Προβλημάτων 1
 Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Κεφάλαιο 6. Ικανοποίηση Περιορισµών. Τεχνητή Νοηµοσύνη - Β' Έκδοση. Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η.
 Κεφάλαιο 6 Ικανοποίηση Περιορισµών Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Ικανοποίηση Περιορισµών Ένα πρόβληµα ικανοποίησης περιορισµών (constraint
Κεφάλαιο 6 Ικανοποίηση Περιορισµών Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Ικανοποίηση Περιορισµών Ένα πρόβληµα ικανοποίησης περιορισµών (constraint
ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ. Ενότητα 6: Προβλήματα ικανοποίησης περιορισμών. Ρεφανίδης Ιωάννης Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 6: Προβλήματα ικανοποίησης περιορισμών Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα 6: Προβλήματα ικανοποίησης περιορισμών Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΙΚΑΝΟΠΟΙΗΣΗ ΠΕΡΙΟΡΙΣΜΩΝ
 ΙΚΑΝΟΠΟΙΗΣΗ ΠΕΡΙΟΡΙΣΜΩΝ (ΜΕ ΒΑΣΗ ΤΟ ΚΕΦ. 6 ΤΟΥ ΒΙΒΛΙΟΥ «ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ» ΤΩΝ ΒΛΑΧΑΒΑ, ΚΕΦΑΛΑ, ΒΑΣΙΛΕΙΑ Η, ΚΟΚΚΟΡΑ & ΣΑΚΕΛΛΑΡΙΟΥ) Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ ΠΡΟΒΛΗΜΑΤΑ ΙΚΑΝΟΠΟΙΗΣΗΣ ΠΕΡΙΟΡΙΣΜΩΝ Είναι γνωστές µερικές
ΙΚΑΝΟΠΟΙΗΣΗ ΠΕΡΙΟΡΙΣΜΩΝ (ΜΕ ΒΑΣΗ ΤΟ ΚΕΦ. 6 ΤΟΥ ΒΙΒΛΙΟΥ «ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ» ΤΩΝ ΒΛΑΧΑΒΑ, ΚΕΦΑΛΑ, ΒΑΣΙΛΕΙΑ Η, ΚΟΚΚΟΡΑ & ΣΑΚΕΛΛΑΡΙΟΥ) Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ ΠΡΟΒΛΗΜΑΤΑ ΙΚΑΝΟΠΟΙΗΣΗΣ ΠΕΡΙΟΡΙΣΜΩΝ Είναι γνωστές µερικές
(50 μον.) πάντοτε Διατυπώστε
 ΑΣΚΗΣΗ 1 Α. (50 μον.) Σας δίνεται ο ακόλουθος γράφος, το οποίο πρέπει να χρωματίσετε χρησιμοποιώντας 3 χρώματα (R,G,B), ώστε δύο γειτονικές κορυφές να μην έχουν το ίδιο χρώμα. Θεωρείστε ότι ο χρωματισμός
ΑΣΚΗΣΗ 1 Α. (50 μον.) Σας δίνεται ο ακόλουθος γράφος, το οποίο πρέπει να χρωματίσετε χρησιμοποιώντας 3 χρώματα (R,G,B), ώστε δύο γειτονικές κορυφές να μην έχουν το ίδιο χρώμα. Θεωρείστε ότι ο χρωματισμός
Μεταβλητες: Q, NSW, V, T, SA, WA, NT. Πεδίο Ορισμού: Για κάθε μεταβλητη το ίδιο. D i ={R, G, B} όπου i= Q, NSW,., NT.
 1. Στην άσκηση μας, μας έχει δωθεί ένας γράφος, ο οποίος αντιπροσωπεύει ένα χάρτη και μάλιστα αυτόν της Αυστραλίας. Στον γράφο αυτό υπάρχουν και κόμβοι, οι οποίοι αφορούν με τη σειρά τους τις διάφορες
1. Στην άσκηση μας, μας έχει δωθεί ένας γράφος, ο οποίος αντιπροσωπεύει ένα χάρτη και μάλιστα αυτόν της Αυστραλίας. Στον γράφο αυτό υπάρχουν και κόμβοι, οι οποίοι αφορούν με τη σειρά τους τις διάφορες
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems
 HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems Ημερομηνία Παράδοσης: 0/1/017 την ώρα του μαθήματος ή με email: mkarabin@csd.uoc.gr Γενικές Οδηγίες α) Επιτρέπεται η αναζήτηση στο Internet και στην βιβλιοθήκη
HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems Ημερομηνία Παράδοσης: 0/1/017 την ώρα του μαθήματος ή με email: mkarabin@csd.uoc.gr Γενικές Οδηγίες α) Επιτρέπεται η αναζήτηση στο Internet και στην βιβλιοθήκη
===========================================================================
 =========================================================================== Α. (50 µον.) Σας δίνεται ο ακόλουθος γράφος, το οποίο πρέπει να χρωµατίσετε χρησιµοποιώντας 4 χρώµατα (R,G,B,Υ), ώστε δύο γειτονικές
=========================================================================== Α. (50 µον.) Σας δίνεται ο ακόλουθος γράφος, το οποίο πρέπει να χρωµατίσετε χρησιµοποιώντας 4 χρώµατα (R,G,B,Υ), ώστε δύο γειτονικές
Ασκήσεις μελέτης της 4 ης διάλεξης. ), για οποιοδήποτε μονοπάτι n 1
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Πρόβληµα ικανοποίησης περιορισµών
 Προβλήµατα ικανοποίησης περιορισµών Constraint Satisfaction Problems Πρόβληµα ικανοποίησης περιορισµών Μεταβλητές: X 1, X 2,, X n, Πεδία ορισµού: D 1, D 2, D n Περιορισµοί: C 1, C 2,, C m Ανάθεση τιµών:
Προβλήµατα ικανοποίησης περιορισµών Constraint Satisfaction Problems Πρόβληµα ικανοποίησης περιορισµών Μεταβλητές: X 1, X 2,, X n, Πεδία ορισµού: D 1, D 2, D n Περιορισµοί: C 1, C 2,, C m Ανάθεση τιµών:
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Λογική. Δημήτρης Πλεξουσάκης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: Μελέτη παραλλαγών του αλγόριθμου minconflicts για προβλήματα ικανοποίησης περιορισμών ΒΑΡΚΑΣ ΙΩΑΝΝΗΣ,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: Μελέτη παραλλαγών του αλγόριθμου minconflicts για προβλήματα ικανοποίησης περιορισμών ΒΑΡΚΑΣ ΙΩΑΝΝΗΣ,
Τεχνητή Νοημοσύνη. 4η διάλεξη ( ) Ίων Ανδρουτσόπουλος.
 Τεχνητή Νοημοσύνη 4η διάλεξη (2016-17) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται κυρίως στα βιβλία Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β.
Τεχνητή Νοημοσύνη 4η διάλεξη (2016-17) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται κυρίως στα βιβλία Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β.
Αντισταθμιστική ανάλυση
 Αντισταθμιστική ανάλυση Θεωρήστε έναν αλγόριθμο Α που χρησιμοποιεί μια δομή δεδομένων Δ : Κατά τη διάρκεια εκτέλεσης του Α η Δ πραγματοποιεί μία ακολουθία από πράξεις. Παράδειγμα: Θυμηθείτε το πρόβλημα
Αντισταθμιστική ανάλυση Θεωρήστε έναν αλγόριθμο Α που χρησιμοποιεί μια δομή δεδομένων Δ : Κατά τη διάρκεια εκτέλεσης του Α η Δ πραγματοποιεί μία ακολουθία από πράξεις. Παράδειγμα: Θυμηθείτε το πρόβλημα
Επίλυση προβληµάτων. Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης
 Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Ασκήσεις μελέτης της 6 ης διάλεξης
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 6 ης διάλεξης 6.1. (α) Το mini-score-3 παίζεται όπως το score-4,
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 6 ης διάλεξης 6.1. (α) Το mini-score-3 παίζεται όπως το score-4,
ΗΥ180: Λογική Διδάσκων: Δημήτρης Πλεξουσάκης. Φροντιστήριο 8 Επίλυση για Horn Clauses Λογικός Προγραμματισμός Τετάρτη 9 Μαΐου 2012
 ΗΥ180: Λογική Διδάσκων: Δημήτρης Πλεξουσάκης Φροντιστήριο 8 Επίλυση για Horn Clauses Λογικός Προγραμματισμός Τετάρτη 9 Μαΐου 2012 Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει
ΗΥ180: Λογική Διδάσκων: Δημήτρης Πλεξουσάκης Φροντιστήριο 8 Επίλυση για Horn Clauses Λογικός Προγραμματισμός Τετάρτη 9 Μαΐου 2012 Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει
Προγραμματισμός Ι (ΗΥ120)
 Προγραμματισμός Ι (ΗΥ120) Διάλεξη 17: Λύση Προβλημάτων με Αναδρομή Οι πύργοι του Hanoi Δίνεται ένα χώρος με τρεις θέσεις αποθήκευσης. Δίνεται μια στοίβα από Ν πλάκες σε φθίνον μέγεθος, σε μια από τις τρεις
Προγραμματισμός Ι (ΗΥ120) Διάλεξη 17: Λύση Προβλημάτων με Αναδρομή Οι πύργοι του Hanoi Δίνεται ένα χώρος με τρεις θέσεις αποθήκευσης. Δίνεται μια στοίβα από Ν πλάκες σε φθίνον μέγεθος, σε μια από τις τρεις
Αλγόριθµοι CSPs Κώδικας. Μάθηµα Τεχνητής Νοηµοσύνης ΥΣ02 Χειµερινό εξάµηνο
 Αλγόριθµοι CSPs Κώδικας Μάθηµα Τεχνητής Νοηµοσύνης ΥΣ02 Χειµερινό εξάµηνο 2008-2009 CSPLIB Βιβλιοθήκη µε ρουτίνες για την επίλυση δυαδικών προβληµάτων ικανοποίησης περιορισµών http://ai.uwaterloo.ca/~vanbeek/software.h
Αλγόριθµοι CSPs Κώδικας Μάθηµα Τεχνητής Νοηµοσύνης ΥΣ02 Χειµερινό εξάµηνο 2008-2009 CSPLIB Βιβλιοθήκη µε ρουτίνες για την επίλυση δυαδικών προβληµάτων ικανοποίησης περιορισµών http://ai.uwaterloo.ca/~vanbeek/software.h
Ευχαριστίες. Τέλος θα ήθελα να ευχαριστήσω όλους όσους ήταν δίπλα μου όλα αυτά τα χρόνια και με βοήθησαν να πραγματοποιήσω τους στόχους μου.
 Ευχαριστίες Θα ήθελα να ευχαριστήσω τον καθηγητή μου, Δρ Γιάννη Δημόπουλο, ο οποίος ήταν ο επιβλέπον καθηγητής της διπλωματικής αυτής εργασίας και με βοήθησε ώστε να ολοκληρωθεί με επιτυχία. Επίσης θα
Ευχαριστίες Θα ήθελα να ευχαριστήσω τον καθηγητή μου, Δρ Γιάννη Δημόπουλο, ο οποίος ήταν ο επιβλέπον καθηγητής της διπλωματικής αυτής εργασίας και με βοήθησε ώστε να ολοκληρωθεί με επιτυχία. Επίσης θα
Πληρότητα της μεθόδου επίλυσης
 Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει ένα αρνητικό γράμμα, τότε το σύνολο είναι ικανοποιήσιμο. Άρα για να είναι μη-ικανοποιήσιμο, θα πρέπει να περιέχει τουλάχιστον
Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει ένα αρνητικό γράμμα, τότε το σύνολο είναι ικανοποιήσιμο. Άρα για να είναι μη-ικανοποιήσιμο, θα πρέπει να περιέχει τουλάχιστον
Κεφάλαιο 1 Συστήματα γραμμικών εξισώσεων
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
1.3 Συστήματα γραμμικών εξισώσεων με ιδιομορφίες
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών θα πρέπει να
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών θα πρέπει να
Για παράδειγμα η αρχική και η τελική κατάσταση αναπαριστώνται ως εξής: (ένα λίτρο)
 8 1 η ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Απάντηση 1ης άσκησης Κατάσταση (κόμβοι): Αναπαριστούμε μια κατάσταση του προβλήματος με ένα διατεταγμένο ζεύγος (X,Y) όπου X είναι τα λίτρα στο βάζο Α (χωρητικότητα
8 1 η ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Απάντηση 1ης άσκησης Κατάσταση (κόμβοι): Αναπαριστούμε μια κατάσταση του προβλήματος με ένα διατεταγμένο ζεύγος (X,Y) όπου X είναι τα λίτρα στο βάζο Α (χωρητικότητα
Θεωρήστε ένα puzzle (παιχνίδι σπαζοκεφαλιάς) με την ακόλουθη αρχική διαμόρφωση : b b b w w w e
 Άσκηση 1 Θεωρήστε ένα puzzle (παιχνίδι σπαζοκεφαλιάς) με την ακόλουθη αρχική διαμόρφωση : b b b w w w e Υπάρχουν τρία μαύρα τετραγωνάκια (b), τρία άσπρα (w) και ένα κενό (e). Η σπαζοκεφαλιά έχει τις ακόλουθες
Άσκηση 1 Θεωρήστε ένα puzzle (παιχνίδι σπαζοκεφαλιάς) με την ακόλουθη αρχική διαμόρφωση : b b b w w w e Υπάρχουν τρία μαύρα τετραγωνάκια (b), τρία άσπρα (w) και ένα κενό (e). Η σπαζοκεφαλιά έχει τις ακόλουθες
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Λύσεις 2η σειράς ασκήσεων Προθεσμία παράδοσης: 18 Μαίου 2015 Πρόβλημα 1. (14
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Λύσεις 2η σειράς ασκήσεων Προθεσμία παράδοσης: 18 Μαίου 2015 Πρόβλημα 1. (14
Ακέραιος Γραμμικός Προγραμματισμός
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Δομές Δεδομένων & Αλγόριθμοι
 Θέματα Απόδοσης Αλγορίθμων 1 Η Ανάγκη για Δομές Δεδομένων Οι δομές δεδομένων οργανώνουν τα δεδομένα πιο αποδοτικά προγράμματα Πιο ισχυροί υπολογιστές πιο σύνθετες εφαρμογές Οι πιο σύνθετες εφαρμογές απαιτούν
Θέματα Απόδοσης Αλγορίθμων 1 Η Ανάγκη για Δομές Δεδομένων Οι δομές δεδομένων οργανώνουν τα δεδομένα πιο αποδοτικά προγράμματα Πιο ισχυροί υπολογιστές πιο σύνθετες εφαρμογές Οι πιο σύνθετες εφαρμογές απαιτούν
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 1: Εισαγωγή- Χαρακτηριστικά Παραδείγματα Αλγορίθμων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 1: Εισαγωγή- Χαρακτηριστικά Παραδείγματα Αλγορίθμων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α :
ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α :
Εφαρμόζονται σε προβλήματα στα οποία δεν υπάρχει πληροφορία που να επιτρέπει την αξιολόγηση των καταστάσεων του χώρου αναζήτησης.
 Ανάλογα με το αν ένας αλγόριθμος αναζήτησης χρησιμοποιεί πληροφορία σχετική με το πρόβλημα για να επιλέξει την επόμενη κατάσταση στην οποία θα μεταβεί, οι αλγόριθμοι αναζήτησης χωρίζονται σε μεγάλες κατηγορίες,
Ανάλογα με το αν ένας αλγόριθμος αναζήτησης χρησιμοποιεί πληροφορία σχετική με το πρόβλημα για να επιλέξει την επόμενη κατάσταση στην οποία θα μεταβεί, οι αλγόριθμοι αναζήτησης χωρίζονται σε μεγάλες κατηγορίες,
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 1 Εισαγωγή 1 / 14 Δομές Δεδομένων και Αλγόριθμοι Δομή Δεδομένων Δομή δεδομένων είναι ένα σύνολο αποθηκευμένων
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 1 Εισαγωγή 1 / 14 Δομές Δεδομένων και Αλγόριθμοι Δομή Δεδομένων Δομή δεδομένων είναι ένα σύνολο αποθηκευμένων
Ενότητες 3 & 4: Δένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις
 Ενότητες 3 & 4: Δένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις Άσκηση 1 Γράψτε μία αναδρομική συνάρτηση που θα παίρνει ως παράμετρο ένα δείκτη στη ρίζα ενός δυαδικού δένδρου και θα επιστρέφει το βαθμό του
Ενότητες 3 & 4: Δένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις Άσκηση 1 Γράψτε μία αναδρομική συνάρτηση που θα παίρνει ως παράμετρο ένα δείκτη στη ρίζα ενός δυαδικού δένδρου και θα επιστρέφει το βαθμό του
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
K24 Ψηφιακά Ηλεκτρονικά 6: Πολυπλέκτες/Αποπολυπλέκτες
 K24 Ψηφιακά Ηλεκτρονικά 6: Πολυπλέκτες/Αποπολυπλέκτες TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 4 Λειτουργία Πολυπλέκτης (Mul plexer) Ο
K24 Ψηφιακά Ηλεκτρονικά 6: Πολυπλέκτες/Αποπολυπλέκτες TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 4 Λειτουργία Πολυπλέκτης (Mul plexer) Ο
HY Λογική Διδάσκων: Δ. Πλεξουσάκης Εαρινό Εξάμηνο. Φροντιστήριο 6
 HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Εαρινό Εξάμηνο 2015-2016 Φροντιστήριο 6 Α) ΘΕΩΡΙΑ Μέθοδος Επίλυσης (Resolution) Στη μέθοδο της επίλυσης αποδεικνύουμε την ικανοποιησιμότητα ενός συνόλου προτάσεων,
HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Εαρινό Εξάμηνο 2015-2016 Φροντιστήριο 6 Α) ΘΕΩΡΙΑ Μέθοδος Επίλυσης (Resolution) Στη μέθοδο της επίλυσης αποδεικνύουμε την ικανοποιησιμότητα ενός συνόλου προτάσεων,
Ακέραιος Γραμμικός Προγραμματισμός
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος Γραμμικός Προγραμματισμός Όταν για
Αριθμητική Ανάλυση & Εφαρμογές
 Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Ψευδοκώδικας. November 7, 2011
 Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Διακριτά Μαθηματικά. Ενότητα 4: Εισαγωγή / Σύνολα
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Διακριτά Μαθηματικά Ενότητα 4: Εισαγωγή / Σύνολα Αν. Καθηγητής Κ. Στεργίου e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Διακριτά Μαθηματικά Ενότητα 4: Εισαγωγή / Σύνολα Αν. Καθηγητής Κ. Στεργίου e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
Εισαγωγή στην Αριθμητική Ανάλυση
 Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
3η Σειρά Γραπτών Ασκήσεων
 1/48 3η Σειρά Γραπτών Ασκήσεων Αλγόριθμοι και Πολυπλοκότητα ΣΗΜΜΥ, Εθνικό Μετσόβιο Πολυτεχνείο 2/48 1 Άσκηση 1: Πομποί και Δέκτες 2 Άσκηση 2: Διακοπές στην Ικαρία 3 Άσκηση 3: Επιστροφή στη Γη 4 Άσκηση
1/48 3η Σειρά Γραπτών Ασκήσεων Αλγόριθμοι και Πολυπλοκότητα ΣΗΜΜΥ, Εθνικό Μετσόβιο Πολυτεχνείο 2/48 1 Άσκηση 1: Πομποί και Δέκτες 2 Άσκηση 2: Διακοπές στην Ικαρία 3 Άσκηση 3: Επιστροφή στη Γη 4 Άσκηση
Εργαστήριο 6 ο 7 ο / Ερωτήματα Ι
 Εργαστήριο 6 ο 7 ο / Ερωτήματα Ι Απλά ερωτήματα Επιλογής Ερωτήματα με Ενώσεις πινάκων Ερωτήματα με Παραμετρικά Κριτήρια Ερωτήματα με Υπολογιζόμενα πεδία Απλά ερωτήματα Επιλογής Τα Ερωτήματα μας επιτρέπουν
Εργαστήριο 6 ο 7 ο / Ερωτήματα Ι Απλά ερωτήματα Επιλογής Ερωτήματα με Ενώσεις πινάκων Ερωτήματα με Παραμετρικά Κριτήρια Ερωτήματα με Υπολογιζόμενα πεδία Απλά ερωτήματα Επιλογής Τα Ερωτήματα μας επιτρέπουν
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 9 P vs NP 1 / 13 Δυσκολία επίλυσης υπολογιστικών προβλημάτων Κάποια προβλήματα είναι εύκολα να λυθούν με
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 9 P vs NP 1 / 13 Δυσκολία επίλυσης υπολογιστικών προβλημάτων Κάποια προβλήματα είναι εύκολα να λυθούν με
Rule Based systems Συστήματα Βασισμένα σε κανόνες
 Rule Based systems Συστήματα Βασισμένα σε κανόνες Τμήματα ενός έμπειρου συστήματος βασισμένου σε κανόνες Βάση Γνώσης (Κανόνες) Μηχανισμός Εξαγωγής Συμπερασμάτων Χώρος Εργασίας (Γεγονότα) Μηχανισμός Επεξήγησης
Rule Based systems Συστήματα Βασισμένα σε κανόνες Τμήματα ενός έμπειρου συστήματος βασισμένου σε κανόνες Βάση Γνώσης (Κανόνες) Μηχανισμός Εξαγωγής Συμπερασμάτων Χώρος Εργασίας (Γεγονότα) Μηχανισμός Επεξήγησης
Κατανεμημένα Συστήματα Ι
 Συναίνεση χωρίς την παρουσία σφαλμάτων Κατανεμημένα Συστήματα Ι 4η Διάλεξη 27 Οκτωβρίου 2016 Παναγιώτα Παναγοπούλου Κατανεμημένα Συστήματα Ι 4η Διάλεξη 1 Συναίνεση χωρίς την παρουσία σφαλμάτων Προηγούμενη
Συναίνεση χωρίς την παρουσία σφαλμάτων Κατανεμημένα Συστήματα Ι 4η Διάλεξη 27 Οκτωβρίου 2016 Παναγιώτα Παναγοπούλου Κατανεμημένα Συστήματα Ι 4η Διάλεξη 1 Συναίνεση χωρίς την παρουσία σφαλμάτων Προηγούμενη
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΠΙΠΕΔΟ ΣΠΟΥΔΩΝ Προπτυχιακό ΚΩΔΙΚΟΣ ΜΑΘΗΜΑΤΟΣ GD2670
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΠΙΠΕΔΟ ΣΠΟΥΔΩΝ Προπτυχιακό ΚΩΔΙΚΟΣ ΜΑΘΗΜΑΤΟΣ GD2670 ΕΞΑΜΗΝΟ ΣΠΟΥΔΩΝ Έκτο ΤΙΤΛΟΣ ΜΑΘΗΜΑΤΟΣ Δομές Δεδομένων και Αλγόριθμοι ΑΥΤΟΤΕΛΕΙΣ ΔΙΔΑΚΤΙΚΕΣ
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΠΙΠΕΔΟ ΣΠΟΥΔΩΝ Προπτυχιακό ΚΩΔΙΚΟΣ ΜΑΘΗΜΑΤΟΣ GD2670 ΕΞΑΜΗΝΟ ΣΠΟΥΔΩΝ Έκτο ΤΙΤΛΟΣ ΜΑΘΗΜΑΤΟΣ Δομές Δεδομένων και Αλγόριθμοι ΑΥΤΟΤΕΛΕΙΣ ΔΙΔΑΚΤΙΚΕΣ
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { R η R είναι μια κανονική έκφραση η οποία παράγει μια μη πεπερασμένη γλώσσα} (β) { G η G είναι μια CFG η οποία
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { R η R είναι μια κανονική έκφραση η οποία παράγει μια μη πεπερασμένη γλώσσα} (β) { G η G είναι μια CFG η οποία
4.3 Ορθότητα και Πληρότητα
 4.3 Ορθότητα και Πληρότητα Συστήματα αποδείξεων όπως η μορφολογική παραγωγή και η κατασκευή μοντέλων χρησιμοποιούνται για να δείξουμε την εγκυρότητα εξαγωγών συμπερασμάτων. Ένα σύστημα αποδείξεων μπορεί
4.3 Ορθότητα και Πληρότητα Συστήματα αποδείξεων όπως η μορφολογική παραγωγή και η κατασκευή μοντέλων χρησιμοποιούνται για να δείξουμε την εγκυρότητα εξαγωγών συμπερασμάτων. Ένα σύστημα αποδείξεων μπορεί
Το Πρόβλημα του Περιοδεύοντος Πωλητή - The Travelling Salesman Problem
 Το Πρόβλημα του Περιοδεύοντος Πωλητή - The Travelling Salesman Problem Έλενα Ρόκου Μεταδιδακτορική Ερευνήτρια ΕΜΠ Κηρυττόπουλος Κωνσταντίνος Επ. Καθηγητής ΕΜΠ Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Το Πρόβλημα του Περιοδεύοντος Πωλητή - The Travelling Salesman Problem Έλενα Ρόκου Μεταδιδακτορική Ερευνήτρια ΕΜΠ Κηρυττόπουλος Κωνσταντίνος Επ. Καθηγητής ΕΜΠ Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
HY Λογική Διδάσκων: Δ. Πλεξουσάκης
 HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει ένα αρνητικό γράμμα, τότε το σύνολο είναι ικανοποιήσιμο. Άρα για να είναι μη-ικανοποιήσιμο,
HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει ένα αρνητικό γράμμα, τότε το σύνολο είναι ικανοποιήσιμο. Άρα για να είναι μη-ικανοποιήσιμο,
Αλγόριθµοι Οπισθοδρόµησης
 Αλγόριθµοι Οπισθοδρόµησης Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: Η οπισθοδρόµηση στο σχεδιασµό αλγορίθµων Το πρόβληµα των σταθερών γάµων και ο αλγόριθµος των Gale-Shapley Το πρόβληµα
Αλγόριθµοι Οπισθοδρόµησης Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: Η οπισθοδρόµηση στο σχεδιασµό αλγορίθµων Το πρόβληµα των σταθερών γάµων και ο αλγόριθµος των Gale-Shapley Το πρόβληµα
Pascal, απλοί τύποι, τελεστές και εκφράσεις
 Pascal, απλοί τύποι, τελεστές και εκφράσεις 15 Νοεμβρίου 2011 1 Γενικά Στην standard Pascal ορίζονται τέσσερις βασικοί τύποι μεταβλητών: integer: Παριστάνει ακέραιους αριθμούς από το -32768 μέχρι και το
Pascal, απλοί τύποι, τελεστές και εκφράσεις 15 Νοεμβρίου 2011 1 Γενικά Στην standard Pascal ορίζονται τέσσερις βασικοί τύποι μεταβλητών: integer: Παριστάνει ακέραιους αριθμούς από το -32768 μέχρι και το
ΕΘΝΙΚΟ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΕΘΝΙΚΟ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Καθηγητής : Κουμπαράκης Μανόλης Ημ/νία παράδοσης: 11/01/2011 Ονομ/μο φοιτητή : Μπεγέτης Νικόλαος Α.Μ.:
ΕΘΝΙΚΟ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Καθηγητής : Κουμπαράκης Μανόλης Ημ/νία παράδοσης: 11/01/2011 Ονομ/μο φοιτητή : Μπεγέτης Νικόλαος Α.Μ.:
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων
 K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ»
 ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ» Νικόλαος Μπαλκίζας 1. ΕΙΣΑΓΩΓΗ Σκοπός του σχεδίου μαθήματος είναι να μάθουν όλοι οι μαθητές της τάξης τις έννοιες της ισοδυναμίας των κλασμάτων,
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ» Νικόλαος Μπαλκίζας 1. ΕΙΣΑΓΩΓΗ Σκοπός του σχεδίου μαθήματος είναι να μάθουν όλοι οι μαθητές της τάξης τις έννοιες της ισοδυναμίας των κλασμάτων,
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο
 ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2010-2011 Πρώτη Σειρά Ασκήσεων (20% του συνολικού βαθμού στο μάθημα, Άριστα = 390 μονάδες) Ημερομηνία Ανακοίνωσης: 6/10/2010 Ημερομηνία Παράδοσης: 15/11/2010 σύμφωνα
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2010-2011 Πρώτη Σειρά Ασκήσεων (20% του συνολικού βαθμού στο μάθημα, Άριστα = 390 μονάδες) Ημερομηνία Ανακοίνωσης: 6/10/2010 Ημερομηνία Παράδοσης: 15/11/2010 σύμφωνα
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Διακριτά Μαθηματικά Ι Ενότητα 5: Αρχή Εγκλεισμού - Αποκλεισμού Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Διακριτά Μαθηματικά Ι Ενότητα 5: Αρχή Εγκλεισμού - Αποκλεισμού Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Άσκηση 1 (ανακοινώθηκε στις 20 Μαρτίου 2017, προθεσμία παράδοσης: 24 Απριλίου 2017, 12 τα μεσάνυχτα).
 Κ08 Δομές Δεδομένων και Τεχνικές Προγραμματισμού Διδάσκων: Μανόλης Κουμπαράκης Εαρινό Εξάμηνο 2016-2017. Άσκηση 1 (ανακοινώθηκε στις 20 Μαρτίου 2017, προθεσμία παράδοσης: 24 Απριλίου 2017, 12 τα μεσάνυχτα).
Κ08 Δομές Δεδομένων και Τεχνικές Προγραμματισμού Διδάσκων: Μανόλης Κουμπαράκης Εαρινό Εξάμηνο 2016-2017. Άσκηση 1 (ανακοινώθηκε στις 20 Μαρτίου 2017, προθεσμία παράδοσης: 24 Απριλίου 2017, 12 τα μεσάνυχτα).
Σχέδιο Μαθήματος - "Ευθεία Απόδειξη"
 Σχέδιο Μαθήματος - "Ευθεία Απόδειξη" ΤΑΞΗ: Α Λυκείου Μάθημα: Άλγεβρα Τίτλος Ενότητας: Μέθοδοι Απόδειξης - Ευθεία απόδειξη Ώρες Διδασκαλίας: 1. Σκοποί Να κατανοήσουν οι μαθητές την διαδικασία της ευθείας
Σχέδιο Μαθήματος - "Ευθεία Απόδειξη" ΤΑΞΗ: Α Λυκείου Μάθημα: Άλγεβρα Τίτλος Ενότητας: Μέθοδοι Απόδειξης - Ευθεία απόδειξη Ώρες Διδασκαλίας: 1. Σκοποί Να κατανοήσουν οι μαθητές την διαδικασία της ευθείας
Σχέσεις, Ιδιότητες, Κλειστότητες
 Σχέσεις, Ιδιότητες, Κλειστότητες Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σχέσεις 1 / 26 Εισαγωγή & Ορισµοί ιµελής Σχέση R από
Σχέσεις, Ιδιότητες, Κλειστότητες Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σχέσεις 1 / 26 Εισαγωγή & Ορισµοί ιµελής Σχέση R από
Τσάπελη Φανή ΑΜ: 2004030113. Ενισχυτική Μάθηση για το παιχνίδι dots. Τελική Αναφορά
 Τσάπελη Φανή ΑΜ: 243113 Ενισχυτική Μάθηση για το παιχνίδι dots Τελική Αναφορά Περιγραφή του παιχνιδιού Το παιχνίδι dots παίζεται με δύο παίχτες. Έχουμε έναν πίνακα 4x4 με τελείες, και σκοπός του κάθε παίχτη
Τσάπελη Φανή ΑΜ: 243113 Ενισχυτική Μάθηση για το παιχνίδι dots Τελική Αναφορά Περιγραφή του παιχνιδιού Το παιχνίδι dots παίζεται με δύο παίχτες. Έχουμε έναν πίνακα 4x4 με τελείες, και σκοπός του κάθε παίχτη
ΑΔΙΕΞΟΔΑ. Λειτουργικά Συστήματα Ι. Διδάσκων: Καθ. Κ. Λαμπρινουδάκης ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι
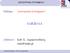 ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Μάθημα: Λειτουργικά Συστήματα Ι ΑΔΙΕΞΟΔΑ Διδάσκων: Καθ. Κ. Λαμπρινουδάκης clam@unipi.gr 1 ΑΔΙΕΞΟΔΑ 2 ΠΟΡΟΙ Υπάρχουν δύο τύποι πόρων σε υπολογιστικά συστήματα: Προεκτοπίσιμοι πόροι
ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Μάθημα: Λειτουργικά Συστήματα Ι ΑΔΙΕΞΟΔΑ Διδάσκων: Καθ. Κ. Λαμπρινουδάκης clam@unipi.gr 1 ΑΔΙΕΞΟΔΑ 2 ΠΟΡΟΙ Υπάρχουν δύο τύποι πόρων σε υπολογιστικά συστήματα: Προεκτοπίσιμοι πόροι
Chapter 9: NP-Complete Problems
 Θεωρητική Πληροφορική Ι: Αλγόριθμοι και Πολυπλοκότητα Chapter 9: NP-Complete Problems 9.3 Graph-Theoretic Problems (Συνέχεια) 9.4 Sets and Numbers Γιώργος Αλεξανδρίδης gealexan@mail.ntua.gr Κεφάλαιο 9:
Θεωρητική Πληροφορική Ι: Αλγόριθμοι και Πολυπλοκότητα Chapter 9: NP-Complete Problems 9.3 Graph-Theoretic Problems (Συνέχεια) 9.4 Sets and Numbers Γιώργος Αλεξανδρίδης gealexan@mail.ntua.gr Κεφάλαιο 9:
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Λογική. Δημήτρης Πλεξουσάκης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 4ο μέρος σημειώσεων: Ακολουθίες Επίλυσης, Επίλυση για όρους Horn, Λογικός Προγραμματισμός Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 4ο μέρος σημειώσεων: Ακολουθίες Επίλυσης, Επίλυση για όρους Horn, Λογικός Προγραμματισμός Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής
 Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
Οι βασικές λειτουργίες (ή πράξεις) που γίνονται σε μια δομή δεδομένων είναι:
 ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ Μια δομή δεδομένων στην πληροφορική, συχνά αναπαριστά οντότητες του φυσικού κόσμου στον υπολογιστή. Για την αναπαράσταση αυτή, δημιουργούμε πρώτα ένα αφηρημένο μοντέλο στο οποίο προσδιορίζονται
ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ Μια δομή δεδομένων στην πληροφορική, συχνά αναπαριστά οντότητες του φυσικού κόσμου στον υπολογιστή. Για την αναπαράσταση αυτή, δημιουργούμε πρώτα ένα αφηρημένο μοντέλο στο οποίο προσδιορίζονται
Προγραμματισμός Ι (ΗΥ120)
 Προγραμματισμός Ι (ΗΥ120) Διάλεξη 17: Λύση Προβλημάτων με Αναδρομή Οι πύργοι του Hanoi Δίνεται ένα χώρος με τρεις θέσεις αποθήκευσης. Δίνεται μια στοίβα από Ν πλάκες σε φθίνον μέγεθος, σε μια από τις τρεις
Προγραμματισμός Ι (ΗΥ120) Διάλεξη 17: Λύση Προβλημάτων με Αναδρομή Οι πύργοι του Hanoi Δίνεται ένα χώρος με τρεις θέσεις αποθήκευσης. Δίνεται μια στοίβα από Ν πλάκες σε φθίνον μέγεθος, σε μια από τις τρεις
Σχέδια μαθημάτων για την δημιουργία συναρτήσεων υπολογισμού του ΜΚΔ και του ΕΚΠ στην MSWLogo
 Σχέδια μαθημάτων για την δημιουργία συναρτήσεων υπολογισμού του Μέγιστου Κοινού Διαιρέτη (ΜΚΔ) και του Ελάχιστου Κοινού Πολλαπλασίου (ΕΚΠ) δύο αριθμών, με την γλώσσα προγραμματισμού Logo Κογχυλάκης Σ.
Σχέδια μαθημάτων για την δημιουργία συναρτήσεων υπολογισμού του Μέγιστου Κοινού Διαιρέτη (ΜΚΔ) και του Ελάχιστου Κοινού Πολλαπλασίου (ΕΚΠ) δύο αριθμών, με την γλώσσα προγραμματισμού Logo Κογχυλάκης Σ.
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Περιγραφή Προβλημάτων Διαισθητικά, σε ένα πρόβλημα υπάρχει μια δεδομένη κατάσταση
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Περιγραφή Προβλημάτων Διαισθητικά, σε ένα πρόβλημα υπάρχει μια δεδομένη κατάσταση
Δομές Δεδομένων. Ενότητα 1 - Εισαγωγή. Χρήστος Γκουμόπουλος. Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων
 Δομές Δεδομένων Ενότητα 1 - Εισαγωγή Χρήστος Γκουμόπουλος Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Αντικείμενο μαθήματος Δομές Δεδομένων (ΔΔ): Στην επιστήμη υπολογιστών
Δομές Δεδομένων Ενότητα 1 - Εισαγωγή Χρήστος Γκουμόπουλος Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Αντικείμενο μαθήματος Δομές Δεδομένων (ΔΔ): Στην επιστήμη υπολογιστών
Επίλυση Προβλημάτων με Χρωματισμό. Αλέξανδρος Γ. Συγκελάκης asygelakis@gmail.com
 Επίλυση Προβλημάτων με Χρωματισμό Αλέξανδρος Γ. Συγκελάκης asygelakis@gmail.com 1 Η αφορμή συγγραφής της εργασίας Το παρακάτω πρόβλημα που τέθηκε στο Μεταπτυχιακό μάθημα «Θεωρία Αριθμών» το ακαδημαϊκό
Επίλυση Προβλημάτων με Χρωματισμό Αλέξανδρος Γ. Συγκελάκης asygelakis@gmail.com 1 Η αφορμή συγγραφής της εργασίας Το παρακάτω πρόβλημα που τέθηκε στο Μεταπτυχιακό μάθημα «Θεωρία Αριθμών» το ακαδημαϊκό
Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 3ο μέρος σημειώσεων: Μέθοδος της Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 3ο μέρος σημειώσεων: Μέθοδος της Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο ΔΙΑΛΕΞΗ 3: Αλγοριθµική Ελαχιστοποίηση (Quine-McCluskey, tabular method)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 3: Αλγοριθµική Ελαχιστοποίηση (Quine-McCluskey, tabular method) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 3: Αλγοριθµική Ελαχιστοποίηση (Quine-McCluskey, tabular method) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
Δέντρα Απόφασης (Decision(
 Δέντρα Απόφασης (Decision( Trees) Το μοντέλο που δημιουργείται είναι ένα δέντρο Χρήση της τεχνικής «διαίρει και βασίλευε» για διαίρεση του χώρου αναζήτησης σε υποσύνολα (ορθογώνιες περιοχές) Ένα παράδειγμα
Δέντρα Απόφασης (Decision( Trees) Το μοντέλο που δημιουργείται είναι ένα δέντρο Χρήση της τεχνικής «διαίρει και βασίλευε» για διαίρεση του χώρου αναζήτησης σε υποσύνολα (ορθογώνιες περιοχές) Ένα παράδειγμα
Αλγόριθμοι και Δομές Δεδομένων (IΙ) (γράφοι και δένδρα)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2016-17 Αλγόριθμοι και Δομές Δεδομένων (IΙ) (γράφοι και δένδρα) http://mixstef.github.io/courses/csintro/ Μ.Στεφανιδάκης Αφηρημένες
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2016-17 Αλγόριθμοι και Δομές Δεδομένων (IΙ) (γράφοι και δένδρα) http://mixstef.github.io/courses/csintro/ Μ.Στεφανιδάκης Αφηρημένες
Κατακερματισμός (Hashing)
 Κατακερματισμός (Hashing) O κατακερματισμός είναι μια τεχνική οργάνωσης ενός αρχείου. Είναι αρκετά δημοφιλής μέθοδος για την οργάνωση αρχείων Βάσεων Δεδομένων, καθώς βοηθάει σημαντικά στην γρήγορη αναζήτηση
Κατακερματισμός (Hashing) O κατακερματισμός είναι μια τεχνική οργάνωσης ενός αρχείου. Είναι αρκετά δημοφιλής μέθοδος για την οργάνωση αρχείων Βάσεων Δεδομένων, καθώς βοηθάει σημαντικά στην γρήγορη αναζήτηση
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
Συνδυαστική Απαρίθμηση
 Παραδείγματα Συνδυαστική Απαρίθμηση Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο n θρανία στη σειρά
Παραδείγματα Συνδυαστική Απαρίθμηση Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο n θρανία στη σειρά
ΠΑΙΓΝΙΑ Παιχνίδια Γενική Θεώρηση μεγιστοποιήσει την πιθανότητά
 ΠΑΙΓΝΙΑ Παιχνίδια Γενική Θεώρηση: Έστω ότι έχουμε τους παίκτες Χ και Υ. Ο κάθε παίκτης, σε κάθε κίνηση που κάνει, προσπαθεί να μεγιστοποιήσει την πιθανότητά του να κερδίσει. Ο Χ σε κάθε κίνηση που κάνει
ΠΑΙΓΝΙΑ Παιχνίδια Γενική Θεώρηση: Έστω ότι έχουμε τους παίκτες Χ και Υ. Ο κάθε παίκτης, σε κάθε κίνηση που κάνει, προσπαθεί να μεγιστοποιήσει την πιθανότητά του να κερδίσει. Ο Χ σε κάθε κίνηση που κάνει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις Πέμπτη 27 Ιουνίου 2013 10:003:00 Έστω το πάζλ των οκτώ πλακιδίων (8-puzzle)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις Πέμπτη 27 Ιουνίου 2013 10:003:00 Έστω το πάζλ των οκτώ πλακιδίων (8-puzzle)
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 19 Hashing - Κατακερματισμός 1 / 23 Πίνακες απευθείας πρόσβασης (Direct Access Tables) Οι πίνακες απευθείας
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 19 Hashing - Κατακερματισμός 1 / 23 Πίνακες απευθείας πρόσβασης (Direct Access Tables) Οι πίνακες απευθείας
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Αναζήτηση Δοθέντος ενός προβλήματος με περιγραφή είτε στον χώρο καταστάσεων
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Αναζήτηση Δοθέντος ενός προβλήματος με περιγραφή είτε στον χώρο καταστάσεων
Τι είναι αλγόριθμος; Υποπρογράμματα (υποαλγόριθμοι) Βασικές αλγοριθμικές δομές
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Το Πρόβλημα της Πινακοθήκης (The Art Gallery Problem)
 Το Πρόβλημα της Πινακοθήκης (The Art Gallery Problem) Διατύπωση Σας ανήκει μια πινακοθήκη και επιθυμείτε να τοποθετήσετε κάμερες ασφαλείας έτσι ώστε όλη η γκαλερί να είναι προστατευμένη από κλέφτες. Σε
Το Πρόβλημα της Πινακοθήκης (The Art Gallery Problem) Διατύπωση Σας ανήκει μια πινακοθήκη και επιθυμείτε να τοποθετήσετε κάμερες ασφαλείας έτσι ώστε όλη η γκαλερί να είναι προστατευμένη από κλέφτες. Σε
Σχεδίαση Αλγορίθμων -Τμήμα Πληροφορικής ΑΠΘ - Εξάμηνο 4ο
 Σχεδίαση Αλγορίθμων Διαίρει και Βασίλευε http://delab.csd.auth.gr/~gounaris/courses/ad auth gounaris/courses/ad 1 Διαίρει και Βασίλευε Η γνωστότερη ρημέθοδος σχεδιασμού αλγορίθμων: 1. Διαιρούμε το στιγμιότυπο
Σχεδίαση Αλγορίθμων Διαίρει και Βασίλευε http://delab.csd.auth.gr/~gounaris/courses/ad auth gounaris/courses/ad 1 Διαίρει και Βασίλευε Η γνωστότερη ρημέθοδος σχεδιασμού αλγορίθμων: 1. Διαιρούμε το στιγμιότυπο
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 3-4 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητες 3 & 4: ένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις Άσκηση 1 Γράψτε
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 3-4 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητες 3 & 4: ένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις Άσκηση 1 Γράψτε
5.1. Προσδοκώμενα αποτελέσματα
 5.1. Προσδοκώμενα αποτελέσματα Όταν θα έχεις ολοκληρώσει τη μελέτη αυτού του κεφαλαίου θα έχεις κατανοήσει τις τεχνικές ανάλυσης των αλγορίθμων, θα μπορείς να μετράς την επίδοση των αλγορίθμων με βάση
5.1. Προσδοκώμενα αποτελέσματα Όταν θα έχεις ολοκληρώσει τη μελέτη αυτού του κεφαλαίου θα έχεις κατανοήσει τις τεχνικές ανάλυσης των αλγορίθμων, θα μπορείς να μετράς την επίδοση των αλγορίθμων με βάση
Β Ομάδα Ασκήσεων "Λογικού Προγραμματισμού" Ακαδημαϊκού Έτους
 Page 1 of 15 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Β Ομάδα Ασκήσεων "Λογικού Προγραμματισμού" Ακαδημαϊκού Έτους 2016-17 Οι ασκήσεις της ομάδας αυτής πρέπει
Page 1 of 15 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Β Ομάδα Ασκήσεων "Λογικού Προγραμματισμού" Ακαδημαϊκού Έτους 2016-17 Οι ασκήσεις της ομάδας αυτής πρέπει
Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός συγκρίσεων π
 Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Κατανεμημένα Συστήματα Ι
 Κατανεμημένα Συστήματα Ι Παναγιώτα Παναγοπούλου 11η Διάλεξη 12 Ιανουαρίου 2017 1 Ανεξάρτητο σύνολο Δοθέντος ενός μη κατευθυνόμενου γραφήματος G = (V, E), ένα ανεξάρτητο σύνολο (independent set) είναι ένα
Κατανεμημένα Συστήματα Ι Παναγιώτα Παναγοπούλου 11η Διάλεξη 12 Ιανουαρίου 2017 1 Ανεξάρτητο σύνολο Δοθέντος ενός μη κατευθυνόμενου γραφήματος G = (V, E), ένα ανεξάρτητο σύνολο (independent set) είναι ένα
Αλγοριθμικές Τεχνικές
 Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Αλγοριθμικές Τεχνικές 1 Τεχνικές Σχεδιασμού Αλγορίθμων Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και
Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Αλγοριθμικές Τεχνικές 1 Τεχνικές Σχεδιασμού Αλγορίθμων Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και
