Μία τετρακτύς εκ της ΑΚΟΥΣΤΙΚΗΣ: 1. Ένταση (W/m 2 ) 2. Στάθμη Έντασης (db) 3. Ακουστότητα (sone) 4. Στάθμη Ακουστότητας (phon) του Ήχου
|
|
|
- Σωφρονία Καραμανλής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Μία τετρακτύς εκ της ΑΚΟΥΣΤΙΚΗΣ:. Ένταση (/ ). Στάθμη Έντασης (db) 3. Ακουστότητα (sone) 4. Στάθμη Ακουστότητας (phon) του Ήχου
2 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Κυρίες και κύριοι σύνεδροι, προκειμένου να καταστήσω καταληπτό το νόημα του τίτλου της εισηγήσεώς μου, οφείλω να πραγματοποιήσω μια αναδρομή στο παρελθόν. Οι Πυθαγόρειοι θεωρούσαν αναγκαίο να πλάθουν λέξεις εσωτερικής σημασίας, όπως είναι οι λέξεις φιλοσοφία, κόσμος, τετρακτύς, κάθαρσις, εχεμύθια, κατάρτυσις, στις οποίες απέδιδαν ιδιαίτερη σημασία. Η ιερά τετρακτύς συμβολικά παριστάνεται με δέκα κουκίδες, που έχουν την εξής κανονική τριγωνική διάταξη: Την τετρακτύ, ως σχήμα, γνώρισε ο Πυθαγόρας στη Βαβυλώνα. Έχει βρεθεί έντυπη η τετρακτύς επάνω σε χρυσή λαβή ξίφους του 700 π.χ. στην πόλη Ουρ. Κάθε κουκίδα της τετρακτύος ήταν και ένα σπουδαιότατο σύμβολο, διότι: Η μία κουκίδα ήταν σύμβολο του ενεργού στοιχείου ή του Δημιουργού. Οι δύο κουκίδες συμβόλιζαν την ύλη, το παθητικό στοιχείο. Οι τρεις κουκίδες συμβόλιζαν τον Κόσμο, δηλαδή την ένωση του ενεργού και του παθητικού στοιχείου. Οι τέσσερις κουκίδες συμβόλιζαν τις ελεύθερες τέχνες, που συμπληρώνουν και τελειοποιούν τον Κόσμο. Η τετρακτύς εταυτίζετο με το Απολλώνιον ΕΙ, αριθμητικώς εξεφράζετο δια του «τριγωνικού» αριθμού 0=++3+4, ενώ ταυτόχρονα οι αριθμοί,, 3, 4 κατεδείκνυαν τη Μουσική αρμονία. Η τετρακτύς όντως εμπεριέχει όλες τις Πυθαγόρειες μουσικές συμφωνίες. 4: είναι ο τετραπλάσιος λόγος και εκφράζει τη συμφωνία, δηλαδή το εύφωνο μουσικό διάστημα της δις διαπασών (δύο οκτάβες), 3: είναι ο ημιόλιος λόγος και εκφράζει τη διά πέντε συμφωνία (διάστημα πέμπτης καθαρής), ο 4:3 είναι ο επίτριτος λόγος και εκφράζει τη διά τεσσάρων συμφωνία (διάστημα τετάρτης καθαρής), : είναι ο διπλάσιος λόγος και εκφράζει την διαπασών συμφωνία (διάστημα οκτάβας). Κατά την τελετή της μυήσεως των Πυθαγορείων οι μυούμενοι νεοφώτιστοι ήσαν υποχρεωμένοι να δίνουν τον περίφημο Πυθαγόρειο όρκο στην ιερά τετρακτύ «Οὐ, μὰ τὸν ἁμετέρα ψυχὰ παραδόντα τετρακτύν, παγὰν ἀενάου φύσιος ριζώματ' ἔχουσαν». Τέλος, «τετρακτύς» εσήμαινε μια τετράδα, δηλαδή τέσσερα πράγματα. Ο Θέων ο Σμυρναίος μας πληροφορεί ότι οι Πυθαγόρειοι διέκριναν και εσέβοντο διαφορετικές τετρακτείς, δηλαδή διαφορετικές τετράδες. Ο τίτλος της εισηγήσεώς μου, κυρίες και κύριοι συνάδελφοι, αναφέρεται σε μια τετράδα μεγεθών της Ακουστικής. Ένταση του Ήχου,. Στάθμη Έντασης του Ήχου, 3. Στάθμη Ακουστότητας του Ήχου, 4. Ακουστότητα του Ήχου με τις αντίστοιχες μονάδες μετρήσεώς των. /,. db, 3. phon, 4. sone Κυρίες και κύριοι Σύνεδροι, εδώ και μερικά χρόνια στο Τμήμα Μουσικών Σπουδών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών παρέχεται ένας αριθμός μαθημάτων ελεύθερης επιλογής με τη φιλοσοφία των προαπαιτουμένων μαθημάτων για την κατάρτιση Ηχοληπτών. Ευελπιστούμε στην κατάρτιση Μουσικολόγων-Ηχοληπτών τριτοβαθμίου Εκπαιδεύσεως, οι οποίοι πλέον των απαραιτήτων γνώσεων ενός
3 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής 3 Μουσικολόγου, που αποκτώνται κατά τις πενταετείς σπουδές τους, θα είναι ικανοί να δαμάσουν ποικιλοτρόπως τον ήχο. Σύμβουλός τους θα είναι η γνώση, που αντλείται από τη Θεωρία, βοηθοί τους δε τα όργανα και οι διατάξεις καταγραφής και αναπαραγωγής του ήχου, που τους παρέχει η σύγχρονη Τεχνολογία του ήχου μέσα σε ένα υπερσύγχρονο και άριστα εξοπλισμένο Studio Ήχου του Εργαστηρίου Μουσικής Ακουστικής Τεχνολογίας του Τμήματός μας. Ένας σωστός επαγγελματίας ηχολήπτης εκτός από το ταλέντο, δηλαδή το προσωπικό συναίσθημα και τη φαντασία, θα πρέπει πρωτίστως να είναι καταρτισμένος με ουσιαστικές θεωρητικές και πρακτικές γνώσεις, οι οποίες θα του επιτρέψουν το ορθότερο κριτικό άκουσμα και την αρτιότερη ηχητική απόδοση αυτού και θα τον οδηγήσουν αξιοκρατικά να διαπρέψει στον εργασιακό του χώρο. Δυστυχώς, κυρίες και κύριοι ΦΥΣΙΚΟΙ, στα Λύκεια της πατρίδας μας δεν διδάσκονται όλα τα πεδία της Φυσικής με πρώτο-πρώτο το πεδίο της Ακουστικής, της επιστήμης των ήχων. Τραγική συνέπεια είναι οι πρωτοετείς φοιτητές των Τμημάτων Μουσικών Σπουδών στα Πανεπιστήμια, αλλά και οι σπουδαστές των Ωδείων, των Σχολών Ηχοληψίας, των Σχολών Ήχου, κ.λπ. να μη γνωρίζουν τα στοιχειώδη περί του ήχου, το υλικό δηλαδή, που καλούνται να δαμάσουν ή να επεξεργασθούν, προκειμένου να δημιουργήσουν. Ορισμένοι, μάλιστα, μη συναισθανόμενοι την άγνοιά τους σχετικά με τα φαινόμενα του ήχου και έχοντας υπερεκτιμήσει τη σύγχρονη Τεχνολογία, έχουν τη νοοτροπία ότι, για να γίνει κανείς π.χ. ένας καλός ηχολήπτης, πρέπει και αρκεί να είναι απλώς και μόνον ένας καλός χειριστής της κονσόλας! Άλλοι αδιαφορούν πλήρως γι αυτή τη θεωρητική γνώση και λειτουργούν ως υποκείμενα-εμπειροτέχνες μπροστά από την κονσόλα με ό,τι αυτό συνεπάγεται! Ένας Ηχολήπτης μπροστά στην κονσόλα και πριν αρχίσει να τοποθετεί τα «κουμπιά» της σε διάφορες θέσεις θα πρέπει να γνωρίζει κάλλιστα τη σημασία των φράσεων «ο ήχος ΕΙΝΑΙ δυνατός» και «ΜΟΥ ΦΑΙΝΕΤΑΙ ότι ο ήχος είναι δυνατός». Με άλλα λόγια θα πρέπει να γνωρίζει για την πρώτη περίπτωση τα ΑΝΤΙΚΕΙΜΕΝΙΚΑ μεγέθη του ήχου (Ένταση και Στάθμη Έντασης) και για τη δεύτερη περίπτωση τα ΥΠΟΚΕΙ- ΜΕΝΙΚΑ μεγέθη του ήχου (Ακουστότητα και Στάθμη Ακουστότητας). Θα πρέπει να γνωρίζει τέσσερα Ακουστικά μεγέθη, δηλαδή μια Ακουστική τετρακτύ.
4 4 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Διάγραμμα : Τα πεδία του επιστητού, στα οποία βρίσκει εφαρμογή η Ακουστική.
5 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής 5 Ένταση του ήχου Ως γνωστόν, κάθε ελεύθερα δονούμενο σύστημα χάνει με το πέρασμα του χρόνου ενέργεια με αποτέλεσμα να εκτελεί φθίνουσα ταλάντωση. Ο ρυθμός απώλειας της ενέργειάς του, δηλαδή Ενέ ργ εια, εκφράζεται με το μέγεθος Ισχύς και μετρείται σε Χ ρόνος Joule μονάδες att =. sec Το μέγεθος της ηχητικής ισχύος που εκπέμπεται από τα διάφορα μουσικά όργανα, παραθέτω στον Πίνακα Ι. Πίνακας Ι: Ακουστικές ισχείς, που εκπέμπουν διάφορα μουσικά όργανα Μουσικό όργανο Κλαρινέτο Κόρνο Φλάουτο Κόντρα Μπάσο Τούμπα Τρομπέτα Πιάνο Τρομπόνι Κύμβαλα Ντραμς Ορχήστρα Ακουστική Ισχύς σε att 0,05 0,05 0,06 0,6 0,0 0,3 0,44 6,00 9,50 5,00 67,00 Αναλογισθείτε ότι ισχύ 00 att, που δίδει ένας λαμπτήρας φωτισμού, ισοδυναμεί με την ισχύ που δίδουν 000 κλαρινέτα μαζί ή 000 κόρνα μαζί ή 667 φλάουτα μαζί ή 65 κόντρα μπάσσα μαζί ή 500 τούμπες μαζί ή 33 τρομπέτες μαζί ή 7 πιάνα μαζί ή 7 τρομπόνια μαζί ή κύμβαλα μαζί ή 4 ντραμς μαζί ή περίπου ορχήστρες μαζί. Πρέπει να τονισθεί με ιδιαίτερη έμφαση ότι κατά μέσον όρο μόνο το % της ενεργείας ενός δονουμένου ηχοπαραγωγού μηχανικού συστήματος μετατρέπεται σε ηχητική ενέργεια! Η ηχητική ενέργεια, διαδιδόμενη ομοιόμορφα στο χώρο, διαπερνά επιφάνεια σφαίρας ολοένα και μεγαλύτερου εμβαδού, με αποτέλεσμα επιφάνειες ίσου εμβαδού σε διαφορετική απόσταση από την ηχητική πηγή να διαπερνώνται από διαφορετική ποσότητα ηχητικής ενέργειας. Για την περιγραφή αυτού του γεγονότος οι Φυσικοί οδηγήθηκαν στην εισαγωγή ενός καινούργιου μεγέθους, αυτού της έντασης (Ιntensity) του ημιτονοειδούς ήχου. Μιλώντας για την ένταση του ημιτονοειδούς ήχου σε ένα σημείο του ηχητικού πεδίου και προς μια συγκεκριμένη κατεύθυνση, σύμφωνα με τον κανονισμό ΕΛΟΤ 556. (.9) θα εννούμε το πηλίκο της ηχητικής ενέργειας (), που διαπερνά κάθετα στη μονάδα του χρόνου (sec) τη μονάδα της επιφάνειας ( ) ή θα εννοούμε το πηλίκο της ηχητικής ισχύος (P), που διαπερνά κάθετα τη μονάδα της επιφάνειας ( ).
6 6 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Σχήμα : Ενέργεια που διαπερνά κάθετα μια επιφάνεια με εμβαδόν. Μονάδα μέτρησης της έντασης του ημιτονοειδούς ήχου είναι το. Όπως έχουμε πει, η ηχητική ισχύς, καθώς απομακρύνεται από τη σημειακή ηχητική πηγή μέσα σ ένα ελεύθερο ηχητικό πεδίο, εξαπλούται ομοιόμορφα στην επιφάνεια σφαίρας με ολοένα αυξανόμενη ακτίνα με αποτέλεσμα η ένταση να μειούται σύμφωνα I r με το νόμο του αντιστρόφου τετραγώνου =. I r Πρέπει να σημειωθεί ότι ο νόμος του αντιστρόφου τετραγώνου είναι γενικός και ισχύει για όλα τα κύματα (μηχανικά και ηλεκτρομαγνητικά). Νόμος Αντιστρόφου Τετραγώνου Μεταβολή Έντασης 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0, 0, Πολλαπλασιασμός Απόστασης Σχήμα : Ο γραμμικός νόμος και ο νόμος του αντιστρόφου τετραγώνου για τα κύματα.
7 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής 7 Σχήμα : Η αύξηση του εμβαδού της επιφανείας επιφέρει τη μείωση της εντάσεως του κύματος. Στάθμη Μεγεθών Κυρίες και κύριοι Σύνεδροι, γνωρίζετε πολύ καλά ότι μέτρηση ενός μεγέθους ονομάζεται η σύγκριση αυτού του μεγέθους με ένα άλλο ομοειδές μέγεθος, το οποίο εμείς είτε αυθαίρετα, είτε με κοινή συμφωνία το εκλάβαμε ως μονάδα μέτρησης. Αποτέλεσμα της μέτρησης ενός μεγέθους είναι το μέτρο του μεγέθους. Το μέτρο πολλαπλασιαζόμενο επί την μονάδα μέτρησης δίνει το μετρούμενο μέγεθος. Μερικές φορές είναι δυνατόν να συγκρίνουμε ένα μέγεθος με ένα άλλο ομοειδές, χωρίς αυτό να είναι η μονάδα μέτρησης, και να σχηματίσουμε μια ιδέα (όχι, όμως, ακριβή) για το μέγεθος, που μας ενδιαφέρει. Λέμε, επί παραδείγματι, ότι ο Γιάννης είναι 0 c ψηλότερος από τον Κώστα, αλλά, αφού δεν γνωρίζουμε το ύψος του Κώστα, δεν μπορούμε να αντιληφθούμε με ακρίβεια πόσο ψηλός είναι ο Γιάννης. Εάν, όμως, μας ήταν γνωστό ότι το ύψος του Κώστα είναι,70, τότε αμέσως θα καταλαβαίναμε ότι το ύψος του Γιάννη είναι,80. Επειδή μεγαλύτερη σχέση με τις ανθρώπινες αισθήσεις έχουν οι λόγοι, παρά οι διαφορές των μεγεθών, είναι δυνατόν να λαμβάνουμε τον λόγο του μετρούμενου μεγέθους προς το μέγεθος ή τη στάθμη αναφοράς. Στα μέσα του 9 ου αιώνα οι Φυσικοί Ernst eber και Gustaf Fechner κατέληξαν σε έναν ψυχοφυσικό νόμο, ο οποίος λέει ότι το αίσθημα είναι ανάλογο του δεκαδικού λογαρίθμου του ερεθίσματος, που το προκαλεί. Δηλαδή Αίσθημα = k log(ερέθισμα) όπου k είναι μια σταθερά αναλογίας που, κατά περίπτωση, έχει κάποια τιμή. Από δύο δοθέντα ομοειδή ερεθίσματα ε και ε τα προκαλούμενα αισθήματα α και α, αντίστοιχα, είναι: α =k log(ε ) α =k log(ε ) H διαφορά α -α των δύο προκαλουμένων αισθημάτων εκφράζεται από τη σχέση: α - α = k log(ε ) - k log(ε ε ) = k log ε
8 8 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Βλέπει κανείς ότι στη σχέση αυτή δεν εισάγεται μόνον ο λόγος των δύο μεγεθών ε και ε, αλλά και ο λογάριθμος του λόγου τους. Εάν το ερέθισμα ε ισούται με το κατώφλι του αισθήματος, οπότε το αίσθημα α =0, η διαφορά α -α των δύο προκαλουμένων αισθημάτων εκφράζει τη στάθμη (level) του προκαλουμένου αισθήματος α από το ερέθισμα ε με αναφορά το ερέθισμα ε και δίνεται από τη σχέση: α - α = α - 0 = α = k log(ε ) - k log(ε ε ) = k log ε Χρησιμοποιώντας τη διαφορά των τιμών δύο μεγεθών είναι δυνατόν το διάστημα τιμών να είναι τρομακτικά μεγάλο και, ως εκ τούτου, δύσχρηστο στους καθημερινούς μας υπολογισμούς και δοσοληψίες. Το ίδιο πρόβλημα, ίσως σε ελαφρώς μικρότερη κλίμακα, εξακολουθεί να υφίσταται, όταν λαμβάνονται οι λόγοι των μεγεθών. Η εισαγωγή, όμως, του λογαρίθμου του λόγου των δύο μεγεθών συμπιέζει το όλο διάστημα τιμών, το εξαιρετικά μεγάλο, σε ένα κατά πάρα πολύ μικρότερο και, ως εκ τούτου, εύχρηστο διάστημα τιμών. Για να καταστούν τα προηγούμενα κατανοητά, παραθέτω το ακόλουθο παράδειγμα: Για κάθε ήχο μιας ορισμένης συχνότητας (ερέθισμα) υπάρχουν δύο όρια ευαισθησίας (α) το κατώτερο όριο ακουστότητας ή κατώφλι ακουστότητας και (β) το ανώτερο όριο ακουστότητας ή όριον πόνου ή ακμή ακουστότητας. Το κατώφλι ακουστότητας αντιπροσωπεύει την ελαχιστότατη και μόλις ακουστή ένταση ήχου για μια συγκεκριμένη συχνότητα. Το όριο πόνου είναι αυτό που, όταν το ξεπερνούμε, προκαλείται πόνος στα αυτιά και, μοιραία, οδηγούμεθα στη φυσιολογική καταστροφή του μηχανισμού της ακοής. Αυτά τα δύο όρια ποικίλουν από άτομο σε άτομο για την κάθε μία συχνότητα, αλλά στην περιοχή των 000 Hz για όλους τους ανθρώπους με «οξεία» ακοή το εύρος των δύο ορίων είναι το μεγαλύτερο. Συγκεκριμένα σε αυτή τη συχνότητα το κατώφλι ακουστότητας αντιστοιχεί στα 0 και το όριο πόνου στο. Η διαφορά των τιμών αυτών των δύο εντάσεων εξακολουθεί να είναι ένταση και ισούται με: 0 = 0, = 0, Ο λόγος αυτών των εντάσεων είναι καθαρός αριθμός (αδιάστατο μέγεθος) και ισούται με: = 0 0 =
9 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής 9 Ο δεκαδικός λογάριθμος του λόγου αυτών των εντάσεων ορίζει τη στάθμη του μεγέθους του αριθμητού με αναφορά το ομοειδές μέγεθος του παρονομαστού και εκφράζεται με έναν μικρό, και, συνεπώς, εύχρηστο αριθμό: log = log0 = 0 Η στάθμη των μεγεθών, εν γένει, καθιερώθηκε από τα Εργαστήρια του εργοστασίου Bell των Ηνωμένων Πολιτειών της Αμερικής στις αρχές του 0ού αιώνα να μετρείται σε μονάδες Bel, η οποία, όμως, ως μεγάλη και δύσχρηστη μονάδα αντικαταστάθηκε από το decibel (db). Η μονάδα decibel (db), που χρησιμοποιείται ευρύτατα στην Ακουστική, αποτελεί δάνειο από την Ηλεκτρική Μηχανολογία. To decibel (db) εν γένει εκφράζει το δεκαπλάσιο του λογαρίθμου του λόγου των αριθμητικών τιμών δύο μεγεθών Αριθµητικ ή Τιµ ή Μεγέθους 0 log db ή ή έ Αριθµητικ Τιµ Μεγ θους και εκφράζει απόλυτες τιμές μεγεθών, στάθμες (levels) μεγεθών, μόνο στην περίπτωση που η αριθμητική τιμή του Μεγέθους, στον παρονομαστή, είναι σταθερή και γνωστή, οπότε εκλαμβάνεται ως αριθμητική τιμή αναφοράς (reference value). Στα διάφορα πεδία έρευνας και μελέτης της Τεχνολογίας του Ήχου χρησιμοποιούνται διάφορες, καθιερωμένες πλέον, κλίμακες decibel, που η καθεμία έχει τη δική της προτυποποιημένη τιμή αναφοράς. Στάθμη ισχύος (PL=Power Level) Αναφερόμενοι στο decibel με την αυστηρή σημασία του όρου στο χώρο της Τεχνολογίας του Ήχου, προκειμένου να μετρήσουμε τη στάθμη ισχύος ενός σήματος (PL=Power Level), εννοούμε το δεκαπλάσιο του λογαρίθμου του λόγου των αριθμητικών τιμών των ισχύων δύο σημάτων, ένα εκ των οποίων εκλαμβάνεται ως σήμα αναφοράς, δηλαδή: ( ) PL db Αριθµητικ ή Τιµ ή Ισχύος Σήµατος = 0 log = ριθµητικ ή ιµ ή σχύος ήµατος Α Τ Ι Σ αναφοράς P = 0 log P αναφοράς Όταν το illiwatt ( ) εκλαμβάνεται ως η ισχύς αναφοράς, τότε η στάθμη ισχύος ενός σήματος εκφράζεται σε μονάδες db. Όταν το att ( ) εκλαμβάνεται ως η ισχύς αναφοράς, τότε η στάθμη ισχύος ενός σήματος εκφράζεται σε μονάδες db. w
10 0 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Στάθμη έντασης (ΙL=Ιntensity Level) Η στάθμη έντασης (IL=Intensity Level) θα υπολογίζεται από τη σχέση: IL ( db) = 0 log I I αναφοράς Ως ένταση αναφοράς εκλαμβάνεται η τιμή Iαναφορ άς = 0, που είναι το κατώφλι ακουστότητας στη συχνότητα των 000 Hz για έναν άνθρωπο με οξεία ακοή. Από την παραπάνω σχέση προκύπτει ότι, εάν διπλασιασθεί η ένταση του ήχου, τότε η προκύπτουσα στάθμη έντασης του ήχου αυξάνει κατά 3 db. Πρόκειται για το ονομαζόμενο σημείο των 3 db (the three db point). Ισοδυνάμως, εάν υποδιπλασιασθεί η ένταση του ήχου, τότε η προκύπτουσα στάθμη έντασης του ήχου ελαττώνεται κατά 3 db. Η στάθμη πίεσης του ήχου (SPL=Sound Pressure Level). Τα περισσότερα μικρόφωνα είναι ευαίσθητα στην πίεση του ήχου παρά στην έντασή του. Όταν τέτοια μικρόφωνα χρησιμοποιούνται σε μετρήσεις ηχητικών σταθμών με ηχόμετρα, οι υπολογισμοί δεν βασίζονται στην ένταση του ήχου, αλλά στην ενεργό πίεση του ήχου. Η σχέση που δίνει τη στάθμη πίεσης του ήχου (SPL) είναι η εξής: SPL ( db) = 0 log P όπου P 0 το πλάτος πίεσης του ηχητικού κύματος και P 0 0 αναφοράς P 0 αναφοράς τα 0 μpa. Για ένα τρέχον ή οδεύον κύμα οι αριθμητικές τιμές που προκύπτουν για την IL και την SPL είναι ταυτόσημες και τα IL και SPL αντιπροσωπεύουν ένα και το αυτό μέγεθος. Στην περίπτωση, όμως, στασίμων κυμάτων, επειδή δεν υπάρχει ροή ενέργειας, δεν μπορεί να προσδιορισθεί η ένταση Ι του ήχου, οπότε η IL χάνει το νόημά της. Πρέπει να τονισθεί με έμφαση ότι οι υπολογισμοί των IL και SPL δεν έχουν να κάνουν καθόλου με τη συχνότητα του ηχητικού κύματος. Στην εικόνα παρουσιάζονται μερικές τυπικές τιμές της στάθμης έντασης που προκαλείται από διάφορες χαρακτηριστικές ηχητικές πηγές, προκειμένου να σχηματίσετε μια άποψη.
11 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής Πρόσθεση σταθμών έντασης ήχου Έστω ότι μας δίδονται n πλήθους ηχητικές πηγές με στάθμες έντασης IL, IL, IL3,..., IL n, αντίστοιχα, οι οποίες συνηχούν σ ένα χώρο. Η πρόσθεση αυτών των σταθμών έντασης αποδεικνύεται ότι πραγματοποιείται, λόγω της εμπεριεχομένης λογαριθμικότητας, με τη διαδικασία που υπαγορεύει η σχέση: IL IL IL3 ILn IL = 0 log ολ. Στην περίπτωση που όλες οι n ηχητικές πηγές έχουν την ίδια ένταση Ι, δηλαδή την ίδια στάθμη έντασης (IL), τότε η παραπάνω σχέση παίρνει τη μορφή: IL ολ = IL + 0 log Εάν σε μία αίθουσα διδασκαλίας με 5 μαθητές κάποια στιγμή φωνάξουν όλοι οι μαθητές μαζί με στάθμη έντασης 80 db ο καθένας, τότε μέσα στην αίθουσα θα δημιουργηθεί ολική στάθμη έντασης ίση με IL = log 5 = 93, 98 db ( n) ολ. Από την παραπάνω σχέση προκύπτει ότι, εάν σ ένα χώρο συνηχήσουν δύο πηγές με την ίδια στάθμη έντασης (IL), τότε η ολική στάθμη έντασης του ήχου αυξάνει κατά 3 db. Πρόκειται και παλι για το σημείο των 3 db (the three db point). Στάθμες ήχου στη Μουσική Συγκεκριμένες στάθμες έντασης ήχου αποδίδονται στις διάφορες σημάνσεις δυναμικής της κλασικής μουσικής, οι οποίες παρέχουν την πληροφορία για το πόσο δυνατά ή απαλά πρέπει να παιχθεί ένα μουσικό κομμάτι. Οι ιταλικές λέξεις forte (δυνατά) και piano (απαλά) συντομογραφικά συμβολίζονται, αντίστοιχα, ως και. Ισχυρότερες διαβαθμίσεις της έντασης εκφράζονται με τους συμβολισμούς (fortissio), (fortissisio), ενώ μεγαλύτερες διαβαθμίσεις της απαλότητας εκφράζονται με τους συμβολισμούς (pianissio), (pianissisio). Στο ενδιάμεσο υπάρχουν οι διαβαθμίσεις (ezzoforte) και (ezzopiano), όπου η λέξη ezzo σημαίνει «μισό-» ή «μέσο-».
12 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Για τις εκφράσεις ή,,, αποδίδονται τυπικές στρογγυλοποιημένες τιμές στάθμης έντασης του ήχου των 00, 90, 80, 70, 60, 50 και 40 db. Στάθμη Ακουστότητας (Loudness Level) Η στάθμη ακουστότητας είναι το υποκειμενικό εκείνο χαρακτηριστικό γνώρισμα του ήχου, το οποίο παρέχει το μέγεθος της ακουστικής εντυπώσεως, που προκαλείται στο ακουστικό σύστημα του ανθρώπου. Γενικά, η στάθμη ακουστότητας (LL), που αντιλαμβάνεται το ανθρώπινο σύστημα ακοής, δεν ταυτίζεται με τη στάθμη της ηχητικής έντασης (IL) ή τη στάθμη της ακουστικής πίεσης (SPL). Αυτό συμβαίνει επειδή το ανθρώπινο αυτί παρουσιάζει διαφορετική ευαισθησία στις διάφορες ακουστές συχνότητες. Ένα προσωπικό μέτρο της στάθμης ακουστότητας επιβάλλεται με ψυχοακουστικά πειράματα κατά τα οποία ερωτάται ένα πλήθος ατόμων, κατάλληλα επιλεγμένων, εάν ήχοι διαφορετικών συχνοτήτων και σταθμών έντασης ηχούν εξίσου δυνατά με έναν πρότυπο ημιτονοειδή ήχο. Ο πρότυπος ημιτονοειδής ήχος έχει ληφθεί με συχνότητα 000 Hz αφενός μεν διότι είναι κοντά στη συχνοτική περιοχή της μεγάλης ευαισθησίας του αυτιού μας ( Hz), αφετέρου δε διότι είναι δύναμη του αριθμού 0 (βάση του δεκαδικού αριθμητικού συστήματος) διευκολύνοντας τους υπολογισμούς και την ανάγνωση των διαφόρων διαγραμμάτων, που στην πλειοψηφία τους είναι λογαριθμικά. Ως μονάδα μέτρησης της στάθμης ακουστότητας ορίσθηκε από τον Barkhausen το 96 το phon. Με βάση τα παραπάνω, η κλίμακα της στάθμης ακουστότητας σε μονάδες phon ταυτίζεται αριθμητικά με την κλίμακα της στάθμης έντασης σε db (αναφορά 0 ) ΜΟΝΟ στη συχνότητα αναφοράς, δηλαδή στη συχνότητα των 000 Hz. Για παράδειγμα, λέμε ότι ένας ημιτονοειδής ήχος έχει στάθμη ακουστότητας 60 phon, εάν ηχεί εξίσου δυνατά με έναν ημιτονοειδή ήχο συχνότητας 000 Hz και στάθμης έντασης 60 db. Για όλες τις άλλες συχνότητες η μετάβαση από την κλίμακα της στάθμης ακουστότητας στην κλίμακα της στάθμης έντασης γίνεται με τη βοήθεια του διαγράμματος των ισοακουστικών καμπυλών, δημιούργημα των H. Fletcher και. A. Munson.
13 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής 3 Σχήμα 3: Διάγραμμα ισοακουστικών καμπυλών Των Fletcher-Munson ανά 0 phon για ημιτονοειδείς ήχους σε λογαριθμική χάραξη κατάλληλο για τη λήψη πληροφοριών που αφορούν συχνότητα (μουσικό ύψος), στάθμη έντασης και στάθμη ακουστότητας. Η ισοακουστική καμπύλη των μηδέν (0) phon ονομάζεται «κατώφλι ακουστότητας» και είναι αυτή που περνά από το σημείο με συντεταγμένες 000 Hz για τη συχνότητα και 0 db SPL για τη στάθμη έντασης, όταν πρόκειται για ακούσματα από το ένα αυτί μέσω ακουστικού. Για τα αμφιωτικά ακούσματα αυτή η καμπύλη είναι ελαφρώς υπερυψωμένη και περνά από το σημείο με συντεταγμένες 000 Hz για τη συχνότητα και 4, db SPL για τη στάθμη έντασης και συναντάται και με την ονομασία «καμπύλη ελαχίστου ακουστού πεδίου». Όλα τα σημεία αυτής της ισοακουστικής καμπύλης, παρόλο που ηχούν εξίσου δυνατά, δηλαδή έχουν την ίδια στάθμη ακουστότητας (0 phon ή 4, phon), απαιτούν διαφορετικές στάθμες έντασης db SPL, ιδιαίτερα στις ακραίες συχνοτικές περιοχές απ ό,τι στις κεντρικές Hz και αυτό διότι το αυτί μας παρουσιάζει διαφορετική ευαισθησία στις διάφορες συχνοτικές περιοχές και είναι αδρανέστερο στις πολύ υψηλές και στις πολύ χαμηλές συχνότητες. Ακουστότητα (Loudness) Η ακουστότητα είναι ένα ψυχοφυσικό μέγεθος. Χαρακτηρίζει τους σύνθετους ήχους, όπως ακριβώς η ένταση, που είναι φυσικό μέγεθος, χαρακτηρίζει τους ημιτονοειδείς ήχους. Η ακουστότητα έχει σχέση με το πόσο έντονα ακούγεται ο ήχος, δηλαδή χαρακτηρίζει το ποσοτικό αίσθημα ακοής, που προκαλεί ένας ήχος στο αισθητήριο της ακοής. Η ακουστότητα εξαρτάται από τη συχνότητα και τη στάθμη έντασης του ήχου και, ως ψυχοφυσικό μέγεθος, στηρίζεται σε υποκειμενικά κριτήρια.
14 4 0ο Πανελλήνιο Συνέδριο Φυσικής, Λουτράκι, 9/-//0004 Προκειμένου να μετρήσουμε την αντίληψη των ήχων από τον άνθρωπο, χρειαζόμαστε οπωσδήποτε μια καλώς ορισμένη μονάδα για την ακουστότητα που γίνεται αντιληπτή, και αυτή η μονάδα ονομάζεται sone. Εάν ένας ακροατής, που διαθέτει κανονική ακοή, βρίσκεται μέσα σε έναν ανηχοϊκό θάλαμο και στέκεται απέναντι από ένα μεγάφωνο, θα λέμε ότι αντιλαμβάνεται έναν ήχο ακουστότητας sone, όταν ακούει ημιτονοειδή ήχο συχνότητας 000 Hz και στάθμης έντασης 40 db SPL, ή, ισοδύναμα, όταν ακούει ημιτονοειδή ήχο συχνότητας 000 Hz και στάθμης ακουστότητας 40 phon. Το προσόν που διαθέτει το μέγεθος ακουστότητα έναντι της στάθμης έντασης είναι ότι υπακούει στην πράξη της πρόσθεσης κατά την γνωστή μας πρακτική αριθμητική, πράγμα που δεν ισχύει για τη στάθμη έντασης. Επί παραδείγματι ακουστότητα sones από κάποια ηχητική πηγή και ακουστότητα sones από κάποια άλλη ηχητική πηγή, που συνηχεί, ισοδυναμούν με ακουστότητα +=4 sones, που προκαλεί από μόνη της μια κάποια τρίτη ηχητική πηγή. Ενώ στάθμη έντασης 60 db από κάποια ηχητική πηγή και στάθμη έντασης 60 db από κάποια άλλη ηχητική πηγή, που συνηχεί, ισοδυναμούν με στάθμη έντασης 63 db και όχι 60+60=0 db, που προκαλεί από μόνη της μια κάποια τρίτη ηχητική πηγή. Η Ακουστότητα (σε μονάδες sone) και η στάθμη Ακουστότητας (σε μονάδες phon) συνδέονται με τη σχέση L = LL 40 0 Κυρίες και κύριοι σύνεδροι, καταλήγων την εισήγησή μου, θα επιθυμούσα με ένα παράδειγμα να υποδείξω τον τρόπο διαχείρισης των μεγαθών αυτής της τετρακτύος κατά τη λύση ασκήσεων.
15 Χαράλαμπος Χ. Σπυρίδης, Καθηγητής Μουσικής Ακουστικής-Πληροφορικής 5 Ημιτονοειδής ήχος συχνότητας 00 Hz έχει στάθμη έντασης 50 db. Θα υπολογίσουμε τη στάθμη της ακουστότητάς του και την ακουστότητά του. Σε ποια στάθμη έντασης πρέπει να μεταφερθεί αυτός ο ήχος, ώστε να διπλασιασθεί η ακουστότητά του; Λύση Από το διάγραμμα των ισοακουστικών καμπυλών των Fletcher-Munson για συχνότητα f=00 Hz και στάθμη έντασης IL=50 db προκύπτει στάθμη ακουστότητας (LL) 50 phon. ( LL 40) 0 Με στάθμη ακουστότητας (LL) 50 phon από τη σχέση S = υπολογίζουμε την ακουστότητα του ημιτονοειδούς ήχου, η οποία προκύπτει ίση με ( 50 40) S = 0 = sone. Ένας ημιτονοειδής ήχος συχνότητας f=00 Hz για να μας φαίνεται διπλάσια δυνατός από τον δοθέντα, θα πρέπει να έχει διπλάσια ακουστότητα από αυτόν, δηλαδή θα πρέπει να έχει ακουστότητα ίση με = 4 sone. ( LL 40) 0 Λογαριθμίζοντας τη σχέση S =, προκύπτει ότι η τιμή της στάθμης ακουστότητας του ημιτονοειδούς ήχου συναρτήσει της τιμής της ακουστότητάς του είναι: log S LL = phons. log Για τιμή ακουστότητας 4 sone προκύπτει από την παραπάνω σχέση τιμή στάθμης ακουστότητας ίση με 60 phon. Τέλος, από το διάγραμμα των ισοακουστικών καμπυλών των Fletcher-Munson για συχνότητα f=00 Hz και στάθμη ακουστότητας (LL) 60 phon προκύπτει στάθμη έντασης ίση με 60 db. Σας ευχαριστώ
Ψηφιακή Επεξεργασία Σηµμάτων
 Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα: Τεχνολογίες και Συστήµματα Ευρυζωνικών Εφαρµμογών και Υπηρεσιών 1 Προεπισκόπηση
Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα: Τεχνολογίες και Συστήµματα Ευρυζωνικών Εφαρµμογών και Υπηρεσιών 1 Προεπισκόπηση
Δυστυχώς, κάποτε, κάποιοι «αρμόδιοι» απεφάσισαν να μη διδάσκονται στο Λύκειο όλα τα πεδία της Φυσικής! Μεταξύ αυτών καταλέγεται και το πεδίο της
 ΠΡΟΛΟΓΟΣ Το βιβλίο αυτό με τίτλο «Λυμένες Ασκήσεις Μουσικής Ακουστικής» απευθύνεται κυρίως στους φοιτητές μου στο Τμήμα Μουσικών Σπουδών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών, στους φοιτητές
ΠΡΟΛΟΓΟΣ Το βιβλίο αυτό με τίτλο «Λυμένες Ασκήσεις Μουσικής Ακουστικής» απευθύνεται κυρίως στους φοιτητές μου στο Τμήμα Μουσικών Σπουδών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών, στους φοιτητές
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΕΣ ΣΤΑΘΜΕΣ, ΜΕΤΡΗΣΕΙΣ, ΘΟΡΥΒΟΣ, ΗΧΟΜΟΝΩΣΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΕΣ ΣΤΑΘΜΕΣ, ΜΕΤΡΗΣΕΙΣ, ΘΟΡΥΒΟΣ, ΗΧΟΜΟΝΩΣΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΕΣ ΣΤΑΘΜΕΣ, ΜΕΤΡΗΣΕΙΣ, ΘΟΡΥΒΟΣ, ΗΧΟΜΟΝΩΣΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ
Δομικά Υλικά Μάθημα ΙΙΙ. Ηχος & Ηχητικά Φαινόμενα
 Δομικά Υλικά Μάθημα ΙΙΙ Ηχος & Ηχητικά Φαινόμενα Ηχος: Μια μηχανική διαταραχή η οποία προκαλείται από μια πηγή και διαδίδεται με ορισμένη ταχύτητα σε ένα ελαστικό μέσο. Μια περιοδική ταλάντωση των μορίων
Δομικά Υλικά Μάθημα ΙΙΙ Ηχος & Ηχητικά Φαινόμενα Ηχος: Μια μηχανική διαταραχή η οποία προκαλείται από μια πηγή και διαδίδεται με ορισμένη ταχύτητα σε ένα ελαστικό μέσο. Μια περιοδική ταλάντωση των μορίων
Υπερβολικός ή ανεπιθύμητος ήχος με αποτέλεσμα ενόχληση ή απώλεια ακοής (φυσικής ή τεχνητής προέλευσης)
 Θόρυβος Υπερβολικός ή ανεπιθύμητος ήχος με αποτέλεσμα ενόχληση ή απώλεια ακοής (φυσικής ή τεχνητής προέλευσης) Ηχος: Διαταραχή πίεσης που διαδίδεται σαν κύμα στον αέρα και ανιχνεύεται από το αυτί. Η διαταραχή
Θόρυβος Υπερβολικός ή ανεπιθύμητος ήχος με αποτέλεσμα ενόχληση ή απώλεια ακοής (φυσικής ή τεχνητής προέλευσης) Ηχος: Διαταραχή πίεσης που διαδίδεται σαν κύμα στον αέρα και ανιχνεύεται από το αυτί. Η διαταραχή
Ενότητα 9: Θεωρητικός υπολογισμός έντασης ήχου σε εγκατάσταση υποθετικού στούντιο
 Ενότητα 9: Θεωρητικός υπολογισμός έντασης ήχου σε εγκατάσταση υποθετικού στούντιο Α. Αραβαντινός - Μ. Καραγιάννη Σελίδα 1 1. Σκοπός Πρόκειται για άσκηση θεωρητικού χαρακτήρα στην οποία πραγματοποιούνται
Ενότητα 9: Θεωρητικός υπολογισμός έντασης ήχου σε εγκατάσταση υποθετικού στούντιο Α. Αραβαντινός - Μ. Καραγιάννη Σελίδα 1 1. Σκοπός Πρόκειται για άσκηση θεωρητικού χαρακτήρα στην οποία πραγματοποιούνται
Ψηφιακός ήχος και κινούμενα γραφικά
 ΕΣΔ200 Δημιουργία Περιεχομένου ΙI Ψηφιακός ήχος και κινούμενα γραφικά Εισαγωγή Το παρακάτω σχήμα περιγράφει τους δυνατούς τρόπους δημιουργίας αποθήκευσης και. αναπαραγωγής ψηφιακού ήχου Ο Ήχος από φυσική
ΕΣΔ200 Δημιουργία Περιεχομένου ΙI Ψηφιακός ήχος και κινούμενα γραφικά Εισαγωγή Το παρακάτω σχήμα περιγράφει τους δυνατούς τρόπους δημιουργίας αποθήκευσης και. αναπαραγωγής ψηφιακού ήχου Ο Ήχος από φυσική
1/3/2009. ιδάσκων. Ορολόγιο πρόγραμμα του μαθήματος. Φλώρος Ανδρέας Επίκ. Καθηγητής. Εκπόνηση εργασίας / εργασιών. ιαλέξεις. Εργαστηριακό / Εργαστήριο
 Πληροφορίες για το μάθημα ιδάσκων Μάθημα: «Ηλεκτροακουστική & Ακουστική Χώρων» Διάλεξη 1 η :«Διαδικασία μαθήματος και Εισαγωγή» Φλώρος Ανδρέας Επίκ. Καθηγητής Ανδρέας Φλώρος (floros@ionio.gr) Μιχάλης Αρβανίτης
Πληροφορίες για το μάθημα ιδάσκων Μάθημα: «Ηλεκτροακουστική & Ακουστική Χώρων» Διάλεξη 1 η :«Διαδικασία μαθήματος και Εισαγωγή» Φλώρος Ανδρέας Επίκ. Καθηγητής Ανδρέας Φλώρος (floros@ionio.gr) Μιχάλης Αρβανίτης
ΘΟΡΥΒΟΣ ΗΧΟΔΟΣΙΜΕΤΡΙΑ Σιδερής Ευστάθιος
 ΘΟΡΥΒΟΣ ΗΧΟΔΟΣΙΜΕΤΡΙΑ Σιδερής Ευστάθιος 1. Θόρυβος Θόρυβος είναι κάθε υπερβολικός ή ανεπιθύμητος ήχος ο οποίος προκαλεί στον αποδέκτη άνθρωπο δυσφορία ή ακόμα και απώλεια ακοής. Δεκάδες εκατομμύρια εργαζόμενοι
ΘΟΡΥΒΟΣ ΗΧΟΔΟΣΙΜΕΤΡΙΑ Σιδερής Ευστάθιος 1. Θόρυβος Θόρυβος είναι κάθε υπερβολικός ή ανεπιθύμητος ήχος ο οποίος προκαλεί στον αποδέκτη άνθρωπο δυσφορία ή ακόμα και απώλεια ακοής. Δεκάδες εκατομμύρια εργαζόμενοι
ΗΧΟΣ : ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ, ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΑΧΥΤΗΤΑΣ
 Α1 ΗΧΟΣ : ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ, ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΑΧΥΤΗΤΑΣ 1. Σκοπός Στην εργαστηριακή αυτή άσκηση παρουσιάζεται η δράση ενός µεγάφωνου που τροφοδοτείται κατάλληλα µε εναλλασσόµενο ρεύµα από µονάδα γεννήτριας
Α1 ΗΧΟΣ : ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ, ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΑΧΥΤΗΤΑΣ 1. Σκοπός Στην εργαστηριακή αυτή άσκηση παρουσιάζεται η δράση ενός µεγάφωνου που τροφοδοτείται κατάλληλα µε εναλλασσόµενο ρεύµα από µονάδα γεννήτριας
ΘΟΡΥΒΟΣ Αξιολόγηση και µέτρα αντιµετώπισης
 TEE TKM ΣΕΜΙΝΑΡΙΑ ΜΙΚΡΗΣ ΙΑΡΚΕΙΑ ΣΤ ΚΥΚΛΟΣ2005 ΥΓΕΙΑ ΚΑΙ ΑΣΦΑΛΕΙΑ ΕΡΓΑΖΟΜΕΝΩΝ ΣΤΗΝ ΒΙΟΜΗΧΑΝΙΑ ΘΟΡΥΒΟΣ Αξιολόγηση και µέτρα αντιµετώπισης Ν. Μαραγκός Μηχανολόγος Mηχ. Msc ΚΙΛΚΙΣ 2005 ΘΟΡΥΒΟΣ Αξιολόγηση
TEE TKM ΣΕΜΙΝΑΡΙΑ ΜΙΚΡΗΣ ΙΑΡΚΕΙΑ ΣΤ ΚΥΚΛΟΣ2005 ΥΓΕΙΑ ΚΑΙ ΑΣΦΑΛΕΙΑ ΕΡΓΑΖΟΜΕΝΩΝ ΣΤΗΝ ΒΙΟΜΗΧΑΝΙΑ ΘΟΡΥΒΟΣ Αξιολόγηση και µέτρα αντιµετώπισης Ν. Μαραγκός Μηχανολόγος Mηχ. Msc ΚΙΛΚΙΣ 2005 ΘΟΡΥΒΟΣ Αξιολόγηση
ΠΕΡΙΕΧΟΜΕΝΑ. ΕΙΣΑΓΩΓΗ: Γνωριμία με την ΑΚΟΥΣΤΙΚΗ 1 ΜΕΡΟΣ ΠΡΩΤΟ: ΘΕΩΡΙΑ 5. 1 ος ΘΕΜΑΤΙΚΟΣ ΑΞΟΝΑΣ: ΤΑΛΑΝΤΩΣΕΙΣ 7 Προσδοκώμενα αποτελέσματα 8
 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ: Γνωριμία με την ΑΚΟΥΣΤΙΚΗ 1 ΜΕΡΟΣ ΠΡΩΤΟ: ΘΕΩΡΙΑ 5 1 ος ΘΕΜΑΤΙΚΟΣ ΑΞΟΝΑΣ: ΤΑΛΑΝΤΩΣΕΙΣ 7 Προσδοκώμενα αποτελέσματα 8 1.1. Περιοδική κίνηση Περιοδικά φαινόμενα 9 1.2. Ταλάντωση - Ταλαντούμενα
ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ: Γνωριμία με την ΑΚΟΥΣΤΙΚΗ 1 ΜΕΡΟΣ ΠΡΩΤΟ: ΘΕΩΡΙΑ 5 1 ος ΘΕΜΑΤΙΚΟΣ ΑΞΟΝΑΣ: ΤΑΛΑΝΤΩΣΕΙΣ 7 Προσδοκώμενα αποτελέσματα 8 1.1. Περιοδική κίνηση Περιοδικά φαινόμενα 9 1.2. Ταλάντωση - Ταλαντούμενα
Ο Ήχος. Υπεύθυνος Καθηγητής: Παζούλης Παναγιώτης
 ιαθεµατική Εργασία µε Θέµα: Οι Φυσικές Επιστήµες στην Καθηµερινή µας Ζωή Ο Ήχος Τµήµα: β1 Γυµνασίου Υπεύθυνος Καθηγητής: Παζούλης Παναγιώτης Συντακτική Οµάδα: Γεώργιος Ελευθεριάδης Ο Ήχος Έχει σχέση ο
ιαθεµατική Εργασία µε Θέµα: Οι Φυσικές Επιστήµες στην Καθηµερινή µας Ζωή Ο Ήχος Τµήµα: β1 Γυµνασίου Υπεύθυνος Καθηγητής: Παζούλης Παναγιώτης Συντακτική Οµάδα: Γεώργιος Ελευθεριάδης Ο Ήχος Έχει σχέση ο
Ανακαλύπτεται το μικρόφωνο!
 ΠΡΟΛΕΓΟΜΕΝΑ Το ΕΠΕΑΕΚ είναι το Επιχειρησιακό Πρόγραμμα, το οποίο σχεδιάστηκε για την Εκπαίδευση και την Αρχική Επαγγελματική Κατάρτιση με στόχο να ανταποκριθεί η Ελλάδα στις προκλήσεις που διαμορφώνονται
ΠΡΟΛΕΓΟΜΕΝΑ Το ΕΠΕΑΕΚ είναι το Επιχειρησιακό Πρόγραμμα, το οποίο σχεδιάστηκε για την Εκπαίδευση και την Αρχική Επαγγελματική Κατάρτιση με στόχο να ανταποκριθεί η Ελλάδα στις προκλήσεις που διαμορφώνονται
Εισαγωγή στα χαρακτηριστικά των μικροφώνων
 ΕΙΔΗ ΜΙΚΡΟΦΩΝΩΝ Επιμέλεια: Νίκος Σκιαδάς ΠΕ 17.13 Μουσικής Τεχνολογίας Το μικρόφωνο πήρε την ονομασία του από τον Ντέιβιντ Χιουζ, ο οποίος επινόησε μια διάταξη μεταφοράς ήχου που ήταν τόσο ευαίσθητη, που
ΕΙΔΗ ΜΙΚΡΟΦΩΝΩΝ Επιμέλεια: Νίκος Σκιαδάς ΠΕ 17.13 Μουσικής Τεχνολογίας Το μικρόφωνο πήρε την ονομασία του από τον Ντέιβιντ Χιουζ, ο οποίος επινόησε μια διάταξη μεταφοράς ήχου που ήταν τόσο ευαίσθητη, που
Ευαισθησία (dβ) VS Απόδοση (ακουστική ευαισθησία) (%)
 Ευαισθησία (dβ) S Απόδοση (ακουστική ευαισθησία) (%) Στις παρακάτω γραμμές θα προσπαθήσομε να αναλύσομε τη σχέση μεταξύ ευαισθησίας και βαθμού απόδοσης ενός ηχείου. Η ευαισθησία και ο βαθμός απόδοσης είναι
Ευαισθησία (dβ) S Απόδοση (ακουστική ευαισθησία) (%) Στις παρακάτω γραμμές θα προσπαθήσομε να αναλύσομε τη σχέση μεταξύ ευαισθησίας και βαθμού απόδοσης ενός ηχείου. Η ευαισθησία και ο βαθμός απόδοσης είναι
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΑ ΗΧΟΥ εισαγωγή
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΑ ΗΧΟΥ εισαγωγή ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΑ ΗΧΟΥ εισαγωγή ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Ο Ήχος ως Σήμα & η Ακουστική Οδός ως Σύστημα
 Εθνκό & Καποδιστριακό Πανεπιστήμιο Αθηνών Ο Ήχος ως Σήμα & η Ακουστική Οδός ως Σύστημα Βασικές Έννοιες Θάνος Μπίμπας Επ. Καθηγητής ΕΚΠΑ Hon. Reader UCL Ear InsUtute Διαταραχές Φωνής & Ακοής στις Ερμηνευτικές
Εθνκό & Καποδιστριακό Πανεπιστήμιο Αθηνών Ο Ήχος ως Σήμα & η Ακουστική Οδός ως Σύστημα Βασικές Έννοιες Θάνος Μπίμπας Επ. Καθηγητής ΕΚΠΑ Hon. Reader UCL Ear InsUtute Διαταραχές Φωνής & Ακοής στις Ερμηνευτικές
Συστήματα Πολυμέσων. Ενότητα 11: Χαρακτηριστικά Ψηφιακού Ήχου. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 11: Χαρακτηριστικά Ψηφιακού Ήχου Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 11: Χαρακτηριστικά Ψηφιακού Ήχου Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Κλινική χρήση των ήχων
 Κλινική χρήση των ήχων Ήχοι και ακουστότητα Κύματα υπερήχων Ακουστικά κύματα, Ήχοι, Είδη ήχων Ήχους υπό την ευρεία έννοια καλούμε κάθε κύμα πίεσης που υπάρχει και διαδίδεται στο εσωτερικό των σωμάτων.
Κλινική χρήση των ήχων Ήχοι και ακουστότητα Κύματα υπερήχων Ακουστικά κύματα, Ήχοι, Είδη ήχων Ήχους υπό την ευρεία έννοια καλούμε κάθε κύμα πίεσης που υπάρχει και διαδίδεται στο εσωτερικό των σωμάτων.
ΨΥΧΟΑΚΟΥΣΤΙΚΗ σύνδεσης φυσικού φαινομένου/ήχος υποκειμενικού αισθήματος πως συμπεράσματα
 4 2 ΨΥΧΟΑΚΟΥΣΤΙΚΗ Κάτω από τον όρο «Ψυχοακουστική» κρύβεται ένας πολύ ενδιαφέρον επιστημονικός κλάδος. Το αντικείμενό του είναι περίπου φανερό απλά και μόνο από το όνομα: Εξετάζει τις ιδιομορφίες της σύνδεσης
4 2 ΨΥΧΟΑΚΟΥΣΤΙΚΗ Κάτω από τον όρο «Ψυχοακουστική» κρύβεται ένας πολύ ενδιαφέρον επιστημονικός κλάδος. Το αντικείμενό του είναι περίπου φανερό απλά και μόνο από το όνομα: Εξετάζει τις ιδιομορφίες της σύνδεσης
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Μουσική και Μαθηματικά!!!
 Μουσική και Μαθηματικά!!! Η μουσική είναι ίσως από τις τέχνες η πιο δεμένη με τα μαθηματικά, με τη μαθηματική σκέψη, από την ίδια τη φύση της. Η διατακτική δομή μπορεί να κατατάξει τα στοιχεία ενός συνόλου,
Μουσική και Μαθηματικά!!! Η μουσική είναι ίσως από τις τέχνες η πιο δεμένη με τα μαθηματικά, με τη μαθηματική σκέψη, από την ίδια τη φύση της. Η διατακτική δομή μπορεί να κατατάξει τα στοιχεία ενός συνόλου,
ΠΟΜΠΟΣ ΕΚΤΗΣ ΑΝΙΧΝΕΥΤΗΣ
 Σαν ήχος χαρακτηρίζεται οποιοδήποτε μηχανικό ελαστικό κύμα ή γενικότερα μία μηχανική διαταραχή που διαδίδεται σε ένα υλικό μέσο και είναι δυνατό να ανιχνευθεί από τον άνθρωπο μέσω της αίσθησης της ακοής.
Σαν ήχος χαρακτηρίζεται οποιοδήποτε μηχανικό ελαστικό κύμα ή γενικότερα μία μηχανική διαταραχή που διαδίδεται σε ένα υλικό μέσο και είναι δυνατό να ανιχνευθεί από τον άνθρωπο μέσω της αίσθησης της ακοής.
ΑΠΟ ΤΟΥΣ : Γιάννης Πετσουλας-Μπαλής Στεφανία Ολέκο Χριστίνα Χρήστου Βασιλική Χρυσάφη
 ΑΠΟ ΤΟΥΣ : Γιάννης Πετσουλας-Μπαλής Στεφανία Ολέκο Χριστίνα Χρήστου Βασιλική Χρυσάφη Ο ΠΥΘΑΓΟΡΑΣ (572-500 ΠΧ) ΗΤΑΝ ΦΟΛΟΣΟΦΟΣ, ΜΑΘΗΜΑΤΙΚΟΣ ΚΑΙ ΘΕΩΡΗΤΙΚΟΣ ΤΗΣ ΜΟΥΙΣΚΗΣ. ΥΠΗΡΞΕ Ο ΠΡΩΤΟΣ ΠΟΥ ΕΘΕΣΕ ΤΙΣ ΒΑΣΕΙΣ
ΑΠΟ ΤΟΥΣ : Γιάννης Πετσουλας-Μπαλής Στεφανία Ολέκο Χριστίνα Χρήστου Βασιλική Χρυσάφη Ο ΠΥΘΑΓΟΡΑΣ (572-500 ΠΧ) ΗΤΑΝ ΦΟΛΟΣΟΦΟΣ, ΜΑΘΗΜΑΤΙΚΟΣ ΚΑΙ ΘΕΩΡΗΤΙΚΟΣ ΤΗΣ ΜΟΥΙΣΚΗΣ. ΥΠΗΡΞΕ Ο ΠΡΩΤΟΣ ΠΟΥ ΕΘΕΣΕ ΤΙΣ ΒΑΣΕΙΣ
Στάσιμα κύματα - Μέτρηση της ταχύτητας του ήχου με το σωλήνα Kundt
 Στάσιμα κύματα - Μέτρηση της ταχύτητας του ήχου με το σωλήνα Kundt Η χρησιμοποιούμενη διάταξη φαίνεται στο ακόλουθο σχήμα: Το μεγάφωνο του σωλήνα Kundt συνδέεται στην έξοδο SIGNAL OUT της γεννήτριας συχνοτήτων.
Στάσιμα κύματα - Μέτρηση της ταχύτητας του ήχου με το σωλήνα Kundt Η χρησιμοποιούμενη διάταξη φαίνεται στο ακόλουθο σχήμα: Το μεγάφωνο του σωλήνα Kundt συνδέεται στην έξοδο SIGNAL OUT της γεννήτριας συχνοτήτων.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ ΘΕΜΑ 1 ο (βαθµοί 2) Σώµα µε µάζα m=5,00 kg είναι προσαρµοσµένο στο ελεύθερο άκρο ενός κατακόρυφου ελατηρίου και ταλαντώνεται εκτελώντας πέντε (5) πλήρης ταλαντώσεις σε χρονικό
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ ΘΕΜΑ 1 ο (βαθµοί 2) Σώµα µε µάζα m=5,00 kg είναι προσαρµοσµένο στο ελεύθερο άκρο ενός κατακόρυφου ελατηρίου και ταλαντώνεται εκτελώντας πέντε (5) πλήρης ταλαντώσεις σε χρονικό
Κεφάλαιο 5 ο : Μηχανικά Κύματα
 Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan g g Εισαγωγή Η ενέργεια μεταφέρεται με μεταφορά μάζας Αν ρίξεις μια μπάλα προς ένα αμαξάκι, το αμαξάκι
Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan g g Εισαγωγή Η ενέργεια μεταφέρεται με μεταφορά μάζας Αν ρίξεις μια μπάλα προς ένα αμαξάκι, το αμαξάκι
ΗΧΟΣ : ΕΞΑΣΘΕΝΗΣΗ ΗΧΟΥ, ΜΕΤΡΗΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΝΤΕΛΕΣΤΗ ΕΞΑΣΘΕΝΗΣΗΣ
 Α3 ΗΧΟΣ : ΕΞΑΣΘΕΝΗΣΗ ΗΧΟΥ, ΜΕΤΡΗΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΝΤΕΛΕΣΤΗ ΕΞΑΣΘΕΝΗΣΗΣ Σκοπός Αντικείµενο της άσκησης αυτής είναι η µελέτη του φαινοµένου της εξασθένησης ή- χου κατά τη διέλευσή του από απορροφητή δεδοµένου
Α3 ΗΧΟΣ : ΕΞΑΣΘΕΝΗΣΗ ΗΧΟΥ, ΜΕΤΡΗΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΝΤΕΛΕΣΤΗ ΕΞΑΣΘΕΝΗΣΗΣ Σκοπός Αντικείµενο της άσκησης αυτής είναι η µελέτη του φαινοµένου της εξασθένησης ή- χου κατά τη διέλευσή του από απορροφητή δεδοµένου
ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. ΜΕΡΟΣ Α : Άλγεβρα. Κεφάλαιο 2 ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Ειδικότερα:
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
Ένα ταχέως µεταβαλλόµενο διάµηκες κύµα πίεσης που διαδίδεται σε ένα υλικό µέσον (αέρια, υγρά, στερεά).
 Ένα ταχέως µεταβαλλόµενο διάµηκες κύµα πίεσης που διαδίδεται σε ένα υλικό µέσον (αέρια, υγρά, στερεά). ( ωt kx) y = yoηµ ιάµηκες κύµα. Η κίνηση των µορίων είναι παράλληλη προς τη διεύθυνση διάδοσης του
Ένα ταχέως µεταβαλλόµενο διάµηκες κύµα πίεσης που διαδίδεται σε ένα υλικό µέσον (αέρια, υγρά, στερεά). ( ωt kx) y = yoηµ ιάµηκες κύµα. Η κίνηση των µορίων είναι παράλληλη προς τη διεύθυνση διάδοσης του
Μάθημα: Τεχνολογία Ήχου
 Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Τεχνολογία Ήχου Εργαστηριακή Άσκηση 3 «Καταγραφή της επίπτωσης της κατευθυντικότητας ηλεκτροακουστικών μετατροπέων» Διδάσκων: Φλώρος Ανδρέας Δρ.
Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Τεχνολογία Ήχου Εργαστηριακή Άσκηση 3 «Καταγραφή της επίπτωσης της κατευθυντικότητας ηλεκτροακουστικών μετατροπέων» Διδάσκων: Φλώρος Ανδρέας Δρ.
Ειδικά Θέματα Ηλεκτρονικών 1
 Ειδικά Θέματα Ηλεκτρονικών 1 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 3...2 ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ...2 3.1 Απόκριση συχνότητας ενισχυτών...2 3.1.1 Παραμόρφωση στους ενισχυτές...5 3.1.2 Πιστότητα των ενισχυτών...6 3.1.3
Ειδικά Θέματα Ηλεκτρονικών 1 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 3...2 ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ...2 3.1 Απόκριση συχνότητας ενισχυτών...2 3.1.1 Παραμόρφωση στους ενισχυτές...5 3.1.2 Πιστότητα των ενισχυτών...6 3.1.3
Φυσική και Μουσική Ακουστική
 Φυσική και Μουσική Ακουστική Στο υποχρεωτικό αυτό µάθηµα οι φοιτητές θα έλθουν για πρώτη φορά σε επαφή µε την Ακουστική -µια από τις κύριες υποδιαιρέσεις της κλασικής Φυσικής που, δυστυχώς, δεν διδάσκεται
Φυσική και Μουσική Ακουστική Στο υποχρεωτικό αυτό µάθηµα οι φοιτητές θα έλθουν για πρώτη φορά σε επαφή µε την Ακουστική -µια από τις κύριες υποδιαιρέσεις της κλασικής Φυσικής που, δυστυχώς, δεν διδάσκεται
Δρ.Κων. Κων.Λαμπρόπουλος. Χειρουργός ΩΡΛ Φωνίατρος Πρόεδρος Επιστημονικού Συμβουλίου
 Δρ.Κων Κων.Λαμπρόπουλος Χειρουργός ΩΡΛ Φωνίατρος Πρόεδρος Επιστημονικού Συμβουλίου Πρόεδρος Ελληνικής Φωνιατρικής Εταιρείας Αθήνα, 17 νοεμβρίου 2010 πέντε αισθήσεις όραση αφή όσφρηση γεύση ακοή η ακοή
Δρ.Κων Κων.Λαμπρόπουλος Χειρουργός ΩΡΛ Φωνίατρος Πρόεδρος Επιστημονικού Συμβουλίου Πρόεδρος Ελληνικής Φωνιατρικής Εταιρείας Αθήνα, 17 νοεμβρίου 2010 πέντε αισθήσεις όραση αφή όσφρηση γεύση ακοή η ακοή
Τ Ε Ι Κ Ρ Η Τ Η Σ Π Α Ρ Α Ρ Τ Η Μ Α Ρ Ε Θ Υ Μ Ν Ο Υ ΤΜΗΜΑ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΑΚΟΥΣΤΙΚΗΣ ΙΟΥΛΙΟΣ 2013
 Τ Ε Ι Κ Ρ Η Τ Η Σ Π Α Ρ Α Ρ Τ Η Μ Α Ρ Ε Θ Υ Μ Ν Ο Υ ΤΜΗΜΑ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΑΚΟΥΣΤΙΚΗΣ ΗΧΟΛΗΨΙΑ Ι ΞΕΝΙΚΑΚΗΣ ΔΗΜΗΤΡΗΣ ΙΟΥΛΙΟΣ 2013 1 1 ΕΙΣΑΓΩΓΗ 1.1 ΗΧΟΛΗΨΙΑ 1.1.1 ΓΕΝΙΚΑ 1. Προϋπόθεση πραγματοποίησης
Τ Ε Ι Κ Ρ Η Τ Η Σ Π Α Ρ Α Ρ Τ Η Μ Α Ρ Ε Θ Υ Μ Ν Ο Υ ΤΜΗΜΑ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΑΚΟΥΣΤΙΚΗΣ ΗΧΟΛΗΨΙΑ Ι ΞΕΝΙΚΑΚΗΣ ΔΗΜΗΤΡΗΣ ΙΟΥΛΙΟΣ 2013 1 1 ΕΙΣΑΓΩΓΗ 1.1 ΗΧΟΛΗΨΙΑ 1.1.1 ΓΕΝΙΚΑ 1. Προϋπόθεση πραγματοποίησης
2. ΤΟ ΠΛΕΟΝΕΚΤΗΜΑ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ SYNTHESIS ΣΤΗΝ ΑΠΟ ΟΣΗ ΤΩΝ ΙΑΣΤΗΜΑΤΩΝ ΚΑΙ Η ΑΙΤΙΟΛΟΓΗΣΗ ΤΟΥ
 2. ΤΟ ΠΛΕΟΝΕΚΤΗΜΑ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ SYNTHESIS ΣΤΗΝ ΑΠΟ ΟΣΗ ΤΩΝ ΙΑΣΤΗΜΑΤΩΝ ΚΑΙ Η ΑΙΤΙΟΛΟΓΗΣΗ ΤΟΥ Tο σύστηµα γραφής που χρησιµοποιεί ο χρήστης στο πρόγραµµα Synthesis προσφέρει αρκετές από τις δυνατότητες
2. ΤΟ ΠΛΕΟΝΕΚΤΗΜΑ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ SYNTHESIS ΣΤΗΝ ΑΠΟ ΟΣΗ ΤΩΝ ΙΑΣΤΗΜΑΤΩΝ ΚΑΙ Η ΑΙΤΙΟΛΟΓΗΣΗ ΤΟΥ Tο σύστηµα γραφής που χρησιµοποιεί ο χρήστης στο πρόγραµµα Synthesis προσφέρει αρκετές από τις δυνατότητες
ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΑΠΡΙΛΙΟΥ 2011 Γ ΤΑΞΗΣ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ Μ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΑΠΡΙΛΙΟΥ 2011 Γ ΤΑΞΗΣ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ Μ. ΤΡΙΤΗ 19 ΑΠΡΙΛΙ ΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ : ΟΧΤΩ (8) ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΑΠΡΙΛΙΟΥ 2011 Γ ΤΑΞΗΣ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ Μ. ΤΡΙΤΗ 19 ΑΠΡΙΛΙ ΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ : ΟΧΤΩ (8) ΘΕΜΑ Α Στις ημιτελείς προτάσεις
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηχητικά Κύματα Εικόνα: Τα αυτιά του ανθρώπου έχουν εξελιχθεί να ακούν και να ερμηνεύουν ηχητικά κύματα ως φωνή ή ως ήχους. Κάποια ζώα, όπως το είδος αλεπούς με τα αυτιά νυχτερίδας,
Φυσική για Μηχανικούς Ηχητικά Κύματα Εικόνα: Τα αυτιά του ανθρώπου έχουν εξελιχθεί να ακούν και να ερμηνεύουν ηχητικά κύματα ως φωνή ή ως ήχους. Κάποια ζώα, όπως το είδος αλεπούς με τα αυτιά νυχτερίδας,
Τι είναι ο ήχος? Στα στερεά διαδίδονται διαμήκη & εγκάρσια κύματα. Ένα ταχέως μεταβαλλόμενο διάμηκες κύμα πίεσης που διαδίδεται σε
 Τι είναι ο ήχος? Στα στερεά διαδίδονται διαμήκη & εγκάρσια κύματα Ένα ταχέως μεταβαλλόμενο διάμηκες κύμα πίεσης που διαδίδεται σε ένα υλικό μέσο (αέρια, υγρά, στερεά) : y yot kx 1 1 όπου ω=πν [rad/sec]
Τι είναι ο ήχος? Στα στερεά διαδίδονται διαμήκη & εγκάρσια κύματα Ένα ταχέως μεταβαλλόμενο διάμηκες κύμα πίεσης που διαδίδεται σε ένα υλικό μέσο (αέρια, υγρά, στερεά) : y yot kx 1 1 όπου ω=πν [rad/sec]
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Κεφάλαιο T3. Ηχητικά κύµατα
 Κεφάλαιο T3 Ηχητικά κύµατα Εισαγωγή στα ηχητικά κύµατα Τα κύµατα µπορούν να διαδίδονται σε µέσα τριών διαστάσεων. Τα ηχητικά κύµατα είναι διαµήκη κύµατα. Διαδίδονται σε οποιοδήποτε υλικό. Είναι µηχανικά
Κεφάλαιο T3 Ηχητικά κύµατα Εισαγωγή στα ηχητικά κύµατα Τα κύµατα µπορούν να διαδίδονται σε µέσα τριών διαστάσεων. Τα ηχητικά κύµατα είναι διαµήκη κύµατα. Διαδίδονται σε οποιοδήποτε υλικό. Είναι µηχανικά
Δομικά Υλικά Μάθημα ΙV. Ηχος & Ηχητικά Φαινόμενα II
 Δομικά Υλικά Μάθημα ΙV Ηχος & Ηχητικά Φαινόμενα II Συντελεστής Ανάκλασης r Συντελεστής Ανάκλασης r Ο λόγος της ανακλώμενης (W r ) ηχητικής ενέργειας από την επιφάνεια προς την προσπίπτουσα (W i ) Συντελεστής
Δομικά Υλικά Μάθημα ΙV Ηχος & Ηχητικά Φαινόμενα II Συντελεστής Ανάκλασης r Συντελεστής Ανάκλασης r Ο λόγος της ανακλώμενης (W r ) ηχητικής ενέργειας από την επιφάνεια προς την προσπίπτουσα (W i ) Συντελεστής
Μάθημα: Τεχνολογία Ήχου
 Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Τεχνολογία Ήχου Εργαστηριακή Άσκηση 3 «Καταγραφή της επίπτωσης της κατευθυντικότητας ηλεκτροακουστικών μετατροπέων» Διδάσκων: Φλώρος Ανδρέας Δρ.
Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Τεχνολογία Ήχου Εργαστηριακή Άσκηση 3 «Καταγραφή της επίπτωσης της κατευθυντικότητας ηλεκτροακουστικών μετατροπέων» Διδάσκων: Φλώρος Ανδρέας Δρ.
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / Ε Π Ω Ν Υ Μ Ο :...
 Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
ΠΑΡΟΥΣΙΑΣΗ ΣΤΑΤΙΣΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ
 ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
Φυσική Εικόνας & Ήχου ΙΙ (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου ΙΙ (Ε) Ενότητα 1: Ήχος Μελέτη χαρακτηριστικών, Προσδιορισμός ταχύτητας Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας &
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου ΙΙ (Ε) Ενότητα 1: Ήχος Μελέτη χαρακτηριστικών, Προσδιορισμός ταχύτητας Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας &
Συστήματα Πολυμέσων. Ενότητα 12: Συμπίεση Ψηφιακού Ήχου. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 12: Συμπίεση Ψηφιακού Ήχου Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 12: Συμπίεση Ψηφιακού Ήχου Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τι είναι η Ψυχοακουστική;
 Τι είναι η Ψυχοακουστική; Γιώργος Παπαδέλης papadeli@mus.auth.gr Τμήμα Μουσικών Σπουδών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Κύκλος διαλέξεων Μουσικής Ακουστικής Cb + tbn 1/37 Γνωσιοεπιστήμη: Ηδιεπιστημονική
Τι είναι η Ψυχοακουστική; Γιώργος Παπαδέλης papadeli@mus.auth.gr Τμήμα Μουσικών Σπουδών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Κύκλος διαλέξεων Μουσικής Ακουστικής Cb + tbn 1/37 Γνωσιοεπιστήμη: Ηδιεπιστημονική
ΕΦΑΡΜΟΣΜΕΝΗ ΑΚΟΥΣΤΙΚΗ II
 ΕΦΑΡΜΟΣΜΕΝΗ ΑΚΟΥΣΤΙΚΗ II (Έκδοση 1.1, 12/10/2012) ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ... 1. ΤΟΝΙΚΟ ΥΨΟΣ ΚΑΙ ΧΡΟΙΑ... 1.1. Κλίμακες... 1.2 Διάκριση του τονικού ύψους... 1.3 Το τονικό ύψος των καθαρών τόνων... 1.4 Τονικό
ΕΦΑΡΜΟΣΜΕΝΗ ΑΚΟΥΣΤΙΚΗ II (Έκδοση 1.1, 12/10/2012) ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ... 1. ΤΟΝΙΚΟ ΥΨΟΣ ΚΑΙ ΧΡΟΙΑ... 1.1. Κλίμακες... 1.2 Διάκριση του τονικού ύψους... 1.3 Το τονικό ύψος των καθαρών τόνων... 1.4 Τονικό
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ Θέµα ο ΚΕΦΑΛΑΙΟ 2 ο : ΚΥΜΑΤΑ Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασµένες; α Η υπέρυθρη ακτινοβολία έχει µήκη κύµατος µεγαλύτερα από
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ Θέµα ο ΚΕΦΑΛΑΙΟ 2 ο : ΚΥΜΑΤΑ Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασµένες; α Η υπέρυθρη ακτινοβολία έχει µήκη κύµατος µεγαλύτερα από
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
Μελέτη και εικονική διαμόρφωση ακουστικής σε αίθουσα διδασκαλίας
 Μελέτη και εικονική διαμόρφωση ακουστικής σε αίθουσα διδασκαλίας Ιωάννης Γ. Μαλαφής, Π.Δ. 407/82 Εργαστήριο Μουσικής Ακουστικής Τεχνολογίας, Τμήμα Μουσικών Σπουδών, Πανεπιστήμιο Αθηνών. Παναγιώτης Ε. Χατζημανολάκης
Μελέτη και εικονική διαμόρφωση ακουστικής σε αίθουσα διδασκαλίας Ιωάννης Γ. Μαλαφής, Π.Δ. 407/82 Εργαστήριο Μουσικής Ακουστικής Τεχνολογίας, Τμήμα Μουσικών Σπουδών, Πανεπιστήμιο Αθηνών. Παναγιώτης Ε. Χατζημανολάκης
Κεφάλαιο 5 ο : Μηχανικά Κύματα
 Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Εισαγωγή Η ενέργεια μεταφέρεται με Μεταφορά μάζας Κύματα Μέσω του σκοινιού ύδιαδίδεται δίδ ένα κύμα το
Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Εισαγωγή Η ενέργεια μεταφέρεται με Μεταφορά μάζας Κύματα Μέσω του σκοινιού ύδιαδίδεται δίδ ένα κύμα το
Διαγώνισμα 1 Α στα Μηχανικά κύματα
 ΔΙΑΓΩΝΙΣΜΑ 4 5 ου ΚΕΦΑΛΑΙΟΥ ΘΕΜΑ 1 Από τις παρακάτω προτάσεις ποιες είναι σωστές και ποιες είναι λανθασμένες; α) Όταν ένα σώμα που ταλαντώνεται περνάει από τη θέση ισορροπίας, η τιμή της συνολικής δύναμης
ΔΙΑΓΩΝΙΣΜΑ 4 5 ου ΚΕΦΑΛΑΙΟΥ ΘΕΜΑ 1 Από τις παρακάτω προτάσεις ποιες είναι σωστές και ποιες είναι λανθασμένες; α) Όταν ένα σώμα που ταλαντώνεται περνάει από τη θέση ισορροπίας, η τιμή της συνολικής δύναμης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 24 ΑΠΡΙΛΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που
Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΑΚΟΥΣΤΙΚΗΣ Τ.Ε. ΕΙΣΑΓΩΓΗ ΣΤΑ ΗΧΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι
 Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΑΚΟΥΣΤΙΚΗΣ Τ.Ε. ΕΙΣΑΓΩΓΗ ΣΤΑ ΗΧΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι ΚΕΧΡΑΚΟΣ ΚΩΣΤΑΣ ΧΟΥΣΙΔΗΣ ΧΡΗΣΤΟΣ ΡΕΘΥΜΝΟ 2013 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 Ο
Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΜΟΥΣΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΑΚΟΥΣΤΙΚΗΣ Τ.Ε. ΕΙΣΑΓΩΓΗ ΣΤΑ ΗΧΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι ΚΕΧΡΑΚΟΣ ΚΩΣΤΑΣ ΧΟΥΣΙΔΗΣ ΧΡΗΣΤΟΣ ΡΕΘΥΜΝΟ 2013 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 Ο
 Ηχοπροστασία Ήχος Ήχος είναι καθετί που ακούμε. Ο ήχος γενικότερα υπήρξε ένα μέσο έκφρασης και πληροφόρησης του ανθρώπου με το περιβάλλον του. Ο ήχος ανήκει στο φυσικό περιβάλλον του ανθρώπου. Με την καταγραφή
Ηχοπροστασία Ήχος Ήχος είναι καθετί που ακούμε. Ο ήχος γενικότερα υπήρξε ένα μέσο έκφρασης και πληροφόρησης του ανθρώπου με το περιβάλλον του. Ο ήχος ανήκει στο φυσικό περιβάλλον του ανθρώπου. Με την καταγραφή
Η ζωή και ο Θάνατος στο Υλικό Σύμπαν
 Η ζωή και ο Θάνατος στο Υλικό Σύμπαν Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής- Πανεπιστήμιο Αθηνών Η Γεωμετρία Του Σύμπαντος Όταν αναφερόμαστε σε μια γεωμετρία, θεωρούμε ως αυτονόητη
Η ζωή και ο Θάνατος στο Υλικό Σύμπαν Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής- Πανεπιστήμιο Αθηνών Η Γεωμετρία Του Σύμπαντος Όταν αναφερόμαστε σε μια γεωμετρία, θεωρούμε ως αυτονόητη
ΤΕΧΝΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ
 ΤΕΧΝΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ Κατασκευή: Το μονόχορδο του Πυθαγόρα 2005-2006 Τόλιας Γιάννης Α1 Λ Υπεύθυνη Καθηγήτρια: Α. Τσαγκογέωργα Περιεχόμενα: Τίτλος Εργασίας Σκοπός Υπόθεση (Περιγραφή Κατασκευής) Ορισμός Μεταβλητών
ΤΕΧΝΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ Κατασκευή: Το μονόχορδο του Πυθαγόρα 2005-2006 Τόλιας Γιάννης Α1 Λ Υπεύθυνη Καθηγήτρια: Α. Τσαγκογέωργα Περιεχόμενα: Τίτλος Εργασίας Σκοπός Υπόθεση (Περιγραφή Κατασκευής) Ορισμός Μεταβλητών
Α6 ΗΧΟΣ : ΜΕΤΡΗΣΗ ΤΗΣ ΣΤΑΘΜΗΣ ΕΝΤΑΣΗΣ ΤΟΥ ΗΧΟΥ ΑΠΟ ΥΟ Ή ΠΕΡΙΣΣΟΤΕΡΕΣ ΑΝΕΞΑΡΤΗΤΕΣ ΠΗΓΕΣ
 Α6 ΗΧΟΣ : ΜΕΤΡΗΣΗ ΤΗΣ ΣΤΑΘΜΗΣ ΕΝΤΑΣΗΣ ΤΟΥ ΗΧΟΥ ΑΠΟ ΥΟ Ή ΠΕΡΙΣΣΟΤΕΡΕΣ ΑΝΕΞΑΡΤΗΤΕΣ ΠΗΓΕΣ Σκοπός Σκοπός της άσκησης είναι η µέτρηση της στάθµης έντασης του ήχου που παράγεται από την ταυτόχρονη λειτουργία
Α6 ΗΧΟΣ : ΜΕΤΡΗΣΗ ΤΗΣ ΣΤΑΘΜΗΣ ΕΝΤΑΣΗΣ ΤΟΥ ΗΧΟΥ ΑΠΟ ΥΟ Ή ΠΕΡΙΣΣΟΤΕΡΕΣ ΑΝΕΞΑΡΤΗΤΕΣ ΠΗΓΕΣ Σκοπός Σκοπός της άσκησης είναι η µέτρηση της στάθµης έντασης του ήχου που παράγεται από την ταυτόχρονη λειτουργία
Το παρακάτω διάγραμμα παριστάνει την απομάκρυνση y ενός σημείου Μ (x Μ =1,2 m) του μέσου σε συνάρτηση με το χρόνο.
 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
Ηλεκτρομαγνητικά Διαδίδονται στο κενό
 Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 15 Μάθημα: ΦΥΣΙΚΗ 4ωρο Τ.Σ. Ημερομηνία και ώρα εξέτασης: Παρασκευή 1 Ιουνίου 15 8:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 15 Μάθημα: ΦΥΣΙΚΗ 4ωρο Τ.Σ. Ημερομηνία και ώρα εξέτασης: Παρασκευή 1 Ιουνίου 15 8:
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
ΔΙΔΑΣΚΩΝ: Δρ. Στυλιανός Τσίτσος
 ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΔΙΚΤΥΑ ΥΨΗΛΩΝ ΣΥΧΝΟΤΗΤΩΝ (Θ) Ενότητα 10: Μικροκυματική Τεχνολογία ΔΙΔΑΣΚΩΝ: Δρ. Στυλιανός Τσίτσος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν
ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΔΙΚΤΥΑ ΥΨΗΛΩΝ ΣΥΧΝΟΤΗΤΩΝ (Θ) Ενότητα 10: Μικροκυματική Τεχνολογία ΔΙΔΑΣΚΩΝ: Δρ. Στυλιανός Τσίτσος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν
β. δημιουργούνται από πηγή η οποία ταλαντώνεται κάθετα στη διεύθυνση διάδοσης.
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 18/11/2017 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ-DOPPLER ΘΕΜΑ Α 1. Τα εγκάρσια μηχανικά κύματα : α. διαδίδονται σε όλα τα μέσα. β.
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 18/11/2017 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ-DOPPLER ΘΕΜΑ Α 1. Τα εγκάρσια μηχανικά κύματα : α. διαδίδονται σε όλα τα μέσα. β.
Φαινόμενο Doppler (Γ. Μ.) Φαινόμενο Doppler. Φαινόμενο Doppler είναι η διαφορά των συχνοτήτων που μετρούν οι παρατηρητές
 Φαινόμενο Doppler Για την κατανόηση του φαινομένου αυτού εισάγουμε τα παρακάτω σύμβολα και πρέπει να εξηγήσουμε τη σημασία τους. : πηγή ηχητικών κυμάτων : ανιχνευτής ηχητικών κυμάτων : συχνότητα ηχητικών
Φαινόμενο Doppler Για την κατανόηση του φαινομένου αυτού εισάγουμε τα παρακάτω σύμβολα και πρέπει να εξηγήσουμε τη σημασία τους. : πηγή ηχητικών κυμάτων : ανιχνευτής ηχητικών κυμάτων : συχνότητα ηχητικών
ΕΝΟΤΗΤΑ 5 5.0 ΡΑΔΙΟΦΩΝΙΑ
 ΕΝΟΤΗΤΑ 5 5.0 ΡΑΔΙΟΦΩΝΙΑ ΕΙΣΑΓΩΓΗ Η ανάγκη των ανθρώπων για ασύρματη επικοινωνία από απόσταση έδωσε το έναυσμα στους επιστήμονες της εποχής, πριν περίπου 116 χρόνια, να ασχοληθούν περαιτέρω με την εξέλιξη
ΕΝΟΤΗΤΑ 5 5.0 ΡΑΔΙΟΦΩΝΙΑ ΕΙΣΑΓΩΓΗ Η ανάγκη των ανθρώπων για ασύρματη επικοινωνία από απόσταση έδωσε το έναυσμα στους επιστήμονες της εποχής, πριν περίπου 116 χρόνια, να ασχοληθούν περαιτέρω με την εξέλιξη
κριτήρια αξιολόγησης ΚΕΦΑΛΑΙΟ 5 1o Κριτήριο αξιολόγησης
 1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
Μάθημα: Ακουστική και Ψυχοακουστική
 Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Ακουστική και Ψυχοακουστική Εργαστηριακή Άσκηση 1 «Ποσοτική εκτίμηση ελαχίστου κατωφλίου ακουστότητας» Διδάσκων: Φλώρος Ανδρέας Δρ. Ηλ/γος Μηχ/κός
Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Ακουστική και Ψυχοακουστική Εργαστηριακή Άσκηση 1 «Ποσοτική εκτίμηση ελαχίστου κατωφλίου ακουστότητας» Διδάσκων: Φλώρος Ανδρέας Δρ. Ηλ/γος Μηχ/κός
6.2.2 Χαρακτηριστικά κεραιών 1 / 18
 6.2.2 Χαρακτηριστικά κεραιών 1 / 18 Για κάθε κεραία υπάρχουν μια σειρά από μεγέθη που χαρακτηρίζουν τη λειτουργία της και την καταλληλότητά της για κάθε περίπτωση χρήσης. 2 / 18 Η ιδιοσυχνότητα fo Η ιδιοσυχνότητα
6.2.2 Χαρακτηριστικά κεραιών 1 / 18 Για κάθε κεραία υπάρχουν μια σειρά από μεγέθη που χαρακτηρίζουν τη λειτουργία της και την καταλληλότητά της για κάθε περίπτωση χρήσης. 2 / 18 Η ιδιοσυχνότητα fo Η ιδιοσυχνότητα
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 23/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 23/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο
ΕΡΕΥΝΗΤΙΚΗ ΕΡΓΑΣΙΑ ΜΟΥΣΙΚΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ
 1ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΩΝ ΕΡΕΥΝΗΤΙΚΗ ΕΡΓΑΣΙΑ ΜΟΥΣΙΚΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ Α Β ΤΕΤΡΑΜΗΝΟ ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ ΚΟΡΟΝΤΖΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΠΕ03 ΟΜΑΔΑ : ΑΝΔΡΩΝΑ ΕΙΡΗΝΗ ΚΕΦΑΛΑ ΑΘΑΝΑΣΙΑ ΜΙΛΙΔΑΚΗ ΜΕΛΙΝΑ ΖΕΡΒΑΣ ΧΡΗΣΤΟΣ
1ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΩΝ ΕΡΕΥΝΗΤΙΚΗ ΕΡΓΑΣΙΑ ΜΟΥΣΙΚΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ Α Β ΤΕΤΡΑΜΗΝΟ ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ ΚΟΡΟΝΤΖΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΠΕ03 ΟΜΑΔΑ : ΑΝΔΡΩΝΑ ΕΙΡΗΝΗ ΚΕΦΑΛΑ ΑΘΑΝΑΣΙΑ ΜΙΛΙΔΑΚΗ ΜΕΛΙΝΑ ΖΕΡΒΑΣ ΧΡΗΣΤΟΣ
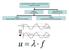
1kHz=10 3 Hz, 1MHz=10 6 Hz, 1GHz=10 9 Hz, κ.ο.κ.
 Α5 ΗΧΟΣ : ΘΕΩΡΗΤΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ ΕΝΤΑΣΗΣ ΗΧΟΥ ΑΠΟ ΥΟ ΑΝΕΞΑΡΤΗΤΕΣ, ΓΝΩΣΤΕΣ ΠΗΓΕΣ ΣΕ ΕΓΚΑΤΑΣΤΑΣΗ ΥΠΟΘΕΤΙΚΟΥ ΣΤΟΥΝΤΙΟ Σκοπός Πρόκειται για άσκηση θεωρητικού χαρακτήρα στην οποία πραγµατοποιούνται υπολογισµοί
Α5 ΗΧΟΣ : ΘΕΩΡΗΤΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ ΕΝΤΑΣΗΣ ΗΧΟΥ ΑΠΟ ΥΟ ΑΝΕΞΑΡΤΗΤΕΣ, ΓΝΩΣΤΕΣ ΠΗΓΕΣ ΣΕ ΕΓΚΑΤΑΣΤΑΣΗ ΥΠΟΘΕΤΙΚΟΥ ΣΤΟΥΝΤΙΟ Σκοπός Πρόκειται για άσκηση θεωρητικού χαρακτήρα στην οποία πραγµατοποιούνται υπολογισµοί
Μάθημα: Ακουστική και Ψυχοακουστική
 Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Ακουστική και Ψυχοακουστική Εργαστηριακή Άσκηση 1 «Ποσοτική εκτίμηση ελαχίστου κατωφλίου ακουστότητας» Διδάσκων: Φλώρος Ανδρέας Δρ. Ηλ/γος Μηχ/κός
Τμήμα Τεχνών Ήχου και Εικόνας Ιόνιο Πανεπιστήμιο Μάθημα: Ακουστική και Ψυχοακουστική Εργαστηριακή Άσκηση 1 «Ποσοτική εκτίμηση ελαχίστου κατωφλίου ακουστότητας» Διδάσκων: Φλώρος Ανδρέας Δρ. Ηλ/γος Μηχ/κός
Ύψος Συχνότητα Ένταση Χροιά. Ο ήχος Ο ήχος είναι μια μορφή ενέργειας. Ιδιότητες του ήχου. Χαρακτηριστικά φωνής
 Ο ήχος Ο ήχος είναι μια μορφή ενέργειας Είναι οι παλμικές δονήσεις που δημιουργούνται από ένα οποιοδήποτε σώμα, όταν τεθεί σε κίνηση, σε κραδασμό Την κίνηση σε ένα σώμα που βρίσκεται σε αδράνεια, μπορεί
Ο ήχος Ο ήχος είναι μια μορφή ενέργειας Είναι οι παλμικές δονήσεις που δημιουργούνται από ένα οποιοδήποτε σώμα, όταν τεθεί σε κίνηση, σε κραδασμό Την κίνηση σε ένα σώμα που βρίσκεται σε αδράνεια, μπορεί
«Μουσικό διάστημα: Μήκος ή λόγος μηκών;»
 «Μουσικό διάστημα: Μήκος ή λόγος μηκών;» Η έννοια «διάστημα» ως σχέσεως δύο αριθμών προς αλλήλους. Η σχέση μεταξύ δύο αριθμών στη Πυθαγόρειο θεωρία της Μουσικής και σ αυτήν ακόμη την Κατατομή Κανόνος του
«Μουσικό διάστημα: Μήκος ή λόγος μηκών;» Η έννοια «διάστημα» ως σχέσεως δύο αριθμών προς αλλήλους. Η σχέση μεταξύ δύο αριθμών στη Πυθαγόρειο θεωρία της Μουσικής και σ αυτήν ακόμη την Κατατομή Κανόνος του
KEΦΑΛΑIΟ 1: ΤΟ ΦΥΣΙΚΟ ΦΑΙΝΟΜΕΝΟ ΤΟΥ ΗΧΟΥ KAI H ANTIΛΗΨΗ AYTOY
 KEΦΑΛΑIΟ 1: ΤΟ ΦΥΣΙΚΟ ΦΑΙΝΟΜΕΝΟ ΤΟΥ ΗΧΟΥ KAI H ANTIΛΗΨΗ AYTOY 13 1.1. ΠΕΡΙΓΡΑΦΗ ΤΟΥ ΦΥΣΙΚΟΥ ΦΑΙΝΟΜΕΝΟΥ ΤΟΥ ΗΧΟΥ 1.1.1. ΓΕΝΕΣΗ ΤΟΥ ΗΧΟΥ Ήχος είναι ό,τι ακούμε. Ο ήχος είναι μια μορφή ενέργειας που μεταδίδεται
KEΦΑΛΑIΟ 1: ΤΟ ΦΥΣΙΚΟ ΦΑΙΝΟΜΕΝΟ ΤΟΥ ΗΧΟΥ KAI H ANTIΛΗΨΗ AYTOY 13 1.1. ΠΕΡΙΓΡΑΦΗ ΤΟΥ ΦΥΣΙΚΟΥ ΦΑΙΝΟΜΕΝΟΥ ΤΟΥ ΗΧΟΥ 1.1.1. ΓΕΝΕΣΗ ΤΟΥ ΗΧΟΥ Ήχος είναι ό,τι ακούμε. Ο ήχος είναι μια μορφή ενέργειας που μεταδίδεται
Ψηφιακή Επεξεργασία Σηµμάτων
 Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα: Τεχνολογίες και Συστήµματα Ευρυζωνικών Εφαρµμογών και Υπηρεσιών 1 Προεπισκόπηση
Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα: Τεχνολογίες και Συστήµματα Ευρυζωνικών Εφαρµμογών και Υπηρεσιών 1 Προεπισκόπηση
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 2 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 2
 Εργαστήριο Ηλεκτρoακουστικής Άσκηση 2 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 2 MEΤΡΗΣΗ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΘΟΡΥΒΟΥ ΚΑΙ ΗΧΟΜΟΝΩΣΗΣ 1. ΕΙΣΑΓΩΓΗ Σαν θόρυβος ορίζεται συνήθως η κατηγορία των ανεπιθύμητων ήχων, που
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 2 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 2 MEΤΡΗΣΗ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΘΟΡΥΒΟΥ ΚΑΙ ΗΧΟΜΟΝΩΣΗΣ 1. ΕΙΣΑΓΩΓΗ Σαν θόρυβος ορίζεται συνήθως η κατηγορία των ανεπιθύμητων ήχων, που
ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ
 ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΚΑΘΗΓΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΙΑΡΚΕΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΣΟΜΟΙΩΣΗ ΝΕΟ ΦΡΟΝΤΙΣΤΗΡΙΟ 3 ΩΡΕΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΚΑΘΗΓΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΙΑΡΚΕΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΣΟΜΟΙΩΣΗ ΝΕΟ ΦΡΟΝΤΙΣΤΗΡΙΟ 3 ΩΡΕΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
1.1 Δραστηριότητα: Εισαγωγή στις άπειρες διαδικασίες
 1.1 Δραστηριότητα: Εισαγωγή στις άπειρες διαδικασίες Θέμα της δραστηριότητας Η δραστηριότητα αυτή είναι μια εισαγωγή στις άπειρες διαδικασίες. Η εισαγωγή αυτή επιτυγχάνεται με την εφαρμογή της μεθόδου
1.1 Δραστηριότητα: Εισαγωγή στις άπειρες διαδικασίες Θέμα της δραστηριότητας Η δραστηριότητα αυτή είναι μια εισαγωγή στις άπειρες διαδικασίες. Η εισαγωγή αυτή επιτυγχάνεται με την εφαρμογή της μεθόδου
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
ΚΥΜΑ ΗΧΟΣ ΙΑΘΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΣΥΜΒΟΛΗ
 ΗΧΟΣ ΚΥΜΑ ΙΑΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΣΥΜΒΟΛΗ Έχουμε ανάκλαση κάθε φορά που ένα κύμα το οποίο διαδίδεται σε υλικό μέσο συναντά άλλο μέσο που έχει διαφορετική πυκνότητα απότοπρώτο. Εισερχόμενος παλμός ιερχόμενος
ΗΧΟΣ ΚΥΜΑ ΙΑΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΣΥΜΒΟΛΗ Έχουμε ανάκλαση κάθε φορά που ένα κύμα το οποίο διαδίδεται σε υλικό μέσο συναντά άλλο μέσο που έχει διαφορετική πυκνότητα απότοπρώτο. Εισερχόμενος παλμός ιερχόμενος
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 1. Στερεό σώμα περιστρέφεται γύρω από σταθερό άξονα, υπό την επίδραση σταθερής ροπής. Ο ρυθμός παραγωγής έργου: α) ισούται με τη μεταβολή της ενέργειας του σώματος.
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 1. Στερεό σώμα περιστρέφεται γύρω από σταθερό άξονα, υπό την επίδραση σταθερής ροπής. Ο ρυθμός παραγωγής έργου: α) ισούται με τη μεταβολή της ενέργειας του σώματος.
Κεφάλαιο 9. Έλεγχοι υποθέσεων
 Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
1 ο ΤΕΣΤ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια (20-4903576) ΤΑΞΗ... Γ ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ... ο ΤΕΣΤ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ. Στην απλή αρµονική ταλάντωση, το ταλαντούµενο
ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια (20-4903576) ΤΑΞΗ... Γ ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ... ο ΤΕΣΤ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ. Στην απλή αρµονική ταλάντωση, το ταλαντούµενο
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
Μάθημα Ακουστικής. Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ
 Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
1. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ):
 1. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ): 1) Ηλεκτρισμένα ονομάζουμε τα σώματα τα οποία, αφού τα τρίψουμε έχουν την ιδιότητα να έλκουν μικρά αντικείμενα. 2) Οι ηλεκτρικές
1. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ): 1) Ηλεκτρισμένα ονομάζουμε τα σώματα τα οποία, αφού τα τρίψουμε έχουν την ιδιότητα να έλκουν μικρά αντικείμενα. 2) Οι ηλεκτρικές
ΘΕΜΑ Α ΕΡΩΤΗΣΕΙΣ ΘΕΜΑ Α
 ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
Κύκλος διαλέξεων ακουστικής. Εισαγωγή στα θέματα
 Κύκλος διαλέξεων ακουστικής Εισαγωγή στα θέματα In memoriam Χρήστου Κουτσοδημάκη Τι είναι ήχος? Ότι ακούω. (?) ΕΛΟΤ 263.1 Ήχος ορίζεται ως η μηχανική διαταραχή που διαδίδεται με ορισμένη ταχύτητα
Κύκλος διαλέξεων ακουστικής Εισαγωγή στα θέματα In memoriam Χρήστου Κουτσοδημάκη Τι είναι ήχος? Ότι ακούω. (?) ΕΛΟΤ 263.1 Ήχος ορίζεται ως η μηχανική διαταραχή που διαδίδεται με ορισμένη ταχύτητα
