Γραφική με Υπολογιστή Computer Graphics
|
|
|
- Σπύρος Καζαντζής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Γραφική με Υπολογιστή Computer Graphics 1. Βασικοίγραφικοίαλγόριθμοι 2. Αρχέςγραφικώνπλεγματικώνοθονώνraster 3. Μετασχηματισμοί2 και3 διαστάσεωνκαι συστήματασυντεταγμένων 4. Προβολέςκαιμετασχηματισμοίπαρατήρησης 5. Aλγόριθμοιαπόκρυψηςεπιφανειώνκαι αλγόριθμοιφωτισμού διαφάνειεςαπόβιβλίοθεοχάρημπέμ, Συμμετρία, Αθήνα1999
2 Ιστορικήαναδρομή
3 Περιοχές σχετικές με την Εικόνα Γραφική με Υπολογιστές (Computer Graphics) Επεξεργασία - ΑνάλυσηΕικόνων (Image Processing -Analysis) Τεχνητήόραση(Computer vision) Αλληλεπίδραση Ανθρώπου - Υπολογιστή
4 Περιοχέςεφαρμογών Γραφικήαλληλεπίδρασημεχρήστη (GUI). Σχεδίαση(CAD): πχαρχιτεκτονική, VLSI design ΓεωγραφικάΣυστήματαΠληροφοριών(GIS). Προσομοιώσεις(π.χ. πτήσεων). Συνθετικές ταινίες& διαφήμιση Computer Animation. Επαυξημένη Πραγματικότητα -Augmented Reality Εικονική Πραγματικότητα Virtual Reality Ιατρικέςεφαρμογές. Οπτικοποίησηδεδομένων. Τέχνη(π.χ. fractals). Παιχνίδια.
5 Γραφικόσύστημαεπεξεργασίας
6 Πλεγματικήήδιανυσματικήαπεικόνιση
7 Πλεγματικήοθόνη (raster display) Σάρωσητηςοθόνηςανάγραμμήκαισε συγκεκριμένοχρονικόρυθμό
8 Πλεγματικήοθόνη: αποθήκευσηεικόναςστημνήμη Αποθήκευσητηςεικόναςστημνήμηως πίνακατριώνδιαστάσεων (πλάτοςx ύψοςx χρώμα) Χρήσηπαλέταςγιαμείωσηαπαιτήσεων χρώματος.
9 Χρήσηπαλέταςχρωμάτων
10 Πλεγματικήοθόνη/ 2 2-Δπλέγμαχρωματιζόμενωνεικονοστοιχείων(pixels) Φρεσκάρισμασεσταθερόρυθμόαπόμνήμη Κανέναςπεριορισμόςσεεικόνα Αποδέσμευσηφρεσκαρίσματοςαπόάλλεςλειτουργίες Μεγάλη(;) απαίτησημνήμης (1024 x 1024 x 24= 3MB) Μείωσημεχρήσηπαλέτας(lookuptable) Προβλήματαταύτισης(aliasing) Νέεςτεχνολογίες(LCD, plasma)
11 Πλεγματικήοθόνη /3 Απαιτούνται αλγόριθμοι απεικόνισης ευθείας, καμπύλης, πλήρωσης πολυγώνου σε πλεγματική οθόνη
12 Αλγόριθμοςγραφικήςαπεικόνισης
13 Παράστασησχημάτων ΠΑΡΑΣΤΑΣΗΣΤΗΝΟΘΟΝΗ Σάρωση Αντιταύτιση Φωτισμός Υφή
14 ΑπεικόνισηΕυθύγραμμουτμήματος Αλγόριθμοιυποστηρίζονταικαιαπό hardware. Κριτήρια «καλού» αλγορίθμου: Όσογίνεταιπιοκοντάστημαθηματικήπορεία Πάχοςσταθερόκαιανεξάρτητοαπόμήκοςκαι κλίση. Μεόσοτοδυνατόνμικρότερουπολογιστικό κόστος(μεγαλύτερηταχύτητα).
15 Αλγόριθμος 1 Έστωευθύγραμμοτμήμαμεταξύpixels P 1 (x 1,y 1 ), P n (x n,y n ) στοπρώτοοκταμόριο. Τότε: όπου y=s*x+b
16 Υλοποίηση void line1( x1, y1, xn, yn, colour) intx1,y1, xn, yn, colour; /* colour: ακέραιααναπαράστασητουχρώματος*/ { float s, b, y; intx; s=( yn-y1)/( xn-x1); b=( y1* xn-yn* x1)/( xn-x1); for (x= x1; x<= xn; x++){ y= s* x+ b; setpixel( x, round( y), colour); } }
17 Αλγόριθμος 2 (αποδοτικότερος) Οπολλαπλασιασμόςμέσαστοβρόγχο μπορείνααποφευχθείμετατρέπονταςτον τύποσεαναδρομικό:
18 Υλοποίηση line2 (x1, y1, xn, yn, colour) intx1,y1, xn, yn, colour; { float s, y; intx; s=( yn-y1)/( xn-x1); y= y1; for (x= x1; x<= xn; x++){ setpixel( x, round( y), colour); y= y+ s; } }
19 Αλγόριθμος 3 Αποφυγήτηςστρογγυλοποίησηςμέσα στο βρόγχομεχωρισμότουy σεακέραιοκαι δεκαδικόμέρος(error)καιχρήσημόνοτου ακεραίουγιαεύρεσητουεπομένου σημείου. Σφάλμα = απόστασηpixel απόιδεατήπορεία.
20 line3 (x1, y1, xn, yn, colour) intx1,y1, xn, yn, colour; Υλοποίηση { float s, error; intx, y; s=( yn-y1)/( xn-x1); y= y1; error= 0; for (x= x1; x<= xn; x++){ setpixel( x, y, colour); error= error+ s; if(error>= 0.5){ y++; error--} } }
21 Αλγόριθμος 4 (Bresenham) Πολλαπλασιάζονταςμεdx=xn-x1, οιμεταβλητές s και error γίνονται ακέραιες. Η σύγκρισηγιατηνεπιλογήτουεπόμενουpixel γίνεταιμεfloor(dx/2). Επίσης, αφαιρώνταςαπό τηναρχικήτιμήτουerrordx, ησύγκρισημπορεί ναγίνεικαιμετο 0. Λειτουργείγιαθετικέςκλίσεις.
22 Υλοποίηση line4 (x1, y1, xn, yn, colour) intx1,y1, xn, yn, colour; { interror, x, y, dx, dy; dx= xn-x1; dy= yn-y1; error=-dx/ 2; y= y1; for (x= x1; x<= xn; x++){ setpixel( x, y, colour); error= error+ dy; if(error>= 0){ y++; error= errordx} } }
23 Περιορισμοί Μόνοστο 1ο ογδοημόριο. Εύκολαμπορείνα επεκταθείκαισταάλλαμεκατάλληλεςεναλλαγές τωνρόλωνx, y,αρχικούκαιτελικούσημείου. Άξονας ταχύτερηςκίνησηςκαιείδοςμεταβολήςτουάλλου άξοναδίνονταιστοσχήμα.
24 Περιορισμοί (συνέχεια) Ευθύγραμματμήματαδιαφορετικώνκλίσεων μπορείναέχουνδιαφορετικήφωτεινότητα. Τοφαινόμενοαυτόμπορείναδιορθωθείμε τεχνικέςαντι-ταύτισης(anti-aliasing).
25 Τοφαινόμενοτηςταύτισης (aliasing) προβλήματαδειγματοληψίας Τεθλασμένηεμφάνισηευθυγράμμωντμημάτωνκαι ακμώνπολυγώνων Λανθασμένηεμφάνισηεπαναλαμβανόμενων τμημάτωνενόςσχήματος Λανθασμένηεμφάνισημικρώνσχημάτωνπου μπορείναεμφανίζονταιήναεξαφανίζονταιανάλογα μετηθέσητους Μέθοδοιαντιταύτισης: Pitteway&Watkinson, postfiltering, stochastic sampling, A-buffer )
26 Αλγόριθμοςσχεδίασηςκύκλουσε πλεγματικήοθόνη Εκμετάλλευση 8-πλής συμμετρίας:
27 Συμμετρίακύκλου circle_ symmetry(x, y, colour) intx, y, colour; { setpixel( x, y, colour); setpixel( y, x, colour); setpixel( y,-x, colour); setpixel( x,-y, colour); setpixel(-x,-y, colour); setpixel(-y,-x, colour); setpixel(-y, x, colour); setpixel(-x, y, colour); }
28 Αλγόριθμος Bresenham Έστωότιεπελέγητοσημείο(x i,y i ). Το επόμενοθαείναι(x i +1,y i ) ή(x i +1,y i -1);
29 Αλγόριθμος Μεταβλητήαπόφασης: e i = d 1 d 2 όπου d 1 = y 2 i -y 2, d 2 = y 2 -(y i -1) 2 Εάνe i 0, επιλέγεταιτο(x i +1,y i -1) αλλιώς επιλέγεταιτο(x i +1,y i )
30 Υπολογισμόςτου e Γιαx=x i +1 ισχύειότιy 2 =r 2, οπότε: e i = y i2 -r 2 + (x i +1) 2 + (y i -1) 2 -r 2 + (x i +1) 2 e i =2 (x i +1) 2 + y i2 + (y i -1) 2 2 r 2
31 Αναδρομικόςυπολογισμός e e i+1 = 2 (x i+1 +1) 2 + y i+12 + (y i+1-1) 2-2 r 2 = 2 (x i +2) 2 + y i+12 + (y i+1-1) 2-2 r 2 = 2x i2 + 8x i + 8+ y i+12 + y i+12-2 y i r 2 = 2(x i +1) 2 + 4x i y i+12-2y i r 2 = e i + 4x i (y i+12 -y i2 ) 2(y i+1 -y i )
32 Τελικόςτύποςυπολογισμού Αν e i <0 y i+1 = y i e i+1 = e i + 4(x i + 1)+ 2 Ανei 0 y i+1 = y i 1 e i+1 = e i + 4x i ((y i -1) 2 -y i2 ) 2(y i -1- y i ) e i+1 = e i + 4(x i +1) + 2 4(y i 1)
33 Παρατηρήσεις Αρχικήτιμή: e 1 =2+ r 2 + (r 1) 2 2r 2 = 3 2r Γιαμεταφοράτουκύκλουαπότο(0,0) στο (x 0,y 0 ) αρκείνααντικατασταθείηκλήση circle_symmetry(x,y,colour); από: circle_symmetry(x-x 0,y-y 0,colour);
34 circle (r, colour) intr, colour; { intx, y, e; x= 0; y= r; e= 3-2* r; while (x<= y){ circle_ symmetry( x, y, colour); x++; if (e>= 0) { y--; e= e-4* y } e= e+ 4* x+ 2; } } Υλοποίηση
35 Λειτουργίεςσεπλεγματικήοθόνη RasterOp Πλεγματικήοθόνη: εικόνααποθηκεύεταιστη μνήμηοθόνης(frame buffer) Πολλέςδιαδικασίεςμεμετακίνησηήσυνδυασμούς στημνήμηοθόνης. (π.χ. επεξεργασίακειμένου)
36 RasterOp Γενικήρουτίναμετακίνησης/συνδυασμού παραλληλογράμμωντμημάτωνεικόνας. Βελτιστοποιημένη, γρήγορηυλοποίηση.
37 Υλοποίηση RasterOp( src_x_min, src_y_min, dst_x_min, dst_y_min, sizex, sizey, funct) intsrc_x_min, src_y_min, dst_x_min, dst_y_min, sizex,sizey; ftypefunct) /* (src_x_min, src_y_min) και(dst_x_min, dst_y_min) */ /* ήκάτωαριστερήγωνίατωνsourceκαιdestination */ /* sizex, sizeyοιx καιy διαστάσειςσεpixel */ /* function κάποιοςτελεστής με pixel */ { inti, j; for (i= 0; i< sizex; i++) } for (j= 0; j< sizey; j++) }} set_pixel( dst_x_min+ i, dst_y_min+ j, funct( read_pixel( dst_x_min+ i, dst_y_min+ j) read_pixel( dst_x_min+ i, dst_y_min + j)));
38 Παράδειγμα: exchange μεχρήσηxor Αντιμετάθεσησχημάτωνχωρίςχρήσηβοηθητικούχώρου. void exchange (src_ x_ min, src_ y_ min, dst_ x_ min, dst_y_ min, sizex, sizey) intsrc_ x_ min, src_ y_ min, dst_ x_ min, dst_ y_ min, sizex, sizey; { RasterOp (src_ x_ min, src_ y_ min, dst_ x_ min, dst_ y_ min, sizex, sizey, XOR); RasterOp (dst_ x_ min, dst_ y_ min, src_ x_ min, src_ y_ min, sizex, sizey, XOR); RasterOp (src_ x_ min, src_ y_ min, dst_ x_ min, dst_ y_ min, sizex, sizey, XOR); }
39 RasterOp: Μετακίνηση Η exchangeμπορείναχρησιμεύσειγια διαδοχικέςμετακινήσειςαντικειμένων (π.χ.cursor)
40 move move (from_x_min, from_y_min, to_x_min, to_y_min, back_x_min, back_y_min, sizex, sizey) intfrom_x_min, from_y_min, to_x_min,to_y_min, back_x_min, back_y_min, sizex, sizey; { exchange (to_x_min, to_y_min,back_x_min,back_y_min, sizex, sizey); exchange (from_x_min, from_y_min,to_x_min, to_y_min, sizex, sizey); }
41 Μετασχηματισμοί 2Δ& 3Δ Συνδυασμοίβασικώνμετασχηματισμών: μετατόπιση,αλλαγήκλίμακας, περιστροφή, στρέβλωση.
42 Σημείακαι Διανύσματα Ε 3 ο3δ Ευκλείδειοςχώροςσημείων, p σημείο. R 3 ο3δ Ευκλείδειοςχώροςδιανυσμάτων, v διάνυσμα. Βασικέςιδιότητες: p 1, p 2 Ε 3, u R 3 με u = p 1 -p 2. p Ε 3, u R 3, p +u = q Ε 3 p, q, r Ε 3, (p q) + (q r) = (p r)
43 Διανυσματικοίχώροι ΣεκάθεδιανυσματικόχώροΔ(π.χ. R 3 ) ορίζονται2 πράξεις Διανυσματικήπρόσθεση(q+ v) Βαθμωτός(scalar) πολλαπλασιασμός(λv) Ιδιότητεςπρόσθεσης: Αντιμεταθετική: q + v = v + q Προσεταιριστική: (p + q) + v = p + (q + v) Ύπαρξηουδετέρου: 0 Δ: 0 + v = v + 0 = v Ύπαρξηαντιθέτου: p Δ -p Δ: p + (-p) = 0
44 Διανυσματικοίχώροι Ιδιότητεςβαθμωτούπολλαπλασιασμού (β.π.) Επιμερισμόςωςπροςτηνπρόσθεση: λ(v + q) = λv + λq Επιμερισμόςπρόσθεσηςωςπροςβαθμωτό πολλαπλασιασμό: (λ + μ) v = λv + μv Προσεταιρισμός: (λμ) v = λ(μv) Ουδέτεροστοιχείο: 1 Δ: v 1 = 1 v =v
45 Διανυσματικοίχώροι Παραδείγματα: 2Δκαι3Δ Ευκλείδειοιχώροι. Πολυώνυμαδιαφόρωνβαθμών. Γραμμικόςσυνδυασμόςx 1, x 2, x ν Δ: y = λ 1 x 1 + λ 2 x λ ν x ν Γραμμικήανεξαρτησίαx 1, x 2, x ν, Δ: αν λ 1 x 1 + λ 2 x λ ν x ν = 0, έχειμόνηλύσητην λ 1 = λ 2 = = λ ν = 0 Παράδειγματα(1,0,0), (0,1,0), (0,0,1) του Ε 3
46 Διανυσματικοίχώροι Βάση: κάθεολοκληρωμένοσύνολο γραμμικώς ανεξαρτήτωνδιανυσμάτων. Τοπλήθοςτουςκαλείταιδιάστασητουχώρου. Ανy = λ 1 i + λ 2 j + λ 3 k όπου(i, j, k) βάση τότε(λ 1, λ 2, λ 3 ) συντεταγμένες. (Ο, i, j, k) ονομάζεταισύστημασυντεταγμένωνμε βάσητοσημείοο, καιβάση(i, j, k) (i, j, k) ορίζουνάξονεςσυντεταγμένων Μήκος: διανύσματος(x,y,z)
47 Διανυσματικοίχώροι Απόστασημεταξύδύοσημείων p 1, p 2
48 Διανυσματικοίχώροι Εσωτερικόγινόμενο (πραγματικόςαριθμός) v w= Σ(v i w i ) π.χ. Ευκλείδειος3Δ: v w= v x w x + v y w y + v z w z Ιδιότητες: Αντιμεταθετική: v w= w v v v= 0 v= 0 v/ v = v, μοναδιαίοδιάνυσμα(κανονικοποίηση) ισχύειv w= v w cos(θ), απ όπουμπορείνα υπολογιστείκαιηγωνίαμεταξύδιανυσμάτων.
49 Διανυσματικοίχώροι Εξωτερικόγινόμενο (διάνυσμα) v x w = (v y w z + v z w y ) i + (v x w z + v z w x )j + (v x w y + v y w x )k v x w είναικάθετοστοεπίπεδοπουορίζουν ταδύοάλλαδιανύσματα. δενισχύειηαντιμεταθετικήιδιότητα. v x w = - w x v
50 Συσχετισμένοι (Affine) Μετασχηματισμοί Συσχετισμένοςήβαρυκεντρικόςμετασχηματισμός σημείωνp 0 p n Ε 3 : p = Σα j p j όπου α j R και Σα j = 1 αποτέλεσμαp Ε 3. {αj} ονομάζονταιοισυσχετισμένεςσυντεταγμένεςτουpως προςp 0 p n. Ομετασχηματισμόςείναικυρτόςανα j 0 Συσχετισμένοςμετασχηματισμός Φ: Ε 3 Ε 3 πουαφήνει τουςσυσχετισμένουςμετασχηματισμούςαναλλοίωτους: Φ(p) = Σα j Φ(p j )
51 Συσχετισμένοι Μετασχηματισμοί π.χ. εφαρμογήσυσχετισμένουμετασχηματισμού πάνωσεευθύγραμμοτμήμαs απεικονίζειτο μέσον του στο μέσο της συσχετισμένης εικόνας Φ(s). Συσχετισμένοςμετασχηματισμόςμεμορφήπίνακα: Φ(p) = Α p + t (A πίνακας, 3x3 γιατο Ε 3 ) Απόδειξη: Φ(Σαjpj) = Α(Σα j p j ) + t = ΣAα j p j + Σα j t = Σα j (A p j + t) = Σα j Φ(p)
52 2D Μετασχηματισμοί Μετατόπιση: x =x+a, y =y+b
53 Μετασχηματισμοί Αλλαγήκλίμακας (διαφορετικήανάάξονα): x =x*a, y =y*b
54 Μετασχηματισμοί Στροφήκατάγωνίαθ (+veαντίθετααπόδείκτεςρολογιού)
55 Μετασχηματισμοί Στρέβλωσηκατάάξονα x καιyμεπαράγοντα2: x =x+2y, y =y+2x
56 Μετασχηματισμοί Οποιοσδήποτεάλλοςμετασχηματισμός, δημιουργείταισανσυνδυασμόςτωντεσσάρων βασικώνμετασχηματισμών: Μμετατόπιση, R στροφή, H στρέβλωση, S αλλαγήκλίμακος.
57 Μετασχηματισμοί: άσκηση Στρέβλωση(shearing), Ναβρεθούνοισχέσεις μετασχηματισμούκατάx καιy με z σταθερό: Απάντηση SH(p) = H x,y p, όπου:
58 Ομογενείςσυντεταγμένες Προβλήματα: Μεταφοράδενυλοποιείταιμεπολλαπλασιασμό πινάκων. ΎπαρξησταθερούσημείουΟ, σταθερούγιαόλους τουςμετασχηματισμούς. Ομογενείςσυντεταγμένες: (x,y) (x,y,w) με w 0. (x,y,w) παριστάνειτο(x/w,y/w) Άπειρεςτριάδεςγιακάθεσημείο. Βασικήπαράσταση: (x,y,1)
59 Ομογενείςσυντεταγμένες
60 ΟμογενείςΣυντεταγμένες Συσχετισμένοιμετασχηματισμοί: πίνακες3x3 Μεταφορά:
61 ΟμογενείςΣυντεταγμένες Αλλαγήκλίμακας (ανsi< 1 σμίκρυνση)
62 Στροφή Ομογενείςσυντεταγμένες
63 Ομογενείςσυντεταγμένες Στρέβλωση (κατάάξονεςx καιy):
64 Σύνθεσημετασχηματισμών Σύνθεσημετασχηματισμών: π.χ. Αλλαγήκλίμακας, ωςπροςc=(cx,cy,1) μεταφοράκατά c= -(O -C) αλλαγήκλίμακας μεταφοράκατάc Γενικάδενισχύειηαντιμετάθεση. Πρώτοςεκτελείται οτελεστήςπουγράφεταιτελευταίος. Σύνθεση: Εκτέλεσησειράςμετασχηματισμώναπόένα τελικόπίνακα. Αυξάνειτηναπόδοση(μειώνειτηνπολυπλοκότητα)
65 Σύνθεσημετασχηματισμών Ιδιότητες: T(x 1,y 1 ) T(x 2,y 2 ) = T(x 2,y 2 ) T(x 1,y 1 ) = T(x1 +x2,y 1 +y 2 ) S(s x1,s y1 ) S(s x2,s y2 )= S(s x2,s y2 ) S(s x1,s y1 ) = S(s x1 s x2,s y1 s y2 ) R(θ 1 ) R(θ 2 ) = R(θ 2 ) R(θ 1 ) = R(θ 1 + θ 2 ) S(s x,s y ) R(θ) = R(θ) S(s x,s y ) μόνοανs x = s y
66 ΓεωμετρικέςΙδιότητες Γιακάθεσυσχετισμένομετασχηματισμό F και σημεία pκαι q ισχύει: F(λp+(1-λ)q) = λf(p)+ (1-λ) F(q) για 0 λ 1 λp+(1-λ)q είναι το ευθύγραμμο τμήμα μεταξύp και q. ΗF παράγειπάλιευθύγραμμοτμήμα. Η σχέσηλ/(1-λ) παραμένειαναλλοίωτηαπό F. Εξακολουθείνααρκείαπεικόνισηάκρωνμόνο. Παράλληλεςευθείεςπαραμένουνπαράλληλες. π.χ. οιμετασχηματισμοίπουείδαμενωρίτερα.
67 Γεωμετρικέςιδιότητες Ορθογώνιοςμετασχηματισμός: ΜετασχηματισμόςΑλέγεταιορθογώνιοςαν α 1 = α 2 = 1 α 1 α 2 = 0 ΟρίζουσατουΑ= 1
68 Γεωμετρικέςιδιότητες ΟΜείναιμετασχηματισμόςομοιότηταςανοΑείναι ορθογώνιος. Έναςμετασχηματισμόςομοιότηταςδιατηρείαναλλοίωταμήκη καιγωνίες. ΟποιαδήποτεσύνθεσηΤ& R είναιμετασχηματισμός ομοιότητας. ΑνστησύνθεσηέχουμεS και Η, έχουμεσυσχετισμένο μετασχηματισμόαλλάόχιομοιότητας(διατηρείταιπαραλληλία αλλάόχιμήκηκαιγωνίες).
69 Άσκηση Ζητείταιναυπολογιστείοπίνακας μετασχηματισμούτηςσυμμετρικήςαπεικόνισης εικόναςως προς τονάξονα w ο οποίος σχηματίζειγωνίαθμετονθετικόάξονατωνχ Βοήθεια: Ομετασχηματισμόςμπορείνα προκύψειαπό: στροφήτηςεικόναςκατά θ ΣυμμετρίαωςπροςτονάξοναΧ Στροφήτηςεικόναςκατάθ
70 Φροντιστηριακήάσκηση #4 1. Ναμελετήσετεκαιναπεριγράψετετην τρέχουσατεχνολογίακαρτώνγραφικών 2. ΔίδεταισημείοΑ(χ=3,ψ=2). Ζητείταινα βρεθείτοσημείοα πουπροκύπτειαπότην περιστροφήτουσημείουαωςπροςσημείοβ ο μεσυντεταγμένεςβ(χ=1, ψ=1)κατάγωνία θ=30
71 2-ΔΜετασχηματισμόςΠαρατήρησης
72 2-ΔΜετασχηματισμόςΠαρατήρησης
73 2-ΔΜετασχηματισμόςΠαρατήρησης
74 Αποκοπή / clipping Αποκοπήαντικειμένου(π.χ. πολυγώνου, πυραμίδας, κύβου) ω.π. σημείοαποκοπής: Αποφυγήαντεστραμμένηςεμφάνισηςαντικειμένων (π.χ. 3-Δ, όπισθενπαρατηρητή). Μείωσητουόγκουδεδομένων(φίλτρο).
75 Αποκοπή 2-Δ: στηναντιταύτιση, απόκρυψη, παράλληλη επεξεργασία, 2Δπακέτα. 3-Δ: γραφικήσωλήνωση(γενίκευση2-δαποκοπής) 2-Δαποκοπήσημείου: εντόςεάνx min x x max και y min y y max.
76 Αποκοπή Ευθύγραμματμήματα: Αλγόριθμοςμέσου. Διαδοχικήδιάσπασηευθυγράμμουτμήματοςστημέση (ολίσθηση). Χρήση «φθηνών» ελέγχωνεντός/ εκτός. Κωδικοποίηση 9 περιοχών τουεπιπέδου Τέλοςεάνp 1 p 2 < pixel.
77 Αλγόριθμος Μέσου typedefstruct {float x, y} point; midpoint (P1, P2, xmin, xmax, ymin, ymax) point P1, P2; float xmin, xmax, ymin, ymax; { point M; /* ΥπολογισμόςΙΧ1, ΙΥ 1, ΙΧ2, ΙΥ 2 */ if (( IX1== 0)&&( IY1== 0)&&( IX2== 0)&&( IY2== 0)) /* ΤοP1P2 είναιεντόςπαραθύρου */ else if (( IX1== IX2)&&( IX1!= 0)) (( IY1== IY2)&&(IY1!= 0)) /* ToP1P2 είναιεκτόςπαραθύρου */ else { M. x=( P1. x+ P2.x)/ 2; M. y=( P1. y+ P2.y)/ 2; midpoint (P1,M, xmin, xmax, ymin, ymax); midpoint (M, P2, xmin, xmax, ymin, ymax); } }
78 Αποκοπήευθυγράμμωντμημάτων Αλγόριθμος Cohen-Sutherland: Αρχικά «φθηνός» έλεγχος γιατιςαπλέςπεριπτώσεις. π.χ. AB έξω, CD μέσα. Γιαάλλαευθύγραμμα τμήματα, κόψιμομε ευθείαπαραθύρουκαι αναδρομή.
79 Αλγόριθμος Cohen-Sutherland Αντιστοίχησηκωδικών σε9 περιοχέςτου επιπέδου. Κώδικεςπροκύπτουναπόταπρόσημαδιαφορών (π.χ. 1 ο bit y max y). Πρώτο bit1, περιοχήπάνωαπότηνευθείαy = y max Δεύτερο bit1, περιοχήκάτωαπότηνευθείαy = y min Τρίτο bit1, περιοχήδεξιάαπότηνευθείαx = x max Τέταρτο bit1, περιοχή αριστερά απότηνευθείαx = x min
80 Αλγόριθμος Cohen-Sutherland Υπολόγισεκώδικεςc 1, c 2 γιαp 1 p 2. Ανc 1 c 2 = 0000, p 1 p 2 είναιεντός(π.χ. CD). Ανc 1 c 2 = 0000, p 1 p 2 είναιεκτός(π.χ. ΑΒ). Διαφορετικά: Εύρεσηευθείαςτουπαραθύρου πουαντιστοιχείσε bit μεδιαφορετικέςτιμές. τομήp 1 p 2 μεευθεία. Αναδρομικήκλήσηγιατοένααπότατμήματαως προςτηνευθείατμήμα(εκείνομε bit=0)
81 Αλγόριθμος Cohen-Sutherland void CS (P1,P2, xmin, xmax, ymin, ymax) point P1, P2; float xmin, xmax, ymin, ymax; { intc1, c2; point I; c1= code( P1); /* ΕύρεσηκώδικαP1*/ c2= code( P2); /* ΕύρεσηκώδικαP2*/ if(( c1 c2)== 0) /* ΤοP1P2 είναιεντόςπαραθύρου */ elseif(( c1& c2)!= 0) /* ΤοP1P2 είναιεκτόςπαραθύρου */ else { intersect (P1,P2,I,xmin,xmax,ymin,ymax); if exoteriko(p1) CS( I,P2,xmin,xmax,ymin,ymax); else CS( P1, I, xmin, xmax, ymin, ymax); } }
82 Αλγόριθμος Sutherland-Hodgman 2-Δ αποκοπήςπολυγώνων Κατάλληλοςγιααποκοπήτυχαίουπολυγώνουμε κυρτόπολύγωνο(παράθυρο) αποκοπής. m βήματα για m πλευρές παραθύρου αποκοπής. είσοδοςστοβήμαi (i = 1 m) μετάαπόαποκοπήμε πλευράi-1.
83 Αλγόριθμος Sutherland-Hodgman2-Δ αποκοπήςπολυγώνων πολύγωνοορίζεταιαπότιςκορυφέςτουp 1, p 2 p n μεθετικήμαθηματικήφορά. Βήμαi εξετάζεισχέσηπλευράςsp μεακμή παραθύρουi.
84 Αλγόριθμος Sutherland-Hodgman2-Δ ΑποκοπήςΠολυγώνων ΠαράδειγμαβήματοςSutherland-Hodgman:
85 Αποκοπήσε 3-Δ Αντικείμενοαποκοπής: Περιορισμένηπυραμίδα(προοπτική) Κύβος(παράλληλη) 6 επίπεδααποκοπήςγιαυτάτααντικείμενα.
86 Cohen Sutherland 3-Δ 6 bit κωδικοίγιακάθεάκροp(x, y, z) Έστωκύβοςαποκοπής: πρώτο bit = 1, z p > z max, σημείοπίσωαπόκύβο. δεύτερο bit = 1, z p < z min, σημείοεμπρόςαπόκύβο τρίτο bit = 1, y p > y max, σημείοπάνωαπόκύβο τέταρτο bit = 1, y p < y min, σημείοκάτωαπόκύβο πέμπτο bit = 1, x p > x max, σημείοδεξιάαπόκύβο έκτο bit = 1, x p < x min, σημείοαριστεράαπόκύβο
87 Αλγόριθμος Cohen Sutherland 3-Δ ΑνC 1 C 2 = , p 1 p 2 εντός. ΑνC 1 C , p 1 p 2 εκτός. Διαφορετικά: Εύρεσηεπιφάνειαςκύβουπουαντιστοιχείσε bit μεδιαφορετικέςτιμές. τομήp 1 p 2 μεεπιφάνεια Αναδρομικήκλήσηγιατοεσωτερικότμήμαως προςεπιφάνεια..
88 Αλγόριθμος Cohen Sutherland 3-Δ Τομή ευθυγράμμου τμήματοςp1p2 με επίπεδο βάσει τηςπαραμετρικήςεξίσωσης: x(t) = x1 + t(x2 x1) = x1 + t Δx y(t) = y1 + t(y2 y1) = y1 + t Δy z(t) = z1 + t(z2 z1) = z1 + t Δz π.χ. τομήμεy = Υ Y = y(t) = y 1 + t Δt t = (Y y 1 ) / Δy Αν t [0,1], υπάρχεισημείο τομής με συντεταγμένες: (x 1 + t Δx, Y, z 1 + t Δz) = (x 1 + (Y y 1 ) Δx/Δy, Y, z 1 + (Y y 1 )Δz/Δy)
89 Αλγόριθμος Sutherland-Hodgman3-Δ 6 στάδιααποκοπήςγιατα 6 επίπεδα έλεγχοςανp(x,y,z) εσωτερικόεπιπέδου (a,b,c,d) απότοπρόσημο f(x,y,z) = ax + by + cz+ d Υπολογισμόςτομήςευθυγράμμουτμήματος μεεπίπεδο: π.χ. όπωςστηπερίπτωσηcohen- Sutherland
90 Μετασχηματισμοί 3-Δ Ομογενείςσυντεταγμένεςσημείων Ε 3 : (x,y,z,w) Βασικήπαράσταση: (x,y,z,1) Δεξιόστροφα(εδώ) ήαριστερόστροφα συστήματα.
91 Μετασχηματισμοί 3-Δ
92 Μετασχηματισμοί 3-Δ Στροφή: Ανάγκηκαθορισμούθετικής / αρνητικήςφοράς Ορθογώνιοιμετασχηματισμοί
93 Μετασχηματισμοί 3-Δ
94 Φροντιστηριακήάσκηση Φ5 Μετασχηματισμοί 3 διαστάσεων Σελ119 (Θεοχάρης) άσκησηα.3.9 Περιστροφήπυραμίδαςωςπροςάξονα
95 ΜΑΘΗΜΑ #9 Προβολές Απαραίτητεςαφού3Δαντικείμενα απεικονίζονταισε2δσυσκευές.
96 Προβολές Προοπτική: πεπερασμένηαπόστασηκέντρου προβολήςαπόεπίπεδοπροβολής. Παράλληλη: άπειρηαπόστασηκέντρου προβολήςαπόεπίπεδοπροβολής. Ιδιότητεςπροβολών: Ευθείεςπροβάλλονταισεευθείες. Αποστάσειςαλλάζουν(γενικά). 3Δπαράλληλεςευθείες, μηπαράλληλεςμεεπίπεδο προβολής, δενπροβάλλονταισεπαράλληλεςευθείες. Γωνίαμεταξύευθειώναλλάζει, εκτόςανεπίπεδο γωνίαςπαράλληλομεεπίπεδοπροβολής.
97 ΠροοπτικήΠροβολή Έστωπροβολήστοεπίπεδο ΧΥμεκέντρο προβολής
98 ΠροοπτικήΠροβολή Δενείναιγραμμικόςμετασχηματισμός (διαίρεσημε z). Δενμπορείναδοθείμεμορφήπίνακα. Ωστόσομπορούμεναχρησιμοποιήσουμεμεταβολήτου w. Ακολουθείδιαίρεσημε w (αφούπρέπειw=1)
99 ΠροοπτικήΠροβολή Χαρακτηριστικό: κεντρικήσμίκρυνση (όπωςτοανθρώπινομάτι).
100 ΠαράλληληΠροβολή Κέντροπροβολήςστοάπειρο, δίνεταικατεύθυνση προβολής. Διατηρείαποστάσεις, χρήσιμοστοιχείο π.χ. στηναρχιτεκτονική. Ορθογώνιαπαράλληληπροβολή: πάνωσεένααπό ταβασικάεπίπεδαμεκάθετεςακτίνεςπροβολής. Πίνακαςμετασχηματισμού γιαορθογώνια π.χ. στο ΧΥ
101 ΠαράλληληΠροβολή Παράλληλεςπροβολέςδιακρίνονταισε: Ορθογραφικές: ακτίνεςπροβολής κάθετεςστοεπίπεδοπροβολής. Πλάγιες: ακτίνεςόχικάθετες. Ορθογραφικέςδιακρίνονταισε: Ορθογώνιες: ακτίνεςπροβολήςπαράλληλεςμε Χ, ΥήΖ. Αξονομετρικές: μηορθογώνιες. Ισομετρικές: ακτίνεςπροβολήςπαράλληλεςμεκύρια διαγώνιοχώρου.
102 Παράδειγμα -άσκηση ΠροβολήμοναδιαίουκύβουστοεπίπεδοΧΥ για προοπτικήπροβολή μεd=1 καιd=10 (μοναδιαίοςκύβοςέχειμιακορυφήστο 0,0,0 καιμίακορυφήστο(1,1,1), περιγράφεταιαπό 8 σημεία, μήτρα 8*4 )
103 ΜετασχηματισμόςΠαρατήρησης ΠαγκόσμιοΣύστημαΣυντεταγμένωνΣύστημα ΣυντεταγμένωνΠαρατηρητή. Σύνθεσηβασικώνμετασχηματισμών. Καθορίζειόριααποκοπής& παραμέτρουςπροβολής ΘαεξετάσουμεΜΠΙ
104 ΜετασχηματισμόςΠαρατήρησηςΙ ΜΠΙχρησιμοποιείπροοπτικήπροβολήκαικαθορίζεταιαπό: α. ΣημείοπαρατήρησηςΟ β. 2 ανύσματαγια Υ Π καιζ Π (αριστερόστροφο). Από Παγκόσμιο Σύστημα Συντεταγμένων(ΠΣΣ) σεσύστημα συντεταγμένων παρατηρητή(σσπ) : 1. ΜεταφοράστηναρχήΠΣΣ. 2. Στροφέςγύρωαπό Χ, ΥκαιΖτουΠΣΣώστεναταυτισθούν με αντίστοιχουςσσπ. 3. Αποκοπή. 4. ΠροοπτικήΠροβολή. Χρησιμοποιούνται 3 ακόμα παράμετροι για καθορισμό ορίωναποκοπής: γ. Μέγεθοςπαραθύρουπροβολής 2h. δ. Απόσταση d έμπροσθενεπιπέδουαποκοπήςαπό (κάθετοστονζ Π ). ε. Απόσταση f όπισθενεπιπέδουαποκοπήςαπό (κάθετοστονζ Π ).
105 ΜετασχηματισμόςΠαρατήρησηςΙ
106 ΜετασχηματισμόςΠαρατήρησηςΙ ΧαρακτηριστικάΜΠΙ: Επίπεδοπροβολήςταυτόσημομεέμπροσθενεπίπεδο αποκοπής z Π =d. Κέντροπροβολήςταυτόσημομεσημείοπαρατήρησης. Προοπτικήπροβολή. Τετράγωνοπαράθυρο, συμμετρικόωςπρος Ζ Π. Πληροφορίαz διατηρείταικατάτηνπροβολή για2 λόγους: 3Δαποκοπήευκολότερησανενδιάμεσοστάδιοτης προβολής. Απόκρυψηαπαιτεί z πληροφορία. (Z-Buffer)
107 Προβολήστον ΜΠΙ Θα χρειαστούμε PΜΠ1 από ΣΣΠ σε ΣΣ Οθόνης(ΣΣΟ):
108 Προβολήστον ΜΠΙ Οπαραπάνωμετασχηματισμόςμπορείναχωρισθείσε: Γραμμικόμέρος(πίνακας). Διαίρεσημεομογενήσυντεταγμένη(= z Π )
109 Προβολήστον ΜΠΙ
110 Προβολήστον ΜΠΙ
111 Φροντιστηριακήάσκηση Φ6 (παραδοτέα-τελευταία) Ναβρεθείημήτραμετασχηματισμούενός σημείου(x,y,z) απόσύστημασυντεταγμένων φυσικούσυστήματοςσεένασύστημασ εταγμένωνπαρατήρησης(σσπ) με χαρακτηριστικά: οάξονας Ζ τουσσπναδείχνεικατευθείανστηναρχήτου φυσικούσυστήματοςκαιοάξοναςχναείναι παράλληλοςστοεπίπεδοχυτουφυσικούσυστήματοςοι δεάξονεςχ,υ τουσσπναείναιπαράλληλοιστουςάξονες τηςοθόνηςπουαποτελείτοεπίπεδοπροβολής
112 Άσκηση (συνέχεια) Χρησιμοποιείστετοσχήμαγιατιςεξισώσεις μετασχηματισμού x= ρ*sinφ* cosθ y= ρ*sinφ* sinθ z = ρ* cosφ
113 Άσκηση (συνέχεια) Στησυνέχειαχρησιμοποιήσατετημήτραμετασχηματισμού καθώςκαιτιςεξισώσειςτηςπροοπτικήςπροβολήςγιανα λύσετετοεξήςπρόβλημα: Ανυποθέσουμεκύβοτουοποίου τοκέντροβρίσκεταιστηναρχήτουφυσικούσυστήματος συντεταγμένων με ακμή 1 εκ, έστω ότι παρατηρούμε τον κύβοαπό σημείο 6,10,8 μετονάξοναπαρατήρησης z να δείχνειπροςτηναρχήτουφυσικούσυστήματος συντεταγμένων. Υποθέτουμεότιοάξοναςτωνχβρίσκεται στοεπίπεδο z=8. Επίσηςυποθέστεότιβλέπουμετο αντικείμενο από απόσταση 0,6 μ. Καιότι ηοθόνη(πεδίο προβολής) είναιδιαστάσεων 0,3*0,3 μ. Μεσυντεταγμένες 1024*1024. Ναβρεθείκαιναυπολογιστείηπροοπτική προβολήτουκύβουστοεπίπεδοτηςοθόνης
114 Αποκοπήστο ΜΠΙ Τιμήορίζεικαιταόριααποκοπής: w x w w y w 0 z w Αποκοπήγίνεταιμετάτηνεφαρμογή P ΜΠΙ αλλάπριντηδιαίρεσημετο w
115 #10 ΠρόβλημαΑπόκρυψης Ποιοείναιτοεμφανέςαντικείμενο(χρώμα) σεκάθε σημείοτουεπιπέδουπροβολής; Χωρίζονταισεαλγόριθμουςαπόκρυψηςακμώνκαι επιφανειών. Χρησιμοποιούνάμεσαήέμμεσαταξινόμησηστις διαστάσεις X Y καιz.
116 ΑλγόριθμοιΑπόκρυψης Χωρίζονταισε αλγόριθμουςχώρουαντικειμένων και αλγόριθμουςχώρουεικόνας. ΑλγόριθμοιχώρουαντικειμένωνείναιO(Π 2 ) ενώαλγόριθμοιχώρουεικόναςείναιο(π-ρ) όπου Ποαριθμόςτωνπολυγώνων και P οαριθμόςτωνpixels.
117 Αλγόριθμοιχώρουαντικειμένων Αλγόριθμοιχώρουαντικειμένωνσυγκρίνουν αντικείμεναμεταξύτουςγιαναβρουντοπλησιέστερο σεκάθεσημείοτουεπιπέδουπροβολής: Γιακάθεαντικείμενοπ { Εύρεσητωνορατώντμημάτωντουπμέσωσύγκρισης (Χ,Υ,Ζ) μεόλαταάλλααντικείμενα; Χρωματισμόςτωνορατώντμημάτωντουπστηνοθόνη }
118 Αλγόριθμοιχώρουεικόνας Αλγόριθμοιχώρουεικόναςέχουντηνεξήςμορφή: Γιακάθεpixelρτηςεικόνας { Εύρεσητουπλησιέστερουαντικειμένουπουτέμνεται απότηνακτίναπροβολήςπουπερνάαπότορ; Χρωματισμόςτουρμετοχρώματουπλησιέστερου αντικειμένουστοσημείοτομής }
119 ΑλγόριθμοιΑπόκρυψης Υπολογιστικήακρίβεια. Αλγόριθμοιχώρουεικόνας: ακρίβειαπουαπαιτείηανάλυσητης εικόνας. Αλγόριθμοιχώρουαντικειμένων: ακρίβειαορισμούαντικειμένων (=ακρίβειαυπολογιστή). Θέσηστηγραφικήσωλήνωσηεξόδου. Αλγόριθμοιχώρουαντικειμένων: μετάτηνπροβολή (διακεκομμένηγραμμή). Αλγόριθμοιχώρουεικόνας: ενσωματώνονταιστηδιαδικασία παράστασηςστηνοθόνη. Διαγραφήπίσωεπιφανειών.
120 ΑλγόριθμοιΑπόκρυψης Τεχνικέςβελτίωσηςαποτελεσματικότητας αλγορίθμωναπόκρυψης. Εκμετάλλευσηπροοπτικούμετασχηματισμού. Εκμετάλλευσησυνάφειας. Περιβάλλοντεςόγκοι. Διαμερισμόςχώρου.
121 Προοπτικός Μετασχηματισμός ΖήτημααπόκρυψηςμεταξύδύοσημείωνΣ 1 (x 1,y 1,z 1 ) καισ 2 (x 2,y 2,z 2 ) υπάρχει μόνοανταδύοσημείαβρίσκονταιπάνωστηνίδιαακτίναπροβολής. Συνθήκηαπόκρυψηςστηνπαράλληληπροβολή: (x 1 =x 2 ) και(y 1 =y 2 ) Συνθήκηαπόκρυψηςστηνπροοπτικήπροβολή:(x 1 /z 1 =x 2 /z 2 ), (y 1 /z 1 =y 2 /z 2 ) Απαιτεί(ακριβή) διαίρεσημε z. Η διαίρεσηαυτήγίνεταικατάτηνπροοπτικήπροβολή. Η προοπτικήπροβολήμετατρέπειτιςακτίνεςπροβολήςσεπαράλληλες. Φυλάμε z συντεταγμένηγιασύγκρισηβάθους.
122 Συνάφεια Συνάφεια: ιδιότηταγεωμετρικώνοντοτήτωννα διατηρούντοπικάσταθερέςτιςτιμέςτων χαρακτηριστικώντουςήνατιςμεταβάλλουν ομαλά. π.χ. αυξητικόςυπολογσμός z σημείωνπολυγώνου. Είδησυνάφειας: Συνάφειαακμής. Συνάφειαεπιφάνειας. Συνάφειαγραμμώνσάρωσης. Συνάφειακαρέ.
123 Περιβάλλοντες Όγκοι Απλούστεροιόγκοιαπότααντικείμεναπου περιβάλλουνγιαμείωσηκόστουςσυγκρίσεωνκατά τηνταξινόμηση στις διαστάσεις Χ, ΥκαιΖ. Συχνάέχουντημορφήορθογώνιουπαραλληλογράμμου (2Δ) ήορθογώνιουπαραλληλεπιπέδου(3δ). Οχιαπαραίτητακλειστοί. Ανοιπεριβάλλοντεςόγκοιδύοαντικειμένωνδεν τέμνονταιτότεούτετααντικείμενατέμνονται. Τοαντίθετοδενισχύειπάντα.
124 ΔιαμερισμόςΧώρου Διαμερισμόςχώρουσεσύνολο διατεταγμένωνμερών (π.χ. voxels). Ταμέρητουχώρουπουκαταλαμβάνειένα αντικείμενοορίζουνέμμεσατηδιάταξήτου σεσχέσημεάλλααντικείμενα.
125 ΔιαγραφήΠίσωΕπιφανειών Ανηγωνίαμεταξύκαιείναιτότεηεπιφάνειαείναι Μιαεπιφάνειαείναιορατήαν Μειώνειόγκοδεδομένωνκατά ~50%. Λύνειπρόβλημααπόκρυψηςγιαένακυρτό αντικείμενο.πίσω(αόρατη).
126 ΔιαγραφήΠίσωΕπιφανειών ΛειτουργείστοχώροαντικειμένωνκαιείναιΟ(Π). V μπορείναυπολογισθείαπόμίακορυφήp της επιφάνειας. ΑνοπαρατηρητήςβρίσκεταιστοκέντροτουΣΣΠτότεV=-P N μπορεί να υπολογισθεί από 3 διαδοχικές, μη συγγραμμικέςκορυφέςp 1, P 2, P 3 και ΠΡΟΣΟΧΗ: Χρήσησειράςκορυφών
127 ΑλγόριθμοιΑπόκρυψηςΕπιφανειών Ακολούθησαντηνεμφάνισητηςπλεγματικής οθόνης. 4 Βασικέςκατηγορίες. z-buffer (πιοδιαδεδομένος). scanline. ταξινόμησηκατάβάθος. υποδιαίρεσηεπιφάνειας.
128 ΑλγόριθμοιΑπόκρυψηςΕπιφανειών Βασικήπράξη: σύγκρισηβάθους 2 στοιχείων μείδιο ΧΥ. Η προοπτικήπροβολή διευκολύνει. Μετατρέπειακτίνεςπροβολής ώστεναείναιπαράλληλεςτου Z. Ίσεςαποστάσειςστον Ζ π δεν μετασχηματίζονταισείσες αποστάσειςστονζ ο. Ζ ο μεταβάλλεταιταχύτερακαθώς πλησιάζειτημέγιστητιμήτου(1).
129 Αλγόριθμος z-buffer Απαιτεί ύπαρξη μνήμης βάθους (z-buffer) για κάθεpixel. Οιτιμέςβάθουςβρίσκονται(γιαταπερισσότερα σχήματα) μεπαρεμβολή. Έμμεσηταξινόμηση. Γιακάθεpixelοz-bufferφυλάειτηνελάχιστη(ως τώρα) τιμήβάθουςστοpixelαυτό. Αρχικοποίηση στο μέγιστο z (πίσωεπίπεδο αποκοπής).
130 Αλγόριθμος z-buffer /* Αρχικοποίηση: m,nοιδιαστάσειςτηςοθόνης */ for (x=0; x<m; x++) { } for (y=0; y<n; y++) { } z_buffer[x,y]=f; /*μέγιστοβάθος*/ frame_buffer[x,y]=background; /*φόντο*/ /*Επεξεργασίαπολυγώνων*/ for (π=0; π<number_of_polygons(); π++) { /*Επεξεργασίαscanlinesπολυγώνουymin ymax*/ for(y=ymin; y<=ymax; y++) { /*Βρεςμεγραμμικήπαρεμβολήμεταξύτωναντίστοιχωνκορυφών, τιςτιμέςτομήςμε scanliney :xleft,xrightτις τιμές βάθους στις τομές:zleft,zrightτις τιμές χρωματισμού στιςτομές:cleft,cright*/ for (x=xleft; x<=xright; x++) { /*Βρεςμεγραμμικήπαρεμβολήμεταξύxleftκαιxrightτηντιμήβάθους z καιχρώματος c σεκάθεpixelx,y*/ if (z<z_buffer[x,y]) { z_buffer[x,y]=z; frame_buffer[x,y]=c;
131 Αλγόριθμος z-buffer Τομέςπλευρώνπολυγώνουμεscanlines βρίσκονταιμελίσταενεργώνπλευρών. Γραμμικήπαρεμβολή z.
132 Αλγόριθμος z-buffer Ο(Π,S), όπου ΠοαριθμόςπολυγώνωνκαιS o μέσοςαριθμόςpixelανάπολύγωνο. Γιατυπικέςσκηνές (σταθερό). Πλεονεκτήματα z-buffer: Ευκολίαυλοποίησηςσε H/W ήs/w. Επεξεργασίαπολυγώνωνμετυχαίασειρά. Δυνατότηταχρήσηςγιαμηπολυγωνικάαντικείμενα (μεσυνάρτησηβάθους). Ανάγκησεμνήμη: Έναςκαλός z-buffer απαιτεί32 bits/pixel. Γιαανάλυση1024x1024 αυτόσυνεπάγεται4mbytes.
133 ΕιδικέςΕφαρμογές z-buffer Συνδυασμόςεικόνων Έστω οι frame και z-buffer εικόνων A και Β. ΑκαιΒμπορείναδημιουργήθηκανχωριστά. Συνδυασμός: for (x=0; x<m; x++) for (y=0; y<n; y++) {Z C [x,y]=(z A [x,y]<z B [x,y])?z A [x,y]:z B [x,y]; F C [x,y]=(z A [x,y]<z B [x,y])?f A [x,y]:f B [x,y];} Τοποθέτηση3Δαντικειμένων σεσκηνήμεχρήση z-buffer. 3Δcursor. Δενμεταβάλλουμεπεριεχόμενα z-buffer.
134 ΑλγόριθμοιΛίσταςΠροτεραιότητας (αλγόριθμοι ζωγράφου) Ταξινόμησηπολυγώνωνκατάβάθοςκαιεμφάνιση μεσωστήσειρά: Οχιπάνταδυνατή(επικάλυψη z-έκτασης, τεμνόμενα πολύγωνα). Διαμερισμόςπολυγώνων. Μεγάληπολυπλοκότητα. Χώροςαντικειμένων, αναποτέλεσμαθεωρηθείη ταξινομημένηλίστα. 1. Αλγόριθμοςταξινόμησηςκατάβάθος(Newell 1972). 2. ΑλγόριθμοςBSP δένδρου(fuchs 1983).
135 ΑλγόριθμοςΤαξινόμησηςκατά Βάθος Ταξινόμησηκατάφθίνουσααπόστασηαπό κέντροπροβολής. Σύγκριση P προq δενείναιπάνταεύκολη. Χρήσηπεριβάλλοντοςπαραλληλεπιπέδου [x min (P), y min (P), z min (P)],[x max (P), y max (P), z max (P)].
136 ΑλγόριθμοιΥποδιαίρεσηςΕπιφάνειας Αναδρομικήδιαίρεσηεπιπέδουπροβολής: Αν1 πολύγωνοκαλύπτειτμήμαπλήρως, τότεαυτόπαίρνειτοχρώματουπολυγώνου. Αναδρομήσταματάεπίσηςστομέγεθοςτουpixel. Εκμετάλλευσησυνάφειαςεπιφάνειας(μεγάλαπολύγωνα, σταθερούχρώματος). Αλγόριθμος Warnock: Αναδρομήσταματά αναπόένα τμήμα περνά τοπολύ1 ακμή πολυγώνου. ΣυγκρίσειςπροβολήςπολυγώνουP μεπεριοχήοθόνηςβ. Χρήσηπεριβάλλοντωνορθογωνίων: 4 περιπτώσειςσχέσης P καιb: (D: Disjoint) P εξωτερικότηςβ. (C: Contained) P εσωτερικότηςβ. (S: Surrounding) P καλύπτονπλήρωςτηνβ. (I: Intersecting) P τέμνοντηνβ. Π.χ.σχέση D εξασφαλίζεται εάνισχύει:
137 ΑλγόριθμοιΥποδιαίρεσηςΕπιφάνειας Αναδρομικές διαιρέσεις Warnock: Μείωσηυποδιαιρέσεων μεβάσηκορυφέςπολυγώνων (Weiler-Atherton):
138 Σύγκριση ΜεθόδωνΑπόκρυψης
139 ΑπόκρυψηκαιΠαρακολούθηση Ακτίνας (Ray Tracing) Αλγόριθμοςπαρακολούθησηςακτίνας(Whitted): Ακτίνεςπουορίζονταιαπόσημείοπαρατήρησηςκαι κάθεpixelακολουθούνταιώσπουνασυναντήσουν αντικείμενο. Εκείδιασπώνταιανάλογαμεμοντέλο. Ουσιαστικάλύνειπρόβλημααπόκρυψης.
#9 Γραφική Υπολογιστή
 #9 Γραφική Υπολογιστή 1. Βασικοί γραφικοί αλγόριθµοι, 2. Αρχές γραφικών πλεγµατικών οθονών raster 3. Μετασχηµατισµοί 2 και 3 διαστάσεων και συστήµατα συντεταγµένων, 4. Προβολές και µετασχηµατισµοί παρατήρησης,
#9 Γραφική Υπολογιστή 1. Βασικοί γραφικοί αλγόριθµοι, 2. Αρχές γραφικών πλεγµατικών οθονών raster 3. Μετασχηµατισµοί 2 και 3 διαστάσεων και συστήµατα συντεταγµένων, 4. Προβολές και µετασχηµατισµοί παρατήρησης,
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ. 3ο Μάθημα Αποκοπή. Γραφικα. Ευάγγελος Σπύρου
 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
Διδάσκων: Φοίβος Μυλωνάς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Πρόβληµα Απόκρυψης. Ποιο είναι το εµφανές αντικείµενο (χρώµα) σε κάθε σηµείο του επιπέδου προβολής;
 Πρόβληµα Απόκρυψης Ποιο είναι το εµφανές αντικείµενο (χρώµα) σε κάθε σηµείο του επιπέδου προβολής; Σ Εµφανές αντικείµενο στο σηµείο Σ Επίπεδο προβολής Χωρίζονται σε αλγόριθµους απόκρυψης ακµών και επιφανειών.
Πρόβληµα Απόκρυψης Ποιο είναι το εµφανές αντικείµενο (χρώµα) σε κάθε σηµείο του επιπέδου προβολής; Σ Εµφανές αντικείµενο στο σηµείο Σ Επίπεδο προβολής Χωρίζονται σε αλγόριθµους απόκρυψης ακµών και επιφανειών.
Γραφικά με υπολογιστές
 Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων
 2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων
 Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pixels: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pixels: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Τι είναι Αποκοπή (clip)?
 Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων
 5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
Γραφικά με Η/Υ / Εισαγωγή
 Γραφικά με Η/Υ Εισαγωγή Πληροφορίες μαθήματος (1/4) Υπεύθυνος μαθήματος: Μανιτσάρης Αθανάσιος, Καθηγητής ιδάσκοντες: Μανιτσάρης Αθανάσιος: email: manits@uom.gr Μαυρίδης Ιωάννης: email: mavridis@uom.gr
Γραφικά με Η/Υ Εισαγωγή Πληροφορίες μαθήματος (1/4) Υπεύθυνος μαθήματος: Μανιτσάρης Αθανάσιος, Καθηγητής ιδάσκοντες: Μανιτσάρης Αθανάσιος: email: manits@uom.gr Μαυρίδης Ιωάννης: email: mavridis@uom.gr
Αποκοπή 4.1. Εργα: : & ΣΚΕΠΣΙΣ (ΕΠΕΑΚ - ΥΠΕΠΘ) Τµήµα Πληροφορικής 1 2 (SCS) Θέση παρατηρητή. Θέσεις αντικειµένων και φωτεινών πηγών
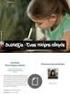 Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε 2Δ συσκευές. Θέση παρατηρητή. 3Δ Μετασχ/σμός Παρατήρησης
 Προβολές Προβολές Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε Δ συσκευές. Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3Δ Μαθηματικά Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης
Προβολές Προβολές Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε Δ συσκευές. Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3Δ Μαθηματικά Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης
Μετασχηµατισµοί 2 &3
 Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Γραφικά με Η/Υ Αποκοπή
 Γραφικά με Η/Υ Αποκοπή Αποκοπή Οι αλγόριθμοι αποκοπής έχουν σχεδιαστεί έτσι ώστε να είναι αποτελεσματικοί στο να εντοπίζουν τα τμήματα μίας σκηνής ή ενός αντικειμένου σε συντεταγμένες προβολής που βρίσκονται
Γραφικά με Η/Υ Αποκοπή Αποκοπή Οι αλγόριθμοι αποκοπής έχουν σχεδιαστεί έτσι ώστε να είναι αποτελεσματικοί στο να εντοπίζουν τα τμήματα μίας σκηνής ή ενός αντικειμένου σε συντεταγμένες προβολής που βρίσκονται
Εισαγωγή. Γραφικά. Μοντέλο (Πληροφορίες για Περιεχόµενο εικόνας. Επεξεργασία Εικόνων. Εικόνα. Τεχνητή Όραση 1.1. Εργα: : 2000+1 & ΣΚΕΠΣΙΣ (ΕΠΕΑΚ
 Εισαγωγή Μιάεικόνααξίζει1000 λέξεις : Ανθρώπινοοπτικόκανάλι: 30-40 Μbits/s (=64-85 M λέξεις /min µε 4 γράµµατα/λέξη, 7bits/γράµµα). Γραπτό κείµενο: 600-1200 λέξεις/min. 100.000 αποδοτικότερη επικοινωνία
Εισαγωγή Μιάεικόνααξίζει1000 λέξεις : Ανθρώπινοοπτικόκανάλι: 30-40 Μbits/s (=64-85 M λέξεις /min µε 4 γράµµατα/λέξη, 7bits/γράµµα). Γραπτό κείµενο: 600-1200 λέξεις/min. 100.000 αποδοτικότερη επικοινωνία
Σχεδίαση με Ηλεκτρονικούς Υπολογιστές
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 13: Τεχνικές απεικόνισης στην οθόνη του ΗΥ Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα Αγρονόμων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 13: Τεχνικές απεικόνισης στην οθόνη του ΗΥ Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα Αγρονόμων
Γραφικά με Η/Υ Αποκοπή
 Γραφικά με Η/Υ Αποκοπή Βασικές λειτουργίες απεικόνισης μετατροπή των φυσικών συντεταγμένων, ενός αντικειμένου, σε συντεταγμένες της συσκευής απεικόνισης (δημιουργία μετασχηματισμού απεικόνισης) αφαίρεση
Γραφικά με Η/Υ Αποκοπή Βασικές λειτουργίες απεικόνισης μετατροπή των φυσικών συντεταγμένων, ενός αντικειμένου, σε συντεταγμένες της συσκευής απεικόνισης (δημιουργία μετασχηματισμού απεικόνισης) αφαίρεση
Μετασχηματισμός Παρατήρησης
 Μετασχηματισμός Παρατήρησης Παγκόσμιο Σύστημα Συντεταγμένων Σύστημα Συντεταγμένων Παρατηρητή. Σύνθεση βασικών μετασχηματισμών. Καθορίζει όρια αποκοπής & παραμέτρους προβολής Θα εξετάσουμε ΜΠ Ι και Θέσεις
Μετασχηματισμός Παρατήρησης Παγκόσμιο Σύστημα Συντεταγμένων Σύστημα Συντεταγμένων Παρατηρητή. Σύνθεση βασικών μετασχηματισμών. Καθορίζει όρια αποκοπής & παραμέτρους προβολής Θα εξετάσουμε ΜΠ Ι και Θέσεις
ΘΕΜΑ: Υλοποίηση Αλγορίθμων Γραφικής σε Περιβάλλον Οπτικού Προγραμματισμού
 Τ.Ε.Ι. ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗ ΠΛΗΡΟΦΟΡΙΩΝ ΘΕΜΑ: Υλοποίηση Αλγορίθμων Γραφικής σε Περιβάλλον Οπτικού Προγραμματισμού ΣΠΟΥΔΑΣΤΡΙΑ: ΚΛΑΔΑΚΗ ΕΙΡΗΝΗ 275 ΚΑΒΑΛΑ, 2006 ΠΕΡΙΕΧΟΜΕΝΑ
Τ.Ε.Ι. ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗ ΠΛΗΡΟΦΟΡΙΩΝ ΘΕΜΑ: Υλοποίηση Αλγορίθμων Γραφικής σε Περιβάλλον Οπτικού Προγραμματισμού ΣΠΟΥΔΑΣΤΡΙΑ: ΚΛΑΔΑΚΗ ΕΙΡΗΝΗ 275 ΚΑΒΑΛΑ, 2006 ΠΕΡΙΕΧΟΜΕΝΑ
Μετασχηματισμοί Μοντελοποίησης (modeling transformations)
 Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods)
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods) Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods) Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch
 Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
Προβολές. Απαραίτητες αφού 3 αντικείµενα απεικονίζονται σε 2 συσκευές.
 ροβολές Απαραίτητες αφού 3 αντικείµενα απεικονίζονται σε συσκευές. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή 3 Μαθηµατικά Μοντέλα ΣΣΑ 3 Μετασχ/σµοί Μοντέλου ΣΣ (WCS) 3 Μετασχ/σµός αρατήρησης
ροβολές Απαραίτητες αφού 3 αντικείµενα απεικονίζονται σε συσκευές. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή 3 Μαθηµατικά Μοντέλα ΣΣΑ 3 Μετασχ/σµοί Μοντέλου ΣΣ (WCS) 3 Μετασχ/σµός αρατήρησης
Σχεδίαση γραµµών στην οθόνη του Υπολογιστή Γέµισµα πολυγώνων Αποκοπή
 Σχεδίαση γραµµών στην οθόνη του Υπολογιστή Γέµισµα πολυγώνων Αποκοπή 1 1η προσέγγιση: εφαρµογή της εξίσωσης της ευθείας Έστω ότι επιθυµούµε να σχεδιάσουµε ευθεία y=mx+b Προσέγγιση 1: δίνουµε τιµές στο
Σχεδίαση γραµµών στην οθόνη του Υπολογιστή Γέµισµα πολυγώνων Αποκοπή 1 1η προσέγγιση: εφαρµογή της εξίσωσης της ευθείας Έστω ότι επιθυµούµε να σχεδιάσουµε ευθεία y=mx+b Προσέγγιση 1: δίνουµε τιµές στο
Διαλέξεις #05 & #06. Διδάσκων: Φοίβος Μυλωνάς. Γραφικά με υπολογιστές. Αλγόριθμος Σχεδίασης Κύκλου Αλγόριθμος Σχεδίασης Έλλειψης
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διαλέξεις #05 & #06 Αλγόριθμος Σχεδίασης Κύκλου Αλγόριθμος Σχεδίασης Έλλειψης Φοίβος
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διαλέξεις #05 & #06 Αλγόριθμος Σχεδίασης Κύκλου Αλγόριθμος Σχεδίασης Έλλειψης Φοίβος
4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης
 4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Προοπτική Προβολή Παράλληλη Προβολή Ορθογραφικές Προβολές Πλάγιες Παράλληλες
4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Προοπτική Προβολή Παράλληλη Προβολή Ορθογραφικές Προβολές Πλάγιες Παράλληλες
Γραφικά Ι. Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή
Γραφικά Ι Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 22D D σχημάτων (ευθεία
 Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά Υπολογιστών & Εικονική Πραγματικότητα. Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής
 Γραφικά Υπολογιστών & Εικονική Πραγματικότητα Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής Βασικές λειτουργίες απεικόνισης μετατροπή του παγκόσμιου συστήματος συντεταγμένων, ενός αντικειμένου, σε
Γραφικά Υπολογιστών & Εικονική Πραγματικότητα Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής Βασικές λειτουργίες απεικόνισης μετατροπή του παγκόσμιου συστήματος συντεταγμένων, ενός αντικειμένου, σε
Γραφικά Υπολογιστών: Θέαση στις 3D
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Θέαση στις 3D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Σήμερα θα δούμε τα παρακάτω θέματα: Μετασχηματισμοί
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Θέαση στις 3D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Σήμερα θα δούμε τα παρακάτω θέματα: Μετασχηματισμοί
Διαλέξεις #13-#14 Εισαγωγικά στοιχεία Προοπτική, Παράλληλη, Πλάγια Υπολογισμός Παράλληλης Προβολής Υπολογισμός Προοπτικής Προβολής Παραδείγματα
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διαλέξεις #13-#14 Εισαγωγικά στοιχεία Προοπτική, Παράλληλη, Πλάγια Υπολογισμός
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διαλέξεις #13-#14 Εισαγωγικά στοιχεία Προοπτική, Παράλληλη, Πλάγια Υπολογισμός
Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering)
 Υφή Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering) Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3D Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης Απομάκρυνση Πίσω Επιφανειών
Υφή Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering) Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3D Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης Απομάκρυνση Πίσω Επιφανειών
Εργαστήριο Τεχνολογίας Πολυμέσων & Γραφικών, Τ.Ε.Π Π.Μ, Μάθημα: Γραφικά με Η/Υ
 ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
Γραφικά με Η/Υ Αλγ λ ό γ ρ ό ιθ ρ μοι κύκλου & έλλειψης
 Γραφικά με Η/Υ Αλγόριθμοι κύκλου & έλλειψης Τεχνική μέσου σημείου (μέσο έ σημείο Q) NE pixel Q Μέσο σημείο M E pixel P = ( x p, y p ) x x + 1 = p Προηγούμενο pixel Επιλογές για το Επιλογές για το τρέχων
Γραφικά με Η/Υ Αλγόριθμοι κύκλου & έλλειψης Τεχνική μέσου σημείου (μέσο έ σημείο Q) NE pixel Q Μέσο σημείο M E pixel P = ( x p, y p ) x x + 1 = p Προηγούμενο pixel Επιλογές για το Επιλογές για το τρέχων
Μάθημα 10 ο. Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 10 ο Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Η περιγραφή μίας περιοχής μπορεί να γίνει: Με βάση τα εξωτερικά χαρακτηριστικά (ακμές, όρια). Αυτή η περιγραφή προτιμάται όταν μας ενδιαφέρουν
Μάθημα 10 ο Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Η περιγραφή μίας περιοχής μπορεί να γίνει: Με βάση τα εξωτερικά χαρακτηριστικά (ακμές, όρια). Αυτή η περιγραφή προτιμάται όταν μας ενδιαφέρουν
Αλγόριθμοι παράστασης βασικών σχημάτων σε πλεγματικές οθόνες
 Αλγόριθμοι παράστασης βασικών σχημάτων σε πλεγματικές οθόνες Αλγόριθμοι Παράστασης Βασικών Σχημάτων Προσέγγιση μαθηματικών σχημάτων από διακριτά pxels: Ευθύγραμμο τμήμα, κύκλος, κωνικές τομές, πολύγωνο.
Αλγόριθμοι παράστασης βασικών σχημάτων σε πλεγματικές οθόνες Αλγόριθμοι Παράστασης Βασικών Σχημάτων Προσέγγιση μαθηματικών σχημάτων από διακριτά pxels: Ευθύγραμμο τμήμα, κύκλος, κωνικές τομές, πολύγωνο.
Μετασχηματισμοί Παρατήρησης και Προβολές
 Μετασχ. Γραφικά Παρατήρησης Υπολογιστών και Προβολές Μετασχηματισμοί Παρατήρησης και Προβολές Γ. Γ. Παπαϊωάννου, - 2008 Στάδια Προβολής στο Επίπεδο Περνάμε από WCS στοτοπικόσύστημα συντεταγμένων του παρατηρητή
Μετασχ. Γραφικά Παρατήρησης Υπολογιστών και Προβολές Μετασχηματισμοί Παρατήρησης και Προβολές Γ. Γ. Παπαϊωάννου, - 2008 Στάδια Προβολής στο Επίπεδο Περνάμε από WCS στοτοπικόσύστημα συντεταγμένων του παρατηρητή
Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Ο πολλαπλασιασμός Ax μπορεί να ειδωθεί σαν μετασχηματισ
 Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Ο πολλαπλασιασμός
Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Ο πολλαπλασιασμός
Μετασχηµατισµοί 2 & 3
 Μετασχηµατισµοί & 3 Περιγράφονται σαν σύνεση βασικών: µετατόπιση αλλαγή κλίµακαςπεριστροφή στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών Θέση
Μετασχηµατισµοί & 3 Περιγράφονται σαν σύνεση βασικών: µετατόπιση αλλαγή κλίµακαςπεριστροφή στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών Θέση
ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ - ΕΛΛΕΙΨΗΣ
 ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ - ΕΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ - ΕΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
Κλασσική παρατήρηση & παρατήρηση με υπολογιστή
 Κλασσική παρατήρηση & παρατήρηση με υπολογιστή Πολλέςαπότιςεργασίεςσχεδίασης (αρχιτεκτονικό, μηχανολογικό σχέδιο, κινούμενα σχέδια) γίνονται με υπολογιστή Ο χρήστης θα πρέπει να μπορεί να παράξει «κλασικές»
Κλασσική παρατήρηση & παρατήρηση με υπολογιστή Πολλέςαπότιςεργασίεςσχεδίασης (αρχιτεκτονικό, μηχανολογικό σχέδιο, κινούμενα σχέδια) γίνονται με υπολογιστή Ο χρήστης θα πρέπει να μπορεί να παράξει «κλασικές»
Γραφικά Υπολογιστών. Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης. Γραφικά Υπολογιστών ΣΤ Εξάμηνο. Δρ Κωνσταντίνος Δεμερτζής
 Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Σχεδίαση Πολυγώνων και Καμπυλών kdemertz@fmenr.duth.gr Σχεδίαση Πολυγώνων Τα ευθύγραμμα τμήματα
Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Σχεδίαση Πολυγώνων και Καμπυλών kdemertz@fmenr.duth.gr Σχεδίαση Πολυγώνων Τα ευθύγραμμα τμήματα
Θεωρία μετασχηματισμών
 Μήτρα Μετασχηματισμού Η γεωμετρία ενός αντικειμένου μπορεί να παρουσιαστεί από ένα σύνολο σημείων κατανεμημένων σε διάφορα επίπεδα. Έτσι λοιπόν ένα πλήθος δεδομένων για κάποιο αντικείμενο μπορεί να αναπαρασταθεί
Μήτρα Μετασχηματισμού Η γεωμετρία ενός αντικειμένου μπορεί να παρουσιαστεί από ένα σύνολο σημείων κατανεμημένων σε διάφορα επίπεδα. Έτσι λοιπόν ένα πλήθος δεδομένων για κάποιο αντικείμενο μπορεί να αναπαρασταθεί
Γραφικά Ι. Ενότητα 2: Αλγόριθμοι Σχεδίασης. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 2: Αλγόριθμοι Σχεδίασης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δ οθόνες αποτελούνται από διακριτά πλέγματα
Γραφικά Ι Ενότητα 2: Αλγόριθμοι Σχεδίασης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δ οθόνες αποτελούνται από διακριτά πλέγματα
Γραφικά Υπολογιστών και Συστήματα Αλληλεπίδρασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Γραφικά Υπολογιστών και Συστήματα Αλληλεπίδρασης Γεωμετρικοί μετασχηματισμοί Διδάσκων: Αν. Καθ. Ιωάννης Φούντος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Γραφικά Υπολογιστών και Συστήματα Αλληλεπίδρασης Γεωμετρικοί μετασχηματισμοί Διδάσκων: Αν. Καθ. Ιωάννης Φούντος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Εισαγωγή /4 Το σχήμα και το μέγεθος των δισδιάστατων αντικειμένων περιγράφονται με τις καρτεσιανές συντεταγμένες x, y. Με εφαρμογή γεωμετρικών μετασχηματισμών στο μοντέλο
ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Εισαγωγή /4 Το σχήμα και το μέγεθος των δισδιάστατων αντικειμένων περιγράφονται με τις καρτεσιανές συντεταγμένες x, y. Με εφαρμογή γεωμετρικών μετασχηματισμών στο μοντέλο
Γραφικά με υπολογιστές. Διδάσκων: Φοίβος Μυλωνάς. Διάλεξη #07
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Μετασχηµατισµοί. Μετασχηµατισµοί είναι πράξεις (Τελεστές) που επιδρούν πάνω στις συντεταγµένες των σηµείων που απαρτίζουν ένα γεωµετρικό σχήµα M(V)
 Μετασχηµατισµοί Μετασχηµατισµοί είναι πράξεις (Τελεστές) που επιδρούν πάνω στις συντεταγµένες των σηµείων που απαρτίζουν ένα γεωµετρικό σχήµα V M(V) 2.1 Αναπαράσταση 3Δ µοντέλων Κάθε 3Δ µοντέλο αποτελείται
Μετασχηµατισµοί Μετασχηµατισµοί είναι πράξεις (Τελεστές) που επιδρούν πάνω στις συντεταγµένες των σηµείων που απαρτίζουν ένα γεωµετρικό σχήµα V M(V) 2.1 Αναπαράσταση 3Δ µοντέλων Κάθε 3Δ µοντέλο αποτελείται
ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ
 ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ Ένα γεωμετρικό μοντέλο είναι μια αριθμητική περιγραφή ενός αντικειμένου, που περιλαμβάνει το μέγεθος, το σχήμα, καθώς και άλλες ιδιότητές του. Η περιγραφή του μοντέλου
ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ Ένα γεωμετρικό μοντέλο είναι μια αριθμητική περιγραφή ενός αντικειμένου, που περιλαμβάνει το μέγεθος, το σχήμα, καθώς και άλλες ιδιότητές του. Η περιγραφή του μοντέλου
Γραφικά Υπολογιστών: Εμφάνιση σε 2D
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εμφάνιση σε 2D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Έννοιες παραθύρων (windowing) Αποκοπή (clipping)
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εμφάνιση σε 2D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Έννοιες παραθύρων (windowing) Αποκοπή (clipping)
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Απεικόνιση Υφής. Μέρος Α Υφή σε Πολύγωνα
 Απεικόνιση Γραφικά ΥφήςΥπολογιστών Απεικόνιση Υφής Μέρος Α Υφή σε Πολύγωνα Γ. Γ. Παπαϊωάννου, - 2008 Τι Είναι η Υφή; Η υφή είναι η χωρική διαμόρφωση των ποιοτικών χαρακτηριστικών της επιφάνειας ενός αντικειμένου,
Απεικόνιση Γραφικά ΥφήςΥπολογιστών Απεικόνιση Υφής Μέρος Α Υφή σε Πολύγωνα Γ. Γ. Παπαϊωάννου, - 2008 Τι Είναι η Υφή; Η υφή είναι η χωρική διαμόρφωση των ποιοτικών χαρακτηριστικών της επιφάνειας ενός αντικειμένου,
Εισαγωγή. Γιατί γραφικά υπολογιστών; Προσέγγιση «από πάνω προς τα κάτω» (top-down). Βαθµίδα διασύνδεσης προγραµµατιστή εφαρµογών (API)
 Εισαγωγή Γιατί γραφικά υπολογιστών; Προσέγγιση «από πάνω προς τα κάτω» (top-down). Βαθµίδα διασύνδεσης προγραµµατιστή εφαρµογών (API) Γιατί OpenGL; Άλλα APIs: PHIGS (ANSI), GKS, Direct3D, VRML, JAVA-3D
Εισαγωγή Γιατί γραφικά υπολογιστών; Προσέγγιση «από πάνω προς τα κάτω» (top-down). Βαθµίδα διασύνδεσης προγραµµατιστή εφαρµογών (API) Γιατί OpenGL; Άλλα APIs: PHIGS (ANSI), GKS, Direct3D, VRML, JAVA-3D
ΚΕΦΑΛΑΙΟ 2: ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ -ΈΛΛΕΙΨΗΣ
 ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ -ΈΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
ΚΕΦΑΛΑΙΟ : ΑΛΓΟΡΙΘΜΟΙ ΕΥΘΕΙΑΣ ΚΥΚΛΟΥ -ΈΛΛΕΙΨΗΣ Μια εικόνα μπορεί να περιγραφεί με πολλούς τρόπους. Αν υποθέσουμε ότι έχουμε μια προβολή ψηφιδοπλέγματος, μια εικόνα καθορίζεται πλήρως από το σύνολο των
Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε
 Κεφάλαιο 6 Αποκοπή (clipping) Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε η διαδικασία προβολής µεµονωµένων σηµείων και µόνο προς το τέλος του κεφαλαίου
Κεφάλαιο 6 Αποκοπή (clipping) Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε η διαδικασία προβολής µεµονωµένων σηµείων και µόνο προς το τέλος του κεφαλαίου
Γεωμετρικοί μετασχηματιμοί εικόνας
 Γεωμετρικοί μετασχηματιμοί εικόνας Μάθημα: Υπολογιστική Οραση 1 Γεωμετρικοί Μετασχηματισμοί Ορισμός σημείου στονευκλείδιοχώρο: p=[x p,y p,z p ] T, όπου x p, y p, z p πραγματικοί αριθμοί. ΕστωΕ 3 τοσύνολοτωνp.
Γεωμετρικοί μετασχηματιμοί εικόνας Μάθημα: Υπολογιστική Οραση 1 Γεωμετρικοί Μετασχηματισμοί Ορισμός σημείου στονευκλείδιοχώρο: p=[x p,y p,z p ] T, όπου x p, y p, z p πραγματικοί αριθμοί. ΕστωΕ 3 τοσύνολοτωνp.
Γραφικά & Οπτικοποίηση. Κεφάλαιο 1. Εισαγωγή. Γραφικά & Οπτικοπίηση: Αρχές & Αλγόριθμοι Κεφάλαιο 1
 Γραφικά & Οπτικοποίηση Κεφάλαιο 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 2 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και GPU 3 Εφαρμογές Ειδικά εφέ για ταινίες & διαφημίσεις Επιστημονική εξερεύνηση μέσω οπτικοποίησης
Γραφικά & Οπτικοποίηση Κεφάλαιο 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 2 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και GPU 3 Εφαρμογές Ειδικά εφέ για ταινίες & διαφημίσεις Επιστημονική εξερεύνηση μέσω οπτικοποίησης
ισδιάστατοι μετασχηματισμοί ΚΕΦΑΛΑΙΟ 4: ισδιάστατοι γεωμετρικοί μετασχηματισμοί
 ΚΕΦΑΛΑΙΟ 4: ισδιάστατοι γεωμετρικοί μετασχηματισμοί Πολλά προβλήματα λύνονται μέσω δισδιάστατων απεικονίσεων ενός μοντέλου. Μεταξύ αυτών και τα προβλήματα κίνησης, όπως η κίνηση ενός συρόμενου μηχανισμού.
ΚΕΦΑΛΑΙΟ 4: ισδιάστατοι γεωμετρικοί μετασχηματισμοί Πολλά προβλήματα λύνονται μέσω δισδιάστατων απεικονίσεων ενός μοντέλου. Μεταξύ αυτών και τα προβλήματα κίνησης, όπως η κίνηση ενός συρόμενου μηχανισμού.
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
Γραφικά με υπολογιστές. Διδάσκων: Φοίβος Μυλωνάς. Διαλέξεις #11-#12
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmlonas@ionio.gr Διαλέξεις #-# Σύνθεση Δ Μετασχηματισμών Ομογενείς Συντεταγμένες Παραδείγματα Μετασχηματισμών
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmlonas@ionio.gr Διαλέξεις #-# Σύνθεση Δ Μετασχηματισμών Ομογενείς Συντεταγμένες Παραδείγματα Μετασχηματισμών
Γραφικά Υπολογιστών. Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης. Γραφικά Υπολογιστών ΣΤ Εξάμηνο. Δρ Κωνσταντίνος Δεμερτζής
 Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Παραμετρική Αναπαράσταση Γεωμετρικών Σχημάτων και Σχεδίαση ευθείας kdemertz@fmenr.duth.gr Αξιολόγηση
Τμήμα Μηχανικών Πληροφορικής ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΣΤ Εξάμηνο Δρ Κωνσταντίνος Δεμερτζής η Παραμετρική Αναπαράσταση Γεωμετρικών Σχημάτων και Σχεδίαση ευθείας kdemertz@fmenr.duth.gr Αξιολόγηση
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων
 Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pls: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pls: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Πολλαπλασιαστές Lagrange Δυνάμεις δεσμών
 ΦΥΣ - Διαλ.08 Πολλαπλασιαστές Lagrange Δυνάμεις δεσμών q q Το μεγάλο πλεονέκτημα του Lagrangian φορμαλισμού είναι ότι δεν χρειάζεται να υπολογισθούν οι δυνάμεις των δεσμών Ø Υπάρχουν περιπτώσεις που χρειαζόμαστε
ΦΥΣ - Διαλ.08 Πολλαπλασιαστές Lagrange Δυνάμεις δεσμών q q Το μεγάλο πλεονέκτημα του Lagrangian φορμαλισμού είναι ότι δεν χρειάζεται να υπολογισθούν οι δυνάμεις των δεσμών Ø Υπάρχουν περιπτώσεις που χρειαζόμαστε
ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design) Ενότητα # 2: Στερεοί Μοντελοποιητές (Solid Modelers) Δρ Κ. Στεργίου
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design) Ενότητα # 2: Στερεοί Μοντελοποιητές (Solid Modelers) Δρ Κ. Στεργίου
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων
 Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pls: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
Αλγόριθµοι Παράστασης Βασικών Σχηµάτων Προσέγγιση µαθηµατικών σχηµάτων από διακριτά pls: Ευθύγραµµο τµήµα, κύκλος, κωνικές τοµές, πολύγωνο. S/W ή H/W. Θέσεις αντικειµένων και φωτεινών πηγών Θέση παρατηρητή
ΠΡΩΤΟ ΘΕΜΑ ΕΞΕΤΑΣΕΩΝ
 ΠΡΩΤΟ ΘΕΜΑ ΕΞΕΤΑΣΕΩΝ 1. Α. Έστω x, y και x, y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. i. Να εκφράσετε (χωρίς απόδειξη) το εσωτερικό γινόμενο των διανυσμάτων και συναρτήσει των συντεταγμένων τους.
ΠΡΩΤΟ ΘΕΜΑ ΕΞΕΤΑΣΕΩΝ 1. Α. Έστω x, y και x, y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. i. Να εκφράσετε (χωρίς απόδειξη) το εσωτερικό γινόμενο των διανυσμάτων και συναρτήσει των συντεταγμένων τους.
Τάξη B. Μάθημα: Η Θεωρία σε Ερωτήσεις. Επαναληπτικά Θέματα. Επαναληπτικά Διαγωνίσματα. Επιμέλεια: Κώστας Κουτσοβασίλης. α Ε
 Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
Λύσεις στο Επαναληπτικό Διαγώνισμα 2
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο Επαναληπτικό Διαγώνισμα 2 Για τυχόν παρατηρήσεις, απορίες ή λάθη που θα βρείτε, στείλτε μου
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο Επαναληπτικό Διαγώνισμα 2 Για τυχόν παρατηρήσεις, απορίες ή λάθη που θα βρείτε, στείλτε μου
Αλγόριθμοι Σχεδίασης
 Γραφικά & Οπτικοποίηση Κεφάλαιο 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δοθόνες αποτελούνται από διακριτά πλέγματα εικονοστοιχείων (pixels) Σχεδίαση: μετατροπή 2Δ στοιχειωδών σχημάτων σε διακριτή παράσταση εικονοστοιχείων
Γραφικά & Οπτικοποίηση Κεφάλαιο 2 Αλγόριθμοι Σχεδίασης Σχεδίαση 2Δοθόνες αποτελούνται από διακριτά πλέγματα εικονοστοιχείων (pixels) Σχεδίαση: μετατροπή 2Δ στοιχειωδών σχημάτων σε διακριτή παράσταση εικονοστοιχείων
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
0 SOLID_LINE 1 DOTTED_LINE 2 CENTER_LINE 3 DASHED_LINE 4 USERBIT_LINE
 1. Η κωδικοποίηση των χρωµάτων για σύστηµα γραφικών µε 16 χρώµατα Κωδικός Χρώµα Χρώµατος 0 BLACK 1 BLUE 2 GREEN 3 CYAN 4 RED 5 MAGENTA 6 BROWN 7 LIGHTGRAY 8 DARKGRAY 9 LIGHTBLUE 10 LIGHTGREEN 11 LIGHTCYAN
1. Η κωδικοποίηση των χρωµάτων για σύστηµα γραφικών µε 16 χρώµατα Κωδικός Χρώµα Χρώµατος 0 BLACK 1 BLUE 2 GREEN 3 CYAN 4 RED 5 MAGENTA 6 BROWN 7 LIGHTGRAY 8 DARKGRAY 9 LIGHTBLUE 10 LIGHTGREEN 11 LIGHTCYAN
Απεικόνιση δεδομένων (data visualization)
 Απεικόνιση δεδομένων (data visualization) Χρήση γραφικών για την αναπαράσταση δεδομένων από διάφορες πηγές Ιατρικές εφαρμογές (π.χ. αξονική τομογραφία) Μαθηματικά μοντέλα και συναρτήσεις Προσομοίωση διεργασιών
Απεικόνιση δεδομένων (data visualization) Χρήση γραφικών για την αναπαράσταση δεδομένων από διάφορες πηγές Ιατρικές εφαρμογές (π.χ. αξονική τομογραφία) Μαθηματικά μοντέλα και συναρτήσεις Προσομοίωση διεργασιών
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 A ΦΑΣΗ ΜΑΘΗΜΑΤΙΚΑ
 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν α= ( x,y ), β= ( x,y) γ= x,y α β+ γ =
ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν α= ( x,y ), β= ( x,y) γ= x,y α β+ γ =
Γραφικά Ι. Ενότητα 1: Εισαγωγή. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 1: Εισαγωγή Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 3 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και
Γραφικά Ι Ενότητα 1: Εισαγωγή Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 3 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και
Σχεδίαση με Ηλεκτρονικούς Υπολογιστές
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 2: Μετασχηματισμοί συντεταγμένων στις 2 διαστάσεις Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 2: Μετασχηματισμοί συντεταγμένων στις 2 διαστάσεις Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα
ΛΥΣΕΙΣ 6. a2 x 2 y 2. = y
 ΛΥΣΕΙΣ 6. Οι ασκήσεις από το βιβλίο των Marsden - romba. 7.5. Θεωρούμε την παραμετρικοποίηση rx, y = x, y, a 2 x 2 y 2, όπου το x, y διατρέχει τον δίσκο στο xy-επίπεδο που ορίζεται από την x 2 +y 2 a 2.
ΛΥΣΕΙΣ 6. Οι ασκήσεις από το βιβλίο των Marsden - romba. 7.5. Θεωρούμε την παραμετρικοποίηση rx, y = x, y, a 2 x 2 y 2, όπου το x, y διατρέχει τον δίσκο στο xy-επίπεδο που ορίζεται από την x 2 +y 2 a 2.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΓΡΑΦΙΚΑ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκων: Ν. ΝΙΚΟΛΑΙΔΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΓΡΑΦΙΚΑ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκων: Ν. ΝΙΚΟΛΑΙΔΗΣ 1 η Σειρά Ασκήσεων Πλαίσια, γεωμετρικοί μετασχηματισμοί και προβολές 1. Y B (-1,2,0) A (-1,1,0) A (1,1,0)
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΓΡΑΦΙΚΑ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκων: Ν. ΝΙΚΟΛΑΙΔΗΣ 1 η Σειρά Ασκήσεων Πλαίσια, γεωμετρικοί μετασχηματισμοί και προβολές 1. Y B (-1,2,0) A (-1,1,0) A (1,1,0)
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας
 Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ. Ενότητα 5 η : Παραδείγµατα 3 µηχανισµών. χώρο (3 )
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ Ενότητα 5 η Παραδείγµατα µηχανισµών στο χώρο (3 ) Παράδειγµα 1 ο : Ροµποτικός βραχίονας RPPRR R: revolute pair P: prismatic pair Βραχίονας Τηλεσκοπικός βραχίονας
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ Ενότητα 5 η Παραδείγµατα µηχανισµών στο χώρο (3 ) Παράδειγµα 1 ο : Ροµποτικός βραχίονας RPPRR R: revolute pair P: prismatic pair Βραχίονας Τηλεσκοπικός βραχίονας
Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή
 Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή Oι οπτικές επιδράσεις, που μπορεί να προκαλέσει μια εικόνα στους χρήστες, αποτελούν ένα από τα σπουδαιότερα αποτελέσματα των λειτουργιών γραφικών με Η/Υ. Τον όρο της οπτικοποίησης
Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή Oι οπτικές επιδράσεις, που μπορεί να προκαλέσει μια εικόνα στους χρήστες, αποτελούν ένα από τα σπουδαιότερα αποτελέσματα των λειτουργιών γραφικών με Η/Υ. Τον όρο της οπτικοποίησης
Κεφάλαιο 2 - Σχεδίαση
 Κεφάλαιο 2 - Σχεδίαση Σύνοψη Στον τομέα των γραφικών, υπάρχει από τη μια μεριά η μαθηματική περιγραφή των σχημάτων που χαρακτηρίζεται από την ανάλογη αυστηρότητα και από την άλλη οι περιορισμοί της πλεγματικής
Κεφάλαιο 2 - Σχεδίαση Σύνοψη Στον τομέα των γραφικών, υπάρχει από τη μια μεριά η μαθηματική περιγραφή των σχημάτων που χαρακτηρίζεται από την ανάλογη αυστηρότητα και από την άλλη οι περιορισμοί της πλεγματικής
Έγχρωµο και Ασπρόµαυρο Φως
 Έγχρωµο και Ασπρόµαυρο Φως Χρώµα: κλάδος φυσικής, φυσιολογίας, ψυχολογίας, τέχνης. Αφορά άµεσα τον προγραµµατιστή των γραφικών. Αν αφαιρέσουµε χρωµατικά χαρακτηριστικά, λαµβάνουµε ασπρόµαυρο φως. Μόνο
Έγχρωµο και Ασπρόµαυρο Φως Χρώµα: κλάδος φυσικής, φυσιολογίας, ψυχολογίας, τέχνης. Αφορά άµεσα τον προγραµµατιστή των γραφικών. Αν αφαιρέσουµε χρωµατικά χαρακτηριστικά, λαµβάνουµε ασπρόµαυρο φως. Μόνο
Αντικείμενα και γεωμετρικοί μετασχηματισμοί
 Αντικείμενα και γεωμετρικοί μετασχηματισμοί Τα βασικά γεωμετρικά αντικείμενα και οι μεταξύ τους σχέσεις μπορούν να περιγραφούν με τρεις βασικές γεωμετρικές οντότητες: σημεία, βαθμωτά μεγέθη, διανύσματα
Αντικείμενα και γεωμετρικοί μετασχηματισμοί Τα βασικά γεωμετρικά αντικείμενα και οι μεταξύ τους σχέσεις μπορούν να περιγραφούν με τρεις βασικές γεωμετρικές οντότητες: σημεία, βαθμωτά μεγέθη, διανύσματα
Ταξινόμηση καμπυλών και επιφανειών με τη βοήθεια των τετραγωνικών μορφών.
 Ταξινόμηση καμπυλών και επιφανειών με τη βοήθεια των τετραγωνικών μορφών (βλ ενότητες 8 και 8 από το βιβλίο Εισαγωγή στη Γραμμική Άλγεβρα, Ι Χατζάρας, Θ Γραμμένος, 0) (Δείτε τα παραδείγματα 8 (, ) και
Ταξινόμηση καμπυλών και επιφανειών με τη βοήθεια των τετραγωνικών μορφών (βλ ενότητες 8 και 8 από το βιβλίο Εισαγωγή στη Γραμμική Άλγεβρα, Ι Χατζάρας, Θ Γραμμένος, 0) (Δείτε τα παραδείγματα 8 (, ) και
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2009
 ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ Μάθημα: ΜΑΘΗΜΑΤΙΚΑ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 009 Ημερομηνία και ώρα εξέτασης: ευτέρα, 1 Ιουνίου 009 7:30 10:30
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ Μάθημα: ΜΑΘΗΜΑΤΙΚΑ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 009 Ημερομηνία και ώρα εξέτασης: ευτέρα, 1 Ιουνίου 009 7:30 10:30
Αποκοπή ευθυγράμμων τμημάτων
 Αλγόριθμος των Cohen-Sutherland Αποκοπή ευθυγράμμων τμημάτων Χαρακτηριστικά (Attrbutes LEFT : αριστερά της ευθείας LEFT RIGHT: δεξιά της ευθείας RIGHT ΤΟΡ : άνω της ευθείας TO BOTTO: κάτω της ευθείας BOTTO
Αλγόριθμος των Cohen-Sutherland Αποκοπή ευθυγράμμων τμημάτων Χαρακτηριστικά (Attrbutes LEFT : αριστερά της ευθείας LEFT RIGHT: δεξιά της ευθείας RIGHT ΤΟΡ : άνω της ευθείας TO BOTTO: κάτω της ευθείας BOTTO
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 A ΦΑΣΗ ΜΑΘΗΜΑΤΙΚΑ
 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. Απόδειξη σχολικού βιβλίου σελίδα 43 Α. Ο
ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. Απόδειξη σχολικού βιβλίου σελίδα 43 Α. Ο
Διάλεξη #10. Διδάσκων: Φοίβος Μυλωνάς. Γραφικά με υπολογιστές. Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο.
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmlonas@ionio.gr Διάλεξη # Δ Μετασχηματισμοί (γενικά) Γραμμικοί Μετασχηματισμοί Απλοί Συσχετισμένοι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmlonas@ionio.gr Διάλεξη # Δ Μετασχηματισμοί (γενικά) Γραμμικοί Μετασχηματισμοί Απλοί Συσχετισμένοι
Γ5. Αν για τα α, β έχουµε α β= 0, ισχύει πάντα ότι α = 0 ή β= 0. Μονάδες 10
 7 ο Γενικό Λύκειο Περιστερίου ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ: Β ΛΥΚΕΙΟΥ ΤΜΗΜΑ: ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΗΜΕΡΟΜΗΝΙΑ:
7 ο Γενικό Λύκειο Περιστερίου ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ: Β ΛΥΚΕΙΟΥ ΤΜΗΜΑ: ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΗΜΕΡΟΜΗΝΙΑ:
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
Γραφικά Υπολογιστών: Εισαγωγή
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εισαγωγή Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή Γραφικά Υπολογιστών Τι είναι? Περιοχές εφαρμογής
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εισαγωγή Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή Γραφικά Υπολογιστών Τι είναι? Περιοχές εφαρμογής
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα. Παπαπαύλου Χρήστος ΑΜ: 6609
 Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών
 Γραφικά & Οπτικοποίηση Κεφάλαιο 5 Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών Εισαγωγή Το οπτικό μας πεδίο είναι περιορισμένο ενώ παράλληλα υπάρχει παρεμπόδιση μεταξύ αντικειμένων βλέπουμε
Γραφικά & Οπτικοποίηση Κεφάλαιο 5 Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών Εισαγωγή Το οπτικό μας πεδίο είναι περιορισμένο ενώ παράλληλα υπάρχει παρεμπόδιση μεταξύ αντικειμένων βλέπουμε
Επαναληπτικές Ασκήσεις στην Αναλυτική Γεωμετρία
 Επαναληπτικές Ασκήσεις στην Αναλυτική Γεωμετρία (Από παλαιά bac και prebac) 1) Θεωρούμε το σημείο Α(3, 2, 0) και το επίπεδο α: 3x+2y+pz=3, όπου το p είναι ένας πραγματικός αριθμός. Να βρεθεί η τιμή του
Επαναληπτικές Ασκήσεις στην Αναλυτική Γεωμετρία (Από παλαιά bac και prebac) 1) Θεωρούμε το σημείο Α(3, 2, 0) και το επίπεδο α: 3x+2y+pz=3, όπου το p είναι ένας πραγματικός αριθμός. Να βρεθεί η τιμή του
Αρχιτεκτονική Υπολογιστών
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Αρχιτεκτονική Υπολογιστών Ενότητα 11: Γραφικά VGA Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Αρχιτεκτονική Υπολογιστών Ενότητα 11: Γραφικά VGA Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
OpenGL. Μετασχηματισμοί. Μάθημα: Γραφικά Υπολογιστών και Εικονική Πραγματικότητα. Κατερίνα Παπαδοπούλου /
 OpenGL Μετασχηματισμοί Κατερίνα Παπαδοπούλου / pakate@unipi.gr Μάθημα: Γραφικά Υπολογιστών και Εικονική Πραγματικότητα Τύποι μετασχηματισμών Μετασχηματισμοί μοντέλου (modeling transformations) με glmatrixmode
OpenGL Μετασχηματισμοί Κατερίνα Παπαδοπούλου / pakate@unipi.gr Μάθημα: Γραφικά Υπολογιστών και Εικονική Πραγματικότητα Τύποι μετασχηματισμών Μετασχηματισμοί μοντέλου (modeling transformations) με glmatrixmode
Γενικό Ενιαίο Λύκειο Μαθ. Κατ. Τάξη B
 151 Θέματα εξετάσεων περιόδου Μαΐου - Ιουνίου στα Μαθηματικά Κατεύθυνσης Τάξη - B Λυκείου 15 Α. Αν α, β, γ ακέραιοι ώστε α/β και α/γ, να δείξετε ότι α/(β + γ). Μονάδες 13 Β. α. Δώστε τον ορισμό της παραβολής.
151 Θέματα εξετάσεων περιόδου Μαΐου - Ιουνίου στα Μαθηματικά Κατεύθυνσης Τάξη - B Λυκείου 15 Α. Αν α, β, γ ακέραιοι ώστε α/β και α/γ, να δείξετε ότι α/(β + γ). Μονάδες 13 Β. α. Δώστε τον ορισμό της παραβολής.
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
