θα επιβρα δύνεται. Επειδή η F! /Μ και θα ισχύει η σχέση: /t!
|
|
|
- Πλούτων Ιωάννου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ξύλινο κιβώτιο µάζας M κινείται πάνω σε λείο οριζόντιο δάπεδο µε ταχύτητα µέτρου v 0. Ένα βλήµα µάζας m, κινούµενο αντίρροπα προς το κιβώτιο προσπίπτει σ αυτό µε ταχύ τητα µέτρου v 0 και εξέρχεται από αυτό µε ταχύτητα µέτρου v 0 /5. i) Να βρείτε την συνθήκη, ώστε το κιβώτιο λόγω της κρούσεως να αλλάξει φορά κινήσεως. ii) Εάν η αναστροφή κινήσεως του κιβωτίου συµβεί ύστερα απο χρόνο t α από την έναρξη της κρούσεως, να βρέθουν οι µετατοπίσεις του κιβωτίου και του βλήµατος ως προς το ακίνητο δάπεδο, κατά τον χρόνο εισχώρησης του βλήµατος στο κιβώτιο. Nα δεχθείτε ότι η δύναµη που δέχεται το βλήµα από το ξύλο κατά την διεύθυνση της εισχώρησής του µέσα σ αυτό είναι σταθερή. ΛYΣH: i) Στην διάρκεια της εισχώρησης του βλήµατος στο ξύλινο κιβώτιο η συνισταµένη των εξωτερικών δυνάµεων επί του συστήµατος είναι µηδε νική, που σηµαίνει ότι η ορµή του διατηρείται κατά τον χρόνο αυτόν, δηλα δή ισχύει η σχέση: mv 0 - Mv 0 = MV + mv 0 /5 8mv 0-5Mv 0 = 5MV V = v 0 ( 8m - 5M) / 5M (1) όπου V η αλγεβρική τιµή της ταχύτητας V του κιβωτίου αµέσως µετα την έξοδο του βήµατος. Για να αναστραφεί η κίνηση του κιβωτίου πρέπει: Σχήµα 1 (1) V > 0 v 0 ( 8m - 5M) / 5M > 0 8m - 5M > 0 m / M > 5 / 8 ()
2 H () αποτελεί την ζητούµενη συνθήκη. ii) Eάν F είναι η δύναµη που δέχεται το κιβώτιο από το βλήµα στην διάρ κεια της εισχώρησής του µέσα σ αυτό, τότε κατά το αξίωµα της ισότητας µεταξύ δράσεως-αντιδράσεως η δύναµη που δέχεται το βλήµα από το κιβώ τιο θα είναι - F. Tο κιβώτιο υπό την επίδραση της F αρχικά θα επιβραδύ νεται µέχρις ότου µηδενιστεί η ταχύτητα του την στιγµή t α που θα αναστραφεί η κίνησή του και στην συνέχεια θα επιταχύνεται µέχρις ότου το βλήµα εξέλθει από αυτό, ενώ το βλήµα υπό την επίδραση της - F θα επιβρα δύνεται. Επειδή η F είναι σταθερή η κίνηση του κιβωτίου είναι οµαλά µεταβαλλόµενη µε επιτάχυνση F /Μ και θα ισχύει η σχέση: 0 = -v 0 + Ft / M F = Mv 0 /t () όπου F το µέτρο της F. Εφαρµόζοντας για το βλήµα το θεώρηµα κινητικής ενέργειας-έργου κατά τον χρόνο εισχώρησής του παίρνουµε: ( ) (" K ) ($ B - K ) B = W - m v / 5 0 F - m ( v 0 ) = -FS B () mv mv 0 = -FS B 48mv 0 5 = Mv 0 t S B S B = 48mv 0 t 5M (3) όπου S B η ζητούµενη µετατόπιση του βλήµατος ως προς το ακίνητο δάπεδο. Εφαρµόζοντας εξάλλου για το κιβώτιο το ίδιο θεώρηµα και για τον ίδιο χρό νο, παίρνουµε την σχέση: K K (" ) - K K ($ ) = W F MV - Mv (1) 0 = FS K Mv 0 8m - 5M$ " 5M - Mv () 0 = FS K Mv 0 8m " 5M - 1 $ ) ( ) * - 1, +, = Mv 0 S t K v 0-8m " 5M - $ 8m 5M = S K t S K = 8m 4m 5M " 5M - 1 $ v 0 t (4) όπου S K η ζητούµενη µετατόπιση του κιβωτίου ως προς το ακίνητο δάπεδο. P.M. fysikos
3 Mια σφαίρα είναι δεµένη στο άκρο αβαρούς και µη εκτατού νήµατος, του οποίου το άλλο άκρο είναι στερεωµένο σε ακλόνητο σηµείο Ο. Η σφαίρα κρατείται στην θέση Α όπου το νήµα είναι τεντωµένο και σχηµατίζει γωνία φ=π/4 µε την κατακόρυφη διεύθυνση (σχ. α). Κάποια στιγµή η σφαίρα αφήνεται ελεύθερη και όταν φθάνει στην θέση Β συµµετρική της Α ως προς την κατα κόρυφη συγκρούεται µε όµοια σφαίρα που προσπίπτει σ αυτήν κατακόρυφα µε ταχύτητα v 0, κατά δε την επαφή των σφαιρών η διάκεντρός τους είναι κάθετη στο νήµα. Εάν οι σφαίρες είναι λείες και τελείως ελαστικές να βρεθει το µέτρο της v 0, ώστε η σφαίρα που είναι δεµένη στο νήµα να φθάσει σε µια ανώτατη θέση Γ µε το νήµα τεντωµένο και µε κλiση θ=5π/1 ως προς την κατακόρυφη διεύθυνση. Δίνεται η απόσταση L του κέντρου της σφαίρας από το Ο και η επιτάχυνση g της βαρύτητας. ΛΥΣΗ: H σφαίρα που είναι δεµένη στο νήµα όταν αφεθεί ελεύθερη στην θέση Α εκτελεί κυκλική κίνηση µε κέντρο το Ο και ακτίνα L, φθάνει δε στην θέση Β µε µηδενική ταχύτητα. Σύµφωνα µε τα δεδοµένα του προβλή µατος η σφαίρα αυτή συγκρούεται ελαστικά µε όµοια σφαίρα η κρούση δε αυτή είναι πλάγια κεντρική, διότι η ταχύτητα προσκρουσης σχηµατίζει γωνία φ=π/4 µε την διάκεντρο των δύο σφαιρών η οποία αποτελεί και την ευθεία κρουσης (n) αυτών (σχ. β). Επειδή οι σφαίρες έχουν την ίδια µάζα συµβαίνει αµέσως µετά την ελαστική κρούση τους ανταλλαγή ταχυτήτων, κατά την διεύθυνση (n). Έτσι η ταχύτητα της σφαίρας που είναι δεµένη στο Σχήµα α Σχήµα β νήµα αµέσως µετά την κρούση είναι ίση µε την συνιστώσα v n της ταχύτη τας v 0 κατά την διεύθυνση (n), η δε αντίστοιχη ταχύτητα της άλλης σφαίρας είναι µηδενική. Είναι προφανές ότι η ταχύτητα v n ως κάθετη στο νήµα είναι συµβατή µε τον δεσµό που επιβάλλει το νήµα στην σφαίρα. Η σφαίρα έχοντας αρχική ταχύτητα v n στην θέση Β κινείται υπό την επίδραση του βάρους της και της τάσεως του νήµατος επί κυκλικής τροχιάς κέντρου Ο και ακτίνας L (σχ. 3) και φθάνει στην θέση Γ µε µηδενική ταχύτητα, όπου το νήµα σχηµατίζει µε την κατακόρυφη διεύθυνση γωνία θ=5π/1. Εφαρµόζοντας για την σφαίρα το θεώρηµα διατήρησης της µηχανικής ενέργειας µεταξύ των θέσεων Β και Γ παίρνουµε την σχέση:
4 K B + U B = K + U mv n / + 0 = 0 + mgh ( ) ( v 0 "$ ) = g( L"$ - L" ) v n = g O B - O " v 0 " ($ / 4) = gl ["($ / 4) - "(5$ /1)] (1) Όµως έχουµε: Σχήµα 3 " 5$ ( 1) * = " $ 4 + $ ( 6 ) * = " $ ( 4 ) * " $ ( 6 ) * - +µ $ ( 4 ) * +µ $ ( 6 * ) " 5$ ( * = 1) 3-1 = 4 ( 3-1) οπότε η σχέση (1) γράφεται: $ v 0 " ( ) = gl 3-1 * ) -, ) 4, () +, v 0 = ( 3-3)gL v 0 = ( 3-3)gL P.M. fysikos Σφαιρίδιο µάζας m, προσκρούει πλάγια µε ταχύτητα v πάνω σε σφαίρα µάζας M (M>m) και ακτίνας r, που είναι δεµένη στο ένα άκρο αβαρούς και µη εκτατού νήµατος µή κους L, του οποίου το άλλο άκρο έχει στερεωθεί σε ακλόνητο σηµείο Ο (σχ. 4α). i) Eάν οι δύο σφαίρες είναι λείες, η κρούση τους ελαστική και µετωπική διαρκεί δε πολύ µικρό χρόνο Δt, να βρεθεί η µέση τάση του νήµατος για τον χρόνο αυτό. ii) Nα βρεθεί η τάση του νήµατος αµέσως µετά την κρούση.
5 Δίνεται η γωνία φ που σχηµατίζει ο φορέας της ταχύτητας v µε την οριζόντια διεύθυνση, η επιτάχυνση g της βαρύτητας και ότι η µετα τόπιση των δύο σφαιρών στον χρόνο Δt είναι αµελητέα. ΛYΣH: i) Επειδή οι δύο σφαίρες είναι λείες η ωστική δύναµη κρούσεως f 1 που δέχεται το σφαιρίδιο µάζας m είναι αντίρροπη της ταχύτητας πρόσκρου σής του v, που σηµαίνει ότι η ταχύτητα ανάκλασής του v θα είναι συνευ θειακή της v και έστω ότι η φορά της είναι αυτή του σχήµατος (4γ). Εξάλλου αµέσως µετά την κρούση η ταχύτητα V της σφαίρας µάζας Μ θα είναι αναγκαστικά οριζόντια, λόγω του δεσµού που επιβάλλει στην σφαίρα αυτή το κατακόρυφο νήµα (σχ. 4γ). Πρέπει να παρατηρήσουµε ότι στην διάρ Σχήµα 4α Σχήµα 4β Σχήµα 4γ κεια της κρούσεως το σύστηµα των δύο σφαιρών είναι µηχανικά µονωµένο κατά τον οριζόντιο άξονα x, διότι δεν δέχεται οριζόντιες εξωτερικές δυνά µεις. Έτσι η ορµή του συστήµατος στον οριζόντιο άξονα δεν µεταβάλλεται στη διάρκεια του χρόνου Δt της κρούσεως, δηλαδή ισχύει: mv x + 0 = -m v x + MV mv"$ = -m v "$ + MV m( v + v )"$ = MV v + v = MV/m"$ (1) όπου v x, v x οι οριζόντιες συνιστώσες των ταχυτήτων v και v αντιστοίχως. Επειδή η κρούση των δύο σφαιρών είναι ελαστική η κινητική ενέργεια του συστήµατος λίγο πριν την κρούση είναι ίση µε την κινητική του ενέργεια αµέσως µετά την κρούση, δηλαδή έχουµε την σχέση: mv v + 0 = m + MV m ( v - v ) = MV ( )( v - v ) = MV () m v + v Διαιρώντας κατά µέλη τις (1) και () παίρνουµε: v - v = V"$ (3)
6 Προσθέτοντας κατά µέλη τις (1) και (3) παίρνουµε: v = MV/m"$ + V"$ v = V"$ ( 1 + M/m) V = v ( 1 + M/m)"$ = mv ( m + M)"$ (4) Συνδυάζοντας τις (3) και (4) τελικώς θα έχουµε: ( ) v = v M - m m + M > 0 (5) δηλαδή η φορά του διανύσµατος v σχεδιάστηκε σωστά. Λόγω της πολύ µικρής διάρκειας της κρούσεως η µετατόπιση των σφαιρών στον χρόνο Δt είναι ασήµαντη, οπότε µπορούµε να ισχυριστούµε ότι κατά την κρούση το νήµα παραµένει περίπου κατακόρυφο, δηλαδή η κατεύθυνση της τάσεως T του νήµατος δεν µεταβάλλεται, όµως µεταβάλλεται το µέτρο της µε αποτέλεσµα να συµβάλλει µε ουσιαστικό τρόπο στην µεταβολή της ορµής του συστήµατος κατά την κρούση. Στο σηµείο αυτό είναι απαραίτητο να διευκρινήσουµε την έννοια της µέσης τιµής του µέτρου της τάσεως T για τον χρόνο Δt. Ας φανταστούµε ότι το µέτρο της T µένει σταθερό κατά τον χρόνο Δt µε τιµή T µ τέτοια, ώστε η σταθερή πλέον τάση του νήµατος να συµβάλλει στην διαµόρφωση της µεταβολής της ορµής του συστήµατος όσο και η πραγµατική µεταβλητή τάση. Η σταθερή αυτή τιµή T µ εξ ορισµού αποτελεί το µέτρο της µέσης τάσεως του νήµατος για τον χρόνο Δt. Mε βάση τον ορισµό αυτό µπορούµε να δεχτούµε ότι η µεταβολή της ορµής του συστήµατος κατά την κατακόρυφη διεύθυνση y στον χρόνο Δt οφείλεται στα σταθερά βάρη m g, M g των δύο σφαιρών και στην σταθερή µέση τάση T µ του νήµατος. Εφαρµόζοντας κατά την κατακόρυφη διεύθυνση y για κάθε σφαίρα τον ο νόµο του Νεύτωνα υπό την γενικευµένη µορφή του παίρνου µε: P 1,y /t = -mg + f 1,y " [ m v - ( -mv )] /"t = -mg + f y y 1,y $ P,y /t = -Mg - f,y + T µ $ 0 = -Mg - f,y + T µ m ( v + v)"µ /$t = -mg + f 1,y 0 = -Mg - f,y + T µ ( (+ ) m ( v + v)"µ $t = -( m + M)g + f 1,y - f,y + T µ (6) όπου f 1,y f,y οι µέσες τιµές των µέτρων των κατακόρυφων συνιστώσων των δυνάµεων κρούσεως f 1 και f αντιστοίχως. Όµως κάθε στιγµή οι δυνάµεις κρούσεως είναι αντίθετες, οπότε θα ισχύει f 1,y =f,y και η (6) γράφεται:
7 m ( v + v)"µ $t T µ = m ( v + v )"µ $t = -( m + M)g + T µ (5) + ( m + M)g T µ = mv M - m " m + M + 1 $ µ( )t + ( m + M )g T µ = mmvµ" ( m + M)t + ( m + M )g (7) Παρατήρηση: Λόγω της εµφάνισης του χρόνου Δt στον παρονοµαστή του κλάσµατος στον πρώτο όρο του δεύτερου µέλους της (7) ο όρος αυτός είναι πολύ µεγαλύτερος του όρου (M+m)g και η σχέση (7) µε καλή προσέγγιση παίρνει την µορφή: F µ mmv"µ ( m + M)$t ii) Eάν T είναι η τάση του νήµατος αµέσως µετά την κρούση, τότε η συνι σταµένη αυτής και του βάρους M g της δεµένης στο νήµα σφαίρας αποτελεί κεντροµόλο δύναµη για την σφαίρα την στιγµή αυτή, δηλαδή ισχύει: (8) T - Mg = MV L + r (4) M $ T = Mg + " L + r 4m v ( m + M) () * 4Mm v T = Mg + ( L + r) m + M ( ) " $ (9) P.M. fysikos Το σώµα A του σχήµατος (5α) έχει µάζα M και ηρεµεί πάνω σε λείο οριζόντιο δάπεδο. Κάποια στιγµή προσπίπτει στην λεία κεκλιµένη επιφάνεια του σώµατος ελαστική σφαίρα µάζας m<m µε ταχύτητα v, της οποίας ο φορέας είναι κάθετος στην κεκλιµένη επιφάνεια του σώµατος και ανακλάται. i) Να βρεθεί ποιο κλάσµα της κινητικής ενέργειας της σφαίρας µεταφέρεται µέσω της κρούσεως στο σώµα. ii) Eάν o χρόνος επαφής της σφαιρας µε την κεκλιµένη επιφάνεια είναι Δt µε Δt 0, να βρεθεί η µέση δύναµη κρούσεως που δέχεται η σφαίρα κατά τον χρόνο Δt.
8 Δίνεται η γωνία κλίσεως φ της κεκλιµένης επιφάνειας του σώµατος ως προς την οριζόντια διεύθυνση. ΛΥΣΗ: i) Επειδή η κεκλιµένη επιφάνεια επί της οποίας προσπίπτει η σφαίρα είναι λεία η ωστική δύναµη κρούσεως f 1 που δέχεται η σφαίρα είναι αντίρροπη της ταχύτητας πρόσκρουσής της v, που σηµαίνει ότι η ταχύτητα ανάκλασής της v θα είναι συνευθειακή της v (σχ. 5γ). Εξάλλου αµέσως µετά την κρούση η ταχύτητα V του σώµατος A θα είναι αναγκαστικά οριζόντια, λόγω του δεσµού που επιβάλλει η επαφή του µε το λείο οριζόντιο δάπεδο. Παρατηρούµε ακόµη ότι κατά τον χρόνο Δt της κρούσεως το σύστη µα σφαίρα-σώµα A είναι µηχανικά µονωµένο κατά τον οριζόντιο άξονα x, διότι δεν δέχεται οριζόντιες εξωτερικές δυνάµεις. Έτσι η ορµή του συστή µατος κατά τον άξονα αυτόν δεν µεταβάλλεται στην διάρκεια του χρόνου Δt, δηλαδή ισχύει: -mv x + 0 = -MV + m v x -mvµ" = -MV + m v µ" m( v + v )"µ = MV (1) Σχήµα 5α Σχήµα 5β Σχήµα 5γ όπου v x, v x οι οριζόντιες συνιστώσες των ταχυτήτων v και v αντιστοίχως. Επειδή η κρούση είναι ελαστική η κινητική ενέργεια του συστήµατος λίγο πριν την κρούση είναι ίση µε την κινητική του ενέργεια αµέσως µετά την κρούση, δηλαδή έχουµε την σχέση: mv v + 0 = m + MV m ( v - v ) = MV ( )( v - v ) = MV () m v + v Διαιρώντας κατά µέλη τις (1) και () παίρνουµε: ( v - v ) / "µ = V v - v = V"µ (3) Προσθέτοντας κατά µέλη τις (1) και (3) παίρνουµε: v = MV/mµ" + Vµ" v = Vµ" ( 1 + M/m)
9 v V = ( 1 + M/m)µ" = mv ( m + M)µ" (4) Συνδυάζοντας τις (3) και (4) τελικώς θα έχουµε: ( ) v = v M - m m + M > 0 (5) δηλαδή η φορά του διανύσµατος v είναι αυτή που εξ αρχής σχεδιάστηκε. H κινητική ενέργεια Κ Α που αποκτά το σώµα Α µέσω της κρούσεως, δίνεται από την σχέση: K A = MV (4) K A = 4Mm v ( ) µ " m + M K A = mv 4Mm ( m + M) µ " K 4Mm A = K m + M ( ) "µ K A K = 4Mm ( m + M) "µ (6) όπου Κ Σ η κινητική ενέργεια της σφαίρας λίγο πριν την κρούση. Η σχέση (6) παρέχει το ζητούµενο κλάσµα. ii) Λόγω της πολύ µικρής διάρκειας της κρούσεως η µετατόπιση της σφαιρας και του σώµατος Α είναι ασήµαντη, οπότε µπορούµε να ισχυριστού µε ότι κατά τον χρόνο Δt η δύναµη κρούσεως f 1 που δέχεται η σφαίρα διατη ρεί σχεδόν σταθερή κατεύθυνση, ενώ το µέτρο της µεταβάλλεται. Η µέση τιµή της f 1 για τον χρόνο Δt είναι εξ ορισµού η σταθερή εκείνη δύναµη f 1(µ ) η οποία συµβάλλει στην διαµόρφωση της µεταβολής της ορµής της σφαίρας στον χρόνο Δt όσο και η πραγµατική δύναµη κρούσεως f 1. Εφαρµόζοντας κατά την κατακόρυφη διεύθυνση y για την σφαίρα τον ο νόµο του Νεύτω να υπό την γενικευµένη µορφή του παίρνουµε: y P 1,y /t = -mg + f 1(µ ) y [ ( )] /"t = -mg + f 1(µ ) m v y - -mv y m ( v + v)"$ /t = -mg + f 1(µ ) "$ (7) y όπου f 1(µ ) η µέση τιµή του µέτρου της κατακόρυφης συνιστώσας της δύνα µης κρούσεως f 1 και m g το βάρος της σφαίρας. Συνδυάζοντας την σχέση (7) µε την (5) παίρνουµε: mv M - m " m + M + 1 $ ()* +t = -mg + f 1(µ ) ()*
10 f 1(µ ) "$ = mmv"$ m + M ( )t + mg (8) Όµως η παρουσία του χρόνου Δt στον παρονοµαστή του κλάσµατος στον πρώτο όρο του δεύτερου µέλους της (8) καθιστά τον όρο αυτόν πολύ µεγα λύτερο του όρου mg ο οποίος µπορεί να παραληφθεί και η σχέση (8) µε καλή προσέγγιση γράφεται: f 1(µ ) "$ mmv"$ m + M ( )t f 1(µ ) mmv m + M ( )"t P.M. fysikos Στην διάταξη του σχήµατος (6) οι τροχαλίες τ 1, τ έχουν αντίστοιχες µάζες Μ 1, Μ και ακτίνες R, R/, µπορούν δε να στρέφονται περί σταθερούς οριζόντιους άξονες που διέρχονται από τα κέντρα τους. Από τα αυλάκια των τροχαλίών διέρχεται αβαρές και µη εκτατό νήµα στις ελεύθερες άκρες του οποίου είναι στερεωµένα τα σώµατα Σ 1, Σ µε αντίστοιχες µάζες m 1, m (m 1 >m ). Κάποια στιγµή τα σώµατα αφήνονται ελεύθερα να κινηθούν. Nα βρεθούν: i) οι επιταχύνσεις των δύο σωµάτων και ii) η τάση του οριζόντιου τµήµατος ΜΝ του νήµατος. Δίνoνται οι ροπές αδράνειας I 1 =Μ 1 R / και Ι =(Μ /)(R/) των τρο χαλιών τ 1 τ αντιστοίχως ως προς τους άξονες περιστροφής τους, η επιτάχυνση g της βαρύτητας και ότι το νήµα δεν ολισθαίνει στα αυλάκια τους. ΛYΣH: i) Εάν το σώµα Σ 1 ανέρχεται µε επιτάχυνση a τότε το σώµα Σ θα κατέρχεται µε επιτάχυνση - a, διότι το νήµα που διέρχεται από τα αυλάκια των δύο τροχαλιών είναι µη εκτατό. Τα σώµατα Σ 1 και Σ δέχονται τα βάρη τους m 1 g, m g αντιστοίχως και τις αντίστοιχες τάσεις T 1, T των νηµάτων που τα συγκρατούν (σχ. 6) σύµφωνα δε µε τον δεύτερο νόµο κίνησης του Νεύτωνα θα έχουµε τις σχέσεις: T 1 - m 1 g = m 1 a " m g - T = m a (1) Eξάλλου oι τροχαλίες τ 1 και τ στρέφονται περί τους σταθερούς άξονές τους δεξιόστροφα, η µεν τ 1 υπό την επίδραση των ροπών περί το κέντρο της των τάσεων T 1 και F του νήµατος που περιβάλλει το αυλάκι της, η δε τ υπό την επίδραση των αντίστοιχων ροπών των τάσεων T και - F του αντίστοι χου νήµατος. Εφαρµόζοντας για τις τροχαλίες τον θεµελιώδη νόµο της στροφικής κίνησης παίρνουµε τις σχέσεις:
11 FR - T 1 R = I 1 " 1 $ T R/ - FR/ = I " FR - T 1 R = M 1 R " 1 / T R/ - FR/ = M R " /8 $ F - T 1 = M 1 R " 1 / T - F = M R " /4 $ () Σχήµα 6 όπου " 1, " οι γωνιακές επιταχύνσεις των τροχαλιών τ 1 και τ αντιστοίχως. Όµως το νήµα είναι αβαρές, οπότε θα ισχύει T 1 =- T 1 και T =- T και επειδή κάθε στιγµή τα σηµεία M και Ν των τροχαλιών έχουν την ίδια ταχύτητα θα ισχύει ακόµη η σχέση: 1 R = R/ 1 = / " 1 = " / (3) όπου 1, οι γωνιακές ταχύτητες των τροχαλιών τ 1 και τ αντιστοίχως. Έτσι οι σχέσεις () σε συνδυασµό και µε την ω 1 R=a παίρνουν την µορφή: F - T 1 = M 1 R " 1 / T - F = M R " 1 / $ F - T = M a/ 1 1 " T - F = M a/ (4) Προσθέτοντας κατά µέλη τις (4) έχουµε: (1) T - T 1 = ( M 1 + M )a/ m g - m a - ( m 1 g + m 1 a) = ( M 1 + M )a/ ( m - m 1 )g = ( M 1 / + M / + m 1 + m )a
12 ( m - m 1 )g = ( M 1 + M + m 1 + m )a a = ( m - m 1 )g ( ) M 1 + M + m 1 + m (5) ii) Συνδυάζοντας µεταξύ τους τις πρώτες σχέσεις των (4) και (1), παίρνουµε: (5) F - ( m 1 g + m 1 a) = M 1 a/ F = m 1 g + ( M 1 / + m 1 )a F = m 1 g + ( m - m 1 )( M 1 / + m 1 )g M 1 + M + m 1 + m ( ) ( F = m 1 g + m - m 1 )( M 1 + m 1 )g M 1 + M + m 1 + m ( ) ( )( M 1 + m 1 ) ( ) F = m 1 + m - m 1 " M 1 + M + m 1 + m $ g P.M. fysikos Μια τροχαλία µάζας m και ακτίνας R εδράζεται πάνω σε δύο λεία ακλόνητα σφαιρίδια Α και Β, που οι επιβατικές τους ακτίνες ως προς το κέντρο Κ της τροχαλίας σχηµατίζουν µε την κατακόρυφη διεύθυνση Κx γωνία φ=π/1 (σχ. 7). Στο αυλάκι της τροχαλίας έχει περιτυλιχθεί αβαρές και µη εκτατό νήµα του οποίου το ελεύθερο άκρο έλκεται κατακόρυφα µε σταθερή δύναµη F, η οποία θέτει την τροχαλία σε περιστροφική κίνηση. i) Εάν σε χρόνο Τ ξετυλίγεται νήµα µήκους L, να βρεθεί η δύναµη έλξεως F. ii) Να υπολογιστούν οι δυνάµεις επαφής των σφαιριδίων επί της τροχαλίας. Δίνεται η ροπή αδράνειας I Κ =mr / της τροχαλίας ως προς άξονα που διέρχεται από το κέντρο της Κ και είναι κάθετος στο επίπεδό της, η επιτάχυνση g της βαρύτητας και ότι το νήµα δεν ολισθαίνει στο αυλάκι της τροχαλίας. ΛYΣH: i) H τροχαλία δέχεται το βάρος της w, την δύναµη έλξεως F η οποία είναι εφαπτοµενική του αυλακιού της και τις δυνάµεις επαφής F A, F B από τα σφαιρίδια A και Β αντιστοίχως, των οποίων οι φορείς διέρχονται από το κέντρο της K. H κίνηση της τροχαλίας είναι γνήσια περιστροφή περί τον γεωµετρικό της άξονα και σύµφωνα µε τον θεµελιώδη νόµο της στροφικής κίνησης ισχύει η σχέση:
13 " (K) = I K $ FR = mr " / F = mr " / " = F / mr (1) Από την (1) παρατηρούµε ότι η γωνιακή επιτάχυνση " της τροχαλίας είναι σταθερή, δηλαδή η περιστροφή της είναι οµαλά επιταχυνόµενη, οπότε η γωνία στροφής θ Τ αυτής σε χρόνο Τ θα υπολογίζεται από την σχέση: () T = " T / T = FT / mr () To µήκος L του νήµατος που θα ξετυλιχθεί σε χρόνο Τ είναι: () L = T R L = FT / m F = ml/t (3) Σχήµα 7 ii) Εξάλλου η συνισταµένη δύναµη που δέχεται η τροχαλία κατά την οριζόν τια και κατακόρυφη διεύθυνση είναι µηδενική, δηλαδή ισχύουν οι σχέσεις: F (x) = 0" F (y) = 0$ F Ax - F Bx = 0 " -F Ay - F By + F + mg = 0 F A µ" = F B µ" F A $" + F B $" = F + mg ( F = F A B ( F A + F B )"$ = F + mg (3) F A "$ = F + mg F A = F B = m ( L + ) gt T "$ F A "$ = ml/ T + mg (4) Παρατήρηση: Για τον υπολογισµό του συνφ θα χρησιµοποιήσουµε την τρι γωνοµετρική ταυτότητα "$ = " $ - µ $ = " $ - 1
14 η οπoία για φ=π/1 δίνει: " $ ( $ ( * = " * - 1 6) 1) 3 = $ ( " * - 1 1) $ ( 3 + = 4" 1) * "$ = " ) ( 1 + = * 3 + P.M. fysikos Στο καρούλι του σχήµατος (8) ενεργεί η δύναµη F, η οποία εφαρµόζεται στο άκρο A του νήµατος που περιβάλλει την κεντρική περιοχή του τυµπάνου του καρουλιού. To νήµα παρουσιάζει κλίση φ (0<φ<π/) ως προς την οριζόντια διεύθυνση είναι αβαρές και µη εκτατό και δεν ολισθαίνει πάνω στο καρούλι, ενώ οι κυκλικές βάσεις του καρουλιού εφάπτονται οριζόντιου δαπέ δου. i) Nα βρείτε τις αναγκαίες συνθήκες, ώστε το καρούλι να κυλίεται χωρίς ολίσθηση πάνω στο οριζόντιο δάπεδο, στην περίπτωση που αυτό είναι λείο. ii) Εάν αλλάξουµε την διεύθυνση του νήµατος όπως δείχνεται στο σχήµα 9α, να βρείτε τις αναγκαίες συνθήκες, ώστε το καρούλι να κυλίεται χωρίς ολίσθηση µε µετατόπιση του άξονά του προς τα δεξιά, στην περίπτωση που το οριζόντιο δάπεδο δεν είναι λείο. iii) Tι συµβαίνει µε την κίνηση του καρουλιού, όταν ο φορέας της δύναµης F προεκτεινόµενος τέµνει την ευθεία επαφής του καρου λιού µε το οριζόντιο έδαφος; Δίνονται οι ακτίνες r, R του τυµπάνου και των κυκλικών βάσεων αντιστοίχως του καρουλιού (R>r), η ακτίνα αδράνειας Κ αυτού ως προς τον γεωµετρικό του άξονα και η µάζα του m. ΛΥΣΗ i) Έστω ότι το καρούλι κυλίεται στην περίπτωση που το οριζόντιο δάπεδο είναι λείο. Στο καρούλι ενεργεί το βάρος του w, η τάση του νήµατος που περιβάλει το αυλάκι του, ίση µε την δύναµη F που εφαρµόζεται στο άκρο του Α, η οποία αναλύεται στην οριζόντια συνιστώσα F x και στην κατα κόρυφη συνιστώσα F y και τέλος η κατακόρυφη δύναµη επαφής N απο το δάπεδο (σχ. 8). Η κύλιση του καρουλιού µπορεί να θεωρηθεί ως επαλληλία µιας οριζόντιας µεταφορικής κίνησης µε επιτάχυνση a C και µιας περιστρο φικής κίνησης περί τον οριζόντιο άξονά του µε γωνιακή επιτάχυνση. Εφαρµόζοντας για την µεταφορική κίνηση τον δεύτερο νόµο του Νεύτωνα έχουµε την σχέση: F x = ma C F"$ = ma C (1)
15 Εφαρµόζοντας εξάλλου για την περιστροφική κίνηση του καρουλιού τον θεµελιώδη νόµο της στροφικής κίνησης παίρνουµε την σχέση: Fr = I C " Fr = mk " Fr = mk a C / R () όπου τέθηκε " =a C /R λόγω της κυλίσεως του καρουλιού. Διαιρώντας κατά µέλη τις (1) και () παίρνουµε: "$ r = R Rr "$ = K K (3) Σχήµα 8 Επειδή κατά την κατακόρυφη διεύθυνση το καρούλι ισορροπεί ισχύει η σχέ ση: N + F y - mg = 0 N = mg - Fµ" (4) Όµως για να διατηρεί συνεχώς το καρούλι επαφή µε το δάπεδο πρέπει Ν 0, οπότε από την (4) προκύπτει: (3) mg F"µ mg > F 1 - " $ mg F 1 - R r K 4 F mgk K 4 - R r (5) µε K >Rr. Η (5) αποτελει την αναγκαία συνθήκη ώστε το καρούλι να κυλί εται πάνω στο λείο οριζόντιο δάπεδο. Παρατηρούµε ότι η κύλιση δεσµέυεται µόνο από το µέτρο της δύναµης F και όχι από την διεύθυνσή της, αφού η (5) είναι ανεξάρτητη της γωνίας φ. ii) Ας δεχθούµε ότι το µέτρο της δύναµης F και η τιµή της γωνίας φ προ καλούν έναρξη κύλισης χωρίς ολίσθηση του καρουλιού, µε µετατόπιση του γεωµετρικού του άξονα προς τα δεξιά. Τότε θα πρέπει το καρούλι να αρχίσει περιστρεφόµενο περί τον άξονά του δεξιόστροφα, ώστε να είναι δυνατός ο
16 µηδενισµός της εφαπτοµενικής επιτάχυνσης των σηµείων επαφής του E µε το οριζόντιο έδαφος. Στο καρούλι ενεργεί το βάρος του w, η δύναµη F που αναλύεται στην οριζόντια συνιστώσα F x και στην κατακόρυφη συνιστώσα F y και η δύναµη επαφής από το έδαφος που αναλύεται στην κάθετη αντίδραση N και στην στατική τριβή T (σχ. 9α). Εάν a C είναι η επιτάχυνση του κέντρου µάζας του καρουλιού, σύµφωνα µε τον δεύτερο νόµο κίνησης του Νεύτωνα θα έχουµε: F x - T = ma C F"$ - T = ma C (6) Εφαρµόζοντας εξάλλου για την περιστροφική κίνηση του καρουλιού τον θεµελιώδη νόµο της στροφικής κίνησης παίρνουµε την σχέση: TR - Fr = I C TR - Fr = mk TR - Fr = mk a C /R T - Fr / R = mk a C /R (7) όπου η αντίστοιχη γωνιακή του επιτάχυνση, της οποίας το µέτρο λόγω της κύλισης είναι ίσο µα a C /R. Συνδυάζοντας τις σχέσεις (6) και (7) παίρνου µε: F"$ - ma C = Fr / R + mk a C /R ( ) ( ) F "$ - r ( * = m 1 + K ( R ) R * ) a a = F "$ - r / R C C m 1 + K / R (8) Σχήµα 9α Σχήµα 9β Όµως για να εξασφαλίζεται η κύλιση προς τα δεξιά πρέπει: (8) a C >0 "$ - r / R > 0 "$ > r / R Ακόµη πρέπει να συµβαίνουν τα εξής: α) Το καρούλι να µη χάνει την επαφή του µε το έδαφος, δηλαδή πρέπει:
17 N 0 mg-fηµφ 0 F mg/ηµφ (9) β) Το καρούλι να µη ολισθαίνει, δηλαδή πρέπει: T nn T n(mg - F"µ) (10) όπου n o συντελεστής οριακής τριβής καρουλιού-δαπέδου. Εξάλλου διαιρών τας κατά µέλη τις (6) και (7) παίρνουµε: T - Fr / R F"$ - T = K R TR - FrR = FK "$ - TK T( R + K ) = F( rr + K "$ ) T = F rr + K "$ Συνδυάζοντας την (10) µε την (11) έχουµε: F rr + K "$( R + K * + n(mg - F,µ$) ) R + K ( * (11) ) F( rr + K "$ + nr µ$ + nk µ$ ) nmg( R + K ) F nmg( R + K ) ( ) + K ( $ + n"µ ) R r + R"µ (1) H σχέση συνφ>r/r σε συνδυασµό µε τις (9) και (1) εξασφαλίζουν την κύλι ση χωρίς ολίσθηση του καρουλιού, µε µετατόπιση του άξονά του προς τα δεξιά. iii) Eάν ο φορέας της δύναµης F προεκτεινόµενος συναντά την ευθεία επαφής του καρουλιού µε το έδαφος (σχ. 9β), τότε θα ισχύει συνφ=r/r και η σχέση (8) δίνει a C =0, µε αποτέλεσµα να είναι και ω =0. Τότε η (7) επιβάλλει την σχέση: T - Fr / R = 0 T = Fr/ R (13) η οποία είναι συµβιβαστή µε την (6). Αν ακόµη απαιτήσουµε η τριβή να είναι στατική πρέπει: (13) T nn Fr / R n(mg - F"µ) F(r / R + nµ") nmg F(r + nrµ") nmrg F nmrg r + nr"µ F nmrg r + nr 1 - "$
18 F nmrg r + nr 1 - r /R F nmrg r + n R - r (14) Τέλος για να µη χάνει το καρούλι την επαφή του µε το έδαφος πρέπει: N 0 w - Fµ" 0 mg F 1 - "$ F mg 1 - r / R F mgr R - r (15) Άρα, όταν ο φορέας της δύναµης F προεκτεινόµενος διέρχεται από την ευθεία επαφής του καρουλιού µε το έδαφος και το µέτρο της ικανοποιεί τις σχέσεις (14) και (15) το καρούλι θα ισορροπεί. P.M. fysikos Στο καρούλι του σχήµατος (10) ενεργεί η δύνα µη F, η οποία εφαρµόζεται στο άκρο A του νήµατος που περιβάλ λει την κεντρική περιοχή του κυλινδρικου κορµού του καρουλιού. To νήµα παρουσιάζει κλίση φ ως προς την οριζόντια διεύθυνση (0<φ<π/), είναι αβαρές και µη εκτατό και δεν ολισθαίνει πάνω στο καρούλι, ενώ οι κυκλικές βάσεις του καρουλιού εφάπτονται µη λείου οριζόντιου δαπέδου. i) Nα βρείτε τις αναγκαίες συνθήκες, ώστε το καρούλι να εκτελεί γνήσια περιστροφική κίνηση περί τον γεωµετρικό του άξονα. ii) Υπό ποία συνθηκη η γνήσια περιστροφή του καρουλιού επιτυγ χά νεται µε την ελάχιστη τιµή του µέτρου της F και ποια είναι η ελάχιστη αυτή τιµή;. Δίνονται η µάζα m του καρουλιού, οι ακτίνες r, R του κυλινδρι κού κορµου και των κυκλικών του βάσεων αντιστοίχως (R>r) και o συντελεστής n τριβής ολισθήσεως καρουλιού-δαπέδου. ΛΥΣΗ i) Στο καρούλι ενεργεί το βάρος του w, η τάση του νήµατος ίση µε την δύναµη F που ασκείται στο άκρο του A και αναλύεται στην οριζόντια συνιστώ σα F x και στην κατακόρυφη συνιστώσα F y τέλος δε η δύναµη επα φής από το δάπεδο που αναλύεται στην κάθετη αντίδραση N και στην τριβή T η οποία είναι τριβή ολισθήσεως (σχ. 10). Επειδη απαιτησή µας είναι το καρούλι να εκτελεί γνήσια περιστροφική κίνηση περί τον γεωµετρικό του άξονα, πρέπει η συνισταµένη δύναµη που δέχεται κατά την οριζόντια και κατακόρυφη διεύυνση να είναι µηδενική, δηλαδή πρέπει να ισχύουν οι σχέσεις: F (x) = 0" F (y) = 0$ F - T= 0 x " F y + N - mg = 0 F"$ = T N = mg - Fµ$ (
19 F"$ = nn N = mg - Fµ$ ( F"$ = n( mg - Fµ$ ) F ("$ + nµ$ ) = nmg F = nmg "$ + nµ$ (1) Εξάλλου σύµφωνα µε τον θεµελιώδη νόµο της στροφικής κίνησης θα έχουµε για το καρούλι την σχέση: " (C) = I C $ Fr - TR = I C " () Σχήµα 10 όπου " η γωνιακή του επιτάχυνση του καρουλιού και Ι C η ροπή αδράνειάς του ως προς τον άξονά του. Όµως πρέπει να ισχύει > 0, οπότε η () δίνει: Fr - TR > 0 F > nnr/r F > nr r ( mg - Fµ" ) F 1 + nrµ" ( > nrmg $ r r (1) nmg ) ( nrµ$ ) ( + > nrmg "$ + nµ$ * r * r 1 + nrµ" r > R ($" + nµ" ) r r + nrµ" > R$" + nrµ" "$ < r / R (3) Τέλος πρέπει να εξετάσουµε αν η τιµή που προκύπτει για το µέτρο της δύνα µης F από την σχέση (1) εξασφαλίζει ότι το καρούλι δεν χάνει την επαφή του µε το έδαφος. Αν δεχθούµε ότι αυτό συµβαίνει, τότε το µέτρο της κάθε της αντίδρασης N θα είναι: (1) N = mg - Fµ" N = mg - nmgµ" $" + nµ"
20 N = mg"$ + nmgµ$ - nmgµ$ "$ + nµ$ = mg"$ "$ + nµ$ > 0 δηλαδή το καρούλι δεν χάνει την επαφή του µε το έδαφος. Η παραπάνω ανά λυση µας επιτρέπει να συµπεράνουµε ότι, αν ισχύει: "$ < r / R και F = nmg "$ + nµ$ τότε το καρούλι θα έχει γνήσια περιστροφική κίνηση µε γωνιακή επιτάχυν ση που καθορίζεται από τον θεµελιώδη νόµο της στροφικής κίνησης, σε συνδυασµό βέβαια µε τις δύο προηγούµενες δεσµεύσεις. ii) Θέτοντας στην σχέση (1) όπου n=εφθ, αυτή µετασχηµατίζεται ως εξής: F = nmg "$ + $µ$ = nmg "$ + µµ$ /" F = nmg"$ ""$ + µ$µ = nmg"$ "( - $) (4) Από την (4) παρατηρούµε ότι αν η γωνία φ λάβει την τιµή που ικανοποιεί την σχέση εφφ=εφθ=n, τότε το µέτρο της F παίρνει την µικρότερη τιµή του: F min = nmg"$ = nmg 1 + $ = nmg (5) 1 + n Αν λοιπόν ισχύει: "$ < r/r ή n < r R τότε η γνήσια περιστροφή του καρουλιού επιτυγχάνεται µε την ελάχιστη τιµή του µέτρου της F, η οποία υπολογίζεται από την (5). P.M. fysikos Ένας εργάτης προκαλεί κύλιση ενός κυλίνδρου µάζας Μ σε οριζόντιο έδαφος µε την βοήθεια ενός δοκαριού µάζας m και µήκους L, φροντίζοντας ώστε το δοκάρι να είναι οριζόντιο και να εφάπτεται του κυλίνδρου. Tην χρονική στιγµή t=0 το ένα άκρο B του δοκαριού είναι σ επαφή µε τον κύλινδρο. Nα δείξετε ότι για να µετακινείται το δοκάρι µε σταθερη επιτάχυνση a χωρίς να ολισθαίνει επί του κυλίνδρου, πρέπει ο εργάτης να εξασκεί στο άκρο του Α δύναµη, της οποίας η µεν οριζόντια συνιστώσα είναι σταθερή, ένω η κατακόρυφη συνιστώσα της µεταβάλλεται χρονικά.
21 Δίνεται η ροπή αδράνειας Ι=ΜR / του κυλίνδρου ως προς τον γεω µετρικό του άξονα και η επιτάχυνση g της βαρύτητας. ΛΥΣΗ: Eξετάζουµε το σύστηµα δοκάρι-κυλινδρος την τυχαία χρονική στιγµή t που ο άξονας του κυλίνδρου έχει µετατοπιστεί κατά x απο την αρχι κή του θέση Ο, που βρίσκεται ακριβώς πάνω από το άκρο Β του δοκαριού. To δοκάρι δέχεται το βάρος του w, την δύναµη F από τον εργάτη που αναλύε ται στην οριζόντια συνιστώσα F x και στην κατακόρυφη συνιστώσα F y και τέλος την δύναµη επαφής από τον κύλινδρο που αναλύεται στην κάθετη Σχήµα 11α Σχήµα 11β αντίδραση N και στην τριβή T που είναι στατική τριβή, διότι το δοκάρι δεν ολισθαίνει επί του κυλίνδρου. Εφαρµόζοντας για την µεταφορική κίνη ση του δοκαριού τον δεύτερο νόµο του Νεύτωνα κατα την οριζόντια και κατακόρυφη διεύθυνση παίρνουµε τις σχέσεις: F x - T = ma " F y + N E - mg = 0 $ F x = T + ma " N E = mg - F y $ Ο κύλινδρος δέχεται το βάρος του W, την δύναµη επαφής από το οριζόντιο έδαφος που αναλύεται στην κάθετη αντίδραση N E και στην τριβή T E που είναι στατική τριβή, διότι ο κύλινδρος κυλίεται πάνω στο οριζόντιο έδαφος και τέλος την δύναµη επαφής από το δοκάρι που αναλύεται στην τριβή T " και στην κάθετη αντίδραση N " που είναι αντίθετες των T E, N E αντιστοίχως, λόγω του αξιώµατος της ισότητας δράσεως-αντιδράσεως (σχ. 11β). Όµως η επίπεδη κίνηση του κυλίνδρου µπορεί να θεωρηθεί ως επαλληλία µιας οριζόντιας µεταφορικής κίνησης και µιας περιστροφής περί τον γεωµετρικό του άξονα, εφαρµόζοντας δε για την µεταφορική κίνηση τον δεύτερο νόµο του Νεύτωνα και για την περιστροφή του τον θεµελιώδη νόµο της στροφι κής κίνησης παίρνουµε τις σχέσεις: (1) T " - T E = Ma C T " R + T E R = I $ T - T = Ma E C T R + T E R = MR " / $ T - T E = Ma C T + T E = MR " / $ T - T E = Ma C T + T E = Ma C / " $ ()
22 όπου " η γωνιακή επιτάχυνση του κυλίνδου και a C η επιτάχυνση του άξο νά του, της οποίας το µέτρο είναι ίσο µε ω R λόγω της κυλίσεως του κυλίν δρου πάνω στο οριζόντιο έδαφος. Όµως η επιτάχυνση a του δοκαριού είναι καθε στιγµή ίση µε την εφαπτοµενική επιτάχυνση του σηµείου επαφής Ε του κυλίνδρου µε το δοκάρι, η οποία είναι ίση µε a C. Έτσι οι σχέσεις () γράφονται: T - T E = Ma/ T + T E = Ma / 4 " $ (+ ) T = 3Ma/4 T = 3Ma/8 (3) Συνδυάζοντας την πρώτη εκ των σχέσεων (1) µε την (3) παίρνουµε: F x - 3Ma/8 = ma F x = ( m + 3M/8)a (4) Από την (4) παρατηρούµε ότι το µέτρο της οριζόντιας συνιστώσας της F είναι σταθερό, αφου η επιτάχυνση a είναι σταθερή. Εξάλλου το δοκάρι δεν περιστρέφεται, που σηµαίνει ότι η συνολική ροπή περί το κέντρο µάζας του Κ των δυνάµεων που δέχεται είναι µηδενική, δηλαδή µπορούµε να γράψουµε την σχέση: (1) " (K) = 0 F y L/ - N E ( K ) = 0 F y L/ - ( mg - F y )( K ) = 0 (4) Eπείδη κάθε στιγµή η ταχύτητα του δοκαριού είναι διπλάσια της ταχύτητας του κέντρου µάζας του κυλίνδρου η µετατόπιση του άκρου Β του δοκαριου σε χρόνο t είναι διπλάσια της αντίστοιχης µετατόπισης x του κέντρου του κυλίνδρου, οπότε η απόσταση ΚΕ είναι ίση µε L/-x και η (4) γράφεται: F y L/ - ( mg - F y )( L/ - x) = 0 F y L/ - mgl/ + F y L/ + mgx - F y x = 0 F y ( L - x) = mg L/ - x ( ) F y = mg( L/ - x) L - x Από την (6) παρατηρούµε ότι το µέτρο της κατακόρυφης συνιστώσας της F µεταβάλλεται χρονικά, διότι η απόσταση x µεταβάλλεται. P.M. fysikos (6)
από τον κατακόρυφο τοίχο, της οποίας ο φορέας είναι οριζόντιος και την δύναµη επα φής N!
 Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
i) Nα δείξετε ότι, κάθε στιγµή οι ταχύτητες των δύο πιθήκων ως προς το ακίνητο έδαφος είναι ίσες.
 Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δίνεται η ροπή αδράνειας I=mL 2 /3 της ράβδου ως προς τον άξονα περιστροφής της, η επιτάχυνση! g της βαρύτητας και ότι π 2!10.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
, της οποίας το µέτρο ικανοποιεί τη σχέση:
 Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή
 Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση.
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
ii) ii) Nα καθορίσετε το είδος της ισορροπίας της ράβδου.
 Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
ΛΥΣΗ: Κατά τον πολύ µικρό χρόνο Δt (Δt 0) που ενεργεί επί του σφαιριδίου Γ η ώθηση Ω. =mv. το σφαιρίδιο Β δέχεται τις κρουστικές δυνάµεις F
 Τρία µικρά σφαιρίδια της ίδιας µάζας είναι αρθρωµένα στις άκρες δύο συνεχόµεων ράβδων ΑΒ και ΒΓ αµελητέας µάζας, όπως φαίνεται στο σχήµα (1), το δε σύστηµα ισορροπεί εκτός πεδίου βαρύτητας. Στο σφαιρίδιο
Τρία µικρά σφαιρίδια της ίδιας µάζας είναι αρθρωµένα στις άκρες δύο συνεχόµεων ράβδων ΑΒ και ΒΓ αµελητέας µάζας, όπως φαίνεται στο σχήµα (1), το δε σύστηµα ισορροπεί εκτός πεδίου βαρύτητας. Στο σφαιρίδιο
ΛΥΣΗ: Έστω O η θέση ισορροπίας του σφαιριδίου. Στη θέση αυτή το σφαι ρίδιο δέχεται το βάρος του w!, τη δύναµη F
 Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
Ένα ιδανικό ελατήριο σταθεράς k κόβεται σε δύο τµήµατα µε µήκη L και L. Η µία άκρη κάθε τµήµατος συνδέεται στέρεα µε µικρό σφαιρίδιο µάζας m και οι ελέυθερες άκρες τους στερεώνονται σε ακλόνητα σηµεία
i) Nα βρεθεί η επιτάχυνση του κέντρου Κ της τροχαλίας την στιγµή t=0 αµέσως µετά την θραύση του νήµατος.
 H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
της οποίας ο φορέας σχηµατί ζει γωνία φ=π/6 µε την κατακόρυφη διεύθυνση και ανακλάται µε αντίστοιχη γωνία φ=π/4.
 Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
διέρχεται από το σηµείο τοµής Ο των φορέων του βάρους w! της ράβδου και της οριζόντιας αντίδρασης A!
 Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
. Αυτό σηµαίνει ότι το κέντρο µάζας κινείται ευθύγραµµα µε σταθερή επιτάχυνση a! = F!
 Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
ii) Nα υπολογιστεί η κινητική ενέργεια του συστήµατος σε συνάρτηση µε τον χρόνο. Δίνεται η επιτάχυνση! g της βαρύτητας.
 Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
i) το πλάτος ταλάντωσης του καροτσιού µετά την ενσωµάτωση του σφαιριδίου σ' αυτό και
 Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
Ένα καροτσάκι που περιέχει άµµο, συνολικής µάζας M, εκτελεί οριζόντια αρµονική ταλάντωση σε λείο επίπεδο, µε τη βοήθεια ιδανικού οριζόντιου ελατηρίου σταθεράς k. Ένα σφαιρίδιο µάζας m
και όταν φθάσει στο σηµείο Γ αρχίζει να κινείται στο κυκλικό του τµήµα που έχει την µορφή λείου τεταρτο κυκλίου ακτίνας R.
 Το σώµα Σ του σχήµατος (α) έχει µάζα και µπορεί να ολισθαίνει πάνω σε λείο οριζόντιο έδαφος. Ένα µικρό σφαιρίδιο µάζας m κινείται αρχικά πάνω στο οριζόντιο τµήµα του σώµατος µε ταχύτητα v 0 και όταν φθάσει
Το σώµα Σ του σχήµατος (α) έχει µάζα και µπορεί να ολισθαίνει πάνω σε λείο οριζόντιο έδαφος. Ένα µικρό σφαιρίδιο µάζας m κινείται αρχικά πάνω στο οριζόντιο τµήµα του σώµατος µε ταχύτητα v 0 και όταν φθάσει
που εξασκείται στο άκρο της Γ και των αντιδράσεων A! , A 2
 Oµογενής ράβδος BΓ βάρους w, ισορροπεί ώστε τα άκρα της να εφάπτονται σε µια λεία και ακίνητη κοίλη σφαίρα ακτί νας R, όπως φαίνεται στο σχήµα (1). Eάν η κατακόρυφη δύναµη F που εξασκείται στο άκρο Γ της
Oµογενής ράβδος BΓ βάρους w, ισορροπεί ώστε τα άκρα της να εφάπτονται σε µια λεία και ακίνητη κοίλη σφαίρα ακτί νας R, όπως φαίνεται στο σχήµα (1). Eάν η κατακόρυφη δύναµη F που εξασκείται στο άκρο Γ της
Οµογενής σφαίρα µάζας m και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση!!
 Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
Οµογενής σφαίρα µάζας και ατίνας R, ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγµή ενεργεί στην σφαίρα οριζόντια ώθηση βραχείας διάρκειας, της οποίας ο φορέας βρίσκε ται άνωθεν του κέντρου της
όπου Α το πλάτος της ταλάντωσης, φ η αρχική της φάση και ω η γωνιακή της συχνότητα. Οι σχέσεις (2) εφαρµοζόµενες τη χρονική στιγµή t=0 δίνουν:
 Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ
 Ονοµατεπώνυµο: Διάρκεια: (3 45)+5=50 min Τµήµα: ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ Ζήτηµα ο Ένα στερεό µπορεί να στρέφεται γύρω από σταθερό άξονα και αρχικά ηρεµεί. Σε µια στιγµή δέχεται (ολική) ροπή
Ονοµατεπώνυµο: Διάρκεια: (3 45)+5=50 min Τµήµα: ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ Ζήτηµα ο Ένα στερεό µπορεί να στρέφεται γύρω από σταθερό άξονα και αρχικά ηρεµεί. Σε µια στιγµή δέχεται (ολική) ροπή
( ) ( ) 2 1 K = K = m 2. ! = v 2 + v 1 R + r (3) H (1) λόγω της (3) γράφεται: R - v 2. + v 1. v 2. r > 0 (4) ! v K. + v 1 )R - v 2. = v 2. - v.
 Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
από την άρθρωση και της δύναµης επαφής από τον τοίχο που αναλύεται στην στατική τριβη T!
 Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
i) Να δείξετε ότι: F max = (m 1 + m 2 όπου! g η επιτάχυνση της βαρύτητας.
 Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
Q του νήµατος που το συγκρατεί, συµφωνα δε µε τον δεύτερο νό µο κίνησης του Νεύτωνα θα ισχύει η σχέση: της τάσεως!
 Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
i) Nα βρείτε την ταχύτητα του κέντρου της στεφάνης αµέσως µετά την κρού ση, η οποία θεωρείται βραχείας διάρκειας.
 Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
(σχ. 1). Εφαρ µόζοντας για την µεταφορική συνιστώσα της κύλισης του δίσκου τον
 Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο
 Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
i) Nα βρείτε την επιτάχυνση του κέντρου της τροχαλίας τ 1.
 Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
περί το κέντρο της σφαίρας, ονοµάζεται δε τριβή κυλίσεως. Tο µέτρο της τρι βής κυλίσεως είναι προφανώς ανάλογο του µέτρου της N,!
 Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου.
 Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
i) Nα δείξετε ότι αν το σύστηµα αφεθεί ελεύθερο η τροχαλία τ 1 δεν µπορεί να κυλίεται, άλλά µόνο να ισσρροπεί ή να ολισθαίνει.
 Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
όπου Μ η µάζα της Γης την οποία θεωρούµε σφαίρα οµογενή, G η παγκόσµια σταθερά της βαρύτητας και L!
 Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
Eάν L 1, L 2 είναι τα αντίστοιχα φυσικά µήκη των ελατηρίων ε 1 και ε 2 τότε για την απόσταση ΑΒ των σηµείων στήριξης των ελατηρίων θα έχουµε:
 Tο µικρό σώµα του σχήµατος (1) έχει µάζα m και συγκρατείται στο λείο οριζόντιο έδαφος σε τέτοια θέση, ώστε τα ελατήρια ε 1 και ε να είναι τεντωµένα κατά α απο την φυσική τους κατάσταση. i) Eάν k, k είναι
Tο µικρό σώµα του σχήµατος (1) έχει µάζα m και συγκρατείται στο λείο οριζόντιο έδαφος σε τέτοια θέση, ώστε τα ελατήρια ε 1 και ε να είναι τεντωµένα κατά α απο την φυσική τους κατάσταση. i) Eάν k, k είναι
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
ii) Να δείξετε ότι το σφαιρίδιο εκτελεί µια µη αρµονική περιοδική ταλάντωση, της οποίας να υπολογίσετε την περίοδο.
 Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
i) Το επίπεδο της τροχαλίας είναι οριζόντιο και το έδαφος λείο.
 Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ. Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται.
 ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ Διερεύνηση της σχέσης L=ω Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται. Η ροπή αδράνειας Ι
ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ Διερεύνηση της σχέσης L=ω Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται. Η ροπή αδράνειας Ι
i) Nα αποδείξετε ότι το σώµα τελικά θα ηρεµήσει ως προς το δοκάρι και να βρείτε την κοινή τους ταχύτητα στο σύστηµα αναφοράς του εδάφους.
 Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
Ένα δοκάρι µεγάλου µήκους και µάζας M, είναι ακίνητο πάνω σε λείο οριζόντιο έδαφος. Στο ένα άκρο του δοκαριού βρίσκεται ξύλινο σώµα µάζας m, το οποίο παρουσιάζει µε την επιφά νεια του δοκαριού συντελεστή
(τρίτος νόµος του Νεύτωνα) και την πλάγια αντίδραση του οριζόντιου εδάφους, η οποία αναλύεται στην τριβή ολίσθησης T!
 Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
. Εάν η σφαίρα κυλίεται πάνω στο δοκάρι να βρείτε: i) την επιτάχυνση του δοκαριού και του κέντρου της σφαίρας, στο σύστηµα αναφοράς του δαπέδου και
 Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
Eφαρµόζοντας στο τρίγωνο OAΣ το θεώρηµα του συνηµιτόνου παίρνουµε:
 ΘΕΜΑ 6o Η κυκλική τροχαλία του σχήµατος (1) έχει µάζα Μ και ακτίνα R, είναι σε επαφή µε οριζόντιο δάπεδο (ε), ενώ στον άξονά της έχει πακτωθεί αβαρής ράβδος µήκους L, στο ελεύθερο ακρο της οποίας έχει
ΘΕΜΑ 6o Η κυκλική τροχαλία του σχήµατος (1) έχει µάζα Μ και ακτίνα R, είναι σε επαφή µε οριζόντιο δάπεδο (ε), ενώ στον άξονά της έχει πακτωθεί αβαρής ράβδος µήκους L, στο ελεύθερο ακρο της οποίας έχει
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ii) Nα βρεθεί η κινητική ενέργεια της σφαίρας, όταν το δοκάρι έχει µετατοπιστεί κατά S ως προς το έδαφος.
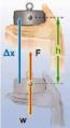 Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
ΜΕΡΟΣ Γ! 2η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ΟΡΟΣΗΜΟ >Ι 3. δ. Ι Οι τροχοί (1) και (2) του σχήματος είναι ίδιοι. Τότε: και Ι 2
 ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
# $ + L " = ml " ml! = ML " $ + ml " $ L " = ML/2(M + m) # $ (1) Eξάλλου, εάν L' α, L' σ είναι οι τελικές αποστάσεις του κέντρου µάζας C του
 Mία σανίδα, µήκους L καί µάζας M, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Στο ένα άκρο της σανίδας πατάει άνθ ρωπος µάζας m και αρχίζει να κινείται προς το άλλο άκρο της. Kατά πόσο θα µετατοπιστεί η
Mία σανίδα, µήκους L καί µάζας M, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Στο ένα άκρο της σανίδας πατάει άνθ ρωπος µάζας m και αρχίζει να κινείται προς το άλλο άκρο της. Kατά πόσο θα µετατοπιστεί η
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V!
 Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
) ω ω. L λίγο πριν. . Nα βρεθούν:
 Δύο σφαιρίδια A, B µάζας m το καθένα συνδέονται µεταξύ τους µε αβαρές και µη εκτατό νήµα µήκους L, ηρεµούν δε πάνω σε οριζόντιο τραπέζι ευρισκόµενα σε απόσταση α
Δύο σφαιρίδια A, B µάζας m το καθένα συνδέονται µεταξύ τους µε αβαρές και µη εκτατό νήµα µήκους L, ηρεµούν δε πάνω σε οριζόντιο τραπέζι ευρισκόµενα σε απόσταση α
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1. ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 24 Γενάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 24 Γενάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
του σφαιριδίου κατευθύνεται προς τα κάτω και σχηµατίζει µε την κατακόρυφη διεύθυνση γωνία φ.
 Μικρό σφαιρίδιο µάζας m, προσπίπτει σε σηµεί ο Α της περιφέρειας ενός δακτυλιδιού ακτίνας R, το οποίο µπορεί να περιστρέφεται περί οριζόντιο άξονα που διέρχεται από ένα σηµείο του Ο. Η ταχύτητα πρόσπτωσης
Μικρό σφαιρίδιο µάζας m, προσπίπτει σε σηµεί ο Α της περιφέρειας ενός δακτυλιδιού ακτίνας R, το οποίο µπορεί να περιστρέφεται περί οριζόντιο άξονα που διέρχεται από ένα σηµείο του Ο. Η ταχύτητα πρόσπτωσης
i) την µέγιστη ροπή του ζεύγους δυνάµεων που επιτρέπεται να ενερ γήσει επί του κυλίνδρου, ώστε αυτός να ισορροπεί και
 Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
i) Nα εκφράσετε σε συνάρτηση µε τον χρόνο την γωνιακή ταχύτητα της τροχαλίας.
 Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
ταχύτητα μέτρου. Με την άσκηση κατάλληλης σταθερής ροπής, επιτυγχάνεται
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ 26. Δύο σημειακές σφαίρες που η καθεμιά έχει μάζα συνδέονται μεταξύ τους με οριζόντια αβαρή ράβδο. Το σύστημα περιστρέφεται γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ 26. Δύο σημειακές σφαίρες που η καθεμιά έχει μάζα συνδέονται μεταξύ τους με οριζόντια αβαρή ράβδο. Το σύστημα περιστρέφεται γύρω από κατακόρυφο
% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου
![% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου % ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου](/thumbs/53/30956495.jpg) 1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ. ΘΕΜΑ Α (μοναδες 25)
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]
![ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου] ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]](/thumbs/52/29790189.jpg) ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ Σ ένα στερεό ασκούνται ομοεπίπεδες δυνάμεις. Όταν το στερεό ισορροπεί, δηλαδή ισχύει ότι F 0 και δεν περιστρέφεται τότε το αλγεβρικό άθροισμα των ροπών είναι μηδέν Στ=0,
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ Σ ένα στερεό ασκούνται ομοεπίπεδες δυνάμεις. Όταν το στερεό ισορροπεί, δηλαδή ισχύει ότι F 0 και δεν περιστρέφεται τότε το αλγεβρικό άθροισμα των ροπών είναι μηδέν Στ=0,
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ. Δίνεται ότι η ροπή αδράνειας του δίσκου ως προς τον άξονα Κ είναι Ι= M R
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
Διαγώνισμα Φυσικής Α Λυκείου
 Διαγώνισμα Φυσικής Α Λυκείου Δυναμιική.. Θέμα 1 ο 1. Συμπληρώστε την παρακάτω πρόταση. H αρχή της αδράνειας λέει ότι όλα ανεξαιρέτως τα σώματα εκδηλώνουν μια τάση να διατηρούν την... 2. Ένα αυτοκίνητο
Διαγώνισμα Φυσικής Α Λυκείου Δυναμιική.. Θέμα 1 ο 1. Συμπληρώστε την παρακάτω πρόταση. H αρχή της αδράνειας λέει ότι όλα ανεξαιρέτως τα σώματα εκδηλώνουν μια τάση να διατηρούν την... 2. Ένα αυτοκίνητο
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
ακτινικής διεύθυνσης και στην οριακή τριβή T!"
 Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]
![ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%] ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]](/thumbs/65/53613594.jpg) 1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος. και Α 2
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
Ασκήσεις. Φυσική Γ Λυκείου - Μηχανική στερεού σώματος
 - Μηχανική στερεού σώματος Ασκήσεις 1. Στερεό στρέφεται γύρω Ένας δίσκος μπορεί να περιστρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο και είναι κάθετος στο επίπεδο του. Ο δίσκος είναι
- Μηχανική στερεού σώματος Ασκήσεις 1. Στερεό στρέφεται γύρω Ένας δίσκος μπορεί να περιστρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο και είναι κάθετος στο επίπεδο του. Ο δίσκος είναι
ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 23/2/2014 ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3-4
 ΚΕΝΤΡΟ Αγίας Σοφίας 39 3 ΝΤΕΠΩ Β Όλγας 3 38 ΕΥΟΣΜΟΣ ΜΑλεξάνδρου 5 37736 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3// ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3- ΘΕΜΑ A Στις ερωτήσεις - να γράψετε
ΚΕΝΤΡΟ Αγίας Σοφίας 39 3 ΝΤΕΠΩ Β Όλγας 3 38 ΕΥΟΣΜΟΣ ΜΑλεξάνδρου 5 37736 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3// ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3- ΘΕΜΑ A Στις ερωτήσεις - να γράψετε
mu R mu = = =. R Γενική περίπτωση ανακύκλωσης
 Γενική περίπτωση ανακύκλωσης Με τον όρο ανακύκλωση εννοούμε την κίνηση ενός σώματος σε κατακόρυφο επίπεδο σε κυκλική τροχιά. Χαρακτηριστικό παράδειγμα τέτοιας κίνησης είναι η κίνηση στο roller coaster,
Γενική περίπτωση ανακύκλωσης Με τον όρο ανακύκλωση εννοούμε την κίνηση ενός σώματος σε κατακόρυφο επίπεδο σε κυκλική τροχιά. Χαρακτηριστικό παράδειγμα τέτοιας κίνησης είναι η κίνηση στο roller coaster,
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
1. Για το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και. = (x σε μέτρα).
 Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα.
 Δίσκος Σύνθετη Τρίτη 01 Μαϊου 2012 ΑΣΚΗΣΗ 5 Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα. ΠΕΙΡΑΜΑ Α Θα εκτοξευθεί με ταχύτητα από τη βάση του κεκλιμένου
Δίσκος Σύνθετη Τρίτη 01 Μαϊου 2012 ΑΣΚΗΣΗ 5 Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα. ΠΕΙΡΑΜΑ Α Θα εκτοξευθεί με ταχύτητα από τη βάση του κεκλιμένου
Κρούσεις. 1 ο ΘΕΜΑ.
 ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
i) Nα βρεθεί η επιτάχυνση του κέντρου του δακτυλιδιού. Σχήµα 1 Σχήµα 2 L C
 Ένα στερεό σώµα αποτελείται από λεπτό δακτυ λίδι µάζας m και ακτίνας R και από δύο όµοιες λεπτές ράβδους µαζάς m η κάθε µια, των οποίων τα κέντρα έχουν ηλεκτροκολυθεί µε το δακτυλίδι, σε αντιδιαµετρικά
Ένα στερεό σώµα αποτελείται από λεπτό δακτυ λίδι µάζας m και ακτίνας R και από δύο όµοιες λεπτές ράβδους µαζάς m η κάθε µια, των οποίων τα κέντρα έχουν ηλεκτροκολυθεί µε το δακτυλίδι, σε αντιδιαµετρικά
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση 19-05-08 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Συµπαγής κύλινδρος µάζας Μ συνδεδεµένος σε ελατήριο σταθεράς k = 3. N / και αµελητέας µάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Συµπαγής κύλινδρος µάζας Μ συνδεδεµένος σε ελατήριο σταθεράς k = 3. N / και αµελητέας µάζας, κυλίεται, χωρίς να
Nα δείξετε τις εξής προτάσεις:
 Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1.
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1.
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο:
 6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
