4 ο Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης
|
|
|
- Μελίνα Γιάγκος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 4 ο Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης
2 ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΕΞΙΣΩΣΗ ΑΠΟΜΑΚΡΥΝΣΗΣ :. ( t ) ΕΞΙΣΩΣΗ ΤΑΧΥΤΗΤΑΣ :.. ( t ), υ. ΕΞΙΣΩΣΗ ΕΠΙΤΑΧΥΝΣΗΣ : max.. ( t ), α. 2 2 max ΔΥΝΑΜΗ ΕΠΑΝΑΦΟΡΑΣ : 2 F=-D.x, D=m.ω, Fmax D.A m ΠΕΡΙΟΔΟΣ : 2 D 1 ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ : U Dx 2 Θ.Ι της ταλάντωσης. 1 2 ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ : K m 2 2, όπου χ η απομάκρυνση από τη ΟΛΙΚΗ ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ : Ε=Κ+U, 1 1 U m DA max max max ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Όταν απομακρύνω το σώμα από τη Θ.Ι κατά χ και το αφήνω ελεύθερο, τότε η μετατόπιση χ είναι το πλάτος Α της ταλάντωσης 2. Όταν το σώμα απομακρύνεται από τη Θ.Ι κατά χ και ταυτόχρονα το εκτοξεύουμε με ταχύτητα υ, τότε το χ δεν είναι το πλάτος της ταλάντωσης, οπότε για να το υπολογίσω εφαρμόζω την Α.Δ.Ε.Τ στη θέση αυτή : E K U DA Dx m Από την γραφική παράσταση ενός μεγέθους χ, υ, α,κ.τ.λ, συναρτήσει του χρόνου μπορώ να υπολογίσω την περίοδο της ταλάντωσης, την μέγιστη τιμή αυτού του μεγέθους και την αρχική του φάση. 4. Για να υπολογίσω την απομάκρυνση χ=f(t), την ταχύτητα υ=f(t) κ.τ.λ θα πρέπει να υπολογίσω το πλάτος Α το ω και την αρχική φάση της ταλάντωσης. Για την αρχική φάση γράφω τις αρχικές συνθήκες για την ταλάντωση : Για t=0 το σώμα που βρίσκεται π.χ : χ=+α/2 και προς τα πού κινείται, προς τη θετική φορά κίνησης υ >0 ή την αρνητική φορά κίνησης υ<0. Κατόπιν ή με τις εξισώσεις ή με το περιστρεφόμενο διάνυσμα βρίσκω την αρχική φάση. 5. Σε μια περίοδο Τ ο ταλαντωτής περνά από τη θέση ισορροπίας αλλά και από οποιαδήποτε άλλη θέση δύο 2 φορές. Ισχύει : Τ αντιστοιχεί 2 φορές t N 1
3 6. Για δύο θέσεις συμμετρικές ως προς τη Θ.Ι, το σώμα έχει την ίδια ταχύτητα κατά μέτρο και την ίδια επιτάχυνση κατά μέτρο. 7. Μέσα σε μια περίοδο Τ ο ταλαντωτής έχει την ίδια ταχύτητα ( και επιτάχυνση) κατά μέτρο τέσσερις 4 φορές. 8. Η δυναμική ενέργεια ταλάντωσης π.χ είναι ίση με την κινητική U=K σε δύο θέσεις συμμετρικές ως προς τη Θ.Ι. 9. Μέσα σε μια περίοδο Τ ο ταλαντωτής έχει δυναμική ενέργεια ταλάντωσης είναι ίση με την κινητική U=K τέσσερις (4 ) φορές. 10. Μέσα σε μια περίοδο Τ ο ταλαντωτής παίρνει την μέγιστη κινητική του ενέργεια (μέγιστη ταχύτητα ή επιτάχυνση) καθώς και την μέγιστη δυναμική δύο (2) φορές. 11. Ο χρόνος μεταξύ δύο διαδοχικών μεγιστοποιήσεων της ταχύτητας, της επιτάχυνσης κ.τ.λ είναι Τ/ Όταν το σώμα εκτοξευθεί από τη Θ.Ι ή περνά από τη Θ.Ι με ταχύτητα υ, τότε η ταχύτητα αυτή είναι μέγιστη για την ταλάντωση. 13. Η μεταβολή της ταχύτητας (ή επιτάχυνσης ) για δύο διαδοχικά περάσματα του ταλαντωτή από τη Θ.Ι είναι Δυ=2.υ max.(γιατί ;) 14. Να γνωρίζω ότι για να αποδείξω ότι ένα σώμα εκτελεί απλή αρμονική ταλάντωση θα πρέπει: Α. Στη Θ.Ι να σημειώσω τις δυνάμεις που ενεργούν, να γράψω τη σχέση ΣF=0 και Β. Στη τυχαία θέση, αφού απομακρύνω το σώμα κατά χ από τη Θ.Ι και το αφήσω ελεύθερο, σημειώνω πάλι τις δυνάμεις που ενεργούν στο σώμα κατά τη διεύθυνση της κίνησης και θα πρέπει να αποδείξω ότι : F=-D.x. 15. Η δύναμη του ελατηρίου F ελ υπολογίζεται από τη σχέση F ελ = - k. x, όπου χ είναι η απομάκρυνση από τη θέση φυσικού μήκους του ελατηρίου ενώ η δύναμη ΣF της ταλάντωσης από τη σχέση ΣF=- D. x, όπου χ η απομάκρυνση από τη θέση ισορροπίας της ταλάντωσης. 16. Το έργο της δύναμης του ελατηρίου είναι : 1 1 WF U ελατ αρχ U τελ kx kx όπου χ είναι η απομάκρυνση από τη θέση φυσικού μήκους του ελατηρίου, ενώ το έργο της δύναμης επαναφοράς της ταλάντωσης ΣF είναι : W F U U Dx D, όπου χ η απομάκρυνση από τη θέση ισορροπίας 2 2 της ταλάντωσης. Ακόμη για το έργο της δύναμης επαναφοράς ισχύει : 1 1 W K.m.υ.m.υ ΣF τελ τελ αρχ 2
4 17. Όταν σε κάποια θέση χ, π.χ, χ=- 10 cm ζητείται η ταχύτητα του σώματος ή αντιστρόφως γνωρίζω την ταχύτητα σε κάποια θέση ή χρονική στιγμή, τότε για να την υπολογίσω εφαρμόζω (συνήθως )την Α.Δ.Ε.Τ. : E K U DA Dx m Αν δοθεί η σχέση μεταξύ της δυναμικής και της κινητικής ενέργειας της ταλάντωσης π.χ K=3U και ζητηθεί η θέση χ όπου συμβαίνει αυτό, τότε γράφω την Α.Δ.Ε.Τ ως εξής : 1 1 E K U E U U E U DA Dx και υπολογίζω τη θέση χ. Αντίστοιχα αν μου ζητηθεί η ταχύτητα τότε, K 4K E K U E K E DA m Για τον υπολογισμό της χρονικής στιγμής που το σώμα διέρχεται από κάποια θέση χ, ή χρονικού διαστήματος Δt χρησιμοποιώ ή το περιστρεφόμενο διάνυσμα (Δφ=ω.Δt) ή λύνω την τριγωνομετρική εξίσωση και υπολογίζω το χρόνο, π.χ : π.ημ(ωt+ ) Όταν στο σώμα ενεργήσει σταθερή δύναμη F και απομακρυνθεί κατά χ από τη Θ.Ι, τότε το έργο της δύναμης F θα ισούται με την ολική ενέργεια ταλάντωσης 1 2 : WF DA =F.x=F.A, οπότε μπορώ να υπολογίσω το πλάτος της ταλάντωσης Α. Ακόμη 2 χρησιμοποιώ το Θ.Μ.Κ.Ε για να βρω την ταχύτητα στη θέση που αποσύρεται η δύναμη και μετά με Α.Δ.Ε.Τ βρίσκω το πλάτος της ταλάντωσης. 21. Πρέπει να γνωρίζω τις θέσεις όπου τα μεγέθη χ, υ, α, Κ, U, T, λαμβάνουν τη μέγιστη τιμή τους και που μηδενίζονται. t=t x<0 υ>0 α>0 t=0 x>0, υ>0, α<0 t=t/4 -Α Ο +Α t=3t/4 α>0 υ<0 x<0 t=t/2 x>0, α<0,υ<0 α=ω 2 Α, υ=0 α=0, υmax=±ωα υ=0, α=-ω 2 Α K=0, Umax=1/2DA 2 U=0, Kmax=1/2mυ 2 max K=0, Umax=1/2DA 2 3
5 22. ΡΥΘΜΟΙ ΜΕΤΑΒΟΛΗΣ ΜΕΓΕΘΩΝ Όλοι οι ρυθμοί είναι στιγμιαίοι, αναφέρονται σε μια συγκεκριμένη χρονική στιγμή t 1 και συνήθως ζητείται η απόλυτος τιμή τους. ( με απόδειξη ) 1. Ρυθμός μεταβολής μετατόπισης και ρυθμός μεταβολής ταχύτητας Δχ Δυ A. Mετατόπισης : ( ) t (ταχύτητα) και Β. Ταχύτητας : ( ) t (επιτάχυνση) Δt 1 Δt 1 2. Ρυθμός μεταβολής της ορμής p m. p ( ) t m. a, οπότε ( ) t F Dx t 1 t t 1 3. Ρυθμός μεταβολής της κινητικής ενέργειας της ταλάντωσης. ( W ) F F t F., Άρα ( ) t = F. Ό ΣF=-D.x t 1 t t t 1 και χ η απομάκρυνση από τη Θ.Ι της ταλάντωσης. 4. Ρυθμός μεταβολής της δυναμικής ενέργειας της ταλάντωσης ΔU. Ε=Κ+U άρα ΔΚ+ΔU=0 (E=σταθ), οπότε Δt Δt ΔU W. ΔU. ( ) F F t F., άρα ( ) t F. Δt 1 Δt Δt Δt 1 5. Ρυθμός μεταβολής της δυναμικής ενέργειας του ελατηρίου U W. ( F F U ) t F., άρα ( ) t F., όπου F. t 1 t t t 1 και χ η απομάκρυνση από τη Θ.Φ.Μ του ελατηρίου. 6. Ρυθμός μεταβολής της βαρυτικής δυναμικής του σώματος U W mg.. U ( ) m. g., άρα ( B t ) t m. g. t 1 t t t 1 4
6 ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΡΟΒΛΗΜΑΤΩΝ 1. Προσδιορίζω το αντικείμενο- το σώμα ή σώματα που αναφέρονται στο πρόβλημα. 2. Εντοπίζω το φαινόμενο ή τα φαινόμενα που παρουσιάζονται. Π.χ Ταλάντωση φθίνουσα ταλάντωση, κρούση, συμβολή κυμάτων κ.τ.λ 3. Καταγράφω όλα τα δεδομένα της άσκησης και επισημαίνω τις φράσεις κλειδιά που θα με βοηθήσουν για την επίλυση του προβλήματος. 4. Συνδυάζω τις έννοιες και τους νόμους που αναφέρονται στο παραπάνω φαινόμενο ή φαινόμενα του προβλήματος. Π.χ Ταχύτητα ταλάντωσης, Δυναμική ενέργεια, Αρχή διατήρησης της ενέργειας, Αρχή διατήρησης της ορμής, αρχή της επαλληλίας κ.τ.λ. 5. Ανακαλώ από την μνήμη μου τις εξισώσεις, τις σχέσεις που αναφέρονται στα παραπάνω 6. Ανατρέχω στις παρατηρήσεις και την μεθοδολογία που έχουμε μάθει για το συγκεκριμένο φαινόμενο ή κεφάλαιο. 7. Συνθέτω όλα τα παραπάνω, διοχετεύω λίγο από το περίσσευμα της αυτενέργειάς μου, αυτοσυγκεντρώνομαι και καταστρώνω το σχέδιο λύσης στο μυαλό μου. 8. Ακολουθώ μια συγκεκριμένη πορεία επίλυσης που θα μάθουμε για κάθε κεφάλαιο και για κάθε φαινόμενο. 9. Προσέχω να εκμεταλλευτώ όλα τα δεδομένα του προβλήματος. 10. Δεν χάνω την ψυχραιμία μου ούτε και βιάζομαι, προσέχω τέλος, να απαντήσω σε όλες τις ερωτήσεις με όποια σειρά επιθυμώ ( αν αυτό είναι δυνατό!) 11. Δεν παραλείπω τις μονάδες μέτρησης και προσέχω να εργάζομαι στο ίδιο σύστημα μονάδων, συνήθως στο S.I. 12. Κάθε λύση επιστημονικά τεκμηριωμένη είναι και αποδεκτή. 5
7 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΞΙΣΩΣΕΙΣ ΕΛΑΤΗΡΙΑ 1. Η γραφική παράσταση της ταχύτητας, σε συνάρτηση με τον χρόνο, για ένα σημειακό αντικείμενο μάζας m= 1 kg που εκτελεί απλή αρμονική ταλάντωση φαίνεται στο σχήμα. Τη χρονική στιγμή t1=2/3 s το σώμα βρίσκεται στη θέση χ1= m. Α) Να γράψετε την εξίσωση της ταχύτητας και της απομάκρυνσης σε σχέση με το χρόνο. Β) Να βρείτε τη δύναμη επαναφοράς τη χρονική στιγμή t2=4 s και όταν βρίσκεται στη θέση χ1 Γ) Να κάνετε το διάγραμμα της επιτάχυνσης συναρτήσει της απομάκρυνσης χ και συναρτήσει του χρόνου. (υ=π.10-2 συνπt/4, ημπt/4, 0Ν ) 2. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση μεταξύ δύο ακραίων θέσεων, σι οποίες απέχουν μεταξύ τους απόσταση d = 20 cm. Τη χρονική στιγμή t=0 το σώμα βρίσκεται στη θέση ισορροπίας, κινείται προς τη θετική κατεύθυνση και ύστερα από χρόνο t=1, 5 s επανέρχεται για τρίτη φορά στη θέση ισορροπίας του. Α. Να βρείτε το πλάτος και την περίοδο της ταλάντωσης Β. Να γράψετε την εξίσωση της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης της ταλάντωσης του σώματος σε συνάρτηση με το χρόνο Γ. Να γράψετε την εξίσωση της συνισταμένης δύναμης που δέχεται το σώμα σε συνάρτηση με την απομάκρυνσή του και να σχεδιάσετε το αντίστοιχο διάγραμμα Δ. Να υπολογίσετε την ταχύτητα του σώματος όταν αυτό βρίσκεται για πρώτη φορά στη θέση χ1=-0,05 m Ε. Να υπολογίσετε την επιτάχυνση του σώματος τη χρονική στιγμή t1=2 s. Θεωρήστε για τις πράξεις: π 2 = 10. (0,1ημ2πt, 0.2π συν2πt, -80x, -8.ημ2πt ) 3. * Ένα μικρό σώμα μάζας m= 0,1 kg εκτελεί απλή αρμονική ταλάντωση μεταξύ δύο ακραίων θέσεων, οι οποίες απέχουν μεταξύ τους απόσταση d = 20 cm. Το μικρό σώμα εκτελεί 4 πλήρεις ταλαντώσεις σε χρονική διάρκεια Δt = 0,4 sec και η απομάκρυνσή του από τη θέση ισορροπίας του, κάθε χρονική στιγμή, δίνεται από τη σχέση χ = Α ημωt. α) Να γράψετε την εξίσωση της ταχύτητας και της επιτάχυνσης της ταλάντωσης του σώματος σε συνάρτηση με το χρόνο και να σχεδιάσετε τις γραφικές τους παραστάσεις σε συνάρτηση με το χρόνο σε βαθμολογημένους άξονες. β) Ποια είναι η απομάκρυνση και η ταχύτητά του τη χρονική στιγμή t=3/40 sec ; γ) Ποια η δυναμική και η κινητική ενέργεια του σώματος τη χρονική στιγμή t2=1/120 s. δ) Να υπολογίσετε τη δύναμη που δέχεται το μικρό σώμα τη χρονική στιγμή που διέρχεται από τη θέση χ1 = - 0,05 m. ε) Να υπολογίσετε το μέτρο της επιτάχυνσης και το μέτρο της ταχύτητας του μικρού σώματος, τη στιγμή που η δύναμη επαναφοράς έχει μέτρο 10 Ν. Θεωρήστε για τις πράξεις: π 2 = 10. (2πσυν20πt, -400ημ20πt, -0.1 m, 0.5J, 1.5 J, 20 N, 100 m/s 2 ) 6
8 4. * Υλικό σημείο μάζας m=0,2kg εκτελεί απλή αρμονική ταλάντωση. Όταν η απομάκρυνσή του από τη θέση ισορροπίας του είναι x1= m η ταχύτητά του έχει μέτρο υ1= m/ s ενώ όταν η απομάκρυνση είναι x2= m η ταχύτητα έχει μέτρο υ2= m/s., Να βρείτε: Α. Την κυκλική συχνότητα ω και το πλάτος Α της ταλάντωσης Β. Την δύναμη επαναφοράς και την επιτάχυνση της ταλάντωσης στη χ=+α/2. Γ. Σε ποια θέση θα είναι U=(3/4).E ( 1 r/s, 0,1 m, m ) 5. * Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση, τη χρονική στιγμή t=0 βρίσκεται στη θέση ισορροπίας και κινείται προς τη θετική κατεύθυνση. Το σώμα περνάει από τη θέση ισορροπίας 10 φορές το δευτερόλεπτο και τη χρονική στιγμή t=1/20 sec βρίσκεται στη θέση χ=+0,2 m. Α. Να βρείτε την περίοδο και το πλάτος της ταλάντωσης Β. Να γράψετε τις εξισώσεις της δυναμικής και κινητικής ενέργειας σε συνάρτηση με το χρόνο και να κάνετε τις αντίστοιχες γραφικές παραστάσεις. Γ. Να υπολογίσετε την απομάκρυνση του σώματος από τη θέση ισορροπίας τις χρονικές στιγμές που η ταχύτητά του είναι υ= π m/s. Δ. Να βρείτε το μέτρο της δύναμης επαναφοράς της ταλάντωσης τη στιγμή που η δυναμική ενέργεια του είναι U= π 2 J. (0,2 s, 0.2 m, 40.ημ 2 10πt, m, 200N ) 6. * Ένα μικρό σώμα μάζας m = 0,2 kg εκτελεί απλή αρμονική ταλάντωση και τη χρονική στιγμή t = 0 διέρχεται από τη θέση χ1 = + 0,5 m με ταχύτητα υ1 = m/s και έχοντας επιτάχυνση α1 = - 50 m/s 2. α) Να υπολογίσετε την περίοδο και το πλάτος της ταλάντωσης. β) Να γράψετε την εξίσωση της δυναμικής και της κινητικής ενέργειας της ταλάντωσης σε συνάρτηση με το χρόνο. γ) Να υπολογίσετε την απομάκρυνση του σώματος τις χρονικές στιγμές που η κινητική ενέργεια του σώματος ισούται με τη δυναμική ενέργεια της ταλάντωσης. δ) Επί πόσο χρόνο στη διάρκεια μιας περιόδου η δυναμική ενέργεια είναι μεγαλύτερη της κινητικής; (0,2πs, 1m, 10ημ 2 (10t+π/6), 2/2m, 0,1πs) 7. *Υλικό σημείο μάζας m = 0,01 kg εκτελεί απλή αρμονική ταλάντωση και η ολική του ενέργεια είναι Ε = J. Η απομάκρυνση χ του υλικού σημείου από τη θέση ισορροπίας του είναι ημιτονική συνάρτηση του χρόνου και η επιτάχυνσή του α συνδέεται με την απομάκρυνση από τη θέση ισορροπίας του με τη σχέση α = -16χ (στο SI). α. Να βρείτε την περίοδο και το πλάτος της ταλάντωσης. β. Να γράψετε την εξίσωση της απομάκρυνσης χ σε συνάρτηση με το χρόνο αν για tο =0 το υλικό σημείο έχει U= K, χ>0 και κινείται κατά τη αρνητική κατεύθυνση. [Τ =π/2 s, Α = 0,2 m, χ= 0,2 ημ (4t+ 3π/4) (SI) 8. *Σώμα μάζας εκτελεί απλή αρμονική ταλάντωση. Η επιτάχυνση του σώματος στη θέση Κ και στη θέση Λ είναι ακ=αmax 3/2 και αλ=- αmax 2/2 αντίστοιχα. Αν ο ελάχιστος χρόνος μετάβασης του σώματος από τη θέση Κ στη θέση Λ είναι Δt=7/12 s, Α) Να βρεθούν η συχνότητα και η περίοδος της ταλάντωσης. Β) Αν η μέγιστη ταχύτητα είναι υmax= π m/s και το σώμα τη χρονική στιγμή t=0 βρίσκεται στη θέση Λ κινούμενο κατά τη αρνητική φορά, να γράψετε την εξίσωση της απομάκρυνσης της ταλάντωσης συναρτήσει του χρόνου. (2 sec, 0.5 Hz, 1.ημ(πt+3π/4) 7
9 9. Το διάγραμμα του σχήματος απεικονίζει την κινητική ενέργεια ενός σώματος μάζας m= 2 kg που εκτελεί απλή αρμονική ταλάντωση, σε συνάρτηση με την απομάκρυνσή του από τη θέση ισορροπίας του. Τη χρονική στιγμή t =0 το σώμα βρίσκεται στη θέση χ1=- 0,3 m και τη χρονική στιγμή t=π/20 s βρίσκεται για πρώτη φορά στη θέση χ1=+ 0,3 m α) Να βρείτε τη σχέση που περιγράφει τη συνάρτηση του διαγράμματος β) Να υπολογίσετε τη μέγιστη τιμή της δύναμης επαναφοράς που δέχεται το σώμα κατά την ταλάντωσή του και την εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο γ) Να υπολογίσετε τη δυναμική ενέργεια της ταλάντωσης στις θέσεις όπου η ταχύτητά του έχει μέτρο ίσο με υ=3 2 m/s και τη χρονική στιγμή στην οποία αποκτάται αυτή η τιμή για δεύτερη φορά. δ) Να παραστήσετε γραφικά τη δυναμική ενέργεια της ταλάντωσης σε συνάρτηση με την αλγεβρική τιμή της ταχύτητας. ( Κ=36- υ 2, 240 Ν, 0,3 ημ(20t+3π/2), 18 J, 3π/80 s ) 10. Η κινητική ενέργεια ενός σώματος που εκτελεί απλή αρμονική ταλάντωση μεταβάλλεται με το χρόνο, όπως στο διάγραμμα του σχήματος. Τη χρονική στιγμή t=0 το σώμα δέχεται δύναμη επαναφοράς που έχει αλγεβρική τιμή F= Ν. α) Να βρεθεί η μάζα του σώματος. β) Να γράψετε την εξίσωση της δύναμης επαναφοράς σε συνάρτηση με το χρόνο και να σχεδιάσετε το διάγραμμά της σε σχέση με το χρόνο γ) Να υπολογίσετε τη χρονική στιγμή που η δυναμική ενέργεια του σώματος μηδενίζεται για πρώτη φορά. (0.5 kg, ημ(20t+3π/4), π/80 s ) 11. *Σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση. Η στιγμιαία ταχύτητα υ του σώματος συνδέεται με την απομάκρυνση χ του σώματος με τη σχέση: υ 2 = 0,16-4 χ 2 (S.I). Ι. Να υπολογίσετε: α. Την περίοδο της ταλάντωσης. β. Την ενέργεια της ταλάντωσης. 2. Αν το σώμα μεταβεί από τη θέση χ1 = - 0,1 m στη θέση χ2 = +0,2 m, να υπολογίσετε το ελάχιστο και το μέγιστο χρονικό διάστημα που απαιτείται για την μετάβαση αυτή. ( π s, 0,16 J, π/3 s, 2π/3 s ) 12. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση με πλάτος Α. Η γραφική παράσταση της απομάκρυνσης σε συνάρτηση με το χρόνο δίνεται από το διάγραμμα. α) Να γραφεί η εξίσωση της ταχύτητας σε συνάρτηση με το χρόνο. β) Να γίνει η γραφική παράσταση της επιτάχυνσης σε συνάρτηση με το χρόνο. γ) Αν η μάζα του σώματος είναι m=1 kg να βρείτε την κινητική ενέργεια του σώματος στη θέση χ1=α/2 και να κάνετε το διάγραμμα της δυναμικής ενέργειας συναρτήσει της απομάκρυνσης χ. (2.συν(20t+3π/2), -40.ημ(20t+3π/2), 1,5 J) 8
10 13. Στο διπλανό σχήμα φαίνεται το διάγραμμα επιτάχυνσης χρόνου για ένα σώμα που εκτελεί απλή αρμονική ταλάντωση. Το μέτρο της μεταβολής της αλγεβρικής τιμής της ορμής ανάμεσα σε δύο διαδοχικές διελεύσεις του σώματος από τη θέση ισορροπίας είναι Δp=2π kgm/s. Να βρεθούν: Α. η αρχική φάση της ταλάντωσης. B. το πλάτος της ταλάντωσης και η μάζα του σώματος Γ. ο ρυθμός μεταβολής της ορμής του σώματος τη χρονική στιγμή t1 που η επιτάχυνση είναι 25 m/s 2 Δ. ο ελάχιστος χρόνος για να μεταβεί το σώμα από τη θέση που έχει επιτάχυνση α1= 50 m/s 2 στη θέση που έχει επιτάχυνση α2= 25 3 m/s 2. Δίνεται π 2 = * Στο διπλανό σχήμα φαίνεται η γραφική παράσταση της δύναμης επαναφοράς που δέχεται ένα σώμα κατά τη διάρκεια της απλής αρμονικής ταλάντωσής του, σε συνάρτηση με την απομάκρυνσή του από τη θέση ισορροπίας. Τη χρονική στιγμή t = 0 το σώμα βρίσκεται στη θέση χ1 = - 0,1 m και επιβραδύνεται με επιβράδυνση α1 = + 2,5 m/s 2. Να υπολογίσετε: α) τη γωνιακή συχνότητα και την ολική ενέργεια της ταλάντωσης β) την αρχική φάση της ταλάντωσης,να γράψετε την εξίσωση της απομάκρυνσης σε συνάρτηση με τον χρόνο και να σχεδιάσετε το διάγραμμα της. γ) την κινητική ενέργεια του σώματος τη στιγμή που το μέτρο της δύναμης επαναφοράς ισούται με το μισό της μέγιστης τιμής της. (5r/s, 1J, 0,2ημ(5t+7π/6), 0,75 J ) 15. * Σώμα μάζας m = 1 kg είναι δεμένο στο ένα άκρο οριζόντιου ελατηρίου σταθεράς k = 100 Ν/m, το άλλο άκρο του οποίου είναι στερεωμένο σε κατακόρυφο τοίχο. Το σώμα μπορεί να κινείται πάνω σε οριζόντιο επίπεδο χωρίς τριβές. Εκτρέπουμε το σώμα από τη θέση ισορροπίας του κατά χ1 = 0,1 3 m και τη χρονική στιγμή t= 0 το εκτοξεύουμε από τη θέση αυτή με ταχύτητα μέτρου υ1 = 1 m/s, όπως φαίνεται στο σχήμα. α) Να υπολογίσετε το πλάτος και την αρχική φάση της ταλάντωσής του. β) Να γράψετε τις εξισώσεις της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης του σώματος σε συνάρτηση με το χρόνο και να σχεδιάσετε το διάγραμμα της επιτάχυνσης σε συνάρτηση με το χρόνο και τη μετατόπιση γ) Να υπολογίσετε το έργο της δύναμης επαναφοράς από τη στιγμή της εκτόξευσης του σώματος μέχρι τη στιγμή που διέρχεται για πρώτη φορά από τη θέση χ2 =- Α / 2 όπου Α το πλάτος της ταλάντωσης. (0,2m, π/3, 0,2ημ(10t+π/3), 1J ) 9
11 16. * Ένα σώμα ισορροπεί δεμένο στο κάτω άκρο ιδανικού ελατηρίου του οποίου το πάνω άκρο είναι ακλόνητα συνδεδεμένο. Στη θέση ισορροπίας του σώματος το ελατήριο είναι επιμηκυμένο κατά Δχ = 0,1 m. Απομακρύνουμε το σώμα προς τα κάτω από τη θέση ισορροπίας του κατά d = 0,2 m και το αφήνουμε τη χρονική στιγμή t=0 ελεύθερο να κινηθεί χωρίς να έχει αρχική ταχύτητα. Α. Να αποδείξετε ότι το σώμα θα εκτελέσει απλή αρμονική ταλάντωση και να υπολογίσετε την περίοδo Β. Να βρείτε τις εξισώσεις της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης σαν συνάρτηση του χρόνου επιλέγοντας σαν θετική φορά τη φορά του βάρους του σώματος. Γ. Να βρείτε το χρονικό διάστημα που το ελατήριο είναι συμπιεσμένο μέσα σε μια περίοδο Δ. Να υπολογίσετε την ταχύτητα του σώματος όταν το ελατήριο δεν ασκεί δύναμη στο σώμα. Ε. Να υπολογίσετε την ταχύτητα του σώματος όταν το βάρος του είναι ίσο με την δύναμη του ελατηρίου. Δίνονται: g = 10 m/s 2. Θεωρήστε αμελητέες τις τριβές.. (π/5 sec, 0.2ημ(10t+π/2), π/15 sec,± 3m/s, ±2m/s ) 17. * Το ένα άκρο κατακόρυφου ελατηρίου σταθεράς Κ = 100 Ν/m στερεώνεται ακλόνητα σε οροφή, ενώ στο ελεύθερο άκρο του προσδένεται σώμα μάζας m = 1 kg. Ανυψώνουμε το σώμα κατακόρυφα, ώστε το ελατήριο να αποκτήσει το φυσικό του μήκος, και του δίνουμε ταχύτητα υ= 3m/s με φορά προς τη θέση ισορροπίας του συστήματος, τη στιγμή t=0, λαμβάνοντας σαν θετική φορά αυτή προς τα πάνω. Α. Nα βρείτε την εξίσωση της απομάκρυνσης χ=f(t) του συστήματος Β. Πότε το σύστημα σταματάει στιγμιαία για πρώτη φορά ;Πόση είναι τότε η δυναμική ενέργεια του ελατηρίου; Γ. Να γραφεί η σχέση που δίνει την κινητική ενέργεια του συστήματος με το χρόνο ; Δ. Που βρίσκεται το σώμα, πόση είναι η ταχύτητα και πόση η συνισταμένη δύναμη πάνω του τη στιγμή t1=π/6s ; E. Να υπολογίσετε το έργο της δύναμης του ελατηρίου κατά την μετατόπιση του σώματος από το σημείο εκκίνησης μέχρι το κατώτερo σημείο της τροχιάς του Δίνεται g=10m/s 2. (0,2ημ(10t+5π/6), π/15s, 4,5J, 0,2m, 0, -20N, - 4,5J) 18. Σώμα μάζας m=1 kg είναι στερεωμένο στο ελεύθερο άκρο του κατακόρυφου ελατηρίου και το άλλο άκρο είναι στερεωμένο στο έδαφος. Το σύστημα εκτελεί απλή αρμονική ταλάντωση και θωρούμε θετική φορά κίνησης προς τα πάνω. Στο διάγραμμα του σχήματος δίνεται η γραφική παράσταση ταχύτητας χρόνου για την ταλάντωση του σώματος. α) Να υπολογίσετε το πλάτος της ταλάντωσης και τη σταθερά k του ελατηρίου. β) Να γράψετε την εξίσωση επιτάχυνσης χρόνου και να την παραστήσετε γραφικά. γ) Να υπολογίσετε τις ελάχιστες και τις μέγιστες (κατά μέτρο) τιμές της δύναμης επαναφοράς και της δύναμης που ασκεί το ελατήριο στο σώμα, κατά τη διάρκεια της ταλάντωσής του. δ) Να υπολογίσετε τη μεταβολή της δυναμικής ενέργειας της ταλάντωσης από τη χρονική στιγμή t=0 έως τη χρονική στιγμή t1 = π/30 s ε) Να υπολογίσετε την επί τοις εκατό μεταβολή της κινητικής ενέργειας του σώματος από τη χρονική t= 0 μέχρι τη χρονική στιγμή t2 = π/40 s. Δίνεται g=10 m/s 2 (0.1 m, 100 N/m, 0 N, 10 N, 0 N, 20 N, J, -50% ) 10
12 19. Σώμα μάζας m = 2 kg είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k και ισορροπεί με το ελατήριο επιμηκυμένο κατά χ1 = 0,1 m, όπως φαίνεται στο διπλανό σχήμα. Μετακινούμε το σώμα προς τα πάνω κατά Δχ = 0,2 m, μέχρι μία θέση όπου μηδενίζεται στιγμιαία η ταχύτητά του και τη στιγμή εκείνη, που τη θεωρούμε t = 0, το αφήνουμε ελεύθερο. α) Να αποδείξετε ότι το σώμα θα εκτελέσει απλή αρμονική ταλάντωση από τη στιγμή που το αφήσαμε ελεύθερο και να υπολογίσετε την περίοδο της ταλάντωσης. β) Να βρείτε την εξίσωση της απομάκρυνσης χ και της ταχύτητας ταλάντωσης σε σχέση με το χρόνο και να κάνετε το διάγραμμα της απομάκρυνσης για δύο περιόδους. Θεωρήστε θετική φορά αυτή προς τα πάνω. γ) Να υπολογίσετε τη δυναμική ενέργεια του ελατηρίου και τη δυναμική ενέργεια της ταλάντωσης τη χρονική στιγμή t1 = Τ/2, όπου Τ η περίοδος της ταλάντωσης.. δ) Να υπολογίσετε το έργο της δύναμης επαναφοράς και το έργο της δύναμης του ελατηρίου από τη χρονική στιγμή t= 0 μέχρι τη χρονική στιγμή που το σώμα διέρχεται από τη θέση ισορροπίας του για πρώτη φορά. ε) Να βρείτε τη χρονική στιγμή που το σώμα διέρχεται για πρώτη φορά από τη θέση χ= -0,1m. Στ) Να βρείτε τη θέση όπου η κινητική ενέργεια ταλάντωσης είναι τριπλάσια της δυναμικής ενέργειας ταλάντωσης για πρώτη φορά. Πόση είναι στη θέση αυτή η δυναμική ενέργεια του ελατηρίου ; Δίνεται: g = 10 m/s 2. Θεωρήστε αμελητέες τις πάσης φύσεως τριβές. 20. Ένα σώμα μάζας m=2 kg ισορροπεί δεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=50 N/m, του οποίου το κάτω άκρο είναι στερεωμένο στο δάπεδο. Εκτρέπουμε κατακόρυφα το σώμα προς τα πάνω μέχρι το φυσικό μήκος του ελατηρίου (βλέπε σχήμα) και το αφήνουμε ελεύθερο. Να βρεθούν: Α) το πλάτος της ταλάντωσης του σώματος. Β) η ενέργεια που δαπανήθηκε για να εκτρέψουμε το σώμα από τη θέση ισορροπίας του μέχρι τη θέση του φυσικού μήκους του ελατηρίου. Γ) η μέγιστη δυναμική ενέργεια της ταλάντωσης και η μέγιστη δυναμική ενέργεια του ελατηρίου κατά τη διάρκεια της ταλάντωσης. Δ) η χρονική στιγμή κατά την οποία το σώμα θα αποκτήσει ταχύτητα μέτρου υ= 3 m/s για δεύτερη φορά. Θεωρείστε θετική φορά προς τα πάνω. Δίνεται g = 10 m/s 2 11
13 21. * Το σώμα μάζας m = 2 kg του διπλανού σχήματος είναι στερεωμένο στο ένα άκρο ελατηρίου σταθεράς k, το άλλο άκρο του οποίου είναι δεμένο σε ακλόνητο σημείο. Το σώμα βρίσκεται σε επαφή με το λείο κεκλιμένο επίπεδο και αρχικά ισορροπεί ακίνητο. Εκτρέπουμε το σώμα από τη θέση ισορροπίας του κατά χ1 με φορά προς τα πάνω και τη χρονική στιγμή t = 0 το αφήνουμε ελεύθερο να κινηθεί χωρίς αρχική ταχύτητα από τη θέση που το εκτρέψαμε. Το σώμα εκτελεί ταλάντωση, η μέγιστη κινητική ενέργεια της οποίας ισούται με Kmax = 9 J και επιτυγχάνεται μετά από χρόνο Δt = 0,05π s αφότου τ' αφήσαμε ελεύθερο. α) Να αποδείξετε ότι η ταλάντωση του σώματος είναι απλή αρμονική και να υπολογίσετε τη μέγιστη ταχύτητά του. β) Να γράψετε την εξίσωση της απομάκρυνσης του σώματος από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο. γ) Να υπολογίσετε το μέτρο του ρυθμού μεταβολής της ορμής του σώματος, τη στιγμή που η δυναμική ενέργεια της ταλάντωσης ισούται με το μισό της μέγιστης τιμής της. δ) Να υπολογίσετε το ρυθμό μεταβολής της ταχύτητας τις χρονικές στιγμές που η δυναμική ενέργεια γίνεται μέγιστη. ε) Να βρείτε τη χρονική στιγμή που περνά για πρώτη φορά από τη θέση χ=-α/2. Δίνεται: g = 10 m/s 2. Θεωρήστε αμελητέες τις τριβές. (3 m/s, 0,3ημ (10t+π/2), 30 2 Ν) 22. Στο διπλανό σχήμα, το ένα άκρο του ελατηρίου σταθεράς k=200 N/m είναι ακλόνητα στερεωμένο στη βάση λείου κεκλιμένου επιπέδου, ενώ στο ελεύθερο άκρο του ισορροπεί δεμένο σώμα μάζας m = 2 kg. Το κεκλιμένο επίπεδο σχηματίζει γωνία φ = 30 o με τον ορίζοντα. Συμπιέζουμε το ελατήριο επιπλέον κατά.χο = 0,1 m και τη χρονική στιγμή t=0, εκτοξεύουμε το σώμα με ταχύτητα υο = 3 m/s όπως στο σχήμα. α) Να αποδείξετε ότι το σύστημα εκτελεί απλή αρμονική ταλάντωση και να γράψετε την εξίσωση της απομάκρυνσης του σώματος. Θεωρήστε θετική φορά τη φορά της ταχύτητας υο. β) Να υπολογίσετε την επιτάχυνση του σώματος τη στιγμή που το ελατήριο αποκτά το φυσικό του μήκος για πρώτη φορά. γ) Να υπολογίσετε το λόγο της κινητικής ενέργειας του σώματος προς τη δυναμική ενέργεια ταλάντωσης τις στιγμές που ο ρυθμός μεταβολής της ταχύτητας του σώματος έχει μέτρο, ίσο με 10 m/s 2. δ) Να βρείτε τη χρονική στιγμή που ο ταλαντωτής διέρχεται από τη θέση +Α για πρώτη φορά. Δίνεται g=10 m/s 2. [ 0.2 ημ(10t+11π/6), -5 m/s 2, 3, π/15 s ) 12
14 23. Η μια άκρη ιδανικού ελατηρίου σταθεράς k=100n/m είναι στερεωμένη στο πάνω μέρος του πλάγιου επιπέδου γωνίας φ=30 ο, όπως στο σχήμα. Από ένα σημείο του πλάγιου επιπέδου που απέχει s=0,25m από το ελεύθερο άκρο του ελατηρίου, εκτοξεύεται με αρχική ταχύτητα υο=2m/s, κατά μήκος του άξονα του ελατηρίου προς τα πάνω ένα σώμα Σ μάζας m=2kg. Όταν το σώμα ακουμπήσει στο ελατήριο, ενώνεται με αυτό και αρχίζει να εκτελεί αρμονική ταλάντωση α) Να βρείτε την ταχύτητα του σώματος τη στιγμή που έρχεται σε επαφή με το ελατήριο. β) Να βρείτε τη μέγιστη ταχύτητα του σώματος. γ) Να γράψετε τη συνάρτηση της απομάκρυνσης της ταλάντωσης σε σχέση με το χρόνο, θεωρώντας t=0 τη στιγμή της ένωσης του σώματος με το ελατήριο και τα θετικά προς τα πάνω. δ) Να βρείτε το ρυθμό μεταβολής κινητικής ενέργειας του σώματος τη στιγμή που διέρχεται από το σημείο εκτόξευσης για δεύτερη φορά. Δίνεται g=10m/s Σώμα μάζας m=1 kg ισορροπεί πάνω σε λείο οριζόντιο επίπεδο, στερεωμένο στα άκρα δύο οριζόντιων ελατηρίων της ίδιας σταθεράς Κ, όπως φαίνεται στο σχήμα. Τα δύο ελατήρια έχουν το φυσικό τους μήκος. Όταν το σώμα εκτραπεί από τη θέση ισορροπίας του κατά μήκος του κοινού άξονα των δύο ελατηρίων, εκτελεί απλή αρμονική ταλάντωση. Το διάγραμμα του σχήματος παριστάνει τη μεταβολή της δύναμης επαναφοράς F που δέχεται το σώμα, σε συνάρτηση με το χρόνο α. Γιατί το σύστημα εκτελεί απλή αρμονική ταλάντωση; Να υπολογίσετε το πλάτος της ταλάντωσης του σώματος. β. Να αποδείξετε ότι η ταλάντωση έχει αρχική φάση και να προσδιορίσετε την τιμή της ταλάντωσης. γ. Να γράψετε την εξίσωση της απομάκρυνσης του σώματος από τη θέση ισορροπίας του, σε συνάρτηση με το χρόνο, και να παραστήσετε γραφικά την απομάκρυνση, σε συνάρτηση με το χρόνο. δ. Να υπολογίσετε τη σταθερά Κ του κάθε ελατηρίου. (0,2 m, 3π/2, 0,2ημ(20t+3π/2), 200 Ν/m) 13
15 25. Ένα σώμα μάζας m = 1 kg ισορροπεί πάνω σε λείο οριζόντιο επίπεδο, στερεωμένο στα άκρα δύο οριζόντιων ελατηρίων σταθεράς Κ1=250 Ν/ m και Κ2 αντίστοιχα, όπως φαίνεται στο σχήμα. Το μήκος κάθε ελατηρίου είναι μεγαλύτερο από το φυσικό του μήκος στη θέση ισορροπίας., δηλαδή είναι επιμηκυμένα. Απομακρύνουμε το σώμα από τη θέση ισορροπίας του προς τα δεξιά κατά χ (θετική φορά )και μετά το αφήνουμε ελεύθερο. Το σώμα τη χρονική στιγμή t=0 βρίσκεται στη θέση χ1=- Α/2 (Α πλάτος ταλάντωσης) κινούμενο προς την ακραία θέση ταλάντωσης χ= - Α και φθάνει στη θέση ισορροπίας του για πρώτη φορά τη χρονική στιγμή t = π/24 s, έχοντας ταχύτητα στη θέση αυτή υ=+ 8 m/s. Α) Να αποδείξετε ότι το σώμα θα εκτελέσει απλή αρμονική ταλάντωση και να υπολογίσετε την τιμή της σταθεράς Κ2 του ελατηρίου. Β) Να γράψετε την εξίσωση της ταχύτητας του σώματος από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο Γ) Να βρεθεί η χρονική στιγμή κατά την οποία η δυναμική και η κινητική ενέργεια ταλάντωσης θα γίνουν για πρώτη φορά ίσες. Δ) Να υπολογίσετε το μέτρο της ταχύτητας του σώματος τη στιγμή που η δύναμη επαναφοράς ισούται με F= Ν. 26. Σώμα μάζας m=1kg ισορροπεί συνδεδεμένο στα άκρα δύο κατακόρυφων ιδανικών ελατηρίων, έχοντας το ίδιο φυσικό μήκος, όπως φαίνεται στο σχήμα. Στη θέση που η μάζα ισορροπεί το ελατήριο σταθεράς k1 είναι τεντωμένο και το ελατήριο σταθεράς k2 είναι συσπειρωμένο. Οι σταθερές των ελατηρίων είναι k1 = 25 Ν/m και k2 = 75 Ν/m. Απομακρύνουμε τη μάζα από τη θέση ισορροπίας της κατά τη διεύθυνση του άξονα των ελατηρίων και από τη θέση φυσικού μήκους των δύο ελατηρίων και τη χρονική στιγμή t=0, την προσδίνουμε ταχύτητα υ= 3 m/s με φορά προς τη θέση ισορροπίας, οποία θεωρείται αρνητική. α. Να δείξετε ότι το σύστημα θα εκτελέσει απλή αρμονική ταλάντωση και να υπολογίστε την περίοδο Τ. β. Να γράψετε την εξίσωση της απομάκρυνσης της ταλάντωσης και να σχεδιάσετε το διάγραμμα της σε συνάρτηση με το χρόνο γ. Να βρείτε τη χρονική στιγμή που το σώμα περνά για 3 η φορά από τη θέση ισορροπίας της ταλάντωσης και τον ρυθμό μεταβολής της κινητικής ενέργειας στη θέση αυτή. δ. Κάποια χρονική στιγμή που το σώμα περνά από τη θέση ισορροπίας, κόβουμε και απομακρύνουμε το ελατήριο σταθεράς Κ2, χωρίς απώλειες ενέργειας. Να βρείτε τη μέγιστη ταχύτητα της νέας ταλάντωσης και τη μέγιστη δύναμη του ελατηρίου. (g = 10 m/s 2 ). 14
16 27. Στα δύο άκρα λείου επιπέδου στερεώνουμε τα άκρα δύο ιδανικών ελατηρίων με σταθερές k1=60 N/m και k2=140 N/m, αντίστοιχα. Στα ελεύθερα άκρα των ελατηρίων, δένουμε ένα σώμα Σ μάζας m = 2 kg ώστε τα ελατήρια να έχουν το φυσικό τους μήκος (όπως φαίνεται στο σχήμα). Εκτρέπουμε το σώμα Σ κατά Α = 0,2 m προς τα δεξιά και τη χρονική στιγμή tο=0 αφήνουμε το σώμα ελεύθερο. Δ1. Να αποδείξετε ότι το σώμα Σ εκτελεί απλή αρμονική ταλάντωση και να γράψετε τη σχέση που δίνει την απομάκρυνση του σώματος Σ από τη θέση ισορροπίας σε συνάρτηση με το χρόνο. Να θεωρήσετε θετική την φορά προς τα δεξιά Δ2. Να βρείτε το ρυθμό μεταβολής της κινητικής ενέργειας τη χρονική στιγμή t1=π/60 sec. Δ3. Να υπολογίσετε την ταχύτητα του σώματος στη θέση χ=+α/2. Δ4. Τη στιγμή που το ελατήριο βρίσκεται στη θέση x = +Α/2 αφαιρείται ακαριαία το ελατήριο k2, χωρίς απώλειες ενέργειας. Να υπολογίσετε την ενέργεια της νέας ταλάντωσης. 28. Το σύστημα που φαίνεται στο διπλανό σχήμα ισορροπεί στο λείο κεκλιμένο επίπεδο που έχει γωνία κλίσης φ=30. Οι σταθερές των ελατηρίων είναι k1 = 150 Ν/m και k2 = 250 Ν/m, ενώ η μάζα του σώματος είναι m = 4 kg. Στη θέση ισορροπίας το ελατήριο k1 είναι συσπειρωμένο κατά χ1 ενώ το ελατήριο k2 επιμηκυμένο, φυσικά πάλι κατά χ1. Σπρώχνουμε το σώμα παράλληλα στο κεκλιμένο επίπεδο, έτσι ώστε τα ελατήρια να αποκτήσουν το φυσικό τους μήκος, και τη χρονική στιγμή t=0 το αφήνουμε ελεύθερο, με θετική φορά προς τα πάνω. α) Να βρείτε τη δυναμική ενέργεια κάθε ελατηρίου όταν το σώμα ισορροπεί. β) Να αποδείξετε ότι, μόλις αφήσουμε το σώμα ελεύθερο, θα εκτελέσει απλή αρμονική ταλάντωση, της οποίας να βρείτε την περίοδο. γ) Να γράψετε τη χρονική εξίσωση της επιτάχυνσης και να την παραστήσετε γραφικά για μια περίοδο. δ) Να βρείτε το μέγιστο ρυθμό μεταβολής της ορμής του σώματος. Δίνεται: g = 10 m/s 2. [α) 3/16 J, 5/16 J, β) Τ = π/5 s, γ) α = -5ημ (l0t +π/ 2) (S.I.), 20 Ν] 29. Σώμα μάζας m = 1 kg είναι δεμένο στο ελεύθερο άκρο οριζόντιου ελατηρίου σταθεράς k = 100 N/m και μπορεί να κινείται σε λείο οριζόντιο επίπεδο. Το σώμα δέχεται συνεχώς σταθερή οριζόντια δύναμη μέτρου F = 10Ν όπως στο σχήμα. Τη χρονική στιγμή t=0 το σώμα βρίσκεται σε απόσταση x1=+0,3 m από τη θέση φυσικού μήκους του ελατηρίου και κινείται προς την αρνητική κατεύθυνση με ταχύτητα υ1=-2 3 m/s. α) Να αποδείξετε ότι η σταθερά επαναφοράς της ταλάντωσης είναι ίση με τη σταθερά k του ελατηρίου. β) Να γράψετε την εξίσωση της απομάκρυνσης χ σε συνάρτηση με το χρόνο και να την παραστήσετε γραφικά σε σχέση με το χρόνο. γ) Τη χρονική στιγμή που η δυναμική ενέργεια ταλάντωσης είναι ίση με την κινητική για πρώτη φορά να βρείτε το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος. δ) Κάποια στιγμή που η δύναμη του ελατηρίου είναι μέγιστη, η δύναμη F καταργείται. Να υπολογίσετε το νέο πλάτος της ταλάντωσης του σώματος. 15
17 30. Tο σώμα μάζας m=1 kg του σχήματος ισορροπεί δεμένο στο άκρο κατακόρυφου ελατηρίου σταθεράς k = 100 N/m, που κρέμεται από οροφή, με την επίδραση κατακόρυφης δύναμης μέτρου F = 10 Ν, όπως στο σχήμα. Τη χρονική στιγμή t =0 η δύναμη καταργείται, και το σώμα εκτελεί κατακόρυφη απλή αρμονική ταλάντωση. α) Να υπολογίσετε το πλάτος της ταλάντωσης του σώματος. β) Να υπολογίσετε τη δύναμη επαναφοράς στη θέση που το σώμα βρίσκεται σε απόσταση Δl = 15 cm κάτω από τη θέση φυσικού μήκους (Θ. Φ.Μ.) του ελατηρίου. γ) Να παραστήσετε γραφικά την αλγεβρική τιμή της δύναμης του ελατηρίου σε συνάρτηση με την απομάκρυνση χ του σώματος από τη θέση ισορροπίας του. δ) Να παραστήσετε γραφικά την κινητική ενέργεια του σώματος συναρτήσει του χρόνου. Θεωρήστε θετική φορά προς τα κάτω. Δίνεται g = 10 m/s 2. (0.1 m, - 5 N, -100 x-10, 0.5 συν 2 (10t+π/2) 31. Κύβος μάζας m=10 kg ισορροπεί τοποθετημένος πάνω σε λείο οριζόντιο επίπεδο. Στη μια κατακόρυφη έδρα του κύβου είναι δεμένη η μια άκρη ιδανικού οριζόντιου ελατηρίου σταθεράς Κ = 250 Ν / m, του οποίου η άλλη άκρη είναι δεμένη σε σταθερό σημείο κατακόρυφου τοίχου. Το ελατήριο βρίσκεται στο φυσικό του μήκος. Στην απέναντι κατακόρυφη έδρα του κύβου είναι δεμένο μη ελαστικό και αβαρές νήμα το οποίο έχει όριο θραύσης Τθρ =120 Ν. Μέσω του νήματος ασκούμε στο σώμα δύναμη κατά τη διεύθυνση του άξονα του ελατηρίου και με φορά τέτοια ώστε το ελατήριο να επιμηκύνεται. Το μέτρο της δύναμης μεταβάλλεται με την επιμήκυνση χ του ελατηρίου σύμφωνα με την εξίσωση F = x (S.Ι). Να βρείτε α. τη δυναμική ενέργεια του ελατηρίου τη στιγμή που κόβεται το νήμα. β. το πλάτος της ταλάντωσης που θα εκτελέσει το σύστημα ελατήριο κύβος, καθώς και την εξίσωση της απομάκρυνσης της ταλάντωσης σε συνάρτηση με το χρόνο, αν για t=0 είναι η στιγμή κόβεται το νήμα και θετική φορά αυτή της επιμήκυνσης του ελατηρίου. γ. μετά πόσο χρόνο από τη στιγμή t=0 που κόβεται το νήμα θα περάσει ο κύβος από τη θέση ισορροπίας του για πρώτη φορά; Να θεωρήσετε άξονα χ χ με αρχή τη θέση ισορροπίας του κύβου και θετική φορά εκείνη κατά την οποία το ελατήριο επιμηκύνεται. (5 J, 0.4 m, 0,4ημ(5t+π/6), π/6 s) 32. Δύο σώματα με μάζες m1 = 2 kg και m2 = 6 kg είναι αναρτημένα από το ελατήριο σταθεράς k = 200 Ν/m του ακόλουθου σχήματος. Εκτρέπουμε το σώμα μάζας m2 από τη θέση ισορροπίας του κατά ψ = 0,2 m προς τα κάτω και στη συνέχεια το αφήνουμε ελεύθερο Α) Να υπολογίσετε την περίοδο της ταλάντωσης που θα εκτελέσει το σύστημα των δύο σωμάτων. Β) Να γράφετε την εξίσωση που δίνει την απομάκρυνση του σώματος μάζας m2 από τη θέση ισορροπίας του, καθώς και την εξίσωση που υπολογίζει την τάση του νήματος Ν, συναρτήσει του χρόνου. Να θεωρήσετε ως αρχή των χρόνων τη στιγμή κατά την οποία αφήσαμε τo σώμα μάζας m2 ελεύθερο. Γ) Να υπολογίσετε το μέγιστο πλάτος ταλάντωσης του σώματος m2, ώστε να μη χαλαρώνει το νήμα Δίνεται g = 10 m/s 2. Το νήμα είναι μη εκτατό με μεγάλο όριο θραύσης. (0,4π s, 0.2ημ(5t+π/2), ημ(5t+π/2), 0,4 m) 16
18 33. Τα σώματα του διπλανού σχήματος έχουν μάζες m1 =10 kg και m2 = 4 kg, είναι ενωμένα με αβαρές νήμα και αρχικά ισορροπούν ακίνητα με το σώμα μάζας m2 να απέχει από το έδαφος απόσταση h = 1,25 m. Το ένα άκρο του ελατηρίου σταθεράς k είναι στερεωμένο στην οροφή, ενώ στο άλλο άκρο είναι δεμένο το σώμα μάζας m1. Τη χρονική στιγμή t = 0 κόβουμε το νήμα. Τη στιγμή που το σώμα μάζας m2 φτάνει στο έδαφος, το σώμα μάζας m1 φτάνει για πρώτη φορά σε θέση μέγιστης απομάκρυνσης. Να υπολογίσετε: α) την περίοδο της ταλάντωσης του σώματος μάζας m1, β) τη μέγιστη ταχύτητα του σώματος μάζας m1, γ) την εξίσωση απομάκρυνσης του σώματος μάζας m1 από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο. δ) τη χρονικό διάστημα από τη θέση χ1=-α/2 μέχρι τη θέση χ2=+α/2 για πρώτη φορά. Δίνονται: g = 10 m/s 2, π 2 = 10. Θεωρήστε αμελητέες τις τριβές. ( 1s, 0,2π m/s, 0,1ημ(2πt + 3π/2)] 34. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k1=40ν/m, ενώ εφάπτεται στο ελεύθερο άκρο ενός δεύτερου ελατηρίου σταθεράς k2=120ν/m (χωρίς να έχει δεθεί), το οποίο έχει το φυσικό μήκος του, όπως στο διπλανό σχήμα. Εκτρέπουμε το σώμα, παράλληλα στο επίπεδο, προς τα πάνω κατά 0,4m και τη στιγμή t=0 αφήνεται να κινηθεί. i) Να υπολογιστεί η περίοδος της ταλάντωση ii) Να βρεθεί η εξίσωσης της απομάκρυνσης x=f(t) από την αρχική θέση ισορροπίας του και να γίνει η γραφική της παράσταση, σε βαθμολογημένους άξονες, μέχρι να ολοκληρωθεί μια ταλάντωση, παίρνοντας την αρχική απομάκρυνση ως θετική. iii) Για τη στιγμή που το σώμα έχει διανύσει διάστημα s=0,5m, να υπολογιστούν: α) Η δυναμική ενέργεια ταλάντωσης και β) Ο ρυθμός μεταβολής της. Δίνονται g=10m/s 2 και π Ένα σώμα είναι δεμένο στο κατώτερο άκρο ελατηρίου και εκτελεί αρμονική ταλάντωση με θετικά προς τα κάτω. Στο διάγραμμα βλέπουμε τη μεταβολή της δυναμικής ενέργειας λόγω παραμόρφωσης του ελατηρίου σε συνάρτηση με την απομάκρυνση χ της ταλάντωσης του σώματος. α. Να βρεθεί η σταθερά του ελατηρίου και η περίοδος της ταλάντωσης. β. Με τι ρυθμό μεταβάλλεται η δυναμική ενέργεια λόγω παραμόρφωσης του ελατηρίου τη στιγμή που το σώμα διέρχεται από τη θέση ισορροπίας του κινούμενο προς τα θετικά; γ. Αν τη χρονική στιγμή t= 0 η δυναμική ενέργεια του ελατηρίου είναι ίση με τη μέγιστη κινητική ενέργεια του σώματος και αυξάνεται, να βρεθεί η αρχική φάση της ταλάντωσης. Δίνεται: g= 10 m/s 2. ( 200 Ν/m, 0,2π s, 40 J/s, π/6 ) 17
19 36. *Το σύστημα των δύο μαζών με το ελατήριο ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο, όπως φαίνεται στο σχήμα. Το ελατήριο θεωρείται ιδανικό με σταθερά Κ = 100 Ν/m, η μάζα του Α σώματος είναι m1 = 1 kg και του δευτέρου σώματος B είναι m2=2m1 και η γωνία κλίσης του κεκλιμένου επιπέδου είναι φ = 30. Ενώ το σύστημα είναι ακίνητο στη θέση ισορροπίας του, κόβουμε το νήμα, απομακρύνουμε το σώμα Β από τη θέση του και το σώμα Α αφήνεται ελεύθερο. α. Να δείξετε ότι το σύστημα ελατήριο -σώμα Α θα εκτελέσει απλή αρμονική ταλάντωση, να υπολογίσετε την περίοδο Τ και το πλάτος Α της ταλάντωσης. β. Να γράψετε την εξίσωση της δυναμικής ενέργειας της ταλάντωσης σε σχέση με το χρόνο, αν θεωρήσουμε ότι για t=0 το ταλαντούμενο σώμα διέρχεται από τη θέση χ=+α/2 κινούμενο κατά την αρνητική κατεύθυνση και να σχεδιάσετε το διάγραμμά της σε σχέση με το χρόνο. γ. Τη δύναμη του ελατηρίου και τη δύναμη ΣF επαναφοράς στις ακραίες θέσεις της ταλάντωσης. δ. Τη χρονική στιγμή που το σώμα Α περνά για δεύτερη φορά από τη θέση ισορροπίας της ταλάντωσης. Δίνεται g=10m/s 2. (0.2 π s, 0.1 m, 0.5ημ 2 (10t+5π/6), 7π/60 s) 37. Το ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωμένο σε οριζόντιο επίπεδο. Στο άλλο άκρο του συνδέεται σταθερά σώμα Σ1 μάζας Μ = 3kg. Πάνω στο σώμα Α είναι τοποθετημένο σώμα Σ2 μάζας m = 1 kg και το σύστημα ισορροπεί με το ελατήριο συσπειρωμένο από το φυσικό του μήκος κατά ψ1 = 0,4m. Στη συνέχεια εκτρέπουμε το σύστημα κατακόρυφα προς τα κάτω κατά ψ2 = 0,8m από τη θέση ισορροπίας του το αφήνουμε ελεύθερο τη χρονική στιγμή t = 0, θεωρώντας θετική φορά αυτή προς τα πάνω α) Να υπολογίσετε την γωνιακή συχνότητα ω της ταλάντωσης του συστήματος και τη σταθερά επαναφοράς D καθεμίας μάζας ξεχωριστά. β) Να δείξετε άτι το σώμα Β θα εγκαταλείψει το σώμα Α και να βρείτε τη θέση και την ταχύτητα που έχει εκείνη τη χρονική στιγμή. γ) Να υπολογίσετε τη χρονική στιγμή που το σώμα Β θα εγκαταλείψει το σώμα A Δίνεται η επιτάχυνση της βαρύτητας g = 10 m/s 2 (5r/s, 25N/m, 75 N/m, 0,4m, 2 3 m/s, 2π/15 s) 18
20 38. * Ένα σώμα Σ1 μάζας m1= 4,5 kg ισορροπεί σε λείο οριζόντιο επίπεδο στερεωμένο στο ελεύθερο άκρο οριζόντιου ελατηρίου σταθεράς K= 50 N/m όπως φαίνεται στο σχήμα. Τοποθετούμε δεύτερο σώμα Σ2 μάζας m2 = 3,5 kg δίπλα στο Σ1 και το σπρώχνουμε αργά, ώστε το ελατήριο να συμπιεστεί κατά d = 0,4 m, και την t = 0 αφήνουμε το σύστημα ελεύθερο να κινηθεί. Να βρείτε: Α. Σε ποια θέση χάνεται η επαφή μεταξύ των σωμάτων και ποια στιγμή συμβαίνει αυτό. Β. Την ταχύτητα του σώματος Σ2 μόλις χάνεται η επαφή.. Γ. Την περίοδο και το πλάτος της ταλάντωσης του Σ1 μετά το χάσιμο της επαφής. Δ. Την απόσταση μεταξύ των σωμάτων όταν το ελατήριο έχει τη μέγιστη επιμήκυνσή του για πρώτη φορά. ( π/5 s, 1 m/s, 0.6π s, 0.3 m ) 39. Το αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=400 N/mστερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ1 μάζας m1=3 kg, το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ1 τοποθετείται δεύτερο σώμα Σ2 μάζας m1=1 kg. Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου V και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή στη διάρκεια της ταλάντωσης. α) Να υπολογίσετε τη γωνιακή συχνότητα της ταλάντωσης καθώς και τις σταθερές ταλάντωσης D, D 1και D2 του συστήματος και των σωμάτων Σ1 και Σ2 αντίστοιχα. β) Να τοποθετήσετε το σύστημα σε μια τυχαία θέση της ταλάντωσής του, να σχεδιάσετε και να περιγράψετε σε τρία κατάλληλα σχήματα τις δυνάμεις, που δέχονται: i) το σύστημα Σ1 Σ2, ii) το Σ1 και iii) το Σ2. γ) Να παραστήσετε γραφικά την αλγεβρική τιμή της στατικής τριβής από το Σ1 στο Σ2 σε συνάρτηση με την απομάκρυνση από τη θέση ισορροπίας του, για πλάτος ταλάντωσης A=3cm. δ) Να υπολογίσετε τη μέγιστη τιμή της αρχικής ταχύτητας εκτόξευσης Vmax, του συστήματος των Σ1, Σ2 ώστε το σώμα Σ2 να μην ολισθήσει πάνω στο σώμα Σ1. Δίνεται η επιτάχυνση της βαρύτητας g= 10 m/s 2 και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ1 και Σ2 είναι μ=0,5. 19
21 ΕΙΔΙΚΕΣ ΠΕΡΙΠΩΣΕΙΣ 1 ) Ένα σώμα μάζας 2kg, είναι δεμένο στο άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k1=200ν/m. Ανεβάζουμε το σώμα κατακόρυφα προς τα πάνω φέρνοντάς το σε μια θέση Θ, όπου το ελατήριο έχει συσπειρωθεί κατά Δl=0,1m. Κάτω ακριβώς από το σώμα υπάρχει ένα δεύτερο ιδανικό ελατήριο, το πάνω άκρο του οποίου απέχει κατά d=0,2m από το σώμα, όπως στο σχήμα. Σε μια στιγμή tο=0, αφήνουμε το σώμα ελεύθερο να κινηθεί και παρατηρούμε ότι σταματά την προς τα κάτω κίνησή του, αφού μετατοπισθεί κατά 0,3m. i) Να αποδείξετε ότι το σώμα θα εκτελέσει ΑΑΤ, μέχρι να έρθει σε επαφή με το κάτω ελατήριο, υπολογίζοντας το πλάτος και την περίοδο ταλάντωσης. ii) Να αποδείξτε ότι η κίνηση του σώματος, όταν βρίσκεται σε επαφή με το κάτω ελατήριο είναι μια νέα ΑΑΤ, υπολογίζοντας επίσης το πλάτος και την περίοδο ταλάντωσης. iii) Ποια χρονική στιγμή το σώμα θα επανέρθει για πρώτη φορά στη θέση Θ; iv) Να υπολογιστούν οι ρυθμοί μεταβολής της ορμής του σώματος στην ανώτερη και στην κατώτερη θέση της τροχιάς του. Δίνεται g=10m/s 2. 2) Ένα σώμα Σ μάζας 1kg, βρίσκεται δεμένο στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου, το οποίο κρέμεται μέσα σε έναν ανελκυστήρα (ασανσέρ) το οποίο κατέρχεται με σταθερή επιτάχυνση α=2m/s 2. Στη διάρκεια της κίνησης το σώμα παραμένει «ακίνητο» ως προς το θάλαμο του ανελκυστήρα, απέχοντας 1m από τη βάση του. Σε μια στιγμή και ενώ η ταχύτητά του είναι υ=4m/s, ο θάλαμος συγκρούεται με το έδαφος, όπου και ακινητοποιείται ακαριαία. Δίνεται η σταθερά του ελατηρίου k=20ν/m και η επιτάχυνση της βαρύτητας g=10m/s 2. i) Στη διάρκεια της πτώσης του θαλάμου, το ελατήριο έχει το φυσικό του μήκος ή όχι; ii) Να περιγράψετε την κίνηση που θα κάνει το σώμα Σ, μετά την ακινητοποίηση του ανελκυστήρα. iii) Να αποδειχτεί ότι η κίνηση αυτή θα είναι ΑΑΤ. iv) Να εξετάσετε αν το σώμα Σ θα φτάσει στο δάπεδο του θαλάμου. 20
22 3) 4) 21
23 5) 6) 22
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
1. Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα.
 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
4. Σώμα Σ 1 μάζας m 1 =1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ=30 ο. Το σώμα Σ 1 είναι δεμένο στην άκρη
 1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο.
 1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
Εκφώνηση 1. α). β). γ). Επιλέξτε τη σωστή πρόταση και αιτιολογείστε.
 Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ.
 1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1 Κινηματική προσέγγιση
 1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 .. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
.. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΟΡΟΣΗΜΟ Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση x 5 3 cm. Να βρείτε την αρχική φάση φ 0
 Απλή Αρμονική Ταλάντωση ΚΕΦΑΛΑΙΟ 1 Σώμα που εκτελεί απλή αρμονική ταλάντωση και χρησιμοποιούμε τις εξισώσεις. 1.56 Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση
Απλή Αρμονική Ταλάντωση ΚΕΦΑΛΑΙΟ 1 Σώμα που εκτελεί απλή αρμονική ταλάντωση και χρησιμοποιούμε τις εξισώσεις. 1.56 Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Δ.
 1.1. Μηχανικές. Ομάδα Δ. 1.1.51. Συνάντηση σωμάτων που ταλαντώνονται. Τα σώματα Α και Β του σχήματος έχουν ίσες μάζες m 1 =m 2 =m=1kg. Τα δύο σώματα ισορροπούν πάνω στο λείο οριζόντιο δάπεδο, με τα ελατήρια
1.1. Μηχανικές. Ομάδα Δ. 1.1.51. Συνάντηση σωμάτων που ταλαντώνονται. Τα σώματα Α και Β του σχήματος έχουν ίσες μάζες m 1 =m 2 =m=1kg. Τα δύο σώματα ισορροπούν πάνω στο λείο οριζόντιο δάπεδο, με τα ελατήρια
α. β. γ. δ. Μονάδες 5 α. β. γ. δ. Μονάδες 5 α. ελαστική β. ανελαστική γ. πλαστική δ. έκκεντρη
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ. =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1. =8m /s συγκρούεται κεντρικά
 ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
5. Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με τον χρόνο.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης
 4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης 1 ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά κινείται με ταχύτητα
4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης 1 ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά κινείται με ταχύτητα
Ημερομηνία: Τετάρτη 26 Οκτωβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ 6/0/06 ΕΩΣ 30/0/06 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 6 Οκτωβρίου 06 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ 6/0/06 ΕΩΣ 30/0/06 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 6 Οκτωβρίου 06 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 2ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ
 F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F Στεφάνου Μ. 1 Φυσικός
 F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ
 ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. Α1. Κατά τη διάρκεια μιας
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. Α1. Κατά τη διάρκεια μιας
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΤΑΛΑΝΤΩΣΕΙΣ. . Ερωτήσεις αντιστοίχισης. Σχήμα 2 από τη θέση ισορροπίας του δίνεται από την εξίσωση x = Aημωt.
 ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
2. Σώμα εκτελεί Α.Α.Τ. και η εξίσωση της απομάκρυνσης σε σχέση με το χρόνο είναι:
 1. Σώμα εκτελεί Α.Α.Τ. με περίοδο 2 s και πλάτος ταλάντωσης 0,1 m. Τη χρονική στιγμή 0 το σώμα διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Να υ πολογιστούν: α) η συχνότητα και η γωνιακή συχνότητα
1. Σώμα εκτελεί Α.Α.Τ. με περίοδο 2 s και πλάτος ταλάντωσης 0,1 m. Τη χρονική στιγμή 0 το σώμα διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Να υ πολογιστούν: α) η συχνότητα και η γωνιακή συχνότητα
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ - ΑΣΚΗΣΕΙΣ
 ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΚΑΙ ΤΑΛΑΝΤΩΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΚΑΙ ΤΑΛΑΝΤΩΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α (μονάδες 25) Α1. Σε μια Α.Α.Τ. η εξίσωση της απομάκρυνσης είναι x=a.συνωt. Τη χρονική στιγμή
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΚΑΙ ΤΑΛΑΝΤΩΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α (μονάδες 25) Α1. Σε μια Α.Α.Τ. η εξίσωση της απομάκρυνσης είναι x=a.συνωt. Τη χρονική στιγμή
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
προς ένα ακίνητο σωμάτιο α (πυρήνας Ηe), το οποίο είναι ελεύθερο να κινηθεί,
 ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 24/09/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
Κρούσεις. Ομάδα Γ. Κρούσεις Ενέργεια Ταλάντωσης και Ελαστική κρούση Κρούση και τριβές Κεντρική ανελαστική κρούση
 . Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
. Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΛΥΣΕΙΣ. Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 01-013 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΟΦΟΙΤΟΙ ΗΜΕΡΟΜΗΝΙΑ: /10/1 ΘΕΜΑ 1 ο ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 01-013 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΟΦΟΙΤΟΙ ΗΜΕΡΟΜΗΝΙΑ: /10/1 ΘΕΜΑ 1 ο ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
α. Από τη μάζα του σώματος που ταλαντώνεται. β. Μόνο από τα πλάτη των επιμέρους απλών αρμονικών ταλαντώσεων.
 ιαγώνισμα στη φυσική θετικού προσανατολισμού Ύλη: μηχανικές ταλαντώσεις ιάρκεια 3 ώρες ΘΕΜΑ Α Στις προτάσεις Α1 έως Α8 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ιαγώνισμα στη φυσική θετικού προσανατολισμού Ύλη: μηχανικές ταλαντώσεις ιάρκεια 3 ώρες ΘΕΜΑ Α Στις προτάσεις Α1 έως Α8 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΚΕΦΑΛΑΙΟ 1ο: ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Όλα τα θέματα των πανελληνίων στις μηχανικές ταλαντώσεις έως και το 2014 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ. Ερωτήσεις Πολλαπλής Επιλογής
 έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
4.1. Κρούσεις. Κρούσεις. 4.1.Ταχύτητες κατά την ελαστική κρούση Η Ορμή είναι διάνυσμα. 4.3.Κρούση και Ενέργεια.
 4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
Φυσική Γ Λυκείου Θετικού Προσανατολισμού Σχ. έτος ο Διαγώνισμα Κρούσεις - Ταλαντώσεις Θέμα 1ο
 1ο Διαγώνισμα Κρούσεις - Ταλαντώσεις Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη ϕράση που τη συμπληρώνει σωστά.
1ο Διαγώνισμα Κρούσεις - Ταλαντώσεις Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη ϕράση που τη συμπληρώνει σωστά.
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
Θέμα 1 ο (Μονάδες 25)
 ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β
 1 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β 1) Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας ma, κινούμενο με ταχύτητα υα=3 m/s κατά
1 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β 1) Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας ma, κινούμενο με ταχύτητα υα=3 m/s κατά
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 4. α. β. ii. iii. 6. α.
 Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ F 2 F 3 F 1 F 4
 1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16
 ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16 Θέμα Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που
ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16 Θέμα Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ 2. έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε σταθερό σημείο.
 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση ΙΙ - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση ΙΙ - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Η απλή αρµονική ταλάντωση είναι κίνηση : (δ) ευθύγραµµη περιοδική Α.2. Σώµα εκτελεί απλή αρµονική
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση ΙΙ - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Η απλή αρµονική ταλάντωση είναι κίνηση : (δ) ευθύγραµµη περιοδική Α.2. Σώµα εκτελεί απλή αρµονική
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
Ημερομηνία: Παρασκευή 27 Οκτωβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
12ο ΓΕΛ ΠΕΙΡΑΙΑ 12/10/2010 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ
 1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]
![ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%] ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]](/thumbs/65/53613594.jpg) 1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
Ενδεικτικές Λύσεις. Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
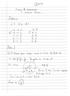 ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί στη
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί στη
ΟΡΟΣΗΜΟ. 1ο Κριτήριο αξιολόγησης στα κεφ Θέμα 1. Κριτήρια αξιολόγησης Ταλαντώσεις - Κύματα.
 1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Α.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ
 ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
ΤΑΛΑΝΤΩΣΕΙΣ (23 ΠΕΡΙΟΔΟΙ)
 α (cm/s ) ΚΕΦΑΛΑΙΟ 3 Κατηγορία Α ΤΑΛΑΝΤΩΣΕΙΣ (3 ΠΕΡΙΟΔΟΙ) 1. Να προσδιορίσετε ποια από τα πιο κάτω φυσικά μεγέθη μπορεί να έχουν την ίδια κατεύθυνση για ένα απλό αρμονικό ταλαντωτή: α. θέση και ταχύτητα,
α (cm/s ) ΚΕΦΑΛΑΙΟ 3 Κατηγορία Α ΤΑΛΑΝΤΩΣΕΙΣ (3 ΠΕΡΙΟΔΟΙ) 1. Να προσδιορίσετε ποια από τα πιο κάτω φυσικά μεγέθη μπορεί να έχουν την ίδια κατεύθυνση για ένα απλό αρμονικό ταλαντωτή: α. θέση και ταχύτητα,
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η ΗΜΕΡΟΜΗΝΙΑ: 24/07/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η ΗΜΕΡΟΜΗΝΙΑ: 4/07/014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η ΗΜΕΡΟΜΗΝΙΑ: 4/07/014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ ΣΤΟ ΦΑΙΝΟΜΕΝΟ DOPPLER
 ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ ΣΤΟ ΦΑΙΝΟΜΕΝΟ DOPPLER Ερώτηση 6 Ερώτηση 7 Α. σταθερή συχνότητα Β. αυξανόμενη συχνότητα Γ. μειούμενη συχνότητα Ερώτηση 9 Ερώτηση 8 Ερώτηση 10 Ερώτηση 11 Ερώτηση 12 Ερώτηση 13 α. 9/10
ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ ΣΤΟ ΦΑΙΝΟΜΕΝΟ DOPPLER Ερώτηση 6 Ερώτηση 7 Α. σταθερή συχνότητα Β. αυξανόμενη συχνότητα Γ. μειούμενη συχνότητα Ερώτηση 9 Ερώτηση 8 Ερώτηση 10 Ερώτηση 11 Ερώτηση 12 Ερώτηση 13 α. 9/10
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΟΥΛΙΟY 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΟΥΛΙΟY 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΟΥΛΙΟY 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
Το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας και είναι συνεχώς τεντωμένο. Η αντίσταση του αέρα θεωρείται αμελητέα.
 Ένα γιο γιο σε ταλάντωση Ομογενής κύλινδρος Σ, (γιο γιο) ισορροπεί έχοντας το νήμα τυλιγμένο γύρω της πολλές φορές. Η μία άκρη του νήματος είναι στερεωμένη στην οροφή Ο και η άλλη στο σώμα Σ, το οποίο
Ένα γιο γιο σε ταλάντωση Ομογενής κύλινδρος Σ, (γιο γιο) ισορροπεί έχοντας το νήμα τυλιγμένο γύρω της πολλές φορές. Η μία άκρη του νήματος είναι στερεωμένη στην οροφή Ο και η άλλη στο σώμα Σ, το οποίο
Σάββατο 12 Νοεμβρίου Απλή Αρμονική Ταλάντωση - Κρούσεις. Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες. Θέμα Α.
 Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
=2m /s. Να βρείτε: a. Τη σταθερά επαναφοράς D. b. Την περίοδο T της ταλάντωσης c. Την ενέργεια της ταλάντωσης d. Το πλάτος A της ταλάντωσης.
 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m/ s, ενώ στη θέση με απομάκρυνση x 2 =+4m το μέτρο
1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m/ s, ενώ στη θέση με απομάκρυνση x 2 =+4m το μέτρο
ΔΙΑΡΚΕΙΑ: 180min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ 1 ο ΘΕΜΑ 2 ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ
 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 80min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΜΟΝΑΔΕΣ ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΘΕΜΑ Α:. Κατά την διάρκεια της φθίνουσας ταλάντωσης ενός αντικειμένου, το
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 80min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΜΟΝΑΔΕΣ ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΘΕΜΑ Α:. Κατά την διάρκεια της φθίνουσας ταλάντωσης ενός αντικειμένου, το
Συλλογή θεμάτων 3 & 4
 Συλλογή θεμάτων 3 & 4 1)Η ταχύτητα ενός κινητού μεταβάλλεται με το χρόνο όπως φαίνεται στο διπλανό διάγραμμα. 20 u(m/s) α. Αφού περιγράψετε την κίνηση του κινητού, να υπολογίσετε τη συνολική του μετατόπιση.
Συλλογή θεμάτων 3 & 4 1)Η ταχύτητα ενός κινητού μεταβάλλεται με το χρόνο όπως φαίνεται στο διπλανό διάγραμμα. 20 u(m/s) α. Αφού περιγράψετε την κίνηση του κινητού, να υπολογίσετε τη συνολική του μετατόπιση.
Ενδεικτικές Λύσεις. Θέµα Α
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ 5 ΚΑΙ 1 (ΚΡΟΥΣΕΙΣ - ΤΑΛΑΝΤΩΣΕΙΣ) ΚΥΡΙΑΚΗ 15 ΝΟΕΜΒΡΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 3
 ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ 5 ΚΑΙ 1 (ΚΡΟΥΣΕΙΣ - ΤΑΛΑΝΤΩΣΕΙΣ) ΚΥΡΙΑΚΗ 15 ΝΟΕΜΒΡΙΟΥ 015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 3 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ 5 ΚΑΙ 1 (ΚΡΟΥΣΕΙΣ - ΤΑΛΑΝΤΩΣΕΙΣ) ΚΥΡΙΑΚΗ 15 ΝΟΕΜΒΡΙΟΥ 015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 3 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ
 2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ 207-208 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΝΟΕΜΒΡΙΟΥ 207 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΟΝΟΜΑΤΕΠΩΝΥΜΟ Τμήμα Γθετ.
2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ 207-208 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΝΟΕΜΒΡΙΟΥ 207 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΟΝΟΜΑΤΕΠΩΝΥΜΟ Τμήμα Γθετ.
Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον)
 Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον) 1. Σε μια φθίνουσα ταλάντωση ποιο από τα παρακάτω μεγέθη παραμένει σταθερό: α) το πλάτος
Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον) 1. Σε μια φθίνουσα ταλάντωση ποιο από τα παρακάτω μεγέθη παραμένει σταθερό: α) το πλάτος
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
