Αλγοριθμική Προσέγγιση της Μετατροπής από μία Εντολή Επανάληψης σε Άλλη
|
|
|
- Άνεμονη Δημητρακόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Αλγοριθμική Προσέγγιση της Μετατροπής από μία Εντολή Επανάληψης σε Άλλη Αθανάσιος Πέρδος 1, Σπύρος Δουκάκης 2, Νάγια Γιαννοπούλου 3 1 Δρ. Καθηγητής Πληροφορικής, Ελληνογαλλική Σχολή Καλαμαρί perdos@kalamari.gr 2 Υπ. Διδάκτορας, Πανεπιστήμιο Αιγαίου sdoukakis@rhodes.aegean.gr 3 Καθηγήτρια Πληροφορικής, Λεόντειο Λύκειο Πατησίων nagia@math.ntua.gr Περίληψη Η διερεύνηση της δυνατότητας μετατροπής και στη συνέχεια η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που διδάσκεται στο μάθημα Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον και αρκετές φορές έχει εξεταστεί σε πανελλαδικό επίπεδο. Στην εργασία επιχειρείται μία συνολική προσέγγιση των μετατροπών από μία εντολή επανάληψης στις άλλες δύο εντολές επανάληψης εφόσον μπορούν να πραγματοποιηθούν, με στόχο τη βελτίωση της διδασκαλίας και μάθησης των μαθητών/τριών. Αν και παρατίθενται μεθοδολογίες που καλύπτουν όλες τις δυνατές περιπτώσεις μετατροπών, σημειώνεται ότι οι συγκεκριμένοι κανόνες δεν είναι απόλυτοι και για αυτό σε περίπτωση που κάποιος δεν τους ακολουθήσει είναι καθοριστικής σημασίας η εικονική εκτέλεση (στο χαρτί) ή η εκτέλεση στον υπολογιστή του αρχικού τμήματος αλγόριθμου και του τμήματος αλγόριθμου που δημιουργήθηκε από την μετατροπή, ώστε για τις ίδιες εισόδους να δίνουν τα ίδια αποτελέσματα. Λέξεις κλειδιά: Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον, δομή επανάληψης, μετατροπές εντολών επανάληψης 1. Εισαγωγή Ένας από τους διδακτικούς στόχους του μαθήματος Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον (ΑΕΠΠ) είναι οι μαθητές/τριες να μπορούν να επιλέγουν την κατάλληλη εντολή επανάληψης και να έχουν γνώσεις σωστής σύνταξης της εντολής που θα επιλέξουν. Στο βιβλίο μαθητή αναφέρει ότι «Πολύ συχνά η ίδια επαναληπτική διαδικασία μπορεί να γραφεί εξίσου σωστά χρησιμοποιώντας είτε την εντολή ΟΣΟ ΕΠΑΝΑΛΑΒΕ είτε την εντολή ΜΕΧΡΙΣ_ΟΤΟΥ» (Βακάλη κ.α., 2009, σ. 176) και, επίσης, ότι «Κάθε επανάληψη που εκτελείται με μία εντολή ΓΙΑ ΑΠΟ ΜΕΧΡΙ, μπορεί να υλοποιηθεί και με τη χρήση των βασικών εντολών επανάληψης ΟΣΟ...ΕΠΑΝΑΛΑΒΕ και ΜΕΧΡΙΣ_ΟΤΟΥ» (Βακάλη κ.α., 2009, σ. 179). Ταυτόχρονα, για την επίτευξη αυτών των δύο στόχων, στο τετράδιο μαθητή, εκτός από την ύπαρξη ενός πλήθους δραστηριοτήτων, υπάρχει
2 και μία δραστηριότητα που έχει ως στόχο την συγγραφή ενός τμήματος αλγόριθμου από μία εντολή επανάληψης στις άλλες δύο (ΔΤ4, Κεφ. 8). Η συγκεκριμένη δραστηριότητα έδωσε το έναυσμα στους θεματοδότες να αξιολογήσουν τις γνώσεις των μαθητών/τριών στην ικανότητα μετατροπής ενός αλγόριθμου ή ενός τμήματος αλγόριθμου από μία εντολή επανάληψης σε μία άλλη ή και στις δύο άλλες εντολές επανάληψης, εφόσον αυτή είναι εφικτή. Έτσι, κατά την πανελλαδική εξέταση του μαθήματος, η συγκεκριμένη γνώση έχει εξεταστεί αρκετές φορές με θέματα διαφορετικού βαθμού δυσκολίας και διαφορετικής μοριοδότησης λαμβάνοντας από 4 μέχρι και 10 μόρια στα 100. Η δυσκολία των θεμάτων που έχουν επιλεγεί για την αξιολόγηση της συγκεκριμένης γνώσης, όπου μερικές φορές οδήγησε ακόμα και την επιτροπή εξετάσεων να μη δώσει ολοκληρωμένη προτεινόμενη λύση (Θέμα επαναληπτικών εξετάσεων ημερησίων λυκείων, 2001), προκάλεσε συζητήσεις και κατεύθυνε τους διδάσκοντες/ουσες, πάντα με στόχο τη βελτίωση της γνώσης των μαθητών/τριών, να προσπαθήσουν να αναδείξουν τις μετατροπές από την μία εντολή επανάληψης σε άλλη (Τσιωτάκης & Δουκάκης, 2005) ή να προσπαθήσουν να κατηγοριοποιήσουν τις δυνατές μετατροπές (Δρίμτζιας, 2010). Ένα ακόμα σημαντικό ζήτημα που έχει προκύψει από την αξιολόγηση της συγκεκριμένης γνώσης, είναι η έννοια της ισοδυναμίας του αλγόριθμου που προκύπτει από την μετατροπή με τον αρχικό αλγόριθμο. Έτσι, στα θέματα εξετάσεων έχουν χρησιμοποιηθεί φράσεις όπως «Να μετατρέψετε την παραπάνω δομή σε ισοδύναμη δομή επανάληψης» (Θέμα εξετάσεων ημερησίων λυκείων, 2001), «Να δώσετε τη δομή επανάληψης Για από μέχρι βήμα η οποία τυπώνει ακριβώς τις ίδιες τιμές με το πιο πάνω τμήμα αλγορίθμου» (Θέμα επαναληπτικών εξετάσεων ημερησίων λυκείων, 2001), «Να ξαναγράψετε το παραπάνω τμήμα αλγορίθμου χρησιμοποιώντας την εντολή ΓΙΑ αντί της εντολής ΟΣΟ» (Θέμα επαναληπτικών εξετάσεων ημερησίων λυκείων, 2007), «Να γράψετε τμήμα αλγορίθμου, που θα έχει το ίδιο αποτέλεσμα με το παρακάτω τμήμα» (Θέμα εξετάσεων ημερησίων λυκείων, 2009). Ωστόσο, στις περισσότερες περιπτώσεις η φρασεολογία που χρησιμοποιείται είναι αυτή της μετατροπής σε ισοδύναμο τμήμα αλγόριθμου. Στην παρούσα εργασία οι συγγραφείς ενστερνίζονται την πρόταση των Ολυμπιάδων πληροφορικής ότι δηλαδή: «ισοδύναμα προγράμματα είναι αυτά που για τις ίδιες εισόδους, δίνουν τα ίδια αποτελέσματα» (International Olympiad in Informatics, 2010). Αυτό έρχεται σε συμφωνία και με το στόχο του μαθήματος που είναι οι μαθητές να αναπτύξουν αναλυτική και συνθετική σκέψη καθώς και ικανότητες μεθοδολογικού χαρακτήρα. Η εργασία αυτή έχει ως στόχο από τη μία πλευρά να καλύψει όλες τις δυνατές μετατροπές από μία εντολή επανάληψης σε άλλη, όταν αυτή μπορεί να πραγματοποιηθεί και από την άλλη να παρέχει στους μαθητές μία αλγοριθμική προσέγγιση των μετατροπών ώστε να τους διευκολύνει στη μελέτη τους και στην αντιμετώπιση των θεμάτων των πανελλαδικών εξετάσεων. Για να επιτευχθούν τα 165
3 παραπάνω λαμβάνονται υπόψη τα θέματα των εξετάσεων, η υπάρχουσα βιβλιογραφία κυρίως ελληνική αφού τόσο η ψευδογλώσσα όσο και η ΓΛΩΣΣΑ ορίζονται στο συγκεκριμένο διδακτικό πακέτο και αξιοποιούνται ορισμένες γενικές αρχές που αν ακολουθηθούν μπορούν να δώσουν σωστή λύση σε τέτοιου είδους θέματα. Αν και καλύπτονται όλες οι δυνατές μετατροπές από τις μεθοδολογίες που προτείνονται, οι συγγραφείς δέχονται ότι οι κανόνες που προτείνουν δεν είναι απόλυτοι. Μπορεί κάποιος μαθητής ή καθηγητής σε ένα θέμα μετατροπής, να δημιουργήσει ισοδύναμο τμήμα αλγόριθμου που για τις ίδιες εισόδους να δίνει τα ίδια αποτελέσματα. Σε αυτή την περίπτωση, οι συγγραφείς θεωρούν ότι είναι καθοριστικής σημασίας η εικονική εκτέλεση (στο χαρτί) ή η εκτέλεση στον υπολογιστή (με τη χρήση κάποιου εκπαιδευτικού λογισμικού, όπως pseudoglossa.gr (Στέργου, 2010), Διερμηνευτής της Γλώσσας (Γεωργόπουλος, 2005), και Γλωσσομάθεια (Νικολαΐδης, 2010), τόσο του αρχικού τμήματος αλγόριθμου όσο και του τμήματος αλγόριθμου που δημιουργήθηκε από την μετατροπή(δουκάκης & Ψαλτίδου, 2011). 2. Πλαίσιο 2.1. Συντομογραφίες Για τις ανάγκες της εργασίας, την καλύτερη παρουσίαση και την ευκολότερη κατανόηση είναι απαραίτητες ορισμένες συντομογραφίες που θα χρησιμοποιηθούν στις επόμενες παραγράφους. Οι συντομογραφίες είναι οι ακόλουθες: μτ: μεταβλητή τ1: αρχική τιμή τ2: τελική τιμή β: τιμή βήματος 2.2. Γενικές αρχές Οι εντολές που περιέχονται στην εντολή Όσο επανάλαβε και στην εντολή Για από μέχρι, υπάρχει περίπτωση να εκτελεστούν καμία φορά, ενώ οι εντολές που περιέχονται στην εντολή Μέχρις_ότου θα εκτελεστούν τουλάχιστον μία φορά. Στον πίνακα 1 παρουσιάζονται οι περιπτώσεις που οι εμπεριεχόμενες εντολές των εντολών επανάληψης θα εκτελεστούν καμία φορά. 166
4 Πίνακας 1: Οι περιπτώσεις που εκτελούνται καμία φορά οι εμπεριεχόμενες εντολές των εντολών επανάληψης Εντολή επανάληψης Περίπτωση να εκτελεστούν οι εντολές καμία φορά Όσο επανάλαβε Κατά τον πρώτο έλεγχο της συνθήκης που περιλαμβάνει η εντολή επανάληψης, αυτή να είναι Ψευδής. Για μτ από τ1 μέχρι τ2 με_βήμα β β > 0 και τ1 > τ2 είτε β < 0 και τ1 < τ2 Στις τρεις εντολές επανάληψης υπάρχει περίπτωση ο βρόχος να εκτελείται άπειρες φορές. Στον πίνακα 2 παρουσιάζονται οι περιπτώσεις που οι εμπεριεχόμενες εντολές των εντολών επανάληψης θα εκτελεστούν άπειρες φορές. Πίνακας 2: Οι περιπτώσεις που εκτελούνται άπειρες φορές οι εμπεριεχόμενες εντολές των εντολών επανάληψης Εντολή επανάληψης Όσο επανάλαβε Μέχρις_ότου Για από μέχρι με_βήμα Περίπτωση να εκτελεστούν οι εντολές άπειρες φορές Κατά τον πρώτο έλεγχο η συνθήκη είναι Αληθής και παραμένει σε κάθε επανάληψη Αληθής. Η συνθήκη παραμένει σε κάθε επανάληψη Ψευδής. Όταν το βήμα είναι μηδέν. Στην εντολή Για μτ από τ1 μέχρι τ2 με_βήμα β όταν το βήμα είναι μηδέν σύμφωνα με το διδακτικό πακέτο «ο βρόχος εκτελείται επ άπειρον» (Βακάλη κ.α., 2009, σ. 44). Ωστόσο, είναι απαραίτητο στο σημείο αυτό να διευκρινιστεί ότι στο διδακτικό πακέτο και κατά την περιγραφή της λειτουργίας της εντολής ΓΙΑ ΑΠΟ ΜΕΧΡΙ στο επίπεδο της ΓΛΩΣΣΑΣ δεν είναι εμφανές ότι όταν το βήμα είναι μηδέν ο βρόχος εκτελείται άπειρες φορές. Αντίθετα, φαίνεται από τα συμφραζόμενα (Βακάλη κ.α., 2009, σ. 178) ότι ο βρόχος εκτελείται άπειρες φορές στην περίπτωση που β = 0 και τ1 <= τ2, ενώ ο βρόχος εκτελείται καμία φορά αν β = 0 και τι > τ2 (Τσιωτάκης κ.α., 2010). Η μετατροπή από την εντολή Όσο επανάλαβε στην εντολή Μέχρις_ότου και αντιστρόφως έχει νόημα μόνο αν δεν παραβιάζεται το κριτήριο της περατότητας στην αρχική εντολή. Ωστόσο, ακόμα και σε τέτοια περίπτωση η μετατροπή είναι πάλι εφικτή, όμως οδηγούμαστε ξανά σε ατέρμονα βρόγχο. Η μετατροπή από τις εντολές Όσο επανάλαβε και Μέχρις_ότου στην Για από μέχρι είναι δυνατή μόνο αν στην αρχική εντολή υπάρχει μία μεταβλητή (μτ) που λαμβάνει κάποια αρχική τιμή (τ1) πριν από την εντολή επανάληψης, ενώ η συνθήκη είναι της μορφής: 167
5 μτ συγκριτικός_τελεστής τ2 5 ο Πανελλήνιο Συνέδριο Καθηγητών Πληροφορικής όπου ο συγκριτικός τελεστής είναι ένας εκ των, >,, <. Στην περίπτωση είτε του = είτε του θα γίνει ειδική αναφορά και τ2 είναι η τελική τιμή που μπορεί να φτάσει η μεταβλητή και για την οποία εκτελούνται οι εντολές της επανάληψης. Ακόμη η μεταβλητή πρέπει μέσα στο σώμα της εντολής επανάληψης να αλλάζει μόνο κατά την τιμή κάποιου βήματος (β). Επίσης θα πρέπει να είναι γνωστές εκ των προτέρων η αρχική (τ1) και η τελική τιμή (τ2) της μεταβλητής, καθώς και η τιμή του βήματος (β) με την οποία αλλάζει η μεταβλητή κάθε φορά στην επανάληψη, ενώ θα πρέπει να διατηρούν σταθερή την τιμή τους σε όλη τη διάρκεια εκτέλεσης της επανάληψης. Τέλος, η μετατροπή έχει νόημα μόνο αν στην αρχική εντολή δεν παραβιάζεται το κριτήριο της περατότητας. Έτσι, αν οι τιμές των τ1, τ2 και β είναι τυχαίες, δηλαδή δεν είναι γνωστές ποιες συγκεκριμένες σταθερές τιμές έχουν στο ορατό τμήμα του αρχικού αλγόριθμου, θα πρέπει να διερευνηθεί με τη χρήση εντολών επιλογής αν ικανοποιούνται όλα τα παραπάνω. 3. Μετατροπές 3.1 Από την εντολή Όσο επανάλαβε στην εντολή Μέχρις_ότου Η γενική μορφή της εντολής Όσο επανάλαβε είναι η ακόλουθη: Όσο συνθήκη επανάλαβε Αν από την εικονική εκτέλεση του αλγόριθμου είναι βέβαιο ότι κατά τον πρώτο έλεγχο της συνθήκης αυτή είναι Αληθής, τότε η μετατροπή έχει ως εξής: Αρχή_επανάληψης Μέχρις_ότου όχι(συνθήκη) Αν από την εικονική εκτέλεση του αλγόριθμου δεν είναι βέβαιο ότι κατά τον πρώτο έλεγχο της συνθήκης αυτή είναι Αληθής, τότε πρέπει να χρησιμοποιηθεί μία εντολή απλής επιλογής για να ελέγχει αυτήν τη συνθήκη. Οπότε η μετατροπή έχει ως εξής: Αν συνθήκη τότε Αρχή_επανάληψης Μέχρις_ότου όχι(συνθήκη) Τέλος_αν 3.2 Από την εντολή Μέχρις_ότου στην εντολή Όσο επανάλαβε Η γενική μορφή της εντολής Μέχρις_ότου είναι η ακόλουθη: 168
6 Αρχή_επανάληψης Μέχρις_ότου συνθήκη 5 ο Πανελλήνιο Συνέδριο Καθηγητών Πληροφορικής Μία προτεινόμενη μέθοδος μετατροπής που δίνει πάντοτε λύση είναι η ακόλουθη: Όσο όχι(συνθήκη) επανάλαβε Θα πρέπει να επισημανθεί ότι η προτεινόμενη μέθοδος μπορεί πάντα να εφαρμοστεί, ωστόσο υπάρχουν και άλλοι τρόποι (πιο κατανοητοί και με λιγότερες γραμμές κώδικα) για να μετατραπεί η Μέχρις_ότου σε Όσο επανάλαβε, αρκεί η αρχική εντολή επανάληψης και η τελική να προκύψουν ισοδύναμες. Υπάρχουν λοιπόν περιπτώσεις όπου αν η λογική έκφραση (όχι(συνθήκη)) είναι αληθής την πρώτη φορά που θα ελεγχθεί όπως προκύπτει από εικονική εκτέλεση τότε οι εντολές πριν από το σώμα της επανάληψης είναι δυνατόν να παραλειφθούν. 3.3 Από την εντολή Για από μέχρι στις άλλες δύο εντολές επανάληψης Η γενική μορφή της εντολής Για από μέχρι είναι η ακόλουθη: Για μτ από τ1 μέχρι τ2 με_βήμα β Η προτεινόμενη μέθοδος μετατροπής βασίζεται στο πρόσημο της τιμής του βήματος, όπου αν β > 0 τότε η συνθήκη στην εντολή Όσο επανάλαβε θα είναι της μορφής μτ τ2, ενώ αν β < 0 τότε η συνθήκη στην εντολή Όσο επανάλαβε θα είναι της μορφής μτ τ2. Αν χρησιμοποιηθούν οι παραπάνω προτεινόμενες συνθήκες τότε σίγουρα οι μετατροπές είναι σωστές, αφού για παράδειγμα αν τ1 > τ2 και β > 0 η Για από μέχρι δεν εκτελείται, ενώ η Όσο επανάλαβε εκτελείται άπειρες φορές. Έτσι, θεωρώντας ότι β 0, η μετατροπή μπορεί να γίνει ως εξής: 169
7 Αν β > 0 τότε μτ τ1 Όσο μτ τ2 επανάλαβε αλλιώς_αν β < 0 τότε μτ τ1 Όσο μτ τ2 επανάλαβε Τέλος_αν Αν β > 0 και τ1 τ2 τότε μτ τ1 Αρχή_επανάληψης Μέχρις_ότου μτ > τ2 αλλιώς_αν β < 0 και τ1 τ2 τότε μτ τ1 Αρχή_επανάληψης Μέχρις_ότου μτ < τ2 Τέλος_αν Η παραπάνω προτεινόμενη μετατροπή έχει πραγματοποιηθεί λαμβάνοντας υπόψη όλες τις δυνατές τιμές που μπορούν να έχουν οι τ1, τ2 και β. Είναι χρήσιμο να επισημανθεί ότι η προτεινόμενη μετατροπή χρειάζεται να εφαρμοστεί στις περιπτώσεις που δεν είναι γνωστό αν το βήμα είναι θετικό ή αρνητικό. Αν όμως είναι γνωστό το πρόσημο του βήματος, τότε χρειάζεται να αξιοποιηθεί μόνο το αντίστοιχο τμήμα αλγόριθμου και χωρίς την εντολή επιλογής. Επίσης, είναι άξιο αναφοράς, ότι αν η εντολή Για...από...μέχρι εκτελείται καμία φορά, τότε καμία φορά θα εκτελεστεί και η εντολή Όσο...επανάλαβε. Για την μετατροπή της εντολής Για από μέχρι στην εντολή Μέχρις_ότου προτείνεται η μετατροπή της Για σε Όσο επανάλαβε και στη συνέχεια μετατροπή της Όσο επανάλαβε στην εντολή Μέχρις_ότου, σύμφωνα με τη μέθοδο που παρουσιάστηκε στην παράγραφο 3.1. Ωστόσο για λόγους πληρότητας η μετατροπή παρουσιάζεται στην δεύτερη στήλη. 3.4 Από την εντολή Όσο επανάλαβε στην εντολή Για από μέχρι Όπως ήδη αναφέρθηκε, η μετατροπή από την εντολή Όσο επανάλαβε στην εντολή Για από μέχρι μπορεί να γίνει μόνο αν ισχύουν οι προϋποθέσεις που παρουσιάστηκαν στις γενικές αρχές. Έτσι σε περίπτωση που το βήμα (β) δεν έχει συγκεκριμένη αριθμητική τιμή θα πρέπει να γίνει διερεύνηση για το πότε είναι εφικτή η μετατροπή. Για αυτό το λόγο απαιτείται και η χρήση κατάλληλων εντολών επιλογής ώστε η Όσο επανάλαβε και η Για στην οποία μετατρέπεται να είναι ισοδύναμες, δηλαδή να δίνουν ίδια αποτελέσματα. Για την μετατροπή είναι απαραίτητη η διάκριση στις ακόλουθες περιπτώσεις: Ο συγκριτικός τελεστής της εντολής Όσο επανάλαβε είναι είτε μικρότερος ή ίσος ( ), είτε μεγαλύτερος ή ίσος ( ) Στην περίπτωση που ο συγκριτικός τελεστής της συνθήκης στην εντολή Όσο επανάλαβε είναι είτε ο (μικρότερος ή ίσος), είτε ο (μεγαλύτερος ή ίσος) τότε η εντολή μπορεί να είναι μία από τις ακόλουθες δύο: α) μτ τ1 β) μτ τ1 Όσο μτ τ2 επανάλαβε Όσο μτ τ2 επανάλαβε Για να μπορεί να γίνει η μετατροπή, στην (α) περίπτωση πρέπει να ισχύει β > 0, αφού αν δεν ισχύει είναι πιθανό ο βρόχος να είναι ατέρμων στην περίπτωση που τ1 τ2. Για να μπορεί να γίνει η μετατροπή, στην (β) περίπτωση πρέπει να ισχύει β < 0, αφού αν δεν ισχύει είναι πιθανό ο βρόχος να είναι ατέρμων στην περίπτωση που τ1 τ2. Αν ισχύουν τα παραπάνω, τότε η μετατροπή είτε του (α), είτε του (β) τμήματος αλγόριθμου είναι η ακόλουθη: 170
8 Για μτ από τ1 μέχρι τ2 με_βήμα β Αν στην περίπτωση (α) δεν ισχύει τ1 τ2 τότε η επανάληψη εκτελείται καμία φορά με την εντολή Όσο επανάλαβε και καμία φορά με την εντολή Για...από...μέχρι. Αν στην περίπτωση (β) δεν ισχύει τ1 τ2 τότε η επανάληψη εκτελείται καμία φορά με την εντολή Όσο επανάλαβε και καμία φορά με την εντολή Για...από...μέχρι. Έτσι και στις δύο περιπτώσεις προκύπτουν ισοδύναμα τμήματα αλγόριθμου Ο συγκριτικός τελεστής της εντολής Όσο επανάλαβε είναι είτε αυστηρά μικρότερος (<) είτε αυστηρά μεγαλύτερος (>) Αν στη συνθήκη της εντολής Όσο επανάλαβε ο τελεστής σύγκρισης είναι αυστηρά μικρότερος ή αυστηρά μεγαλύτερος, τότε οι εντολές του βρόχου δεν εκτελούνται όταν η μεταβλητή της συνθήκης λάβει την τιμή τ2 και άρα είναι πιθανό να είναι λάθος η μετατροπή σε Για μτ από τ1 μέχρι τ2 με_βήμα β. Για το λόγο αυτό, χρειάζεται διερεύνηση για την εύρεση της τελικής τιμής που λαμβάνει πραγματικά η μεταβλητή στην εντολή Όσο επανάλαβε ώστε να βρεθεί η αντίστοιχη τελική τιμή που θα γραφεί στο τμήμα αλγόριθμου με την εντολή Για από μέχρι. Για λόγους παρουσίασης, η τελική τιμή που λαμβάνει πραγματικά η μεταβλητή στην εντολή Όσο επανάλαβε και θα αξιοποιηθεί στην εντολή Για από μέχρι θα αναφέρεται ως τπ2. Ο υπολογισμός της τιμής τπ2, ανεξάρτητα αν το β είναι θετικό ή αρνητικό μπορεί να πραγματοποιηθεί ως εξής: Έστω η γενική μορφή της εντολής Όσο επανάλαβε στην οποία δεν υπάρχει αυστηρή ανισότητα και κ ένας ακέραιος που εκφράζει πόσες φορές αλλάζει μέσα στο βρόχο η μεταβλητή (μτ)κατά το βήμα για να πλησιάσει ή να φτάσει την τελική τιμή (τ2), όχι όμως να την ξεπεράσει. Η τιμή της, θα είναι: κ = (τ2 - τ1) / β. Ωστόσο, η τιμή του κ θα πρέπει να είναι ακέραια, ενώ η συγκεκριμένη διαίρεση μπορεί να δώσει και πραγματικό αποτέλεσμα. Για το λόγο αυτό, τελικά η τιμή του κ θα δίνεται από τη σχέση: κ = Α_Μ((τ2 - τ1) / β) (1) όπου Α_Μ(x) συνάρτηση που επιστρέφει το ακέραιο μέρος του x. Έτσι η πραγματικά τελική τιμή για την οποία εκτελείται η εντολή Όσο επανάλαβε είναι η τπ2 = τ1 + κ * β (2) Στην περίπτωση όμως της εντολής Όσο επανάλαβε με αυστηρή ανισότητα, (τπ2 < τ2 για θετικό β ή τπ2 > τ2 για αρνητικό β), δεν υπάρχει πρόβλημα στη μετατροπή σε Για μτ από τ1 μέχρι τ2 με_βήμα β αφού η μεταβλητή δεν φτάνει στην τ2. Αν όμως τπ2 = τ2 τότε η πραγματικά τελική τιμή της μεταβλητής στην εντολή Όσο επανάλαβε δεν είναι η προαναφερόμενη, αλλά η αμέσως προηγούμενή της. Έτσι αν η τιμή τπ2 που υπολογίζεται από την παραπάνω σχέση είναι ίση με την τ2 τότε για τον τελικό υπολογισμό της τιμής τπ2, αφαιρείται από τη σχέση (2) το βήμα (β) και άρα η νέα σχέση είναι η: Συνοψίζοντας τα βήματα που ακολουθούνται είναι: Βήμα 1: Βήμα 2: Βήμα 3: τπ2 = τ1 + κ * β - β (3) Υπολογισμός των φορών που αλλάζει η μεταβλητή κατά το βήμα για να πλησιάσει ή να φτάσει την τελική τιμή, όχι όμως να την ξεπεράσει, στη γενική μορφή της εντολής Όσο επανάλαβε: κ = Α_Μ((τ2 - τ1) / β) Εύρεση της τελευταίας τιμής που λαμβάνει πραγματικά η μεταβλητή της εντολής Όσο επανάλαβε στη γενική της μορφή: τπ2 = τ1 + κ * β Εύρεση της πραγματικά τελικής τιμής αν στην περίπτωση της αυστηρής ανισότητας ισχύει τπ2 = τ2, από τον τύπο τπ2 = τ1 + κ * β - β 171
9 Το τμήμα αλγόριθμου που υλοποιεί τα παραπάνω σε περίπτωση τυχαίων τιμών των τ1, τ2 και β, είναι το ακόλουθο: κ Α_Μ((τ2 - τ1) / β) τπ2 τ1 + κ * β Αν τπ2 = τ2 τότε τπ2 τπ2 - β Σύμφωνα με τον εκπαιδευτικό Δρίμτζια (2010), μία άλλη προτεινόμενη μεθοδολογία στην περίπτωση που ο συγκριτικός τελεστής είναι αυστηρά μικρότερος ή αυστηρά μεγαλύτερος βασίζεται στην παρατήρηση ότι η μτ δεν μπορεί να φτάσει στην τ2. Έτσι, αναφέρει ότι αν η τιμή του βήματος είναι ακέραια τότε τίθεται τ2 = τ2 ± 1, ενώ αν η τιμή του βήματος είναι πραγματική και έχει ένα δεκαδικό ψηφίο τότε τίθεται τ2 = τ2 ± 0,1, ή αν έχει δύο δεκαδικά ψηφία τίθεται τ2 = τ2 ± 0,01 κ.ο.κ. Ωστόσο, είναι χρήσιμο να επισημανθεί ότι δεν αρκεί να ελεγχθεί μόνο το βήμα αν λαμβάνει ακέραια ή πραγματική τιμή για να εντοπιστεί η διαφορά από την τελική τιμή, αλλά πρέπει να ελεγχθούν και οι τρεις τιμές τ1, τ2 και β. Έτσι, αν και τα τρία είναι ακέραια τότε τ2 = τ2 ± 1, ενώ αν η τ1 ή η τ2, ή το β ή κάποια από αυτά είναι πραγματικές η νέα τελική τιμή στην εντολή Για θα πρέπει να διαφέρει από την τελική τιμή στην εντολή Όσο κατά 0,1 αν κάποιο πραγματικό μέρος έχει ένα σημαντικό ψηφίο μετά την υποδιαστολή, 0,01 αν κάποιο πραγματικό μέρος έχει δύο σημαντικά ψηφία μετά την υποδιαστολή κ.ο.κ. Επιπλέον, αν κάποια από τις μεταβλητές τ1, τ2 και β δεν έχει συγκεκριμένη αριθμητική τιμή, η παραπάνω προσέγγιση αποτυγχάνει να δώσει λύση, αφού δεν είναι γνωστός ο αριθμός των ψηφίων του πραγματικού μέρους Στην εντολή Όσο επανάλαβε υπάρχουν εντολές μετά την αλλαγή της μεταβλητής κατά το βήμα. Στην περίπτωση που υπάρχουν εντολές μετά την αλλαγή της τιμής της μεταβλητής κατά το βήμα στην Όσο επανάλαβε, τότε είναι απαραίτητο να εντοπιστούν οι εντολές που χρησιμοποιείται η τιμή της μεταβλητής μετά την αλλαγή της και στις αντίστοιχες εντολές της Για από μέχρι να χρησιμοποιηθεί η τιμή της μεταβλητής αλλαγμένη κατά το βήμα. 3.5 Από την εντολή Μέχρις_ότου στην εντολή Για...από...μέχρι Για την μετατροπή της εντολής Μέχρις_ότου στην εντολή Για...από...μέχρι προτείνεται η μετατροπή της Μέχρις_ότου σε Όσο...επανάλαβε και στη συνέχεια μετατροπή της Όσο...επανάλαβε στην εντολή Για...από...μέχρι, σύμφωνα με τα προηγούμενα. 4. Περιορισμοί και προβληματισμοί Όλες οι προτεινόμενες μέθοδοι βασίζονται στην παραδοχή ότι η μετατροπή από μία εντολή επανάληψης σε μία άλλη είναι εφικτή. Για αυτό παρουσιάστηκε αναλυτικά πότε είναι δυνατόν να μετατραπεί μία εντολή επανάληψης σε μία άλλη ενώ συνιστάται να ελέγχεται πάντα με εικονική εκτέλεση πότε είναι εφικτή η μετατροπή. Υπάρχουν όμως και κάποιοι περιορισμοί που αφορούν κυρίως τη μετατροπή από και σε Για...από...μέχρι. Αν πρόκειται να μετατραπεί η εντολή Για...από...μέχρι στην εντολή Όσο επανάλαβε, όπως παρουσιάστηκε πρέπει να συνταχθεί με βάση το πρόσημο του βήματος η συνθήκη στην εντολή Όσο επανάλαβε, αλλιώς θα είναι λανθασμένη. Αν ζητείται να μετατραπεί η εντολή Μέχρις_ότου στην εντολή Για...από...μέχρι και στην Μέχρις_ότου υπάρχει η συνθήκη μτ > τ2 ενώ τ1 τ2 και β < 0 υπάρχουν δύο περιπτώσεις: α) Δεν τερματίζει ποτέ εφόσον τ1 + β τ2, β) εκτελείται μόνο μία φορά εφόσον τ1 + β > τ2. Και στις δύο περιπτώσεις δεν μπορεί η εντολή Μέχρις_ότου να μετατραπεί σε Για...από...μέχρι. Το συμπέρασμα είναι το ίδιο αν μτ < τ2 ενώ τ1 τ2 και β > 0. Αν ζητείται να μετατραπεί η εντολή Όσο επανάλαβε στην εντολή Για...από...μέχρι και υπάρχει ο τελεστής του διάφορου ( ) στην συνθήκη τότε θα πρέπει να εξακριβωθεί αν στην εντολή Όσο επανάλαβε η μεταβλητή παίρνει κάποια στιγμή την τ2 γιατί διαφορετικά 172
10 παραβιάζεται η περατότητα, οπότε η μετατροπή δεν θα έχει νόημα. Αυτό μπορεί να γίνει με τη μέθοδο που παρουσιάστηκε πριν στην περίπτωση της αυστηρής ανισότητας στην συνθήκη κατά τη μετατροπή από την εντολή Όσο επανάλαβε στην εντολή Για...από...μέχρι. Στο ίδιο μήκος, εντάσσεται και ένα πιθανό ζήτημα μετατροπής μίας εντολής Όσο επανάλαβε στην εντολή Για με τον τελεστή της ισότητας (=) στην συνθήκη. Στην περίπτωση αυτή η μετατροπή έχει νόημα αν τ1 = τ2 όποτε και οι δυο εντολές εκτελούνται ακριβώς μία φορά. Αποτελεί όμως και προβληματισμό, αν είναι παιδαγωγικά χρήσιμο και διδακτικά σημαντικό να ζητείται από τους μαθητές/τριες να διερευνούν περιπτώσεις ατέρμονα βρόχου κατά την αξιολόγησή τους σε θέματα μετατροπών από μία εντολή επανάληψης σε μία άλλη. 5. Επίλογος Η παρούσα εργασία έχει σκοπό α) να αναδείξει την ποικιλία των μετατροπών από μία εντολή επανάληψης σε μία άλλη, β) να παρουσιάσει γενικευμένους τρόπους μετατροπής από μία εντολή επανάληψης σε μία άλλη και γ) να συνεισφέρει στον εκπαιδευτικό διάλογο για τη διδακτική προσέγγιση του τρόπου μετατροπής από μία εντολή επανάληψης σε μία άλλη. Αναδεικνύεται ότι δεν μπορεί να μετατραπεί κάθε εντολή επανάληψης σε οποιαδήποτε άλλη εντολή επανάληψης και επιπλέον παρατηρείται η ανάγκη διερεύνησης για να είναι εφικτή η γενικευμένη μετατροπή από μία εντολή επανάληψης σε μία άλλη, κάτι που συνεισφέρει στην ανάπτυξη αναλυτικής και συνθετικής σκέψης, καθώς και στην απόκτηση ικανοτήτων μεθοδολογικού χαρακτήρα, λαμβάνοντας όμως υπόψη κάθε φορά την παιδαγωγική αξία της αξιολόγησης σχετικών θεμάτων. Βιβλιογραφία International Olympiad in Informatics (2010). ioinformatics.org, Ανακτήθηκε στις 30 Δεκεμβρίου 2010, από Βακάλη, Α., Γιαννόπουλος, Η., Ιωαννίδης, Χ., Κοίλιας, Χ., Μάλαμας, Κ., Μανωλόπουλος, Ι., & Πολίτης, Π. (2009). Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον. Αθήνα: ΠΙ. Γεωργόπουλος, Ά., Τσέλιος, Ν., Κόμης, Β., & Πολίτης, Π. (2005). Ολοκληρωμένο προγραμματιστικό περιβάλλον διδακτικής υποστήριξης μαθημάτων Πληροφορικής Γυμνασίου-Λυκείου. Πρακτικά 3ου Πανελλήνιου Συνεδρίου «Διδακτική της Πληροφορικής», Κόρινθος, , Εκδόσεις Νέων Τεχνολογιών. Δουκάκης, Σ., & Ψαλτίδου, Α. (2011). Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον, Τόμος Α, Εκδόσεις Πατάκη. Δρίμτζιας, Β. (2010). Μεθοδολογία Μετατροπής ενός Τμήματος Αλγορίθμου που χρησιμοποιεί την Εντολή Όσο επανάλαβε σε Ισοδύναμη Μορφή χρησιμοποιώντας την Εντολή Για από μέχρι με_βήμα Στο Γρηγοριάδου, Μ. (Επιμ.), Πρακτικά 5ου Πανελλήνιου Συνεδρίου Διδακτικής της Πληροφορικής, Αθήνα, Νικολαΐδης, Σ. (2010). Τελευταία προσπέλαση στις 30 Δεκεμβρίου 2010, από Στέργου, Σ. (2010). pseudoglossa.gr - Online διερμηνευτής για την Ψευδογλώσσα του μαθήματος Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον. Στο Δουκάκης Σ. (Επιμ.) Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον, Παρελθόν, Παρόν και Μέλλον, ΕΠΥ, Αθήνα, Εκδόσεις Νέων Τεχνολογιών, Τσιωτάκης, Π. & Δουκάκης, Σ. (2005). Πρόταση διδασκαλίας των δομών επανάληψης για το μάθημα ανάπτυξης εφαρμογών σε προγραμματιστικό περιβάλλον στο εργαστήριο. Στο Γιαλαμά, Α., Τζιμόπουλος, Ν. & Χλωρίδου, Α. (Επιμ.), Πρακτικά 3ου Πανελληνίου Συνεδρίου των εκπαιδευτικών για τις ΤΠΕ «Αξιοποίηση των Τεχνολογιών της Πληροφορίας και της Επικοινωνίας στη Διδακτική Πράξη», Σύρος, , Εκδόσεις Νέων Τεχνολογιών. Τσιωτάκης, Π., Στέργου, Σ., Αδαμόπουλος, Ν., & Ψαλτίδου, Α. (2010). Το διδακτικό πακέτο του μαθήματος «Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον». Ασάφειες και επακόλουθα προβλήματα. Στο Δουκάκης Σ. (Επιμ.) Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον, Παρελθόν, Παρόν και Μέλλον, ΕΠΥ, Αθήνα, Εκδόσεις Νέων Τεχνολογιών,
4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη.
 4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη. Η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που αρκετές φορές έχει εξεταστεί σε πανελλαδικό
4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη. Η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που αρκετές φορές έχει εξεταστεί σε πανελλαδικό
Επαναληπτικές Διαδικασίες
 Επαναληπτικές Διαδικασίες Οι επαναληπτικές δομές ( εντολές επανάληψης επαναληπτικά σχήματα ) χρησιμοποιούνται, όταν μια ομάδα εντολών πρέπει να εκτελείται αρκετές- πολλές φορές ανάλογα με την τιμή μιας
Επαναληπτικές Διαδικασίες Οι επαναληπτικές δομές ( εντολές επανάληψης επαναληπτικά σχήματα ) χρησιμοποιούνται, όταν μια ομάδα εντολών πρέπει να εκτελείται αρκετές- πολλές φορές ανάλογα με την τιμή μιας
Η Δομή Επανάληψης. Εισαγωγή στην δομή επανάληψης Χρονική διάρκεια: 3 διδακτικές ώρες
 Η Δομή Επανάληψης Εισαγωγή στην δομή επανάληψης Χρονική διάρκεια: 3 διδακτικές ώρες Οι 2 πρώτες διδακτικές ώρες στην τάξη Η τρίτη διδακτική ώρα στο εργαστήριο Γενικός Διδακτικός Σκοπός Ενότητας Να εξοικειωθούν
Η Δομή Επανάληψης Εισαγωγή στην δομή επανάληψης Χρονική διάρκεια: 3 διδακτικές ώρες Οι 2 πρώτες διδακτικές ώρες στην τάξη Η τρίτη διδακτική ώρα στο εργαστήριο Γενικός Διδακτικός Σκοπός Ενότητας Να εξοικειωθούν
Ανάπτυξη εφαρμογών Σχετικά με την εντολή επανάληψης «Για από μέχρι με_βήμα»
 Ανάλυση λειτουργίας Ανάπτυξη εφαρμογών Σχετικά με την εντολή επανάληψης «Για από μέχρι με_βήμα» Για i από ΑΡΧ_ΤΙΜΗ μέχρι ΤΕΛ_ΤΙΜΗ με_βήμα ΒΗΜΑ Η μεταβλητή Iκαι οι τιμές ΑΡΧ_ΤΙΜΗ, ΤΕΛ_ΤΙΜΗ και
Ανάλυση λειτουργίας Ανάπτυξη εφαρμογών Σχετικά με την εντολή επανάληψης «Για από μέχρι με_βήμα» Για i από ΑΡΧ_ΤΙΜΗ μέχρι ΤΕΛ_ΤΙΜΗ με_βήμα ΒΗΜΑ Η μεταβλητή Iκαι οι τιμές ΑΡΧ_ΤΙΜΗ, ΤΕΛ_ΤΙΜΗ και
Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2. Α1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων πληροφορικής
 Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2 Α1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων πληροφορικής Α2. Ο αλγόριθμος αποτελείται από ένα πεπερασμένο σύνολο εντολών Α3. Ο αλγόριθμος
Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2 Α1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων πληροφορικής Α2. Ο αλγόριθμος αποτελείται από ένα πεπερασμένο σύνολο εντολών Α3. Ο αλγόριθμος
1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες εντολές (μορφές) της;
 1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες (μορφές) της; Η δομή επανάληψης χρησιμοποιείται όταν μια σειρά εντολών πρέπει να εκτελεστεί σε ένα σύνολο περιπτώσεων, που έχουν κάτι
1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες (μορφές) της; Η δομή επανάληψης χρησιμοποιείται όταν μια σειρά εντολών πρέπει να εκτελεστεί σε ένα σύνολο περιπτώσεων, που έχουν κάτι
2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ 1) Πότε χρησιμοποιείται η δομή επανάληψης
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ 1) Πότε χρησιμοποιείται η δομή επανάληψης
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α : Α1
ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α : Α1
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον 2o Επαναληπτικό Διαγώνισμα Κεφ: 2 ο 7 ο 8 ο ΗΜΕΡΟΜΗΝΙΑ 21/ 10/ 2017
 ΜΑΘΗΜΑ Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον ΔΙΑΓΩΝΙΣΜΑ 2o Επαναληπτικό Διαγώνισμα ΥΛΗ Κεφ: 2 ο 7 ο 8 ο ΗΜΕΡΟΜΗΝΙΑ 21/ 10/ 2017 Θέμα Α A1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΜΑΘΗΜΑ Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον ΔΙΑΓΩΝΙΣΜΑ 2o Επαναληπτικό Διαγώνισμα ΥΛΗ Κεφ: 2 ο 7 ο 8 ο ΗΜΕΡΟΜΗΝΙΑ 21/ 10/ 2017 Θέμα Α A1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΟΚΤΩΒΡΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΣΠΟΥΔΕΣ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΟΚΤΩΒΡΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Α
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ. i. Η συνθήκη α > β ή α <= β α) είναι πάντα Αληθής β) είναι πάντα Ψευδής γ) δεν υπολογίζεται δ) τίποτα από τα προηγούμενα
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΟΚΤΩΒΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 (ΕΞΙ) ΘΕΜΑ Α : A1. Να γράψετε στο φύλλο απαντήσεων τον αριθμό καθεμιάς
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΟΚΤΩΒΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 (ΕΞΙ) ΘΕΜΑ Α : A1. Να γράψετε στο φύλλο απαντήσεων τον αριθμό καθεμιάς
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΗΡΕΣΙΩΝ 2005
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΗΡΕΣΙΩΝ 2005 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΗΡΕΣΙΩΝ 2005 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον
 Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον 2.4.5 8.2 Δομή Επανάληψης Δομές Επανάληψης Οι δομές επανάληψης χρησιμοποιούνται στις περιπτώσεις όπου μια συγκεκριμένη ακολουθία εντολών πρέπει να εκτελεστεί
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον 2.4.5 8.2 Δομή Επανάληψης Δομές Επανάληψης Οι δομές επανάληψης χρησιμοποιούνται στις περιπτώσεις όπου μια συγκεκριμένη ακολουθία εντολών πρέπει να εκτελεστεί
Παράδειγμα 2. Λύση & Επεξηγήσεις. Τέλος_επανάληψης Εμφάνισε "Ναι" Τέλος Α2
 Διδακτική πρόταση ΕΝΟΤΗΤΑ 2η, Θέματα Θεωρητικής Επιστήμης των Υπολογιστών Κεφάλαιο 2.2. Παράγραφος 2.2.7.4 Εντολές Όσο επανάλαβε και Μέχρις_ότου Η διαπραγμάτευση των εντολών επανάληψης είναι σημαντικό
Διδακτική πρόταση ΕΝΟΤΗΤΑ 2η, Θέματα Θεωρητικής Επιστήμης των Υπολογιστών Κεφάλαιο 2.2. Παράγραφος 2.2.7.4 Εντολές Όσο επανάλαβε και Μέχρις_ότου Η διαπραγμάτευση των εντολών επανάληψης είναι σημαντικό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΕΠΠ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ / Γ3 Γ4 ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : ΕΞΙ (6)
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ A : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΕΠΠ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ / Γ3 Γ4 ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : ΕΞΙ (6) A1. Να γράψετε στο φύλλο απαντήσεων τον αριθμό καθεμιάς
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ A : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΕΠΠ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ / Γ3 Γ4 ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : ΕΞΙ (6) A1. Να γράψετε στο φύλλο απαντήσεων τον αριθμό καθεμιάς
2ο ΓΕΛ ΑΓ.ΔΗΜΗΤΡΙΟΥ ΑΕΠΠ ΘΕΟΔΟΣΙΟΥ ΔΙΟΝ ΠΡΟΣΟΧΗ ΣΤΑ ΠΑΡΑΚΑΤΩ
 ΠΡΟΣΟΧΗ ΣΤΑ ΠΑΡΑΚΑΤΩ ΣΤΑΘΕΡΕΣ είναι τα μεγέθη που δεν μεταβάλλονται κατά την εκτέλεση ενός αλγόριθμου. Εκτός από τις αριθμητικές σταθερές (7, 4, 3.5, 100 κλπ), τις λογικές σταθερές (αληθής και ψευδής)
ΠΡΟΣΟΧΗ ΣΤΑ ΠΑΡΑΚΑΤΩ ΣΤΑΘΕΡΕΣ είναι τα μεγέθη που δεν μεταβάλλονται κατά την εκτέλεση ενός αλγόριθμου. Εκτός από τις αριθμητικές σταθερές (7, 4, 3.5, 100 κλπ), τις λογικές σταθερές (αληθής και ψευδής)
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον και Μαθηματικά: Μια αλγοριθμική προσέγγιση του θεωρήματος Bolzano
 Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον και Μαθηματικά: Μια αλγοριθμική προσέγγιση του θεωρήματος Bolzano Πέρδος Αθανάσιος 1, Σαράφης Ιωάννης 2, Δουκάκης Σπυρίδων 3, Ντρίζος Δημήτριος 4 1 Δρ.
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον και Μαθηματικά: Μια αλγοριθμική προσέγγιση του θεωρήματος Bolzano Πέρδος Αθανάσιος 1, Σαράφης Ιωάννης 2, Δουκάκης Σπυρίδων 3, Ντρίζος Δημήτριος 4 1 Δρ.
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 26 ΑΠΡΙΛΙΟΥ 2012 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΛΥΣΕΙΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: 7 Α1. Κάθε σωστή απάντηση
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 26 ΑΠΡΙΛΙΟΥ 2012 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΛΥΣΕΙΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: 7 Α1. Κάθε σωστή απάντηση
i 1 Όσο i <> 100 επανάλαβε i i + 2 Γράψε A[i] Τέλος_επανάληψης
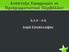
![i 1 Όσο i <> 100 επανάλαβε i i + 2 Γράψε A[i] Τέλος_επανάληψης i 1 Όσο i <> 100 επανάλαβε i i + 2 Γράψε A[i] Τέλος_επανάληψης](/thumbs/71/65910122.jpg) ΘΕΜΑ Α A1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις α-δ και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή, ή τη λέξη ΛΑΘΟΣ, αν είναι λανθασμένη. a. Σε μία εντολή εκχώρησης του αποτελέσματος
ΘΕΜΑ Α A1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις α-δ και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή, ή τη λέξη ΛΑΘΟΣ, αν είναι λανθασμένη. a. Σε μία εντολή εκχώρησης του αποτελέσματος
ΘΕΜΑ 1 ο. Στήλη Β Προτάσεις. β. Ο βρόχος επανάληψης τερµατίζεται, όταν η συνθήκη είναι αληθής. όταν η συνθήκη είναι ψευδής.
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ): ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ): ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 05/01/2010 ΘΕΜΑ 1 ο Α) Δίνεται η παρακάτω ακολουθία εντολών αλγορίθμου: ΑΛΓΟΡΙΘΜΟΣ Θέμα1 ΔΙΑΒΑΣΕ Ν Σ 0 π 0 ΓΙΑ ψ ΑΠΟ -1 ΜΕΧΡΙ
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 05/01/2010 ΘΕΜΑ 1 ο Α) Δίνεται η παρακάτω ακολουθία εντολών αλγορίθμου: ΑΛΓΟΡΙΘΜΟΣ Θέμα1 ΔΙΑΒΑΣΕ Ν Σ 0 π 0 ΓΙΑ ψ ΑΠΟ -1 ΜΕΧΡΙ
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΡΠΕΝΗΣΙΟΥ ΔΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ 19/12/2008. Τμήμα ΓΤ1 Όνομα:...
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΡΠΕΝΗΣΙΟΥ ΔΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ 19/12/2008 Τμήμα ΓΤ1 Όνομα:... ΘΕΜΑ 1 ο. Α) Να γράψετε στο φύλλο απαντήσεών σας Σ εάν κρίνετε ότι η πρόταση είναι σωστή και
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΡΠΕΝΗΣΙΟΥ ΔΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ 19/12/2008 Τμήμα ΓΤ1 Όνομα:... ΘΕΜΑ 1 ο. Α) Να γράψετε στο φύλλο απαντήσεών σας Σ εάν κρίνετε ότι η πρόταση είναι σωστή και
Διάγραμμα Ροής. Σελίδα 1 από 10
 Θεωρία επισκόπηση 3 Επανάληψη Σημείωση: Οι εντολές που συγκροτούν μια εντολή επανάληψης αποκαλούνται βρόχος 1. Εντολή Όσο.επανάλαβε Σύνταξη Όσο συνθήκη επανάλαβε εντολές Πώς Λειτουργεί. Αρχικά ελέγχεται
Θεωρία επισκόπηση 3 Επανάληψη Σημείωση: Οι εντολές που συγκροτούν μια εντολή επανάληψης αποκαλούνται βρόχος 1. Εντολή Όσο.επανάλαβε Σύνταξη Όσο συνθήκη επανάλαβε εντολές Πώς Λειτουργεί. Αρχικά ελέγχεται
Στήλη Β Προτάσεις. 1. Όσο συνθήκη επανάλαβε εντολές Τέλος_επανάληψης 2. Αρχή_επανάληψης εντολές Μέχρις_ότου συνθήκη
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ)
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ)
2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΣΚΗΣΕΙΣ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ Σημειώστε αν είναι
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΣΚΗΣΕΙΣ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ Σημειώστε αν είναι
Επιλογή και επανάληψη. Λογική έκφραση ή συνθήκη
 Επιλογή και επανάληψη Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως, ότι στο
Επιλογή και επανάληψη Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως, ότι στο
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 03-11-2013 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-4 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 03-11-2013 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-4 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη
ΤΡΙΩΡΗ ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ
 ΤΡΙΩΡΗ ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 ο Α. Δίνεται η εντολή εκχώρησης: τ κ < λ Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος. Να δικαιολογήσετε
ΤΡΙΩΡΗ ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 ο Α. Δίνεται η εντολή εκχώρησης: τ κ < λ Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος. Να δικαιολογήσετε
Προτεινόμενα Θέματα ΑΕΠΠ
 Προτεινόμενα Θέματα ΑΕΠΠ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε αν κάθε μία από τις παρακάτω προτάσεις είναι σωστή (Σ) ή λανθασμένη (Λ). Αιτιολογήσετε κάθε σας απάντηση 1. Η μερικώς περιορισμένη εμβέλεια προσφέρει
Προτεινόμενα Θέματα ΑΕΠΠ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε αν κάθε μία από τις παρακάτω προτάσεις είναι σωστή (Σ) ή λανθασμένη (Λ). Αιτιολογήσετε κάθε σας απάντηση 1. Η μερικώς περιορισμένη εμβέλεια προσφέρει
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ονοματεπώνυμο: Βαθμός:
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ονοματεπώνυμο: Βαθμός: Θέμα 1ο Α) Απαντήστε στις παρακάτω ερωτήσεις επιλέγοντας Σ (Σωστό) ή Λ (Λάθος). 1. Η ομάδα εντολών μέσα στην Αρχή_επανάληψης..μέχρις_ότου
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ονοματεπώνυμο: Βαθμός: Θέμα 1ο Α) Απαντήστε στις παρακάτω ερωτήσεις επιλέγοντας Σ (Σωστό) ή Λ (Λάθος). 1. Η ομάδα εντολών μέσα στην Αρχή_επανάληψης..μέχρις_ότου
Θέματα ΑΕΠΠ Πανελλήνιες Εξετάσεις 2007
 Θέματα ΑΕΠΠ Πανελλήνιες Εξετάσεις 2007 ΣΤΑΤΙΣΤΙΚΑ Αποτελέσματα γραπτής εξέτασης στο μάθημα ΑΕΠΠ (Ιούλιος 2007) 18-20 15-17,9 12-14,9 10-11,9 5-9,9 0-4,9 13,96% 13,90% 12,36% 10,19% 28,34% 21,22% ΘΕΜΑ 1
Θέματα ΑΕΠΠ Πανελλήνιες Εξετάσεις 2007 ΣΤΑΤΙΣΤΙΚΑ Αποτελέσματα γραπτής εξέτασης στο μάθημα ΑΕΠΠ (Ιούλιος 2007) 18-20 15-17,9 12-14,9 10-11,9 5-9,9 0-4,9 13,96% 13,90% 12,36% 10,19% 28,34% 21,22% ΘΕΜΑ 1
ΟΜΑΔΑ Ε ΓΕΩΡΓΙΟΥ ΦΩΤΕΙΝΗ ΗΛΙΟΥΔΗ ΑΦΡΟΔΙΤΗ ΜΕΤΑΛΛΙΔΟΥ ΧΡΥΣΗ ΝΙΖΑΜΗΣ ΑΛΕΞΑΝΔΡΟΣ ΤΖΗΚΑΛΑΓΙΑΣ ΑΝΔΡΕΑΣ ΤΡΙΓΚΑΣ ΑΓΓΕΛΟΣ
 ΟΜΑΔΑ Ε ΓΕΩΡΓΙΟΥ ΦΩΤΕΙΝΗ ΗΛΙΟΥΔΗ ΑΦΡΟΔΙΤΗ ΜΕΤΑΛΛΙΔΟΥ ΧΡΥΣΗ ΝΙΖΑΜΗΣ ΑΛΕΞΑΝΔΡΟΣ ΤΖΗΚΑΛΑΓΙΑΣ ΑΝΔΡΕΑΣ ΤΡΙΓΚΑΣ ΑΓΓΕΛΟΣ Η ΔΙΔΑΣΚΑΛΙΑ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΤΟ ΛΥΚΕΙΟ Εισαγωγή Η μεγάλη ανάπτυξη και ο ρόλος που
ΟΜΑΔΑ Ε ΓΕΩΡΓΙΟΥ ΦΩΤΕΙΝΗ ΗΛΙΟΥΔΗ ΑΦΡΟΔΙΤΗ ΜΕΤΑΛΛΙΔΟΥ ΧΡΥΣΗ ΝΙΖΑΜΗΣ ΑΛΕΞΑΝΔΡΟΣ ΤΖΗΚΑΛΑΓΙΑΣ ΑΝΔΡΕΑΣ ΤΡΙΓΚΑΣ ΑΓΓΕΛΟΣ Η ΔΙΔΑΣΚΑΛΙΑ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΤΟ ΛΥΚΕΙΟ Εισαγωγή Η μεγάλη ανάπτυξη και ο ρόλος που
ΠΕΡΙΕΧΟΜΕΝΑ. Εντολές επιλογής Εντολές επανάληψης
 ΠΕΡΙΕΧΟΜΕΝΑ Εντολές επιλογής Εντολές επανάληψης Εισαγωγή Στο προηγούμενο κεφάλαιο αναπτύξαμε προγράμματα, τα οποία ήταν πολύ απλά και οι εντολές των οποίων εκτελούνται η μία μετά την άλλη. Αυτή η σειριακή
ΠΕΡΙΕΧΟΜΕΝΑ Εντολές επιλογής Εντολές επανάληψης Εισαγωγή Στο προηγούμενο κεφάλαιο αναπτύξαμε προγράμματα, τα οποία ήταν πολύ απλά και οι εντολές των οποίων εκτελούνται η μία μετά την άλλη. Αυτή η σειριακή
Δομές Επανάληψης. Όσο μέχρις ότου για. 22/11/08 Ανάπτυξη εφαρμογών 1
 Δομές Επανάληψης Όσο μέχρις ότου για 22/11/08 Ανάπτυξη εφαρμογών 1 Όσο. επανάλαβε Όσο Συνθήκη επανάλαβε Εντολή1 Εντολή2.. Ομάδα εντολών Συνθήκη Αληθής Ομάδα εντολών Εντολή Ν Τέλος_Επανάληψης Ψευδής 1.
Δομές Επανάληψης Όσο μέχρις ότου για 22/11/08 Ανάπτυξη εφαρμογών 1 Όσο. επανάλαβε Όσο Συνθήκη επανάλαβε Εντολή1 Εντολή2.. Ομάδα εντολών Συνθήκη Αληθής Ομάδα εντολών Εντολή Ν Τέλος_Επανάληψης Ψευδής 1.
ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 18/02/2013 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 18/02/2013 ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α1. α. Παραβιάζει τα κριτήρια της καθοριστικότητας και της περατότητας β. Αιτιολόγηση: ο αλγόριθμος παραβιάζει το κριτήριο
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 18/02/2013 ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α1. α. Παραβιάζει τα κριτήρια της καθοριστικότητας και της περατότητας β. Αιτιολόγηση: ο αλγόριθμος παραβιάζει το κριτήριο
Ημερομηνία: Τρίτη 27 Δεκεμβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΕΠΠ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τρίτη 27 Δεκεμβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΕΠΠ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τρίτη 27 Δεκεμβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε
8. Επιλογή και επανάληψη
 8. Επιλογή και επανάληψη 8.1 Εντολές Επιλογής ΕΣΕΠ06-Θ1Β5 Η ιεραρχία των λογικών τελεστών είναι µικρότερη των αριθµητικών. ΕΣ07-Θ1Γ5 Η σύγκριση λογικών δεδοµένων έχει έννοια µόνο στην περίπτωση του ίσου
8. Επιλογή και επανάληψη 8.1 Εντολές Επιλογής ΕΣΕΠ06-Θ1Β5 Η ιεραρχία των λογικών τελεστών είναι µικρότερη των αριθµητικών. ΕΣ07-Θ1Γ5 Η σύγκριση λογικών δεδοµένων έχει έννοια µόνο στην περίπτωση του ίσου
Μάριος Αγγελίδης
 Δομή Επανάληψης Ενότητες βιβλίου: 2.4.5, 8.2, 8.2.1, 8.2.2, 8.2.3 Ώρες διδασκαλίας: 5 Η δομή επανάληψης χρησιμοποιείται όταν έχουμε μία ομάδα εντολών που θέλουμε να εκτελεστούν πολλές φορές. Υπάρχουν τρείς
Δομή Επανάληψης Ενότητες βιβλίου: 2.4.5, 8.2, 8.2.1, 8.2.2, 8.2.3 Ώρες διδασκαλίας: 5 Η δομή επανάληψης χρησιμοποιείται όταν έχουμε μία ομάδα εντολών που θέλουμε να εκτελεστούν πολλές φορές. Υπάρχουν τρείς
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ. i. Η συνθήκη α > β ή α <= β α) είναι πάντα Αληθής β) είναι πάντα Ψευδής γ) δεν υπολογίζεται δ) τίποτα από τα προηγούμενα
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΤΑΞΗ / ΤΜΗΜΑ : ΑΠΟΦΟΙΤΟΙ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 (ΕΞΙ) ΘΕΜΑ Α : A1. Να γράψετε στο φύλλο απαντήσεων τον αριθμό καθεμιάς
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΤΑΞΗ / ΤΜΗΜΑ : ΑΠΟΦΟΙΤΟΙ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 (ΕΞΙ) ΘΕΜΑ Α : A1. Να γράψετε στο φύλλο απαντήσεων τον αριθμό καθεμιάς
Δρίμτζιας Βασίλειος MSc, Καθηγητής Πληροφορικής ΠΕ19, 1ο Γενικό Λύκειο Ηγουμενίτσας
 Μεθοδολογία Μετατροπής ενός τμήματος αλγορίθμου που χρησιμοποιεί την εντολή Όσο επανάλαβε σε ισοδύναμη μορφή χρησιμοποιώντας την εντολή Για από μέχρι... με_βήμα Δρίμτζιας Βασίλειος MSc, Καθηγητής Πληροφορικής
Μεθοδολογία Μετατροπής ενός τμήματος αλγορίθμου που χρησιμοποιεί την εντολή Όσο επανάλαβε σε ισοδύναμη μορφή χρησιμοποιώντας την εντολή Για από μέχρι... με_βήμα Δρίμτζιας Βασίλειος MSc, Καθηγητής Πληροφορικής
ΘΕΜΑΤΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 1/12/2013
 ΘΕΜΑΤΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 1/12/2013 ΘΕΜΑ 1 ο Α. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη Σωστό,
ΘΕΜΑΤΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 1/12/2013 ΘΕΜΑ 1 ο Α. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη Σωστό,
Ψευδοκώδικας. November 7, 2011
 Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Σημείωση: Για τα θέματα που ακολουθούν ο παρακάτω πίνακας παρουσιάζει ισοδύναμα μεταξύ τους σύμβολα και εκφράσεις. := ή =
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 9 ΙΟΥΛΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 9 ΙΟΥΛΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ
Παλλατίδειο ΓΕΛ Σιδηροκάστρου
 Δομή Επανάληψης 2000 Θέμα 2 ο Έστω τμήμα αλγορίθμου με μεταβλητές A, B, C, D, X και Υ. D 2 Για Χ από 2 μέχρι 5 με_βήμα 2 Α 10 * Χ Β 5 * Χ + 10 C Α + Β (5 * Χ) D 3 * D - 5 Υ A + B C + D Να βρείτε τις τιμές
Δομή Επανάληψης 2000 Θέμα 2 ο Έστω τμήμα αλγορίθμου με μεταβλητές A, B, C, D, X και Υ. D 2 Για Χ από 2 μέχρι 5 με_βήμα 2 Α 10 * Χ Β 5 * Χ + 10 C Α + Β (5 * Χ) D 3 * D - 5 Υ A + B C + D Να βρείτε τις τιμές
Γ ΤΑΞΗ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ÑÏÌÂÏÓ
 Γ ΤΑΞΗ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1ο Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό,αν είναι σωστή,
Γ ΤΑΞΗ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1ο Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό,αν είναι σωστή,
Φάσμα. προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι.
 σύγχρονο Φάσμα προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο 25ης Μαρτίου 111 - ΠΕΤΡΟΥΠΟΛΗ - 210 50 20 990-210 50 27 990 25ης Μαρτίου 74 - ΠΕΤΡΟΥΠΟΛΗ - 210 50 50 658-210 50 60 845 Γραβιάς 85 -
σύγχρονο Φάσμα προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο 25ης Μαρτίου 111 - ΠΕΤΡΟΥΠΟΛΗ - 210 50 20 990-210 50 27 990 25ης Μαρτίου 74 - ΠΕΤΡΟΥΠΟΛΗ - 210 50 50 658-210 50 60 845 Γραβιάς 85 -
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) 2004
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) 2004 ΘΕΜΑ 1ο ΕΚΦΩΝΗΣΕΙΣ Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) 2004 ΘΕΜΑ 1ο ΕΚΦΩΝΗΣΕΙΣ Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις
Θέμα 1 ο. Επαναληπτικό ΛΥΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΣΤΡΙΤΣΙΟΥ ΠΑΡΑΣΚΕΥΗ 5 Μαΐου 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΣΤΡΙΤΣΙΟΥ ΠΑΡΑΣΚΕΥΗ 5 Μαΐου 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΙΟΥΝΙΟΥ 2005
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΙΟΥΝΙΟΥ 2005 ΘΕΜΑ 1ο Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα να ικανοποιεί ένας αλγόριθµος. Μονάδες 5 2. Ποιο κριτήριο
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΙΟΥΝΙΟΥ 2005 ΘΕΜΑ 1ο Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα να ικανοποιεί ένας αλγόριθµος. Μονάδες 5 2. Ποιο κριτήριο
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ
 Θέμα Α ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2016-2017 Πάτρα 3/5/2017 Ονοματεπώνυμο:.. Α1. Να γράψετε στην κόλλα σας τον αριθμό
Θέμα Α ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2016-2017 Πάτρα 3/5/2017 Ονοματεπώνυμο:.. Α1. Να γράψετε στην κόλλα σας τον αριθμό
ΘΕΜΑ Α. Α2. Να αναφέρετε από τι εξαρτάται η επιλογή του καλύτερου αλγορίθμου ταξινόμησης. Μονάδες 4. Σελίδα 1 από 8
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 2013 Γ Λυκείου Τεχνολογική Κατεύθυνση ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 2013 Γ Λυκείου Τεχνολογική Κατεύθυνση ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5
Τ και τιµή του Β θετική µετατρέπεται ισοδύναµα στην εντολή Όσο ως εξής:
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 12 ΙΑΝΟΥΑΡΙΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 12 ΙΑΝΟΥΑΡΙΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ
Για Ι από 2 μέχρι 10 με_βήμα 0 S S+I Τέλος_επανάληψης Εμφάνισε S Μονάδες 5
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΙΟΥΝΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΙΟΥΝΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΕΠΠ ΤΡΙΤΗ 18 ΑΠΡΙΛΙΟΥ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7)
 ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΕΠΠ ΤΡΙΤΗ 18 ΑΠΡΙΛΙΟΥ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) Θέμα Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΕΠΠ ΤΡΙΤΗ 18 ΑΠΡΙΛΙΟΥ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) Θέμα Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ
 1ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ Α ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 26 ΑΠΡΙΛΙΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ
1ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ Α ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 26 ΑΠΡΙΛΙΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ
ΑΕΠΠ Ερωτήσεις θεωρίας
 ΑΕΠΠ Ερωτήσεις θεωρίας Κεφάλαιο 1 1. Τα δεδομένα μπορούν να παρέχουν πληροφορίες όταν υποβάλλονται σε 2. Το πρόβλημα μεγιστοποίησης των κερδών μιας επιχείρησης είναι πρόβλημα 3. Για την επίλυση ενός προβλήματος
ΑΕΠΠ Ερωτήσεις θεωρίας Κεφάλαιο 1 1. Τα δεδομένα μπορούν να παρέχουν πληροφορίες όταν υποβάλλονται σε 2. Το πρόβλημα μεγιστοποίησης των κερδών μιας επιχείρησης είναι πρόβλημα 3. Για την επίλυση ενός προβλήματος
Κεφάλαια Εντολές επανάληψης. Τρεις εντολές επανάληψης. Επιλογή εντολής επανάληψης ΟΣΟ...ΕΠΑΝΑΛΑΒΕ. Σύνταξη στη ΓΛΩΣΣΑ
 Εντολές επανάληψης Κεφάλαια 02-08 οµές Επανάληψης Επιτρέπουν την εκτέλεση εντολών περισσότερες από µία φορά Οι επαναλήψεις ελέγχονται πάντοτε από κάποια συνθήκη η οποία καθορίζει την έξοδο από το βρόχο
Εντολές επανάληψης Κεφάλαια 02-08 οµές Επανάληψης Επιτρέπουν την εκτέλεση εντολών περισσότερες από µία φορά Οι επαναλήψεις ελέγχονται πάντοτε από κάποια συνθήκη η οποία καθορίζει την έξοδο από το βρόχο
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΡΠΕΝΗΣΙΟΥ ΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ 16/12/2008. Τµήµα ΓΤ2 Όνοµα:...
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΡΠΕΝΗΣΙΟΥ ΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ 16/12/2008 Τµήµα ΓΤ2 Όνοµα:... ΘΕΜΑ 1 ο. Α) Να γράψετε στο φύλλο απαντήσεών σας Σ εάν κρίνετε ότι η πρόταση είναι σωστή και
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΡΠΕΝΗΣΙΟΥ ΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ 16/12/2008 Τµήµα ΓΤ2 Όνοµα:... ΘΕΜΑ 1 ο. Α) Να γράψετε στο φύλλο απαντήσεών σας Σ εάν κρίνετε ότι η πρόταση είναι σωστή και
ΑΕΠΠ 4o Επαναληπτικό Διαγώνισμα
 ΑΕΠΠ 4o Επαναληπτικό Διαγώνισμα Ονοματεπώνυμο: ΘΕΜΑ 1 A. Να γράψετε τους κανόνες που πρέπει να ακολουθούνται στη χρήση των εμφωλευμένων βρόχων. B. Να χαρακτηρίσετε ως σωστή (Σ) ή λάθος (Λ) καθεμία από
ΑΕΠΠ 4o Επαναληπτικό Διαγώνισμα Ονοματεπώνυμο: ΘΕΜΑ 1 A. Να γράψετε τους κανόνες που πρέπει να ακολουθούνται στη χρήση των εμφωλευμένων βρόχων. B. Να χαρακτηρίσετε ως σωστή (Σ) ή λάθος (Λ) καθεμία από
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον
 Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον 2.4.5 8.2 Βασικές Ασκήσεις στις Δομές Επανάληψης Έλεγχος Εισαγόμενων Τιμών Εύρεση Αθροισμάτων - Μέσων όρων Εύρεση Μέγιστου- Ελάχιστου Εύρεση Πλήθους Ποσοστών
Ανάπτυξη Εφαρμογών σε Προγραμματιστικό Περιβάλλον 2.4.5 8.2 Βασικές Ασκήσεις στις Δομές Επανάληψης Έλεγχος Εισαγόμενων Τιμών Εύρεση Αθροισμάτων - Μέσων όρων Εύρεση Μέγιστου- Ελάχιστου Εύρεση Πλήθους Ποσοστών
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 Σάββατο, 4 Ιουνίου 2005 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1o Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα να ικανοποιεί ένας αλγόριθµος.
Σάββατο, 4 Ιουνίου 2005 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1o Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα να ικανοποιεί ένας αλγόριθµος.
Ημερομηνία: Τετάρτη 27 Δεκεμβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΕΠΠ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 27 Δεκεμβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΕΠΠ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 27 Δεκεμβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα
Τρίτη, 1 Ιουνίου 2004 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ
 ΘΕΜΑ 1 ο ο Τρίτη, 1 Ιουνίου 2004 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό, αν είναι
ΘΕΜΑ 1 ο ο Τρίτη, 1 Ιουνίου 2004 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό, αν είναι
ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 05/03/2012
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 05/03/2012 ΘΕΜΑ Α Α1. Να γράψετε τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 05/03/2012 ΘΕΜΑ Α Α1. Να γράψετε τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι
Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2
 Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2 1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων Πληροφορικής 2. Ο αλγόριθμος αποτελείται από ένα πεπερασμένο σύνολο εντολών 3. Ο αλγόριθμος
Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2 1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων Πληροφορικής 2. Ο αλγόριθμος αποτελείται από ένα πεπερασμένο σύνολο εντολών 3. Ο αλγόριθμος
Πληροφορική ΙΙ. Τ.Ε.Ι. Ιονίων Νήσων Σχολή Διοίκησης και Οικονομίας - Λευκάδα
 Πληροφορική ΙΙ Τ.Ε.Ι. Ιονίων Νήσων Σχολή Διοίκησης και Οικονομίας - Λευκάδα Στέργιος Παλαμάς, Υλικό Μαθήματος «Πληροφορική ΙΙ», 2015-2016 Μάθημα 1: Εισαγωγή στους Αλγόριθμους Αλγόριθμος είναι μια πεπερασμένη
Πληροφορική ΙΙ Τ.Ε.Ι. Ιονίων Νήσων Σχολή Διοίκησης και Οικονομίας - Λευκάδα Στέργιος Παλαμάς, Υλικό Μαθήματος «Πληροφορική ΙΙ», 2015-2016 Μάθημα 1: Εισαγωγή στους Αλγόριθμους Αλγόριθμος είναι μια πεπερασμένη
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ (2ος Κύκλος) ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ (2ος Κύκλος) ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΘΕΜΑΤΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 Θέμα 1 ο ΘΕΜΑΤΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις ως
Θέμα 1 ο ΘΕΜΑΤΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις ως
ΠΡΟΣ: Τηλέφωνο: 210-3443422 Ινστιτούτο Εκπαιδευτικής Πολιτικής ΚΟΙΝ.:
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ----- Βαθμός Ασφαλείας: Να διατηρηθεί μέχρι: Βαθ. Προτεραιότητας: ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ Π/ΘΜΙΑΣ ΚΑΙ Δ/ΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ----- Βαθμός Ασφαλείας: Να διατηρηθεί μέχρι: Βαθ. Προτεραιότητας: ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ Π/ΘΜΙΑΣ ΚΑΙ Δ/ΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ,
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1 ο ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΑΒΒΑΤΟ 23 ΙΑΝΟΥΑΡΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1 ο ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΑΒΒΑΤΟ 23 ΙΑΝΟΥΑΡΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΟΜΗ ΕΠΑΝΑΛΗΨΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: 6
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΟΜΗ ΕΠΑΝΑΛΗΨΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: 6 ΘΕΜΑ 1 ο Α. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) η λανθασµένες
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΟΜΗ ΕΠΑΝΑΛΗΨΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: 6 ΘΕΜΑ 1 ο Α. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) η λανθασµένες
Ο αλγόριθμος πρέπει να τηρεί κάποια κριτήρια
 Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών, αυστηρά καθορισμένων και εκτελέσιμων σε πεπερασμένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήματος. Ο αλγόριθμος πρέπει να τηρεί κάποια κριτήρια Είσοδος:
Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών, αυστηρά καθορισμένων και εκτελέσιμων σε πεπερασμένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήματος. Ο αλγόριθμος πρέπει να τηρεί κάποια κριτήρια Είσοδος:
Εκπαιδευτικό Σενάριο για την Διδασκαλία των Δομών Επανάληψης
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Εκπαιδευτικό Σενάριο για την Διδασκαλία των Δομών Επανάληψης Παπαδημητρίου Ηλίας Σιψά Γρηγορία Καλαμάτα 20/06/2013 Εκπαιδευτικό Σενάριο Για Την Διδασκαλία
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Εκπαιδευτικό Σενάριο για την Διδασκαλία των Δομών Επανάληψης Παπαδημητρίου Ηλίας Σιψά Γρηγορία Καλαμάτα 20/06/2013 Εκπαιδευτικό Σενάριο Για Την Διδασκαλία
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ. Εξετάσεις Προσομοίωσης 24/04/2019
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Εξετάσεις Προσομοίωσης 24/04/2019 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-4 και δίπλα τη λέξη ΣΩΣΤΟ, αν
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Εξετάσεις Προσομοίωσης 24/04/2019 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-4 και δίπλα τη λέξη ΣΩΣΤΟ, αν
ΤΕΛΙΚΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ
 ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΛΙΚΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Επιμέλεια: Ομάδα Διαγωνισμάτων από Το στέκι των πληροφορικών Θέμα 1 ο Α. Να χαρακτηρίσετε κάθε μία από
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΛΙΚΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Επιμέλεια: Ομάδα Διαγωνισμάτων από Το στέκι των πληροφορικών Θέμα 1 ο Α. Να χαρακτηρίσετε κάθε μία από
Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΜΑΘΗΜΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 15 / 01 / 2012
 ΘΕΜΑ 1 ο Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΜΑΘΗΜΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 15 / 01 / 2012 A. Να σημειώσετε αν είναι σωστή ή λανθασμένη η καθεμιά από τις παρακάτω
ΘΕΜΑ 1 ο Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΜΑΘΗΜΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 15 / 01 / 2012 A. Να σημειώσετε αν είναι σωστή ή λανθασμένη η καθεμιά από τις παρακάτω
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ/Γ ΟΙΚΟΝΟΜΙΚΩΝ & ΠΛΗΡΟΦΟΡΙΚΗΣ-ΘΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 12/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΚΑΤΡΑΚΗ Α.-ΣΙΟΤΡΟΠΟΣ Π.-ΛΙΟΔΑΚΗΣ Ε.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 2017-2018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ/Γ ΟΙΚΟΝΟΜΙΚΩΝ & ΠΛΗΡΟΦΟΡΙΚΗΣ-ΘΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 12/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΚΑΤΡΑΚΗ Α.-ΣΙΟΤΡΟΠΟΣ Π.-ΛΙΟΔΑΚΗΣ Ε. ΘΕΜΑ Α Α1. Να γράψετε τον αριθμό
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 2017-2018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ/Γ ΟΙΚΟΝΟΜΙΚΩΝ & ΠΛΗΡΟΦΟΡΙΚΗΣ-ΘΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 12/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΚΑΤΡΑΚΗ Α.-ΣΙΟΤΡΟΠΟΣ Π.-ΛΙΟΔΑΚΗΣ Ε. ΘΕΜΑ Α Α1. Να γράψετε τον αριθμό
ΔΙΑΓΩΝΙΣΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ:- Γ ΛΥΚΕΙΟΥ ΤΜΗΜΑΤΑ: ΓΟ4 ΓΟ7 (ΖΩΓΡΑΦΟΥ) ΓΟ5 ΓΟ6 (ΧΟΛΑΡΓΟΣ) HM/NIA: 15/1/2017
 ΔΙΑΓΩΝΙΣΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ:- Γ ΛΥΚΕΙΟΥ ΤΜΗΜΑΤΑ: ΓΟ4 ΓΟ7 (ΖΩΓΡΑΦΟΥ) ΓΟ5 ΓΟ6 (ΧΟΛΑΡΓΟΣ) HM/NIA: 15/1/2017 ΘΕΜΑ Α (Α1) Δίνεται η παρακάτω ακολουθία εντολών αλγορίθμου:
ΔΙΑΓΩΝΙΣΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΑΞΗ:- Γ ΛΥΚΕΙΟΥ ΤΜΗΜΑΤΑ: ΓΟ4 ΓΟ7 (ΖΩΓΡΑΦΟΥ) ΓΟ5 ΓΟ6 (ΧΟΛΑΡΓΟΣ) HM/NIA: 15/1/2017 ΘΕΜΑ Α (Α1) Δίνεται η παρακάτω ακολουθία εντολών αλγορίθμου:
ΚΕΦΑΛΑΙΑ & 8.2 (ΔΟΜΕΣ ΕΠΑΝΑΛΗΨΗΣ) ΘΕΩΡΙΑ
 ΚΕΦΑΛΑΙΑ 2.4.5 & 8.2 (ΔΟΜΕΣ ΕΠΑΝΑΛΗΨΗΣ) ΘΕΩΡΙΑ Ερωτήσεις Σωστό / Λάθος 1. Στη δομή Για... από... μέχρι η αρχική τιμή του μετρητή πρέπει να είναι πάντα μικρότερη από την τελική. 2. Η δομή Όσο... επανάλαβε
ΚΕΦΑΛΑΙΑ 2.4.5 & 8.2 (ΔΟΜΕΣ ΕΠΑΝΑΛΗΨΗΣ) ΘΕΩΡΙΑ Ερωτήσεις Σωστό / Λάθος 1. Στη δομή Για... από... μέχρι η αρχική τιμή του μετρητή πρέπει να είναι πάντα μικρότερη από την τελική. 2. Η δομή Όσο... επανάλαβε
Γκύζη 14-Αθήνα Τηλ :
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ)
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ)
Κεφαλαιο 2.2 ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΑΛΓΟΡΙΘΜΟΙ
 Κεφαλαιο 2.2 ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΑΛΓΟΡΙΘΜΟΙ 1.Σ, 2.Σ, 3. Λ, 4.Σ, 5.Σ Στο α) ανήκουν: 1,2,5,6,7 Στο β) ανήκουν: 3,4,8,9,10 1.-Λ, 2.-Λ, 3.-Σ, 4.-Σ, 5.-Σ 1. -Πραγματικός, 2. -Αρφαριθμητικός, 3.-Αλφαριθμητικός,
Κεφαλαιο 2.2 ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΑΛΓΟΡΙΘΜΟΙ 1.Σ, 2.Σ, 3. Λ, 4.Σ, 5.Σ Στο α) ανήκουν: 1,2,5,6,7 Στο β) ανήκουν: 3,4,8,9,10 1.-Λ, 2.-Λ, 3.-Σ, 4.-Σ, 5.-Σ 1. -Πραγματικός, 2. -Αρφαριθμητικός, 3.-Αλφαριθμητικός,
Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ. Ημερομηνία: Σάββατο 5 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ημερομηνία: Σάββατο 5 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ημερομηνία: Σάββατο 5 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2011-2012 Επιμέλεια: Ομάδα Διαγωνισμάτων από το Στέκι των Πληροφορικών Θέμα Α Α1. Να γράψετε στο τετράδιό σας τον
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2011-2012 Επιμέλεια: Ομάδα Διαγωνισμάτων από το Στέκι των Πληροφορικών Θέμα Α Α1. Να γράψετε στο τετράδιό σας τον
ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ Γ Α... Β
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 11 ΑΠΡΙΛΙΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 11 ΑΠΡΙΛΙΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ
2. Ένα από τα στάδια αντιμετώπισης ενός προβλήματος είναι η ανάλυση.
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΕΣΠΕΡΙΝΟΥ ΕΠΑΛ (ΟΜΑΔΑΣ Β ) ΣΑΒΒΑΤΟ 22 ΜΑΪΟΥ 2010 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΕΣΠΕΡΙΝΟΥ ΕΠΑΛ (ΟΜΑΔΑΣ Β ) ΣΑΒΒΑΤΟ 22 ΜΑΪΟΥ 2010 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε
ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ & Δ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ KAI Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 5 ΣΕΠΤΕΜΒΡΙΟΥ 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ & Δ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ KAI Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 5 ΣΕΠΤΕΜΒΡΙΟΥ 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 30 MAΪΟΥ ΑΕΠΠ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 30 MAΪΟΥ 2008 - ΑΕΠΠ ΘΕΜΑ 1ο Α. 1. Ποια είναι τα κυριότερα χρησιμοποιούμενα γεωμετρικά σχήματα σε ένα διάγραμμα ροής και τι ενέργεια ή
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 30 MAΪΟΥ 2008 - ΑΕΠΠ ΘΕΜΑ 1ο Α. 1. Ποια είναι τα κυριότερα χρησιμοποιούμενα γεωμετρικά σχήματα σε ένα διάγραμμα ροής και τι ενέργεια ή
Αλγόριθμοι Αναπαράσταση αλγορίθμων Η αναπαράσταση των αλγορίθμων μπορεί να πραγματοποιηθεί με:
 Αλγόριθμοι 2.2.1. Ορισμός: Αλγόριθμος είναι μια πεπερασμένη σειρά εντολών, αυστηρά καθορισμένων και εκτελέσιμων σε πεπερασμένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήματος. Τα κυριότερα χρησιμοποιούμενα
Αλγόριθμοι 2.2.1. Ορισμός: Αλγόριθμος είναι μια πεπερασμένη σειρά εντολών, αυστηρά καθορισμένων και εκτελέσιμων σε πεπερασμένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήματος. Τα κυριότερα χρησιμοποιούμενα
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 A ΦΑΣΗ
 ΤΑΞΗ: ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ημερομηνία: Πέμπτη 3 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
ΤΑΞΗ: ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ημερομηνία: Πέμπτη 3 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) 2004
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) 2004 ΘΕΜΑ 1ο Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) 2004 ΘΕΜΑ 1ο Α. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΘΕΜΑ Α. Λύση: 1. Σωστό, 2. Λάθος, 3. Σωστό, 4. Λάθος, 5. Λάθος. Ποια η διαφορά μεταξύ διερμηνευτή και μεταγλωττιστή; Απάντηση:
 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη Λάθος, αν είναι λανθασμένη. 1. Η ταξινόμηση είναι μια από τις βασικές
ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη Λάθος, αν είναι λανθασμένη. 1. Η ταξινόμηση είναι μια από τις βασικές
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ ΑΕΠΠ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 - ΑΕΠΠ ΘΕΜΑ 1ο Α. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-6 και δίπλα τη λέξη Σωστό, αν
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 - ΑΕΠΠ ΘΕΜΑ 1ο Α. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-6 και δίπλα τη λέξη Σωστό, αν
ΘΕΜΑ 1ο Α. 1-6 Σωστό Λάθος Μονάδες 12 Β. Στήλης Στήλης Β Στήλης Α Στήλης Β).
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) ΘΕΜΑ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) ΘΕΜΑ
Διαγώνισμα Ανάπτυξης Εφαρμογών Σε Προγραμματιστικό Περιβάλλον
 Διαγώνισμα Ανάπτυξης Εφαρμογών Σε Προγραμματιστικό Περιβάλλον ΘΕΜΑ Α A1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη
Διαγώνισμα Ανάπτυξης Εφαρμογών Σε Προγραμματιστικό Περιβάλλον ΘΕΜΑ Α A1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ)
 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (7) 25/7/2012 Θέμα Α Α1. Να γράψετε στο τετράδιό
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (7) 25/7/2012 Θέμα Α Α1. Να γράψετε στο τετράδιό
Ι. ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Της Γ τάξης Ημερησίου Γενικού Λυκείου
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ----- ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ Π/ΘΜΙΑΣ ΚΑΙ Δ/ΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ, ΠΡΟΓΡΑΜΜΑΤΩΝ ΚΑΙ ΟΡΓΑΝΩΣΗΣ Δ/ΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΤΜΗΜΑ Α -----
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ----- ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ Π/ΘΜΙΑΣ ΚΑΙ Δ/ΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ, ΠΡΟΓΡΑΜΜΑΤΩΝ ΚΑΙ ΟΡΓΑΝΩΣΗΣ Δ/ΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΤΜΗΜΑ Α -----
ΔΙΑΓΩΝΙΣΜΑ 1ο Γ Τάξη Ενιαίου Λυκείου Σχολικό Έτος ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 ΔΙΑΓΩΝΙΣΜΑ 1ο Γ Τάξη Ενιαίου Λυκείου Σχολικό Έτος 2017 2018 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ Α Α1. Απαντήστε στις παρακάτω προτάσεις με το γράμμα Σ αν η πρόταση είναι Σωστή ή με το
ΔΙΑΓΩΝΙΣΜΑ 1ο Γ Τάξη Ενιαίου Λυκείου Σχολικό Έτος 2017 2018 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ Α Α1. Απαντήστε στις παρακάτω προτάσεις με το γράμμα Σ αν η πρόταση είναι Σωστή ή με το
Αλγοριθμική Δομή Επανάληψης
 Ημερίδα : «Διδακτικές προσεγγίσεις στα μαθήματα Ανάπτυξη εφαρμογών και Προγραμματιμός» Αλγοριθμική Δομή Επανάληψης Γεώργιος Χρ. Μακρής Διδακτικοί στόχοι στις δομές επανάληψης Να μπορούν να ξεχωρίζουν οι
Ημερίδα : «Διδακτικές προσεγγίσεις στα μαθήματα Ανάπτυξη εφαρμογών και Προγραμματιμός» Αλγοριθμική Δομή Επανάληψης Γεώργιος Χρ. Μακρής Διδακτικοί στόχοι στις δομές επανάληψης Να μπορούν να ξεχωρίζουν οι
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 02/11/2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι. ΜΙΧΑΛΕΑΚΟΣ - Π. ΣΙΟΤΡΟΠΟΣ- Α. ΚΑΤΡΑΚΗ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 02/11/2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι. ΜΙΧΑΛΕΑΚΟΣ - Π. ΣΙΟΤΡΟΠΟΣ- Α. ΚΑΤΡΑΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 02/11/2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι. ΜΙΧΑΛΕΑΚΟΣ - Π. ΣΙΟΤΡΟΠΟΣ- Α. ΚΑΤΡΑΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα
