Spriahnute oscilatory
|
|
|
- Σωφρονία Βιτάλη
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Spriahnute oscilatory Juraj Tekel 1 Tema spriahnutych oscilatorov je na strednej skole vacsinou vynechana. Je vsak velmi zaujimava a velmi dolezita. Ide o situaciu, ked sa sustava sklada z viacerych telies, na ktore posobia pruzne sily, tj. sily majuce tvar k suradnica, avsak sily posobia aj medzi tymito telesami. V rovniciach sa tento fakt prejavi tak, ze v pohybovej rovnici pre teleso sa objavia suradnice ineho, pripadne inych telies. Na uvod si povedzme cosi vseobecne o suradniciach. Neskor sa to ukaze neocakave dolezite. Slovo suradnica v kazdom z nas pravdepodobne vzbudzuje predstavu vzdialenosti od nejakeho referencneho bodu. Napriklad suradnice kvetinaca v izbe, vzdialenost, ktoru po ceste preslo auto, vseobecne popis miesta, kde sa nejake teleso nachadza. Avsak popisovat polohu telesa mozme aj inak, ako vzdialenostou, napriklad zemepisna sirka a dlza. Zas ale potrebujeme referencne miesto, vzhladom na ktore tieto uhly meriame. Suradnice su teda vseobecne sada cisel, ktore spolu s dobre znamim sposobom, ako tieto cisla zistujeme hovori, kde sa teleso nachadza. Aspon sa tak zda. Avsak situacie su vo fyzike casto zlozitejsie. Zvacsa je ulohou fyzika popisat, ako sa bude spravat nejaka sustava. V uz spomenutych pripadoch kvetinac, auto na ceste ci na zemeguli. V niektorych pripadoch je vsak neprakticke popisovat stav sustavy, ktora nas zaujima, popisovat vzdialenostou. Napriklad pre kondenzator je najlepsie popisany jeho stav nabojom, ktory sa na nom nazbieral. Pre cely elektrck obvod to moze byt prud a napatie na jednotlyvych jeho castiach. Fyzik potom hlada rovnice, ktore popsiuju ako sa menia tieto suradnice v case. Takze nasa povodna definicia suradnice prechadza na o nieco vseobecnejsi pripad. Suradnice su sada cisel, ktore spolu s dobre znamim sposobom, ako tieto cisla zistujeme hovori, v ktorom zo svojich moznych stavov sa popisovana sustava nachadza. Riesenim rovnic pre suradnice potom zistime, ako sa bude stav telesa menit. Suradnice su teda sposob, ako zmatematizovat popis sustavy do reci cisel a funkcii, pre ktore vieme napisat a riesit rovnice. Teraz prichadza klucove vsimnutie tejto prednasky. Na popis sustavy neexistuju iba jedine suradnice. Naopak suradnic, ktore mozme vybrat na popis sustavy je nekonecne vela uz len napriklad vdaka moznej zmene referenceho miesta. Aby bolo jasne, o com hovorime, majme len jeden hmotny bod v priestore. Jeho polohu mozme popisat napriklad tak, ze zvolime pravouhlu suradnicou sustavu a zadame suradnice miesta, kde sa bod nachadza (x, y, z). Tento pod mozme popisat ale aj inak, napriklad sferickymi suradnicami, teda vzdialenostou od zvoleneho bodu a uhlami od x-ovej a z-ovej osy (r, φ, θ). Mozme ale zvolit suradnice inak. Polohu telesa by rovnako dobre popisovala aj trojica (x + y, x y, z) alebo trojica (x + 2y z, x + y 2z, y + z). Mohli sme ale zvolit aj zlozitejsiu zavyslost ako napriklad (sin(x), log(y), z 4 7 ). Upllne vseobecne mozu mat suradnice tvar (f x (x, y, z), f y (x, y, z), f z (x, y, z)) za istych podmienok na funkcie f x, f y, f z, aby tieto suradnice boli nezavysle. V roznych suradniciach samozrejme vyzeraju rovnice, popisujuce pohyb sustavy rozne. Maju teda aj ine vysledky, ale vyznam tycht vysledkov, teda pohyb, ktory suradnice popisuju musi byt rovnaky. A to nam dava do ruk silnu zbran. Mozme si lubovole vybrat suradnice tak, aby rovnice, ktore v nich popisuju ako sa meni stav sustavy boli co najjednoduchsie a my sme ich vedeli vyriesit. Uvidime, ako nam tento fakt pomoze pri popise pohybu sprahnutych oscilatorov. Este budeme potrebovat nieco malo o harmonickych oscilatoroch. Majme teleso, ktoreho pohyb je viazany na priamku. Ak na teleso posobi sila, ktora sa da zapisat v tvare F = kx, kde k je nejaka 1 Akekolvek pripomienky, upozornenia alebo namety uvitam na adrese juraj.tekel@gmail.com 1
2 kladna konstanta, potom je pohybova rovnica a = ω 2.x kde ω = k/m. Tym sa zdoraznuje, ze cislo, stojace na pravej strane pred x je zaporne. Takato rovnica ma potom riesenie 2 x(t) = X 0 sin(ωt + φ) v(t) = X 0 ω cos(ωt + φ) a fyzici tomu radi hovoria harmonicke kmity. Perioda tohto pohybu je T = 2π/ω. Ak by bola poloha telesa, pripadne stav sustavy popisanou suradnicou, ale rovnica, popisujuca zmeny tejto suradnice by bola v tvare zrychleniesuradnice = ω 2 suradnica, jej riesenim su harmonicke kmity a plati pre nu predchadzajuce a nasledovne. Je dobre si ujasnit vyznam konstant X 0, ω, φ, ktore su postupne maximalna vychylka, nejak zakodovana perioda a zaciatocna faza Prve dve teda popisuju pohyb telesa ako taky a tretia situaciu, v akej teleso svoj pohyb zacina v case t = 0. Rovnice sa pouzitim suctoveho vzorca pre sinus daju prepisat do tvaru pripadne najcastejsie x(t) = A 0 sin ωt + B 0 cos ωt v(t) = A 0 ω cos ωt + B 0 ω sin ωt x(t) = A sin ωt + B cos ωt ω v(t) = A cos ωt + Bω sin ωt V konstantach A, B je zakodovana infotmacia o pociatocnych podmienkach. Lahko sa presvedcime, ze B je vychylka v case t = 0 a A je pociatocna rychlost. Pouzivaju sa oba tvary rieseni a zalezi od konkretnej situacie, ktora z dvoch sad je pre nas vyhodnejsia. A samozrejme budme potrebovat vediet, ze F = ma. No a mozme sa konecne venovat spriahnutym oscilatorom. Ilustrujme to na jednoduchom pripade. Neskor si povieme, ako nas postup zovseobecnime na vseobecny pripad. Dve telesa hmotnosti m na troch pruzinach, tak ze kazde je na jednej strane pripevnene jednou pruzinou k stene a medzi sebou maju dalsiu pruzinu. Nech je na zaciatku cela sustava v rovnovovahe a nech sa telesa mozu pohybovat len po jedne priamke. Polohu tejto sustavy opisuju dve suradnice, napriklad vychylka z rovnovaznej polhy prveho telesa x a duheho telesa y. Na kazde z telies posobi silou pruzinka, ktorou je teleso uchytene k stene velkosti kx resp. ky a pruzinka medzi nimi silou velkosti k(x y). Ked si dobre premyslime smery, ktorymi tieto sily posobia, dostaneme pohybove rovnice pre telesa ma x = kx k(x y) ma y = ky k(y x) Ked zavedieme oznacenie k m = ω2, rovnice prejdu na tvar a x = 2ω 2 x + ω 2 y (1) a y = 2ω 2 y + ω 2 x (2) 2 Je to diferencialna rovnica a na jej riesenia treba vediet vela netrivialnej matematiky. Treba sa preto na tejto urovni uspokojit s tym, ze niekto tu rovnicu za nas zratal a my sme vdacni, ze to nemusime robit zas a znova sami a toto riesenie si radsej zapamatame. Pri tom samozrejme pekne podakujeme. 2
3 Vidime, ze rovnice pre pohyb telies nemaj tvar rovnice pre LHO, ktory by sa nam pacil, nakolko by sme hned vedeli napisat jej riesenia. Dokonca su tieto rovnice previazane, teda v rovnici pre jedno teleso vystupuje suradnica druheho telesa. Taketo rovnice zatial riesit nevieme. Preto vyskusajme takuto vec. Skusme do rovnic dosadit riesnie v tvare harmonickych kmitov, tj. v tvare x = A x sin (Ωt + Φ x ), kde Ω je vseobecne cosi ine ako ω. A rovnake riesenie pre y 3. Co nas opravnuje k takemuto kroku? V prvom rade do pohybovych rovnic mozme dosadit akekovlek riesnie v tvare cohokolvek. Rovnice nam potom povedia, ci takyto pohyb moze alebo nemoze teleso vykonavat. Ak by sme dosadili naprikad riesenie v tvare rovnmerne zrychleneho pohybu 4, rovnice by povedali ze takyto pohyb mozny nie. Ak v navrhovanom rieseni nechame nejake volne parametre, v nasom pripadne to je A x,y, Ω, Φ x,y, rovnice nam povedia, pre ake, ak nejake, hodnoty tychto parametrov je riesenie takehoto tvaru pripustne. V pripade neuspechu sme nic nestratili, v pripadne uspechu sme ziskali konkretny tvar mozneho riesenia pohybovych rovnic. V druhom rade mame istotu, ze ked takto najdeme nejake risenie, ktore vyhovuje nejakym konkretnym pociatocnym podmienkam, ine riesenie tymto pociatocnym podmienkam vyhovovat nebude. Bolo by neprijemne, keby sme dva krat nastavili sustavu do rovnakej polohy a ona sa pohybovala inak. Keby to neplatilo, vsetci fyzici by prisli o pracu, lebo by stratila zmysel 5. Porozmyslajte, ako je to s hadzanim kockou a ako nahodnost vstupuje do hry. Dosadme teda navrhovane riesenia do rovnic (1). Ω 2 A x sin (Ωt + Φ x ) = 2ω 2 A x sin (Ωt + Φ x ) + ω 2 A y sin (Ωt + Φ y ) ( Ω 2 + 2ω 2 )A x sin (Ωt + Φ x ) = ω 2 A y sin (Ωt + Φ y ) Ω 2 A y sin (Ωt + Φ y ) = 2ω 2 A y sin (Ωt + Φ y ) + ω 2 A x sin (Ωt + Φ x ) ( Ω 2 + 2ω 2 )A y sin (Ωt + Φ y ) = ω 2 A x sin (Ωt + Φ x ) 3 Tu treba poznamenat, ze riesnie by sme mohli dosadzat aj tvare suctu sinusu a kosinusu. Takato cesta je vsak schodnejsia 4 Pre ilustraciu to spravme. Pre rovnomerne zrychelny pohyb x = x 0 + v x0t at2 y = y 0 + v y0t bt2 a x = a a y = b Dosadime toto riesenie do rovnic (1) a zistime, ze a = 2ω 2 ( x 0 + v x0t at2 ) + ω 2 ( y 0 + v y0t bt2 ) 0 = ω 2 ( 2x 0 + y 0) a + ω 2 ( 2v x0 + v y0)t + ω 2 ( a b)t2 Vidime, ze sme dosatli kvadraticku rovnicu pre cas. Vseobecne je tada platna iba pre dva konkretne casi. Jedniny pripad, kedy plati v kazdom case (co je presne to co chceme) je, ked v skutocnosti nepojde o kvadraticku rovnicu, ale o identitu, teda ked 0 = ω 2 ( 2x 0 + y 0) a ω 2 ( 2x 0 + y 0) = a 0 = ω 2 ( 2v x0 + v y0) 2v x0 = v y0 0 = ω 2 ( a + 1 b) 2a = b 2 Z druhej rovnice by sme dostali podobne podmienky, len s vymenenymi parametrami pre suradnice x a y. Tie su zjavne splnene iba v pripade a = b = v x0 = v y0 = x 0 = y 0 = 0. Takze jediny rovnomerne zrychleny pohyb, ktory je riesnim tychto rovnic je statie. 5 V kvanotvej teorii to prestava byt pravda a aj pri rovnakych podmienkach mozu nastat ine veci. Tu vsak vieme presne povedat s akou pradvepodobnostou ta ktora vec nastane, takze praca fyzika je istym sposobom zmysluplna. 3
4 Vydelenim tychto dvoch rovnic sa zbavime casu dostavame podmienku (2ω 2 Ω 2 ) 2 = ω 4 Ktora ma dve riesenia Ω 2 = ω 2 a Ω 2 = 3ω 2. Toto dosadime do povodnych podmienok a dostaneme V prvom a A x sin (Ωt + Φ x ) = A y sin (Ωt + Φ y ) A y sin (Ωt + Φ y ) = A x sin (Ωt + Φ x ) v druhom pripade. Nakolko tieto rovnice maju platit pre lubovolne t, na to, aby nase navrhovane riesnie bolo riesenim rovnice (1), musia byt splnene podmienky alebo A x = A y, Φ x = Φ y, Ω 2 = ω 2 A x = A y, Φ x = Φ y + π, Ω 2 = 3ω 2 Dostali sme teda dve mozne riesenia v tvare hamronickych kmitov. Premyslite si, ze to znamena, nasledovne. V prvom priadne vychylime obe telesa rovnako na rovnaku stranu a udelime im rovnaku rychlost. Vtedy sa streda pruzina nebude vobec predlzovat a telesa kmitaju akoby tam druhe teleso vobec nebolo. Druha moznost po preskumani vztahu parametrov pre prve a druhe teleso znamena, ze telesa vychylime za zaciatku rovnako opacnym smerom a udelime im rovnaku rychlost proti sebe. Vtedy bude stred strednej pruziny stat a telesa budu kmitat akoby tam druhe teleso nebolo a pruziny mali tuhost k a 2k. Z tvaru rovnic vyplyva, ze ked by sme scitali tieto dve riesenia a dostali riesenie v tvare ( ) x = A sin (ωt + Φ 1 ) + B sin 3ωt + Φ2 ( ) y = A sin (ωt + Φ 1 ) + B sin 3ωt + Φ2 + π aj toto bude riesenie rovnic. To preto, ze rovnice su linearne, teda v nich vystupuju suradnice iba v prvej mocnine. A teraz pride jeden z najvacsich zazrakov fyziky. Akekolvek riesenie uvedenych pohybovych rovnic sa da napisat ako sucet nejakych nasobkov nasich dvoch natypovanych rieseni! To sa da nahliadnut napriklad tak, ze akekolvek pociatocne podmienky sme schopny splnit tymto riesenim. Mame totiz styry pociatocne podmienky, tj. dve pociatocne suradnice a dve pociatocne rychlosti, a styry parametre v navrhovanom sucte A, B, Φ 1,2 6. Uz zo spominanej jednoznacnosti fyzikalnych procesov vyplyva, ze ine riesenie potom mat nebudeme. Napriak tomu, ze viedlo k uzastnemu a uplnemu vysledku, cele toto typovanie rieseni vyzera dost pofiderne. Podme sa na to teda pozriet z ineho uhlu. Najskro si musime spomenut na diskusiu o suradniciach z uvodu a zamysliet sa, ci ina volba suradnic nie je pre nas pripad vhodnejsia. Po niekolkych neuspesnych pokusom prideme na to, ze ked namiesto x, y zvolime suradnice q = x + y w = x y 6 Tato uvaha je samozrejem neuplna a nemame zarucene, ze pre lubovolny tvar x, y so styrmi volnymi parametrami sme schopny splnit styry pociatecone pdomeinky, ale podrobnejsia analyza, ktoru si zvedavy citatel isto rad urobi sam, ukaze, ze to nie je nas pripad. 4
5 pohybove rovnice prejdu na tvar a podobne pre a w. a q = a x + a y = [ 2ω 2 + ω 2] [ x + 2ω 2 + ω 2] y a q = ω 2 q (3) a w = 3ω 2 w (4) Vidime, cim su teda dobre tieto nove suradnice. Nemaju sidce ziadnu interpretaciu ako nejaka konkretna vychlka niecoho, ale ak nimi popisujeme system, prideme k rovniciam, ktore vieme riesnit. Mozme teda smelo pisat q = A q sin(ωt + Φ q ) w = A w sin( 3ωt + Φ w ) Ak chceme vidiet, ako sa telesa pohybuju v nasich povodnych suradniciach 7 staci riesit sustavu rovnic x + y = A q sin(ωt + Φ q ) (5) x y = w = A w sin(3ωt + Φ w ) (6) ktora ma riesenie x = 1 2 A q sin(ωt + Φ q ) A w sin( 3ωt + Φ w ) Ked sa teraz s tymito rieseniami trochu pohrame y = 1 2 A q sin(ωt + Φ q ) 1 2 A w sin( 3ωt + Φ w ) x = A sin(ωt + Φ q ) + B sin( 3ωt + Φ w ) (7) y = A sin(ωt + Φ q ) B sin( 3ωt + Φ w ) = A sin(ωt + Φ q ) + B sin( 3ωt + Φ w + π) (8) Postup, aky mse sa k tomu vysledku dostali zavysel od toho, ako sme vybrali q, w a ake boli cisla K, L, vysledok vsak od toho uz zavysly nie je. Vidime, ze sme dostali vseobecne riesnie v tvare lineranej kombinacie dvoch rieseni. Nikoho asi neprekvapuje, ze su to presne tie riesenia, ktore sme natypovali v prvej casti. Naslim ale uplne vseobnecne a uplne riesenie v suradniciach x, y, nakolko presne take bolo riesenie v suradniciach q, w, pomocou ktoreho sme k nemu dosli. Po tom, ako opadol vsetok prach, pozbierali sa mrtvy a raneny, dotiekla krv a prestalo prsat si strucne zhrnme, co sa vlastne udialo. Na zaciatku sme mali vcelku zlozitu situaciu. Zviazane rovnice a tak. Avsak prechodom k inym, vhodnejsim suradniciam sme presli k rovniciam, ktore nie len ze boli nezviazane ale vedeli sme ich aj jednoducho riesit. Najst potom riesenie v povodnych suradniach bola malina. Rieseniam, z ktorych su poskladane vysledne vseobence riesenia, teda tym, tkore sme najskor natypovali a potom nasli suradnice, v ktorych sa tak sustava skutocne hybe, sa hovori mody. Prave sme sa presvedcili, ze lubovolny pohyb sustavy je nejaka kombinacia modov. Ak teda tieto mody najdeme, vyhrali sme, nakolko vieme popisat kazdy jej mozny pohyb. To sa ale lahko povie... Este si na zaver spomenme, ze pri spriahnutych oscilatoroch, teda v sustave, kde posobia iba pruzne sily, ale vseobecne aj medzi castami sustavy, sa vzdy take suradnice, v ktorych sustava kona harmonicke kmity, daju najst a je ich prirodzene tolko, kolko bolo povodnych suradnic. Teda tolko, z kolkych casti sa sustava sklada krat pocet suradnic, potrebnych na opisanie polohy jednej casti. Tomuto poctu, teda poctu vsetkych suradnic potrebnych na opisanie polohy celej sustavy, sa hovori pocet stupnov volnosti. A spriahnute oscilatory maju presne tolko modov, kolko je stupnov volnosti. 7 Co zvacsa chceme, lebo len v nich si vieme predstavit, ako sa telesa pohybuju 5
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
3. Striedavé prúdy. Sínusoida
 . Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
. Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
MIDTERM (A) riešenia a bodovanie
 MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
Motivácia pojmu derivácia
 Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
x x x2 n
 Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
PRIEMER DROTU d = 0,4-6,3 mm
 PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
6 Limita funkcie. 6.1 Myšlienka limity, interval bez bodu
 6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
Súradnicová sústava (karteziánska)
 Súradnicová sústava (karteziánska) = sú to na seba kolmé priamky (osi) prechádzajúce jedným bodom, na všetkých osiach sú jednotky rovnakej dĺžky-karteziánska sústava zavedieme ju nasledovne 1. zvolíme
Súradnicová sústava (karteziánska) = sú to na seba kolmé priamky (osi) prechádzajúce jedným bodom, na všetkých osiach sú jednotky rovnakej dĺžky-karteziánska sústava zavedieme ju nasledovne 1. zvolíme
7 Derivácia funkcie. 7.1 Motivácia k derivácii
 Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Súčtové vzorce. cos (α + β) = cos α.cos β sin α.sin β cos (α β) = cos α.cos β + sin α.sin β. tg (α β) = cotg (α β) =.
 Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
3. prednáška. Komplexné čísla
 3. predáška Komplexé čísla Úvodé pozámky Vieme, že existujú také kvadratické rovice, ktoré emajú riešeie v obore reálych čísel. Študujme kvadratickú rovicu x x + 5 = 0 Použitím štadardej formule pre výpočet
3. predáška Komplexé čísla Úvodé pozámky Vieme, že existujú také kvadratické rovice, ktoré emajú riešeie v obore reálych čísel. Študujme kvadratickú rovicu x x + 5 = 0 Použitím štadardej formule pre výpočet
Tomáš Madaras Prvočísla
 Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Diferenciálne rovnice
 Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
Goniometrické substitúcie
 Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Deliteľnosť a znaky deliteľnosti
 Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Obyčajné diferenciálne rovnice
 (ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
(ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín. Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť.
 Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich
 Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Chí kvadrát test dobrej zhody. Metódy riešenia úloh z pravdepodobnosti a štatistiky
 Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
1.4 Rovnice, nerovnice a ich sústavy
 1. Rovnice, nerovnice a ich sústavy Osah Pojmy: rovnica, nerovnica, sústava rovníc, sústava nerovníc a ich riešenie, koeficient, koreň, koreňový činiteľ, diskriminant, doplnenie do štvorca, úprava na súčin,
1. Rovnice, nerovnice a ich sústavy Osah Pojmy: rovnica, nerovnica, sústava rovníc, sústava nerovníc a ich riešenie, koeficient, koreň, koreňový činiteľ, diskriminant, doplnenie do štvorca, úprava na súčin,
STRIEDAVÝ PRÚD - PRÍKLADY
 STRIEDAVÝ PRÚD - PRÍKLADY Príklad0: V sieti je frekvencia 50 Hz. Vypočítajte periódu. T = = = 0,02 s = 20 ms f 50 Hz Príklad02: Elektromotor sa otočí 50x za sekundu. Koľko otáčok má za minútu? 50 Hz =
STRIEDAVÝ PRÚD - PRÍKLADY Príklad0: V sieti je frekvencia 50 Hz. Vypočítajte periódu. T = = = 0,02 s = 20 ms f 50 Hz Príklad02: Elektromotor sa otočí 50x za sekundu. Koľko otáčok má za minútu? 50 Hz =
Budený oscilátor s tlmením
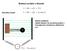 Budený oscilátor s tlmením Špeciálny prípad Možná realizácia: Nabité teliesko na nevodivej pružine v homogénnom striedavom elektrickom poli Budený oscilátor s tlmením Použijeme trik s komplexnými fázormi
Budený oscilátor s tlmením Špeciálny prípad Možná realizácia: Nabité teliesko na nevodivej pružine v homogénnom striedavom elektrickom poli Budený oscilátor s tlmením Použijeme trik s komplexnými fázormi
Volny pad s odoporom vzduchu (ako uvod do poruchovych vypoctov)
 Volny pad s odoporom vzduchu (ako uvod do poruchovych vypoctov) Juro Tekel juraj(dot)tekel(at)gmail(dot)com Text o tom, ako sa da priblizne poratat volny pad s odporom vzduchu a o tom, ze sa to rovnako
Volny pad s odoporom vzduchu (ako uvod do poruchovych vypoctov) Juro Tekel juraj(dot)tekel(at)gmail(dot)com Text o tom, ako sa da priblizne poratat volny pad s odporom vzduchu a o tom, ze sa to rovnako
Definícia parciálna derivácia funkcie podľa premennej x. Definícia parciálna derivácia funkcie podľa premennej y. Ak existuje limita.
 Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Príklady na precvičovanie Fourierove rady
 Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY Strojnícka fakulta, Žilinská Univerzita
 132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti
 4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
18. kapitola. Ako navariť z vody
 18. kapitola Ako navariť z vody Slovným spojením navariť z vody sa zvyknú myslieť dve rôzne veci. Buď to, že niekto niečo tvrdí, ale nevie to poriadne vyargumentovať, alebo to, že niekto začal s málom
18. kapitola Ako navariť z vody Slovným spojením navariť z vody sa zvyknú myslieť dve rôzne veci. Buď to, že niekto niečo tvrdí, ale nevie to poriadne vyargumentovať, alebo to, že niekto začal s málom
Numerické metódy matematiky I
 Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie ) Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc
Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie ) Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc
Obsah. 1.1 Reálne čísla a ich základné vlastnosti... 7 1.1.1 Komplexné čísla... 8
 Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY. Pomôcka pre prípravný kurz
 KATEDRA APLIKOVANEJ MATEMATIKY A INFORMATIKY STROJNÍCKA FAKULTA TU KOŠICE PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY Pomôcka pre prípravný kurz 8 ZÁKLADNÉ ALGEBRAICKÉ VZORCE ) (a±b)
KATEDRA APLIKOVANEJ MATEMATIKY A INFORMATIKY STROJNÍCKA FAKULTA TU KOŠICE PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY Pomôcka pre prípravný kurz 8 ZÁKLADNÉ ALGEBRAICKÉ VZORCE ) (a±b)
AerobTec Altis Micro
 AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
1 Prevod miestneho stredného slnečného času LMT 1 na iný miestny stredný slnečný čas LMT 2
 1 Prevod miestneho stredného slnečného času LMT 1 na iný miestny stredný slnečný čas LMT 2 Rozdiel LMT medzi dvoma miestami sa rovná rozdielu ich zemepisných dĺžok. Pre prevod miestnych časov platí, že
1 Prevod miestneho stredného slnečného času LMT 1 na iný miestny stredný slnečný čas LMT 2 Rozdiel LMT medzi dvoma miestami sa rovná rozdielu ich zemepisných dĺžok. Pre prevod miestnych časov platí, že
AFINNÉ TRANSFORMÁCIE
 AFINNÉ TRANSFORMÁCIE Definícia0..Zobrazenie f: R n R m sanazývaafinné,ak zachováva kolinearitu(t.j. priamka sa zobrazí buď na priamku alebo na jeden bod), zachovávadeliacipomer(t.j.akprekolineárnebody
AFINNÉ TRANSFORMÁCIE Definícia0..Zobrazenie f: R n R m sanazývaafinné,ak zachováva kolinearitu(t.j. priamka sa zobrazí buď na priamku alebo na jeden bod), zachovávadeliacipomer(t.j.akprekolineárnebody
DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c)
 Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Matematika 2. časť: Funkcia viac premenných Letný semester 2013/2014
 Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Zložené funkcie a substitúcia
 3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
Numerické metódy Učebný text pre bakalárske štúdium
 Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej transformácie,
 Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Goniometrické nerovnice
 Ma-Go--T List Goniometrické nerovnice RNDr. Marián Macko U: Problematiku, ktorej sa budeme venovať, začneme úlohou. Máme určiť definičný obor funkcie f zadanej predpisom = sin. Máš predstavu, s čím táto
Ma-Go--T List Goniometrické nerovnice RNDr. Marián Macko U: Problematiku, ktorej sa budeme venovať, začneme úlohou. Máme určiť definičný obor funkcie f zadanej predpisom = sin. Máš predstavu, s čím táto
,Zohrievanie vody indukčným varičom bez pokrievky,
 Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
RIEŠENIE WHEATSONOVHO MOSTÍKA
 SNÁ PMYSLNÁ ŠKOL LKONKÁ V PŠŤNO KOMPLXNÁ PÁ Č. / ŠN WSONOVO MOSÍK Piešťany, október 00 utor : Marek eteš. Komplexná práca č. / Strana č. / Obsah:. eoretický rozbor Wheatsonovho mostíka. eoretický rozbor
SNÁ PMYSLNÁ ŠKOL LKONKÁ V PŠŤNO KOMPLXNÁ PÁ Č. / ŠN WSONOVO MOSÍK Piešťany, október 00 utor : Marek eteš. Komplexná práca č. / Strana č. / Obsah:. eoretický rozbor Wheatsonovho mostíka. eoretický rozbor
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR. Michal Zajac. 3 T b 1 = T b 2 = = = 2b
 VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Priamkové plochy. Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava
 Priamkové plochy Priamkové plochy Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava Priamkové plochy rozdeľujeme na: Rozvinuteľné
Priamkové plochy Priamkové plochy Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava Priamkové plochy rozdeľujeme na: Rozvinuteľné
Vzorové riešenia 3. kola zimnej série 2014/2015
 riesky@riesky.sk Riešky matematický korešpondenčný seminár Vzorové riešenia. kola zimnej série 04/05 Príklad č. (opravovali Tete, Zuzka): Riešenie: Keďže číslo má byť deliteľné piatimi, musí končiť cifrou
riesky@riesky.sk Riešky matematický korešpondenčný seminár Vzorové riešenia. kola zimnej série 04/05 Príklad č. (opravovali Tete, Zuzka): Riešenie: Keďže číslo má byť deliteľné piatimi, musí končiť cifrou
16. Základne rovinné útvary kružnica a kruh
 16. Základne rovinné útvary kružnica a kruh Kružnica k so stredom S a polomerom r nazývame množinou všetkých bodov X v rovine, ktoré majú od pevného bodu S konštantnú vzdialenosť /SX/ = r, kde r (patri)
16. Základne rovinné útvary kružnica a kruh Kružnica k so stredom S a polomerom r nazývame množinou všetkých bodov X v rovine, ktoré majú od pevného bodu S konštantnú vzdialenosť /SX/ = r, kde r (patri)
Smernicový tvar rovnice priamky
 VoAg1-T List 1 Smernicový tvar rovnice priamk RNDr.Viera Vodičková U: Medzi prevratné objav analtickej geometrie patrí to, že s priamkou nenarábame ako s geometrickým objektom, ale popisujeme ju rovnicou.
VoAg1-T List 1 Smernicový tvar rovnice priamk RNDr.Viera Vodičková U: Medzi prevratné objav analtickej geometrie patrí to, že s priamkou nenarábame ako s geometrickým objektom, ale popisujeme ju rovnicou.
Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus
 KrAv11-T List 1 Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus RNDr. Jana Krajčiová, PhD. U: Najprv si zopakujme, ako znie definícia logaritmu. Ž: Ja si pamätám, že logaritmus súvisí
KrAv11-T List 1 Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus RNDr. Jana Krajčiová, PhD. U: Najprv si zopakujme, ako znie definícia logaritmu. Ž: Ja si pamätám, že logaritmus súvisí
Základné vzťahy medzi hodnotami goniometrických funkcií
 Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
ZADANIE 1_ ÚLOHA 3_Všeobecná rovinná silová sústava ZADANIE 1 _ ÚLOHA 3
 ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
Analytická geometria
 Analytická geometria Analytická geometria je oblasť matematiky, v ktorej sa študujú geometrické útvary a vzťahy medzi nimi pomocou ich analytických vyjadrení. Praktický význam analytického vyjadrenia je
Analytická geometria Analytická geometria je oblasť matematiky, v ktorej sa študujú geometrické útvary a vzťahy medzi nimi pomocou ich analytických vyjadrení. Praktický význam analytického vyjadrenia je
Kontrolné otázky z jednotiek fyzikálnych veličín
 Verzia zo dňa 6. 9. 008. Kontrolné otázky z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej odpovede sa môže v kontrolnom teste meniť. Takisto aj znenie nesprávnych odpovedí. Uvedomte si
Verzia zo dňa 6. 9. 008. Kontrolné otázky z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej odpovede sa môže v kontrolnom teste meniť. Takisto aj znenie nesprávnych odpovedí. Uvedomte si
Vzorové príklady s riešeniami k lineárnej algebre a geometrie pre aplikovaných informatikov k písomke
 Vzorové príklady s riešeniami k lineárnej algebre a geometrie pre aplikovaných informatikov k písomke 23.5.26 Príklad č. Riešte sústavu Bx = r (B r) 2 3 4 2 3 4 6 8 8 2 (B r) = 6 9 2 6 3 9 2 3 4 2 3 2
Vzorové príklady s riešeniami k lineárnej algebre a geometrie pre aplikovaných informatikov k písomke 23.5.26 Príklad č. Riešte sústavu Bx = r (B r) 2 3 4 2 3 4 6 8 8 2 (B r) = 6 9 2 6 3 9 2 3 4 2 3 2
Ján Buša Štefan Schrötter
 Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Kompilátory. Cvičenie 6: LLVM. Peter Kostolányi. 21. novembra 2017
 Kompilátory Cvičenie 6: LLVM Peter Kostolányi 21. novembra 2017 LLVM V podstate sada nástrojov pre tvorbu kompilátorov LLVM V podstate sada nástrojov pre tvorbu kompilátorov Pôvodne Low Level Virtual Machine
Kompilátory Cvičenie 6: LLVM Peter Kostolányi 21. novembra 2017 LLVM V podstate sada nástrojov pre tvorbu kompilátorov LLVM V podstate sada nástrojov pre tvorbu kompilátorov Pôvodne Low Level Virtual Machine
Goniometrické rovnice riešené substitúciou
 Ma-Go-10-T List 1 Goniometrické rovnice riešené substitúciou RNDr. Marián Macko U: Okrem základných goniometrických rovníc, ktorým sme sa už venovali, existujú aj zložitejšie goniometrické rovnice. Metódy
Ma-Go-10-T List 1 Goniometrické rovnice riešené substitúciou RNDr. Marián Macko U: Okrem základných goniometrických rovníc, ktorým sme sa už venovali, existujú aj zložitejšie goniometrické rovnice. Metódy
ELEKTRICKÉ POLE. Elektrický náboj je základná vlastnosť častíc, je viazaný na častice látky a vyjadruje stav elektricky nabitých telies.
 ELEKTRICKÉ POLE 1. ELEKTRICKÝ NÁBOJ, COULOMBOV ZÁKON Skúmajme napr. trenie celuloidového pravítka látkou, hrebeň suché vlasy, mikrotén slabý prúd vody... Príčinou spomenutých javov je elektrický náboj,
ELEKTRICKÉ POLE 1. ELEKTRICKÝ NÁBOJ, COULOMBOV ZÁKON Skúmajme napr. trenie celuloidového pravítka látkou, hrebeň suché vlasy, mikrotén slabý prúd vody... Príčinou spomenutých javov je elektrický náboj,
Technická univerzita v Košiciach. Zbierka riešených a neriešených úloh. z matematiky. pre uchádzačov o štúdium na TU v Košiciach
 Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Spojité rozdelenia pravdepodobnosti. Pomôcka k predmetu PaŠ. RNDr. Aleš Kozubík, PhD. 26. marca Domovská stránka. Titulná strana.
 Spojité rozdelenia pravdepodobnosti Pomôcka k predmetu PaŠ Strana z 7 RNDr. Aleš Kozubík, PhD. 6. marca 3 Zoznam obrázkov Rovnomerné rozdelenie Ro (a, b). Definícia.........................................
Spojité rozdelenia pravdepodobnosti Pomôcka k predmetu PaŠ Strana z 7 RNDr. Aleš Kozubík, PhD. 6. marca 3 Zoznam obrázkov Rovnomerné rozdelenie Ro (a, b). Definícia.........................................
Diferenciálne rovnice. Základný jazyk fyziky
 Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa padajúceho v gravitačnom poli.
Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa padajúceho v gravitačnom poli.
Základné poznatky molekulovej fyziky a termodynamiky
 Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Gramatická indukcia a jej využitie
 a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
23. Zhodné zobrazenia
 23. Zhodné zobrazenia Zhodné zobrazenie sa nazýva zhodné ak pre každé dva vzorové body X,Y a ich obrazy X,Y platí: X,Y = X,Y {Vzdialenosť vzorov sa rovná vzdialenosti obrazov} Medzi zhodné zobrazenia patria:
23. Zhodné zobrazenia Zhodné zobrazenie sa nazýva zhodné ak pre každé dva vzorové body X,Y a ich obrazy X,Y platí: X,Y = X,Y {Vzdialenosť vzorov sa rovná vzdialenosti obrazov} Medzi zhodné zobrazenia patria:
FUNKCIE N REÁLNYCH PREMENNÝCH
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
Matematický model robota s diferenciálnym kolesovým podvozkom
 Matematický model robota s diferenciálnym kolesovým podvozkom Demonštračný modul Úlohy. Zostavte matematický model robota s diferenciálnym kolesovým podvozkom 2. Vytvorte simulačný model robota v simulačnom
Matematický model robota s diferenciálnym kolesovým podvozkom Demonštračný modul Úlohy. Zostavte matematický model robota s diferenciálnym kolesovým podvozkom 2. Vytvorte simulačný model robota v simulačnom
HASLIM112V, HASLIM123V, HASLIM136V HASLIM112Z, HASLIM123Z, HASLIM136Z HASLIM112S, HASLIM123S, HASLIM136S
 PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
Úvod do lineárnej algebry
 Katedra matematiky Fakulta elektrotechniky a informatiky Technická Univerzita v Košiciach Úvod do lineárnej algebry Monika Molnárová, Helena Myšková 005 RECENZOVALI: RNDr. Štefan Schrötter, CSc. RNDr.
Katedra matematiky Fakulta elektrotechniky a informatiky Technická Univerzita v Košiciach Úvod do lineárnej algebry Monika Molnárová, Helena Myšková 005 RECENZOVALI: RNDr. Štefan Schrötter, CSc. RNDr.
TREDNÁ ODBORNÁ ŠKOLA STRÁŽSKE PRACOVNÝ ZOŠIT. k predmetu Matematika pre
 TREDNÁ ODBORNÁ ŠKOLA STRÁŽSKE PRACOVNÝ ZOŠIT k predmetu Matematika pre 2. ročník SOŠ v Strážskom, študijný odbor 3760 6 00 prevádzka a ekonomika dopravy Operačný program: Vzdelávanie Programové obdobie:
TREDNÁ ODBORNÁ ŠKOLA STRÁŽSKE PRACOVNÝ ZOŠIT k predmetu Matematika pre 2. ročník SOŠ v Strážskom, študijný odbor 3760 6 00 prevádzka a ekonomika dopravy Operačný program: Vzdelávanie Programové obdobie:
Analytická geometria pre tých, ktorí jej potrebujú rozumieť
 Škola pre Mimoriadne Nadané Deti a Gymnázium, Teplická 7, 831 02 Bratislava Anino BELAN Analytická geometria pre tých, ktorí jej potrebujú rozumieť učebný text pre septimu osemročného gymnázia BRATISLAVA
Škola pre Mimoriadne Nadané Deti a Gymnázium, Teplická 7, 831 02 Bratislava Anino BELAN Analytická geometria pre tých, ktorí jej potrebujú rozumieť učebný text pre septimu osemročného gymnázia BRATISLAVA
Úvod. Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...
 Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
URČENIE MOMENTU ZOTRVAČNOSTI FYZIKÁLNEHO KYVADLA
 54 URČENE MOMENTU ZOTRVAČNOST FYZKÁLNEHO KYVADLA Teoretický úvod: Fyzikálnym kyvadlom rozumieme teleso (napr. dosku, tyč), ktoré vykonáva periodický kmitavý pohyb okolo osi, ktorá neprechádza ťažiskom.
54 URČENE MOMENTU ZOTRVAČNOST FYZKÁLNEHO KYVADLA Teoretický úvod: Fyzikálnym kyvadlom rozumieme teleso (napr. dosku, tyč), ktoré vykonáva periodický kmitavý pohyb okolo osi, ktorá neprechádza ťažiskom.
DOMÁCE ZADANIE 1 - PRÍKLAD č. 2
 Mechanizmy s konštantným prevodom DOMÁCE ZADANIE - PRÍKLAD č. Príklad.: Na obrázku. je zobrazená schéma prevodového mechanizmu tvoreného čelnými a kužeľovými ozubenými kolesami. Určte prevod p a uhlovú
Mechanizmy s konštantným prevodom DOMÁCE ZADANIE - PRÍKLAD č. Príklad.: Na obrázku. je zobrazená schéma prevodového mechanizmu tvoreného čelnými a kužeľovými ozubenými kolesami. Určte prevod p a uhlovú
FUNKCIE. Funkcia základné pojmy. Graf funkcie
 FUNKCIE Funkcia základné pojm. Graf funkcie V prai sa často stretávame so skúmaním závislosti veľkosti niektorých veličín od veľkosti iných veličín, napríklad dĺžka kružnice l závisí od jej priemeru d
FUNKCIE Funkcia základné pojm. Graf funkcie V prai sa často stretávame so skúmaním závislosti veľkosti niektorých veličín od veľkosti iných veličín, napríklad dĺžka kružnice l závisí od jej priemeru d
Zrýchľovanie vesmíru. Zrýchľovanie vesmíru. o výprave na kraj vesmíru a čo tam astronómovia objavili
 Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
M8 Model "Valcová a kužeľová nádrž v sérií bez interakcie"
 M8 Model "Valcová a kužeľová nádrž v sérií bez interakcie" Úlohy: 1. Zostavte matematický popis modelu M8 2. Vytvorte simulačný model v prostredí: a) Simulink zostavte blokovú schému, pomocou rozkladu
M8 Model "Valcová a kužeľová nádrž v sérií bez interakcie" Úlohy: 1. Zostavte matematický popis modelu M8 2. Vytvorte simulačný model v prostredí: a) Simulink zostavte blokovú schému, pomocou rozkladu
MATEMATICKÁ ANALÝZA 1
 UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied Božena Mihalíková, Ján Ohriska MATEMATICKÁ ANALÝZA Vysokoškolský učebný text Košice, 202 202 doc. RNDr. Božena
UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied Božena Mihalíková, Ján Ohriska MATEMATICKÁ ANALÝZA Vysokoškolský učebný text Košice, 202 202 doc. RNDr. Božena
Termodynamika. Doplnkové materiály k prednáškam z Fyziky I pre SjF Dušan PUDIŠ (2008)
 ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
Teoretická mechanika
 Univerzita Komenského, Bratislava Fakulta matematiky, fyziky a informatiky Teoretická mechanika Bratislava, 4 B. Rabatin Obsah Úvod Matematický aparát teoretickej mechaniky. Einsteinova sumačná konvencia.....................................
Univerzita Komenského, Bratislava Fakulta matematiky, fyziky a informatiky Teoretická mechanika Bratislava, 4 B. Rabatin Obsah Úvod Matematický aparát teoretickej mechaniky. Einsteinova sumačná konvencia.....................................
Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus
 1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
