Teorinė mechanika I. Uždavinių sprendimo vadovas
|
|
|
- Τελεσφόρος Μελετόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00
2 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS oomoji nga. V.: Technia, p. Kngoje pateitos žinios apie teoretinės mechanios statios principų taimą įvairiems uždaviniams spręsti. Pateiiami svarbiausių tipinių uždavinių sprendimo pavzdžiai, išsamūs jų omentarai. Nagrinėjama susiertančiųjų, ploščiųjų ir erdvinių jėgų sistemų pusiausvra, ūnų sistemos pusiausvra bei aptariami sldimo trinties uždavinių sprendimo patumai. Leidins sirtas VGTU pagrindinių studijų studentams spręsti savaranišo darbo užduotis. Leidinį reomendavo undamentinių moslų faulteto studijų omitetas Recenzavo habil. dr. prof. G. Kulvietis habil. dr. prof.. Leonavičius VGTU leidlos Technia 487 moomosios metodinės literatūros nga R. aušs, J. Kasnausas, 00 VGTU leidla Technia, 00
3 TURINYS TURINYS...3 Pratarmė...4. Statios uždavinių sprendimo principai...5. Susiertančiųjų jėgų sistemos pusiausvra Ploščioji jėgų sistema Kūnų sistemos pusiausvra Sldimo trintis Ploščiųjų santvarų saičiavimas Erdvinė jėgų sistema...45 Literatūra
4 PRTRĖ Teorinė mechania ra viena iš svarbiausių disciplinų, rengiant auštos valifiacijos inžinerijos specialistus. Ja remiasi toios bendrosios inžinerinės disciplinos, aip medžiagų mechania, taiomoji mechania, mašinų ir prietaisų elementai. Remiantis teorinės mechanios principais sprendžiami daugelis inžinerinių uždavinių, projetuojamos mašinos ir statiniai. oantis teorinės mechanios, reiia įgti uždavinių sprendimo įgūdžių. Todėl būtina savaranišai spręsti paanamai uždavinių. Šiame leidinje pateiiami statios uždavinių sprendimo pavzdžiai ir savaranišo darbo užduots. Kartu pateiiami savaranišai spręsti sirtų uždavinių teisingi sprendimo rezultatai. Knga sirta visų specialbių ir momo formų (dieninio ir neaivaizdinio) VGTU studentams. Tai pirmasis toio pobūdžio leidins, uriame pateiiami savaranišo sprendimo užduočių variantai ir jų rezultatai. utoriai atsiprašo už pasitaiančius netislumus. 4
5 . STTIKOS UŽDVINIŲ SPRENDIO PRINIPI Sprendžiant teorinės mechanios uždavinius, taiomi įvairūs modeliai, aprašants supaprastintų (idealizuotų) inžinerinių objetų būvį. Šie modeliai būtini norint sėmingai taiti mechanios principus. Sėmingas modelio suūrimas leidžia efetviai išspręsti inžinerinėje pratioje pasitaiančius mechanios uždavinius. endrieji teorinės mechanios uždavinių sprendimo etapai būtų toie:. tliti inžinerinio uždavinio analizę ir susieti tiriamą fizinį uždavinį su atitinamais teorinės mechanios principais.. Sudarti uždavinio modelį ir pateiti idealizacijos schemas. 3. Taiant būtinus teorinės mechanios principus, sudarti idealizuoto objeto būvį aprašančias lgtis. 4. Saitišai išspręsti sudartą lgčių sistemą. ūtina taiti bendrąją parametrų dimensijų sistemą. 5. tliti gautų saitinių rezultatų inžinerinį įvertinimą. 6. Išsprendus problemą, atliti trinėto teorinės mechanios uždavinio papildomą analizę ar nėra itų galimų uždavinio sprendimo būdų. Sudarant teorinės mechanios uždavinių saitinius modelius taiomi šie supaprastinimai (idealizacijos): materialusis tašas ir standusis ūnas. aterialusis tašas turi masę, bet jo geometriniai matmens ra be galo maži. Kai trinėjamas inžinerinis objetas modeliuojamas materialiuoju tašu, lgts, gautos taiant teorinės mechanios principus, labai supaprastėja, nes nereiia įvertinti objeto geometrijos. Standusis ūnas suprantamas aip be galo didelio materialiųjų tašų saičiaus ombinacija. Visi šie materialieji tašai išlaio tuos pačius atstumus vienas nuo ito, pridėjus išorines aprovas. Taigi analizuojant ūną veiiančias jėgas nereiia atsižvelgti į objeto medžiagos savbes. Paprastai sprendžiant statios uždavinius taiomas analizinis metodas. Standžiojo ūno pusiausvra suprantama aip rimties būsena itų jį supančių ūnų atžvilgiu. Laisvąjį ūną veiiančių jėgų atsisvėrimas ra būtina, bet nepaanama pusiausvros sąlga. Veiiant atsvertai jėgų sistemai, laisvasis ūnas titai išsaugo buvusią rimties būseną. Taiant analizinį saičiavimo metodą, spręsti pradedame išsiaišindami uždavinio esmę, nustatdami žinomus ir saičiuojamuosius parametrus, sudarome objeto brėžinį. Tolesnę sprendimo eigą galima susirstti į šiuos etapus: nustatoma tašas ar ūnas, urio pusiausvra trinėjama: brėžinje parodomos žinomos atviosios jėgos; ūnas atpalaiduojamas nuo ršių, jie paeičiami evivalentišomis reacijos jėgomis; nustatomas bendras nežinomųjų ddžių saičius ir tiriamas uždavinio statinis išsprendžiamumas; pasirenamos oordinačių ašs ir sudaromos pusiausvros lgts, įvertinant visų ūną veiiančių jėgų (atviųjų ir ršių reacijos) poveiį; sprendžiant pusiausvros lgtis nustatomos nežinomosios jėgos. Daugumoje statios uždavinių iš ansto negalima žinoti ne ti jėgos didumo, bet ir tislios reacijos jėgos rpties. Šiais atvejais reacijos jėga paprastai saidoma į omponentes, sutampančias su pasirintų oordinačių ašių rptimis. Jeigu saičiavimo metu urios nors jėgos ar jos omponentės didumas gaunamas su neigiamu algebriniu ženlu, tai žinome, ad tiroji šios jėgos rptis ra priešinga pasirintajai. Jei uždavinio sąlga reialauja rasti ūno poveiį į urį nors ršį, tai galima nustatti ršio reaciją, o ūno poveiis į ršį visada ra toio pat didumo ti priešingos rpties jėga. Nagrinėjant ūnų sistemos pusiausvrą, galima tirti ievieno atsiro sistemos ūno pusiausvrą. Šiuo atveju ūnų sąveios jėgos ra vienodo didumo ir priešingų rpčių. Galima trinėti visą ūnų sistemą aip geometrišai neintamą standųjį objetą, jeigu gautos pusiausvros lgts tina ai urioms nežinomoms jėgoms saičiuoti.. SUSIKERTNČIŲJŲ JĖGŲ SISTEOS PUSIUSVYR Sprendžiant teorinės mechanios uždavinius dažnai taioma materialiojo tašo idealizacija. Ši prielaida leidžia geroai supaprastinti pagrindinių lgčių sistemą. aterialiojo tašo idealizacija taioma, ai 5
6 objeto saičiuojamojoje schemoje atviųjų ir reatviųjų jėgų veiimo linijos ertasi viename taše. Šiuo atveju turime susiertančiųjų jėgų sistemą. Susiertančiųjų jėgų sistemos būtina ir paanama pusiausvros sąlga ra atstojamosios R (.) lgbė nuliui. Ši sąlga ploščiajai susiertančiųjų jėgų sistemai išreišiama dviem analizinėmis lgtimis 0, 0 (.) arba momentų pusiausvros lgtimis ( ) 0, ( ) 0. (.3) Šiuo atveju tašai ir negali būti vienoje tiesėje su jėgų susiirtimo tašu. Erdvinei susiertančiųjų jėgų sistemai atstojamoji R 0 išreišiama trimis pusiausvros sąlgų lgtimis z 0, 0, 0. (.4). uždavins Krovins, urio svoris G0 N, paabintas lnu. Lnas per mažą sridinį gali būti vniojamas ant ritės D. psaičiuoti eltuvo strpų ir reacijas. Strpinės onstrucijos bei lno išdėstmo ampas parodtas. brėžinje. 60 G D. brėž. Pradžioje sudarome uždavinio sprendimo saičiuojamąją schemą. Žinodami, ad strpų reacijos nureiptos išilgai strpų, o lno reacija sutampa su lno rptimi, tašą atpalaiduojame nuo ršių.. brėžinje parodtos visos tašą veiiančios jėgos. 6
7 S G T S. brėž. Čia S ir S strpų reacijos, T lno reacija. Parenamos oordinačių ašs ir, ir užrašomos statinės pusiausvros lgts, projetuojant visas jėgas į šias ašis: 0, 0, S + S cos60 T cos60 0, S cos30 + G + T cos30 0. Lno reacija T G, adangi lnas visuose tašuose įtemptas vienoda jėga. Todėl + T( + cos30 ) 0, ( + cos30 ) 0( + 0,866) S cos30 S S T cos30 0,866,55 N, ( T S ) cos60 ( 0 +,55) 0,5 5,78 N. Neigiamas reacijos S ženlas rodo, ad šis strpas ra gniuždomas.. uždavins Standusis rėmas (.3 brėž.), įtvirtintas nejudriuoju šarnru ir judriuoju šarnru, veiiamas horizontaliosios jėgos 0 N. Saičiuojamos šarnrų reacijos brėž. 7
8 Sudardami uždavinio sprendimo saičiuojamąją schemą, rėmo ršius paeičiame atitinamomis reacijos jėgomis. Šioje saičiuojamojoje schemoje rėmą veiia trs nelgiagrečios jėgos. Tai išorinės aprovos jėga ir šarnrų reacijos. Pusiausvra įmanoma, ai šios jėgos ertasi viename taše. Sudarta saičiuojamoji schema parodta.4 brėž. 3 D 3 5 R 45 R α.4 brėž. Šiam uždaviniui spręsti taiome momentų pusiausvros lgtis (.3). Tašai ir nėra vienoje tiesėje su jėgų susiirtimo tašu D, todėl momentų lgts rašomos šių tašų atžvilgiu. Gaunamos šios pusiausvros lgts: ( ) 0, ( ) 0, 3 + 4R 5 + R Iš pirmosios lgties išreišiame R 3 4cos α R sin α. cos α R cos R sin α cos 45 0, 0. D Čia tg α 0,, α arctg 0,,3, sin α 0.97, cos α 0, 98. Taigi R 7 N. 4 0,98 0,97 Iš antrosios lgties gauname R 3,57 N. 6cos ,707 Sprendinį galima patirinti užrašius jėgų projecijų pusiausvros lgtį R cos 45 R sinα 0 3,57 0, ,97 0. (Lgtis teninama).3 uždavins Šiame uždavinje nagrinėjama erdvinės susiertančiųjų jėgų sistemos pusiausvra, taiant lgtis (.4). Krovins, urio svoris G 0 N, laiomas lnu, permestu per sridinį ir užvniotu ant ritės H. Konstrucijos schema pateita.5 brėž. Sistemos geometrija aprašoma taip: E E,. E 60, DH 30, 90. Saičiuojamos onstrucijos trijų strpų, ir D reacijos. 8
9 z E S S S 3 L T D 3 G H.5 brėž. Pradžioje sudarome uždavinio sprendimo saičiuojamąją schemą. Laiome strpų reacijas nureiptomis išilgai jų ašių, o lno įtempimo jėgą išilgai lno. Spręsdami šį uždavinį trinėjame tašą. Šį laisvąjį tašą veiiančios jėgos parodtos.5 brėž. Tai erdvinė susiertančių jėgų sistema. Užrašome tašo pusiausvros lgtis z 0, 0, 0, S S S 3 cos 45 sin 45 S S cos 45 sin 45 0, S cos60 T cos30 G 0. 3 cos30 T cos60 0, Pirmoji lgtis rodo, ad S S. Iš trečiosios lgties, įvertinant T G, randama S 3 G ( + cos30 ) 0( + 0,866) 74,64 N. Iš antrosios lgties randame S3 cos30 T cos60 74,64 0, ,5 S S 38,64 N. cos 45 0,707 Pagal saičiavimo rezultatus, trečiasis strpas ra gniuždomas, o iti du tempiami. 9
10 3. PLOKŠČIOJI JĖGŲ SISTE endruoju atveju, ai trinėjamą objetą veiiančių jėgų sistema neturi joių patumų, taioma standžiojo ūno idealizacija. Daugelje inžinerinių uždavinių veiiančios aprovos ra simetrinės, todėl jų sprendimas gali būti supaprastintas. Šiuo atveju visos trinėjamą objetą veiiančios jėgos projetuojamos į vieną ploštumą. Taip gaunama ploščioji jėgų sistema. Jėgų sistemos, veiiančios standųjį ūną ir išdėsttos vienoje ploštumoje, pusiausvros būtina ir paanama sąlga ra suminės jėgos ir suminio momento lgbė nuliui, t.. 0, O ( ) 0. (3.) naliziniu pavidalu šios pusiausvros sąlgos gali būti išreištos trimis būdais:. O 0, 0, ( ) 0. (3.) 0,. ( ) 0, ( ) ( ) 0, ( ) 0, ( ) 0. (3.3) (3.4) Pirmajame variante tašu O gali būti bet uris ploštumos tašas. ntrajame variante ašis negali būti statmena atarpai. Trečiajame variante tašai, ir negali būti vienoje tiesėje. tsiro varianto pasirinimas galimas bet uriam statios uždaviniui, ai trinėjama ploščiosios jėgų sistemos pusiausvra. 3. uždavins Vienaltė horizontalioji sija, urios svoris G N, įtvirtinta judriuoju šarnru, o tašuose ir atremta strpais J ir L. Strpų galuose ra šarnriniai sujungimai. Strpų svoriai atlieant saičiavimus neįvertinami. Konstrucijos schema parodta 3. brėž. Čia pateiti ir sijos matmens. Jėgos ddis ra 6 N. Saičiuojamos sijos atramų reacijos. Sprendimo pradžioje sudarome uždavinio saičiuojamąją schemą. Kadangi sija vienaltė ir vienodo serspjūvio, svorio jėgos G pridėties tašas ra sijos vidurje. tpalaiduojame siją nuo visų ršių. Strpų reacijos jėgų rpts sutampa su jų rptimis, o judriojo šarnro reacijos jėga statmena nuožulniajai ploštumai. Laisvosios sijos schema parodta 3. brėžinje. Pradžioje užrašome momentų pusiausvros lgtį E ( ) 0, ur tašas E ra jėgų R ir R susiirtimo tašas. Čia E tg 60,73 3,46 m. Taigi ši momentų pusiausvros lgtis turės pavidalą G 3 cos45 + 3,46 cos R cos30 3,46R cos
11 3 45 G 30 3 J 60 L 3. brėž. E 30 R R 60 H 45 R G 3. brėž. Taidami šią lgtį apsaičiuojame reacijos jėgos R ddį G 0,46 cos 45 0,46 6 0,707 R 3,93 N. 4cos30 3,46cos60 4 0,866 3,46 0,5 Po to užrašome siją veiiančių jėgų projecijų lgtis 0, R R cos 60 + cos45 cos60 0, R cos 45 R cos60 cos60 6 0,707 3,93 0,5 0,5 0, R R cos 30 R G cos 45 + R cos30 0, R cos30 G cos 45 + R cos30 8,69 N, 8,69 0, , ,93 0,866 36,N.
12 Patirinimui užrašome momentų pusiausvros lgtį H ( ) 0, 3 R cos30 + R cos45 + 3R cos30 0, 3 8,69 0,866 36, 6 0, ,93 0,866 0, Šis rezultatas leidžia tiėti sprendiniais. 3. uždavins Uždavins sirtas rėmo, įtvirtinto nejudriuoju ir judriuoju šarnrais, atramų reacijoms saičiuoti. Galimi rėmų variantai pateiti 3. lentelėje. 3. lentelė. Uždavinių variantų schemos 3. lentelėje išspausdintos saitmeninės atsirų variantų duomenų reišmės. Lentelėje nurodtas onrečios schemos numeris (SH), matmens metrais, jėgų, pasirsttųjų aprovų, porų momentų ir
13 ampų reišmės. Kai urios jėgos duotam variantui gali būti lgios nuliui. Tuo atveju nuliui lgi aprova ar momentas neturi būti vaizduojama sprendžiant onrečią užduotį. 3. lentelė. Uždavinių variantų pradiniai duomens 3
14 Ši užduotis sirta ploščiosios jėgų sistemos pusiausvros uždavinių sprendimo įgūdžiams įtvirtinti. Sprendžiant šią užduotį patogiausia pirmąja f užrašti momentų sumos lgtį centro atžvilgiu, nes jame veiia dvi saičiuojamos reacijų omponentės ir. Nustatoma judriojo šarnro reacija R. Komponentės ir nesaičiuojamos projetuojant rėmą, aip laisvą ūną veiiančios jėgos į pasirintas oordinačių ašis. Saičiavimui patirinti užrašoma momentų sumos lgtis apie bet urį ploštumos tašą, per urį nepraeina reacijų veiimo tiesės. Teisingai apsaičiavus reacijas ir užrašius patirinimo lgtį, ši lgtis turi virsti tapatbe (momentų suma prilgti nuliui). 3.3 lentelėje išspausdintos pateitų uždavinių reacijų reišmės. 3.3 lentelė. Uždavinių variantų reacijų reišmės 3. uždavinio sprendimo pavzds Pateiiamas uždavinio, sudarto pagal analogišus duomenis, sprendimas. Uždavinio schemą, sudartą pagal užduoties duomenis, pateiiame 3.4 brėžinje. Trinėjamo rėmo matmens pateiiami brėžinje. Lgios nuliui aprovos nėra parodtos brėžinje. Čia: 6 Nm, P 7 N, P3 9 N, q N m. Sudarome saičiuojamąją uždavinio schemą, ršius paeisdami atitinamomis reacijos jėgomis. 3.5 brėžinje ršių reacijos jėgos parenamos taip: R statmena atraminei ploštumai, o šarnro reacija pateiiama omponentėmis,. Pasirsttąją aprovą paeičiame suteltąja jėga Q q l,5 5 N. 5 4
15 4 8 P q 60 P brėž. P Q,5 P R 3.5 brėž. Pradžioje užrašome momentų, veiiančių centro atžvilgiu, pusiausvros lgtį: 0, 3P 5,5Q 8P3 cos60 P3 cos30 + R cos45 + 8R cos45 0. Čia P 3 ir R vertinamos dviem omponentėmis. Lgtje esanti viena nežinomoji reacijos jėga R saičiuojama taip: 3P + 5,5Q + 8P3 cos60 + P3 cos30 R, 0cos 45 3, , , ,866 R 4,33 N. 0 0,707 Tada užrašome veiiančių jėgų projecijų į oordinačių ašis lgtis: 5
16 P 0, R cos45 + P3 cos60 0, P 0, P Q P3 cos30 + R cos Spręsdami šias lgtis saičiuojame atramos reacijų omponentes: R cos45 P3 cos60, 4,33 0, ,5,,70 N, P + Q + P3 cos30 cos 45 0, ,866 4,33 0,707, R,59 N. Patirinimui užrašome momentų sumos lgtį centro D atžvilgiu: D P + 6,5Q 6R cos 45 4R cos 45,59 + 8, , ,33 0,707 0,007. Šis rezultatas vertinamas aip aptislio saičiavimo palaida, o sprendinius galime laiti teisingais Gembinio rėmo, veiiamo ploščiosios jėgų sistemos, reacijos Gembiniu vadinamas standžiai viename taše įtvirtintas rėmas. Standžiojo įtvirtinimo reacijas sudaro jėga ir jėgų pora. Kadangi reacijos jėgos rptis paprastai nežinoma, ši reacijos jėga išsaidoma į dvi omponentes. 3.3 uždavins Rėmas standžiai įtvirtintas taše parodtas 3.6 brėžinje. Šį rėmą veiia jėgos P, P ir jėgų pora, urios momento ddis, ir pasirsttoji aprova, urios intensvumas q. Saičiuojame standžiojo įtvirtinimo reacijas. 0 4 P 30 q 3 5 P 3.6 brėž. 9 6
17 Saičiuojamoji rėmo schema pateiiama 3.7 brėžinje. Šioje schemoje pasirsttoji aprova paeista suteltąja Q 5 q 5 0 N bei atraminiai ršiai paeisti atitinamomis reacijos jėgomis. P 30 Q,5 3 9 P 3.7 brėž. Užrašome rėmo pusiausvros lgtis: P P 0, 0, + P cos60 + P 0, + P cos30 Q 0, 0, + P cos60 +,5Q + 7P 0. Spręsdami šias lgtis apsaičiuojame reacijos jėgų ddžius: P cos60 P 0,5 9 0 N, Q cos30 0 0,866 8,7 N, P P cos60 +,5Q 7P, 0,5 9 +, Nm. Sprendimą patiriname užrašdami momentų pusiausvros lgtį 7 5P cos60 9P cos , Q 9 5 ( 0) 5 0, 5 9 0, , , Tai leidžia tiėti sprendimo rezultatais. 7
18 Savaranišam sprendimui pateiiamas gembinių sijų schemų rinins parodtas 3.4 lentelėje, o duomens 3.5 lentelėje. Šių užduočių atsamai išspausdinti 3.6 lentelėje. 3.4 lentelė. Gembinių sijų schemos 8
19 3.5 lentelė. Gembinių sijų pradiniai duomens 9
20 3.6 lentelė. Gembinių sijų saičiavimo rezultatai 4. KŪNŲ SISTEOS PUSIUSVYR Ršiai ūnų sistemoje sirstomi į vidinius ir išorinius. Vidiniais vadinami ršiai, jungiants ūnus į sistemą. Išoriniai tai ršiai, jungiants tiriamos sistemos ūnus prie itų ūnų. Vidinių ršių reacijos, būdamos ūnų tarpusavio sąveios jėgomis, ra vienodo didumo ir priešingų rpčių. Čia nagrinėjamos ūnų sistemos, veiiamos ploščiosios jėgų sistemos, todėl sprendžiant uždavinius šiai jėgų sistemai taiomos įprastos statinės pusiausvros lgts. Visai ūnų sistemai gali būti užrašomos 3 statinės pusiausvros lgts, į urias neįeina vidinių ršių reacijos, nes būdamos vienodo didumo ir priešingų rpčių jos viena itą eliminuoja. Paprastai lgčių, užraštų visai sistemai, nepaana išorinių ršių reacijoms nustatti. Kievienos sistemos ūnas gali būti nagrinėjamas atsirai. Šiuo atveju ievienam ūnui užrašome po 3 statines pusiausvros lgtis, urios leidžia saičiuoti išorinių ir vidinių ršių reacijas. Kūnų sistema ra statišai sprendžiama, ai nežinomųjų jėgų saičius neviršija 3n (n ūnų saičius). 4. uždavins Vienaltė horizontalioji sija, urios svoris G 4 N, įtvirtinta šarnru ir remiasi į atraminę siją D. Šios sijos svoris G 5 N. Ji įtvirtinta šarnru D ir palaioma lnu EL. Konstrucijos matmens pateiiami 4. brėžinje. Taše veiianti jėga P 8 N. Saičiuojamos šarnrų reacijos, lno įtempimo jėga ir sijų tarpusavio sąveios taše jėga. 0
21 5 h E,5 H T 30 P 60 D 60 3 G G 4. brėž. Konstruciją sudaro du standieji ūnai ir D. Kievieną iš šių sijų galima nagrinėti atsirai. 4. ir 4.3 brėžiniuose pateiiamos šių ūnų saičiuojamosios schemos, gautos pašalinus išorinius ir vidinius ršius. Šarnrų reacijos vertinamos dviem omponentėmis. Sąveios jėga taše privalo būti statmena sijos ploštumai, o lno įtempimo jėga sutampa su lno rptimi. G P 60,5 R 3, brėž. tlię 4.3 brėžinio geometrinę analizę, apsaičiuojame D cos ,866 3, 46 m, h L sin 30 0,5 0,5 m. Kadangi siją veiia ti trs nežinomos jėgos,, R, spręsti pradedame nuo šios sijos. Pradžioje sudarome tašo atžvilgiu momentų pusiausvros lgtį: ( ) 0,,5G + 3,46R 5P cos30 0.
22 h 3 60 T R 30 P D 60 P G brėž. Taidami šią lgtį, apsaičiuojame reacijos jėgą R : 5P cos30 +,5G R, 3, ,866 +,5 4 R,89 N. 3,46 jėgas Tada sudarome jėgų projecijų į oordinačių ašis pusiausvros lgtis ir apsaičiuojame reacijos ir : 0, 0, P cos 60 0, P cos ,5 G + R G R 4 N, P cos 30 0, + P cos 30 4, ,866,97 N. Nagrinėjame siją D. Žinodami, ad R R,89 N, užrašome statinės pusiausvros lgtis: ( ) 0, G cos30 + 3T cos60 4 cos30 0, D 0, T 0, D 0, D G R 0. ' R ' Išsprendę šias lgtis, apsaičiuojame ' 0 ( G + 4R ) cos30 ( 5 + 4,89) T 0 3cos 60 D T 35,54 N, ' 3 0,5 D G + R 5 +,89 7,89 N. 0,866 35,54 N, Patirinimui užrašome visai nagrinėjamai sistemai momentų pusiausvros lgtį, uri įvertina ti išorines jėgas. entru parenamas tašas H, uriame nesierta išorinių ršių reacijos jėgos.
23 H ( P ),73 0,77G + P cos60 3,7P cos30 + 0,5T + P, D 73 (,97) 0, ,5 3,7 8 0, ,5 35, ,54,73 7,89 0,033. 4,73 Šioje lgtje geometriniai parametrai atsirai neparodti, tačiau jie nustatomi remiantis elementariais saičiavimais. 4. uždavins Šiame uždavinje nagrinėjama dviejų ūnų sistema, parodant, ad ai uriais atvejais pusiausvros lgts, užraštos visai sistemai, gali būti sėmingai panaudojamos atsiroms reacijos jėgoms saičiuoti. Konstrucijos schema parodta 4.4 brėžinje. q P 60 P brėž. Čia P N, P 9 N, 0 Nm, q, N. 7 m Pašalinus ršius, sudarta onstrucijos saičiuojamoji schema, parodta 4.5 brėžinje. Saičiuojamojoje schemoje išsirsttas rūvis paeičiamas oncentruota jėga Q 3 q 3, 3,6 N. Vertindami ti išorines jėgas, užrašome momentų pusiausvros lgtis ūnų sistemai; ( ) 0, ( ) 0,,5Q P 5P cos60 + P cos ,5Q + 4P + P cos Taidami šias lgtis apsaičiuojame reacijos jėgų ir reišmes,5q + P + + 5P cos60 P cos30,5 3, ,5 9 0,866 7,86 N, 5 5,5Q + 4P + P cos30,5 3, ,866 3,64 N
24 3 Q P D 60 P, brėž. Tada sudarome jėgų projecijų pusiausvros lgtį: 0, (ašis nestatmena atarpai ) + Q P cos Ši lgtis negali būti išspręsta, tačiau išreišiame Q + P cos30. nalizuojame atsirai sijos pusiausvrą (šios sijos schema parodta 4.6 brėžinje): : 60 P 4.6 brėž. 4
25 Užrašome statinės pusiausvros lgtis sijai ir apsaičiuojame nežinomųjų reacijos jėgų reišmes: ( ) 0, 3 P cos30 0, P cos30 9 0,866,6 N, 3 3 0, P cos30 + 0, P cos30 9 0,866,6 5, N, 0, P cos60 + 0, P cos60 Saičiuojame panaudodami sudartos lgties išraišą 3, ,866,6,59 N. 9 0,5 7,86 3,36 N. Patirinimui sudarome momentų pusiausvros lgtį visai ūnų sistemai, centru pasirinę jėgos P veiimo tašą D. D ( ) + +,5Q 4P cos60 P cos , , + 5, 3, , 5 9 0, , , 6 0, 0. Reacijų reišmės laitinos teisingomis. 4.3 uždavins Nagrinėjama trijų dalių horizontalioji sija. Sijos dals jungiamos šarnrais ir. Siją veiia atviosios jėgos P 5 N, P 7,5 N, išsirstta aprova, urios intensvumas q,5 N m ir 5 Nm. ūtina saičiuoti išorinių ir vidinių ršių reacijas. Sijos schema parodta 4.7 brėžinje E 35 0,5 P 0,5,5 P q H,5 4 D 4.7 brėž. Šarnre D tena saičiuoti dvi išorinių ršių reacijų omponentes, šarnruose ir po dvi vidinių ršių reacijų dedamąsias, atramas, E ir H paeičiame reacijos jėgomis, turinčiomis po vieną omponentę. endras saičiuojamų reacijų saičius lgus 9. Kadangi siją sudaro 3 ūnai, bendras lgčių saičius prilgsta nežinomųjų saičiui. Uždavins ra statišai sprendžiamas. 5
26 35 P 4 P 3,5,5 4.8 brėž. Pradėti saičiavimą reomenduojame nuo ūno, urį veiia mažiausias nežinomų jėgų saičius, arba šios jėgos išdėsttos mažiausiame tašų saičiuje. Pagal pasutinį riterijų tos ūnas ra (vidinių ršių reacijos veiia dviejuose tašuose ir ). Nagrinėjame šį ūną. Šios sijos dalies schema parodta 4.8 brėžinje. Reacijų,,, rpts parenamos laisvai. Sudarome šio ūno statinės pusiausvros lgtis ir sprendžiame: ( ) 0, 0, 0,,5P cos55,5p 4 0, 0 P cos55 P 0, + P cos35 0. Spręsdami pirmąją ir antrąją lgtis, apsaičiuojame ir reišmes 0,5P cos55,5p 0,5 7,5 0,574,5 5 3,66 N, 4 4 P cos55 + P + 7,5 0, ,66 5,65 N. Trečioji lgtis palieama tolesniam sprendimui. Tada nagrinėtume sijos dalį, ur liusių nežinomų jėgų būtų ti 3. Šios dalies schema parodta 4.9 brėžinje. ' ' ' Čia,. Užrašome šios dalies pusiausvros lgtis ir saičiuojame R R, : ( ) 0, ' E 0 + 3, 5R 4, ' , 65 RE, 3, 5 3, 5 R E,7 N., E 6
27 60 R R E 3,5 0,5 ' ' 4.9 brėž. 0, R R cos 60 ' + RE ' RE R 3,03 N, 0, R cos30 ' ' R cos30 ',8 N. 0,,65,7, 0, 3,03 0,866, Taidami ūno ansčiau nespręstą lgtį, apsaičiuojame + P cos35,,8 + 7,5 0,89, 5,4 N. Tada saičiuojame sijos dalį D, urioje lię trs nežinomos jėgos. Šios sijos dalies schema pateiiama 4.0 brėžinje. : Q P R H P 0,5 0,5 4.0 brėž. 7
28 Pirmąja užrašome momentų pusiausvros lgtį, centru pasirinę tašą D : D ( ) 0,,5 R + Q 0. H Vadinasi, Q RH, Q q,5,5 N,,5,5 + 3,66 5 R H 0, N.,5 Projetuojame jėgas į oordinačių ašis ir sudarę atitinamas pusiausvros lgtis, apsaičiuojame reacijos jėgų D ir D reišmes: 0, + D D 0, 0, 5,4 N, Q + RH + D 0, D Q R,5 + 3,66 + 0,, H D 6,8 N. Saičiavimą patiriname nagrinėdami visos sijos pusiausvrą. Veiiančių išorinių jėgų schema parodta 4. brėžinje. L 60 R 3,5 4 R E P 45,5 0,5 P,5 R H Q 0,5 0,5 P P 4. brėž. Tašas L parintas centru, adangi per jį nepraeina išorinių jėgų veiimo tiesės. ( ) cos R ,5R 4,5P cos55 + P cos35 6,5P + 8,5R 9Q + D + D L E H 0 ( 0, ) 9, 5 + 5, + 3, 03 0, , 5 7, 4, 5 7, 5 0, , 5 0, 89 6, , , 8 5 0, 00. Šis rezultatas leidžia saičiavimo rezultatus laiti patiimais. 4. lentelėje pateiiami duomens trijų dalių sijoms sudarti ir savaranišai tobulinti sprendimo įgūdžius. 8
29 4. lentelė. Trijų dalių sijos užduočių variantų pradiniai duomens 9
30 Lentelėje pateiti duomens L, L, L 3 nusao atsirų sijos dalių ilgius metrais, KP ir DP sijos airiojo ir dešiniojo dalių įtvirtinimo variantus, P, P, q, q, lq, /, /j atviosios aprovas veiiančios siją. Čia ir j nurodo, urią sijos dalį veiia atitinamas monetas. XP, XP, Xq, lq nurodo atitinamų jėgų pridėties oordinates ir aprautos dalies ilgį (lq). Koordinačių pradžia laiomas airsis sijos galas (tašas ). Schemai sudarti reialinga informacija pateita 4. brėžinje. L L L3 X X D KP 0 DP 0 KP DP α KP DP α P P q α D α XP XP Xq Lq 4. brėž. Jeigu X 0, antros judriosios šarnrinės atramos nėra. omento algebrinis ženlas parodo jo rptis sudarant schemą. Jėga P visais atvejais nureipta vertialia rptimi (žemn). Šių užduočių sprendimo rezultatai pateiiami 4. lentelėje. 30
31 4. lentelė. Trijų dalių sijos užduočių variantų saičiavimo rezultatai 3
32 5. SLYDIO TRINTIS Sldimo trintimi vadinamas pasipriešinimas, atsirandantis liečiantis dviem ūnams ir esant reliatviojo sldimo galimbei. Trinties jėga veiia priešinga rptimi galimai ūno sldimo rpčiai. asimali galima trinties jėga ra f s N. (5.) Čia f s trinties oeficientas, prilausantis nuo besiliečiančių ūnų medžiagų, jų besiliečiančių paviršių glotnumo ir N ontato jėgos. Trinties oeficientas, atitinantis didžiausią trinties jėgą, ūnui nejudant, vadinamas statinės trinties oeficientu. Trinties oeficientas, atitinantis slstantį ūną veiiančią jėgą, vadinamas inetinės trinties oeficientu. Jis aptisliai 5% mažesnis už statinės trinties oeficientą. Sprendžiant statios uždavinius, taiomos ūnų pusiausvros lgts. e itų atviųjų ir reacijos jėgų, vertinamos ir trinties jėgos, apsaičiuotos pagal (5.) formulę. 5. uždavins P brėž. Kūnas, urio svoris G 5 N, esantis ant šiurščios nuožulnios ploštumos, veiiamas horizontaliosios jėgos P. Jo statinės trinties oeficientas f 0,4. Saičiuoti minimalią ir masimalią jėgos P reišmes, užtirinančias ūno rimties būseną. Jėgų schema, atitinanti atvejį, ai ūnas jėgos P sulaiomas nuo sldimo žemn ploštuma, parodtas 5. brėžinje. P 60 N G brėž. Užrašome susiertančių jėgų sistemos pusiausvros lgtis: 0, P cos30 + G cos 60 0, 0, N P cos60 G cos30 0. Nustatome masimalią galimą trinties jėgos fn reišmę. Taidami antrąją pusiausvros lgtį, randame ontato ir trinties jėgų išraišas 3
33 N P cos60 + G cos30, o fn fpcos60 + fg cos30. Šią išraišą statome į pirmą lgtį: P cos 30 + fp cos60 + fg cos30 G cos60 0. Vadinasi, ( cos60 f cos30 ) 5( 0,5 0,4 0,866) G P 0,7 N. cos30 + f cos60 0, ,4 0,5 Ši jėgos P reišmė užtirina, ad ūnas nesls žemn ploštuma. Ji aivaizdžiai minimali. Jėgų schema, nustatant jėgos P masimalią reišmę, parodta 5.3 brėžinje. P 60 N 30 G brėž. Šiuo atveju pusiausvros lgts sudaromos taip: 0, P cos30 G cos60 0, 0, N P cos 60 G cos30 0. Trinties jėgos ddis saičiuojamas taiant išraišą: fn Pf cos 60 + Gf cos 30. Įstačius šią trinties jėgos išraišą į pirmąją pusiausvros lgtį, apsaičiuojamas jėgos P ddis P cos 30 G cos60 Pf cos60 Gf cos30 0, ( cos60 + f cos30 ) 5( 0,5 + 0,4 0,866) G P 6,35 N. cos30 f cos60 0,866 0,4 0,5 Pusiausvra išlis, ai jėga P is nuo didumas ir rptis. P 0,7 N ii P 6,35 N, artu eisis trinties jėgos min ma 33
34 5. uždavins Sldimo trinties oeficientas tarp visų paviršių ra vienodas f 0,3. ūtina nustatti masimalią jėgos P reišmę, užtirinančią ūnų sistemos pusiausvrą. (5.4 brėžins) G,5 N, G N. Taip pat saičiuosime lno įtempimo jėgą, esant masimaliai P jėgos reišmei. P 5.4 brėž. Nagrinėjame pirmojo ir antrojo ūnų pusiausvros sąlgas. Šiam tislui sudarome atsiriems ūnams saičiuojamąsias schemas, pavaizduotas 5.5 brėžinje. N ` G T P N ' G 5.5 brėž. Šiose saičiuojamosiose schemose G G + G,5 +,,6 N ir '. Trinėjant antrojo ūno pusiausvros sąlgas, sudaromos šios lgts: 0, T 0,, N G 0. ' 0 Spręsdami šias pusiausvros lgtis, apsaičiuojame ' fn 0,3 0,3 N, ' T 0,3 N. ' ir T reišmes Trinėjant antrojo ūno pusiausvros sąlgas, sudaromos šios lgts: 0, P 0, N G 0. 0, 34
35 psaičiuojame jėgų ir P reišmes Nf,5 0,3 0,75 N, P + 0,75 + 0,35,05 N. ivaizdu, ad pusiausvra galima, ai P,05 N. 5.3 uždavins ilindras, urio svoris G 4 N, o spinduls r 0, m, remiasi į horizontaliąją ir vertialiąją ploštumas, esant vienodiems abiejų ploštumų sldimo trinties oeficientams f 0,4. Nustatsime masimalų galimą jėgų poros momentą, užtirinantį cilindro pusiausvros būseną (5.6 brėžins). r G 5.6 brėž. Esant masimaliam jėgų poros momentui, sldimo trintis vertinama masimaliomis galimomis jėgomis. Laisvą cilindrą veiiančios jėgos parodtos 5.7 brėžinje. N c N G 5.7 brėž. 35
36 ilindrą veiianti jėgų sistema ra ploščioji. Todėl spręsdami uždavinį taisime šias jėgų sistemai būdingas pusiausvros sąlgas:, + N 0, 0 0, N G 0,, c ( ) 0, r r 0. nalizuodami pirmąją lgtį, gauname, ad N, N f. Iš antrosios lgties randame, ad N G ir N f, N f, arba N G N f. psaičiuojame veiiančių jėgų reišmes G Gf Gf, o bei. + f + f + f N Įstatome šias jėgų išraišas į trečiąją pusiausvros lgtį: Gf r Gfr 0, + f + f Gfr 4 0,4 0, + f + 0,4 ( f + ) ( 0,4 + ) 0,39 N. Tai masimali poros momento reišmė. 5.4 uždavins Vienaltė sija, urios svoris G 4 N, o ilgis L, m remiasi į šiurščią horizontaliąją ploštumą, o parodtoje padėtje laioma lno. Žinant trinties oeficientą sijos į ploštumą f 0,35, nustatti, ar sija lis pusiausvroje, taip pat rasti lno įtempimo jėgą ir trinties jėgos didumą (5.8 brėžins). α α L 30 G 5.8 brėž. Šios sijos saičiuojamoji schema parodta 5.9 brėžinje. 36
37 T 30 G N 5.9 brėž. Kampai ir lgūs pusiausvros lgtis: α 75. Turime ploščiąją jėgų sistemą, uriai užrašome šias 0, T cos5 0, 0, N G + T cos 75 0, ( ) 0, 0,5G cos60 + T cos5 0. Taidami trečiąją lgtį, apsaičiuojame lno tempimo jėgą T: 0,5G cos60 0,5 4 0,5 T,04 N. cos5 0,966 Taidami antrąją lgtį, apsaičiuojame ontato jėgą N: N G T cos75 N 3,73 N. 4,04 0,6, Taidami pirmąją lgtį, nustatome būtinąją trinties jėgos reišmę pusiausvrai užtirinti T cos 5,04 0,966 N. Galima masimali trinties jėgos reišmė m fn 0,35 3,73,3N. Kadangi tiroji trinties jėgos reišmė neviršija masimalios galimos, sija gali būti pusiausvroje, esant trinėtai padėčiai. 6. PLOKŠČIŲJŲ SNTVRŲ SKIČIVIS Santvara laioma ploščiąja, ai visi strpai ir mazgai bei veiiančios juose jėgos išdėsttos vienoje ploštumoje. Santvaros strpai gali būti tempiami arba gniuždomi. Saičiuojant visi strpai laiomi tempiamais. Jų įrąžos nureiptos išilgai strpo nuo mazgo. Saičiavimui gali būti taiomi du metodai:. azgų išpjovimo,. Pjūvių (Riterio). 37
38 Taiant mazgų išpjovimą, pirmiausia nustatomos išorinių ršių reacijos. Santvara šiame etape laioma standžiuoju ūnu. Užrašomos statinės pusiausvros lgts visai santvarai. Taiant mazgų išpjovimą, pradedama nuo mazgo, į urį sueina ne daugiau aip du strpai, o ievienas itas mazgas gali turėti ne daugiau aip strpus su nežinomomis įrąžomis. Kieviename mazge turima ploščioji susiertančių jėgų sistema. Taiant šios sistemos pusiausvros lgtis, saičiuojamos dvi strpų įrąžos. Taiant pjūvių metodą, santvara dalijama į dvi dalis. Pjūviu ertama ne daugiau aip tris strpus. Nagrinėjant vienos atpjautos santvaros dalies pusiausvrą, gaunama ploščioji jėgų sistema. Ją sudaro išorinės jėgos mazguose ir į pjūvį pateusių strpų įrąžos. Sprendžiant šios jėgų sistemos pusiausvrą, galima saičiuoti ii 3 strpų įrąžų ievienam atlitam pjūviui. 6. uždavins Saičiuojame santvaros, parodtos 6. brėžinje, strpų įrąžas. Čia P N, P N, P N E P P 3 3 P 3 D 4 6. brėž. Nustatant išorinių ršių reacijas, santvara laioma standžiuoju ūnu ir šio etapo saičiuojamoji schema pavaizduota 6. brėžinje E P P α P 3 D R 6. brėž. Užrašome visos santvaros pusiausvros lgtis: ( ) 0, 8P + 4P + 3P3 R 0, 38
39 0, + P 0, 3 0, P + P + R 0. Spręsdami šią lgčių sistemą, apsaičiuojame ršių reacijų jėgų ddžius: 8P + 4P + 3P R,5 N, N, P 3 P + P R 4 +,5 5,54 N. Įrąžų saičiavimą pradedame mazgu, urį veiia dvi nežinomos jėgos (6.3 brėž.). Tai strpų ir 3 įrąžos. Strpų įrąžas paprastai žmime raide S. Čia tg α, α 56,3. S α S 6.3 brėž. Užrašome ir sprendžiame šios viename taše susiertančių jėgų sistemos pusiausvros lgtis: 0, S sinα 0, S sinα 5,5 0,83 0, S S cosα 0, 8,63 N, S S cosα + 8,63 0,554 9,3 N. Po to trinėjame mazgo pusiausvrą. azgo išpjovimo saičiuojamoji schema pateita 6.4 brėžinje. S D S α α R S 6.4 brėž. Užrašome ir sprendžiame mazgo susiertančių jėgų sistemos pusiausvros lgtis: 39
40 0, R + S sin α+ S sin α 0, R,5 S S + 8,63 7,N, sinα 0,83 0, S S cos α+ S cos α 0, S D D ( S S ) cos α ( 8,63 + 7,) 0,554 6,3 N. Liusieji santvaros mazgai gali būti nagrinėjami bet uria tvara, nes juos veiia po dvi nežinomas strpų įrąžas. Kai jau nustattos išorinių ršių reacijos, pasutinių santvaros mazgų išpjovimas leidžia patirinti saičiavimo teisingumą. Šiuo atveju nustattos strpų įrąžos turi teninti mazgų pusiausvros sąlgas. Trinėjame itą D mazgą, urio saičiuojamoji schemą, taiant mazgų išpjovimo metodą, pateita 6.5 brėžinje. S S D ED α α P3 S D 6.5 brėž Sudarome mazgo D pusiausvros lgtis: 0, P S cos α+ S cos α+ S 0, 3 ED D D 0, S ED sin α S sin α 0. + D Išsprendę šią pusiausvros lgčių sistemą, apsaičiuojame strpų S ED ir S D įrąžas: S arba P S D cosα+ S 0, ED S D P 3 S S cos α S ED 4,80 N. 3 + D + 6,3 0,554 D D 4,80 N, Tada trinėjame mazgą. Taiant mazgų išpjovimo metodą, sudarome šio mazgo saičiuojamąją schemą (6.6 brėžins). S E α S D P S α S 6.6 brėž. Sudarome mazgo vieną pusiausvros lgtį ir apsaičiuojame S E įrąžą P 0, S E S D cos α+ S + S cos α 0, 40
41 S E SD cos α+ S + S cos α 4,8 0, ,3 7, 0,554,6 N. Tiriame šio mazgo pusiausvrą: P ( S + S ) sin α + P ( 4,80 7,) 0,83 + 0,005. D nalizuodami mazgą E, sudarome saičiuojamąją schemą (6.7 brėžins). P E α S ED S E 6.7 brėž. Užrašomos šios pusiausvros lgts: P P S E + S ED cos α,6 4,80 0,554 0,04, P + S ED sin α 4 4,80 0,83 0,006. Pusiausvra teninama su nedidelėmis palaidomis. 6. uždavins Saičiuoti santvaros, parodtos 6.8 brėžinje, strpų EG, E ir D įrąžas. Čia P P,5 N, P 5 N. 3 E P G I P J P3, D H,8,8,8,8 6.8 brėž. Saičiuodami šarnro reacijas, nagrinėjame santvarą, taidami standžiojo ūno prielaidą. Saičiuojamoji schema pateita 6.9 brėžinje. 4
42 P P P3, R,8,8,8,8 6.9 brėž. Užrašome visos santvaros pusiausvros lgtis ir apsaičiuojame reacijų jėgas ( ) 0, P 0, 7, + 5,4P +,8 P +, P3 0, 5,4P +,8 P +, P3 5,4 5 +,8 5 +, 5 5,83 N, 7, 7, P 3 0, 5 N. P 3 Šarnro reacijos, sprendžiant šį uždavinį, nėra reialingos. Daromas santvaros pjūvis per užduotje nurodtus strpus. Nagrinėjame airiosios nupjautos santvaros dalies pusiausvrą. Ši santvaros dalis parodta 6.0 brėžinje. α E P S EG α, S E D S D,8 6.0 brėž. 4
43 Šiuo atveju turime bendrojo tipo ploščiąją jėgų sistemą, uriai užrašomos vienos santvaros dalies pusiausvros lgts, ir apsaičiuojamos strpų įrąžos S D, S E ir S ED : E ( ) 0,,8 +, +, S 0, S 0,,8,, D,8 5,83, 5, D P S E sin α 0, D, +,8,6 m,, sinα 0,555,,6,8 cosα 0,833,,6 P 5,83 5 S sinα 0,555 0, E + S D + S E cosα + S EG 0, S S S cos α, ED S ED D E,50 N, 5 8,75,5 0,833 5 N. Strpas ED ra gniuždomas, o du iti tempiami. 6.3 uždavins 8,75 N, Saičiuosime santvaros, pateiiamos 6. brėžinje, strpų E, ir P įrąžas. P P P3 P4 0 N. Sprendžiant šį uždavinį parodoma, ad išorinių ršių išanstinis saičiavimas gali būti nereialingas. P4 β E P3 G P α I P 5 β H D brėž. Pjūvis atlieamas per strpus, uriuose reiia rasti įrąžas, ir nagrinėjama pjūvio dešinėje liusios santvaros dalies pusiausvra (6. brėžins). 43
44 S E E P3 P P α S β α 3 3 S D 6. brėž. įrąžos: Trinėjamai santvaros daliai užrašomos pusiausvros lgts ir apsaičiuojamos reiiamų strpų ( ) 0, 3P 6P + E SE 5 tg α 0,47, T 0, I m, 5 sinα 0,385, I 3 I cos α 0,93, I 3 E EI tg α 6 0,47,5 m, 3P + 6P S E 7 N,,5,5 0, S 0, E S cos β S cos α 0, D P + P + P3 + S D sinα S sinβ 0. Sprendžiant 0 lgtį, apsaičiuojame įrąžos S išraišą: S SE S D cosα. cos β cos β Šią išraišą įstatome į 0 lgtį: P + P + P3 + S D sinα+ SE tg β+ S D cosα tg β 0, S D P + P + P3 + SE tg β, sinα + cosα tg β E,5 tg β 0,833, E 3 44
45 ,833 S D 03,34 N, 0, ,93 0,833 E cos β, 3 +,5 3,9m, 3 cos β 0,768, 3,9 7 03,34 0,93 S + 30,45 N. 0,768 0,768 Strpai E ir tempiami, o strpas D gniuždomas. 7. ERDVINĖ JĖGŲ SISTE et uri erdvinė jėgų sistema gali būti reduuota į suminę jėgą, lgią visų jėgų vetorių sumai, ir jėgų porą, urios momentas vadinamas suminiu momentu. n R, 0 0 ( ). (7.) Suminė jėga neprilauso nuo centro padėties, o suminis momentas paprastai prilauso nuo centro pasirinimo. Jėgų sistema pusiausvroji, ai R 0 ir o 0 bet uriam pasirintam centrui O. Šios pusiausvros sąlgos nusaomos šešiomis analizinėmis lgtimis: z Oz 0, 0, 0, O O ( ) 0, ( ) 0, ( ) 0. (7.) Kai ūną veiia erdvinė lgiagrečių jėgų sistema, ašį z parinus lgiagrečia jėgoms, pusiausvra nustatoma trimis lgtimis: z 0, O O ( ) 0, ( ) 0. (7.3) Sprendžiant erdvinės jėgų sistemos uždavinius, jėgos paprastai saidomos į omponentes pasirintų oordinačių ašių rptimis. Jėgos momentas ašies atžvilgiu lgus nuliui, ai ji erta ašį arba ra lgiagreti ašiai. Dažnai patogu naudoti analizines formules jėgų momentams saičiuoti: O O Oz ( ) z z ( ) z z ( ),, (7.4). Čia,, z ra jėgos pridėties tašo oordinatės. 45
46 7. uždavins Standžiai taše įtvirtinta erdvinė gembinė sija, veiiama jėgų P N, P 5 N ir poros, urios momentas 7 Nm. a 4,5 m, b 4 m, c,5 m, α 65, β 5 (7. brėžins). Saičiuosime sijos reacijas standžiojo įtvirtinimo taše. z D P β G E α P 7. brėž. Sudarant uždavinio saičiuojamąją schemą, standžiojo įtvirtinimo ršį galima paeisti reacijos jėga ir pora. Reacijos jėga ir poros momentas erdvėje gali turėti bet urią rptį. Todėl šią jėgą ir poros momentą paeičiame trimis vetorinėmis dedamosiomis oordinačių ašių rptimis (7. brėžins). Sudarant saičiuojamąją schemą, jėgos P ir P išsaidtos į dedamąsias: P P sinα sin 65,8N, P P cosα cos65 0,85 N, P z P sinβ 5sin 5, N, P P cosβ 5cos 5 4,53 N. Sudarome šios erdvinės jėgų sistemos statinės pusiausvros lgtis ir apsaičiuojame reacijos jėgų omponentes: z 0, 0, 0, P 0, P,8N, P P 0, P P 0,85 4,53 3,68 N, + z P z 0, z P z, N. 46
47 P β P G Pz z z D E P z P α P z ( ) 0, 7. brėž. ( ED) P 0, ( ED) P, ( 4,5,5) 0,85 3,39 Nm, + Gc P z P + Gc P + P z,5, + 4,5 4,53 ( ) 0, z ( ) 0, z z z ( ED) P + P z 0, ( ED) P P z, ( 4,5,5),8,5,,68 Nm, + E P E z + D P + P + P z D P P,,5,8 4 0,85,5 4,53 7 6,5 Nm. tlieant saičiavimo patirinimą, parenama ita oordinačių sistema. Užrašomos momentų pusiausvros lgts. Šiame uždavinje parinta oordinačių sistema,, z : ( ) E + ( ED) ED P + ( G + E) P z 3,39,5, + ( 4,5,5) ( 3,68),5 4,53 + (,5 +,5), 0,005, ( ) ( ED) D + ( D) P z,68 ( 4,5,5),8 4, + (,5 + 4), 0, ( ) z + + E + D + ( + D) P 6, ,5,8 4 3,68 + (,5 + 4) 4,53 0. z Patirinimo rezultatai leidžia teigti, ad reacijų omponentės nustattos teisingai. Šį uždavinį galima spręsti naudojant vetorinių algebros lgčių sistemą (7.). Sprendžiant šiuo būdu saičiavimus reomenduojame atliti sudarius 7. lentelę. 0, 47
48 7. lentelė. Vetorinių pusiausvros lgčių omponentės Duomens ir Jėgos tarpiniai rezultatai z P P , ,5 -,5 z , ,8 4, ,85 4,53 z 0 0 z 0 -, z ,3 z ,7 0,385 z ,3 0 z , ,4, ,55 0 nalizuojant atitinamas lentelės eilutes, sudaromos ir sprendžiamos pusiausvros lgts: z 0, 0,,8 0,,8N, 0, z 0,85 + 4,53 0, 0,85 4,53 3,68 N, z, 0, z, N, ( ) 0, + 5,3 +,7 0,385 0, 0,385 5,8,7 3,39 Nm, ( ) 0, ( ) 0, 3,6 + 5,3 0, 3,6 5,3,68 Nm, z + + 3,4 +,35 + 4,55 0, z 3,4,35 4,55, 7 3,4,35 4,55 6,5 Nm. z Užrašant ievieną momentų pusiausvros lgtį, naudojamos dvi gretimos 7. lentelės eilutės. Savaranišam sprendimui erdvinių gembinių sijų schemos pateiiamos 7. lentelėje. Šių schemų duomens pateiti 7.3 lentelėje. Šioje lentelėje nurodoma, uriai iš šešių sijos variantų siriami atitinami duomens. Gembinių sijų saičiavimo rezultatai atspausdinti 7.4 lentelėje. Tai leidžia tobulinti erdvinių sistemų analizės įgūdžius. 48
49 7. lentelė. Erdvinių gembinių sijų schemos 49
50 7.3 lentelė. Gembinių sijų pradiniai duomens 50
51 7.4 lentelė. Gembinių sijų saičiavimo rezultatai 7. uždavins lūninis velenas gali sutis įtvirtintas guoliuose ir. Veleno gale esantį rumpliaratį veiia jėga. Krumpliaračio spinduls R 0, m. lūnę veiianti jėga ra ploštumoje, statmenoje veleno ašiai. 0 N. lūnės spinduls r 0,5 m. Veleno schema pateiiama 7.3 brėžinje. Šiame uždavinje saičiuojamas jėgos didumas ir guolių reacijos. tramų reacijos, ai atramos statmenos veleno ašiai parodtos 7.4 brėžinje. Šios lgts visai sutampa su šiam uždaviniui užraštomis ir spręstomis pusiausvros lgtimis. Saičiuojant veleno atramų reacijas, reomenduojama pirmąja užrašti momentų pusiausvros lgtį atžvilgiu ašies, sutampančios su suimosi ašimi: ( ) 0, R Rr cos30 0, r cos30 0 0,5 0,866,99 N. R 0, 5
52 z 0,5 0, 0,5 r R brėž. z z 0,5 0, z 0,5 r R z brėž. Užrašomos momentų pusiausvros lgts itų dviejų onrečių oordinačių ašių atžvilgiu: ( ) 0, 0, cos30 + 0,35 0, 0, cos30 0, 0 0,866 z 9,9 N, 0,35 0,35 z 5
53 z ( ) 0, 0,5 0, cos60 0,35 0, 0,5 0, cos60 0,35 0,5,99 0, 0 0,5 0,5 N. 0,35 Kai oordinačių ašs z ir parenamos taip, ad eitų per vieną iš veleno atramų, momentų pusiausvros lgts turi po vieną nežinomą jėgą ir ra lengvai sprendžiamos. Sudarome jėgų projecijų į oordinačių ašis pusiausvros lgtis ir jas sprendžiame: z 0, 0, + z + cos60 + 0, cos60 z cos ,,99 0 0,5 + 0,5,84 N, z cos 30 z 0 0,866 9,9 7,4 N. Saičiavimo patirinimui užrašome momentų pusiausvros lgtis atžvilgiu ašių ir z. ( ) 0,z + 0,5z 0, 7,4 + 0,5 9,9 0,00, ( ),35 + 0, 0,5 0,35,99 + 0, (,84) 0,5 ( 0,5) 0,00. z 0 Tai leidžia tiėti saičiavimo rezultatais. Šį uždavinį galima spręsti vetorinės algebros metodu. Šiuo atveju tarpinius saičiavimus surašome į 7.5 lentelę. 7.5 lentelė. Vetorinių pusiausvros lgčių omponentės Duomens ir tarpiniai JĖGOS rezultatai z z 0 0 0,35 0,35 0, 0, ,5 0 z , cos60 z 0 z 0 z cos30 0 z ,5 cos30 0 z , z z ,35 z 0, cos ,35 0 0, cos 60 0, Pagal lentelės duomenis užrašome vetorinės momentų pusiausvros lgties omponentes: ( ) 0, 0,5 cos30 + 0, 0, 53
54 z ( ) 0, 0,35 0, cos30 0, z ( ) 0, 0,35 0, cos ,5 0. Gauti rezultatai rodo, ad reacijos jėgų omponenčių reišmės ra teisingos. 6.3 uždavins 4 N svorio vienaltį stačiaampio gretasienio formos ūną, pritvirtintą rutuliniu šarnru, cilindriniu šarnru ir strpu EO, veiia jėga 6 N, jėga 8 N ir pora, urios momentas Nm. Jėga nureipta išilgai atarpos EL, tiese D, o momento vetorius D. a,6 m, b 0,8 m, c 0,4 m, β 30. Strpo svoris atlieant saičiavimus nevertinamas. Saičiuosime ūno atramų reacijas. z E β K G L b c D a 7.5 brėž. Šarnro reacija gali būti bet urios rpties erdvėje. Šią reaciją saidome į tris dedamąsias. ilindrinio šarnro reacijos jėga turi dvi dedamąsias, statmenas cilindro ašiai. Strpo reacija sutampa su jo geometrine ašimi. Iš viso turime 6 nežinomas reacijos jėgas, urios nustatomos analizuojant erdvinės jėgų sistemos pusiausvros sąlgas. Kūną veiiančios jėgos parodtos 7.6 brėžinje. Jėgos, ir S išsaidomos į dedamąsias: cosα, sin α, cos γ, sin γ, S S cosβ, Sz S sin β. 54
55 z S S K L 0,4 S z E D z,6 G N z 0,8 7.6 brėž. Čia EL,6 + 0,8,79 m, 0,8,6 sinα 0,447, cosα 0,894,,79,79 DN,6 + 0,4,65 m, 0,4,6 sinγ 0,4, cosγ 0,970.,65,65 Šį uždavinį sprendžiame vetorinės algebros metodu. Tarpinius saičiavimo rezultatus pateiiame 7.6 lentelėje. Duomens ir tarpiniai rezultatai 7.6 lentelė. Vetorinių pusiausvros lgčių omponentės z JĖGOS z G S ,8 0,8 0, ,8,6,6, , 0,4 0 0, sin α S cos cosα cos γ 0 z 0 0 z 0 β 0 z G 0 sin γ z ,8G 0,6 sin γ,6 S z ,4 cosα 0 z ,4 sin α 0,4S z ,8 0,4G , ,6 sin α z S sin β sin β cosβ,6s cosβ 55
56 Remdamiesi 7.6 lentelės duomenimis sudarome erdvinio ūno pusiausvros lgtis ir apsaičiuojame reacijos jėgas bei strpo įrąžą: z z ( ) 0, 0,8G,6 sinγ,6s sinβ 0,4 cosα 0,8G,6 sinγ 0,4 cosα 0,8 S ( ) 0,,6 sinβ 0,8 0,4 sinα 0,4S cosβ 0,4G 0, 0, 4,6 8 0,4 0,4 6 0,894,55 N,,6 0,5 z 0,4 sinα+ 0,4S cosβ+ 0,4G + 0,4 6 0, ,4 (,55) 0, ,4 4 + z 7,4 N, 0,8 0,8 ( ) 0, 0,8,6 sinα,6 S cosβ 0, 0, 0, 0,,6 sinα,6 S cosβ,6 6 0,447,6 (,55) 0,8 0,8 sinα S cosβ 0, sinα+ S cosβ 6 0,447,55 0,866 0,47 N, 0,866 0,95 N, + + cosα+ cosγ 0, cosα cosγ 0,95 6 0, ,97,7 N, z + z G + sinγ+ S sinβ 0, + G sinγ S sinβ 7, ,4 +,55 0,5 3,9 N. z z Patirinimui užrašome momentų pusiausvros lgtis atžvilgiu ašių ir ( ) 0,4 cos γ 0,8G +,6 z +,6 z + 0,4 + 0, 0,4 8 0,97 0,8 4 +,6 ( 3,9) +,6 7,4 + 0,4 (,7) + 0,4 ( 0,95) 0, ( ) 0,8 sin γ 0,8S sinβ+ 0,4G 0,8 z 0, 0,8 8 0,4 0,8 (,55) 0,5 + 0,4 4 0,8 ( 3,9) 0,4 0,47 0, Patirinimas parodo, ad saičiavimo rezultatai ra patiimi. LITERTŪR. R.. Hibbeler. Engineering echanics. Statics and Dnamics. acmillan Publishing ompan, IN, New Yor, p... P. eer, E. R. Johnston. Vector echanics for Engineers. Statics, cgraw-hill oo o, p. 3. V. Paliūnas. Teorinė mechania. Vilnius: Žuvėdra, p. 56
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
2.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS
 .5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
9. Sukimas Bendrosios žinios
 9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
2015 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
9. KEVALŲ ELEMENTAI. Pavyzdžiai:
 9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
r F F r F = STATIKA 1 Q = qmax 2
 STTIK Mechanika fizinių moksų šaka, naginėjanti mateiaiuosius objektus: kūnus, kūnų sistemas, tų sistemų pusiausvyą, judėjimo dėsnius i mechaninę tapusavio sąveiką. Statika moksas apie pavienius mateiaiuosius
STTIK Mechanika fizinių moksų šaka, naginėjanti mateiaiuosius objektus: kūnus, kūnų sistemas, tų sistemų pusiausvyą, judėjimo dėsnius i mechaninę tapusavio sąveiką. Statika moksas apie pavienius mateiaiuosius
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
Ketvirtos eilės Rungės ir Kutos metodo būsenos parametro vektoriaus {X} reikšmės užrašomos taip:
 PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
2009 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 1 6 uždavinių atsakymai
 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
06 Geometrin e optika 1
 06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
Arenijaus (Arrhenius) teorija
 Rūgštys ir bazės Arenijaus (Arrhenius) teorija Rūgštis: Bazė: H 2 O HCl(d) H + (aq) + Cl - (aq) H 2 O NaOH(k) Na + (aq) + OH - (aq) Tuomet neutralizacijos reakcija: Na + (aq) + OH - (aq) + H + (aq) + Cl
Rūgštys ir bazės Arenijaus (Arrhenius) teorija Rūgštis: Bazė: H 2 O HCl(d) H + (aq) + Cl - (aq) H 2 O NaOH(k) Na + (aq) + OH - (aq) Tuomet neutralizacijos reakcija: Na + (aq) + OH - (aq) + H + (aq) + Cl
0.1. Bendrosios sąvokos
 0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
2008 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija
 008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
LIETUVOS RESPUBLIKOS ŠVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINŲ CENTRAS 2013 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ
 LIETUVS RESPUBLIKS ŠVIETIM IR MKSL MINISTERIJ NINLINIS EGZMINŲ ENTRS 03 METŲ MTEMTIKS VLSTYBINI BRNS EGZMIN REZULTTŲ STTISTINĖ NLIZĖ 03 m. birželio 5 d. matematikos valstbinį brandos egzaminą leista laikti
LIETUVS RESPUBLIKS ŠVIETIM IR MKSL MINISTERIJ NINLINIS EGZMINŲ ENTRS 03 METŲ MTEMTIKS VLSTYBINI BRNS EGZMIN REZULTTŲ STTISTINĖ NLIZĖ 03 m. birželio 5 d. matematikos valstbinį brandos egzaminą leista laikti
0.1. Bendrosios sąvokos
 .1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
.1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
3 modulis. Funkcijos sąvoka. Laipsninė, rodiklinė ir logaritminė funkcija
 P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
Diskrečioji matematika
 VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
Matematinės analizės egzamino klausimai MIF 1 kursas, Bioinformatika, 1 semestras,
 MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
A priedas. Diagnostikoje naudojami tarptautiniai ISO standartai
 Priedai A priedas. Diagnostikoje naudojami tarptautiniai ISO standartai B priedas. Patikslintas tiesiakrumplės pavaros matematinis modelis C priedas. Patikslintas tiesiakrumplė pavaros matematinis modelis
Priedai A priedas. Diagnostikoje naudojami tarptautiniai ISO standartai B priedas. Patikslintas tiesiakrumplės pavaros matematinis modelis C priedas. Patikslintas tiesiakrumplė pavaros matematinis modelis
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos
 Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
TEORIJOS PRADMENYS PROGRAMA
 DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės inducijos principas 2 Dauginimo taisylė 3 Gretiniai, ėliniai ir deriniai 4 Kartotiniai
DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės inducijos principas 2 Dauginimo taisylė 3 Gretiniai, ėliniai ir deriniai 4 Kartotiniai
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
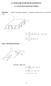 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
AIBĖS, FUNKCIJOS, LYGTYS
 AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
Statistinė termodinamika. Boltzmann o pasiskirstymas
 Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Praeita paskaita. Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje. Praeita paskaita. 2D Transformacijos. Grafika ir vizualizavimas, VDU, 2010
 Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
DEFORMUOJAMO KŪNO MECHANIKA 1 dalis
 DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
KADETAS (VII ir VIII klasės)
 ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
MEDŽIAGŲ ATSPARUMAS. Jonas Juodis. Tatjana Sankauskienė
 LETUVOS ŽEĖS ŪKO UVERSTETS Vanens ūo r žemėtvaros faultetas Statbnų onstrucjų atera Jonas Juos Tatjana Sanausenė EDŽGŲ TSPRUS Pratnų arbų aprašas aemja 009 UDK 59 / (07)(00) Jonas Juos, Tatjana Sanausenė
LETUVOS ŽEĖS ŪKO UVERSTETS Vanens ūo r žemėtvaros faultetas Statbnų onstrucjų atera Jonas Juos Tatjana Sanausenė EDŽGŲ TSPRUS Pratnų arbų aprašas aemja 009 UDK 59 / (07)(00) Jonas Juos, Tatjana Sanausenė
KENGŪRA SENJORAS
 KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS VU MATEMATIKOS IR INFORMATIKOS FAKULTETAS VU MATEMATIKOS IR INFORMATIKOS INSTITUTAS LIETUVOS MATEMATIKŲ DRAUGIJA KENGŪRA 2016. SENJORAS TARPTAUTINIO MATEMATIKOS
KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS VU MATEMATIKOS IR INFORMATIKOS FAKULTETAS VU MATEMATIKOS IR INFORMATIKOS INSTITUTAS LIETUVOS MATEMATIKŲ DRAUGIJA KENGŪRA 2016. SENJORAS TARPTAUTINIO MATEMATIKOS
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
Laboratorinis darbas Nr. 2
 M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
III.Termodinamikos pagrindai
 III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
Papildomo ugdymo mokykla Fizikos olimpas. Mechanika Dinamika 1. (Paskaitų konspektas) 2009 m. sausio d. Prof.
 Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
Cheminės kinetikos kurso KONSPEKTAS
 VILNIUS PEDGOGINIS UNIVERSITETS Gamtos moslų faultetas Chemijos atedra lbertas alinausas Cheminės inetios urso KONSPEKTS etodinė priemonė Vilnius 5 etodinė priemonė buvo aprobuota:. Chemijos atedros posėdyje
VILNIUS PEDGOGINIS UNIVERSITETS Gamtos moslų faultetas Chemijos atedra lbertas alinausas Cheminės inetios urso KONSPEKTS etodinė priemonė Vilnius 5 etodinė priemonė buvo aprobuota:. Chemijos atedros posėdyje
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
EKONOMETRIJA 1 (Regresinė analizė)
 EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė
 Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
 728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
KŪNŲ PUSIAUSVYRA. PAPRASTIEJI MECHANIZMAI. SLĖGIS. KŪNAI SKYSČIUOSE (DUJOSE)
 LIETUVOS IZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ IZIKŲ MOKYKLA OTONAS KŪNŲ PUSIAUSVYRA. PAPRASTIEJI MECHANIZMAI. SLĖGIS. KŪNAI SKYSČIUOSE (DUJOSE) I KURSO I TURO UŽDAVINIŲ SPRENDIMŲ METODINIAI NURODYMAI
LIETUVOS IZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ IZIKŲ MOKYKLA OTONAS KŪNŲ PUSIAUSVYRA. PAPRASTIEJI MECHANIZMAI. SLĖGIS. KŪNAI SKYSČIUOSE (DUJOSE) I KURSO I TURO UŽDAVINIŲ SPRENDIMŲ METODINIAI NURODYMAI
PNEUMATIKA - vožtuvai
 Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Stiklo pluošto laikikliai - gali būti sprendimas langams/durims tvirtinti šiltinimo sluoksnyje
 Stiklo pluošto laikikliai - gali būti sprendimas langams/durims tvirtinti šiltinimo sluoksnyje Lango vieta angoje Reguliuojami stiklo pluošto laikikliai Sukurta mūsų, pagaminta mūsų Geram rezultatui
Stiklo pluošto laikikliai - gali būti sprendimas langams/durims tvirtinti šiltinimo sluoksnyje Lango vieta angoje Reguliuojami stiklo pluošto laikikliai Sukurta mūsų, pagaminta mūsų Geram rezultatui
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 2014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ
 LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
TEORINĖ ELEKTROTECHNIKA
 Zita SAVICKIENĖ TEORINĖ ELEKTROTECHNIKA Prjekt kdas VP1-2.2-ŠMM-07-K-01-047 VGTU Elektrniks fakultet I pakps studijų prgramų esminis atnaujinimas Vilnius Technika 2012 VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS
Zita SAVICKIENĖ TEORINĖ ELEKTROTECHNIKA Prjekt kdas VP1-2.2-ŠMM-07-K-01-047 VGTU Elektrniks fakultet I pakps studijų prgramų esminis atnaujinimas Vilnius Technika 2012 VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS
Vilniaus universitetas Gamtos mokslų fakultetas Kartografijos centras. Giedrė Beconytė. Mokomoji knyga geomokslų specialybių studentams
 Vilniaus universitetas Gamtos mokslų fakultetas Kartografijos centras Giedrė Beconytė DUOMENŲ BAZIŲ PROJEKTAVIMAS Mokomoji knyga geomokslų specialybių studentams Vilnius 2012 Aprobuota VU Gamtos mokslų
Vilniaus universitetas Gamtos mokslų fakultetas Kartografijos centras Giedrė Beconytė DUOMENŲ BAZIŲ PROJEKTAVIMAS Mokomoji knyga geomokslų specialybių studentams Vilnius 2012 Aprobuota VU Gamtos mokslų
M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra. Juozas Navickas FIZIKA. I dalis MOKOMOJI KNYGA
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra Juozas Navickas FIZIKA I dalis MOKOMOJI KNYGA KAUNAS, ARDIVA 8 UDK 53(75.8) Na95 Juozas Navickas FIZIKA, I dalis
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra Juozas Navickas FIZIKA I dalis MOKOMOJI KNYGA KAUNAS, ARDIVA 8 UDK 53(75.8) Na95 Juozas Navickas FIZIKA, I dalis
V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI
 V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI Uždirbtų palūkanų suma priklauso ne tik nuo palūkanų normos dydžio, bet ir nuo palūkanų kapitalizavimo dažnio Metinė palūkanų norma nevisada atspindi
V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI Uždirbtų palūkanų suma priklauso ne tik nuo palūkanų normos dydžio, bet ir nuo palūkanų kapitalizavimo dažnio Metinė palūkanų norma nevisada atspindi
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
4.3. Minimalaus dengiančio medžio radimas
 SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
2014 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija
 PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 04 m. birželio 6 d. Nr. (.)-V-69birželio 4 04 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA I dalis Kiekvieno I dalies klausimo
PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 04 m. birželio 6 d. Nr. (.)-V-69birželio 4 04 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA I dalis Kiekvieno I dalies klausimo
. (2 taškai) (1 taškas) . (2 taškai) . (2) (2 taškai)
 0 m. ietuvos 6-ojo fizikos čempionato UŽDUOČŲ SPRENDMA 0 m. gruodžio 6 d. (Kiekvienas uždavinys vertinamas 0 taškų, visa galimų taškų suma 00). Pervyniojant transformatoriaus ritę buvo pastebėta, kad ritėje
0 m. ietuvos 6-ojo fizikos čempionato UŽDUOČŲ SPRENDMA 0 m. gruodžio 6 d. (Kiekvienas uždavinys vertinamas 0 taškų, visa galimų taškų suma 00). Pervyniojant transformatoriaus ritę buvo pastebėta, kad ritėje
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA. Algoritmų teorija. Paskaitų konspektas
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
Skalbimo mašina Vartotojo vadovas Πλυντήριο Ρούχων Εγχειρίδιο Χρήστη Mosógép Használati útmutató Automatická pračka Používateľská príručka
 WMB 71032 PTM Skalbimo mašina Vartotojo vadovas Πλυντήριο Ρούχων Εγχειρίδιο Χρήστη Mosógép Használati útmutató utomatická pračka Používateľská príručka Dokumentu Nr 2820522945_LT / 06-07-12.(16:34) 1 Svarbūs
WMB 71032 PTM Skalbimo mašina Vartotojo vadovas Πλυντήριο Ρούχων Εγχειρίδιο Χρήστη Mosógép Használati útmutató utomatická pračka Používateľská príručka Dokumentu Nr 2820522945_LT / 06-07-12.(16:34) 1 Svarbūs
Algoritmai. Vytautas Kazakevičius
 Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
10. Lenkimas. 10.1. Bendrosios žinios
 10. Lenkimas 10.1. Bendrosios žinios Lenkimu vadinamas deformavimo tipas, apibūdinamas strpo ašies išsikreivinimu nuo lenkimo momento. Skersinio lenkimo atveu sios ašies išsikreivinimo priežastis ra ir
10. Lenkimas 10.1. Bendrosios žinios Lenkimu vadinamas deformavimo tipas, apibūdinamas strpo ašies išsikreivinimu nuo lenkimo momento. Skersinio lenkimo atveu sios ašies išsikreivinimo priežastis ra ir
Matematinis modeliavimas
 ALGIRDAS AMBRAZEVIƒIUS Matematinis modeliavimas Vilniaus universitetas 2006 2 TURINYS 1 SKYRIUS PAPRASƒIAUSI MATEMATINIAI MODELIAI 4 11 Pagrindines s vokos 4 12 Fundamentaliu gamtos desniu taikymas 10
ALGIRDAS AMBRAZEVIƒIUS Matematinis modeliavimas Vilniaus universitetas 2006 2 TURINYS 1 SKYRIUS PAPRASƒIAUSI MATEMATINIAI MODELIAI 4 11 Pagrindines s vokos 4 12 Fundamentaliu gamtos desniu taikymas 10
1 Įvadas Neišspręstos problemos Dalumas Dalyba su liekana Dalumo požymiai... 3
 Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
II dalis Teisingas atsakymas į kiekvieną II dalies klausimą vertinamas 1 tašku g/mol
 PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 05 m. birželio 8 d. įsakymu Nr. (.3.)-V-73 05 M. CHEMIJOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA. Pagrindinė sesija I dalis Teisingas
PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 05 m. birželio 8 d. įsakymu Nr. (.3.)-V-73 05 M. CHEMIJOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA. Pagrindinė sesija I dalis Teisingas
1. Klasifikavimo su mokytoju metodai
 1. Klasifikavimo su mokytoju metodai Klasifikacijos uždavinys yra atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, garso, asmens, proceso) skaitinius duomenis priskirti ji kokiai nors
1. Klasifikavimo su mokytoju metodai Klasifikacijos uždavinys yra atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, garso, asmens, proceso) skaitinius duomenis priskirti ji kokiai nors
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
Matematinė logika. 1 skyrius Propozicinės formulės. žodį, Graikiškas žodis logos (λóγoς) reiškia
 1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
JONAS DUMČIUS TRUMPA ISTORINĖ GRAIKŲ KALBOS GRAMATIKA
 JONAS DUMČIUS (1905 1986) TRUMPA ISTORINĖ GRAIKŲ KALBOS GRAMATIKA 1975 metais rotaprintu spausdintą vadovėlį surinko klasikinės filologijos III kurso studentai Lina Girdvainytė Aistė Šuliokaitė Kristina
JONAS DUMČIUS (1905 1986) TRUMPA ISTORINĖ GRAIKŲ KALBOS GRAMATIKA 1975 metais rotaprintu spausdintą vadovėlį surinko klasikinės filologijos III kurso studentai Lina Girdvainytė Aistė Šuliokaitė Kristina
PUSLAIDININKINIŲ PRIETAISŲ TYRIMAS
 laboratorinis darbas PSLAIDININKINIŲ PIETAISŲ TIMAS Darbo tikslas susipažinti su puslaidininkinių diodų, stabilitronų ir švietukų struktūra, veikimo principu, ištirti jų charakteristikas. Teorinės žinios
laboratorinis darbas PSLAIDININKINIŲ PIETAISŲ TIMAS Darbo tikslas susipažinti su puslaidininkinių diodų, stabilitronų ir švietukų struktūra, veikimo principu, ištirti jų charakteristikas. Teorinės žinios
Sieninis auksto efektyvumo "Inverter" tipo kondicionierius
 YORK kondicionieriai 2007 KONIONIRII Sieninis "Inverter Mimetic" tipo kondicionierius YVH 09 to 12 from 2.5 to 3.5 kw PINT TH RONT TH OLOR YOU WNT Modelis 09 12 Saldymo galia kw 2.5 (1.0-3.2) 3.5 (1.4-4.6)
YORK kondicionieriai 2007 KONIONIRII Sieninis "Inverter Mimetic" tipo kondicionierius YVH 09 to 12 from 2.5 to 3.5 kw PINT TH RONT TH OLOR YOU WNT Modelis 09 12 Saldymo galia kw 2.5 (1.0-3.2) 3.5 (1.4-4.6)
KLASIKIN E MECHANIKA
 KLASIKIN E MECHANIKA Algirdas MATULIS Puslaidininkiu zikos institutas Vadoveliu serijos papildymas auk²tuju mokyklu tiksliuju mokslu specialybiu studentams Email: amatulis@takas.lt Mob.: +370 654 543 06
KLASIKIN E MECHANIKA Algirdas MATULIS Puslaidininkiu zikos institutas Vadoveliu serijos papildymas auk²tuju mokyklu tiksliuju mokslu specialybiu studentams Email: amatulis@takas.lt Mob.: +370 654 543 06
STOGO ŠILUMINIŲ VARŽŲ IR ŠILUMOS PERDAVIMO KOEFICIENTO SKAIČIAVIMAS
 STOGO ŠILUMINIŲ VAŽŲ I ŠILUMOS PEDAVIMO KOEFICIENTO SKAIČIAVIMAS ST 2.05.02:2008 2 priedas 1. Stogo suminė šiluminė varža s (m 2 K/W) apskaičiuojama pagal formulę [4.6]: s 1 2... n ( g q ); (2.1) čia:
STOGO ŠILUMINIŲ VAŽŲ I ŠILUMOS PEDAVIMO KOEFICIENTO SKAIČIAVIMAS ST 2.05.02:2008 2 priedas 1. Stogo suminė šiluminė varža s (m 2 K/W) apskaičiuojama pagal formulę [4.6]: s 1 2... n ( g q ); (2.1) čia:
IV. FUNKCIJOS RIBA. atvira. intervala. Apibrėžimas Sakysime, kad skaičius b yra funkcijos y = f(x) riba taške x 0, jei bet kokiam,
 41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
Taikomieji optimizavimo metodai
 Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
NEKILNOJAMOJO TURTO VERTINIMAS
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Žemėtvarkos katedra Audrius ALEKNAVIČIUS NEKILNOJAMOJO TURTO VERTINIMAS Metodiniai patarimai Akademija, 2007 UDK 332.6(076) Spausdino UAB Judex, Europos pr. 122, LT-46351
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Žemėtvarkos katedra Audrius ALEKNAVIČIUS NEKILNOJAMOJO TURTO VERTINIMAS Metodiniai patarimai Akademija, 2007 UDK 332.6(076) Spausdino UAB Judex, Europos pr. 122, LT-46351
6. Konstrukcijų patikimumo įvertinimo metodai
 6. Kostrukcijų patikimumo įvertiimo metodai 6.1. Bedrieji kostrukcijų patikimumo įvertiimo pricipai 6.1 tekstas Eksploatuojamoje kostrukcijoje, kaip ir visur gamtoje, vyksta priešybių kova: iš vieos pusės,
6. Kostrukcijų patikimumo įvertiimo metodai 6.1. Bedrieji kostrukcijų patikimumo įvertiimo pricipai 6.1 tekstas Eksploatuojamoje kostrukcijoje, kaip ir visur gamtoje, vyksta priešybių kova: iš vieos pusės,
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
 1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
GEOMETRINĖS OPTIKOS PAGRINDAI
 OPTINĖS SISTEMOS GEOMETRINĖS OPTIKOS PAGRINDAI sites.google.com/site/optinessistemos/ I. ĮVADAS Ženklai geometrinėje optikoje LABAI SVARBU! Fizikinė optika ir geometrinė optika Fizikinė optika - bangų
OPTINĖS SISTEMOS GEOMETRINĖS OPTIKOS PAGRINDAI sites.google.com/site/optinessistemos/ I. ĮVADAS Ženklai geometrinėje optikoje LABAI SVARBU! Fizikinė optika ir geometrinė optika Fizikinė optika - bangų
III. MATRICOS. DETERMINANTAI. 3.1 Matricos A = lentele žymėsime taip:
 III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas. Algirdas Antanavičius. Mokomoji knyga
 Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI Mokomoji knyga Akademija, 2007 Redaktorė: M. Židonienė turinys ĮVADAS... 1. Geodezijos
Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI Mokomoji knyga Akademija, 2007 Redaktorė: M. Židonienė turinys ĮVADAS... 1. Geodezijos
2018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ
 N A C I O N A L I N I S E G Z A M I N Ų C E N T R A S 018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 018 m. birželio 9 d. įvyko matematikos valstybinis brandos egzaminas.
N A C I O N A L I N I S E G Z A M I N Ų C E N T R A S 018 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 018 m. birželio 9 d. įvyko matematikos valstybinis brandos egzaminas.
Patekimo į darbo vietas aukštyje priemonės
 Patekimo į darbo vietas aukštyje priemonės Patekimo į darbo vietas aukštyje priemonės Turinys Pratarmė... 5 I. Fiksuotų priėjimo priemonių tarp dviejų lygių darbo vietų parinkimas... 6 1. Pagrindinės
Patekimo į darbo vietas aukštyje priemonės Patekimo į darbo vietas aukštyje priemonės Turinys Pratarmė... 5 I. Fiksuotų priėjimo priemonių tarp dviejų lygių darbo vietų parinkimas... 6 1. Pagrindinės
