Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
|
|
|
- Ἀδράστεια Νικολάκος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
2 Πολυπλοκότητα Περιεχόμενα 1 Υπολογισιμότητα 2 Αυτόματα και Τυπικές Γλώσσες 3 Πολυπλοκότητα Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
3 I Θεωρία Υπολογισμού: Μας ενδιαφέρει μόνον αν ένα πρόβλημα είναι υπολογίσιμο ή όχι Θεωρία Πολυπλοκότητας: Θεωρούμε μόνο υπολογίσιμα προβλήματα και προσπαθούμε να δούμε αν μπορούν να επιλυθούν με περιορισμούς στους διαθέσιμους υπολογιστικούς πόρους, όπως ο χρόνος υπολογισμού, ο επιπλέον χώρος μνήμης που απαιτείται για ενδιάμεσα αποτελέσματα κατά την επίλυση, και άλλοι Αυτοί οι περιοριμοί, καθώς και άλλα χαρακτηριστικά των υπολογισμών ορίζουν κλάσεις πολυπλοκότητας μέσα στις οποίες τοποθετούμε τα διάφορα προβλήματα Παρά τις συνεχείς και μακροχρόνιες προσπάθειες πολλών επιστημόνων, υπάρχουν αρκετά ανοιχτά ερωτήματα Πχ, υπάρχουν προβλήματα για τα οποία, αν και ανήκουν στο NP, δεν έχει βρεθεί πολυωνυμικός αλγόριθμος, αλλά ούτε απόδειξη ότι είναι NP-complete Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
4 II GRAPH ISOMORPHISM (το πιο γνωστό ανοιχτό πρόβλημα): Δεδομένων δύο γράφων είναι ισομορφικοί; (παράβαλε με το SUBGRAPH ISOMORPHISM το οποίο είναι γνωστό ότι είναι NP-complete) LINEAR PROGRAMMING (παρέμενε για χρόνια ανοιχτό): δεδομένου ενός συστήματος γραμμικών εξισώσεων και ανισοτήτων και μιας γραμμικής αντικειμενικής συνάρτησης (μεγιστοποίηση ή ελαχιστοποίηση) να ευρεθεί μια βέλτιστη εφικτή λύση; Μέθοδος Simplex (Dantzig): Στη χειρότερη περίπτωση χρειαζόταν εκθετικό χρόνο Ελλειψοειδής μέθοδος (Khachiyan): Ο πρώτος πολυωνυμικός αλγόριθμος για τον γραμμικό προγραμματισμό Δεν είχε μεγάλο πρακτικό ενδιαφέρον Αλγόριθμος Karmarkar: Πολυωνυμικός αλγόριθμος που είχε και πρακτικά αποτελέσματα καλύτερα από τη μέθοδο Simplex PRIMALITY: Δίνεται ένας ακέραιος Είναι πρώτος ή όχι; Πρόσφατα (2002 από τους Agrawal, Kayal, Saxena AKS) απεδείχθη και ότι το πρόβλημα αυτό, που παρέμενε για αρκετό καιρό ανοικτό, είναι στο P Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
5 Βασικοί Ορισμοί I Ορισμός Στην κλάση TIME(t(n)) (ή DTIME(t(n))) ανήκουν τα προβλήματα που μπορούν να επιλυθούν από ντετερμινιστική μηχανή Turing σε χρόνο t(n) Ορισμός Στην κλάση NTIME(t(n)) ανήκουν τα προβλήματα που μπορούν να επιλυθούν από μη ντετερμινιστική μηχανή Turing σε χρόνο t(n) Ορισμός Στην κλάση SPACE(s(n)) (ή DSPACE(s(n))) ανήκουν τα προβλήματα που μπορούν να επιλυθούν από ντετερμινιστική μηχανή Turing χρησιμοποιώντας επιπλέον χώρο s(n) Ορισμός Στην κλάση NSPACE(s(n)) ανήκουν τα προβλήματα που μπορούν να επιλυθούν από μη ντετερμινιστική μηχανή Turing χρησιμοποιώντας επιπλέον χώρο s(n) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
6 Βασικοί Ορισμοί II Με βάση τα παραπάνω, ορίζουμε: P = PTIME = Ť iě1 DTIME(ni ) NP = NPTIME = Ť iě1 NTIME(ni ) PSPACE = Ť iě1 DSPACE(ni ) NPSPACE = Ť iě1 NSPACE(ni ) L = DSPACE(log n) NL = NSPACE(log n) EXP = Ť iě1 DTIME(2ni ) EXPSPACE = Ť iě1 DSPACE(2ni ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
7 Βασικοί Ορισμοί III Παρατήρηση Μία συνάρτηση f ονομάζεται συνάρτηση πολυπλοκότητας (constructible) αν υπάρχει μία TM τέτοια input x με x = n, αποδέχεται το input σε χρόνο O(n + f(n)) (time-constructible) ή working space O(f(n)) (space-constructible) Αν η f είναι μία συνάρτηση πολυπλοκότητας τότε ισχύουν: DSPACE(f(n)) Ď NSPACE(f(n)) DTIME(f(n)) Ď NTIME(f(n)) διότι κάθε ντετερμινιστική μηχανή Turing μπορεί να θεωρηθεί ως μη ντετερμινιστική με μία μόνο επιλογή σε κάθε βήμα Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
8 Βασικοί Ορισμοί IV DTIME(f(n)) Ď DSPACE(f(n)) NTIME(f(n)) Ď DSPACE(f(n)) διότι σε χρόνο f(n) δεν μπορεί να εξεταστεί χώρος (αριθμός θέσεων στην ταινία της TM) παραπάνω από f(n) NSPACE(f(n)) Ď DTIME(k log n+f(n) ) Αν f(n) ą log n τότε: DSPACE(f(n)) Ď DTIME(c f(n) ) NTIME(f(n)) Ď DTIME(c f(n) ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
9 Βασικοί Ορισμοί V Το παρακάτω θεώρημα οφείλεται στον Savitch (1970): Θεώρημα Αν f(n) ě log n τότε NSPACE(f(n)) Ď DSPACE(f 2 (n)) Άμεσα από το θεώρημα του Savitch προκύπτει ότι PSPACE = NPSPACE Από τις παραπάνω σχέσεις προκύπτει η εξής ιεραρχία: L Ď NL Ď P Ď NP Ď PSPACE = NPSPACE Γνωρίζουμε ότι L PSPACE και NL PSPACE (αυτό προκύπτει από το θεώρημα ιεραρχίας για χωρικές κλάσεις πολυπλοκότητας, που αναφέρεται παρακάτω) Ανοιχτά παραμένουν τα προβλήματα: L Ě NL Ě P Ě NP Ě PSPACE Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
10 Πολυπλοκότητα Βασικοί Ορισμοί VI Ο κόσμος μοιάζει, ως τώρα, να είναι όπως στο παρακάτω σχήμα L NL P NP PSPACE = NPSPACE Σχήμα: Κλάσεις πολυπλοκότητας Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
11 Βασικοί Ορισμοί VII Επίσης, πρέπει να αναφέρουμε ότι οι παραπάνω κλάσεις πολυπλοκότητας αφορούν προβλήματα απόφασης Μπορούμε επίσης να ορίσουμε κλάσεις πολυπλοκότητας για μηχανές Turing που υπολογίζουν συναρτήσεις Ένα χαρακτηριστικό παράδειγμα είναι η παρακάτω κλάση: Ορισμός FP = το σύνολο των συναρτήσεων που υπολογίζεται από ντετερμινιστική μηχανή Turing σε πολυωνυμικό χρόνο Η κλάση FP θα φανεί χρήσιμη παρακάτω στον ορισμό των αναγωγών, αφού περιλαμβάνει τις εύκολα υπολογιζόμενες συναρτήσεις Μία άλλη επίσης χρήσιμη κλάση πολυπλοκότητας που αφορά συναρτήσεις είναι η εξής: Ορισμός FL = το σύνολο των συναρτήσεων που υπολογίζεται από ντετερμινιστική μηχανή Turing σε λογαριθμικό χώρο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
12 Θεωρήματα ιεραρχίας I Ισχύουν τα παρακάτω θεωρήματα για το μοντέλο της ντετερμινιστικής μηχανής Turing με τρεις ταινίες (θεωρούμε πάντοτε συναρτήσεις πολυπλοκότητας t 1, t 2, s 1, s 2 ): Θεώρημα (Fürer, 1982) Έστω t 2 (n) ą n Τότε υπάρχει γλώσσα που γίνεται αποδεκτή σε χρόνο t 2, αλλά όχι σε χρόνο t 1 για οποιοδήποτε t 1 = o(t 2 (n)) Θεώρημα (Hartmanis, Lewis, Stearns, 1965) Έστω s 2 (n) ą log n Τότε υπάρχει γλώσσα που γίνεται αποδεκτή σε χώρο s 2, αλλά όχι σε χώρο s 1 για οποιοδήποτε s 1 = o(s 2 (n)) Οι τεχνικές αποδείξεις παραλείπονται Παρόμοια θεωρήματα ισχύουν και για μη ντετερμινιστικές μηχανές Turing Οι αποδείξεις μάλιστα είναι πιο εύκολες Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
13 Πολυπλοκότητα Θεωρήματα ιεραρχίας II Οι εμμονή μας σε constructible συναρτήσεις πολυπλοκότητας οφείλεται στο γεγονός ότι αν επιτρέψουμε οποιαδήποτε συνάρτηση στην θέση των t(n), s(n), τότε προκύπτουν διάφορα παθολογικά φαινόμενα, όπως το παρακάτω: Θεώρημα (Gap theorem) Υπάρχει αναδρομική συνάρτηση t(n), τέτοια ώστε TIME(t(n)) = TIME(2 t(n) ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
14 Συμπληρωματικές κλάσεις πολυπλοκότητας I Ορισμός Έστω γλώσσα L Ως γνωστόν, το συμπλήρωμα της γλώσσας συμβολίζεται και ορίζεται ως εξής: L = tx x R Lu Τώρα, για μία κλάση γλωσσών C, ορίζουμε (με την βοήθεια του συμπληρώματος): coc = tl L P Cu Παράδειγμα: η κλάση conp αποτελείται από τις γλώσσες που είναι συμπληρώματα γλωσσών στοnp Ένα πρόβλημα που ανήκει στην κλάση conp είναι το SAT ή το στενά συσχετιζόμενο με αυτό πρόβλημα της ταυτολογίας, αν δηλαδή ένας λογικός τύπος που δίνεται είναι ταυτολογία Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
15 Συμπληρωματικές κλάσεις πολυπλοκότητας II Έχει ενδιαφέρον να δούμε ποιες κλάσεις πολυπλοκότητας είναι κλειστές ως προς συμπλήρωμα, δηλαδή για ποιες κλάσεις C ισχύει C = coc Γενικά, οι ντετερμινιστικές κλάσεις πολυπλοκότητας (είτε χρονικές, είτε χωρικές) είναι κλειστές ως προς συμπλήρωμα, δηλαδή, οι DTIME(t(n)) και DSPACE(s(n)) είναι κλειστές ως προς συμπλήρωμα Αν θεωρήσουμε μη ντετερμινισμό, το πρόβλημα είναι ανοιχτό στην περίπτωση της χρονικής πολυπλοκότητας Για παράδειγμα δεν γνωρίζουμε αν conp NP Μάλιστα, το τελευταίο συνδέεται και με το πρόβλημα αν P NP, αφού προφανώς αν conp NP, τότε P NP Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
16 Συμπληρωματικές κλάσεις πολυπλοκότητας III Θεώρημα (Immerman-Szelepcsényi) Η κλάση NSPACE(s(n)) είναι κλειστή ως προς συμπλήρωμα Για s(n) = n έχουμε την κλάση προβλημάτων που επιλύονται από μηχανή Turing που χρησιμοποιεί γραμμικό χώρο, αλλιώς γνωστό και ως LBA (linearly bounded automaton), οπότε το παραπάνω θεώρημα έλυσε και ένα, για πολλά χρόνια, ανοικτό πρόβλημα, αν δηλαδή η κλάση των LBA (ή ισοδύναμα η κλάση των context sensitive γλωσσών, από ένα αποτέλεσμα του Kuroda, του 1964) είναι κλειστή ως προς συμπλήρωμα Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
17 Αναγωγές I Η έννοια της αναγωγής σε πολυωνυμικό χρόνο πρέπει να συνδέει μεταξύ τους προβλήματα με υπολογιστικά εύκολο τρόπο Θεωρούμε εύκολες συναρτήσεις (και προβλήματα) που υπολογίζονται σε πολυωνυμικό χρόνο Θα θέλαμε: Αν οι συναρτήσεις f και g είναι εύκολες, τότε και η σύνθεσή τους f g είναι εύκολη Αν η f είναι υπολογίσιμη σε χρόνο O(n 2 ), τότε θεωρείται εύκολη Άρα θεωρούμε εύκολα προβλήματα (και συναρτήσεις) αυτά που υπολογίζονται σε πολυωνυμικό χρόνο (έστω και σε O(n 1000 )) Για τους παραπάνω λόγους, ορίζουμε την αναγωγή κατά Karp: Ορισμός (Αναγωγή κατά Karp) A ď P m B: Df P P A ðñ f(x) P B) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
18 Αναγωγές II Υπάρχουν και άλλες χρήσιμες αναγωγές, όπως η λεγόμενη log-space, που χρησιμοποιεί λογαριθμικό χώρο, και η οποία είναι χρήσιμη για αναγωγές προβλημάτων σε μικρότερες κλάσεις πολυπλοκότητας, όπως η P: Ορισμός (Log-space Αναγωγή) A ď L m B: Df P P A ðñ f(x) P B) Ισχύει: A ď L m B ùñ A ď P m B, αλλά όχι το αντίστροφο Μία επιθυμητή ιδιότητα μίας αναγωγής είναι να είναι κλειστή ως προς διάφορες κλάσεις γλωσσών: Ορισμός Λέμε ότι μία κλάση γλωσσών C είναι κλειστή ως προς μία αναγωγή ď αν A ď B ^ B P C ùñ A P C Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
19 Αναγωγές III Μερικές από τις κλάσεις πολυπλοκότητας που είναι κλειστές ως προς την αναγωγή κατά Karp (ď P m) είναι οι εξής: P, PSPACE, EXP, EXPSPACE (βλέπε παραπάνω για τους ορισμούς τους) Ορισμός (Hardness) Λέμε ότι A είναι C-hard (C-δύσκολο), ως προς την ď, P C : B ď A Η έννοια της hardness δίνει ένα κάτω όριο για την πολυπλοκότητα ενός προβλήματος, δεδομένου ότι το πρόβλημα A είναι τουλάχιστον τόσο δύσκολο όσο οποιοδήποτε πρόβλημα μίας κλάσης C Ορισμός (Completeness) Λέμε ότι A είναι C-complete (C-πλήρες), ως προς την ď, αν: A είναι C hard ως προς ď ^ A P C Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
20 Αναγωγές IV Παρακάτω δίνουμε πλήρη προβλήματα για μερικές από τις σημαντικότερες κλάσεις πολυπλοκότητας: NL: το πρόβλημα Reachability (log-space αναγωγές) P: Circuit-Value και Linear Programming (πάλι με log-space αναγωγές) NP: το 3SAT PSPACE: το QBF (Quantified Boolean Formula satisfiability problem) EXP: το n ˆ n Go EXPSPACE: το RegExp(Y,,, 2 ), που είναι το πρόβλημα ελέγχου ισοδυναμίας regular expressions, που χρησιμοποιούν τους τελεστές Y (ένωση), (παράθεση), (άστρο του Kleene) και 2, όπου α 2 = α α Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
21 Παράμετροι για ορισμό κλάσεων πολυπλοκότητας I Concrete Complexity: Θεωρούμε κάποιο συγκεκριμένο μοντέλο υπολογισμού, κάποιο συγκεκριμένο πρόβλημα και κάποιον συγκεκριμένο αλγόριθμο για το πρόβλημα σε αυτό το μοντέλο Έτσι καθορίζουμε την ακριβή πολυπλοκότητα του αλγορίθμου (οι σταθερές φυσικά δεν παίζουν ρόλο) Abstract ή αλλιώς structural complexity: Θεωρούμε κλάσεις πολυπλοκότητας με διάφορες υπολογιστικές παραμέτρους και συγκρίνουμε τις κλάσεις μεταξύ τους (ως προς εγκλεισμό, διαχωρισμό κτλ) Χρήσιμο για τις συγκρίσεις είναι να βρούμε αναγωγές και προβλήματα που είναι πλήρη σε αυτές τις κλάσεις ως προς αυτές τις αναγωγές Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
22 Παράμετροι για ορισμό κλάσεων πολυπλοκότητας II Αναφέρουμε επιγραμματικά μερικές παραμέτρους με τις οποίες ορίζονται κλάσεις πολυπλοκότητας: μοντέλο υπολογισμού: Μηχανή Turing (TM), Random Access Machine (RAM), πεπερασμένο αυτόματο, Linearly Bounded Automaton (LBA), Παράλληλη RAM (PRAM), μονότονα κυκλώματα (monotone circuits) μέθοδος λειτουργίας/αποδοχής: ντετερμινιστική, μη ντετερμινιστική, πιθανοτική, εναλλασσόμενη (alternating), παράλληλη είδος μοντέλου/λειτουργίας: αποφασιστής (decider), αποδέκτης (acceptor), γεννήτρια (generator), μετατροπέας (transducer) αγαθά: αριθμός βημάτων, αριθμός συγκρίσεων, αριθμός πολλαπλασιασμών, χρόνος, χώρος μνήμης, πλήθος επεξεργαστών, αριθμός εναλλαγών στο υπολογιστικό δένδρο, μέγεθος (size) κυκλώματος, βάθος (depth) κυκλώματος άλλα εργαλεία: τυχαιότητα (randomness), μαντεία (oracles), διαλογική αλληλεπίδραση (interactivity), υπόσχεση (promise), τελεστές (operators) φράγματα (bounds) ως προς το μήκος της εισόδου: για παράδειγμα O(n 3 ) ή πολυωνυμικό, time/space (t(n), s(n)) tradeoff (αντιστάθμισμα), Probabilistic Checkable Proofs: PCP(r(n), q(n)) (με χρήση r(n) τυχαίων bits και q(n) queries, ερωτήσεων, στην απόδειξη) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
23 Μοντέλα δένδρων υπολογισμού για TM I Για να μελετήσουμε την συμπεριφορά μηχανών Turing, θα κωδικοποιήσουμε τους υπολογισμούς μίας μηχανής Turing με ένα δέντρο υπολογισμού Ο υπολογισμός ξεκινά στην ρίζα του δένδρου Θεωρούμε ότι αν σε κάποιο σημείο του υπολογισμού έχουμε μία μη ντετερμινιστική επιλογή τότε έχουμε μία διακλάδωση στο δένδρο Στα φύλλα της μηχανής ΤΜ έχουμε τις απαντήσεις της μηχανής Turing Κάθε μονοπάτι από την ρίζα του δένδρου μέχρι κάποιο φύλλο επομένως κωδικοποιεί έναν πιθανό υπολογισμό Χωρίς βλάβη της γενικότητας, υποθέτουμε ότι το δένδρο είναι δυαδικό, πλήρες και γεμάτο όλα τα φύλλα του είναι στο ίδιο επίπεδο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
24 Μοντέλα δένδρων υπολογισμού για TM II yes no yes yes Σχήμα: Μοντέλο δένδρων υπολογισμού Επίσης, έχει ενδιαφέρον το μήκος του υπολογιστικού μονοπατιού από την ρίζα μέχρι το φύλλο να έχει πολυωνυμικό μήκος ως προς το μήκος της εισόδου (να αντιστοιχεί δηλαδή το κάθε μονοπάτι σε κάποιον «εύκολο», δηλαδή πολυωνυμικό, υπολογισμό) Θεωρώντας το παραπάνω μοντέλο, θα ορίσουμε μερικές από τις γνωστές κλάσεις υπολογισμού, καθώς και μερικές καινούριες Πιο συγκεκριμένα, Θα χρησιμοποιήσουμε ποσοδείκτες στα μονοπάτια Επειδή εννοείται πάντοτε ο περιορισμός του μήκους των μονοπατιών, θα γράφουμε πχ Dy, αντί για Dy: y ď p( x ), όπου y: μεταβλητή για τα μονοπάτια, x: μεταβλητή για την είσοδο, p: πολυώνυμο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
25 Μοντέλα δένδρων υπολογισμού για TM III Για παράδειγμα, η κλάση P μπορεί να οριστεί ως εξής: # x P L y) L P P ðñ DR P P: x R L R(x, y) Περισσότερο ενδιαφέρον έχει η κλάση NP που μπορεί να οριστεί ως εξής: # x P L ùñ DyR(x, y) L P NP ðñ DR P P: x R L R(x, y) Δηλαδή, αν x P L υπάρχει τουλάχιστον ένας υπολογισμός που αποδέχεται, ενώ αν x R L κανένας υπολογισμός δεν αποδέχεται Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
26 Μοντέλα δένδρων υπολογισμού για TM IV Παρομοίως, η κλάση conp ορίζεται ως εξής: # x P L y) L P conp ðñ DR P P: x R L ùñ Dy R(x, y) Παρατηρούμε ότι οι ποσοδείκτες που χρησιμοποιούνται και αντιστοιχούν στο «x P L» και στο «x R L» καθορίζουν πλήρως την αντίστοιχη κλάση πολυπλοκότητας Έτσι, εισαγάγουμε τον παρακάτω συμβολισμό: P = NP = conp = (@, D) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
27 Προσεγγιστικοί Αλγόριθμοι I Ένα πρόβλημα βελτιστοποίησης είναι: (I, S, v, goal) I: τα στιγμιότυπα του προβλήματος S: μία συνάρτηση που αντιστοιχίζει σε κάθε στιγμιότυπο τις εφικτές λύσεις v: η αντικειμενική συνάρτηση αντιστοιχίζει σε κάθε εφικτή λύση, έναν θετικό ακέραιο goal: min ή max, για πρόβλημα ελαχιστοποίησης ή μεγιστοποίησης της αντικειμενικής συνάρτησης, αντίστοιχα Η τιμή της αντικειμενικής συνάρτησης για την βέλτιστη λύση με είσοδο x συμβολίζεται με OPT(x) και είναι ίση με goaltv(y) y P S(x)u Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
28 Προσεγγιστικοί Αλγόριθμοι II Επίσης, ορίζουμε για κάθε πρόβλημα βελτιστοποίησης το αντίστοιχο (underlying) πρόβλημα απόφασης ως εξής: Δίδεται επιπλέον της εισόδου x ένα φράγμα k Ερώτηση: είναι OPT(x) ě k; (για πρόβλημα μεγιστοποίησης ανάλογα για πρόβλημα ελαχιστοποίησης) Παράδειγμα Στο πρόβλημα MAX-CLIQUE το στιγμιότυπο είναι ένας γράφος x, οι εφικτές λύσεις είναι όλοι οι πλήρεις υπογράφοι του x (κλίκες), η αντικειμενική συνάρτηση είναι το πλήθος των κόμβων της κλίκας και goal = max Το αντίστοιχο πρόβλημα απόφασης είναι το γνωστό CLIQUE Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
29 Προσεγγιστικοί Αλγόριθμοι III Ορίζουμε τις παρακάτω βασικές κλάσεις πολυπλοκότητας για προβλήματα βελτιστοποίησης: Ορισμός NPO: η κλάση των προβλημάτων βελτιστοποίησης, για τα οποία το αντίστοιχο πρόβλημα απόφασης είναι στο NP (με την προϋπόθεση ότι υπάρχουν εφικτές λύσεις για κάθε στιγμιότυπο) Ορισμός PO: η κλάση των προβλημάτων βελτιστοποίησης, για τα οποία το αντίστοιχο πρόβλημα απόφασης είναι στο P Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
30 Προσεγγιστικοί Αλγόριθμοι IV Πολλά προβλήματα βελτιστοποίησης είναι NP-δύσκολα Για αυτό αναζητούμε προσεγγιστικούς πολυωνυμικούς αλγόριθμους που επιλύουν τέτοια προβλήματα Ορισμός Ένας πολυωνυμικός αλγόριθμος M είναι ρ-προσεγγιστικός για ένα πρόβλημα μεγιστοποίησης αν για κάθε x P I επιστρέφει μια λύση M(x) P S(x) τέτοια ώστε: v(m(x)) OPT(x) ď ρ Αντίστοιχα ορίζεται ρ-προσεγγιστικός αλγόριθμος για πρόβλημα ελαχιστοποίησης Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
31 Προσεγγιστικοί Αλγόριθμοι V Οι πιο γνωστές υποκλάσεις της NPO, εκτός της PO, είναι οι εξής: poly-apx: περιέχει προβλήματα για τα οποία υπάρχει p(n)-προσεγγιστικός αλγόριθμος για κάποιο πολυώνυμο p (όπου n είναι το μήκος της εισόδου: n = x ) log-apx: περιέχει προβλήματα για τα οποία υπάρχει log n-προσεγγιστικός αλγόριθμος (όπου n είναι το μήκος της εισόδου: n = x ) APX: περιέχει προβλήματα για τα οποία υπάρχει ρ-προσεγγιστικός αλγόριθμος για κάποια σταθερά ρ ą 0 PTAS: περιέχει προβλήματα για τα οποία υπάρχει πολυωνυμικού χρόνου προσεγγιστικό σχήμα, δηλαδή (1+ε)-προσεγγιστικός αλγόριθμος για κάθε σταθερά ε ą 0 FPTAS: περιέχει προβλήματα για τα οποία υπάρχει πλήρως πολυωνυμικού χρόνου προσεγγιστικό σχήμα, δηλαδή (1+ε)-προσεγγιστικός αλγόριθμος για κάθε σταθερά ε ą 0, που επιπλέον ο χρόνος που χρειάζεται είναι πολυωνυμικός και ως προς το 1/ε Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
32 Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι VI Σχήμα: Κλάσεις προβλημάτων βελτιστοποίησης Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ & Πολυπλ Απρίλιος / 32
Τυχαιότητα (Randomness) I
 I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
Στοιχεία Θεωρίας Υπολογισμού
 Κεφάλαιο 3 Στοιχεία Θεωρίας Υπολογισμού Στο κεφάλαιο αυτό παρουσιάζεται μια εισαγωγή σε βασικές έννοιες της θεωρίας υπολογισμού, με έμφαση στην υπολογιστική πολυπλοκότητα. Η εξοικείωση με τις έννοιες αυτές
Κεφάλαιο 3 Στοιχεία Θεωρίας Υπολογισμού Στο κεφάλαιο αυτό παρουσιάζεται μια εισαγωγή σε βασικές έννοιες της θεωρίας υπολογισμού, με έμφαση στην υπολογιστική πολυπλοκότητα. Η εξοικείωση με τις έννοιες αυτές
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 14. Χρονική Πολυπλοκότητα 17, 20, 24 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 14. Χρονική Πολυπλοκότητα 17, 20, 24 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Μάιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ &
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Μάιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ &
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Chapter 7, 8 : Time, Space Complexity
 CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 19 December 2008 1 1 Κλάση NP 2 Μη-Ντετερμινιστικές Μηχανές Turing: Eίναι δυνατόν σε μια συνολική κατάσταση να υπάρχουν πολλές δυνατές επόμενες
CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 19 December 2008 1 1 Κλάση NP 2 Μη-Ντετερμινιστικές Μηχανές Turing: Eίναι δυνατόν σε μια συνολική κατάσταση να υπάρχουν πολλές δυνατές επόμενες
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κλάσεις P, NP NP-πληρότητα 15 Απριλίου 2008 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να περιγράψουμε με
Θεωρία Υπολογισμού και Πολυπλοκότητα Κλάσεις P, NP NP-πληρότητα 15 Απριλίου 2008 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να περιγράψουμε με
Chapter 7, 8 : Time, Space Complexity
 CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 12 December 2008 1 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτεμπορούμεναπεριγράψουμεμεένααλγόριθμο μπορεί να
CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 12 December 2008 1 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτεμπορούμεναπεριγράψουμεμεένααλγόριθμο μπορεί να
Μηχανές Turing (T.M) I
 Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Το 10ο πρόβλημα του Hilbert I
 Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Υπολογιστική Πολυπλοκότητα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 18: Χρονική και Χωρική Πολυπλοκότητα
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 18: Χρονική και Χωρική Πολυπλοκότητα Τι θα κάνουμε σήμερα Εισαγωγικά Χρονική Πολυπλοκότητα (7) Κλάση P (7.2) Κλάση ΝΡ (7.3) ΝΡ-πληρότητα (7.4) Χωρική
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 18: Χρονική και Χωρική Πολυπλοκότητα Τι θα κάνουμε σήμερα Εισαγωγικά Χρονική Πολυπλοκότητα (7) Κλάση P (7.2) Κλάση ΝΡ (7.3) ΝΡ-πληρότητα (7.4) Χωρική
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές.
 Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Γιατί κάποια (επιλύσιμα) προβλήματα είναι δύσκολο
Υπολογιστική Πολυπλοκότητα ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Γιατί κάποια (επιλύσιμα) προβλήματα είναι δύσκολο
ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ
 ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ Επιμέλεια : Γεωργίου Κωστής Παρουσίαση στα πλαίσια του μαθήματος: Δίκτυα και πολυπλοκότητα Φεβρουάριος 004 μπλ Κίνητρα για τη μελέτη της μη προσεγγισιμότητας Ο πληρέστερος
ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ Επιμέλεια : Γεωργίου Κωστής Παρουσίαση στα πλαίσια του μαθήματος: Δίκτυα και πολυπλοκότητα Φεβρουάριος 004 μπλ Κίνητρα για τη μελέτη της μη προσεγγισιμότητας Ο πληρέστερος
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα Υπολογιστική πολυπλοκότητα αλγόριθµου Α: Ποσότητα υπολογιστικών πόρων που απαιτεί Α ως αύξουσα συνάρτηση µεγέθους στιγµιότυπου εισόδου. Χρόνος, µνήµη, επεξεργαστές, επικοινωνία,
Υπολογιστική Πολυπλοκότητα Υπολογιστική πολυπλοκότητα αλγόριθµου Α: Ποσότητα υπολογιστικών πόρων που απαιτεί Α ως αύξουσα συνάρτηση µεγέθους στιγµιότυπου εισόδου. Χρόνος, µνήµη, επεξεργαστές, επικοινωνία,
Ασυμπτωτικός Συμβολισμός
 Ασυμπτωτικός Συμβολισμός ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Ασυμπτωτικός Συμβολισμός ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Ασυμπτωτικός Συμβολισμός
 Ασυμπτωτικός Συμβολισμός Επιμέλεια διαφανειών: Δημήτρης Φωτάκης (λίγες προσθήκες: Άρης Παγουρτζής) Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα
Ασυμπτωτικός Συμβολισμός Επιμέλεια διαφανειών: Δημήτρης Φωτάκης (λίγες προσθήκες: Άρης Παγουρτζής) Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα
Κλάσεις Πολυπλοκότητας
 Κλάσεις Πολυπλοκότητας Παύλος Εφραιμίδης pefraimi ee.duth.gr Κλάσεις Πολυπλοκότητας 1 Οι κλάσεις πολυπλοκότητας P και NP P: Polynomial ΗκλάσηP περιλαμβάνει όλα τα υπολογιστικά προβλήματα που μπορούν
Κλάσεις Πολυπλοκότητας Παύλος Εφραιμίδης pefraimi ee.duth.gr Κλάσεις Πολυπλοκότητας 1 Οι κλάσεις πολυπλοκότητας P και NP P: Polynomial ΗκλάσηP περιλαμβάνει όλα τα υπολογιστικά προβλήματα που μπορούν
Σχήματα McCarthy I. Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα:
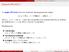 Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
CSC 314: Switching Theory
 CSC 314: Switching Theory Course Summary 9 th January 2009 1 1 Θέματα Μαθήματος Ερωτήσεις Τι είναι αλγόριθμος? Τι μπορεί να υπολογιστεί? Απαντήσεις Μοντέλα Υπολογισμού Δυνατότητες και μη-δυνατότητες 2
CSC 314: Switching Theory Course Summary 9 th January 2009 1 1 Θέματα Μαθήματος Ερωτήσεις Τι είναι αλγόριθμος? Τι μπορεί να υπολογιστεί? Απαντήσεις Μοντέλα Υπολογισμού Δυνατότητες και μη-δυνατότητες 2
Αλγόριθμοι Προσέγγισης για NP-Δύσκολα Προβλήματα
 Αλγόριθμοι Προσέγγισης για NP-Δύσκολα Προβλήματα Διδάσκοντες: E. Ζάχος, Α. Παγουρτζής Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
Αλγόριθμοι Προσέγγισης για NP-Δύσκολα Προβλήματα Διδάσκοντες: E. Ζάχος, Α. Παγουρτζής Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός συγκρίσεων π
 Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Μη επιλυσιμότητα I. Απόδειξη. Ορίζουμε # # =
 Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Διαλογικά Συσ τήματα Αποδείξεων Διαλογικά Συστήματα Αποδείξεων Αντώνης Αντωνόπουλος Κρυπτογραφία & Πολυπλοκότητα 17/2/2012
 Αντώνης Αντωνόπουλος Κρυπτογραφία & Πολυπλοκότητα 17/2/2012 Εισαγωγή Ορισμός Επέκταση του NP συστήματος αποδείξεων εισάγωντας αλληλεπίδραση! Ενα άτομο προσπαθεί να πείσει ένα άλλο για το ότι μία συμβολοσειρά
Αντώνης Αντωνόπουλος Κρυπτογραφία & Πολυπλοκότητα 17/2/2012 Εισαγωγή Ορισμός Επέκταση του NP συστήματος αποδείξεων εισάγωντας αλληλεπίδραση! Ενα άτομο προσπαθεί να πείσει ένα άλλο για το ότι μία συμβολοσειρά
conp and Function Problems
 conp and Function Problems 1 Ένα πρόβλημα απόφασης λέμε ότι επιλύεται σε μηντετερμινιστικό πολυωνυμικό χρόνο αν υπάρχει ένας μηντετερμινιστικός αλγόριθμος που, εκμεταλλευόμενος μια τυχαία επιλογή, μπορεί
conp and Function Problems 1 Ένα πρόβλημα απόφασης λέμε ότι επιλύεται σε μηντετερμινιστικό πολυωνυμικό χρόνο αν υπάρχει ένας μηντετερμινιστικός αλγόριθμος που, εκμεταλλευόμενος μια τυχαία επιλογή, μπορεί
Εισαγωγή στους Αλγόριθμους. Παύλος Εφραιμίδης, Λέκτορας
 Εισαγωγή στους Αλγόριθμους Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr 1 Περιεχόμενα Μαθήματος Εισαγωγή στου Αλγόριθμους Πολυπλοκότητα Αλγορίθμων Ασυμπτωτική Ανάλυση Θεωρία Γράφων Κλάσεις Πολυπλοκότητας
Εισαγωγή στους Αλγόριθμους Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr 1 Περιεχόμενα Μαθήματος Εισαγωγή στου Αλγόριθμους Πολυπλοκότητα Αλγορίθμων Ασυμπτωτική Ανάλυση Θεωρία Γράφων Κλάσεις Πολυπλοκότητας
Ασυμπτωτικός Συμβολισμός
 Ασυμπτωτικός Συμβολισμός ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Υπολογιστική πολυπλοκότητα αλγόριθμου Α: Ποσότητα
Ασυμπτωτικός Συμβολισμός ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Υπολογιστική πολυπλοκότητα αλγόριθμου Α: Ποσότητα
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 13: Παραλλαγές Μηχανών Turing και Περιγραφή Αλγορίθμων
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 13: Παραλλαγές Μηχανών Turing και Περιγραφή Αλγορίθμων Τι θα κάνουμε σήμερα Εισαγωγή Πολυταινιακές Μηχανές Turing (3.2.1) Μη Ντετερμινιστικές Μηχανές
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 13: Παραλλαγές Μηχανών Turing και Περιγραφή Αλγορίθμων Τι θα κάνουμε σήμερα Εισαγωγή Πολυταινιακές Μηχανές Turing (3.2.1) Μη Ντετερμινιστικές Μηχανές
ILP-Feasibility conp
 Διάλεξη 19: 23.12.2014 Θεωρία Γραμμικού Προγραμματισμού Γραφέας: Χαρίλαος Τζόβας Διδάσκων: Σταύρος Κολλιόπουλος 19.1 Θεωρία Πολυπλοκότητας και προβλήματα απόφασης Για να μιλήσουμε για προβλήματα και τον
Διάλεξη 19: 23.12.2014 Θεωρία Γραμμικού Προγραμματισμού Γραφέας: Χαρίλαος Τζόβας Διδάσκων: Σταύρος Κολλιόπουλος 19.1 Θεωρία Πολυπλοκότητας και προβλήματα απόφασης Για να μιλήσουμε για προβλήματα και τον
ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ Φεβρουάριος 2005 Σύνολο μονάδων: 91
 Ε.Μ.Πoλυτεχνείο ΣΗΜΜΥ, ΣΕΜΦΕ Τομέας Τεχνολογίας Πληροφορικής & Υπολογιστών Διδάσκων: Ε.Ζαχος Ονοματεπώνυμο:... Αριθμός Μητρώου:... Σχολή:... εξάμηνο:... ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ Φεβρουάριος 005 Σύνολο
Ε.Μ.Πoλυτεχνείο ΣΗΜΜΥ, ΣΕΜΦΕ Τομέας Τεχνολογίας Πληροφορικής & Υπολογιστών Διδάσκων: Ε.Ζαχος Ονοματεπώνυμο:... Αριθμός Μητρώου:... Σχολή:... εξάμηνο:... ΑΛΓΟΡΙΘΜΟΙ ΚΑΙ ΠΟΛΥΠΛΟΚΟΤΗΤΑ Φεβρουάριος 005 Σύνολο
Τεχνικές Αποδείξεις Κάτω Φραγμάτων
 Τεχνικές Αποδείξεις Κάτω Φραγμάτων Θέλουμε να δείξουμε κυκλωματικά κάτω φράγματα για ομοιόμορφες κλάσεις επειδή: Δίνουν μεγάλη πληροφορία για τις κλάσεις αυτές: π.χ. αν EXP P /poly σημαίνει Ότι παρότι
Τεχνικές Αποδείξεις Κάτω Φραγμάτων Θέλουμε να δείξουμε κυκλωματικά κάτω φράγματα για ομοιόμορφες κλάσεις επειδή: Δίνουν μεγάλη πληροφορία για τις κλάσεις αυτές: π.χ. αν EXP P /poly σημαίνει Ότι παρότι
Πολυπλοκότητα. Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης. Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης. Προσπάθεια υλοποίησης
 Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης Προσπάθεια υλοποίησης Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι
Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης Προσπάθεια υλοποίησης Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι
Κεφάλαιο 8. NP και Υπολογιστική Δυσεπιλυσιμότητα. Παύλος Εφραιμίδης V1.1,
 Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Παύλος Εφραιμίδης V1.1, 2015-01-19 Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα
Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Παύλος Εφραιμίδης V1.1, 2015-01-19 Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Ανάλυση Αλγορίθμων Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ανάλυση Αλγορίθμων Η ανάλυση αλγορίθμων περιλαμβάνει τη διερεύνηση του τρόπου
Αλγόριθμοι και Πολυπλοκότητα Ανάλυση Αλγορίθμων Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ανάλυση Αλγορίθμων Η ανάλυση αλγορίθμων περιλαμβάνει τη διερεύνηση του τρόπου
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Προσεγγιστικοί Αλγόριθμοι
 Κεφάλαιο 12 Προσεγγιστικοί Αλγόριθμοι 12.1 Προβλήματα Βελτιστοποίησης Σε ένα πρόβλημα βελτιστοποίησης σε κάθε στιγμιότυπο του προβλήματος αντιστοιχούν κάποιες εφικτές (feasible) -δηλαδή επιτρεπτές- λύσεις,
Κεφάλαιο 12 Προσεγγιστικοί Αλγόριθμοι 12.1 Προβλήματα Βελτιστοποίησης Σε ένα πρόβλημα βελτιστοποίησης σε κάθε στιγμιότυπο του προβλήματος αντιστοιχούν κάποιες εφικτές (feasible) -δηλαδή επιτρεπτές- λύσεις,
Θεωρήµατα Ιεραρχίας Ειδικά Θέµατα Υπολογισµού και Πολυπλοκότητας, Μάθηµα Βασικής Επιλογής Εαρινού Εξαµήνου Τοµέας Εφαρµογών και Θεµελιώσεων
 Θεωρήµατα Ιεραρχίας Ειδικά Θέµατα Υπολογισµού και Πολυπλοκότητας, Μάθηµα Βασικής Επιλογής Εαρινού Εξαµήνου Τοµέας Εφαρµογών και Θεµελιώσεων Απόστολος Φίλιππας Τµήµα Μηχανικών Η/Υ και Πληροφορικής 19 Μαΐου,
Θεωρήµατα Ιεραρχίας Ειδικά Θέµατα Υπολογισµού και Πολυπλοκότητας, Μάθηµα Βασικής Επιλογής Εαρινού Εξαµήνου Τοµέας Εφαρµογών και Θεµελιώσεων Απόστολος Φίλιππας Τµήµα Μηχανικών Η/Υ και Πληροφορικής 19 Μαΐου,
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 1η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 1η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Επιχειρησιακή Έρευνα Θεωρητική Θεμελίωση της Μεθόδου Simplex
 Επιχειρησιακή Έρευνα Θεωρητική Θεμελίωση της Μεθόδου Simplex Νίκος Τσάντας ιατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών Τμήμ. Μαθηματικών Μαθηματικά των Υπολογιστών και των Αποφάσεων Ακαδημαϊκό έτος 2006-07
Επιχειρησιακή Έρευνα Θεωρητική Θεμελίωση της Μεθόδου Simplex Νίκος Τσάντας ιατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών Τμήμ. Μαθηματικών Μαθηματικά των Υπολογιστών και των Αποφάσεων Ακαδημαϊκό έτος 2006-07
Όρια Αλγόριθμων Ταξινόμησης. Εισαγωγή στην Ανάλυση Αλγορίθμων Μάγια Σατρατζέμη
 Όρια Αλγόριθμων Ταξινόμησης Εισαγωγή στην Ανάλυση Αλγορίθμων Μάγια Σατρατζέμη Όρια Αλγόριθμων Ταξινόμησης Μέχρι στιγμής εξετάσθηκαν μέθοδοι ταξινόμησης µε πολυπλοκότητα της τάξης Θ ) ή Θlog ). Τι εκφράζει
Όρια Αλγόριθμων Ταξινόμησης Εισαγωγή στην Ανάλυση Αλγορίθμων Μάγια Σατρατζέμη Όρια Αλγόριθμων Ταξινόμησης Μέχρι στιγμής εξετάσθηκαν μέθοδοι ταξινόμησης µε πολυπλοκότητα της τάξης Θ ) ή Θlog ). Τι εκφράζει
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Ιούνιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Ιούνιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 3: Ασυμπτωτικός συμβολισμός Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 3: Ασυμπτωτικός συμβολισμός Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος στη δεύτερη έκδοση
 Πρόλογος του επιµελητή xiii Πρόλογος στην πρώτη έκδοση xv Προς τους ϕοιτητές.......................... xv Προς τους διδάσκοντες........................ xvii Ηπρώτηέκδοση........................... xviii
Πρόλογος του επιµελητή xiii Πρόλογος στην πρώτη έκδοση xv Προς τους ϕοιτητές.......................... xv Προς τους διδάσκοντες........................ xvii Ηπρώτηέκδοση........................... xviii
ΣΧΕΣΕΙΣ ΜΕΤΑΞΥ ΚΛΑΣΕΩΝ ΠΟΛΥΠΛΟΚΟΤΗΤΑΣ
 ΣΧΕΣΕΙΣ ΜΕΤΑΞΥ ΚΛΑΣΕΩΝ ΠΟΛΥΠΛΟΚΟΤΗΤΑΣ Κλάσεις Πολυπλοκότητας Περιλαµβάνουν αναδροµικές γλώσσες Οι γλώσσες ταξινοµούνται στις κλάσεις πολυπλοκότητας ανάλογα µε τη δυσκολία απόφασης τους (ποσότητα απαιτούµενων
ΣΧΕΣΕΙΣ ΜΕΤΑΞΥ ΚΛΑΣΕΩΝ ΠΟΛΥΠΛΟΚΟΤΗΤΑΣ Κλάσεις Πολυπλοκότητας Περιλαµβάνουν αναδροµικές γλώσσες Οι γλώσσες ταξινοµούνται στις κλάσεις πολυπλοκότητας ανάλογα µε τη δυσκολία απόφασης τους (ποσότητα απαιτούµενων
ΚΕΦΑΛΑΙΟ 12: Θεωρία υπολογισµών
 ΚΕΦΑΛΑΙΟ 12: Θεωρία υπολογισµών 1 Συναρτήσεις και ο υπολογισµός τους 2 Μηχανές Turing 3 Καθολικές γλώσσες προγραµµατισµού 4 Μια µη υπολογίσιµη συνάρτηση 5 Πολυπλοκότητα προβληµάτων 1 Συναρτήσεις Μία συνάρτηση
ΚΕΦΑΛΑΙΟ 12: Θεωρία υπολογισµών 1 Συναρτήσεις και ο υπολογισµός τους 2 Μηχανές Turing 3 Καθολικές γλώσσες προγραµµατισµού 4 Μια µη υπολογίσιµη συνάρτηση 5 Πολυπλοκότητα προβληµάτων 1 Συναρτήσεις Μία συνάρτηση
Παραλλαγές και επεκτάσεις αυτομάτων I
 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως
Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνο ΣHMΜY
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνο ΣHMΜY 2η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνο ΣHMΜY 2η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Προσεγγιστικοί Αλγόριθμοι
 Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
NP-πληρότητα. Λεωνίδας Παληός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων
 NP-πληρότητα Λεωνίδας Παληός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων Πολυωνυμικός μετασχηματισμός Ένας πολυωνυμικός μετασχηματισμός από την L 1 Σ 1 * στην L 2 Σ 2 * είναι μια συνάρτηση
NP-πληρότητα Λεωνίδας Παληός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων Πολυωνυμικός μετασχηματισμός Ένας πολυωνυμικός μετασχηματισμός από την L 1 Σ 1 * στην L 2 Σ 2 * είναι μια συνάρτηση
Κεφάλαιο 5 Ανάλυση Αλγορίθμων
 Κεφάλαιο 5 Ανάλυση Αλγορίθμων 5.1 Επίδοση αλγορίθμων Τα πρωταρχικά ερωτήματα που προκύπτουν είναι: 1. πώς υπολογίζεται ο χρόνος εκτέλεσης ενός αλγορίθμου; 2. πώς μπορούν να συγκριθούν μεταξύ τους οι διάφοροι
Κεφάλαιο 5 Ανάλυση Αλγορίθμων 5.1 Επίδοση αλγορίθμων Τα πρωταρχικά ερωτήματα που προκύπτουν είναι: 1. πώς υπολογίζεται ο χρόνος εκτέλεσης ενός αλγορίθμου; 2. πώς μπορούν να συγκριθούν μεταξύ τους οι διάφοροι
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Μη Ντετερμινισμός και NP-Πληρότητα
 Μη Ντετερμινισμός και NP-Πληρότητα Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μη Ντετερμινιστικές Μηχανές Turing Μη ντετερμινιστική
Μη Ντετερμινισμός και NP-Πληρότητα Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μη Ντετερμινιστικές Μηχανές Turing Μη ντετερμινιστική
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { G,k η G είναι μια ασυμφραστική γραμματική η οποία παράγει κάποια λέξη 1 n όπου n k } (β) { Μ,k η Μ είναι
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { G,k η G είναι μια ασυμφραστική γραμματική η οποία παράγει κάποια λέξη 1 n όπου n k } (β) { Μ,k η Μ είναι
Εφαρμοσμένη Κρυπτογραφία Ι
 Εφαρμοσμένη Κρυπτογραφία Ι Κωνσταντίνου Ελισάβετ ekonstantinou@aegean.gr http://www.icsd.aegean.gr/ekonstantinou Η συνάρτηση φ(.) του Euler Για κάθε ακέραιο n > 0, έστω φ(n) το πλήθος των ακεραίων στο
Εφαρμοσμένη Κρυπτογραφία Ι Κωνσταντίνου Ελισάβετ ekonstantinou@aegean.gr http://www.icsd.aegean.gr/ekonstantinou Η συνάρτηση φ(.) του Euler Για κάθε ακέραιο n > 0, έστω φ(n) το πλήθος των ακεραίων στο
Προσεγγιστικοί Αλγόριθμοι
 Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
Λύσεις 4ης Σειράς Ασκήσεων
 Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 3η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 3η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
για NP-Δύσκολα Προβλήματα
 Προσεγγιστικοί Αλγόριθμοι για NP-Δύσκολα Προβλήματα Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Προσεγγιστικοί Αλγόριθμοι για NP-Δύσκολα Προβλήματα Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Υπολογιστικό Πρόβληµα
 Υπολογιστικό Πρόβληµα Μετασχηµατισµός δεδοµένων εισόδου σε δεδοµένα εξόδου. Δοµή δεδοµένων εισόδου (έγκυρο στιγµιότυπο). Δοµή και ιδιότητες δεδοµένων εξόδου (απάντηση ή λύση). Τυπικά: διµελής σχέση στις
Υπολογιστικό Πρόβληµα Μετασχηµατισµός δεδοµένων εισόδου σε δεδοµένα εξόδου. Δοµή δεδοµένων εισόδου (έγκυρο στιγµιότυπο). Δοµή και ιδιότητες δεδοµένων εξόδου (απάντηση ή λύση). Τυπικά: διµελής σχέση στις
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών 6
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Ασυμπτωτικός Συμβολισμός
 Ασυμπτωτικός Συμβολισμός ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Υπολογιστική
Ασυμπτωτικός Συμβολισμός ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Υπολογιστική
Κεφάλαιο 8. NP και Υπολογιστική Δυσεπιλυσιμότητα. Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα αναζήτησης είναι ένα πρόβλημα στο
Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιμότητα Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβλημα αναζήτησης (search problem) Ένα πρόβλημα αναζήτησης είναι ένα πρόβλημα στο
Εισαγωγή στους Αλγόριθµους. Αλγόριθµοι. Ιστορικά Στοιχεία. Ο πρώτος Αλγόριθµος. Παραδείγµατα Αλγορίθµων. Τι είναι Αλγόριθµος
 Εισαγωγή στους Αλγόριθµους Αλγόριθµοι Τι είναι αλγόριθµος; Τι µπορεί να υπολογίσει ένας αλγόριθµος; Πως αξιολογείται ένας αλγόριθµος; Παύλος Εφραιµίδης pefraimi@ee.duth.gr Αλγόριθµοι Εισαγωγικές Έννοιες
Εισαγωγή στους Αλγόριθµους Αλγόριθµοι Τι είναι αλγόριθµος; Τι µπορεί να υπολογίσει ένας αλγόριθµος; Πως αξιολογείται ένας αλγόριθµος; Παύλος Εφραιµίδης pefraimi@ee.duth.gr Αλγόριθµοι Εισαγωγικές Έννοιες
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { D το D είναι ένα DFA το οποίο αποδέχεται όλες τις λέξεις στο Σ * } (α) Για να διαγνώσουμε το πρόβλημα μπορούμε
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { D το D είναι ένα DFA το οποίο αποδέχεται όλες τις λέξεις στο Σ * } (α) Για να διαγνώσουμε το πρόβλημα μπορούμε
Εισαγωγικές Έννοιες. ημήτρης Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών. Εθνικό Μετσόβιο Πολυτεχνείο
 Εισαγωγικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εισαγωγικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς όρους όλες οι μεταβλητές είναι μη αρνητικές
 Ένα τυχαίο π.γ.π. maximize/minimize z=c x Αx = b x 0 Τυπική μορφή του π.γ.π. maximize z=c x Αx = b x 0 b 0 είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς
Ένα τυχαίο π.γ.π. maximize/minimize z=c x Αx = b x 0 Τυπική μορφή του π.γ.π. maximize z=c x Αx = b x 0 b 0 είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς
Κεφάλαιο 8. NP και Υπολογιστική Δυσεπιλυσιµότητα. Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιµότητα Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβληµα αναζήτησης (search problem) Ένα πρόβληµα αναζήτησης είναι ένα πρόβληµα στο
Κεφάλαιο 8 NP και Υπολογιστική Δυσεπιλυσιµότητα Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 πρόβληµα αναζήτησης (search problem) Ένα πρόβληµα αναζήτησης είναι ένα πρόβληµα στο
ΑΚΕΡΑΙΟΣ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΑΚΕΡΑΙΟΣ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ολοκληρωμένη μαθηματική τεχνική βελτιστοποίησης Ευρύτατο φάσμα εφαρμογών Εισαγωγή ακέραιων/λογικών/βοηθητικών μεταβλητών Δυνατότητα γραμμικοποίησης με 0-1 μεταβλητές
ΑΚΕΡΑΙΟΣ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ολοκληρωμένη μαθηματική τεχνική βελτιστοποίησης Ευρύτατο φάσμα εφαρμογών Εισαγωγή ακέραιων/λογικών/βοηθητικών μεταβλητών Δυνατότητα γραμμικοποίησης με 0-1 μεταβλητές
t M (w) T ( w ) O( n) = O(n 2 )
 Κεφάλαιο 9 Υπολογιστική Πολυπλοκότητα Σύνοψη Πέρα από το ερώτημα του αν για ένα πρόβλημα υπάρχει Μηχανή Turing, που το επιλύει, μας απασχολεί επίσης και το ερώτημα του αν ένα πρόβλημα είναι «πρακτικά»
Κεφάλαιο 9 Υπολογιστική Πολυπλοκότητα Σύνοψη Πέρα από το ερώτημα του αν για ένα πρόβλημα υπάρχει Μηχανή Turing, που το επιλύει, μας απασχολεί επίσης και το ερώτημα του αν ένα πρόβλημα είναι «πρακτικά»
Κυκλώματα και βασικές Ιδιότητες
 Κυκλώματα και βασικές Ιδιότητες Κύκλωμα C Κατευθυνόμενος ακυκλικός γράφος με n πηγές (κάθε μία αντιστοιχεί σε ένα bit εισόδου) και μία καταβόθρα (το bit εξόδου). Οι ενδιάμεσοι κόμβοι αντιστοιχούν σε κάποια
Κυκλώματα και βασικές Ιδιότητες Κύκλωμα C Κατευθυνόμενος ακυκλικός γράφος με n πηγές (κάθε μία αντιστοιχεί σε ένα bit εισόδου) και μία καταβόθρα (το bit εξόδου). Οι ενδιάμεσοι κόμβοι αντιστοιχούν σε κάποια
Προσεγγιστικοί Αλγόριθμοι για NP- ύσκολα Προβλήματα
 Προσεγγιστικοί Αλγόριθμοι για NP- ύσκολα Προβλήματα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια
Προσεγγιστικοί Αλγόριθμοι για NP- ύσκολα Προβλήματα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 3ο μέρος σημειώσεων: Μέθοδος της Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 3ο μέρος σημειώσεων: Μέθοδος της Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 7β: Όρια Αλγόριθμων Ταξινόμησης Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos.
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 7β: Όρια Αλγόριθμων Ταξινόμησης Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos.
Εισαγωγή στην Ανάλυση Αλγορίθμων (2-3)
 Εισαγωγή στην Ανάλυση Αλγορίθμων (2-3) 3.1 Ασυμπτωτικός συμβολισμός (Ι) Οι ορισμοί που ακολουθούν μας επιτρέπουν να επιχειρηματολογούμε με ακρίβεια για την ασυμπτωτική συμπεριφορά. Οι f(n) και g(n) συμβολίζουν
Εισαγωγή στην Ανάλυση Αλγορίθμων (2-3) 3.1 Ασυμπτωτικός συμβολισμός (Ι) Οι ορισμοί που ακολουθούν μας επιτρέπουν να επιχειρηματολογούμε με ακρίβεια για την ασυμπτωτική συμπεριφορά. Οι f(n) και g(n) συμβολίζουν
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Υπολογίσιμες Συναρτήσεις
 Υπολογίσιμες Συναρτήσεις Σ Π Υ Ρ Ι Δ Ω Ν Τ Ζ Ι Μ Α Σ Δ Τ Ο Μ Ε Α Σ Τ Μ Η Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Σ Χ Ο Λ Η Θ Ε Τ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Ι Ω Α Ν Ν Ι Ν Ω Ν Υπολογίσιμες Συναρτήσεις
Υπολογίσιμες Συναρτήσεις Σ Π Υ Ρ Ι Δ Ω Ν Τ Ζ Ι Μ Α Σ Δ Τ Ο Μ Ε Α Σ Τ Μ Η Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Σ Χ Ο Λ Η Θ Ε Τ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Ι Ω Α Ν Ν Ι Ν Ω Ν Υπολογίσιμες Συναρτήσεις
Προηγμένα Θέματα Αλγορίθμων (ΣΗΜΜΥ ΕΜΠ) Αλγόριθμοι Δικτύων και Πολυπλοκότητα (ΕΜΠ - ΑΛΜΑ) Προσεγγιστικοί Αλγόριθμοι.
 Προηγμένα Θέματα Αλγορίθμων (ΣΗΜΜΥ ΕΜΠ) Αλγόριθμοι Δικτύων και Πολυπλοκότητα (ΕΜΠ - ΑΛΜΑ) Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άνοιξη 2018 Προσεγγιστικοί Αλγόριθμοι Αφορούν κυρίως σε προβλήματα βελτιστοποίησης:
Προηγμένα Θέματα Αλγορίθμων (ΣΗΜΜΥ ΕΜΠ) Αλγόριθμοι Δικτύων και Πολυπλοκότητα (ΕΜΠ - ΑΛΜΑ) Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άνοιξη 2018 Προσεγγιστικοί Αλγόριθμοι Αφορούν κυρίως σε προβλήματα βελτιστοποίησης:
Αναδρομικές Συναρτήσεις και Σχέσεις I
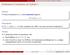 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Ορισµός. Εστω συναρτήσεις: f : N R και g : N R. η f(n) είναι fi( g(n) ) αν υπάρχουν σταθερές C 1, C 2 και n 0, τέτοιες ώστε:
 Συµβολισµός Ω( ) Τάξη των Συναρτήσεων () Εκτίµηση Πολυπλοκότητας Αλγορίθµων Ορέστης Τελέλης telelis@unipi.gr Ορισµός. Εστω συναρτήσεις: f : N R και g : N R η f(n) είναι Ω( g(n) ) αν υπάρχουν σταθερές C
Συµβολισµός Ω( ) Τάξη των Συναρτήσεων () Εκτίµηση Πολυπλοκότητας Αλγορίθµων Ορέστης Τελέλης telelis@unipi.gr Ορισµός. Εστω συναρτήσεις: f : N R και g : N R η f(n) είναι Ω( g(n) ) αν υπάρχουν σταθερές C
Chapter 9: NP-Complete Problems
 Θεωρητική Πληροφορική Ι: Αλγόριθμοι και Πολυπλοκότητα Chapter 9: NP-Complete Problems 9.3 Graph-Theoretic Problems (Συνέχεια) 9.4 Sets and Numbers Γιώργος Αλεξανδρίδης gealexan@mail.ntua.gr Κεφάλαιο 9:
Θεωρητική Πληροφορική Ι: Αλγόριθμοι και Πολυπλοκότητα Chapter 9: NP-Complete Problems 9.3 Graph-Theoretic Problems (Συνέχεια) 9.4 Sets and Numbers Γιώργος Αλεξανδρίδης gealexan@mail.ntua.gr Κεφάλαιο 9:
ΑΛΓΟΡΙΘΜΟΙ. Ενότητα 11: Περιορισμοί της Αλγοριθμικής Ισχύος
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 11: Περιορισμοί της Αλγοριθμικής Ισχύος Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 11: Περιορισμοί της Αλγοριθμικής Ισχύος Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες
Εφαρμοσμένη Κρυπτογραφία Ι
 Εφαρμοσμένη Κρυπτογραφία Ι Κωνσταντίνου Ελισάβετ ekonstantinou@aegean.gr http://www.icsd.aegean.gr/ekonstantinou Ησυνάρτησηφ(.) του Euler Για κάθε ακέραιο n> 0, έστω φ(n) το πλήθος των ακεραίων στο διάστημα
Εφαρμοσμένη Κρυπτογραφία Ι Κωνσταντίνου Ελισάβετ ekonstantinou@aegean.gr http://www.icsd.aegean.gr/ekonstantinou Ησυνάρτησηφ(.) του Euler Για κάθε ακέραιο n> 0, έστω φ(n) το πλήθος των ακεραίων στο διάστημα
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα 7ο εξάμηνο ΣHMΜY Εισαγωγή Διδάσκοντες: Άρης Παγουρτζής, Δώρα Σούλιου Στάθης Ζάχος, Δημήτρης Σακαβάλας Επιμέλεια διαφανειών: Άρης Παγουρτζής www.corelab.ntua.gr/courses/algorithms
Αλγόριθμοι και Πολυπλοκότητα 7ο εξάμηνο ΣHMΜY Εισαγωγή Διδάσκοντες: Άρης Παγουρτζής, Δώρα Σούλιου Στάθης Ζάχος, Δημήτρης Σακαβάλας Επιμέλεια διαφανειών: Άρης Παγουρτζής www.corelab.ntua.gr/courses/algorithms
Θεωρία Υπολογισμού και Πολυπλοκότητα Αναγωγές
 Θεωρία Υπολογισμού και Πολυπλοκότητα Αναγωγές Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Ανεπίλυτα Προβλήματα από τη Θεωρία Γλωσσών (5.1) To Πρόβλημα της Περάτωσης Το Πρόβλημα της Κενότητα
Θεωρία Υπολογισμού και Πολυπλοκότητα Αναγωγές Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Ανεπίλυτα Προβλήματα από τη Θεωρία Γλωσσών (5.1) To Πρόβλημα της Περάτωσης Το Πρόβλημα της Κενότητα
8. Πολλαπλές μερικές παράγωγοι
 94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό ) είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό ) είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνο ΣΕΜΦΕ
 Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνο ΣΕΜΦΕ 2η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνο ΣΕΜΦΕ 2η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
8. Πολλαπλές μερικές παράγωγοι
 94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών. Προδιαγραφές
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσ.h.m.μ.y. & Σ.Ε.Μ.Φ.Ε. http://www.corelab.ece.ntua.gr/courses/ 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές Στάθης Ζάχος Συνεργασία: Κωστής Σαγώνας Επιμέλεια:
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσ.h.m.μ.y. & Σ.Ε.Μ.Φ.Ε. http://www.corelab.ece.ntua.gr/courses/ 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές Στάθης Ζάχος Συνεργασία: Κωστής Σαγώνας Επιμέλεια:
Αλγόριθμοι Ταξινόμησης Μέρος 4
 Αλγόριθμοι Ταξινόμησης Μέρος 4 Μανόλης Κουμπαράκης Δομές Δεδομένων και Τεχνικές 1 Μέθοδοι Ταξινόμησης Βασισμένοι σε Συγκρίσεις Κλειδιών Οι αλγόριθμοι ταξινόμησης που είδαμε μέχρι τώρα αποφασίζουν πώς να
Αλγόριθμοι Ταξινόμησης Μέρος 4 Μανόλης Κουμπαράκης Δομές Δεδομένων και Τεχνικές 1 Μέθοδοι Ταξινόμησης Βασισμένοι σε Συγκρίσεις Κλειδιών Οι αλγόριθμοι ταξινόμησης που είδαμε μέχρι τώρα αποφασίζουν πώς να
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Επανάληψη Μαθήματος
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Επανάληψη Μαθήματος Το Μάθημα σε μια Διαφάνεια Υπολογιστικά μοντέλα Κανονικές Γλώσσες Ντετερμινιστικά Αυτόματα Μη Ντετερμινιστικά Αυτόματα Κανονικές Εκφράσεις
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Επανάληψη Μαθήματος Το Μάθημα σε μια Διαφάνεια Υπολογιστικά μοντέλα Κανονικές Γλώσσες Ντετερμινιστικά Αυτόματα Μη Ντετερμινιστικά Αυτόματα Κανονικές Εκφράσεις
Το πρόβλημα μονοδρόμησης (The One-Way Street Problem)
 Το πρόβλημα μονοδρόμησης (The One-Way Street Problem) Το πρόβλημα Σχετίζεται με τη διαχείριση της κίνησης οχημάτων στους δρόμους Αν δεν υπήρχαν καθυστερήσεις στην κίνηση στις πόλεις Αποφυγή σπατάλης ενέργειας
Το πρόβλημα μονοδρόμησης (The One-Way Street Problem) Το πρόβλημα Σχετίζεται με τη διαχείριση της κίνησης οχημάτων στους δρόμους Αν δεν υπήρχαν καθυστερήσεις στην κίνηση στις πόλεις Αποφυγή σπατάλης ενέργειας
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Επίπεδα Γραφήματα : Προβλήματα και Υπολογιστική Πολυπλοκότητα
 Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
