ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΚΑΙ ΚΙΝΗΣΗ ΣΤΟ ΑΝΘΡΩΠΙΝΟ ΣΩΜΑ
|
|
|
- ÏΚάϊν Δουρέντης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΚΑΙ ΚΙΝΗΣΗ ΣΤΟ ΑΝΘΡΩΠΙΝΟ ΣΩΜΑ Οι Μοχλοί είναι ένα παράδειγμα συστήματος παράλληλων δυνάμεων και συναντώνται πολύ συχνά στο ανθρώπινο σώμα. Ο μοχλός είναι μια στερεή δοκός η οποία μπορεί να στρέφεται γύρω από ένα σταθερό σημείο ή άξονα. Σ ένα μοχλό υπάρχουν : 1. Ο άξονας ή υπομόχλιο (Fulcrum) που στο ανθρώπινο σώμα είναι συνήθως ο άξονας μιας άρθρωσης. 2.Η αντίσταση ή βάρος (Resistance) που μπορεί να είναι το βάρος ενός τμήματος ενός οστού ή μια εξωτερικά εφαρμοζόμενη δύναμη ή βάρος, η οποία αντιτίθεται στην κίνηση. 3.Η δύναμη ή προσπάθεια (Effort) η οποία κινεί ή στηρίζει και στο ανθρώπινο σώμα συνήθως προέρχεται από τη συστολή ενός μυ που συμβάλλει έτσι στην ισορροπία ή στην πρόκληση κίνησης. Το σημείο εφαρμογής της δύναμης είναι συχνά το σημείο κατάφυσης του μυός. Υπάρχουν τρία είδη μοχλών. ΜΟΧΛΟΣ Α ΕΙΔΟΥΣ Το υπομόχλιο βρίσκεται μεταξύ της δύναμης και της αντίστασης (φορτίο). Με αυτό το είδος μοχλού μπορούμε να επιτύχουμε είτε κέρδος σε δύναμη είτε κέρδος σε ταχύτητα.μεγαλύτερη δύναμη επιτυγχάνεται, όταν ο άξονας περιστροφής βρίσκεται πλησιέστερα προς την δύναμη αντίστασης αντίθετα μεγαλύτερη ταχύτητα επιτυγχάνουμε όταν ο άξονας περιστροφής βρίσκεται πλησιέστερα στη δύναμη. Παράδειγμα μοχλού Α είδους (Εικόνα 1α) είναι η τραμπάλα όπου το βαρύτερο παιδί κάθεται πλησιέστερα στον άξονα περιστροφής, με αποτέλεσμα μικρότερη δύναμη να αντισταθμίζει μεγαλύτερο βάρος (φορτίο).άλλα παραδείγματα είναι το πόμολο και το ψαλίδι (Εικόνα 1β). (Εικόνα 1α) (Εικόνα 1β) Στο ανθρώπινο σώμα παραδείγματα μοχλού Α Είδους είναι η στήριξη της κεφαλής όπου ρόλο υπομόχλιου παίζει η ατλαντοινιακή άρθρωση, δύναμη ασκούν οι σπληνοειδείς μύες και δύναμη αντίστασης είναι το βάρος της κεφαλής (Εικόνα 1γ) και ο τρικέφαλος μυς που δρά στην ωλένη ως δύναμη με υπομόχλιο την άρθρωση του αγκώνα και δύναμη αντίστασης το βάρος του πήχυ,όταν ο πήχυς εκτείνεται. Στο ανθρώπινο σώμα τα παραδείγματα μοχλού Α είδους είναι σπάνια. (Εικόνα 1γ) 1
2 ΜΟΧΛΟΣ B ΕΙΔΟΥΣ Η αντίσταση (φορτίο) βρίσκεται μεταξύ του υπομόχλιου και της δύναμης (Εικόνα 2α). Χρησιμοποιείται για τη στήριξη ή κίνηση ενός μεγάλου βάρους από μια μικρότερη δύναμη και ο μοχλοβραχίονας της δύναμης είναι μεγαλύτερος από τον μοχλοβραχίονα της δύναμης αντίστασης, γι αυτό και θεωρείται ως μεγεθυντής δύναμης. Παραδείγματα μοχλού Β είδους είναι η χειράμαξα (Εικόνα 2β) και ο καρυοθραύστης. Στο ανθρώπινο σώμα παραδείγματα μοχλού Β Είδους είναι η στήριξη του σώματος στα άκρα των δακτύλων με το μεγάλο δάκτυλο να θεωρείται ως υπομόχλιο- άξονας, τους μυς που καταφύονται στη φτέρνα να ασκούν τη δύναμη και το βάρος του σώματος που ασκείται στον αστράγαλο να είναι η δύναμη αντίστασης (φορτίο) (Εικόνα 2γ). Επίσης, ο πήχυς και ο βραχιόνιος (brachialis) μυς είναι μοχλός Β Είδους, διότι το βάρος του πήχυ ασκείται μεταξύ της άρθρωσης του αγκώνα και της δύναμης που ασκεί ο βραχιόνιος μυς. Στο ανθρώπινο σώμα τα παραδείγματα μοχλού Β είδους είναι σπάνια. (Εικόνα 2α) (Εικόνα 2β) ΣΗΜΕΙΩΣΗ: (Εικόνα 2γ) Στη βιβλιογραφία διατυπώνεται και η άποψη ότι κακώς αναφέρεται ως παράδειγμα μοχλού Β ΕΙΔΟΥΣ η στήριξη του σώματος στα άκρα των δακτύλων του ποδιού, διότι το σημείο εφαρμογής της δύναμης, της δύναμης φορτίου και το υπομόχλιο δε βρίσκονται στο ίδιο επίπεδο στήριξης. 2
3 ΜΟΧΛΟΣ Γ ΕΙΔΟΥΣ Η δύναμη είναι μεταξύ του υπομόχλιου άξονα και της δύναμης αντίστασης.ο μοχλός Γ ΕΙΔΟΥΣ (Εικόνα 3α) επιτρέπει την ανάπτυξη ταχύτητας η κίνησης ενός μικρού βάρους για μεγάλη απόσταση και ο μοχλοβραχίονας της δύναμης είναι μικρότερος από τον μοχλοβραχίονα της δύναμης αντίστασης γι αυτό και θεωρείται και μειωτής δύναμης, αφού η δύναμη είναι μεγαλύτερη από τη δύναμη αντίστασης (φορτίο).το καλάμι του ψαρέματος και η λαβίδα (Εικόνα 3β) είναι παραδείγματα μοχλού Γ ΕΙΔΟΥΣ. Στο ανθρώπινο σώμα παραδείγματα μοχλού Γ Είδους είναι ο Δικέφαλος μυς του βραχίονα του άνω άκρου που καταφύεται στον πήχυ (Κερκίδα) μεταξύ της άρθρωσης του αγκώνα (υπομόχλιο) και του βάρους του πήχυ. (Εικόνα 3γ) Στο ανθρώπινο σώμα τα παραδείγματα μοχλών στην συντριπτική τους πλειοψηφία είναι Γ είδους. (Εικόνα 3α) (Εικόνα 3β) (Εικόνα 3γ) ΜΗΧΑΝΙΚΟ ΠΛΕΟΝΕΚΤΗΜΑ Το Μηχανικό Πλεονέκτημα (ΜΠ) ορίζεται ως το πηλίκο του μοχλοβραχίονα της δύναμης προς τον μοχλοβραχίονα της δύναμης αντίστασης : Μοχλοβραχίονας δύναμης MΠ= Μοχλοβραχίονας δύναμης αντίστασης Στους μοχλούς Α είδους το Μηχανικό Πλεονέκτημα διαφέρει και εξαρτάται από τη θέση του υπομόχλιου (άξονα) σε σχέση με τη δύναμη και τη δύναμη αντίστασης. Στους μοχλούς Β είδους όπου ο Μοχλοβραχίονας δύναμης είναι μεγαλύτερος από τον Μοχλοβραχίονας δύναμης αντίστασης το Μηχανικό Πλεονέκτημα είναι ΜΠ>1, δηλαδή υφίσταται πάντα. 3
4 Στους μοχλούς Γ είδους όπου ο Μοχλοβραχίονας δύναμης είναι μικρότερος από τον Μοχλοβραχίονας δύναμης αντίστασης, το Μηχανικό Πλεονέκτημα είναι ΜΠ<1,δηλαδή δεν υπάρχει. Το παράδοξο στο ανθρώπινο σώμα είναι ότι οι μοχλοί που προσφέρουν μεγάλο Μηχανικό Πλεονέκτημα είναι σπάνιοι. Αυτό οφείλεται στο ότι τα σώματα μας δεν μεταφέρουν συχνά μεγάλα βάρη και μάλιστα αργά. Αν αυτό συνέβαινε θα μας ενδιέφερε το ΜΠ. Αντίθετα, τα σώματα μας χρησιμοποιούνται πολύ συχνά σε δραστηριότητες που απαιτούν μικρά βάρη να κινούνται γρήγορα. Αυτός είναι ο λόγος για τον οποίο στο ανθρώπινο σώμα κυριαρχεί η παρουσία μοχλών Γ είδους. Άλλα κλινικά παραδείγματα μοχλών είναι οι νάρθηκες (splints).(εικόνα 4).Η άρθρωση που περιβάλλει ο νάρθηκας είναι το υπομόχλιο, ένα τμήμα του αποτελεί τον μοχλοβραχίονα της δύναμης και το άλλο το μοχλοβραχίονα της δύναμης αντίστασης.η περιοχή που ενσωματώνεται στο νάρθηκα πρέπει να δέχεται καλά σχεδιασμένη κατανομή της πίεσης και η δύναμη να αντισταθμίζει τη δύναμη αντίστασης, διαφορετικά ο νάρθηκας γίνεται άβολος και αναποτελεσματικός. Η σύγκριση των εικόνων (4α) και (4β) δείχνει ότι η αύξηση του μοχλοβραχίονα της δύναμης (FA) σε σχέση με το μοχλοβραχίονα της δύναμης αντίστασης (RA) προκαλεί αύξηση του Μηχανικού Πλεονεκτήματος. Ο νάρθηκας εκ του τρόπου κατασκευής του ασκεί και τη δύναμη (που είναι ίσου μέτρου με τη δύναμη που ασκεί ο μυς) και τη δύναμη αντίστασης (που είναι ίση με το βάρος του τμήματος του χεριού). Στην εικόνα (4γ) φαίνεται ένας νάρθηκας στην περιοχή του πήχυ και του άκρου χεριού. F F A (Εικόνα 4α) A (Εικόνα 4β) R R (Εικόνα 4γ) 4
5 ΣΥΜΠΕΡΑΣΜΑ ΜΗΧΑΝΙΚΟ ΠΛΕΟΝΕΚΤΗΜΑ ΤΑΧΥΤΗΤΑ. ΔΥΟ ΑΝΤΙΠΑΛΟΙ. Όταν η δύναμη καταβάλλεται από ένα μυ και ο μοχλοβραχίονάς της είναι μικρότερος από τον μοχλοβραχίονα της δύναμης αντίστασης, τότε το μέτρο της δύναμης είναι μεγάλο, αλλά η δαπάνη σε μυική δύναμη αντισταθμίζεται από το κέρδος σε ταχύτητα και σε μήκος τροχιάς των μακρινότερων αναλογικά από τον άξονα περιστροφής τμημάτων. Αυτό συμβαίνει στους μοχλούς Γ είδους όπου: Μοχλοβραχίονας δύναμης < Μοχλοβραχίονας δύναμης αντίστασης Επειδή το σημείο εφαρμογής της δύναμης αντίστασης βρίσκεται μακρύτερα από τον άξονα περιστροφής σε σχέση με αυτό της δύναμης, θα ταξιδεύει μεγαλύτερη απόσταση στον ίδιο χρόνο, αλλά μεγαλύτερη απόσταση στον ίδιο χρόνο σημαίνει μεγαλύτερη ταχύτητα. Επομένως, οι μοχλοί Γ είδους είναι κατάλληλοι για ρίψη αντικειμένων, λακτίσματα κ.λ.π Όταν η δύναμη είναι μια εξωτερική δύναμη και ο μοχλοβραχίονάς της είναι μεγαλύτερος από τον μοχλοβραχίονα της δύναμης αντίστασης, τότε το μέτρο της δύναμης είναι μικρό σε σχέση με το μέτρο της δύναμης αντίστασης, αλλά μικρό είναι τότε και το κέρδος σε ταχύτητα και μήκος τροχιάς. Αυτό συμβαίνει με τους μοχλούς Β είδους και σε όσους από τους μοχλούς Α είδους ισχύει: Μοχλοβραχίονας δύναμης > Μοχλοβραχίονας δύναμης αντίστασης Οι ιδέες αυτές είναι βαθύτατα συνδεδεμένες αφ ενός με την λογική προστασίας των αρθρώσεων, καθώς και με την χρήση, όσο το δυνατόν δυνατότερων αρθρώσεων για δραστηριότητες και αφ ετέρου με τις αρχές της μηχανικής του σώματος οι οποίες συνηγορούν υπέρ της διατήρησης των αντικειμένων κοντά στο σώμα, όχι μόνο για λόγους μεγαλύτερης σταθερότητας αλλά και για λόγους καταβολής μικρότερης δύναμης για την ανύψωση αντικειμένων και τη μεταφορά τους. ΣΤΟΙΧΕΙΑ ΓΙΑ ΤΗΝ ΑΝΑΤΟΜΙΑ ΚΑΙ ΤΗ ΦΥΣΙΟΛΟΓΙΑ ΤΟΥ ΑΝΩ ΑΚΡΟΥ Ο σκελετός του άνω άκρου αποτελείται από τα οστά της ωμικής ζώνης δηλαδή του ώμου, με τα οποία το άνω άκρο συνδέεται με τον κορμό,το βραχίονα, τον πήχη (αντιβραχίονα) και το άκρο χέρι. Για την καλύτερη κατανόηση του παραδείγματος που ακολουθεί θα περιοριστούμε στα εξής : Ο βραχίονας(upper arm) αποτελείται από ένα οστό,το βραχιόνιο οστό (humerus), ο πήχυς (forearm) από δύο οστά την κερκίδα (radius) και την ωλένη(ulna), με την ωλένη να είναι μεγαλύτερη σε μήκος από την κερκίδα.τα οστά του βραχίονα και του πήχυ συνδέονται με την άρθρωση του αγκώνα (elbow). Οι μύες του άνω άκρου είναι γραμμωτοί, όπως όλοι οι σκελετικοί μύες, οι οποίοι ονομάζονται έτσι, επειδή προσφύονται σε οστά. Η πρόσφυση στο πιο ακίνητο οστό ονομάζεται έκφυση και η πρόσφυση στο πιο κινητό κατάφυση. Εδώ, δε θα αποφύγω τον πειρασμό να σχολιάσω τις αντίστοιχες λέξεις της σημερινής Διεθνούς Γλώσσας (έκφυση origin= πηγή, αρχή, καταγωγή, προέλευση, προέρχομαι, κατάγομαι και κατάφυση insertion = εισαγωγή, παρεμβολή, καταχώρηση ). Αν κάποιος δεν έχει διαβάσει τίποτα από τα προηγούμενα και του πω ο μυς εκφύεται, αν το συνδέσει με το φύομαι συμπεραίνει ότι κάτι που φυτρώνει είναι λογικό να είναι πιο σταθερό (ακίνητο) στο σημείο από το οποίο φυτρώνει (ρίζα) και ο μυς καταφύεται είναι λογικό να έχει να κάνει με την κατάληξη αυτού που φύτρωσε, άρα αυτή η η κατάληξη είναι πιο ελεύθερη να κινείται (φύλλα). 5
6 Είναι αυτοτελή όργανα και νευρώνονται από νεύρα του εγκεφαλονωτιαίου νευρικού συστήματος και γι αυτό λέγονται εκούσιοι μύες. Οι μύες προκείμένου να γίνει μια κίνηση μόνο συστέλλονται, γι αυτό εμφανίζονται κατά ζεύγη με τον ανταγωνιστή τους μυ. Ακόμη και σε κατάσταση πλήρους χαλάρωσης οι μύες έχουν μια μικρή σύσπαση που λέγεται μυικός τόνος. Στο σώμα οι μύες είναι έτσι τοποθετημένοι, ώστε το μήκος ηρεμίας (relaxing length) τους να είναι περίπου το βέλτιστο μήκος (optimal length) τους. Το βέλτιστο μήκος (optimal length) είναι αυτό στο οποίο μπορεί να επιτευχθεί η μέγιστη δύναμη κατά τη διάρκεια μιας τετανικής συστολής,ο όρος τετανική δεν έχει καμία σχέση με το βακτήριο clostridium tetani που προκαλεί την ασθένεια του τετάνου, αλλά με την κανονική ανταπόκριση του μυ από τη νευρική διέγερση. Ισοτονική συστολή είναι αυτή στην οποία η τάση του μυ αρχικά αυξάνεται και έπειτα παραμένει σταθερή καθώς αλλάζει το μήκος του, οπότε παράγει μηχανικό έργο π.χ ανύψωση ενός αντικειμένου. Πιο συγκεκριμένα, κρατάω ένα δέμα και το σηκώνω για να το αποθέσω στο τραπέζι. Κατά τη διάρκεια αυτής της κίνησης συστέλλονται, κυρίως, ο Βραχιόνιος μυς και ο Δικέφαλος μυς, οι οποίοι εκτελούν ισοτονική συστολή. Οι ισοτονικές συστολές χωρίζονται σε ομόκεντρες (concentric) στις οποίες η τάση του μυ υπερνικά την αντίσταση και ο μυς συστέλλεται και σε έκκεντρες (eccentric) συστολές όπου η μέγιστη τάση που αναπτύσσει ο μυς είναι μικρότερη από την αντίσταση και ο μυς επιμηκύνεται, λόγω της συστολής κάποιου άλλου μυ ή της έλξης της βαρύτητας. Οι ισομετρικές συστολές είναι αυτές στις οποίες το μήκος του μυ δε μικραίνει (βραχύνεται), με αποτέλεσμα η τάση του μυ να αναπτύσσεται σε σταθερό μήκος μυ, να ασκεί έλξη στους τένοντες, χωρίς να παράγει μηχανικό έργο και να μην υπερβαίνει ποτέ την αντίσταση. Για παράδειγμα, όταν προσπαθούμε να ανυψώσουμε ένα μεγάλο βάρος, το μήκος του μυ παραμένει σταθερό καθώς συστέλλεται και η τάση αυξάνεται. Στο προηγούμενο παράδειγμα, αν δεν αποθέσω το δέμα στο τραπέζι, αλλά το κρατάω πάνω από την επιφάνεια του τραπεζιού, οι δύο μύες (Βραχιόνιος -Δικέφαλος) εκτελούν ισομετρική συστολή για την κάμψη του αντιβράχιου (πήχυ) προς τον βραχίονα (κάμψη του αγκώνα) και δεν παράγουν έργο. Οι ισομετρικές συστολές είναι σημαντικές για τη διατήρηση μιας στάσης, όπως η στήλωση των ποδιών όταν στεκόμαστε ή η συγκράτηση ενός ποτού που το πίνουμε σε γουλιές. Ο μυικός τόνος αυξάνεται σε ψυχρό περιβάλλον, με αποτέλεσμα η ισομετρική συστολή να μετατρέπεται σε τρομώδη ισοτονική συστολή (ρίγος) που εξαναγκάζει τους μύες σε παραγωγή μηχανικού έργου, δηλαδή καύσεις στους μύες, άρα και παραγωγή θερμότητας. Οι έκκεντρες συστολές, είναι πολύ σπουδαίες σε πολλές συνηθισμένες κινήσεις. Μέσω αυτών μπορούμε να ασκήσουμε ακριβή έλεγχο στο μέγεθος της παραγόμενης από το μυ τάσης. Όταν μεταβάλλουμε την τάση του μυ σε μία έκκεντρη συστολή μπορούμε να ελέγξουμε το μέγεθος της επιμήκυνσης του μυ, όπως ακριβώς μπορούμε να μεταβάλλουμε την τάση σε μια ομόκεντρη συστολή π.χ έκκεντρες συστολές προκύπτουν καλώς κατεβαίνουμε τα σκαλιά μιας σκάλας και κύκλους από έκκεντρες και ομόκεντρες συστολές εκτελούμε κατά τη φυσική άσκηση στην οποία, κρατώντας ένα βάρος (αλτήρα), κάμπτουμε και εκτείνουμε το σύστημα αγκώνας πήχυς. Στο διπλανό διάγραμμα φαίνεται η μεταβολή της ταχύτητας συστολής ενός μυ σε σχέση με το φορτίο: ταχύτητα συστολής του μυ Μέγιστη ταχύτητα συστολής (μηδενικό φορτίο) Μέγιστη φορτίο, μηδενική ταχύτητα συστολής 6 φορτίο
7 Από το διάγραμμα προκύπτει ότι όταν σηκώνουμε μικρά βάρη ελαφρά σώματα- η ανύψωση γίνεται με μεγάλη ταχύτητα, όσο αυξάνεται το βάρος η ταχύτητα ανύψωσης μικραίνει μέχρι που μηδενίζεται. Στο παράδειγμα που ακολουθεί μας ενδιαφέρει ο Δικέφαλος μυς (biceps brachii) του βραχίονα, ανταγωνιστής του οποίου είναι ο Τρικέφαλος μυς (triceps brachii). Ο Δικέφαλος μυς εκφύεται με δύο εκφυτικές κεφαλές, τη μακρά και τη βραχεία από την ωμοπλάτη και καταφύεται στον πήχυ. Όταν ο Δικέφαλος μυς συστέλλεται με την ενέργειά του κάμπτει τον πήχυ προς τον βραχίονα και συγχρόνως μπορεί να τον υπτιάζει. Αντίθετα, στην έκταση του πήχυ συστέλλεται ο Τρικέφαλος. Άλλοι μυς που παίζουν ρόλο στην κίνηση του άνω άκρου είναι ο Βραχιόνιος μυς (brachialis) ο οποίος εκφύεται από το βραχιόνιο οστούν και καταφύεται στην ωλένη και κάμπτει τον πήχυ και ο βραχιονοκερκιδικός (brachioradialis) μυς ο οποίος εκφύεται από το βραχιόνιο οστούν και καταφύεται στην κερκίδα, ο οποίος κάμπτει τον πήχυ και βοηθάει στον πρηνισμό του. Μυς του Άνω Άκρου- Πρόσθια Επιφάνεια Μυς του Άνω Άκρου- Οπίσθια Επιφάνεια ΟΣΤΑ ΤΟΥ ΑΝΩ ΑΚΡΟΥ 7
8 Οι σκελετικοί μύες προσφύονται στα οστά μέσω των τενόντων (tendons) που είναι τα ακραία τμήματα των μυών και αποτελούν τον συνδετικό τους κρίκο με τα οστά. Λόγω των ελαστικών ιδιοτήτων που παρουσιάζει ο τένοντας του Δικέφαλου, σε μελέτες που έχουν γίνει φαίνεται ότι το σύστημα τένοντας - μάζα πήχυ μπορεί να θεωρηθεί ως σύστημα ελατηρίου μάζας με φυσική συχνότητα από 2,2-2,5 Hz. ΠΑΡΑΔΕΙΓΜΑ Στην εικόνα φαίνεται το άνω άκρο ενός ενήλικα άνδρα που κρατά στο χέρι του ομογενή σφαίρα μάζας m= 5Kg, το Δικέφαλος μυς κέντρο μάζας της οποίας, απέχει από την άρθρωση του αγκώνα Ε απόσταση d= 36 cm.το σύστημα πήχυς άκρο χέρι μάζας Μ=3Kg βρίσκεται σε d=36cm οριζόντια θέση και είναι κάθετος προς τον βραχίονα και το κέντρο μάζας του C απέχει από την άρθρωση του αγκώνα Ε απόσταση l=18,4cm. Ο Δικέφαλος μυς καταφύεται μέσω του τένοντα στο Ε Β C L σημείο Β του πήχυ που απέχει από την άρθρωση του αγκώνα Ε απόσταση γ=4cm και σχηματίζει με την διεύθυνση του βραχίονα γωνία θ=12 0. Να υπολογιστούν: γ=4cm α. Το μέτρο της δύναμης που ασκεί ο Δικέφαλος στον πήχυ. β. Το μέτρο της δύναμης που ασκείται από τον βραχίονα στον πήχυ στην άρθρωση του αγκώνα. γ. Ανυψώνουμε τον πήχυ και το σώμα, έτσι, ώστε το σημείο L να βρεθεί στη θέση L 1 που απέχει από την αρχική του θέση κατακόρυφη απόσταση h=(ll 1 )=18cm.Ποια η κατακόρυφη ανύψωση ΒΒ 1 του σημείου Β. Τι παρατηρείτε; δ. Υποθέτουμε ότι το σύστημα τένοντας του Δικέφαλου μυ πήχυς άκρο χέρι - σφαίρα αντιστοιχεί σε σύστημα <<ελατηρίου μάζας>> σταθεράς κ. Αν ο πήχυς εκτελέσει περιοδική κίνηση μεταξύ των θέσεων L 1 και L 2 που είναι συμμετρικές ως προς τη θέση L (curls), παρατηρείται ότι φθάνει από τη θέση L στην ανώτερη θέση L 1 σε χρόνο Δt=0,1s, οπότε ο Δικέφαλος μυς φτάνει στην κατάσταση μέγιστης συστολής του. Θεωρώντας ότι η κίνηση του συστήματος είναι τμήμα περιοδικής κίνησης περιόδου Τ 0 =2π Μ + m, να υπολογίσετε τη σταθερά κ του «ισοδύναμου ελατηρίου» κ και τη συχνότητα της κίνησης του συστήματος «τένοντας Δικεφάλου πήχυς». Δίνεται g=10 m/s 2, π 2 =10. Να αγνοήσετε τις δυνάμεις που ασκούν ο Τρικέφαλος μυς (ανταγωνιστής μυς) και ο Βραχιόνιος μυς στον πήχυ. Να θεωρήσετε ότι ημ12 0 =0,20 και συν12 0 =0,98. 8
9 ΛΥΣΗ α. Από την ισορροπία του πήχυ έχουμε: Στ (Ε) =0 Τ y (EB) W(EC) W Σ (ΕL)=0 Τ y , =0 Τ y =588 N.(1) T Αλλά Τ y =Τσυν12 0 (1) y Τ= 0 συν12 Τ=600Ν (2) β. Επίσης, ΣF x =0 T x =F x F x =T ημ12 0 (2) F x =120N(3) ΣF x =0 Τ y =W+W Σ +F (1) y F y = F y =508N (4). Επομένως η δύναμη που δέχεται η άρθρωση του αγκώνα είναι: 2 2 F= F + F (3) F=521,98Ν 522Ν x y (4) γ. Από τα όμοια τρίγωνα (ΕΒΒ 1) 1 και (ΕCC 1) 9 προκύπτει: (BB ) 1 (EB) (BB ) 2cm.Το σημείο Β που βρίσκεται πλησιέστερα στον άξονα 1 (LL ) (EL) περιστροφής που διέρχεται από το Ε και είναι κάθετος στο επίπεδο της κίνησης του πήχυ, ανυψώνεται 9 φορές λιγότερο σε σχέση με το σημείο L. Δηλαδή, το σημείο L κινείται 9 φορές ταχύτερα από το σημείο Β αφού στον ίδιο χρόνο ανυψώνεται 9 φορές περισσότερο. Αυτό είναι «το κέρδος» που προκύπτει από «το τίμημα» της καταβολής πολύ μεγαλύτερης δύναμης από τον Δικέφαλο (Τ=600Ν ) σε σχέση με τη δύναμη φορτίου W Σ =50Ν. δ. Ο χρόνος κίνησης του πήχυ από τη θέση L στη θέση L 1, Δt αντιστοιχεί σε ένα Τ τέταρτο της περιόδου, Δt= 0 4. Άρα Τ 0=4Δt T 0 =0,4s (5) Αλλά Τ 0 = 2π 1 f= =2,5Hz. T 0 2 (5) Μ + m 4π (Μ + m) κ= κ=2000n/m. Η συχνότητα είναι κ T 2 0 γ=4cm Δικέφαλος μυς d=36cm Β C L ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Είναι προφανές ότι η παραπάνω προσέγγιση της κίνησης του συστήματος πήχυς Δικέφαλος μυς στο δ. ερώτημα είναι μια υπεραπλούστευση. Υπάρχουν διάφορα μοντέλα προσεγγίσεις του θέματος. Οι S. J. Fellows και P. Rack σε σχετική δημοσίευση (v. 383; Feb 1989, The Journal of physiology ) μεταξύ των άλλων αναφέρουν τα εξής: Ο συνδυασμός πήχυ και τενόντων συμπεριφέρεται σε σχετικά πειράματα ως σύστημα «ελατηρίου - μάζας» με φυσική συχνότητα μεταξύ των 2-2,5Hz. Κατά τη διάρκεια αυθορμήτων κινήσεων είναι ενεργοί ο Δικέφαλος, ο Βραχιόνιος, ο Βραχιονιοκερκιδικός και επιπροσθέτως ο Τρικέφαλος. Επειδή κατά την κάμψη του πήχυ οι δυνάμεις κατανέμονται μεταξύ των τενόντων των παραπάνω μυών και λειτουργούν ως ελατήρια σε παράλληλη σύνδεση, αυτό στην πραγματικότητα αποτελεί ένα σκληρότερο ισοδύναμο ελατήριο από αυτό που αντιστοιχεί στον τένοντα του Δικεφάλου μόνο. Αυτό έχει ως αποτέλεσμα η φυσική συχνότητα του συστήματος τένοντας μάζα πήχυ να είναι υψηλότερη με αποτέλεσμα να μην Ε T F x F y T x T y B 1 W C 1 L 1 W Σ L 2
10 είναι εύκολο να επιτευχθούν αυθόρμητες κινήσεις με συχνότητες μεγαλύτερες από 5Hz. 2. Σε άλλα μοντέλα το σύστημα πήχυς άκρο χέρι θεωρείται ως στερεό με ροπή αδρανείας που δίνεται από τον τύπο της ροπής αδρανείας ελλειψοειδούς, το οποίο όταν στρέφεται περί άξονα που διέρχεται από την άρθρωση του αγκώνα M 2 2 και είναι κάθετος στο επίπεδο της περιστροφής έχει ροπή αδρανείας Ι= (b +c ) 5 όπου Μ= η μάζα του συστήματος πήχυς άκρο χέρι και b, c= οι δύο άξονες του ελλειψοειδούς που είναι κάθετοι στον τρίτο άξονα περιστροφής. 3. Σε πειραματικές διατάξεις ο υπολογισμός της ροπής αδρανείας του 2 T Mgd προηγούμενου συστήματος γίνεται από τη σχέση Ι= όπου Τ = η περίοδος 2 4π της στροφικής ταλάντωσης που θεωρείται ότι εκτελεί το σύστημα, M= η μάζα του πήχυ και του άκρου χεριού και d= η απόσταση του κέντρου μάζας του συστήματος από την άρθρωση του αγκώνα. ΣΧΟΛΙΟ Μελέτες έχουν δείξει ότι η δυνατότητα ανάπτυξης της περιμέτρου του Δικεφάλου μυ (κοινώς «ποντίκι») εξαρτάται από γενετικούς παράγοντες όπως είναι η φύση των μυικών ινών και κυρίως από την απόσταση της κατάφυσης του Δικέφαλου μυ από τον αγκώνα. Όσο πιο μακριά καταφύεται ο Δικέφαλος από την άρθρωση του αγκώνα τόσο μικρότερη είναι η δυνατότητα ανάπτυξης της περιμέτρου του Δικεφάλου. Ας το έχουν λοιπόν αυτό υπόψη τους όσοι ενδιαφέρονται πριν καταφύγουν στην αλόγιστη χρήση διαφόρων «ουσιών» Βιβλιογραφία 1. Occupational therapy for physical Dysfunction Mary Vining Radomski Katherine A. Trombly 2. Human Physiology Lauralee Sherwood 3. S. J. Fellows και P. Rack Changes in the length of the human biceps brachii muscle during elbow movements ( The Journal of physiology, v. 383; Feb 1989) Ξ. Στεργιάδης 10
Στέφανος Πατεράκης - Φυσικοθεραπευτής
 ΚΙΝΗΣΙΟΛΟΓΙΑ Ορισμός : Είναι η επιστήμη που μελετά την ανθρώπινη κίνηση. Χρησιμοποιεί γνώσεις από τη μηχανική της φυσικής, την ανατομία και τη φυσιολογία. Η Βαρύτητα Έλκει όλα τα σώματα προς το έδαφος.
ΚΙΝΗΣΙΟΛΟΓΙΑ Ορισμός : Είναι η επιστήμη που μελετά την ανθρώπινη κίνηση. Χρησιμοποιεί γνώσεις από τη μηχανική της φυσικής, την ανατομία και τη φυσιολογία. Η Βαρύτητα Έλκει όλα τα σώματα προς το έδαφος.
Εμβιομηχανική. Σοφία Ξεργιά PT, MSc, PhD
 Εμβιομηχανική Σοφία Ξεργιά PT, MSc, PhD Λειτουργία των σκελετικών μυών Γραμμή έλξης Γωνία πρόσφυσης Είδη συστολής Επίδραση της βαρύτητας Μηκοδυναμική σχέση Ταχοδυναμική σχέση Ελαστικές ιδιότητες Γραμμή
Εμβιομηχανική Σοφία Ξεργιά PT, MSc, PhD Λειτουργία των σκελετικών μυών Γραμμή έλξης Γωνία πρόσφυσης Είδη συστολής Επίδραση της βαρύτητας Μηκοδυναμική σχέση Ταχοδυναμική σχέση Ελαστικές ιδιότητες Γραμμή
ΣΧΟΛΙΑ ΙΑΦΑΝΕΙΩΝ ΙΑΛΕΞΗΣ ΜΕ ΤΙΤΛΟ: «ΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ ΣΤΙΣ ΑΡΘΡΩΣΕΙΣ ΤΟΥ ΣΩΜΑΤΟΣ»
 ΣΧΟΛΙΑ ΙΑΦΑΝΕΙΩΝ ΙΑΛΕΞΗΣ ΜΕ ΤΙΤΛΟ: «ΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ ΣΤΙΣ ΑΡΘΡΩΣΕΙΣ ΤΟΥ ΣΩΜΑΤΟΣ» ιαφάνεια 4 Ας θυµηθούµε τι είναι η ροπή. Στο σχήµα έχουµε µια ράβδο, η οποία µπορεί να περιστρέφεται γύρω από έναν άξονα
ΣΧΟΛΙΑ ΙΑΦΑΝΕΙΩΝ ΙΑΛΕΞΗΣ ΜΕ ΤΙΤΛΟ: «ΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ ΣΤΙΣ ΑΡΘΡΩΣΕΙΣ ΤΟΥ ΣΩΜΑΤΟΣ» ιαφάνεια 4 Ας θυµηθούµε τι είναι η ροπή. Στο σχήµα έχουµε µια ράβδο, η οποία µπορεί να περιστρέφεται γύρω από έναν άξονα
ΕΜΒΙΟΜΗΧΑΝΙΚΟΙ ΠΑΡΑΓΟΝΤΕΣ. Σοφία Α. Ξεργιά PT, MSc, PhD
 ΕΜΒΙΟΜΗΧΑΝΙΚΟΙ ΠΑΡΑΓΟΝΤΕΣ Σοφία Α. Ξεργιά PT, MSc, PhD Ανάλυση της Ανθρώπινης Κίνησης Εμβιομηχανική Κινησιολογία Κινηματική Κινητική Λειτουργική Ανατομική Γραμμική Γωνιακή Γραμμική Γωνιακή Θέση Ταχύτητα
ΕΜΒΙΟΜΗΧΑΝΙΚΟΙ ΠΑΡΑΓΟΝΤΕΣ Σοφία Α. Ξεργιά PT, MSc, PhD Ανάλυση της Ανθρώπινης Κίνησης Εμβιομηχανική Κινησιολογία Κινηματική Κινητική Λειτουργική Ανατομική Γραμμική Γωνιακή Γραμμική Γωνιακή Θέση Ταχύτητα
ΕΠΕΑΕΚ ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ Τ.Ε.Φ.Α.Α. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΘΕΣΣΑΛΙΑΣ - ΑΥΤΕΠΙΣΤΑΣΙΑ
 ΕΠΕΑΕΚ ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ Τ.Ε.Φ.Α.Α. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΘΕΣΣΑΛΙΑΣ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΜΚ 0903 «Κινησιολογία» 7η Διάλεξη: «Άνω
ΕΠΕΑΕΚ ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ Τ.Ε.Φ.Α.Α. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΘΕΣΣΑΛΙΑΣ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΜΚ 0903 «Κινησιολογία» 7η Διάλεξη: «Άνω
ΜΥΟΛΟΓΙΑ. 1. Σκελετικοί µύες
 ΜΥΟΛΟΓΙΑ Μυϊκός ιστός και Μυϊκό σύστηµα Ι. Γενικά Α. Μύες = όργανα µαλακά συσταλτά 1. οι συσπάσεις των µυϊκών ινών κινούν τα µέρη του σώµατος 2. προσδίδει το σχήµα του σώµατος 3. τρία είδη µυών α. Σκελετικοί
ΜΥΟΛΟΓΙΑ Μυϊκός ιστός και Μυϊκό σύστηµα Ι. Γενικά Α. Μύες = όργανα µαλακά συσταλτά 1. οι συσπάσεις των µυϊκών ινών κινούν τα µέρη του σώµατος 2. προσδίδει το σχήµα του σώµατος 3. τρία είδη µυών α. Σκελετικοί
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
Στέφανος Πατεράκης (Φυσικ/τής)
 ΜΥΣ Οι μύες είναι όργανα του ανθρωπίνου σώματος. Σχηματίζονται από μυϊκό ιστό. Μαζί με τους τένοντες συμβάλουν στην κίνηση των οστών. Είδη των μυών Ο μυς της καρδιάς, Οι λείοι, και Οι γραμμωτοί. Ο μυς
ΜΥΣ Οι μύες είναι όργανα του ανθρωπίνου σώματος. Σχηματίζονται από μυϊκό ιστό. Μαζί με τους τένοντες συμβάλουν στην κίνηση των οστών. Είδη των μυών Ο μυς της καρδιάς, Οι λείοι, και Οι γραμμωτοί. Ο μυς
Γκύζη 14-Αθήνα Τηλ :
 Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Κινησιολογία Ενότητα 7: Άνω άκρο - αγκώνας Αθανάσιος Τσιόκανος Τμήμα Επιστήμης Φυσικής Αγωγής και Αθλητισμού Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Κινησιολογία Ενότητα 7: Άνω άκρο - αγκώνας Αθανάσιος Τσιόκανος Τμήμα Επιστήμης Φυσικής Αγωγής και Αθλητισμού Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Στέφανος Πατεράκης (Φυσικ/τής)
 Η Ελαστικότητα Είναι η ικανότητα της αύξησης του μήκους ενός μυός, κάτω από την επίδραση μιας δύναμης και η επιστροφή στο αρχικό μήκος του, όταν σταματήσει η επίδραση της δύναμης αυτής. Η ιδιότητα αυτή
Η Ελαστικότητα Είναι η ικανότητα της αύξησης του μήκους ενός μυός, κάτω από την επίδραση μιας δύναμης και η επιστροφή στο αρχικό μήκος του, όταν σταματήσει η επίδραση της δύναμης αυτής. Η ιδιότητα αυτή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 10 ΙΟΥΝΙΟΥ 2014 ΕΚΦΩΝΗΣΕΙΣ
 Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 10 ΙΟΥΝΙΟΥ 2014 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία
Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 10 ΙΟΥΝΙΟΥ 2014 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη
 Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Τετάρτη 12 Απριλίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2008 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 00 ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Τα
ΘΕΜΑ ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 00 ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Τα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2016-2017 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2016-2017 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον
, συγκρούεται μετωπικά και ελαστικά με ακίνητη σφαίρα μάζας m 2. Οι ταχύτητες υ και υ των σφαιρών μετά την κρούση
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 13 ΙΟΥΝΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 13 ΙΟΥΝΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
Επαναληπτικη άσκηση στην Μηχανική Στερεού-Κρούσεις
 Επαναληπτικη άσκηση στην Μηχανική Στερεού-Κρούσεις Σφαίρα Σ 2 µάζας m 2 =m=2kg ηρεµεί στερεωµένη στο αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m το άλλο άκρο του οποίου είναι στερεωµένο
Επαναληπτικη άσκηση στην Μηχανική Στερεού-Κρούσεις Σφαίρα Σ 2 µάζας m 2 =m=2kg ηρεµεί στερεωµένη στο αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m το άλλο άκρο του οποίου είναι στερεωµένο
5 ΛΥΚΕΙΟ ΧΑΛΑΝΔΡΙΟΥ 2013-2014 ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ ΒΙΟΛΟΓΙΑ. H άρθρωση του ώμου
 5 ΛΥΚΕΙΟ ΧΑΛΑΝΔΡΙΟΥ 2013-2014 ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ ΒΙΟΛΟΓΙΑ H άρθρωση του ώμου Μαθητής Μ. Γεώργιος Ανατομία ώμου Τα κύρια οστά του ώμου είναι το βραχιόνιο και η ωμοπλάτη.η αρθρική κοιλότητα προστατεύεται
5 ΛΥΚΕΙΟ ΧΑΛΑΝΔΡΙΟΥ 2013-2014 ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ ΒΙΟΛΟΓΙΑ H άρθρωση του ώμου Μαθητής Μ. Γεώργιος Ανατομία ώμου Τα κύρια οστά του ώμου είναι το βραχιόνιο και η ωμοπλάτη.η αρθρική κοιλότητα προστατεύεται
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Τα δύο
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Τα δύο
Μαθημα 1 ο : ΑΡΧΕΣ ΕΜΒΙΟΜΗΧΑΝΙΚΗΣ, ΚΑΤΗΓΟΡΙΟΠΟΙΗΣΗ ΚΑΙ ΚΡΙΤΗΡΙΑ ΕΠΙΛΟΓΗΣ ΤΩΝ ΑΣΚΗΣΕΩΝ
 ΑΣΚΗΣΗ ΜΕ ΑΝΤΙΣΤΑΣΕΙΣ (Κ.Μ. Μ 161) Μαθημα 1 ο : ΑΡΧΕΣ ΕΜΒΙΟΜΗΧΑΝΙΚΗΣ, ΚΑΤΗΓΟΡΙΟΠΟΙΗΣΗ ΚΑΙ ΚΡΙΤΗΡΙΑ ΕΠΙΛΟΓΗΣ ΤΩΝ ΑΣΚΗΣΕΩΝ Με την ολοκλήρωση του μαθήματος οι φοιτητές πρέπει να είναι σε θέση να: περιγράψουν
ΑΣΚΗΣΗ ΜΕ ΑΝΤΙΣΤΑΣΕΙΣ (Κ.Μ. Μ 161) Μαθημα 1 ο : ΑΡΧΕΣ ΕΜΒΙΟΜΗΧΑΝΙΚΗΣ, ΚΑΤΗΓΟΡΙΟΠΟΙΗΣΗ ΚΑΙ ΚΡΙΤΗΡΙΑ ΕΠΙΛΟΓΗΣ ΤΩΝ ΑΣΚΗΣΕΩΝ Με την ολοκλήρωση του μαθήματος οι φοιτητές πρέπει να είναι σε θέση να: περιγράψουν
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
Γ ΛΥΚΕΙΟΥ ΟΙ ΚΙΝΗΣΕΙΣ ΤΩΝ ΣΤΕΡΕΩΝ ΣΩΜΑΤΩΝ
 Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ
 F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
Περιεχόμενα. Λεξιλόγιο
 Περιεχόμενα ΜΕΡΟΣ I: ΑΡΧΕΣ ΕΜΒΙΟΜΗΧΑΝΙΚΗΣ 1 Εισαγωγή στην Εμβιομηχανική Ανάλυση 2 Μηχανικές Ιδιότητες των Υλικών 3 Εμβιομηχανική των Οστών 4 Εμβιομηχανική των Σκελετικών Μυών 5 Εμβιομηχανική των Χόνδρων
Περιεχόμενα ΜΕΡΟΣ I: ΑΡΧΕΣ ΕΜΒΙΟΜΗΧΑΝΙΚΗΣ 1 Εισαγωγή στην Εμβιομηχανική Ανάλυση 2 Μηχανικές Ιδιότητες των Υλικών 3 Εμβιομηχανική των Οστών 4 Εμβιομηχανική των Σκελετικών Μυών 5 Εμβιομηχανική των Χόνδρων
ΣΕΙΡΑ: 3 Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής
 ΜΑΘΗΜΑ /ΤΑΞΗ: Φυσική Κατεύθυνσης Γ Λυκείου ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 16/03/014 ΣΕΙΡΑ: 3 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής ΘΕΜΑ Α Να γράψετε στο τετράδιό
ΜΑΘΗΜΑ /ΤΑΞΗ: Φυσική Κατεύθυνσης Γ Λυκείου ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 16/03/014 ΣΕΙΡΑ: 3 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής ΘΕΜΑ Α Να γράψετε στο τετράδιό
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή Αδράνειας) Γ ΛΥΚΕΙΟΥ. Α)Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση.
 ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή δράνειας) Γ ΛΥΚΕΙΟΥ ΘΕΜ 1 Ο : )Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση. 1. Για ένα ζεύγος δυνάμεων Η ροπή του, εξαρτάται
ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή δράνειας) Γ ΛΥΚΕΙΟΥ ΘΕΜ 1 Ο : )Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση. 1. Για ένα ζεύγος δυνάμεων Η ροπή του, εξαρτάται
Μηχανική και Παθομηχανική της Μυϊκής Δραστηριότητας στον Αγκώνα
 Μηχανική και Παθομηχανική της Μυϊκής Δραστηριότητας στον Αγκώνα ΚΕΦΑΛΑΙΟ 12 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ ΚΑΜΠΤΗΡΕΣ ΜΥΕΣ ΤΟΥ ΑΓΚΩΝΑ...00 Δικέφαλος Βραχιόνιος Μυς...00 Πρόσθιος Βραχιόνιος...00 Βραχιονοκερκιδικός...00
Μηχανική και Παθομηχανική της Μυϊκής Δραστηριότητας στον Αγκώνα ΚΕΦΑΛΑΙΟ 12 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ ΚΑΜΠΤΗΡΕΣ ΜΥΕΣ ΤΟΥ ΑΓΚΩΝΑ...00 Δικέφαλος Βραχιόνιος Μυς...00 Πρόσθιος Βραχιόνιος...00 Βραχιονοκερκιδικός...00
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ-ΟΜΟΓΕΝΩΝ 10/7/2015
 ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:... ΤΣΙΜΙΣΚΗ &ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 270727 222594 ΑΡΤΑΚΗΣ 2 - Κ. ΤΟΥΜΠΑ THΛ: 993 949422 www.syghrono.gr ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ-ΟΜΟΓΕΝΩΝ 0/7/205
ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:... ΤΣΙΜΙΣΚΗ &ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 270727 222594 ΑΡΤΑΚΗΣ 2 - Κ. ΤΟΥΜΠΑ THΛ: 993 949422 www.syghrono.gr ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ-ΟΜΟΓΕΝΩΝ 0/7/205
ΛΥΚΕΙΟ ΑΓΙΟΥ ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΛΥΚΕΙΟ ΑΓΙΟΥ ΠΥΡΙΔΩΝΑ ΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕ ΠΡΟΑΓΩΓΙΚΕ ΕΞΕΤΑΕΙ ΦΥΙΚΗ ΚΑΤΕΥΘΥΝΗ Β ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 31-05-2012 ΔΙΑΡΚΕΙΑ: 07.45 10.15 Οδηγίες 1. Το εξεταστικό δοκίμιο αποτελείται από 9 σελίδες.
ΛΥΚΕΙΟ ΑΓΙΟΥ ΠΥΡΙΔΩΝΑ ΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕ ΠΡΟΑΓΩΓΙΚΕ ΕΞΕΤΑΕΙ ΦΥΙΚΗ ΚΑΤΕΥΘΥΝΗ Β ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 31-05-2012 ΔΙΑΡΚΕΙΑ: 07.45 10.15 Οδηγίες 1. Το εξεταστικό δοκίμιο αποτελείται από 9 σελίδες.
A4. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
υ λ γ. λ δ. λ 0 υ. Μονάδες 5
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 1 ΙΟΥΝΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 1 ΙΟΥΝΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ
ΦΥΣΙΚΗ Ο.Π Β Λ-Γ Λ ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ
 ΦΥΣΙΚΗ Ο.Π Β Λ-Γ Λ 25/11/2018 ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Ο.Π Β Λ-Γ Λ 25/11/2018 ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 3 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 3 να γράψετε στο τετράδιό
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ
 ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΦΥΣΙΚΗ Ο.Π Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Εισαγωγή στην άσκηση με αντίσταση. Ισομετρική Ενδυνάμωση. Δρ. Φουσέκης Κων/νος. Καθηγητής Εφαρμογών. Kων/νος Φουσέκης, Καθηγητης Εφ.
 Εισαγωγή στην άσκηση με αντίσταση Ισομετρική Ενδυνάμωση Δρ. Φουσέκης Κων/νος. Καθηγητής Εφαρμογών Άσκηση με αντίσταση Αντίσταση με αντίσταση είναι μια ενεργητική εκγύμναση (δυναμική ή στατική μυϊκή συστολή)
Εισαγωγή στην άσκηση με αντίσταση Ισομετρική Ενδυνάμωση Δρ. Φουσέκης Κων/νος. Καθηγητής Εφαρμογών Άσκηση με αντίσταση Αντίσταση με αντίσταση είναι μια ενεργητική εκγύμναση (δυναμική ή στατική μυϊκή συστολή)
γραπτή εξέταση στη ΦΥΣΙΚΗ B κατεύθυνσης
 η εξεταστική περίοδος από 4/0/5 έως 08//5 γραπτή εξέταση στη ΦΥΣΙΚΗ B κατεύθυνσης Τάξη: Β Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α A Στις ερωτήσεις Α-Α4 να επιλέξετε τη σωστή απάντηση.
η εξεταστική περίοδος από 4/0/5 έως 08//5 γραπτή εξέταση στη ΦΥΣΙΚΗ B κατεύθυνσης Τάξη: Β Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α A Στις ερωτήσεις Α-Α4 να επιλέξετε τη σωστή απάντηση.
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2004
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε
δ. έχουν πάντα την ίδια διεύθυνση.
 Διαγώνισμα ΦΥΣΙΚΗ Κ.Τ Γ ΛΥΚΕΙΟΥ ΖΗΤΗΜΑ 1 ον 1.. Σφαίρα, μάζας m 1, κινούμενη με ταχύτητα υ1, συγκρούεται μετωπικά και ελαστικά με ακίνητη σφαίρα μάζας m. Οι ταχύτητες των σφαιρών μετά την κρούση α. έχουν
Διαγώνισμα ΦΥΣΙΚΗ Κ.Τ Γ ΛΥΚΕΙΟΥ ΖΗΤΗΜΑ 1 ον 1.. Σφαίρα, μάζας m 1, κινούμενη με ταχύτητα υ1, συγκρούεται μετωπικά και ελαστικά με ακίνητη σφαίρα μάζας m. Οι ταχύτητες των σφαιρών μετά την κρούση α. έχουν
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
ΟΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 3.1 Στο σχήμα φαίνεται μία πόρτα και οι δυνάμεις που δέχεται. Ροπή ως προς τον άξονα z z έχει η δύναμη:
 3.1 Στο σχήμα φαίνεται μία πόρτα και οι δυνάμεις που δέχεται. Ροπή ως προς τον άξονα z z έχει η δύναμη: α. F 1 β. F 2 γ. F 3 δ. F 4 3. 2 Ένα σώμα δέχεται πολλές ομοεπίπεδες δυνάμεις. Τότε: α. οι ροπές
3.1 Στο σχήμα φαίνεται μία πόρτα και οι δυνάμεις που δέχεται. Ροπή ως προς τον άξονα z z έχει η δύναμη: α. F 1 β. F 2 γ. F 3 δ. F 4 3. 2 Ένα σώμα δέχεται πολλές ομοεπίπεδες δυνάμεις. Τότε: α. οι ροπές
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σώμα εκτελεί ταυτόχρονα τις ταλαντώσεις με εξισώσεις x1 A2 f1t και x1 A2 f2t. Οι ταλαντώσεις έχουν την ίδια διεύθυνση, την ίδια θέση ισορροπίας
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σώμα εκτελεί ταυτόχρονα τις ταλαντώσεις με εξισώσεις x1 A2 f1t και x1 A2 f2t. Οι ταλαντώσεις έχουν την ίδια διεύθυνση, την ίδια θέση ισορροπίας
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΕΚΦΩΝΗΣΕΙΣ. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικά Θέµατα ΟΕΦΕ 008 1 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που
Επαναληπτικά Θέµατα ΟΕΦΕ 008 1 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
υ r 1 F r 60 F r A 1
 2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ
 ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
F Στεφάνου Μ. 1 Φυσικός
 F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Μυς κεφαλής - τραχήλου άνω άκρου
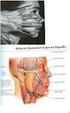 Μυς κεφαλής - τραχήλου άνω άκρου Μύες του προσώπου. Λέγονται και «μιμικοί». Κινητική νεύρωση Προσωπικό νεύρο -VII Αισθητική νεύρωση τρίδυμο νεύρο -V Α) Κογχική ομάδα 1. Σφιγκτήρας των βλεφάρων 2. Επισκύνιος
Μυς κεφαλής - τραχήλου άνω άκρου Μύες του προσώπου. Λέγονται και «μιμικοί». Κινητική νεύρωση Προσωπικό νεύρο -VII Αισθητική νεύρωση τρίδυμο νεύρο -V Α) Κογχική ομάδα 1. Σφιγκτήρας των βλεφάρων 2. Επισκύνιος
Προτεινόμενα θέματα για τις εξετάσεις 2011
 Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 12 ΙΟΥΝΙΟΥ 2017 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1 ΙΟΥΝΙΟΥ 017 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1 ΙΟΥΝΙΟΥ 017 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την
ΦΥΣ. 111 Τελική Εξέταση: 17-Δεκεµβρίου-2017
 ΦΥΣ. 111 Τελική Εξέταση: 17-Δεκεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται
ΦΥΣ. 111 Τελική Εξέταση: 17-Δεκεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 20 ΑΠΡΙΛΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 20 ΑΠΡΙΛΙΟΥ 2016-1 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΟΧΤΩ (8) Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 20 ΑΠΡΙΛΙΟΥ 2016-1 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΟΧΤΩ (8) Στις ερωτήσεις 1-4 να γράψετε
Θέμα Α Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλάντωση Doppler Ρευστά -Στερεό Ονοματεπώνυμο Μαθητή: Ημερομηνία: 04-03-2019 Επιδιωκόμενος Στόχος: 80/100 Θέμα Α Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλάντωση Doppler Ρευστά -Στερεό Ονοματεπώνυμο Μαθητή: Ημερομηνία: 04-03-2019 Επιδιωκόμενος Στόχος: 80/100 Θέμα Α Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2004
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση..
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση..
ΑΠΑΝΤΗΣΕΙΣ. Η κινητική ενέργεια του κυλίνδρου λόγω της μεταφορικής του κίνησης δίνεται από την σχέση: Κ μετ = 1 m u 2 cm
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΟΥ ΛΥΕΙΟΥ Μ.ΤΕΤΑΡΤΗ 0 ΑΠΡΙΛΙΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΗ ΘΕΤΙΗΣ - ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ Θέμα 1 ο 1. γ. γ 3. α 4. δ 5. α) Λ β) Σ γ)
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΟΥ ΛΥΕΙΟΥ Μ.ΤΕΤΑΡΤΗ 0 ΑΠΡΙΛΙΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΗ ΘΕΤΙΗΣ - ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ Θέμα 1 ο 1. γ. γ 3. α 4. δ 5. α) Λ β) Σ γ)
Ποια μπορεί να είναι η κίνηση μετά την κρούση;
 Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5o ΔΙΑΓΩΝΙΣΜΑ ΔΙΑΓΩΝΙΣΜΑ - ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5o ΔΙΑΓΩΝΙΣΜΑ ΔΙΑΓΩΝΙΣΜΑ - ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5o ΔΙΑΓΩΝΙΣΜΑ ΔΙΑΓΩΝΙΣΜΑ - ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΡΟΠΕΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ
 ΡΟΠΕΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ Ροπή Δύναμης Θα έχετε παρατηρήσει πως κλείνετε ευκολότερα μια πόρτα, αν την σπρώξετε σε μια θέση που βρίσκεται σχετικά μακρύτερα από τον άξονα περιστροφής της (τους μεντεσέδες
ΡΟΠΕΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ Ροπή Δύναμης Θα έχετε παρατηρήσει πως κλείνετε ευκολότερα μια πόρτα, αν την σπρώξετε σε μια θέση που βρίσκεται σχετικά μακρύτερα από τον άξονα περιστροφής της (τους μεντεσέδες
Το μυϊκό σύστημα αποτελείται από τους μύες. Ο αριθμός των μυών του μυϊκού συστήματος ανέρχεται στους 637. Οι μύες είναι όργανα για τη σωματική
 Μύες Το μυϊκό σύστημα αποτελείται από τους μύες. Ο αριθμός των μυών του μυϊκού συστήματος ανέρχεται στους 637. Οι μύες είναι όργανα για τη σωματική κινητικότητα, την σπλαχνική κινητικότητα και τη κυκλοφορία
Μύες Το μυϊκό σύστημα αποτελείται από τους μύες. Ο αριθμός των μυών του μυϊκού συστήματος ανέρχεται στους 637. Οι μύες είναι όργανα για τη σωματική κινητικότητα, την σπλαχνική κινητικότητα και τη κυκλοφορία
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα
 Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ F 2 F 3 F 1 F 4
 1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
Επαναληπτικό Διαγώνισμα Ι Φυσικής Γ Λυκείου
 Επαναληπτικό Διαγώνισμα Ι Φυσικής Γ Λυκείου Διάρκεια: 3 ώρες Θέμα Α 1) Ένα στερεό σώμα περιστρέφεται γύρω από ακλόνητο άξονα. Αν διπλασιαστεί η στροφορμή του, χωρίς να αλλάξει ο άξονας περιστροφής γύρω
Επαναληπτικό Διαγώνισμα Ι Φυσικής Γ Λυκείου Διάρκεια: 3 ώρες Θέμα Α 1) Ένα στερεό σώμα περιστρέφεται γύρω από ακλόνητο άξονα. Αν διπλασιαστεί η στροφορμή του, χωρίς να αλλάξει ο άξονας περιστροφής γύρω
2) Βάρος και κυκλική κίνηση. Β) Κυκλική κίνηση
 Β) Κυκλική κίνηση 1) Υπολογισμοί στην ομαλή κυκλική κίνηση. Μια μικρή σφαίρα, μάζας 2kg, εκτελεί ομαλή κυκλική κίνηση, σε κύκλο κέντρου Ο και ακτίνας 0,5m, όπως στο σχήμα. Τη χρονική στιγμή t=0 η σφαίρα
Β) Κυκλική κίνηση 1) Υπολογισμοί στην ομαλή κυκλική κίνηση. Μια μικρή σφαίρα, μάζας 2kg, εκτελεί ομαλή κυκλική κίνηση, σε κύκλο κέντρου Ο και ακτίνας 0,5m, όπως στο σχήμα. Τη χρονική στιγμή t=0 η σφαίρα
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1ο: ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1ο: ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΟΡΟΣΗΜΟ. 3.1 Στο σχήμα φαίνεται μία πόρτα και οι δυνάμεις που δέχεται. Ροπή ως προς τον άξονα z z έχει η δύναμη: α. σχήμα 1, β. σχήμα 2, γ.
 ÑïðÞ äýíáìçò - Ióïññïðßá óôåñåïý óþìáôïò ÊÅÖÁËÁÉÏ 4.1 Στο σχήμα φαίνεται μία πόρτα και οι δυνάμεις που δέχεται. Ροπή ως προς τον άξονα z z έχει η δύναμη: α. F 1 β. F 2 γ. F δ. F 4.2 Ένα σώμα δέχεται πολλές
ÑïðÞ äýíáìçò - Ióïññïðßá óôåñåïý óþìáôïò ÊÅÖÁËÁÉÏ 4.1 Στο σχήμα φαίνεται μία πόρτα και οι δυνάμεις που δέχεται. Ροπή ως προς τον άξονα z z έχει η δύναμη: α. F 1 β. F 2 γ. F δ. F 4.2 Ένα σώμα δέχεται πολλές
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣ. 131 Τελική εξέταση: 10-Δεκεμβρίου-2005
 ΦΥΣ. 131 Τελική εξέταση: 10-Δεκεμβρίου-2005 Πριν αρχίσετε συμπληρώστε τα στοιχεία σας (ονοματεπώνυμο και αριθμό ταυτότητας). Ονοματεπώνυμο Αριθμός ταυτότητας Σας δίνονται 20 ισότιμα προβλήματα (10 βαθμοί
ΦΥΣ. 131 Τελική εξέταση: 10-Δεκεμβρίου-2005 Πριν αρχίσετε συμπληρώστε τα στοιχεία σας (ονοματεπώνυμο και αριθμό ταυτότητας). Ονοματεπώνυμο Αριθμός ταυτότητας Σας δίνονται 20 ισότιμα προβλήματα (10 βαθμοί
F r. www.ylikonet.gr 1
 3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2019 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 019 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 019 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΠΕΡΙΣΤΡΟΦΗ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΕΠΙΒΡΑΔΥΝΟΜΕΝΟΣ ΑΠΟ ΔΥΟ ΑΒΑΡΗΣ ΡΑΒΔΟΥΣ
 ΠΕΡΙΣΤΡΟΦΗ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΕΠΙΒΡΑΔΥΝΟΜΕΝΟΣ ΑΠΟ ΔΥΟ ΑΒΑΡΗΣ ΡΑΒΔΟΥΣ Κυκλικός δίσκος ακτίνας R και μάζας m, περιστρέφεται με σταθερή γωνιακή ταχύτητα ω 0 (η τριβή στον άξονα περιστροφής θεωρείται αμελητέα).
ΠΕΡΙΣΤΡΟΦΗ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΕΠΙΒΡΑΔΥΝΟΜΕΝΟΣ ΑΠΟ ΔΥΟ ΑΒΑΡΗΣ ΡΑΒΔΟΥΣ Κυκλικός δίσκος ακτίνας R και μάζας m, περιστρέφεται με σταθερή γωνιακή ταχύτητα ω 0 (η τριβή στον άξονα περιστροφής θεωρείται αμελητέα).
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 10 ΣΕΠΤΕΜΒΡΙΟΥ 2015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 10 ΣΕΠΤΕΜΒΡΙΟΥ 2015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Τίτλος Κεφαλαίου: Στερεό σώµα. Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως. Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1
 Τίτλος Κεφαλαίου: Στερεό σώµα ιδακτική Ενότητα: Κινηµατική του Στερεού Σώµατος Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως Θέµα 3ο: Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1 ιδακτική Ενότητα: Ροπή
Τίτλος Κεφαλαίου: Στερεό σώµα ιδακτική Ενότητα: Κινηµατική του Στερεού Σώµατος Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως Θέµα 3ο: Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1 ιδακτική Ενότητα: Ροπή
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΠΕΜΠΤΗ 3 ΙΟΥΝΙΟΥ 2004 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΠΕΜΠΤΗ 3 ΙΟΥΝΙΟΥ 2004 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που
Εσωτερικές Αλληλεπιδράσεις Νο 3.
 Το θέμα του 05, (επαναληπτικές) Εσωτερικές λληλεπιδράσεις Νο 3. Δύο ράβδοι είναι συνδεδεμένες στο άκρο τους και σχηματίζουν σταθερή γωνία 60 ο μεταξύ τους, όπως φαίνεται στο Σχήμα. Οι ράβδοι είναι διαφορετικές
Το θέμα του 05, (επαναληπτικές) Εσωτερικές λληλεπιδράσεις Νο 3. Δύο ράβδοι είναι συνδεδεμένες στο άκρο τους και σχηματίζουν σταθερή γωνία 60 ο μεταξύ τους, όπως φαίνεται στο Σχήμα. Οι ράβδοι είναι διαφορετικές
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 3 Ο ΔΥΝΑΜΕΙΣ
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 3 Ο ΔΥΝΑΜΕΙΣ 3.1 Η έννοια της δύναμης ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Στο κεφάλαιο των κινήσεων ασχοληθήκαμε με τη μελέτη της κίνησης χωρίς να μας απασχολούν τα αίτια που προκαλούν την κίνηση
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 3 Ο ΔΥΝΑΜΕΙΣ 3.1 Η έννοια της δύναμης ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Στο κεφάλαιο των κινήσεων ασχοληθήκαμε με τη μελέτη της κίνησης χωρίς να μας απασχολούν τα αίτια που προκαλούν την κίνηση
3.3. Δυναμική στερεού.
 3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος. και Α 2
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
