που δέχονται οι τροχοί αυτοί αποτελούν κινητήριες δυνάµεις για το αυτοκί νητο, δηλαδή είναι δυνάµεις οµόρροπες προς την κίνησή του, ένω οι τριβές T!
|
|
|
- Τάνις Χατζηιωάννου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Tο κέντρο µάζας ενός επιβατηγού αυτοκινήτου απέχει από το οριζόντιο έδαφος απόσταση h. Δίνεται η µάζα Μ του αυτοκινήτου η µάζα m και η ακτίνα R κάθε τροχού, η επιτάχυνση g της βαρύτητας και οι αποστάσεις b, b των οπισθίων και εµπροσθίων τροχών αντιστοίχως, από την κατακόρυφη διεύθυνση που διέρχεται από το κέντρο µάζας του αυτοκινήτου. i) Mε την προϋπόθεση ότι η κίνηση του αυτοκινήτου είναι στους πίσω τροχούς του, µε αποτέλεσµα να εξασκείται σταθερή στρεπτική ροπή περί τον άξονα τους µέτρου τ κ και ότι οι τροχοί κυλίωνται χωρίς ολίσθηση, να βρεθεί η επιτάχυνση εκκίνησης του αυτοκινήτου. ii) Να υπολογίσετε τις κάθετες αντιδράσεις επί των τροχών του αυτο κινήτου και να βρείτε την συνθήκη ώστε να µην ανασηκώνεται το µπροστινό του µέρος κατά την εκκίνησή του, µε την προϋπόθεση ότι ο συντελεστής οριακής τριβής µεταξύ του εδάφους και των τροχών είναι αρκετά µεγάλος, ώστε να αποφεύγεται η ολίσθησή τους. iii) Eάν ο συντελεστής τριβής ολίσθησης µεταξύ των τροχών και του οδοστρώµατος είναι n, να βρεθεί η µέγιστη τιµή της επιτάχυνσης εκ κίνησής του, ώστε οι τροχοί του να µη ολισθαίνουν, υπό την προϋπό θεση ότι οι µπροστινοί τροχοί του δεν ανασηκώνονται. Δίνεται η ροπή αδράνειας Ι=mR / κάθε τροχού ως προς τον άξονα περιστροφής του. ΛYΣH: i) Το αυτοκίνητο κατά την εκκίνησή του δέχεται το βάρος του W και τις αντιδράσεις του οδοστρώµατος στους τέσσερις τροχούς του, οι οποίες αναλύονται στην στατική τριβή και την κάθετη αντίδραση. Επειδή η µηχανή του αυτοκινήτου δίνει περιστροφική κίνηση στους πίσω τροχούς του, οι τριβές T που δέχονται οι τροχοί αυτοί αποτελούν κινητήριες δυνάµεις για το αυτοκί νητο, δηλαδή είναι δυνάµεις οµόρροπες προς την κίνησή του, ένω οι τριβές T στους µπροστινούς τροχούς είναι δυνάµεις αντίρροπες προς την κίνησή του (σχήµα ). Eφαρµόζοντας για την µεταφορική κίνηση του κέντρου µάζας C του αυτοκι νήτου το δεύτερο νόµο κίνησης του Nεύτωνα, παίρνουµε τη σχέση: T - T = Μa C ()
2 όπου a C η επιτάχυνση του κέντρου µάζας. Εξάλλου κάθε οπίσθιος τροχός του αυτοκινήτου δέχεται περί τον άξονά του την στρεπτική ροπή ", η οποία οφείλεται στην σύζευξη του άξονα µε τον κινητήρα του αυτοκινήτου και την Σχήµα ροπή της τριβής T, η οποία αντιτίθεται στην περιστροφή του. Σύµφωνα µε τον θεµελιώδη νόµο της περιστροφικής κίνησης για κάθε οπίσθιο τροχό θα ισχύει: " - T R = I#' " - T R = mr #'/ T R = " - mr(r#')/ T = " / R- ma C / () όπου η ' γωνιακή επιτάχυνση του τροχού, της οποίας το µέτρο είναι ίσο µε a C /R, αφου ο τροχός κυλίεται χωρίς ολίσθηση. Εφαρµόζοντας τον ίδιο νόµο για κάθε µπροστινό τροχό παίρνουµε την σχέση: T R = I' T R = mr '/ T = ma C / (3) H () λόγω των () και (3) δίνει: " / R - ma C - ma C = Ma C " / R = (M + m)a C a C = " R(M + m) (4) ii) Eίναι γνωστό ότι η στροφορµή ενός συστήµατος σωµάτων περί ένα σηµείο είναι το διανυσµατικό άθροισµα των αντίστοιχων στροφορών των σωµάτων που το αποτελούν. Στην περίπτωση του αυτοκινήτου η στροφορµή του περί το κέντρο µάζας του C θα είναι το διανυσµατικό άθροισµα των αντίστοιχων στρο φορµών των τεσσάρων τροχών του, της στροφορµής της στροφορµής = * του υπόλοιπου µέρους του, δηλαδή θα ισχύει: L () C + L () C + L (3) C + L (4) ( C + L ) C + * Όµως η στροφορµή του τροχού () περί το C είναι: () = L O + ( r m v ) = mr " + ( r m 0 ) = mr ( ) του κινητήρα του και (5) " (6)
3 όπου m, R η µάζα και η ακτίνα αντιστοίχως του τροχού, r το διάνυσµα θέσεως του κέντρου Ο του τροχού ως προς το C, η γωνιακή ταχύτητα περιστροφής του τροχού περί το Ο και v η ταχύτητα του Ο στο σύστηµα αναφοράς του κέντρου µάζας C, η οποία είναι µηδενική διότι οι ταχύτητες των C και Ο είναι ίδιες στο σύστηµα αναφοράς του εδάφους. Όµοια εργαζόµενοι για τους άλλους τρεις τροχούς βρίσκουµε ότι: () = (3) = (4) = mr / (7) Εξάλλου εύκολα προκύπτει ότι L * C = 0, διότι δεν υπάρχει περιστροφή του υπό λοιπου µέρους του οχήµατος περί το δικό του κέντρο µάζας, ενώ για την στροφορµή του κινητήρα περί το C ισχύει: ( ) = I " (8) όπου Ι κ η ροπή αδράνειας του κινητήρα περί τον άξονα περιστροφής του και " η γωνιακή ταχύτητα περιστροφής του περί τον άξονα αυτόν. Με βάση τα παρα πάνω η σχέση (5) γράφεται: = 4mR / + I " " = mr + I " " (9) Παραγωγίζοντας την (9) ως προς τον χρόνο t παίρνουµε την σχέση: d = mr d + I " d " d " d = mr '+I " (0) Αν δεχθούµε ότι ο κινητήρας του αυτοκινήτου στρέφεται µε σταθερή γωνιακή ταχύτητα, θα ισχύει d " /= 0 και η (6) παίρνει την µορφή: d = mr ' () Όµως στο σύστηµα αναφοράς του εδάφους ισχύει η σχέση: d = (" (7) C ) ( " C ) = mr # ' () όπου ( " C ) η συνισταµένη εξωτερική ροπή περί το C που δέχεται το όχηµα, δηλαδή στο άθροισµα αυτό δεν υπεισέρχεται η κινητήρια ροπή στους τροχούς διότι αυτή αποτελεί εσωτερική ροπή για το αυτοκίνητο. Παρατήρηση: Πρέπει να τονίσουµε ότι η σχέση: dl / = (" )
4 ισχύει και στην περίπτωση που η στροφορµή και η συνισταµένη ροπή θεωρούν ται περί ένα σηµείο που είναι ακίνητο ή κινείται µε την ταχύτητα του κέντρου µάζας C, λογουχάρη για τα σηµεία του άξονα περιστροφής κάθε τροχού. Η διανυσµατική σχέση () µετατρέπεται σε σχέση αλγεβρικών τιµών αν λάβου µε αυθαίρετα ως θετική φορά, την φορά που προχωρεί δεξιόστροφος κοχλίας στρεφόµενος όπως οι τροχοί, οπότε θα έχουµε την σχέση: N b - T h + T h - N b = mr ' () N b - N b - h(t - T ) = mra C N b - N b - hma C / = mra C N b - N b = ( mr + Mh/)a C (3) Eξάλλου το αυτοκίνητο δεν έχει κίνηση κατά την κατακόρυφη διεύθυνση, οπό τε ισχύει η σχέση: N + N = Mg/ (4) Oι σχέσεις (3) και (4) αποτελούν ένα σύστηµα πρώτου βαθµού ως προς Ν και Ν, η λύση του οποίου δίνει: και N = N = Mgb mr + Mh + (b + b ) (b + b ) a C (5) Mgb mr + Mh - (b + b ) (b + b ) a C (6) Από την (5) προκύπτει ότι κατα την εκκίνηση του αυτοκινήτου ισχύει Ν >0 που σηµαίνει ότι οι πίσω τροχοί του δεν ανασηκώνονται. Για να µην ανασηκώ νονται και οι µπροστινοί τροχοί πρέπει να ισχύει Ν 0, η οποία µε βάση την (6) δίνει: (4) Mgb mr + Mh - (b + b ) (b + b ) a C 0 Mgb (b + b ) mr + M " # (b + b ) R(M + m) Mgb " # (mr + Mh) R(M + m) " # MgRb $ M + m ' & ) (7) % mr + Mh( H (7) αποτελεί την ζητούµενη συνθήκη για να µην ανασηκώνεται το µπροστι νό µέρος του αυτοκινήτου κατα την εκκίνησή του.
5 iii) Για να µην ολισθαίνουν οι τροχοί του αυτοκινήτου κατα την εκκίνησή του πρέπει τα µέτρα των τριβών T και T να µην υπερβαίνουν τις αντίστοιχες οριακές τριβές nn και nn, δηλαδή πρέπει να ισχύει: T nn " # T nn $ (),(3) " / R- ma C / # nn $ % ma C / # nn & (+ ) " / R# n(n + N ) " # nrmg / (8) H (8) αποτελεί την ζητούµενη συνθήκη για να µην ολισθαίνουν οι τροχοί του αυτοκινήτου κατα την εκκίνησή του. P.M. fysikos Ένας ποδηλατιστής κινείται οµαλά σε κατηφορικό δρόµο γωνίας κλίσεως φ, χωρίς να χρησιµοποιεί το πεντάλ του ποδήλατου. Η τριβή µεταξύ των τροχών του ποδήλατου και του οδοστώµατος έχει τιµή που επιτρέπει στους τροχούς να κυλίωνται χωρίς ολίσθηση, ενώ θεω ρείται αµελητέα η παραµόρφωση του εδάφους και των τροχών στις επιφάνειες συνεπαφής τους. i) Εάν Μ είναι η συνολική µάζα του συστήµατος ποδήλατο-ποδηλατισ τής, h η απόσταση του κέντρου µάζας του από το οδόστρωµα και L, L οι αποστάσεις των κέντρων του πίσω και του µπροστινού τροχού αντιστοίχως από την ευθεία που διέρχεται από το κέντρο µάζας και είναι κάθετη στο οδόστρωµα, να βρεθεί η επιτάχυνση του κέντρου µάζας του συστήµατος. ii) Nα βρεθεί η συνθήκη, ώστε να µην ανασηκώνεται ο πίσω τροχός του ποδήλατου. Δίνεται η µάζα m κάθε τροχού που θεωρείται οµοιό µορφα κατανεµηµένη στην περιφέρειά του, η ακτίνα του R, ενώ παραλείπεται η αντίσταση του αέρα. ΛΥΣΗ: i) To σύστηµα ποδήλατο-ποδηλατιστής στην διάρκεια της καθοδικής του κίνησης δέχεται το βάρος του W, που αναλύεται στην παράλληλη προς το οδόστρωµα συνιστώσα W x και στην κάθετη προς αυτό συνιστώσα W y και τις αντιδράσεις του εδάφους στους δύο τροχούς του, που αναλύονται στις στατικές τριβές T, T επί του οπίσθιου και του µπροστινού τροχού αντιστοιχως και στις αντίστοιχες κάθετες αντιδράσεις N, N οι φορείς των οποίων διέρχονται από τα κέντρα των τροχών (σχήµα ). Εφαρµόζοντας για το κέντρο µάζας C του συστήµατος τον δεύτερο νόµο κίνησης του Νεύτωνα, παίρνουµε την σχέση: W x - T - T = Ma C Mgµ" - T - T = Ma C ()
6 όπου a C η επιτάχυνση του κέντρου µάζας. Εξάλλου ο θεµελιώδης νόµος της στροφικής κίνησης δίνει για την περιστροφή των δύο τροχών τις σχέσεις: T R= mr '" # T R= mr ' $ T = mr' " # T = mr' $ T = ma C " T = ma C # () Σχήµα όπου ' η γωνιακή επιτάχυνση περιστροφής κάθε τροχού, της οποίας το µέτρο έιναι ίσο µε a C /R διότι οι τροχοί κυλίωνται. Συνδυάζοντας τις σχέσεις () και () παίρνουµε: Mgµ" - ma C = Ma C a C = Mgµ" (3) M + m ii) Επειδή το κέντρο µάζας δεν κινείται κάθετα προς το κεκλιµένο οδόστρωµα, µπορούµε να γράψουµε την σχέση: N + N = W y N + N = Mg"#$ (4) Μια άλλη σχέση µεταξύ των Ν, Ν θα προκύψει αν χρησιµοποιήσουµε την έννοια της στροφορµής του συστήµατος περί το κέντρο µάζας του C. H στρο φορµή του συστήµατος περί το C είναι ίση µε το διανυσµατικό άθροισµα των αντίστοιχων στροφορµών (), αντιστοίχως και της στροφορµής δηλαδή ισχύει η σχέση: = L () C + L () C + + Όµως για τις στροφορµές * () και L () C = L O + ( r m v ) " L () C = L O + ( r m v $ # ) % $ * () του πίσω και του µπροστινού τροχού του υπόλοιπου µέρους του συστήµατος, () ισχύουν οι σχέσεις: L () C = mr + ( r " m 0 ) # L () C = mr + ( r " m 0 % $ ) &% (5)
7 () = () = mr (6) όπου, L O, L O οι ιδιοστροφορµές του πίσω και του µπροστινού τροχού αντι στοίχως, r, r τα διανύσµατα θέσεως των κέντρων Ο και Ο των τροχών αυτών ως προς το C, η κοινή γωνιακή ταχύτητα περιστροφής τους και v, v οι ταχύτητες των Ο και Ο στο σύστηµα αναφοράς του κέντρου µάζας C, οι οποίες είναι µηδενικές, διότι οι ταχύτητες των C, Ο, Ο είναι ίδιες στο σύστηµα αναφοράς του εδάφους. Εξάλλου εύκολα προκύπτει ότι L * C = 0, διότι δεν υπάρ χει περιστροφή του υπολοίπου µέρους του συστήµατος περί το δικό του κέντρο µάζας. Με βάση τα παραπάνω η σχέση (5) παίρνει την µορφή: = mr Παραγωγίζοντας την (7) ως προς τον χρόνο t παίρνουµε την σχέση: d = mr d d (7) = mr ' (8) Όµως στο σύστηµα αναφοράς του εδάφους ισχύει η σχέση: d = (" (8) C ) ( " C ) = mr # ' (9) όπου ( " C ) η συνισταµένη εξωτερική ροπή περί το C που δέχεται το σύτηµα. Η διανυσµατική σχέση (9) µετατρέπεται σε σχέση αλγεβρικών τιµών αν λάβου µε αυθαίρετα ως θετική φορά, την φορά που προχωρεί δεξιόστροφος κοχλίας στρεφόµενος όπως οι τροχοί, οπότε θα έχουµε την σχέση: () -N L + N L + ht + ht = mra C L(-N + N ) + hma C = mra C L(N - N ) = m(h - R)a C (0) Oι σχέσεις (4) και (0) αποτελούν ένα σύστηµα πρώτου βαθµού ως προς Ν και Ν, η λύση του οποίου δίνει: και N N = Mg"#$ 3 = Mg"#$ 3 + m(h - R)a C 3L - m(h - R)a C 3L () () Από την () προκύπτει ότι κατα την κίνηση του συστήµατος ισχύει Ν >0, που σηµαίνει ότι ο µπροστινός τροχος του ποδήλατου δεν ανασηκώνεται. Για να
8 µην ανασηκώνεται και ο πίσω τροχός πρέπει να ισχύει Ν 0, η οποία µε βάση την () δίνει: Mg"#$ 3 - m(h - R)a C 3L (3) % 0 Mg"#$ % m(h - R) L Mg&µ$ M + m "#$ %µ$ & ' h - R * ), ( L + m M + m "# $ % h - R ( ' * & L ) m M + m (3) H (3) αποτελεί την ζητούµενη συνθήκη για να µην ανασηκώνεται ο πίσω τρο χός του ποδήλατου. P.M. fysikos Ένας ποδηλατιστής κινείται οµαλά σε κατηφορικό δρόµο γωνίας κλί σεως φ, χωρίς να χρησιµοποιεί το πεντάλ του ποδήλατου. Στη συνέ χεια κινείται οµαλά σε ανηφορικό δρόµο γωνίας κλίσεως φ, εξασκών τας στο πεντάλ δύναµη που είναι κάθετη στο άκρο του στρφάλου και έχει σταθερό µέτρο. Eάν το βάρος του ποδηλατιστή και του ποδηλά του είναι w, το µήκος του στρόφαλου του πεντάλ L και η γωνιακή ταχύτητα περιστροφής του ", να βρεθεί το µέτρο της δύναµης στο πεντάλ, ώστε το σύστηµα ποδήλατο-ποδηλατιστής να κινείται στον ανηφορικό δρόµο µε σταθερή ταχύτητα v C. H αντίσταση του αέρα να θεωρηθεί αµελητέα, οι δε τροχοί του ποδήλατου κυλίωνται χωρίς ολίσθηση. ΛYΣH: Tο σύστηµα ποδήλατο-ποδηλατιστής κατά την κίνησή του στον κατη φορικό δρόµο δέχεται το βάρος του w, που αναλύεται στην κάθετη προς τον δρόµο συνιστώσα w y και στην παράλληλη προς αυτόν συνιστώσα w x (σχ. 3) και τις αντιδράσεις των τροχών, οι οποίες αναλύονται στις στατικές τριβές T, T παράλληλες προς τον δρόµο και αντίθετης φοράς προς την κίνηση και στις κά Σχήµα 3 θετες αντιδράσεις N N (σχ 3). Λόγω της ισοταχούς κύλισης των τροχών του ποδη λάτου η περιστροφή κάθε τροχού περί τον άξονά του είναι οµαλή, που ση µαίνει ότι η ροπή της αντίστοιχης στατικής τριβής περί τον άξονα αυτόν αντι
9 σταθµίζεται από την αντίστοιχη τριβή κυλίσεως. Δηλαδή υπάρχει παραµόρφω ση στην επιφάνεια επαφής εδάφους-τροχού που µετατοπίζει την κάθετη αντίδ Σχήµα 4 ραση µε αποτέλεσµα ο φορέας της να µην διέρχεται από το κέντρο του τρο χού και µε τον τρόπο αυτόν δηµιουργείται τριβή κύλισης που είναι ροπή αντιτιθέ µενη στην περιστροφή του. Αν δεχθούµε ότι ο συντελεστής τριβής κυλίσεως έχει την ίδια τιµή b και στους δύο τροχούς, τότε θα έχουµε τις σχέσεις: T R = N b " T R = N b # T = N b/r " T = N b/r# () Eξάλλου η ισοταχής µεταφορική κίνηση του συστήµατος κατά µήκος του κεκλιµένου δρόµου και η ανυπαρξία κίνησης κάθετα προς τον δρόµο επιβάλλει τις σχέσεις: T + T = w x " N + N = w y # T + T = wµ" & ' N + N = w#$%" ( () N b R + N b R = wµ" # $ % () b ( R N + N ) = wµ" b R w"#$ = w%µ$ b = R µ" #$%" () Όταν το σύστηµα ποδήλατο-ποδηλατιστής κινείται στον ανηφορικό δρόµο, δέχε ται ακριβώς τις ίδιες δυνάµεις, µε µόνη διαφορά ότι, τώρα η στατική τριβή T ' στον πίσω τροχό αποτελεί προωθητική δύναµη για την µεταφορική κίνηση του συστήµατος, δηλαδή είναι οµόρροπη της κίνησής του, ενώ η στατική τριβή T ' επί του µπροστινού τροχού εξακολουθεί να είναι αντίρροπη της µεταφορικής κίνησης (σχ. 6). Αν δεχθούµε ότι ο ανηφορικός δρόµος είναι της ίδιας κατασ κευής µε τον κατηφορικό, τότε οι κάθετες αντιδράσεις N ', N ' επί των τρο χών δηµιουργούν τριβές κύλισης που αντιτίθενται στην περιστροφή τους. Αν επικεντώσουµε την προσοχή µας στον µπροστινό τροχό, λογω της οµαλής περιστροφής του περί τον άξονά του, µπορούµε να γράψουµε την σχέση: T' R = N' b T' = N' b/r (3)
10 Αν αναφερθούµε στο σύστηµα του πίσω τροχού και του κυκλικού γραναζιού που είναι οµοαξονικά συσσωµατοµένο µε αυτόν, το σύστηµα δέχεται την ροπή της στατικής τριβής T ' και τις ροπές των δυνάµεων F, F που ασκούν οι δύο κλά δοι της αλυσίδας που συνδέει το γρανάζι του πίσω τροχού µε το κυκλικό γρα Σχήµα 5 νάζι του πεντάλ του ποδήλατου (σχ. 6) Λόγω της οµαλής περιστροφής του συστήµατος (βλέπε προηγούµενο θέµα) ισχύει η σχέση: F R - F R - T' R - N' b = 0 R (F - F ) = T' R + N' b (4) όπου R η ακτίνα του γραναζιού. Eξάλλου το σύστηµα του πεντάλ και του γρα ναζιού που είναι συσσωµατωµένο µε αυτό, δέχεται την ροπή της δύναµης F που ασκεί µε τα πόδια του ο ποδηλάτης στα άκρα των δύο στροφάλων και τις Σχήµα 6 Σχήµα 7 ροπές των δυνάµεων - F, - F που δέχεται το γρανάζι από τους δύο κλάδους της αλυσίδας σύζευξης των δύο γραναζιών. Λόγω της οµαλής περιστροφής του συστήµατος αυτού ισχύει η σχέση: FL + F R - R F = 0 FL = R (F - F ) (5) όπου R η ακτίνα του γραναζιού του πεντάλ. Συνδυάζοντας τις σχέσεις (4) και (5) παίρνουµε: R R = T' R + N' b FL T' R + N' b = FL R R (6) Όµως, λόγω της οµαλής µεταφορικής κίνησης του συστήµατος στον ανηφορικό δρόµο θα ισχύει:
11 (3) T' - T' = wµ" T' - N' b/r = wµ" T' R - N' b= wrµ" T' R =N' b+ wrµ" (7) Συνδυάζοντας τις σχέσεις (6) και (7) παίρνουµε: N' b+ wrµ" + N' b = FL R R b(n' + N' ) = FL R R - wrµ" bw"#$ = FL R () - wr%µ$ R R µ" #$%" w#$%" + wrµ" = FL R R Rw (%µ$ "#$ "#$ + %µ$ "#$ ) = FL R R Rw %µ ( $ "#$ + $ ) = FL R (8) R Το γεγονός ότι η αλυσίδα δεν ολισθαίνει πάνω στα γρανάζια όλα τα σηµεία της έχουν κάθε στιγµή ταχύτητες του ίδιου µέτρου, και το γεγονός αυτό µας επιτ ρέπει να γράψουµε την σχέση: R = " R R /R = " / όπου η γωνιακή ταχύτητα περιστροφής των τροχών του ποδήλατου. Έτσι η σχέση (8) παίρνει την µορφή: F = Rw 'µ (& L " #$%& + & ) F = διότι λόγω της κυλίσεως των τροχών ισχύει v C =ωr. v C w 'µ (& L " #$%& + & ) P.M. fysikos Ένα βαγόνι φέρει κ το πλήθος τροχούς της ίδιας ακτίνας R, οι οποίοι βρίσκονται σε συµµετρικές θέσεις, ώστε το βάρος W του βαγονιού να
12 ισοκατανέµεται πάνω στους τροχούς. Eάν ο συντελεστής τριβής κυλί σεως µεταξύ κάθε τροχού και των σιδηροτροχιών πάνω στις οποίες κυλίεται είναι b, να βρεθεί η δύναµη έλξεως στο βαγόνι, ώστε αυτό να κινείται οριζόντια µε επιτάχυνση µέτρου a. Nα θεωρήσετε ότι, κάθε τροχός έχει µάζα m, που είναι συγκεντρωµένη στην περιφέρειά του. ΛYΣH: Eπειδή οι τροχοί του βαγονιού κυλίονται πάνω στις σιδηροτροχιές, η τριβή T πάνω σε κάθε τροχό είναι στατική τριβή, ενώ η αντίστοιχη κάθετη αντί δραση N της σιδηροτροχιάς δεν διέρχεται από τον άξονα περιστροφής του τροχού, αλλά ο φορέας της είναι µετατοπισµένος δεξιότερα κατά b (σχήµα 7) Eξάλλου το σύστηµα βαγόνι-τροχοί δέχεται τις ακόλουθες εξωτερικές δυνά µεις. Tο βάρος του W, την οριζόντια δύναµη έλξεως F, τις αντιδράσεις του εδά φους επί των τροχών του, οι οποίες αναλύονται στις στατικές τριβές T και στις κάθετες αντιδράσεις N, που για λόγους συµµετρίας είναι ίδιες σε κάθε τροχό. Σχήµα 8 Eφαρµόζοντας για την µεταφορική κίνηση του συστήµατος τον δεύτερο νόµο κίνησης του Νεύτωνα, παίρνουµε τη σχέση: F - κt = wa/g () Eξάλλου, εφαρµόζοντας για κάθε κυλιόµενο τροχό του βαγονιού τον θεµελιώ δη νόµο της στροφικής κίνησης έχουµε: TR - Nb = Iω TR - Nb = mr ω () όπου I η ροπή αδράνειας κάθε τροχού, ως προς τον άξονα περιστροφής του, η οποία είναι ίση µε mr (η µάζα του m θεωρείται συγκεντρωµένη στην περιφέ ρειά του) και ' η γωνιακή του επιτάχυνση. Όµως κατά τον κατακόρυφο άξο να το βαγόνι δεν έχει κίνηση, οπότε ισχύει κn=w δηλ. N=W/κ, και η () γράφε ται: TR - Wb/κ = mr ω' (3) Λόγω της κύλισης των τροχών ισχύει Rω = a και η (3) γράφεται: TR - Wb/κ = mra T = Wb/κR + ma (4) Συνδυάζοντας τις σχέσεις () και (4) έχουµε: F - (Wb/R + ma) = Wa/g F = a(w/g + m) + wb/r P.M. fysikos
περί το κέντρο της σφαίρας, ονοµάζεται δε τριβή κυλίσεως. Tο µέτρο της τρι βής κυλίσεως είναι προφανώς ανάλογο του µέτρου της N,!
 Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
Θεωρούµε µια βαρειά σφαίρα, η οποία ισορροπεί επί σχετικά µαλακού εδάφους, ώστε να προκαλεί σ αυτό µια µικρή παραµόρφωση. Λόγω της συµµετρίας που παρουσιάζει η παραµόρφωση αυτή, ως προς την κατακόρυφη
, της οποίας το µέτρο ικανοποιεί τη σχέση:
 Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση.
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση. i) Εάν Κ είναι το στιγµιαίο κέντρο περιστροφής του στερεού κάποια στιγµή και C η αντίστοιχη θέση του κέντρου µάζας
Δίνεται η ροπή αδράνειας I=mL 2 /3 της ράβδου ως προς τον άξονα περιστροφής της, η επιτάχυνση! g της βαρύτητας και ότι π 2!10.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας της εφαρµόζεται
από τον κατακόρυφο τοίχο, της οποίας ο φορέας είναι οριζόντιος και την δύναµη επα φής N!
 Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
Οµογενής συµπαγής κύβος ακµής α και µάζας m, ισορροπεί ακουµπώντας µε µια ακµή του σε κατακόρυφο τοίχο και µε µια του έδρα σε κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, όπως φαίνεται στο
i) Nα βρείτε την επιτάχυνση του κέντρου της τροχαλίας τ 1.
 Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
Στην διάταξη του σχήµατος 1) οι τροχαλίες τ 1 και τ έχουν την ίδια µάζα Μ που θεωρείται συγκεντρωµένη στην περι φέρειά τους και την ίδια ακτίνα R. Στο αυλάκι της σταθερής τροχα λίας τ έχει περιτυλιχθεί
i) Nα δείξετε ότι, κάθε στιγµή οι ταχύτητες των δύο πιθήκων ως προς το ακίνητο έδαφος είναι ίσες.
 Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
Δύο πιθηκάκια της ίδιας µάζας αναρριχώνται εκ της ηρεµίας κατά µήκος των τµηµάτων του αβαρούς σχοινιού, που διέρχεται από τον λαιµό µιας σταθερής τροχαλίας (σχ. ). H τροχαλία έχει αµελητέα µάζα και µπορεί
ΜΕΡΟΣ Γ! 2η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ΜΕΡΟΣ Γ η οµάδα λυµένων παραδειγµάτων Στις άκρες αβαρούς και λεπτής ράβδου µηκούς L, έχουν στερεωθεί δύο όµοιες σφαίρες, µάζας m και ακτίνας R, το δε σύστηµα στρέφεται µε σταθερή γωνιακή ταχύτητα περί
ακτινικής διεύθυνσης και στην οριακή τριβή T!"
 Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
Λεπτή κυκλική στεφάνη ακτίνας R και µάζας m, ισορρο πεί εφαπτόµενη σε δύο υποστηρίγµατα A και Γ, όπως φαίνεται στο σχήµα (1. Eάν ο συντελεστής οριακής τριβής µεταξύ της στεφάνης και των υποστη ριγµάτων
(τρίτος νόµος του Νεύτωνα) και την πλάγια αντίδραση του οριζόντιου εδάφους, η οποία αναλύεται στην τριβή ολίσθησης T!
 Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
Επί της κεκλιµένης έδρας µιας ορθογώνιας και ισοσκελούς σφήνας µάζας m, η οποία ισορροπεί πάνω σε οριζόντιο έδαφος, αφήνεται µικρός κύβος µάζας m. Μεταξύ του κύβου και της σφήνας δεν υπάρχει τριβή, ενώ
i) Nα βρεθεί η επιτάχυνση του κέντρου Κ της τροχαλίας την στιγµή t=0 αµέσως µετά την θραύση του νήµατος.
 H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
H τροχαλία του σχήµατος () µάζας m και ακτίνας R, ισορροπεί εξαρτηµένη από τα νήµατα ΑΒ και ΓΔ τα οποία είναι ισο κεκλιµένα ως προς την οριζόντια διεύθυνση κατα γωνία φ. Κάποια στιγµή κόβουµε το νήµα ΑΒ
ii) ii) Nα καθορίσετε το είδος της ισορροπίας της ράβδου.
 Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Oµογενής ράβδος Γ, βάρους w και µήκους L, είναι αρθρωµένη στο ένα άκρο της όπως φαίνεται στο σχήµα (), ενώ το άλλο άκρο της είναι δεµένο σε νήµα που διέρχεται από µικρή ακίνητη τροχαλία O, η οποία βρίσκεται
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή
 Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
Ένα σώµα µε µεγάλη µάζα Μ, κινείται µε σταθερή ταχύτητα µέτρου V 0 πάνω σε λείο οριζόντιο έδαφος κατευθυνόµενο προς κατακόρυφο τοίχο. Το σώµα κάποια στιγµή συγκρούεται ελα στικά και µετωπικά µε µια µπάλα
( ) ω ( ) = 0. Aπό τις σχέσεις (2) προκύπτει ή ότι το διάνυσµα v K. είναι κάθετο στα διανύσµα τα r A
 Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση και έστω (S) η κύρια* τοµή του στερεού κατά µια τυχαία χρονική στιγµή t. Να δείξετε ότι το αντίστοιχο προς την κύρια
Θεωρούµε στερεό σώµα που εκτελεί ως προς ένα αδρανειακό σύστηµα αναφοράς επίπεδη κίνηση και έστω (S) η κύρια* τοµή του στερεού κατά µια τυχαία χρονική στιγµή t. Να δείξετε ότι το αντίστοιχο προς την κύρια
i) τον λόγο των µαζών των δύο σφαιριδίων, ώστε αυτά µετά την κρού ση τους να φθάνουν στις αρχικές τους θέσεις και
 Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
Δύο αβαρή και µη εκτατά νήµατα του ίδιου µή κους είναι στερεωµένα στο ίδιο σηµείο Ο, ενώ στις ελεύθερες άκρες των νηµάτων είναι δεµένα δύο σφαιρίδια, µε µάζες 1 και. Eκτρέ πουµε τα σφαιρίδια από την θέση
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
( ) ( ) 2 1 K = K = m 2. ! = v 2 + v 1 R + r (3) H (1) λόγω της (3) γράφεται: R - v 2. + v 1. v 2. r > 0 (4) ! v K. + v 1 )R - v 2. = v 2. - v.
 Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
Το καρούλι του σχήµατος κυλίεται χωρίς ολίσ θηση πάνω σε οριζόντιο δοκάρι, που ολισθαίνει επί οριζοντίου έδα φους µε ταχύτητα v η οποία έχει την κατεύθυνση του δοκαριού. Η κύλιση του καρουλιού επιτυγχάνεται
την αρχή Ο του ΟΧY, που είναι ένα αδρανειακό σύστηµα αναφοράς. Εάν
 Ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε, παραµένουν αµετάβλητες µε τον χρόνο. Για την µελέτη της επίπεδης κίνησης στερεού
Ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε, παραµένουν αµετάβλητες µε τον χρόνο. Για την µελέτη της επίπεδης κίνησης στερεού
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο:
 6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
ΘΕΩΡΗΜΑ Α! του σώ µατος ισχύει η σχέση: η επιβατική ακτίνα ως προς το σηµείο P του τυχαίου υλικού σηµείου του στερεού µάζας m i και v!
 ΘΕΩΡΗΜΑ Α Ο ρυθµός µεταβολής της στροφορµής στερεού σώµατος, θεωρούµενης περί ένα σηµείο του ή της επεκτάσεώς του και αναφερόµενης σε κάποιο αδρανειακό σύστηµα, είναι κάθε στιγµή ίσος µε την συνολική ροπή
ΘΕΩΡΗΜΑ Α Ο ρυθµός µεταβολής της στροφορµής στερεού σώµατος, θεωρούµενης περί ένα σηµείο του ή της επεκτάσεώς του και αναφερόµενης σε κάποιο αδρανειακό σύστηµα, είναι κάθε στιγµή ίσος µε την συνολική ροπή
διέρχεται από το σηµείο τοµής Ο των φορέων του βάρους w! της ράβδου και της οριζόντιας αντίδρασης A!
 Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
Η οµογενής ράβδος ΑΒ του σχήµατος έχει βά ρος w και στηρίζεται διά του άκρου της Α σε τραχύ κεκλιµένο επί πεδο γωνίας κλίσεως φ ως προς τον ορίζοντα, ενώ το άλλο της άκρο Β ακουµπάει σε λείο κατακόρυφο
Kινηµατική άποψη της επίπεδης κίνησης
 Kινηµατική άποψη της επίπεδης κίνησης Θα λέµε ότι ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε), παραµέ νουν αµετάβλητες µε το
Kινηµατική άποψη της επίπεδης κίνησης Θα λέµε ότι ένα στερεό σώµα εκτελεί επίπεδη κίνηση, όταν οι αποστάσεις των υλικών του σηµείων από ένα ορισµένο επίπεδο αναφοράς (ε), παραµέ νουν αµετάβλητες µε το
ii) Nα υπολογιστεί η κινητική ενέργεια του συστήµατος σε συνάρτηση µε τον χρόνο. Δίνεται η επιτάχυνση! g της βαρύτητας.
 Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
Στην διάταξη του σχήµατος () η ράβδος ΑΒ είναι οµογενής, έχει µήκος L και µπορεί να στρέφεται περί οριζόντιο άξο να, που διέρχεται από σηµείο Ο ευρισκόµενο σε απόσταση 3L/4 από το άκρο της Α. Η τροχαλία
i) την µέγιστη ροπή του ζεύγους δυνάµεων που επιτρέπεται να ενερ γήσει επί του κυλίνδρου, ώστε αυτός να ισορροπεί και
 Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Oµογενής κύλινδρος µάζας m και ακτίνας R εφάπ τεται στα τοιχώµατα ενός αυλακιού, τα οποία είναι επίπεδες σταθερές επιφάνειες που η τοµή τους είναι οριζόντια. Τα τοιχώµατα είναι ισο κεκλιµένα ως προς τον
Q του νήµατος που το συγκρατεί, συµφωνα δε µε τον δεύτερο νό µο κίνησης του Νεύτωνα θα ισχύει η σχέση: της τάσεως!
 Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
Αβαρής ράβδος αποτελείται από δύο συνεχόµενα τµήµατα ΟΑ και ΑΒ που είναι ορθογώνια µεταξύ τους. Το άκρο Ο της ράβδου είναι αρθρωµένο σε οριζόντιο έδαφος το δε τµήµα της ΟΑ είναι κατακόρυφο και εφάπτεται
i) Να δείξετε ότι: F max = (m 1 + m 2 όπου! g η επιτάχυνση της βαρύτητας.
 Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
Δύο σώµατα Σ και Σ µε αντίστοιχες µάζες m και m, είναι στερεωµένα στις άκρες ενός κατακόρυφου αβαρούς ελατηρίου, όπως φαίνεται στο σχήµα. Εξασκούµε στο σώµα Σ κατακόρυφη δύναµη µε φορά προς τα κάτω, της
από την άρθρωση και της δύναµης επαφής από τον τοίχο που αναλύεται στην στατική τριβη T!
 Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
Tο ένα άκρο A οµογενούς ράβδου AB αρθρώνεται σε οριζόντιο επίπεδο, ενώ το άλλο της άκρο Β εφάπτεται κατακόρυ φου τοίχου, µε τον οποίο η ράβδος παρουσιάζει συντελεστή οριακής τριβής µ. H άρθρωση της ράβδου
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Ενδεικτικές Λύσεις Θέµα Α Α.1. Ενας δίσκος στρέφεται γύρω από άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδό του. Η τιµή
ΚΥΛΙΣΗ ΣΤΕΡΕΟΥ ΚΑΤΑ ΜΗΚΟΣ ΠΛΑΓΙΟΥ ΕΠΙΠΕΔΟΥ
 ΚΥΛΙΣΗ ΣΤΕΡΕΟΥ ΚΑΤΑ ΜΗΚΟΣ ΠΛΑΙΟΥ ΕΠΙΠΕΔΟΥ Σε ένα πλάγιο επίπεδο γωνίας κλίσης κυλίεται χωρίς να ολισθαίνει προς τα κάτω, ένα στερεό σώµα µε κατανοµή µάζας συµµετρική ως προς το κέντρο του. ( Το στερεό
ΚΥΛΙΣΗ ΣΤΕΡΕΟΥ ΚΑΤΑ ΜΗΚΟΣ ΠΛΑΙΟΥ ΕΠΙΠΕΔΟΥ Σε ένα πλάγιο επίπεδο γωνίας κλίσης κυλίεται χωρίς να ολισθαίνει προς τα κάτω, ένα στερεό σώµα µε κατανοµή µάζας συµµετρική ως προς το κέντρο του. ( Το στερεό
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
i) Nα δείξετε ότι αν το σύστηµα αφεθεί ελεύθερο η τροχαλία τ 1 δεν µπορεί να κυλίεται, άλλά µόνο να ισσρροπεί ή να ολισθαίνει.
 Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
Στην διάταξη του σχήµατος η τροχαλία τ 1 έχει µάζα m 1 και ακτίνα R και στο αυλάκι της έχει περιτυλιχθεί αβαρές νήµα, το οποίο διέρ χεται από τον λαιµό της µικρής τροχαλίας τ στο δε άκρο του έχει δε θεί
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V!
 Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
Ένα διαστηµόπλοιο µάζας M, κινείται στο διά στηµα µε σταθερή ταχύτητα V 0. O πιλότος του θέλει ν αλλάξει τη διεύθυνση κίνησης του διαστηµόπλοιου, ώστε η νέα διεύθυνση να γίνει κάθετη προς την αρχική. Για
ii) Nα βρεθεί η κινητική ενέργεια της σφαίρας, όταν το δοκάρι έχει µετατοπιστεί κατά S ως προς το έδαφος.
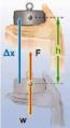 Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
Στην διάταξη του σχήµατος () το δοκάρι Δ έχει µάζα Μ και µπορεί να ολισθαίνει πάνω σε λείο κεκλιµένο επίπεδο γωνίας κλίσεως φ ως προς τον ορίζοντα. Κάποια στιγµή που λαµβά νεται ως αρχή µέτρησης του χρόνου
ΣΤΡΕΦΟΜΕΝΟΙ ΙΣΚΟΙ & ΠΕΡΙ ΣΤΡΟΦΟΡΜΗΣ
 ΣΤΡΕΦΜΕΝΙ ΙΣΚΙ & ΠΕΡΙ ΣΤΡΦΡΜΗΣ Ένας οµογενής και συµπαγής δίσκος µάζας m και ακτίνας =,2m στρέφεται γύρω από σταθερό οριζόντιο άξονα που διέρχεται από το κέντρο του µε γωνιακή ταχύτητα µέτρου ω =1 ra/sec.
ΣΤΡΕΦΜΕΝΙ ΙΣΚΙ & ΠΕΡΙ ΣΤΡΦΡΜΗΣ Ένας οµογενής και συµπαγής δίσκος µάζας m και ακτίνας =,2m στρέφεται γύρω από σταθερό οριζόντιο άξονα που διέρχεται από το κέντρο του µε γωνιακή ταχύτητα µέτρου ω =1 ra/sec.
i) Το επίπεδο της τροχαλίας είναι οριζόντιο και το έδαφος λείο.
 Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
Πάνω σε οριζόντιο έδαφος ηρεµεί µια τροχαλία µάζας m και ακτίνας R. Στο αυλάκι της τροχαλίας έχει περιτυλιχ θεί αβαρές νήµα στο ελεύθερο άκρο Α του οποίου εξασκείται σταθε ρή οριζόνια δύναµη F. Eάν µέχρις
ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 23/2/2014 ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3-4
 ΚΕΝΤΡΟ Αγίας Σοφίας 39 3 ΝΤΕΠΩ Β Όλγας 3 38 ΕΥΟΣΜΟΣ ΜΑλεξάνδρου 5 37736 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3// ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3- ΘΕΜΑ A Στις ερωτήσεις - να γράψετε
ΚΕΝΤΡΟ Αγίας Σοφίας 39 3 ΝΤΕΠΩ Β Όλγας 3 38 ΕΥΟΣΜΟΣ ΜΑλεξάνδρου 5 37736 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3// ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3- ΘΕΜΑ A Στις ερωτήσεις - να γράψετε
A! Κινηµατική άποψη. Σχήµα 1 Σχήµα 2
 A Κινηµατική άποψη Θεωρούµε στερεό σώµα σε τυχαία κίνηση, η οποία εξέταζεται από ένα αδρα νειακό σύστηµα αναφοράς ΟXYZ. Εφοδιάζουµε το σώµα µε κινητό σύστηµα συντεταγµένων xyz ακλόνητα συνδεδεµένο µε αυτό,
A Κινηµατική άποψη Θεωρούµε στερεό σώµα σε τυχαία κίνηση, η οποία εξέταζεται από ένα αδρα νειακό σύστηµα αναφοράς ΟXYZ. Εφοδιάζουµε το σώµα µε κινητό σύστηµα συντεταγµένων xyz ακλόνητα συνδεδεµένο µε αυτό,
i) Nα βρείτε την ταχύτητα του κέντρου της στεφάνης αµέσως µετά την κρού ση, η οποία θεωρείται βραχείας διάρκειας.
 Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
Mια κυκλική στεφάνη ακτίνας R, της οποίας η µάζα θεωρείται συγκεντρωµένη στην περιφέρεια της, κυλίεται ισοταχώς πάνω σε οριζόντιο επίπεδο το δε κέντρο της έχει ταχύτητα v. Kάποια στιγµή η στε φάνη προσκρούει
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ii) Nα βρείτε την µέγιστη γωνιακή ταχύτητα της ράβδου.
 Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
Oµογενής ράβδος σταθερής διατοµής, µάζας m και µήκους L, µπορεί να στρέφεται περί οριζόντιο άξονα που διέρχεται από το ένα άκρο της. Όταν η ράβδος βρίσκεται στην θέση ευσταθούς ισορροπίας εφαρµόζεται στο
της οποίας ο φορέας σχηµατί ζει γωνία φ=π/6 µε την κατακόρυφη διεύθυνση και ανακλάται µε αντίστοιχη γωνία φ=π/4.
 Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
Οριζόντιος δίσκος µάζας Μ ισορροπεί στηριζόµε νος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, του οποίου το άλλο άκρο στηρίζεται στο έδαφος (σχήµα 1). Ένα µικρό σφαιρίδιο µάζας m, προσκρούει
( σφόνδυλος : τροχαλία με μεγάλη μάζα)
 Ζήτημα 1 ο (μια σωστή στα ερωτήματα α,β,γ,) α) Οι πόλοι της γης βρίσκονται στα ίδια σημεία της επιφάνειας της γης Η σταθερότητα των πόλων οφείλεται; Στο γεγονός ότι ασκείται από τον ήλιο ελκτική δύναμη
Ζήτημα 1 ο (μια σωστή στα ερωτήματα α,β,γ,) α) Οι πόλοι της γης βρίσκονται στα ίδια σημεία της επιφάνειας της γης Η σταθερότητα των πόλων οφείλεται; Στο γεγονός ότι ασκείται από τον ήλιο ελκτική δύναμη
ΟΡΟΣΗΜΟ >Ι 3. δ. Ι Οι τροχοί (1) και (2) του σχήματος είναι ίδιοι. Τότε: και Ι 2
 ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
, σταθερής κατεύθυνσης, της οποίας το µέτρο µεταβάλλεται µε τον χρόνο t, σύµφωνα µε την σχέση:
 Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
Σώµα µάζας m σχήµατος ορθογώνιου κιβωτίου, ισορροπεί πάνω σε τραχύ οριζόντιο επίπεδο και στην άνω επιφάνειά του έχει τοποθετηθεί σώµα µάζας m/. Κάποια στιγµή που λαµβάνε ται ως αρχή µέτρησης του χρόνου
όπου Α το πλάτος της ταλάντωσης, φ η αρχική της φάση και ω η γωνιακή της συχνότητα. Οι σχέσεις (2) εφαρµοζόµενες τη χρονική στιγµή t=0 δίνουν:
 Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
Tο ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωµένο στο οριζόντιο έδαφος, ενώ το άλλο του άκρο είναι ελεύθερο. Mικρό σφαιρίδιο, µάζας m, αφήνεται σε ύψος h από το άκρο Β. Το σφαιρίδιο πέφτοντας
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2018: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 018: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1α. (δ) Α1β. (α) Αα. (α) Αβ. (δ) Α3α. (β) Α3β. (γ) Α4α. (β)
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 018: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1α. (δ) Α1β. (α) Αα. (α) Αβ. (δ) Α3α. (β) Α3β. (γ) Α4α. (β)
i) Nα βρεθεί η επιτάχυνση του κέντρου του δακτυλιδιού. Σχήµα 1 Σχήµα 2 L C
 Ένα στερεό σώµα αποτελείται από λεπτό δακτυ λίδι µάζας m και ακτίνας R και από δύο όµοιες λεπτές ράβδους µαζάς m η κάθε µια, των οποίων τα κέντρα έχουν ηλεκτροκολυθεί µε το δακτυλίδι, σε αντιδιαµετρικά
Ένα στερεό σώµα αποτελείται από λεπτό δακτυ λίδι µάζας m και ακτίνας R και από δύο όµοιες λεπτές ράβδους µαζάς m η κάθε µια, των οποίων τα κέντρα έχουν ηλεκτροκολυθεί µε το δακτυλίδι, σε αντιδιαµετρικά
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ Σ ένα στερεό ασκούνται ομοεπίπεδες δυνάμεις. Όταν το στερεό ισορροπεί, δηλαδή ισχύει ότι F 0 και δεν περιστρέφεται τότε το αλγεβρικό άθροισμα των ροπών είναι μηδέν Στ=0,
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: ΔΥΝΑΜΕΙΣ ΚΑΙ ΡΟΠΕΣ Σ ένα στερεό ασκούνται ομοεπίπεδες δυνάμεις. Όταν το στερεό ισορροπεί, δηλαδή ισχύει ότι F 0 και δεν περιστρέφεται τότε το αλγεβρικό άθροισμα των ροπών είναι μηδέν Στ=0,
Ενδεικτική λύση 3 ου θέματος
 Ενδεικτική λύση ου θέματος ΘΕΜΑ ο Η διάταξη του παρακάτω σχήματος αποτελείται από μία κεκλιμένη επιφάνεια (περιοχή Α), μία οριζόντια επιφάνεια (περιοχή Β) και ένα τεταρτοκύκλιο (περιοχή Γ). Ομογενής και
Ενδεικτική λύση ου θέματος ΘΕΜΑ ο Η διάταξη του παρακάτω σχήματος αποτελείται από μία κεκλιμένη επιφάνεια (περιοχή Α), μία οριζόντια επιφάνεια (περιοχή Β) και ένα τεταρτοκύκλιο (περιοχή Γ). Ομογενής και
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι. Θέµα Α
 6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
ΜΕΡΟΣ Γ! 1η οµάδα λυµένων παραδειγµάτων
 ΜΕΡΟΣ Γ 1η οµάδα λυµένων παραδειγµάτων Ένας τροχός, µάζας m η οποία θεωρείται συγ κεντωµενη στην περιφέρειά του, περιστρέφεται περί οριζόντιο άξονα ασήµαντης µάζας, ο οποίος διέρχεται από το κέντρο του
ΜΕΡΟΣ Γ 1η οµάδα λυµένων παραδειγµάτων Ένας τροχός, µάζας m η οποία θεωρείται συγ κεντωµενη στην περιφέρειά του, περιστρέφεται περί οριζόντιο άξονα ασήµαντης µάζας, ο οποίος διέρχεται από το κέντρο του
EΡΓΑΣΙΑ 5 η Καταληκτική ηµεροµηνία παράδοσης: 20 Ιουλίου 2003
 1 EΡΓΑΣΙΑ 5 η Καταληκτική ηµεροµηνία παράδοσης: 20 Ιουλίου 2003 1. Από την ίδια γραµµή αφετηρίας(από το ίδιο ύψος) ενός κεκλιµένου επιπέδου αφήστε να κυλήσουν, ταυτόχρονα προς τα κάτω, δύο κυλίνδροι της
1 EΡΓΑΣΙΑ 5 η Καταληκτική ηµεροµηνία παράδοσης: 20 Ιουλίου 2003 1. Από την ίδια γραµµή αφετηρίας(από το ίδιο ύψος) ενός κεκλιµένου επιπέδου αφήστε να κυλήσουν, ταυτόχρονα προς τα κάτω, δύο κυλίνδροι της
. Αυτό σηµαίνει ότι το κέντρο µάζας κινείται ευθύγραµµα µε σταθερή επιτάχυνση a! = F!
 Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
Διαγώνισμα: Μηχανική Στερεού Σώματος
 Διαγώνισμα: Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
Διαγώνισμα: Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
ii) Να δείξετε ότι το σφαιρίδιο εκτελεί µια µη αρµονική περιοδική ταλάντωση, της οποίας να υπολογίσετε την περίοδο.
 Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
Το σύστηµα του σχήµατος αποτελείται από δύο όµοια ελατήρια στα θεράς και φυσικού µήκους α, των οποίων οι άξονες βρίσκονται πάνω στην ευθεία ΑΒ, όπου Α, Β είναι δύο ακλόνητα σηµεία του επιπέδου. Εκτρέπουµε
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Κεφάλαιο 4 Θέμα 1ο Α. Να επιλέξετε τη σωστή απάντηση που ακολουθεί κάθε μια από τις πιο κάτω προτάσεις α. Ένα σώμα ηρεμεί εκτός πεδίου βαρύτητας. Ασκούμε
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Κεφάλαιο 4 Θέμα 1ο Α. Να επιλέξετε τη σωστή απάντηση που ακολουθεί κάθε μια από τις πιο κάτω προτάσεις α. Ένα σώμα ηρεμεί εκτός πεδίου βαρύτητας. Ασκούμε
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ. Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται.
 ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ Διερεύνηση της σχέσης L=ω Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται. Η ροπή αδράνειας Ι
ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΣΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ Διερεύνηση της σχέσης L=ω Η στροφορμή ενός στερεού σώματος είναι μηδενική, όταν το σώμα δεν περιστρέφεται. Η ροπή αδράνειας Ι
Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 2 0 Κεφάλαιο
 Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 0 Κεφάλαιο Περιέχει: Αναλυτική Θεωρία Ερωτήσεις Θεωρίας Ερωτήσεις Πολλαπλής Επιλογής Ερωτήσεις Σωστού - λάθους Ασκήσεις ΘΕΩΡΙΑ 4- ΕΙΣΑΓΩΓΗ Στην μέχρι τώρα
Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 0 Κεφάλαιο Περιέχει: Αναλυτική Θεωρία Ερωτήσεις Θεωρίας Ερωτήσεις Πολλαπλής Επιλογής Ερωτήσεις Σωστού - λάθους Ασκήσεις ΘΕΩΡΙΑ 4- ΕΙΣΑΓΩΓΗ Στην μέχρι τώρα
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ. ΘΕΜΑ Α (μοναδες 25)
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα.
 Δίσκος Σύνθετη Τρίτη 01 Μαϊου 2012 ΑΣΚΗΣΗ 5 Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα. ΠΕΙΡΑΜΑ Α Θα εκτοξευθεί με ταχύτητα από τη βάση του κεκλιμένου
Δίσκος Σύνθετη Τρίτη 01 Μαϊου 2012 ΑΣΚΗΣΗ 5 Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα. ΠΕΙΡΑΜΑ Α Θα εκτοξευθεί με ταχύτητα από τη βάση του κεκλιμένου
ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
i) Nα εκφράσετε σε συνάρτηση µε τον χρόνο την γωνιακή ταχύτητα της τροχαλίας.
 Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Στην διάταξη του σχήµατος ) οι δύο κυκλικοί δίσκοι Δ, Δ έχουν την ιδια ακτίνα R και αντίστοιχες µάζες m, m µπορούν δε να κυλίωνται χωρίς ολίσθηση κατά µήκος δύο κεκλιµέ νων επιπέδων που είναι µεταξύ τους
Γ ΤΑΞΗ ΤΜΗΜΑ ΟΝΟΜΑ. ΘΕΜΑ 1ο. 7 mr 5. 1 mr. Μονάδες 5. α. 50 W β. 100 W γ. 200 W δ. 400 W
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
(σχ. 1). Εφαρ µόζοντας για την µεταφορική συνιστώσα της κύλισης του δίσκου τον
 Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
Oµογενής λεπτός δίσκος ακτίνας R και µάζας m, ακινητεί επί οριζόντιου εδάφους µε το οποίο παρουσιάζει συντελεστή οριακής τριβής µ το δε επιπεδό του είναι κατακόρυφο,. Κάποια στιγµή εφαρµόζεται στο κέντρο
όπου Μ η µάζα της Γης την οποία θεωρούµε σφαίρα οµογενή, G η παγκόσµια σταθερά της βαρύτητας και L!
 Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
Είναι γνωστό ότι, όταν ένα σώµα κινείται µέσα στο βαρυτικό πεδίο της Γης υπό την επίδραση µόνο της Νευτώνειας έλξεως, η τροχιά που διαγράφει το κέντρο µάζας του είναι επίπεδη και µάλιστα το επίπεδό της
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
που δέχεται από την παράπλευρη επιφάνεια του κώνου, της οποίας ο φορέας είναι κάθετος στην επιφάνεια αυτή, αφού θεωρείται λεία και των δυνάµεων T
 Mιά κυκλική σπείρα εύκαµπτης αλυσίδας βάρους w, είναι τοποθετηµένη πάνω σε λείο ορθό κώνο ύψους h, του οποίου η βάση έχει ακτίνα R (σχ. 9). O κατακόρυφος άξονας του κώνου διέρ χεται από το κέντρο της αλυσίδας
Mιά κυκλική σπείρα εύκαµπτης αλυσίδας βάρους w, είναι τοποθετηµένη πάνω σε λείο ορθό κώνο ύψους h, του οποίου η βάση έχει ακτίνα R (σχ. 9). O κατακόρυφος άξονας του κώνου διέρ χεται από το κέντρο της αλυσίδας
. Εάν η σφαίρα κυλίεται πάνω στο δοκάρι να βρείτε: i) την επιτάχυνση του δοκαριού και του κέντρου της σφαίρας, στο σύστηµα αναφοράς του δαπέδου και
 Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
Οµογενής σφαίρα µάζας m και ακτίνας R είναι ακίνητη πάνω σε οριζόντιο δοκάρι µάζας Μ και µήκους L, που µπορεί να ολισθαίνει χωρίς τριβή επί οριζοντίου δαπέδου. Η σφαίρα εφάπτεται στο δεξιό άκρο Β του δοκαριού
ιονύσης Μητρόπουλος Ζ Ο
 Πρισµατικό σώµα και κύλινδρος (ΙΙ) Κίνηση σε οριζόντιο επίπεδο (Σ 2 ) (Σ 1 ) A F εξ Ζ Ο Πρισµατικό σώµα (Σ 2 ) µάζας m = 4kg και κύλινδρος (Σ 1 ) ίσης µάζας m και ακτίνας R = 0,2m βρίσκονται πάνω σε οριζόντιο
Πρισµατικό σώµα και κύλινδρος (ΙΙ) Κίνηση σε οριζόντιο επίπεδο (Σ 2 ) (Σ 1 ) A F εξ Ζ Ο Πρισµατικό σώµα (Σ 2 ) µάζας m = 4kg και κύλινδρος (Σ 1 ) ίσης µάζας m και ακτίνας R = 0,2m βρίσκονται πάνω σε οριζόντιο
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Τετάρτη 12 Απριλίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Ενδεικτικές Λύσεις Κυριακή 28 Φλεβάρη 2016 Θέµα Α Α.1. Ενα στερεό σώµα περιστρέφεται γύρω από ακλόνητο άξονα. Εάν διπλασιαστεί η στροφορµή
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
, που είναι στατική τριβή µε κατεύθυνση αντίθετη της ταχύτητας του κέντρου µάζας C 1 της σφαίρας (σχήµα 1) και η δύναµη επαφής!
 Δύο οµογενείς σφαίρες Α και Β, της ίδιας ακτίνας R µε αντίστοιχες µάζες m και m είναι ακίνητες επί οριζοντίου εδάφους και εφάπ τονται µεταξύ τους. Κάποια στιγµή που λαµβάνεται ως αρχή µέτρη σης του χρόνου
Δύο οµογενείς σφαίρες Α και Β, της ίδιας ακτίνας R µε αντίστοιχες µάζες m και m είναι ακίνητες επί οριζοντίου εδάφους και εφάπ τονται µεταξύ τους. Κάποια στιγµή που λαµβάνεται ως αρχή µέτρη σης του χρόνου
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
F r. www.ylikonet.gr 1
 3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
ΧΡΗΣΙΜΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΣΤΕΡΕΟ ΣΩΜΑ
 ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΧΡΗΣΙΜΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΣΤΕΡΕΟ ΣΩΜΑ Παρατηρήσεις : I a. Όσο μεγαλύτερη είναι η ροπή αδράνειας ενός σώματος τόσο πιο δύσκολα αλλάζει η περιστροφική κατάσταση του σώματος.. Εάν η συνισταμένη
ο ΓΕΛ ΓΑΛΑΤΣΙΟΥ ΧΡΗΣΙΜΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΣΤΕΡΕΟ ΣΩΜΑ Παρατηρήσεις : I a. Όσο μεγαλύτερη είναι η ροπή αδράνειας ενός σώματος τόσο πιο δύσκολα αλλάζει η περιστροφική κατάσταση του σώματος.. Εάν η συνισταμένη
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
ΦΥΣΙΚΗ. α) έχουν κάθε χρονική στιγμή την ίδια οριζόντια συνιστώσα ταχύτητας, και την ίδια κατακόρυφη συνιστώσα ταχύτητας.
 Β Λυκείου 14 / 04 / 2019 ΦΥΣΙΚΗ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις A1 A4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Η ορμή ενός σώματος :
Β Λυκείου 14 / 04 / 2019 ΦΥΣΙΚΗ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις A1 A4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Η ορμή ενός σώματος :
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο
 Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
# $ + L " = ml " ml! = ML " $ + ml " $ L " = ML/2(M + m) # $ (1) Eξάλλου, εάν L' α, L' σ είναι οι τελικές αποστάσεις του κέντρου µάζας C του
 Mία σανίδα, µήκους L καί µάζας M, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Στο ένα άκρο της σανίδας πατάει άνθ ρωπος µάζας m και αρχίζει να κινείται προς το άλλο άκρο της. Kατά πόσο θα µετατοπιστεί η
Mία σανίδα, µήκους L καί µάζας M, βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Στο ένα άκρο της σανίδας πατάει άνθ ρωπος µάζας m και αρχίζει να κινείται προς το άλλο άκρο της. Kατά πόσο θα µετατοπιστεί η
Nα δείξετε τις εξής προτάσεις:
 Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
Nα δείξετε τις εξής προτάσεις: i) Εάν ένα υλικό σηµείο µάζας m κινείται πάνω σ ένα άξονα x x, ώστε κάθε στιγµή η ταχύτητά του v και η αποµάκρυνσή του x ως προς µια αρχή Ο του άξονα, να ικανοποιούν τη σχέση:
A) Να βρεθεί η γωνιακή επιτάχυνση του τροχού, καθώς και ο αριθµός των στροφών
 Άσκηση ολίσθηση-κύλιση µε ολίσθηση-κύλιση χωρίς ολίσθηση Ο τροχός του σχήµατος έχει ακτίνα R0,m και αφήνεται τη χρονική στιγµή t0 µε αρχική γωνιακή ταχύτητα ω ο 300 rad/sec σε επαφή µε τα δύο κάθετα τοιχώµατα,
Άσκηση ολίσθηση-κύλιση µε ολίσθηση-κύλιση χωρίς ολίσθηση Ο τροχός του σχήµατος έχει ακτίνα R0,m και αφήνεται τη χρονική στιγµή t0 µε αρχική γωνιακή ταχύτητα ω ο 300 rad/sec σε επαφή µε τα δύο κάθετα τοιχώµατα,
Ένθετη θεωρία για την αδρανειακή δύναµη D Alempert
 Ένθετη θεωρία για την αδρανειακή δύναµη D Alempert Είναι γνωστό ότι ο δεύτερος νόµος κίνησης του Νεύτωνα ισχύει µόνο για τα λεγόµενα αδρανεικά συστήµατα αναφοράς, δηλαδή για τα συστήµατα εκείνα που είναι
Ένθετη θεωρία για την αδρανειακή δύναµη D Alempert Είναι γνωστό ότι ο δεύτερος νόµος κίνησης του Νεύτωνα ισχύει µόνο για τα λεγόµενα αδρανεικά συστήµατα αναφοράς, δηλαδή για τα συστήµατα εκείνα που είναι
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου.
 Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
Οµογενής ράβδος µάζας m και µήκους L, κρατεί ται οριζόντια ακουµπώντας σε σταθερή ακίδα που απέχει απόσταση x από το κέντρο µάζας C της ράβδου. i) Να βρεθεί η απόσταση x, ώστε την στιγµή που η ράβδος αφήνεται
Υλικό σηµείο µάζας m, κινείται εντός δυναµικού πεδίου δεχόµενο ελκτική κεντρική δύναµη F!
 Υλικό σηµείο µάζας, κινείται εντός δυναµικού πεδίου δεχόµενο ελκτική κεντρική δύναµη F (), η οποία ακολουθεί τον νόµο του αντιστρόφου τετραγώνου της απόστασης από το ελκτι κό κέντρο Ο, δηλαδή περιγράφεται
Υλικό σηµείο µάζας, κινείται εντός δυναµικού πεδίου δεχόµενο ελκτική κεντρική δύναµη F (), η οποία ακολουθεί τον νόµο του αντιστρόφου τετραγώνου της απόστασης από το ελκτι κό κέντρο Ο, δηλαδή περιγράφεται
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1. ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]
![ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου] ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]](/thumbs/52/29790189.jpg) ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Στις ερωτήσεις -4 να βρείτε τη σωστή πρόταση.. Η ροπή αδράνειας ενός στερεού σώµατος εξαρτάται: α. Από τη ροπή της δύναµης που ασκείται στο στερεό. β. από
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Στις ερωτήσεις -4 να βρείτε τη σωστή πρόταση.. Η ροπή αδράνειας ενός στερεού σώµατος εξαρτάται: α. Από τη ροπή της δύναµης που ασκείται στο στερεό. β. από
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
i) Να δείξετε ότι αν για µια τιµή της γωνίας θ η ράβδος ισορροπεί, η ισορροπία αυτή είναι αδιάφορη.
 Η ράβδος του σχήµατος έχει µήκος L, βάρος w και στηρίζεται διά του άκρου της Α επί λείου τοίχου, ενώ το άλλο άκρο της Β ακουµπά ει σε λεία κοίλη επιφάνεια. Η τοµή της επιφάνειας µε κατακόρυφο επίπεδο που
Η ράβδος του σχήµατος έχει µήκος L, βάρος w και στηρίζεται διά του άκρου της Α επί λείου τοίχου, ενώ το άλλο άκρο της Β ακουµπά ει σε λεία κοίλη επιφάνεια. Η τοµή της επιφάνειας µε κατακόρυφο επίπεδο που
διέρχεται από το σηµείο Ο της ράβδου, υπό την επίδραση των βαρών m 1 από τον άξονα περιστροφής, που αναλύεται στην οριζόντια συνιστώσα!
 Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
Θεωρήστε οριζόντια ράβδο αµελητέας µάζας, η οποία µπορεί να περιστρέφεται περί σταθερό οριζόντιο άξονα κάθετο στη ράβδο. Στα άκρα της υπάρχουν δυο διαφορετικές σηµειακές µάζες m, m, που οι αντίστοιχες
όπως φαίνεται στο σχήµα (1).
 Οµογενής δίσκος βάρους w και ακτίνας R, κυλίεται χωρίς ολίσθη ση σε τραχύ οριζόντιο έδαφος, ελκόµενος µε αβαρές και µή εκτατό νήµα που είναι κατάλληλα δεµένο στο κέντρο του δίσκου. Το νήµα διέρχεται από
Οµογενής δίσκος βάρους w και ακτίνας R, κυλίεται χωρίς ολίσθη ση σε τραχύ οριζόντιο έδαφος, ελκόµενος µε αβαρές και µή εκτατό νήµα που είναι κατάλληλα δεµένο στο κέντρο του δίσκου. Το νήµα διέρχεται από
! =A'B=C!! C! = R" (1)
 Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
Οµογενής κύβος ακµής α ισορροπεί επί ακλό νητης σφαιρικής επιφάνειας ακτίνας R, µε το κέντρο µάζας του ακριβώς πάνω από την κορυφή Α της επιφάνειας. Εάν µεταξύ του κύβου και της σφαιρικής επιφάνειας υπάρχει
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 03 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. c Α. d Α3. c Α4. c Α5. Σ, Λ, Σ, Σ, Λ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (γ). Γνωρίζουμε (σχολικό βιβλίο, σελ. 3) ότι ένα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 03 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. c Α. d Α3. c Α4. c Α5. Σ, Λ, Σ, Σ, Λ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (γ). Γνωρίζουμε (σχολικό βιβλίο, σελ. 3) ότι ένα
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3/2/2016 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3/2/2016 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ 2 ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m 0.25 Kg κινείται στο επίπεδο xy, με τις εξισώσεις κίνησης
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3/2/2016 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ 2 ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m 0.25 Kg κινείται στο επίπεδο xy, με τις εξισώσεις κίνησης
