Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
|
|
|
- Στέφανος Κουταλιανός
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην µερική ικανοποίηση ων απαιήσεων για ην απόκηση ιδακορικού ιπλώµαος ΜΑΝΩΛΗΣ Γ. ΙΑΜΑΝΤΗΣ ΧΑΝΙΑ 00
2 Copyright υπό Μανώλη Γ. ιαµανή Χανιά 00
3 Η διαριβή ου Μανώλη ιαµανή εγκρίνεαι: Καθ. Μάρκος Παπαγεωργίου (Επιβλέπων) Αναπ. Καθ. Ηλίας Κοσµαόπουλος (µέλος ριµελούς) Καθ. Γεώργιος Σαυρουλάκης (µέλος ριµελούς) Καθ. Γεώργιος Χαµηλοθώρης Καθ. Γεώργιος Σαυρακάκης Επ. Καθ. Ιάσων Καραφύλλης Επ. Καθ. Ιωάννης Παπαµιχαήλ 3
4 ΕΥΧΑΡΙΣΤΙΕΣ Θα ήθελα να ευχαρισήσω όλα α µέλη ου εργασηρίου υναµικών Συσηµάων και Προσοµοίωσης ου µήµαος Μηχανικών Παραγωγής και ιοίκησης, για ην άψογη συνεργασία και βοήθεια που υπήρξε όλα αυά α χρόνια σε διάφορους οµείς. Ξεχωρισά θα ήθελα να ευχαρισήσω ον καθηγηή Μάρκο Παπαγεωργίου, υπεύθυνο ου εργασηρίου, αλλά και επιβλέπων καθηγηή και επισηµονικό υπεύθυνο σο ερευνηικό έργο «Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο» σα πλαίσια ου οποίου πραγµαοποιήθηκε αυή η διαριβή, για η σήριξη και ην υποµονή ου, αλλά και για ην οικονοµική βοήθεια που είχα καά η διάρκεια ων σπουδών. Ένα πολύ µεγάλο ευχαρισώ σο αναπληρωή καθηγηή Ηλία Κοσµαόπουλο για ην πολύιµη βοήθεια και καθοδήγηση ου. Χωρίς αυόν αυή η διδακορική διαριβή δεν θα είχε έρθει εις πέρας. Επίσης θα ήθελα να ευχαρισήσω α µέλη ης επαµελούς επιροπής που συµµεείχαν σην διόρθωση και αξιολόγηση αυής ης διαριβής. Η παρούσα διαριβή είναι µέρος ου ερευνηικού έργου 03Ε 899, ο οποίο υλοποιήθηκε σα πλαίσια ου Προγράµµαος Ενίσχυσης Ερευνηικού υναµικού (ΠΕΝΕ ) που συν-χρηµαοδοήθηκε από εθνικούς και κοινοικούς πόρους (75% από ο Ευρωπαϊκό Κοινοικό αµείο και 5% από ο Ελληνικό Υπουργείο Ανάπυξης, Γενική Γραµµαεία Έρευνας και Τεχνολογίας.) 4
5 ΠΕΡΙΕΧΟΜΕΝΑ ΠΕΡΙΛΗΨΗ...7. ΕΙΣΑΓΩΓΗ...9. ΕΠΙΣΚΟΠΗΣΗ ΜΕΘΟ ΩΝ ΕΛΕΓΧΟΥ ΓΙΑ ΑΠΟΧΕΤΕΥΤΙΚΑ ΙΚΤΥΑ. 3. ΕΠΙΣΚΟΠΗΣΗ ΜΕΘΟ ΩΝ ΕΛΕΓΧΟΥ ΓΙΑ ΙΚΤΥΑ ΑΡ ΕΥΣΗΣ ΕΠΙΛΟΓΗ ΜΕΤΑΒΛΗΤΩΝ ΕΛΕΓΧΟΜΕΝΕΣ ΜΕΤΑΒΛΗΤΕΣ Ροές Επίπεδα σάθµης υδάων Όγκοι αποθήκευσης ΜΕΤΡΗΣΙΜΕΣ ΜΕΤΑΒΛΗΤΕΣ ΜΕΤΑΒΛΗΤΕΣ ΕΛΕΓΧΟΥ ΛΟΓΙΚΗ ΤΟΥ ΕΛΕΓΧΟΥ ΕΛΕΓΧΟΣ ΚΛΕΙΣΤΟΥ ΒΡΟΧΟΥ ΕΛΕΓΧΟΣ ΑΝΟΙXΤΟΥ ΒΡΟΧΟΥ ΣΥΜΠΕΡΑΣΜΑΤΑ ΣΧΕ ΙΑΣΤΙΚΕΣ ΜΕΘΟ ΟΙ ΕΙΣΟ ΟΙ /ΕΞΟ ΟΙ ΜΟΝΟΜΕΤΑΒΛΗΤΕΣ ΜΕΘΟ ΟΙ ΠΟΛΥΜΕΤΑΒΛΗΤΕΣ ΜΕΘΟ ΟΙ ΕΠΙΣΚΟΠΗΣΗ ΑΠΟΧΕΤΕΥΤΙΚΩΝ ΙΚΤΥΩΝ ΣΤΟΝ ΕΛΛΑ ΙΚΟ ΧΩΡΟ 6 4. ΤΥΠΟΙ ΑΠΟΧΕΤΕΥΤΙΚΩΝ ΙΚΤΥΩΝ ΣΤΟΝ ΕΛΛΑ ΙΚΟ ΧΩΡΟ ΚΑΙ ΕΝ ΥΝΑΜΕΙ ΕΦΑΡΜΟΓΗ ΜΕΤΡΩΝ ΕΛΕΓΧΟΥ ΠΑΡΑΣΙΤΙΚΕΣ ΕΙΣΡΟΕΣ ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΑΛΓΟΡΙΘΜΟΣ ΓΙΑ ΤΟΝ ΣΧΕ ΙΑΣΜΟ ΣΤΡΑΤΗΓΙΚΗΣ ΕΛΕΓΧΟΥ ΤΗΣ ΡΟΗΣ ΛΑΜΒΑΝΟΝΤΑΣ ΥΠΟΨΗ ΤΗ ΧΡΟΝΙΚΗ ΥΣΤΕΡΗΣΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΟΙ ΥΝΑΜΙΚΕΣ ΤΗΣ ΡΟΗΣ Υ ΑΤΩΝ: ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΑΛΓΟΡΙΘΜΟΣ ΕΚΤΙΜΗΣΗΣ ΠΡΑΚΤΙΚΕΣ Ο ΗΓΙΕΣ ΠΡΟΣΟΜΟΙΩΣΕΙΣ (Α) ΣΥΜΠΕΡΑΣΜΑΤΑ (Α)
6 5.7 ΚΑΤΑΣΚΕΥΗ ΕΛΕΓΚΤΗ ΠΡΟΣΟΜΟΙΩΣΕΙΣ (B) ΣΥΜΠΕΡΑΣΜΑΤΑ (Β) ΣΧΕ ΙΑΣΜΟΣ ΚΥΡΤΟΥ ΕΛΕΓΧΟΥ ΓΙΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 5 6. ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ-ΣΥΜΒΟΛΙΣΜΟΙ Ο ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΣΕΙΣ-ΑΠΟΤΕΛΕΣΜΑΤΑ ΙΚΤΥΟ ΟΚΙΜΗΣ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΒΑΣΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΡΟΣΕΓΓΙΣΕΙΣ ΣΤΟΙΧΕΙΑ ΤΗΣ ΜΟΝΤΕΛΟΠΟΙΗΣΗΣ ΑΡΧΙΚΟΠΟΙΗΣΗ ΣΕΝΑΡΙΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΕΠΙΛΟΓΗ ΤΗΣ ΣΤΑΘΕΡΑΣ L ΑΠΟΤΕΛΕΣΜΑΤΑ ΣΥΜΠΕΡΑΣΜΑΤΑ...70 ΣΥΝΟΨΗ...7 ΒΙΒΛΙΟΓΡΑΦΙΑ
7 ΠΕΡΙΛΗΨΗ Τις ελευαίες δεκαείες έχουν εναθεί οι προσπάθειες για η διαχείριση υδάων, είε πρόκειαι για αρδευικά, είε για αποχεευικά δίκυα. Οι µεγάλες ανάγκες σε νερό, η µόλυνση ου υδροφόρου ορίζονα, η αλλαγή ων κλιµαικών συνθηκών, η ασυφιλία και η ανάπυξη ης βιοµηχανίας έχουν µειώσει δρασικά α αποθέµαα πόσιµου νερού ή νερού άρδευσης. Αυό κάνει αναγκαία ην ανάπυξη µεθόδων βέλισης διαχείρισης ων αποθεµάων νερού. Σα ασικά κένρα από ην άλλη (αλλά και α βιοµηχανικά), παραηρείαι ο φαινόµενο ης µόλυνσης ου υδροφόρου ορίζονα από ην µη καλή διαχείριση ων αποχεευικών δικύων. Όαν υπάρχουν εγκαασάσεις βιολογικού καθαρισµού, βελιώνεαι η καάσαση. Το κόσος όµως για να φιαχεί ένα δίκυο που θα µεαφέρει α απόβληα και πολλές φορές και α όµβρια ύδαα, σον βιολογικό καθαρισµό είναι εράσιο. Χρειάζεαι αρκεή µελέη, καλό και αυσηρό πολεοδοµικό σχέδιο και καασκευή υπόγειου δικύου σωληνώσεων και αποθηκευικών χώρων λυµάων. Τα πανορροϊκά δίκυα εκός από α ασικά και βιοµηχανικά λύµαα, µεαφέρουν και α βρόχινα ύδαα σε εγκαασάσεις βιολογικού καθαρισµού, για επεξεργασία πριν από ην απόθεση ους σε ποάµια λίµνες ή η θάλασσα. Όαν οι βροχοπώσεις είναι ισχυρές, µπορεί να οδηγηθούµε σε υπερχείλιση ου συσήµαος και απόθεση ων λυµάων καευθείαν σον υδροφόρο ορίζονα. Μια σωσά σχεδιασµένη υποδοµή αποχεευικών δικύων, και η χρήση µιας καλής πολιικής ελέγχου ης ροής ων λυµάων θα µπορούσε να µειώσει και σε κάποιες περιπώσεις να εξαφανίσει ις όποιες υπερχειλίσεις. Τα προβλήµαα που ενοπίζοναι είναι πολλά. Από η µία η µη οικολογική συνείδηση ων ιθυνόνων, από ην άλλη ο µεγάλο κόσος καασκευής. Τα ελευαία χρόνια όµως που οι λαϊκές πιέσεις είναι περισσόερες και που η οικολογική συνείδηση αρχίζει να κερδίζει έδαφος, η επισηµονική κοινόηα σε συνεργασία µε δήµους, εκµεαλλευόµενη και ην πιο αυσηρή νοµοθεσία (ουλάχισον σε άλλες ευρωπαϊκές χώρες), χρησιµοποιεί η θεωρία ελέγχου και άλλες εχνικές για να δώσει λύση σο πρόβληµα µε ο ελάχισο κόσος. Έχουν χρησιµοποιηθεί από α αρχαία χρόνια πολλές µέθοδοι διαχείρισης υδάων σε δίκυα, αλλά ις ελευαίες δεκαείες µε ην ανάπυξη ων υπολογισών, πολλές νέες και πιο αποελεσµαικές (αλλά και πολύπλοκες) µέθοδοι χρησιµοποιούναι και πολύ περισσόερες έχουν προαθεί. Όλες µε α πλεονεκήµαα και α µειονεκήµαά ους. Σε αυήν ην εργασία γίνεαι µια προσπάθεια να αναγνωρισούν κάποια από α βασικά προβλήµαα που ενοπίζοναι σις µεθόδους ελέγχου ης ροής υδάων σε δίκυα (αποχεευικά και αρδευικά) και να δοθούν κάποια εργαλεία ικανά να αναπεξέλθουν σε αυά α προβλήµαα. 7
8 Θα δοθεί αρχικά µια επισκόπηση µεθόδων που έχουν χρησιµοποιηθεί σο παρελθόν για α αποχεευικά και αρδευικά δίκυα, α προβλήµαα που ενοπίζοναι κυρίως όσο αφορά η χρονική υσέρηση ων συσηµάων. Η χρονική υσέρηση έχει να κάνει µε ο χρόνο που χρειάζεαι ένα σύσηµα να αποκριθεί σε µια απόφαση ελέγχου και ις διάφορες δυναµικές που δηµιουργούναι καά ην υλοποίησή ης. Για α αρδευικά δίκυα π.χ. ο άνοιγµα ης πύλης ενός φράγµαος, δε θα φέρει καευθείαν ην ποσόηα ου ύδαος που χρειαζόµασε σε ένα συγκεκριµένο σηµείο ενός αρδευικού δικύου. Θα χρειασεί κάποιος χρόνος. Αν ο άνοιγµα ης πύλης γίνει αρκεά «νωρίς», θα δηµιουργηθεί ένα δυναµικό κύµα µε αποέλεσµα να επισπευεί η µεαφορά, αλλά να υπερβεί ην απαιούµενη ποσόηα και να χαθεί πολύιµο νερό. Από ην άλλη, αν ο άνοιγµα ης πύλης γίνει αρκεά «αργά» δεν θα µπορούν οι καλλιεργηές να καλύψουν ις ανάγκες ους ην ώρα που ο επιθυµούν. Τέοιου είδους ανικρουόµενα συµφέρονα είναι κυρίως αυά που πρέπει να ρυθµίσουµε µέσω µέρων ελέγχου ροής ων υδάων. Το πρόβληµα γίνεαι πιο πολύπλοκο σις περιπώσεις δικύων υδάων, όπου πέραν ου γεγονόος όι ο ελεγκής πρέπει να λάβει υπόψη ην χρονική υσέρηση, θα πρέπει να ληφθεί υπόψη και ο γεγονός όι οι αποφάσεις σε ένα µήµα ου δικύου επηρεάζουν µερικές φορές σηµανικά ην καάσαση σο υπόλοιπο µήµα ου δικύου. Επίσης, περιορισµοί χωρηικόηας, περιορισµοί ελάχισου και µέγισου ελέγχου, κλπ, καθισούν ο πρόβληµα βέλισου ελέγχου σε δίκυα υδάων εξαιρεικά πολύπλοκο, µε ις υπάρχουσες µεθοδολογίες να µην είναι ικανές να δώσουν υπολογισικά εφικές λύσεις. Σην παρούσα διαριβή προείνοναι δύο µέθοδοι για ον έλεγχο υδάων σε αποχεευικά και αρδευικά δίκυα. Η πρώη είναι εφαρµόσιµη σε αποκενρωµένο έλεγχο. Το πλεονέκηµά ης είναι όι λαµβάνει υπόψη ην µεαβολή ης χρονικής υσέρησης σις αποφάσεις ελέγχου. Πιο συγκεκριµένα, χρησιµοποιείαι η θεωρία ων προσαρµοσικών αλγορίθµων για ην εκίµηση ης µεαβολής ης υσέρησης. Θεωρηική ανάλυση όσο και πειράµαα προσοµοίωσης δείχνουν όι η γνώση ης χρονικής υσέρησης είναι ένα χρήσιµο εργαλείο που οδηγεί σο σχεδιασµό ελεγκών αρκεά καλύερων και πιο αποελεσµαικών από ους απλούς PI ελεγκές, που ευρέως χρησιµοποιούναι σην πράξη. Η δεύερη µέθοδος είναι µια µέθοδος κενρικού ελέγχου η οποία παράγει ελεγκές που δύναναι να προσεγγίσουν ους βέλισους µε «αυθαίρεη» ακρίβεια. Τµηµαοποιούµε ο χώρο ων καασάσεων και για κάθε µήµα σχεδιάζουµε έναν γραµµικό ελεγκή. Χρησιµοποιώνας η θεωρία ου δυναµικού προγραµµαισµού (HJB συναρήσεις) και η θεωρία ευσάθειας καά Lyapunov αποδεικνύουµε όι η απόδοση ου προεινόµενου ελεγκή µπορεί να προσεγγίσει αυή ου βέλισου ελεγκή µε «αυθαίρεη» ακρίβεια. Το βασικό πλεονέκηµα αυής ης µεθόδου είναι όι οι χρονοβόροι υπολογισµοί γίνοναι σε µη πραγµαικό χρόνο. Σε πραγµαικό χρόνο οι απαιούµενες πράξεις ανισοιχούν σε αυές ενός απλού γραµµικού ελεγκή. 8
9 . ΕΙΣΑΓΩΓΗ Σην προσπάθεια ελέγχου δικύων ροής έχουν χρησιµοποιηθεί αρκεές µέθοδοι. Τα κυριόερα προβλήµαά ους είναι ο σχεικά απλοποιηµένος σχεδιασµός ων δυναµικών ης ροής, που διευκολύνει από η µια ις υπολογισικές ανάγκες, αλλά θυσιάζει ην πλήρη απεικόνιση ων δυναµικών και άρα οδηγεί σε µη βέλισο έλεγχο. ιάφορες µέθοδοι προσπάθησαν να προσεγγίσουν ις µερικές διαφορικές εξισώσεις Saint Venant (που δίνουν ην πλήρη απεικόνιση ων δυναµικών ης ροής) µε γραµµικά µονέλα λαµβάνονας υπόψη η χρονική υσέρηση ου συσήµαος. Λαµβάνουν όµως υπόψη η χρονική υσέρηση σαν µια σαθερά βασισµένοι κυρίως σε ισορικά δεδοµένα κλπ. Από ην άλλη, πιο περίπλοκα δυναµικά συσήµαα προσέγγισης δεν οδηγούν σε εφαρµόσιµες µεθόδους λόγω ου µεγάλου υπολογισικού φόρου που απαιούν. Σην παρούσα διαριβή προείνοναι δύο µέθοδοι. Η πρώη απευθύνεαι σε αποκενρωµένο έλεγχο. Το πλεονέκηµά ης είναι όι λαµβάνεαι υπόψη η µεαβολή ης χρονικής υσέρησης σις αποφάσεις ελέγχου. Χρησιµοποιείαι η θεωρία ων προσαρµοσικών αλγορίθµων για ην εκίµηση ης µεαβολής ης υσέρησης. Τα αποελέσµαα δείχνουν όι η γνώση ης χρονικής υσέρησης είναι ένα δυναό εργαλείο που οδηγεί σο σχεδιασµό ελεγκών αρκεά καλύερων και πιο αποελεσµαικών από ους απλούς PI ελεγκές, που ευρέως χρησιµοποιούναι σην πράξη. Η δεύερη µέθοδος είναι µια µέθοδος κενρικού ελέγχου για ην οποία εγγυόµασε προσέγγιση ου βέλισου ελεγκή µε «αυθαίρεη» ακρίβεια. Τµηµαοποιούµε ο χώρο ων καασάσεων και για κάθε µήµα σχεδιάζουµε έναν γραµµικό ελεγκή. Χρησιµοποιώνας η θεωρία ου δυναµικού προγραµµαισµού (HJB συναρήσεις) και η θεωρία ευσάθειας καά Lyapunov αποδεικνύουµε όι η απόδοση ου ελεγκή µας µπορεί να προσεγγίσει αυή ου βέλισου ελεγκή µε «αυθαίρεη» ακρίβεια. Το βασικό πλεονέκηµα αυής ης µεθόδου είναι όι οι χρονοβόροι υπολογισµοί γίνοναι σε µη πραγµαικό χρόνο. Σε πραγµαικό χρόνο οι απαιούµενες πράξεις ανισοιχούν σε αυές ενός απλού γραµµικού ελεγκή. Η δοµή ης παρούσας διαριβής είναι η παρακάω. Αρχικά γίνεαι επισκόπηση ων µεθόδων ελέγχου για αποχεευικά δίκυα και αρδευικά (κεφάλαια και 3). Αναφέροναι πλειάδα µεθόδων που έχουν προαθεί σηριζόµενες σε διάφορες σχεδιασικές µεθόδους και διαφορεικά µαθηµαικά εργαλεία. Μεά σο κεφάλαιο 4 ακολουθεί µια επισκόπηση ων αποχεευικών δικύων σον ελλαδικό χώρο. Αναφέροναι α προβλήµαα που ενοπίζοναι και οι ήδη υπάρχουσα υποδοµή. Μεγαλύερο βάρος πέφει σο αποχεευικό δίκυο ης πρωεύουσας. Σο 5 ο κεφάλαιο προείνεαι µια µεθοδολογία σχεδιασµού αποκενρωµένου ελέγχου η οποία σηρίζεαι σην, σε πραγµαικό χρόνο, εκίµηση ης χρονικής υσέρησης. Αποδεικνύουµε όµως όι η εκίµηση ης χρονικής υσέρησης που προείνουµε λειουργεί ικανοποιηικά. Επίσης η χρήση αυής ης εκίµησης µας οδηγεί ση δηµιουργία οικογένειας ελεγκών πολύ καλύερων και πιο αποελεσµαικών από 9
10 ους απλούς PI ελεγκές ή ους ελεγκές που θεωρούν η χρονική υσέρηση ως σαθερά. Η προσπάθεια η προηγούµενη µέθοδος να επεκαθεί ώσε να κααλήξουµε σε κενρικό έλεγχο δεν απέδωσε καρπούς. Γι αυό ο λόγο σο κεφάλαιο 6 προείνεαι µια άλλη µεθοδολογία ελέγχου. Σε αυήν προσεγγίζουµε γραµµικά-καά-όπους ον βέλισο ελεγκή κάνονας διακριοποίηση ου χώρου ων καασάσεων και προσεγγίζουµε ο βέλισο κόσος µεαφοράς µε µια πολυωνυµική συνάρηση. Αποδεικνύουµε ελικά όι η απόδοση ου ελεγκή σε σχέση µε η βέλιση εξαράαι µόνο από ο πόσο «καλές» προσεγγίσεις θα κάνουµε. Οπόε αν επιλεγεί µεγάλης άξης πολυώνυµο για ην προσέγγιση και ο χώρος ων καασάσεων διακριοποιηθεί σε πολλά διασήµαα µπορούµε να προσεγγίσουµε µε πολλή καλή ακρίβεια ον βέλισο ελεγκή. Οι υπολογισµοί ων ελεγκών γίνοναι µε ην επίλυση ενός κυρού προβλήµαος σε µη πραγµαικό χρόνο. Σο κεφάλαιο 7, αξιολογείαι η η µέθοδος µέσω προσοµοιώσεων σε ένα δίκυο δοκιµής που ανικαοπρίζει µήµα ου αποχεευικού δικύου ης Αθήνας. ίνοναι κάποια πρώιµα αποελέσµαα που αποδεικνύουν ους ισχυρισµούς µας. 0
11 . ΕΠΙΣΚΟΠΗΣΗ ΜΕΘΟ ΩΝ ΕΛΕΓΧΟΥ ΓΙΑ ΑΠΟΧΕΤΕΥΤΙΚΑ ΙΚΤΥΑ Ο σχεδιασµός ενός συσήµαος ελέγχου για αποχεευικά δίκυα έχει σαν σόχο ην προσασία ου υδροφόρου ορίζονα που δέχεαι ις εξόδους ου συσήµαος. Γι αυό ο λόγο, κύριος σόχος ου ελέγχου θα πρέπει να είναι η ελαχισοποίηση ων υπερχειλίσεων καά η διάρκεια βροχοπώσεων και άλλων πιθανών διααραχών. Αυός ο σόχος µπορεί να επιευχθεί µε Τη µέγιση δυναή χρήση ου αποθηκευικού χώρου πριν επιευχθεί κάποια υπερχείλιση ου συσήµαος. Αν καά η διάρκεια κάποιας ισχυρής βροχόπωσης δεν είναι δυναή η αποφυγή υπερχειλίσεων, αυές θα πρέπει να διανεµηθούν ισόποσα σε όλο ο δίκυο (σε όλα α σηµεία υπερχείλισης). Αν υπάρχουν αποθηκευικοί χώροι χωρίς ην δυναόηα υπερχείλισης, θα πρέπει να αποφευχθεί η υπερβολική χρήση ους. Το αχύερο δυναό άδειασµα ου συσήµαος (µε αυόχρονη υπερεκµεάλλευση ης ικανόηας καθαρισµού ου βιολογικού καθαρισµού) έσι ώσε ο δίκυο να είναι έοιµο να ανιδράσει ικανοποιηικά σε µια µελλονική βροχόπωση. Κάποιοι υποσόχοι που λειουργούν συµπληρωµαικά µε α παραπάνω είναι: Ο διαµοιρασµός ης συνολικής αποθηκευµένης ποσόηας λυµάων σε όλους ους αποθηκευικούς χώρους, έσι ώσε να υπάρχει καά η διάρκεια ου αδειάσµαος ου δικύου, αποθηκευικός χώρος πανού, για ην περίπωση βροχόπωσης. Η αποφυγή απόοµων αλλαγών ων εκροών ου συσήµαος. Η ανάπυξη εχνικών βελισοποίησης για ο σχεδιασµό και η διαχείριση συσηµάων ροής υδάων σε κλεισά κανάλια (αποχεευικά δίκυα ή δίκυα ύδρευσης), έχει ερευνηθεί σε πολλά µέρη ου κόσµου και από διάφορες οµάδες. Η επιλογή ης µεθόδου που θα χρησιµοποιηθεί, εξαράαι από α χαρακηρισικά ων αποθηκευικών χώρων, ην διαθεσιµόηα δεδοµένων και φυσικά ους σόχους ου ελέγχου και ους ανάλογους περιορισµούς. Έχουν αναπυχθεί µέθοδοι βασισµένες κυρίως σε πένε βασικές καηγορίες. Γραµµικός προγραµµαισµός Ο γραµµικός προγραµµαισµός είναι ένα αρκεά δυναό εργαλείο βελισοποίησης και εύκολο ση χρήση. Σο [39] περιγράφεαι η λειουργία ενός γραµµικού ρυθµισή, σε µια διαδικασία ανοιχού βρόχου, µε σκοπό ον έλεγχο σε πραγµαικό χρόνο, µιας εργασηριακής διαδικασίας δεξαµενών υδάων, και ης
12 σάθµης ου ύδαος σε µια δεξαµενή αποθήκευσης µε σόχο ην παραγωγή υδροηλεκρικής ενέργειας. Για αποχεευικά δίκυα, ο γραµµικός προγραµµαισµός χρησιµοποιείαι σο [3] για ην ανάπυξη ενός αλγορίθµου για αυόµαο έλεγχο ης αποθηκευµένης ποσόηας λυµάων σε πανορροϊκά δίκυα και σο [7] για έλεγχο σε πραγµαικό χρόνο, ασικών δικύων βρόχινου νερού. Το πραγµαικά, µη γραµµικό πρόβληµα, ανικαθίσααι από διαδοχικά γραµµικά προβλήµαα. υναµικός προγραµµαισµός Ο δυναµικός προγραµµαισµός έχει χρησιµοποιηθεί ευρέως ση βελισοποίηση συσηµάων ροής υδάων, καθώς οι µη γραµµικές και σοχασικές διαδικασίες που λαµβάνουν χώρα σε ένα έοιο πολύπλοκο σύσηµα, µπορούν να εκφρασούν µε όρους δυναµικού προγραµµαισµού. Όαν όµως µιλάµε για συσήµαα µε πολλούς αποθηκευικούς χώρους, η χρήση ου δυναµικού προγραµµαισµού είναι περιορισµένη εξαιίας ου όγκου πληροφοριών που πρέπει να αποθηκευούν. Σε αυές ις περιπώσεις µπορούµε να χωρίσουµε ο πρόβληµά µας σε µικρόερα υποπροβλήµαα που συµβαίνουν σε χρονική σειρά ο ένα µε ο άλλο. Π.χ. σο [] για ον έλεγχο δικύου ύδρευσης, χρησιµοποιείαι µια έοια επαναληπική δυναµική διαδικασία. Ο αλγόριθµος επιλύεαι για κάθε υποσύσηµα ου δικύου και για κάθε χρονικό βήµα. Σο [7] γίνεαι χρήση διαφορικού δυναµικού προγραµµαισµού µε περιορισµούς για έλεγχο σε σύσηµα µε πολλούς αποθηκευικούς χώρους. Επίσης πολλές φορές χρησιµοποιούναι µέθοδοι που συνδυάζουν γραµµικό και δυναµικό προγραµµαισµό. Τέοια παραδείγµαα βρίσκοναι σα [38] και [09]. υναµικός προγραµµαισµός έχει χρησιµοποιηθεί σο [88], για βέλισο σχεδιασµό αποχεευικού δικύου, σο [05] για ον πιο οικονοµικό σχεδιασµό αποχεευικού δικύου, σο [35] για ο σχεδιασµό ου πιο οικονοµικού δικύου αποχέευσης µε ύπαρξη και δεξαµενών αποθήκευσης και σο [54] για ον έλεγχο ου πανορροϊκού δικύου ου San Francisco. Μη γραµµικός προγραµµαισµός Ο µη γραµµικός προγραµµαισµός προσφέρει µια πιο αυσηρή µαθηµαική προσέγγιση ων συναρήσεων, ων περιορισµών και ων δυναµικών που εκφράζουν ένα σύσηµα ροής υδάων, σε σχέση µε ο δυναµικό προγραµµαισµό ή ις απλοποιήσεις ου γραµµικού. Μερικά παραδείγµαα βρίσκοναι σα [], [8], [40], [70], [73], [9]. Σο [34] παρουσιάζεαι ένας αλγόριθµος που συνδυάζει σοιχεία διακριού δυναµικού προγραµµαισµού µε σοιχεία βελισοποίησης υπό περιορισµούς (µη γραµµικός προγραµµαισµός µε περιορισµούς ισόηας). Σο [0] εφαρµόζεαι αυόµαος έλεγχος, σε πραγµαικό χρόνο, για πανορροϊκά αποχεευικά δίκυα, µε χρήση ης θεωρίας ελέγχου. Τέλος, αναπύχθηκε αλγόριθµος επίλυσης για αποχεευικά δίκυα σα [65], [74], [75], [76], [77], [78], [79], [80], [8]. Γραµµικός εραγωνικός έλεγχος Η θεωρία ου γραµµικού εραγωνικού ελέγχου έχει χρησιµοποιηθεί ευρέως για η λύση πολλών ειδών προβληµάων. Πολλοί είναι οι ερευνηές που ανέρεξαν
13 σον γραµµικό εραγωνικό έλεγχο για να επιλύσουν προβλήµαα σχεικά µε η λειουργία δεξαµενών αποθήκευσης σε δίκυα ροής. Ένα έοιο παράδειγµα βρίσκεαι σο [68]. Σο [36] αναπύχθηκε µια διαδικασία αναπλήρωσης ύδαος για δίκυα µε πολλά κανάλια, µε η χρήση γραµµικού εραγωνικού ελέγχου. Σο [08] χρησιµοποιείαι πολυµεαβληός έλεγχος κλεισού βρόχου για πανορροϊκά αποχεευικά δίκυα, και έλος παρόµοιας λογικής ελεγκής χρησιµοποιείαι σα [64], [65], [69], [76], [77] και [79]. Γενεικοί αλγόριθµοι Αυοί οι αλγόριθµοι προσπαθούν να µιµηθούν η διαδικασία ης φυσικής επιλογής, µε λίγα λόγια ης εξελικικής θεωρίας. Κααφέρνουν να κραούν ένα σύνολο καλών λύσεων µε αποέλεσµα να µην εγκλωβισούµε σε κάποιο οπικό ελάχισο. Επειδή είναι µια ευρεική µέθοδος περισσόερο, παρά µια αυσηρά µαθηµαική διαδικασία δεν εγγυάαι ο ολικό και απόλυο ελάχισο, αλλά µια αρκεά ικανοποιηική λύση. Μερικές υπικές εφαρµογές έοιων µεθόδων µπορούν να βρεθούν σα [55], [6], και [06]. Ανάλογα µε ην πολυπλοκόηα ου συσήµαος µπορούµε να δούµε και συνδυασµό ων παραπάνω µεθόδων. Γενικά ο γραµµικός προγραµµαισµός είναι πιο εύχρησος, αλλά δεν µπορεί να αναλύσει πισά ις εξισώσεις και ις δυναµικές ου συσήµαος. Ο δυναµικός προγραµµαισµός για να εφαρµοσεί πρέπει να αναλύσουµε ο πολύπλοκο συνήθως πρόβληµα σε διάφορα πιο απλά υποσυσήµαα που συµβαίνουν σε χρονική αλυσίδα. Ούε εδώ µπορούµε να αναλύσουµε πλήρως ις δυναµικές. Ο µη γραµµικός προγραµµαισµός είναι ένα πολύ αυσηρά καθορισµένο µαθηµαικό εργαλείο που µπορεί πράγµαι να εκφράσει πλήρως κάθε δυναµική καάσαση ου συσήµαος, αλλά είναι πιο δύσκολη και πολύπλοκη η ανάπυξή ου. ιάφορες ευρεικές µέθοδοι ερευνήθηκαν καά καιρούς. Είναι µέθοδοι απλοποιηµένες που προσπαθούν να δώσουν καλές λύσεις και να διαχειρισούν µε έµµεσο ρόπο ις δυναµικές ου συσήµαος. Είναι πολύ εύρωσες και ευέλικες µέθοδοι, αλλά ο όι δε µας εγγυώναι η βέλιση λύση είναι ένα σηµανικό µειονέκηµα. 3
14 3. ΕΠΙΣΚΟΠΗΣΗ ΜΕΘΟ ΩΝ ΕΛΕΓΧΟΥ ΓΙΑ ΙΚΤΥΑ ΑΡ ΕΥΣΗΣ Έχουν χρησιµοποιηθεί αρκεές µέθοδοι διαχείρισης αρδευικών δικύων. Από χώρα σε χώρα και από περιοχή σε περιοχή οι µέθοδοι αυές διαφέρουν σε αρκεά σηµεία. Συνανούναι οι απλούσερες µέθοδοι οι οποίες χρησιµοποιήθηκαν από α αρχαία χρόνια, αλλά και πιο σύγχρονες και πολύπλοκες µέθοδοι. Εδώ θα ασχοληθούµε µε µεθόδους αυοµάου ελέγχου και θα αναφερθούµε σις κυριόερες καηγοριοποιήσεις. Για να φιάξουµε καηγοριοποιήσεις θα πρέπει να επιλέξουµε α βασικά ανεξάρηα κριήρια που διαφοροποιούν ις µεθόδους. Επιλέγουµε λοιπόν α παρακάω ρία ουσιασικά και κύρια κριήρια: επιλογή µεαβληών, λογική ου ελέγχου, µέθοδος σχεδιασµού. (Malaterre Pierre-Olivier regulation of irrigation canals: Characterization and classification [63] ) 3. ΕΠΙΛΟΓΗ ΜΕΤΑΒΛΗΤΩΝ Ση θεωρία ελέγχου ένα σύσηµα συνήθως αναπαρισάαι όπως σο σχήµα 3.. Με U συµβολίζοναι οι µεαβληές ελέγχου (άνοιγµα πυλών, ροές κλπ) που ενεργοποιούναι ώσε να επηρεάσουν ην καάσαση ου συσήµαος. Με Y συµβολίζοναι οι προς έλεγχο µεαβληές ου συσήµαος, οι µεαβληές καάσασης (π.χ επίπεδο ύδαος, αχύηα ύδαος, ροή κλπ). U System Y Σχήµα 3.. Συνήθης παρουσίαση ενός συσήµαος. Οι µεαβληές καάσασης Y δε δίνοναι πάνα καευθείαν από ο σύσηµα, αλλά καµιά φορά υπολογίζοναι µέσω συναρήσεων g, από ις φυσικές µεαβληές Ζ όπως αυές µερούναι σο σύσηµά µας. (Σχήµα 3.) Ένα έοιο παράδειγµα έχουµε µε η µεαβληή ελέγχου Υ=αy up +(-α)y dn ση µέθοδο BIVAL, όπου οι µερήσιµες µεαβληές Z είναι α ανάνη και καάνη ύψη ης σάθµης ου ύδαος σο κανάλι. Η σάθµη µπορεί να µερηθεί µε πολλούς ρόπους. Αυό που µας ενδιαφέρει κάθε φορά είναι ο ύπος, ο αριθµός και η οποθέηση ων κάθε είδους µερήσεων. Παροµοίως, οι µεαβληές ελέγχου U, µερικές φορές δε µπορούν να εφαρµοσούν άµεσα σο σύσηµα. Σε αυές ις περιπώσεις κάνουµε χρήση µιας συνάρησης f, ώσε να εξάγουµε βασικές εφαρµόσιµες ενολές ελέγχου V για ους επενεργοποιηές 4
15 µας. Αυή η συνάρηση f µπορεί να χωρισεί σε δύο συναρήσεις f και f. Η f µεαρέπει ις µεαβληές ελέγχου U σε κάποιο επιθυµηό άνοιγµα πύλης (φράγµαος) και η f ο επιθυµηό άνοιγµα πύλης σις µεαβληές V. Γενικόερα οι επίσηµοι PID ελεγκές µε γρήγορα εναλλασσόµενες δυναµικές, χρησιµοποιούν έοιους f αναδρασικούς µηχανισµούς ελέγχου. Εποµένως η ανίσοιχη δυναµική παραµελείαι και οι εξεαζόµενες σοιχειώδεις ενολές V είναι µόνο ανοίγµαα πυλών. Έσι θεωρούµε όι είναι δυναόν να µεακινήσουµε ις πύλες σε οποιαδήποε θέση και µε άπειρη αχύηα. U f System g Y Σχήµα 3.. Λεποµερής παρουσίαση ενός συσήµαος. 3.. ΕΛΕΓΧΟΜΕΝΕΣ ΜΕΤΑΒΛΗΤΕΣ Οι ελεγχόµενες µεαβληές είναι οι µεαβληές καάσασης που πρέπει σο έλος ου ελέγχου να έχουν µια επιθυµηή ιµή. Θέλουµε λοιπόν να ρυθµίσουµε αυές ις µεαβληές, είε η επιθυµηή ιµή είναι σαθερή, είε µεαβάλλεαι σο χρόνο. Οι ελεγχόµενες µεαβληές σε αρδευικά δίκυα µπορεί να είναι δύο ειδών: ροές ή σάθµες ύδαος, σύµφωνα µε ην ορολογία που χρησιµοποιείαι ση µονελοποίηση έοιων συσηµάων. Μπορούν εξίσου να είναι όγκοι ύδαος, που σηµαίνει χρονικό ολοκλήρωµα ροών, ή χωρικό ολοκλήρωµα ων σάθµεων ύδαος Ροές Οι ανάγκες ων χρησών ενός δικύου άρδευσης καθορίζοναι κυρίως µε όρους ροών. Για ου λόγου ο αληθές, οι ανάγκες ων αγροών εκφράζοναι σε όρους ροών που οδηγούναι καευθείαν σα χωράφια ους, σε ένα δευερεύον κανάλι ή σε µια εγκαάσαση ανλιών. Οι επιχειρήσεις προσασίας ου περιβάλλονος ενδιαφέροναι για όσο ο δυναόν λιγόερες απώλειες ροών και οι πολίες ενδιαφέροναι για ις ροές που κααλήγουν σο ασικό υδρευικό δίκυο ή σε εγκαασάσεις φιλραρίσµαος. Σε πολλές περιπώσεις υπάρχουν φυσικά ή εχνηά συσήµαα αποθήκευσης ύδαος. Οι ανάγκες ων χρησών σε αυή ην περίπωση µπορούν να εκφρασούν πιο πολύπλοκα ως ο όγκος ύδαος που ους διανέµεαι σε κάποιο χρονικό ορίζονα. Εδώ οι ελεγχόµενες µεαβληές δεν έχουν µια δοσµένη ιµή ροής, αλλά µεριέαι ως όγκος (χρονικό ολοκλήρωµα ης ροής σε καθορισµένη περίοδο). Οι διακυµάνσεις ης ροής καθορίζοναι από η χωρηικόηα ου αποθηκευικού χώρου. Αυές οι 5
16 υδάινες αποθήκες έχουν όµως σηµανικούς περιορισµούς όσο αφορά ο κόσος αλλά και ο µέγεθός ους µε αποέλεσµα να µην χρησιµοποιούναι ευρέως. Συχνά όλα α επιφανειακά υδραυλικά συσήµαα χρειάζοναι άµεση ή έµµεση διαχείριση προκειµένου να επιευχθεί η κάλυψη ων αναγκών σε ροές. εδοµένου ου φυσικού φαινοµένου που λαµβάνει χώρα (λόγω ης βαρύηας έχουµε ροή από ο ανάνη µέρος σο καάνη), αυές οι ανάγκες µπορούν να καλυφθούν µόνο από ην είσοδο ανάνη ου συσήµαος, µε αποσράγγιση ου ανάνη αποθηκευικού χώρου. Οι GPC ([89],[93],[94],[95],[96],[97]), CAGG ([84],[85],[4]) και SIMBAK ([]) είναι µερικά παραδείγµαα µεθόδων ελέγχου ων ροών Επίπεδα σάθµης υδάων Ανίθεα µε ις ροές, ο ύψος ων υδάων σο κανάλι µπορεί να µερηθεί πολύ εύκολα σε ανοικά επιφανειακά κανάλια. Επίσης όλοι οι περιορισµοί (κλίσης, αποθήκευσης κλπ) εκφράζοναι σε επίπεδο σάθµης ου ύδαος. Η ελεγχόµενη σάθµη y µπορεί να είναι ανάνη (y up σχήµα 3.3), καάνη (y dn σχήµα 3.4) ή ενδιάµεσα ου καναλιού (y in σχήµα 3.5). Σα σχήµαα 3.3 και 3.4, οι ιµές ης σάθµης ου ύδαος είναι ίσες µε η µηδενική και ην µέγιση ροή. Αυό βέβαια δεν ισχύει σε όλες ις περιπώσεις (π.χ. GEC Alsthom Gates [3],[4]). Το πώς θα χειρισούµε ο πρόβληµα έχει να κάνει καά πολύ από η θέση ου y. Σχήµα 3.3. Έλεγχος ου ανάνη ύψους (σάθµης) ου καναλιού. Σχήµα 3.4. Έλεγχος ου καάνη ύψους (σάθµης) ου καναλιού. 6
17 Σχήµα 3.5. Έλεγχος ης σάθµης σο µέσο ου καναλιού Ένα από α πλεονεκήµαα ου ελέγχου ων ανάνη υψών ου ύδαος, είναι όι ένας όγκος αποθήκευσης V είναι διαθέσιµος µεαξύ ου µηδενικού όγκου ροών και ου µέγισου όγκου ροών. Αυό επιρέπει η γρήγορη αναπόκριση σε απρόβλεπες ζηήσεις ή και ην αποθήκευση ύδαος σε περίπωση µείωσης ης καανάλωσης. Το πρόβληµα σε αυή ην περίπωση είναι ο σχεικά υψηλό κόσος εξαιίας ης οριζόνιας ροφοδόησης. Οι AVIS και AVIO ([3],[4],[37]), είναι µερικά παραδείγµαα έοιων µεθόδων. Όαν έχουµε έλεγχο ης καάνη σάθµης ύδαος, η ροφοδόηση ων καναλιών ακολουθεί η φυσική κλίση ου εδάφους, γεγονός που µειώνει ο κόσος καασκευής. Όµως ο κανάλι δε µπορεί πλέον να λειουργεί και σαν χώρος αποθήκευσης, µε αποέλεσµα η µη γρήγορη ανίδραση σε απρόβλεπες ζηήσεις. Τα παραπάνω ύδαα δε µπορούν να αποθηκευούν οπικά και πηγαίνουν σα παρακάω µήµαα ου καναλιού. Οι ΑΜΙL ([3],[4],[37]), ELFLO ([00],[5]), PIR ([9]) είναι µερικές από ις χαρακηρισικές µεθόδους ελέγχου ων καάνη σάθµεων ου ύδαος. Ασκώνας ον έλεγχο σε ένα ενδιάµεσο σηµείο ου καναλιού, συνήθως κονά ση µέση, είναι σαν να ελέγχουµε ην αποθηκευµένη ποσόηα ου ύδαος σο συγκεκριµένο µήµα ου καναλιού. Μπορούµε άµεσα να µερήσουµε ο ύψος ης σάθµης σο ενδιάµεσο σηµείο, ή να ο εκιµήσουµε µε ένα γραµµικό συνδυασµό ων ανάνη και καάνη υψών. (BIVAL). Με ον έλεγχο σε κάποιο ενδιάµεσο σηµείο εξισορροπούµε α µειονεκήµαα και πλεονεκήµαα ων παραπάνω µεθόδων. Η µοναδική έοια µέθοδος που βρέθηκε είναι η BIVAL ([3],[9]) Όγκοι αποθήκευσης Σε αυήν ην περίπωση, οι ελεγκές είναι λιγόερο ευαίσθηοι σις διααραχές, αλλά οι χρόνοι απόκρισης έχουν αυξηθεί. Αυές οι µέθοδοι εφαρµόζοναι σε δίκυα άρδευσης µε αρκεά µεγάλους αποθηκευικούς χώρους, και εξοπλισµένα µε εξόδους ων οποίων η ροφοδόηση δεν εξαράαι από ις σάθµες ύδαος σο κύριο κανάλι. (π.χ. εγκαασάσεις ανλιών). Παραδείγµαα έοιων µεθόδων είναι η υναµική ρύθµιση (Dynamic regulation: [], [9]) και οι ελεγχόµενοι όγκοι (Controlled Volumes: [6] ). 7
18 3.. ΜΕΤΡΗΣΙΜΕΣ ΜΕΤΑΒΛΗΤΕΣ Όαν µιλάµε για µερήσιµες µεαβληές εννοούµε κυρίως ο ύψος ης σάθµης ου ύδαος (π.χ ELFLO, PIR). Σε κάποιες περιπώσεις µπορούµε να µερήσουµε και η ροή (π.χ. CACG). Η ροή µπορεί να µερηθεί µε χρήση καάλληλων εργαλείων, όπως ηλεκροµαγνηικές ή υπερηχηικές συσκευές. Επίσης οι όγκοι ύδαος µπορούν να µερηθούν µερώνας αρκεά ύψη επιπέδου ύδαος καά µήκος ου δικύου (π.χ. Dynamic Regulation) ΜΕΤΑΒΛΗΤΕΣ ΕΛΕΓΧΟΥ Οι µεαβληές ελέγχου U µεαφράζοναι συνήθως σε ανοίγµαα πύλης (ή ποσοσιαία αλλαγή ου ανοίγµαος ης πύλης) και σε ροές (ή ποσοσιαία αλλαγή ης ροής). Τα ανοίγµαα πύλης σε ένα µήµα ου δικύου, έχουν ως πλεονέκηµα ην ικανόηα να λαµβάνουν υπόψη ις πολύπλοκες δυναµικές που δηµιουργούναι από ο άνοιγµα ης πύλης ση ροή ου συγκεκριµένου µήµαος, καθώς και σα ανάνη και καάνη ύψη ης σάθµης ου ύδαος. Αυές οι δυναµικές ου συσήµαος είναι ουσιώδεις και πρέπει να ληφθούν οπωσδήποε υπόψη µε κάποιο ρόπο. Το να θεωρήσουµε η ροή ως µεαβληή ελέγχου µας επιρέπει να µην ασχοληθούµε µε ο συνδυασµό ων διάφορων υποσυσηµάων, αλλά να αρκεσούµε σε οπικούς ελέγχους ου κάθε µήµαος. Αυή είναι µια πολύ σηµανική διαπίσωση σε περιπώσεις µονοδιάσαων ελεγκών. Ωσόσο, αυές οι δυναµικές δεν είναι δυναόν να παρθούν υπόψη από ον κενρικό έλεγχο. Αφού λοιπόν καά ο σχεδιασµό ου κενρικού ελεγκή αγνοούµε ις πολύπλοκες οπικές δυναµικές, δεν είναι δυναόν να κρίνουµε ην ποιόηα ης συµπεριφοράς ου. Αν ως µεαβληή ελέγχου U επιλέξουµε η ροή, είναι απαραίηο να µεαφρασεί σε άνοιγµα πύλης ώσε να υπάρχει συµβαόηα µε ο σύσηµα. Αυή η µεαροπή γίνεαι µε κάποια καάλληλη συνάρηση ή µε κάποιον οπικό δυναµικό ελεγκή (π.χ. ελεγκής PID ). 3. ΛΟΓΙΚΗ ΤΟΥ ΕΛΕΓΧΟΥ Ο καθορισµός ης λογικής ου ελέγχου εξαράαι από ις πληροφορίες που χρησιµοποιούναι για ον υπολογισµό ων µεαβληών ελέγχου ου συσήµαος. Έχουµε δύο περιπώσεις, η λογική ανοιχού βρόχου ή η λογική κλεισού βρόχου (δηλαδή µε ανάδραση). 3.. ΕΛΕΓΧΟΣ ΚΛΕΙΣΤΟΥ ΒΡΟΧΟΥ Σε κλεισούς βρόχους οι µεαβληές ελέγχου U υπολογίζοναι από ο σφάλµα ανάµεσα σις πραγµαικές ιµές ων ελεγχόµενων µεαβληών καάσασης Y και ου ανίσοιχου σόχου Yc δηλαδή ης επιθυµηής ιµής (σχήµα 3.6). Οι διααραχές P, ακόµα και όαν είναι άγνωσες, λαµβάνοναι υπόψη έµµεσα, µέσω ων επιδράσεών ους σις εξόδους Y ου συσήµαος. Ση θεωρία ελέγχου αυή η έννοια 8
19 είναι ουσιώδης αφού ανισοιχεί ις ιµές ων µεαβληών ελέγχου µε ις ιµές ων µεαβληών καάσασης. Έλεγχος κλεισού βρόχου µπορεί να γίνει ανεξαρήως ης επιλογής ων ελεγχόµενων µεαβληών καάσασης. Παραδείγµαα εφαρµογής ελέγχου κλεισού βρόχου όσο αφορά η ροή είναι η GPC ([93], [89]), η CACG ([85]), CARA ([67],[90]) και η Liu ([60]). U P System Y FB Y c Σχήµα 3.6. Έλεγχος κλεισού βρόχου (αναροφοδόηση-feedbac) Έχουν καθορισεί δύο ύποι ελέγχου κλεισού βρόχου σο ύψος σάθµης ου ύδαος, όσο αφορά η σχεική θέση ης µεαβληής ελέγχου και ης ελεγχόµενης µεαβληής καάσασης. Σο ύψος ης σάθµης µπορεί να ασκηθεί έλεγχος είε µέσω µεαροπής ης ανάνη ροής, είε µέσω ης µεαροπής ου καάνη ύψους ης σάθµης ου ύδαος. Αυοί οι δύο ύποι φαίνοναι σα σχήµαα 3.7 και 3.8. Παραδόξως, εξαιίας ισορικών λόγων, α ονόµαα ων µεθόδων είναι ανάποδα από ο αναµενόµενο. Η µεαροπή ης ανάνη ροής ονοµάζεαι καάνη έλεγχος κλεισού βρόχου και η µεαροπή ου καάνη ύψους ονοµάζεαι ανάνη έλεγχος κλεισού βρόχου. Σχήµα 3.7. Καάνη έλεγχος Σχήµα 3.8. Ανάνη έλεγχος Ο καάνη έλεγχος ης σάθµης ου ύδαος δηµιουργεί έµµεσα έλεγχο κλεισού βρόχου ης ροής, αφού επιυγχάνεαι από ην ανίσοιχη µεαροπή ης ανάνη ροής. Αυό ο χαρακηρισικό είναι πολύ σηµανικό σοιχείο ου καάνη ελέγχου ης ροής. Εξαιίας αυού ου χαρακηρισικού είναι εφικός ο καάνη έλεγχος ης σάθµης ου ύδαος, χωρίς να χρειάζεαι επιπλέον έλεγχος ης ροής. Παραδείγµαα έοιων µεθόδων είναι οι AVIS, AVIO, ELFLO ([00]), CARDD ([4]), CARA ([67]), PID ([9]) PIR ([9]) Liu ([60]) και άλλες. 9
20 Ανίθεα µε ον καάνη έλεγχο ης σάθµης ου ύδαος, ο ανάνη έλεγχος δεν παράγει έλεγχο ροής, αφού επιυγχάνεαι µε µεαροπές ου καάνη ύψους ης σάθµης ου ύδαος. Έσι ο ανάνη έλεγχος ης σάθµης ου ύδαος χρειάζεαι να συµπληρωθεί από έναν έλεγχο ροής. Παράδειγµα έοιων µεθόδων είναι η AMIL. Κάποιες µέθοδοι ελέγχου ης σάθµης ου ύδαος συνδυάζουν και η λογική ου ανάνη και ου καάνη ελέγχου (σχήµα 3.9). Παράδειγµα έοιων µεθόδων είναι η LQR ([7], [8], [3], [4], [5], [6], [6]). Ελεγχόµενο ύψος υδάων Σχήµα 3.9. Έλεγχος ανάνη και καάνη Σην περίπωση κλεισού βρόχου σους όγκους ύδαος, ο έλεγχος επιυγχάνεαι συναρήσει ου σφάλµαος ανάµεσα σους ελεγχόµενους όγκους σε ποικίλα µήµαα ου καναλιού και ις ανίσοιχες επιθυµηές ιµές. Γενικά ο όγκος ύδαος ενός µήµαος ου καναλιού ελέγχεαι µέσω µιας µεαροπής ης ανάνη ροής. Εποµένως ο έλεγχος ου όγκου δηµιουργεί έµµεσα έλεγχο ροής. Η δυναµική ρύθµιση SCP και η µέθοδος ων ελεγχόµενων όγκων USBR είναι δύο παραδείγµαα έοιων µεθόδων. Οι όγκοι ύδαος σε κάποιο κανάλι θα µπορούσαν να ελεγχθούν και µε µια µεαροπή ου καάνη ύψους ης σάθµης ου ύδαος. Για πολύπλοκες διαδικασίες, όπως διαδικασίες µε χρονική υσέρηση ([53]), οι κλεισοί βρόχοι δεν δίνουν ικανοποιηικά αποελέσµαα. Για α αρδευικά δίκυα, οι χρονικές υσερήσεις παίζουν σηµανικό ρόλο αφού µιλάµε για διασήµαα λίγων λεπών ή και αρκεών ωρών. Ένας κλεισός βρόχος µπορεί να λειουργήσει σωσά µόνο αν υπάρχουν µεγάλοι αποθηκευικοί χώροι υδάων, πράγµα που αυξάνει ο συνολικό κόσος καασκευής καά πολύ. Πάνως σε αυήν ην περίπωση µπορούµε να εγγυηθούµε όι η υσέρηση ου ελέγχου θα ισούαι µε ην υσέρηση ου συσήµαος. Σύµφωνα µε ον ([0]) η προσθήκη ενός ανοικού βρόχου βελιώνει αισθηά η λειουργία ου ελέγχου. 3.. ΕΛΕΓΧΟΣ ΑΝΟΙXΤΟΥ ΒΡΟΧΟΥ Σε ανοιχούς βρόχους, ο έλεγχος U υπολογίζεαι λαµβάνονας υπόψη ις δυναµικές ου συσήµαος (µε η χρήση ειδικού µονέλου), ις επιθυµηές ιµές Y c και ην εκίµηση ων διααραχών Pˆ (σχήµα 3.0). Ο έλεγχος ανοιχού βρόχου µπορεί να ανισαθµίσει ην εγγενή χρονική υσέρηση ου συσήµαος προβλέπονας ις ανάγκες ων χρησών. Η πρόβλεψη αυή θα πρέπει να έχει αρκεά καλή ακρίβεια. 0
21 Για να επιευχθεί κάι έοιο θα πρέπει να ληφθούν υπόψη κλιµαικά, κοινωνικά και γεωπονικά δεδοµένα. Επίσης θα πρέπει να χρησιµοποιηθούν και ισορικά δεδοµένα καανάλωσης ([83]). Έλεγχος ανοιχού βρόχου µπορεί να εφαρµοσεί για ον έλεγχο όλων ων µεαβληών καάσασης: ροή, σάθµη υδάων και όγκο υδάων. P Pˆ FF U System Y Y c Σχήµα 3.0. Έλεγχος ανοιχού βρόχου (Feed-forword) Ανάλογα ην µέθοδο υπολογισµού δίνοναι α παρακάω παραδείγµαα ελέγχου ανοικού βρόχου ης εκροής: Με µονέλο ανασροφής: κινηµαικό κύµα (CARA, [90]), κύµα διάχυσης (CACG, [93]), δυναµικό κύµα ([9]) Με βελισοποίηση: ([56]) Παραδείγµαα ελέγχου ανοιχού βρόχου ης σάθµης ων υδάων είναι: Με ανασροφή µονέλου δυναµικού κύµαος ([33]) Με βελισοποίηση ([03]) Με προσοµοίωση ([9]) Για ους όγκους ένα παράδειγµα µπορεί να βρεθεί σο ([9]) ΣΥΜΠΕΡΑΣΜΑΤΑ Και η λογική ου ανοικού αλλά και ου κλεισού βρόχου, έχουν πλεονεκήµαα και περιορισµούς όσο αφορά ην αποελεσµαικόηά ους. Συχνά λοιπόν συνανάµε συνδυασµό ων δύο µεθόδων (σχήµα 3.), όπου ο κλεισός βρόχος χρησιµοποιείαι για να µειώσει α σφάλµαα ου ανοικού βρόχου. Για πολυµεαβληά προβλήµαα συχνά συνανούναι διάφορων ειδών έλεγχοι για διαφορεικές µεαβληές ελέγχου. P Pˆ FF U System Y Y c FB Υ c Σχήµα 3.. Έλεγχος ανοιχού και κλεισού βρόχου
22 Ο καάνη έλεγχος ης σάθµης και ων όγκων ων υδάων, ανισοιχεί έµµεσα έλεγχο ροής. Σις υπόλοιπες περιπώσεις χρειάζεαι και δεύερος έλεγχος για η ροή. Συνήθως για η ροή χρησιµοποιείαι ανοιχός βρόχος, ενώ για ο ύψος ης σάθµης κλεισός βρόχος. Αυό συµβαίνει γιαί η σάθµη ων υδάων είναι εύκολο να µερηθεί και ο κλεισός βρόχος χρησιµοποιεί µερήσεις, ενώ ο ανοικός εκιµήσεις. 3.3 ΣΧΕ ΙΑΣΤΙΚΕΣ ΜΕΘΟ ΟΙ Η θεωρία ελέγχου εµπεριέχει ρία βασικά βήµαα: η µονελοποίηση ου συσήµαος, ην ανάλυση ου συσήµαος και ο σχεδιασµό ου ελεγκή. Οι πρώες υπολογισικές µέθοδοι αναπύχθηκαν προηγούµενους αιώνες. Τις ελευαίες δεκαείες µε ην ανάπυξη ων υπολογισών υπάρχει µεγάλη άνθιση σις µεθόδους σχεδιασµού και σα υπολογισικά εργαλεία. Αρκεί να αναφέρουµε όι κυκλοφορούν ευρέως δεκάδες σχεικοί προσοµοιωές. Αποέλεσµα αυού είναι πλέον α αναλογικά µονοδιάσαα προβλήµαα ελέγχου να ανικαασαθούν από ψηφιακά και πολυδιάσαα, γεγονός που περιπλέκει α πράγµαα, αλλά κάνει ην εφαρµογή ελέγχου πιο αποελεσµαική ΕΙΣΟ ΟΙ /ΕΞΟ ΟΙ Οι µεαβληές καάσασης και ελέγχου έχουν ήδη ορισεί σε προηγούµενες ενόηες. Οι µεαβληές U είναι είσοδοι ου συσήµαος και έξοδοι ου ελεγκή. Σε αυήν ην επισκόπησή κάνουµε αξινόµηση µε βάση ους ελεγκές και όχι ο σύσηµα. Σο σχήµα 3. φαίνοναι οι διάφοροι ύποι εισόδων και εξόδων. Όπου: U είναι µεαβληές που ενεργούν σο σύσηµα, αλλά δεν δίνοναι από ον ελεγκή (µη ελεγχόµενες είσοδοι, διααραχές κλπ). U µεαβληές που δίνοναι από ον ελεγκή αλλά δεν επιδρούν σο σύσηµα (π,χ, έλεγχος σε κάποιο άλλο σύσηµα). Y µεαβληές που δίνοναι από ο σύσηµα, αλλά δε χρησιµοποιούναι άµεσα από ον ελεγκή (µερήσιµες µεαβληές Z). Y µεαβληές που χρησιµοποιούναι από ον ελεγκή, αλλά δεν προκύπουν από ο σύσηµα (µερήσιµες µεαβληές Ζ, έλεγχος που προκύπει από κάποιον άλλο ελεγκή κλπ) Οι είσοδοι ου ελεγκή εποµένως είναι οι µεαβληές Y και Y και οι έξοδοι U και U.
23 U U System Υ Y U Ελεγκής Y Σχήµα 3.. Είσοδοι και έξοδοι ενός ελεγχόµενου συσήµαος Ένας µονοµεαβληός ελεγκής έχει µία είσοδο και µία έξοδο. Αυές οι µέθοδοι ονοµάζοναι SISO. (Single Input Single Output). Ένας πολυµεαβληός ελεγκής έχει αρκεές εισόδους και εξόδους και ονοµάζεαι ΜΙΜΟ (Multiple Inputs Multiple Outputs). Οι ελεγκές µπορεί να είναι πολυµεαβληοί µόνο ση είσοδο (MISO), ή µόνο σην έξοδο (SIMO). Συνήθως µια µέθοδος που έχει µοναδική έξοδο λέγεαι µονοµεαβληή ακόµα και αν έχει πολλές εισόδους, ανίσοιχα µια µέθοδος µε πολλές εξόδους πολυµεαβληή. Αυή η απλοποίηση έχει να κάνει µε ο γεγονός όι ο µαθηµαικό υπόβαθρο ων µεθόδων ελέγχου συνδέεαι περισσόερο µε ον αριθµό ων εξόδων, παρά ις εισόδους. Αυή η απλοποιηµένη ονοµασία χρησιµοποιείαι σα δύο παρακάω υποκεφάλαια ΜΟΝΟΜΕΤΑΒΛΗΤΕΣ ΜΕΘΟ ΟΙ Έχουν αναπυχθεί πολλές ευρεικές µονοµεαβληές µέθοδοι βασισµένες σην ρευσοµηχανική και όχι ση θεωρία ελέγχου (π.χ [3] CARDD [4]). Αν και έοιες µέθοδοι βρίσκοναι ση παγκόσµια βιβλιογραφία, δεν είναι λειουργικές. Π.χ η µέθοδος Littleman (USBR,[5]) είναι µια εµπειρική µέθοδος βασισµένη σε έναν three position controller. Οι περισσόερες µέθοδοι ελέγχου σε αρδευικά δίκυα που βασίζοναι σην κλασική θεωρία ελέγχου, χρησιµοποιούν ον γραµµικό µονοµεαβληό ελεγκή PID. Παραδείγµαα µεθόδων σχεικών µε ον PID ελεγκή είναι: P: AMIL, AVIS, AVIO PI: ELFLO, BIVAL, PI Sogreah PID: PID UMA Enginnering. Αν και συνήθως οι PID ελεγκές είναι πολύ αποελεσµαικοί, δεν λαµβάνουν καθόλου υπόψη ις χρονικές υσερήσεις. Ο Shand ([00]) µελεώνας ο κανάλι Corning ης Καλιφόρνια ων Η.Π.Α. µελέησε ην πιθανόηα να χρησιµοποιηθεί η µέθοδος πρόβλεψης ου Smith έσι ώσε να ξεπερασούν οι δυσκολίες ης χρονικής υσέρησης. Ανιµεώπισε δυσκολίες και ελικά επιλέγει η όχι και όσο αποελεσµαική µέθοδος ELFLO. Το 99 όµως ένας έοιος συνδυασµός έγινε εφικός ([9]). Αυός ο ελεγκής ονοµάζεαι PIR και καάφερε να ξεπεράσει ις δυσκολίες ου Shand εκµεαλλευόµενος ην ανάπυξη ης εχνολογίας σους προσωπικούς υπολογισές. 3
24 Άλλοι γραµµικοί ελεγκές που έχουν χρησιµοποιηθεί σε συσήµαα ποαµών µε µεγάλες χρονικές υσερήσεις είναι οι CACG, µε χρήση συναρήσεων µεαφοράς µεγάλου βαθµού. Η γενικευµένη µέθοδος πρόβλεψης (GPC), µια µονοµεαβληή µέθοδος βελισοποίησης, αναπύχθηκε από ους Sawadogo ([93],[94],[95],[96],[97]) και Rodellar ([89]). ε βασίζεαι σε µέθοδο κλεισού βρόχου, αλλά σην ελαχισοποίηση ενός κριηρίου J, που έχει να κάνει µε ις µεαβληές U και ο σφάλµα από ις µεαβληές καάσασης και ις επιθυµηές ους ιµές. Οι µέθοδοι GPC χρησιµοποιούν µονέλα συναρήσεων µεαφοράς και συνήθως εµπεριέχουν συνδυασµό ανοιχού και κλεισού βρόχου. Επίσης έχουν αναπυχθεί και µέθοδοι που χρησιµοποιούν ην ασαφή λογική (π.χ. CNABRL) και α νευρωνικά δίκυα (π.χ.[98]). Οι µονοµεαβληές µέθοδοι για να εφαρµοσούν, θεωρούν ο συνολικό σύσηµα σαν ένα σύνολο υποσυσηµάων που δεν αλληλεπιδρούν µεαξύ ους. Όµως α αρδευικά δίκυα είναι συσήµαα πολυµεαβληά µε πολύ ισχυρές αλληλεπιδράσεις ανάµεσα σα διάφορα υποσυσήµαα. Ένα άνοιγµα πύλης, επηρεάζει όλα α ανάνη και καάνη µήµαα ου συνολικού δικύου. Αυή η εχνική ης αποσύνδεσης εφαρµόσηκε σον ελεγκή ELFLO ([99]). Περιορίζει, όσο ο δυναό, ην επίδραση ης εφαρµογής ου ελέγχου ση µία και µοναδική έξοδο. Έσι µπορούµε να θεωρήσουµε ο πολυµεαβληό µας σύσηµα σαν µία σειρά µονοµεαβληών συηµάων, ανεξάρηων µεαξύ ους, που ενεργούν παράλληλα. Αυό µπορεί να γίνει µόνο όαν οι είσοδοι είναι περισσόερες ή ουλάχισον ίσες µε ις εξόδους ([]). Η αποσύνδεση ων υποσυσηµάων µπορεί να βελιώσει αισθηά ην αποελεσµαικόηα ενός ελεγκή. Μειώνουν όµως ην αποελεσµαικόηά ου, άγνωσες διααραχές και σφάλµαα µονελοποίησης. Μέθοδοι όπως η RIP ([9]) µπορεί να µη λαµβάνουν υπόψη ις συνέπειες ης αλληλεπίδρασης ων υποσυσηµάων, αλλά προσπαθούν να ις µειώσουν. Ως µεαβληή ελέγχου επιλέγεαι η ροή και όχι ο άνοιγµα πύλης και όαν επιλέγουµε να ανοίξουµε (κλείσουµε) µια πύλη, ένα ποσοσό ου ανοίγµαος (κλεισίµαος) εκελείαι σο προηγούµενο ανάνη µήµα ΠΟΛΥΜΕΤΑΒΛΗΤΕΣ ΜΕΘΟ ΟΙ Η θεωρία ελέγχου περιέχει πολλές πολυµεαβληές µεθόδους. Πολύ λίγες από αυές έχουν χρησιµοποιηθεί σα αρδευικά δίκυα. (Π.χ. η πολυµεαβληή PID) Οι περισσόερες από αυές ακολουθούν η λογική ου κλεισού βρόχου ([9]) και ελάχισες αυή ου ανοικού βρόχου ([60]). Επίσης έχουν αναπυχθεί αρκεές µέθοδοι βελισοποίησης. Αυές είναι ως επί ο πλείσον πολυµεαβληές. Αυές χωρίζοναι σε 3 κύριες καηγορίες: Γραµµικές ([9]) Μη γραµµικές ([03], [56]) LQR ([8], [6], [6]) 4
25 Η κλασική µη γραµµική βελισοποίηση οδηγεί αποκλεισικά σε λογική ανοιχού βρόχου µε αποέλεσµα ην αυξηµένη ευαισθησία ου ελεγκή, σε λάθη µονελοποίησης και διααραχές. Για να εισάγουµε έλεγχο κλεισού βρόχου, ο έλεγχος θα πρέπει να γίνεαι περιοδικά. Αυό περιπλέκει η µέθοδο και περιορίζει ην εφαρµοσιµόηά ης, εξαιίας ων πολλών περιορισµών που υπάρχουν σε πραγµαικό χρόνο. Επίσης δεν είναι εύκολος ο καθορισµός ων αρχικών συνθηκών, που απαιείαι για η βελισοποίηση. Οι µέθοδοι LQR περιέχουν και έλεγχο κλεισού και ανοιχού βρόχου. Γενικά οι πολυµεαβληές µέθοδοι είναι πιο πολύπλοκες από ις µονοµεαβληές. 5
26 4 ΕΠΙΣΚΟΠΗΣΗ ΑΠΟΧΕΤΕΥΤΙΚΩΝ ΙΚΤΥΩΝ ΣΤΟΝ ΕΛΛΑ ΙΚΟ ΧΩΡΟ 4. ΤΥΠΟΙ ΑΠΟΧΕΤΕΥΤΙΚΩΝ ΙΚΤΥΩΝ ΣΤΟΝ ΕΛΛΑ ΙΚΟ ΧΩΡΟ ΚΑΙ ΕΝ ΥΝΑΜΕΙ ΕΦΑΡΜΟΓΗ ΜΕΤΡΩΝ ΕΛΕΓΧΟΥ Σην Ελλάδα υπήρξε σηµανική καθυσέρηση σην καασκευή σύγχρονων αποχεευικών συσηµάων [6]. Η ανάπυξη σην καασκευή σύγχρονων αποχεευικών συσηµάων ξεκίνησε περί α µέσα ης δεκαείας ου 960 όαν και είχε εγκααλειφθεί παγκοσµίως η άση για καασκευή πανορροϊκών δικύων. Αποέλεσµα ούου είναι όι, µε εξαίρεση κάποια µήµαα ου δικύου ης Αθήνας και ης Θεσσαλονίκης και κάποια παλαιά µικρά µήµαα επαρχιακών πόλεων (π.χ. Νεάπολη Κρήης) [6] που είναι πανορροϊκά δίκυα, η πλειοψηφία ων αποχεευικών δικύων ση χώρα µας είναι χωρισικού ύπου. Για αυό ο λόγο, η εργασία αυή επικενρώνεαι µόνο σε αποχεευικά συσήµαα χωρισικού ύπου. Πρέπει να σηµειωθεί εδώ, όι σε ανίθεση µε α πανορροϊκά δίκυα για α οποία έχουν αναπυχθεί µονέρνες και αρκεά προηγµένες µεθοδολογίες όσο κενρικού όσο και αποκενρωµένου ελέγχου [66], κάι έοιο δεν ισχύει σην περίπωση ων χωρισικών δικύων. Η πλειοψηφία ων αποχεευικών δικύων ακαθάρων ης χώρας µας, διαθέει κενρικούς αγωγούς σους οποίους διοχεεύοναι α λύµαα από ο πρωεύον, ο δευερεύον και ο ριεύον δίκυο. Αυό σε ανίθεση µε α δίκυα όµβριων, α οποία συνήθως δεν διαθέουν κενρικούς αγωγούς, πράγµα που δυσχεραίνει ην εφαρµογή µεθόδων ελέγχου. Θα πρέπει να σηµειωθεί εδώ όι η πλειοψηφία ων συσηµάων ελέγχου διεθνώς υλοποιούναι µόνο σους κενρικούς αγωγούς. Οι παραπάνω λόγοι σε συνδυασµό µε ην ανυπαρξία µεθόδων και εχνολογιών ελέγχου σα αποχεευικά δίκυα ης χώρας µας, καθώς και ου γεγονόος όι µηχανισµοί παρακολούθησης (monitoring) ων δικύων ης χώρας µας είναι εγκαασηµένοι καά κύριο λόγο σους κενρικούς αγωγούς, µας οδήγησαν σο να επικενρωθούµε σε προβλήµαα ελέγχου κενρικών αγωγών δικύων ακαθάρων. Ένα σηµανικό γεγονός ο οποίο πρέπει επίσης να ληφθεί υπόψη όσο ση µονελοποίηση όσο και σον έλεγχο ων χωρισικών δικύων ακαθάρων σα οποία επικενρώνεαι η εργασία µας, είναι όι λόγω ων πολύ σηµανικών παρασιικών εισροών, αυά α δίκυα λειουργούν εν µέρει σαν πανορροϊκά. Σο πρόβληµα ων παρασιικών εισροών θα αναφερθούµε σο επόµενο κεφάλαιο. Τα γεωµερικά όσο και άλλα χαρακηρισικά ων κενρικών αγωγών ων δικύων ακαθάρων ης χώρας µας ποικίλουν. Ενδεικικά αναφέρουµε α εξής: Ο Κενρικός Αποχεευικός Αγωγός (ΚΑΑ) ης Αθήνας είναι ένας µεγάλος και βασικός συλλεκήρας µε ωοειδή διαοµή,60 µ. επί,90 µ. ου πανορροϊκού συσήµαος που ξεκινάει από ην περιοχή ης σχολής χωροφυλακής (οδός Ζαγοράς) και ακολουθεί ην οδό Μιχαλακοπούλου µέχρι ην οδό Πονοηρακλείας. Από εκεί συνεχίζει µε µεγαλύερη διαοµή,80 µ. επί 3,0 µ. µέχρι ην οδό Νυµφαίου []. 6
27 Σο παραπάνω σηµείο διά ης οδού Παπαδιαµανοπούλου συµβάλλει και ο αγωγός ου ρέµαος Ζωγράφου. Από εκεί και κάω ο αγωγός γίνεαι δίδυµος µςε διάµερο κάθε κλάδου 3,80 µ. φάνονας µέχρι η συµβολή ου σο όε ρέµα Ηριδανού. Από εκεί και κάω ο αγωγός καασκευάσηκε µε διαοµή 4,0 µ. µέχρι ο ύψος ης Σαδίου και οδεύει καά µήκος ης λεωφόρου Βας. Κωνσανίνου µε αποδέκη ο ρέµα που κάποε ήαν ο Ιλισός ποαµός, ενώ ένα σηµανικό µέρος ων παροχών ξηράς περιόδου εκρέπεαι προς ον ΚΑΑ. Η παροχή βροχής συνεχίζει µέσω υπερχειλισών και οδεύει µέχρι ην ανοική κοίη και εκβολή ου Ιλισού []. 3 Ο Συµπληρωµαικός Κενρικός Αποχεευικός Αγωγός (ΣΚΑΑ) καασκευάσηκε µέσα ση δεκαεία ου 980. Αρχίζει από ον ΚΑΑ από σηµείο ου σο µήµα που διέρχεαι από ην περιοχή ης Αγίας Άννης σο δήµο Αγ. Ιωάννη Ρένη και απολήγει σον Ακροκέραµο. Ο ΣΚΑΑ συµπληρώνει ην παροχεευική ικανόηα ου ΚΑΑ. Είναι κυκλικός αγωγός από οπλισµένο σκυρόδεµα µήκους 7,5 χλµ. και παροχεευικόηας 5 κ.µ. ανά δευερόλεπο. Ο ΣΚΑΑ έχει διάµερο 3,3 µ. []. 4 Ο Παρακηφίσιος ξεκινά από ον ΚΑΑ σο ύψος ης περιοχής ου Αγ. Ιωάννη Ρένη και ελειώνει σην περιοχή ης Εκάλης. Η διαοµή ου σην εκβολή είναι,4 µ. επί,7 µ., σκουφοειδής σε µήκος 3,6 χλµ. Το µήκος ου φάνει α 6 περίπου χιλιόµερα, ενώ η παροχεευική ου ικανόηα σην εκβολή είναι 0, κ.µ. ανά δευερόλεπο. Σήµερα βρίσκεαι υπό καασκευή ο ελευαίο µήµα ου που κααλήγει σον Άγιο Σέφανο []. 5 Ο Ανακουφισικός Κααθλιπικός Αγωγός (ΑΚΑ) άγει α λύµαα ων περιοχών ου Μοσχάου, ης Νέας Σµύρνης, ου Παλαιού Φαλήρου σον ΚΑΑ, ανακουφίζονας ις περιοχές αυές που εξυπηρεούναι σήµερα από ον Κενρικό Παραλιακό Συλλεκήρα ης ακής Σαρωνικού. Η διαοµή ου σην εκβολή είναι,9 µ. και ο συνολικό µήκος ου φάνει α 6 χλµ. Η παροχεευική ου ικανόηα σην εκβολή φάνει α 7 κ.µ. ανά δευερόλεπο []. 6 Κενρικοί αγωγοί παρόµοιων γεωµερικών χαρακηρισικών συνανώναι και σην περιοχή ης Θεσσαλονίκης. Πιο συγκεκριµένα, ο ΚΑΑ Θεσσαλονίκης (µήκους µ.) εκείνεαι από ο σαθµό επεξεργασίας λυµάων σο Γαλλικό ποαµό µέχρι ην συµβολή ων οδών Σόλωνος και Μπόσαρη. ιασχίζεαι µε µία µέση διαοµή διαµέρου,70 µ. και σε βάθος που κυµαίνεαι από 0 µ. έως 30 µ. περίπου. Με ον ΚΑΑ συνδέεαι όλο ο υφισάµενο δίκυο αποχέευσης ης πόλης. Επιπλέον συνδέοναι ο αγωγός ης εαιρίας ΕΚΟ, ο προσαγωγός ακαθάρων ου δήµου Θέρµης και ο προσαγωγός.. Καλοχωρίου []. 7 Ανίθεα οι κενρικοί αγωγοί ων επαρχιακών πόλεων διαφέρουν σηµανικά. Ενδεικικά αναφέρουµε ο αποχεευικό σύσηµα ων δήµων Άργους και Ναυπλίου. Ο κενρικός αγωγός ου Άργους αποελείαι από σιµενοσωλήνες µήκους δύο µέρων ( µ.) κυκλικής διαοµής διαµέρου 000mm. Ο ανίσοιχος αγωγός ου Ναυπλίου αποελείαι από σωλήνες πολυαιθυλενίου (PE) και κάθε σωλήνας έχει µήκος δώδεκα µέρων ( µ.), είναι κυκλικής διαοµής και διαµέρου 800mm. Ο δήµος Νέας Κίου συµβάλλει σην εγκαάσαση επεξεργασίας λυµάων ου παραπάνω συσήµαος µέσω κααθλιπικών 7
28 πλασικών αγωγών από PVC. Οι αγωγοί προσαγωγή ου Ναυπλίου και ου Άργους, που είναι κύριοι ροφοδόες ης εγκαάσασης επεξεργασίας λυµάων, είναι οποθεηµένοι κάω από η σάθµη ου υδροφόρου ορίζονα, ο οποίος βρίσκεαι σε σάθµη µ. κάω από ην επιφάνεια ου εδάφους. Καά µέσον όρο ο βάθος οποθέησης ου κενρικού αγωγού µεαφοράς ων λυµάων ου δήµου Άργους είναι 5 µ. κάω από ην επιφάνεια ου εδάφους [5]. Παρόµοιων γεωµερικών χαρακηρισικών κενρικούς αγωγούς συνανάµε σις περισσόερες επαρχιακές πόλεις ης χώρας µας [4], [6], [7], [8] [9] [0]. Σις περισσόερες περιπώσεις ων επαρχιακών δικύων, η διαοµή ων κενρικών αγωγών είναι mm ενώ ο µήκος ους κυµαίνεαι σα µ. 4. ΠΑΡΑΣΙΤΙΚΕΣ ΕΙΣΡΟΕΣ Ένα από α σοβαρόερα προβλήµαα που καλούναι να ανιµεωπίσουν οι µεθοδολογίες ελέγχου αποχεευικών δικύων ακαθάρων ση χώρα µας, είναι η σηµανική παρουσία παρασιικών εισροών, οι οποίες σε µερικές περιπώσεις φάνουν και σο 00% ης παροχής λυµάων [4],[5],[7]. Σε σχεική µελέη που έγινε από ην Ε..Ε.Υ.Α σε δείγµα 5 ΕΥΑ που µελεήθηκαν, διαπισώθηκε όι ο πρόβληµα ων παρασιικών εισροών είναι κοινό και πολύ σηµανικό για όλες. Σύµφωνα µε ην µελέη η γενική εκίµηση είναι όι α δίκυα ακαθάρων λειουργούν εν µέρει ως πανορροϊκά, αλλά σε ποια έκαση και βαθµό, αυό είναι άγνωσο. Το πρόβληµα ων παρασιικών εισροών σύµφωνα µε ις εκιµήσεις ων ΕΥΑ- οφείλεαι σις βροχοπώσεις και σε εισροές από ους αύλειους χώρους και ις υδρορροές ων καοικιών. Επίσης από µη σεγανά δίκυα ακαθάρων που βρίσκεαι κονά σε θάλασσα, ποαµό ή λίµνη ή σε κάποιες περιπώσεις και από ον υδροφόρο ορίζονα. Σε µια άλλη µελέη [4], [5] παρουσιάζεαι µια πιο εµπερισαωµένη ανάλυση ου προβλήµαος ων παρασιικών εισροών. Η σηµανικόηα και ο µέγεθος ων παρασιικών εισροών, σύµφωνα µε ην µελέη αυή, διαπισώνεαι από ο γεγονός όι η παροχή ακαθάρων σα δίκυα ων Ιωαννίνων και ης Καρδίσας καά ις υγρές περιόδους µπορεί να είναι έως και 60% µεγαλύερη από αυή ων ξηρών περιόδων. Πέραν ου ενοπισµού ου προβλήµαος και ης ποσοικής ου εκίµησης, οι εργασίες [5], [7] προχωρούν και σην ανάπυξη ενός µαθηµαικού µονέλου επίδρασης ων παρασιικών εισροών. Σύµφωνα µε αυό ο µονέλο, η συνολική παροχή ακαθάρων (ΣΠΑ) δίνεαι από η σχέση: ΣΠΑ=α+βΥ δ +βπ ε +γβ εζ +Ε 4. όπου α, β, γ, δ, ε είναι οι συνελεσές ου µονέλου, α+βυ δ είναι η παροχή λυµάων, βπ ε είναι η εισροή υπόγειων ρευµάων και γβ εζ +Ε είναι η εισροή όµβριων ρευµάων (όπου όλες οι παροχές/εισροές είναι κανονικοποιηµένες). Ενδεικικές ιµές για ους συνελεσές α, β, γ, δ, ε είναι οι 0.8, 0.4, , 0.4 και 0.7 ανίσοιχα []. 8
29 5 ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΑΛΓΟΡΙΘΜΟΣ ΓΙΑ ΤΟΝ ΣΧΕ ΙΑΣΜΟ ΣΤΡΑΤΗΓΙΚΗΣ ΕΛΕΓΧΟΥ ΤΗΣ ΡΟΗΣ ΛΑΜΒΑΝΟΝΤΑΣ ΥΠΟΨΗ ΤΗ ΧΡΟΝΙΚΗ ΥΣΤΕΡΗΣΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ 5. ΕΙΣΑΓΩΓΗ Η εισαγωγή ων µεθοδολογιών αυόµαου ελέγχου σε ανοιχά δίχυα ροής ις ελευαίες δεκαείες, έχει βελιώσει αρκεά ην αποδοικόηα ων συσηµάων διαχείρισης υδάων. Για παράδειγµα, η εφαρµογή ων αυόµαων συσηµάων ελέγχου σην άρδευση και σα φράγµαα έχουν µειώσει σηµανικά ην απώλεια υδάων σε σύγκριση µε α µη ελεγχόµενα συσήµαα. Οµοίως, οι σραηγικές ελέγχου για α αποχεευικά δίκυα έχουν µειώσει αρκεά ις υπερχειλίσεις λυµάων µε σηµανικές επιπώσεις σο περιβάλλον και ην υγεία ων ανθρώπων. Οι περισσόερες από ις υπάρχουσες προσεγγίσεις για ον έλεγχο ων συσηµάων ροής, υποθέουν ένα γραµµικό µονέλο µε µια σαθερή χρονική υσέρηση για η δυναµική ης ροής. Ένα έοιο µονέλο µπορεί να ληφθεί κάνονας αρχικά γραµµικοποίηση ων µη γραµµικών µερικών διαφορικών εξισώσεων Saint Venant και έπεια προσεγγίζονας ο προκύπον απειρο-διάσαο µονέλο, µε ένα γραµµικό µονέλο χρονικής υσέρησης (πρώης ή δεύερης άξης). Η προσέγγιση ων δυναµικών ης ροής από ένα γραµµικό σαθερό µονέλο χρονικής υσέρησης ισχύει µόνο όαν λειουργεί ο σύσηµα κονά σε µια ονοµασική εκροή. Ενούοις, σε περίπωση µεγάλων αποκλίσεων ης πραγµαικής εκροής όσον αφορά ην ονοµασική ιµή, η χρονική υσέρηση ου συσήµαος µπορεί να διαφοροποιείαι σηµανικά σε σχέση µε ην σαθερή ιµή που υποθέσαµε σο αρχικό σχεδιασµό ου µονέλου. Είναι βεβαιωµένο όι η χρονική υσέρηση αυξάνεαι, όσο αυξάνεαι και ο µήκος ου καναλιού ο οποίο µελεάµε. Σο γράφηµα 5. φαίνεαι η γραφική παράσαση ης χρονικής υσέρησης σε σχέση µε ην εκροή για κανάλια ροής µήκους 0 και 30 χιλιοµέρων ανίσοιχα. Για ο γράφηµα 5. χρησιµοποιήθηκε για ον υπολογισµό ης χρονικής υσέρησης ο µη γραµµικό µονέλο ων Litrico & Georges (999) [58]. Οι σηµανικές διακυµάνσεις ης χρονικής υσέρησης θέουν αυσηρούς περιορισµούς σο σχεδιασµό ελέγχου µε ην υπόθεση ης σαθερής χρονικής υσέρησης, που πρέπει να ανιµεωπίσει ο ερώηµα: ευρωσία ή απόδοση. Σην πραγµαικόηα, όπως αναφέρεαι σο [07], «µεγάλη ποσόηα υδάων χάνεαι σα κανάλια άρδευσης. Ένας λόγος για ον οποίο οι απώλειες είναι µεγάλες είναι όι σα κανάλια άρδευσης χρησιµοποιείαι συνηρηική πολιική, µε η διέλευση µεγάλων ποσοήων υδάων προκειµένου να µπορούµε σχεδόν πάνα να εγγυηθούµε ον ανεφοδιασµό ων αγροών, όαν αυοί ην έχουν ανάγκη. Ως εκ ούου υπάρχει µια σύγκρουση µεαξύ ης ελαχισοποίησης ων απωλειών υδάων σα κανάλια άρδευσης και ην αξιοπισία ης παροχής υδάων». Η προαναφερθείσα ανεπάρκεια ενός σραηγικού ελέγχου που υποθέει σαθερή χρονική υσέρηση, οδηγεί σην ανάγκη ανάπυξης µιας σραηγικής ελέγχου που (i) 9
30 θα είναι βασισµένη σε ένα ακριβέσερο µονέλο για ις διακυµάνσεις ης χρονικής υσέρησης και (ii) θα µπορεί αποελεσµαικά να εξεάσει ις διακυµάνσεις ης χρονικής υσέρησης χωρίς να «θυσιάζει» ην απόδοση προς χάριν ης ευρωσίας. Ένα πρώο βήµα για αυόν ο σκοπό είναι η ανάπυξη ενός µαθηµαικού µονέλου, καάλληλου για ην εφαρµογή αξιόπισων αλγορίθµων εκίµησης και εχνικών ελέγχου. Γράφηµα 5.: η χρονική υσέρηση σαν συνάρηση ης εκροής για ένα µήµα µήκους 0 χλµ. (µπλε καµπύλη) και ένα µήκους 30 χλµ. (κόκκινη καµπύλη) Ένας ακριβής αλγόριθµος εκίµησης είναι κρίσιµος, δεδοµένου όι α µονέλα που βασίζοναι σε ονοµασικές παραµέρους, απουγχάνουν συνήθως να προσεγγίσουν αποελεσµαικά ην πραγµαική δυναµική ου συσήµαος. Σις περισσόερες περιπώσεις, απαιείαι µια διαδικασία εκίµησης που χρησιµοποιεί πραγµαικές µερήσεις, προκειµένου να ληφθεί ένα ακριβές µονέλο ου πραγµαικού συσήµαος. Προείνουµε και αναλύουµε µια νέα προσέγγιση, µε η βοήθεια αυσηρών µαθηµαικών και πειραµαικών προσοµοιώσεων, µε σόχο ην ανάπυξη µιας σραηγικής ελέγχου για συσήµαα ροής που να βασίζεαι σε ακριβή και σε πραγµαικό χρόνο ενηµερωµένα µονέλα, για ο σύσηµα χρονικής υσέρησης. Η προεινόµενη προσέγγιση χρησιµοποιεί µια γενίκευση ου ΕΚΕΥ ( ιαφορικές Εξισώσεις Καασαικά Εξαρώµενης Υσέρησης) µονέλου ροής προεινόµενου σο [59] συνδυασµένο µε µια νέα καασαική προσαρµοσική µέθοδο που υπολογίζει και κάνει εκίµηση ων µη γραµµικών χαρακηρισικών ης χρονικής υσέρησης. Με καάλληλη εκµεάλλευση ων ιδιοήων ων δυναµικών ης ροής, αναπύσσεαι ένας απλός υπολογισικά αλλά και ακριβής ευρεικός αλγόριθµος που είναι παρόµοιος µε αυόν που χρησιµοποιείαι σο [43]. Αποδεικνύεαι όι ο 30
31 προεινόµενο µονέλο εγγυάαι η γενική σύγκλιση, δηλαδή επικραούν οι συνθήκες -Επιµονής ση ιέγερση- (Persistence of Excitation - PE). Ενούοις, ανίθεα µε α γραµµικά συσήµαα, όπου αρκεί ο καάλληλος σχεδιασµός ου σήµαος εισόδου, προκειµένου να εγγυηθούµε ην ύπαρξη ων συνθηκών PE, βλέπε π.χ. ην παράγραφο 5.. [43], σην περίπωσή µας η µη γραµµική εξάρηση ου ευρεικού αλγορίθµου µε ις άγνωσες παραµέρους δεν µας εγγυάαι κάι παρόµοιο. Ενούοις, βασισµένοι σην εµπειρία που αποκήθηκε από πειραµαικές προσοµοιώσεις, µπορούµε να δώσουµε κάποιες πρακικές οδηγίες για (α) η µονελοποίηση ου εισαγµένου σήµαος, καθώς επίσης και για (β) ην επιλογή ων παραµέρων ου αλγορίθµου εκίµησης, έσι ώσε οι συνθήκες PE να ισχύουν. Αξίζει επίσης να ειπωθεί όι α αποελέσµαα προσοµοιώσεων που έγιναν εξακριβώνουν ην αποελεσµαικόηα και ην ευκολία εφαρµογής ης προεινόµενης προσέγγισης. Αφού λοιπόν καασκευάσουµε ο µονέλο µε ο οποίο θα µπορούµε να βρούµε η σχέση ανάµεσα σην καασαική εξίσωση ενός συσήµαος ροής και η χρονική υσέρηση, θα δείξουµε όι ένα έοιο µονέλο µπορεί να χρησιµοποιηθεί ως προσαρµοσικός αλγόριθµος για ον σχεδιασµό σραηγικής ελέγχου ης ροής. Με λίγα λόγια χρησιµοποιώνας η γνώση που µας δίνει ένας έοιος αλγόριθµος για α µη γραµµικά χαρακηρισικά ης χρονικής υσέρησης, µπορούµε να σχεδιάσουµε έναν προσαρµοσικό έλεγχο ο οποίος θα µπορεί να ανιληφθεί γρήγορα ις απόοµες αλλαγές ση σάθµη ου καναλιού ακόµα και αν προέρχοναι από εξωερικές διααραχές και θα παίρνει ις καάλληλες αποφάσεις ελέγχου παίρνονας υπόψη η δυναµική ου συσήµαος. 5. ΟΙ ΥΝΑΜΙΚΕΣ ΤΗΣ ΡΟΗΣ Υ ΑΤΩΝ: ΜΟΝΤΕΛΟΠΟΙΗΣΗ Θεωρούµε έναν ενιαίο ποαµό ή ένα κανάλι ροής µήκους Χ µε εισροή (ανάνη ροή) u(t) και y(t) η εκροή (καάνη ροή) σο καάνη έλος ου καναλιού. Όπως συµβαίνει σε υπικές εφαρµογές σα ελεγχόµενα κανάλια άρδευσης, α φράγµαα ποαµών, α αποχεευικά δίκυα, κ.λπ., έσι και η προεινόµενη προσέγγιση κάνει χρήση ης υπόθεσης όι ολόκληρο ο σύσηµα είναι εξοπλισµένο µε σαθµούς µέρησης σους οποίους µεράαι ο u(t) και ο y(t). Προκειµένου να απλοποιήσουµε ακόµα περισσόερο ο σύσηµα, η προεινόµενη προσέγγιση θα υποθέσει όι η ροή σο έλος ου καάνη καναλιού δεν υπόκειαι σε έλεγχο. Ενούοις, ο προεινόµενος αλγόριθµος µπορεί να επεκαθεί εύκολα σην περίπωση όπου υπάρχουν ενδιάµεσοι σαθµοί µέρησης που παρέχουν µερήσεις ης εκροής (ή ης εισροής υδάων) σε πραγµαικό χρόνο σις ενδιάµεσες θέσεις. Για ην αποελεσµαική µονελοποίηση ων δυναµικών ης ροής µπορούν να χρησιµοποιηθούν οι γνωσές µερικές διαφορικές εξισώσεις Saint-Venant, βλέπε π.χ. [0] ή η µέθοδος Diffusive Wave, βλέπε π.χ. [6], [57]. Όπως ήδη αναφέρθηκε, είναι πολύ δύσκολο να ληφθούν και να αναλυθούν πρακικές σραηγικές ελέγχου που χρησιµοποιούν µερικές διαφορικές εξισώσεις (NPDEs). Για αυόν ον λόγο, ανί ου µονέλου NPDE, προείνεαι η χρήση ου ακόλουθου ΕΚΕΥ µονέλου για ην προσέγγιση ων δυναµικών ης ροής: 3
32 ( Y ) + G( Y ) u ( ) w( Y ) y+ = F Υ +, 5. Όπου ο εκφράζει ον διακριοποιηµένο χρόνο, ο ( ) εκφράζει ην χωρική χρονική υσέρηση, ο Y είναι ο διάνυσµα ων προηγούµενων µερήσεων εκροής, και α F, G, w είναι καάλληλα καθορισµένες µη γραµµικές συναρήσεις, µε ην w να απεικονίζει ις επιδράσεις ων µη µερήσιµων εξωγενών διααραχών ή α σχεδιασικά λάθη λόγω ης προσέγγισης ων πραγµαικών δυναµικών ροής µέσω ης (5.). Η σχέση (5.) ανιπροσωπεύει µια γενίκευση ενός ΕΚΕΥ µονέλου όπως προείνεαι σο [59]. Μπορούν να χρησιµοποιηθούν αυσηρά θεωρήµαα βασισµένα ση θεωρία ων ηµισυνόλων [] και η θεωρία ων αριθµηικών προσεγγίσεων ων λύσεων ων ΕΚΕΥ, βλέπε π.χ. [], για να αποδειχθεί όι η σχέση (5.) µπορεί να προσεγγίσει µε αρκεή ακρίβεια ις µερικές διαφορικές εξισώσεις ου Saint-Venant ή ου Diffusive Wave, υπό ον όρο όι η διάσαση ου διανύσµαος Y είναι αρκεά µεγάλη. Επίσης µε α ίδια θεωρηικά βοηθήµαα µπορούµε να αποδείξουµε όι η σχέση (5.) ικανοποιεί ην ακόλουθη ανισόηα: G(Y ) >0 για όλα α αποδεκά διανύσµαα Y. Όπως θα δούµε και παρακάω, η ανισόηα αυή είναι απαραίηο να ισχύει για ην ανάπυξη ου προεινόµενου αλγόριθµου. Παραήρηση : Το µονέλο (5.) είναι καάλληλο για ο σχεδιασµό σραηγικών ελέγχου. Το µονέλο αυό ισχύει για αρκεές ισχυρές θεωρηικά µεθοδολογίες σχεδιασµού σραηγικών ελέγχου, όπως η IMC βλέπε [3], ή οι µη γραµµικές επεκάσεις ου ελεγκή Smith, βλέπε [5]. Η προεινόµενη προσέγγιση κάνει επίσης, χρήση ης υπόθεσης όι οι άγνωσες µη γραµµικές συναρήσεις F, G,, µπορούν να προσεγγισούν από γραµµικά παραµεροποιηµένες µη γραµµικές συναρήσεις ου διανύσµαος Υ: Τ Τ Τ F Υ) θ α( Υ), G( Y ) θ β ( Υ), ( Υ) θ γ ( ) 5. ( 3 Υ Όπου θ i, i=,,3, είναι ένα άγνωσο σαθερό διάνυσµα και α,β,γ είναι γνωσές µη γραµµικές διανυσµαικές συναρήσεις. Μια έοια υπόθεση έχει νόηµα, αν α α,β,γ επιλεγούν από µια οικογένεια κλασικών προσεγγισικών συναρήσεων, όπως π.χ. οι πολυωνυµικές ή α σιγµοειδή νευρωνικά δίκυα µε υχαίους κόµβους, βλέπε [4], και άλλες. Σε αυήν ην περίπωση η ακρίβεια ης προσέγγισης µπορεί να επιλεγεί διαλέγονας ις διασάσεις ων διανυσµαικών συναρήσεων α, β, γ. Με βάση ην παραπάνω υπόθεση οι (5.), (5.) µπορούν να γραφούν ως εξής : y + = + θ α = α( Y θ α ), θ β u β = β ( Y 3γ ), + w γ = γ ( Y ) 5.3 3
33 Όπου w = w( Y, ) + σφάλµα µονελοποίησης εξαιίας ης προσέγγισης (5.). Το µονέλο (5.3) µας βοηθά να προείνουµε ο παρακάω µονέλο εκίµησης ης δυναµικής ης ροής: ) ) = 5.4 yˆ θ α θ β u ) + + θ 3γ Όπου ο y ˆ + είναι η εκίµηση ου y και ο ) + θ η εκίµηση ου i θ. Το πρόβληµα i είναι να υπολογίσουµε α ) θ έσι ώσε οι εκιµήσεις i y ˆ + να είναι όσο πιο κονά γίνεαι σις πραγµαικές µερήσεις y, δεδοµένου όι έχουµε αρκεές µερήσεις για + α y και u. Ένας ρόπος να λύσουµε ο πρόβληµα αυό είναι µέσω ης ελαχισοποίησης ης ) ) ) ) ) J ( θ, θ, θ ) ( y u ) 3 = θα θβ + θ3γ ) Προφανώς, ο πρόβληµα δεν είναι κυρό πρόβληµα βελισοποίησης και έσι οι αλγόριθµοι µη γραµµικής βελισοποίησης εφαρµοζόµενοι σε αυό ο πρόβληµα µπορούν να παγιδευούν σε οπικά ελάχισα. Επιπλέον, λόγω ης ασυνέχειας ου J όσον αφορά ο ) θ, δείε [6], οι µη γραµµικοί αλγόριθµοι βελισοποίησης µπορούν 3 να απούχουν ακόµη και ση σύγκλιση σε ένα οπικό ελάχισο ου J. Παρακάω δίνεαι µια εναλλακική µεθοδολογία που ανιπαρέρχεαι αυό ο πρόβληµα. 5.3 ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΑΛΓΟΡΙΘΜΟΣ ΕΚΤΙΜΗΣΗΣ Σε αυήν ην ενόηα θα παρουσιασεί και θα αναλυθεί ο προεινόµενος αλγόριθµος εκίµησης. Με ην αφαίρεση ης (5.4) από ην (5.3) παίρνουµε ην εξίσωση ου σφάλµαος εκίµησης: e ) ~ ~ = + y+ y+ = θ α + θ β u ) + θ ( u u ) θ γ β θ γ ˆ θ γ w 5.5 Όπου ~ θ = θ ˆ θ εκφράζει α διανύσµαα σφάλµαος σην εκίµηση παραµέρων. i i i Ας σηµειωθεί όι ανίθεα µε ους κλασικούς αλγορίθµους εκίµησης, βλέπε π.χ. [43] σην περίπωσή µας η εξίσωση ου σφάλµαος εκίµησης δεν είναι γραµµική όσον αφορά ο % θ 3. Για να παρακάµψουµε αυό ο πρόβληµα εισάγουµε ην ακόλουθη προσέγγιση ης εισροής u - ως συνάρηση ου, υποθέονας όι για µια δεδοµένη καάνη εκροή y, υπάρχει ένα ανώαο και ένα καώαο όριο ου, u c + d + ε ( y ) ( y ) c 5.6 =, min max Όπου α c, d ελαχισοποιούν ην 33
34 = ( y max ( min ( y ) c + d u ), ) Τα ) και ) εκφράζουν α εξαρώµενα από ην καάνη εκροή min ( y max ( y καώαα και ανώαα όρια ανίσοιχα, και ο ε εκφράζει ο προσεγγισικό σφάλµα που προκύπει εξαιίας ης προσέγγισης ου u - από η γραµµική συνάρηση c +d. εν είναι δύσκολο να δει κανείς όι ο µέγεθος ου σφάλµαος προσέγγισης ε εξαράαι από (D) ην σενόηα ων ορίων ( y ), ( y ). Όσο πιο σενά είναι αυά α όρια min όσο πιο µικρό είναι ο µέγεθος ου ε. Σο επόµενο κεφάλαιο δίνεαι µια απλή µεθοδολογία για η λήψη ων ορίων. (D) ην διακύµανση ου u σε σχέση µε ο χρόνο. Όσο µικρόερη είναι η διακύµανση όσο µικραίνει και ο µέγεθος ου ε. Οι (5.6), (5.5) µπορούν να γραφούν: e ~ ~ max ~ ) + w = θα + θ β u + θ β c ( θ γ ) + ε θ γ 3 3 όπου ˆ ε = θβ ( εθ3γ εθ3γ ). Προφανώς ο µέγεθος ουε εξαράαι από α (D), (D) που περιγράφηκαν προηγούµενα. Η εξίσωση σφάλµαος (5.7) είναι παρόµοιας µορφής µε αυήν που χρησιµοποιείαι για ην εκίµηση γραµµικών συσηµάων µε άγνωσο κέρδος (βλέπε ην παράγραφο 4.5. σο [43]), σύµφωνα µε ην οποία ο θ β ανισοιχεί σο άγνωσο κέρδος ου συσήµαος. Γενικά οι συγκλίνονες αλγόριθµοι για αυά α συσήµαα έχουν προαθεί υπό ην υπόθεση όι ο σήµα ου κέρδους είναι γνωσό. Σην περίπωση ης προεινόµενης προσέγγισης, αυοί οι αλγόριθµοι µπορούν να εφαρµοσούν µιας και θα ισχύει θ β G( Y ) 0 όπως είδαµε παραπάνω. Μια ιδιαίερη µορφή > αυών ων αλγορίθµων, όπως εφαρµόζεαι σο πρόβληµα µας, είναι η ακόλουθη: ) ˆ θ ( ) ( ) ( ) ˆ + = θ + nα e+ + nσ θ( ) ) ˆ θ ( ) ( ) ( ) ˆ + = θ + nβ u ˆ e n ( ) 3 ( ) + σ θ θ γ + ) ˆ θ ( ) = θ ( ) + nc γ e + nσ ( ) ˆ θ ( ) Όπου n είναι µια θεικά ορισµένη σαθερά (προσαρµοσικό κέρδος) και σ i (), βλέπε [43], χρησιµοποιείαι για να διαηρήσει α διανύσµαα εκίµησης παραµέρων ˆ θ i ( t ) µέσα σε κάποια όρια. Το σ i () καθορίζεαι από η σχέση: ) 0 αν θi Μ σ i ( ) = σ 0 αλλιώς
35 Όπου Μ,σ 0 είναι θεικές σαθερές που ορίζοναι από ον χρήση. Το παρακάω θεώρηµα καθιερώνει ιδιόηες σύγκλισης σον προσαρµοσικό αλγόριθµο (5.8). Αξίζει να σηµειωθεί όι ση πρόασή µας ο «κέρδος» θ β δεν θεωρείαι σαθερά, σε ανίθεση µε ους γραµµικούς αλγορίθµους εκίµησης. Για αυόν ον λόγο, η ανάλυση σύγκλισης ων βασικών γραµµικών αλγορίθµων εκίµησης, πρέπει να ροποποιηθεί καάλληλα. Θεώρηµα 5. θεωρήσε ον προεινόµενο προσαρµοσικό αλγόριθµο εκίµησης παραµέρων (5.4), (5.6), (5.8). Υπάρχει µια θεική σαθερά η * έοια ώσε, αν * n (0, η ], η παρακάω δήλωση ισχύει: (α) ο σφάλµα εκίµησης e + µεά από άπειρα βήµαα συγκλίνει σο υποσύνολο D και παραµένει εκεί. Με D { e+ : e+ c( + w ) + c β + } ε 5.9 = β + = β + β, για κάποια θεικά και σαθερά δυναµικές που αναπύσσοναι σο πραγµαικό σύσηµα. c,c ανεξάρηα από ις (β) ας ορίσουµε α ()=α(), α ()= β u ), α 3 ()=c γ και θ 3 ( ) γ Φ()=[ a ), a ( ), a ( ). Αν ο διάνυσµα Φ() ακολουθεί ις συνθήκες P.E. ( 3 ] (persistency of excitation) όε υπάρχουν πραγµαικές θεικές σαθερές c,c και ένας θεικός ακέραιος Τ έοιος ώσε T + l= Τ c I Φ( l) Φ ( l) ci, 5.0 Όπου Ι ο µοναδιαίος πίνακας, όε ο σφάλµα εκίµησης ων παραµέρων ~ ~ ~ ~ θ ( ) = [ θ ( ), θ ( ), θ ( )] 3 και ο σφάλµα e + συγκλίνουν εκθεικά σα υποσύνολα Ε και D, ανίσοιχα, όπου % { θ ( ) : % θ ( ) ( ε ) } β E = c + w + c και c,c 3 4, κάποιες θεικές σαθερές ανεξάρηες από ις δυναµικές που αναπύσσοναι σο πραγµαικό σύσηµα. Απόδειξη: η απόδειξη ακολουθεί α κλασικά θεωρήµαα σην ανάλυση ων προσαρµοσικών αλγόριθµων. Γι αυό ο λόγο δίνεαι µόνο ένα µικρό κοµµάι αυής. Αρχικά θεωρούµε ην παρακάω συνάρηση Lapunov: ~ V = θ ~ ( ) + θ ( ) + θ β θ3( ) ~ 35
36 Όπως ήδη αναφέρθηκε ο όρος θ β είναι θεικός και γι αυό η συνάρηση Lapunov είναι θεικά ορισµένη. Χρησιµοποιώνας ις (5.7), (5.8) και ην ανισόηα x( x+y ) -x / + y /, θα έχουµε: V + ~ ~ ~ ~ = θ ( + ) θ ( + ) + θ ( + ) θ ( + ) + θ β ~ ~ ~ ~ = θ ( + ) θ ( + ) + θ ( + ) θ ( + ) ~ + θ β θ ( + ) θ ( + ) + θ ( β + ~ ~ θ ( + ) θ ( + ) ~ ~ β ) θ ( + ) θ ( + ) = % θ + % θ + θ β % θ ( ) ( ) 3( ) 3 3 n% θ ( ) α e n% θ ( ) β u e ) + θ 3 ( ) γ + nθ β % θ ( ) cγ e nα e + nσ ( ) % θ ( ) ˆ θ ( ) + + nβ u e + nσ ( ) % θ ( ) ˆ θ ( ) ˆ θ 3 ( ) γ + + θ β ncγ e + nσ ( ) % θ ( ) ˆ θ ( ) n σ ( ) % θ ( ) ˆ θ ( ) i= + θ ( β β )% θ ( + ) % θ ( + ) = V n( e ε w ) e n αe+ σ θ θ n βu ) e σ θ θ θ3γ + nθβ cγ e+ σ 3 θ3 θ3 i= i i i ( )% ( ) ˆ ( ) ( )% ( ) ˆ ( ) ( )% ( ) ˆ ( ) 3 3 n σ i ( ) % σ i ( ) % i ( ) i θi ( ) % θ θ θi ( ) n i= + θ ( β + β ) % θ 3 ( + ) % θ 3( + ) n n V e + + ( ε + w ) + + ( ) % ( ) ˆ ( ) n α e + σ θ θ 36
37 + β + σ ( ) θ% ( ) θˆ ( ) n u ˆ e ( ) θε γ + ) + θ β γ + σ ( ) θ% ( ) θ ( ) n c e n σ ( ) θ% ( ) + n σ ( ) θ ( ) i i i i i= i= + θ ( β β ) θ% ( + ) θ% ( + ) Όπου σ i ( ) = σ i ( ) for i=,, σ 3( ) = θβσ 3( ). Η παραπάνω ανισόηα είναι κλασικής µορφής σην θεωρία ανάπυξης προσαρµοσικών συσηµάων, βλέπε θεώρηµα σο [43]. Με ην ανισόηα που κααλήξαµε και ο θεώρηµα ων [43] η απόδειξη µπορεί να θεµελιωθεί. Παραήρηση : Από πρακικής απόψεως, ο θεώρηµα 5. δηλώνει όι, εάν η δυναµική ενός συσήµαος ροής έχει αργή διακύµανση σο χρόνο, οπόε σε αυή ην περίπωση η επίδραση ων όρων ε, β + β είναι αµεληέα, ο σφάλµα εκίµησης e + και (σε περίπωση που οι συνθήκες PE ικανοποιούναι) ο σφάλµα εκίµησης ~ παραµέρου θ ( ) συγκλίνουν σε ιµές ανάλογες προς ο µέγεθος w, ο οποίο εξαράαι από ις µη µερήσιµες διααραχές και ους όρους σφάλµαος ης µονελοποίησης. Αξίζει επίσης να σηµειωθεί όι οι συνθήκες PE (5.0) είναι αναγκαία και ικανή ~ συνθήκη για η σύγκλιση ου σφάλµαος εκίµησης ων παραµέρων θ ( ), ανεξάρηα από ον αλγόριθµο που προείνουµε, βλέπε []. Σα γραµµικά συσήµαα µπορεί να εγγυηθεί η ικανοποίηση ων συνθηκών PE (5.0) µε καάλληλη επιλογή ακολουθίας u. Σα µη γραµµικά συσήµαα ο πρόβληµα ου σχεδιασµού ων δεδοµένων u, έσι ώσε η σχέση (5.0) να ισχύει, παραµένει ένα ανοικό και περίπλοκο πρόβληµα. Παρακάω, αυό ο ζήηµα θα εξεασεί περαιέρω µε ην παρουσίαση µερικών πρακικών και ρεαλισικών οδηγιών για ην ισχύ ων συνθηκών PE (5.0) µόνο για ο συγκεκριµένο πρόβληµα που ανιµεωπίζουµε. 5.4 ΠΡΑΚΤΙΚΕΣ Ο ΗΓΙΕΣ Σε αυήν ην ενόηα δίνοναι πρακικές οδηγίες για ην εφαρµογή ου προεινόµενου αλγορίθµου. Κάποιες από αυές είναι κρίσιµες για ην υλοποίηση ου. Υπολογισµός ων y), ( y) : για ον υπολογισµό ων άνω και κάω ορίων ης min ( max χρονικής υσέρησης µπορούµε να χρησιµοποιήσουµε ένα προσεγγισικό µονέλο, βασισµένο σε κάποιες ονοµασικές παραµέρους ου δικύου. Σις πειραµαικές προσοµοιώσεις χρησιµοποιήθηκαν α παρακάω όρια: min ( y) = ( y) 50min nom ( y) = ( y) 50min 5. max nom + 37
38 Όπου nom (y) είναι µια προσέγγιση ης υσέρησης βασισµένη σε ονοµασικές παραµέρους: X nom ( y) = S( y) 5. Θ( y) Όπου y E( y) = LI 0.4 y 5I Θ( y) = 0.4 3L n S( y) = XE( y) P( y) = 3 ( y) Θ π Φ( y) = + arctan XE( y) cos( Φ( y) / 3) 3 Θ( y) 3E( y) S( y) Θ( y) 9E( y) XΘ( y) 9E( y) 5.3 και Χ, Ι, L,n εκφράζουν ο µήκος, ην κλίση, ο πλάος και η σαθερά ριβής ου καναλιού ανίσοιχα. Η προσέγγιση (5.), (5.3) ης χρονικής υσέρησης πάρθηκε από ο [58], µε µηµαική γραµµικοποίηση ων µερικών διαφορικών εξισώσεων ου Diffusive Wave. Ο αλγόριθµός πάνως, όπως θα φανεί και παρακάω, έχει µεγάλη ευρωσία όσο αφορά α άνω και κάω όρια ης χρονικής υσέρησης. Επιλογή ου διανύσµαος Y : Όσο αφορά ο διάνυσµα Y, ο οποίο αποελείαι από παρελθονικές ιµές εκροών που θα χρησιµοποιηθούν σον αλγόριθµό (5.3), η επιλογή θα πρέπει να γίνει πολύ προσεκικά. Συγκεκριµένα, η διάσαση ου Y θα πρέπει να είναι αρκεά µεγάλη έσι ώσε ο µονέλο (5.3) να µπορεί να προσεγγίσει αξιόπισα ις δυναµικές ων ροών ου πραγµαικού συσήµαος. Επίσης α σοιχεία ου διανύσµαος Y θα πρέπει να αναφέροναι σε ιµές όχι όσο κονά χρονικά σις ωρινές µερήσεις (για να ισχύουν οι PE συνθήκες), αλλά ούε και πολύ µακριά (για ην αποφυγή εµφάνισης µη πραγµαικών καθυσερήσεων, λόγω ης υπέρπαραµεροποίησης). Έχονας αυά σο µυαλό και βλέπονας και α αποελέσµαα ων προσοµοιώσεων για διάφορες επιλογές σε σχέση µε ο Y, παραθέουµε ην παρακάω επιλογή ή οποία δείχνει να οδηγεί σε πιο ικανοποιηικά αποελέσµαα: Y = [ y µ / Τ, y µ / Τ,..., y Τ / Τ ] Όπου Τ η διακριοποίηση ου χρόνου, Τ = Χ/00 (min) και Χ είναι ο µήκος ου καναλιού (σε µέρα) και µ µια θεική σαθερά που εξαράαι από ο µήκος Χ (επιλέγεαι αναλογικά ου µήκους). Για ο παράδειγµα που παραθέουµε, για µήκος Χ=0000 µέρα επιλέχθηκε µ=5 min. 38
39 Επιλογή ων αναδροµικών όρων α, β, γ: Οι εξισώσεις ων α, β µπορούν να αναπαρασαθούν µε η χρήση νευρωνικών δικύων δευέρου βαθµού, βλέπε [49]. Πιο συγκεκριµένα οι συναρήσεις ων α, β µπορούν να επιλεγούν από: a a β β di, d i, l di, δι, l a ( Y ) = Y K Y, ( Y = Y KΥ i β l i ) l Όπου α i (Y), β i (Y) εκφράζουν ις i-οσές κααχωρήσεις ων α(υ), β(υ) ανίσοιχα. a β Το l είναι η διάσαση ου Υ και α d 0,, είναι θεικοί ακέραιοι που d,, { } i j a β ικανοποιούν ην d d {0,, }, j i, j, j i, j i, j i. Για α πειραµαικά αποελέσµαα που παραθέοναι σην επόµενη ενόηα, α α i (Y), β i (Y) επιλέγηκαν υχαία από ην παραπάνω περιγραφείσα λίσα. Όσο αφορά ο διάνυσµα γ(υ) βρέθηκε όι η παρακάω απλή επιλογή προσφέρει ικανοποιηικά αποελέσµαα: γ(υ)= [,Υ,/Υ ] όπου Υ = y -5/T εκφράζει ο πρώο σοιχείο ου διανύσµαος Υ. Μια πιο πολύπλοκη επιλογή ου διανυσµαικού όρου γ(υ) θα προκαλούσε πρόβληµα σην εκίµηση ης χρονικής υσέρησης ( ) εξαιίας ης υπέρ-παραµεροποίησης. Αξίζει να σηµειωθεί όι οι παραπάνω προεινόµενες επιλογές για α διανύσµαα α, β, γ δουλεύουν ικανοποιηικά για οποιοδήποε κανάλι ροής υδάων, ενώ η επιλογή ου l γίνεαι µε βάση ο µήκος ου καναλιού. Αρχικοποίηση ων παραµέρων εκίµησης: Η αρχική ιµή ης παραµέρου ) θ 3που αναποκρίνεαι σην εκίµηση ης χρονικής υσέρησης, θα πρέπει να επιλεγεί ως ένα διάνυσµα µε µεγάλες θεικές ιµές. Αν δεν γίνει αυό, υπάρχει κίνδυνος ο αλγόριθµος εκίµησης να µας δώσει αρνηικές ιµές ης υσέρησης κααλήγονας σε εξωπραγµαικά αποελέσµαα. Τα ) θ, ) θ µπορούν να επιλεγούν αυθαίρεα. Επιλογή ου προσαρµοσικού κέρδους n: προκειµένου να συµψηφίσουµε ις παρενέργειες που προκαλεί η διακριοποίηση ου χρόνου ων όρων θ3 β, ε, θα πρέπει να επιλέξουµε ο n πολύ µικρό (π.χ n<0-8 ). Αυή η επιλογή οδηγεί σε πολύ αργή σύγκλιση ου αλγόριθµου εκίµησης ων παραµέρων. Για ην αποφυγή αυού ου προβλήµαος, ο αλγόριθµος εκίµησης θα πρέπει να κάνει αρκεές επαναλήψεις µε η χρήση ων ίδιων κάθε φορά δεδοµένων. Αυό έγινε και σην περίπωση ων πειραµαικών αποελεσµάων που παραίθεναι παρακάω. Επιλογή ων σαθερών ου προσαρµοσικού αλγόριθµου σ 0, Μ: Η επιλογή σ 0 =η και Μ=0 0 (ο Μ πρέπει να επιλεγεί ίσο µε έναν µεγάλο αριθµό) βοηθούν σην αποελεσµαικόηα ου προεινόµενου αλγορίθµου. Επιλογή ης εισροής u : Το βασικό µειονέκηµα ου προεινόµενου αλγόριθµου, είναι η αδυναµία ου να χρησιµοποιηθεί σε περιπώσεις όπου η εισροή u παραµένει σαθερή για µεγάλα χρονικά διασήµαα (Καά Τόπους Σαθερή - ΚΤΣ), π.χ. για χρονικές περιόδους µεγαλύερες από ην ελάχιση χρονική υσέρηση. Σε αυήν ην περίπωση ο όρος c σην (5.6) µηδενίζεαι πράγµα που οδηγεί σε αναποελεσµαικόηα ο µονέλο (5.5) (δεν ικανοποιούναι οι PE συνθήκες). Όπως θα φανεί και σο κεφάλαιο ων προσοµοιώσεων ο αλγόριθµος δεν κααφέρνει να 39
40 δώσει ικανοποιηικά αποελέσµαα όαν ο u παραµένει σαθερό για µεγάλα χρονικά διασήµαα. Όαν αυό δεν συµβαίνει, όε αποδεικνύεαι πειραµαικά όι ισχύουν πάνα οι PE συνθήκες. Γι αυό ο λόγο α δεδοµένα που θα χρησιµοποιηθούν από ον αλγόριθµο θα πρέπει να είναι έσι επιλεγµένα ώσε να αποφεύγεαι η καάσαση ΚΤΣ ου u. 5.5 ΠΡΟΣΟΜΟΙΩΣΕΙΣ (Α) Για να µπορέσουµε να αξιολογήσουµε ον προεινόµενο αλγόριθµο, ον εφαρµόσαµε για ην µονελοποίηση ενός καναλιού µήκους 0 χιλιοµέρων. Οι παράµεροι ου καναλιού είναι οι ίδιες µε αυές που χρησιµοποιούναι σο [59], δηλαδή l=8m, n=0.05, I= Οι µερικές διαφορικές εξισώσεις ου Diffusive Wave (DW) χρησιµοποιήθηκαν για η µονελοποίηση ων δυναµικών ροής. Για ην αριθµηική λύση ου µονέλου DW χρησιµοποιήθηκε ο αλγόριθµος Musingum- Cunge [7]. Γράφηµα 5.: ισορικά δεδοµένα εισροής που χρησιµοποιήθηκαν σις προσοµοιώσεις. Οι µη διακεκοµµένες καµπύλες ανισοιχούν σε αυές που χρησιµοποιήθηκαν για εκπαίδευση ου αλγορίθµου. Σα πειράµαα που κάναµε η αρχική ροή θεωρήθηκε σαθερή και ίση µε m 3 /s. Η εισροή που χρησιµοποιήθηκε σις προσοµοιώσεις ήαν µια από ις 4 καµπύλες που παρουσιάζοναι σο γράφηµα 5.. Μια από αυές ις καµπύλες εµπεριέχει ο πρόβληµα που αναφέραµε παραπάνω (σαθερόηα για µεγάλα χρονικά διασήµαα). Σε όλα α αποελέσµαα που παρουσιάζοναι, ο προεινόµενος αλγόριθµος εκίµησης παραµέρων (5.8) εφαρµόσηκε για α δεδοµένα εισροών/εκροών (training data) ης ροής ης µιας από ις µη διακεκοµµένες καµπύλες ου γραφήµαος
41 Το προκύπον µονέλο µε ις παραµέρους ) θ i που προέκυψαν αξιολογήθηκε µε η χρήση ων υπόλοιπων καµπυλών (evaluation data). Προκααρκικά αποελέσµαα µε η χρήση ου µονέλου µερικών διαφορικών εξισώσεων ων Litrico και Pomet Οι µερικές διαφορικές εξισώσεις ου DW δεν ενσωµαώνουν ένα µονέλο διαχείρισης για ις µη γραµµικές αυξοµειώσεις ης χρονικής υσέρησης. Γι αυό ο λόγο είναι πολύ δύσκολο να εκιµήσουµε ην αποελεσµαικόηα ου προεινόµενου αλγορίθµου όσο αφορά ην εκίµηση ων χαρακηρισικών ης χρονικής υσέρησης. Για ην αποφυγή αυού ου προβλήµαος αρχικά εφαρµόζουµε ον αλγόριθµό µας σο µονέλο ων Litrico και Pomet (LP) που εµπεριέχει ένα µονέλο για ην χρονική υσέρηση, ο οποίο αναπαρισάαι σην παρακάω σχέση: S( y( t)) ( LP) :&& y( t) = y& ( t) y( t) P( y( t)) P( y( t)) + u( t P( y( t)) nom ( y( t))) Όπου οι µη γραµµικοί όροι P(y), S(y), nom (y) δίνοναι από ις σχέσεις (5.), (5.3). Πρέπει να σηµειωθεί όι ο παραπάνω µονέλο προσεγγίζει ις δυναµικές ης ροής µε µεγάλη δυσκολία. Επίσης καά ην εφαρµογή ου προεινόµενου αλγορίθµου σο µονέλο (LP) ο διάνυσµα Y που χρησιµοποιήθηκε επιλέχθηκε σύµφωνα µε ην Y =[y,y - ]. Σα γραφήµαα 5.3 και 5.4 παρουσιάζοναι α αποελέσµαα ου προεινόµενου αλγορίθµου όπως εφαρµόσηκε σο µονέλο (LP). Σο γράφηµα 5.3, α δεδοµένα εκπαίδευσης (training data) που χρησιµοποιήθηκαν, ήαν αυά ης µη διακεκοµµένης και µε µη µεγάλες χρονικές περιόδους σαθερόηας, ου γραφήµαος 5., ενώ σο γράφηµα 5.4 α δεδοµένα εκπαίδευσης που χρησιµοποιήθηκαν, ήαν αυά ης καµπύλης µε ις συνθήκες ΚΤΣ. Σην περίπωση ου γραφήµαος 5.3 α εκιµώµενα δεδοµένα (εκροή και χρονική υσέρηση) προσεγγίζουν σχεδόν άψογα α πραγµαικά δεδοµένα. Σην περίπωση ου γραφήµαος 5.4 ο µονέλο µας δεν παρουσιάζει ακρίβεια λόγω ης έλλειψης ων PE συνθηκών, όπως εξηγήθηκε προηγούµενα. Τα χαµηλόερα διαγράµµαα ου γραφήµαος 5.3 ανισοιχούν σις δυναµικές ης ροής από ην ΚΤΣ καµπύλη εισροών ου γραφήµαος 5.. Όπως φαίνεαι από ο γράφηµα 5.3 όαν α δεδοµένα εκπαίδευσης δεν είναι ΚΤΣ εισροές, ο αλγόριθµος µπορεί να εκιµήσει αποελεσµαικά ις δυναµικές ης ροής. 4
42 Γράφηµα 5.3: Αποελέσµαα προσοµοίωσης µε η χρήση ου (LP) µονέλου και µια µη ΚΤΣ ροή. Η κόκκινη διακεκοµµένη καµπύλη είναι η εκίµηση, ενώ η µπλε α πραγµαικά δεδοµένα. Τα πάνω γραφήµαα ανισοιχούν σα δεδοµένα εκπαίδευσης, ενώ α υπόλοιπα (3 γραµµές) ανισοιχούν σα δεδοµένα αξιολόγησης. Γράφηµα 5.4: Αποελέσµαα προσοµοίωσης µε η χρήση ου (LP) µονέλου και µια ΚΤΣ ροή. Η κόκκινη διακεκοµµένη καµπύλη είναι η εκίµηση, ενώ η µπλε α πραγµαικά δεδοµένα. Τα πάνω γραφήµαα ανισοιχούν σα δεδοµένα εκπαίδευσης, ενώ α υπόλοιπα ( γραµµές) ανισοιχούν σα δεδοµένα αξιολόγησης. 4
43 Αποελέσµαα µε η χρήση ου µονέλου DW Αφού οι ΚΤΣ εισροές δεν είναι και όσο καάλληλες για ην εφαρµογή ου προεινόµενου αλγόριθµου για ο απλό µονέλο (LP), είναι αναµενόµενο να είναι ακόµα χειρόερα α πράγµαα για ο πιο πολύπλοκο DW µονέλο. Ως λοιπόν δεδοµένα εκπαίδευσης θα χρησιµοποιηθούν α δεδοµένα ης µη διακεκοµµένης και µη ΚΤΣ καµπύλης ου γραφήµαος 5.. Οι παράµεροι ου µονέλου µας χρησιµοποιήθηκαν όπως περιγράφηκαν σην ενόηα 5.4. Σο γράφηµα 5.5 φαίνοναι α αποελέσµαα ης εφαρµογής ου προεινόµενου αλγορίθµου σο µονέλο DW. Για να µπορέσουµε να συγκρίνουµε α αποελέσµαα µεαξύ ου DW µε χρήση ου προεινόµενου αλγόριθµου, και ου προσεγγισικού µονέλου (LP), α αποελέσµαα που προέκυψαν από ο µονέλο (LP) βρίσκοναι και αυά σο γράφηµα 5.5 (διακεκοµµένη καµπύλη). Όπως φαίνεαι από ο γράφηµα 5.5, ο προεινόµενος αλγόριθµος εκιµά µε καλύερη ακρίβεια ις δυναµικές ου πραγµαικού συσήµαος σε σχέση µε ο (LP) µονέλο. Επισηµαίνουµε επίσης ην µεγάλη απόκλιση που υπάρχει µεαξύ ων χρονικών υσερήσεων που εκιµήθηκαν µε ον έναν ή ον άλλο αλγόριθµο. Παίρνονας υπόψη ην σχεδόν έλεια εκίµηση ων πραγµαικών παραµέρων ου συσήµαος συµπεραίνουµε όι και σην εκίµηση ης χρονικής υσέρησης ο προεινόµενος αλγόριθµος πρέπει να προσεγγίζει καλύερα ην πραγµαική ης ροχιά. Γράφηµα 5.5: Αποελέσµαα προσοµοίωσης µε η χρήση ου DW NPDE µονέλου και µια µη ΚΤΣ ροή. Η κόκκινη διακεκοµµένη καµπύλη είναι η εκίµηση, ενώ η µπλε α πραγµαικά δεδοµένα. Τα πάνω γραφήµαα ανισοιχούν σα δεδοµένα εκπαίδευσης, ενώ α υπόλοιπα (3 γραµµές) ανισοιχούν σα δεδοµένα αξιολόγησης. Η πράσινη καµπύλη ανισοιχεί σα δεδοµένα που δηµιουργήθηκαν µε η χρήση ου LP µονέλου. 43
44 Πριν κλείσουµε µε α αποελέσµαά µας θα πρέπει να πούµε και δύο λόγια για ην ευρωσία ου προεινόµενου αλγόριθµου όσον αφορά α πάνω και κάω όρια ης υσέρησης ( ) όπως αυά υπολογίζοναι σην (5.). Όπως φαίνεαι και από ο γράφηµα η εκίµηση ης υσέρησης ξεπερνά α όρια που θέσαµε ση χρονική περίοδο µεαξύ ων χρονικών ιµών 8 και 0 (γράφηµα 5.3α). Παρόλα αυά, δηλαδή ο γεγονός όι δεν ισχύει ο περιορισµός (5.6) για ένα µικρό διάσηµα, ο αλγόριθµος κααφέρνει να εκιµήσει ις πραγµαικές δυναµικές ου συσήµαος µε µεγάλη ακρίβεια. Αυό ο γεγονός από µόνο ου δείχνει ην ευρωσία ου αλγόριθµού µας. 5.6 ΣΥΜΠΕΡΑΣΜΑΤΑ (Α) Μέχρι σιγµής προείναµε και αναλύσαµε έναν νέο αλγόριθµο εκίµησης ων δυναµικών που αναπύσσοναι σε ένα σύσηµα ροής µε η χρήση ενός µονέλου µερικών διαφορικών εξισώσεων, µε αυσηρά θεωρηικά εργαλεία αλλά και πειραµαικές προσοµοιώσεις. Ο προεινόµενος αλγόριθµος, σε ανίθεση µε ους υπόλοιπους ης βιβλιογραφίας, εγγυάαι σύγκλιση εφόσον οι συνθήκες Persistence of excitation ικανοποιούναι. Επίσης δόθηκαν οδηγίες για ο σχεδιασµό πειραµαικού µονέλου, έσι ώσε οι PE συνθήκες να ικανοποιούναι πάνα. 5.7 ΚΑΤΑΣΚΕΥΗ ΕΛΕΓΚΤΗ Αφού καασκευάσαµε και αποδείξαµε ην ικανοποιηική λειουργία ου προεινόµενου προσαρµοσικού αλγορίθµου εκίµησης παραµέρων, θα ον χρησιµοποιήσουµε ώρα και για ην καασκευή ελεγκή ης ροής. Σε ένα υπικό σύσηµα ελέγχου ροής, ο ελεγκής καλείαι να ρυθµίσει ην εκροή ή ο επίπεδο (ύψος σάθµης) ων υδάων σο κανάλι ροής σε ένα επιθυµηό επίπεδο y, παίρνονας αποφάσεις για ην εισροή u. Συνήθως ο επιθυµηό επίπεδο r (setpoint) δίνεαι από ένα εποπικό σύσηµα διαχείρισης που βασίζεαι ση ζήηση και η χωρηικόηα ου δικύου, βλέπε [7], [66]. Συνήθως, ο επιθυµηό επίπεδο y παραµένει σαθερό για µεγάλα χρονικά διασήµαα. r Παραήρηση 3: Τα προβλήµαα ης ροής και ης ρύθµισης ου επιπέδου ων υδάων είναι αρκεά παρόµοια, βλέπε [8]. Εµείς θα επικενρωθούµε σο πρόβληµα ελέγχου ης ροής, αλλά όι θα επακολουθήσει µπορεί εύκολα να επεκαθεί και σην περίπωση ου ελέγχου ης σάθµης ων υδάων. Για ην επίλυση ου προβλήµαος διαήρησης επιθυµηού επιπέδου που περιγράφηκε πριν, θεωρούµε όι ο ελεγκής θα έχει η µορφή: u = Ζ 5.4 x 44
45 όπου ο x εκφράζει ο διάνυσµα ων παραµέρων ελέγχου και Ζ ένα διάνυσµα που εµπεριέχει ις µερήσεις που έχουν γίνει η χρονική σιγµή (π.χ. µερήσεις εκροής, µερήσεις εισροής, επιθυµηή εκροή ) καθώς και ις διάφορες σαθερές π.χ. r r T Z = [ y,... y p, u y =,... u p,, r,... r u p ] r r,...rpr Όπου α p y, p u, p r είναι µη αρνηικοί ακέραιοι και περιοδικές συναρήσεις (π.χ. ηµιονοειδής). Η ενσωµάωση ου σαθερού όρου σο διάνυσµα γίνεαι έσι ώσε ο ελεγκής (5.4) να µπορέσει να ανισαθµίσει ις επιδράσεις ων σαθερών ή αργά εναλλασσόµενων διααραχών. Οι όροι r,...rp χρησιµοποιούναι για ην r ανισάθµιση ων περιοδικών διααραχών. Πρέπει να ονισεί όι οι διααραχές είε είναι σχεδόν σαθερές (διαχείριση βρόχινου νερού ή λιώσιµο πάγου κλπ) είε περιοδικές (λύµαα για α αποχεευικά δίκυα, απόσυρση νερού από α αρδευικά δίκυα κλπ), είε συνδυασµός και ων δύο. Παραήρηση 4: Ο προεινόµενος προσαρµοσικός αλγόριθµος δεν εφαρµόζεαι µόνο για γραµµικούς ελεγκές ης µορφής (5.4), αλλά και για µη γραµµικής µορφής. Σε αυήν ην περίπωση ο διάνυσµα Ζ θα είναι ένα µη γραµµικό διάνυσµα ων µερήσεων και ων όρων, r,...rp. Εµείς θα επικενρωθούµε σην υπόθεση ου r γραµµικού ελεγκή καθώς από ην εµπειρία µας, αλλά και από α αποελέσµαα που δίνοναι σε παρακάω ενόηα, είναι προφανές όι µε ην καάλληλη επιλογή ων παραµέρων ελέγχου, ένας γραµµικός ελεγκής, µε παραµέρους που έχουν εκιµηθεί µε η βοήθεια ου προεινόµενου προσαρµοσικού αλγορίθµου που αναλύσαµε σε προηγούµενη ενόηα, µπορεί να οδηγήσει σε πολύ ικανοποιηικά αποελέσµαα ελέγχου κλεισού βρόχου. Προσαρµοσικός αλγόριθµος ελέγχου Ο προεινόµενος ελεγκής χρησιµοποιεί ην υπόθεση όι ο προεινόµενος προσαρµοσικός αλγόριθµος ης ενόηας 5.3 έχει ήδη χρησιµοποιηθεί σο µονέλο ) ροής (5.) και έχουµε ήδη ση διάθεσή µας ην εκίµηση ( Y ) ˆ =θ3γ ( Y ). Πρέπει να δοθεί έµφαση σο γεγονός όι η χρονική υσέρηση ου καασαικού µονέλου (5.), όπως αυή εκφράζεαι από η συνάρηση (Υ ), είναι πολύ ευαίσθηη σις εξωερικές διααραχές και σις αλλαγές απόφασης ελέγχου. Γι αυό ο λόγο η ) ακρίβεια ης εκίµησής µας ( Y ) ( Y ) δεν περιµένουµε να βελιωθεί αρκεά καά η διάρκεια ης εφαρµογής ου προεινόµενου ελέγχου. Για να ο αποφύγουµε αυό µπορούµε αυόχρονα µε ην εφαρµογή ου ελέγχου να θέσουµε σε λειουργία και ον προσαρµοσικό αλγόριθµο εκίµησης ης χρονικής υσέρησης. Σε αυήν ην περίπωση ο προσαρµοσικό κέρδος n ου αλγορίθµου εκίµησης πρέπει να είναι µικρόερο από αυό ου αλγορίθµου ελέγχου. r Έσω eο σφάλµα ης ρύθµισης σο επιθυµηό επίπεδο (setpoint). Χρησιµοποιώνας ις (5.) και (5.4) βρίσκουµε όι η εξίσωση που περιγράφει η δυναµική ου σφάλµαος είναι η παρακάω: 45
46 r r r e+ = y+ y+ = F + G xζ ( Y w y ) r r r Έσω V V( e e,..., e ), όπου m θεικός ακέραιος. Η συνάρηση V µπορεί να m r r r επιλεγεί από ον χρήση έσι ώσε ( e, e,..., e m) 0 r r r r r r V ( e e,..., e ) 0 e = e =... = e 0, m = m = r r επιλεγεί ως V ( e ) = ( e ). V και επιπλέον. Για απλόηα η V µπορεί να Το παρακάω θεώρηµα θα φανεί πολύ χρήσιµο σην ανάπυξη ου προεινόµενου προσαρµοσικού αλγορίθµου ελέγχου. Θεώρηµα 5.: δεδοµένων αρχικών ιµών : y < Y <, l { 0,...,} y και µιας l l ακολουθίας διααραχών ελαχισοποίησης έχει λύση: w < W <, ο ακόλουθο περιορισµένο πρόβληµα x * =arg-min x (ρ +ρ ) 5.6 όπου ρ, ρ ικανοποιούν ους παρακάω περιορισµούς 0 ρ <, ρ < ( r r r r r r ( Υ ),,..., ) (,,..., ) + m+ ρ m ρ V F + G x Ζ + w y e e < V e e e Έχονας ο θεώρηµα καά νου προείνουµε ον παρακάω κανόνα ελέγχου για η ρύθµιση ου x : x + =x -κζ -ˆ (Y)ε + +π 5.9 V r όπου ε + = (, r r e e,..., e m ), r + + ο κ εκφράζει ο προσαρµοσικό κέρδος και e+ δίνεαι από ο χρήση και ο π, βλέπε [43] υπολογίζεαι από: 0 εάν x < M ή x 0 και x Z ˆ( Υ ) ε 0 + π = κz ε αλλιώς ˆ( Υ ) + όπου Μ ένας πολύ µεγάλος θεικός αριθµός. Το παρακάω θεώρηµα αποδεικνύει ις ιδιόηες σύγκλισης ου προεινόµενου προσαρµοσικού αλγόριθµου ελέγχου. Θεώρηµα 5.3: θεωρούµε ο µονέλο (5.4) (5.9) και υποθέουµε όι ο Μ είναι αρκεά µεγάλος αριθµός ώσε x * < Μ. Τόε οι δυναµικές ου συσήµαος κλεισού βρόχου ικανοποιούν: 46
47 * εg M lim V ˆ ρ + O( ) + O + + ( κ) κ O O κ και εg M sup V ˆ ρ + O( ) + O + + ( κ) + x0 x κ O O O κ ( ) * * Παραήρηση 5: βασισµένοι σις προσοµοιώσεις που έγιναν, η επιλογή r r V ( e ) = ( e ), βοηθά ον ελεγκή µας να δώσει ικανοποιηικά αποελέσµαα. Παρόλα αυά, µια πιο πολύπλοκη µορφή ης συνάρησης V θα µπορούσε να βοηθήσει σην ακρίβεια ου ελέγχου. Παραήρηση 6: Όπως είδαµε σο θεώρηµα 5.3, ο προσαρµοσικός αλγόριθµος ελέγχου απαιεί µια προσεκική επιλογή ου προσαρµοσικού κέρδουςκ : Αν ο κ ε επιλεγεί πολύ µικρό, οι όροι G M O + κ O µπορούν να γίνουν υπερβολικά κ µεγάλοι, ενώ η επιλογή ενός µεγάλου κµπορεί να κάνει ον όρο O ( κ) πολύ µεγάλο. Παραήρηση 7: σηµειώσε όι ο βέλισο διάνυσµα x * όπως ορίσηκε από ο θεώρηµα 5., είναι µια συνάρηση ης αρχικής καάσασης, αλλά και ων εξωερικών διααραχών w. 5.8 ΠΡΟΣΟΜΟΙΩΣΕΙΣ (B) Προκειµένου να αξιολογήσουµε ην απόδοση ου προεινόµενου αλγόριθµου ον εφαρµόσαµε σε ένα κανάλι ροής µήκους 0 χιλιοµέρων. Οι παράµεροι ου καναλιού είναι οι ίδιες µε προηγουµένως. Για ην µονελοποίηση ων δυναµικών ου συσήµαος χρησιµοποιήθηκε ο µονέλο DW ου [59]. Για ην αριθµηική επίλυση ων µερικών διαφορικών εξισώσεων ου DW χρησιµοποιήθηκε ο µονέλο Musingun-Cunge, βλέπε [7]. Χρησιµοποιήθηκαν 4 σενάρια για ις προσοµοιώσεις: S: Αρχικά η ροή είναι ίση µε Q 0 =5m 3 /s σε όλο ο κανάλι ροής. Ο κανόνας για αλλαγή ου επιθυµηού σηµείου (setpoint) είναι y r = Q + 0 m 3 /s ή y r = Q 0 m 3 /s. Καά η διάρκεια ης εφαρµογής ου ελέγχου εµφανίζεαι µια διααραχή ης µορφής w =w +w, όπου w είναι ένας σαθερός υχαίος όρος και w, είναι επίσης υχαίος Gauss-ιανής µορφής και µικρόερος σε σχέση µε ο w. S: Ίδιο σενάριο µε ο S µε η διαφορά όι εδώ Q 0 =m 3 /s 47
48 S3: Αρχικά η ροή είναι ίση µε Q 0 =5m 3 /s σε όλο ο κανάλι ροής. Ο κανόνας για αλλαγή ου επιθυµηού σηµείου (setpoint) είναι y r = Q + 0 m 3 /s ή y r = Q 0 m 3 /s. Καά η διάρκεια ης εφαρµογής ου ελέγχου εµφανίζεαι µια διααραχή ης µορφής w =w +w, +w 3, όπου w,w είναι ίδια µε αυά ων σεναρίων S, S και w 3, είναι ένα περιοδικό σήµα (ηµιονοειδές) µε µέγεθος ίδια άξης µε ου w και περίοδο 6 ώρες S4: Ίδιο σενάριο µε ο S3 µε η διαφορά όι εδώ Q 0 =m 3 /s Για να συγκρίνουµε ην απόδοση ου προεινόµενου προσαρµοσικού αλγορίθµου ελέγχου µε ην απόδοση ενός γραµµικού ελεγκή, δηµιουργούµε έναν απλό PI ελεγκή ης µορφής: r r u ( ) = u + y + Ke + K y y 5.0 Όπου Κ,Κ εκφράζουν α κέρδη ου PI ελεγκή. Με πειράµαα, και αφού δοκιµάσαµε διάφορες ιµές, επιλέξαµε α βέλισα Κ,Κ για ον ελεγκή (5.0). Ο προσαρµοσικός αλγόριθµος που χρησιµοποιήθηκε για ις προσοµοιώσεις δίνεαι: u = + Όπου r r u + y + x, e + x, ( y y ) + x3, + x4, r ( ) + x5, r ( ) x6, r3 ( ) 5. x, είναι οι προς ρύθµιση παράµεροι ου ελεγκή και () είναι περιοδικά i σήµαα µε περιόδους, 8 και 5 ώρες ανίσοιχα. Ας σηµειωθεί όι ο προσαρµοσικός αλγόριθµος (5.) δε γνωρίζει ην περίοδο ης περιοδικής διααραχής w 3, ων σεναρίων S3 και S4. Οι παράµεροι ελέγχου επιλέχθηκαν ως εξής: r i r r V ( e ) = ( e ) Το προσαρµοσικό κέρδος κ =0-3 και Μ= Σε όλα α πειράµαα οι αρχικές ιµές ων παραµέρων ου ελεγκή ήαν µηδενικές. ( x i, 0 = 0 i ). Πρέπει να δοθεί έµφαση σο όι οι αποφάσεις ελέγχου και ων ελεγκών (5.0), (5.) περιορίσηκαν σο διάσηµα [,0]m 3 λόγω φυσικών περιορισµών. Τα γραφήµαα δείχνουν ην απόδοση ου PI ελεγκή (ελείες) και ου προσαρµοσικού ελεγκή (παύλες) συγκρινόµενους µε ην απόφαση ελέγχου για όλα α σενάρια. Για όλα α σενάρια έγιναν 3 προσοµοιώσεις και κάθε γράφηµα έχει 3 γραφικές παρασάσεις. Όπως είναι εµφανές από α γραφήµαα, σε όλες ις περιπώσεις µε εξαίρεση ην µεσαία γραφική παράσαση ου γραφήµαος 5.8, ο προεινόµενος προσαρµοσικός αλγόριθµος ελέγχου υπερέχει ου PI ελεγκή και όσο αφορά ην ικανόηά ου να 48
49 προσεγγίζει καλύερα ην επιθυµηή καάσαση, αλλά και παρουσιάζει λιγόερες ασοχίες. Λέγονας ασοχία εννοούµε ην υπέρβαση ης µπλε γραµµής σα γραφήµαα η οποία δείχνει ην ενολή ελέγχου u =. r y 5.9 ΣΥΜΠΕΡΑΣΜΑΤΑ (Β) Συµπεραίνουµε λοιπόν όι ο προσαρµοσικός αλγόριθµος ης ενόηας 5.3 µπορεί να χρησιµοποιηθεί και για η δηµιουργία προσαρµοσικού ελεγκή, ο οποίος λειουργεί καλύερα από ους διαδεδοµένους γραµµικούς ελεγκές µιας και µπορεί να πάρει υπόψη ου πιο ρεαλισικές απεικονίσεις ων δυναµικών που παρουσιάζει ο σύσηµα. Ο συνδυασµός ων αλγορίθµων, από η µια δηλαδή η προσαρµοσική εκίµηση ων χαρακηρισικών ων δυναµικών ου συσήµαος, και από ην άλλη ο προσαρµοσικός ελεγκής που παίρνει σε πραγµαικό χρόνο µερήσεις και εκιµήσεις ης καασαικής ου συσήµαος, µπορεί να γίνει ένα πολύ δυναό εργαλείο σα προβλήµαα ροής, είε αυά είναι προβλήµαα αποχεευικών, είε αρδευικών δικύων. Γράφηµα 5.6: Σενάριο : ζηούµενο σήµα (µπλε γραµµή), απόκριση ανοιχού βρόχου κάω από ην επίδραση ελέγχου u =y γ (πράσινη καµπύλη), απόκριση ου PI ελεγκή (πράσινη διακεκοµµένη καµπύλη) και ο προσαρµοσικός ελεγκής (κόκκινη καµπύλη). 49
50 Γράφηµα 5.7: Σενάριο : ζηούµενο σήµα (µπλε γραµµή), απόκριση ανοιχού βρόχου κάω από ην επίδραση ελέγχου u =y γ (πράσινη καµπύλη), απόκριση ου PI ελεγκή (πράσινη διακεκοµµένη καµπύλη) και ο προσαρµοσικός ελεγκής (κόκκινη καµπύλη). Γράφηµα 5.8: Σενάριο 3: ζηούµενο σήµα (µπλε γραµµή), απόκριση ανοιχού βρόχου κάω από ην επίδραση ελέγχου u =y γ (πράσινη καµπύλη), απόκριση ου PI ελεγκή (πράσινη διακεκοµµένη καµπύλη) και ο προσαρµοσικός ελεγκής (κόκκινη καµπύλη). 50
51 Γράφηµα 5.9: Σενάριο 4: ζηούµενο σήµα (µπλε γραµµή), απόκριση ανοιχού βρόχου κάω από ην επίδραση ελέγχου u =y γ (πράσινη καµπύλη), απόκριση ου PI ελεγκή (πράσινη διακεκοµµένη καµπύλη) και ο προσαρµοσικός ελεγκής (κόκκινη καµπύλη). 5
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Ολοκλήρωση διεργασίας χρησιμοποιώντας την τεχνολογία σύγκλισης (Pinch Technology)
 Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Μέθοδοι ανάλυσης οικονοµικής σκοπιµότητας έργων. Κοινωνικο- οικονοµικές. Ο ορισµός του έργου. Τεχνική αξιολόγησης έργων
 Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΚΗΠΟΣ & ΒΕΡΑ. τα «πώς ντας σε όλα μας ό πλούσιο φωτογρ. λίδα 3. όλης. Διαβάστε στη σελ. 7 για ένα βιβλίο που θα κάνει τις ιδέες σας...
 μ Κηπο ανία Π ΕΡ Ι Ο Δ Ι ΚΗ ΕΚ Δ ΟΣΗ ΓΙΑ ΤΗ ΦΥΣΗ ΚΑ Ι ΤΟ ΠΕ ΡΙ ΒΑ ΛΛΟ Ν Αγαπηοί φίλοι ου πράσινου, Όλοι μας διαπισώνουμε καθημερινά ο έλλειμμα που υπάρχει σε καθαρό νερό και αέρα, σο πράσινο, ση διαχείριση
μ Κηπο ανία Π ΕΡ Ι Ο Δ Ι ΚΗ ΕΚ Δ ΟΣΗ ΓΙΑ ΤΗ ΦΥΣΗ ΚΑ Ι ΤΟ ΠΕ ΡΙ ΒΑ ΛΛΟ Ν Αγαπηοί φίλοι ου πράσινου, Όλοι μας διαπισώνουμε καθημερινά ο έλλειμμα που υπάρχει σε καθαρό νερό και αέρα, σο πράσινο, ση διαχείριση
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πανελή Α. Δείρογλου Πυχιούχου Παιδαγωγικού Τήαος Δηοικής Εκπαίδευσης Το Ολοήερο Δηοικό Σχολείο από η σκοπιά ων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πανελή Α. Δείρογλου Πυχιούχου Παιδαγωγικού Τήαος Δηοικής Εκπαίδευσης Το Ολοήερο Δηοικό Σχολείο από η σκοπιά ων
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΙΓΝΙΟΘΕΩΡΗΤΙΚΗ ΜΕΛΕΤΗ ΠΟΛΥΕΠΙΠΕ ΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ WEB CACHING
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΜΕΤΑΠΤΥΧΙΑΚΗ ΕΞΕΙ ΙΚΕΥΣΗ ΣΤΑ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΑΙΓΝΙΟΘΕΩΡΗΤΙΚΗ ΜΕΛΕΤΗ ΠΟΛΥΕΠΙΠΕ ΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΜΕΤΑΠΤΥΧΙΑΚΗ ΕΞΕΙ ΙΚΕΥΣΗ ΣΤΑ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΑΙΓΝΙΟΘΕΩΡΗΤΙΚΗ ΜΕΛΕΤΗ ΠΟΛΥΕΠΙΠΕ ΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
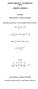 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
25 χρόνια από την πτώση του τείχους του Βερολίνου
 25 χρόνια από ην πώση ου είχους ου Βερολίνου Πόσα γνωρίζουμε για ο είχος που χώριζε ην σημανικόερη πόλη ης Γερμανίας σε Αναολικό και Δυικό μπλοκ; Με αφορμή ην 25η επέειο ης πώσης ου είχους ου Βερολίνου
25 χρόνια από ην πώση ου είχους ου Βερολίνου Πόσα γνωρίζουμε για ο είχος που χώριζε ην σημανικόερη πόλη ης Γερμανίας σε Αναολικό και Δυικό μπλοκ; Με αφορμή ην 25η επέειο ης πώσης ου είχους ου Βερολίνου
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΕΙΣΑΓΩΓΗ Γενικότερος σκοπός του Προγράμματος NETCASTLE
 Τ οδι ασυν ορι ακ όπρογ ραμμαi P A ηςε υρωπαϊ κ ήςέν σωης-ε λ λ άδας Αλ βαν ί ας-20072013 γ ι α ην Αλ βαν ί α Τ Ε ΛΙ ΚΗΕ ΚΘΕ ΣΗ Προόδουκ αι Αξ ι ολ όγ ησης ουπρογ ράμμα ος NET CAS T L E γ ι α ην Αλ βαν
Τ οδι ασυν ορι ακ όπρογ ραμμαi P A ηςε υρωπαϊ κ ήςέν σωης-ε λ λ άδας Αλ βαν ί ας-20072013 γ ι α ην Αλ βαν ί α Τ Ε ΛΙ ΚΗΕ ΚΘΕ ΣΗ Προόδουκ αι Αξ ι ολ όγ ησης ουπρογ ράμμα ος NET CAS T L E γ ι α ην Αλ βαν
ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ
 8ο Πανελλήνιο Συμποσιο Ωκεανογαφίας & Αλιείας ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ Χισόφοος Γ. Κουίας*, Αχιλλέας Γ. Σαμαάς** *Ο.Λ.Θ. Α.Ε.,
8ο Πανελλήνιο Συμποσιο Ωκεανογαφίας & Αλιείας ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ Χισόφοος Γ. Κουίας*, Αχιλλέας Γ. Σαμαάς** *Ο.Λ.Θ. Α.Ε.,
Ενότητα Ζ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ
 Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Κεφάλαιο 8: Μαγνητικά Υλικά και Ιδιότητες ΙΙ. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
? Συμπεριφορά ψαθυρών υλικών 11/6/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας
 11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
ιόδευση των πληµµυρών
 ιόδευση των πληµµυρών Με τον όρο διόδευση εννοούµε τον υπολογισµό του πληµµυρικού υδρογραφήµατος σε µια θέση Β στα κατάντη ενός υδατορρεύµατος, όταν αυτό είναι γνωστό σε µια θέση Α στα ανάντη ή αντίστοιχα
ιόδευση των πληµµυρών Με τον όρο διόδευση εννοούµε τον υπολογισµό του πληµµυρικού υδρογραφήµατος σε µια θέση Β στα κατάντη ενός υδατορρεύµατος, όταν αυτό είναι γνωστό σε µια θέση Α στα ανάντη ή αντίστοιχα
Multi Post. Ενδοριζικοί άξονες ανασύστασης
 Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
ΜΑΘΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΓΙΑ ΤΗΝ ΕΝΑΝΘΡΑΚΩΣΗ ΚΑΙ ΣΚΥΡΟΔΕΜΑΤΟΣ
 ΜΑΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΓΙΑ ΤΗΝ ΕΝΑΝΡΑΚΩΣΗ ΚΑΙ ΤΗ ΧΛΩΡΙΩΣΗ ΣΚΥΡΟΔΕΜΑΤΟΣ Η Διπλωμαική Εργαία παρουιάηκε ενώπιον ου Διδακικού Προωπικού ου Πανεπιημίου Αιγαίου Για ην Εκπλήρωη ων Απαιήεων για ο Δίπλωμα Ειδίκευης
ΜΑΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΓΙΑ ΤΗΝ ΕΝΑΝΡΑΚΩΣΗ ΚΑΙ ΤΗ ΧΛΩΡΙΩΣΗ ΣΚΥΡΟΔΕΜΑΤΟΣ Η Διπλωμαική Εργαία παρουιάηκε ενώπιον ου Διδακικού Προωπικού ου Πανεπιημίου Αιγαίου Για ην Εκπλήρωη ων Απαιήεων για ο Δίπλωμα Ειδίκευης
Απλοποίηση υπολογισμών σε σωλήνες υπό πίεση
 Υδραυλική & Υδραυλικά Έργα Απλοποίηση υπολογισμών σε σωλήνες υπό πίεση Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Καθιερωμένοι τύποι της υδραυλικής για μόνιμη ομοιόμορφη ροή
Υδραυλική & Υδραυλικά Έργα Απλοποίηση υπολογισμών σε σωλήνες υπό πίεση Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Καθιερωμένοι τύποι της υδραυλικής για μόνιμη ομοιόμορφη ροή
ασκήσεις υποταγής στη δεν αντεχει: σχολική καθημερινότητα ο επιθετικός προσδιορισμός περιεχομενα
 ο επιθεικός προσδιορισμός δεν ανεχει: καθηγηές, άξεις, βαθμούς, κουδούνια, γονείς, μαθήμαα, καριέρα, συλλόγους, κηδεμόνες, απουσιολόγια, προσευχή, πειθαρχία, μάθεε-ξεχάσε ην ορισική, ην υποακική ις προσαγές
ο επιθεικός προσδιορισμός δεν ανεχει: καθηγηές, άξεις, βαθμούς, κουδούνια, γονείς, μαθήμαα, καριέρα, συλλόγους, κηδεμόνες, απουσιολόγια, προσευχή, πειθαρχία, μάθεε-ξεχάσε ην ορισική, ην υποακική ις προσαγές
ΕΠΙΡΡΟΗ ΕΥΤΕΡΟΓΕΝΩΝ ΣΤΡΕΠΤΙΚΩΝ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΣΤΗΝ ΑΝΑΛΥΣΗ ΡΑΒ ΩΝ ΤΥΧΟΥΣΑΣ ΙΑΤΟΜΗΣ
 ΕΠΙΡΡΟΗ ΕΥΤΕΡΟΓΕΝΩΝ ΣΤΡΕΠΤΙΚΩΝ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΣΤΗΝ ΑΝΑΛΥΣΗ ΡΑΒ ΩΝ ΤΥΧΟΥΣΑΣ ΙΑΤΟΜΗΣ Ε.Ι. Σαπουνζάκης Αναπληρωής Καθηγηής Σχολή Πολιικών Μηχανικών, Εθνικό Μεσόβιο Πολυεχνείο Πολυεχνειούπολη Ζωγράφου, Αθήνα
ΕΠΙΡΡΟΗ ΕΥΤΕΡΟΓΕΝΩΝ ΣΤΡΕΠΤΙΚΩΝ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΣΤΗΝ ΑΝΑΛΥΣΗ ΡΑΒ ΩΝ ΤΥΧΟΥΣΑΣ ΙΑΤΟΜΗΣ Ε.Ι. Σαπουνζάκης Αναπληρωής Καθηγηής Σχολή Πολιικών Μηχανικών, Εθνικό Μεσόβιο Πολυεχνείο Πολυεχνειούπολη Ζωγράφου, Αθήνα
MATLAB. Εισαγωγή στο SIMULINK. Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής
 MATLAB Εισαγωγή στο SIMULINK Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής Εισαγωγή στο Simulink - Βιβλιοθήκες - Παραδείγματα Εκκίνηση BLOCKS click ή Βιβλιοθήκες Νέο αρχείο click ή Προσθήκη block σε αρχείο
MATLAB Εισαγωγή στο SIMULINK Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής Εισαγωγή στο Simulink - Βιβλιοθήκες - Παραδείγματα Εκκίνηση BLOCKS click ή Βιβλιοθήκες Νέο αρχείο click ή Προσθήκη block σε αρχείο
Copyright - Υδρομέντωρ
 - Υδ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΡΟΓΡΑΜΜΑΤΑ «ΑΝΤΑΓΩΝΙΣΤΙΚΟΤΗΤΑ & ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΤΗΤΑ» ΚΑΙ ΠΕΡΙΦΕΡΕΙΩΝ ΣΕ ΜΕΤΑΒΑΣΗ ΠΑΡΑΔΟΤΕΟ 6.3 ΕΘΝΙΚΟ ΣΤΡΑΤΗΓΙΚΟ
- Υδ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΡΟΓΡΑΜΜΑΤΑ «ΑΝΤΑΓΩΝΙΣΤΙΚΟΤΗΤΑ & ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΤΗΤΑ» ΚΑΙ ΠΕΡΙΦΕΡΕΙΩΝ ΣΕ ΜΕΤΑΒΑΣΗ ΠΑΡΑΔΟΤΕΟ 6.3 ΕΘΝΙΚΟ ΣΤΡΑΤΗΓΙΚΟ
«Προσβλητική» και «απαξιωτική» ενέργεια
 Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου 67 ΧΡΟΝΙΑ αφιερωµένα σην ενηµέρωση Παρασκευή 1 Οκωβρίου 2010 Φύλλο 127 www.fonitisparou.gr Έος 65 ο Νέα Περίοδος
Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου 67 ΧΡΟΝΙΑ αφιερωµένα σην ενηµέρωση Παρασκευή 1 Οκωβρίου 2010 Φύλλο 127 www.fonitisparou.gr Έος 65 ο Νέα Περίοδος
ΤΟ ΝΕΡΟ ΣΤΗΝ ΠΟΛΗ ΜΑΣ ΑΝΑΚΥΚΛΩΣΗ ΝΕΡΟΥ ΗΡΩ ΓΚΑΝΤΑ ΕΛΣΑ ΜΕΜΜΟΥ
 ΤΟ ΝΕΡΟ ΣΤΗΝ ΠΟΛΗ ΜΑΣ ΑΝΑΚΥΚΛΩΣΗ ΝΕΡΟΥ ΗΡΩ ΓΚΑΝΤΑ ΕΛΣΑ ΜΕΜΜΟΥ Μέχρι πριν από 100 χρόνια ή και µέχρι πριν από λίγα χρόνια, σε ορισµένες περιοχές το πόσιµο νερό προερχόταν από πηγάδια και πηγές. Σήµερα,
ΤΟ ΝΕΡΟ ΣΤΗΝ ΠΟΛΗ ΜΑΣ ΑΝΑΚΥΚΛΩΣΗ ΝΕΡΟΥ ΗΡΩ ΓΚΑΝΤΑ ΕΛΣΑ ΜΕΜΜΟΥ Μέχρι πριν από 100 χρόνια ή και µέχρι πριν από λίγα χρόνια, σε ορισµένες περιοχές το πόσιµο νερό προερχόταν από πηγάδια και πηγές. Σήµερα,
Αριθμητική Ανάλυση & Εφαρμογές
 Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Ιωάννα Ανυφαντή, Μηχανικός Περιβάλλοντος Επιβλέπων: Α. Ευστρατιάδης, ΕΔΙΠ ΕΜΠ. Αθήνα, Ιούλιος 2018
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Δ.Π.Μ.Σ. «ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΥΔΡΟΛΟΓΙΑ & ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Ιωάννα Ανυφαντή, Μηχανικός Περιβάλλοντος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Δ.Π.Μ.Σ. «ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΥΔΡΟΛΟΓΙΑ & ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Ιωάννα Ανυφαντή, Μηχανικός Περιβάλλοντος
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
Σειρά Ασκήσεων στην Αντοχή των Υλικών
 Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
3. Δίκτυο διανομής επιλύεται για δύο τιμές στάθμης ύδατος της δεξαμενής, Η 1 και
 ΕΜΠ Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά Υδραυλικά Έργα Επαναληπτική εξέταση 10/2011 1 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ (Μονάδες 3, Διάρκεια 20') ΠΑΡΑΛΛΑΓΗ Α Απαντήστε στις ακόλουθες ερωτήσεις, σημειώνοντας
ΕΜΠ Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά Υδραυλικά Έργα Επαναληπτική εξέταση 10/2011 1 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ (Μονάδες 3, Διάρκεια 20') ΠΑΡΑΛΛΑΓΗ Α Απαντήστε στις ακόλουθες ερωτήσεις, σημειώνοντας
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
τρόπος για να εμπεδωθεί η θεωρία. Για την επίλυση των παραδειγμάτων χρησιμοποιούνται στατιστικά πακέτα, ώστε να είναι δυνατή η ανάλυση μεγάλου όγκου
 ΠΡΟΛΟΓΟΣ Η γραμμική παλινδρόμηση χρησιμοποιείται για την μελέτη των σχέσεων μεταξύ μετρήσιμων μεταβλητών. Γενικότερα, η γραμμική στατιστική συμπερασματολογία αποτελεί ένα ευρύ πεδίο της στατιστικής ανάλυσης
ΠΡΟΛΟΓΟΣ Η γραμμική παλινδρόμηση χρησιμοποιείται για την μελέτη των σχέσεων μεταξύ μετρήσιμων μεταβλητών. Γενικότερα, η γραμμική στατιστική συμπερασματολογία αποτελεί ένα ευρύ πεδίο της στατιστικής ανάλυσης
Υπενθύµιση εννοιών από την υδραυλική δικτύων υπό πίεση
 Υπενθύµιση εννοιών από την υδραυλική δικτύων υπό πίεση Σηµειώσεις στα πλαίσια του µαθήµατος: Τυπικά υδραυλικά έργα Ακαδηµαϊκό έτος 2005-06 Ανδρέας Ευστρατιάδης & ηµήτρης Κουτσογιάννης Εθνικό Μετσόβιο Πολυτεχνείο
Υπενθύµιση εννοιών από την υδραυλική δικτύων υπό πίεση Σηµειώσεις στα πλαίσια του µαθήµατος: Τυπικά υδραυλικά έργα Ακαδηµαϊκό έτος 2005-06 Ανδρέας Ευστρατιάδης & ηµήτρης Κουτσογιάννης Εθνικό Μετσόβιο Πολυτεχνείο
Υφαλμύρινση Παράκτιων Υδροφορέων - προσδιορισμός και αντιμετώπιση του φαινομένου με συνδυασμό μοντέλων προσομοίωσης και μεθόδων βελτιστοποίησης
 Υφαλμύρινση Παράκτιων Υδροφορέων - προσδιορισμός και αντιμετώπιση του φαινομένου με συνδυασμό μοντέλων προσομοίωσης και μεθόδων βελτιστοποίησης Καθ. Καρατζάς Γεώργιος Υπ. Διδ. Δόκου Ζωή Σχολή Μηχανικών
Υφαλμύρινση Παράκτιων Υδροφορέων - προσδιορισμός και αντιμετώπιση του φαινομένου με συνδυασμό μοντέλων προσομοίωσης και μεθόδων βελτιστοποίησης Καθ. Καρατζάς Γεώργιος Υπ. Διδ. Δόκου Ζωή Σχολή Μηχανικών
ΣΤΟΧΟΣ ΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ Η ιερεύνηση της επιρροής του φωτισµού αστικών και υπεραστικών οδών στη συχνότητα και σοβαρότητα των ατυχηµάτων µε χρήση λο
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΜΕΤΑΦΟΡΩΝ ΚΑΙ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΥΠΟ ΟΜΗΣ Νικόλαος Μιτζάλης Επιβλέπων: Γιώργος Γιαννής, Αναπληρωτής Καθηγητής ΕΜΠ ΣΤΟΧΟΣ ΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ Η
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΜΕΤΑΦΟΡΩΝ ΚΑΙ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΥΠΟ ΟΜΗΣ Νικόλαος Μιτζάλης Επιβλέπων: Γιώργος Γιαννής, Αναπληρωτής Καθηγητής ΕΜΠ ΣΤΟΧΟΣ ΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ Η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ. Μέρος Α (2007-08)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ Μέρος Α (2007-08) ΕΙΣΑΓΩΓΗ I-1 Ρευσοµηχανική (Fluid Mechanics) είναι ο κλάδος ης εφαρµοσµένης µηχανικής (applied
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ Μέρος Α (2007-08) ΕΙΣΑΓΩΓΗ I-1 Ρευσοµηχανική (Fluid Mechanics) είναι ο κλάδος ης εφαρµοσµένης µηχανικής (applied
Περί χασμάτων. Ελένη Μάνου, νεφρολόγος Επιμελήτρια Α' ΓΝ Παπαγεωργίου Θεσσαλονίκη
 Περί χασμάων Ελένη Μάνυ, νεφρλόγς Επιμελήρια Α' ΓΝ Παπαγεωργίυ Θεσσαλνίκη Χάσμα ανιόνων (ΧΑ) ρύ: ένα δύσκλ και παραμελημέν κεφάλαι! "Gamblegram" Η σημασία ης ηλεκρικής υδεερόηας σε σχέση με η σύγχυση πυ
Περί χασμάων Ελένη Μάνυ, νεφρλόγς Επιμελήρια Α' ΓΝ Παπαγεωργίυ Θεσσαλνίκη Χάσμα ανιόνων (ΧΑ) ρύ: ένα δύσκλ και παραμελημέν κεφάλαι! "Gamblegram" Η σημασία ης ηλεκρικής υδεερόηας σε σχέση με η σύγχυση πυ
Η επίδραση της δειγματοληπτικής αβεβαιότητας των εισροών στη στοχαστική προσομοίωση ταμιευτήρα
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Η επίδραση της δειγματοληπτικής αβεβαιότητας των εισροών στη στοχαστική προσομοίωση ταμιευτήρα Ελένη Ζαχαροπούλου
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Η επίδραση της δειγματοληπτικής αβεβαιότητας των εισροών στη στοχαστική προσομοίωση ταμιευτήρα Ελένη Ζαχαροπούλου
