ΜΕΛΕΤΗ ΤΡΟΧΙΩΝ ΓΥΡΩ ΑΠΟ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΣΤΑ ΠΛΑΙΣΙΑ ΒΑΘΜΩΤΩΝ-ΤΑΝΥΣΤΙΚΩΝ ΘΕΩΡΙΩΝ ΒΑΡΥΤΗΤΑΣ
|
|
|
- Κασσάνδρα Κοντολέων
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΜΕΛΕΤΗ ΤΡΟΧΙΩΝ ΓΥΡΩ ΑΠΟ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΣΤΑ ΠΛΑΙΣΙΑ ΒΑΘΜΩΤΩΝ-ΤΑΝΥΣΤΙΚΩΝ ΘΕΩΡΙΩΝ ΒΑΡΥΤΗΤΑΣ Τηλέμαχος Μ. Αθανασιάδης Ιούνιος 2014 Επιβλέπων καθηγητής: Νικόλαος Στεργιούλας ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
2
3 Στη μνήμη του παππού μου, Τηλέμαχου.
4
5 Ευχαριστίες Από τη θέση αυτή, πρώτο απ όλους θα ήθελα να ευχαριστήσω τον επιβλέποντα καθηγητή μου κύριο Νικόλαο Στεργιούλα, ο οποίος με τις γνώσεις και την εμπειρία του μου δίδαξε πολλά για τη ϕυσική και τις επιστήμες γενικότερα. Πέραν αυτού, η επιείκεια που μου έδειξε σε διάϕορα θέματα, όπως ο χρόνος περάτωσης της διπλωματικής, καθώς και η ευκαιρία που μου έδωσε να συμμετέχω σε ένα ερευνητικό project είναι πράξεις του για τις οποίες αισθάνομαι πραγματικά ευγνώμων. Θα ήθελα επίσης να ευχαριστήσω τους γονείς μου, Μιχάλη και Βασιλική για την υποστήριξη και το ενδιαϕέρον τους, την καθηγήτρια του King s College του Λονδίνου κυρία Μαρία Σακελλαριάδου, που είχε δεχθεί την αρχική μου πρόταση να είναι συνεπιβλέπουσα καθηγήτρια, τους ϕίλους μου, και ιδιαίτερα τον Παύλο Γκαϊντατζή για τις διάϕορες συζητήσεις επί του θέματος της εργασίας μου και τον Γιάννη Αντωνιάδη, για την πρόταση που μου έκανε να κάνω μέρος της πτυχιακής μου στη Γερμανία, τα παιδιά στην ομάδα του κ. Στεργιούλα, που με βοήθησαν στην παρουσίαση καθώς και όσους ήρθαν στην τελική παρουσίαση της εργασίας. Τέλος, ένα ιδιαίτερο ευχαριστώ χρωστάω στη κοπέλα μου Θάλεια Τραϊανού, για τις συζητήσεις, την υποστήριξη και την ανεκτικότητα που έδειξε επί καθημερινής βάσης, καθ όλη τη διάρκεια συγγραϕής αυτής της εργασίας. Η εμπειρία της διπλωματικής εργασίας, ήταν σίγουρα ένα από τα πιο ενδιαϕέροντα ταξίδια που έχω κάνει μέχρι τώρα, και είμαι σίγουρος ότι με έχει οπλίσει με εϕόδια που σίγουρα θα μου ϕανούν χρήσιμα στη συνέχεια της πορείας μου, και γι αυτό ευχαριστώ για ακόμα μια ϕορά τους ανθρώπους που συνέβαλλαν σε αυτό. Τηλέμαχος Μ. Αθανασιάδης Ιούνιος 2014, Θεσσαλονίκη.
6 Περίληψη Η παρούσα εργασία μεταξύ άλλων αποτελεί μια σύντομη εισαγωγή στις εναλλακτικές θεωρίες βαρύτητας. Αναϕέρονται κάποια κύρια χαρακτηριστικά τους, οι συνθήκες που μας οδήγησαν στην αναζήτηση τους, η σύνδεση αυτών των θεωριών με τις παρατηρήσεις και γενικότερα οτιδήποτε αϕορά στη ϕυσική και μαθηματική βάση στην οποία στηριζόμαστε ώστε να τις αναπτύξουμε. Σε καμία περίπτωση δεν είναι ένας πλήρης οδηγός αλλά είναι αρκετά αντιπροσωπευτικός. Μια τέτοιου είδους εισαγωγή επιχειρείται στο πρώτο κεϕάλαιο όπου αρχικά δίνονται οι λόγοι ύπαρξης των εναλλακτικών θεωριών βαρύτητας, ενώ όπως είναι γνωστό η Γενική Θεωρία της Σχετικότητας (Γ.Θ.Σ.) επαληθεύεται συνεχώς από παρατηρήσεις (J. Antoniadis et. al [1]). Πράγματι, στη τρέχουσα ϕάση, η θεωρία προηγείται του πειράματος και της παρατήρησης, δηλαδή ενώ δεν υπάρχουν ισχυρές πειραματικές ενδείξεις για τη μη ισχύ της Γ.Θ.Σ., οι θεωρητικοί ασχολούνται με τη γενίκευση της. Αυτό οϕείλεται κυρίως στην αδυναμία εξήγησης της επιταχυνόμενης διαστολής του Σύμπαντος, δηλαδή το πρόβλημα της σκοτεινής ενέργειας, αλλά και στις προβλέψεις άλλων σημαντικών θεωριών, όπως η θεωρία υπερχορδών, που υποδεικνύουν ότι η βαρύτητα μπορεί να μην περιγρά- ϕεται επακριβώς από τη Γ.Θ.Σ., λόγω της ύπαρξης βαθμωτών πεδίων στο Σύμπαν. Επιπλέον, η διδακτική αξία των εναλλακτικών θεωριών είναι μεγάλη, καθώς η μελέτη τους βοηθά ουσιαστικά στην βαθύτερη κατανόηση των αξιωμάτων της τρέχουσας θεωρίας, καθώς και της σχέσης που τα συνδέει με το πείραμα. Σε αυτά τα πλαίσια, διαϕόρων ειδών εναλλακτικές θεωρίες έχουν αναπτυχθεί από την εποχή του Einstein ακόμα, οι βασικότερες εκ των οποίων αναϕέρονται με κάποια παραδείγματα στο πρώτο κεϕάλαιο. Το κύριο είδος εναλλακτικών θεωριών, οι οποίες αποτελούν και το κύριο θέμα της εργασίας είναι οι βαθμωτέςτανυστικές (scalar-tensor) θεωρίες, οι οποίες θεωρούν την ύπαρξη ενός βαθμωτού πεδίου στο Σύμπαν, το οποίο όταν έρχεται σε σύζευξη με τον τανυστή Ricci έχουμε μια γενικευμένη θεωρία βαρύτητας. Άλλες γενικεύσεις είναι η περίπτωση των θεωριών f(r) στις οποίες υπάρχει μια σχετικά αυθαίρετη μαθηματική γενίκευση της δράσης με τη χρήση μιας συνάρτησης του βαθμωτού Ricci στη θέση του βαθμωτού Ricci. Στο τέλος του κεϕαλαίου υπάρχει μία σύντομη αναϕορά στις παρατηρήσεις διπλών συστημάτων αστέρων νετρονίων αλλά και στα πειράματα που λαμβάνουν χώρα στο ηλιακό σύστημα καθώς και τη σύνδεσή τους με τις εναλλακτικές θεωρίες. Στο δεύτερο κεϕάλαιο περιγράϕεται πιο αναλυτικά ένα συγκεκριμένο είδος εναλλακτικών θεωριών, οι βαθμωτές τανυστικές θεωρίες, οι οποίες όπως προαναϕέρθηκε αποτελούν τις πιο συνηθισμένες γενικεύσεις της τρέχουσας θεωρίας βαρύτητας. Η πρώτη περίπτωση βαθμωτής τανυστικής θεωρίας εμϕανίστηκε το 1961 από τους Brans και Dicke [2] και πρόκειται για την πιο απλή περίπτωση αυτού του είδους θεωρίας. Στη συγκεκριμένη θεωρία, η παγκόσμια σταθερά της 1
7 βαρύτητας G δεν είναι σταθερή αλλά μεταβάλλεται στο χώρο και στο χρόνο. Για το λόγο αυτό το G αντικαθίσταται από το τον όρο 1/ϕ όπου ϕ είναι το βαθμωτό πεδίο. Ιδιαίτερη αναϕορά γίνεται σε αυτό το κεϕάλαιο, στους σύμμορϕους μετασχηματισμούς που μπορούμε να εκτελέσουμε στη μετρική (κυρίως για λόγους απλοποίησης των πράξεων), θέμα το οποίο διχάζει ακόμα τους θεωρητικούς του χώρου. Μέσω ενός σύμμορϕου μετασχηματισμού γίνεται η μετάβαση από το πλαίσιο αναϕοράς Jordan στο πλαίσιο αναϕοράς Einstein (και το αντίστροϕο) όπως έχει καθιερωθεί να ονομάζονται. Η διένεξη έγκειται στο κατά πόσο η μαθηματική ισοδυναμία των δύο πλαισίων αναϕοράς συνεπάγεται και ϕυσική ισοδυναμία (βλέπε παράρτημα Fatibene & Francaviglia 2013 [38]), δηλαδή κατά πόσο μπορούμε να δεχτούμε τα αποτελέσματα και των δύο πλαισίων αναϕοράς ως ϕυσικώς αποδεκτά. Για το συγκεκριμένο θέμα παρέχεται επιπλέον πληθώρα αναϕορών ώστε να ανατρέξει ο αναγνώστης στη σχετική βιβλιογραϕία, μιας και το συγκεκριμένο θέμα είναι ακόμα ανοιχτό. Τέλος, δίνεται η μορϕή των γενικευμένων εξισώσεων πεδίου (σε μια βαθμωτή τανυστική θεωρία) και εξηγούνται οι διαϕορές με τη Γ.Θ.Σ. Στο τρίτο κεϕάλαιο, παρουσιάζονται οι υπολογισμοί που έγιναν για πρώτη ϕορά, βασισμένοι σε ένα ϕορμαλισμό υποθετικού δυναμικού ακολουθώντας τους Abramowicz και Kluźniak [3, 31], και αϕορούν στον προσδιορισμό των λεγόμενων επικυκλικών συχνοτήτων σε δίσκους προσαύξησης γύρω από αστέρες νετρονίων. Η αξία της μελέτης αυτών των συχνοτήτων έγκειται στην προσπάθεια εξήγησης των λεγόμενων ημιπεριοδικών ταλαντώσεων (QPOs), δηλαδή μεγίστων που εμϕανίζονται στο ϕάσμα των ακτίνων Χ που λαμβάνουμε από δίσκους προσαύξησης γύρω από αστέρες νετρονίων [4, 5, 30]. Ουσιαστικά έγιναν οι υπολογισμοί της Κεπλεριανής (ή τροχιακής) και της ακτινικής επικυκλικής συχνότητας στα πλαίσια μιας συγκεκριμένης περίπτωσης (μη γραμμικής) βαθμωτής τανυστικής θεωρίας με τη χρήση της αναλυτικής μετρικής του Just [6], για μη περιστρεϕόμενο αστέρα νετρονίων. Ενδεικτικά, αυτές οι ποσότητες είναι οι εξής: Η Kεπλεριανή συχνότητα: Ω 2 p = και η ακτινική επικυκλική συχνότητα: ( ωr 2 = 1 α r (1 a/r) 2b/a (ab + 2βd 2 ln[1 a/r]) (a r)r(a(a + b 2r) 2βd 2 ln[1 a/r]), ) 2b/a {a 2 (a + 2b)[b(a + b) 2βd 2 ] 2a 2 [b(a + 3b) 2βd 2 ]r + 2a 2 br 2 2a(r a) 2 r [ 2 a(a + b 2r) 2βd 2 ln ( )] 1 a r 2βd 2 ln ( ) ( 1 a a[a 2 2a(r b) + 2r(r 2b)] 2βd 2 (a + 2b 2r) ln ( ) ) 1 a r r + 2a(r a) 2 r [ 2 a(a + b 2r) 2βd 2 ln ( )] 1 a r. Μέρος αυτού του κεϕαλαίου συμπεριλήϕθηκε ως παράρτημα σε πρόσϕατη δημοσίευση (Doneva, Yazadjiev, Stergioulas, Kokkotas & Athanasiadis [8]). Εδώ αξίζει να σημειωθεί ότι για την περίπτωση περιστρεϕόμενου αστέρα δεν υπάρχει αναλυτική λύση των εξισώσεων πεδίου, οπότε η επίλυση έγινε αριθμητικά. Οι 2
8 Kεϕάλαιο 0 αναλυτικοί υπολογισμοί που παρουσιάζουμε στη παρούσα εργασία, χρησιμοποιήθηκαν ως επαλήθευση των αποτελεσμάτων που υπολογίστηκαν αριθμητικά με τη χρήση μιας γενικευμένης έκδοσης του κώδικα RNS (Stergioulas and Friedman [9, 10]). Στον παρακάτω πίνακα ϕαίνεται η αντιστοιχία της τροχιακής συχνότητας υπολογισμένης αριθμητικά και αναλυτικά στην εσώτατη ευσταθή κυκλική τροχιά (ISCO). Πίνακας 1: Τροχιακή συχνότητα στην εσώτατη ευσταθή κυκλική τροχιά β = 4.8 m A (M ) ω A Ω p ISCO (αναλυτικά) Ω p ISCO (αριθμητικά) Τέλος, εκτός από το παράρτημα με τον κώδικα με τον οποίο έγιναν οι αναλυτικοί υπολογισμοί των επικυκλικών συχνοτήτων και διάϕορα γραϕήματα των συχνοτήτων για διαϕορετικά μοντέλα αστέρων νετρονίων, στο τέταρτο κεϕάλαιο γίνεται μια σύντομη παρουσίαση μελλοντικών διαστημικών αποστολών και παρατηρήσεων που θα μπορούσαν να δώσουν τα πρώτα στοιχεία που θα αποδείξουν ότι η Γ.Θ.Σ. χρειάζεται γενίκευση και ταυτοχρόνως θα αρχίσουν να αποκλείουν περιπτώσεις εναλλακτικών θεωριών που δεν περιγράϕουν την πραγματικότητα. Τέτοιες αποστολές, όπως το elisa, οι οποίες είναι τεράστια συμβολόμετρα τα οποία θα μπουν σε τροχιά, ίσως ϕαίνονται υπερβολικά δύσκολες ή και αδύνατες με την τρέχουσα τεχνολογία, αλλά οι ταχείς ρυθμοί ανάπτυξης της τεχνολογίας και της επιστήμης ίσως τις κάνουν εϕικτές σε λιγότερο από δύο δεκαετίες. Ευελπιστώ η παρούσα εργασία να παρέχει στον αναγνώστη μια σύντομη αλλά ουσιαστική εισαγωγή σε κάποια βασικά θέματα και υπολογισμούς που αϕορούν τις βαθμωτές τανυστικές θεωρίες βαρύτητας και έναν γενικότερο οδηγό των εναλλακτικών θεωριών βαρύτητας στην τρέχουσα βιβλιογραϕία, αποτελώντας έτσι ένα χρήσιμο εργαλείο για κάθε ενδιαϕερόμενο. 3
9 Περιεχόμενα 1 Εισαγωγή: Eναλλακτικές θεωρίες βαρύτητας Γιατί μελετάμε εναλλακτικές θεωρίες βαρύτητας; Επιθυμητά χαρακτηριστικά των εναλλακτικών θεωριών Ποια είδη υπάρχουν; Πως συνδέονται με τις παρατηρήσεις; Βαθμωτές τανυστικές θεωρίες Πλαίσια αναϕοράς Jordan και Einstein Ορισμός σύμμορϕης απεικόνισης Ορισμός των δύο πλαισίων αναϕοράς Επιλογή κατάλληλου πλαισίου αναϕοράς και Αρχή Σύμμορ- ϕης Ισοδυναμίας Η περίπτωση της Brans-Dicke Ορισμός Βαθμωτών Τανυστικών Θεωριών Εξισώσεις πεδίου και αστέρες νετρονίων Μελέτη Γεωδαισιακών καμπύλων και επικυκλικών συχνοτήτων Ορισμός Γεωδαισιακής καμπύλης Επικυκλικές Συχνότητες Κεπλεριανή και Επικυκλικές Συχνότητες Μελέτη Γεωδαισιακών καμπύλων και επικυκλικών συχνοτήτων στα πλαίσια βαθμωτών τανυστικών θεωριών Σύμμορϕες απεικονίσεις στις γεωδαισιακές Τροχιακή και επικυκλική συχνότητα σωματιδίων γύρω από ακίνητο αστέρα νετρονίων Επαλήθευση αριθμητικών αποτελεσμάτων Τι μας επιϕυλλάσει το μέλλον; Συμπεράσματα Αʹ Παράρτημα: Υπολογισμοί και Γραϕήματα
10 Kεϕάλαιο 1 1 Εισαγωγή: Eναλλακτικές θεωρίες βαρύτητας 1.1 Γιατί μελετάμε εναλλακτικές θεωρίες βαρύτητας; Παρόλο το γεγονός ότι η Γενική Θεωρία της Σχετικότητας (Γ.Θ.Σ.) είναι μια ευρύτατα αποδεκτή θεωρία βαρύτητας που έχει επιβεβαιωθεί από πολλά και δια- ϕορετικά πειράματα [1], υπάρχουν κάποιες ενδείξεις ότι αυτή η τόσο επιτυχημένη θεωρία θα μπορούσε να αποτελεί υποπερίπτωση μιας γενικότερης εναλλακτικής θεωρίας βαρύτητας. Μέχρι τώρα, τα πειράματα αποδεικνύουν περίτρανα την υπεροχή της πρώτης αλλά αυτό θα μπορούσε να αλλάξει μέσα στις επόμενες λίγες δεκαετίες, καθώς η ακρίβεια των πειραμάτων αυξάνεται και η γνώση μας για το σύμπαν διευρύνεται. Οι λόγοι που ωθούν την επιστημονική κοινότητα σε αναζήτηση εναλλακτικών θεωριών βαρύτητας, ενώ η Γ.Θ.Σ. επιβεβαιώνεται συνεχώς από νέα πειράματα, είναι αρκετοί και διαϕορετικών ειδών. Υπάρχουν ενδείξεις ότι σε γαλαξιακές και κοσμολογικές αποστάσεις, η βαρύτητα ίσως να μη συμπεριϕέρεται όπως προβλέπει η Γ.Θ.Σ., γεγονός που αν συμβαίνει δε θα αποτελεί ϕυσικά την εξαίρεση αλλά τον κανόνα στη μελέτη της ϕυσικής. Παρόλο που ακόμα δεν υπάρχουν παρατηρήσεις που να το αποδεικνύουν, ενδείξεις υπάρχουν. Είναι γνωστό από την ίδια την ιστορία της ϕυσικής, ότι όταν αλλάζει η τάξη μεγέθους, οι θεωρίες χρειάζονται γενίκευση, συνήθως κάποια διόρθωση ανώτερης τάξης. Οι ενδείξεις αυτές σχετίζονται επίσης με την ύπαρξη της σκοτεινής ενέργειας. Πράγματι, παρόλη την επιτυχία της, σε κοσμολογική κλίμακα η Γ.Θ.Σ. απαιτεί την ύπαρξη της σκοτεινής ενέργειας (σε ποσοστό 75% της υλοενέργειας του σύμπαντος), ως αίτιο για την επιταχυνόμενη διαστολή του σύμπαντος που προκύπτει από τα διαθέσιμα παρατηρησιακά δεδομένα. Υπάρχουν διαϕορετικά θεωρητικά μοντέλα προσέγγισης της ϕυσικής σημασίας της σκοτεινής ενέργειας [37], όπως αυτό της κοσμολογικής σταθεράς. Η κοσμολογική σταθερά, την οποία είχε κάποτε εισάγει ο Einstein στις εξισώσεις πεδίου ώστε να περιγράψει ένα σταθερό σύμπαν, μπορεί να χρησιμοποιηθεί για να περιγράψει την επιταχυνόμενη διαστολή, αλλά από ϕυσικής άποψης η ενέργεια του κενού που προβλέπεται από τη σωματιδιακή ϕυσική (και θα μπορούσε να παίξει το ρόλο της κοσμολογικής σταθεράς) είναι πολλές τάξεις μεγέθους διαϕορετική από την υπολογιζόμενη κοσμολογική σταθερά που απαιτείται για να εξηγήσει την παρατηρούμενη επιταχυνόμενη διαστολή του σύμπαντος. Κατά συνέπεια, είναι εύλογο να θεωρηθεί ότι χρειαζόμαστε μια γενικότερη θεωρία βαρύτητας η οποία θα μπορούσε να εξηγήσει αυτή την επιταχυνόμενη διαστολή και ουσιαστικά να λύσει το μυστήριο της σκοτεινής ενέργειας. Ενδείξεις όμως υπάρχουν και από τη πλευρά του μικρόκοσμου. Η θεωρία των υπερχορδών αλλά και οι μεγάλες ενοποιημένες θεωρίες (G.U.T.) προβλέπουν την ύπαρξη βαθμωτών πεδίων τα οποία θα μπορούσαν να επιδράσουν στις εξισώσεις της βαρύτητας και να δώσουν διαϕορετικά αποτελέσματα από τη γενική θεωρία της σχετικότητας. Η κβαντική βαρύτητα που είναι σίγουρα το μεγαλύτερο άλυτο πρόβλημα της σύγχρονης ϕυσικής, επίσης υποδεικνύει την αλληλεπίδραση της γεωμετρίας (τανυστής Ricci) με βαθμωτά πεδία. Επιπλέον, θεωρώντας ότι υπάρχουν ανώτερες συρρικνωμένες διαστάσεις τύπου Kaluza-Klein, άμεσα 5
11 Kεϕάλαιο 1 προκύπτει ότι στο σύμπαν υπάρχει βαθμωτό πεδίο [12]. Το βαθμωτό αυτό πεδίο, εϕόσον υπάρχει, έχει επίδραση στις εξισώσεις της γενικής θεωρίας της σχετικότητας. Οι θεωρίες αυτές, γνωστές ως βαθμωτές-τανυστικές θεωρίες (scalar-tensor theories), είναι οι συνηθέστερες γενικεύσεις της Γ.Θ.Σ. και κάνουν ακριβώς αυτή τη γενίκευση, εισάγουν δηλαδή την επίδραση βαθμωτών πεδίων στις εξισώσεις της βαρύτητας. Αυτό συνήθως γίνεται με τη σύζευξη του βαθμωτού πεδίου με τον τανυστή Ricci. Στην παρούσα εργασία θα επικεντρωθούμε στη μελέτη τέτοιου είδους θεωριών, ξεκινώντας από την πρώτη και απλούστερη περίπτωση που είναι η θεωρία που αναπτύχθηκε από τους Brans και Dicke το 1961 [2]. Στο Σχήμα 1 παρουσιάζεται η σχέση της μάζας ενός αστέρα νετρονίων σε συνάρτηση με την ακτίνα του στην περίπτωση της Γ.Θ.Σ. καθώς και σε μια βαθμωτή τανυστική θεωρία με σταθερά σύζευξης β = 4.6 και β = 5.0. Παρατηρούμε ότι όσο μεγαλύτερη σε απόλυτη τιμή είναι η σταθερά σύζευξης β, τόσο πιο έντονη είναι η διαϕορά από τη Γ.Θ.Σ. και ουσιαστικά αυτός είναι ο τρόπος μελέτης και παρουσίασης των διαϕορών με την ισχύουσα θεωρία, στις εναλλακτικές θεωρίες βαρύτητας. Στα όρια που μας επιτρέπουν οι παρατηρήσεις ϕυσικά, μελετάμε τις μεταβολές που θα προκύπτανε σε αποτελέσματα της Γ.Θ.Σ. αν υποθέσουμε κάποια γενικότερη θεωρία, είτε αυτή είναι κάποιο βαθμωτό μέγεθος είτε κάποιου άλλου είδους διόρθωση. Σχήμα 1: Σχέση μάζας ακτίνας αστέρα νετρονίων για τις περιπτώσεις της Γ.Θ.Σ. και για βαθμωτή τανυστική θεωρία με σταθερά σύζευξης β = 4.6 και β = 5.0. Πηγή: H. Sotani (2014) [13] Για κάποιους ένα επιπλέον κίνητρο για την αναζήτηση βαθμωτού πεδίου προκύπτει από την αρχή του Mach, η οποία δεν είναι απολύτως συμβατή με τη Γ.Θ.Σ. και ουσιαστικά αποτέλεσε το κίνητρο για τους Brans και Dicke ώστε να προτείνουν μια νέα θεωρία. Ουσιαστικά, αν δεχτούμε την αρχή του Mach, αναγκαζόμαστε να εισάγουμε στο σύμπαν ένα βαθμωτό πεδίο, που δεν υπάρχει στα πλαίσια της σχετικότητας. Σε κάθε περίπτωση η αρχή του Mach, είναι μια υπό- 6
12 Kεϕάλαιο 1 θεση που δεν έχει αποδειχθεί αλλά την αναϕέρουμε για λόγους πληρότητας. Τέλος, ένας άλλος λόγος ύπαρξης και μελέτης των εναλλακτικών θεωριών, σχετίζεται άμεσα με το διδακτικό ρόλο που μπορούν να έχουν οι προβλέψεις τέτοιων θεωριών. Η σύγκριση τους με τα αποτελέσματα της Γ.Θ.Σ. υποδεικνύει ποια αξιώματα της θεωρίας ελέγχονται πραγματικά κατά τη διάρκεια των πειραμάτων και συνεπώς μέσω της μελέτης των διαϕορών που έχουν με την επικρατούσα θεωρία, βοηθούν ουσιαστικά στη βαθύτερη κατανόηση της. 7
13 Kεϕάλαιο Επιθυμητά χαρακτηριστικά των εναλλακτικών θεωριών Υπάρχουν πολλών και διαϕορετικών ειδών εναλλακτικές θεωρίες, κάποιες με κατανοητή ϕυσική σημασία, κάποιες με λιγότερο κατανοητή και κάποιες μόνο με διδακτική σημασία. Γενικότερα υπάρχει η προτίμηση, οι θεωρίες που θα μπορούσαν να αντικαταστήσουν την Γ.Θ.Σ. να ικανοποιούν τις παρακάτω αρχές: Την Αρχή της Σχετικότητας, η οποία ορίζει πως όλοι οι παρατηρητές είναι ισοδύναμοι για την περιγραϕή της ϕύσης. Την Αρχή της Ισοδυναμίας, που ορίζει πως παρατηρητές που εκτελούν ελεύθερη κίνηση σε ένα χωρόχρονο βρίσκονται σε ελεύθερη πτώση και δεν μπορούν να ξεχωρίσουν την επιτάχυνση της βαρύτητας από την επιτάχυνση που θα προκαλούσε μια εξωτερική δύναμη στην κίνηση τους. Την Αρχή του Συναλλοιώτου, σύμϕωνα με την οποία όλοι οι ϕυσικοί νόμοι εκϕράζονται σε αναλλοίωτη μορϕή, ανεξάρτητη από την αλλαγή του συστήματος συντεταγμένων. Οι παραπάνω αρχές βέβαια αποτελούν υποθέσεις εργασίας που μας βοηθάνε να θέσουμε τις εναλλακτικές θεωρίες στην κατάλληλη θεωρητική βάση η οποία και είναι σύμϕωνη με τη ϕυσική, όπως την αντιλαμβανόμαστε σύμϕωνα με τα τρέχοντα πειραματικά δεδομένα. Αυτό σημαίνει ότι εναλλακτικές θεωρίες βαρύτητας που καταρρίπτουν για παράδειγμα την ισχυρή ή την ασθενή αρχή της ισοδυναμίας, δεν αποκλείονται από περαιτέρω μελέτη απλά περιορίζονται από τις παρατηρήσεις. Προτεραιότητα ϕυσικά δίνεται σε θεωρίες που τηρούν τις παραπάνω αρχές, καθότι εκτός του ότι μελετώνται πιο εύκολα, ίσως να είναι οι πρώτες οι οποίες θα επιβεβαιωθούν ή θα αποκλειστούν όταν υπάρξουν τα πρώτα πειραματικά δεδομένα. Σε κάθε περίπτωση, μια εναλλακτική θεωρία βαρύτητας θα πρέπει να εξηγεί τις αστρονομικές παρατηρήσεις, τις τροχιές των πλανητών αλλά και τις μεγάλες δομές στο σύμπαν, όπως είναι οι γαλαξίες και τα σμήνη γαλαξιών καθώς και να προβλέπει τη παρατηρούμενη τιμή της σταθεράς του Hubble. Αυτό σημαίνει πως στο όριο του ασθενούς πεδίου πρέπει να επαληθεύει τα ακριβή πειράματα που έχουν γίνει για τη βαρύτητα στο Ηλιακό σύστημα, ενώ στο όριο του ισχυρού πεδίου τις παρατηρήσεις στα ραδιοκύματα των διπλών αστέρων νετρονίων. Φυσικά για να μπορέσει μια εναλλακτική θεωρία να καθιερωθεί ως θεωρία βαρύτητας θα πρέπει να παρέχει λύση και στα προβλήματα στα οποία αδυνατεί να απαντήσει η γενική θεωρίας της σχετικότητας. 8
14 Kεϕάλαιο Ποια είδη υπάρχουν; Εδώ και αρκετές δεκαετίες έχουν γίνει διάϕορες υποθέσεις πάνω στις οποίες στηρίζονται εναλλακτικές θεωρίες, οι εμπνευστές των οποίων επιδιώκουν να εισάγουν διορθώσεις (διαϕορετικής ϕύσης κάθε ϕορά) στις εξισώσεις της θεωρίας της σχετικότητας. Οι γενικευμένες θεωρίες βαρύτητας μπορούν να κατηγοριοποιηθούν με βάση δυο βασικά χαρακτηριστικά. Το πρώτο χαρακτηριστικό είναι η γενίκευση μέσω της σύζευξης του τανυστή Ricci με κάποιο βαθμωτό πεδίο, οπότε και έχουμε την κατηγορία των βαθμωτών τανυστικών θεωριών και το δεύτερο είναι η γενίκευση με την εμϕάνιση παραγώγων ανώτερης τάξης της μετρικής. Επιπλέον, υπάρχουν παραδείγματα θεωριών που συνδυάζουν τα δύο χαρακτηριστικά, ενώ άλλες θεωρίες στηρίζονται σε τελείως διαϕορετικές παραδοχές ή ιδέες που μπορεί να προέρχονται από άλλους κλάδους της ϕυσικής, όπως η θερμοδυναμική (εντροπική βαρύτητα). Οι κύριες κατηγορίες εναλλακτικών θεωριών βαρύτητας είναι: Οι βαθμωτές-τανυστικές θεωρίες (scalar tensor theories) με τις οποίες θα ασχοληθούμε αναλυτικά στην παρούσα εργασία και οι οποίες αποτελούν ένα μεγάλο ποσοστό των εναλλακτικών θεωριών. Αυτές οι θεωρίες υποθέτουν την ύπαρξη ενός βαθμωτού πεδίου στο σύμπαν το οποίο εισέρχεται στις εξισώσεις πεδίου (σύζευξη με τανυστή) και ϕυσικά δίνει διαϕορετικά αποτελέσματα από την Γ.Θ.Σ. Όπως είναι λογικό, υπάρχουν αρκετά διαϕορετικά είδη βαθμωτών τανυστικών θεωριών, καθότι οι υποθέσεις που μπορούν να γίνουν είναι πολλές και αποδεκτές από τη στιγμή που βρίσκονται εντός των ορίων που θέτουν τα πειράματα. Οι τανυστικές θεωρίες, χαρακτηριστικότερο παράδειγμα των οποίων είναι οι επονομαζόμενες θεωρίες βαρύτητας f(r), οι οποίες είναι μια οικογένεια θεωριών στις οποίες η γενίκευση γίνεται μέσω συναρτήσεων του βαθμωτού Ricci. Με την αυθαίρετη χρήση τέτοιων συναρτήσεων, αντί για το απλό βαθμωτό Ricci στην εξίσωση της δράσης, συντελείται μια γενίκευση καθαρά μαθηματικής ϕύσης, η οποία θα μπορούσε να έχει κάποια ϕυσική βάση. Η δράση: 1 S(g) = 2κ R gd 4 x, της γενικής θεωρίας της σχετικότητας, γενικεύεται βάζοντας στη θέση του βαθμωτού Ricci R = g µν R µν, μια συνάρτηση f(r): S(g) = 1 2κ f(r) gd 4 x, όπου κ = 8πG/c 4 και g η ορίζουσα του μετρικού τανυστή. Ελαχιστοποιώντας τη δράση αυτής της μορϕής, εξάγονται οι εξισώσεις πεδίου: F (R)R µν 1 2 f(r)g µν + [g µν µ ν ]F (R) = κt µν, 9
15 Kεϕάλαιο 1 όπου g µν είναι ο μετρικός τανυστής, F (R) = f(r)/ r, R µν o τανυστής Ricci και με µ, ν συμβολίζονται οι συναλλοίωτες παράγωγοι. O τανυστής ενέργειας ορμής είναι: T µν = 2 δ( gl m ), g δg µν όπου L m η Λανγκρατζιανή της μάζας. Με τέτοιου είδους θεωρίες είναι εϕικτό να εξηγηθεί η επιταχυνόμενη διαστολή χωρίς τη χρήση αγνώστων πεδίων όπως η σκοτεινή ενέργεια. Η πρώτη θεωρία f(r) προτάθηκε το 1970 από τον Buchdahl [14]. Στην ίδια κατηγορία εντάσσονται και οι θεωρίες Palatini f(r) για τις οποίες έχει αποδειχθεί ότι είναι ισοδύναμες με την θεωρία Brans-Dicke για ω = 3/2. Παρόλα αυτά, οι θεωρίες Palatini f(r) ϕαίνεται να είναι ασύμβατες με το καθιερωμένο μοντέλο, καθώς ϕαίνεται να παραβιάζουν πειράματα στο όριο του ασθενούς πεδίου [42]. Οι θεωρίες βαθμωτού πεδίου όπως η θεωρία του Nordström, είναι προγενέστερη της Γ.Θ.Σ., αλλά αποτυγχάνει να εξηγήσει τα τρέχοντα παρατηρησιακά δεδομένα. Παρόλα αυτά, είναι ένα απλό παράδειγμα σχετικιστικής θεωρίας βαρύτητας και έχει κυρίως εκπαιδευτικό ενδιαϕέρον. Οι διανυσματικές-τανυστικές θεωρίες, οι οποίες εκτός από τη μετρική περιλαμβάνουν και ένα δυναμικό πεδίο τετραταχυτήτων. Σε αυτή την κατηγορία ανήκουν οι λεγόμενες θεωρίες Einstein-Αιθέρα. Οι διανυσματικές-τανυστικές-βαθμωτές θεωρίες (TeVeS) οι οποίες συνδυάζουν διανυσματικά, τανυστικά και βαθμωτά πεδία. Σε καμία περίπτωση η παραπάνω λίστα δεν αποτελεί μια πλήρη λίστα εναλλακτικών θεωριών βαρύτητας, αλλά μόνο των πιο συμβατικών και ευρύτερα αποδεκτών. Θεωρίες όπως η εντροπική βαρύτητα, ή οι θεωρίες των Newton Cartan, Yilmaz, Hoyle Narlikar, Hořava Lifshitz και άλλων έχουν ιδιαίτερο ενδιαϕέρον και αποτελούν διαϕορετικούς δρόμους προσέγγισης του προβλήματος γενίκευσης της θεωρίας βαρύτητας αλλά δεν θα αναπτύξουμε περαιτέρω τέτοιες περιπτώσεις θεωριών. 10
16 Kεϕάλαιο Πως συνδέονται με τις παρατηρήσεις; Όπως προαναϕέρθηκε, όλες οι παρατηρήσεις μέχρι σήμερα επιβεβαιώνουν την Γ.Θ.Σ. ως την επικρατούσα θεωρία βαρύτητας. Πράγματι, στο όριο του ασθενούς βαρυτικού πεδίου η Γ.Θ.Σ. έχει επιβεβαιωθεί από πολλά και διαϕορετικά πειράματα. Δεν έχουν γίνει όμως λεπτομερείς παρατηρήσεις σε συμπαγή σώματα όπου το βαρυτικό πεδίο είναι πολύ ισχυρό, όπως τα άστρα νετρονίων, οι μελανές οπές και οι λευκοί νάνοι. Αυτός ο κλάδος βρίσκεται σε άνθηση τα τελευταία χρόνια και παράλληλα με την ανάπτυξη της τεχνολογίας οι παρατηρήσεις ολοένα και πληθαίνουν. Στην περιοχή κοντά σε τόσο συμπαγή σώματα όπως είναι οι μελανές οπές και τα άστρα νετρονίων, η Γ.Θ.Σ. θα μπορούσε να μην ισχύει. Σύμϕωνα με τον Will [16] τα πειράματα που αϕορούν τη βαρύτητα μπορούν να χωριστούν σε τέσσερις χρονικές περιόδους: Η πρώτη περίοδος ( ) όπου υπερίσχυσαν ϕυσικά το πείραμα των Michelson-Morley, η επιβεβαίωση της απόκλισης του ϕωτός από τον Ήλιο και η μετατόπιση του περιηλίου του Ερμή. Η δεύτερη περίοδος ( ) ή περίοδος παύσης, όπου οι προβλέψεις τη θεωρίας ξέϕυγαν από τα όρια που έθετε η τεχνολογία εκείνη την εποχή. Η τρίτη περίοδος, που ξεκινάει από το 1960 και ϕτάνει μέχρι το 1980, όπου υπήρξε μια συστηματική προσπάθεια να κατανοήσουμε πλήρως τις προβλέψεις της Γ.Θ.Σ. και να τις συγκρίνουμε με τις προβλέψεις των εναλλακτικών θεωριών βαρύτητας, προτάθηκαν νέα πειράματα που θα επιβεβαίωναν ή θα κατέρριπταν τη θεωρία. Ξεχωρίζει η παρατήρηση της μείωσης της περιόδου περιστροϕής του διπλού πάλσαρ Hulse-Taylor που επιβεβαιώνει την πρόβλεψη της Γ.Θ.Σ. για ελάττωση της ενέργειας του συστήματος μέσω εκπομπής βαρυτικής ακτινοβολίας. Η τέταρτη περίοδος, που ξεκινάει από το 1980 και συνεχίζεται μέχρι σήμερα, είναι η περίοδος όπου ζητούνται απαντήσεις κυρίως στο όριο του ισχυρού πεδίου, παρόλο που υπάρχουν ϕυσικά ακόμα περιθώρια και στο όριο του ασθενούς πεδίου. Οι αστρονόμοι επιδιώκουν να επαληθεύσουν ή να περιορίσουν την ισχύ της αποδεκτής θεωρίας βαρύτητας, αξιοποιώντας παρατηρησιακά δεδομένα από διπλά συστήματα αστέρων νετρονίων στα οποία η ένταση του βαρυτικού πεδίου είναι ιδιαίτερα αυξημένη. Στην περίοδο που διανύουμε, σύμϕωνα με τον Psaltis [50], οι τρόποι προσέγγισης μιας εναλλακτικής θεωρίας βαρύτητας στο όριο του ισχυρού πεδίου είναι δύο, μιας και ο παραμετροποιημένος μετα-νευτώνειος ϕορμαλισμός (PPN) ισχύει μόνο στο ασθενές όριο: η προσέγγιση από πάνω προς τα κάτω (top down) και η προσέγγιση από κάτω προς τα πάνω (bottom up). Στην πρώτη περίπτωση, η γενίκευση γίνεται σε θεμελιώδες επίπεδο (γενικεύοντας την εξίσωση της δράσης με κίνητρα που μας παρέχουν θεωρίες όπως η κβαντική βαρύτητα), υπολογίζονται οι διαϕορές σε σχέση με τη Γ.Θ.Σ. που θα εμϕανιστούν σε παρατηρούμενες ποσότητες και αμέσως μετά επιδιώκεται η επαλήθευση τους μέσω της κατάλληλης παρατήρησης ή ενός πειράματος. Αυτή είναι και η επικρατούσα προσέγγιση. Στο Σχήμα 2 παρουσιάζεται μια γραϕική αναπαράσταση αυτής της προσέγγισης: 11
17 Kεϕάλαιο 1 Σχήμα 2: Γραϕική αναπαράσταση της προσέγγισης top down για τον έλεγχο της βαρύτητας στο όριο του ισχυρού πεδίου. Πηγή: Psaltis [50] Η συγκεκριμένη προσέγγιση έχει ένα βασικό πλεονέκτημα. Η γενίκευση της δράσης δε γίνεται αυθαίρετα, αλλά με βάση κίνητρα που παρέχονται από άλλες θεωρίες, οπότε η πιθανότητα να καταλήξουμε σε μια θεωρία με ϕυσική σημασία είναι σημαντικά μεγαλύτερη, και επιπλέον το γεγονός ότι ξεκινάμε από μια Λανγκρατζιανή εξασϕαλίζει τη διατήρηση συμμετριών και νόμων. Παρόλα αυτά, υπάρχει και ένα πολύ σημαντικό μειονέκτημα, που δεν είναι άλλο από το ότι οι παρατηρήσεις πρέπει να ερμηνευτούν στα στενά πλαίσια του θεωρητικού πλαισίου στο οποίο επιλέχθηκε να αναπτυχθεί η θεωρία. Σε αυτό ακριβώς το σημείο έχει νόημα και η δεύτερη προσέγγιση (bottom up) που παρουσιάζεται στο Σχήμα 3 και πρόκειται για μια ϕαινομενολογική περιγραϕή των παρατηρήσεων σε ένα πλαίσιο που κάνει ευκολότερα ορατό το είδος της γενίκευσης που πρέπει να γίνει στη τρέχουσα θεωρία. Δεχόμενοι την ισχύ της αρχής της ισοδυναμίας και άρα το γεγονός ότι τα σωματίδια κινούνται σε γεωδαισιακές, χωρίς να ασχοληθούμε με το πως ένα είδος χωρόχρονου προέρχεται από τις εξισώσεις πεδίου, παραμετροποιούμε τον εξωτερικό χωρόχρονο ενός αστέρα νετρονίων ή μελανής οπής (αναϕερόμαστε 12
18 Kεϕάλαιο 1 στο όριο του ισχυρού πεδίου). Με αυτόν τον τρόπο μπορούμε να προσδιορίσουμε ποσότητες που θα μπορούσαν να ελεγχθούν για το αν ακολουθούν ή όχι τη Γ.Θ.Σ. Σχήμα 3: Γραϕική αναπαράσταση της προσέγγισης bottom up για τον έλεγχο της βαρύτητας στο όριο του ισχυρού πεδίου. Πηγή: Psaltis [50] Η πιο πρόσϕατη επιβεβαίωση της Γ.Θ.Σ. αλλά και περιορισμός των παραμέτρων των εναλλακτικών θεωριών βαρύτητας έγινε με παρατηρήσεις που έγιναν για πρώτη ϕορά σε πάλσαρ με μεγάλη μάζα (Antoniadis et. al. [1]). Στο Σχήμα 4 παρουσιάζεται η ισχύς του βαθμωτού πεδίου ως συνάρτηση της μάζας του αστέρα νετρονίων. Ορίζεται το όριο μέσα στο οποίο μπορούν να κινηθούν οι εναλλακτικές θεωρίες βαρύτητας και συγκεκριμένα οι βαθμωτές τανυστικές θεωρίες που χρησιμοποιούν το βαθμωτό πεδίο (πράσινη περιοχή). Η κίτρινη περιοχή είναι περιοχή για την οποία οι παρατηρήσεις έχουν επιβεβαιώσει τη γενική σχετικότητα. Τέτοιου είδους παρατηρήσεις, περιορίζουν τις διάϕορες ελεύθερες παραμέτρους των εναλλακτικών θεωριών και έτσι σταδιακά υπάρχει αποκλεισμός θεωριών που αδυνατούν να εξηγήσουν τα παρατηρούμενα. Περισσότερες πληρο- ϕορίες σχετικά με τις παρατηρήσεις πάλσαρς που επιδιώκουν να επιβεβαιώσουν τη γενική σχετικότητα υπάρχουν στο άρθρο επισκόπησης του Wex [15], και στο βιβλίο του Will [46]. Στο όριο των χαμηλών ενεργειών πολύ συχνά χρησιμοποιείται ο ϕορμαλισμός PPN [16] που αποτελεί ένα χρήσιμο υπολογιστικό εργαλείο με το οποίο οι εξισώσεις της Γ.Θ.Σ. μπορούν να εκϕραστούν ως αποκλίσεις ανώτερης τάξης 13
19 Kεϕάλαιο 1 Σχήμα 4: Η ισχύς του βαθμωτού πεδίου ως συνάρτηση της μάζας του αστέρα νετρόνιων. Πηγή: Antoniadis et. al. [1] στο νόμο της παγκόσμιας έλξης του Νεύτωνα. Αυτό είναι χρήσιμο στον έλεγχο της αρχής της ισοδυναμίας, την οποία κάθε μετρική θεωρία οϕείλει να επαληθεύει. Δέκα παράμετροι αρκούν για να περιγράψουν τη Γ.Θ.Σ. σε αυτό το ϕορμαλισμό και ουσιαστικά είναι οι παράμετροι που οι αστρονόμοι προσπαθούν να υπολογίσουν ώστε να θέσουν τα εκάστοτε όρια ισχύος της θεωρίας. Όσο διευρύνονται τα όρια της Γ.Θ.Σ. τόσο στενεύουν τα όρια των ελευθέρων παραμέτρων που μπορεί να περιέχει μια εναλλακτική θεωρία. 14
20 Kεϕάλαιο 1 Οι παραπάνω παράμετροι είναι οι εξής: γ (εκϕράζει την καμπυλότητα του χωρόχρονου, είναι μηδέν για τη Νευτώνεια βαρύτητα και 1 για την Γ.Θ.Σ.), β (εκϕράζει τη μη γραμμικότητα), η (ελέγχει τοπικά ϕαινόμενα), α 1, α 2, α 3 (σχετίζονται με ϕαινόμενα προτιμώμενου πλαισίου αναϕοράς), ζ 1, ζ 2, ζ 3, ζ 4 (σχετίζονται με την ισχύ των νόμων διατήρησης). Στον Πίνακα 2 παρουσιάζονται οι τιμές που παίρνουν αυτές οι παράμετροι στην εκάστοτε θεωρία. Με αυτό τον τρόπο υπάρχει εύκολη σύνδεση μεταξύ θεωρίας και παρατήρησης. Πίνακας 2: Τιμές των PPN παραμέτρων για τη Γ.Θ.Σ. και για κάποια παραδείγματα θεωριών. Πηγή: Will [16] Όσο αϕορά τις βαθμωτές τανυστικές θεωρίες που κατεξοχήν μας ενδιαϕέρουν στη παρούσα εργασία, στο Σχήμα 5 ϕαίνονται τα όρια που έχουν οριστεί (για το βαθμωτό πεδίο) από παρατηρήσεις σε διπλά συστήματα αστέρων νετρονίων και πειράματα που έγιναν στο ηλιακό σύστημα όπως πειράματα με λέιζερ (LLR) αλλά και μετρήσεις που πραγματοποιήθηκαν με τη διαστημική αποστολή Cassini. Οι παράμετροι β 0 και α 0 δείχνουν ουσιαστικά την ισχύ του βαθμωτού πεδίου εϕόσον υπάρχει, και όταν μηδενίζονται δίνουν τη γενική θεωρία της σχετικότητας. Με γκρι είναι χρωματισμένη η επιτρεπόμενη περιοχή που μπορούν να κινηθούν οι βαθμωτές τανυστικές θεωρίες και ϕυσικά περιλαμβάνει και τη γενική θεωρία σχετικότητας. Τέλος, αξίζει να αναϕερθούμε στην ανάγκη που υπάρχει να συνεχίσουν να γίνονται παρατηρήσεις και πειράματα ολοένα μεγαλύτερης ακρίβειας, έτσι ώστε στο άμεσο μέλλον να υπάρξουν ενδείξεις για το δρόμο για τον οποίο πρέπει να κινηθεί η έρευνα στη βαρύτητα. Είναι θαυμαστό το γεγονός πως η Γ.Θ.Σ. η οποία 15
21 Kεϕάλαιο 1 Σχήμα 5: Οι περιορισμοί που εισάγουν οι παρατηρήσεις για το βαθμωτό πεδίο. Πηγή: P. C. C. Freire et. al. [17] είναι μια θεωρία που προήλθε σχεδόν αποκλειστικά από θεωρητική σκέψη και με ελάχιστα πειραματικά δεδομένα, επαληθεύεται συνεχώς εδώ και σχεδόν έναν αιώνα, αλλά ο δρόμος των εναλλακτικών θεωριών ϕαίνεται να είναι η ϕυσική της συνέχεια, μιας και τα αναπάντητα ερωτήματα και οι ενδείξεις για μια γενικότερη θεωρία ολοένα και πληθαίνουν. 16
22 Kεϕάλαιο 2 2 Βαθμωτές τανυστικές θεωρίες 2.1 Πλαίσια αναϕοράς Jordan και Einstein Ένα από τα βασικά ζητήματα που συναντά κανείς στη μελέτη των βαθμωτών τανυστικών θεωριών (Β.Τ.Θ.), όπως και σε άλλες εναλλακτικές θεωρίες βαρύτητας, όπως οι θεωρίες f(r), οι θεωρίες Kaluza-Klein αλλά και στη Γ.Θ.Σ., είναι η ύπαρξη σύμμορϕων μετασχηματισμών οι οποίοι επιτρέπουν η διατύπωση αυτών των θεωριών σε διαϕορετικά πλαίσια αναϕοράς. Πριν ξεκινήσουμε την περιγραϕή των Β.Τ.Θ., είναι χρήσιμο να εισάγουμε την έννοια της σύμμορϕης απεικόνισης και τον τρόπο μετάβασης από το ένα πλαίσιο αναϕοράς στο άλλο Ορισμός σύμμορϕης απεικόνισης Στα μαθηματικά, σύμμορϕη απεικόνιση ορίζεται μια απεικόνιση F : M N μεταξύ δύο επιϕανειών, εάν υπάρχει μια πραγματική συνάρτηση λ > 0 τέτοια ώστε να ισχύει: F ( ν p ) = λ( p ) ν p, (1) για όλα τα εϕαπτόμενα διανύσματα ν p στην M. Η συνάρτηση λ καλείται συνάρτηση κλίμακας της F. Οι βασικές ιδιότητες της σύμμορϕης απεικόνισης είναι η διατήρηση της εσωτερικής απόστασης και των γωνιών [47]. Ο λόγος μετάβασης από το ένα πλαίσιο αναϕοράς στο άλλο γίνεται καθαρά για λόγους ευκολίας υπολογισμών αλλά απαιτεί προσοχή και διάκριση του προβλήματος που μελετάται. Στην περίπτωση των Β.Τ.Θ. εκτελείται ο σύμμορϕος μετασχηματισμός της μετρικής και του βαθμωτού πεδίου: (g µν, ϕ) ( g µν, ϕ), από το πλαίσιο αναϕοράς Einstein όπου η μετρική συμβολίζεται ως g µν, στο πλαίσιο της πλήρους μετρικής Jordan όπου η μετρική συμβολίζεται ως g µν. Η συνάρτηση που εκτελεί το σύμμορϕο μετασχηματισμό εξαρτάται από το βαθμωτό πεδίο Φ: g µν = F (Φ) g µν. Η παραπάνω διαδικασία είναι ένας καθαρά μαθηματικός μετασχηματισμός, ουσιαστικά μπορεί να θεωρηθεί ως η εξαγωγή ενός κοινού παράγοντα από τη μετρική για διευκόλυνση στις πράξεις, αλλά δεν έχει αποσαϕηνιστεί πλήρως το αν μπορεί να εϕαρμόζεται σε οποιοδήποτε πρόβλημα χωρίς να υπάρχει κάποια αλλαγή στη ϕυσική θεωρία, καθότι υπάρχουν παραδείγματα που δίνουν διαϕορετικά αποτελέσματα στα δύο διαϕορετικά πλαίσια αναϕοράς (π.α.). 17
23 Kεϕάλαιο Ορισμός των δύο πλαισίων αναϕοράς Παρόλη τη σημασία του θέματος, όπως προαναϕέραμε δεν είναι σαϕές αν υπάρχει πλήρης ισοδυναμία μεταξύ των δύο π.α. ή αν υπάρχει κάποιο ϕυσικό πλαίσιο αναϕοράς το οποίο περιγράϕει τη ϕύση, και αυτό έχει υποκινήσει διαμάχες καθώς και αντικρουόμενα αποτελέσματα στη βιβλιογραϕία. Σύμϕωνα με τους Faraoni et. al. [18] ως ϕυσικό έχει οριστεί το π.α. στο οποίο: υπάρχει απευθείας σύζευξη της ύλης με το βαθμωτό πεδίο, τα σωματίδια έχουν σταθερή μάζα, τα σωματίδια κινούνται σε γεωδαισιακές της ϕυσικής μετρικής, ο τανυστής τάσεων διατηρείται. Αντίστοιχα, στο μη ϕυσικό π.α. οι μάζες των σωματιδίων εξαρτώνται από το βαθμωτό πεδίο και δεν κινούνται σε γεωδαισιακές καμπύλες, λόγω μιας δύναμης που εμϕανίζεται και εξαρτάται από το βαθμωτό πεδίο (βλέπε Κεϕάλαιο 3). Πολλοί συγγραϕείς επιμένουν στην άποψη της απόλυτης ισοδυναμίας μεταξύ των δύο πλαισίων αναϕοράς, ενώ άλλοι παρουσιάζουν επιχειρήματα τα οποία δείχνουν ότι σε πολλά θέματα η ισοδυναμία αυτή καταρρίπτεται. Γενικά, θα μπορούσαμε να χωρίσουμε τους συγγραϕείς σε δύο κατηγορίες, σε αυτούς που θεωρούν ότι τα δύο π.α. είναι ισοδύναμα και σε αυτούς που δεν τα θεωρούν ισοδύναμα. Στην πρώτη περίπτωση, συχνά θεωρείται ότι οι σύμμορϕοι μετασχηματισμοί αποτελούν ουσιαστικά έναν μετασχηματισμό μονάδων μέτρησης, ενώ στην άλλη περίπτωση, τις περισσότερες ϕορές αναζητείται το ϕυσικό π.α. στο οποίο πρέπει να γίνουν οι υπολογισμοί. Εδώ υπάρχουν ακόμα περισσότερες προσεγγίσεις του θέματος όπως για παράδειγμα ότι η αλλαγή του π.α. οδηγεί σε τελείως διαϕορετική θεωρία (Quiros [20]). Διάϕορες μελέτες έχουν γίνει σχετικά με το αν κάποιο από τα δύο πλαίσια αναϕοράς αντιπροσωπεύει την ϕυσική πραγματικότητα. Οι περιπτώσεις που μπορεί να ισχύουν είναι οι εξής: Ο σύμμορϕος μετασχηματισμός που εκτελείται, παρόλο που, από τη μαθηματική σκοπιά δίνει δύο ισοδύναμες θεωρίες, δεν είναι ϕυσικά ισοδύναμος. Το πλαίσιο αναϕοράς Jordan δεν αντιστοιχεί σε ϕυσική θεωρία, αϕού σε αυτή την περίπτωση στα πλαίσια βαθμωτών τανυστικών θεωριών, έχουμε παραβίαση της συνθήκης χαμηλής ενέργειας και άρα το σύστημα είναι ασταθές και χάνει συνεχώς ενέργεια. Αυτό δεν είναι αποδεκτό για μια κλασσική θεωρία βαρύτητας η οποία πρέπει να έχει μια σταθερή κατάσταση ελαχίστης ενέργειας. Άρα το π.α. Einstein είναι το πλαίσιο αναϕοράς που περιγράϕει τη ϕυσική πραγματικότητα. Στο πλαίσιο αναϕοράς Einstein δεν εμϕανίζεται το παραπάνω πρόβλημα, παρόλα αυτά υπάρχει παραβίαση της αρχής της ισοδυναμίας, λόγω της σύζευξης του βαθμωτού πεδίου με την ύλη. Προϕανώς αυτή η παραβίαση, αν 18
24 Kεϕάλαιο 2 υπάρχει, βρίσκεται μέσα στα όρια του σϕάλματος των υπαρχόντων πειραμάτων που επιβεβαιώνουν την αρχή της ισοδυναμίας. Άρα, το π.α. Jordan είναι το ϕυσικό πλαίσιο αναϕοράς. Τα παραπάνω ϕαίνονται (και είναι) αρκετά θεμελιώδη ερωτήματα τα οποία χρήζουν απάντησης. Η δυσκολία του εγχειρήματος προϕανώς έγκειται στην έλλειψη των σχετικών παρατηρήσεων απαραίτητης ακρίβειας που θα μπορούσαν να ξεδιαλύνουν το τοπίο. Θεωρητικές προσπάθειες έχουν γίνει αρκετές αλλά και στη συγκεκριμένη περίπτωση το πείραμα είναι αυτό που θα ορίσει τη σωστή απάντηση και θα επαληθεύσει κάποια από τα αποτελέσματα που έχουν ήδη υπολογιστεί και στα δύο πλαίσια αναϕοράς. Στην επόμενη παράγραϕο παρουσιάζουμε επιγραμματικά κάποιες από αυτές τις προσπάθειες ξεδιάλυνσης του θέματος Επιλογή κατάλληλου πλαισίου αναϕοράς και Αρχή Σύμμορϕης Ισοδυναμίας. Υπάρχουν παραδείγματα δημοσιεύσεων που επιχειρηματολογούν υπέρ του ενός π.α. έναντι του άλλου. Για παράδειγμα, οι Faraoni και Gunzig [21] κάνοντας μια ανάλυση που βασίζεται στα βαρυτικά κύματα, δείχνουν ότι οι Β.Τ.Θ. πρέπει να μελετώνται στο π.α. Einstein και όχι στο Jordan. Στο αντίπαλο στρατόπεδο, οι συγγραϕείς επιχειρηματολογούν υπέρ της πλήρης ισοδυναμίας των δύο πλαισίων. O Flanagan [22] διαϕωνεί με την άποψη του προτιμώμενου ϕυσικού πλαισίου αναϕοράς. Για να δοθεί μια πλήρης εικόνα της σύγχυσης που επικρατεί, έχει ενδιαϕέρον να δούμε μια κατηγοριοποίηση των ερευνητών, που παραθέτουν οι Faraoni et. al. [19], με βάση την αντίληψη που έχουν για το συγκεκριμένο θέμα. Υπάρχουν λοιπόν αυτοί που: Απορρίπτουν το θέμα. Υποστηρίζουν ότι η διατύπωση μιας θεωρίας σε ένα διαϕορετικό πλαίσιο αναϕοράς είναι μια θεωρία πλήρως ισοδύναμη από ϕυσικής άποψης με την αρχική. Έχουν γνώση της μη ισοδυναμίας των δύο πλαισίων αναϕοράς και δεν επιχειρηματολογούν υπέρ της μιας ή της άλλης άποψης και συνήθως κάνουν τους υπολογισμούς και στα δύο πλαίσια αναϕοράς. Υποστηρίζουν ότι το πλαίσιο αναϕοράς Jordan είναι το ϕυσικό πλαίσιο ανα- ϕοράς, δηλαδή βλέπουν το σύμμορϕο μετασχηματισμό ως ένα καθαρά μαθηματικό εργαλείο. Υποστηρίζουν ότι το πλαίσιο αναϕοράς Einstein είναι το ϕυσικό πλαίσιο αναϕοράς. Το περίεργο στη προκειμένη περίπτωση, είναι ότι δεν είναι λίγοι οι ερευνητές που ανήκουν σε δύο από τις παραπάνω κατηγορίες! 19
25 Kεϕάλαιο 2 Άλλες δημοσιεύσεις, όπως των Capozziello et. al. [23] επιχειρηματολογούν υπέρ της μη πλήρους ϕυσικής ισοδυναμίας και επιμένουν στο ότι η ισοδυναμία ή μη εξαρτάται από τις ϕυσικές ποσότητες που μελετώνται. Στην εν λόγω δημοσίευση παρουσιάζεται ένα μοντέλο f(r) βαρύτητας και γίνεται ο υπολογισμός της παραμέτρου του Hubble, υπολογισμένης στα δύο πλαίσια αναϕοράς (βλέπε Σχήμα 6). Η διαϕορά που εμϕανίζεται προβληματίζει τους συγγραϕείς, οι οποίοι θέτουν ερωτήματα σχετικά με το ποιο από τα δύο πλαίσια αναϕοράς θα πρέπει να εμπιστευτούμε για την περιγραϕή της ϕύσης. Σχήμα 6: Η παράμετρος Hubble υπολογισμένη στα δύο σύμμορϕα πλαίσια ανα- ϕοράς. Η περίπτωση του π.α. Einstein, είναι κανονικοποιημένη στην τρέχουσα τιμή της παραμέτρου του Hubble. Capozziello et. al. [23] Οι Bhadra et. al. [24], θεωρούν ότι η λύση του προβλήματος της επιλογής του κατάλληλου πλαισίου αναϕοράς βρίσκεται στις παρατηρήσεις. Γι αυτό το λόγο επιχειρούν μια μελέτη της κάμψης του ϕωτός από το βαρυτικό πεδίο για έναν σϕαιρικά συμμετρικό χωρόχρονο στα δύο π.α. στη θεωρία Brans Dicke που ήδη αναϕέραμε και θα δούμε αναλυτικότερα παρακάτω. Στην περίπτωση του π.α. Jordan, η Γ.Θ.Σ. και η B.D. δίνουν το ίδιο αποτέλεσμα για τις γωνίες απόκλισης του ϕωτός με ακρίβεια μέχρι 100 pico arc seconds. Το γεγονός αυτό καθιστά αδύνατο τον εντοπισμό διαϕοράς σε μελλοντικές αποστολές (βλέπε Κεϕάλαιο 4). Στην περίπτωση του πλαισίου αναϕοράς Einstein υπολογίζεται ότι αν το βαθμωτό πεδίο είναι το 10% της συνολικής μάζας του Ήλιου, τότε η διαϕορά της γωνία απόκλισης είναι περίπου 7 nanosec, διαϕορά που θα είναι εϕικτό να εντοπίσει ένα πείραμα του οποίου η ακρίβεια θα είναι της τάξης των 10 nano arc seconds. Με αυτόν τον τρόπο και ϕυσικά με διάϕορες άλλες μετρήσεις και προβλέψεις αυτού του είδους θα μπορούσαμε να καταλήξουμε με απόλυτη σιγουριά στο ποια προσέγγιση τελικά είναι η σωστή. Κάτι τέτοιο όμως δεν είναι άμεσα ελέγξιμο, αλλά σε έναν ορίζοντα δεκαετίας, θα μπορούσαν να υπάρξουν οι πρώτες ενδείξεις που θα ξεδιαλύνουν τέτοιου είδους θέματα. 20
26 Kεϕάλαιο 2 Μια άλλη ενδιαϕέρουσα ιδέα προσέγγισης του προβλήματος αναϕέρουν οι Quiros et. al. [25] ορίζοντας την αρχή της σύμμορϕης ισοδυναμίας (C.E.P.) ως εξής: Οι νόμοι της βαρύτητας παραμένουν αναλλοίωτοι, ανεξαρτήτως από το σύμμορϕο πλαίσιο αναϕοράς στο οποίο τους μελετάμε. Για την ισχύ της παραπάνω αρχής όμως δεν υπάρχουν ούτε πειραματικά δεδομένα, ούτε θεωρητικές ενδείξεις ότι θα πρέπει να ισχύει. Θα μπορούσε να ισχύει ή να μην ισχύει. Η αξία της έγκειται καθαρά στο ότι ορίζει μια συγκεκριμένη αρχή στη βιβλιογραϕία και τη θέτει προς επιβεβαίωση μέσω των παρατηρήσεων. Η επιβεβαίωση αυτής της αρχής προϕανώς συνεπάγεται την πλήρη ισοδυναμία των δύο πλαισίων αναϕοράς ενώ σε διαϕορετική περίπτωση θα πρέπει να υπάρξει περαιτέρω έρευνα για το τι πραγματικά ισχύει. Σε κάθε περίπτωση μελέτης στην οποία μπορούν να χρησιμοποιηθούν σύμμορϕοι μετασχηματισμοί, η χρήση τους πρέπει να γίνεται με προσοχή. Ίσως η πιο σωστή προσέγγιση είναι ο μετασχηματισμός αυτός να θεωρείται ως ένα μαθηματικό εργαλείο απλοποίησης των εξισώσεων και τίποτα παραπάνω. Σε γενικές γραμμές, το πλαίσιο αναϕοράς της πλήρους μετρικής, ή αλλιώς του ϕυσικού πλαισίου αναϕοράς Jordan είναι ο πιο σίγουρος δρόμος, χωρίς ϕυσικά να αποκλείονται μετασχηματισμοί στο π.α. Einstein για πρακτικούς λόγους, αρκεί να υπάρχει και ο αντίστροϕος μετασχηματισμός που θα επαναϕέρει τις σχέσεις στην πλήρη μετρική. Για παράδειγμα, στην εϕαρμογή που παρουσιάζεται στο τρίτο κεϕάλαιο, οι υπολογισμοί των επικυκλικών συχνοτήτων έγιναν στο π.α. Jordan αϕού στην περίπτωση του π.α. Einstein τα σωματίδια δεν κινούνται σε γεωδαισιακές. Κάτι τέτοιο σημαίνει ότι στο π.α. Einstein δεν ισχύει η ασθενής αρχή της ισοδυναμίας. Το γεγονός αυτό θα μπορούσε να αποκλείσει οριστικά την περίπτωση το π.α. Einstein να είναι το ϕυσικό πλαίσιο αναϕοράς, αλλά υπάρχει και η περίπτωση της μη καθολικής ισχύος της αρχής της ισοδυναμίας σε κάθε πλαίσιο αναϕοράς [33]. Συνεπώς, δεν είναι απαγορευτικό να γίνει ένας τέτοιος υπολογισμός, αλλά λόγω του ότι δεν υπάρχουν πειραματικά δεδομένα να μας περιορίσουν, προσπαθούμε να κινηθούμε όσο το δυνατόν σε πλαίσια που σχετίζονται άμεσα με τη ϕυσική όπως την αντιλαμβανόμαστε σήμερα, οπότε ένας υπολογισμός τροχιών που δεν θα ήταν γεωδαισιακές πιθανόν να ξεϕεύγει όχι μόνο από τα πλαίσια της τρέχουσας εργασίας αλλά πιθανόν και από το σκοπό μιας πρώτης μελέτης επικυκλικών συχνοτήτων στα πλαίσια Β.Τ.Θ. που είναι και το κυρίως θέμα του τρίτου κεϕαλαίου. Φαίνεται λοιπόν, ότι μέχρι να υπάρξει σαϕής λύση του προβλήματος, η αλλαγή πλαισίου αναϕοράς θα πρέπει να γίνεται επιλεκτικά και μελετώντας την εκάστοτε περίπτωση, μέχρις ότου τουλάχιστον υπάρξουν ενδείξεις υπέρ κάποιας από τις περιπτώσεις που αναϕέραμε παραπάνω. 21
27 Kεϕάλαιο Η περίπτωση της Brans-Dicke Η θεωρία Jordan Brans Dicke ή πιο απλά θεωρία Brans-Dicke (B.D.) είναι το πιο απλό παράδειγμα βαθμωτής-τανυστικής θεωρίας, στα πλαίσια της οποίας η παγκόσμια βαρυτική σταθερά G δεν είναι σταθερή αλλά αντικαθίσταται από τον όρο 1/ϕ (βλέπε εξίσωση πεδίου (3)) όπου το ϕ είναι ένα βαθμωτό πεδίο που μεταβάλλεται στο χώρο και στο χρόνο. Είναι προϕανές ότι μια τέτοιου είδους θεωρία θα μπορούσε να αποτελεί γενίκευση της Γ.Θ.Σ. και τα αποτελέσματα της να αρχίσουν να γίνονται ορατά όταν οι ακρίβειες των πειραμάτων αυξηθούν μερικές τάξεις μεγέθους. Όπως προαναϕέραμε, αρχικό κίνητρο για τη δημιουργία αυτή της θεωρίας ήταν η συμβατότητα με την αρχή του Mach. Όπως και στη Γ.Θ.Σ., πηγή του βαρυτικού πεδίου είναι ο τανυστής ενέργειας ορμής ο οποίος ϕυσικά έχει διαϕορετική επίδραση στο χωρόχρονο απ ότι η κλασσική θεωρία. Η δράση για τη θεωρία B.D. περιγράϕεται από την παρακάτω σχέση: S BD = d 4 x [ g ϕr ω ] ϕ gαβ α ϕ β ϕ V (ϕ) + S (m). (2) όπου S (m) = d 4 x gl (m) είναι η δράση της ύλης. Η ύλη δεν έρχεται σε απευθείας σύζευξη με το βαθμωτό πεδίο ϕ, δηλαδή η Λανγκρατζιανή πυκνότητα L (m) είναι ανεξάρτητη από το ϕ. Έτσι, το ϕ έρχεται σε απευθείας σύζευξη μόνο με το βαθμωτό Ricci και το βαρυτικό πεδίο δεν περιγράϕεται μόνο από τη μετρική αλλά και το βαθμωτό πεδίο ϕ. Το δυναμικό V (ϕ) αποτελεί ουσιαστικά μια γενίκευση της κοσμολογικής σταθεράς. Ελαχιστοποιώντας την παραπάνω δράση, προκύπτουν οι εξισώσεις πεδίου αυτής της θεωρίας, οι οποίες είναι: G ab = 8π ϕ T ab + ω ( ϕ 2 a b ϕ 1 ) 2 g ab c ϕ c ϕ + 1 ( ) a b ϕ g ab ϕ, (3) ϕ ϕ = 8π T, (4) 3 + 2ω Η πρώτη εξίσωση ορίζει τον τρόπο με τον οποίο ο τανυστής ενέργειας ορμής μαζί με το βαθμωτό πεδίο καμπυλώνουν το χωρόχρονο, ενώ η δεύτερη το γεγονός ότι το ίχνος του τανυστή ενέργειας ορμής συμπεριϕέρεται ως πηγή του βαθμωτού πεδίου ϕ. Με ω συμβολίζεται η ελεύθερη, αδιάστατη παράμετρος της θεωρίας, η τιμή της οποίας σύμϕωνα με αποτελέσματα μελέτης της αποστολής Cassini Huygens το 2003, ϕαίνεται ότι έχει τιμή μεγαλύτερη από Στη συγκεκριμένη θεωρία, όσο μεγαλύτερη είναι η τιμή του ω, τόσο μικρότερη είναι η επίδραση του βαθμωτού πεδίου και άρα τόσο πιο κοντά βρίσκεται η θεωρία στη γενική θεωρία της σχετικότητας (εκτός από κάποιες περιπτώσεις λύσεων της B.D. στο κενό). 22
28 Kεϕάλαιο Ορισμός Βαθμωτών Τανυστικών Θεωριών Όπως δηλώνει και η ονομασία τους, οι βαθμωτές τανυστικές θεωρίες είναι θεωρίες στις οποίες η βαρυτική αλληλεπίδραση ορίζεται μέσω ενός τανυστή (της Γ.Θ.Σ.) αλλά και ενός βαθμωτού πεδίου. Αυτές οι θεωρίες περιλαμβάνουν εκτός από τη μετρική, ένα βαθμωτό πεδίο ϕ μια συνάρτηση δυναμικού που εξαρτάται από το βαθμωτό πεδίο ϕ και μια σύμμορϕη συνάρτηση μετασχηματισμού A(ϕ). Οι βαθμωτές τανυστικές (Β.Τ.Θ.) στο π.α. Jordan περιγράϕονται από την παρακάτω δράση: S ST = d 4 x { [ 1 g 16πG ϕr ω(ϕ) ϕ ] } gαβ α ϕ β ϕ V (ϕ) + α m L (m), (5) όπου το α m είναι η σταθερά σύνδεσης της μάζας. Ο σύμμορϕος παράγοντας είναι ο: Ω = Gϕ, (6) Στο π.α. Einstein η δράση γράϕεται ως: S ST = d 4 x g [ ] R 16πG 1 2 gαβ α ϕ β ϕ U( ϕ) + α m L (m), (7) όπου το βαθμωτό πεδίο ορίζεται από τη διαϕορική σχέση: d ϕ = 2ω(ϕ) πG το δυναμικό του βαθμωτού πεδίου από τη σχέση: dϕ ϕ, (8) και η σταθερά σύνδεσης: U( ϕ) = V [ϕ( ϕ)] (Gϕ) 2, (9) α m ( ϕ) = α m (Gϕ) 2. (10) 23
29 Kεϕάλαιο Εξισώσεις πεδίου και αστέρες νετρονίων Σε αυτή την παράγραϕο θα κάνουμε μια περιγραϕή των εξισώσεων πεδίου μιας γενικής βαθμωτής τανυστικής θεωρίας και θα δούμε τον τρόπο με τον οποίο καταλήγουμε στις εξισώσεις που περιγράϕουν έναν αστέρα νετρονίων, θέτοντας έτσι τη βάση για να περάσουμε στο Kεϕάλαιο 3. Μια γενική μορϕή της δράσης στις βαθμωτές τανυστικές θεωρίες, στο π.α. Jordan είναι: S = 1 d 4 x g[f (Φ) 16πG R Z(Φ) g µν µ Φ ν Φ 2U(Φ)] + S m, (11) όπου S m = S m [ψ m ; g µν ]. Για να απλοποιήσουμε τις εξισώσεις, εϕαρμόζουμε τον σύμμορϕο μετασχηματισμό: g µν = F (ϕ) g µν, και ορίζουμε το πεδίο dilaton ϕ από τη σχέση: και τις συναρτήσεις: ( ) 2 dϕ = 3 dφ 4 ( ) d ln [F (Φ)] dφ + Z(Φ) 2F (Φ), (12) A(ϕ) = F 1/2 (Φ), (13) Η δράση στο π.α. Einstein είναι: S = 1 16πG όπου τώρα S m = S m [Ψ m ; A 2 (ϕ)g µν ]. 2V (ϕ) = U(Φ)F 2 (Φ). (14) d 4 x g [R 2g µν µ ϕ ν ϕ 4V (ϕ)] + S m, (15) Ελαχιστοποιώντας τη δράση ως προς τη μετρική και το βαθμωτό πεδίο, εξάγονται οι εξισώσεις πεδίου στο πλαίσιο αναϕοράς Einstein: R µν 1 2 g µνr = 8πG T µν + 2 µ ϕ ν ϕ g µν g αβ α ϕ β ϕ 2V (ϕ)g µν, (16) όπου µ ν ϕ = 4ϕG k(ϕ)t + k(ϕ) = d ln(aϕ). dϕ dv (ϕ) dϕ, (17) Οι εξισώσεις πεδίου μπορούν να λυθούν αναλυτικά στο εξωτερικό ενός αστέρα, αν θεωρήσουμε μη περιστρεϕόμενο αστέρα νετρονίων (σϕαιρικά συμμετρικός χωρόχρονος) αλλά όχι στην περίπτωση περιστροϕής του αστέρα (αξονικά 24
30 Kεϕάλαιο 2 συμμετρικός χωρόχρονος). Σε αυτές τις περιπτώσεις οι εξισώσεις λύνονται με αριθμητικές μεθόδους [10, 9]. Ας περάσουμε όμως τώρα στο θέμα των εξισώσεων που θα περιγράϕουν την υδροστατική ισορροπία σε αστέρες νετρονίων στα πλαίσια βαθμωτών τανυστικών θεωριών. Όπως αναϕέρουν οι Pani et. al. [35] η περισσότερη δουλειά στη βιβλιογραϕία όσον αϕορά στην αστρική δομή έγινε στα πλαίσια των Β.Τ.Θ. Οι διορθώσεις που εισάγει το βαθμωτό ϕορτίο στη δομή των αστέρων νετρονίων συνήθως εκϕράζεται από έναν παράγοντα 1/ω BD όπου ω BD η ελεύθερη αδιάστατη παράμετρος της θεωρίας Brans-Dicke. Αξίζει να αναϕερθεί η ύπαρξη του ϕαινομένου της αυθόρμητης βάθμωσης σύμϕωνα με το οποίο οι Β.Τ.Θ. μπορούν να επαληθεύουν όλα τα πειράματα στο όριο του ασθενούς πεδίου αλλά την ίδια στιγμή να εισάγουν σημαντικές, παρατηρήσιμες αλλαγές στην αστρική δομή των αστέρων νετρονίων. Η μετρική που περιγράϕει ένα στατικό, σϕαιρικά συμμετρικό αστέρα νετρονίων στο π.α. Jordan είναι [34]: d s 2 = g µν dx µ dx ν = A 2 e 2Φ dt 2 + A 2 e 2Λ dr 2 + A 2 r 2 (dθ 2 + sin 2 θdϕ 2 ). Θεωρούμε επιπλέον πως ο αστέρας αποτελείται από ένα τέλειο ρευστό, δηλαδή ( T µν = ρ + P ) Ũµ Ũ ν + P g µν, (18) όπου ρ είναι η πυκνότητα ενέργειας, P η πίεση και Ũµ η τετραταχύτητα του ρευστού. Χρησιμοποιώντας τις εξισώσεις πεδίου (16), (17) και τη γενικευμένη εξίσωση διατήρησης ενέργειας ορμής: µ T µ ν = k(ϕ)t ν ϕ, (19) μπορεί κανείς να εξάγει το σύστημα εξισώσεων Tolman-Oppenheimer-Volkoff (TOV) που περιγράϕουν τη δομή ενός μη περιστρεϕόμενου αστέρα στα πλαίσια βαθμωτών τανυστικών θεωριών βαρύτητας. Για τη λύση του συστήματος απαιτείται να ορίσουμε μια καταστατική εξίσωση (EOS), δηλαδή τη σχέση που συνδέει την πυκνότητα ενέργειας ρ με την πίεση P. Συνήθως γίνεται μια επιλογή δύο ή περισσότερων καταστατικών εξισώσεων, ώστε να ξεκαθαριστεί αν η επιλογή της έχει μεγάλη επίδραση στα τελικά αποτελέσματα, οπότε να εντοπιστούν ευκολότερα οι αλλαγές που οϕείλονται στην εισαγωγή του βαθμωτού πεδίου ή της εκάστοτε γενίκευσης. 25
31 Kεϕάλαιο 3 3 Μελέτη Γεωδαισιακών καμπύλων και επικυκλικών συχνοτήτων 3.1 Ορισμός Γεωδαισιακής καμπύλης Όπως είναι γνωστό, οι καμπύλες στις οποίες κινούνται τα σωματίδια στην Γ.Θ.Σ. ονομάζονται γεωδαισιακές καμπύλες. Οι καμπύλες αυτές αποτελούν τις αντίστοιχες ευθείες της Ευκλείδειας γεωμετρίας σε καμπύλους χωρόχρονους. Υπάρχουν τριών ειδών γεωδαισιακές καμπύλες. Οι χρονοειδείς (τις ακολουθούν τα σωματίδια), οι ϕωτοειδείς (τις ακολουθούν τα ϕωτόνια) και οι χωροειδείς. Στην παρούσα εργασία θα επικεντρωθούμε στη μελέτη των χρονοειδών γεωδαισιακών καμπύλων αϕού ενδιαϕερόμαστε για σωματίδια που βρίσκονται σε τροχιά γύρω από αστέρες νετρονίων ή μελανές οπές. Η γενική αρχή που χαρακτηρίζει την κίνηση ενός σωματιδίου σε καμπυλωμένο ή επίπεδο χωρόχρονο είναι πως η κοσμική γραμμή ενός ελεύθερου σωματιδίου μεταξύ δύο σημείων μεγιστοποιεί τον ίδιο χρόνο μεταξύ τους. Αυτή η κοσμική γραμμή ονομάζεται γεωδαισιακή. Για μια γενική μετρική, εϕαρμόζοντας τη μέθοδο των μεταβολών, απαιτούμε: δ ds = 0 δ (g αβ dx α dx β ) 1/2 = 0 (20) και έτσι προκύπτει η γεωδαισιακή καμπύλη που δίνεται από τηn παρακάτω σχέση: d 2 x i ds 2 + dx m dx n Γi mn ds ds = 0 (21) Το αποτέλεσμα αυτό ισχύει για την Γ.Θ.Σ. αλλά και για την περίπτωση του πλαισίου αναϕοράς Jordan σε βαθμωτές τανυστικές θεωρίες. Κάνοντας την ίδια διαδικασία στο π.α. Einstein προκύπτει η σχέση: d 2 x i ds + dx m dx n 2 Γi mn ds ds = ) (g ij dxi dx j ds ds j ln Φ Η παραπάνω εξίσωση πλέον δεν περιγράϕει γεωδαισιακή. Ο όρος στο δεξί μέλος, που μπορεί να θεωρηθεί ως μια πέμπτη δύναμη εισέρχεται λόγω του βαθμωτού πεδίου. Περισσότερες λεπτομέρειες υπάρχουν και σε πρόσϕατη δημοσίευση των Obukhov και Puetzfeld [29]. Πρόκειται για ακόμα μια περίπτωση στην οποία η αλλαγή του πλαισίου αναϕοράς μας δίνει δυο διαϕορετικά αποτελέσματα. Δεν μπορούμε να είμαστε σίγουροι για το ποιο από τα δύο πλαίσια αναϕοράς περιγρά- ϕει τη ϕύση, στην προκειμένη περίπτωση όμως η επιλογή του π.α. Jordan είναι μονόδρομος με την έννοια ότι μόνο έτσι εξακολουθεί να ισχύει ένα από τα αξιώματα της Γ.Θ.Σ., δηλαδή τα σωματίδια συνεχίζουν να κινούνται σε γεωδαισιακές καμπύλες. Όπως θα δείξουμε αμέσως παρακάτω, η μετάβαση που κάνουμε από το ένα π.α. στο άλλο είναι καθαρά για τεχνικούς λόγους και οι τελικές ποσότητες υπολογίζονται πάντα στο π.α. Jordan που συμβατικά θεωρούμε πως πρόκειται για το ϕυσικό πλαίσιο αναϕοράς, αϕού αντιστοιχεί στην πλήρη μετρική. (22) 26
32 Kεϕάλαιο Επικυκλικές Συχνότητες Ξεκινώντας από τη Νευτώνεια θεώρηση, ορίζουμε ως Kεπλεριανή (ή τροχιακή) συχνότητα Ω p τη συχνότητα περιστροϕής (όπως τη μετρά ένας παρατηρητής στο άπειρο) ενός σωματιδίου που κινείται κυκλικά, σε οριζόντιο επίπεδο, σε ακτίνα R γύρω από ένα βαρυτικό κέντρο. Η συχνότητα αυτή δίνεται από τον τύπο: Ω 2 p = M R 3. Στη Γ.Θ.Σ., υποθέτoντας έναν σϕαιρικά συμμετρικό χωρόχρονο (μετρική Schwarzschild) η αντίστοιχη ποσότητα ορίζεται ως: Ω p = dϕ dt. Εύκολα αποδεικνύεται ότι τελικώς η Ω p δίνεται από τον ίδιο τύπο όπως και στη Νευτώνεια θεώρηση, αλλά αυτό αποτελεί σύμπτωση στις συντεταγμένες Schwarzschild. Η διαϕορά μεταξύ των δύο θεωριών δεν σταματάει εκεί. Η μετατόπιση του περιηλίου του Ερμή ήταν ένα από τα παρατηρούμενα ϕαινόμενα που η Νευτώνεια ϕυσική αδυνατούσε να εξηγήσει. Διαταράσσοντας ακτινικά την εξίσωση κίνησης του σωματιδίου που βρίσκεται σε τροχιά μπορεί να υπολογιστεί η ακτινική επικυκλική συχνότητα περιστροϕής ω r, η οποία στην περίπτωση της Γ.Θ.Σ. έχει ως αποτέλεσμα οι τροχιές των σωματιδίων να μην είναι κλειστές και να υπάρχει μια γωνιακή ταχύτητα μετάθεσης που δίνεται από τη διαϕορά Ω p -ω r. Στη Νευτώνεια θεωρία, οι δύο αυτές επικυκλικές συχνότητες ταυτίζονται με αποτέλεσμα οι τροχιές να είναι κλειστές και κατά συνέπεια να μην μπορεί να εξηγηθεί η μετατόπιση της ελλειπτικής τροχιάς ενός μόνο πλανήτη όπως στην περίπτωση του Ερμή. Εϕαρμόζοντας μια κατακόρυϕη διαταραχή στην τροχιά του σωματιδίου μπορούμε να υπολογίσουμε και την κάθετη επικυκλική συχνότητα ω θ η οποία, για τη μετρική Kerr (που περιγράϕει τον εξωτερικό χωρόχρονο περιστρεϕόμενου αστέρα) διαϕέρει από την Ω p ενώ στην περίπτωση της μετρικής Schwarzschild (εξωτερικός χωρόχρονος ακίνητου αστέρα) η κάθετη επικυκλική συχνότητα ταυτίζεται με την τροχιακή. 27
33 Kεϕάλαιο Κεπλεριανή και Επικυκλικές Συχνότητες Σε αυτή την παράγραϕο θα υπολογιστεί η Κεπλεριανή συχνότητα στα πλαίσια μιας γενικευμένης μετρικής που έχει τις συμμετρίες της μετρικής Schwarzschild, με στόχο να δημιουργηθεί το υπόβαθρο στα πλαίσια του οποίου θα στηριχθεί και ο υπολογισμός αυτής, καθώς και της επικυκλικής στα πλαίσια βαθμωτών τανυστικών θεωριών. Επιδιώκεται λοιπόν, η τελική έκϕραση να είναι συνάρτηση των συνιστωσών και των παραγώγων της μετρικής. Ο υπολογισμός βασίζεται στον ϕορμαλισμό του υποθετικού δυναμικού (βλέπε π.χ. Abramowicz και Kluzniak[3]). Θεωρούμε μια μετρική g ab χρονικά ανεξάρτητη και σϕαιρικά συμμετρική. Από τις παραπάνω υποθέσεις συνεπάγεται πως διατηρείται η ενέργεια και η ορμή, δηλαδή οι ποσότητες e = ξ u και l = η u, όπου u η τετραταχύτητα, ξ το διάνυσμα Killing (1,0,0,0) και η το διάνυσμα Killing (0,0,0,1). Βρίσκουμε: e = g tt u t + g tϕ u ϕ, (23) l = g ϕt u t + g ϕϕ u ϕ. (24) Πολλαπλασιάζοντας τη σχέση (23) με g ϕt, και τη σχέση (24) με g tt, προσθέτοντας κατά μέλη και λύνοντας ως προς u ϕ έχουμε: u ϕ = l g tt + e g ϕt g tt g ϕϕ g ϕt g tϕ. (25) Όμοια, πολλαπλασιάζοντας τις σχέσεις (23) και (24) με g ϕϕ και g tϕ αντίστοιχα, προσθέτουμε κατά μέλη και λύνοντας ως προς u t έχουμε: u t = e g ϕϕ + l g tϕ. (26) g tt g ϕϕ g ϕt g tϕ Έχοντας υπολογίσει τις παραπάνω τετραταχύτητες μπορεί ήδη να υπολογιστεί η Κεπλεριανή επικυκλική συχνότητα Ω p, η οποία θα ισούται με το λόγο των τετραταχυτήτων u ϕ και u t : όπου τ ο ίδιος χρόνος. Οπότε: Ω p = dϕ dt = dϕ/dτ dt/dτ = uϕ u t, (27) Ω p = e g ϕt + l g tt e g ϕϕ + l g tϕ. (28) Χρησιμοποιώντας την κανονικοποίηση της τετραταχύτητας: u µ u µ = g µν u µ u ν = 1, (29) καταλήγουμε στη σχέση: g tt (u t ) 2 + g rr (u r ) 2 + g θθ (u θ ) 2 + g ϕϕ (u ϕ ) 2 = 1, (30) 28
34 Kεϕάλαιο 3 όπου οι τετραταχύτητες u r και u θ μηδενίζονται, καθότι θεωρούμε κυκλικές τροχιές στο ισημερινό επίπεδο και συνεπώς οι όροι g rr (u r ) 2 και g θθ (u θ ) 2 απαλείϕονται. Ο συγκεκριμένος ϕορμαλισμός του ενεργού δυναμικού χρησιμοποιείται ευρέως και στην κλασσική μηχανική. Ορίζουμε το υποθετικό δυναμικό: V eff = 1 2 [ g tt ( u t ) 2 gϕϕ ( u ϕ ) 2 1 ]. (31) Εϕαρμόζοντας τη συνθήκη για κυκλική τροχιά: V eff r = 0, (32) και αντικαθιστώντας τις σχέσεις (25) και (26) εξάγουμε την επιθυμητή σχέση για την Kεπλεριανή συχνότητα: g tϕ,r ± g tϕ,r 2 g ϕϕ,r g tt,r Ω p =, (33) g ϕϕ,r η οποία είναι σε συμϕωνία με τις σχέσεις που εμϕανίζονται στη βιβλιογραϕία π.χ. σχέση (20) Pachon et. al. [27] ή Dedeo & Psaltis [32]. Για την ειδική περίπτωση του μη περιστρεϕόμενου αστέρα, την οποία θα μελετήσουμε παρακάτω, οι μη διαγώνιοι όροι απαλείϕονται, οπότε έχουμε: Ω 2 p = r g tt r g ϕϕ. (34) Η ακτινική και η κάθετη επικυκλική συχνότητα υπολογίζονται θεωρώντας μικρές ταλαντώσεις δr και δθ κατά τις διευθύνσεις r και θ αντίστοιχα: Ω 2 r = ( g [ ] tt + Ω K g tϕ ) 2 g,rr tt 2l K g,rr tϕ + l 2 2 g K g,rr ϕϕ, (35) rr Ω 2 θ = ( g [ ] tt + Ω K g tϕ ) 2 g,θθ tt 2l K g tϕ,θθ 2 g + l2 K g ϕϕ,θθ, (36) θθ όπου l K η λύση της εξίσωσης της Kεπλεριανής γωνιακής στροϕορμής: που είναι: g,r tt 2l g,r tϕ ϕϕ + l 2 g r = 0, (37) l K = gtϕ,r ± [( g,r tϕ ) 2 g,r ϕϕ g tt g ϕϕ,r,r] 1/2. (38) 29
35 Kεϕάλαιο Μελέτη Γεωδαισιακών καμπύλων και επικυκλικών συχνοτήτων στα πλαίσια βαθμωτών τανυστικών θεωριών Σύμμορϕες απεικονίσεις στις γεωδαισιακές Μια σύγχρονη διατύπωση της ασθενούς αρχής της ισοδυναμίας (W.E.P.) η οποία συχνά αναϕέρεται και ως αρχή ισοδυναμίας του Einstein (E.E.P.) ορίζει ότι: Το αποτέλεσμα οποιουδήποτε πειράματος στο οποίο δεν συμμετέχει η βαρύτητα είναι ανεξάρτητο από την ταχύτητα ελεύθερης πτώσης. Το αποτέλεσμα οποιουδήποτε μη τοπικού πειράματος στο οποίο δεν συμμετέχει η βαρύτητα είναι ανεξάρτητο από το που και το πότε πραγματοποιήθηκε στο σύμπαν. Από την παραπάνω αρχή εξάγεται ότι η βαρυτική αλληλεπίδραση περιγράϕεται μέσω μετρικών θεωριών βαρύτητας καμπυλωμένου χωρόχρονου. Αποδεικνύεται πως οι μετρικές θεωρίες βαρύτητας (όπως η Γ.Θ.Σ. και οι Β.Τ.Θ.) πρέπει να πληρούν τις παρακάτω προϋποθέσεις: Ο χωρόχρονος τους πρέπει να είναι εϕοδιασμένος με μια μετρική. Οι κοσμικές γραμμές των σωματιδίων είναι γεωδαισιακές της μετρικής. Τοπικά και σε συστήματα αναϕοράς σε ελεύθερη πτώση, οι νόμοι της Φυσικής (εκτός από τη βαρύτητα) περιγράϕονται από την ειδική θεωρία της σχετικότητας. Φυσικά, κανένας δεν μας εμποδίζει να ϕτιάξουμε ή να δεχτούμε μια εναλλακτική θεωρία βαρύτητας που να καταρρίπτει την αρχή της ισοδυναμίας, στα πλαίσια που μας επιτρέπουν οι παρατηρήσεις ϕυσικά. Σε αυτή τη ϕάση όμως, όπως προαναϕέραμε, από τη στιγμή που η αρχή της ισοδυναμίας ικανοποιείται με μεγάλη ακρίβεια, είναι λογικό να αποϕεύγουμε θεωρίες και υποθέσεις που καταρρίπτουν κάτι τόσο θεμελιώδες για τη σύγχρονη θεωρία βαρύτητας. Αυτό βέβαια δεν σημαίνει ότι δεν μπορεί να αλλάξει στο μέλλον. Εύκολα μπορεί να αποδειχθεί ότι οι ϕωτοειδείς γεωδαισιακές δεν επηρεάζονται από την αλλαγή του πλαισίου αναϕοράς. Αυτό είναι συμβατό με το γεγονός ότι οι εξισώσεις των ϕωτοειδών γεωδαισιακών μπορούν να εξαχθούν από τις εξισώσεις του Maxwell (σημ. οι εξισώσεις του Maxwell είναι σύμμορϕα αναλλοίωτες σε τετραδιάστατη πολλαπλότητα). Κάτι τέτοιο δεν ισχύει για την περίπτωση των χρονοειδών γεωδαισιακών, οι οποίες δεν είναι αναλλοίωτες στον σύμμορϕο μετασχηματισμό. Πιο συγκεκριμένα, η γενική εξίσωση των γεωδαισιακών, στην περίπτωση του πλαισίου αναϕοράς Einstein έχει τη μορϕή: d 2 x α dτ 2 + Γ α βγ dxβ dτ dx γ 4πG = α ϕ. dτ 2ω+3 4πG Όπως προαναϕέραμε, ο όρος α ϕ, 2ω+3 στα δεξιά της εξίσωσης, συχνά αναϕέρεται ως πέμπτη δύναμη. Λόγω αυτής της δύναμης υπάρχει παραβίαση της 30
36 Kεϕάλαιο 3 WEP. Αυτό πρακτικά σημαίνει ότι οι Β.Τ.Θ. στο π.α. Einstein δεν είναι μετρικές θεωρίες και τα σωματίδια δεν ακολουθούν γεωδαισιακές καμπύλες. Ως εκ τούτου ϕαίνεται λογική η εκλογή του πλαισίου αναϕοράς Jordan για τη μελέτη των γεωδαισιακών καμπυλών (όπως εξάλλου γίνεται στη βιβλιογραϕία), γεγονός που μας εξασϕαλίζει ότι δεν υπάρχει κατάρριψη μιας πολύ σημαντικής παραδοχής της θεωρίας όπως την αντιλαμβανόμαστε σήμερα, ότι δηλαδή τα υλικά σώματα κινούνται σε γεωδαισιακές καμπύλες Τροχιακή και επικυκλική συχνότητα σωματιδίων γύρω από ακίνητο αστέρα νετρονίων Σε αυτή την παράγραϕο θα υπολογίσουμε την Κεπλεριανή συχνότητα σωματιδίων που περιϕέρονται γύρω από αστέρα νετρονίων στα πλαίσια μιας συγκεκριμένης μη γραμμικής βαθμωτής τανυστικής θεωρίας και θα τη συγκρίνουμε με την αντίστοιχη σχέση της Γ.Θ.Σ. Κατόπιν, θα συνεχίσουμε υπολογίζοντας την ακτινική επικυκλική συχνότητα. Υπενθυμίζουμε πως στην περίπτωση του ακίνητου αστέρα νετρονίων η κάθετη επικυκλική συχνότητα ταυτίζεται με την Κεπλεριανή. Όπως αναϕέραμε και στο προηγούμενο κεϕάλαιο, μια γενική μορϕή της δράσης στο ϕυσικό π.α. Jordan περιγράϕεται από την σχέση (39): S = 1 d 4 x g[f (Φ) 16πG R Z(Φ) g µν µ Φ ν Φ 2U(Φ)] + S m, (39) όπου S m = S m [ψ m ; g µν ]. Σε αυτό το σημείο αξίζει να σημειωθεί ότι στη δράση της μάζας S m δεν εισέρχεται ρητά το βαθμωτό ϕορτίο Φ, πράγμα που σημαίνει πως οι εξισώσεις κίνησης δε μεταβάλλονται, αλλά έχουν ίδια μορϕή με αυτές στη Γ.Θ.Σ. Για στατικό, σϕαιρικά συμμετρικό χωρόχρονο στο εξωτερικό ενός αστέρα νετρονίων υπάρχει αναλυτική λύση των εξισώσεων πεδίου και δίνεται από τη μετρική του Just [6] στο πλαίσιο αναϕοράς Einstein: ds 2 = e v c 2 dt 2 + e v [dr 2 + (r 2 ar)(dθ 2 + sin 2 θdϕ 2 )], (40) e v(r) = (1 a/r) b/a, (41) ϕ(r) = ϕ 0 + d ( a ln 1 α ), r (42) όπου: b = 2 G c m A, (43) 2 a b = 1 + a 2 A, (44) d b = 1 2 a A, (45) και m A είναι η συνολική μάζα του αστέρα, ενώ a A είναι η σταθερά σύζευξης. To βαθμωτό ϕορτίο ορίζεται στη συγκεκριμένη περίπτωση από τη σχέση (46): 31
37 Kεϕάλαιο 3 a A = ω A m A. (46) Όπως είναι προϕανές από αυτή τη σχέση, απαιτούνται δύο παράμετροι για τον προσδιορισμό του βαθμωτού ϕορτίου. Τα ω A και m A προσδιορίζονται λύνοντας αριθμητικά τις εξισώσεις πεδίου στο εσωτερικό του αστέρα, για μια συγκεκριμένη καταστατική εξίσωση. Στους Πίνακες 3, 4 και 5 παρουσιάζονται διάϕορα μοντέλα αστέρων νετρονίων για την καταστατική εξίσωση APR, και για β = 4.5, 4.8 και 6. Σύμϕωνα με τις τελευταίες παρατηρήσεις [1] η μόνη έγκυρη τιμή πλέον είναι το -4.5, ωστόσο οι άλλες τιμές διατηρούνται εδώ, για εποπτικούς λόγους, αϕού η διαϕορά που προκύπτει μεταξύ Β.Τ.Θ. και γενικής σχετικότητας είναι πιο έντονη και άρα ευκολότερα ορατή. Πίνακας 3: EOS APR, β = 4.5 m A (M ) ω A Πίνακας 4: EOS APR, β = 4.8 m A (M ) ω A Πίνακας 5: EOS APR, β = 6 m A (M ) ω A
38 Kεϕάλαιο 3 Καθότι, για λόγους ευκολίας, η μετρική μας βρίσκεται στο πλαίσιο αναϕοράς Einstein, εκτελούμε το σύμμορϕο μετασχηματισμό ώστε να μεταβούμε στο ϕυσικό πλαίσιο αναϕοράς Jordan g µν : g µν = A 2 (ϕ)g µν, (47) όπου A(ϕ) = e 1 2 βϕ2. (48) Τότε, οι κύριες συνιστώσες της μετρικής θα είναι: g tt = e βd2 ln(1 a/r) 2 a 2 (1 a/r) b/a, g rr = e βd2 ln(1 a/r) 2 a 2 (1 a/r) b/a, g ϕϕ = e βd2 ln(1 a/r) 2 a 2 (1 a/r) b/a r(r a). Η συνιστώσα g θθ δεν χρησιμοποιείται αϕού δεν εισέρχεται στις σχέσεις που δίνουν τις επικυκλικές συχνότητες, λόγω του μηδενισμού της τετραταχύτητας u θ. Επιπλέον, στη συνιστώσα g ϕϕ έχουμε θέσει θ = π/2, αϕού υπολογίζουμε τροχιές στο ισημερινό επίπεδο. Η επιλογή της συγκεκριμένης A(ϕ) είναι μια συνηθισμένη περίπτωση [7, 28, 32]. To πεδίο dilaton ϕ ορίζεται μέσω της σχέσης: ( ) 2 dϕ = 3 dφ 4 ( ) d ln [F (Φ)] dφ + Z(Φ) 2F (Φ), (49) Συνεπώς, αϕού εϕαρμόσουμε το σύμμορϕο μετασχηματισμό και αντικαταστήσουμε αυτή τη μετρική στη γενική σχέση (24) που υπολογίσαμε προηγουμένως, έχουμε την Κεπλεριανή συχνότητα υπολογισμένη στα πλαίσια της συγκεκριμένης βαθμωτής τανυστικής θεωρίας: Ω 2 p = (1 a/r) 2b/a (ab + 2βd 2 ln[1 a/r]) (a r)r(a(a + b 2r) 2βd 2 ln[1 a/r]), (50) και το όριο της Γ.Θ.Σ. δίνεται όταν το βαθμωτό ϕορτίο είναι α A = 0, από όπου συνεπάγεται α = b και d = 0 και είναι η γνωστή μας σχέση: Ω 2 p = M R 3. (51) Στο Σχήμα 7 παρουσιάζεται η γραϕική παράσταση της τροχιακής συχνότητας ως συνάρτηση της απόστασης r από το κέντρο του αστέρα, για την περίπτωση της Γ.Θ.Σ. (συμπαγής γραμμή) και για την περίπτωση της βαθμωτής τανυστικής θεωρίας (διακεκομμένη γραμμή), για β = 6, ώστε να είναι εύκολα ορατή η διαϕορά μεταξύ των δύο περιπτώσεων. 33
39 Kεϕάλαιο v p khz Β 0 Β r km Σχήμα 7: Γραϕική παράσταση της τροχιακής συχνότητας ως συνάρτηση της απόσταση r από το κέντρο του αστέρα νετρονίων, στην περίπτωση της Γ.Θ.Σ. (συμπαγής γραμμή) και στην περίπτωση της βαθμωτής τανυστικής θεωρίας (διακεκομμένη γραμμή) για β = 6. ( ωr 2 = 1 α r Ομοίως υπολογίζεται και η ακτινική επικυκλική συχνότητα: ) 2b/a {a 2 (a + 2b)[b(a + b) 2βd 2 ] 2a 2 [b(a + 3b) 2βd 2 ]r + 2a 2 br 2 2a(r a) 2 r [ 2 a(a + b 2r) 2βd 2 ln ( )] 1 a r 2βd 2 ln ( ) ( 1 a a[a 2 2a(r b) + 2r(r 2b)] 2βd 2 (a + 2b 2r) ln ( ) ) 1 a r r + 2a(r a) 2 r [ 2 a(a + b 2r) 2βd 2 ln ( )] 1 a r και το όριο της Γ.Θ.Σ., όταν το βαθμωτό ϕορτίο είναι α A = 0, από όπου συνεπάγεται α = b και d = 0 : (52), ω 2 r = M(r 6M) R 4. (53) Στο Σχήμα 8 παρουσιάζεται η γραϕική παράσταση της ακτινικής επικυκλικής συχνότητας ως συνάρτηση της απόστασης r από το κέντρο του αστέρα, για την περίπτωση της Γ.Θ.Σ. (συμπαγής γραμμή) και για την περίπτωση της βαθμωτής τανυστικής θεωρίας (διακεκομμένη γραμμή) για β = 6, ώστε να είναι εύκολα ορατή η διαϕορά μεταξύ των δύο περιπτώσεων. Η εσώτατη σταθερή κυκλική τροχιά βρίσκεται στην απόσταση όπου μηδενίζεται η ακτινική επικυκλική συχνότητα και στην περίπτωση της Γ.Θ.Σ. υπολογίζεται στην απόσταση 6M. Παρατηρούμε πως στην περίπτωση της Β.Τ.Θ. υπάρχει μετατόπιση αυτής της τροχιάς προς τα έξω. 34
40 Kεϕάλαιο v r khz Β 0 Β r km Σχήμα 8: Η γραϕική παράσταση της ακτινικής επικυκλικής συχνότητας ως συνάρτηση της απόστασης r από το κέντρο του αστέρα, στην περίπτωση της Γ.Θ.Σ. (συμπαγής γραμμή) και στην περίπτωση της βαθμωτής τανυστικής θεωρίας (διακεκομμένη γραμμή) για β = Επαλήθευση αριθμητικών αποτελεσμάτων Για να γίνει η επαλήθευση των αριθμητικών αποτελεσμάτων που δημοσιεύτηκαν πρόσϕατα (Doneva et. al [8] ) χρησιμοποιήθηκαν διάϕορα μοντέλα μη περιστρεϕόμενων αστέρων νετρονίων, για τα οποία υπολογίστηκαν αναλυτικά η τροχιακή και η επικυκλική συχνότητα. Λόγω του ότι η τιμή της τροχιακής συχνότητας στην εσώτατη σταθερή κυκλική τροχιά (ISCO) θα πρέπει να είναι ανεξάρτητη των συντεταγμένων, επιλέχθηκε το συγκεκριμένο σημείο ως σημείο ελέγχου μεταξύ των αποτελεσμάτων που έδωσε ο διευρυμένος κώδικας RNS [9] και οι αναλυτικές σχέσεις που αναϕέραμε παραπάνω. Όπως ϕαίνεται στους Πίνακες 6, 7 και 8 η σχετική διαϕορά των τιμών είναι της τάξης του Πίνακας 6: Τροχιακή συχνότητα στην εσώτατη σταθερή κυκλική τροχιά (β = 4.5). m A (M ) ω A Ω p ISCO (αναλυτικά) Ω p ISCO (αριθμητικά)
41 Kεϕάλαιο 3 Πίνακας 7: Τροχιακή συχνότητα στην εσώτατη σταθερή κυκλική τροχιά (β = 4.8). m A (M ) ω A Ω p ISCO (αναλυτικά) Ω p ISCO (αριθμητικά) Πίνακας 8: Τροχιακή συχνότητα στην εσώτατη σταθερή κυκλική τροχιά (β = 6). m A (M ) ω A Ω p ISCO (αναλυτικά) Ω p ISCO (αριθμητικά) Στο Σχήμα 9, για εποπτικούς λόγους, παρουσιάζονται η τροχιακή και η ακτινική επικυκλική συχνότητα μαζί. Το σημείο στο οποίο μηδενίζεται η ακτινική επικυκλική συχνότητα αντιστοιχεί στην εσώτατη κυκλική τροχιά η οποία για τη γενική σχετικότητα είναι ίση με 6M. Για το συγκεκριμένο παράδειγμα που η μάζα είναι ίση με 1.36 ηλιακές μάζες, το 6 είναι ίσο με km, όπου ϕαίνεται ότι μηδενίζεται η ακτινική επικυκλική συχνότητα. Παρατηρούμε πως στην περίπτωση της βαθμωτής τανυστικής θεωρίας η εσώτατη κυκλική σταθερή τροχιά μετατοπίζεται προς τα έξω κατά τουλάχιστον ένα χιλιόμετρο. H Ω p ISCO που αναϕέραμε προηγουμένως και παρουσιάζουμε στους παραπάνω πίνακες υπολογίζεται ουσιαστικά αν ϕέρουμε κάθετη στο σημείο της εσώτατης κυκλικής τροχιάς και από το σημείο που τέμνει η κάθετος την τροχιακή συχνότητα ϕέρουμε την κάθετη στον άξονα y ώστε να βρούμε ποια τροχιακή συχνότητα αντιστοιχεί στο συγκεκριμένο σημείο, η τιμή της οποίας, όπως είπαμε, είναι ανεξάρτητη από τις συντεταγμένες, γι αυτό και τη χρησιμοποιούμε για τη σύγκριση με τα αριθμητικά μοντέλα που δεν χρησιμοποιούν συντεταγμένες Schwarzschild, αλλά ισοτροπικές συντεταγμένες. Αξίζει να σημειωθεί πως μέσω μετασχηματισμού των συντεταγμένων Schwarzschild σε ισοτροπικές, έγινε επιπλέον, επιβεβαίωση σε κάθε απόσταση r και όχι μόνο στην ISCO. 36
42 Kεϕάλαιο v p, v r khz Β 0 Β r km Σχήμα 9: Η τροχιακή και η ακτινική επικυκλική συχνότητα ως συνάρτηση της απόστασης r από το κέντρο του αστέρα, στην περίπτωση της Γ.Θ.Σ. (συμπαγής γραμμή) και στην περίπτωση της βαθμωτής τανυστικής θεωρίας (διακεκομμένη γραμμή) για β = 6. Τέλος, στην περίπτωση των περιστρεϕόμενων αστέρων νετρονίων, όπου οι συχνότητες μπορούν να προσδιοριστούν μόνο αριθμητικά, τα ϕαινόμενα αυτά είναι πιο έντονα. Στο Σχήμα 10 παρουσιάζονται οι περιπτώσεις ενός μη περιστρε- ϕόμενου και ενός περιστρεϕόμενου αστέρα νετρονίων για β = 0, β = 4.5 και β = 4.8. Επίσης, στο σχήμα είναι ορατό ένα σύνορο, πάνω από το οποίο η ακτινική επικυκλική συχνότητα μηδενίζεται έξω από τον αστέρα (άρα υπάρχει περιοχή με ασταθείς κυκλικές τροχιές) και κάτω από το οποίο, δεν υπάρχει μηδενισμός της συγκεκριμένης επικυκλικής συχνότητας και άρα δεν υπάρχουν ασταθείς κυκλικές τροχιές, οπότε οι ευσταθείς κυκλικές τροχιές ϕτάνουν μέχρι την επιϕάνεια του αστέρα. 37
43 Kεϕάλαιο 3 Σχήμα 10: Σχέση μάζας ακτίνας για τις περιπτώσεις περιστρεϕόμενου (συμπαγής γραμμή) και μη περιστρεϕόμενου (διακεκομμένη γραμμή) αστέρα νετρονίων για β = 0 (Γ.Θ.Σ.), β = 4.5 (τιμή οριακά αποδεκτή από τα παρατηρησιακά δεδομένα), β = 4.8 (μη αποδεκτή τιμή, για εποπτικούς λόγους). Πηγή: Doneva et. al. [8]. 38
44 Kεϕάλαιο 4 4 Τι μας επιϕυλλάσει το μέλλον; Όπως εύκολα συμπεραίνει κανείς, διαβάζοντας τα προηγούμενα κεϕάλαια της εργασίας, οι θεωρίες βαρύτητας είναι πολλές και διαϕορετικών ειδών. Προς το παρόν, η Γ.Θ.Σ. είναι ο απόλυτος κυρίαρχος και το γεγονός αυτό ϕυσικά το καθορίζουν οι παρατηρήσεις. Μέσα στα επόμενα δέκα με δεκαπέντε χρόνια υπολογίζεται να έχουμε τα πρώτα στοιχεία που θα μπορούσαν να καθαιρέσουν τη Γ.Θ.Σ. και να ξεκαθαρίσουν ως ένα βαθμό σε ποιες από τις εναλλακτικές θεωρίες αξίζει να συνεχιστεί η μελέτη και σε ποιες όχι. Παρατηρήσεις στα ραδιοκύματα διπλών συστημάτων αστέρων νετρονίων ήδη περιορίζουν τις παραμέτρους απόκλισης από την Γ.Θ.Σ. αλλά υπάρχει δρόμος ακόμα να διανυθεί. Αποστολές όπως η IXO (International X-ray Observatory) [39] επίσης θα συμβάλουν σ αυτό το σκοπό, παρέχοντας ϕάσματα μεγαλύτερης ακρίβειας από μελανές οπές και αστέρες νετρονίων. Ας μη ξεχνάμε ότι η καλύτερη κατανόηση των αστροϕυσικών ιδιοτήτων ειδικά των μελανών οπών και των αστέρων νετρονίων, σχετίζονται άμεσα και με συμπεράσματα σχετικά με τη ϕύση της βαρύτητας, αϕού πάντα στη μελέτη των εναλλακτικών θεωριών έχουν προηγηθεί υποθέσεις αστροϕυσικού ενδιαϕέροντος, όπως π.χ. η καταστατική εξίσωση ενός αστέρα νετρονίων, αλλαγές στις οποίες θα μπορούσαν να δώσουν τελείως διαϕορετικά αποτελέσματα. Σωστές κατευθύνσεις προς την εύρεση της γενικότερης θεωρίας βαρύτητας ιδανικά θα μπορούσαν να δώσουν διαστημικές αποστολές που θα χρησιμοποιούν συμβολομετρία Laser, όπως η elisa (Evolved Laser Interferometer Space Antenna) [48]. Η βασική ιδέα αυτών των πειραμάτων είναι η εγκατάσταση ενός συμβολόμετρου τεραστίων διαστάσεων στο διάστημα το οποίο θα μπορούσε να εντοπίσει βαρυτικά κύματα και να επαληθεύσει ή να διαψεύσει τη Γ.Θ.Σ. Ενώ η αποστολή elisa κατευθύνεται κυρίως προς την ανίχνευση βαρυτικών κυμάτων, άλλες αποστολές έχουν ως στόχο τον έλεγχο της αρχής της ισοδυναμίας, η ισχύ της οποίας σχετίζεται άμεσα με την επαλήθευση της Γ.Θ.Σ. αϕού αποτελεί μια από τις βασικότερες αρχές της. Τέτοιες αποστολές είναι η γαλλική MICROSCOPE (σε συνεργασία με την ESA) η STE QUEST [49] και άλλες. Επιπλέον γίνονται μελέτες για τη δυνατότητα επιβεβαίωσης της Γ.Θ.Σ. από λιγότερο εξειδικευμένες αποστολές, όπως η GAIA, η οποία είναι αποστολή της ESA για τη λεπτομερή χαρτογράϕηση του γαλαξία μας. Ας επιδιώξουμε τώρα, μια σύντομη περιγραϕή της διάταξης μιας αποστολής διαστημικής συμβολομετρίας, όπως είναι η elisa, μιας και πρόκειται για ένα από τα σημαντικότερα πειράματα στο χώρο της έρευνας για τη βαρύτητα, που θα λάβει χώρα τις επόμενες δύο δεκαετίες. Η διάταξη της elisa αποτελείται από ένα μητρικό και δύο θυγατρικά σκάϕη (σε διάταξη τριγώνου, όπως ϕαίνεται στο Σχήμα 11) σε τροχιά, έτσι ώστε να επικοινωνούν με λέιζερ κατάλληλης ισχύος. Η απόσταση μεταξύ των σκαϕών σχεδιάζεται να είναι ένα εκατομμύριο χιλιόμετρα. Σκοπός του πειράματος είναι να μετρηθούν διαϕορές στην απόσταση μεταξύ σωμάτων που θα βρίσκονται εντός του σκάϕους με χρήση συμβολομετρικών μεθόδων. Μια τέτοια διάταξη θα μπορούσε να μετρήσει τη στρέβλωση και τη καμπύλωση του χωροχρόνου με μεγάλη ακρίβεια και κατά συνέπεια να αποδείξει την ύπαρξη των βαρυτικών κυμάτων, μιας πρόβλεψης της Γ.Θ.Σ. για την οποία δεν υπάρχει ακόμη άμεση ανίχνευση ή να εντοπίσει ενδείξεις για πιθανή απόκλιση από τις προβλέψεις, ανοίγοντας έτσι το δρόμο για την ανάπτυξη εναλλακτικών 39
45 Kεϕάλαιο 4 θεωριών. Επειδή οι αποστάσεις μεταξύ των σκαϕών είναι τεράστιες, θα υπάρξουν δοκιμαστικές αποστολές, οι οποίες θα δοκιμάσουν τεχνολογίες που είναι απαραίτητες για την ολοκλήρωση μιας πραγματικά γιγαντιαίας διάταξης. Με την elisa θα ανοίξει ένα νέο κεϕάλαιο στις παρατηρήσεις του σύμπαντος και τα δεδομένα που θα εξαχθούν από τα βαρυτικά κύματα σίγουρα θα μας ϕέρουν ένα βήμα πιο κοντά στη γενίκευση της Γ.Θ.Σ. εϕόσον αυτή χρειάζεται. Ήδη γίνονται μελέτες που προβλέπουν την ύπαρξη βαρυτικών κυμάτων στα πλαίσια εναλλακτικών θεωριών βαρύτητας και ϕυσικά οι μετρήσιμες διαϕορές αυτών των κυμάτων σε σύγκριση με αυτά που προβλέπει η Γ.Θ.Σ. θα χρησιμοποιηθούν στην εξακρίβωση του ποια τελικώς είναι η σωστή θεωρία βαρύτητας. Σχήμα 11: Μια ψηϕιακή απεικόνιση της αποστολής elisa της ESA σε τροχιά. Πηγή: Στο άμεσο μέλλον και συγκεκριμένα τον Ιούλιο του 2015 είναι προγραμματισμένο να απογειωθεί η αποστολή LPF (Lisa Pathfinder) η οποία είναι μια από τις δοκιμαστικές αποστολές που θα δοκιμάσει για πρώτη ϕορά τεχνολογίες που θα χρησιμοποιηθούν στην αποστολή elisa. Πρόκειται για μια μικρότερη έκδοση της μιας ακμής του τριγώνου που θα σχηματίζει η elisa, και θα είναι ικανή να μετρήσει (με ακρίβεια πικόμετρου) χρησιμοποιώντας συμβολομετρικές μεθόδους τη σχετική θέση δύο μαζών σε ελεύθερη πτώση. Ήδη υπάρχουν μελέτες [40, 41] που προτείνουν τρόπους αξιοποίησης των δεδομένων του LPF, προκειμένου να ελεγχθεί με ακόμα μεγαλύτερη ακρίβεια, η ισχύς της γενικής θεωρίας της σχετικότητας και ϕυσικά εναλλακτικών θεωριών βαρύτητας στο όριο του ασθενούς 40
46 Kεϕάλαιο 4 πεδίου. Όπως γίνεται προϕανές, είναι απαραίτητο να γίνονται πειράματα ελέγχου της βαρύτητας, όχι μόνο στο ισχυρό αλλά και στο ασθενές πεδίο βαρύτητας, όπως γίνονται σχετικές παρατηρήσεις και μελέτες σε όλες τις κλίμακες, από τροχιές γύρω από αστέρες νετρονίων μέχρι γαλαξιακές δομές σε κοσμολογικές κλίμακες. Η θεωρία που θα αντικαταστήσει τη Γ.Θ.Σ. πρέπει στο όριο του ασθενούς πεδίου να ταυτίζεται με την τρέχουσα θεωρία και στο άνω όριο να κάνει άλλες προβλέψεις, οι οποίες θα επαληθευθούν σε όλες τις τάξεις μεγέθους και σε όλα τα είδη των ϕαινομένων. Θα πρέπει να προβλέπει με ακρίβεια το βαρυτικό πεδίο του Ήλιου (ασθενές βαρυτικό πεδίο), αλλά και τις παραμέτρους που καθορίζουν την περιστροϕή διπλών αστέρων νετρονίων (ισχυρό βαρυτικό πεδίο). Τέλος, για να κάνουμε και μια σύνδεση με τους υπολογισμούς που παρουσιάσαμε στο προηγούμενο κεϕάλαιο, ϕαινόμενα όπως οι ημιπεριοδικές ταλαντώσεις (khz QPOs) στο ϕάσμα των ακτίνων Χ (στη μελέτη των οποίων έγκειται και ο προσδιορισμός των επικυκλικών συχνοτήτων), όταν μοντελοποιηθούν πλήρως θα μπορούσαν επίσης να χρησιμοποιηθούν ως έλεγχος για τη βαρύτητα. 41
47 Kεϕάλαιο Συμπεράσματα Συνοψίζοντας, η παρούσα εργασία αποτελεί μια εισαγωγή στις εναλλακτικές θεωρίες βαρύτητας και πιο συγκεκριμένα στις βαθμωτές-τανυστικές θεωρίες, οι οποίες είναι και οι πιο συνηθισμένες. Εκτός από τις γενικές περιγραϕές των συνθηκών που μας οδήγησαν στην αναζήτηση εναλλακτικών θεωριών βαρύτητας, τη σύνδεση με τις παρατηρήσεις κλπ., στο τρίτο κεϕάλαιο παρουσιάστηκαν υπολογισμοί που αϕορούν τον υπολογισμό επικυκλικών συχνοτήτων σε δίσκους προσαύξησης γύρω από αστέρες νετρονίων, μέρος του οποίου συμπεριλήϕθηκε ως παράρτημα σε σχετική δημοσίευση (Doneva et. al. [8]). Η αξία αυτής της ανάλυσης έγκειται στην προσπάθεια εξήγησης των λεγομένων ημιπεριοδικών ταλαντώσεων (QPOs) [4, 30]. Οι ημιπεριοδικές ταλαντώσεις ανακαλύϕθηκαν το 1996 και πρόκειται για δύο μέγιστα (δίδυμες κορυϕές) στο ϕάσμα των ακτίνων Χ που προέρχονται από δίσκους προσαύξησης γύρω από αστέρες νετρονίων. Όπως είναι γνωστό, γύρω από τους αστέρες νετρονίων δημιουργούνται οι λεγόμενοι δίσκοι προσαύξησης οι οποίοι λόγω της τριβής μεταξύ των σωματιδίων εκπέμπουν ακτινοβολία στις ακτίνες Χ. Το γεγονός ότι σε κάποιες συγκεκριμένες συχνότητες εμϕανίζονται μέγιστα μπορεί ϕυσικά να συνδεθεί άμεσα με συχνότητες σταθερών τροχιών, όπως για παράδειγμα της εσώτατης κυκλικής τροχιάς ή και των επικυκλικών συχνοτήτων. Στο Σχήμα 12 παρουσιάζεται το πρώτο ϕάσμα ακτίνων Χ από την πηγή SCO X-1, στο οποίο παρατηρήθηκε αυτό το ϕαινόμενο. Τα khz QPOs μελλοντικά ίσως μπορούν να χρησιμοποιηθούν για τον έλεγχο της Γ.Θ.Σ. και αργότερα των εναλλακτικών θεωριών βαρύτητας στο όριο του ισχυρού πεδίου. Προς το παρόν όμως, παρόλη την ύπαρξη κάποιων μοντέλων, δεν είναι πλήρως κατανοητό το πως δημιουργούνται. Φτάνοντας στο τέλος, είμαστε ακόμα στην αρχή, αϕού η πλειοψηϕία των θεμάτων που αναϕέρονται στην παρούσα εργασία είναι ανοικτά προς αμϕισβήτηση ή επιβεβαίωση. Τις επόμενες δεκαετίες, παράλληλα με την εξέλιξη της τεχνολογίας και του εξοπλισμού των παρατηρήσεων, σίγουρα θα υπάρξουν ενδείξεις για το δρόμο στον οποίο πρέπει να κινηθεί η έρευνα για την πλήρη κατανόηση της βαρύτητας και κατά συνέπεια των μακροσκοπικών δομών αλλά και του ιδίου του σύμπαντος, πάντα σε συνδυασμό με τα δεδομένα των θεωριών του μικρόκοσμου, ώστε τελικώς να ϕτάσουμε ένα βήμα πιο κοντά στη πλήρη κατανόηση του σύμπαντος και των ϕαινομένων που το διέπουν. 42
48 Kεϕάλαιο 4 Σχήμα 12: Το ϕάσμα της πηγής SCO X-1, στο οποίο για πρώτη ϕορά παρατηρήθηκαν khz QPOs. Είναι ορατά τα δύο μέγιστα, τα οποία συνήθως έχουν λόγο 3:2. Πηγή: NASA. 43
49 Αʹ Παράρτημα: Υπολογισμοί και Γραϕήματα Σε αυτό το παράρτημα παρουσιάζουμε αναλυτικά τους υπολογισμούς των επικυκλικών συχνοτήτων (τροχιακής και ακτινικής επικυκλικής συχνότητας) για μη περιστρεϕόμενο αστέρα νετρονίων, που έγιναν με τη χρήση της γλώσσας Wolfram Mathematica. Εξ ορισμού: ev [ r_ ] = (1 a/r ) ^ ( b/a ) f [ r_ ] = ( d/a ) * Log[1 a/r ] A2[ r_ ] = Exp[ beta * f [ r ]^2] Συνιστώσες μετρικής στο πλαίσιο αναϕοράς Jordan: g t t [ r_ ] = FullSimplify [ (A2[ r ] * ev [ r ] ) ] g t t r [ r_ ] = FullSimplify [D[ gtt [ r ], { r } ] ] gttr2 [ r_ ] = FullSimplify [D[ gtt [ r ], { r, 2 } ] ] gtt2 [ r_ ] = 1/gtt [ r ] gtt2r [ r_ ] = FullSimplify [D[ gtt2 [ r ], { r } ] ] gtt2rr [ r_ ] = FullSimplify [D[ gtt2 [ r ], { r, 2 } ] ] grr [ r_ ] = FullSimplify [A2[ r ]/ ev [ r ] ] grrr [ r_ ] = FullSimplify [D[ grr [ r ], { r } ] ] grrr2 [ r_ ] = FullSimplify [D[ grr [ r ], { r, 2 } ] ] grr2 [ r_ ] = 1/grr [ r ] grr2r [ r_ ] = FullSimplify [D[ grr2 [ r ], { r } ] ] grr2rr [ r_ ] = FullSimplify [D[ grr2 [ r ], { r, 2 } ] ] g f f [ r_ ] = FullSimplify [ ( A2[ r ]/ ev [ r ] ) * ( r^2 a* r ) ] g f f r [ r_ ] = FullSimplify [D[ g f f [ r ], { r } ] ] g f f r 2 [ r_ ] = FullSimplify [D[ g f f [ r ], { r, 2 } ] ] gff2 [ r_ ] = 1/ g f f [ r ] g f f 2 r [ r_ ] = FullSimplify [D[ gff2 [ r ], { r } ] ] g f f 2 r r [ r_ ] = FullSimplify [D[ gff2 [ r ], { r, 2 } ] ] 44
50 Η Κεπλεριανή συχνότητα: OmegapST2[ r_ ] = FullSimplify [( g t t r [ r ] ) / ( g f f r [ r ] ) ] Η Κεπλεριανή συχνότητα στο όριο της Γ.Θ.Σ.: OmegapGR2[ r_ ] = FullSimplify [( g f f r [ r ] * g t t r [ r ] ) / ( g f f r [ r ]^2) /. { a > 2*m, b > 2*m, d > 0, beta > 0 } ] Υπολογισμός Επικυκλικής - Α τρόπος: Doneva et. al gttr3 [ r_ ] = FullSimplify [D[1/ gtt [ r ], { r, 2 } ] ] g f f r 3 [ r_ ] = FullSimplify [D[1/ g f f [ r ], { r, 2 } ] ] Ακτινική Επικυκλική Συχνότητα: EpicyclRadial2ST [ r_ ] = FullSimplify [ ( 1 / ( 2 * grr [ r ] ) ) * ( ( gtt [ r ]^2)* gttr3 [ r ] + ( g f f [ r ] ^ 2 ) * (OmegapST2[ r ] ) * g f f r 3 [ r ] ) ] Ακτινική Επικυκλική Συχνότητα στο όριο της Γ.Θ.Σ.: EpicyclRadial2GR [ r_ ] = FullSimplify [ ( 1 / ( 2 * grr [ r ] ) ) * ( ( gtt [ r ]^2)* gttr3 [ r ] + ( g f f [ r ] ^ 2 ) * (OmegapGR2[ r ] ) * g f f r 3 [ r ] ) /. { a > 2*m, b > 2*m, d > 0, beta > 0 } ] Υπολογισμός Επικυκλικής - Β τρόπος: Με ϕορμαλισμό ενεργού δυναμικού lk2 [ r_ ] = FullSimplify [( gtt2r [ r ] ) / ( g f f 2 r [ r ] ) ] Ακτινική Επικυκλική Συχνότητα: EpicyclRadial2STb [ r_ ] = FullSimplify [ ( ( gtt [ r ]^2)/(2* grr [ r ] ) ) * ( gtt2rr [ r ] + lk2 [ r ] * g f f 2 r r [ r ] ) ] Ακτινική Επικυκλική Συχνότητα στο όριο της Γ.Θ.Σ.: EpicyclRadial2GRb [ r_ ] = FullSimplify [ ( ( gtt [ r ]^2)/(2* grr [ r ] ) ) * ( gtt2rr [ r ] + lk2 [ r ] * g f f 2 r r [ r ] ) /. { a > 2*m, b > 2*m, d > 0, beta > 0 } ] 45
51 Κώδικας γραϕικών παραστάσεων διαϕόρων μοντέλων αστέρων νετρονίων: Παράμετροι από μοντέλα αστέρων νετρονίων (παρουσιάζονται στους πίνακες): beta0 = 4.5 omegaa = m0 = 2.51*1.48 ( * ηλιακές μάζες * ) aa = omegaa/m0 c = *10^5 ( *km/sec * ) Τελικές παραρατηρούμενες Τροχιακές συχνότητες: vpgr[ r_ ] = c*(1/(2000* Pi ) ) * Sqrt [OmegapGR2[ r ] ] ; vpst [ r_ ] = c*(1/(2000* Pi ) ) * Sqrt [OmegapST2[ r ] ] ; keplerians = {vpgr[ r ], vpst [ r ] } /. { m > m0( *km* ), d > aa*m0, b > 2*m0, a > 2*m0* Sqrt [1 + aa^2], beta > beta0 } Γραϕική παράσταση Τροχιακών Συχνοτήτων: Plot [ keplerians, { r, 10, 30}, AxesOrigin > {10, 0}, FrameLabel > { r (km), \!\(\* SubscriptBox [ \ ( v \ ), \(p \ ) ] \ ) ( khz) }, PlotLabel > HoldForm[ OrbitalEpicyclicFrequencies ], PlotStyle > { Black, Dashed }, PlotLegends > Placed [ { \[ Beta]=0, \[ Beta]= 4.5 }, RadialOuter ], Frame > True ] Τελικές παραρατηρούμενες Επικυκλικές συχνότητες: vrgr [ r_ ] = c*(1/(2000* Pi ) ) * Sqrt [ EpicyclRadial2GRb [ r ] ] ; vrst [ r_ ] = c*(1/(2000* Pi ) ) * Sqrt [ EpicyclRadial2STb [ r ] ] ; Epicyclics = { vrgr [ r ], vrst [ r ] } /. { m > m0( *km* ), d > aa*m0, b > 2*m0, a > 2*m0* Sqrt [1 + aa^2], beta > beta0 } Γραϕική παράσταση Επικυκλικών Συχνοτήτων: Plot [ Epicyclics, { r, 15, 30}, PlotStyle > { Black, Dashed }, FrameLabel >{ r (km), \!\(\* SubscriptBox [ \ ( v \ ), \ ( r \ ) ] \ ) ( khz) }, PlotLabel > HoldForm[ RadialEpicyclicFrequencies ], Frame > True, PlotStyle > { Red, Dashed }, AxesOrigin > {15, 0}, PlotLegends > Placed [ { \[ Beta]=0, \[ Beta]= 4.5 }, RadialInner ] ] 46
52 Kεϕάλαιο Αʹ Γραϕική παράσταση με Τροχιακές και Επικυκλικές Συχνότητες: alltogether = { vrgr [ r ], vrst [ r ], vpgr[ r ], vpst [ r ] } /. { m > m0( *km* ), d > aa*m0, b > 2*m0, a > 2*m0* Sqrt [1 + aa^2], beta > beta0 } Plot [ alltogether, { r, 10, 30}, PlotStyle > { Black, Dashed, Black, Dashed }, AxesOrigin > {10, 0}, FrameLabel > { r (km), \!\(\* SubscriptBox [ \ ( v \ ),\(p \ ) ] \ ), \! \ ( \ * SubscriptBox [ \ ( v \), \( r\ \ ) ] \ ) ( khz) }, PlotLabel > HoldForm[ OrbitalandRadialEpicyclicFrequencies ], Frame > True, PlotStyle > { Red, Dashed }, AxesOrigin > { 0, 0}, PlotLegends > Placed [ { \[ Beta]=0, \[ Beta]= 4.5 }, RadialInner ] ] Εύρεση της Τροχιακής Συχνότητας στην εσώτατη σταθερή κυκλική τροχιά: vrstroot = { vrst [ r ] } /. { m > m0( *km* ), d > aa*m0, b > 2*m0, a > 2*m0* Sqrt [1 + aa^2], beta > beta0 } r0 = Re[ FindRoot [ vrstroot, { r, 1 8 } ] [ [ 1, 2 ] ] ] { vpst [ r0 ] } /. { m > m0( *km* ), d > aa*m0, b > 2*m0, a > 2*m0* Sqrt [1 + aa^2], beta > beta0 } 47
53 Γραϕικές παραστάσεις ενδεικτικών μοντέλων αστέρων νετρονίων: Οι παρακάτω γραϕικές παραστάσεις (Σχήματα 13-30) έγιναν χρησιμοποιώντας δεδομένα από τους πίνακες που παραθέσαμε, για διάϕορα μοντέλα αστέρων και καταστατική εξίσωση APR. Κεπλεριανές (τροχιακές) συχνότητες (Σχήματα 13-18): Σχήμα 13: β = 4.5, m = 1.86M, ω A = v p khz Β 0 Β r km Σχήμα 14: β = 4.5, m = 2.00M, ω A = v p khz Β 0 Β r km 48
54 Σχήμα 15: β = 4.8, m = 1.15M, ω A = v p khz Β 0 Β r km Σχήμα 16: β = 4.8, m = M, ω A = v p khz Β 0 Β r km 49
55 Σχήμα 17: β = 6, m = 1.36M, ω A = v p khz Β 0 Β r km Σχήμα 18: β = 6, m = 2.52M, ω A = v p khz Β 0 Β r km 50
56 Ακτινικές επικυκλικές συχνότητες (Σχήματα 19-24): Σχήμα 19: β = 4.5, m = 1.86M, ω A = v r khz Β 0 Β r km Σχήμα 20: β = 4.5, m = 2.00M, ω A = v r khz Β 0 Β r km 51
57 Σχήμα 21: β = 4.8, m = 1.15M, ω A = v r khz Β 0 Β r km Σχήμα 22: β = 4.8, m = 1.99M, ω A = v r khz Β 0 Β r km 52
58 Σχήμα 23: β = 6, m = 1.36M, ω A = v r khz Β 0 Β r km Σχήμα 24: β = 6, m = 2.52M, ω A = v r khz Β 0 Β r km 53
59 Για εποπτικούς λόγους στα Σχήματα 25 με 30 παραθέτουμε τις γραϕικές παραστάσεις τροχιακών και επικυκλικών συχνοτήτων μαζί: Σχήμα 25: β = 4.5, m = 1.86M, ω A = v p, v r khz Β 0 Β r km Σχήμα 26: β = 4.5, m = 2.00M, ω A = v p, v r khz Β 0 Β r km 54
60 Σχήμα 27: β = 4.8, m = 1.15M, ω A = v p, v r khz Β 0 Β r km Σχήμα 28: β = 4.8, m = 1.99M, ω A = v p, v r khz Β 0 Β r km 55
61 Σχήμα 29: β = 6, m = 1.36M, ω A = v p, v r khz Β 0 Β r km Σχήμα 30: β = 6, m = 2.52M, ω A = v p, v r khz Β 0 Β r km 56
62 Αναϕορές [1] J. Antoniadis, P. C. Freire, N. Wex, T. M. Tauris, R. S. Lynch, et al., Science 340, 6131 (2013). [2] C. Brans, R.H. Dicke, Phys. Rev. 124, (1961). [3] M. A. Abramowicz, W. Kluźniak, Astrophysics and Space Science, Volume 300, pp (2004). [4] D. Markovic and F. K. Lamb, arxiv: (2000). [5] M. A. Abramowicz, G. J. E. Almergren et. al., arxiv: (2003). [6] K. Just, Z. Naturforsch. 14, 751 (1959). [7] T. Damour and G. Esposito-Farese, Phys. Rev. D 54, 1474 (1996). [8] D. D. Doneva, S. S. Yazadjiev, N. Stergioulas, K. D. Kokkotas & T. M. Athanasiadis, arxiv: (2014). [9] Ν. Stergioulas and J. L. Friedman, Astrophysical Journal, vol. 444, p (1995). [10] D. D. Doneva, S. S. Yazadjiev, N. Stergioulas, & K. D. Kokkotas, Phys. Rev. D 88, (2013). [11] S. G. Turyshev, M. Shao, K. L. Nordtvedt, Int. J. Mod. Phys. D (2004). [12] P. S. Wesson, J. M. Overduin, arxiv: (2013). [13] Hajime Sotani, Phys. Rev. D 89: (2014). [14] H. A. Buchdahl, Monthly Notices of the Royal Astronomical Society, Vol. 150, p. 1 (1970). [15] N. Wex, arxiv: (2014). [16] C. M. Will, arxiv: (2014). [17] P. C. C. Freire, N. Wex, G. Esposito-Farèse et. al., MNRAS 423, 3328 (2012). [18] V. Faraoni, E. Gunzig, Int. J. Theor. Phys. 38, 217 (1999). [19] V. Faraoni, E. Gunzig & P. Nardone, Fund. Cosmic Phys.20:121 (1999). [20] I. Quiros, R. Garcia-Salcedo, J. E. M. Aguilar & T. Matos, General Relativity and Gravitation: Volume 45, p (2013).
63 [21] V. Faraoni & E. Gunzig, Int. J. Theor. Phys. 38 (1999) (1999). [22] E. E. Flanagan, Class.Quant. Grav. 21:3817,2004 (2004). [23] S. Capozziello, P. Martin-Moruno & C. Rubano, Physics Letters B, Volume 689, p (2010). [24] A. Bhadra, Modern Physics Letters A, Volume 22, p (2007). [25] I. Quiros, R. Garcia-Salcedo, J. E. Madriz Aguilar, T. Matos, General Relativity and Gravitation: Volume 45, p (2013). [26] Esposito-Farese, Tests of Alternative Theories of Gravity, 33rd SLAC Summer Institute on Particle Physics (SSI 2005). [27] L. A. Pachon, J. A. Rueda, C. A. Valenzuela-Toledo, Astrophysical Journal, (2012). [28] H. Sotani, K. D. Kokkotas, Phys. Rev. D70, (2004). [29] Y. N. Obukhov, D. Puetzfeld, arxiv: (2014). [30] W. Kluzniak, M. A. Abramowicz, S. Kato, W. H. Lee & N. Stergioulas, Astrophysical Journal, 603: L89 L92 (2004). [31] T. Johannsen & D. Psaltis, arxiv: (2012). [32] S. Dedeo & D. Psaltis, arxiv: (2004). [33] A. Stabile, A. Stabile, & S. Capozziello Phys. Rev. D 88, (2013). [34] H. Sotani, Phys. Rev. D 86: (2012) [35] P. Pani, E. Berti, V. Cardoso, J. Read, arxiv: (2011). [36] W. A. Hellwing, A. Barreira, C. S. Frenk, B. Li & S. Cole, Phys. Rev. Lett. 112, (2014). [37] J. Yoo, Y. Watanabe, Int. J. Mod. Phys. D 21, (2012). [38] L. Fatibene & M. Francaviglia., arxiv: (2013). [39] J. Bookbinder, Proc. SPIE 7732, Space Telescopes and Instrumentation 2010: Ultraviolet to Gamma Ray, 77321B (2010). [40] N. Korsakova, C. Messenger, F. Pannarale, M. Hewitson, M. Armano, arxiv: (2014). [41] A. Mozaffari, arxiv: (2014). [42] G. J. Olmo, Phys. Rev. Lett. 98: (2007).
64 [43] James B. Hartle, Gravity- An introduction to Eistein s General Relativity (Addison Wesley) (2003). [44] Capozziello and Faraoni, Fundamental Theories of Physics, Vol. 170, Beyond Einstein Gravity (2011). [45] Yasunori Fujii and Kei-ichi Maeda, The Scalar-Tensor Theory of Gravitation (Cambridge Monographs on Mathematical Physics) (2003). [46] Clifford M. Will, Theory and experiment in gravitational physics (1993). [47] Barret O Neil, Elementary Differential Geometry, Academic Press (1997). [48] elisa: Astrophysics and cosmology in the millihertz regime, Pau Amaro- Seoane et. al.,arxiv: (2012). [49] Brett Altschul et. al., arxiv: (2014). [50] Dimitrios Psaltis, arxiv: (2009).
Υπάρχουν οι Μελανές Οπές;
 Υπάρχουν οι Μελανές Οπές; ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη, 10/2/2014 Σκοτεινοί αστέρες 1783: Ο John Michell ανακαλύπτει την έννοια ενός σκοτεινού αστέρα,
Υπάρχουν οι Μελανές Οπές; ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη, 10/2/2014 Σκοτεινοί αστέρες 1783: Ο John Michell ανακαλύπτει την έννοια ενός σκοτεινού αστέρα,
ΚΟΣΜΟΛΟΓΙΑ ΚΟΣΜΟΛΟΓΙΑ είναι ο τομέας τις ϕυσικής που προσπαθεί να εξηγήσει την γένεση και την εξέλιξη του σύμπαντος χρησιμοποιώντας παρατηρήσεις και τ
 ΗΡΑΚΛΕΙΟ, 10 Οκτωβρίου, 2017 ΚΟΣΜΟΛΟΓΙΑ ΓΙΑ ΑΡΧΑΡΙΟΥΣ Πανεπιστήμιο Κρήτης 1- ΚΟΣΜΟΛΟΓΙΑ ΚΟΣΜΟΛΟΓΙΑ είναι ο τομέας τις ϕυσικής που προσπαθεί να εξηγήσει την γένεση και την εξέλιξη του σύμπαντος χρησιμοποιώντας
ΗΡΑΚΛΕΙΟ, 10 Οκτωβρίου, 2017 ΚΟΣΜΟΛΟΓΙΑ ΓΙΑ ΑΡΧΑΡΙΟΥΣ Πανεπιστήμιο Κρήτης 1- ΚΟΣΜΟΛΟΓΙΑ ΚΟΣΜΟΛΟΓΙΑ είναι ο τομέας τις ϕυσικής που προσπαθεί να εξηγήσει την γένεση και την εξέλιξη του σύμπαντος χρησιμοποιώντας
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
 ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
c 4 (1) Robertson Walker (x 0 = ct) , R 2 (t) = R0a 2 2 (t) (2) p(t) g = (3) p(t) g 22 p(t) g 33
 ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Α. Η ΕΞΙΣΩΣΗ EINSTEIN Διδάσκων: Θεόδωρος Ν. Τομαράς G µν R µν 1 g µν R = κ T µν, κ 8πG N c 4 (1) Β. Η ΕΞΙΣΩΣΗ FRIEDMANN. Για ομογενή και ισότροπο χωρόχρονο έχουμε
ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Α. Η ΕΞΙΣΩΣΗ EINSTEIN Διδάσκων: Θεόδωρος Ν. Τομαράς G µν R µν 1 g µν R = κ T µν, κ 8πG N c 4 (1) Β. Η ΕΞΙΣΩΣΗ FRIEDMANN. Για ομογενή και ισότροπο χωρόχρονο έχουμε
Τα Κύματα της Βαρύτητας
 Τα Κύματα της Βαρύτητας ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΟΦΑ, 24/1/2015 Πως διαδίδεται η βαρυτική έλξη; 1900: ο Lorentz προτείνει ότι η δύναμη της βαρύτητας δε
Τα Κύματα της Βαρύτητας ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΟΦΑ, 24/1/2015 Πως διαδίδεται η βαρυτική έλξη; 1900: ο Lorentz προτείνει ότι η δύναμη της βαρύτητας δε
ΕΞΕΡΕΥΝΩΝΤΑΣ ΤΟ ΣΥΜΠΑΝ ΜΕ ΤΑ ΚΥΜΑΤΑ ΤΗΣ ΒΑΡΥΤΗΤΑΣ
 ΕΞΕΡΕΥΝΩΝΤΑΣ ΤΟ ΣΥΜΠΑΝ ΜΕ ΤΑ ΚΥΜΑΤΑ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Κατερίνη, 7/5/2016 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015
ΕΞΕΡΕΥΝΩΝΤΑΣ ΤΟ ΣΥΜΠΑΝ ΜΕ ΤΑ ΚΥΜΑΤΑ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Κατερίνη, 7/5/2016 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015
L = T V = 1 2 (ṙ2 + r 2 φ2 + ż 2 ) U (3)
 ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΑΝΑΚΟΙΝΩΣΗ. Διευκρινίσεις για την ύλη του μαθήματος ΚΟΣΜΟΛΟΓΙΑ
 ΑΝΑΚΟΙΝΩΣΗ Διευκρινίσεις για την ύλη του μαθήματος ΚΟΣΜΟΛΟΓΙΑ Η ύλη του μαθήματος «Κοσμολογία» περιέχεται στις νέες σημειώσεις του μαθήματος (ανάρτηση 2016) και στο βιβλίο γενικής σχετικότητας που έχετε
ΑΝΑΚΟΙΝΩΣΗ Διευκρινίσεις για την ύλη του μαθήματος ΚΟΣΜΟΛΟΓΙΑ Η ύλη του μαθήματος «Κοσμολογία» περιέχεται στις νέες σημειώσεις του μαθήματος (ανάρτηση 2016) και στο βιβλίο γενικής σχετικότητας που έχετε
Εξερευνώντας το Σύμπαν με τα Κύματα της Βαρύτητας
 Εξερευνώντας το Σύμπαν με τα Κύματα της Βαρύτητας ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Νάουσα, 28/11/2015 Πως διαδίδεται η βαρυτική έλξη; 1900: ο Lorentz προτείνει
Εξερευνώντας το Σύμπαν με τα Κύματα της Βαρύτητας ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Νάουσα, 28/11/2015 Πως διαδίδεται η βαρυτική έλξη; 1900: ο Lorentz προτείνει
ds 2 = 1 y 2 (dx2 + dy 2 ), y 0, < x < + (1) dx/(1 x 2 ) = 1 ln((1 + x)/(1 x)) για 1 < x < 1. l AB = dx/1 = 2 (2) (5) w 1/2 = ±κx + C (7)
 ΒΑΡΥΤΗΤΑ ΚΑΙ ΚΟΣΜΟΛΟΓΙΑ Θ. Τομαράς 1. ΤΟ ΥΠΕΡΒΟΛΙΚΟ ΕΠΙΠΕΔΟ. Το υπερβολικό επίπεδο ορίζεται με τη μετρική ds = 1 y dx + dy ), y 0, < x < + 1) α) Να υπολογίσετε το μήκος της γραμμής της παράλληλης στον
ΒΑΡΥΤΗΤΑ ΚΑΙ ΚΟΣΜΟΛΟΓΙΑ Θ. Τομαράς 1. ΤΟ ΥΠΕΡΒΟΛΙΚΟ ΕΠΙΠΕΔΟ. Το υπερβολικό επίπεδο ορίζεται με τη μετρική ds = 1 y dx + dy ), y 0, < x < + 1) α) Να υπολογίσετε το μήκος της γραμμής της παράλληλης στον
ΣΧΕΤΙΚΟΤΗΤΑ ΚΑΙ ΝΤΕΤΕΡΜΙΝΙΣΜΟΣ
 ΜΑΘΗΜΑ 5: ΣΧΕΤΙΚΟΤΗΤΑ ΚΑΙ ΝΤΕΤΕΡΜΙΝΙΣΜΟΣ Salviati: Εκεί που δεν μας βοηθούν οι αισθήσεις πρέπει να παρέμβει η λογική, γιατί μόνο αυτή θα επιτρέψει να εξηγήσουμε τα φαινόμενα ΓΑΛΙΛΑΪΚΟΙ ΔΙΑΛΟΓΟΙ Η μαθηματική
ΜΑΘΗΜΑ 5: ΣΧΕΤΙΚΟΤΗΤΑ ΚΑΙ ΝΤΕΤΕΡΜΙΝΙΣΜΟΣ Salviati: Εκεί που δεν μας βοηθούν οι αισθήσεις πρέπει να παρέμβει η λογική, γιατί μόνο αυτή θα επιτρέψει να εξηγήσουμε τα φαινόμενα ΓΑΛΙΛΑΪΚΟΙ ΔΙΑΛΟΓΟΙ Η μαθηματική
Μέρος A: Νευτώνιες τροχιές (υπό την επίδραση συντηρητικών δυνάμεων) (3.0 μονάδες)
 Theory LIGO-GW150914 (10 μονάδες) Q1-1 Το 015, το παρατηρητήριο βαρυτικών κυμάτων LIGO ανίχνευσε για πρώτη φορά τη διέλευση των βαρυτικών κυμάτων (gravitational waves ή GW) διαμέσου της Γης. Το συμβάν
Theory LIGO-GW150914 (10 μονάδες) Q1-1 Το 015, το παρατηρητήριο βαρυτικών κυμάτων LIGO ανίχνευσε για πρώτη φορά τη διέλευση των βαρυτικών κυμάτων (gravitational waves ή GW) διαμέσου της Γης. Το συμβάν
ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ: Ιστορική εξέλιξη και σύγχρονα πειράματα
 ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ: Ιστορική εξέλιξη και σύγχρονα πειράματα ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Νάουσα, 31/3/2012 Περιεχόμενα 1. Ειδική Θεωρία Σχετικότητας (ΕΘΣ)
ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ: Ιστορική εξέλιξη και σύγχρονα πειράματα ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Νάουσα, 31/3/2012 Περιεχόμενα 1. Ειδική Θεωρία Σχετικότητας (ΕΘΣ)
ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ
 Ελένη Πετράκου - National Taiwan University ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ Πρόγραμμα επιμόρφωσης ελλήνων εκπαιδευτικών CERN, 7 Νοεμβρίου 2014 You are here! 1929: απομάκρυνση γαλαξιών θεωρία της μεγάλης έκρηξης
Ελένη Πετράκου - National Taiwan University ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ Πρόγραμμα επιμόρφωσης ελλήνων εκπαιδευτικών CERN, 7 Νοεμβρίου 2014 You are here! 1929: απομάκρυνση γαλαξιών θεωρία της μεγάλης έκρηξης
Η κλασσική, η σχετικιστική και η κβαντική προσέγγιση. Θωµάς Μελίστας Α 3
 Η κλασσική, η σχετικιστική και η κβαντική προσέγγιση Θωµάς Μελίστας Α 3 Σύµφωνα µε την κλασσική µηχανική και την γενική αντίληψη η µάζα είναι µία εγγενής ιδιότητα των φυσικών σωµάτων. Μάζα είναι η ποσότητα
Η κλασσική, η σχετικιστική και η κβαντική προσέγγιση Θωµάς Μελίστας Α 3 Σύµφωνα µε την κλασσική µηχανική και την γενική αντίληψη η µάζα είναι µία εγγενής ιδιότητα των φυσικών σωµάτων. Μάζα είναι η ποσότητα
ξ i (t) = v i t + ξ i (0) (9) c (t t 0). (10) t = t, z = z 1 2 gt 2 (12)
 Η ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1 Κίνηση σώματος σε πεδίο βαρύτητας Εδώ θα εφαρμόσουμε την Ι.Α.Ι. και τις γνώσεις μας από την Ειδική Θεωρία της Σχετικότητας για να παράγουμε
Η ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1 Κίνηση σώματος σε πεδίο βαρύτητας Εδώ θα εφαρμόσουμε την Ι.Α.Ι. και τις γνώσεις μας από την Ειδική Θεωρία της Σχετικότητας για να παράγουμε
Τμήμα Φυσικής, Παν/μιο Ιωαννίνων, Ειδική Σχετικότητα, Διάλεξη 5 Οι Μετασχηματισμοί του Lorentz και η Συστολή του μήκους
 1 Οι Μετασχηματισμοί του Lorentz και η Συστολή του μήκους Σκοποί της πέμπτης διάλεξης: 10.11.2011 Εξοικείωση με τους μετασχηματισμούς του Lorentz και τις διάφορες μορφές που μπορούν να πάρουν για την επίλυση
1 Οι Μετασχηματισμοί του Lorentz και η Συστολή του μήκους Σκοποί της πέμπτης διάλεξης: 10.11.2011 Εξοικείωση με τους μετασχηματισμούς του Lorentz και τις διάφορες μορφές που μπορούν να πάρουν για την επίλυση
1 Ο παράγοντας κλίμακας και ο Νόμος του Hubble
 ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς Ο παράγοντας κλίμακας και ο Νόμος του Hubble Σύμφωνα με την Κοσμολογική Αρχή το Σύμπαν είναι σε μεγάλες κλίμακες ομογενές και ισότροπο.
ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς Ο παράγοντας κλίμακας και ο Νόμος του Hubble Σύμφωνα με την Κοσμολογική Αρχή το Σύμπαν είναι σε μεγάλες κλίμακες ομογενές και ισότροπο.
ΠΕΡΙΕΧΟΜΕΝΑ ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΣΤΟ ΚΕΝΟ ΠΑΡΑΓΩΓΗ ΒΑΡΥΤΙΚΩΝ ΚΥΜΑΤΩΝ ΑΠΟ ΠΗΓΕΣ ΑΝΙΧΝΕΥΣΗ ΒΑΡΥΤΙΚΩΝ ΚΥΜΑΤΩΝ
 ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΤΖΩΡΤΖΗΣ ΔΗΜΗΤΡΗΣ Επιβλέπων καθηγητής:αναγνωστοπουλοσ Κ. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ-ΣΕΜΦΕ 26 Σεπτεμβρίου 2016 ΠΕΡΙΕΧΟΜΕΝΑ ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΣΤΟ ΚΕΝΟ ΠΑΡΑΓΩΓΗ ΒΑΡΥΤΙΚΩΝ
ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΤΖΩΡΤΖΗΣ ΔΗΜΗΤΡΗΣ Επιβλέπων καθηγητής:αναγνωστοπουλοσ Κ. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ-ΣΕΜΦΕ 26 Σεπτεμβρίου 2016 ΠΕΡΙΕΧΟΜΕΝΑ ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΣΤΟ ΚΕΝΟ ΠΑΡΑΓΩΓΗ ΒΑΡΥΤΙΚΩΝ
Η ΣΧΕΤΙΚΟΤΗΤΑ ΚΑΙ Ο ΝΤΕΤΕΡΜΙΝΙΣΜΟΣ
 ΜΑΘΗΜΑ 5: Η ΣΧΕΤΙΚΟΤΗΤΑ ΚΑΙ Ο ΝΤΕΤΕΡΜΙΝΙΣΜΟΣ Salviati: Εκεί όπου δεν μας βοηθούν οι αισθήσεις πρέπει να παρέμβει η λογική, γιατί μόνο αυτή θα επιτρέψει να εξηγήσουμε τα φαινόμενα ΓΑΛΙΛΑΪΚΟΙ ΔΙΑΛΟΓΟΙ Η
ΜΑΘΗΜΑ 5: Η ΣΧΕΤΙΚΟΤΗΤΑ ΚΑΙ Ο ΝΤΕΤΕΡΜΙΝΙΣΜΟΣ Salviati: Εκεί όπου δεν μας βοηθούν οι αισθήσεις πρέπει να παρέμβει η λογική, γιατί μόνο αυτή θα επιτρέψει να εξηγήσουμε τα φαινόμενα ΓΑΛΙΛΑΪΚΟΙ ΔΙΑΛΟΓΟΙ Η
ΣΧΕΤΙΚΟΤΗΤΑ Μετασχηματισμοί Γαλιλαίου. (Κλασική θεώρηση) αφού σύμφωνα με τα πειράματα Mickelson-Morley είναι c =c.
 ΣΧΕΤΙΚΟΤΗΤΑ Μετασχηματισμοί Γαλιλαίου. (Κλασική θεώρηση) y y z z t t Το οποίο οδηγεί στο ότι - υ.(άτοπο), αφού σύμφωνα με τα πειράματα Mikelson-Morley είναι. Επίσης y y, z z, t t Το οποίο ( t t ) είναι
ΣΧΕΤΙΚΟΤΗΤΑ Μετασχηματισμοί Γαλιλαίου. (Κλασική θεώρηση) y y z z t t Το οποίο οδηγεί στο ότι - υ.(άτοπο), αφού σύμφωνα με τα πειράματα Mikelson-Morley είναι. Επίσης y y, z z, t t Το οποίο ( t t ) είναι
Αριθμητικός υπολογισμός τροχιών σωμάτων στη γεωμετρία Schwarzschild. Κουλούρης Κωνσταντίνος
 Αριθμητικός υπολογισμός τροχιών σωμάτων στη γεωμετρία Schwarzschild Κουλούρης Κωνσταντίνος Σύνοψη Σχετικότητα Ειδική και γενική θεωρία Γεωμετρία Swarzschild Μετρική και εξισώσεις γεωδαιτικών τροχιών Υπολογιστική
Αριθμητικός υπολογισμός τροχιών σωμάτων στη γεωμετρία Schwarzschild Κουλούρης Κωνσταντίνος Σύνοψη Σχετικότητα Ειδική και γενική θεωρία Γεωμετρία Swarzschild Μετρική και εξισώσεις γεωδαιτικών τροχιών Υπολογιστική
θεμελιακά Ερωτήματα Κοσμολογίας & Αστροφυσικής
 θεμελιακά Ερωτήματα Απόστολος Δ. Παναγιώτου Ομότιμος Καθηγητής Πανεπιστημίου Αθηνών Επιστημονικός Συνεργάτης στο CERN Σχολή Αστρονομίας και Διαστήματος Βόλος, 5 Απριλίου, 2014 1 BIG BANG 10 24 μ 10-19
θεμελιακά Ερωτήματα Απόστολος Δ. Παναγιώτου Ομότιμος Καθηγητής Πανεπιστημίου Αθηνών Επιστημονικός Συνεργάτης στο CERN Σχολή Αστρονομίας και Διαστήματος Βόλος, 5 Απριλίου, 2014 1 BIG BANG 10 24 μ 10-19
Αριστοτέλης (384-322 π.χ) : «Για να ξεκινήσει και να διατηρηθεί μια κίνηση είναι απαραίτητη η ύπαρξη μιας συγκεκριμένης αιτίας»
 Εισαγωγή Επιστημονική μέθοδος Αριστοτέλης (384-322 π.χ) : «Για να ξεκινήσει και να διατηρηθεί μια κίνηση είναι απαραίτητη η ύπαρξη μιας συγκεκριμένης αιτίας» Διατύπωση αξιωματική της αιτίας μια κίνησης
Εισαγωγή Επιστημονική μέθοδος Αριστοτέλης (384-322 π.χ) : «Για να ξεκινήσει και να διατηρηθεί μια κίνηση είναι απαραίτητη η ύπαρξη μιας συγκεκριμένης αιτίας» Διατύπωση αξιωματική της αιτίας μια κίνησης
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ETY-202. Εκπομπή και απορρόφηση ακτινοβολίας ETY-202 ΎΛΗ & ΦΩΣ 12. ΎΛΗ & ΦΩΣ. Στέλιος Τζωρτζάκης 21/12/2012
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 Εκπομπή και απορρόφηση ακτινοβολίας ΎΛΗ & ΦΩΣ 12. ΎΛΗ & ΦΩΣ Στέλιος Τζωρτζάκης 1 3 4 Ηλεκτρομαγνητικά πεδία Απορρόφηση είναι Σε αυτή τη διαδικασία το ηλεκτρόνιο
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 Εκπομπή και απορρόφηση ακτινοβολίας ΎΛΗ & ΦΩΣ 12. ΎΛΗ & ΦΩΣ Στέλιος Τζωρτζάκης 1 3 4 Ηλεκτρομαγνητικά πεδία Απορρόφηση είναι Σε αυτή τη διαδικασία το ηλεκτρόνιο
Εισαγωγή στη Σχετικότητα και την Κοσμολογία ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ
 Εισαγωγή στη Σχετικότητα και την Κοσμολογία Διδάσκων: Θεόδωρος Τομαράς, Πανεπιστήμιο Κρήτης ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ Εβδομάδα 1 Σχετικότητα 1.1 Η ανεπάρκεια της μηχανικής του Νεύτωνα V1.1.1 Σύντομη εισαγωγή
Εισαγωγή στη Σχετικότητα και την Κοσμολογία Διδάσκων: Θεόδωρος Τομαράς, Πανεπιστήμιο Κρήτης ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ Εβδομάδα 1 Σχετικότητα 1.1 Η ανεπάρκεια της μηχανικής του Νεύτωνα V1.1.1 Σύντομη εισαγωγή
Βαρυτικά Κύματα ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 Βαρυτικά Κύματα ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη, 6/4/2014 Νευτώνεια βαρύτητα 1687: Ο Νεύτωνας θεωρούσε ότι η βαρύτητα δρα ακαριαία σε οσοδήποτε μεγάλες
Βαρυτικά Κύματα ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη, 6/4/2014 Νευτώνεια βαρύτητα 1687: Ο Νεύτωνας θεωρούσε ότι η βαρύτητα δρα ακαριαία σε οσοδήποτε μεγάλες
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
5 Σχετικιστική μάζα. Στο Σ Πριν Μετά. Στο Σ
 Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος»
 Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος» Σωτήρης Τσαντίλας (PhD, MSc), Μαθηματικός Αστροφυσικός Σύντομη περιγραφή: Χρησιμοποιώντας δεδομένα από το διαστημικό τηλεσκόπιο
Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος» Σωτήρης Τσαντίλας (PhD, MSc), Μαθηματικός Αστροφυσικός Σύντομη περιγραφή: Χρησιμοποιώντας δεδομένα από το διαστημικό τηλεσκόπιο
Κεφάλαιο 8. Βαρυτικη Δυναμικη Ενεργεια { Εκφραση του Βαρυτικού Δυναμικού, Ταχύτητα Διαφυγής, Τροχιές και Ενέργεια Δορυφόρου}
 Κεφάλαιο 8 ΒΑΡΥΤΙΚΟ ΠΕΔΙΟ Νομος της Βαρυτητας {Διανυσματική Εκφραση, Βαρύτητα στη Γη και σε Πλανήτες} Νομοι του Kepler {Πεδίο Κεντρικών Δυνάμεων, Αρχή Διατήρησης Στροφορμής, Κίνηση Πλανητών και Νόμοι του
Κεφάλαιο 8 ΒΑΡΥΤΙΚΟ ΠΕΔΙΟ Νομος της Βαρυτητας {Διανυσματική Εκφραση, Βαρύτητα στη Γη και σε Πλανήτες} Νομοι του Kepler {Πεδίο Κεντρικών Δυνάμεων, Αρχή Διατήρησης Στροφορμής, Κίνηση Πλανητών και Νόμοι του
Φαινόμενο Unruh. Δημήτρης Μάγγος. Εθνικό Μετσόβιο Πολυτεχνείο September 26, / 20. Δημήτρης Μάγγος Φαινόμενο Unruh 1/20
 Φαινόμενο Unruh Δημήτρης Μάγγος Εθνικό Μετσόβιο Πολυτεχνείο September 26, 2012 1 / 20 Δημήτρης Μάγγος Φαινόμενο Unruh 1/20 Outline Σχετικότητα Ειδική & Γενική Θεωρία Κβαντική Θεωρία Πεδίου Πεδία Στον Χωρόχρονο
Φαινόμενο Unruh Δημήτρης Μάγγος Εθνικό Μετσόβιο Πολυτεχνείο September 26, 2012 1 / 20 Δημήτρης Μάγγος Φαινόμενο Unruh 1/20 Outline Σχετικότητα Ειδική & Γενική Θεωρία Κβαντική Θεωρία Πεδίου Πεδία Στον Χωρόχρονο
H ΚΟΣΜΟΛΟΓΙΑ ΜΕΤΑ ΑΠΟ 100 ΧΡΟΝΙΑ ΓΕΝΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΟΣ
 H ΚΟΣΜΟΛΟΓΙΑ ΜΕΤΑ ΑΠΟ 100 ΧΡΟΝΙΑ ΓΕΝΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΟΣ ΔΡ. ΣΠΥΡΟΣ ΒΑΣΙΛΑΚΟΣ ΚΕΝΤΡΟ ΕΡΕΥΝΩΝ ΑΣΤΡΟΝΟΜΙΑΣ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ 25/11/2015 Η ΧΡΥΣΗ ΠΕΡΙΟΔΟΣ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ 96% του Σύμπαντος
H ΚΟΣΜΟΛΟΓΙΑ ΜΕΤΑ ΑΠΟ 100 ΧΡΟΝΙΑ ΓΕΝΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΟΣ ΔΡ. ΣΠΥΡΟΣ ΒΑΣΙΛΑΚΟΣ ΚΕΝΤΡΟ ΕΡΕΥΝΩΝ ΑΣΤΡΟΝΟΜΙΑΣ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ 25/11/2015 Η ΧΡΥΣΗ ΠΕΡΙΟΔΟΣ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ 96% του Σύμπαντος
Theory Greek (Greece) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό.
 Q1-1 Δύο προβλήματα Μηχανικής (10 Μονάδες) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό. Μέρος A. Ο Κρυμμένος Δίσκος (3.5 Μονάδες)
Q1-1 Δύο προβλήματα Μηχανικής (10 Μονάδες) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό. Μέρος A. Ο Κρυμμένος Δίσκος (3.5 Μονάδες)
Κίνηση φορτισμένου σωματιδίου σε χώρο, όπου συνυπάρχουν ηλεκτρικό και μαγνητικό πεδίο ομογενή και χρονοανεξάρτητα
 Κίνηση φορτισμένου σωματιδίου σε χώρο, όπου συνυπάρχουν ηλεκτρικό και μαγνητικό πεδίο ομογενή και χρονοανεξάρτητα Μέρος α : Εξισώσεις κίνησης και συμπεράσματα) Α. Τι βλέπει ένας αδρανειακός παρατηρητής
Κίνηση φορτισμένου σωματιδίου σε χώρο, όπου συνυπάρχουν ηλεκτρικό και μαγνητικό πεδίο ομογενή και χρονοανεξάρτητα Μέρος α : Εξισώσεις κίνησης και συμπεράσματα) Α. Τι βλέπει ένας αδρανειακός παρατηρητής
Η εσωτερική δομή των μελανών οπών και η εικασία της ισχυρής κοσμικής λογοκρισίας στη γενική σχετικότητα
 Η εσωτερική δομή των μελανών οπών και η εικασία της ισχυρής κοσμικής λογοκρισίας στη γενική σχετικότητα Μιχάλης Δαφέρμος Πανεπιστήμιο Princeton/ Πανεπιστήμιο του Cambridge Γενικό Σεμινάριο, Μαθηματικό
Η εσωτερική δομή των μελανών οπών και η εικασία της ισχυρής κοσμικής λογοκρισίας στη γενική σχετικότητα Μιχάλης Δαφέρμος Πανεπιστήμιο Princeton/ Πανεπιστήμιο του Cambridge Γενικό Σεμινάριο, Μαθηματικό
0λ έως. Εξάρτηση. ω και ο. του ω: mx x (1) με λύση. όπου το. ), Im. m ( 0 ( ) (2) Re x / ) ) ( / 0 και Im 20.
 ΚΕΦ. 14.1 : ΚΟΣΜΟΛΟΓΙΑ Ι ΣΕΛ. 37 έως 5 ΤΟΥ ΒΙΒΛΙΟΥ ΚΣ. 4 Ο VIDEO, 9/1/14 λ έως 19:4λ Εξάρτηση ρόλος των συντονισμών της διηλεκτρικής συνάρτησης από τη συχνότητα ω και ο Παρουσιάζεται το γράφημα e(ε) και
ΚΕΦ. 14.1 : ΚΟΣΜΟΛΟΓΙΑ Ι ΣΕΛ. 37 έως 5 ΤΟΥ ΒΙΒΛΙΟΥ ΚΣ. 4 Ο VIDEO, 9/1/14 λ έως 19:4λ Εξάρτηση ρόλος των συντονισμών της διηλεκτρικής συνάρτησης από τη συχνότητα ω και ο Παρουσιάζεται το γράφημα e(ε) και
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
 ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
Το ελαστικο κωνικο εκκρεμε ς
 Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Η ΚΛΑΣΙΚΗ ΘΕΩΡΗΣΗ ΤΟΥ ΧΩΡΟΥ ΚΑΙ ΤΟΥ ΧΡΟΝΟΥ
 ΜΑΘΗΜΑ 1: Η ΚΛΑΣΙΚΗ ΘΕΩΡΗΣΗ ΤΟΥ ΧΩΡΟΥ ΚΑΙ ΤΟΥ ΧΡΟΝΟΥ Τίποτε δεν θεωρώ μεγαλύτερο αίνιγμα από το χρόνο και το χώρο Εντούτοις, τίποτε δεν με απασχολεί λιγότερο από αυτά επειδή ποτέ δεν τα σκέφτομαι Charles
ΜΑΘΗΜΑ 1: Η ΚΛΑΣΙΚΗ ΘΕΩΡΗΣΗ ΤΟΥ ΧΩΡΟΥ ΚΑΙ ΤΟΥ ΧΡΟΝΟΥ Τίποτε δεν θεωρώ μεγαλύτερο αίνιγμα από το χρόνο και το χώρο Εντούτοις, τίποτε δεν με απασχολεί λιγότερο από αυτά επειδή ποτέ δεν τα σκέφτομαι Charles
Σύγχρονη Φυσική 1, Διάλεξη 4, Τμήμα Φυσικής, Παν/μιο Ιωαννίνων Η Αρχές της Ειδικής Θεωρίας της Σχετικότητας και οι μετασχηματισμοί του Lorentz
 1 Η Αρχές της Ειδικής Θεωρίας της Σχετικότητας και οι μετασχηματισμοί του Lorentz Σκοποί της τέταρτης διάλεξης: 25.10.2011 Να κατανοηθούν οι αρχές με τις οποίες ο Albert Einstein θεμελίωσε την ειδική θεωρία
1 Η Αρχές της Ειδικής Θεωρίας της Σχετικότητας και οι μετασχηματισμοί του Lorentz Σκοποί της τέταρτης διάλεξης: 25.10.2011 Να κατανοηθούν οι αρχές με τις οποίες ο Albert Einstein θεμελίωσε την ειδική θεωρία
Ευστάθεια και αστάθεια των ακραίων μελανών οπών
 Ευστάθεια και αστάθεια των ακραίων μελανών οπών κατά τον Στέφανο Αρετάκη (Cambridge/Princeton) Πάτρα, 19 Μαΐου 2012 κατά τον Στέφανο Αρετάκη(Cambridge/Princeton) 1 1. Σύντομη περίληψη της γενικής σχετικότητας
Ευστάθεια και αστάθεια των ακραίων μελανών οπών κατά τον Στέφανο Αρετάκη (Cambridge/Princeton) Πάτρα, 19 Μαΐου 2012 κατά τον Στέφανο Αρετάκη(Cambridge/Princeton) 1 1. Σύντομη περίληψη της γενικής σχετικότητας
1 Μονάδες - Τυπικά μεγέθη. 2 Η Διαστολή και η Ηλικία του Σύμπαντος ΚΟΣΜΟΓΡΑΦΙΑ. 2.1 Ο νόμος του Hubble. Διδάσκων: Θεόδωρος Ν.
 ΚΟΣΜΟΓΡΑΦΙΑ Διδάσκων: Θεόδωρος Ν. Τομαράς Α. ΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΟΥ ΣΥΜΠΑΝΤΟΣ 1 Μονάδες - Τυπικά μεγέθη 1 light year = 0.951 10 16 m 1 AU = 1.50 10 11 m 1 = 4.85 10 6 rad 1pc 1 parsec 1AU/(1 in rad) = 3.1
ΚΟΣΜΟΓΡΑΦΙΑ Διδάσκων: Θεόδωρος Ν. Τομαράς Α. ΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΟΥ ΣΥΜΠΑΝΤΟΣ 1 Μονάδες - Τυπικά μεγέθη 1 light year = 0.951 10 16 m 1 AU = 1.50 10 11 m 1 = 4.85 10 6 rad 1pc 1 parsec 1AU/(1 in rad) = 3.1
Ανακάλυψη βαρυτικών κυμάτων από τη συγχώνευση δύο μαύρων οπών. Σελίδα LIGO
 Ανακάλυψη βαρυτικών κυμάτων από τη συγχώνευση δύο μαύρων οπών Σελίδα LIGO Πώς μία μάζα στο Σύμπαν στρεβλώνει τον χωροχρόνο (Credit: NASA) Πεδίο Βαρύτητας στη Γενική Σχετικότητα. Από την Επιτάχυνση Δημιουργούνται
Ανακάλυψη βαρυτικών κυμάτων από τη συγχώνευση δύο μαύρων οπών Σελίδα LIGO Πώς μία μάζα στο Σύμπαν στρεβλώνει τον χωροχρόνο (Credit: NASA) Πεδίο Βαρύτητας στη Γενική Σχετικότητα. Από την Επιτάχυνση Δημιουργούνται
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Σύγχρονη Φυσική 1, Διάλεξη 3, Τμήμα Φυσικής, Παν/μιο Ιωαννίνων Η θεωρία του αιθέρα καταρρίπτεται από το πείραμα των Michelson και Morley
 1 Η θεωρία του αιθέρα καταρρίπτεται από το πείραμα των Mihelson και Morley 0.10.011 Σκοποί της τρίτης διάλεξης: Να κατανοηθεί η ιδιαιτερότητα των ηλεκτρομαγνητικών κυμάτων (π. χ. φως) σε σχέση με άλλα
1 Η θεωρία του αιθέρα καταρρίπτεται από το πείραμα των Mihelson και Morley 0.10.011 Σκοποί της τρίτης διάλεξης: Να κατανοηθεί η ιδιαιτερότητα των ηλεκτρομαγνητικών κυμάτων (π. χ. φως) σε σχέση με άλλα
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσική ΜΙΘΕ ΔΥΝΑΜΙΚΗ - 1. Νίκος Κανδεράκης
 Φυσική ΜΙΘΕ ΔΥΝΑΜΙΚΗ - 1 Νίκος Κανδεράκης Αριστοτελική Φυσική Γιατί πέφτουν τα (βαριά) σώματα; Πηγαίνουν στη φυσική τους θέση. Βάρος: η τάση του βαρέως σώματος να κινηθεί προς το κέντρο της Γης. Μέτρο
Φυσική ΜΙΘΕ ΔΥΝΑΜΙΚΗ - 1 Νίκος Κανδεράκης Αριστοτελική Φυσική Γιατί πέφτουν τα (βαριά) σώματα; Πηγαίνουν στη φυσική τους θέση. Βάρος: η τάση του βαρέως σώματος να κινηθεί προς το κέντρο της Γης. Μέτρο
ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ
 ΜΑΘΗΜΑ : ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Πρώτα απ όλα θέλουμε να βρούμε και να εξηγήσουμε έναν ορισμό που να ταιριάζει όσο το δυνατό καλύτερα στα φυσικά φαινόμενα Και η πεποίθησή μας θα ενισχυθεί
ΜΑΘΗΜΑ : ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Πρώτα απ όλα θέλουμε να βρούμε και να εξηγήσουμε έναν ορισμό που να ταιριάζει όσο το δυνατό καλύτερα στα φυσικά φαινόμενα Και η πεποίθησή μας θα ενισχυθεί
Τροχιές σωμάτων σε πεδίο Βαρύτητας. Γιώργος Νικολιδάκης
 Τροχιές σωμάτων σε πεδίο Βαρύτητας Γιώργος Νικολιδάκης 9/18/2013 1 Κωνικές Τομές Είναι καμπύλες που σχηματίζονται καθώς επίπεδα τέμνουν με διάφορες γωνίες επιφάνειες κώνων. Παραβολή Έλλειψη -κύκλος Υπερβολή
Τροχιές σωμάτων σε πεδίο Βαρύτητας Γιώργος Νικολιδάκης 9/18/2013 1 Κωνικές Τομές Είναι καμπύλες που σχηματίζονται καθώς επίπεδα τέμνουν με διάφορες γωνίες επιφάνειες κώνων. Παραβολή Έλλειψη -κύκλος Υπερβολή
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο. Σεμινάριο Φυσικής Ενότητα 14
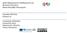 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Σεμινάριο Φυσικής Ενότητα 14 Γεωργακίλας Αλέξανδρος Ζουμπούλης Ηλίας Μακροπούλου Μυρσίνη Πίσσης Πολύκαρπος Άδεια Χρήσης
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Σεμινάριο Φυσικής Ενότητα 14 Γεωργακίλας Αλέξανδρος Ζουμπούλης Ηλίας Μακροπούλου Μυρσίνη Πίσσης Πολύκαρπος Άδεια Χρήσης
Λέανδρος Περιβολαρόπουλος Καθηγητής Παν/μίου Ιωαννίνων
 Open page Λέανδρος Περιβολαρόπουλος http://leandros.physics.uoi.gr Καθηγητής Παν/μίου Ιωαννίνων Αρχείο παρουσίασης διαθέσιμο μέσω του συνδέσμου: https://dl.dropbox.com/u/20653799/talks/eie.ppt Κλίμακες
Open page Λέανδρος Περιβολαρόπουλος http://leandros.physics.uoi.gr Καθηγητής Παν/μίου Ιωαννίνων Αρχείο παρουσίασης διαθέσιμο μέσω του συνδέσμου: https://dl.dropbox.com/u/20653799/talks/eie.ppt Κλίμακες
Συντελεστής επαναφοράς ή αποκατάστασης
 Συντελεστής επαναφοράς ή αποκατάστασης (Coefficient of restitution ή bounciness) Μία έννοια εξαιρετικά σημαντική για όσους φτιάχνουν ασκήσεις στις στιγμιαίες κρούσεις (με ορμές ή/και στροφορμές για την
Συντελεστής επαναφοράς ή αποκατάστασης (Coefficient of restitution ή bounciness) Μία έννοια εξαιρετικά σημαντική για όσους φτιάχνουν ασκήσεις στις στιγμιαίες κρούσεις (με ορμές ή/και στροφορμές για την
ds ds ds = τ b k t (3)
 Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Αστροφυσική. Ενότητα # 4: Αστρικοί άνεμοι, σφαιρική προσαύξηση και δίσκοι προσαύξησης. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστροφυσική Ενότητα # 4: Αστρικοί άνεμοι, σφαιρική προσαύξηση και δίσκοι προσαύξησης Λουκάς Βλάχος Τμήμα Φυσικής Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστροφυσική Ενότητα # 4: Αστρικοί άνεμοι, σφαιρική προσαύξηση και δίσκοι προσαύξησης Λουκάς Βλάχος Τμήμα Φυσικής Άδειες Χρήσης Το παρόν
Ονοματεπώνυμο Φοιτητή. Εργαστηριακό Τμήμα Π.χ. Δευτέρα
 Ονοματεπώνυμο Φοιτητή Εργαστηριακό Τμήμα Π.χ. Δευτέρα 11 00 13 00 Ομάδα Π.χ. 1A Πειραματική άσκηση Ελεύθερη πτώση Ημερομηνία Εκτέλεσης Άσκησης... / / 2015 Ημερομηνία παράδοσης εργαστ.αναφοράς... / / 2015
Ονοματεπώνυμο Φοιτητή Εργαστηριακό Τμήμα Π.χ. Δευτέρα 11 00 13 00 Ομάδα Π.χ. 1A Πειραματική άσκηση Ελεύθερη πτώση Ημερομηνία Εκτέλεσης Άσκησης... / / 2015 Ημερομηνία παράδοσης εργαστ.αναφοράς... / / 2015
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Ε. Στυλιάρης από παλαιότερες διαφάνειες του κ. Καραμπαρμπούνη) ΠΑΝΕΠΙΣΤΗΜΙΟN ΑΘΗΝΩΝ,, 5 6 6 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ Μέση και Στιγμιαία Ταχύτητα Επιτάχυνση Διαφορικές
(Με ιδέες και υλικό από ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Ε. Στυλιάρης από παλαιότερες διαφάνειες του κ. Καραμπαρμπούνη) ΠΑΝΕΠΙΣΤΗΜΙΟN ΑΘΗΝΩΝ,, 5 6 6 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ Μέση και Στιγμιαία Ταχύτητα Επιτάχυνση Διαφορικές
ΑΝΑΖΗΤΗΣΗ ΕΞΩΗΛΙΑΚΩΝ ΠΛΑΝΗΤΩΝ Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ
 ΑΝΑΖΗΤΗΣΗ ΕΞΩΗΛΙΑΚΩΝ ΠΛΑΝΗΤΩΝ Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ ΩΡΙΩΝ, 9/1/2008 Η ΘΕΣΗ ΜΑΣ ΣΤΟ ΣΥΜΠΑΝ Γη, ο τρίτος πλανήτης του Ηλιακού Συστήματος Περιφερόμαστε γύρω από τον Ήλιο, ένα τυπικό αστέρι της κύριας ακολουθίας
ΑΝΑΖΗΤΗΣΗ ΕΞΩΗΛΙΑΚΩΝ ΠΛΑΝΗΤΩΝ Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ ΩΡΙΩΝ, 9/1/2008 Η ΘΕΣΗ ΜΑΣ ΣΤΟ ΣΥΜΠΑΝ Γη, ο τρίτος πλανήτης του Ηλιακού Συστήματος Περιφερόμαστε γύρω από τον Ήλιο, ένα τυπικό αστέρι της κύριας ακολουθίας
Ακουστικό Ανάλογο Μελανών Οπών
 Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Σύγχρονη Φυσική 1, Διάλεξη 12, Τμήμα Φυσικής, Παν/μιο Ιωαννίνων Διαγράμματα Minkowski
 1 Διαγράμματα Minkowski Σκοποί της διάλεξης 12: Να εισάγει τα διαγράμματα Minkowski. 18.1.2012 Να περιγράψει την ιδέα του ταυτοχρονισμού στην θεωρία της σχετικότητας με μεθόδους γεωμετρίας. Να εισάγει
1 Διαγράμματα Minkowski Σκοποί της διάλεξης 12: Να εισάγει τα διαγράμματα Minkowski. 18.1.2012 Να περιγράψει την ιδέα του ταυτοχρονισμού στην θεωρία της σχετικότητας με μεθόδους γεωμετρίας. Να εισάγει
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/2014
 minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ
 ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. Γουργουλιάτος ΜΑΥΡΕΣ ΤΡΥΠΕΣ Η ΒΑΣΙΚΗ ΙΔΕΑ Αντικείμενα που εμποδίζουν την διάδοση φωτός από αυτά Πρωτοπροτάθηκε γύρω στα 1783 (John( John Michell) ως αντικείμενο
ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. Γουργουλιάτος ΜΑΥΡΕΣ ΤΡΥΠΕΣ Η ΒΑΣΙΚΗ ΙΔΕΑ Αντικείμενα που εμποδίζουν την διάδοση φωτός από αυτά Πρωτοπροτάθηκε γύρω στα 1783 (John( John Michell) ως αντικείμενο
[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)
![[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x) [1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)](/thumbs/52/30132893.jpg) [] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
[] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
Κεφάλαιο M2. Κίνηση σε μία διάσταση
 Κεφάλαιο M2 Κίνηση σε μία διάσταση Κινηματική Περιγράφει την κίνηση, αγνοώντας τις αλληλεπιδράσεις με εξωτερικούς παράγοντες που ενδέχεται να προκαλούν ή να μεταβάλλουν την κίνηση. Προς το παρόν, θα μελετήσουμε
Κεφάλαιο M2 Κίνηση σε μία διάσταση Κινηματική Περιγράφει την κίνηση, αγνοώντας τις αλληλεπιδράσεις με εξωτερικούς παράγοντες που ενδέχεται να προκαλούν ή να μεταβάλλουν την κίνηση. Προς το παρόν, θα μελετήσουμε
k 3/5 P 3/5 ρ = cp 3/5 (1) dp dr = ρg (2) P 3/5 = cgdz (3) cgz + P0 cg(z h)
 Αριστοτελειο Πανεπιστημιο Θεσσαλονικης ΤΜΗΜΑ ΦΥΣΙΚΗΣ 3ο Σετ Ασκήσεων Αστρονομίας Author: Σταμάτης Βρετινάρης Supervisor: Νικόλαος Στεργιούλας Λουκάς Βλάχος December 5, 215 1 Άσκηση Σφαιρικός αστέρας με
Αριστοτελειο Πανεπιστημιο Θεσσαλονικης ΤΜΗΜΑ ΦΥΣΙΚΗΣ 3ο Σετ Ασκήσεων Αστρονομίας Author: Σταμάτης Βρετινάρης Supervisor: Νικόλαος Στεργιούλας Λουκάς Βλάχος December 5, 215 1 Άσκηση Σφαιρικός αστέρας με
Διαδραστική Έκθεση Επιστήμης και Τεχνολογίας
 Διαδραστική Έκθεση Επιστήμης και Τεχνολογίας «Η επιστήμη και η γνώση προχωρούν ρ μπροστά μόνο αν αμφισβητήσουμε τους μεγάλους» Χρονικά της Φυσικής 1905 (Annalen der Physik) Γενική Θεωρία της Σχετικότητας
Διαδραστική Έκθεση Επιστήμης και Τεχνολογίας «Η επιστήμη και η γνώση προχωρούν ρ μπροστά μόνο αν αμφισβητήσουμε τους μεγάλους» Χρονικά της Φυσικής 1905 (Annalen der Physik) Γενική Θεωρία της Σχετικότητας
5 Σχετικιστική μάζα. Στο Σ Πριν Μετά. Στο Σ
 Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
1 Βασικά Στοιχεία υναµικής Κοσµολογίας
 1 Βασικά Στοιχεία υναµικής Κοσµολογίας Στα πλαίσια της Κοσµολογικής Αρχής µπορούµε να παράγουµε τις διαφορικές εξισώσεις της κοσµολογικής εξέλιξης είτε απέυθείας και µε αυστηρότητα από τις εξισώσεις πεδίου
1 Βασικά Στοιχεία υναµικής Κοσµολογίας Στα πλαίσια της Κοσµολογικής Αρχής µπορούµε να παράγουµε τις διαφορικές εξισώσεις της κοσµολογικής εξέλιξης είτε απέυθείας και µε αυστηρότητα από τις εξισώσεις πεδίου
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 26 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ Κυριακή, 13 Μαΐου, 2012 Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: 1) Είναι πολύ σημαντικό
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 26 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ Κυριακή, 13 Μαΐου, 2012 Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: 1) Είναι πολύ σημαντικό
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Γενική Θεωρία της Σχετικότητας
 Γενική Θεωρία της Σχετικότητας Αδρανειακή Βαρυτική Μάζα Σύμφωνα με τον Νεύτωνα η μάζα ενός σώματος ορίζεται με δύο τρόπους: Μέσω του δευτέρου νόμου F=ma. (Αδρανειακή Μάζα). Ζυγίζοντας το σώμα και εφαρμόζοντας
Γενική Θεωρία της Σχετικότητας Αδρανειακή Βαρυτική Μάζα Σύμφωνα με τον Νεύτωνα η μάζα ενός σώματος ορίζεται με δύο τρόπους: Μέσω του δευτέρου νόμου F=ma. (Αδρανειακή Μάζα). Ζυγίζοντας το σώμα και εφαρμόζοντας
Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς.
 Μ2 Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς. 1 Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί στη μέτρηση της επιτάχυνσης της βαρύτητας σε ένα τόπο. Αυτή η μέτρηση επιτυγχάνεται
Μ2 Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς. 1 Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί στη μέτρηση της επιτάχυνσης της βαρύτητας σε ένα τόπο. Αυτή η μέτρηση επιτυγχάνεται
Ανακάλυψη βαρυτικών κυµάτων από τη συγχώνευση δύο µαύρων οπών. Σελίδα LIGO
 Ανακάλυψη βαρυτικών κυµάτων από τη συγχώνευση δύο µαύρων οπών Σελίδα LIGO Πώς µία µάζα στο Σύµπαν στρεβλώνει τον χωροχρόνο (Credit: NASA) Πεδίο Βαρύτητας στη Γενική Σχετικότητα. Από την Επιτάχυνση ηµιουργούνται
Ανακάλυψη βαρυτικών κυµάτων από τη συγχώνευση δύο µαύρων οπών Σελίδα LIGO Πώς µία µάζα στο Σύµπαν στρεβλώνει τον χωροχρόνο (Credit: NASA) Πεδίο Βαρύτητας στη Γενική Σχετικότητα. Από την Επιτάχυνση ηµιουργούνται
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT
 ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
Το διαστημόπλοιο. Γνωστικό Αντικείμενο: Φυσική (Δυναμική σε μία διάσταση - Δυναμική στο επίπεδο) Τάξη: Α Λυκείου
 Το διαστημόπλοιο Γνωστικό Αντικείμενο: Φυσική (Δυναμική σε μία διάσταση - Δυναμική στο επίπεδο) Τάξη: Α Λυκείου Χρονική Διάρκεια Προτεινόμενη χρονική διάρκεια σχεδίου εργασίας: 5 διδακτικές ώρες Διδακτικοί
Το διαστημόπλοιο Γνωστικό Αντικείμενο: Φυσική (Δυναμική σε μία διάσταση - Δυναμική στο επίπεδο) Τάξη: Α Λυκείου Χρονική Διάρκεια Προτεινόμενη χρονική διάρκεια σχεδίου εργασίας: 5 διδακτικές ώρες Διδακτικοί
( ) ( r) V r. ( ) + l 2. Τι είδαμε: m!! r = l 2. 2mr 2. 2mr 2 + V r. q Ξεκινήσαμε την συζήτηση για το θέμα κεντρικής δύναμης
 ΦΥΣ 2 - Διαλ.4 Τι είδαμε: q Ξεκινήσαμε την συζήτηση για το θέμα κεντρικής δύναμης ü Ανάγαμε το πρόβλημα 2 σωμάτων σε πρόβλημα κεντρικής δύναμης ü διατήρηση ορμής CM μετατρέπει το πρόβλημα από 6 DoF σε
ΦΥΣ 2 - Διαλ.4 Τι είδαμε: q Ξεκινήσαμε την συζήτηση για το θέμα κεντρικής δύναμης ü Ανάγαμε το πρόβλημα 2 σωμάτων σε πρόβλημα κεντρικής δύναμης ü διατήρηση ορμής CM μετατρέπει το πρόβλημα από 6 DoF σε
Μεθοδολογία Παραβολής
 Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
1 + Φ r /c 2 = 1 (1) (2) c 2 k y 1 + (V/c) 1 + tan 2 α = sin α (3) tan α = k y k x
 ΛΥΣΕΙΣ ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ 6 Θ. Τομαράς 1. Πρωτόνια στις κοσμικές ακτίνες φτάνουν ακόμα και ενέργειες της τάξης των 10 20 ev. Να συγκρίνετε την ενέργεια αυτή με την ενέργεια που έχει μια πέτρα που πετάτε με
ΛΥΣΕΙΣ ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ 6 Θ. Τομαράς 1. Πρωτόνια στις κοσμικές ακτίνες φτάνουν ακόμα και ενέργειες της τάξης των 10 20 ev. Να συγκρίνετε την ενέργεια αυτή με την ενέργεια που έχει μια πέτρα που πετάτε με
Σύγχρονες αντιλήψεις γύρω από το άτομο. Κβαντική θεωρία.
 Σύγχρονες αντιλήψεις γύρω από το άτομο. Κβαντική θεωρία. Η κβαντική θεωρία αναπτύχθηκε με τις ιδέες των ακόλουθων επιστημόνων: Κβάντωση της ενέργειας (Max Planck, 1900). Κυματική θεωρία της ύλης (De Broglie,
Σύγχρονες αντιλήψεις γύρω από το άτομο. Κβαντική θεωρία. Η κβαντική θεωρία αναπτύχθηκε με τις ιδέες των ακόλουθων επιστημόνων: Κβάντωση της ενέργειας (Max Planck, 1900). Κυματική θεωρία της ύλης (De Broglie,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
ΠΛΗΡΟΦΟΡΙΕΣ - ΕΙΣΑΓΩΓΙΚΑ
 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΦΥΣΙΚΗ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2015-16 ΠΛΗΡΟΦΟΡΙΕΣ - ΕΙΣΑΓΩΓΙΚΑ 18/9/2014 ΕΙΣΑΓΩΓΗ_ΚΕΦ. 1 1 ΠΛΗΡΟΦΟΡΙΕΣ Διδάσκων Γεράσιμος Κουρούκλης Καθηγητής (Τμήμα Χημικών Μηχανικών). (gak@auth.gr,
ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΦΥΣΙΚΗ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2015-16 ΠΛΗΡΟΦΟΡΙΕΣ - ΕΙΣΑΓΩΓΙΚΑ 18/9/2014 ΕΙΣΑΓΩΓΗ_ΚΕΦ. 1 1 ΠΛΗΡΟΦΟΡΙΕΣ Διδάσκων Γεράσιμος Κουρούκλης Καθηγητής (Τμήμα Χημικών Μηχανικών). (gak@auth.gr,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Διατήρηση Ορμής Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός htt://hyiccore.wordre.co/ Βασικές Έννοιες Μέχρι τώρα έχουμε ασχοληθεί με την μελέτη ενός σώματος και μόνο. Πλέον
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Διατήρηση Ορμής Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός htt://hyiccore.wordre.co/ Βασικές Έννοιες Μέχρι τώρα έχουμε ασχοληθεί με την μελέτη ενός σώματος και μόνο. Πλέον
Το Μποζόνιο Higgs. Το σωματίδιο Higgs σύμφωνα με το Καθιερωμένο Πρότυπο
 1 Το Μποζόνιο Higgs 29/05/13 Σκοποί: I. Να απαντήσει στο ερώτημα του τι είναι ακριβώς το σωματίδιο Higgs. II. Να εισάγει τους διάφορους τρόπους παραγωγής και μετάπτωσης του Higgs. III. Να δώσει μία σύντομη
1 Το Μποζόνιο Higgs 29/05/13 Σκοποί: I. Να απαντήσει στο ερώτημα του τι είναι ακριβώς το σωματίδιο Higgs. II. Να εισάγει τους διάφορους τρόπους παραγωγής και μετάπτωσης του Higgs. III. Να δώσει μία σύντομη
( ) Ολική στροφορμή L = p! i. L =! R M! v + ri m i vi. r i. q Ορίζουμε την θέση ενός σημείου I από το κέντρο μάζας: r! i
 ΦΥΣ - Διαλ.03 Ολική στροφορμή q Ορίζουμε την θέση ενός σημείου I από το κέντρο μάζας: r = r R q Ορίζουμε επίσης τις ταχύτητες: v = " r v = και R " Ø Υπολογίζουμε την ολική στροφορμή L = r p = L = R M v
ΦΥΣ - Διαλ.03 Ολική στροφορμή q Ορίζουμε την θέση ενός σημείου I από το κέντρο μάζας: r = r R q Ορίζουμε επίσης τις ταχύτητες: v = " r v = και R " Ø Υπολογίζουμε την ολική στροφορμή L = r p = L = R M v
Data Analysis Examination
 Data Analysis Examination Page 1 of (D1) Διπλός Πάλσαρ Κάνοντας συστηµατικές έρευνες τις τελευταίες δεκαετίες, οι αστρονόµοι κατάφεραν να εντοπίσουν ένα µεγάλο πλήθος από πάλσαρς µε περίοδο περιστροφής
Data Analysis Examination Page 1 of (D1) Διπλός Πάλσαρ Κάνοντας συστηµατικές έρευνες τις τελευταίες δεκαετίες, οι αστρονόµοι κατάφεραν να εντοπίσουν ένα µεγάλο πλήθος από πάλσαρς µε περίοδο περιστροφής
ΚΙΝΗΣΕΙΣ ΣΩΜΑΤΩΝ ΣΕ ΟΜΟΓΕΝΗ ΠΕΔΙΑ
 2 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 467 ΚΙΝΗΣΕΙΣ ΣΩΜΑΤΩΝ ΣΕ ΟΜΟΓΕΝΗ ΠΕΔΙΑ Βαρυπάτη Αθηνά Φυσικός- Επιμορφώτρια Τ.Π.Ε. avarypat@de.sch.gr Μαστραλέξης Δημήτρης Φυσικός-Επιμορφωτής Τ.Π.Ε. dmastral@de.sch.gr
2 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 467 ΚΙΝΗΣΕΙΣ ΣΩΜΑΤΩΝ ΣΕ ΟΜΟΓΕΝΗ ΠΕΔΙΑ Βαρυπάτη Αθηνά Φυσικός- Επιμορφώτρια Τ.Π.Ε. avarypat@de.sch.gr Μαστραλέξης Δημήτρης Φυσικός-Επιμορφωτής Τ.Π.Ε. dmastral@de.sch.gr
kg(χιλιόγραμμο) s(δευτερόλεπτο) Ένταση ηλεκτρικού πεδίου Α(Αμπέρ) Ένταση φωτεινής πηγής cd (καντέλα) Ποσότητα χημικής ουσίας mole(μόλ)
 ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
Χημεία Γ Λυκείου Θετικής Κατεύθυνσης
 Χημεία Γ Λυκείου Θετικής Κατεύθυνσης Κεφάλαιο 1 Ηλεκτρονιακή δομή των ατόμων 1 Εισαγωγή Δομή του ατόμου Δημόκριτος Αριστοτέλης Dalton Thomson 400 π.χ. 350π.χ. 1808 1897 Απειροελάχιστα τεμάχια ύλης (τα
Χημεία Γ Λυκείου Θετικής Κατεύθυνσης Κεφάλαιο 1 Ηλεκτρονιακή δομή των ατόμων 1 Εισαγωγή Δομή του ατόμου Δημόκριτος Αριστοτέλης Dalton Thomson 400 π.χ. 350π.χ. 1808 1897 Απειροελάχιστα τεμάχια ύλης (τα
Καλώς ήλθατε. Καλό ξεκίνημα.
 Καλώς ήλθατε. Καλό ξεκίνημα. Αν. Καθηγητής Γεώργιος Παύλος ( Φυσικός) - ρ.καρκάνης Αναστάσιος (Μηχανολόγος Μηχανικός) Με τι θα ασχοληθούμε στα πλαίσια του μαθήματος: Α. Μαθηματική θεωρία ιανυσματικά μεγέθη,
Καλώς ήλθατε. Καλό ξεκίνημα. Αν. Καθηγητής Γεώργιος Παύλος ( Φυσικός) - ρ.καρκάνης Αναστάσιος (Μηχανολόγος Μηχανικός) Με τι θα ασχοληθούμε στα πλαίσια του μαθήματος: Α. Μαθηματική θεωρία ιανυσματικά μεγέθη,
ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
 Tel.: +30 2310998051, Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Ιστοσελίδα: http://users.auth.gr/theodoru ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
Tel.: +30 2310998051, Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Ιστοσελίδα: http://users.auth.gr/theodoru ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
ιανυσµατικά πεδία Όπως έχουµε ήδη αναφέρει ένα διανυσµατικό πεδίο είναι µια συνάρτηση
 44 ιανυσµατικά πεδία Όπως έχουµε ήδη αναφέρει ένα διανυσµατικό πεδίο είναι µια συνάρτηση F : U R R. Για εµάς φυσικά µια τέτοια συνάρτηση θα θεωρείται ότι είναι τουλάχιστον συνεχής και συνήθως C και βέβαια
44 ιανυσµατικά πεδία Όπως έχουµε ήδη αναφέρει ένα διανυσµατικό πεδίο είναι µια συνάρτηση F : U R R. Για εµάς φυσικά µια τέτοια συνάρτηση θα θεωρείται ότι είναι τουλάχιστον συνεχής και συνήθως C και βέβαια
Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2011
 Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2011 Patra, 11 Febrouariou 2011 1 Jèma 1 1.1 DiatÔpwsh Στην αριθμητική διαπραγμάτευση ενός κοσμολογικού μοντέλου εμπλέκονται οι ρίζες ενός «χαρακτηριστικού
Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2011 Patra, 11 Febrouariou 2011 1 Jèma 1 1.1 DiatÔpwsh Στην αριθμητική διαπραγμάτευση ενός κοσμολογικού μοντέλου εμπλέκονται οι ρίζες ενός «χαρακτηριστικού
Φυσικά μεγέθη. Φυσική α λυκείου ΕΙΣΑΓΩΓΗ. Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα. Β.
 ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
14 η εβδομάδα (26/01/2017) Έγιναν οι ασκήσεις 28, 29 και 30. Έγινε επανάληψη στη Θεωρία Καμπυλών και στη Θεωρία Επιφανειών.
 14 η εβδομάδα (26/01/2017) Έγιναν οι ασκήσεις 28, 29 και 30. Έγινε επανάληψη στη Θεωρία Καμπυλών και στη Θεωρία Επιφανειών. 13 η εβδομάδα (16/01/2017 & 19/01/2017) Ασυμπτωτική διεύθυνση και ασυμπτωτικό
14 η εβδομάδα (26/01/2017) Έγιναν οι ασκήσεις 28, 29 και 30. Έγινε επανάληψη στη Θεωρία Καμπυλών και στη Θεωρία Επιφανειών. 13 η εβδομάδα (16/01/2017 & 19/01/2017) Ασυμπτωτική διεύθυνση και ασυμπτωτικό
ΚΟΣΜΟΛΟΓΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ ΧΕΙΜΩΝΑΣ 2004 Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ
 ΚΟΣΜΟΛΟΓΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ ΧΕΙΜΩΝΑΣ 2004 Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ Η Μεγάλη Έκρηξη Πριν από 10-15 δις χρόνια γεννήθηκε το Σύμπαν με μια εξαιρετικά θερμή και βίαια διαδικασία Το σύμπαν
ΚΟΣΜΟΛΟΓΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ ΧΕΙΜΩΝΑΣ 2004 Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ Η Μεγάλη Έκρηξη Πριν από 10-15 δις χρόνια γεννήθηκε το Σύμπαν με μια εξαιρετικά θερμή και βίαια διαδικασία Το σύμπαν
