Κεφάλαιο Προσοµοιώσεις
|
|
|
- Γῆ Ανδρέου
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 4 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όλες οι ακιβείς επιστήµες κυιαχούνται από την ιδέα της ποσέγγισης. Bertrad Russell 4. Ποσοµοιώσεις Σκοπός του παόντος κεφαλαίου είναι η παουσίαση της υπολογιστικής ποσέγγισης των πειαµατικών αποτελεσµάτων του ποηγούµενου κεφαλαίου. Παουσιάζονται οι τόποι µοντελοποίησης του αναπτυσσόµενου δυναµικού και της µεταβατικής αντίστασης διαφόων συστηµάτων γείωσης. Τα αποτελέσµατα της υπολογιστικής ποσέγγισης συγκίνονται µε τα πειαµατικά αποτελέσµατα του ποηγούµενου κεφαλαίου, καθώς και µε αποτελέσµατα ποσοµοίωσης και πειαµάτων άλλων εευνητών. Η αντίσταση γείωσης και τα άλλα χαακτηιστικά (της απόκισης) των συστηµάτων γείωσης στη µόνιµη κατάσταση µποούν να υπολογιστούν απ` ευθείας στο πεδίο του χόνου µε κλειστού τύπου µαθηµατικές εκφάσεις. Τούτο, επίσης, είναι δυνατό να γίνει, βάσει της υπάχουσας βιβλιογαφίας [45], στην πείπτωση της µεταβατικής απόκισης του οιζόντιου ηλεκτοδίου γείωσης. Στο εγαστήιο Υψηλών Τάσεων παγµατοποιήθηκε κυκλωµατική και πεδιακή ανάλυση ηλεκτοδίων γείωσης τοποθετηµένων σε οµοιογενές αλλά και σε πολυστωµατικό έδαφος. Στη συνέχεια, παουσιάζονται οι τόποι µοντελοποίησης του ηλεκτοδίου γείωσης, οι µέθοδοι για τον υπολογισµό των πααµέτων των µοντέλων του ηλεκτοδίου γείωσης, αλλά και η µέθοδος υπολογισµού των πααµέτων της πολυστωµατικής δοµής του εδάφους. Για τις υπολογιστικές ποσεγγίσεις χησιµοποιήθηκαν τα πακέτα λογισµικού PC- Opera D (versio 8.5) [5] και PSCAD/EMTDC (versio 3.) [6]. Επίσης, χησιµοποιήθηκε κώδικας υλοποιηµένος σε Matlab [7] και γλώσσα C [8]. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ
2 Το PC Opera είναι ένα πακέτο πογαµµάτων ανάλυσης ποβληµάτων ηλεκτοµαγνητικού πεδίου. Για την ανάλυση ακολουθείται η µέθοδος των πεπεασµένων στοιχείων και επίλυση των µεικών διαφοικών εξισώσεων που πειγάφουν τη συµπειφοά του πεδίου [5]. Το EMTDC είναι ένας ποσοµοιωτής µεταβατικής κατάστασης που εξελίσσεται από τα µέσα της δεκαετίας του `7. Η δηµιουγία του είναι εµπνευσµένη από το κλασσικό άθο του Dommel [9]. Το PSCAD/EMTDC είναι ένα επαγγελµατικό εγαλείο ποσοµοίωσης για την ανάλυση συστηµάτων ισχύος, το PSCAD είναι το γαφικό πειβάλλον και το EMTDC είναι η µηχανή ποσοµοίωσης [6]. 4. Ανάλυση κατακόυφων άβδων γείωσης 4.. Θεωητική ποσέγγιση κατακόυφων άβδων γείωσης (κυκλωµατική) Το πιο απλό σύστηµα γείωσης αποτελείται από ένα χάλκινο, συνήθως, ηλεκτόδιο τοποθετηµένο κατακόυφα, όπως φαίνεται µαζί µε το ισοδύναµο κύκλωµα του στο Σχήµα 4..α. (α) (β) Σχήµα 4.: Ισοδύναµο κύκλωµα (α) ενός κατακόυφου ηλεκτόδιου (β) ενός τιγώνου γείωσης Η διαφοική εξίσωση που πειγάφει τη διαφοά δυναµικού µεταξύ του σηµείου έγχυσης του κουστικού εύµατος και της άπειης γης είναι: u(t) = R i L di R (4.) dt ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ
3 Τα κουστικά εύµατα που ποσοµοιώνουν τα κεαυνικά πλήγµατα, συνήθως, ποσοµοιώνονται µε διπλοεκθετικές συνατήσεις [3-8]: at bt ( ) i() t = I e e o (4.) Η εξίσωση του δυναµικού, λαµβάνοντας υπόψη τη µοφή του κουστικού εύµατος, εκφάζεται στο πεδίο της συχνότητας ως εξής: L s L s u ( s) = ( ) ( ) ( ) ( ) (4.3) C s a s τ C s b s τ s a s b όπου τ = R C Εφαµόζοντας αντίστοφο µετασχηµατισµό Laplace, η εξίσωση δυναµικού εκφάζεται στο πεδίο του χόνου: u( t) = I o R τ τt e ( b a) ( τ a) ( τ b) bt at ( ) e τ at bt ( τ b) e ( τ a) ( τ a) ( τ b) I L be ae (4.4) o Η κουστική σύνθετη αντίσταση (σχέση 3.) οίζεται ως ο λόγος της κουστικής τάσης πος το κουστικό εύµα. Η µαθηµατική εξίσωση 4.5.α, που πειγάφει τη συµπειφοά ενός συγκεκιµένου συστήµατος, εξάγεται από την κυκλωµατική ανάλυση θεωώντας τα στοιχεία συγκεντωµένα και είναι η ακόλουθη: z ( t) at ( τ b) e ( τ a) ( b a) bt tτ e e = R τ at bt ( τ a) ( τ b) ( e e ) at b t ( τ - a) ( τ - b) ( e e ) bt at b e a e L at b t (4.5.α) e e Ένα άλλο κοινώς χησιµοποιούµενο σύστηµα γείωσης είναι το τίγωνο γείωσης, το οποίο αποτελείται από τεις κατακόυφες χάλκινες άβδους, όπως φαίνεται στο σχήµα 4..β µαζί µε το ισοδύναµο κύκλωµά του. Η εξίσωση 4.5.β, που πειγάφει τη συµπειφοά ενός συστήµατος αποτελούµενου από τεις παάλληλες κατακόυφες άβδους και η οποία ποκύπτει από την κυκλωµατική ανάλυση ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ
4 θεωώντας συγκεντωµένα στοιχεία -όπως στη διάταξη του σχήµατος 4..β- και ανάλογη µεθοδολογία µε αυτή της µίας κατακόυφης άβδου, δίνεται παακάτω: z ( t) at ( τ b) e ( τ a) ( b a) bt tτ R e e ( ) ( ) ( ) ( ) ( ) ( ) τ at bt at b t 3 τ a τ b e e τ - a τ - b e e bt at L be ae at bt 3 e e (4.5.β) = Η αντίσταση µόνιµης κατάστασης µίας κατακόυφης άβδου υπολογίζεται από την ακόλουθη σχέση, υποθέτοντας οµοιόµοφο εύµα κατά µήκος της άβδου [8]: R = l 8 l π l d, (4.6.α) ενώ η αντίσταση µόνιµης κατάστασης κάθε κατακόυφης άβδου του τιγώνου γείωσης υπολογίζεται από την σχέση [8]: R = l 3 l 4 π l d d d d l 6 l (4.6.β) Η χωητικότητα µίας κατακόυφης άβδου δίνεται από τη σχέση [8]: C r o = π ε ε l l 4, (4.7.α) l d ενώ η χωητικότητα κάθε κατακόυφης άβδου της διάταξης των τιών άβδων µε τη χήση των ισοδυνάµων αποστάσεων υπολογίζεται από την σχέση [, ]: C r o = π ε ε l l d d (4.7.β) Η επαγωγή µίας κατακόυφης άβδου δίνεται από τη σχέση [8]: L l 4 7 l = l, d (4.8.α) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 3
5 ενώ η επαγωγή κάθε κατακόυφης άβδου, συνυπολογίζοντας και την αµοιβαία επαγωγή, δίνεται από την ακόλουθη σχέση [, ]: L l 7 = π l l( d ) (4.8.β) r όπου η ειδική αντίσταση του εδάφους l το µήκος της άβδου d η διάµετος της άβδου ε o η διηλεκτική σταθεά του κενού ε r η σχετική διηλεκτική σταθεά του εδάφους r η ακτίνα της άβδου d η απόσταση µεταξύ δύο άβδων r =,7788 rη ισοδύναµη ακτίνα Στην πααπάνω σχέση η ισοδύναµη ακτίνα r χησιµοποιείται ποκειµένου να αντισταθµίσει τον ιονισµό του εδάφους. 4.. Θεωητική ποσέγγιση κατακόυφων άβδων γείωσης (πεδιακή) Θεωείται η τιστωµατική δοµή του εδάφους του σχήµατος 4. [8]. Τα δύο οµόκεντα ηµισφαίια ακτίνων α και α, χωίζουν το έδαφος σε τεις πειοχές I, II και III, οι οποίες έχουν ειδική αντίσταση, και 3 αντίστοιχα. Στην παούσα ανάλυση το σύστηµα γείωσης υποτίθεται ότι είναι τοποθετηµένο οπουδήποτε στον χώο του εδάφους (σχήµα 4.) και µποεί, επίσης, να εκτείνεται σε διαφοετικές πειοχές. Για την επίλυση που ακολουθεί, θεωείται η πείπτωση µιας σηµειακής πηγής εύµατος ευισκοµένης στο κέντο µίας σφαιικής πειοχής, η οποία χωίζεται από δύο οµόκεντες σφαίες σε τεις τοµείς. Η πείπτωση αυτή, λόγω της συµµετίας που παουσιάζει, είναι ποτιµότεη από το µοντέλο που πειγάφηκε στο σχήµα 4., στο οποίο η µισή σφαία είναι στο έδαφος και η άλλη µισή στον αέα. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 4
6 Επιφάνεια εδάφους α φ θ 3 Ι ΙΙ ΙΙΙ α Σχήµα 4.: Εδάφη µε ηµισφαιική διαστωµάτωση Πόκειται για ένα γενικευµένο πόβληµα της συνάτησης Gree [8]: ύπαξη µίας σηµειακής πηγής µε τη συνθήκη ότι το δυναµικό πααµένει µεταξύ των οίων r = και r = (όπου r είναι η σφαιική συντεταγµένη του σηµείου αναφοάς) και µε οιακές συνθήκες και συνθήκες συνέχειας στα όια των διαφοετικών εδαφών. Ο στόχος είναι να υπολογιστεί το ηλεκτικό δυναµικό εξαιτίας της σηµειακής πηγής εύµατος, οπουδήποτε στο έδαφος. Για το σκοπό αυτό οιοθετούνται τεις διαφοετικές πειοχές για την πηγή: r <α, α <r <α και r >α, όπου r είναι η ακτινική σφαιική συντεταγµένη της σηµειακής πηγής. Στη συνέχεια, εξάγονται εκφάσεις εξατώµενες από τις πειοχές που βίσκεται τόσο η πηγή, όσο και το σηµείο αναφοάς. Ξεκινώντας µε την υπόθεση πως η λύση σε γενικευµένη µοφή είναι µια πολλαπλή σειά σε ένα σφαιικό σύστηµα συντεταγµένων και λαµβάνοντας υπ όψιν τις πειοχές της πηγής και του σηµείου αναφοάς, τίθενται οι οιακές συνθήκες και οι συνθήκες συνέχειας και εκφάζονται οι ελεύθεες µεταβλητές ως µια διπλή σειά όων των σχετιζόµενων συνατήσεων Legedre, όπου είναι απααίτητο. Τελικά, η διαδικασία επίλυσης καταλήγει στις εκφάσεις που δίνουν τα ηλεκτικά δυναµικά εξαιτίας της σηµειακής πηγής εύµατος, για τις διάφοες πειοχές τοποθέτησής της. Για το ηµισφαιικό µοντέλο, που φαίνεται στο σχήµα 4., η λύση µποεί εύκολα να βεθεί µε τη µέθοδο των ειδώλων, αξιοποιώντας τα αποτελέσµατα από την πείπτωση των σφαιών. Αν η παγµατική πηγή δυναµικού εντοπίζεται στο (r, θ, φ ), τότε το είδωλο της πηγής εντοπίζεται στο (r, π-θ, φ ) και έχει την ίδια ένταση µε την παγµατική πηγή. Το z ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 5
7 δυναµικό οπουδήποτε στον χώο οφείλεται τόσο στις παγµατικές, όσο και στις φανταστικές πηγές (στο µοντέλο του εδάφους µε τις δυο οµόκεντες σφαίες). Η συνεισφοά της φανταστικής πηγής εύκολα υπολογίζεται, αντικαθιστώντας το θ µε το π-θ στη λύση της πείπτωσης µε την παγµατική πηγή. Όταν η σηµειακή πηγή είναι στην πειοχή I, οι µεικές διαφοικές εξισώσεις που ισχύουν για κάθε πειοχή είναι [8]: V I r r = I δ ( ), για r<α (4.9.α) V =, για α <r<α (4.9.β) II V =, για r>α (4.9.γ) III Ποκειµένου να λυθεί η πώτη εξίσωση του πααπάνω συστήµατος εξισώσεων, η οποία είναι Poisso, γίνεται η αντικατάσταση [8]: V I I = V I r r 4 π, (4.) οπότε µετατέπεται σε Laplace, και το σύστηµα γίνεται: V I =, για r<α (4..α) V =, για α <r<α (4..β) II V =, για r>α (4..γ) III Ακολουθώντας την διαδικασία που πειγάφεται αναλυτικά στο Παάτηµα 4 η λύση που ποκύπτει είναι: V V I II = = = m= = m= r m Im A (cos ) cos[ ( m r P θ m φ φ)] (4..α) r B m r C m m P (cos ) cos[ ( θ m φ φ)] (4..β) r ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 6
8 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 7 = = = )] ( cos[ ) (cos m m m III m P r D V φ φ θ (4..γ) όπου ) (cos θ m P και ) (cosθ m P είναι τα πολυώνυµα ή συνατήσεις Legedre πώτου είδους. Οι συνατήσεις Legedre ) (cosθ m Q δευτέου είδους (οι οποίες απειίζονται) δεν εµφανίζονται στη λύση γιατί αναζητούνται φαγµένες λύσεις. Ο υπολογισµός των συντελεστών (A m, B m, C m, D m ) παουσιάζεται αναλυτικά στο Παάτηµα 4. Οι συντελεστές (A m, B m, C m, D m ) δίνονται από τις σχέσεις (4.3): = = = = m m m m m m m m r I D r I C a a r I B a a r a a r I A ) ( ) ( (4.3) µε τον συντελεστή να δίνεται από τη σχέση (4.4): = 3 3 a a (4.4) Η λύση που ποέκυψε έχει την ίδια µοφή µε τη λύση στην εγασία [8], µόνο που διαφέουν οι όοι στη σχέση (4.3). Στο Παάτηµα 4 υπολογίζεται το δυναµικό και για την πείπτωση στην οποία θεωείται ότι η σηµειακή πηγή εύµατος βίσκεται στην πειοχή ΙΙ του σχήµατος 4..
9 4..3 Πααδείγµατα της ποσέγγισης σε κατακόυφες άβδους γείωσης Εφαµόζοντας την ποσέγγιση της ποηγούµενης πααγάφου υπολογίζεται η µεταβατική σύνθετη αντίσταση συνηθισµένων συστηµάτων γείωσης που αποτελούνται από µία ή πεισσότεες κατακόυφες άβδους []. Η µελέτη εφαµόστηκε σε ακετά συστήµατα γείωσης, στα οποία έγινε έγχυση κεαυνικού εύµατος. Οι συντελεστές a, b της διπλοεκθετικής εξίσωσης (εξίσωση 4.) παίνουν τις τιµές 999s - και s - αντίστοιχα. Χησιµοποιώντας την εξίσωση 4.5.α η µεταβολή της κουστικής σύνθετης αντίστασης µίας κατακόυφης άβδου παουσιάζεται στα σχήµατα 4.3α 4.6α, ενώ µε χήση της εξίσωσης 4.5.β η µεταβολή της κουστικής σύνθετης αντίστασης ενός τιγώνου (µε µήκος πλευάς d ) αποτελούµενο από τεις κατακόυφες άβδους απεικονίζεται στα σχήµατα 4.3β 4.6β. Είναι εµφανές από τα σχήµατα ότι και η αντίσταση µονίµου καταστάσεως και η σύνθετη κουστική αντίσταση παουσιάζουν µικότεες τιµές για το τίγωνο γείωσης σε σχέση µε τη µία κατακόυφη άβδο. Από το σχήµα 4.5 είναι εµφανές ότι η µεταβολή της διαµέτου του ηλεκτοδίου δεν επιδά σηµαντικά, ιδιαίτεα στην πείπτωση του τιγώνου, ούτε στην αντίσταση µονίµου καταστάσεως, ούτε στη σύνθετη κουστική αντίσταση Z [Ω] Z [Ω] l=.5 m l=.5 m (α) µία κατακόυφη άβδο (β) τίγωνο Σχήµα 4.3: Κουστική σύνθετη αντίσταση συνατήσει του χόνου µεταβάλλοντας το µήκος του ηλεκτοδίου (=3 Ωm, d=mm, d =m, l =.5,.,.5,.m) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 8
10 Z [Ω] Z [Ω] 5 5 = Ωm =75 Ωm =3 Ωm = Ωm t [µsec] 4 3 =3 Ωm = Ωm =75 Ωm = Ωm t [µsec] (α) µία κατακόυφη άβδο (β) τίγωνο Σχήµα 4.4: Κουστική σύνθετη αντίσταση συνατήσει του χόνου µεταβάλλοντας την ειδική αντίσταση του εδάφους ( l =.5m, d=mm, d =m, =, 3, 75, Ωm) 4 Z [Ω] Z [Ω] d=5 mm d= mm d=4 mm t [µsec] d=5 mm d= mm d=4 mm t [µsec] (α) µία κατακόυφη άβδο (β) τίγωνο Σχήµα 4.5: Κουστική σύνθετη αντίσταση συνατήσει του χόνου µεταβάλλοντας τη διάµετο του ηλεκτοδίου ( l =.5m, d =m, =3Ωm, d=5,, 4mm) (α) µία κατακόυφη άβδο (β) τίγωνο Σχήµα 4.6: Κουστική σύνθετη αντίσταση συνατήσει του χόνου και του µήκους για µία κατακόυφη άβδο (d=mm, =3Ωm, d =m) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 9
11 4.3 Κυκλωµατική ποσέγγιση συστηµάτων γείωσης Ένα ηλεκτόδιο τοποθετηµένο οιζόντια ή κατακόυφα αποτελεί µια απλή διάταξη γείωσης. Επιπλέον, αποτελεί στοιχειώδες τµήµα ενός συστήµατος γείωσης. Η ανάλυση της συµπειφοάς του, υπό µεταβατικές συνθήκες, θέτει τη βάση για τον υπολογισµό της συµπειφοάς µιας γείωσης µε σύνθετη γεωµετία. Στη συνέχεια, επιχειείται µια ποσπάθεια κυκλωµατικής ποσοµοίωσης των συστηµάτων γείωσης. Στη διεθνή βιβλιογαφία παουσιάζονται συχνά κυκλωµατικές ποσεγγίσεις. Στη συγκεκιµένη µελέτη χησιµοποιήθηκε το µοντέλο των π-ισοδύναµων κυκλωµάτων. Στο µοντέλο αυτό το ηλεκτόδιο διαµοιάζεται σε ίσα τµήµατα, καθένα από τα οποία παιστάνεται µε ένα π-κύκλωµα. Ποκειµένου να ποσοµοιωθούν οι επιµέους αγωγοί των πλεγµάτων µε τα αντίστοιχα Τ, Γ και Π ισοδύναµα κυκλώµατα, θα υπολογιστούν τα στοιχεία αυτών. Απώτεος σκοπός της µαθηµατικής αυτής ποσέγγισης των στοιχείων είναι ο υπολογισµός της συνολικής σύνθετης αντίστασης γείωσης του πλέγµατος. Το πλέγµα αποτελείται από οιζόντιους και κάθετους στοιχειώδεις αγωγούς. Κάθε στοιχειώδης αγωγός του πλέγµατος µποεί να αντικατασταθεί µε ένα από τα τία ισοδύναµα κυκλώµατα Γ, Π και Τ [, ]. Τα κυκλώµατα αυτά αποτελούνται από στοιχεία συνδεδεµένα σε σειά ή παάλληλα, τα οποία µποούν να υπολογιστούν µε τον ίδιο τόπο και για τα τία κυκλώµατα. Η διαφοετική ονοµασία του καθενός ποκύπτει ανάλογα µε τη θέση του εγκάσιου κλάδου, όπως φαίνεται στο σχήµα 4.7. R L R L R/ L/ L/ R/ G C G/ G/ C/ G C Σχήµα 4.7: Ισοδύναµα κυκλώµατα. Όλα πειλαµβάνουν στον οιζόντιο κλάδο την ωµική αντίσταση και την αυτεπαγωγή του στοιχείου του συστήµατος και στον εγκάσιο κλάδο την εγκάσια αγωγιµότητα και τη χωητικότητα του στοιχείου. Τα στοιχεία σειάς, που είναι η ωµική αντίσταση R και η επαγωγή L, οιοθετούν το εύµα. Τα παάλληλα στοιχεία, που ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ
12 είναι η εγκάσια αγωγιµότητα G και η χωητικότητα C, εκφάζουν τις απώλειες εύµατος πος τη γη. Από τα εν σειά στοιχεία το πιο σηµαντικό από πλευάς µεγέθους είναι η επαγωγή, ενώ η ωµική αντίσταση που εκφάζει τις απώλειες του αγωγού πολλές φοές µποεί να αµεληθεί χωίς σηµαντικό σφάλµα. Από τα παάλληλα στοιχεία σπουδαιότεο όλο παίζει η αγωγιµότητα. Η επίδαση της χωητικότητας είναι, συνήθως, πολύ µική σε σύγκιση µε αυτή της εγκάσιας αγωγιµότητας και, συνεπώς, πολύ συχνά αγνοείται Ωµική αντίσταση ευθύγαµµου τµήµατος Η κατανοµή του εύµατος ενός κυλινδικού αγωγού που διαέεται από εύµα µηδενικής συχνότητας είναι οµοιόµοφη και η ωµική του αντίσταση R δίνεται από τη σχέση [, ]: l R = π r (4.5) όπου η ειδική αντίσταση του αγωγού l το µήκος του αγωγού r η ακτίνα του αγωγού Η ωµική αντίσταση ενός αγωγού επηεάζεται όχι µόνο από την ειδική αντίσταση του υλικού και τις διαστάσεις του αγωγού, αλλά και από τη συχνότητα του εύµατος που τον διαέει. Η κατανοµή του εύµατος µέσα στον αγωγό είναι ανοµοιόµοφη και η ανοµοιοµοφία αυτή γίνεται τόσο εντονότεη, όσο αυξάνεται η συχνότητα [, ]. Το εύµα συγκεντώνεται στην επιφάνεια του αγωγού µε αποτέλεσµα η παγµατική διατοµή του αγωγού που διαέεται από εύµα να είναι µικότεη. Αυτό οδηγεί σε αύξηση της αποτελεσµατικής αντίστασης ενός συµπαγούς αγωγού. Σε πολύ υψηλές συχνότητες η αύξηση αυτή είναι έντονη και η αντίσταση του αγωγού µποεί να γίνει µέχι και είκοσι φοές µεγαλύτεη από την αντίσταση που θα είχε αν διαεόταν από συνεχές εύµα. Το φαινόµενο αυτό ονοµάζεται «επιδεµικό φαινόµενο». Το επιδεµικό φαινόµενο µποεί να εκτιµηθεί ποσεγγιστικά µε τη βοήθεια ενός παάγοντα δ, ο οποίος ονοµάζεται βάθος διείσδυσης και εκφάζει το πάχος του ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ
13 τοιχώµατος ενός σωληνωτού αγωγού (ίσης εξωτεικής διαµέτου µε εκείνητου παγµατικού αγωγού) του οποίου η αντίσταση, όταν αυτός διαέεται από εύµα µηδενικής συχνότητας, θα ήταν πείπου ίση µε την αντίσταση του παγµατικού αγωγού, όταν αυτός διαέεται από εύµα µη µηδενικής συχνότητας f. Το βάθος διείσδυσης δ δίνεται από τη σχέση [,,,.]: Ro δ =. r (4.6) f όπου R o η αντίσταση συνεχούς εύµατος που δίνεται από τη σχέση (4.5) r η ακτίνα του αγωγού f η συχνότητα του εύµατος Εναλλακτικά, χησιµοποιείται για το βάθος διείσδυσης δ η σχέση [69]: δ = (4.7) ω µ σ όπου ω = π f η κυκλική συχνότητα του εύµατος µ η µαγνητική διαπεατότητα του αγωγού σ η ειδική αγωγιµότητα του αγωγού Ο λόγος της εξατώµενης από τη συχνότητα αντίστασης γείωσης πος την αντίσταση συνεχούς εύµατος δίνεται από τη σχέση [69]: R Ro 4 r δ = 48 r 3 δ 4 3 r δ για για r < δ r > δ (4.8) Εποµένως, για r δ ο λόγος R τείνει στο R o r δ. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ
14 Γαφικά ο λόγος της εξατώµενης από τη συχνότητα αντίστασης γείωσης πος την αντίσταση συνεχούς εύµατος συνατήσει του παάγοντα r ω µ σ αναπαίσταται στο σχήµα 4.8. Li L io,,8 L L i io 5, 4, R R o ω Li, R o,6 3,,4, R R o ω Li R o,, r ω µ σ Σχήµα 4.8: Γαφική παάσταση R συνατήσει του παάγοντα R o r ω µ σ [69] 4.3. Εγκάσια αγωγιµότητα ευθυγάµµου τµήµατος Η εγκάσια αγωγιµότητα οιζοντίου ηλεκτοδίου του σχήµατος 4.9 δίνεται στη βιβλιογαφία από πολλές εναλλακτικές σχέσεις. Αέας d l h Σχήµα 4.9: Οιζόντιο ηλεκτόδιο σε διστωµατικό έδαφος Ο Sirotijskij [69, 3] για τον υπολογισµό της εγκάσιας αγωγιµότητας οιζοντίου ηλεκτοδίου χησιµοποιεί τη σχέση: ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 3
15 G = π l l l s l l r d l l r (4.9) όπου s η ειδική αντίσταση του εδάφους l το µήκος του αγωγού r η ακτίνα του αγωγού d το βάθος τοποθέτησης του αγωγού Ο Ajekov [69, 4] για τον υπολογισµό της εγκάσιας αγωγιµότητας οιζοντίου ηλεκτοδίου ποτείνει τη σχέση: G = π l l s l r d (4.) Οι Verma και Mukhedkar [6] δηµοσίευσαν σε άθο τους ότι, ανάλογα µε το βάθος τοποθέτησης του οιζόντιου αγωγού, η αγωγιµότητά του δίνεται από τους τύπους: π l l s l r G = π l l s l r ( ισχύει για µεγάλο βάθος) ( ισχύει για µικό βάθος) (4.) Οι Mazzetti και Veca [6] ποτείνουν έναν τύπο για τον υπολογισµό της ανά µονάδα µήκους αντίστασης γείωσης R (που είναι το αντίστοφο της αγωγιµότητας) οιζοντίου ηλεκτοδίου: R = s l π r [Ω/m] (4.) Ο Sude [] ποτείνει τη σχέση (4.3) για τον υπολογισµό της αγωγιµότητας στην πείπτωση ενός αγωγού τοποθετηµένου οιζόντια στην επιφάνεια της γης. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 4
16 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 5 = l r G s l l π (ισχύει για r >> l ) (4.3) Στην πείπτωση που ο αγωγός είναι τοποθετηµένος σε βάθος h, τότε στη σχέση (4.3) η ακτίνα r του αγωγού αντικαθίσταται µε την ισοδύναµη ακτίνα d r. Συνεπώς, η αγωγιµότητα στην πείπτωση που ο αγωγός είναι τοποθετηµένος σε βάθος d δίνεται από τη σχέση [, 76]: = l d r G s l l π (ισχύει για l << h ) (4.4) Η εγκάσια αγωγιµότητα του ηλεκτοδίου του σχήµατος 4.9 υπολογίζεται από τη σχέση [46]: = d r L G s l l l l π (4.5) όπου L το µήκος των τµηµάτων στα οποία έχει χωιστεί το ηλεκτόδιο Σύµφωνα µε τον Tagg [] το αντίστοφο της αγωγιµότητας (η µοφή των επόµενων σχέσεων (4.6) έως και (4.8), εξηγεί αφ' εαυτής γιατί ο Tagg ποτιµάει να δώσει τύπους για το αντίστοφο της αγωγιµότητας) οιζοντίου ηλεκτοδίου τοποθετηµένου σε διστωµατικό έδαφος πλησίον της επιφανείας, όπως στο σχήµα 4.9, δίνεται από τη σχέση: ( ) ( ) = l l l l l l l 4 4 l l d d d d r G π = = 4 8 l 4 l l l l h h h h k R R α = (4.6)
17 όπου h το πάχος του πώτου στώµατος (πλησιέστεο στην επιφάνεια του εδάφους) η ειδική αντίσταση του πώτου στώµατος η ειδική αντίσταση του πώτου στώµατος k = ο συντελεστής αντικατοπτισµού Ο πώτος όος R εκφάζει την αντίσταση που θα είχε το ηλεκτόδιο αν ήταν τοποθετηµένο σε οµοιογενές έδαφος, ενώ ο δεύτεος όος επιπόσθετη αντίσταση λόγω της ύπαξης του δεύτεου στώµατος. R α εκφάζει την Στην πείπτωση κατακόυφου ηλεκτοδίου (σχήµα 4.), ο Tagg [] ποτείνει τη σχέση: = = 4 l k l G π l r = h l h l l (4.7) Αέας l h Σχήµα 4.: Kατακόυφο ηλεκτόδιο Όταν το ηλεκτόδιο εκτείνεται σε δύο στώµατα του εδάφους, όπως στο σχήµα 4., ο Tagg [] υπολογίζει την αντίσταση του ηλεκτοδίου από τη σχέση: = G π l l k l = h l ( ) l k l h α ( ) = h l k k (4.8) Αέας l h Σχήµα 4.: Κατακόυφο ηλεκτόδιο σε διστωµατικό έδαφος ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 6
18 Η εξατηµένη από τη συχνότητα εγκάσια αγωγιµότητα οιζοντίου ηλεκτοδίου σύµφωνα µε τον Sude [] δίνεται από τη σχέση: G = π l.58 s l γ r d (4.9) όπου γ η σταθεά εξάπλωσης Η σταθεά εξάπλωσης δίνεται από τη σχέση []: ( σ j ω ) γ = j ω µ ε o ε r (4.3) όπου ω η κυκλική συχνότητα του εύµατος µ η µαγνητική διαπεατότητα του εδάφους σ η ειδική αγωγιµότητα του εδάφους ε o η διηλεκτική επιτεπτότητα του κενού ε r η διηλεκτική σταθεά του εδάφους Επαγωγή ευθυγάµµου τµήµατος Όταν ένας αγωγός διαέεται από εύµα, τότε γύω από τον αγωγό δηµιουγείται µαγνητικό πεδίο. Αν η τιµή του εύµατος αυτού µεταβληθεί, θα µεταβληθεί η µαγνητική του οή και θα πααχθεί µία τάση εξ επαγωγής. Το φαινόµενο αυτό εκφάζεται µέσω της αυτεπαγωγής. Η αυτεπαγωγή L ενός ευθύγαµµου αγωγού µήκους l δίνεται από τη σχέση [93, ]: l L =. l l [µη] (4.3) r όπου r η ακτίνα του αγωγού Η αυτεπαγωγή ενός αγωγού µποεί να εκφαστεί ως το άθοισµα δύο όων, όπως στη σχέση [53]: ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 7
19 L = L it L ext (4.3) όπου L it είναι η εσωτεική αυτεπαγωγή και L ext η εξωτεική αυτεπαγωγή. Ο πώτος όος L it οφείλεται στη µαγνητική οή στο εσωτεικό του αγωγού, ενώ ο δεύτεος στη οή που αναπτύσσεται στο εξωτεικό του αγωγού. Η εσωτεική αυτεπαγωγή ενός αγωγού, εξαιτίας του επιδεµικού φαινοµένου, επηεάζεται από τη συχνότητα του εύµατος που τον διαέει. Η εξωτεική αυτεπαγωγή καθώς και η αλληλεπαγωγή µεταξύ δύο αγωγών δεν επηεάζονται από το επιδεµικό φαινόµενο [53]. Η εσωτεική αυτεπαγωγή ενός κυλινδικού αγωγού µήκους l που διαέεται από εύµα µηδενικής συχνότητας δίνεται από τη σχέση [, ]: µ l L it,o = (4.33) 4 π όπου µ η µαγνητική διαπεατότητα του αγωγού Ο λόγος της εσωτεικής αυτεπαγωγής ενός αγωγού, που διαέεται από εύµα µη µηδενικής συχνότητας, πος την εσωτεική αυτεπαγωγή αγωγού, που διαέεται από εύµα µηδενικής συχνότητας, δίνεται από τη σχέση (4.34) και η µεταβολή του συνατήσει του παάγοντα r ω µ σ, απεικονίζεται στο σχήµα 4.8 [69]. L L it it,o 4 r δ = δ 3 δ r 8 r δ 8 r για για r δ r δ < > (4.34) όπου δ το βάθος διείσδυσης. Εποµένως, για r δ ο λόγος R τείνει στο rδ R o. Η εξωτεική αυτεπαγωγή ενός αγωγού που είναι τοποθετηµένος στην επιφάνεια του εδάφους δίνεται από τη σχέση []: L ext µ l = [ γ r K( γ r) ] (4.35) π γ r όπου µ η µαγνητική διαπεατότητα του εδάφους γ η σταθεά εξάπλωσης ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 8
20 r η ακτίνα του αγωγού Κ η πώτης τάξης τοποποιηµένη συνάτηση Bessel δευτέου είδους Για γ r <. 5, από την επίλυση της (4.35) ποκύπτει: L ext = µ l j π. l 85 π 4 γ r (4.36) Στην πείπτωση που ο αγωγός µήκους l και ακτίνας r είναι τοποθετηµένος σε βάθος h από την επιφάνεια της γης, τότε η ποηγούµενη σχέση τοποποιείται ως εξής []: L ext = µ l K 4 π α u h α e cos ( ) ( ) ( u r) γ r K γ r 4 h du (4.37) όπου α = u γ και Κ η µηδενικής τάξης συνάτηση Bessel δευτέου είδους. Όταν ο αγωγός είναι τοποθετηµένος σε πολύ µεγάλο βάθος, οι δύο τελευταίοι όοι της πααπάνω σχέσης µποούν να πααλειφθούν: L ext µ l = K γ 4 π ( r) για γ h >> (4.38) Επιλύοντας την 4.38 για γ r <. 5 έχουµε: µ l L ext = l Ψ () 4 π για γ h >> και γ r <. 5 (4.39) γ r Ο όος Ψ() ποκύπτει από τη συνάτηση Γάµµα ή συνάτηση πααγοντικού, η οποία οίζεται ως το όιο για της σχέσης []: ( u ) 3K( ) ( u ) ( u ) K( u ) u = (4.4) u! = Γ Η παάγωγος του λογαίθµου της συνάτησης Γάµµα οίζεται ως: d ( ) ( u! ) Ψ u = logu! = ή ( u) =Ψ ( u ) du u! Ψ (4.4) u ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 9
21 Για u = ποκύπτει η σταθεά του Euler: Ψ () =.577 = logγ, όπου γ =. 78 Η εξωτεική αυτεπαγωγή ενός αγωγού τοποθετηµένου σε άπειο βάθος από την επιφάνεια του εδάφους είναι λιγότεο από 5% µικότεη από την τιµή που θα είχε αν ο αγωγός βισκόταν κοντά στην επιφάνεια []. Συνεπώς, για αγωγούς σε µικό βάθος µποούν να χησιµοποιηθούν οι τύποι (4.35) και (4.36), που ισχύουν για την επιφάνεια. Η µαγνητική σύζευξη µεταξύ δύο αγωγών µήκους l i και αλληλεπαγωγής, η οποία µποεί να υπολογιστεί από τη σχέση [53]: l j εκφάζεται µέσω της L ij = µ 4 π l l dl i i j ij dl d j (4.4) όπου d ij η απόσταση µεταξύ των αγωγών i και j µ η µαγνητική διαπεατότητα του µέσου d l δ l β α Σχήµα 4.: ιάταξη δύο πααλλήλων αγωγών οιζόντιας απόστασης δ και κατακόυφης d. Η αλληλεπαγωγή µεταξύ δύο πααλλήλων αγωγών µε µήκος l και l αντίστοιχα και µε διάταξη όπως εικονίζονται στο σχήµα 4., δίνεται από τη σχέση [8, 83, 93]: γ L ij =. a sih α β sih d β γ sih d γ δ sih d α d β d γ d δ d [µh] (4.43) ) δ d όπου δ η οιζόντια απόσταση των δύο αγωγών ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 3
22 d η κατακόυφη απόσταση των δύο αγωγών a = l l β = l δ γ = l δ δ Ποσεγγιστικά ισχύει: sih ( y y ) y l (4.44) Αντικαθιστώντας τη σχέση (4.44) στη σχέση (4.43), ποκύπτει: L ij α α β β =. a l β l d d d d γ γ δ δ γ l δ l d d d d α d β d γ d δ d [µh] (4.45) Εάν οι αγωγοί υπεκαλύπτονται, τότε η οιζόντια απόσταση δ λαµβάνεται µε ανητικό πόσηµο. Στην πείπτωση που η κατακόυφη απόσταση των δύο αγωγών είναι µηδέν, ενώ η οιζόντια απόσταση τους είναι διάφοη του µηδενός, µεταξύ τους η αλληλλεπαγωγή δίνεται από τη σχέση [93, 69]: { a l[ a] β l( β ) γ l( γ ) δ l( δ )} L ij =. [µh] (4.46) } Στην πείπτωση που η οιζόντια και η κατακόυφη απόσταση των δύο αγωγών είναι µηδέν η µεταξύ τους αλληλεπαγωγή δίνεται από τη σχέση [93, 69]: {( l l ) l( l l ) l l l l } L =. l [µη] (4.47) ij l Αναφέεται [69] ότι στην πείπτωση που η οιζόντια απόσταση είναι µηδέν, ενώ η κατακόυφη απόσταση είναι διάφοη του µηδενός η αλληλλεπαγωγή µεταξύ των ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 3
23 δύο αγωγών δίνεται από τη γενική σχέση (4.45). Για την πείπτωση µηδενικής οιζόντιας απόστασης και µη µηδενικής κατακόυφης απόστασης χησιµοποιήθηκε η σχέση (4.47) γεγονός που οδήγησε στον υπολογισµό συµµετικών τιµών, οι οποίες έχονται σε καλύτεη συµφωνία µε τα πειάµατα υπό κλίµακα που έχουν γίνει στο εγαστήιο. H αλληλεπαγωγή µεταξύ δύο αγωγών δεν επηεάζεται από το επιδεµικό φαινόµενο [53], µε αποτέλεσµα να µένει αµετάβλητη όταν ο αγωγός διαέεται από εύµα µη µηδενικής συχνότητας. Στο Παάτηµα Π5. παουσιάζονται αναλυτικά οι σχέσεις για τον υπολογισµό της επαγωγής οιζοντίων αγωγών στην πείπτωση ύπαξης αγωγού επιστοφής εύµατος. Στην Π5. αναλύεται η διαδικασία υπολογισµού της σύνθετης αντίστασης αγωγών που διαέονται από εύµα µη µηδενικής συχνότητας για την ίδια πείπτωση ύπαξης αγωγού επιστοφής εύµατος Εγκάσια χωητικότητα ευθυγάµµου τµήµατος Σε οµοιογενές διηλεκτικό µέσο η χωητικότητα C του στοιχείου k ως πος τη γη µποεί να υπολογιστεί από τη σχέση που συνδέει την αγωγιµότητα G µε τη χωητικότητα [56]. C = ε ε G (4.48) o r s όπου ε ο η διηλεκτική επιτεπτότητα του κενού ε r η διηλεκτική σταθεά του εδάφους s η ειδική αντίσταση του εδάφους Σε ανοµοιογενές διηλεκτικό µέσο µε διηλεκτικές σταθεές εκαι ε και ειδικές αντιστάσεις s και s ισχύει ο λόγος [69]: s s ε = ε (4.49) Η εξατηµένη από τη συχνότητα εγκάσια χωητικότητα αγωγού, τοποθετηµένου σε οµοιογενές έδαφος, δίνεται από τη σχέση (4.48). Στη σχέση αυτή η αγωγιµότητα G ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 3
24 πέπει να αντικατασταθεί από τη σχέση (4.9), η οποία συµπειλαµβάνει και την εξάτηση της αγωγιµότητας από τη συχνότητα του εύµατος που διαέει τον αγωγό. Εναλλακτικά, σε ένα σύστηµα δύο ή πεισσοτέων αλληλοσυνδεδεµένων αγωγών που διαέονται από ποσότητα φοτίου είναι αναπόφευκτη η ύπαξη χωητικότητας. Ο λόγος της µεταβολής του φοτίου πος τη µεταβολή τάσης που επιβάλλεται σε έναν αγωγό (είναι στην παγµατικότητα συνάτηση της τοπολογίας του συστήµατος και της επιτεπτότητας του υλικού) οίζεται ως χωητικότητα. Το αντίστοφο της χωητικότητας του αγωγού k εξατάται από τις διαστάσεις του αγωγού και δίνεται από τη σχέση []: P k = l π ε l r k (4.5) όπου r k η ακτίνα του αγωγού l το µήκος του αγωγού ε η επιτεπτότητα του υλικού Η αντίστοφη χωητικότητα που οφείλεται στην αλληλεπίδαση του αγωγού k µε τον αγωγό p εξατάται από την απόσταση των δύο αγωγών και εκφάζεται από τη σχέση: P kp = l π ε l D kp (4.5) όπου D kp η απόσταση µεταξύ των δύο αγωγών Χησιµοποιώντας τις σχέσεις (4.5) και (4.5) µποούµε να δηµιουγήσουµε µία µήτα Ρ αντιστόφων χωητικοτήτων, στην οποία τα διαγώνια στοιχεία Ρ ii εκφάζουν την αντίστοφη χωητικότητα που οφείλεται στον ίδιο τον αγωγό, ενώ τα µη διαγώνια στοιχεία Ρ ij εκφάζουν την αντίστοφη χωητικότητα που οφείλεται στην αλληλεπίδαση του αγωγού i µε τον αγωγό j. Για ένα σύστηµα µε αγωγούς η µήτα Ρ έχει τη µοφή: ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 33
25 P P P = P3 L P P P P L P 3 P P P L P L L L L L P P P 3 L P (4.5) Στη συνεχεία, για να υπολογίσουµε τις χωητικότητες των αγωγών ακεί να αντιστέψουµε τη µήτα Ρ, οπότε θα ποκύψει ένας πίνακας C της µοφής: C = P C C = C3 L C C C C L C 3 C C C L C L L L L L C C C C 3 L (4.53) Πααδείγµατα στην κυκλωµατική ποσέγγιση Χησιµοποιώντας τον τόπο υπολογισµού των πααµέτων του π-ισοδύναµου κυκλώµατος που παουσιάζεται στην 4.3 γίνεται ποσοµοίωση σε οισµένα κλασσικά συστήµατα γείωσης. Το εγχυόµενο εύµα είναι διπλοεκθετικής µοφής και εκφάζεται από την εξίσωση (4.). Οι συντελεστές α, β παίνουν τιµές από τον πίνακα 4., ενώ η µέγιστη τιµή του εύµατος είναι µονάδα για να είναι εύκολη η σύγκιση µε πειαµατικά ή θεωητικά αποτελέσµατα άλλων εευνητών. α/α α [s - ] β [s - ] T crest [µs] T half [µs] 6667, , , , , , , , 9 5 5, , , , Πίνακας 4.: Χαακτηιστικά µεγέθη εγχυόµενου εύµατος ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 34
26 Τα συστήµατα τα οποία µελετώνται είναι οιζόντια ηλεκτόδια µία κατακόυφη άβδος; καθώς και τεταγωνικά πλέγµατα γείωσης Εφαµογή σε οιζόντια ηλεκτόδια Τα δεδοµένα του εδάφους και των ηλεκτοδίων τα οποία µελετούνται δίνονται στον πίνακα 4.: Πείπτωση Α Β Γ Ε Ειδική αντίσταση εδάφους [Ωm] Σχετική διηλεκτική σταθεά εδάφους ε r Μήκος ηλεκτοδίου l [m] 5 4 Βάθος τοποθέτησης ηλεκτοδίου h [m],6,6,6,6,6 Ακτίνα ηλεκτοδίου r [mm],5,5 9 9 Πίνακας 4.: Χαακτηιστικά εδάφους και ηλεκτοδίων Στα σχήµατα 4.3 και 4.4 παουσιάζεται για την πείπτωση Α, του πίνακα 4., η χονική µεταβολή του εγχυόµενου εύµατος (πάνω τµήµα του σχήµατος), της διαφοάς δυναµικού ως πος την άπειη γη (µεσαίο τµήµα του σχήµατος) και της σύνθετης µεταβατικής αντίστασης (κάτω τµήµα του σχήµατος) του οιζοντίου ηλεκτοδίου. Σε κάθε σχήµα υπάχουν τεις γαφικές πααστάσεις, µία για καθένα από τα πααπάνω µεγέθη αντιστοίχως. Η µαύη καµπύλη αναφέεται σε σηµείο του ηλεκτοδίου που βίσκεται στην αχή του (στο σηµείο που γίνεται η έγχυση του κεαυνικού εύµατος), η κόκκινη καµπύλη αναφέεται σε σηµείο που απέχει 3,5m από την αχή του ηλεκτοδίου, ενώ η πάσινη καµπύλη αναφέεται σε σηµείο που απέχει 7m από την αχή του ηλεκτοδίου. Το γάµµα που βίσκεται δεξιά από κάθε σχήµα πααπέµπει, µε ελληνικό τόπο γαφής, στη µοφή του εύµατος (από τον αύξοντα αιθµό του πίνακα 4.). Το µήκος του ηλεκτοδίου, το µήκος της διαµέισής του, ο χόνος µεγίστου και ο χόνος ηµίσεος εύους ουάς αναφέονται στην επικεφαλίδα κάθε σχήµατος. Η επίδαση του χόνου µετώπου του εγχυόµενου εύµατος φαίνεται στο σχήµα 4.3. Όπως παατηείται από τη µελέτη των γαφικών πααστάσεων του σχήµατος 4.3, η µείωση του χόνου µετώπου του εγχυόµενου εύµατος για σταθεό χόνο ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 35
27 ηµίσεος εύους ουάς ποκαλεί αύξηση της µέγιστης τιµής της µεταβατικής τάσεως. Αύξηση υπάχει και στη µέγιστη τιµή της µεταβατικής σύνθετης αντίστασης. Η τελική τιµή της τάσεως δεν εξατάται από τη µοφή του εύµατος. Ποφανώς, και η τελική τιµή της µεταβατικής σύνθετης αντίστασης δεν εξατάται από τη µοφή του εύµατος, αλλά τείνει στην τιµή της αντίστασης γείωσης µονίµου καταστάσεως. Από τη µελέτη της επίδασης του χόνου ουάς του εγχυόµενου εύµατος στη µοφή των αντίστοιχων µεγεθών του σχήµατος 4.4 ποκύπτει ότι η επίδασή της είναι αµελητέα συγκινόµενη µε την επίδαση που έχει ο χόνος µετώπου. Στο σχήµα 4.5 παουσιάζεται, για τις πειπτώσεις Β και Γ των οιζοντίων ηλεκτοδίων του πίνακα 4., η επίδαση του χόνου µεγίστου του εγχυόµενου εύµατος, για σταθεό (ίσο µε 43µs) χόνο ηµίσεος εύους στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Παατηείται ότι η µείωση του χόνου µεγίστου του εγχυόµενου εύµατος ποκαλεί αύξηση στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Ανάλογα συµπεάσµατα ποκύπτουν από το σχήµα 4.6, για τις πειπτώσεις και Ε των οιζοντίων ηλεκτοδίων του πίνακα 4.. Στις πειπτώσεις Β και Γ των οιζοντίων ηλεκτοδίων του πίνακα 4. µεταβάλλεται η τιµή της ειδικής αντίστασης. Στη µόνιµη κατάσταση λειτουγίας, δηλαδή µετά από µεικά µs, η αύξηση της ειδικής αντίστασης του εδάφους ποκαλεί ανάλογη ποσοστιαία αύξηση στην τιµή της αντίστασης µονίµου καταστάσεως ή της αναπτυσσόµενης τάσης, ενώ στο µεταβατικό στάδιο παατηείται ότι δεκαπλασιασµός της ειδικής αντίστασης (από Ωm σεωm) ποκαλεί από διπλασιασµό (στην έγχυση πολύ γήγοου εύµατος) έως τεταπλασιασµό (στην πείπτωση που ο χόνος µεγίστου του εύµατος ισούται µε 3µs) της µέγιστης αναπτυσσόµενης τάσης (σχήµα 4.5). Ποφανώς, αν εξεταστεί µία πολύ αγή κυµατοµοφή τότε αφενός υπάχει πολύ µική αύξηση της τάσης σε σχέση µε την τάση µετά από κάποια µs και αφετέου η αύξηση της ειδικής αντίστασης του εδάφους ποκαλεί ανάλογη ποσοστιαία αύξηση στην τιµή της µέγιστης αναπτυσσόµενης τάσης. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 36
28 (α) (β) (γ) (δ) (ε) (στ) Σχήµα 4.3: Γαφικές πααστάσεις (επίδαση χόνου µετώπου) ηλεκτοδίου Α ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 37
29 (ζ) (η) (θ) (ι) (ια) (ιβ) Σχήµα 4.4: Γαφικές πααστάσεις (επίδαση χόνου ουάς) ηλεκτοδίου Α ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 38
30 Μέγιστη τάση [V] Β Γ,5,5,5 3 Xόνος µεγίστου εύµατος [µs] Σχήµα 4.5: Επίδαση του χόνου µεγίστου του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση στην πείπτωση του οιζόντιου ηλεκτοδίου Β και Γ 4 Μέγιστη τάση [V] ,5,5,5 3 Xόνος µεγίστου εύµατος [µs] Ε Σχήµα 4.6: Επίδαση του χόνου µεγίστου του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση στην πείπτωση του οιζόντιου ηλεκτοδίου και Ε Από το σχήµα 4.6 εξάγεται το συµπέασµα ότι η αύξηση του µήκους του ηλεκτοδίου ποκαλεί µείωση της µέγιστης τιµής της αναπτυσσόµενης τάσης. Για διπλασιασµό του µήκους του ηλεκτοδίου παατηείται µείωση της αναπτυσσόµενης τάσης έως και κατά 35%, ποσοστό µειούµενο όταν µειώνεται ο χόνος µεγίστου εύµατος. Αυτό συµβαίνει γιατί το µήκος του ηλεκτοδίου το οποίο ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 39
31 παγµατικά συµµετέχει στο µεταβατικό στάδιο είναι το µικότεο από το παγµατικό µήκος του ηλεκτοδίου και το ενεγό του µήκος. Το ενεγό µήκος le ενός ηλεκτοδίου δίνεται από την σχέση [8, 6]: l e = K Τ (4.54) είναι η ειδική αντίσταση του εδάφους (σε Ωm), Τ ο χόνος µετώπου της κυµατοµοφής (σε µs) και Κ είναι µία σταθεά που εξατάται από το ηλεκτόδιο ή το πλέγµα και παίνει τιµές από έως [8, 6]. Όταν το µήκος του ηλεκτοδίου γίνει µεγαλύτεο από το ενεγό µήκος τότε ενδεχόµενη αύξηση του µήκους του δεν επιφέει καµία βελτίωση στη µέγιστη τιµή τη; αναπτυσσόµενης τάσης. 4 Μέγιστη τάση [V] Β Γ Χόνος ηµίσεος εύους [µs] Σχήµα 4.7: Επίδαση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση στην πείπτωση του οιζόντιου ηλεκτοδίου Β και Γ Στο σχήµα 4.7 παουσιάζεται, για τις πειπτώσεις Β και Γ των οιζοντίων ηλεκτοδίων του πίνακα 4.., η επίδαση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος, για χόνο µεγίστου σταθεό (ίσο µε,µs) στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Παατηείται ότι η αύξηση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος ποκαλεί αύξηση στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Η αύξηση της ειδικής αντίστασης ποκαλεί την ίδια επίδαση για όλους τους χόνους ηµίσεος εύους (για τη συγκεκιµένη πείπτωση ο ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 4
32 δεκαπλασιασµός της ειδικής αντίστασης του εδάφους ποκαλεί τιπλασιασµό στην τιµή της µέγιστης αναπτυσσόµενης τάσης). Μέγιστη τάση [V] Χόνος ηµίσεος εύους [µs] Ε Σχήµα 4.8: Επίδαση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση στην πείπτωση του οιζόντιου ηλεκτοδίου και Ε. Από το σχήµα 4.8 παατηείται ότι η αύξηση του χόνου ηµίσεος εύους (για σταθεό χόνο µεγίστου ίσο µε,µs) ποκαλεί αύξηση της τιµής της µέγιστης αναπτυσσόµενης τάσης. Επιπλέον, ο διπλασιασµός του µήκους του ηλεκτοδίου (πείπτωση Ε έναντι της ) ποκαλεί µείωση της αναπτυσσόµενης τάσης πεί το 35% (σχήµα 4.8) Εφαµογή σε κατακόυφη άβδο Τα δεδοµένα του εδάφους και των κατακόυφων άβδων οι οποίοι µελετώνται παουσιάζονται στον πίνακα 4.3: Πείπτωση Α Β Γ Ε Ειδική αντίσταση εδάφους [Ωm] 3 Σχετική διηλεκτική σταθεά εδάφους ε r Μήκος άβδου l [m] 4 4 Ακτίνα ηλεκτοδίου r [mm] Πίνακας 4.3: Χαακτηιστικά εδάφους και άβδων ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 4
33 Στο σχήµα 4.9 παουσιάζεται, για τις πειπτώσεις Α, Β και των κατακόυφων άβδων του πίνακα 4.3, η επίδαση του χόνου µεγίστου του εγχυόµενου εύµατος, για σταθεό χόνο ηµίσεος εύους (ίσο µε 43µs) στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Παατηείται ότι η µείωση του χόνου ανόδου του εγχυόµενου εύµατος ποκαλεί αύξηση στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Ανάλογα συµπεάσµατα ποκύπτουν από το σχήµα 4., για τις πειπτώσεις Γ και Ε του πίνακα 4.3. Στο σχήµα 4. παουσιάζεται, για τις πειπτώσεις Α, Β και των κατακόυφων άβδων η επίδαση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος, για χόνο µεγίστου σταθεό (ίσο µε,µs) στη µέγιστη τιµή της αναπτυσσόµενης τάσης. Αντίστοιχη µεταβολή παουσιάζεται στο σχήµα 4. για τις πειπτώσεις Γ και Ε των κατακόυφων άβδων. Παατηείται ότι η αύξηση του χόνου ηµίσεος εύους ουάς για σταθεό χόνο µεγίστου του εγχυόµενου εύµατος ποκαλεί αύξηση στην µέγιστη τιµή της αναπτυσσόµενης τάσης. Με σύγκιση των αποτελεσµάτων (σχήµατα ) για τις κατακόυφες άβδους των πειπτώσεων Β και Γ αφενός και των πειπτώσεων και Ε αφετέου ποκύπτει πως η αύξηση της ειδικής αντίστασης ποκαλεί ανάλογη ποσοστιαία αύξηση της µέγιστης τιµής της αναπτυσσόµενης τάσης. Μέγιστη τάση [V] ,5,5,5 3 Xόνος µεγίστου εύµατος [µs] Α Β Σχήµα 4.9: Επίδαση του χόνου µεγίστου του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση (πείπτωση των κατακόυφων άβδων Α, Β και ) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 4
34 5 Μέγιστη τάση [V] Γ Ε,5,5,5 3 Xόνος µεγίστου εύµατος [µs] Σχήµα 4.: Επίδαση του χόνου µεγίστου του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση (πείπτωση των κατακόυφων άβδων Γ και Ε) Μέγιστη τάση [V] Χόνος ηµίσεος εύους [µs] Α Β Σχήµα 4.: Επίδαση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση (πείπτωση των κατακόυφων άβδων Α, Β και ) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 43
35 5 Μέγιστη τάση [V] Γ Ε Χόνος ηµίσεος εύους [µs] Σχήµα 4.: Επίδαση του χόνου ηµίσεος εύους ουάς του εγχυόµενου εύµατος στη µέγιστη εµφανιζόµενη τάση ( πείπτωση των κατακόυφων άβδων Γ και Ε) Εφαµογή σε πλέγµατα Τα δεδοµένα του εδάφους και των πλεγµάτων τα οποία εξετάζονται παουσιάζονται στους πίνακες 4.4 και 4.5. Τα πλέγµατα του πίνακα 4.4 είναι όλα τεταγωνικά και αποτελούνται από εννέα τεταγωνικούς βόχους. Οι τεταγωνικοί βόχοι του κάθε πλέγµατος έχουν ίδιες διαστάσεις. Αυτό που εξετάζεται µε την βοήθεια των ποσοµοιώσεων των πλεγµάτων του πίνακα 4.4 είναι η επίδαση του µήκους της πλευάς του πλέγµατος, της ειδικής αντίστασης του εδάφους και της µοφής του εγχυόµενου εύµατος στην αναπτυσσόµενη τάση. Πείπτωση Α Β Γ Ε ΣΤ Ειδική αντίσταση εδάφους [Ωm] Σχετική διηλεκτική σταθεά εδάφους ε r Αιθµός τεταγώνων πλέγµατος Μήκος πλευάς πλέγµατος l [m] Βάθος τοποθέτησης πλέγµατος h [m],5,5,5,5,5,5 Ακτίνα ηλεκτοδίου πλέγµατος r [mm] Πίνακας 4.4: Χαακτηιστικά εδάφους και πλεγµάτων ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 44
36 Πείπτωση Ζ Η Θ Ι Ειδική αντίσταση εδάφους [Ωm] Σχετική διηλεκτική σταθεά εδάφους ε r Αιθµός τεταγώνων πλέγµατος Μήκος πλευάς πλέγµατος l [m] 4 4 Βάθος τοποθέτησης πλέγµατος h [m],5,5,5,5 Ακτίνα ηλεκτοδίου πλέγµατος r [mm] Πίνακας 4.5: Χαακτηιστικά εδάφους και πλεγµάτων Τα πλέγµατα του πίνακα 4.5 είναι και αυτά τεταγωνικά, αλλά αποτελούνται από διαφοετικό αιθµό τεταγωνικών βόχων. Η κάθε πλευά οποιουδήποτε βόχου σε όλα τα πλέγµατα του πίνακα 4.5 έχει µήκος m. Εποµένως, χησιµοποιώντας τις αντίστοιχες ποσοµοιώσεις για τα τέσσεα πλέγµατα του πίνακα 4.5 και τα δύο πλέγµατα των πειπτώσεων Γ και του πίνακα 4.4 εξετάζεται η επίδαση του αιθµού των τεταγωνικών βόχων του πλέγµατος, της ειδικής αντίστασης του εδάφους και της µοφής του εγχυόµενου εύµατος στην αναπτυσσόµενη τάση. Στο σχήµα 4.3 παουσιάζονται για το 3x3 πλέγµα της πείπτωσης, του πίνακα 4.4, η χονική µεταβολή του εγχυόµενου εύµατος στη γωνία του πλέγµατος (πάνω τµήµα του σχήµατος), της διαφοάς δυναµικού ως πος την άπειη γη (µεσαίο τµήµα του σχήµατος) και της σύνθετης µεταβατικής αντίστασης (κάτω τµήµα του σχήµατος) του οιζοντίου ηλεκτοδίου. Στο σχήµα που παουσιάζεται η διαφοά δυναµικού ως πος την άπειη γη υπάχουν τέσσεις γαφικές πααστάσεις που αναφέονται στα αντίστοιχα σηµεία του σχήµατος 3..β. Η µαύη καµπύλη αναφέεται στη γωνία Α του πλέγµατος (η οποία είναι το σηµείο που γίνεται η έγχυση του κεαυνικού εύµατος), η κόκκινη καµπύλη αναφέεται στο σηµείο C, ενώ η πάσινη καµπύλη αναφέεται στο σηµείο G και τέλος η καφέ καµπύλη αναφέεται στην απέναντι από το σηµείο έγχυσης γωνία (αντιδιαγώνιο σηµείο). Το γάµµα που βίσκεται δεξιά από κάθε σχήµα πααπέµπει, µε ελληνικό τόπο γαφής, στη µοφή του εύµατος (από τον αύξοντα αιθµό του πίνακα 4.). Το σηµείο έγχυσης, το είδος του πλέγµατος, ο χόνος µεγίστου και ο χόνος ηµίσεος εύους ουάς αναφέονται στην επικεφαλίδα κάθε σχήµατος. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 45
37 (α) (β) (γ) (δ) (ε) (στ) Σχήµα 4.3: Γαφικές πααστάσεις (επίδαση χόνου µετώπου) στο πλέγµα ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 46
38 Στο σχήµα 4.3 παατηείται ότι όσο ταχύτεα φθάνει στο µέγιστό του το εγχυόµενο εύµα (για δεδοµένο πάντα χόνο ηµίσεος εύους ουάς) τόσο µεγαλύτεη είναι η αναπτυσσόµενη τάση σε όλα τα σηµεία του πλέγµατος. Επίσης, γίνεται εύκολα αντιληπτό ότι όσο µεγαλύτεη απόσταση απέχει το σηµείο που µελετάµε από το σηµείο έγχυσης του κουστικού εύµατος τόσο µικότεη είναι η αναπτυσσόµενη τάση στο συγκεκιµένο σηµείο. Το δυναµικό σε όλα τα σηµεία του πλέγµατος για χόνο µεγαλύτεο των 3µs τείνει να ταυτιστεί. Ο χόνος στον οποίο επιτυγχάνεται αυτή η σύγκλιση είναι σε άµεση εξάτηση µε τον χόνο µεγίστου του εγχυοµένου εύµατος. Όσο µικότεος είναι ο χόνος µεγίστου τόσο γηγοότεα επιτυγχάνεται η σύγκλιση των δυναµικών αλλά και η εκ των άνω ποσέγγιση της µεταβατικής σύνθετης αντίστασης στην αντίστοιχη τιµή της µονίµου καταστάσεως Μέγιστη τάση [kv] A (γωνία) Γ (γωνία) Ε (γωνία) Α (κέντο) Γ (κέντο) Ε (κέντο),5,5,5 3 Τcrest [µs] Σχήµα 4.4: Μεταβολή της µέγιστης τάσης που αναπτύσσεται στα πλέγµατα των πειπτώσεων Α, Γ και Ε συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος Στο σχήµατα 4.4 και 4.5 παουσιάζεται η µεταβολή της µεγίστης αναπτυσσοµένης τάσης για τα πλέγµατα του πίνακα 4.4 στο σηµείο που γίνεται η έγχυση του κουστικού εύµατος. Είναι εµφανές ότι όσο ταχύτεο είναι το εγχυόµενο εύµα τόσο µεγαλύτεη είναι η αναπτυσσόµενη µέγιστη τάση. Επίσης, παατηείται ότι η έγχυση του εύµατος στο κέντο δηµιουγεί µικότεη ανύψωση δυναµικού σε σχέση µε την έγχυση σε γωνία του πλέγµατος. Η αύξηση της ειδικής αντίστασης του εδάφους, για το ίδιο πάντα εγχυόµενο εύµα, οδηγεί σε αύξηση της ανύψωσης του δυναµικού. Από την εξίσωση (4.54), όπως αναφέθηκε, ποκύπτει πως η αύξηση της ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 47
39 ειδικής αντίστασης του εδάφους οδηγεί σε αύξηση του ενεγού µήκους των αγωγών. Εποµένως, η αύξηση της ειδικής αντίστασης του εδάφους πέπει να οδηγεί τους κατασκευαστές συστηµάτων γείωσης στην αύξηση των διαστάσεων των κατασκευαζόµενων γειώσεων. Μέγιστη τάση [kv] ,5,5,5 3 Τcrest [µs] Β (γωνία) Β (κέντο) (γωνία) (κέντο) ΣΤ (γωνία) ΣΤ (κέντο) Σχήµα 4.5: Μεταβολή της µέγιστης τάσης που αναπτύσσεται στα πλέγµατα των πειπτώσεων Β, και ΣΤ συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος U=/U= ,5,5,5 3 Χόνος µεγίστου εύµατος [µs] Α-Β Γ- Ε-ΣΤ Σχήµα 4.6: Μεταβολή του λόγου των µέγιστων τάσεων (για =Ωm πος =Ωm) που αναπτύσσεται στα πλέγµατα του πίνακα 4.4 συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος για έγχυση στη γωνία του πλέγµατος ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 48
40 Στο σχήµα 4.6 παουσιάζεται η µεταβολή του λόγου των µέγιστων τάσεων (για πλέγµα τοποθετηµένο σε έδαφος ειδικής αντίστασης Ωm και ειδικής αντίστασης Ωm) που αναπτυσσόταν στα πλέγµατα του πίνακα 4.4 συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος για έγχυση στη γωνία του πλέγµατος. Στο σχήµα 4.7 παουσιάζεται η µεταβολή των µεγίστων τάσεων για τις πειπτώσεις Γ, Ζ και Θ των πλεγµάτων των πινάκων 4.4 και 4.5 συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος. Στο σχήµα 4.8 παουσιάζεται η µεταβολή των µέγιστων τάσεων για τις πειπτώσεις, Η και Ι των πλεγµάτων των πινάκων 4.4 και 4.5 συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος. Οι συνεχείς γαµµές αναφέονται σε έγχυση του εύµατος στη γωνία του εξεταζόµενου πλέγµατος, ενώ οι διακεκοµµένες γαµµές αφοούν έγχυση στο κέντο του πλέγµατος. Σαφέστατα, φαίνεται ότι η έγχυση στη γωνία ποκαλεί σχεδόν διπλάσια ανύψωση δυναµικού σε σχέση µε αυτή που θα ποκαλούσε έγχυση στο κέντο. Επίσης, παουσιάζεται και η επίδαση του µεγέθους του πλέγµατος. 3 5 Μέγιστη τάση [V] 5 5 Θ Γ Ζ,5,5,5 3 3,5 Tcrest [µs] Σχήµα 4.7: Μεταβολή των µέγιστων τάσεων για τις πειπτώσεις Γ, Ζ και Θ των πλεγµάτων των πινάκων 4.4 και 4.5 συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος, για ειδική αντίσταση εδάφους =Ωm Συγκίνοντας τα σχήµατα 4.7 και 4.8 µποεί εύκολα να διακίνει κανείς την επίδαση της ειδικής αντίστασης στη µέγιστη αναπτυσσόµενη τάση. Στο σχήµα 4.7, όπου η ειδική αντίσταση του εδάφους είναι δέκα φοές µικότεη από την ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 49
41 αντίστοιχη του σχήµατος 4.8, οι αναπτυσσόµενες τάσεις είναι σαφέστατα µικότεες σε σύγκιση µε αυτές του σχήµατος 4.8. Μέγιστη τάση [V] ,5,5,5 3 Tcrest [µs] Ι Η Σχήµα 4.8: Μεταβολή των µέγιστων τάσεων για τις πειπτώσεις, Η και Ι των πλεγµάτων των πινάκων 4.4 και 4.5 συνατήσει του χόνου µεγίστου του εγχυόµενου εύµατος, για ειδική αντίσταση εδάφους =Ωm Συµπεάσµατα για την κυκλωµατική ποσέγγιση Παουσιάστηκε µία µεθοδολογία για τον υπολογισµό των πααµέτων του π- ισοδύναµου κυκλώµατος που µποεί να χησιµοποιηθεί για να παγµατοποιηθεί ποσοµοίωση σε κάθε σύστηµα γείωσης. Η µεθοδολογία αυτή εφαµόστηκε για τον υπολογισµό της µεταβατικής ανύψωσης δυναµικού και της µεταβατικής σύνθετης αντίστασης σε σειά από συστήµατα γείωσης (µε διαφοετικές διαστάσεις, βάθος τοποθέτησης και τόπο κατασκευής). Για τις ποσοµοιώσεις χησιµοποιήθηκε πληθώα διαφοετικών κυµατοµοφών του εγχυόµενου εύµατος ποκειµένου να µελετηθεί η επίδαση των πααµέτων του εύµατος. Επίσης, µεταβλήθηκε η ειδική αντίσταση του εδάφους για να διεευνηθεί η συµβολή της στα υπό έευνα φαινόµενα. Για να δειχθεί η αξία και η καταλληλότητα της µεθοδολογίας στο σηµείο αυτό κίνεται σκόπιµη η σύγκιση των αποτελεσµάτων των ποσοµοιώσεων που έγιναν αφενός µεν µε αποτελέσµατα πειαµάτων και ποσοµοιώσεων άλλων εευνητών, αφετέου δε µε τα πειαµατικά αποτελέσµάτα που ποέκυψαν κατά τη διάκεια της παούσης διατιβής. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 5
42 Τα πλέον χησιµοποιούµενα διεθνώς πειαµατικά αποτελέσµατα έχουν ποκύψει από την EDF [78] και καλύπτουν ακετά διαφοετικά συστήµατα γείωσης. Τα πειαµατικά αυτά δεδοµένα έχουν χησιµοποιηθεί από πλήθος εευνητών, οι οποίοι ποτείνουν διάφοους τόπους ποσοµοίωσης. Στα επόµενα σχήµατα παουσιάζονται τα αποτελέσµατα αυτών µαζί και µε τα αποτελέσµατα της µεθοδολογίας που αναπτύχθηκε στα πλαίσια της παούσης εγασίας. Στο σχήµα 4.9α παατίθενται τα πειαµατικά αποτελέσµατα για ένα οιζόντιο ηλεκτόδιο (ακτίνας mm, µήκους 5m, τοποθετηµένο σε βάθος,6m από την επιφάνεια εδάφους ειδικής αντίστασης 7Ωm) [78] µαζί µε τα αποτελέσµατα της ποσοµοίωσης του Grcev [5], ενώ στο σχήµα 4.9β παουσιάζονται τα αντίστοιχα δικά µας αποτελέσµατα. Στα αποτελέσµατα της ποσοµοίωσης µε το EMTDC παουσιάζονται γαφικές πααστάσεις µε τία χώµατα. Το µαύο χώµα αντιστοιχεί στην αχή του ηλεκτοδίου, το κόκκινο σε απόσταση 3,5m από την αχή του ηλεκτοδίου και το πάσινο σε απόσταση 7m από την αχή του ηλεκτοδίου, έτσι ώστε να είναι δυνατή η σύγκιση µε τα αντίστοιχα πειαµατικά αποτελέσµατα [78]. Από τα αποτελέσµατα της συγκεκιµένης ποσοµοίωσης, που φαίνονται στα σχήµατα 4.9.α και 4.9.β, διαπιστώνεται ότι η σύγκλιση της ποσοµοίωσης που ποτείνεται είναι καλύτεη από την αντίστοιχη του Grcev [5]. (α) (β) Σχήµα 4.9: (α) Παουσίαση αποτελεσµάτων Grcev [5] (β) Παουσίαση αποτελεσµάτων από το PSCAD/EMTDC για οιζόντιο ηλεκτόδιο. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 5
43 Στο σχήµα 4.3.α παατίθενται τα πειαµατικά αποτελέσµατα για µία κατακόυφη άβδο (ακτίνας 6mm, µήκους 6m, τοποθετηµένης σε έδαφος ειδικής αντίστασης 5Ωm) [78] µαζί µε τα αποτελέσµατα της ποσοµοίωσης του Grcev [5], ενώ στο σχήµα 4.3.β τα αντίστοιχα αποτελέσµατα από το PSCAD/EMTDC. Παατηείται ότι η ποσοµοίωση που έγινε στα πλαίσια της παούσης εγασίας βίσκεται πλησιέστεα στα πειαµατικά αποτελέσµατα [78] (α) (β) Σχήµα 4.3: (α) Παουσίαση αποτελεσµάτων Grcev [5] (β) Παουσίαση αποτελεσµάτων από το PSCAD/EMTDC για κατακόυφη άβδο. Για την πείπτωση των πλεγµάτων Γ, Ζ και Θ των πινάκων 4.4 και 4.5 τα αποτελέσµατα της ποσοµοίωσης συγκίνονται µε τα αποτελέσµατα του άθου των Grcev και Heimbach [54]. Τα αποτελέσµατα αυτά παουσιάζονται στο σχήµα 4.3.α, ενώ στο σχήµα 4.3.β παουσιάζονται τα αντίστοιχα δικά µας. Παατηείται ότι υπάχει πολύ καλή σύγκλιση ανάµεσα στα αποτελέσµατα των δύο ποσοµοιώσεων, ενώ, επιπλέον, η µεθοδολογία που χησιµοποιήθηκε στην ποσοµοίωση µε το PSCAD/EMTDC είναι σαφέστατα απλούστεη από τη µεθοδολογία των άλλων [54]. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 5
44 6 x Τάση 4 x 3x3 4x4 5 5 Χόνος [µ s] (α) (β) Σχήµα 4.3: (α) Παουσίαση αποτελεσµάτων Grcev [54] (β) Παουσίαση αποτελεσµάτων από το PSCAD/EMTDC για πλέγµατα γείωσης. Στο σχήµα 4.3 συγκίνονται τα πειαµατικά αποτελέσµατα (κόκκινη καµπύλη) που παουσιάστηκαν στην για οιζόντια ηλεκτόδια µε τα αποτελέσµατα της ποσοµοίωσης (πάσινη καµπύλη) της µε πολύ καλή σύγκλιση µεταξύ τους. O ι ζ όντ ι ο η λεκτ όδι ο m O ι ζ όντ ι ο η λεκτ όδι ο 4m Τάση [kv] 8 6 Τάση [kv] X όνος [µ s] X όνος [µ s] (α) (β) Σχήµα 4.3: Σύγκιση πειαµατικών αποτελεσµάτων (κόκκινη καµπύλη) και αποτελεσµάτων ποσοµοίωσης (πάσινη καµπύλη) για την τάση που αναπτύσσεται σε οιζόντιο ηλεκτόδιο (α) µήκους m (β) µήκους 4m Αντίστοιχα στο σχήµα 4.33 για την πείπτωση της κατακόυφης άβδου τα πειαµατικά αποτελέσµατα (κόκκινη καµπύλη) που παουσιάστηκαν στην 3.3. συγκίνονται µε τα αποτελέσµατα της ποσοµοίωσης (πάσινη καµπύλη) της µε πολύ καλή σύγκλιση ανάµεσα σε πειαµατικά αποτελέσµατα και αποτελέσµατα ποσοµοίωσης. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 53
45 9 8 7 Τάση [kv] X όνος [µ s] Σχήµα 4.33: Σύγκιση πειαµατικών αποτελεσµάτων (κόκκινη καµπύλη) και αποτελεσµάτων ποσοµοίωσης για την τάση που αναπτύσσεται σε µία κατακόυφη άβδο Τέλος, στο σχήµα 4.34 συγκίνονται, για την πείπτωση των πλεγµάτων, τα πειαµατικά αποτελέσµατα (κόκκινη καµπύλη) που παουσιάστηκαν στην 3. µε τα αποτελέσµατα της ποσοµοίωσης (πάσινη καµπύλη) της διαπιστώνοντας ικανοποιητική ταύτιση µεταξύ των αποτελεσµάτων..6 G4(Io=5A, γ ωνί α, =4Ω m) G9 (Io=A, κ έντο, =,5Ω m) Tά ση [kv].8 Tά ση [kv] X όνος [µ s] X όνος [µ s] (α) (β) Σχήµα 4.34: Σύγκιση πειαµατικών αποτελεσµάτων (κόκκινη καµπύλη) και αποτελεσµάτων ποσοµοίωσης (πάσινη καµπύλη) για την τάση που αναπτύσσεται στα πλέγµατα (α) G4 (β) G9 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 54
46 4.4 Πεδιακή ποσέγγιση συστηµάτων γείωσης 4.4. Εισαγωγή στο PC Opera Το PC Opera είναι ένα πακέτο πογαµµάτων ανάλυσης ποβληµάτων ηλεκτοµαγνητικού πεδίου. Μια πλήης λύση ενός ποβλήµατος µε το PC Opera [5] διενεγείται σε τεις φάσεις: α) τη φάση της πο- επεξεγασίας, κατά την οποία γίνεται η ποετοιµασία και η εισαγωγή των δεδοµένων που πειγάφουν το πόβληµα, όπως η γεωµετία του ποβλήµατος, οι ιδιότητες των υλικών, η πλεγµατοποίηση και οι οιακές συνθήκες, β) τη φάση της ανάλυσης, κατά την οποία επιλέγεται ο επιλύτης που θα χησιµοποιηθεί, η ανοχή σύγκλισης και ο επαναληπτικός τύπος και γ) τη φάση της µετ- επεξεγασίας, κατά την οποία εµφανίζονται τα υπολογισθέντα αποτελέσµατα και εκτελείται ο υπολογισµός των απααίτητων πααγώγων µεγεθών. Τα πογάµµατα ανάλυσης του PC Opera [5] υπολογίζουν τα πεδιακά µεγέθη µε βάση τη µέθοδο των πεπεασµένων στοιχείων. Η φιλοσοφία της µεθόδου των πεπεασµένων στοιχείων συνοπτικά είναι η ακόλουθη: Το στοιχείο κατασκευής, µέσα στο οποίο πέπει να βεθεί η κατανοµή ενός πεδιακού µεγέθους, αντικαθίσταται µε πλήθος στοιχείων πεπεασµένων διαστάσεων, στα οποία αντιστοιχίζονται ιδιότητες ίδιες µε τις αντίστοιχες του κατασκευαστικού στοιχείου (πχ. η ίδια διηλεκτική σταθεά). Η µέθοδος των πεπεασµένων στοιχείων µποεί να εφαµοσθεί γενικά σε οποιοδήποτε πόβληµα µε οποιοδήποτε είδος µη γαµµικότητας. Βασίζεται στην διαίεση του χώου, στον οποίο ικανοποιείται η εξίσωση, σε στοιχειώδη στοιχεία όγκου (τα πεπεασµένα στοιχεία). Μέσα σε κάθε πεπεασµένο στοιχείο χησιµοποιείται ένα απλό πολυώνυµο που ποσεγγίζει την λύση. Η γενική ιδέα που χησιµοποιείται στην ανάλυση των πεπεασµένων στοιχείων είναι ανεξάτητη των διαστάσεων του χώου. Αφετηία της ανάλυσης αποτελεί η εξίσωση Poisso που πειγάφει το δυναµικό σε µια διάσταση [5]: ε φ = (4.55) Η συνάτηση δυναµικού µποεί να είναι ένα ηλεκτοστατικό δυναµικό. Σε αυτή την πείπτωση, το θα είναι γαµµική πυκνότητα φοτίου. Για να οιστεί το δυναµικό ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 55
47 χειάζονται οιακές συνθήκες που µποεί να είναι είτε τιµές του δυναµικού, είτε της πααγώγου του, για παάδειγµα: φ = x (4.56) Για τη λύση της εξίσωσης µε την µέθοδο των πεπεασµένων στοιχείων ο χώος διαιείται σε στοιχεία όγκου. Μέσα σε κάθε τέτοιο στοιχείο το δυναµικό ποσεγγίζεται από το γαµµικό πολυώνυµο: ( x) = α β x φ (4.57) Το ηλεκτοστατικό δυναµικό είναι συνεχές στο χώο, πα` όλο που η παάγωγος του µποεί να είναι ασυνεχής αν η επιτεπτότητα ε είναι ασυνεχής. Η µέθοδος των πεπεασµένων στοιχείων πέπει να ποσοµοιώσει αυτή την συµπειφοά, έτσι είναι βολικό η εξίσωση (4.57) να χαακτηίζεται από τις τιµές του δυναµικού στους κόµβους του στοιχείου και να χησιµοποιεί τις ίδιες τιµές για τα υπόλοιπα πολυώνυµα που έχουν κοινό κόµβο. Μία πεαιτέω απλοποίηση µποεί να γίνει τοποποιώντας την εξίσωση (4.57) µε όους κοµβικών συνατήσεων Ν i, που καθοίζονται ως εξής: ( x) = N i xi ( x) = x = x=x i N i x = x j j i (4.58) όπου x i είναι η x συντεταγµένη του κόµβου i. Η εξίσωση (4.57) παίνει τη µοφή: ( ) = N( x) φ N( x) φ φ x (4.59) Οι συνατήσεις Ν i εκφάζονται σε όους τοπικών συντεταγµένων µέσα στο στοιχείο. Χησιµοποιώντας το σύστηµα τοπικών συντεταγµένων ξ οι συνατήσεις Ν i γάφονται ως εξής: N N = ( ξ ) = - ξ ( ξ ) (4.6) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 56
48 Οι συνατήσεις Ν i κάθε κόµβου οίζονται µόνο εντός των στοιχείων που πειλαµβάνουν αυτόν τον κόµβο και είναι µηδενικές εκτός των στοιχείων αυτών. Η µέθοδος υπολογισµού του δυναµικού φ µε χήση χαακτηιστικών τιµών δυναµικού των κόµβων και συνατήσεων Ν i αποτελεί τη βάση, στην οποία πολλές εναλλακτικές διαδικασίες µποούν να στηιχθούν για την επίλυση της εξίσωσης (4.56). Οι µέθοδοι διακύµανσης (variatioal methods), ελαχίστων τεταγώνων και συντελεστών βαύτητας (weighted residual) είναι τεις από τις ευύτεα χησιµοποιούµενες µεθόδους. Οι συντελεστές βαύτητας έχουν διαδεδοµένη εφαµογή σε πογάµµατα λογισµικού ποκειµένου να υλοποιηθεί µία αιθµητική επίλυση. Μία ποσεγγιστική επίλυση ως πος φ καθοίζεται από την απαίτηση να ικανοποιείται η παακάτω συνάτηση: ( φ ) W ε dx = (4.6) όπου W είναι η συνάτηση βάους, από την οποία παίνει το όνοµά της και η µέθοδος. Ολοκληώνοντας την (4.6) κατά τµήµατα, ποκειµένου να µειωθεί η τάξη της διαφόισης που εφαµόζεται στο φ, ποκύπτει µια ποσεγγιστική λύση για το δυναµικό φ : b a ϑφ b ( W ε φ W) dx [ Wε ] a = (4.6) ϑχ όπου α, b τα όια ολοκλήωσης της εξίσωσης. Η εξίσωση (4.6) οδηγεί κατευθείαν σε αιθµητικό υπολογισµό της λύσης χησιµοποιώντας τα πεπεασµένα στοιχεία και τις συνατήσεις Ν i που πειγάφηκαν πιο πάνω. Η συγκεκιµένη µέθοδος επίλυσης πλεονεκτεί έναντι των άλλων, αφού οι συνατήσεις W και φ δεν χειάζονται συνεχή πααγώγιση και επιπλέον καθοίζονται εύκολα οι φυσικές οιακές συνθήκες στην επιφάνεια της πειοχής φ. x ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 57
49 Ο τοµέας από α εώς b διαιείται σε γαµµικά στοιχεία και οι αντίστοιχοι κόµβοι δίνουν ένα συνδυασµό ανεξάτητων συνατήσεων βάους. Από αυτές τις συνατήσεις βάους µποούν να αναπτυχθούν εξισώσεις µε την απαίτηση η εξίσωση (4.6) να ικανοποιείται για κάθε συνάτηση βάους. Η εξίσωση για την συνάτηση βάους W i εξάγεται από την: j b a b ( N i ε N jφ j N i ) ϑx - N = ε ϑφ i ϑ x (4.63) a για όλα τα στοιχεία που πειέχουν τον κόµβο i. Παίνοντας όλες τις εξισώσεις για τις διαφοετικές συνατήσεις βάους ποκύπτει ένα σύστηµα γαµµικών εξισώσεων, που σε µητική µοφή γάφεται ως: K Φ = S (4.64) όπου Κ ο πίνακας των συντελεστών, Φ το διάνυσµα των άγνωστων τάσεων στους κόµβους και S το διάνυσµα των οιακών συνθηκών ή των πυκνοτήτων φοτίου. Οι συντελεστές στον πίνακα Κ έχουν τη µοφή: b K = N ε N dx (4.65) ij a i j Αξίζει να σηµειωθεί, ότι, πα όλο που η ολοκλήωση στην εξίσωση (4.65) γίνεται για όια από α έως b, µόνο τα στοιχεία που πειλαµβάνουν και τους δύο κόµβους i και j συνεισφέουν. Ο εξισώσεις της σχέσης (4.64) συχνά δεν είναι γαµµικές επειδή η επιτεπτότητα ε εξατάται από την ένταση του πεδίου, που ποφανώς δεν είναι γαµµική. Για την επίλυση αυτών των µη γαµµικών εξισώσεων χησιµοποιείται η µέθοδος Newto-Raphso. ίνεται µια αχική τιµή στα δυναµικά Φ και υπολογίζεται µια νέα λύση Φ επιλύοντας το γαµµικοποιηµένο Ιακωβιανό σύστηµα: Φ = Φ J R (4.66) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 58
50 όπου το υπόλοιπο R δίνεται από την: R = K Φ S (4.67) και η Ιακωβιανή J από την: J ϑ = ϑ Φ ( K Φ S ) (4.68) Με διαδοχικές επαναλήψεις της µεθόδου Newto-Raphso ποσεγγίζεται η ζητούµενη τιµή του δυναµικού. Στην εγασία αυτή το πόγαµµα καλείται να εφαµόσει ηλεκτοστατική ανάλυση. Η διαδικασία εξισώσεων που ακολουθείται είναι η εξής: Η διηλεκτική µετατόπιση (D) και η πυκνότητα φοτίου συνδέονται µε τη σχέση: D = (4.69) και η ένταση ηλεκτικού πεδίου και η επιτεπτότητα συνδέονται µε τη διηλεκτική µετατόπιση µέσω της: D = ε E (4.7) Το ηλεκτικό δυναµικό (V) οίζεται από την γνωστή σχέση: E = V (4.7) Η απόκλιση της πυκνότητας εύµατος (J) ισούται µε µηδέν: J = (4.7) Η στατική ανάλυση των πεδίων του PC-Opera επιλύει µη χονικά µεταβαλλόµενο µαγνητικό ή ηλεκτικό πεδίο. Το µοντέλο µποεί να πειέχει υλικά µε µη γαµµική διαπεατότητα µ ή επιτεπτότητα ε σε σύστηµα κατεσιανών ή κυλινδικών συντεταγµένων. Μποούν, επίσης, να επιλυθούν και άλλοι τύποι πεδίων, όπως για παάδειγµα πεδία που πειγάφονται από µη-γαµµικές εξισώσεις Poisso ή από οή ηλεκτικών ευµάτων. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 59
51 Το Opera-d/St υπολογίζει το βαθµωτό ή διανυσµατικό δυναµικό που καθοίζεται από µια µη γαµµική εξίσωση Poisso. Το διανυσµατικό δυναµικό συνήθως χησιµοποιείται για ανάλυση µαγνητικών πεδίων, επειδή τα αποτελέσµατα του βαθµωτού δυναµικού δεν µποούν να πειέχουν εύµα σαν πηγή των πεδίων, ωστόσο, αν ένα µοντέλο έχει ως διέγεση µόνο οιακές συνθήκες ή µόνιµους µαγνήτες, µποούν να χησιµοποιηθούν και οι δύο µοφές δυναµικού. Η εξίσωση που πέπει να επιλυθεί στην πείπτωση υπολογισµού βαθµωτού δυναµικού είναι: ( φ ) µ H = (4.73) c όπου το φ είναι βαθµωτό ηλεκτικό δυναµικό και το είναι πυκνότητα φοτίου. Ο όος H c παιστάνει µόνιµους µαγνήτες για ανάλυση µαγνητικών πεδίων και ηλεκτίτες για ανάλυση ηλεκτικών πεδίων Κατανοµή δυναµικού στην επιφάνεια του εδάφους Το δυναµικό V o σε κάθε σηµείο x στην επιφάνεια οµοιογενούς εδάφους (µε ειδική αντίσταση χώµατος ο ) και για εύµα τιµής Ι, που εισέχεται σε άβδο κατακόυφα τοποθετηµένη στο έδαφος, δίνεται από τη λύση της γενικής εξίσωσης []: o I λ z Vo ( x) = e J o ( λ x) λ (4.74) π όπου J ο είναι η συνάτηση Bessel πώτου είδους, µηδενικής τάξης. Αναλυτική λύση της κατανοµής του δυναµικού V υπάχει και στην πείπτωση που η κατακόυφη άβδος είναι τοποθετηµένη σε διστωµατικό έδαφος µε χήση της διστωµατικής µεθόδου του Tagg []. I V π x ( x) = [ F ( x)] (4.75) όπου F k e λh ( x) = x J ( λ x λh o k e ) λ (4.76) ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 6
52 και k είναι ο συντελεστής ανάκλασης µεταξύ του πώτου στώµατος του εδάφους (µε ειδική αντίσταση εδάφους ) και του δευτέου στώµατος του εδάφους (µε ειδική αντίσταση εδάφους ). k = (4.77) Για πολυστωµατικά εδάφη έχει αναπτυχθεί µία θεωητική µέθοδος που ποτάθηκε από τους Takahashi και Kawase [7, 8] και υπολογίζει το δυναµικό της επιφάνειας του εδάφους. Το θεωητικό µοντέλο για δοµή εδάφους Ν οιζόντιων στωµάτων παουσιάζεται στο σχήµα I x h h... h N- Ν- Ν z Σχήµα 4.35: Πολυστωµατική δοµή Το δυναµικό σε κάθε σηµείο x στην επιφάνεια της γης για εύµα Ι που διεισδύει σε επιφανειακό σηµειακό ηλεκτόδιο µποεί να εκφαστεί µε την εξίσωση (4.78) [7, 8]: V I π x ( x) = [ F ( x)] N N (4.78) όπου λh K N e FN ( x) = x J ( λ x) λ λ o (4.79) h K e N ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 6
53 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 6 και h N h N N e K k e K k K = λ λ h N h N N e K k e K k K = λ λ = S S h NS S h NS S NS e K k e K k K λ λ = N N h NN N h NN N NN e K k e K k K λ λ = N k K NN (4.8) Επιπόσθετα, για <i<n- οι συντελεστές ανάκλασης µεταξύ των διαδοχικών στωµάτων του εδάφους δίνονται από τη σχέση: i i i i k i = (4.8) όπου i η ειδική αντίσταση του i-οστού στώµατος του εδάφους Επίλυση ποβληµάτων κατανοµής δυναµικού µε χήση του PC Opera Με τη βοήθεια του λογισµικού πακέτου PC Opera της VectorField ποσοµοιώθηκαν διάφοες διατάξεις εδάφους πολυστωµατικής δοµής και µελετήθηκε η κατανοµή του δυναµικού στην επιφάνεια του εδάφους. Έγινε σειά ποσοµοιώσεων στο πόγαµµα PC Opera και συγκίθηκαν µε τις θεωητικές καµπύλες των Takahashi και Kawase [7, 8] που ποκύπτουν από την εξίσωση (4.77). Το πόγαµµα δέχεται σαν παάµετο τη διηλεκτική σταθεά ε r και όχι την ειδική αντίσταση. Τα στώµατα που εξετάστηκαν είχαν ειδικές αντιστάσεις των Ωm και Ωm, γιατί υπάχει στη βιβλιογαφία [54, 56, 84] αντιστοιχία µε τη διηλεκτική σταθεά ε r, (για =Ωm αντιστοιχεί ε r =36 και για =Ωm αντιστοιχεί ε r =9 [54, 56, 84]). Βάσει αυτών των συγκίσεων βέθηκε η βέλτιστη
54 πλεγµατοποίηση, σύµφωνα µε τη µέθοδο πεπεασµένων στοιχείων, δηλαδή τέτοια ώστε να σηµειώνεται η µικότεη δυνατή απόκλιση ποσοµοίωσης-θεωίας. Στη συνέχεια, συγκίθηκαν διάφοα αποτελέσµατα ποσοµοιώσεων και θεωητικές καµπύλες διαφόων δοµών πολυστωµατικού εδάφους, οι ειδικές αντιστάσεις των στωµάτων, του οποίου έπαιναν ποικίλες τιµές, όχι µόνο Ωm και Ωm. Τα αποτελέσµατα αυτής της διαδικασίας παουσιάζονται στη γαφική παάσταση του σχήµατος Έχοντας τώα την επιθυµητή αντιστοιχία τιµών, είναι εφικτή η ποσοµοίωση των ποβληµάτων µε το PC Opera. ιηλεκτική σταθεά εr Ειδική αντίσταση [Ωm] Σχήµα 4.36: Μεταβολή της διηλεκτικής σταθεάς ε r συνατήσει της ειδική αντίστασης του εδάφους Τεταστωµατικό έδαφος (Πόβληµα ) Το σύστηµα γείωσης αποτελείται από µια άβδο, η οποία βίσκεται τοποθετηµένη κατακόυφα µέσα σε τεταστωµατικό έδαφος. Το πόβληµα είναι συµµετικό ως πος τον κατακόυφο άξονα, οπότε ακεί η σχεδίαση του µοντέλου στο ένα ηµιεπίπεδο (σχήµα 4.37). Η εξεταζόµενη δοµή εδάφους αποτελείται από 4 στώµατα µε ειδικές αντιστάσεις ως 4 και τα πάχη των στωµάτων είναι αντίστοιχα 5m, m, m και άπειο (σχήµα 4.35). Εναλλάσσοντας τις τιµές των ειδικών αντιστάσεων των στωµάτων µελετήθηκαν τέσσεις διαφοετικές διατάξεις (από Α έως ), όπως καταγάφονται στον παακάτω πίνακα: ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 63
55 ιάταξη [Ωm] Ρ [Ωm] 3 [Ωm] 4 [Ωm] Α 5 Β 5 5 Γ Πίνακας 4.6: ιατάξεις ποβλήµατος Σχήµα 4.37: Η γεωµετία του ποβλήµατος Στο σχήµα 4.37 παουσιάζεται η γεωµετία του ποβλήµατος και του πλέγµατος που χησιµοποιήθηκε κατά την επίλυση. Στο σχήµα 4.38 παουσιάζεται η µεταβολή του δυναµικού στην επιφάνεια του εδάφους ως πος την οιζόντια απόσταση από το ηλεκτόδιο για κάθε µία από τις πειπτώσεις του πίνακα 4.6. Η πάσινη καµπύλη αντιστοιχεί στον υπολογισµό του δυναµικού µε χήση της εξίσωσης (4.74), θεωώντας ότι το έδαφος είναι οµοιόµοφο µε ειδική αντίσταση ίση µε την ειδική αντίσταση του επάνω στώµατος. Η µωβ καµπύλη αντιστοιχεί στον υπολογισµό του δυναµικού µε χήση της εξίσωσης (4.75), θεωώντας ότι το έδαφος είναι διστωµατικό µε επάνω στώµα ίδιο µε το επάνω στώµα του υπό µελέτη εδάφους, ενώ το κάτω στώµα θεωείται απείου βάθους και ειδικής αντίστασης εδάφους ίσης µε την ειδική αντίσταση του δευτέου στώµατος της διάταξής µας. Η µπλε ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 64
56 καµπύλη αντιστοιχεί στον υπολογισµό του δυναµικού µε χήση της εξίσωσης (4.78) και της θεώησης τεταστωµατικού εδάφους. Τέλος, η γαλάζια καµπύλη αντιστοιχεί στο αποτέλεσµα της ποσοµοίωσης µε τη χήση του PC Opera Τάση [V] 5 4 Τάση [V] Απόσταση [m] (Α) Απόσταση [m] (Β) Τάση [V] 5 4 Τάση [V] Απόσταση [m] Απόσταση [m] (Γ) ( ) Σχήµα 4.38: Η µεταβολή του δυναµικού στην επιφάνεια του εδάφους ως πος την οιζόντια απόσταση από το ηλεκτόδιο : θεωητική ανάλυση Takahashi Kawase [7,8], : διστωµατική µέθοδος [], : ποσοµοίωση µε PC Opera, : µονοστωµατικό έδαφος [] Τεταστωµατικό έδαφος (Πόβληµα ) Το σύστηµα γείωσης και σε αυτό το πόβληµα αποτελείται από µια κατακόυφη άβδο τοποθετηµένη σε τεταστωµατικό έδαφος. Το πόβληµα είναι συµµετικό ως πος τον κατακόυφο άξονα, οπότε ακεί η σχεδίαση του µοντέλου στο ένα ηµιεπίπεδο (σχήµα 4.39). Στο πόβληµα αυτό εξετάζονται δύο διαφοετικές διατάξεις εδάφους Α και Β, των οποίων οι ειδικές αντιστάσεις ως και 4 των στωµάτων τους παουσιάζονται στον πίνακα 4.7. Τα πάχη των τιών πώτων στωµάτων είναι 7,5m, ενώ του τετάτου και τελευταίου στώµατος είναι άπειο. ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 65
57 Στο σχήµα 4.4 παουσιάζεται η µεταβολή του δυναµικού στην επιφάνεια του εδάφους ως πος την οιζόντια απόσταση από το ηλεκτόδιο για κάθε µία από τις πειπτώσεις του πίνακα 4.7. ιάταξη [Ωm] [Ωm] 3 [Ωm] 4 [Ωm] Α Β Πίνακας 4.7: ιατάξεις ποβλήµατος Σχήµα 4.39: Η γεωµετία του ποβλήµατος Τάση [V] 5 4 Τάση [V] Απόσταση [m] Απόσταση [m] (Α) (Β) Σχήµα 4.4: Η µεταβολή του δυναµικού στην επιφάνεια του εδάφους ως πος την οιζόντια απόσταση από το ηλεκτόδιο : θεωητική ανάλυση Takahashi Kawase [7,8], : διστωµατική µέθοδος [], : ποσοµοίωση µε PC Opera, : µονοστωµατικό έδαφος [] ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 66
58 Πενταστωµατικό έδαφος (Πόβληµα ) Μία κατακόυφη άβδος τοποθετηµένη σε πενταστωµατικό έδαφος εξετάζεται σε αυτό το πόβληµα. Tα πάχη των στωµάτων είναι αντίστοιχα 5m, m, m, 4m και άπειο. Το πόβληµα είναι συµµετικό ως πος τον κατακόυφο άξονα, οπότε ακεί η σχεδίαση του µοντέλου στο ένα ηµιεπίπεδο. Εναλλάσσοντας τις τιµές των ειδικών αντιστάσεων των στωµάτων µελετήθηκαν τέσσεις διαφοετικές διατάξεις (από Α έως ), οι οποίες παουσιάζονται στον παακάτω πίνακα: ιάταξη [Ωm] [Ωm] 3 [Ωm] 4 [Ωm] 5 [Ωm] Α Β Γ Πίνακας 4.8: ιατάξεις ποβλήµατος Η γεωµετία του ποβλήµατος και το χησιµοποιούµενο κατά την επίλυση πλέγµα παουσιάζονται στο σχήµα 4.4. Τα αποτελέσµατα για την κατανοµή δυναµικού που εξάγονται από την στατική ανάλυση, δίνονται στα παακάτω σχήµατα. Σχήµα 4.4: Το πλέγµα της γεωµετίας του ποβλήµατος ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 67
1) Ηλεκτρικό πεδίο φορτισμένου φύλλου απείρων διαστάσεων
 1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
Μαθηματι ά ατεύθυνσης
 Β Λυκείου Μαθηματι ά ατεύθυνσης Ο Κύκλος Θεωία Μεθοδολογία -Ασκήσεις Σ υ ν ο π τ ι κ ή Θ ε ω ί α Ονομασία Διατύπωση Σχόλια Σχήμα Α. Κύκλος Οισμός: Ονομάζεται κύκλος με κέντο Ο και ακτίνα το σύνολο των
Β Λυκείου Μαθηματι ά ατεύθυνσης Ο Κύκλος Θεωία Μεθοδολογία -Ασκήσεις Σ υ ν ο π τ ι κ ή Θ ε ω ί α Ονομασία Διατύπωση Σχόλια Σχήμα Α. Κύκλος Οισμός: Ονομάζεται κύκλος με κέντο Ο και ακτίνα το σύνολο των
H 2 + x 2 cos ϕ. cos ϕ dϕ =
 . Άπειη γαμμική κατανομή ϕοτίου λ Θεωούμε την γαμμική κατανομή ϕοτίου στον άξονα των x και ζητάμε το ηλεκτικό πεδίο στο σημείο A που απέχει από την κατανομή. Το στοιχειώδες τμήμα dx της κατανομής στη θέση
. Άπειη γαμμική κατανομή ϕοτίου λ Θεωούμε την γαμμική κατανομή ϕοτίου στον άξονα των x και ζητάμε το ηλεκτικό πεδίο στο σημείο A που απέχει από την κατανομή. Το στοιχειώδες τμήμα dx της κατανομής στη θέση
ΠΕΙΡΑΜΑ 10. Aεροδυναµική Στερεών Σωµάτων
 ΠΕΙΡΑΜΑ 10 Aεοδυναµική Στεεών Σωµάτων Σκοπός του πειάµατος Σκοπός του πειάµατος αυτού είναι η µελέτη της αντίστασης που αναπτύσσεται κατά τη σχετική κίνηση ενός αντικειµένου µέσα σε ένα αέιο. Οι εξισώσεις
ΠΕΙΡΑΜΑ 10 Aεοδυναµική Στεεών Σωµάτων Σκοπός του πειάµατος Σκοπός του πειάµατος αυτού είναι η µελέτη της αντίστασης που αναπτύσσεται κατά τη σχετική κίνηση ενός αντικειµένου µέσα σε ένα αέιο. Οι εξισώσεις
ΣΥΓΚΡΙΤΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΕΠΙ ΡΑΣΗΣ ΠΑΡΑΜΕΤΡΩΝ ΣΧΕ ΙΑΣΜΟΥ ΣΥΣΤΗΜΑΤΩΝ ΓΕΙΩΣΗΣ
 ΣΥΓΚΡΙΤΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΕΠΙ ΡΑΣΗΣ ΠΑΡΑΜΕΤΡΩΝ ΣΧΕ ΙΑΣΜΟΥ ΣΥΣΤΗΜΑΤΩΝ ΓΕΙΩΣΗΣ M. Λοέντζου* Γ. Γεωγαντζής Ν. Χατζηαγυίου ΕΣΜΗΕ Α.Ε. / Ε ΑΣΣ ΕΗ Α.Ε. / ΚΣ Ε.Μ.Π. / ΣΜΗ&ΜΥ Στόχος του σχεδιασµού των συστηµάτων
ΣΥΓΚΡΙΤΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΕΠΙ ΡΑΣΗΣ ΠΑΡΑΜΕΤΡΩΝ ΣΧΕ ΙΑΣΜΟΥ ΣΥΣΤΗΜΑΤΩΝ ΓΕΙΩΣΗΣ M. Λοέντζου* Γ. Γεωγαντζής Ν. Χατζηαγυίου ΕΣΜΗΕ Α.Ε. / Ε ΑΣΣ ΕΗ Α.Ε. / ΚΣ Ε.Μ.Π. / ΣΜΗ&ΜΥ Στόχος του σχεδιασµού των συστηµάτων
Επανέλεγχος ηλεκτρικής εγκατάστασης
 Επανέλεγχος ηλεκτικής εγκατάστασης Οδηγίες διεξαγωγής μετήσεων και δοκιμών για επανελέγχους ηλεκτικών εγκαταστάσεων με τη χήση σύγχονων ογάνων 1. Εισαγωγή στις απαιτήσεις των επανελέγχων Τα οφέλη του τακτικού
Επανέλεγχος ηλεκτικής εγκατάστασης Οδηγίες διεξαγωγής μετήσεων και δοκιμών για επανελέγχους ηλεκτικών εγκαταστάσεων με τη χήση σύγχονων ογάνων 1. Εισαγωγή στις απαιτήσεις των επανελέγχων Τα οφέλη του τακτικού
B ρ (0, 1) = {(x, y) : x 1, y 1}
 Κεφάλαιο 3 Τοπολογία μετικών χώων 3.1 Ανοικτά και κλειστά σύνολα 3.1.1 Ανοικτά σύνολα Οισμοί 3.1.1. Εστω (X, ) μετικός χώος και έστω x 0 X. (α) Η ανοικτή -μπάλα με κέντο το x 0 και ακτίνα ε > 0 είναι το
Κεφάλαιο 3 Τοπολογία μετικών χώων 3.1 Ανοικτά και κλειστά σύνολα 3.1.1 Ανοικτά σύνολα Οισμοί 3.1.1. Εστω (X, ) μετικός χώος και έστω x 0 X. (α) Η ανοικτή -μπάλα με κέντο το x 0 και ακτίνα ε > 0 είναι το
Να βρίσκουμε τις σχετικές θέσεις δύο κύκλων, όταν γνωρίζουμε τις ακτίνες τους και το μήκος της διακέντρου.
 Ενότητα 6 Κύκλος Στην ενότητα αυτή θα μάθουμε: Να βίσκουμε τις σχετικές θέσεις δύο κύκλων, όταν γνωίζουμε τις ακτίνες τους και το μήκος της διακέντου. Να αποδεικνύουμε και να εφαμόζουμε τις σχέσεις εγγεγαμμένων
Ενότητα 6 Κύκλος Στην ενότητα αυτή θα μάθουμε: Να βίσκουμε τις σχετικές θέσεις δύο κύκλων, όταν γνωίζουμε τις ακτίνες τους και το μήκος της διακέντου. Να αποδεικνύουμε και να εφαμόζουμε τις σχέσεις εγγεγαμμένων
Κεφάλαιο 3: Μοντέλα Θεωρίας Αναμονής
 Κεφάλαιο 3: Μοντέλα Θεωίας Αναμονής Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Γιάννης Γαοφαλάκης Αν. Καθηγητής Οισμός συστημάτων αναμονής Συστήματα αναμονής (Queueing Syses): Συστήματα στα οποία οι αφίξεις
Κεφάλαιο 3: Μοντέλα Θεωίας Αναμονής Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Γιάννης Γαοφαλάκης Αν. Καθηγητής Οισμός συστημάτων αναμονής Συστήματα αναμονής (Queueing Syses): Συστήματα στα οποία οι αφίξεις
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ιπλωµατική Εγασία : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΚΩ ΙΚΑ ΕΠΙΛΥΣΗΣ ΑΞΟΝΟΣΥΜΜΕΤΡΙΚΩΝ ΠΕ ΙΩΝ ΡΟΗΣ ΓΙΑ ΟΜΗΜΕΝΑ ΚΑΙ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ιπλωµατική Εγασία : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΚΩ ΙΚΑ ΕΠΙΛΥΣΗΣ ΑΞΟΝΟΣΥΜΜΕΤΡΙΚΩΝ ΠΕ ΙΩΝ ΡΟΗΣ ΓΙΑ ΟΜΗΜΕΝΑ ΚΑΙ
Συλλογή Ασκήσεων Υδροστατικής
 Συλλογή Ασκήσεων Υδοστατικής Άσκηση. ℵ Να βεθεί η τιμή της πίεσης που δείχνει το πιεσόμετο, σε mmhg. Δίνονται οι πυκνότητες υδαγύου Hg 600kg/m, νεού Ν 000 kg/m και αέα Α,9 kg/m. 0 cm cm + 0 Επίλυση Αχικά
Συλλογή Ασκήσεων Υδοστατικής Άσκηση. ℵ Να βεθεί η τιμή της πίεσης που δείχνει το πιεσόμετο, σε mmhg. Δίνονται οι πυκνότητες υδαγύου Hg 600kg/m, νεού Ν 000 kg/m και αέα Α,9 kg/m. 0 cm cm + 0 Επίλυση Αχικά
υναµική Μηχανών Ι Ακαδηµαϊκό έτος : Ε. Μ. Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 14.
 υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών - Εγαστήιο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 4. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών
υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών - Εγαστήιο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 4. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών
x D 350 C D Co x Cm m m
 Υ ΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΘΗΓΗΤΗΣ : Ν ΚΩΤΣΟΒΙΝΟΣ ΛΕΚΤΟΡΑΣ : Π. ΑΓΓΕΛΙ ΗΣ ΛΥΣΕΙΣ B ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΚΟΡ ΟΠΟΥΛΟΣ ΗΜΗΤΡΙΟΣ ΑΜ 585 ΑΣΚΗΣΗ Θαλασσινό νεό από ένα εγοστάσιο, βεβαηµένο
Υ ΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΘΗΓΗΤΗΣ : Ν ΚΩΤΣΟΒΙΝΟΣ ΛΕΚΤΟΡΑΣ : Π. ΑΓΓΕΛΙ ΗΣ ΛΥΣΕΙΣ B ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΚΟΡ ΟΠΟΥΛΟΣ ΗΜΗΤΡΙΟΣ ΑΜ 585 ΑΣΚΗΣΗ Θαλασσινό νεό από ένα εγοστάσιο, βεβαηµένο
x όπου Ε είναι η ολική ενέργεια ανά µονάδα µάζας και Η είναι η ολική ενθαλπία για τις οποίες ισχύει
 ΜΕΘΟ ΟΙ ΑΕΡΟ ΥΝΑΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Κ.Χ. ΓΙΑΝΝΑΚΟΓΛΟΥ, Αν. Καθηγητής, Τοµέας Ρευστών, Σχολή Μηχανολόγων Ε.Μ.Π. ΜΟΝΟ ΙΑΣΤΑΤΕΣ ΕΞΙΣΩΣΕΙΣ EULER ιαφοετικές Γαφές των Εξισώσεων
ΜΕΘΟ ΟΙ ΑΕΡΟ ΥΝΑΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Κ.Χ. ΓΙΑΝΝΑΚΟΓΛΟΥ, Αν. Καθηγητής, Τοµέας Ρευστών, Σχολή Μηχανολόγων Ε.Μ.Π. ΜΟΝΟ ΙΑΣΤΑΤΕΣ ΕΞΙΣΩΣΕΙΣ EULER ιαφοετικές Γαφές των Εξισώσεων
Ανάληψη αξονικού φορτίου από πάσσαλο
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΔΙΑΛΕΞΕΩΝ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «Αλληλεπίδαση Εδάφους Κατασκευής» 8 ο Εξ. ΠΟΛ. ΜΗΧ. - Ακαδ. Ετος 6 7 Διδάσκοντες : Γ. Γκαζέτας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΔΙΑΛΕΞΕΩΝ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «Αλληλεπίδαση Εδάφους Κατασκευής» 8 ο Εξ. ΠΟΛ. ΜΗΧ. - Ακαδ. Ετος 6 7 Διδάσκοντες : Γ. Γκαζέτας
Υπολογισμός γεωστροφικών ρευμάτων με τη χρήση δεδομένων από CTD. Σύγκριση με αποτελέσματα από A.D.C.P. & Drifters.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΘΑΛΑΣΣΑΣ Υπολογισμός γεωστοφικών ευμάτων με τη χήση δεδομένων από CTD. Σύγκιση με αποτελέσματα από A.D.C.P. & Drifters. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ (Επιβλέπων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΘΑΛΑΣΣΑΣ Υπολογισμός γεωστοφικών ευμάτων με τη χήση δεδομένων από CTD. Σύγκιση με αποτελέσματα από A.D.C.P. & Drifters. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ (Επιβλέπων:
Κεφάλαιο 2 Εισαγωγή στα ροϊκά φαινόμενα
 Κεφάλαιο Εισαγωγή στα οϊκά φαινόμενα Σύνοψη Η έννοια του ανοικτού συστήματος (όγκος ελέγχου) Ρυθμός μεταβολής των ιδιοτήτων του συστήματος Νόμος της συνέχειας Νόμος της ομής (δυνάμεις) Γενικευμένη εξίσωση
Κεφάλαιο Εισαγωγή στα οϊκά φαινόμενα Σύνοψη Η έννοια του ανοικτού συστήματος (όγκος ελέγχου) Ρυθμός μεταβολής των ιδιοτήτων του συστήματος Νόμος της συνέχειας Νόμος της ομής (δυνάμεις) Γενικευμένη εξίσωση
Απόδειξη. Θέτουµε τώρα δ= Απόδειξη. 1 συν. 4α + 4β. 3. Απόδειξη Σύµφωνα µε την 2 έχουµε. οπότε προκύπτει. και τελικά
 1., β R ΤΟ ΤΡΙΓΩΝΟ ΜΕΓΙΣΤΟΥ ΕΜΒΑ ΟΥ ΕΓΓΕΓΡΑΜΜΕΝΟΥ ΣΕ ΚΥΚΛΟ a ισχύει ηµα ηµβ ηµ ηµα ηµβ ηµ ηµα ηµβ 1 συν ηµα ηµβ 1- συνα συνβ +ηµα ηµβ συν(α-β) 1 ηµα ηµβ 1- συν (α+β) + γ + δ. α, β, γ, δ (0, π ) ισχύει:
1., β R ΤΟ ΤΡΙΓΩΝΟ ΜΕΓΙΣΤΟΥ ΕΜΒΑ ΟΥ ΕΓΓΕΓΡΑΜΜΕΝΟΥ ΣΕ ΚΥΚΛΟ a ισχύει ηµα ηµβ ηµ ηµα ηµβ ηµ ηµα ηµβ 1 συν ηµα ηµβ 1- συνα συνβ +ηµα ηµβ συν(α-β) 1 ηµα ηµβ 1- συν (α+β) + γ + δ. α, β, γ, δ (0, π ) ισχύει:
ΑΣΚΗΣΗ 14. έκδοση DΥΝI-EXC b
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΣΚΗΣΗ 14 έκδοση DΥΝI-EXC14-016b Copyright Ε.Μ.Π. - 016 Σχολή
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΣΚΗΣΗ 14 έκδοση DΥΝI-EXC14-016b Copyright Ε.Μ.Π. - 016 Σχολή
Εύρωστοι Γεωμετρικοί Αλγόριθμοι Robust algorithms in Computational Geometry
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ Εύωστοι Γεωμετικοί Αλγόιθμοι Roust lgorithms in Computtionl Geometr Ζαχάου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ Εύωστοι Γεωμετικοί Αλγόιθμοι Roust lgorithms in Computtionl Geometr Ζαχάου
ΚΕΦΑΛΑΙΟ 10 ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ. Εξισώσεις Maxwell Όπως έχουµε, ήδη, αναφέει, ένα ηλεκτοστατικό πεδίο E µποεί να υφίσταται ανεξάτητα από την παουσία ή όχι µαγνητικού πεδίου H, όπως για
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ. Εξισώσεις Maxwell Όπως έχουµε, ήδη, αναφέει, ένα ηλεκτοστατικό πεδίο E µποεί να υφίσταται ανεξάτητα από την παουσία ή όχι µαγνητικού πεδίου H, όπως για
Σχήµα ΒΣ-6. Προφίλ πάχους, ταχύτητας και θερµοκρασίας υµένα κατά την συµπύκνωση
 υθµοί µετάοσης θεµότητας παουσιάζονται πολύ µεγαλύτεοι από τους αντίστοιχους στην συµπύκνωση τύπου υµένα. Κατά την συµπύκνωση υµένα, το υγό συµπύκνωµα ηµιουγείται αχικά στην επιφάνεια, από την οποία στην
υθµοί µετάοσης θεµότητας παουσιάζονται πολύ µεγαλύτεοι από τους αντίστοιχους στην συµπύκνωση τύπου υµένα. Κατά την συµπύκνωση υµένα, το υγό συµπύκνωµα ηµιουγείται αχικά στην επιφάνεια, από την οποία στην
1 r ολοκληρώνοντας αυτή τη σχέση έχουµε:
 Σελ-- ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΣΤΟΝ ΙΑΓΩΝΙΣΜΟ ΤΩΝ ΕΚΠΑΙ ΕΥΤΙΚΩΝ Α.Σ.Ε.Π 998 ΕΡΩΤΗΜΑ ο Με βάση τα χαακτηιστικά των βαυτικών δυνάµεων, ποια µεγέθη συµπεαίνετε ότι διατηούνται κατά τη κίνηση των πλανητών υπό την επίδαση
Σελ-- ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΣΤΟΝ ΙΑΓΩΝΙΣΜΟ ΤΩΝ ΕΚΠΑΙ ΕΥΤΙΚΩΝ Α.Σ.Ε.Π 998 ΕΡΩΤΗΜΑ ο Με βάση τα χαακτηιστικά των βαυτικών δυνάµεων, ποια µεγέθη συµπεαίνετε ότι διατηούνται κατά τη κίνηση των πλανητών υπό την επίδαση
Χειμερινό εξάμηνο 2007 1
 ΜΜΚ 3 Μεταφοά Θεμότητας Φυσική Συναγωγή ΜΜΚ 3 Μεταφοά Θεμότητας Τμήμα Μηχανολόγων Μηχανικών και Μηχανικών Πααγωγής ΜΜK 3 Μεταφοά Θεμότητας Φυσική Συναγωγή (r convction) Στα ποηγούμενα ύο κεφάλαια ασχοληθήκαμε
ΜΜΚ 3 Μεταφοά Θεμότητας Φυσική Συναγωγή ΜΜΚ 3 Μεταφοά Θεμότητας Τμήμα Μηχανολόγων Μηχανικών και Μηχανικών Πααγωγής ΜΜK 3 Μεταφοά Θεμότητας Φυσική Συναγωγή (r convction) Στα ποηγούμενα ύο κεφάλαια ασχοληθήκαμε
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΠΟΛΙΤΙΚΕΣ ΕΛΕΓΧΟΥ ΑΠΟΘΕΜΑΤΩΝ ΚΑΙ ΠΩΛΗΣΕΩΝ ΓΙΑ ΑΠΛΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ ΠΕΛΑΤΕΣ ΠΟΥ ΑΠΟΘΑΡΡΥΝΟΝΤΑΙ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΠΟΛΙΤΙΚΕΣ ΕΛΕΓΧΟΥ ΑΠΟΘΕΜΑΤΩΝ ΚΑΙ ΠΩΛΗΣΕΩΝ ΓΙΑ ΑΠΛΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ ΠΕΛΑΤΕΣ ΠΟΥ ΑΠΟΘΑΡΡΥΝΟΝΤΑΙ ιατιβή που υπεβλήθη για την µεική ικανοποίηση των απαιτήσεων για την απόκτηση Μεταπτυχιακού
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΠΟΛΙΤΙΚΕΣ ΕΛΕΓΧΟΥ ΑΠΟΘΕΜΑΤΩΝ ΚΑΙ ΠΩΛΗΣΕΩΝ ΓΙΑ ΑΠΛΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ ΠΕΛΑΤΕΣ ΠΟΥ ΑΠΟΘΑΡΡΥΝΟΝΤΑΙ ιατιβή που υπεβλήθη για την µεική ικανοποίηση των απαιτήσεων για την απόκτηση Μεταπτυχιακού
Σημειώσεις IV: Μαθηματικά Υπολογιστικής Τομογραφίας
 HY 673 - Ιατική Απεικόνιση Στέλιος Οφανουδάκης Κώστας Μαιάς Σημειώσεις IV: Μαηματικά Υπολογιστικής Τομογαφίας Σεπτέμβιος 2003-Φεβουάιος 2004 Αχές Υπολογιστικής Τομογαφίας 1. Η ανάγκη απεικόνισης στις 3-Διαστάσεις
HY 673 - Ιατική Απεικόνιση Στέλιος Οφανουδάκης Κώστας Μαιάς Σημειώσεις IV: Μαηματικά Υπολογιστικής Τομογαφίας Σεπτέμβιος 2003-Φεβουάιος 2004 Αχές Υπολογιστικής Τομογαφίας 1. Η ανάγκη απεικόνισης στις 3-Διαστάσεις
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ. Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ.
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
Μελέτη της Άνωσης. Α = ρ υγρού g V βυθ..
 Μελέτη της Άνωσης F 1 h 1 h 2 Α) Η Άνωση οφείλεται στην βαύτητα. Αν ένα σώμα βίσκεται μέσα σε υγό με πυκνότητα υγού η επάνω επιφάνειά του με εμβαδό S δέχεται δύναμη F 1 = P 1 S και η ίσου εμβαδού κάτω
Μελέτη της Άνωσης F 1 h 1 h 2 Α) Η Άνωση οφείλεται στην βαύτητα. Αν ένα σώμα βίσκεται μέσα σε υγό με πυκνότητα υγού η επάνω επιφάνειά του με εμβαδό S δέχεται δύναμη F 1 = P 1 S και η ίσου εμβαδού κάτω
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ»
 ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 005-06 ΔΙΑΛΕΞΗ Θεμελιώσεις με πασσάλους : Ομάδες πασσάλων.05.005. Κατηγοίες πασσάλων. Αξονική φέουσα ικανότητα μεμονωμένου πασσάλου.
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 005-06 ΔΙΑΛΕΞΗ Θεμελιώσεις με πασσάλους : Ομάδες πασσάλων.05.005. Κατηγοίες πασσάλων. Αξονική φέουσα ικανότητα μεμονωμένου πασσάλου.
3. Μετρήσεις GPS Προβλήµατα
 . Μετήσεις GPS Ποβλήµατα.. Μετήσεις G.P.S. και ποβλήµατα. Οι παατηήσεις που παγµατοποιούνται µε το σύστηµα GPS, όπως έχουµε άλλωστε ήδη αναφέει, διακίνονται σε δύο κατηγοίες: α) σε µετήσεις ψευδοαποστάσεων
. Μετήσεις GPS Ποβλήµατα.. Μετήσεις G.P.S. και ποβλήµατα. Οι παατηήσεις που παγµατοποιούνται µε το σύστηµα GPS, όπως έχουµε άλλωστε ήδη αναφέει, διακίνονται σε δύο κατηγοίες: α) σε µετήσεις ψευδοαποστάσεων
Εργ.Αεροδυναμικής, ΕΜΠ. Καθ. Γ.Μπεργελές
 ΠΡΟΤΥΠΑ ΡΕΥΣΤΟΜΗΧΑΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ (Υπολογιστική Ρευστομηχανική-Πεπεασμένες διαφοές) Γ. Μπεγελές Ιανουάιος 6 C 5 4 3 Z 3 3 4 5 6 7 ZC CON:..5..5.3.35.4.45.5.55.6.65.7.75.8.85.9.95 C ΠΕΡΙΕΧΟΜΕΝΑ. Παάδειγμα
ΠΡΟΤΥΠΑ ΡΕΥΣΤΟΜΗΧΑΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ (Υπολογιστική Ρευστομηχανική-Πεπεασμένες διαφοές) Γ. Μπεγελές Ιανουάιος 6 C 5 4 3 Z 3 3 4 5 6 7 ZC CON:..5..5.3.35.4.45.5.55.6.65.7.75.8.85.9.95 C ΠΕΡΙΕΧΟΜΕΝΑ. Παάδειγμα
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΑΣΚΗΣΕΙΣ
 ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ Η μέτηση της ταχύτητας οής ενός εστού μέσα σε ένα σωλήνα γίνεται με τη σσκεή Prandtl (σωλήνας Pitot) (βλέπε Σχήμα). Η σσκεή ατή αποτελείται από δο πολύ λεπτούς σωλήνες,
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ Η μέτηση της ταχύτητας οής ενός εστού μέσα σε ένα σωλήνα γίνεται με τη σσκεή Prandtl (σωλήνας Pitot) (βλέπε Σχήμα). Η σσκεή ατή αποτελείται από δο πολύ λεπτούς σωλήνες,
Bernoulli P ρ +gz Ω2 ϖ 2 2
 Εθνικό και Καποιστιακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Δυναμική των Ρευστών, 6 Φεβουαίου 08 Απαντήστε σε 3 από τα 4 θέματα ιάκεια εξέτασης ώες Καλή επιτυχία = bonus εωτήματα) Θέμα ο :
Εθνικό και Καποιστιακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Δυναμική των Ρευστών, 6 Φεβουαίου 08 Απαντήστε σε 3 από τα 4 θέματα ιάκεια εξέτασης ώες Καλή επιτυχία = bonus εωτήματα) Θέμα ο :
Μοντέλα Ταχέως Περιστρεφόµενων Αστέρων Νετρονίων
 ιπλωµατική Εγασία Μοντέλα Ταχέως Πειστεφόµενων Αστέων Νετονίων Πασχαλίδης Βασίλειος Α.Ε.Μ.: 1188 Κατεύθυνση Αστονοµίας Αστοφυσικής Επιβλέποντες Καθηγητές: Κ. Κόκκοτας, Ν. Στεγιούλας 8 Ιουλίου 3 Πλάνο Παουσίασης
ιπλωµατική Εγασία Μοντέλα Ταχέως Πειστεφόµενων Αστέων Νετονίων Πασχαλίδης Βασίλειος Α.Ε.Μ.: 1188 Κατεύθυνση Αστονοµίας Αστοφυσικής Επιβλέποντες Καθηγητές: Κ. Κόκκοτας, Ν. Στεγιούλας 8 Ιουλίου 3 Πλάνο Παουσίασης
( ) ( ) ( ) 1 ( ) ( ) Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN
 Γαµµική Άλγεβα ΙΙ Σελίδα από Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Έστω λ είναι ιδιοτιµή του ν ν πίνακα, αλγεβικής πολλαπλότητας ν > Ένα διάνυσµα τάξης x, διάφοο του µηδέν, ονοµάζεται γενικευµένο ιδιοδιάνυσµα,,
Γαµµική Άλγεβα ΙΙ Σελίδα από Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Έστω λ είναι ιδιοτιµή του ν ν πίνακα, αλγεβικής πολλαπλότητας ν > Ένα διάνυσµα τάξης x, διάφοο του µηδέν, ονοµάζεται γενικευµένο ιδιοδιάνυσµα,,
Άσκηση 1. R y. R x. Επίλυση (2.1) (2.2) Q 1 1 = 1 1
 Ασκήσεις εφαµογής ισοζυγίου οής γαµ. οµής Άσκηση Ακοφύσιο Α εκτοξεύει κυλινδική φλέβα νεού διαµέτου d c µε υθµό l/. H φλέβα του νεού εισέχεται σε ένα διαχύτη και χωίζεται σε κυλινδικές φλέβες µε διατοµές
Ασκήσεις εφαµογής ισοζυγίου οής γαµ. οµής Άσκηση Ακοφύσιο Α εκτοξεύει κυλινδική φλέβα νεού διαµέτου d c µε υθµό l/. H φλέβα του νεού εισέχεται σε ένα διαχύτη και χωίζεται σε κυλινδικές φλέβες µε διατοµές
ΠΡΟΣΟΜΟΙΩΣΗ ΙΦΑΣΙΚΗΣ ΡΟΗΣ ΑΕΡΑ ΚΑΙ ΣΩΜΑΤΙ ΙΩΝ ΣΕ ΕΣΩΤΕΡΙΚΟΥΣ ΧΩΡΟΥΣ
 ΠΡΟΣΟΜΟΙΩΣΗ ΙΦΑΣΙΚΗΣ ΡΟΗΣ ΑΕΡΑ ΚΑΙ ΣΩΜΑΤΙ ΙΩΝ ΣΕ ΕΣΩΤΕΡΙΚΟΥΣ ΧΩΡΟΥΣ. Π. Κααδήµου, Ν.Χ Μακάτος Εθνικό Μετσόβιο Πολυτεχνείο, Σχολή Χηµικών Μηχανικών, Τοµέας ΙΙ, Πολυτεχνειούπολη Ζωγάφου 15780 Αθήνα ΠΕΡΙΛΗΨΗ
ΠΡΟΣΟΜΟΙΩΣΗ ΙΦΑΣΙΚΗΣ ΡΟΗΣ ΑΕΡΑ ΚΑΙ ΣΩΜΑΤΙ ΙΩΝ ΣΕ ΕΣΩΤΕΡΙΚΟΥΣ ΧΩΡΟΥΣ. Π. Κααδήµου, Ν.Χ Μακάτος Εθνικό Μετσόβιο Πολυτεχνείο, Σχολή Χηµικών Μηχανικών, Τοµέας ΙΙ, Πολυτεχνειούπολη Ζωγάφου 15780 Αθήνα ΠΕΡΙΛΗΨΗ
P l+1 (cosa) P l 1 (cosa) 2δ l,0 1
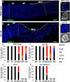 Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
_ Τ.Ε.Ι. ΚΑΒΑΛΑΣ Σχολή Τεχνολογικών Εφαρμογών Τμήμα Ηλεκτρολογίας
 _ Τ.Ε.Ι. ΚΑΒΑΛΑΣ Σχολή Τεχνολογικών Εφαμογών Τμήμα Ηλεκτολογίας Υπετάσεις και Απαιτήσεις Μόνωσηςί \Λ - 'V k - O 6 Μια πειοχή μεγάλης σημαοτίας κατά το σχεδίασμά συστημάτων ισχύος είναι η μελέτη των απαιτήσεων
_ Τ.Ε.Ι. ΚΑΒΑΛΑΣ Σχολή Τεχνολογικών Εφαμογών Τμήμα Ηλεκτολογίας Υπετάσεις και Απαιτήσεις Μόνωσηςί \Λ - 'V k - O 6 Μια πειοχή μεγάλης σημαοτίας κατά το σχεδίασμά συστημάτων ισχύος είναι η μελέτη των απαιτήσεων
Ανάλυση σε Πεπερασμένο Όγκο Αναφοράς. Τρόποι επίλυσης προβλημάτων Μηχανικής Ρευστών. Θεωρητική ανάλυση συστήματος
 Ανάλυση σε Πεπεασμένο Όκο Αναφοάς Τόποι επίλυσης ποβλημάτων Μηχανικής Ρευστών Θεωητική ανάλυση συστήματος Πεπεασμένοόκοαναφοάς Διαφοική ανάλυση σε απειοστό όκο Πειαματική ανάλυση Συστήματα Οι νόμοι της
Ανάλυση σε Πεπεασμένο Όκο Αναφοάς Τόποι επίλυσης ποβλημάτων Μηχανικής Ρευστών Θεωητική ανάλυση συστήματος Πεπεασμένοόκοαναφοάς Διαφοική ανάλυση σε απειοστό όκο Πειαματική ανάλυση Συστήματα Οι νόμοι της
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ
 ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ ΜΕΡΟΣ Ι Ν. ΔΕΡΒΑΚΟΥ Σημειώσεις Πααδόσεων Αθήνα 23 ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ Ι. ΕΙΣΑΓΩΓΗ Βασική Δομή Ποβλημάτων Αναμονής Σύστημα Αναμονής Πηγή ποσέλευσης
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ ΜΕΡΟΣ Ι Ν. ΔΕΡΒΑΚΟΥ Σημειώσεις Πααδόσεων Αθήνα 23 ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ Ι. ΕΙΣΑΓΩΓΗ Βασική Δομή Ποβλημάτων Αναμονής Σύστημα Αναμονής Πηγή ποσέλευσης
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ. Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ A Α. α Α. β Α3. γ Α4. δ Α5. α. Λάθος ΘΕΜΑ Β ΦΥΣΙΚΗ Ηµεοµηνία: Μ. Τετάτη Απιλίου 07 β. Σωστό γ. Λάθος δ. Λάθος
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ A Α. α Α. β Α3. γ Α4. δ Α5. α. Λάθος ΘΕΜΑ Β ΦΥΣΙΚΗ Ηµεοµηνία: Μ. Τετάτη Απιλίου 07 β. Σωστό γ. Λάθος δ. Λάθος
1. ΕΙΣΑΓΩΓΗ. 1.1 Ερευνητικό ενδιαφέρον. 1.2 Επισηµάνσεις από τη βιβλιογραφία. 1.3 Προσέγγιση λύσης προβληµάτων:
 . Εευνητικό ενδιαφέον. ΕΙΣΑΓΩΓΗ. Επισηµάνσεις από τη βιβλιογαφία α) Ελλιπείς γνώσεις των πολύπλοκων φυσικών διεγασιών β) Ελάχιστα εφαµόζονται οι νόµοι της Μηχανικής των Ρευστών γ)ελάχιστα βιβλία διεθνώς
. Εευνητικό ενδιαφέον. ΕΙΣΑΓΩΓΗ. Επισηµάνσεις από τη βιβλιογαφία α) Ελλιπείς γνώσεις των πολύπλοκων φυσικών διεγασιών β) Ελάχιστα εφαµόζονται οι νόµοι της Μηχανικής των Ρευστών γ)ελάχιστα βιβλία διεθνώς
Μάθηµα: ΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ. Ασκήσεις
 Μάθηα: ΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ 7 ου εξαήνου ΣΕΜΦΕ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ - ΑΝΑΛΥΣΗ ΕΠΙ ΟΣΗΣ ΙΚΤΥΩΝ Ασκήσεις Αποστέλλονται πακέτα σταθεού ήκους ytes από τον κόβο # στον κόβο #4 έσω των κόβων # και #3 σε σειά, όπως
Μάθηα: ΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ 7 ου εξαήνου ΣΕΜΦΕ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ - ΑΝΑΛΥΣΗ ΕΠΙ ΟΣΗΣ ΙΚΤΥΩΝ Ασκήσεις Αποστέλλονται πακέτα σταθεού ήκους ytes από τον κόβο # στον κόβο #4 έσω των κόβων # και #3 σε σειά, όπως
ΡΕΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM
 Q ΡΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM Ισοοπία σε αγωγό μόνον όταν στο εσωτεικό του αγωγού είναι =0 λεύθεο Ηλεκτόνιο Πείσεια ελευθέων ηλεκτονίων ξωτεικό ηλεκτικό πεδίο εσ εξ = εσ = 0 εξ σωτεικό ηλ. πεδίο Ποσθήκη εξωτεικού
Q ΡΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM Ισοοπία σε αγωγό μόνον όταν στο εσωτεικό του αγωγού είναι =0 λεύθεο Ηλεκτόνιο Πείσεια ελευθέων ηλεκτονίων ξωτεικό ηλεκτικό πεδίο εσ εξ = εσ = 0 εξ σωτεικό ηλ. πεδίο Ποσθήκη εξωτεικού
4.4 Η Επιδοµή της Γραµµής
 4. Η Υποδοµή της Γαµµής Η κατασκευή που βίσκεται κάτω από την επιδοµή, ονοµάζεται υποδοµή ή υπόβαση και αποτελείται από την στώση διαµόφωσης και την κυίως υποδοµή ή υπόβαση ή έδαφος θεµελίωσης. 4.4 Η Επιδοµή
4. Η Υποδοµή της Γαµµής Η κατασκευή που βίσκεται κάτω από την επιδοµή, ονοµάζεται υποδοµή ή υπόβαση και αποτελείται από την στώση διαµόφωσης και την κυίως υποδοµή ή υπόβαση ή έδαφος θεµελίωσης. 4.4 Η Επιδοµή
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΝΑΚΛΑΣΗ & ΔΙΑΔΟΣΗ ΚΥΜΑΤΩΝ ΣΕ ΑΣΥΝΕΧΕΙΑ ΧΟΡΔΗΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 96778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΝΑΚΛΑΣΗ & ΔΙΑΔΟΣΗ ΚΥΜΑΤΩΝ ΣΕ ΑΣΥΝΕΧΕΙΑ ΧΟΡΔΗΣ Σγγαφή Επιμέλεια: Παναγιώτης Φ. Μοίας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 96778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 96778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΝΑΚΛΑΣΗ & ΔΙΑΔΟΣΗ ΚΥΜΑΤΩΝ ΣΕ ΑΣΥΝΕΧΕΙΑ ΧΟΡΔΗΣ Σγγαφή Επιμέλεια: Παναγιώτης Φ. Μοίας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 96778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
" Θεωρητική και υπολογιστική µελέτη της βαροκλινικής αστάθειας "
 Αιστοτέειο Πανεπιστήµιο Θεσσαονίκης Σχοή ετικών επιστηµών Τµήµα Φυσικής " Θεωητική και υποογιστική µεέτη της βαοκινικής αστάειας " ιπωµατική εγασία Πόγαµµα µεταπτυχιακών σπουδών Υποογιστική Φυσική Καογεάς
Αιστοτέειο Πανεπιστήµιο Θεσσαονίκης Σχοή ετικών επιστηµών Τµήµα Φυσικής " Θεωητική και υποογιστική µεέτη της βαοκινικής αστάειας " ιπωµατική εγασία Πόγαµµα µεταπτυχιακών σπουδών Υποογιστική Φυσική Καογεάς
Εισαγωγή στην Αστρονομία
 Παπαδόπουλος Μιλτιάδης ΑΕΜ: 4 Εξάμηο: 7 ο Ασκήσεις: -4 Εισαγωγή στη Αστοομία Έα ομογεές μεσοαστικό έφος έχει μάζα Μ ΜΗ (μία μάζα Ηλίου) και πυκότητα ^ mp/m^ Η πείοδος αξοικής πειστοφής του είαι έτη Ποια
Παπαδόπουλος Μιλτιάδης ΑΕΜ: 4 Εξάμηο: 7 ο Ασκήσεις: -4 Εισαγωγή στη Αστοομία Έα ομογεές μεσοαστικό έφος έχει μάζα Μ ΜΗ (μία μάζα Ηλίου) και πυκότητα ^ mp/m^ Η πείοδος αξοικής πειστοφής του είαι έτη Ποια
Υπάρχει σηµείο χ 0 τέτοιο ώστε να ισχύει..
 Υπάχει σηµείο χ 0 τέτοιο ώστε να ισχύει.. ( ή διαφοετικά πεί ιζών εξίσωσης ) I. Για να δείξουµε ότι µια εξίσωση f(χ)=0 έχει µία τουλάχιστον ίζα στο διάστηµα (α, β) µποούµε να εγασθούµε ως εξής: 1 0ς τόπος:
Υπάχει σηµείο χ 0 τέτοιο ώστε να ισχύει.. ( ή διαφοετικά πεί ιζών εξίσωσης ) I. Για να δείξουµε ότι µια εξίσωση f(χ)=0 έχει µία τουλάχιστον ίζα στο διάστηµα (α, β) µποούµε να εγασθούµε ως εξής: 1 0ς τόπος:
3. Αρμονικά Κύματα Χώρου και Επιφανείας. P, S, Rayleigh και Love
 3. Αμονικά Κύματα Χώου και Επιφανείας P, S, Rayleigh και Lve ΠΕΡΙΕΧΟΜΕΝΑ 3. Κύματα (P & S) σε ομοιογενή χώο 3. Κύματα σε ανομοιογενή μέσα με δι-επιφάνεια 3.3. Επιφανειακά κύματα Πόσθετο ιάβασμα Steven
3. Αμονικά Κύματα Χώου και Επιφανείας P, S, Rayleigh και Lve ΠΕΡΙΕΧΟΜΕΝΑ 3. Κύματα (P & S) σε ομοιογενή χώο 3. Κύματα σε ανομοιογενή μέσα με δι-επιφάνεια 3.3. Επιφανειακά κύματα Πόσθετο ιάβασμα Steven
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΠΕΙΡΑΜΑΤΙΚΗ Υ ΡΑΥΛΙΚΗ ΤΟΜΕΑΣ Υ ΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ Υ ΡΑΥΛΙΚΗΣ Ακ. Έτος 0-. ΜΕΤΡΗΣΕΙΣ ΑΠΩΛΕΙΩΝ ΕΝΕΡΓΕΙΑΣ ΣΕ ΑΓΩΓΟΥΣ ΥΠΟ ΠΙΕΣΗ. Γενικά - αντικείµενο του πειάµατος Οι αγωγοί υπό πίεση αποτελούν ένα από τα βασικά αντικείµενα των Πολιτικών
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ Υ ΡΑΥΛΙΚΗΣ Ακ. Έτος 0-. ΜΕΤΡΗΣΕΙΣ ΑΠΩΛΕΙΩΝ ΕΝΕΡΓΕΙΑΣ ΣΕ ΑΓΩΓΟΥΣ ΥΠΟ ΠΙΕΣΗ. Γενικά - αντικείµενο του πειάµατος Οι αγωγοί υπό πίεση αποτελούν ένα από τα βασικά αντικείµενα των Πολιτικών
Η Βουλή των Αντιπροσώπων ψηφίζει ως ακολούθως:
 5 Ε.Ε. Πα. Ι(II) Α. 461, 18.1.8 Ν. 57(II)/8 Ο πεί Συμπληωματικού Ποϋπολογισμού της Αχής Λιμένων Κύπου Νόμος (Α. 1) του 8 εκδίδεται με δημοσίευση στην Επίσημη Εφημείδα της Κυπιακής Δημοκατίας σύμφωνα με
5 Ε.Ε. Πα. Ι(II) Α. 461, 18.1.8 Ν. 57(II)/8 Ο πεί Συμπληωματικού Ποϋπολογισμού της Αχής Λιμένων Κύπου Νόμος (Α. 1) του 8 εκδίδεται με δημοσίευση στην Επίσημη Εφημείδα της Κυπιακής Δημοκατίας σύμφωνα με
ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΧΑΡΤΟΓΡΑΦΙΚΩΝ ΠΡΟΒΟΛΩΝ ΕΓΚΑΡΣΙΑ ΜΕΡΚΑΤΟΡΙΚΗ ΠΡΟΒΟΛΗ
 ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΧΑΡΤΟΓΡΑΦΙΚΩΝ ΠΡΟΒΟΛΩΝ ΕΓΚΑΡΣΙΑ ΜΕΡΚΑΤΟΡΙΚΗ ΠΡΟΒΟΛΗ Οι σχέσεις της Εγκάσιας Μεκατοικής Ποβοής στο εειψοειδές µποούν να ποκύψουν από την Εγκάσια Ισαπέχουσα Ποβοή Cassii εαµόζοντας
ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΧΑΡΤΟΓΡΑΦΙΚΩΝ ΠΡΟΒΟΛΩΝ ΕΓΚΑΡΣΙΑ ΜΕΡΚΑΤΟΡΙΚΗ ΠΡΟΒΟΛΗ Οι σχέσεις της Εγκάσιας Μεκατοικής Ποβοής στο εειψοειδές µποούν να ποκύψουν από την Εγκάσια Ισαπέχουσα Ποβοή Cassii εαµόζοντας
2 i d i(x(i), y(i)),
 Κεφάλαιο 2 Σύγκλιη ακολουθιών και υνέχεια υνατήεων 2.1 Σύγκλιη ακολουθιών Στον Απειοτικό Λογιμό μελετήαμε τη ύγκλιη ακολουθιών παγματικών αιθμών. Με τον όο ακολουθία παγματικών αιθμών εννοούμε κάθε υνάτηη
Κεφάλαιο 2 Σύγκλιη ακολουθιών και υνέχεια υνατήεων 2.1 Σύγκλιη ακολουθιών Στον Απειοτικό Λογιμό μελετήαμε τη ύγκλιη ακολουθιών παγματικών αιθμών. Με τον όο ακολουθία παγματικών αιθμών εννοούμε κάθε υνάτηη
Τα κύρια σηµεία της παρούσας διδακτορικής διατριβής είναι: Η πειραµατική µελέτη της µεταβατικής συµπεριφοράς συστηµάτων γείωσης
 Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
ΚΕΦΑΛΑΙΟ 4 Ο ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ
 Σχεδίαση με τη χήση Η/Υ ΚΕΦΛΙ 4 ΓΕΩΜΕΤΡΙΚΕΣ ΚΤΣΚΕΥΕΣ ΔΡ ΛΕΩΝΙΔΣ ΝΘΠΥΛΣ, ΕΠΙΚΥΡΣ ΚΘΗΓΗΤΗΣ ΤΜΗΜ ΔΙΙΚΗΣΗΣ ΚΙ ΔΙΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΡΙΣΣ Θέμα 24 ο : κατασκευή ασκευή κύκλου εφαπτομένου στις πλευές γωνίας Έστω
Σχεδίαση με τη χήση Η/Υ ΚΕΦΛΙ 4 ΓΕΩΜΕΤΡΙΚΕΣ ΚΤΣΚΕΥΕΣ ΔΡ ΛΕΩΝΙΔΣ ΝΘΠΥΛΣ, ΕΠΙΚΥΡΣ ΚΘΗΓΗΤΗΣ ΤΜΗΜ ΔΙΙΚΗΣΗΣ ΚΙ ΔΙΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΡΙΣΣ Θέμα 24 ο : κατασκευή ασκευή κύκλου εφαπτομένου στις πλευές γωνίας Έστω
Τµήµα Ηλεκτρονικής. Πτυχιακή εργασία. Προσοµοιώσεις Προβληµάτων Σκέδασης Ηλεκτροµαγνητικών Κυµάτων από Τραχείες Επιφάνειες µε Τυχαία Χαρακτηριστικά
 T.Ε.Ι. Κήτης Παάτηµα Χανίων Τµήµα Ηλεκτονικής Πτυχιακή εγασία µε θέµα Ποσοµοιώσεις Ποβληµάτων Σκέδασης Ηλεκτοµαγνητικών Κυµάτων από Ταχείες Επιφάνειες µε Τυχαία Χαακτηιστικά από τον Αθανάσιο Λέκκα, Σπουδαστή
T.Ε.Ι. Κήτης Παάτηµα Χανίων Τµήµα Ηλεκτονικής Πτυχιακή εγασία µε θέµα Ποσοµοιώσεις Ποβληµάτων Σκέδασης Ηλεκτοµαγνητικών Κυµάτων από Ταχείες Επιφάνειες µε Τυχαία Χαακτηιστικά από τον Αθανάσιο Λέκκα, Σπουδαστή
ΕΞΑΣΘΕΝΗΣΗ ΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ
 ΕΞΑΣΘΕΝΗΣΗ ΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ Διάδοση κυλινδικού κύματος Καταγαφή σεισμού (Μ5.9) σε διαφοετικό πειβάλλον εξασθένησης ΗΕΞΑΣΘΕΝΗΣΗΤΩΝΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΧΕΣΗ ΜΕ ΤΟ ΜΕΣΟ ΔΙΑΔΟΣΗΣ ΓΕΩΜΕΤΡΙΚΗ ΔΙΑΣΠΟΡΑ ΑΠΟΣΒΕΣΗ
ΕΞΑΣΘΕΝΗΣΗ ΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ Διάδοση κυλινδικού κύματος Καταγαφή σεισμού (Μ5.9) σε διαφοετικό πειβάλλον εξασθένησης ΗΕΞΑΣΘΕΝΗΣΗΤΩΝΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΧΕΣΗ ΜΕ ΤΟ ΜΕΣΟ ΔΙΑΔΟΣΗΣ ΓΕΩΜΕΤΡΙΚΗ ΔΙΑΣΠΟΡΑ ΑΠΟΣΒΕΣΗ
Προσομοίωση Monte Carlo
 Κλασσική ατομιστική ποσομοίωση Ποσομοίωση Mot Crlo Δ.Γ. Παπαγεωγίου Λίγη ιστοία 777 Gorgs Lous LClrc, Cot d Buffo: Θεωητική πόβλεψη για το πείαμα τυχαίας ίψης βελόνας. 90 Lzzr: Πειαματική επιβεβαίωση της
Κλασσική ατομιστική ποσομοίωση Ποσομοίωση Mot Crlo Δ.Γ. Παπαγεωγίου Λίγη ιστοία 777 Gorgs Lous LClrc, Cot d Buffo: Θεωητική πόβλεψη για το πείαμα τυχαίας ίψης βελόνας. 90 Lzzr: Πειαματική επιβεβαίωση της
ΕΠΙΣΗΜΗ ΕΦΗΜΕΡΙΔΑ ΤΗΣ ΚΥΠΡΙΑΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΠΑΡΑΡΤΗΜΑ ΠΡΩΤΟ ΝΟΜΟΘΕΣΙΑ - ΜΕΡΟΣ ΙI. Αριθμός 4312 Παρασκευή, 9 Δεκεμβρίου
 N. 4(II)/016 ΕΠΙΣΗΜΗ ΕΦΗΜΕΡΙΔΑ ΤΗΣ ΚΥΠΡΙΑΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΠΑΡΑΡΤΗΜΑ ΠΡΩΤΟ ΝΟΜΟΘΕΣΙΑ - ΜΕΡΟΣ ΙI Αιθμός 431 Παασκευή, 9 Δεκεμβίου 016 815 Ο πεί Συμπληωματικού Ποϋπολογισμού της Αχής Λιμένων Κύπου Νόμος (Α.
N. 4(II)/016 ΕΠΙΣΗΜΗ ΕΦΗΜΕΡΙΔΑ ΤΗΣ ΚΥΠΡΙΑΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΠΑΡΑΡΤΗΜΑ ΠΡΩΤΟ ΝΟΜΟΘΕΣΙΑ - ΜΕΡΟΣ ΙI Αιθμός 431 Παασκευή, 9 Δεκεμβίου 016 815 Ο πεί Συμπληωματικού Ποϋπολογισμού της Αχής Λιμένων Κύπου Νόμος (Α.
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΘΗΜ / ΤΞΗ : ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙ: ΣΕΙΡ: (ΛΥΣΕΙΣ) ΘΕΜ Οδηγία: Να γάψετε στο τετάδιό σας τον αιθμό καθεμιάς από τις παακάτω εωτήσεις -4 και δίπλα το γάμμα που αντιστοιχεί στη σωστή απάντηση..
ΜΘΗΜ / ΤΞΗ : ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙ: ΣΕΙΡ: (ΛΥΣΕΙΣ) ΘΕΜ Οδηγία: Να γάψετε στο τετάδιό σας τον αιθμό καθεμιάς από τις παακάτω εωτήσεις -4 και δίπλα το γάμμα που αντιστοιχεί στη σωστή απάντηση..
Μελέτη του υδατικού ισοζυγίου υδροφορέα στην περιοχή της Ελασσόνας
 Μελέτη του υδατικού ισοζυγίου υδοφοέα στην πειοχή της Ελασσόνας Χήστος Τζιµόπουλος, Πλιάτσικα ήµητα Τοµέας Συγκοινωνιακών και Υδαυλικών Έγων, Τµήµα Αγονόµων & Τοπογάφων Μηχανικών, Πολυτεχνική Σχολή, Αιστοτέλειο
Μελέτη του υδατικού ισοζυγίου υδοφοέα στην πειοχή της Ελασσόνας Χήστος Τζιµόπουλος, Πλιάτσικα ήµητα Τοµέας Συγκοινωνιακών και Υδαυλικών Έγων, Τµήµα Αγονόµων & Τοπογάφων Μηχανικών, Πολυτεχνική Σχολή, Αιστοτέλειο
Διάνυσμα μετατόπισης. Στοιχεία Διανυσματικής Ανάλυσης
 Στοιχεία Διανυσματικής νάλυσης Συστήματα Συντεταγμένων (D) Διανυσματικά και αμωτά Μεγέη Πάξεις και ιδιότητες διανυσμάτων Διανυσματικές συνατήσεις Πααγώγιση Διανυσματικών συνατήσεων Ολοκλήωση Διανυσματικών
Στοιχεία Διανυσματικής νάλυσης Συστήματα Συντεταγμένων (D) Διανυσματικά και αμωτά Μεγέη Πάξεις και ιδιότητες διανυσμάτων Διανυσματικές συνατήσεις Πααγώγιση Διανυσματικών συνατήσεων Ολοκλήωση Διανυσματικών
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ»
 ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 25-6 ΔΙΑΛΕΞΗ 11 Θεμελιώσεις με πασσάλους : Καθιζήσεις πασσάλων 5.1.26 1. Κατηγοίες πασσάλων 2. Αξονική φέουσα ικανότητα μεμονωμένου
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 25-6 ΔΙΑΛΕΞΗ 11 Θεμελιώσεις με πασσάλους : Καθιζήσεις πασσάλων 5.1.26 1. Κατηγοίες πασσάλων 2. Αξονική φέουσα ικανότητα μεμονωμένου
= = σταθ. Ι. που είναι. Η ροπή αδράνειας ενός σώματος μετρά την κατανομή της μάζας γύρω από τον άξονα περιστροφής, έτσι όσο
 Απαντήσεις ΘΕΜΑ Α Α. γ, Α. α, Α3. γ, Α4. α, Α5. Σ, Λ, Λ, Λ, Σ. ΘΕΜΑ Β Β. Σωστή απάντηση είναι η γ. Σε μία τυχαία θέση θα έχουμε: Στ = τf τ w = F g ηµθ θ F Στ = ( c + 0,5g ηµθ) g ηµ θ = c = σταθ. g Άα λοιπό
Απαντήσεις ΘΕΜΑ Α Α. γ, Α. α, Α3. γ, Α4. α, Α5. Σ, Λ, Λ, Λ, Σ. ΘΕΜΑ Β Β. Σωστή απάντηση είναι η γ. Σε μία τυχαία θέση θα έχουμε: Στ = τf τ w = F g ηµθ θ F Στ = ( c + 0,5g ηµθ) g ηµ θ = c = σταθ. g Άα λοιπό
Μάθημα: Ρομποτικός Έλεγχος
 Διατμηματικό Πόγαμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 0 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
Διατμηματικό Πόγαμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 0 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
ΚΕΦΑΛΑΙΟ 2 Ο. 7.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ ω ΜΕ
 ΚΕΦΛΙΟ Ο ΤΡΙΓΩΝΟΜΕΤΡΙ 7.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ ΓΩΝΙΣ ω ΜΕ o ω 18 o 1. Πώς οίζονται οι τιγωνομετικοί αιθμοί μίας οξείας γωνίας σε οθογώνιο τίγωνο; ΠΝΤΗΣΗ Γ β α γ Το ημίτονο της οξείας γωνίας σε οθογώνιο
ΚΕΦΛΙΟ Ο ΤΡΙΓΩΝΟΜΕΤΡΙ 7.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ ΓΩΝΙΣ ω ΜΕ o ω 18 o 1. Πώς οίζονται οι τιγωνομετικοί αιθμοί μίας οξείας γωνίας σε οθογώνιο τίγωνο; ΠΝΤΗΣΗ Γ β α γ Το ημίτονο της οξείας γωνίας σε οθογώνιο
1. Ανατοκισμός. 2. Ονομαστικό επιτόκιο
 Ε5. ΣΥΝΕΧΗΣ ΑΝΑΤΟΚΙΣΜΟΣ-ΠΑΡΟΥΣΕΣ ΑΞΙΕΣ.Ανατοισμός.Ονομαστιό επιτόιο 3.Παγματιό επιτόιο 4.Χόνος διπλασιασμού 5.Συνεχής ανατοισμός 6.Παούσα αξία οής 7.Εξέλιξη δημόσιου χέους 8.Νεολασσιό υπόδειγμα ανάπτυξης
Ε5. ΣΥΝΕΧΗΣ ΑΝΑΤΟΚΙΣΜΟΣ-ΠΑΡΟΥΣΕΣ ΑΞΙΕΣ.Ανατοισμός.Ονομαστιό επιτόιο 3.Παγματιό επιτόιο 4.Χόνος διπλασιασμού 5.Συνεχής ανατοισμός 6.Παούσα αξία οής 7.Εξέλιξη δημόσιου χέους 8.Νεολασσιό υπόδειγμα ανάπτυξης
5. Μετασχηµατισµοί συντεταγµένων
 5. Μετασχηµατισµοί συντεταγµένν 5. Στοιχεία από την ελλειψοειδή Γεδαισία Η γήινη επιφάνεια έχει πολύπλοκη µοφή και δεν είναι δυνατό να πειγαφή µε µαθηµατικές εξισώσεις. Στην ποσπάθεια να πειγάψουν την
5. Μετασχηµατισµοί συντεταγµένν 5. Στοιχεία από την ελλειψοειδή Γεδαισία Η γήινη επιφάνεια έχει πολύπλοκη µοφή και δεν είναι δυνατό να πειγαφή µε µαθηµατικές εξισώσεις. Στην ποσπάθεια να πειγάψουν την
University of Crete. School of Science Department of Mathematics. Master Thesis. Lie Groups, Lie Algebras and the Hydrogen Atom
 Πανεπιστήµιο Κήτης Σχολή Θετικών Επιστηµών Τµήµα Μαθηµατικών Μεταπτυχιακή εγασία Le οµάδες, Le άλγεβες και το Άτοµο του Υδογόνου Νίκος Κωνσταντίνου Ανδιανός Επιβλέπων καθηγητής Μιχάλης Κολουντζάκης Ηάκλειο
Πανεπιστήµιο Κήτης Σχολή Θετικών Επιστηµών Τµήµα Μαθηµατικών Μεταπτυχιακή εγασία Le οµάδες, Le άλγεβες και το Άτοµο του Υδογόνου Νίκος Κωνσταντίνου Ανδιανός Επιβλέπων καθηγητής Μιχάλης Κολουντζάκης Ηάκλειο
ιείσδυση Θάλασσας στη Λιµνοθάλασσα Βιστωνίδα και η Περιβαλλοντική Σηµασία της
 Ολοκληωµένη ιαχείιση Υδατικών Πόων 21 ιείσδυση Θάλασσας στη Λιµνοθάλασσα Βιστωνίδα και η Πειβαλλοντική Σηµασία της ΚΟΓΙΑ Φ. ΚΟΝΙ ΑΡΗΣ Α. ΑΓΓΕΛΙ ΗΣ Π. MSc. Φυσικός Α.Π.Θ. MSc. Πολιτικός Μηχ..Π.Θ. Λέκτοας.Π.Θ.
Ολοκληωµένη ιαχείιση Υδατικών Πόων 21 ιείσδυση Θάλασσας στη Λιµνοθάλασσα Βιστωνίδα και η Πειβαλλοντική Σηµασία της ΚΟΓΙΑ Φ. ΚΟΝΙ ΑΡΗΣ Α. ΑΓΓΕΛΙ ΗΣ Π. MSc. Φυσικός Α.Π.Θ. MSc. Πολιτικός Μηχ..Π.Θ. Λέκτοας.Π.Θ.
Κεφάλαιο 2 Ηλεκτρικά Χαρακτηριστικά Γραµµών Μεταφοράς
 Κεφάλαιο Ηλεκτρικά Χαρακτηριστικά Γραµµών Μεταφοράς Σύνοψη Το κεφάλαιο αυτό είναι εστιασµένο στην ανάλυση και στους υπολογισµούς των παραµέτρων των γραµµών µεταφοράς Για τις κυριότερες από αυτές, την αυτεπαγωγή
Κεφάλαιο Ηλεκτρικά Χαρακτηριστικά Γραµµών Μεταφοράς Σύνοψη Το κεφάλαιο αυτό είναι εστιασµένο στην ανάλυση και στους υπολογισµούς των παραµέτρων των γραµµών µεταφοράς Για τις κυριότερες από αυτές, την αυτεπαγωγή
Περιεχόμενα. Πρόλογος...13
 Περιεχόμενα Πρόλογος...3 Κεφάλαιο : Στοιχεία ηλεκτρικών κυκλωμάτων...5. Βασικά ηλεκτρικά μεγέθη...5.. Ηλεκτρικό φορτίο...5.. Ηλεκτρικό ρεύμα...5..3 Τάση...6..4 Ενέργεια...6..5 Ισχύς...6..6 Σύνοψη...7.
Περιεχόμενα Πρόλογος...3 Κεφάλαιο : Στοιχεία ηλεκτρικών κυκλωμάτων...5. Βασικά ηλεκτρικά μεγέθη...5.. Ηλεκτρικό φορτίο...5.. Ηλεκτρικό ρεύμα...5..3 Τάση...6..4 Ενέργεια...6..5 Ισχύς...6..6 Σύνοψη...7.
Ασκήσεις στο µάθηµα «Ευέλικτα Συστήµατα Μεταφοράς» του 7 ου εξαµήνου
 EΘΝΙΚΟ MΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΏΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Αναπλ. Καθηγητής Γ. Κορρές Άσκηση 1 Ασκήσεις στο µάθηµα «Ευέλικτα Συστήµατα Μεταφοράς» του 7
EΘΝΙΚΟ MΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΏΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Αναπλ. Καθηγητής Γ. Κορρές Άσκηση 1 Ασκήσεις στο µάθηµα «Ευέλικτα Συστήµατα Μεταφοράς» του 7
Περιεχόμενα. Πρόλογος...13
 Περιεχόμενα Πρόλογος...3 Κεφάλαιο : Στοιχεία ηλεκτρικών κυκλωμάτων...5. Βασικά ηλεκτρικά μεγέθη...5.. Ηλεκτρικό φορτίο...5.. Ηλεκτρικό ρεύμα...5..3 Τάση...6..4 Ενέργεια...6..5 Ισχύς...6..6 Σύνοψη...7.
Περιεχόμενα Πρόλογος...3 Κεφάλαιο : Στοιχεία ηλεκτρικών κυκλωμάτων...5. Βασικά ηλεκτρικά μεγέθη...5.. Ηλεκτρικό φορτίο...5.. Ηλεκτρικό ρεύμα...5..3 Τάση...6..4 Ενέργεια...6..5 Ισχύς...6..6 Σύνοψη...7.
ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΙΚΤΥΑ ΚΙΝΗΤΩΝ ΚΑΙ ΠΡΟΣΩΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για τη διαχείιση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΙΚΤΥΑ ΚΙΝΗΤΩΝ ΚΑΙ ΠΡΟΣΩΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για τη διαχείιση
Κλάσεις καθολικών και Αμφιμονοσήμαντων Συναρτήσεων
 ΑΝΝΑ ΚΟΥΤΡΟΥΜΠΟΥΧΟΥ ΜΑΘΗΜΑΤΙΚΟΣ Κλάσεις καθολικών και Αμφιμονοσήμαντων Συνατήσεων ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΜΕΑΣ ΘΕΩΡΗΤΙΚΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Επιβλέπουσα: Β Βλάχου, Λέκτοας ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ-ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ
ΑΝΝΑ ΚΟΥΤΡΟΥΜΠΟΥΧΟΥ ΜΑΘΗΜΑΤΙΚΟΣ Κλάσεις καθολικών και Αμφιμονοσήμαντων Συνατήσεων ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΜΕΑΣ ΘΕΩΡΗΤΙΚΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Επιβλέπουσα: Β Βλάχου, Λέκτοας ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ-ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ
6. ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΣΤΗ ΓΡΑΜΜΙΚΗ ΣΥΣΧΕΤΙΣΗ
 6. ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΣΤΗ ΓΡΑΜΜΙΚΗ ΣΥΣΧΕΤΙΣΗ Είναι φυικό ότι ο δειγματικός υντελετής R, ως μια τατιτική υνάτηη, είναι μιά τυχαία μεταβλητή. Οπως είπαμε ήδη μποεί να χηιμοποιηθεί αν εκτιμήτια του. Για να
6. ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΣΤΗ ΓΡΑΜΜΙΚΗ ΣΥΣΧΕΤΙΣΗ Είναι φυικό ότι ο δειγματικός υντελετής R, ως μια τατιτική υνάτηη, είναι μιά τυχαία μεταβλητή. Οπως είπαμε ήδη μποεί να χηιμοποιηθεί αν εκτιμήτια του. Για να
Μηχανές Πλοίου ΙΙ (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδυµα Αθήνας Μηχανές Πλοίου ΙΙ Ε Άσκηση 2 Γεώγιος Κ. Χατζηκωνσταντής Επίκουος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδυµα Αθήνας Μηχανές Πλοίου ΙΙ Ε Άσκηση 2 Γεώγιος Κ. Χατζηκωνσταντής Επίκουος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας
2012 : (307) : , 29 2012 : 11.00 13.30
 ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2012 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑ : Εφαρµοσµένη Ηλεκτρολογία
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2012 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑ : Εφαρµοσµένη Ηλεκτρολογία
Σύνδεση µε µη αβαρή ράβδο
 Σύνδεση µε µη αβαή άβδο Με τη βοήθεια µιας άβδου µάζας Μ kg και µήκους L συνδέουµε τα κέντα µάζας ενός δίσκου µάζας 4kg και ενός δακτυλίου µάζας m 6kg, όπως αίνεται στο σχήµα. Ο m δίσκος και η άβδος έχουν
Σύνδεση µε µη αβαή άβδο Με τη βοήθεια µιας άβδου µάζας Μ kg και µήκους L συνδέουµε τα κέντα µάζας ενός δίσκου µάζας 4kg και ενός δακτυλίου µάζας m 6kg, όπως αίνεται στο σχήµα. Ο m δίσκος και η άβδος έχουν
R, B Borel σύνολο, τότε αν ο µετασχηµατισµός fourier του ν µ είναι στον L 2, (E) > 0. Η τεχνική που ανέπτυξε
 ΑΠΟΣΒΕΣΗ ΚΥΚΛΙΚΩΝ ΜΕΣΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER ΜΕΤΡΩΝ ΧΡΗΣΤΟΣ ΧΑΤΖΗΦΟΥΝΤΑΣ ΤΜΗΜΑ ΜΑΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Από την ϑεωεία µέτου γνωίζουµε το ϑεώηµα του stainhaus που χαακτηίζει όλα τα σύνολα ϑετικού
ΑΠΟΣΒΕΣΗ ΚΥΚΛΙΚΩΝ ΜΕΣΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER ΜΕΤΡΩΝ ΧΡΗΣΤΟΣ ΧΑΤΖΗΦΟΥΝΤΑΣ ΤΜΗΜΑ ΜΑΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Από την ϑεωεία µέτου γνωίζουµε το ϑεώηµα του stainhaus που χαακτηίζει όλα τα σύνολα ϑετικού
Φυσική Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου 2001
 Φυσική Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου 00 Ζήτηµα ο. Η εξίσωση της αποµάκρυνσης σε έναν απλό αρµονικό ταλαντωτή, πλάτους χ 0 και κυκλικής συχνότητας ω, δίνεται από τη σχέση: χ χ 0 ηµωt. Η εξίσωση
Φυσική Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου 00 Ζήτηµα ο. Η εξίσωση της αποµάκρυνσης σε έναν απλό αρµονικό ταλαντωτή, πλάτους χ 0 και κυκλικής συχνότητας ω, δίνεται από τη σχέση: χ χ 0 ηµωt. Η εξίσωση
ΑΣΚΗΣΗ 4. Ωµική αντίσταση αυτεπαγωγή πηνίου
 ΑΣΚΗΣΗ 4 Ωµική αντίσταση αυτεπαγωγή πηνίου ΣΥΣΚΕΥΕΣ: Ένα πηνίο, ένα βολτόµετρο (AC-DC), ένα αµπερόµετρο (AC-DC), τροφοδοτικό (AC-DC). ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ Το πηνίο είναι µια πυκνή σπειροειδής περιέλιξη ενός
ΑΣΚΗΣΗ 4 Ωµική αντίσταση αυτεπαγωγή πηνίου ΣΥΣΚΕΥΕΣ: Ένα πηνίο, ένα βολτόµετρο (AC-DC), ένα αµπερόµετρο (AC-DC), τροφοδοτικό (AC-DC). ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ Το πηνίο είναι µια πυκνή σπειροειδής περιέλιξη ενός
Φυσική Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου 2001 ΕΚΦΩΝΗΣΕΙΣ
 Φυσική Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου 00 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα ο. Η εξίσωση της αποµάκρυνσης σε έναν απλό αρµονικό ταλαντωτή, πλάτους χ 0 και κυκλικής συχνότητας ω, δίνεται από τη σχέση: χ χ
Φυσική Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου 00 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα ο. Η εξίσωση της αποµάκρυνσης σε έναν απλό αρµονικό ταλαντωτή, πλάτους χ 0 και κυκλικής συχνότητας ω, δίνεται από τη σχέση: χ χ
ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1 γ Α2 β Α3 γ Α4 β Α5. α Σ, β Σ, γ Λ, δ Λ, ε Σ.
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΑΔΑ Β) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 0 ΕΞΕΤΑΖΟΕΝΟ ΑΘΗΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΑ Α Α γ Α β Α γ Α β Α5. α Σ, β Σ, γ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΑΔΑ Β) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 0 ΕΞΕΤΑΖΟΕΝΟ ΑΘΗΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΑ Α Α γ Α β Α γ Α β Α5. α Σ, β Σ, γ
ΕΞΑΝΑΓΚΑΣΜΕΝΗ ΗΛΕΚΤΡΙΚΗ ΤΑΛΑΝΤΩΣΗ Ο ΣΥΝΤΟΝΙΣΜΟΣ ΚΑΙ ΟΙ ΕΚ ΟΧΕΣ ΤΟΥ
 η ΠΕΡΙΠΤΩΣΗ ΕΞΑΝΑΓΚΑΣΜΕΝΗ ΗΛΕΚΤΡΙΚΗ ΤΑΛΑΝΤΩΣΗ Ο ΣΥΝΤΟΝΙΣΜΟΣ ΚΑΙ ΟΙ ΕΚ ΟΧΕΣ ΤΟΥ ΣΥΝΤΟΝΙΣΜΟΣ ΣΕ ΚΥΚΛΩΜΑ -L-C ΣΕ ΣΕΙΡΑ Κύκλωµα που αποτελείται από ωµική αντίσταση,ιδανικό πηνίο µε συντελεστή αυτεπαγωγής L
η ΠΕΡΙΠΤΩΣΗ ΕΞΑΝΑΓΚΑΣΜΕΝΗ ΗΛΕΚΤΡΙΚΗ ΤΑΛΑΝΤΩΣΗ Ο ΣΥΝΤΟΝΙΣΜΟΣ ΚΑΙ ΟΙ ΕΚ ΟΧΕΣ ΤΟΥ ΣΥΝΤΟΝΙΣΜΟΣ ΣΕ ΚΥΚΛΩΜΑ -L-C ΣΕ ΣΕΙΡΑ Κύκλωµα που αποτελείται από ωµική αντίσταση,ιδανικό πηνίο µε συντελεστή αυτεπαγωγής L
ΔΙΑΛΕΞΗ 11 Συνδυασμός περιστροφής και στρωμάτωσης (Quasi-geostrophic dynamics in stratified fluids)
 ΙΑΛΕΞΗ Συνδυασμός πειστοφής και στωμάτωσης (Qus-eosrophc dnmcs n sred luds) Πειεχόμενα: Qus-eosrophc dnmcs Broclnc ossb wves Broclnc nsbl eulbrum dens surce osclln dens surce
ΙΑΛΕΞΗ Συνδυασμός πειστοφής και στωμάτωσης (Qus-eosrophc dnmcs n sred luds) Πειεχόμενα: Qus-eosrophc dnmcs Broclnc ossb wves Broclnc nsbl eulbrum dens surce osclln dens surce
ΔΙΑΛΕΞΗ 8 Kύματα βαρύτητας απουσία περιστροφής
 ΔΙΑΛΕΞΗ 8 Kύματα βαύτητας απουσία πειστοφής Πειεχόμενα: Χαακτηιστικά μεγέθη τν κυμάτν Εξισώσεις τν επιφανειακών κυμάτν Ποσεγγίσεις βαχέν/μακών κυμάτν Το κυματικό φάσμα Εστεικά κύματα βαύτητας Χαακτηιστικά
ΔΙΑΛΕΞΗ 8 Kύματα βαύτητας απουσία πειστοφής Πειεχόμενα: Χαακτηιστικά μεγέθη τν κυμάτν Εξισώσεις τν επιφανειακών κυμάτν Ποσεγγίσεις βαχέν/μακών κυμάτν Το κυματικό φάσμα Εστεικά κύματα βαύτητας Χαακτηιστικά
Εξισώσεις οριακού στρώματος και μη συνεκτικής ροής Το διακριτό πρόβλημα
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΕΡΟΔΥΝΑΜΙΚΗ Διάσκων: Δ. Ριζιώτης Βασίλης Εξισώσεις οιακού στώματος και μη συνεκτικής οής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΕΡΟΔΥΝΑΜΙΚΗ Διάσκων: Δ. Ριζιώτης Βασίλης Εξισώσεις οιακού στώματος και μη συνεκτικής οής
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
ΜΟΝΑ ΕΣ, ΣΤΑΘΕΡΕΣ, ΧΡΗΣΙΜΕΣ ΣΧΕΣΕΙΣ
 ΠΑΡΑΡΤΗΜΑ ΙΙ ΠΑΡΑΡΤΗΜΑ ΙΙ ΜΟΝΑ ΕΣ, ΣΤΑΘΕΡΕΣ, ΧΡΗΣΙΜΕΣ ΣΧΕΣΕΙΣ ΠΙΝΑΚΑΣ ΜΟΝΑ ΕΣ ΜΕΓΕΘΩΝ ΣΤΟ MK ΣΥΜΒΟΛΟ ΜΕΓΕΘΟΥΣ M (ή L ) Αλληλεπαγωγή (hen) H ΟΝΟΜΑ ΜΕΓΕΘΟΥΣ (ΜΟΝΑ Α) ΣΥΜΒΟΛΟ ΜΟΝΑ ΑΣ ΙΑΣΤΑΣΕΙΣ L Αυτεπαγωγή
ΠΑΡΑΡΤΗΜΑ ΙΙ ΠΑΡΑΡΤΗΜΑ ΙΙ ΜΟΝΑ ΕΣ, ΣΤΑΘΕΡΕΣ, ΧΡΗΣΙΜΕΣ ΣΧΕΣΕΙΣ ΠΙΝΑΚΑΣ ΜΟΝΑ ΕΣ ΜΕΓΕΘΩΝ ΣΤΟ MK ΣΥΜΒΟΛΟ ΜΕΓΕΘΟΥΣ M (ή L ) Αλληλεπαγωγή (hen) H ΟΝΟΜΑ ΜΕΓΕΘΟΥΣ (ΜΟΝΑ Α) ΣΥΜΒΟΛΟ ΜΟΝΑ ΑΣ ΙΑΣΤΑΣΕΙΣ L Αυτεπαγωγή
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ
 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 2 Ισοδύναμο Ηλεκτρικό Κύκλωμα Σύγχρονων Μηχανών Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Υπολογισμός Αυτεπαγωγής και αμοιβαίας επαγωγής Πεπλεγμένη μαγνητική ροή συναρτήσει των
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 2 Ισοδύναμο Ηλεκτρικό Κύκλωμα Σύγχρονων Μηχανών Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Υπολογισμός Αυτεπαγωγής και αμοιβαίας επαγωγής Πεπλεγμένη μαγνητική ροή συναρτήσει των
ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ. ηµήτρης Ιψάκης. ρ.χηµικός Μηχανικός. Τριµελής Συµβουλευτική Επιτροπή
 ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΛΕΓΚΤΩΝ PID ΣΕ ΚΑΙΝΟΤΟΜΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΞΙΟΠΟΙΗΣΗ Υ ΡΟΓΟΝΟΥ ηµήτης Ιψάκης.Χηµικός Μηχανικός Τιµελής Συµβουλευτική Επιτοπή Αναπλ. Καθηγητής Ν. Κααµπετάκης
ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΛΕΓΚΤΩΝ PID ΣΕ ΚΑΙΝΟΤΟΜΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΞΙΟΠΟΙΗΣΗ Υ ΡΟΓΟΝΟΥ ηµήτης Ιψάκης.Χηµικός Μηχανικός Τιµελής Συµβουλευτική Επιτοπή Αναπλ. Καθηγητής Ν. Κααµπετάκης
υναµική Μηχανών Ι Ακαδηµαϊκό έτος : Ε. Μ. Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 22.
 υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι -. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 Cprigh ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 0. Με επιφύλαξη παντός
υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι -. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 0-0 Cprigh ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 0. Με επιφύλαξη παντός
ΣΥΝΟΠΤΙΚΗΣ ΚΑΙ ΔΥΝΑΜΙΚΗΣ ΜΕΤΕΩΡΟΛΟΓΙΑΣ
 ΘΕΟΔΩΡΟΣ Σ. ΚΑΡΑΚΩΣΤΑΣ ΚΑΘΗΓΗΤΗΣ Αιστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών, Τμήμα Γελογίας Τομέας Μετεολογίας και Κλιματολογίας Σ Η Μ Ε Ι Ω Σ Ε Ι Σ ΣΥΝΟΠΤΙΚΗΣ ΚΑΙ ΔΥΝΑΜΙΚΗΣ ΜΕΤΕΩΡΟΛΟΓΙΑΣ
ΘΕΟΔΩΡΟΣ Σ. ΚΑΡΑΚΩΣΤΑΣ ΚΑΘΗΓΗΤΗΣ Αιστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών, Τμήμα Γελογίας Τομέας Μετεολογίας και Κλιματολογίας Σ Η Μ Ε Ι Ω Σ Ε Ι Σ ΣΥΝΟΠΤΙΚΗΣ ΚΑΙ ΔΥΝΑΜΙΚΗΣ ΜΕΤΕΩΡΟΛΟΓΙΑΣ
εν απαιτείται οπλισµός διάτµησης για διατµητική δύναµη µικρότερη ή ίση µε την τιµή V Rd,c
 Χ. Κααγιάννης, Πολιτικός Μηχ. ΕΜΠ,. Μηχ. ΚΑΘΗΓΗΤΗΣ Κατασκευών Ωπλισµένου Σκυοδέµατος και Αντισεισµικού Σχεδιασµού ΠΡΟΕ ΡΟΣ ΤΜΗΜΑΤΟΣ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΘ Συνοπτική Παουσίαση Σχεδιασµού έναντι ιάτµησης
Χ. Κααγιάννης, Πολιτικός Μηχ. ΕΜΠ,. Μηχ. ΚΑΘΗΓΗΤΗΣ Κατασκευών Ωπλισµένου Σκυοδέµατος και Αντισεισµικού Σχεδιασµού ΠΡΟΕ ΡΟΣ ΤΜΗΜΑΤΟΣ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΘ Συνοπτική Παουσίαση Σχεδιασµού έναντι ιάτµησης
