110 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ 3.1 Ελάχιστα ΠΑ Οταν χρησιμοποιούμε ΠΑ σε διάφορες εφαρμογές και προβλήματα, μας ενδιαφέρει να βρούμε

Transcript

1 Κεφάλαιο 3 Ελαχιστοποίηση και Μη Κανονικές Γλώσσες Σύνοψη Στο συγκεκριμένο κεφάλαιο, θα έχουμε την ευκαιρία να δούμε πώς μπορούμε να βρούμε την πιο σύντομη και οικονομική περιγραφή μιας κανονικής γλώσσας, δηλαδή το ελάχιστο ΠΑ για τη γλώσσα. Υπάρχουν γλώσσες, που δεν είναι κανονικές και άρα δε μπορούν να αναπαρασταθούν από ΠΑ ή ΚΕ. Στο κεφάλαιο αυτό θα περιγράψουμε τεχνικές, που δίνουν απάντηση στο ερώτημα: για μια γλώσσα L, πώς μπορούμε να ξέρουμε αν αυτή είναι κανονική ή όχι; Τέλος, θα ασχοληθούμε με ενδιαφέροντα προβλήματα απόφασης, που αφορούν τις κανονικές γλώσσες και θα προτείνουμε χρήσιμους αλγορίθμους, για την επίλυσή τους. Προαπαιτούμενη γνώση Για την κατανόηση του κεφαλαίου θα πρέπει ο αναγνώστης να έχει αφομοιώσει τις μαθηματικές έννοιες του Παραρτήματος I, καθώς και τους ορισμούς και τα αποτελέσματα του Κεφαλαίου 2. Για καλύτερη εξοικείωση με τους αλγορίθμους μετασχηματισμού στους ο- ποίους στηρίζονται τα θεμελιώδη θεωρήματα του κεφαλαίου, προτείνεται η διαδραστική προσομοίωση των παραδειγμάτων με το ανοικτό λογισμικό JFLAP. Στο Παράρτημα II γίνεται μία εισαγωγή στη χρήση του λογισμικού JFLAP. 109

2 110 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ 3.1 Ελάχιστα ΠΑ Οταν χρησιμοποιούμε ΠΑ σε διάφορες εφαρμογές και προβλήματα, μας ενδιαφέρει να βρούμε τη μικρότερη μηχανή, για την αναπαράσταση μιας γλώσσας. Λέμε ότι έν ΝΠΑ M είναι ελάχιστο, αν και μόνο αν δεν υπάρχει κάποιο άλλο ΝΠΑ με M με L(M) = L(M ) τέτοιο ώστε το M να έχει λιγότερες καταστάσεις από το M. Κάποια από τα ερωτήματα, που σχετίζονται με την εύρεση του ελάχιστου ΝΠΑ για μία γλώσσα είναι τα εξής: 1. Δοθείσης μιας γλώσσας L υπάρχει ένα ελάχιστο ΝΠΑ, που αποδέχεται την L; 2. Αν υπάρχει μία ελάχιστη μηχανή, είναι αυτή μοναδική; 3. Δοθέντος ενός ΝΠΑ M, που αποδέχεται κάποια γλώσσα L, μπορούμε ν αποφανθούμε αν αυτό είναι ελάχιστο; 4. Δοθέντος ενός ΝΠΑ M, μπορούμε να δημιουργήσουμε ένα ισοδύναμο ελάχιστο ΝΠΑ M ; Οι απαντήσεις σ όλα τα παραπάνω ερωτήματα είναι καταφατικές και η ελαχιστοποίηση ΠΑ παίζει σημαντικό ρόλο στην αποδοτική σχεδίαση συστημάτων και λογισμικού. Στην Ενότητα θα δώσουμε απαντήσεις στα δύο πρώτα ερωτήματα, στην Ενότητα στα δύο επόμενα και στην Ενότητα θ αναφερθούμε σε εφαρμογές Ελάχιστο ΝΠΑ για μια γλώσσα Ορισμός 3.1 (Διάκριση συμβολοσειρών ως προς μία γλώσσα) Δύο συμβολοσειρές x και y δε διακρίνονται ως προς τη γλώσσα L και αυτό το γράφουμε ως x L y αν και μόνο αν z Σ, (xz L και yz L) ή (xz L και yz L) Αντίθετα, θα λέμε ότι οι x και y διακρίνονται μεταξύ τους ως προς την L, αν και μόνο αν υπάρχει τουλάχιστο μία συμβολοσειρά z, τέτοια ώστε τόσο η xz όσο και η yz ανήκουν στην L. Σημειώνουμε ότι η σχέση L είναι σχέση ισοδυναμίας, καθώς εύκολα αποδεικνύεται ότι είναι ανακλαστική, συμμετρική και μεταβατική. Κατά συνέπεια, οι κλάσεις ισοδυναμίας αποτελούν μία διαμέριση του Σ, που σημαίνει ότι (i) καμία από τις κλάσεις ισοδυναμίας της L δεν είναι κενή και (ii) κάθε συμβολοσειρά του Σ ανήκει ακριβώς σε μία κλάση ισοδυναμίας της L.

3 3.1. ΕΛΑΧΙΣΤΑ ΠΑ 111 Θα δούμε στη συνέχεια ότι οι κλάσεις ισοδυναμίας της L αντιστοιχούν ακριβώς στις καταστάσεις του ελάχιστου ΝΠΑ, που αποδέχεται την L. Αυτό σημαίνει ότι κάθε συμβολοσειρά του Σ οδηγεί το ΝΠΑ σε μία συγκεκριμένη κατάσταση. Δοθείσης μιας γλώσσας L, τίθεται το ερώτημα του πώς μπορούμε να ο- ρίσουμε τη σχέση L. Ενας τρόπος για να γίνει αυτό είναι να ξεκινήσουμε μία λεξικογραφική απαρίθμηση των συμβολοσειρών του Σ και να συνεχίσουμε μέχρις ότου προκύψει ένα πρότυπο. Παράδειγμα 3.1 (Εύρεση της σχέσης L για τη γλώσσα L) Ας θεωρήσουμε τη γλώσσα με αλφάβητο Σ = {, }: L = {w Σ : δύο διαδοχικοί χαρακτήρες δε μπορεί να είναι ίδιοι} Οι κλάσεις ισοδυναμίας της σχέσης L είναι: [1] [ɛ] [ɛ] [2] [,,,...] [όλες οι μη κενές συμβολοσειρές, που τελειώνουν σε και δεν έχουν δύο διαδοχικούς ίδιους χαρακτήρες] [3] [,,,,...] [όλες οι μη κενές συμβολοσειρές, που τελειώνουν σε και δεν έχουν δύο διαδοχικούς ίδιους χαρακτήρες] [4] [,,,...] [όλες οι συμβολοσειρές, που περιέχουν τουλάχιστο δύο διαδοχικούς ίδιους χαρακτήρες] Από το Παράδειγμα 3.1 παρατηρούμε τα εξής: Καμία κλάση ισοδυναμίας δεν περιέχει ταυτόχρονα συμβολοσειρές, που ανήκουν στην L και συμβολοσειρές, που δεν ανήκουν στην L. Αυτό είναι εύκολο να το δείξουμε, αν θεωρήσουμε τη συμβολοσειρά παράθεσης ɛ. Αν x L τότε xɛ L και αν y L τότε yɛ L. Επομένως οι x και y διακρίνονται από την ɛ. Αν υπάρχουν συμβολοσειρές, που οδηγούν ένα ΝΠΑ για την L σε αδιέξοδη κατάσταση (δηλαδή συμβολοσειρές που δεν ανήκουν στην L ανεξάρτητα από το τι ακολουθεί), τότε θα υπάρχει μία κλάση ισοδυναμίας της L, που αντιστοιχεί στην αδιέξοδη κατάσταση.

4 112 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ Κάποια κλάση ισοδυναμίας περιέχει την ɛ. Αυτή αντιστοιχεί στην αρχική κατάσταση του ελάχιστου ΝΠΑ, που αποδέχεται την L. Μπορεί να υπάρχουν περισσότερες από μία κλάσεις ισοδυναμίας με συμβολοσειρές της γλώσσας L. Εφτασε η στιγμή ν αναφερθούμε σε ΝΠΑ και να εξετάσουμε το πώς σχετίζεται η L μ ένα ΝΠΑ, που αποδέχεται την L. Θα λέμε ότι μία κατάσταση q ενός ΝΠΑ M περιέχει το σύνολο των συμβολοσειρών w, τέτοιων ώστε ξεκινώντας η M από την αρχική της κατάσταση προσεγγίζει την q μετά από την ανάγνωση της w. Θεώρημα 3.1 Εστω L μία κανονική γλώσσα και έστω M = (K, Σ, δ, s, A) ένα ΝΠΑ, που αποδέχεται την L. Ο αριθμός των καταστάσεων του M είναι μεγαλύτερος ή ίσος από τον αριθμό των κλάσεων ισοδυναμίας της L. Απόδειξη: Ας υποθέσουμε ότι ο αριθμός των καταστάσεων του M είναι μικρότερος από τον αριθμό των κλάσεων ισοδυναμίας της L. Τότε, από την αρχή του «περιστερώνα» (βλ. Παράρτημα I.5), πρέπει να υπάρχει τουλάχιστο μία κατάσταση q, που περιέχει συμβολοσειρές από τουλάχιστο δύο κλάσεις ισοδυναμίας της L. Σ αυτή την περίπτωση, η συμπεριφορά του M στη συνέχεια, γι αυτές τις συμβολοσειρές, δε διαφοροποιείται. Αυτό όμως έρχεται σε αντίφαση με το γεγονός ότι οι συγκεκριμένες συμβολοσειρές ανήκουν σε διαφορετικές κλάσεις ισοδυναμίας της L. Ετσι, η υπόθεση ότι ο αριθμός των καταστάσεων του M είναι μικρότερος από τον αριθμό των κλάσεων ισοδυναμίας της L οδηγεί σε άτοπο. Γνωρίζουμε λοιπόν ένα κάτω όριο στον αριθμό των καταστάσεων, που απαιτούνται, για ένα ΝΠΑ, που θα αποδέχεται τη γλώσσα L. Το επόμενο ερώτημα, που καλούμαστε ν απαντήσουμε είναι αν είναι πάντα εφικτό να βρούμε ένα ΝΠΑ M με ακριβώς τόσες καταστάσεις όσες είναι οι κλάσεις ισοδυναμίας της L. Και σ αυτή την περίπτωση η απάντηση είναι καταφατική. Θεώρημα 3.2 Εστω L μία κανονική γλώσσα ορισμένη ως προς ένα αλφάβητο Σ. Υπάρχει ένα ΝΠΑ M, που αποδέχεται την L και έχει ακριβώς n καταστάσεις, όπου n είναι ο αριθμός των κλάσεων ισοδυναμίας της L. Οποιοδήποτε άλλο ΝΠΑ αποδέχεται τη L θα πρέπει είτε να έχει περισσότερες καταστάσεις από το M, είτε να είναι ισοδύναμο με το M ακόμη και αν οι καταστάσεις ονομάζονται διαφορετικά.

5 3.1. ΕΛΑΧΙΣΤΑ ΠΑ 113 Απόδειξη: Η απόδειξη στηρίζεται στην κατασκευή ενός κατάλληλου M = (K, Σ, δ, s, A) στο οποίο: το K περιέχει n καταστάσεις, δηλαδή μία για κάθε κλάση ισοδυναμίας της L s = [ɛ], δηλαδή η κλάση ισοδυναμίας για την ɛ της σχέσης L A = {[x] : x L} δ([x], ) = [x], δηλαδή αν το M βρίσκεται σε κατάσταση, που περιέχει κάποια συμβολοσειρά x, τότε μετά από την ανάγνωση του επόμενου συμβόλου θα βρίσκεται στην κατάσταση, που περιέχει τη συμβολοσειρά x Τώρα για ν αποδείξουμε την αλήθεια του θεωρήματος γι αυτό το κατασκευασμένο M πρέπει να δείξουμε ότι: το K είναι πεπερασμένο Πράγματι, εφόσον η L είναι κανονική γλώσσα, γίνεται αποδεκτή από κάποιο ΝΠΑ, έστω M, μ ένα πεπερασμένο αριθμό καταστάσεων, έστω m. Τότε όμως με βάση το Θεώρημα 3.1, n m και επομένως το K είναι επίσης πεπερασμένο. η δ είναι συνάρτηση Η κατασκευή, που περιγράψαμε, ορίζει την τιμή της δ για όλα τα ζεύγη (κατάσταση, είσοδος). Επιπλέον, το γεγονός ότι η κατασκευή εγγυάται μία μοναδική τιμή για κάθε τέτοιο ζεύγος, προκύπτει από τον ορισμό της L. L = L(M) Για ν αποδειχθεί ο ισχυρισμός, πρέπει πρώτα να δείξουμε ότι u, v Σ, ([ɛ], uv) M ([u], v). Εφαρμόζουμε επαγωγή ως προς το u. Αν u = 0, τότε έχουμε ([ɛ], ɛv) M ([ɛ], v), που αληθεύει, αφού το M δεν εκτελεί καμία μετάβαση. Ας υποθέσουμε ότι η σχέση ισχύει και για u = k, οπότε εξετάζουμε τι γίνεται για u = k + 1, u 1. Εστω u = yc, όπου y Σ και c Σ. Τότε έχουμε: ([ɛ], ycv) M ([y], cv) (από την επαγωγική υπόθεση, αφού y = k) ([y], cv) M ([yc], v) (από τον ορισμό της δ) ([ɛ], ycv) M ([yc], v) (τις παραπάνω και τη μεταβατικότητα της M ) ([ɛ], sv) M ([s], v) (επειδή u = yc)

6 114 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ Τώρα, έστω ότι η v είναι ɛ και έστω u οποιαδήποτε συμβολοσειρά του Σ. Από το αποτέλεσμα της επαγωγής, γνωρίζουμε ότι ([ɛ], u) M ([u], ɛ) και άρα το M αποδέχεται την u, αν και μόνο αν [u] A. Το τελευταίο όμως εξασφαλίζεται από την κατασκευή του M, αν οι συμβολοσειρές, που περιέχονται στην [u] ανήκουν στην L. Άρα, το M αποδέχεται ακριβώς εκείνες τις συμβολοσειρές, που ανήκουν στην L. δεν υπάρχει μικρότερο ΝΠΑ M, που αποδέχεται την L Αυτό είναι άμεση συνέπεια του Θεωρήματος 3.1, που λέει ότι ο αριθμός των κλάσεων ισοδυναμίας της L είναι ένα κάτω όριο στον αριθμό των καταστάσεων, για κάθε ΝΠΑ M, που αποδέχεται την L. δεν υπάρχει άλλο ΝΠΑ M, με n καταστάσεις, που αποδέχεται την L Ας θεωρήσουμε ένα οποιοδήποτε άλλο ΝΠΑ M με n καταστάσεις, που αποδέχεται την L. Αφού δε μας ενδιαφέρουν τα ονόματα καταστάσεων, μπορούμε να τα τυποποιήσουμε. Ονομάζουμε την αρχική κατάσταση των M και M 1. Ορίζουμε μία λεξικογραφική διάταξη των στοιχείων του Σ και αριθμούμε τις υπόλοιπες καταστάσεις των M και M ως εξής: 1: repet 2: Εστω q η κατάσταση με το μικρότερο αριθμό με μεταβάσεις, που οδηγούν σε κατάσταση, που δεν έχει ακόμη αριθμηθεί. 3: Επέλεξε τις εξερχόμενες μεταβάσεις από την q σε μη αριθμημένη κατάσταση. Ταξινόμησε αυτές τις μεταβάσεις λεξικογραφικά με βάση το σύμβολο με το οποίο επιγράφονται. 4: Για όλες αυτές τις μεταβάσεις (q,, p) σύμφωνα με τη σειρά ταξινόμησής τους, εκχώρησε τον επόμενο αχρησιμοποίητο αριθμό στην κατάσταση p. 5: until έχουν αριθμηθεί όλες οι καταστάσεις Σημειώνουμε ότι το M έχει n καταστάσεις και ότι υπάρχουν n κλάσεις ισοδυναμίας ως προς την L. Επειδή καμία από τις κλάσεις ισοδυναμίας δε μπορεί να είναι κενή (κάθε σχέση ισοδυναμίας είναι μία διαμέριση), είτε κάθε κατάσταση του M περιέχει τουλάχιστο μία συμβολοσειρά είτε, αν υπάρχει κατάσταση χωρίς συμβολοσειρές, τότε έχουμε τουλάχιστο μία κατάσταση, που περιέχει συμβολοσειρές από διαφορετικές κλάσεις ισοδυναμίας της L. Στη δεύτερη περίπτωση θα ίσχυε L L(M) και γι αυτό εξετάζουμε μόνο την πρώτη εκδοχή. Για να είναι το M διαφορετικό από το M υπάρχει τουλάχιστο μία κατάσταση q και ένα σύμβολο εισόδου c με το M να έχει μία μετάβαση (q, c, r) και το M μία μετάβαση (q, c, t) με r t. Καλούμε [r] το σύνολο των συμβολοσειρών, που περιέχει

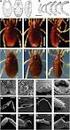
7 3.1. ΕΛΑΧΙΣΤΑ ΠΑ 115 η κατάσταση r. Αφού το M δεν έχει καταστάσεις, που δεν περιέχουν καμία συμβολοσειρά, από την αρχή του «περιστερώνα» η μετάβαση (q, c, t) του M θα πρέπει να στέλνει κάποια συμβολοσειρά u που περιέχεται στην [r] σε μία κατάσταση t, που περιέχει συμβολοσειρές, οι οποίες δεν περιέχονται στην [r]. Τότε, όλες οι συμβολοσειρές της [t] θα έχουν την ίδια συμπεριφορά με την u. Από την άλλη, η u διακρίνεται από τις συμβολοσειρές, που περιέχονται στην [t]. Αν όμως δύο συμβολοσειρές, που διακρίνονται ως προς την L έχουν την ίδια συμπεριφορά στο M, τότε L(M ) L, οπότε οδηγούμαστε σε άτοπο. Η κατασκευή, που χρησιμοποιήσαμε στην απόδειξη του Θεωρήματος 3.2 μπορεί να χρησιμοποιηθεί αν γνωρίζουμε την L, για να δημιουργήσουμε ένα ελάχιστο ΝΠΑ για την L. Παράδειγμα 3.2 (Δημιουργία ελάχιστου ΝΠΑ από την L ) Ας θεωρήσουμε τη γλώσσα του Παραδείγματος 3.1: L = {w Σ : δύο διαδοχικοί χαρακτήρες δε μπορεί να είναι ίδιοι} και τις τέσσερις κλάσεις ισοδυναμίας της L, που καταγράψαμε. Δημιουργούμε ένα ελάχιστο ΝΠΑ M, που αποδέχεται την L ως εξής: Οι κλάσεις ισοδυναμίας της L αποτελούν τις καταστάσεις του M. Αρχική κατάσταση είναι η [ɛ] = [1]. Καταστάσεις αποδοχής είναι όλες οι κλάσεις ισοδυναμίας, που περιέχουν συμβολοσειρές της L, δηλαδή οι [1], [2] και [3]. δ([x], ) = [x], για παράδειγμα, η κλάση ισοδυναμίας [1] περιλαμβάνει τη συμβολοσειρά ɛ. Αν το σύμβολο ακολουθεί την ɛ, τότε το αποτέλεσμα, δηλαδή η συμβολοσειρά ανήκει στην κλάση ισοδυναμίας [2]. Γι αυτό δημιουργούμε μία μετάβαση από την [1] στην [2], που επιγράφεται με. Η κλάση ισοδυναμίας [2] περιέχει τη συμβολοσειρά. Αν το σύμβολο ακολουθεί το, το αποτέλεσμα της παράθεσης, δηλαδή η συμβολοσειρά, ανήκει στην κλάση ισοδυναμίας [3]. Γι αυτό λοιπόν δημιουργούμε μία μετάβαση από την [2] στην [3], που επιγράφεται με κ.λ.π. Το αποτέλεσμα της κατασκευής είναι αυτό που απεικονίζεται στο Σχήμα 3.1.

8 116 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ 2, Σχήμα 3.1: Ελάχιστο ΝΠΑ για τη γλώσσα του Παραδείγματος 3.1 Το θεώρημα, που μόλις αποδείξαμε εκτός από τη χρήσιμη κατασκευή μας δίνει επίσης έναν εύκολο τρόπο, για να αποδείξουμε το παρακάτω αποτέλεσμα, το διάσημο θεώρημα, που για πρώτη φορά εισηγήθηκαν οι Myhill [3] και Nerode [4]. Θεώρημα 3.3 (Θεώρημα Myhill και Nerode) Μία γλώσσα είναι κανονική αν και μόνο αν ο αριθμός των κλάσεων ισοδυναμίας της L είναι πεπερασμένος. Απόδειξη: Διατυπώνουμε δύο αποδείξεις, μία για κάθε κατεύθυνση της διπλής συνεπαγωγής. Αν η L είναι κανονική γλώσσα, τότε ο αριθμός των κλάσεων ισοδυναμίας ως προς την L είναι πεπερασμένος. Αν η L είναι κανονική, τότε υπάρχει ένα ΝΠΑ M, που αποδέχεται την L με ένα πεπερασμένο αριθμό καταστάσεων, έστω m. Ομως από το Θεώρημα 3.1, ο αριθμός των κλάσεων ισοδυναμίας ως προς την L είναι μικρότερος ή ίσος προς το m. Συμπεραίνουμε λοιπόν ότι ο αριθμός των κλάσεων ισοδυναμίας της L είναι πεπερασμένος. Αν ο αριθμός των κλάσεων ισοδυναμίας της L είναι πεπερασμένος, τότε η L είναι κανονική γλώσσα. Αν ο αριθμός των κλάσεων ισοδυναμίας της L είναι πεπερασμένος, τότε η κατασκευή, που περιγράψαμε στην απόδειξη του Θεωρήματος 3.2 δίνει ένα ΝΠΑ, που αποδέχεται την L. Άρα η L είναι κανονική γλώσσα.

9 3.1. ΕΛΑΧΙΣΤΑ ΠΑ Ελαχιστοποίηση ενός ΝΠΑ Παράδειγμα 3.3 (ΝΠΑ με πλεονασματικές καταστάσεις) Ας θεωρήσουμε το ΝΠΑ του Σχήματος 3.2, που αποδέχεται τη γλώσσα της κανονικής έκφρασης: ( ) () Με μία πιο προσεκτική ματιά οι καταστάσεις q 3 και q 8 δε διαφοροποιούνται, q 0 q 1 q 3 q 4, q 5 q 6 q 7 q 8 Σχήμα 3.2: ΝΠΑ για τη γλώσσα της κανονικής έκφρασης ( ) () καθώς είναι καταστάσεις αποδοχής, ενώ αμφότερες οδηγούν στην q 7 με είσοδο και στην q 4 με είσοδο. Θα μπορούσαν λοιπόν να συνενωθούν, ώστε να έχουμε ένα μικρότερο ΝΠΑ. Με τον ίδιο τρόπο θα μπορούσαμε να επιχειρηματολογήσουμε για τη συνένωση των q 0 και q 6. Συνενώνοντας καταστάσεις μ αυτό τον τρόπο δημιουργούμε τελικά ένα πιο μικρό ΝΠΑ, που αναπαριστά την ίδια γλώσσα, όπως και το αρχικό. Παρατηρούμε ότι το κλειδί για μία αναπαράσταση της γλώσσας από ένα μικρότερο αυτόματο είναι ν αναγνωρίσουμε και να συνενώσουμε τις ισοδύναμες καταστάσεις. Ξεκινάμε λοιπόν ορίζοντας μία σχέση ισοδυναμίας των καταστάσεων [2]: Ορισμός 3.2 (Ισοδύναμες καταστάσεις σε ΠΑ) Δύο καταστάσεις p, q σ ένα ΠΑ M είναι ισοδύναμες, δηλαδή p q, αν και μόνο αν για κάθε συμβολοσειρά εισόδου w στο M όταν αυτό βρίσκεται σε οποιαδήποτε από τις p, q, το M είτε αποδέχεται τη w και στις δύο περιπτώσεις, είτε την απορρίπτει.

10 118 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ Θα μπορούσαμε μ άλλα λόγια να πούμε ότι το ΠΑ εκτελεί την ίδια λειτουργία, όταν αρχίζει έναν υπολογισμό σε οποιαδήποτε από τις δύο καταστάσεις. Από το ορισμό προκύπτει ότι αν δύο καταστάσεις είναι ισοδύναμες, τότε οι συμβολοσειρές, που αυτές περιέχουν, είναι υποσύνολα της ίδιας κλάσης ισοδυναμίας της L(M). Εδώ όμως καλούμαστε να απαντήσουμε σε δύο ανοικτά ερωτήματα. Πρώτον, πώς βρίσκει κάποιος ισοδύναμες καταστάσεις και στη συνέχεια, πόσο σημαντική είναι αυτή η πληροφορία; Αρχικά απαντάμε στο δεύτερο ερώτημα παραθέτοντας ένα πόρισμα από το Θεώρημα των Myhill και Nerode (Θεώρημα 3.3). Πόρισμα 3.1 Για ένα ΝΠΑ M, ο ελάχιστος αριθμός καταστάσεων σ ένα ισοδύναμο ΝΠΑ είναι ίσος με τον αριθμό των κλάσεων ισοδυναμίας της για το M. Μία ακόμη παρατήρηση είναι σημαντική, για να οδηγηθούμε σ έναν αλγόριθμο μετατροπής ενός ΝΠΑ σε μία ελάχιστη ισοδύναμη μηχανή: οι ισοδύναμες καταστάσεις οδηγούν για όλες τις εισόδους σε καταστάσεις, που είναι επίσης ισοδύναμες. Τώρα λοιπόν γνωρίζουμε ότι αν μπορούμε να βρούμε τις κλάσεις ισοδυναμίας (δηλ. τις ομάδες με ισοδύναμες καταστάσεις) για ένα ΝΠΑ, τότε μπορούμε να τις χρησιμοποιήσουμε ως καταστάσεις της ελάχιστης ισοδύναμης μηχανής. Παράδειγμα 3.4 (Ελαχιστοποίηση ΝΠΑ) Θα χρησιμοποιήσουμε ως παράδειγμα για τη συζήτηση, που ακολουθεί, το ΝΠΑ του Σχήματος 3.2. Ας διαιρέσουμε αρχικά το χώρο καταστάσεων της μηχανής ε δύο ομάδες καταστάσεων: τις καταστάσεις αποδοχής A = {q 3, q 8 } και τις καταστάσεις απόρριψης B = {q 0, q 1, q 4, q 5, q 6, q 7 }. Σημειώνουμε ότι οι καταστάσεις σ αυτές τις δύο ομάδες είναι ισοδύναμες ως προς την κενή συμβολοσειρά ως είσοδο. Ας δούμε ώρα αν οι καταστάσεις σ αυτές τις δύο ομάδες οδηγούν στην ίδια ομάδα στις περιπτώσεις εισόδου και. Σχετικά με την ομάδα A, ήδη αναφέρθηκε στο Παράδειγμα 3.3 ότι τόσο η q 3, όσο και η q 8 οδηγούν στην q 7 με και στην q 4 με, δηλαδή και στις δύο περιπτώσεις οδηγούν σε καταστάσεις της ομάδας B. Σ ότι αφορά την ομάδα B, δεν ισχύει κάτι αντίστοιχο. Ο παρακάτω πίνακας δείχνει το αποτέλεσμα της εφαρμογής των δύο εισόδων σ αυτές τις καταστάσεις (για παράδειγμα, η είσοδος οδηγεί από την q 1 στην q 6 της ομάδας B και η είσοδος οδηγεί στην q 3 της ομάδας A). Από την κατάσταση: q 0 q 1 q 4 q 5 q 6 q 7 το οδηγεί στο B B B B B B το οδηγεί στο B A B B B A

11 3.1. ΕΛΑΧΙΣΤΑ ΠΑ 119 Κοιτάζοντας πιο προσεκτικά τον πίνακα παρατηρούμε ότι η είσοδος μας βοηθάει να διακρίνουμε δύο από τις καταστάσεις (τις q 1 και q 7 ) από τις υ- πόλοιπες καταστάσεις της ομάδας, καθώς με ανάγνωση αυτού του χαρακτήρα οι πρώτες οδηγούν στο A σε αντίθεση με τις υπόλοιπες, που οδηγούν στο B. Κατά συνέπεια, οι καταστάσεις του συνόλου {q 0, q 4, q 5, q 6 } δε μπορεί να είναι ισοδύναμες μ αυτές του {q 1, q 7 } και έτσι πρέπει να διασπάσουμε την B σε δύο ομάδες καταστάσεων. q 0 q 1 q 2 q 3 q 4, Σχήμα 3.3: Ελάχιστο ΝΠΑ για τη γλώσσα ( ) () Τώρα λοιπόν έχουμε τις ομάδες A = {q 3, q 8 }, B = {q 0, q 4, q 5, q 6 }, C = {q 1, q 7 } και μία αντίστοιχη ανάλυση του που οδηγούν οι είσοδοι δείχνει ότι η q 4 δεν είναι ισοδύναμη με τις υπόλοιπες καταστάσεις της ομάδας B. Για μία ακόμη φορά διασπούμε την ομάδα B. Αυτή η διαδικασία μπορεί να συνεχιστεί μέχρι το σημείο, στο οποίο δεν είναι δυνατό να διακριθούν μεταξύ τους οι καταστάσεις σε κάποια ομάδα και ολοκληρώνεται έχοντας στο τέλος τις ομάδες: A = {q 3, q 8 }, B = {q 0, q 5, q 6 }, C = {q 1 }, D = {q 4 }, E = {q 7 } Από τους ορισμούς και τα θεωρητικά αποτελέσματα, που αναφέραμε, μπορούμε να συμπεράνουμε ότι όλες οι καταστάσεις σε κάθε ομάδα είναι ισοδύναμες, αφού όλες οδηγούν στις ίδιες ομάδες με τις εισόδους και. Επομένως οι καταστάσεις μέσα σε κάθε ομάδα δε μπορούν να διακριθούν μεταξύ τους με τον τρόπο, που περιγράφεται στον Ορισμό 3.2. Μπορούμε επίσης να ισχυριστούμε ότι εξαιτίας του Πορίσματος από το Θεώρημα Myhill-Nerode, ένα οποιοδήποτε ΝΠΑ για τη γλώσσα ( ) () θα πρέπει να έχει τουλάχιστο πέντε καταστάσεις. Η κατασκευή τώρα του ΝΠΑ με τον ελάιστο αριθμό καταστάσεων είναι μάλλον εύκολη. Χρησιμοποιούμε αποκλειστικά τις κλάσεις ισοδυναμίας (δηλ. τις

12 120 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ Αλγόριθμος 3.1 Ελαχιστοποίηση (M) Είσοδος: ένα ΝΠΑ M Εξοδος: το μικρότερο ισοδύναμο ΝΠΑ M 1: ομάδα A := {καταστάσεις αποδοχής του M} 2: ομάδα B := {καταστάσεις απόρριψης του M} 3: repet 4: for ll ομάδα καταστάσεων do 5: for ll κατάσταση στην ομάδα do 6: βρες σε ποιες ομάδες καταστάσεων οδηγούν οι είσοδοι 7: if υπάρχουν διαφορές then 8: διάσπασε την ομάδα σε σύνολα με τις καταστάσεις που οδηγούν στις ίδιες ομάδες για όλες τις εισόδους 9: until δε διασπάται κάποια ομάδα καταστάσεων 10: κατασκεύασε ένα νέο ΝΠΑ M με καταστάσεις τις ομάδες καταστάσεων του M ομάδες) των καταστάσεων και βρίσκουμε απ αυτές τις κατάλληλες μεταβάσεις. Ως αποτέλεσμα αυτής της διαδικασίας παίρνουμε τελικά το ΝΠΑ του Σχήματος 3.3. Τα βήματα, που ακολουθήσαμε, για την ελαχιστοποίηση του ΝΠΑ του Σχήματος 3.2 συνοψίζονται στον Αλγόριθμο 3.1. Ο Αλγόριθμος 3.1 έχει πολυπλοκότητα O(n 2 Σ ), όπου Σ το μέγεθος του αλφαβήτου, καθώς σε κάθε επανάληψη του βρόγχου repet θα πρέπει να ελέγχονται όλες οι n καταστάσεις και ο βρόγχος μπορεί να χρειάζεται να εκτελεστεί n φορές. Εχουν προταθεί και πιο γρήγοροι αλγόριθμοι για την ελαχιστοποίηση ε- νός ΝΠΑ, όπως για παράδειγμα αυτός του Hopcroft [1] με πολυπλοκότητα O(n Σ logn) Εφαρμογές Ψηφιακή σχεδίαση Τα ψηφιακά κυκλώματα περιλαμβάνουν διασυνδεδεμένες λογικές πύλες, που όλες μαζί εκτελούν μία λειτουργία με ένα ή περισσότερα σήματα εισόδου. Οταν έχουμε αλλαγή σ ένα σήμα εισόδου, η αλλαγή μεταδίδεται μέσω των πυλών, προκαλώντας μία δραστηριότητα διακοπών σε κάθε σημείο, όπου έχουμε διάδοση του σήματος. Αυτή η δραστηριότητα διακοπών έχει ως συνέπεια το ρεύμα

13 3.1. ΕΛΑΧΙΣΤΑ ΠΑ 121 να φορτίζει ή ν αποφορτίζει το χωρητικό φορτίο των CMOS (Complementry Metl Oxide Semiconductor) πυλών προκαλώντας έτσι κατανάλωση ισχύος. Το επίπεδο της κατανάλωσης εξαρτάται από την CMOS τεχνολογία κατασκευής, τη συχνότητα λειτουργίας, αλλά πάνω απ όλα τη δραστηριότητα διακοπών ανά κύκλο ρολογιού μέσα στο ψηφιακό κύκλωμα. Τα σύγχρονα ολοκληρωμένα κυκλώματα σε διάφορες εφαρμογές, όπως τους πολυεπεξεργαστές, την ψηφιακή μετάδοση, τα ψηφιακά φίλτρα και την ψηφιακή επεξεργασία σήματος σχεδιάζονται για να εκτελούν ένα μεγάλο αριθμό σύνθετων λειτουργιών. Για να διασφαλιστεί η ορθή αλληλεπίδραση των λειτουργιών είναι απαραίτητη κάποια λογική ελέγχου της διαχείρισης των λειτουργιών. Α- κόμη και στις περιπτώσεις σχεδίασης, που περιλαμβάνουν ένα σημαντικό αριθμό στοιχείων μετάδοσης δεδομένων, ο ελεγκτής καταλαμβάνει ένα διόλου ευκαταφρόνητο μέρος. Αυτή η λογική ελέγχου συχνά υλοποιείται ως μία μηχανή πεπερασμένων καταστάσεων, που παρακολουθεί την «κατάσταση» του ολοκληρωμένου κυκλώματος χρησιμοποιώντας έναν καταχωρητή κατάστασης (βλ. Ε- νότητα 2.7.1). Η έξοδος του ελεγκτή (μηχανής πεπερασμένων καταστάσεων) εξαρτάται από την κατάσταση, στην οποία αυτός βρίσκεται. Για να υλοποιηθεί μία μηχανή πεπερασμένων καταστάσεων σ ένα ψηφιακό κύκλωμα, θα πρέπει ν αποδοθούν μοναδικές τιμές δυαδικών κωδικών, για την αναπαράσταση των διακριτών καταστάσεων στον καταχωρητή κατάστασης. Η κωδικοποίηση των καταστάσεων καθορίζει τις λειτουργίες ελέγχου, που επιδρούν στον καταχωρητή κατάστασης και γι αυτό επηρεάζει τη δραστηριότητα διακοπών και κατά συνέπεια την κατανάλωση ισχύος στη μηχανή πεπερασμένων καταστάσεων και σ ολόκληρο το κύκλωμα. Στις μέρες μας, πολλές συσκευές για τις οποίες σχεδιάζονται τέτοιου ε- ίδους κυκλώματα είναι μεταφέρσιμες ή συσκευές χειρός και ο περιορισμός της κατανάλωσης ισχύος έχει αναδειχθεί ως πρώτη προτεραιότητα στη VLSI (Very Lrge Scle Integrtion) σχεδίαση. Γι αυτό το σκοπό, επιλέγεται να τερματίζεται η λειτουργία των στοιχείων μετάδοσης δεδομένων, όταν αυτά δε χρησιμοποιούνται. Από την άλλη, οι ελεγκτές είναι κατ ανάγκη πάντα ενεργοί με συνέπεια να καταναλώνουν ένα σημαντικό μέρος της ισχύος του συστήματος. Ετσι, η σύνθεση μηχανών πεπερασμένων καταστάσεων για μικρή κατανάλωση ενέργειας έχει εξελιχθεί σ ένα ιδιαίτερα σημαντικό πρόβλημα, που προσελκύει μεγάλο ερευνητικό ενδιαφέρον. Η σύνθεση μηχανών πεπερασμένων καταστάσεων περιλαμβάνει τα εξής βήματα: 1. Ελαχιστοποίηση καταστάσεων. Περιορίζεται ο αριθμός των καταστάσεων αναγνωρίζοντας και συνενώνοντας τις ισοδύναμες καταστάσεις. Η μηχανή πεπερασμένων καταστάσεων, που θα προκύψει, υλοποιείται πιο

14 122 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ εύκολα. 2. Κωδικοποίηση ή εκχώρηση καταστάσεων. Σε κάθε κατάσταση της μηχανής εκχωρείται ένας μοναδικός δυαδικός κωδικός. Η επιλογή της κατάλληλης τεχνικής κωδικοποίησης παίζει κρίσιμο ρόλο. Μία λάθος επιλογή μπορεί να έχει ως αποτέλεσμα μία μηχανής πεπερασμένων καταστάσεων, που είναι πολύ αργή ή καταναλώνει περισσότερη ισχύ από όσο χρειάζεται ή ακόμη έχουμε και έναν συνδυασμό των δύο. 3. Ελαχιστοποίηση συνδυαστικής λογικής. Οι κωδικοί, που δεν έχουν εκχωρηθεί σε καταστάσεις, χρησιμοποιούνται ως «αδιάφοροι» για τον περιορισμό της συνδυαστικής λογικής. 3.2 Λήμμα της Άντλησης και Μη Κανονικές Γλώσσες Στο Κεφάλαιο 2 είδαμε ότι η κλάση των κανονικών γλωσσών είναι κλειστή ως προς διάφορες πράξεις και οι γλώσσες αυτές μπορούν να περιγραφούν από (ντεντερμινιστικά ή μη ντεντερμινιστικά) πεπερασμένα αυτόματα και κανονικές εκφράσεις. Σε αυτές τις πολύ σημαντικές ιδιότητες στηρίχτηκε η ανάπτυξη διάφορων τεχνικών, που χρησιμοποιούνται για να δείξουμε ότι μία γλώσσα είναι κανονική. Παρατηρήστε ότι για μία κανονική γλώσσα: 1. Η ποσότητα της μνήμης,που χρειάζεται για να αποφασιστεί αν μία δοθείσα συμβολοσειρά ανήκει στη γλώσσα είναι πεπερασμένη και ανεξάρτητη από το μήκος της συμβολοσειράς. 2. Αν η γλώσσα αποτελείται από έναν άπειρο αριθμό συμβολοσειρών, τότε αυτή η γλώσσα θα πρέπει να περιέχει άπειρα υποσύνολα με μία αρκετά επαναλαμβανόμενη δομή. Διαισθητικά, οι γλώσσες που δεν πληρούν τα δύο προαναφερόμενα κριτήρια θα πρέπει να μην είναι κανονικές γλώσσες. Για παράδειγμα, ας δούμε τη γλώσσα: {0 n 1 n : n 0} Αυτή η γλώσσα δε θα μπορούσε να είναι κανονική, επειδή φαίνεται απίθανο ένα ΝΠΑ να μπορεί να θυμάται το πόσα 0 θα έχει διαβάσει τη στιγμή που προσεγγίζει το όριο ανάμεσα στα 0 και τα 1. Παρομοίως, η γλώσσα {0 n : n είναι ένας πρώτος αριθμός}

15 3.2. ΛΗΜΜΑ ΑΝΤΛΗΣΗΣ 123 δε μπορεί να είναι κανονική, επειδή οι πρώτοι αριθμοί δε φαίνεται να εμφανίζονται με κάποια επαναληπτική δομή, που θα μπορούσε να χρησιμοποιηθεί σε ένα ΝΠΑ. Σε μία πιο τυπική προσέγγιση, θα αποδείξουμε μία ιδιότητα, που έχουν όλες οι κανονικές γλώσσες, που θα τη λέμε λήμμα της άντλησης. Αν μία γλώσσα δεν έχει αυτή την ιδιότητα, τότε δε θα είναι μία κανονική γλώσσα. Το λήμμα της άντλησης ορίζει ότι η οποιαδήποτε αρκετά μεγάλου μήκους συμβολοσειρά μιας κανονικής γλώσσας μπορεί να «αντληθεί», δηλαδή υπάρχει ένα τμήμα της, που είναι δυνατό να επαναλαμβάνεται για έναν οποιοδήποτε αριθμό φορών, έτσι ώστε οι συμβολοσειρές που προκύπτουν να ανήκουν όλες στη γλώσσα. Θεώρημα 3.4 (Λήμμα της Άντλησης για Κανονικές Γλώσσες) Εστω ότι L είναι μία κανονική γλώσσα. Τότε θα υπάρχει ένας ακέραιος p 1, που θα λέγεται μήκος άντλησης, ώστε κάθε συμβολοσειρά w L με w p να μπορεί να γραφεί ως w = xyz και 1. y ɛ 2. xy p 3. για όλα τα i 0, xy i z L Με άλλα λόγια, το λήμμα της άντλησης ορίζει ότι με αντικατάσταση του μέρος y της συμβολοσειράς w από μηδέν ή περισσότερα αντίγραφα, η συμβολοσειρά που προκύπτει θα ανήκει επίσης στη γλώσσα L. Απόδειξη: Εστω Σ το αλφάβητο της γλώσσας L. Αφού η L είναι μία κανονική γλώσσα, θα υπάρχει ένα ΝΠΑ M = (K, Σ, δ, s, A), που θα αποδέχεται την L. Ορίζουμε p να είναι ο αριθμός των καταστάσεων στο σύνολο K. Εστω w = w 1 w 2... w n μία οποιαδήποτε συμβολοσειρά της L τέτοια ώστε n p. Ορίζουμε r 1 = s, r 2 = δ(r 1, w 1 ), r 3 = δ(r 2, w 2 ),..., r n+1 = δ(r n, w n ). Ετσι, όταν το ΝΠΑ M διαβάζει τη συμβολοσειρά w από τα αριστερά προς τα δεξιά, επισκέπτεται διαδοχικά τις καταστάσεις r 1, r 2,..., r n+1. Αφού η w είναι μία συμβολοσειρά της L, γνωρίζουμε ότι r n+1 A. Ας εστιάσουμε στις πρώτες p + 1 καταστάσεις r 1, r 2,..., r p+1 αυτής της ακολουθίας. Αφού ο αριθμός των καταστάσεων του M είναι p, θα πρέπει να υπάρχει μία κατάσταση, που εμφανίζεται δύο φορές. Τότε όμως θα υπάρχουν δείκτες j και l τέτοιοι ώστε 1 j < l p + 1 και r j = r l. Ορίζουμε ως x = w 1 w 2... w j 1, y = w j..., w l 1 και z = w l... w n. Αφού j < l θα έχουμε y ɛ, αποδεικνύοντας έτσι τον πρώτο ισχυρισμό του θεωρήματος. Επειδή l p+1 θα έχουμε xy = l 1 p και έτσι αποδεικνύεται

16 124 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ ο δεύτερος ισχυρισμός του θεωρήματος. Για να διαπιστώσουμε ότι είναι επίσης αληθής και ο τρίτος ισχυρισμός, υπενθυμίζουμε ότι η συμβολοσειρά w = xyz γίνεται αποδεκτή από το M. Καθώς λοιπόν διαβάζεται η x, το M μετακινείται από την αρχική κατάσταση s στην κατάσταση r j. Καθώς διαβάζεται η y, το αυτόματο μετακινείται από την κατάσταση r j στην κατάσταση r l = r j, δηλαδή όταν θα έχει διαβαστεί η y το M θα βρίσκεται πάλι στην κατάσταση r j. Τέλος, καθώς διαβάζεται η z, το M μετακινείται από την κατάσταση r j στην κατάσταση αποδοχής r n+1. Ετσι, η υποσυμβολοσειρά y θα μπορούσε να επαναλαμβάνεται για έναν οποιοδήποτε αριθμό i 0 φορών και οι αντίστοιχες συμβολοσειρές xy i z να είναι επίσης αποδεκτές από το M. Προκύπτει λοιπόν ότι xy i z L για όλα τα i 0. ανάγνωση s ανάγνωση ανάγνωση Παράδειγμα 3.5 (Η γλώσσα {0 n 1 n : n 0}) Για τη γλώσσα L = {0 n 1 n : n 0} θα αποδείξουμε με εις άτοπο απαγωγή ότι δεν είναι κανονική. Ας υποθέσουμε λοιπόν ότι η L είναι μία κανονική γλώσσα και ας ορίσουμε ως p 1 το μήκος άντλησης, που αναφέρεται στο λήμμα της άντλησης. Εξετάζουμε τη συμβολοσειρά w = 0 p 1 p. Είναι ξεκάθαρο ότι w L και w = 2p p. Επομένως, από το λήμμα της άντλησης, η w μπορεί να γραφεί ως w = xyz, όπου y ɛ, xy p και xy i z L για όλα τα i 0.

17 3.2. ΛΗΜΜΑ ΑΝΤΛΗΣΗΣ 125 Παρατηρούμε ότι αφού xy p, η συμβολοσειρά y θα περιέχει μόνο 0. Επίσης, καθώς y ɛ η y θα περιέχει τουλάχιστο ένα 0. Τότε όμως, σύμφωνα με το λήμμα της άντλησης οι συμβολοσειρές xy 0 z = xz, xy 2 z = xyyz, xy 3 z = xyyyz,... θα έπρεπε επίσης να περιέχονται στην L πράγμα που δε συμβαίνει. Εχοντας φτάσει σε ένα άτοπο συμπεραίνουμε ότι η αρχική υπόθεση πως η L είναι κανονική δεν ισχύει. Παράδειγμα 3.6 (Η γλώσσα {ss : s {0, 1} }) Για τη γλώσσα L = {ss : s {0, 1} } θα αποδείξουμε με εις άτοπο απαγωγή ότι δεν είναι κανονική. Ας υποθέσουμε λοιπόν ότι η L είναι μία κανονική γλώσσα και ας ορίσουμε ως p 1 το μήκος άντλησης, που αναφέρεται στο λήμμα της άντλησης. Εξετάζουμε τη συμβολοσειρά w = 0 p 10 p 1. Είναι ξεκάθαρο ότι w L και w = 2p + 2 p. Επομένως, από το λήμμα της άντλησης, η w μπορεί να γραφεί ως w = xyz, όπου y ɛ, xy p και xy i z L για όλα τα i 0. Παρατηρούμε ότι αφού xy p, η συμβολοσειρά y θα περιέχει μόνο 0. Επίσης, καθώς y ɛ η y θα περιέχει τουλάχιστο ένα 0. Τότε όμως, σύμφωνα με το λήμμα της άντλησης η συμβολοσειρά xy 2 z = xyyz θα έπρεπε επίσης να περιέχεται στην L πράγμα που δε συμβαίνει. Εχοντας φτάσει σε ένα άτοπο συμπεραίνουμε ότι η αρχική υπόθεση πως η L είναι κανονική δεν ισχύει. Επισημαίνουμε ότι επιλέγοντας w = 0 2p, που είναι επίσης μία συμβολοσειρά της L με μήκος τουλάχιστο p, δεν καταλήγουμε σε άτοπο. Ο λόγος είναι ότι η συμβολοσειρά y μπορεί να έχει ένα άρτιο μήκος. Ετσι, η 0 2p δεν είναι η «κατάλληλη» συμβολοσειρά για να οδηγηθούμε σε άτοπο. Επιλέγοντας w = 0 p 10 p 1 οδηγούμαστε σε άτοπο και επομένως αυτή είναι μία «κατάλληλη» συμβολοσειρά για να δείξουμε ότι η L δεν είναι κανονική. Παράδειγμα 3.7 (Η γλώσσα {1 n2 : n 0}) Για τη γλώσσα L = {1 n2 : n 0} θα αποδείξουμε με εις άτοπο απαγωγή ότι δεν είναι κανονική. Ας υποθέσουμε λοιπόν ότι η L είναι μία κανονική γλώσσα και ας ορίσουμε ως p 1 το μήκος άντλησης, που αναφέρεται στο λήμμα της άντλησης.

18 126 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ Εξετάζουμε τη συμβολοσειρά w = 1 p2. Είναι ξεκάθαρο ότι w L και w = p 2 p. Επομένως, από το λήμμα της άντλησης, η w μπορεί να γραφεί ως w = xyz, όπου y ɛ, xy p και xy i z L για όλα τα i 0. Παρατηρούμε ότι και w = xyz = p 2 xy 2 z = xyyz = xyyz + y = p 2 + y Αφού xy p έχουμε y p. Επίσης, καθώς y ɛ ισχύει ότι y 1. Προκύπτει ότι p 2 < xy 2 z p 2 + p < (p + 1) 2 Επομένως, το μήκος της συμβολοσειράς xy 2 z είναι ένας αριθμός, που βρίσκεται αυστηρά ανάμεσα σε δύο συνεχόμενα τετράγωνα. Προκύπτει λοιπόν ότι το συγκεκριμένο μήκος δεν δίνεται ως τετράγωνο κάποιου αριθμού και γι αυτό η xy 2 z δεν περιέχεται στην L. Εχοντας φτάσει σε ένα άτοπο, συμπεραίνουμε ότι η αρχική υπόθεση πως η L είναι κανονική δεν ισχύει. Παράδειγμα 3.8 (Η γλώσσα {1 n : n είναι πρώτος}) Για τη γλώσσα L = {1 n : n είναι πρώτος} θα αποδείξουμε με εις άτοπο απαγωγή ότι δεν είναι κανονική. Ας υποθέσουμε λοιπόν ότι η L είναι μία κανονική γλώσσα και ας ορίσουμε ως p 1 το μήκος άντλησης, που αναφέρεται στο λήμμα της άντλησης. Εστω επίσης n p ένας πρώτος αριθμός και ας εξετάσουμε τη συμβολοσειρά w = 1 n. Είναι ξεκάθαρο ότι w L και w = n p. Επομένως, από το λήμμα της άντλησης, η w μπορεί να γραφεί ως w = xyz, όπου y ɛ, xy p και xy i z L για όλα τα i 0. Εστω k ένας ακέραιος τέτοιος ώστε y = 1 k. Αφού y ɛ, έχουμε k 1. Για κάθε i 0, n + (i 1)k θα είναι ένας πρώτος αριθμός, επειδή xy i z = 1 n+(i 1)k L. Ομως για i = n + 1 έχουμε n + (i 1)k = n + nk = n(1 + k) που δεν είναι ένας πρώτος αριθμός, αφού n 2 και 1+k 2. Εχοντας φτάσει σε ένα άτοπο, συμπεραίνουμε ότι η αρχική υπόθεση πως η L είναι κανονική δεν ισχύει.

19 3.3. ΑΠΟΦΑΣΙΣΙΜ ΟΤΗΤΑ ΠΡΟΒΛΗΜΆΤΩΝ & ΑΛΓ ΟΡΙΘΜΟΙ ΠΑ Αποφασισιμότητα προβλημάτων & αλγόριθμοι ΠΑ Στην ενότητα αυτή επιχειρούμε να απαντήσουμε στα εξής ερωτήματα: 1. Υπάρχει αλγόριθμος, που βρίσκει αν η γλώσσα, που γίνεται αποδεκτή από ένα ΠΑ είναι το κενό σύνολο; 2. Υπάρχει αλγόριθμος, που βρίσκει αν δύο ΠΑ αποδέχονται την ίδια γλώσσα; 3. Υπάρχει αλγόριθμος, που βρίσκει αν δύο κανονικές γλώσσες είναι ίδιες; 4. Υπάρχει αλγόριθμος, που βρίσκει αν η γλώσσα που γίνεται αποδεκτή από ένα ΠΑ είναι άπειρη; Για όλα τα παραπάνω ερωτήματα απαιτείται να υπάρχει ένας αλγόριθμος, που τερματίζει για όλες τις εισόδους με μία απάντηση «ναι» ή «όχι». Δε μας απασχολεί η αποδοτικότητα του αλγορίθμου, που επιλύει το πρόβλημα, αλλά μόνο αν αυτός απαντάει στο ερώτημα μέσα σε πεπερασμένο χρόνο. Θεώρημα 3.5 (ΠΑ με κενή γλώσσα) Υπάρχει αλγόριθμος που βρίσκει αν η γλώσσα L(M) ενός ΠΑ M είναι κενή. Απόδειξη: Εστω ότι το M αποτελείται από n καταστάσεις. Η πιο μικρή συμβολοσειρά, που γίνεται αποδεκτή από το M δε μπορεί να εισέρχεται στην ίδια κατάσταση περισσότερες από μία φορές και επομένως θα έχει μήκος μικρότερο από n. Η L(M) θα είναι κενή, αν και μόνο αν η αρχική κατάσταση του M δεν είναι κατάσταση αποδοχής και καμία από τις συμβολοσειρές με μήκος μικρότερο του n δε γίνεται αποδεκτή. Επειδή ο αριθμός των συγκεκριμένων συμβολοσειρών είναι πεπερασμένος, αυτές μπορούν να ελεγχθούν και επομένως υπάρχει αλγόριθμος, που βρίσκει αν η γλώσσα L(M) είναι κενή. Θεώρημα 3.6 (ΠΑ με ίδια γλώσσα) Υπάρχει αλγόριθμος που βρίσκει αν δύο ΠΑ αποδέχονται την ίδια γλώσσα. Απόδειξη: Ας θεωρήσουμε δύο ΠΑ M 1 και M 2, που αποδέχονται αντίστοιχα τις γλώσσες L(M 1 ) και L(M 2 ). Οι δύο αυτές γλώσσες είναι ίδιες, αν L(M 1 ) L(M 2 ) =, όπου L(M 1 ) L(M 2 ) είναι η συμμετρική διαφορά των δύο γλωσσών: (L(M 1 ) L(M 2 )) (L(M 2 ) L(M 1 )) =

20 128 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ (L(M 1 ) L(M 2 )) (L(M 2 ) L(M 1 )) Γνωρίζουμε όμως από τις ιδιότητες κλειστότητας των κανονικών γλωσσών ότι δοθέντων δύο ΠΑ M 1 και M 2, που αποδέχονται αντίστοιχα τις γλώσσες L(M 1 ) και L(M 2 ), μπορούμε να δημιουργήσουμε ΠΑ, που αποδέχονται το συμπλήρωμα μιας γλώσσας, καθώς και τις γλώσσες L(M 1 ) L(M 2 ) και L(M 1 ) L(M 2 ). Άρα μπορούμε να κατασκευάσουμε ένα αυτόματο, που αποδέχεται τη γλώσσα L(M 1 ) L(M 2 ) και σύμφωνα με το Θεώρημα 3.5 υπάρχει αλγόριθμος για να ελέγξουμε αν αυτή είναι κενή. Θεώρημα 3.7 ( Ιδιες κανονικές γλώσσες) Υπάρχει αλγόριθμος που βρίσκει αν δύο κανονικές γλώσσες είναι ίδιες. Απόδειξη: Δοθέντων δύο κανονικών εκφράσεων για τις γλώσσες L 1 και L 2 κατασκευάζουμε τα ΝΠΑ M 1 και M 2, που αποδέχονται αντίστοιχα τις L 1 και L 2. Από το Θεώρημα 3.6 είναι σαφές ότι υπάρχει αλγόριθμος, για να ελεγχθεί αν οι γλώσσες, που αποδέχονται τα M 1 και M 2 είναι ίδιες. Πριν από την απόδειξη του επόμενου θεωρήματος χρειάζεται να αποδείξουμε το παρακάτω Λήμμα. Λήμμα 3.1 Για ένα ΠΑ M με n καταστάσεις η L(M) είναι άπειρη αν και μόνο αν υπάρχει μία συμβολοσειρά της L(M) με μήκος μεγαλύτερο από n και μικρότερο από 2n. Απόδειξη: Παρατηρούμε ότι η L(M) είναι άπειρη αν και μόνο αν περιλαμβάνει συμβολοσειρές, που οδηγούν το M στην εκτέλεση των μεταβάσεων κάποιου βρόγχου. Κάθε συμβολοσειρά με μήκος μεγαλύτερο από n, δηλαδή όσες οι καταστάσεις του M, οδηγεί τη μηχανή στην εκτέλεση ενός τέτοιου βρόγχου. Επομένως το M αποδέχεται τουλάχιστο μία συμβολοσειρά με μήκος μεγαλύτερο από n, αλλά επειδή ένας τέτοιος βρόγχος μπορεί να εκτελείται για έναν οποιοδήποτε αριθμό επαναλήψεων η γλώσσα θα περιέχει άπειρες συμβολοσειρές με μήκος μεγαλύτερο από n. Θεωρούμε μία συμβολοσειρά, που αποδέχεται το M εκτελώντας ένα τέτοιο βρόγχο δύο φορές. Απ αυτή τη συμβολοσειρά μπορούμε ν «αντλήσουμε» την υποσυμβολοσειρά, που αντιστοιχεί σε μία μόνο εκτέλεση των μεταβάσεων του βρόγχου. Σ αυτή την περίπτωση θα έχουμε μία μικρότερη συμβολοσειρά, που

21 3.3. ΑΠΟΦΑΣΙΣΙΜΟΤΗΤΑ ΠΡΟΒΛΗΜΑΤΩΝ & ΑΛΓΟΡΙΘΜΟΙ ΠΑ 129 είναι επίσης αποδεκτή από το M. Κατά συνέπεια, αν το M αποδέχεται κάποιες συμβολοσειρές, απ αυτές που οδηγούν στην εκτέλεση ενός βρόγχου δύο φορές, θ αποδέχεται επίσης τουλάχιστο μία συμβολοσειρά, που οδηγεί στην εκτέλεση ενός βρόγχου για μία μόνο φορά. Ο μεγαλύτερος βρόγχος, που μπορεί να περιέχει το M θα μπορούσε να οδηγήσει στο πέρασμα απ όλες τις καταστάσεις για δεύτερη φορά. Ετσι, η L(M) είναι άπειρη αν και μόνο αν το M αποδέχεται τουλάχιστο μία συμβολοσειρά w τέτοια ώστε: n w 2n Θεώρημα 3.8 (ΠΑ με άπειρη γλώσσα) Υπάρχει αλγόριθμος που βρίσκει αν η γλώσσα που γίνεται αποδεκτή από ένα ΠΑ M είναι άπειρη. Απόδειξη: Εστω ότι το M έχει n καταστάσεις. Τότε, σύμφωνα με το Λήμμα 3.1 η L(M) είναι άπειρη, αν και μόνο αν το M αποδέχεται μία συμβολοσειρά w μήκους n w 2n. Επειδή όμως έχουμε μόνο ένα πεπερασμένο αριθμό τέτοιων συμβολοσειρών, μπορεί κάθε μία απ αυτές να ελεγχθεί αν γίνεται αποδεκτή από το αυτόματο. Θεώρημα 3.9 (ΠΑ με πεπερασμένη γλώσσα) Υπάρχει αλγόριθμος που βρίσκει αν η γλώσσα που γίνεται αποδεκτή από ένα ΠΑ M είναι πεπερασμένη. Απόδειξη: Με βάση την απόδειξη του Θεωρήματος 3.8, αν δεν υπάρχει συμβολοσειρά w, που να είναι αποδεκτή από την M με n w 2n, τότε η L(M) είναι πεπερασμένη (σ αυτές τις γλώσσες συμπεριλαμβάνονται η κενή γλώσσα και η γλώσσα, που αποτελείται μόνο από την κενή συμβολοσειρά). Θεώρημα 3.10 (Υποσύνολο κανονικής γλώσσας) Υπάρχει αλγόριθμος που βρίσκει αν για δύο κανονικές γλώσσες L 1 L 2. Απόδειξη: Γνωρίζουμε από τις ιδιότητες κλειστότητας των κανονικών γλωσσών ότι από δύο ΠΑ M 1 και M 2 με γλώσσες L 1 και L 2 αντίστοιχα, μπορούμε να δημιουργήσουμε ΠΑ, που αποδέχεται τη γλώσσα L = L 1 L 2. Ομως το αν η L είναι κενή μπορούμε να το διαπιστώσουμε με βάση το Θεώρημα 3.5 και αυτό θα ισχύει αν και μόνο αν L 1 L 2. Άρα υπάρχει αλγόριθμος, που βρίσκει αν η L 1 είναι υποσύνολο της L 2.

22 130 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ Στο Παράδειγμα 2.3 παρουσιάσαμε τον αλγόριθμο εκτέλεσης ενός ΝΠΑ. Για ένα δοθέν αυτόματο M, ο αντίστοιχος αλγόριθμος εξαρτάται από τις καταστάσεις K και το αλφάβητο Σ της μηχανής και το πρόγραμμα θα έχει μήκος 2 + ( K ( Σ + 2)) εντολές. Ο απαιτούμενος χρόνος για την ανάλυση μιας συμβολοσειράς εισόδου w είναι O( w Σ). Ομως το πιο σημαντικό πρόβλημα μ αυτή την προσέγγιση είναι ότι θα πρέπει να δημιουργείται ένα νέο πρόγραμμα, για κάθε ΝΠΑ, που πρόκειται να εκτελεστεί. Εναλλακτικά, μπορούμε να προσομοιώσουμε την εκτέλεση οποιουδήποτε ΝΠΑ μέσω ενός διερμηνευτή, όπως φαίνεται στον Αλγόριθμο 3.2. Αλγόριθμος 3.2 Προσομοίωση-ΝΠΑ (M, w) Είσοδος: ένα ΝΠΑ M = (K, Σ, δ, s, A) και μία συμβολοσειρά w Σ Εξοδος: η w είναι αποδεκτή ή απορρίπτεται 1: st:=s 2: repet 3: c:=get-next-symol(w) 4: if c null then 5: st:=δ(st, c) 6: until c == null 7: if st A then 8: η w είναι αποδεκτή 9: else 10: η w απορρίπτεται Ο αλγόριθμος Προσομοίωση-ΝΠΑ (M, w) εκτελείται σε χρόνο O( w ), αν βέβαια η προσπέλαση στον πίνακα της δ στο βήμα 5 εκτελείται σε σταθερό χρόνο. Ο αλγόριθμος Προσομοίωση-ΝΠΑ (M, w) είναι βασικό συστατικό των αλγορίθμων για τα προβλήματα των θεωρημάτων αυτής της ενότητας. Στις περισσότερες περιπτώσεις στηριζόμαστε στον έλεγχο των κριτηρίων, που αναφέρονται στις αποδείξεις των αντίστοιχων θεωρημάτων, για ένα πεπερασμένο αριθμό συμβολοσειρών ακόμη και αν η γλώσσα του αυτομάτου είναι άπειρη. Ετσι, εξασφαλίζουμε ότι ο αλγόριθμος τερματίζει σε έναν πεπερασμένο αριθμό βημάτων, για όλες τις πιθανές εξόδους. Για παράδειγμα, ο Αλγόριθμος 3.3 δίνει απάντηση στο πρόβλημα τους Θεωρήματος 3.5. Ο αλγόριθμος ΚενήΓλώσσα-ΝΠΑ (M) υλοποιεί τον έλεγχο, που προτείνεται στην απόδειξη του Θεωρήματος 3.5: η L(M) είναι κενή αν και μόνο αν

23 3.3. ΑΠΟΦΑΣΙΣΙΜΟΤΗΤΑ ΠΡΟΒΛΗΜΑΤΩΝ & ΑΛΓΟΡΙΘΜΟΙ ΠΑ 131 Αλγόριθμος 3.3 ΚενήΓλώσσα-ΝΠΑ (M) Είσοδος: ένα ΝΠΑ M = (K, Σ, δ, s, A) Εξοδος: η L(M) είναι κενή ή όχι 1: for ech w Σ με w < K do 2: Προσομοίωση-ΝΠΑ (M, w) 3: if το M αποδέχεται τουλάχιστο μία τέτοια w then 4: η L(M) δεν είναι κενή 5: else 6: η L(M) είναι κενή καμία από τις συμβολοσειρές με μήκος μικρότερο από τον αριθμό καταστάσεων του M δεν είναι αποδεκτή. Εναλλακτικά, το πρόβλημα θα μπορούσε να απαντηθεί, αν αντί της προσομοίωσης του M γίνει μία κατάλληλη στατική ανάλυση της συνάρτησης μετάβασης. Σε αυτή την περίπτωση, το M δε χρειάζεται να εκτελεστεί για κάποια συμβολοσειρά. Ο Αλγόριθμος 3.4 υλοποιεί τη συγκεκριμένη προσέγγιση. Αλγόριθμος 3.4 ΚενήΓλώσσαΓραφ-ΝΠΑ (M) Είσοδος: ένα ΝΠΑ M = (K, Σ, δ, s, A) Εξοδος: η L(M) είναι κενή ή όχι 1: Σημείωσε τις καταστάσεις, που προσεγγίζονται με μονοπάτι από την s 2: if τουλάχιστο μία σημειωμένη κατάσταση είναι κατάσταση αποδοχής then 3: η L(M) δεν είναι κενή 4: else 5: η L(M) είναι κενή Η γλώσσα L(M) είναι μη κενή αν το K περιέχει τουλάχιστο μία κατάσταση αποδοχής. Αυτό όμως δεν είναι αρκετό από μόνο του: θα πρέπει αυτή η κατάσταση αποδοχής να είναι προσεγγίσιμη μέσω ενός μονοπατιού από την αρχική κατάσταση. Ο αλγόριθμος ΚενήΓλώσσαΓραφ-ΝΠΑ (M) κάνει αυτόν τον έλεγχο στο γράφο, που ορίζει η συνάρτηση μετάβασης του M. Ενας άλλος έλεγχος στο γράφο της συνάρτησης μετάβασης του ΝΠΑ είναι η βάση ενός αλγορίθμου, για το πρόβλημα του Θεωρήματος 3.9. Παρατηρούμε ότι η γλώσσα ενός ΝΠΑ M είναι πεπερασμένη, αν η συνάρτηση μετάβασης δεν περιέχει βρόγχους πάνω σε μονοπάτια προς τις καταστάσεις αποδοχής. Ε- πιπλέον, οι βρόγχοι σε καταστάσεις, που δεν προσεγγίζονται από την αρχική κατάσταση, δεν επηρεάζουν το αποτέλεσμα. Για να αποφευχθεί ο έλεγχος τέτοιων καταστάσεων εκτελείται πρώτα ο αλγόριθμος Ελαχιστοποίηση (M). Ο Αλγόριθμος 3.5 αποδίδει τον πλήρη έλεγχο του γράφου της συνάρτησης

24 132 ΚΕΦΑΛΑΙΟ 3. ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ - ΜΗ ΚΑΝ. ΓΛΩΣΣΕΣ μετάβασης, για να διαπιστωθεί αν η γλώσσα ενός ΝΠΑ M είναι πεπερασμένη. Αλγόριθμος 3.5 ΠεπερΓλώσσαΓραφ-ΝΠΑ (M) Είσοδος: ένα ΝΠΑ M = (K, Σ, δ, s, A) Εξοδος: η L(M) είναι πεπερασμένη ή όχι 1: M :=Ελαχιστοποίηση (M) 2: Σημείωσε όλες τις καταστάσεις του M, πάνω σε μονοπάτι προς κατάσταση αποδοχής 3: Ελεγξε αν υπάρχουν κύκλοι σε κάποια από τις σημειωμένες καταστάσεις του M 4: if υπάρχουν κύκλοι then 5: η L(M) δεν είναι πεπερασμένη 6: else 7: η L(M) είναι πεπερασμένη Εναλλακτικά, το ίδιο πρόβλημα λύνεται ελέγχοντας το κριτήριο, που α- ναφέρεται στην απόδειξη του Θεωρήματος 3.9: για ένα κατάλληλα επιλεγμένο πεπερασμένο σύνολο συμβολοσειρών w Σ καλείται ο αλγόριθμος Προσομοίωση-ΝΠΑ (M, w). Ο έλεγχος αυτός φαίνεται στον Αλγόριθμο 3.6. Αλγόριθμος 3.6 ΠεπερΓλώσσα-ΝΠΑ (M) Είσοδος: ένα ΝΠΑ M = (K, Σ, δ, s, A) Εξοδος: η L(M) είναι πεπερασμένη ή όχι 1: for ech w Σ με K w 2 K 1 do 2: Προσομοίωση-ΝΠΑ (M, w) 3: if το M αποδέχεται τουλάχιστο μία τέτοια w then 4: η L(M) δεν είναι πεπερασμένη 5: else 6: η L(M) είναι πεπερασμένη 3.4 Βιντεοδιαλέξεις Στην ενότητα αυτή, ο αναγνώστης μπορεί να παρακολουθήσει... βιντεοδιαλέξεις

25 3.5. ΔΙΑΔΡΑΣΤΙΚ Ο ΤΕΣΤ Διαδραστικό τεστ Στο διαδραστικό τεστ, που ακολουθεί καλείστε να απαντήσετε σε μία ερώτηση πολλαπλής επιλογής πάνω στην ύλη του Κεφαλαίου 3. Αν επιλέξετε λάθος απάντηση, τότε μπορείτε να επαναλάβετε την προσπάθεια. Ο βαθμός με τον οποίο αξιολογείστε σε κάθε ερώτηση εξαρτάται από το πόσες προσπάθειες θα χρειαστείτε για να βρείτε τη σωστή απάντηση. Για κάθε σωστή απάντηση, εμφανίζεται στην οθόνη ο μέσος όρος των επιδόσεων σας στις ερωτήσεις, που έχουν απαντηθεί μέχρι εκείνη τη στιγμή. Βιβλιογραφία - Αναφορές [1] John E. Hopcroft. An n log n lgorithm for minimizing sttes in finite utomton. Technicl report, Stnford, CA, USA, [2] Edwrd F. Moore. Gednken-experiments on sequentil mchines. In Clude Shnnon nd John McCrthy, editors, Automt Studies, pges Princeton University Press, Princeton, NJ, [3] John R. Myhill. Finite Automt nd the Representtion of Events. Technicl Report WADC TR , Wright-Pterson Air Force Bse, [4] A. Nerode. Liner utomton trnsformtions. Proceedings of the Americn Mthemticl Society, 9(4): , 1958.