ΘΕΜΑ Γ, Δ. γ. 0,3 m δ. 112,5 rad] 3. Η ράβδος του σχήματος περιστρέφεται με σταθερή γωνιακή
|
|
|
- Λαδων Θεοδωρίδης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΘΕΜΑ Γ, Δ 1. Μια ευθύγραμμη ράβδος ΑΒ αρχίζει από την ηρεμία να περιστρέφεται με σταθερή γωνιακή επιτάχυνση 4 rad/s. Η ράβδος έχει μήκος l 1 m. 0 άξονας περιστροφής της ράβδου είναι κάθετος στη ράβδο και διέρχεται από ένα σημείο της Ο. Τη χρονική στιγμή 2 s το άκρο Α της ράβδου έχει γραμμική ταχύτητα 2,4 m/s. α. Πόση γραμμική ταχύτητα έχει το σημείο Β της ράβδου τη χρονική στιγμή 3 s; β. Πόσες περιστροφές έχει εκτελέσει η ράβδος μέχρι τη χρονική στιγμή ; γ. Πόση σταθερή γωνιακή επιβράδυνση πρέπει να αποκτήσει η ράβδος τη χρονική στιγμή 5 s, ώστε να σταματήσει την περιστροφή της τη χρονική στιγμή 7 s; δ. Να κάνετε τα διαγράμματα και για τη ράβδο από τη χρονική στιγμή 0 s έως 7 s. [απ. α. 8,4 m/s β. 9/ στροφές γ. 10 rad/s ] 2. Ομογενής δίσκος ακτίνας 40 cm αρχίζει να περιστρέφεται γύρω από άξονα κάθετο στον δίσκο και διερχόμενο από το κέντρο του, με γωνιακή ταχύτητα που μεταβάλλεται, ό πως στο διάγραμμα του σχήματος. Να υπολογίσετε: α. Τη γωνιακή επιτάχυνση του δίσκου τις χρονικές στιγμές 6 s και 12 s. β. Το μέτρο της γραμμικής ταχύτητας ενός σημείου της περιφέρειας του δίσκου τις ίδιες χρονικές στιγμές. γ. Την απόσταση που απέχει από το κέντρο του δίσκου ένα σημείο Σ που τη χρονική στιγμή το μέτρο της γραμμικής του ταχύτητας μειώνεται με ρυθμό 0,9 m/s. δ. Τη συνολική γωνιακή μετατόπιση του δίσκου. [απ. α., 1,5 rad/s,, 3 rad/s β. 3,6 m/s γ. 0,3 m δ. 112,5 rad] 3. Η ράβδος του σχήματος περιστρέφεται με σταθερή γωνιακή επιτάχυνση 4 rad/s γύρω από σταθερό άξονα κάθετο στη ράβδο και διερχόμενο από κάποιο σημείο της Ο. Τη χρονική στιγμή 0 η ράβδος ήταν ακίνητη και τη χρονική στιγμή 0,5 s η ράβδος έχει τη διεύθυνση του σχήματος. Τη στιγμή το άκρο Κ έχει ταχύτητα 0,8 m/s και το μέσο Μ της ράβδου έχει ταχύτητα 0,2 m/s, όπως στο σχήμα. α. Πόσο απέχει από το άκρο Κ το σημείο Ο; β. Πόσο είναι το μήκος της ράβδου και πόσο απέχει τη στιγμή το σημείο Κ από την αρχική του θέση; γ. Πόση ταχύτητα έχει το σημείο Λ τη στιγμή που η ράβδος έχει ολοκληρώσει μια περιστροφή μετά τη χρονική στιγμή 0 s; δ. Πόσες περιστροφές έχει εκτελέσει η ράβδος τη στιγμή που η ταχύτητα του σημείου Λ θα είναι δεκαπλάσια της ταχύτητας που έχει το σημείο Κ τη χρονική στιγμή ; [απ. α. 40 cm β. ΚΛ 0,6 m, 40 2 cm γ. 0,8 m/s δ. 100 περιστροφές] 4. Ένας τροχός ακτίνας 20 cm κυλάει χωρίς ολίσθηση πάνω σε οριζόντια επιφάνεια με σταθερή ταχύτητα 8 m/s. α. Να βρείτε το μέτρο και την κατεύθυνση της ταχύτητας των σημείων της περιφέρειας του τροχού που απέχουν 20 cm από την οριζόντια επιφάνεια. ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 1
2 β. Πόσο θα μετατοπιστεί το κέντρο μάζας του τροχού, όταν αυτός έχει εκτελέσει 10 περιστροφές; γ. Να αποδείξτε ότι, αν Ο το σημείο επαφής του τροχού με το έδαφος κάποια στιγμή και Σ ένα τυχαίο σημείο της περιφέρειας του τροχού, τότε η ταχύτητα του σημείου Σ είναι κάθετη στο ευθύγραμμο τμήμα ΟΣ. Αν το σημείο Σ απέχει από το 0 απόσταση 30 cm, να υπολογίσετε το μέτρο της ταχύτητας του Σ. δ. Κάποια στιγμή ο τροχός αποκτά σταθερή επιβράδυνση και σταματά μετά από 16 m. Να βρείτε την επιβράδυνση που απέκτησε. Πόση ταχύτητα είχε το ανώτερο σημείο του τροχού 1 s πριν αυτός σταματήσει; [απ. α. 8 m/s β. 4 m γ. 12 m/s δ. 2 m/s, 4 m/s] 5. Μία ράβδος ΟΑ μήκους 60 cm και μάζας 5 kg μπορεί να περιστρέφεται γύρω από άξονα κάθετο στη ράβδο και διερχόμενο από το ένα της άκρο Ο. Αρχικά η ράβδος είναι ακίνητη και τη χρονική στιγμή 0 s αρχίζει να περιστρέφεται με σταθερή γωνιακή επιτάχυνση, 0,4 rad/s. Τη χρονική στιγμή 10 s η ράβδος αποκτά σταθερή γωνιακή επιβράδυνση, 0,8 rad/s. α. Να υπολογίσετε τη γωνιακή ταχύτητα της ράβδου και τη γραμμική ταχύτητα του ά κρου Α τη χρονική στιγμή. β. Να βρείτε πόσες περιστροφές πραγματοποίησε η ράβδος μέχρι να σταματήσει. γ. Να σχεδιάσετε τις γραφικές παραστάσεις της γωνιακής ταχύτητας και της γωνιακής μετατόπισης της ράβδου σε συνάρτηση με τον χρόνο. δ. Να βρείτε το μέτρο της σταθερής ροπής που δέχθηκε η ράβδος πριν και μετά τη χρονική στιγμή. Για τη ράβδο δίνεται /12. [απ. 4 rad/s, Α 2,4 m/sβ. περιστροφές δ. 0,24 Ν m, 0,48 Ν m] 6. Στο σχήμα φαίνεται ένα καρούλι μάζας 5 kg και ακτίνας 20 cm, Στο καρούλι είναι τυλιγμένο νήμα με μήκος 2,5 m και ακτίνα περιέλιξης 10 cm. Το νήμα είναι οριζόντιο και τραβάμε το άκρο του Α με οριζόντια επιτάχυνση 0,6 m/s. Αρχικά το σύστημα είναι ακίνητο. Να υπολογίσετε: α. Τη γωνιακή και τη μεταφορική επιτάχυνση του καρουλιού, αν αυτό κυλάει χωρίς ολίσθηση. β. Τη γωνιακή και τη μεταφορική ταχύτητα με την οποία θα κυλάει το καρούλι, καθώς και την ταχύτητα του ανώτερου σημείου της περιφέρειάς του τη χρονική στιγμή που θα ξετυλιχτεί εντελώς το νήμα. γ. Το πλήθος των περιστροφών του καρουλιού μέχρι τη χρονική στιγμή. δ. Τη δύναμη που ασκούμε στο καρούλι μέσω του νήματος, αν η ροπή αδράνειας του καρουλιού είναι 0,04 kg m. [απ. α. 2 rad/s, 0,4 m/s β. 10 rad/s, 2 m/s, 4 m/s γ., στροφές δ. 1,6 Ν] 7. Ο διπλός τροχός του σχήματος έχει ακτίνες 30 cm και 20 cm. Στη περιφέρεια κάθε τροχού είναι τυλιγμένο αβαρές νήμα και ο τροχός βρίσκεται σε οριζόντιο δάπεδο με το οποίο παρουσιάζει συντελεστή τριβής ολίσθησης 0,4. Τραβάμε τα ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 2
3 άκρα των δύο νημάτων με σταθερές ταχύτητες 4 m/s και 1 m/s, όπως στο σχήμα διατηρώντας τα νήματα διαρκώς οριζόντια. α. Να υπολογίσετε τη γωνιακή ταχύτητα του τροχού. β. Να βρείτε την ταχύτητα του κέντρου μάζας του διπλού τροχού, καθώς και την ταχύτητα του σημείου επαφής του με το δάπεδο. γ. Αν ο τροχός έχει μάζα 2 kg να υπολογίσετε τα μέτρα των δυνάμεων που α σκούμε με τα νήματα στον τροχό. δ. Με ποιον ρυθμό εκλύεται θερμότητα λόγω τριβής στο περιβάλλον; [απ. α. 10 rad/s β. cm 1 m/s, υ 2 m/s γ. 1,6 N, 9,6 N δ. 16 J/s] 8. Η ομογενής και ισοπαχής ράβδος του σχήματος έχει μάζα 2 kg μήκος 3 m και είναι αρθρωμένη στο σημείο Α, ενώ στο άλλο της άκρο έχει προσδεθεί μικρή σφαίρα ίδιας μάζας με τη ράβδο. Κατά μήκος της ράβδου μπορεί να ολισθαίνει χωρίς τριβές λείος αβαρής δακτύλιος Δ, στον οποίο είναι δεμένο το ένα άκρο αβαρούς νήματος το άλλο άκρο του οποίου είναι δεμένο στον κατακόρυφο τοίχο. Η ράβδος ισορροπεί σχηματίζοντας γωνία 30 με την οριζόντια διεύθυνση και ο δακτύλιος βρίσκεται στο μέσο της. α. Να βρείτε τη ροπή αδράνειας της ράβδου ως προς την άρθρωση. β. Να δικαιολογήσετε γιατί στην κατάσταση ισορροπίας το νήμα θα είναι κάθετο στη ράβδο. γ. Να υπολογίσετε την τάση του νήματος και το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση. δ. Αν κόψουμε το νήμα, να βρείτε τη γωνιακή επιτάχυνση που θα αποκτήσει αμέσως η ράβδος. ε. Πόση ταχύτητα θα έχει το σφαιρίδιο τη στιγμή που η ράβδος γίνεται κατακόρυφη; Για τη ράβδο δίνεται /12. [απ. α. 24 kg m γ N, 10 7 N δ. rad/s ε. 4,5 5 m/s] 9. Η ομογενής ράβδος του σχήματος έχει μάζα 4 kg και μήκος 2 m. Η ράβδος ισορροπεί οριζόντια με το άκρο της Α αρθρωμένο σε κατακόρυφο τοίχο. Στο άλλο της άκρο Β είναι κρεμασμένο σώμα μάζας. Στο σημείο Γ που απέχει 50 cm από το άκρο Β, η ράβδος είναι δεμένη με νήμα που το άλλο του άκρο είναι δεμένο σε σώμα μάζας. Το σώμα είναι με τη σειρά του δεμένο στο κάτω άκρο κατακόρυφου ελατήριου σταθεράς 1200 N/m. Αν κόψουμε το νήμα στο σημείο Γ, το σώμα θα ανέβει κατά 25 cm μέχρι στιγμιαία να σταματήσει σε χρόνο /20 s. Να υπολογίσετε: α. Τη μάζα και την αρχική παραμόρφωση του ελατηρίου β. Τη μάζα. γ. Τη δύναμη που δέχεται η ράβδος από την άρθρωση. δ. Τη γωνιακή επιτάχυνση που θα αποκτήσει η ράβδος μόλις κόψουμε το νήμα στο σημείο Γ. Για τη ράβδο δίνεται /12 [απ. α. 3 kg, 15 cm β. 9,25 kg γ. 17,5 Ν δ. 7,5 rad/s ] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 3
4 10. Ο ομογενής κύλινδρος του σχήματος έχει μάζα 4 kg, ακτίνα 50 cm και μπορεί να περιστρέφεται γύρω από ακλόνητο οριζόντιο άξονα που διέρχεται από το κέντρο του. Στην περιφέρεια του κυλίνδρου είναι τυλιγμένο νήμα μήκους 8 m. Τη χρονική στιγμή 0 s τραβάμε με σταθερή δύναμη 1 Ν το νήμα και αυτό ξετυλίγεται, χωρίς να ολισθαίνει στην επιφάνεια του κυλίνδρου. Μόλις το νήμα ξετυλιχτεί εντελώς, ο κύλινδρος αποκτά σταθερή γωνιακή επιβράδυνση, λόγω των δυνάμεων τριβής που δέχεται από τον άξονα περιστροφής. Αν η μεγίστη συχνότητα που απέκτησε ο κύλινδρος είναι 2/ Hz: α. Να υπολογίσετε τη σταθερή ροπή λόγω τριβών με τον άξονα. β. Να βρείτε τη χρονική στιγμή που ο κύλινδρος σταματά. γ. Να κάνετε τη γραφική παράσταση της γωνιακής ταχύτητας του κυλίνδρου σε συνάρτηση με τον χρόνο. δ. Να βρείτε το πλήθος των περιστροφών που εκτέλεσε ο κύλινδρος κατά τη διάρκεια της περιστροφής του. Για τον κύλινδρο δίνεται /2 [απ. α. 0,25 Ν m β. 16 s γ.16/ στροφές] 11. Πάνω σε οριζόντιο δάπεδο με συντελεστή τριβής 0,2 μπορεί να κυλάει τροχός, που θεωρείται ομογενής δίσκος, μάζας 2 kg και ακτίνας 0,4 m. Εφαπτομενικά στην περιφέρεια του τροχού και στο ανώτερο σημείο του ενεργεί σταθερή οριζόντια δύναμη 6 Ν. α. Να υπολογίσετε τη μεταφορική και τη γωνιακή επιτάχυνση του τροχού. β. Να βρείτε τη δύναμη τριβής που δέχεται ο τροχός από το δάπεδο και να προσδιορίσετε τη φορά της. γ. Να υπολογίσετε τη μεταφορική και τη γωνιακή επιτάχυνση του τροχού στην περίπτωση που η δύναμη έχει μέτρο 16 Ν. δ. Στην περίπτωση γ. να βρείτε τον αριθμό των περιστροφών που εκτελεί ο τροχός, ό ταν έχει μετατοπιστεί κατά 45 m. Για τον κύλινδρο δίνεται /2 [απ. 4 m/s, 10 rad/s β. 2 N γ. 10 m/s, 30 rad/s δ. 67,5/ στροφές] 12. Δύο δίσκοι ακτίνας 20 cm και 10 cm είναι ομόκεντρα κολλημένοι και μπορούν να περιστρέφονται γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο τους. Στην περιφέρεια κάθε δίσκου είναι τυλιγμένο νήμα, στο άλλο άκρο του οποίου είναι δεμένο βαρίδι μάζας 2 kg. Τη χρονική στιγμή 0 s αφήνουμε το σύστημα ελεύθερο και το ένα βαρίδι αποκτά επιτάχυνση 2 m/s με φορά προς τα κάτω. α. Να υπολογίσετε την επιτάχυνση του άλλου βαριδιού. β. Να βρείτε τις τάσεις των νημάτων στα βαρίδια. γ. Να υπολογίσετε τη ροπή αδράνειας του διπλού δίσκου ως προς τον άξονα περιστροφής του. δ. Αν το μήκος του τυλιγμένου νήματος στον μεγάλο δίσκο είναι 4 m, και μόλις ξετυλιχτεί φεύγει από τον δίσκο, ποια χρονική στιγμή η γωνιακή ταχύτητα του διπλού δίσκου θα μηδενιστεί στιγμιαία και πόσες στροφές θα έχει εκτελέσει ο δίσκος μέχρι τότε. [απ. 1 m/s β. 16 Ν, 22 N γ. 0,1kg m δ. 3,2 s, 16/ στροφές] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 4
5 13. Στη διάταξη του σχήματος ο δίσκος είναι ομογενής μάζας 2 kg και ακτίνας 20 cm. Ο δίσκος φέρει αυλάκι ακτίνας 10 cm γύρω από το οποίο είναι τυλιγμένο λεπτό αβαρές νήμα στο άλλο άκρο του οποίου είναι δεμένο σώμα Σ μάζας 1 kg. Η ομογενής ράβδος πάνω από τον δίσκο έχει μάζα 4 kg καί μπορεί να περιστρέφεται χωρίς τριβές γύρω από το ένα της άκρο, που είναι αρθρωμένο στο σημείο Α στον κατακόρυφο τοίχο. Το άλλο άκρο της ράβδου συγκρατείται ακριβώς πάνω από το κέντρο του δίσκου, έτσι ώστε, αν το αφήσουμε, εφάπτεται στον δίσκο με τη ράβδο σε οριζόντια θέση. Η επιφάνεια επαφής ράβδου και δίσκου παρουσιάζει συντελεστή τριβής 0,5, Αφήνουμε ελεύθερο το σώμα Σ να κινηθεί και μετά από 5 s αφήνουμε τη ράβδο να ακουμπήσει στον δίσκο. α. Να υπολογίσετε την επιτάχυνση του σώματος Σ, πριν ακουμπήσουμε τη ράβδο πάνω στον δίσκο. β. Να βρείτε τη μέγιστη ταχύτητα που θα αποκτήσει το σώμα Σ και την απόσταση που θα κατέβει. γ. Με ποιον ρυθμό αυξάνεται η κινητική ενέργεια του δίσκου λίγο πριν αφήσουμε τη ράβδο; δ. Πόσες συνολικά περιστροφές θα εκτελέσει ο δίσκος μέχρι τελικά να σταματήσει; (Ο άξονας περιστροφής του δίσκου είναι σταθερός και η ροπή αδράνειας του δίσκου μάζας και ακτίνας είναι ). [απ. α. 2 m/s β. 10 m/s, 25 m γ. 80 J/s δ. 250/ στροφές] 14. Ο κύλινδρος του σχήματος με μάζα 240 g βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας 45, με συντελεστή τριβής. Στην περιφέρεια του κυλίνδρου είναι τυλιγμένο λεπτό νήμα που το άλλο του άκρο είναι δεμένο σε σταθερό σημείο, έτσι ώστε το τμήμα του νήματος που δεν είναι σε επαφή με τον κύλινδρο να είναι παράλληλο στο κεκλιμένο επίπεδο. α. Να βρείτε την ελάχιστη τιμή του συντελεστή τριβής, ώστε ο κύλινδρος να ισορροπεί. β. Αν ο συντελεστής τριβής έχει τιμή ίση με το μισό της ε λάχιστης, να υπολογίσετε την επιτάχυνση με την οποία θα κατέρχεται ο κύλινδρος, γ. Να βρείτε την τάση του νήματος όσο ο κύλινδρος κατέρχεται. δ. Πόσο θα είναι το έργο της τριβής από τη στιγμή που αφέθηκε ο κύλινδρος μέχρι τη χρονική στιγμή 3 s. Για τον κύλινδρο δίνεται. [απ. α. 0,5 β. 5 2/3 γ. 0,5 2, δ. 9 J] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 5
6 15. Ομογενής και ισοπαχής ράβδος μήκους 4 m και μάζας 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου αβαρούς νήματος σταθερού μήκους, με το επάνω άκρο του συνδεδεμένο στην οροφή, όπως φαίνεται στο σχήμα, Στο σημείο Γ ισορροπεί ομογενής σφαίρα μάζας 2,5 kg και ακτίνας 0,2 m. Δίνονται ΑΚ /4 και ΑΓ 3 /4. α. Να υπολογίσετε το μέτρο της δύναμης που ασκεί το νήμα στη ράβδο. Τη χρονική στιγμή 0 s ασκείται στο κέντρο μάζας της σφαίρας με κατάλληλο τρόπο σταθερή οριζόντια δύναμη μέτρου 7 Ν, με φορά προς το άκρο Β. Η σφαίρα κυλιέται, χωρίς να ολισθαίνει. β. Να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας της σφαίρας κατά την κίνησή της. γ. Να υπολογίσετε το μέτρο της ταχύτητας του κέντρου μάζας της σφαίρας όταν φθάσει στο άκρο Β. δ. Να υπολογίσετε το μέτρο της στροφορμής της σφαίρας, όταν φθάσει στο άκρο Β. H ροπή αδράνειας της σφαίρας μάζας ως προς το κέντρο μάζας της και 10 m/s. [απ. α. 115 Ν β. 2 m/s γ. 2 m/s δ. 0,4 kg m /s] 16. Ο δίσκος (1) περιστρέφεται με γωνιακή ταχύτητα 10 rad/s και ο δίσκος (2) περιστρέφεται κατά την αντίθετη φορά με γωνιακή ταχύτητα μέτρου 20 rad/s. Ο δίσκος έχει ροπή αδράνειας ως προς τον άξονα περιστροφής του 16 kg m και ο δίσκος έχει ροπή αδράνειας 4 kg m. Κάποια στιγμή ο δίσκος (2) ακουμπά πάνω στον δίσκο (1) και δέχεται σταθερή ροπή λόγω τριβών με μέτρο 4Ν m. α. Να υπολογίσετε τη γωνιακή ταχύτητα του ενός τη στιγμή που θα μηδενιστεί η γωνιακή ταχύτητα του άλλου. β. Να βρείτε την κοινή γωνιακή ταχύτητα των δύο δίσκων και σε πόσο χρόνο οι δύο δίσκοι θα την αποκτήσουν. γ. Να κάνετε τη γραφική παράσταση σε συνάρτηση με τον χρόνο του ρυθμού απώλειας μηχανικής ενέργειας στο σύστημα των δύο δίσκων. δ. Πόση θερμότητα εκλύεται στο περιβάλλον λόγω της επαφής των δύο δίσκων; [απ. α. 5 rad/s β. 4 rad/s 24 s γ SI δ J] 17. Πάνω σε οριζόντιο δάπεδο μπορεί να κυλάει χωρίς ολίσθηση ομογενής κύλινδρος μάζας 2 kg και ακτίνας 0,3 m. Αρχικά ο κύλινδρος είναι ακίνητος και στη περιφέρειά του είναι τυλιγμένο λεπτό νήμα. Τη χρονική στιγμή 0 s ασκούμε στο ανώτερο σημείο της κυλινδρικής επιφάνειας μέσω του νήματος σταθερή οριζόντια εφαπτομενική δύναμη 10 Ν. Να υπολογίσετε: α. Την επιτάχυνση του κέντρου μάζας του κυλίνδρου, β. Το έργο της, όταν ο κύλινδρος μετατοπιστεί κατά 30 m. γ. Τη μεταφορική ταχύτητα του κυλίνδρου εκείνη τη στιγμή και τον ρυθμό μεταβολής της στροφορμής του ως προς το κέντρο μάζας του. ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 6
7 δ. Το ποσοστό της ενέργειας που έχει προσφέρει μέχρι εκείνη τη στιγμή η δύναμη και έχει μετατραπεί σε κινητική ενέργεια λόγω περιστροφής. Για τον κύλινδρο δίνεται. [απ. α. m/s β. 600 J γ. 20 m/s, 2 kg m /s δ. 33,3%] 18. Μια μικρή σφαίρα ακτίνας 2 cm και μάζας 350 g αφήνεται από ένα σημείο να κυλήσει χωρίς ολίσθηση κατά μήκος της κεκλιμένης τροχιάς του σχήματος, που σχηματίζει γωνία 60 με το οριζόντιο δάπεδο. α. Να υπολογίσετε την επιτάχυνση του κέντρου μάζας της σφαίρας όσο αυτή κινείται στο ευθύγραμμο τμήμα της τροχιάς. β. Να βρείτε το ελάχιστο αρχικό ύψος του κέντρου μάζας της μικρής σφαίρας από το οριζόντιο δάπεδο, ώστε η σφαίρα να εκτελέσει πλήρη ανακύκλωση ακτίνας 40 cm. γ. Αν η σφαίρα αφεθεί από το ελάχιστο ύψος που βρέθηκε, πόση κάθετη δύναμη επαφής θα δέχεται από την τροχιά τη στιγμή που θα βρίσκεται στο ίδιο ύψος με το κέντρο της; δ. Σε εκείνη τη θέση με ποιον ρυθμό θα μεταβάλλεται η κινητική ενέργεια της σφαίρας; Για την σφαίρα δίνεται. [απ. α. 3 m/s β. 104,6 cm γ. 8,5 Ν δ. 10,6 J/s] 19. Ο κύλινδρος του σχήματος ακτίνας και μάζας 4 kg βρίσκεται σε οριζόντιο δάπεδο με συντελεστή τριβής 0,2. Ο άξονας του κυλίνδρου συνδέεται κατάλληλα με ιδανικό ελατήριο σταθεράς 150 N/m, που είναι οριζόντιο και το άλλο του άκρο είναι ακλόνητο. Εκτρέπουμε τον κύλινδρο κατά 10 cm από τη θέση ισορροπίας του και τον αφήνουμε ελεύθερο. α. Να αποδείξετε ότι το κέντρο μάζας του κυλίνδρου θα εκτελέσει αρμονική, ταλάντωση. β. Να γράψετε την εξίσωση της απομάκρυνσης της αρμονικής ταλάντωσης που θα ε κτελέσει. γ. Πόση είναι η μέγιστη κινητική ενέργεια του κυλίνδρου; δ. Ποιο είναι το μέγιστο πλάτος των αρμονικών ταλαντώσεων που μπορεί να εκτελεί ο κύλινδρος; Για τον κύλινδρο δίνεται. [απ. β. 0,1 ημ 5 γ. 0,75 J δ. 16 cm] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 7
8 20. Οι δύο ράβδοι του σχήματος έχουν μήκος 1 m η μικρή και 2 m η μεγάλη και μάζες 2 kg και 2 αντίστοιχα. Οι δύο ράβδοι είναι κολλημένες στο ένα τους άκρο σχηματίζοντας σταθερή ορθή γωνία και η μικρή ράβδος έχει στο άλλο της άκρο κολλημένο μικρό σφαιρίδιο μάζας. Το σύστημα μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το σημείο ένωσης των δύο ράβδων και αρχικά συγκρατείται με τη μεγάλη ράβδο οριζόντια και τη μικρή, κατακόρυφη ράβδο όπως στο σχήμα. Κάποια στιγμή αφήνουμε το σύστημα ελεύθερο. Να υπολογίσετε: α. Τη ροπή αδράνειας του συστήματος ως προς τον άξονα περιστροφής. β. Τη γωνιακή επιτάχυνση του συστήματος στην αρχική του θέση. γ. Τη γωνιακή μετατόπιση Δ στη θέση όπου η γωνιακή επιτάχυνση θα μηδενιστεί. δ. Τη μέγιστη γωνιακή ταχύτητα που θα αποκτήσει. Για μια ομογενή ράβδο είναι. [απ. α. 8 kg m β. 5 rad/s γ. tan Δ 4/3 δ. 5 rad/s] 21. Η ομογενής και ισοπαχής ράβδος ΚΛ του σχήματος έχει μήκος 60 cm και μάζα 1,2 kg. Η ράβδος μπορεί να περιστρέφεται γύρω από οριζόντιο σταθερό άξονα που διέρχεται από το σημείο της Ο το οποίο απέχει απόσταση 20 cm από το άκρο της Λ. Το άκρο Κ της ράβδου ακουμπά σε λείο οριζόντιο δάπεδο μεγάλης έκτασης και η ράβδος σχηματίζει γωνία 30 με το δάπεδο. α. Να βρείτε τη δύναμη επαφής που ασκείται στη ράβδο από το δάπεδο και τη δύναμη που ασκείται στη ράβδο από τον σταθερό άξονα Ο. Από ύψος 0,15 m πάνω από το άκρο Λ αφήνουμε να πέσει ένα μικρό σφαιρίδιο μάζας 600 g, το οποίο συγκρούεται πλαστικά με τη ράβδο στο άκρο της Λ. β. Να υπολογίσετε την ταχύτητα που θα αποκτήσει το άκρο Κ της ράβδου μετά την κρούση. γ. Να βρείτε τη μηχανική ενέργεια που χάθηκε κατά την κρούση. δ. Σε πόσο χρόνο μετά την κρούση το άκρο Κ θα ακουμπήσει ξανά στο οριζόντιο δάπεδο; Για μια ομογενή ράβδο είναι [απ. α. 3 N, 9 N β. 1 m/s γ. 0,675 J δ. s] 22. Μια ομογενής ράβδος ΟΑ μήκους l 0,45 m και μάζας 2 kg μπορεί να περιστρέφεται γύρω από οριζόντιο σταθερό άξονα κάθετο στη ράβδο, που διέρχεται από το ένα της άκρο Ο. Η ράβδος αρχικά ισορροπεί σε κατακόρυφη θέση, όπως στο σχήμα. Μια σφαίρα ίδιας μάζας με τη ράβδο κινούμενη με οριζόντια ταχύτητα 3 m/s σφηνώνεται στο κατώτερο άκρο Α της ράβδου. Το επίπεδο που ορίζει η ταχύτητα της σφαίρας και η ράβδος είναι κάθετο στον άξονα περιστροφής. α. Να βρείτε τη γωνία που θα σχηματίσει η ράβδος με την κατακόρυφη τη στιγμή που θα μηδενιστεί η γωνιακή της ταχύτητα. β. Να υπολογίσετε τη μηχανική ενέργεια που χάθηκε κατά την ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 8
9 κρούση, γ. Να βρείτε την ταχύτητα της σφαίρας, ώστε η ράβδος να εκτελέσει πλήρη ανακύκλωση. δ. Αν η σφαίρα συγκρουστεί με την ελάχιστη ταχύτητα για ανακύκλωση, να υπολογίσετε τον ρυθμό μεταβολής της κινητικής ενέργειας του συστήματος τη στιγμή που η ράβδος διέρχεται από την οριζόντια θέση. Για μια ομογενή ράβδο είναι [απ. α. 60 β. 2,25 J γ. 6 m/s δ. 67,5 2 J/s] 23. Ο κύλινδρος του σχήματος έχει μάζα 6 kg και ακτίνα 20 cm. Στην περιφέρεια του είναι τυλιγμένο λεπτό νήμα που το άκρο του Α αρχίζουμε να τραβάμε με σταθερή οριζόντια επιτάχυνση, έτσι ώστε σε 2 s το άκρο Α να μετατοπιστεί κατά 8 m. α. Να θεωρήσετε ότι το δάπεδο είναι ιδανικά λείο. α1. Να υπολογίσετε την επιτάχυνση του κέντρου μάζας του κυλίνδρου και τη δύναμη που ασκούμε στο νήμα α2. Πόση ενέργεια (εκφρασμένη σε κλάσμα) που προσφέραμε στον κύλινδρο έγινε κινητική ενέργεια λόγω στροφικής κίνησης; α3. Όταν ο κύλινδρος έχει μετατοπιστεί κατά 2 m, πόσο έχει αυξηθεί η απόσταση του χεριού μας από τον κύλινδρο; β. Να θεωρήσετε ότι το δάπεδο έχει τριβές, ώστε ο κύλινδρος να κυλά χωρίς ολίσθηση, β1. Να υπολογίσετε τη δύναμη που ασκούμε στο νήμα β2. Να βρείτε τον ρυθμό αύξησης της στροφορμής του κυλίνδρου ως προς το κέντρο μάζας του, β3. Να βρείτε τον ρυθμό αύξησης της κινητικής ενέργειας λόγω στροφικής κίνησης τη χρονική στιγμή που ο κύλινδρος έχει μετατοπιστεί κατά 9 m. Για τον κύλινδρο [απ. α1. m/s, 8 N α2. 2/3 α3. 4 m β1. 9 Ν β2. 1,2 kg m /s β3. 36 J/s] 24. Ο κυλινδρικός τροχός του σχήματος έχει α κτίνα 30 cm και διαθέτει μια κεντρική εγκοπή ακτίνας 20 cm γύρω από την οποία είναι τυλιγμένο νήμα που το τραβάμε, ασκώντας έτσι στον τροχό μια σταθερή δύναμη παράλληλη στο κεκλιμένο επίπεδο, γωνίας 30. Ο τροχός συγκρατείται ακίνητος, όταν η δύναμη έχει μέτρο 6 Ν. Ο συντελεστής τριβής μεταξύ τροχού και ε πιπέδου είναι 3/2. α. Αν ασκήσουμε τη χρονική στιγμή 0 s στον τροχό δύναμη 15 Ν, να υπολογίσετε την επιτάχυνση με την οποία θα ανέρχεται αυτός στο κεκλιμένο επίπεδο κυλώντας χωρίς ολίσθηση. β. Να βρείτε το έργο της δύναμης μέχρι τη χρονική στιγμή 0,6 s. γ. Να βρείτε τον ρυθμό μεταβολής της κινητικής ενέργειας του τροχού τη στιγμή. δ. Να υπολογίσετε τη μέγιστη τιμή της δύναμης, ώστε ο τροχός να ανέρχεται κυλώντας και μη ολισθαίνοντας. ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 9
10 Για τον κύλινδρο. [απ. α. 5 m/s β. 22,5 J γ. 45 J/s δ. 105 N] 25. Η ομογενής ράβδος ΚΛ του οχήματος έχει μάζα 3 kg και μήκος 4 m. Στο άκρο Λ της ράβδου έχει προσαρμοστεί μικρό ροδάκι αμελητέας μάζας και έτσι το άκρο Λ μπορεί να κινείται χωρίς τριβές κατά μήκος μιας λείας σταθερής και οριζόντιας μεταλλικής τροχιάς (ε). Το άλλο άκρο Κ της ράβδου σύρεται στο οριζόντιο έδαφος με το οποίο παρουσιάζει συντελεστή τριβής 0,5. Όταν το άκρο Κ α κουμπά στο έδαφος, η ράβδος σχηματίζει γωνία 45 με αυτό. Ασκούμε στο άκρο Λ μια σταθερή οριζόντια δύναμη και η ράβδος αρχίζει να κινείται με σταθερή ταχύτητα. α. Να υπολογίσετε το μέτρο της δύναμης. β. Αν αυξήσουμε το μέτρο της δύναμης στην τιμή 15 Ν να υπολογίσετε την επιτάχυνση που θα αποκτήσει η ράβδος. γ. Για ποια τιμή της δύναμης το άκρο Κ θα χάσει την επαφή του με το έδαφος; δ. Για ποια τιμή της δύναμης το άκρο Κ θα βρίσκεται σε ύψος 0,8 m από το έδαφος, καθώς η ράβδος κινείται; Δίνονται 10 m/s 2 1,4, 3 1,7. [απ. α. 5 N β. 4 m/s γ. 30 Ν δ. 51 Ν] 26. Η ομογενής και συμπαγής σφαίρα του σχήματος έχει μάζα 2 kg και ακτίνα 20 cm. Η σφαίρα είναι ακίνητη στην άκρη μιας οριζόντιας σανίδας μήκους 6 m και ίδιας μάζας με τη σφαίρα. Η σανίδα είναι ακίνητη σε λεία οριζόντια επιφάνεια. Τη χρονική στιγμή 0 s χτυπάμε τη σφαίρα ασκώντας της μια στιγμιαία οριζόντια δύναμη, που ο φορέας της διέρχεται από το κέντρο μάζας της σφαίρας. Αμέσως η σφαίρα αποκτά ταχύτητα 9 m/s. Μεταξύ της σφαίρας και της σανίδας υπάρχει συντελεστής τριβής ολίσθησης 0,4. α. Να βρείτε ποια χρονική στιγμή η σφαίρα θα αρχίσει να κυλάει χωρίς ολίσθηση πάνω στη σανίδα. β. Να υπολογίσετε τις ταχύτητες που θα έχουν η σφαίρα και η σανίδα τότε. γ. Ποια χρονική στιγμή η σφαίρα θα φθάσει στην άλλη άκρη της σανίδας; δ. Πόση θερμότητα εκλύεται λόγω της τριβής μεταξύ της σφαίρας και της σανίδας; Ροπή αδράνειας της σφαίρας. [απ. α. 0,5 s β. 7 m/s, 2 m/s γ. 1 s δ. 18 J] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 10
11 27. Η ομογενής ράβδος ΑΒ του σχήματος έχει μάζα 2 kg και μήκος 2 m και είναι αρθρωμένη στο σημείο Α. Στο σημείο Γ που απέχει από το άκρο Α απόσταση 0,5 m είναι δεμένο ένα ελατήριο σταθερός 200 N/m, στο άλλο του άκρο του οποίου έχει δεμένο σώμα ίδιας μάζας με τη ράβδο, Η ράβδος συγκρατείται οριζόντια με τη βοήθεια νήματος που είναι δεμένο στο άκρο της Β και σχηματίζει με τη ράβδο γωνία 30. Το ελατήριο συγκρατείται συμπιεσμένο με τη βοήθεια ενός άλλου νήματος που είναι δεμένο στη ράβδο και στο σώμα. α. Να βρείτε την τάση του νήματος στο σημείο Β. Κάποια χρονική στιγμή 0 s κόβουμε το νήμα που συγκροτεί συμπιεσμένο το ελατήριο. Αν είναι γνωστό ότι η τάση του νήματος στο σημείο Β αμέσως μετά το κόψιμο του νήματος μηδενίζεται στιγμιαία, χωρίς να μετακινηθεί η ράβδος; β. Να υπολογίσετε την αρχική παραμόρφωση του ελατηρίου, γ. Να γράψετε την εξίσωση της αρμονικής ταλάντωσης που θα εκτελέσει το σώμα. δ. Αν είναι γνωστό ότι το όριο θραύσης του νήματος στο σημείο Β είναι 45 Ν, ποια χρονική στιγμή θα σπάσει αυτό το νήμα; ε. Πόση γωνιακή επιτάχυνση θα αποκτήσει η ράβδος αμέσως μετά το σπάσιμο του νήματος στο σημείο Β; Για μια ομογενή ράβδο είναι. [απ. α. 30 Ν β. 20 cm γ. 0,3 ημ 10 δ. s ε. 16,875 rad/s ] 28. Μια σανίδα μήκους 4 m και μάζας 2 kg ακουμπά πάνω σε δύο ί διους κυλίνδρους μάζας 2 kg ο καθένας, οι οποίοι είναι ακίνητοι πάνω σε οριζόντια επιφάνεια, όπως στο σχήμα. Τα σημεία επαφής των κυλίνδρων με τη σανίδα απέχουν από το κέντρο της 1 m. Ασκούμε στο κέντρο του ενός κυλίνδρου σταθερή οριζόντια δύναμη 28 Ν και τσ σύστημα αρχίζει να κινείται, χωρίς να υπάρχει ολίσθηση σε καμία επαφή. α. Να υπολογίσετε την επιτάχυνση κάθε κυλίνδρου και της σανίδας. β. Πόση ταχύτητα θα έχει η σανίδα, όταν το άκρο της φτάσει στο ανώτερο σημείο του πίσω κυλίνδρου; γ. Αν η επαφή των κυλίνδρων με τη σανίδα παρουσίαζε συντελεστή τριβής ολίσθησης 0,5, πόση ταχύτητα θα είχε η σανίδα τη στιγμή που θα άρχιζε να ολισθαίνει πάνω σε έναν κύλινδρο; Δίνεται για τον κύλινδρο. [απ. α. 2 m/s και 4 m/s β. 4 m/s γ. 2,53 m/s] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 11
12 29. Στη διάταξη του σχήματος τα σώματα Σ1 και Σ2 και η τροχαλία έχουν ίδια μάζα 5 kg. Η τροχαλία έχει α κτίνα 20 cm και το ελατήριο έχει σταθερά 200 N/m. Αρχικά το σύστημα ισορροπεί και το οριζόντιο δάπεδο είναι λείο. α. Πόση είναι η αρχική παραμόρφωση του ελατηρίου; Κατεβάζουμε το σώμα Σ2 κατά 20 cm και τη χρονική στιγμή 0 s το αφήνουμε ελεύθερο. β. Να αποδείξετε ότι, όταν αφήσουμε ελεύθερο το θα εκτελέσει αρμονική ταλάντωση και να βρείτε την περίοδό της. γ. Να γράψετε την εξίσωση της γωνιακής ταχύτητας της τροχαλίας σε συνάρτηση με τον χρόνο, θεωρώντας θετική φορά τη φορά των δεικτών του ρολογιού. δ. Πόση είναι η μέγιστη ενέργεια της ταλάντωσης του Σ2 και πόση, επίσης, είναι η ε νέργεια που ξοδέψαμε, για να κατεβάσουμε το Σ2; ε. Ποιο είναι το μέγιστο πλάτος της ταλάντωσης που μπορεί να εκτελεί το Σ2; Να θεωρήσετε την τροχαλία ως ομογενή δίσκο με και άτι το νήμα δεν ολισθαίνει στην περιφέρεια της τροχαλίας [απ. α. 25 cm β. 0,5 s γ. 4συν 4 δ. 1,6 J και 4 J ε. m] 30. Ομογενής κύλινδρος μάζας 2 kg και ακτίνας 0,1 m ισορροπεί σε οριζόντιο δάπεδο με τον άξονα παράλληλο στο δάπεδο. Τη στιγμή 0 ασκούμε στον κύλινδρο ζεύγος δυνάμεων, μέτρου 4 N η κάθε μια των οποίων οι φορείς βρίσκονται στο ίδιο κατακόρυφο επίπεδο που διέρχεται από το κέντρο μάζας του κυλίνδρου και είναι κάθετο στον άξονα. Οι φορείς των δύο δυνάμεων του ζεύγους απέχουν /2. Α. Αν το οριζόντιο δάπεδο είναι λείο: α. Τι είδους κίνηση θα κάνει ο κύλινδρος και γιατί; β. Να βρείτε το μέτρο της ταχύτητας των ανωτέρων σημείων του κυλίνδρου τη στιγμή t=3 s. γ. Να βρείτε το ρυθμό με τον οποίο το ζεύγος των δυνάμεων προσφέρει ενέργεια στον κύλινδρο τη στιγμή 3 s. Β. Αν το δάπεδο δεν είναι λείο και ο συντελεστής μέγιστης στατικής τριβής μεταξύ δαπέδου και κυλίνδρου είναι 0,5 να βρείτε: δ. Για ποιες τιμές του μέτρου της κάθε δύναμης του ζεύγους, ο κύλινδρος κυλίεται χωρίς να ολισθαίνει. ε. Να βρείτε το μέτρο της ταχύτητας των ανώτερων σημείων του κυλίνδρου τη χρονική στιγμή 3 s, αν η 4 Ν. Δίνονται και 10 m/s [απ. β. 6 m/s γ. 12 W δ. 30 Ν ε. 4 m/s] 31. Ομογενής ράβδος ΑΒ μήκους 3 m μάζας 12 kg μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που περνάει από το σημείο Ο και είναι κάθετος σε αυτήν. Η απόσταση ΑΟ είναι ΑΟ 1 m. Στο άκρο Β υπάρχει σταθερά στερεωμένη σημειακή μάζα 2 kg. Στο άκρο Α η ράβδος συνδέεται με τεντωμένο ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 12
13 νήμα ΑΔ με σώμα μάζας 1 kg που είναι στερεωμένο και δεμένο στο άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς 400 Ν/m, όπως φαίνεται στο σχήμα. Όλο το σύστημα αρχικά ισορροπεί. Α. Να υπολογιστούν: α. Η ροπή αδράνειας του συστήματος ράβδου σώματος ως προς τον άξονα περιστροφής, Ο. β. Το μέτρο της τάσης του νήματος και το μέτρο της δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής, όταν ισορροπεί. Β. Τη χρονική στιγμή 0 κόβουμε το νήμα και το σώμα αρχίζει να ταλαντώνεται αρμονικά, ενώ η ράβδος με το να περιστρέφεται χωρίς τριβές. Να υπολογιστούν: γ. Το μέτρο του ρυθμού μεταβολής της στροφορμής του συστήματος ράβδου τη στιγμή που κόβεται το νήμα. δ. Τη γωνιακή ταχύτητα του συστήματος τη στιγμή που περνάει από την κατακόρυφη θέση. ε. Το πλάτος και την περίοδο της ταλάντωσης του σώματος. στ. Το ρυθμό μεταβολής της κινητικής ενέργειας του σώματος τη χρονική στιγμή s. Δίνονται, η ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το κέντρο της και είναι κάθετος σ αυτήν, και το 10 m/s. [απ. α. 20 kg m, β. 100 Ν, 240 N, γ. 100 kg m /s, δ. 10 rad/s, ε. 0,25 m, 0,1 s, στ J/s.] 32. Στο σχήμα δίνονται 4 kg, 0,5 m, 0,1 m, 0,5kg m, 30 και 10 m/s. α. Πόσο πρέπει να είναι η δύναμη και η δύναμη της στατικής τριβής ώστε ο κύλινδρος να ισορροπεί; β. Πόση πρέπει να είναι η δύναμη ώστε η στατική τριβή να είναι μηδέν και το στερεό να κυλίεται προς τα κάτω χωρίς να ολισθαίνει; Πόση θα είναι τότε η επιτάχυνση του κέντρου μάζας; γ. Αν ο συντελεστής μέγιστης στατική τριβής είναι, για ποιες τιμές της είναι δυνατή η κύλιση χωρίς ολίσθηση; [απ. α. 25 N. 5 Ν β. Ν, m/s, Ν Ν] 33. Δύο κυλινδρικοί δίσκοι έχουν ίδια μάζα 2 kg και ίδια ακτίνα 0,2 m και ροπή αδράνεια ως προς τον άξονα συμμετρίας τους και περιστροφής τους. O ένας δίσκος μπορεί να στρέφεται χωρίς τριβές γύρω από σταθερό άξονα, όπως φαίνεται στο σχήμα, ενώ αβαρές λεπτό νήμα είναι τυλιγμένο γύρω και από τους δύο δίσκους. Αν αφήσουμε τη χρονική στιγμή 0 το δεύτερο δίσκο ελεύθερο αυτός πέφτει ενώ ταυτόχρονα περιστρέφεται. Να υπολογιστούν: α. Η επιτάχυνση του κέντρου μάζας του κάτω δίσκου. β. Η τάση του νήματος. γ. Η γωνιακή επιτάχυνση του κάθε δίσκου. δ. Το μήκος του νήματος που ξετυλίχτηκε μέχρι τη χρονική στιγμή 2 s. ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 13
14 ε. Το ρυθμό μεταβολής της κινητικής ενέργειας του κάθε δίσκου αλλά και του συστήματος τη χρονική στιγμή 2 s. στ. Τη μεταβολή της κινητικής ενέργειας του συστήματος των δύο δίσκων τη χρονική στιγμή. Δίνεται 10 m/s. [α. 8 m/s, β. 4 Ν, γ. 20 rad/s, δ. 16 m, ε. 32 J/s, 288 J/s, 320 J/s, στ. 320 J] 34. Στο λούκι δίσκου μάζας 0,4 kg, ακτίνας 0,4 m είναι τυλιγμένο αβαρές νήμα. Τη στιγμή 0 αφήνουμε το δίσκο ελεύθερο ενώ α σκούμε στο ελεύθερο άκρο Α του νήματος κατακόρυφη δύναμη 2,4 N με φορά προς τα πάνω. Το νήμα ξετυλίγεται και ο δίσκος περιστρέφεται γύρω από οριζόντιο άξονα. Να βρείτε: α. Τις επιταχύνσεις του σημείου Α και του κέντρου μάζας του δίσκου. β. Το μέτρο του ρυθμού μεταβολής της στροφορμής του δίσκου. γ. Το μήκος του νήματος που ξετυλίχτηκε μέχρι τη στιγμή 4 s. δ. Το έργο της στο χρονικό διάστημα 0 έως 4 s και την κινητική ενέργεια του δίσκου τη χρονική στιγμή 4 s. ε. Το ρυθμό με τον οποίο παρέχει ενέργεια η δύναμη και το ρυθμό μεταβολής κινητικής ενέργειας του δίσκου τη στιγμή 4 s. στ. Τη χρονική στιγμή το νήμα κόβεται. Πόση θα είναι η ταχύτητα του κέντρου μάζας τη χρονική στιγμή 10 s; Δίνονται και 10 m/s. [απ. α. 8 m/s, 4 m/s, β. 0,96 kg m /s, γ. 96 m, δ. 153,6 J, 281,6 J, ε. 76,8 J/s, 140,8 J/s, στ.76 m/s] 35. Στο σύστημα που φαίνεται στο σχήμα η μικρή τροχαλία είναι αμελητέας μάζας, και το αβαρές σχοινί συνδέει το σώμα Σ μάζας 1 kg με τον τροχό μάζας 4 kg και ακτίνας 0,1 m, ενώ το οριζόντιο επίπεδο πάνω στο οποίο κινείται το σώμα είναι τελείως λείο. Αν αφήσουμε το σύστημα ε λεύθερο τη χρονική στιγμή 0, να υπολογιστούν: α. Η επιτάχυνση του κέντρου, Κ του τροχού. β. Η επιτάχυνση του σώματος Σ. γ. Η πτώση του κέντρου μάζας, Κ και η μετατόπιση του σώματος Σ, τη χρονική στιγμή 2 s. δ. Η γωνία στροφής ενός σημείου του τροχού τη χρονική στιγμή, 2 s. ε. Το ποσοστό της δυναμικής ενέργειας του τροχού που μετατράπηκε σε κινητική ε νέργεια περιστροφής του μέχρι τη χρονική στιγμή 2 s. στ. Ο ρυθμός μεταβολής κινητικής ενέργειας του τροχού τη χρονική στιγμή 2 s. Δίνονται και 10 m/s. [απ. α. 4 m/s, β. 8 m/s, γ. 8 m, 16 m, δ. 80 rad, ε. 20%, στ. 192 J/s] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 14
15 36. Ομογενής ράβδος μάζας 3 kg και μήκους l 1,6 m συγκρατείται ακίνητη σε οριζόντια θέση. Η ράβδος μπορεί να στρέφεται γύρω από την άρθρωση Ο χωρίς τριβές. Η ράβδος αφήνεται ελεύθερη και όταν φτάνει στην κατακόρυφη θέση, το κατώτερο άκρο της Α συγκρούεται ελαστικά με το σώμα (Σ1) μάζας 1 kg,το οποίο είναι ακίνητο σε λείο οριζόντιο επίπεδο. Κατά μήκος του λείου οριζοντίου επιπέδου υπάρχει δεύτερο σώμα (Σ2) μάζας 1kg το οποίο εκτελεί απλή αρμονική ταλάντωση (Α.Α.Τ.), δεμένο στο ένα άκρο ιδανικού ελατηρίου σταθεράς 400 N/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο, όπως στο σχήμα. Ο άξονας του ελατηρίου είναι στη διεύθυνση κίνησης του σώματος (Σ1). Τα δύο σώματα (Σ1) και (Σ2) συγκρούονται μετωπικά και ελαστικά. Η ολική ενέργεια ταλάντωσης του σώματος (Σ2) πριν την κρούση είναι, 8 J. Την στιγμή της κρούσης για την απομάκρυνση του σώματος (Σ2) ισχύει 0. Δίνεται ότι στη θέση η ολική ενέργεια της Α.Α.Τ. που εκτελεί το σώμα (Σ2), μετά την κρούση με το σώμα (Σ1), έχει τη μέγιστη δυνατή τιμή. Να υπολογίσετε: α. Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση, ακριβώς πριν την κρούση με το σώμα (Σ1). β. Τη θέση που έγινε η ελαστική κρούση μεταξύ των σωμάτων (Σ1) και (Σ2). γ. Τα δύο σώματα (Σ1) και (Σ2) συγκρούονται ξανά; Αν ναι να προσδιορίσετε το ελάχιστο χρονικό διάστημα που μεσολάβησε από την πρώτη μέχρι την δεύτερη ελαστική μετωπική κρούση των σωμάτων (Σ1) και (Σ2). δ. Ποια είναι η μέγιστη δυναμική ενέργεια που θα αποκτήσει η ράβδος, μετά τη δωδέκατη κρούση των σωμάτων (Σ1), (Σ2) και ράβδου. Θεωρήστε επίπεδο αναφοράς (Σ1), (Σ2) και ράβδου το οριζόντιο επίπεδο της ταλάντωσης. Δίνονται: η ροπή αδράνειας της ράβδου ως προς το κέντρο μάζας l, η επιτάχυνση της βαρύτητας 10 m/s. Οι διαστάσεις των σωμάτων (Σ1) και (Σ2) θεωρούνται αμελητέες. [απ. α. 75 N, β. 0,2 m, γ. Δ /15 s δ. 48 J] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 15
16 37. Το μικρό σώμα μάζας 5 kg του διπλανού σχήματος είναι δεμένο στο ένα άκρο αβαρούς και μη εκτατού νήματος και περιστρέφεται χωρίς τριβές με γωνιακή ταχύτητα, διαγράφοντας οριζόντια, κυκλική τροχιά ακτίνας 0,4 m. Το νήμα διέρχεται μέσα από έναν κατακόρυφο σωλήνα και στο ελεύθερο άκρο του Ζ ασκούμε κατακόρυφη δύναμη μέτρου 50 Ν. ώστε να παραμένει συνεχώς α κίνητο. Κάποια στιγμή, μεγαλώνοντας το μέτρο της κατακόρυφης δύναμης που ασκούμε στο άκρο Ζ του νήματος, μετακινούμε προς τα κάτω κατά το άκρο Ζ, μειώνοντας την ακτίνα της κυκλικής τροχιάς του μικρού σώματος. Η ενέργεια που ξοδέψαμε για τη μετακίνηση αυτή ισούται με 150 J. Να υπολογίσετε: α. το μέτρο της γωνιακής ταχύτητας. β. το μέτρο της νέας στροφορμής του μικρού σώματος μετά την κατακόρυφη μετακίνηση του άκρου Ζ. γ. την απόσταση. δ. τη μάζα ενός σώματος που πρέπει να κρεμάσουμε στο άκρο Ζ, μετά τη μετακίνηση κατά, ώστε το σώμα αυτό να παραμένει ακίνητο στη θέση του χωρίς να του α σκούμε κάποια κατακόρυφη δύναμη. Η επιτάχυνση της βαρύτητας ισούται με 10 m/s. [απ. α. 5 rad/s, β. 4 kg m /s, γ. 0,3 m δ. 320 kg] ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 6 16
% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου
![% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου % ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου](/thumbs/53/30956495.jpg) 1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 1
 1. Ένα βλήμα μάζας 0,1 kg που κινείται οριζόντια με ταχύτητα 100 m/s σφηνώνεται σε ακίνητο ξύλο μάζας 1,9 kg. Να βρεθεί η απώλεια ενέργειας που οφείλεται στην κρούση, όταν το ξύλο είναι: α. πακτωμένο στο
1. Ένα βλήμα μάζας 0,1 kg που κινείται οριζόντια με ταχύτητα 100 m/s σφηνώνεται σε ακίνητο ξύλο μάζας 1,9 kg. Να βρεθεί η απώλεια ενέργειας που οφείλεται στην κρούση, όταν το ξύλο είναι: α. πακτωμένο στο
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
ΤΕΣΤ 16. Να επιλέξετε τη σωστή απάντηση. Να δικαιολογήσετε την επιλογή σας. Να επιλέξετε τη σωστή απάντηση. Να δικαιολογήσετε την επιλογή σας.
 Επαναληπτικό 4 ΘΕΜ aa ΤΕΣΤ 16 1. Στη διάταξη του σχήματος, ασκούμε κατακόρυφη δύναμη σταθερού μέτρου F στο άκρο του νήματος, ώστε ο τροχός () να ανέρχεται κυλιόμενος χωρίς ολίσθηση στο κεκλιμένο επίπεδο.
Επαναληπτικό 4 ΘΕΜ aa ΤΕΣΤ 16 1. Στη διάταξη του σχήματος, ασκούμε κατακόρυφη δύναμη σταθερού μέτρου F στο άκρο του νήματος, ώστε ο τροχός () να ανέρχεται κυλιόμενος χωρίς ολίσθηση στο κεκλιμένο επίπεδο.
Προτεινόμενα ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ
 ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος. και Α 2
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ. Δίνεται ότι η ροπή αδράνειας του δίσκου ως προς τον άξονα Κ είναι Ι= M R
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ταχύτητα μέτρου. Με την άσκηση κατάλληλης σταθερής ροπής, επιτυγχάνεται
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ 26. Δύο σημειακές σφαίρες που η καθεμιά έχει μάζα συνδέονται μεταξύ τους με οριζόντια αβαρή ράβδο. Το σύστημα περιστρέφεται γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ 26. Δύο σημειακές σφαίρες που η καθεμιά έχει μάζα συνδέονται μεταξύ τους με οριζόντια αβαρή ράβδο. Το σύστημα περιστρέφεται γύρω από κατακόρυφο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε.
 ΚΕΦΑΛΑΙΟ 4 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -OΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ ΘΕΜΑ 3 o 00 Ομογενής και ισοπαχής ράβδος ΑΓ, μήκους L=1 m και μάζας m=10 kg, μπορεί να στρέφεται γύρω από ακλόνητο οριζόντιο
ΚΕΦΑΛΑΙΟ 4 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -OΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ ΘΕΜΑ 3 o 00 Ομογενής και ισοπαχής ράβδος ΑΓ, μήκους L=1 m και μάζας m=10 kg, μπορεί να στρέφεται γύρω από ακλόνητο οριζόντιο
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
το άκρο Β έχει γραμμική ταχύτητα μέτρου.
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ 1. Μια ράβδος ΑΒ περιστρέφεται με σταθερή γωνιακή ταχύτητα γύρω από έναν σταθερό οριζόντιο άξονα που περνάει από ένα σημείο πάνω
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ 1. Μια ράβδος ΑΒ περιστρέφεται με σταθερή γωνιακή ταχύτητα γύρω από έναν σταθερό οριζόντιο άξονα που περνάει από ένα σημείο πάνω
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
Τίτλος Κεφαλαίου: Στερεό σώµα. Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως. Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1
 Τίτλος Κεφαλαίου: Στερεό σώµα ιδακτική Ενότητα: Κινηµατική του Στερεού Σώµατος Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως Θέµα 3ο: Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1 ιδακτική Ενότητα: Ροπή
Τίτλος Κεφαλαίου: Στερεό σώµα ιδακτική Ενότητα: Κινηµατική του Στερεού Σώµατος Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως Θέµα 3ο: Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1 ιδακτική Ενότητα: Ροπή
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΘΕΜΑΤΑ ΑΠΟ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 4 ΘΕΜΑΤΑ ΑΠΟ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -O.Ε.Φ.Ε 196 ΘΕΜΑ 4 ο 00 Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΒ, που έχουν μάζα Μ = 4 Κg και μήκος L =
ΚΕΦΑΛΑΙΟ 4 ΘΕΜΑΤΑ ΑΠΟ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -O.Ε.Φ.Ε 196 ΘΕΜΑ 4 ο 00 Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΒ, που έχουν μάζα Μ = 4 Κg και μήκος L =
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
Ασκήσεις. Φυσική Γ Λυκείου - Μηχανική στερεού σώματος
 - Μηχανική στερεού σώματος Ασκήσεις 1. Στερεό στρέφεται γύρω Ένας δίσκος μπορεί να περιστρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο και είναι κάθετος στο επίπεδο του. Ο δίσκος είναι
- Μηχανική στερεού σώματος Ασκήσεις 1. Στερεό στρέφεται γύρω Ένας δίσκος μπορεί να περιστρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο και είναι κάθετος στο επίπεδο του. Ο δίσκος είναι
ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]
![ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%] ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]](/thumbs/65/53613594.jpg) 1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
3.6. Σύνθετα θέματα στερεού. Ομάδα Δ.
 3.5.61. Μια κινούμενη τροχαλία. 3.6. Σύνθετα θέματα στερεού. Ομάδα Δ. Γύρω από μια τροχαλία μάζας Μ=0,8kg έχουμε τυλίξει ένα αβαρές νήμα, στο άκρο του οποίου έχουμε δέσει ένα σώμα Σ μάζας m=0,1kg. Συγκρατούμε
3.5.61. Μια κινούμενη τροχαλία. 3.6. Σύνθετα θέματα στερεού. Ομάδα Δ. Γύρω από μια τροχαλία μάζας Μ=0,8kg έχουμε τυλίξει ένα αβαρές νήμα, στο άκρο του οποίου έχουμε δέσει ένα σώμα Σ μάζας m=0,1kg. Συγκρατούμε
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]
![ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου] ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]](/thumbs/52/29790189.jpg) ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΘΕΜΑ Α Α. Στις ερωτήσεις 1-5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α. Στις ερωτήσεις 1-5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση 1.
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α. Στις ερωτήσεις 1-5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση 1.
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. = 2r, τότε:
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Διατήρηση της στροφορμής) Η Γη στρέφεται σε ελλειπτική τροχιά γύρω από τον Ήλιο. Το κοντινότερο σημείο στον Ήλιο ονομάζεται Περιήλιο (π) και το πιο απομακρυσμένο Αφήλιο (α).
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Διατήρηση της στροφορμής) Η Γη στρέφεται σε ελλειπτική τροχιά γύρω από τον Ήλιο. Το κοντινότερο σημείο στον Ήλιο ονομάζεται Περιήλιο (π) και το πιο απομακρυσμένο Αφήλιο (α).
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
 ΘΕΜΑ Α 018 Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση. A1. Δύο μικρά σώματα με
ΘΕΜΑ Α 018 Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση. A1. Δύο μικρά σώματα με
ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΦΥΣΙΚΗ Ο.Π Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
Για τις παραπάνω ροπές αδράνειας ισχύει: α. β. γ. δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 3 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 3 να γράψετε στο τετράδιό
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΟΡΟΣΗΜΟ. Ισχύει: α. L 1. και Κ 1 β. 2L 1 =2L 2 =L 2. και 2Κ 1 γ. L 1
 61 Η κινητική ενέργεια ενός δίσκου μάζας m και ακτίνας R που εκτελεί στροφική κίνηση, εξαρτάται: α Μόνο από την γωνιακή του ταχύτητα β Μόνο από την μάζα και την ακτίνα του γ Μόνο από την γωνιακή του ταχύτητα,
61 Η κινητική ενέργεια ενός δίσκου μάζας m και ακτίνας R που εκτελεί στροφική κίνηση, εξαρτάται: α Μόνο από την γωνιακή του ταχύτητα β Μόνο από την μάζα και την ακτίνα του γ Μόνο από την γωνιακή του ταχύτητα,
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2016-2017 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2016-2017 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 4. α. β. ii. iii. 6. α.
 Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2019 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 019 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 019 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ. =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1. =8m /s συγκρούεται κεντρικά
 ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Τετάρτη 12 Απριλίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΡΙΤΗ 18 ΑΠΡΙΛΙΟΥ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΡΙΤΗ 8 ΑΠΡΙΛΙΟΥ 07 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ A Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό κάθε
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΡΙΤΗ 8 ΑΠΡΙΛΙΟΥ 07 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ A Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό κάθε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
4. Σώμα Σ 1 μάζας m 1 =1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ=30 ο. Το σώμα Σ 1 είναι δεμένο στην άκρη
 1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β.
 ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1.
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1.
ΜΟΝΑΔΕΣ 5. A4. Σώμα περιστρέφεται γύρω από σταθερό άξονα έχοντας στροφορμή μέτρου L. Τη χρονική στιγμή t=0 ασκούμε στο σώμα ροπή δύναμης μέτρου τ
 ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΑΒΒΑΤΟ 31 ΜΑΡΤΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΑΒΒΑΤΟ 31 ΜΑΡΤΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΕΝΩΣΗ ΦΥΣΙΚΩΝ ΚΥΠΡΟΥ
 33 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α Φάση) Κυριακή, 16 Δεκεμβρίου 2018 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) σελίδες και πέντε (5) θέματα. 2) Να απαντήσετε σε όλα τα
33 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α Φάση) Κυριακή, 16 Δεκεμβρίου 2018 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) σελίδες και πέντε (5) θέματα. 2) Να απαντήσετε σε όλα τα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα
 Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 3 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 01: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το
3 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 01: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤ. & ΤΕΧΝ. ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
Για τις παραπάνω ροπές αδράνειας ισχύει: α. β. γ. δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ-A ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ-A ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή Αδράνειας) Γ ΛΥΚΕΙΟΥ. Α)Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση.
 ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή δράνειας) Γ ΛΥΚΕΙΟΥ ΘΕΜ 1 Ο : )Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση. 1. Για ένα ζεύγος δυνάμεων Η ροπή του, εξαρτάται
ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή δράνειας) Γ ΛΥΚΕΙΟΥ ΘΕΜ 1 Ο : )Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση. 1. Για ένα ζεύγος δυνάμεων Η ροπή του, εξαρτάται
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 Β ΦΑΣΗ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 08 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Απριλίου 08 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 08 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Απριλίου 08 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 17/4/2016 ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 7/4/06 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη σωστή απάντηση:
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 7/4/06 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη σωστή απάντηση:
Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~
 Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~ Θέμα Α 1. Σε χορδή έχει δημιουργηθεί στάσιμο κύμα. Δύο σημεία Α και Β που δεν είναι δεσμοί απέχουν μεταξύ τους απόσταση
Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~ Θέμα Α 1. Σε χορδή έχει δημιουργηθεί στάσιμο κύμα. Δύο σημεία Α και Β που δεν είναι δεσμοί απέχουν μεταξύ τους απόσταση
Γκύζη 14-Αθήνα Τηλ :
 Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ:
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ: 20-4-2017 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ: 20-4-2017 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ
ΣΤΕΡΕΟ. 1. Στο σχήμα φαίνεται πως μεταβάλλεται η γωνιακή ταχύτητα ενός δίσκου που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής.
 1. Στο σχήμα φαίνεται πως μεταβάλλεται η γωνιακή ταχύτητα ενός δίσκου που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής. Δίνεται ακτίνα δίσκου 0,5 m. α) Να βρεθούν οι γωνιακές επιταχύνσεις
1. Στο σχήμα φαίνεται πως μεταβάλλεται η γωνιακή ταχύτητα ενός δίσκου που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής. Δίνεται ακτίνα δίσκου 0,5 m. α) Να βρεθούν οι γωνιακές επιταχύνσεις
ΦΥΣΙΚΗ Ο.Π. ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΓΕΛ / 04 / 09 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Σώμα εκτελεί απλή αρμονική ταλάντωση
Γ ΓΕΛ / 04 / 09 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Σώμα εκτελεί απλή αρμονική ταλάντωση
ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 Κανάρη 36, Δάφνη Τηλ. 1 9713934 & 1 9769376 ΘΕΜΑ Α ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Α. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Κανάρη 36, Δάφνη Τηλ. 1 9713934 & 1 9769376 ΘΕΜΑ Α ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Α. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 1 ΙΟΥΝΙΟΥ 019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 1 ΙΟΥΝΙΟΥ 019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Δίνονται: π=3,14 και συν3π/4 = 2
 1. Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές Π 1 και Π 2, που δημιουργούν στην επιφάνεια του υγρού εγκάρσια αρμονικά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται
1. Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές Π 1 και Π 2, που δημιουργούν στην επιφάνεια του υγρού εγκάρσια αρμονικά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται
α.- β. γ. δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 13/11/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 13/11/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
3.3. Δυναμική στερεού.
 3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 23/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 23/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ. ΘΕΜΑ Α (μοναδες 25)
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 28/2/2016
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 8//06 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΣΤΕΡΕΟ ΚΑΙ Doppler ΘΕΜΑ Α Α Μικρότερη συχνότητα ακούει ένας παρατηρητής σε σχέση με την πραγματική συχνότητα
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 8//06 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΣΤΕΡΕΟ ΚΑΙ Doppler ΘΕΜΑ Α Α Μικρότερη συχνότητα ακούει ένας παρατηρητής σε σχέση με την πραγματική συχνότητα
προς ένα ακίνητο σωμάτιο α (πυρήνας Ηe), το οποίο είναι ελεύθερο να κινηθεί,
 ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
Κρούσεις. Ομάδα Γ. Κρούσεις Ενέργεια Ταλάντωσης και Ελαστική κρούση Κρούση και τριβές Κεντρική ανελαστική κρούση
 . Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
. Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
2) Ομογενής δίσκος μάζας m και ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο
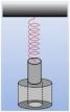 - 1 - Επώνυμο.. Όνομα.. Αγρίνιο 22/3/2015 Ζήτημα 1 0 Να επιλεγεί η σωστή πρόταση 1) Ομογενής δίσκος μάζας m και ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο επίπεδο. Ο δίσκος στρέφεται γύρω
- 1 - Επώνυμο.. Όνομα.. Αγρίνιο 22/3/2015 Ζήτημα 1 0 Να επιλεγεί η σωστή πρόταση 1) Ομογενής δίσκος μάζας m και ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο επίπεδο. Ο δίσκος στρέφεται γύρω
ΦΥΣΙΚΗ Ο.Π. Αν η κρούση της σφαίρας με τον κατακόρυφο τοίχο είναι ελαστική, τότε ισχύει:. = και =.. < και =. γ. < και <. δ. = και <.
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
ΘΕΜΑ 1 ο Στις ερωτήσεις 1 4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 2013 Γ Λυκείου Θετική & Τεχνολογική Κατεύθυνση ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1 4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1. Σώμα
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 2013 Γ Λυκείου Θετική & Τεχνολογική Κατεύθυνση ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1 4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1. Σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. (Θέμα Δ) Άσκηση 2. (Κύλιση χωρίς ολίσθηση, σχέση υ cm και ω, σχέση α cm και a γων )
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Γωνιακή ταχύτητα, γωνιακή επιτάχυνση, σύνθετη κίνηση, κέντρο μάζας) Δύο δίσκοι οριζόντιοι Δ 1 και Δ εκτελούν περιστροφική κίνηση γύρω από κατακόρυφο άξονα που περνά από το
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Γωνιακή ταχύτητα, γωνιακή επιτάχυνση, σύνθετη κίνηση, κέντρο μάζας) Δύο δίσκοι οριζόντιοι Δ 1 και Δ εκτελούν περιστροφική κίνηση γύρω από κατακόρυφο άξονα που περνά από το
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 14/4/2019
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 14/4/2019 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 14/4/2019 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 Κανάρη 6, Δάφνη Τηλ. 10 97194 & 10 976976 ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α Ι. Στις ερωτήσεις A1-A4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Κανάρη 6, Δάφνη Τηλ. 10 97194 & 10 976976 ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α Ι. Στις ερωτήσεις A1-A4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
Διαγώνισμα Μηχανική Στερεού Σώματος
 Διαγώνισμα Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
Διαγώνισμα Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
ΦΥΣΙΚΗ. α) έχουν κάθε χρονική στιγμή την ίδια οριζόντια συνιστώσα ταχύτητας, και την ίδια κατακόρυφη συνιστώσα ταχύτητας.
 Β Λυκείου 14 / 04 / 2019 ΦΥΣΙΚΗ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις A1 A4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Η ορμή ενός σώματος :
Β Λυκείου 14 / 04 / 2019 ΦΥΣΙΚΗ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις A1 A4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Η ορμή ενός σώματος :
