Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption
|
|
|
- Ευφήμιος Καραμήτσος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption
2 Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης
3 Συνήθως δίνονται: Ρυθμός ροής αερίου (GG iiii ) Σύσταση τροφοδοσίας yy iiii Σύσταση διαλύτη xx iiii Βαθμός διαχωρισμού A. Επιλογή Ρυθμού Ροής Διαλύτη Ανάκτηση = yy iiii yy oooooo yy iiii yy oooooo = yy iiii (1 Ανάκτηση) ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΤΑΛΛΗΛΟΥ ΡΥΘΜΟΥ ΡΟΗΣ ΔΙΑΛΥΤΗ (L in ) ΑΠΟ ΚΛΙΣΗ ΓΡΑΜΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ
4 Καθώς μειώνεται η ποσότητα του διαλύτη (L), η κλίση της γραμμής λειτουργίας μειώνεται και ο αριθμός των σταδίων αυξάνεται.
5 Γνωστές Παράμετροι: Εύρεση ελάχιστου λόγου ροής Υγρού/Αερίου yy 1, yy NN+1 : Είσοδος, έξοδος αερίου που θέλουμε να απομακρύνουμε xx oo : Σύσταση εισόδου του διαλύτη 1 y N+1 είσοδος αερίου y y 1 έξοδος αερίου 0 Καθορισμένο (L/G)= Κορυφή Κ x o είσοδος υγρού (L/G) min (L/G) y e =f(x) x N (max) 0 1 x LL GG = yy NN+1 yy 1 mmmmmm xx NN mmmmmm xx oo Ο ελάχιστος λόγος ροής αντιστοιχεί σε άπειρο ύψος ή άπειρο αριθμό θεωρητικών βαθμίδων Στο διάγραμμα ισορροπίας y-x, ο ελάχιστος λόγος ροής βρίσκεται από το σημείο τομής της γραμμής λειτουργίας με την καμπύλη ισορροπίας
6 Β. Θερμοκρασία Απορρόφηση Εξώθερμη Διεργασία Βελτιώνεται με μείωση της θερμοκρασίας Ψύξη υγρού διαλύτη πριν την είσοδο του στη στήλη απορρόφησης Η αύξηση της θερμοκρασίας έχει ως αποτέλεσμα: Η καμπύλη ισορροπίας ανεβαίνει και μειώνεται η ισχύς απορρόφησης. Για ίδιο Υ, ο διαχωρισμός μειώνεται με την αύξηση της θερμοκρασίας Τ 3 > Τ 2 > Τ 1 xx 3 < xx 2 < xx 1
7 Για τον ίδιο λόγο (L/G), ο αριθμός των βαθμίδων ισορροπίας αυξάνεται με την αύξηση της θερμοκρασίας Μεγάλο ύψος στήλης Κακές συνθήκες Υψηλό κόστος
8 Για τον ίδιο λόγο (L/G), η κινητήρια δύναμη μειώνεται με την αύξηση της θερμοκρασίας και ο διαχωρισμός γίνεται δυσκολότερος.
9 Γ. Πίεση Καθώς η πίεση αυξάνεται, η ισχύς απορρόφησης αυξάνεται. pp ii = HH ii xx ii (Νόµος Henry) Η αύξηση της πίεσης έχει ως αποτέλεσμα: Η καμπύλη ισορροπίας κατεβαίνει και βελτιώνεται η ισχύς απορρόφησης. Για ίδιο Υ, ο διαχωρισμός αυξάνεται με την αύξηση της πίεσης P 3 < PP 2 < PP 1 xx 3 < xx 2 < xx 1
10 Για τον ίδιο λόγο (L/G), ο αριθμός των βαθμίδων ισορροπίας μειώνεται με την αύξηση της πίεσης Μικρό ύψος στήλης Καλές συνθήκες Χαμηλό κόστος
11 Για τον ίδιο λόγο (L/G), η κινητήρια δύναμη αυξάνεται με την αύξηση της πίεσης και ο διαχωρισμός γίνεται ευκολότερος.
12 Διεργασία Απορρόφησης- Πυκνά Μίγματα Πυκνά μίγματα: yy NN+1 αρκετά μεγάλο GG NN+1 > GG 1 κκκκκκ LL NN > LL oo Ορισμός ροής αδρανούς αερίου GG και αδρανούς διαλύτη LL ως βάση καθώς θεωρούνται σταθερές σε όλο το μήκος της στήλης. Έκφραση ολικών παροχών G nn και LL nn συναρτήσει των αδρανών παροχών GG και LL : Είσοδος υγρού LL oo, xx oo Έξοδος αερίου GG 1, yy 1 GG = GG nn (1 yy nn ) LL = LL nn (1 xx nn ) G YY NN+1 YY 1 για κάθε n της στήλης Ολικό ισοζύγιο μάζας συστατικού: όπου: XX nn = = LL XX NN XX oo xx nn 1 xx nn YY nn = yy nn 1 yy nn Λόγοι γραμμομοριακών κλασμάτων NN mmmmmm ssssssssssss iiii gggggg YY = mmmmmm pppppppp cccccccccccccc gggggg CC Έξοδος υγρού Είσοδος αερίου LL NN, xx NN GG N+1, yy NN+1 mmmmmm ssssssssssss iiii llllllllllll XX = mmmmmm pppppppp ssssssssssssss SS
13 Μέθοδος McCabe - Thiele για στήλες απορρόφησης με δίσκους 1 y e =f(x) y y N+1 y 1 Κ (y 1, x o ) (y 3, x 2 ) (y 2, x 1 ) (L/G) 1 (y 1, x 1 ) 2 (y 2, x 2 ) 3 (y 3, x 3 ) x N (max) 0 0 x o 0,2 0,4 0,6 0,8 1 x Μεθοδολογία: 1. Σχεδιασμός καμπύλης ισορροπίας 2. Σχεδιασμός γραμμής λειτουργίας Κ yy 1, xx oo Κλίση LL GG 3. Κατασκευή θεωρητικών βαθμίδων ξεκινώντας από την κορυφή του πύργου Κ χρησιμοποιώντας ως όρια τη γραμμή λειτουργίας και την καμπύλη ισορροπίας
14 Μέθοδος Kremser υπολογισμού βαθμίδων απορρόφησης Παραδοχές: Αραιά Μίγματα Νόμος Raoult ή Henry Εξίσωση Kremser: όπου: yy NN+1 yy 1 yy 1 yy 1 = mm ii : κλίση της εξίσωσης ισορροπίας 1 LL mm ii GG 1 LL mm ii GG NN+1 mm ii = HH ii (Νόμος Henry) mm P ή ii = pp ii oo PP (Νόμος Raoult) Αριθμός βαθμίδων απορρόφησης: NN = ln 1 mm GG LL ln yy NN+1 yy 1 yy 1 yy 1 LL mm GG + mm GG LL όπου: yy 1 = mm xx oo + bb The vapor composition is the value that would be in equilibrium with the inlet liquid, x 0.
15 Μέθοδος Kremser υπολογισμού βαθμίδων- Μη Ιδανικά Διαλύματα όπου: Εξίσωση Kremser: yy NN+1 yy 1 yy 1 yy 1 = i. Για μη ιδανικά διαλύματα με γνωστό το συντελεστή ενεργότητας (γγ iiii ): mm ii = γγ iiii pp ii oo PP 1 LL mm ii GG 1 LL mm ii GG NN+1 ii. Για μη ιδανικά διαλύματα με διαθέσιμα δεδομένα διαλυτότητας υπό μορφή γραμμομοριακών κλασμάτων xx ii : mm ii = pp ii oo xx ii PP όπου: p io η τάση ατμών του καθαρού διαλύτη στη θερμοκρασία του διαλύματος P η ολική πίεση xx ii Γραμμομοριακό κλάσμα του i στην υγρή φάση σε ισορροπία
16 Απορρόφηση πολυσυστατικών μιγμάτων Γραμμή Λειτουργίας: yy nn+11,ii = LL GG xx nn,ii + yy 11,ii LL GG xx oo,ii Είσοδος υγρού LL oo, xx oo,ii Έξοδος αερίου GG 1, yy 1,ii Τα προβλήματα με πολυσυστατικά μίγματα αντιμετωπίζονται ως ξεχωριστά προβλήματα για κάθε συστατικό! NN Έξοδος υγρού LL NN, xx NN,ii Είσοδος αερίου GG N+1, yy NN+1,ii
17 Απορρόφηση πολυσυστατικών μιγμάτων Έστω μίγμα 3 συστατικών Λύση 3 προβλημάτων για κάθε συστατικό Γνωστά: xx oo,aa xx oo,bb xx oo,cc yy NN+1,AA yy NN+1,BB yy NN+1,CC Είσοδος υγρού LL oo xx oo,aa xx oo,bb xx oo,cc Έξοδος αερίου GG 1 yy 1,AA yy 1,BB yy 1,CC yy 1,BB L, G Για το συστατικό B γνωρίζουμε και τη σύστασή του στη φάση του αερίου στην έξοδο της στήλης απορρόφησης, επομένως ορίζεται ως «συστατικό κλειδί». NN? Σύσταση συστατικού Β στην έξοδο της στήλης απορρόφησης στη φάση του υγρού (xx NN,BB ) Έξοδος υγρού LL NN xx NN,AA xx NN,BB xx NN,CC Είσοδος αερίου GG N+1 yy NN+1,AA yy NN+1,BB yy NN+1,CC
18 Υπολογισμός xx nn,bb : Απορρόφηση πολυσυστατικών μιγμάτων yy nn+11,ββ = LL GG xx nn,ββ + yy 11,BB LL GG xx oo,bb xx nn,ββ Γραφική μέθοδος- McCabe Thiele - Αριθμός Βαθμίδων Ισορροπίας i. Σχεδιασμός γραμμής ισορροπίας με κλίση τις σταθερές KK BB ή mm BB ii. Σχεδιασμός γραμμής λειτουργίας με κλίση L/G iii. Γραφικός υπολογισμός Βαθμίδων Ισορροπίας yy nn+11,ββ y yy 11,BB xx oo,bb x xx nn,ββ
19 Απορρόφηση πολυσυστατικών μιγμάτων Οι γραμμές λειτουργίας των υπόλοιπων συστατικών κατασκευάζονται ώστε να είναι παράλληλες με τη γραμμή λειτουργίας του συστατικού κλειδιού. Ο αριθμός των θεωρητικών βαθμίδων για τα υπόλοιπα συστατικά πρέπει να είναι ίδιος με το «συστατικό κλειδί». Σχεδιασμός γραμμής ισορροπίας με κλίση KK ii ή mm ii Έστω yy 1,ii xx nn,ii : Από γραμμή λειτουργίας Όχι Σχεδιασμός γραμμής λειτουργίας με κλίση L/G Αριθμός Βαθμίδων Ισορροπίας-McCabe Thiele N i =N Συστ. κλειδί Ναι Τέλος
20 Αριθμός Βαθμίδων Ισορροπίας Απορρόφηση πολυσυστατικών μιγμάτων 1. Γραφική μέθοδος- McCabe Thiele i. Κατασκευάζονται οι γραμμές ισορροπίας των διαφόρων συστατικών του μίγματος με κλίσεις τις σταθερές KK ii ή mm ii (Έστω τα συστατικά προπάνιο, βουτάνιο και πεντάνιο) ii. iii. iv. Επιλογή ενός συστατικού ως «συστατικό κλειδί» Η γραμμή ισορροπίας του είναι κατά το δυνατόν παράλληλη με τη γραμμή λειτουργίας (K i ή m i περίπου ίση με G o ). (Οικονομικός διαχωρισμός) M Οι γραμμές λειτουργίας των υπόλοιπων συστατικών κατασκευάζονται ώστε να είναι παράλληλες με τη γραμμή λειτουργίας του συστατικού κλειδιού. Υπολογίζεται ο αριθμός των απαιτούμενων βαθμίδων για το «συστατικό κλειδί» μέσω της μεθοδολογίας McCabe- Thiele. Ο αριθμός των θεωρητικών βαθμίδων για τα υπόλοιπα συστατικά πρέπει να είναι ίδιος με το «συστατικό κλειδί» και συγχρόνως να ικανοποιούνται τα δεδομένα σύστασης του μίγματος στα άκρα του πύργου. L M S
21 Απορρόφηση πολυσυστατικών μιγμάτων Οι διαδικασίες για την πολλαπλή απορρόφηση είναι ταυτόσημες για τα δυαδικά μίγματα. Αντί να έχουμε μια ενιαία καμπύλη ισορροπίας και γραμμή λειτουργίας, υπάρχουν τώρα μια καμπύλη ισορροπίας και μια γραμμή λειτουργίας για κάθε απορροφημένο συστατικό του αερίου. Ο ρυθμός ροής αερίου (G) και ο ρυθμός ροής υγρού (L) είναι περίπου σταθεροί διαμέσου της στήλης. Η γραμμή λειτουργίας βρίσκεται μέσω του σημείου (xin, yout) και της κλίσης (L / G) για το συστατικό κλειδί και επειδή η σύσταση της τροφοδοσίας είναι γνωστή μπορούμε να εντοπίσουμε το τερματικό σημείο της γραμμής λειτουργίας (xout, yin). Ο αριθμός των απαιτούμενων βαθμίδων για το «συστατικό κλειδί» μέσω της μεθοδολογίας McCabe- Thiele. Ακριβώς ο ίδιος αριθμός απαιτούμενων βαθμίδων είναι διαθέσιμος για τα άλλα συστατικά. Οι γραμμές λειτουργίας των συστατικών πρέπει να έχουν την ίδια κλίση. Έτσι, μπορούμε να υπολογίσουμε την ανάκτηση για κάθε συστατικό που εισέρχεται.
22
23 Απορρόφηση πολυσυστατικών μιγμάτων 2. Αλγεβρική μέθοδος- Kremser Περιπτώσεις i. Όταν Εξίσωση Kremser: LL mm ii GG yy NN+1 yy 1 yy 1 yy 1 = LL mm ii GG << 1 και το Ν πολύ μεγάλο τότε η Εξ. (1): yy NN+1 yy 1 yy 1 yy 1 = LL mm ii GG LL mm ii GG 1 LL mm ii GG Εφαρμόζεται για την εκτίμηση του βαθμού απορρόφησης των πλέον πτητικών συστατικών του πολυσύνθετου μίγματος NN+1 (1) ii. Όταν LL mm ii GG >> 1 και το Ν πολύ μεγάλο τότε η Εξ. (1): yy NN+1 yy 1 yy 1 yy 1 = 1 Το αέριο εγκαταλείπει τον πύργο σε κατάσταση ισορροπίας με το υγρό απορρόφησης Για συστατικά λιγότερο πτητικά από το συστατικό κλειδί γίνεται η παραδοχή ότι αυτά απορροφούνται πλήρως από το διαλύτη
24 Αλγεβρική μέθοδος- Kremser Μεθοδολογία: 1. Υπολογίζονται οι απαιτούμενες βαθμίδες για το συστατικό κλειδί 2. Εφαρμόζεται η εξίσωση Kremser για τα υπόλοιπα συστατικά για την εύρεση του βαθμού απορρόφησης του κάθε συστατικού
25 Ορισμός Εκρόφησης ή εξάντλησης ή απογύμνωσης Η εκρόφηση είναι το αντίθετο της απορρόφησης και συνεπάγεται την απομάκρυνση διαλυμένων αερίων σε υγρό μέσω ενός παράγοντα εκρόφησης. Σκοπός: 1. Ανάκτηση της διαλυμένης ουσίας. 2. Ανάκτηση του διαλύτη. 3. Ανάκτηση τόσο της διαλυμένης ουσίας όσο και του διαλύτη. Συνήθως η απορρόφηση ακολουθείται από την εκρόφηση. Ο πιο συχνά χρησιμοποιούμενος παράγοντας εκρόφησης είναι ο ατμός.
26 Διεργασία Εκρόφησης- Αραιά Μίγματα Αραιά μίγματα: xx NN+1 αρκετά μικρό Παραδοχή: GG 1 = GG 2 = = GG NN = GG L 1 = LL 2 = = LL NN = LL Ολικό ισοζύγιο μάζας συστατικού: LL nn+1 xx nn+1 + GG oo yy oo = LL 1 xx 1 + GG nn yy nn LL xx nn+1 xx 1 = GG yy nn yy oo Είσοδος υγρού LL Ν+1, xx Ν+1 Ν LL nn+1, xx nn+1 nn Έξοδος αερίου GG Ν, yy Ν GG nn, yy nn yy nn = LL GG xx nn+1 + yy 0 LL GG xx 1 Εξίσωση Λειτουργίας Πύργου Εκρόφησης 2 1 Έξοδος υγρού LL 1, xx 1 Είσοδος αερίου GG 0, yy 0
27 Διεργασία Εκρόφησης- Αραιά Μίγματα L N+1, x N+1 G N, y N N L n+1, x n+1 G n, y n n 2 1 L 1, x 1 G o, y o Γραμμή Λειτουργίας: yy nn = LL GG xx nn+1 + yy 0 LL GG xx 1
28 Απορρόφηση vs Εκρόφηση y N+1 είσοδος αερίου y 1 y 1 έξοδος αερίου 0 Καθορισμένο Καθορισμένο Κορυφή Κ (y 1, x o ) x o είσοδος υγρού (L/G) Πυθμένας Π (y Ν+1, x Ν ) x N ζητούμενο Καμπύλη ισορροπίας y e =f(x) 0 1 x 1. Η γραμμή λειτουργίας στην απορρόφηση βρίσκεται πάνω από την καμπύλη ισορροπίας (αντίθετα στην εκρόφηση) 2. Στην διεργασία απορρόφησης, το σημείο που αντιστοιχεί στον πυθμένα Π(yy 0, xx 1 ) είναι καθορισμένο σε αντίθεση με τη διεργασία εκρόφησης, όπου είναι το σημείο που αντιστοιχεί στην κορυφή KK(yy 1, xx 0 )
29 Διεργασία Εκρόφησης- Πυκνά Μίγματα Πυκνά μίγματα: xx NN+1 αρκετά μεγάλο LL NN+1 > LL 1 κκκκκκ GG NN > GG oo Ορισμός ροής αδρανούς αερίου GG και αδρανούς διαλύτη LL ως βάση καθώς θεωρούνται σταθερές σε όλο το μήκος της στήλης. Έκφραση ολικών παροχών G nn και LL nn συναρτήσει των αδρανών παροχών GG και LL : GG = GG nn (1 yy nn ) LL = LL nn (1 xx nn ) L XX NN+1 XX 1 για κάθε n της στήλης Ολικό ισοζύγιο μάζας συστατικού: όπου: XX nn = = GG YY NN YY oo xx nn 1 xx nn YY nn = yy nn 1 yy nn Είσοδος υγρού LL Ν+1, xx Ν+1 Ν LL nn+1, xx nn+1 nn 2 1 Έξοδος υγρού LL 1, xx 1 Έξοδος αερίου GG Ν, yy Ν GG nn, yy nn Είσοδος αερίου GG 0, yy 0 Λόγοι γραμμομοριακών κλασμάτων
30 Μέθοδος McCabe-Thiele για στήλες εκφόφησης αερίων με δίσκους L, x N+1 G, y N N n 2 1 L, x 1 G, y o
31 Μέθοδος Kremser υπολογισμού βαθμίδων εκρόφησης Εξίσωση Kremser: xx 1 xx 1 xx NN+1 xx 1 = mm 1 ii GG LL 1 mm iigg LL NN+1 Αριθμός βαθμίδων εκρόφησης: NN = ln 1 LL xx NN+1 xx 1 mm ii GG + LL xx 1 xx 1 mm ii GG ln mm iigg LL όπου: mm ii : κλίση της εξίσωσης ισορροπίας xx 1 = yy oo bb mm xx NN+1 = yy NN bb mm
32 Στήλες Απορρόφησης Βασιζόμενες στο Ρυθμό Μεταφοράς Μάζας Θεωρία του Διπλού φιλμ Διεπιφάνεια Υμένας αερίου y Υμένας υγρού y δ x δ Συγκέντρωση N A x Αέρια Φάση (G) Υγρή Φάση (L) Απόσταση όπου: NN ii mmmmmm mm 3 ss NN ii = kk GG,ΟΛ aa yy yy ee = kk LL,ΟΛ aa (xx ee xx), ρυθμός μεταφοράς μάζας του συστατικού i από τη μια φάση στην άλλη kk GG,ΟΛ αα, kk LL,ΟΛ αα mmmmmm, ολικοί συντελεστές μεταφοράς μάζας ανά μονάδα όγκου του cccc 3 ss συστατικού i στη φάση του αερίου και υγρού, αντίστοιχα αα cccc2 cccc 3, ειδική επιφάνεια που αναπαριστά τη μονάδα επιφάνειας μεταφοράς μάζας ανά μονάδα όγκου μέσα στην οποία γίνεται η μεταφορά
33 Σχεδιασμός Στηλών Απορρόφησης με Πληρωτικά Υλικά Αραιά Μίγματα [Διαφορική μάζα του i που εγκαταλείπει το αέριο] = [Διαφορική μάζα του i που πηγαίνει στο υγρό ] L in, x in G out, y out GG dddd = LL dddd aa = dddd AAAAAA A dz GG dddd = LL dddd = NN ii dddd = NN ii AA ddzz dv L out, x out G in, y in GG dddd = kk GG,ΟΛ aa yy yy ee A dz Αέρια φάση Η κύρια αντίσταση στη μεταφορά μάζας βρίσκεται στην αέρια φάση όπου: Α: επιφάνεια κάθετης διατομής στήλης LL dddd = kk GG,ΟΛ aa xx ee xx A dz Υγρή φάση Η κύρια αντίσταση στη μεταφορά μάζας βρίσκεται στην υγρή φάση
34 Συνολικό Ύψος Στήλης (z) zz = yy iiii GG kk GG,ΟΛ aa AA yy oooooo dddd (yy yy ee ) zz = xx oooooo LL kk LL,ΟΛ aa AA xx iiii dddd (xx ee xx) HH OOOO = HH OOOO = GG kk GG,ΟΛ aa AA LL kk LL,ΟΛ aa AA «Ύψος μονάδος μεταφοράς» (m) NN OOOO = yy iiii yy oooooo xx oooooo NN OOLL = xx iiii dddd (yy yy ee ) dddd (xx ee xx) «Αριθμός μονάδων μεταφοράς» (Αδιάστατο) Αποτελεί το μέτρο δυσκολίας μεταφοράς μάζας για δεδομένη μεταβολή των συγκεντρώσεων
35 NN OOOO = yy iiii yy oooooo dddd (yy yy ee ) (1) Ισοζύγιο Μάζας σε όγκο ελέγχου 1:? GG yy yy oooooo = LL xx xx iiii Υπολογισμός Ολοκληρώματος L in, x in G out, y out (1) xx = GG LL yy + xx iiii GG LL yy oooooo (2) Νόμος Henry: yy ee = mm xx yy yy ee = yy mm xx 2 yy yy ee = yy mm GG LL yy mmxx iiii + mm GG LL yy oooooo A dz dv yy yy ee = 1 mm GG LL yy mm(xx iiii GG LL yy oooooo) CC L out, x out G in, y in Άρα, (1) NN OOOO = 1 1 mm GG LL ln 1 mm GG LL yy iiii + CC 1 mm GG LL yy oooooo + CC
36 Σχεδιασμός Στηλών Απορρόφησης με Πληρωτικά Υλικά L Πυκνά Μίγματα in, x in Ρυθμός μεταφοράς Ni για πυκνά μίγματα NN ii = kk GG,ΟΛ αα yy yy ee 1, όπου 1 yy 1 yy llll = 1 yy (1 yy ee) llll (1 yy) ln (1 yy ee ) Διαφορικό Ισοζύγιο Μάζας dd GGyy = dd LLxx = NN ii AA ddzz GG = GG (1 yy nn ) LL = LL (1 xx nn ) Ισοζύγιο Μάζας GG GG YY iiii YY oooooo = LL XX oooooo XX iiii (3) L out, x out dddd (1 yy) 2 = LL dddd (1 xx) 2 = NN ii AA dddd (2) A G out, y out dz dv G in, y in 1, 2, 3 GG dddd 1 yy 2 = kk GG,ΟΛ αα AA yy yy ee dddd = GG 1 yy llll dddd kk GG,ΟΛ ααaa(1 yy) (1 yy)(yy yy ee ) 1 yy llll dddd
37 Συνέχεια dddd = GG 1 yy llll dddd kk GG,ΟΛ ααaa(1 yy) (1 yy)(yy yy ee ) zz = HH OOOO yy iiii yy oooooo 1 yy llll dddd (1 yy)(yy yy ee ) όπου: GG kk GG,ΟΛ ααaa(1 yy) = G kk GG,ΟΛ ααaa = HH OOOO NN OOOO = yy iiii yy oooooo yy iiii 1 yy llll dddd (1 yy)(yy yy ee ) = yy oooooo dddd (yy yy ee ) ln 1 yy oooooo 1 yy iiii
38 Όπου: ηη οο = Απόδοση Στηλών Απορρόφησης πππππππππππππππππππππ δδδδδδδδδδδδδδδδδδδδδ δδδδδδδδδδδδδδδδδδδδδ ππππππ θθθθ εεεεεεεεεεεεεεεεεεooνννννννν σσσσ σσσσσσσσσσ αααααααααααααα ύψψψψψψψψ ή ηη oo = yy iiii yy oooooo yy iiii yy oooooo,ee (1) yy oooooo,ee είναι η σύσταση του αερίου που θα ήταν σε ισορροπία με τη σύσταση εισόδου xx iiii του υγρού στη στήλη Αν xx iiii = 0 (Καθαρός διαλύτης στην είσοδο), τότε: Επίσης: LL GG = ββ LL GG mmmmmm = ββ ηη oo = yy oooooo yy iiii yy oooooo yy iiii yy oooooo = ββ yy iiii yy oooooo xx oooooo,mmmmmm xx iiii xx oooooo,mmmmmm = β m ηη oo = ββ mm yy iiii yy oooooo yy oooooo ηη oo = 1 LL ββ mm GG ββ: Συντελεστής οικονομικής λειτουργίας 1.25 < ββ < 1.5
Λύση Παραδείγματος 1. Διάγραμμα ροής διεργασίας. Εκρόφηση χλωριούχου βινυλίου από νερό στους 25 C και 850 mmhg. Είσοδος υγρού.
 Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Energy resources: Technologies & Management
 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Απορρόφηση Αερίων. 1. Εισαγωγή
 1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ. -Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση
 ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ -Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Απορρόφηση αερίων φυσική και χημική Παραδείγματα βιομηχανικών εφαρμογών ) Απορρόφηση SΟ 3 κατά την παραγωγή
ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ -Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Απορρόφηση αερίων φυσική και χημική Παραδείγματα βιομηχανικών εφαρμογών ) Απορρόφηση SΟ 3 κατά την παραγωγή
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ. ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ (MSc)
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ (MSc) ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΠΣΕ60 Ακαδημαϊκό Έτος: 207-208 η Γραπτή Εργασία Επιβλέπων
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ (MSc) ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΠΣΕ60 Ακαδημαϊκό Έτος: 207-208 η Γραπτή Εργασία Επιβλέπων
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Απορρόφηση (Absorption)
 Απορρόφηση (Absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσο-absorbate) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσοabsorbent) με το οποίο βρίσκεται σε επαφή. Βασίζεται
Απορρόφηση (Absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσο-absorbate) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσοabsorbent) με το οποίο βρίσκεται σε επαφή. Βασίζεται
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ. Απορρόφηση 1
 ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ 1. Ισορροπία αερίων- υγρού 2. Ανάλυση διεργασίας Απορρόφησης 3. Απορρόφηση Πολυσύνθετων Μιγμάτων 4. Στήλες Απορρόφησης με πληρωτικά υλικά Απορρόφηση 1 Απορρόφηση Απορρόφηση Αερίων (Gas
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ 1. Ισορροπία αερίων- υγρού 2. Ανάλυση διεργασίας Απορρόφησης 3. Απορρόφηση Πολυσύνθετων Μιγμάτων 4. Στήλες Απορρόφησης με πληρωτικά υλικά Απορρόφηση 1 Απορρόφηση Απορρόφηση Αερίων (Gas
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
Κεφάλαιο 6 Απορρόφηση
 Κεφάλαιο 6 Απορρόφηση Σύνοψη Απορρόφηση αεριών ονομάζεται η φυσική διεργασία απομάκρυνσης ενός ή περισσοτέρων συστατικών ενός αερίου ρεύματος προς ένα μη πτητικό υγρό, το οποίο διαλύει αυτό(α) το(α) συστατικό(α).
Κεφάλαιο 6 Απορρόφηση Σύνοψη Απορρόφηση αεριών ονομάζεται η φυσική διεργασία απομάκρυνσης ενός ή περισσοτέρων συστατικών ενός αερίου ρεύματος προς ένα μη πτητικό υγρό, το οποίο διαλύει αυτό(α) το(α) συστατικό(α).
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΥΤΙΚΕ ΔΙΕΡΓΑΙΕ ΜΕΣΑΥΟΡΑ ΜΑΖΑ. - Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση
 ΥΤΙΚΕ ΔΙΕΡΓΑΙΕ ΜΕΣΑΥΟΡΑ ΜΑΖΑ - Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Εκχύλιση : εκχύλιση υγρών εκχύλιση στερεών διαχωρισμός αναμίξιμων υγρών παραπλήσια σ.ζ. ή α ΑΒ =1 έκπλυση ή διαλυτοποίηση
ΥΤΙΚΕ ΔΙΕΡΓΑΙΕ ΜΕΣΑΥΟΡΑ ΜΑΖΑ - Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Εκχύλιση : εκχύλιση υγρών εκχύλιση στερεών διαχωρισμός αναμίξιμων υγρών παραπλήσια σ.ζ. ή α ΑΒ =1 έκπλυση ή διαλυτοποίηση
Είδη ΙΦΥΥ δυαδικών μιγμάτων
 Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης
 ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης
 σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
Electronic Analysis of CMOS Logic Gates
 Electronic Analysis of CMOS Logic Gates Dae Hyun Kim EECS Washington State University References John P. Uyemura, Introduction to VLSI Circuits and Systems, 2002. Chapter 7 Goal Understand how to perform
Electronic Analysis of CMOS Logic Gates Dae Hyun Kim EECS Washington State University References John P. Uyemura, Introduction to VLSI Circuits and Systems, 2002. Chapter 7 Goal Understand how to perform
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης 2. Ενέργεια Ενεργοποίησης
 Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ. Σχεδιασµός της Στήλης µε Χρήση ενός Προσοµοιωτή. K.A. Μάτης
 ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Σχεδιασµός της Στήλης µε Χρήση ενός Προσοµοιωτή K.A. Μάτης Εισαγωγή Στη διεργασία της απορρόφησης ένα αέριο µίγµα έρχεται σε επαφή µε ένα υγρό (το διαλύτη ή απορροφητικό) ώστε να διαλυθεί
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Σχεδιασµός της Στήλης µε Χρήση ενός Προσοµοιωτή K.A. Μάτης Εισαγωγή Στη διεργασία της απορρόφησης ένα αέριο µίγµα έρχεται σε επαφή µε ένα υγρό (το διαλύτη ή απορροφητικό) ώστε να διαλυθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ. Ενότητα #7: Σύστημα Ασαφούς Λογικής Μαθηματικές Εκφράσεις
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #7: Σύστημα Ασαφούς Λογικής Μαθηματικές Εκφράσεις Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #7: Σύστημα Ασαφούς Λογικής Μαθηματικές Εκφράσεις Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
Συστήματα Αυτομάτου Ελέγχου Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ι Ενότητα #7: Άλγεβρα Βαθμίδων (μπλόκ) Ολική Συνάρτηση Μεταφοράς Δημήτριος Δημογιαννόπουλος Τμήματος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ι Ενότητα #7: Άλγεβρα Βαθμίδων (μπλόκ) Ολική Συνάρτηση Μεταφοράς Δημήτριος Δημογιαννόπουλος Τμήματος
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 6-ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ
 ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 6-ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ 1. Σε δοχείο σταθερού όγκου και σε σταθερή θερμοκρασία, εισάγονται κάποιες ποσότητες των αερίων Η 2(g) και Ι 2(g) τα οποία αντιδρούν σύμφωνα με
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 6-ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ 1. Σε δοχείο σταθερού όγκου και σε σταθερή θερμοκρασία, εισάγονται κάποιες ποσότητες των αερίων Η 2(g) και Ι 2(g) τα οποία αντιδρούν σύμφωνα με
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
Ομογενής και Ετερογενής Ισορροπία
 Ομογενής και Ετερογενής Ισορροπία Ομογενής ισορροπία : N 2(g) + O 2(g) 2NO (g) Ετερογενής ισορροπία : Zn (s) + 2H (aq) + Zn (aq) ++ + H 2(g) Σταθερά χηµικής ισορροπίας Kc: Για την αµφίδροµη χηµική αντίδραση:
Ομογενής και Ετερογενής Ισορροπία Ομογενής ισορροπία : N 2(g) + O 2(g) 2NO (g) Ετερογενής ισορροπία : Zn (s) + 2H (aq) + Zn (aq) ++ + H 2(g) Σταθερά χηµικής ισορροπίας Kc: Για την αµφίδροµη χηµική αντίδραση:
ΓΡΑΜΜΙΚΑ ΜΟΝΤΕΛΑ ΚΑΙ ΣΧΕΔΙΑΣΜΟΙ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ I
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΑ ΜΟΝΤΕΛΑ ΚΑΙ ΣΧΕΔΙΑΣΜΟΙ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ I Άσκηση 1 Ερώτημα (i) HH 0 : μμ 1 = μμ = μμ 3 = μμ 4 = μμ HH 1 : τουλάχιστον
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΑ ΜΟΝΤΕΛΑ ΚΑΙ ΣΧΕΔΙΑΣΜΟΙ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ I Άσκηση 1 Ερώτημα (i) HH 0 : μμ 1 = μμ = μμ 3 = μμ 4 = μμ HH 1 : τουλάχιστον
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ
 3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ
 Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
8.3 Πύργος Απορρόφησης
 26 8.3 Πύργος Απορρόφησης Ορισμός του μοριακού κλάσματος του Α στην αέρια φάση και στην υγρή φάση, με βάση τα αδρανή σε κάθε σημείο του πύργου απορρόφησης. Αντίστοιχα για το Β στην υγρή φάση: p A Y A x
26 8.3 Πύργος Απορρόφησης Ορισμός του μοριακού κλάσματος του Α στην αέρια φάση και στην υγρή φάση, με βάση τα αδρανή σε κάθε σημείο του πύργου απορρόφησης. Αντίστοιχα για το Β στην υγρή φάση: p A Y A x
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Ακαδημαϊκό έτος ΜΕΡΟΣ Α : ΘΕΩΡΙΑ/ΕΡΩΤΗΜΑΤΑ Τελική Εξέταση ΦΥΕ22 ΒΑΡΥΤΗΤΑ: 30%
 Ακαδημαϊκό έτος 03-04 7.06.04 ΜΕΡΟΣ Α : ΘΕΩΡΙΑ/ΕΡΩΤΗΜΑΤΑ Τελική Εξέταση ΦΥΕ ΒΑΡΥΤΗΤΑ: 30% ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΕΙΑ - ΘΕΩΡΙΑ ΔΙΑΡΚΕΙΑ: ώρα (4:00-5:00) Α. Χημική Θερμοδυναμική
Ακαδημαϊκό έτος 03-04 7.06.04 ΜΕΡΟΣ Α : ΘΕΩΡΙΑ/ΕΡΩΤΗΜΑΤΑ Τελική Εξέταση ΦΥΕ ΒΑΡΥΤΗΤΑ: 30% ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΕΙΑ - ΘΕΩΡΙΑ ΔΙΑΡΚΕΙΑ: ώρα (4:00-5:00) Α. Χημική Θερμοδυναμική
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ. Ενότητα #8: Βελτιστοποίηση Συστημάτων Ασαφούς Λογικής. Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #8: Βελτιστοποίηση Συστημάτων Ασαφούς Λογικής Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΥΦΥΗΣ ΕΛΕΓΧΟΣ Ενότητα #8: Βελτιστοποίηση Συστημάτων Ασαφούς Λογικής Αναστάσιος Ντούνης Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Άδειες
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Πίνακες Ορίζουσες. Πίνακας: ορθογώνια διάταξη αριθμών που αποτελείται από γραμμές και στήλες.
 1 Πίνακες Ορίζουσες Πίνακας: ορθογώνια διάταξη αριθμών που αποτελείται από γραμμές και στήλες. Παράδειγμα (χορήγηση Βαλασικλοβιρης (αντιυπερτασικό) σε νήπια) Ηλικία (μήνες) Μέσο Cmax (μg/ml) Μέσο βάρος
1 Πίνακες Ορίζουσες Πίνακας: ορθογώνια διάταξη αριθμών που αποτελείται από γραμμές και στήλες. Παράδειγμα (χορήγηση Βαλασικλοβιρης (αντιυπερτασικό) σε νήπια) Ηλικία (μήνες) Μέσο Cmax (μg/ml) Μέσο βάρος
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΕΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΕΙΟΥ ΘΕΜΑ Α Α1. Έστω μια συνάρτηση ff που έχει πεδίο ορισμού το ΔΔ. 1. Πότε η ffλέγεται συνεχής στο xx 0 ΔΔ ; 2. Πότε η ff λέγεται συνεχής; (Μονάδες
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΕΙΟΥ ΘΕΜΑ Α Α1. Έστω μια συνάρτηση ff που έχει πεδίο ορισμού το ΔΔ. 1. Πότε η ffλέγεται συνεχής στο xx 0 ΔΔ ; 2. Πότε η ff λέγεται συνεχής; (Μονάδες
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΤΥΠΟΠΟΙΗΣΗ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΤΥΠΟΠΟΙΗΣΗ 1 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Προβλήματα Αδιαστατοποίησης - Δυναμικής Πληθυσμών Άσκηση 3.3, σελίδα 32 από
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΤΥΠΟΠΟΙΗΣΗ 1 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Προβλήματα Αδιαστατοποίησης - Δυναμικής Πληθυσμών Άσκηση 3.3, σελίδα 32 από
Λύσεις. ΘΕΜΑ Α A1. Απόδειξη σελ. 144 Α2. Α. ii. B. iv A3. Ορισμός σελ. 162 Α4. i. Λ ii. Σ iii. Λ iv. Σ v. Σ ΘΕΜΑ Β Β1. Διακρίνουμε τις περιπτώσεις:
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΡΕΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α A. Απόδειξη σελ. 44 Α. Α. ii. B. iv A3. Ορισμός σελ. 6 Α4. i. Λ ii. Σ iii.
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΡΕΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α A. Απόδειξη σελ. 44 Α. Α. ii. B. iv A3. Ορισμός σελ. 6 Α4. i. Λ ii. Σ iii.
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α
 ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 5: Διαγράμματα σημείων ζέσεως συνθέσεως Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 Σελίδα 2 1. Θεωρία
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 5: Διαγράμματα σημείων ζέσεως συνθέσεως Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 Σελίδα 2 1. Θεωρία
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Συστήματα Αυτομάτου Ελέγχου Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ι Ενότητα #9: Σύστημα ης τάξης: Χρονική Απόκριση και Χαρακτηριστικά Μεγέθη (Φυσικοί Συντελεστές) Δημήτριος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ι Ενότητα #9: Σύστημα ης τάξης: Χρονική Απόκριση και Χαρακτηριστικά Μεγέθη (Φυσικοί Συντελεστές) Δημήτριος
Για αραιά διαλύματα : x 1 0 : μ i = μ i 0 RTlnx i χ. όπου μ i φ =μ i 0 χ
 Για ιδανικά διαλύματα : μ i = μ i lnx i x= γ=1 Για αραιά διαλύματα : x 1 : μ i = μ i lnx i χ μ i = μ i φ lnx i όπου μ i φ =μ i χ Χημική Ισορροπία λ Από σελ. 7 Χημική Ισορροπία όταν ν i μ i = (T,P σταθερό)
Για ιδανικά διαλύματα : μ i = μ i lnx i x= γ=1 Για αραιά διαλύματα : x 1 : μ i = μ i lnx i χ μ i = μ i φ lnx i όπου μ i φ =μ i χ Χημική Ισορροπία λ Από σελ. 7 Χημική Ισορροπία όταν ν i μ i = (T,P σταθερό)
ΑΠΟΡΡΟΦΗΣΗ (absorption)
 Εισαγωγή ΑΠΟΡΡΟΦΗΣΗ (absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσοabsorbate ή solute) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσο - absorbent), με το οποίο
Εισαγωγή ΑΠΟΡΡΟΦΗΣΗ (absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσοabsorbate ή solute) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσο - absorbent), με το οποίο
Υποθέστε ότι ο ρυθμός ροής από ένα ακροφύσιο είναι γραμμική συνάρτηση της διαφοράς στάθμης στα δύο άκρα του ακροφυσίου.
 ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
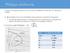 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Τρίτο πακέτο ασκήσεων
 ΕΚΠΑ Ακαδημαϊκό έτος 018-019 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Τρίτο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 18 Ιανουαρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
ΕΚΠΑ Ακαδημαϊκό έτος 018-019 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι Τρίτο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 18 Ιανουαρίου (στο μάθημα της κ. Κουραντή, του κ. Παπανδρέου
ΚΕΦΑΛΑΙΟ 4 ΑΠΟΡΡΟΦΗΣΗ- ΕΚΡΟΦΗΣΗ ΑΕΡΙΩΝ
 ΚΕΦΑΛΑΙΟ 4 ΑΠΟΡΡΟΦΗΣΗ- ΕΚΡΟΦΗΣΗ ΑΕΡΙΩΝ Η απορρόφηση αερίων είναι η διεργασία κατά την οποία μία ή περισσότερες συνιστώσες ενός αέριου μείγματος διαλύονται κατά την επαφή με ένα υγρό (Beet & Mers, 96).
ΚΕΦΑΛΑΙΟ 4 ΑΠΟΡΡΟΦΗΣΗ- ΕΚΡΟΦΗΣΗ ΑΕΡΙΩΝ Η απορρόφηση αερίων είναι η διεργασία κατά την οποία μία ή περισσότερες συνιστώσες ενός αέριου μείγματος διαλύονται κατά την επαφή με ένα υγρό (Beet & Mers, 96).
Εκπομπές και πορεία των χημικών ουσιών στο περιβάλλον
 Εκπομπές και πορεία των χημικών ουσιών στο περιβάλλον 4 Εκπομπές και πορεία των χημικών ουσιών στο περιβάλλον Enve-Lab Enve-Lab, 2015 1 Παράδειγμα μοντέλου πολλαπλών φάσεων: Μοντέλο πτητικότητας πολλαπλών
Εκπομπές και πορεία των χημικών ουσιών στο περιβάλλον 4 Εκπομπές και πορεία των χημικών ουσιών στο περιβάλλον Enve-Lab Enve-Lab, 2015 1 Παράδειγμα μοντέλου πολλαπλών φάσεων: Μοντέλο πτητικότητας πολλαπλών
Πρόρρηση Ισορροπίας Φάσεων. Υψηλές Πιέσεις
 Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων.
 25/9/27 Εισαγωγή Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων. Οι ρυθμοί δεν μπορούν να μετρηθούν απευθείας => συγκεντρώσεις των αντιδρώντων και των προϊόντων
25/9/27 Εισαγωγή Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων. Οι ρυθμοί δεν μπορούν να μετρηθούν απευθείας => συγκεντρώσεις των αντιδρώντων και των προϊόντων
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
M V n. nm V. M v. M v T P P S V P = = + = σταθερή σε παραγώγιση, τον ορισµό του συντελεστή διαστολής α = 1, κυκλική εναλλαγή 3
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΩΝ Separation Processes. Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens
 ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΩΝ Separation Processes Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens Διεργασίες Διαχωρισμών Ορισμός Φυσικές διεργασίες οι οποίες
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΩΝ Separation Processes Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens Διεργασίες Διαχωρισμών Ορισμός Φυσικές διεργασίες οι οποίες
Απρίλιος Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6F, L = 0.4F, F = 1 kmol/s. Ζητούμενα: x Fi, x Li
 Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Πίνακες Γραμμικά Συστήματα
 Πίνακες Γραμμικά Συστήματα 1. Είδη Πινάκων Οι πίνακες είναι ένα χρήσιμο μαθηματικό εργαλείο, με εφαρμογές και διασυνδέσεις σε πολλές επιστήμες. Η σημαντικότερη εφαρμογή των πινάκων είναι στην επίλυση συστημάτων
Πίνακες Γραμμικά Συστήματα 1. Είδη Πινάκων Οι πίνακες είναι ένα χρήσιμο μαθηματικό εργαλείο, με εφαρμογές και διασυνδέσεις σε πολλές επιστήμες. Η σημαντικότερη εφαρμογή των πινάκων είναι στην επίλυση συστημάτων
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ημερομηνία: Σάββατο 4 Μαΐου 2019 Διάρκεια Εξέτασης: 3 ώρες Α.1 α) ΣΩΣΤΟ ΑΠΑΝΤΗΣΕΙΣ ΟΜΑΔΑ ΠΡΩΤΗ
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ημερομηνία: Σάββατο 4 Μαΐου 2019 Διάρκεια Εξέτασης: 3 ώρες Α.1 α) ΣΩΣΤΟ ΑΠΑΝΤΗΣΕΙΣ ΟΜΑΔΑ ΠΡΩΤΗ
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ
 ΤΑΞΗ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ Ημερομηνία: Σάββατο 11 Μαΐου 019 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α Α1. Θεωρία. Σχολικό βιβλίο σελίδα 90 ΑΠΑΝΤΗΣΕΙΣ Α. α. (αα 1) β. (ββ 3) γ. (γγ ) δ. (δδ 5) Α3. α.
ΤΑΞΗ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ Ημερομηνία: Σάββατο 11 Μαΐου 019 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α Α1. Θεωρία. Σχολικό βιβλίο σελίδα 90 ΑΠΑΝΤΗΣΕΙΣ Α. α. (αα 1) β. (ββ 3) γ. (γγ ) δ. (δδ 5) Α3. α.
Κεφάλαιο 5: Διεργασίες απόσταξης
 92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
ΒΡΑΧΥΧΡΟΝΙΑ ΠΕΡΙΟΔΟΣ
 ΒΡΑΧΥΧΡΟΝΙΑ ΠΕΡΙΟΔΟΣ 1. Έστω ένας κλάδος όπου nn επιχειρήσεις έχουν την ίδια τεχνολογία. Η συνάρτηση κόστους της κάθε μιας επιχείρησης είναι CC() = 100 + 2. Η συνάρτηση ζήτησης του κλάδου είναι QQ DD =
ΒΡΑΧΥΧΡΟΝΙΑ ΠΕΡΙΟΔΟΣ 1. Έστω ένας κλάδος όπου nn επιχειρήσεις έχουν την ίδια τεχνολογία. Η συνάρτηση κόστους της κάθε μιας επιχείρησης είναι CC() = 100 + 2. Η συνάρτηση ζήτησης του κλάδου είναι QQ DD =
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα. Εισαγωγική Χημεία
 Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
ΟΡΓΑΝΙΚΟΙ ΡΥΠΟΙ - ΙΔΙΟΤΗΤΕΣ, ΚΑΤΑΝΟΜΗ ΣΤΟ ΕΔΑΦΟΣ
 ΟΡΓΑΝΙΚΟΙ ΡΥΠΟΙ - ΙΔΙΟΤΗΤΕΣ, ΚΑΤΑΝΟΜΗ ΣΤΟ ΕΔΑΦΟΣ ΛΙΓΑ ΣΤΟΙΧΕΙΑ ΟΡΓΑΝΙΚΗΣ ΧΗΜΕΙΑΣ ΦΥΣΙΚΟΧΗΜΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΟΡΓΑΝΙΚΩΝ ΡΥΠΩΝ ΚΑΤΑΝΟΜΗ ΦΑΣΕΩΝ ΣΤΑ ΕΔΑΦΗ ΑΠΟΚΑΤΑΣΤΑΣΗ ΡΥΠΑΣΜΕΝΩΝ ΕΔΑΦΩΝ 2α-1 ΣΤΟΙΧΕΙΑ ΟΡΓΑΝΙΚΗΣ
ΟΡΓΑΝΙΚΟΙ ΡΥΠΟΙ - ΙΔΙΟΤΗΤΕΣ, ΚΑΤΑΝΟΜΗ ΣΤΟ ΕΔΑΦΟΣ ΛΙΓΑ ΣΤΟΙΧΕΙΑ ΟΡΓΑΝΙΚΗΣ ΧΗΜΕΙΑΣ ΦΥΣΙΚΟΧΗΜΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΟΡΓΑΝΙΚΩΝ ΡΥΠΩΝ ΚΑΤΑΝΟΜΗ ΦΑΣΕΩΝ ΣΤΑ ΕΔΑΦΗ ΑΠΟΚΑΤΑΣΤΑΣΗ ΡΥΠΑΣΜΕΝΩΝ ΕΔΑΦΩΝ 2α-1 ΣΤΟΙΧΕΙΑ ΟΡΓΑΝΙΚΗΣ
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
Γεωργικά Φάρμακα ΙΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Έλεγχος φυτοπροστατευτικών προϊόντων Διαχωριστικές τεχνικές: χρωματογραφία Ουρανία Μενκίσογλου-Σπυρούδη Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Έλεγχος φυτοπροστατευτικών προϊόντων Διαχωριστικές τεχνικές: χρωματογραφία Ουρανία Μενκίσογλου-Σπυρούδη Άδειες Χρήσης Το παρόν
Από τις (1) και (2) έχουμε:
 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΚΑΝΟΝΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ 3 ΣΤΟ ΜΑΘΗΜΑ «ΔΙΗΛΕΚΤΡΙΚΕΣ, ΟΠΤΙΚΕΣ, ΜΑΓΝΗΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΥΛΙΚΩΝ» ΤΟΥ ΠΑΤΡΙΚ ΑΣΕΝΟΒ (OR STEVE HARRIS FOR MY FRIENDS FROM THE SHMMY FORUM) Θέμα ον : Έχουμε ιοντικό
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΚΑΝΟΝΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ 3 ΣΤΟ ΜΑΘΗΜΑ «ΔΙΗΛΕΚΤΡΙΚΕΣ, ΟΠΤΙΚΕΣ, ΜΑΓΝΗΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΥΛΙΚΩΝ» ΤΟΥ ΠΑΤΡΙΚ ΑΣΕΝΟΒ (OR STEVE HARRIS FOR MY FRIENDS FROM THE SHMMY FORUM) Θέμα ον : Έχουμε ιοντικό
Προβλήματα εκχύλισης
 Προβλήματα εκχύλισης Πηγή: Μαρίνου-Κουρή, Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, εκδ. Παπασωτηρίου, Αθήνα, 1994 1. Εκχύλιση ακετόνης από νερό με χλωροβενζόλιο σε μονοβάθμιο εκχυλιστήρα. 100 kg διαλύματος
Προβλήματα εκχύλισης Πηγή: Μαρίνου-Κουρή, Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, εκδ. Παπασωτηρίου, Αθήνα, 1994 1. Εκχύλιση ακετόνης από νερό με χλωροβενζόλιο σε μονοβάθμιο εκχυλιστήρα. 100 kg διαλύματος
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction Ορισμός Εκχύλισης Υγρού- Υγρού Αποτελεί μια διεργασία
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction Ορισμός Εκχύλισης Υγρού- Υγρού Αποτελεί μια διεργασία
Ε.Α.Υ. Υπολογιστική Όραση. Κατάτμηση Εικόνας
 Ε.Α.Υ. Υπολογιστική Όραση Κατάτμηση Εικόνας Γεώργιος Παπαϊωάννου 2015 ΚΑΤΩΦΛΙΩΣΗ Κατωφλίωση - Γενικά Είναι η πιο απλή μέθοδος segmentation εικόνας Χωρίζουμε την εικόνα σε 2 (binary) ή περισσότερες στάθμες
Ε.Α.Υ. Υπολογιστική Όραση Κατάτμηση Εικόνας Γεώργιος Παπαϊωάννου 2015 ΚΑΤΩΦΛΙΩΣΗ Κατωφλίωση - Γενικά Είναι η πιο απλή μέθοδος segmentation εικόνας Χωρίζουμε την εικόνα σε 2 (binary) ή περισσότερες στάθμες
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ
 Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Υπολογισμός & Πρόρρηση. Θερμοδυναμικών Ιδιοτήτων
 Υπολογισμός & Πρόρρηση Θερμοδυναμικών Ιδιοτήτων d du d Θερμοδυναμικές Ιδιότητες d dh d d d du d d dh U A H G d d da d d dg d du dq dq d / d du dq Θεμελιώδεις Συναρτήσεις περιέχουν όλες τις πληροφορίες
Υπολογισμός & Πρόρρηση Θερμοδυναμικών Ιδιοτήτων d du d Θερμοδυναμικές Ιδιότητες d dh d d d du d d dh U A H G d d da d d dg d du dq dq d / d du dq Θεμελιώδεις Συναρτήσεις περιέχουν όλες τις πληροφορίες
(β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele
 Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
ΕΞΙΣΩΣΗ CLAUSIUS-CLAPEYRON ΘΕΩΡΙΑ
 ΕΞΙΣΩΣΗ CLAUSIUS-CLAEYRON ΘΕΩΡΙΑ Περιεχόμενα 1. 3D Διάγραμμα Φάσης 2. Λανθάνουσα θερμότητα 3. Εξίσωση Clausius Clapeyron 4. Συμπιεστότητα 5. Θερμική διαστολή 6. Θερμοχωρητικότητα 1 στερεό στερεό+υγρό υγρό
ΕΞΙΣΩΣΗ CLAUSIUS-CLAEYRON ΘΕΩΡΙΑ Περιεχόμενα 1. 3D Διάγραμμα Φάσης 2. Λανθάνουσα θερμότητα 3. Εξίσωση Clausius Clapeyron 4. Συμπιεστότητα 5. Θερμική διαστολή 6. Θερμοχωρητικότητα 1 στερεό στερεό+υγρό υγρό
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 8 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 8 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ
 ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Μαΐου 09 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α Α. β Α. γ Α3. γ Α4. γ ΑΠΑΝΤΗΣΕΙΣ Α5. α. Σωστό β. Λάθος γ. Λάθος δ. Λάθος ε. Λάθος ΘΕΜΑ Β Β. β. Άπο τη
ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Μαΐου 09 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α Α. β Α. γ Α3. γ Α4. γ ΑΠΑΝΤΗΣΕΙΣ Α5. α. Σωστό β. Λάθος γ. Λάθος δ. Λάθος ε. Λάθος ΘΕΜΑ Β Β. β. Άπο τη
MIKΡΕΣ ΟΠΕΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm MIKΡΕΣ ΟΠΕΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Μικρές Οπές. Ασκήσεις ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm MIKΡΕΣ ΟΠΕΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Μικρές Οπές. Ασκήσεις ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm
Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ
 Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 pulis@chem.auth.gr phtcatalysisgrup.web.auth.gr Διαλύματα και Συστήματα υγρών Διαμόρφωση μαθήματος Θεωρία/Ασκήσεις
Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 pulis@chem.auth.gr phtcatalysisgrup.web.auth.gr Διαλύματα και Συστήματα υγρών Διαμόρφωση μαθήματος Θεωρία/Ασκήσεις
Φυσική Ι. Ενότητα 3: Μηχανικές δυνάμεις. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική Ι Ενότητα 3: Μηχανικές δυνάμεις Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Περιγραφή και παρουσίαση μηχανικών δυνάμεων Βαρύτητα Τριβή (στατική και ολίσθησης) Τάση
Φυσική Ι Ενότητα 3: Μηχανικές δυνάμεις Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Περιγραφή και παρουσίαση μηχανικών δυνάμεων Βαρύτητα Τριβή (στατική και ολίσθησης) Τάση
