Η γλώσσα προγραµµατισµού Prolog Αλγόριθµοι αναζήτησης σε Prolog
|
|
|
- Ἡρωδίωνν Δαμασκηνός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Λογικός Προγραµµατισµός Η γλώσσα προγραµµατισµού Prolog Αλγόριθµοι αναζήτησης σε Prolog Προτάσεις Horn (1/2) Οι προτάσεις Horn ή Οριστικές Προτάσεις (Definite Clauses) αποτελούν ένα περιορισµένο υποσύνολο της λογικής πρώτης τάξης. Ειδικότερα, µια πρόταση Horn µπορεί να έχει τη µορφή: A1 A2... AN B ή όπως συνηθέστερα γράφεται: B A1 A2... AN ήακόµη: B A1 A2... AN Ηπρόταση B δηλώνει ότι η πρόταση Β είναι αληθής. εν µπορούν όλες οι βάσεις γνώσεις να µεταφραστούν σε προτάσεις Horn, λόγω της µη δυνατότητας ύπαρξης αρνητικών συµβόλων Γιάννης Ρεφανίδης 2
2 Προτάσεις Horn (2/2) Η µορφή που έχουν οι προτάσεις Horn έχει ως αποτέλεσµα ναµην είναι δυνατόν να αποδεικνύονται αρνητικές προτάσεις. Για το λόγο αυτό, οι ερωτήσεις που κάνουµε σεένασύστηµα προτάσεων Horn αφορούν την απόδειξη θετικών µόνο προτάσεων. Έτσι ένα σύστηµα προτάσεωνhorn δεν µπορεί ποτέ να πέσει σε αντίφαση, µε την έννοια ότι δεν µπορεί ποτέ να αποδείξει τις προτάσεις P και P ταυτόχρονα. «Καταχρηστικά» πολλές φορές θεωρούµε ότι η µη δυνατότητα απόδειξης της πρότασης P ισοδυναµεί µε την απόδειξη της πρότασης P. Γιάννης Ρεφανίδης 3 Λογικός προγραµµατισµός (1/2) Ο λογικός προγραµµατισµός αποτελεί την πιο διαδεδοµένη υλοποίηση της λογικής πρώτης τάξης µέσω της γλώσσας λογικού προγραµµατισµού Prolog. Ο λογικός προγραµµατισµός βασίζεται στις προτάσεις Horn. Η γλώσσα Prolog (όπως και η γλώσσα συναρτησιακού προγραµµατισµού LISP) βοηθά στη γρήγορη ανάπτυξη εφαρµογών τεχνητής νοηµοσύνης. Παρέχει: Ευκολία στο χειρισµό συµβόλων Ενσωµατωµένο µηχανισµό ταυτοποίησης/ενοποίησης Ενσωµατωµένο αλγόριθµο αναζήτησης πρώτα-κατά-βάθος Χρήσιµο link: Γιάννης Ρεφανίδης 4
3 Λογικός προγραµµατισµός (2/2) Οι προτάσεις στο λογικό προγραµµατισµό µπορούν να περιέχουν µεταβλητές, οι οποίες όµως θεωρούνται όλες καθολικά ποσοτικοποιηµένες. Πατέρας(x,y) Γονιός(x,y) Άρεν(x) Το σύµβολο του καθολικού ποσοδείκτη το παραλείπουµε. Υπάρχουν ενσωµατωµένες συναρτήσεις για αριθµητικές πράξεις. Υπάρχουν κατηγορήµατα διαδικαστικής υφής όπως π.χ. κατηγορήµατα εισόδου/εξόδου. Η στρατηγική αναζήτησης είναι πρώτα-κατά-βάθος. Έχει σηµασία η σειρά µε την οποία είναι γραµµένες οι προτάσεις στη βάση γνώσης. Ηαναζήτησηµπορεί να παγιδευθεί σε κλαδιά άπειρου βάθους. Γιάννης Ρεφανίδης 5 Σύνταξη (1/2) Τα ονόµατα των κατηγορηµάτων, των αντικειµένων και των συναρτησιακών όρων ξεκινούν µε πεζά γράµµατα. Τα ονόµατα των µεταβλητών ξεκινούν µε κεφαλαίο γράµµα. Κάθε πρόταση τερµατίζει µε τελεία. Γεγονότα (απλές προτάσεις) : άνθρωπος (σωκράτης). Κανόνες (σύνθετες προτάσεις): θνητός(χ) :- άνθρωπος(χ). Για κάθε Χ, εάν το Χ είναι άνθρωπος τότε το Χ είναι θνητός. πατέρας(χ,υ) :- γονιός(χ,υ), άρεν(χ). Για κάθε Χ και Υ, το Χ είναι πατέρας του Υ εάν το Χ είναι γονιός του Υ και επιπλέον το φύλο του Χ είναι αρσενικό. Γιάννης Ρεφανίδης 6
4 Σύνταξη (2/2) Συγκρίνοντας τις προτάσεις: πατέρας(χ,υ) :- γονιός(χ,υ), άρεν(χ). Πατέρας(x,y) Γονιός(x,y) Άρεν(x) βλέπουµε ότιχρησιµοποιείται το :- αντί για και το κόµµα αντίγια το. Προτάσεις σαν την παραπάνω ονομάζονται κανόνες και ερμηνεύονται ως εξής: Γιαναισχύειτοπατέρας(X,Y) πρέπει να ισχύουν ταυτόχρονα τα γονιός(χ,υ) και άρεν(χ). ήισοδύναμα Για κάθε Χ,Υ, εάν ισχύουν τα γονιός(χ,υ) και άρεν(χ) τότε ισχύει και το πατέρας(χ,υ). Το συμπέρασμα ( πατέρας(χ,υ) ) ονομάζεται κεφαλή (head) του κανόνα ενώ οι προϋποθέσεις (γονιός(χ,υ), άρεν(χ) ) ονοµάζονται σώµα του κανόνα. Γιάννης Ρεφανίδης 7 ιαδικασίες Ένα σύνολο από προτάσεις, γεγονότα ή κανόνες, όπου στην κεφαλή τους έχουν όλες το ίδιο κατηγόρηµα καιµε τον ίδιο αριθµό ορισµάτων, ονοµάζεται διαδικασία. Παρακάτω φαίνεται µια διαδικασία που αφορά το κατηγόρηµα uncle/2 καιορίζειπότεέναςάνθρωποςείναιθείοςενόςάλλου. uncle(x,y) :- brother(x,z), father(z,y). uncle(x,y):- brother(x,z), mother(z,y). Γιάννης Ρεφανίδης 8
5 Υποβολή ερωτήσεων (1/6) Η Prolog είναι συνήθως µια διερµηνευόµενη γλώσσα. Ο χρήστης φορτώνει το πρόγραµµα στη µνήµη και στη συνέχεια υποβάλλει ερωτήσεις για τις οποίες περιµένει απάντηση. Ο διερµηνέας της Prolog εµφανίζει την προτροπή:?- για την υποβολή ερωτήσεων. Οι ερωτήσεις µπορούν να αποτελούνται από σύζευξη ενός ή περισσοτέρων κατηγορηµάτων µε ή χωρίς µεταβλητές. Κάθε ερώτηση πρέπει να τερµατίζει µε τελεία. Γιάννης Ρεφανίδης 9 Υποβολή ερωτήσεων (2/6) Για παράδειγµα, έστω η παρακάτω βάση γνώσης (το "πρόγραµµα") σε Prolog: parent(nick,maria). parent(nick, george). male(nick). male(george). female(maria). father(x,y):-parent(x,y), male(x). mother (X,Y):-parent(X,Y), female(x). Υποβάλλουµε την ερώτηση:?-father(nick,maria)....και παίρνουµε την απάντηση: yes. Προσοχή: Οι µεταβλητές διαφορετικών προτάσεων θεωρούνται πάντα διαφορετικές, ακόµη και αν έχουν το ίδιο όνοµα. Γιάννης Ρεφανίδης 10
6 Υποβολή ερωτήσεων (3/6) Παρόµοια, υποβάλλουµε την ερώτηση:?-father(maria,nick)....και παίρνουµε την απάντηση: no. Μια ερώτηση µπορεί να περιέχει µεταβλητές, όπως π.χ.:?- father(nick,z). Το νόηµα µιας τέτοιας ερώτησης είναι να ελεγχθεί εάν υπάρχουν τιµές για τη µεταβλητή Ζ, για τις οποίες να ισχύει το father(nick,z). Βλέπουµε δηλαδήότιοιµεταβλητές στις ερωτήσεις θεωρούνται υπαρξιακά ποσοτικοποιηµένες. ΠΡΟΣΟΧΗ: Οι µεταβλητές στις ερωτήσεις είναι διαφορετικές από τις µεταβλητές των προτάσεων της βάσης γνώσης, ακόµη καιανέχουν ίδια ονόµατα. Γιάννης Ρεφανίδης 11 Υποβολή ερωτήσεων (4/6) Στην περίπτωση ερώτησης µε µεταβλητές και εφόσον υπάρχουν τιµές για τις µεταβλητές για τις οποίες να ισχύει η ερώτηση, η Prolog απαντά µε την ανάθεση των τιµών στις µεταβλητές (αντί για ένα απλό yes):?- father(nick,z). Z=maria Αφού εµφανίσει µιαπρώτηδυνατήανάθεσητιµών στις µεταβλητές, µπορούµε να ζητήσουµε να ψάξει για άλλες τέτοιες "λύσεις". Για το σκοπό αυτό πατάµε το πλήκτρο; ή το κενό(spacebar), οπότε η Prolog απαντά: Ζ=george Στην παραθυρική έκδοση της ECLiPSe ζητούµε επιπλέον λύσεις πατώντας το κουµπί More. Γιάννης Ρεφανίδης 12
7 Υποβολή ερωτήσεων (5/6) Εάν για µια ερώτηση µε µεταβλητές η Prolog δεν µπορέσει να βρει καµία δυνατή ανάθεση τιµών σε αυτές, τότε απαντά αρνητικά:?- father(x,nick). no Μπορούµε να έχουµε περισσότερες από µια µεταβλητές σε µια ερώτηση:?- father(a,b). οπότε η απάντηση, εφόσον υπάρχει, µας δίνει τιµές για όλες τις µεταβλητές: Α=nick, B=maria και αν ζητήσουµε και δεύτερη λύση παίρνουµε την: Α=nick, B=george Γιάννης Ρεφανίδης 13 Υποβολή ερωτήσεων (6/6) Τέλος, µια ερώτηση µπορεί να είναι σύζευξη 2 ή περισσότερων απλών προτάσεων (µε ή και χωρίς µεταβλητές):?- male(z), father (nick,z). Η ερώτηση αυτή ερµηνεύεται ως: Βρες τα αντικείµενα εκείνα Ζ για τα οποία ισχύουν ταυτόχρονα οι σχέσεις father (nick,z) και male(z). ή σε απλά ελληνικά: Βρες τα παιδιά του nick τα οποία είναι αγόρια. Η Prolog θα απαντήσει: Z=george Γιάννης Ρεφανίδης 14
8 Εξαγωγή συµπερασµάτων (1/3) Η διαδικασία απόδειξης ξεκινά µε την υποβολή µιας ερώτησης, έστω π.χ.: male(z), father(nick,z). Η Prolog προσπαθεί να "αποδείξει" µία-µία τις επιµέρους προτάσεις της ερώτησης. Για να αποδειχθεί µια πρόταση, πρέπει αυτή να ταυτοποιηθεί είτε: µε ένα γεγονός της βάσης γνώσης, είτε µε την κεφαλή ενός κανόνα της βάσης γνώσης. Στην περίπτωση ταυτοποίησης µε την κεφαλή ενός κανόνα, το πρόβληµα "µετατίθεται" στην απόδειξη όλων των επιµέρους προτάσεων στο σώµα του κανόνα. Γιάννης Ρεφανίδης 15 Εξαγωγή συµπερασµάτων (2/3) Για παράδειγµα, η πρότασηmale(z) ταυτοποιείται µε την πρόταση: male(nick). µε την αντικατάσταση {Z/nick}. Στη συνέχεια η πρόταση father(nick,z), η οποία πλέον έχει γίνει father(nick,nick), ταυτοποιείται µε την κεφαλή του κανόνα: father(x,y):-parent(x,y), male(x). µε την αντικατάσταση {X/nick, Y/nick}, οπότε πλέον το πρόβληµα µετατίθεται στην απόδειξη των προτάσεων: parent(nick,nick), male(nick) Γιάννης Ρεφανίδης 16
9 Εξαγωγή συµπερασµάτων (3/3) Η προσπάθεια απόδειξης της προτάσης: parent(nick,nick) θα αποτύχει, οπότε ο µηχανισµός αναζήτησης της Prolog θα αναζητήσει εναλλακτικούς τρόπους απόδειξης. Θα βρει ότι η αρχική πρόταση: male(z) µπορούσε να ταυτοποιηθεί και µε το γεγονός: male(george) της βάσης γνώσης, κάτι που οδηγούσε στην ανάγκη για απόδειξη των γεγονότων: parent(nick,george), male(george) τα οποία υπάρχουν στη βάση γνώσης. Η απάντηση που τελικά παίρνουµε είναιη: Z=george Γιάννης Ρεφανίδης 17 Παρατηρήσεις Κατά την προσπάθεια απάντησης της ερώτησης του χρήστη, η Prolog προσπαθεί να ταυτοποιήσει την ερώτηση µε κάποιο γεγονός ή την κεφαλή κάποιου κανόνα. Κατά την ταυτοποίηση οι µεταβλητές που υπάρχουν στην ερώτηση του χρήστη παίρνουν τιµές (δεσµεύονται). Μια µεταβλητή που έχει πάρει κάποια τιµήδεν µπορεί να την αλλάξει στο τρέχον µονοπάτι (κλαδί) αναζήτησης. Ο µόνος τρόπος µια µεταβλητή να αλλάξει τιµή είναιτο µονοπάτι αναζήτησης στο οποίο έγινε η δέσµευση να αποτύχει. Σε αυτή την περίπτωση όλες οι µεταβλητές που είχαν πάρει τιµές σε αυτό το µονοπάτι αναζήτησης, τις χάνουν. Η Prolog θα δοκιµάσει εναλλακτικά µονοπάτια αναζήτησης, στα οποία θα γίνουν νέες αποδόσεις τιµών. Η διαδικασία επιστροφής σε εναλλακτικά µονοπάτια αναζήτησης, ύστερα από µια αποτυχία, ονοµάζεται backtracking (υπαναχώρηση). Γιάννης Ρεφανίδης 18
10 Στρατηγική αναζήτησης Η στρατηγική αναζήτησης που ακολουθεί η Prolog είναι η πρώτακατά-βάθος. Για παράδειγµα, έστω η παρακάτω ερώτηση:?- a, b. Θα προσπαθήσει λοιπόν η Prolog να «αποδείξει» πρώτα το a και µετά το b. Έστω ότι στο τρέχον πρόγραµµα υπάρχει ο κανόνας: a:-a1, a2. Άρα, γιανααποδείξειηprolog το a, πρέπει να αποδείξει τα a1 και a2. Η Prolog θα προσπαθήσει να αποδείξει τα a1 και a2 πριν το b. ηλαδή, τα «παιδιά» του τρέχοντος στόχου έχουν προτεραιότητα έναντι των υπόλοιπων παλαιότερων στόχων. Γιάννης Ρεφανίδης 19 Ανώνυµη µεταβλητή (1/3) Τόσο στα προγράµµατα, όσο και στις ερωτήσεις µας στην Prolog, µπορούµε ναχρησιµοποιούµε τηνανώνυµη µεταβλητή. Ως «ανώνυµη» χαρακτηρίζεται η µεταβλητή _ (χωρίς τα εισαγωγικά) καθώς και οποιαδήποτε µεταβλητή έχει όνοµα που ξεκινά µε τοσύµβολο _. Ηεµφάνιση της ανώνυµης µεταβλητής σε µια ερώτηση, για παράδειγµα στην:?- male(_). ερµηνεύεται ως εξής: Υπάρχει κάποιο «αντικείµενο» του προγράµµατος το οποίο να είναι male ; Εάν υπάρχει κάποιο τέτοιο αντικείµενο, η Prolog θα αποκριθεί yes (χωρίς να µας αναφέρει το όνοµά του), ειδάλλως θα αποκριθεί no. Γιάννης Ρεφανίδης 20
11 Ανώνυµη µεταβλητή (2/3) Η ανώνυµη µεταβλητή µπορεί να εµφανίζεται και µέσα σε κανόνες. Για παράδειγµα, έστω ότι έχουµε τον κανόνα: parent(x,y):- ο οποίος δηλώνει ότι ο Χ είναι γονιός του Υ. Έστω ότι θέλουµε να ορίσουµε µε κανόνες το κατηγόρηµα children_benefit(x), το οποίο ορίζει ότι ο Χ δικαιούται επίδοµα τέκνων. Αυτό ισχύει µόνο εφόσον ο Χ είναι γονιός κάποιου Υ, χωρίς να µας ενδιαφέρει το όνοµα του Υ. Το γράφουµε ωςεξής: children_benefit(x) :- parent(x,_). Γιάννης Ρεφανίδης 21 Ανώνυµη µεταβλητή (3/3) ΠΡΟΣΟΧΗ: Σε περίπτωση που σε έναν κανόνα ή σε µια ερώτηση ή ακόµη και µέσα στο ίδιο το κατηγόρηµα εµφανίζονται περισσότερες από µια ανώνυµες µεταβλητές, αυτές θεωρούνται διαφορετικές. Ένας απλός τρόπος να ανιχνεύουµε πότεχρειάζεταινα χρησιµοποιήσουµε µια ανώνυµη µεταβλητή είναι ο εξής: Εάν σε ένα γεγονός ή κανόνα το όνοµα µιας µεταβλητής εµφανίζεται µία και µόνο µια φορά, τότε αυτή η µεταβλητή µπορεί να γίνει ανώνυµη. Τέτοιες µεταβλητές που εµφανίζονται µόνο µια φορά σε κάποιο γεγονός ή κανόνα ονοµάζονται µοναδικές µεταβλητές (singleton variables). Επειδή µοναδικές µεταβλητές µπορεί να προκύψουν από ακούσιο αναγραµµατισµό, όλες οι Prolog εµφανίζουν προειδοποιήσεις (warnings) για αυτές κατά τη διαδικασία µετάφρασης (compile) ενός προγράµµατος. Γιάννης Ρεφανίδης 22
12 Σύνθετοι όροι (1/3) Τα ορίσµατα των κατηγορηµάτων µπορεί να είναι σύνθετοι όροι (ή αλλιώς «συναρτησιακοί όροι»). Ένας σύνθετος όρος αποτελείται από το συναρτησιακό σύµβολο και τα ορίσµατα: f(k1, k2,, kn) Τα ορίσµατα ενός σύνθετου όρου µπορεί να είναι και αυτά σύνθετοι όροι. Οι σύνθετοι όροι χρησιµεύουν στην οµαδοποίηση των ορισµάτων ενός κατηγορήµατος και τελικά στην αναγνωσιµότητα του προγράµµατος. Οποιοδήποτε πρόγραµµα µε σύνθετους όρους µπορεί πολύ εύκολα να µετατραπεί σε ένα πρόγραµµα χωρίς σύνθετους όρους. Γιάννης Ρεφανίδης 23 Σύνθετοι όροι (2/3) Για παράδειγµα, έστω ότι στην αναλυτική γεωµετρία θέλουµε να αναπαραστήσουµε ευθύγραµµα τµήµατα στο επίπεδο. Για κάθε ευθ.τµήµα χρειάζεται να αναπαραστήσουµε τις δύο κορυφές του, άρα χρειαζόµαστε 4 αριθµούς. Για παράδειγµα: segment (2,1,5,4). όπου το segment είναι ένα κατηγόρηµα τάξης4. Εναλλακτικά µπορούµε ναοµαδοποιήσουµε τις τέσσερις παραµέτρους του segment, χρησιµοποιώντας σύνθετους όρους. Για παράδειγµα: segment (point(2,1), point(5,4) ). όπου το segment είναι πλέον ένα κατηγόρηµα τάξης2 και έχουµε επιπλέον ορίσει/χρησιµοποιήσει και τον συναρτησιακό όρο point µε δύοορίσµατα. Αυτό που κερδίσαµε είναι η αναγνωσιµότητα του προγράµµατος. Γιάννης Ρεφανίδης 24
13 Σύνθετοι όροι (3/3) Προσοχή χρειάζεται όταν ενοποιούµε κατηγορήµατα που περιλαµβάνουν σύνθετους όρους. Παρακάτω δίνονται µερικά παραδείγµατα. segment(point(2,3), point(5,4) ) segment(point(2,3), point(5,4) ) segment(point(2,3), point(5,4) ) segment(x,y) segment(x, point(y,z)) segment(3,4,5,4) {point(2,3)/x, point(5,4)/y} {point(2,3)/x, 5/Y, 4/Z} αποτυχία Γιάννης Ρεφανίδης 25 Αναδροµή (1/3) Ένας κανόνας στην Prolog που περιλαµβάνει στο σώµα του κάποια κλήση στο κατηγόρηµα της κεφαλής του κανόνα ονοµάζεται αναδροµικός. Για παράδειγµα, έστω το παρακάτω πρόγραµµα: father(nick, george). father(george, john). father(john, jim). ancestor(x,y) :- father(x,y). ancestor(x,y) :- father(x,z), ancestor(z,y). Ο κανόνας που ορίζει τη σχέση ancestor είναι αναδροµικός.?- ancestor(nick, jim). yes Γιάννης Ρεφανίδης 26
14 Αναδροµή (2/3) Χωρίς τη χρήση αναδροµικού κανόνα, θα έπρεπε να ορίσουµε πολλούς µη αναδροµικούς κανόνες της µορφής: ancestor(x,y) :- father(x,y). ancestor(x,y) :- father(x,z), father(z,y). ancestor(x,y) :- father(x,z1), father(z1,z2),, father(zn,y). Είναι φανερό ότι οι παραπάνω κανόνες, εκτός από το ότι είναι πάρα πολλοί, δεν καλύπτουν και όλες τις περιπτώσεις. Γιάννης Ρεφανίδης 27 Αναδροµή (3/3) Με τη χρήση αναδροµικών κανόνων, είναι δυνατόν η Prolog να παγιδευτεί σε ατέρµονα κλαδιά αναζήτησης και να µην δώσει καµία απάντηση (είτε θετική είτε αρνητική), όση ώρα και αν περιµένουµε. Σε περίπτωση θετικής αναµενόµενης απάντησης, αυτό θα µπορούσε να αποφευχθεί εάν η Prolog ακολουθούσε µια αναζήτηση πρώτα-κατάπλάτος (αντί για την αναζήτηση πρώτα-κατά-βάθος) που υιοθετεί. Αλλάζοντας τη σειρά συγγραφής των κανόνων της βάσης γνώσης, καθώς και των κλήσεων στο σώµα κάθεκανόνα, συνήθως αποφεύγουµε τέτοια προβλήµατα. Για παράδειγµα, ο παρακάτω αναδροµικός ορισµός της διαδικασίας ancestor, όπου έχει αλλάξει η σειρά των δύο κανόνων αλλά και στο σώµα του κανόνα, «κολλάει» σε οποιαδήποτε κλήση στο ancestor/2. ancestor(x,y) :- ancestor(z,y), father(x,z). ancestor(x,y) :- father(x,y). Γιάννης Ρεφανίδης 28
15 Λίστες (1/3) Οι λίστες είναι η σηµαντικότερη δοµή δεδοµένων της Prolog. Μια λίστα είναι ένας δυναµικός µονοδιάστατος πίνακας µε στοιχεία του αριθµούς, σύµβολα, σύνθετους όρους ή και άλλες λίστες. Τα στοιχεία µιας λίστας δεν είναι απαραίτητο να είναι του ίδιου τύπου. Μερικά παραδείγµατα λιστών: [physics, 8, maths, 9] [ nick, 3, 12, ball, point(1,2), [a, b] ] Γιάννης Ρεφανίδης 29 Λίστες (2/3) Μια λίστα µπορεί να ενοποιηθεί µε µια µεταβλητή: Χ= [physics, 8, maths, 9] Τιςπερισσότερεςφορέςθέλουµε ναχειριστούµε ταστοιχείαµιας λίστας ένα-ένα. Σε αυτή την περίπτωση έχουµε τη δυνατότητα να ενοποιήσουµε µια µεταβλητή µε το πρώτο στοιχείο της λίστας(κεφαλή) και µια άλλη µεταβλητή µε τα υπόλοιπα στοιχεία της λίστας(ουρά). Έτσι η προσπάθεια ταυτοποίησης: [Χ Y] = [physics, 8, maths, 9] µας δίνει: Χ = physics Y = [8, maths, 9] Γιάννης Ρεφανίδης 30
16 Λίστες (3/3) Παρακάτω φαίνονται διάφορες προσπάθειες ενοποίησης µε λίστες. 1ος όρος [a, b, c] [a, b, c] [a, b] [a,b] [f(1), k, [m] ] [f(1), k, [m] ] 2ος όρος [a, b, c, d] [X, Y] [a,x] [a X ] [ f(x), Y, Z ] [ f(x), Y Z ] Ενοποίηση αποτυχία αποτυχία { b / X } { [b] / X } {1/X, k/y, [m] /Z } {1/X, k/y, [[m]] /Z } [[a]] [X Y] { [a] / X, []/Y } Γιάννης Ρεφανίδης 31 Παρατήρηση Οι λίστες στην Prolog µπορείναθεωρηθείότιείναισύνθετοιόροι τάξης 2, όπου το πρώτο όρισµα είναι η κεφαλή της λίστας και το δεύτερο η ουρά της (σε µορφή λίστας). Ως συναρτησιακό σύµβολο χρησιµοποιείται η τελεία. Έτσι ισχύουν οι παρακάτω ισοδυναµίες. [a, b] =.(a,.(b) ) [a] =.(a, [ ] ) [a, b, c] =.(a,.(b,.(c, [ ] ) ) ) [ [a], b] =.(.(a, [ ] ),.(b, [ ] ) ) Ουσιαστικά δηλαδή η αναπαράσταση µε αγκύλες είναι για την ευκολία του προγραµµατιστή και την αναγνωσιµότητα των προγραµµάτων. Γιάννης Ρεφανίδης 32
17 Παράδειγµα: Έλεγχος συµπερίληψης σε λίστα Το κατηγόρηµα member παρακάτω ελέγχει εάν ένα στοιχείο (πρώτο όρισµα) ανήκει σε µία λίστα (το δεύτερο όρισµα): member(x, [ X Y ] ). member(x, [ Head Tail ] ) :- member(x, Tail). Πιθανές ερωτήσεις:?- member( 2, [ 1, 2, 3] ). yes?- member(4, [ 1, 2, 3 ] ). no?- member(x, [1, 2, 3]). X=1 X=2 X=3 Κατηγορήµατα σαν το παραπάνω υπάρχουν ενσωµατεµένα στις περισσότερες υλοποιήσεις της Prolog καιέτσιδενχρειάζεταιναορίζονται ξανά από τον προγραµµατιστή. Γιάννης Ρεφανίδης 33 Παράδειγµα: Εύρεση τελευταίου στοιχείου λίστας (1/2) Το παρακάτω κατηγόρηµα, last(x,l) επιστρέφει ως Χ το τελευταίο στοιχείο της λίστας L. last(x, [X]). last(x, [ _Head Tail] ):- last(x,tail). Μπορούµε να κάνουµε κλήσεις στο last/2 µε το πρώτο όρισµα ελεύθερο και το δεύτερο δεσµευµένο. Για παράδειγµα, µια τέτοια κλήση είναι η:?- last( Z, [2, 3, 4] ). η οποία επιστρέφει Z=4 Εάν καλέσουµε τοκατηγόρηµα καιµε ταδύοορίσµατα δεσµευµένα, η απάντηση που θα πάρουµε θαείναιyes ή no, ανάλογα µε τοαντο πρώτο όρισµα είναι το τελευταίο στοιχείο της λίστα τους δεύτερου ορίσµατος ή όχι. Γιάννης Ρεφανίδης 34
18 Παράδειγµα: Εύρεση τελευταίου στοιχείου λίστας (2/2) Για παράδειγµα, η κλήση:?- last( 4, [2, 3, 4]). επιστρέφει yes, ενώ η κλήση:?- last( 1, [2, 3, 4]). επιστρέφει no. Το κατηγόρηµα last θα λειτουργήσει ακόµη και αν το καλέσουµε µε το πρώτο όρισµα δεσµευµένο και το δεύτερο ελεύθερο! Σε αυτή την περίπτωση θα επιστρέψει (άπειρες στο πλήθος) λίστες των οποίων το τελευταίο στοιχείο είναι το πρώτο όρισµα. Μπορούµε ακόµη νατοκαλέσουµε καιµε ταδύοορίσµατα ελεύθερα. Σε αυτή την περίπτωση θα επιστρέψει (άπειρες στο πλήθος) λίστες των οποίων το τελευταίο στοιχείο είναι ενοποιηµένο µε το πρώτο όρισµα (µολονότι και τα δύο εξακολουθούν να είναι µεταβλητές). Γιάννης Ρεφανίδης 35 Παράδειγµα: Συνένωση λιστών (1/3) Θα ορίσουµε ένα κατηγόρηµα append(l1,l2,l3), το οποίο επιτυγχάνει όταν η λίστα L3 είναι η ένωση (παράθεση) των L1 και L2. Θα µπορούµε νατοκαλούµε µε οποιοδήποτε όρισµά τουδεσµευµένο ή ελεύθερο. Οι βασικές ιδέες είναι οι εξής: Ησυνένωσηµιας λίστας L2 µε την κενή λίστα είναι η ίδια λίστα L2. append([ ], L2, L2). Ησυνένωση µιας λίστας ενός στοιχείου και µιας λίστας L2 δίνεται από τον παρακάτω κανόνα: append([a], L2, [A L2]). Παρατήρηση: Η παραπάνω δήλωση θα µπορούσε πιο περιφραστικά να γραφεί ισοδύναµα καιως: append(l1, L2, L3) :- L1=[A], L3=[A L2]. Γιάννης Ρεφανίδης 36
19 Παράδειγµα: Συνένωση λιστών (2/3) (συνέχεια...) Για τη συνένωση µιας λίστας L1 πολλών στοιχείων µε τηλίσταl2 σκεφτόµαστε ως εξής: Αφαιρούµε απότηνl1 τοπρώτοστοιχείοτηςχ και κάνουµε συνένωση της ουράς της L1 (έστω Τ1 το όνοµά της)µετην L2. Στο αποτέλεσµα προσθέτουµε και το πρώτο στοιχείο. append( L1, L2 L3 ) :- L1=[X T1], append(t1, L2, L30), L3=[X L30]. Ο παραπάνω κανόνας είναι αρκετά περιφρατικός. Πιο σύντοµα µπορεί να γραφεί και ως: append( [Χ Τ1], L2, [Χ L30]) :- append(t1,l2, L30). Άρα τελικά το πρόγραµµά µας γράφεται: append([ ], L2, L2). append([a], L2, [A L2]). append( L1, L2 L3 ) :- L1=[X T1], append(t1,l2, L30), L3=[X L30]. Γιάννης Ρεφανίδης 37 Παράδειγµα: Συνένωση λιστών (3/3) Το πρόγραµµα πουβρήκαµε : append([ ], L2, L2). append([a], L2, [A L2]). append( L1, L2 L3 ) :- L1=[X T1], append(t1,l2, L30), L3=[X L30]. µπορεί τελικά να απλοποιηθεί στο ισοδύναµο: append([ ], L, L). append( [X T1], L2, [X L3] ) :- append(t1,l2,l3). Ουσιαστικά η περίπτωση που η L1 έχει ένα µόνοστοιχείοδεν χρειάζεται, µιας και µπορείνακαλυφθείαπότουςδύοάλλουςκανόνες. Γιάννης Ρεφανίδης 38
20 Παράδειγµα: ιαγραφή στοιχείων από λίστα (1/2) Θέλουµε να φτιάξουµε το κατηγόρηµα delete(x,l1,l2), όπου Χ είναι ένα στοιχείο, L1 µια λίστα και L2 ηλίσταl1 από την οποία έχουν εµφανιστεί όλες οι εµφανίσεις του Χ. Οι βασικές ιδέες είναι οι εξής: Εάν η L1 είναι κενή, τότε και η L2 είναι κενή: delete( _X, [ ], [ ] ). Πιο περιφραστικά µπορεί κανείς να γράψει: delete( _X, L1, L2] ) :- L1=[ ], L2=[ ]. Εάν το στοιχείο Χ ταυτίζεται µε το πρώτο στοιχείο της L1, τότε η L2 ισούται µε την ουρά της L1, από την οποία όµως έχουν αφαιρεθεί όλα τα X. delete( X, [ X T1], L2) :- delete(x, Τ1, L2). Γιάννης Ρεφανίδης 39 Παράδειγµα: ιαγραφή στοιχείων από λίστα (2/2) (συνέχεια...) Εάν τέλος το πρώτο στοιχείο της L1 δεν ταυτίζεται µε τοχ, τότε η L2 αποτελείται από το πρώτο στοιχείο της L1 και από όσα από τα υπόλοιπα στοιχεία της L1 είναι διαφορετικά από το Χ. delete(x, [ X1 T1], [ X1 T2] ) :- X \=X1, delete(x, T1, T2). Άρα το συνολικό πρόγραµµα έχειωςεξής: delete( _X, [ ], [ ] ). delete( X, [ X T1], L2) :- delete(x, Τ1, L2). delete(x, [ X1 T1], [ X1 T2] ) :- X \=X1, delete(x, T1, T2). Γιάννης Ρεφανίδης 40
21 Παράδειγµα: Αναστροφή λίστας Θέλουµε να ορίσουµε το κατηγόρηµα reverse(l1, L2), το οποίο επιτυγχάνει όταν η λίστα L1 είναι η ανάστροφη της L2. Οι βασικές ιδέες είναι οι εξής: Η ανάστροφη της κενής λίστας είναι η κενή λίστα. reverse( [ ], [ ] ). Για να αναστρέψουµε τηνl1, ξεχωρίζουµε το πρώτο στοιχείο της H1 από την ουρά της T1, αναστρέφουµε την ουρά της και έστω RT1 η ανεστραµµένη ουρά. Τότε η L2 ισούται µε τηνένωσητηςrt2 και του στοιχείου H1. reverse( [ H1 T1], L2):- reverse(t1, RT1), append(rt1, [H1], L2). Γιάννης Ρεφανίδης 41 Παρατηρήσεις Πολλά από τα κατηγορήµατα χειρισµού λιστών που είδαµε στις προηγούµενες διαφάνειες υπάρχουν ενσωµατωµένα στις περισσότερες υλοποιήσεις της γλώσσας Prolog. Σε αυτές τις περιπτώσεις καλό είναι να χρησιµοποιούµε τα υπάρχοντα κατηγορήµατα, τα οποία είναι πιο αποτελεσµατικά. Όσον αφορά τις δικές µας υλοποιήσεις, αυτές που παρουσιάστηκαν στις προηγούµενες διαφανειες δεν είναι οι µοναδικές. Θα µπορούσε κανείς να βρει και εναλλακτικές ισοδύναµες υλοποιήσεις, οι οποίες ενδεχοµένως να ήταν αποτελεσµατικότερες (δηλ. γρηγορότερες). Γιάννης Ρεφανίδης 42
22 Αριθµητικές διαδικασίες (1/4) Ως ορίσµατα κατηγορηµάτων µπορούν να χρησιµοποιηθούν και αριθµοί. Μπορούµε µάλιστα να κατασκευάζουµε αριθµητικές εκφράσεις χρησιµοποιώντας τις γνωστές πράξεις +, -, *, /, καθώς και συναρτήσεις όπως sin(), cos(), exp() κλπ. Μια µεταβλητή µπορεί να ενοποιηθεί µε έναν αριθµό ή µία αριθµητική έκφραση. Μπορούµε να συγκρίνουµε αριθµούς / αριθµητικές εκφράσεις (που περιέχουν µεταβλητές) χρησιµοποιώντας τους παρακάτω τελεστές (κατηγορήµατα), µε τηγνωστήτουςσηµασία: >, >=, <, =<, =:= και =/=. Γιάννης Ρεφανίδης 43 Αριθµητικές διαδικασίες (2/4) Προσοχή χρειάζεται στη διάκριση των τελεστών =:= και =. Ο απλός τελεστής = συγκρίνει όρους προσπαθώντας να εκτελέσει ενοποίηση. Για παράδειγµα, η κλήση: parent(x,y) = parent(nick, maria) επιτυγχάνει. Αντίθετα οι κλήσεις: 2+1 = = 1+4 αποτυγχάνουν. Πετυχαίνει όµως η κλήση: 2+1 = 2+1 θεωρώντας την έκφραση 2+1 ως τον σύνθετο όρο +(2,1). Γιάννης Ρεφανίδης 44
23 Αριθµητικές διαδικασίες (3/4) Για σύγκριση αριθµητικών εκφράσεων µε ταυτόχρονη εκτέλεση πράξεων χρησιµοποιούµε τον τελεστή =:=, ο οποίος πετυχαίνει σε όλες τις παρακάτω περιπτώσεις: 2+1 =:= =:= =:= 2+1 Παρόµοια, για να ελέγξουµε εάν δύο αριθµητικές εκφράσεις καταλήγουν σε διαφορετικό αριθµητικό αποτέλεσµα χρησιµοποιούµε τον τελεστή =\=. Ο αντίστοιχος τελεστής \= ελέγχει εάν δύο όροι δεν είναι ενοποιήσιµοι, χωρίς να εκτελέσει καµία πράξη. ΠΡΟΣΟΧΗ: Όλοι οι αριθµητικοί τελεστές ισότητας/ανισότητας απαιτούν κατά την κλήση τους όλες οι µεταβλητές που εµπλέκονται στις αριθµητικές εκφράσεις να είναι δεσµευµένες. Γιάννης Ρεφανίδης 45 Αριθµητικές διαδικασίες (4/4) Για να εκτελέσουµε µια αριθµητική πράξη και να αποδώσουµε το αποτέλεσµα σε µια µεταβλητή χρησιµοποιούµε τον τελεστή is : X is 2+3 όπου το αποτέλεσµα είναι η µεταβλητή Χ να πάρει την τιµή 5. Αντίθετα αν χρησιµοποιήσουµε τοντελεστή=, δηλαδή: Χ=2+3 το αποτέλεσµα θαείναιηµεταβλητή Χ να πάρει ως τιµή τοσύνθετο όρο 2+3. Ή σε προθεµατική µορφή: +(2,3). Γιάννης Ρεφανίδης 46
24 Ενσωµατωµένα κατηγορήµατα (1/5) Μέχρι τώρα είδαµε προγράµµατα της Prolog, όπου όλα τα κατηγορήµατα ορίστηκαν από τον χρήστη. Η Prolog διαθέτει όµως πολλά ενσωµατωµένα κατηγορήµατα, τα οποία επιτελούν ειδικές λειτουργίες. Για παράδειγµα, το κατηγόρηµα member(x,y) επιστρέφει yes όταν το Y είναι λίστα και το Χ είναι στοιχείο αυτής της λίστας, ειδάλλως επιστρέφει no. Γιάννης Ρεφανίδης 47 Ενσωµατωµένα κατηγορήµατα (2/5) Μπορούµε να χωρίσουµε τα ενσωµατωµένα κατηγορήµατα σε δύο οµάδες: Αυτά που έχουν λογική σηµασία: Επιστρέφουν yes ή no, ανάλογα µε την περίπτωση. Παράδειγµα είναι το member(x,y). Αυτά που έχουν διαδικαστική σηµασία: Εκτελούν µια συγκεκριµένη δουλειά και επιστρέφουν (σχεδόν) πάντα yes. Παράδειγµα: Το κατηγόρηµα write(χ) τυπώνει τον όρο Χ στην οθόνη και επιστρέφει yes. Παρόµοια το κατηγόρηµα nl αλλάζει παράγραφο στην οθόνη. Γιάννης Ρεφανίδης 48
25 Ενσωµατωµένα κατηγορήµατα (3/5) Μπορούµε να διακρίνουµε τα ορίσµατα των ενσωµατωµένων κατηγορηµάτων σε δύο κατηγορίες: Αυτά που κατά την κλήση του κατηγορήµατος πρέπει να έχουν πάρει τιµή. Για παράδειγµα, η κλήση Χ>Υ θα προκαλέσει τερµατισµό προγράµµατος, εάν ένα από τα δύο ορίσµατα του κατηγορήµατος '>' δεν έχει πάρει τιµή. Αυτά που κατά την κλήση του κατηγορήµατος δεν είναι υποχρεωτικό να έχουν πάρει τιµή. Για παράδειγµα, η κλήση member(x,[ 1 2 3]), εάν το Χ δεν έχει πάρει τιµή, θα επιστρέψει διαδοχικά: Χ=1, Χ=2 και Χ=3. Γιάννης Ρεφανίδης 49 Ενσωµατωµένα κατηγορήµατα (4/5) Παρακάτω αναφέρουµε µερικά από τα ενσωµατωµένα κατηγορήµατα που βρίσκουµε στις περισσότερες Prolog, µαζί µε µια σύντοµη ερµηνεία τους. get(x): ιαβάζει από το πληκτρολόγιο τον επόµενο χαρακτήρα που πληκτρολογεί ο χρήστης και τον επιστρέφει στη µεταβλητή Χ. read(x): ιαβάζει από το πληκτρολόγιο τον επόµενο όρο που πληκτρολογεί ο χρήστης και τον επιστρέφει στη µεταβλητή Χ. put(x): Τυπώνει στην οθόνη τον χαρακτήρα Χ. write(x): Τυπώνει στην οθόνη τον όρο Χ. nl : Αλλάζει γραµµή στην οθόνη. Γιάννης Ρεφανίδης 50
26 Ενσωµατωµένα κατηγορήµατα (5/5) Οχειρισµός (ανάγνωση και εγγραφή) αρχείων δίσκου γίνεται µε τις ίδιες εντολές που γίνεται η είσοδος/έξοδος από/σε πληκτρολόγιο/οθόνη. Χρησιµοποιούνται ειδικές εντολές για να ανακατευθύνουν την είσοδο και την έξοδο από και σε αρχείο. Ειδικότερα: see(stream): ΣτοεξήςηείσοδοςδιαβάζεταιαπότοStream. seen : Στο εξής είσοδος γίνεται ξανά το πληκτρολόγιο και όλα τα ανοικτά αρχεία εισόδου κλείνουν. seeing(stream): Επιστρέφει στη µεταβλητή Stream το όνοµα του τρέχοντος ρεύµατος εισόδου. tell(stream) : Το Stream γίνεται το τρέχον ρεύµα εξόδου. told: Τρέχον ρεύµα εξόδου γίνεται η οθόνη και όλα τα ανοικτά αρχεία εξόδου κλείνουν. telling(stream): Επιστρέφει στη µεταβλητή Stream το όνοµα του τρέχοντος ρεύµατος εξόδου. Γιάννης Ρεφανίδης 51 Αποκοπή (1/3) Έχουµε ορίσει ως διαδικασία ένα σύνολο κανόνων (συµπεριλαµβανοµένων και γεγονότων) που έχουν το ίδιο κατηγόρηµα στηνκεφαλήτους. Για παράδειγµα, οι παρακάτω κανόνες αποτελούν µια διαδικασία: uncle(x,y) :- brother(x,z), father(z,y). uncle(x,y):- brother(x,z), mother(z,y). η οποία ορίζει πότε ο Χ είναι θείος του/της Υ. Γιάννης Ρεφανίδης 52
27 Αποκοπή (2/3) Έστω επίσης ότι έχουµε τα παρακάτω γεγονότα: brother(bob, john). brother(bob, nick). father(john,ann). Θέλουµε να ελέγξουµε εάνοbob είναι θείος της ann. Εκτελούµε λοιπόν την ερώτηση: uncle(bob,ann). Στον πρώτο κανόνα της διαδικασίας uncle/2 η παραπάνω ερώτηση πετυχαίνει, µε τις ενοποιήσεις X=bob, Y=ann και Z=john. Η διαδικασία επιστρέφει επιτυχώς, ωστόσο θυµάται ότι πρέπει κάποια στιγµή στοµέλλον να ελέγξει και το δεύτερο κανόνα της διαδικασίας uncle. Γιάννης Ρεφανίδης 53 Αποκοπή (3/3) Με την αποκοπή µπορούµε να καθορίσουµε ότι εάν επιτύχει ο πρώτος κανόνας της διαδικασίας uncle/2 δεν χρειάζεται να ελεγχθεί και ο δεύτερος. Αυτό γίνεται ως εξής: uncle(x,y) :- brother(x,z), father(z,y),!. uncle(x,y):- brother(x,z), mother(z,y). Γενικά όταν η Prolog συναντήσει µια αποκοπή, δεν ελέγχει τους επόµενους κανόνες της τρέχουσας διαδικασίας, ενώ «ξεχνά» όλα τα εναλλακτικά µονοπάτια που ενδεχοµένως αποµένει να ελέγξει από προηγούµενες κλήσεις της ίδιας διαδικασίας (στην προκειµένη περίπτωση εναλλακτικές κλήσεις στα borher(x,z) και father(z,y), καθώς και από προηγούµενους κανόνες της uncle/2, εφόσον υπήρχαν). Γιάννης Ρεφανίδης 54
28 Παράδειγµα αποκοπής: Βηµατική συνάρτηση Έστω ότι θέλουµε να ορίσουµε τοκατηγόρηµα step(x,y), το οποίο προσοµοιώνει τη βηµατική συνάρτηση: Εάν το Χ είναι µικρότερο από το 0, το Υ είναι µηδέν, ειδάλλως το Υ είναι 1. Η έκδοση του προγράµµατος χωρίς αποκοπή είναι η εξής: step(x,0):- X<0. step(x,1):- X>=0. Η έκδοση του προγράµµατος µε αποκοπή είναι η εξής: step(x,0):- X<0,!. step(x,1). Η πρώτη έκδοση ελέγχει πάντα και τον δεύτερο κανόνα, ακόµη και αν έχει επιτύχει ο πρώτος. Η δεύτερη έκδοση ελέγχει τον δεύτερο κανόνα µόνο αν αποτύχει ο πρώτος. Μάλιστα, σε αυτή την περίπτωση ο δεύτερος κανόνας έχει µετατραπεί σε απλό γεγονός! (δηλαδή αφαιρέθηκε ο ανισοτικός έλεγχος). Γιάννης Ρεφανίδης 55 Παράδειγµα αποκοπής: Ηδιαδικασίαmember (1/3) Ορίσαµε σε προηγούµενη διαφάνεια τη διαδικασία member(x,l), η οποία επιτυγχάνει όταν το Χ είναι µέλος της λίστας L. Το πρόγραµµα που παρουσιάσαµε ήταν το εξής: member(x, [ X Y ] ). member(x, [ Head Tail ] ) :- member(x, Tail). Έστω ότι κάνουµε την ερώτηση:?- member(2, [1,2,3,4]). Η παραπάνω διαδικασία λειτουργει ως εξής: Ο πρώτος κανόνας συγκρίνει το 2 µε το πρώτο στοιχείο της λίστας. Επειδή δεν ταυτίζονται αποτυγχάνει. Ο δεύτερος κανόνας καλεί αναδροµικά τη διαδικασία, έχοντας αφαιρέσει το πρώτο στοιχείο της λίστας. Η αναδροµική κλήση πετυχαίνει αµέσως και έτσι πετυχαίνει και η αρχική κλήση. Γιάννης Ρεφανίδης 56
29 Παράδειγµα αποκοπής: Ηδιαδικασίαmember (2/3) Αφού η διαδικασία επιστρέψει επιτυχώς, διατηρεί στη µνήµη εναλλακτικά µονοπάτια απόδειξης. Τα µονοπάτια αυτά προκύπτουν από το γεγονός ότι η πρώτη αναδροµική κλήση µπορούσε ενδεχοµένως να ικανοποιηθεί από τον δεύτερο κανόνα, δηλαδή πάλι αναδροµικά, κοκ. Ουσιαστικά η διαδικασία θα συνεχίσει να ελέγχει εάν το 2 υπάρχει στη λίστα [1,2,3,4] µέχρι να ελέγξει ολόκληρη τη λίστα. Ενδεχοµένως θα θέλαµε η διαδικασία member να τερµατίζει µόλις ανακαλύψει την πρώτη εµφάνιση του στοιχείου που αναζητούµε στη λίστα. Αυτό επιτυγχάνεται µε το παρακάτω πρόγραµµα: member(x, [ X Y ] ) :-!. member(x, [ Head Tail ] ) :- member(x, Tail). Γιάννης Ρεφανίδης 57 Παράδειγµα αποκοπής: Ηδιαδικασίαmember (3/3) Η προσθήκη της αποκοπής στον πρώτο κανόνα της member/2 αυξάνει την αποτελεσµατικότητα του κανόνα, έχει όµως ένα πολύ σοβαρό µειονέκτηµα: Εάν υποβάλλουµε την ερώτηση:?- member(x, [1,2,3,4]). παίρνουµε µόνο την απάντηση Χ=1 Αντίθετα, εάν δεν υπήρχε η αποκοπή, η ίδια ερώτηση θα έδινε διαδοχικά τις απαντήσεις: Χ=1 Χ=2 Χ=3 Χ=4 Γιάννης Ρεφανίδης 58
30 Παρατηρήσεις Η χρήση της αποκοπής: Αυξάνει την αποτελεσµατικότητα των προγραµµάτων όταν οι κλήσεις µας γίνονται χωρίς µεταβλητές. εν µας επιστρέφει όλες τις εναλλακτικές λύσεις όταν οι κλήσεις γίνονται µε µεταβλητές. Γενικότερα, θεωρείται ότι η χρήση της αποκοπής περιορίζει τη δηλωτικότητα (declarativeness) των προγραµµάτων, καθιστώντας τα πιο διαδικαστικά (procedural). Ηδιαδικασίαmember υλοποιείται από όλες τις Prolog χωρίς αποκοπή. Γιάννης Ρεφανίδης 59 ΗάρνησηστηνProlog Είδαµε ότιµε τιςπροτάσειςhorn δεν µπορούµε νααποδεικνύουµε αρνητικές προτάσεις. Ωστόσο, η Prolog επιτρέπει τη χρήση άρνησης στο σώµα των κανόνων, µε χρήση της δεσµευµένης λέξης not: alive(x) :- not dead(x). Η λέξη not µπορεί να εµφανίζεται µόνο στο σώµα των κανόνων (όχι δηλαδή στην κεφαλή), και ερµηνεύεται ως εξής: Εάν µε βάση όσα γνωρίζει το πρόγραµµα ως τώρα δεν µπορέσει να αποδείξει το dead(x), τότε µπορεί να υποθέσει ότι ισχύει το not dead(x). Η παραπάνω προσέγγιση ονοµάζεται "υπόθεση του κλειστού κόσµου", αφού υποθέτει ότι γνωρίζουµε ταπάντασεσχέσηµε το συγκεκριµένο πρόβληµα, άρα ό,τι δεν µπορούµε να το αποδείξουµε δεν ισχύει. Γιάννης Ρεφανίδης 60
31 υναµική τροποποίηση προγράµµατος (1/2) Μπορούµε να προσθέτουµε και να αφαιρούµε γεγονότα και κανόνες από τη µνήµη κατά την εκτέλεση του προγράµµατος. Αυτό επιτυγχάνεται µε τα παρακάτω κατηγορήµατα: assert( Clause ) : Προσθέτει στη µνήµη το γεγονός ή τον κανόνα Clause. assert( city(thessaloniki) ). assert( (brother(x,y):- father(z,x), father(z,y), male(x) ) ). Η πρόταση Clause τοποθετείται ύστερα από όλες τις προτάσεις του ίδιου κατηγορήµατος. asserta( Clause ) : Ίδιο µε το assert/1, µε µοναδική διαφορά ότι προσθέτει την πρόταση Clause πριν από άλλες προτάσεις του ίδιου κατηγορήµατος. retract( Clause ) : ιαγράφει από τη µνήµη το πρώτο γεγονός ή κανόνα που ταυτοποιείται µε τοclause. retract_all( Clause ) : ιαγράφει από τη µνήµη όλα τα γεγονότα / κανόνες που ταυτοποιούνται µε το Clause. Γιάννης Ρεφανίδης 61 υναµική τροποποίηση προγράµµατος (2/2) Η δυνατότητα δυναµικής τροποποίησης ενός προγράµµατος µας επιτρέπει, µεταξύ άλλων, να έχουµε καθολικές µεταβλητές στην Prolog. Για παράδειγµα, έστω ότι χρειαζόµαστε έναν καθολικό µετρητή, ο οποίος θα ενηµερώνεται από διάφορα σηµεία του προγράµµατος. Μπορούµε να δηλώσουµε ένα γεγονός: counter(0). Στη συνέχεια, εάν σε κάποιο σηµείο του προγράµµατος θέλουµε να αυξήσουµε τηντιµή τουκατά1, προσθέτουµε τις παρακάτω εντολές:... retract( counter(x) ), X1 is X + 1, assert( counter(x1) ), Γιάννης Ρεφανίδης 62
32 Παρατήρηση Προσοχή: Για να µπορούµε να προσθέτουµε / αφαιρούµε δυναµικά προτάσεις που αφορούν ένα συγκεκριµένο κατηγόρηµα, αυτό το κατηγόρηµα πρέπει να δηλωθεί ως δυναµικό. Αυτό γίνεται µε δήλωση στην αρχή του προγράµµατος: :-dynamic όνοµα_κατηγορήµατος/τάξη. Στο παράδειγµα της προηγούµενης διαφάνειας, θα έπρεπε στην αρχή του προγράµµατος να υπάρχει η δήλωση: :-dynamic counter/1. Για όσα κατηγορήµατα δεν υπάρχει η παραπάνω δήλωση, η Prolog τα θεωρεί στατικά και δεν µας επιτρέπει να προσθέτουµε και να αφαιρούµε προτάσεις δυναµικά κατά την εκτέλεση του προγράµµατος. Γιάννης Ρεφανίδης 63 Συγκέντρωση λύσεων (1/2) Πολλές φορές χρειαζόµαστε να µαζέψουµε σε µία λίστα όλες τις πιθανές απαντήσεις µιας ερώτησης. Για παράδειγµα, έστω το παρακάτω πρόγραµµα: father(nick, george) father(nick, mary) father(john, elen) Έστω ότι θέλουµε να βρούµε ταπαιδιάτουnick. Ηερώτηση:?- father(nick, X) µας επιστρέφει ένα-έναταπαιδιάτου, χωρίς να µας δίνει τη δυνατότητα να τα χειριστούµεόλα µαζί ταυτόχρονα. Γιάννης Ρεφανίδης 64
33 Συγκέντρωση λύσεων (2/2) Μπορούµε να ζητήσουµε από την Prolog να µας επιστρέψει ταυτόχρονα όλες τις δυνατές απαντήσεις σε µια ερώτηση. Αυτό γίνεται µε το κατηγόρηµα findall/3: findall( Term, Goal, List ) : Κατά την κλήση της findall, η Prolog βρίσκει όλες τις πιθανές απαντήσεις στην ερώτηση Goal. Για κάθε απάντηση που βρίσκει τοποθετει στο List ένα αντίγραφο του Term, µε τις µεταβλητές του Term να έχουν πάρει τιµές από την εκάστοτε απάντηση του Goal. Για παράδειγµα:?- findall( X, father(nick,x), List). List= [george, mary] Εναλλακτικά: findall( child(x), father(nick,x), List). List= [ child(george), child(mary) ] Γιάννης Ρεφανίδης 65 Λογικός Προγραµµατισµός Η γλώσσα προγραµµατισµού Prolog Αλγόριθµοι αναζήτησης σε Prolog
34 Το πρόβληµα του ίππου Στις επόµενες διαφάνειες θα χρησιµοποιήσουµε τηνprolog για να λύσουµε προβλήµατα µε χρήση αλγορίθµων αναζήτησης. Θα χρησιµοποιήσουµε ως παράδειγµα το πρόβληµα του ίππου στο σκάκι, το οποίο ορίζεται ως εξής: εδοµένης µια σκακιέρας ΝxN και ενός ίππου σε κάποια θέση της σκακιέρας, να βρεθεί µια διαδροµή τουίππουµε την οποία αυτός επισκέπεται όλα τα τετράγωνα της σκακιέρας, µια φορά το καθένα, ξεκινώντας από συγκεκριµένη θέση (π.χ. µια γωνία). Το πρόβληµα έχει λύση για σκακιέρες µε µήκος πλευράς τουλάχιστον 5. Γιάννης Ρεφανίδης 67 Αναπαράσταση θέσεων Θα χρησιµοποιήσουµε σύνθετους όρους της µορφής pos(x,y) για να αναφερόµαστε στη θέση X,Y της σκακιέρας. Για παράδειγµα, pos(1,1), pos(2,3) κλπ Ορίσουµε τη µέγιστη διάσταση της σκακιέρας µε το γεγονός: size(5). Γιάννης Ρεφανίδης 68
35 Αναπαράσταση κινήσεων (1/4) Οι επιτρεπτές κινήσεις του ίππου από ένα τυχαίο τετράγωνο είναι το πολύ 8. Για όσους δεν γνωρίζουν σκάκι, κάθε κίνηση του ίππου αντιστοιχεί σε µετακίνησή του κατά ένα τετράγωνο στη µία διάσταση και δύο τετράγωνα στην άλλη, αρκεί να µην βγει έξω από την σκακιέρα. Φυσικά στο πραγµατικό σκάκι η νέα θέση δεν πρέπει να κατέχεται από πιόνι του ίδιου χρώµατος, ενώ η µετακίνηση του ίππου δεν θα πρέπει να αφήνει εκτεθειµένο τον βασιλιά του ίδιου χρώµατος. Στην εικόνα δίπλα ο µαύρος ίππος µπορεί να µετακινηθεί σε οποιαδήποτε από τις θέσεις που είναι σηµειωµένες Γιάννης Ρεφανίδης Αναπαράσταση κινήσεων (2/4) Ο παρακάτω κανόνας µας δίνει µια από τις επιτρεπτές κινήσεις του ίππου: move( pos(x,y), pos(x1,y1) ) :- X>2, Y>1, X1 is X-2, Y1 is Y-1. Ο παρακάτω κανόνας µας δίνει ακόµη µια µετακίνηση προς την αντίθετη κατεύθυνση. move( pos(x,y), pos(x1,y1) ) :- X1 is X+2, Y1 is Y+1, size(s), Χ1=<S, Υ1=<S. Γιάννης Ρεφανίδης 70
36 Αναπαράσταση κινήσεων (3/4) Ακολουθούν οι ορισµοί των υπολοίπων έξι κινήσεων. move( pos(x,y), pos(x1,y1) ) :- X>1, Y>2, X1 is X-1, Y1 is Y-2. move( pos(x,y), pos(x1,y1) ) :- X>1, X1 is X-1, Y1 is Y+2, size(s), Υ1=<S. move( pos(x,y), pos(x1,y1) ) :- X>2, X1 is X-2, Y1 is Y+1, size(s), Υ1=<S. Γιάννης Ρεφανίδης 71 Αναπαράσταση κινήσεων (4/4) (συνέχεια...) move( pos(x,y), pos(x1,y1) ) :- X1 is X+1, size(s), Χ1=<S, Υ>2, Y1 is Y-2. move( pos(x,y), pos(x1,y1) ) :- X1 is X+2, size(s), Χ1=<S, Υ>1, Y1 is Y-1. move( pos(x,y), pos(x1,y1) ) :- X1 is X+1, Y1 is Y+2, size(s), Χ1=<S, Υ1=<S. Γιάννης Ρεφανίδης 72
37 Αναπαράσταση σκακιέρας (1/3) Θα χρειαστούµε έναν τρόπο να αναπαριστούµε τησκακιέρα, ώστε να θυµόµαστε ποια τετράγωνα δεν έχουµε επισκεφθεί ακόµη ή ποια έχουµε επισκεφθεί. Ο πιο απλός τρόπος είναι µια λίστα, για παράδειγµα: [ pos(1,1), pos(1,2),, pos(2,1),, pos(5,5) ] Για ευκολότερη δηµιουργία της λίστας, µπορούµε να φτιάξουµε µια διαδικασία που θα επιστρέφει την παραπάνω λίστα, όταν της δώσουµε τη διάσταση της σκακιέρας. Η διαδικασία gen_table/1 στις επόµενες διαφάνειες επιστρέφει στη µεταβλητή Table έναν πίνακα µε στοιχεία του όλες τις θέσεις της σκακιέρας. Η διάσταση της σκακιέρας λαµβάνεται από το γεγονός size(5). Γιάννης Ρεφανίδης 73 Αναπαράσταση σκακιέρας (2/3) gen_table(table):- size(s), gen_table(1,s,table). gen_table(s, S, Table ):- gen_row(s, S, Table, 1),!. gen_table(row,s,table):- gen_row(row, S, TableRow, 1), Next_Row is Row+1, gen_table(next_row, S, Rest_Table), append(tablerow, Rest_Table, Table). Γιάννης Ρεφανίδης 74
38 Αναπαράσταση σκακιέρας (3/3) gen_row(row, S, [ pos(row,s)], S) :-!. gen_row(row, S, [ pos(row,col) Rest], Col ):- Next_Col is Col + 1, gen_row(row, S, Rest, Next_Col). Γιάννης Ρεφανίδης 75 Αναπαράσταση καταστάσεων Σε κάθε κατάσταση του χώρου αναζήτησης θα πρέπει να γνωρίζουµε: Σε ποια θέση βρισκόµαστε. Ποιες θέσεις δεν έχουµε ακόµη επισκεφθεί. Μπορούµε νααναπαραστήσουµε καταστάσεις µε τονπαρακάτω σύνθετο όρο: state(current_pos, Rest) όπου Current_pos είναι η τρέχουσα θέση, π.χ. pos(1,1). Rest είναι µια λίστα µε τις θέσεις που αποµένει να επισκεφθούµε. Για παράδειγµα: state(pos(4,2), [pos(1,2),,pos(5,5)] ) Γιάννης Ρεφανίδης 76
39 Τελεστής µετάβασης Χρειαζόµαστε µια διαδικασία η οποία για κάθε κατάσταση βρίσκει, ένα-ένα, όλαταπαιδιάτης. next_state( state(current_pos, Rest), state(new_pos, New_rest):- move(current_pos, New_pos), member(new_pos, Rest), delete(new_pos,rest,new_rest). Γιάννης Ρεφανίδης 77 Αναζήτηση πρώτα κατά βάθος (1/3) Σε κάθε κατάσταση κατά την αναζήτηση θα πρέπει: Να βρίσκουµε όλες τις δυνατές καταστάσεις-παιδιά. Να επιλέγουµε µια κατάσταση-παιδί και να συνεχίζουµε απόαυτήν. Να θυµόµαστε από ποιες θέσεις περάσαµε µέχρι να φτάσουµε στην τρέχουσα θέση. Θα υλοποιήσουµε τον αλγόριθµο αναζήτησης πρώτα κατά βάθος βασιζόµενοι στον ενσωµατωµένο µηχανισµό αναζήτησηςτης Prolog, οοποίοςλειτουργείµε την στρατηγική πρώτα κατά βάθος. Γιάννης Ρεφανίδης 78
40 Αναζήτηση πρώτα κατά βάθος (2/3) Ηδιαδικασίαdfs_tour/2 υλοποιεί τον αλγόριθµο αναζήτησηςπρώτα κατά βάθος: dfs_tour( state(current_pos, [ ] ), [Current_pos] ). dfs_tour( state(current_pos, Rest), [ Current_pos Path ] ):- next_state(state(current_pos, Rest), state(new_pos, New_rest) ), dfs_tour( state(new_pos, New_rest), Path ). Το πρώτο όρισµα τηςdfs_tour/2 είναι η τρέχουσα κατάσταση, συµπεριλαµβανοµένης της τρέχουσας θέσης και των θέσεων που αποµένει να επισκεφθούµε. Στο δεύτερο όρισµα της dfs_tour/2 επιστρέφονται οι θέσεις που επισκέπτεται ο αλγόριθµος, διαταγµένες µε τη σειρά επίσκεψης. Καλούµε τηνdfs_tour/2 ως: dfs_tour( state(pos(1,1), [pos(1,2), pos(1,3),, pos(5,5)] ), Path). Γιάννης Ρεφανίδης 79 Αναζήτηση πρώτα κατά βάθος (3/3) Για πιο εύκολη κλήση της dfs_tour/2 ορίζουµε τη βοηθητική διαδικασία run_dfs/1 ως εξής: run_dfs(path):- gen_table(table), delete(pos(1,1),table,rest), dfs_tour(state(pos(1,1),rest), Path). Παρακάτω φαίνεται η λύση που επιστρέφει ο αλγόριθµος: Path=[pos(1, 1), pos(3, 2), pos(5, 3), pos(4, 1), pos(2, 2), pos(1, 4), pos(3, 5), pos(5, 4), pos(3, 3), pos(4, 5), pos(2, 4), pos(1, 2), pos(3, 1), pos(5, 2), pos(4, 4), pos(2, 5), pos(1, 3), pos(2, 1), pos(4, 2), pos(2, 3), pos(1, 5), pos(3, 4), pos(5, 5), pos(4, 3), pos(5, 1)] Γιάννης Ρεφανίδης 80
41 Παρατηρήσεις Όπως έχουµε δει στους αλγορίθµους αναζήτησης, κάθε αλγόριθµος αναζήτησης πρέπει να διατηρεί το µέτωπο αναζήτησης, µια λίστα όπου υπάρχουν οι καταστάσεις εκείνες που έχουν συναντηθεί αλλά δεν έχουν επεκταθεί ακόµη. Στην υλοποίηση του αλγορίθµου αναζήτησης πρώτα κατά βάθος που παρουσιάστηκε στις προηγούµενες διαφάνειες, δεν χρειάστηκε το πρόγραµµά µας να υλοποιήσει το µέτωπο αναζήτησης. Αντίθετα, χρησιµοποιήσαµε το εσωτερικό«µέτωπο αναζήτησης» της Prolog, το οποίο λειτουργεί µε τη στρατηγική πρώτα-κατά-βάθος. Εάν θελήσουµε όµως να υλοποιήσουµε οποιονδήποτε άλλο αλγόριθµο, θα πρέπει να υλοποιήσουµε δικό µας µέτωπο αναζήτησης. Γιάννης Ρεφανίδης 81 Αναζήτηση πρώτα κατά πλάτος (1/5) Γιαναυλοποιήσουµε την αναζήτηση πρώτα κατά πλάτος, πρέπει να κατασκευάσουµε µόνοι µας το µέτωπο αναζήτησης του αλγορίθµου, ως µια λίστα καταστάσεων που έχει επισκεφθεί ο αλγόριθµος αλλά δεν έχει ακόµη βρει τα παιδιά τους. Λόγω της υλοποίησης της ατζέντας, χρειάζεται σε κάθε κατάσταση να προσθέσουµε καιτηδιαδροµή µε την οποία ο ίππος έφθασε στην τρέχουσα θέση. Έτσι η περιγραφή µιας κατάστασης γίνεται: state(current_pos, Rest, Path) όπου Current_pos είναι η τρέχουσα θέση, π.χ. pos(1,1). Rest είναι µια λίστα µε τις θέσεις που αποµένει να επισκεφθούµε. Path είναι η λίστα των θέσεων από τις οποίες έχει περάσει ο ίππος. Γιάννης Ρεφανίδης 82
42 Αναζήτηση πρώτα κατά πλάτος (2/5) Θεωρούµε ότι το µέτωπο αναζήτησης παριστάνεται ως ένα γεγονός της µορφής: agenda( [state(..), state( ),, state( ) ] ). Αρχικά το µέτωπο αναζήτησης πρέπει να περιέχει µόνο την αρχική κατάσταση: agenda( [ state( pos(1,1), [ pos(1,2),..., pos(5,5) ], [pos(1,1)] ) ] ). Το πρόγραµµα θα πρέπει, σε κάθε βήµα, να αφαιρεί από το µέτωπο αναζήτησης την πρώτη κατάσταση, να βρίσκει τα παιδιά της, και να τα προσθέτει στο τέλος του µετώπου αναζήτησης. Η τροποποίηση του παραπάνω γεγονότος είναι δυνατή µε τις εντολές retract και assert. Γιάννης Ρεφανίδης 83 Αναζήτηση πρώτα κατά πλάτος (3/5) Η διαδικασία του αλγορίθµου αναζήτησης πρώτα κατά πλάτος είναι ηεξής: bfs_tour(path):- retract( agenda( [ state( Current_pos, [ ], Path ) _ ] )),!. bfs_tour(path):- retract( agenda( [ State Rest_agenda ] )), find_children(state, Children), append(rest_agenda, Children, New_agenda), assert( agenda(new_agenda) ), bfs_tour(path). Ο πρώτος κανόνας επιτυγχάνει όταν η πρώτη κατάσταση στην agenda έχει επισκεφθεί όλες τις θέσεις. Ο δεύτερος κανόνας σβήνει (αφού τη διαβάσει πρώτα) την παλιά agenda, βρίσκει τα παιδιά της πρώτης κατάστασης και τα προσθέτει στο τέλος της νέας agenda. Γιάννης Ρεφανίδης 84
43 Αναζήτηση πρώτα κατά πλάτος (4/5) Παρακάτω ορίζουµε τη διαδικασία find_children, η οποία επιστρέφει σε λίστα όλα τα παιδιά µιας κατάστασης. find_children(current_state,children):- findall( Next_state, next_state(current_state, Next_state), Children). όπου η διαδικασία next_state έχει πλέον γίνει ως εξής: next_state( state(current_pos, Rest, Path), state(new_pos, New_rest, [New_pos Path]):- move(current_pos, New_pos), member(new_pos, Rest), delete(new_pos,rest,new_rest). Γιάννης Ρεφανίδης 85 Αναζήτηση πρώτα κατά πλάτος (5/5) Για πιο εύκολη κλήση της bfs_tour/2 ορίζουµε τη βοηθητική διαδικασία run_bfs/1 ως εξής: run_bfs(path):- gen_table(table), delete(pos(1,1),table,rest), assert(agenda([ state( pos(1,1), Rest, [pos(1,1)] ) ] )), bfs_tour(path1), reverse(path1,path). Ο αλγόριθµος αναζήτησης πρώτα κατά πλάτος δεν µπορεί να λύσει το συγκεκριµένο πρόβληµα. Ο λόγος είναι ότι για να βρει µια λύση, η οποία έχει µήκος 25, θα πρέπει πρώτα να εξετάσει όλες τις διαδροµές µε µήκος 24, οι οποίες είναι πάρα πολλές (της τάξης του 8 24 ). Γιάννης Ρεφανίδης 86
44 Παρατήρηση Θα µπορούσαµε πολύεύκολαναµετατρέψουµε τον αλγόριθµο αναζήτησης πρώτα κατά πλάτος σε πρώτα κατά βάθος µε δικόµας µέτωπο αναζήτησης. Αυτό µπορεί να γίνει αν η κλήση: append(rest_agenda, Children, New_agenda) στον δεύτερο κανόνα της διαδικασίας bfs_tour/1 άλλαζε σε: append(children, Rest_agenda, New_agenda) Γιάννης Ρεφανίδης 87 Αναζήτηση πρώτα στο καλύτερο (1/5) Η αναζήτηση πρώτα στο καλύτερο απαιτεί µια µικρή τροποποίηση στο πρόγραµµα της αναζήτησης πρώτα κατά πλάτος: Κάθε κατάσταση πρέπει να συνοδεύεται από έναν αριθµό, που να δηλώνει το πόσο «καλή» είναι αυτή η κατάσταση. Οι καταστάσεις στο µέτωπο αναζήτησης (agenda) πρέπει να είναι ταξινοµηµένες. Αλλάζουµε λοιπόν τον ορισµό τωνκαταστάσεωνωςεξής: state(score, Current_pos, Rest, Path) όπου Score είναι ο βαθµός κάθε κατάστασης Γιάννης Ρεφανίδης 88
45 Αναζήτηση πρώτα στο καλύτερο (2/5) Χρειαζόµαστε και ένα µηχανισµό βαθµολόγησης των καταστάσεων. Η βασική ιδέα είναι η εξής: Προτιµούνται οι καταστάσεις για τις οποίες: Το τρέχον τετράγωνο είναι στην άκρη της σκακιέρας. Έχουν ήδη διανύσει µεγαλύτερα µονοπάτια. Η παρακάτω διαδικασία βαθµολογεί καταστάσεις: heuristic( state(score, pos(x,y), Rest, Path) ):- size(s), DistX is min(x-1, S-X), DistY is min(y-1, S-Y), length(rest, LR), Score is DistX*DistY+4*LR. Γιάννης Ρεφανίδης 89 Αναζήτηση πρώτα στο καλύτερο (3/5) Οι νέες καταστάσεις θα πρέπει να βαθµολογούνται µόλις δηµιουργούνται. Ηδιαδικασίαnext_state τροποποιείται ως εξής: next_state( state(_, Current_pos, Rest, Path), state(score, New_pos, New_rest, [New_pos Path]):- move(current_pos, New_pos), member(new_pos, Rest), delete(new_pos,rest,new_rest) heuristic(state(score, New_pos, New_rest,_)). Η κλήση στον κανόνα heuristic γίνεται µε τηνέακατάστασηναέχει δεσµευµένες όλες τις παραµέτρους της εκτός από την Score. Ο κανόνας heuristic πετυχαίνει δεσµεύοντας την παράµετρο Score στην ευρετική τιµή της κατάστασης. Γιάννης Ρεφανίδης 90
46 Αναζήτηση πρώτα στο καλύτερο (4/5) Οαλγόριθµος πρώτα στο καλύτερο θα πρέπει να διατηρεί το µέτωπο αναζήτησης ταξινοµηµένο. bestfs_tour(path):- retract( agenda( [ state( _, Current_pos, [ ], Path ) _ ] )),!. bestfs_tour(path):- retract( agenda( [ State Rest_agenda ] )), find_children(state, Children), append(rest_agenda, Children, New_agenda), sort(new_agenda, Sorted_agenda), assert( agenda(sorted_agenda) ), bestfs_tour(path). Η ενσωµατωµένη διαδικασία sort/2 της Prolog ταξινοµεί µια λίστα αλφαβητικά. Στην προκειµένη περίπτωση, όλοι οι όροι της λίστας είναι τύπου state/4, και το πρώτο σηµείο στο οποίο διαφέρουν είναι η βαβµολογία των καταστάσεων. Γιάννης Ρεφανίδης 91 Αναζήτηση πρώτα στο καλύτερο (5/5) Τέλος, για πιο εύκολη κλήση της bestfs_tour/2 ορίζουµε τη βοηθητική διαδικασία run_bestfs/1 ως εξής: run_bestfs(path):- gen_table(table), delete(pos(1,1),table,rest), heuristic(state(score, pos(1,1), Rest, _)), assert(agenda([state( Score, pos(1,1), Rest, [pos(1,1)] )] )), bfs_tour(path1), reverse(path1,path). Γιάννης Ρεφανίδης 92
47 Παρατηρήσεις Οαλγόριθµος αναζήτησης πρώτα στο καλύτερο βρίσκει τη λύση σε σηµαντικά µικρότερο αριθµό επαναλήψεων. Συγκεκριµένα, ο αλγόριθµος πρώτα στο καλύτερο βρήκε λύση µετά από 32 επαναλήψεις, ενώ ο αλγόριθµος πρώτα κατά βάθος µετά από Γιάννης Ρεφανίδης 93 Γνωστές υλοποιήσεις της γλώσσας Prolog Eclipse Imperial College, London Prolog+Constraints Ελεύθερη διανοµή για πανεπιστήµια/φοιτητές Sicstus Prolog Prolog+Constraints Trial version SWI Απλή Prolog Ελεύθερη διανοµή LPA Prolog Απλή Prolog Εµπορική Γιάννης Ρεφανίδης 94
Παράδειγµα: Οικονοµικός Σύµβουλος
 Παράδειγµα: Οικονοµικός Σύµβουλος Περιγραφή του προβλήµατος (1/3)! Στις επόµενες διαφάνειες θα παρουσιαστεί ένα απλό παράδειγµα κατασκευής ενός οικονοµικού συµβούλου χρησιµοποιώντας λογική πρώτης τάξης
Παράδειγµα: Οικονοµικός Σύµβουλος Περιγραφή του προβλήµατος (1/3)! Στις επόµενες διαφάνειες θα παρουσιαστεί ένα απλό παράδειγµα κατασκευής ενός οικονοµικού συµβούλου χρησιµοποιώντας λογική πρώτης τάξης
Επιλογή και επανάληψη. Λογική έκφραση ή συνθήκη
 Επιλογή και επανάληψη Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως, ότι στο
Επιλογή και επανάληψη Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως, ότι στο
2ο ΓΕΛ ΑΓ.ΔΗΜΗΤΡΙΟΥ ΑΕΠΠ ΘΕΟΔΟΣΙΟΥ ΔΙΟΝ ΠΡΟΣΟΧΗ ΣΤΑ ΠΑΡΑΚΑΤΩ
 ΠΡΟΣΟΧΗ ΣΤΑ ΠΑΡΑΚΑΤΩ ΣΤΑΘΕΡΕΣ είναι τα μεγέθη που δεν μεταβάλλονται κατά την εκτέλεση ενός αλγόριθμου. Εκτός από τις αριθμητικές σταθερές (7, 4, 3.5, 100 κλπ), τις λογικές σταθερές (αληθής και ψευδής)
ΠΡΟΣΟΧΗ ΣΤΑ ΠΑΡΑΚΑΤΩ ΣΤΑΘΕΡΕΣ είναι τα μεγέθη που δεν μεταβάλλονται κατά την εκτέλεση ενός αλγόριθμου. Εκτός από τις αριθμητικές σταθερές (7, 4, 3.5, 100 κλπ), τις λογικές σταθερές (αληθής και ψευδής)
ΠΑΡΑ ΕΙΓΜΑΤΑ ΣΤΗ ΓΛΩΣΣΑ PROLOG ΠΑΡΑ ΕΙΓΜΑ 1
 ΠΑΡΑ ΕΙΓΜΑΤΑ ΣΤΗ ΓΛΩΣΣΑ PROLOG ΠΑΡΑ ΕΙΓΜΑ 1 Έστω ότι µας ζητούν να γράψουµε ένα πρόγραµµα Prolog που να εκτυπώνει την οποιαδήποτε υπο-λίστα της παρακάτω λίστας: red blue green yellow gray χρησιµοποιώντας
ΠΑΡΑ ΕΙΓΜΑΤΑ ΣΤΗ ΓΛΩΣΣΑ PROLOG ΠΑΡΑ ΕΙΓΜΑ 1 Έστω ότι µας ζητούν να γράψουµε ένα πρόγραµµα Prolog που να εκτυπώνει την οποιαδήποτε υπο-λίστα της παρακάτω λίστας: red blue green yellow gray χρησιµοποιώντας
Επίλυση προβληµάτων. Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης
 Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L. να αναγνωρίζει (ηµιαποφασίζει) µια γλώσσα L. 1. Η TM «εκτελεί» τον απαριθµητή, E.
 Οι γλώσσες των Μηχανών Turing Αποφασισιµότητα / Αναγνωρισιµότητα Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L Αποδέχεται όταν (η είσοδος στην TM) w L. Ορέστης Τελέλης telelis@unipi.gr Τµήµα
Οι γλώσσες των Μηχανών Turing Αποφασισιµότητα / Αναγνωρισιµότητα Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L Αποδέχεται όταν (η είσοδος στην TM) w L. Ορέστης Τελέλης telelis@unipi.gr Τµήµα
! όπου το σύµβολο έχει την έννοια της παραγωγής, δηλαδή το αριστερό µέρος ισχύει ενώ το δεξιό µέρος συµπεραίνεται και προστίθεται στη βάση γνώσης.
 Αποδείξεις (1/2)! Χρησιµοποιούµε τις συνεπαγωγές της βάσης γνώσης για να βγάλουµε νέα συµπεράσµατα. Για παράδειγµα:! Από τις προτάσεις:! Ακαι Α Β! µπορούµε να βγάλουµε το συµπέρασµα (τεχνική modus ponens
Αποδείξεις (1/2)! Χρησιµοποιούµε τις συνεπαγωγές της βάσης γνώσης για να βγάλουµε νέα συµπεράσµατα. Για παράδειγµα:! Από τις προτάσεις:! Ακαι Α Β! µπορούµε να βγάλουµε το συµπέρασµα (τεχνική modus ponens
Κεφάλαιο 5ο: Εντολές Επανάληψης
 Χρήστος Τσαγγάρης ΕΕ ΙΠ Τµήµατος Μαθηµατικών, Πανεπιστηµίου Αιγαίου Κεφάλαιο 5ο: Εντολές Επανάληψης Η διαδικασία της επανάληψης είναι ιδιαίτερη συχνή, αφού πλήθος προβληµάτων µπορούν να επιλυθούν µε κατάλληλες
Χρήστος Τσαγγάρης ΕΕ ΙΠ Τµήµατος Μαθηµατικών, Πανεπιστηµίου Αιγαίου Κεφάλαιο 5ο: Εντολές Επανάληψης Η διαδικασία της επανάληψης είναι ιδιαίτερη συχνή, αφού πλήθος προβληµάτων µπορούν να επιλυθούν µε κατάλληλες
επιµέλεια Θοδωρής Πιερράτος
 Βασικές έννοιες προγραµµατισµού Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως,
Βασικές έννοιες προγραµµατισµού Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ
 ΘΕΜΑ ο 2.5 µονάδες ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 2 Σεπτεµβρίου 2005 5:00-8:00 Σχεδιάστε έναν αισθητήρα ercetro
ΘΕΜΑ ο 2.5 µονάδες ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 2 Σεπτεµβρίου 2005 5:00-8:00 Σχεδιάστε έναν αισθητήρα ercetro
Επιµέλεια Θοδωρής Πιερράτος
 Ερωτήσεις Σωστό - Λάθος 1. Ο αλγόριθµος πρέπει να τερµατίζεται µετά από εκτέλεση πεπερασµένου αριθµού εντολών. 2. Η είσοδος σε έναν αλγόριθµο µπορεί να είναι έξοδος σε έναν άλλο αλγόριθµο. 3. Ένας αλγόριθµος
Ερωτήσεις Σωστό - Λάθος 1. Ο αλγόριθµος πρέπει να τερµατίζεται µετά από εκτέλεση πεπερασµένου αριθµού εντολών. 2. Η είσοδος σε έναν αλγόριθµο µπορεί να είναι έξοδος σε έναν άλλο αλγόριθµο. 3. Ένας αλγόριθµος
int array[10]; double arr[5]; char pin[20]; Προγραµµατισµός Ι
![int array[10]; double arr[5]; char pin[20]; Προγραµµατισµός Ι int array[10]; double arr[5]; char pin[20]; Προγραµµατισµός Ι](/thumbs/53/30869683.jpg) Εισαγωγή Στον Προγραµµατισµό «C» Πίνακες Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Πίνακες στη C Ένας πίνακας στη C είναι
Εισαγωγή Στον Προγραµµατισµό «C» Πίνακες Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Πίνακες στη C Ένας πίνακας στη C είναι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΠΜΣ «ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ 2006-2007 2η Σειρά Ασκήσεων ΑΠΑΝΤΗΣΕΙΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΠΜΣ «ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ 2006-2007 2η Σειρά Ασκήσεων ΑΠΑΝΤΗΣΕΙΣ 1. ίνεται το γνωστό πρόβληµα των δύο δοχείων: «Υπάρχουν δύο δοχεία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΠΜΣ «ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ 2006-2007 2η Σειρά Ασκήσεων ΑΠΑΝΤΗΣΕΙΣ 1. ίνεται το γνωστό πρόβληµα των δύο δοχείων: «Υπάρχουν δύο δοχεία
Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΚΦΩΝΗΣΕΙΣ ÏÅÖÅ
 1 Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ Α. Να γράψετε στην κόλλα σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1 5 και δίπλα τη λέξη
1 Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ Α. Να γράψετε στην κόλλα σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1 5 και δίπλα τη λέξη
Εισαγωγή στην C. Μορφή Προγράµµατος σε γλώσσα C
 Εισαγωγή στην C Μορφή Προγράµµατος σε γλώσσα C Τµήµα Α Με την εντολή include συµπεριλαµβάνω στο πρόγραµµα τα πρότυπα των συναρτήσεων εισόδου/εξόδου της C.Το αρχείο κεφαλίδας stdio.h είναι ένας κατάλογος
Εισαγωγή στην C Μορφή Προγράµµατος σε γλώσσα C Τµήµα Α Με την εντολή include συµπεριλαµβάνω στο πρόγραµµα τα πρότυπα των συναρτήσεων εισόδου/εξόδου της C.Το αρχείο κεφαλίδας stdio.h είναι ένας κατάλογος
HY118- ιακριτά Μαθηµατικά. Παράδειγµα. Από τα συµπεράσµατα στις υποθέσεις Αποδείξεις - Θεωρία συνόλων. Από τις υποθέσεις στα συµπεράσµατα...
 HY118- ιακριτά Μαθηµατικά Παρασκευή, 11/03/2016 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/15/2016
HY118- ιακριτά Μαθηµατικά Παρασκευή, 11/03/2016 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/15/2016
ΣΕΤ ΑΣΚΗΣΕΩΝ 4. Προθεσµία: 8/1/12, 22:00
 ΣΕΤ ΑΣΚΗΣΕΩΝ 4 ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2011-2012 Προθεσµία: 8/1/12, 22:00 Περιεχόµενα Διαβάστε πριν ξεκινήσετε Εκφώνηση άσκησης Οδηγίες αποστολής άσκησης Πριν ξεκινήσετε (ΔΙΑΒΑΣΤΕ
ΣΕΤ ΑΣΚΗΣΕΩΝ 4 ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2011-2012 Προθεσµία: 8/1/12, 22:00 Περιεχόµενα Διαβάστε πριν ξεκινήσετε Εκφώνηση άσκησης Οδηγίες αποστολής άσκησης Πριν ξεκινήσετε (ΔΙΑΒΑΣΤΕ
C: Από τη Θεωρία στην Εφαρµογή 2 ο Κεφάλαιο
 C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 2 ο Τύποι Δεδοµένων Δήλωση Μεταβλητών Έξοδος Δεδοµένων Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Μνήµη και Μεταβλητές Σχέση Μνήµης Υπολογιστή και Μεταβλητών Η µνήµη (RAM) ενός
C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 2 ο Τύποι Δεδοµένων Δήλωση Μεταβλητών Έξοδος Δεδοµένων Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Μνήµη και Μεταβλητές Σχέση Μνήµης Υπολογιστή και Μεταβλητών Η µνήµη (RAM) ενός
lab13grades Άσκηση 2 -Σωστά απελευθερώνετε ολόκληρη τη λίστα και την κεφαλή
 ΑΕΜ ΒΑΘΜΟΣ ΣΧΟΛΙΑ 00497 -Δεν ελέγχετε αν η createlist εκτελλέστικε σωστά και δεν τερµατίζετε το πρόγραµµα σε διαφορετική -Σωστά βρίσκετε το σηµείο στο οποίο πρέπει να προστεθεί ο κόµβος. -Σωστά τερµατίζετε
ΑΕΜ ΒΑΘΜΟΣ ΣΧΟΛΙΑ 00497 -Δεν ελέγχετε αν η createlist εκτελλέστικε σωστά και δεν τερµατίζετε το πρόγραµµα σε διαφορετική -Σωστά βρίσκετε το σηµείο στο οποίο πρέπει να προστεθεί ο κόµβος. -Σωστά τερµατίζετε
Λογικός Προγραµµατισµός: Η Γλώσσα Prolog
 Λογικός Προγραµµατισµός: Η Γλώσσα Prolog 1 Βασικά Στοιχεία Γλώσσας Prolog Ορισµοί (statements): Επιτελούν το ρόλο εντολών στις κλασσικές γλώσσες προγραµµατισµού Γεγονότα Κανόνες Ερωτήσεις Όροι (terms):
Λογικός Προγραµµατισµός: Η Γλώσσα Prolog 1 Βασικά Στοιχεία Γλώσσας Prolog Ορισµοί (statements): Επιτελούν το ρόλο εντολών στις κλασσικές γλώσσες προγραµµατισµού Γεγονότα Κανόνες Ερωτήσεις Όροι (terms):
Θεώρηµα: Z ( Απόδειξη: Περ. #1: Περ. #2: *1, *2: αποδεικνύονται εύκολα, διερευνώντας τις περιπτώσεις ο k να είναι άρτιος ή περιττός
 HY118- ιακριτά Μαθηµατικά Την προηγούµενη φορά Τρόποι απόδειξης Τρίτη, 07/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter,
HY118- ιακριτά Μαθηµατικά Την προηγούµενη φορά Τρόποι απόδειξης Τρίτη, 07/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter,
Προγραµµατισµός Ι (ΗΥ120)
 Προγραµµατισµός Ι (ΗΥ120) Διάλεξη 15: Διασυνδεµένες Δοµές - Λίστες Δοµές δεδοµένων! Ένα τυπικό πρόγραµµα επεξεργάζεται δεδοµένα Πώς θα τα διατάξουµε? 2 Τι λειτουργίες θέλουµε να εκτελέσουµε? Πώς θα υλοποιήσουµε
Προγραµµατισµός Ι (ΗΥ120) Διάλεξη 15: Διασυνδεµένες Δοµές - Λίστες Δοµές δεδοµένων! Ένα τυπικό πρόγραµµα επεξεργάζεται δεδοµένα Πώς θα τα διατάξουµε? 2 Τι λειτουργίες θέλουµε να εκτελέσουµε? Πώς θα υλοποιήσουµε
Επαναληπτικές δοµές. µτ α.τ. Όχι. ! απαγορεύεται µέσα σε µία ΓΙΑ να µεταβάλλουµε τον µετρητή! διότι δεν θα ξέρουµε µετά πόσες επαναλήψεις θα γίνουν
 Επαναληπτικές δοµές Η λογική των επαναληπτικών διαδικασιών εφαρµόζεται όπου µία ακολουθία εντολών εφαρµόζεται σε ένα σύνολο περιπτώσεων που έχουν κάτι κοινό. Όταν ψάχνουµε θέση για να παρκάρουµε κοντά
Επαναληπτικές δοµές Η λογική των επαναληπτικών διαδικασιών εφαρµόζεται όπου µία ακολουθία εντολών εφαρµόζεται σε ένα σύνολο περιπτώσεων που έχουν κάτι κοινό. Όταν ψάχνουµε θέση για να παρκάρουµε κοντά
υναµικές οµές εδοµένων
 υναµικές οµές εδοµένων Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: υναµικές οµές εδοµένων Γενικά υναµική έσµευση Μνήµης οµή τύπου structure αυτοαναφορικές δοµές Η δήλωση typedef στη C Αναπαράσταση
υναµικές οµές εδοµένων Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: υναµικές οµές εδοµένων Γενικά υναµική έσµευση Μνήµης οµή τύπου structure αυτοαναφορικές δοµές Η δήλωση typedef στη C Αναπαράσταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ. ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 24 Ιουνίου 2004
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙ ΜΑΚΕ ΝΙΑΣ ΙΚΝΜΙΚΩΝ ΚΑΙ ΚΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΣΜΕΝΗΣ ΠΛΗΡΦΡΙΚΗΣ ΤΕΝΗΤΗ ΝΗΜΣΥΝΗ Τελικές εξετάσεις 24 Ιουνίου 2004 ιάρκεια: 3 ώρες α) Αναφέρετε τη σειρά µε την
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙ ΜΑΚΕ ΝΙΑΣ ΙΚΝΜΙΚΩΝ ΚΑΙ ΚΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΣΜΕΝΗΣ ΠΛΗΡΦΡΙΚΗΣ ΤΕΝΗΤΗ ΝΗΜΣΥΝΗ Τελικές εξετάσεις 24 Ιουνίου 2004 ιάρκεια: 3 ώρες α) Αναφέρετε τη σειρά µε την
FAIL PASS PASS οριακά
 AEM 0001 0002 COMMENTS οριακά -Το πρόγραµµά σου δουλεύει λάθος για τις εισόδους: 7 -Δεν έχεις µεριµνήσει για την περίπτωση step=1. Μπορούσες να θεωρήσεις ειδική περίπτωση και να την υλοποιείς σε άλλον
AEM 0001 0002 COMMENTS οριακά -Το πρόγραµµά σου δουλεύει λάθος για τις εισόδους: 7 -Δεν έχεις µεριµνήσει για την περίπτωση step=1. Μπορούσες να θεωρήσεις ειδική περίπτωση και να την υλοποιείς σε άλλον
for for for for( . */
 Εισαγωγή Στον Προγραµµατισµό «C» Βρόχοι Επανάληψης Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Ο βρόχος for Η εντολή for χρησιµοποιείται
Εισαγωγή Στον Προγραµµατισµό «C» Βρόχοι Επανάληψης Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Ο βρόχος for Η εντολή for χρησιµοποιείται
a = 10; a = k; int a,b,c; a = b = c = 10;
 C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 4 ο Τελεστές Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Ο τελεστής εκχώρησης = Ο τελεστής = χρησιµοποιείται για την απόδοση τιµής (ή αλλιώς ανάθεση τιµής) σε µία µεταβλητή Π.χ.
C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 4 ο Τελεστές Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Ο τελεστής εκχώρησης = Ο τελεστής = χρησιµοποιείται για την απόδοση τιµής (ή αλλιώς ανάθεση τιµής) σε µία µεταβλητή Π.χ.
Ασκήσεις μελέτης της 4 ης διάλεξης. ), για οποιοδήποτε μονοπάτι n 1
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
char name[5]; /* define a string of characters */
![char name[5]; /* define a string of characters */ char name[5]; /* define a string of characters */](/thumbs/54/33866219.jpg) Συµβολοσειρές (Strings) Συµβολοσειρά (string) είναι µια σειρά αλφαριθµητικών χαρακτήρων (γενικά εκτυπώσιµων συµβόλων ASCII). Όταν λέµε σειρά εννοούµε διαδοχικές θέσεις µνήµης που µπορούν να αντιµετωπισθούν
Συµβολοσειρές (Strings) Συµβολοσειρά (string) είναι µια σειρά αλφαριθµητικών χαρακτήρων (γενικά εκτυπώσιµων συµβόλων ASCII). Όταν λέµε σειρά εννοούµε διαδοχικές θέσεις µνήµης που µπορούν να αντιµετωπισθούν
o AND o IF o SUMPRODUCT
 Πληροφοριακά Εργαστήριο Management 1 Information Συστήματα Systems Διοίκησης ΤΕΙ Τμήμα Ελεγκτικής Ηπείρου Χρηματοοικονομικής (Παράρτημα Πρέβεζας) και Αντικείµενο: Μοντελοποίηση προβλήµατος Θέµατα που καλύπτονται:
Πληροφοριακά Εργαστήριο Management 1 Information Συστήματα Systems Διοίκησης ΤΕΙ Τμήμα Ελεγκτικής Ηπείρου Χρηματοοικονομικής (Παράρτημα Πρέβεζας) και Αντικείµενο: Μοντελοποίηση προβλήµατος Θέµατα που καλύπτονται:
2.2.3 Η εντολή Εκτύπωσε
 2.2.3 Η εντολή Εκτύπωσε Η εντολή Εκτύπωσε χρησιµοποιείται προκειµένου να εµφανίσουµε κάτι στην οθόνη του υπολογιστή. Για τον λόγο αυτό ονοµάζεται και εντολή εξόδου. Ισοδύναµα µπορεί να χρησιµοποιηθεί και
2.2.3 Η εντολή Εκτύπωσε Η εντολή Εκτύπωσε χρησιµοποιείται προκειµένου να εµφανίσουµε κάτι στην οθόνη του υπολογιστή. Για τον λόγο αυτό ονοµάζεται και εντολή εξόδου. Ισοδύναµα µπορεί να χρησιµοποιηθεί και
Γενικές Παρατηρήσεις. Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα (1) Το Λήµµα της Αντλησης. Χρήση του Λήµµατος Αντλησης.
 Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
ΓΛΩΣΣΑ ΑΛΦΑΒΗΤΟ ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΣΤΑΘΕΡΕΣ ΜΕΤΑΒΛΗΤΕΣ
 ΓΛΩΣΣΑ ΑΛΦΑΒΗΤΟ Κεφαλαία και μικρά γράμματα ελληνικού αλφαβήτου: Α Ω και α ω Κεφαλαία και μικρά γράμματα λατινικού αλφαβήτου: A Z και a z Αριθμητικά ψηφία: 0 9 Ειδικοί χαρακτήρες: + - * / =. ( ),! & κενός
ΓΛΩΣΣΑ ΑΛΦΑΒΗΤΟ Κεφαλαία και μικρά γράμματα ελληνικού αλφαβήτου: Α Ω και α ω Κεφαλαία και μικρά γράμματα λατινικού αλφαβήτου: A Z και a z Αριθμητικά ψηφία: 0 9 Ειδικοί χαρακτήρες: + - * / =. ( ),! & κενός
ΚΕΦΑΛΑΙΟ 7 ο. Έτσι ο προγραµµατισµός µε τη ΓΛΩΣΣΑ εστιάζεται στην ανάπτυξη του αλγορίθµου και τη µετατροπή του σε σωστό πρόγραµµα.
 ΚΕΦΑΛΑΙΟ 7 ο 1. Επιλογή της κατάλληλης γλώσσας προγραµµατισµού Εκατοντάδες γλώσσες προγραµµατισµού χρησιµοποιούνται όπως αναφέρθηκε σήµερα για την επίλυση των προβληµάτων µε τον υπολογιστή, τη δηµιουργία
ΚΕΦΑΛΑΙΟ 7 ο 1. Επιλογή της κατάλληλης γλώσσας προγραµµατισµού Εκατοντάδες γλώσσες προγραµµατισµού χρησιµοποιούνται όπως αναφέρθηκε σήµερα για την επίλυση των προβληµάτων µε τον υπολογιστή, τη δηµιουργία
Τίτλος Υποέργου: Εφαρµογές Τεχνητής Νοηµοσύνης στην Τεχνολογία Λογισµικού και στην Ιατρική
 Αρχιµήδης ΙΙ Ενίσχυση Ερευνητικών Οµάδων του ΤΕΙ Κρήτης Τίτλος Υποέργου: Εφαρµογές Τεχνητής Νοηµοσύνης στην Τεχνολογία Λογισµικού και στην Ιατρική Επιστηµονικός Υπεύθυνος: ρ Εµµανουήλ Μαρακάκης ραστηριότητα
Αρχιµήδης ΙΙ Ενίσχυση Ερευνητικών Οµάδων του ΤΕΙ Κρήτης Τίτλος Υποέργου: Εφαρµογές Τεχνητής Νοηµοσύνης στην Τεχνολογία Λογισµικού και στην Ιατρική Επιστηµονικός Υπεύθυνος: ρ Εµµανουήλ Μαρακάκης ραστηριότητα
ΚΕΦΑΛΑΙΟ 8 Η ΓΛΩΣΣΑ PASCAL
 8.1. Εισαγωγή ΚΕΦΑΛΑΙΟ 8 Η ΓΛΩΣΣΑ PACAL Πως προέκυψε η γλώσσα προγραμματισμού Pascal και ποια είναι τα γενικά της χαρακτηριστικά; Σχεδιάστηκε από τον Ελβετό επιστήμονα της Πληροφορικής Nicklaus Wirth to
8.1. Εισαγωγή ΚΕΦΑΛΑΙΟ 8 Η ΓΛΩΣΣΑ PACAL Πως προέκυψε η γλώσσα προγραμματισμού Pascal και ποια είναι τα γενικά της χαρακτηριστικά; Σχεδιάστηκε από τον Ελβετό επιστήμονα της Πληροφορικής Nicklaus Wirth to
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Τρίτη, 07/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/7/2017
HY118- ιακριτά Μαθηµατικά Τρίτη, 07/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/7/2017
Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5)
 Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στον Κατηγορηματικό Λογισμό Σύνταξη Κανόνες Συμπερασμού Σημασιολογία ΕΠΛ 412 Λογική στην
Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στον Κατηγορηματικό Λογισμό Σύνταξη Κανόνες Συμπερασμού Σημασιολογία ΕΠΛ 412 Λογική στην
ΑΕΠΠ Ερωτήσεις θεωρίας
 ΑΕΠΠ Ερωτήσεις θεωρίας Κεφάλαιο 1 1. Τα δεδομένα μπορούν να παρέχουν πληροφορίες όταν υποβάλλονται σε 2. Το πρόβλημα μεγιστοποίησης των κερδών μιας επιχείρησης είναι πρόβλημα 3. Για την επίλυση ενός προβλήματος
ΑΕΠΠ Ερωτήσεις θεωρίας Κεφάλαιο 1 1. Τα δεδομένα μπορούν να παρέχουν πληροφορίες όταν υποβάλλονται σε 2. Το πρόβλημα μεγιστοποίησης των κερδών μιας επιχείρησης είναι πρόβλημα 3. Για την επίλυση ενός προβλήματος
Κεφάλαιο 10 ο Υποπρογράµµατα
 Κεφάλαιο 10 ο Υποπρογράµµατα Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον Η αντιµετώπιση των σύνθετων προβληµάτων και η ανάπτυξη των αντίστοιχων προγραµµάτων µπορεί να γίνει µε την ιεραρχική σχεδίαση,
Κεφάλαιο 10 ο Υποπρογράµµατα Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον Η αντιµετώπιση των σύνθετων προβληµάτων και η ανάπτυξη των αντίστοιχων προγραµµάτων µπορεί να γίνει µε την ιεραρχική σχεδίαση,
Γραµµικός Προγραµµατισµός - Μέθοδος Simplex
 Γραµµικός Προγραµµατισµός - Μέθοδος Simplex Η πλέον γνωστή και περισσότερο χρησιµοποιηµένη µέθοδος για την επίλυση ενός γενικού προβλήµατος γραµµικού προγραµµατισµού, είναι η µέθοδος Simplex η οποία αναπτύχθηκε
Γραµµικός Προγραµµατισµός - Μέθοδος Simplex Η πλέον γνωστή και περισσότερο χρησιµοποιηµένη µέθοδος για την επίλυση ενός γενικού προβλήµατος γραµµικού προγραµµατισµού, είναι η µέθοδος Simplex η οποία αναπτύχθηκε
Παλαιότερες ασκήσεις
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY6 - Συστήµατα Ανάκτησης Πληροφοριών Παλαιότερες ασκήσεις η Σειρά Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Άσκηση ( η σειρά ασκήσεων
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY6 - Συστήµατα Ανάκτησης Πληροφοριών Παλαιότερες ασκήσεις η Σειρά Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Άσκηση ( η σειρά ασκήσεων
3 Αναδροµή και Επαγωγή
 3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
ÔÏÕËÁ ÓÁÑÑÇ ÊÏÌÏÔÇÍÇ
 ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ (2ος Κύκλος) ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ηµεροµηνία: Παρασκευή 25 Απριλίου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ (2ος Κύκλος) ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ηµεροµηνία: Παρασκευή 25 Απριλίου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
if(συνθήκη) {... // οµάδα εντολών } C: Από τη Θεωρία στην Εφαρµογή 5 ο Κεφάλαιο
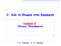 C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 5 ο Έλεγχος Προγράµµατος Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Η εντολή if (Ι) Η εντολή if είναι µία από τις βασικότερες δοµές ελέγχου ροής στη C, αλλά και στις περισσότερες
C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 5 ο Έλεγχος Προγράµµατος Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Η εντολή if (Ι) Η εντολή if είναι µία από τις βασικότερες δοµές ελέγχου ροής στη C, αλλά και στις περισσότερες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ ΜΕΡΟΣ ΤΕΤΑΡΤΟ Insert, Update, Delete, Ένωση πινάκων Γιώργος Μαρκοµανώλης Περιεχόµενα Group By... 1 Having...1 Οrder By... 2 Εντολή Insert...
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ ΜΕΡΟΣ ΤΕΤΑΡΤΟ Insert, Update, Delete, Ένωση πινάκων Γιώργος Μαρκοµανώλης Περιεχόµενα Group By... 1 Having...1 Οrder By... 2 Εντολή Insert...
ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις Παρασκευή 28 Σεπτεµβρίου 2007 ιάρκεια: 13:00-16:00
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις Παρασκευή 28 Σεπτεµβρίου 2007 ιάρκεια: 13:00-16:00
Διαδικασιακός Προγραμματισμός
 Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 2 η Τύποι Δεδομένων Δήλωση Μεταβλητών Έξοδος Δεδομένων Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα
Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 2 η Τύποι Δεδομένων Δήλωση Μεταβλητών Έξοδος Δεδομένων Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Θέµα 1 ο Α. Να απαντήσετε τις παρακάτω ερωτήσεις τύπου Σωστό Λάθος (Σ Λ) 1. Σκοπός της συγχώνευσης 2 ή περισσοτέρων ταξινοµηµένων πινάκων είναι η δηµιουργία
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Θέµα 1 ο Α. Να απαντήσετε τις παρακάτω ερωτήσεις τύπου Σωστό Λάθος (Σ Λ) 1. Σκοπός της συγχώνευσης 2 ή περισσοτέρων ταξινοµηµένων πινάκων είναι η δηµιουργία
Βαθμός Σχόλια. lab5 PASS PASS PASS PASS PASS. Οριακά PASS - Καλή δουλειά
 Α. Μ. Βαθμός Σχόλια 1183 1194 1238 1239 1240 1241 - Καλή δουλειά 1242 1243 1244 1245 - Κακή χρήση συναρτήσεων. Κάνεις τον ίδιο έλεγχο και εντός και εκτός της συνάρτησης. Θα έπρεπε να έχεις βρεί ένα τρόπο
Α. Μ. Βαθμός Σχόλια 1183 1194 1238 1239 1240 1241 - Καλή δουλειά 1242 1243 1244 1245 - Κακή χρήση συναρτήσεων. Κάνεις τον ίδιο έλεγχο και εντός και εκτός της συνάρτησης. Θα έπρεπε να έχεις βρεί ένα τρόπο
Ενδεικτικές Ερωτήσεις Θεωρίας
 Ενδεικτικές Ερωτήσεις Θεωρίας Κεφάλαιο 2 1. Τι καλούμε αλγόριθμο; 2. Ποια κριτήρια πρέπει οπωσδήποτε να ικανοποιεί ένας αλγόριθμος; 3. Πώς ονομάζεται μια διαδικασία που δεν περατώνεται μετά από συγκεκριμένο
Ενδεικτικές Ερωτήσεις Θεωρίας Κεφάλαιο 2 1. Τι καλούμε αλγόριθμο; 2. Ποια κριτήρια πρέπει οπωσδήποτε να ικανοποιεί ένας αλγόριθμος; 3. Πώς ονομάζεται μια διαδικασία που δεν περατώνεται μετά από συγκεκριμένο
ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Κεφάλαιο 8 : H γλώσσα προγραµµατισµού Pascal 1 ο Μέρος σηµειώσεων (Ενότητες 8.1 & 8.2 σχολικού βιβλίου)
 ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Κεφάλαιο 8 : H γλώσσα προγραµµατισµού Pascal 1 ο Μέρος σηµειώσεων (Ενότητες 8.1 & 8.2 σχολικού βιβλίου) 1. Εισαγωγή Χαρακτηριστικά της γλώσσας Τύποι δεδοµένων Γλώσσα προγραµµατισµού
ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Κεφάλαιο 8 : H γλώσσα προγραµµατισµού Pascal 1 ο Μέρος σηµειώσεων (Ενότητες 8.1 & 8.2 σχολικού βιβλίου) 1. Εισαγωγή Χαρακτηριστικά της γλώσσας Τύποι δεδοµένων Γλώσσα προγραµµατισµού
Sheet2. Σωστή, και µπράβο που µεριµνήσατε για λίστες διαφορετικών µεγεθών.
 Α.Μ. ΒΑΘΜΟΣ ΣΧΟΛΙΑ Δεν κάνει compile και το λάθος είναι σηµαντικό: Το head1 είναι δείκτης σε struct, εποµένως η προσπέλαση πεδίου γίνεται 321 FAIL µε head1->next και όχι head1.next. Επιπλέον, έχετε λάθος
Α.Μ. ΒΑΘΜΟΣ ΣΧΟΛΙΑ Δεν κάνει compile και το λάθος είναι σηµαντικό: Το head1 είναι δείκτης σε struct, εποµένως η προσπέλαση πεδίου γίνεται 321 FAIL µε head1->next και όχι head1.next. Επιπλέον, έχετε λάθος
ΦΥΣ-151. Ηλεκτρονικοί Υπολογιστές Ι (FORTRAN 77) (Άνοιξη 2004)
 8 ΦΥΣ-151. Ηλεκτρονικοί Υπολογιστές Ι (FORTRAN 77) (Άνοιξη 2004) ιάλεξη 2 2.1 ΜΕΤΑΒΛΗΤΕΣ (ΜΕΡΟΣ Β) Στην προηγούµενη διάλεξη µάθαµε ότι µπορούµε να χρησιµοποιούµε τη ρητή ή την αυτονόητη δήλωση µεταβλητών
8 ΦΥΣ-151. Ηλεκτρονικοί Υπολογιστές Ι (FORTRAN 77) (Άνοιξη 2004) ιάλεξη 2 2.1 ΜΕΤΑΒΛΗΤΕΣ (ΜΕΡΟΣ Β) Στην προηγούµενη διάλεξη µάθαµε ότι µπορούµε να χρησιµοποιούµε τη ρητή ή την αυτονόητη δήλωση µεταβλητών
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
Σχήµα 3.1: Εισαγωγή shift register σε βρόγχο for-loop.
 Η δοµή «Shift register» 1. Η δοµή «Shift register» εισάγεται στο βρόγχο for-loop αλλά και σε άλλους βρόγχους που θα δούµε στη συνέχεια, όπως ο βρόγχος «While loop». Ο τρόπος εισαγωγής και λειτουργίας της
Η δοµή «Shift register» 1. Η δοµή «Shift register» εισάγεται στο βρόγχο for-loop αλλά και σε άλλους βρόγχους που θα δούµε στη συνέχεια, όπως ο βρόγχος «While loop». Ο τρόπος εισαγωγής και λειτουργίας της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΜΣΕ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ ΚΑΙ ΕΞΕΛΙΚΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΜΣΕ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ ΚΑΙ ΕΞΕΛΙΚΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΟΜΑ Α ΑΣΚΗΣΕΩΝ ΑΣΚΗΣΗ Στην εικόνα παρακάτω φαίνεται ένα νευρωνικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΜΣΕ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ ΚΑΙ ΕΞΕΛΙΚΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΟΜΑ Α ΑΣΚΗΣΕΩΝ ΑΣΚΗΣΗ Στην εικόνα παρακάτω φαίνεται ένα νευρωνικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 21 Σεπτεµβρίου 2004 ιάρκεια: 3 ώρες Το παρακάτω σύνολο
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 21 Σεπτεµβρίου 2004 ιάρκεια: 3 ώρες Το παρακάτω σύνολο
Εντολές της LOGO (MicroWorlds Pro)
 Εντολές της LOGO (MicroWorlds Pro) Εντολές εμφάνισης (εξόδου) και αριθμητικές πράξεις δείξε Εμφανίζει στην οθόνη έναν αριθμό, το αποτέλεσμα πράξεων, μια λέξη ή μια λίστα (ομάδα) λέξεων. δείξε 200 200 δείξε
Εντολές της LOGO (MicroWorlds Pro) Εντολές εμφάνισης (εξόδου) και αριθμητικές πράξεις δείξε Εμφανίζει στην οθόνη έναν αριθμό, το αποτέλεσμα πράξεων, μια λέξη ή μια λίστα (ομάδα) λέξεων. δείξε 200 200 δείξε
Α. Ερωτήσεις Ανάπτυξης
 οµηµένος Προγραµµατισµός-Κεφάλαιο 7 Σελίδα 1 α ό 10 ΕΝΟΤΗΤΑ ΙΙΙ (ΠΡΟΓΡΑΜΜΑΤΑ) ΚΕΦΑΛΑΙΟ 7: Είδη, Τεχνικές και Περιβάλλοντα Προγραµµατισµού Α. Ερωτήσεις Ανάπτυξης 1. Τι ονοµάζουµε γλώσσα προγραµµατισµού;
οµηµένος Προγραµµατισµός-Κεφάλαιο 7 Σελίδα 1 α ό 10 ΕΝΟΤΗΤΑ ΙΙΙ (ΠΡΟΓΡΑΜΜΑΤΑ) ΚΕΦΑΛΑΙΟ 7: Είδη, Τεχνικές και Περιβάλλοντα Προγραµµατισµού Α. Ερωτήσεις Ανάπτυξης 1. Τι ονοµάζουµε γλώσσα προγραµµατισµού;
Προβλήµατα ικανοποίησης περιορισµών
 Προβλήµατα Ικανοποίησης Περιορισµών Προβλήµατα ικανοποίησης περιορισµών Λογικός προγραµµατισµός µε περιορισµούς Προβλήµατα Ικανοποίησης Περιορισµών Ένα πρόβληµα ικανοποίησης περιορισµών (constraint satisfaction
Προβλήµατα Ικανοποίησης Περιορισµών Προβλήµατα ικανοποίησης περιορισµών Λογικός προγραµµατισµός µε περιορισµούς Προβλήµατα Ικανοποίησης Περιορισµών Ένα πρόβληµα ικανοποίησης περιορισµών (constraint satisfaction
Οι πράξεις που χρειάζονται για την επίλυση αυτών των προβληµάτων (αφού είναι απλές) µπορούν να τεθούν σε µια σειρά και πάρουν µια αλγοριθµική µορφή.
 Η Αριθµητική Ανάλυση χρησιµοποιεί απλές αριθµητικές πράξεις για την επίλυση σύνθετων µαθηµατικών προβληµάτων. Τις περισσότερες φορές τα προβλήµατα αυτά είναι ή πολύ περίπλοκα ή δεν έχουν ακριβή αναλυτική
Η Αριθµητική Ανάλυση χρησιµοποιεί απλές αριθµητικές πράξεις για την επίλυση σύνθετων µαθηµατικών προβληµάτων. Τις περισσότερες φορές τα προβλήµατα αυτά είναι ή πολύ περίπλοκα ή δεν έχουν ακριβή αναλυτική
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
(α) Ζητείται να αναπαρασταθεί η παραπάνω γνώση σε Prolog, ώστε να δημιουργηθεί αντίστοιχο πρόγραμμα.
 1. Δίνονται τα εξής γεγονότα «Ο Παύλος είναι πατέρας του Γιάννη και της Γεωργίας» και «Η Ελένη είναι μητέρα της Μαρίας και του Πέτρου». Επίσης, μας δίνεται και η εξής γνώση τύπου κανόνα, που αφορά το πότε
1. Δίνονται τα εξής γεγονότα «Ο Παύλος είναι πατέρας του Γιάννη και της Γεωργίας» και «Η Ελένη είναι μητέρα της Μαρίας και του Πέτρου». Επίσης, μας δίνεται και η εξής γνώση τύπου κανόνα, που αφορά το πότε
Αριθµητική Ολοκλήρωση
 Κεφάλαιο 5 Αριθµητική Ολοκλήρωση 5. Εισαγωγή Για τη συντριπτική πλειοψηφία των συναρτήσεων f (x) δεν υπάρχουν ή είναι πολύ δύσχρηστοι οι τύποι της αντιπαραγώγου της f (x), δηλαδή της F(x) η οποία ικανοποιεί
Κεφάλαιο 5 Αριθµητική Ολοκλήρωση 5. Εισαγωγή Για τη συντριπτική πλειοψηφία των συναρτήσεων f (x) δεν υπάρχουν ή είναι πολύ δύσχρηστοι οι τύποι της αντιπαραγώγου της f (x), δηλαδή της F(x) η οποία ικανοποιεί
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Προγραμματισμός ΙI (Θ)
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Προγραμματισμός ΙI (Θ) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Μάρτιος 2017 Δρ. Δημήτρης Βαρσάμης Μάρτιος 2017
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Προγραμματισμός ΙI (Θ) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Μάρτιος 2017 Δρ. Δημήτρης Βαρσάμης Μάρτιος 2017
Προγραμματισμός Υπολογιστών & Υπολογιστική Φυσική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Προγραμματισμός Υπολογιστών & Υπολογιστική Φυσική Ενότητα 7: Συναρτήσεις Νικόλαος Στεργιούλας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Προγραμματισμός Υπολογιστών & Υπολογιστική Φυσική Ενότητα 7: Συναρτήσεις Νικόλαος Στεργιούλας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ (2ος Κύκλος) ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ηµεροµηνία: Παρασκευή 25 Απριλίου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ (2ος Κύκλος) ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Ηµεροµηνία: Παρασκευή 25 Απριλίου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
ΚΕΦΑΛΑΙΟ 6 - ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ
 ΚΕΦΑΛΑΙΟ 6 - ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ Προγραµµατισµός Η/Υ Ο προγραµµατισµός είναι η διατύπωση του αλγορίθµου σε µορφή κατανοητή από τον Η/Υ ώστε να τον εκτελέσει («τρέξει» όπως λέµε στην ορολογία της
ΚΕΦΑΛΑΙΟ 6 - ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ Προγραµµατισµός Η/Υ Ο προγραµµατισµός είναι η διατύπωση του αλγορίθµου σε µορφή κατανοητή από τον Η/Υ ώστε να τον εκτελέσει («τρέξει» όπως λέµε στην ορολογία της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 17 Φεβρουαρίου 2004 ιάρκεια: 2 ώρες (15:00-17:00)
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 17 Φεβρουαρίου 2004 ιάρκεια: 2 ώρες (15:00-17:00)
HY118- ιακριτά Μαθηµατικά. Νόµοι ισοδυναµίας. Κατηγορηµατικός Λογισµός. ιακριτά Μαθηµατικά, Εαρινό εξάµηνο Παρασκευή, 24/02/2017
 HY118- ιακριτά Μαθηµατικά Παρασκευή, 24/02/2017 Κατηγορηµατικός Λογισµός Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University
HY118- ιακριτά Μαθηµατικά Παρασκευή, 24/02/2017 Κατηγορηµατικός Λογισµός Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University
οµή Επιλογής Α. Κατηγορία προβληµάτων Β. Κριτήριο Αλγορίθµου Γ. Τρόπος αναπαράστασης αλγορίθµων . Είδος σταθεράς Ε. Λογική τιµή
 οµή Επιλογής Θέµα Α Α1. Να χαρακτηρίσετε κάθε µία από τις παρακάτω προτάσεις µε Σ αν είναι σωστή ή Λ αν είναι λανθασµένη. 1. Όλες οι δοµές επιλογής κλείνουν µε την εντολή. 2. Η παρακάτω εντολή είναι σωστή
οµή Επιλογής Θέµα Α Α1. Να χαρακτηρίσετε κάθε µία από τις παρακάτω προτάσεις µε Σ αν είναι σωστή ή Λ αν είναι λανθασµένη. 1. Όλες οι δοµές επιλογής κλείνουν µε την εντολή. 2. Η παρακάτω εντολή είναι σωστή
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
PROJECT ΣΤΟ ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΕΥΡΕΤΙΚΕΣ ΜΕΘΟ ΟΥΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ PROJECT ΣΤΟ ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΕΥΡΕΤΙΚΕΣ ΜΕΘΟ ΟΥΣ ΜΕΡΟΣ ΕΥΤΕΡΟ Πολίτη Όλγα Α.Μ. 4528 Εξάµηνο 8ο Υπεύθυνος Καθηγητής Λυκοθανάσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ PROJECT ΣΤΟ ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΕΥΡΕΤΙΚΕΣ ΜΕΘΟ ΟΥΣ ΜΕΡΟΣ ΕΥΤΕΡΟ Πολίτη Όλγα Α.Μ. 4528 Εξάµηνο 8ο Υπεύθυνος Καθηγητής Λυκοθανάσης
Τεχνητή Νοημοσύνη. 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος. http://www.aueb.gr/users/ion/
 Τεχνητή Νοημοσύνη 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία: Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Τεχνητή Νοημοσύνη 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία: Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Γραµµική Άλγεβρα. Εισαγωγικά. Μέθοδος Απαλοιφής του Gauss
 Γραµµική Άλγεβρα Εισαγωγικά Υπάρχουν δύο βασικά αριθµητικά προβλήµατα στη Γραµµική Άλγεβρα. Το πρώτο είναι η λύση γραµµικών συστηµάτων Aλγεβρικών εξισώσεων και το δεύτερο είναι η εύρεση των ιδιοτιµών και
Γραµµική Άλγεβρα Εισαγωγικά Υπάρχουν δύο βασικά αριθµητικά προβλήµατα στη Γραµµική Άλγεβρα. Το πρώτο είναι η λύση γραµµικών συστηµάτων Aλγεβρικών εξισώσεων και το δεύτερο είναι η εύρεση των ιδιοτιµών και
Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΚΦΩΝΗΣΕΙΣ ÏÅÖÅ
 1 Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ Α. Να γράψετε στην κόλλα σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1 5 και δίπλα τη λέξη
1 Γ' ΛΥΚΕΙΟΥ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ Α. Να γράψετε στην κόλλα σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις 1 5 και δίπλα τη λέξη
Κεφάλαιο Αλφαριθµητικές Σειρές Χαρακτήρων (Strings)
 Κεφάλαιο 9.1-9.2 Αλφαριθµητικές Σειρές Χαρακτήρων (Strings) ( ιάλεξη 19) ιδάσκων: ηµήτρης Ζεϊναλιπούρ 1) Strings στη C Ένα string είναι µία ακολουθία αλφαριθµητικών χαρακτήρων, σηµείων στίξης κτλ. Π.χ.
Κεφάλαιο 9.1-9.2 Αλφαριθµητικές Σειρές Χαρακτήρων (Strings) ( ιάλεξη 19) ιδάσκων: ηµήτρης Ζεϊναλιπούρ 1) Strings στη C Ένα string είναι µία ακολουθία αλφαριθµητικών χαρακτήρων, σηµείων στίξης κτλ. Π.χ.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 2: Εκφράσεις, πίνακες και βρόχοι 14 Απριλίου 2016 Το σημερινό εργαστήριο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 2: Εκφράσεις, πίνακες και βρόχοι 14 Απριλίου 2016 Το σημερινό εργαστήριο
ΕΡΩΤΗΜΑΤΑ σε ΓΝΩΣΗ ΚΑΤΗΓΟΡΗΜΑΤΙΚΗ ΛΟΓΙΚΗ. ηµήτρης Ψούνης ΠΛΗ31, Απαντήσεις Ερωτήσεων Quiz - ΓΝΩΣΗ 1. ΣΩΣΤO τo (b): NAI ΕΞΗΓΗΣΗ: ΤΕΣΤ 7 / ΑΣΚΗΣΗ 1.
 ηµήτρης Ψούνης ΠΛΗ31, Απαντήσεις Ερωτήσεων Quiz - ΓΝΩΣΗ 1 ΕΡΩΤΗΜΑΤΑ σε ΓΝΩΣΗ ΚΑΤΗΓΟΡΗΜΑΤΙΚΗ ΛΟΓΙΚΗ ΚΑΤΗΓΟΡΗΜΑΤΙΚΗ ΛΟΓΙΚΗ 1 Η πρόταση «εν είναι όλα τα άλογα τετράποδα» είναι ισοδύναµη µε την πρόταση. a.
ηµήτρης Ψούνης ΠΛΗ31, Απαντήσεις Ερωτήσεων Quiz - ΓΝΩΣΗ 1 ΕΡΩΤΗΜΑΤΑ σε ΓΝΩΣΗ ΚΑΤΗΓΟΡΗΜΑΤΙΚΗ ΛΟΓΙΚΗ ΚΑΤΗΓΟΡΗΜΑΤΙΚΗ ΛΟΓΙΚΗ 1 Η πρόταση «εν είναι όλα τα άλογα τετράποδα» είναι ισοδύναµη µε την πρόταση. a.
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2013-2014
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2013-2014 Επιμέλεια: Ομάδα Διαγωνισμάτων από το Στέκι των Πληροφορικών Θέμα Α A1. Να γράψετε στο τετράδιό σας τους
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2013-2014 Επιμέλεια: Ομάδα Διαγωνισμάτων από το Στέκι των Πληροφορικών Θέμα Α A1. Να γράψετε στο τετράδιό σας τους
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 1 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΚΕΦΑΛΑΙΟ 3ο: ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΜΕΡΟΣ 2 ο : ΣΤΟΙΒΑ & ΟΥΡΑ ΙΣΤΟΣΕΛΙΔΑ ΜΑΘΗΜΑΤΟΣ: http://eclass.sch.gr/courses/el594100/ ΣΤΟΙΒΑ 2 Μια στοίβα
1 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΚΕΦΑΛΑΙΟ 3ο: ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΜΕΡΟΣ 2 ο : ΣΤΟΙΒΑ & ΟΥΡΑ ΙΣΤΟΣΕΛΙΔΑ ΜΑΘΗΜΑΤΟΣ: http://eclass.sch.gr/courses/el594100/ ΣΤΟΙΒΑ 2 Μια στοίβα
ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ
 ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ ΣΕΝΑΡΙΟ ΠΑΙΧΝΙ ΙΟΥ Το παιχνίδι θα αποτελείται από δυο παίκτες, οι οποίοι θα βρίσκονται αντικριστά στις άκρες ενός γηπέδου δεξιά και αριστερά, και µια µπάλα.
ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ ΣΕΝΑΡΙΟ ΠΑΙΧΝΙ ΙΟΥ Το παιχνίδι θα αποτελείται από δυο παίκτες, οι οποίοι θα βρίσκονται αντικριστά στις άκρες ενός γηπέδου δεξιά και αριστερά, και µια µπάλα.
τη µέθοδο της µαθηµατικής επαγωγής για να αποδείξουµε τη Ϲητούµενη ισότητα.
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
ΕΙΣΑΓΩΓΗ ΣΤΟ MATLAB- SIMULINK
 ΕΙΣΑΓΩΓΗ ΣΤΟ MATLAB- SIMULINK ρ. Γεώργιος Φ. Φραγκούλης Καθηγητής Ver. 0.2 9/2012 ιανύσµατα & ισδιάστατοι πίνακες Ένα διάνυσµα u = (u1, u2,, u ) εισάγεται στη MATLAB ως εξής : u=[ u1, u2,, un ] ή u=[ u1
ΕΙΣΑΓΩΓΗ ΣΤΟ MATLAB- SIMULINK ρ. Γεώργιος Φ. Φραγκούλης Καθηγητής Ver. 0.2 9/2012 ιανύσµατα & ισδιάστατοι πίνακες Ένα διάνυσµα u = (u1, u2,, u ) εισάγεται στη MATLAB ως εξής : u=[ u1, u2,, un ] ή u=[ u1
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Τρίτη, 21/02/2017 Το υλικό των διαφανειών έχει βασιστεί σε Αντώνης διαφάνειες Α. Αργυρός του Kees van e-mail: argyros@csd.uoc.gr Deemter, από το University of Aberdeen 2/21/2017
HY118- ιακριτά Μαθηµατικά Τρίτη, 21/02/2017 Το υλικό των διαφανειών έχει βασιστεί σε Αντώνης διαφάνειες Α. Αργυρός του Kees van e-mail: argyros@csd.uoc.gr Deemter, από το University of Aberdeen 2/21/2017
Περιεχόμενα Πρόλογος 1. Εισαγωγή 2. Τα Βασικά Μέρη ενός Προγράμματος Prolog
 Περιεχόμενα Πρόλογος... xxv 1. Εισαγωγή... 1 1.1. Ιστορική Εξέλιξη της Prolog.... 2 1.2. Προστακτικός και Δηλωτικός Προγραμματισμός.... 2 1.3. Δηλωτική και διαδικαστική έννοια ενός προγράμματος Prolog....
Περιεχόμενα Πρόλογος... xxv 1. Εισαγωγή... 1 1.1. Ιστορική Εξέλιξη της Prolog.... 2 1.2. Προστακτικός και Δηλωτικός Προγραμματισμός.... 2 1.3. Δηλωτική και διαδικαστική έννοια ενός προγράμματος Prolog....
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2015-2016 Θέμα Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις προτάσεις 1-4 και δίπλα τη λέξη ΣΩΣΤΟ,
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 2015-2016 Θέμα Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις προτάσεις 1-4 και δίπλα τη λέξη ΣΩΣΤΟ,
Ο Προγραμματισμός στην Πράξη
 Ο Προγραμματισμός στην Πράξη Το περιβάλλον προγραμματισμού MicroWorlds Pro Μενού επιλογών Γραμμή εργαλείων Επιφάνεια εργασίας Περιοχή Καρτελών Κέντρο εντολών Καρτέλες Οι πρώτες εντολές Εντολές εμφάνισης
Ο Προγραμματισμός στην Πράξη Το περιβάλλον προγραμματισμού MicroWorlds Pro Μενού επιλογών Γραμμή εργαλείων Επιφάνεια εργασίας Περιοχή Καρτελών Κέντρο εντολών Καρτέλες Οι πρώτες εντολές Εντολές εμφάνισης
ΦΥΣ-151. Ηλεκτρονικοί Υπολογιστές Ι (FORTRAN 77) (Άνοιξη 2004)
 1 ΦΥΣ-151. Ηλεκτρονικοί Υπολογιστές Ι (FORTRAN 77) (Άνοιξη 2004) ιάλεξη 1 1.1 ΕΙΣΑΓΩΓΗ ΣΤΗ FORTRAN 77 Ένα πρόγραµµα σε οποιαδήποτε γλώσσα προγραµµατισµού δεν τίποτα άλλο από µια σειρά εντολών που πρέπει
1 ΦΥΣ-151. Ηλεκτρονικοί Υπολογιστές Ι (FORTRAN 77) (Άνοιξη 2004) ιάλεξη 1 1.1 ΕΙΣΑΓΩΓΗ ΣΤΗ FORTRAN 77 Ένα πρόγραµµα σε οποιαδήποτε γλώσσα προγραµµατισµού δεν τίποτα άλλο από µια σειρά εντολών που πρέπει
υναµικές οµές εδοµένων (συν.) Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα:
 υναµικές οµές εδοµένων (συν.) Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: Ταξινοµηµένες Λίστες µε δυναµική δέσµευση µνήµης Αναδροµκές συναρτήσεις ΕΠΛ 12 Αρχές Προγραµµατισµού ΙΙ 1 Λίστες
υναµικές οµές εδοµένων (συν.) Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: Ταξινοµηµένες Λίστες µε δυναµική δέσµευση µνήµης Αναδροµκές συναρτήσεις ΕΠΛ 12 Αρχές Προγραµµατισµού ΙΙ 1 Λίστες
Εισαγωγή στην Τοπολογία
 Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Εφαρμοσμένη Πληροφορική ΙΙ (Θ) Είσοδος/Έξοδος Μεταβλητές Τύποι Μεταβλητών Τελεστές και Προτεραιότητα Μετατροπές Μεταξύ Τύπων
 Εφαρμοσμένη Πληροφορική ΙΙ (Θ) Είσοδος/Έξοδος Μεταβλητές Τύποι Μεταβλητών Τελεστές και Προτεραιότητα Μετατροπές Μεταξύ Τύπων 1 Είσοδος/Έξοδος Είσοδος/Έξοδος ανάλογα με τον τύπο του προγράμματος Πρόγραμμα
Εφαρμοσμένη Πληροφορική ΙΙ (Θ) Είσοδος/Έξοδος Μεταβλητές Τύποι Μεταβλητών Τελεστές και Προτεραιότητα Μετατροπές Μεταξύ Τύπων 1 Είσοδος/Έξοδος Είσοδος/Έξοδος ανάλογα με τον τύπο του προγράμματος Πρόγραμμα
ΚΕΦΑΛΑΙΟ 7 ΕΙ Η, ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 ΚΕΦΑΛΑΙΟ 7 ΕΙ Η, ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ 7.1. Ανάπτυξη Προγράµµατος Τι είναι το Πρόγραµµα; Το Πρόγραµµα: Είναι ένα σύνολο εντολών για την εκτέλεση ορισµένων λειτουργιών από τον υπολογιστή.
ΚΕΦΑΛΑΙΟ 7 ΕΙ Η, ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ 7.1. Ανάπτυξη Προγράµµατος Τι είναι το Πρόγραµµα; Το Πρόγραµµα: Είναι ένα σύνολο εντολών για την εκτέλεση ορισµένων λειτουργιών από τον υπολογιστή.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ
 ΘΕΜΑ ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις Παρασκευή 9 Ιανουαρίου 2007 5:00-8:00 εδοµένου ότι η
ΘΕΜΑ ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις Παρασκευή 9 Ιανουαρίου 2007 5:00-8:00 εδοµένου ότι η
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ PROLOG Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ PROLOG Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ ΓΕΝΙΚΑ PROLOG PROgramming in LOGic Πρώτη υλοποίηση: Alain Colmerauer, Μασσαλία (Αρχή Επίλυσης, Εργασία R. Kowalski) εύτερη υλοποίηση: D. Warren, Εδιµβούργο
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ PROLOG Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ ΓΕΝΙΚΑ PROLOG PROgramming in LOGic Πρώτη υλοποίηση: Alain Colmerauer, Μασσαλία (Αρχή Επίλυσης, Εργασία R. Kowalski) εύτερη υλοποίηση: D. Warren, Εδιµβούργο
Επαναληπτικό ιαγώνισµα Πληροφορικής Γ Γυµνασίου Γιώργος Λιακέας Σχολικός Σύµβουλος Πληροφορικής Ερωτήσεις
 Επαναληπτικό ιαγώνισµα Πληροφορικής Γ Γυµνασίου (νέο βιβλίο Πληροφορικής Γυµνασίου Αράπογλου, Μαβόγλου, Οικονοµάκου, Φύτρου) Γιώργος Λιακέας Σχολικός Σύµβουλος Πληροφορικής Ερωτήσεις 1. Τι είναι ο Αλγόριθµος;
Επαναληπτικό ιαγώνισµα Πληροφορικής Γ Γυµνασίου (νέο βιβλίο Πληροφορικής Γυµνασίου Αράπογλου, Μαβόγλου, Οικονοµάκου, Φύτρου) Γιώργος Λιακέας Σχολικός Σύµβουλος Πληροφορικής Ερωτήσεις 1. Τι είναι ο Αλγόριθµος;
