ΠΑΝΕΠΙΣΤΗΜΙΑΚΕΣ ΠΑΡΑ ΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΓΙΑ ΚΙΝΗΣΗ ΚΑΙ ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΗ Ι
|
|
|
- Ἄρτεμις Λιάπης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΝΕΡΓΕΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΛΕΚΤΟΡΑΣ ΑΘΑΝΑΣΙΟΣ. ΚΑΡΛΗΣ Τριφασική πηγή τάσης Διέγερση Κύκλωμα Παλμών Τύμπανο Ελεγκτής Ταχύτητας Ελεγκτής Ρεύματος Ταχ. Μετατροπέας ΠΑΝΕΠΙΣΤΗΜΙΑΚΕΣ ΠΑΡΑ ΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΓΙΑ ΚΙΝΗΣΗ ΚΑΙ ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΗ Ι ΞΑΝΘΗ 00
2 Περιεχόμενα Κεφάλαιο. Γενικά στοιχεία του μαθήματος Κεφάλαιο. Στοιχεία φυσικής και μηχανικής 4. Μετάδοση κίνησης 3.3 Χαρακτηριστικές φορτίων 6.4 Επίδραση των χαρακτηριστικών στη δυναμική ευστάθεια 8 Κεφάλαιο 3 3. Μετασχηματιστές 3. Μηχανές συνεχούς ρεύματος Κινητήρες Σ.Ρ. ξένης (ή παράλληλης) διέγερσης Κινητήρες Σ.Ρ. διέγερσης σειράς Ηλεκτρονικά ελεγχόμενα κινητήρια συστήματα με κινητήρες Σ.Ρ Ψαλιδιστές Ανορθωτικές διατάξεις Κινητήρες Univerl Μηχανές συνεχούς ρεύματος μόνιμου μαγνήτη Μηχανές συνεχούς ρεύματος μόνιμου μαγνήτη χωρίς ψήκτρες 97
3 Γενικά στοιχεία του μαθήματος Συστήματα ηλεκτροπαραγωγής είναι τα συστήματα που χρησιμοποιούνται για τη μετατροπή της μηχανικής ενέργειας σε ηλεκτρική, προκειμένου να τροφοδοτηθούν ηλεκτρικά φορτία. Ηλεκτρικά κινητήρια συστήματα είναι τα συστήματα που χρησιμοποιούνται για τη δημιουργία κίνησης, δηλαδή τη μετατροπή της ηλεκτρικής ενέργειας σε μηχανική, προκειμένου να παραχθεί ορισμένο έργο. Η κατάλληλη ζεύξη ενός ηλεκτρικού και ενός μηχανικού συστήματος καθιστά δυνατή τη μετατροπή της ενέργειας από τη μια μορφή στην άλλη. Συνδετικό κρίκο μεταξύ των δύο αυτών συστημάτων αποτελεί μια συσκευή ηλεκτρομηχανικής μετατροπής της ενέργειας βασικό στοιχείο της οποίας αποτελεί η στρεφόμενη ηλεκτρική μηχανή. Η ηλεκτρική μηχανή έχει τη δυνατότητα να λειτουργεί είτε ως γεννήτρια, είτε ως κινητήρας, δηλαδή η διαδικασία της μετατροπής της ενέργειας σε μια μηχανή είναι αντιστρεπτή, αν και ορισμένο μέρος της ενέργειας «χάνεται μη αντιστρεπτά» σε θερμότητα. Η δομή ενός συστήματος ηλεκτροπαραγωγής και ενός συστήματος ηλεκτρικής κίνησης παρουσιάζονται στο Σχ... Σχήμα. Σύστημα ηλεκτροπαραγωγής.
4 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Τροφοδοσία δικτύου Σήμα ελέγχου Μονάδα Ελέγχου Μετατροπέας Ισχύος V, I T, ω Κινητήρας Φορτίο Σύστημα Ανάδρασης Σχήμα.b Στοιχειώδες σύστημα κίνησης. Η σωστή σχεδίαση των παραπάνω συστημάτων απαιτεί πλήρη γνώση της στατικής και δυναμικής συμπεριφοράς όλων των επιμέρους συνιστωσών του. Στο σχήμα. ο στρόβιλος (Turbine) μαζί με τη γεννήτρια (Genr.) αποτελούν το ηλεκτροπαραγωγό ζεύγος. Βασικές μεταβλητές ελέγχου μπορεί να είναι οι εξής: Ταχύτητα Τάση Συνδυασμός των παραπάνω Ο στρόβιλος, μέσω του συστήματος ελέγχου της ταχύτητας, τροφοδοτεί τη γεννήτρια (σύγχρονη) με την κατάλληλη μηχανική ισχύ έτσι ώστε να ικανοποιηθούν οι απαιτήσεις για σταθερή ταχύτητα της γεννήτριας άρα για σταθερή συχνότητα δικτύου. Η τάση της γεννήτριας ελέγχεται μέσω του συστήματος ελέγχου της διέγερσής της. Στο σχήμα.b ο κινητήρας μαζί με το μετατροπέα ισχύος αποτελούν το σύστημα οδήγησης του μηχανικού φορτίου. Βασικές μεταβλητές ελέγχου μπορεί να είναι οι εξής: Ροπή Επιτάχυνση Ταχύτητα Θέση Συνδυασμός των παραπάνω
5 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Ο μετατροπέας ισχύος, μέσω του συστήματος ελέγχου, τροφοδοτεί τον κινητήρα με το κατάλληλο ρεύμα και τάση έτσι ώστε να ικανοποιηθούν οι απαιτήσεις του μηχανικού φορτίου. Τα συστήματα ηλεκτρικής κίνησης χρησιμοποιούνται σε μια πολύ ευρεία περιοχή ισχύος, από μερικά Wtt μέχρι πολλές χιλιάδες kwtt. Βρίσκουν δε εφαρμογές από τους πολύ ακριβείς ελεγκτές θέσης των ρομπότ μέχρι τα κινητήρια συστήματα μεταβλητής ταχύτητας των αντλιών για τη ρύθμιση της ροής. Άλλες εφαρμογές τους είναι οι εξής: Στη χαρτοβιομηχανία Στις εργαλειομηχανές Στο ηλεκτρικό αυτοκίνητο Στη τσιμεντοβιομηχανία Στους ταινιόδρομους Στην κλωστοϋφαντουργία Στους ηλεκτρικούς σιδηροδρόμους, κ.λ.π. Τις προηγούμενες δεκαετίες χρησιμοποιούνταν στα ηλεκτρικά κινητήρια συστήματα κινητήρες συνεχούς ρεύματος, λόγω του πλεονεκτήματος τους να ελέγχεται η μαγνητική τους ροή (μέσω του ρεύματος διέγερσης) ανεξάρτητα από την ηλεκτρική ροπή (έλεγχος μέσω του ρεύματος τυμπάνου). Τα συστήματα ελέγχου των κινητήρων συνεχούς ρεύματος είναι απλούστερα και οικονομικότερα από τα αντίστοιχα των κινητήρων εναλλασσόμενου ρεύματος, όμως οι τελευταίοι παρουσιάζουν αρκετά πλεονεκτήματα σε σύγκριση με τους κινητήρες συνεχούς. Οι κινητήρες συνεχούς είναι ογκωδέστεροι, έχουν μεγαλύτερο κόστος, απαιτούν μεγαλύτερο χρόνο και κόστος συντήρησης, έχουν περιορισμένα λειτουργικά όρια σε τάση και ταχύτητα και δεν ενδείκνυται η λειτουργία τους σε εκρηκτικό ή διαβρωτικό περιβάλλον. Τα παραπάνω περιόρισαν τη χρήση τους σε ειδικές εφαρμογές και έδωσαν ώθηση κυρίως στους ασύγχρονους κινητήρες βραχυκυκλωμένου δρομέα. Εξάλλου, η εξέλιξη των ηλεκτρονικών ισχύος και της μικροηλεκτρονικής είχε σαν αποτέλεσμα την υλοποίηση πιο σύνθετων και πιο αποδοτικών συστημάτων ελέγχου και οδήγησης των τελευταίων. 3
6 . Στοιχεία φυσικής και μηχανικής Γραμμική κίνηση Σχήμα. Γραμμική κίνηση Για να υπερνικηθεί μια ύναμη F σε N με μία Ταχύτητα v σε /ec απαιτείται μηχανική ισχύς P σε Wtt: P v F (.) Σαν δύναμη μπορεί να θεωρηθεί κάποιο βάρος, τριβή ή αντίσταση στον αέρα σε ανυψωτικά μηχανήματα, οχήματα, εργαλειομηχανές κ.λ.π. Εάν είναι η Μάζα σε kg και α η Επιτάχυνση σε /ec τότε ισχύει για τη δύναμη: F (.) Εάν η δύναμη αντιδρά στο βάρος τότε ισχύει: F g (.3) όπου g είναι η επιτάχυνση της βαρύτητας (9,8 /ec ). Φυσικά το κινητήριο σύστημα που θα κινήσει το φορτίο έχει κάποιες απώλειες, οι οποίες εκφράζονται με το βαθμό απόδοσης η της μηχανής. Κατά συνέπεια η ισχύς που απαιτείται για μια γραμμική κίνηση του φορτίου δίνεται από τον τύπο:
7 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο P L v F (.4) Περιστροφική κίνηση Σχήμα. Περιστροφική κίνηση Στο συγκεκριμένο είδος κίνησης πρέπει να αναπτυχθεί μία ροπή σε N: M F r (.5) Η εφαπτομενική δύναμη F δρα πάνω στην ακτίνα r. Ο τύπος της γωνιακής ταχύτητας είναι: n (.6) Η εφαπτομενική ταχύτητα που δρα πάνω στην ακτίνα περιστροφής είναι: v r n r (.7) Από τις εξισώσεις (.5) και (.7) προκύπτει για τη μηχανική ισχύ: P F v M n M (.8) Εάν είναι γνωστός και ο βαθμός απόδοσης του κινητήρα τότε η απαραίτητη ισχύς του κινητήρα για την κάλυψη του φορτίου είναι: M n M (.9) P L Η ροπή Μ δίνεται συνήθως σε N (N=J=W=0,0 kp), οπότε η περιστροφική ταχύτητα πρέπει να εκφράζεται σε στροφές/δευτερόλεπτο. Σε ορισμένα κινητήρια συστήματα συνυπάρχουν η γραμμική και η περιστροφική κίνηση. Για να απλουστευθούν οι υπολογισμοί οι δύο τύποι κινήσεων ανάγονται σε ένα κοινό είδος κίνησης. Συγκεκριμένα, 5
8 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο μετασχηματίζονται τα μεγέθη της γραμμικής κίνησης στα αντίστοιχα της περιστροφικής. Εφόσον λοιπόν η μηχανική ισχύς είναι το μέγεθος το οποίο δεν μπορεί να αλλαχθεί, υπολογίζεται η απαιτούμενη ροπή από την εξίσωση (.8): M F v F v n (.0) Σε συστήματα όπου υπάρχει μετάδοση της κίνησης από έναν άξονα σε άλλον αντιστοιχούν διαφορετικές τιμές της ροπής και της ταχύτητας σε κάθε άξονα. Και σε αυτή την περίπτωση είναι σωστό να συσχετιστούν τα διάφορα μεγέθη με τη μηχανική ισχύ του κινητήρα. Ροή Ισχύος Σχήμα.3 Μετάδοση κίνησης Εάν η G είναι ο βαθμός απόδοσης του συστήματος μετάδοσης κίνησης (στα συστήματα με γρανάζια είναι περίπου 0,95 ενώ με ιμάντες κυμαίνεται από 0,60 έως 0,85) ισχύει: P P G (.) M M G M M G M M G n n (.) Ο λόγος i = n /n είναι ο λόγος μετάδοσης της κίνησης, οπότε: M M (.3) i G 6
9 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Ροπή αδρανείας Σύμφωνα με την εξίσωση.7 η ταχύτητα ενός στοιχειώδους σωματιδίου ενός περιστρεφόμενου σώματος είναι: v Από την εξίσωση αυτή μπορεί να υπολογισθεί η κινητική ενέργεια του περιστρεφόμενου σωματιδίου: r r r W K (.4) v Η συνολική ενέργεια του περιστρεφόμενου σώματος είναι το άθροισμα των ενεργειών όλων των στοιχειωδών σωματιδίων και, εφόσον η ταχύτητα ω είναι ίδια για όλα τα σωματίδια, ισχύει: Wtotl K totl r (.5) Η τιμή του αθροίσματος που βρίσκεται μέσα στην παρένθεση είναι το «στρεφόμενο ισοδύναμο» της μάζας και ονομάζεται περιστρεφόμενη αδράνεια ή ροπή αδρανείας και συμβολίζεται στη βιβλιογραφία είτε με I είτε με J. Στη γενική περίπτωση ενός στερεού σώματος τυχαίου σχήματος, το οποίο θεωρούμε ότι αποτελείται από στοιχειώδη σωματίδια μάζας Δ το καθένα και τα οποία απέχουν διαφορετική απόσταση (r) το καθένα από τον άξονα περιστροφής, η ροπή αδρανείας ως προς τυχαίο άξονα περιστροφής δίνεται από τη σχέση: I J li r r d (.6) 0 Εάν υποθέσουμε ότι το σώμα έχει σταθερή πυκνότητα ρ και με τη χρήση του μεγέθους V του όγκου του σώματος η παραπάνω εξίσωση γίνεται: J r d r dv r dv (.7) Οι συγκεκριμένες ροπές αδρανείας της ράβδου, καθώς και οι ροπές αδρανείας άλλων σχημάτων και αξόνων παρουσιάζονται στον παρακάτω πίνακα: 7
10 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Περιγραφή σχήματος Άξονας περιστροφής Σχήμα Ροπή αδρανείας ακτύλιος Άξονας που περνά από το κέντρο του δακτυλίου. J MR ακτύλιος Άξονας που περνά από οποιαδήποτε διάμετρο του δακτυλίου. J MR ακτυλιοειδής κύλινδρος Άξονας που περνά από το κέντρο του J M R R κυλίνδρου. Συμπαγής κύλινδρος Άξονας που περνά από το κέντρο του κυλίνδρου. J MR Συμπαγής κύλινδρος Άξονας που περνά από κεντρική διάμετρο του J 4 MR ML κυλίνδρου. Λεπτή ράβδος Άξονας που περνά J ML από το μέσο της ράβδου και είναι κάθετος στο μήκος της. 8
11 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Λεπτή ράβδος Άξονας που περνά από το ένα άκρο της ράβδου και είναι κάθετος στο μήκος της. J ML 3 Συμπαγής σφαίρα Άξονας που περνά από οποιαδήποτε διάμετρο της σφαίρας. J MR 5 Λεπτό σφαιρικό κέλυφος Άξονας που περνά από οποιαδήποτε διάμετρο του κελύφους. J MR 3 Πλάκα Κάθετος άξονας που περνά από το κέντρο της πλάκας. J b M Λεπτός ίσκος Άξονας που περνά από το κέντρο του δίσκου J MR R Πίνακας. Ροπές αδρανείας διαφόρων σχημάτων. Για το λεπτό δίσκο του παραπάνω πίνακα ισχύει: J R 0 r d R R 4 M M 3 M R r rdr r dr MR 4 0 R R 0 R ενώ για το συμπαγή κύλινδρο με άξονα περιστροφής που περνά από το κέντρο του ισχύει: J R 0 r d R R 4 M M 3 M R r rldr r dr MR 4 0 R L R 0 R 9
12 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο δηλαδή η ροπή αδρανείας του συμπίπτει με αυτή του δίσκου, όπως άλλωστε αναμενόταν διότι ο κύλινδρος μπορεί να θεωρηθεί ένα σύνολο από δίσκους. Η δομή όμως του δρομέα μιας ηλεκτρικής μηχανής δεν είναι γνωστή ώστε να υπολογίζεται εύκολα η ροπή αδρανείας του. Στην πράξη θεωρούμε το συνολικό βάρος του δρομέα (G = g) συγκεντρωμένο σε ένα δακτύλιο με διάμετρο (D = r), οπότε ισχύει: J r G D g 4 GD 4g kp 4 9,8 / (.8) 0,055 kp 0,5 kg 0,5 W 3 Πολλές φορές χρησιμοποιείται αντί του J το μέγεθος GD που λέγεται ροπή ορμής και μετριέται σε kp. Επίσης, μπορεί να μετρηθεί πειραματικά η ροπή αδρανείας των στρεφόμενων μερών μιας μηχανής. Συγκεκριμένα η μηχανή (ή ολόκληρο το κινητήριο σύστημα) αφήνεται να περιστραφεί εν κενώ, χωρίς τροφοδοσία. Σ αυτή την περίπτωση δρουν στη μηχανή όλες οι αδράνειες και τριβές, τόσο του δρομέα της όσο και του φορτίου με συνέπεια η περιστροφική ταχύτητα να ελαττώνεται μέχρι την πλήρη ακινησία της μηχανής. Χωρίς φορτίο Σχήμα.4 Καμπύλη επιβράδυνσης 0
13 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Για κάθε τιμή της γωνιακής ταχύτητας ω της καμπύλης ω = (t) (βλ. σχήμα.4) προσδιορίζουμε, μέσω της εφαπτομένης, την κλίση Δω/Δt. Εάν είναι γνωστή η ροπή επιβράδυνσης Μ Βω (π.χ. με μέτρηση μέσω ενός ροπόμετρου) προκύπτει η εξής σχέση για τη ροπή αδρανείας: J M B t / (.9) Στο σχήμα.5 παρουσιάζονται πραγματικές τιμές της ροπής αδρανείας από διάφορες μηχανές. Σχήμα.5 Τιμές της ροπής αδρανείας ασύγχρονων μηχανών βραχυκυκλωμένου κλωβού ( ) και μηχανών συνεχούς ( ) σε σχέση με την ονομαστική τους ισχύ Ρ Ν για ταχύτητες n d = 000 in - (καμπύλη ), 500 in - () και 3000 in - (3). Σύμφωνα με την εξίσωση.5 η κινητική ενέργεια μιας στρεφόμενης μάζας είναι W και συνεπώς η αλλαγή στην ταχύτητα περιστροφής J της μάζας αντιστοιχεί σε μία ενέργεια W J αρχική και ω η τελική ταχύτητα αντίστοιχα., όπου ω είναι η Εάν σε ένα κινητήριο σύστημα συνυπάρχουν στρεφόμενες μάζες με διαφορετικές ροπές αδρανείας ή αν συνυπάρχει ευθύγραμμη και περιστροφική κίνηση, τότε είναι χρήσιμο η επίδραση όλων των μαζών να ενοποιηθεί μέσω μιας ενιαίας ροπής αδρανείας. Η βάση για αυτή τη θεώρηση είναι η αρχή διατήρησης της κινητικής ενέργειας. Εάν η ροπή αδρανείας J που αντιστοιχεί στην ταχύτητα ω πρέπει να μετατραπεί σε J που αντιστοιχεί σε ταχύτητα ω τότε ισχύει: W W J J
14 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο W W G όπου η G είναι ο βαθμός απόδοσης του συστήματος μετάδοσης κίνησης και τελικά: J J G J G n n J i G (.0) Για τη μετατροπή μιας ευθύγραμμης κίνησης μιας μάζας σε αντίστοιχη περιστροφική ισχύει: W v W J και εφόσον οπότε: v r γίνεται: W r J r (.) Ανάλογα με την επιτάχυνση στην ευθύγραμμη κίνηση ισχύει για την επιτάχυνση στην περιστροφική κίνηση μιας μάζας αδρανείας J μια αντίστοιχη επιτάχυνση περιστροφής α=dω/dt (με ω=πn) και μια ροπή επιτάχυνσης: M B J Jd/ dt J dn / dt (.) Ένα κινητήριο σύστημα περιγράφεται συχνά και από τη λεγόμενη σταθερά αδρανείας, η οποία δίνεται από τον τύπο: M N S J / U I H J / (.3) N Όπου η συσσωρευμένη κινητική ενέργεια στο δρομέα J / διαιρείται με την ονομαστική ισχύ της μηχανής. M N N N M N Συστήματα μεταβλητής μάζας Σύμφωνα με την εξίσωση., για σώματα με σταθερή μάζα προκύπτει η σχέση F =, δηλαδή η δύναμη είναι ο χρονικός ρυθμός μεταβολής της
15 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο ορμής του. Όμως η ορμή ενός σώματος είναι το γινόμενο της μάζας του επί την ταχύτητά του. Επομένως γενικά ισχύει: F dp dt dv dt v d dt (.4) Όπου p είναι η ορμή και Δν είναι η μεταβολή της ταχύτητας από την αρχική στην τελική κατάσταση.. Μετάδοση της κίνησης Οι συνηθέστεροι τρόποι μετάδοσης της κίνησης από έναν άξονα σε έναν άλλο είναι μέσω οδοντωτών τροχών (γρανάζια), μέσω ιμάντων και με αλυσοκίνηση. Επίσης, σε μηχανές μικρής ισχύος η σύνδεση μπορεί να γίνει απευθείας με ειδικό σύνδεσμο (κόμπλερ). Οδοντωτοί τροχοί ) Παράλληλοι οδοντωτοί τροχοί. Χρησιμοποιούνται στις περιπτώσεις όπου οι άξονες είναι παράλληλοι μεταξύ τους. b) Κωνικοί οδοντωτοί τροχοί. Χρησιμοποιούνται στις περιπτώσεις όπου οι άξονες βρίσκονται στο ίδιο επίπεδο και τέμνονται σε ένα σημείο. c) Ελικοειδείς οδοντωτοί τροχοί. Χρησιμοποιούνται στις περιπτώσεις όπου οι άξονες διασταυρώνονται στο χώρο χωρίς όμως να τέμνονται. Στην κατηγορία αυτή εντάσσεται και το σύστημα οδοντωτού τροχού ατέρμονα κοχλία. Η περιφερειακή ταχύτητα οδοντωτού τροχού, διαμέτρου «D», ο οποίος περιστρέφεται με «n» στροφές ανά λεπτό, δίνεται από τη σχέση: v R n R 60 Dn 60 / ec (.5) Έστω ότι δυο οδοντωτοί τροχοί, με διαμέτρους D, D και στροφές ανά λεπτό n, n αντίστοιχα, βρίσκονται σε εμπλοκή. 3
16 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Σχήμα.6 Μετάδοση κίνησης με τροχούς Η περιφερειακή ταχύτητα είναι η ίδια και στους δύο τροχούς. ηλαδή: v R v R (.6) Επομένως, R n D (.7) N R n D όπου Ν η σχέση μετάδοσης της κίνησης. Από τις παραπάνω σχέσεις είναι προφανές ότι ο τροχός με τη μεγαλύτερη διάμετρο θα στρέφεται με λιγότερες στροφές και αντίστροφα. Έστω Ζ, Ζ οι αριθμοί των δοντιών των δύο οδοντωτών τροχών και «t» το κοινό τους βήμα. Ισχύει ότι: D tz και D tz άρα Z n n (.8) ηλαδή η σχέση μετάδοσης είναι ανάλογη του λόγου του αριθμού των δοντιών των δύο γραναζιών. Εάν αμελήσουμε τις απώλειες οι δύο τροχοί φέρουν την ίδια ισχύ και κατά συνέπεια τα δόντια του γραναζιού με τη μικρότερη διάμετρο δέχονται πολύ μεγαλύτερη φόρτιση, με αποτέλεσμα για μεγάλες σχέσεις μεταφοράς να απαιτείται ανθεκτικότερη κατασκευή των δοντιών του μικρού γραναζιού. Σχήμα.7α) Μηχανισμός σύζευξης με γρανάζια β) ατέρμων κοχλίας 4
17 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Σύμφωνα με τα παραπάνω, θεωρώντας το σύστημα οδοντωτών τροχών του σχήματος.7α χωρίς απώλειες, ισχύει για τις ροπές στις δύο πλευρές του παραπάνω συστήματος: T T L L L n n L N (.9) Στον ατέρμονα κοχλία του σχήματος.7β η ροπή και η δύναμη συνδέονται με τη σχέση: T F L v L x L N (.30) Όπου v L x είναι η γραμμική ταχύτητα, είναι το βήμα (πάσο) του L ατέρμονα κοχλία και Ν είναι ο συντελεστής μετάδοσης της κίνησης (ή σύζευξης). Η ηλεκτρομαγνητική ροπή Τ e που απαιτείται από τον κινητήρα μπορεί να υπολογισθεί με βάση ενεργειακές θεωρήσεις και να εκφρασθεί ως προς τη ροπή αδρανείας, την επιτάχυνση του φορτίου, το συντελεστή μετάδοσης κίνησης και την ωφέλιμη ροπή ή δύναμη. Στο σχήμα.7α Τ WL είναι η ωφέλιμη ροπή στο φορτίο και επιτάχυνση του φορτίου. Έτσι : e L J N J NT B N B L η (.3) L L WL L N N Η εξίσωση αυτή μπορεί να γραφεί ως προς την ταχύτητα του κινητήρα ( L N ), την ισοδύναμη ροπή αδρανείας J eq J N J L, την ισοδύναμη ιξώδη τριβή TWeq NT WL : B eq B N B και την ισοδύναμη ωφέλιμη ροπή e eq L L J B T (.3) eq L Weq Ομοίως για το σύστημα του ατέρμονα κοχλία του σχήματος.7β η ηλεκτρομαγνητική ροπή Τ e δίνεται από τη σχέση: J J N M T M W ( NFWL v (.33) N L e ) Όπου F WL είναι η ωφέλιμη δύναμη και Μ W και Μ T οι μάζες του δοκιμίου και του τραπεζιού αντίστοιχα. Από τις εξισώσεις.9 και.30 προκύπτει ότι η επιλογή του συντελεστή μετάδοσης της κίνησης επιδρά στην ταχύτητα του κινητήρα. Επίσης, από 5
18 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο τις εξισώσεις.3 και.33 προκύπτει ότι ο ίδιος συντελεστής επιδρά και στην ηλεκτρομαγνητική ροπή που απαιτείται από τον κινητήρα. Κίνηση με ιμάντες Στην περίπτωση αυτή, κάθε άξονας φέρει από μία τουλάχιστον τροχαλία και όλες μαζί συνδέονται μέσω κατάλληλου ιμάντα. Για την εξασφάλιση καλής λειτουργίας, συνήθως ο κάτω κλάδος του ιμάντα εκλέγεται να έλκει και ο επάνω να έλκεται. Η σχέση μετάδοσης της κίνησης είναι η ίδια με n εκείνη των οδοντωτών τροχών ( N n ). Για την αποφυγή φαινομένων ολίσθησης, ο ιμάντας πρέπει να είναι καλά τανυσμένος, δηλαδή να εφάπτεται δυνατά στις επιφάνειες των τροχαλιών. Η ολίσθηση αυτή, η οποία έχει ως αποτέλεσμα τη μείωση των στροφών του κινούμενου συστήματος, συνήθως αντιμετωπίζεται μέσω ειδικών τανυστήρων, αυξάνοντας τη γωνία επαφής του ιμάντα με τις τροχαλίες. Τα χαρακτηριστικά του ιμάντα (πλάτος, πάχος) καθορίζονται από τη μεταφερόμενη ισχύ και βάσει αυτών, στη συνέχεια καθορίζονται οι διαστάσεις των τροχαλιών. Τροχαλίες μικρής διαμέτρου προκαλούν την πρόωρη φθορά του ιμάντα λόγω ισχυρών καμπτικών δυνάμεων. Αλυσοκίνηση Ο τρόπος αυτός είναι ανάλογος της μετάδοσης της κίνησης με ιμάντες. Οι άξονες αντί τροχαλιών φέρουν ειδικού τύπου γρανάζια, τα οποία εμπλέκονται μέσω ειδικής αλυσίδας κίνησης. Η μέθοδος αυτή συνήθως εφαρμόζεται σε χαμηλόστροφα συστήματα και όταν η απόσταση μεταξύ των αξόνων είναι μεγάλη..3 Χαρακτηριστικές φορτίων Η χαρακτηριστική ροπής στροφών του φορτίου αποτελεί ένα από τα πλέον βασικά κριτήρια επιλογής του κινητήρα. Συνήθως δίνεται από τους κατασκευαστές και παρέχει πληροφορίες για τις απαιτήσεις του φορτίου σε 6
19 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο ροπή σε μία ευρεία περιοχή στροφών. Τυπικές μορφές χαρακτηριστικών παρουσιάζονται στα σχήματα.8 και.9. Μ (N) Μ~n 3 δ Μ~n γ Μ~n β Μ=σταθ α Σχήμα.8 Χαρακτηριστικές ροπής στροφών διαφόρων φορτίων α β γ Σχήμα.9 Χαρακτηριστικές ροπής/ισχύος στροφών διαφόρων φορτίων δ 7
20 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Στην πρώτη κατηγορία (σχήμα.9α), όπου η ισχύς του φορτίου είναι σταθερή, ανήκουν ελάχιστες περιπτώσεις φορτίων και συγκεκριμένα σε μηχανές περιελίξεως ή ξετυλίγματος χαρτιού, λαμαρίνας, υφάσματος ή άλλων υλικών, όπου θα πρέπει να διατηρείται σταθερή η δύναμη έλκυσης F του αντίστοιχου υλικού όταν η διάμετρος D=r του τυλιγμένου υλικού ελαττώνεται (ή αυξάνεται) ενώ η περιφερειακή ταχύτητα περιέλιξης v παραμένει σταθερή M L ~ ~ r και P L F v cont. n Στη δεύτερη κατηγορία (σχήμα.8α και.9β), όπου η ροπή του φορτίου είναι σταθερή, ανήκουν ανυψωτικά μηχανήματα, ανελκυστήρες ανθρώπων, μεταφορικές ταινίες, ορισμένοι τύποι ανεμιστήρων και εργαλειομηχανές με σταθερή κοπτική μορφή. Στην τρίτη κατηγορία (σχήμα.8β και.9γ), όπου η ροπή του φορτίου είναι ανάλογη της ταχύτητας, ανήκουν κυρίως έλαστρα, έμβολα και ορισμένοι τύποι αντλιών. Επίσης, την ιδιότητα αυτή παρουσιάζουν οι ηλεκτρικές γεννήτριες και η ηλεκτρική πέδη. Στην τέταρτη κατηγορία (σχήμα.8γ και.9δ), όπου η ροπή του φορτίου είναι ανάλογη του τετραγώνου της ταχύτητας, ανήκουν κυρίως παλινδρομικές μηχανές, φυγοκεντρικές αντλίες, ορισμένοι τύποι ανεμιστήρων, όπως φυσητήρες, εξαεριστήρες, συμπιεστές και προπέλες πλοίων. Στην πέμπτη κατηγορία (σχήμα.8δ), όπου η ροπή του φορτίου είναι ανάλογη του κύβου της ταχύτητας, ανήκουν κυρίως εργαλειομηχανές, όπως τόρνοι, φρέζες κ.λ.π., περιελικτικές μηχανές και μηχανές κατεργασίας ξύλου. Όταν είναι λοιπόν γνωστή η χαρακτηριστική ροπής στροφών του φορτίου το επόμενο βήμα είναι η επιλογή του κατάλληλου κινητήρα (μέσω της αντίστοιχης χαρακτηριστικής του), έτσι ώστε να υπάρξει η βέλτιστη δυνατή συνεργασία από οικονομοτεχνικής άποψης..4 Επίδραση των χαρακτηριστικών στη δυναμική ευστάθεια Η μορφή των χαρακτηριστικών ροπής στροφών του φορτίου και του κινητήρα παίζουν σημαντικό ρόλο στη δυναμική συμπεριφορά και στην ευστάθεια του συστήματος (σχήμα.0). 8
21 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Σχήμα.0 Επίδραση των χαρακτηριστικών στη δυναμική ευστάθεια Εάν και είναι οι χαρακτηριστικές του κινητήρα και του φορτίου αντίστοιχα, τότε το σημείο τομής τους Α(n ο, Τ ο ) είναι το σημείο λειτουργίας στη στάσιμη κατάσταση. Εάν για κάποιο λόγο ελαττωθεί η ταχύτητα από n ο σε n, τότε αναπτύσσεται θετική δυναμική ροπή η οποία τείνει να επαναφέρει το σύστημα στην αρχική του κατάσταση. Ανάλογα, αύξηση των στροφών από n ο σε n έχει ως αποτέλεσμα την ανάπτυξη αρνητικής δυναμικής ροπής, η οποία επίσης τείνει να επαναφέρει το σύστημα στην αρχική του κατάσταση. Εάν όμως η χαρακτηριστική του φορτίου περιγράφεται από την καμπύλη 3 τότε τυχόν ελάττωση των στροφών έχει ως αποτέλεσμα την εμφάνιση αρνητικής ροπής, η οποία έχει ως συνέπεια την περαιτέρω ελάττωση των στροφών μέχρι τελικά το μηδενισμό τους. Προκαλείται δηλαδή αποσυγχρονισμός του συστήματος. Από τις χαρακτηριστικές - και -3 βγαίνει το συμπέρασμα ότι για την ευσταθή λειτουργία θα πρέπει να ικανοποιείται η συνθήκη: dt dn dtl dn Όπου Τ L η ροπή του φορτίου και Τ η κινούσα ροπή. (.34) 9
22 Συστήματα ηλεκτρικών μηχανών για κίνηση και ηλεκτροπαραγωγή I Κεφάλαιο Τέλος, όσο μεγαλύτερη είναι η γωνία τομής των δύο χαρακτηριστικών (ιδανική γωνία 90 ), τόσο μικρότερες θα είναι οι διακυμάνσεις των στροφών του συστήματος για αντίστοιχες μεταβολές του φορτίου (σχήμα.). Σχήμα. ιακύμανση των στροφών λόγω μεταβολής του φορτίου σαν συνάρτηση της γωνίας τομής των δύο χαρακτηριστικών. 0
23 3. Μετασχηματιστές Γενικά Για τη μοντελοποίηση και προσομοίωση της δυναμικής συμπεριφοράς των μετασχηματιστών απαιτείται κατάλληλο μαθηματικό μοντέλο (σύστημα διαφορικών εξισώσεων), η επίλυση του οποίου (μετά από καθορισμό των συγκεκριμένων αρχικών συνθηκών) αποδίδει την εξέλιξη στο χρόνο του εκάστοτε μεταβατικού φαινομένου που συμβαίνει στο μετασχηματιστή. Μεταβατικά φαινόμενα εξαιρετικής σημασίας για το μετασχηματιστή είναι η ενεργοποίησή του (σύνδεση του πρωτεύοντος με το δίκτυο) και το βραχυκύκλωμα του δευτερεύοντος (υπό πλήρη τάση στο πρωτεύον). Σε αυτές τις δύο περιπτώσεις δημιουργούνται μεγάλα ρεύματα, επικίνδυνα για τη θερμική και μηχανική καταπόνηση των τυλιγμάτων του μετασχηματιστή, η μέγιστη τιμή των οποίων προσδιορίζει και τα όργανα ασφαλείας που θα πρέπει να τοποθετηθούν στη διάταξη συνδεσμολογίας του μετασχηματιστή. Το δυναμικό μαθηματικό μοντέλο ενός μονοφασικού μετασχηματιστή με πυρήνα σταθερής διαπερατότητας δίνεται από τις εξισώσεις: di di (3.) Ri L M dt dt di di (3.) Ri L M dt dt Όπου L = αυτεπαγωγή πρωτεύοντος, L = αυτεπαγωγή δευτερεύοντος, Μ = αλληλεπαγωγή δευτερεύοντος ως προς το πρωτεύον, Μ = αλληλεπαγωγή πρωτεύοντος ως προς το δευτερεύον. Οι παραπάνω εξισώσεις γράφονται σε μορφή πινάκων ως εξής: L M M L di dt R 0 i di 0 R i 0 dt ή (3.3)
24 di dt L di M dt M L R 0 0 R i i L M M L Όταν είναι γνωστές οι αριθμητικές τιμές των παραμέτρων του μετασχηματιστή, οι εφαρμοζόμενες τάσεις και οι αρχικές συνθήκες τότε οι παραπάνω εξισώσεις μπορούν εύκολα να επιλυθούν (είτε με μετασχηματισμό Lplce, είτε με μεθόδους επίλυσης διαφορικών εξισώσεων, είτε σε Η/Υ με μεθόδους ολοκλήρωσης, όπως π.χ. κανόνας τραπεζίου, Runge-Kutt, κ.λ.π.). Ρεύμα εισροής (Inruh current) μετασχηματιστή Στη στάσιμη κατάσταση (υπό κανονικές συνθήκες) το ρεύμα διέγερσης ενός μετασχηματιστή είναι συνήθως πολύ χαμηλό, λιγότερο από 5% του ονομαστικού. Τη χρονική στιγμή όμως της σύνδεσης του μετασχηματιστή στο δίκτυο θα ρεύσει ένα μεγάλο ρεύμα εισροής σε αυτόν για όσο χρόνο διαρκεί το μεταβατικό φαινόμενο. Αυτό το ρεύμα μπορεί να είναι 0 με 0 φορές μεγαλύτερο του ονομαστικού. Ο ακριβής προσδιορισμός αυτού του ρεύματος απαιτείται για τη σωστή σχεδίαση του συστήματος προστασίας του μετασχηματιστή. Το εύρος του ρεύματος εισροής εξαρτάται από το χρονικό σημείο στην κυματομορφή της τάσης, στο οποίο γίνεται η σύνδεση του μετασχηματιστή με το δίκτυο. Θεωρήστε ένα μετασχηματιστή στον οποίο αρχικά δεν υπήρχε παραμένουσα ροή στον πυρήνα και το πρωτεύον του οποίου συνδέεται σε μία τάση : v V in t (3.4) Εάν αμελήσουμε τις απώλειες του πυρήνα και την αντίσταση του πρωτεύοντος ισχύει: d (3.5) v N dt (3.6) vdt Ας εξετάσουμε τις παρακάτω δύο περιπτώσεις:. Ο μετασχηματιστής συνδέεται όταν η τάση είναι μέγιστη. Η διακύμανση της τάσης και της ροής παρουσιάζονται στο σχήμα 3.. Ας
25 σημειωθεί ότι δεν παρατηρείται μεταβατικό φαινόμενο στη ροή, η χρονική μεταβολή της οποίας είναι: x in t 90 (3.7) V (3.8) όπου x N Το ρεύμα μαγνήτισης, το οποίο μπορεί να βρεθεί από τη χαρακτηριστική Β-Η (μαγνήτισης) του πυρήνα του μετασχηματιστή, παρουσιάζεται επίσης στο σχήμα 3.. Όπως είναι φανερό δεν ρέει κάποιο ρεύμα εισροής και το σύστημα είναι από την αρχή στη στάσιμη κατάσταση. Σχήμα 3. Ρεύμα εισροής μετασχηματιστή όταν συνδεθεί τη χρονική στιγμή της μέγιστης τάσης.. Ο μετασχηματιστής συνδέεται όταν η τάση είναι μηδέν. Η διακύμανση της τάσης του ρεύματος εισροής και της ροής παρουσιάζονται στο σχήμα 3.. Από τις εξισώσεις 3.4 και 3.6 η ροή υπολογίζεται ως εξής: x V tdt t in co 0 (3.9) cot V t x Η μέγιστη ροή έχει διπλασιαστεί και το αντίστοιχο μέγιστο ρεύμα μαγνήτισης είναι πολύ μεγάλο εξαιτίας του κορεσμού του πυρήνα. Στην πράξη, το μεγάλο ρεύμα εισροής θα αποσβεσθεί γρήγορα (σχήμα 3.3) λόγω της αντίστασης των τυλιγμάτων του μετασχηματιστή. Σε έναν τριφασικό μετασχηματιστή πάντα δημιουργείται ένα ρεύμα εισροής, διότι, ακόμα και αν η τάση είναι στη μέγιστη τιμή σε μία φάση όταν συνδέεται ο μετασχηματιστής, δεν είναι στη μέγιστη τιμή στις άλλες δύο φάσεις. 3
26 Σχήμα 3. Ρεύμα εισροής μετασχηματιστή όταν συνδεθεί τη χρονική στιγμή της μηδενικής τάσης. Σχήμα 3.3 Επίδραση της αντίστασης τυλιγμάτων στο ρεύμα εισροής μετασχηματιστή. 4
27 3. Μηχανές συνεχούς ρεύματος Γενικά Οι μηχανές συνεχούς ρεύματος ανάλογα με τη συνδεσμολογία του τυλίγματος διέγερσης διακρίνονται σε ξένης διέγερσης, παράλληλης διέγερσης (σχήμα 3.4), διέγερσης σειράς (σχήμα 3.4b) και σύνθετης διέγερσης (σχήμα 3.4c) Σε πολλές εφαρμογές χρησιμοποιούνται κινητήρες συνεχούς ρεύματος για να οδηγήσουν μηχανικά φορτία. Σε μερικές από αυτές τις εφαρμογές απαιτείται η ταχύτητα της μηχανής να παραμένει σταθερή στις μεταβολές του φορτίου. Σε άλλες, αντιθέτως, απαιτείται η ταχύτητα να ρυθμίζεται σε μια ευρεία περιοχή τιμών. Σε κάθε περίπτωση πρέπει να είναι γνωστή η σχέση ροπής στροφών της μηχανής. Σχήμα 3.4 Συνδεσμολογίες D.C. μηχανών ) παράλληλης διέγερσης, b) διέγερσης σειράς, c) σύνθετης διέγερσης. Η μηχανή συνεχούς ρεύματος μπορεί να λειτουργήσει τόσο σαν κινητήρας, όσο και σαν γεννήτρια. Στην πράξη όμως χρησιμοποιείται 5
28 περισσότερο ως κινητήρας (εξαιτίας της ευρείας διάδοσης των γεννητριών εναλλασσόμενου ρεύματος) παρέχοντας τη δυνατότητα για ακριβή έλεγχο της ταχύτητας και της ροπής σε μια ευρεία κλίμακα τιμών. Κινητήρες συνεχούς ρεύματος μεγάλου μεγέθους (δεκάδων ή εκατοντάδων ίππων) χρησιμοποιούνται σε εργαλειομηχανές, εκτυπωτικές πρέσες, ταινίες μεταφοράς, ανεμιστήρες, αντλίες, ανυψωτικές μηχανές, γερανούς, μηχανές κατεργασίας χάρτου και υφάσματος, κ.λ.π. Επίσης, οι κινητήρες συνεχούς χρησιμοποιούνται ως επί το πλείστον στην έλξη ηλεκτρικών οχημάτων (αυτοκινήτων και σιδηροδρόμων). Κινητήρες συνεχούς ρεύματος μικρού μεγέθους (υποδιαιρέσεων του ίππου) χρησιμοποιούνται κυρίως ως συσκευές ελέγχου, όπως ταχογεννήτριες για μέτρηση της ταχύτητας και σερβοκινητήρες για ακριβή τοποθέτηση και κατανομή. 3.. Κινητήρες Σ.Ρ. ξένης (ή παράλληλης) διέγερσης Χαρακτηριστική ροπής - στροφών Οι «εξωτερικές» χαρακτηριστικές ενός κινητήρα συνεχούς ρεύματος συνδέουν την περιστροφική ταχύτητα και τη ροπή που αναπτύσσεται στον άξονά του για να οδηγήσει ένα μηχανικό φορτίο. Συνήθως, εκτιμώνται ή προσδιορίζονται με δοκιμές σε διάφορες καταστάσεις σταθερής λειτουργίας με διάφορα ηλεκτρικά και μηχανικά μεγέθη. Οι εξισώσεις που αναφέρονται στο συγκεκριμένο κινητήρα συνεχούς ρεύματος είναι οι εξής: V T K (3.0) e I Από τις εξισώσεις 3. και 3. προκύπτει: E K (3.) E I r (3.) V r V I r T K K K Αντίστοιχα από τις εξισώσεις 3.0 και 3.3 προκύπτει: T e K V r K e (3.3) (3.4) Εάν η τάση τυμπάνου V και η μαγνητική ροή Φ παραμείνουν σταθερές τότε η χαρακτηριστική ροπής στροφών είναι η ακόλουθη: 6
29 κλίση r Σχήμα 3.5 Χαρακτηριστική ροπής στροφών. Η πτώση στην τιμή της ταχύτητας, όσο η αναπτυσσόμενη ροπή αυξάνεται, είναι μικρή παρέχοντας ουσιαστικά μια πολύ καλή ρύθμιση της ταχύτητας. Σε μία πραγματική μηχανή η μαγνητική ροή θα ελαττωθεί με την αύξηση της ροπής ή του ρεύματος τυμπάνου εξαιτίας της αντίδρασης τυμπάνου και κατά συνέπεια η παραπάνω πτώση στην ταχύτητα θα είναι ακόμα μικρότερη. Με άλλα λόγια η αντίδραση του τυμπάνου βελτιώνει τη ρύθμιση της ταχύτητας. Από την εξίσωση 3.3 βγαίνει το συμπέρασμα ότι ο έλεγχος της ταχύτητας στον κινητήρα μπορεί να επιτευχθεί με τους εξής τρόπους: Με ρύθμιση της τάσης τυμπάνου (V ). Με ρύθμιση της διέγερσης (Φ). Με ρύθμιση της αντίστασης τυμπάνου (r ). Σε γενικές γραμμές η ταχύτητα αυξάνει με την αύξηση της τάσης τυμπάνου και μειώνεται με την αύξηση της μαγνητικής ροής ή της αντίστασης τυμπάνου. Ρύθμιση της τάσης τυμπάνου Σε αυτή τη μέθοδο ελέγχου των στροφών η αντίσταση τυμπάνου (r ) παραμένει αμετάβλητη, το ρεύμα διέγερσης (Ι ) διατηρείται σταθερό (συνήθως στην ονομαστική του τιμή) και ρυθμίζεται η τάση τυμπάνου ώστε να μεταβάλλεται η ταχύτητα του κινητήρα. Εάν θεωρηθεί αμελητέα η αντίδραση τυμπάνου τότε από την εξίσωση 3.3 προκύπτει: Όπου K / K V K T (3.5) K και r K K / 7
30 Η ρύθμιση αυτή της τάσεως τυμπάνου μπορεί να γίνει είτε μέσω ελεγχόμενων ανορθωτικών διατάξεων (εάν τροφοδοτείται από δίκτυο εναλλασσόμενης τάσης π.χ. της ΕΗ), είτε μέσω γεννητριών συνεχούς ρεύματος. Όταν η ροπή φορτίου είναι σταθερή, όπως αυτή ενός ανελκυστήρα ή μίας γερανογέφυρας, τότε η ταχύτητα θα μεταβάλλεται γραμμικά με την τάση V, όπως φαίνεται στο σχήμα 3.6. Εάν η τάση στους ακροδέκτες της μηχανής διατηρείται σταθερή και μεταβάλλεται η ροπή φορτίου, τότε η ταχύτητα μπορεί να ρυθμίζεται με την τάση V, όπως φαίνεται στο σχήμα 3.6b. Σχήμα 3.6 Έλεγχος της τάσης τυμπάνου μιας D.C. μηχανής ) σταθερή ροπή φορτίου, b) σταθερή τάση, c) σταθερό ρεύμα τυμπάνου, d) r = 0 ( V t V R r ) Σε μία πραγματική εφαρμογή, όπου η ταχύτητα μεταβάλλεται με τη μεταβολή της τάσης V, το ρεύμα τυμπάνου διατηρείται σταθερό (γεγονός το οποίο απαιτεί έλεγχο κλειστού βρόγχου cloed loop opertion). Από τις εξισώσεις 3. και 3. προκύπτει ότι, εάν το ρεύμα Ι α είναι σταθερό τότε: 8
31 E V Κατά συνέπεια, όσο αυξάνει το V τόσο αυξάνει γραμμικά η ταχύτητα (σχήμα 3.6c). Από την εξίσωση 3.0 προκύπτει ότι εάν το ρεύμα Ι α παραμένει σταθερό, παραμένει και η ροπή σταθερή. Επίσης, και η ισχύς εισόδου από την πηγή τροφοδοσίας (Ρ = V Ι α ) μεταβάλλεται γραμμικά με την ταχύτητα. Για ταχύτητες μεγαλύτερες της ονομαστικής, και για αποφυγή υπερφόρτισης του κινητήρα, η τάση τυμπάνου παραμένει σταθερή στην ονομαστική της τιμή και διατηρείται πλέον σταθερή η ηλεκτρομαγνητική ισχύς και όχι η ροπή. Αυτό επιτυγχάνεται με τον έλεγχο της μαγνητικής ροής του πεδίου διέγερσης (μειώνοντας τα ρεύμα διέγερσης) κατά τέτοιο τρόπο ώστε το γινόμενο Τω να παραμένει σταθερό (σχήμα 3.7 και 3.8d). Σχήμα 3.7 Σχέση ροπής ταχύτητας για όλη την περιοχή ταχυτήτων Εάν θεωρηθεί αμελητέα η αντίσταση τυμπάνου r τότε οι τιμές των Ρ, V και Ι α είναι μηδενικές όταν η ταχύτητα είναι μηδέν και μεταβάλλονται γραμμικά με την ταχύτητα (σχήμα 3.6d). Η μέθοδος ελέγχου της τάσης τυμπάνου προσφέρεται για μία ομαλή μεταβολή της ταχύτητας της μηχανής από τη μηδενική τιμή μέχρι την ονομαστική. Παρ όλα αυτά η μέθοδος αυτή είναι αρκετά δαπανηρή διότι απαιτεί μια μεταβαλλόμενη πηγή συνεχούς ρεύματος για το κύκλωμα του τυμπάνου. 9
32 Ρύθμιση της διέγερσης Σε αυτή τη μέθοδο η αντίσταση τυμπάνου r και η τάση στους ακροδέκτες της μηχανής V διατηρούνται σταθερές και η ταχύτητα ελέγχεται μεταβάλλοντας το ρεύμα Ι στο κύκλωμα διέγερσης. Αυτό συνήθως επιτυγχάνεται χρησιμοποιώντας ένα ρεοστάτη (R c ) στο κύκλωμα διέγερσης, όπως φαίνεται στο σχήμα 3.8. Σχήμα 3.8 Έλεγχος της διέγερσης μιας D.C. μηχανής Εάν θεωρήσουμε ότι βρισκόμαστε στη γραμμική περιοχή της καμπύλης μαγνήτισης, τότε η μαγνητική ροή εντός της μηχανής (Φ) θα είναι ανάλογη του ρεύματος διέγερσης (Ι ), συνεπώς: K K I (3.6) Όπου K η σταθερά αναλογίας μεταξύ της μαγνητικής ροής και του ρεύματος διέγερσης. Από τις εξισώσεις 3.4 και 3.6 προκύπτει: 30
33 K V I r T K I (3.7) Σε περίπτωση που δεν υπάρχει φορτίο Τ 0, και σύμφωνα με την εξίσωση V 3.7: K I. Όπως φαίνεται στο σχήμα 3.8b η ταχύτητα μεταβάλλεται αντίστροφα με το ρεύμα διέγερσης. Να σημειωθεί ότι εάν το κύκλωμα διέγερσης διακοπεί τότε η ταχύτητα μπορεί να γίνει επικίνδυνα υψηλή. Για μια συγκεκριμένη τιμή του ρεύματος διέγερσης (Ι ) ισχύει από την εξίσωση 3.7: Όπου η σταθερά K T (3.8) K 3 4 V K 3 αντιπροσωπεύει την εν κενώ ταχύτητα και K I K 4. K I r Σε μια συγκεκριμένη τιμή του ρεύματος διέγερσης (Ι ) η ταχύτητα παραμένει ουσιαστικά σταθερή σε μία συγκεκριμένη τιμή όσο αυξάνει η ροπή. Η συγκεκριμένη αυτή τιμή της ταχύτητας μπορεί να ρυθμιστεί από το ρεύμα διέγερσης, όπως φαίνεται στο σχήμα 3.5c. Όπως ακριβώς συνέβη με τον έλεγχο της τάσης τυμπάνου, ο έλεγχος της διέγερσης δίνει τη δυνατότητα τόσο για μεταβαλλόμενη ταχύτητα, όσο και για ρύθμιση της ταχύτητας σε συγκεκριμένη τιμή. Η ρύθμιση της ταχύτητας από τη μηδενική τιμή ως την ονομαστική συνήθως επιτυγχάνεται με τον έλεγχο της τάσης τυμπάνου. Για τη ρύθμιση της ταχύτητας πέραν της ονομαστικής της τιμής χρησιμοποιείται η μέθοδος ελάττωσης του ρεύματος διέγερσης, η οποία ονομάζεται «ελάττωση ή εξασθένιση του πεδίου». Στην ονομαστική ταχύτητα η τάση τυμπάνου έχει την ονομαστική της τιμή. Εάν για λόγους υπερθέρμανσης το ρεύμα τυμπάνου δεν πρέπει να ξεπεράσει την ονομαστική του τιμή, τότε η ρύθμιση της ταχύτητας πέραν της ονομαστικής της τιμής περιορίζεται από το όριο σταθερής ισχύος: P V I I I I ό ό 3
34 άρα η ροπή ελαττώνεται με την ταχύτητα στην περιοχή εξασθένιση του πεδίου (σχήμα 3.8d και 3.7). Ο έλεγχος της διέγερσης είναι εύκολο να υλοποιηθεί και είναι λιγότερο δαπανηρός διότι εφαρμόζεται στη μεριά χαμηλής κατανάλωσης ισχύος, όπως είναι αυτή του κυκλώματος διέγερσης. Παρ όλα αυτά, λόγω της μεγάλης αυτεπαγωγής στο κύκλωμα της διέγερσης η μεταβολή του ρεύματος διέγερσης θα είναι σχετικά αργή, γεγονός το οποίο θα έχει επίπτωση και στην απόκριση της ρύθμισης της ταχύτητας. Ρύθμιση της αντίστασης τυμπάνου Σε αυτή τη μέθοδο η τάση στους ακροδέκτες της μηχανής V και το ρεύμα Ι διέγερσης (άρα και η μαγνητική ροή) διατηρούνται σταθερά στις ονομαστικές τους τιμές και η ταχύτητα ελέγχεται μεταβάλλοντας την αντίσταση τυμπάνου r. Αυτό συνήθως επιτυγχάνεται χρησιμοποιώντας ένα ρεοστάτη (R e ) στο κύκλωμα του τυμπάνου, όπως φαίνεται στο σχήμα 3.9. Σχήμα 3.9 Έλεγχος της αντίστασης τυμπάνου μιας D.C. μηχανής 3
35 Από την εξίσωση 3.4 προκύπτει: V r R (3.9) e T K K Εάν η τάση στους ακροδέκτες της μηχανής V και η μαγνητική ροή Φ διατηρούνται σταθερές: K K T (3.0) K 5 6 V Όπου η σταθερά K 5 αντιπροσωπεύει την εν κενώ ταχύτητα και K 6 r R K e. Οι χαρακτηριστικές ταχύτητας ροπής για διάφορες τιμές της εξωτερικής αντίστασης τυμπάνου παρουσιάζονται στο σχήμα 3.9b. Η τιμή της αντίστασης (R e ) μπορεί να ρυθμίζεται για τη δημιουργία διαφόρων ταχυτήτων, τέτοιες ώστε το ρεύμα τυμπάνου (άρα και η ροπή) να παραμένει σταθερό. Αυτή την περίπτωση δείχνει το σχήμα 3.9b. Η αντίστοιχη χαρακτηριστική ταχύτητας αντίστασης για λειτουργία με σταθερή ροπή παρουσιάζεται στο σχήμα 3.9c. Η ταχύτητα μπορεί να ρυθμιστεί από τη μηδενική τιμή ως τη μέγιστη, μεταβάλλοντας την αντίσταση (R e ), όπως φαίνεται στο σχήμα 3.9d. Η μέθοδος ελέγχου της αντίστασης τυμπάνου είναι εύκολη στην υλοποίηση, όμως είναι λιγότερο αποδοτική εξαιτίας των απωλειών πάνω στην αντίσταση (R e ). Πολλά μεταφορικά οχήματα ελέγχονται ακόμα με αυτή τη μέθοδο. Η αντίσταση (R e ) πρέπει να σχεδιασθεί να αντέχει το ρεύμα τυμπάνου. Άρα είναι κατά πολύ ακριβότερη από τον αντίστοιχο ρεοστάτη (R c ) στη μέθοδο ελέγχου της διέγερσης. Ένα από τα κύρια προσόντα των μηχανών ξένης διέγερσης είναι η ευκολία με την οποία ρυθμίζεται η αναπτυσσόμενη ροπή. Η ροπή είναι ευθέως ανάλογη του ρεύματος τυμπάνου, το οποίο αντίστοιχα εξαρτάται από τη διαφορά μεταξύ της εφαρμοζόμενης τάσης V και της αναπτυσσόμενης εσωτερικής τάσης Ε. Έτσι, μπορούμε να εξαναγκάσουμε τη μηχανή να κινηθεί δεξιόστροφα ή αριστερόστροφα και να αναπτύξει θετική (κινητήρας) ή αρνητική (γεννήτρια) ροπή, ελέγχοντας απλώς το κατά πόσο θα είναι μεγαλύτερη ή μικρότερη η εφαρμοζόμενη τάση V από την αναπτυσσόμενη εσωτερική τάση Ε. 33
36 Μια, ελεγχόμενης τάσης τυμπάνου, μηχανή συνεχούς ρεύματος είναι κατά συνέπεια κατάλληλη για λειτουργία στα λεγόμενα «4 τεταρτημόρια», όπως αυτό δείχνεται στο σχήμα 3.0. Σχήμα 3.0 Λειτουργία μιας D.C. μηχανής στα 4 τεταρτημόρια των χαρακτηριστικών ροπής - στροφών Όταν η μηχανή λειτουργεί σαν κινητήρας στρεφόμενος δεξιόστροφα, βρισκόμαστε στο τεταρτημόριο. Η εφαρμοζόμενη τάση V είναι μεγαλύτερη από την αναπτυσσόμενη εσωτερική τάση Ε και ένα θετικό ρεύμα ρέει εντός της μηχανής. Η ισχύς που αντλείται από το δίκτυο (V Ι) είναι θετική και εάν οι συνθήκες είναι σταθερές το μεγαλύτερο μέρος της ισχύος θα μεταδοθεί στο φορτίο. Εάν στη μηχανή που λειτουργεί στο σημείο Α ελαττώσουμε ξαφνικά την τάση τροφοδοσίας σε μία τιμή V b, η οποία είναι μικρότερη της αναπτυσσόμενης εσωτερικής τάσης, τότε το ρεύμα (άρα και η ροπή) θα αλλάξει κατεύθυνση και το σημείο λειτουργίας θα ολισθήσει στο Β. Σε αυτό το τεταρτημόριο η μηχανή συμπεριφέρεται σαν γεννήτρια επιστρέφοντας ισχύ στο δίκτυο. Εάν η μηχανή αφεθεί ως έχει είναι σαφές ότι δεν θα παραμείνει στο σημείο Β. Η ταυτόχρονη επίδραση της ροπής του φορτίου και της αρνητικής ροπής της μηχανής θα οδηγήσουν τη μηχανή σε επιβράδυνση, έτσι ώστε η αναπτυσσόμενη εσωτερική τάση να ξαναγίνει μικρότερη της τάσης τροφοδοσίας και το ρεύμα θα ξαναγίνει θετικό οδηγώντας τη μηχανή ξανά στο πρώτο 34
37 τεταρτημόριο σε ένα σημείο λειτουργίας με μικρότερη ταχύτητα εξαιτίας της μικρότερης τάσης τροφοδοσίας. Κατά τη διάρκεια της επιβράδυνσης κινητική ενέργεια από την αδράνεια της μηχανής και του φορτίου επιστρέφει στην πηγή τροφοδοσίας. Αυτό είναι ένα παράδειγμα αναγεννητικής πέδησης και εμφανίζεται κάθε φορά που θα μειώσουμε την τάση ώστε να μειώσουμε τις στροφές της μηχανής. Η μετάβαση από το πρώτο στο δεύτερο τεταρτημόριο μπορεί επίσης να γίνει αν, διατηρώντας την ίδια φορά περιστροφής και την τάση τροφοδοσίας, αντιστρέψουμε τη ροπή φορτίου σε μια ταχύτητα μεγαλύτερη από αυτή της εν κενώ λειτουργίας. Ακόμα, το ίδιο αποτέλεσμα θα είχε και η αύξηση του πεδίου της διέγερσης, η οποία με τη σειρά της θα αυξήσει την εσωτερική τάση της μηχανής πάνω από την τιμή της τάσης τροφοδοσίας, αντιστρέφοντας έτσι το ρεύμα τυμπάνου, τη ροπή και τη ροή ισχύος. Εάν θέλουμε να λειτουργούμε τη μηχανή συνεχώς στο σημείο Β η μηχανή θα πρέπει να οδηγηθεί από μία πηγή μηχανικής ισχύος. Είδαμε πριν ότι η μηχανή τείνει φυσικά να περιστραφεί με μικρότερη ταχύτητα από αυτή που αντιστοιχεί στο σημείο Β, άρα θα πρέπει να την εξαναγκάσουμε να περιστραφεί γρηγορότερα και να αναπτύξει έτσι μια μεγαλύτερη από την V b εσωτερική τάση εάν θέλουμε συνεχή λειτουργία της μηχανής σαν γεννήτρια. Εντελώς ανάλογα είναι και τα συμπεράσματα που εξάγονται από τη λειτουργία της μηχανής σε αριστερόστροφη περιστροφή (η τάση τροφοδοσίας V είναι ανάστροφη). Λειτουργία σαν κινητήρας υπάρχει στο τρίτο τεταρτημόριο ενώ μετάπτωση (με αναγεννητική πέδηση) στο τέταρτο τεταρτημόριο έχουμε όταν μειώσουμε την τάση για να μειώσουμε την περιστροφική ταχύτητα. Επίσης, το ίδιο επιτυγχάνουμε εάν αντιστρέψουμε τις συνδεσμολογίες του τυλίγματος της διέγερσης. Ένα παραδοσιακό κινητήριο σύστημα που λειτουργεί σε τέσσερα τεταρτημόρια παρουσιάζεται στο σχήμα 3. και ονομάζεται σύστημα Wrd-Leonrd. Το κινητήριο αυτό σύστημα εμπλέκει τρεις μηχανές, στις οποίες συμπεριλαμβάνονται δύο μηχανές συνεχούς ρεύματος ξένης διέγερσης, οι οποίες έχουν ηλεκτρικά συνδεδεμένα τα κυκλώματα τυμπάνου τους. 35
38 Σχήμα 3. Γενική διάταξη κινητηρίου συστήματος Wrd-Leonrd Η μηχανή συνεχούς είναι μηχανικά συνδεδεμένη σε μια κινητήρια μηχανή, η οποία παρέχει σταθερή ονομαστική ταχύτητα. Επίσης, η εσωτερική τάση της μηχανής ελέγχεται από ένα εξωτερικό ρεύμα διέγερσης. Η μηχανή συνεχούς είναι μηχανικά συνδεδεμένη στο φορτίο. Απόλυτες και σχετικές ρυθμίσεις στα ρεύματα διέγερσης των δύο μηχανών ελέγχουν τη χαρακτηριστική ροπής στροφών της μηχανής, όπως φαίνεται στο σχήμα 3.c. Σχήμα 3.b Ισοδύναμο κύκλωμα και (c) χαρακτηριστική ροπής στροφών κινητηρίου συστήματος Wrd-Leonrd 36
39 Παρόλο που το συγκεκριμένο κινητήριο σύστημα παρέχει όλες τις δυνατότητες ελέγχου, έχει το μειονέκτημα ότι απαιτεί τρεις ογκώδεις στρεφόμενες μηχανές, κάτι που μειώνει τη συνολική απόδοση του συστήματος και παρουσιάζει περιορισμένο χρόνο απόκρισής λόγω των χρονικών σταθερών των κυκλωμάτων διέγερσης. Πέδηση σε ηλεκτρική κίνηση Σχήμα 3. Πέδηση ηλεκτρικής μηχανής Ο όρος πέδηση χρησιμοποιείται όταν: ) Κατά τη λειτουργία της μηχανής ως γεννήτρια, η ροπής της (αντιροπή) πεδεί την κινητήρια μηχανή, η οποία με τη ροπή της κινεί τη γεννήτρια και επιβάλλει την φορά περιστροφής (π.χ. η κάθοδος βάρους ανυψωτικού μηχανήματος πεδείται από την αντιροπή της συμπλεγμένης μηχανής, η οποία λειτουργεί ως γεννήτρια (περιοχή ΙΙ). ) Η ηλεκτρική μηχανή φορτίζεται όπως στην περίπτωση του κινητήρα (δηλαδή αντίθετα προς τη φορά περιστροφής της ως κινητήρας), η ροπή φόρτισής της όμως (πέδηση) είναι τόσο μεγάλη ώστε εξαναγκάζει τη μηχανή να περιστραφεί αντίθετα (ω <0). Η κατάσταση αυτή προκαλεί μηχανικές και θερμικές βλάβες (λόγω του πολύ μεγάλου ρεύματος) και είναι επιτρεπτή μόνο ως μεταβατική υπό 37
40 ορισμένες συνθήκες, π.χ. στην πέδηση με αλλαγή πολικότητας (περιοχή ΙΙΙ). Ωφέλιμη πέδηση Η ηλεκτρική μηχανή λειτουργεί ως γεννήτρια και πεδεί τη μηχανή εργασίας (φορτίο). Έτσι, γίνεται εκμετάλλευση της δυναμικής ή κινητικής ενέργειας με τη μετατροπή της σε ηλεκτρική. Εφαρμογές αυτού του τύπου της πέδησης βρίσκουμε στις εξής περιπτώσεις: Α) Ηλεκτρικός σιδηρόδρομος σε κατήφορο Η κίνηση του οχήματος προκαλείται από τη συνιστώσα F του βάρους που είναι παράλληλη προς το κεκλιμένο επίπεδο της τροχιάς. Στη μόνιμη κατάσταση η ταχύτητα υ είναι σταθερή διότι ισχύει: Τ εξ =Τ τρ +Τ Όπου Τ εξ η ροπή κίνησης που προκαλεί το βάρος Τ τρ Τ η ροπή τριβών και η ροπή της γεννήτριας Η κινητήρια ισχύς είναι Ρ = F υ. Η ηλεκτρική μηχανή λειτουργεί ως γεννήτρια δίνοντας στο δίκτυο την ισχύ Ρ = Ρ-ΣΡ, όπου ΣΡ οι συνολικές απώλειες. Για την εκμετάλλευση αυτής της ισχύος πρέπει να είναι συνδεδεμένα στο δίκτυο και άλλα οχήματα, των οποίων οι ηλεκτρικές μηχανές να λειτουργού ως κινητήρες. Σχήμα 3.3 Κίνηση οχήματος στον κατήφορο 38
41 Β) Ταπείνωση βαρών Όπως και στην προηγούμενη περίπτωση, σε κάθοδο βάρους W με ταχύτητα υ με ανυψωτικό μηχάνημα ή ανελκυστήρα, η κινητήρια ισχύς είναι Ρ=Wυ. Πέδηση με αντίσταση Πρόκειται για την περίπτωση που αναφέρθηκε προηγουμένως, όπου δεν γίνεται μετατροπή μηχανικής ενέργειας σε ηλεκτρική. Σύμφωνα με το σχήμα 3.4 η ηλεκτρική μηχανή χωρίζεται από το δίκτυο όπου ήταν πριν συνδεδεμένη και κλείνει το κύκλωμά της με ωμική αντίσταση R, ενώ η διέγερση δεν μεταβάλλεται (ξένη ή παράλληλη διέγερση). Η δυναμική ή κινητική ενέργεια του φορτίου μετατρέπεται από την ηλεκτρική μηχανή (που λειτουργεί ως γεννήτρια) σε ηλεκτρική ενέργεια, η οποία χάνεται υπό μορφή θερμότητας πάνω στην αντίσταση R. Σχήμα 3.4 Πέδηση με αντίσταση Σύμφωνα με τις εξισώσεις των μηχανών συνεχούς ρεύματος ξένης διέγερσης ισχύει (αφού η τάση V=0): r T R K (3.) 39
42 Εφαρμογές αυτού του τύπου της πέδησης βρίσκουμε στις εξής περιπτώσεις: Α) Πέδηση οχήματος Σχήμα 3.5 Πέδηση οχήματος με αντίσταση Υποθέτουμε ότι το αρχικό σημείο λειτουργίας της μηχανής ως κινητήρα ήταν το ΑΙ και το όχημα έχει μια ορισμένη κινητική ενέργεια. Αμέσως μετά τη μετατροπή της συνδεσμολογίας (t=0 + ) η περιστροφική ταχύτητα παραμένει αμετάβλητη λόγω της αδράνειας των περιστρεφόμενων μαζών, άρα το νέο σημείο λειτουργίας είναι το ΑΙΙ. Η ροπή της μηχανής (που λειτουργεί πλέον ως γεννήτρια) πεδεί το όχημα και μειώνει την περιστροφική ταχύτητα. Σύμφωνα με την καμπύλη όμως μειώνεται και η ίδια η ροπή. Για αποτελεσματικότερη πέδηση χρησιμοποιείται κλιμακωτή αντίσταση (όπως στην εκκίνηση) με την οποία επιτυγχάνεται μεγάλη ροπή πέδησης ακόμα και όταν έχει μειωθεί πολύ η περιστροφική ταχύτητα. Την πέδηση ενισχύει επίσης και η εξωτερική ροπή (ροπή τριβών του οχήματος). Στην κίνηση ηλεκτρικών οχημάτων (έλξη) εφαρμόζεται συχνά η πέδηση με αντίσταση κινητήρων διέγερσης σειράς. Η μηχανή λειτουργεί ως αυτοδιεγειρόμενη γεννήτρια. Επειδή στις μηχανές διέγερσης σειράς η φορά της εσωτερικής ροπής είναι ίδια στη λειτουργία κινητήρα και γεννήτριας (αλλάζουν πρόσημο και το ρεύμα και η μαγνητική ροή) η φορά περιστροφής της γεννήτριας είναι αντίθετη από αυτή του κινητήρα. Για να διατηρείται ίδια η φορά περιστροφής πρέπει να αντιστραφεί η πολικότητα της διέγερσης με αλλαγή της συνδεσμολογίας. 40
43 Β) Ταπείνωση βαρών Σχήμα 3.6 Σχέση ροπής ταχύτητας στην πέδηση με αντίσταση Λόγω της σταθερότητας της ροπής κίνησης (Τ εξ =rw, όπου r είναι η ακτίνα της τροχαλίας και W το βάρος), επιτυγχάνεται σταθερή περιστροφική ταχύτητα, άρα και σταθερή ταχύτητα καθόδου. Η ταχύτητα είναι ανάλογη με την ολική αντίσταση του δρομέα. Άρα με την κατάλληλη εξωτερική αντίσταση επιτυγχάνεται η επιθυμητή ταχύτητα. Πέδηση με αλλαγή πολικότητας Πρόκειται για την περίπτωση όπου, ενώ περιστρέφεται ο κινητήρας, αλλάζουμε την πολικότητα της διέγερσης με συνέπεια να αντιστραφεί η μαγνητική ροή και η ΗΕ Ε (η περιστροφική ταχύτητα δεν μεταβάλλεται αμέσως λόγω αδράνειας), άρα και το ρεύμα γίνεται πολύ μεγάλο: I V E (3.) r Επίσης, και η αναπτυσσόμενη ροπή είναι πολύ μεγάλη και έχει αντίθετη φορά (ροπή πέδησης) από τη φορά περιστροφής της μηχανής. Η ροπή αυτή όχι μόνο πεδεί τη μηχανή μέχρι την ακινητοποίηση αλλά εκκινεί τη μηχανή με την αντίθετη φορά περιστροφής. 4
44 Σχήμα 3.7 Σχέση ροπής ταχύτητας στην πέδηση με αλλαγή πολικότητας Έστω κινητήρας που κινεί όχημα προς μία κατεύθυνση με σταθερή ταχύτητα. Η χαρακτηριστική του κινητήρα παράλληλης διέγερσης είναι : T r 0 (3.3) K V Όπου 0 και Α το σημείο λειτουργίας για Τ=Τ εξ, με Τ εξ τη ροπή K φόρτισης λόγω τριβών. Εάν αντιστραφεί η πολικότητα της διέγερσης ο κινητήρας αποκτά τη χαρακτηριστική: T r 0 (3.4) K Η στιγμιαία ροπή πέδησης (σημείο Β) είναι πολύ μεγάλη, ακινητοποιεί ταχύτατα τον κινητήρα (σημείο Γ) και τον εκκινεί προς την αντίθετη φορά έως το σημείο, όπου και ισορροπεί. Το όχημα κινείται τώρα με ταχύτητα ίση με την αρχική, ενώ και η ροπή φόρτισης έχει αντιστραφεί. Η παραπάνω μέθοδος είναι ανεπίτρεπτη, προπαντός για μεγάλες μηχανές και υπό πλήρη τάση. Μπορεί όμως να εφαρμοσθεί με μειωμένη τάση ή με την παρεμβολή ωμικής αντίστασης. Εάν είναι επιθυμητή η ακινητοποίηση του οχήματος θα πρέπει να ληφθεί μέριμνα για τη διακοπή της τάσης όταν γίνει 0. Το ίδιο αποτέλεσμα έχουμε εάν δεν μεταβάλλουμε τη διέγερση αλλά αλλάξουμε την πολικότητα των ψηκτρών, οπότε αντιστρέφεται η φορά του ρεύματος στο τύλιγμα του δρομέα. Για το λόγο αυτό η μέθοδος ονομάζεται 4
45 και αντιθέτου ρεύματος. Για τη γρήγορη αλλαγή της φοράς περιστροφής στις μηχανές ξένης και παράλληλης διέγερσης προτιμάται γενικά η αλλαγή της πολικότητας του τυμπάνου και όχι της διέγερσης, διότι το τύλιγμα της διέγερσης έχει μεγάλη αυτεπαγωγή και κατά συνέπεια μεγάλη χρονική σταθερά (τάξης μεγέθους δεκαπλάσιας της αντίστοιχης του τυμπάνου), πράγμα που μειώνει την ταχύτητα ελέγχου. υσκολία παρουσιάζει και η διακοπή μεγάλων ρευμάτων γι αυτό συνήθως συνδέεται σε σειρά με τα τυλίγματα του τυμπάνου μια μεγάλη αντίσταση. Μια παραλλαγή της μεθόδου πέδης με αντίθετο ρεύμα παρουσιάζεται στο σχήμα 3.8. Στην περίπτωση αυτή η πολικότητα της τάσης τυμπάνου δεν αλλάζει, αλλά με τη σύνδεση των αντιστάσεων σε σειρά ελαττώνεται ο αριθμός στροφών και σε μια τιμή της ροπής (θετική) επιτυγχάνεται η αλλαγή της φοράς περιστροφής. Για τη δημιουργία αρνητικού αριθμού στροφών θα πρέπει: R r V T (3.5) K K V (R τυχαίο) Φορτίο V I Τ R = 4r R = 6r R = 8r α) β) Σχήμα 3.8α) Συνδεσμολογία, β) σχέση ταχύτητας/ρεύματος ροπής στην πέδηση με αντίθετο ρεύμα. 43
46 Εκκίνηση Εάν μια μηχανή συνεχούς ρεύματος συνδεθεί κατευθείαν σε μία πηγή συνεχούς ρεύματος τότε το ρεύμα εκκίνησης είναι επικίνδυνα υψηλό (σχήμα 3.9α). I V E (3.6) R Η αντι-ηε δύναμη E K ) είναι μηδέν στην εκκίνηση. Άρα ισχύει: ( I V (3.7) R Συνεπώς, εφόσον η αντίσταση R είναι μικρή το ρεύμα εκκίνησης είναι πολύ μεγάλο. Για να περιορισθεί το ρεύμα εκκίνησης σε μια ασφαλή τιμή χρησιμοποιούνται οι ακόλουθες μέθοδοι:. Εισάγεται μία εξωτερική αντίσταση R e στην εκκίνηση (σχήμα 3.9b).. Χρησιμοποιείται μια μειωμένη τάση ακροδεκτών στην εκκίνηση. Αυτό βέβαια απαιτεί μια πηγή μεταβλητής τάσης. V V + V _ Σχήμα 3.9 Συνδεσμολογία εκκινητή μηχανής συνεχούς ρεύματος. 44
47 Με την εξωτερική αντίσταση συνδεδεμένη στο κύκλωμα του τυμπάνου το ρεύμα του τυμπάνου στην εκκίνηση γίνεται: Η αντι-ηε δύναμη I V E (3.8) R Re E αυξάνει όσο αυξάνει η ταχύτητα της μηχανής. Συνεπώς η εξωτερική αντίσταση μπορεί να αφαιρείται βαθμιαία όσο επιταχύνεται η μηχανή χωρίς το ρεύμα να υπερβαίνει κάποιο συγκεκριμένο όριο. Αυτό επιτυγχάνεται με τη χρήση ενός εκκινητή (σχήμα 3.9c). Στην εκκίνηση το χειριστήριο (hndle) μετακινείται στη θέση, στην οποία όλες οι αντιστάσεις R, R, R 3, R 4, είναι συνδεδεμένες σε σειρά με την αντίσταση τυμπάνου και έτσι περιορίζεται το ρεύμα τυμπάνου. Όσο επιταχύνεται η μηχανή το χειριστήριο μετακινείται στις θέσεις, 3, 4 και τελικά 5, στην οποία όλες οι αντιστάσεις του εκκινητή έχουν αποσυνδεθεί από το κύκλωμα του τυμπάνου. Το χειριστήριο θα παραμείνει στη θέση 5 μέσω του ηλεκτρομαγνήτη ο οποίος διεγείρεται από το ρεύμα του πεδίου διέγερσης Ι. υναμική συμπεριφορά γεννήτριας συνεχούς ρεύματος ξένης διέγερσης Στη μελέτη της δυναμικής συμπεριφοράς μιας μηχανής συνεχούς ρεύματος λαμβάνονται υπόψιν οι επιδράσεις των αυτεπαγωγών, των αλληλεπαγωγών και της αδράνειας της μηχανής, οι οποίες δεν υφίστανται στη στάσιμη (μόνιμη) κατάσταση. Από τη φύση της (λόγω κατασκευής) η λειτουργία των στρεφόμενων μηχανών είναι μη γραμμική και κατά συνέπεια η μοντελοποίησή τους γίνεται με συστήματα μη γραμμικών διαφορικών εξισώσεων. Στην προκειμένη περίπτωση θα εξετασθούν γραμμικοποιημένες διαφορικές εξισώσεις μοντελοποίησης της δυναμικής συμπεριφοράς των μηχανών συνεχούς ρεύματος. Για το λόγο αυτό γίνονται οι παρακάτω παραδοχές: Ο μαγνητικός κορεσμός αμελείται, δηλαδή οι αυτεπαγωγές είναι σταθερές, ανεξάρτητες του ρεύματος. εν υπάρχει ζεύξη μεταξύ των μαγνητικών πεδίων του τυμπάνου και της διέγερσης, επειδή οι άξονές τους είναι κάθετοι. 45
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΓΚΙΟΚΑΣ ΠΑΝΑΓΙΩΤΗΣ. ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας μιας ηλεκτρικής γεννήτριας Σ.Ρ. με διέγερση σειράς.
 ΓΚΙΟΚΑΣ ΠΑΝΑΓΙΩΤΗΣ ΑΜ:6749 ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας μιας ηλεκτρικής γεννήτριας Σ.Ρ. με διέγερση σειράς. ΣΚΟΠΟΣ: Για να λειτουργήσει μια γεννήτρια, πρέπει να πληρούνται οι παρακάτω βασικές
ΓΚΙΟΚΑΣ ΠΑΝΑΓΙΩΤΗΣ ΑΜ:6749 ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας μιας ηλεκτρικής γεννήτριας Σ.Ρ. με διέγερση σειράς. ΣΚΟΠΟΣ: Για να λειτουργήσει μια γεννήτρια, πρέπει να πληρούνται οι παρακάτω βασικές
10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
 10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Ηλεκτρική μηχανή ονομάζεται κάθε διάταξη η οποία μετατρέπει τη μηχανική ενεργεια σε ηλεκτρική ή αντίστροφα ή μετατρεπει τα χαρακτηριστικά του ηλεκτρικού ρεύματος. Οι ηλεκτρικες
10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Ηλεκτρική μηχανή ονομάζεται κάθε διάταξη η οποία μετατρέπει τη μηχανική ενεργεια σε ηλεκτρική ή αντίστροφα ή μετατρεπει τα χαρακτηριστικά του ηλεκτρικού ρεύματος. Οι ηλεκτρικες
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 2: Ασύγχρονος Τριφασικός Κινητήρας Αρχή Λειτουργίας Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 2: Ασύγχρονος Τριφασικός Κινητήρας Αρχή Λειτουργίας Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών
Τμήμα Ηλεκτρολόγων Μηχανικών ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΡΟΠΗΣ ΤΑΧΥΤΗΤΑΣ ΕΠΑΓΩΓΙΚΩΝ ΚΙΝΗΤΗΡΩΝ
 Ένας που κατασκευάζεται ώστε να παρουσιάζει μεγάλη αντίσταση δρομέα η ροπή εκκίνησης του είναι αρκετά υψηλή αλλά το ίδιο υψηλή είναι και η ολίσθηση του στις κανονικές συνθήκες λειτουργίας Όμως επειδή Pconv=(1-s)PAG,
Ένας που κατασκευάζεται ώστε να παρουσιάζει μεγάλη αντίσταση δρομέα η ροπή εκκίνησης του είναι αρκετά υψηλή αλλά το ίδιο υψηλή είναι και η ολίσθηση του στις κανονικές συνθήκες λειτουργίας Όμως επειδή Pconv=(1-s)PAG,
2. ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ
 28 2. ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι γεννήτριες εναλλασσόµενου ρεύµατος είναι δύο ειδών Α) οι σύγχρονες γεννήτριες ή εναλλακτήρες και Β) οι ασύγχρονες γεννήτριες Οι σύγχρονες γεννήτριες παράγουν
28 2. ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι γεννήτριες εναλλασσόµενου ρεύµατος είναι δύο ειδών Α) οι σύγχρονες γεννήτριες ή εναλλακτήρες και Β) οι ασύγχρονες γεννήτριες Οι σύγχρονες γεννήτριες παράγουν
ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ. 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα.
 Σκοπός της άσκησης: ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα. 1. Γενικά Οι
Σκοπός της άσκησης: ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα. 1. Γενικά Οι
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6
5. ΜΟΝΟΦΑΣΙΚΟΙ ΚΑΙ ΑΛΛΟΙ ΚΙΝΗΤΗΡΕΣ
 73 5. ΜΟΝΟΦΑΣΙΚΟΙ ΚΑΙ ΑΛΛΟΙ ΚΙΝΗΤΗΡΕΣ Στην συνέχεια εξετάζονται οι µονοφασικοί επαγωγικοί κινητήρες αλλά και ορισµένοι άλλοι όπως οι τριφασικοί σύγχρονοι κινητήρες που υπάρχουν σε µικρό ποσοστό σε βιοµηχανικές
73 5. ΜΟΝΟΦΑΣΙΚΟΙ ΚΑΙ ΑΛΛΟΙ ΚΙΝΗΤΗΡΕΣ Στην συνέχεια εξετάζονται οι µονοφασικοί επαγωγικοί κινητήρες αλλά και ορισµένοι άλλοι όπως οι τριφασικοί σύγχρονοι κινητήρες που υπάρχουν σε µικρό ποσοστό σε βιοµηχανικές
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι γεννήτριες συνεχούς ρεύματος διαχωρίζονται στις ακόλουθες κατηγορίες: Ανεξάρτητης (ξένης) διέγερσης. Παράλληλης διέγερσης. Διέγερσης σειράς. Αθροιστικής σύνθετης διέγερσης.
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι γεννήτριες συνεχούς ρεύματος διαχωρίζονται στις ακόλουθες κατηγορίες: Ανεξάρτητης (ξένης) διέγερσης. Παράλληλης διέγερσης. Διέγερσης σειράς. Αθροιστικής σύνθετης διέγερσης.
Γεννήτρια συνεχούς ρεύματος παράλληλης. διέγερσης
 ΑΣΚΗΣΗ 6 Γεννήτρια συνεχούς ρεύματος παράλληλης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Στις γεννήτριες παράλληλης διέγερσης το τύλιγμα διέγερσης συνδέεται παράλληλα με το κύκλωμα του δρομέα, όπως φαίνεται
ΑΣΚΗΣΗ 6 Γεννήτρια συνεχούς ρεύματος παράλληλης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Στις γεννήτριες παράλληλης διέγερσης το τύλιγμα διέγερσης συνδέεται παράλληλα με το κύκλωμα του δρομέα, όπως φαίνεται
Τμήμα Ηλεκτρολόγων Μηχανικών ΕΛΕΓΧΟΣ ΤΑΧΥΤΗΤΑΣ ΣΤΟΥΣ ΕΠΑΓΩΓΙΚΟΥΣ ΚΙΝΗΤΗΡΕΣ
 Το κανονικό εύρος λειτουργίας ενός τυπικού επαγωγικού κινητήρα (κλάσης Α, Β και C) περιορίζεται κάτω από 5% για την ολίσθηση ενώ η μεταβολή της ταχύτητας πέρα από αυτό το εύρος είναι σχεδόν ανάλογη του
Το κανονικό εύρος λειτουργίας ενός τυπικού επαγωγικού κινητήρα (κλάσης Α, Β και C) περιορίζεται κάτω από 5% για την ολίσθηση ενώ η μεταβολή της ταχύτητας πέρα από αυτό το εύρος είναι σχεδόν ανάλογη του
ΑΣΚΗΣΗ 6 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 6 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α), η κατανόηση της λειτουργίας της γεννήτριας
ΑΣΚΗΣΗ 6 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α), η κατανόηση της λειτουργίας της γεννήτριας
Οι μηχανές ΕΡ είναι γεννήτριες που μετατρέπουν τη μηχανική ισχύ σε ηλεκτρική και κινητήρες που μετατρέπουν την ηλεκτρική σε μηχανική
 Οι μηχανές ΕΡ είναι γεννήτριες που μετατρέπουν τη μηχανική ισχύ σε ηλεκτρική και κινητήρες που μετατρέπουν την ηλεκτρική σε μηχανική Υπάρχουν 2 βασικές κατηγορίες μηχανών ΕΡ: οι σύγχρονες και οι επαγωγικές
Οι μηχανές ΕΡ είναι γεννήτριες που μετατρέπουν τη μηχανική ισχύ σε ηλεκτρική και κινητήρες που μετατρέπουν την ηλεκτρική σε μηχανική Υπάρχουν 2 βασικές κατηγορίες μηχανών ΕΡ: οι σύγχρονες και οι επαγωγικές
ΑΣΚΗΣΗ 6 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ
 ΑΣΚΗΣΗ 6 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Ο πειραματικός προσδιορισμός των απωλειών σιδήρου και των μηχανικών απωλειών
ΑΣΚΗΣΗ 6 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Ο πειραματικός προσδιορισμός των απωλειών σιδήρου και των μηχανικών απωλειών
ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ
 ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ Σκοπός της άσκησης: Σκοπός της άσκησης είναι: 1. Να εξοικειωθεί ο σπουδαστής με την διαδικασία εκκίνησης ενός σύγχρονου τριφασικού
ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ Σκοπός της άσκησης: Σκοπός της άσκησης είναι: 1. Να εξοικειωθεί ο σπουδαστής με την διαδικασία εκκίνησης ενός σύγχρονου τριφασικού
ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΟΥΝΙΟΥ 2007
 ΤΕΙ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΣΤΕΦ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΔΙΔΑΣΚΩΝ: Δρ. Π. Β. Μαλατέστας, Καθηγητής ΗΜΕΡΟΜΗΝΙΑ : 5//7 Μάθημα : Ηλεκτρική Κίνηση ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΟΥΝΙΟΥ 7 ΘΕΜΑ ο (4%) Κινητήρας με γραμμική χαρακτηριστική
ΤΕΙ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΣΤΕΦ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΔΙΔΑΣΚΩΝ: Δρ. Π. Β. Μαλατέστας, Καθηγητής ΗΜΕΡΟΜΗΝΙΑ : 5//7 Μάθημα : Ηλεκτρική Κίνηση ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΟΥΝΙΟΥ 7 ΘΕΜΑ ο (4%) Κινητήρας με γραμμική χαρακτηριστική
ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ
 ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς ρεύματος
ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς ρεύματος
3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Διατάξεις εκκίνησης κινητήρων ΣΡ
 Διατάξεις εκκίνησης κινητήρων ΣΡ Η διάταξη ελέγχου και προστασίας του κινητήρα ΣΡ πρέπει: 1. Να προστατεύει τον κινητήρα από βραχυκυκλώματα στην ίδια τη διάταξη προστασίας 2. Να προστατεύει τον κινητήρα
Διατάξεις εκκίνησης κινητήρων ΣΡ Η διάταξη ελέγχου και προστασίας του κινητήρα ΣΡ πρέπει: 1. Να προστατεύει τον κινητήρα από βραχυκυκλώματα στην ίδια τη διάταξη προστασίας 2. Να προστατεύει τον κινητήρα
ΑΣΚΗΣΗ 1 η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ. Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την:
 Σκοπός της Άσκησης: ΑΣΚΗΣΗ η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την: α. Κατασκευή μετασχηματιστών. β. Αρχή λειτουργίας μετασχηματιστών.
Σκοπός της Άσκησης: ΑΣΚΗΣΗ η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την: α. Κατασκευή μετασχηματιστών. β. Αρχή λειτουργίας μετασχηματιστών.
3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
Τμήμα Ηλεκτρολόγων Μηχανικών ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΚΑΤΆ ΤΗ ΛΕΙΤΟΥΡΓΙΑ ΣΓ
 Όταν κατά τη λειτουργία μιας ΣΓ η ροπή στον άξονα της ή το φορτίο της μεταβληθούν απότομα, η λειτουργία της παρουσιάζει κάποιο μεταβατικό φαινόμενο για κάποια χρονική διάρκεια μέχρι να επανέλθει στη στάσιμη
Όταν κατά τη λειτουργία μιας ΣΓ η ροπή στον άξονα της ή το φορτίο της μεταβληθούν απότομα, η λειτουργία της παρουσιάζει κάποιο μεταβατικό φαινόμενο για κάποια χρονική διάρκεια μέχρι να επανέλθει στη στάσιμη
ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ
 ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ Σκοπός της άσκησης: 1. Ο πειραματικός προσδιορισμός της χαρακτηριστικής λειτουργίας
ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ Σκοπός της άσκησης: 1. Ο πειραματικός προσδιορισμός της χαρακτηριστικής λειτουργίας
ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ. Κινητήρες ΣΡ. Άγγελος Μπουχουράς - Μηχανές Ι
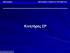 Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 7: Μέθοδοι Εκκίνησης και Πέδησης Ασύγχρονων Τριφασικών Κινητήρων Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 7: Μέθοδοι Εκκίνησης και Πέδησης Ασύγχρονων Τριφασικών Κινητήρων Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 3: Εξισώσεις Μόνιμης Κατάστασης Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 3: Εξισώσεις Μόνιμης Κατάστασης Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΙΙ
 ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΙΙ ΣΥΓΧΡΟΝΕΣ ΜΗΧΑΝΕΣ Ε.Ρ. 1. Μια σύγχρονη γεννήτρια με ονομαστικά στοιχεία: 2300V, 1000kV, 60Hz, διπολική με συντελεστής ισχύος 0,8 επαγωγικό και σύνδεση σε αστέρα έχει σύγχρονη
ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΙΙ ΣΥΓΧΡΟΝΕΣ ΜΗΧΑΝΕΣ Ε.Ρ. 1. Μια σύγχρονη γεννήτρια με ονομαστικά στοιχεία: 2300V, 1000kV, 60Hz, διπολική με συντελεστής ισχύος 0,8 επαγωγικό και σύνδεση σε αστέρα έχει σύγχρονη
ΑΣΚΗΣΗ 11 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 11 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας
ΑΣΚΗΣΗ 11 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας
ΑΣΚΗΣΗ 1 ΜΟΝΟΦΑΣΙΚΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗΣ
 ΑΣΚΗΣΗ 1 ΜΟΝΟΦΑΣΙΚΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗΣ Α.1 ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΜΟΝΟΦΑΣΙΚΟ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗ Ο μετασχηματιστής είναι μια ηλεκτρική διάταξη που μετατρέπει εναλλασσόμενη ηλεκτρική ενέργεια ενός επιπέδου τάσης
ΑΣΚΗΣΗ 1 ΜΟΝΟΦΑΣΙΚΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗΣ Α.1 ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΜΟΝΟΦΑΣΙΚΟ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗ Ο μετασχηματιστής είναι μια ηλεκτρική διάταξη που μετατρέπει εναλλασσόμενη ηλεκτρική ενέργεια ενός επιπέδου τάσης
Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 2013/2014, Ημερομηνία: 24/06/2014
 Θέμα ο Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 03/04, Ημερομηνία: 4/06/04 Σε μονοφασικό Μ/Σ ονομαστικής ισχύος 60kA, 300/30, 50Hz, ελήφθησαν
Θέμα ο Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 03/04, Ημερομηνία: 4/06/04 Σε μονοφασικό Μ/Σ ονομαστικής ισχύος 60kA, 300/30, 50Hz, ελήφθησαν
Μηχανές εναλλασσομένου ρεύματος
 Μηχανές εναλλασσομένου ρεύματος 1 Εισαγωγή Οι μηχανές εναλλασσόμενου ρεύματος (Ε.Ρ.) αποτελούν τη συντριπτική πλειονότητα των ηλεκτρικών μηχανών που χρησιμοποιούνται στη βιομηχανία, κυρίως λόγω της επικράτησης
Μηχανές εναλλασσομένου ρεύματος 1 Εισαγωγή Οι μηχανές εναλλασσόμενου ρεύματος (Ε.Ρ.) αποτελούν τη συντριπτική πλειονότητα των ηλεκτρικών μηχανών που χρησιμοποιούνται στη βιομηχανία, κυρίως λόγω της επικράτησης
μετασχηματιστή. ΤΜΗΜΑ: ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας ενός μονοφασικού
 ΤΜΗΜΑ: ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας ενός μονοφασικού μετασχηματιστή. ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: κ. Δημήτριος Καλπακτσόγλου ΕΡΓΑΣΙΑ ΤΗΣ: Αικατερίνης-Χρυσοβαλάντης Γιουσμά Α.Ε.Μ:
ΤΜΗΜΑ: ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας ενός μονοφασικού μετασχηματιστή. ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: κ. Δημήτριος Καλπακτσόγλου ΕΡΓΑΣΙΑ ΤΗΣ: Αικατερίνης-Χρυσοβαλάντης Γιουσμά Α.Ε.Μ:
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 6: Επίδραση της Μεταβολής της Συχνότητας στη Χαρακτηριστική Ροπής - Στροφών Ηρακλής Βυλλιώτης Τμήμα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 6: Επίδραση της Μεταβολής της Συχνότητας στη Χαρακτηριστική Ροπής - Στροφών Ηρακλής Βυλλιώτης Τμήμα
ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ)
 ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ) Περιγραφή Λειτουργίας Σύγχρονου Κινητήρα Σκοπός: Η παρούσα εργασία έχει σκοπό να περιγράψει τη λειτουργία ενός
ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ) Περιγραφή Λειτουργίας Σύγχρονου Κινητήρα Σκοπός: Η παρούσα εργασία έχει σκοπό να περιγράψει τη λειτουργία ενός
ΑΣΚΗΣΗ 7 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 7 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς
ΑΣΚΗΣΗ 7 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς
ΣΥΜΠΙΕΣΤΕΣ ΗΛΕΚΤΡΙΚΟ ΣΥΣΤΗΜΑ
 9. Ηλεκτρικό Σύστημα Συμπιεστών Ανάλογα με την κατασκευή τους και το είδος του εναλλασσόμενου ρεύματος που απαιτούν για τη λειτουργία τους, οι ηλεκτροκινητήρες διακρίνονται σε: Μονοφασικούς. Τριφασικούς.
9. Ηλεκτρικό Σύστημα Συμπιεστών Ανάλογα με την κατασκευή τους και το είδος του εναλλασσόμενου ρεύματος που απαιτούν για τη λειτουργία τους, οι ηλεκτροκινητήρες διακρίνονται σε: Μονοφασικούς. Τριφασικούς.
Στον άπειρο ζυγό και μέσω μιας γραμμής μεταφοράς ισχύος συνδέεται κάποια βιομηχανία
 ΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Στον άπειρο ζυγό και μέσω μιας γραμμής μεταφοράς ισχύος συνδέεται κάποια βιομηχανία Οι 2 από τους 3 κινητήρες αυτής της βιομηχανίας είναι επαγωγικοί και διαθέτουν επαγωγικούς συντελεστές
ΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Στον άπειρο ζυγό και μέσω μιας γραμμής μεταφοράς ισχύος συνδέεται κάποια βιομηχανία Οι 2 από τους 3 κινητήρες αυτής της βιομηχανίας είναι επαγωγικοί και διαθέτουν επαγωγικούς συντελεστές
ΘΕΜΑ 1ο Για τις ερωτήσεις να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Κακαζιάνης Πέτρος ΘΕΜΑ 1ο Για τις ερωτήσεις 1.1 1.13 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Κακαζιάνης Πέτρος ΘΕΜΑ 1ο Για τις ερωτήσεις 1.1 1.13 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΗΛΕΚΤΡΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Α. ΑΣΚΗΣΕΙΣ ΕΛΕΓΧΟΥ ΤΑΧΥΤΗΤΑΣ D.C. ΚΙΝΗΤΗΡΑ
 ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ. ΓΕΝΙΚΑ ΗΛΕΚΤΡΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Α. ΑΣΚΗΣΕΙΣ ΕΛΕΓΧΟΥ ΤΑΧΥΤΗΤΑΣ D.C. ΚΙΝΗΤΗΡΑ Σε ένα ανοιχτό σύστημα με συνάρτηση μεταφοράς G η έξοδος Υ και είσοδος Χ συνδέονται με τη σχέση: Y=G*Χ
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ. ΓΕΝΙΚΑ ΗΛΕΚΤΡΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Α. ΑΣΚΗΣΕΙΣ ΕΛΕΓΧΟΥ ΤΑΧΥΤΗΤΑΣ D.C. ΚΙΝΗΤΗΡΑ Σε ένα ανοιχτό σύστημα με συνάρτηση μεταφοράς G η έξοδος Υ και είσοδος Χ συνδέονται με τη σχέση: Y=G*Χ
ΙΤ=ΙS RT RS. Uεπ. Άσκηση 5 Ηλεκτρικοί κινητήρες DC
 Άσκηση 5 Ηλεκτρικοί κινητήρες DC 5.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη του τρόπου λειτουργίας και ελέγχου των ηλεκτρικών κινητήρων DC. Αναλύονται ο τρόπος εκκίνησης και ρύθμισης της
Άσκηση 5 Ηλεκτρικοί κινητήρες DC 5.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη του τρόπου λειτουργίας και ελέγχου των ηλεκτρικών κινητήρων DC. Αναλύονται ο τρόπος εκκίνησης και ρύθμισης της
Άσκηση 4 Αρχή λειτουργίας Μηχανών DC
 Άσκηση 4 Αρχή λειτουργίας Μηχανών DC 4.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη της αρχής λειτουργίας των μηχανών DC. Οι μηχανές DC μπορούν να λειτουργήσουν είτε ως γεννήτριες είτε ως κινητήρες.
Άσκηση 4 Αρχή λειτουργίας Μηχανών DC 4.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη της αρχής λειτουργίας των μηχανών DC. Οι μηχανές DC μπορούν να λειτουργήσουν είτε ως γεννήτριες είτε ως κινητήρες.
Γεννήτρια συνεχούς ρεύματος ξένης διέγερσης
 ΑΣΚΗΣΗ 5 Γεννήτρια συνεχούς ρεύματος ξένης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Μια ηλεκτρική μηχανή συνεχούς ρεύματος παράγει τάση συνεχούς μορφής όταν χρησιμοποιείται ως γεννήτρια, ενώ ένας κινητήρας
ΑΣΚΗΣΗ 5 Γεννήτρια συνεχούς ρεύματος ξένης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Μια ηλεκτρική μηχανή συνεχούς ρεύματος παράγει τάση συνεχούς μορφής όταν χρησιμοποιείται ως γεννήτρια, ενώ ένας κινητήρας
Γεννήτριες ΣΡ Κινητήρες ΣΡ
 Κινητήρες ΣΡ Ως γεννήτρια ΣΡ χαρακτηρίζεται η ηλεκτρική μηχανή που κατά τη λειτουργία της λαμβάνει κινητική ενέργεια και τη μετατρέπει σε ηλεκτρική με τη μορφή συνεχούς ρεύματος Η ΗΕΔ που δημιουργείται
Κινητήρες ΣΡ Ως γεννήτρια ΣΡ χαρακτηρίζεται η ηλεκτρική μηχανή που κατά τη λειτουργία της λαμβάνει κινητική ενέργεια και τη μετατρέπει σε ηλεκτρική με τη μορφή συνεχούς ρεύματος Η ΗΕΔ που δημιουργείται
Κινητήρας παράλληλης διέγερσης
 Κινητήρας παράλληλης διέγερσης Ισοδύναμο κύκλωμα V = E + I T V = I I T = I F L R F I F R Η διέγερση τοποθετείται παράλληλα με το κύκλωμα οπλισμού Χαρακτηριστική φορτίου Έλεγχος ταχύτητας Μεταβολή τάσης
Κινητήρας παράλληλης διέγερσης Ισοδύναμο κύκλωμα V = E + I T V = I I T = I F L R F I F R Η διέγερση τοποθετείται παράλληλα με το κύκλωμα οπλισμού Χαρακτηριστική φορτίου Έλεγχος ταχύτητας Μεταβολή τάσης
Γεννήτριες ΣΡ Ξένης Διέγερσης
 Γεννήτριες ΣΡ Ξένης Διέγερσης Γεννήτριες ΣΡ Γεννήτριες ανεξάρτητης διέγερσης: το κύκλωμα που παράγει το κύριο πεδίο (κύκλωμα διέγερσης) τροφοδοτείται από μία ξεχωριστή πηγή, ανεξάρτητη από τη γεννήτρια
Γεννήτριες ΣΡ Ξένης Διέγερσης Γεννήτριες ΣΡ Γεννήτριες ανεξάρτητης διέγερσης: το κύκλωμα που παράγει το κύριο πεδίο (κύκλωμα διέγερσης) τροφοδοτείται από μία ξεχωριστή πηγή, ανεξάρτητη από τη γεννήτρια
ΑΣΚΗΣΗ 2 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΑΥΤΟΝΟΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΗΣ ΤΡΙΦΑΣΙΚΗΣ ΓΕΝΝΗΤΡΙΑΣ ΜΕ ΦΟΡΤΙΟ
 ΑΣΚΗΣΗ 2 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΑΥΤΟΝΟΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΗΣ ΤΡΙΦΑΣΙΚΗΣ ΓΕΝΝΗΤΡΙΑΣ ΜΕ ΦΟΡΤΙΟ Σκοπός της άσκησης: Σκοπός της άσκησης είναι η μελέτη των χαρακτηριστικών λειτουργίας μιας σύγχρονης γεννήτριας
ΑΣΚΗΣΗ 2 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΑΥΤΟΝΟΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΗΣ ΤΡΙΦΑΣΙΚΗΣ ΓΕΝΝΗΤΡΙΑΣ ΜΕ ΦΟΡΤΙΟ Σκοπός της άσκησης: Σκοπός της άσκησης είναι η μελέτη των χαρακτηριστικών λειτουργίας μιας σύγχρονης γεννήτριας
Κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης. α) αθροιστικής σύνθετης διέγερσης
 ΑΣΚΗΣΗ 10 Κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης α) αθροιστικής σύνθετης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Ο κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης συνδυάζει τα πλεονεκτήματα του κινητήρα
ΑΣΚΗΣΗ 10 Κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης α) αθροιστικής σύνθετης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Ο κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης συνδυάζει τα πλεονεκτήματα του κινητήρα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ MM505 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΒΙΟΜΗΧΑΝΙΚΟΙ ΑΥΤΟΜΑΤΙΣΜΟΙ Εργαστήριο ο - Θεωρητικό Μέρος Βασικές ηλεκτρικές μετρήσεις σε συνεχές και εναλλασσόμενο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ MM505 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΒΙΟΜΗΧΑΝΙΚΟΙ ΑΥΤΟΜΑΤΙΣΜΟΙ Εργαστήριο ο - Θεωρητικό Μέρος Βασικές ηλεκτρικές μετρήσεις σε συνεχές και εναλλασσόμενο
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 4: Μέθοδος Μικρών Μεταβολών Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 4: Μέθοδος Μικρών Μεταβολών Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: 2 η
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: 2 η Τίτλος Άσκησης: ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ και ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ «Λειτουργία Γεννήτριας Συνεχούς Ρεύματος Ξένης διέγερσης και σχεδίαση της χαρακτηριστικής φορτίου» «Λειτουργία
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: 2 η Τίτλος Άσκησης: ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ και ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ «Λειτουργία Γεννήτριας Συνεχούς Ρεύματος Ξένης διέγερσης και σχεδίαση της χαρακτηριστικής φορτίου» «Λειτουργία
ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ
 ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ 1 Η γεννήτρια ή ηλεκτρογεννήτρια είναι μηχανή που βασίζεται στους νόμους της
ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ 1 Η γεννήτρια ή ηλεκτρογεννήτρια είναι μηχανή που βασίζεται στους νόμους της
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Μαγνητικό Πεδίο. μαγνητικό πεδίο. πηνίο (αγωγός. περιστραμμένος σε σπείρες), επάγει τάση στα άκρα του πηνίου (Μετασχηματιστής) (Κινητήρας)
 Ένας ρευματοφόρος αγωγός παράγει γύρω του μαγνητικό πεδίο Ένα χρονικά μεταβαλλόμενο μαγνητικό πεδίο, του οποίου οι δυναμικές γραμμές διέρχονται μέσα από ένα πηνίο (αγωγός περιστραμμένος σε σπείρες), επάγει
Ένας ρευματοφόρος αγωγός παράγει γύρω του μαγνητικό πεδίο Ένα χρονικά μεταβαλλόμενο μαγνητικό πεδίο, του οποίου οι δυναμικές γραμμές διέρχονται μέσα από ένα πηνίο (αγωγός περιστραμμένος σε σπείρες), επάγει
ΑΣΚΗΣΗ 9 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 9 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: α) η ασφαλής εκκίνηση β) η χάραξη της χαρακτηριστικής
ΑΣΚΗΣΗ 9 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: α) η ασφαλής εκκίνηση β) η χάραξη της χαρακτηριστικής
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦΑΛΑΙΟ 3 3.1 ΕΙΣΑΓΩΓΗ Μια ηλεκτρική µηχανή συνεχούς ρεύµατος χρησιµοποιείται ως γεννήτρια, όταν ο άξονάς της στρέφεται από µια κινητήρια µηχανή (prim movr). Η κινητήρια µηχανή
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦΑΛΑΙΟ 3 3.1 ΕΙΣΑΓΩΓΗ Μια ηλεκτρική µηχανή συνεχούς ρεύµατος χρησιµοποιείται ως γεννήτρια, όταν ο άξονάς της στρέφεται από µια κινητήρια µηχανή (prim movr). Η κινητήρια µηχανή
Μέθοδοι Ελέγχου Ηλεκτρικών Κινητήρων Σ.Ρ.
 Μέθοδοι Ελέγχου Ηλεκτρικών Κινητήρων Σ.Ρ. Ευθυμίου Σωτήρης Δέδες Παναγιώτης 26/06/2014 Εισαγωγή Σκοπός αυτής της παρουσίασης είναι η συνοπτική περιγραφή τριών διαφορετικών μεθόδων ελέγχου κινητήρων Σ.Ρ.
Μέθοδοι Ελέγχου Ηλεκτρικών Κινητήρων Σ.Ρ. Ευθυμίου Σωτήρης Δέδες Παναγιώτης 26/06/2014 Εισαγωγή Σκοπός αυτής της παρουσίασης είναι η συνοπτική περιγραφή τριών διαφορετικών μεθόδων ελέγχου κινητήρων Σ.Ρ.
25.2. Εισαγωγή Θεωρητικές Επεξηγήσεις Λειτουργίας
 φαρμογή 5 Τριφασικός παγωγικός Κινητήρας : Με Τυλιγμένο Δρομέα ( ο μέρος) 5.. Σκοποί της φαρμογής Μαθησιακοί Στόχοι Να μπορείτε να εξετάζετε την κατασκευή ενός τριφασικού επαγωγικού κινητήρα με τυλιγμένο
φαρμογή 5 Τριφασικός παγωγικός Κινητήρας : Με Τυλιγμένο Δρομέα ( ο μέρος) 5.. Σκοποί της φαρμογής Μαθησιακοί Στόχοι Να μπορείτε να εξετάζετε την κατασκευή ενός τριφασικού επαγωγικού κινητήρα με τυλιγμένο
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α
Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές μαγνητικό πεδίο
 Στον ΣΚ 2 πόλων το μαγνητικό πεδίο του δρομέα BR παράγεται από το ρεύμα διέγερσης IF Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές
Στον ΣΚ 2 πόλων το μαγνητικό πεδίο του δρομέα BR παράγεται από το ρεύμα διέγερσης IF Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές
Εργαστήριο Ανάλυσης Συστημάτων Ηλεκτρικής Ενέργειας
 Εργαστήριο Ανάλυσης Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 5: Η σύγχρονη μηχανή (γεννήτρια/κινητήρας ) Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Εργαστήριο Ανάλυσης Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 5: Η σύγχρονη μηχανή (γεννήτρια/κινητήρας ) Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
ΑΣΚΗΣΗ 7 η ΧΑΡΑΚΤΗΡΙΣΤΙΚΗ ΡΟΠΗΣ ΣΤΡΟΦΩΝ ΑΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ
 ΑΣΚΗΣΗ 7 η ΧΑΡΑΚΤΗΡΙΣΤΙΚΗ ΡΟΠΗΣ ΣΤΡΟΦΩΝ ΑΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη του τρόπου εκκίνησης και λειτουργίας
ΑΣΚΗΣΗ 7 η ΧΑΡΑΚΤΗΡΙΣΤΙΚΗ ΡΟΠΗΣ ΣΤΡΟΦΩΝ ΑΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη του τρόπου εκκίνησης και λειτουργίας
Τμήμα Ηλεκτρολόγων Μηχανικών ΜΟΝΟΦΑΣΙΚΟΙ ΚΙΝΗΤΗΡΕΣ
 Το βασικό μειονέκτημα που εμφανίζεται στη σχεδίαση των μονοφασικών επαγωγικών κινητήρων είναι ότι αντίθετα από τις 3-φασικές πηγές ισχύος οι 1-φασικές πηγές δεν παράγουν στρεφόμενο μαγνητικό πεδίο Το μαγνητικό
Το βασικό μειονέκτημα που εμφανίζεται στη σχεδίαση των μονοφασικών επαγωγικών κινητήρων είναι ότι αντίθετα από τις 3-φασικές πηγές ισχύος οι 1-φασικές πηγές δεν παράγουν στρεφόμενο μαγνητικό πεδίο Το μαγνητικό
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Τ.Ε.Ι. ΠΑΤΡΑΣ / Σ.Τ.ΕΦ. Πάτρα Τμήμα: ΜΗΧΑΝΟΛΟΓΙΑΣ. Εξέταση στο μάθημα «Ηλεκτρικές Μηχανές»
 Τ.Ε.Ι. ΠΑΤΡΑΣ / Σ.Τ.ΕΦ. Πάτρα 26-1-2012 Τμήμα: ΜΗΧΑΝΟΛΟΓΙΑΣ Εξέταση στο μάθημα «Ηλεκτρικές Μηχανές» ΠΡΟΣΟΧΗ: Για οποιοδήποτε σύμβολο χρησιμοποιήσετε στις πράξεις σας, να γράψετε ξεκάθαρα τι αντιπροσωπεύει
Τ.Ε.Ι. ΠΑΤΡΑΣ / Σ.Τ.ΕΦ. Πάτρα 26-1-2012 Τμήμα: ΜΗΧΑΝΟΛΟΓΙΑΣ Εξέταση στο μάθημα «Ηλεκτρικές Μηχανές» ΠΡΟΣΟΧΗ: Για οποιοδήποτε σύμβολο χρησιμοποιήσετε στις πράξεις σας, να γράψετε ξεκάθαρα τι αντιπροσωπεύει
Πείραμα επαγόμενου ρεύματος
 Επαγόμενα πεδία Ένα μαγνητικό πεδίο μπορεί να μην είναι σταθερό, αλλά χρονικά μεταβαλλόμενο. Πειράματα που πραγματοποιήθηκαν το 1831 (από τους Michael Faraday και Joseph Henry) έδειξαν ότι ένα μεταβαλλόμενο
Επαγόμενα πεδία Ένα μαγνητικό πεδίο μπορεί να μην είναι σταθερό, αλλά χρονικά μεταβαλλόμενο. Πειράματα που πραγματοποιήθηκαν το 1831 (από τους Michael Faraday και Joseph Henry) έδειξαν ότι ένα μεταβαλλόμενο
ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας ενός
ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας ενός
Ηλεκτροκινητήρας Εναλλασσόμενου Ρεύματος τύπου κλωβού. Άσκηση 9. Ηλεκτροκινητήρας εναλλασσόμενου ρεύματος τύπου κλωβού
 ANTIKEIMENO: Άσκηση 9 Ηλεκτροκινητήρας εναλλασσόμενου ρεύματος τύπου κλωβού ΣΤΟΧΟΙ ΑΥΤΟΥ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ: Κατανόηση της λειτουργίας του ηλεκτροκινητήρα εναλλασσόμενου ρεύματος τύπου κλωβού Υπολογισμός μηχανικών
ANTIKEIMENO: Άσκηση 9 Ηλεκτροκινητήρας εναλλασσόμενου ρεύματος τύπου κλωβού ΣΤΟΧΟΙ ΑΥΤΟΥ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ: Κατανόηση της λειτουργίας του ηλεκτροκινητήρα εναλλασσόμενου ρεύματος τύπου κλωβού Υπολογισμός μηχανικών
Ηλεκτρικές Μηχανές ΙΙ Εργαστήριο
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Εργαστήριο Ενότητα 1: Προσδιορισμός των Σταθερών του Ισοδύναμου Κυκλώματος Ασύγχρονης Μηχανής Ηρακλής Βυλλιώτης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Εργαστήριο Ενότητα 1: Προσδιορισμός των Σταθερών του Ισοδύναμου Κυκλώματος Ασύγχρονης Μηχανής Ηρακλής Βυλλιώτης
Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών
 Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών Το εκπαιδευτικό υλικό που ακολουθεί αναπτύχθηκε στα πλαίσια του έργου «Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», του Μέτρου «Εισαγωγή
Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών Το εκπαιδευτικό υλικό που ακολουθεί αναπτύχθηκε στα πλαίσια του έργου «Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», του Μέτρου «Εισαγωγή
Τμήμα Ηλεκτρολόγων Μηχανικών ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΑΡΑΜΕΤΡΩΝ ΣΤΟ ΙΣΟΔΥΝΑΜΟ ΚΥΚΛΩΜΑ
 Το ισοδύναμο κύκλωμα ενός επαγωγικού κινητήρα αποτελεί ένα πολύ σημαντικό εργαλείο για τον προσδιορισμό της απόκρισης του κινητήρα στις αλλαγές του φορτίου του Για να χρησιμοποιηθεί αυτό το ισοδύναμο θα
Το ισοδύναμο κύκλωμα ενός επαγωγικού κινητήρα αποτελεί ένα πολύ σημαντικό εργαλείο για τον προσδιορισμό της απόκρισης του κινητήρα στις αλλαγές του φορτίου του Για να χρησιμοποιηθεί αυτό το ισοδύναμο θα
Γεννήτριες ΣΡ Κινητήρες ΣΡ
 Γεννήτριες ΣΡ Κινητήρες ΣΡ - Στοιχειώδεις Ηλεκτρικές Μηχανές Επαγωγή λέγεται το φαινόμενο κατά το οποίο αναπτύσσεται ΗΕΔ: a. Στα άκρα αγωγού όταν αυτός κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο επαγωγής
Γεννήτριες ΣΡ Κινητήρες ΣΡ - Στοιχειώδεις Ηλεκτρικές Μηχανές Επαγωγή λέγεται το φαινόμενο κατά το οποίο αναπτύσσεται ΗΕΔ: a. Στα άκρα αγωγού όταν αυτός κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο επαγωγής
Αφεντουλίδου Όλγα ΑΜ:6904. Ηλεκτρικές Μηχανές. Μέθοδοι εκκίνησης τριφασικού επαγωγικού κινητήρα
 Αφεντουλίδου Όλγα ΑΜ:6904 Ηλεκτρικές Μηχανές Μέθοδοι εκκίνησης τριφασικού επαγωγικού κινητήρα 1 Εισαγωγή Από τα διάφορα είδη ηλεκτρικών μηχανών εναλλασσόμενου ρεύματος, ο τριφασικός ασύγχρονος ή επαγωγικός
Αφεντουλίδου Όλγα ΑΜ:6904 Ηλεκτρικές Μηχανές Μέθοδοι εκκίνησης τριφασικού επαγωγικού κινητήρα 1 Εισαγωγή Από τα διάφορα είδη ηλεκτρικών μηχανών εναλλασσόμενου ρεύματος, ο τριφασικός ασύγχρονος ή επαγωγικός
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Ηλεκτρικές Μηχανές Ι. Ενότητα 4: Εύρεση Παραμέτρων. Τσιαμήτρος Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών Τ.Ε
 Ηλεκτρικές Μηχανές Ι Ενότητα 4: Εύρεση Παραμέτρων Τσιαμήτρος Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών Τ.Ε Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Ηλεκτρικές Μηχανές Ι Ενότητα 4: Εύρεση Παραμέτρων Τσιαμήτρος Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών Τ.Ε Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
Ανύψωση τάσης στην έξοδο της γεννήτριας παραγωγής. Υποβιβασμός σε επίπεδα χρησιμοποίησης. Μετατροπή υψηλής τάσης σε χαμηλή με ρεύματα χαμηλής τιμής
 Είδη μετασχηματιστών Μετασχηματιστές Ισχύος Μετασχηματιστές Μονάδος Ανύψωση τάσης στην έξοδο της γεννήτριας παραγωγής Μετασχηματιστές Υποσταθμού Υποβιβασμός σε επίπεδα διανομής Μετασχηματιστές Διανομής
Είδη μετασχηματιστών Μετασχηματιστές Ισχύος Μετασχηματιστές Μονάδος Ανύψωση τάσης στην έξοδο της γεννήτριας παραγωγής Μετασχηματιστές Υποσταθμού Υποβιβασμός σε επίπεδα διανομής Μετασχηματιστές Διανομής
Ηλεκτρικές Μηχανές ΙΙ Εργαστήριο
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Εργαστήριο Ενότητα 6: Χαρακτηριστική Φόρτισης Σύγχρονης Γεννήτριας Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Εργαστήριο Ενότητα 6: Χαρακτηριστική Φόρτισης Σύγχρονης Γεννήτριας Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 8: Θεωρία των δυο Στρεφόμενων Πεδίων Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 8: Θεωρία των δυο Στρεφόμενων Πεδίων Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 2014/2015, Ημερομηνία: 16/06/2015
 Θέμα ο Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 04/05, Ημερομηνία: 6/06/05 Τα δεδομένα που ελήφθησαν από τις δοκιμές βραχυκύκλωσης και
Θέμα ο Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 04/05, Ημερομηνία: 6/06/05 Τα δεδομένα που ελήφθησαν από τις δοκιμές βραχυκύκλωσης και
Εργαστήριο Ελέγχου και Ευστάθειας Συστημάτων Ηλεκτρικής Ενέργειας
 Εργαστήριο Ελέγχου και Ευστάθειας Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 4 Συμπεριφορά σύγχρονου κινητήρα υπό φορτίο Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών
Εργαστήριο Ελέγχου και Ευστάθειας Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 4 Συμπεριφορά σύγχρονου κινητήρα υπό φορτίο Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Λειτουργικά χαρακτηριστικά γεννητριών
 Λειτουργικά χαρακτηριστικά γεννητριών Η φασική τάση στο εσωτερικό μιας μηχανής (στα τυλίγματα του στάτη) δίνεται από τη σχέση: E 2 N φ f A = π C Συχνότητα περιστροφής μηχανής Πλήθος σπειρών στο τύλιγμα
Λειτουργικά χαρακτηριστικά γεννητριών Η φασική τάση στο εσωτερικό μιας μηχανής (στα τυλίγματα του στάτη) δίνεται από τη σχέση: E 2 N φ f A = π C Συχνότητα περιστροφής μηχανής Πλήθος σπειρών στο τύλιγμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
4. ΤΡΙΦΑΣΙΚΟΙ ΑΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ
 56 4. ΤΡΙΦΑΣΙΚΟΙ ΑΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Οι ασύγχρονοι κινητήρες που ονοµάζονται και επαγωγικοί κινητήρες διακρίνονται σε µονοφασικούς και τριφασικούς. Στην συνέχεια θα εξετασθούν οι τριφασικοί ασύγχρονοι
56 4. ΤΡΙΦΑΣΙΚΟΙ ΑΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Οι ασύγχρονοι κινητήρες που ονοµάζονται και επαγωγικοί κινητήρες διακρίνονται σε µονοφασικούς και τριφασικούς. Στην συνέχεια θα εξετασθούν οι τριφασικοί ασύγχρονοι
Εξεταστική περίοδος χειμερινού εξαμήνου
 Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ Διδάσκων: Δρ. Π. Β. Μαλατέστας, Καθηγητής Ημερομηνία : 06/0/0 Διάρκεια: h 5in Ονοματεπώνυμο σπουδαστή: Αριθμός μητρώου: Μάθημα : Ηλεκτρική
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ Διδάσκων: Δρ. Π. Β. Μαλατέστας, Καθηγητής Ημερομηνία : 06/0/0 Διάρκεια: h 5in Ονοματεπώνυμο σπουδαστή: Αριθμός μητρώου: Μάθημα : Ηλεκτρική
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Γεννήτριες ΣΡ Παράλληλης Διέγερσης
 Παράλληλης Διέγερσης Το κύκλωμα διέγερσης συνδέεται στα άκρα της και τροφοδοτείται από την τάση εξόδου της μηχανής Σε αυτό το κύκλωμα το ρεύμα οπλισμού τροφοδοτεί τόσο το κύκλωμα διέγερσης όσο και το φορτίο
Παράλληλης Διέγερσης Το κύκλωμα διέγερσης συνδέεται στα άκρα της και τροφοδοτείται από την τάση εξόδου της μηχανής Σε αυτό το κύκλωμα το ρεύμα οπλισμού τροφοδοτεί τόσο το κύκλωμα διέγερσης όσο και το φορτίο
Γ ΛΥΚΕΙΟΥ ΟΙ ΚΙΝΗΣΕΙΣ ΤΩΝ ΣΤΕΡΕΩΝ ΣΩΜΑΤΩΝ
 Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 1: Βασικές Αρχές Ηλεκτρικών Μηχανών Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 1: Βασικές Αρχές Ηλεκτρικών Μηχανών Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
Άσκηση 1 ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ
 Άσκηση 1 ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ 1.1 Μέτρηση του λόγου μετασχηματισμού και προσδιορισμός παραμέτρων ισοδύναμου κυκλώματος μονοφασικών μετασχηματιστών 1.2 Αυτομετασχηματιστές 1.3 Τριφασικοί μετασχηματιστές Σελίδα
Άσκηση 1 ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ 1.1 Μέτρηση του λόγου μετασχηματισμού και προσδιορισμός παραμέτρων ισοδύναμου κυκλώματος μονοφασικών μετασχηματιστών 1.2 Αυτομετασχηματιστές 1.3 Τριφασικοί μετασχηματιστές Σελίδα
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
Στα τυλίγματα απόσβεσης ενός ΣΚ μπορεί να αναπτυχθεί κάποια ροπή εκκίνησης χωρίς εξωτερική τροφοδοσία του κυκλώματος διέγερσης
 Στα τυλίγματα απόσβεσης ενός ΣΚ μπορεί να αναπτυχθεί κάποια ροπή εκκίνησης χωρίς εξωτερική τροφοδοσία του κυκλώματος διέγερσης Μια μηχανή που κατασκευάζεται με τυλίγματα απόσβεσης ονομάζεται επαγωγική
Στα τυλίγματα απόσβεσης ενός ΣΚ μπορεί να αναπτυχθεί κάποια ροπή εκκίνησης χωρίς εξωτερική τροφοδοσία του κυκλώματος διέγερσης Μια μηχανή που κατασκευάζεται με τυλίγματα απόσβεσης ονομάζεται επαγωγική
Ηλεκτρικές Μηχανές Ι. Ενότητα 7: Εισαγωγή στις Μηχανές Συνεχούς Ρεύματος Τσιαμήτρος Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών Τ.Ε
 Ηλεκτρικές Μηχανές Ι Ενότητα 7: Εισαγωγή στις Μηχανές Συνεχούς Ρεύματος Τσιαμήτρος Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών Τ.Ε Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Ηλεκτρικές Μηχανές Ι Ενότητα 7: Εισαγωγή στις Μηχανές Συνεχούς Ρεύματος Τσιαμήτρος Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών Τ.Ε Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
Βασικά στοιχεία μετασχηματιστών
 Βασικά στοιχεία μετασχηματιστών 1. Εισαγωγικά Οι μετασχηματιστές (transformers) είναι ηλεκτρικές διατάξεις, οι οποίες μετασχηματίζουν (ανυψώνουν ή υποβιβάζουν) την τάση και το ρεύμα. Ο μετασχηματιστής
Βασικά στοιχεία μετασχηματιστών 1. Εισαγωγικά Οι μετασχηματιστές (transformers) είναι ηλεκτρικές διατάξεις, οι οποίες μετασχηματίζουν (ανυψώνουν ή υποβιβάζουν) την τάση και το ρεύμα. Ο μετασχηματιστής
ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444
 ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444 DC ΔΙΑΚΟΠΤΙΚA ΤΡΟΦΟΔΟΤΙΚΑ, ΜΕΤΑΤΡΟΠΕΙΣ ΜΕ ΗΛΕΚΤΡΙΚΗ ΑΠΟΜΟΝΩΣΗ Δρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444 DC ΔΙΑΚΟΠΤΙΚA ΤΡΟΦΟΔΟΤΙΚΑ, ΜΕΤΑΤΡΟΠΕΙΣ ΜΕ ΗΛΕΚΤΡΙΚΗ ΑΠΟΜΟΝΩΣΗ Δρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
Ερωτήσεις. 2. Η ροπή αδράνειας μιας σφαίρας μάζας Μ και ακτίνας R ως προς άξονα που διέρχεται
 - Μηχανική στερεού σώματος Ερωτήσεις 1. Στερεό στρέφεται γύρω από σταθερό άξονα. Η γωνιακή ταχύτητα του στερεού μεταβάλλεται με το χρόνο όπως στο διπλανό διάγραμμα ω -. Να χαρακτηρίσετε τις παρακάτω προτάσεις
- Μηχανική στερεού σώματος Ερωτήσεις 1. Στερεό στρέφεται γύρω από σταθερό άξονα. Η γωνιακή ταχύτητα του στερεού μεταβάλλεται με το χρόνο όπως στο διπλανό διάγραμμα ω -. Να χαρακτηρίσετε τις παρακάτω προτάσεις
