στρώµατα του ρευστού έχουν κοινή επιφάνεια Α και βαθµίδα ταχύτητας
|
|
|
- בַּעַל־זְבוּל Βιτάλη
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Γενικά Ιξώδες Κατά τν ροή ρευστού µέσα από αγωγό απαιτείται άσκσ διαφοράς πιέσεως µεταξύ των άκρων του αγωγού για να υπερνικθούν οι δυνάµεις συνοχής µεταξύ των µορίων του ρευστού. Το ιξώδες, το οποίο είναι µέτρο αυτής τς τριβής, είναι εντατική ιδιόττα του ρευστού οποία χαρακτρίζει τν ροή. Όσο πιο µεγάλο το ιξώδες του ρευστού, τόσο πιο αργή ροή για δεδοµέν διαφορά πιέσεως. Το ιξώδες ορίζεται από τ σχέσ (1). Η ταχύττα του ρευστού είναι µικρότερ καθώς πλσιάζει τα τοιχώµατα του δοχείου και µδενίζεται σε αυτά. Παρατρείται, δλαδή, βαθµίδα ταχύττας κάθετα στν διεύθυνσ z τς κινήσεως του ρευστού. Αν δυο διαδοχικά στρώµατα του ρευστού έχουν κοινή επιφάνεια Α και βαθµίδα ταχύττας ένα στρώµα στο άλλο δύναµ: v, ασκείται από το x v F= A (1) x όπου είναι το ιξώδες του ρευστού. Η σχέσ (1) ονοµάζεται νόµος του Poiseuille και γενικεύεται για όλες τις διευθύνσεις στο χώρο. Η µονάδα του ιξώδους είναι 1 Pa s = 1 N s m -2 = 1 kg m -1 s -1, αλλά χρσιµοποιείται και µονάδα poise µε σχέσ 1 poise = 1 g cm -1 s -1 = 0.1 Pa s. Αν ο αγωγός είναι κυλινδρικός σωλήνας µήκους L και ακτίνας R, µπορεί να υπολογιστεί παροχή του ρευστού (όγκος ρευστού ανά µονάδα χρόνου) για ορισµέν διαφορά πιέσεως στα άκρα του αγωγού p. Κατά τν στρωτή ροή δύναµ Poiseuille οποία ασκείται σε ακτίνα r επάνω σε κυλινδρική επιφάνεια A = 2πrL (2) εξισορροπείται από τν διαφορά των πιέσεων οποία ασκείται σε επιφάνεια πr 2. λαδή: v 2πrL = pπr r 2 Μετά από πράξεις καταλήγουµε στν εξίσωσ Poiseuille: V πr p V& = () t 8L Στο ιξωδόµετρο τύπου Ostwald, το οποίο χρσιµοποιούµε σε αυτή τν άσκσ, ως κινούσα δύναµ επενεργεί υδροστατική πίεσ τς στήλς του µετρούµενου υγρού, δλαδή p = ρ g h (5), όπου ρ πυκνόττα του υγρού, g επιτάχυνσ τς βαρύττας και h το ύψος τς στήλς του υγρού. Μετρείται ο χρόνος t για τν εκροή σταθερού όγκου του υγρού V. Από τ σχέσ () έχουµε: V πr ρgh = (6) t 8L απ όπου προκύπτει: (3) 5-1
2 ή απλούστερα: 8LV t= (7) πr gh ρ t= C (8) ρ όπου σταθερά C εξαρτάται µόνο από τν κατασκευή του ιξωδοµέτρου 8LV C= (9) πr gh Μετρώντας το χρόνο ροής ενός πρότυπου υγρού, δλαδή ενός του οποίου είναι γνωστά από τ βιβλιογραφία το ιξώδες και πυκνόττα σε ορισµέν θερµοκρασία προσδιορίζουµε τν σταθερά C. Κατόπιν αρκεί µέτρσ του χρόνου ροής για το µετρούµενο υγρό για να προσδιοριστεί το ιξώδες του σε θερµοκρασία για τν οποία γνωρίζουµε και τν πυκνόττά του. Από σειρά µετρήσεων του ιξώδους σε διάφορες θερµοκρασίες είναι δυνατό να βρούµε τν εξάρτσή του από τν θερµοκρασία. Η εξάρτσ αυτή ακολουθεί συνήθως τν µορφή τς εξισώσεως του Arrhenius: E vis = Ae RT (10) όπου R παγκόσµια σταθερά των ιδανικών αερίων και Α και Ε vis παράµετροι που εξαρτώνται από το µετρούµενο υγρό. Η Ε vis ονοµάζεται ενέργεια ενεργοποιήσεως ροής. Παραδείγµατα διαγραµµάτων Arrhenius µε αριθµτικές τιµές για τν ενέργεια ενεργοποιήσεως ροής δίνονται στο επόµενο σχήµα. ln() E visc (kj/mol) H 2 O (0.8) [16.38 (0.19)] EtOH (0.06) n-proh (0.06) i-proh (0.08) CH 3 COCH (0.03) x10-3 1/T (K -1 ) Σχήµα 1: ιάγραµµα Arrhenius για νερό, αιθανόλ, προπανόλ-1, προπανόλ-2 και ακετόν µε δεδοµένα τς βιβλιογραφίας [CRC Handbook of Chemistry and Physics, 83 rd Ed., 2002, p ]. Αναγράφονται οι τιµές τς ενέργειας ενεργοποιήσεως ροής όπως υπολογίζονται από το διάγραµµα µε τιµές αβεβαιόττας (τυπική απόκλισ) σε παρένθεσ. 5-2
3 Οδγίες εκτέλεσς Από κάθε οµάδα λαµβάνονται 3- µετρήσεις χρόνου ροής µε χρονόµετρο ακριβείας για νερό και για τν (ίδια για τις 3 οµάδες) µετρούµεν ουσία σε µια θερµοκρασία. Κάθε οµάδα εκτελεί τις µετρήσεις σε διαφορετική θερµοκρασία και οι 3 θερµοκρασίες πρέπει να απέχουν 5 10 C µεταξύ τους. Συµπλρώνεται πίνακας µε τις θερµοκρασίες (θ), τις αντίστροφες απόλυτες θερµοκρασίες (1/Τ), τους µέσους χρόνους ροής (t), τις αντίστοιχες υπολογισµένες (από εξίσωσ ή πίνακα) πυκνόττες τς µετρούµενς ουσίας (ρ) και του ιξώδους () τς ουσίας. Eπεξεργασία µετρήσεων Κατασκευάζονται 2 διαγράµµατα: α) = f(θ), β) ln = f(1/t). Από το πρώτο διάγραµµα πρέπει να είναι σαφής ποιοτικά εξάρτσ του ιξώδους από τν θερµοκρασία. Από το δεύτερο διάγραµµα προσδιορίζονται οι παράµετροι τς εξισώσεως Arrhenius σύµφωνα µε τν (11) που αποτελεί τν λογαριθµική έκφρασ τς (10). E vis ln= ln A+ (11) RT ίνονται τα αποτελέσµατα για τν ενέργεια ενεργοποιήσεως ροής (Ε vis ) και τον αντίστοιχο προεκθετικό συντελεστή τς εξισώσεως Arrhenius (A) και υπολογίζεται το ιξώδες τς ουσίας στους 20 C. Συγκρίνονται οι τιµές µε τν βιβλιογραφία. Συµπλρώνετε τα πεδία τς τελευταίας σελίδας. Για κάθε τύπο υπολογισµού δίνετε αναλυτικό παράδειγµα µε εµφανείς τις επιµέρους πράξεις, τις µονάδες των φυσικών µεγεθών και σωστή χρήσ των σµαντικών ψφίων. Πίνακας Ι. Πυκνόττα και ιξώδες του νερού σε διάφορες θερµοκρασίες θ ( C) ρ (g cm -3 ) (mpa s) Το ιδώδες () του νερού µπορεί να υπολογισθεί και από τον τύπο: ln 0 = a a θ ( C) ρ (g cm -3 ) (mpa s) a (12) T0 + θ ( T ) θ όπου 0 = 1 mpa s, T 0 = K, a 0 = , a 1 = K, a 2 = K 2 5-3
4 ίνεται εξάρτσ τς πυκνόττας (ρ) ή του όγκου (V) από τ θερµοκρασία (θ) για µερικές ενώσεις: νερό: ρ(θ) =[ θ θ θ 3 ] g cm -3 για 18 C < θ < 0 C µεθανόλ αιθανόλ προπανόλ-1 προπανόλ-2 βουτανόλ-1 βουτανόλ-2 ρ(15 C)= g cm -3, για -38 C<θ<70 C: V(θ)/V(0 C)= θ x10-6 θ x10-9 θ 3 ρ(20 C)= g cm -3, για 0 C<θ<30 C: V(θ)/V(0 C)= θ ρ(20 C)=0.80 g cm -3, για 0 C<θ<9 C: V(θ)/V(0 C)= θ+.9689x10-6 θ x10-9 θ 3 ρ(20 C)=0.785g cm -3, για 0 C<θ<83 C: V(θ)/V(0 C)= θ+.303x10e -7 θ x10-8 θ 3 ρ(20 C)= g cm -3, για 6 C<θ<108 C: V(θ)/V(0 C)= x10 - θ+2.863x10-6 θ x10-9 θ 3 ρ(20 C)=0.806 g cm -3, για 0 C<θ<20 C: V(θ)/V(0 C)=1+9.0x10 - θ για 20 C<θ<30 C: V(θ)/V(20 C)= x10-3 θ οξεικός µεθυλεστέρας ρ(25 C)=0.927 g cm -3, για 0 C<θ<58 C: V(θ)/V(0 C)= θ x10-7 θ x10-8 θ 3 οξεικός αιθυλεστέρας ρ(20 C)=0.901 g cm -3, για -36 C<θ<72 C: V(θ)/V(0 C)= θ x10-6 θ 2 κυκλοεξάνιο εξάνιο ρ(20 C)= g cm -3, για 25 C<θ<3 C: ρ(θ)=[ x10 - θ] g cm -3 για 0 C<θ<69 C: ρ(θ)=[ x10 - θ-1.08x10-6 θ x10-10 θ 3 ] g cm -3 επτάνιο ρ(20 C)=0.683 g cm -3, ρ(0 C)=0.67 g cm -3 τολουόλιο χλωροφόρµιο τετραχλωράνθρακας ρ(20.89 C)= g cm -3, για 0 C<θ<90 C: V(θ)/V(0 C)= θ+1.779x10-6 θ 2 ρ(25 C)=1.790 g cm -3, για 0 C<θ<63 C: V(θ)/V(0 C)= θ+.6673x10-6 θ x10-8 θ 3 για 0 C<θ<0 C: ρ(θ)=[ x10-3 θ-6.90x10-7 θ 2 ] g cm -3 5-
5 Θέµα Άσκσς: H 2 O θ ( C) (mpa s) t 1 (s) t 2 (s) t 3 (s) t µέσο (s) ρ (g/cm 3 ) C Χµική ένωσ: θ ( C) t 1 (s) t 2 (s) t 3 (s) t µέσο (s) ρ (g/cm 3 ) (mpa s) ln T (K) T -1 (K -1 ) (mpa s) θ ( C) ln /T (x10-3 K -1 ) κλίσ = E visc = Α = (20 C) =
Παραδείγµατα ροής ρευστών (Moody κλπ.)
 Παραδείγµατα ροής ρευστών (Mooy κλπ.) 005-006 Παράδειγµα 1. Να υπολογισθεί η πτώση πίεσης σε ένα σωλήνα από χάλυβα του εµπορίου µήκους 30.8 m, µε εσωτερική διάµετρο 0.056 m και τραχύτητα του σωλήνα ε 0.00005
Παραδείγµατα ροής ρευστών (Mooy κλπ.) 005-006 Παράδειγµα 1. Να υπολογισθεί η πτώση πίεσης σε ένα σωλήνα από χάλυβα του εµπορίου µήκους 30.8 m, µε εσωτερική διάµετρο 0.056 m και τραχύτητα του σωλήνα ε 0.00005
Να υπολογίσετε τη μάζα 50 L βενζίνης. Δίνεται η σχετική πυκνότητά της, ως προς το νερό ρ σχ = 0,745.
 1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ
 Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ Σκοπός του πειράματος είναι να μελετηθεί
Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ Σκοπός του πειράματος είναι να μελετηθεί
Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης
 Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης ΘΕΜΑ Α Α1. Το ανοιχτό κυλινδρικό δοχείο του σχήματος βρίσκεται εντός πεδίο βαρύτητας με
Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης ΘΕΜΑ Α Α1. Το ανοιχτό κυλινδρικό δοχείο του σχήματος βρίσκεται εντός πεδίο βαρύτητας με
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
Α Σ Κ Η Σ Η 2 ΜΕΤΡΗΣΗ ΤΟΥ ΣΥΝΤΕΛΕΣΤΗ ΙΞΩΔΟΥΣ ΥΓΡΟΥ ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ
 Α Σ Κ Η Σ Η 2 ΜΕΤΡΗΣΗ ΤΟΥ ΣΥΝΤΕΛΕΣΤΗ ΙΞΩΔΟΥΣ ΥΓΡΟΥ ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ ΣΥΝΤΕΛΕΣΤΗΣ ΙΞΩΔΟΥΣ Κατά την κίνηση των υγρών, εκτός από την υδροστατική πίεση που ενεργεί κάθετα σε όλη την επιφάνεια, έχουμε και
Α Σ Κ Η Σ Η 2 ΜΕΤΡΗΣΗ ΤΟΥ ΣΥΝΤΕΛΕΣΤΗ ΙΞΩΔΟΥΣ ΥΓΡΟΥ ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ ΣΥΝΤΕΛΕΣΤΗΣ ΙΞΩΔΟΥΣ Κατά την κίνηση των υγρών, εκτός από την υδροστατική πίεση που ενεργεί κάθετα σε όλη την επιφάνεια, έχουμε και
Το μισό του μήκους του σωλήνα, αρκετά μεγάλη απώλεια ύψους.
 Πρόβλημα Λάδι πυκνότητας 900 kg / και κινηματικού ιξώδους 0.000 / s ρέει διαμέσου ενός κεκλιμένου σωλήνα στην κατεύθυνση αυξανομένου υψομέτρου, όπως φαίνεται στο παρακάτω Σχήμα. Η πίεση και το υψόμετρο
Πρόβλημα Λάδι πυκνότητας 900 kg / και κινηματικού ιξώδους 0.000 / s ρέει διαμέσου ενός κεκλιμένου σωλήνα στην κατεύθυνση αυξανομένου υψομέτρου, όπως φαίνεται στο παρακάτω Σχήμα. Η πίεση και το υψόμετρο
6 Εξαναγκασμένη ροή αέρα
 6 Εξαναγκασμένη ροή αέρα 6.1 Εισαγωγή Όταν θέτουμε σε κίνηση κάποια μόρια ενός ρευστού μέσω μιας αντλίας ή ενός φυσητήρα, η κίνηση μεταδίδεται και στα υπόλοιπα μόρια του ρευστού μέσω των αλληλεπιδράσεων
6 Εξαναγκασμένη ροή αέρα 6.1 Εισαγωγή Όταν θέτουμε σε κίνηση κάποια μόρια ενός ρευστού μέσω μιας αντλίας ή ενός φυσητήρα, η κίνηση μεταδίδεται και στα υπόλοιπα μόρια του ρευστού μέσω των αλληλεπιδράσεων
Διαγώνισμα Φυσικής Γ Λυκείου 5/3/2017
 Διαγώνισμα Φυσικής Γ Λυκείου 5/3/2017 ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΠΙΛΟΓΗ Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
Διαγώνισμα Φυσικής Γ Λυκείου 5/3/2017 ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΠΙΛΟΓΗ Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Ρευστά. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός. https://physicscourses.wordpress.com
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Ρευστά Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscourses.wordpress.com Βασικές έννοιες Πρώτη φορά συναντήσαμε τη φυσική των ρευστών στη Β Γυμνασίου. Εκεί
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Ρευστά Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscourses.wordpress.com Βασικές έννοιες Πρώτη φορά συναντήσαμε τη φυσική των ρευστών στη Β Γυμνασίου. Εκεί
Μιχαήλ Π. Μιχαήλ Φυσικός
 3. ΜΗΧΑΝΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ - Ρευστά σε κίνηση Είδη ροής - Ρευµατικές γραµµές και εξίσωση συνέχειας - Διατήρηση ενέργειας, εξίσωση Bernoulli - Πραγµατικά ρευστά Εσωτερική τριβή ιξώδες, Νόµος Poiseuille 3.
3. ΜΗΧΑΝΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ - Ρευστά σε κίνηση Είδη ροής - Ρευµατικές γραµµές και εξίσωση συνέχειας - Διατήρηση ενέργειας, εξίσωση Bernoulli - Πραγµατικά ρευστά Εσωτερική τριβή ιξώδες, Νόµος Poiseuille 3.
Διαγώνισμα Φυσικής Γ Λυκείου ~~ Ρευστά ~~
 Διαγώνισμα Φυσικής Γ Λυκείου ~~ Ρευστά ~~ Διάρκεια: 3 ώρες Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
Διαγώνισμα Φυσικής Γ Λυκείου ~~ Ρευστά ~~ Διάρκεια: 3 ώρες Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
3. Τριβή στα ρευστά. Ερωτήσεις Θεωρίας
 3. Τριβή στα ρευστά Ερωτήσεις Θεωρίας Θ3.1 Να συμπληρωθούν τα κενά στις προτάσεις που ακολουθούν: α. Η εσωτερική τριβή σε ένα ρευστό ονομάζεται. β. Η λίπανση των τμημάτων μιας μηχανής οφείλεται στις δυνάμεις
3. Τριβή στα ρευστά Ερωτήσεις Θεωρίας Θ3.1 Να συμπληρωθούν τα κενά στις προτάσεις που ακολουθούν: α. Η εσωτερική τριβή σε ένα ρευστό ονομάζεται. β. Η λίπανση των τμημάτων μιας μηχανής οφείλεται στις δυνάμεις
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Ρευστά. Τετάρτη 12 Απριλίου Θέμα 1ο
 Διαγώνισμα Ρευστά Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Στον πυθμένα των δύο δοχείων 1 και 2 του διπλανού σχήματος, που
Διαγώνισμα Ρευστά Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Στον πυθμένα των δύο δοχείων 1 και 2 του διπλανού σχήματος, που
v = 1 ρ. (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ: ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ
 ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ: ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ 27 Φεβρουαρίου 2006 Διάρκεια εξέτασης : 2.5 ώρες Ονοματεπώνυμο: ΑΕΜ Εξάμηνο: (α) Επιτρέπονται: Τα βιβλία
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ: ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ 27 Φεβρουαρίου 2006 Διάρκεια εξέτασης : 2.5 ώρες Ονοματεπώνυμο: ΑΕΜ Εξάμηνο: (α) Επιτρέπονται: Τα βιβλία
Άσκηση 9. Προσδιορισμός του συντελεστή εσωτερικής
 1.Σκοπός Άσκηση 9 Προσδιορισμός του συντελεστή εσωτερικής τριβής υγρών Σκοπός της άσκησης είναι ο πειραματικός προσδιορισμός του συντελεστή εσωτερικής τριβής (ιξώδες) ενός υγρού. Βασικές θεωρητικές γνώσεις.1
1.Σκοπός Άσκηση 9 Προσδιορισμός του συντελεστή εσωτερικής τριβής υγρών Σκοπός της άσκησης είναι ο πειραματικός προσδιορισμός του συντελεστή εσωτερικής τριβής (ιξώδες) ενός υγρού. Βασικές θεωρητικές γνώσεις.1
ΔΙΑΓΩΝΙΣΜΑ 4- ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ( ) ΚΕΦΑΛΑΙΟ 3 ΡΕΥΣΤΑ ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ A ΔΙΑΓΩΝΙΣΜΑ 4- ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (2016-17) ΚΕΦΑΛΑΙΟ 3 ΡΕΥΣΤΑ ΕΚΦΩΝΗΣΕΙΣ Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΘΕΜΑ A ΔΙΑΓΩΝΙΣΜΑ 4- ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (2016-17) ΚΕΦΑΛΑΙΟ 3 ΡΕΥΣΤΑ ΕΚΦΩΝΗΣΕΙΣ Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Σελίδα 1 από 6
 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,, 3, 4 δείχνουν
ΘΕΜΑ Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,, 3, 4 δείχνουν
Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι
 Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
ΜΕΤΡΗΣΗ ΣΥΝΤΕΛΕΣΤΗ ΕΣΩΤΕΡΙΚΗΣ ΤΡΙΒΗΣ
 ΜΕΤΡΗΣΗ ΣΥΝΤΕΛΕΣΤΗ ΕΣΩΤΕΡΙΚΗΣ ΤΡΙΒΗΣ Σκοπός της άσκησης Σε αυτή την άσκηση θα μετρήσουμε τον συντελεστή εσωτερικής τριβής ή ιξώδες ρευστού προσδιορίζοντας την οριακή ταχύτητα πτώσης μικρών σφαιρών σε αυτό
ΜΕΤΡΗΣΗ ΣΥΝΤΕΛΕΣΤΗ ΕΣΩΤΕΡΙΚΗΣ ΤΡΙΒΗΣ Σκοπός της άσκησης Σε αυτή την άσκηση θα μετρήσουμε τον συντελεστή εσωτερικής τριβής ή ιξώδες ρευστού προσδιορίζοντας την οριακή ταχύτητα πτώσης μικρών σφαιρών σε αυτό
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Ρευστά - Μηχανική Στερεού Σώματος. Κυριακή 5 Μαρτίου Θέμα 1ο
 Διαγώνισμα Ρευστά - Μηχανική Στερεού Σώματος Κυριακή 5 Μαρτίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Στον πυθμένα των δύο δοχείων 1 και 2
Διαγώνισμα Ρευστά - Μηχανική Στερεού Σώματος Κυριακή 5 Μαρτίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Στον πυθμένα των δύο δοχείων 1 και 2
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΜΕΤΑΦΟΡΑ ΟΡΜΗΣ - ΡΕΟΛΟΓΙΑ
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΜΕΤΑΦΟΡΑ ΟΡΜΗΣ - ΡΕΟΛΟΓΙΑ Ρεολογία Επιστήµη που εξετάζει την ροή και την παραµόρφωση των υλικών κάτω από την άσκηση πίεσης. Η µεταφορά των υγρών στην βιοµηχανία τροφίµων συνδέεται άµεσα
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΜΕΤΑΦΟΡΑ ΟΡΜΗΣ - ΡΕΟΛΟΓΙΑ Ρεολογία Επιστήµη που εξετάζει την ροή και την παραµόρφωση των υλικών κάτω από την άσκηση πίεσης. Η µεταφορά των υγρών στην βιοµηχανία τροφίµων συνδέεται άµεσα
Ροή πραγµατικών ρευστών: Επιβεβαίωση του νόµου του Poiseuille
 237 Ιωάννης Α. Σιανούδης Ροή πραγµατικών ρευστών: Επιβεβαίωση του νόµου του Poiseuille Σκοπός Σκοπός της άσκησης αυτής είναι η επιβεβαίωση ενός ιδιαίτερα χρήσιµου νόµου, του νόµου Poiseuille, ο οποίος
237 Ιωάννης Α. Σιανούδης Ροή πραγµατικών ρευστών: Επιβεβαίωση του νόµου του Poiseuille Σκοπός Σκοπός της άσκησης αυτής είναι η επιβεβαίωση ενός ιδιαίτερα χρήσιµου νόµου, του νόµου Poiseuille, ο οποίος
Ορμή και Δυνάμεις. Θεώρημα Ώθησης Ορμής
 501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 23 ΜΑΪOY 2016 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 17/4/2016 ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 7/4/06 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη σωστή απάντηση:
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 7/4/06 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη σωστή απάντηση:
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 : ΜΕΛΕΤΗ ΣΥΝΤΕΛΕΣΤΗ ΙΞΩΔΟΥΣ ΥΓΡΩΝ. Επιμέλεια άσκησης : Μισοπολινού-Τάταλα Δουκαίνη
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 : ΜΕΛΕΤΗ ΣΥΝΤΕΛΕΣΤΗ ΙΞΩΔΟΥΣ ΥΓΡΩΝ Επιμέλεια άσκησης : Μισοπολινού-Τάταλα Δουκαίνη Σκοπός : Θα μετρηθεί ο συντελεστής ιξώδους του νερού με τη μέθοδο ιξωδομέτρου του Όστβαλντ (Ostwald)
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 : ΜΕΛΕΤΗ ΣΥΝΤΕΛΕΣΤΗ ΙΞΩΔΟΥΣ ΥΓΡΩΝ Επιμέλεια άσκησης : Μισοπολινού-Τάταλα Δουκαίνη Σκοπός : Θα μετρηθεί ο συντελεστής ιξώδους του νερού με τη μέθοδο ιξωδομέτρου του Όστβαλντ (Ostwald)
Λίγη Φυσική. για τη σοκολάτα Ζωή Ευθυμιάδου 1, Βικτωρία Κελαναστάση 2, Αγγελική Κοσμά 3 1 ο Πρότυπο Πειραματικό Λύκειο Θες/νίκης «Μανόλης Ανδρόνικος»
 Λίγη Φυσική. για τη σοκολάτα Ζωή Ευθυμιάδου 1, Βικτωρία Κελαναστάση 2, Αγγελική Κοσμά 3 1 ο Πρότυπο Πειραματικό Λύκειο Θες/νίκης «Μανόλης Ανδρόνικος» 1 zoeefth@hotmail.com, 2 viktwria444@hotmail.com, 3
Λίγη Φυσική. για τη σοκολάτα Ζωή Ευθυμιάδου 1, Βικτωρία Κελαναστάση 2, Αγγελική Κοσμά 3 1 ο Πρότυπο Πειραματικό Λύκειο Θες/νίκης «Μανόλης Ανδρόνικος» 1 zoeefth@hotmail.com, 2 viktwria444@hotmail.com, 3
A3. Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F.
 ΘΕΜΑ Α ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ-ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ- ΚΕΦΑΛΑΙΟ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ
ΘΕΜΑ Α ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ-ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ- ΚΕΦΑΛΑΙΟ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO Ε.Κ.Φ.Ε. Νέας Σμύρνης
 ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2015-2016 Ε.Κ.Φ.Ε. Νέας Σμύρνης Εξέταση στη Φυσική ΛΥΚΕΙΟ: Τριμελής ομάδα μαθητών: 1. 2. 3. Αναπληρωματικός: Β Σειρά Θεμάτων (Φυσική) Μέτρηση του συντελεστή ιξώδους
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2015-2016 Ε.Κ.Φ.Ε. Νέας Σμύρνης Εξέταση στη Φυσική ΛΥΚΕΙΟ: Τριμελής ομάδα μαθητών: 1. 2. 3. Αναπληρωματικός: Β Σειρά Θεμάτων (Φυσική) Μέτρηση του συντελεστή ιξώδους
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
(1) v = k[a] a [B] b [C] c, (2) - RT
![(1) v = k[a] a [B] b [C] c, (2) - RT (1) v = k[a] a [B] b [C] c, (2) - RT](/thumbs/57/40855227.jpg) Χηµική Κινητική Αντικείµενο της Χηµικής Κινητικής είναι η µελέτη της ταχύτητας µιας αντιδράσεως, ο καθορισµός των παραγόντων που την επηρεάζουν και η εύρεση ποσοτικής έκφρασης για τον κάθε παράγοντα, δηλ.
Χηµική Κινητική Αντικείµενο της Χηµικής Κινητικής είναι η µελέτη της ταχύτητας µιας αντιδράσεως, ο καθορισµός των παραγόντων που την επηρεάζουν και η εύρεση ποσοτικής έκφρασης για τον κάθε παράγοντα, δηλ.
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 3) ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 3) ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ Στις παρακάτω ερωτήσεις Α-Α4 να σημειώσετε την σωστή απάντηση Α. Νερό διαρρέει έναν κυλινδρικό σωλήνα, ο οποίος στενεύει σε κάποιο σημείο του χωρίς να διακλαδίζεται. Ποια
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ Στις παρακάτω ερωτήσεις Α-Α4 να σημειώσετε την σωστή απάντηση Α. Νερό διαρρέει έναν κυλινδρικό σωλήνα, ο οποίος στενεύει σε κάποιο σημείο του χωρίς να διακλαδίζεται. Ποια
Ρευστά σε Κίνηση. Επιµέλεια: ρ. Μιχάλης Ε. Καραδηµητρίου, Φυσικός.
 Ρευστά σε Κίνηση - Μάρτης 2017 Επιµέλεια: ρ. Μιχάλης Ε. Καραδηµητρίου, Φυσικός http://www.perifysikhs.com 1. Θέµα Α - Ερωτήσεις πολλαπλής επιλογής 1.1. Ενας άνθρωπος στέκεται όρθιος πάνω σε οριζόντιο έδαφος.
Ρευστά σε Κίνηση - Μάρτης 2017 Επιµέλεια: ρ. Μιχάλης Ε. Καραδηµητρίου, Φυσικός http://www.perifysikhs.com 1. Θέµα Α - Ερωτήσεις πολλαπλής επιλογής 1.1. Ενας άνθρωπος στέκεται όρθιος πάνω σε οριζόντιο έδαφος.
Παραδείγµατα ροής ρευστών (Bernoulli)
 Παραδείγµατα ροής ρευστών (Bernolli) 005-006 Παράδειγµα. Γάλα ρέει µέσα από σωλήνα διαµέτρου.5 c, µε παροχή 0 L.in - σε θερµοκρασία C. Η ροή είναι νµατώδς, τυρβώδς ή µεταβατική? µ.0 Pa s, ρ 09 kg -3..
Παραδείγµατα ροής ρευστών (Bernolli) 005-006 Παράδειγµα. Γάλα ρέει µέσα από σωλήνα διαµέτρου.5 c, µε παροχή 0 L.in - σε θερµοκρασία C. Η ροή είναι νµατώδς, τυρβώδς ή µεταβατική? µ.0 Pa s, ρ 09 kg -3..
R T ενώ σε ολοκληρωµένη, αν θεωρήσουµε ότι οι ενθαλπίες αλλαγής φάσεως είναι σταθερές στο διάστηµα θερµοκρασιών που εξετάζουµε, είναι
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Εργαστήριο Μηχανικής Ρευστών. Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής
 Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2012 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος B Λυκείου
 B Λυκείου Θεωρητικό Μέρος Θέμα ο 0 Μαρτίου 0 A. Ποια από τις παρακάτω προτάσεις για μια μπαταρία είναι σωστή; Να εξηγήσετε πλήρως την απάντησή σας. α) Η μπαταρία εξαντλείται πιο γρήγορα όταν τη συνδέσουμε
B Λυκείου Θεωρητικό Μέρος Θέμα ο 0 Μαρτίου 0 A. Ποια από τις παρακάτω προτάσεις για μια μπαταρία είναι σωστή; Να εξηγήσετε πλήρως την απάντησή σας. α) Η μπαταρία εξαντλείται πιο γρήγορα όταν τη συνδέσουμε
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ ÅÐÉËÏÃÇ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 017 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Μ Τετάρτη 1 Απριλίου 017 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 017 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Μ Τετάρτη 1 Απριλίου 017 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
Μηχανική των Ρευστών. Επιµέλεια: ρ. Μιχάλης Ε. Καραδηµητρίου, Φυσικός.
 Μηχανική των Ρευστών - Μάρτης 2018 Επιµέλεια: ρ. Μιχάλης Ε. Καραδηµητρίου, Φυσικός http://www.perifysikhs.com 1. Θέµα Α - Ερωτήσεις πολλαπλής επιλογής 1.1. Ενας άνθρωπος στέκεται όρθιος πάνω σε οριζόντιο
Μηχανική των Ρευστών - Μάρτης 2018 Επιµέλεια: ρ. Μιχάλης Ε. Καραδηµητρίου, Φυσικός http://www.perifysikhs.com 1. Θέµα Α - Ερωτήσεις πολλαπλής επιλογής 1.1. Ενας άνθρωπος στέκεται όρθιος πάνω σε οριζόντιο
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 10 η : Μεταβατική Διάχυση και Συναγωγή Μάζας
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 10 η : Μεταβατική Διάχυση και Συναγωγή Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 10 η : Μεταβατική Διάχυση και Συναγωγή Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΡΕΥΣΤΑ -ΣΤΕΡΕΟ 24/02/2019
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΡΕΥΣΤΑ -ΣΤΕΡΕΟ 24/02/2019 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΡΕΥΣΤΑ -ΣΤΕΡΕΟ 24/02/2019 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
Κινηματική ρευστών. Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του
 301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
ΡΕΥΣΤΑ. Φυσική Θετικού Προσανατολισμου Γ' Λυκείου
 ΡΕΥΣΤΑ ΕΙΣΑΓΩΓΗ Ρευστά Με τον όρο ρευστά εννοούμε τα ΥΓΡΑ και τα ΑΕΡΙΑ τα οποία, αντίθετα από τα στερεά, δεν έχουν καθορισμένο όγκο ούτε σχήμα. Τα υγρά είναι ασυμπίεστα και τα αέρια συμπιεστά. Τα υγρά
ΡΕΥΣΤΑ ΕΙΣΑΓΩΓΗ Ρευστά Με τον όρο ρευστά εννοούμε τα ΥΓΡΑ και τα ΑΕΡΙΑ τα οποία, αντίθετα από τα στερεά, δεν έχουν καθορισμένο όγκο ούτε σχήμα. Τα υγρά είναι ασυμπίεστα και τα αέρια συμπιεστά. Τα υγρά
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 4 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2019: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ A Α1α. (β) Α1β. (β) Αα. (γ) Αβ. (α) Αα. (γ) Αβ. (δ) Α4α. (α) Α4β. (γ) Α5. α. Σ β. Λ γ. Λ δ. Σ ΘΕΜΑ Β Β1.
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ A Α1α. (β) Α1β. (β) Αα. (γ) Αβ. (α) Αα. (γ) Αβ. (δ) Α4α. (α) Α4β. (γ) Α5. α. Σ β. Λ γ. Λ δ. Σ ΘΕΜΑ Β Β1.
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Ενδεικτικές Λύσεις Θέµα Α Α.1. Καθώς µια στοιχειώδης επιφάνεια αλλάζει προσανατολισµό χωρίς όµως το κέντρο της να αλλάξει ϐάθος εντός του υγρού, τότε αλλάζει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Ενδεικτικές Λύσεις Θέµα Α Α.1. Καθώς µια στοιχειώδης επιφάνεια αλλάζει προσανατολισµό χωρίς όµως το κέντρο της να αλλάξει ϐάθος εντός του υγρού, τότε αλλάζει
α. 0 β. mωr/2 γ. mωr δ. 2mωR (Μονάδες 5) γ) στην ισόθερμη εκτόνωση δ) στην ισόχωρη ψύξη (Μονάδες 5)
 ΜΑΘΗΜΑ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ Φυσική Β Λυκείου Προσανατολισμού Γκικόντης Λαμπρος ΗΜΕΡΟΜΗΝΙΑ 5 - - 07 ΔΙΑΡΚΕΙΑ ώρες ΘΕΜΑ ο Α. Στις παρακάτω ερωτήσεις -5 να επιλέξετε τη σωστή απάντηση. Α. Μικρό σώμα μάζας m εκτελεί
ΜΑΘΗΜΑ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ Φυσική Β Λυκείου Προσανατολισμού Γκικόντης Λαμπρος ΗΜΕΡΟΜΗΝΙΑ 5 - - 07 ΔΙΑΡΚΕΙΑ ώρες ΘΕΜΑ ο Α. Στις παρακάτω ερωτήσεις -5 να επιλέξετε τη σωστή απάντηση. Α. Μικρό σώμα μάζας m εκτελεί
Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ
 1 Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ερωτήσεις 1 έως 4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθµό το γράµµα που αντιστοιχεί στη σωστή
1 Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ερωτήσεις 1 έως 4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθµό το γράµµα που αντιστοιχεί στη σωστή
F el = z k e 0 (3) F f = f k v k (4) F tot = z k e 0 x f kv k (5)
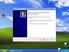 Κίνηση των ιόντων υπό την επίδραση ηλεκτρικού πεδίου Αντώνης Καραντώνης 15 Μαρτίου 2011 1 Σκοπός της άσκησης Σκοπός της άσκησης είναι ο προσδιορισμός της οριακής ταχύτητας των ιόντων υπό την επίδραση ηλεκτρικού
Κίνηση των ιόντων υπό την επίδραση ηλεκτρικού πεδίου Αντώνης Καραντώνης 15 Μαρτίου 2011 1 Σκοπός της άσκησης Σκοπός της άσκησης είναι ο προσδιορισμός της οριακής ταχύτητας των ιόντων υπό την επίδραση ηλεκτρικού
5 Μετρητές παροχής. 5.1Εισαγωγή
 5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
Υπολογισμός συνάρτησης μεταφοράς σε Υδραυλικά συστήματα. Αντίσταση ροής υγρού. Μανομετρικό Υψος h. Υψος h2. Ροή q
 Υπολογισμός συνάρτησης μεταφοράς σε Υδραυλικά συστήματα. Αντίσταση ροής υγρού Υψος h Μανομετρικό Υψος h Υψος h Σχήμα.4 Ροή q Ας υποθέσουμε ότι έχουμε δύο δεξαμενές που επικοινωνούν με ένα σωλήνα όπως ακριβώς
Υπολογισμός συνάρτησης μεταφοράς σε Υδραυλικά συστήματα. Αντίσταση ροής υγρού Υψος h Μανομετρικό Υψος h Υψος h Σχήμα.4 Ροή q Ας υποθέσουμε ότι έχουμε δύο δεξαμενές που επικοινωνούν με ένα σωλήνα όπως ακριβώς
Θέμα Α Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλάντωση Doppler Ρευστά -Στερεό Ονοματεπώνυμο Μαθητή: Ημερομηνία: 04-03-2019 Επιδιωκόμενος Στόχος: 80/100 Θέμα Α Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλάντωση Doppler Ρευστά -Στερεό Ονοματεπώνυμο Μαθητή: Ημερομηνία: 04-03-2019 Επιδιωκόμενος Στόχος: 80/100 Θέμα Α Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της
Δυναμική των ρευστών Στοιχεία θεωρίας
 Δυναμική των ρευστών Στοιχεία θεωρίας 1. Ρευστά σε ισορροπία Πίεση, p: Ορίζεται ως το πηλίκο του μέτρου της δύναμης df που ασκείται κάθετα σε μια επιφάνεια εμβαδού dα προς το εμβαδόν αυτό. p= df da Η πίεση
Δυναμική των ρευστών Στοιχεία θεωρίας 1. Ρευστά σε ισορροπία Πίεση, p: Ορίζεται ως το πηλίκο του μέτρου της δύναμης df που ασκείται κάθετα σε μια επιφάνεια εμβαδού dα προς το εμβαδόν αυτό. p= df da Η πίεση
Σημειώσεις Εγγειοβελτιωτικά Έργα
 4. ΚΛΕΙΣΤΟΙ ΑΓΩΓΟΙ 4.1. Γενικά Για τη μελέτη ενός δικτύου κλειστών αγωγών πρέπει να υπολογιστούν οι απώλειες ενέργειας λόγω τριβών τόσο μεταξύ του νερού και των τοιχωμάτων του αγωγού όσο και μεταξύ των
4. ΚΛΕΙΣΤΟΙ ΑΓΩΓΟΙ 4.1. Γενικά Για τη μελέτη ενός δικτύου κλειστών αγωγών πρέπει να υπολογιστούν οι απώλειες ενέργειας λόγω τριβών τόσο μεταξύ του νερού και των τοιχωμάτων του αγωγού όσο και μεταξύ των
Διατήρηση της Ύλης - Εξίσωση Συνέχειας
 Διατήρηση της Ύλης - Εξίσωση Συνέχειας Α. Ερωτήσεις Πολλαπλής Επιλογής 1. Ένα ρευστό χαρακτηρίζεται ως πραγματικό όταν α. κατά τη ροή του δεν παρουσιάζει εσωτερικές τριβές. β. κατά τη ροή του δεν παρουσιάζονται
Διατήρηση της Ύλης - Εξίσωση Συνέχειας Α. Ερωτήσεις Πολλαπλής Επιλογής 1. Ένα ρευστό χαρακτηρίζεται ως πραγματικό όταν α. κατά τη ροή του δεν παρουσιάζει εσωτερικές τριβές. β. κατά τη ροή του δεν παρουσιάζονται
Στοιχεία Μηχανολογικού Εξοπλισμού
 Στοιχεία Μηχανολογικού Εξοπλισμού Σκοπός Η γνωριμία και η εξοικείωση των φοιτητών με τον μηχανολογικό εξοπλισμό (σωληνώσεις, αντλίες, ανεμιστήρες, συμπιεστές, μετρητικά όργανα) που χρησιμοποιείται στη
Στοιχεία Μηχανολογικού Εξοπλισμού Σκοπός Η γνωριμία και η εξοικείωση των φοιτητών με τον μηχανολογικό εξοπλισμό (σωληνώσεις, αντλίες, ανεμιστήρες, συμπιεστές, μετρητικά όργανα) που χρησιμοποιείται στη
Απόδειξη της σχέσης 3.17 που αφορά στην ακτινωτή ροή µονοφασικού ρευστού σε οµογενές πορώδες µέσο
 ΜΗΧΑΝΙΚΗ ΠΕΤΡΕΛΑΙΩΝ ΚΕΦΑΛΑΙΟ 3 Ασκήσεις Απόδειξη της σχέσης 3.7 που αφορά στην ακτινωτή ροή µονοφασικού ρευστού σε οµογενές πορώδες µέσο Νόµος Darcy: A dp π rh dp Q Q µ dr µ dr I e Q µ dr Q µ dr dp dp
ΜΗΧΑΝΙΚΗ ΠΕΤΡΕΛΑΙΩΝ ΚΕΦΑΛΑΙΟ 3 Ασκήσεις Απόδειξη της σχέσης 3.7 που αφορά στην ακτινωτή ροή µονοφασικού ρευστού σε οµογενές πορώδες µέσο Νόµος Darcy: A dp π rh dp Q Q µ dr µ dr I e Q µ dr Q µ dr dp dp
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΚΙΝΗΜΑΤΙΚΟ ΙΞΩΔΕΣ ΔΙΑΦΑΝΩΝ ΚΑΙ ΑΔΙΑΦΑΝΩΝ ΥΓΡΩΝ (ASTM D 445, IP 71)
 ΘΕΩΡΙΑ Ιξώδες ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΚΙΝΗΜΑΤΙΚΟ ΙΞΩΔΕΣ ΔΙΑΦΑΝΩΝ ΚΑΙ ΑΔΙΑΦΑΝΩΝ ΥΓΡΩΝ (ASTM D 445, IP 71) Το ιξώδες είναι η ιδιότητα που έχει ένα ρευστό να παρουσιάζει αντίσταση κατά τη ροή του, ως αποτέλεσμα
ΘΕΩΡΙΑ Ιξώδες ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΚΙΝΗΜΑΤΙΚΟ ΙΞΩΔΕΣ ΔΙΑΦΑΝΩΝ ΚΑΙ ΑΔΙΑΦΑΝΩΝ ΥΓΡΩΝ (ASTM D 445, IP 71) Το ιξώδες είναι η ιδιότητα που έχει ένα ρευστό να παρουσιάζει αντίσταση κατά τη ροή του, ως αποτέλεσμα
Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου /3
 Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου 2014 1/3 Πρόβλημα 2. Καταστατική Εξίσωση Van der Waals (11 ) Σε ένα πολύ γνωστό μοντέλο του ιδανικού αερίου, του οποίου η καταστατική εξίσωση περιγράφεται από το νόμο
Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου 2014 1/3 Πρόβλημα 2. Καταστατική Εξίσωση Van der Waals (11 ) Σε ένα πολύ γνωστό μοντέλο του ιδανικού αερίου, του οποίου η καταστατική εξίσωση περιγράφεται από το νόμο
Θέρµανση Ψύξη ΚλιµατισµόςΙΙ
 Θέρµανση Ψύξη ΚλιµατισµόςΙΙ ίκτυα διανοµής αέρα (αερισµού ή κλιµατισµού) Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Μέρηδικτύουδιανοµήςαέρα Ένα δίκτυο διανοµής αέρα εγκατάστασης
Θέρµανση Ψύξη ΚλιµατισµόςΙΙ ίκτυα διανοµής αέρα (αερισµού ή κλιµατισµού) Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Μέρηδικτύουδιανοµήςαέρα Ένα δίκτυο διανοµής αέρα εγκατάστασης
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Φαινόμενα μεταφοράς Ορισμοί. Ενεργός διατομή 3. Ενεργός διατομή στο μοντέλο των σκληρών σφαιρών
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Φαινόμενα μεταφοράς Ορισμοί. Ενεργός διατομή 3. Ενεργός διατομή στο μοντέλο των σκληρών σφαιρών
Ασκήσεις στην Μηχανική των Ρευστών
 1 η Οµάδα Ερωτήσεις Πολλαπλής Επιλογής 1. Ιξώδες ενός ρευστού ονομάζουμε α. τις δυνάμεις που αντιτίθενται στην κίνησή του όταν αυτό είναι ιδανικό. β. τις δυνάμεις που αντιτίθενται στην κίνησή του όταν
1 η Οµάδα Ερωτήσεις Πολλαπλής Επιλογής 1. Ιξώδες ενός ρευστού ονομάζουμε α. τις δυνάμεις που αντιτίθενται στην κίνησή του όταν αυτό είναι ιδανικό. β. τις δυνάμεις που αντιτίθενται στην κίνησή του όταν
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
Εφαρμοσμένη Υδραυλική. ΕΔΙΠ, Τμήμα Αγρονόμων και Τοπογράφων Μηχανικών, ΑΠΘ
 Εφαρμοσμένη Υδραυλική Πατήστε για προσθήκη Γ. Παπαευαγγέλου κειμένου ΕΔΙΠ, Τμήμα Αγρονόμων και Τοπογράφων Μηχανικών, ΑΠΘ 1 Εισαγωγή Ρευστομηχανική = Μηχανικές ιδιότητες των ρευστών (υγρών και αερίων) Υδρομηχανική
Εφαρμοσμένη Υδραυλική Πατήστε για προσθήκη Γ. Παπαευαγγέλου κειμένου ΕΔΙΠ, Τμήμα Αγρονόμων και Τοπογράφων Μηχανικών, ΑΠΘ 1 Εισαγωγή Ρευστομηχανική = Μηχανικές ιδιότητες των ρευστών (υγρών και αερίων) Υδρομηχανική
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΙΑΓΩΝΙΣΜΑ
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΙΑΓΩΝΙΣΜΑ ΘΕΜΑ 1 Α) Τί είναι µονόµετρο και τί διανυσµατικό µέγεθος; Β) Τί ονοµάζουµε µετατόπιση και τί τροχιά της κίνησης; ΘΕΜΑ 2 Α) Τί ονοµάζουµε ταχύτητα ενός σώµατος και ποιά η µονάδα
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΙΑΓΩΝΙΣΜΑ ΘΕΜΑ 1 Α) Τί είναι µονόµετρο και τί διανυσµατικό µέγεθος; Β) Τί ονοµάζουµε µετατόπιση και τί τροχιά της κίνησης; ΘΕΜΑ 2 Α) Τί ονοµάζουµε ταχύτητα ενός σώµατος και ποιά η µονάδα
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
Α3. ύο οµόσηµα σηµειακά φορτία q 1, q 2 βρίσκονται σε αϖόσταση r µεταξύ τους. Αν τα δύο φορτία βρεθούν σε διϖλάσια αϖόσταση, τότε η δυναµική τους ενέρ
 ΠΡΟΣΟΜΟΙΩΣΗ ΕΞΕΤΑΣΕΩΝ Β ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 22 ΑΠΡΙΛΙΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς αϖό τις ϖαρακάτω ερωτήσεις Α1 - Α4 και δίϖλα το γράµµα
ΠΡΟΣΟΜΟΙΩΣΗ ΕΞΕΤΑΣΕΩΝ Β ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 22 ΑΠΡΙΛΙΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς αϖό τις ϖαρακάτω ερωτήσεις Α1 - Α4 και δίϖλα το γράµµα
ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 109 ΙΔΑΝΙΚΑ (ΤΕΛΕΙΑ) ΑΕΡΙΑ Το αέριο που οι συγκρούσεις των μορίων του είναι τελείως ελαστικές
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 109 ΙΔΑΝΙΚΑ (ΤΕΛΕΙΑ) ΑΕΡΙΑ Το αέριο που οι συγκρούσεις των μορίων του είναι τελείως ελαστικές
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 25/02/2018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 25/02/2018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Ρευστά: ρέουν Υγρά Αέρια
 ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Ρευστά: Υλικά που δεν έχουν καθορισμένο σχήμα (ρέουν), αλλά παίρνουν εκείνο του δοχείου μέσα στο οποίο βρίσκονται. Υγρά (έχουν καθορισμένο όγκο) Αέρια (καταλαμβάνουν ολόκληρο τον όγκο που
ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Ρευστά: Υλικά που δεν έχουν καθορισμένο σχήμα (ρέουν), αλλά παίρνουν εκείνο του δοχείου μέσα στο οποίο βρίσκονται. Υγρά (έχουν καθορισμένο όγκο) Αέρια (καταλαμβάνουν ολόκληρο τον όγκο που
Δραστηριότητα A3 - Φυσική Ιξώδες και δείκτης διάθλασης ελαιόλαδου
 Δραστηριότητα A3 - Φυσική Ιξώδες και δείκτης διάθλασης ελαιόλαδου Πολλές από τις φυσικές ιδιότητες του ελαιόλαδου ήταν γνωστές στους αρχαίους Έλληνες και τις χρησιμοποιούσαν για να ελέγχουν την ποιότητά
Δραστηριότητα A3 - Φυσική Ιξώδες και δείκτης διάθλασης ελαιόλαδου Πολλές από τις φυσικές ιδιότητες του ελαιόλαδου ήταν γνωστές στους αρχαίους Έλληνες και τις χρησιμοποιούσαν για να ελέγχουν την ποιότητά
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΔΙΑΓΩΝΙΣΜΟΥ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΔΙΑΓΩΝΙΣΜΟΥ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ ΘΕΜΑ Α Σε κάθε κουτάκι που βρίσκεται δεξιά από τον αριθµό, να σηµειώσετε το γράµµα Σ αν η αντίστοιχη πρόταση είναι σωστή ή το γράµµα Λ αν είναι λανθασµένη.
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΔΙΑΓΩΝΙΣΜΟΥ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ ΘΕΜΑ Α Σε κάθε κουτάκι που βρίσκεται δεξιά από τον αριθµό, να σηµειώσετε το γράµµα Σ αν η αντίστοιχη πρόταση είναι σωστή ή το γράµµα Λ αν είναι λανθασµένη.
ΦΥΣΙΚΗ ΧΗΜΕΙΑ ΙΙΙ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΕΠΙΔΡΑΣΗ ΘΕΡΜΟΚΡΑΣΙΑΣ ΣΤΗ ΣΤΑΘΕΡΑ ΤΑΧΥΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΟΧΗΜΕΙΑΣ Γραφείο 211 Επίκουρος Καθηγητής: Δ. Τσιπλακίδης Τηλ.: 2310 997766 e mail: dtsiplak@chem.auth.gr url:
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΟΧΗΜΕΙΑΣ Γραφείο 211 Επίκουρος Καθηγητής: Δ. Τσιπλακίδης Τηλ.: 2310 997766 e mail: dtsiplak@chem.auth.gr url:
ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 Κανάρη 36, Δάφνη Τηλ 0 973934 & 0 9769376 ΘΕΜΑ Α ΦΥΣΙΚΗ ΟΠ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Ι Οδηγία: Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Κανάρη 36, Δάφνη Τηλ 0 973934 & 0 9769376 ΘΕΜΑ Α ΦΥΣΙΚΗ ΟΠ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Ι Οδηγία: Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ
 166 Α. ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΚΤΟΥ ΤΥΠΟΥ: ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ 1. Να αναφέρεται παραδείγματα φαινομένων που μπορούν να ερμηνευτούν με την μελέτη των ρευστών σε ισορροπία. 2. Ποια σώματα ονομάζονται ρευστά;
166 Α. ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΚΤΟΥ ΤΥΠΟΥ: ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ 1. Να αναφέρεται παραδείγματα φαινομένων που μπορούν να ερμηνευτούν με την μελέτη των ρευστών σε ισορροπία. 2. Ποια σώματα ονομάζονται ρευστά;
PP οι στατικές πιέσεις στα σημεία Α και Β. Re (2.3) 1. ΑΝΤΙΚΕΙΜΕΝΟ ΚΑΙ ΣΚΟΠΟΣ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2: ΡΟΗ ΣΕ ΑΓΩΓΟΥΣ 1. ΑΝΤΙΚΕΙΜΕΝΟ ΚΑΙ ΣΚΟΠΟΣ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ Η πειραματική εργασία περιλαμβάνει 4 διαφορετικά πειράματα που σκοπό έχουν: 1. Μέτρηση απωλειών πίεσης σε αγωγό κυκλικής διατομής.
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2: ΡΟΗ ΣΕ ΑΓΩΓΟΥΣ 1. ΑΝΤΙΚΕΙΜΕΝΟ ΚΑΙ ΣΚΟΠΟΣ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ Η πειραματική εργασία περιλαμβάνει 4 διαφορετικά πειράματα που σκοπό έχουν: 1. Μέτρηση απωλειών πίεσης σε αγωγό κυκλικής διατομής.
Ρευστά σε κίνηση. Α. ΕΡΩΤΗΣΕΙΣ Υγρά σε ισορροπία F 1 F 2 F 3
 1. Ο υδραυλικός ανυψωτήρας του σχήματος περιλαμβάνει τρία αβαρή κυλινδρικά έμβολα 1, και 3. Η διάμετρος του εμβόλου 3 είναι διπλάσια της διαμέτρου του εμβόλου. F 1 F F 3 Ρευστά σε κίνηση Α. ΕΡΩΤΗΣΕΙΣ Υγρά
1. Ο υδραυλικός ανυψωτήρας του σχήματος περιλαμβάνει τρία αβαρή κυλινδρικά έμβολα 1, και 3. Η διάμετρος του εμβόλου 3 είναι διπλάσια της διαμέτρου του εμβόλου. F 1 F F 3 Ρευστά σε κίνηση Α. ΕΡΩΤΗΣΕΙΣ Υγρά
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 12 ΙΟΥΝΙΟΥ 2017 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1 ΙΟΥΝΙΟΥ 017 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1 ΙΟΥΝΙΟΥ 017 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την
2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά
 2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά 2.1 Εισαγωγή Η θερμοκρασιακή διαφορά μεταξύ δυο σημείων μέσα σ' ένα σύστημα προκαλεί τη ροή θερμότητας και, όταν στο σύστημα αυτό περιλαμβάνεται ένα ή περισσότερα
2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά 2.1 Εισαγωγή Η θερμοκρασιακή διαφορά μεταξύ δυο σημείων μέσα σ' ένα σύστημα προκαλεί τη ροή θερμότητας και, όταν στο σύστημα αυτό περιλαμβάνεται ένα ή περισσότερα
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΜΑΘΗΜΑ ΤΑΞΗ Γ ΛΥΚΕΙΟΥ ΟΝΟΜ/ΜΟ: ΗΜΕΡ/ΝΙΑ ΚΑΘ/ΤΕΣ ΓΙΑΡΕΝΟΠΟΥΛΟΣ Λ. ΚΟΥΣΟΥΛΗΣ Δ.
 ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΤΑΞΗ Γ ΛΥΚΕΙΟΥ ΟΝΟΜ/ΜΟ: ΗΜΕΡ/ΝΙΑ 15-1-017 ΚΑΘ/ΤΕΣ ΓΙΑΡΕΝΟΠΟΥΛΟΣ Λ. ΚΟΥΣΟΥΛΗΣ Δ. ΒΑΘΜΟΣ: /100, /0 Θέμα 1ο 1. Αν η εξίσωση ενός αρμονικού κύματος είναι y =10ημ(6πt
ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΤΑΞΗ Γ ΛΥΚΕΙΟΥ ΟΝΟΜ/ΜΟ: ΗΜΕΡ/ΝΙΑ 15-1-017 ΚΑΘ/ΤΕΣ ΓΙΑΡΕΝΟΠΟΥΛΟΣ Λ. ΚΟΥΣΟΥΛΗΣ Δ. ΒΑΘΜΟΣ: /100, /0 Θέμα 1ο 1. Αν η εξίσωση ενός αρμονικού κύματος είναι y =10ημ(6πt
Γρηγόρης Δρακόπουλος. Φυσικός Ελληνογαλλική Σχολή Καλαμαρί. Επιλεγμένες ασκήσεις στη. Μηχανική Ρευστών. νω ν Φυσικών.
 Γρηγόρης Δρακόπουλος Φυσικός Ελληνογαλλική Σχολή Καλαμαρί Επιλεγμένες ασκήσεις στη Μηχανική Ρευστών Έ ν ω σ η Ε λ λ ή νω ν Φυσικών Θεσσαλονίκη 06 Ισορροπία υγρού Α. Στο διπλανό σχήμα, φαίνεται δοχείο που
Γρηγόρης Δρακόπουλος Φυσικός Ελληνογαλλική Σχολή Καλαμαρί Επιλεγμένες ασκήσεις στη Μηχανική Ρευστών Έ ν ω σ η Ε λ λ ή νω ν Φυσικών Θεσσαλονίκη 06 Ισορροπία υγρού Α. Στο διπλανό σχήμα, φαίνεται δοχείο που
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Μάρτη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Μάρτη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε
Γραµµοµοριακός όγκος. Ο Νόµος του Avogadro
 ΤΟ MOL ΣΤΑ ΑΕΡΙΑ Γραµµοµοριακός όγκος Ο Νόµος του Avogadro Ελένη ανίλη, Χηµικός, Msc., Ph.D 2 Η ΧΡΗΣΙΜΟΤΗΤΑ ΤΟΥ MOL ΣΤΑ ΑΕΡΙΑ Όπως ήδη ξέρεις τα αέρια είναι πολύ ελαφρά. Είναι δύσκολο να τα ζυγίσουµε όµως
ΤΟ MOL ΣΤΑ ΑΕΡΙΑ Γραµµοµοριακός όγκος Ο Νόµος του Avogadro Ελένη ανίλη, Χηµικός, Msc., Ph.D 2 Η ΧΡΗΣΙΜΟΤΗΤΑ ΤΟΥ MOL ΣΤΑ ΑΕΡΙΑ Όπως ήδη ξέρεις τα αέρια είναι πολύ ελαφρά. Είναι δύσκολο να τα ζυγίσουµε όµως
μεταβάλλουμε την απόσταση h της μιας τρύπας από την επιφάνεια του υγρού (π.χ. προσθέτουμε ή αφαιρούμε υγρό) έτσι ώστε h 2 =2 Α 2
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΡΕΥΣΤΑ 1 Μια κυλινδρική δεξαμενή ακτίνας 6m και ύψους h=5m είναι γεμάτη με νερό, βρίσκεται στην κορυφή ενός πύργου ύψους 45m και χρησιμοποιείται για το πότισμα ενός χωραφιού α Ποια η παροχή
ΑΣΚΗΣΕΙΣ ΣΤΑ ΡΕΥΣΤΑ 1 Μια κυλινδρική δεξαμενή ακτίνας 6m και ύψους h=5m είναι γεμάτη με νερό, βρίσκεται στην κορυφή ενός πύργου ύψους 45m και χρησιμοποιείται για το πότισμα ενός χωραφιού α Ποια η παροχή
Εργαστήριο Μηχανικής Ρευστών
 Εργαστήριο Μηχανικής Ρευστών Αργυρόπουλος Αθανάσιος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Β Ημ/νία εκτέλεσης Πειράματος: 26-11-1999 Ημ/νία παράδοσης Εργασίας: 16-12-1999 1 Θεωρητική Εισαγωγή: 1. Εισαγωγικές έννοιες
Εργαστήριο Μηχανικής Ρευστών Αργυρόπουλος Αθανάσιος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Β Ημ/νία εκτέλεσης Πειράματος: 26-11-1999 Ημ/νία παράδοσης Εργασίας: 16-12-1999 1 Θεωρητική Εισαγωγή: 1. Εισαγωγικές έννοιες
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. Καθηγητής Δ. Ματαράς
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url Ludwig Prandtl (1875 1953) 3. ΦΑΙΝΟΜΕΝΑ ΤΗΣ ΡΟΗΣ ΤΩΝ ΡΕΥΣΤΩΝ Δυναμική Ροή Δυναμική Ροή (potential flow): η ροή ιδανικού ρευστού
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url Ludwig Prandtl (1875 1953) 3. ΦΑΙΝΟΜΕΝΑ ΤΗΣ ΡΟΗΣ ΤΩΝ ΡΕΥΣΤΩΝ Δυναμική Ροή Δυναμική Ροή (potential flow): η ροή ιδανικού ρευστού
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
Οδηγίες προς υποψηφίους ΚΑΛΗ ΕΠΙΤΥΧΙΑ!
 ΠΡΟΣΟΜΟΙΩΣΗ ΕΞΕΤΑΣΕΩΝ Β ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΑΠΡΙΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς αϖό τις ϖαρακάτω ερωτήσεις 1-4 και δίϖλα το γράµµα
ΠΡΟΣΟΜΟΙΩΣΗ ΕΞΕΤΑΣΕΩΝ Β ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΑΠΡΙΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς αϖό τις ϖαρακάτω ερωτήσεις 1-4 και δίϖλα το γράµµα
B' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ ÅÐÉËÏÃÇ
 1 B' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό κάθε µιας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη
1 B' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό κάθε µιας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2004 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 ο Στις ερωτήσεις Α, Β, Γ και, να επιλέξετε τον αριθµό που αντιστοιχεί στην σωστή απάντηση Α. Ένα φορτισµένο σωµατίδιο εκτοξεύεται
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2004 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 ο Στις ερωτήσεις Α, Β, Γ και, να επιλέξετε τον αριθµό που αντιστοιχεί στην σωστή απάντηση Α. Ένα φορτισµένο σωµατίδιο εκτοξεύεται
ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΧΤΩΝ ΚΑΙ ΚΛΕΙΣΤΩΝ ΑΓΩΓΩΝ
 ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΧΤΩΝ ΚΑΙ ΚΛΕΙΣΤΩΝ ΑΓΩΓΩΝ Π. Σιδηρόπουλος Δρ. Πολιτικός Μηχανικός Εργαστήριο Υδρολογίας και Ανάλυσης Υδατικών Συστημάτων Τμήμα Πολιτικών Μηχανικών Π.Θ. E-mail: psidirop@teilar.gr ΕΓΓΕΙΟΒΕΛΤΙΩΤΙΚΑ
ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΧΤΩΝ ΚΑΙ ΚΛΕΙΣΤΩΝ ΑΓΩΓΩΝ Π. Σιδηρόπουλος Δρ. Πολιτικός Μηχανικός Εργαστήριο Υδρολογίας και Ανάλυσης Υδατικών Συστημάτων Τμήμα Πολιτικών Μηχανικών Π.Θ. E-mail: psidirop@teilar.gr ΕΓΓΕΙΟΒΕΛΤΙΩΤΙΚΑ
Περι-Φυσικής. Θέµα Α. Θετικής & Τεχν. Κατεύθυνσης - Επαναληπτικό ΙΙ. Ονοµατεπώνυµο: Βαθµολογία % (α) η ϑερµοκρασία του παραµένει σταθερή.
 Θετικής & Τεχν. Κατεύθυνσης - Επαναληπτικό ΙΙ Ηµεροµηνία : Μάης 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστή απάντηση [4 5 = 20 µονάδες] Α.1. Στην
Θετικής & Τεχν. Κατεύθυνσης - Επαναληπτικό ΙΙ Ηµεροµηνία : Μάης 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστή απάντηση [4 5 = 20 µονάδες] Α.1. Στην
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Νευτώνια και μη Νευτώνια ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 15 Απριλίου 2019 1 Καταστατικές εξισώσεις Νευτώνιου ρευστού Νευτώνια ή Νευτωνικά
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Νευτώνια και μη Νευτώνια ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 15 Απριλίου 2019 1 Καταστατικές εξισώσεις Νευτώνιου ρευστού Νευτώνια ή Νευτωνικά
p = p n, (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
