ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
|
|
|
- Φιλύρη Βουγιουκλάκης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΥΓΚΡΙΣΗ ΜΕΘΟΔΩΝ ΠΡΟΒΛΕΨΗΣ ΜΕΤΑΞΥ ΠΛΑΙΣΙΩΝ ΓΙΑ ΤΗΝ ΚΩΔΙΚΟΠΟΙΗΣΗ VIDEO Kιοσσές Στέργιος Επιβλέπων Καθηγητής : Παπανικολάου Γεώργιος ΘΕΣΣΑΛΟΝΙΚΗ, ΝΟΕΜΒΡΙΟΣ 2017
2 2
3 ΠΕΡΙΛΗΨΗ Στην παρούσα διατριβή εξετάζεται η προτεινόμενη μέθοδος πρόβλεψης μεταξύ πλαισίων με όνομα BLU-ME, ή Block Unshifting Motion Estimation, στο πλαίσιο του προτύπου κωδικοποίησης MPEG. Κύριος στόχος είναι η μελέτη των αποτελεσμάτων τόσο σε ποιότητα όσο και σε μέγεθος σε bits που προσφέρει η BLU-ME σε σχέση με την κανονική μέθοδο πρόβλεψης του MPEG. Η κωδικοποίηση και αποκωδικοποίηση των αποτελεσμάτων της πρόβλεψης βασίζεται και για τις δύο περιπτώσεις στο πρότυπο MPEG, ώστε να υπάρχει κοινό κριτήριο αξιολόγησης. Σε πρώτο στάδιο, περιγράφονται θεωρητικά οι δύο μέθοδοι πρόβλεψης αλλά και οι τεχνικές της κωδικοποίησης. Στο επόμενο στάδιο, υλοποιείται σε κώδικα Matlab μια προσέγγιση του MPEG σύμφωνα με κατάλληλη βιβλιογραφία, πάνω στην οποία βασίζεται και η υλοποίηση της BLU-ME. Τέλος, πραγματοποιούνται πειράματα από τα οποία εξάγονται και συγκρίνονται τα αποτελέσματα των δύο μεθόδων. ABSTRACT The aim of the present thesis is the evaluation of the proposed motion estimation method, BLU-ME or Block Unshifting Motion Estimation, in the context of the MPEG codec. The evaluation takes account of both the quality and the size in bits of the results that BLU-ME gives, in comparison with the standard motion estimation method MPEG uses. The coding and decoding techniques for both methods are based in the MPEG standard, so that the final review of the results may have a common ground. In the first step, the motion estimation methods as well as the coding techniques are thoroughly examined. The next step is about the practical implementation using Matlab, of the MPEG coding standard, according to proper sources, on which the BLU-ME implementation is based. Finally, experiments are run and the final results of both methods are extracted and compared for evaluation. 3
4 ΠΕΡΙΕΧΟΜΕΝΑ ΠΕΡΙΛΗΨΗ...3 ABSTRACT...3 ΠΡΟΛΟΓΟΣ...6 ΚΕΦΑΛΑΙΟ 1 - Εισαγωγή Θεωρία Πληροφοριών Χρήσιμες Έννοιες της Θεωρίας Πληροφοριών Εικόνα και Βίντεο Ανθρώπινη αντίληψη της εικόνας και του βίντεο Εικόνα Βίντεο...11 ΚΕΦΑΛΑΙΟ 2 - ΣΥΜΠΙΕΣΗ ΕΙΚΟΝΑΣ Επισκόπηση της συμπίεσης εικόνας Τεχνικές κωδικοποίησης χωρίς απώλειες Κωδικοποίηση Ηuffman Κωδικοποίηση Μήκους Διαδρομής Τεχνικές κωδικοποίησης με απώλειες Κβάντιση Διαφορική Κωδικοποίηση Κωδικοποίηση Μετασχηματισμού Χρωματικοί χώροι και υποδειγματοληψία Πρότυπο κωδικοποίησης εικόνας JPEG Μετρικές Συμπίεσης...20 ΚΕΦΑΛΑΙΟ 3 - ΣΥΜΠΙΕΣΗ ΒΙΝΤΕΟ Επισκόπηση της συμπίεσης βίντεο Τμηματική Πρόβλεψη Πλαισίων και Αντιστάθμιση Κίνησης Αλγόριθμοι αναζήτησης Βελτιστοποίηση πρόβλεψης Πρόβλεψη και αντιστάθμιση σε υποστοιχειακό επίπεδο Είδη Πλαισίων Group of Pictures Πρότυπα κωδικοποίησης βίντεο, MPEG/MPEG ΚΕΦΑΛΑΙΟ 4 - Η μέθοδος BLU-ME Αντιστροφή της μετατόπισης ή unshifting Ο αλγόριθμος BLU-ME...29 KΕΦΑΛΑΙΟ 5 - ΥΛΟΠΟΙΗΣΗ
5 5.1 Κώδικας για το πρότυπο MPEG Συνάρτηση για την υλοποίηση του codec Συνάρτηση για τη κωδικοποίηση των Ι πλαισίων Συναρτήσεις για τη κωδικοποίηση των P και Β πλαισίων Συναρτήσεις για αποκωδικοποίηση P και Β πλαισίων Συναρτήσεις για υπολογισμό bits αναπαράστασης Κώδικας για το πρότυπο με τη μέθοδο BLU-ME...33 ΚΕΦΑΛΑΙΟ 6 - ΠΕΙΡΑΜΑΤΑ Πρώτο Πείραμα Αποτελέσματα και σχόλια για το MPEG Αποτελέσματα και σχόλια για τη BLU-ME Σύγκριση μεταξύ των μεθόδων Δεύτερο Πείραμα Τρίτο Πείραμα...75 ΚΕΦΑΛΑΙΟ 7 ΣΥΝΟΨΗ...76 ΠΑΡΑΡΤΗΜΑ Α ΠΙΝΑΚΕΣ ΚΒΑΝΤΙΣΗΣ...77 ΠΑΡΑΡΤΗΜΑ B ΛΕΞΙΛΟΓΙΑ HUFFMAN...78 Βιβλιογραφία:
6 ΠΡΟΛΟΓΟΣ Σε αυτή την εργασία υλοποιείται ο κλασικός αλγόριθμος συμπίεσης του προτύπου MPEG/MPEG-2 με βάση τον οποίο υλοποιείται και ένας άλλος, εναλλακτικός αλγόριθμος συμπίεσης στον οποίο εφαρμόζεται η μέθοδος πρόβλεψης κίνησης με το όνομα Block Unshifting Motion Estimation, ή BLU ME [8]. Με είσοδο ένα δείγμα βίντεο, κύριος στόχος είναι η σύγκριση της αρχικής μεθόδου πρόβλεψης κίνησης που χρησιμοποιεί το MPEG με αυτή που προτείνει η BLU ME, με κριτήρια την τελική ποιότητα του αποσυμπιεσμένου δείγματος, σε σύγκριση με το αρχικό, και το βαθμό συμπίεσης που επιτυγχάνεται. Η κωδικοποίηση πέρα της πρόβλεψης κίνησης είναι κοινή μεταξύ των αλγορίθμων και βασίζεται στη λογική του MPEG, έτσι ώστε να υπάρχει ένας κοινός άξονας για την τελική αξιολόγηση και σχολιασμό των αποτελεσμάτων. Στο πρώτο κεφάλαιο, παρουσιάζονται βασικές έννοιες άμεσα και έμμεσα σχετικές με το αντικείμενο της εργασίας. Αρχικά, γίνεται μια σύντομη εισαγωγή στη θεωρία πληροφοριών, έτσι ώστε να στηθεί ένα γενικότερο θεωρητικό πλαίσιο πίσω από την έννοια της συμπίεσης. Παραθέτονται, επιπλέον, βασικοί όροι που θα απασχολήσουν το κείμενο σε όλη του την έκταση. Στη συνέχεια του κεφαλαίου, ακολουθεί περιγραφή της οπτικής αντίληψης του ανθρώπου των σημάτων της εικόνας και κατ επέκταση του βίντεο. Τέλος, ορίζονται ως έννοιες του ψηφιακού χώροι τόσο η εικόνα όσο και το βίντεο με παράθεση τον κυρίων χαρακτηριστικών τους. Στο δεύτερο κεφάλαιο, γίνεται μια γενική επισκόπηση της συμπίεση της εικόνας. Δίνεται ένα παράδειγμα για την ανάγκη της συμπίεσης και στη συνέχεια ορίζονται τα είδη του πλεονασμού της πληροφορίας μιας εικόνας. Ακολουθεί η περιγραφή βασικών τεχνικών κωδικοποίησης που χρησιμοποιούνται κατά τον αλγόριθμο συμπίεσης και τέλος γίνεται ανάλυση του πρότυπο συμπίεσης JPEG. Κρίθηκε απαραίτητη η αρχική αναφορά στην εικόνα καθώς αποτελεί τη βάση για το επόμενο κεφάλαιο. Στο τρίτο κεφάλαιο, λοιπόν, γίνεται αντίστοιχη ανάλυση για το βίντεο, όσον αφορά την ανάγκη για συμπίεση, τους πλεονασμούς της πληροφορίας και των τεχνικών κωδικοποίησης. Ιδιαίτερη έμφαση δίνεται στη τεχνική πρόβλεψης της κίνησης που αποτελεί και από τα κυριότερα αντικείμενα της εργασίας. Τέλος παρουσιάζονται τα πρότυπα MPEG/MPEG-2 πάνω και στα οποία βασίζεται το πειραματικό μέρος. Στο τέταρτο κεφάλαιο, αναλύεται η προτεινόμενη μέθοδος BLU ME ενώ στο πέμπτο περιγράφεται το κομμάτι της υλοποίησης των αλγορίθμων για κάθε μέθοδο. Στο έκτο κεφάλαιο παρουσιάζονται τα πειράματα με αξιολόγηση και σχολιασμό των αποτελεσμάτων και στο έβδομο η εργασία λήγει με μια σύντομη σύνοψη. Τέλος, περιλαμβάνονται δύο παραρτήματα, Α και Β, που περιέχουν ειδικούς πίνακες στους οποίους γίνονται αναφορές κατά την έκταση της εργασίας. 6
7 ΚΕΦΑΛΑΙΟ 1 - Εισαγωγή 1.1 Θεωρία Πληροφοριών Ο όρος πληροφορία εξελίχθηκε από μια έννοια αυθαίρετη σε μια μετρήσιμη, διακριτή και ορισμένη ποσότητα, με το paper του Claude Shannon, A Mathematical Theory of Communication, το οποίο εκδόθηκε το 1948 [6, σ.2], ιδρύοντας έτσι ένα νέο πεδίο ερευνών, τη Θεωρία Πληροφοριών. Το αντικείμενο της θεωρίας αυτής αφορά την αποδοτικότητα και την αξιοπιστία της μετάδοσης πληροφορίας από μια πηγή σε ένα προορισμό μέσω ενός καναλιού. Ως μονάδα της πληροφορίας συνήθως ορίζεται το bit, ή δυαδικό ψηφίο, 1 ή 0, ενώ ο ρυθμός μετάδοσης εκφράζει τόσο τη ποσότητα της πληροφορία που μεταδίδεται ανά μια μονάδα χρόνου από μια πηγή καθώς και τη δυνατότητα μετάδοσης από ένα κανάλι. Για να χαρακτηριστεί η μετάδοση αποδοτική πρέπει η πληροφορία να μεταδίδεται με τον ελάχιστο δυνατό ρυθμό, δηλαδή με μια μορφή λιγότερων bits ενώ η αξιοπιστία αφορά την ποιότητα της τελικής μετάδοσης. Στην πράξη κάθε κανάλι, ή μέσο μετάδοσης διαθέτει ένα βαθμό χωρητικότητας που περιορίζει τη ποσότητα που μπορεί να μεταφέρει ανά κάποια μονάδα χρόνου ενώ ενδέχεται να περιέχει και σήμα θορύβου που αλλοιώνει την ποιότητα της μετάδοσης. Για παράδειγμα, άμα η πηγή εκπέμπει δεδομένα με μεγαλύτερο ρυθμό απ ότι υποστηρίζει το κανάλι τότε η εμφάνιση σφαλμάτων κατά τη μετάδοση είναι εγγυημένη. Για την περιγραφή του παραπάνω προβλήματος, ο Shannon εισήγαγε ένα ειδικό μοντέλο το οποίο αποτελείται από την πηγή της πληροφορίας, τον κωδικοποιητή, το κανάλι, τον αποκωδικοποιητή και το δέκτη. Η πηγή θεωρείται ότι παράγει πληροφορία, έτσι ώστε να μπορεί να περιγραφεί με μοντέλο πιθανοτήτων. [1,σ.177] Ο κωδικοποιητής, είτε ως hardware, είτε ως λογισμικό, αναλαμβάνει την μετατροπή μιας δεδομένης πληροφορίας από την αρχική της μορφή σε μια πιο κατάλληλη, συνήθως μια που αναπαρίσταται με λιγότερα bits, προκειμένου να μεταδοθεί, όσο πιο αποδοτικά και αξιόπιστα γίνεται, μέσα από ένα κανάλι. Για ένα κανάλι, ο περιορισμός στο μέγεθος της πληροφορίας που μεταδίδει ανά κάποια χρονική περίοδο, μετριέται σε Hz (bandwitdh ή εύρος ζώνης) ή σε bits per second (data rate ή ρυθμός δεδομένων). Ο αποκωδικοποιητής, τέλος, παίρνει την κωδικοποιημένη πληροφορία από το κανάλι, την οποία και αποκωδικοποιεί, ώστε να τη φέρει όσο πιο κοντά στην αρχική της μορφή, καθώς ενδέχεται να έχει υποστεί απώλειες κατά την κωδικοποίηση.[1,σ.177] Σύμφωνα με τη παραπάνω παράγραφο μπορεί να οριστεί και η έννοια της συμπίεσης δεδομένων. Συμπίεση δηλαδή είναι η μετατροπή της πληροφορίας, είτε είναι κείμενο, ήχος, εικόνα ή βίντεο, από το αρχικό της μέγεθος σε bits σε μια μορφή που χρειάζεται λιγότερα bits αναπαράστασης τόσο για ανάγκες μετάδοσης όσο και για αποθήκευσης. Η ποιότητα της συμπίεσης εξαρτάται από την απώλεια των δεδομένων κατά την κωδικοποίηση και μετριέται συγκρίνοντας την ποιότητα της αποσυμπιεσμένης πληροφορίας σε σχέση με την αρχική. Η ανάγκη για συμπίεση είναι ένα πρόβλημα που συνεχώς εμφανίζεται όσο η απαίτηση για μετάδοση και αποθήκευση πληροφορίας αυξάνεται. Ειδικά για εικόνες και βίντεο, όσο η ποιότητα τους αυξάνεται με τις νέες τεχνολογίες λήψης και καταγραφής τόσα περισσότερα bits αναπαράστασης χρειάζονται και επομένως αυξάνεται και η απαίτηση για επαρκή συμπίεση. Στα επόμενο κεφάλαια θα αναλυθούν με λεπτομέρεια τεχνικές και πρότυπα κωδικοποίησης/ αποκωδικοποίησης τόσο για εικόνα όσο και για βίντεο. 7
8 1.1.1 Χρήσιμες Έννοιες της Θεωρίας Πληροφοριών Στην παράγραφο που ακολουθεί ορίζονται κάποιες θεμελιώδης έννοιες της θεωρίας πληροφοριών που θα εμφανίζονται στα επόμενο κεφάλαια : Σύμβολα, ή λέξεις, είναι διακριτά σύνολα δυαδικών ψηφίων, μεταβλητού ή σταθερού μήκους. Για παράδειγμα, ένα σύμβολο είναι το s1=1001, μήκους τεσσάρων bits. [1,σ.178] Αλφάβητο είναι ένα διακριτό, μη κενό σύνολο από σύμβολα, το οποίο αναπαρίσταται ως, S = { s1, s2, s3,..., sn}. [1,σ.178] Ακολουθία ή συμβολοσειρά, με δεδομένο ένα αλφάβητο, είναι μια σειρά αποτελούμενη από διακριτά σύμβολα. Για παράδειγμα, μια τέτοια ακολουθία ορίζεται ως s1s2s3.[1,σ.179] Κώδικες προθέματος, ή prefix code, είναι ειδικά σύμβολα που περιέχονται σε ένα σύνολο, το λεξικό. Μέσα σε ένα λεξικό κάθε κώδικας είναι μοναδικός. Χρησιμοποιούνται ως ειδικά σημεία σε μια ακολουθία, με λέξεις μεταβλητού μήκους, που επιτρέπουν τον αποκωδικοποιητή να ξεχωρίζει μεταξύ διακριτών λέξεων. [1,σ ] Ένας ακόμα σημαντικός όρος είναι η εντροπία, όρος δανεισμένος από τη φυσική, και αφορά την ποσοτικοποίηση της πληροφορίας που περιέχεται σε ένα σύνολο συμβόλων, δηλαδή εξαρτάται από τις πιθανότητες εμφάνισης Pi, i συμβόλων.[1,181] Η εντροπία ορίζεται ως, H= Pi log 2 ( ) 1 = Pi log 2 ( Pi ) Pi Άρα για ένα δεδομένο σύμβολο s i, ορίζεται η έννοια της φερόμενης πληροφορίας ως lo g2 ( ) 1 Pi, η οποία αναπαριστά το μέγεθος σε bits της πληροφορίας που περιέχει το σύμβολο. Όπως φαίνεται από τη σχέση, υψηλή πιθανότητα σημαίνει μικρότερη πληροφορία και αντίστροφα. [1,σ.182] Επομένως μέγιστη εντροπία σε ένα σύνόλο συμβόλων μιας ακολουθίας εμφανίζεται για ίσες ανά μεταξύ τους πιθανότητες, ενώ ελάχιστη εντροπία προκύπτει από την συνεχή εμφάνιση μόνο ενός συμβόλου. Για ενδιάμεσες καταστάσεις, υψηλή εντροπία σημαίνει εμφάνιση περισσότερων διακριτών συμβόλων άρα και ανάγκη περισσότερων δυαδικών ψηφίων για την αναπαράσταση τους. Αντιθέτως, όταν η ακολουθία περιέχει πιο διακριτά μοτίβα συμβόλων, το πληροφορικό περιεχόμενο της ελαττώνεται μαζί με την απαίτηση για bits αναπαράστασης. [1,σ ] 1.2 Εικόνα και Βίντεο Η εικόνα μπορεί αρχικά να οριστεί ως στατική, οπτική πληροφορία που αναπαριστά ένα στιγμιότυπο του κόσμου που μας περιβάλλει. Το βίντεο, με τη σειρά του, ορίζεται ως μια συνεχόμενη αλληλουχία εικόνων και μπορεί να οριστεί με τη σειρά του ως χρονικά μεταβαλλόμενη οπτική πληροφορία. Το βίντεο μπορεί να περιέχει και ακουστική πληροφορία αλλά αυτό είναι πέρα του αντικείμενου του παρόντος εγγράφου. 8
9 1.2.1 Ανθρώπινη αντίληψη της εικόνας και του βίντεο Η οπτική πληροφορία είτε της εικόνας είτε του βίντεο λαμβάνεται από το ανθρώπινο μάτι ως αναλογικό ηλεκτρομαγνητική ακτινοβολία και επεξεργάζεται από ειδικά αισθητήρια όργανα, ή φωτοϋποδοχείς. Το μάτι μπορεί να αντιληφθεί κυματομορφές μήκους μεταξύ 380 nm και 780nm, το λεγόμενο ορατό φάσμα του φωτός. Το σύστημα με το οποίο το μάτι σχηματίζει την εικόνα από το σήμα αποτελείται από την ίριδα, την κόρη και το φακό. Στον αμφιβληστροειδή βρίσκονται δύο είδη φωτοϋποδοχών, τα ραβδία, σύνολο εκατομμυρίων, και τα κωνία, γύρω στα 7 με 8 εκατομμύρια. Τα πρώτα είναι ευαίσθητα στην αλλαγή της φωτεινότητας, δηλαδή την ένταση του φωτός που αντιλαμβάνεται το μάτι ενώ τα δεύτερα επιτρέπουν την αντίληψη της χρωματικής πληροφορίας. Ειδικότερα, τα κωνία χωρίζονται σε τρεις κατηγορίες, τα S κωνία, ευαίσθητα σε φωτόνια μικρού μήκους κύματος,που αντιστοιχούν στο μπλε χρώμα, τα Μ κωνία ευαίσθητα σε μεσαίου μήκους, δηλαδή στο πράσινο χρώμα, και τα L κωνία ευαίσθητα σε υψηλού μήκους φωτόνια, που συνθέτουν το κόκκινο χρώμα. [7] Με την εκπόνηση πειραμάτων, διαπιστώθηκε ότι τα τρία αυτά χρώματα άμα προστεθούν μεταξύ τους με διάφορες τιμές έντασης μπορούν να σχηματίσουν όλα τα υπόλοιπα χρώματα του ορατού φάσματος. Για το λόγο αυτό το κόκκινο, το μπλε και το πράσινο ονομάζονται πρωτεύοντα χρώματα. Εντέλει, η επιλεκτική χρωματική αντίληψη σε συνδυασμό με την υψηλότερη ευαισθησία του ανθρώπινου ματιού στην φωτεινή πληροφορία αποτελούν σημαντικούς παράγοντες κατά τη διαδικασία της συμπίεσης. [7] Εικόνα Όπως κάθε αναλογικό σήμα, η εικόνα μπορεί να εισαχθεί στο ψηφιακό χώρο με τη διαδικασία της ψηφιοποίησης. Η ψηφιοποίηση αποτελείται από τα στάδια της δειγματοληψίας και της κβάντισης, δηλαδή της αντιστοίχισης των συνεχών τιμών του σήματος σε ένα περιορισμένο, διακριτό σύνολο τιμών. Γενικά, για την καταγραφή των δειγμάτων μιας συνεχής εικόνας χρησιμοποιούνται στη διάταξη μιας ψηφιακής κάμερας, ειδικοί φωτοευαίσθητοι αισθητήρες, όπως οι CCD ή οι CMOS, οι οποίοι μετατρέπουν το φως που δέχονται στην είσοδο σε ηλεκτρικό φορτίο. Ο αριθμός των αισθητήρων αυτό, που αποτελεί βασικό χαρακτηριστικό μιας ψηφιακής κάμερας, καθορίζει των αριθμών δειγμάτων που θα ληφθούν συνολικά κατά τη λήψη ενός στιγμιότυπου. Η διάταξη τους είναι σε μορφή δισδιάστατου πίνακα. Η τιμή έντασης της εξόδου του κάθε αισθητήρα κβαντίζεται, δηλαδή αντιστοιχίζεται σε μια διακριτή τιμή ανάλογα με ορισμένες στάθμες. Ο αριθμός των σταθμών αυτών εξαρτάται από τις δυνατότητες της συσκευής και έχει να κάνει με τον αριθμό των bits που θα χρησιμοποιούνται για την αναπαράσταση του κάθε δείγματος. [7] Συνοψίζοντας, λοιπόν, η ψηφιακή εικόνα αναπαρίσταται από ένα πίνακα με διακριτές, ακέραιες τιμές, διαστάσεων MxN, F ( i, j ),ό πουi=1... Mκαιj=1... N. Οι διαστάσεις του πίνακα αυτού αποτελούν την ανάλυση, ή resolution, της εικόνας, όπου Μ το ύψος σε γραμμές και Ν το πλάτος σε στήλες. Κάθε κελί του πίνακα αποτελεί ένα pixel ή εικονοστοιχείο, που ορίζεται ως η ελάχιστη ποσότητα πληροφορίας της εικόνας. Σε κάθε pixel αντιστοιχεί και μια τιμή έντασης στο εύρος [ 0,2κ 1 ], όπου κ το σύνολο των bits αναπαράστασης για ένα εικονοστοιχείο. Για παράδειγμα, οι εικόνες που αναπαρίστανται με ένα bit ανά pixel, ονομάζονται δυαδικές με τιμές στα pixels, 0 ή 1, μαύρο ή άσπρο. Αντίστοιχα εικόνες των 8 bits ανά pixel, έχουν ως τιμές έντασης από το εύρος. Το 0 αντιστοιχεί στο μαύρο, το 255 στο λευκό 9
10 ενώ οι ενδιάμεσες τιμές αντιστοιχούν σε αποχρώσεις του γκρι, για αυτό και αυτές οι εικόνες ονομάζονται greyscale. Για την αναπαράσταση των έγχρωμων εικόνων σχεδιάστηκαν ειδικοί χρωματικοί χώροι, δηλαδή μαθηματικά μοντέλα που προσεγγίζουν την ανθρώπινη χρωματική αντίληψη όπως περιγράφηκε στην προηγούμενη ενότητα. Ο πιο βασικός χρωματικός χώρος είναι ο RGB, ή Red Green Blue, που όπως φαίνεται από το όνομα, βασίζεται στα τρία βασικά χρώματα όπως και τα κωνία του ματιού. Αποκαλείται και προσθετικός χώρος καθώς ο προσθετικός συνδυασμός των διάφορων εντάσεων των χρωματικών συνιστωσών σχηματίζει, ή πιο συγκεκριμένα, προσεγγίζει το υπόλοιπο ορατό φάσμα. Μια έγχρωμη εικόνα, λοιπόν, αναπαρίσταται στο χώρο RGB, με τρεις διακριτούς greyscale πίνακες ίδιων διαστάσεων MxN, όπου κάθε ένας περιέχει τιμές έντασης για το κόκκινο, πράσινο και μπλε αντίστοχα. Αυτό επίσης σημαίνει ότι κάθε pixel είναι πλέον ένα διάνυσμα με τρεις συνιστώσες, όπου η κάθε μια αναπαριστάται με 8 bits. Ο τελικός πίνακας δηλαδή είναι πλέον διαστάσεων MxNx 3. Προκύπτει και η έννοια του βάθος εικονοστοιχείου ή pixel depth, όπου στην περίπτωση του RGB λέγεται ότι κάθε pixel έχει βάθος 24 bit. [7] Αναφορικά, υπάρχει και ο χώρος RGBA, όπου προστίθεται ένα νέο κανάλι, το Alpha, που δίνει την πληροφορία της αδιαφάνειας, με τιμές στο σύνολο [ 0.0,1.0 ], όπου 0 σημαίνει απόλυτη διαφάνεια και 1 απόλυτη αδιαφάνεια. Σε αυτή την περίπτωση ο πίνακας θα είχε διαστάσεις MxNx 4. Στα επόμενα κεφάλαια θα φανεί και η χρήση εναλλακτικών χρωματικών μοντέλων για την επίτευξη περισσότερης συμπίεσης. [7] Εικόνα 1.1 Παράδειγμα εικόνας για διάφορες τιμές βάθους pixel Εικόνα 1.2 Η γνωστή εικόνα, Lena, σε έγχρωμη μορφή 10
11 1.3 Βίντεο Το βίντεο αναπαρίσταται ως αλληλουχία διακριτών εικόνων στο χρόνο. Κάθε εικόνα καλείται πλαίσιο και διαθέτει τα γνωστά χαρακτηριστικά του πλάτους, ύψους και του βάθους εικονοστοιχείου. Ειδικότερα, χρησιμοποιείται ο όρος aspect ratio, ο λόγος του πλάτους προς το ύψος, ως ένα εύκολο κριτήριο διαχωρισμού των βίντεο σε κατηγορίες. Ο ρυθμός με τον οποίο προβάλλονται τα πλαίσια ανά ένα δευτερόλεπτο ή πιο απλά, ο ρυθμός πλαισίων, frame rate, είναι κύριο χαρακτηριστικό του σήματος βίντεο που καθορίζει την ομαλότητα της κίνησης όπως την αντιλαμβάνεται ο άνθρωπος. Για παράδειγμα, συνήθως οι κινηματογραφικές ταινίες διαθέτουν ρυθμό 24 πλαισίων το δευτερόλεπτο, ο οποίος καλύπτει τις ανάγκες της ανθρώπινης όρασης ενώ προσφέρει και εξοικονόμηση κόστους για την παραγωγή της ταινίας. Αν μειωθεί η τιμή του ρυθμού αρκετά εντέλει θα σπάσει η αίσθηση της ομαλή κίνησης. Για την τηλεοπτική μετάδοση τα κλασικά αναλογικά πρότυπα NTSC και PAL χρησιμοποιούν 30 και 25 πλαίσια το δευτερόλεπτο αντίστοιχα, ενώ πλέον η μετάδοση γίνεται ψηφιακά με το HDTV πρότυπο, δηλαδή τηλεόραση υψηλής ευκρίνειας, που υποστηρίζει και υψηλότερους ρυθμούς.[1,σ.83] Η λήψη του αναλογικού βίντεο γίνεται με βάση τεχνική σάρωσης και μετατρέπεται ουσιαστικά σε ένα μονοδιάστατο σήμα το οποίο διαμορφώνεται και εκπέμπεται ή καταγράφεται σε κάποιο μέσο. Στη περίπτωση έγχρωμου βίντεο που βρίσκεται πιο συχνό χώρο RGB εφαρμόζεται πριν την εκπομπή και μετασχηματισμός στο χρωματικό μοντέλο YUV. Το μοντέλο αυτό διαχωρίζει την πληροφορία στη φωτεινή συνιστώσα Υ και τις χρωματικές UV, οι οποίες υποδειγματολειπτούνται, δηλαδή εκπέμπονται για κάθε εικονοστοιχείο οι μισές ή λιγότερες χρωματικές συνιστώσες σε σχέση με τις φωτεινές. Επιτυγχάνεται έτσι μείωση της απαίτησης για εύρος ζώνης. Η λογική της υποδειγματοληψίας βασίζεται στο γεγονός ότι ο άνθρωπος είναι πιο ευαίσθητος στη μεταβολή της φωτεινότητας παρά στα χρώματα. Στην περίπτωση της ασπρόμαυρης τηλεόρασης μεταφέρεται μόνο η συνιστώσα Υ. [1,σ.84-85] Κάθε πλαίσιο του βίντεο σχηματίζεται από την πλευρά του δέκτη, όπου στην περίπτωση αυτή είναι η αναλογική τηλεόραση, και πάλι με τεχνική σάρωσης. Το μονοδιάστατο συνεχές σήμα δηλαδή σαρώνεται ανά διακριτές γραμμές έτσι ώστε να σχηματιστεί η τελική διάταξη της εικόνας. Η σάρωση χωρίζεται σε δύο κατηγορίες, την προοδευτική και τη διεμπλεγμένη. Η πρώτη αποτελεί τη συνεχή σάρωση των γραμμών που συγχρονίζονται ανάλογα με το ρυθμό ανανέωσης της τηλεόρασης (60 Hz για το NTSC και 50Hz για PAL). Η διεμπλεγμένη σάρωση από την άλλη αφορά το διαχωρισμό του πλαισίου σε δύο ημιπλαίσια ή πεδία, όπου το ένα αποτελείται από τις γραμμές σάρωσης άρτιας αρίθμησης και το άλλο της περιττής. Στην περίπτωση του NTSC χρειάζεται 1/60οστό του δευτερολέπτου για τη σχεδίαση των πεδίων άρα συνολικά ένα πλαίσιο σχηματίζεται στο 1/30οστό του δευτερόλεπτου. Προκύπτει έτσι και ο συνήθης ρυθμός των 30 πλαισίων το δευτερόλεπτο ή 60 πεδίων το δευτερόλεπτο. Για το PAL η λογική είναι η αντίστοιχη όπου χρειάζεται το 1/25οστό του δευτερολέπτου για τη συνολική διαδικασία.[1,σ.85-86] Πλέον όμως η ψηφιακή τηλεόραση έχει εδραιωθεί ως το νέο στάνταρντ, που υποστηρίζει σήμα βίντεο υψηλής ευκρίνειας, του οποίου η επεξεργασία και μετάδοση γίνεται με πρότυπα κωδικοποίησης/αποκωδικοποίησης όπως το MPEG-2. Πέρα του προτύπου HDTV, που χαρακτηρίζεται από λόγο διαστάσεων, 16:9, διαστάσεων 720x1280 για HD ή 1080x1920 για fullhd, υπάρχουν ενδεικτικά το πρότυπο ψηφιακού κινηματογράφου με λόγο 47:20 ή τα πρότυπα CIF και QCIF με λόγους 4:3 για χρήση σε μετάδοση βίντεο χαμηλών απαιτήσεων, όπως είναι οι τηλεδιασκέψεις [1,σ.90-91]. 11
12 Εικόνα 1.3 Οι κυριότερες τιμές aspect-ratio Εικόνα 1.4 Μια γραφική επεξήγηση των μεθόδων σάρωσης 12
13 ΚΕΦΑΛΑΙΟ 2 - ΣΥΜΠΙΕΣΗ ΕΙΚΟΝΑΣ Για μια έγχρωμη RGB εικόνα,με διαστάσεις 1080x1920 όπου κάθε pixel χρειάζεται 24 bits, 8 για κάθε συνιστώσα, εύκολα υπολογίζεται ο συνολικός αριθμός των bits αναπαράστασης ως 1080*1920*24= bits ή περίπου 50Μbits. Για μια μόνο εικόνα, αυτή η ποσότητα είναι αρκετά μεγάλη τόσο για μετάδοση όσο και αποθήκευση. Η υψηλή αυτή απαίτηση προκύπτει από την ύπαρξη πλεονασμού στην πληροφορία της, ο οποίος μπορεί να απομακρυνθεί με ειδικές τεχνικές κωδικοποίησης έτσι ώστε να μειωθεί η απαίτηση αυτή σε bits, είτε με απώλειες είτε χωρίς. 2.1 Επισκόπηση της συμπίεσης εικόνας Κύριος στόχος της συμπίεσης, όπως ορίζεται από τη θεωρία πληροφοριών, είναι η ελαχιστοποίηση της πλεονάζουσας πληροφορίας που περιέχει μια εικόνα προκειμένου να είναι πιο εφικτή και αποδοτική η μεταφορά της μέσω ενός δεδομένου μέσου. Αυτός ο πλεονασμός, ή redundancy, μπορεί να διακριθεί στις παρακάτω κατηγορίες Πλεονασμός κωδικοποίησης, που έχει να κάνει με το πλεονασμό στη αναπαράσταση με bits του κάθε εικονοστοιχείου της εικόνας. Ουσιαστικά, στην περίπτωση που η ανάθεση bits δεν εκμεταλλεύεται τις συχνότητες ή πιθανότητες εμφάνισης των τιμών έντασης των εικονοστοιχείων, θα υπάρχουν περισσότερα bits από ότι χρειάζονται. Προκειμένου, λοιπόν, να βελτιστοποιηθεί η κατανομή των bits ανά εικονοστοιχείο χρησιμοποιούνται τεχνικές κωδικοποίησης που εκμεταλλεύονται την εντροπία μιας δεδομένης εικόνας.[2,σ.748] Χωρικός πλεονασμός, ότι δηλαδή στις περισσότερες εικόνες, τα pixels παρουσιάζουν ομοιότητες ή εξαρτώνται από τα γειτονικά τους, με αποτέλεσμα να προκύπτει περιττή επανάληψη της πληροφορίας. Σε αυτή την περίπτωση ένα συχνό εργαλείο συμπίεσης είναι η κωδικοποίηση μετασχηματισμού, πιο συχνά στο χώρο των συχνοτήτων.[2,σ.748] Ψυχο-οπτικός πλεονασμός, που αφορά την οπτική αντίληψη του ανθρώπου. Όπως αναφέρθηκε στην εισαγωγή,το ανθρώπινο μάτι είναι πιο ευαίσθητο στη φωτεινότητα παρά στα επιμέρους χρώματα μιας εικόνας, άρα οι χρωματικές πληροφορίες της εικόνας θεωρούνται πλεονάζουσες. Η συμπίεση των χρωμάτων γίνεται με το μετασχηματισμό χρωματικού χώρου και, στη συνέχεια, με κάποιο βαθμού υποδειγματοληψίας των χρωματικών συνιστωσών ανά εικονοστοιχείο [2,σ ]. 2.2 Τεχνικές κωδικοποίησης χωρίς απώλειες Οι τεχνικές κωδικοποίησης χωρίς απώλειες επιτρέπουν τη διατήρηση της πληροφορίας κατά την κωδικοποίηση, έτσι ώστε η αποκωδικοποίηση να επιστρέψει την αρχική πληροφορία αυτούσια [1,σ.220]. Συνήθως τεχνικές της κατηγορίας αυτής χρησιμοποιούν λεξικά με τα οποία αναθέτουν κωδικές λέξεις στα σύμβολα εισόδου. Έτσι μια τιμή έντασης ενός pixel μπορεί να αναπαρασταθεί από ένα μοναδικό δυαδικό κώδικα. Τα λεξικά αυτά δημιουργούνται με βάση τη στατιστική μελέτη των δειγμάτων της πληροφορίας, με τη λογική ότι τα πιο συχνά σύμβολα θα αντιστοιχούν σε κώδικες μικρότερου μήκους έναντι των λιγότερο πιθανών συμβόλων. Σε αυτή την περίπτωση είναι 13
14 κωδικοποίηση μεταβλητού μήκους, ή variable length coding. Εναλλακτικά μπορεί να γίνει αντιστοίχιση σε σταθερού μήκους κωδικών, το οποίο είναι λιγότερο ευέλικτο [3,σ.133]. Ακολουθούν οι κυριότερες τεχνικές κωδικοποίησης χωρίς απώλειες που χρησιμοποιούνται και στο πειραματικό μέρος της εργασίας: Κωδικοποίηση Ηuffman Κωδικοποίηση Huffman, η οποία αποτελεί μια από τις πιο δημοφιλείς και ευρέως χρησιμοποιημένες τεχνικές. Ο αλγορίθμος του Huffman παίρνει ως είσοδο τα σύμβολα μιας πληροφορίας και τις πιθανότητες εμφανίσεις τους και επιστρέφει μια κωδικοποιημένη συμβολοσειρά αποτελούμενη από δυαδικά ψηφία. Η διαδικασία μπορεί να θεωρηθεί ότι κατασκευάζει ένα δέντρο: αρχικά, τα δύο σύμβολα με τις μικρότερες πιθανότητες εμφάνισης προστίθενται σε ένα κοινό κόμβο, με τιμή το άθροισμα των πιθανοτήτων τους, όπου το ένα σύμβολο αντιστοιχεί σε ένα κλαδί με τιμή 0 και το άλλο σε κλαδί με τιμή 1. Στη συνέχεια, ο πρώτος κόμβος αποτελεί ένα νέο σύμβολο, που αντικαθιστά τα δύο προηγούμενα, με τη δικιά του πιθανότητα, η οποία συγκρίνεται με τις υπόλοιπες πιθανότητες. Στο επόμενο βήμα, θα σχηματιστεί ο επόμενος κόμβος των δύο ελάχιστων πιθανοτήτων και ούτε μέχρι να εξαντληθούν τα σύμβολα. Προκύπτει, έτσι το συνολικό δέντρο Ηuffman από το οποίο εξάγονται οι τελικοί κώδικες αναπαράστασης ως εξής: ξεκινώντας από τον κόμβο- κορυφή και ακολουθώντας τη διαδρομή του 0 ή του 1, ο αλγόριθμος καταλήγει είτε σε άλλο κόμβο όπου και επιλέγει νέα διαδρομή ή καταλήγει σε ένα από τα χαμηλότερα σύμβολα, όπου ο συνολικός συνδυασμός δυαδικών ψηφίων που οδήγησε σε αυτό αποτελεί τον κώδικα αναπαράστασης. Ο κώδικας αυτός θα είναι μικρότερος σε μήκος για τα πιο συχνοεμφανιζόμενα σύμβολα, καθώς θα βρίσκονται πιο ψηλά στη δομή του δέντρου. Τα λιγότερο πιθανά, από την άλλη, στον πάτο του δέντρου θα αντιστοιχούν σε μακρύτερους κώδικες. [4,σ.41-46]. Στην παρακάτω εικόνα φαίνεται ένα παράδειγμα δέντρου Huffman. Εικόνα 2.1 Ένα παράδειγμα δέντρου Huffman, όπου φαίνονται οι κόμβοι με τα σύμβολα και τις συχνότητες εμφάνισης τους. Τα 0 και 1 καθορίζουν το κώδικα για κάθε σύμβολο. 14
15 Πρακτικά, δημιουργείται ένα ειδικό μοντέλο αναπαράστασης, ή βιβλίο κωδικών/λεξιλόγιο, όπου κάθε σύμβολο αντιστοιχεί σε ένα μοναδικό κώδικα, και οι επιμέρους κώδικες συνδυάζονται σε μια ενιαία συμβολοσειρά. Ο αποκωδικοποιητής, με τη σειρά του, παίρνει στην είσοδο τη συμβολοσειρά αυτή, καθώς και το μοντέλο, και ανακατασκευάζει την αρχική πληροφορία. Η αποκωδικοποίηση γίνεται με τη σάρωση της κωδικοποιημένης συμβολοσειράς, ένα ψηφίο τη φορά, όπου και ο αλγόριθμος προσπαθεί να αντιστοιχίσει τους κώδικες του μοντέλου στα αρχικά σύμβολα σύμφωνα με το λεξιλόγιο Κωδικοποίηση Μήκους Διαδρομής Κωδικοποίηση μήκους διαδρομής, ή run length encoding, που είναι μια πολύ απλή τεχνική απομάκρυνσης του πλεονασμού. Η κύρια ιδέα της βασίζεται στο ότι μια σειρά συμβόλων περιέχει ακολουθίες του ίδιου συμβόλου. Για παράδειγμα, μια σειρά ΑΑΑΒΒΒCCCD, βλέπουμε πως έχει επαναλήψεις οι οποίες μπορούν να αναπαριστούν με ένα μετρητή των επαναλήψεων και το ίδιο το σύμβολο. Το παράδειγμα μας κωδικοποιείται, λοιπόν, ως 3A3B3C1D. Το αρνητικό με τη τεχνική αυτή είναι πως, πρακτικά, δεν είναι εύκολη η αναπαράσταση με δυαδικά ψηφία σε περίπτωση που τα σύμβολα είναι αριθμοί, όπως γίνεται με την εικόνα, ή και γενικά δεν είναι προφανές πότε ξεκινάει ο μετρητής και πότε το σύμβολο. Για αυτό, όπως θα φανεί και παρακάτω, χρησιμοποιείται σε συνδυασμό με άλλες τεχνικές, σε συγκεκριμένες περιπτώσεις χαμηλής εντροπίας. [1,σ ] 2.3 Τεχνικές κωδικοποίησης με απώλειες Στις περιπτώσεις είναι αναγκαίο να θυσιαστεί κάποιο κομμάτι της πληροφορίας ώστε να επιτευχθεί ο στόχος αποθήκευσης ή μετάδοσης. Ως αντίτιμο αυτής της θυσίας, όμως, είναι η εισαγωγή της έννοιας της παραμόρφωσης. Από τη στιγμή, δηλαδή, που η αρχική πληροφορία δε πρόκειται να ανακατασκευαστεί με απόλυτη ακρίβεια θα υπάρχει ένας βαθμός σφάλματος. Παρακάτω, αναλύονται ορισμένες τεχνικές συμπίεσης με απώλειες: Κβάντιση Κβάντιση, είναι η αντιστοίχιση των τιμών των εικονοστοιχείων από το αρχικό, μεγάλο σύνολο τιμών τους σε ένα πιο μικρό σύνολο τιμών. Βασικό παράδειγμα είναι η βαθμωτή κβάντιση, ορίζονται ειδικά σύνολα τιμών ή στάθμες στις οποίες αντιστοιχίζεται μία τιμή τη φορά. Για παράδειγμα μια στάθμη [1,5] θα αντιστοιχίζει όλες τις τιμές των εικονοστοιχείων που ανήκουν στο σύνολο αυτό σε ένα κοινό σύμβολο. Η απώλεια προέρχεται κατά την αντιστροφή της διαδικασίας όπου δεν είναι δυνατό να γνωρίζει ο αποκωδικοποιητής από ποια ακριβώς τιμή του εύρους προήλθε ένα σύμβολο. Σε άλλες εφαρμογές που θα αναλυθούν στην πορεία, η κβάντιση περιλαμβάνει τη διαίρεση των τιμών έντασης των εικονοστοιχείων με ειδικούς συντελεστές και τη στρογγυλοποίηση των αποτελεσμάτων. Μπορεί να μην υπάρχουν στάθμες αλλά το τελικό αποτέλεσμα είναι πάλι η μείωση του εύρους των τιμών των δειγμάτων της εικόνας. Για την ανακατασκευή οι συντελεστές πολλαπλασιάζονται με τα κβαντισμένα δείγματα όπου και θα προκύψει σφάλμα σε σχέση με τις αρχικές Διαφορική Κωδικοποίηση 15
16 Διαφορική κωδικοποίηση, ή DPCM, που εφαρμόζεται σε περιπτώσεις που τα διαδοχικά δείγματα του σήματος/ πληροφορίας παρουσιάζουν μεταξύ τους στατιστική συσχέτιση. Η συσχέτιση αυτή που αποτελεί μορφή πλεονασμού μπορεί να αντιμετωπιστεί κωδικοποιώντας τις προβλέψεις μεταξύ των δειγμάτων καθώς και τα σφάλματα τους με τις πραγματικές τιμές. Ως πρόβλεψη σε αυτή την τεχνική θεωρείται το ίδιο το σήμα, δηλαδή, υποθέτοντας πως το ν-oστό δείγμα είναι το y(n-1) τότε η πρόβλεψη του είναι το y(n), με σφάλμα μεταξύ τους το d(n)=y(n)-y(n-1). Η απώλεια της πληροφορίας προέρχεται από τυχόν κβαντισμό του σφάλματος d(n), που συμβολίζεται πλέον ως d (n). Επομένως, στον αποκωδικοποιητή η διαδικασία εκτελείται αντίστροφα, ως y (n)=d (n)+y(n-1) και, στη συνέχεια, τα δείγματα αποκβαντίζονται. Προφανώς, τα πρώτα δείγματα, δηλαδή για n=1, που αποτελούν την αρχική πρόβλεψη απλά κβαντίζονται ανεξάρτητα. Μια απλή μετατροπή που βοηθά στην ελάττωση πιθανής συσσώρευσης σφάλματος κβάντισης κατά τη διαδικασία είναι η κβάντιση του δείγματος n-1, για τον υπολογισμό,δηλαδή, του σφάλματος ως d(n)=y(n)-y (n-1).[1,σ ] Κωδικοποίηση Μετασχηματισμού Κωδικοποίηση μετασχηματισμού, Discrete Cosine Fourier: Πρόκειται για ένα δημοφιλή μετασχηματισμό που χρησιμοποιείται τόσο στη συμπίεση εικόνας όσο και στο βίντεο. Η λογική του είναι η μεταφορά της εικόνας εισόδου από το πεδίο των εικονοστοιχείων στο πεδίο των συχνοτήτων. Είναι παρόμοιος με το διακριτό μετασχηματισμό fourier με τη διαφορά ότι αποτελείται μόνο από άθροισμα συνημιτόνων διαφορετικών συχνοτητών πολλαπλασιασμένων με συντελεστές, δηλαδή μόνο από πραγματικούς αριθμούς. Πρακτικά, ο μετασχηματισμός δε γίνεται σε ολόκληρη την εικόνα αλλα σε μικρότερα κομμάτια της διαστάσεων συνθως 8x8 ή 16x16. Ως παράδειγμα, στη πρώτη περίπτωση προκύπτουν ανά τμήμα σε δομή πίνακα ίδιων διαστάσεων, 64 συντελεστές ή coefficients, που αναπαριστούν το εύρος των συχνοτήτων του κάθε τμήματος της εικόνας. Το πρώτο κέλι πάνω αριστερά αποτελεί το λεγομενο DC συντελεστης, δηλαδή μηδενικης συχνότητας, ενώ οι υπόλοιποι ονομάζονται AC συντελεστές και αναπαριστούν τις υπόλοιπες, υψηλότερες τιμές συχνότητας που συνθέτουν το τμήμα κατά το κάθετο και οριζόντια αξονα. Εικόνα 2.2 Ένα παράδειγμα εφαρμογής DCT πάνω σε τμήμα εικόνας 16
17 Η δυνατότητα αντιστροφής του μετασχηματισμού είναι ένα ακόμα πλεονέκτημα της μεθόδου. Η αντιστροφή αυτή επιστρέφει αυτούσιο αρχικό κομμάτι της εικόνας άμα εφαρμοστεί με απόλυτη ακρίβεια των συντελεστών. Πρακτικά, όμως, πάντα ακολουθεί κβάντιση των όρων ώστε να είναι σε μορφή πραγματικού ακέραιου για την μετέπειτα κωδικοποίηση. [1,σ.200] 2.4 Χρωματικοί χώροι και υποδειγματοληψία Όπως αναφέρθηκε στην εισαγωγή, το ανθρώπινο μάτι είναι πολύ πιο ευαίσθητο στη φωτεινότητα παρά στο χρώμα μιας εικόνας. Επομένως μια μορφή συμπίεσης γίνεται αρχικά με το μετασχηματισμό από τον αρχικό χρωματικό χώρο RGB στο YCbCr, και στη συνέχεια με τη υποδειγματοληψίας των συνιστωσών χρώματος, Cb και Cr. Ο χώρος αυτός είναι παρόμοιος με το YUV, δηλαδή δίνει έμφαση στη φωτεινότητα έναντι των χρωμάτων, με τη διαφορά ότι χρησιμοποιείται στο ψηφιακό χώρο. Με το RGB συνδέονται μέσω εξισώσεων με συγκεκριμένους συντελεστές και ο μετασχηματισμός από το ένα μοντέλο στο άλλο είναι σχετικά απλός. Εικόνα 2.3 H Lena μετασχηματισμένη στο μοντέλο YcbCr Πρακτικά ενώ κωδικοποιούνται όλες οι τιμές έντασης φωτεινότητας Υ των εικονοστοιχείων. οι αντίστοιχες χρωματικές εντάσεις αφαιρούνται από τη διαδικασία, βέβαια ως ένα βαθμό, όπως φαίνεται στα πρότυπα που ακολουθούν: 4:4:4, εδώ δεν παρουσιάζεται ουσιαστικά υποδειγματοληψία, αλλά γενικά δεν απολαμβάνει κοινή χρήση. 4:2:2, όπου οι χρωματικές συνιστώσες δειγματολειπτούνται ως μισές της φωτεινότητας, 4:2:0, όπου οι χρωματικές συνιστώσες είναι το ένα τέταρτο της φωτεινότητας. Στην εικόνα 2.4 φαίνονται οι παραπάνω περιπτώσεις για το YUV αλλά με την ακριβώς ίδια λογική ισχύουν και στο YCbCr. 17
18 Εικόνα 2.4 Υποδειγματοληψία YUV και αντίστοιχη για το YCbCr 2.5 Πρότυπο κωδικοποίησης εικόνας JPEG Ως πρότυπο κωδικοποίησης, ουσιαστικά, ορίζεται ένα μοντέλο που συνδυάζει τεχνικές κωδικοποίησης, καθώς και ένα σύνολο από χαρακτηριστικά, που καθορίζονται από τον κατασκευαστή. Τα πρότυπα αυτά συνεχώς εξελίσσονται, ή χρησιμοποιούνται ως βάσεις για νέα πρότυπα, όσο διευρύνονται οι ανάγκες για βέλτιστη διαχείριση όλο και μεγαλύτερων ποσοτήτων δεδομένων. Σε αυτή την ενότητα γίνεται μια σύντομη προεπισκόπηση για ένα πολύ κλασικό πρότυπο, το JPEG, το οποίο θα συνεχίσει να εμφανίζεται σε όλη την έκταση της εργασίας. To πρότυπο JPEG δημιουργήθηκε από το Joint Photographic Experts Group, από όπου προκύπτει και το όνομα, και αναγνωρίστηκε επίσημα το Πρόκειται για ένα από τα πιο ευρέως γνωστά και χρησιμοποιημένα πρότυπα, με κύρια χρήση την κωδικοποίηση φωτογραφιών σε ψηφιακές μηχανές και εικόνων για χρήση στο διαδίκτυο. Η κύρια λειτουργία συνδυάζει τεχνικές κωδικοποίησης με και χωρίς απώλειες, άρα το τελικό αποτέλεσμα πάντα θα παρουσιάζει κάποιο βαθμό απώλειας μετά την αποκωδικοποίηση. Η διαδικασία κωδικοποίησης, λοιπόν, χωρίζεται στα βήματα που ακολουθούν. Σε περίπτωση έγχρωμης εικόνας, γίνεται μετασχηματισμός στο χρωματικό χώρο, YCbCr, και πραγματοποιείται υποδειγματοληψία τύπου 4:2:0. Στη συνέχεια σε κάθε συνιστώσα φωτεινότητας και χρώματος εφαρμόζονται ξεχωριστά τα υπόλοιπα βήματα. Σε περίπτωση grayscale εικόνας το πρότυπο παραλείπει το παρών βήμα και ξεκινάει από το αμέσως επόμενο [1,σ.224].Κάθε συνιστώσα, ως δισδιάστατος πίνακας, χωρίζεται σε τμήματα, ή blocks, διαστάσεων 8x8, τα οποία με τη σειρά τους επεξεργάζονται ξεχωριστά. Σε περίπτωση, που οι διαστάσεις δεν είναι πολλαπλάσιες του 8, τα πιθανά κενά συμπληρώνονται με μηδενικά [1,σ.224]. Σε κάθε block κάθε συνιστώσας εφαρμόζεται DCT μετασχηματισμός και από τις τιμές έντασης των εικονοστοιχείων προκύπτουν αντίστοιχοι συντελεστές DCT, ή DCT coefficients. Το μετασχηματισμένο πλέον block, περιέχει τη πιο σημαντική πληροφορία στα πρώτα κελιά, προς τα πάνω και αριστερά, δηλαδή όπου αναπαρίστανται η μηδενική και οι χαμηλότερες συχνότητες. Οι υψηλότερες συχνότητες αποτελούν με τη σειρά τους τη λιγότερη σημαντική πληροφορία [1,σ.224]. 18
19 Οι συντελεστές σε κάθε μετασχηματισμένο block, στην συνέχεια, κβαντίζονται με ειδικούς πίνακες κβάντισης που ορίζει το πρότυπο (πίνακας Α.1 στο παράρτημα Α). Σύμφωνα με τη λογική του προηγούμενου βήματος οι τιμές των πινάκων είναι μικρότερες για τις χαμηλότερες συχνότητες και μεγαλύτερες για τις υψηλότερες. Για τις συνιστώσες της φωτεινότητας και των χρωμάτων χρησιμοποιούνται διαφορετικοί πίνακες, με τους χρωματικούς πίνακες κβάντισης να περιλαμβάνουν μεγαλύτερης έντασης συντελεστές, ουσιαστικά θυσιάζοντας σε μεγαλύτερο βαθμό την πληροφορία χρώματος. Προκειμένου να προκύπτουν διαφορετικές βαθμίδες κβάντισης, οι πίνακες αυτοί πολλαπλασιάζονται με ένα θετικό πραγματικό συντελεστή. Αν είναι ίσος με 1 ή μεγαλύτερος προκύπτει μεγαλύτερη συμπίεση ενώ μικρότερη για την αντίθετη περίπτωση. Η τελική αλγοριθμική πράξη αποτελείται από απλή διαίρεση ένα προς ένα των κελιών μεταξύ του block και του πίνακα κβάντισης και την μετέπειτα στρογγυλοποίηση των νέων κελιών [1,σ.225]. Ακολουθεί η κωδικοποίηση των κβαντισμένων συντελεστών σε μια ενδιάμεση δυαδική αναπαράσταση. Εδώ, οι συντελεστές χωρίζονται σε DC, δηλαδή το πρώτο κελί του κάθε τμήματος 8x8, στη θέση (0,0), και AC όλοι οι υπόλοιποι. Οι DC συντελεστές του κάθε τμήματος κωδικοποιούνται με, ειδικό χωρίς απώλειες,dpcm, καθώς παρουσιάζουν μεταξύ τους συσχέτιση. Χωρίς απωλειες σημαίνει ότι δε γίνεται περαιτέρω κβάντιση του συντελεστή διαφοράς. Από την άλλη, οι AC συντελεστές σαρώνονται σε ένα διάνυσμα με ζιγκ ζαγκ μοτίβο, το οποίο κωδικοποιείται με RLE, με γνώμονα τα στατιστικά συχνότερα μηδενικά που προκύπτουν σε αυτούς λόγω κβάντισης, όπως περιγράφεται στη προηγούμενη παράγραφο. [2,σ.828] Η τελική κωδικοποίηση βασίζεται στη μέθοδο Huffman, με τη διαφορά ότι υπάρχει έτοιμοι πίνακες/λεξιλόγια που αντιστοιχούν κατάλληλες συμβολοσειρές δυαδικών ψηφίων. Στους DC και AC όρους έχουν ανατεθεί διαφορετικοί πίνακες και λογική ανάθεσης ψηφίων, όπως φαίνονται στο παράρτημα Β. Για κάθε DC όρο βρίσκεται το ακριβές μέγεθος του σε bits, και σύμφωνα με αυτό αντιστοιχεί στον πίνακα Β.1 στις ειδικές κατηγορίες μεγέθους η καθεμία με ένα μοναδικό κώδικα prefix. Το τελικό αποτέλεσμα αποτελείται από μια συμβολοσειρά που αποτελείται από τον κατάλληλο κώδικα που προηγείται της τιμής του όρου σε δυαδικό σύστημα. Έτσι κατά την αποκωδικοποίηση θα διαβαστεί πρώτα ο μοναδικός κώδικας που ουσιαστικά λέει στον αποκωδικοποιητή τον αριθμό των αμέσως επόμενων bits που θα διαβαστούν ώστε να προκύψει ο DC όρος. Για τους AC όρους η λογική είναι παρόμοια με τη διαφορά ότι ο κώδικας prefix αναφέρεται σε συνδυασμό των μηδενικών που προηγούνται ενός μη μηδενικού όρου και το μέγεθος σε bits του όρου αυτού. Και πάλι η τελική συμβολοσειρά αποτελείται πρώτα από τον μοναδικό κώδικα και μετά την τιμή του όρου σε δυαδικό σύστημα. Υπάρχει επίσης και ένας ειδικό κωδικός που ορίζει το τέλος του κάθε block ώστε να ξέρει ο αποκωδικοποιητής πότε να ψάχνει για τον επόμενο DC όρο [2,σ ]. Στο πίνακα Β.1 φαίνεται επίσης κομμάτι του πίνακα κωδικών για τους AC συντελεστές. Τέλος, τα παραπάνω βήματα με την ανάποδη σειρά δίνουν την αποκωδικοποιημένη εικόνα, η οποία θα συγκριθεί με την αρχική ώστε να κριθεί η ποιότητα της συμπίεσης.[2,σ.831] Ανατρέχοντας στο αρχικό παράδειγμα όπου μια εικόνα χρειάζεται 24 bits για κάθε pixel, 8 για κάθε συνιστώσα χρώματος, με τη συμπίεση του JPEG μπορεί να επιτευχθεί μείωση της απαίτησης αυτής για παράδειγμα, κατά μέσο όρο, σε 1 με 1,5 bit ανά pixel για κάθε συνιστώσα ή και λιγότερο για τις χρωματικές. Σε μια τέτοια περίπτωση το τελικό αποτέλεσμα θα ήταν 1080*1920*3*1.5= περίπου 9,3 Μbits έναντι των αρχικών 50 Mbits. Σαφώς υπάρχει και περισσότερο περιθώριο για μικρότερα μεγέθη αλλά υπάρχει και ως αντίκτυπο η τελική ποιότητα της αποσυμπιεσμένης εικόνας. 19
20 Εικόνα 2.5 Αριστερά η αρχική εικόνα, δεξιά η αποσυμπιεσμένη εκδοχή της με εφαρμογή JPEG 2.6 Μετρικές Συμπίεσης Με ποιο κριτήριο, όμως, αξιολογείται η ποιότητα του αποτελέσματος ενός προτύπου συμπίεσης; Σε περίπτωση συμπίεσης χωρίς απώλειες αρκεί ο απλός λόγος συμπίεσης, δηλαδή ο λόγος του αποσυμπιεσμένου μεγέθους σε bits προς το συμπιεσμένο μέγεθος, αλλά στην περίπτωση των απωλειών δε καλύπτει και την έννοια της παραμόρφωσης. Συνεπώς, πέρα από το λόγο συμπίεσης, ο βαθμός της παραμόρφωσης είναι ένα ακόμα βασικό κριτήριο της συμπίεσης αλλά χρειάζεται, με τη σειρά του, μια αντίστοιχη μετρική. Οι πιο δημοφιλείς μετρικές παραμόρφωσης εκφράζονται με τις παρακάτω συναρτήσεις: Μέσο τετραγωνικό σφάλμα ή Mean Squared Error (MSE), που ορίζεται ως n 2 1 MSE= ( y i ~ yi). n i=1 Λόγος κορύφωσης σήματος προς θόρυβο ή Peak-to-Signal-Ratio (PSNR), που ορίζεται ως PSNR=10 log 10 ( MAX 2 / MSE ), και αποτελεί ένα αντικειμενικό κριτήριο της τελικής ποιότητας μιας αποσυμπιεσμένης εικόνας. MAX, είναι η μέγιστη ένταση ενός pixel, όπως 255 για εικόνες 8-bit. Όπως φαίνεται είναι αντιστρόφως ανάλογη του σφάλματος, επομένως, υψηλότερο PSNR σημαίνει και καλύτερη ποιότητα συμπίεσης. Στο λογαριθμικό σκέλος συνήθως το εύρος τιμών είναι μεταξύ 30dB και 50dB για εικόνες 8-bit. Ο συνήθης τρόπος παρουσίασης των παραπάνω μετρικών είναι οι λεγόμενες Rate-Distortion καμπύλες, όπου στον κάθετο άξονα αντιστοιχεί μια παράμετρος παραμόρφωσης όπως το σφάλμα ή ακόμα και το PSNR και στον οριζόντιο μια παράμετρος μέτρησης του ρυθμού της πληροφορίας, συνήθως την ποσότητα των bits κωδικοποίησης. 20
21 ΚΕΦΑΛΑΙΟ 3 - ΣΥΜΠΙΕΣΗ ΒΙΝΤΕΟ Το βίντεο ορίζεται ως ένα σήμα διαδοχικών εικόνων, όπου για κάθε εικόνα ισχύουν οι έννοιες του πλεονασμού και οι τεχνικές κωδικοποίησης που αναλύθηκαν στο κεφάλαιο 2. Εισέρχεται, λόγω της διαδοχής, και η έννοια του χρονικού πλεονασμού που αντιμετωπίζεται με την τεχνική της πρόβλεψης κίνησης, την οποία θα καλύψει το παρών κεφάλαιο. Το δεύτερο αντικείμενο του κεφαλαίου αυτού είναι το πρότυπο MPEG, πάνω στο οποίο βασίζεται και το πειραματικό μέρος. Η ανάγκη για συμπίεση του σήματος βίντεο φαίνεται εύκολα, ανατρέχοντας στο αντίστοιχο παράδειγμα της εικόνας. Για τη μια RGB εικόνα διαστάσεων 1080x1920 χρειάζονται κοντά 50Μ bits. Αν το βίντεο αποτελείται από πολλαπλές τέτοιες εικόνες με ρυθμό μετάδοσης 30 πλαισίων το δευτερόλεπτο, τότε θα χρειάζονται 50Μ*30=1500Μ ή 1,5 Gbits το δευτερόλεπτο. Τέτοια απαίτηση είναι πρακτικά αδύνατο για ένα ρεαλιστικό δίκτυο με μέση δυνατότητη στο εύρος των 10 με 100 Mbits το δευτερόλεπτο. 3.1 Επισκόπηση της συμπίεσης βίντεο Γνωρίζοντας, λοιπόν, πως η εικόνα συμπιέζεται ως σύνολο στατικών τμημάτων με τους γνωστούς τύπους πλεονασμού, στην περίπτωση του βίντεο, μια προφανή ιδέα είναι να εφαρμοστούν οι γνωστές τεχνικές κωδικοποίησης σε κάθε εικόνα ξεχωριστά για τη συνoλική έκταση του. Το τελευταίο, όντως, εφαρμόστηκε με το πρότυπο MJPEG, το οποίο κωδικοποιούσε κάθε πλαίσιο του βίντεο ως εικόνα JPEG. Από την άλλη, αγνοείται έτσι ένα νέο είδος πλεονασμού που εισάγει το στοιχείο του χρόνου, το χρονικό πλεονασμό. Με την αντίστοιχη λογική του χωρικού πλεονασμού εξηγείται και ο χρονικός. Όπως δηλαδή τα γειτονικά pixels σε μια μεμονωμένη εικόνα είναι σχετικά μεταξύ τους, έτσι και σε μια ακολουθία πλαισίων σε ένα βίντεο, υπάρχει επίσης συσχέτιση. Για παράδειγμα, σε ένα κομμάτι ενός βίντεο, μπορεί τα pixels μεταξύ γειτονικών πλαισίων να μην αλλάζουν σημαντικά, ή ακόμα και να παραμένουν σχεδόν ίδια. Τότε λέγεται ότι εμφανίζεται χαμηλής κίνηση μεταξύ των πλαισίων. Συνεπώς, ακούγεται πιο αποτελεσματικό να κωδικοποιούνται οι διαφορές μεταξύ πλαισίων όπως, για παράδειγμα, με εφαρμογή DPCM. Όντως μεταξύ ομοίων πλαισίων υπό συνθήκες χαμηλής κίνησης η διαφορά του ενός ως προς το άλλο θα παρουσιάζει μικρότερες τιμές έντασης και ως αποτέλεσμα θα κωδικοποιείται με λιγότερα bits.[1,σ ] Οι περιπτώσεις υψηλής κίνησης, που συνήθως αφορούν τη ύπαρξη ενός αντικειμένου στο βίντεο που μετακινείται, εμφανίζεται ή εξαφανίζεται μεταξύ πλαισίων αποτελούν την κύρια πρόκληση της κωδικοποίησης βίντεο. Το πλαίσιο διαφοράς τότε θα εμφανίζει στις ανόμοιες περιοχές μεγαλύτερο σφάλμα έναντι των ομοίων περιοχών. Η απαίτηση της κωδικοποίησης τότε αυξάνεται με απρόβλεπτο τρόπο. Η πιο ακραία περίπτωση είναι η ολική αλλαγή σκηνικού μεταξύ πλαισίων [1,σ ]. Φαίνεται, λοιπόν, ότι δεν αρκεί η απλή αφαιρετική μέθοδος. Για αυτό το λόγο, σχεδιάστηκε η μέθοδος πρόβλεψης και αντιστάθμισης κίνησης, motion estimation και motion compensation αντίστοιχα, που ακολουθεί στην επόμενη ενότητα. 3.2 Τμηματική Πρόβλεψη Πλαισίων και Αντιστάθμιση Κίνησης 21
22 Με δεδομένα τα πλαίσια Ν και Ν+1, όπου το πρώτο αποτελεί το πλαίσιο αναφοράς, ή reference frame, και το δεύτερο το πλαίσιο στόχου, ή target frame, η διαδικασία της πρόβλεψης, αρχικά, χωρίζει το πλαίσιο Ν+1 σε τμήματα, που λέγονται macroblocks, τα οποία με τη σειρά τους αποτελούνται από μικρότερα τμήματα τα blocks. Το πιο συχνό μέγεθος macroblock είναι το 16x16, όπου και αποτελείται από τέσσερα 8x8 blocks, αλλά γενικά εξαρτάται από το εκάστοτε πρότυπο. [5,24] Κάθε macroblock του πλαισίου Ν+1, ή macroblock στόχου, συγκρίνεται ξεχωριστά με την αντίστοιχη σε συντεταγμένες περιοχή του πλαισίου Ν, δηλαδή το macroblock αναφοράς, και προκύπτει ένα πρώτο σφάλμα, που ορίζεται ως το ελάχιστο. Η πιο συχνή μέθοδος μέτρησης του σφάλματος αυτού είναι το κλασικό μέσο τετραγωνικό σφάλμα, ενώ μπορούν να χρησιμοποιηθούν και άλλες μέθοδοι. Σε μια ορισμένη περιοχή αναζήτησης, ανάλογα με μια ακέραιη παράμετρο βήματος, το macroblock αναφοράς θα μετατοπιστεί κατά το κάθετο και οριζόντιο άξονα ξεχωριστά ή και ταυτόχρονα, εφόσον βέβαια το επιτρέπουν οι οριακές συνθήκες. Αν δηλαδή οι αρχικές συνταγμένες γραμμών είναι 1 έως 16, η μετατόπιση κατά δύο pixels θα φέρει το macroblock αναφοράς στις συντεταγμένες 3 έως 18. Στη συνέχεια, λοιπόν, το macroblock στόχου θα συγκριθεί με το νέο macroblock αναφοράς και θα προκύψει ένα νέο σφάλμα, το οποίο θα συγκριθεί με το αρχικό. Αν το νέο σφάλμα είναι μικρότερο τότε ορίζεται αυτό ως το ελάχιστο σφάλμα αλλιώς το υπάρχων ελάχιστο παραμένει ως έχει. Η παραπάνω διαδικασία θα επαναληφθεί με ένα νέο βήμα, έως ότου εξαντληθούν οι πιθανές μετατοπίσεις.[5,σ.24-25] Στο τέλος της διαδικασίας το βήμα που οδήγησε στο ελάχιστο σφάλμα αποθηκεύεται ως το διάνυσμα κίνησης, ή motion vector, με δύο συνιστώσες που εκφράζουν μετατόπιση κατά τον κάθετο και οριζόντιο άξονα αντίστοιχα. Συνήθως αρνητικό πρόσημο μιας συνιστώσας σημαίνει κάθετη κίνηση προς τα πάνω και οριζόντια προς τα αριστερά ενώ το θετικό πρόσημο, προφανώς, σημαίνει το αντίστροφο. Στη περιοχή επίσης με το μικρότερο σφάλμα, το macroblock του Ν αφαιρείται από το αντίστοιχο του Ν+1 και έτσι προκύπτει το macroblock διαφορά ή σφάλματος. Σαν τελικό αποτέλεσμα θα έχουν ένα συνολικό πλαίσιο διαφοράς, όπου σε κάθε macroblock αντιστοιχεί και ένα διάνυσμα κίνησης, όπου pixels και διανύσματα θα περάσουν εντέλει στο στάδιο κωδικοποίησης.[5,σ.24-25] Εικόνα 3.1 Πρόβλεψη και αντιστάθμιση κίνησης Όλα τα παραπάνω συνθέτουν τη διαδικασία πρόβλεψης, την αναζήτηση δηλαδή των πιο ομοίων τμημάτων μεταξύ δύο πλαισίων, και την αντιστάθμιση κίνησης, όπου με τη χρήση των διανυσμάτων κίνησης πάνω στο πλαίσιο Ν, δημιουργείται ένα πλαίσιο πρόβλεψης πιο κοντά στο πλαίσιο στόχο 22
23 και έτσι το τελικό πλαίσιο διαφοράς μπορεί να κωδικοποιηθεί στη θέση του πλαισίου στόχου, εξασφαλίζοντας μικρότερη απαίτηση σε bits αναπαράστασης. Η αντίστροφη διαδικασία είναι απλή, καθώς παίρνοντας το άθροισμα του πλαισίου διαφοράς με το αντισταθμισμένο πλαίσιο Ν, προκύπτει το πλαίσιο Ν Αλγόριθμοι αναζήτησης Στην ποιότητα της πρόβλεψης παίζει επίσης ρόλο και ο αλγόριθμος αναζήτησης. Παρακάτω ακολουθούν κάποιοι βασικοί αλγόριθμοι αναζήτησης: Εξαντλητική αναζήτηση, όπου για ένα δεδομένο σύνολο τιμών, που ορίζεται ως [-βήμα, βήμα] όπου βήμα η μέγιστη πιθανή τιμή μετατόπισης για κάθε άξονα. Για κάθε τιμή στο εύρος αυτό κάθε macroblock θα μετατοπιστεί προς όλες τις πιθανές κατευθύνσεις, κρατώντας σε κάθε επανάληψη το διάνυσμα που έδωσε ελάχιστο σφάλμα κριτηρίου. [1,273] Λογαριθμική αναζήτηση, όπου η λογική είναι παρόμοια με την παραπάνω με την κύρια διαφορά ότι υπάρχει κάθε βήμα είναι το μισό του προηγουμένου. Ξεκινώντας από την αρχική του θέση το macroblock θα μετατοπιστεί για ένα πρώτο βήμα x, με όλους τους πιθανούς συνδυασμούς για τους δύο άξονες, μέχρι να βρεθεί η πρώτη θέση που επιστρέφει το ελάχιστο κριτήριο σφάλματος. Στη συνέχεια, ξεκινώντας από τη νέα θέση η διαδικασία επαναλαμβάνεται για το μισό βήμα, x/2, μέχρι να εντοπίσει την επόμενη θέση. [1, ] Βελτιστοποίηση πρόβλεψης Υπάρχουν, βέβαια, περιπτώσεις που από το ένα πλαίσιο στο άλλο εμφανίζεται ή εξαφανίζεται ένα αντικείμενο, ή και αλλάζει ολόκληρη η σκηνή. Σε αυτή την περίπτωση η πρόβλεψη μπορεί να επιφέρει μεγαλύτερο σφάλμα άρα και περισσότερη πληροφορία από το να έμενε όπως έχει το macroblock. Μια απλή μέθοδος βελτιστοποίησης της πρόβλεψης αποτελεί η εισαγωγή μιας τιμής κατωφλίου, όπου στη περίπτωση που το σφάλμα μεταξύ δύο macroblock θα το ξεπεράσει, τότε απλά το macroblock αναφοράς αφήνεται ίδιο. Προκύπτει δηλαδή ένα πλαίσιο συνδυασμός του αρχικού της αναφοράς και του πλαισίου διαφοράς. Το αρνητικό της μεθόδου αυτής είναι ότι δεν υπάρχει τρόπος να είναι πάντα βέλτιστη η τιμή του κατωφλίου, άρα μπορεί να εφαρμοστεί μια διαδικασία επανάληψης για ποικίλες τιμές κατωφλίου μέχρι να βρεθεί η κατάλληλη για κάθε macroblock. Βέβαια, αυξάνεται έτσι και ο χρόνος εκτέλεσης και η πολυπλοκότητα του αλγορίθμου καθώς και η ανάγκη για επιπλέον πληροφορία για να σταλθεί στον αποκωδικοποιητή, με τη μορφή ειδικών σημαιών που θα δείχνουν, για ένα δεδομένο πλαίσιο διαφοράς, ποια macroblocks έμειναν ίδια και ποια όχι Πρόβλεψη και αντιστάθμιση σε υποστοιχειακό επίπεδο Μια επιπλέον μέθοδος βελτίωσης του τελικού αποτελέσματος της πρόβλεψης κίνησης αποτελεί η χρήση παρεμβολής στο πλαίσιο αναφοράς ώστε να πάρουμε τις τιμές μεταξύ των εικονοστοιχείων 23
24 ανά macroblock. Το υποστοιχειακό επίπεδο ή subpixel μπορεί να σημαίνει ακρίβεια μισού pixel, ενός τετάρτου του pixel και ούτω καθεξής. Ουσιαστικό, το διακριτό σήμα του macroblock της εικόνας με τη χρήση οποιαδήποτε μεθόδου παρεμβολής μετατρέπεται σε ένα συνεχές, καθώς εμφανίζονται όλες οι ενδιάμεσες τιμές των αρχικών δειγμάτων. Η ακρίβεια που επιλέγεται καθορίζει το βαθμό της μετατόπισης, shift, ώστε να προκύψει ένα νέο macroblock, και πάλι διαστάσεων 16x16, που περιέχει τα ενδιάμεσα αυτά δείγματα. Μπορεί να θεωρηθεί λοιπόν ως μια νέα δειγματοληψία.[8] Η διαδικασία δέχεται ως είσοδο κάθε macroblock και τα διανύσματα κίνησης από την αρχική πρόβλεψη κίνησης, κατά ακέραιο pixel. Έτσι για ένα macroblock με τα αντίστοιχα αρχικά διανύσματα κεντράρει στην ήδη καλύτερη πιθανή περιοχή του πλαισίου αναφοράς, ακρίβειας ακέραιου pixel. Τώρα, όμως, macroblock αναφοράς δέχεται padding και παρεμβολή, για παράδειγμα γραμμική ή δι-γραμμική. Στη συνέχεια, για κάθε βήμα μετατόπισης της δεδομένης ακριβείας δειγματολειπτούνται οι νέες τιμές στο νέο macroblock αναφοράς, το οποίο και συγκρίνεται με το macroblock στόχου. Και πάλι σύμφωνα με κριτήριο σφάλματος επιλέγεται η πιο κατάλληλη μετατοπισμένη θέση. Το τελικό αποτέλεσμα είναι ένα νέο σύνολο διανυσμάτων κίνησης μαζί με το νέο πλαίσιο διαφοράς. Η παραπάνω διαδικασία αυξάνει την τελική ακρίβεια της πρόβλεψης, προσφέροντας αποτελεσματικότερη συμπίεση. Μειονεκτήματα της μεθόδου είναι η αυξημένη απαίτηση για κωδικοποίηση των διανυσμάτων κίνησης κινητής υποδιαστολής καθώς και πιθανά σφάλματα παρεμβολής, όπως η εμφάνιση θολούρας ή η απώλεια αντίθεσης στο πλαίσιο πρόβλεψης.[8] Εικόνα 3.2 Υποστοιχειακό επίπεδο και ακρίβειες pixel. 3.3 Είδη Πλαισίων Όπως αναφέρθηκε προηγουμένως κατά την πρόβλεψη κίνησης έχουμε ένα λεγόμενο πλαίσιο αναφοράς και ένα πλαίσιο στόχου από τα οποία προκύπτει ένα πλαίσιο διαφοράς για κωδικοποίηση. Αυτό το είδος εξάρτησης μεταξύ δυο πλαισίων σίγουρα περιπλέκει τη διαδικασία αποκωδικοποίησης, καθώς το πλαίσιο στόχος θα πρέπει να είναι έτοιμο πριν την αποκωδικοποίηση του πλαισίου αναφοράς, αφού χρειάζεται για το άθροισμα με το πλαίσιο διαφοράς. Προκύπτει λοιπόν και η ανάγκη για κατηγορίες πλαισίων, οι οποίες ορίζονται ως εξής: Ι frames, τα οποία αποτελούν τα πλαίσια αναφοράς. Κωδικοποιούνται ακριβώς με τον ίδιο τρόπο με το πρότυπο jpeg έτσι ώστε να μπορούν να αποκωδικοποιηθούν ανεξάρτητα. Η περίπτωση αυτή αποκαλείται και ενδοπλαισιακή κωδικοποίηση ή intra-coding. Το αρνητικό είναι ότι περιέχουν μεγαλύτερη ποσότητα πληροφορίας από τις άλλες κατηγορίες αλλά είναι αναγκαίο κακό.[5,σ.26] 24
25 P frames, είναι ουσιαστικά τα πλαίσια διαφοράς ενός πλαισίου αναφοράς και ενός πλαισίου στόχου, τύπου Ι ή τύπου P, τα οποία έχουν ήδη προηγηθεί. Μετά τη διαδικασία πρόβλεψης και αντιστάθμισης κίνησης, η διαδικασία κωδικοποίησης του πλαισίου διαφοράς είναι ολόιδια με αυτή των πλαισίων Ι με μόνη διαφορά και τα διανύσματα κίνησης που συμπεριλαμβάνονται στη συνολική πληροφορία του πλαισίου P καθώς και διαφορετικούς πίνακες κβάντισης. Αντίστοιχα με παραπάνω, η διαδικασία αποκαλείται κωδικοποίηση μεταξύ πλαισίων ή inter-coding.[5,σ.26] B frames, είναι παρόμοια με τα P, με τη διαφορά ότι συγκρίνονται με πλαίσια στόχους τόσο παρελθοντικά όσο και μελλοντικά. Σε επίπεδο macroblock δηλαδή γίνεται σύγκριση μεταξύ του αντίστοιχου macroblock ενός προηγούμενου Ι ή P πλαισίου και ομοίως με αυτό ενός επόμενου I ή P, και επιλέγεται το πιο μικρό σφάλμα από τα δύο. Κατά την αποκωδικοποίηση θα χρειαστούν και ειδικά bits σημαίας που θα δείχνουν αν το κάθε macroblock διαφοράς προέκυψε από προηγούμενο ή επόμενο frame. Από τη μία, λοιπόν, υπάρχει πιθανότητα επίτευξης συνολικά χαμηλότερου σφάλματος άρα και μείωση της γενικής πληροφορίας αλλά με αυξημένη πολυπλοκότητα και χρόνο εκτέλεσης.[5,26] 3.4 Group of Pictures Ένα σύνολο εικόνων ή group of pictures, GOP, είναι ειδική δομή η οποία ορίζει τη σειρά με την οποία στοιχίζονται τα πλαίσια Ι, P και Β. Η ροή του βίντεο κατά την είσοδο στον κωδικοποιητή ουσιαστικά αποτελείται από ένα σύνολο από GOPs, που καθορίζουν πόσα πλαίσια αναφοράς και πλαίσια διαφοράς θα κωδικοποιηθούν. Με αντίστοιχη σειρά πραγματοποιείται και η αποκωδικοποίηση των συνόλων αυτών. Ένα συχνό παράδειγμα συνόλου είναι το IBPBPI, ή το IPPPI, όπου κάθε νέο Ι πλαίσιο αποτελεί και την αρχή του επόμενου gop. Το σύνολο των πλαισίων από το αρχικό Ι μέχρι το επόμενο, ονομάζεται μέγεθος του GOP. Κατά την αποκωδικοποίηση, τα GOPS προσφέρουν ευελιξία καθώς κάθε σύνολο πλαισίων διαφοράς εξαρτάται πάντα από ένα ανεξάρτητο πλαίσιο αναφοράς που βρίσκεται σε μια γνωστή θέση στη ροή. Έτσι σε περίπτωση σφάλματος ο αποκωδικοποιητής μπορεί να ανατρέξει στο τελευταίο πλαίσιο αναφοράς και να προσπαθήσει ξανά. Επιπλέον, υπάρχει και η δυνατότητα ο αποκωδικοποιητής να πηδήξει σε διαφορετικά σημεία της ροής, δηλαδή σε κάποιο άλλο GOP, και να συνεχίσει από εκεί ομαλά τη λειτουργία του ή να διορθώσει πιθανό σφάλμα χωρίς να πρέπει να ξεκινήσει από την αρχή της ροής. [1, ] Εικόνα 3.3 Παράδειγμα ενός GOP. 3.5 Πρότυπα κωδικοποίησης βίντεο, MPEG/MPEG-2 Το πρότυπο MPEG-1 αποτελεί από τα πιο διαδεδομένα και γνωστά πρότυπα συμπίεσης ήχου και βίντεο. Δημιουργήθηκε από την ομάδα MPEG, ή Moving Picture Experts Group και έγινε αποδεκτό το Νοέμβριο του 1991 από την ISO. Χρησιμοποιείται κυρίως για τη συμπίεση ήχου-βίντεο για 25
26 αποθήκευση σε CD καθώς και για μετάδοση με ροή γύρω 1.5 Mbits/s, ποιότητας γενικά συγκρίσιμης με το αναλογικό VHS. [1,σ.277] Το πρότυπο MPEG-2 είναι η συνέχεια του πρώτου προτύπου το οποίο έγινε αποδεκτό με τη σειρά του το Σχεδιάστηκε τόσο για συμπίεση όσο και για μετάδοση ροών ήχου και βίντεο. Υποστηρίζει μεγαλύτερο εύρος ζώνης από τον προκάτοχο του, ροή δεδομένων από 4Mbps με 9Mbps και γενικά καλύτερη ποιότητα, καθώς χρησιμοποιείται και για μετάδοση βίντεο υψηλής ανάλυσης.[1,σ.278] Η βασική λειτουργία και των δύο προτύπων είναι ουσιαστικά ίδια και δεν αποτελεί παρά μια σύνοψη όλων των ενοτήτων του κεφαλαίου αυτού. Έχοντας, λοιπόν, μια ροή βίντεο προς τον κωδικοποιητή, κάθε GOP που περιέχει Ι, P ή Β πλαίσια κωδικοποιεί αρχικά το κάθε πλαίσιο ενδοπλαισιακά ή μεταξύ πλαισίων αναλόγως της κατηγορίας του, και μεταφέρει τη νέα κωδικοποιημένη ροή δυαδικών ψηφίων στον αποκωδικοποιητή για την ανάκτηση του βίντεο. Όπως και στο JPEG, χρησιμοποιούνται ξεχωριστοί πίνακες κβάντισης για τις συνιστώσες φωτεινότητας και χρώματος του κάθε πλαισίου, αλλά και για τις διαφορετικές κατηγορίες πλαισίων. Στους πίνακες Α.2 και Α.3 του παραρτήματος Α, φαίνονται οι βασικοί αυτοί πίνακες. Με σταθερούς τους πίνακες αυτούς, χρησιμοποιείται και πάλι ένας αριθμός που πολλαπλασιάζεται με κάθε πίνακα ώστε να αυξήσει ή ελαττώσει τους συντελεστές ώστε να προκύψει μεγαλύτερος ή μικρότερος βαθμός συμπίεσης αντίστοιχα. [1,σ.279] Στη συνέχεια, ακολουθεί η κωδικοποίηση χωρίς απωλειών των κβαντισμένων συντελεστών, η οποία όπως στο JPEG, βασίζεται στο συνδυασμό των τεχνικών Ηuffman και RLE, με διαφορετικούς πινάκων με μοναδικούς variable length ή μεταβλητού μήκους κώδικες. Όπως και προηγουμένως στο JPEG, οι DC συντελεστές κωδικοποιούνται με βάση το μέγεθος τους σε bits και σύμφωνα με τον πίνακα Β.2 τους αντιστοιχούν και οι κατάλληλη prefix κωδικοί που δηλώνουν το μέγεθος αυτό. Η τελική συμβολοσειρά του DC όρου θα αποτελείται από το μοναδικό κωδικό και την αναπαράσταση της τιμής σε δυαδικό σύστημα. Για τους AC όρους αφού δεχθούν ζιγκ ζαγκ σάρωση και RLE κωδικοποίηση μετριέται το σύνολο των μηδενικών πριν κάθε άλλο μη μηδενικό όρο. Ανάλογα με τον αριθμό των μηδενικών και την ίδια την τιμή του όρου αντιστοιχεί και μια ολική, μοναδική συμβολοσειρα που περιέχει ως το δεξιότερο bit το πρόσημο του κωδικοποιημένου αριθμού. Στο πίνακα Β.3 φαίνεται ο συνολικό πίνακας με τις συμβολοσειρές. Η διαφορά με τον αντίστοιχο του jpeg είναι ακριβώς ότι περιέχεται μέσα στο κώδικα αναπαράστασης η ίδια η τιμή του αριθμού. Και προφανώς ο αποκωδικοποιητής διαβάζει τους μοναδικούς κώδικες και αντίστοιχα βγάζει την ακέραιη τιμή με το κατάλληλο πρόσημο. [1,σ ] Πέρα από την πληροφορία της κάθε εικόνας μεταφέρονται και ειδικά bits που ενημερώνουν τον αποκωδικοποιητή για το πότε ξεκινάει και τελειώνει ένα GOP, στη συνέχεια μέσα σε ένα GOP ποια πλαίσια ανήκουν σε κάθε κατηγορία, πότε αρχίζουν και πότε τελειώνουν, και τέλος μέσα σε κάθε εικόνα ορίζει και πάλι αρχή και τέλος για κάθε macroblock, και το ίδιο για τα blocks του κάθε macroblock. Επίσης περιέχεται και με αντίστοιχα bits ό,τι άλλη πληροφορία χρειάζεται ο αποκωδικοποιητής, όπως τα διανύσματα κίνησης για τα P και B πλαίσια, τις τιμές του κβαντιστή, το bit rate, ειδικές σημαίες, οι διαστάσεις των πλαισίων, των macroblocks και των blocks και άλλα. Αυτά τα bits αποτελούν τις επικεφαλίδες ή headers και γενικά σαν συνολικό μέγεθος πληροφορίας είναι αμελητέα σε σχέση με μια μεμονωμένη εικόνα. Επίσης, χρησιμοποιείται ένας buffer ώστε να αποθηκεύεται κάθε ανακατασκευασμένο πλαίσιο Ι ώστε την πληροφορία αυτή να την παίρνει τόσο ο κωδικοποιητής για τη διαδικασία πρόβλεψης και αντιστάθμισης κίνησης όσο και ο αποκωδικοποιητής για την αντίστροφη διεργασία. 26
27 Κάποια επιπλέον χαρακτηριστικά του MPEG είναι η δυνατότητα πρόβλεψης και αντιστάθμισης σε υποστοιχειακό επίπεδο με ακρίβεια μισού εικονοστοιχείου ενώ διαθέτει και μηχανισμό ελέγχου ροής των δεδομένων έτσι ώστε κατά τη μετάδοση να μπορεί να προσαρμόζεται γύρω από τις απαιτήσεις συμπίεσης και την διατήρηση μιας επιθυμητής ποιότητας. Επίσης ορίζει ειδικές τομές, που αποτελούνται από ένα σύνολο macroblock τις οποίες μπορεί να κβαντίσει με διαφορετικές τιμές. Έτσι υπάρχει ευελιξία κατά τον έλεγχο του ρυθμού δεδομένων καθώς και μέσα σε ένα πλαίσιο ενδέχεται κάποιες περιοχές να μπορούν να συμπιεσθούν περισσότερο ή λιγότερο. Από την άλλη, το MPEG-2 έχει όλα τα παραπάνω αλλά προσθέτει και μια νέα λειτουργία, τη κλιμακούμενη κωδικοποίηση ή scalable encoding, η οποία περιλαμβάνει την προεπεξεργασία του βίντεο σε ένα βασικό στρώμα και σε ένα εμπλουτισμένο, τα οποία κωδικοποιούνται ξεχωριστά σε διακριτές ροές. Έτσι ένας αποκωδικοποιητής θα ανακτήσει σίγουρα το βασικό στρώμα με μια αρχική, ικανοποιητική ποιότητα και άμα έχει μετά τη δυνατότητα θα ανακτήσει και την επόμενη ροή που θα προσφέρει και περισσότερη ποιότητα στο τελικό αποτέλεσμα.[1, ] Εικόνα 3.4 Παράδειγμα κωδικοποίησης με MPEG, όπου πάνω δεξιά φαίνεται το πλαίσιο στόχου, πάνω αριστερά το πλαίσιο αναφοράς ενώ κάτω δεξιά και αριστερά είναι το πλαίσιο πρόβλεψης και σφάλματος αντίστοιχα. 27
28 ΚΕΦΑΛΑΙΟ 4 - Η μέθοδος BLU-ME Η κλασική μέθοδος πρόβλεψης/αντιστάθμισης κίνησης κάνει την εξής υπόθεση: για ένα δεδομένο block από την εικόνα Α, που ορίζεται ως εικόνα αναφοράς, και ένα από την εικόνα Β, η εικόνα στόχου, το block Α θα υποστεί παρεμβολή και ως συνεχές σήμα θα δειγματοληφθεί για νέες διακριτές κατά μια μετατόπιση σε υποστοιχειακό επίπεδο. Το μετατοπισμένο block θα προσεγγίζει το block Β με το μικρότερο δυνατό σφάλμα. Σε ένα GOP η πλειοψηφία πλαισίων θα είναι τύπου P ή B τα οποία θα προσεγγίζονται από 1 ή 2 πλαίσια αναφοράς αναφοράς αντίστοιχα. Η αντιμετώπιση των διάφορων πλαισίων, όπως φαίνεται, δεν μπορεί να θεωρηθεί συμμετρική. Η μέθοδος BLU-ME, Block Unshifting-Motion Estimation, προτείνει μια εναλλακτική υπόθεση, σύμφωνα με την οποία για τα ίδια δεδομένα blocks των πλαίσιων Α και Β θα υπάρχει ένα τρίτο ιδεατό block Ι, το οποίο με συγκριμένες μετατοπίσεις θα προσεγγίζει τα blocks των A και B, και πάλι σε υποστοιχειακό επίπεδο. Και τα δύο πλαίσια δηλαδή θα δέχονται την ίδια αντιμετώπιση. Υπονοείται ότι μεταξύ των Α και Β έχει ήδη ακολουθήσει πρόβλεψη και αντιστάθμιση για ακρίβεια ακέραιου pixel, δηλαδή τα αντίστοιχα blocks τους αναπαριστούν μια όσο γίνεται ίδια εικόνα. Το ιδεατό block I κατασκευάζεται με την εφαρμογή της τεχνικής block unshifting πάνω στα block των A και Β. Στο υπόλοιπο του κεφαλαίου θα ακολουθήσει μια σύντομη ανάλυση της τεχνικής αυτής, που βασίζεται στην αντιστροφή της διαδικασίας της μετατόπισης και η περιγραφή του αλγορίθμου της μεθόδους BLU-ME. 4.1 Αντιστροφή της μετατόπισης ή unshifting Σύμφωνα με την ανάλυση στο προηγούμενο κεφάλαιο, η πρόβλεψη κίνησης σε υποστοιχειακό επίπεδο αποτελείται από την μετατροπή του διακριτού σήματος της ψηφιακής εικόνας σε ένα συνεχές σήμα, με τη χρήση γραμμικής παρεμβολής, και την μετέπειτα νέα δειγματοληψία τιμών κατά κάποιο βήμα μετατόπισης, όπως για μισό ή για ένα τέταρτο του pixel. Πιο απλουστευμένα, αν θεωρηθεί ένα διάνυσμα a, που αποτελεί γραμμή μιας εικόνας. Αν το διάνυσμα αυτό είναι μήκους Ν τότε μετά τη μετατόπιση του θα προκύψει ένα νέο διάνυσμα b, μήκους Ν-1. Προκειμένου να γίνει η κατάλληλη μετατόπιση ώστε από το b να προκύψει το αρχικό a, παρουσιάζονται προβλήματα καθώς από Ν-1 δείγματα πρέπει να εμφανιστούν κάποια συγκεκριμένα Ν δείγματα. Πρόκειται δηλαδή για ένα σύστημα Ν-1 εξισώσεων με Ν αγνώστους. Επιπλέον υπάρχουν άπειρα πιθανά διανύσματα a που μπορούν να μετατοπιστούν για να προκύψει το ίδιο διάνυσμα b. Η τεχνική του unshifting προτείνει λοιπόν ένα κριτήριο επιλογής ενός από των πιθανών διανυσμάτων a που θα είναι η πιο κοντινή αρχική μορφή του b. Το κριτήριο αυτό βασίζεται στον υπολογισμό της χωρικής συχνότητας των διανυσμάτων με τον τύπο, N i d ( a )= ( ai=1 ai ) ( 1 ) =a1 2 a2+ 3 a3 + ( 1 ) i=2 N +1 an. Επομένως επιλέγεται η αρχική εικόνα a με χωρική συχνότητα πληροφορίας πιο όμοια με το b. 28
29 4.2 Ο αλγόριθμος BLU-ME Οι εικόνες εισόδου, λοιπόν, Α και Β έχουν ήδη υποστεί μεταξύ τους πρόβλεψη και αντιστάθμιση κίνησης σε ακρίβεια ακέραιου pixel. Ο αλγόριθμος BLU-ME εκτελείται για κάθε block του Β και το αντίστοιχο, μετατοπισμένο κατά ακέραια διανύσματα, block του Α. Υποθέτει επίσης την ύπαρξη του ιδεατού block, έτσι ώστε όταν μετατοπιστεί κατά διανύσματα (xα,yα) θα προσεγγίζει το block του Α ενώ όταν μετατοπιστεί κατά (xβ,yβ) θα προσεγγίζει το block του Β. Επομένως, προκύπτουν δύο διανύσματα κίνησης (xα,yα) και (xβ,yβ) μεταξύ των αρχικών blocks και του ιδεατού. Με κριτήριο το συνολικό μέσο τετραγωνικό σφάλμα μεταξύ των shifted blocks και των αρχικών, επαναλαμβάνει τη διαδικασία για διαφορετικές μετατοπίσεις μέχρι να βρεθούν τα (xα,yα) και (xβ,yβ) που αντιστοιχούν στο ελάχιστο σφάλμα. Οι νέες τιμές των διανυσμάτων υπολογίζονται με τον αλγόριθμο NelderMead[9][10]. Η μέθοδος εφαρμόζεται ομοίως για όλα τα υπόλοιπα block των Α και Β ώστε να προκύψει το συνολικό ιδεατό πλαίσιο Ι με όλα τα τελικά ζευγάρια διανυσμάτων κίνησης, (xα,yα) και (xβ,yβ), ανά block [8]. Ως τονισμένα Α, Β και Ι εννοούνται τα blocks των πλαισίων Α, Β και Ι αντίστοιχα. Επομένως ο αναλυτικός αλγόριθμος της BLU-ME, σύμφωνα με την παραπάνω περιγραφή, αποτελείται από τα εξής βήματα: 1. Οι τιμές των (xα,yα) και (xβ,yβ) αρχικοποιούνται με την τιμή Σε κάθε επανάληψη του αλγορίθμου, τα blocks Α και B, αντι-μετατοπίζονται, (unshifted), κατά (xα,yα) και (xβ,yβ) αντίστοιχα. Ο μέσος όρος των παράγωγων, unshifted blocks δημιουργεί το ιδεατό block I. To ιδεατό block Ι μετατοπίζεται κατά (xα,yα) και (xβ,yβ) ώστε να παράγει τα blocks Α και Β, τις προσεγγίσεις δηλαδή των A και Β αντίστοιχα. Υπολογίζονται τα μέσα τετραγωνικά σφάλματα μεταξύ των Α,A' και B,B' και προστίθενται ώστε να προκύψει το κριτήριο για την παύση της διαδικασίας. Ελέγχεται το κριτήριο και αν δεν ικανοποιηθεί τότε μετατοπίζονται ξανά τα αρχικά blocks με ανανεωμένα διανύσματα κίνησης, σύμφωνα με τον αλγόριθμο Nelder-Mead, και υπολογίζεται εκ νέου το ιδεατό block και το επόμενο κριτήριο. Εφόσον ικανοποιηθεί το κριτήριο, αν υπολογίσει αμελητέα διαφορά με το προηγούμενο σφάλμα, τότε ο αλγόριθμος επιστρέφει τα τελικά διανύσματα (x Α,yΑ) και (xβ,yβ) και το τελικό ιδεατό block.[8] 29
30 KΕΦΑΛΑΙΟ 5 - ΥΛΟΠΟΙΗΣΗ Η υλοποίηση πραγματοποιήθηκε στο προγραμματιστικό περιβάλλον της Matlab. Χωρίζεται σε δύο κύρια τμήματα: Το πρώτο αφορά τη συγγραφή κώδικα για το σχεδιασμό ενός προτύπου κωδικοποίησης/αποκωδικοποίησης βασισμένο όσο πιο πιστά στο πρότυπο mpeg, σύμφωνα με βιβλιογραφία που κυκλοφορεί ανοικτά στο διαδίκτυο και σε συγγράμματα. Το δεύτερο αποτελείται από την υλοποίηση αντίστοιχου πρότυπου, αυτή τη φορά με πυρήνα τη μέθοδο BLU-ME που περιγράφηκε στην προηγούμενη ενότητα, καθώς και τη συγγραφή κώδικα για την εξαγωγή και σύγκριση των τελικών αποτελεσμάτων. 5.1 Κώδικας για το πρότυπο MPEG Η υλοποίηση του MPEG χωρίζεται σε διάφορες συναρτήσεις οι οποίες θα αναλυθούν παρακάτω. Η γενική ροή του κώδικα ξεκινάει με το script, codec, το οποίο καλεί για κάθε πλαίσιο εισόδου τις συναρτήσεις encodei και encodep οι οποίες με τη σειρά τους εκτελούν το κύριο αλγόριθμο του MPEG όπως αυτός παρουσιάστηκε στο προηγούμενο κεφάλαιο. Με περισσότερη λεπτομέρεια εξηγείται η λειτουργία τους στις επόμενες ενότητες Συνάρτηση για την υλοποίηση του codec Η συνάρτηση codec δέχεται ως είσοδο το ψηφιακό βίντεο τα πλαίσια του οποίου περιέχονται σε ειδική δομή τύπου structure. Για την εξαγωγή των πλαισίων από ένα βίντεο υπάρχουν ειδικές συναρτήσεις της Μatlab, ανάλογα και με το είδος πάντα του βίντεο. Η δεύτερη είσοδος είναι οι μεταβλητές που ρυθμίζουν την τελική ποιότητα της συμπίεσης, όπως οι συντελεστές κβάντισης, το βήμα της πρόβλεψης κίνησης και ειδική σημαία για τη μέθοδο πρόβλεψης, δηλαδή σε ακρίβεια ακεραίου ή μισού εικονοστοιχείου. Τέλος η τρίτη είσοδος είναι το μοτίβο που θα ακολουθούν τα GOPs, ορισμένο ως string με κατάλληλο συνδυασμό των χαρακτήρων, I, P ή B. Το κύριο σώμα του αλγορίθμου διαβάζει πρώτα το μήκος σε χαρακτήρες του μοτίβου και εκτελεί ένα βρόγχο επανάληψης για το σύνολο των εικόνων με βήμα το μήκος αυτό. Σε κάθε επανάληψη, στη συνέχεια, εκτελεί ένα δεύτερο βρόγχο επανάληψης όπου σε κάθε πλαίσιο αντιστοιχεί και ένα τύπο πλαισίου από το ορισμένο GOP. Για παράδειγμα, με είσοδο το μοτίβο IPPP, για κάθε 4 εικόνες του συνόλου πλαισίων, η πρώτη θα παίρνει τον τύπο Ι και οι υπόλοιπες το P. Μετά, η I εικόνα κωδικοποιείται με ειδική συνάρτηση που επιστρέφει την αποκωδικοποιημένη εικόνα. Έτσι όταν έρθει η σειρά του πλαισίου P θα γίνει, μέσω αντίστοιχης συνάρτησης, κατάλληλη κωδικοποίηση με αναφορά το αποκωδικοποιημένο πλαίσιο Ι, όπως ορίζεται και στη θεωρία. Σε περίπτωση που βρεθεί ένα πλαίσιο B, για παράδειγμα με μοτίβο ΙBPBP, γίνεται μια διαδικασία pre-emption, όπου το Β, και κάθε άλλο Β που θα το ακολουθήσει, θα μείνουν στην άκρη ώσπου να έρθει το επόμενο P πλαίσιο. Αφού κωδικοποιηθεί το P πλαίσιο με αναφορά στο αρχικό πλαίσιο Ι, θα αποκωδικοποιηθεί αμέσως μετά και τότε τα πλαίσια Β επανέρχονται στο προσκήνιο όπου και θα κωδικοποιηθούν με την κανονική τους σειρά με βάση τα δύο πλαίσια αναφοράς. Πρακτικά οι δείκτες των πλαισίων που αντιστοιχούν στα Β αποθηκεύονται σε ένα διάνυσμα και ενεργοποιείται 30
31 μια ειδική σημαία όπου με σχέση λογικού AND με την αντίστοιχη σημαία ότι είναι έτοιμο το αμέσως επόμενο P πλαίσιο, θα εκκινήσει το βρόγχο κωδικοποίησης των Β. Οι σημαίες και το διάνυσμα μηδενίζονται και η σάρωση του επόμενου πλαισίου συνεχίζεται από το τελευταίο P μέχρι το τέλος του GOP. Τέλος αποκωδικοποιούνται και τα B πλαίσια, και κάθε ένα ανακατασκευασμένο αποθηκεύεται σε μια δομή structure που είναι και η έξοδος του αλγορίθμου Συνάρτηση για τη κωδικοποίηση των Ι πλαισίων Η συνάρτηση αυτή αναλαμβάνει την κωδικοποίηση των Ι πλαισίων. Βασίζεται στον αλγόριθμο του JPEG, με τη διαφορά στους βασικούς πίνακες κβάντισης που χρησιμοποιούνται από τα δύο πρότυπα (πίνακες Α.2 και Α.3). Μια αρχική υλοποίηση του κώδικα δημιουργήθηκε από το μηδέν αλλά μια αντίστοιχη που βρέθηκε στο σύγγραμα [3, ] ήταν αρκετά πιο ολοκληρωμένη άρα προσαρμόστηκε καταλλήλως. Αρχικά, λοιπόν, γίνεται μετατροπή της εικόνας εισόδου σε τύπο double της Μatlab, καθώς συνήθως είναι τύπου uint8, δηλαδή ακέραιοι μεγέθους 8 bit. Αν η εικόνα έχει και χρωματικές συνιστώσες γίνετα και αντίστοιχη μετατροπή από το χώρο RGB στο YCbCr, με ειδική συνάρτηση της Μatlab. Στη συνέχεια οι πίνακες των χρωματικών συνιστωσών δέχονται υποδειγματοληψία, ουσιαστικά με μέθοδο αλλαγής των διαστάσεων τους και τέλος κάθε συνιστώσα αποθηκεύεται σε ξεχωριστές μεταβλητές. Στη συνέχεια, ξεκινώντας από τη συνιστώσα φωτεινότητας, με χρήση βρόγχων επανάληψης για κάθε block 8x8 της συνιστώσας εφαρμόζεται μετασχηματισμός DCT με τη χρήση της συνάρτησης dct2 της Matlab, που είναι ειδικά σχεδιασμένη για πίνακες ΜxN. Το μετασχηματισμένο block διαιρείται με το πίνακα κβάντισης, πολλαπλασιασμένο με το συντελεστή κβάντισης. Ο DC όρος του κβαντισμένου block εισέρχεται σε ειδική συνάρτηση που υπολογίζει, σύμφωνα με τον κατάλληλο πίνακα Ηuffman (Β.2), πόσα bits του αντιστοιχούν. Οι AC όροι με τη σειρά τους περνάνε πρώτα σε συνάρτηση που τους σαρώνει με ζιγκ ζαγκ τρόπο και τους επιστρέφει σε μορφή διανύσματος, το οποίο εισέρχεται σε αντίστοιχη συνάρτηση που υπολογίζει τα συνολικά bits αναπαράστασης, σύμφωνα με τη λογική που εξηγήθηκε σε προηγούμενα κεφάλαια. Η ίδια διαδικασία ακολουθεί και για τις συνιστώσες χρώματος. Τέλος, οι έξοδοι είναι τα συνολικά bits όλων των συνιστωσών, καθώς και ένα πλαίσιο που αποτελείται από τις αποκωδικοποιημένες συνιστώσες. Να σημειωθεί ότι η αποκωδικοποίηση των χρωματικών περιλαμβάνει και την επιστροφή τους στις αρχικές διαστάσεις με μέθοδο παρεμβολής. Οι συναρτήσεις υπολογισμού των bits αναπαράστασης αναλύονται σε επόμενη ενότητα Συναρτήσεις για τη κωδικοποίηση των P και Β πλαισίων Η συνάρτηση encodep βασίζεται στην encodei με τη διαφορά ότι πριν τη διαδικασία συμπίεσης δημιουργείται πρώτα το πλαίσιο διαφοράς. Ως εισόδους παίρνει το πλαίσιο στόχου, το πλαίσιο αναφοράς Ι, το βήμα της πρόβλεψης, την τιμή του threshold, συντελεστή κβάντισης για το πλαίσιο Ι, συντελεστή κβάντισης για το πλαίσιο διαφοράς και μια σημαία που δηλώνει αν θα γίνει πρόβλεψη με ακρίβεια ενός ή μισού pixel. Άρα όπως πριν το πλαίσιο στόχου δέχεται χρωματική επεξεργασία ή απλά γίνεται τύπου double ανάλογα με το αν είναι RGB ή grayscale. Στη συνέχεια, το πλαίσιο στόχου, με βρόγχους επανάληψης, χωρίζεται σε macroblocks, διαστάσεων 16x16. Κάθε macroblock εισέρχεται μαζί με τις συντεταγμένες του, δηλαδή δύο διανύσματα που δηλώνουν αριθμούς γραμμών και στηλών, το πλαίσιο αναφοράς, τις τιμές βήματος και του κατωφλίου στη συνάρτηση motion. 31
32 Η motion αναλαμβάνει να κάνει την πρόβλεψη και αντιστάθμιση κίνησης ένα macroblock τη φορά. Ο αλγόριθμος αναζήτησης είναι ο εξαντλητικός, όπου για το δεδομένο βήμα εκτελεί δύο βρόγχους επανάληψης, μια για κάθε άξονα, για τις τιμές [-βήμα, βήμα]. Σύμφωνα με τις συντεταγμένες που δέχεται αντισταθμίζει το αντίστοιχο macroblock του πλαισίου αναφοράς και υπολογίζει το σφάλμα του από το macroblock στόχου με τη μέθοδο του μέσου τετραγωνικού σφάλματος. Εξαντλεί όλες τις επαναλήψεις και καταλήγει στα διανύσματα κίνησης που δίνουν το μικρότερο σφάλμα, άρα και με αυτά αφαιρεί κανονικά το αντισταθμισμένο macroblock αναφοράς από αυτό του στόχου. Σε περίπτωση που το τελικό σφάλμα είναι πάλι μεγαλύτερο του threshold, τότε το αρχικό macroblock στόχου μένει ίδιο, δηλαδή είναι I-macroblock. Σε αυτή την περίπτωση η σημαία παίρνει τιμή 1 αλλιώς μένει 0. Συνοψίζοντας έχει ως εξόδους το τελικό macroblock διαφοράς ή το αρχικό στόχου, τα αντίστοιχα διανύσματα κίνησης, το τελικό υπολογισμένο σφάλμα, που θα φανεί η χρήση του σε λίγο, και μια σημαία, για να ενημερώνει τον αποκωδικοποιητή σχετικά με το αποτέλεσμα της σύγκρισης με το κατώφλι. Στην έξοδο της motion, σε περίπτωση που το macroblock είναι τύπου Ι τότε ορίζεται ένας πίνακα κβαντισμού, διαστάσεων ίδιου με των πλαισίων, στις αντίστοιχες 16x16 συντεταγμένες το κατάλληλο πίνακα κβαντισμού για τα 4 block του macroblock αυτού, πολλαπλασιασμένου με το συντελεστή κβαντισμού του Ι. Αντίστοιχα αν το macroblock είναι τύπου P, ο πίνακας κβάντισης παίρνει την τιμή του κβαντιστή των P πλαισίων, πολλαπλασιασμένο με τον συντελεστή κβαντισμού του P. Παράλληλα τα macroblock συνθέτουν σιγά σιγά το νέο πλαίσιο διαφοράς/σφάλματος. Σημειώνεται πως η διαδικασία πρόβλεψης και αντιστάθμισης γίνεται μόνο για τη συνιστώσα φωτεινότητας, και απλά αφαιρούνται τα χρώματα κατά τη τελική επιλογή διανυσμάτων κίνησης. Επίσης αν η σημαία για την ακρίβεια πρόβλεψης ισούται με 2, τότε καλείται η συνάρτηση exhaustsp που με είσοδο το συνολικό πλαίσιο διαφοράς, το πλαίσιο αναφοράς και τα διανύσματα κίνησης εκτελεί την ίδια διαδικασία κατά μισό pixel (μόνο για τα P macroblocks) και επιστρέφει το νέο πλαίσιο διαφοράς καθώς και τα νέα διανύσματα. Αφού τελειώσει η παραγωγή του πλαισίου διαφοράς/σφάλματος τότε ακολουθεί η διαδικασία που περιγράφεται στην προηγούμενη ενότητα. Σε επίπεδο κώδικα, πρώτα γίνεται η εφαρμογή dct2 ανά 8x8 block στο πλαίσιο και μετά γίνεται διαίρεση, κελί με κελί, με το συνολικό πίνακα κβάντισης. Ακολουθεί ο υπολογισμός των bits αναπαράστασης και η αποκωδικοποίηση με τις συναρτήσεις jpegdcbits και jpegacbits ή mpegdcbits και mpegacbits, που περιγράφονται σε επόμενη ενότητα. Εδώ περιλαμβάνεται και ειδική συνάρτηση που υπολογίζει τα bits των διανυσμάτων κίνησης, η οποία θα αναλυθεί αργότερα. Και πάλι, λοιπόν, η έξοδος επιστρέφει το αποκωδικοποιημένο πλαίσιο διαφοράς, τα διανύσματα κίνησης και τα συνολικά bits, με και χωρίς τα διανύσματα κίνησης. Η συνάρτηση για τα B πλαίσια, encodeb, είναι ίδια με την encodei με ορισμένες διαφορές. Πρώτον δέχεται δύο πλαίσια αναφοράς ως είσοδο, ένα αρχικό Ι ή και ένα μελλοντικό Ι ή P. Για την πρόβλεψη και αντιστάθμιση χρησιμοποιεί καλεί δύο φορές τη συνάρτηση motion για κάθε macroblock, μια με πλαίσιο αναφοράς το I και μια για το P. Εδώ χρησιμεύει και το τελικό σφάλμα κάθε δοκιμής ως έξοδος της motion, καθώς συγκρίνονται τα σφάλματα μεταξύ των δύο καλεσμάτων και εκεί αποφασίζει ποιο από τα δύο macroblock διαφοράς θα χρησιμοποιήσει. Ένας νέος πίνακας με σημαίες παίρνει τις τιμές 0 ή 1 για κάθε macroblock, όπου το 0 σημαίνει ότι ως αναφορά έχει το πλαίσιο Ι και το 1 ότι η αναφορά είναι ως προ το πλαίσιο P. Τώρα, αν και τα δύο σφάλματα είναι μεγαλύτερα του threshold, επιλέγεται και πάλι απλά το αρχικό macroblock. Ο υπόλοιπος αλγόριθμος λειτουργεί με τον ίδιο τρόπο με παραπάνω. 32
33 5.1.4 Συναρτήσεις για αποκωδικοποίηση P και Β πλαισίων Η συνάρτηση reversesp δέχεται ως είσοδο το αποκωδικοποιημένο πλαίσιο διαφοράς/σφάλματος, τα διανύσματα κίνησης και το επίσης αποκωδικοποιημένο πλαίσιο αναφοράς και επιστρέφει το ανακατασκευασμένο πλαίσιο P. Η reversesp εκτελεί την ίδια λειτουργία απλά με ένα ακόμα όρισμα το δεύτερο πλαίσιο αναφοράς. Η ακρίβεια πρόβλεψης σαν είσοδος δεν χρειάζεται καθώς ο αλγόριθμος εκτελεί τη διαδικασία αυτόματα με κριτήριο το κάθε διάνυσμα κίνησης, δηλαδή αν είναι ακέραιο ή έχει και δεκαδικό μέρος. Επίσης ελέγχει τις σημαίες που περιλαμβάνονται στην τρίτη διάσταση του πίνακα των διανυσμάτων κίνησης. Για κάθε macroblock του πλαισίου διαφοράς, αν η σημαία είναι 0 τότε προστίθεται με το αντισταθμισμένο macroblock αναφοράς και προκύπτει το ανακτασκευασμένο macroblock P. Αν η σημαία είναι 1 τότε απλά το macroblock είναι τύπου Ι. Στο τέλος της διαδικασίας προκύπτει το πλαίσιο P, το οποίο αν είναι σε YCbCr μορφή θα μετασχηματιστεί σε RGB και θα γίνει τύπου uint8, ή αν είναι graysclae τότε απλά αλλάζει τύπο Συναρτήσεις για υπολογισμό bits αναπαράστασης Οι συναρτήσεις jpegacbits και jpegdcbits, δανείστηκαν από τη πηγή [3, ]. Καλούνται από τις συναρτήσεις κωδικοποίησης μετά το στάδιο της κβάντισης. Η πρώτη δέχεται ως είσοδο ένα κβαντισμένο 8x8 DCT block, όπου αρχικά εφαρμόζει ζιγκ ζαγκ σάρωση και το φέρνει σε μορφή διανύσματος μήκους 64 κελιών. Στη συνέχεια διαβάζει το κάθε κελί του διανύσματος μέσα σε ένα βρόγχο επανάληψης όπου από το δεύτερο κελί ως το τελευταίο, μετράει τον αριθμό των μηδενικών μέχρι να βρει έναν μη μηδενικό ακέραιο. Τότε αφού υπολογίσει το μέγεθος του ακεραίου σε bits, το συνδυάζει με το σύνολο των μηδενικών ως δείκτες σε ένα structure που περιέχει τα μήκη των συμβολοσειρών/ κωδικών Ηuffman για κάθε πιθανό συνδυασμό αυτό. Όπως αναφέρθηκε σε προηγούμενο κεφάλαιο οι κωδικοί και τα μήκη τους φαίνονται στο πίνακα B.1. Έτσι πραγματοποιεί run length encoding μαζί με κωδικοποίηση Ηuffman, χωρίς να ξοδεύει χρόνο να αντικαταστήσει τα στοιχεία με τις ίδιες τις συμβολοσειρές. Η δεύτερη συνάρτηση υπολογίζει το μέγεθος σε bits του DC όρου κάθε block, αφού τον έχει αφαιρέσει από το προηγούμενο DC όρο, εφόσον υπάρχει κάποιος. Και πάλι με δείκτη το μέγεθος επιλέγει από ειδικό structure το μήκος του συνολικού κωδικού που αντιστοιχεί στον όρο. Με πρότυπο τις παραπάνω, δημιουργήθηκαν και οι συναρτήσεις mpegacbits και mpegdcbits, που λειτουργούν με παρόμοιο τρόπο με προσαρμοσμένα τα structures ώστε να είναι σύμφωνα με τους πίνακες Ηuffman του MPEG, Β.2 και Β.3 στο παράρτημα Β. Επίσης δημιουργήθηκε και η συνάρτηση cbits που υπολογίζει το μέγεθος των διανυσμάτων κίνησης αναλόγως. Δε χρειάζεται προηγούμενη επεξεργασία των δεδομένων, δηλαδή είσοδος είναι απευθείας ο πίνακας των διανυσμάτων. Στο παράρτημα Β (σελ.82) υπάρχει εκτενής εξήγηση της κωδικοποίησης αυτής. 5.2 Κώδικας για το πρότυπο με τη μέθοδο BLU-ME Η κύρια μέθοδος BLU-ME υλοποιείται με τη συνάρτηση calculate, η οποία δέχεται σαν είσοδο δύο αντίστοιχα blocks, διαστάσεων 16x16, από ένα ζευγάρι πλαισίων. Σύμφωνα με τον αλγόριθμο που περιγράφηκε στο κεφάλαιο 4, ένα από τα δύο πλαίσια δέχεται πρόβλεψη και αντιστάθμιση κίνησης με ακρίβεια ενός pixel, με στόχο το άλλο. Αν οριστούν οι εικόνες εισόδου ως Α και Β, τότε κάθε 33
34 block της Β εισέρχεται αυτούσιο ενώ το αντίστοιχο του στην εικόνα Α είναι μετατοπισμένο με τα κατάλληλα διανύσματα κίνησης. Η συνάρτηση στη συνέχεια εφαρμόζει τη διαδικασία του block unshifting και παράγει ένα νέο block, μεγέθους 17x17, με τα αντίστοιχα διανύσματα κίνησης x A,yA,xB και yb. Η διαδικασία συνεχίζεται μέχρι να εξαντληθούν τα blocks των εικόνων όπου και πλέον έχει παραχθεί το ιδεατό πλαίσιο όπως ορίζει η μέθοδος. Για λόγους συμπίεσης, έτσι ώστε δηλαδή το ιδεατό πλαίσιο, διαστάσεων (M+9)x(Ν+11) να είναι ίδιων διαστάσεων με τα πλαίσια εισόδου, διαστάσεων MxN, ακολουθεί η εξής διαδικασία: η τελευταία στήλη του κάθε block προστίθεται με τη νέα στήλη του γειτονικού του block από τα δεξιά, και το άθροισμα διαιρείται διά δύο, και προκύπτει μια κοινή στήλη με τους μέσους όρους των pixels. Η δεύτερη στήλη μέχρι την τελευταία του γειτονικού block στοιχίζονται δίπλα στη κοινή στήλη αυτή. Πλέον προκύπτει ένα νέο block, διαστάσεων 17x18.Η διαδικασία επαναλαμβάνεται μεταξύ της δομής αυτής και του επόμενου γειτονικού block μέχρι αυτά να εξαντληθούν. Ομοίως επεξεργάζεται κάθε επόμενη σειρά από blocks. Στη συνέχεια, η τελευταία γραμμή κάθε συνολικής δομής 17xN+1 θα προστεθεί με την πρώτη γραμμή της γειτονικής συνολικής δομής κατά το κάθετο άξονα. Και πάλι το άθροισμα θα διαιρεθεί με το δύο και θα προκύψει μια κοινή γραμμή με το μέσο όρο των pixels μεταξύ των δύο δομών. Στο τέλος της διαδικασίας, θα προκύψει ένα νέο ιδεατό πλαίσιο M+1xN+1, όπου και αφαιρούνται η τελευταία γραμμή και στήλη ώστε να γίνει διαστάσεων MxN. Να σημειωθεί ότι ο αλγόριθμος της μεθόδου είναι πρακτικά πολύ αργός. Επομένως έγινε πρώτα κατασκευή των ιδεατών πλαισίων για τα δεδομένα ζευγάρια πλαισίων, τα οποία αποθηκεύτηκαν σε μια δομή πίνακα. Αφού έχει παραχθεί το ιδεατό πλαίσιο, μένει να υπολογισθούν και τα πλαίσια σφάλματος των πλαισίων Α και Β σε σχέση με αυτό. Αυτό γίνεται με τη χρήση της συνάρτησης difab, που δέχεται ως είσοδο τα Α και Β καθώς και το αντίστοιχο τους ιδεατό πλαίσιο και τα διανύσματα x A,yA,xB και yb. Σε αυτό το σημείο προστίθενται μια ακόμα γραμμή και στήλη στο ιδεατό πλαίσιο, με τιμές ίσες της γραμμής Μ και στήλης Ν αντίστοιχα. Κάθε block του ιδεατού πλαισίου θα αφαιρεθεί από τα αντίστοιχα των Α και Β, μετατοπισμένο κατά τα διανύσματα x A,yA και xb,yb αντίστοιχα, μέσω της συνάρτησης movehv. Η συνάρτηση αυτή δέχεται είσοδο διαστάσεων (M+1)x(N+1) και παράγει M x N, ενώ όλα τα blocks πρέπει να είναι 16x16. Συνεπώς, σαν είσοδο η movehv παίρνει blocks από το ιδεατό πλαίσιο, μεγέθους 17x17, που μοιράζονται μεταξύ τους τις γραμμές και στήλες με τους μέσους όρους, ώστε να προκύψουν 16x16 blocks για την τελική αφαίρεση. Η ανακατασκευή των Α και Β γίνεται με την αντιστροφή της παραπάνω διαδικασία με τη συνάρτηση undifab. Για μια δεδομένη, λοιπόν, ροή πλαισίων εισόδου στον κωδικοποιητή, για κάθε ζευγάρι θα παράγεται ένα ιδεατό πλαίσιο, δύο σετ από διανύσματα κίνησης και δύο πλαίσια διαφοράς/σφαλμάτων. Τα ιδεατά πλαίσια θα χωρίζονται σε GOP και θα δέχονται παρόμοια επεξεργασία όπως περιγράφηκε στην ενότητα 5.1. Τα πλαίσια διαφοράς θα δέχονται κωδικοποίηση ως πλαίσια P και τα διανύσματα κίνησης θα κωδικοποιούνται σταθερά με 4 bits το καθένα, αφού στρογγυλοποιηθούν. Καθώς τα διανύσματα κίνησης είναι θετικές τιμές μεταξύ του 0 και του 1, με μεγάλη ακρίβεια, στρογγυλοποιούνται στο 1 δεκαδικό. Έτσι προκύπτουν τιμές 0, 0.1, 0.2,..., 1.0 που κωδικοποιούνται με 4 bits. Για παράδειγμα στο 0 θα αντιστοιχεί 0000, στο 0,1 0001, στο και ούτω καθεξής. 34
35 ΚΕΦΑΛΑΙΟ 6 - ΠΕΙΡΑΜΑΤΑ 6.1 Πρώτο Πείραμα Ως δείγμα χρησιμοποιήθηκε η αλληλουχία/βίντεο foreman σε πρότυπο QCIF, με διαστάσεις δηλαδή 144x176 και στο χρωματικό χώρο του greyscale. Η επιλογή των διαστάσεων είναι καθαρά λόγω εξοικονόμησης υπολογιστικού χρόνου καθώς ο κώδικας στη Matlab είναι σχετικά αργός. Εξάλλου η λογική του αλγορίθμου είναι ίδια για οποιαδήποτε είσοδο. Επιλέχτηκε επίσης ο χώρος του greyscale γιατί το κύριο αντικείμενο που εξετάζεται στην εργασία αυτή είναι η εναλλακτική μέθοδος πρόβλεψης και αντιστάθμισης κίνησης, η οποία και εκτελείται μόνο στη φωτεινή συνιστώσα σε περίπτωση έγχρωμης εικόνας. Το αρχείο περιέχει 300 πλαίσια συνολικά από τα οποία επιλέχτηκε δείγμα των 32 πρώτων πλαισίων. Κύριο χαρακτηριστικό της αλληλουχίας είναι η σταθερότητα του παρασκηνίου με κίνηση να παρατηρείται μόνο πάνω στον πρωταγωνιστή που κουνάει το κεφάλι και αλλάζει εκφράσεις. Για το μέγεθος αυτός του δείγματος επιλέχτηκε το μοτίβο GOP, IPPPI, ώστε να προκύψουν 8 συνολικά που είναι αρκετά για παρατηρήσεις. Το κάθε P εξαρτάται από το παγκόσμιο Ι της ομάδας του καθώς θεωρείται ότι τα γειτονικά πλαίσια ανά τετράδα θα διαφέρουν ελάχιστα ανά μεταξύ τους. Για τον ίδιο λόγο δε χρησιμοποιείται και το κριτήριο του κατωφλίου, ο οποίος είναι αρκετά αυθαίρετος και θέλει πολλαπλές δοκιμές για ένα μόνο ζευγάρι εικόνων. Προφανώς αποκλίσεις είναι πιθανές και θα σχολιασθούν αναλόγως Αποτελέσματα και σχόλια για το MPEG Ως ακρίβεια της εξαντλητικής πρόβλεψης/αντιστάθμισης χρησιμοποιείται η συνθήκη μισού και ενός τετάρτου του pixel σε ξεχωριστές δοκιμές. Τα I frames κωδικοποιούνται με το πίνακα κβάντισης Α.2 και τα P με το πίνακα Α.3, του παραρτήματος Α. Οι δύο πίνακες χρησιμοποιούνται γιατί είναι οι βασικοί του MPEG-2. Τέλος για επίτευξη πολλαπλών βαθμών συμπίεσης χρησιμοποιούνται συντελεστές κβάντισης στο εύρος τιμών [0.7, 2.2] με βήμα 0.1. Με χρήση του ίδιου συντελεστή για όλα τα Ι και P frames ανά δοκιμή προκύπτουν οι εικόνες 6.1 με 6.16 όπου φαίνονται για κάθε τιμή συντελεστή, στο σύνολο των δειγμάτων τα υπολογισμένα bits αναπαράστασης ανά πλαίσιο, στη συμπιεσμένη του μορφή, και οι τιμές του κριτηρίου PSNR μεταξύ των ανακατασκευασμένων και των αρχικών μορφών τους. Περιλαμβάνονται γραφήματα τόσο για ακρίβεια half pixel, με χρώμα μπλε, όσο και για quarter pixel, με χρώμα πορτοκαλί. Τα πλαίσια I παρουσιάζουν γενικά μεγαλύτερη απαίτηση σε bits παρόλο που κβαντίζονται με πιο δυνατό κβαντιστή. Προφανώς δεν διαφέρουν τα Ι πλαίσια μεταξύ των δοκιμών των δύο ακριβειών πρόβλεψης. Ο κβαντιστής αυτός έχει και ως συνέπεια και χαμηλότερο PSNR για τα I σε σχέση με τα P. Τα παραπάνω φαίνονται πως ισχύουν για κάθε τιμή συντελεστή με τα γραφήματα να υποχωρούν ομοιόμορφα ανά δοκιμή μεγαλύτερου συντελεστή. Αντίστοιχα οι τιμές PSNR πέφτουν για μεγαλύτερους συντελεστές που είναι λογικό καθώς αυξάνονται οι απώλειες. Από την άλλη όσο μικραίνει ο συντελεστής φαίνεται η αντίστροφη λειτουργία δηλαδή μικρότερη συμπίεση με περισσότερα bits και αυξημένο PSNR. 35
36 Εικόνα 6.1 Αλληλουχία των πλαισίων ως προς τα bits αναπαράστασης για τιμές συντελεστή 0.7, 0.8, 0.9 και 1.0. Εικόνα 6.2 Αλληλουχία των πλαισίων ως προς τα bits αναπαράστασης συντελεστή 1.1, 1.2, 1.3 και
37 Εικόνα 6.3 Αλληλουχία των πλαισίων ως προς τα bits αναπαράστασης για τιμές συντελεστή 1.5, 1.6, 1.7 και 1.8. Εικόνα 6.4 Αλληλουχία των πλαισίων ως προς τα bits αναπαράστασης για τιμές συντελεστή 1.9, 2.0, 2.1 και
38 Εικόνα 6.5 Αλληλουχία των πλαισίων ως προς τις τιμές PSNR για τιμές συντελεστή 0.7, 0.8, 0.9 και 1.0. Εικόνα 6.6 Αλληλουχία των πλαισίων ως προς τις τιμές PSNR για τιμές συντελεστή 1.1, 1.2, 1.3 και
39 Εικόνα 6.7 Αλληλουχία των πλαισίων ως προς τις τιμές PSNR για τιμές συντελεστή 1.5, 1.6, 1.7 και 1.8. Εικόνα 6.8 Αλληλουχία των πλαισίων ως προς τις τιμές PSNR για τιμές συντελεστή 1.9, 2.0, 2.1 και
40 Γενικά, λοιπόν, προκύπτει πτώση σε bits αναπαράστασης. Μια ασυμπίεστη εικόνα για το σύνολο των 32 θα χρειαζόταν 144*176*8= bits ή 203 Κ bits, ενώ για το μικρότερο συντελεστή 0.7 φαίνεται μέσος όρος περίπου 32 K bits, ο οποίος μειώνεται για μεγαλύτερους συντελεστές. Η υπόθεση για την επιλογή του GOP, IPPP, παρουσιάζει ενδιαφέροντα αποτελέσματα. Από τη μία φαίνεται ότι κάθε P πλαίσιο χρειάζεται σε γενικές γραμμές λιγότερα bits από το αντίστοιχο I πλαίσιο της ομάδας και ταυτόχρονα η ανακατασκευή τους παρουσιάζει και υψηλότερο PSNR. Αυτό αποδεικνύει και την αποτελεσματικότητα της πρόβλεψης κίνησης σε υποστοιχειακό επίπεδο. Από την άλλη υπάρχει και απόκλιση, για κάθε διαδοχικό P πλαίσιο του GOP. Φαίνεται σε κάθε ομάδα ότι το πρώτο P έχει λιγότερα bits και μεγαλύτερο PSNR, ενώ το δεύτερο και το τρίτο έχουν περισσότερα και μικρότερο αντίστοιχα. Ειδικά το τρίτο φαίνεται να πλησιάζει το I πλαίσιο, αλλά πάλι καλύτερο από το να κωδικοποιούνται όλα ως I. Το φαινόμενο αυτό εξαρτάται πάντα από το εκάστοτε δείγμα βίντεο και είναι δύσκολο να προβλεφθεί ακριβώς. Πιθανές λύσεις είναι η χρήση του κατωφλίου που είναι χρονοβόρα διαδικασία λόγω της αυθαιρεσίας στη λογική της. Πιο σωστή είναι η χρήση B πλαισίων, που δημιουργήθηκαν για ακριβώς αυτό το σκοπό, δηλαδή να κωδικοποιούνται πιο ευέλικτα σύμφωνα με μια μελλοντική αναφορά. Από την άλλη B πλαίσια δε χρησιμοποιούνται στα πειράματα γιατί η μέθοδος BLU-ME στη παρούσα μορφή της δε περιέχει παρόμοια λειτουργία μελλοντικής πρόβλεψης. Γενικά μπορούν να δοκιμαστούν πολλαπλοί συνδυασμοί πλαισίων σε ένα GOP ή η πρόβλεψη να γίνεται ανά διαδοχικό P πλαίσιο και όχι με ένα κοινό I πλαίσιο για όλα. Πρακτικά η τελευταία πρόταση σημαίνει μεγαλύτερη εξάρτηση ανά πλαίσιο που αυξάνει απαίτηση στο να αποθηκεύεται στο buffer πιο συχνά ένα νέο ανακατασκευασμένο πλαίσιο. Εντέλει στόχος του πειράματος είναι να βρεθεί μια ικανοποιητική κατάσταση ώστε να εφαρμοστεί με ίδιο τρόπο με τη μέθοδο BLU-ME. Μεταξύ των ακριβειών half και quarter pixel, και οι δυο παρουσιάζουν κοινά αποτελέσματα. Γενικά φαίνεται για αυτό το δείγμα εικόνων ότι η δεύτερη ακρίβεια παρουσιάζει για κάθε βήμα συντελεστή κβάντισης μικρότερες μέσες απαιτήσεις σε bits ενώ περίπου ίδια αποτελέσματα PSNR σε σχέση με τη πρώτη. Και σε περιπτώσεις μεν που υπάρχει πτώση ή αύξηση PSNR είναι αμελητέα. Ωστόσο, τα διανύσματα κίνησης της ακρίβειας quarter pixel κωδικοποιούνται χωρίς απώλειες με περισσότερα bits σε σχέση την περίπτωση του half pixel, όπως ορίστηκε με το αυτοσχέδιο πρότυπο της παρούσας εργασίας. Είναι πιθανό για μια πιο βελτιστοποιημένη κωδικοποίηση των διανυσμάτων να προκύπτει πιο μεγάλη συνολική πτώση στα bits αλλά γενικά και χωρίς τα διανύσματα τα υπολογισμένα bits μόνο των pixels δεν παρουσιάζουν σημαντική διαφορά. Στην πορεία των δοκιμών θα κρατηθεί η ακρίβεια μισού pixel λόγω των μικρών διαφορών στα αποτελέσματα αλλά και γιατί χρειάζεται λιγότερο υπολογιστικό χρόνο. Μολονότι ο συντελεστής είναι ίδιος για όλα τα είδη πλαισίων, είναι δυνατή και η επιλογή διαφορετικού συντελεστή για τα Ι και τα P. Εναλλακτικά για παράδειγμα, για περισσότερη συμπίεση των P χωρίς να χαθεί πολύ ποιότητα από το πλαίσιο αναφοράς τους ανά GOP, μπορεί να κρατηθεί σταθερός ο συντελεστής του Ι και να αυξηθεί ανά βήμα ο αντίστοιχος των P. Όσο πιο πολύ συμπιέζεται το πλαίσιο αναφοράς τόσο πιο πολύ θα διαφέρει από την αρχική του μορφή και αυτό οδηγεί σε μεγαλύτερα σφάλματα στο πλαίσιο διαφοράς που μπορεί να έχει επιπτώσεις όπου το ένα πλαίσιο P να προσεγγίζει ή να ξεπερνάει το Ι πλαίσιο σε bits. Για παράδειγμα, το πρώτο πλαίσιο κωδικοποιείται με συντελεστή 1.5 ως Ι, ενώ το δεύτερο ως P με συντελεστή 1. Το αποτέλεσμα είναι για το Ι είναι bits ενώ για το P, bits. Από τη μία το ανακατασκευασμένο P παρουσιάζει υψηλότερο PSNR και πάλι σε σχέση με το Ι. Για συντελεστή από 1.1 και μετά φαίνεται πιο επιτυχημένη μείωση των bits του P με αντίστοιχη πτώση πάντα του PSNR. Γενικά, πάντως θα παίζει 40
41 ρόλο και η ίδια η εικόνα άρα είναι θέμα δοκιμών και απόκρισης κάθε φορά. Μπορεί στην τελική να συμφέρει αυτός ο συνδυασμός 1.5 και 1, όσον αφορά τα συνολικά bits. Αν όμως θεωρείται απαγορευτικό τα P να χρειάζονται περισσότερα bits από το I, τότε θα χρειαστούν πιο κατάλληλοι συνδυασμοί συντελεστών. Σε εμπορικές υλοποιήσεις του MPEG, που δεν κυκλοφορούν μεν σε βιβλιογραφία όντας ιδιόκτητες, θα υπάρχουν σίγουρα και πιο εξιδανικευμένοι μηχανισμοί για δυναμικότερη συμπίεση ανά συγκεκριμένα τμήματα μέσα σε ένα block. Τέλος, φαίνονται και οι καμπύλες R-D για κάθε εικόνα για τις δύο ακρίβειες, με το PSNR στο κάθετο άξονα και τα bits στον οριζόντιο και το συνδυασμό των τιμών τους να σχηματίζουν τα σημεία της καμπύλης για κάθε συντελεστή κβάντισης. Παρατηρείται, όπως είναι και επιθυμητή, πτώση του PSNR για λιγότερα bits, κάποιες φορές πιο ομαλή και άλλες πιο απότομη, τόσο για την ακρίβεια half pixel όσο και για την quarter pixel. Σε γενικές γραμμές είναι παρόμοιες οι καμπύλες μεταξύ τους με το quarter pixel να δίνει μεγαλύτερη αίσθηση ομαλότητας για τα περισσότερα δείγματα και ελαφρώς καλύτερα αποτελέσματα. Είναι εντέλει θέμα μεταξύ υπολογιστικού χρόνου και λίγο πιο καλής συμπίεσης με αμελητέες διαφορές στην τελική ποιότητα. Εικόνα 6.9 Rate-Distortion καμπύλες ανά πλαίσιο για το πρώτο GOP. 41
42 Εικόνα 6.10 Rate-Distortion καμπύλες ανά πλαίσιο για το δεύτερο GOP. Εικόνα 6.11 Rate-Distortion καμπύλες ανά πλαίσιο για το τρίτο GOP. 42
43 Εικόνα 6.12 Rate-Distortion καμπύλες ανά πλαίσιο για το τέταρτο GOP. Εικόνα 6.13 Rate-Distortion καμπύλες ανά πλαίσιο για το πέμπτο GOP. 43
44 Εικόνα 6.14 Rate-Distortion καμπύλες ανά πλαίσιο για το έκτο GOP. Εικόνα 6.15 Rate-Distortion καμπύλες ανά πλαίσιο για το έβδομο GOP. 44
45 Εικόνα 6.16 Rate-Distortion καμπύλες ανά πλαίσιο για το όγδοο GOP. Παρακάτω φαίνεται και ένα οπτικό παράδειγμα των αποτελεσμάτων: Εικόνα 6.17 Το πρώτο πλαίσιο του δείγματος βίντεο, ακατέργαστο. 45
46 Εικόνα 6.18 Το πρώτο πλαίσιο του δείγματος βίντεο κωδικοποιημένο ως Ι με συντελεστή 1, παρατηρείται ελαφριά αλλοίωση. Εικόνα 6.19 Το πρώτο πλαίσιο του δείγματος βίντεο κωδικοποιημένο ως Ι με συντελεστή 2. Όπως φαίνεται η αλλοίωση της ποιότητας της εικόνας φαίνεται να προκαλεί ένα block effect, όπου δηλαδή φαίνονται διακριτά τμήματα της εικόνας. Για την αντιμετώπιση αυτού του 46
47 φαινομένου υπάρχει ειδικός αλγόριθμος βελτιστοποίησης ώστε να απομακρύνονται οι έντονες αυτές αλλοιώσεις. Θέματα βελτιστοποίησης όμως δεν απασχολούν την παρούσα εργασία. Εικόνα 6.20 Το δεύτερο πλαίσιο του δείγματος βίντεο, ακατέργαστο. Εικόνα 6.21 Το δεύτερο πλαίσιο κωδικοποιημένο ως P για συντελεστή 1. 47
48 Εικόνα 6.22 Το δεύτερο πλαίσιο κωδικοποιημένο ως P για συντελεστή 2. Και πάλι παρατηρείται αλλοίωση αλλά σε μικρότερο βαθμό από το Ι, καθώς ως P παρουσιάζει υψηλότερο PSNR, πάντα, για κοινό συντελεστή κβάντισης. Όπως ήδη εξηγήθηκε για μη συμμετρικούς συντελεστές μεταξύ I και P πλαισίων, τα τελευταία μπορούν να συμπιεσθούν περισσότερο με περισσότερη θυσία της οπτικής ποιότητας Αποτελέσματα και σχόλια για τη BLU-ME Κατά τη διάρκεια της υλοποίησης της BLU-ME, ήταν αναμενόμενο το ιδεατό πλαίσιο να καθιστά αδύνατη την σοβαρή μείωση της απαίτησης σε bits, καθώς για κάθε ζεύγος πλαισίων αντιστοιχεί και ένα ακόμα που θα χρειαστεί bits αναπαράστασης. Για τη συνολική έκταση των 32 πλαισίων προκύπτουν και άλλα 16, συνολικά 48 πλαίσια. Άρα πιο σημαντικό κρίθηκε να συγκριθεί η τελική ποιότητα της εναλλακτικής πρόβλεψης πάνω στα πραγματικά πλαίσια του δείγματος σε σχέση με το ΜPEG. Ο στόχος δηλαδή είναι περισσότερο μια αρχική σύγκριση ως ένα σημείο αναφοράς για πιθανή μελλοντική επεξεργασία του αλγορίθμου παρά η σχεδίαση ενός προτύπου που θα αντικαταστήσει εντελώς το MPEG. Ένα ακόμα θέμα της μεθόδου είναι ότι από τα πλαίσια εισόδου Α και Β μόνο ένα θα μεταφερθεί αυτούσιο ενώ το άλλοι θα μπει με μετατοπισμένα τα blocks του. Το ιδεατό πλαίσιο δηλαδή θα προσεγγίζει πάντα το Β σε καλύτερο βαθμό απ ότι το Α. Για αυτό στη πορεία υπάρχουν δύο περιπτώσεις, ο υπολογισμός της διαφοράς του Α με το ιδεατό με τα διανύσματα x Α και yα όπως προκύπτουν από τη BLU-ME και η κωδικοποίηση του Α ως P, όπως στο MPEG, με αναφορά το ιδεατό για ακρίβεια μισού pixel. Η επιλογή αυτή έγινε λόγω υπολογιστικού χρόνου. Στην τελευταία περίπτωση τα xα,yα διανύσματα δε κωδικοποιούνται αλλά αντικαθίστανται από τα νέα διανύσματα της κλασικής πρόβλεψης. 48
49 Αρχικά για το ιδεατό πλαίσιο για τα πρώτα δύο πλαίσια του δείγματος, εφαρμόστηκε intraκωδικοποίηση με το βασικό πίνακα κβάντισης του MPEG-2, με συντελεστή 1. Το τελικό αποτέλεσμα σε bits αναπαράστασης των συμπιεσμένων πλαισίων είναι 35076, μέγεθος αρκετά μεγαλύτερο, κατά 20% περίπου, από τα bits του πρώτου πλαισίου ως Ι στην περίπτωση του MPEG. Για σύγκριση, το πλαίσιο μέσου όρου μεταξύ του μετατοπισμένου πλαισίου 1 και του πλαισίου 2, δηλαδή όπως εισέρχονται στη BLU-ME, κωδικοποιήθηκε ως Ι με ίδιο συντελεστή και επέστρεψε bits. Άρα απ ότι φαίνεται ο αλγόριθμος που υπολογίζει το ιδεατό πλαίσιο προσθέτει επιπλέον πληροφορία σε σχέση με μια πιο απλή πράξη. Για τα υπόλοιπα ιδεατά πλαίσια για τα συνολικά 16 ζευγάρια πλαισίων παρατηρούνται παρόμοια αποτελέσματα σε bits για την intraκωδικοποίηση με συντελεστή 1. Επιβεβαιώνεται, λοιπόν, και η αρχική υποψία. Επόμενο βήμα ήταν να δημιουργηθούν GOP για τα ιδεατά πλαίσια με τρόπο ίδιο όπως στο πείραμα του MPEG, δηλαδή μοτίβο IPPP, όπου το Ι είναι κοινή αναφορά για τα υπόλοιπα. Αρχικά χρησιμοποιήθηκαν οι βασικοί πίνακες κβάντισης αλλά το αποτέλεσμα δεν ήταν ικανοποιητικό καθώς τα ιδεατά P πλαίσια χρειάζονταν περισσότερα bits από το Ι, για κοινό συντελεστή κβάντισης. Αυτό σημαίνει ότι δεν υπάρχει αρκετή συσχέτιση μεταξύ των ιδεατών πλαισίων ώστε να συμπιεσθεί. Ένας τρόπος να αντιμετωπιστεί η περίπτωση αυτή είναι να χρησιμοποιούνται ξεχωριστοί συντελεστές για τα I και P. Προκειμένου, όμως, να τρέξουν δοκιμές παρόμοιες με το MPEG πείραμα, χρησιμοποιήθηκε ο πίνακας κβάντισης του Ι (Α.2) και για τα P. Έτσι, παρουσιάζεται συμπεριφορά όμοια με το προηγούμενο πείραμα, για κάθε ομοιόμορφο συντελεστή κβάντισης. Σε ένα GOP, κάθε P κωδικοποιείται με λιγότερα bits από το επόμενό του με το τρίτο να παρουσιάζει μια πιο απότομη απόκλιση με περισσότερα bits, πάλι όμως λιγότερα από το πλαίσιο Ι. Για τον υπολογισμό των πλαισίων διαφοράς μεταξύ των Α και B και του αντίστοιχου τους ιδεατού πλαισίου αναφοράς, παρουσιάζονται οι δυο πιθανές περιπτώσεις, μια για τα BLU-ME διανύσματα και η άλλη για τα διανύσματα του κανονικού ME (motion estimation). Σε γενικές γραμμές η δεύτερη περίπτωση επιστρέφει πιο ικανοποιητικά και ομοιόμορφα αποτελέσματα κατά τη συνολική έκταση του δείγματος. Από την άλλη δεν είναι κακή και η απόκριση της πρώτης περίπτωσης, εμφανίζονται όμως outliers στα πλαίσια 23 και 25, όπου το Α έχει αρκετά πιο υψηλή απαίτηση σε bits από όλα τα άλλα. Αυτό οφείλεται και στη παρατήρηση σχετικά με τη μορφή των blocks του Α κατά την κατασκευή των ιδεατών. Είναι πιθανό ότι και σε άλλο κομμάτι του βίντεο μπορεί να προκύπτουν τέτοια outliers. Ακολουθούν τα γραφήματα 6.23 με 6.38 όπου φαίνονται οι απαιτήσεις σε bits των συμπιεσμένων πλαισίων Α και Β όπως και οι τιμές του κριτηρίου PSNR μεταξύ των αποσυμπιεσμένων και των αρχικών εκδοχών τους. Με μπλε χρώμα φαίνονται τα Α πλαίσια με τα διανύσματα της μεθόδου BLU ME ενώ με πορτοκαλί τα κανονικά διανύσματα ακρίβειας μισού pixel. Τα Β πλαίσια είναι παντού ίδια άρα αναπαρίστανται από ένα μόνο χρώμα. Καθώς η αρχική εικόνα έχει βάθος pixel 8 bit τότε κατά μέσο όρο κάθε εικόνα θα χρειαζόταν 144*176*8= bits ή περίπου 203 Κ bits. Κοιτώντας την εικόνα 6.23 για το συντελεστή 1 τότε μέσος όρος για όλες τις εικόνες είναι bits αναπαράστασης ή περίπου 19 Κ bits. Φαίνεται δηλαδή μια σημαντική πτώση στην απαίτηση που όλο και μειώνεται για μεγαλύτερους συντελεστές κβάντισης. 49
50 Εικόνα 6.23 Απαίτηση σε bits για συντελεστές κβάντισης 1, 1.1 και 1.2. Εικόνα 6.24 Απαίτηση σε bits για συντελεστές κβάντισης 1.3, 1.4 και
51 Εικόνα 6.25 Απαίτηση σε bits για συντελεστές κβάντισης 1.6, 1.7 και 1.8. Εικόνα 6.26 Απαίτηση σε bits για συντελεστές κβάντισης 1.9 και 2.0. Όπως και στην ενότητα των αποτελεσμάτων του MPEG φαίνεται μια ομαλή μείωση των bits για όλα τα πλαίσια όσο αυξάνεται ο συντελεστής κβάντισης. Στα επόμενα γραφήματα του PSNR με μπλε και πορτοκαλί χρώματα διακρίνονται και πάλι οι δυο περιπτώσεις για τα πλαίσια Α, ενώ τα Β είναι πάντα ίδια. 51
52 Εικόνα 6.27 Τιμές PSNR για συντελεστές κβάντισης 1, 1.1 και 1.2. Εικόνα 6.28 Τιμές PSNR για συντελεστές κβάντισης 1.3, 1.4 και
53 Εικόνα 6.29 Τιμές PSNR για συντελεστές κβάντισης 1.6, 1.7 και 1.8. Εικόνα 6.30 Τιμές PSNR για συντελεστές κβάντισης 1.9 και 2. Από τις μέσες τιμές PSNR για κάθε σύνολο φαίνεται ότι η περίπτωση για τα κανονικά ME παρουσιάζει πιο ομοιόμορφα αποτελέσματα. Σε γενικές γραμμές είναι καλύτερη λύση από την προτεινόμενη της μεθόδου, πάντα για τα πλαίσια Α. Τέλος, ακολουθούν και οι καμπύλες R-D και για τις δύο περιπτώσεις. 53
54 Εικόνα 6.31 R-D καμπύλες για τα πλαίσια 1,2,3,4. Εικόνα 6.32 R-D καμπύλες για τα πλαίσια 5,6,7,8. 54
55 Εικόνα 6.33 R-D καμπύλες για τα πλαίσια 9,10,11,12. Εικόνα 6.34 R-D καμπύλες για τα πλαίσια 13,14,15,16. 55
56 Εικόνα 6.35 R-D καμπύλες για τα πλαίσια 17,18,19,20 Εικόνα 6.36 R-D καμπύλες για τα πλαίσια 21,22,23,24 56
57 Εικόνα 6.37 R-D καμπύλες για τα πλαίσια 25,26,27,28 Εικόνα 6.38 R-D καμπύλες για τα πλαίσια 29,30,31,32 57
58 Φαίνεται ότι στις περισσότερες περιπτώσεις η πορτοκαλί καμπύλη, για την περίπτωση των ME διανυσμάτων, προηγείται της μπλε, δηλαδή αντιστοιχεί σε μικρότερες τιμές bits ανά πλαίσιο και ταυτόχρονα αντιστοιχεί σε μεγαλύτερες τιμές PSNR. Γενικά, η καλύτερη δυνατή συμπίεση για όλα τα ζεύγη γίνεται με ενδοπλαισιακή κωδικοποίηση του κάθε ιδεατού πλαισίου αναφοράς όπου και τα Α και Β θα δίνουν καλύτερα αποτελέσματα PSNR σε σχέση με το πείραμα στο MPEG αλλά όχι σε ιδιαίτερα σημαντικό βαθμό. Από την άλλη θα προκύπτει και αρκετή αύξηση στον αριθμό των bits που δε θα δικαιολογεί τις συγκριτικά μικρές αυξήσεις σε PSNR Σύγκριση μεταξύ των μεθόδων Για τη τελική σύγκριση των αποτελεσμάτων PSNR και bits, συνεπώς, χρησιμοποιείται η περίπτωση των διανυσμάτων της ME έναντι αυτών της BLU ME, πάντα μόνο για την περίπτωση του Α πλαισίου. Αυτό εντέλει δεν αναιρεί εντελώς τη μέθοδο BLU ME, καθώς η υπόθεση της λέει ότι ιδεατό πλαίσιο θα προσφέρει πιο ακριβή πρόβλεψη. Φαίνεται, όσον αφορά την ποιότητα των ανακατασκευασμένων πλαισίων, ότι η μέθοδος BLU-ME παρουσιάζει γενικά καλύτερα αποτελέσματα με γενική αύξηση του μέσου PSNR των πλαισίων ανά συντελεστή κβάντισης, κατά 1 περίπου db σε σχέση με τα αποτελέσματα του MPEG (για half pixel). Για την αντίστοιχη σύγκριση των bits, παρουσιάζεται τόσο το καθαρό μέγεθος του κάθε ζεύγους A και B αλλά και το συνολικό μέγεθος μαζί με το ιδεατό πλαίσιο, του οποίου τα bits προστίθενται σε κάθε πλαίσιο Α ανά ζεύγος των 32 πλαισίων. Γενικά, η πρόβλεψη της BLU ME χρησιμοποιεί λιγότερα bits αναπαράστασης για τις μεμονωμένες κωδικοποιημένες διαφορές μεταξύ των Α και Β και του ιδεατού σε σχέση με τα πλαίσια όπως κωδικοποιούνται στο MPEG. Σε συνδυασμό με τον ελαφρώς αυξημένο PSNR δείχνει ότι η πρόβλεψη είναι όντως πιο ακριβής. Πρακτικά όμως για την αποκωδικοποίηση θα χρειαστεί το ιδεατό πλαίσιο το οποίο αυξάνει κατά μεγάλο βαθμό τη μέση απαίτηση σε bitς για όλα τα ζεύγη Α, Β. Eικόνα 6.39 Απαίτηση σε bits μεταξύ των μεθόδων για συντελεστές κβάντισης 1, 1.1 και
59 Εικόνα 6.40 Απαίτηση σε bits μεταξύ των μεθόδων για συντελεστές κβάντισης 1.3, 1.4 και 1.5. Εικόνα 6.41 Απαίτηση σε bits μεταξύ των μεθόδων για συντελεστές κβάντισης 1.6, 1.7 και
60 Εικόνα 6.42 Απαίτηση σε bits μεταξύ των μεθόδων για συντελεστές κβάντισης 1.9 και 2. Αν υπολογιστεί και το μέγεθος του ιδεατού πλαισίου φαίνεται πως δεν υπάρχει σύγκριση. Η BLU-ME δε καταφέρνει καλύτερη συμπίεση. Και οι αντίστοιχες εικόνες για το PSNR: Εικόνα 6.43 Τιμές PSNR μεταξύ των μεθόδων για συντελεστές κβάντισης 1, 1.1 και
61 Εικόνα 6.44 Τιμές PSNR μεταξύ των μεθόδων για συντελεστές κβάντισης 1.3, 1.4 και 1.5 Εικόνα 6.45 Τιμές PSNR μεταξύ των μεθόδων για συντελεστές κβάντισης 1.6, 1.7 και
62 Εικόνα 6.46 Τιμές PSNR μεταξύ των μεθόδων για συντελεστές κβάντισης 1.9 και 2 Συγκρίνοντας τις μέσες τιμές PSNR για κάθε σύνολο πλαισίων φαίνεται μια σταθερή αύξηση 1dB με τη μέθοδο BLU-ME για κάθε συντελεστή κβάντισης. Ακόμα και με τη περίπτωση χρήσης των BLU ME διανυσμάτων xα,yα για την κωδικοποίηση του Α τότε και πάλι θα φαίνεται τέτοια σταθερή αύξηση. Ακόμα και συγκριτικά με την περίπτωση των διανυσμάτων ακρίβειας quarter pixel στο MPEG, η BLU ME παρουσιάζει σταθερή αύξηση στο PSNR. Η εναλλακτική μέθοδος πρόβλεψης κίνησης μπορεί να θεωρηθεί επιτυχημένη όσον αφορά την τελική ποιότητα των πλαισίων αλλά με μεγάλο κόστος σε ποσότητα πληροφορίας. Τέλος, ακολουθούν κάποια οπτικά παραδείγματα της BLU-ME: Εικόνα 6.47 Παράδειγμα ενός ιδεατού πλαισίου όπως κατασκευάστηκε από τα πλαίσια 1 και 2, ως Α και Β αντίστοιχα. 62
63 Εικόνα 6.48 Το ανακατασκευασμένο πλαίσιο Α από το ιδεατό πλαίσιο της εικόνας 6.47 για συντελεστή κβάντισης 1. Εικόνα 6.49 Το ανακατασκευασμένο πλαίσιο Α από το ιδεατό πλαίσιο της εικόνας 6.47 για συντελεστή κβάντισης 2. 63
64 Εικόνα 6.50 Το ανακατασκευασμένο πλαίσιο Β από το ιδεατό πλαίσιο της εικόνας 6.47 για συντελεστή κβάντισης 1. Εικόνα 6.51 Το ανακατασκευασμένο πλαίσιο Β από το ιδεατό πλαίσιο της εικόνας 6.47 για συντελεστή κβάντισης 2. 64
65 6.2 Δεύτερο Πείραμα Ένα σύντομο δεύτερο πείραμα πραγματοποιήθηκε όμοιο με το πρώτο με τη μόνη διαφορά στην εξάρτηση μεταξύ των πλαισίων ενός GOP. Αντί το Ι να είναι το κοινό πλαίσιο αναφοράς για όλα τα P πλαίσια, παρουσιάζουν μεταξύ τους διαδοχική εξάρτηση δηλαδή κάθε πλαίσιο εκτός του Ι εξαρτάται από το ακριβώς προηγούμενό του. Κωδικοποίηση έγινε για τιμές συντελεστών κβάντισης από 1 έως 1.6 με βήμα 0.1, τόσο με τη χρήση MPEG (για half pixel ακρίβεια) όσο και με BLU-ME, όπου 16 ιδεατά πλαίσια αποτελούν 4 GOPS με μοτίβο IPPP. Το γενικό συμπέρασμα είναι ότι βελτιώνονται τα αποτελέσματα της πρόβλεψης και στις δύο μεθόδους με αποτέλεσμα υψηλότερες τιμές PSNR στα δύο τελευταία P πλαίσια ενός GOP και ταυτόχρονα λιγότερα bits κωδικοποίησης, για κάθε βαθμίδα κβάντισης. Αντίστοιχα τα Α και Β πλαίσια στη BLU-ME παρουσιάζουν επίσης μικρή αύξηση στο PSNR. Αυτό οφείλεται και στα καλύτερα αποτελέσματα των ιδεατών πλαισίων από την εναλλακτική εξάρτηση μεταξύ των πλαισίων ενός GOP. Όσο πιο υψηλό PSNR παρουσιάζει ένα ιδεατό πλαίσιο τόσο πιο ποιοτικά ανακατασκευασμένα Α και Β επιστρέφει η BLU-ME. Επομένως για το MPEG προκύπτουν τα αποτελέσματα στις παρακάτω εικόνες, όπου Case 1 αναφέρεται στο πρώτο πείραμα και Case 2 στο παρών. Εικόνα 6.52 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1. 65
66 Εικόνα 6.53 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.1. Εικόνα 6.54 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης
67 Εικόνα 6.55 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.3. Εικόνα 6.56 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης
68 Εικόνα 6.57 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.5. Εικόνα 6.58 Απαιτήσεις σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης
69 Eικόνα 6.59 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1. Εικόνα 6.60 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης
70 Εικόνα 6.61 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.2. Εικόνα 6.62 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης
71 Εικόνα 6.63 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.4. Εικόνα 6.64 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης
72 Εικόνα 6.65 Τιμές PSNR μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.6. Παρατηρείται, λοιπόν, γενική, μικρή αύξηση του PSNR για λιγότερα bits. Τώρα, σχετικά με το BLU ME, παρατηρείται αρχικά το καλύτερο αποτέλεσμα της πρόβλεψης σε σχέση με το πείραμα 1, όπου τα ιδεατά πλαίσια ανά GOP δίνουν λιγότερα bits στο παρών πείραμα (Case 2, πορτοκαλί) έναντι του πρώτου (Case 1, μπλε). Εικόνα 6.66 Απαίτηση σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1, 1.1 και
73 Εικόνα 6.67 Απαίτηση σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.3, 1.4 και 1.5. Εικόνα 6.68 Απαίτηση σε bits μεταξύ των δύο πειραμάτων για συντελεστή κβάντισης 1.6. Όσον αφορά το PSNR, για ένα GOP με ιδεατά πλαίσια, τα πρώτα 2 μένουν ίδια με το πρώτο πείραμα άρα θα εξεταστούν ενδεικτικά δύο παραδείγματα ενός 3ου και ενός 4ου P πλαισίου από δύο GOPs. Αυτά διαφέρουν από το πρώτο πείραμα επειδή εξαρτώνται από το 2ο και 3ο P πλαίσιο του GOP τους αντίστοιχα, και όχι από το 1ο πλαίσιο, που δέχεται ενδοπλαισιακή κωδικοποίηση. Στο παρακάτω πίνακα φαίνονται τιμές PSNR για το τρίτο αποκωδικοποιημένο ιδεατό πλαίσιο του πρώτου GOP, που αντιστοιχεί στα πλαίσια 5 και 6, 73
74 Εικόνα 6.69 Τιμές PSNR για το ιδεατό πλαίσιο του ζεύγους πλαισίων 5 και 6. Στον επόμενο πίνακα, το ίδιο με παραπάνω αλλά για το τέταρτο αποκωδικοποιημένο ιδεατό πλαίσιο του τελευταίου GOP, που αντιστοιχεί στα πλαίσια 31 και 32. Εικόνα 6.70 Τιμές PSNR για το ιδεατό πλαίσιο του ζεύγους πλαισίων 31 και 32. Επομένως, φαίνεται ότι για λιγότερα bits επιτυγχάνονται και καλύτερες τιμές PSNR για το δεύτερο πείραμα. Αυτό ισχύει και για τα υπόλοιπα αποκωδικοποιημένα τρίτα και τέταρτα P πλαίσια των GOPs. Συνεπώς και τα αποκωδικοποιημένα Α και Β πλαίσια θα παρουσιάζουν μεγαλύτερο PSNR. Στην επόμενη εικόνα φαίνονται οι μέσες τιμές PSNR για κάθε συνολική αλληλουχία των 16 ζεύγων Α και Β, ή αλλιώς των 32 πραγματικών πλαισίων μεταξύ των πειραμάτων. Στις πρώτες δύο στήλες της εικόνας 6.71 εμφανίζονται τα αποτελέσματα για τη BLU-ME και στην τρίτη τα αντίστοιχα του πειράματος 2 στο MPEG. Ισχύει επίσης όπου / το εξής: περίπτωση BLUE διανυσμάτων / περίπτωση ME διανυσμάτων. Εικόνα 6.71 Μέσες τιμές PSNR ανά ακολουθία μεταξύ των πειραμάτων Συνοψίζοντας, παρουσιάζονται και για τις δύο περιπτώσεις διανυσμάτων στο BLU ME ελαφρώς καλύτερα αποτελέσματα στο PSNR, που ενώ δεν είναι σημαντικά πρακτικά, αποδεικνύουν την καλύτερη πρόβλεψη στο πείραμα 2. Και πάλι μεταξύ MPEG και BLU-ME εμφανίζεται καλύτερη μέση τιμή PSNR ανά συντελεστή κβάντισης αλλά η BLU-ME θα απαιτεί πάντα περισσότερα bits κωδικοποίησης. 74
75 6.3 Τρίτο Πείραμα Ένα τελευταίο πείραμα έγινε πάνω στη πρόβλεψης κίνησης του MPEG, αυτή τη φορά με άπειρη ακρίβεια διανυσμάτων στο υποστοιχειακό επίπεδο. Η συνάρτηση που χρησιμοποιήθηκε ονομάζεται SPMSE και, για είσοδο, δύο πλαίσια, ένα αναφοράς και ένα στόχου, και τα μεταξύ τους ακέραια διανύσματα κίνησης επιστρέφει το πλαίσιο διαφοράς και νέα διανύσματα με τιμές, για παράδειγμα, ή Κατά την ανακατασκευή όμως του αρχικού πλαισίου στόχους, χωρίς ενδιάμεση συμπίεση και αποσυμπίεση, δηλαδή με τη πρόσθεση του πλαισίου διαφοράς με το μετατοπισμένο πλαίσιο αναφοράς δεν επιστρέφει αυτούσιο αποτέλεσμα. Λόγω σφαλμάτων ακρίβειας προκύπτουν δηλαδή αλλοιώσεις στην εικόνα στόχου όπως φαίνεται στην παρακάτω εικόνα.συνεπώς και με ενδιάμεση συμπίεση θα προστίθεται και αναμενόμενη αλλοίωση. Εντέλει δεν είναι προτιμότερη πρόβλεψη από την κανονική και συμφέρει περισσότερο η μέθοδος BLU-ME όσον αφορά διανύσματα κίνησης άπειρης ακρίβειας. Εικόνα 6.72 Αριστερά το αρχικό πλαίσιο στόχου ενώ δεξιά το ανακατασκευασμένο. Ενδεικτικά η κωδικοποίηση του πλαισίου διαφοράς για συντελεστή κβάντισης 1 με τον πίνακα Α.3, δίνει καλό αποτέλεσμα σε bits σε σχέση με τη κωδικοποίηση του πλαισίου αναφοράς. Από την άλλη, το PSNR του ανακατασκευασμένου είναι db, πολύ χαμηλότερο από όλες τις προηγούμενες δοκιμές. Είναι προφανές, σύμφωνα με τις προηγούμενες ενότητες του κεφαλαίου, ότι για περισσότερη συμπίεση θα παρουσιάζεται και μεγαλύτερη πτώση της ποιότητας. Συνεπώς, δε φαίνεται κάποιο όφελος στην περαιτέρω μελέτη αυτού τους είδους πρόβλεψης όσον αφορά το κανονικό MPEG. Στην εικόνα 6.73 φαίνεται και το ανακατασκευασμένο πλαίσιο. 75
76 Εικόνα 6.73 Η ανακατασκευασμένη εικόνα για συντελεστή κβάντισης 1 που αντιστοιχεί σε PSNR, περίπου, 29 db. ΚΕΦΑΛΑΙΟ 7 ΣΥΝΟΨΗ Συνοψίζοντας, λοιπόν, η εναλλακτική μέθοδος πρόβλεψης που προσφέρει η μέθοδος BLU-ME φαίνεται να έχει ικανοποιητικά αποτελέσματα όσον αφορά την ποιότητα των ανακατασκευασμένων πλαισίων σε σύγκριση με το πρότυπο MPEG. Η υψηλότερη όμως απαίτηση σε bits που εμφανίζει δε τη καθιστά ικανή να ανταγωνιστεί το MPEG. Εξάλλου, ο κύριος στόχος ήταν, η μελέτη και μια αρχική αξιολόγηση με τις γνωστές μεθόδους κωδικοποίησης του τμηματικού μετασχηματισμός DCT και της κβάντισης όπως γίνεται και στο MPEG. Ως πρόταση για περαιτέρω βελτίωση της μεθόδου θα ήταν, για παράδειγμα, προσπάθεια για δημιουργία ενός κοινού, ιδεατού πλαισίου αναφοράς για περισσότερα των δύο πλαισίων της ροής ενός βίντεο. Έτσι θα μειωνόταν η απαίτηση σε bits ενώ θα συντηρούταν η ομοιόμορφη αύξηση της ποιότητας σε ένα GOP. Ένα άλλο ελάττωμα είναι και o πολύ αργός χρόνος εκτέλεσης της για κάθε ζεύγος πλαισίων, θέμα που χρήζει βελτίωσης άμα είναι να χρησιμοποιηθεί υπό ρεαλιστικές συνθήκες συμπίεσης βίντεο η μέθοδος αυτή. 76
77 ΠΑΡΑΡΤΗΜΑ Α ΠΙΝΑΚΕΣ ΚΒΑΝΤΙΣΗΣ Πίνακας Α.1 Πίνακας κβάντισης στο JPEG Πίνακας Α.2 Πίνακας κβάντισης για intra-coding στο MPEG [ ] Πίνακας Α.3 Πίνακας κβάντισης για inter-coding στο MPEG, ομοιόμορφο 16 77
78 ΠΑΡΑΡΤΗΜΑ B ΛΕΞΙΛΟΓΙΑ HUFFMAN (α) (β) Πίνακας Β.1 (α) Κώδικες προθέματος για τους DC συντελεστές στο JPEG, (β) Δείγμα των κωδικών προθέματος για τους AC συντελεστές στο JPEG [3, ] Πίνακας Β.2 Κώδικες προθέματος για τους DC συντελεστές στο MPEG [3,367] 78
79 Πίνακας Β.3 Κώδικες κωδικοποίησης για τους συντελεστές AC στο MPEG (συνεχίζεται) [3,369] 79
80 Πίνακας Β.3(συνέχεια) Κώδικες κωδικοποίησης για τους AC συντελεστές στο MPEG (συνεχίζεται) [3, 370] 80
81 Πίνακας Β.3 (τέλος) Κώδικες κωδικοποίησης για τους AC συντελεστές στο MPEG [3,371] Πίνακας Β.4 Κώδικες προθέματος για τους χρωματικούς DC συντελεστές στο MPEG [3,220] Η κωδικοποίηση των διανυσμάτων κίνησης υλοποιήθηκε με αυτοσχέδια μέθοδο που αναπτύχθηκε για την εργασία αυτή με βάση τον πίνακα Β.4. Γενικά δε βρέθηκε σε κάποιο βιβλίο επαρκής 81
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ. Κωδικοποίηση εικόνας
 ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 2 Κωδικοποίηση εικόνας Ακολουθία από ψηφιοποιημένα καρέ (frames) που έχουν συλληφθεί σε συγκεκριμένο ρυθμό frame rate (π.χ. 10fps,
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 2 Κωδικοποίηση εικόνας Ακολουθία από ψηφιοποιημένα καρέ (frames) που έχουν συλληφθεί σε συγκεκριμένο ρυθμό frame rate (π.χ. 10fps,
Συµπίεση Εικόνας: Το πρότυπο JPEG
 ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων ΒΕΣ Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση Εικόνας: Το πρότυπο JPEG ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Εισαγωγή Σχεδιάστηκε από την οµάδα Joint Photographic Experts
ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων ΒΕΣ Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση Εικόνας: Το πρότυπο JPEG ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Εισαγωγή Σχεδιάστηκε από την οµάδα Joint Photographic Experts
ΒΕΣ 04: Συµπίεση και Μετάδοση Πολυµέσων. Περιεχόµενα. Βιβλιογραφία. Συµπίεση εικόνων: Το πρότυπο JPEG. Εισαγωγή. Ευθύς µετασχηµατισµός DCT
 ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Περιεχόµενα Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση
ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Περιεχόµενα Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση
Περιεχόµενα. ΕΠΛ 422: Συστήµατα Πολυµέσων. Βιβλιογραφία. Εισαγωγή. Συµπίεση εικόνων: Το πρότυπο JPEG. Εισαγωγή. Ευθύς µετασχηµατισµός DCT
 Περιεχόµενα ΕΠΛ : Συστήµατα Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση ηµιουργία
Περιεχόµενα ΕΠΛ : Συστήµατα Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση ηµιουργία
Κωδικοποίηση βίντεο (H.261 / DVI)
 Κωδικοποίηση βίντεο (H.261 / DVI) Αρχές κωδικοποίησης βίντεο Εισαγωγή στο H.261 Κωδικοποίηση βίντεο Ροή δεδοµένων Εισαγωγή στο DVI Κωδικοποίηση ήχου και εικόνων Κωδικοποίηση βίντεο Ροή δεδοµένων Τεχνολογία
Κωδικοποίηση βίντεο (H.261 / DVI) Αρχές κωδικοποίησης βίντεο Εισαγωγή στο H.261 Κωδικοποίηση βίντεο Ροή δεδοµένων Εισαγωγή στο DVI Κωδικοποίηση ήχου και εικόνων Κωδικοποίηση βίντεο Ροή δεδοµένων Τεχνολογία
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας. Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Group (JPEG) το 1992.
 Μέθοδοι Συμπίεσης Εικόνας Πρωτόκολλο JPEG Συμπίεση Εικόνας: Μείωση αποθηκευτικού χώρου Ευκολία στη μεταφορά αρχείων Δημιουργήθηκε από την ομάδα Joint Photographic Experts Group (JPEG) το 1992. Ονομάστηκε
Μέθοδοι Συμπίεσης Εικόνας Πρωτόκολλο JPEG Συμπίεση Εικόνας: Μείωση αποθηκευτικού χώρου Ευκολία στη μεταφορά αρχείων Δημιουργήθηκε από την ομάδα Joint Photographic Experts Group (JPEG) το 1992. Ονομάστηκε
Μάθημα 7 ο. Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Βίντεο και κινούµενα σχέδια
 Βίντεο και κινούµενα σχέδια Περιγραφή του βίντεο Ανάλυση του βίντεο Κωδικοποίηση των χρωµάτων Μετάδοση τηλεοπτικού σήµατος Συµβατικά τηλεοπτικά συστήµατα Τεχνολογία Πολυµέσων 06-1 Περιγραφή του βίντεο
Βίντεο και κινούµενα σχέδια Περιγραφή του βίντεο Ανάλυση του βίντεο Κωδικοποίηση των χρωµάτων Μετάδοση τηλεοπτικού σήµατος Συµβατικά τηλεοπτικά συστήµατα Τεχνολογία Πολυµέσων 06-1 Περιγραφή του βίντεο
Βίντεο. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 06-1
 Βίντεο Εισαγωγή Χαρακτηριστικά του βίντεο Απόσταση θέασης Μετάδοση τηλεοπτικού σήματος Συμβατικά τηλεοπτικά συστήματα Ψηφιακό βίντεο Εναλλακτικά μορφότυπα Τηλεόραση υψηλής ευκρίνειας Κινούμενες εικόνες
Βίντεο Εισαγωγή Χαρακτηριστικά του βίντεο Απόσταση θέασης Μετάδοση τηλεοπτικού σήματος Συμβατικά τηλεοπτικά συστήματα Ψηφιακό βίντεο Εναλλακτικά μορφότυπα Τηλεόραση υψηλής ευκρίνειας Κινούμενες εικόνες
Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε Απώλειες. Πρότυπα Συµπίεσης Εικόνων
 ΤΨΣ 5: Ψηφιακή Επεξεργασία Εικόνας ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε απώλειες Πρότυπα Συµπίεσης Εικόνων Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο
ΤΨΣ 5: Ψηφιακή Επεξεργασία Εικόνας ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε απώλειες Πρότυπα Συµπίεσης Εικόνων Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Αρχές κωδικοποίησης. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ,
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται από δύο µέρη. Το πρώτο περιλαµβάνει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται από δύο µέρη. Το πρώτο περιλαµβάνει
Τεχνολογία Πολυμέσων. Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
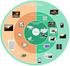 Τεχνολογία Πολυμέσων Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων. Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων. Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
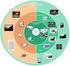 Τεχνολογία Πολυμέσων Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Συστήματα Πολυμέσων. Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
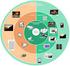 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
DIP_06 Συμπίεση εικόνας - JPEG. ΤΕΙ Κρήτης
 DIP_06 Συμπίεση εικόνας - JPEG ΤΕΙ Κρήτης Συμπίεση εικόνας Το μέγεθος μιας εικόνας είναι πολύ μεγάλο π.χ. Εικόνα μεγέθους Α4 δημιουργημένη από ένα σαρωτή με 300 pixels ανά ίντσα και με χρήση του RGB μοντέλου
DIP_06 Συμπίεση εικόνας - JPEG ΤΕΙ Κρήτης Συμπίεση εικόνας Το μέγεθος μιας εικόνας είναι πολύ μεγάλο π.χ. Εικόνα μεγέθους Α4 δημιουργημένη από ένα σαρωτή με 300 pixels ανά ίντσα και με χρήση του RGB μοντέλου
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
Συστήματα Πολυμέσων. Ενότητα 7: Συμπίεση Εικόνας κατά JPEG. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Συμπίεση Εικόνας κατά JPEG Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Συμπίεση Εικόνας κατά JPEG Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Συστήματα Πολυμέσων. Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τεράστιες ανάγκες σε αποθηκευτικό χώρο
 ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Τμήμα Επιστήμης Υπολογιστών ΗΥ-474. Ψηφιακό βίντεο. Αναλογικό βίντεο / ψηφιοποίηση Διεπαφές Εκτίμηση κίνησης μπλοκ
 Ψηφιακό βίντεο Αναλογικό βίντεο / ψηφιοποίηση Διεπαφές Εκτίμηση κίνησης μπλοκ Αναλογικό βίντεο SECAM PAL NTSC Ρυθμός πλεγμάτων (Hz) 50 50 59,94 Αριθμός ενεργών γραμμών ανά καρέ 576 576 480 Σχήμα εικονοστοιχείου
Ψηφιακό βίντεο Αναλογικό βίντεο / ψηφιοποίηση Διεπαφές Εκτίμηση κίνησης μπλοκ Αναλογικό βίντεο SECAM PAL NTSC Ρυθμός πλεγμάτων (Hz) 50 50 59,94 Αριθμός ενεργών γραμμών ανά καρέ 576 576 480 Σχήμα εικονοστοιχείου
Κεφάλαιο 2. Οργάνωση και διαχείριση της Πληροφορίας στον. Υπολογιστή
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 2 Οργάνωση και διαχείριση της Πληροφορίας στον Υπολογιστή Δεδομένα και Εντολές πληροφορία δεδομένα εντολές αριθμητικά δδ δεδομένα κείμενο εικόνα Επιλογή Αναπαράστασης
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 2 Οργάνωση και διαχείριση της Πληροφορίας στον Υπολογιστή Δεδομένα και Εντολές πληροφορία δεδομένα εντολές αριθμητικά δδ δεδομένα κείμενο εικόνα Επιλογή Αναπαράστασης
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
χωρίςναδηµιουργείταιαίσθησηαπώλειαςτηςποιότηταςτηςανακατασκευασµένηςεικόνας.
 Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intra- frame Coding): Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
 ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intraframe Coding): κάθε εικόνα αντιμετωπίζεται και κωδικοποιείται ανεξάρτητα από τις υπόλοιπες (όπως στο JPEG) Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intraframe Coding): κάθε εικόνα αντιμετωπίζεται και κωδικοποιείται ανεξάρτητα από τις υπόλοιπες (όπως στο JPEG) Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
Κεφάλαιο 3 Συμπίεση Βίντεο
 Κεφάλαιο 3 Συμπίεση Βίντεο Σύνοψη Στο κεφάλαιο αυτό εξετάζουμε τους βασικούς τρόπους με τους οποίους το πρότυπο MPEG (και συγκεκριμένα το MPEG-2) προβλέπει τη συμπίεση του σήματος βίντεο. Η ανάγκη για
Κεφάλαιο 3 Συμπίεση Βίντεο Σύνοψη Στο κεφάλαιο αυτό εξετάζουμε τους βασικούς τρόπους με τους οποίους το πρότυπο MPEG (και συγκεκριμένα το MPEG-2) προβλέπει τη συμπίεση του σήματος βίντεο. Η ανάγκη για
Επεξεργασία Πολυµέσων. Δρ. Μαρία Κοζύρη Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας
 Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Τεχνολογία Πολυμέσων. Ενότητα # 6: Βίντεο Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 6: Βίντεο Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 6: Βίντεο Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Εικόνα. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 05-1
 Εικόνα Εισαγωγή Ψηφιακή αναπαράσταση Κωδικοποίηση των χρωμάτων Συσκευές εισόδου και εξόδου Βάθος χρώματος και ανάλυση Συμβολική αναπαράσταση Μετάδοση εικόνας Σύνθεση εικόνας Ανάλυση εικόνας Τεχνολογία
Εικόνα Εισαγωγή Ψηφιακή αναπαράσταση Κωδικοποίηση των χρωμάτων Συσκευές εισόδου και εξόδου Βάθος χρώματος και ανάλυση Συμβολική αναπαράσταση Μετάδοση εικόνας Σύνθεση εικόνας Ανάλυση εικόνας Τεχνολογία
Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω:
 Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Εφαρμογές Πληροφορικής
 Εφαρμογές Πληροφορικής Κεφάλαιο 11 Πολυμέσα ΜΕΡΟΣ Α 1. Υπερκείμενο Ποιός είναι ο κόμβος, ποιός ο σύνδεσμος και ποιά η θερμή λέξη; 1 2. Υπερμέσα Χαρακτηριστικά Κόμβος (Node) Αποτελεί τη βάση πληροφοριών
Εφαρμογές Πληροφορικής Κεφάλαιο 11 Πολυμέσα ΜΕΡΟΣ Α 1. Υπερκείμενο Ποιός είναι ο κόμβος, ποιός ο σύνδεσμος και ποιά η θερμή λέξη; 1 2. Υπερμέσα Χαρακτηριστικά Κόμβος (Node) Αποτελεί τη βάση πληροφοριών
Δ10. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 203-204 Κωδικοποίηση εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Ανάλυση Οθονών Δρ. Ν. Π. Σγούρος 3 Πρωτόκολλα μετάδοσης εικονοροών Πρωτόκολλο Ρυθμός (Hz) Φίλμ 23.976 ATSC 24 PAL,DVB-SD,DVB-HD
Συμπίεση Δεδομένων 203-204 Κωδικοποίηση εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Ανάλυση Οθονών Δρ. Ν. Π. Σγούρος 3 Πρωτόκολλα μετάδοσης εικονοροών Πρωτόκολλο Ρυθμός (Hz) Φίλμ 23.976 ATSC 24 PAL,DVB-SD,DVB-HD
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #5: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 7 Νοεµβρίου 2005 Επανάληψη Θεωρία Πληροφορίας Εντροπία: H ( P) i= 0 Κωδικοποίηση Huffman 3
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #5: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 7 Νοεµβρίου 2005 Επανάληψη Θεωρία Πληροφορίας Εντροπία: H ( P) i= 0 Κωδικοποίηση Huffman 3
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
Δ11 Δ12. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 Κωδικοποιητές εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Κωδικοποιητές Εικονοροών ITU-T VCEG H.261 (1990) ISO/IEC MPEG H.263 (1995/9 6) MPEG-2 (H.262) (1994/9 5) H.263+ (1997/98)
Συμπίεση Δεδομένων 2013-2014 Κωδικοποιητές εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Κωδικοποιητές Εικονοροών ITU-T VCEG H.261 (1990) ISO/IEC MPEG H.263 (1995/9 6) MPEG-2 (H.262) (1994/9 5) H.263+ (1997/98)
Τμήμα Επιστήμης Υπολογιστών ΗΥ-474. Ψηφιακή Εικόνα. Χωρική ανάλυση Αρχεία εικόνων
 Ψηφιακή Εικόνα Χωρική ανάλυση Αρχεία εικόνων Ψηφιοποίηση εικόνων Δειγματοληψία περιοδική, ορθογώνια (pixel = picture element) πυκνότητα ανάλογα με τη λεπτομέρεια (ppi) Κβαντισμός τιμών διακριτές τιμές,
Ψηφιακή Εικόνα Χωρική ανάλυση Αρχεία εικόνων Ψηφιοποίηση εικόνων Δειγματοληψία περιοδική, ορθογώνια (pixel = picture element) πυκνότητα ανάλογα με τη λεπτομέρεια (ppi) Κβαντισμός τιμών διακριτές τιμές,
Αρχές κωδικοποίησης. Τεχνολογία Πολυµέσων 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Μοντέλο Επικοινωνίας Δεδομένων. Επικοινωνίες Δεδομένων Μάθημα 6 ο
 Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
2. ΨΗΦΙΟΠΟΙΗΣΗ ΠΛΗΡΟΦΟΡΙΑΣ
 2. ΨΗΦΙΟΠΟΙΗΣΗ ΠΛΗΡΟΦΟΡΙΑΣ Περιγραφή πληροφορίας. Η πληροφορία περιγράφεται σαν μία ή περισσότερες χρονικές ή χωρικές μεταβλητές. Μετατρέπει την φυσική ποσότητα σε ηλεκτρικό σήμα To σήμα αναπαριστά το
2. ΨΗΦΙΟΠΟΙΗΣΗ ΠΛΗΡΟΦΟΡΙΑΣ Περιγραφή πληροφορίας. Η πληροφορία περιγράφεται σαν μία ή περισσότερες χρονικές ή χωρικές μεταβλητές. Μετατρέπει την φυσική ποσότητα σε ηλεκτρικό σήμα To σήμα αναπαριστά το
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Αντοχή (ruggedness) στο θόρυβο μετάδοσης Αποτελεσματική αναγέννηση (regeneration) Δυνατότητα ομοιόμορφου σχήματος (uniform format) μετάδοσης Όμως:
 ΨΗΦΙΑΚΗ ΑΝΑΠΑΡΑΣΤΑΣΗ Πλεονεκτήματα: Αντοχή (ruggedness) στο θόρυβο μετάδοσης Αποτελεσματική αναγέννηση (regeneration) Δυνατότητα ομοιόμορφου σχήματος (uniform format) μετάδοσης Όμως: Αύξηση απαίτησης εύρους
ΨΗΦΙΑΚΗ ΑΝΑΠΑΡΑΣΤΑΣΗ Πλεονεκτήματα: Αντοχή (ruggedness) στο θόρυβο μετάδοσης Αποτελεσματική αναγέννηση (regeneration) Δυνατότητα ομοιόμορφου σχήματος (uniform format) μετάδοσης Όμως: Αύξηση απαίτησης εύρους
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Διαφορική Παλμοκωδική Διαμόρφωση + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Διαφορική Παλμοκωδική Διαμόρφωση + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
MPEG-4: Βασικά Χαρακτηριστικά
 MPEG-4 MPEG-4: Βασικά Χαρακτηριστικά Σχεδιάστηκε ώστε να καλύπτει ευρύ φάσμα ρυθμών, από 5 kbps εώς 10 Mbps Εκτός από τη συμπίεση δίνει έμφαση και στην αλληλεπίδραση με το χρήστη Χρησιμοποιεί αντικείμενα
MPEG-4 MPEG-4: Βασικά Χαρακτηριστικά Σχεδιάστηκε ώστε να καλύπτει ευρύ φάσμα ρυθμών, από 5 kbps εώς 10 Mbps Εκτός από τη συμπίεση δίνει έμφαση και στην αλληλεπίδραση με το χρήστη Χρησιμοποιεί αντικείμενα
ΑΣΚΗΣΗ 2 ΒΑΣΙΚΑ ΚΑΙ ΣΥΝΘΕΤΑ ΣΗΜΑΤΑ ΔΥΟ ΔΙΑΣΤΑΣΕΩΝ - ΕΙΚΟΝΑΣ
 ΑΣΚΗΣΗ 2 ΒΑΣΙΚΑ ΚΑΙ ΣΥΝΘΕΤΑ ΣΗΜΑΤΑ ΔΥΟ ΔΙΑΣΤΑΣΕΩΝ - ΕΙΚΟΝΑΣ Αντικείμενο: Κατανόηση και αναπαράσταση των βασικών σημάτων δύο διαστάσεων και απεικόνισης αυτών σε εικόνα. Δημιουργία και επεξεργασία των διαφόρων
ΑΣΚΗΣΗ 2 ΒΑΣΙΚΑ ΚΑΙ ΣΥΝΘΕΤΑ ΣΗΜΑΤΑ ΔΥΟ ΔΙΑΣΤΑΣΕΩΝ - ΕΙΚΟΝΑΣ Αντικείμενο: Κατανόηση και αναπαράσταση των βασικών σημάτων δύο διαστάσεων και απεικόνισης αυτών σε εικόνα. Δημιουργία και επεξεργασία των διαφόρων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Θεωρητικές Ασκήσεις (# 3): 1. Ο διακριτός µετασχηµατισµός συνηµίτονου (Discrete Cosine Transform)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Θεωρητικές Ασκήσεις (# 3): 1. Ο διακριτός µετασχηµατισµός συνηµίτονου (Discrete Cosine Transform)
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Πληροφορική Ι. Μάθημα 9 ο Συμπίεση δεδομένων. Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας. Δρ.
 Οι διαφάνειες έχουν βασιστεί στο βιβλίο «Εισαγωγή στην επιστήμη των υπολογιστών» του B. Forouzanκαι Firoyz Mosharraf(2 η έκδοση-2010) Εκδόσεις Κλειδάριθμος Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου
Οι διαφάνειες έχουν βασιστεί στο βιβλίο «Εισαγωγή στην επιστήμη των υπολογιστών» του B. Forouzanκαι Firoyz Mosharraf(2 η έκδοση-2010) Εκδόσεις Κλειδάριθμος Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Κωδικοποίηση εικόνων κατά JPEG
 Κωδικοποίηση εικόνων κατά JPEG Εισαγωγή Προετοιµασία της εικόνας ρυθµός Ακολουθιακός απωλεστικός ρυθµός Εκτεταµένος απωλεστικός ρυθµός Μη απωλεστικός ρυθµός Ιεραρχικός ρυθµός Τεχνολογία Πολυµέσων 09-1
Κωδικοποίηση εικόνων κατά JPEG Εισαγωγή Προετοιµασία της εικόνας ρυθµός Ακολουθιακός απωλεστικός ρυθµός Εκτεταµένος απωλεστικός ρυθµός Μη απωλεστικός ρυθµός Ιεραρχικός ρυθµός Τεχνολογία Πολυµέσων 09-1
Συστήµατα Πολυµέσων Ενδιάµεση Εξέταση: Οκτώβριος 2004
 Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ
 3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ ΑΝΑΓΚΗ ΣΥΜΠΙΕΣΗΣ ΔΕΔΟΜΕΝΩΝ Local Multimedia Π.χ. Μία ταινία 90 min απαιτεί 120 GB, και τα σημερινά μέσα αποθήκευσης < 25 GB. Άρα σήμερα είναι αδύνατη η αποθήκευση και η
3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ ΑΝΑΓΚΗ ΣΥΜΠΙΕΣΗΣ ΔΕΔΟΜΕΝΩΝ Local Multimedia Π.χ. Μία ταινία 90 min απαιτεί 120 GB, και τα σημερινά μέσα αποθήκευσης < 25 GB. Άρα σήμερα είναι αδύνατη η αποθήκευση και η
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Α.Τ.Ε.Ι. Ηρακλείου Ψηφιακή Επεξεργασία Εικόνας ιδάσκων: Βασίλειος Γαργανουράκης. Ανθρώπινη Όραση - Χρωµατικά Μοντέλα
 Ανθρώπινη Όραση - Χρωµατικά Μοντέλα 1 Τι απαιτείται για την όραση Φωτισµός: κάποια πηγή φωτός Αντικείµενα: που θα ανακλούν (ή διαθλούν) το φως Μάτι: σύλληψη του φωτός σαν εικόνα Τρόποι µετάδοσης φωτός
Ανθρώπινη Όραση - Χρωµατικά Μοντέλα 1 Τι απαιτείται για την όραση Φωτισµός: κάποια πηγή φωτός Αντικείµενα: που θα ανακλούν (ή διαθλούν) το φως Μάτι: σύλληψη του φωτός σαν εικόνα Τρόποι µετάδοσης φωτός
Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση
 Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 5 η Παρουσίαση : Ψηφιακή Επεξεργασία Εικόνας Διδάσκων: Γιάννης Ντόκας Σύνθεση Χρωμάτων Αφαιρετική Παραγωγή Χρώματος Χρωματικά
Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 5 η Παρουσίαση : Ψηφιακή Επεξεργασία Εικόνας Διδάσκων: Γιάννης Ντόκας Σύνθεση Χρωμάτων Αφαιρετική Παραγωγή Χρώματος Χρωματικά
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ.
 Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας. Παρουσίαση 12 η. Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση 12 η Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων Εισαγωγή (1) Το χρώμα είναι ένας πολύ σημαντικός παράγοντας περιγραφής, που συχνά απλουστεύει κατά
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση 12 η Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων Εισαγωγή (1) Το χρώμα είναι ένας πολύ σημαντικός παράγοντας περιγραφής, που συχνά απλουστεύει κατά
Πολυμέσα. Συμπίεση δεδομένων Κωδικοποίηση JPEG. Δρ. Γεώργιος Π. Παυλίδης ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ
 Πολυμέσα Συμπίεση δεδομένων Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης JPEG, Οικογένεια H.26x, H.32x Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη
Πολυμέσα Συμπίεση δεδομένων Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης JPEG, Οικογένεια H.26x, H.32x Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ. Εισαγωγή
 ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 1 Εισαγωγή Το μάθημα «Αρχές Ψηφιακής Τηλεόρασης» εξετάζει τις τεχνολογίες και τους μηχανισμούς που παρεμβάλλονται για να διανεμηθεί
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 1 Εισαγωγή Το μάθημα «Αρχές Ψηφιακής Τηλεόρασης» εξετάζει τις τεχνολογίες και τους μηχανισμούς που παρεμβάλλονται για να διανεμηθεί
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Αρχές συµπίεσης δεδοµένων Ήδη συµπίεσης Συµπίεση εικόνων Αλγόριθµος JPEG Γιατί χρειαζόµαστε συµπίεση; Τα σηµερινά αποθηκευτικά µέσα αδυνατούν
Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Αρχές συµπίεσης δεδοµένων Ήδη συµπίεσης Συµπίεση εικόνων Αλγόριθµος JPEG Γιατί χρειαζόµαστε συµπίεση; Τα σηµερινά αποθηκευτικά µέσα αδυνατούν
Ψηφιακές Τηλεπικοινωνίες. Θεωρία Ρυθμού Παραμόρφωσης
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Κωδικοποίηση βίντεο (MPEG)
 (MEG) Εισαγωγή στο MEG-1 Κωδικοποίηση βίντεο οµή βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MEG-1 MEG (Motion ictures Experts Group) ίντεο και ήχος υψηλής ποιότητας ιανοµή
(MEG) Εισαγωγή στο MEG-1 Κωδικοποίηση βίντεο οµή βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MEG-1 MEG (Motion ictures Experts Group) ίντεο και ήχος υψηλής ποιότητας ιανοµή
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
DIP_01 Εισαγωγή στην ψηφιακή εικόνα. ΤΕΙ Κρήτης
 DIP_01 Εισαγωγή στην ψηφιακή εικόνα ΤΕΙ Κρήτης Πληροφορίες Μαθήματος ιαλέξεις Πέμπτη 12:15 15:00 Αιθουσα Γ7 ιδάσκων:. Κοσμόπουλος Γραφείο: Κ23-0-15 (ισόγειο( κλειστού γυμναστηρίου) Ωρες γραφείου Τε 16:00
DIP_01 Εισαγωγή στην ψηφιακή εικόνα ΤΕΙ Κρήτης Πληροφορίες Μαθήματος ιαλέξεις Πέμπτη 12:15 15:00 Αιθουσα Γ7 ιδάσκων:. Κοσμόπουλος Γραφείο: Κ23-0-15 (ισόγειο( κλειστού γυμναστηρίου) Ωρες γραφείου Τε 16:00
Συστήματα Πολυμέσων. Ενότητα 16: Διαμορφώσεις και Πρότυπα Ψηφιακού Βίντεο. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 16: Διαμορφώσεις και Πρότυπα Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 16: Διαμορφώσεις και Πρότυπα Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν
ΠΛΗΡΟΦΟΡΙΚΗ I. 7 η ΔΙΑΛΕΞΗ Γραφικά με Υπολογιστή
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ - ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΣΑΓΩΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΤΟΥΡΙΣΤΙΚΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΚΑΙ ΕΠΙΧΕΙΡΗΣΕΩΝ ΦΙΛΟΞΕΝΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗ I 7 η ΔΙΑΛΕΞΗ Γραφικά με Υπολογιστή ΧΑΣΑΝΗΣ ΒΑΣΙΛΕΙΟΣ
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ - ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΣΑΓΩΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΤΟΥΡΙΣΤΙΚΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΚΑΙ ΕΠΙΧΕΙΡΗΣΕΩΝ ΦΙΛΟΞΕΝΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗ I 7 η ΔΙΑΛΕΞΗ Γραφικά με Υπολογιστή ΧΑΣΑΝΗΣ ΒΑΣΙΛΕΙΟΣ
ιαφορική εντροπία Σεραφείµ Καραµπογιάς
 ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Βασικά στοιχεία εικονοστοιχείου (pixel) Φυσική λειτουργία όρασης Χηµική και ψηφιακή σύλληψη (Κλασσικές και ψηφιακές φωτογραφικές µηχανές)
Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Βασικά στοιχεία εικονοστοιχείου (pixel) Φυσική λειτουργία όρασης Χηµική και ψηφιακή σύλληψη (Κλασσικές και ψηφιακές φωτογραφικές µηχανές)
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
Ανάλυση Διατάξεων Εκπομπής σε Συστήματα Ψηφιακής Τηλεόρασης Υψηλής Ευκρίνειας
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Ανάλυση Διατάξεων Εκπομπής σε Συστήματα Ψηφιακής Τηλεόρασης Υψηλής Ευκρίνειας Φλώρος Άγγελος ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Ανάλυση Διατάξεων Εκπομπής σε Συστήματα Ψηφιακής Τηλεόρασης Υψηλής Ευκρίνειας Φλώρος Άγγελος ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ,
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 422: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2004 2005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το τρέχον έγγραφο αποτελεί υπόδειγµα τελικής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 422: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2004 2005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το τρέχον έγγραφο αποτελεί υπόδειγµα τελικής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας Διδάσκων: Αναγνωστόπουλος Χρήστος Κώδικες μετρήσεων αντικειμένων σε εικόνα Χρωματικά μοντέλα: Munsell, HSB/HSV, CIE-LAB Κώδικες μετρήσεων αντικειμένων σε εικόνες Η βασική
Επεξεργασία Χαρτογραφικής Εικόνας Διδάσκων: Αναγνωστόπουλος Χρήστος Κώδικες μετρήσεων αντικειμένων σε εικόνα Χρωματικά μοντέλα: Munsell, HSB/HSV, CIE-LAB Κώδικες μετρήσεων αντικειμένων σε εικόνες Η βασική
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Συστήματα Πολυμέσων. Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Θεώρημα κωδικοποίησης πηγής
 Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Δ13b. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Εκτίμηση ποιότητας Εικόνας Ι Αντικειμενική Αξιολόγηση Χρήση μετρικών εκτίμησης ποιότητας Βασίζονται στη σύγκριση μεταξύ εικονοστοιχείων αρχικής και ανασυσταμένης εικόνας Υποκειμενική
Συμπίεση Δεδομένων 2014-2015 Εκτίμηση ποιότητας Εικόνας Ι Αντικειμενική Αξιολόγηση Χρήση μετρικών εκτίμησης ποιότητας Βασίζονται στη σύγκριση μεταξύ εικονοστοιχείων αρχικής και ανασυσταμένης εικόνας Υποκειμενική
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 Κωδικοποίηση ζωνών συχνοτήτων Δρ. Ν. Π. Σγούρος 2 Φαινόμενο Μπλόκ (Blocking Artifact) Η χρήση παραθύρων για την εφαρμογή των μετασχηματισμών δημιουργεί το φαινόμενο μπλόκ Μειώνεται
Συμπίεση Δεδομένων 2013-2014 Κωδικοποίηση ζωνών συχνοτήτων Δρ. Ν. Π. Σγούρος 2 Φαινόμενο Μπλόκ (Blocking Artifact) Η χρήση παραθύρων για την εφαρμογή των μετασχηματισμών δημιουργεί το φαινόμενο μπλόκ Μειώνεται
Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης
 Πανεπιστήμιο Πατρών Τμήμα Μηχ. Η/Υ & Πληροφορικής Ακαδημαϊκό Έτος 009-010 Ψ Η Φ Ι Α Κ Ε Σ Τ Η Λ Ε Π Ι Κ Ο Ι Ν Ω Ν Ι ΕΣ η Εργαστηριακή Άσκηση: Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης Στην άσκηση
Πανεπιστήμιο Πατρών Τμήμα Μηχ. Η/Υ & Πληροφορικής Ακαδημαϊκό Έτος 009-010 Ψ Η Φ Ι Α Κ Ε Σ Τ Η Λ Ε Π Ι Κ Ο Ι Ν Ω Ν Ι ΕΣ η Εργαστηριακή Άσκηση: Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης Στην άσκηση
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Μετάδοση πληροφορίας - Διαμόρφωση
 Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Τμήμα Λογιστικής. Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. Μαθήματα 6 και 7 Αναπαράσταση της Πληροφορίας στον Υπολογιστή. 1 Στέργιος Παλαμάς
 ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Τμήμα Λογιστικής Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές Μαθήματα 6 και 7 Αναπαράσταση της Πληροφορίας στον Υπολογιστή 1 1. Αριθμοί: Το Δυαδικό Σύστημα Οι ηλεκτρονικοί υπολογιστές
ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Τμήμα Λογιστικής Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές Μαθήματα 6 και 7 Αναπαράσταση της Πληροφορίας στον Υπολογιστή 1 1. Αριθμοί: Το Δυαδικό Σύστημα Οι ηλεκτρονικοί υπολογιστές
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοημοσύνη Ι» 5 o Φροντιστήριο
 Πρόβλημα ο Ασκήσεις Φροντιστηρίου 5 o Φροντιστήριο Δίνεται το παρακάτω σύνολο εκπαίδευσης: # Είσοδος Κατηγορία 0 0 0 Α 2 0 0 Α 0 Β 4 0 0 Α 5 0 Β 6 0 0 Α 7 0 Β 8 Β α) Στον παρακάτω κύβο τοποθετείστε τα
Πρόβλημα ο Ασκήσεις Φροντιστηρίου 5 o Φροντιστήριο Δίνεται το παρακάτω σύνολο εκπαίδευσης: # Είσοδος Κατηγορία 0 0 0 Α 2 0 0 Α 0 Β 4 0 0 Α 5 0 Β 6 0 0 Α 7 0 Β 8 Β α) Στον παρακάτω κύβο τοποθετείστε τα
2.0 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ-ΟΡΟΛΟΓΙΕΣ
 2.0 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ-ΟΡΟΛΟΓΙΕΣ Η σάρωση ενός εγγράφου εισάγει στον υπολογιστή μια εικόνα, ενώ η εκτύπωση μεταφέρει στο χαρτί μια εικόνα από αυτόν. Για να αντιληφθούμε επομένως τα χαρακτηριστικά των σαρωτών
2.0 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ-ΟΡΟΛΟΓΙΕΣ Η σάρωση ενός εγγράφου εισάγει στον υπολογιστή μια εικόνα, ενώ η εκτύπωση μεταφέρει στο χαρτί μια εικόνα από αυτόν. Για να αντιληφθούμε επομένως τα χαρακτηριστικά των σαρωτών
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Χωρικά φίλτρα Χωρικά φίλτρα Γενικά Σε αντίθεση με τις σημειακές πράξεις και μετασχηματισμούς, στα
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Χωρικά φίλτρα Χωρικά φίλτρα Γενικά Σε αντίθεση με τις σημειακές πράξεις και μετασχηματισμούς, στα
