2. Rotacija krutog tijela. Kinematika krutog tijela. 11. dio. Kinematika krutog tijela. 1. Translacija krutog tijela. a) Krivocrtna b) Pravocrtna
|
|
|
- Αμάρανθος Δημαράς
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Kod kruog ijel udljeosu bilo kojih diju ok ijel osje ijekom gibj epromijeje. Kiemik kruog ijel 11. dio Kiemik gibj: ) kruog šp b) krue ploe c) kruog ijel. Rzlikujemo: ) slobodo ijelo b) eslobodo ijelo 1 Slobodo gibje kruog ijel Priudo gibje kruog ijel moguos gibj ogrie je jskim ezm. Kiemik kruog ijel Gibje mehizm sus ssljeih od iše meusobo ezih kruih ijel. 1. Trslcij. Rocij Riski mehizmi kod kojih se si loi gibju u rim prlelim s jedom epomiom, refereom riom. Kriocr Procr Trslcij kruog ijel ) Kriocr b) Procr. Rocij kruog ijel ) oko epomie osi b) oko reue osi c) oko epomie oke O slobode osi 5 6 1
2 . Rocij kruog ijel c) Rocij kruog ijel oko epomie oke O ) oko epomie osi b) oko reue osi 7 Gibje zrk - sfero gibje ω r i ω p imju isi smjer rocije 8 c) Rocij kruog ijel oko epomie oke O 1. Trslcijsko gibje Gibje Zemlje oko Suc rerogrd precesij duži 1 1 kos. ω r i ω p imju supro smjer rocije 9 10 d() 0 r r + d() d( ) d(r ) d(r ) d() + slijedi : slijedi : 1. Trslcijsko gibje Se oke kruog ijel pri rslcijskom gibju opisuju kogruee puje i imju u skom reuku reme jedke brzie i ubrzj po prcu, smjeru i iezieu. Dooljo je pozi zko gibj smo jede oke ijel. Kruž rslcij je poseb sluj kriocre rslcije rzi : Ubrzje: 11 1
3 Duži C izodi. gibje Duži izodi.. gibje Primjer rslcijskog gibj: Gibje klip u beziskom ili dizel-mooru Gibje go rom dijelu pu Rocijsko gibje ) oko epomie osi b) oko reue osi ) Rocijsko gibje oko epomie osi gibj zupik, remeic, zmšjk, kružih pil id. Zko rocijskog gibj: ϕ ϕ () 15 Rocij oko epomie osi Gibje ijel pri kojemu se oke ijel duž osi rocije osju epomie. Se osle oke ijel opisuju kružice oko epomie osi u rim okomiim os rocije i s središem oj osi. 16 Sredj ku brzi: ω sr ϕ 1 s Treu ku brzi: Ku brzi ω Prem kuoj brzii ω rzlikujemo slijede gibj: Promjeljio ω f () Jedoliko ω kos. (Smjer: Prilo dese ruke) ω lim( ω sr 0 ϕ dϕ ) lim
4 Promjelji rocij: Sredje kuo ubrzje: Kuo ubrzje: Kuo ubrzje ε ω εsr ω dω ε lim εsr lim 0 0 d 1 s Slujei rocijskih gibj: 1. ε >0 jedoliko ubrzo gibje (dω ε. >0). ε <0 jedoliko usporeo gibje (dω ε. <0) 3. ε 0 ω kos. jedoliko gibje (dω ε. 0) Jedoliko ubrzo rocijsko gibje Vekori ω i ε isog su smjer. Jedoliko usporeo rocijsko gibje Vekori ω i ε suproi su po smjeru Kuo ubrzje : ε > 0; ε kos. Kuo ubrzje: ε < 0; ε kos. Ku brzi : ω ω + ε 0 Ku brzi : ω ω ε 0 Zko gibj : 1 ϕ ϕ0 + ω0 + ε Zko gibj : 1 ϕ ϕ0 + ω0 ε 1 3. Jedoliko rocijsko gibje roj okre u miui Kuoubrzje: Ku brzi: Zko gibj: ε 0 ω kos. ϕ ϕ0 + ω Vez izmeu kue brzie ω (1/s ili rd/s) i broj okre ijel (okr./mi): π ω
5 rzi ok ijel pri rociji Obod brzi Obode brzie ok ijel proporciole su jihoim udljeosim od osi rocije. ds r dϕ ds dϕ r r ω rr ω ω 5 6 Ubrzje ok ijel pri rociji Kompoee ubrzj: d r ε r ω gα Iezie ubrzj: ε ω Odredie krker rocijskog gibj kruog ijel oko epomie osi: ) ε 5 rd/s b) ε 0 c) ω 150 (rd/s) + r ε + ω 4 7 d) ω 0. (rd/s) 8 Primjer 1: Vrilo elekromoor okree se kosim brojem okrej 1400 okr./mi. ko promjer ril izosi 100 mm odredie: ) kuu brziu ril (ω?) b) obodu brziu oke obodu ril (?) c) ubrzje oke obodu ril (?). Zdo: 1400 okr./mi. d 100 mm; r d/50 mm0,050 m Zdo: 1400 okr./mi. d 100 mm; r d/ 50 mm 0,050 m Rješeje: π π 1400 ) ω 147 rd / s b) r ω 0, ,35 m/s c) jedoliko gibje + r ε 0 ( r ω) r ω r r 1080 m / s ε 0 0, m / s
6 Sk ok ijel i gib se u rii prleloj s ekom epomiom (refereom) riom Π 0. Risko ili plro gibje kruog ijel Se oke okomici opisuju ideie meusobo prlele puje i u skom reuku imju jedke ekore brzi i ubrzj Položj presjek S u rii Oxy može se odredii ko je poz položj eke oke presjek S i ku Risko gibje kruog ijel možemo sesi prouje gibj krue figure.j. presjek S u rii Položj presjek S u rii Oxy može se odredii ko je poz položj eke oke presjek S i ku Gibje re krue figure S u rii odreeo je jeddžbm: To su ujedo kiemske jeddžbe riskog gibj kruog ijel: x x() y y() ϕ ϕ () kos. x y x() y() ϕ ϕ ()
7 Sko gibje presjek S može se rzložii : ) rslcijsko gibje i b) rocijsko gibje oko oke proizoljo odbrog pol (ili oko oke ) Odreije puj ok ijel Tok (x ; y ) Tok (x; y ) Jeddžbe gibj oke : r x i + y j Odreije brzi ok ijel r r + r x x y y + d cos( ϕ + α) + d si( ϕ + α) 39 r x i + y j d r d r d r + 40 Odreije brzi ok ijel r d d r d r + d r d r + + ω + ω
8 + + ω Teorem o projekcijm brzi Orogole projekcije ekor brzi spojicu ok i meusobo su jedke. N ' ' kos. rzi oke kruog ijel kod riskog gibj jedk je ekorskom zbroju brzie oke i brzie oke pri rociji ijel oko oke - pol. 43 N ω PN 44 ' ' cos α ω P cos α ω PN cosβ ω P cosβ ω PN N N Korljje O P + OP rzie: O ω PO ω r ω P ω r C ω PC ω r Pr ojekcije spojicu OC ' cos 45 ' ω r ω r ' C ω r 45 Tok P reui pol brzi P 0 46 Treui pol brzi P i - pozo Treui pol brzi je ok P u presjeku S kruog ijel ij je brzi u odreeom reuku jedk uli. P Z odreije reuog pol brzi P porebo je pozi prce i smjeroe brzi bilo kojih diju ok kruog ijel koje se lze presjeku S pr. i P 0 P 47 Treui pol P lzi se u sjecišu okomic poueih brzie i (sjecišu prc i b) 48 8
9 rzi bilo koje oke kruog ijel koj leži u presjeku S jedk je jeoj obodoj brzii pri rociji oko reuog pol brzi P. rzie pojediih ok ijel proporciole su jihoim udljeosim od reuog pol brzi. ω P P ω P ω P P 0 P P + P + P P P Odreije brzi ok ijel pomou reuog pol P Zdo: Iezie i prc brzie i smo prc Z odreije brzie bilo koje oke kruog ijel presjeku S porebo je pozi iezie i prc brzie jede oke i prc brzie druge oke ijel. ω ω Trži se iezie? P ω 51 P ω ω P 5 Slujei odreij reuog pol brzi Treu rslcij: Treui pol: C C? PC ω r ω ω r P 53 P P
10 Primjer riskog gibj kruog ijel: Korljje bez klizj ljksog ijel po poršii drugog ijel Trslcij + Rocij Korljje - reui pol Korljje rocij oko reue osi Ubrzje ok ijel r r + r d r r d r d + + d r d r Podsjeik: Ubrzje ok kod kružog gibj Kompoee ubrzj: d r ε r ω ε gα ω Ubrzje oke pri rociji ijel oko pol : + Tgecijl kompoe ubrzj: ( r ) ε Norml kompoe ubrzj: Iezie ubrzj: + r 4 ε + ω 59 ω 60 10
11 ε gα ω 4 ( ) + ( ) ε + ω Ubrz rocij Uspore rocij + Ubrz rocij 61 6 Primjer 1: Šp dužie m izodi plro gibje. U jedom reuku brzi oke zr s osi šp ku od 30 i izosi 5 m/s. U isom reuku brzi oke zr s osi šp ku od 60. Odredie: ) izos brzie oke (grfiki i liiki) b) položj reuog pol P (grfiki) c) kuu brziu ω. )? - grfiki ( je okomio spojicu ) b) Treui pol P )? Teorem o jedkosi projekcij brzi c) ω? cos30 cos cos30 8,66 1 cos60 (m /s) 65 P si30 0,5 1 (m) 5 P ω ω P 1 5 (1/s) Dom zd: Odredie brziu središ šp oke C (grfiki i liiki)
Kinematika materijalne toke. 2. Prirodni koordinatni sustav. 1. Vektorski nain definiranja gibanja. Krivocrtno gibanje materijalne toke
 Kioco gibje meijle oke Kiemik meijle oke. dio ) Zje kiocog gibj b) Bi i ubje Položj meijle oke u skom euku eme možemo defiii slijedee ie:. Vekoski i defiij gibj (). Piodi i defiij gibj s s (). Vekoski
Kioco gibje meijle oke Kiemik meijle oke. dio ) Zje kiocog gibj b) Bi i ubje Položj meijle oke u skom euku eme možemo defiii slijedee ie:. Vekoski i defiij gibj (). Piodi i defiij gibj s s (). Vekoski
Zadatak: Kolika je obodna brzina toka A koja se giba po kružnici promjera 240 cm s 60 okreta u minuti?
 Kiemik Zdk: Kojom bziom e gib pješk ko 4 km pijee z 35 mi. 4 km 35 mi? Jedoliko poco gibje:. 4,9 (m/) 35 3 Zdk: Kolik je obod bzi ok koj e gib po kužici pomje 4 cm oke u miui? d 4 cm d/ cm, m o/mi π π
Kiemik Zdk: Kojom bziom e gib pješk ko 4 km pijee z 35 mi. 4 km 35 mi? Jedoliko poco gibje:. 4,9 (m/) 35 3 Zdk: Kolik je obod bzi ok koj e gib po kužici pomje 4 cm oke u miui? d 4 cm d/ cm, m o/mi π π
Kinematika materijalne toke. 3. dio a) Zadavanje krivocrtnog gibanja b) Brzina v i ubrzanje a
 Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
a) Kosi hitac Krivolinijsko gibanje materijalne toke Sastavljeno gibanje Specijalni sluajevi kosog hica: b) Horizontalni hitac c) Vertikalni hitac
 ) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i
 Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Dinamika krutog tijela ( ) Gibanje krutog tijela. Gibanje krutog tijela. C. Složeno gibanje. Pojmovi: A. Translacijsko gibanje krutog tijela. 12.
 Pojmo:. Vekor sle F (ranslacja). omen sle (roacja) Dnamka kruog jela. do. omen romos masa. Rad kruog jela A 5. Kneka energja k 6. omen kolna gbanja L 7. u momena kolne gbanja momena sle L f ( ) Gbanje
Pojmo:. Vekor sle F (ranslacja). omen sle (roacja) Dnamka kruog jela. do. omen romos masa. Rad kruog jela A 5. Kneka energja k 6. omen kolna gbanja L 7. u momena kolne gbanja momena sle L f ( ) Gbanje
Analitička geometrija i linearna algebra. Kartezijev trodimenzionalni pravokutni koordinatni sustav čine 3 međusobno okomite osi: Ox os apscisa,
 Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
GIBANJE (m h) giba miruje giba giba miruje miruje h 1000 :1000 h 1 h h :1000 1
 GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
Dinamika krutog tijela ( ) Gibanje krutog tijela. Gibanje krutog tijela. Pojmovi: C. Složeno gibanje. A. Translacijsko gibanje krutog tijela. 14.
 Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Geometrijske karakteristike poprenih presjeka nosaa. 9. dio
 Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.
 Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
α =. n n n Vježba 001 Koliko stranica ima pravilni mnogokut ako jedan njegov unutarnji kut iznosi 144? Rezultat: n = 10.
 Zdtk (Mrij, gimzij) Koliko stric im prvili mogokut ko jed jegov uutrji kut izosi 8? Rješeje Formul z veličiu jedog uutrjeg kut prvilog mogokut je: ( ) 8 α = ( ) 8 8 = / 8 = ( ) 8 8 = 8 6 8 8 = 6 7 = 6
Zdtk (Mrij, gimzij) Koliko stric im prvili mogokut ko jed jegov uutrji kut izosi 8? Rješeje Formul z veličiu jedog uutrjeg kut prvilog mogokut je: ( ) 8 α = ( ) 8 8 = / 8 = ( ) 8 8 = 8 6 8 8 = 6 7 = 6
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
 ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
FURIJEOVI REDOVI ZADACI ( II
 FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
dužina usmjerena (orijentirana) dužina (zna se koja je točka početna, a koja krajnja) vektor
 I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo
 GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
1. Duljinska (normalna) deformacija ε. 2. Kutna (posmina) deformacija γ. 3. Obujamska deformacija Θ
 Deformaije . Duljinska (normalna) deformaija. Kutna (posmina) deformaija γ 3. Obujamska deformaija Θ 3 Tenor deformaija tenor drugog reda ij γ γ γ γ γ γ 3 9 podataka+mjerna jedinia 4 Simetrinost tenora
Deformaije . Duljinska (normalna) deformaija. Kutna (posmina) deformaija γ 3. Obujamska deformaija Θ 3 Tenor deformaija tenor drugog reda ij γ γ γ γ γ γ 3 9 podataka+mjerna jedinia 4 Simetrinost tenora
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
 w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
PRAVAC. riješeni zadaci 1 od 8 1. Nađite parametarski i kanonski oblik jednadžbe pravca koji prolazi točkama. i kroz A :
 PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Dinamika krutog tijela. 14. dio
 Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (
Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (
A MATEMATIKA Zadana je z = x 3 y + 1
 A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
m i N 1 F i = j i F ij + F x
 N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
2.6 Nepravi integrali
 66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Cenovnik spiro kanala i opreme - FON Inžinjering D.O.O.
 Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
VAŽNO. Posmino naprezanje τ
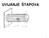 UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
VALJAK. Valjak je geometrijsko telo ograničeno sa dva kruga u paralelnim ravnima i delom cilindrične površi čije su
 ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
Vrijedi relacija: Suma kvadrata cosinusa priklonih kutova sile prema koordinatnim osima jednaka je jedinici.
 Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
J. Brnić & G. Turkalj: Nauka o čvrstoći I, Tehnički fakultet Sveučilišta u Rijeci, Rijeka, 2004.
 /5 Ispravci u knjii: J. rnić & G. Turkalj: Nauka o čvrsoći I, Tehnički fakule Sveučiliša u Rijeci, Rijeka,. Daum adnje promjene:. svibnja 5. Redni broj roj sranice. 9 Ispravak Na sl..9a prikaana su poiivna
/5 Ispravci u knjii: J. rnić & G. Turkalj: Nauka o čvrsoći I, Tehnički fakule Sveučiliša u Rijeci, Rijeka,. Daum adnje promjene:. svibnja 5. Redni broj roj sranice. 9 Ispravak Na sl..9a prikaana su poiivna
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

= + injekcija. Rješenje 022 Kažemo da funkcija f ima svojstvo injektivnosti ili da je ona injekcija ako vrijedi
 Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
ZASTORI SUNSET CURTAIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
Odred eni integrali. Osnovne osobine odred enog integrala: f(x)dx = 0, f(x)dx = f(x)dx + f(x)dx.
 Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Magneti opis i namena Opis: Napon: Snaga: Cena:
 Magneti opis i namena Opis: Napon: Snaga: Cena: Magnet fi 9x22x28x29,5 mm 12 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V AC 9 Magnet fi 9x22x28x29,5 mm 110 V DC 15 Magnet
Magneti opis i namena Opis: Napon: Snaga: Cena: Magnet fi 9x22x28x29,5 mm 12 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V AC 9 Magnet fi 9x22x28x29,5 mm 110 V DC 15 Magnet
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
 1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Deformacije. Tenzor deformacija tenzor drugog reda. Simetrinost tenzora deformacija. 1. Duljinska deformacija ε. 1. Duljinska (normalna) deformacija ε
 Deformae. Duljinska (normalna) deformaa. Kutna (posmina) deformaa. Obujamska deformaa Θ Tenor deformaa tenor drugog reda 9 podatakamjerna jedinia Simetrinost tenora deformaa 6 podataka 4. Duljinska deformaa
Deformae. Duljinska (normalna) deformaa. Kutna (posmina) deformaa. Obujamska deformaa Θ Tenor deformaa tenor drugog reda 9 podatakamjerna jedinia Simetrinost tenora deformaa 6 podataka 4. Duljinska deformaa
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]
![c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata] c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]](/thumbs/92/108578155.jpg) Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Magneti opis i namena Opis: Napon: Snaga: Cena:
 Magneti opis i namena Opis: Napon: Snaga: Cena: Magnet fi 9x22x28x29,5 mm 12 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V AC 9 Magnet fi 9x22x28x29,5 mm 110 V DC 15 Magnet
Magneti opis i namena Opis: Napon: Snaga: Cena: Magnet fi 9x22x28x29,5 mm 12 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V DC 9 Magnet fi 9x22x28x29,5 mm 24 V AC 9 Magnet fi 9x22x28x29,5 mm 110 V DC 15 Magnet
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
Nacionalni centar za vanjsko vrednovanje obrazovanja MATEMATIKA
 Ncioli cetr z vjsko vredovje orzovj MATEMATIKA viš rzi KNJIŽICA FORMULA VIŠA VIŠA RAZINA RAZINA Kopleks roj: i i Mtetik Kopleks roj: Kopleks roj: i z i i z i i z R Kjižic forul VIŠA (cos RAZINA si Kopleks
Ncioli cetr z vjsko vredovje orzovj MATEMATIKA viš rzi KNJIŽICA FORMULA VIŠA VIŠA RAZINA RAZINA Kopleks roj: i i Mtetik Kopleks roj: Kopleks roj: i z i i z i i z R Kjižic forul VIŠA (cos RAZINA si Kopleks
( ) 2. određuje se izrazom S = 4 π
 Zdtk 8 (Ml, gimzij) Itezitet Sučev zrčej udljeosti od.5 0 m od središt Suc izosi 00 W/m. Z koliko se smji ms Suc tijekom 365 d uz pretpostvku d se eergij koju Suce zrči u potpuosti doiv uklerim izgrjem
Zdtk 8 (Ml, gimzij) Itezitet Sučev zrčej udljeosti od.5 0 m od središt Suc izosi 00 W/m. Z koliko se smji ms Suc tijekom 365 d uz pretpostvku d se eergij koju Suce zrči u potpuosti doiv uklerim izgrjem
Chapter 1 Fundamentals in Elasticity
 D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
1.PRIZMA ( P=2B+M V=BH )
 .RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
 Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Dijagrami: Greda i konzola. Prosta greda. II. Dijagrami unutarnjih sila. 2. Popre nih sila TZ 3. Momenata savijanja My. 1. Uzdužnih sila N. 11.
 Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
a C 1 ( ) = = = m.
 Zdtk 4 (Petr, gimzij) Dvije tke leće, koverget jkosti + dpt i diverget jkosti 5 dpt, slijepljee su zjedo Predmet se lzi 5 cm ispred kovergete leće Odredite gdje je slik predmet ješeje 4 C = + m -, C =
Zdtk 4 (Petr, gimzij) Dvije tke leće, koverget jkosti + dpt i diverget jkosti 5 dpt, slijepljee su zjedo Predmet se lzi 5 cm ispred kovergete leće Odredite gdje je slik predmet ješeje 4 C = + m -, C =
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ŽUPANIJSKO NATJECANJE IZ FIZIKE 2012/2013 Srednje škole 1. skupina. Zadatak 1 (10bodova)
 ŽUPANIJSKO NATJECANJE IZ FIZIKE / Srednje škole. skupin Zdk (bodo) Iic i ric urkuju se n szi duljine s ko d isoremeno kreu s sr. Iic jednoliko ubrz pru peinu ukupnog remen rnj od sr do cilj, posiže brzinu
ŽUPANIJSKO NATJECANJE IZ FIZIKE / Srednje škole. skupin Zdk (bodo) Iic i ric urkuju se n szi duljine s ko d isoremeno kreu s sr. Iic jednoliko ubrz pru peinu ukupnog remen rnj od sr do cilj, posiže brzinu
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa
 .vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
M p f(p, q) = (p + q) O(1)
 l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Παρασκευή 1 Νοεμβρίου 2013 Ασκηση 1. Λύση. Παρατήρηση. Ασκηση 2. Λύση.
 (, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R
(, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Levizja ne dy dhe tre dimensione
 Kpiulli, Leizj e d dhe re dimesioe Leizj e d dhe re dimesioe. Nje mkie udheo km e peredim dhe km e ju-peredim. S eshe zhedosj rezule e mkies e lidhje me pike e isjes (drejimi dhe ler e sj )? S S S S cos
Kpiulli, Leizj e d dhe re dimesioe Leizj e d dhe re dimesioe. Nje mkie udheo km e peredim dhe km e ju-peredim. S eshe zhedosj rezule e mkies e lidhje me pike e isjes (drejimi dhe ler e sj )? S S S S cos
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Gauss, Stokes, Maxwell. Vektorski identiteti ( ),
 Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
 1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
ČETVOROUGAO. β 1. β B. Četvorougao je konveksan ako duž koja spaja bilo koje dve tačke unutrašnje oblasti ostaje unutar četvorougla.
 Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
, 81, 5?J,. 1o~",mlt. [ BO'?o~ ~Iel7L1 povr.sil?lj pt"en:nt7 cf~ ~ <;). So. r~ ~ I~ + 2 JA = (;82,67'11:/'+2-[ 4'33.10'+ 7M.
 J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
6.642 Continuum Electromechanics
 MIT OpenCourseWre http://ocw.mit.edu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.edu/terms. 6.64, Continuum Electromechnics,
MIT OpenCourseWre http://ocw.mit.edu 6.64 Continuum Electromechnics Fll 8 For informtion out citing these mterils or our Terms of Use, visit: http://ocw.mit.edu/terms. 6.64, Continuum Electromechnics,
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
m 1, m 2 F 12, F 21 F12 = F 21
 m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
jqa=mêççìåíë=^âíáéåöéëéääëåü~ñí= =p~~êäêωåâéå= =déêã~åó
 L09 cloj=klk=tsvjmosopa jqa=mêççìåíë=^âíáéåöéëéääëåü~ñí= =p~~êäêωåâéå= =déêã~åó 4 16 27 38 49 60 71 82 93 P Éå Ñê ÇÉ áí dbq=ql=hklt=vlro=^mmif^k`b mo pbkq^qflk=ab=slqob=^mm^obfi ibokbk=pfb=feo=dboûq=hbkkbk
L09 cloj=klk=tsvjmosopa jqa=mêççìåíë=^âíáéåöéëéääëåü~ñí= =p~~êäêωåâéå= =déêã~åó 4 16 27 38 49 60 71 82 93 P Éå Ñê ÇÉ áí dbq=ql=hklt=vlro=^mmif^k`b mo pbkq^qflk=ab=slqob=^mm^obfi ibokbk=pfb=feo=dboûq=hbkkbk
P l+1 (cosa) P l 1 (cosa) 2δ l,0 1
 Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
➆t r r 3 r st 40 Ω r t st 20 V t s. 3 t st U = U = U t s s t I = I + I
 tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ
 Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ 2/2012
 ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /0 Έστω r rx, y, z, I a, b συνάρτηση C τάξης και r r r x y z Nα αποδείξετε ότι: d dr r (α) r r, I r r r d dr d r (β) r r, I dr (γ) Αν r 0, για κάθε I κάθε I d (δ)
ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /0 Έστω r rx, y, z, I a, b συνάρτηση C τάξης και r r r x y z Nα αποδείξετε ότι: d dr r (α) r r, I r r r d dr d r (β) r r, I dr (γ) Αν r 0, για κάθε I κάθε I d (δ)
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Proračun potrebne glavne snage rezanja i glavnog strojnog vremena obrade
 Zaod a tehnologiju Katedra a alatne strojee Proračun potrebne glane snage reanja i glanog strojnog remena obrade Sadržaj aj ježbe be: Proračun snage kod udužnog anjskog tokarenja Glano strojno rijeme kod
Zaod a tehnologiju Katedra a alatne strojee Proračun potrebne glane snage reanja i glanog strojnog remena obrade Sadržaj aj ježbe be: Proračun snage kod udužnog anjskog tokarenja Glano strojno rijeme kod
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
SLIČNOST TROUGLOVA. kažemo da su slične ( sa koeficijentom sličnosti k ) ako postoji transformacija sličnosti koja figuru F prevodi u figuru F
 SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
