Uvr{tavaju}i u prvu, tre}u i petu jedna~inu x = L, a u preostale x = 0, dobivamo: EA L
|
|
|
- Δράκων Νικολαΐδης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 eora lsh osa~a II eoda deformaca 6. EODA DEFORACIJA eoda deformaca e meoda oom se mog prora~a sv sa~ ca od lsh ssema, bez obzra a o ao s zada rb ve. U s{ meodom deformaca se ra~a pomeraa odre eh a~aa lsog ssema z slova ravoe`e ra{h vash sla. Obzrom da se meodom oa~h elemeaa ra~a pomeraa slo`eh ssema (lsh, dvo- rodmezoalh) z slova ravoe`e, pozavae meode deformaca mogome ola{ava shvaae meode oa~h elemeaa, oa e daas sadardo prme pr aalz slo`eh osrca. Soga e za~a dealog pozavaa meode deformaca poslede vreme veoma porasao. Sve glave procedre oe se vr{e pr or{e meode deformaca s do meode oa~h elemeaa. 6.. Veza zme sla pomeraa {apa. arca ros {apa. Jaso, da b zra~al pomeraa z slova ravoe`e porebo e zraz ra{e sle preo pomeraa, odoso sposav dre vez zme pomeraa ra{h sla poedm a~ama osove {apa. a osov preposave o learm osvm geomersm eda~ama, dobl smo eda~e (.5), (.8), (.) (.) za Beroll-ev model grede. Rad edosaveg zvo ea, odvo}emo cae pomeraa ~vorova od caa vasog opere}ea. ame, sva {ap e do eog ssema ao aav ma pomeraa ~vorovma mo`e b zlo`e vasom opere}e. Uolo `elmo zra~a sle a om {ap, mo`emo sors prcp sperpozce zra~a prese~e sle od pomeraa ~vorova vash caa odvoeo posle dobvee rezlae sabra. U prvom ora preposav}emo da posmara {ap e zlo`e opere}e prome emperare, pa pomee eda~e ma obl: x ( x) = x x x( x) = x ( x) y ( x) = y ϕx x x EI ϕ( x) = ϕ x x EI EI y ( x) = y ϕ ( x) ( x) ( x) EI ϕ( x) = ϕ ( x) ( x) EI EI Uvr{ava} prv, re} pe eda~ x =, a preosale x =, dobvamo: x = x = ( x x ) x = x = ( ) x x 87
2 eora lsh osa~a II EI y y y = y ϕ = ϕ ϕ EI ( ) ϕ = ϕ y y = EI EI ϕ ϕ EI ( y y ) y = y ϕ = ϕ ϕ EI ( y y ) ϕ = ϕ = EI EI ϕ ϕ eoda deformaca ( ) Ove eda~e s dobvee pod preposavom da s pozve sle, slad sa `ersom ovecom, oa e prazaa a slc 6.. Po{o se meod deformaca posavla ravoe`a ompleog ssema, pogodo e predzae svh sla pomeraa defsa odos a loal oorda ssem {apa. Sla 6.. o za~ da pozve prese~e sle a {ap del pravc oordah osova, ao e prazao a slc 6.. Ovav ovec za prese~e sle }emo ors za meod deformaca oa e ob~aea za sve sofverse paee o sl`e za aalz osrca. apome se da pravlo o cra momeaa osae epromeeo,. mome se cra a oo sra gde s zaega vlaa. y x Sla 6.. o za~ da }e se gorm eda~ama prome predzac za sle:,,, {o dae: = ( x x ) ( ) EI y = ϕ ϕ y = ϕ ϕ ( ) y y Uolo dobvee eda~e za prese~e sle ~vorovma ap{emo mar~om obl, dobvamo: 88
3 eora lsh osa~a II eoda deformaca l: = EI EI f= 4EI EI EI EI x y EI ϕ x y ϕ 4EI (6.) (6.) arca azva se marca ros {apa. arcom ros {apa se povez prese~e sle pomeraa osove {apa a egovm raevma loalom oordaom ssem,. oordaom ssem o vred za a {ap. Dmeze marce ros e obl zavse od preposavleog sepea slobode reaa {apa. Jeda~om (6.) e prazaa marca ros za {ap rav, ~ ~vorov ma po r sepea slobode reaa (dve raslace eda roaca). Uolo preposavmo da e {ap asalo r, {o odgovara zaemare ormalh sla meod deformaca ( A I ), ada veor pomeraa {apa ma samo ~er ~laa razl~a od le: y, ϕ, y, ϕ, pa se preo pomeraa mog zraz samo mome rasverzale sle (ormale sle e mora b edae l!): EI EI 4EI EI y ϕ = EI EI y ϕ EI 4EI (6.) Dale, pod preposavom da {ap rav ema asal deformac, marca ros {apa se redcra a 4x4. Uolo posmaramo {ap re{ee rav, preposavlamo da e a {ap opere}e samo asalm slam, {o za~ da ma sl~vo pomeraa pravc x loalog oordaog ssema. o za~ da sva ~vor ma samo po eda sepe slobode reaa,. {ap ma po dva sepea slobode reaa. Posledca e o da marca ros ma dmeze x: = (6.4) 89
4 eora lsh osa~a II eoda deformaca [ap prosor ma po sepe slobode reaa, er sva ~vor ma po r roace r raslace, ao da marca ros avog {apa ma dmeze x. Veza zme prese~h sla pomeraa se mo`e zraz eda~om: x x y z = y z z y z y x x ϕ x ϕ x y ϕ z y ϕ z z ϕ y z ϕ y GI gde e: =, x EI z z 4EI z =, 55 =, 56 =, 66 =, 67 = EI y y 4EI y EI y =, 78 =, 88 =, 89 =. 77 EI z Da b dobl oa~e zraze za prese~e sle a {ap o e zlo`e delova opere}ea l promee emperare, posmara}emo {ap praza a slc 6.. Po{o s pomeraa a raevma {apa edaa l, pra~o se rad o obosrao le{eom {ap. Za aav {ap }emo poovo prme eda~e (.5), (.8), (.) (.), s m da }e sada fgrra samo ~laov veza za opere}ee. x( ) = x = α ( s) px( s) ds = x( ) = x = α spx( s) ds= Δ y( ) y ( ) y( ) EI α h = = s p s ds = Δ ϕ( ) = ϕ = ( s) py( s) ds α EI EI EI = h s p s ds Δ y( ) = y = y( ) α EI = h Δ ϕ( ) = ϕ = s py( s) ds α EI EI EI = h 9
5 eora lsh osa~a II eoda deformaca Iz gorh eda~a se edosavo mog dob vredos prese~h sla ~vorovma. Uzma} obzr ovec za meod sla (promea predzaa sla,, ) dobvamo: x ( ) x( ) α = s p s ds = ( ) α = sp s ds = s = s p ( s) ds EIα Δ = h y s s = py( s) ds = s s py( s) ds EI m = α Δ = m h s s = p ( s) ds = y Dale, gorm eda~ama s praza zraz za prese~e sle a raevma obosrao le{eog {apa sled delovaa vasog opere}ea promee emperare. Ove sle se ob~o ra~a ao reace obosrao le{ee grede, a e preo prazah eda~a. Sada se mog apsa eda~e za prese~e sle a raevma opere}eog {apa preo pomeraa: EI EI x 4EI EI y ϕ m = x y EI EI ϕ m EI 4EI (6.5) l: f= f (6.6) Jeda~e oma se mome zra`ava preo pomeraa azva se o{ aabey-eve eda~e. U eda~ (6.6) veor f se azva veor opere}ea {apa. Ova eda~a vred za {ap o e a oba raa ro veza za e drg {ap. Poseb zraz za prese~e sle se mog apsa za {apove, o a edom ra 9
6 eora lsh osa~a II eoda deformaca ma zada rb ve po slama. U s{ ave eda~e se dobva ao da se z zadaog rbog vea po slama zraz pomerae oe e vezao za sl, oda se a zraz bac osale eda~e. Ova pospa se a~e azva sa~a odezaca me se, op{em sl~a, mog z ssema eda~a zbac sve eda~e ~ e slobod ~la eda l, z elmsae svh epozah oe se alaze z dagoale ~laove zba~eh eda~a. Preposavmo da e zada ssem od eda~a sa epozah: = f ( x) ( x) ( x) Ao m eda~a ma sloboda ~la razl~ od le, a eda~a sloboda ~la eda l, ada gor eda~ mo`emo apsa ao: m m m mxm mx mx fmx m = xm x x x Iz drge mar~e eda~e }emo zraz pomeraa oa s vezaa za le slobode m ~laove: x = x xm m mx bac h prv: m m m m m mxm mx mx x xm mx = m f ( ) = f =f m m m m mxm mx x xm mx mx me e orgala marca odezovaa marc, ~ e rag za ma od raga orgale marce. aravo, odezovam ssemom eda~a e mog}e zra~a epozae oe s zba~ee. U sac damc osrca, ova pospa se ors olo `elmo zra~a prese~e sle svm a~ama eog ssema samo oa pomeraa oa s eophoda za prora~ prese~h sla. Ovo }emo poas a slede}m prmerma. [AP SA ZGOBO A JEDOJ SRAI E,A,I, Iz pozae ~ece da momea a~ mora b eda l, mamo: m = ϕ ϕ ( y y) m = ϕ = ϕ ( y y) m =.5 ϕ ( y y) m.5 m = ϕ ( y y ).5 m = ϕ ( y y ) Prssvo zgloba ema caa a ormale sle., EI = 9
7 eora lsh osa~a II eoda deformaca Jeda~a {apa mar~o form ma obl: 6 EI EI EI x m y 4EI m ϕ m = x y m EI EI ϕ (6.7) [AP SA UI POJE ZA RASVERZAU SIU E,A,I, U s{ prmeemo s pospa. rasverzala sla a~ mora b edaa l: ( y y ) = ϕ ϕ = y = y ( ϕ ϕ ) EI = EI ( ) ϕ ϕ m = EI ( ) ϕ ϕ m = x 4 EI EI y ϕ m = x y ϕ EI 4EI m (6.8) 9
8 eora lsh osa~a II eoda deformaca a s a~ se mog dob eda~e {apa za drge rbe vee a raevma l za hov ombac. 6.. Idefaca mmalog broa epozah pomeraa ssema. Sve prazae eda~e {apa marce ros s zvedee pod preposavom da e {ap zme ~vorova prav, osaog popre~og presea bez lh pola za blo o prese~ sl. Drgm re~ma, zme ~vorova la pomeraa e oala glaa. Ovm veom se pra~o defra mmala bro a~aa-~vorova oma e porebo zra~a pomeraa da b se dobl a~ rezla meodom deformaca. Uolo e posoe la pola za pomeraa eda ~vor ma dve raslace ed roac,. r epozaa pomeraa l r sepea slobode reaa. a slc 6.. praza s ~vorov sa zglobovma (lm polem za momea) odgovara} bro sepe slobode reaa. U prcp {ap o e zglobo veza za e ~vor om ~vor ma gao zaorea o e eovsa o gl zaorea ~vora. SSK= SSK=6 SSK=4 Sla 6.. Dale, za e zada ls ssem rav, pa bro pomeraa se ra~a ao zbr slobodh raslaca - pomaa roaca - glova zaorea ~vorova. Bro pomaa e eda bro ~vorova pomo`eom sa dva. Od ovog broa se odzma bro pomaa o e zada rbm vema (pore epore osloc). Bro glova zaorea e eda bro ~vorova, ve}aom za bro zglobh veza. Od ovog broa reba odze bro ~vorova gde e rbm vema defsao le{ee. Sve ovo se mo`e predsav slede}om eda~om: Prmer: SSK = SP SU; SP = rp; SU = sz r a) =6, r p =5, s z =, r =, SP=7 SU=4 epozaa pomeraa:,,,,,, x y x y x y x epozae roace: ϕ, ϕ, ϕ, ϕ 5 b) =6, r p =6, s z =, r =, SP=6 SU=7 epozaa pomeraa: x, y, x, y, x, y epozae roace: ϕ, ϕ, ϕ5, ϕ, ϕ, ϕ4, ϕ5 94
9 eora lsh osa~a II eoda deformaca U em sl~aevma mog se ves doda ~vorov, da b se meoda deformaca mogla prme. p~a sl~a e prora~ pomaa ee a~e obosrao le{ee grede meodom deformaca. Uvo eem ovog ~vora a mes gde se ra` poma dobvamo po r ~vora, a epozae s pomac gao zaorea ~vora. Idefaca epozah pomeraa e prv ora pr prme meode deformaca. Praza meod vr vaa broa epozah pomeraa zasva se a preposavc da s sv {apov deformabl. eoda deformaca zasovaa a ovavo preposavc azva se a~a l sroga meoda deformaca. Za razl od e poso eh~a meoda deformaca, gde se preposavla da s {apov asalo r. Opravdae za prme ove meode deformaca e so ao pr zaemare caa ormalh sla meod sla. ame, marc ros {apa, ~laov veza za asala pomeraa sle s mogo ve} od osalh ~laova. Uvr vae broa epozah pomaa e e{o omplovae za eh~ meod deformaca, er bro epozah pomeraa zavs od polo`aa broa {apova. Po{o sada {apov ma mal ros a savae odos a asal ros, ova zadaa se mo`e sves a vr vae sepea slobode reaa mehazma sa rm {apovma. ame, sva ~vor ssema se mo`e bac fv zglob, ~me se dobva mehazam o se ob~o azva zgloba {ema. Sada se bro epozah pomaa eda sepe slobode reaa avog mehazma. U prmer a) b posoala dva epozaa pomaa o: horzoal poma ~vora 5 horzoal poma ~vorova,. Jaso e da horzoal poma ovh ~vorova mora b edsve rad asale ros grede. Sv veral pomac s eda l rad oga {o s sbov asalo r. epoza glov zaorea se odre a s a~ za eh~ za a~ meod deformaca. Prmer: P 4 Zgloba {ema Prema a~o meod deformaca praza ssem ma 8 epozah pomaa - svaom od slobodh ~vorova po dva. Prema eh~o meod deformaca s ssem ma eda epoza poma, er e zgloba {ema mehazam sa edm sepeom slobode reaa, oe e {emas prazao a slc. 95
10 eora lsh osa~a II eoda deformaca 6.. Posavlae vea ravoe`e. Asemblrae marce ros. Kao e vod ovog poglavla re~eo, epozaa pomeraa se dobva z ssema eda~a o se formra z slova ravoe`e. Prese~e sle a raevma {apova, dale ~vorovma, s zra`ee preo pomeraa ~vorova. Opere}ea promee emperare oe del a {apove s, ao er, redovaa a ~vorove preo veora opere}ea za sva {ap. Posavla} vee ravoe`e za sva ~vor o ma pomerae dobva se eda~e oma s epozaa pomeraa. Uve ravoe`e se mog posav a v{e a~a: dreo - secaem ~vorova posavlaem vea da e sma sla ( momeaa) za sva ~vor edaa l. Po{o se slov ravoe`e posavla pravc svaog epozaog pomeraa, dobva se oolo eda~a olo ma epozah pomeraa. Prmer : q α Prema a~o meod deformaca ova ssem ma 5 epozah pomeraa: X, Y, X,, ϕ ϕ. Uve ravoe`e o se mog posav s: =, X =, Y = za ~vor =, X = za ~vor. Rasavla} ssem a ~vorove {apove, ~vorovma posavlamo se sle ao a raevma {apova, sa sprom predzaom. o za~ da s sle oe del a ~vor pozve ao: del odozgo prema dole, s desa levo pravc azale a sa, {o e pravo sproo od ovece oa vred za {ap oal oorda ssem {apa e zarora za gao α odos a global. Po{o s eda~e {apa zvedee loalom oordaom ssem, porebo e pomeraa praza loalom oordaom ssem {apa (vd eda~.8): x = Xcosα Ysα x cosα sα X = y Ycosα Xsα = y sα cosα = Y Rad ra}eg psaa ve{}emo slede}e ozae: 96
11 eora lsh osa~a II eoda deformaca 4 EI 6 ; EI ; = = = ; = EI EI = ϕ ; = ϕ ; = x y y Za {ap mamo: EI = ϕ ϕ m ; = ϕ ϕ ; = ( ) Y Y X X EI = ϕ ϕ m ; = ϕ ϕ ; = X X q q gde s: m= m= ; = = ( ) Y Y Uslov ravoe`e: ( ) = ϕ ϕ ( cosα) Y sαx m = cosα sα = ( ) ( ) sαϕ cosα sα s α cos α X = Y X sα cosα = ( ) ( ) ( ) cosα ϕ ϕ s α cos α sαcosα = Y X = ϕ ϕ Y m = = = X X cosα sα ϕ m ϕ m s α Y cosα d ( ) = X s α ( ) s X α d44 l: K F= (6.9) arca K se azva globala marca ros. o e ve smer~a, vadraa marca ~ e rag eda bro epozah pomeraa. Globala marca ros e zvedea z vea ravoe`e, o s posavle dreo. Jaso, a ova a~ se e mo`e dob op{ zraz za dobvae globale marce ros. 97
12 eora lsh osa~a II eoda deformaca Kao e poazao prehodm poglavlma, ve ravoe`e se mog posav a drge a~e. Korse} agrage-ov prcp vrelh radova l eerges rer ravoe`e, dobl smo slede} eda~ ravoe`e mar~om obl: δq q δq Q= (6.) gde se δ q mo`e erprera l ao veor vrelh pomeraa l ao varaca veora pomeraa ompleog ssema. Po{o s epozaa pomeraa svara pomeraa oa s edo vrela. Ao ra`ea pomeraa ~vorova pra`emo preo veora pomeraa, marc ros oza~mo sa K veor geeralsah sla oe odgovara ra`em pomerama sa, eda~a (6.) se mo`e apsa ao: F δ K δ F = (6.) Prv sabra eda~e (6.) predsavla rad ra{h sla a vrelm pomerama ~vorova, a drg rad vash sla oe del ~vorovma. Ura{e sle ~vorovma s prazae pomo} eda~e {apa (6.6). U op{em sl~a ls ssem se saso od {apova. Za sva {ap mo`emo apsa eda~ {apa: f = f δ f = δ δf = = = (6.) U goro eda~ f e veor ra{h sla, e marca ros {apa, e veor pomeraa, a f veor opere}ea {apa. Komplea eda~a e daa loalom oordaom ssem {apa. Vrel rad ra{h sla a pomerama mo`e se zraz ao sma vrelh radova ra{h sla a {apovma. Pod preposavom da se ssem saso od {apova, mamo: (6.) Sada se agrage-ov prcp ravoe`e mo`e apsa ombovaem eda~a (6.) (6.): = δ = δ f δ F = (6.4) Problem sa eda~om (6.4) e ome da e rad ra{h sla da preo veora o s defsa loalm oordam ssemma, a rad vash sla preo veora pomeraa ompleog ssema, ao da se ova eda~a a mo`e dreo sors za prora~ pomeraa. Da b o blo mog}e porebo e veore pomeraa o s da loalm oordam ssemma praza preo edsveog veora pomeraa o se def{e edsveom globalom oordaom ssem. Prv ora e a} proece veora pomeraa {apa globalom oordaom ssem. Jeda~e {apa s zvedee loalom oordaom ssem, o e op{em sl~a zarora za gao α odos a global oorda ssem. 98
13 eora lsh osa~a II eoda deformaca y Y x α X Sla 6.4 Korse} eda~e za preslavae veora z loalog global oorda ssem, oe s zvedee drgom poglavl, mo`emo zraz veor pomeraa {apa globalom oordaom ssem: x cosα y sα ϕ = x y ϕ sα cosα cosα sα sα cosα X Y ϕ X Y ϕ e l: = (6.5) arca se azva marca rasformace {apa {apa odos a global oorda ssem. Veor zavs sl~vo od agba predsavla veor pomeraa {apa globalom oordaom ssem. O~gledo, ada se loal global oorda ssem polapa marca rasformace e ed~a. Isom marcom rasformace se preslava veor vrelh pomeraa z loalog global oorda ssem: δ = δ e Uvr{avaem eda~a (6.4) (6.5) eda~ (6.) dobvamo: = δ e = δ e f e δ F = (6.6) (6.7) U eda~ (6.7) veor pomeraa s da globalom oordaom ssem. Preosalo e veore pomeraa {apova zraz preo veora pomeraa e ompleog ssema. Sva od {es ~laova veora predsavla pomerae prvog l drgog ~vora {apa pravc osova globalog oordaog ssema. Po{o s pomeraa svh ~vorova globalom oordaom ssem sadr`aa veor pomeraa ssema, sve {o e porebo rad e defsa meso svaog ~laa veora e veor pomeraa ssema. o e mog}e rad sposavlaem veze obl: e = (6.8) 99
14 eora lsh osa~a II eoda deformaca arca azva se marca ompablos. Ova marca ma {es vrsa, a bro oloa e eda bro epozah pomeraa ssema. U svao vrs ma av{e eda ~la o e eda, do s osal eda l. Bro oloe (pr. drgo vrs) oo se alaz eda e bro vrse veora pomeraa ssema oo se alaz pomerae {apa a oe se drga vrsa odos. Dale, marca ompablos edog {apa ma oolo edca olo ~vorov {apa ma pomeraa (za~ masmalo {es), a sve osalo s le. Uolo e eo pomerae {apa spre~eo rbm vema po pomerama, ada s odgovara}o vrs sve le. Dale, marca ompablos zavs sl~vo od polo`aa {apa ssem {apova rbh vea. Prme} eda~ (6.8) a vrela pomeraa vr{ava} e eda~ (6.7) dobva se: = δ = δ f δ F = (6.9) o`e} gor eda~ sa = = δ f dobvamo: F = (6.) Izraz glaso zagrad eda~ (6.) predsavla zbr vadrah marca dmeza mxm, gde e m bro epozah pomeraa. Drga sma e sma veora odgovara}h dmeza. Ao vedemo ozae: K = F = f = = mo`emo apsa: K F = F (6.) (6.) Jeda~a (6.) predsavla ssem eda~a z oeg se ra~a epozaa pomeraa,. odre e se veor. arca K se azva globala marca ros ssema, ao smo vdel, dobva se z vea ravoe`e. Proces dobvaa globale marce ros z marca ros {apova azva se asemblrae. Veor F e veor slobodh ~laova predsavla vaso opere}ee redovao ~vorove. Ovaav a~ formraa ssema eda~a meode deformaca }emo poaza a prmer. Ssem se saso od dva {apa. Za sva {ap }emo apsa veore sla, pomeraa opere}ea loalom oordaom ssem, e marce ros, rasformaca ompablos. Korse} se ozae prmeee prmer., mamo: f = ; = ; f =
15 eora lsh osa~a II eoda deformaca x y ϕ =, x y ϕ cosα sα sα cosα = cosα sα sα cosα arc ompablos dobvamo a osov veze veora pomeraa {apa veora pomeraa ssema: X ϕ Y ϕ ϕ e = = ; = Y X X Y X ϕ = Prve r vrse s vezaa za dva pomaa roac prvg ~vora {apa. Po{o se om ~vor alaz le{ee (rb ve) sva ova pomeraa s edaa l, pa ovm vrsama ema edca. ^evrom vrsom se defra meso horzoalog pomeraa drgog ~vora {apa (~vor ). Po{o se o pomeraa alaz 4. vrs veora pomeraa ssema, edca se alaz 4. olo. Ism rezoom se formra pea {esa vrsa marce ompablos {apa. = s α s α cos α s α ( ) sα cos α s α ( ) sα s α s α ( ) s α cos α cosα ( ) s α cos α cosα sα cosα sα cosα / s α s α cos α s α ( ) s α cos α s α ( ) s α s α s α ( ) s α cos α cosα ( ) s α cos α cosα sα cos α / sα cosα
16 eora lsh osa~a II eoda deformaca cosα sα s α cosα s α cos α ( ) = s α sα ( ) cos s α α q q f = ; = ; f = q q x y ϕ =, = = I = x y ϕ [ap. ma spre~eo samo veralo pomerae drgog ~vora (pea vrsa), a marca rasformace e ed~a. Soga e: = = q q f = q Uvr{ava} dobvee rezlae eda~ (6.) dobvamo marc ros ssema veor ~vorh sla.
17 eora lsh osa~a II eoda deformaca cosα sα K = s α cosα d ( ) s α sα ( ) d44 q q F = q Kao e vdlvo, dobvea e sa marca ros ssema, odoso s ssem eda~a meode deformaca, ao pr prme dreh slova ravoe`e (eda~a 6.9). Praza a~ dobvaa marce ros ssema z marca ros {apova e ao pogoda za zrad sofversog modla. a osov zadah lazh podaaa: oordae ~vorova, araersa maerala popre~og presea za sva {ap lao e zra~a marce ros marce rasformace za sva {ap. a osov geomere ssema rbh vea (veze zme {apova osloc) lao se defcra epozaa pomeraa (sva pomeraa ~vorova zzev oh o s spre~e oslocma), oa se sme{a a prozvola a~ (prema merac ~vorova) veor pomeraa ssema. Ova pomeraa se prdr` poedm {apovma a osov oga se formra marce ompablos za sva {ap. Osaa procesa asemblraa marce ros veora ~vorh sla se svod a mo`ee sabrae marca Re{avae ssema eda~a. ao formraa ssema eda~a porebo e sysem eda~a re{ da b se dobla epozaa pomeraa ssema. Re{avae ssema eda~a ob~o odzma av{e vremea proces prora~a. Ssem eda~a se mo`e re{ l eravm l drem meodama. a~e{}e or{e dre meod ese meod Gass-ove elmace. Preposavmo da reba re{ ssem od eda~ia sa epozah zada mar~om obl ao: K = F (6.) eod Gass-ove elmace se saso od r faze. U prvo faz, oa se azva raglara deompozca marca K se zamee prozvodom dve marce. Jeda od h e doa rogaoa, a drga gora rogaoa. Ao prv oza~mo sa S, a drg sa R mamo:.. s..... K = S R; S =.... s s.. s ( ) r r... r r... r. R =..... r ( ).. r
18 eora lsh osa~a II eoda deformaca Dale, prva faza se saso odre va marca S R z marce K. Ove marce se odre ora po ora. U prvom ora se odre e prva vrsa marce S prva oloa marce R : Prv vrs marce obl veora: R = s r = s r = r r = = = s r = s r s = = / R, odoso prv olo marce S, mo`emo praza r s r s = = ; S = = r s U drgom ora mo`emo modfova orgal marc K e odze prozvod S R : ao {o }emo od ( ) ( ) K = KS R = (6.4) Iz eda~e (6.4) vd se }e prvo olo prvo vrs ove marce b samo ( ) le, {o pra~o za~ da marca K ma - vrsa oloa. Drga vrsa marce R mo`e se odred a osov zraza za drg vrs marce K : s r s r r r r (6.4) = = = = = Drga oloa marce S dobva se ao: sr s r s r s r s s (6.4) = = = = = = r r Obzrom da e prva vrsa marce ( ) ( ) ( ) K edaa l, ( ) ( ) ( ) ( ) s ~laov prve ele vrse marce K, a s ~laov prve ele oloe. o za~ da se drgom ora drga vrsa drga oloa marca S R ra~a a s a~a ao e o ra eo prvom ora, samo se meso orgale marce K, ors modfovaa - ( ) odezovaa marca K. Prema ome, osale vrse oloe se mog zra~a poavlaem drgog oraa. U posledem ora odezovaa marca ma samo eda ~la razl~ od le: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) = (6.5) Deompozcom marce K, oa se vr{ oraa zavr{ea e prva faza Gass-ove meode elmace. Sada eda~ (6.) mo`emo apsa obl: Sy = F y= R (6.6) 4
19 eora lsh osa~a II eoda deformaca Ssem eda~a S y = F se mo`e edosavo re{, ao {o }e se prvo re{ prva eda~a ssema, oa ma samo ed epoza: y = f Drga eda~a ma obl: sy y = f Korse} re{ee prehode eda~e ovo e eda~a sa samo edom epozaom y, o e lao zra~a. ao oga se prelaz a slede} eda~ gde se z zra~ae y y avla ope samo eda epozaa y. Pospa proala`ea veora y se zavr{ava ada se z poslede eda~e zra~a y. me se zavr{ava drga faza Gass-ovog meoda., oa se azvca preda redca. re}a, posleda faza se azva zada spsca svod se a re{avae ssema eda~a: R = y (6.7) Po{o e veor y poza, ova ssem eda~a se re{ava od poslede eda~e oa ma obl: y r = y = r Preposleda eda~a sada ma samo ed epoza, oa se lao zra~ava edosavm algebarsm operacama. Ova pospa se asavla sve do se z prve eda~e e zra~a {o e posleda epozaa daog ssema eda~a. Prmer: Re{ ssem eda~a Gass-ovom meodom. Re{ee: Prva faza = { 4 }; {.5} R = S = K ( ) = { }; { } R = S = K ( ) =
20 eora lsh osa~a II 7 4 { } ; { } R = S = K ( 4) eoda deformaca = 7 { 7 }; { } R4 = S 4 = 4 S= ; R = y = 6, y = 6 6 = 6, y = 6 =, y = = = = 7 4 = = = ( ) = 8.57 = ( ) = 9.4 {o s re{ea goreg ssema eda~a. Predos ove meode e {o se apred za bro ra~sh operaca oe e porebo zvr{ za re{avae ssema eda~a, a samm m ompersog vremea. Usavr{avae ove meode ma cl da se a aefas a~ pohra samo ompoee razl~e od le, ~me se pos`e za~aa {eda ro{ ompersog vremea prosora za prora~ velh ssema eda~a Prora~ prese~h sla {apovma. Re{avaem ssema eda~a dobva se pomeraa svh ~vorova ssema, a samm m pomeraa ~vorova svaog {apa. Korse} eda~e {apa mog se zra~a veor prese~h sla svaom {ap: f = f (6.8) Jed problem e {o gora eda~a podrazmeva da e veor pomeraa da loalom oordaom ssem -og {apa, a re{avaem ssema eda~a dobl smo veor pomeraa ssema. Prema ome, porebo e sors zraze oma se povez veor pomeraa svaog {apa sa veorom pomeraa ssema. Iz eda~a (6.5) (6.8) dobva se: 6
21 eora lsh osa~a II eoda deformaca = Uvr{avaem (6.9) (6.8) dobva se: f = f (6.9) (6.) Pomo} eda~e (6.) mog se dob sve prese~e sle a po~e a ra {apa edosavm ra~sm operacama sa marcama. Uolo s slov ravoe`e posavle dreo, ada se orse poeda~o eda~e za sva prese~ sl ada e porebo zra~a proece poedh pomaa a osove loalh oordah ssema, oe osm glova zaorea fgrra m eda~ama. Kada se sra~a sle ~vorovma, z slova ravoe`e se lao mog zra~a sle svm presecma {apa ao dob dagram prese~h sla. apome se o{ edom da e ovo faz porebo vod ra~a da predzac dobveh prese~h sla odgovara ovec oa va` za meod deformaca. me se zavr{ava proces re{avaa elas~og lsog ssema a~om meodom deformaca. 7
Dvostrukom integracijom jedna~ine c) dobiva se: M (6.38)
 Stata ostrca I Prora~ pomeraa 63 Deformacoa la {tapa Deformacoa la {tapa predstavla dmeze obl {tapa ao deformace Uolo aalzramo delovae popre~og optere}ea a prav {tap rav, {tap mea samo obl La oom se praze
Stata ostrca I Prora~ pomeraa 63 Deformacoa la {tapa Deformacoa la {tapa predstavla dmeze obl {tapa ao deformace Uolo aalzramo delovae popre~og optere}ea a prav {tap rav, {tap mea samo obl La oom se praze
5. POTENCIJALNA ENERGIJA ELASTI^NOG SISTEMA Pojam potencijalne energije elasti~nog sistema
 eora lh oa~a II Potecala eerga elat~og tema 5. POECIJAA EERGIJA EASI^OG SISEA 5.. Poam potecale eerge elat~og tema U predmetu ehaa II defa e poam potecalog pola egove oobe, ao poam potecale eerge. Ovde
eora lh oa~a II Potecala eerga elat~og tema 5. POECIJAA EERGIJA EASI^OG SISEA 5.. Poam potecale eerge elat~og tema U predmetu ehaa II defa e poam potecalog pola egove oobe, ao poam potecale eerge. Ovde
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
transformacija j y i x x promatramo dva koordinatna sustava S i S sa zajedničkim ishodištem z z Homogene funkcije Ortogonalne transformacije
 promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
Modeliranje turbulencije u cilju primene numeričkih simulacija u hidrotehnici
 Modelrane rblence cl prmene nmerčh smlaca hdroehnc nverze Beorad Građevns fale - Krs Mehane flda na doorsm sdama - Nenad Jaćmovć Ma, 03. CFD Compaonal Fld Mechancs Račnsa mehana flda Prmena meoda nmerče
Modelrane rblence cl prmene nmerčh smlaca hdroehnc nverze Beorad Građevns fale - Krs Mehane flda na doorsm sdama - Nenad Jaćmovć Ma, 03. CFD Compaonal Fld Mechancs Račnsa mehana flda Prmena meoda nmerče
pismeni br.4 4.2: Izračunati yds, gdje je K luk parabole y 2 = 2 px od ishodišta to točke
 Prakkm Maemaka III Prredo DJočć smen br : Raz Forero red nkc eroda dan ormom za < za < : Izračna ds gde e k araboe od shodša o očke M : Izračna koordnae ežsa homogenog ka ckode a sn a ; : Izračna I e [
Prakkm Maemaka III Prredo DJočć smen br : Raz Forero red nkc eroda dan ormom za < za < : Izračna ds gde e k araboe od shodša o očke M : Izračna koordnae ežsa homogenog ka ckode a sn a ; : Izračna I e [
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
TEHNIČKI FAKULTET SVEUČILIŠTA U RIJECI Zavod za elektroenergetiku. Prijelazne pojave. Osnove elektrotehnike II: Prijelazne pojave
 THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK
 SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
 w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
!"!# ""$ %%"" %$" &" %" "!'! " #$!
 " "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.
 Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Newtonovi aksiomi: MEHANIKA II. Zadaci dinamike: I. Aksiom: Zakon inercije. II. Aksiom: Osnovni zakon dinamike. III. Aksiom: Zakon akcije i reakcije
 Newoo ao: MHANIKA II. do: D Aebero prcp Zao dae I. ao: Zao ercje II. ao: Zao baja III. ao: Zao acje reacje (poajaje z ae) I. Ao: Zao ercje Maerjao jeo oa bez djeoaja ajh a zadržaa aje roaja jedoo praocro
Newoo ao: MHANIKA II. do: D Aebero prcp Zao dae I. ao: Zao ercje II. ao: Zao baja III. ao: Zao acje reacje (poajaje z ae) I. Ao: Zao ercje Maerjao jeo oa bez djeoaja ajh a zadržaa aje roaja jedoo praocro
Mašinski fakultet, Beograd - Mehanika 3 Predavanje 10 i 11 1
 Mš fule Beog - Meh 3 Peve lee lče ehe Geele ooe o e o e o elh č č olož e oeđe 3 Deovh oo ( o e elue holooh ecoh žvućh ve ( f α (α e olož e oeđe evh oo ev e o u ouo oeđuu olož elog e u oou vu e geele ooe
Mš fule Beog - Meh 3 Peve lee lče ehe Geele ooe o e o e o elh č č olož e oeđe 3 Deovh oo ( o e elue holooh ecoh žvućh ve ( f α (α e olož e oeđe evh oo ev e o u ouo oeđuu olož elog e u oou vu e geele ooe
Identitet filter banke i transformacije transformacije sa preklapanjem
 OASDSP: asoacije i ile bae asoacije disei sigala File bae Ideie ile bae i asoacije asoacije sa elaaje Uslov eee eosucije ovi Sad 6 saa OASDSP: asoacije i ile bae ovi Sad 6 saa DF: vadaa asoacija DF IF
OASDSP: asoacije i ile bae asoacije disei sigala File bae Ideie ile bae i asoacije asoacije sa elaaje Uslov eee eosucije ovi Sad 6 saa OASDSP: asoacije i ile bae ovi Sad 6 saa DF: vadaa asoacija DF IF
Da se podsetimo Algoritam optimizacije. Odrediti vrednosti parametara kola koje će garantovati da odziv F(x, p) ima željenu vrednost F * (x).
 Aotam otmzac Da s odstmo Aotam otmzac Aotam otmzac Aotam otmzac : Oddt vdost aamtaa oa [,... ] o ć aatovat da odzv (x, ma žu vdost * (x. Mtod: až mmuma fuc š E(x,; (oma za vattatvu ocu odstuaa dobo od
Aotam otmzac Da s odstmo Aotam otmzac Aotam otmzac Aotam otmzac : Oddt vdost aamtaa oa [,... ] o ć aatovat da odzv (x, ma žu vdost * (x. Mtod: až mmuma fuc š E(x,; (oma za vattatvu ocu odstuaa dobo od
Parcijalne molarne veličine
 arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Aritmetički i geometrijski niz
 Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
SWOT 1. Analysis and Planning for Cross-border Co-operation in Central European Countries. ISIGInstitute of. International Sociology Gorizia
 SWOT 1 Analysis and Planning for Cross-border Co-operation in Central European Countries ISIGInstitute of International Sociology Gorizia ! " # $ % ' ( )!$*! " "! "+ +, $,,-,,.-./,, -.0",#,, 12$,,- %
SWOT 1 Analysis and Planning for Cross-border Co-operation in Central European Countries ISIGInstitute of International Sociology Gorizia ! " # $ % ' ( )!$*! " "! "+ +, $,,-,,.-./,, -.0",#,, 12$,,- %
Elementi energetske elektronike
 ELEKTRIČNE MAŠINE Elemen energeske elekronke Uvod Čme se bav energeska elekronka? Energeska elekronka se bav konverzjom (prevaranjem) razlčh oblka elekrčne energje. Uvod Gde se kors? Elemen energeske elekronke
ELEKTRIČNE MAŠINE Elemen energeske elekronke Uvod Čme se bav energeska elekronka? Energeska elekronka se bav konverzjom (prevaranjem) razlčh oblka elekrčne energje. Uvod Gde se kors? Elemen energeske elekronke
Građevinski fakultet, Beograd
 Građesk fakule Beogra Eksploaaa zaša pozeh oa Obašea ežbe VEŽBA Pree ežbe e raspor aere u porozo sre. raspora eača presala zako oržaa ase pree a supsau koa se rasporue. Oržae ase rasporoae supsae ože a
Građesk fakule Beogra Eksploaaa zaša pozeh oa Obašea ežbe VEŽBA Pree ežbe e raspor aere u porozo sre. raspora eača presala zako oržaa ase pree a supsau koa se rasporue. Oržae ase rasporoae supsae ože a
Ekonometrija 5. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET
 TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
MEHANIKA FLUIDA. Složeni cevovodi
 MEHANIKA FLUIDA Složeni cevovoi.zaata. Iz va velia otvorena rezervoara sa istim nivoima H=0 m ističe voa roz cevi I i II istih prečnia i užina: =00mm, l=5m i magisalni cevovo užine L=00m, prečnia D=50mm.
MEHANIKA FLUIDA Složeni cevovoi.zaata. Iz va velia otvorena rezervoara sa istim nivoima H=0 m ističe voa roz cevi I i II istih prečnia i užina: =00mm, l=5m i magisalni cevovo užine L=00m, prečnia D=50mm.
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA
 RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA PREDAVANJE
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
Dijagrami: Greda i konzola. Prosta greda. II. Dijagrami unutarnjih sila. 2. Popre nih sila TZ 3. Momenata savijanja My. 1. Uzdužnih sila N. 11.
 Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
ITU-R P (2009/10)
 ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
Prema tome, kao sredstva koja uvrštavamo u portfolio pojavljuju se sredstvo 3, sa najvećim iznosom Sharpe-ovog indeksa, i sredstvo 2.
 Prmer 7. 1) Da su podac za r sredsva u peroda osmarana, R 1,518 R 3, 031 R3 3, 9533 r 1 1, 0383 r 0, 837 r 3 1, 48 r 1 r 0,1919 r 1 r 3 0, 698 r r 3 0, 1801 na osnovu dah sumranh vrednos odred očekvanu
Prmer 7. 1) Da su podac za r sredsva u peroda osmarana, R 1,518 R 3, 031 R3 3, 9533 r 1 1, 0383 r 0, 837 r 3 1, 48 r 1 r 0,1919 r 1 r 3 0, 698 r r 3 0, 1801 na osnovu dah sumranh vrednos odred očekvanu
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
 1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Trigonometrijske nejednačine
 Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο
 18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
Đường tròn : cung dây tiếp tuyến (V1) Đường tròn cung dây tiếp tuyến. Giải.
 Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
Trigonometrijski oblik kompleksnog broja
 Trgnmetrjsk blk kmpleksng brja Da se pdsetm: Kmpleksn brj je blka je realn de, je magnarn de kmpleksng brja, - je magnarna jednca, ( Dva kmpleksna brja su jednaka ak je Za brj _ je knjugvan kmpleksan brj.
Trgnmetrjsk blk kmpleksng brja Da se pdsetm: Kmpleksn brj je blka je realn de, je magnarn de kmpleksng brja, - je magnarna jednca, ( Dva kmpleksna brja su jednaka ak je Za brj _ je knjugvan kmpleksan brj.
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK
 OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
Elektrotehnički fakultet univerziteta u Beogradu 26. jun Katedra za Računarsku tehniku i informatiku
 Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Mašinski fakultet, Beograd - Mehanika 2 Predavanje 9 1 DINAMIKA
 Mašsk fakle, eogad - Mehaka Pedavaje 9 DINAMIKA Damka je deo eojske mehake koj počava mehačka keaja ejalh ojekaa sposavljajć vez zmeđ keaja zoka koj zazvaj o keaje. Najjedosavj model ealog ela jese ejala
Mašsk fakle, eogad - Mehaka Pedavaje 9 DINAMIKA Damka je deo eojske mehake koj počava mehačka keaja ejalh ojekaa sposavljajć vez zmeđ keaja zoka koj zazvaj o keaje. Najjedosavj model ealog ela jese ejala
Rešenje: X C. Efektivne vrednosti struja kroz pojedine prijemnike su: I R R U I. Ekvivalentna struja se određuje kao: I
 . Otnik tnsti = 00, kalem induktivnsti = mh i kndenzat kaacitivnsti = 00 nf vezani su aaleln, a između njihvih kajeva je usstavljen steidični nan efektivne vednsti = 8 V, kužne učestansti = 0 5 s i četne
. Otnik tnsti = 00, kalem induktivnsti = mh i kndenzat kaacitivnsti = 00 nf vezani su aaleln, a između njihvih kajeva je usstavljen steidični nan efektivne vednsti = 8 V, kužne učestansti = 0 5 s i četne
Difuzija supstance u vazduhu analitičko i numeričko rešavanje
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA FIZIKU Dfuzja supsace u vazduhu aalčko umerčko rešavaje - dplomsk rad - Meor: Dr Mla Pać Kadda: Mlea Brakovć Nov Sad, 00 Sadržaj UVOD
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA FIZIKU Dfuzja supsace u vazduhu aalčko umerčko rešavaje - dplomsk rad - Meor: Dr Mla Pać Kadda: Mlea Brakovć Nov Sad, 00 Sadržaj UVOD
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
( ) π. I slučaj-štap sa zglobovima na krajevima F. Opšte rešenje diferencijalne jednačine (1): min
 Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Chapter 1 Fundamentals in Elasticity
 D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
i b, onda postoje jedinstveni q (kvocijent) (ostatak) takvi da je a = bq + r. , broj 5 dijeli broj n 5 n
 4 Cel broev Sup prrodh broeva { 3K } Sup prrodh broeva ule 0 { 0} { 03K } Sup celh broeva { K 3 03 K} 4 Delvost u supu celh broeva Defca Nea su tao da e b a Svostva: Za \ { 0} Za b \ { 0} 3 Za b \ { 0}
4 Cel broev Sup prrodh broeva { 3K } Sup prrodh broeva ule 0 { 0} { 03K } Sup celh broeva { K 3 03 K} 4 Delvost u supu celh broeva Defca Nea su tao da e b a Svostva: Za \ { 0} Za b \ { 0} 3 Za b \ { 0}
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
cele mai ok referate
 Permur www.refereo.ro cele m o refere.noue de permure. Fe A o mulme f de elemee, dc A{,, 3,, }. O fuce becv σ:aàa e umee permure ubue de grdul. P:Numrul uuror permurlor de ord ee egl cu!..produul compuere
Permur www.refereo.ro cele m o refere.noue de permure. Fe A o mulme f de elemee, dc A{,, 3,, }. O fuce becv σ:aàa e umee permure ubue de grdul. P:Numrul uuror permurlor de ord ee egl cu!..produul compuere
FUNKCIJE UTJECAJA I UTJECAJNE LINIJE
 FUNKCIJE UTJECJ I UTJECJNE LINIJE Funkcje ujecaja ujecajne lnje korse se kod proračuna konsrukcja na djelovanje pokrenh operećenja. Zadaak: odred onaj položaj pokrenog operećenja koj će da najnepovoljnj
FUNKCIJE UTJECJ I UTJECJNE LINIJE Funkcje ujecaja ujecajne lnje korse se kod proračuna konsrukcja na djelovanje pokrenh operećenja. Zadaak: odred onaj položaj pokrenog operećenja koj će da najnepovoljnj
1.1. Napisati relaciju kojom je moguće odrediti ukupan broj elektrona na nekoj orbiti: n
 I ES EES - VAIJANA Zadatak bro... Nasat relacu koom e moguće odredt ukua bro elektroa a eko orbt: l 0 ( Z 0 l + ) [ + 3 + 5 + ( ) ].. Nasat relacu koa ovezue kocetrace elektroa šula kod čstog (trsc) oluvodča:.3.
I ES EES - VAIJANA Zadatak bro... Nasat relacu koom e moguće odredt ukua bro elektroa a eko orbt: l 0 ( Z 0 l + ) [ + 3 + 5 + ( ) ].. Nasat relacu koa ovezue kocetrace elektroa šula kod čstog (trsc) oluvodča:.3.
Metoda najmanjih kvadrata
 Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
SONATA D 295X245. caza
 SONATA D 295X245 caza 01 Γωνιακός καναπές προσαρμόζεται σε όλα τα μέτρα σε όλους τους χώρους με μηχανισμούς ανάκλησης στα κεφαλάρια για περισσότερή αναπαυτικότητα στην χρήση του-βγαίνει με κρεβάτι η χωρίς
SONATA D 295X245 caza 01 Γωνιακός καναπές προσαρμόζεται σε όλα τα μέτρα σε όλους τους χώρους με μηχανισμούς ανάκλησης στα κεφαλάρια για περισσότερή αναπαυτικότητα στην χρήση του-βγαίνει με κρεβάτι η χωρίς
GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo
 GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Problemas resueltos del teorema de Bolzano
 Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Moto armonico: T : periodo, ω = pulsazione A: ampiezza, φ : fase
 Moo armonico: equazione del moo: d x ( ) = x ( ) soluzione: x ( ) = A s in ( + φ ) =π/ Τ T : periodo, = pulsazione A: ampiezza, φ : fase sposameno: x ( ) = X s in ( ) velocià: dx() v () = = X cos( ) accelerazione:
Moo armonico: equazione del moo: d x ( ) = x ( ) soluzione: x ( ) = A s in ( + φ ) =π/ Τ T : periodo, = pulsazione A: ampiezza, φ : fase sposameno: x ( ) = X s in ( ) velocià: dx() v () = = X cos( ) accelerazione:
Dimenzioniranje SN/NN kabela i transformatora
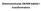 Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
ČETVOROUGAO. β 1. β B. Četvorougao je konveksan ako duž koja spaja bilo koje dve tačke unutrašnje oblasti ostaje unutar četvorougla.
 Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
Hemijska kinetika. Hemijska kinetika. Hemijska kinetika. Hemijska kinetika. Eksperimentalne osnove hemijske kinetike
 Zašo se izučava ieia hemijsih reaija? raiča i fudameala začaj Ša obuhvaa HK? formaa hemijsa ieia reaioa diamia Eserimeae osove hemijse ieie. uvrñivaje sehiomerijse jedačie hemijse reaije (reba ideifiovai
Zašo se izučava ieia hemijsih reaija? raiča i fudameala začaj Ša obuhvaa HK? formaa hemijsa ieia reaioa diamia Eserimeae osove hemijse ieie. uvrñivaje sehiomerijse jedačie hemijse reaije (reba ideifiovai
SKEMA PERCUBAAN SPM 2017 MATEMATIK TAMBAHAN KERTAS 2
 SKEMA PERCUBAAN SPM 07 MATEMATIK TAMBAHAN KERTAS SOALAN. a) y k ( ) k 8 k py y () p( ) ()( ) p y 90 0 0., y,, Luas PQRS 8y 8 y Perimeter STR y 8 7 7 y66 8 6 6 6 6 8 0 0, y, y . a).. h( h) h h h h h h 0
SKEMA PERCUBAAN SPM 07 MATEMATIK TAMBAHAN KERTAS SOALAN. a) y k ( ) k 8 k py y () p( ) ()( ) p y 90 0 0., y,, Luas PQRS 8y 8 y Perimeter STR y 8 7 7 y66 8 6 6 6 6 8 0 0, y, y . a).. h( h) h h h h h h 0
Deformacije. Tenzor deformacija tenzor drugog reda. Simetrinost tenzora deformacija. 1. Duljinska deformacija ε. 1. Duljinska (normalna) deformacija ε
 Deformae. Duljinska (normalna) deformaa. Kutna (posmina) deformaa. Obujamska deformaa Θ Tenor deformaa tenor drugog reda 9 podatakamjerna jedinia Simetrinost tenora deformaa 6 podataka 4. Duljinska deformaa
Deformae. Duljinska (normalna) deformaa. Kutna (posmina) deformaa. Obujamska deformaa Θ Tenor deformaa tenor drugog reda 9 podatakamjerna jedinia Simetrinost tenora deformaa 6 podataka 4. Duljinska deformaa
1. Duljinska (normalna) deformacija ε. 2. Kutna (posmina) deformacija γ. 3. Obujamska deformacija Θ
 Deformaije . Duljinska (normalna) deformaija. Kutna (posmina) deformaija γ 3. Obujamska deformaija Θ 3 Tenor deformaija tenor drugog reda ij γ γ γ γ γ γ 3 9 podataka+mjerna jedinia 4 Simetrinost tenora
Deformaije . Duljinska (normalna) deformaija. Kutna (posmina) deformaija γ 3. Obujamska deformaija Θ 3 Tenor deformaija tenor drugog reda ij γ γ γ γ γ γ 3 9 podataka+mjerna jedinia 4 Simetrinost tenora
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
!"#$ "%&$ ##%&%'()) *..$ /. 0-1$ )$.'-
 !!" !"# "%& ##%&%',-... /. -1.'- -13-',,'- '-...4 %. -5"'-1.... /..'-1.....-"..'-1.. 78::8
!!" !"# "%& ##%&%',-... /. -1.'- -13-',,'- '-...4 %. -5"'-1.... /..'-1.....-"..'-1.. 78::8
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Dinamika krutog tijela. 14. dio
 Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (
Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (
OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA
 OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA OSNOVI HEMIJSKE TERMODINAMIKE Hemjska termodnamka proučava promene energje (toplotn efekat) pr odgravanju hemjskh reakcja. MATERIJA ENERGIJA? Energja je dskontnualna
OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA OSNOVI HEMIJSKE TERMODINAMIKE Hemjska termodnamka proučava promene energje (toplotn efekat) pr odgravanju hemjskh reakcja. MATERIJA ENERGIJA? Energja je dskontnualna
Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1
 Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
tel , version 1-7 Feb 2013
 !"## $ %&' (") *+ '#),! )%)%' *, -#)&,-'" &. % /%%"&.0. )%# "#",1 2" "'' % /%%"&30 "'' "#", /%%%" 4"," % /%%5" 4"," "#",%" 67 Y% !"!"# $ %& & # &$ ' '#( ''# ))'%&##& *'#$ ##''' "#$ %% +, %'# %+)% $
!"## $ %&' (") *+ '#),! )%)%' *, -#)&,-'" &. % /%%"&.0. )%# "#",1 2" "'' % /%%"&30 "'' "#", /%%%" 4"," % /%%5" 4"," "#",%" 67 Y% !"!"# $ %& & # &$ ' '#( ''# ))'%&##& *'#$ ##''' "#$ %% +, %'# %+)% $
!"#$ %"&'$!&!"(!)%*+, -$!!.!$"("-#$&"%-
 !"#$ %"&$!&!"(!)%*+, -$!!.!$"("-#$&"%-.#/."0, .1%"("/+.!2$"/ 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333 4.)!$"!$-(#&!- 33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333
!"#$ %"&$!&!"(!)%*+, -$!!.!$"("-#$&"%-.#/."0, .1%"("/+.!2$"/ 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333 4.)!$"!$-(#&!- 33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
 728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
Ekonometrija 4. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Priveznice W re r R e o R p o e p S e l S ing n s
 Priveznice Wire Rope Slings PRIVEZNICE OD ČEIČNO UŽEA (RAE) jenosruke SINE WIRE ROPE SINS Sanar EN P P P P P P P P P P P P ozvoljeno operećenje kg elemeni priveznice prekina jenokrako vešanje ) ouvaanje
Priveznice Wire Rope Slings PRIVEZNICE OD ČEIČNO UŽEA (RAE) jenosruke SINE WIRE ROPE SINS Sanar EN P P P P P P P P P P P P ozvoljeno operećenje kg elemeni priveznice prekina jenokrako vešanje ) ouvaanje
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
