T O P L I N A P l i n s k i z a k o n i
|
|
|
- Χρυσάνθη Μαυρίδης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 1. Da bi mogli matematički oisati lin uvodimo ojam tzv. idealnog lina. Koji odgovor nije točan? Idealni lin o retostavci je onaj lin kod kojeg: a) možemo zanemariti međudjelovanje između molekula, tj. njihovu otencijalnu energiju. b) se molekule kaotično gibaju u svim smjerovima otuno međusobno neovisno, osim u trenutku sudara. c) su sudari sa stjenkom osude savršeno elastični. d) molekule zamišljamo kao materijalne točke zanemarujući njihov volumen e) molekule zamišljamo kao materijalne točke zanemarujući njihovu masu. 2. U cilindru se nalazi 10 m 3 kisika [M(O2) = 32 g/mol] ri standardnim uvjetima. Kolika je to količina tvari iskazana u molima? Kolika je masa kisika? (R: 446 mol; 14,3 kg) 3. Cilindar s omičnim kliom sadrži 1 mol idealnog lina. Plinu se mijenja volumen ri stalnoj temeraturi, dakle izotermna romjena. Pri temeraturi okoline Stjekica je dobila vrijednosti: / dm / 10 5 Pa dok je Fili za drugu temeraturu okoline s istim ostalim očetnim uvjetima kao i Stjekica dobio vrijednosti: / dm / 10 5 Pa a) Tko je mjerio kod više temerature? b) Često se umjesto rikaza u, grafu izotermička romjena stanja lina rikazuje u, 1/ grafu. Nacrtajte kako izgledaju grafovi izotermi različitih temeratura u oba grafa, te označite koja je temeratura najveća, a koja najmanja.
2 4. Koji je od redloženih - grafova oisuje izotermni roces određene mase idealnog lina za dvije različite temerature i ri čemu je <. a) b) c) d) e) 5. Koji je od redloženih grafova oisuje izotermni roces određene mase idealnog lina za dvije različite temerature i ri čemu je <. 1/ 1/ 1/ 1/ 1/ a) b) c) e) e)
3 6. Balon u obliku kugle olumjera 18 cm naunjen je helijem temerature 20 C i tlaka 1,05 atm. Koliko molova helija sadrži balon i kolika je masa helija u balonu? (R = 8,314 J/molK) (R: 1,066 mol; 4,26 g) 7. Tlak u automobilskoj gumi je 301 kpa ri temeraturi 10 C. Nakon rijeđenih 100 km temeratura u gumi se oveća na vrijednost 40 C. Koliki je sada tlak u gumi, smatramo li da se volumen gume nije romijenio? (R: 333 kpa) 8. Zatvorena osuda sadrži određenu količinu dušika [M(N 2) = 28 g/mol] ri tlaku od 3,65 atm. Koliki će biti tlak u osudi, iskazan u atmosferama, ako dušik zamijenimo jednakom masom ugljičnog dioksida CO 2 [M(CO 2)=44 g/mol] ri konstantnoj temeraturi? (R: 2,32 atm)
4 9. U cilindru se nalazi 25,5 mola helija temerature 10 C i tlaka 1,35 atm. Koliki je volumen helija? (R: 0,439) 10. Tlak u automobilskoj gumi unjenoj kod temerature 15 C je 1233 kpa. Ako temeratura naraste na 38 C, koliko zraka iskazanog u % moramo iz gume isustiti da bi tlak ostao jednak kao i rije? olumen gume je konstantan. (R: (n 1 n 2)/n 1 = 7,4 %) 11. Automobilsku gumu volumena 10 litara treba naumati do tlaka Pa. Temeratura zraka je 0 C i atmosferski tlak je 10 5 Pa. Ako uma izbacuje 500 cm 3 zraka o jednom stisku, koliko uta treba ritisnuti ručicu ume ako je guma na očetku bila : a) razna b) una zraka od atmosferskim tlakom? Smatrajte da se temeratura i volumen gume ne mijenjaju tijekom umanja. (R; a) 60; b) 40)
5 12. Zatvoreni cilindar sadrži zrak na temeraturi 100 C. Na kojoj bi temeraturi trebao biti zrak u osudi da tlak bude dva uta veći? (R: 473 C) 13. Idealni lin mase m zatvoren u cilindru volumena ima temeraturu T i tlak. Ako se masa lina oveća na 3m, temeratura snizi na T/3 i volumen smanji na /3, tlak lina u cilindru će biti: a) /3 b) c) 3 d) 9 e) Idealni lin temerature 300 K ri izotermnoj eksanziji oveća svoj volumen dva uta i zatim se izohorno zagrijava tako da mu tlak bude jednak onom rije eksanzije. Kolika je konačna temeratura lina nakon zagrijavanja? (R: 600 K) 15. U zatvorenoj osudi nalazi se lin na temeraturi 27 C i tlaku 0. Ako se lin zagrije na temeraturu 327 C tlak će biti: a) P 0/2 b) 3 0 c) 4 0 d) 2 0 e) P 0
6 16. Za određenu masu idealnog lina tražimo ovisnost između temerature T i gustoće ρ ri konstantnom tlaku, ri čemu je 2 > 1. Koji od redloženih grafova rikazuje tu ovisnost? T 1 T 2 T T T ρ ρ 2 ρ 1 ρ ρ a) b) c) 17. Mjehurić idealnog lina oveća svoj volumen kada se s dna jezera enje rema ovršini dva uta. Kolika je dubina jezera od retostavkom da je temeratura vode jednaka na svim dubinama? (g 10 m/s 2 ; ρ vode = 10 3 kg/m 3 ; a = 10 5 Pa) (R: 10 m) d) e) 18. Za određenu masu idealnog lina rikazana je ovisnost između temerature T i reciročne vrijednosti gustoće 1/ρ ri konstantnom tlaku, ri čemu je 2 > 1. Koji od redloženih grafova rikazuje tu ovisnost? T 1 T 2 T T T /ρ 1/ρ 2 1/ρ 1 1/ρ 1/ρ a) b) c) d) e)
7 19. Za određenu masu idealnog lina rikazana je ovisnost gustoće ρ i tlaka ri konstantnoj temeraturi T (K), ri čemu je <. Koji od redloženih grafova rikazuje tu ovisnost? ρ ρ ρ ρ ρ a) b) c) d) e) 20. U zatvorenoj osudi nalazi se zrak ri tlaku Pa. Ako temeratura u osudi naraste od 100 C na 200 C, novi tlak iznosi: a) 1, Pa b) 2, Pa c) 2, Pa d) 4, Pa e) 6, Pa 21. Za koliko stunjeva se romijenila temeratura lina ako izobarno ovećamo volumen lina dva uta? Početna temeratura lina je bila 0 C. a) 273 C b) 0 C c) 2 C d) 546 C e) 546 K 22. Za koliko stunjeva se romijenila temeratura lina ako izohorno ovećamo volumen lina dva uta? Početna temeratura lina je bila 27 C. a) 54 C b) 300 C c) 27 C d) 573 C e) 600 K
8 23. Određena masa lina ima temeraturu 27 C, tlak 1,7 bara ri volumenu 6,5 litara. Kolika će biti temeratura lina ako se tlak oveća na 3,5 bara, a volumen smanji na 4,2 litre? a) 117 K b) 35 K c) 35 C d) 390 C e) 126 C 24. Iz osude naunjene vodikom H 2 (M = 2 g/mol), volumena 10 l zbog okvarenog ventila izlazi lin. Na temeraturi t 1 = 7 C manometar je okazivao tlak od 5 MPa. Nakon nekog vremena na temeraturi t 2 = 17 C manometar okazuje jednak tlak kao i na rijašnjoj temeraturi t 1. Kolika je masa lina istekla iz osude? (R = 8,314 J/molK) a) 24,8 g b) 1,48 kg c) 14,8 g d) 1,48 g e) 174 g 25. U nekoj boci nalazi se lin od tlakom 10 6 Pa na temeraturi 27 C. Iz boce se isusti četvrtina mase lina i temeratura ovisi na 127 C. Koliki će biti tlak lina u boci ako je volumen konstantan? (R: 10 6 Pa) 26. Balon sadrži 500 m3 helija na temeraturi 27 C i tlaku 10 5 Pa. Izračunaj volumen balona na visini 6000 m gdje je tlak 0, Pa, a temeratura -3 C. (R: 900 m)
9 27. Temeratura u sobi volumena 50 m 3 ovisi se od 10 C na 20 C. Pri tom je tlak stalan i iznosi 10 5 Pa. Za koliko se romijeni masa zraka u sobi? (M zraka = 29 g/mol) /Pa /Pa a) 2,1 g b) 2,1 kg c) 12,2 kg d) g e) kg 28. Idealni lin odvrgnut je kružnom rocesu rikazanog,t grafom. Nacrtaj taj roces u, grafu. /m 3 B C A /m Na,T grafu rikazan je kružni roces jednog mola idealnog lina. Temeratura lina iskazana je u kelvinima. Nacrtaj taj isti roces u,1/ grafu. A B D C 1/ 30. Idealni lin odvrgnut je kružnom rocesu rikazanim,t grafom. Nacrtaj taj roces u,t grafu gdje je temeratura iskazana u kelvinima. /m 3 B C A
10 31. Na crtežu je rikazan kružni roces jednog mola idealnog lina u,t grafu. Nacrtaj taj isti roces u,1/ grafu. A B D C 1/ 32. Tijekom vožnje zrak u automobilskim gumama se grije. Na očetku vožnje temeratura zraka u gumama je bila 27 C, a na kraju vožnje 57 C. Uz retostavku da se volumen u gumama nije romijenio, izračunaj omjer tlakova na kraju i na očetku vožnje. (R: 1,1) 33. Zrak se nalazi u rostoriji na temeraturi 11 C. Prostorija se zagrije na 23 C ri stalnom tlaku i određena masa zraka izađe. Koliki je omjer masa zraka u rostoriji rije i nakon zagrijavanja? a) 1,64 b) 1,08 c) 3,04 d) 2,04 e) 1,04
11 34. U gumenom balonu nalazi se zrak od tlakom 1 = 0,1 MPa. Temeratura zraka je t 1 = 20 C, dok je njegova gustoća ρ 1 = 1,22 kg/m 3. Kolika će biti gustoća zraka u balonu kad se on one na visinu gdje je tlak zraka 2 = 3 kpa, a temeratura t 2 = -45 C? a) 4, kg/m 3 b) 4, kg/m 3 c) 4, kg/m 3 d) 4,7 kg/m 3 e) 47 kg/m Koji od redloženih,t grafova najbolje oisuje izobarni roces određene mase idealnog lina tlaka 1 i 2 za dva različita tlaka ri čemu je 1< 2? a) b) c) d) e) 36. Koji od redloženih,t grafova najbolje oisuje izobarni roces određene mase idealnog lina za dva različita tlaka 1 i 2 ri čemu je 1< 2? C a) t/ C 0 C t/ C 0 C t/ C 0 C b) c) d) t/ C
12 37. Balon volumena 224 m 3 i mase 145 kg uni se tolim zrakom ri normiranom atmosferskom tlaku. Kolika mora biti najmanja temeratura zraka u balonu da bi se on očeo dizati vertikalno uvis, ako je temeratura okolnog zraka 0 C, a molna masa zraka iznosi 29 g/mol? a) 73 C b) 273 C c) 27 C d) 100 C e) 150 C 38. Tlak u žarulji ri temeraturi 20 C iznosi 0, Pa. Koliki je tlak u žarulji kad se zrak u njoj ugrije na 127 C? a) 5, Pa b) 1, Pa c) 6, Pa d) 2, Pa e) 0, Pa 39. Otvorenu staklenu tikvicu volumena 250 cm 3 zagrijavamo nad lamenom do 127 C. Cijelu tikvicu uronimo otvorom rema dolje u osudu s vodom temerature 7 C, tako da je grlo tikvice isod razine vode (crtež). oda uđe u tikvicu tako da je razina vode u tikvici 20 cm isod ovršine. Atmosferski tlak je 10 5 Pa, gustoća vode 10 3 kg/m 3, a g 10 m/s 2. Kolika će masa vode ući u tikvicu od retostavkom da je cijeli sustav na temeraturi 7 C? (R: 78 g)
13 40. Na crtežu je rikazan kružni roces jednog mola idealnog lina tzv.,t graf. Nacrtaj taj isti roces u 1/, grafu. A B 1/ D C 41. Na crtežu je rikazan kružni roces jednog mola idealnog lina u,t grafu. Nacrtaj taj isti roces u 1/, grafu. A B 1/ D C 42. Koji od redloženih,t grafova rikazuje izohornu romjenu stanja lina za linove različitih molarnih masa M 1<M 2, ri čemu su mase linova jednake, tj. m 1 = m 2? M 1 M 2 M 2 M 1 M 1 M 2 M 2 M 1 M 1 M 2 a) b) c) d) e) 43. Koji od redloženih,t grafova rikazuje izotermni roces određene mase idealnog lina za dvije različite temerature i, ri čemu je <? 1/ 1/ 1/ 1/ 1/ a) b) c) d) e)
14 44. Unutar cilindra zatvorenog na oba kraja nalazi se okretni kli. S jedne strane kia nalazi se m kilograma kisika ( 16 O), a s druge strane 2m kilograma dušika ( 14 N). Koliki dio ukunog volumena zauzima kisik ako je sustav u tolinskoj ravnoteži? a) 7/16 b) 32/38 c) 7/23 d) 28/32 e) 14/ Mjehurić zraka giba se od dna osude s vodom rema ovršini. Kako se ri tom mijenja sila uzgona koja otiskuje mjehurić zraka? Pretostavljamo da je temeratura vode osvuda jednaka. a) ovećava se b) ostaje stalna c) smanjuje se d) veća je ri dnu, manja ri ovršini e) ri dnu je veća, a zatim je stalna 46. Kolika je temeratura lina u zatvorenoj osudi ako mu se tlak ovećao za 1 % ri romjeni temerature za 3 K? a) 250 K b) 273 K c) 380 K d) 300 K e) 323 K 47. Zatvorena osuda sadrži zrak temerature 100 C. Do koje temerature treba zagrijati zrak da se tlak u osudi udvostruči? a) 200 C b) 300 C c) 375 C d) 473 C e) 700 C
15 48. Na kojoj će dubini u vodi mjehurić zraka imati ribližno dva uta manji romjer nego na ovršini? Atmosferski tlak je 10 5 Pa, gustoća vode 10 3 kg/m 3. Neka je temeratura vode svuda jednaka. a) 125 m b) 18 m c) 35 m d) 9 m e) 70 m 49. Mjehurić zraka volumena 1 cm 3 nalazi se na dubini 10 m. Temeratura vode na toj dubini je 4 C. Koliki će biti volumen mjehurića ri ovršini vode ako je tamo temeratura 23 C?? Atmosferski tlak je 10 5 Pa, gustoća vode 10 3 kg/m 3, a g 10 m/s 2. (R: 2,137 cm 3 ) 50. Koji od redloženih grafova oisuje izohorni roces određene mase idealnog lina za dva različita volumena 1 i 2 ri čemu je 1 < a) b) c) d) e) 51. Koji od redloženih,t grafova najbolje oisuje izohorni roces određene mase idealnog lina za dva različita volumena 1 i 2 ri čemu je 1 < a) t/ C 0 C t/ C 0 C t/ C 0 C b) c) d) t/ C
16 52. Tri grama vodika nalaze se od tlakom 400 kpa na temeraturi 1800 C. odik se hladi dok mu tlak i volumen ne adnu na olovinu rijašnje vrijednosti. Kolika je konačna temeratura vodika? M(H 2) = 2 g/mol. a) 214 K b) 412 K c) 518 K d) 778 K e) 1000 K 53. U staklenoj cijevi duljine 100 cm zatvorenoj na oba kraja (crtež) nalazi se stuac žive duljine 20 cm. Kad je cijev horizontalna, živa se nalazi na sredini cijevi. Kad se cijev ostavi u vertikalni oložaj, stuac žive se susti za 10 cm. Izračunaj očetni tlak u cijevi ako se temeratura nije mijenjala. Gustoća žive je kg/m 3. Zaokruži točan odgovor. a) 3, Pa b) 5, Pa c) 2, Pa d) 4, Pa e) 6, Pa Tri grama vodika nalaze se u osudi od tlakom 400 kpa na temeraturi 1800 C. odik se hladi dok mu tlak i temeratura ne adnu na olovinu rijašnje vrijednosti. Koliki je konačni volumen vodika? M(H 2) = 2 g/mol. a) 3,2 litre b) 42 litre c) 4,2 litre d) 5,2 litre e) 32 litre
17 /Pa T O P L I N A 55. Za koliko uta se romijeni volumen mjehurića lina koji s dubine 100 m isliva na ovršinu vode ako je atmosferski tlak 10 5 Pa, dok temeratura vode na dubini od 100 m iznosi 2 C, a ri ovršini je temeratura 27 C. Gustoća vode je 10 3 kg/m 3, a g 10 m/s 2. a) 12 uta b) 11 uta c) 10 uta d) 9 uta e) 8 uta 56. Na crtežu su rikazane dvije izoterme u, grafu temeratura i idealnog lina zatvorenog u cilindru s omičnim kliom. Možeš li s grafa zaključiti o odnosu temeratura i? a) Ne, jer ne znamo koji je to lin. b) Da, točno, temeratura = 2 c) Da, ribližno, samo da je >. d) Da, točno, temeratura = 2? e) Da, ribližno, samo da je >. 57. Idealni lin odvrgnut je kružnom rocesu rikazanog,t grafom. Nacrtaj taj roces u,t grafu, gdje je temeratura T iskazana u kelvinima. B C /m 3 A
18 58. Možemo li idealni lin revesti u tekuće stanje? a) Da, ako ovećamo tlak b) Da, ako ga ohladimo na vrlo nisku temeraturu c) Ne, jer nema sila rivlačenja koje djeluju među molekulama d) Ne, jer nema tako velikih tlakova i to je čisto tehnički roblem e) Da, ako lin jako stlačimo i ri tom jako ohladimo 59. Plin komrimiramo izotermno na tri uta manji volumen, ri čemu iz cilindra objegne jedna trećina mase lina. Konačni tlak lina je: a) tri uta veći od očetnog. b) tri uta manji od očetnog. c) dva uta veći od očetnog. d) dva uta manji od očetnog. e) neromijenjen. 60. Plin se širi izotermno na tri uta veći volumen, ri čemu iz cilindra objegne dvije trećine mase lina. Konačni tlak lina je: a) tri uta veći od očetnog. b) devet uta manji od očetnog. c) dva uta veći od očetnog. d) tri uta manji od očetnog. e) neromijenjen. 61. Mjehurić zraka u jezeru ima na dubini 43,5 m volumen 1 cm 3. Ako je temeratura na toj dubini 5,5 C, a ri vrhu 21 C, koliki će biti volumen mjehurića neosredno rije izranjanja? Atmosferski tlak iznosi a = Pa, gustoća vode je 10 3 kg/m 3, a g 10 m/s 2. (R: 5,5 cm 3 ) 62. Ako luća ronioca imaju kaacitet 5,5 litara kada se nalazi 10 m isod razine vode, za koliki će dio volumena luća eksandirati kada brzo izroni na ovršinu? Temeratura je stalna. Koje su moguće osljedice? (R: 2 = 11 litara, dakle 2 uta. Posljedice su kobne o život!)
19 63. Dvije osude sojene su kao na slici i odvojene zatvorenim ventilom. U manjoj osudi volumena 4 litre je lin od tlakom Pa, a u većoj volumena 6 litara tlak je 10 5 Pa. Koliki će biti tlakovi u osudi ako ventil olagano otvorimo? Smatraj da je romjena izotermna. (R: 1, Pa) 64. Najniži tlak koji možemo ostići tehnikom vakumiranja iznosi Pa. Koliko se molekula zraka nalazi u 1 cm 3 ri tom tlaku ako je temeratura 0 C? (N A = 6, mol-1) (R: 265 molekula o cm 3 ) 65. U kući volumena 800 m 3 nalazi se zrak. a) Kolika je masa zraka u kući ri temeraturi 27 C i tlaku od 10 5 Pa? b) Kolika masa zraka će ući ili izaći iz kuće ako tlak ostane jednak, a temeratura se snizi na 0 C? (M zraka= 28 g/mol) (R: a) 898 kg; b) Ući će 89 kg)
20 /Pa /Pa T O P L I N A 66. Idealni lin odvrgnut je kružnom rocesu rikazanom,t grafom. Nacrtaj taj roces u, grafu. B C A /m Da se izbjegne oasnost od narkoze dušikom, boce za ronjenje se une smjesom kisika i helija. Međutim, kisik od tlakom većim od 10 5 Pa (=1 bar) je toksičan. Zbog toga arcijalni tlak kisika ne smije relaziti tu vrijednost. Ako se ronilac nalazi na dubini gdje je tlak 11 bara, koliki mora biti omjer kisika i helija u boci iskazan u %? (M helija = 4 g/mol, M kisika = 32 g/mol) (R: kisika = 1 bar; helija = 10 bara 56 % He i 44 % kisika) 68. U staklenoj cjevčici rikazanoj na slici nalazi se stuac žive visine 15 cm. On sabija stuac zraka visine 15 cm. Kolika će biti visina stuca zraka x ako cjevčicu okrenemo s otvorom rema dolje? Smatraj da se temeratura nije romijenila. Gustoća žive je 13, kg/m 3, atmosferski tlak 10 5 Pa a g 10 m/s 2. (R: 22,7 cm) x cm 15 cm 15 cm 15 cm
21 69. U staklenoj cjevčici rikazanoj na slici nalazi se stuac žive visine 15 cm. On sabija stuac zraka visine 15 cm. Kolika će biti visina stuca zraka x ako cjevčicu oložimo horizontalno? Smatraj da se temeratura nije romijenila. Gustoća žive je 13, kg/m 3, atmosferski tlak 10 5 Pa a g 10 m/s 2. (R: 18,06 cm) x cm 15 cm 15 cm 15 cm 70. U uskoj cjevčici otvorenoj na jednom a zatvorenom na drugom kraju nalazi se stuac žive visine h. Ako je cjevčica okrenuta s otvorom rema gore, visina stuca lina iznosi h 1, a ako je cjevčica okrenuta otvorom rema dolje, visina tog stuca je h 2. a) Ako znamo gustoću žive ρ i akceleraciju sile teže g, kako možemo odrediti atmosferski tlak a, od retostavkom da se ri okretanju cjevčice temeratura nije romijenila. b) Koliki bi bio tlak lina u cjevčici da je ona ostavljena horizontalno? h 2 h h h 1
22 71. U staklenoj cjevčici, čiji je jedan kraj zataljen a drugi otvoren, nalazi se određena količina zraka. Cjevčica je uronjena u osudu u kojoj se nalazi živa. Kada je duljina cjevčice iznad žive 13 cm, živa u osudi i u cjevčici je na istoj razini. Kolika će biti visina stuca žive x iznad razine u osudi kada se cjevčica izvuče iz žive za još 12 cm? Atmosferski tlak je 10 5 Pa, a gustoća žive ρ = 13, kg/m 3. Promjena je izotermna. (R: x = 9,9 cm) 72. Pokažite da se efektivna brzina (ili srednja kvadratična brzina) o molekuli idealnog lina može iskazati jednadžbom: v ef = 3RT M
23 73. Posuda sadrži 2 mola helija temerature 20 C. Molna masa helija iznosi kg mol -1. Ako smatramo da se helij onaša kao idealni lin odredite: a) srednju kinetičku energiju čestice helija b) ukunu unutarnju energiju sustava c) efektivnu brzinu čestice helija (R: a) 6, ; b) 7,3 kj; c) 1351 m/s) 74. Posuda sadrži 10 litara jednoatomnog idealnog lina mase 0,02 kg, temerature 50 C i tlaka Pa. a) Koliko molova lina sadrži osuda? b) Kolika je efektivna brzina molekule lina? (R: a) 1,12 mola; b) 671 m/s) 75. Pet čestica idealnog lina helija ima brzine iskazane u m/s: 500, 600, 700, 800, 900. Izračunaj: a) srednju brzinu, b) efektivnu brzinu o čestici, c) temeraturu lina ako je molna masa lina 4 g/mol. (R: a) 700 m/s; b) 714 m/s; c) 8107 K)
24 76. Izračunaj srednju kinetičku energiju translacijskog gibanja lemenitog lina argona 40 Ar i efektivnu brzinu čestice lina na temeraturi 27 C. (R: 6, J; 432 m/s) 77. Kolika je unutarnja energija jednog mola idealnog lina na temeraturi 300 K? (R: 3741 J) 78. Na kojoj temeraturi je efektivna brzina molekula dušika jednaka efektivnoj brzini molekula vodika koje su na temeraturi 0 C? Molne mase su: M(N 2) = 28,01 g/mol i M(H 2) = 2,02 g/mol. (R: 3510 C) 79. U osudi se nalazi smjesa kritona (M 1 = 83,8 g/mol), neona (M 2 = 20,18 g/mol) i helija (M 3 = 4,00 g/mol): Usoredite efektivne brzine i rosječne kinetičke energije molekula lina.
25 80. Izotoe urana dobivamo onekad i rocesima difuzije koristeći činjenicu da za uran 238 U i 235 U ostoji različita brzina difuzije. Koliki je omjer srednjih brzina čestica tih dvaju izotoa? (R: 1,006) 81. Kisik ima gustoću 1,4 kg/m 3 kod tlaka 10 5 Pa. Kolika je efektivna brzina molekula kisika na toj temeraturi? a) 5 m/s b) 18 m/s c) 123 m/s d) 273 m/s e) 463 m/s 82. Kad se temeratura idealnog lina oveća sa 250 K na 500 K, molekule lina odvostruče svoju: a) veličinu b) rosječnu translacijsku kinetičku energiju c) rosječnu brzinu d) rosječnu količinu gibanja e) masu 83. Kad se temeratura idealnog lina oveća sa 10 C na 100 C, molekule lina romijene svoju rosječnu translacijsku kinetičku energiju: a) 1,32 uta b) 10 uta c) 100 uta d) 90 uta e) 0,1 uta 84. Ako se efektivna brzina čestica lina udvostruči, tada asolutna temeratura lina: a) ostaje ista b) dva uta se oveća c) dva uta se smanji d) četiri uta se oveća e) osam uta se oveća
26 85. olumen kod idealnog lina direktno je roorcionalan: I. tlaku kod stalne temerature i mase II. Temeraturi (u kelvinima) ako su masa i tlak stalni III. Masi lina ako su tlak i temeratura stalni Koja od tvrdnji je točna: a) sve b) samo I. i II. c) samo II. i III. d) samo I. e) samo I. i III. 86. U osudi se nalaze dva lina A i B kod konstantne temerature. Relativna molekularna masa molekula lina B je 8 uta veća od relativne molekularne mase lina A. Koliki je omjer efektivnih brzina molekula lina A i B (v efa/v efb=?) a) 2 b) 2 2 c) 4 d) 8 e) Unutarnja energija jednoatomnog idealnog lina sastoji se uglavnom od: a) međumolekulske otencijalne energije b) energije rotacije atoma c) energije titranja atoma d) translacijske kinetičke energije kaotičnog gibanja atoma e) translacijske kinetičke energije kaotičnog gibanja elektrona 88. Određena masa lina eksandira ri stalnoj temeraturi. Koje se od navedenih svojstava molekula idealnog lina ovećava? a) srednja kinetička energija b) srednja efektivna brzina c) srednji efektivni razmak između molekula d) srednji broj sudara u jedinici vremena e) tlak lina 89. Uzimajući u obzir kinetičku teoriju idealnih linova, od navedenih tvrdnji samo jedna nije točna. Koja? a) Molekule su savršeno elastične kuglice. b) Ne ostoji jaka sila rivlačenja između molekula. c) Molekule se međusobno ne sudaraju. d) Molekule se kaotično gibaju. e) Molekule ri istoj temeraturi imaju jednaku translacijsku kinetičku energiju.
27 90. Pet molekula idealnog lina ima brzine; 1, 2, 2, 3 i 4 (u jedinicama brzine). a) Kolika je efektivna brzina molekula? b) Kolika je srednja brzina molekula lina? (R: a) v ef = 2,6 jedinica brzine; b) v = 2,4 jedinica brzine) 91. U zatvorenoj osudi zagrijavamo vodik koji se nalazi ri normalnom tlaku 0. Koliko uta treba ovećati tlak lina da bi se efektivna brzina njegovih molekula udvostručila? a) 2 uta b) za 2 c) 4 uta d) za 0 e) za Koja od navedenih tvrdnji nije točna? a) Plin zauzima sav njemu ristuačan volumen. b) Nakon difuzije gustoća lina u čitavom volumenu ostaje jednaka. c) Molekule lina ri danoj temeraturi imaju određenu rasodjelu o brzinama koju nazivamo Maxwellova rasodjela d) Izjednačenje temerature je osljedica izjednačavanja srednje kinetičke energije čestica lina. e) Statistički zakoni su objektivni zakoni rirode i njima možemo redvidjeti onašanje svake ojedine čestice lina. 93. Na crtežu je rikazana romjena otencijalne energije E s udaljenosti r između dvaju atoma u dvoatomnoj molekuli. Točka P označava: a) najmanji razmak između atoma. b) najmanju silu međudjelovanja atoma. c) najmanju akceleraciju atoma. d) najmanju kinetičku energiju atoma. e) najveću silu međudjelovanja atoma. 94. Na crtežu je rikazana romjena sile F o udaljenosti r između dvaju atoma u dvoatomnoj molekuli. Koja tvrdnja nije točna: a) U točki A sila između čestica je odbojna. b) U točki B sila između čestica je nula a otencijalna energija najveća. c) U točkama C i D sila između čestica je rivlačna. d) U točki B sila između čestica je nula a otencijalna energija je najmanja. e) Površina u F,r grafu desno od točke B označava energiju za otuno odvajanje čestica.
28 95. Koliki je omjer srednje kinetičke energije atoma lina helija 4 He i atoma lina neona 20 Ne ri jednakoj temeraturi? a) 10 b) 2,5 c) 1/5 d) 5 e) Koliki je omjer srednjih kvadratičnih brzina (efektivnih brzina) atoma lina helija 2He i atoma lina neona 10Ne ri jednakoj temeraturi? a) 4 b) 5 1/2 c) 1/5 d) 5 e) U svezi s molekulskim međudjelovanjem romotrite sljedeće tvrdnje: I. Molekule se mogu rivlačiti ili odbijati s obzirom na njihovu međusobnu udaljenost. II. Na krivulji otencijalne energije dviju molekula o njihovoj međusobnoj udaljenosti ojavljuje se tzv. otencijalna jama. Što je dubina jame veća, to je na ravnotežnoj udaljenosti veća energija međumolekulske veze. III. Doseg rivlačne sile manji je od dosega odbojne sile. Od navedenih tvrdnji točne su: a) sve b) samo I. i II. c) samo I. i III. d) samo II. i III. e) samo II. 98. U svezi s molekulskim međudjelovanjem romotrite sljedeće tvrdnje: I. Molekule se mogu rivlačiti ili odbijati s obzirom na njihovu međusobnu udaljenost. II. Na krivulji otencijalne energije dviju molekula o njihovoj međusobnoj udaljenosti ojavljuje se tzv. otencijalna jama. Što je dubina jame veća, to je na ravnotežnoj udaljenosti manja energija međumolekulske veze. III. Doseg rivlačne sile veći je od dosega odbojne sile. Od navedenih tvrdnji točne su: f) sve g) samo I. i II. h) samo I. i III. i) samo II. i III. j) samo II.
29 99. U svezi s molekulskim međudjelovanjem romotrite sljedeće tvrdnje: I. Na ravnotežnoj udaljenosti otencijalna energija je međumolekularnog djelovanja najmanja. II. Kada bi molekule mirovale, one bi se rasoredile tako da im ukuna otencijalna energija bude najmanja. III. Doseg rivlačne sile manji je od dosega odbojne sile. Od navedenih tvrdnji točne su: k) sve l) samo I. i II. m) samo II. i III. n) samo I. i III. o) samo II Promotrite sljedeće tvrdnje: I. Stanje lina otuno je određeno tlakom, volumenom i brojem čestica N ojedinog lina. II. Srednja kinetička energija molekulskog gibanja ovećava se s ovišenjem temerature lina. III. Pri sudaru molekula sa stjenkom osude mijenja se smjer i iznos brzine ojedine molekule. Od navedenih tvrdnji točne su: ) sve q) samo II. i III. r) samo I. i III. s) samo II. t) samo I. i II Posuda volumena 5 litara sadrži jednoatomni idealni lin od tlakom Pa. Kolika je ukuna translacijska kinetička energija svih čestica lina? (R: 1500 J) 102. Pri temeraturi 27 C efektivna brzina molekula lina iznosi 500 m/s. Kolika je temeratura ri kojoj molekule lina imaju dva uta veću efektivnu brzinu? (R: 927 C) 103. Neki lin ima temeraturu 27 C. Ako linu ovisimo temeraturu dva uta, koliki joj je odnos efektivnih brzina molekula lina rije i nakon zagrijavanja? (R: 1,41 uta)
30 104. Kod idealnog lina retostavili smo da su sudari molekula u zatvorenoj osudi savršeno elastični. Što bi se dogodilo s tlakom lina kada bi sudari bili neelastični? (R: tlak bi se sam o sebi smanjivao) 105. Za idealne jednoatomne linove ri zadanoj temeraturi vrijedi: a) srednja kinetička energija ne ovisi o vrsti lina. b) srednja kinetička energija veća je kada je masa molekule lina veća. c) srednja kinetička energija veća je kada je masa molekule lina manja. d) srednja kinetička energija veća je kada je volumen molekule lina veći. e) srednja kinetička energija veća je kada je volumen molekule lina manji Ako se srednja kvadratična brzina molekula (efektivna brzina) idealnog lina koji je zagrijan na temeraturu 300 K odvostruči, temeratura lina iznosi: a) 327 K b) 424 K c) 600 K d) 1200 K e) K 107. Idealni lin temerature 300 K grijemo u zatvorenoj osudi a se srednja kinetička energija molekula odvostruči. Koja je od navedenih tvrdnji točna? a) Srednja kvadratična brzina molekula (efektivna brzina) se udvostruči. b) Temeratura lina oraste na 600 K. c) Količina gibanja molekula se odvostruči. d) Temeratura lina jednaka je 900 K. e) Srednja brzina molekula se udvostruči.
31 108. U osudi zagrijavamo tri mola idealnog jednoatomnog lina temerature 300 K do temerature 900 K. Koliko molova lina mora 'objeći' iz osude da bi unutarnja energija lina ostala jednaka kao i rije zagrijavanja? a) 2,3 b) 0,3 c) 1,3 d) 1,0 e) 2,0
Zadatci za vježbanje - termičko širenje / plinski zakoni / tlak idealnog plina
 Zadatci za vježbanje - termičko širenje / plinski zakoni / tlak idealnog plina Pun spremnik benzina sadrži 60 litara. Ako je napunjen pri temperaturi 5 C i ostavljen na suncu tako da se temperatura povisi
Zadatci za vježbanje - termičko širenje / plinski zakoni / tlak idealnog plina Pun spremnik benzina sadrži 60 litara. Ako je napunjen pri temperaturi 5 C i ostavljen na suncu tako da se temperatura povisi
PITANJA IZ TERMIČKIH POJAVA I MOLEKULARNO-KINETIČKE TEORIJE
 PITANJA IZ TERMIČKIH POJAVA I MOLEKULARNO-KINETIČKE TEORIJE 1. Što je temperatura i kako je mjerimo? 2. Na koji način se mjeri temperatura i kakva je Celzijeva termometrijska ljestvica? 3. Napišite i objasnite
PITANJA IZ TERMIČKIH POJAVA I MOLEKULARNO-KINETIČKE TEORIJE 1. Što je temperatura i kako je mjerimo? 2. Na koji način se mjeri temperatura i kakva je Celzijeva termometrijska ljestvica? 3. Napišite i objasnite
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Fakultet kemijskog inženjerstva i tehnologije Sveučilišta u Zagrebu Seminar 06 Plinski zakoni dr. sc. Biserka Tkalčec dr. sc.
 Fakultet kemijskog inženjerstva i tehnologije Sveučilišta u Zagrebu Seminar 06 Plinski zakoni dr. sc. Biserka Tkalčec dr. sc. Lidija Furač Pri normalnim uvjetima tlaka i temperature : 11 elemenata su plinovi
Fakultet kemijskog inženjerstva i tehnologije Sveučilišta u Zagrebu Seminar 06 Plinski zakoni dr. sc. Biserka Tkalčec dr. sc. Lidija Furač Pri normalnim uvjetima tlaka i temperature : 11 elemenata su plinovi
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Q = m c ( t t Neka je m 2 masa leda koja se tom toplinom može rastaliti. Tada vrijedi jednadžba: J m c t t 0. kg C
 Zadatak 4 (Ivica, tehnička škola) U osudi se nalazi litara vode na teeraturi 8 ºC. Ako u ovu količinu vode uronio 3 kg leda teerature ºC, onda će se led istoiti. Hoće li se istoiti sva količina leda? (secifični
Zadatak 4 (Ivica, tehnička škola) U osudi se nalazi litara vode na teeraturi 8 ºC. Ako u ovu količinu vode uronio 3 kg leda teerature ºC, onda će se led istoiti. Hoće li se istoiti sva količina leda? (secifični
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Priprema za državnu maturu
 Priprema za državnu maturu Toplina / Molekularno-kinetička teorija / Termodinamika 1. Temperatura apsolutne nule iznosi C. Temperatura od 37 C iznosi K. Ako se temperatura tijela povisi od 37 C na 39 C
Priprema za državnu maturu Toplina / Molekularno-kinetička teorija / Termodinamika 1. Temperatura apsolutne nule iznosi C. Temperatura od 37 C iznosi K. Ako se temperatura tijela povisi od 37 C na 39 C
ρ =. 3 V Vježba 081 U posudi obujma 295 litara nalazi se kisik pri normiranom tlaku. Izračunaj masu tog kisika. V =
 Zadatak 8 (Ajax, ginazija) U osudi obuja 59 litara nalazi se kisik ri norirano tlaku Izračunaj asu tog kisika (gustoća kisika ρ 4 / ) Rješenje 8 V 59 l 59 d 59, ρ 4 /,? Gustoću ρ neke tvari definirao ojero
Zadatak 8 (Ajax, ginazija) U osudi obuja 59 litara nalazi se kisik ri norirano tlaku Izračunaj asu tog kisika (gustoća kisika ρ 4 / ) Rješenje 8 V 59 l 59 d 59, ρ 4 /,? Gustoću ρ neke tvari definirao ojero
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
12. SKUPINA ZADATAKA IZ FIZIKE I 6. lipnja 2016.
 12 SKUPIN ZDK IZ FIZIKE I 6 linja 2016 Zadatak 121 U osudi - sremniku očetnog volumena nalazi se n molova dvoatomnog lina na temeraturi rema slici) Plin izobarno ugrijemo na temeraturu, adijabatski ga
12 SKUPIN ZDK IZ FIZIKE I 6 linja 2016 Zadatak 121 U osudi - sremniku očetnog volumena nalazi se n molova dvoatomnog lina na temeraturi rema slici) Plin izobarno ugrijemo na temeraturu, adijabatski ga
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
T O P L I N A. Termičko širenje čvrstih tijela i tekućina
 Termičko širenje čvrstih tijela i tekućina 1. Tijelo A ima temperaturu 0 C. Tijelo B ima dva puta višu temperaturu. Kolika je temperatura tijela B iskazana u C? 2. Brownovo gibanje dokazuje: a) kaotično
Termičko širenje čvrstih tijela i tekućina 1. Tijelo A ima temperaturu 0 C. Tijelo B ima dva puta višu temperaturu. Kolika je temperatura tijela B iskazana u C? 2. Brownovo gibanje dokazuje: a) kaotično
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Rad, energija i snaga
 Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Repetitorij-Dinamika. F i Zakon očuvanja impulsa (ZOI): i p i = j p j. Zakon očuvanja energije (ZOE):
 Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Toplina Q koju predamo sustavu voda aluminijski lonac utroši se na njihovo zagrijavanje.budući da nema gubitaka topline, vrijedi.
 Zadatak 6 (Viki, srednja škola) Voda se zagrijava u aluminijskome loncu uz stalno miješanje. Početno su voda i lonac na temeraturi od 0 ºC. Nakon što zajedno rime 75. k toline, temeratura vode i lonca
Zadatak 6 (Viki, srednja škola) Voda se zagrijava u aluminijskome loncu uz stalno miješanje. Početno su voda i lonac na temeraturi od 0 ºC. Nakon što zajedno rime 75. k toline, temeratura vode i lonca
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
VOLUMEN ILI OBUJAM TIJELA
 VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
ZADATCI S OPĆINSKIH NATJECANJA
 ZADATCI S OPĆINSKIH NATJECANJA Tlak i sila, idrostatski, idraulički i atmosferski tlak 1. U-cijev jednolikog poprečnog presjeka otvorena je prema atmosferi i dijelom napunjena živom. Zatim se u oba njena
ZADATCI S OPĆINSKIH NATJECANJA Tlak i sila, idrostatski, idraulički i atmosferski tlak 1. U-cijev jednolikog poprečnog presjeka otvorena je prema atmosferi i dijelom napunjena živom. Zatim se u oba njena
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Zadatci za vježbanje Termodinamika
 Zadatci za vježbanje Termodinamika 1. Električnim bojlerom treba zagrijati 22 litre vode 15 ⁰C do 93 ⁰C. Koliku snagu mora imati grijač da bi se to postiglo za 2 sata zagrijavanja? Specifični toplinski
Zadatci za vježbanje Termodinamika 1. Električnim bojlerom treba zagrijati 22 litre vode 15 ⁰C do 93 ⁰C. Koliku snagu mora imati grijač da bi se to postiglo za 2 sata zagrijavanja? Specifični toplinski
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
TOPLINA I TEMPERATURA:
 GEOMETRIJSKA OPTIKA 1. U staklenoj posudi s ravnim dnom nalazi se sloj vode (n v =1,33) debljine 5 cm, a na njemu sloj ulja (n u =1,2) debljine 3 cm. Iz zraka na ulje upada svjetlost pod kutom 45, prolazi
GEOMETRIJSKA OPTIKA 1. U staklenoj posudi s ravnim dnom nalazi se sloj vode (n v =1,33) debljine 5 cm, a na njemu sloj ulja (n u =1,2) debljine 3 cm. Iz zraka na ulje upada svjetlost pod kutom 45, prolazi
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
=1), što znači da će duljina cijevi L odgovarati kritičnoj duljini Lkr. koji vlada u ulaznom presjeku, tako da vrijedi
 Primjer. Zrak (R=87 J/(kg K), κ=,4) se iz atmosfere ( =, bar, T =88 K) usisava oz cijev romjera D = mm, duljine L = m, rema slici. Treba odrediti maksimalno mogući maseni rotok m max oz cijev uz retostavku
Primjer. Zrak (R=87 J/(kg K), κ=,4) se iz atmosfere ( =, bar, T =88 K) usisava oz cijev romjera D = mm, duljine L = m, rema slici. Treba odrediti maksimalno mogući maseni rotok m max oz cijev uz retostavku
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Q = m c t + m r Q = m c t t
 Zadatak (Edo, ginazija) Koliko toline treba da se iz litre vode od 5 C dobije destilirana voda? (secifični tolinski kaacitet vode c = 4.9 J/(kg K), secifična tolina isaravanja r =.6 5 J/kg, vrelište vode
Zadatak (Edo, ginazija) Koliko toline treba da se iz litre vode od 5 C dobije destilirana voda? (secifični tolinski kaacitet vode c = 4.9 J/(kg K), secifična tolina isaravanja r =.6 5 J/kg, vrelište vode
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
C 273,15, T 273,15, 1 1 C 1 50 C 273,15 K 50K 323,15K 50K 373,15K C 40 C 40 K
 1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
8 O H = =
 Zadatak (arko, ginazija) U zatvorenoj osudi obuja nalazi se. kg vode i.6 kg kisika. Odredi tlak u osudi ri C ako znao da ri toj teeraturi sva voda rijeñe u aru. (linska konstanta R = 8. J/(ol K)) Rješenje
Zadatak (arko, ginazija) U zatvorenoj osudi obuja nalazi se. kg vode i.6 kg kisika. Odredi tlak u osudi ri C ako znao da ri toj teeraturi sva voda rijeñe u aru. (linska konstanta R = 8. J/(ol K)) Rješenje
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA
 Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Unutarnji je volumen čaše V 1. Budući da je do polovice napunjena vodom masa te vode iznosi: 2 Ukupna masa čaše i vode u njoj je 1 kg
 Zadatak 6 (Josi, ginazija) Staklena čaša nalazi se u sudoeru naunjena vodo. Čaša je do olovice naunjena vodo. Unutarnji voluen čaše je 5 c, a njezina asa kada je razna iznosi 9 g. Ako oduzeo sao alo vode
Zadatak 6 (Josi, ginazija) Staklena čaša nalazi se u sudoeru naunjena vodo. Čaša je do olovice naunjena vodo. Unutarnji voluen čaše je 5 c, a njezina asa kada je razna iznosi 9 g. Ako oduzeo sao alo vode
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Kinetička teorija plinova
 Kinetička teorija plinova «Uvod u statističku fiziku» Ivo Batistić ivo@phy.hr Fizički odsjek, PMF Sveučilište u Zagrebu predavanja 2005/2006 Pregled predavanja Kratki uvod Osnovne fizikalne veličine Klasična
Kinetička teorija plinova «Uvod u statističku fiziku» Ivo Batistić ivo@phy.hr Fizički odsjek, PMF Sveučilište u Zagrebu predavanja 2005/2006 Pregled predavanja Kratki uvod Osnovne fizikalne veličine Klasična
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Primjeri zadataka iz Osnova fizike
 Mjerne jedinice 1. Koja je od navedenih jedinica osnovna u SI-sustavu? a) džul b) om c) vat d) amper 2. Koja je od navedenih jedinica osnovna u SI-sustavu? a) kut b) brzina c) koncentracija d) količina
Mjerne jedinice 1. Koja je od navedenih jedinica osnovna u SI-sustavu? a) džul b) om c) vat d) amper 2. Koja je od navedenih jedinica osnovna u SI-sustavu? a) kut b) brzina c) koncentracija d) količina
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
10. STATIKA FLUIDA Uvod. -ionizirani plin (visoka temperatura) kvantnomehanički. -odreñen oblik i volumen. -poprimaju oblik posude
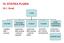 10. STATIKA FLUIDA 10.1. Uvod TVARI KRUTINE TEKUĆINE (KAPLJEVINE) PLINOVI PLAZMA BOSE- EINSTEINOV KONDENZAT -odreñen oblik i volumen -orimaju oblik osude volumennestlačiv -ionizirani lin (visoka temeratura)
10. STATIKA FLUIDA 10.1. Uvod TVARI KRUTINE TEKUĆINE (KAPLJEVINE) PLINOVI PLAZMA BOSE- EINSTEINOV KONDENZAT -odreñen oblik i volumen -orimaju oblik osude volumennestlačiv -ionizirani lin (visoka temeratura)
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
šupanijsko natjecanje iz zike 2017/2018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova)
 šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Gravitacija. Gravitacija. Newtonov zakon gravitacije. Odredivanje gravitacijske konstante. Keplerovi zakoni. Gravitacijsko polje. Troma i teška masa
 Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Pripreme za predavanja iz Fizike 1 doc. dr. sc. Sanda Pleslić
 . Mehanika tekućina: statika.. Tlak. Pascalov zakon. Hidrostatski tlak Tvar može ostojati u 3 agregatna stanja: čvrstom, tekućem i linovitom. Čvrsta tijela zadržavaju određeni volumen i oblik zbog relativno
. Mehanika tekućina: statika.. Tlak. Pascalov zakon. Hidrostatski tlak Tvar može ostojati u 3 agregatna stanja: čvrstom, tekućem i linovitom. Čvrsta tijela zadržavaju određeni volumen i oblik zbog relativno
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Nastavna jedinica. Gibanje tijela je... tijela u... Položaj točke u prostoru opisujemo pomoću... prostor, brzina, koordinatni sustav,
 1. UVOD 1. * Odgovorite na sljedeća pitanja tako da dopunite tvrdnje. 1.1 Što je gibanje tijela? Gibanje tijela je... tijela u... 1.2 Osnovni parametri u kinematici su... i... 1.3 Na koji način opisujemo
1. UVOD 1. * Odgovorite na sljedeća pitanja tako da dopunite tvrdnje. 1.1 Što je gibanje tijela? Gibanje tijela je... tijela u... 1.2 Osnovni parametri u kinematici su... i... 1.3 Na koji način opisujemo
( ) Φ = Hɺ Hɺ. 1. zadatak
 7.vježba iz ermodiamike rješeja zadataka. zadatak Komresor usisava 30 m 3 /mi zraka staja 35 o C i 4 bar te ga o ravotežoj romjei staja v kost. komrimira a tlak 8 bar. Komresor se hladi vodom koja tijekom
7.vježba iz ermodiamike rješeja zadataka. zadatak Komresor usisava 30 m 3 /mi zraka staja 35 o C i 4 bar te ga o ravotežoj romjei staja v kost. komrimira a tlak 8 bar. Komresor se hladi vodom koja tijekom
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
