ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και ΧΑΟΣ. Ioannis E. Antoniou
|
|
|
- Κῆρες Βασιλόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και ΧΑΟΣ 2. MΗNYMATA ως Χρονοσειρες. Αναλογικα και Ψηφιακα Μηνυματα. Δειγματοληψια Ioannis E. Antoniou Mathematics Department Aristotle University 54124,Thessaloniki,Greece
2 Mηνυματα και Γλωσσα Επικοινωνιας Μετατροπη Ψηφιακου σε Αναλογικο Σημα Μετατροπη Αναλογικου σε Ψηφιακο Σημα Δειγματοληψια
3 MHNYMATA και ΓΛΩΣΣΑ ΕΠΙΚΟΙΝΩΝΙΑΣ Επικοινωνια είναι η ανταλλαγη Μηνυματων Τα Μηνυματα είναι χρονοσειρες συμβολων σ από το συνολο Σ Σε διακριτο χρονο ακολουθιες ψ: T Σ: t ψ t, T Z (digital signals) Σε συνεχη χρονο συναρτησεις ψ: T Σ: t ψ(t), T R (analog signals) T = o Xρονος = το διαταγμενο συνολο καταγραφων του Χρονου Ο χρονος μπορει να είναι συνεχης, t, η διακριτος t=nτ, n, τ η μοναδα χρονου = ο στοιχειωδης χρονος = το χρονον (chronon). Τα Μηνυματα είναι στοιχεια του συνολου Σ T των απεικονισεων με πεδιο ορισμου το χρονο T (δεικτες χρονου) και πεδιο τιμων τα συμβολα από το Σ Το συμβολο Σ T περιλαμβανει ολες τις κλασεις Μηνυματων
4 Παραδειγματα Μηνυματων - Συμβολων Μηνυμα Μετρηση Θερμοκρασιας, Πιεσης, Ηλεκτρικου Ρευματος Τηλεγραφημα του 1902 Συμβολα Ρητοι Αριθμοι., _, ΚΕΝΟ Δυαδικο 0,1 Ηχος, Moυσικη Νοτες, Υψη, Διαρκειες Εικονα, Video, Aκολουθια Pixels Κειμενο βιβλιου Εmails, Περιεχομενο Iστοσελιδων Προγραμμα Ενταση (Red, Green, Blue) ASKII χαρακτηρες τα Συμβολα μιας Γλωσσας Προγραμματισμου Πχ. ΜathML DNA Tα 4 Νουκλεοτιδια Α,G,C,T Πρωτεινες Τα 20 Αμινοξεα Α,C,D,E,F,G,H,I, K, L,M,N,P,Q, R,S,T,V,W,Y Παιγνιο με Ζαρια 1,2,3,4,5,6 Βιβλιοθηκη της Βαβελ 22 letters, comma, period, space Βοrges J. L Ficciones, Grove Press 1962
5 The 20 Amino Acids directly encoded by the universal genetic code NAME ΟΝΟΜΑ Abbreviation Symbol Produced by Organism Alanine αλανινη ALA A Non Essential Arginine αργινινη ARG R Conditional Asparagine Ασπαραγινη ΑSN N Non Essential Aspartic acid ασπαρτικο οξυ ASP D Non Essential Cysteine Κυστεινη CYS C Conditional Glutamin acid γλουταμικο οξυ GLU E Non Essential Glutamine γλουταμινη GLN Q Conditional Glycine Γλυκινη GLY G Conditional Histidine ιστιδινη HIS H Essential Isoleucine ισολευκινη ILE I Essential Leucine Λευκινη LEU L Essential Lysine Λυσινη LYS K Essential Methionine μεθειονινη MET M Essential Phenylalanine φαινυλαλανινη PHE F Essential Proline προλινη PRO P Conditional Serine σερινη SER S Conditional Threonine θρεονινη THR T Essential Tryptophan τρυπτοφανη TRP W Essential Tyrosine τυροσινη TYR Y Conditional Valine βαλινη VAL V Essential
6 Ορισμος Μηνυμα μηκους m είναι κάθε πεπερασμενη ακολουθια (ψ) = (ψ t+1, ψ t+2,..., ψ t+m ), ορων που λαμβανονται από n Συμβολα Σ={σ 1, σ 2,... σ n }, ψ t Σ (ψ) Σ m Σ F Xωροι Μηνυματων: Σ m = οι πεπερασμενες ακολουθιες συμβολων από το Σ με m ορους Σ m = οι πεπερασμενες ακολουθιες συμβολων από το Σ με το πολυ m ορους Σ F = οι πεπερασμενες ακολουθιες συμβολων από το Σ Σ N = οι μονοπλευρες (unilateral) ακολουθιες συμβολων από το Σ Σ Z = οι αμφιπλευρες (bilateral) ακολουθιες συμβολων από το Σ
7 Kαθε m-αδα (ψ t+1, ψ t+2,..., ψ t+m ) ειναι ενα διαταγμενο δειγμα μεγεθους m, εκ των n συμβολων {σ 1, σ 2,... σ n }, οπου καθε συμβολο μπορει να επαναλαμβανεται. Ισοδυναμα: (ψ t+1, ψ t+2,..., ψ t+m ) ειναι Επαναληπτικη Διαταξη (σ k1, σ k2,..., σ km ) των n συμβολων {σ 1, σ 2,... σ n } ανα m Το πληθος των μηνυματων μηκους m είναι Το πληθος των Επαναληπτικων Διαταξεων n Στοιχειων ανα m: Υ m = n m
8 Ορισμος Η Κλασση Σ F των πεπερασμενων ακολουθιων συμβολων από το Σ Σ F = Σ * = m N Kleene Closure {A} Σ m To συνολο Σ * εχει απειρο πληθος στοιχειων, ενώ καθε στοιχειο του εχει πεπερασμενο μηκος Παραδειγμα Σ = {0, 1}, Σ* = {ε, 0, 1, 00, 01, 10, 11, 000, 001, 010, 011, }.
9 Ορισμος Γλωσσα με Αλφαβητο Σ (L, Σ, G) 1) Σ={σ 1, σ 2,... σ n } το συνολο συμβολων, ψηφιων, γραμματων της Γλωσσας 2) G = η Γραμματικη της Γλωσσας = οι κανονες συνταξης λεξεων-προτασεων που οριζουν ποιες λεξεις (ακολουθιες συμβολων) είναι συντακτικα αποδεκτες (syntactically admissible,valid) 3) L Σ F L(Σ) ένα συνολο μηνυματων = λεξεων με συμβολα από το Σ. Τα δυνατα κειμενα, η «Γραμματεια» της Γλωσσας
10 Παραδειγμα: Η Βιβλιοθηκη της Βαβελ που περιεχει τα βιβλια που γραφτηκαν και θα γραφτουν «the Library is total and that its shelves register all the possible combinations of the twenty-odd orthographical symbols (a number which, though extremely vast, is not infinite): Everything: the minutely detailed history of the future, the archangels' autobiographies, the faithful catalogues of the Library, thousands and thousands of false catalogues, the demonstration of the fallacy of those catalogues, the demonstration of the fallacy of the true catalogue, the Gnostic gospel of Basilides, the commentary on that gospel, the commentary on the commentary on that gospel, the true story of your death, the translation of every book in all languages, the interpolations of every book in all books.» Βοrges J. L Ficciones, Grove Press 1962 The Babel Library has x books the alphabet has 25 symbols. Each book has 410 pages, with 40 lines of 80 characters on each page. Number of symbols in a Book: = Bloch W. G.2008, The Unimaginable Mathematics of Borges Library Of Babel, Oxford University Press The Library of Congress has 3 x 10 7 Books Number of Orthographically correct Books written in English: = Number of English Words: Number of Words per line (including comma, period, space): 30 Number of Words per Book: 410 x 30 x 40 =
11 Symbols Grammar = Rules for Syntax Syntax = message (φραση) construction Μessages, Φρασεις, Logical Forms, Σχηματα Λογου Axioms Inference Rules = Transformation Rules Semantics, Meaning Language Formal System Logic = Logical System Gerber A., Van der Merwe A.,Barnard A. 2008, A Functional Semantic Web architecture, European Semantic Web Conference, ESWC 08, Tenerife
12 ΣΧΟΛΙΑ Συντακτικα Φιλτρα, πχ Ορθογραφος Microsoft Word Η συντακτικη επεξεργασια μεσω της Γραμματικης είναι αναγκαια για την Νοηματοδοτηση (Meaning) των Μηνυματων-κειμενων, αλλα δεν επαρκει Νοηματικη Επεξεργασια (Semantic Processing) Σημασιολογικα Φιλτρα (Semantic Filters) ΕΦΑΡΜΟΓΕΣ Λογικη, Υπολογιστες, Προγραμματισμος, Διαδικτυο Γλωσσολογια Βιολογια Μουσικη
13 References Ginsburg Σ. 1975, Algebraic and automata theoretic properties of formal languages, North-Holland Harrison Μ. 1978, Introduction to Formal Language Theory, Addison-Wesley. Hopcroft J. and Ullman J. 1979, Introduction to Automata Theory, Languages and Computation, Addison-Wesley Publishing, Reading Massachusetts Rozenberg G., Salomaa A. 1997, Handbook of Formal Languages: Volumes I-III, Springer
14 Digital to Analog Conversion = Curve fitting = Smoothing = finding a curve which has the best fit to a series of data points and possibly other constraints includes interpolation (exact fit) regression analysis (approximate fit) extrapolation Interpolation = Παρεμβολη Reconstruction of a function from discrete samples Representation of a function in terms of discrete samples Given the points (y 1, t 1 ), (y 2, t 2 ),, (y N, t N ) Find an Interpolation function f within a specific Class A of functions : y n = f(t n ), n=1,2,,n Regression = Παλινδρομιση Construct a function within a specific Class A of functions with minimal distance from discrete samples Least Squares Regression = Least Squares Fit: the Distance is the L 2 distance Extrapolation is the extension of f (constructed by Interpolation or by Regression) for t > t N
15 Regression, Interpolation, Function Basis of A Extrapolation are called Polynomial Polynomials Rational Fractions of Polynomials Trigonometric Periodic Functions Fourier Analysis Exponential Exponentials Smoothing = Εξομαλυνση A C r is a Class of Smooth functions Wavelet Wavelets Wavelet Analysis
16 Analog to Digital Conversion Sampling = Δειγματοληψια The conversion of Continuous Functions (Signals) to Numerical Sequences (Time Series)
17 Both DAC (Interpolation) and ADC (Sampling) are based on Function Expansion Formulas Harmonic Analysis Ηarmonic Analysis Function Expansion Formulas f(t)= f ν u ν ( ν t) u ν οrthonormal basis of Functions in some HS of real functions on some interval (a,b) f ν = <f, u ν > = (a,b) dt w(t) f(t) u ν (t) w(t)dt = dν(t) the measure on (a,b) L 2 ([a,b), w) the Hilbert Space of square integrable Functions on [a,b) with respect to the measure w(t)dt = dν(t)
18 Approximations of functions with Function Expansion Formulas Ν f [N] (t) = f ν u ν (t) ν=1 Approximation Error: ε Ν = f f [N] (t) Ν f [N] (t) = f ν u ν (t) ν= N Expansions Taylor Expansion Weierstrass Theorem Fourier Series Special Function Expansions Wavelet Expansions
19 Taylor Expansion f(t+x)= f(x)= ν=0 ν=0 1 ν! f(ν) (t)x ν 1 ν! f(ν) (0)x ν Weierstrass Theorem every continuous function defined on a closed interval [a,b] can be uniformly approximated as closely as desired by a polynomial function. Polynomials are among the simplest functions, Computers directly evaluate polynomials Polynomial interpolation. v r = x r is a basis (non-orthonormal) of the Hilbert Space L 2 ([a,b), w(t)dt) generalization to several real variables
20 Fourier Series of the T-Periodic Real Function f (Temporal), T>0 Theorem Riesz-Fisher 1907 f is square integrable lim N f f [N] 2 = lim N dt with f [N] (t) = +N n= N C n e inωt, C n = dt T 0 T f(t) f [N] (t) 2 = 0 T 0 T e inωt f(t) Proof Dym H., McKean Η.1972, Fourier Series and Integrals, Academic Press, New York Dunford, N.,Schwartz, J.T. 1958, Linear operators, Part I, Wiley, New York (IV I3) Corollary u n = e inωt, n Z οrthonormal basis of L 2 (0,T), ω = 2π Τ = the Cyclic Frequency
21 Fourier Transform: L 2 (0,T) l 2 (Z) : f f n = < e inωt, f > Scalar Product of L 2 (0,T): < f, g > = dt T 0 T f (t)g(t) Scalar Product of l 2 (Z): < (f n ), (g n ) > l 2 (Z) = n= f n g n Exponential Expansion Formula for real periodic functions f with period T>0: with + f(t) = C n e inωt T 0 n= C n = < e inωt, f > = dt e inωt f(t) = the n-fourier Amplitude of f, n Z T 0 C 0 =< 1, f > = dt T T f(t) = the Average Value of f over the Period T
22 Definition Trigonometric Series Expansion for real periodic functions f with period T: + f(t) = [α n cos(nωt) + β n sin(nωt)] n=0 The Fourier Coefficients are T 0 α 0 = dt T f(t) T α n = 2 T dt 0 β n = 2 T dt 0 T f(t) cos(nωt), n = 1,2, f(t) si n(nωt), n = 1,2, Aσκηση: {0.1} Δειξτε τους τυπους των συντελεστων Fourier με την παραδοχη ότι ισχυει η ιδιοτητα εναλλαγης Ολοκληρωματος που εχει η Ομοιομορφη συγκλιση Σειρων Συναρτησεων: Τ dt 0 + [α n cos (nωt) + β n sin (nωt)] n=0 + Τ = dt n=0 0 [α n cos (nωt) + β n sin (nωt)]
23 Σχεση Τριγωνομετρικης Εκθετικης Σειρας Fourier α 0 = C 0 α n = 2ReC n, n=1,2, β n = 2ImC n, n=1,2, C n = 1 2 (α n + i β n ), n=1,2, C n =(C n )* = 1 2 (α n i β n ), n=1,2, Proof f(t) = + C n e inωt 1 = C 0 + C n e inωt + + C n e inωt + == C 0 + C n e +inωt + C n e inωt n= n= n=1 n=1 + n=1 ] f real (C n )* = C n : f(t) = C n=1 2Re[C n e inωt ] = C 0 + [α n cosωt + β n sin ωt
24 EXAMPLES Aσκηση: Υπολογιστε το Αναπτυγμα Fourier {0.1} Aσκηση: Υπολογιστε το Αναπτυγμα Fourier {0.1}
25 f(x) = 4 sin(2n 1)x π 2n 1 n=1 Aσκηση: Υπολογιστε το Αναπτυγμα Fourier {0.1} f(x) = θ( x) [2νπ, 2νπ + 2π), ν Z = sin (2n 1)x π 2n 1 Aσκηση: Υπολογιστε το Αναπτυγμα Fourier {0.1} n=1
26 f(x) = π sin n 2π Τ x n n=1 Aσκηση: Υπολογιστε το Αναπτυγμα Fourier {0.1} f(x) = e x (2ν 1)π, (2ν + 1)π, ν Z = 2sinh(π) π ( 1)n 1 + n 2 cos (nx) sin(nx) n=1 Aσκηση: Υπολογιστε το Αναπτυγμα Fourier {0.1}
27 Theorem The Fourier Transform is Unitary < f, g > = < (f n ), (g n ) > l 2 (Z) T dt T 0 f (t)g(t) = f n g n n= Αποδειξη Aσκηση 0.1 Σχεση Διαφορισιμοτητας και Προσεγγισης Fourier Aσκηση: {1} Υπολογιστε τα Αναπτυγματα Fourier σε καποιο διαστημα [0, Τ] f [5] (t) = 5 [α n (f) cos (nωt) + β n (f) sin (nωt) n=0 5 g [5] (t) = [α n (g) cos (nωt) + β n (g) sin (nωt) n=0 των 5 πρωτων ορων μιας λειας συναρτησης f και μιας μη λειας συναρτησης g με 2 ακμες Συγκρινατε τις 2 προσεγγισεις f [5] (t) και g [5] (t) με τις f(t) και g(t) αντιστοιχα.
28 Power of the Periodic function The Norm Square Parseval's Formula T f 2 = dt T 0 f(t) 2 = f n 2 n=
29 Theorem Τhe Fourier basis is an orthonormal basis of eigenfunctions of the differentiation operators Self-Adjoint Differentiation: i d dx e iωt = ωe iωt Laplace Operator: d2 dx 2 e iωt = ω 2 e iωt Early ideas about the Trigonometric Series Expansion of Periodic Functions go back to Pythagoras Solutions of Wave Equation of Strings 2 ψ = t 2 c2 2 ψ x2 as Trigonometric Series Expansions were obtained by J.R. D Alembert 1747 and D. Bernoulli 1853 Solutions of the Heat Equation ψ 2 as Trigonometric Series Expansions were obtained by J.B. Fourier Fourier J.B. 1822, Theorie Analytique de la Chaleur, Didot, Paris. English translation by Freeman E. 1955, Dover, New York. = β 2 ψ t x The notions of Convergence and the classes of functions that can be represented as Trigonometric Series were clarified later Dym H., McKean Η.1972, Fourier Series and Integrals, Academic Press, New York
30 Special Function Expansions Orthonormal bases on spaces of integrable functions solutions of differential equations integrals of elementary functions Sturm-Liouville Equation Second order Linear Eigenvalue Equation: SL[ψ]=λψ a(x) d2 ψ dψ + b(x) dx2 dx = λψ Οι ιδιοσυναρτησεις (Eιδικες Συναρτησεις) αποτελουν oρθοκανονικη βαση στους Χωρους L 2 [(α,β),w] {Tαξινομιση Ειδικων Συναρτησεων. Θεωρημα Rodriguez} Dennery P., Krzywicki A. 1969, Mathematics for Physicists, Harper, New York Miller 1968, Lie Theory and Special Functions, Academic Press, New York Wawrzynczyk Α. 1984, Group Representations and Special Functions, D.Reidel Publishing Company, Dordrecht
31 Oι 3 βασικες Ειδικες Συναρτησεις ως βασεις ιδιοσυναρτησεων Τελεστων Sturm-Liouville Interval Sturm-Liouville Equation (, ) Hermite Equation [0, ) Laguerre Equation a(x) d2 y dy + b(x) dx2 dx = λy Eigenfunctions Basis Weight in the Scalar Product w(x) d2 y dy + 2x dx2 dx = 2n y Hermite Polynomials e x2 x d2 y dy + [ γ + x 1] dx2 dx = λy Laguerre Functions e x [ 1,1] Legendre Equation [ (1 x 2 )] d2 y dy + [2x] dx2 dx = n(n + 1)y Legendre Polynomials 1
32 Κατασκευη βασεων σε Xωρους Συναρτησεων επι οιουδηποτε διαστηματος (α,β) Μετασχηματισμοι Von Neumann Definition Von Neumann Transforms of Functions on (t 1, t 2 ) to functions on (x 1, x 2 ) are the Unitary Transformations of square Integrable functions supported on (t 1, t 2 ) to square Integrable functions supported on (x 1, x 2 ) V: L 2 (t 1, t 2 ) L 2 (x 1, x 2 ) : f Vf with f (t) (Vf)(x): < Vf, Vg > = < f, g > dx (Vf) (x)(vg)(x) x 2 x 1 t 2 = dt f t 1 (t)g(t) Misra B., Speiser D.,Targonski G. 1961, Integral Operators in the Theory of Scattering, Helv. Phys. Acta 36, Von Neumann J. 1935, Charakterisierung des Spektrums eines Integraloperators, Actualites Scientifiques et Industrielles No. 229
33 VN Transforms Example 1: V: L 2 (-, ) L 2 (0, ) : f Vf with f (t) (Vf)(x) = 1 x f(lnx) V -1 : L 2 (0, ) L 2 (-, ) : f V -1 f with f (t) (V -1 f)(x) = e x 2f(e x ) Aσκηση: Δειξτε ότι ο Μετασχηματισμος V είναι Unitary {0.5} VN Transforms Example 2: V: L 2 (0, ) L 2 1 (0, 1) : f Vf with f (t) (Vf)(x) = f x 1 x 1 x V -1 : L 2 (0, 1) L 2 (0, ) : f V -1 f with f (t) (V -1 1 f)(x) = f x 1+x 1+x Aσκηση: Δειξτε ότι ο Μετασχηματισμος V είναι Unitary {0.5} VN Transforms Example 3: V: L 2 [0,T) L 2 [a,b) : f Vf : with f (t) Vf(x)= T b a f x a b a T V -1 : L 2 [a,b) L 2 [0,T) : f Vf : Vf(t)= b a T f b a T t + a Aσκηση: Δειξτε ότι ο Μετασχηματισμος V είναι Unitary {0.5}
34 Wavelet Expansions Wavelets are functions ψ(x) whose translations and dilations ψ β,α βψ(βx α) provide bases for expansion of integrable functions Μultiresolution Analysis
35 Haar Wavelet Στις Αρχες του 20 ου αιωνα πιστευαν πως ολες οι ορθοκανονικες βασεις συναρτησεων ειναι ιδιοσυναρτησεις Διαφορικων Τελεστων ως λειες συναρτησεις Υπαρχουν Μη Διαφορισιμες βασεις συναρτησεων? Ηaar Wavelets Haar A. 1910, Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen 69 no. 3, ψ(x) = 1, 0 x < 1 2 1, 1 2 x < 1 0, otherwise
36 ψ ν α = ψ(2 ν x α), ν, α Integers Antoniou I., Gustafson K. 1998, Haar s Wavelets and Differential Equations, J. Diff. Equations Antoniou I., Gustafson K. 1999, Wavelets and Stochastic Processes, Math.and Computers in Simulation 49, Antoniou I., Gustafson K. 2000, The Time Operator of Wavelets, Chaos, Solitons and Fractals 11, Antoniou I., Suchanecki Z. 2000, Non-uniform Time Operator, Chaos and Wavelets on the Interval, Chaos, Solitons and Fractals 11, Walter G. 1994, Wavelets and other Orthogonal Systems With Applications, CRC, Boca Raton Frazier M. 1999, An Introduction to Wavelets Through Linear Algebra, Springer, New York Jorgensen P. 2006, Analysis and Probability Wavelets, Signals, Fractals, Springer, New York Fractals, Generalized Functions, Chaos
37 Shannon Wavelet Shannon Interpolation Formula If a function f(t) contains no frequencies higher than W hertz, f(t) = 1 2π dω F(ω)eiωt = 1 2π 2πW dω F(ω)eiωt 2πW the Fourier Amplitudes F(ω) vanish outside [ πw, πw]: F(ω) = 0, for ω > πw Then it is completely determined by giving its ordinates at a series of points spaced 1/(2W) seconds apart. f(t) = + f n sin π(2wt n) n= = + f(nt) sin π T n = + 2W π(2wt n) n= f(nt) u π t n (t) T n n= where: f n = f n = f(nt) the samples 2W t T = 1 2W the sampling period u n (t) = sin π t T n π t T n = sinc π t n the Shannon Wavelet T
38 sinc(x) = sinx x = the sinus cardinalis function
39 Shannon C. 1949, Communication in the presence of Noise, Proc. Institute of Radio Engineers 37, Reprint as classic paper in: Proc. IEEE, Vol. 86, No. 2, (Feb 1998) Jerri A. 1977, "The Shannon sampling theorem: its various extensions and applications: A tutorial review" Proc. IEEE 65, pp Higgins J. 1985, "Five short stories about the Cardinal Series" Bull. Amer. Math. Soc. 12, pp Marks II R. 1991, Introduction to Shannon Sampling and Interpolation Theory, Springer, New York. Higgins J. 1996, Sampling Theory in Fourier and Signal Analysis Foundations, Clarendon Press, Oxford, New York Smale S., Zhou D.-X. 2004, Shannon Sampling and Function Reconstruction from Point Values, Bulletin AMS 41 (3), Pages Aσκηση: {0.8} Παραδειγμα Δειγματοληψιας Shannon
40 Theorem 1) {sinc(t k), k inz } is an orthonormal basis of bandlimited real functions with highest frequency π 2) sinλx λx, solutions of the Differential Equation: Aποδειξη: Aσκηση {0.1}
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
 ΜΙΝΟΠΕΤΡΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΦΥΣΙΚΟΣ - Ρ/Η ΚΑΘΗΓΗΤΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΥΠΕΥΘΥΝΟΣ ΣΕΦΕ 2 ου ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΡΑΜΑΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΒΙΟΛΟΓΙΑΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
ΜΙΝΟΠΕΤΡΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΦΥΣΙΚΟΣ - Ρ/Η ΚΑΘΗΓΗΤΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΥΠΕΥΘΥΝΟΣ ΣΕΦΕ 2 ου ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΡΑΜΑΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΒΙΟΛΟΓΙΑΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΑΝΤΙΓΡΑΦΗ ΚΑΙ ΕΚΦΡΑΣΗ ΤΗΣ ΓΕΝΕΤΙΚΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
 DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
Κεφάλαιο 1. Οι δομικοί λίθοι
 Κεφάλαιο 1 Οι δομικοί λίθοι Κεφάλαιο 1 Οι Δομικοί Λίθοι των Πρωτεϊνών Εικόνα 1.1 Η αμινοξική αλληλουχία μιας πρωτεϊνικής πολυπεπτιδικής αλυσίδας ονομάζεται πρωτοταγής δομή. Διαφορετικές περιοχές της αλληλουχίας
Κεφάλαιο 1 Οι δομικοί λίθοι Κεφάλαιο 1 Οι Δομικοί Λίθοι των Πρωτεϊνών Εικόνα 1.1 Η αμινοξική αλληλουχία μιας πρωτεϊνικής πολυπεπτιδικής αλυσίδας ονομάζεται πρωτοταγής δομή. Διαφορετικές περιοχές της αλληλουχίας
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
ExpIntegralE. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 ExpIntegralE Notations Traditional name Exponential integral E Traditional notation E Mathematica StandardForm notation ExpIntegralE, Primary definition 06.34.0.000.0 E t t t ; Re 0 Specific values Specialied
ExpIntegralE Notations Traditional name Exponential integral E Traditional notation E Mathematica StandardForm notation ExpIntegralE, Primary definition 06.34.0.000.0 E t t t ; Re 0 Specific values Specialied
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Fundamentals of Signals, Systems and Filtering
 Fundamentals of Signals, Systems and Filtering Brett Ninness c 2000-2005, Brett Ninness, School of Electrical Engineering and Computer Science The University of Newcastle, Australia. 2 c Brett Ninness
Fundamentals of Signals, Systems and Filtering Brett Ninness c 2000-2005, Brett Ninness, School of Electrical Engineering and Computer Science The University of Newcastle, Australia. 2 c Brett Ninness
Arithmetical applications of lagrangian interpolation. Tanguy Rivoal. Institut Fourier CNRS and Université de Grenoble 1
 Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ
 BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΜΟΡΙΑΚΑ ΜΟΝΤΕΛΑ 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING) 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING)
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΜΟΡΙΑΚΑ ΜΟΝΤΕΛΑ 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING) 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING)
ECE 468: Digital Image Processing. Lecture 8
 ECE 468: Digital Image Processing Lecture 8 Prof. Sinisa Todorovic sinisa@eecs.oregonstate.edu 1 Image Reconstruction from Projections X-ray computed tomography: X-raying an object from different directions
ECE 468: Digital Image Processing Lecture 8 Prof. Sinisa Todorovic sinisa@eecs.oregonstate.edu 1 Image Reconstruction from Projections X-ray computed tomography: X-raying an object from different directions
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation. Mathematica StandardForm notation
 KelvinKei Notations Traditional name Kelvin function of the second kind Traditional notation kei Mathematica StandardForm notation KelvinKei Primary definition 03.5.0.000.0 kei kei 0 Specific values Values
KelvinKei Notations Traditional name Kelvin function of the second kind Traditional notation kei Mathematica StandardForm notation KelvinKei Primary definition 03.5.0.000.0 kei kei 0 Specific values Values
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ
 BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΜΟΡΙΑΚΑ ΜΟΝΤΕΛΑ 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING) 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING)
BIOXHMEIA, TOMOΣ I ΠANEΠIΣTHMIAKEΣ EKΔOΣEIΣ KPHTHΣ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΑΠΕΙΚΟΝΙΣΗ ΜΟΡΙΑΚΩΝ ΔΟΜΩΝ ΜΟΡΙΑΚΑ ΜΟΝΤΕΛΑ 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING) 1: ΧΩΡΟΠΛΗΡΩΤΙΚΟ ΜΟΝΤΕΛΟ (SPACE-FILLING)
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2
![If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2 If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2](/thumbs/53/31933086.jpg) Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Homomorphism in Intuitionistic Fuzzy Automata
 International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
If we restrict the domain of y = sin x to [ π 2, π 2
 Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
J. of Math. (PRC) Banach, , X = N(T ) R(T + ), Y = R(T ) N(T + ). Vol. 37 ( 2017 ) No. 5
 Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Elements of Information Theory
 Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
Ποια είναι κατά τη γνώμη σας τα 30 μικρομόρια που συνιστούν τα πρόδρομα μόρια των βιομακρομορίων; Πώς μπορούν να ταξινομηθούν;
 Ποια είναι κατά τη γνώμη σας τα 30 μικρομόρια που συνιστούν τα πρόδρομα μόρια των βιομακρομορίων; Πώς μπορούν να ταξινομηθούν; Γενικά Για να προσδιορίσουμε τα 30 πρόδρομα μόρια των βιομακρομορίων θα πρέπει
Ποια είναι κατά τη γνώμη σας τα 30 μικρομόρια που συνιστούν τα πρόδρομα μόρια των βιομακρομορίων; Πώς μπορούν να ταξινομηθούν; Γενικά Για να προσδιορίσουμε τα 30 πρόδρομα μόρια των βιομακρομορίων θα πρέπει
4 ο ΚΕΦΑΛΑΙΟ. Γ ε ν ε τ ι κ ή
 4 ο ΚΕΦΑΛΑΙΟ Γ ε ν ε τ ι κ ή 1. Κύκλος της ζωής του κυττάρου 3ο Γελ. Ηλιούπολης επιμέλεια: Αργύρης Γιάννης 2 2. Μοριακή Γενετική i). Ροή της γενετικής πληροφορίας DNA RNA πρωτεΐνες νουκλεΐκά οξέα ή πρωτεΐνες
4 ο ΚΕΦΑΛΑΙΟ Γ ε ν ε τ ι κ ή 1. Κύκλος της ζωής του κυττάρου 3ο Γελ. Ηλιούπολης επιμέλεια: Αργύρης Γιάννης 2 2. Μοριακή Γενετική i). Ροή της γενετικής πληροφορίας DNA RNA πρωτεΐνες νουκλεΐκά οξέα ή πρωτεΐνες
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙΔΕΣ
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 19 ΙΟΥΝΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) Να γράψετε στο τετράδιό
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 19 ΙΟΥΝΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΒΙΟΛΟΓΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) Να γράψετε στο τετράδιό
MAΘΗΜΑ 4 ο AMINOΞΕΑ-ΠΕΠΤΙ ΙΑ-ΠΡΩΤΕΪΝΕΣ
 MAΘΗΜΑ 4 ο AMIΞΕΑ-ΠΕΠΤΙ ΙΑ-ΠΡΩΤΕΪΝΕΣ Αλανίνη (Αla) Αλανυλοσερίνη (Αla-Ser) Αλβουµίνη ρα. Κουκουλίτσα Αικατερίνη Χηµικός Εργαστηριακός Συνεργάτης Τ.Ε.Ι Αθήνας ckoukoul@teiath.gr AMIΞΕΑ 2 λειτουργικές οµάδες
MAΘΗΜΑ 4 ο AMIΞΕΑ-ΠΕΠΤΙ ΙΑ-ΠΡΩΤΕΪΝΕΣ Αλανίνη (Αla) Αλανυλοσερίνη (Αla-Ser) Αλβουµίνη ρα. Κουκουλίτσα Αικατερίνη Χηµικός Εργαστηριακός Συνεργάτης Τ.Ε.Ι Αθήνας ckoukoul@teiath.gr AMIΞΕΑ 2 λειτουργικές οµάδες
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
The Spiral of Theodorus, Numerical Analysis, and Special Functions
 Theo p. / The Spiral of Theodorus, Numerical Analysis, and Special Functions Walter Gautschi wxg@cs.purdue.edu Purdue University Theo p. 2/ Theodorus of ca. 46 399 B.C. Theo p. 3/ spiral of Theodorus 6
Theo p. / The Spiral of Theodorus, Numerical Analysis, and Special Functions Walter Gautschi wxg@cs.purdue.edu Purdue University Theo p. 2/ Theodorus of ca. 46 399 B.C. Theo p. 3/ spiral of Theodorus 6
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Sampling Basics (1B) Young Won Lim 9/21/13
 Sampling Basics (1B) Copyright (c) 2009-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
Sampling Basics (1B) Copyright (c) 2009-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Paper Reference. Paper Reference(s) 6665/01 Edexcel GCE Core Mathematics C3 Advanced. Thursday 11 June 2009 Morning Time: 1 hour 30 minutes
 Centre No. Candidate No. Paper Reference(s) 6665/01 Edexcel GCE Core Mathematics C3 Advanced Thursday 11 June 2009 Morning Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae
Centre No. Candidate No. Paper Reference(s) 6665/01 Edexcel GCE Core Mathematics C3 Advanced Thursday 11 June 2009 Morning Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Fourier Analysis of Waves
 Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
On the Galois Group of Linear Difference-Differential Equations
 On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field
 Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field Supplementary Information Michael J. Robertson, Julian Tirado-Rives, and William L. Jorgensen* Department of Chemistry, Yale
Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field Supplementary Information Michael J. Robertson, Julian Tirado-Rives, and William L. Jorgensen* Department of Chemistry, Yale
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Review Test 3. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
A summation formula ramified with hypergeometric function and involving recurrence relation
 South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
University of Illinois at Urbana-Champaign ECE 310: Digital Signal Processing
 University of Illinois at Urbana-Champaign ECE : Digital Signal Processing Chandra Radhakrishnan PROBLEM SET : SOLUTIONS Peter Kairouz Problem Solution:. ( 5 ) + (5 6 ) + ( ) cos(5 ) + 5cos( 6 ) + cos(
University of Illinois at Urbana-Champaign ECE : Digital Signal Processing Chandra Radhakrishnan PROBLEM SET : SOLUTIONS Peter Kairouz Problem Solution:. ( 5 ) + (5 6 ) + ( ) cos(5 ) + 5cos( 6 ) + cos(
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
is like multiplying by the conversion factor of. Dividing by 2π gives you the
 Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Ψηφιακή Επεξεργασία Φωνής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Φωνής Ενότητα 1η: Ψηφιακή Επεξεργασία Σήματος Στυλιανού Ιωάννης Τμήμα Επιστήμης Υπολογιστών CS578- Speech Signal Processing Lecture 1: Discrete-Time
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Φωνής Ενότητα 1η: Ψηφιακή Επεξεργασία Σήματος Στυλιανού Ιωάννης Τμήμα Επιστήμης Υπολογιστών CS578- Speech Signal Processing Lecture 1: Discrete-Time
BandPass (4A) Young Won Lim 1/11/14
 BandPass (4A) Copyright (c) 22 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later version
BandPass (4A) Copyright (c) 22 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later version
ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΜΟΡΙΑΚΗΣ ΒΙΟΛΟΓΙΑΣ ΚΑΙ ΓΕΝΕΤΙΚΗΣ ΓΟΝΙ ΙΑΚΗ ΕΚΦΡΑΣΗ ΚΑΙ ΣΗΜΑΤΟ ΟΤΗΣΗ
 ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΜΟΡΙΑΚΗΣ ΒΙΟΛΟΓΙΑΣ ΚΑΙ ΓΕΝΕΤΙΚΗΣ ΓΟΝΙ ΙΑΚΗ ΕΚΦΡΑΣΗ ΚΑΙ ΣΗΜΑΤΟ ΟΤΗΣΗ ρ. Α. ΓΑΛΑΝΗΣ agalanis@mbg.duth.gr Figure 6.1 The Biology of Cancer ( Garland Science 2007) Figure
ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΜΟΡΙΑΚΗΣ ΒΙΟΛΟΓΙΑΣ ΚΑΙ ΓΕΝΕΤΙΚΗΣ ΓΟΝΙ ΙΑΚΗ ΕΚΦΡΑΣΗ ΚΑΙ ΣΗΜΑΤΟ ΟΤΗΣΗ ρ. Α. ΓΑΛΑΝΗΣ agalanis@mbg.duth.gr Figure 6.1 The Biology of Cancer ( Garland Science 2007) Figure
The k-α-exponential Function
 Int Journal of Math Analysis, Vol 7, 213, no 11, 535-542 The --Exponential Function Luciano L Luque and Rubén A Cerutti Faculty of Exact Sciences National University of Nordeste Av Libertad 554 34 Corrientes,
Int Journal of Math Analysis, Vol 7, 213, no 11, 535-542 The --Exponential Function Luciano L Luque and Rubén A Cerutti Faculty of Exact Sciences National University of Nordeste Av Libertad 554 34 Corrientes,
g-selberg integrals MV Conjecture An A 2 Selberg integral Summary Long Live the King Ole Warnaar Department of Mathematics Long Live the King
 Ole Warnaar Department of Mathematics g-selberg integrals The Selberg integral corresponds to the following k-dimensional generalisation of the beta integral: D Here and k t α 1 i (1 t i ) β 1 1 i
Ole Warnaar Department of Mathematics g-selberg integrals The Selberg integral corresponds to the following k-dimensional generalisation of the beta integral: D Here and k t α 1 i (1 t i ) β 1 1 i
Τάξη. Γνωστικό αντικείµενο: Ειδικοί διδακτικοί στόχοι
 Αµινοξέα και πεπτίδια Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος Χηµεία,Βιοχηµεία. Αµινοξέα και πεπτίδια 2 διδακτικές ώρες Ειδικοί διδακτικοί στόχοι Οι διδακτικοί στόχοι αυτών
Αµινοξέα και πεπτίδια Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος Χηµεία,Βιοχηµεία. Αµινοξέα και πεπτίδια 2 διδακτικές ώρες Ειδικοί διδακτικοί στόχοι Οι διδακτικοί στόχοι αυτών
Formal Semantics. 1 Type Logic
 Formal Semantics Principle of Compositionality The meaning of a sentence is determined by the meanings of its parts and the way they are put together. 1 Type Logic Types (a measure on expressions) The
Formal Semantics Principle of Compositionality The meaning of a sentence is determined by the meanings of its parts and the way they are put together. 1 Type Logic Types (a measure on expressions) The
GAUSS-LAGUERRE AND GAUSS-HERMITE QUADRATURE ON 64, 96 AND 128 NODES
 GAUSS-LAGUERRE AND GAUSS-HERMITE QUADRATURE ON 64, 96 AND 128 NODES RICHARD J. MATHAR Abstract. The manuscript provides tables of abscissae and weights for Gauss- Laguerre integration on 64, 96 and 128
GAUSS-LAGUERRE AND GAUSS-HERMITE QUADRATURE ON 64, 96 AND 128 NODES RICHARD J. MATHAR Abstract. The manuscript provides tables of abscissae and weights for Gauss- Laguerre integration on 64, 96 and 128
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Notations. Primary definition. Specific values. General characteristics. Series representations. Traditional name. Traditional notation
 Pi Notations Traditional name Π Traditional notation Π Mathematica StandardForm notation Pi Primary definition.3... Π Specific values.3.3.. Π 3.5965358979338663383795889769399375589795937866868998683853
Pi Notations Traditional name Π Traditional notation Π Mathematica StandardForm notation Pi Primary definition.3... Π Specific values.3.3.. Π 3.5965358979338663383795889769399375589795937866868998683853
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spectrum Representation (5A) Young Won Lim 11/3/16
 Spectrum (5A) Copyright (c) 2009-2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Spectrum (5A) Copyright (c) 2009-2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Introduction to Time Series Analysis. Lecture 16.
 Introduction to Time Series Analysis. Lecture 16. 1. Review: Spectral density 2. Examples 3. Spectral distribution function. 4. Autocovariance generating function and spectral density. 1 Review: Spectral
Introduction to Time Series Analysis. Lecture 16. 1. Review: Spectral density 2. Examples 3. Spectral distribution function. 4. Autocovariance generating function and spectral density. 1 Review: Spectral
The circle theorem and related theorems for Gauss-type quadrature rules
 OP.circle p. / The circle theorem and related theorems for Gauss-type quadrature rules Walter Gautschi wxg@cs.purdue.edu Purdue University OP.circle p. 2/ Web Site http : //www.cs.purdue.edu/ archives/22/wxg/codes
OP.circle p. / The circle theorem and related theorems for Gauss-type quadrature rules Walter Gautschi wxg@cs.purdue.edu Purdue University OP.circle p. 2/ Web Site http : //www.cs.purdue.edu/ archives/22/wxg/codes
Computing the Macdonald function for complex orders
 Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Differential equations
 Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής
 Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Οι πρωτεΐνες δομούνται από ένα σύνολο αμινοξέων. 1/10/2015 Δ.Δ. Λεωνίδας
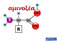 αμινοξέα Οι πρωτεΐνες δομούνται από ένα σύνολο αμινοξέων Λυσίνη CORN Ισομερές L Ισομερές D R = πλευρική αλυσίδα (side chain) Τα περισσότερα αμινοξέα είναι ασύμμετρα Όλα τα αμινοξέα που βρίσκονται στις
αμινοξέα Οι πρωτεΐνες δομούνται από ένα σύνολο αμινοξέων Λυσίνη CORN Ισομερές L Ισομερές D R = πλευρική αλυσίδα (side chain) Τα περισσότερα αμινοξέα είναι ασύμμετρα Όλα τα αμινοξέα που βρίσκονται στις
Commutative Monoids in Intuitionistic Fuzzy Sets
 Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
