Να οδηγηθούμε σε μια αρχιτεκτονική που έχει μεγάλο αριθμό καταχωρητών και να εφαρμόσουμε τεχνική ελαχιστοποίησης καταχωρητών
|
|
|
- Ἴκαρος Λύκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Folding
2 Να καθορίσουμε συστηματικά τα κυκλώματα ελέγχου μιας DSP αρχιτεκτονικής χρησιμοποιώντας folding μετασχηματισμό ώστε να πραγματοποιούμε πολλαπλές αλγοριθμικές πράξεις σε ένα λειτουργικό στοιχείο με ένα πολυπλεγμένο στο χρόνο μηχανισμό. Να μειώσουμε τον αριθμό των hardware λειτουργικών στοιχείων functional units (FUs) κατά ένα παράγοντα N αυξάνοντας τον χρόνο υπολογισμών κατά αντίστοιχο παράγοντα N. Να οδηγηθούμε σε μια αρχιτεκτονική που έχει μεγάλο αριθμό καταχωρητών και να εφαρμόσουμε τεχνική ελαχιστοποίησης καταχωρητών
3 Λειτουργικό Στοιχείο Functional Unit (FU)
4 Μια συστηματική τεχνική ώστε να σχεδιάζουμε hardware κυκλώματα ελέγχου (συνήθως) όπου αρκετές αλγοριθμικές λειτουργίες πραγματοποιούνται στο ίδιο λειτουργικό στοιχείο με ένα πολυπλεγμένο στο χρόνο μηχανισμό. U, V: κόμβοι (λειτουργίες) του αρχικού DFG H U, H V : κόμβοι (λειτουργικά στοιχεία) του folded DFG W (x) : x-th επανάληψη του κόμβου W U e V: μια ακμή e από τον κόμβο U στον V w(e): αριθμός στοιχείων καθυστέρησης στην ακμή e Παράγοντας Folding N Ο αριθμός των λειτουργιών που πραγματοποιούνται χρησιμοποιώντας ένα FU Folding Σύνολο Ένα ταξινομημένο σύνολο από λειτουργίες που θα εκτελούνται στο ίδιο FU H θέση της λειτουργίας U στο folding σύνολο λέμε ότι είναι η folding τάξη του U Το folding σύνολο αναπαριστά τον χρησιμοποιούμενο folding μετασχηματισμό
5 P U : αριθμός pipeline επιπέδων του H U. P U = 0 σημαίνει ότι H U δεν είναι pipelined. e D F (U V): (folding εξίσωση) αριθμός κύκλων για τους οποίους το αποτέλεσμα του H U πρέπει να είναι αποθηκευμένο D F (U V ) = [N(l + w(e))] + v] [Nl + P U + u] = Nw(e) P U + v u Αρνητική τιμή στην folding εξίσωση D F είναι δυνατή πριν από retiming των folding εξισώσεων κόμβοι (λειτουργικά στοιχεία) e Lan-Da Van VL
6 Ο Folding Μετασχηματισμός U (l) w(e) V (l+w(e)) N folded N folded H U (Nl+u) P U +D F H V (N(l+w(e))+v) Lan-Da Van VLSI - DSP- 6-6
7 Folding factor N = 4 Folding Σύνολο S 1 = {4, 2, 3, 1}, S 2 = {5, 8, 6, 7}, όπου S 1 αναφέρεται σε όλες τις προσθέσεις και S 2 αναφέρεται σε όλους τους πολλαπλασιασμούς. Υποθέτω ότι Πρόσθεση: 1 u.t. Πολλαπλασιασμός: 2 u.t. Lan-Da Van Χρησιμοποιώ αθροιστές 1-επιπέδου πολλ/στες 2-επιπέδων pipeline
8 Folding Retimed Biquad Φίλτρο folding εξισώσεις e D F (U V ) = [N(l + w(e))] + v] [Nl + P+ u] = Nw(e) P U + v u Για να είναι εφικτό το folding πρέπει D F (U V ) 0 για όλες τις ακμές
9 Lan-Da Van VLSI- DSP- 6-9
10 Είναι μια διαδικασία ώστε να υπολογίζω τον ελάχιστο αριθμό καταχωρητών που χρειάζονται στην υλοποίηση ενός DSP αλγορίθμου σε υλικό. Γραμμική Ανάλυση Χρόνου Ζωής Κυκλική Ανάλυση Χρόνου Ζωής Υπολογίζεται ο αριθμός των ενεργών μεταβλητών σε κάθε χρονικό unit Ο μέγιστος αριθμός των ενεργών μεταβλητών προσδιορίζεται Τεχνική κατανομής καταχωρητών Forward-backward Lan-Da Van VLSI- DSP- 6-10
11 Μεταβλητές {a, b, c} max {0,1,2,2,2,2,2,2}=2 Έμμεση περιοδικότητα Τρείς επαναλήψεις με N=6
12 a b c d e f g h i Ανάστροφος a d g b e h c f i i h g f e d c b a Matrix Transpose i f c h e b g d a
13 VLSI Digital Signal Processing Systems T zlout = zero-latency χρόνος εξόδου T diff = T zlout T input T output = T zlout + max{-t diff }
14 Γραμμικό Lifetime διάγραμμα Κυκλικό Lifetime διάγραμμα Ο ελάχιστος αριθμός καταχωρητών είναι 4.
15 Βήμα 1: Βρίσκω τον ελάχιστο αριθμό καταχωρητών με lifetime ανάλυση. Βήμα 2: Βάζω κάθε μεταβλητή εισόδου στο χρονικό βήμα που αντιστοιχεί στην αρχή της διάρκειας ζωής της Βήμα 3: Κάθε μεταβλητή κατανέμεται με forward τρόπο μέχρι να απενεργοποιηθεί (να είναι νεκρή) ή να φτάσει τον τελευταίο καταχωρητή. Βήμα 4: Μια και η κατανομή είναι περιοδική, η κατανομή της συγκεκριμένης επανάληψης θα επαναλαμβάνεται και στις μελλοντικές επαναλήψεις. Άρα αρκεί να κατανήμουμε τις θέσεις των καταχωρητών στα πλαίσια μιας περιόδου N. Βήμα 5: Αν μια μεταβλητή που φτάσει στον τελευταίο καταχωρητή είναι ακόμα ενεργή, τότε αυτή η μεταβλητή κατανέμεται σε καταχωρητή με backward τρόπο. Βήμα 6: Επαναλαμβάνω τα βήματα 4 και 5 όσες φορές χρειάζεται μέχρι η κατανομή ολοκληρωθεί.
16
17 Βήμα 1: Κάνω retiming για την folded αρχιτεκτονική Βήμα 2 Γράφω τις folding εξισώσεις Βήμα 3: Χρησιμοποιώ τις folding εξισώσεις για να φτιάξω το τον lifetime πίνακα Βήμα 4: Φτιάχνω το lifetime διάγραμμα και καθορίζω τον αριθμό των απαραίτητων καταχωρητών Βήμα 5: Κάνω forward-backward κατανομή καταχωρητών Βήμα 6: σχεδιάζω την folded αρχιτεκτονική με τον ελάχιστο αριθμό καταχωρητών
18
19
20 Step 1: Retiming Retiming Invalid folding: DF(1 2) = -3 DF(6 4) = -4 DF(8 4) = -3 DF(7 3) = -3
21 Step 2: Folding Equations D F (U V) = Nw(e) P u + v u D F (1 2) = 4(1) = 1 D F (1 5) = 4(1) = 0 Step 3: Construct the lifetime table D F (1 6) = 4(1) = 2 D F (1 7) = 4(1) = 3 D F (1 8) = 4(2) = 5 D F (3 1) = 4(0) = 0 D F (4 2) = 4(0) = 0 D F (5 3) = 4(0) = 0 D F (6 4) = 4(1) = 4 D F (7 3) = 4(1) = 1 D F (8 4) = 4(1) = 1 T input T output = u + P u = u + P u + max v {D F (U V) }
22 Step 4: Draw the Lifetime Chart Folding Factor = 4 Step 5: Register Allocation Ο ελάχιστος Αριθμός των καταχωρητών είναι 2.
23 Step 6: Folded Architecture VLSI Digital Signal Processing Systems
24 Step 1: Retiming Retiming Invalid folding: DF(3 1) = -3 DF(4 1) = -2
25 Step 2: Folding Equations Step 3: Construct the lifetime table D F (U V) = Nw(e) P u + v - u D F (1 2) = 4(1) = 0 D F (2 3) = 4(1) = 5 D F (2 4) = 4(1) = 2 D F (3 1) = 4(1) = 1 D F (4 1) = 4(2) = 0 T input T output = u + P u = u + P u + max v {D F (U V) }
26 Step 4: Draw the Lifetime Chart Step 5: Register Allocation Folding Factor = 2 The minimum number of registers is 3.
27 Step 6: Folded Architecture
Pipelining και Παράλληλη Επεξεργασία
 Pipelining και Παράλληλη Επεξεργασία Εισαγωγή Σωλήνωση - Pipelining Βασισμένη στην ιδέα σωλήνα που στέλνει νερό χωρίς να περιμένει το νερό που μπαίνει σε ένα σωλήνα να τελειώσει water pipe Μπορεί να οδηγήσει
Pipelining και Παράλληλη Επεξεργασία Εισαγωγή Σωλήνωση - Pipelining Βασισμένη στην ιδέα σωλήνα που στέλνει νερό χωρίς να περιμένει το νερό που μπαίνει σε ένα σωλήνα να τελειώσει water pipe Μπορεί να οδηγήσει
Το ολοκληρωμένο κύκλωμα μιας ΚΜΕ. «Φέτα» ημιαγωγών (wafer) από τη διαδικασία παραγωγής ΚΜΕ
 Το ολοκληρωμένο κύκλωμα μιας ΚΜΕ Η Κεντρική Μονάδα Επεξεργασίας (Central Processing Unit -CPU) ή απλούστερα επεξεργαστής αποτελεί το μέρος του υλικού που εκτελεί τις εντολές ενός προγράμματος υπολογιστή
Το ολοκληρωμένο κύκλωμα μιας ΚΜΕ Η Κεντρική Μονάδα Επεξεργασίας (Central Processing Unit -CPU) ή απλούστερα επεξεργαστής αποτελεί το μέρος του υλικού που εκτελεί τις εντολές ενός προγράμματος υπολογιστή
Σύνθεση Data Path. ιασύνδεσης. Μονάδες. Αριθµό Μονάδων. Τύπο Μονάδων. Unit Selection Unit Binding. λειτουργιών σε. Μονάδες. Αντιστοίχιση µεταβλητών &
 Data Path Allocation Σύνθεση Data Path Το DataPath είναι ένα netlist που αποτελείται από τρεις τύπους µονάδων: (α) Λειτουργικές Μονάδες, (β) Μονάδες Αποθήκευσης και (γ) Μονάδες ιασύνδεσης Αριθµό Μονάδων
Data Path Allocation Σύνθεση Data Path Το DataPath είναι ένα netlist που αποτελείται από τρεις τύπους µονάδων: (α) Λειτουργικές Μονάδες, (β) Μονάδες Αποθήκευσης και (γ) Μονάδες ιασύνδεσης Αριθµό Μονάδων
Κάθε functional unit χρησιμοποιείται μια φορά σε κάθε κύκλο: ανάγκη για πολλαπλό hardware = κόστος υλοποίησης!
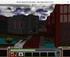 Single-cyle υλοποίηση: Διάρκεια κύκλου ίση με τη μεγαλύτερη εντολή-worst case delay (εδώ η lw) = χαμηλή απόδοση! Αντιβαίνει με αρχή: Κάνε την πιο απλή περίπτωση γρήγορη (ίσως και εις βάρος των πιο «σύνθετων»
Single-cyle υλοποίηση: Διάρκεια κύκλου ίση με τη μεγαλύτερη εντολή-worst case delay (εδώ η lw) = χαμηλή απόδοση! Αντιβαίνει με αρχή: Κάνε την πιο απλή περίπτωση γρήγορη (ίσως και εις βάρος των πιο «σύνθετων»
Multi Cycle Datapath. Αρχιτεκτονική Υπολογιστών. 5ο εξάμηνο ΣΗΜΜΥ ακ. έτος: Νεκ. Κοζύρης
 Αρχιτεκτονική Υπολογιστών 5ο εξάμηνο ΣΗΜΜΥ ακ. έτος: 2014-2015 Νεκ. Κοζύρης nkoziris@cslab.ece.ntua.gr Multi Cycle Datapath http://www.cslab.ece.ntua.gr/courses/comparch/ Άδεια Χρήσης Το παρόν εκπαιδευτικό
Αρχιτεκτονική Υπολογιστών 5ο εξάμηνο ΣΗΜΜΥ ακ. έτος: 2014-2015 Νεκ. Κοζύρης nkoziris@cslab.ece.ntua.gr Multi Cycle Datapath http://www.cslab.ece.ntua.gr/courses/comparch/ Άδεια Χρήσης Το παρόν εκπαιδευτικό
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
Μηχανοτρονική. Τμήμα Μηχανικών Παραγωγής και Διοίκησης 7 ο Εξάμηνο,
 Τμήμα Μηχανικών Παραγωγής και Διοίκησης 7 ο Εξάμηνο, 2016-2017 ΜΙΚΡΟΕΠΕΞΕΡΓΑΣΤΕΣ Μικροϋπολογιστής Υπολογιστής που χρησιμοποιείται για την είσοδο, επεξεργασία και έξοδο πληροφοριών. Είδη μικροϋπολογιστών:
Τμήμα Μηχανικών Παραγωγής και Διοίκησης 7 ο Εξάμηνο, 2016-2017 ΜΙΚΡΟΕΠΕΞΕΡΓΑΣΤΕΣ Μικροϋπολογιστής Υπολογιστής που χρησιμοποιείται για την είσοδο, επεξεργασία και έξοδο πληροφοριών. Είδη μικροϋπολογιστών:
Είναι το «μυαλό» του υπολογιστή μας. Αυτός κάνει όλους τους υπολογισμούς και τις πράξεις. Έχει δική του ενσωματωμένη μνήμη, τη λεγόμενη κρυφή
 1 Είναι το «μυαλό» του υπολογιστή μας. Αυτός κάνει όλους τους υπολογισμούς και τις πράξεις. Έχει δική του ενσωματωμένη μνήμη, τη λεγόμενη κρυφή μνήμη(cache). Η cache είναι πολύ σημαντική, πολύ γρήγορη,
1 Είναι το «μυαλό» του υπολογιστή μας. Αυτός κάνει όλους τους υπολογισμούς και τις πράξεις. Έχει δική του ενσωματωμένη μνήμη, τη λεγόμενη κρυφή μνήμη(cache). Η cache είναι πολύ σημαντική, πολύ γρήγορη,
Στοιχεία αρχιτεκτονικής μικροεπεξεργαστή
 Στοιχεία αρχιτεκτονικής μικροεπεξεργαστή Αριθμός bit δίαυλου δεδομένων (Data Bus) Αριθμός bit δίαυλου διευθύνσεων (Address Bus) Μέγιστη συχνότητα λειτουργίας (Clock Frequency) Τύποι εντολών Αριθμητική
Στοιχεία αρχιτεκτονικής μικροεπεξεργαστή Αριθμός bit δίαυλου δεδομένων (Data Bus) Αριθμός bit δίαυλου διευθύνσεων (Address Bus) Μέγιστη συχνότητα λειτουργίας (Clock Frequency) Τύποι εντολών Αριθμητική
9. Συστολικές Συστοιχίες Επεξεργαστών
 Κεφάλαιο 9: Συστολικές συστοιχίες επεξεργαστών 208 9. Συστολικές Συστοιχίες Επεξεργαστών Οι συστολικές συστοιχίες επεξεργαστών είναι επεξεργαστές ειδικού σκοπού οι οποίοι είναι συνήθως προσκολλημένοι σε
Κεφάλαιο 9: Συστολικές συστοιχίες επεξεργαστών 208 9. Συστολικές Συστοιχίες Επεξεργαστών Οι συστολικές συστοιχίες επεξεργαστών είναι επεξεργαστές ειδικού σκοπού οι οποίοι είναι συνήθως προσκολλημένοι σε
ΤΕΧΝΙΚΕΣ ΑΥΞΗΣΗΣ ΤΗΣ ΑΠΟΔΟΣΗΣ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ I
 ΤΕΧΝΙΚΕΣ ΑΥΞΗΣΗΣ ΤΗΣ ΑΠΟΔΟΣΗΣ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ I MIPS Η MIPS (Microprocessor without Interlocked Pipeline Stages) είναι μία αρχιτεκτονική συνόλου εντολών (ISA) γλώσσας μηχανής που αναπτύχθηκε από την εταιρεία
ΤΕΧΝΙΚΕΣ ΑΥΞΗΣΗΣ ΤΗΣ ΑΠΟΔΟΣΗΣ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ I MIPS Η MIPS (Microprocessor without Interlocked Pipeline Stages) είναι μία αρχιτεκτονική συνόλου εντολών (ISA) γλώσσας μηχανής που αναπτύχθηκε από την εταιρεία
Πρότυπο περιφερειακής ολίσθησης για ψηφιακά. Std ) Δημήτρης Νικολός, Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν.
 Πρότυπο περιφερειακής ολίσθησης για ψηφιακά κυκλώματα (Digital boundary scan, IEEE Std. 1149.1) Δημήτρης Νικολός, Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών Περίγραμμα παρουσίασης
Πρότυπο περιφερειακής ολίσθησης για ψηφιακά κυκλώματα (Digital boundary scan, IEEE Std. 1149.1) Δημήτρης Νικολός, Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών Περίγραμμα παρουσίασης
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
ιαµέριση - Partitioning
 ιαµέριση - Partitioning ιαµέριση ιαµέριση είναι η διαµοίραση αντικειµένων σε οµάδες µε στόχο την βελτιστοποίηση κάποιας συνάρτησης. Στην σύνθεση η διαµέριση χρησιµοποιείται ως εξής: Οµαδοποίηση µεταβλητών
ιαµέριση - Partitioning ιαµέριση ιαµέριση είναι η διαµοίραση αντικειµένων σε οµάδες µε στόχο την βελτιστοποίηση κάποιας συνάρτησης. Στην σύνθεση η διαµέριση χρησιµοποιείται ως εξής: Οµαδοποίηση µεταβλητών
Graph Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βάλια
 Graph Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βάλια Περιεχόμενα Μεταβατικό Κλείσιμο Συνεκτικές συνιστώσες Συντομότερα μονοπάτια Breadth First Spanning
Graph Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βάλια Περιεχόμενα Μεταβατικό Κλείσιμο Συνεκτικές συνιστώσες Συντομότερα μονοπάτια Breadth First Spanning
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 4: Συστηματικές μέθοδοι επίλυσης κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 4: Συστηματικές μέθοδοι επίλυσης κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
ΠΛΗ10 Κεφάλαιο 2. ΠΛH10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: : Αριθμητική περιοχή της ALU 2.5: Κυκλώματα Υπολογιστών
 ΠΛH10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.3 : Αριθμητική περιοχή της ALU 2.5: Κυκλώματα Υπολογιστών Στόχοι Μαθήματος: Να γνωρίσετε τις βασικές αρχές αριθμητικής των Η/Υ. Ποια είναι τα κυκλώματα
ΠΛH10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.3 : Αριθμητική περιοχή της ALU 2.5: Κυκλώματα Υπολογιστών Στόχοι Μαθήματος: Να γνωρίσετε τις βασικές αρχές αριθμητικής των Η/Υ. Ποια είναι τα κυκλώματα
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Ανάλυση Ακολουθιακών Κυκλωμάτων 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Ανάλυση Ακολουθιακών Κυκλωμάτων Ανάλυση: Ο καθορισμός μιας κατάλληλης περιγραφής η οποία επιδεικνύει
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Ανάλυση Ακολουθιακών Κυκλωμάτων Ανάλυση: Ο καθορισμός μιας κατάλληλης περιγραφής η οποία επιδεικνύει
Σχεδίαση υψηλών επιδόσεων pipelining παράλληλη επεξεργασία
 Σχεδίαση υψηλών επιδόσεων pipelining παράλληλη επεξεργασία Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Ρυθμός εκτέλεσης εργασιών
Σχεδίαση υψηλών επιδόσεων pipelining παράλληλη επεξεργασία Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Ρυθμός εκτέλεσης εργασιών
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX
 ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
Βασική Εφικτή Λύση. Βασική Εφικτή Λύση
 Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n µεταβλητών και m περιορισµών Εστω πραγµατικοί αριθµοί a ij, b j, c i R µε 1 i m, 1 j n Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n
Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n µεταβλητών και m περιορισµών Εστω πραγµατικοί αριθµοί a ij, b j, c i R µε 1 i m, 1 j n Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n
2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ 1) Πότε χρησιμοποιείται η δομή επανάληψης
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ 1) Πότε χρησιμοποιείται η δομή επανάληψης
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Κυκλική Συνέλιξη. Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Κυκλική Συνέλιξη Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Διακριτού Χρόνου Σειρές Fourier Περιοδική Επέκταση Σήµατος Πεπερασµένης Χρονικής Διάρκειας.
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Κυκλική Συνέλιξη Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Διακριτού Χρόνου Σειρές Fourier Περιοδική Επέκταση Σήµατος Πεπερασµένης Χρονικής Διάρκειας.
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Graph Algorithms. Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βασιλική
 Graph Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βασιλική Περιεχόμενα minimum weight spanning tree connected components transitive closure shortest paths
Graph Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βασιλική Περιεχόμενα minimum weight spanning tree connected components transitive closure shortest paths
27-Ιαν-2009 ΗΜΥ (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό
 ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 2 Βασικά μέρη συστήματος ΨΕΣ Φίλτρο αντι-αναδίπλωσης
ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 2 Βασικά μέρη συστήματος ΨΕΣ Φίλτρο αντι-αναδίπλωσης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Καταχωρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
Μετρικές & Επιδόσεις. Κεφάλαιο V
 Μετρικές & Επιδόσεις Κεφάλαιο V Χρόνος εκτέλεσης & επιτάχυνση Σειριακός χρόνος εκτέλεσης: Τ (για τον καλύτερο σειριακό αλγόριθμο) Παράλληλος χρόνος εκτέλεσης: (με επεξεργαστές) Επιτάχυνση (speedup): S
Μετρικές & Επιδόσεις Κεφάλαιο V Χρόνος εκτέλεσης & επιτάχυνση Σειριακός χρόνος εκτέλεσης: Τ (για τον καλύτερο σειριακό αλγόριθμο) Παράλληλος χρόνος εκτέλεσης: (με επεξεργαστές) Επιτάχυνση (speedup): S
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Xρονισμός ψηφιακών κυκλωμάτων
 Xρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Καθυστέρηση λογικών πυλών και των συνδυαστικών κυκλωμάτων
Xρονισμός ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Φθινόπωρο 2008 ΗΥ220 1 Περιεχόμενα μαθήματος Καθυστέρηση λογικών πυλών και των συνδυαστικών κυκλωμάτων
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών Απόδοση ΚΜΕ. (Μέτρηση και τεχνικές βελτίωσης απόδοσης)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 2016-17 Απόδοση ΚΜΕ (Μέτρηση και τεχνικές βελτίωσης απόδοσης) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Κεντρική Μονάδα Επεξεργασίας
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 2016-17 Απόδοση ΚΜΕ (Μέτρηση και τεχνικές βελτίωσης απόδοσης) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Κεντρική Μονάδα Επεξεργασίας
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Παράδειγµα: Καταχωρητής 2-bit. Καταχωρητής 4-bit. Μνήµη Καταχωρητών
 ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
HY Λογική Διδάσκων: Δ. Πλεξουσάκης Εαρινό Εξάμηνο. Φροντιστήριο 6
 HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Εαρινό Εξάμηνο 2015-2016 Φροντιστήριο 6 Α) ΘΕΩΡΙΑ Μέθοδος Επίλυσης (Resolution) Στη μέθοδο της επίλυσης αποδεικνύουμε την ικανοποιησιμότητα ενός συνόλου προτάσεων,
HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Εαρινό Εξάμηνο 2015-2016 Φροντιστήριο 6 Α) ΘΕΩΡΙΑ Μέθοδος Επίλυσης (Resolution) Στη μέθοδο της επίλυσης αποδεικνύουμε την ικανοποιησιμότητα ενός συνόλου προτάσεων,
13/5/2015 ΟΥΡΕΣ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ. Δομές Δεδομένων. Ουρές Προτεραιότητας
 ΟΥΡΕΣ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ Δομές Δεδομένων Τι θα δούμε Ουρές προτεραιότητας Πράξεις Διωνυμικές Ουρές Διωνυμικά Δέντρα Διωνυμικοί Σωροί Ουρές Fibonacci Αναπαράσταση Πράξεις Ανάλυση Συγκρίσεις Ουρές προτεραιότητας
ΟΥΡΕΣ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ Δομές Δεδομένων Τι θα δούμε Ουρές προτεραιότητας Πράξεις Διωνυμικές Ουρές Διωνυμικά Δέντρα Διωνυμικοί Σωροί Ουρές Fibonacci Αναπαράσταση Πράξεις Ανάλυση Συγκρίσεις Ουρές προτεραιότητας
Κάθε functional unit χρησιµοποιείται µια φορά σε κάθε κύκλο: ανάγκη για πολλαπλό hardware = κόστος υλοποίησης!
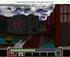 Single-cyle υλοποίηση: ιάρκεια κύκλου ίση µε τη µεγαλύτερη εντολή-worst case delay (εδώ η lw) = χαµηλή απόδοση! Αντιβαίνει µε αρχή: Κάνε την πιο απλή περίπτωση γρήγορη (ίσως και εις βάρος των πιο «σύνθετων»
Single-cyle υλοποίηση: ιάρκεια κύκλου ίση µε τη µεγαλύτερη εντολή-worst case delay (εδώ η lw) = χαµηλή απόδοση! Αντιβαίνει µε αρχή: Κάνε την πιο απλή περίπτωση γρήγορη (ίσως και εις βάρος των πιο «σύνθετων»
Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
Μοντέλο Perceptron πολλών στρωμάτων Multi Layer Perceptron (MLP)
 Μοντέλο Perceptron πολλών στρωμάτων Multi Layer Perceptron (MLP) x -0,5 a x x 2 0 0 0 0 - -0,5 y y 0 0 x 2 -,5 a 2 θ η τιμή κατωφλίου Μία λύση του προβλήματος XOR Multi Layer Perceptron (MLP) x -0,5 Μία
Μοντέλο Perceptron πολλών στρωμάτων Multi Layer Perceptron (MLP) x -0,5 a x x 2 0 0 0 0 - -0,5 y y 0 0 x 2 -,5 a 2 θ η τιμή κατωφλίου Μία λύση του προβλήματος XOR Multi Layer Perceptron (MLP) x -0,5 Μία
Σημειωματάριο Δευτέρας 4 Δεκ. 2017
 Σημειωματάριο Δευτέρας 4 Δεκ. 2017 Ο αλγόριθμος Floyd-Warshall για την έυρεση όλων των αποστάσεων σε ένα γράφημα με βάρη στις ακμές Συνεχίσαμε σήμερα το θέμα της προηγούμενης Τετάρτης. Έχουμε ένα γράφημα
Σημειωματάριο Δευτέρας 4 Δεκ. 2017 Ο αλγόριθμος Floyd-Warshall για την έυρεση όλων των αποστάσεων σε ένα γράφημα με βάρη στις ακμές Συνεχίσαμε σήμερα το θέμα της προηγούμενης Τετάρτης. Έχουμε ένα γράφημα
1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες εντολές (μορφές) της;
 1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες (μορφές) της; Η δομή επανάληψης χρησιμοποιείται όταν μια σειρά εντολών πρέπει να εκτελεστεί σε ένα σύνολο περιπτώσεων, που έχουν κάτι
1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες (μορφές) της; Η δομή επανάληψης χρησιμοποιείται όταν μια σειρά εντολών πρέπει να εκτελεστεί σε ένα σύνολο περιπτώσεων, που έχουν κάτι
Γραμμικός Προγραμματισμός Μέθοδος Simplex
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
Γραµµικός Προγραµµατισµός (ΓΠ)
 Γραµµικός Προγραµµατισµός (ΓΠ) Περίληψη Επίλυση δυσδιάστατων προβληµάτων Η µέθοδος simplex Τυπική µορφή Ακέραιος Προγραµµατισµός Προγραµµατισµός Παραγωγής Προϊόν Προϊόν 2 Παραγωγική Δυνατότητα Μηχ. 4 Μηχ.
Γραµµικός Προγραµµατισµός (ΓΠ) Περίληψη Επίλυση δυσδιάστατων προβληµάτων Η µέθοδος simplex Τυπική µορφή Ακέραιος Προγραµµατισµός Προγραµµατισµός Παραγωγής Προϊόν Προϊόν 2 Παραγωγική Δυνατότητα Μηχ. 4 Μηχ.
Προβλήματα Ελάχιστου Κόστους Ροής σε Δίκτυο. Δίκτυα Ροής Ελάχιστου Κόστους (Minimum Cost Flow Networks)
 Προβλήματα Ελάχιστου Κόστους Ροής σε Δίκτυο Ορισμοί Παραδείγματα Δικτυακή Simplex (προβλήματα με και χωρίς φραγμούς). Δίκτυα Ροής Ελάχιστου Κόστους (Minimum ost Flow Networks) Ένα δίκτυο μεταφόρτωσης αποτελείται
Προβλήματα Ελάχιστου Κόστους Ροής σε Δίκτυο Ορισμοί Παραδείγματα Δικτυακή Simplex (προβλήματα με και χωρίς φραγμούς). Δίκτυα Ροής Ελάχιστου Κόστους (Minimum ost Flow Networks) Ένα δίκτυο μεταφόρτωσης αποτελείται
Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής
 Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής Βασισμένο σε μια εργασία των Καζαρλή, Καλόμοιρου, Μαστοροκώστα, Μπαλουκτσή, Καλαϊτζή, Βαλαή, Πετρίδη Εισαγωγή Η Εξελικτική Υπολογιστική
Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής Βασισμένο σε μια εργασία των Καζαρλή, Καλόμοιρου, Μαστοροκώστα, Μπαλουκτσή, Καλαϊτζή, Βαλαή, Πετρίδη Εισαγωγή Η Εξελικτική Υπολογιστική
Σύστημα και Μαθηματικά μοντέλα συστημάτων
 Σύστημα και Μαθηματικά μοντέλα συστημάτων Όταν μελετούμε έναν συγκεκριμένο μηχανισμό η μια φυσική διεργασία επικεντρώνουμε το ενδιαφέρον μας στα φυσικά μεγέθη του μηχανισμού τα οποία μας ενδιαφέρει να
Σύστημα και Μαθηματικά μοντέλα συστημάτων Όταν μελετούμε έναν συγκεκριμένο μηχανισμό η μια φυσική διεργασία επικεντρώνουμε το ενδιαφέρον μας στα φυσικά μεγέθη του μηχανισμού τα οποία μας ενδιαφέρει να
i Throughput: Ο ρυθμός ολοκλήρωσης έργου σε συγκεκριμένο χρόνο
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 6-7 Απόδοση ΚΜΕ (Μέτρηση και τεχνικές βελτίωσης απόδοσης) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Κεντρική Μονάδα Επεξεργασίας
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 6-7 Απόδοση ΚΜΕ (Μέτρηση και τεχνικές βελτίωσης απόδοσης) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Κεντρική Μονάδα Επεξεργασίας
ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ
 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς όρους όλες οι μεταβλητές είναι μη αρνητικές
 Ένα τυχαίο π.γ.π. maximize/minimize z=c x Αx = b x 0 Τυπική μορφή του π.γ.π. maximize z=c x Αx = b x 0 b 0 είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς
Ένα τυχαίο π.γ.π. maximize/minimize z=c x Αx = b x 0 Τυπική μορφή του π.γ.π. maximize z=c x Αx = b x 0 b 0 είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς
καθ. Βασίλης Μάγκλαρης
 ΣΤΟΧΑΣΤΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ & ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Αίθουσα 005 - Νέα Κτίρια ΣΗΜΜΥ Ε.Μ.Π. Ενισχυτική Μάθηση - Δυναμικός Προγραμματισμός: 1. Markov Decision Processes 2. Bellman s Optimality Criterion 3. Αλγόριθμος
ΣΤΟΧΑΣΤΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ & ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Αίθουσα 005 - Νέα Κτίρια ΣΗΜΜΥ Ε.Μ.Π. Ενισχυτική Μάθηση - Δυναμικός Προγραμματισμός: 1. Markov Decision Processes 2. Bellman s Optimality Criterion 3. Αλγόριθμος
Επίλυση 1 ης Εργασίας. Παραδόθηκαν: 11/12 15%
 Επίλυση 1 ης Εργασίας Παραδόθηκαν: 11/12 15% ΘΕΜΑ 1 ΑΠΑΝΤΗΣΗ Α) Συνθήκη συντήρησης της αρχικής ροής Το φορτίο που μεταφέρεται από τον r είναι 3 (r->1=1) + (r->3=0) + (r- >4=2) Το φορτίο που φθάνει στον
Επίλυση 1 ης Εργασίας Παραδόθηκαν: 11/12 15% ΘΕΜΑ 1 ΑΠΑΝΤΗΣΗ Α) Συνθήκη συντήρησης της αρχικής ροής Το φορτίο που μεταφέρεται από τον r είναι 3 (r->1=1) + (r->3=0) + (r- >4=2) Το φορτίο που φθάνει στον
ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 2004., η οποία όµως µπορεί να γραφεί µε την παρακάτω µορφή: 1 e
 ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη)
 Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Ταυτόχρονη εκτέλεση Ο προγραμματιστής δεν ελέγχει (άμεσα) την εκτέλεση/εναλλαγή των νημάτων Δεν γνωρίζει πότε θα αρχίσει
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Ταυτόχρονη εκτέλεση Ο προγραμματιστής δεν ελέγχει (άμεσα) την εκτέλεση/εναλλαγή των νημάτων Δεν γνωρίζει πότε θα αρχίσει
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ
 Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Μηχανές Πεπερασμένων Καταστάσεων
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
ΟΥΡΕΣ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ
 ΟΥΡΕΣ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ Δομές Δεδομένων Παπαγιαννόπουλος Δημήτριος 30 Μαρτίου 2017 18 Μαΐου 2017 papagianno@ceid.upatras.gr 1 Περιεχόμενα Ουρές προτεραιότητας Πράξεις Διωνυμικές Ουρές Διωνυμικά Δέντρα Διωνυμικοί
ΟΥΡΕΣ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ Δομές Δεδομένων Παπαγιαννόπουλος Δημήτριος 30 Μαρτίου 2017 18 Μαΐου 2017 papagianno@ceid.upatras.gr 1 Περιεχόμενα Ουρές προτεραιότητας Πράξεις Διωνυμικές Ουρές Διωνυμικά Δέντρα Διωνυμικοί
Αρχιτεκτονική υπολογιστών
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Αρχιτεκτονική υπολογιστών Ενότητα 10 : Ομάδες εντολών: Τρόποι Διευθυνσιοδότησης και Μορφοποιήσεις Ευάγγελος Καρβούνης Τρίτη, 19/01/2016 2 Διευθυνσιοδότηση
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Αρχιτεκτονική υπολογιστών Ενότητα 10 : Ομάδες εντολών: Τρόποι Διευθυνσιοδότησης και Μορφοποιήσεις Ευάγγελος Καρβούνης Τρίτη, 19/01/2016 2 Διευθυνσιοδότηση
Μάθημα 4: Κεντρική Μονάδα Επεξεργασίας
 Μάθημα 4: Κεντρική Μονάδα Επεξεργασίας 4.1 Γενικά Ο υπολογιστής επεξεργάζεται δεδομένα ακολουθώντας βήμα βήμα, τις εντολές ενός προγράμματος. Το τμήμα του υπολογιστή, που εκτελεί τις εντολές και συντονίζει
Μάθημα 4: Κεντρική Μονάδα Επεξεργασίας 4.1 Γενικά Ο υπολογιστής επεξεργάζεται δεδομένα ακολουθώντας βήμα βήμα, τις εντολές ενός προγράμματος. Το τμήμα του υπολογιστή, που εκτελεί τις εντολές και συντονίζει
Εισαγωγικές έννοιες. Κατηγορίες προβλημάτων (σε μια διάσταση) Προβλήματα εύρεσης μεγίστου. Συμβολισμοί
 Κατηγορίες προβλημάτων (σε μια διάσταση) Εισαγωγικές έννοιες Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Το πρόβλημα
Κατηγορίες προβλημάτων (σε μια διάσταση) Εισαγωγικές έννοιες Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Το πρόβλημα
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο 28 8//28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα
ΗΜΥ 2: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο 28 8//28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα
Μαθηµατικοί Υπολογισµοί στην R
 Κεφάλαιο 3 Μαθηµατικοί Υπολογισµοί στην R Ενα µεγάλο µέρος της ανάλυσης δεδοµένων απαιτεί διάφορους µαθηµατικούς υπολογισµούς. Αυτό το κεφάλαιο εισαγάγει τον αναγνώστη στις διάφορες δυνατότητες που έχει
Κεφάλαιο 3 Μαθηµατικοί Υπολογισµοί στην R Ενα µεγάλο µέρος της ανάλυσης δεδοµένων απαιτεί διάφορους µαθηµατικούς υπολογισµούς. Αυτό το κεφάλαιο εισαγάγει τον αναγνώστη στις διάφορες δυνατότητες που έχει
Digital Image Processing
 Digital Image Processing Φιλτράρισμα στο πεδίο των Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008. Φίλτρο: μια διάταξη ή
Digital Image Processing Φιλτράρισμα στο πεδίο των Πέτρος Καρβέλης pkarvelis@gmail.com Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008. Φίλτρο: μια διάταξη ή
Στον παρακάτω πίνακα παρουσιάζονται οι διάφορες δραστηριότητες που απαιτούνται στο πλαίσιο υλοποίησης ενός μικρού έργου:
 Εκφώνηση Στον παρακάτω πίνακα παρουσιάζονται οι διάφορες δραστηριότητες που απαιτούνται στο πλαίσιο υλοποίησης ενός μικρού έργου: Οι άμεσες σχέσεις προτεραιότητας είναι: Activity Number Activity Completion
Εκφώνηση Στον παρακάτω πίνακα παρουσιάζονται οι διάφορες δραστηριότητες που απαιτούνται στο πλαίσιο υλοποίησης ενός μικρού έργου: Οι άμεσες σχέσεις προτεραιότητας είναι: Activity Number Activity Completion
Υλοποιήσεις Ψηφιακών Φίλτρων
 Ψηφιακή Επεξεργασία Σηµάτων 10 Υλοποιήσεις Ψηφιακών Φίλτρων Α. Εισαγωγή Οποιοδήποτε γραµµικό χρονικά αµετάβλητο σύστηµα διακριτού χρόνου χαρακτηρίζεται πλήρως από τη συνάρτηση µεταφοράς του η οποία έχει
Ψηφιακή Επεξεργασία Σηµάτων 10 Υλοποιήσεις Ψηφιακών Φίλτρων Α. Εισαγωγή Οποιοδήποτε γραµµικό χρονικά αµετάβλητο σύστηµα διακριτού χρόνου χαρακτηρίζεται πλήρως από τη συνάρτηση µεταφοράς του η οποία έχει
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ. Κεφάλαιο 3
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 3 Κεντρική Μονάδα Επεξεργασίας Κεντρική Μονάδα Επεξεργασίας Μονάδα επεξεργασίας δεδομένων Μονάδα ελέγχου Μονάδα επεξεργασίας δεδομένων Δομή Αριθμητικής Λογικής Μονάδας
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 3 Κεντρική Μονάδα Επεξεργασίας Κεντρική Μονάδα Επεξεργασίας Μονάδα επεξεργασίας δεδομένων Μονάδα ελέγχου Μονάδα επεξεργασίας δεδομένων Δομή Αριθμητικής Λογικής Μονάδας
Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυϊκότητα. Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα. τελευταία ενημέρωση: 1/12/2016
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Δυϊκότητα Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 1/12/2016 1 Το δυϊκό πρόβλημα Για κάθε πρόβλημα Γραμμικού Προγραμματισμού υπάρχει
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Δυϊκότητα Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 1/12/2016 1 Το δυϊκό πρόβλημα Για κάθε πρόβλημα Γραμμικού Προγραμματισμού υπάρχει
Network Algorithms and Complexity Παραλληλοποίηση του αλγορίθμου του Prim. Αικατερίνη Κούκιου
 Network Algorithms and Complexity Παραλληλοποίηση του αλγορίθμου του Prim Αικατερίνη Κούκιου Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Network Algorithms and Complexity Παραλληλοποίηση του αλγορίθμου του Prim Αικατερίνη Κούκιου Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
z = c 1 x 1 + c 2 x c n x n
 Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
HMY 102 Ανάλυση Ηλεκτρικών Κυκλωμάτων
 HM Ανάλυση Ηλεκτρικών Κυκλωμάτων Δρ. Σταύρος Ιεζεκιήλ iezekiel@ucy.ac.cy reen Park, Γραφείο Τηλ. 899 Διάλεξη 4 Από την προηγούμενη διάλεξη Πραγματικές πηγές τάσης και πραγματικές πηγές ρεύματος έχουν εσωτερική
HM Ανάλυση Ηλεκτρικών Κυκλωμάτων Δρ. Σταύρος Ιεζεκιήλ iezekiel@ucy.ac.cy reen Park, Γραφείο Τηλ. 899 Διάλεξη 4 Από την προηγούμενη διάλεξη Πραγματικές πηγές τάσης και πραγματικές πηγές ρεύματος έχουν εσωτερική
Συστήματα VLSI. Εισαγωγή. Γιώργος Δημητρακόπουλος. Δημοκρίτειο Πανεπιστήμιο Θράκης. Άνοιξη 2014
 Συστήματα VLSI Εισαγωγή Γιώργος Δημητρακόπουλος Δημοκρίτειο Πανεπιστήμιο Θράκης Άνοιξη 2014 Συστήματα VLSI 1 Τα ολοκληρωμένα κυκλώματα από «μέσα» Συστήματα VLSI 2 Τα εργαλεία της σχεδίασης Algorithms-Applications
Συστήματα VLSI Εισαγωγή Γιώργος Δημητρακόπουλος Δημοκρίτειο Πανεπιστήμιο Θράκης Άνοιξη 2014 Συστήματα VLSI 1 Τα ολοκληρωμένα κυκλώματα από «μέσα» Συστήματα VLSI 2 Τα εργαλεία της σχεδίασης Algorithms-Applications
Κεφάλαιο 2.4 Matrix Algorithms
 Κεφάλαιο 2.4 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βασιλική Κατασκευή ΝxNxN Mesh of trees (1/3) Στον ΝxNxN κύβο προσθέτω τους εξής κόμβους:
Κεφάλαιο 2.4 Matrix Algorithms Παρουσίαση στα πλαίσια του μαθήματος «Παράλληλοι Αλγόριθμοι» Καούρη Γεωργία Μήτσου Βασιλική Κατασκευή ΝxNxN Mesh of trees (1/3) Στον ΝxNxN κύβο προσθέτω τους εξής κόμβους:
Σήματα και Συστήματα ΙΙ
 Σήματα και Συστήματα ΙΙ Ενότητα 3: Διακριτός και Ταχύς Μετασχηματισμός Fourier (DTF & FFT) Α. Ν. Σκόδρας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής
Σήματα και Συστήματα ΙΙ Ενότητα 3: Διακριτός και Ταχύς Μετασχηματισμός Fourier (DTF & FFT) Α. Ν. Σκόδρας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής
Β. Βασιλειάδης. Επιχειρησιακή Έρευνα Διάλεξη 5 η -Αλγόριθμος Simplex
 Β. Βασιλειάδης Επιχειρησιακή Έρευνα Διάλεξη 5 η -Αλγόριθμος Simplex Περιεχόμενα Ο αλγόριθμος Simplex Βασικά Βήματα Παραδείγματα Συμπεράσματα 1o Bήμα: εξάλειψη των ανισοτήτων Στη μαθηματική διατύπωση του
Β. Βασιλειάδης Επιχειρησιακή Έρευνα Διάλεξη 5 η -Αλγόριθμος Simplex Περιεχόμενα Ο αλγόριθμος Simplex Βασικά Βήματα Παραδείγματα Συμπεράσματα 1o Bήμα: εξάλειψη των ανισοτήτων Στη μαθηματική διατύπωση του
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 22D D σχημάτων (ευθεία
 Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Μέθοδοι μονοδιάστατης ελαχιστοποίησης
 Βασικές αρχές μεθόδων ελαχιστοποίησης Μέθοδοι μονοδιάστατης ελαχιστοποίησης Οι μέθοδοι ελαχιστοποίησης είναι επαναληπτικές. Ξεκινώντας από μια αρχική προσέγγιση του ελαχίστου (την συμβολίζουμε ) παράγουν
Βασικές αρχές μεθόδων ελαχιστοποίησης Μέθοδοι μονοδιάστατης ελαχιστοποίησης Οι μέθοδοι ελαχιστοποίησης είναι επαναληπτικές. Ξεκινώντας από μια αρχική προσέγγιση του ελαχίστου (την συμβολίζουμε ) παράγουν
Θέματα Προγραμματισμού Η/Υ
 Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 7: Θεματική Ενότητα: Δομές επανάληψης ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική Ενότητα 7 Δομές επανάληψης
Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 7: Θεματική Ενότητα: Δομές επανάληψης ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική Ενότητα 7 Δομές επανάληψης
Στ Τάξη. Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1
 Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 11: Εφαρμογές DFT Ταχύς Μετασχηματισμός Fourier (FFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Διακριτός Μετασχηματισμός Fourier Υπολογισμός Γραμμικής Συνέλιξης
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 11: Εφαρμογές DFT Ταχύς Μετασχηματισμός Fourier (FFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Διακριτός Μετασχηματισμός Fourier Υπολογισμός Γραμμικής Συνέλιξης
Κεφαλαιο 2.2 ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΑΛΓΟΡΙΘΜΟΙ
 Κεφαλαιο 2.2 ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΑΛΓΟΡΙΘΜΟΙ 1.Σ, 2.Σ, 3. Λ, 4.Σ, 5.Σ Στο α) ανήκουν: 1,2,5,6,7 Στο β) ανήκουν: 3,4,8,9,10 1.-Λ, 2.-Λ, 3.-Σ, 4.-Σ, 5.-Σ 1. -Πραγματικός, 2. -Αρφαριθμητικός, 3.-Αλφαριθμητικός,
Κεφαλαιο 2.2 ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΑΛΓΟΡΙΘΜΟΙ 1.Σ, 2.Σ, 3. Λ, 4.Σ, 5.Σ Στο α) ανήκουν: 1,2,5,6,7 Στο β) ανήκουν: 3,4,8,9,10 1.-Λ, 2.-Λ, 3.-Σ, 4.-Σ, 5.-Σ 1. -Πραγματικός, 2. -Αρφαριθμητικός, 3.-Αλφαριθμητικός,
Ενδεικτικές Ερωτήσεις Θεωρίας
 Ενδεικτικές Ερωτήσεις Θεωρίας Κεφάλαιο 2 1. Τι καλούμε αλγόριθμο; 2. Ποια κριτήρια πρέπει οπωσδήποτε να ικανοποιεί ένας αλγόριθμος; 3. Πώς ονομάζεται μια διαδικασία που δεν περατώνεται μετά από συγκεκριμένο
Ενδεικτικές Ερωτήσεις Θεωρίας Κεφάλαιο 2 1. Τι καλούμε αλγόριθμο; 2. Ποια κριτήρια πρέπει οπωσδήποτε να ικανοποιεί ένας αλγόριθμος; 3. Πώς ονομάζεται μια διαδικασία που δεν περατώνεται μετά από συγκεκριμένο
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 2013 Διάρκεια εξέτασης : 160 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών:
 Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Δ Ι Α Φ Ο Ρ Ι Κ Ο Σ Λ Ο Γ Ι Σ Μ Ο Σ Πεδίο Ορισμού Συνάρτησης
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ / ΕΠΑΝΑΛΗΨΗΣ Δ Ι Α Φ Ο Ρ Ι Κ Ο Σ Λ Ο Γ Ι Σ Μ Ο Σ Πεδίο Ορισμού Συνάρτησης 1 Τι πρέπει να γνωρίζω για τα πεδία ορισμού; Χωρίς πολλές φιλοσοφίες: όταν μιλάμε για το πεδίο ορισμού μιας συνάρτησης,
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ / ΕΠΑΝΑΛΗΨΗΣ Δ Ι Α Φ Ο Ρ Ι Κ Ο Σ Λ Ο Γ Ι Σ Μ Ο Σ Πεδίο Ορισμού Συνάρτησης 1 Τι πρέπει να γνωρίζω για τα πεδία ορισμού; Χωρίς πολλές φιλοσοφίες: όταν μιλάμε για το πεδίο ορισμού μιας συνάρτησης,
Στο σχήμα 3.1 δίνεται μια μονάδα επεξεργασίας δεδομένων σταθερής υποδιαστολής που εκτελεί οποιαδήποτε από τις κάτωθι εντολές σε ένα κύκλο ρολογιού.
 1 Ασκήσεις Αρχιτεκτονικής Υπολογιστών, Δημήτρης Νικολός, Απρίλης 2011 Άσκηση 3 Στο σχήμα 3.1 δίνεται μια μονάδα επεξεργασίας δεδομένων σταθερής υποδιαστολής που εκτελεί οποιαδήποτε από τις κάτωθι εντολές
1 Ασκήσεις Αρχιτεκτονικής Υπολογιστών, Δημήτρης Νικολός, Απρίλης 2011 Άσκηση 3 Στο σχήμα 3.1 δίνεται μια μονάδα επεξεργασίας δεδομένων σταθερής υποδιαστολής που εκτελεί οποιαδήποτε από τις κάτωθι εντολές
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
26-Nov-09. ΗΜΥ 210: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο Καταχωρητές 1. Διδάσκουσα: Μαρία Κ. Μιχαήλ
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 6: Συμπίεση Έργου
 Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 6: Συμπίεση Έργου Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.)
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 6: Συμπίεση Έργου Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.)
Γενική οργάνωση υπολογιστή «ΑΒΑΚΑ»
 Περιεχόμενα Γενική οργάνωση υπολογιστή «ΑΒΑΚΑ»... 2 Καταχωρητές... 3 Αριθμητική-λογική μονάδα... 3 Μονάδα μνήμης... 4 Μονάδα Εισόδου - Εξόδου... 5 Μονάδα ελέγχου... 5 Ρεπερτόριο Εντολών «ΑΒΑΚΑ»... 6 Φάση
Περιεχόμενα Γενική οργάνωση υπολογιστή «ΑΒΑΚΑ»... 2 Καταχωρητές... 3 Αριθμητική-λογική μονάδα... 3 Μονάδα μνήμης... 4 Μονάδα Εισόδου - Εξόδου... 5 Μονάδα ελέγχου... 5 Ρεπερτόριο Εντολών «ΑΒΑΚΑ»... 6 Φάση
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων 15/11/2010. Σχεδιασμός Ακολουθιακών Κυκλωμάτων 1
 ΗΜΥ 20: Σχεδιασμός Ψηφιακών Συστημάτων 5//200 ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Σχεδιασμός Ακολουθιακών Κυκλωμάτων Αρχή: Μια λίστα/περιγραφή
ΗΜΥ 20: Σχεδιασμός Ψηφιακών Συστημάτων 5//200 ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Σχεδιασμός Ακολουθιακών Κυκλωμάτων Αρχή: Μια λίστα/περιγραφή
Εργαστήριο Εισαγωγής στη Σχεδίαση Συστημάτων VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
3η Σειρά Γραπτών Ασκήσεων
 1/48 3η Σειρά Γραπτών Ασκήσεων Αλγόριθμοι και Πολυπλοκότητα ΣΗΜΜΥ, Εθνικό Μετσόβιο Πολυτεχνείο 2/48 1 Άσκηση 1: Πομποί και Δέκτες 2 Άσκηση 2: Διακοπές στην Ικαρία 3 Άσκηση 3: Επιστροφή στη Γη 4 Άσκηση
1/48 3η Σειρά Γραπτών Ασκήσεων Αλγόριθμοι και Πολυπλοκότητα ΣΗΜΜΥ, Εθνικό Μετσόβιο Πολυτεχνείο 2/48 1 Άσκηση 1: Πομποί και Δέκτες 2 Άσκηση 2: Διακοπές στην Ικαρία 3 Άσκηση 3: Επιστροφή στη Γη 4 Άσκηση
Πληροφορική 2. Αλγόριθμοι
 Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων
 Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων Με τον όρο ανάλυση ενός κυκλώματος εννοούμε τον προσδιορισμό της συμπεριφοράς του κάτω από συγκεκριμένες συνθήκες λειτουργίας. Έτσι, για ένα συνδυαστικό κύκλωμα,
Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων Με τον όρο ανάλυση ενός κυκλώματος εννοούμε τον προσδιορισμό της συμπεριφοράς του κάτω από συγκεκριμένες συνθήκες λειτουργίας. Έτσι, για ένα συνδυαστικό κύκλωμα,
Minimum Spanning Tree: Prim's Algorithm
 Minimum Spanning Tree: Prim's Algorithm 1. Initialize a tree with a single vertex, chosen arbitrarily from the graph. 2. Grow the tree by one edge: of the edges that connect the tree to vertices not yet
Minimum Spanning Tree: Prim's Algorithm 1. Initialize a tree with a single vertex, chosen arbitrarily from the graph. 2. Grow the tree by one edge: of the edges that connect the tree to vertices not yet
Μάθημα 3.2: Κεντρική Μονάδα Επεξεργασίας
 Κεφάλαιο 3 ο Αρχιτεκτονική Υπολογιστών Μάθημα 3.: Κεντρική Μονάδα Επεξεργασίας Όταν ολοκληρώσεις το κεφάλαιο θα μπορείς: Να σχεδιάζεις την εσωτερική δομή της ΚΜΕ και να εξηγείς τη λειτουργία των επιμέρους
Κεφάλαιο 3 ο Αρχιτεκτονική Υπολογιστών Μάθημα 3.: Κεντρική Μονάδα Επεξεργασίας Όταν ολοκληρώσεις το κεφάλαιο θα μπορείς: Να σχεδιάζεις την εσωτερική δομή της ΚΜΕ και να εξηγείς τη λειτουργία των επιμέρους
ΠΛΗ10 Κεφάλαιο 2. ΠΛΗ10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.1: Bασική Δομή του Υπολογιστή
 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.1: Bασική Δομή του Υπολογιστή Στόχοι Μαθήματος: Να γνωρίσετε τις βασικές λειτουργίες ενός Η/Υ. Να γνωρίσετε τις έννοιες δεδομένα, πληροφορία, επεξεργασία,
Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.1: Bασική Δομή του Υπολογιστή Στόχοι Μαθήματος: Να γνωρίσετε τις βασικές λειτουργίες ενός Η/Υ. Να γνωρίσετε τις έννοιες δεδομένα, πληροφορία, επεξεργασία,
Κεφάλαιο 4ο: Δικτυωτή Ανάλυση
 Κεφάλαιο ο: Δικτυωτή Ανάλυση. Εισαγωγή Η δικτυωτή ανάλυση έχει παίξει σημαντικό ρόλο στην Ηλεκτρολογία. Όμως, ορισμένες έννοιες και τεχνικές της δικτυωτής ανάλυσης είναι πολύ χρήσιμες και σε άλλες επιστήμες.
Κεφάλαιο ο: Δικτυωτή Ανάλυση. Εισαγωγή Η δικτυωτή ανάλυση έχει παίξει σημαντικό ρόλο στην Ηλεκτρολογία. Όμως, ορισμένες έννοιες και τεχνικές της δικτυωτής ανάλυσης είναι πολύ χρήσιμες και σε άλλες επιστήμες.
Θέματα Διπλωματικών Εργασιών
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. & Μηχ. Υπολογιστών Τομέας Τεχνολογίας Πληροφορικής & Υπολογιστών Εργαστήριο Μικροϋπολογιστών & Ψηφιακών Συστημάτων Τηλ.: 210 772-2500, Γραμμ.: 210 772-3548,
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. & Μηχ. Υπολογιστών Τομέας Τεχνολογίας Πληροφορικής & Υπολογιστών Εργαστήριο Μικροϋπολογιστών & Ψηφιακών Συστημάτων Τηλ.: 210 772-2500, Γραμμ.: 210 772-3548,
ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΑΛΓΟΡΙΘΜΟΥΣ ΚΑΙ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ
 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΑΛΓΟΡΙΘΜΟΥΣ ΚΑΙ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΣΜΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ Διδάσκουσα Δρ Β. Καβακλή Χειμερινό Εξάμηνο 2001 1 Δοκιμή Έλεγχος Αλγορίθμου Για να
ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΑΛΓΟΡΙΘΜΟΥΣ ΚΑΙ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΣΜΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ Διδάσκουσα Δρ Β. Καβακλή Χειμερινό Εξάμηνο 2001 1 Δοκιμή Έλεγχος Αλγορίθμου Για να
