Τοµέας Περιφερειακής Ανάλυσης, Τ.Θ. 1527, 71110, Ηράκλειο Κρήτης. Τηλ: , Fax:

Transcript

1 ΧΑΡΤΕΣ ΚΙΝ ΥΝΟΥ ΓΙΑ ΤΗ ΜΕΛΕΤΗ ΤΗΣ ΛΕΪΣΜΑΝΙΑΣΗΣ ΣΤΗΝ ΚΕΝΤΡΙΚΗ ΤΥΝΗΣΙΑ Γιάννης Καµαριανάκης 1*, Πουλίκος Πραστάκος 1, Afif Ben Salah 2, Sadok Schlif 2, Nissaf Ben Alaya 2 1 Ίδρυµα Τεχνολογίας και Έρευνας, Ινστιτούτο Υπολογιστικών Μαθηµατικών, Τοµέας Περιφερειακής Ανάλυσης, Τ.Θ. 1527, 71110, Ηράκλειο Κρήτης 2 Institut Pasteur Tunis, Tunisia kamarian@iacm.forth.gr, Τηλ: , Fax: ΠEΡΙΛΗΨΗ Η λεϊσµανίαση (Zonotic Cutaneous Lishmaniasis- ZCL) είναι µια ασθένεια που απαντάται συχνά σε χώρες της νότιας και ανατολικής Μεσογείου. Σε αυτό το άρθρο παρουσιάζουµε την εξέλιξη της ασθένειας στο χώρο και το χρόνο και εστιάζουµε στους παράγοντες που συµβάλλουν ώστε µια περιοχή να χαρακτηρίζεται από υψηλό επιδηµιολογικό κίνδυνο. Τα δεδοµένα αφορούν ενενήντα τέσσερις επαρχίες της περιοχής Sidi-Bouzid στην κεντρική Τυνησία για την περίοδο από το 1999 έως το Αρχικά εξετάζουµε την χωρική και χρονική οµογένεια του κινδύνου µέσω κατάλληλων στατιστικών ελέγχων. Μετά την απόρριψη των δύο υποθέσεων ελέγχουµε την (στατιστικά σηµαντική) ύπαρξη περιοχών στο χώρο και το χρόνο µε υψηλή εµφάνιση της ασθένειας (spatial clustering tests). Για το σκοπό αυτό χρησιµοποιούµε στατιστικές χωρικής, χρονικής και χωρο-χρονικής ανίχνευσης. Τα αποτελέσµατα υποδεικνύουν ότι το 2004 ήταν χρονιά που η ασθένεια βρισκόταν σε έξαρση και ότι υπήρχε µια περιοχή µε ιδιαίτερα υψηλά ποσοστά εµφάνισης της ασθένειας. Η συγκεκριµένη περιοχή που αποτελείται από επτά επαρχίες και σε αυτήν κατοικεί περίπου το πέντε τοις εκατό των κατοίκων του Sidi-Bouzid, γειτονεύει µε το φράγµα Sidi-Saad. Η κατασκευή του συγκεκριµένου φράγµατος στις αρχές της δεκαετίας του ογδόντα αναφέρεται από προηγούµενες επιδηµιολογικές µελέτες ως ο κύριος λόγος εµφάνισης της ασθένειας στην περιοχή. Στη συνέχεια εφαρµόζουµε µοντέλα χωρικής παλινδρόµησης Poisson µε επεξηγηµατικούς παράγοντες την πληθυσµιακή πυκνότητα κάθε επαρχίας, έναν δείκτη αστικότητας και τον αριθµό κατοίκων ανά κατοικία. Μόνο ο δείκτης αστικότητας προκύπτει ως στατιστικά σηµαντικός παράγοντας για την επεξήγηση των χωρικών µεταβολών της ασθένειας. Μέσω των συγκεκριµένων στατιστικών µοντέλων κατασκευάζουµε χάρτες εξοµαλυσµένου κινδύνου. ΛΕΞΕΙΣ ΚΛΕΙ ΙΑ Χάρτες Επιδηµιολογικού Κινδύνου, Χωρικές Συστάδες (Spatial Clusters), Στατιστικά Μοντέλα Επιδηµιολογικού Κινδύνου 1.ΕΙΣΑΓΩΓΗ Η λεϊσµανίαση (Zoonotic cutaneous leishmaniasis-zcl) απαντάται σε πολλές χώρες της νότιας και ανατολικής Μεσογείου. Θεωρείται σηµαντικό πρόβληµα υγείας µε κλινικές εκδηλώσεις που κυρίως είναι δερµατικές πληγές. Η ασθένεια µεταδίδεται στον άνθρωπο µέσω της µύγας Phlebotomus papatazi από δύο είδη ποντικιών (Psammomys obesus, Meriones spp.). Υπάρχει πληθώρα παραγόντων που σχετίζονται µε την

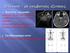
2 αυξηµένη εµφάνιση της ασθένειας στην περιοχή. Σύµφωνα µε προηγούµενες επιδηµιολογικές µελέτες η πλειοψηφία τους σχετίζεται µε ανθρώπινες δραστηριότητες κυρίως περιβαλλοντικές επεµβάσεις και µετακινήσεις πληθυσµών. Για παράδειγµα η έξαρση της ασθένειας στην Τυνησία στις αρχές της δεκαετίας του ογδόντα σχετίζεται µε την κατασκευή του φράγµατος Sidi-Saad. Οι βασικές µέθοδοι ελέγχου της µετάδοσης της ασθένειας στηρίζονται στον έλεγχο των πληθυσµών των ποντικιών. Μια πρακτική που εφαρµόστηκε στην Τυνησία και την Ιορδανία είναι η καταστροφή ενός είδους µικρού θάµνου (chenopod) το οποίο είναι η βασική πηγή τροφής και στέγη για τα Psammomys obesus και η εµφύτευση δέντρων σε περιοχές ακτίνας δύο µέχρι τριών χιλιοµέτρων γύρω από ανθρώπινες κοινότητες. Σε αυτό το άρθρο παρουσιάζουµε τα αποτελέσµατα της ανάλυσης µιας καταγραφής κρουσµάτων ZCL στην περιοχή Sidi-Bouzid στην κεντρική Τυνησία από το 1999 έως το Ελέγχουµε τη χωρική και χρονική οµογένεια (ανά επαρχία) του κινδύνου και τον συσχετίζουµε µε κοινωνικούς και γεωγραφικούς παράγοντες. Στην επόµενη ενότητα εξετάζουµε την ασθένεια µε µεθόδους περιγραφικής στατιστικής. Στην τρίτη ενότητα εξετάζουµε την ύπαρξη περιοχών στο χώρο µελέτης (spatial clusters) µε στατιστικά σηµαντικό κίνδυνο λεϊσµανίασης. Στην τέταρτη ενότητα υποδειγµατοποιούµε τη χωρική και χρονική µεταβλητότητα του κινδύνου µε µοντέλα παλινδρόµησης Poisson. Στην πέµπτη ενότητα συνοψίζουµε τα συµπεράσµατα της µελέτης. Μια παρόµοια µελέτη της λεϊσµανίασης στη νότια Αµερική έγινε από τους Assunção et al (1999,2001). 2. ΠΕΡΙΓΡΑΦΙΚΗ ΑΝΑΛΥΣΗ Το Sidi-Bouzid καλύπτει περίπου 7,5 χιλιάδες τετραγωνικά χιλιόµετρα και βρίσκεται στην κεντρική Τυνησία µεταξύ των συντεταγµένων 34 o 30 και 35 o 29 S, 8 o 55 και 10 o 04 W. Η περιοχή (εικόνα 1) υποδιαιρείται σύµφωνα µε την εθνική στατιστική υπηρεσία σε 94 επαρχίες (sectors). Ο πληθυσµός της σύµφωνα µε την απογραφή του 2005 είναι κάτοικοι. Συνολικά περιπτώσεις λεϊσµανίασης αναφέρθηκαν στην υπό µελέτη περιοχή (από το 1999 ως το 2004 µε µέση εµφάνιση 669,7 περιπτώσεων τη χρονιά ανά εκατό χιλιάδες κατοίκους. Περίπου 63,4 τοις εκατό των περιπτώσεων αναφέρθηκαν σε (ογδόντα τρεις) αγροτικές επαρχίες που περιέχουν το εβδοµήντα ένα τοις εκατό του πληθυσµού του Sidi-Bouzid. Η εξέλιξη του φαινοµένου στο χρόνο απεικονίζεται στο αριστερό µέρος της δεύτερης εικόνας και στην τρίτη εικόνα Στην τρίτη εικόνα µπορεί κάποιος να παρατηρήσει µια τάση υψηλής εµφάνισης της ασθένειας στο ανατολικό µέρος της υπό µελέτη περιοχής όπως εξελίσσεται ο χρόνος. Το 2004 η ασθένεια ήταν σε έξαρση όπως επιβεβαιώνεται από τον έλεγχο χ 2 και τη στατιστική χρονικής ανίχνευσης. Οι παρατηρούµενες περιπτώσεις ήταν 1,66 φορές περισσότερες από τις αναµενόµενες κάτω από την υπόθεση της χρονικής οµογένειας. Επίσης, όπως υποδεικνύεται από το γράφηµα στο αριστερό µέρος της δεύτερης εικόνας, υπάρχει η τάση, επαρχίες µε υψηλή εµφάνιση της ασθένειας την πρώτη χρονιά της µελέτης, να παρουσιάζουν υψηλή εµφάνιση της ασθένειας καθ όλη τη διάρκεια της µελέτης.

3 Εικόνα 1. Αριστερά: Οι γεωγραφικές περιφέρειες της Τυνησίας και η υπό µελέτη περιοχή (Sidi Bouzid). εξιά: ορυφορική εικόνα LandSat του Sidi Bouzid µε προβεβληµένα τα σύνορα των επαρχιών. Το κόκκινο χρώµα αντιπροσωπεύει βλάστηση, το γκρι χέρσα γη, πράσινοι τόνοι αντιπροσωπεύουν αραιή βλάστηση και το γαλάζιο χρώµα αντιστοιχεί σε αστικές περιοχές. Εικόνα 2. Αριστερά: Κρούσµατα λεϊσµανίασης στο Sidi Bouzid από το 1999 ως το εξιά: Γραµµική συσχέτιση µεταξύ του αριθµού κρουσµάτων το 1999 και του ολικού αριθµού κρουσµάτων κατά την περίοδο για τις 94 επαρχίες του Sidi Bouzid.

4 Εικόνα 3. Ποσοστά εµφάνισης λεϊσµανίασης επί του συνόλου του πληθυσµού κάθε επαρχίας. 2.ΧΩΡΙΚΗ ΟΜΑ ΟΠΟΙΗΣΗ ΕΠΑΡΧΙΩΝ ΜΕ ΣΤΑΤΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΧΩΡΙΚΗΣ ΚΑΙ ΧΩΡΟ-ΧΡΟΝΙΚΗΣ ΑΝΙΧΝΕΥΣΗΣ Αρχικά ελέγξαµε τη χωρική οµογένεια του αθροίσµατος των κρουσµάτων ανά επαρχία καθ όλη την περίοδο µελέτης και στη συνέχεια εφαρµόσαµε ξεχωριστούς ελέγχους ανά χρονιά. Ο έλεγχος χ 2 εφαρµόστηκε και στις δύο περιπτώσεις. Η αρχική υπόθεση της χωρικής οµογένειας όσον αφορά τον κίνδυνο, απορρίπτεται ισχυρά σε κάθε περίπτωση (p-value<0.0001). Εφόσον έχουµε σαφή ένδειξη ανοµοιογενούς κατανοµής του κινδύνου στο χώρο προχωρούµε στην ανίχνευση περιοχών σύνολα γειτονικών επαρχιών που µπορούν να χαρακτηριστούν ως περιοχές (στατιστικά) σηµαντικού κινδύνου. Για αυτό το σκοπό χρησιµοποιούµε στατιστικές χωρικής ανίχνευσης. H µεθοδολογία που χρησιµοποιούµε, προβάλλει ένα «κυκλικό παράθυρο» στο χάρτη και µεταβάλλει το κέντρο του, ώστε το παράθυρο να περικλείει διαφορετικά σύνολα γειτονικών επαρχιών. Για πρακτικούς λόγους το κέντρο του παραθύρου τοποθετείται µόνο στο κέντρο των επαρχιών. Για κάθε θέση του κυκλικού παραθύρου η ακτίνα του

5 µεταβάλλεται από το µηδέν ως ένα µέγιστο, έτσι ώστε το παράθυρο να µην περικλείει παραπάνω από το πενήντα τοις εκατό του συνολικού πληθυσµού. Είναι προφανές ότι η µέθοδος κατασκευάζει ένα µεγάλο αριθµό παραθύρων, το καθένα αποτελούµενο από διαφορετικά σύνολα γειτονικών επαρχιών και το καθένα υποψήφιο να περιέχει µια στατιστικά σηµαντική περιοχή υψηλού κινδύνου. Για κάθε παράθυρο η µέθοδος ελέγχει την υπόθεση ότι υπάρχει στατιστικά σηµαντικά µεγαλύτερος (ή µικρότερος) κίνδυνος για την ασθένεια µέσα στο παράθυρο απ ότι έξω. Για την ανίχνευση των περιοχών υψηλού κινδύνου ταυτίζεται το κέντρο µιας οµάδας επαρχιών µε αυτό µιας άλλης. Η στατιστική χωρικής ανίχνευσης έχει χρησιµοποιηθεί σε µεγάλο αριθµό επιδηµιολογικών µελετών για παράδειγµα στους Chaput, Meek και Heimer (2002), Bakker κ.α.(2004), Jennings κ.α. (2005). Η εφαρµογή της διευκολύνεται σηµαντικά από το ελεύθερο λογισµικό SatScan ( Οι στατιστικές µέθοδοι χωρικής ανίχνευσης αναπτύχθηκαν από τον Kulldorff (1997, 1999, 2005). Οι εικόνες 4 και 5 παρουσιάζουν γειτονιές επαρχιών που οµαδοποιούνται στο χώρο, όσον αφορά την εµφάνιση υψηλού η χαµηλού επιδηµιολογικού κινδύνου. Και στις δύο περιπτώσεις το µοντέλο πιθανότητας που χαρακτηρίζει τη χωρική κατανοµή της ασθένειας είναι Poisson. H εικόνα 4 προέκυψε µε το κριτήριο της µη επικάλυψης των οµάδων κα η εικόνα 5 µε το κριτήριο του να µη συµπίπτουν τα κέντρα των οµάδων. Και οι δύο µέθοδοι υποδεικνύουν µια γειτονιά επαρχιών µε στατιστικά σηµαντικά συχνότερη εµφάνιση της ασθένειας σε σχέση µε τις υπόλοιπες. Οι συγκεκριµένες (επτά) επαρχίες βρίσκονται στο βόρειο-ανατολικό τµήµα του Sidi-Bouzid, κοντά στο φράγµα Sidi-Saad η κατασκευή του οποίου στις αρχές της δεκαετίας του ογδόντα σχετίζεται σύµφωνα µε προηγούµενες µελέτες µε την εµφάνιση της ασθένειας στην περιοχή. Οι παρατηρούµενες περιπτώσεις λεϊσµανίασης στην περιοχή είναι τέσσερις φορές περισσότερες σε σχέση µε τις αναµενόµενες κάτω από την υπόθεση της οµογενούς κατανοµής της ασθένειας. Ο πληθυσµός της συγκεκριµένης περιοχής υψηλού ρίσκου είναι κάτοικοι. Η πλειοψηφία των επαρχιών που απαρτίζουν την περιοχή (έξι) είναι αγροτικές. Όταν επιτρέψουµε χωρική επικάλυψη µεταξύ των οµάδων επαρχιών, τα αποτελέσµατα της χωρικής ανίχνευσης υποδεικνύουν τρεις ακόµα οµάδες επαρχιών µε (στατιστικά σηµαντικό) υψηλό κίνδυνο λεϊσµανίασης. Συνολικά είκοσι επαρχίες περιέχονται στις τρεις αυτές οµάδες και οι παρατηρούµενες περιπτώσεις λεϊσµανίασης στην περιοχή είναι δύο φορές περισσότερες σε σχέση µε τις αναµενόµενες κάτω από την υπόθεση της (χωρικά) οµογενούς κατανοµής της ασθένειας. Ο κίνδυνος λεϊσµανίασης εµφανίζεται σηµαντικά χαµηλός σε επαρχίες του βόρειου και δυτικού Sidi-Bouzid. Όταν επιτρέπουµε την επικάλυψη µεταξύ των στατιστικά σηµαντικών οµάδων επαρχιών (clusters) πρακτικά όλο το βορειοδυτικό τµήµα του Sidi-Bouzid καλύπτεται από επαρχίες χαµηλού επιδηµιολογικού κινδύνου. Για την εκτίµηση του χρονικού ορίζοντα όσον αφορά τη χωρική οµαδοποίηση των επαρχιών χρησιµοποιήθηκε η στατιστική τεχνική χωρο-χρονικής ανίχνευσης που προτάθηκε από τον Kulldorff (2005). Και εδώ, το µέτρο πιθανότητας που σχετίζεται µε τον στατιστικό έλεγχο, είναι Poisson. Η στατιστική χωρο-χρονικής ανίχνευσης ορίζεται µέσω κυλινδρικών παραθύρων, µε κυκλική γεωγραφική βάση και ύψος που αντιστοιχεί σε µονάδες χρόνου. Η βάση του εστιάζεται σε ένα από τα πιθανά κέντρα (επαρχιών) και η ακτίνα της µεταβάλλεται σε µέγεθος.

6 Εικόνα 4. Γειτονικές οµάδες επαρχιών µε οµογενή επιδηµιολογικό κίνδυνο (spatial clusters) όπως προέκυψαν µε στατιστικές τεχνικές χωρικής ανίχνευσης µε το κριτήριο της µη επικάλυψης µεταξύ των οµάδων. Εικόνα 5. Γειτονικές οµάδες επαρχιών µε οµογενή επιδηµιολογικό κίνδυνο (spatial clusters) όπως προέκυψαν µε στατιστικές τεχνικές χωρικής ανίχνευσης µε το κριτήριο της µη ταύτισης του κέντρου δύο οµάδων. Οι επαρχίες µε µαύρο χρώµα ανήκουν τουλάχιστον σε δύο οµάδες.

7 Εικόνα 6. Γειτονικές οµάδες επαρχιών µε οµογενή επιδηµιολογικό κίνδυνο (spatial clusters) στο χώρο και το χρόνο όπως προέκυψαν µε στατιστικές τεχνικές χωροχρονικής ανίχνευσης µε το κριτήριο της µη επικάλυψης µεταξύ των οµάδων. Εικόνα 7. Γειτονικές οµάδες επαρχιών µε οµογενή επιδηµιολογικό κίνδυνο (spatial clusters) στο χώρο και το χρόνο όπως προέκυψαν µε στατιστικές τεχνικές χωροχρονικής ανίχνευσης µε το κριτήριο της µη ταύτισης του κέντρου δύο οµάδων. Οι επαρχίες µε µαύρο χρώµα ανήκουν τουλάχιστον σε δύο οµάδες.

8 Το ύψος του κυλίνδρου αντιπροσωπεύει πιθανά χρονικά διαστήµατα µέσα στην περίοδο µελέτης. Το κυλινδρικό, αυτή τη φορά παράθυρο, µετακινείται στο χώρο και το χρόνο και τελικά προκύπτουν κύλινδροι διαφορετικού µεγέθους που καλύπτουν όλη τη γεωγραφική περιοχή και όλα τα πιθανά χρονικά υποδιαστήµατα. Η αρχική υπόθεση είναι ότι ο (Poisson κατανεµηµένος) αριθµός των κρουσµάτων ανά κύλινδρο σχετίζεται µε οµογενή κίνδυνο στο χώρο και το χρόνο, ενώ σύµφωνα µε την εναλλακτική υπόθεση τουλάχιστον ένας κύλινδρος έχει διαφορετικό επιδηµιολογικό κίνδυνο στο εσωτερικό του από ότι στο εξωτερικό του. Έτσι, για κάθε κύλινδρο υπολογίζεται ο αριθµός των κρουσµάτων στο εσωτερικό και εξωτερικό του µαζί µε τον αναµενόµενο αριθµό κρουσµάτων σύµφωνα µε την αρχική υπόθεση. Τελικά, υπολογίζεται η πιθανοφάνεια κάθε κυλίνδρου να αποτελεί σηµαντική χωρο-χρονική συστάδα (cluster) και ο κύλινδρος µε τη µέγιστη πιθανοφάνεια αποτελεί την πιο πιθανή συστάδα. Όπως και πριν χρησιµοποιήσαµε δύο εναλλακτικά κριτήρια για το σχηµατισµό των συστάδων: το πρώτο ήταν η µη επικάλυψη µεταξύ συστάδων και το δεύτερο η µη ταύτιση των κέντρων δύο συστάδων (εδώ η επικάλυψη επιτρέπεται). Τα αποτελέσµατα της τεχνικής στατιστικής χωρο-χρονικής ανίχνευσης µοιάζουν µε τα προηγούµενα µόνο που σε αυτή την περίοδο υπάρχει ένα χρονικό παράθυρο µέσα στο οποίο η χωρική συστάδα απέκλινε σηµαντικά σε σχέση µε το µέσο όρο. Για παράδειγµα η δεύτερη οµάδα επαρχιών υψηλού κινδύνου, που βρίσκεται στο κέντρο της υπό µελέτη περιοχής απέκλινε σηµαντικά κατά το χρονικό διάστηµα από το 1999 ως το 2003 ενώ για την πρώτη οµάδα επαρχιών η αντίστοιχη περίοδος ξεκινά το 2000 και τελειώνει το εν υπάρχει ένδειξη σηµαντικού χωρικής ή χωρο-χρονικής οµαδοποίησης επαρχιών στο νότιο ή νοτιοδυτικό τµήµα της υπό µελέτη περιοχής. 4. ΜΟΝΤΕΛΑ ΧΩΡΙΚΗΣ ΠΑΛΙΝ ΡΟΜΗΣΗΣ POISSON ΚΑΤΑ BAYES ΚΑΙ ΧΑΡΤΕΣ ΕΞΟΜΑΛΥΣΜΕΝΟΥ ΚΙΝ ΥΝΟΥ Για την επεξήγηση µέρους της χωρικής µεταβλητότητας της λεϊσµανίασης, εκτιµήθηκαν υποδείγµατα χωρικής παλινδρόµησης Poisson κατά Bayes. Σύµφωνα µε τα συγκεκριµένα µοντέλα τα παρατηρούµενα κρούσµατα είναι Poisson κατανεµηµένα και ο λογάριθµος των κρουσµάτων κάθε επαρχίας σχετίζεται µε τον αναµενόµενο αριθµό κρουσµάτων κάτω από την υπόθεση οµογενούς κινδύνου και µε τρεις επεξηγηµατικές µεταβλητές: την πληθυσµιακή πυκνότητα, τον αριθµό των ανθρώπων ανά κατοικία και έναν δείκτη αστικότητας. Υποδείγµατα όπως το παραπάνω έχουν εφαρµοστεί σε µεγάλο πλήθος επιδηµιολογικών µελετών. Για εκτεταµένες βιβλιογραφικές αναφορές όπως και για µια λεπτοµερή παρουσίαση αυτού του µέρους της εφαρµογής το οποίο έχει αρκετές τεχνικές λεπτοµέρειες, ο ενδιαφερόµενος αναγνώστης µπορεί να ανατρέξει στους Kamarianakis et al. (2006). Εδώ θα αρκεστούµε να σηµειώσουµε ότι η εφαρµογή υποδειγµάτων όπως αυτό που χρησιµοποιήσαµε διευκολύνεται σηµαντικά από τη χρήση αλγορίθµων τύπου MCMC. Για τη δική µας εφαρµογή, χρησιµοποιήσαµε το ελεύθερο λογισµικό WINBUGS, που αναπτύσσεται την τελευταία δεκαετία από την οµάδα βιοστατιστικής και επιδηµιολογίας του Cambridge.

9 Tα αποτελέσµατα της εκτίµησης του µοντέλου, υποδεικνύουν σηµαντική εξάρτηση των παρατηρούµενων κρουσµάτων ανά επαρχία µε το δείκτη αστικότητας. Η αρνητική τιµή του συγκεκριµένου συντελεστή υποδεικνύει λιγότερα κρούσµατα σε αγροτικές περιοχές, κάτι που φαίνεται περίεργο αρχικά, αλλά είναι συνεπές µε προηγούµενες εργασίες που αναφέρουν υψηλό επιδηµιολογικό κίνδυνο σε περι-αστικές περιοχές. Για του λόγου το αληθές, η εικόνα 8 δείχνει τη γεωγραφική αποτύπωση των κρουσµάτων λεϊσµανίασης στην πόλη του Sidi-Bouzid κατά το H πληθυσµιακή πυκνότητα εµφανίζεται ως µη σηµαντικός επεξηγηµατικός παράγοντας ενώ ο συντελεστής που σχετίζεται µε τον αριθµό κατοίκων ανά οικία παίρνει αρνητικές τιµές αντίθετα µε τις αρχικές µας προβλέψεις. Για µια πιο πλήρη επισκόπηση των αποτελεσµάτων ο ενδιαφερόµενος αναγνώστης µπορεί να ανατρέξει στους Kamarianakis et al. (2006). Εικόνα 8. Αποτύπωση του τόπου κατοικίας των κρουσµάτων λεϊσµανίασης στην πόλη Sidi Bouzid κατά το 2004.

10 Εικόνα 9. Αριστερά: Παρατηρούµενα (αθροιστικά) κρούσµατα λεϊσµανίασης κατά την περίοδο εξιά: Αναµενόµενα (αθροιστικά) κρούσµατα λεϊσµανίασης κατά την περίοδο κάτω από την υπόθεση οµογενούς χωρικής κατανοµής της ασθένειας Εικόνα 10. Αριστερά: Προβλέψεις (αθροιστικών) κρουσµάτων λεϊσµανίασης κατά την περίοδο από το στατιστικό µοντέλο. εξιά: Εκτιµώµενος σχετικός κίνδυνος ανά επαρχία.

11 5. ΣΥΜΠΕΡΑΣΜΑΤΑ Η λεϊσµανίαση, αποτελεί µαζί µε τη φυµατίωση και την ηπατίτιδα ένα από τα σηµαντικότερα προβλήµατα υγείας στην Τυνησία. Εµφανίστηκε αρχικά στο κεντρικό τµήµα της χώρας στις αρχές της δεκαετίας του ογδόντα και σήµερα έχει εξαπλωθεί στο µεγαλύτερο µέρος του κεντρικού και νότιου τµήµατος της. Περίπου δύο µε τρεις χιλιάδες κρούσµατα καταγράφονται κάθε χρόνο, και ανά πέντε µε έξι χρόνια η ασθένεια βρίσκεται σε έξαρση για µια χρονιά µε τους επακριβείς λόγους να είναι µέχρι στιγµής άγνωστοι. Πιθανοί παράγοντες σχετίζονται µε τις δυναµικές των πληθυσµών των τρωκτικών και των εντόµων και το πώς αλληλεπιδρούν µε τις αλλαγές στο κλίµα. Έτσι η δυνατότητα πρόβλεψης των εξάρσεων και της χωρικής διασποράς της ασθένειας, φαίνεται για την ώρα πολύ µακρινή. Η αποτίµηση της σηµαντικότητας διαφόρων επεξηγηµατικών παραγόντων είναι αποφασιστικής σηµασίας για την αποτελεσµατική κατανόηση των επιδηµιολογικών χαρακτηριστικών της λεϊσµανίασης και την πρόβλεψη της εξέλιξης της ασθένειας στο χώρο και το χρόνο. Παλαιότερες µελέτες υποδεικνύουν ότι οι ανθρώπινες επεµβάσεις στο φυσικό περιβάλλον µπορεί να επιδράσουν δραστικά όσον αφορά τους ρυθµούς µετάδοσης της ασθένειας στον άνθρωπο. Στην περιοχή µελέτης, λόγω της κατασκευής του φράγµατος του Sidi Saad το 1982, σε πολλά από τα αποξηραµένα εδάφη ευδοκίµησε ένα είδος θάµνου το οποίο αποτελεί τροφή για τα ποντίκια P. Obesus µε αποτέλεσµα τη σηµαντική αύξηση του πληθυσµού τους. Εκείνη την περίοδο πρωτοεµφανίστηκε η λεϊσµανίαση στην περιοχή. Το 1992 η ασθένεια ήταν σε έξαρση στην πόλη του Sidi- Bouzid και οι υγειονοµικές αρχές δοκίµασαν µέτρα ελέγχου και πρόληψης κυρίως µέσω της δενδροφύτευσης σε περιοχές κοντά σε πόλεις όπου η προηγούµενη βλάστηση ήταν chenopods. Παρ όλα τα µέτρα ελέγχου ο αριθµός κρουσµάτων ανά χρονιά παραµένει σηµαντικός. Επιπλέον, όπως φαίνεται από αυτή την εργασία οι περιοχές που βρίσκονται κοντά στο φράγµα εξακολουθούν να έχουν σηµαντικά αυξηµένο αριθµό κρουσµάτων. Οι παρατηρήσεις µας συµπίπτουν µε προηγούµενες που αναφέρουν ότι η ασθένεια εξαπλώνεται µε εξάρσεις στο χώρο και το χρόνο και αυξηµένο αριθµό κρουσµάτων σε περι-αστικές περιοχές. 6. ΕΥΧΑΡΙΣΤΙΕΣ Η παρούσα εργασία πραγµατοποιήθηκε στα πλαίσια του ευρωπαϊκού ερευνητικού προγράµµατος EMPHIS ( Οφείλουµε θερµές ευχαριστίες σε όλους τους συνεργάτες και ειδικά σε εκείνους που µας παρείχαν τα δεδοµένα της µελέτης. ΒΙΒΛΙΟΓΡΑΦΙΑ Assunção, R.M, Reis, I.A, Oliveira, CL., 2001, Diffusion and prediction of leishmaniasis in a large metropolitan area in Brazil with a Bayesian space-time model. Statistics in Medicine, 20: Bakker, M.I., Hatta, M., Kwenang, A., Faber, W.R., van Beers, S.M., Klatser, P.R., Oskam,

12 L., 2004, Population survey to determine risk factors for Mycobacterium leprae transmission and infection. International Journal of Epidemiology, 33: Chaput, E.K., Meek, J.I., Heimer, R., 2002, Spatial analysis of human granulocytic ehrlichiosis near Lyme, Connecticut. Emerging Infectious Diseases, 8: Jennings, J.M., Curriero, F.C., Celentano, D., Ellen, J.M., 2005, Geographic identification of high gonorrhea transmission areas in Baltimore, Maryland. American Journal of Epidemiology, 161: Kamarianakis, Y., Chlif, S., Ben Salah, A., Ben Alaya, N., Prastacos, P., 2006, Zoonotic cutaneous leishmaniasis in Central Tunisia: spatio-temporal dynamics. Submitted for publication. Kulldorff, M., 1997, A spatial scan statistic. Communications in Statistics: Theory and Methods, 26: Kulldorff, M., 1999, Spatial scan statistics: Models calculations and applications. In Balakrisnan and Glaz (eds), Recent Advances on Scan Stastics and Applications. Boston, USA: Birkhauser, Kulldorff, M., 1999, Spatial scan statistics: Models calculations and applications. In Balakrisnan and Glaz (eds), Recent Advances on Scan Stastics and Applications. Boston, USA: Birkhauser, Kulldorff, M., and Information Management Services, Inc. SaTScan TM v6.0: software for the spatial and space-time scan statistics. Machado-Coelho, G.L.L., Assunção, R,M, Mayrink, W., Caiaffa, W.T., 1999 American cutaneous leishmaniasis in southeast Brazil: space-time clustering. International Journal of Epidemiology, 28: